Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2013-12 Screen Reader version ^♣

Welfare Costs of Shifting Trend Inflation^†

Taisuke Nakata*

Federal Reserve Board

Keywords: Great inflation, second-order approximation, trend inflation, welfare.

Abstract:

This paper studies the welfare consequences of exogenous variations in trend inflation in a New Keynesian economy. Consumption and leisure respond asymmetrically to a rise and a decline in trend inflation. As a result, an increase in the variance of shocks to the trend inflation process decreases welfare not only by increasing the volatilities of consumption and leisure, but also by decreasing their average levels. I find that the welfare cost of drifting trend inflation is modest and that it comes mainly from reduced average levels of consumption and leisure, not from their increased volatilities.

JEL Classification: C63, E31, E52

1 Introduction

Despite nearly two decades of low and stable inflation in the United States, memory of the Great Inflation of the 1970s still looms large in the minds of economists and policymakers. A sustained increase in energy prices during the 2000s generated discussions on the extent to energy inflation passes through to core inflation.¹ More recently, even under today's environment of zero short-term nominal interest rate and potential deflation, the accommodative stance of monetary policy has generated concerns regarding the possibility of a sustained rise in future inflation.²

Many researchers have used a highly persistent trend inflation process, interpreted as the Federal Reserve's slowly-moving implicit inflation target, to model the sustained rise of inflation during the Great Inflation period and its subsequent decline, and have studied its implications for various aspects of macroeconomic dynamics. In an early contribution, Kozicki & Tinsley (2001) explored the implications of drifting trend inflation for the term structure of interest rates. Ireland (2007) analyzed the consequences of the variation in trend inflation for output and overall inflation using an estimated New Keynesian model, while Cogley et al. (2009) explored its implications for the predictability of inflation. Cogley & Sbordone (2008) examined the effect of incorporating shifting trend inflation on the estimated parameter of the Calvo model. However, this literature has been silent about its welfare consequences.

To fill in the gap, this paper studies the implications of exogenous variations in trend inflation for welfare. The analysis is conducted in a standard New Keynesian model with Calvo price setting. The central bank sets the nominal interest rate according to a Taylor rule in which the interest rate responds to the deviation of inflation from trend inflation rate. In the spirit of the aforementioned papers, I model trend inflation--interpreted as the central bank's target inflation rate--as a highly persistent AR(1) process. I then compare the welfare of an economy in which the variance of innovations to the trend inflation process is zero with that of an economy in which the variance is positive.

I find that an increase in the variance of shocks to the trend inflation process reduces welfare and that it does so mainly through its effect on average consumption and leisure. This result arises due to an asymmetry in the consumption and leisure responses to fluctuations in trend inflation. A rise in trend inflation increases price dispersion, the main source of aggregate production inefficiency in the model, by more than a decline in trend inflation of the same size would reduce it. As a result, the household reduces consumption and leisure in response to an increase in trend inflation by more than s/he would increase them in response to reduction in trend inflation. Thus, a mean preserving spread in the shocks to the trend inflation processes decreases the average level of consumption and leisure. An increase in the variance of shocks to the trend inflation process also reduces welfare by increasing the variances of consumption and leisure, but this volatility effect is quantitatively less important compared to the average level effect.

I find that the welfare cost of variation in trend inflation is modest in this model. In the baseline parametrization, the compensating variation in consumption required to make the representative household indifferent to living in the economy with drifting trend inflation, as opposed to an economy with low and stable trend inflation, is about 0.1 percent. This is substantially smaller than the welfare cost of business cycles computed in the spirit of Lucas (1987), which is about 0.5 percent in the model studied in this paper.³ For a wide range of plausible parameter values, the welfare cost of shifting trend inflation is less than 1 percent. Only when the price friction is sufficiently large and the trend inflation process is upward biased, the welfare cost exceeds one percent.

This paper is closely related to a set of papers that examines the effects of non-zero trend inflation on macroeconomic dynamics in New Keynesian models. In an early contribution, Ascari (2004) showed that the level of trend inflation affects inflation and output dynamics in quantitatively important ways. Ascari & Ropele (2007) study the implications of non-zero trend inflation for optimal monetary policy, while Amano et al. (2009) investigate the implications for the optimal rate of inflation. Amano et al. (2007) explore the implications for the time-series properties of macro variables, while Kiley (2007), Ascari & Ropele (2009), and Coibion & Gorodnichenko (2011) study the effect of trend inflation on the determinacy of the model. This paper differ from these papers because it studies the model with shifting trend inflation, while these early papers analyze models with constant non-zero trend inflation.

The rest of the paper is organized as follows. Section 2 presents the model. Section 3 defines the measures of welfare and discusses the solution method. Section 4 discusses parametrization. Section 5 presents the results. Section 6 makes several remarks related to the model's determinacy. The last section concludes.

2 Model

The model is given by a New Keynesian economy populated by four main actors: The household, the final-good producer, and a continuum of intermediate goods producers, and the government.

2.1 The household

There is a representative household who maximizes the expected discounted sum of future period utility

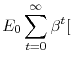$\displaystyle E_{0} \sum_{t=0}^{\infty}\beta^{t} [$ log $\displaystyle (C_{t} - h C_{t-1}) - \frac{N_{t}^{1+v}}{1+v}]$

subject to the household's budget constraint

$\displaystyle P_{t}C_{t} + R_{t}^{-1}B_{t} \leq W_{t}N_{t} + B_{t-1} - P_{t}T_{t} + P_{t}\Gamma_{t}$

$C_{t}$ is consumption of final goods and $N_{t}$ is labor supply. $P_{t}$ is the nominal price, $W_{t}$ is the nominal wage, $T_{t}$ is a lump-sum tax, and $\Gamma_{t}$ is the profit due to owning the intermediate goods firms. $B_{t}$ is the holding of risk-free one-period bonds carried over from period t, paying one unit of consumption in period t+1. $R_{t}$ denotes the gross nominal return on bonds purchased in period t. A lump-sum tax is levied to finance government spending $G_{t}$ period by period so that $T_{t}=G_{t}$ . Government spending is given exogenously and specified as a fraction of aggregate output $Y_{t}$ :

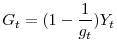$\displaystyle G_{t} = (1-\frac{1}{g_{t}})Y_{t}$

where log $(g_{t})$ follows an AR(1) process.

log $\displaystyle (g_{t}) = (1-\rho_{g})$ log $\displaystyle (\bar{g}) + \rho_{g}$ log $\displaystyle (g_{t-1}) + \sigma_{g}\epsilon_{g,t}$

$\epsilon_{g,t}$ is a standard normal and independent across time.

2.2 Firms

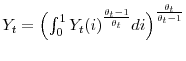There is a representative final good producer and a continuum of intermediate goods producers indexed by $i \in [0,1]$ . The representative final good producer purchases the intermediate goods, and combines them into the final good using CES technology $Y_{t} = \Bigl( \int_{0}^{1} Y_{t}(i)^{\frac{\theta_{t}-1}{\theta_{t}}} di \Bigr)^{\frac{\theta_{t}}{\theta_{t}-1}}$ . $\theta_{t}$ measures the substitutability of intermediate goods and evolves according to an AR(1) process.

log $\displaystyle (\theta_{t}) = (1-\rho_{\theta})$ log $\displaystyle (\bar{\theta}) + \rho_{\theta}$ log $\displaystyle (\theta_{t-1}) + \sigma_{\theta,t}\epsilon_{\theta,t}$

$\epsilon_{\theta,t}$ is a standard normal and independent across time. A monopolistically competitive firm, i, produces an intermediate good $Y_{t}(i)$ using a linear production technology.

$\displaystyle Y_{t}(i) = A_{t} N_{t}(i)$

where $N_{t}(i)$ is the labor input and $A_{t}$ evolves according to an AR(1) process

log $\displaystyle (A_{t}) = \rho_{A}$ log $\displaystyle (A_{t-1}) + \sigma_{A,t}\epsilon_{A,t}$

$\epsilon_{A,t}$ is a standard normal and independent across time. Intermediate goods producers are assumed to set nominal prices in a staggered fashion. Every period, a fraction $\alpha$ of firms cannot optimize their prices, and a fraction $1-\alpha$ of firms can. When they cannot optimize their prices, they update their prices mechanically according to

$\displaystyle P_{t}(i) = \Pi_{t-1}^{\rho}P_{t-1}(i)$

where $\Pi_{t} = \frac{P_{t}}{P_{t-1}}$ and $\rho$ measures the degree of indexation.⁴ When intermediate goods producers get an opportunity to optimize, they choose $P_{t}^{*}(i)$ to maximize the expected discounted sum of future profits over all future states in which it cannot re-optimize:

$\displaystyle E_{t} \sum_{s=0}^{\infty} \alpha^{s} D_{t,t+s} \Bigl[ P_{t}^{*}(i)\Pi_{t,t+s-1}^{\rho} - \frac{W_{t+s}}{A_{t+s}} \Bigr] Y_{t+s}(i)$

subject to a sequence of demand functions

$\displaystyle Y_{t+s}(i) = \Bigl[ \frac{P_{t}^{*}(i)\Pi_{t,t+s-1}^{\rho} } {P_{t+s}} \Bigr]^{-\theta_{t}} Y_{t+s}$

where $\Pi_{t,t+s-1} = 1$ if and $\Pi_{t,t+s-1} = \frac{P_{t}}{P_{t-1}}\frac{P_{t+1}}{P_{t}}...\frac{P_{t+s-1}}{P_{t+s-2}}$ otherwise. Since the representative household owns the intermediate goods producers, the future profits are discounted by the stochastic discount factor, $D_{t,t+s}$ , associated with the household's intertemporal optimization problem. The stochastic discount factor is given by

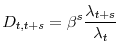$\displaystyle D_{t,t+s} = \beta^{s}\frac{\lambda_{t+s}}{\lambda_{t}}$

where $\lambda_{t}$ is the Lagrangian multiplier on the household budget constraint at time t.

2.3 Monetary Policy

The central bank sets the nominal interest rate $R_{t}$ according to the following Taylor rule.

$\displaystyle \frac{R_{t}}{\bar{R}_{t}} = (\frac{R_{t-1}}{\bar{R}_{t-1}})^{\phi_{R}}\Bigl[ (\frac{\Pi_{t}}{\bar{\Pi}_{t}})^{\phi_{\Pi}} (\frac{y_{t}}{\bar{y}_{t}})^{\phi_{y}} \Bigr]^{1-\phi_{R}}e^{\sigma_{R}\epsilon_{R,t}}$

where $\bar{\Pi}_{t}$ is trend inflation, and $y_{t} = \frac{Y_{t}}{A_{t}}$ . $\Pi_{t} = \frac{P_{t}}{P_{t-1}}$ , $\bar{R}_{t}$ and $\bar{y}_{t}$ are the deterministic steady-state levels of $R_{t}$ and $y_{t}$ associated with an economy in which $\bar{\Pi}^{*} = \bar{\Pi}_{t}$ . $\epsilon_{R,t}$ is an iid monetary policy shock.

In the spirit of Kozicki & Tinsley (2001), Ireland (2007), and Cogley et al. (2009), I model trend inflation as a highly persistent AR(1) process.

log $\displaystyle (\bar{\Pi}_{t}) = (1 - \rho_{\bar{\pi}})$ log $\displaystyle (\bar{\Pi}^{*}) + \rho_{\bar{\pi}}$ log $\displaystyle (\bar{\Pi}_{t-1}) + \sigma_{\bar{\Pi}}\epsilon_{\bar{\Pi},t}$

(1)

$\epsilon_{\bar{\Pi},t}$ is a standard normal and independent across time. The main exercise of the paper will be to compare an economy in which $\sigma_{\bar{\Pi}}$ is zero with an economy in which $\sigma_{\bar{\Pi}}$ is positive.

2.4 Market Clearing Conditions

The market clearing conditions for labor, final goods, and the government bond are given by

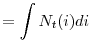$\displaystyle N_{t}$	$\displaystyle = \int N_{t}(i) di$
$\displaystyle Y_{t}$	$\displaystyle = C_{t} + G_{t}$
$\displaystyle B_{t}$	$\displaystyle = 0$

3 Welfare Measure and Solution Method

Welfare is measured by the unconditional expected utility of the representative household, $E[ \sum_{t=0}^{\infty} \beta^{t} u(C_{t},C_{t-1},N_{t})]$ . The welfare cost of shifting trend inflation is measured by the compensating variation in consumption that makes the representative household in an economy with no variation in trend inflation as well-off as the one in another economy with variation in trend inflation. Specifically, is defined through

$\displaystyle E [ \sum_{t=0}^{\infty} \beta^{t} u( C_{A,t}+wc, C_{A,t-1}+wc, N_{A,t}) ] = E [ \sum_{t=0}^{\infty} \beta^{t} u(C_{B,t}, C_{B,t-1}, N_{B,t})]$

$C_{k,t}$ and $N_{k,t}$ are consumption and labor supply plans in the economy $k \in {A,B}$ where A is an economy with $\sigma_{\bar{\Pi}} > 0$ and B is an economy with $\sigma_{\bar{\Pi}} = 0$ .

I use a perturbation method to compute the second-order approximations to the policy functions around the deterministic steady-state, and use these to compute the second-order accurate welfare.⁵ Using the second-order Taylor expansion of the household's utility function around the deterministic steady-state, the welfare can be decomposed as follows.

$\displaystyle W$	$\displaystyle \equiv E [ \sum_{t=0}^{\infty} \beta^{t} u(z_{t})] \nonumber$
	$\displaystyle \approx \sum_{t=0}^{\infty} \beta^{t} u(\bar{z}) + \sum_{t=0}^{\infty}\beta^{t} Du(\bar{z}) E[z_{t}- \bar{z}] + \sum_{t=0}^{\infty}\beta^{t} Hu(\bar{z}) E[(z_{t}- \bar{z}) \otimes (z_{t}- \bar{z})] \nonumber$
	$\displaystyle \equiv W_{d} + W_{l} + W_{vol}$

where $z_{t}:= [C_{t},C_{t-1},N_{t}]$ , and $Du(\bar{z})$ and $Hu(\bar{z})$ are vectors containing the first and second derivatives, respectively, of $u(\cdot)$ evaluated at $\bar{z}$ , the deterministic steady-state of . I call $W_{d}$ , $W_{l}$ , and $W_{vol}$ the deterministic, level, and volatility components of the welfare, respectively. $W_{d}$ depends only on the deterministic steady-state quantities, $\bar{z}$ . $W_{l}$ depends on the mean of $E[z_{t}]$ , which reflects the nonlinearity in the policy functions. This term would always be zero if policy functions are evaluated up to a first-order approximation. $W_{vol}$ depends on the volatility of $z_{t}$ and captures the household's risk aversion. I will use this decomposition to identify the source of the welfare costs of shifting trend inflation. Following Kim et al. (2008), I compute the level and volatility components without simulation using the idea of "pruning." The appendix describes the details of the computation.

4 Parametrization

Table 1 lists baseline parameter values. The household's preference parameters, coefficients in the Taylor rule, the persistence and the standard deviations of exogenous shocks are set to the posterior median estimates of a medium-size DSGE models with constant volatilities from Justiniano & Primiceri (2008). Their estimates of these parameters are in line with the estimates from other similar New Keynesian DSGE models found in the literature.

For the parameters governing the production sector, I use the estimates from Cogley & Sbordone (2008) as the baseline since this is the only study that estimates the parameters of the Calvo model allowing for imperfect indexation and shifting trend inflation.⁶ Their posterior medians are roughly 0, 0.6, and 10 for the degree of indexation ( $\rho$ ), the probability of non-optimization ( $\alpha$ ), and the elasticity of substitution ( $\bar{\theta}$ ), respectively. Their estimate of zero degree of indexation is consistent with the literature on constant non-zero trend inflation discussed in the introduction which assumes this parameter to be zero. I will conduct sensitivity analysis with respect to alternative degrees of indexation as well as alternative Calvo parameter values.

The steady-state level of trend inflation is set to 2 annualized percent (i.e., $\bar{\Pi}^{*}=1.02^{0.25}$ ). For the persistence and standard deviation of the trend inflation process, I follow Cogley et al. (2009) who set the AR(1) coefficient to 0.995 and estimated the standard deviation of the innovation to the trend process to be $\frac{0.08}{100}$ for their Great Inflation subsample. This process implies an unconditional standard deviation of trend inflation of 3.2 percent annualized.⁷ I will consider other values for these two parameters as well.

5 Results

I first discuss the welfare cost of constant non-zero trend inflation. Understanding the welfare costs of constant trend inflation is a useful step toward understanding the source of the welfare costs of shifting trend inflation. I then describe the paper's main results on the welfare costs of shifting trend inflation.

5.1 Welfare Costs of Constant Non-Zero Inflation

Table 2 compares the welfare and a few other properties of an economy in which trend inflation is constant at 0 annualized percent and an economy in which trend inflation is constant at 6 annualized percent.

Welfare is lower in the high trend inflation economy than in the zero trend inflation economy, and the welfare difference comes mainly from the deterministic component, $W_{d}$ . In particular, the deterministic steady-state consumption/labor supply are lower/higher in the high trend inflation economy (0.821/1.067 in the high trend inflation economy versus 0.818/1.068 in the zero trend inflation economy). To understand why trend inflation affects the steady-state consumption/labor supply, notice that the main inefficiency of the economy can be captured by the cross sectional price dispersion across intermediate goods $s_{t} := \int_{0}^{1} (\frac{P_{t}(i)}{P_{t}})^{-\theta_{t}} di$ . By aggregating the production function for intermediate goods producers, we obtain the following aggregate production function

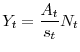$\displaystyle Y_{t} = \frac{A_{t}}{s_{t}} N_{t}$

This expression says that, the larger the price dispersion is, the less efficient the aggregate production is. In the high trend inflation economy, the deterministic steady-state level of price dispersion is high as non-optimizing firms cannot index their prices, and the aggregate production is therefore less efficient.⁸ Thus, the household needs to work more to maintain the same consumption level, or needs to reduce consumption if s/he were to work the same hours. In equilibrium, the agent decides to work more and consume less.

The welfare difference also comes from the level and volatility components, albeit to a substantially smaller degree. Volatilities of consumption and labor supply are larger in the high trend inflation economy than in the constant trend inflation economy (1.349/1.949 versus 1.447/2.135). Volatilities directly reduce welfare through $W_{vol}$ , but also indirectly reduce welfare through $W_{l}$ , by affecting the average levels of consumption and labor supply due to precautionary motives.⁹ This result is consistent with the analysis of Amano et al. (2007) in which they document higher volatilities and lower average levels of consumption and leisure when trend inflation is high.

The top left panel of Figure 1 reports how the welfare costs vary with the level of trend inflation. An important feature is that the relationship between trend inflation and welfare cost is nonlinear; a given amount of increase in the steady-state level of trend inflation leads to a larger increase in the welfare cost when trend inflation is higher. To help us understand this relationship, the top right panel plots the deterministic steady-state levels of price dispersion at various trend inflation rates. A given amount of increase in trend inflation leads to a larger increase in the steady state levels of price dispersion when trend inflation is higher. As a result, the steady state levels of consumption and labor supply also exhibit the nonlinearity. With the deterministic components the main driver of welfare, such nonlinearity in the steady-state quantities leads to the aforementioned relationship between trend inflation and welfare. This nonlinearity will be a key factor in understanding the welfare costs of shifting trend inflation, which we turn to now.

5.2 Welfare Costs of Shifting Trend Inflation

The first and second columns of Table 3 present the properties of an economy with drifting trend inflation (i.e. $\sigma_{\bar{\Pi}}=\frac{0.08}{100}$ ) and an economy with constant trend inflation (i.e. $\sigma_{\bar{\Pi}} = 0$ ). In both economies, the steady-state trend inflation is set to 2 annualized percent (i.e., $\bar{\Pi}^{*}=1.02^{0.25}$ ).

Welfare is lower in the economy with shifting trend inflation than in the constant trend economy. Under the baseline parametrization, welfare cost of shifting trend inflation is roughly 0.1 percent. Since the deterministic steady-states of the two economies are the same, the deterministic components of welfare, $W_{d}$ , are the same. The main welfare difference comes from the level component, $W_{l}$ , reflecting the reduced average consumption and the increase average labor supply. While the volatility component, $W_{vol}$ , also contributes to the welfare difference, this effect is relatively minor.

A mean-preserving spread on the shock distribution reduces average consumption and increases average labor supply because the policy functions for consumption and labor supply are respectively concave and convex functions of trend inflation. To understand this feature of policy functions, consider the bottom two panels in Figure 1 again. Since trend inflation is highly persistent, a shock to trend inflation can be thought of as taking the economy to a new steady state with a different level of trend inflation. The concavity of the policy function for consumption means that a positive shock to trend inflation decreases consumption by more than a negative shock increases it. The convexity of the policy function for labor supply means that a positive shock to trend inflation increases labor supply by more than a negative shock decrease it. Thus, an increase in the variance of shocks to trend inflation decreases consumption and increases labor supply.

This channel is distinct from how business cycle fluctuations reduce welfare. The third column of Table 3 presents the welfare and other properties of an economy in which the variances of all exogenous shocks are set to zero, except for the shocks to the trend inflation process. The welfare gain of eliminating the variation in the business cycle shocks mainly comes from the reduced volatilities of consumption and leisure. The volatility component of the welfare is -0.04 in the economy without any business cycles shocks while it is -4.19 in the model with them. While the differences in their average levels also contribute to the welfare gain, their effects are relatively less important.

Welfare costs depend importantly on the parameters governing the pricing environment. The top panels of Figure 2 show how the welfare costs of shifting trend inflation vary with the degree of price indexation and the frequency of price adjustment. Since price indexation allows non-optimizing firms to catch up with price changes by optimizing firms, the larger degree of price indexation means that prices are less dispersed at any trend inflation rate. As a result, when firms are allowed to index their prices, consumption and labor supply are less affected by the level of trend inflation. Welfare costs of shifting trend inflation are therefore lower in the economy with higher price indexation. Top right panel shows the effect of price adjustment frequency on the welfare costs of shifting trend inflation. With less frequent price adjustment (i.e., larger $\alpha$ ), the welfare costs of constant nonzero trend inflation increases and so does the welfare cost of shifting trend inflation. With $\alpha=0.8$ , the welfare cost exceeds one percent.

The bottom left panel of Figure 2 demonstrates the degree to which the welfare cost of shifting trend inflation depends on the variance of the shocks to trend inflation. Perhaps obviously, the larger the variance is, the larger the welfare cost of shifting trend inflation is. The right end of the panel ( $\sigma_{\Pi}=\frac{0.1}{100}$ ) roughly corresponds to the estimate in Ireland (2007) and 25th percentile of the posterior estimate from Cogley et al. (2009) which implies the unconditional standard deviation of trend inflation is 4 percent annualized. The welfare cost of shifting trend inflation remains modest even at this high estimate. Finally, the bottom right panel shows the effect of varying persistence of trend inflation process while keeping the unconditional variance of the trend inflation process constant. While the welfare costs are smaller when the trend inflation process is less persistent, the effects are quantitatively small.

An alternative price friction: quadratic price adjustment costs

This subsection examines the welfare costs of shifting trend inflation in the Rotemberg pricing model, another common pricing setup used in the literature. In the Rotemberg model, intermediate good producers choose their prices in order to maximize the expected discounted future profits subject to quadratic price adjustment costs. Firm i's objective function is given by

$\displaystyle E_{t} \sum_{s=0}^{\infty} D_{t,t+s} P_{t+s} \Bigl[ \frac{P_{t+s}(i)}{P_{t+s}}Y_{t+s}(i) - \frac{W_{t}(i)}{P_{t+s}}N_{t+s}(i) - \frac{AC_{t+s}(i)}{P_{t+s}} \Bigr]\\$

where the adjustment cost, $AC_{t}(i)$ , is given by

$\displaystyle AC_{t}(i) = \frac{\varphi}{2} \Bigl[ \frac{P_{t}(i)}{ \Pi_{t-1}^{\rho} P_{t-1}(i)} - 1\Bigr]^{2} Y_{t}(i)$

The welfare cost of shifting trend inflation arises in this model through its effects on average consumption and labor supply as in the Calvo model. The price adjustment cost increases with the level of trend inflation in an accelerating way due to the quadratic nature of adjustment costs. Accordingly, consumption and labor supply decisions respond asymmetrically to a rise and fall in trend inflation. Thus, variations in trend inflation reduces welfare by lowering average consumption and increasing the average level of labor supply.

Figure 3 compares the welfare costs between Rotemberg and Calvo models for various parameter values. For the top left panel, for each Calvo parameter value, I compute the price adjustment cost parameter in the Rotemberg model that would imply the same slope for the log-linearized Phillips curve. The welfare costs are smaller in the Rotemberg model than in the Calvo model by a modest amount for most parameter values. However, the differences can be very large when the price frictions are large, as demonstrated in the top left panel. With the Calvo parameter of 0.8, the welfare costs of shifting trend inflation is about 1.6 percent while it is about 0.8 percent in the Rotemberg model with a corresponding degree of price friction.

An asymmetric trend inflation process

The specification of the trend inflation process in equation (1) implies that the trend inflation fluctuates symmetrically around 2 percent steady-state level.¹⁰ While widely employed in the literature, this symmetric assumption may not be realistic as the instability in trend inflation is often associated with concerns that the inflation becomes higher, not lower. The specification also implies that the central bank aims at negative trend inflation with some probability, which again is not realistic. Accordingly, I consider a modified process for trend inflation in which (i) the instability in trend inflation is associated with an increase in the average trend inflation and (ii) the inflation rate is bounded to be positive. The modified process is given by

log $\displaystyle (\bar{\Pi}_{t}-1) = (1-\rho_{\bar{\Pi}})$ log $\displaystyle (\bar{\Pi}^{*}-1) + \rho_{\bar{\pi}}$ log $\displaystyle (\bar{\Pi}_{t-1}-1) + e_{\bar{\Pi},t}$

where $e_{\bar{\Pi},t} \sim N(0,\kappa\sigma_{\bar{\Pi}}^{2})$ and the constant $\kappa$ is chosen so that the variance of trend inflation in this modified process is the same as that in the baseline specification. In this formulation of trend inflation, a positive innovation leads to a larger increase in trend inflation than a negative innovation does, and therefore, an increase in the variance of the innovation raises the average trend inflation.

Figure 4 compares the welfare costs of shifting trend inflation under the baseline and modified trend inflation processes. By construction, the welfare costs of shifting trend inflation are larger under the modified process than under the baseline process as the variation in trend inflation also increases the average level of trend inflation under the modified process. The welfare costs are typically about 50-100 percent larger with the asymmetric trend inflation process. With the welfare costs being modest under the baseline trend inflation process, the differences are modest in absolute terms. However, for sufficiently large Calvo parameter values implying large welfare costs, the absolute differences are large. When $\alpha=0.8$ , the welfare cost of drifting trend inflation is 1.7 percent under the alternative process as opposed to 1.2 percent under the baseline process.

6 Discussion

6.1 Determinacy

Ascari & Ropele (2009), Coibion & Gorodnichenko (2011), and Kiley (2007) have studied the determinacy properties of the New Keynesian model with constant non-zero trend inflation and found that the set of central bank's reaction functions consistent with determinacy shrinks as trend inflation increases. On a related note, Ascari (2004) and Bakhshi et al. (2007) have pointed out that the Calvo model implies an upper bound of trend inflation above which the model is not well-defined.

While a comprehensive analysis of determinacy properties for models with drifting trend inflation is outside the scope of this paper, a few comments are in order. First, for all the parameter values considered in this paper, the model has a unique rational expectation solution when the steady-state level of trend inflation is 2 percent. Second, since the trend inflation process is mean-reverting, the extent to which trend inflation becomes arbitrarily high in this model is limited compared to the model in which trend inflation follows a random walk. For example, under the baseline parametrization, the probability of trend inflation going above 10 percent is less than one percent. However, with non-negligible probability that trend inflation becomes as high as double digits, it is important to check how good the locally approximated solution is in capturing the large increase in cross-sectional price dispersion associated with such a high trend inflation rate.

To understand how accurate the second-order approximation to the model's solution is, I computed a third-order accurate law of motion using PerturbationAIM of Anderson et al. (2005), and calculated a third-order accurate welfare from it by extending the method of Kim et al. (2008). Welfare costs did not change in a quantitatively important way. I interpret this as indicating that second-order approximation captures the nonlinearity of the model reasonably well. Nevertheless, as pointed out in de Winds & den Haan (2009), perturbation methods cannot control the radius of convergence, and the appropriateness of local approximation is entirely problem specific. Thus, caution is needed in using second-order approximate solutions when applying the analysis of this paper to alternative pricing models.

6.2 State-Dependent Pricing Models

One feature of the Calvo pricing model is that the frequency of price adjustment does not vary with the level of trend inflation. While micro-price data in the U.S. is not available during the episode of the Great Inflation, micro data from other countries show that price adjustment is more frequent during the period of a high inflation (Barros et al. (2009) and Gagnon (2009)). A class of state-dependent pricing models are consistent with this observation, and it would be useful to extend the analysis of this paper to those models. Such analysis is left for future research. The welfare costs of inflation and shifting trend inflation are most likely lower in those models with endogenous frequency of price adjustment than in the Calvo model. Readers can think of the welfare cost calculated with the Calvo-model as an upper bound estimate of the welfare cost of drifting trend inflation under state-dependent pricing models.

7 Conclusion

This paper has studied the welfare consequences of variation in trend inflation. I showed that the welfare cost of shifting trend inflation is modest, and that it comes mainly from the reduced average levels of consumption and leisure. A larger variation in trend inflation leads to a reduction in the average levels of consumption and leisure because a rise in trend inflation decreases consumption and leisure more than a reduction of the same size increases them. For a large range of parameter values, the welfare costs of shifting trend inflation is less than one percent. However, when the price friction is sufficiently large and when the trend inflation process is upward-biased, the welfare cost can exceed than one percent.

Bibliography

R. A. Amano, et al. (2007).

`The Macroeconomic Effects of Nonzero Trend Inflation'.
Journal of Money, Credit and Banking 39(7):1821-1838.

R. A. Amano, et al. (2009).

`Trend inflation, wage and price rigidities, and productivity growth'.
Journal of Monetary Economics 56(3):353-364.

G. Anderson, et al. (2005).

`Higher-Order Perturbation Solutions to Dynamic, Discrete-Time Rational Expectations Models'.
Working Paper .

G. Ascari (2004).

`Staggered Prices and Trend Inflation: Some Nuisances'.
Review of Economic Dynamics 7(3):642-667.

G. Ascari & T. Ropele (2007).

`Optimal Monetary Policy under Low Trend Inflation'.
Journal of Monetary Economics 54(8):2568-2583.

G. Ascari & T. Ropele (2009).

`Trend Inflation, Taylor Principle and Indeterminacy'.
Journal of Money, Credit and Banking 41(8):1557-1584.

H. Bakhshi, et al. (2007).

`The New Keynesian Phillips Curve Under Trend Inflation and Strategic Complementarity'.
Journal of Macroeconomics 29:37-59.

R. Barros, et al. (2009).

`Price Setting in a Variable Macroeconomic Environment: Evidence from Brazilian CPI'.
Working Paper .

B. Bernanke (2006).

`Energy and the Economy'.
Remarks at the Economic Club of Chicago.

T. Cogley, et al. (2009).

`Inflation-Gap Persistence in the U.S.'.
American Economic Journal: Macroeconomics .

T. Cogley & A. Sbordone (2008).

`Trend Inflation, Indexation, and Inflation Persistence in the New Keynesian Phillips Curve'.
American Economic Review 98(5):2101-2126.

O. Coibion & Y. Gorodnichenko (2011).

`Monetary Policy, Trend Inflation and the Great Moderation: An Alternative Interpretation'.
American Economic Review pp. 341-370.

J. de Winds & W. J. den Haan (2009).

`How Well-Behaved Are Higher-Order Perturbation Solutions?'.
Working Paper .

C. L. Evans (2009).

`The Great Inflation 2.0 Debate'.
Remarks at Council on Foreign Relations .

E. Gagnon (2009).

`Price Setting During Low and High Inflation: Evidence from Mexico'.
Quarterly Journal of Economics 124(3):1221-1263.

P. N. Ireland (2007).

`Changes in the Federal Reserve's Inflation Target: Causes and Consequences'.
Journal of Money, Credit and Banking 39(8):1851-1882.

A. Justiniano & G. Primiceri (2008).

`Time-Varying Volatilities and Macroeconomics Fluctuations'.
American Economic Review 98(3):604-641.

M. Kiley (2007).

`Is Moderate-To-High Inflation Inherently Unstable?'.
International Journal of Central Banking 3(2):173-201.

J. Kim, et al. (2008).

`Calculating and Using Second Order Accurate Solutions of Discrete Time Dynamic Equilibrium Models'.
Journal of Economic Dynamics and Control 32:3397-3414.

S. Kozicki & P. Tinsley (2001).

`Shifting Endpoints in the Term Structure of Interest Rates'.
Journal of Monetary Economics 47(3):613-652.

R. E. Lucas, Jr. (1987).

Models of Business Cycles.
Blackwell.

Table 1: Baseline Parameter Values
Parameter	Description	Value
$\beta$	Discount factor	0.9974
	Consumption habit	0.81
	Inverse Frisch elasticity	1.59
$\alpha$	Probability of not being able to optimize	0.6
$\rho$	Degree of price indexation	0.0
$\bar{\theta}$	Elasticity of substitution	10
$\phi_{R}$	AR(1) coefficient for monetary policy shock	0.81
$\phi_{\Pi}$	Taylor coefficient on inflation gap	1.92
$\phi_{y}$	Taylor coefficient on output gap	0.08
$1-\bar{g}^{-1}$	Steady-state share of government expenditure	0.26
(Exogenous shock specific parameter) $\rho_{A}$	AR(1) coefficient for TFP shock	0.8
(Exogenous shock specific parameter) $\rho_{\theta}$	AR(1) coefficient for markup shock	0.0
(Exogenous shock specific parameter) $\rho_{g}$	AR(1) coefficient for government spending shock	0.98
(Exogenous shock specific parameter) $100\sigma_{A}$	Std. Deviation of TFP shock	1.10
(Exogenous shock specific parameter) $100\sigma_{\theta}$	Std. Deviation of markup shock	0.55
(Exogenous shock specific parameter) $100\sigma_{g}$	Std. Deviation of government spending shock	0.55
(Exogenous shock specific parameter) $100\sigma_{R}$	Std. Deviation of monetary policy shock	0.25
(Trend inflation process specific parameter) $\bar{\Pi}^{*}$	Steady-state level of trend inflation	$1.02^{0.25}$
(Trend inflation process specific parameter) $\rho_{\bar{\Pi}}$	Persistence of trend inflation	0.995
(Trend inflation process specific parameter) $100\sigma_{\bar{\Pi}}$	Std. deviation of shocks to trend inflation	0.08
(Trend inflation process specific parameter)	Implied unconditional std. deviation of trend inflation	3.2 (Ann. %)

Table 2: Welfare Cost of Constant Non-Zero Trend Inflation
	Model with $\bar{\Pi}^{*}=1.0$	Model with $\bar{\Pi}^{*}=1.06^{0.25}$
Welfare costs of constant trend inflation		0.59 %
	-894.84	-899.46
$W_{d}$	-889.96	-892.40
$W_{l}$	-0.67	-2.15
$W_{vol}$	-4.21	-4.91
Steady-State C	0.821	0.818
Steady-State N	1.067	1.068
$E[C]^{*}$	-0.161	-0.539
$E[N]^{*}$	0.012	0.016
	1.349	1.447
	1.949	2.135

*Expressed as a percentage deviation from the deterministic steady-state.

Table 3: Welfare Cost of Shifting Trend Inflation
	Model with all shocks	Model with $\sigma_{\bar{\Pi}} = 0$	Model with $\sigma_{A},\sigma_{\theta},\sigma_{g},\sigma_{R} =0$
Welfare costs of shifting trend inflation		0.09 %
Welfare costs of business cycles			0.57 %
	-895.31	-894.59	-890.90
$W_{d}$	-890.17	-890.17	-890.17
$W_{l}$	-0.95	-0.27	-0.68
$W_{vol}$	-4.19	-4.15	-0.04
Steady-State C	0.821	0.821	0.821
Steady-State N	1.067	1.067	1.067
$E[C]^{*}$	-0.233	-0.057	-0.176
$E[N]^{*}$	0.013	0.011	0.001
	1.343	1.336	0.136
	1.993	1.993	0.017

*Expressed as a percentage deviation from the deterministic steady-state.

Figure 1: Welfare Costs of Constant Non-Zero Trend Inflation

Figure 2: Welfare Costs of Shifting Trend Inflation

*A blue vertical line indicates the baseline parameter value.
**For the bottom right panel, the standard deviation of shocks to trend inflation is adjusted as I vary persistence so as to keep the unconditional variance of trend inflation unchanged.

Figure 3: Welfare Costs of Shifting Trend Inflation: Rotemberg pricing model

*Black lines are for the Calvo model and red lines are for the Rotemberg model. For the top right panel, the welfare cost in the Rotemberg model is computed for the value of price adjustment cost parameter that would imply the same slope of the log-linearized Phillips curve as in the Calvo model with corresponding frequency of price adjustment.
**See the footnotes in Figure 2

Figure 4: Welfare Costs of Shifting Trend Inflation: An asymmetric trend inflation process

*Black lines are for the baseline trend inflation process and red lines are for the asymmetric trend inflation process.
**See the footnotes in Figure 2

Appendix

This appendix describes the method of Kim et al. (2008) that allows us to compute second-order accurate welfare measure without simulation. Suppose that you have found the coefficient matrices in the following canonical form.

$\displaystyle y_{t}$	$\displaystyle =$	$\displaystyle F_{c} + F_{f}x_{t} + \frac{1}{2}F_{s}[x_{t}\otimes x_{t}]$
$\displaystyle x_{t+1}$	$\displaystyle =$	$\displaystyle P_{c} + P_{f}x_{t} + \frac{1}{2}P_{s}[x_{t}\otimes x_{t}] + Q e_{t+1}$

$y_{t}$ contains model's forward-looking variables, $x_{t}$ contains exogenous variables and pre-determined variables, and $e_{t}$ contains all exogenous shocks in the economy. Elements of Q contain standard deviation of $e_{t}$ .

Noticing that you only need first-order accurate $x_{t}$ in order to compute second-order accurate $[x_{t}\otimes x_{t}]$ , Kim et al. (2008) write

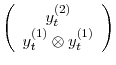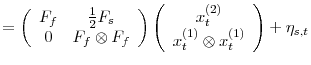$\displaystyle \left( \begin{array}{c} y_{t}^{(2)}\\ y_{t}^{(1)} \otimes y_{t}^{(1)}\\ \end{array} \right)$	$\displaystyle = \left( \begin{array}{cc} F_{f}& \frac{1}{2}F_{s} \\ 0 & F_{f} \otimes F_{f}\\ \end{array} \right) \left( \begin{array}{c} x_{t}^{(2)}\\ x_{t}^{(1)} \otimes x_{t}^{(1)}\\ \end{array} \right) + \eta_{s,t} \nonumber$
	$\displaystyle \Leftrightarrow Y_{s,t} = A_{y,s} X_{s,t} + \eta_{s,t+1}$
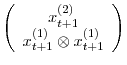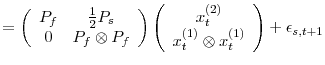$\displaystyle \left( \begin{array}{c} x_{t+1}^{(2)}\\ x_{t+1}^{(1)} \otimes x_{t+1}^{(1)}\\ \end{array} \right)$	$\displaystyle = \left( \begin{array}{cc} P_{f} & \frac{1}{2}P_{s}\\ 0 & P_{f} \otimes P_{f}\\ \end{array} \right) \left( \begin{array}{c} x_{t}^{(2)}\\ x_{t}^{(1)} \otimes x_{t}^{(1)}\\ \end{array} \right) + \epsilon_{s,t+1} \nonumber$
	$\displaystyle \Leftrightarrow X_{s,t+1} = A_{x,s} X_{s,t} + \epsilon_{s,t+1}$

where $x_{t}^{(i)}$ and $y_{t}^{(i)}$ denotes i-th order accurate solution to $x_{t}$ and $y_{t}$ , respectively. Elements of $T_{y,s} = E_{0}[\eta_{s,t+1}]$ are given by

$\displaystyle T_{y,s,1}$	$\displaystyle = F_{c}$
$\displaystyle T_{y,s,2}$	$\displaystyle = 0$

and elements of $T_{x,s} = E_{0}[\epsilon_{s,t+1}]$ are given by

$\displaystyle T_{x,s,1}$	$\displaystyle = P_{c}$
$\displaystyle T_{x,s,2}$	$\displaystyle = (Q \otimes Q)vec(I_{n_{\epsilon}})$

A second-order accurate welfare can then be computed using these VAR representation as follows.

	$\displaystyle E[\sum_{t=0}^{\infty}\beta^{t}u(y_{t},x_{t})] \nonumber$
	$\displaystyle \approx \frac{u(\bar{y},\bar{x})}{1-\beta} + E\sum_{t=0}^{\infty}\beta^{t}[Du_{y}(\bar{y},\bar{x}) y_{t}^{(2)} + \frac{1}{2}Hu_{y}(\bar{y},\bar{x})(y_{t}^{(1)} \otimes y_{t}^{(1)})] \nonumber$
	$\displaystyle + E\sum_{t=0}^{\infty}\beta^{t}[Du_{x}(\bar{y},\bar{x}) x_{t}^{(2)} + \frac{1}{2}Hu_{x}(\bar{y},\bar{x})(x_{t}^{(1)} \otimes x_{t}^{(1)})] \nonumber$
	$\displaystyle = \frac{u(\bar{y},\bar{x})}{1-\beta} + E[\sum_{t=0}^{\infty}\beta^{t} \left[ \begin{array}{c} Du_{y}(\bar{y},\bar{x})\\ \frac{1}{2}Hu_{y}(\bar{y},\bar{x})\\ \end{array} \right]' Y_{s,t}] + E[\sum_{t=0}^{\infty}\beta^{t} \left[ \begin{array}{c} Du_{x}(\bar{y},\bar{x})\\ \frac{1}{2}Hu_{x}(\bar{y},\bar{x})\\ \end{array} \right]' X_{s,t}] \nonumber$
	$\displaystyle = \frac{u(\bar{y},\bar{x})}{1-\beta} + \left[\begin{array}{c} Du_{y}(\bar{y},\bar{x})\\ \frac{1}{2}Hu_{y}(\bar{y},\bar{x})\\ \end{array} \right]' \sum_{t=0}^{\infty}\beta^{t} EY_{s,t} + \left[\begin{array}{c} Du_{x}(\bar{y},\bar{x})\\ \frac{1}{2}Hu_{x}(\bar{y},\bar{x})\\ \end{array} \right]' \sum_{t=0}^{\infty}\beta^{t} EX_{s,t} \nonumber$
	$\displaystyle = \frac{u(\bar{y},\bar{x})}{1-\beta} + \left[\begin{array}{c} Du_{y}(\bar{y},\bar{x})\\ \frac{1}{2}Hu_{y}(\bar{y},\bar{x})\\ \end{array} \right]' \sum_{t=0}^{\infty}\beta^{t} E[A_{y,s}X_{s,t-1}+\eta_{t}] + \left[\begin{array}{c} Du_{x}(\bar{y},\bar{x})\\ \frac{1}{2}Hu_{x}(\bar{y},\bar{x})\\ \end{array} \right]' (I - \beta A_{x,s})^{-1}\frac{\beta}{1-\beta}T_{x,s} \nonumber$
	$\displaystyle = \frac{u(\bar{y},\bar{x})}{1-\beta} + \left[\begin{array}{c} Du_{y}(\bar{y},\bar{x})\\ \frac{1}{2}Hu_{y}(\bar{y},\bar{x})\\ \end{array} \right]'[A_{y,s}(I - \beta A_{x,s})^{-1}\frac{\beta}{1-\beta}T_{x,s} + \frac{\beta}{1-\beta}T_{y,s}] \nonumber$
	$\displaystyle + \left[\begin{array}{c} Du_{x}(\bar{y},\bar{x})\\ \frac{1}{2}Hu_{x}(\bar{y},\bar{x})\\ \end{array} \right]' (I - \beta A_{x,s})^{-1}\frac{\beta}{1-\beta}T_{x,s}$

Footnotes

† The previous version of the paper was titled "Quantifying the Welfare Costs of the Great Inflation." I thank Tim Cogley for his advice, Jesse Perla and Matt Smith for helpful conversation on computation, and Saki Bigio, Oliver de Groot, John Roberts, Christopher Tonetti, and seminar participants at New York University for thoughtful comments. The views expressed in this paper, and all errors and omissions, should be regarded as those solely of the author, and are not necessarily those of the Federal Reserve Board of Governors or the Federal Reserve System. Return to Text

* Division of Research and Statistics, Federal Reserve Board, 20th Street and Constitution Avenue N.W. Washington, D.C. 20551; Email: [email protected]. Return to Text

1. See Bernanke (2006) Return to Text

2. See, for example, the discussion in Evans (2009) Return to Text

3. This number is large compared to the typical numbers computed in the representative agent model largely due to consumption habit formation. I find that the welfare cost of business cycles is reduced to about 0.1 percent in the absence of consumption habits. Return to Text

4. In the literature estimating New Keynesian models, it has become common to assume that today's price is perfectly indexed to a weighted average of past inflation and today's trend inflation as such assumption implies a log-linearized Phillips curve that is invariant to the level of trend inflation. However, as later discussed in Section 4, Cogley & Sbordone (2008) present evidence against perfect indexation. Return to Text

5. For the baseline parametrization, I also solved the model by a third-order approximation to confirm that the second-order approximation capture the key nonlinearities of the model. See Section 6 for more details. Return to Text

6. In the literature on the estimation of New Keynesian DSGE models, it is commonly assumed that no-optimizing firms can perfectly index their prices to a weighted average of past inflation and steady-state inflation so that the level of trend inflation does not affect the dynamics of the economy. Return to Text

7. When this AR(1) coefficient is one, i.e. when trend inflation is a random walk, the model does not possess a well-defined deterministic steady-state. Even though a subset of variables in the model can be transformed into stationary variables, such transformation will make other variables non-stationary unless the degree of indexation is unity. Return to Text

8. If non-optimizing firms can fully index their prices to past inflation, the steady-state price dispersion is unity regardless of the level of trend inflation. If so, the welfare costs of constant trend inflation is zero. Return to Text

9. This effect is present whenever the household's utility function possesses the property of declining absolute risk aversion. Return to Text

10. To be precise, $\bar{\Pi}$ is slightly asymmetric because $\textit{log}(\bar{\Pi})$ is symmetric. For the variance of shocks considered in this paper, this asymmetry is negligible. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text

Welfare Costs of Shifting Trend Inflation†