
The Response of Equity Prices to Movements in Long-term Interest Rates Associated With Monetary Policy Statements: Before and After the Zero Lower Bound
Keywords: Monetary policy, stock market
Abstract:
Monetary policy actions since 2008 have influenced long-term interest rates through forward guidance and quantitative easing. We propose a strategy to identify the comovement between interest rate and equity price movements induced by monetary policy when an observable representing policy changes, such as changes in the interbank rate, is not available. A decline in long-term interest rates induced by monetary policy statements prior to 2009 is accompanied by a 6- to 9-percent increase in equity prices. This association is substantially attenuated in the period since the zero-lower bound has been binding - with a policy-induced 100 basis-point decline in 10-year Treasury yields associated with a 1½- to 3-percent increase in equity prices. Empirical analysis suggests this attenuation does not represent a change in responses to monetary-policy induced movements in interest rates, but reflects the importance of both short- and long-term interest rates.
The influence of monetary policy actions on equity prices is a key aspect of the monetary transmission mechanism (e.g., the overview in Boivin, Kiley, and Mishkin (2010)). As a result, past research considered the impact of decisions by the Federal Open Market Committee regarding the federal funds rate on equity prices (e.g., Bernanke and Kuttner (2005) and Gurkaynak, Sack, and Swanson (2005), to highlight two important examples). In the period prior to 2008, it was widely acknowledged that the central policy instrument used by the Federal Reserve was the federal funds rate, which implied that these earlier studies could focus directly on the link between equity prices and changes in short-term interest rates to identify the associations between interest rates and equity prices associated with monetary policy actions (subject to an identification strategy, which in the case of Bernanke and Kuttner (2005) and Gurkaynak, Sack, and Swanson (2005) involved an event-study approach).
Recently, assessing the association between the changes in interest rates from monetary policy actions and equity price changes has been complicated by the binding zero-lower bound: Since the end of 2008, the target federal funds rate has been "stuck" at effectively zero, and monetary policy has attempted to influence interest rates and equity prices through non-traditional actions such as forward guidance on the path of the federal funds rate and balance sheet expansion targeted at altering long-term interest rates by changing the supply of assets held by the public (which may influence yields through non-classical channels, such as imperfect substitutability across Treasury securities of different duration). In this environment, there is no simple measure of a monetary policy surprise (such as the surprise in the short-term interest rate). The absence of a simple measure of the monetary policy surprise begs the question of how to assess whether policy efforts to, for example, lower long-term Treasury yields have been accompanied by a change in equity (or other) asset prices similar to that which would have prevailed during earlier periods when more traditional monetary policy instruments - changes in the current federal funds rate target - were available.
We propose a strategy to identify the comovement between long-term interest rates and equity prices associated with monetary policy actions when there is no directly observable indicator of the policy action (or degree of surprise in the policy action). Specifically, we model monetary policy surprises as an unobserved process. We then highlight how simple regressions of surprise changes in equity prices on surprise changes in interest rates may lead to inaccurate inferences on the comovement of equity prices and interest rates following monetary policy actions. More importantly, we show how a simple instrumental variables approach provides accurate inference.
We implement the proposed identification scheme. Using data prior to 2009, our proposed approach shows that the strategy followed by Gurkaynak, Sack, and Swanson (2005), using the first-principal component of short-term interest rates, is robust to the possible inaccuracies associated with an unobserved monetary policy process, as should be expected given the conduct of policy in this period - a time at which changes in the federal funds rate were a good indicator of the size of a policy surprise. (Indeed, on this issue we find the discussion of Gurkaynak, Sack, and Swanson (2005) persuasive and refer the reader to their discussion to understand the state of play prior to the zero-lower bound period.)
However, a simple regression approach involving surprises in long-term interest rates appears biased in the direction our framework suggests is likely, illustrating the value of our approach. Implementation of our identification strategy suggests that, prior to 2009, monetary policy actions that would reduce the 10-year Treasury yield by 100 basis points were associated with a 6- to 9-percent increase in equity prices. In contrast, similar-sized declines in the 10-year Treasury yield associated with monetary policy actions since the end of 2008 have been accompanied by increases in equity prices of 1-½ to 3-percent - a notably smaller association. While the analysis herein is empirical and hence subject to interpretation, these results may suggest that policy efforts to reduce long-term interest rates since 2008 have provided less stimulus than that associated with similar-sized declines in the earlier period; a variety of researchers have suggested this is likely (e.g, Woodford (2012)) because the impact of quantitative easing on overall financial conditions, for a given move in long-term interest rates, is of a different nature than that of declines in long-term interest rates associated with movements in short-term interest rates. Loosely speaking, such a difference could arise because declines in long-term interest rates induced by actions that exploit the imperfect substitutability of long-duration assists with short duration assets is, because of imperfect substitutability, less pervasive than the impact of changes in short-term interest rates. The penultimate section explores this possibility, and suggests that the recent attenuated association of long-term interest rates and equity prices is to be expected given the historical role for both short- and long-term interest rates in determining the overall impact on equity prices of monetary policy statements.
Broadly speaking, our analysis employs a novel method, but reaches conclusions similar to that in a couple of other studies. For example, Rosa (2012) examines the response of Treasury yields and equity prices to announcements of asset purchases by the Federal Reserve: The results suggest that the effect of asset purchases on 10-year Treasury yields is disproportionately large relative to that on equity prices - consistent with the finding herein that the movement of equity prices associated with monetary policy announcements in recent years is attenuated relative to that prior to 2009, although the estimates in this study are very imprecise.2 Such imprecision may arise because Rosa (2012) addresses the problem of an unobservable monetary policy surprise by relying on press reports and scoring announcements as either positive or negative surprises - that is, as a dummy variable with values of 1 or -1. Our identification approach provides an alternative to this dummy-variable approach. Wright (2012) considers the response of equity prices to surprise changes in the first principal component of futures on long-term Treasury yields, but does not formally consider experience before and after the zero-lower bound period; the use of principal components has some similarities to the approach herein, as discussed in the next section.
1 Data and identification strategy
Data
Estimating the response of equity prices to monetary policy actions that alter the shape of the term structure is complicated by the fact that the market is unlikely to respond to anticipated policy actions, making it essential to distinguish between expected and unexpected policy actions. To obtain exogenous, surprise variation in monetary policy actions, we focus on movements in asset prices within the day of an FOMC announcement-that is, changes in interest rates and equity prices in short windows around policy actions associated with regularly scheduled FOMC meetings, as well as any intermeeting policy moves. We consider a 30-minute window beginning 10 minutes prior to the FOMC communication and ending 20 minutes after the FOMC communication.
In our analysis, we consider a range of interest rates. With regard to short-term interest rates, we use surprise changes in the federal funds rate, constructed as in Kuttner (2001), Bernanke and Kuttner (2005), and Gurkaynak, Sack, and Swanson (2005), along with changes in the Eurodollar futures rate 1- to 4-quarters ahead. With regard to long-term interest rates, our focus is on movements in the 10-year Treasury yield, as this yield has received the most attention in the literature, especially the literature on quantitative easing.3 For reasons outlined below, our identification strategy will also use data on 2-year and 5-year Treasury yields. Note that the simple change in the price of these securities within the event windows is a very good measure of the surprise change, as anticipated changes over a 30-minute window have trivial effects on the value of 2- or 5- or 10-year securities.4
Changes in equity prices are collected for the same time window surrounding FOMC communications. We use the change in the S&P500, as this data are available for the longest time window, facilitating comparison to studies of data before the end of 2008. Given the short time window surrounding FOMC announcements used in the analysis, it is unlikely that other factors could systematically affect the comovement between equity prices and the term structure. As a result, it seems plausible that the relationships in this window across the term-structure and with equity prices reflect the effect of policymaker communications.
In looking at the comovement between equity prices and interest rates, we divide the sample into two subperiods. The pre-"zero-lower bound" (ZLB) period extends from July, 1991 through December 16, 2008, as the latter date is the day on which the FOMC lowered the target federal funds rate to effectively zero. This period contains 157 FOMC announcements. The zero-lower bound period includes all FOMC announcements after December 16, 2008 (through December 2012) - for a total of 32 announcements.
Figure 1 presents some key aspects of the data on changes in the federal funds rate, 10-year Treasury yields, and the S&P500 around FOMC announcements. The most notable feature is that surprises in the federal funds rate essentially disappear during the ZLB period - reflecting the binding zero-lower bound over this period. In contrast, there remains substantial variability in long-term interest rates and equity prices around FOMC statements in the ZLB period. More generally, we see a decline in the correlation of short-term and long-term interest rates across these subperiods. This can be seen in table 1, which presents the correlation matrix across surprises in the federal funds rate, 1-quarter ahead Eurodollar future, and the 2-, 5-, and 10-year Treasury yields. The decline in correlation is notable, as, for example, the surprise in the two-year Treasury yield is substantially less correlated with that in the 5- or 10-year yields over the ZLB period; additionally, the first two principal components of the surprises in these interest rates accounts for over 95 percent of the variation in these rates in the pre-ZLB period, but less than 80 percent in the ZLB period (not shown). In addition to the economic logic for the subperiods, these changes in correlations suggest it is valuable to distinguish between these periods.5
Identification Strategy
We assume that the scale of monetary policy actions is unobservable: It is known that policy actions are revealed with FOMC communications, but the scale of the action is not quantifiable. This seems eminently reasonable for the recent period, where it may be difficult to think of a scalar summary for the degree of surprise in forward guidance and changes in asset purchases by the Federal Reserve. In earlier periods (prior to 2009), it was sometimes assumed in similar studies that the surprise in short-term interest rates was the observable surprise in monetary policy; we compare our approach to that of Gurkaynak, Sack, and Swanson (2005) in the next sub-section.
Denote the unobservable surprise in monetary policy by ![]() X(t). This surprise influences interest rates (R(t)) and equity prices (P(t)), with some (independently-distributed) errors,
according to the following equations
X(t). This surprise influences interest rates (R(t)) and equity prices (P(t)), with some (independently-distributed) errors,
according to the following equations
(1) ![]() R(t) = b
R(t) = b![]()
![]() X(t) + e(t).
X(t) + e(t).
(2) ![]() ln(P(t)) = b
ln(P(t)) = b![]()
![]() X(t) + v(t).
X(t) + v(t).
Note that we assume there are errors in these relationships, but they are independent; in other words, any correlation between equity prices and interest rates within the monetary-policy event window owes to monetary policy actions, as seems reasonable given the narrow window we consider.
Our interest is in the degree by which equity prices move because of a monetary policy action that changes interest rates by 100 basis points or 1 percentage point - that is, in the change in equity prices associated with a change in monetary policy (![]() X(t)) of size 1/b
X(t)) of size 1/b![]() ; using (1) and (2), this change in equity prices equals b
; using (1) and (2), this change in equity prices equals b![]() /b
/b![]() .
.
Because the scale of the monetary policy action is unobservable, we cannot estimate (1) and (2). But we can insert (1) into (2), yielding
(3) ![]() ln(P(t)) = (b
ln(P(t)) = (b![]() /b
/b![]() )
)![]() R(t) + w(t).
R(t) + w(t).
Clearly, equation (3) cannot be estimated by least squares, as the error term w(t) is a composite of the error in the interest rate equation (1) and that in the equity price equation (2), and is therefore correlated with ![]() R(t). Nonetheless, we can uncover the coefficient of interest by instrumental variables estimation, using instruments correlated with the change in the interest rate of interest (but uncorrelated with the error term in (1)).
R(t). Nonetheless, we can uncover the coefficient of interest by instrumental variables estimation, using instruments correlated with the change in the interest rate of interest (but uncorrelated with the error term in (1)).
Therefore, our identification strategy is the following:
- Specify the interest rate of interest for equations (1)-(3); for the most part, this will be the 10-year Treasury yield, although we also consider the federal funds rate for comparison with Bernanke and Kuttner (2005) and Gurkaynak, Sack, and Swanson (2005).
- Choose a set of other interest rates as instruments: We will use the Eurodollar futures rate 1-quarter ahead, the yield on the 2-year Treasury, and the yield on the 5-year Treasury; as emphasized earlier, it seems plausible that, within the narrow windows we consider, the comovement of these interest rates with those of interest in step one is determined by the monetary policy action.
- Estimate (3) by instrumental variables (via generalized method of moments, accounting for heteroskedasticity), with attention to tests of the relevance of the instruments and the degree to which they satisfy the expected orthogonality conditions.6
Comparison to the Approach of Gurkaynak, Sack, and Swanson (2005)
Before turning to the results for the relationship between equity prices and the yield on the 10-year Treasury before and after 2009, it is useful to consider whether our identification strategy yields results similar to that of Gurkaynak, Sack, and Swanson (2005) (and the similar strategy of Bernanke and Kuttner (2005)). Gurkaynak, Sack, and Swanson found that equity prices respond to the first principal component of surprises in short-term interest rates: Specifically, they find that a surprise decline in the first principal component of short-term interest rates, scaled to imply a one-for-one movement with the surprise in the federal funds rate, has a coefficient of -5 in a regression where equity prices surprises are the dependent variable - that is, a 100bp surprise decline in the federal funds rate leads to a rise in equity prices of 5 percent. We reproduce this analysis for the pre-ZLB period using the first principal component (PC(t)) of surprises in the federal funds rate and Eurodollar futures 1- to 4-quarters ahead. This regression yields (with standard error in parentheses)
![]() ln(P(t)) = -5.34 (0.96)
ln(P(t)) = -5.34 (0.96) ![]() PC(t).
PC(t).
Our instrumental variables approach, using the surprise in the federal funds rate as the regressor and the instruments outlined above, yields
![]() ln(P(t)) = -5.09 (0.97)
ln(P(t)) = -5.09 (0.97) ![]() R
R
![]() (t).
(t).
Clearly, these approaches yield essentially identical results for the pre-ZLB period. Moreover, the size of the estimated coefficient is essentially the same as that found by Gurkaynak, Sack, and Swanson (2005).
The similarity is not surprising: Principal components, by combining the information in a variety of interest rate measures, lowers the influence of possible measurement error; moreover, the monetary policy regime clearly involved adjustments in short-term interest rates in this period, so the use of short-term interest rates should provide good results.7
Finally, we note that Wright (2012) also considers creating a monetary policy surprise by examining the first-principal component of changes in asset prices (in his case, futures on Treasury yields) around an FOMC announcement, but does not consider experience before and after the zero-lower bound period.
2 Results on Comovement Between Long-term Interest Rates and Equity Prices
We now turn to the comovement between the 10-year Treasury yield and equity prices around monetary policy statements. Table 2 presents results for the pre-ZLB and the ZLB periods. Columns 1 and 2 include instrumental variables and least squares results for the first period; columns 3 and 4 include results for the ZLB period.
As can be seen in the second column, a 100 basis point decline in the 10-year Treasury yield around a monetary policy announcement is associated with a 7 percent increase in equity prices (that is, the coefficient is -6.8 and is overwhelmingly statistically significant) prior to the ZLB period. The size of this effect is larger than that revealed by least squares (column (1)): This is to be expected in large samples (according to our model/identification strategy in the previous section), as the problem with estimating equation (3) by least squares is one of classical measurement error.
Moreover, the association in the ZLB period is notably smaller, with a 100bp decline in 10-year Treasury rates associated with a 3 percent rise in equity prices. While this difference is clearly economically significant, we also consider whether this difference is statistically significant via two tests of parameter stability: The Andrews-Fair (1988) approach tests the null hypothesis that the parameters are constant across the two samples; the Hall-Sen (1999) statistics tests for instability in the overidentifying restrictions, a possibility which seems salient given the changes in comovement across the yield curve induced by the zero lower bound (and documented in table 1). The tests of parameter stability clearly reject the null hypothesis of stability, validating the split in sample periods analyzed (for the IV estimates). Interestingly, the tests of parameter instability fail to reject the null of stability for the least-squares estimates: Given the biases inherent in least squares under the identification assumptions, the stability of the least squares estimates is not of interest other than to cast further doubt on using simple least squares regressions in this context.8
With regard to specification checks, the Cragg-Donald statistics suggest that weak instruments are not a concern. The overidentification restrictions associated with the multiple instruments are of slight concern in the pre-ZLB period (as can be seen by the p-value of the reported J-statistic). Examination of the C-statistic for individual instruments suggests that the orthogonality condition is most problematic for the Eurodollar rate 1-quarter ahead (not reported). Therefore, table 3 includes instrumental variables estimates using only the 2-year Treasury yield as an instrument (columns (1) and (2)) and using only the 5-year Treasury yield as an instrument (columns (3) and (4)). On balance, these results are similar to those in table 1: Prior to the ZLB period, a decline in the 10-year Treasury yield of 100bp associated with a monetary policy statement was accompanied by a 6 percent (column (3)) or 9 percent (column (1)) increase in equity prices; during the ZLB period, a similar-sized decline in the 10-year Treasury rate associated with a monetary policy statement was accompanied by a 1½ percent (column (2)) or 2 percent (column (4)) increase in equity prices.9 (Note that use of the 2-year Treasury yield as an instrument for the ZLB period is somewhat questionable, as the Cragg-Donald statistic suggests it is a weak instrument - consistent with the overall thrust emphasized earlier that shorter-term rates have become somewhat divorced from long-term rates because of the ZLB). The Andrews-Fair tests show clear indications that the parameters are not constant across sample periods.
Overall, our analysis suggests that, prior to 2009, a policy-induced 100 basis-point decline in 10-year Treasury yields was associated with a 6- to 9-percent increase in equity prices. This association is substantially attenuated in the period since the zero-lower bound on the federal funds rate has been binding - with a policy-induced 100 basis-point decline in 10-year Treasury yields associated with a 1½- to 3-percent increase in equity prices over this period.
3 Interpretation
We now provide some speculation on how to interpret these results. A wide variety of researchers have noted that there is no reason, a priori, to expect that movements in Treasury yields associated with a lower path for short-term interest rates should have the same effect on other asset prices or economic activity as such movements induced by Quantitative Easing (QE). For example, Woodford (2012) (who expresses considerable skepticism with regard to the efficacy of QE in affecting long-term interest rates) notes that the spillovers of declines in asset prices to other assets - especially risky assets like equities - may be minimal if the "preferred habitat" or "portfolio balance" channels through which Quantitative Easing influence long-term Treasury yields reflect special features of Treasuries such as those associated with safety or duration (which are channels emphasized in the QE literature; see footnote 1).
Our simple identification strategy from section 1 cannot directly address such different channels - rather, a structural model is required. As a first step, we pursue an empirical strategy, and simply posit that the response of equity prices to monetary policy statements depends both on the impact of such statements on short-term interest rates, as in Bernanke and Kuttner (2005) and Gurkaynak, Sack, and Swanson (2005), and on the movement in long-term interest rates, as in section 2. Specifically, we posit the following equation
(4) ![]() ln(P(t)) = d
ln(P(t)) = d![]()
![]()
![]() R
R
![]() (t) + d
(t) + d![]()
![]()
![]() R
R
![]() (t) + u(t).
(t) + u(t).
This structure is (obviously) inconsistent with the single (unobserved) factor structure used in our identification scheme, but also represents a natural step to go beyond existing work that focuses on one interest rate. For the same reasons as emphasized earlier, we pursue an instrumental variables strategy using the same base instrument set as above.
Table 3 reports results for the pre-ZLB period and the ZLB period. Focusing first on the pre-ZLB period, the results appear quite informative: As shown in column 1, declines in short-term interest rates (the federal funds rate) of 100bp around FOMC statements are associated with an increase in equity prices of 4 percent - not far from the value reported in section 1 or that in Bernanke and Kuttner (2005) and Gurkaynak, Sack, and Swanson (2005); declines in the 10-year Treasury yields of 100bp around FOMC statements are associated with an increase in equity prices of 3 percent - close to the value reported in section 2 for the ZLB period, when short-term interest rates were stuck at zero and hence the comovement of equity prices and long-term rates would likely solely reflect long-term rate movements. Notably, the 10-year Treasury yield is not quite significant at conventional levels (the t-statistic is -1.65, yielding a p-value of 0.1003) - although it is slightly closer to significant than the "path factor" in Gurkaynak, Sack, and Swanson (2005); this is perhaps not that surprising, as the path factor focused on interest rates at a one0year horizon, and movements in interest rates of a more persistent nature may be more economically relevant. Nonetheless, the fact that the 10-year Treasury yield is not quite statistically significant echoes, at least partially, the finding in Gurkaynak, Sack, and Swanson (2005) that only one "monetary policy factor" appears to significantly affect equity prices - consistent with our model/identification strategy from section 2.
Turning to the ZLB period, the coefficient on the 10-year Treasury yield is identical to that in the pre-ZLB period - about -3; the coefficient on the federal funds rate surprise jumps substantially and is very imprecisely estimated, consistent with figure 1 - where variation in the surprise in the federal funds rate collapses during the ZLB period. (The Cragg-Donald statistic indicates that the ZLB period results should be treated with caution: This reflects the ZLB on the short rate, as the instruments for surprises in the federal funds rate are poor.) Finally, the stability tests suggest changes in the parameters across the samples - which reflects the change in the behavior of the short rate, as the coefficient on the Treasury yield is the same across sample periods.
Overall, this data-based exploration is consistent with the results in section 2: Declines in 10-year Treasury yields of 100 basis points that are unaccompanied by declines in short-term interest rates are accompanied by a rise in equity prices of perhaps 3 percent (which is clear both in the multivariate regressions of this section or the univariate regression on 10-year yields in the ZLB period, when short rates respond little to monetary policy statements). Outside of the zero-lower bound period, declines in Treasury yields are generally associated with larger effects, as such movements in Treasury yields are accompanied by declines in short-term interest rates, which affect equity prices in addition to any effects of long rates.
Finally, we emphasize that these reduced-form results are consistent with macroeconomic models of the effects of QE, which emphasize roles for both long- and short-term interest rates in determining overall financial conditions (e.g., Andres, Lopez-Salido, and Nelson (2005); Chen, Curdia, and Ferrero (2012); and Kiley (2012)).
4 Summary
Our results are very clear and robust to a variety of cross-checks. A policy-induced 100 basis-point decline in 10-year Treasury yields was associated with a 6- to 9-percent increase in equity prices prior to the ZLB period. This association is substantially attenuated in the period since the zero-lower bound on the federal funds rate has been binding - with a policy-induced 100 basis-point decline in 10-year Treasury yields associated with a 1½- to 3-percent increase in equity prices over this period. Additional empirical analysis suggests the recent attenuation may not represent a change in the interrelations among equity prices and long-term Treasury yields. Rather, the recent attenuation stems from the binding lower zero-lower-bound and the importance of both short- and long-term interest rates in determining the impact on equity prices of monetary policy statements, consistent with some theoretical models.
Even these clear results are subject to caveats. On the one hand, theoretical considerations suggest it is likely that declines in long-term interest rates from Quantitative Easing may impart less stimulus than decline in such rates from the expected path of the short-term policy interest rate (as discussed in the previous section), and the results are certainly consistent with such a prediction. On the other hand, these results only consider correlations in surprises around FOMC communications, and it is possible that the effects of QE could arise in other windows. (Of course, proponents of such a view would need to acknowledge that much of the evidence regarding the effects of Quantitative Easing on interest rates, which we take as given (see footnote 1), stems from a similar methodology.) Moreover, it is possible that FOMC announcements in the ZLB period have communicated more information about the economic outlook than about the policy stance: If FOMC communications provided previously unappreciated information about the outlook, then it is possible that such information would attenuate the response of equity prices to a policy announcement (because, for example, announcements communicating an easing in policy also communicated a worse economic outlook, with the former factor boosting equity prices and the latter factor depressing equity prices). While future work is clearly needed, these results do suggest some caution in evaluating the degree to which efforts to lower long-term interest rates may boost equity prices and, through this channel, stimulate activity.
References
Andres, Javier, David Lopez-Salido, and Edward Nelson (2004). "Tobin's Imperfect Asset Substitution in Optimizing General Equilibrium." Journal of Money, Credit, and Banking, Vol. 36(4), 665690.
Andrews, Donald W. K. and Ray C. Fair (1988) "Inference in Nonlinear Econometric Models with Structural Change." Review of Economics Studies 55:615-40.
Bernanke, B. S. and K. N. Kuttner, 2005. "What Explains the Stock Market's Reaction to Federal Reserve Policy?" Journal of Finance, 60(3), pp. 1221-1257.
Boivin, Jean, Michael T. Kiley, and Frederic S. Mishkin, 2010. "How Has the Monetary Transmission Mechanism Evolved Over Time?," Handbook of Monetary Economics, in: Benjamin M. Friedman & Michael Woodford (ed.), Handbook of Monetary Economics, edition 1, volume 3, chapter 8, pages 369-422 Elsevier.
Chen, Han, Vasco Cúrdia, and Andrea Ferrero, 2011. "The macroeconomic effects of large-scale asset purchase programs," Staff Reports 527, Federal Reserve Bank of New York.
D'Amico, Stefania, and Thomas B. King (Forthcoming). "Flow and Stock Effects of Large-Scale Treasury Purchases: Evidence on the Importance of Local Supply," Journal of Financial Economics.
Eichenbaum, M., L.P. Hansen, and K.J. Singleton (1988). "A Time Series Analysis of Representative Agent Models of Consumption and Leisure Choice under Uncertainty," The Quarterly Journal of Economics, 103(1), 51-78.
English, William B., Skander J. Van den Heuvel, and Egon Zakrajsek, 2012. "Interest rate risk and bank equity valuations," Finance and Economics Discussion Series 2012-26, Board of Governors of the Federal Reserve System (U.S.).
Gagnon, Joseph, Matthew Raskin, Julie Remache, and Brian Sack, 2011. "The Financial Market Effects of the Federal Reserve's Large-Scale Asset Purchases," International Journal of Central Banking, International Journal of Central Banking, vol. 7(1), pages 3-43, March.
Gurkaynak, Refet S., Brian Sack, and Eric T. Swanson (2005) "Do Actions Speak Louder Than Words? The Response of Asset Prices to Monetary Policy Actions and Statements" International Journal of Central Banking, 55-93.
Hall, Alastair R. and Amit Sen (1999) "Structural Stability Testing in Models Estimated by Generalized Method of Moments." Journal of Business & Economic Statistics, Vol. 17, No. 3 (Jul., 1999), pp. 335-348.
Kiley, Michael T., 2012. "The aggregate demand effects of short- and long-term interest rates," Finance and Economics Discussion Series 2012-54, Board of Governors of the Federal Reserve System (U.S.).
Krishnamurthy, Arvind and Annette Vissing-Jorgenson (2011) The Effects of Quantitative Easing on Interest Rates: Channels and Implications for Policy, Brookings Papers on Economic Activity, Fall 2011.
Krishnamurthy, Arvind and Annette Vissing-Jorgenson (2012) The Aggregate Demand for Treasury Debt, with Arvind Krishnamurthy, Journal of Political Economy, April 2012.
Kuttner, Kenneth N., 2001. "Monetary policy surprises and interest rates: Evidence from the Fed funds futures market," Journal of Monetary Economics, Elsevier, vol. 47(3), pages 523-544, June.
Li, Canlin and Min Wei, 2012. "Term structure modelling with supply factors and the Federal Reserve's Large Scale Asset Purchase programs," Finance and Economics Discussion Series 2012-37, Board of Governors of the Federal Reserve System (U.S.).
Rosa, Carlo, 2012. "How "unconventional" are large-scale asset purchases? The impact of monetary policy on asset prices," Staff Reports 560, Federal Reserve Bank of New York.
Stock, James H. and Motohiro Yogo, 2002. "Testing for Weak Instruments in Linear IV Regression," NBER Technical Working Papers 0284, National Bureau of Economic Research, Inc.
Woodford, Michael (2012) Methods of Policy Accommodation at the Interest-Rate Lower Bound. Prepared for 2012 Jackson Hole Symposium sponsored by the Federal Reserve Bank of Kansas City.
Wright, Jonathan (2012) "What does Monetary Policy do to Long-Term Interest Rates at the Zero Lower Bound?" Mimeo, Johns Hopkins University (May).
Figure 1: Surprises in Selected Interest Rates and Equity Prices Around FOMC Announcements Pre-ZLB and ZLB Period
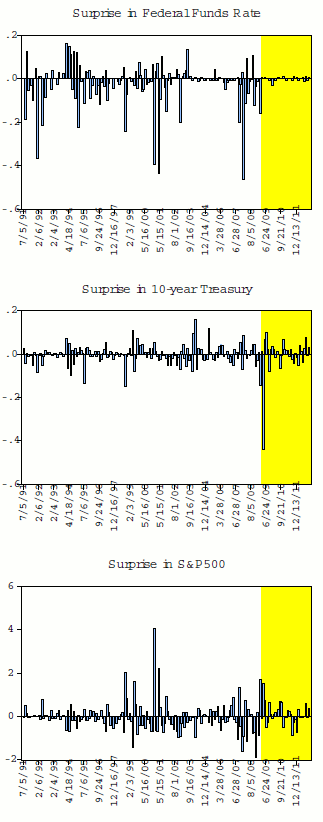
Figure 1 Data
Table 1: Correlation Across Surprises in Interest Rates Around FOMC Announcements
Pre-ZLB Period and ZLB Period
Pre- ZLB period (157 observations)
| Federal Funds | Eurodollar, 1-qtr ahead | 2-yr Treasury | 5-yr Treasury | 10-yr Treasury | |
| Federal Funds | 1.00 | ||||
| Eurodollar, 1-qtr ahead | 0.81 | 1.00 | |||
| 2-yr Treasury | 0.56 | 0.77 | 1.00 | ||
| 5-yr Treasury | 0.34 | 0.62 | 0.92 | 1.00 | |
| 10-yr Treasury | 0.17 | 0.47 | 0.82 | 0.95 | 1.00 |
ZLB period (32 observations)
| Federal Funds | Eurodollar, 1-qtr ahead | 2-yr Treasury | 5-yr Treasury | 10-yr Treasury | |
| Federal Funds | 1.00 | ||||
| Eurodollar, 1-qtr ahead | 0.18 | 1.00 | |||
| 2-yr Treasury | 0.20 | 0.50 | 1.00 | ||
| 5-yr Treasury | 0.06 | 0.52 | 0.85 | 1.00 | |
| 10-yr Treasury | -0.00 | 0.53 | 0.52 | 0.83 | 1.00 |
Table 2: Association of 10-year Treasury Yield Surprises and Equity Price Surprises
Pre-ZLB and ZLB Periods, Baseline Instruments
| Estimation Method | (1) Prior to ZLB LS | (2) Prior to ZLB IV | (3) ZLB LS | (4) ZLB IV |
| Coefficient on: Surprise in 10-yr Treasury | -4.77 | -6.81 | -2.91 | -3.19 |
| Standard error on: Surprise in 10-yr Treasury | 1.70 | 1.73 | 0.55 | 0.71 |
|---|---|---|---|---|
| Test of Overidentifying Restrictions: (J-test, p-value) | na | 0.03 | na | 0.15 |
| Weak Instrument test: Cragg-Donald F-statistic | na | 656.7 | na | 43.9 |
| Weak Instrument test: Stock-Yogo critical value | 22.3 | 22.3 | ||
| Tests of Stability Across Samples: Andrews-Fair test for Tests of Stability Across Samples: parameter stability (p-value) | 0.00 | 0.17 | ||
| Hall-Sen test for stability in overidentifying restrictions (p-value) | 0.03 | na | ||
| Number of observations | 157 | 157 | 32 | 32 |
Note: LS refers to least squares regression. IV refers to instrumental variables via 2-step GMM with heteroskedastic errors. Baseline instruments include the surprises in 1-qtr Eurodollar futures, the 2-year Treasury yield, and the 5-year Treasury yield. Weak instrument test refers to the test based on the size of a 5-percent test being no greater than 10 percent, from Stock and Yogo (2002). Both stability tests refer to a breakpoint at the beginning of the ZLB period (that is, after December 16, 2008). Andrews-Fair test is the Wald test from Andrews and Fair (1988). Hall-Sen test is the test for stability in the overidentifying restrictions from Hall and Sen (1999).
Table 3: Association of 10-year Treasury Yield Surprises and Equity Price Surprises
Pre-ZLB and ZLB Periods, Alternative Instruments
| (1) Instrument: 2-year Treasury yield Pre-ZLB | (2) Instrument: 2-year Treasury yield ZLB | (3) Instrument: 5-year Treasury yield Pre-ZLB | (4) Instrument: 5-year Treasury yield ZLB | |
| Coefficient on: Surprise in 10-yr Treasury | -8.99 | -1.65 | -6.41 | -2.14 |
| Standard error on: Surprise in 10-yr Treasury | 2.14 | 2.55 | 1.72 | 1.48 |
|---|---|---|---|---|
| Weak Instrument test: Cragg-Donald F-statistic | 313.5 | 10.9 | 1426.5 | 64.9 |
| Weak Instrument test: Stock-Yogo critical value | 16.4 | 16.4 | 16.4 | 16.4 |
| Test of Stability Across Samples: Andrews-Fair test for parameter stability (p-value) | 0.00 | 0.02 | ||
| Number of observations | 157 | 32 | 157 | 32 |
Note: Estimation by instrumental variables via 2-step GMM with heteroskedastic errors. Weak instrument test refers to the test based on the size of a 5-percent test being no greater than 10 percent, from Stock and Yogo (2002). Stability test refers to a breakpoint at the beginning of the ZLB period (that is, after December 16, 2008). Andrews-Fair test is the Wald test from Andrews and Fair (1988).
Table 4: Association of Federal Funds Rate and 10-year Treasury Yield Surprises with Equity Price Surprises
Pre-ZLB and ZLB Periods
| (1) Pre-ZLB | (2) ZLB | |
| Coefficient on: Surprise in Federal Funds Rate | -4.06 | -37.58 |
| Standard error on: Surprise in Federal Funds Rate | 1.18 | 18.11 |
| Coefficient on: Surprise in 10-yr Treasury | -3.40 | -3.40 |
| Standard error on: Surprise in 10-yr Treasury | 2.06 | 0.85 |
|---|---|---|
| Test of Overidentifying Restrictions: (J-test, p-value) | 0.24 | 0.21 |
| Weak Instrument test: Cragg-Donald F-statistic | 116.5 | 1.0 |
| Weak Instrument test: Stock-Yogo critical value | 13.4 | 13.4 |
| Tests of Stability Across Samples: Andrews-Fair test for parameter stability (p-value) | 0.01 | |
| Tests of Stability Across Samples: Hall-Sen test for stability in overidentifying restrictions (p-value) | 0.23 | |
| Number of observations | 157 | 32 |
Note: Estimation by instrumental variables via 2-step GMM with heteroskedastic errors. Instruments include the surprises in 1-qtr Eurodollar futures, the 2-year Treasury yield, and the 5-year Treasury yield. Weak instrument test refers to the test based on the size of a 5-percent test being no greater than 10 percent, from Stock and Yogo (2002). Both stability tests refer to a breakpoint at the beginning of the ZLB period (that is, after December 16, 2008). Andrews-Fair test is the Wald test from Andrews and Fair (1988). Hall-Sen test is the test for stability in the overidentifying restrictions from Hall and Sen (1999).