Exchange Rates, Monetary Policy Statements, and Uncovered Interest Parity: Before and After the Zero Lower Bound
Keywords: Monetary policy, exchange rates
Abstract:
While uncovered interest parity (UIP) fails unconditionally, UIP conditional on monetary policy actions remains a cornerstone of macroeconomic models used for monetary policy analysis. We posit that monetary policy actions are partially revealed by FOMC statements and propose a new identification strategy to uncover the degree to which such policy actions induce comovement in exchange rates and long-term interest rates consistent with uncovered interest parity. We reach three conclusions. First, there is evidence in favor of UIP at long horizons, conditional on monetary policy actions, for Dollar/Euro and Dollar/Yen exchange rates. Second, short-run movements in exchange rates following monetary policy surprises are consistent with the overshooting prediction of Dornbusch (1976), although our approach cannot test UIP at short horizons. Finally, we examine the degree to which monetary policy statements since the onset of the zero-lower bound (ZLB) on the short-term interest rate in the United States have engendered different comovement between long-term interest rates and exchange rates and find little evidence for a change in relationships.
Uncovered interest parity (UIP) remains a cornerstone of the monetary policy transmission mechanism, following the influential contribution of Dornbusch (1976) embedded in the core models used at central banks around the world (which build on Obstfeld and Rogoff (1995); see the overview in Boivin, Kiley, and Mishkin (2010)). This influence remains despite the fact that there is overwhelming evidence that UIP fails unconditionally (e.g., Fama (1984) and Rogoff (2002)).
It is possible that the unconditional failure of UIP reflects the influence of factors other than monetary policy, and hence some research has asked whether UIP holds conditional on monetary policy actions - again finding strong evidence against UIP conditional on monetary policy shocks (e.g., Eichenbaum and Evans (1995), Kim and Roubini (2001), Faust and Rogers (2003), Faust, Swanson, and Wright (2005), and Scholl and Uhlig (2010)). This research overwhelming uses a vector-autoregression approach (albeit with different identifying assumptions).
We revisit whether UIP holds conditional on monetary policy shocks using a novel identification scheme. The first aspect of our strategy involves an event study approach in which we focus on surprises in asset prices around monetary policy statements. On top of this, we model monetary policy surprises as an unobserved process affecting asset prices, where the observations in the data may contain noise. We then highlight how simple regressions of surprise changes in exchange rates on surprise changes in interest rates may lead to inaccurate inferences on the comovement of exchange rates and interest rates following monetary policy actions. More importantly, we show how a simple instrumental variables (IV) approach provides accurate inference.
We implement the proposed identification scheme. Using data prior to 2009, a simple regression approach involving surprises in long-term interest rates appears biased in the direction our framework suggests is likely, illustrating the value of our IV approach. This bias results in strong rejections of UIP, even using long-term interest rates, conditional on monetary shocks.
In contrast, implementation of our identification strategy suggests that, prior to 2009, monetary policy actions induced movements in the exchange value of the dollar (relative to the Euro/Deutsche Mark and Yen) and the 5-year or 10-year Treasury yield largely in line with the predictions of uncovered interest parity. This confirmation of UIP, conditional on a monetary policy action, provides evidence that a central prediction of arbitrage across assets denominated in different currencies holds up well under at least some conditions - and indeed under conditions highly relevant for monetary policy.
In addition, we consider the relationship between movements in the U.S. dollar and interest rates at shorter horizons. This analysis finds strong support for overshooting of the type suggested in Dornbusch (1976). (It also finds that a least squares approach is biased against finding overshooting, again illustrating the value of the approach introduced herein). That said, our approach is not amenable to a full examination of UIP (conditional on monetary surprises) at short horizons, as the range of necessary high frequency financial market quotes is beyond that available for this study.
The analysis also considers UIP since the onset of the zero-lower bound (ZLB) in the United States at the end of 2008. This focus is of particular interest, as monetary policy actions in the United States since that time have employed unconventional tools - forward guidance and quantitative easing. Overall, the results indicate that UIP is a good approximation of the relationship between declines in long-term interest rates and exchange rates during this period as well. This finding suggests that monetary policy actions to lower long-term interest rates since 2008 have contributed to a lower exchange value of the dollar - supporting both the views of U.S. policymakers, who have emphasized the positive effects of policy measures in U.S. economic performance, and the concerns regarding "competitive devaluations" of some foreign policymakers.
Finally, the results comparing the pre-ZLB and ZLB period do not suggest that the stimulus from monetary policy to real activity from the exchange rate channel has been attenuated in the ZLB period. This is notable, as a variety of researchers have suggested attenuation of some of the stimulus from recent monetary policy actions (relative to more conventional, pre-ZLB period measures) is likely (e.g., Woodford (2012)); these researchers suggest attenuation because the impact of quantitative easing on overall financial conditions, for a given move in long-term interest rates, is of a different nature than that of declines in long-term interest rates associated with movements in short-term interest rates. Loosely speaking, such a difference could arise because declines in long-term interest rates induced by actions that exploit the imperfect substitutability of long-duration assists with short duration assets is, because of imperfect substitutability, less pervasive than the impact of changes in short-term interest rates.2 While we do not find such evidence for the exchange rate channel, Kiley (2013) suggests that recent monetary policy actions have had unusually small effects on equity values, consistent with some attenuation.
Broadly speaking, our analysis breaks new ground. However, there is some other recent research emphasizing how quantitative easing has contributed to a recent decline in the exchange value of the dollar (Neely (2012) and Rosa (2012)). In addition, our focus on long-term interest rates is in line with the strategy pursued in Chinn and Meredith (2004) and Chinn (2006), who find that the support for UIP is stronger when the focus is on the comovement between exchange rates and long-term interest rates. In this respect, it is important to remember that our analysis does not alter the conclusion that the short-term interest rate differential is a biased predictor of changes in the exchange rate, despite UIP conditional on monetary policy shocks holding at long horizons, similar to the bottom-line emphasized by Chinn (2006). Finally, our emphasis on using an instrumental variables approach and focusing closely on surprises in monetary policy actions (as measures of exogenous changes in interest rates) echoes the common concern that tests of UIP may suffer from problems of endogeneity, particularly if monetary policy responds to the exchange rate as argued by McCallum (1994).
1 Data and identification strategy
Data
Estimating the response of the exchange value of the dollar to monetary policy actions that alter the shape of the term structure is complicated by the fact that the market is unlikely to respond to anticipated policy actions, making it essential to distinguish between expected and unexpected policy actions. To obtain exogenous, surprise variation in monetary policy actions, we focus on movements in asset prices within the day of an FOMC announcement-that is, changes in interest rates and exchange rates in short windows around policy actions associated with regularly scheduled FOMC meetings, as well as any intermeeting policy moves. We consider a 30-minute window beginning 10 minutes prior to the FOMC communication and ending 20 minutes after the FOMC communication. Previous analysis of exchange rates have used similar event windows (e.g., Faust, Swanson, and Wright (2005) and Faust, Rogers, Wang, and Wright (2007)), but have either used such measures to consider UIP conditional on monetary policy shocks in a vector-autoregression analysis (the first study) or have not considered UIP conditional on monetary policy shocks (the second study).
In our analysis, we consider a range of interest rates - some as key regressors and some as instruments in our identification scheme. With regard to short-term interest rates, we use surprise changes in Eurodollar futures 4 quarters ahead (as in, for example, Gurkaynak, Sack, and Swanson (2005), who consider a range of measures of surprises in short-term interest rates). We focus more intensely on longer-term interest rates, as these are central in examining UIP and long horizons and have been the focus on monetary policy actions since the lower bound on short rates became binding in late 2008. With regard to long-term interest rates, our focus is on movements in the 5-year and 10-year Treasury yields. For reasons outlined below, our strategy will also use data on 2-year. Note that the simple change in the price of these securities within the event windows is a very good measure of the surprise change, as anticipated changes over a 30-minute window have trivial effects on the value of 2- or 5- or 10-year securities.3
The majority of FOMC announcements occurred when financial markets in Europe and Japan - the two foreign economic areas analyzed herein - were closed. As a result, we cannot measure changes in foreign interest rates within the same windows as the change in U.S. interest rates, and instead use the daily change from the day of the FOMC announcement to the day after the announcement. As we will highlight below, this data constraint probably introduces some noise in the effect of "monetary surprises" on foreign interest rates - but our identification scheme is designed precisely to address this potential problem.
Changes in the exchange value of the dollar against the Euro/Deutsche Mark and the Yen are collected for the same time window surrounding FOMC communications. (Note that other currency pairs were not available to the author). The exchange rate is measured as dollars per unit of foreign currency, so an increase in the exchange rate represents a depreciation of the currency.
Given the short time window surrounding FOMC announcements used in the analysis, it is unlikely that other factors could systematically affect the comovement between exchange rates and the term structure. As a result, it seems plausible that the relationships in this window across the term-structure and with exchange rates reflect the effect of policymaker communications.
In looking at the comovement between exchange rates and interest rates, we divide the sample into two subperiods. The pre-"zero-lower bound" (ZLB) period extends from July, 1991 through December 16, 2008, as the latter date is the day on which the FOMC lowered the target federal funds rate to effectively zero. (In some regressions using the Euro, the sample period is shorter, reflecting data availability). This period contains 157 FOMC announcements. The zero-lower bound period includes all FOMC announcements after December 16, 2008 (through December 2012) - for a total of 32 announcements.4
Figure 1 presents some key aspects of the data on changes in the 5-year Treasury yields and the exchange value of the dollar against the Euro/Deutsche Mark and Yen around FOMC announcements. There are sizable movements in interest rates and the exchange value of the dollar around FOMC announcements throughout the sample period - both before and after the zero-lower bound.
Table 1 presents the simple correlation matrix for the surprises around FOMC announcements, before and after the zero lower bound. Before the zero lower bound, surprises in short-term interest rates (the Eurodollar future 4-quarters ahead) were very highly correlated with surprise in interest rates at long horizons (e.g., the 10-year Treasury yield); since the onset of the binding zero lower bound, this correlation has decreased. In general, surprises increases in U.S. interest rates have been accompanied by an appreciation of the dollar (i.e., interest rates and the dollar/foreign currency exchange rate are negatively correlated). Note that this correlation increases substantially in the ZLB period, as some FOMC communications led to large movements in interest rates and exchange rates (especially in late 2008 and early 2009). Our analysis will consider carefully whether these changes in correlations are indicative of changes in underlying relationships among the variables.
Identification Strategy
We assume that the scale of monetary policy actions is unobservable: It is known that policy actions are revealed with FOMC communications, but the scale of the action is not quantifiable. This seems eminently reasonable for the recent period, where it may be difficult to think of a scalar summary for the degree of surprise in forward guidance and changes in asset purchases by the Federal Reserve. In earlier periods (prior to 2009), it was sometimes assumed in similar studies that the surprise in short-term interest rates was the observable surprise in monetary policy (e.g., Bernanke and Kuttner (2005) and Gurkaynak, Sack, and Swanson (2005)). Overall, we think it more reasonable, given the fact that FOMC communications reveal information about both the current federal funds rate and the curse of future actions which both affect long-term interest rates, to think of policy surprises as an unobservable process. Of course, our approach, described below, would be robust if an observable process were available - just less efficient; in contrast, assuming an observable process for the policy surprise when one is not, in truth, available would result in biased inference.
Denote the unobservable surprise in monetary policy by 
X(t). This surprise influences interest rates (domestic, R(t), and foreign, R
(t)) and the (natural logarithm of the) exchange rate (e(t)), with some (independently-distributed) errors/noise, according to the following equations
(1a) R(t) = b
X(t) + e(t).
(1b) R(t) = b
X(t) +
e(t).
(2) (e(t)) = b
X(t) + v(t).
Note that we assume there are errors/noise in these relationships, but they are independent; in other words, any correlation between exchange rates and interest rates within the monetary-policy event window owes to monetary policy actions, as seems reasonable given the narrow window we consider.
Our interest is in the degree by which exchange rates move because of a monetary policy action, and particularly whether such movements are consistent with UIP. Specifically, UIP implies (under our convention in which the exchange rates is denominated as dollars in terms of foreign currency)
E
e
(t+k)-e(t) = k(R(t)-R
(t))
where k is the duration of the nominal bonds under consideration and the superscript "T" refers to the "true" measures of interest rates and the exchange rate, uncontaminated by measurement error/noise. Differencing this UIP condition around the monetary policy announcement yields the expression for UIP conditional on a monetary policy surprise,
E e(t+k)- e(t) =
k(R(t)-R(t))
Our data includes e(t), R(t), and R(t) - which include noise/measurement errors (from equations (1-2), but not the true values and not
E e(t+k). At long horizons k, E e(t+k) should be tiny (relative to the other variables considered) - that is, the
permanent change in the nominal exchange rate from a monetary policy surprises will (in standard models) reflect the permanent changes in the (domestic and foreign) price levels, which are likely to be modest. We will return to a discussion of this issue in our section on robustness, and for now
simply assume E e(t+k) is zero, yielding the UIP expression conditional
on a monetary policy surprise,
(3) e(t) = -k(R(t)-R(t))+ w(t).
The prediction is standard - an increase in domestic interest rates leads to an appreciation of the dollar, with the size of the appreciation governed by the magnitude and duration of the change in interest rates; moreover, this exchange rate appreciation embeds Dornbusch's (1976) overshooting,
as the short-run change greatly exceeds any long-run change (i.e., E e(t+k)).
In (3), the error term reflects the measurement errors/noise in observable movements in interest rates and exchange rates (in equations 1 and 2) relative to the true values. Clearly, equation (3) cannot be estimated by least squares, as the error term w(t) is a
composite of the errors in the interest rate equations (1a and 1b) and that in the exchange rate equation (2), and is therefore correlated with R(t) and R(t). Nonetheless, we can uncover the coefficient of interest by instrumental variables estimation,
using instruments correlated with the change in the interest rates of interest (but uncorrelated with the error terms in (1)).
Therefore, our identification strategy is the following:
- Specify the interest rates of interest for equations (1)-(3); for the most part, this will be the 5-year or 10-year Treasury yield and yields on German and Japanese government securities of similar maturity (e.g., k equal to approximately 5 or 10). In both cases, the
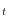
long maturities considered are motivated to a significant degree by the desire to consider cases where E e(t+k) is plausibly near zero. Finally, the effective maturity in each case is approximate, as we use observed movements in coupon yields
in each case, we
compute k using modified duration, assuming the securities trade at par. Under the null hypothesis of UIP, the coefficient from the regression should equal -1. - Choose a set of other interest rates as instruments to control for measurement error: We will use the Eurodollar futures rate 4-quarters ahead and the yield on the 2-year Treasury; as emphasized earlier, it seems plausible that, within the narrow windows we consider, the comovement of these interest rates with those of interest in step one is determined by the monetary policy action.
- Estimate (3) by instrumental variables (via generalized method of moments, accounting for heteroskedasticity), with attention to tests of the relevance of the instruments and the degree to which they satisfy the expected orthogonality conditions.5
The next section presents estimation results.
2 Results on UIP Using Long-term Interest Rates
We first present results estimating (3) by least squares in table 2 for the pre-ZLB and ZLB periods, with the long-horizon interest rate differential given by 5-year yields. The first two columns contain results for the Dollar/(Euro/Deutsche Mark) exchange rate, and the last two contain results for Dollar/Yen exchange rate.
In the period before the ZLB, UIP is rejected for both the Euro and Yen; in contrast, UIP is not rejected in the ZLB period, although the sample size is small and the standard errors are large. Notably, the least squares regression for the Euro does not indicate much evidence of a structural break, although the breakpoint test statistic does indicate some evidence in favor of a break for the Yen.
Table 3 presents IV estimates, using the surprises in the expected Eurodollar rate 4-quarters ahead and the 2-yr Treasury yield as instruments. In the pre-ZLB period, the estimated coefficients are close to -1, highly statistically significant, and not statistically different from -1 for both the Euro (column (1)) and Yen (column (2)). This holds as well for the ZLB period. Our diagnostics suggest that the IV estimates do not suffer from obvious problems - the instruments do not seem correlated with the errors (as suggested by the J-statistic) and the instruments do not appear especially weak for the Yen, although they appear somewhat weak in the case of the Euro (as suggested by the Cragg-Donald statistics). There is no evidence for a break in the estimated coefficient across the pre-ZLB and ZLB sample periods. Finally, the substantially larger coefficients from the IV strategy, especially in the pre-ZLB period when the sample is reasonably large, is exactly what out framework, where least squares suffers from a problem of measurement error that can be corrected by an IV approach, predicts.
Tables 4 and 5 present least squares and instrumental variable results in which the interest differential is measured using 10-year yields. As above, the results are not supportive of UIP using a least squares strategy. In contrast, the results are broadly supportive of UIP using the instrumental variables strategy-again highlighting the value of the approach suggested herein. Moreover, the various diagnostics again suggest the estimation strategy is reasonable, and there is little evidence of a change in the underlying relationships across the pre-ZLB and ZLB periods.
3 Overshooting in the Short-Run and Interpretation
We now consider issues that bear on interpretation and the "robustness" of our results.
As highlighted earlier, the true UIP relationship conditional on a monetary surprise is given by
E e(t+k)- e(t) =
k(R(t)-R(t))
while we have assumed that, at long horizons, E e(t+k) is small and hence can be treated as approximately zero. We now consider this issue in more detail - focusing first on predictions relevant at shorter horizons, when E e(t+k) is plausibly not small - and then turning to a discussion and some empirical evidence on how small E e(t+k) should be at the horizons (5 and 10 years) we consider.
Turning first to the short-run, it is by now a bedrock assumption of monetary economic models that the short-run appreciation of a currency in response to a monetary tightening exceeds the long-run change - i.e., that the nominal exchange rate overshoots its long-run value in response to a
monetary tightening (Dornbusch (1976)) - as initially higher domestic interest rates relative to foreign interest rates dissipate over time, implying that the initial appreciation is followed by an expected depreciation (which ensures that UIP, or the equivalence of expected returns in domestic and
foreign bonds, are equal). This implies that, in the short run, E e(t+k) is positive (an expected depreciation) following an increase in domestic relative to foreign interest rates - and therefore positively correlated with the
interest rate differential. Overshooting therefore implies that, in the short-run, the estimated coefficient in our interest rate regression (3), which omits E e(t+k), should be larger (in absolute value) than -1.
Tables 6 and 7 consider this prediction, focusing on the 2-year horizon (and hence using 2-year yields on the interest rate differential in equation (3)). Table 6 considers least squares, while table 7 tests this prediction using our instrumental variables approach. (In the instrumental variables approach, 2-year interest rates are instrumented with the surprises in the Eurodollar future 4 quarters ahead and the 5-year Treasury yield.) As above, the presence of noise suggests that least squares is biased toward zero in a large sample, and hence we would expect that least squares is less likely to support overshooting than the instrumental variables approach. Looking across the results, this prediction is strongly confirmed: Least squares estimation generally does not support overshooting - that is, the null hypothesis that the regression coefficient is larger, in absolute value, than -1 is not typically supported (especially for the Euro, and less so for the Yen) - while our instrumental variables approach does support overshooting, with estimated coefficients around -3 for the Euro and , during the ZLB period, for the Yen.6
We now consider the assumption that E e(t+k) is small, and hence can be treated as effectively zero, at long horizons. This assumption is likely not literally true, as the expected nominal exchange rate at long horizons should, following a monetary shock
in most macroeconomic models, shift with the permanent changes in the domestic and foreign price levels resulting from such a surprise (thereby leaving the real exchange rate unaffected in the long-run). We made the simplifying assumption that E e(t+k) is
small for several reasons. First, structural models estimated for monetary policy purposes generally find that the "Phillips" curve is very flat, and hence that the effects of monetary policy surprises on the long-run price level are small (e.g., Boivin, Kiley, and Mishkin (2012) and Kiley
(2012), which reference a long literature). These effects are also likely to be small if monetary policy is focused on stabilizing inflation (as found in the analysis of how the evolving response of inflation to monetary actions can be explained by the focus on price stability in the 1980-2005
period in Boivin, Kiley, and Mishkin (2010)), and especially small if monetary policy acts to stabilize the price level (at least somewhat), as found in the empirical analysis of Gordonichenko and Shapiro (2004)). In addition, non-structural investigations, such as those using vector
autoregressions, have found very small effects of monetary policy surprises on the long-run price level in recent data (e.g., figures 2 and 3 in Boivin, Kiley, and Mishkin (2010), or similar results in, for example, Faust and Rogers (2003)).
Overall, each of these considerations suggests that, in the long run, E e(t+k) is small. We also can consider this prediction empirically. Specifically, we use the difference between surprises in nominal yields and
Treasury-inflation-protected securities (that is, the surprise in inflation compensation) to measure the change in the price level expected over 5- or 10-years around FOMC announcements. (This expected change in the price level is, approximately, k times the change in
inflation compensation, where k is the duration of the security; note that inflation compensation includes any risk premiums embedded in asset prices, so this calculation is only approximate, at best.) We regress this change in the expected price level against the
surprise in the U.S. nominal Treasury yields on similar maturity
E p(t+k) = bkR(t) + v(t)
via instrumental variables (for the same reasons as above, and where again the instruments are the surprise in the Eurodollar future 4-quarters ahead and the 2-year Treasury yield). We expect the coefficient b to be small. Results for the 10-year horizons for the pre-ZLB and ZLB periods are reported below (with standard errors in parentheses):
Pre-ZLB: E p(t+k) = 0.12 (0.11)
kR(t) (N equal to 59)
ZLB; E p(t+k) = 0.25 (0.08)kR(t) (N equal to 32)
(Note that the TIPS data is not available for as long a sample period, and hence the pre-ZLB period includes only 59 observations. Also, the results with 5-year yields are largely identical and hence not reported). Before the ZLB period, there is no evidence that price level expectations, at
least as indicated thought TIPS, respond to a change in long-term interest rates around an FOMC communication - consistent with our assumption that E e(t+k) is likely to be small. In contrast, the expected long-run price level appears to have increased with
higher interest rates surrounding FOMC announcements, although the overall change is fairly modest. It is interesting to note that the expected price level increases with higher interest rates surrounding a FOMC announcement, which is not consistent with the expected
contractionary effects of a monetary policy surprise; this could suggest that risk premiums, rather than the expected price level, are dominating moves in inflation compensation. Overall, an analysis of that issue is outside our scope, and we simply conclude by noting that our assumption that
E e(t+k) is likely to be small seems warranted by theory, empirics, and the exploration of TIPS indicators herein, especially for the pre-ZLB period.
4 Summary
We have presented a framework in which monetary policy actions are partially revealed by FOMC statements and proposed a new identification strategy to uncover the degree to which such policy actions induce comovement in exchange rates and long-term interest rates consistent with uncovered interest parity. Our framework suggests that short- and long-run UIP conditions estimated by least squares (conditional on monetary policy surprises) are biased against finding support for UIP and short-run overshooting, and our empirical implementation confirms these predictions. Using our instrumental variables strategy, we find that there is evidence in favor of UIP at long horizons, conditional on monetary policy actions, for Dollar/Euro and Dollar/Yen exchange rates. In addition, short-run movements in exchange rates following monetary policy surprises are consistent with the overshooting prediction of Dornbusch (1976), although our approach cannot test UIP at short horizons. Finally, we examined the degree to which monetary policy statements since the onset of the zero-lower bound (ZLB) on the short-term interest rate in the United States have engendered different comovement between long-term interest rates and exchange rates and find little evidence for a change in relationships.
References
Andres, Javier, David Lopez-Salido, and Edward Nelson (2004). "Tobin's Imperfect Asset Substitution in Optimizing General Equilibrium." Journal of Money, Credit, and Banking, Vol. 36(4), 665690.
Andrews, Donald W. K. and Ray C. Fair (1988) "Inference in Nonlinear Econometric Models with Structural Change." Review of Economics Studies 55:615-40.
Bernanke, B. S. and K. N. Kuttner, 2005. "What Explains the Stock Market's Reaction to Federal Reserve Policy?" Journal of Finance, 60(3), pp. 1221-1257.
Boivin, Jean, Michael T. Kiley, and Frederic S. Mishkin, 2010. "How Has the Monetary Transmission Mechanism Evolved Over Time?," Handbook of Monetary Economics, in: Benjamin M. Friedman & Michael Woodford (ed.), Handbook of Monetary Economics, edition 1, volume 3, chapter 8, pages 369-422 Elsevier.
Chen, Han, Vasco Cúrdia, and Andrea Ferrero, 2011. "The macroeconomic effects of large-scale asset purchase programs," Staff Reports 527, Federal Reserve Bank of New York.
Chinn, M.D., Meredith, G., (2004) "Monetary policy and long horizon uncovered interest parity." IMF Staff Papers 51 (3), 409-430.
Chinn, Menzie D. (2006) "The (partial) rehabilitation of interest rate parity in the floating rate era: Longer horizons, alternative expectations, and emerging markets." Journal of International Money and Finance 25 (2006) 7-21 .
Dornbusch, R., 1976. Expectations and exchange rate dynamics. The Journal of Political Economy 84 (6), 1161-1176.
Eichenbaum, M., Evans, C.L., 1995. Some empirical evidence of shocks to monetary policy on exchange rates. The Quarterly Journal of Economics 110 (4), 975-1010.
Eichenbaum, M., L.P. Hansen, and K.J. Singleton (1988). "A Time Series Analysis of Representative Agent Models of Consumption and Leisure Choice under Uncertainty," The Quarterly Journal of Economics, 103(1), 51-78.
English, William B., Skander J. Van den Heuvel, and Egon Zakrajsek, 2012. "Interest rate risk and bank equity valuations," Finance and Economics Discussion Series 2012-26, Board of Governors of the Federal Reserve System (U.S.).
Fama, E., 1984. Forward and spot exchange rates. Journal of Monetary Economics 14 (3), 319-338.
Faust, J., Rogers, J.H., 2003. Monetary policy's role in exchange rate behaviour. Journal of Monetary Economics 50, 1403-1424.
Faust, Jon & Rogers, John H. & Wang, Shing-Yi B. & Wright, Jonathan H., 2007. "The high-frequency response of exchange rates and interest rates to macroeconomic announcements," Journal of Monetary Economics, Elsevier, vol. 54(4), pages 1051-1068, May.
Faust, J., Swanson, E.T., Wright, J.H., 2004. Identifying VARS based on high frequencyfutures data. Journal of Monetary Economics 51, 1107-1131.
Gorodnichenko, Yuriy & Shapiro, Matthew D., 2007. "Monetary policy when potential output is uncertain: Understanding the growth gamble of the 1990s," Journal of Monetary Economics, Elsevier, vol. 54(4), pages 1132-1162, May.
Gurkaynak, Refet S., Brian Sack, and Eric T. Swanson (2005) "Do Actions Speak Louder Than Words? The Response of Asset Prices to Monetary Policy Actions and Statements" International Journal of Central Banking, 55-93.
Hall, Alastair R. and Amit Sen (1999) "Structural Stability Testing in Models Estimated by Generalized Method of Moments." Journal of Business & Economic Statistics, Vol. 17, No. 3 (Jul., 1999), pp. 335-348.
Kiley, Michael T., 2012. "The aggregate demand effects of short- and long-term interest rates," Finance and Economics Discussion Series 2012-54, Board of Governors of the Federal Reserve System (U.S.).
Kim, S., Roubini, N., 2000. Exchange rate anomalies in the industrial countries: a solution with a structural VAR approach. Journal of Monetary Economics 45 (3), 561-586.
McCallum, B.T. (1994) "A reconsideration of the uncovered interest parity relationship." Journal of Monetary Economics 33, 105-132.
Neely, Christopher J., 2010. "The large scale asset purchases had large international effects," Working Papers 2010-018, Federal Reserve Bank of St. Louis.
Obstfeld, M., Rogoff, K., 1995. Exchange rate dynamics redux. Journal of Political Economy 103, 624-660.
Rogoff, K., 2002. Dornbusch's overshooting model after twenty-five years. IMFWorking Paper. 02/39.
Rosa, Carlo, 2012. "How "unconventional" are large-scale asset purchases? The impact of monetary policy on asset prices," Staff Reports 560, Federal Reserve Bank of New York.
Stock, James H. and Motohiro Yogo, 2002. "Testing for Weak Instruments in Linear IV Regression," NBER Technical Working Papers 0284, National Bureau of Economic Research, Inc.
Woodford, Michael (2012) Methods of Policy Accommodation at the Interest-Rate Lower Bound. Prepared for 2012 Jackson Hole Symposium sponsored by the Federal Reserve Bank of Kansas City.
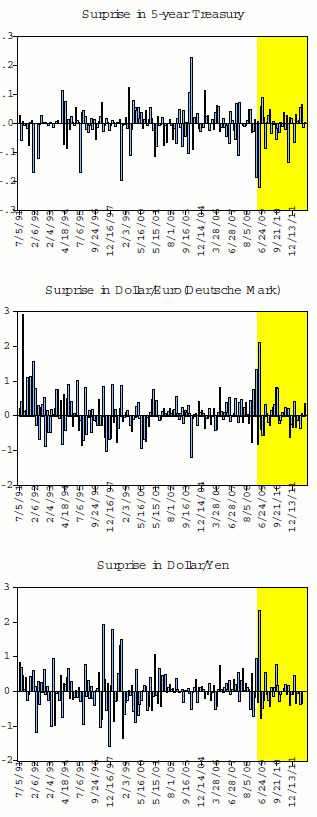
Figure 1 Data
Table 1: Correlation Across Surprises in Interest Rates and Exchange Rates Around FOMC Announcements
Pre-ZLB Period and ZLB Period
Pre- ZLB period (157 observations)
| Eurodollar, 4-qtr ahead | 2-yr Treasury | 5-yr Treasury | 10-yr Treasury | Euro | Yen | |
| Eurodollar, 4-qtr ahead | 1.00 | |||||
| 2-yr Treasury | 0.94 | 1.00 | ||||
| 5-yr Treasury | 0.89 | 0.92 | 1.00 | |||
| 10-yr Treasury | 0.80 | 0.82 | 0.95 | 1.00 | ||
| Euro | -0.36 | -0.37 | -0.35 | -0.28 | 1.00 | |
| Yen | -0.32 | -0.36 | -0.32 | -0.29 | 0.40 | 1.00 |
ZLB period (32 observations)
| Eurodollar, 4-qtr ahead | 2-yr Treasury | 5-yr Treasury | 10-yr Treasury | Euro | Yen | |
| Eurodollar, 4-qtr ahead | 1.00 | |||||
| 2-yr Treasury | 0.93 | 1.00 | ||||
| 5-yr Treasury | 0.71 | 0.90 | 1.00 | |||
| 10-yr Treasury | 0.52 | 0.77 | 0.97 | 1.00 | ||
| Euro | -0.48 | -0.77 | -0.92 | -0.95 | 1.00 | |
| Yen | -0.56 | -0.81 | -0.97 | -0.98 | 0.96 | 1.00 |
Table 2: Association of 5-year Yield Differential Surprises and Exchange Rate Surprises
Pre-ZLB and ZLB Periods, Least Squares
| Estimation Sample | (1) Euro Pre-ZLB | (2) Euro ZLB | (3) Yen Pre-ZLB | (4) Yen ZLB |
| Coefficient on: k(R(t)-R(t)) |
-0.37 | -0.67 | -0.64 | -1.70 |
| Standard error on: k(R(t)-R(t)) |
0.19 | 0.41 | 0.19 | 0.56 |
|---|---|---|---|---|
| Test of Null that UIP holds (coefficient equal to -1) P-value | 0.00 | 0.43 | 0.05 | 0.22 |
| Tests of Stability Across Samples: Andrews-Fair test for parameter stability (p-value) | 0.80 | 0.06 | ||
| Number of observations | 98 | 32 | 146 | 27 |
Note: Least squares regression with heteroskedastic errors. Andrews-Fair stability test is the Wald test from Andrews and Fair (1988) with breakpoint at the beginning of the ZLB period (that is, after December 16, 2008).
Table 3: Association of 5-year Yield Differential Surprises and Exchange Rate Surprises
Pre-ZLB and ZLB Periods, Instrumental Variables
| Estimation Sample | (1) Euro Pre-ZLB | (2) Euro ZLB | (3) Yen Pre-ZLB | (4) Yen ZLB |
| Coefficient on: k(R(t)-R(t)) |
-1.28 | -1.56 | -1.12 | -1.66 |
| Standard error on: k(R(t)-R(t)) |
0.35 | 0.47 | 0.23 | 0.44 |
|---|---|---|---|---|
| Test of Null that UIP holds (coefficient equal to -1) P-value | 0.42 | 0.24 | 0.57 | 0.14 |
| Weak Instrument test: Cragg-Donald F-statistic | 18.89 | 10.30 | 37.32 | 35.53 |
| Weak Instrument test: Stock-Yogo critical value | 8.75 | 8.75 | 8.75 | 8.75 |
| Tests of Stability Across Samples: Andrews-Fair test for parameter stability (p-value) | 0.76 | 0.48 | ||
| Tests of Stability Across Samples: Hall-Sen test for stability in overidentifying restrictions (p-value) | 0.20 | 0.49 | ||
| Number of observations | 98 | 32 | 146 | 27 |
Note: Instrumental variables via 2-step GMM with heteroskedastic errors. Baseline instruments include the surprises in 4-qtr ahead Eurodollar future and the 2-year Treasury yield. Weak instrument test refers to the test based on the size of a 5-percent test being no greater than 20 percent, from Stock and Yogo (2002). Both stability tests refer to a breakpoint at the beginning of the ZLB period (that is, after December 16, 2008). Andrews-Fair test is the Wald test from Andrews and Fair (1988). Hall-Sen test is the test for stability in the overidentifying restrictions from Hall and Sen (1999).
Table 4: Association of 10-year Yield Differential Surprises and Exchange Rate Surprises
Pre-ZLB and ZLB Periods, Least Squares
| Estimation Sample | (1) Euro Pre-ZLB | (2) Euro ZLB | (3) Yen Pre-ZLB | (4) Yen ZLB |
| Coefficient on: k(R(t)-R(t)) |
-0.13 | -0.42 | -0.30 | -0.63 |
| Standard error on: k(R(t)-R(t)) |
0.12 | 0.22 | 0.13 | 0.04 |
|---|---|---|---|---|
| Test of Null that UIP holds (coefficient equal to -1) P-value | 0.00 | 0.00 | 0.05 | 0.00 |
| Tests of Stability Across Samples: Andrews-Fair test for parameter stability (p-value) | 0.51 | 0.02 | ||
| Number of observations | 98 | 32 | 146 | 27 |
Note: Least squares regression with heteroskedastic errors. Andrews-Fair stability test is the Wald test from Andrews and Fair (1988) with breakpoint at the beginning of the ZLB period (that is, after December 16, 2008).
Table 5: Association of 10-year Yield Differential Surprises and Exchange Rate Surprises
Pre-ZLB and ZLB Periods, Instrumental Variables
| Estimation Sample | (1) Euro Pre-ZLB | (2) Euro ZLB | (3) Yen Pre-ZLB | (4) Yen ZLB |
| Coefficient on: k(R(t)-R(t)) |
-0.87 | -0.99 | -0.95 | -0.79 |
| Standard error on: k(R(t)-R(t)) |
0.26 | 0.20 | 0.24 | 0.16 |
|---|---|---|---|---|
| Test of Null that UIP holds (coefficient equal to -1) P-value | 0.61 | 0.94 | 0.82 | 0.19 |
| Weak Instrument test: Cragg-Donald F-statistic | 9.35 | 3.63 | 16.55 | 4.36 |
| Weak Instrument test: Stock-Yogo critical value | 8.75 | 8.75 | 8.75 | 8.75 |
| Tests of Stability Across Samples: Andrews-Fair test for parameter stability (p-value) | 0.80 | 0.64 | ||
| Tests of Stability Across Samples: Hall-Sen test for stability in overidentifying restrictions (p-value) | 0.27 | 0.15 | ||
| Number of observations | 98 | 32 | 146 | 27 |
Note: Instrumental variables via 2-step GMM with heteroskedastic errors. Baseline instruments include the surprises in 4-qtr ahead Eurodollar future and the 2-year Treasury yield. Weak instrument test refers to the test based on the size of a 5-percent test being no greater than 20 percent, from Stock and Yogo (2002). Both stability tests refer to a breakpoint at the beginning of the ZLB period (that is, after December 16, 2008). Andrews-Fair test is the Wald test from Andrews and Fair (1988). Hall-Sen test is the test for stability in the overidentifying restrictions from Hall and Sen (1999).
Table 6: Association of 2-year Yield Differential Surprises and Exchange Rate Surprises
Pre-ZLB and ZLB Periods, Least Squares
| Estimation Sample | (1) Euro Pre-ZLB | (2) Euro ZLB | (3) Yen Pre-ZLB | (4) Yen ZLB |
| Coefficient on: k(R(t)-R(t)) |
-0.98 | -1.18 | -1.55 | -4.68 |
| Standard error on: k(R(t)-R(t)) |
0.38 | 0.62 | 0.39 | 2.33 |
|---|---|---|---|---|
| Tests of Stability Across Samples: Andrews-Fair test for parameter stability (p-value) | 0.87 | 0.17 | ||
| Number of observations | 98 | 32 | 146 | 27 |
Note: Least squares regression with heteroskedastic errors. Andrews-Fair stability test is the Wald test from Andrews and Fair (1988) with breakpoint at the beginning of the ZLB period (that is, after December 16, 2008).
Table 7: Association of 2-year Yield Differential Surprises and Exchange Rate Surprises
Pre-ZLB and ZLB Periods, Instrumental Variables
| Estimation Sample | (1) Euro Pre-ZLB | (2) Euro ZLB | (3) Yen Pre-ZLB | (4) Yen ZLB |
| Coefficient on: k(R(t)-R(t)) |
-3.24 | -3.28 | -1.81 | -3.12 |
| Standard error on: k(R(t)-R(t)) |
0.87 | 1.32 | 0.35 | 1.64 |
|---|---|---|---|---|
| Weak Instrument test: Cragg-Donald F-statistic | 23.32 | 7.45 | 118.46 | 100.18 |
| Weak Instrument test: Stock-Yogo critical value | 8.75 | 8.75 | 8.75 | 8.75 |
| Tests of Stability Across Samples: Andrews-Fair test for parameter stability (p-value) | 0.85 | 0.25 | ||
| Tests of Stability Across Samples: Hall-Sen test for stability in overidentifying restrictions (p-value) | 0.44 | 0.31 | ||
| Number of observations | 98 | 32 | 146 | 27 |
Note: Instrumental variables via 2-step GMM with heteroskedastic errors. Baseline instruments include the surprises in 4-qtr ahead Eurodollar future and the 5-year Treasury yield. Weak instrument test refers to the test based on the size of a 5-percent test being no greater than 20 percent, from Stock and Yogo (2002). Both stability tests refer to a breakpoint at the beginning of the ZLB period (that is, after December 16, 2008). Andrews-Fair test is the Wald test from Andrews and Fair (1988). Hall-Sen test is the test for stability in the overidentifying restrictions from Hall and Sen (1999).