Uncertainty, Risk, and Incentives: Theory and Evidence
Keywords: Executive compensation, optimal contracting, learning, uncertainty, risk-incentive trade-off
Abstract:
1 Introduction
A central prediction of the principal-agent theory is the negative trade-off between risk and incentives (Holmstrom and Milgrom, 1987). Higher performance pay induces greater effort from the agent but increases risk, which, in turn, raises the compensation that must be paid to the agent for bearing risk. The greater the output risk, the higher the compensation for risk, leading to a lower performance pay to the risk-averse agent in the optimal contract. Yet, numerous studies over the past two decades find mixed empirical evidence on such a negative relation between risk and incentives. After reviewing more than two dozen empirical studies and concluding that evidence on the risk-incentive trade-off is inconclusive, Prendergast (2002) argues that in a more uncertain environment, the principal may want to delegate responsibilities to the agent, leading to a positive risk-incentive relation. Other leading explanations for this puzzle includes the idea of endogenous firm risk, where firms offer high powered incentives to induce the agent to take risk (e.g., Core and Guay, 1999; Edmans and Gabaix, 2011a), or the view that risk does not affect incentives because, from the principal's perspective, the cost of risk bearing is outweighed by the benefits of efforts, and thus risk is second order (e.g., Edmans, Gabaix, and Landier, 2009; Edmans and Gabaix, 2011b).
In this paper we offer another plausible theory to explain why the negative risk-incentive trade-off has received mixed empirical support. Empirically measured risk, which is essentially output performance variance, can come from either cash flow risk or project profitability uncertainty, or both. Specifically, in many types of economic environments with agency relationships, output performance not only consists of the agent's effort plus some transitory random noise (i.e., cash flow risk), but also the project's unobserved long-run profitability (i.e., profitability uncertainty).1
We incorporate endogenous learning about the firm's profitability uncertainty into the standard Holmstrom and Milgrom (1987) setting, and show that a potentially positive relation between uncertainty and incentives emerges. In a nutshell, besides the traditional risk channel, the learning channel implies that greater effort, induced by high-powered incentives, leads to more informative signals about uncertain project profitability, improving the firm's future investment decisions. Moreover, somewhat surprisingly, even if one can perfectly separate risk from uncertainty, this learning channel may also overturn the traditional negative risk-incentive relation. Based on several widely used proxies for firm profitability uncertainty, we find empirical support for the positive uncertainty-incentive relation. This suggests that prior mixed empirical results in testing the negative risk-incentive trade-off may be attributable to a positive bias caused by omitting variables that are proxies for profitability uncertainty.
In this paper we develop a two-period investment model, in which the firm hires a manager to manage a project at the beginning of period 1. The project generates an output of
![]() , where
, where ![]() is
capital,
is
capital, ![]() is managerial labor (effort) input, and
is managerial labor (effort) input, and
![]() is exogenous cash flow shock. The parameter
is exogenous cash flow shock. The parameter ![]() is the project's
marginal productivity or profitability. The key departure of our model from standard agency models is that profitability
is the project's
marginal productivity or profitability. The key departure of our model from standard agency models is that profitability ![]() is unknown. Investors learn
is unknown. Investors learn ![]() and then make future investment decisions. Both multiplicative labor with
and then make future investment decisions. Both multiplicative labor with ![]() and additive cash flow noise
and additive cash flow noise
![]() are the drivers of our mechanism; they imply that a greater labor input can increase the information-to-noise ratio of the output signal
are the drivers of our mechanism; they imply that a greater labor input can increase the information-to-noise ratio of the output signal ![]() based on Bayes' rule. At period 2, the firm with a posterior belief of
based on Bayes' rule. At period 2, the firm with a posterior belief of ![]() adjusts capital
adjusts capital ![]() through investment, and resets labor input
through investment, and resets labor input ![]() .
.
To optimize over period-2 investment, investors desire faster learning about ![]() from period-1 output signal
from period-1 output signal ![]() . As a result, for a more informative signal
. As a result, for a more informative signal ![]() , high powered incentives that induce greater effort from the manager are more preferable. Moreover,
the higher the degree of uncertainty, the greater the reduction of the posterior variance of
, high powered incentives that induce greater effort from the manager are more preferable. Moreover,
the higher the degree of uncertainty, the greater the reduction of the posterior variance of ![]() , and thus the greater the benefit in inducing a higher period-1 effort. In other words,
firms with uncertain profitability offer high-powered incentives to their managers for more informative signals to guide their investment policies. This mechanism is similar in spirit to the learning-by-doing literature (e.g., Jovanovic and Lach, 1989; Jovanovic and Nyarko, 1996; and Johnson,
2007). Because uncertainty in
, and thus the greater the benefit in inducing a higher period-1 effort. In other words,
firms with uncertain profitability offer high-powered incentives to their managers for more informative signals to guide their investment policies. This mechanism is similar in spirit to the learning-by-doing literature (e.g., Jovanovic and Lach, 1989; Jovanovic and Nyarko, 1996; and Johnson,
2007). Because uncertainty in ![]() also increases the total volatility of output
also increases the total volatility of output ![]() on the risk-averse manager, when the manager's risk aversion is relatively high, the traditional negative risk-incentive effect dominates and leads to a standard negative uncertainty-incentive relation. However, when the manager's risk aversion is relatively low, the
learning-by-doing effect dominates and leads to a positive uncertainty-incentive relation.2 Moreover, the learning mechanism may also overturn the traditional
negative risk-incentive relation. The higher the risk, the smaller the information-to-noise ratio, and the more the room to learn about the unknown profitability uncertainty. Thus offering high-powered incentives might be desirable.
on the risk-averse manager, when the manager's risk aversion is relatively high, the traditional negative risk-incentive effect dominates and leads to a standard negative uncertainty-incentive relation. However, when the manager's risk aversion is relatively low, the
learning-by-doing effect dominates and leads to a positive uncertainty-incentive relation.2 Moreover, the learning mechanism may also overturn the traditional
negative risk-incentive relation. The higher the risk, the smaller the information-to-noise ratio, and the more the room to learn about the unknown profitability uncertainty. Thus offering high-powered incentives might be desirable.
We empirically test whether the uncertainty-incentive relation is positive in Section 3. Following Pastor and Veronesi (2003) and Korteweg and Polson (2009) we use firm age as our first proxy as older firms usually have lower uncertainty. We also use stock price reaction to earnings announcements (i.e., earnings response coefficient, or ERC) as another proxy for profitability uncertainty (Pastor et al., 2009). Intuitively, investors who are more uncertain about a company's profitability should be more responsive to earnings surprises. Our other proxies for profitability uncertainty are tangibility and market-to-book ratio (Korteweg and Polson, 2009), and analyst forecast error (Lang and Lundholm, 1996). We then run panel regressions of pay-performance sensitivities (PPS henceforth) on these uncertainty proxies and the risk proxy while controlling for other factors known to affect PPS. We find that firm age and tangibility are negatively related to PPS; ERC, market-to-book ratio, and analyst forecast error are positively related to PPS.
Several remarks are worth highlighting in interpreting our empirical results. First, we acknowledge that each individual proxy for uncertainty is imperfect; these proxies may reflect firm characteristics such as growth opportunities. For example, firms with more growth opportunities are often younger, have higher market-to-book ratios, and have more intangible assets. These firms are also harder to analyze and thus are associated with larger ERC and analyst forecast errors. Hence, in all regressions, we control for firm growth using analysts' long-term earnings growth forecast. This is not a perfect solution to remove the effect of growth from the uncertainty proxies, and the results in the paper need to be interpreted with this caveat in mind.
Second, for our analysis, it is important (to try) to separate uncertainty from risk. Fortunately, some uncertainty variables we use are positively correlated with firm volatility, while others (e.g., ERC) are negatively correlated with volatility. Examining all of the different uncertainty variables will help us separate the role of uncertainty from that of volatility. We do, however, acknowledge that the separation of uncertainty from risk in the paper is not perfect.
Third, in our model, profitability uncertainty is taken as exogenous, and firms design endogenous optimal incentive contracts as a response to uncertainty. It could well be possible that the causality goes the other way in practice; that is, incentive contracts affect managers' choices of project uncertainty. This reverse causality problem exists even if we can measure uncertainty perfectly. Although we use fixed effects regressions in the robustness section to address the potential endogeneity problem due to time invariant omitted variables, fixed effects can address neither the problem of time-variant omitted variables nor the reverse causality problem. In this paper we do not claim identification of causality, although we lag our uncertainty proxies by one year in our regression analysis in an attempt to mitigate the reserve causality issue. Because the incentive variables are persistent and some of the uncertainty proxies are forward looking, this treatment is far from perfect.
The contribution of this paper is to propose a new explanation for mixed empirical evidence on the negative risk-incentive trade-off.3 Our learning-based model suggests two reasons: first, the effect of risk on incentives may be confounded by the uncertainty effect if uncertainty is not captured in the model; and second, under learning, the risk-incentive relation becomes ambiguous. On the empirical side, we provide preliminary analysis to see whether the data is consistent with our model. Our analysis suggests that controlling for profitability uncertainty helps partially (if not fully) to restore the negative risk-incentive relation predicted by standard agency theories. Although the coefficients of the risk variable often become less positive or more negative after the uncertainty variables are incorporated in the empirical model, we acknowledge that our analysis cannot fully restore the negative risk-incentive tradeoff and thus is far from resolving Prendagast's statement (2002) that the evidence on the risk-incentive trade-off is inconclusive. We further reiterate that our empirical methodology has several other limitations: our uncertainty proxies are not perfect, the separation of uncertainty from risk is not ideal, and our method does not allow us to establish causality. The attempt to rule out alternative explanations in the robustness section is suggestive rather than conclusive; we await future research on this topic.
The rest of this paper is organized as follows. Section 2 presents the model and its prediction of the positive relation between profitability uncertainty and incentives. Section 3 conducts empirical analysis and Section 4 concludes the paper. All proofs are in the Appendix.
2.1 The Setting
We consider a two-period investment model, where investment consists of capital and (managerial) labor inputs. The risk-free rate is zero. Investors are risk neutral, and managers are risk averse with exponential (CARA) preference. We interpret labor input as the manager's effort. For simplicity, we assume that moral hazard only exists in the first period; the firm matures in the second period and therefore is no longer subject to agency issues.
The output in each period, before investment cost, is modeled as (similar to the standard Cobb-Douglas technology with constant returns to scale)
where
At the beginning of period 1, the firm with a zero outside option decides whether or not to invest ![]() . Given
. Given ![]() , investors hire a manager to provide labor input
, investors hire a manager to provide labor input ![]() , which is unobservable. We interpret
, which is unobservable. We interpret ![]() as managerial effort, and investors offer the manager a compensation contract for proper incentives. We focus on the space of
linear contracts. The contract
as managerial effort, and investors offer the manager a compensation contract for proper incentives. We focus on the space of
linear contracts. The contract
![]() takes the following form with fixed salary
takes the following form with fixed salary ![]() and incentive
and incentive ![]() :
:
Here, the monetary cost for managerial labor
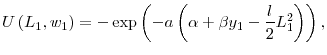 |
(2) |
where
Suppose that the firm induces a labor input of
![]() from the period-1 manager. At the second period the firm makes capital investment and labor investment based on the updated posterior of profitability
from the period-1 manager. At the second period the firm makes capital investment and labor investment based on the updated posterior of profitability
![]() . For period-2 labor investment
. For period-2 labor investment ![]() , the firm hires another manager
with the same cost function
, the firm hires another manager
with the same cost function
![]() , and for simplicity, we assume away any agency problem at period 2 (as the firm's operation becomes more routine). Capital investment is subject to standard
(constant-return-to-scale) quadratic adjustment cost; given initial capital
, and for simplicity, we assume away any agency problem at period 2 (as the firm's operation becomes more routine). Capital investment is subject to standard
(constant-return-to-scale) quadratic adjustment cost; given initial capital ![]() , a (gross) investment of
, a (gross) investment of
![]() leads to a new capital level of
leads to a new capital level of ![]() , where
, where
![]() is a positive constant. As a result, investors at the beginning of period 2 will solve the following problem:
is a positive constant. As a result, investors at the beginning of period 2 will solve the following problem:
![\displaystyle \max_{I,L_{2}}\mathbb{E}\left[ \left. \theta \left( K_{1}+I\right) ^{1-\lambda }L_{2}^{\lambda }+\epsilon _{2}-I-\frac{\kappa }{2K_{1}}I^{2}-% \frac{l}{2}L_{2}^{2}\right\vert y_{1},L_{1}^{\ast }\right]](img39.gif) . . |
We provide a summary of the model timeline as follows; see Figure 1.
- At the beginning of
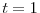 , the firm is deciding whether to take a project. Its outside option is normalized to zero. Thus
, the firm is deciding whether to take a project. Its outside option is normalized to zero. Thus
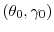 must be sufficiently favorable for the project to be adopted. This stage plays the only role to ensure that
must be sufficiently favorable for the project to be adopted. This stage plays the only role to ensure that
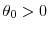 (so maximizing expected output
(so maximizing expected output
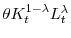 in (1) makes sense), an assumption that holds throughout the paper.4
in (1) makes sense), an assumption that holds throughout the paper.4 - If the firm decides to take this project, investors hire one manager and offer him a linear contract
 , where
, where
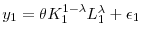 is the project's output in period 1. Investors' period-1 payoff is
is the project's output in period 1. Investors' period-1 payoff is

- Given the outcome
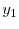 , investors update their belief about
, investors update their belief about  based on the
prior
based on the
prior
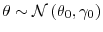 .
. - At
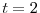 , the firm makes capital investment
, the firm makes capital investment 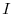 and labor investment
and labor investment 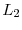 , so that
, so that
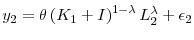 . The period-2 payoff is
. The period-2 payoff is
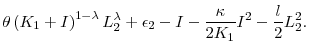
2.2 Discussion of Modeling Assumptions
Before solving the model backwards, we briefly discuss the key assumptions of the model. In particular, we highlight the necessary assumptions for the key model mechanism and discuss the assumptions made for technical convenience as well.
First, two features of production technology in Eq. (1) are important: multiplicative specification between productivity ![]() and managerial labor input
and managerial labor input ![]() , and additive cash flow noise
, and additive cash flow noise
![]() Under this setting, a greater labor input can increase the information-to-noise ratio when investors learn the project's profitability
Under this setting, a greater labor input can increase the information-to-noise ratio when investors learn the project's profitability ![]() from the output signal
from the output signal ![]() using Bayes' rule, resulting in a potentially positive uncertainty-incentive
relation due to the learning-by-doing effect. If instead we assume that output is additive in profitability and labor so that
using Bayes' rule, resulting in a potentially positive uncertainty-incentive
relation due to the learning-by-doing effect. If instead we assume that output is additive in profitability and labor so that
![]() , the learning-by-doing effect disappears. Our learning-by-doing effect also vanishes if we assume a multiplicative cash flow noise, i.e.
, the learning-by-doing effect disappears. Our learning-by-doing effect also vanishes if we assume a multiplicative cash flow noise, i.e.
![]() . This disappearance occurs because increasing effort does not reduce the posterior variance of the unknown parameter
. This disappearance occurs because increasing effort does not reduce the posterior variance of the unknown parameter ![]() in these two alternative settings.
in these two alternative settings.
Second, the common prior on the unknown parameter ![]() indicates that the agent and the principal have the same information regarding
indicates that the agent and the principal have the same information regarding ![]() . It is possible that the agent knows
. It is possible that the agent knows ![]() more than the principal. This is especially true if
more than the principal. This is especially true if ![]() captures the manager's productivity type. Two questions arise under this asymmetric information scenario. The first question is whether the learning-by-doing effect remains. Typically, the
mechanism design approach will first solicit information from the agent in an incentive-compatible manner, and then offer the agent some (potentially different) contract based on the agent's truthful report. If the agent knows
captures the manager's productivity type. Two questions arise under this asymmetric information scenario. The first question is whether the learning-by-doing effect remains. Typically, the
mechanism design approach will first solicit information from the agent in an incentive-compatible manner, and then offer the agent some (potentially different) contract based on the agent's truthful report. If the agent knows ![]() perfectly, then the principal will learn
perfectly, then the principal will learn ![]() immediately, annihilating our learning-by-doing effect. Away from this extreme scenario, as long as
there is uncertainty in
immediately, annihilating our learning-by-doing effect. Away from this extreme scenario, as long as
there is uncertainty in ![]() (either because the agent does not know
(either because the agent does not know ![]() perfectly or the true
perfectly or the true ![]() varies over time), the principal's learning-by-doing effect (that is orthogonal to soliciting the agent's truthful report) remains.
varies over time), the principal's learning-by-doing effect (that is orthogonal to soliciting the agent's truthful report) remains.
Another question is whether information asymmetry leads to an ambiguous uncertainty-incentive relation. A thorough analysis of this question is unavailable. However, from another related angle, Sung (2005) allows for information asymmetry and endogenous project volatility in a setting similar to Holmstrom and Milgrom (1987), and finds that "sometimes the higher the volatility, the higher the sensitivity of the contract." This effect may be complementary to our mechanism.
Third, the assumption of no agency issue in the second period is innocuous and for convenience only. As long as the period-2 managerial labor input has impact on the learning of profitability of period 3, period-2 incentives (if a moral hazard problem still persists) will share the same qualitative feature as period-1 incentives. The important assumption is that the old period 1 manager is replaced by a new manager in period 2, so that the incentive contract is short-term. With long-term employment relationship and endogenous learning, the manager can enjoy some endogenous information rent (as the manager who shirks at period 1 knows that the project actually is better than what investors believe), which makes analysis complicated. See DeMarzo and Sannikov (2010), Prat and Jovanovic (2011), or He, Wei and Yu (2012).
In sum, our main mechanism goes through as long as 1) unknown profitability enters marginal labor productivity, and 2) there is strictly positive cash flow noise that is not scaled with expected output. To highlight the insight, we have chosen to push these two assumptions to extremes so that
![]() .
.
2.3 Learning and Investing in Period 2
Immediately after observing ![]() at period 1, investors update their belief about
at period 1, investors update their belief about ![]() . Given the optimal labor input
. Given the optimal labor input
![]() implemented by the incentive contract at period 1, Bayes' rule implies that the posterior of the project's profitability is characterized by the posterior mean and posterior
variance:
implemented by the incentive contract at period 1, Bayes' rule implies that the posterior of the project's profitability is characterized by the posterior mean and posterior
variance:
Intuitively,
Without loss of generality, we set ![]() to simplify exposition. Solving the model backwards, at period 2 the firm makes capital investment and labor investment so that
to simplify exposition. Solving the model backwards, at period 2 the firm makes capital investment and labor investment so that
![\displaystyle \max_{I,L_{2}}\mathbb{E}\left[ \left. \theta \left( K_{1}+I\right) ^{1-\lambda }L_{2}^{\lambda }+\epsilon _{2}-I-\frac{\kappa }{2K_{1}}I^{2}-% \frac{l}{2}L_{2}^{2}\right\vert y_{1},L_{1}^{\ast }\right] =M\theta _{1}+% \frac{K_{1}}{2}](img69.gif) , , |
where the constant
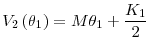 |
is a function of the period 1 posterior mean
However, due to imperfect information, they choose
Standing at time 0, the time-0 expected payoff from period 2 is given by
which is decreasing in
2.4 Optimal Contracting in Period 1
We now solve for the optimal linear contract in period 1. Here, investors offer a linear contract
![]() to implement the optimal labor (effort)
to implement the optimal labor (effort)
![]() , and the optimal contract maximizes their expected total value (including both periods' payoffs):
, and the optimal contract maximizes their expected total value (including both periods' payoffs):
subject to the manager's incentive compatibility and participation constraints:
![\displaystyle L_{1}^{\ast }=\arg \max_{L_{1}}\mathbb{E}\left[ -\exp \left( -a\left( w_{1}-% \frac{l}{2}L_{1}^{2}\right) \right) \right] ,](img77.gif) and and ![\displaystyle \mathbb{E}\left[ -\exp \left( -a\left( w_{1}-\frac{l}{2}L_{1}^{2}\right) \right) \right] \geq \widehat{U}.](img78.gif) |
The following lemma gives the manager's optimal labor (effort) input.
Lemma 1 A contract
![]() implements labor
implements labor
![]() and satisfies the manager's participation constraint, if and only if
and satisfies the manager's participation constraint, if and only if
![]() uniquely solves
uniquely solves
and
Essentially, Lemma 2.4 establishes an important link between implemented labor
![]() and incentive loadings
and incentive loadings ![]() in any incentive-compatible contracts,
which allows the firm to choose implemented
in any incentive-compatible contracts,
which allows the firm to choose implemented
![]() to maximize its value function. In light of Lemma 2.4, we can replace the incentive compatibility and participation constraints in the investors'
problem by Eq. (8) and Eq. (9). Together with Eqs. (3), (4), and (6), we can rewrite the investors' problem in Eq. (7) (for details, see the proof
of Lemma 1 in Appendix A) as:
to maximize its value function. In light of Lemma 2.4, we can replace the incentive compatibility and participation constraints in the investors'
problem by Eq. (8) and Eq. (9). Together with Eqs. (3), (4), and (6), we can rewrite the investors' problem in Eq. (7) (for details, see the proof
of Lemma 1 in Appendix A) as:
![\displaystyle \arg \max_{L_{1}}\left[ \theta _{0}K_{1}^{1-\lambda }L_{1}^{\lambda }-\frac{lL_{1}^{2}}{2}-\frac{a}{2}\beta ^{2}\left( \gamma _{0}K_{1}^{2\left( 1-\lambda \right) }L_{1}^{2\lambda }+\sigma _{\epsilon }^{2}\right) +M\frac{\gamma _{0}^{2}K_{1}^{2\left( 1-\lambda \right) }L_{1}^{2\lambda }}{\sigma _{\epsilon }^{2}+\gamma _{0}K_{1}^{2\left( 1-\lambda \right) }L_{1}^{2\lambda }}\right]](img84.gif)
|
|||
| s.t. 0 |
The first term in the investors' value function is expected period-1 output, the second term is labor cost, the third term is the manager's risk compensation, and the last term is the firm's period 2 payoff. Once we derive the optimal effort level
2.5 Positive Incentive-Uncertainty Relation
In our model, learning could induce a positive relation between incentives and uncertainty. This result is rooted in the fact that investors' expected value of period 2 value,
![]() , depends on learning about profitability
, depends on learning about profitability ![]() from period-1 output
from period-1 output ![]() . As indicated by Eq. (6), maximizing
. As indicated by Eq. (6), maximizing
![]() is equivalent to minimizing the posterior variance of
is equivalent to minimizing the posterior variance of ![]() , i.e.,
, i.e.,
![]() . Because
. Because
![]() is multiplicative with
is multiplicative with ![]() in signal
in signal ![]() as in Eq. (1), implementing a higher effort
as in Eq. (1), implementing a higher effort ![]() raises the
informativeness of the period 1 signal
raises the
informativeness of the period 1 signal ![]() , or equivalently, reduces the posterior variance
, or equivalently, reduces the posterior variance
![]() . Essentially, this mechanism shares a spirit similar to the learning-by-doing literature. For example, Johnson (2007) shows that when return-to-scale in firm's production function
is unknown in advance, overinvestment relative to the full-information case becomes optimal, as overinvestment expedites learning about the unknown production function.
. Essentially, this mechanism shares a spirit similar to the learning-by-doing literature. For example, Johnson (2007) shows that when return-to-scale in firm's production function
is unknown in advance, overinvestment relative to the full-information case becomes optimal, as overinvestment expedites learning about the unknown production function.
Presumably, this learning-by-doing effect is stronger in a more uncertain environment (i.e., a larger
![]() ). The effect is stronger because starting with a larger initial uncertainty
). The effect is stronger because starting with a larger initial uncertainty
![]() , the reduction of the posterior variance will be more significant, which results in a greater benefit of inducing a higher effort. That is, based on Eq. (4), we have
, the reduction of the posterior variance will be more significant, which results in a greater benefit of inducing a higher effort. That is, based on Eq. (4), we have
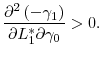 |
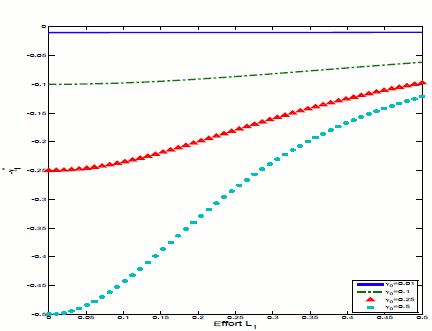
In Figure 2, we plot
Figure 2: The negative posterior variance
![]() as a function of effort in period 1 for different values of
as a function of effort in period 1 for different values of
![]() . Parameters:
. Parameters: ![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() , and
, and
![]() .
.
In Proposition 2 we formally prove the existence of such a positive uncertainty-incentive relation when the manager is sufficiently risk tolerant. Note that higher uncertainty also implies that the manager is bearing larger output volatility, hence a higher incentive provision cost. Therefore, for the positive uncertainty-incentive relation to hold, the manager needs to be sufficiently risk tolerant so that the learning-by-doing effect is dominant.
Proposition 2 For sufficiently small risk aversion coefficient ![]() , a positive relation exists between
, a positive relation exists between
![]() and
and
![]() , i.e.,
, i.e.,
![]() .
.
Figure 3 plots the incentive
![]() as a function of both uncertainty
as a function of both uncertainty
![]() and risk
and risk
![]() . Here, we vary profitability uncertainty
. Here, we vary profitability uncertainty
![]() from 0.2 to 0.3 in the left panels (Panels A and C) and cash flow risk
from 0.2 to 0.3 in the left panels (Panels A and C) and cash flow risk
![]() from 0.05 to 0.15 in the right panels (Panels B and D). We set the absolute risk aversion coefficient to
from 0.05 to 0.15 in the right panels (Panels B and D). We set the absolute risk aversion coefficient to ![]() for the top two panels,5 and
for the top two panels,5 and ![]() for the bottom two panels. Figure 3 indicates that our simple model cannot quantitatively match the very low pay-performance sensitivity observed in the data. However, our focus is the qualitative implications of our model on the relationship between uncertainty
and incentives under realistic parameterizations.
for the bottom two panels. Figure 3 indicates that our simple model cannot quantitatively match the very low pay-performance sensitivity observed in the data. However, our focus is the qualitative implications of our model on the relationship between uncertainty
and incentives under realistic parameterizations.
Panel D shows the traditional negative trade-off between risk
![]() and incentives
and incentives
![]() . In contrast, as predicted by Proposition 2, Panel A shows a positive relation between profitability uncertainty
. In contrast, as predicted by Proposition 2, Panel A shows a positive relation between profitability uncertainty
![]() and incentive
and incentive
![]() when the manager is relatively risk tolerant. Of course, uncertainty also raises the perceived volatility of output. When risk aversion is relatively high as in Panel C, the
traditional negative risk-incentive effects dominate, leading to a negative relation between incentives and uncertainty.
when the manager is relatively risk tolerant. Of course, uncertainty also raises the perceived volatility of output. When risk aversion is relatively high as in Panel C, the
traditional negative risk-incentive effects dominate, leading to a negative relation between incentives and uncertainty.
Figure 3: Incentives
![]() as functions of
as functions of
![]() (left panels A and C) and
(left panels A and C) and
![]() (right panels B and D). Parameters:
(right panels B and D). Parameters: ![]() ,
, ![]() ,
,
![]() ,
,
![]() , and
, and
![]() , In Panel A, we set
, In Panel A, we set ![]() ,
,
![]() , and
, and
![]() . In Panel B, we set
. In Panel B, we set ![]() ,
,
![]() , and
, and
![]() In Panel C, we set
In Panel C, we set ![]() ,
,
![]() , and
, and
![]() . In Panel B, we set
. In Panel B, we set ![]() ,
,
![]() , and
, and
![]()
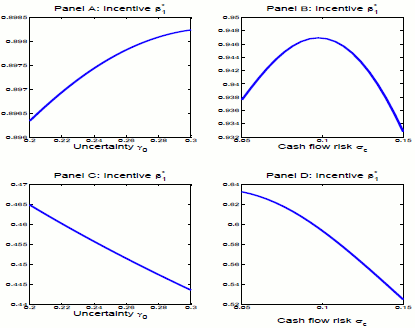
We observe another interesting result in Panel B with ![]() . Here, because of the learning-by-doing effect, even the traditional risk-incentive relation becomes hump shaped. Notice that
investors would like to reduce the posterior variance
. Here, because of the learning-by-doing effect, even the traditional risk-incentive relation becomes hump shaped. Notice that
investors would like to reduce the posterior variance
![]() in Eq. (4), and
in Eq. (4), and
![]() can be viewed as the marginal benefit of expediting learning through raising effort. The higher
can be viewed as the marginal benefit of expediting learning through raising effort. The higher
![]() , the greater the incentive
, the greater the incentive
![]() that investors would like to offer. Linking this benefit to output risk
that investors would like to offer. Linking this benefit to output risk
![]() , in Appendix A we show that
, in Appendix A we show that
![]() if and only if
if and only if
![]() , which explains the nonmonotone incentive-risk relation in Panel B. This
intuition is rooted in the fact that a higher
, which explains the nonmonotone incentive-risk relation in Panel B. This
intuition is rooted in the fact that a higher
![]() implies a lower information-noise ratio. When
implies a lower information-noise ratio. When
![]() so that we are on the right-hand side of the hump shape in Panel B, the
information-noise ratio is low and there is plenty of room for learning. Here, the marginal benefit of expediting learning is positively related to the information-to-noise ratio. Hence, a greater
so that we are on the right-hand side of the hump shape in Panel B, the
information-noise ratio is low and there is plenty of room for learning. Here, the marginal benefit of expediting learning is positively related to the information-to-noise ratio. Hence, a greater
![]() lowers the marginal benefit of learning
lowers the marginal benefit of learning
![]() , and consequently investors offer a lower-powered incentive contract. On the left-hand side of the hump shape where
, and consequently investors offer a lower-powered incentive contract. On the left-hand side of the hump shape where
![]() , the opposite holds. This is because the information-to-noise ratio is
already high and investors have learned a great deal about
, the opposite holds. This is because the information-to-noise ratio is
already high and investors have learned a great deal about ![]() , and a higher
, and a higher
![]() lowers the information-to-noise ratio. This increases the room to learn, leading to a greater marginal benefit from learning. Taken together, Panel B shows that a
potential positive risk-incentive relation due to learning may overturn the traditional negative risk-incentive trade-off when the manager is sufficiently risk tolerant.
lowers the information-to-noise ratio. This increases the room to learn, leading to a greater marginal benefit from learning. Taken together, Panel B shows that a
potential positive risk-incentive relation due to learning may overturn the traditional negative risk-incentive trade-off when the manager is sufficiently risk tolerant.
In sum, in addition to the leading alternative explanations surveyed in the introduction, our model provides another plausible explanation for why it is difficult to identify a negative risk-incentive trade-off in the data. According to our model, there could be two reasons. First, we might have a positive relation between uncertainty and incentives for small risk aversion coefficients (Panel A), and existing empirical analysis does not distinguish uncertainty from risk. Second, even if we can identify risk from uncertainty, with learning there is not necessarily a clear-cut relation between risk and incentives (Panel B).
3 Empirical Analysis
In this section, we empirically test the prediction of a positive relation between uncertainty and incentives. We also investigate how this positive relation affects the traditional trade-off between risk and incentives. In Section 3.1, we describe our data, incentive and risk measures, and profitability uncertainty proxies. We then provide regression results in Section 3.2.
3.1.1 Data and Sample Selection
Our sample consists of a manager-firm matched panel data set from 1992 to 2008. This data set allows us to track the highest paid executives of firms covered by ExecuComp through time. We merge the manager-level ExecuComp data with the firm-level annual accounting variables from Compustat, stock returns from CRSP, corporate board information from RiskMetrics, and analyst forecast information from IBES. We then remove the observations with incomplete data. We also winsorize the continuous variables that present obvious outliers by replacing the extreme values with the 1 and 99 percentile values. The main regressions are estimated based on our full sample, which includes 2,441 firms and 25,999 top executives.
3.1.2 Pay-Performance Sensitivity
The dependent variable in the paper is pay-performance sensitivity (PPS), a standard variable used in the literature to measure managerial incentives. There are three PPS measures in the executive compensation literature. The first measure, dollar-to-dollar measure
(PPS1) (Jensen and Murphy, 1990), is equal to the dollar change in stock and option holdings for a one dollar change in firm value (see also Demsetz and Lehn, 1985; Yermack, 1995; Schaefer, 1998; Palia, 2001; Jin, 2002; and Aggarwal and Samwick, 2003). This measure is essentially
![]() (where
(where ![]() is the CEO's
wealth) and is also called value-sensitivity or share of the money in Becker (2006). The second measure, dollar-to-percentage measure (PPS2) (Hall and Liebman, 1998), is equal to the dollar change in stock and
option holdings for a one percent change in firm value (see also Holmstrom, 1992; and Core and Guay, 2002). The PPS2 measure is equal to
is the CEO's
wealth) and is also called value-sensitivity or share of the money in Becker (2006). The second measure, dollar-to-percentage measure (PPS2) (Hall and Liebman, 1998), is equal to the dollar change in stock and
option holdings for a one percent change in firm value (see also Holmstrom, 1992; and Core and Guay, 2002). The PPS2 measure is equal to
![]() and is also referred to as return-sensitivity or money at stake in Becker (2006). The
third measure, scaled wealth-performance sensitivity measure (PPS3) (Edmans et al., 2009), is equal to PPS2 divided by TDC1, where TDC1 is the total compensation of an executive.6 This incentive measure is similar to the percentage-to-percentage incentives (i.e.,
and is also referred to as return-sensitivity or money at stake in Becker (2006). The
third measure, scaled wealth-performance sensitivity measure (PPS3) (Edmans et al., 2009), is equal to PPS2 divided by TDC1, where TDC1 is the total compensation of an executive.6 This incentive measure is similar to the percentage-to-percentage incentives (i.e.,
![]() ) used (or advocated) by Murphy (1985), Gibbons and Murphy (1992), Rosen (1992), and Peng and Röell (2008), but replaces
flow compensation in the numerator of the Murphy (1985) measure with the change in the executives' wealth.
) used (or advocated) by Murphy (1985), Gibbons and Murphy (1992), Rosen (1992), and Peng and Röell (2008), but replaces
flow compensation in the numerator of the Murphy (1985) measure with the change in the executives' wealth.
3.1.3 Empirical Proxies for Profitability Uncertainty
Despite a large literature studying the effect of parameter uncertainty on asset prices and investment (see Pastor and Veronesi, 2009, for a recent survey), separating uncertainty from risk is empirically challenging. In the existing literature, most of the studies (e.g., Pastor and Veronesi,
2003; Korteweg and Polson, 2009; and Pastor, Taylor, and Veronesi, 2009) use imperfect proxies to test model implications. Following their footsteps, we use five profitability uncertainty proxies in our study. These proxies have been used in the existing literature; for detailed definitions of
these proxies, see Appendix B. We do not use firm size as an uncertainty proxy, although it is proposed by such literature as Korteweg and Polson (2009). There exists a strong empirical relation between size and PPS; that is, firm size is negatively correlated with PPS1
and positively correlated with PPS2 (e.g., Edmans et al., 2009).7 We do, however, include firm size and (size)![]() as control variables in all of our regressions to capture the (potentially nonlinear) size effect.8
as control variables in all of our regressions to capture the (potentially nonlinear) size effect.8
Natural log of firm age
The first proxy that we employ is firm age. Previous studies such as Pastor and Veronesi (2003) and Korteweg and Polson (2009) use firm age as a proxy for profitability uncertainty. Uncertainty declines over a firm's lifetime due to learning, and younger firms have higher uncertainty. Following Pastor and Veronesi (2003), we consider each firm as " born" in the year of its first appearance in the CRSP database. Specifically, we obtain the first occurrence of a valid stock price on CRSP, as well as the first occurrence of a valid market value in the CRSP/COMPUSTAT database, and take the earlier of the two. The firm's age is assigned the value of one in the year in which the firm is born and increases by one in each subsequent year. As in Pastor and Veronesi (2003), we take the natural log of firm age. Log(age) is concave in firm's plain age, and captures the idea that regarding uncertainty, one year of age should matter more for young firms than for old firms.
Earnings response coefficient (ERC)
We follow Pastor et al. (2009) and Cremers and Yan (2010) to use the stock price reaction to earnings announcements (i.e., earnings response coefficient or briefly, ERC). More specifically, ERC is the average of a firm's previous 12 stock price reactions to quarterly earnings surprises.9 Intuitively, investors who are more uncertain about the profitability of a company should respond more strongly to earnings surprises. As noted in Pastor et al. (2009), the ERC measure is ideal to separate uncertainty from volatility because ERC is high when uncertainty is high and earnings volatility is low. When realized earnings are more precise, investors react more to earnings surprises, leading to a higher value of ERC. The shortcoming of the ERC measure is its measurement error. As a result, we also incorporate other empirical proxies of uncertainty in the analysis.
Market-to-book ratio
The third proxy for profitability uncertainty is the market-to-book ratio, which equals market value of equity plus the book value of debt, divided by total assets. Pastor and Veronesi (2003) show that aging in the life of a firm is accompanied by a decrease in the market-to-book ratio. According to Korteweg and Polson (2009), the market-to-book ratio is a proxy for firm growth opportunities, and such opportunities are inherently more difficult to value than the assets in place. As a result, the market-to-book ratio increases with uncertainty about firm profitability.
Tangibility
The fourth proxy is tangibility. Korteweg and Polson (2009) mention that firms with more tangible assets (property, plant, and equipment) are easier to value and thus are related to lower profitability uncertainty. We use net property, plant, and equipment scaled by firm total assets to measure tangibility.
Analyst forecast error
We also construct an analyst forecast error variable as a proxy of profitability uncertainty. Based on Bae et al. (2008) and Lang and Lundholm (1996), for each specific company in each fiscal year, we first obtain the absolute value of the forecast error made by each analyst, where forecast errors are defined as the difference between the forecast value and the actual value of earnings per share. We then use the median value of these absolute forecast errors, scaled by the absolute value of the actual EPS. Using the mean value of the absolute forecast errors gives similar results.10
We end this section by pointing out that uncertainty is hard to measure and could be endogenous. We use five different proxies for uncertainty, hoping that establishing similar results for all of them can raise hurdles for other alternative explanations. Unfortunately, the five proxies we use can be all linked to firm growth. Fast-growing firms have higher marginal benefit of managerial effort and thus should have higher-powered incentives, which can also explain the positive uncertainty-incentive relation.11 To address this issue at least partially, our control variables include the long-term earnings growth forecast from analysts, which gives a more precise measure of firm growth (relative to our five uncertainty proxies). Indeed, in the regressions, the coefficient on long-term earnings growth forecast is always significantly positive, suggesting the validity of this alternative mechanism.
3.1.4 The Risk Variable
Similar to the literature that tests the risk-incentive relation, we take stock return volatility as a measure of risk in our regression analysis. We measure stock return volatility as the standard deviation of daily log (percentage) returns over the past five years, which is then annualized by multiplying by the square root of 254 (Yermack, 1995, and Palia, 2001). We acknowledge that this proxy for firm risk may be imperfect and can also capture profitability uncertainty. We also use the percentage rank of stock dollar return variance (Aggarwal and Samwick, 1999, 2002, 2003, Garvey and Milbourn, 2003, and Jin, 2002) in the empirical analysis, but obtain essentially the same results.
3.1.5 Control Variables
In the regressions, we include various control variables that could potentially affect the incentives a firm provides to its managers; see detailed definitions of all of the following variables in Appendix B. These control variables have been used in the empirical literature on the determinants of managerial incentives (Aggarwal and Samwick, 2003, Core et al., 1999, Jin, 2002, Palia, 2001, etc.). As mentioned at the beginning of Section 3.1.3, since there is a well-established empirical pattern between incentives and firm size, we first include firm size and the square of firm size as controls. Following the literature, we also include profitability, the ratio of capital expenditure to total assets, advertising expenses scaled by total assets, a dummy variable that is set to one whenever advertising expenses are missing, firm leverage, and dividend payout indicator. We further control for corporate governance variables, which include the CEO chair indicator and the proportion of inside directors on the board. Manager-level variables, such as log(tenure), the CEO indicator, and the female indicator, are also controlled in the regressions. Finally, year and industry effects are included to capture the time and industrial differences in the level of managerial incentives.
3.1.6 Summary Statistics and Correlations between Variables
Table 1 contains summary statistics of the variables used in the regression analysis. For instance, the average (median) dollar-to-dollar measure of PPS1 is 1.13% (0.22%), suggesting that the average (median) dollar change in the sample executives' stock and option holdings for a one thousand dollar change in firm value is $11.3 ($2.2). These summary numbers are consistent with those provided in the empirical literature such as Core and Guay (1999), Palia (2001), and Yermack (1995). The statistics also imply a positive skewness in PPS, with a few companies having very high incentives.
The average, median, minimum, and maximum age of the sample firms are 26, 20, 1, and 84 years, respectively, similar to those reported in Pastor and Veronesi (2003). The firms in the sample have an average (median) earnings response coefficient of 4.44 (2.88), market-to-book ratio of 2.08 (1.51), tangibility of 0.29 (0.23), and total assets of $6.6 ($1.3) billion. The average analyst forecast error relative to the actual value is about 16%. In addition, the average (median) annual stock return volatility is 44% (39%).
Table 2 examines the pairwise correlations between the variables. Not surprisingly, the three PPS variables are positively correlated; the correlation coefficient between the dollar-to-dollar PPS1 and the dollar-to-return PPS2 is 0.55, and PPS1 (PPS2) is correlated with PPS3 at 0.21 (0.25). The PPS variables are in general negatively correlated with firm age and tangibility, and are positively correlated with the earnings response coefficient (ERC) and the market-to-book ratio. The correlations between PPS2 and firm age are very low. The low correlations may be due to the fact that PPS2 is PPS1 multiplied by market value of equity, and the negative relation between age and PPS1 is canceled out by the positive relation between age and market value. When we control for firm size in the model, the relation between PPS2 and firm age becomes negative and significant. PPS3 has a very low correlation (-0.03) with firm size, consistent with the property mentioned in Edmans et al. (2009) that the PPS3 measure is independent of firm size.
Table 2 also shows that the uncertainty proxy variables are correlated with each other, with the correlation between firm age and market to book being -0.23 and the correlation between firm age and tangibility around 0.18. These correlations indicate that younger firms tend to be firms with more growth options and lower tangibility ratios. The table also reveals very low correlations between ERC and volatilities and between ERC and firm size, suggesting that ERC serves an ideal proxy variable that separates uncertainty from volatility and firm size. In contrast, the percentage-return and dollar-return volatilities have opposite signs in correlations with other variables. This is perhaps due to the fact that the dollar return volatility, which equals percentage return volatility multiplied by firm market value, captures the firm size effect.
3.2 Empirical Results
This section uses regression analysis to examine the effect of profitability uncertainty and risk on incentives. The main empirical model is as follows:
In the equation, we use
3.2.1 Main Results
Tables 3-5 report the OLS regression results, with each table having different PPS dependent variables. The ![]() -statistics in these regressions are heteroskedasticity robust and are
adjusted for clustering within firms. In all three tables, Column (1) does not include any of the five uncertainty variables, Columns (2)-(6) include one of the five uncertainty variables, and Column (7) includes all five uncertainty variables.
-statistics in these regressions are heteroskedasticity robust and are
adjusted for clustering within firms. In all three tables, Column (1) does not include any of the five uncertainty variables, Columns (2)-(6) include one of the five uncertainty variables, and Column (7) includes all five uncertainty variables.
Positive uncertainty-incentive relation
The results in Tables 3-5 show that firm age is negatively related to incentives (Columns (2) and (7)), indicating that younger firms, i.e., firms with higher uncertainty, are associated with greater managerial incentives. Both the earnings response coefficient (ERC) and the market-to-book ratio are positively associated with the incentive variables in most regressions. The relation between tangibility and PPS is generally negative, suggesting that firms that have more tangible assets are associated with lower incentives. Firms with greater analyst forecast errors (that might be due to greater uncertainty) are weakly related to higher incentives.
All of these results indicate a positive relation between profitability uncertainty and incentives, consistent with our model when the manager's risk aversion is relatively low. This positive relation is not only statistically significant but also economically important. Take Column (7) in
Tables 3-5 as examples. A one-standard-deviation decrease in log(firm age), which is about 0.97 (i.e., firm age reduces by about 3 years), is associated with an increase of approximately 0.23% (=0.97![]() 0.24) in PPS1, 34.09 (=0.97
0.24) in PPS1, 34.09 (=0.97![]() 35.14) in PPS2, and 11.72 (=0.97
35.14) in PPS2, and 11.72 (=0.97![]() 12.08) in PPS3. These increases in PPS are of similar magnitude to that of the median values of PPS. Other uncertainty variables have similar economic significance.
12.08) in PPS3. These increases in PPS are of similar magnitude to that of the median values of PPS. Other uncertainty variables have similar economic significance.
Reexamining the risk-incentive relation
The negative risk-incentive relation is a key prediction from standard agency theories, but with mixed empirical support from existing literature. From the point of view of this paper, the risk proxies used in the previous literature, namely stock volatility and rank of dollar return volatility,
could be contaminated by profitability uncertainty. If profitability uncertainty is positively related to incentives, then it is not surprising that previous research, in which the risk proxy captures both the cash flow risk
![]() and the profitability uncertainty
and the profitability uncertainty
![]() , finds an ambiguous risk-incentive relation.
, finds an ambiguous risk-incentive relation.
The above reasoning suggests that in revealing the negative risk-incentive relation, it is important to control for uncertainty, as it helps correct for the positive bias potentially caused by omitting relevant variables that are proxies for profitability uncertainty. Our empirical results offer evidence for this implication. Compared with the specification that does not include the uncertainty proxies (i.e., Columns(1) of Tables 3-5), when we include the uncertainty variables in the regressions (Columns (7) of Tables 3-5), the relation between volatility and incentives becomes less positive or more negative. This pattern generally holds in other specifications considered in Section 3.2.2 for robustness checks.
Although our results do not fully restore the significantly negative risk-incentive relation from the data (possibly due to such reasons as endogenous matching between firm risk and CEO's risk appetite, the learning-by-doing effect in Figure 3 Panel D of this paper, etc.), it should be safe to say that separating profitability uncertainty from cash flow risk is important when empirically examining the negative risk-incentive relation. Our results also indicate that it may be important to separate the effect of profitability uncertainty from that of risk in other empirical studies.
3.2.2 Robustness Analysis
This section performs additional analysis to investigate the robustness of our empirical results.
Risk measured as dollar return volatility
In addition to measuring firm risk using the variance of stock percentage returns, we attempt to use a different measure of firm risk: volatility of stock dollar returns. Following Aggarwal and Samwick (1999, 2003) and Jin (2002), we use the percentage rank of the variance of dollar returns,12 and report results in Panel A of Table 6. In Column (1), we find that the rank of dollar return volatility is negative and significant, consistent with Aggarwal and Samwick (1999, 2002, 2003), Garvey and Milbourn (2003), and Jin (2002). In Column (2), we include the uncertainty variables, and find that greater profitability uncertainty is related to higher incentives. Moreover, the dollar return volatility (i.e., the risk proxy) continues to be negative and significant after including uncertainty variables. In Columns (3)-(6), in which PPS2 and PPS3 are dependent variables, we continue to find that firms with greater uncertainty provide higher incentives to their executives. The effect of the risk variable is positive and significant when the uncertainty variables are excluded, but the effect becomes insignificant when the uncertainty variables are introduced to the model.
Median regressions
Following Aggarwal and Samwick (1999, 2003) and Jin (2002), we use median regressions to deal with outliers and right skewness in the compensation data. Results are reported in Panel B of Table 6 (with risk measured by the percentage return volatility) and Panel C of Table 6 (with risk measured by the rank of dollar return volatility). Both tables show that in general, uncertainty is positively related to incentives. The coefficient on the risk variable becomes less positive or more negative if profitability uncertainty is captured in the model.
Fixed effect regressions
In Panel D of Table 6, we deal with potential endogeneity issues by adding the firm-manager paired fixed effects in the regressions. For example, it is possible that some unobservable managerial attributes (e.g., risk aversions) are correlated with the explanatory variables, such as firm age and at the same time are correlated with the dependent variable, PPS. The firm-manager fixed effect may also capture time-invariant unobservable factors that potentially affect endogenous matching between the firm and the manager (Graham et al., 2011). We can see from Panel D of Table 6 that the coefficients on the profitability uncertainty proxies continue to show a positive relation between profitability uncertainty and incentives.
Admittedly, the fixed effect specification can only address the potential endogeneity problem due to time invariant omitted variables. Fixed effects cannot address the time-variant omitted variables, nor the reverse causality problem, where some of our proxies of uncertainty (e.g., Market-to-book ratio) are forward looking and thus respond to tomorrow's pay-performance sensitivity (recall that we have lagged uncertainty proxies by one year in regression).
Other robustness checks
Finally, the tables reported so far examine each top executive's incentives. In untabulated analysis, we also examine CEO incentives only, non-CEO incentives, and the average incentives for top executives in each individual company. We also examine the incentives from stock and options, separately. The results, omitted for brevity, provide the same implications as those reported here.
In addition, Pastor and Veronesi (2003) find that the market-to-book ratio increases with uncertainty about average profitability, especially for firms that pay no dividends. We interact the dividend paying dummy with the uncertainty proxy variables, and run regressions with interaction variables. The coefficients of the interaction variables are not significant, suggesting that the positive relation between uncertainty and incentives does not vary significantly between firms that pay dividends and firms that do not.
In all, the empirical results that we obtain offer preliminary support to our theoretical prediction that profitability uncertainty is positively related to incentives.
4 Conclusion
This paper introduces profitability uncertainty into an agency model, and investigates the relation between profitability uncertainty and incentives. Our model predicts a positive uncertainty-incentive relation, in contrast to the negative risk-incentive trade-off obtained in the extant literature. Using several proxies for profitability uncertainty, we find empirically that the data seem to be consistent with our theoretical prediction. Our analysis suggests that controlling for uncertainties helps partially to restore the negative risk-incentive relation predicted by standard agency theories. We acknowledge several limitations in our empirical analysis. Due to these limitations, the empirical results in the paper are suggestive rather than conclusive.
References
Aggarwal, Rajesh K., and Andrew A. Samwick, 1999, The other side of the trade-off: The impact of risk on executive compensation, Journal of Political Economy 107-1, 65-105.
Aggarwal, Rajesh K., and Andrew A. Samwick, 2002, The other side of the trade-off: The impact of risk on executive compensation - A reply, Working Paper, Dartmouth College.
Aggarwal, Rajesh K., and Andrew A. Samwick, 2003, Performance incentives within firms: The effect of managerial responsibility, Journal of Finance 58-4, 1613-1650.
Bae, Kee-Hong, Rene M. Stulz, and Hongping Tan, 2008, Do local analysts know more? A cross-country study of the performance of local analysts and foreign analysts, Journal of Financial Economics 88-3, 581-606.
Baker, George P., and Bjorn Jorgensen, 2003, Volatility, noise and incentives, mimeo, Harvard University and Columbia University.
Baker, Malcolm, and Jeffrey Wurgler, 2006, Investor sentiment and the cross-section of stock returns, Journal of Finance 61-4, 1645-1680.
Becker, Bo, 2006, Wealth and executive compensation, Journal of Finance 61-1, 379-397.
Bitler, Marianne P., Tobias J. Moskowitz, and Annette Vissing-Jorgensen, 2005, Testing agency theory with entrepreneur effort and wealth, Journal of Finance 60-2, 539-576.
Bizjak, John M., James A. Brickley, and Jeffrey L. Coles, 1993, Stock-based incentive compensation and investment behavior, Journal of Accounting and Economics 16, 349-372.
Bushman, Robert M., Raffi J. Indjejikian, and Abbie Smith, 1996, CEO compensation: The role of individual performance evaluation, Journal of Accounting and Economics 21-2, 161-193.
Coles, Jeffrey L., Naveen D. Daniel, and Lalitha Naveen, 2006, Managerial incentives and risk-taking, Journal of Financial Economics 79, 431-468.
Conyon, Martin J., and Kevin J. Murphy, 2000, The prince and the pauper? CEO pay in the United States and United Kingdom, Economic Journal 110-467, 640-671.
Core, John, and Wayne Guay, 1999, The use of equity grants to manage optimal equity incentive levels, Journal of Accounting and Economics 28-2, 151-184.
Core, John, and Wayne Guay, 2002, Estimating the value of employee stock option portfolios and their sensitivities to price and volatility, Journal of Accounting Research 40-3, 613-630.
Core, John, Wayne Guay, and Robert Verrecchia, 2003, Price versus non-price performance measures in optimal CEO compensation contracts, The Accounting Review 78-4, 957-981.
Core, John E., Robert W. Holthausen, and David F. Larcker, 1999, Corporate governance, chief executive officer compensation, and firm performance, Journal of Financial Economics 51-3, 371-406.
Cremers, Martijn, and Hongjun Yan, 2010, Uncertainty and Valuations, working paper, Yale University.
DeMarzo, Peter, and Yuliy Sannikov, 2010, Learning in dynamic incentive contracts, working paper, Stanford University and Princeton University.
Demsetz, Harold, and Kenneth Lehn, 1985, The Structure of Corporate Ownership: Causes and Consequences, Journal of Political Economy 93, 1155-1177.
Dittmann, Ingolf, and Ernst Maug, 2007, Lower Salaries and No Options? On the Optimal Structure of Executive Pay, Journal of Finance 62, 303-342.
Edmans, Alex, and Xavier Gabaix, 2011a, The Effect of Risk on the CEO Market, Review of Financial Studies 24, 2822-2863.
Edmans, Alex, and Xavier Gabaix, 2011b, Tractability in Incentive Contracting, Review of Financial Studies 24, 2865-2894.
Edmans, Alex, Xavier Gabaix, and Augustin Landier, 2009, A multiplicative model of optimal CEO incentives in market equilibrium, Review of Financial Studies 22-12, 4881-4917.
Gabaix, Xavier, and Augustin Landier, 2008, Why has CEO pay increased so much? Quarterly Journal of Economics 123-1, 49-100.
Garen, John E., 1994, Executive compensation and principal-agent theory, Journal of Political Economy 102-6, 1175-1199.
Garvey, Gerald, and Todd Milbourn, 2003, Incentive compensation when executives can hedge the market: Evidence of relative performance evaluation in the cross section, Journal of Finance 58-4, 1557-1582.
Gibbons, Robert and Kevin J. Murphy, 1992, Optimal incentive contracts in the presence of career concerns: Theory and evidence, Journal of Political Economy, 100, 468-505.
Graham, John R., Si Li, and Jiaping Qiu, 2012, Managerial Attributes and Executive Compensation, Review of Financial Studies 25-1, 144-186.
Hall, Brian J., and Jeffrey B. Liebman, 1998, Are CEOs Really Paid Like Bureaucrats?, Quarterly Journal of Economics 113-3, 653-691.
Haubrich, Joseph, 1994. Risk aversion, performance pay, and the principalagent problem. Journal of Political Economy 102, 258-276.
He, Zhiguo, Bin Wei, and Jianfeng Yu, 2012, Optimal Long-term Contracting with Learning, Working paper, University of Chicago.
Himmelberg, Charles P., R. Glenn Hubbard, and Darius Palia, 1999, Understanding the determinants of managerial ownership and the link between ownership and performance, Journal of Financial Economics 53-3, 353-384.
Holmstrom, Bengt, 1992, Comments, in L. Werin and H. Wijkander (eds.), Contract Economics, Cambridge, MA: Blackwell.
Holmstrom, Bengt, and Paul Milgrom, 1987, Aggregation and linearity in the provision of intertemporal incentives, Econometrica 55-2, 303-328.
Jovanovic, Boyan, and Saul Lach, 1989, Entry, Exit, & Diffusion with Learning by Doing, American Economic Review, 79-4, 690-699.
Jovanovic, Boyan, and Yaw Nyarko, 1996, Learning by Doing & the Choice of Technology, Econometrica, 64-6, 1299-1310.
Jensen, Michael C., and Kevin J. Murphy, 1990, Performance pay and top management incentives, Journal of Political Economy 98-2, 225-264.
Jin, Li, 2002, CEO compensation, diversification, and incentives, Journal of Financial Economics 66-1, 29-63.
Johnson, Timothy, 2007, Optimal learning and new technology bubbles, Journal of Monetary Economics, 54, 2486-2511.
Korteweg, Arthur G., and Nicholas Polson, 2009, Corporate credit spreads under parameter uncertainty, working paper, Stanford University and University of Chicago.
Lambert, Richard A., and David F. Larcker, 1987, An analysis of the use of accounting and market measures of performance in executive compensation contracts, Journal of Accounting Research 25, 85-125.
Lang, Mark H., and Russell J. Lundholm, 1996, Corporate disclosure policy and analyst behavior, The Accounting Review 71-4, 467-492.
Murphy, Kevin J., 1985, Corporate Performance and Managerial Remuneration: An Empirical Investigation, Journal of Accounting and Economics, 7, 11-42.
Murphy, Kevin J., 1986, Incentives, learning, and compensation: A theoretical and empirical investigation of managerial labor contracts, Rand Journal of Economics 17, 59-76.
Palia, Darius, 2001, The endogeneity of managerial compensation in firm valuation: A solution, Review of Financial Studies 14-3, 735-764.
Pastor, Lubos, Lucian A. Taylor, and Pietro Veronesi, 2009, Entrepreneurial learning, the IPO decision, and the post-IPO drop in firm profitability, Review of Financial Studies 22-8, 3005-3046.
Pastor, Lubos, and Pietro Veronesi, 2003, Stock valuation and learning about profitability, Journal of Finance 58-5, 1749-1790.
Pastor, Lubos, and Pietro Veronesi, 2009, Learning in financial markets, Annual Review of Financial Economics 1, 361-381.
Peng, Lin, and Ailsa Röell, 2008, Manipulation and Equity-Based Compensation, American Economic Review Papers and Proceedings 98-2, 285-290.
Peng, Lin, and Ailsa Röell, 2012, Managerial Incentives and Stock Price Manipulation, Working paper.
Prat, Julien, and Boyan Jovanovic, 2011, Dynamic contracts when agent's quality is unknown, working paper, NYU.
Prendergast, Canice, 2002, The tenuous trade-off between risk and incentives, Journal of Political Economy 110-5, 1071-1102.
Rosen, Sherwin, 1992, Contracts and the market for executives. In Contract Economics, ed. L Wein, H Wijkander. Cambridge: Blackwell Publishers.
Schaefer, Scott, 1998, The Dependence of Pay-Performance Sensitivity on the Size of the Firm, Review of Economics and Statistics 80, 436-443.
Sung, Jaeyoung, 2005, Optimal Contracts Under Adverse Selection and Moral Hazard: A Continuous-Time Approach, Review of Financial Studies 18, 1021-1073.
Yermack, David, 1995, Do corporations award CEO stock options effectively?, Journal of Financial Economics 39-2, 237-269.
Zabojnik, Jan, 1996, Pay-performance sensitivity and production uncertainty, Economics Letters 53-3, 291-296.
Table 1: Summary Statistics
| Variables | N | Mean | Stdev | Median | Min | Max |
|---|---|---|---|---|---|---|
| Pay-performance sensitivity PPS1 | 179930 | 1.13% | 3.15% | 0.22% | 0% | 22.66% |
| Pay-performance sensitivity PPS2 ($thousands) | 179930 | 168.61 | 476.91 | 27.97 | 0 | 3519.93 |
| Pay-performance sensitivity PPS3 | 169841 | 36.34 | 119.97 | 6.77 | 0 | 939.61 |
| Profitability uncertainty variables Firm age | 143291 | 25.56 | 20.02 | 20 | 1 | 84 |
| Profitability uncertainty variables Earnings response coefficient (ERC) | 117263 | 4.44 | 10.4 | 2.88 | -57.01 | 75.09 |
| Profitability uncertainty variables Market-to-book (M/B) | 141405 | 2.08 | 2.03 | 1.51 | 0.51 | 43.19 |
| Profitability uncertainty variables Tangibility | 139799 | 0.29 | 0.24 | 0.23 | 0 | 0.94 |
| Profitability uncertainty variables Analyst forecast error | 131689 | 0.16 | 0.55 | 0.03 | 0 | 6 |
| Risk variables Stock return volatility | 141623 | 0.44 | 0.2 | 0.39 | 0.18 | 1.14 |
| Risk variables Dollar return volatility ($millions) | 108557 | 1497.2 | 2639.38 | 477.79 | 27.98 | 14382.63 |
| Control variables Total assets ($millions) | 143182 | 6589 | 14022 | 1343 | 0.07 | 72282 |
| Control variables Analysts's long-term growth forecast (%) | 179930 | 15.39 | 6.09 | 15.39 | 1.95 | 60 |
| Control variables Profitability | 140222 | 0.13 | 0.13 | 0.13 | -5.09 | 0.45 |
| Control variables Capital expenditure | 134919 | 0.06 | 0.06 | 0.05 | 0 | 0.48 |
| Control variables Advertisement | 143195 | 0.01 | 0.03 | 0 | 0 | 0.19 |
| Control variables Advertisement missing indicator | 143195 | 0.69 | 0.46 | 1 | 0 | 1 |
| Control variables Leverage | 142528 | 0.23 | 0.2 | 0.21 | 0 | 3.09 |
| Control variables Dividend paying indicator | 143195 | 0.57 | 0.5 | 1 | 0 | 1 |
| Control variables CEO chair indicator | 163936 | 0.65 | 0.48 | 1 | 0 | 1 |
| Control variables Fraction of inside directors | 163936 | 0.27 | 0.14 | 0.25 | 0 | 0.9 |
| Control variables Tenure | 173383 | 9.23 | 5.85 | 8.86 | 0 | 40 |
| Control variables CEO indicator | 179930 | 0.15 | 0.35 | 0 | 0 | 1 |
| Control variables Female indicator | 179930 | 0.05 | 0.22 | 0 | 0 | 1 |
Table 2: Correlations between Variables
| Incentives PPS1 | Incentives PPS2 | Incentives PPS3 | Profitability Uncertainty age | Profitability Uncertainty ERC | Profitability Uncertainty M/B | Profitability Uncertainty tang | Profitability Uncertainty forerr | Risk vol | Risk dolvol | size | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| PPS2 | 0.55 | 1 | |||||||||
| Wealth-performance sensitivity (PPS3) | 0.21 | 0.25 | 1 | ||||||||
| Log(firm age) (age) | -0.16 | 0.003 | -0.1 | 1 | |||||||
| Earnings response coefficient (ERC) | 0.04 | 0.05 | 0.07 | -0.06 | 1 | ||||||
| Market-to-book (M/B) | 0.08 | 0.2 | 0.19 | -0.23 | 0.07 | 1 | |||||
| Tangibility (tang) | -0.05 | -0.08 | -0.03 | 0.18 | -0.06 | -0.12 | 1 | ||||
| Analyst forecast error (forerr) | 0.02 | -0.04 | -0.01 | -0.04 | -0.05 | -0.04 | 0.01 | 1 | |||
| Stock return volatility (vol) | 0.1 | -0.03 | 0.03 | -0.44 | -0.04 | 0.23 | -0.22 | 0.13 | 1 | ||
| Rank of dollar return volatility (dolvol) | -0.14 | 0.29 | 0.09 | 0.23 | 0.01 | 0.16 | -0.06 | -0.12 | -0.12 | 1 | |
| Firm size (size) | -0.2 | 0.19 | -0.03 | 0.44 | -0.01 | -0.24 | 0.03 | -0.1 | -0.48 | 0.73 | 1 |
| Long-term growth forecast | 0.11 | 0.06 | 0.12 | -0.38 | 0.06 | 0.39 | -0.17 | 0.02 | 0.45 | -0.04 | -0.37 |
Table 3: Effects of Profitability Uncertainty and Risk on Incentives (PPS1)
| Dependent variable = PPS1 | (1) | (2) | (3) | (4) | (5) | (6) | (7) |
|---|---|---|---|---|---|---|---|
| Log(firm age) (-) (Profitability uncertainty variable) | -- | -0.20*** | -- | -- | -- | -- | -0.24*** |
| Log(firm age) (-) (Profitability uncertainty variable) (s.e.) | (-6.02) | (-6.80) | |||||
| ERC (+)(Profitability uncertainty variable) | -- | -- | 0.0071*** | -- | -- | -- | 0.007*** |
| ERC (+)(Profitability uncertainty variable) (s.e.) | (4.32) | (4.03) | |||||
| Market-to-book (+)(Profitability uncertainty variable) | -- | -- | -- | 0.007 | -- | -- | -0.002 |
| Market-to-book (+)(Profitability uncertainty variable) (s.e.) | (0.60) | (-0.13) | |||||
| Tangibility (-)(Profitability uncertainty variable) | -- | -- | -- | -- | -0.29* | -- | -0.17 |
| Tangibility (-)(Profitability uncertainty variable) (s.e.) | (-1.65) | (-0.97) | |||||
| Analyst forecast error (+)(Profitability uncertainty variable) | -- | -- | -- | -- | -- | 0.03 | 0.04* |
| Analyst forecast error (+)(Profitability uncertainty variable) (s.e.) | (1.61) | (1.87) | |||||
| Stock return volatility (Risk variable) | 0.0023 | -0.18 | 0.20 | 0.008 | -0.007 | 0.08 | -0.058 |
| Stock return volatility (Risk variable) (s.e.) | (0.01) | (-1.02) | (1.05) | (0.05) | (-0.04) | (0.47) | (-0.31) |
| Firm size (Control variable) | -0.31*** | -0.29*** | -0.29*** | -0.31*** | -0.31*** | -0.30*** | -0.26*** |
| Firm size (Control variable) (s.e.) | (-16.20) | (-13.90) | (-14.91) | (-16.08) | (-15.95) | (-16.04) | (-12.75) |
| Squared firm size (Control variable) | 0.056*** | 0.05*** | 0.05*** | 0.053*** | 0.06*** | 0.06*** | 0.049*** |
| Squared firm size (Control variable) (s.e.) | (8.26) | (8.15) | (6.85) | (7.93) | (8.18) | (8.29) | (7.05) |
| Long-term growth forecast (Control variable) | 0.014*** | 0.01*** | 0.01*** | 0.013*** | 0.013*** | 0.01*** | 0.008*** |
| Long-term growth forecast (Control variable) (s.e.) | (4.77) | (3.68) | (3.88) | (4.69) | (4.53) | (4.92) | (2.77) |
| Profitability (Control variable) | 0.52** | 0.43** | 0.49** | 0.48** | 0.54** | 0.48** | 0.43* |
| Profitability (Control variable) (s.e.) | (2.47) | (2.06) | (2.17) | (2.25) | (2.54) | (2.32) | (1.94) |
| Capital expenditure (Control variable) | 0.90** | 0.75* | 1.00** | 0.92** | 1.33*** | 1.18*** | 1.13*** |
| Capital expenditure (Control variable) (s.e.) | (2.23) | (1.86) | (2.42) | (2.28) | (3.09) | (2.90) | (2.64) |
| Advertisement (Control variable) | 1.14 | 1.23 | 1.30 | 1.14 | 1.08 | 1.43 | 1.36 |
| Advertisement (Control variable) (s.e.) | (0.98) | (1.06) | (1.09) | (0.98) | (0.93) | (1.23) | (1.16) |
| Advertisement missing dummy (Control variable) | -0.01 | -0.01 | 0.04 | -0.02 | -0.01 | 0.02 | 0.04 |
| Advertisement missing dummy (Control variable) (s.e.) | (-0.25) | (-0.20) | (0.66) | (-0.27) | (-0.18) | (0.31) | (0.69) |
| Leverage (Control variable) | 0.03 | 0.02 | -0.06 | 0.005 | 0.07 | -0.06 | -0.03 |
| Leverage (Control variable) (s.e.) | (0.20) | (0.12) | (-0.39) | (0.03) | (0.49) | (-0.44) | (-0.23) |
| Dividend paying indicator (Control variable) | -0.28*** | -0.21*** | -0.26*** | -0.27*** | -0.27*** | -0.27*** | -0.17*** |
| Dividend paying indicator (Control variable) (s.e.) | (-4.65) | (-3.41) | (-4.23) | (-4.65) | (-4.51) | (-4.54) | (-2.78) |
| CEO chair indicator (Control variable) | 0.29*** | 0.29*** | 0.25*** | 0.29*** | 0.29*** | 0.26*** | 0.26*** |
| CEO chair indicator (Control variable) (s.e.) | (6.92) | (6.97) | (6.09) | (6.83) | (6.89) | (6.43) | (6.20) |
| Fraction of inside directors (Control variable) | 2.60*** | 2.57*** | 2.37*** | 2.57*** | 2.57*** | 2.46*** | 2.26*** |
| Fraction of inside directors (Control variable) (s.e.) | (12.45) | (12.38) | (11.44) | (12.42) | (12.21) | (12.02) | (11.01) |
| Log(tenure) (Control variable) | 0.59*** | 0.60*** | 0.59*** | 0.59*** | 0.60*** | 0.58*** | 0.60*** |
| Log(tenure) (Control variable) (s.e.) | (14.75) | (14.99) | (14.66) | (14.82) | (14.74) | (15.13) | (14.88) |
| CEO indicator (Control variable) | 2.80*** | 2.79*** | 2.71*** | 2.80*** | 2.80*** | 2.76*** | 2.71*** |
| CEO indicator (Control variable) (s.e.) | (30.68) | (30.67) | (28.91) | (30.70) | (30.52) | (30.58) | (28.63) |
| Female indicator (Control variable) | -0.21*** | -0.22*** | -0.24*** | -0.21*** | -0.21*** | -0.22*** | -0.25*** |
| Female indicator (Control variable) (s.e.) | (-2.59) | (-2.66) | (-3.25) | (-2.64) | (-2.58) | (-3.05) | (-3.31) |
| Year & 2-digit SIC dummies (Control variable) | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Adjusted R2 | 0.22 | 0.22 | 0.22 | 0.22 | 0.22 | 0.22 | 0.22 |
| Number of observations | 119281 | 119281 | 102537 | 119079 | 118149 | 113496 | 100760 |
Table 4: Effects of Profitability Uncertainty and Risk on Incentives (PPS2)
| Dependent variable = PPS2 | (1) | (2) | (3) | (4) | (5) | (6) | (7) |
|---|---|---|---|---|---|---|---|
| Log(firm age) (-)(Profitability uncertainty variable) | -- | -33.36*** | -- | -- | -- | -- | -35.14*** |
| Log(firm age) (-)(Profitability uncertainty variable) (s.e.) | (-5.89) | (-5.65) | |||||
| ERC (+)(Profitability uncertainty variable) | -- | -- | 1.31*** | -- | -- | -- | 1.01*** |
| ERC (+)(Profitability uncertainty variable) (s.e.) | (4.25) | (3.48) | |||||
| Market-to-book (+)(Profitability uncertainty variable) | -- | -- | -- | 53.53*** | -- | -- | 59.52*** |
| Market-to-book (+)(Profitability uncertainty variable) (s.e.) | (13.83) | (13.65) | |||||
| Tangibility (-)(Profitability uncertainty variable) | -- | -- | -- | -- | -186.15*** | -- | -98.39*** |
| Tangibility (-)(Profitability uncertainty variable) (s.e.) | (-6.12) | (-3.27) | |||||
| Analyst forecast error (+) (Profitability uncertainty variable) | -- | -- | -- | -- | -- | -2.83 | 3.40 |
| Analyst forecast error (+) (Profitability uncertainty variable) (s.e.) | (-0.71) | (1.12) | |||||
| Stock return volatility (Risk variable) | -6.59 | -36.69 | 35.88 | -42.81 | -11.30 | 19.98 | -62.67* |
| Stock return volatility (Risk variable) (s.e.) | (-0.22) | (-1.23) | (1.00) | (-1.54) | (-0.37) | (0.63) | (-1.90) |
| Firm size (Control variable) | 93.35*** | 98.18*** | 97.74*** | 95.59*** | 93.63*** | 96.28*** | 101.61*** |
| Firm size (Control variable) (s.e.) | (19.66) | (19.86) | (19.23) | (21.72) | (19.63) | (19.69) | (21.19) |
| Squared firm size (Control variable) | 11.04*** | 10.83*** | 9.21*** | 7.23*** | 10.32*** | 10.31*** | 5.67*** |
| Squared firm size (Control variable) (s.e.) | (6.66) | (6.58) | (4.94) | (4.44) | (6.36) | (5.91) | (3.25) |
| Long-term growth forecast (Control variable) | 8.39*** | 7.83*** | 8.37*** | 3.86*** | 7.97*** | 8.33*** | 2.63*** |
| Long-term growth forecast (Control variable) (s.e.) | (11.74) | (11.19) | (11.38) | (6.79) | (11.21) | (11.40) | (4.25) |
| Profitability (Control variable) | 294.99*** | 278.55*** | 393.89*** | 134.40*** | 299.38*** | 321.27*** | 79.62** |
| Profitability (Control variable) (s.e.) | (6.05) | (5.74) | (8.69) | (3.69) | (6.14) | (6.50) | (2.24) |
| Capital expenditure (Control variable) | 223.51*** | 197.56*** | 205.42*** | 117.67* | 500.55*** | 207.27*** | 286.90*** |
| Capital expenditure (Control variable) (s.e.) | (3.09) | (2.78) | (2.60) | (1.76) | (6.56) | (2.82) | (3.77) |
| Advertisement (Control variable) | 584.96*** | 599.36*** | 573.61*** | 446.43** | 535.77** | 614.50*** | 426.87** |
| Advertisement (Control variable) (s.e.) | (2.99) | (3.07) | (2.73) | (2.44) | (2.78) | (3.01) | (2.21) |
| Advertisement missing (Control variable)dummy | 3.14 | 3.64 | 6.53 | 6.83 | 3.62 | 6.23 | 7.21 |
| Advertisement missing (Control variable)dummy (s.e.) | (0.30) | (0.35) | (0.59) | (0.69) | (0.35) | (0.57) | (0.71) |
| Leverage (Control variable) | -144.48*** | -146.54*** | -158.20*** | -109.93*** | -129.62*** | -165.64*** | -107.34*** |
| Leverage (Control variable) (s.e.) | (-5.22) | (-5.36) | (-5.09) | (-4.56) | (-4.92) | (-5.57) | (-3.91) |
| Dividend paying indicator (Control variable) | -43.39*** | -31.58*** | -43.56*** | -48.30*** | -38.85*** | -45.91*** | -32.33*** |
| Dividend paying indicator (Control variable) (s.e.) | (-4.10) | (-2.99) | (-3.79) | (-4.83) | (-3.70) | (-4.25) | (-3.01) |
| CEO chair indicator (Control variable) | 20.04*** | 20.18*** | 20.05*** | 19.43*** | 19.10*** | 19.75*** | 18.29*** |
| CEO chair indicator (Control variable) (s.e.) | (2.84) | (2.89) | (2.75) | (2.96) | (2.72) | (2.74) | (2.71) |
| Fraction of inside directors (Control variable) | 318.06*** | 312.53*** | 319.31*** | 324.43*** | 306.52*** | 316.90*** | 301.93*** |
| Fraction of inside directors (Control variable) (s.e.) | (9.79) | (9.69) | (9.15) | (10.32) | (9.52) | (9.36) | (9.07) |
| Log(tenure) (Control variable) | 83.01*** | 84.90*** | 86.82*** | 84.69*** | 83.92*** | 83.93*** | 91.80*** |
| Log(tenure) (Control variable) (s.e.) | (14.11) | (14.38) | (13.62) | (14.62) | (14.19) | (13.80) | (14.33) |
| CEO indicator (Control variable) | 417.28*** | 417.14*** | 424.42*** | 416.30*** | 415.57*** | 424.14*** | 422.89*** |
| CEO indicator (Control variable) (s.e.) | (32.33) | (32.33) | (30.24) | (32.36) | (32.04) | (31.95) | (29.97) |
| Female indicator (Control variable) | -52.13*** | -53.03*** | -54.06*** | -53.90*** | -52.23*** | -53.81*** | -57.52*** |
| Female indicator (Control variable) (s.e.) | (-4.83) | (-4.88) | (-4.51) | (-5.05) | (-4.84) | (-4.84) | (-4.84) |
| Year & 2-digit SIC dummies (Control variable) | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Adjusted R2 | 0.23 | 0.24 | 0.24 | 0.27 | 0.24 | 0.24 | 0.27 |
| Number of observations | 119281 | 119281 | 102537 | 119079 | 118149 | 113496 | 100760 |
Table 5: Effect of Profitability Uncertainty and Risk on Incentives (PPS3)
| Dependent variable = PPS3 | (1) | (2) | (3) | (4) | (5) | (6) | (7) |
|---|---|---|---|---|---|---|---|
| Log(firm age) (-) (Profitability uncertainty variables) | -- | -9.35*** | -- | -- | -- | -- | -12.08*** |
| Log(firm age) (-) (Profitability uncertainty variables) (s.e.) | (-3.80) | (-4.04) | |||||
| ERC (+) (Profitability uncertainty variables) | -- | -- | 0.38*** | -- | -- | -- | 0.34** |
| ERC (+) (Profitability uncertainty variables) (s.e.) | (2.59) | (2.27) | |||||
| Market-to-book (+) (Profitability uncertainty variables) | -- | -- | -- | 9.81*** | -- | -- | 11.39*** |
| Market-to-book (+) (Profitability uncertainty variables) (s.e.) | (5.70) | (4.72) | |||||
| Tangibility (-) (Profitability uncertainty variables) | -- | -- | -- | -- | -7.58 | -- | 13.39 |
| Tangibility (-) (Profitability uncertainty variables) (s.e.) | (-0.54) | (0.85) | |||||
| Analyst forecast error (+) (Profitability uncertainty variables) | -- | -- | -- | -- | -- | 1.62 | 2.01 |
| Analyst forecast error (+) (Profitability uncertainty variables) (s.e.) | (0.81) | (1.30) | |||||
| Stock return volatility (Risk variable) | -6.65 | -15.50 | 1.16 | -13.33 | -6.76 | -2.50 | -21.37 |
| Stock return volatility (Risk variable) (s.e.) | (-0.45) | (-1.02) | (0.07) | (-0.92) | (-0.45) | (-0.16) | (-1.17) |
| Firm size (Control variable) | 5.55*** | 6.89*** | 5.97** | 5.93*** | 5.68*** | 5.93*** | 7.72*** |
| Firm size (Control variable) (s.e.) | (2.64) | (3.11) | (2.56) | (2.88) | (2.66) | (2.72) | (3.15) |
| Squared firm size (Control variable) | -0.14 | -0.20 | -0.21 | -0.83 | -0.13 | -0.24 | -0.70 |
| Squared firm size (Control variable) (s.e.) | (-0.25) | (-0.35) | (-0.33) | (-1.46) | (-0.22) | (-0.41) | (-1.04) |
| Long-term growth forecast (Control variable) | 1.91*** | 1.76*** | 1.92*** | 1.08*** | 1.89*** | 1.93*** | 0.81** |
| Long-term growth forecast (Control variable) (s.e.) | (5.12) | (4.75) | (4.83) | (3.21) | (4.98) | (5.04) | (2.18) |
| Profitability (Control variable) | 71.03*** | 66.26*** | 94.49*** | 40.79** | 70.64*** | 81.80*** | 31.97 |
| Profitability (Control variable) (s.e.) | (3.51) | (3.22) | (3.84) | (2.39) | (3.49) | (3.80) | (1.51) |
| Capital expenditure (Control variable) | 82.70** | 75.48** | 77.75** | 63.68* | 93.35** | 79.71** | 39.03 |
| Capital expenditure (Control variable) (s.e.) | (2.44) | (2.26) | (2.04) | (1.90) | (2.55) | (2.29) | (0.97) |
| Advertisement (Control variable) | 225.72 | 230.51 | 241.75 | 201.76 | 224.88 | 244.70 | 222.15 |
| Advertisement (Control variable) (s.e.) | (1.42) | (1.45) | (1.40) | (1.29) | (1.42) | (1.44) | (1.29) |
| Advertisement missing dummy (Control variable) | -0.87 | -0.66 | 0.32 | -0.21 | -0.62 | 0.33 | 0.49 |
| Advertisement missing dummy (Control variable) (s.e.) | (-0.15) | (-0.12) | (0.05) | (-0.04) | (-0.11) | (0.05) | (0.08) |
| Leverage (Control variable) | -50.53*** | -51.22*** | -55.62*** | -43.79*** | -50.66*** | -53.09*** | -50.13*** |
| Leverage (Control variable) (s.e.) | (-3.87) | (-3.92) | (-3.75) | (-3.51) | (-3.79) | (-3.74) | (-3.34) |
| Dividend paying indicator (Control variable) | -5.20 | -1.91 | -4.49 | -5.96 | -5.12 | -5.16 | -1.17 |
| Dividend paying indicator (Control variable) (s.e.) | (-1.07) | (-0.41) | (-0.84) | (-1.25) | (-1.05) | (-1.05) | (-0.23) |
| CEO chair indicator (Control variable) | 17.78*** | 17.81*** | 18.41*** | 17.63*** | 18.02*** | 17.52*** | 18.54*** |
| CEO chair indicator (Control variable) (s.e.) | (4.79) | (4.81) | (4.54) | (4.83) | (4.82) | (4.56) | (4.59) |
| Fraction of inside directors (Control variable) | 155.76*** | 154.16*** | 148.42*** | 157.18*** | 156.80*** | 151.66*** | 147.22*** |
| Fraction of inside directors (Control variable) (s.e.) | (8.76) | (8.70) | (7.87) | (8.85) | (8.68) | (8.37) | (7.77) |
| Log(tenure) (Control variable) | 3.22** | 3.75*** | 3.41** | 3.52** | 3.28** | 3.01** | 4.50*** |
| Log(tenure) (Control variable) (s.e.) | (2.25) | (2.59) | (2.20) | (2.49) | (2.28) | (2.03) | (2.91) |
| CEO indicator (Control variable) | 0.05 | -0.02 | -0.04 | -0.11 | 0.04 | 0.09 | -0.44 |
| CEO indicator (Control variable) (s.e.) | (0.07) | (-0.03) | (-0.06) | (-0.16) | (0.06) | (0.12) | (-0.63) |
| Female indicator (Control variable) | -3.48 | -3.74 | -2.28 | -3.77 | -3.60 | -3.25 | -3.11 |
| Female indicator (Control variable) (s.e.) | (-0.85) | (-0.91) | (-0.51) | (-0.93) | (-0.87) | (-0.77) | (-0.70) |
| Year & 2-digit SIC dummies | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Adjusted R2 | 0.10 | 0.10 | 0.10 | 0.12 | 0.10 | 0.10 | 0.12 |
| Number of observations | 117238 | 117238 | 101449 | 117130 | 116115 | 112050 | 99730 |
Table 6: Robustness Analysis Panel A: Dollar return volatility and OLS regressions
| Dependent variable = PPS | Expected sign | (1) PPS1 | (2) PPS1 | (3) PPS2 | (4) PPS2 | (5) PPS3 | (6) PPS3 |
|---|---|---|---|---|---|---|---|
| Log(firm age) (Profitability uncertainty variables) | - | -- | -0.27*** | -- | -38.06*** | -- | -10.79*** |
| Log(firm age) (Profitability uncertainty variables) (s.e.) | - | (-6.72) | (-5.03) | (-3.53) | |||
| ERC (Profitability uncertainty variables) | + | -- | 0.006*** | -- | 1.17*** | -- | 0.28* |
| ERC (Profitability uncertainty variables) (s.e.) | + | (3.08) | (3.46) | (1.89) | |||
| Market-to-book (Profitability uncertainty variables) | + | -- | 0.02 | -- | 68.35*** | -- | 9.80*** |
| Market-to-book (Profitability uncertainty variables) (s.e.) | + | (1.34) | (11.69) | (3.71) | |||
| Tangibility (Profitability uncertainty variables) | - | -- | -0.17 | -- | -105.74*** | -- | 20.04 |
| Tangibility (Profitability uncertainty variables) (s.e.) | - | (-0.83) | (-2.93) | (1.14) | |||
| Analyst forecast error (Profitability uncertainty variables) | + | -- | 0.05* | -- | 4.71 | -- | 2.04 |
| Analyst forecast error (Profitability uncertainty variables) (s.e.) | + | (1.94) | (1.23) | (1.40) | |||
| Rank of dollar return volatility (Risk variable) | - | -0.0081*** | -0.0077*** | 2.67*** | -0.28 | 0.66*** | 0.32 |
| Rank of dollar return volatility (Risk variable) (s.e.) | - | (-5.12) | (-5.10) | (8.70) | (-0.70) | (4.05) | (1.53) |
| Control variables year dummies and two digit SIC dummies | Yes | Yes | Yes | Yes | Yes | Yes | |
| Adjusted R2 | 0.23 | 0.24 | 0.26 | 0.30 | 0.11 | 0.12 | |
| Number of observations | 92970 | 80642 | 92970 | 80642 | 92424 | 80425 |
Table 6: Robustness Analysis Panel B: Median regressions
| Dependent variable = PPS | Expected sign | (1) PPS1 | (2) PPS1 | (3) PPS2 | (4) PPS2 | (5) PPS3 | (6) PPS3 |
|---|---|---|---|---|---|---|---|
| Log(firm age) (Profitability uncertainty variable) | - | -- | -0.03*** | -- | -4.98*** | -- | -1.00*** |
| Log(firm age) (Profitability uncertainty variable) (s.e.) | - | (-17.33) | (-18.83) | (-14.51) | |||
| ERC (Profitability uncertainty variable) | + | -- | 0.0008*** | -- | 0.14*** | -- | 0.04*** |
| ERC (Profitability uncertainty variable) (s.e.) | + | (8.22) | (5.24) | (9.50) | |||
| Market-to-book (Profitability uncertainty variable) | + | -- | -0.006*** | -- | 21.55*** | -- | 1.22*** |
| Market-to-book (Profitability uncertainty variable) (s.e.) | + | (-10.17) | (32.57) | (42.91) | |||
| Tangibility (Profitability uncertainty variable) | - | -- | -0.15*** | -- | -24.16*** | -- | -1.92*** |
| Tangibility (Profitability uncertainty variable) (s.e.) | - | (-17.50) | (-14.12) | (-4.88) | |||
| Analyst forecast error (Profitability uncertainty variable) | + | -- | -0.01*** | -- | -0.05 | -- | -0.25*** |
| Analyst forecast error (Profitability uncertainty variable) (s.e.) | + | (-3.42) | (-0.20) | (-3.15) | |||
| Stock return volatility (Risk variable) | - | 0.06*** | 0.06*** | -9.50*** | -12.84*** | -2.75*** | -3.50*** |
| Stock return volatility (Risk variable) (s.e.) | - | (5.20) | (5.97) | (-6.60) | (-8.79) | (-8.61) | (-8.68) |
| Control variables year dummies and two digit SIC dummies | Yes | Yes | Yes | Yes | Yes | Yes | |
| Pseudo R2 | 0.11 | 0.12 | 0.11 | 0.12 | 0.03 | 0.03 | |
| Number of observations | 119281 | 100760 | 119281 | 100760 | 117238 | 99730 |
Table 6: Robustness Analysis Panel C: Dollar return volatility and median regressions
| Dependent variable = PPS | Expected sign | (1) PPS1 | (2) PPS1 | (3) PPS2 | (4) PPS2 | (5) PPS3 | (6) PPS3 |
|---|---|---|---|---|---|---|---|
| Log(firm age) (Profitability uncertainty variable) | - | -- | -0.04*** | -- | -6.46*** | -- | -0.88*** |
| Log(firm age) (Profitability uncertainty variable) (s.e.) | (-17.79) | (-17.29) | (-17.07) | ||||
| ERC (Profitability uncertainty variable) | + | -- | 0.0007*** | -- | 0.18*** | -- | 0.04*** |
| ERC (Profitability uncertainty variable) (s.e.) | (7.13) | (4.79) | (9.64) | ||||
| Market-to-book (Profitability uncertainty variable) | + | -- | -0.002* | -- | 28.35*** | -- | 1.03*** |
| Market-to-book (Profitability uncertainty variable) (s.e.) | (-1.88) | (34.02) | (16.65) | ||||
| Tangibility (Profitability uncertainty variable) | - | -- | -0.19*** | -- | -31.00*** | -- | -1.50*** |
| Tangibility (Profitability uncertainty variable) (s.e.) | (-12.96) | (-15.99) | (-4.99) | ||||
| Analyst forecast error (Profitability uncertainty variable) | + | -- | -0.010*** | -- | 0.55** | -- | -0.23*** |
| Analyst forecast error (Profitability uncertainty variable) (s.e.) | (-3.13) | (2.02) | (-2.95) | ||||
| Rank of dollar return volatility (Risk variable) | - | -0.001*** | -0.002*** | 0.67*** | -0.16*** | 0.05*** | 0.02*** |
| Rank of dollar return volatility (Risk variable) (s.e.) | (-11.08) | (-11.96) | (34.40) | (-5.12) | (30.41) | (5.51) | |
| Control variables year dummies and two digit SIC dummies | Yes | Yes | Yes | Yes | Yes | Yes | |
| Pseudo R2 | 0.12 | 0.13 | 0.12 | 0.14 | 0.03 | 0.03 | |
| Number of observations | 92970 | 80642 | 92970 | 80642 | 92424 | 80425 |
Table 6: Robustness Analysis Panel D: Fixed effect regressions
| Dependent variable = PPS | Expected sign | (1) PPS1 | (2) PPS1 | (3) PPS2 | (4) PPS2 | (5) PPS3 | (6) PPS3 |
|---|---|---|---|---|---|---|---|
| Log(firm age) (Profitability uncertainty variable) | - | -- | -0.42*** | -- | -71.50*** | -- | -29.06*** |
| Log(firm age) (Profitability uncertainty variable) (s.e.) | (-4.51) | (-4.03) | (-6.64) | ||||
| ERC (Profitability uncertainty variable) | + | -- | 0.003*** | -- | 0.20 | -- | 0.25*** |
| ERC (Profitability uncertainty variable) (s.e.) | (3.39) | (0.90) | (5.04) | ||||
| Market-to-book (Profitability uncertainty variable) | + | -- | -0.0001 | -- | 54.85*** | -- | 4.36*** |
| Market-to-book (Profitability uncertainty variable) (s.e.) | (-0.02) | (20.45) | (6.50) | ||||
| Tangibility (Profitability uncertainty variable) | - | -- | -0.60*** | -- | 13.57 | -- | 6.25 |
| Tangibility (Profitability uncertainty variable) (s.e.) | (-3.31) | (0.37) | (0.85) | ||||
| Analyst forecast error (Profitability uncertainty variable) | + | -- | -0.01 | -- | -1.68 | -- | -0.49 |
| Analyst forecast error (Profitability uncertainty variable) (s.e.) | (-0.94) | (-0.89) | (-1.04) | ||||
| Stock return volatility (Risk variable) | - | -0.52*** | -0.82*** | -150.40*** | -147.10*** | -4.42 | 0.08 |
| Stock return volatility (Risk variable) (s.e.) | (-3.57) | (-5.33) | (-5.77) | (-4.62) | (-0.61) | (0.01) | |
| Control variables year dummies and firm-manager paired fixed effects | Yes | Yes | Yes | Yes | Yes | Yes | |
| Adjusted R2 | 0.81 | 0.82 | 0.72 | 0.74 | 0.69 | 0.70 | |
| Number of observations | 119365 | 100835 | 119365 | 100835 | 117238 | 99730 |
Appendix A: Proofs
Proof of Lemma 1 Note that given
![]() and
and ![]() , the manager's expected utility is:
, the manager's expected utility is:
![\displaystyle \mathbb{E}\left[ -e^{-a\left( w_{1}-\frac{l}{2}L_{1}^{2}\right) }\right] =-\exp \left[ -a\left( \alpha +\beta \theta _{0}K_{1}^{1-\lambda }L_{1}^{\lambda }-\frac{l}{2}L_{1}^{2}-\frac{1}{2}a\beta ^{2}\left( \gamma _{0}\left( K_{1}^{1-\lambda }L_{1}^{\lambda }\right) ^{2}+\sigma _{\epsilon }^{2}\right) \right) \right] .](img139.gif)
|
Denote the above function by
![\displaystyle \frac{d\overline{U}\left( L_{1}\right) }{dL_{1}}=\overline{U}\left( L_{1}\right) \left( -a\right) \left[ \lambda \beta \theta _{0}K_{1}^{1-\lambda }L_{1}^{\lambda -1}-lL_{1}-a\gamma _{0}\lambda \beta ^{2}K_{1}^{2\left( 1-\lambda \right) }L_{1}^{2\lambda -1}\right] ,](img141.gif) |
and its second-order condition is
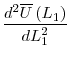 |
![\displaystyle \left( -a\right) ^{2}\overline{U}\left( L_{1}\right) \left[ \lambda \beta \theta _{0}K_{1}^{1-\lambda }L_{1}^{\lambda -1}-lL_{1}-a\gamma _{0}\lambda \beta ^{2}K_{1}^{2\left( 1-\lambda \right) }L_{1}^{2\lambda -1}\right] ^{2}](img143.gif) |
||
The optimal
The assumption
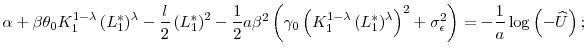
|
or, after substituting the expression of
 |
Proof of Proposition 2 We first prove that
![]() holds when the manager is risk neutral (i.e.,
holds when the manager is risk neutral (i.e., ![]() ); the statement in the proposition immediately follows in light of the continuity of the derivative
); the statement in the proposition immediately follows in light of the continuity of the derivative
![]() in
in ![]() . We can view the maximization problem in terms
of implemented effort
. We can view the maximization problem in terms
of implemented effort
![]() . If the optimal effort increases with uncertainty
. If the optimal effort increases with uncertainty
![]() , i.e.
, i.e.
and if higher effort is linked to higher incentives, which requires that
then we obtain our desired result
From the incentive compatibility condition
![]() , we have
, we have
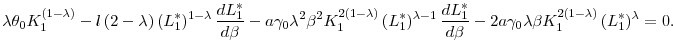
|
Simplifying the above equation, we have
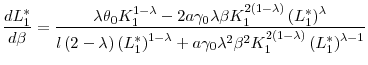 .
. |
Setting
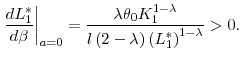 |
Now we use the supermodularity property to prove
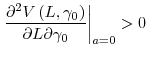 . . |
Recall that the time-0 expected payoff function is given by
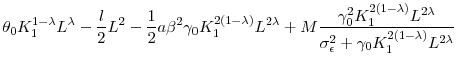
|
|||
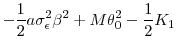 . . |
We thus have
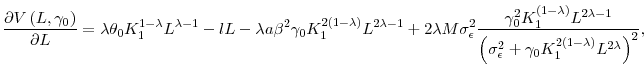
|
and
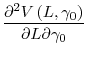 |
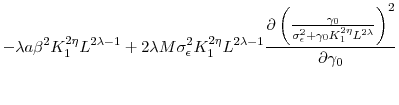 |
||
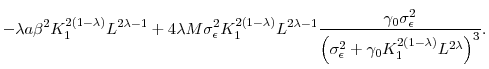
|
Therefore, when
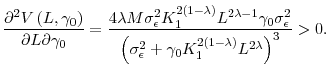
|
This completes the proof.
Appendix of Section 2.4 We have
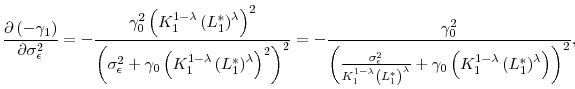
|
therefore
![\displaystyle \frac{\partial \left[ \frac{\sigma _{\epsilon }^{2}}{K_{1}^{1-\lambda }\left( L_{1}^{\ast }\right) ^{\lambda }}+\gamma _{0}K_{1}^{1-\lambda }\left( L_{1}^{\ast }\right) ^{\lambda }\right] }{\partial L_{1}^{\ast }}=% \frac{\lambda \left[ \gamma _{0}K_{1}^{2\left( 1-\lambda \right) }\left( L_{1}^{\ast }\right) ^{2\lambda }-\sigma _{\epsilon }^{2}\right] }{% K_{1}^{1-\lambda }\left( L_{1}^{\ast }\right) ^{\lambda +1}}.](img171.gif)
|
Appendix B: Definition of Variables
- Firm-Level Variables
Firm Age: Based on Pastor and Veronesi (2003), we consider each firm as "born" in the year of its first appearance in the CRSP database. Specifically, we look for the first occurrence of a valid stock price on CRSP, as well as the first occurrence of a valid market value in the CRSP / COMPUSTAT database, and take the earlier of the two. The firm's plain age is assigned the value of one in the year in which the firm is born and increases by one in each subsequent year. We use natural log of firm's plain age as the proxy for uncertainty.
Earnings Response Coefficient (ERC): This variable is the ERC1 as defined in Pastor, et al. (2009) and is equal to the average of the firm's previous 12 stock price reactions to quarterly earnings surprises. Specifically, we first obtain RC, which is the abnormal
return due to a quarterly earnings announcement divided by the unexpected quarterly earnings. The abnormal return is measured as the cumulative return of stock ![]() in excess of stock
in excess of stock
![]() 's industry's return starting one trading day before the firm's earnings announcement and ending one trading day after the same announcement. Quarterly earnings announcement dates are from
IBES. The industry returns are the daily returns of 49 value-weighted industry portfolios from Ken French's website. The unexpected quarterly earnings are equal to the difference between the actual quarterly earnings per share (obtained from the IBES unadjusted actuals file) and the mean of all
analyst forecasts of EPS using IBES's last preannouncement set of forecasts for the given fiscal quarter, deflated by book equity per share of the company. We winsorize RC at 5% and 95% and average the winsorized quarterly RCs over the rolling three-year window to obtain ERC1. Pastor et al. (2009)
contain more detailed information on constructing the ERC variables.
's industry's return starting one trading day before the firm's earnings announcement and ending one trading day after the same announcement. Quarterly earnings announcement dates are from
IBES. The industry returns are the daily returns of 49 value-weighted industry portfolios from Ken French's website. The unexpected quarterly earnings are equal to the difference between the actual quarterly earnings per share (obtained from the IBES unadjusted actuals file) and the mean of all
analyst forecasts of EPS using IBES's last preannouncement set of forecasts for the given fiscal quarter, deflated by book equity per share of the company. We winsorize RC at 5% and 95% and average the winsorized quarterly RCs over the rolling three-year window to obtain ERC1. Pastor et al. (2009)
contain more detailed information on constructing the ERC variables.
Market to Book: (Market value of equity plus the book value of debt)/total assets = (CSHO![]() PRCC_F + AT - CEQ)/AT = (data25
PRCC_F + AT - CEQ)/AT = (data25![]() data199+data6-data60)/data6.
data199+data6-data60)/data6.
Tangibility: Net property, plant, and equipment/total assets = PPENT/AT = data8/data6.
Analyst Forecast Error: For each individual company in each fiscal year, we first obtain the absolute value of the forecast error (equal to the difference between the forecast and the actual EPS values) made by each analyst, and then we use the median value of these absolute forecast errors scaled by the absolute value of the actual EPS. Using the mean value of the absolute forecast errors or scaling by stock price per share gives similar results. The analyst forecast error variable is constructed from the I/B/E/S details database.
Stock Return Volatility: First, we obtain the standard deviation of daily log returns over the past five years, and then annualize the standard deviation by multiplying by the square root of 254. This is the percentage return volatility.
Rank of Dollar Return Volatility: Dollar return volatility is equal to stock percentage return volatility multiplied by the beginning-of-year firm market value. This variable is measured in $millions. Consistent with Aggarwal and Samwick (1999) and Jin (2002), we employ the percentage ranks of dollar return variance in our tests and these percentage ranks range from 0 (lowest risk) to 100 (highest risk).
Firm Size: Natural log of total assets = log(AT) = log(data6). Assets are measured in $millions.
Analysts' Long-Term Growth Forecast: This variable comes from I/B/E/S analysts' forecast of long-term earnings growth (LTG in I/B/E/S). When multiple analysts give LTG forecasts about the same company during the same period, the median forecast is used.
Profitability: Operating income before depreciation and amortization/total assets = OIBDP/AT = data13/data6.
Capital expenditure: Capital expenditures/total assets = CAPX/AT = data128/data6.
Advertisement: Advertising expense/total assets = XAD/AT = data45/data6. This variable is set to zero if it is missing and an advertisement missing indicator is thus included in the regressions to deal with the missing advertisement issue.
Advertisement Missing Indicator: A dummy variable equal to one if the advertisement variable is missing.
Leverage: (Long term debt + debt in current liabilities)/total assets = (DLTT+DLC)/AT = (data9+data34)/data6.
Dividend-Paying Indicator: A dummy variable equal to one if dividends on common stock (data21 or DVC) are strictly positive, and zero otherwise.
CEO Chair Indicator: A dummy variable equal to one if the CEO of the company is also the board chairman, and zero otherwise.
Fraction of Inside Directors: Number of inside board directors divided by board size, where an inside director is defined as a director who is a current or former firm manager or one of his or her family members is a current or former firm manager..
- Manager Level Variables
PPS1: Dollar-to-dollar measure of pay-performance sensitivity. This variable measures the dollar change in stock and option holdings for a one dollar change in firm value. To estimate PPS1, first calculate a variable named totaldelta, which
is obtained from multiplying the Black-Scholes hedge ratio by the shares in options owned by the executive, and then adding the shares in stock owned by the executive. PPS1 in year ![]() is
equal to an executive's totaldelta over fiscal year
is
equal to an executive's totaldelta over fiscal year ![]() divided by total number of shares outstanding (Compustat data item CSHO) of the company at the beginning of year t. The construction of
totaldelta involves lots of details (e.g., how to construct Black-Scholes hedge ratio, how to deal with previously granted options, what to assume for expected life on the options, etc.), and we follow Appendix B in Edmans, et al. (2009) in estimating the totaldelta variable. In the regressions,
PPS1 is in percentages.
divided by total number of shares outstanding (Compustat data item CSHO) of the company at the beginning of year t. The construction of
totaldelta involves lots of details (e.g., how to construct Black-Scholes hedge ratio, how to deal with previously granted options, what to assume for expected life on the options, etc.), and we follow Appendix B in Edmans, et al. (2009) in estimating the totaldelta variable. In the regressions,
PPS1 is in percentages.
PPS2: Dollar-to-percentage measure of pay-performance sensitivity. This variable measures the dollar change in stock and option holdings for a one percent change in firm value. PPS2 in year ![]() is equal to PPS1 in year
is equal to PPS1 in year ![]()
![]() share price
at the beginning of fiscal year t
share price
at the beginning of fiscal year t ![]() total number of shares outstanding at the beginning of
total number of shares outstanding at the beginning of ![]() / 100, where share price is Compustat data item PRCC_F and total number of shares outstanding is Compustat data item CSHO. In the regressions, PPS2 is in $thousands.
/ 100, where share price is Compustat data item PRCC_F and total number of shares outstanding is Compustat data item CSHO. In the regressions, PPS2 is in $thousands.
PPS3: The scaled wealth-performance sensitivity proposed in Edmans et al. (2009). It is available from Alex Edmans' website. Specifically, this sensitivity measure equals the dollar change in executive wealth for a 100 percentage point change in firm value, divided by annual flow compensation (TDC1). This incentive measure is a variant of the percentage-to-percentage incentives used in Murphy (1985), Gibbons and Murphy (1992), and Rosen (1992), and replaces flow compensation in the numerator of the measure in Murphy (1985) with the change in the executives' wealth. By considering the change in wealth, the scaled wealth-performance sensitivity captures the important incentives from changes in the value of previously granted stock and options. See Edmans et al. (2009) for details.
Log(tenure): Natural log of the number of years the manager has been with the company, which equals the difference between the year of the observation and the year when the individual joined the company.
CEO Indicator: A dummy variable that equals one if the manager is the CEO in a particular year and zero if the manager is a non-CEO top executive. This dummy variable is time variant for a given individual because a specific manager could be a CEO in some years and a non-CEO in other years.
Female Indicator: A dummy variable that equals one if the manager is a female and zero otherwise.
![\displaystyle \mathbb{E}\left[ \theta \left\vert y_{1},L_{1}^{\ast }\right. \right] =\theta _{0}+\frac{\gamma _{1}K_{1}^{1-\lambda }\left( L_{1}^{\ast }\right) ^{\lambda }}{\sigma _{\epsilon }^{2}}\left[ y_{1}-\theta _{0}K_{1}^{1-\lambda }\left( L_{1}^{\ast }\right) ^{\lambda }% \right] ,](img62.gif)
![\displaystyle Var\left[ \theta \left\vert y_{1},L_{1}^{\ast }\right. % \right] =\frac{\gamma _{0}\sigma _{\epsilon }^{2}}{\sigma _{\epsilon }^{2}+\gamma _{0}\left( K_{1}^{1-\lambda }\left( L_{1}^{\ast }\right) ^{\lambda }\right) ^{2}}.](img64.gif)
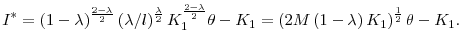
![\displaystyle \mathbb{E}\left[ V_{2}\left( \theta _{1}\right) \right] =M\left( \gamma _{0}-\gamma _{1}\right) +M\theta _{0}^{2}+\frac{K_{1}}{2},](img74.gif)