
The Ins and Outs of Forecasting Unemployment: Using Labor Force Flows to Forecast the Labor Market
Keywords: Unemployment, forecasting, flows
Abstract:
Forecasting the unemployment rate is an important and difficult task for policymakers, especially surrounding economic downturns. Typically, unemployment rate forecasts are made using one of two approaches. The first is based on the historical time-series properties of the unemployment rate and, perhaps, near-term indicators of the labor market. The second is based on the relationship between output growth and unemployment changes known as Okun's law. In this paper we develop a new approach that incorporates information on labor force flows as directed by economic theory to form forecasts for the unemployment rate.
A simple analogy helps explain the main idea behind our approach. Unemployment at a given time can be thought of as the amount of water in a bathtub, a stock. Given an initial water level, the level at some future time is determined by the rate at which water flows into the tub from the faucet and the rate at which water flows out of the tub through the drain. When the inflow rate equals the outflow rate, the amount of water in the tub remains constant. But if the inflow rate increases and the outflow rate does not, we know that the water level will be higher in the future. In other words, the inflow rate and the outflow rate together provide information about the future water level--or in this case, of unemployment.
This insight forms one of two cornerstones of our approach: we exploit this convergence property whereby the actual unemployment rate converges toward the rate implied by the labor force flows. The other is forecasting those underlying flows directly. Because the individual flows have different time-series properties and their contributions change over the business cycle, focusing on the flows allows us to better capture the asymmetric nature of unemployment movements.
For near-term forecasts, our model dramatically outperforms the Survey of Professional Forecasters (SPF), historical forecasts from the Federal Reserve Board's Greenbook, and basic time-series models, achieving a root-mean-squared error (RMSE) about 30 percent below that of the best alternative forecast. Moreover, our model has the highest predictive ability surrounding business cycle turning points and large recessions.
In addition, our model is a particularly useful addition to the existing set of forecasting models because it uses information--data on labor force flows--that is likely not incorporated by other forecasts. Thus, combining the forecasts from our model, the SPF, and a simple time-series model yields a reduction in RMSE, relative to the SPF forecast alone, of about 35 percent for the current-quarter forecast, 15 percent for the next-quarter forecast, and smaller improvements at longer horizons.
Finally, our model can also be used to forecast the labor force participation rate. Here the improvement in forecast performance is more modest than for the unemployment rate: our model improves on the Greenbook only for the current-quarter forecast. Nevertheless, combining the forecasts of our model and the Greenbook yields a sizable reduction in RMSE.
1 Using Labor Force Flows to Forecast Unemployment
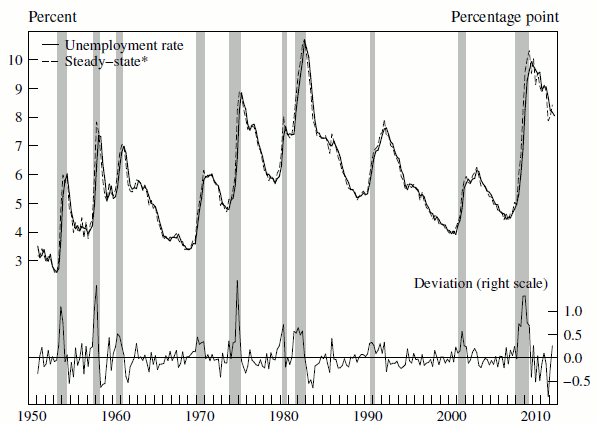
We incorporate information from labor force flows through the concept of the conditional steady-state unemployment rate, which is the rate of unemployment that would eventually prevail were the flows into and out of unemployment to remain at their current rates. In steady state these flows are balanced. However, if the inflow rate were to jump, as tends to happen at the onset of a recession, then the conditional steady-state unemployment rate would also jump. With no additional shocks to either flow, the unemployment rate would progressively rise toward this new steady state. Moreover, because this convergence process occurs typically takes 3 months or more, the conditional steady-state rate provides information about the unemployment rate in the near future.
Figure 1 shows the tight, leading relationship between the steady-state unemployment rate, ![]() , and the actual unemployment rate,
, and the actual unemployment rate, ![]() . As shown by the deviation
. As shown by the deviation ![]() plotted at the bottom of the figure, in periods when
plotted at the bottom of the figure, in periods when
![]() is above the actual rate, the unemployment rate tends to rise, and, conversely, when
is above the actual rate, the unemployment rate tends to rise, and, conversely, when ![]() lies below
lies below ![]() , the unemployment rate tends to fall.
, the unemployment rate tends to fall.
However, relying solely on current labor force flows constrains our approach to very near term forecasts, because the steady state to which the actual unemployment rate converges also changes over time as the underlying flows change. Thus, we forecast the underlying labor force flows using a time-series model and feed those forecasts into a law of motion relating these flows to the unemployment rate to generate unemployment forecasts at longer horizons. Directly forecasting the flows into and out of unemployment rather than the unemployment stock itself, as is customary, is another reason that our model outperforms other approaches. It allows our model to better capture the dynamics of unemployment, because the unemployment stock is driven by flows with different time-series properties, and because the contributions of the different flows change throughout the cycle (Barnichon, 2012).
An additional advantage of focusing on labor force flows is that it allows us to capture the asymmetric nature of unemployment movements--in particular, the fact that increases tend to be steeper than decreases.1 Although our model is not explicitly asymmetric, it relies on the unemployment inflows that are responsible for the asymmetry of unemployment (Barnichon, 2012). By using such information as inputs in the forecasts, our model can incorporate the impulses that generate this asymmetry.2 Thanks to this property, we find that our model outperforms a baseline time-series model around turning points and large recessions (Baghestani, 2008; Montgomery et al., 1998). This is particularly useful since these are the times when accurate unemployment forecasts are most valuable.
This paper builds on the influential work of Montgomery et al. (1998) and extends the growing literature aimed at improving the performance of unemployment forecasting models.3 We draw especially on the recent literature on labor force flows, which has been overlooked by the forecasting literature but has been the subject of numerous studies aimed at understanding the determinants of labor market fluctuations.4 We also weigh in on a debate in this literature over the relative importance of inflows and outflows; using predictive ability as a metric, we find that both are equally important for forecasting unemployment.
2 The Model
Our model is built on two elements: a law of motion describing how the unemployment rate converges to its steady-state value, and a forecast of the labor force flows determining steady-state unemployment and the speed at which actual unemployment converges to steady state. We first present a model with only two labor force states and then expand it to the more general case with three labor force states. We discuss further the intuition behind the model in section 4.5.
2.1 The Labor Market with Two States
The two-state version of our model considers only employment and unemployment. That is, we explicitly assume that there are no movements into or out of the labor force. This approach is consistent with recent literature showing that a two-state model does a good job of capturing unemployment fluctuations. In addition, it provides a simpler framework for understanding the basic flow-based accounting of the conditional steady-state unemployment rate, and it can be estimated over a long period using duration data. However, in section 2.2 we generalize our approach to three states and allow for movements into and out of the labor force.
2.1.1 The Law of Motion for Unemployment
Denote
![]() as the unemployment rate at instant
as the unemployment rate at instant ![]() with
with ![]() indexing months and
indexing months and
![]() a continuous measure of time within a month. Assume that between month
a continuous measure of time within a month. Assume that between month ![]() and month
and month ![]() all unemployed persons are subject to finding a job according to a Poisson process with constant arrival rate
all unemployed persons are subject to finding a job according to a Poisson process with constant arrival rate ![]() , and all employed workers are subject to losing or leaving their job according to a Poisson process with constant arrival rate
, and all employed workers are subject to losing or leaving their job according to a Poisson process with constant arrival rate ![]() .5 The unemployment rate then proceeds according to
.5 The unemployment rate then proceeds according to
as changes in unemployment are given by the difference between the inflows and the outflows. Solving equation 1 yields
where
denotes the conditional steady-state unemployment rate, and
Equation 2 relates variation in the unemployment stock
![]() over the course of a month to variation in the underlying flow hazards,
over the course of a month to variation in the underlying flow hazards, ![]() and
and ![]() . A 1-month-ahead forecast for the unemployment rate,
. A 1-month-ahead forecast for the unemployment rate,
![]() , can thus be obtained from
, can thus be obtained from
where
Over 1951-2011, the sum of monthly unemployment inflow and outflow rates averaged 0.62, implying that the half-life deviation of unemployment from its steady state is slightly more than a month. As a result, 90 percent of the gap between unemployment and its conditional steady-state value is closed in about 4 months, on average. However, as the lower panel of figure 2 shows, this convergence speed varies considerably over the business cycle, as inflow and outflow rates fluctuate. As a result, the time needed to close 90 percent of the gap ranges from about 3 months in tight labor markets to about 5 months in slack markets. In the 2008-09 recession, the drop in the unemployment exit rate was so dramatic that the figure increased to an unprecedented 9 months. It has since edged lower, to just under 8 months in the third quarter of 2012.
Part of the exceptional increase in the last recession owes to a dramatic decline in the job finding rate, the result of exceptionally low job creation and low matching efficiency (Barnichon & Figura, 2010). Moreover, Elsby et al. (2011) show that this exceptional decline was also in part an artifact of measurement error, because not all persons flowing into unemployment had a duration of less than 5 weeks. This phenomenon became much more prevalent in the recent recession, where a larger fraction of persons moving from employment to unemployment reported a duration of more than 5 weeks, leading the duration-based measure of the unemployment exit rate to suffer from a larger downward bias. As we discuss in section 7, to the extent that the bias is stronger than in previous recessions, forecasting performance could deteriorate.
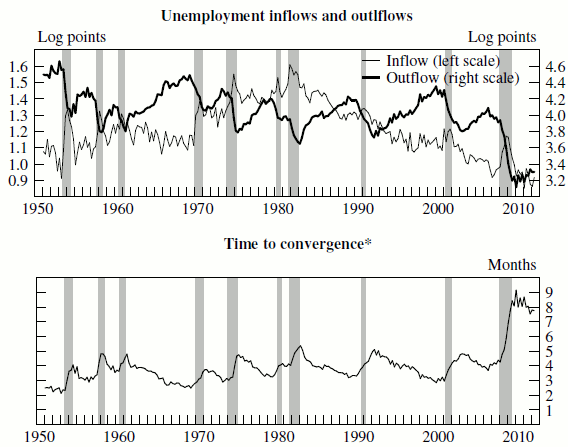 Figure 2 Data
Figure 2 Data
2.1.2 Forecasting Labor Force Flows
Because equation 4 can forecast the unemployment rate only 1 month ahead given the current values of the hazard rates, forecasting the unemployment rate at longer horizons requires making forecasts of the hazard rates. A simple approach is to assume that the
hazard rates remain constant at their last observed value over the forecast horizon. However, in real time a forecaster does not observe ![]() and
and ![]() , but only
, but only ![]() and
and ![]() , because at month
, because at month ![]() one can observe labor force flows only from
one can observe labor force flows only from ![]() to
to ![]() .6 Thus, the
.6 Thus, the ![]() -period-ahead forecast of the unemployment rate can be formed from the month
-period-ahead forecast of the unemployment rate can be formed from the month ![]() values of
values of
![]() and
and ![]() as follows:7
as follows:7
If the hazard rates are persistent enough, equation 5 will provide reasonable forecasts.8 However, as figure 2 shows, the hazard rates do change, and with them the conditional steady-state unemployment rate and the speed of convergence.
Because the hazard rates are not sufficiently persistent, we use a vector autoregression (VAR) to forecast the inflow and outflow rates. We also include two leading indicators of labor force flows: vacancy posting and initial claims for unemployment insurance. Specifically, let
where
| (6) |
over a fifteen-year rolling window.9
After generating forecasts of the hazard rates, we obtain ![]() -period-ahead forecasts of unemployment by iterating on the following:10
-period-ahead forecasts of unemployment by iterating on the following:10
with
and
With month ![]() forecasts of the flow rates in hand, we can calculate the month
forecasts of the flow rates in hand, we can calculate the month ![]() values of
values of ![]() and
and ![]() . The month
. The month ![]() unemployment forecast is then obtained by taking a weighted average of the previous-period (month
unemployment forecast is then obtained by taking a weighted average of the previous-period (month ![]() )
unemployment rate and the current-period (month
)
unemployment rate and the current-period (month ![]() ) conditional steady-state unemployment rate, with the weights determined by the speed of convergence to steady state.
) conditional steady-state unemployment rate, with the weights determined by the speed of convergence to steady state.
2.2 The Labor Market with Three States
So far, we have considered a labor market with only two states: employed or unemployed. However, not all those without jobs are unemployed. Indeed, flows into and out of the labor force dwarf those into and out of unemployment.11 This section considers a model that incorporates flows among all three labor force states.
An important advantage of the three-state model is its ability to capture more accurately the flows taking place in the labor market. For instance, the unemployment inflow rate comprises both those losing or leaving jobs and those entering or reentering the labor force. Since these two flows (and in fact all six flows) display different time-series properties, a three-state model may produce better forecasts than a two-state model.12 In addition, the three-state model can be used to forecast the labor force participation rate.
To generalize our two-state framework to three states, we need to specify and solve the system of differential equations governing the number of people in unemployment, ![]() ; in employment,
; in employment,
![]() ; or out of the labor force,
; or out of the labor force, ![]() .
.
Between month ![]() and month
and month ![]() , individuals can transit from state
, individuals can transit from state
![]() to state
to state
![]() according to a Poisson process with constant arrival rate
according to a Poisson process with constant arrival rate
![]() . The stocks of unemployed, employed, and persons not in the labor force satisfy the following system:13
. The stocks of unemployed, employed, and persons not in the labor force satisfy the following system:13
For instance, as the first line shows, changes in unemployment are given by the difference between the inflows to unemployment (workers losing or quitting their jobs and seeking work, and persons joining or rejoining the labor force) and the outflows from unemployment (unemployed persons finding a job or dropping out of the labor force).
Then, using the initial and terminal conditions, the 1-step-ahead forecasts of the three stocks can be solved as functions of the transition probabilities (the
![]() s in equation 10). The appendix gives the details of the solution. We then use the solution to these equations to generate 1-period-ahead
forecasts of the unemployment rate and the labor force participation rate from
s in equation 10). The appendix gives the details of the solution. We then use the solution to these equations to generate 1-period-ahead
forecasts of the unemployment rate and the labor force participation rate from
| (11) | ![\displaystyle \hat{u}_{t+1\vert t} = \frac{\hat{U}_{t+1\vert t}}{\hat{U}_{t+1\vert t}+\hat{E}_{t+1\vert t}} \\ [1ex]](img64.gif) |
and
| (12) | 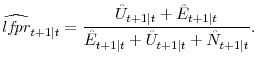 |
Note that, in effect, what we assume for population growth does not affect our forecasts, because we forecast population shares.
As with the two-state model, to construct forecasts beyond one period ahead, we use a VAR to forecast the six transition probabilities. Specifically, we estimate
| (13) |
over a 10-year rolling window, where
Note that in this specification, the unemployment rate and the help-wanted index enter in levels, rather than in changes, because this yielded better forecasts.
3 Data
We construct measures of the transition rates in the two-state and three-state models using different approaches: an indirect one (using information on the stocks of unemployment and of short-term unemployment to infer the transition rates) for the two-state model, and a direct one (using measures of labor force flows) for the three-state model.
For the two-state model, we follow Shimer (2012) and use information on the number of persons unemployed, ![]() , and those unemployed for less than 5 weeks,
, and those unemployed for less than 5 weeks,
![]() , to infer job finding and job separation hazard rates.14Specifically, we calculate the unemployment outflow probability,
, to infer job finding and job separation hazard rates.14Specifically, we calculate the unemployment outflow probability, ![]() , from
, from
with
![\displaystyle U_{t+1} = \frac{\left[1-e^{-\left(f_{t+1}+s_{t+1}\right)}\right]s_{t+1}}{f_{t+1}+s_{t+1}}(U_t+E_t) + e^{-\left(f_{t+1}+s_{t+1}\right)}U_t.](img74.gif) |
Note that in this accounting, given a value for the unemployment outflow rate (which also captures movements out of the labor force) and the stock of unemployed persons, the inflow rate is the rate that explains the observed stock of unemployed persons in the next month. As a result, the inflow rate incorporates all movements in unemployment not accounted for by the unemployment outflow rate.
For the three-state model, we use aggregate labor market transition probabilities among employment, unemployment, and nonparticipation calculated from longitudinally matched Current Population Survey (CPS) micro data. We construct the transition rates from labor market flows as
![]() , where
, where ![]() is the number of persons
observed in state a in month
is the number of persons
observed in state a in month ![]() , and
, and ![]() is the number who transitioned from
state
is the number who transitioned from
state ![]() in month
in month ![]() to state
to state ![]() in month
in month ![]() . (The time series of the
. (The time series of the ![]() s are collectively referred to as "gross flows.") For example,
s are collectively referred to as "gross flows.") For example, ![]() is the number of persons who moved from unemployed to employed, and
is the number of persons who moved from unemployed to employed, and
![]() is the corresponding transition probability. The BLS publishes a research series of gross flows that begins in February 1990. For contemporary forecasts, the published data have
a sufficiently long history to allow estimation of the model. However, to evaluate historical model forecasts before February 2000, we need data with a longer history. Thus, we construct measures of gross flows that cover June 1967 to January 1990, allowing us to begin our evaluation with 1976.
From 1976 to 1990 we construct gross flows from Nekarda (2012) Longitudinal Population Database. Before 1976 we use gross flows tabulated by Joe Ritter (see Shimer, 2012).
is the corresponding transition probability. The BLS publishes a research series of gross flows that begins in February 1990. For contemporary forecasts, the published data have
a sufficiently long history to allow estimation of the model. However, to evaluate historical model forecasts before February 2000, we need data with a longer history. Thus, we construct measures of gross flows that cover June 1967 to January 1990, allowing us to begin our evaluation with 1976.
From 1976 to 1990 we construct gross flows from Nekarda (2012) Longitudinal Population Database. Before 1976 we use gross flows tabulated by Joe Ritter (see Shimer, 2012).
Finally, weekly initial claims for unemployment insurance are published by the Department of Labor's Employment and Training Administration. Our measure of vacancy posting is, as noted before, the composite help-wanted index presented in Barnichon (2010).
4 Forecasting Performance
We evaluate the performance of our flows models by comparing their unemployment rate forecasts with alternative forecasts along two dimensions. First, we assess the RMSEs of out-of-sample forecasts. Second, because it is harder to forecast the unemployment rate around recessions, we assess our model's performance relative to a baseline time-series model over the business cycle. In what follows we refer to the two-state model as "SSUR-2" and the three-state model as "SSUR-3."
4.1 Real-Time Forecasts
Our objective in this section is to evaluate our models' forecasts against the best alternative forecasts, both those of professional forecasters and those derived from other time-series models. We consider five alternative forecasts of the unemployment rate. The first two are from professional forecasters. We consider historical forecasts from the Greenbook, which the literature has generally shown to be the benchmark forecast, and the median forecast from the SPF.15
The other three alternative forecasts are our own estimates from time-series models and are intended to disentangle the mechanisms behind the performance of our model. We consider a basic univariate time-series model, intended as a "naive" forecast that takes into account no other information
but the past unemployment rate. Following Montgomery et al., we use an ARIMA(2,0,1) model for the unemployment rate. We also consider the unemployment rate forecast from a VAR that includes the labor force flows and the two leading indicators, initial
claims and the help-wanted index. By comparing our SSUR models' forecasts against those of the VAR, we can directly evaluate the nonlinear relationship implied by the theory compared with an atheoretical linear time-series model using the same information set. Our last alternative is the
unemployment rate forecast derived from the law of motion for unemployment rate (equation 5), holding the inflow and outflow rates constant at their last known value. We call this the ![]() model. Shutting down the variation in the hazard rates isolates the contribution of the current conditional steady-state unemployment rate. The three alternative time-series models are estimated over a 15-year rolling window.
model. Shutting down the variation in the hazard rates isolates the contribution of the current conditional steady-state unemployment rate. The three alternative time-series models are estimated over a 15-year rolling window.
To reflect the environment within which forecasters must operate, we estimate our models and generate forecasts using real-time data, except for initial claims and the help-wanted index.16 The historical forecasts were necessarily made with only the data in hand at the time. Some economic data, such as real GDP and payroll employment, are subject to substantial revision over time. For these variables, the current-vintage data may differ substantially from the historical data used to make those forecasts. In the case of the unemployment rate, however, the revisions are relatively minor. The labor force data obtained from the CPS are revised only to reflect updated estimates of seasonal fluctuations. Indeed, the not-seasonally-adjusted stocks of employment and unemployment are never revised, reflecting their origin from a point-in-time survey of households. Nevertheless, even the small revisions to seasonal factors may have important consequences for our models' performance.
To construct real-time estimates of the hazard rates, we begin with monthly vintages of the published seasonally-adjusted stocks of employed, unemployed, and short-term unemployed workers.17 For each month, we estimate the time series of the inflow and outflow hazard rates from the real-time stocks as described in section 3. These series are then used in the VAR to forecast the hazard rates. Real-time data for initial claims and the help-wanted index are not available, so current-vintage data are used in the VAR. As with the unemployment rate, revisions to these series are relatively small.18 Nonetheless, in section 4.3 we assess the implications of this limitation.
The SPF sends out its survey questionnaire sometime in the first month of a quarter, and the survey participants are asked to mail back the completed questionnaire by the middle of the second month of the quarter. Thus, the forecasts included in the SPF incorporate labor market data from the first month of each quarter. To make forecasts comparable, our model forecasts are made treating the first month's unemployment rate as data.
The information set for the historical Greenbook forecasts is more irregular. Because the publication of the forecast is dictated by the date of the upcoming Federal Open Market Committee meeting, Greenbook forecasts are made at different points in a quarter; as a result, some forecasts have no
monthly labor market data for the current quarter whereas others have 2 months of data. For example, at the time the March 2004 Greenbook was published, the unemployment rate was known through February 2004, and thus the quarter ![]() forecast was made with data for the first 2 months of the quarter. However, when the April 2004 Greenbook was published, the unemployment rate was known only through March 2004, and thus the quarter
forecast was made with data for the first 2 months of the quarter. However, when the April 2004 Greenbook was published, the unemployment rate was known only through March 2004, and thus the quarter ![]() forecast (for the second quarter of 2004) was made without any published data for the quarter. We are careful to mimic the information set for each Greenbook forecast. Finally, because the Greenbook forecasts are made public with a 5-year
lag, our comparison using the Greenbook ends in 2006.
forecast (for the second quarter of 2004) was made without any published data for the quarter. We are careful to mimic the information set for each Greenbook forecast. Finally, because the Greenbook forecasts are made public with a 5-year
lag, our comparison using the Greenbook ends in 2006.
4.2 Forecast Errors
Table 1 reports the RMSEs of real-time forecasts for quarterly unemployment rates over a 1-year horizon (as well as a forecast of the current quarter, ![]() ). To evaluate the statistical significance of our results, we report the
). To evaluate the statistical significance of our results, we report the ![]() values of the Giacomini & White (2006) unconditional
test statistic of equal predictive ability between our SSUR-2 forecast and the comparison forecast.19
values of the Giacomini & White (2006) unconditional
test statistic of equal predictive ability between our SSUR-2 forecast and the comparison forecast.19
| Model | |||||
| SSUR-2 | 0.12 | 0.35 | 0.54 | 0.70 | 0.86 |
| Greenbook | 0.16*** | 0.39 | 0.54 | 0.65 | 0.78 |
| Greenbook (standard error) | (0.00) | (0.31) | (0.95) | (0.63) | (0.50) |
| SPF | 0.17*** | 0.37 | 0.53 | 0.66 | 0.82 |
| SPF (standard error) | (0.00) | (0.48) | (0.96) | (0.67) | (0.65) |
| No. of observations | 89 | 89 | 89 | 89 | 89 |
|---|
The SSUR-2 model dramatically outperforms the Greenbook and the SPF for short-term forecasts. As the first two rows of table 1 show, the RMSE of the SSUR-2 model forecast for the current quarter is about 0.05 percentage point (more than 30 percent) smaller than those of the other two forecasts. This improvement is statistically significant at the 1 percent level against both. Although the improvement in the next-quarter forecast is of similar magnitude, the RMSE is now only 10 percent smaller than those of the alternatives, and the difference is not statistically significant. At longer horizons the improvement over the SPF and the Greenbook disappears: SSUR-2 performs about 0.05 percentage point worse than either professional forecast on average. Nevertheless, it is striking that our model performs only slightly worse than the Greenbook and the SPF at a 1-year horizon, considering that their forecasts are based on an array of economic data and models of the broader economy, whereas SSUR-2 is a statistical model that incorporates only near-term information about the labor market.
| Model | |||||
| SSUR-2 | 0.15 | 0.38 | 0.60 | 0.83 | 1.06 |
| ARIMA | 0.22*** | 0.52** | 0.84* | 1.14 | 1.41* |
| ARIMA (standard error) | (0.00) | (0.05) | (0.08) | (0.11) | (0.08) |
| VAR | 0.19*** | 0.47*** | 0.73** | 1.03* | 1.30 |
| VAR (standard error) | (0.00) | (0.00) | (0.02) | (0.07) | (0.14) |
|
|
0.20*** | 0.48*** | 0.70** | 0.92 | 1.11 |
|
|
(0.00) | (0.00) | (0.01) | (0.16) | (0.41) |
| SSUR-2-s
|
0.22*** | 0.52*** | 0.75*** | 0.97*** | 1.16 |
| SSUR-2-s
|
(0.00) | (0.00) | (0.00) | (0.03) | (0.18) |
| SSUR-2-f |
0.22*** | 0.52*** | 0.77*** | 1.00*** | 1.23** |
| SSUR-2-f |
(0.00) | (0.00) | (0.00) | (0.00) | (0.01) |
| No. of observations | 432 | 432 | 432 | 429 | 426 |
|---|
Table 2 reports the performance of SSUR-2 against the time-series models. The univariate ARIMA model performs worse than SSUR-2 at all horizons. The same is true of the VAR, showing that the nonlinearity of our model is an important feature. Finally, the
contribution of forecasting the flows is evident from the fourth row, which reports the performance of a forecast based only on convergence to the conditional steady-state unemployment rate (![]() ). This model, too, performs worse than SSUR-2 at all horizons, indicating that time variation in the flow rates is also an important element of our model. It is remarkable that a forecast from the theoretical law of motion (equation 5) that relies
on only the last known value of
). This model, too, performs worse than SSUR-2 at all horizons, indicating that time variation in the flow rates is also an important element of our model. It is remarkable that a forecast from the theoretical law of motion (equation 5) that relies
on only the last known value of ![]() performs as well as or better than both estimated time-series models.20
performs as well as or better than both estimated time-series models.20
Finally, we weigh in on the debate over the relative importance of inflows and outflows to unemployment fluctuations, using predictive ability as a metric. To do so, we evaluate the forecasting performance of variants of the SSUR-2 model in which only one of the hazard rates is allowed to vary.
For example, to evaluate the contribution of the inflow rate, we hold the outflow rate constant at its last known value and allow the inflow rate to vary according to the VAR forecast. We call this variant "SSUR-2-s" and its counterpart that allows only outflows to vary "SSUR-2-f." The bottom
two rows of table 2 show that SSUR-2-s and SSUR-2-f perform about the same at all horizons. However, both models have larger RMSEs than the ![]() model, which
holds both hazard rates constant. Thus, for forecasting unemployment, inflows and outflows are about equally important, in line with the recent consensus in the literature.21
model, which
holds both hazard rates constant. Thus, for forecasting unemployment, inflows and outflows are about equally important, in line with the recent consensus in the literature.21
4.3 Quasi-Real-Time Forecasts and SSUR-3
As we noted earlier, our preferred VAR specification--which includes initial claims for unemployment insurance and the help-wanted index--cannot be estimated in true real time because vintages of these two leading indicators are not available. In work not reported in detail here, we assess
whether this gives our model an unfair advantage over the historical professional forecasters by estimating the VAR for the SSUR-2 model without ![]() and
and
![]() --a true real-time exercise. Over the sample used in the upper panel of table 1, this model still has an RMSE almost 20 percent smaller than the
Greenbook's at quarter
--a true real-time exercise. Over the sample used in the upper panel of table 1, this model still has an RMSE almost 20 percent smaller than the
Greenbook's at quarter ![]() and essentially the same at quarter
and essentially the same at quarter ![]() . We also compare
the performance of the true real-time forecasts of SSUR-2 with the model's "quasi-real-time" forecasts, where we use the same rolling estimation and forecasting procedure as in the real-time exercise but use the current-vintage data at all points; that is, we omit all variation associated with
revisions to the seasonal factors. Over the same sample (results not reported), the truly real-time forecasts are actually slightly better than the quasi-real-time forecasts at all but the current-quarter horizon, where they perform equally well. This suggests that
evaluating the models in quasi-real time likely does not significantly alter the spirit of the real-time exercise.
. We also compare
the performance of the true real-time forecasts of SSUR-2 with the model's "quasi-real-time" forecasts, where we use the same rolling estimation and forecasting procedure as in the real-time exercise but use the current-vintage data at all points; that is, we omit all variation associated with
revisions to the seasonal factors. Over the same sample (results not reported), the truly real-time forecasts are actually slightly better than the quasi-real-time forecasts at all but the current-quarter horizon, where they perform equally well. This suggests that
evaluating the models in quasi-real time likely does not significantly alter the spirit of the real-time exercise.
With this in mind, we assess the quasi-real-time forecasts of the SSUR-3 model. (Because historical records of seasonal revisions to gross flows are not available, we cannot evaluate the performance of the SSUR-3 model in true real time.) Table 3 evaluates the
performance of SSUR-3 against that of SSUR-2 in quasi-real time. Over the period from 1976 to 2006 (upper panel), the three-state model performs a bit worse than SSUR-2 in the current-, next-, and 2-quarter-ahead forecasts, and at longer horizons it performs appreciably worse. However, the gross
flows we calculate from the CPS micro data (from before 1990) are noisier than duration-based hazard rates, in part because of spurious transitions between unemployment and nonparticipation. If we restrict the time period to use only forecasts that were estimated using the published gross flows
data (lower panel), the differences are small at horizons of up to 2 quarters ahead. As with the longer sample, SSUR-3 performs appreciably worse than SSUR-2 at forecast horizons of ![]() and
beyond.
and
beyond.
| Model | |||||
| Greenbook/SPF sample, 1976-2006 SSUR-2 | 0.13 | 0.32 | 0.50 | 0.67 | 0.84 |
|---|---|---|---|---|---|
| Greenbook/SPF sample, 1976-2006 SSUR-3 | 0.15*** | 0.37* | 0.61** | 0.85** | 1.09** |
| Greenbook/SPF sample, 1976-2006 SSUR-3 (standard error) | (0.01) | (0.08) | (0.02) | (0.01) | (0.02) |
| Monthly forecasts, 2000-06 SSUR-2 | 0.10 | 0.23 | 0.30 | 0.44 | 0.54 |
| Monthly forecasts, 2000-06 SSUR-3 | 0.11* | 0.23 | 0.37** | 0.57** | 0.77** |
| Monthly forecasts, 2000-06 SSUR-3 (standard error) | (0.07) | (0.39) | (0.04) | (0.06) | (0.04) |
4.4 Forecasting Performance over the Business Cycle
The unemployment stock is driven by flows with different time-series properties, and the contributions of the different flows change throughout the cycle.22 For instance, inflows are responsible for the sharp increase in unemployment at the onset of recessions, but outflows are the main driving force of unemployment in normal times.
This property suggests that the performance of our flows model may vary over the business cycle. For instance, because the SSUR-2 model incorporates the unemployment inflow rate, which is responsible for the asymmetry of unemployment, it may better capture the asymmetric nature of unemployment than standard models. Thus, it may perform better during recessions, especially compared with standard models, which do not include labor force flows.
To test this idea and evaluate whether SSUR-2 performs differently over the course of the business cycle, we use (Giacomini & Rossi, 2010) predictive ability test in unstable environments. The test develops a measure of the relative local forecasting performance of two models and is ideal for testing whether the performance of our model varies over the cycle relative to that of a benchmark model. We use as the benchmark the ARIMA model presented in table 1. We evaluate local forecasting performance over a 5-year window using monthly forecasts spanning November 1968 to February 2012.
Figure 3 plots the Giacomini & Rossi fluctuation test statistic for current-quarter and 1-quarter-ahead forecasts; the corresponding 5 percent critical value is also shown. The unit of the ![]() axis is the (standardized) rolling difference in mean-squared-error between the two models, a measure of the relative performance, defined such that a positive value indicates a superior performance of SSUR-2.
axis is the (standardized) rolling difference in mean-squared-error between the two models, a measure of the relative performance, defined such that a positive value indicates a superior performance of SSUR-2.
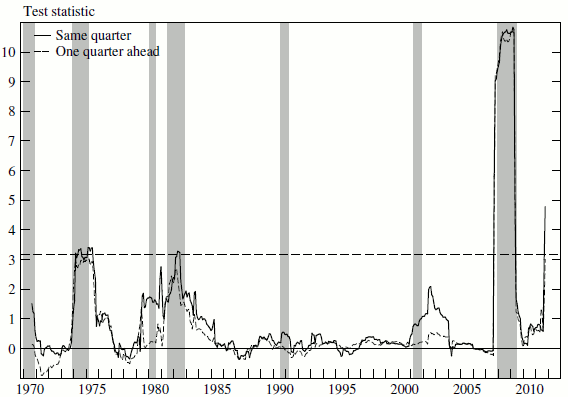 Figure 3 Data
Figure 3 Data
Notes: The Giacomini-Rossi statistic is used here to measure the relative performance of the SSUR-2 and ARIMA(2,0,1) models as the 5-year rolling difference in the mean squared error of their forecasts spanning November 1968 to February 2012. A positive value indicates a superior performance of SSUR-2. Dashed horizontal line indicates 5 percent critical value. Shaded areas represent periods of business recession as determined by the National Bureau of Economic Research.
The SSUR-2 forecasts are almost always more accurate than those of the benchmark model, but SSUR-2 performs especially well around recessions--and particularly during the deep recessions of 1973-75, the early 1980s, and 2008-09--and during times of large and swift movements in the inflow rate. In other words, SSUR-2 yields the greatest improvement over a naive baseline around turning points, precisely when accurate unemployment forecasts are most valuable.
4.5 Intuition for the Model's Performance
Our model's performance is particularly striking in two respects: the model improves significantly upon professional forecasts in the near term, and it performs especially well during recessions. This section discusses the intuition behind this performance.
4.5.1 Average Performance
Our approach to forecasting unemployment rests on the convergence of unemployment toward its steady-state value implied by the labor force flows. Intuitively, if convergence takes place within a couple of months, knowing the current values of the flows provides information on the future level of unemployment, and the SSUR model will perform well over the next couple of months.
In this subsection we develop this intuition further and discuss the reasons behind the quantitative performance of the model. Specifically, our ability to improve forecasting accuracy depends on three parameters: the level of the flows, the persistence of the flows, and whether different flows have different time-series properties.
First, as equation 2 makes clear, the level of the flows governs the speed of convergence to steady state. Since these flows are relatively large in the United States, convergence occurs relatively rapidly (in 3 to 5 months), and the current flows help forecast unemployment in the near term. This explains why, with U.S. data, SSUR-2 performs especially well for current- and next-quarter forecasts. If the flows were larger, the speed of convergence would be even higher, and the model would perform best at an even shorter horizon. At the extreme, if convergence were instantaneous, the current values of the flows would not help forecast unemployment. In contrast, if the flows were much smaller, convergence would occur much more slowly and performance might be best at longer horizons.
If flows were very small, could their current values help us forecast unemployment in the very long run? The reason why this is unlikely comes from the second crucial parameter, the persistence of the flows. The performance of SSUR depends on the interaction between the speed of convergence (the levels of the flows) and the persistence of the flows. The model is good at forecasting unemployment only if the flows are sufficiently persistent that their values can be well predicted over the time needed to converge to steady state. For the U.S. labor market, the model performs well in the near term because the persistence of the flows is sufficiently high.
The third important characteristic behind the performance of SSUR stems from our focus on forecasting the flows rather than the stock. A model of the stock (such as the ARIMA model previously described) cannot perform as well as SSUR, because the flows differ in their time-series properties and because the contributions of the different flows change throughout the cycle. A model of the stock can capture the average time series properties of the stock, but it cannot allow for different time series properties at different stages of the cycle.
4.5.2 Performance over the Business Cycle
The SSUR model performs especially well during recessions and around turning points because the unemployment rate displays steepness asymmetry: increases tend to be steeper than decreases. This asymmetry manifests itself most forcefully during recessions, but a model of the stock is ill equipped to capture it unless one imposes an arbitrary threshold to introduce asymmetry, as is done in threshold autoregressive models. Although SSUR is not explicitly asymmetric, it relies on the labor force flows that are responsible for the asymmetry of unemployment. Indeed, it is the different behavior of the inflows and outflows over the cycle that is responsible for the steepness asymmetry of unemployment (Barnichon, 2012).By incorporating flow information and using it as inputs in the forecasts, our model can incorporate the impulses responsible for the asymmetry of unemployment.
Specifically, the beginning of a recession is typically marked by a sharp increase in the inflow rate: figure 4 plots the impulse responses from our estimated VAR to a shock to the inflow rate.23 Whereas the inflow rate itself displays a sharp increase with fairly rapid reversion to the mean, the outflow rate displays a delayed, U-shaped response with much slower mean reversion. These different impulse responses give rise to the steepness asymmetry of unemployment: following the initial shock, the inflow rate reverts relatively quickly to its mean, but the outflow rate takes longer to return to steady state and thus prevents the unemployment rate from decreasing as rapidly as it increased. By relying on a VAR forecast of the flow rates, following an initial disturbance to the inflow rate at the onset of a recession, SSUR can propagate the cyclical behavior of the flows and thus capture the steepness asymmetry of unemployment.
Source: Authors' calculations using data from Bureau of Labor Statistics.Notes: Impulse response function to a 1-standard-deviation shock to the inflow rate, calculated from a VAR of
5 Combining Forecasts
The array of forecasting models we have considered reflect different information sets. The SSUR models' forecasts rely mainly on labor force flows data and other labor market indicators but not on information from outside the labor market. In contrast, the professional (SPF and Greenbook) forecasts are based on an array of economic data and models beyond the labor market, but they may ignore information on labor force flows. The ARIMA model forecasts unemployment from its past behavior.
Given these different information sets, a natural question is whether these unemployment forecasts can be further improved by combining our flows models' forecasts with a professional forecast such as the SPF and with a simple time-series model such as the ARIMA, to exploit the differences in correlation among the forecast errors (see Granger & Newbold, 1986). We construct such a combined forecast by taking a weighted average of forecasts from SSUR-2, the SPF, and the ARIMA model. The weights are determined by ordinary least squares regression, with a constant included to account for any systematic biases in the estimate. We estimate weights separately for each forecast horizon. The evaluation is a real-time exercise where, for each forecast at a given time, the weights are determined using available history only. These weights allow us to evaluate the marginal contributions of each model over the SPF forecast. If the SSUR-2 model forecast contributes no incremental benefit over the SPF forecast, the weight on the SSUR-2 forecast will be zero.
As table 4 shows, this is not the case: combining the SSUR-2 model with the SPF and the ARIMA improves forecasting performance significantly at horizons up to 2 quarters ahead. Compared with the baseline SPF forecast, the combined forecast achieves a reduction in RMSE of about 35 percent for current-quarter forecasts, 15 percent for 1-quarter-ahead forecasts, and almost 10 percent for 2-quarter-ahead forecasts, with smaller improvements at longer horizons. The combined current-quarter and 1-quarter-ahead forecasts are statistically significantly better than the SPF forecast alone.
| Forecast | |||||
| Root mean squared forecast error (percentage point) |
0.11 | 0.33 | 0.50 | 0.68 | 0.82 |
|---|---|---|---|---|---|
| Root mean squared forecast error (percentage point) |
0.16 | 0.35 | 0.49 | 0.63 | 0.77 |
| Root mean squared forecast error (percentage point) |
0.14 | 0.37 | 0.59 | 0.80 | 0.98 |
| Root mean squared forecast error (percentage point) |
0.11*** | 0.30** | 0.45 | 0.61 | 0.74 |
| Root mean squared forecast error (percentage point) |
(0.00) | (0.03) | (0.15) | (0.35) | (0.37) |
| Optimal weights |
0.80 | 0.48 | 0.42 | 0.35 | 0.40 |
| Optimal weights |
(0.10) | (0.14) | (0.14) | (0.15) | (0.16) |
| Optimal weights |
0.15 | 0.42 | 0.55 | 0.65 | 0.63 |
| Optimal weights |
(0.08) | (0.11) | (0.12) | (0.13) | (0.14) |
| Optimal weights |
0.06 | 0.11 | 0.04 | 0.01 | -0.04 |
| Optimal weights |
(0.11) | (0.12) | (0.12) | (0.12) | (0.13) |
| Optimal weights |
0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Optimal weights |
(0.00) | (0.00) | (0.00) | (0.00) | (0.00) |
The optimal weights reflect the contribution of the SSUR-2 model for short-term forecasting, and the combined forecast puts much more weight on SSUR-2 at short-term horizons.24 Importantly, the fact that the combined forecast performs significantly better than any single forecast indicates that the flows model brings relevant information not contained in the SPF or ARIMA forecasts. In other words, because the forecast errors of the models are not strongly correlated, the combined forecast performs substantially better.
6 Forecasting Labor Force Participation
Compared with the unemployment rate, the labor force participation rate has less of a systematic aggregate relationship with output growth. In fact, aggregate labor force participation has been thought to be acyclical, with changes in the participation rate only weakly related to output growth.25 As a result, forecasting the labor force participation rate was often seen as less of a priority than forecasting the unemployment rate.
The large and unexpected decline in labor force participation during and after the 2008-09 recession challenged that conventional wisdom and highlighted the importance of forecasting the labor force participation rate. However, given the historical absence of a strong relationship between output and labor force participation, forecasters have few models to turn to.
Thus, one advantage of the three-state SSUR model over the two-state model is that it also generates forecasts of the labor force participation rate (and, by extension, the employment-population ratio). Table 5 evaluates the performance of the SSUR-3 model forecasts against that of the Greenbook forecasts.26 SSUR-3 improves on the Greenbook forecast for the current-quarter forecast, although the reduction in RMSE is not statistically significant. At longer forecast horizons, SSUR-3 performs markedly less well than the Greenbook.
| Forecast | |||||
| Root mean squared forecast error (percentage point) |
0.13 | 0.26 | 0.38 | 0.46 | 0.56 |
|---|---|---|---|---|---|
| Root mean squared forecast error (percentage point) |
0.14 | 0.23** | 0.31*** | 0.39* | 0.47 |
| Root mean squared forecast error (percentage point) |
(0.21) | (0.03) | (0.00) | (0.06) | (0.14) |
| Root mean squared forecast error (percentage point) |
0.10*** | 0.15*** | 0.17*** | 0.18*** | 0.19*** |
| Root mean squared forecast error (percentage point) |
(0.00) | (0.00) | (0.00) | (0.00) | (0.00) |
| Optimal weights |
0.40 | 0.36 | 0.67 | 0.85 | 0.69 |
| Optimal weights |
(0.16) | (0.16) | (0.14) | (0.12) | (0.10) |
| Optimal weights |
0.51 | 0.49 | 0.23 | 0.15 | 0.16 |
| Optimal weights |
(0.14) | (0.14) | (0.11) | (0.09) | (0.07) |
| Optimal weights |
0.06 | 0.10 | 0.07 | 0.00 | 0.09 |
| Optimal weights |
(0.02) | (0.04) | (0.05) | (0.05) | (0.06) |
However, SSUR-3 forecast errors need not be correlated with Greenbook forecast errors, so that, again, a combined forecast may generate significant improvement. The third row of table 5 confirms this intuition. The optimal labor force participation rate forecast combining the Greenbook and SSUR-3 forecasts performs significantly better that either alone at all horizons considered, and especially at longer horizons. The reduction in RMSE is trivial for current-quarter forecasts, but grows to between 0.1 and 0.3 percentage point at longer horizons. The large weight on SSUR-3 at all horizons reflects the superior performances of SSUR-3 compared with the Greenbook.27
7 Recent Performance and Near-Term Prospects
Thus far the sample period used in our evaluation against professional forecasts has ended in 2006, shortly before the Great Recession. A crucial question, however, is how the SSUR models perform during that recession and the ongoing recovery. In particular, can the models capture the steep increase in unemployment and the lack of rapid decline following this latest recession compared with other deep recessions?
Beyond 2006, we can no longer compare our models with the Greenbook; we therefore use the SPF as the benchmark instead. As table 1 showed, the SPF and Greenbook forecasts have roughly similar RMSEs over a 1-year forecast horizon.
Table 6 reports the RMSEs for forecasts of both SSUR models and the SPF starting in February 2007 and ending in February 2012. Although the SPF's current-quarter forecast error is roughly comparable to that for the earlier period, forecast errors at longer horizons are 0.1 to 0.8 percentage point larger during this period than over 1976-2006. The flows models' forecast errors are similarly larger. In particular, the two-state model's forecast for the current quarter--by far its comparative advantage--worsens appreciably. Whereas it outperformed the SPF by 25 percent in the earlier period, SSUR-2 now performs only slightly better than the SPF.
| Model | |||||
| SPF | 0.17 | 0.46 | 0.77 | 1.17 | 1.58 |
| SSUR-2 | 0.16 | 0.58 | 0.96 | 1.47 | 1.94 |
| SSUR-3 | 0.13 | 0.45 | 0.93 | 1.50 | 2.11 |
| No. of observations | 23 | 22 | 21 | 20 | 19 |
|---|
In contrast, the three-state model, which performed worse than either the two-state model or the SPF over 1976-2006 at all horizons, now outperforms the SPF by almost 30 percent in the current quarter, and its RMSE is even a bit smaller 1 quarter ahead. We point to three factors to explain this striking difference.
First, the gross flows are much better measured in the published data than in the historical tabulations. Because for much of the 1976-2006 sample the model was estimated using the transitions we calculated from the micro data (rather than from the published data), the three-state model performs worse than the two-state model. Indeed, table 3 showed that SSUR-3 performed about the same as the two-state model when estimated using only the published gross flows data.
Second, the two-state model uses cross-sectional data on unemployment to infer the outflow rate and backs out the inflow rate using an unemployment accounting identity. As Elsby et al. (2011) note, a key assumption needed to derive the hazards appears to have broken down starting in 2009. They show that, historically, the two measures of unemployment outflows moved closely together over the business cycle, but that since 2009, Shimer (2012) measure has exhibited a much larger decline than the flow from the unemployment to employment. They show that the discrepancy is being driven by the large increase in the unemployment duration of persons flowing into unemployment, whereas Shimer's calculation assumes that all unemployment inflows have a duration of 5 weeks or less.
Third, and most important, the two-state model by design abstracts from movements into and out of the labor force. Historically, the labor force participation rate has not exhibited much cycli-cality. However, in the recent recession and recovery, the participation rate has fallen 2![]() percentage points. The Congressional Budget Office's August 2012 estimate of the trend labor force suggests that about 1 percentage point of this decline can be accounted for by declining trend
participation (primarily due to aging of the population). The remainder likely reflects an unusually large cyclical decline. The two-state model cannot account for the cyclical decline and thus projects an employment-population ratio that is systematically too high. In contrast, the flows in the
three-state model reflect the declining participation rate.
percentage points. The Congressional Budget Office's August 2012 estimate of the trend labor force suggests that about 1 percentage point of this decline can be accounted for by declining trend
participation (primarily due to aging of the population). The remainder likely reflects an unusually large cyclical decline. The two-state model cannot account for the cyclical decline and thus projects an employment-population ratio that is systematically too high. In contrast, the flows in the
three-state model reflect the declining participation rate.
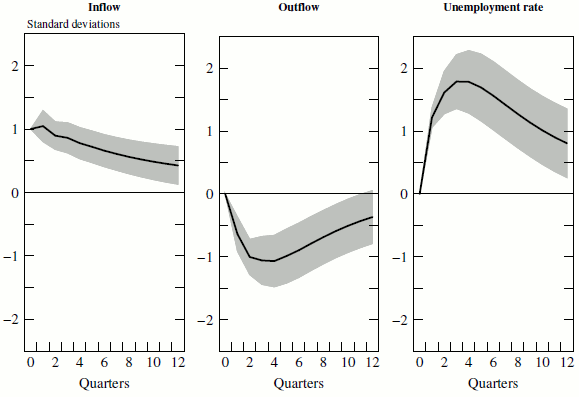
Figure 5 shows the time pattern of recent unemployment rate forecast misses by the SPF and the two SSUR models for both the current-quarter forecast (2 months of forecast; upper panel) and the next-quarter forecast (5 months of forecast; lower panel). A
positive value indicates that the unemployment rate was higher than the model predicted. As the unemployment rate starts to increase, rising from 4.5 percent in the first quarter of 2007 to 4.8 percent at the end of 2007, the SPF and the SSUR models show relatively small upside surprises at both
the ![]() and
and ![]() horizons (the unemployment rate was higher than projected). The
unemployment rate then accelerates over 2008 and the first half of 2009, rising from 5 percent to 9
horizons (the unemployment rate was higher than projected). The
unemployment rate then accelerates over 2008 and the first half of 2009, rising from 5 percent to 9![]() percent. In 2008 the SSUR models and the SPF alike show modestly surprises to the
upside in their current-quarter forecasts, with misses of about
percent. In 2008 the SSUR models and the SPF alike show modestly surprises to the
upside in their current-quarter forecasts, with misses of about ![]() percentage point. However, from 2009 forward the three-state model consistently outperforms the SPF and the two-state
model in the current quarter, with misses to both the upside and the downside. At the 1-quarter-ahead horizon, the two-state model does noticeably worse than the SPF or the three-state model from 2009 on.
percentage point. However, from 2009 forward the three-state model consistently outperforms the SPF and the two-state
model in the current quarter, with misses to both the upside and the downside. At the 1-quarter-ahead horizon, the two-state model does noticeably worse than the SPF or the three-state model from 2009 on.
What do the SSUR models say about the outlook for unemployment 6 months hence as of this writing in November 2012? Table 7 presents their forecasts of the unemployment rate and the labor force participation rate for November 2012 through April 2013. The two-state model projects the unemployment rate to decline over the rest of 2012 and into 2013, from its reported level of 7.9 percent in October to 7.8 percent in December and 7.5 percent in April. This decline reflects a projected increase in the unemployment outflow hazard and a projection of little change in the inflow hazard (not shown). The three-state model projects the unemployment rate to remain at 7.9 percent over the same 6 months, reflecting a slow increase in the job finding rate for unemployed workers and a slight rise in the labor force participation rate.
| Model | Nov. 2012 (Monthly forecast) | Dec. 2012 (Monthly forecast) | Jan. 2013 (Monthly forecast) | Feb. 2013 (Monthly forecast) | Mar. 2013 (Monthly forecast) | Apr. 2013 (Monthly forecast) | Q4 2012 (Quarterly average) | Q1 2013 (Quarterly average) |
| Unemployment rate SSUR-2 | 7.9 | 7.8 | 7.7 | 7.7 | 7.6 | 7.5 | 7.8 | 7.7 |
|---|---|---|---|---|---|---|---|---|
| Unemployment rate SSUR-3 | 7.9 | 7.9 | 7.9 | 7.9 | 7.9 | 7.9 | 7.9 | 7.9 |
| Labor force participation rate SSUR-3 | 64.0 | 64.0 | 64.1 | 64.1 | 64.2 | 64.2 | 63.9 | 64.1 |
8 Conclusion
Although the unemployment rate is typically considered a lagging indicator of the business cycle, increases in the unemployment rate have preceded the last three recessions. Recent research by Fleischman & Roberts (2011) finds that the unemployment rate provides the best single signal about the state of the business cycle in real time. Nevertheless, despite extensive research on the topic, forecasters and policymakers often rely on Okun's law or basic time-series models to forecast the unemployment rate.
This paper has presented a nonlinear unemployment rate forecasting model based on labor force flows that, in real time, dramatically outperforms basic time-series models, the SPF, and the Federal Reserve Board's Greenbook forecast at short horizons. Our model is built on two elements: a nonlinear law of motion describing how the unemployment rate converges to its conditional steady state (the rate of unemployment implied by the flows into and out of unemployment), and forecasts of these labor force flows. The model's performance, in turn, stems from two factors: the convergence of unemployment to its conditional steady state with a lag of 3 to 5 months, and the fact that flows into and out of unemployment have different time-series properties than the stock.
Empirically, the two-state model has a root-mean-squared forecast error about 30 percent smaller than the next-best forecast for the current quarter, and 10 percent smaller for the next-quarter forecast. Moreover, our model has the highest predictive ability of those we analyze surrounding business cycle turning points and large recessions. And because the model brings new information to the forecast, a combination of our model's forecast and the SPF forecast yields an improvement of about 35 percent for the current-quarter forecast and of 25 percent for the next-quarter forecast, with smaller improvements at longer horizons.
The two new models that we propose have both advantages and disadvantages relative to each other. The two-state model is easier to understand conceptually and to implement. The duration-based unemployment inflow and outflow hazard rates have a longer history and are somewhat less noisy. However, these hazard rates are not directly measured but rather inferred from a theoretical model. More important, a key assumption for deriving the hazards appears to have broken down starting in 2009.
The three-state model is a more realistic characterization of the labor market and produces internally consistent forecasts for the unemployment rate, the labor force participation rate, and the employment-population ratio. Although the three-state model's unemployment rate forecasts at longer horizons tend to be worse than those of the two-state model, since 2007 the three-state model outperforms the two-state model--as well as the SPF, in the near term--in part because it accounts for the large decline in labor force participation during this cycle.
Solving the Three-State Model
Denoting
![]() , we can rewrite equation 10 as
, we can rewrite equation 10 as
with
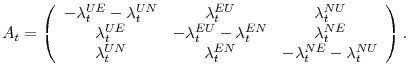
|
Since the columns of ![]() sum to zero,
sum to zero, ![]() has one eigenvalue equal to
zero. Denoting
has one eigenvalue equal to
zero. Denoting ![]() the matrix of eigenvectors of
the matrix of eigenvectors of ![]() corresponding to the
eigenvalues
corresponding to the
eigenvalues
![]() , we can write a solution to equation A.1 as
, we can write a solution to equation A.1 as
with
To find the values of ![]()
![]() and
and ![]() , we use initial conditions
, we use initial conditions
![]() and terminal conditions
and terminal conditions
![]() , the vector of the steady-state numbers of unemployed (
, the vector of the steady-state numbers of unemployed (
![]() ), employed (
), employed (
![]() ), and nonparticipants (
), and nonparticipants (
![]() ). The steady-state stocks are given by
). The steady-state stocks are given by
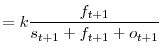 |
||
where
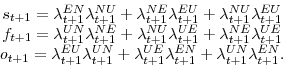
|
Some algebra yields the 1-month-ahead forecasts of unemployment, employment, and nonparticipation:
| (A.4) | 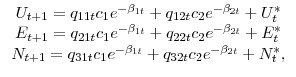
|
where
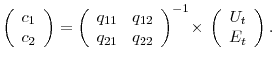 |

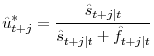
![\displaystyle \left\{ \begin{array}{c} \dot{U}_{t+\tau}=\lambda_{t+1}^{EU}E_{t+\tau}+\lambda_{t+1}^{NU}N_{t+\tau}-(\lambda_{t+1}^{UE}+\lambda_{t+1}^{UN})U_{t+\tau} \\ [1ex] \dot{E}_{t+\tau}=\lambda_{t+1}^{UE}U_{t+\tau}+\lambda_{t+1}^{NE}N_{t+\tau}-(\lambda_{t+1}^{EU}+\lambda_{t+1}^{EN})E_{t+\tau} \\ [1ex] \dot{N}_{t+\tau}=\lambda_{t+1}^{EN}E_{t+\tau}+\lambda_{t+1}^{UN}U_{t+\tau}-(\lambda_{t+1}^{NE}+\lambda_{t+1}^{NU})N_{t+\tau}. \end{array} \right.](img62.gif)
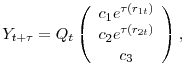
![\displaystyle \left. \begin{array}{rl} r_{1t} \approx -\beta_{1t} &\equiv \lambda_t^{UE}+\lambda_t^{UN}\\ [1ex] r_{2t} \approx -\beta_{2t} &\equiv \lambda_t^{EU}+\lambda_t^{EN}+\lambda_t^{NE}+\lambda_t^{NU}. \end{array} \right.](img150.gif)