Taxation of Human Capital and Wage Inequality: A Cross-Country Analysis
Keywords: Wage inequality, human capital, skill-biased technical change, tax policies
Abstract:
1 Introduction
Why is wage inequality significantly higher in the United States than in continental European countries (CEU)? And why has this inequality gap between the US and the CEU widened substantially since the 1970s (see Table 1)? More broadly, what are the determinants of wage dispersion in modern economies? How do these determinants interact with technological progress and government policies? The goal of this paper is to shed light on these questions by studying the impact of labor market (tax) policies on the determination of wage inequality, focusing on male workers and using cross-country data.
We begin by documenting two new empirical relationships between wage inequality and tax policy. First, we show that countries with more progressive labor income tax schedules have significantly lower wage inequality at different points in time.3 The measure of wages we use is "gross before-tax wages" and can therefore be thought of as a proxy for the marginal product of workers.4 From this perspective, progressivity is associated with a more compressed productivity distribution across workers. Second, we show that countries with more progressive income taxes have also experienced a smaller rise in wage inequality over time, and this relationship is especially strong above the median of the wage distribution. These findings reveal a close relationship between progressivity and wage inequality, which motivates the focus of this paper. However, on their own, these correlations fall short of providing a quantitative assessment of the importance of the tax structure--e.g., what fraction of cross-country differences in wage inequality can be attributed to tax policies? For this purpose, we build a model.
| 1978-1982 average | 2001-2005 average | Change | |
| Denmark | - | 0.97 | - |
| Finland | 0.89 | 0.94 | 0.05 |
| France | 1.22 | 1.14 | -0.08 |
| Germany | 0.93 | 1.06 | 0.07 |
| Netherlands | 0.84 | 1.05 | 0.11 |
| Sweden | 0.73 | 0.87 | 0.14 |
| CEU | 0.92 | 1.01 | 0.06 |
| UK | 0.99 | 1.28 | 0.29 |
| US | 1.28 | 1.60 | 0.32 |
Specifically, we construct a life cycle model that features some key determinants of wages--most notably, human capital accumulation and idiosyncratic shocks. Here is an overview of the framework. Individuals enter the economy with an initial stock of human capital and are able to accumulate more human capital over the life cycle using a Ben-Porath (1967) style technology (which essentially combines learning ability, time, and existing human capital for production). Individuals can choose to either invest in human capital on the job up to a certain fraction of their time or enroll in school where they can invest full time. We assume that skills are general and labor markets are competitive. As a result, the cost of on-the-job investment will be borne by the workers, and firms will adjust the wage rate downward by the fraction of time invested on the job. Therefore, the cost of human capital investment is the forgone earnings while individuals are learning new skills.
We introduce two main features into this framework. First, we assume that individuals differ in their learning ability. As a result, individuals differ systematically in the amount of investment they undertake and, consequently, in the growth rate of their wages over the life cycle. Thus, a key source of wage inequality in this model is the systematic fanning out of the wage profiles.5 Second, we allow for endogenous labor supply choice, which amplifies the effect of progressivity, a point that we return to shortly. Finally, for a comprehensive quantitative assessment, we also allow idiosyncratic shocks to workers' labor efficiency and model differences in consumption taxes and pension systems, which vary greatly across these countries.
The model described here provides a central role for policies that compress the wage structure--such as progressive income taxes--because such policies hamper the incentives for human capital investment. This is because a progressive system reduces after-tax wages at the higher end of the wage distribution compared with the lower end. As a result, it reduces the marginal benefit of investment (the higher wages in the future) relative to the marginal cost (the current forgone earnings), thereby depressing investment. A key observation is that this distortion varies systematically with the ability level--and, specifically, it worsens with higher ability--which then compresses the before-tax wage distribution. These effects of progressivity are compounded by endogenous labor supply and differences in average income tax rates: the higher taxes in the CEU reduce labor supply--and, consequently, the benefit of human capital investment--further compressing the wage distribution.
The main quantitative exercise we conduct is the following. We consider the eight countries listed in Table 1, for which we have complete data for all variables of interest. We assume that all countries have the same innate ability distribution but allow each country to differ in the observable dimensions of its labor market structure, such as in labor income (and consumption) tax schedules and retirement pension system. We then calibrate the model-specific parameters to the US data and keep these parameters fixed across countries. The policy differences we consider explain about half of the observed gap in the log 90-10 wage differential between the US and the CEU in the 2000s and 84% of the wage inequality above the median (log 90-50 differential). The model explains only about 24% of the difference in the lower tail inequality between the US and the CEU, which is consistent with the idea that the human capital mechanism is likely to be more important for higher ability individuals and, therefore, above the median of the distribution. We also provide a decomposition that isolates the roles of (i) the progressivity of income taxes, (ii) average income tax rates, (iii) consumption taxes, and (iv) the pension system. We find that progressivity is by far the most important component, accounting for about 2/3 of the model's explanatory power.
The second question we ask is whether the widening of the inequality gap between the US and the CEU since the late 1970s could also be explained by the same human capital channels discussed earlier. One challenge we face in trying to answer this question is that the country-specific tax schedules that we derive in this paper are only available for the years after 2001 (because the detailed information from OECD sources for taxes is only available after that date), whereas the tax structure has changed over time for several of the countries in our sample. Fortunately, for two countries in our sample--the US and Germany--we are also able to derive tax schedules for 1983, which reveal significantly more flattening of tax schedules in the US compared with Germany from 1983 to 2003. When these changes in progressivity and skill-biased technical change (SBTC) are jointly taken into account, the (recalibrated) model generates a much larger rise in inequality in the US than in Germany, in fact, slightly overestimating the actual widening of the inequality gap between these countries.
Finally, in section 6, we test some key implications of our model for lifecycle behavior using micro data. First, the model predicts that a country with a more progressive tax system should have a flatter age profile of average wages (by dampening human capital accumulation) compared with a less progressive one. Similarly, progressivity will imply a flatter profile of within-cohort wage inequality over the life cycle. We provide a comparison of the United States (using the Panel Study of Income Dynamics, PSID, data) and Germany (using the German Socio-Economic Panel, GSOEP) and find strong support for both predictions.
1.1 Related Literature
The negative relation between inequality and redistribution has also been studied in earlier papers. Among these, Benabou (2000), Moene and Wallerstein (2001), and Hassler et al. (2003) use a political economy framework to explain how countries with high inequality and low redistribution (e.g., the United States) can coexist with countries with low inequality and high redistribution (e.g. continental Europe). Hassler et al. (2003) emphasize the interaction between political economy and human capital investment: redistribution reduces human capital investment by the young, in turn reducing wages throughout the life cycle, and thus implying that a larger share of voters will benefit from redistributive politics. As a result, the model features multiple equilibria. An important implication of this environment is that an increase in pre-tax inequality strengthens the incentives for investment and reduces, ceteris paribus, the fraction of voters supporting redistribution.
Benabou (2000) explores the effects of redistribution in the presence of imperfect credit markets. When inequality is very low, the benefit of redistribution comes mainly from higher output (due to the relaxation of credit constraints for some high productivity individuals). But when inequality is high, the wealthy do not want redistribution. Thus, support for redistribution decreases initially with higher inequality. Moene and Wallerstein (2001) consider the redistributive and insurance aspects of welfare benefits. In their framework, an increased gap between median and mean income increases political support for welfare benefits if benefits are targeted to the employed as redistribution, but decreases the political support if the benefits are targeted to the poor as insurance against income loss. When the targeting of benefits is made endogenous, their model implies that political support for insurance against income risk still declines as the gap between the median and the mean increases. The channels explored in these papers are likely to be complementary to ours.
In terms of methodology, this paper is most closely related to the recent macroeconomics literature that has written fully specified models to address US-CEU differences in labor market outcomes. Prominent examples include Ljungqvist and Sargent (1998), Ljungqvist and Sargent (2008), and Hornstein et al. (2007), who focus on unemployment rates, and Prescott (2004), Ohanian et al. (2008), and Rogerson (2008), who study labor hours differences. Several of these papers rely on representative agent models and are, therefore, silent on wage inequality; and those that do allow for individual-level heterogeneity do not address differences in wage inequality. In terms of modeling choices, the closest framework to ours is Kitao et al. (2008), who study a rich life cycle framework with human capital accumulation and job search and model the benefits system. Their goal is to explain the different unemployment patterns over the life cycle in the US and Europe.
Finally, a number of recent papers share some common modeling elements with ours but address different questions. Important examples include Altig and Carlstrom (1999), Krebs (2003), Caucutt et al. (2006), and Huggett et al. (forthcoming). Altig and Carlstrom (1999) study the quantitative impact of the Tax Reform Act of 1986 on income inequality arising solely from behavioral responses associated with labor supply and saving decisions and find that distortions arising from marginal tax rate changes have sizable effects on income inequality. Krebs (2003) studies the impact of idiosyncratic shocks on human capital investment and shows that reducing income risk can increase growth, in contrast to the standard incomplete markets literature, which typically reaches the opposite conclusion. Caucutt et al. (2006) develop an endogenous growth model with heterogeneity in income. They show that a reduction in the progressivity of tax rates can have positive growth effects even in situations where changes in flat-rate taxes have no effect. Another important contribution is Huggett et al. (forthcoming), who study the distributional implications of the Ben-Porath model and estimate the sources of lifetime inequality using US earnings data. Finally, Erosa and Koreshkova (2007) investigate the effects of replacing the current U.S. progressive income tax system with a proportional one in a dynastic model. They find a large positive effect on steady state output, which comes at the expense of higher inequality. Although our paper has many useful points of contact with this body of work, to our knowledge, our combination of human capital accumulation, ability heterogeneity, progressive taxation, and endogenous labor supply is new, as is the attempt to explain cross-country inequality facts in such a framework.
The next section lays out the main model and explains the various channels through which tax policy affects wage inequality. Section 3 describes how the country-specific tax schedules are estimated and uses the estimates to document two new empirical relationships between taxes and inequality. Sections 4 and 5 discusses the parameterization and the main quantitative results. Section 6 examines a series of micro implications of the human capital mechanism proposed in this paper. Section 7 concludes.
2 The Model
We begin by describing the features of the human capital investment problem. Using this environment, we discuss the various channels through which tax policy affects wage inequality. We then enrich this framework by introducing empirically relevant features (such as idiosyncratic shocks and labor market institutions) that are necessary for a sound quantitative analysis.
2.1 Human Capital Accumulation
Consider an individual who derives utility from consumption and leisure and has access to borrowing and saving at a constant interest rate, ![]() . Let
. Let ![]() be the subjective time discount factor and assume
be the subjective time discount factor and assume
![]() . Each individual has one unit of time in each period, which he can allocate to three different uses: work, leisure, and human capital investment. If an individual chooses to
work, he can allocate a fraction (
. Each individual has one unit of time in each period, which he can allocate to three different uses: work, leisure, and human capital investment. If an individual chooses to
work, he can allocate a fraction (![]() ) of his working hours (
) of his working hours (![]() ) to human capital
investment. At age
) to human capital
investment. At age ![]() new human capital,
new human capital, ![]() is produced according to a
Ben-Porath technology:
is produced according to a
Ben-Porath technology:
where
The opportunity "cost of investment" (in human capital units) is equal to
![]() and, using equation (1), it can be written as
and, using equation (1), it can be written as
![]() , which will play a key role in the optimality conditions that follow.
, which will play a key role in the optimality conditions that follow.
A key parameter in the Ben-Porath technology is ![]() . Heterogeneity in
. Heterogeneity in ![]() implies that individuals will differ systematically in the amount of human capital they accumulate and, consequently, in the growth rate of their wages over the life cycle. This systematic fanning out of wage profiles is the major source of wage inequality in this model.
implies that individuals will differ systematically in the amount of human capital they accumulate and, consequently, in the growth rate of their wages over the life cycle. This systematic fanning out of wage profiles is the major source of wage inequality in this model.
2.2 Inspecting the Mechanisms
We are now ready to discuss how taxation of human capital can affect wage inequality. To this end, it is useful to distinguish between two cases.
Inelastic Labor Supply.
First, suppose that labor supply is inelastic. Assuming an interior solution, the optimality condition for human capital investment is
which equates the after-tax marginal cost of investment on the left hand side to the after-tax marginal benefit on the right.6 To understand the effect of taxes, first consider the case where taxes are flat rate (
Thus, flat-rate taxes have no effect on human capital investment. This is a well-understood insight that goes back to at least Heckman (1976) and Boskin (1977).7
Now consider progressive taxes, i.e.,
![]() . We rearrange equation (4) to get:
. We rearrange equation (4) to get:
With progressivity, as long as the individual's earnings grow over the life cycle, the tax ratios in (5) will be strictly less than one, depressing the marginal benefit of investment, which in turn dampens human capital accumulation. Thus, these tax ratios capture the reduction in the value of future wage earnings compared with the forgone wage earnings today. This observation motivates our first measure of progressivity, what we refer to as the progressivity wedge, defined as:
between any two ages
To understand the effect of progressive taxes on wage inequality, note that the distortion created by progressivity differs systematically across ability levels. At the low end, individuals with very low ability whose optimal plan involves no human capital investment in the absence of taxes would experience no wage growth over the life cycle and, therefore, no distortion from progressive taxation. At the top end, individuals with high ability (whose optimal plan implies low wage earnings early in life and very high earnings later) face very large wedges, which depress their investment. Thus, progressivity reduces the cross-sectional dispersion of human capital and, consequently, wage inequality in an economy, even with inelastic labor supply.
Endogenous Labor Supply.
Second, consider now the the case with elastic labor supply. The first order condition can be shown to be (see Appendix A.1) as follows:
where now the marginal benefit accounts for the utilization rate of human capital, which depends on the labor supply choice. Our second measure of progressivity is precisely motivated by this first order condition subject to a normalization:
where
Now, once again, consider the effect of flat-rate taxes. The intra-temporal optimality condition for labor-leisure choice implies that labor supply depends negatively on the tax rate and positively on the level of human capital. A higher tax rate depresses labor supply choice (as long as the income effect is not too large), which then reduces the marginal benefit of human capital investment, which reduces the optimal level of human capital. But labor supply in turn depends on the level of human capital, which further depresses labor supply, the level of human capital, and so on. Therefore, with endogenous labor supply, even a flat-rate tax has an effect on human capital investment, which can also be large because of the amplification described here.
In summary, the baseline model studied here implies that countries with more progressive tax systems will have lower wage inequality. As will become clear later, these countries will also experience a smaller change in wage inequality in response to technological changes (such as SBTC). In Section 3, we examine these predictions empirically.
2.3 Enriching the Basic Framework
As stated earlier, the main goal of this paper is to provide a quantitative assessment of the importance of the tax structure--e.g., what fraction of cross-country differences in wage inequality can be attributed to tax policies? For this purpose, we introduce several empirically relevant features that are necessary for a sound quantitative analysis.
Upper Bound on On-the-Job Investment.
We impose an upper bound on the fraction of time that can be devoted to on-the-job investment:
![]() , where
, where ![]() Such an upper bound would arise, for example, when
firms incur fixed costs for employing each worker (administrative burden, cost of office space, etc.) or as a result of minimum wage laws. Individuals can invest full-time by attending school (
Such an upper bound would arise, for example, when
firms incur fixed costs for employing each worker (administrative burden, cost of office space, etc.) or as a result of minimum wage laws. Individuals can invest full-time by attending school (![]() ) and enjoy leisure for the rest of the time. Thus, the choice set is
) and enjoy leisure for the rest of the time. Thus, the choice set is
![]() which is non-convex when
which is non-convex when ![]() . Finally, human capital
depreciates every period at rate
. Finally, human capital
depreciates every period at rate ![]() .
.
Idiosyncratic Shocks.
It is difficult to talk about wage inequality without any sort of idiosyncratic shock. In a human capital model, these shocks would interact with investment choice and can greatly affect the quantitative conclusions we draw from the analysis. Thus, we introduce idiosyncratic shocks.
Specifically, when an individual devotes
![]() hours producing for his employer, his effective labor supply becomes
hours producing for his employer, his effective labor supply becomes
![]() , where
, where ![]() is an idiosyncratic Markov shock with a
stationary transition matrix
is an idiosyncratic Markov shock with a
stationary transition matrix
![]() that is identical across agents and over the life cycle. Note that these shocks are not to the stock of human capital (as, for example,
in Huggett et al. (forthcoming)). Instead, these can be viewed as shocks to the rental rate or to the efficiency of labor supply.
that is identical across agents and over the life cycle. Note that these shocks are not to the stock of human capital (as, for example,
in Huggett et al. (forthcoming)). Instead, these can be viewed as shocks to the rental rate or to the efficiency of labor supply.
Market Structure.
A full set of one-period Arrow securities is available for trade at every date and state, allowing markets to be dynamically complete. An Arrow security that promises to deliver one unit of consumption good in state ![]() tomorrow costs
tomorrow costs
![]() in state
in state ![]() today. Individuals completely insure
themselves against consumption risk by trading these securities. Hence, all individuals of a given type
today. Individuals completely insure
themselves against consumption risk by trading these securities. Hence, all individuals of a given type ![]() will have the same (and constant) consumption over the life cycle. However,
individuals will have different realized paths of investment, human capital, labor supply, and wages.
will have the same (and constant) consumption over the life cycle. However,
individuals will have different realized paths of investment, human capital, labor supply, and wages.
Pension Benefits.
It is easy to see from the discussion above of equations (5) and (7) that the existence of a redistributive pension system will have an effect similar to progressive taxation. In addition, the retirement pension system represents a major use of tax revenues collected by governments. Therefore, modeling pensions is important for capturing how funds are returned to households.
During retirement, individuals receive constant pension payments every period. Essentially, the pension of a worker with ability level ![]() depends on two variables: (i) the average lifetime
earnings of workers with the same ability level (denoted by
depends on two variables: (i) the average lifetime
earnings of workers with the same ability level (denoted by
![]() ), and (ii) the total number of years the worker had Social Security eligible earnings by the time he retired, denoted by
), and (ii) the total number of years the worker had Social Security eligible earnings by the time he retired, denoted by ![]() . The pension function is denoted as
. The pension function is denoted as
![]() .9
.9
The Tax System and the Government Budget.
The government imposes a flat-rate consumption tax,
![]() , in addition to the (potentially) progressive labor income tax,
, in addition to the (potentially) progressive labor income tax,
![]() .10 The collected revenues are
used for two main purposes: (i) to finance the benefits system, and (ii) to finance government expenditure, G, that does not yield any direct utility to consumers (because of either corruption or waste). The residual budget surplus or deficit,
.10 The collected revenues are
used for two main purposes: (i) to finance the benefits system, and (ii) to finance government expenditure, G, that does not yield any direct utility to consumers (because of either corruption or waste). The residual budget surplus or deficit, ![]() is distributed in a lump-sum fashion to all households.
is distributed in a lump-sum fashion to all households.
2.4 Individuals' Dynamic Program
Individuals solve the following problem (ability type ![]() is suppressed for clarity):
is suppressed for clarity):
for
After retirement, individuals receive a pension and there is no human capital investment. Since there is no uncertainty during retirement, a riskless bond is sufficient for smoothing consumption. Therefore, the problem at age
![]() can be written as
can be written as
The definition of a stationary recursive competitive equilibrium in this environment is standard, so the formal statement is relegated to Appendix A.
3 Progressivity and Inequality: Two Empirical Facts
This section has two purposes. First, we discuss the derivation of country-specific tax schedules that are used in the rest of the paper. Using these tax schedules, we construct empirical measures of the two progressivity wedges defined in (6) and (8) above. Second, with these wedges on hand, we go on to document two new empirical relationships between wage inequality and the progressivity of (labor income) tax policy that are consistent with the presented model and further motivate the quantitative analysis that follows.11
3.1 Deriving Country-Specific Tax Schedules
For each country, we follow the procedure described here. First, the OECD tax database provides estimates of the total labor income tax for all income levels between half of average wage earnings (hereafter, AW) to two times AW. The
calculation takes into account several types of taxes (central government, local and state, social security contributions made by the employee, and so on), as well as many types of deductions and cash benefits (dependent exemptions, deductions for taxes paid, social assistance, housing assistance,
in-work benefits, etc.).12 Using these estimates, we calculate the average labor income tax rate,
![]() , for 50%, 75%, 100%, 125%, 150%, 175%, and 200% of AW. However, tax rates beyond 200% of AW are also relevant when
individuals solve their dynamic program. Fortunately, another piece of information is available from the OECD: the top marginal tax rate and the top bracket corresponding to it for each country. As described in more detail in Appendix B.1, we use this information to generate average tax rates at income levels beyond two times AW. Then, we fit the following smooth function to the available data points:13
, for 50%, 75%, 100%, 125%, 150%, 175%, and 200% of AW. However, tax rates beyond 200% of AW are also relevant when
individuals solve their dynamic program. Fortunately, another piece of information is available from the OECD: the top marginal tax rate and the top bracket corresponding to it for each country. As described in more detail in Appendix B.1, we use this information to generate average tax rates at income levels beyond two times AW. Then, we fit the following smooth function to the available data points:13
The parameters of the estimated
![]() functions for all countries are reported in Appendix B.1, along with the
functions for all countries are reported in Appendix B.1, along with the ![]() values. Although the assumed functional form allows for various possibilities, all fitted tax schedules turn out to be increasing and concave. The lowest
values. Although the assumed functional form allows for various possibilities, all fitted tax schedules turn out to be increasing and concave. The lowest ![]() is 0.984 and the mean is 0.991, indicating a very good fit. In Figure 1, we plot the estimated functions for three countries: one of the two least progressive (United States), the most progressive (Finland), and one with
intermediate progressivity (Germany).
is 0.984 and the mean is 0.991, indicating a very good fit. In Figure 1, we plot the estimated functions for three countries: one of the two least progressive (United States), the most progressive (Finland), and one with
intermediate progressivity (Germany).
Figure 2 plots the progressivity wedges computed from the estimated tax schedules for all countries in our sample. Specifically, each line plots
![]() and
and
![]() , which are essentially the wedges faced by an individual who starts life at half the average earnings in that country and looks toward an eventual wage level that is up to six
times his initial wage. As seen in the figure, countries are ranked in terms of their progressivity. Consistent with what one could conjecture, the US and the UK have the least progressive tax system, whereas Scandinavian countries have the most progressive ones, and larger continental European
countries are scattered between these two extremes. The differences also appear quantitatively large (although a more precise evaluation needs to await the quantitative analysis in the next section): for example, the marginal benefit of investment for a young worker in the US who invests today when
his wage is
, which are essentially the wedges faced by an individual who starts life at half the average earnings in that country and looks toward an eventual wage level that is up to six
times his initial wage. As seen in the figure, countries are ranked in terms of their progressivity. Consistent with what one could conjecture, the US and the UK have the least progressive tax system, whereas Scandinavian countries have the most progressive ones, and larger continental European
countries are scattered between these two extremes. The differences also appear quantitatively large (although a more precise evaluation needs to await the quantitative analysis in the next section): for example, the marginal benefit of investment for a young worker in the US who invests today when
his wage is
![]() and expects to earn
and expects to earn
![]() in the future is 13% lower than in a flat-tax system. The comparable loss is 27% in Denmark and Finland. These differences grow with the ambition level of the individual,
dampening human capital investment, especially at the top of the distribution.
in the future is 13% lower than in a flat-tax system. The comparable loss is 27% in Denmark and Finland. These differences grow with the ambition level of the individual,
dampening human capital investment, especially at the top of the distribution.
3.2 Taxes and Inequality: Cross-Country Empirical Facts
The wage inequality data come from the OECD's Labour Force Survey database and are derived from the gross (before-tax) wages of full-time, full-year (or equivalent) workers.14 This is the appropriate measure for the purposes of this paper, as it more closely corresponds to the marginal product of each worker (and, hence, his wage) in the model. The fact that the inequality data pertain to before-tax wages is important to keep in mind; if the data were for after-tax wages, the correlation between progressivity and inequality would be mechanical and, thus, not surprising at all. Furthermore, we focus on male workers to avoid potential selection issues that may arise due to wide differences in female labor force participation rates across countries.
We normalize AW in each country to 1 and focus on
![]() as the measure of progressivity. Similarly, when we calculate
as the measure of progressivity. Similarly, when we calculate ![]() for a given country, we use the average hours per person in that country between 2001 and 2005 for
for a given country, we use the average hours per person in that country between 2001 and 2005 for ![]() in equation (8), and the average of
the same variable across all countries for
in equation (8), and the average of
the same variable across all countries for
![]() 15 Finally, for brevity, in the
rest of the paper we will refer to the "log 90-10 wage differential" simply as "L90-10," and similarly for the other wage differentials.
15 Finally, for brevity, in the
rest of the paper we will refer to the "log 90-10 wage differential" simply as "L90-10," and similarly for the other wage differentials.
Figure 3 plots the relationship between L90-10 and the progressivity wedge in the 2000s. Countries with a smaller wedge--meaning a less progressive tax system and, therefore, a smaller distortion in human capital investment--have higher wage inequality. The
relationship is also quite strong with a correlation of -0.82.16 (Repeating the same calculation using ![]() yields the same correlation.) Both relationships are consistent with the human capital model with progressive taxes presented above.
yields the same correlation.) Both relationships are consistent with the human capital model with progressive taxes presented above.
|
We next turn to the change in inequality over time. Figure 4 plots ![]() versus the change in L90-50 (left panel) and
L50-10 (right panel). Countries with a more progressive tax system in the 2000s have experienced a smaller rise in wage inequality since the 1980s. The relationship is especially strong at the top of the wage distribution and weaker at the bottom: the correlation between progressivity and the
change in L90-50 is very strong ( -0.91), whereas the correlation with L50-10 is much weaker (only -0.27); see Figure 4. This result is consistent with the idea that the distortion created by progressivity is likely to be effective especially strongly at the upper end, where human capital accumulation is an important source of wage
inequality, but less so at the lower end, where other factors, such as unionization, minimum wage laws, and so on, could be more important.
versus the change in L90-50 (left panel) and
L50-10 (right panel). Countries with a more progressive tax system in the 2000s have experienced a smaller rise in wage inequality since the 1980s. The relationship is especially strong at the top of the wage distribution and weaker at the bottom: the correlation between progressivity and the
change in L90-50 is very strong ( -0.91), whereas the correlation with L50-10 is much weaker (only -0.27); see Figure 4. This result is consistent with the idea that the distortion created by progressivity is likely to be effective especially strongly at the upper end, where human capital accumulation is an important source of wage
inequality, but less so at the lower end, where other factors, such as unionization, minimum wage laws, and so on, could be more important.
Finally, Table 2 gives a more complete picture of the differences between the two definitions of wedges. The top panel reports the correlation of each wedge measure with log wage differentials, which reveals that the adjustment for utilization rates through labor hours makes little difference in the correlations in 2003. Turning to the change in inequality over time (bottom panel), the simple wedge measure has a somewhat lower correlation with log wage differentials. However, adjusting for average hours per person increases these correlations significantly to -0.66 for the L90-10, and to -0.91 for L90-50 (plotted in the left panel of Figure 4). We conclude that progressivity is strongly correlated with inequality both in the cross-section and over time, especially above the median of the distribution.
Overall, these findings reveal a close relationship between progressivity and wage inequality, which motivates the focus of this paper. However, on their own, these correlations fall short of providing a quantitative assessment of the importance of the tax structure. For this purpose, we now take the model to the data.
| Log wage differentials | Measure of Wedge:
|
Measure of Wedge:
|
| 2003: 90-10 | -.82 | -.82 |
| 2003: 90-50 | -.84 | -.67 |
| 2003: 50-10 | -.70 | -.91 |
| Change from 1980 to 2003: 90-10 | -.35 | -.66 |
| Change from 1980 to 2003: 90-50 | -.58 | -.91 |
| Change from 1980 to 2003: 50-10 | .13 | -.27 |
4 Parameter Choices
We now discuss the parameter choices for the model. We focus on male workers so as to avoid potential selection issues across countries related to different labor market participation rates for female workers. Our basic calibration strategy is to take the United States as a benchmark and pin down a number of parameter values by matching certain targets in the US data.17 We then assume that other countries share the same parameter values with the US along unobservable dimensions (such as the distribution of learning ability), but differ in the dimensions of their labor market policies that are feasible to model and calibrate (specifically, consumption and labor income tax schedules and the retirement pension system). We then examine the differences in economic outcomes--specifically in wage dispersion and labor supply--that are generated by these policy differences alone.
A model period corresponds to one year of calendar time. Individuals enter the economy at age 20 and retire at 65 (![]() ). Retirement lasts for 20 years and everybody dies at age 85. The
net interest rate,
). Retirement lasts for 20 years and everybody dies at age 85. The
net interest rate, ![]() , is set equal to 2%, and the subjective time discount rate is set to
, is set equal to 2%, and the subjective time discount rate is set to
![]() . The curvature of the human capital accumulation function,
. The curvature of the human capital accumulation function, ![]() is set equal to 0.80, broadly consistent with the existing empirical evidence (see Browning et al. (1999, Table 2.3)). In Appendix D, we conduct sensitivity analyses with respect to
is set equal to 0.80, broadly consistent with the existing empirical evidence (see Browning et al. (1999, Table 2.3)). In Appendix D, we conduct sensitivity analyses with respect to
![]() and consider cross-country variation in retirement age
and consider cross-country variation in retirement age ![]() .
.
Utility Function.
Preferences over consumption, ![]() and leisure time,
and leisure time, ![]() are given by this
common separable form:
are given by this
common separable form:
This specification yields two parameters to calibrate: the curvature of leisure, ![]() and the utility weight attached to leisure,
and the utility weight attached to leisure, ![]() . These parameters are jointly chosen to pin down the average hours worked in the economy, as well as the average Frisch labor supply elasticity. In 2003, the average annual hours worked by American males was 1,890 hours, or approximately
5.2 hours per day (Heathcote et al. (2010, figure 2)). Taking the discretionary time endowment of an individual to be 13 hours per day, we get
. These parameters are jointly chosen to pin down the average hours worked in the economy, as well as the average Frisch labor supply elasticity. In 2003, the average annual hours worked by American males was 1,890 hours, or approximately
5.2 hours per day (Heathcote et al. (2010, figure 2)). Taking the discretionary time endowment of an individual to be 13 hours per day, we get
![]() .18
.18
With power utility, the theoretical Frisch elasticity of labor supply is given by
![]() Because in this model, labor supply,
Because in this model, labor supply, ![]() , varies across
individuals, there is a distribution of Frisch elasticities. We simply target the Frisch elasticity implied by the average labor hours,
, varies across
individuals, there is a distribution of Frisch elasticities. We simply target the Frisch elasticity implied by the average labor hours,
![]() . The empirical target we choose is 0.3, which is consistent with the estimates for male workers surveyed by Browning et al. (1999),
which range from zero to 0.5.19 As will become clear later, a higher Frisch elasticity improves the performance of our model, so in our baseline case we
choose the relatively conservative value of 0.3.
. The empirical target we choose is 0.3, which is consistent with the estimates for male workers surveyed by Browning et al. (1999),
which range from zero to 0.5.19 As will become clear later, a higher Frisch elasticity improves the performance of our model, so in our baseline case we
choose the relatively conservative value of 0.3.
| Description | Value | |
| Parameter: |
Curvature of utility of leisure | 5.0 (Frisch = 0.3) |
| Parameter: |
Weight on utility of leisure | 0.20 |
| Parameter: |
Curvature of human capital function | 0.80 |
| Parameter: |
Years spent in the labor market | 45 |
| Parameter: |
Retirement duration (years) | 20 |
| Parameter: |
Interest rate | 0.02 |
| Parameter: |
Time discount factor | |
| Parameter: |
Depreciation rate of skills (annual) | |
| Parameter:
|
Average initial human capital (scaling) | 4.95 |
| Parameters calibrated to match data targets:
|
Average ability | 0.195 |
|---|---|---|
| Parameters calibrated to match data targets:
|
Coeff. of variation of initial human capital | 0.076 |
| Parameters calibrated to match data targets:
|
Coeff. of variation of ability | 0.396 |
| Parameters calibrated to match data targets: |
Dispersion of Markov shock | 0.23 |
| Parameters calibrated to match data targets: |
Transition probability for Markov shock | 0.90 |
| Parameters calibrated to match data targets: |
Maximum investment time on the job | 0.50 |
Distributions: Learning Ability, Initial Human Capital, and Shocks.
Agents have two individual-specific attributes at the time they enter the economy: learning ability and initial human capital endowment. We assume that these two variables are jointly uniformly distributed in the population and are perfectly correlated with each other.20 Although the assumption of perfect correlation is made partly for simplicity, a strong positive correlation is plausible and can be motivated as follows. The
present model is interpreted as applying to human capital accumulation after age 20 and, by that age, high-ability individuals will have invested more than those with low ability, leading to heterogeneity in human capital stocks at that age, which would then be very highly correlated with learning
ability. Indeed, Huggett et al. (forthcoming) estimate the parameters of the standard Ben-Porath model from individual-level wage data and find learning ability and human capital at age 20 to be strongly positively correlated (corr: 0.792). Making the
slightly stronger assumption of perfect correlation allows us to collapse the two-dimensional heterogeneity in ![]() and
and ![]() into one, speeding up computation significantly.
into one, speeding up computation significantly.
Therefore, this jointly uniform distribution of
![]() yields four parameters to be calibrated.
yields four parameters to be calibrated.
![]() is a scaling parameter and is simply set to a computationally convenient value, leaving three parameters: (i) the cross-sectional standard deviation of initial human
capital,
is a scaling parameter and is simply set to a computationally convenient value, leaving three parameters: (i) the cross-sectional standard deviation of initial human
capital,
![]() (ii) the mean learning ability,
(ii) the mean learning ability,
![]() , and (iii) the dispersion of ability,
, and (iii) the dispersion of ability,
![]() The idiosyncratic shock process,
The idiosyncratic shock process, ![]() is assumed
to follow a first-order Markov process, with two possible values,
is assumed
to follow a first-order Markov process, with two possible values,
![]() , and a symmetric transition matrix with
, and a symmetric transition matrix with
![]() . This structure yields two more parameters,
. This structure yields two more parameters, ![]() and
and ![]() , to be calibrated--for a total of five parameters. The sixth and last parameter is
, to be calibrated--for a total of five parameters. The sixth and last parameter is ![]() (maximum investment allowed on the job). Finally, because there is measurement error in individual-level wage data, we add a zero mean i.i.d. disturbance to the wages generated by the model (which has no effect on individuals' optimal
choices).
(maximum investment allowed on the job). Finally, because there is measurement error in individual-level wage data, we add a zero mean i.i.d. disturbance to the wages generated by the model (which has no effect on individuals' optimal
choices).
Data Targets.
Our calibration strategy is to require that the wages generated by the model be consistent with micro-econometric evidence on the dynamics of wages found in panel data on US households. Specifically, these empirical studies begin by writing a stochastic process for log wages (or earnings) of the following general form:
where
We begin with
![]() and assume that it corresponds to the measurement error in the wage data. This is consistent with the finding in Guvenen and Smith (2009)
that the majority of transitory variation in wages is due to measurement error. Based on the results of the validation studies from the US wage data,21 we
take the variance of the measurement error to be 10% of the true cross-sectional variance of wages in each country, which yields
and assume that it corresponds to the measurement error in the wage data. This is consistent with the finding in Guvenen and Smith (2009)
that the majority of transitory variation in wages is due to measurement error. Based on the results of the validation studies from the US wage data,21 we
take the variance of the measurement error to be 10% of the true cross-sectional variance of wages in each country, which yields
![]() for the United States. We then choose the following six moments from the US data to pin down the six parameters identified earlier:
for the United States. We then choose the following six moments from the US data to pin down the six parameters identified earlier:
- the mean log wage growth over the life cycle (informative about
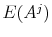 ),
), - the ratio of minimum to mean wage (informative about
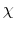 ),
), - the cross-sectional dispersion of wage growth rates,
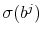 (informative about
(informative about
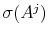 ),
), - the cross-sectional variance of the stochastic component (informative about
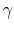 ),
), - the average of the first three autocorrelation coefficients of the stochastic component of wages (informative about
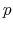 ), and
), and - L90-10 in the population (which, together with the previous moments, is informative about
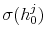 ).
).
The next two moments capture key statistical properties of the stochastic component of wages in the data. These moments are (i) the unconditional variance of the stochastic component, (
![]() , as well as (ii) the average of its first three autocorrelation coefficients. The empirical counterparts for these moments are taken from Haider (2001)Plain Lays the only study that estimates a process for hourly wages and allows for heterogeneous profiles. The figure for the unconditional variance can be calculated to be 0.109 and the average of autocorrelations is calculated to be 0.33, using the estimates in Table 1 of Haider's paper. Further details and justifications for these parameter choices are in Appendix C.23
, as well as (ii) the average of its first three autocorrelation coefficients. The empirical counterparts for these moments are taken from Haider (2001)Plain Lays the only study that estimates a process for hourly wages and allows for heterogeneous profiles. The figure for the unconditional variance can be calculated to be 0.109 and the average of autocorrelations is calculated to be 0.33, using the estimates in Table 1 of Haider's paper. Further details and justifications for these parameter choices are in Appendix C.23
Our sixth, and final, moment is L90-10 in 2003. Adding this moment ensures that the calibrated model is consistent with the overall wage inequality in the US in that year, which is the benchmark against which we measure all other countries. The empirical target value is 1.60 (from the OECD's Labour Force Survey). Table 4 displays the empirical values of the six moments, as well as their counterparts generated by the calibrated model. As can be seen here, all moments are matched fairly well.
One point to note is that even though the average of the first three autocorrelation coefficients is pretty low (0.33), the stochastic component includes measurement error as well, which is iid. The Markov shocks themselves have a first order annual autocorrelation of 0.80 (implied by
![]() , shown in Table 3).
, shown in Table 3).
| Moment | Data | Model |
| Mean log wage growth from age 20 to 55 | 0.45 | 0.44 |
| Ratio of minimum to mean wage rate | 0.29 | 0.30 |
| Cross-sectional standard deviation of wage growth rates | 2.00% | 2.03% |
| Cross-sectional variance of stochastic component | 0.109 | 0.106 |
| Average of first three autocorrelation coeff. of stochastic component | 0.33 | 0.34 |
| L90-10 in 2003 | 1.60 | 1.60 |
Benefits System and the Government Budget.
A great deal of variation can be found across countries in the parameters that control the generosity, the duration, and the insurance component of the benefits system.24 We provide the exact formulas for each country in Appendix B.4. Turning to the government budget, the calibration of ![]() (the surplus wasted by the government) is challenging because of the difficulty of obtaining reliable estimates of its magnitude. In the baseline case, we assume
(the surplus wasted by the government) is challenging because of the difficulty of obtaining reliable estimates of its magnitude. In the baseline case, we assume ![]() . So,
the government returns all the surplus to households in a lump-sum fashion (Tr). Relaxing this assumption and allowing for
. So,
the government returns all the surplus to households in a lump-sum fashion (Tr). Relaxing this assumption and allowing for ![]() has very little effect on the
results (Appendix D).25
has very little effect on the
results (Appendix D).25
Consumption Taxes.
The average tax rate on consumption is taken from McDaniel (2007), who provides estimates for 15 OECD countries for the period 1950 to 2003 by calculating the total tax revenue raised from different types of consumption expenditures and dividing this number by the total amount of corresponding expenditure. McDaniel (2007) does not provide an estimate for Denmark, so we set this country's consumption tax equal to that of Finland, which has a comparable value-added tax (VAT) rate.
5 Quantitative Results
In this section, we begin by presenting the implications of the calibrated model for wage inequality differences across countries at a point in time. We then provide decompositions that quantify the separate effects of progressivity, average income tax rates, consumption taxes, and the pension
system on these results. We next turn to the change in inequality over time and provide a comparison between the United States and Germany from 1983 to 2003. The model statistics below are computed from 10,000 simulated lifecycle paths for individuals drawn from the joint probability distribution
of
![]() .
.
5.1 Cross-Sectional Results: the 2000s
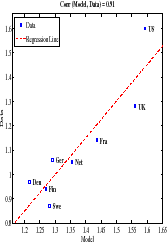
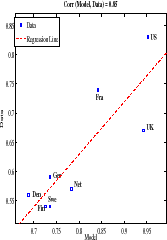
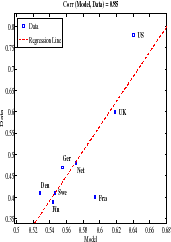
Figure 5 plots L90-10 for each country in the data against the value predicted by the calibrated model. The correlation between the simulated and actual data is 0.91 (and the countries line up nicely along the regression line), suggesting that the model is able to capture the relative ranking of these eight countries in terms of overall wage inequality observed in the data. To explore how the model fares at different parts of the wage distribution, the middle panel of Figure 5 repeats the same exercise for L90-50 and the bottom panel does the same for L50-10. In both cases, the model-data correlations are high: 0.85.
In Table 5, we quantify the importance of taxes for cross-country differences in inequality. The first two columns report L90-10 in the data for all countries, first in levels (second column) and then expressed as a deviation from the US, which is our benchmark
country (third column). For example, in Denmark L90-10 is 0.97, which is 0.63 (i.e., 63 log points) lower than that in the US. The third and fourth columns display the corresponding statistics implied by the calibrated model. Again, for Denmark, the model generates an L90-10 that is 0.38 below what
is implied by the model for the US. Therefore, the model accounts for 60% (![]() ) of the difference in L90-10 between the US and Denmark, reported in column (e). Similar comparisons show
that the model does quite well in explaining the level of wage inequality in Germany but poorly in explaining the UK. The fraction explained by the model ranges from 35% for France to 56% for Germany. Overall, the model accounts for 48% of the actual gap in inequality between the US and the CEU in
2003.
) of the difference in L90-10 between the US and Denmark, reported in column (e). Similar comparisons show
that the model does quite well in explaining the level of wage inequality in Germany but poorly in explaining the UK. The fraction explained by the model ranges from 35% for France to 56% for Germany. Overall, the model accounts for 48% of the actual gap in inequality between the US and the CEU in
2003.
To see which part of the wage distribution is better captured by the model, the next two columns display the same calculation performed in column (e), but now separately for L90-50 (f) and L50-10 (g). For all countries in the CEU, the model explains the upper tail inequality much better than the lower tail inequality. For example, for Denmark, the model explains 97% of L90-50 versus only 31% of L50-10. In fact, the model accounts for at least 65% of L90-50 for all countries in the CEU, averaging 84% across all countries, whereas it accounts for on average only 24% of L50-10.26 That our model does a better job at explaining inequality at the upper end (above the median) will be a recurring theme of this paper. This finding is consistent with the idea that progressive taxation affects the human capital investment of high-ability individuals more than others and, therefore, the mechanism is more effective above the median of the wage distribution. Finally, a notable exception to these generally strong findings is the UK, which is an important outlier: the model explains very little of the difference between the UK and US at the upper tail (6% to be exact) and only slightly more (13%) at the lower end.
| L90-10 Data Level (a) | L90-10 Data |
L90-10 Model Level (c) | L90-10 Model |
L90-10 % explained (d)/(b): (e) | L90-50 % explain. (f) | L50-10 % explain. (g) | |
| Denmark | 0.97 | 0.63 | 1.22 | 0.38 | 0.60 | 0.97 | 0.31 |
| Finland | 0.94 | 0.66 | 1.27 | 0.33 | 0.49 | 0.78 | 0.25 |
| France | 1.14 | 0.46 | 1.44 | 0.16 | 0.35 | 1.23 | 0.12 |
| Germany | 1.06 | 0.54 | 1.29 | 0.30 | 0.56 | 0.90 | 0.28 |
| Netherlands | 1.05 | 0.55 | 1.36 | 0.24 | 0.43 | 0.65 | 0.23 |
| Sweden | 0.87 | 0.73 | 1.28 | 0.31 | 0.43 | 0.75 | 0.26 |
| CEU | 1.00 | 0.59 | 1.31 | 0.29 | 48% | 84% | 24% |
| UK | 1.28 | 0., | 1.56 | 0.03 | 10 | 6 | 13 |
| US | 1.60 | 0.00 | 1.60 | 0.00 |
Decomposing the Effects of Different Policies.
The baseline model incorporates several differences between the labor market policies of the US and those of the CEU countries. Here, we quantify the separate roles played by each of these components for the results presented in the previous section. We conduct three decompositions. First, we assume that countries in the CEU have the same retirement pension system as the US but differ in all other dimensions considered in the baseline model. This experiment separates the role of the tax system for wage inequality from that of the pension system. Second, we also set the consumption taxes of each country equal to that in the US, but each country retains its own income tax schedule as in the baseline model. This experiment quantifies the explanatory power of the model that is coming from the income tax system alone. Third, we go one step further and assume that each country keeps the same progressivity of its income tax schedule but is identical in all other ways to the US, including the average income tax rate. This experiment isolates the role of progressivity alone. In each case, we adjust the lump-sum transfers to balance the government's budget.
Table 6 reports the results. First, in column 2, we assume that all countries have the same pension system as the US. In panel A, the correlation between the data and model is only slightly lower than in the baseline case for all parts of the wage
distribution. Turning to panel B, the fraction of the US-CEU difference explained by the model goes down--but only slightly--indicating that more than 95% of the model's explanatory power is coming from taxes (both income and consumption taxes). Next, in column (3), we also eliminate the
differences in consumption taxes across countries. The model-data correlations go further down but, again, somewhat modestly. In panel B, the explanatory power of the model that is attributable to income taxes alone ranges from 75% to 80% for the three measures of wage inequality. The difference
between columns 2 and 3 provides a useful measure of the role of consumption taxes, which account for about 17% (
![]() ) of the model's explanatory power for L90-10.
) of the model's explanatory power for L90-10.
| Diff. from Benchmark: | Benchmark (1) | All taxes (2) | Lab. Inc. Tax (3) | Progressivity (4) |
| Progressivity | -- | -- | -- | -- |
| Average income taxes | -- | -- | -- | set to US |
| Consumption tax | -- | -- | set to US | set to US |
| Benefits institutions | -- | set to US | set to US | set to US |
| A. Correlation Between Data and Model: 90-10 | 0.91 | 0.90 | 0.85 | 0.88 |
| A. Correlation Between Data and Model: 90-50 | 0.85 | 0.87 | 0.85 | 0.87 |
| A. Correlation Between Data and Model: 50-10 | 0.85 | 0.84 | 0.78 | 0.81 |
| B. Fraction of US-CEU Difference Explained by Model: 90-10 | 0.48 | 0.46 (96%)
|
0.38 (79%) | 0.32 (67%) |
| B. Fraction of US-CEU Difference Explained by Model: 90-50 | 0.84 | 0.79 (94%) | 0.67 (80%) | 0.55 (66%) |
| B. Fraction of US-CEU Difference Explained by Model: 50-10 | 0.24 | 0.23 (96%) | 0.18 (75%) | 0.16 (67%) |
Next, we investigate whether the power of income taxes comes from differences in the average rates across countries or from differences in the progressivity structure. In other words, if continental Europe differed from the US only in the progressivity of its labor income tax system--but had the same average tax rate on labor income--how much of the differences in wage inequality found in the baseline model would still remain? To answer this question, we proceed as follows. First, adjusting the average tax rate to the US level--without affecting progressivity--requires some care. We show in Appendix B.2 how this can be accomplished. Then, using these hypothetical tax schedules, we solve each country's problem, assuming that all countries have identical labor market policies (set to the US benchmark) and their tax schedules generate the same average tax rate as in the US when using individuals' choices made using the US income tax schedule. In panel B of column 4, we see that progressivity alone is responsible for 2/3 of the explanatory power of the model for L90-10.
Notice that the decomposition we conducted here is not invariant to the order in which different features are eliminated. So, a valid question is whether this conclusion--that average tax rate differences do not matter much--is robust to changing this order. To investigate this, we repeated the last experiment reported in column 4, but instead of eliminating average tax rate differences and keeping progressivity intact, we flipped the order (same progressivity as the US, but match each country's average tax rate). In this case, the model only accounts for 14% of L90-10 differences, 20% of L90-50, and 10% of L50-10. This experiment confirms our previous conclusion that average tax rate differences are responsible for only a small fraction of the differences in wage inequality.
In summary, the pension system and consumption taxes together are responsible for about 20% of the model's explanatory power. The more important finding concerns the role of progressivity, which, for all practical purposes, is the key component of the income tax structure for understanding wage inequality differences. Differences in the average income tax rate do not appear to be very important for inequality differences.
The Role of Labor Supply Elasticity.
We now conduct two sensitivity analyses with respect to the value of labor supply elasticity: we consider (i) the case with a high Frisch elasticity of 0.5 and (ii) the case with only an extensive margin:
![]() . In each case, the model is recalibrated to match the same six targets in Table 4. (Appendix D contains further sensitivity analyses with respect to the values of
. In each case, the model is recalibrated to match the same six targets in Table 4. (Appendix D contains further sensitivity analyses with respect to the values of ![]()
![]() ,
, ![]() ,
, ![]() , as well as the treatment of
capital income taxes.)
, as well as the treatment of
capital income taxes.)
| Frisch = 0.5 L90-10 (a) | Frisch = 0.5 L90-50 (b) | Frisch = 0.5 Log 50-10 (c) | Discrete hours:
|
Discrete hours:
|
Discrete hours:
|
|
| Denmark | 0.69 | 1.07 | 0.40 | 0.34 | 0.53 | 0.21 |
| Finland | 0.57 | 0.88 | 0.31 | 0.29 | 0.43 | 0.17 |
| France | 0.39 | 1.32 | 0.16 | 0.17 | 0.56 | 0.07 |
| Germany | 0.68 | 1.01 | 0.40 | 0.29 | 0.42 | 0.17 |
| Netherlands | 0.48 | 0.70 | 0.27 | 0.27 | 0.38 | 0.17 |
| Sweden | 0.52 | 0.87 | 0.33 | 0.22 | 0.38 | 0.15 |
| CEU | 57% | 94% | 31% | 26% | 44% | 16% |
| UK | 13 | 6 | 17 | 2 | 3 | 6 |
In the first experiment we set
![]() which implies a Frisch elasticity of 0.5. Table 7 reports the counterpart of the analysis we conducted for the benchmark model and
reported in Table 5. Comparing the two tables makes it clear that a higher Frisch elasticity improves the model's explanatory power across the board. Now the model can explain 57% of the US-CEU difference in L90-10 (compared with 48% in the benchmark case) and 94%
of the upper tail inequality (from 84% before). However, the improvement in L50-10 is modest, going from 24% in the benchmark case up to 31%.
which implies a Frisch elasticity of 0.5. Table 7 reports the counterpart of the analysis we conducted for the benchmark model and
reported in Table 5. Comparing the two tables makes it clear that a higher Frisch elasticity improves the model's explanatory power across the board. Now the model can explain 57% of the US-CEU difference in L90-10 (compared with 48% in the benchmark case) and 94%
of the upper tail inequality (from 84% before). However, the improvement in L50-10 is modest, going from 24% in the benchmark case up to 31%.
To better understand the role of the intensive margin of labor supply, we now examine another case where workers can only choose between full-time employment at fixed hours (![]() ) and
nonemployment. The parameters of the utility function are the same as in the baseline case. The results are reported in the last three columns of Table 7. Without the amplification provided by an intensive margin--and the resulting dispersion in hours
across countries--the explanatory power of the model falls and, in some cases, it falls significantly. For example, the model accounts for 26% of the difference in L90-10. For the upper-end inequality, the difference is even larger: the model now explains 44%, half of the baseline value, and also
much lower than the 94% in the high Frisch case. Finally, the already low explanatory power at the lower tail falls further from 24% in the baseline case to 16%.
) and
nonemployment. The parameters of the utility function are the same as in the baseline case. The results are reported in the last three columns of Table 7. Without the amplification provided by an intensive margin--and the resulting dispersion in hours
across countries--the explanatory power of the model falls and, in some cases, it falls significantly. For example, the model accounts for 26% of the difference in L90-10. For the upper-end inequality, the difference is even larger: the model now explains 44%, half of the baseline value, and also
much lower than the 94% in the high Frisch case. Finally, the already low explanatory power at the lower tail falls further from 24% in the baseline case to 16%.
These findings underscore the importance of the interaction of endogenous labor supply choice (with an intensive margin) with progressive taxation for understanding wage inequality differences across countries, especially above the median of the distribution.
Inequality Trends over Time: 1983-2003
We now turn from levels in 2003 to the change in wage inequality over time. As shown in Table 1, from early 1980s to the early 2000s, wage inequality increased significantly more in the United States (by 32 log points) compared with the CEU (6 log points). Can the human capital mechanisms studied so far help us understand this "widening" of the inequality gap as well? One challenge we face in trying to answer this question is that the tax schedules we derived above are only available for the years after 2001, whereas the tax structure has changed over time for several of the countries in our sample. Fortunately, for two countries in our sample--the US and Germany--we are also able to derive tax schedules for 1983, which allows us to conduct a two-country comparison in this section.
How to Introduce SBTC?
As noted earlier, in the standard Ben-Porath model studied so far, the price of human capital ![]() was simply a scaling factor and had no effect on any implication of the model, which
is why we normalized it to 1 above. This is an important shortcoming when the goal is to study the changes in human capital investment over time in response to changes in the value of human capital, due to, for example, SBTC. Guvenen and Kuruscu (2010) proposed a tractable way to extend the Ben-Porath model that overcomes this difficulty. This extension basically involves introducing a second factor of production--raw labor (
was simply a scaling factor and had no effect on any implication of the model, which
is why we normalized it to 1 above. This is an important shortcoming when the goal is to study the changes in human capital investment over time in response to changes in the value of human capital, due to, for example, SBTC. Guvenen and Kuruscu (2010) proposed a tractable way to extend the Ben-Porath model that overcomes this difficulty. This extension basically involves introducing a second factor of production--raw labor (![]() )--in addition to human capital,
)--in addition to human capital, ![]() . The key assumption is that, unlike human capital, raw labor cannot be accumulated over the
life cycle (it is fixed). Individuals supply both factors of production for a total hourly wage of
. The key assumption is that, unlike human capital, raw labor cannot be accumulated over the
life cycle (it is fixed). Individuals supply both factors of production for a total hourly wage of
![]() at age
at age ![]() where
where ![]() is now the price (wage) of raw labor. With this two-factor structure, a rise in
is now the price (wage) of raw labor. With this two-factor structure, a rise in ![]() does increase human capital investment. So SBTC could be modeled as a rise in
does increase human capital investment. So SBTC could be modeled as a rise in ![]() over time with
over time with ![]() fixed. The formal statement of this model along with the calibration of SBTC are presented in Appendix D.7. (All parameters other than
fixed. The formal statement of this model along with the calibration of SBTC are presented in Appendix D.7. (All parameters other than ![]() remain essentially unchanged in calibration.)
remain essentially unchanged in calibration.)
Comparing the United States and Germany.
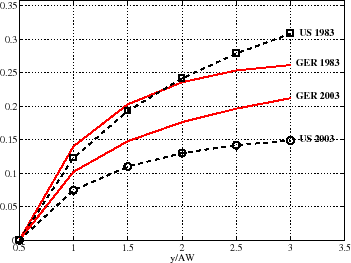
The procedure for constructing the 1983 tax schedules is described in Appendix B.3 and the resulting progressivity wedges are shown in Figure 6. As seen here, in 1983 the progressivity of the tax structure in the US and Germany was similar in both countries up to about twice the average earnings level. And above this point, the US actually had the more progressive system. Over time, the US became much less progressive, whereas the change in Germany was more gradual, making the US tax schedule much flatter than that of Germany over time.
Using these schedules, we conduct three experiments.27 In the first experiment, we assume that the tax schedules remained fixed throughout this period.
We choose one parameter that controls the skill bias of technology, ![]() to match the 32 log points rise in L90-10 in the US during the period. Note from column (1) of Table 8 that, in the data, L90-10 rose by only 13 log points in Germany during the same period. Turning to the model and assuming that Germany has been subject to the same SBTC as the US, the model generates a rise of 19 log points in L90-10 for Germany. Thus, whereas the
inequality gap widens in the data by
to match the 32 log points rise in L90-10 in the US during the period. Note from column (1) of Table 8 that, in the data, L90-10 rose by only 13 log points in Germany during the same period. Turning to the model and assuming that Germany has been subject to the same SBTC as the US, the model generates a rise of 19 log points in L90-10 for Germany. Thus, whereas the
inequality gap widens in the data by ![]() log points, the model predicts
log points, the model predicts ![]() log points, explaining 68% (13/19) of the observed difference in the data.
log points, explaining 68% (13/19) of the observed difference in the data.
| Taxes (SBTC) | Data (1) | Fixed (Calibrated to US) Model (2) | Changing (Fixed) Model (3) | Changing (Calibrated to US) Model (4) |
| Panel A: Change in L90-10 US | 0.32 | 0.32 |
0.21 | 0.32 |
|---|---|---|---|---|
| Panel A: Change in L90-10 GER | 0.13 | 0.19 | 0.01 | 0.09 |
| Panel A: Change in L90-10 |
0.19 | 0.13 | 0.20 | 0.22 |
| Panel B: Change in L90-50 US | 0.22 | 0.23 | 0.15 | 0.23 |
| Panel B: Change in L90-50 GER | 0.05 | 0.14 | 0.01 | 0.06 |
| Panel B: Change in L90-50 |
0.17 | 0.09 | 0.14 | 0.17 |
| Panel C: Change in L50-10 US | 0.10 | 0.09 | 0.06 | 0.09 |
| Panel C: Change in L50-10 GER | 0.07 | 0.05 | 0.00 | 0.03 |
| Panel C: Change in L50-10 |
0.02 | 0.04 | 0.06 | 0.06 |
Second, in column (3), we consider the case where the only change over time is in the tax schedules. We do not recalibrate any parameter to match targets in 1983. In the US, L90-10 rises substantially--by 21 log points--with no SBTC. Hence, the flattening of the tax schedule alone accounts for a
significant fraction (about 2/3) of the rise in US wage inequality during this time. To our knowledge, this result is new in the literature. In contrast to the US, wage inequality barely changes (by 1 log point) in Germany. This experiment suggests that the dramatic fall in progressivity in the US
and the small change in Germany alone could explain almost all of the widening inequality gap! Third, we now incorporate the change in tax schedules and re-calibrate SBTC such that we match the change in L90-10 for the US.28 Now, L90-10 rises by 9 log points in Germany. Thus, the model slightly over-explains--by 16% (
![]() )--the widening gap in the data.
)--the widening gap in the data.
Panels B and C of the table explore how much of the widening gap has occurred at the top and bottom of the distribution. In the data, the L90-50 gap between the US and Germany rose by 17 log points, whereas the L50-10 gap increased by only 2 log points. Therefore, a remarkable fact is that virtually all of the rise in the inequality gap occurred because top-end inequality increased much more in the US (by 0.22) than in Germany (by 0.05). This observation strongly indicates that to understand the widening inequality gap, one needs to understand the economic forces that operate above the median of the wage distribution--and the human capital channels studied here provide one important candidate. To quantify these human capital effects, we turn to column (4): the model generates the same 17 log points rise in the L90-50 gap as in the data, and overstates the L50-10 gap observed in the data by 4 log points.
While these results are encouraging, a caveat must be noted. First, wage inequality in 1983 depends not only on the tax schedule in 1983, but also on the tax schedules that were in place several years prior, since the dispersion in human capital across individuals results from investments made in previous years. Clearly, the same comment applies to 2003. Although in our exercise we do not account for this fact, it is not clear which way this biases the results. This is because the US tax system was even more progressive before the Economic Recovery Tax Act of 1981, whereas the progressivity change in the years preceding 2003 (say, from 1990 to 2003) was more modest. Therefore, if we were to use a time average of tax schedules in our exercise (say, 1973 to 1983 and 1993 to 2003), we conjecture that the reduction in progressivity over time could be larger than we assumed in the experiment just described (which would attribute an even larger role to taxes). A more complete examination of this issue is an exciting topic for future research.
6 Microeconomic Evidence on the Mechanism
The model also makes predictions for how the lifecycle profile of wages and hours varies across countries. In particular, because progressivity dampens human capital investment, average wages should grow more slowly over the life cycle in the CEU. Similarly, because progressivity compresses the cross-sectional distribution of human capital investment, wage inequality should rise less over the life cycle in the CEU. Testing these two predictions requirespanel data on wages (to disentangle the age profile from time or cohort effects), which is difficult to obtain on a comparable basis for the CEU countries in our sample.29 An exception is the German Socio-Economic Panel (GSOEP), which includes information on wages and hours of German individuals and is available to outside (non-European Union) researchers. In this section, we make use of this dataset and the PSID for the United States to provide a two-country comparison of lifecycle profiles.
6.1 Wages and Hours over the Lifecycle: US vs Germany
We focus on male workers who are between 25 and 55 years of age to minimize the effects of early retirement behavior and the consequent fall in employment rates at later ages. The PSID data cover 1968-1992 and the GSOEP data cover 1984 to 2007.
Wages.
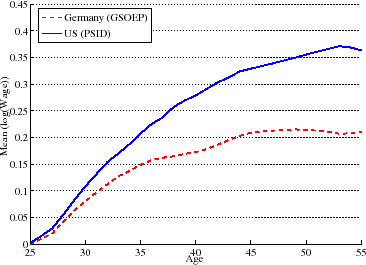
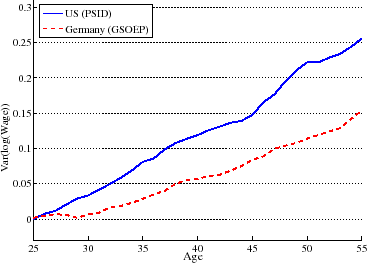
Figure 7 plots the lifecycle profile of mean log wages in the US and Germany. The profiles are extracted from panel data by cleaning cohort effects following the usual procedure in the literature; see Appendix E for details. As seen in the figure, from age 25 to 55 the average wage profile rises by 36 log points in the US, but by only 21 log points in Germany, consistent with the prediction of the model that a more progressive tax system generates a flatter average wage profile. Next, figure 8 plots the lifecycle profile of wage inequality (again controlled for cohort effects) for the two countries. In the US, the variance of log wages rises by 26 log points, compared to 15 log points for Germany. Again, inequality rises more over the lifecycle in the less progressive country, consistent with the mechanism in the model.
Although, in figure 8 we normalized the intercept to zero (to help visual comparison), a relevant question is, how much wage inequality is there at the time workers enter the labor market? To answer this question, we compute the variance of log wages for workers between ages 23 and 27 and find it to be very similar in both countries: 0.251 in the US and 0.260 in Germany.30 This implies that virtually all the difference in wage inequality between Germany and the United States documented in the previous section is generated by the faster rise of inequality over the lifecycle in the US compared to Germany and almost none is due to differences in initial inequality. (Incidentally, this finding is also reassuring, given that our model assumes identical inequality at age 20.)
Finally, instead of controlling for cohort effects as we did above, one can alternatively control for time effects. Using this approach, mean log wages rise by 0.37 in the US compared with 0.27 in Germany. Inequality rises by 0.12 in the US compared with only 0.02 in Germany. Thus, while the magnitudes change, the rankings of the two countries remain the same under this alternative approach.31
A complementary piece of evidence is presented in Domeij and Floden (2010) from Sweden. These authors construct the analog of figure 8 for Sweden and find that the rise in wage inequality over the life cycle is much smaller than in both the US and Germany.32 Given the high progressivity of income taxes in Sweden compared with the US and Germany, this outcome is exactly what is predicted by the present model.
Labor Hours.
We begin with the dispersion in hours. In Germany (GSOEP), the standard deviation of log hours is 0.369 compared with 0.324 in the United States (PSID).33 It is a well-known fact that incomplete markets models without preference heterogeneity severely understate the level of hours inequality (c.f. Erosa et al. (2009)) and our model is no exception. In
the model,
![]() log
log![]() in the US and 0.128 in Germany.34 Despite missing on the levels, the model is consistent with the fact that hours inequality is
somewhat higher in Germany than in the US.
in the US and 0.128 in Germany.34 Despite missing on the levels, the model is consistent with the fact that hours inequality is
somewhat higher in Germany than in the US.
At first blush, it may seem surprising that the model implies higher dispersion in the more progressive country. The reason has to do with lump sum transfers, which happens to work in the opposite direction to progressivity in this two-country comparison. Specifically, the calibrated model implies that lump-sum transfers in Germany are more than twice as large as in the US. By their nature, these transfers create a larger wealth effect on low-income individuals (it is a larger fraction of their income) and, therefore, reduce their labor supply more than that of higher-income individuals. Thus, countries with higher lump-sum payments (or more redistributive government services), ceteris paribus, have higher hours inequality. To illustrate this point, we solve the model for Germany by fixing the lump sum transfers to the same fraction as in the US and assume the rest of the budget surplus yields no utility. The implied standard deviation of log hours falls from 0.128 to 0.098, which is now lower than in the US. Therefore, the predictions of the model regarding hours inequality is in general ambiguous, being driven by progressivity and the size of lump-sum transfers.
As for average hours, the prediction of the model is much clearer: countries with more progressive taxes should have lower average hours. Consistent with this prediction, it is well documented that Americans on average work much longer hours than Europeans (Prescott (2004), Ohanian et al. (2008)). Here we show that the same is true when we focus on male workers. For Germany, Wanger (2006, Table 3) reports that the average hours per (male) worker in 2003 was 1,557 hours. For the same year, Heathcote et al. (2010, figure 2) report that the average hours per (male) person was 1890 hours, or 21% higher than in Germany.35 Given that hours per worker must be higher than hours per person, this provides a lower bound on the gap between German and US males. This gap is even higher than what is predicted by the model (which is 12.3%).
Overall, the lifecycle evidence on wages and hours documented in this section are in line with--and therefore provide further support to--the human capital mechanism that operates in our model.
6.2 Survey Measures of Human Capital Inequality
So far we have focused on the model's implications for variables that are easily measured in the data, such as wages and hours. However, the model also makes very clear predictions about how human capital dispersion should vary by country (or with the progressivity of the country's tax system). We now test three such predictions in the data.
To conduct this analysis, we need an empirical measure of human capital at the individual-level for the countries in our sample. The data source we use is the International Adult Literacy Survey (IALS), which is a large-scale, international comparative assessment designed to measure a range of skills linked to the economic characteristics of the adult population (ages 16 to 65) within and across nations. The IALS has been extensively used as a measure of human capital of the working age population in the literature (see, among others, Leuven et al. (2004); Nickell and Bell (1995); Devroye and Freeman (2000) and the references therein). We use data from the 1998 survey--the latest available--which contains data from seven of the eight countries in our sample, the exception being France.
First, we investigate whether, in the data, higher wage dispersion in a given country is accompanied with larger human capital dispersion, as robustly predicted by our model. Column (1) of Table 9 reports the cross-country correlations between wage and human capital dispersions, the latter measured by the IALS quantitative literacy test score.36 Each correlation is computed using the same measure of dispersion for both variables (L90-10, L90-50, or L50-10). The correlations are strong regardless of the part of the distribution we focus on. Although not reported in the table, the test score dispersion also varies significantly across countries. For example, the country with--by far--the largest dispersion is the US, with a 90-10 percentile ratio of 2.26 (as measured by the quantitative score), followed by the UK with 1.83. At the other end lie the Scandinavian countries with a 90-10 percentile ratio of 1.45. (The prose and document literacy tests reveal even larger gaps.)
| Dispersion measure
|
Cross-Country Correlation of Wage Dispersion (Data) | Test Score Dispersion (Data) with: Human Capital Dispersion (Model) |
| L90-10 | 0.88 | 0.88 |
| L90-50 | 0.89 | 0.78 |
| L50-10 | 0.77 | 0.88 |
Second, we compare the human capital dispersion implied by the model to that found in the data across countries. Column (2) of Table 9 reports the correlations between the human capital dispersion in the model and those measured by the IALS data. The
correlation is robust, ranging from 0.78 to 0.88. Third, and as discussed earlier, our model predicts that countries with a more progressive tax system will have less dispersion in human capital across individuals. Using
![]() , the measure of wedge employed earlier, the correlation with the L90-10 measure of IALS human capital dispersion is -0.79. (Using other test results or alternative wedges (e.g.,
, the measure of wedge employed earlier, the correlation with the L90-10 measure of IALS human capital dispersion is -0.79. (Using other test results or alternative wedges (e.g.,
![]() ,6) yields equally strong results.)
,6) yields equally strong results.)
When these three empirical findings from survey data are put together with the evidence on the lifecycle profiles of wages from US and Germany, they provide strong support to the human capital mechanism that is operational in our model.
7 Conclusions
In this paper, we have studied the effects of progressive labor income taxation on wage inequality when a major source of wage dispersion is differential rates of human capital accumulation. To understand the main mechanisms and their quantitative importance, we have examined differences in wage inequality between the United States and seven European countries, which differ significantly in their income tax structures as well as in other dimensions of their labor market institutions. A common theme in our findings is that the model is significantly better at explaining inequality differences at the upper tail compared to the lower tail. Institutions, such as unionization, minimum wage laws (as in the case of France, discussed earlier), and centralized bargaining, are likely to be more important for the lower tail. However, since changes in the upper tail have been so important during this time (as we have documented), the mechanisms studied in this paper provide a promising direction for understanding US-CEU differences in wage inequality. We also found that the most important policy difference for wage inequality is the progressivity of the income tax system, which is responsible for about two-thirds of the model's explanatory power.37 Finally, we turn to the changes in wage inequality over time. In a two-country the model can account for all of the widening of the inequality gap between the US and Germany, when the actual changes in the tax schedules were also incorporated.
We have also explored the micro implications of the model, which provided further supporting evidence for the model. For example, the lifecycle profile of mean wages is flatter in Germany than in the United States, as implied by the higher progressivity in the former country. A similar result is found for within-cohort wage inequality in Germany and the US. Similarly, average hours for males is much lower in Germany than it is in the US. These observations are consistent with the predictions of the model and provide further support to the empirical relevance of the human capital mechanisms explored in this paper.
An alternative mechanism that is also consistent with the US-Europe inequality gap was proposed by Becker (1985). In his framework, workers choose both hours of work in the market and effort per hour. High ability workers in the US put more effort per hour (and are therefore more productive) than comparable workers in Europe because the return is relatively higher. Thus, wage inequality will be higher in the US than in Europe. An important difference between this mechanism and ours is that our model implies a widening of wage inequality over the life cycle in the US relative to Europe (as documented in Section 6.1), whereas Becker's model implies that wage inequality would be constant over the lifecycle.
An alternative way of modeling for skill acquisition would be through "learning by doing (LBD)," which differs from human capital models in some subtle ways. To understand this, notice that in an LBD model, human capital is acquired by working longer hours. The marginal cost of work is given by the marginal utility of leisure, which is independent of the current tax rate. The marginal benefit is the increase in utility due to higher after-tax earnings both in the current period (higher earnings from longer hours) and future periods (higher wages because of accumulated skills). So, for example, if current taxes are raised without affecting future taxes, this would increase human capital investment in Ben-Porath as we saw in Section 2.2 (because the cost of investment is the current after-tax wage, which is lower now). In contrast, in an LBD model, this will decrease current hours of work because part of the marginal benefit of work (current after-tax earnings) falls. But if there is less work, there is less skill acquisition in an LBD model. This is one example where a change in taxes can increase investment in Ben-Porath while reducing it with learning by doing. However, that this is a carefully selected example. There are many other cases where both models would have qualitatively the same implication (for example if future taxes are raised without affecting current taxes).
Finally, we have made several assumptions to make the quantitative exercise computationally feasible.38 An important direction to extend the current framework would be by carefully modeling the differences between the US and the CEU in the financing of the education system as well as in the types of skills taught in schools in both places. This is a difficult but interesting question that is at the top of our future research agenda.
NOT FOR PUBLICATION
SUPPLEMENTAL APPENDIX
1.0
A.1 Derivation of the Optimal Investment Condition (eq. (7))
Here, we derive the optimal investment condition in the most general framework studied in this paper, described in Section 5.2. The optimality conditions presented earlier in the paper ((4), (5), and (7)) can all be obtained as special cases of this formulation.
Under the assumptions stated in Section 5.2 (i.e., setting
![]() , eliminating pension payments (
, eliminating pension payments (
![]() ), and setting idiosyncratic shocks to their mean value), the problem of the agent is given by
), and setting idiosyncratic shocks to their mean value), the problem of the agent is given by
Note that total tax liability of the agent is given by
![]() . The derivative of tax liability with respect to
. The derivative of tax liability with respect to ![]() gives the
marginal tax rate. Thus,
gives the
marginal tax rate. Thus,
![]() . Using this expression, we obtain the following FOCs for this problem
. Using this expression, we obtain the following FOCs for this problem
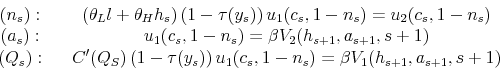
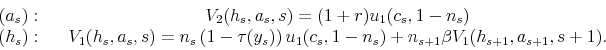
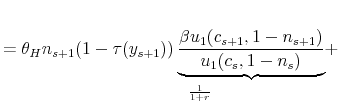 |
||
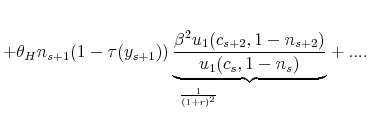 |
Rearranging this expression delivers equation (7):
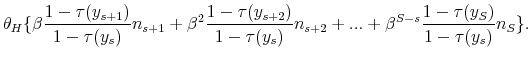
|
A.2 Equilibrium Definition
A stationary recursive competitive equilibrium for this economy is a set of equilibrium decision rules, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and
![]() ; value functions,
; value functions, ![]() and
and ![]() , for working and retirement periods, respectively, where
, for working and retirement periods, respectively, where
![]() (notice the inclusion of
(notice the inclusion of ![]() into this vector); a pricing
function for Arrow securities,
into this vector); a pricing
function for Arrow securities,
![]() , and a measure
, and a measure
![]() such that
such that
- Given the labor income tax function,
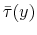 , consumption tax,
, consumption tax,
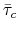 , transfers,
, transfers, 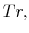 and government's pension function
and government's pension function  , individuals' decision rules and value functions solve problems in (9) to (13) and in (14).
, individuals' decision rules and value functions solve problems in (9) to (13) and in (14). - Asset markets clear:
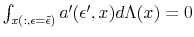 for all combinations of (
for all combinations of (

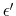 ).39
).39 -
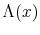 is generated by individuals' optimal choices.
is generated by individuals' optimal choices. - The government budget balances:
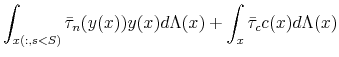
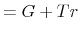
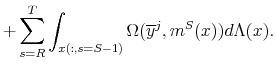
The first term in the government's budget is the total tax revenue from labor income collected from all agents who are working and younger than retirement age. Similarly, the second term is the total tax revenue from the consumption tax, but it is collected from all agents including the
retirees. On the right-hand side, the pension payments only depend on a worker's ability through
![]() and the number of years she worked until retirement (
and the number of years she worked until retirement (![]() ),
which in turn depends on the full state vector
),
which in turn depends on the full state vector ![]() at age
at age ![]() . Therefore, we
integrate the pension payments over the full state vector
. Therefore, we
integrate the pension payments over the full state vector ![]() conditioning on age
conditioning on age ![]() and then sum the same amount over all ages greater than
and then sum the same amount over all ages greater than ![]() to find total pension payments.
to find total pension payments.
B.1 Estimating Country-Specific Average Tax Schedules
Here we provide more details on the estimation of tax schedules described in Section 2.2. Define normalized income as
![]() For each country, denote the top marginal tax rate with
For each country, denote the top marginal tax rate with
![]() and the top bracket
and the top bracket
![]() . The values for these variables are taken from the OECD tax database.40 As noted in the text, we already have average tax rates for all income levels below 2 (i.e., two times AW). For values above this number, we have to consider separately the case where a country's top
marginal tax rate bracket is lower and higher than 2. In the former case (
. The values for these variables are taken from the OECD tax database.40 As noted in the text, we already have average tax rates for all income levels below 2 (i.e., two times AW). For values above this number, we have to consider separately the case where a country's top
marginal tax rate bracket is lower and higher than 2. In the former case (
![]() ), since we know the average tax rate at
), since we know the average tax rate at
![]() , each additional dollar up to 2 is taxed at the rate of
, each additional dollar up to 2 is taxed at the rate of
![]() . Therefore, for
. Therefore, for
![]()
If instead
![]() (which is only the case for the US and France), we do not know the marginal tax rate between
(which is only the case for the US and France), we do not know the marginal tax rate between
![]() and
and
![]() . Thus, we first set
. Thus, we first set
![]() and use linear interpolation between
and use linear interpolation between ![]() and
and
![]() . We have
. We have

|
Then the average tax rate function for
![]() is
is
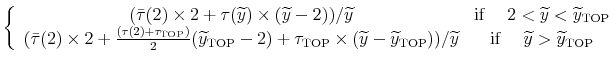
|
We use this expression to compute
![]() for
for
![]() (in addition to the original average tax rate from OECD website). We then fit the functional form given in equation (8) to these 13 data points as explained in the
text. The resulting coefficients are reported in Table A.2.
(in addition to the original average tax rate from OECD website). We then fit the functional form given in equation (8) to these 13 data points as explained in the
text. The resulting coefficients are reported in Table A.2.
| Country: | |||||
| Denmark | 1.4647 | -.01747 | -1.0107 | -.15671 | 0.990 |
| Finland | 1.7837 | -.01199 | -1.4518 | -.11063 | 0.999 |
| France | 0.5224 |
|
-.24249 | -.41551 | 0.993 |
| Germany | 1.8018 | -.01708 | -1.3486 | -.11833 | 0.992 |
| Netherlands | 3.1592 | -.00790 | -2.8274 | -.03985 | 0.984 |
| Sweden | 9.1211 | -.00762 | -8.7763 | -.01392 | 0.985 |
| UK | 0.5920 | -.00390 | -.32741 | -.30907 | 0.989 |
| US | 1.2088 | -.00942 | -.94261 | -.10259 | 0.993 |
B.2 Deriving Tax Schedules with Different Progressivity but Same Average Tax Rate
To change the average tax rates in Europe without changing progressivity, we apply the following procedure. Let
![]() be the marginal tax rate in country
be the marginal tax rate in country ![]() for income level
for income level ![]() We would like to obtain a new tax schedule
We would like to obtain a new tax schedule
![]() with the same progressivity but with a different level. Thus, we need to have (for all
with the same progressivity but with a different level. Thus, we need to have (for all ![]() and
and ![]() )
)
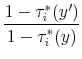 |
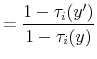 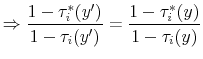 |
Letting this ratio to be equal to a constant
Let the average tax rate be
Plugging this last expression into (20) and solving for
| (19) |
The new schedule
B.3 Constructing Tax Schedules for 1983
Here, we describe the formulas we use to calculate the average tax rate at different income levels for Germany and the United States in 1983. This information is obtained from the OECD (1986) (see pages 104-105 and 244-248 for the US and pages 74-75 and 149-154 for
Germany. In all calculations for Germany, the monetary figures are in Deutsche Mark (DM). Gross income is denoted by
![]() .
.
B.3.1 Germany
Social Security Contributions. In 1983, the social security system in Germany had two brackets with their respective tax rates. Specifically, social security contributions (![]() ) were given by:
) were given by:
Allowances. Each worker receives an allowance (tax exemption) of DM 1080 and an allowance of DM 564 for work-related expenses. The OECD considers other miscellaneous allowances in the amount of DM 1606. We treat this amount as fixed for
all levels of income. Finally, workers are able to deduct part of their social security contributions determined by this formula:
Total Tax. Putting together the taxes and allowances just described gives the taxable income of a worker:
![]()
Now, we can calculate the tax liability to the household. The first step is to round the taxable income.
![]() .
.
We calculate two variables Y and Z that will be used in the calculations that follow. They are defined as
![]() and
and
![]() . To obtain the income tax for a worker, we need to apply Germany's tax schedule in 1983:
. To obtain the income tax for a worker, we need to apply Germany's tax schedule in 1983:
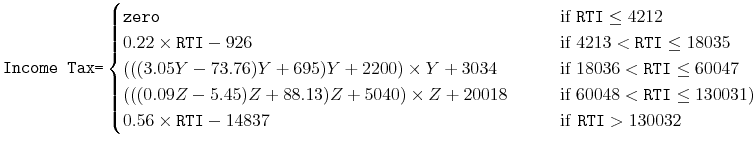
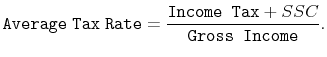
B.3.2 The United States
Social Security Contribution. In 1983, the employee social security contribution in the US was given by
![]()
The employer's social security contribution matches the employee's contribution of ![]() on earnings up to
on earnings up to ![]() . Additionally, employers are required to pay an unemployment tax of
. Additionally, employers are required to pay an unemployment tax of ![]() of earnings up to
of earnings up to ![]() and a nationwide average for state-sponsored tax plan of 2.8% of earnings up to
and a nationwide average for state-sponsored tax plan of 2.8% of earnings up to ![]() .
.
Allowances. The total combined allowances and exemptions amount to $2300 per worker.
![]() .
.
Federal Income Tax. Now, we can calculate the tax liability for the household. We need to apply the US tax schedule in 1983. The first ![]() is not taxed, as discussed earlier. The tax rate is
is not taxed, as discussed earlier. The tax rate is ![]() when taxable income is in
range
when taxable income is in
range
![]() ; is
; is ![]() in range
in range
![]() ; is
; is ![]() in range (4400,8500); 17% in range
in range (4400,8500); 17% in range
![]() ; is 19% in range (10800,12900); is 21% in range
; is 19% in range (10800,12900); is 21% in range
![]() ; is 24% in range (15000,18200); is 28% in range
; is 24% in range (15000,18200); is 28% in range
![]() ; is 32% in range (23500,28800); is 36% in range (28800,34100); is 40% in range (34100,41500); is 45% in range (41500,55300); and 50% above $55,300.
; is 32% in range (23500,28800); is 36% in range (28800,34100); is 40% in range (34100,41500); is 45% in range (41500,55300); and 50% above $55,300.
State and Local Taxes. For the purposes of calculating local and state taxes, the OECD considers a worker that lives in Detroit, Michigan. Detroit allows an exemption of ![]() , then a flat
, then a flat ![]() tax is applied.
tax is applied.
![]() . The formula for Michigan's state income tax is given by
. The formula for Michigan's state income tax is given by
![]()
![]()
Total Tax. The total tax liability is equal to the income tax plus the social security contribution and the local tax. Then, we have
B.4 Pension Systems
The details of the pension benefits system for OECD countries used in this paper are taken from the OECD publication entitled "Pensions at a Glance: 2007." The specific numbers used in this section are from Table I.2 and the unnumbered table on page 35 of that document. Further details of
these pension systems, including the number of years required to qualify for full benefits, and so on, are described more fully on pages 26-35 of the same document. Let
![]() be the lifetime average of net (after-tax) labor earnings of all individuals with ability level
be the lifetime average of net (after-tax) labor earnings of all individuals with ability level ![]() ; and let
; and let
![]() be the same variable averaged across all ability levels. Finally, recall that
be the same variable averaged across all ability levels. Finally, recall that ![]() is the total number of years a worker has been employed up to the retirement age, and let
is the total number of years a worker has been employed up to the retirement age, and let
![]() be the maximum number of years of work that an individual can accumulate retirement credits in a given country. The net retirement earnings of
individual with ability
be the maximum number of years of work that an individual can accumulate retirement credits in a given country. The net retirement earnings of
individual with ability ![]() is given as
is given as
![\displaystyle \Omega(\overline{y}^{j},m^{R})=min\left(1,\frac{m^{R}}{\overline{m}}\right)\left[a\overline{y}+b\overline{y}^{j}\right]](img370.gif)
| Ranges | Ceiling for Pensionable Income (as % of AW) | |||
| DEN | 0.371 | 0.528 | all | -- |
| FIN | 0.011 | 0.695 | all | -- |
| FRA | 0.141 | 0.484 | all | 300% |
| GER | -0.004 | 0.621 | if
|
|
| GER | 0.927 | if
|
150% | |
| NET | 0.005 | 0.928 | all | -- |
| SWE | -0.021 | 0.735 | all | 367% |
| UK | 0.257 | 0.154 | if
|
115% |
| UK | 0.315 | 0.096 | if
|
|
| UK | 0.396 | 0.042 |
|
|
| US | 0.168 | 0.355 | all | 290% |
C.0.0.0.1 Dispersion of wage growth rates.
Using male hourly earnings data, Haider (2001) estimates a value of
![]() and using annual earnings data he estimates it to be 2.02%. Baker (1997, Table 4, rows 6 and 8) uses an annual earnings measure and estimates values of 1.76% and 1.97%
in the two most closely related specifications to the present paper, whereas Guvenen (2009) finds a value of 1.94%, again using male annual earnings data. Finally, Guvenen and Smith (2009) estimate a process for household annual earnings and obtain a value of 1.87%.
and using annual earnings data he estimates it to be 2.02%. Baker (1997, Table 4, rows 6 and 8) uses an annual earnings measure and estimates values of 1.76% and 1.97%
in the two most closely related specifications to the present paper, whereas Guvenen (2009) finds a value of 1.94%, again using male annual earnings data. Finally, Guvenen and Smith (2009) estimate a process for household annual earnings and obtain a value of 1.87%.
C.0.0.0.2 Calibration of the stochastic component.
Over the sample period, Haider estimates the average innovation variance to be 0.074, an AR coefficient of 0.761, and an MA coefficient of -0.42. Using these parameters, the unconditional variance is 0.109. We match the average of the first three autocorrelation coefficients because Haider (2001) estimates an ARMA(1,1) process, whereas in our model we employ a slightly more parsimonious structure (AR(1)+ iid shock). This latter formulation is a common choice in calibrated macroeconomic models because it requires one fewer state variable while still capturing the dynamics of wages quite well. Nevertheless, because of this difference, it is not possible to exactly match each autocorrelation coefficient in the ARMA(1,1) specification and, so, we match the average of the first three. In the calibrated model, the first three autocorrelations are 0.48, 0.33, and 0.20 compared to 0.42, 0.32, and 0.24 in the data.
D. Further Sensitivity Analysis
In all of the following robustness exercises, we recalibrate our model to the empirical targets described in Section 4.
D.1 Taxing Capital Income
In our baseline model, we abstracted from taxation of capital income for two reasons. First, some plausible formulations of capital income taxation substantially complicates the numerical solution of the model by invalidating a relatively fast algorithm we were able to use in its absence. Second, the actual treatment of capital income is quite complex, certainly much more so than labor income. For example, some countries (e.g., the United States) tax certain forms of capital income as ordinary income (i.e., they tax "total" income), whereas some other countries (e.g., France, Finland, and Sweden) allow individuals to pay a lower flat-rate tax on certain types of capital income (such as interest income). See, for example, the discussion in Carey and Rabesona (2002, Table 22) and on pages 158-160. Modeling the complexities of this institutional detail is beyond the scope of this paper, so in the benchmark model studied in the main text we abstracted entirely from capital income taxes.
With these caveats in mind, here we attempt to quantify the effects of taxing capital income in a simple way. Basically, we assume that the government taxes total income--inclusive of capital income--subject to the tax schedules derived in this paper. To understand why taxing total income could matter for ours results, first notice that there are essentially two types of assets in our economy: human capital and financial assets. When capital income is taxed at the flat rate as in our benchmark analysis, progressivity reduces only the return on human capital hindering investment in human capital relative to investment in financial assets. On the other hand, when progressive tax is applied to total income, progressivity reduces both the return on human capital and financial assets. Thus progressivity does not reduce investment in human capital relative to investment in financial asset as much as in the case where progressivity affects only labor income.
To conduct this exercise we have to make some simplifying assumptions to our model and develop a new computational method. The reason is that our computational procedure for the benchmark model relies on the property that the return on savings is independent of the tax rate (which is no longer true in this experiment). This allowed us to compute the human capital investment and consumption-savings decision separately and iteratively. When the progressive tax is applied to total income however, we can no longer use this procedure because we need to compute the total income at each age to compute the tax rate the agent is facing. Thus, we need to solve the human capital investment jointly with consumption-saving decision. However, then it becomes very hard to solve this problem with value function methods, since an individual has to know his borrowing limit in a period to make his optimal choices, which depends on his lifetime human capital and labor supply choices.
To circumvent these problems, we consider a benchmark without idiosyncratic shocks and set ![]() . Since there are no shocks in this version of the model, our target moments reduce to
average wage growth, standard deviation of wage growth rates, and variance of wages due to profile heterogeneity only. The latter two are obtained from Guvenen (2007). Notice that because (i) there are no shocks and (ii) individuals want to invest significantly early on, they would have a very
strong incentive to borrow when utility is separable and hence they want constant consumption. This implies that wealth is negative for many individuals with standard power utility preferences. To mitigate this effect and allow consumption to rise over the lifecycle we use preferences as in
Greenwood et al. (1988) (often called GHH). With this structure, we are able to solve the model both when capital income is and is not taxed.
. Since there are no shocks in this version of the model, our target moments reduce to
average wage growth, standard deviation of wage growth rates, and variance of wages due to profile heterogeneity only. The latter two are obtained from Guvenen (2007). Notice that because (i) there are no shocks and (ii) individuals want to invest significantly early on, they would have a very
strong incentive to borrow when utility is separable and hence they want constant consumption. This implies that wealth is negative for many individuals with standard power utility preferences. To mitigate this effect and allow consumption to rise over the lifecycle we use preferences as in
Greenwood et al. (1988) (often called GHH). With this structure, we are able to solve the model both when capital income is and is not taxed.
The main finding is the following. The new benchmark model with no capital income taxes can account for 69% of the L90-10 gap between the US and CEU in 2003. (This is up from 48% in the baseline model in the text with shocks and ![]() ) Adding capital income taxes to this structure, reduces the explanatory power to 52.8%, for a fall of 23 percent (
) Adding capital income taxes to this structure, reduces the explanatory power to 52.8%, for a fall of 23 percent (![]() ). Thus,
if all capital income was taxed at the same rate as labor income, the model's explanatory power would be about a one quarter lower than in the baseline case.
). Thus,
if all capital income was taxed at the same rate as labor income, the model's explanatory power would be about a one quarter lower than in the baseline case.
Having said that, it should also be stressed that assuming that this exercise is likely to overstate the real effects of capital income taxation. This is because, as mentioned above, in certain CEU countries some capital income is taxed at a flat rate, which is not the case in the United States. Consequently, in those countries, progressivity affects only labor income, making investment in physical assets more attractive than investment in human capital, in turn further compressing the wage distribution. Hence, incorporating such differences would further lower inequality in the CEU and increase the explanatory power of the model. While we do not pursue this approach here, this is an important point to keep in mind.
D.2 Accounting for Cross-Country Variation in Retirement Age
Our baseline model does not allow for variation in retirement age across countries. However, such variation could have important implications for human capital investment by affecting the effective horizon of individuals. Although modeling endogenous retirement is beyond the scope of this paper,
here we explore the effects of allowing for exogenous retirement age differences across countries. We estimate the average retirement age by computing the fraction of people who receive social security pensions and disability benefits at each age.41 We then solve each country's problem using the computed retirement age as an exogenous value for ![]() With this adjustment, the explanatory power for L90-10 increases to 70%, because countries with more progressivity also turn out to have a lower retirement age than less progressive ones. So the two effects reinforce each other.
With this adjustment, the explanatory power for L90-10 increases to 70%, because countries with more progressivity also turn out to have a lower retirement age than less progressive ones. So the two effects reinforce each other.
D.3 Maximum investment on the job
We experiment with two values of ![]() --0.4 and 0.6--one on each side of our baseline choice of 0.5. When
--0.4 and 0.6--one on each side of our baseline choice of 0.5. When ![]() the model's explanatory power for L90-10 and L90-50 fall to 35% and 51% respectively, whereas the explanatory power for L50-10 remains unchanged at 24%. It should be noted however that with this choice of
the model's explanatory power for L90-10 and L90-50 fall to 35% and 51% respectively, whereas the explanatory power for L50-10 remains unchanged at 24%. It should be noted however that with this choice of ![]() , the model implies a minimum to mean wage ratio of 0.24, which is quite a bit lower than the 0.29 value in the data (and what was used to pin down the baseline choice of 0.50 for
, the model implies a minimum to mean wage ratio of 0.24, which is quite a bit lower than the 0.29 value in the data (and what was used to pin down the baseline choice of 0.50 for ![]() ). When
). When ![]() the model explains 61% of the L90-10 difference between the US and CEU, 116% of L90-50, and 24% of L50-10. In
this case, the min to mean wage ratio is a more reasonable 0.30.
the model explains 61% of the L90-10 difference between the US and CEU, 116% of L90-50, and 24% of L50-10. In
this case, the min to mean wage ratio is a more reasonable 0.30.
D.4 Wasteful Government Expenditures versus Transfers
In the baseline model, the surplus was returned back to households in a lump-sum fashion, essentially assuming that government expenditures are perfect substitutes for private consumption. To examine if our results are sensitive to this assumption, we now assume that half of the government
surplus is wasted: ![]() , and each component equals half of the budget surplus (i.e., tax revenues minus benefits payments). This assumption is probably extreme, but it is useful in
illustrating whether the results are sensitive to this scenario. From Table A.3, we see that, qualitatively, the explanatory power of the model is lower for some countries for L90-10 and L90-50 but higher for L50-10. Quantitatively, however, the effect is
minimal across the board. In fact, in some cases, no difference is visible (because of rounding) compared to the benchmark case in Table 5.
, and each component equals half of the budget surplus (i.e., tax revenues minus benefits payments). This assumption is probably extreme, but it is useful in
illustrating whether the results are sensitive to this scenario. From Table A.3, we see that, qualitatively, the explanatory power of the model is lower for some countries for L90-10 and L90-50 but higher for L50-10. Quantitatively, however, the effect is
minimal across the board. In fact, in some cases, no difference is visible (because of rounding) compared to the benchmark case in Table 5.
| L90-10 (a) | L90-50 (b) | L50-10 (c) | |
| Denmark | 63 | 90 | 38 |
| Finland | 49 | 75 | 29 |
| France | 30 | 71 | 14 |
| Germany | 69 | 75 | 60 |
| Netherlands | 45 | 59 | 31 |
| Sweden | 42 | 67 | 23 |
| CEU | 49% | 73% | 29% |
| UK | 21 | 0 | 49 |
D.5 Depreciation of human capital

To check the sensitivity of our results to the choice of the human capital depreciation rate, we have experimented with depreciation rates of 1% and 2%. The model's explanatory power goes down to 44% when
![]() and it increases slightly above 50% when
and it increases slightly above 50% when
![]() . An important point to note is that it is not possible to match two of our targets, mean wage growth and variance of wage growth rate jointly for depreciation rates below 1
percent. For very low values of depreciation rate, when we match the increase in wage inequality over the lifecycle, the wage growth turns out to be very high relative to data. The reason is the following. First note that the learning ability cannot be negative, and as a result the lowest wage
growth is bound by the minus depreciation rate. For a given minimum ability level, we match the variance of
. An important point to note is that it is not possible to match two of our targets, mean wage growth and variance of wage growth rate jointly for depreciation rates below 1
percent. For very low values of depreciation rate, when we match the increase in wage inequality over the lifecycle, the wage growth turns out to be very high relative to data. The reason is the following. First note that the learning ability cannot be negative, and as a result the lowest wage
growth is bound by the minus depreciation rate. For a given minimum ability level, we match the variance of ![]() by adjusting the maximum ability level. However, when we increase the maximum
ability to match the variance of
by adjusting the maximum ability level. However, when we increase the maximum
ability to match the variance of ![]() , the average wage growth turns out to be very high compared to data when we use a very low depreciation rate.
, the average wage growth turns out to be very high compared to data when we use a very low depreciation rate.
D.6 Elasticity of human capital production function
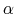
When ![]() is higher, there is less diminishing marginal productivity in human capital production. As a result, human capital investment responds more to changes in incentives due for
example to changes in taxes. The model's explanatory power increases to 65% when we set
is higher, there is less diminishing marginal productivity in human capital production. As a result, human capital investment responds more to changes in incentives due for
example to changes in taxes. The model's explanatory power increases to 65% when we set
![]() and it decreases to 28% when we set it to 0.65. Most of the most recent estimates in the literature are above 0.9 (see, e.g., Heckman et al. (1998); Kuruscu (2006)). Thus, our choice of 0.8 is on the conservative side.
and it decreases to 28% when we set it to 0.65. Most of the most recent estimates in the literature are above 0.9 (see, e.g., Heckman et al. (1998); Kuruscu (2006)). Thus, our choice of 0.8 is on the conservative side.
D.7.0.1 Extended Model with SBTC.
Here is the formal statement of the model studied in Section 5.2:
Notice that the only changes are the introduction of raw labor into the labor earnings equation and human capital accumulation function. The weights
![]() and
and
![]() in the production function in (23) capture the relative efficiency of human capital and raw labor in producing new human capital. As in
Guvenen and Kuruscu (2010) we focus on the case where
in the production function in (23) capture the relative efficiency of human capital and raw labor in producing new human capital. As in
Guvenen and Kuruscu (2010) we focus on the case where
![]() and
and
![]() .
.
| L90-10 | L90-50 + | L50-10 | |
| CEU Data Level | 0.070 | 0.063 | 0.007 |
| CEU Data % | 91% | 9% | |
| CEU Model Level | 0.168 | 0.129 | 0.039 |
| CEU Model % | 77% | 23% | |
| US Data Level | 0.230 | 0.160 | 0.070 |
| US Data % | 70% | 30% | |
| US Model Level | 0.232 | 0.184 | 0.048 |
| US Model % | 79% | 21% | |
| Difference Data: Level | 0.160 | 0.097 | 0.063 |
| Difference Data: % | 61% | 39% | |
| Difference Model: Level | 0.065 | 0.056 | 0.009 |
| Difference Model: % | 87% | 13% | |
| % Explained | 41% | 58% | 14% |
This extended model has some new parameters that need to be calibrated. Except those discussed here, all parameter values are kept at the values given in Table 3. An important point to note is that for the cross-sectional analysis of the previous section, the
two-factor model would have precisely the same implications as the one-factor Ben-Porath model used earlier. This is because
![]() and
and
![]() are constant at a point in time and their values can be normalized to generate exactly the same results as in the previous section. Thus, with proper choices of
are constant at a point in time and their values can be normalized to generate exactly the same results as in the previous section. Thus, with proper choices of
![]() ,
,
![]() , and the distribution of
, and the distribution of ![]() , we do not need to recalibrate any
other parameter and can still obtain the same results for year 2003 as before. This is the route that we follow in this section.42
, we do not need to recalibrate any
other parameter and can still obtain the same results for year 2003 as before. This is the route that we follow in this section.42
For examining the change in inequality over time, we choose
![]() to match the 23 log points in L90-10 in the US from 1980 to 2003. The required change in
to match the 23 log points in L90-10 in the US from 1980 to 2003. The required change in
![]() is 0.236. With this calibration, wage inequality rises by 0.168 in CEU during the same time, compared to 0.070 rise in the data (fourth column
of Table A.4). These results imply that differences in labor market policies, even when they are fixed over time, can generate about 41% (
is 0.236. With this calibration, wage inequality rises by 0.168 in CEU during the same time, compared to 0.070 rise in the data (fourth column
of Table A.4). These results imply that differences in labor market policies, even when they are fixed over time, can generate about 41% (
![]() ) of the widening in the inequality gap between the US and the CEU during this time period.
) of the widening in the inequality gap between the US and the CEU during this time period.
Another dimension of the rise in wage inequality is seen in the last two columns of Table A.4. The substantial part of the rise in wage inequality in the CEU has been at the top: L90-50 is responsible for 91% of the total rise in L90-10, whereas only 9% of the rise took place at the lower end. A similar outcome, somewhat less extreme, is observed in the US where 70% of the rise in L90-10 is due to L90-50. The model generates a similar picture: about 77% of the rise in the CEU and 79% in the US is due to L90-50. An alternative way to express these figures is that the model accounts for 58% of the increase in the inequality gap above the median between the US and the CEU but only 14% of the rising gap below the median. As is clear by now, this is a recurring theme in this paper: the model accounts for cross-country inequality facts at the upper tail quite well, but accounts for a smaller fraction at the lower tail.
E.1 Sample Selection and Data Preparation
The sample period for the German SOEP is 1984-2008 and for the PSID is 1968-1992. We keep only males between 25 and 60 years old, regardless of whether they are heads of household. If an individual does not report hours, wages or income, he is dropped from the sample. To further trim earnings outliers, we exclude observations in which earnings grow by more than 500% or less than -80%, earnings are below 100 Euros (2005) or 2 Dollars (1983) per hour or if they are top-coded. To ensure consistency, we drop those who report zero hours but positive earnings or zero earnings but positive hours. We also drop individuals who report more than 80 hours per week for the entire year, 4160 hours, and flag individuals who work less than one quarter at 40 hours per week, 520 hours. In the PSID, we also drop the SEO oversample.
In the PSID, we have to identify roles within households to pair the "wife" and the "head" of household's hours with that individual. To do so, we use the
![]() variable in 1967 and require that the "wife" is female and the
variable in 1967 and require that the "wife" is female and the
![]() and
and
![]() variables in subsequent years. The household head gets
variables in subsequent years. The household head gets
![]()
![]() , and wives are
, and wives are
![]()
![]() and
and
![]()
![]() until 1982, when they become
until 1982, when they become
![]()
![]() . In a few cases each year, the hours reported from the
household level and matched to the individual do not match individually reported hours, and we drop these. We also create consistent a age variable so that the age increments by 1 each observation even when an individual is surveyed at different times in the year.
. In a few cases each year, the hours reported from the
household level and matched to the individual do not match individually reported hours, and we drop these. We also create consistent a age variable so that the age increments by 1 each observation even when an individual is surveyed at different times in the year.
E.2.1 Residual variables
The lifecycle profiles are based on residual log wages. To obtain residuals we regress log wages on marital status, race in the US case and education level (i.e., dropout, high school or college in the US; and dropout, vocational, high school or college in Germany). In all regressions, the intercept is of an unmarried, white, high school graduate. The regression is repeated for every year of the sample, so the dummy coefficients vary freely over time.
E.2.2 Age Profiles
We construct profiles in much the same way as Deaton and Paxson (1994) and Storesletten et al. (2004b). For each variable, we compute mean and variance within an age-year bin, each defined by a calendar year
and a 5 year window of ages. We label these bins by the year and age in the center of the range. We calculate life-cycle profiles with time effects by using coefficients from regressing these bins on both age and year dummies and weighting by the number of individuals in the year-age bin. That is,
for mean or dispersion of wages within the age-year bin ![]() , we estimate
, we estimate
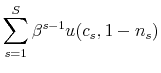
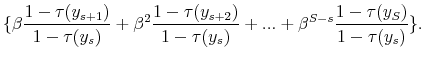
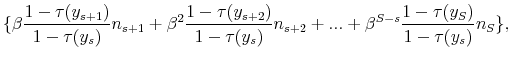
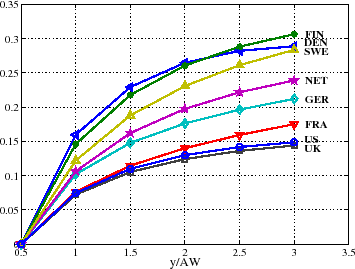
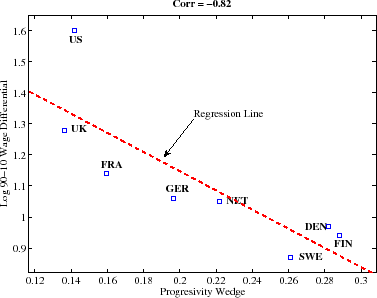
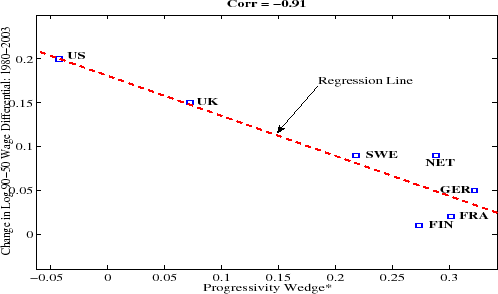
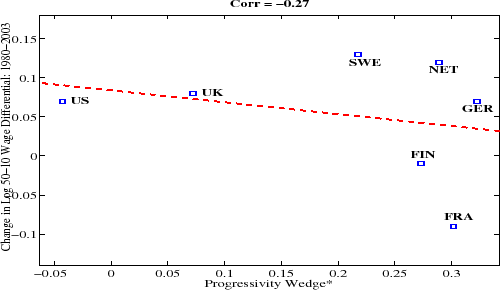
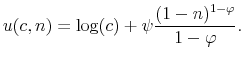
![\displaystyle =\underset{\textrm{systematic comp. }}{\underbrace{\left[a^{j}+b^{j}s\right]}}+\underset{\textrm{stochastic comp.}}{\underbrace{z_{s}^{j}+\varepsilon_{s}^{j}}}](img172.gif)