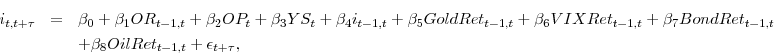The Informational Content of the Embedded Deflation Option in TIPS *
Keywords: TIPS, embedded option, inflation, deflation, term structure
Abstract:
1 Introduction
The market for U. S. Treasury Inflation Protected Securities (TIPS) has experienced significant growth since its inception in 1997. As of May 2010, the face amount of outstanding TIPS was about $563 billion, which was roughly 8% of the size of the nominal U. S. Treasury market. The TIPS market has averaged about $47 billion in new issuances each year and has about $10.6 billion of average daily turnover.1 The main advantage of TIPS over nominal Treasuries is that an investor who holds TIPS is hedged against inflation risk.2 Although there are costs to issuing TIPS (Roush, 2008), there appears to be widespread agreement that the benefits of TIPS outweigh the costs. Campbell, Chan, and Viceira (2003), Kothari and Shanken (2004), Roll (2004), Mamun and Visaltanachoti (2006), Dudley, Roush, and Ezer (2009), Barnes, Bodie, Triest, and Wang (2010), Huang and Zhong (2011), and Bekaert and Wang (2010) all conclude that TIPS offer significant diversification and hedging benefits to risk averse investors.
The main contribution of our paper is to point out an informational benefit of TIPS that has been ignored in the literature. Specifically, we uncover the informational content of the embedded deflation option in TIPS. We develop a model to value the embedded option explicitly and we show that the time variation in the embedded option's value is correlated with periods of deflationary expectations. We also show that the embedded option return is economically important and statistically significant for explaining future inflation, even in the presence of common inflation variables such as the yield spread, the return on gold, the return on crude oil, and lagged inflation. We argue that our results should be useful to anyone who is interested in assessing inflationary expectations.
At the maturity date of a TIPS, the TIPS owner receives the greater of the original principal or the inflation adjusted principal. This contractual feature is an embedded put option since a TIPS investor can force the U.S. Treasury to redeem the TIPS at par if the cumulative inflation over the life of the TIPS is negative (i.e., deflation). The first TIPS auction in 1997 was for a 10-year note. Prior to the auction, Roll (1996) dismissed the importance of the embedded option since the United States had not experienced a decade of deflation for more than 100 years. Our paper directly examines the embedded deflation option in TIPS. Using a sample of 10-year TIPS from 1997 to 2010, we estimate that the value of the embedded option does not exceed $0.0615 per $100 principal amount. If we amortize $0.0615 over the 10-year life of a TIPS, the impact on the TIPS yield is very small, which appears to justify Roll's (1996) comment. However, when we add 5-year TIPS to our sample, we find that the estimated embedded option value is much larger, up to $1.4447 per $100 principal amount. If we amortize $1.4447 over the 5-year life of a TIPS, the impact on the yield is about 29 basis points. Furthermore, we find significant time variation in the embedded option values for both 5-year and 10-year TIPS. We show that this time variation is useful for explaining future inflation, even in the presence of widely used inflation variables such as the return on gold, lagged inflation, the return on crude oil, and the yield spread between nominal Treasuries and TIPS. We call this the informational content of the embedded option in TIPS.
To value the embedded option in TIPS, we use a continuous-time term structure model that has two factors, the nominal interest rate and the inflation rate. Since our two factors are jointly Gaussian, we obtain a closed-form solution for the price of a TIPS. Using our closed-form solution, we decompose the price of each TIPS into two parts, a part that corresponds to the embedded option value and a part that corresponds to the inflation-adjusted coupons and the inflation-adjusted principal. This makes our approach different from what is found in Sun (1992), Bakshi and Chen (1996), Jarrow and Yildirim (2003), Buraschi and Jiltsov (2005), Lioui and Poncet (2005), Chen, Liu, and Cheng (2010), Ang, Bekaert, and Wei (2008), and Haubrich, Pennacchi, and Ritchken (2012). These papers show how to value real bonds, but they ignore the embedded deflation option that is found in TIPS. To the best of our knowledge, we are the first to price the embedded option in TIPS and to use its time variation to explain future inflation. Christensen, Lopez, and Rudebusch (2012) estimate the value of the embedded option in TIPS, but unlike our paper they do not use the time variation in the embedded option value to explain future inflation. In addition, Kitsul and Wright (2012) study options-implied inflation probabilities, but they use CPI caps and floors instead of TIPS to fit their model.
When we fit our model to the data, we find that prior to 2002 the embedded option values are close to zero. From 2002 through 2004, the option values have considerable time variation. The overall trend during this time period is increasing option values followed by decreasing option values, with a peak around November 2003. From 2005 through the first half of 2008, there is some variation in option values, but mostly the values are close to zero. Finally, during the second half of 2008 and all of 2009, there is a surge in option values, which outstrips the previous peak value from 2003. We argue that the time variation in option values is capturing the deflation scare period of 2003-2004 and the deflationary expectations that were associated with the financial crisis in 2008-2009. Our results are consistent with those in Campbell, Shiller, and Viceira (2009), Wright (2009), and Christensen, Lopez, and Rudebusch (2010). However, our approach is different since we explicitly value the embedded option in TIPS and we quantify its time variation.
Although our estimated option values for 10-year TIPS are small economically, the option returns are very large. When we stack our option returns into a vector and perform a Wald test, we strongly reject the null hypothesis that the returns are jointly equal to zero (![]() -value is less than 0.0001). When we perform a similar analysis for 5-year TIPS, we not only reject the null hypothesis that the option returns are jointly equal to zero, but we also reject the null
hypothesis that the option values are jointly equal to zero (both
-value is less than 0.0001). When we perform a similar analysis for 5-year TIPS, we not only reject the null hypothesis that the option returns are jointly equal to zero, but we also reject the null
hypothesis that the option values are jointly equal to zero (both ![]() -values are less than 0.0001). This is consistent with our earlier statement that the embedded option in 5-year TIPS is worth
more than its counterpart in 10-year TIPS. We find similar results when we exclude the period of the financial crisis. Thus our results are not being driven solely by the events of 2008-2009.
-values are less than 0.0001). This is consistent with our earlier statement that the embedded option in 5-year TIPS is worth
more than its counterpart in 10-year TIPS. We find similar results when we exclude the period of the financial crisis. Thus our results are not being driven solely by the events of 2008-2009.
To quantify the informational content of the embedded option in TIPS, we construct several explanatory variables that we use in a regression analysis. We use our estimated option values from 5-year and 10-year TIPS to construct two value-weighted indices, one for the embedded option price level and one for the embedded option return. We show that the coefficient on the embedded option return index is statistically significant for explaining the one-month ahead inflation rate (Table 6). The embedded option return index remains significant even when we include control variables such as lagged inflation, the return on gold, the VIX index, and the yield spread. By itself, the embedded option return index explains up to 25% of the variation in the one-month ahead inflation rate (Table 6). When we include our control variables, this number increases to slightly more than 35%. Using our regression point estimate for 10-year TIPS, we find that a 100% embedded option return (which is less than one standard deviation) is consistent with a 0.52% decrease in the one-month ahead annualized inflation rate. Thus our results are economically significant as well as statistically significant. For completeness, we also analyze the significance of our indices for explaining the one-year ahead inflation rate and the out-of-sample inflation rate. For almost all of these regressions, one or both of our embedded option indices is significant while more common variables, such as the return on gold and the yield spread, are insignificant. This is true both in-sample (Table 6) and out-of-sample (Table 12).
We verify our results by performing several robustness checks. First, we argue that liquidity is not a likely explanation for our results (see section 4.6.1). To investigate this, we eliminate the off-the-run securities from our sample (see section 4.6.2) and we re-construct our embedded option indices using only the on-the-run securities, which are the most liquid TIPS. We show that all of our previous regression results continue to hold with on-the-run TIPS (Table 7). Thus our results are not being driven by possible
illiquidity that surrounds off-the-run TIPS (see Fleming and Krishnan, 2012). Second, we alter the weighting scheme that we use to construct the embedded option indices. Instead of using value weights, we construct the indices with weights that favor shorter-term options, longer-term options,
options that are nearer-the-money, and options that are further out-of-the-money. Upon doing this for both 5-year TIPS (Table 8) and 10-year TIPS (Table 9), we find that our results are robust to different weighting schemes. Third, we construct a new explanatory variable ( ![]() , option return fraction) that captures the fraction of embedded options in each month that has a positive return. This variable is less sensitive to model specification since any other pricing model
that produces the same sign for the embedded option returns will produce the same explanatory variable. We find that
, option return fraction) that captures the fraction of embedded options in each month that has a positive return. This variable is less sensitive to model specification since any other pricing model
that produces the same sign for the embedded option returns will produce the same explanatory variable. We find that ![]() is statistically significant for the full sample of TIPS and for the
on-the-run TIPS, for both the one-month ahead and the one-year ahead inflation rate (Table 10). Thus even if we ignore the magnitude of the option returns and focus solely on the sign of those returns, we find that the embedded option in TIPS contains useful information for explaining the future
inflation rate. Lastly, we examine the ability of our embedded option indices to explain the inflation rate in the presence of other control variables (Table 11), and we use a rolling window empirical technique to examine the out-of-sample performance of our variables (Table 12). After conducting
all of these robustness checks, we find that our main conclusion is not altered - the embedded option in TIPS contains relevant information for explaining the future inflation rate, out to a horizon of at least one year.
is statistically significant for the full sample of TIPS and for the
on-the-run TIPS, for both the one-month ahead and the one-year ahead inflation rate (Table 10). Thus even if we ignore the magnitude of the option returns and focus solely on the sign of those returns, we find that the embedded option in TIPS contains useful information for explaining the future
inflation rate. Lastly, we examine the ability of our embedded option indices to explain the inflation rate in the presence of other control variables (Table 11), and we use a rolling window empirical technique to examine the out-of-sample performance of our variables (Table 12). After conducting
all of these robustness checks, we find that our main conclusion is not altered - the embedded option in TIPS contains relevant information for explaining the future inflation rate, out to a horizon of at least one year.
Explaining future inflation has received a considerable amount of attention in the literature. Many explanatory variables for future inflation have been proposed, such as the interest rate level and lagged inflation (Fama and Gibbons, 1984), the unemployment rate (Stock and Watson, 1999), the money supply (Stock and Watson, 1999; Stockton and Glassman, 1987), inflation surveys (Mehra, 2002; Ang, Bekaert, and Wei, 2007; Chernov and Mueller, 2012; Chun, 2011), the price of gold (Bekaert and Wang, 2010), and the spread between nominal Treasury yields and TIPS yields (Stock and Watson, 1999; Shen and Corning, 2001; Roll, 2004; Christensen, Lopez, and Rudebusch, 2010; Gürkaynak, Sack, and Wright, 2010; D'Amico, Kim, and Wei, 2010; Pflueger and Viceira, 2011). Our paper is different since we focus on the embedded option in TIPS rather than on traditional variables such as the return on gold or the yield spread. However, we include some of these traditional variables as control variables in our regressions. This allows us to analyze the marginal contribution of the variables.
The remainder of our paper is organized as follows. Section 2 introduces our model and derives a closed form solution for TIPS and for nominal Treasury securities. Section 3 describes the data. Section 4 presents our empirical methodology, our model estimation results, and our regression results. We focus on in-sample results, out-of-sample results, and robustness checks. Section 5 gives our concluding remarks. The technical details of our pricing model can be found in the appendix.
2 The model
We use a continuous-time model in which bond prices are driven by two state variables, the nominal interest rate ![]() and the inflation rate
and the inflation rate ![]() . The evolution of
. The evolution of ![]() and
and ![]() is described by the Gaussian system of stochastic processes
is described by the Gaussian system of stochastic processes
where ![]() is a risk neutral probability measure,
is a risk neutral probability measure, ![]() and
and ![]() are independent Brownian motions under
are independent Brownian motions under ![]() , and
, and ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
and
,
and ![]() are parameters. Ang and Piazzesi (2003) show that the inflation rate impacts the mean of the short term nominal interest rate. We use their result as motivation for including the
parameters
are parameters. Ang and Piazzesi (2003) show that the inflation rate impacts the mean of the short term nominal interest rate. We use their result as motivation for including the
parameters ![]() and
and ![]() in equations ( 1)-(2). This makes each of the processes in (1)-(2) more complex than the Vasicek (1977) process, but it allows for a richer set of dynamics between
in equations ( 1)-(2). This makes each of the processes in (1)-(2) more complex than the Vasicek (1977) process, but it allows for a richer set of dynamics between ![]() and
and ![]() .
.
In our empirical estimation below, we use both TIPS and nominal Treasury Notes (T-Notes). Section 2.1 describes our pricing model for TIPS, while section 2.2 describes our pricing model for nominal T-Notes. By including nominal T-Notes in our analysis, we are able to increase the overall size of our sample. As a side benefit, we also avoid overfitting the TIPS market, which may help to control for the issues of TIPS mispricing and illiquidity that are raised by Fleckenstein, Longstaff, and Lustig (2010) and Fleming and Krishnan (2012). We discuss liquidity in more detail later in sections 4.6.1-4.6.2.
Both of our pricing models are derived under the ![]() probability measure, which eliminates the need to be specific about the functional form of the risk premia. For example, the inflation
risk premium may be time varying, as shown in Evans (1998) and Grishchenko and Huang (2012), for the UK and U.S. Treasury markets, respectively. Furthermore, if the risk premia happen to be affine functions of
probability measure, which eliminates the need to be specific about the functional form of the risk premia. For example, the inflation
risk premium may be time varying, as shown in Evans (1998) and Grishchenko and Huang (2012), for the UK and U.S. Treasury markets, respectively. Furthermore, if the risk premia happen to be affine functions of ![]() and
and ![]() , then (1)-(2) are consistent with Barr and Campbell (1997), who show that the expected real
interest rate in the UK is highly variable at short horizons, but it is comparatively stable at long horizons. Our model can support many functional forms for the risk premia since we can always describe the evolution of
, then (1)-(2) are consistent with Barr and Campbell (1997), who show that the expected real
interest rate in the UK is highly variable at short horizons, but it is comparatively stable at long horizons. Our model can support many functional forms for the risk premia since we can always describe the evolution of ![]() and
and ![]() under the true probability measure and then use a prudent change of measure to arrive at (1)-(2). Thus the risk premia are subsumed by
under the true probability measure and then use a prudent change of measure to arrive at (1)-(2). Thus the risk premia are subsumed by ![]() .
.
The advantage of specifying the model under ![]() is that the number of parameters is reduced, which makes our model parsimonious. Since the volatility matrix in (1)-(2) is lower triangular, as in Chun (2011), our model has only 9 parameters. In contrast, Sun (1992, p. 603) uses a model with 13 parameters, Lioui and Poncet (2005, pp. 1269-1270) use 17 parameters, and Christensen, Lopez, and Rudebusch
(2010, Table 7) use 28 to 40 parameters. Given the limited data for TIPS, it is important that we keep the number of parameters as small as possible. To avoid overfitting our model to the TIPS market, we use matching nominal T-Notes in our sample, as mentioned earlier. We also perform several
robustness checks, including the construction of an alternative explanatory variable (
is that the number of parameters is reduced, which makes our model parsimonious. Since the volatility matrix in (1)-(2) is lower triangular, as in Chun (2011), our model has only 9 parameters. In contrast, Sun (1992, p. 603) uses a model with 13 parameters, Lioui and Poncet (2005, pp. 1269-1270) use 17 parameters, and Christensen, Lopez, and Rudebusch
(2010, Table 7) use 28 to 40 parameters. Given the limited data for TIPS, it is important that we keep the number of parameters as small as possible. To avoid overfitting our model to the TIPS market, we use matching nominal T-Notes in our sample, as mentioned earlier. We also perform several
robustness checks, including the construction of an alternative explanatory variable (![]() , option return fraction) that is less sensitive to model specification. We describe these robustness
checks in more detail later.
, option return fraction) that is less sensitive to model specification. We describe these robustness
checks in more detail later.
2.1 TIPS pricing
Consider a TIPS that is issued at time ![]() and matures at time
and matures at time ![]() . We want to
determine the price
. We want to
determine the price ![]() of the TIPS at time
of the TIPS at time ![]() , where
, where ![]() . The principal amount of the TIPS is
. The principal amount of the TIPS is ![]() and the coupon rate is
and the coupon rate is ![]() . Suppose there are
. Suppose there are ![]() coupons yet to be paid, where the coupon payments occur at
coupons yet to be paid, where the coupon payments occur at
![]() . If we let
. If we let
![]() , we can write the TIPS price as
, we can write the TIPS price as
where
![]() denotes expectation at time
denotes expectation at time ![]() under
under ![]() . The right-hand side of (3) has three terms. The first term is the value of the inflation-adjusted coupon payments, the second term is the value of the inflation-adjusted
principal, and the third term is the value of the embedded option. The inflation adjustment in (3) is captured by the exponential term
. The right-hand side of (3) has three terms. The first term is the value of the inflation-adjusted coupon payments, the second term is the value of the inflation-adjusted
principal, and the third term is the value of the embedded option. The inflation adjustment in (3) is captured by the exponential term
for
![]() . In our empirical specification, we use the U.S. Treasury's CPI index ratio to capture the known part of the inflation adjustment.3 The unknown inflation adjustment depends on the stochastic process in (2).
. In our empirical specification, we use the U.S. Treasury's CPI index ratio to capture the known part of the inflation adjustment.3 The unknown inflation adjustment depends on the stochastic process in (2).
Using (1)-(2), the random variables
![]() and
and
![]() for
for
![]() have a joint Gaussian distribution. Thus we can evaluate the expectation in ( 3) to get a closed-form solution for the TIPS price. Our solution
depends on the moments
have a joint Gaussian distribution. Thus we can evaluate the expectation in ( 3) to get a closed-form solution for the TIPS price. Our solution
depends on the moments
![]() ,
,
![]() ,
,
![]() ,
,
![]() , and
, and
![]() for
for
![]() , which are also available in closed-form. We give details in Appendix A.
, which are also available in closed-form. We give details in Appendix A.
2.2 Pricing nominal Treasury Notes
Consider a nominal T-Note that is issued at time ![]() and matures at time
and matures at time ![]() . We want
to determine the T-Note's price
. We want
to determine the T-Note's price ![]() at time
at time ![]() , where
, where ![]() . The principal amount is
. The principal amount is ![]() , the coupon rate is
, the coupon rate is ![]() , and there are
, and there are ![]() coupon payments yet to be paid, at times
coupon payments yet to be paid, at times
![]() . As before, we let
. As before, we let
![]() and thus we can write the T-Note's price as
and thus we can write the T-Note's price as
The price in (5) contains two terms. The first term is the value of the nominal coupon payments, while the second term is the value of the principal amount. Since we are pricing a nominal T-Note, there is no explicit inflation adjustment in (5). However, since ![]() in (1) may not be zero, the price
in (1) may not be zero, the price ![]() depends not only on
depends not only on ![]() and the parameters in (1), but also on
and the parameters in (1), but also on ![]() and the parameters in (2). This sets our model apart from Vasicek (1977).
and the parameters in (2). This sets our model apart from Vasicek (1977).
Like equation (3), our closed-form solution for equation (5) depends on the moments
![]() ,
,
![]() ,
,
![]() ,
,
![]() , and
, and
![]() for
for
![]() . We give details in Appendix B.
. We give details in Appendix B.
3 The data
To estimate our model, we construct a monthly time series for the nominal interest rate and for the inflation rate. We obtain our data from the Federal Reserve Economic Database (FRED) at the Federal Reserve Bank of St. Louis. We use the 3-month Treasury Bill rate
as a proxy for the nominal interest rate. We start with daily observations of the 3-month Treasury Bill rate and we extract the month-end observations to get a monthly time series. Other short-term Treasury Bill rates give similar results. To construct a monthly time series for the inflation rate,
we use the non-seasonally adjusted Consumer Price Index for All Urban Consumers (CPI-U), which is released monthly by the U.S. Bureau of Labor Statistics. This is the same index that is used for inflation adjustments to TIPS. We let ![]() denote the value of the CPI-U that corresponds to month
denote the value of the CPI-U that corresponds to month ![]() . We define the annualized inflation rate for month
. We define the annualized inflation rate for month ![]() as
as
![]() , where 12 is the annualization factor. Thus the inflation rate is the annualized log change in the price level, which is consistent
with (4).
, where 12 is the annualization factor. Thus the inflation rate is the annualized log change in the price level, which is consistent
with (4).
We use Datastream to obtain daily price data for all of the 5-year and 10-year TIPS that have been auctioned by the U.S. Treasury through May 2010. We use this daily data to construct the gross market price for each available TIPS on the last day of each month. We use 10-year TIPS since it gives us the longest possible sample period, from January 1997 (the first ever TIPS auction) through May 2010. However, we include 5-year TIPS since the embedded option values for these TIPS are larger due to the lower cumulative inflation. Each TIPS in Datastream is identified by its International Securities Identification Number (ISIN). To verify the ISIN, we match it with the corresponding CUSIP in Treasury Direct. We use abbreviations to simplify the exposition. For example, the ISIN for the 10-year TIPS that was auctioned in January 1997 is US9128272M3. Since US9128 is common to all of the TIPS, we drop these characters and use the abbreviation 272M3. For each TIPS, we obtain from Datastream the clean price, the settlement date, the coupon rate, the issue date, and the maturity date. At the end of each month, we identify the previous and the next coupon dates, and we count the number of coupons remaining. We construct the gross market price of a TIPS as
In (6), the accrued interest is calculated using the coupon rate, the settlement date, the previous coupon date, and the next coupon date, while the index ratio is the CPI-U inflation adjustment term that is reported on Treasury Direct.
In addition to our sample of 5-year and 10-year TIPS, our estimation uses data on 5-year and 10-year nominal T-Notes. There are 21 ten-year TIPS and 7 five-year TIPS in our sample. For each TIPS, we search for a nominal T-Note with approximately the same issue and maturity dates. We are able to match all but one of our TIPS (the exception is January 1999, for which we cannot identify a matching 10-year nominal T-Note). Thus our sample includes 21 ten-year TIPS and 7 five-year TIPS, plus 20 ten-year matching nominal T-Notes and 7 five-year matching nominal T-Notes. For the matching nominal T-Notes, we obtain our data from Datastream.
We include nominal T-Notes in our sample for several reasons. First, nominal Treasury securities are an important input to any term structure model that is used to assess inflationary expectations. For example, see Campbell and Viceira (2001), Brennan and Xia (2002), Ang and Piazzesi (2003), Sangvinatsos and Wachter (2005), and Kim (2009), to name just a few. Second, by including nominal T-Notes in our estimation, we effectively double our sample size in each month, which helps to estimate the model parameters more precisely. Lastly, since the TIPS market is only about 8% of the size of the nominal Treasury market, we avoid overfitting the TIPS market by including nominal Treasury securities. This helps to control for the trading differences between TIPS and nominal Treasuries (Fleming and Krishnan, 2012) and it helps to address, but does not completely resolve, the issue of relative overpricing in the TIPS market (Fleckenstein, Longstaff, and Lustig, 2010). By including nominal Treasuries in our sample, it is less likely that our fitted parameters are capturing TIPS market imperfections that are present in the data.
To summarize, our data set includes monthly interest rates, monthly inflation rates, and monthly gross prices for TIPS and matching nominal T-Notes. Table 1 shows the TIPS and the nominal T-Notes that are included in our sample. There are 1,405 monthly observations for 10-year TIPS (Panel A), 1,268 monthly observations for 10-year nominal T-Notes (Panel B), 256 monthly observations for 5-year TIPS (Panel C), and 250 monthly observations for 5-year nominal T-Notes (Panel D).
4 Empirical results
Our empirical approach involves several steps. First, we estimate the parameters in (1)-(2) by minimizing the sum of the squared pricing errors for the full sample of 5-year and 10-year TIPS and matching nominal T-Notes (see Table 1). For completeness, we solve similar minimization problems using only 10-year TIPS and matching T-Notes (Panels A and B of Table 1) and using only 5-year TIPS and matching T-Notes (Panels C and D of Table 1). We report results for all three estimations. Second, we use our estimated parameters and our formula for the TIPS embedded option (see equations (42)-(44) in Appendix A) to calculate a set of times series of embedded option values for each TIPS in our sample. We use these time series to construct value-weighted embedded option price indices and value-weighted embedded option return indices. Our option indices, along with various controls, are then used as explanatory variables for in-sample and out-of-sample inflation regressions. In almost all of our regressions, the embedded option return index is statistically significant for explaining the one-month ahead and the one-year ahead inflation rate. We also consider several robustness checks, such as alternative weighting schemes, alternative variable specifications, and additional control variables.
4.1 Parameter estimation
We estimate the parameters in (1)-(2) by minimizing the sum of the squared errors between our model prices and the true market prices. A similar technique is used in Bakshi, Cao, and Chen (1997) and Huang and Wu (2004). Specifically, we solve the problem
where ![]() is the total number of months in the sample,
is the total number of months in the sample, ![]() is the number of TIPS
in the sample for month
is the number of TIPS
in the sample for month ![]() ,
, ![]() is the number of nominal T-Notes in the sample
for month
is the number of nominal T-Notes in the sample
for month ![]() ,
,
![]() is the gross market price of the
is the gross market price of the ![]() th TIPS for month
th TIPS for month ![]() ,
,
![]() is the gross market price of the
is the gross market price of the ![]() th nominal T-Note for month
th nominal T-Note for month
![]() ,
, ![]() is the model price of the
is the model price of the ![]() th TIPS for month
th TIPS for month ![]() , and
, and ![]() is the model price of the
is the model price of the ![]() th nominal T-Note for month
th nominal T-Note for month ![]() .
The model prices
.
The model prices ![]() and
and ![]() are given by (3)
and (5), respectively, and the parameter vector is
are given by (3)
and (5), respectively, and the parameter vector is
![]() .
.
To solve (7), we use Newton's method in the nonlinear least squares (NLIN) routine in SAS. Since (7) is sensitive to the choice of initial conditions, we double check our results by re-solving the problem using the Marquardt method, which is known to be less sensitive to the choice of initial values. In particular, we use a two-step procedure, first using the Marquardt method and then polishing the estimated parameter values using Newton's method. This robustness check provides the same result as using Newton's method alone. For our reported estimates, we verify a global minimum for (7) by checking that the first-order derivatives are zero and all eigenvalues of the Hessian are positive, which implies a positive definite Hessian.
Table 2 summarizes our estimation results. When we estimate our model using all of the TIPS and matching T-Notes from Table 1, we find that the mean absolute pricing error (![]() ) is
$2.717 per $100 face amount. Using only the 10-year TIPS and matching T-Notes, the
) is
$2.717 per $100 face amount. Using only the 10-year TIPS and matching T-Notes, the ![]() increases slightly to $2.953 per $100 face amount. Our mean pricing errors are higher than what is
reported in Chen, Liu, and Cheng (2010), but our sample period is longer than theirs and our model is fit to a wider variation in economic conditions. Our mean absolute yield error (
increases slightly to $2.953 per $100 face amount. Our mean pricing errors are higher than what is
reported in Chen, Liu, and Cheng (2010), but our sample period is longer than theirs and our model is fit to a wider variation in economic conditions. Our mean absolute yield error (![]() ) is
slightly more than 50 basis points, and there is little variation across the three estimations in Table 2. Our
) is
slightly more than 50 basis points, and there is little variation across the three estimations in Table 2. Our ![]() is comparable in magnitude to the RMSE of 74 basis points reported by Chen,
Liu, and Cheng (2010, p. 715). More broadly, our pricing errors are similar to other models in the literature. If we amortize our
is comparable in magnitude to the RMSE of 74 basis points reported by Chen,
Liu, and Cheng (2010, p. 715). More broadly, our pricing errors are similar to other models in the literature. If we amortize our ![]() of $2.717 over a ten year period using semi-annual
compounding, we get about 28 basis points per annum. This is similar to the average pricing errors reported in Dai and Singleton (2000, Table IV) for the swaps market using their
of $2.717 over a ten year period using semi-annual
compounding, we get about 28 basis points per annum. This is similar to the average pricing errors reported in Dai and Singleton (2000, Table IV) for the swaps market using their
![]() model. Our errors appear to be reasonable given that we are using a parsimonious model that is fit simultaneously to two markets, TIPS and nominal T-Notes.
model. Our errors appear to be reasonable given that we are using a parsimonious model that is fit simultaneously to two markets, TIPS and nominal T-Notes.
We also estimated our model using only 5-year TIPS and 5-year matching nominal T-Notes. As shown in Table 1, the number of 5-year TIPS during our sample period is one-third the number of 10-year TIPS. Furthermore, we see in Table 2 that the number of monthly observations for 5-year TIPS and
matching nominal T-Notes is about one-fifth the number of monthly observations for 10-year TIPS and matching nominal T-Notes. There is also a gap in the data using 5-year TIPS since the 5-year TIPS that was issued in July 1997 matured in July 2002, and the next auction of 5-year TIPS occurred in
October 2004. However, in spite of these issues, we went ahead and estimated our model using the available monthly 5-year TIPS data from July 1997 - May 2010. As shown in Table 2, the ![]() from this estimation is $1.416 per $100 face amount. Although this is lower than the
from this estimation is $1.416 per $100 face amount. Although this is lower than the ![]() from the other two estimations, it should be interpreted with caution since there are only seven
5-year TIPS in our sample.
from the other two estimations, it should be interpreted with caution since there are only seven
5-year TIPS in our sample.
To check the economics of our estimations, we compute the long-run means of ![]() and
and ![]() under
under ![]() , which we denote by
, which we denote by ![]() and
and ![]() , respectively. In Appendix C we show how to derive the formulas for
, respectively. In Appendix C we show how to derive the formulas for ![]() and
and ![]() . As Table 2 shows, our estimates of
. As Table 2 shows, our estimates of ![]() and
and
![]() are economically reasonable and are statistically different than zero. For example, using all of the TIPS and matching T-Notes from Table 1, we estimate the long-run mean interest
rate is 5.37% and the long-run mean inflation rate is 2.32%. This implies a long-run mean real rate of 3.05%.
are economically reasonable and are statistically different than zero. For example, using all of the TIPS and matching T-Notes from Table 1, we estimate the long-run mean interest
rate is 5.37% and the long-run mean inflation rate is 2.32%. This implies a long-run mean real rate of 3.05%.
4.2 Time variation in embedded option values
The far right column of Table 2 shows the range of values for the embedded deflation option in TIPS. For all three estimations, the minimum estimated option value is close to zero. For the estimation that uses 10-year TIPS and matching nominal T-Notes, the maximum option value across all TIPS-month observations is $0.0615 per $100 face amount. If we amortize $0.0615 using semi-annual compounding over the 10-year life of a TIPS, we get about 0.6 basis points. Thus on average, ignoring the embedded option on any given trading day has very little impact on the yield of a 10-year TIPS. This may help to explain why most of the existing TIPS literature does not focus on the embedded option.
For the estimation using 5-year TIPS and matching nominal T-Notes, the maximum option value across all TIPS-month observations is $1.3134 per $100 face amount. This is much higher than the $0.0615 per $100 principal amount that we found for 10-year TIPS, but it makes sense because most of the 5-year TIPS were outstanding during the deflationary period in the second half of 2008. In addition, the probability of experiencing cumulative deflation over a 5-year period is higher than the probability of experiencing cumulative deflation over a 10-year period. At the margin, this may be contributing to a higher embedded option value in 5-year TIPS relative to 10-year TIPS. If we amortize $1.3134 over the life of a 5-year TIPS, we find that the embedded option value accounts for up to 27 basis points of the TIPS yield. This is comparable to what is reported in Christensen, Lopez, and Rudebusch (2012), who find that the average value of the TIPS embedded option during 2009 is about 41 basis points.
We find that the estimated value of the embedded deflation option exhibits substantial time variation. Panel A of Figure 1 shows the time series of estimated option values for all 21 ten-year TIPS in our sample. We find a large spike in option values at the end of 2008 and the beginning of 2009. This corresponds to the period of the financial crisis, which was marked by deflationary expectations and negative changes in the CPI index for the second half of 2008. We also find a smaller spike in option values during the 2003-2004 period, which was also marked by deflationary pressure (Ip, 2004). The variation during 2003-2004 is difficult to see in Panel A, but it is more evident in Panel C, which is a zoomed version of Panel A. During most other time periods, the embedded option values are closer to zero. This is intuitive since if cumulative inflation is high, the embedded option will be further out-of-the-money and thus its value should be low.
We find similar results when we estimate our model using the combined sample of 5-year and 10-year TIPS and matching nominal T-Notes. Panel A of Figure 2 shows the estimated option values for all 7 five-year TIPS in our sample, while Panel B of Figure 2 shows the estimated option values for all 21 ten-year TIPS.4 We again find a large spike in option values during the financial crisis (both Panels A and B) and we also find a second spike during the 2003-2004 period (Panel B). Thus including 5-year TIPS does not alter the time variation in the option values.
Our results in Figures 1 and 2 are consistent with the existing literature. Wright (2009), Christensen (2009), and Christensen, Lopez, and Rudebusch (2011) use TIPS to infer the probability of deflation. During the later part of 2008, Wright (2009, Figure 2) shows that the probability of deflation was greater than one-half, which is confirmed by the results in Christensen (2009, Figure 3). Christensen, Lopez, and Rudebusch (2011, Figure 1) provide an estimate of the one-year ahead deflation probability from 1997-2010. Their Figure 1 is strikingly similar to our Figure 1, even though the two figures illustrate different quantities. In particular, their Figure 1 shows the probability that the price level will decrease, while our Figure 1 shows the value of the embedded option in TIPS. We return to this point later in section 4.6.1.
4.3 Joint significance of embedded option values and returns
We use our estimated option values to calculate a time series of option returns for each TIPS in our sample. Although the estimated option values are sometimes small (see Figures 1 and 2), the option returns are economically larger. For example, in Panel A of Figure 1, when the embedded option
value increases from $0.01 to $0.06 during the 2008-2009 period, the return is 500%. To test the joint statistical significance of the estimated option values and the option returns, we perform several Wald tests, which are shown in Table 3. Panel A (Panel B) of Table 3 shows the joint test results
for the option values (returns). In Panel A, for the sample of 10-year TIPS, we cannot reject the null hypothesis that the option values are jointly equal to zero. However, for the 5-year TIPS and for the combined sample of 5-year and 10-year TIPS, we strongly reject the null hypothesis that the
option values are jointly zero (the ![]() -values are less than 0.0001). Evidently, these results are being driven by the larger estimated embedded option values that are contained in 5-year TIPS.
In Panel B of Table 3, we strongly reject the null hypothesis that the option returns are jointly equal to zero (all of the
-values are less than 0.0001). Evidently, these results are being driven by the larger estimated embedded option values that are contained in 5-year TIPS.
In Panel B of Table 3, we strongly reject the null hypothesis that the option returns are jointly equal to zero (all of the ![]() -values are less than 0.0001). This is true for 5-year TIPS, for
10-year TIPS, and for the combined sample of 5-year and 10-year TIPS.
-values are less than 0.0001). This is true for 5-year TIPS, for
10-year TIPS, and for the combined sample of 5-year and 10-year TIPS.
To avoid numerical issues with calculating our option return test statistics in Panel B, we eliminate estimated option values that produce abnormally high returns. These abnormal returns originate in months where the beginning and ending option values have different orders of magnitude, yet both
values are small economically. For example, if an option value moves from ![]() to
to ![]() , the monthly return is very large, but both of the option values are approximately zero. To control for this effect, we discard option values that are smaller than
, the monthly return is very large, but both of the option values are approximately zero. To control for this effect, we discard option values that are smaller than ![]() . We tried other cutoff values, such as
. We tried other cutoff values, such as ![]() and
and ![]() ,
but it does not impact our tests in Table 3, nor does it impact our regression results that are shown below in Sections 4.6-4.8. We use a cutoff of
,
but it does not impact our tests in Table 3, nor does it impact our regression results that are shown below in Sections 4.6-4.8. We use a cutoff of ![]() since it maintains a relatively large sample size while avoiding numerical issues with calculating the option return test statistics. Removing the smallest option values from our sample has the effect of trimming outlier returns. Thus our option return tests in Panel B of
Table 3 are not driven by outliers.
since it maintains a relatively large sample size while avoiding numerical issues with calculating the option return test statistics. Removing the smallest option values from our sample has the effect of trimming outlier returns. Thus our option return tests in Panel B of
Table 3 are not driven by outliers.
4.4 Option-based explanatory variables
We use our estimated option values and option returns to construct explanatory variables for our regression analysis. For the ![]() th TIPS in month
th TIPS in month
![]() , let
, let ![]() denote the estimated value of the embedded option. Thus the option
return in month
denote the estimated value of the embedded option. Thus the option
return in month ![]() for the
for the ![]() th TIPS is
th TIPS is
![]() . For each of our three samples, we construct a value-weighted index for the embedded option price level and a value-weighted index for the embedded option return.
The weight
. For each of our three samples, we construct a value-weighted index for the embedded option price level and a value-weighted index for the embedded option return.
The weight ![]() for the
for the ![]() th TIPS in month
th TIPS in month ![]() is
is
![]() , where
, where ![]() is the number of TIPS in
the sample for month
is the number of TIPS in
the sample for month ![]() . Note that we use the lagged value
. Note that we use the lagged value ![]() when constructing
the weight
when constructing
the weight ![]() for month
for month ![]() . Thus the value-weighted embedded option price index in
month
. Thus the value-weighted embedded option price index in
month ![]() is
is
Panels B and D of Figure 1 show (8) when the model is estimated using 10-year TIPS and matching nominal T-Notes. Likewise, Panel C of Figure 2 shows (8) for 5-year and 10-year TIPS when the model is estimated using all of the bonds in Table
1. We also construct a value-weighted embedded option return index, which for month ![]() is given by
is given by
For robustness, we also checked an alternative definition of the option return index, namely
![]() . Under this alternative definition we found no material impact on our empirical results.
. Under this alternative definition we found no material impact on our empirical results.
4.5 Summary statistics
We examine the informational content of our variables ![]() and
and ![]() for explaining the future inflation rate. Suppose
for explaining the future inflation rate. Suppose ![]() is the value of the CPI-U that corresponds to month
is the value of the CPI-U that corresponds to month ![]() . We define the inflation rate from month
. We define the inflation rate from month ![]() to month
to month ![]() as
as
where ![]() is an annualization factor. Substituting
is an annualization factor. Substituting ![]() in (10) gives the one-month ahead inflation rate, while substituting
in (10) gives the one-month ahead inflation rate, while substituting ![]() in (10) gives the one-year ahead inflation rate. We use ( 10) as the
dependent variable in our regression analysis. In addition to
in (10) gives the one-year ahead inflation rate. We use ( 10) as the
dependent variable in our regression analysis. In addition to ![]() and
and ![]() in (8)-(9), our explanatory variables include: (i) the yield spread
in (8)-(9), our explanatory variables include: (i) the yield spread ![]() , which is the difference between the average yields of the
nominal T-Notes and the TIPS in our sample; (ii) the one-month lagged inflation rate,
, which is the difference between the average yields of the
nominal T-Notes and the TIPS in our sample; (ii) the one-month lagged inflation rate, ![]() ; (iii) the return on gold,
; (iii) the return on gold,
![]() , which we calculate using gold prices from the London Bullion Market Association; (iv) the return on VIX,
, which we calculate using gold prices from the London Bullion Market Association; (iv) the return on VIX,
![]() , which is the return on the S&P 500 implied volatility index; and (v) the value-weighted return on the TIPS in our sample,
, which is the return on the S&P 500 implied volatility index; and (v) the value-weighted return on the TIPS in our sample,
![]() .
.
We include ![]() as an explanatory variable since it is a common measure of inflation expectations. Hunter and Simon (2005) have also shown that the yield spread is correlated with TIPS
returns. We include
as an explanatory variable since it is a common measure of inflation expectations. Hunter and Simon (2005) have also shown that the yield spread is correlated with TIPS
returns. We include
![]() since the fluctuation in the price of gold has long been associated with inflationary expectations. Bekaert and Wang (2010) show that the inflation beta for gold in North
America is about 1.45. We include
since the fluctuation in the price of gold has long been associated with inflationary expectations. Bekaert and Wang (2010) show that the inflation beta for gold in North
America is about 1.45. We include
![]() since its time variation captures the uncertainty associated with macroeconomic activity, as described in Bloom (2009) and David and Veronesi (2011). Lastly, we include
since its time variation captures the uncertainty associated with macroeconomic activity, as described in Bloom (2009) and David and Veronesi (2011). Lastly, we include
![]() as a control variable to see if the TIPS total return has incremental explanatory power beyond that of the embedded option and our other variables. This allows us to compare
the informational content of the embedded option, which is the focus of our study, to that of the TIPS itself, which is examined by Chu, Pittman, and Chen (2007), D'Amico, Kim, and Wei (2010), and Chu, Pittman, and Yu (2011).
as a control variable to see if the TIPS total return has incremental explanatory power beyond that of the embedded option and our other variables. This allows us to compare
the informational content of the embedded option, which is the focus of our study, to that of the TIPS itself, which is examined by Chu, Pittman, and Chen (2007), D'Amico, Kim, and Wei (2010), and Chu, Pittman, and Yu (2011).
Table 4 shows summary statistics for our explanatory variables. For our sample of 5-year TIPS and matching nominal T-Notes, the mean of the embedded option return index is about 0.474, which is a 47.4% monthly average return. The standard deviation of the 5-year embedded option return index is about 1.90, or 190%. For our sample of 10-year TIPS and matching nominal T-Notes, the mean and standard deviation of the option return index are about 135% and 451%, respectively. The fact that the standard deviations are big coincides with our earlier statement that there is substantial time variation in the option returns. This is also apparent by examining the minimum and maximum values for the option return indices, as shown in the last two columns of Table 4.
Table 5 shows the sample correlation matrix for our explanatory variables. Panel A (Panel B) shows the matrix for 5-year (10-year) TIPS, while Panel C shows the matrix for the combined sample of 5-year and 10-year TIPS. The number in parentheses below each correlation is the ![]() -value for a test of the null hypothesis that the correlation coefficient is equal to zero. If we examine the column for the option return index, we see that the return index in all three panels has a
negative sample correlation with the yield spread, the return on gold, and lagged inflation. This is intuitive since the option return index is more likely to be high (low) during periods of deflationary (inflationary) expectations. We also see that the correlation between the option return index
and the TIPS total return is negative. During periods of deflationary expectations, we would expect investors to shun TIPS in favor of nominal bonds. Thus on average, the TIPS total return is low when the embedded option index return is high. Upon examining the
-value for a test of the null hypothesis that the correlation coefficient is equal to zero. If we examine the column for the option return index, we see that the return index in all three panels has a
negative sample correlation with the yield spread, the return on gold, and lagged inflation. This is intuitive since the option return index is more likely to be high (low) during periods of deflationary (inflationary) expectations. We also see that the correlation between the option return index
and the TIPS total return is negative. During periods of deflationary expectations, we would expect investors to shun TIPS in favor of nominal bonds. Thus on average, the TIPS total return is low when the embedded option index return is high. Upon examining the ![]() -values, we cannot reject the null hypothesis that the sample correlation between the yield spread and the option return index is zero. A similar statement holds for the VIX return. For the return on gold, lagged inflation, and
the TIPS total return, the
-values, we cannot reject the null hypothesis that the sample correlation between the yield spread and the option return index is zero. A similar statement holds for the VIX return. For the return on gold, lagged inflation, and
the TIPS total return, the ![]() -values are small and we reject the null that the correlations are zero. However, even for these variables, the magnitude of the coefficients is relatively small.
The numbers vary across Panels A, B, and C, but the gold return and the TIPS total return each have a correlation coefficient with the option return of about -0.25, while lagged inflation has
a correlation coefficient with the option return of about -0.5. Thus it appears that our option return index may be useful for explaining future inflation, even in the presence of these
traditional explanatory variables. We investigate this statement next.
-values are small and we reject the null that the correlations are zero. However, even for these variables, the magnitude of the coefficients is relatively small.
The numbers vary across Panels A, B, and C, but the gold return and the TIPS total return each have a correlation coefficient with the option return of about -0.25, while lagged inflation has
a correlation coefficient with the option return of about -0.5. Thus it appears that our option return index may be useful for explaining future inflation, even in the presence of these
traditional explanatory variables. We investigate this statement next.
4.6 In-sample inflation regressions
which is shown in Table 6. Panel A uses ![]() (one-month ahead) while Panel B uses
(one-month ahead) while Panel B uses ![]() (one-year ahead). In Panel A, our variable
(one-year ahead). In Panel A, our variable ![]() is statistically significant at the 5% level for the sample of 5-year TIPS and is statistically significant at the
1% level for the other two samples.5 This is true even when we include common variables that are known to capture future inflation, such as lagged inflation,
the yield spread, and the return on gold. In Panel B,
is statistically significant at the 5% level for the sample of 5-year TIPS and is statistically significant at the
1% level for the other two samples.5 This is true even when we include common variables that are known to capture future inflation, such as lagged inflation,
the yield spread, and the return on gold. In Panel B, ![]() is statistically significant at the 10% level (5% level) for the sample of 5-year (10-year) TIPS, and is statistically
significant at the 1% level for the combined sample of 5-year and 10-year TIPS. Since
is statistically significant at the 10% level (5% level) for the sample of 5-year (10-year) TIPS, and is statistically
significant at the 1% level for the combined sample of 5-year and 10-year TIPS. Since ![]() is insignificant in both panels, the return index
is insignificant in both panels, the return index ![]() appears to be a more important explanatory variable than the price level index
appears to be a more important explanatory variable than the price level index ![]() .
.
In Panel A of Table 6, note that the VIX return and lagged inflation are statistically significant for all three samples. However, these variables are no longer significant in Panel B. With the exception of a 10% significance for the yield spread in the 5-year sample, the only significant
variable in Panel B is ![]() . While traditional variables are significant for explaining the one-month ahead inflation rate (Panel A), they mostly fail to be significant for the one-year
ahead inflation rate (Panel B). In contrast,
. While traditional variables are significant for explaining the one-month ahead inflation rate (Panel A), they mostly fail to be significant for the one-year
ahead inflation rate (Panel B). In contrast, ![]() is important over both horizons. Since
is important over both horizons. Since ![]() is significant for the one-year horizon, our results are not driven by short-term timing differences between measuring inflation and reporting inflation (i.e., CPI-U announcements).6
is significant for the one-year horizon, our results are not driven by short-term timing differences between measuring inflation and reporting inflation (i.e., CPI-U announcements).6
If we examine the adjusted-![]() values in Panel A, using the combined sample of 5-year and 10-year TIPS, we find that
values in Panel A, using the combined sample of 5-year and 10-year TIPS, we find that ![]() alone explains
alone explains ![]() of the variation in the one-month ahead inflation rate. Once we add all of our control variables, the
adjusted-
of the variation in the one-month ahead inflation rate. Once we add all of our control variables, the
adjusted-![]() increases to 35.6% (see the last column in Panel A). In Panel B,
increases to 35.6% (see the last column in Panel A). In Panel B, ![]() alone explains
alone explains ![]() of the variation in the one-year ahead inflation rate, and this increases to 5.2% when we include the full set of control variables. Furthermore,
for all of our regressions in Table 6, the sign of the coefficient on
of the variation in the one-year ahead inflation rate, and this increases to 5.2% when we include the full set of control variables. Furthermore,
for all of our regressions in Table 6, the sign of the coefficient on ![]() is negative. This is consistent with our economic intuition. Since the embedded TIPS option is a deflation
option, a higher option return this month (as captured by
is negative. This is consistent with our economic intuition. Since the embedded TIPS option is a deflation
option, a higher option return this month (as captured by ![]() ) should be associated with a lower future inflation rate.
) should be associated with a lower future inflation rate.
We find that our results are not only statistically significant, but also economically significant. For example, for the sample of 5-year TIPS in Panel A of Table 6, the coefficient on ![]() is -0.0056 when the control variables are included. Thus a 100% embedded option return, which is less than one standard deviation, predicts a decrease of 56 basis
points in the one-month ahead annualized rate of inflation. If we compare this result to the other variables in the same regression, we find that
is -0.0056 when the control variables are included. Thus a 100% embedded option return, which is less than one standard deviation, predicts a decrease of 56 basis
points in the one-month ahead annualized rate of inflation. If we compare this result to the other variables in the same regression, we find that ![]() is at least as important
economically as the yield spread (coefficient of 0.31 for the 5-year sample) or the lagged inflation (coefficient of 0.28 for the 5-year sample). A one percentage point increase in the yield spread (lagged inflation rate) predicts a 31 basis point (28 basis point) increase in the one-month ahead
annualized rate of inflation.
is at least as important
economically as the yield spread (coefficient of 0.31 for the 5-year sample) or the lagged inflation (coefficient of 0.28 for the 5-year sample). A one percentage point increase in the yield spread (lagged inflation rate) predicts a 31 basis point (28 basis point) increase in the one-month ahead
annualized rate of inflation.
For the sample of 10-year TIPS in Panel A of Table 6, the coefficient on ![]() is -0.0031 when the control variables are included. This is lower than the coefficient of -0.0056 for 5-year TIPS. However, using Table 4, we see that
is -0.0031 when the control variables are included. This is lower than the coefficient of -0.0056 for 5-year TIPS. However, using Table 4, we see that ![]() for 5-year TIPS has a lower mean and standard deviation than
for 5-year TIPS has a lower mean and standard deviation than ![]() for 10-year TIPS. If we multiply
the regression coefficient for
for 10-year TIPS. If we multiply
the regression coefficient for ![]() times the expected option index return, we get 27 basis points (42 basis points) for the sample of 5-year (10-year) TIPS. Likewise, if we multiply the
regression coefficient for
times the expected option index return, we get 27 basis points (42 basis points) for the sample of 5-year (10-year) TIPS. Likewise, if we multiply the
regression coefficient for ![]() times the standard deviation of the option index return, we get 107 basis points (140 basis points) for 5-year (10-year) TIPS. The economic significance
tends to be slightly higher when we estimate our model using 10-year TIPS.
times the standard deviation of the option index return, we get 107 basis points (140 basis points) for 5-year (10-year) TIPS. The economic significance
tends to be slightly higher when we estimate our model using 10-year TIPS.
In Panel B of Table 6, the coefficients on ![]() are lower than their counterparts in Table A. For example, using the 5-year (10-year) sample of TIPS, a 100% embedded option return
predicts a decrease of 14 basis points (6.6 basis points) in the one-year ahead inflation rate when the control variables are included. If we multiply the regression coefficient for
are lower than their counterparts in Table A. For example, using the 5-year (10-year) sample of TIPS, a 100% embedded option return
predicts a decrease of 14 basis points (6.6 basis points) in the one-year ahead inflation rate when the control variables are included. If we multiply the regression coefficient for ![]() times the standard deviation of the option index return in Table 4, we get 27 basis points (30 basis points) for the sample of 5-year (10-year) TIPS. In both cases, the economic significance is lower than what we find in Panel A.
times the standard deviation of the option index return in Table 4, we get 27 basis points (30 basis points) for the sample of 5-year (10-year) TIPS. In both cases, the economic significance is lower than what we find in Panel A.
In summary, it appears that ![]() contains relevant information for future inflation out to a horizon of at least 12 months. The VIX return and lagged inflation are important at the
one-month horizon, but none of the control variables, with the exception of the yield spread for 5-year TIPS, are significant at the one-year horizon. In Table 6, our variable
contains relevant information for future inflation out to a horizon of at least 12 months. The VIX return and lagged inflation are important at the
one-month horizon, but none of the control variables, with the exception of the yield spread for 5-year TIPS, are significant at the one-year horizon. In Table 6, our variable ![]() is
the only variable that is consistently significant. Given the evidence from Table 6, we conclude that the embedded option in TIPS contains useful information about future inflation.
is
the only variable that is consistently significant. Given the evidence from Table 6, we conclude that the embedded option in TIPS contains useful information about future inflation.
4.6.1 Comparison to the literature
Panel C of Table 5 shows that the sample correlation between the option price index and the yield spread is -0.495 (![]() -value is less than 0.0001). We interpret this as evidence that our variable
-value is less than 0.0001). We interpret this as evidence that our variable ![]() is capturing deflationary
expectations - as inflation falls, the yield spread should decrease and the option value should increase. This interpretation coincides with the main results in Christensen, Lopez, and Rudebusch (2011). Their Figure 1, which shows the estimated probability of deflation, is strikingly similar to our
Figure 1, which shows our embedded option values. Both figures have peaks during the 2003-2004 and 2008-2009 periods, which are known periods of deflationary expectations.
is capturing deflationary
expectations - as inflation falls, the yield spread should decrease and the option value should increase. This interpretation coincides with the main results in Christensen, Lopez, and Rudebusch (2011). Their Figure 1, which shows the estimated probability of deflation, is strikingly similar to our
Figure 1, which shows our embedded option values. Both figures have peaks during the 2003-2004 and 2008-2009 periods, which are known periods of deflationary expectations.
We also compare our results to those in Wright (2009). Figure 1 in Wright (2009) shows the yields on two TIPS that have similar maturity dates but different issue dates. The two TIPS are the 1.875% 10-year TIPS with ISIN ending in 28BD1 and the 0.625% 5-year TIPS with ISIN ending in 28HW3. In
spite of the higher real coupon rate on the 10-year TIPS, Wright's Figure 1 shows that the 10-year TIPS yield is higher than the 5-year TIPS yield during the last few months of 2008 and the first half of 2009. Wright (2009, pp. 128-129) argues that the yield difference between these two TIPS is
mostly due to differences in the deflation option value and not due to liquidity. In other words, the embedded deflation option in the 5-year TIPS is worth more than the embedded deflation option in the 10-year TIPS, which coincides with our summary statistics in Table 4. We verify Wright's (2009)
conclusions by using our TIPS option pricing model. The results are shown in our Figure 3. Panel A of Figure 3 reproduces Wright's Figure 1, while Panel B of Figure 3 shows the yield difference, which is the 10-year TIPS yield minus the 5-year TIPS yield. Panel C of Figure 3 plots our estimated
option values for these two TIPS, while Panel D of Figure 3 shows the option value difference, which is the 5-year TIPS option value minus the 10-year TIPS option value. If we compare Panels B and D, we find that the option value difference closely tracks the yield difference. The biggest
difference in yields and option values occurs in the Fall of 2008, which was a deflationary period. When we regress the yield difference in Panel B onto the option value difference in Panel D, we get an adjusted-![]() of 75.5%. Thus our results are consistent with Wright's (2009) conjecture that the yield difference between on-the-run and off-the-run TIPS is mostly due to different embedded option values.
of 75.5%. Thus our results are consistent with Wright's (2009) conjecture that the yield difference between on-the-run and off-the-run TIPS is mostly due to different embedded option values.
4.6.2 Regressions with On-the-run TIPS
To investigate whether liquidity is a contributing factor in our results, we reconstruct the option indices in (8)-(9) using only on-the-run TIPS for each sample. Typically, the on-the-run TIPS is more liquid than any of the off-the-run TIPS. For example, Table 3 and Chart 1 in Fleming and Krishnan (2012) show that trading volume is substantially higher for on-the-run TIPS as compared to off-the-run TIPS. In addition, Fleming and Krishnan (2012, p. 7) report that about 85% of the time, the off-the-run 10-year TIPS has only a one-sided price quote (a bid or an ask, but not both) or no price quote at all. In other words, the quote incidence for off-the-run TIPS is much lower than that of the on-the-run TIPS. Since off-the-run TIPS are not as liquid, we eliminate these bonds from each sample when we reconstruct the indices in ( 8)-(9).
Our regression results using only on-the-run TIPS are shown in Table 7. In Panel A of Table 7, the economic and statistical significance of ![]() is very close to that of Panel A in
Table 6. We continue to find that lagged inflation and the VIX return are significant, but the statistical significance of the VIX return in Panel A of Table 7 for the sample of 10-year TIPS is reduced slightly relative to its counterpart in Table 6. In Panel B of Table 7, the statistical
significance of
is very close to that of Panel A in
Table 6. We continue to find that lagged inflation and the VIX return are significant, but the statistical significance of the VIX return in Panel A of Table 7 for the sample of 10-year TIPS is reduced slightly relative to its counterpart in Table 6. In Panel B of Table 7, the statistical
significance of ![]() is reduced slightly relative to what is shown in Panel B of Table 6. However, our variable
is reduced slightly relative to what is shown in Panel B of Table 6. However, our variable ![]() is the only significant variable in Panel B of Table 7. Traditional variables such as the lagged inflation and the VIX return are significant for explaining the one-month ahead inflation (Panel A of Table 7), but they again fail to be significant for the
one-year ahead inflation (Panel B of Table 7). In contrast, as we showed earlier,
is the only significant variable in Panel B of Table 7. Traditional variables such as the lagged inflation and the VIX return are significant for explaining the one-month ahead inflation (Panel A of Table 7), but they again fail to be significant for the
one-year ahead inflation (Panel B of Table 7). In contrast, as we showed earlier, ![]() is important over both horizons.
is important over both horizons.
The results in Table 7 suggest that illiquidity is not a main driver of our results. Even after discarding the most illiquid TIPS in each sample (i.e., the off-the-run TIPS), we still find that the embedded option index return ![]() is a useful variable for explaining the one-month ahead and the one-year ahead inflation rate.
is a useful variable for explaining the one-month ahead and the one-year ahead inflation rate.
4.7 Robustness
Our prior results suggest that the embedded option in TIPS contains useful information about the future rate of inflation. We now investigate whether our results are robust to changes in our modeling assumptions and our empirical approach. Specifically, we examine alternative weighting schemes for calculating the indices in (8)-(9), we consider an alternative option-based explanatory variable that is less sensitive to our model specification in (1 )-(2), and we consider an additional control variable that helps to capture future inflation. Lastly, in section 4.8 below, we investigate out-of-sample inflation forecasting using our embedded option explanatory variables.
4.7.1 Alternative weighting schemes
In (8)-(9), we used value weights to construct the variables ![]() and
and ![]() . In this section, we reconstruct the variables
. In this section, we reconstruct the variables ![]() and
and ![]() by using a variety of alternative weighting schemes. We then use these reconstructed variables in a regression analysis to see if our earlier results are sensitive to the choice of weights.
by using a variety of alternative weighting schemes. We then use these reconstructed variables in a regression analysis to see if our earlier results are sensitive to the choice of weights.
We first consider weighting schemes that are based on maturity. Following Section 4.4, let ![]() denote the number of TIPS in our sample in month
denote the number of TIPS in our sample in month ![]() . Suppose the
. Suppose the ![]() th TIPS in month
th TIPS in month ![]() has a remaining time to maturity
has a remaining time to maturity ![]() , which is measured in years. We use
, which is measured in years. We use ![]() to construct a set of maturity weights, where the weight assigned to the
to construct a set of maturity weights, where the weight assigned to the ![]() th TIPS in month
th TIPS in month ![]() is
is
Upon substituting (12) into the right-hand side of (8)-(9), we get a new pair of explanatory variables, ![]() and
and
![]() . The variable
. The variable ![]() is a maturity-weighted option price
index while the variable
is a maturity-weighted option price
index while the variable
![]() is a maturity-weighted option return index. Given the weighting scheme in (12), longer term options are assigned larger weights. We also construct a pair
of explanatory variables that favors shorter term options. To do this, the weight assigned to the
is a maturity-weighted option return index. Given the weighting scheme in (12), longer term options are assigned larger weights. We also construct a pair
of explanatory variables that favors shorter term options. To do this, the weight assigned to the ![]() th TIPS in month
th TIPS in month ![]() is
is
where ![]() is the original maturity of the
is the original maturity of the ![]() th TIPS. Upon substituting (13) into the right-hand side of (8)-( 9), we get a new pair of explanatory variables,
th TIPS. Upon substituting (13) into the right-hand side of (8)-( 9), we get a new pair of explanatory variables, ![]() and
and
![]() . The variable
. The variable ![]() (
(
![]() ) is an option price (option return) index that favors shorter term options.
) is an option price (option return) index that favors shorter term options.
Next, we consider weighting schemes that are based on moneyness. Using equation (42) in Appendix A, the embedded option's strike price divided by the inflation-adjusted face value for the ![]() th TIPS in month
th TIPS in month ![]() is
is
where the exponential term in (14) is the inflation adjustment factor. As discussed in Section 2.1, we substitute the U.S. Treasury's CPI-U index ratio for the inflation adjustment factor. Thus ![]() in (14) describes the moneyness of the embedded option. The inflation rate in our sample is usually positive, so almost all of the embedded options are out-of-the-money. However, we can use
in (14) describes the moneyness of the embedded option. The inflation rate in our sample is usually positive, so almost all of the embedded options are out-of-the-money. However, we can use ![]() to construct explanatory variables that depend on the level of option moneyness. For example, to favor nearer-to-the-money (NTM) options, the weight assigned to the
to construct explanatory variables that depend on the level of option moneyness. For example, to favor nearer-to-the-money (NTM) options, the weight assigned to the ![]() th TIPS in month
th TIPS in month ![]() is
is
Alternatively, to favor deeper out-of-the-money (OTM) options, the weight assigned to the ![]() th TIPS in month
th TIPS in month ![]() is
is
where the number 1 represents an at-the-money option. Upon substituting (15) into the right-hand side of (8)-( 9), we get a new pair of explanatory variables, ![]() and
and
![]() . These are the moneyness-weighted option price and option return indices that favor NTM options. Similarly, upon substituting ( 16) into the right-hand
side of (8)-(9 ), we get
. These are the moneyness-weighted option price and option return indices that favor NTM options. Similarly, upon substituting ( 16) into the right-hand
side of (8)-(9 ), we get ![]() and
and
![]() . These are the moneyness-weighted option price and option return indices that favor deeper OTM options.
. These are the moneyness-weighted option price and option return indices that favor deeper OTM options.
Table 8 shows the regression results when we use our alternative weighting schemes for the sample of 5-year TIPS. Panel A (Panel B) shows the results when the dependent variable is the one-month (one-year) ahead inflation rate. Table 9 is similar but shows the results for the sample of 10-year
TIPS. Columns 1, 3, 5, and 7 of each table are univariate regressions that use
![]() ,
,
![]() ,
,
![]() , and
, and
![]() , respectively, as the explanatory variable. In both panels of Tables 8 and 9, the coefficients on these variables have the correct sign and are statistically significant at
either the 1% level or the 5% level. In columns 2, 4, 6, and 8 of each table, we add several additional explanatory variables. In Panel A of Table 8, we see that lagged inflation, the VIX return, and the TIPS total return are statistically significant, which mirrors our results in Panel A of Table
6 for 5-year TIPS. In Panel B of Table 8, the yield spread is statistically significant, which mirrors Panel B of Table 6 for 5-year TIPS. Likewise, the VIX return and lagged inflation are significant in Panel A of Table 9, but none of the control variables are significant in Panel B of Table 9.
This mimics our results in Panels A and B of Table 6 for 10-year TIPS.
, respectively, as the explanatory variable. In both panels of Tables 8 and 9, the coefficients on these variables have the correct sign and are statistically significant at
either the 1% level or the 5% level. In columns 2, 4, 6, and 8 of each table, we add several additional explanatory variables. In Panel A of Table 8, we see that lagged inflation, the VIX return, and the TIPS total return are statistically significant, which mirrors our results in Panel A of Table
6 for 5-year TIPS. In Panel B of Table 8, the yield spread is statistically significant, which mirrors Panel B of Table 6 for 5-year TIPS. Likewise, the VIX return and lagged inflation are significant in Panel A of Table 9, but none of the control variables are significant in Panel B of Table 9.
This mimics our results in Panels A and B of Table 6 for 10-year TIPS.
Chu, Pittman, and Chen (2007) show that the market price of TIPS contains useful information about inflation expectations. Our results in Tables 6-9 provide limited support for their conclusion. Specifically, in Panel A of Table 6, using the sample of 5-year TIPS, we find that the TIPS total
return
![]() is significant for explaining the one-month ahead inflation rate, even in the presence of
is significant for explaining the one-month ahead inflation rate, even in the presence of ![]() ,
, ![]() , and the other control variables. A similar statement holds for all of the regressions in Panel A of Table 8. However, we find that
, and the other control variables. A similar statement holds for all of the regressions in Panel A of Table 8. However, we find that
![]() is not significant in Panel B of Tables 6 and 8, nor is it significant in Panels A or B in Table 7, which uses only on-the-run TIPS. Furthermore,
is not significant in Panel B of Tables 6 and 8, nor is it significant in Panels A or B in Table 7, which uses only on-the-run TIPS. Furthermore,
![]() is not significant in any of our other regressions, such as those using 10-year TIPS or the combined sample of 5-year and 10-year TIPS. Thus it appears that the informational
content of TIPS is coming mostly from the embedded option return and not from the TIPS total return.
is not significant in any of our other regressions, such as those using 10-year TIPS or the combined sample of 5-year and 10-year TIPS. Thus it appears that the informational
content of TIPS is coming mostly from the embedded option return and not from the TIPS total return.
Overall, Tables 8-9 indicate that our earlier results are robust to different weighting schemes. The only exception to this statement occurs in column 8 of Panel A in Tables 8-9, where we use the option return index that favors out-of-the-money options, i.e.,
![]() . We find that this variable is not significant for explaining the one-month ahead inflation rate in the presence of our control variables. Note that
. We find that this variable is not significant for explaining the one-month ahead inflation rate in the presence of our control variables. Note that
![]() favors out-of-the-money options, which are the least sensitive options to movements in inflation. Thus it is perhaps not too surprising that
favors out-of-the-money options, which are the least sensitive options to movements in inflation. Thus it is perhaps not too surprising that
![]() is insignificant. Out of all of our alternative weighting schemes, this is the one that we would have guessed to be least informative. However, this is not to say that
is insignificant. Out of all of our alternative weighting schemes, this is the one that we would have guessed to be least informative. However, this is not to say that
![]() does not contain useful information about future inflation. In panel B of both Tables 8 and 9, we find that
does not contain useful information about future inflation. In panel B of both Tables 8 and 9, we find that
![]() is significant for explaining the one-year ahead inflation rate. Thus even though our control variables drive out of the significance of
is significant for explaining the one-year ahead inflation rate. Thus even though our control variables drive out of the significance of
![]() at the one-month horizon, it remains an important variable at the one-year horizon.
at the one-month horizon, it remains an important variable at the one-year horizon.
4.7.2 Alternative measure of option returns
In the previous sections, we used (8)-(9) to construct ![]() and
and ![]() , where the individual embedded option values were obtained from our TIPS pricing model that uses ( 1)-(2). In this section, we explore an alternative
explanatory variable that is less sensitive to model specification. We use the embedded option returns in each month to compute a new variable,
, where the individual embedded option values were obtained from our TIPS pricing model that uses ( 1)-(2). In this section, we explore an alternative
explanatory variable that is less sensitive to model specification. We use the embedded option returns in each month to compute a new variable, ![]() , which we define as the fraction of
options in month
, which we define as the fraction of
options in month ![]() with a positive return. To calculate
with a positive return. To calculate ![]() , we divide the
number of embedded options with a positive return in month
, we divide the
number of embedded options with a positive return in month ![]() by the total number of embedded options in month
by the total number of embedded options in month ![]() . Using
. Using ![]() instead of
instead of ![]() allows us to
investigate the robustness of our modeling assumptions. Any other model that produces positive (negative) embedded option returns when our model produces positive (negative) embedded option returns will give the same time series for
allows us to
investigate the robustness of our modeling assumptions. Any other model that produces positive (negative) embedded option returns when our model produces positive (negative) embedded option returns will give the same time series for ![]() and thus the same regression results.
and thus the same regression results.
Table 10 shows our regressions results when ![]() is used in place of
is used in place of ![]() . The first two columns of Table 10 use the combined sample of 5-year and 10-year TIPS, while the last two columns use the subsample that includes only on-the-run TIPS. In both Panels A and B of Table 10, we see that
. The first two columns of Table 10 use the combined sample of 5-year and 10-year TIPS, while the last two columns use the subsample that includes only on-the-run TIPS. In both Panels A and B of Table 10, we see that ![]() is statistically significant, although the level of significance is reduced in some cases relative to Tables 6 and 7. In Panel A of Table 10, we see that lagged inflation and the VIX return are significant variables for explaining the
one-month ahead inflation rate, which is also true in Panel A of Tables 6 and 7. Likewise, in Panel B of Table 10, we see that none of the control variables are significant for explaining the one-year ahead inflation rate, which mirrors our results in Panel B of Tables 6 and 7.
is statistically significant, although the level of significance is reduced in some cases relative to Tables 6 and 7. In Panel A of Table 10, we see that lagged inflation and the VIX return are significant variables for explaining the
one-month ahead inflation rate, which is also true in Panel A of Tables 6 and 7. Likewise, in Panel B of Table 10, we see that none of the control variables are significant for explaining the one-year ahead inflation rate, which mirrors our results in Panel B of Tables 6 and 7.
The regressions in Table 10 show that our modeling assumptions in (1)-(2) are not critical to our results. If we were to alter (1)-(2) in such a way that the sign of each
option return did not change, we would get the same variable ![]() and thus the same results in Table 10. Tables 6 and 7 show that the embedded option return index is informationally
relevant for explaining the one-month ahead and the one-year ahead inflation rate. When we ignore the magnitude of the option returns and focus only on the sign of those returns, we get an explanatory variable (namely,
and thus the same results in Table 10. Tables 6 and 7 show that the embedded option return index is informationally
relevant for explaining the one-month ahead and the one-year ahead inflation rate. When we ignore the magnitude of the option returns and focus only on the sign of those returns, we get an explanatory variable (namely, ![]() ) that is also informationally relevant. However, if we compare the adjusted-
) that is also informationally relevant. However, if we compare the adjusted-![]() values in Table 10 to those in Tables 6 and 7, we see that the values
in Table 10 are smaller. But this is exactly what we would expect to find given that
values in Table 10 to those in Tables 6 and 7, we see that the values
in Table 10 are smaller. But this is exactly what we would expect to find given that ![]() captures only the sign of the option returns and not the magnitude. Overall, Table 10 shows that
our results are robust to model specification.
captures only the sign of the option returns and not the magnitude. Overall, Table 10 shows that
our results are robust to model specification.
4.7.3 Additional control variable
In this section we examine the ability of ![]() to explain the future rate of inflation in the presence of an additional control variable, the
return on crude oil
to explain the future rate of inflation in the presence of an additional control variable, the
return on crude oil
![]() . The price of crude oil is impacted by many factors, such as pricing policies in the OPEC cartel, supply disruptions due to weather or political instability, and
speculative demand. The relationship between inflation and the price of crude oil is not necessarily stable over time, a point of view that is supported by Bekaert and Wang (2010) and Hamilton (2009). Because of this, we treat crude oil separately so as to better gauge the marginal impact of
including the crude oil return as a control variable in our regressions.
. The price of crude oil is impacted by many factors, such as pricing policies in the OPEC cartel, supply disruptions due to weather or political instability, and
speculative demand. The relationship between inflation and the price of crude oil is not necessarily stable over time, a point of view that is supported by Bekaert and Wang (2010) and Hamilton (2009). Because of this, we treat crude oil separately so as to better gauge the marginal impact of
including the crude oil return as a control variable in our regressions.
Our results with crude oil are shown in Table 11, where we analyze both the one-month ahead inflation rate (Panel A) and the one-year ahead inflation rate (Panel B) using the 5-year sample of TIPS, the 10-year sample of TIPS, and the 5-year and 10-year combined sample of TIPS. In both panels, we
see that the crude oil return is statistically significant for all three samples. To see the marginal impact of
![]() , we compare Table 11 to Table 6. For the 5-year sample of TIPS, the addition of
, we compare Table 11 to Table 6. For the 5-year sample of TIPS, the addition of
![]() drives out the significance of
drives out the significance of ![]() in both Panels A
and B. It also reduces the significance of the VIX return and lagged inflation, as compared to Panel A in Table 6. For the 10-year sample of TIPS and for the combined sample of 5-year and 10-year TIPS, the addition of
in both Panels A
and B. It also reduces the significance of the VIX return and lagged inflation, as compared to Panel A in Table 6. For the 10-year sample of TIPS and for the combined sample of 5-year and 10-year TIPS, the addition of
![]() reduces, but does not drive out, the significance of
reduces, but does not drive out, the significance of ![]() . This is true in both Panels A and B of Table 11. In the last two columns of Panel B, only the oil return and the embedded option return are statistically significant for explaining the one-year ahead inflation rate.
. This is true in both Panels A and B of Table 11. In the last two columns of Panel B, only the oil return and the embedded option return are statistically significant for explaining the one-year ahead inflation rate.
Overall, our results in Table 11 are mixed since ![]() is not significant in the presence of
is not significant in the presence of
![]() for 5-year TIPS, but it is significant in the presence of
for 5-year TIPS, but it is significant in the presence of
![]() for the other two samples. In spite of this, the results in Table 11 are consistent with our earlier results in Tables 6 and 7. In those two tables,
for the other two samples. In spite of this, the results in Table 11 are consistent with our earlier results in Tables 6 and 7. In those two tables, ![]() is less significant when it is constructed with only 5-year TIPS, as compared to 10-year TIPS or the combined sample of 5-year and 10-year TIPS. We attribute this to the smaller sample size of
5-year TIPS relative to 10-year TIPS, as shown in Table 1. Since
is less significant when it is constructed with only 5-year TIPS, as compared to 10-year TIPS or the combined sample of 5-year and 10-year TIPS. We attribute this to the smaller sample size of
5-year TIPS relative to 10-year TIPS, as shown in Table 1. Since ![]() is significant in the last two columns of Table 11, the embedded option in TIPS contains useful information for
explaining the future inflation rate, even in the presence of
is significant in the last two columns of Table 11, the embedded option in TIPS contains useful information for
explaining the future inflation rate, even in the presence of
![]() .
.
4.8 Out-of-sample inflation regressions
In Section 4.6, we showed that ![]() is significant for explaining the one-month ahead and the one-year ahead
inflation rate. Since our estimation results in Table 2 use data for the entire sample period 1997-2010, our embedded option index variables in (8)-(9) rely on parameter estimates that have a forward looking bias. Thus our results in Section
4.6 should not be interpreted as inflation forecasts - they are simply in-sample results. We now address this issue by using a rolling window approach. We use all of the securities in Table 1 and we re-estimate our model using rolling subsamples. Using the parameter
estimates for each subsample, we calculate the embedded option values and the embedded option returns. We then use the option values and the option returns to explain the future inflation rate, which is a true out-of-sample analysis.
is significant for explaining the one-month ahead and the one-year ahead
inflation rate. Since our estimation results in Table 2 use data for the entire sample period 1997-2010, our embedded option index variables in (8)-(9) rely on parameter estimates that have a forward looking bias. Thus our results in Section
4.6 should not be interpreted as inflation forecasts - they are simply in-sample results. We now address this issue by using a rolling window approach. We use all of the securities in Table 1 and we re-estimate our model using rolling subsamples. Using the parameter
estimates for each subsample, we calculate the embedded option values and the embedded option returns. We then use the option values and the option returns to explain the future inflation rate, which is a true out-of-sample analysis.
More specifically, our full sample period is January 1997 through May 2010, which is 161 months. We use a 48-month rolling window, which allows us to construct 114 subsamples. The first subsample spans January 1997 through December 2000, the second subsample spans February 1997 through January
2001, and so forth. For each subsample, we seek a solution to the optimization problem in (7). We then use the embedded option values from the last month and from the next to the last month of each subsample to calculate ![]() and
and ![]() according to (8)-(9). In the subsample that spans January 1997 -
December 2000, we use the embedded option values from November-December 2000 to calculate
according to (8)-(9). In the subsample that spans January 1997 -
December 2000, we use the embedded option values from November-December 2000 to calculate ![]() and
and ![]() for December 2000; in the subsample that spans February 1997 - January 2001, we use the embedded option values from December 2000 and January 2001 to calculate
for December 2000; in the subsample that spans February 1997 - January 2001, we use the embedded option values from December 2000 and January 2001 to calculate ![]() and
and ![]() for January 2001; and so forth. This gives us a new time series for
for January 2001; and so forth. This gives us a new time series for ![]() and a new time series for
and a new time series for ![]() that do not suffer from forward looking bias.
that do not suffer from forward looking bias.
Table 12 shows the regression results for our out-of-sample approach. Panel A shows our regressions for the one-month ahead out-of-sample inflation rate, while Panel B shows our regressions for the one-year ahead out-of-sample inflation rate. In Panel A of Table 12, ![]() is statistically significant at the 1% level, even in the presence of the control variables. As we saw in the last column of Panel A in Table 6, the VIX return and lagged inflation are also
significant, but unlike Table 6 the yield spread is insignificant. D'Amico, Kim, and Wei (2010) show that the yield spread is a useful measure of inflation expectations, but only after controlling for liquidity in the TIPS market. We do not directly control for TIPS liquidity, but our out-of-sample
analysis focuses on the latter portion of our sample period, where TIPS liquidity is less of a concern relative to the initial years of TIPS trading. In Panel B of Table 12, in the second column where we include the control variables, we find that the only significant variables are
is statistically significant at the 1% level, even in the presence of the control variables. As we saw in the last column of Panel A in Table 6, the VIX return and lagged inflation are also
significant, but unlike Table 6 the yield spread is insignificant. D'Amico, Kim, and Wei (2010) show that the yield spread is a useful measure of inflation expectations, but only after controlling for liquidity in the TIPS market. We do not directly control for TIPS liquidity, but our out-of-sample
analysis focuses on the latter portion of our sample period, where TIPS liquidity is less of a concern relative to the initial years of TIPS trading. In Panel B of Table 12, in the second column where we include the control variables, we find that the only significant variables are ![]() (significant at the 10% level) and
(significant at the 10% level) and ![]() (significant at the 1% level). Although
(significant at the 1% level). Although
![]() is more significant statistically than
is more significant statistically than ![]() , it is less significant
economically. We can see this from the regression coefficients in Panel B and from the summary statistics in Table 4, where the mean and standard deviation of
, it is less significant
economically. We can see this from the regression coefficients in Panel B and from the summary statistics in Table 4, where the mean and standard deviation of ![]() are small relative to the
values for
are small relative to the
values for ![]() . Lastly, upon examining the adjusted-
. Lastly, upon examining the adjusted-![]() values, we see that
values, we see that
![]() ,
, ![]() , and the control variables in Panel A (Panel B) explain 35.3% (
11.7%) of the variation in the one-month (one-year) ahead out-of-sample inflation rate. For Panel A (Panel B), these numbers are about the same as (better than) the corresponding values in Table 6.
, and the control variables in Panel A (Panel B) explain 35.3% (
11.7%) of the variation in the one-month (one-year) ahead out-of-sample inflation rate. For Panel A (Panel B), these numbers are about the same as (better than) the corresponding values in Table 6.
We also use ![]() as an explanatory variable in Table 12. Recall from Section 4.7.2 that
as an explanatory variable in Table 12. Recall from Section 4.7.2 that ![]() is robust to model specification since any other pricing model that produces the same signs for the embedded option returns will produce the same variable
is robust to model specification since any other pricing model that produces the same signs for the embedded option returns will produce the same variable ![]() . Our results with
. Our results with ![]() are shown in the last two columns in Table 12. In Panel A, we find that
are shown in the last two columns in Table 12. In Panel A, we find that ![]() alone is significant at the 1% level, but the significance is driven out by the control variables. Thus it appears that the magnitude of the option returns, and not just the sign of those returns, is important for explaining the one-month ahead
out-of-sample inflation rate. In Panel B, we find that
alone is significant at the 1% level, but the significance is driven out by the control variables. Thus it appears that the magnitude of the option returns, and not just the sign of those returns, is important for explaining the one-month ahead
out-of-sample inflation rate. In Panel B, we find that ![]() alone is significant at the 5% level, and
alone is significant at the 5% level, and ![]() remains significant at the 10% level when the control variables are included. This suggests the sign of the option return contains useful information for forecasting the one-year ahead out-of-sample inflation rate. This is similar to our earlier in-sample
results in Panel B of Table 10.
remains significant at the 10% level when the control variables are included. This suggests the sign of the option return contains useful information for forecasting the one-year ahead out-of-sample inflation rate. This is similar to our earlier in-sample
results in Panel B of Table 10.
If we compare the out-of-sample results in Table 12 to the corresponding in-sample results in Tables 6 and 10, we see that the out-of-sample results are slightly weaker than the in-sample results. There are at least two contributing reasons. First, our rolling subsample is only 48 months long, which is much shorter than our full sample of 161 months. Thus our parameter estimates and our embedded option estimates are noisier in the subsamples, which makes for noisier embedded option explanatory variables. Second, the short length of our window decreases not only the time length of each subsample, but it can also decrease the number of securities that is included in each subsample. For example, in our early subsamples, the number of TIPS and matching nominal Treasuries is reduced since some of these securities have not yet been auctioned. The smaller number of securities implies that there are fewer observations within the subsample for estimating our model parameters, which again will lead to noisier parameter estimates. In spite of these issues, our results in Table 12 suggest that even out-of-sample, the embedded option in TIPS contains information that is useful for explaining future inflation.
5 Concluding remarks
Our paper uncovers the informational content of the embedded deflation option in TIPS. We value the option explicitly and we show that the embedded option return contains relevant information for explaining the one-month ahead and the one-year ahead inflation rate, even in the presence of standard inflation variables. In almost all of our regressions, including our robustness checks, the embedded option return index is statistically and economically important. We argue that the embedded option return should not be ignored. In fact, our results suggest that the time variation in the embedded option return is a valuable tool for anyone who is interested in assessing inflationary expectations.
Our paper contains several new findings. First, we conclude that the embedded option return index is a significant variable for explaining the one-month ahead and the one-year ahead inflation rate, both in-sample and out-of-sample. Using 5-year (10-year) TIPS, our results suggest that a
![]() embedded option return, which is less than one standard deviation, is consistent with a 110 basis point (52 basis point) decrease in the one-month ahead annualized rate of inflation.
For most of our regressions, the traditional inflation variables such as the yield spread and the return on gold are insignificant in the presence of our embedded option return index. However, the lagged inflation rate and the return on the VIX index continue to be important variables. Presumably,
these variables capture additional uncertainty beyond what is contained in the embedded option return. Second, our main conclusions are not altered when we discard off-the-run TIPS, when we use alternative weighting schemes, when we add an additional control variable (the crude oil return), or when
we use our variable
embedded option return, which is less than one standard deviation, is consistent with a 110 basis point (52 basis point) decrease in the one-month ahead annualized rate of inflation.
For most of our regressions, the traditional inflation variables such as the yield spread and the return on gold are insignificant in the presence of our embedded option return index. However, the lagged inflation rate and the return on the VIX index continue to be important variables. Presumably,
these variables capture additional uncertainty beyond what is contained in the embedded option return. Second, our main conclusions are not altered when we discard off-the-run TIPS, when we use alternative weighting schemes, when we add an additional control variable (the crude oil return), or when
we use our variable ![]() , which is less sensitive to model specification. Third, we present evidence to show that our results continue to hold out-of-sample (Table 12). Lastly, we analyze
5-year TIPS, 10-year TIPS, and the combined sample of 5-year and 10-year TIPS. Although our results are somewhat weaker for 5-year TIPS, perhaps due to the smaller sample size, we find that the evidence from 5-year TIPS is not enough to alter our main conclusions. In summary, our paper shows that
the embedded deflation option in TIPS is informationally relevant for explaining future inflation, both in-sample and out-of-sample, out to a horizon of twelve months.
, which is less sensitive to model specification. Third, we present evidence to show that our results continue to hold out-of-sample (Table 12). Lastly, we analyze
5-year TIPS, 10-year TIPS, and the combined sample of 5-year and 10-year TIPS. Although our results are somewhat weaker for 5-year TIPS, perhaps due to the smaller sample size, we find that the evidence from 5-year TIPS is not enough to alter our main conclusions. In summary, our paper shows that
the embedded deflation option in TIPS is informationally relevant for explaining future inflation, both in-sample and out-of-sample, out to a horizon of twelve months.
There are several areas for future research. First, our TIPS pricing model is a traditional asset pricing model in the sense that we do not directly model liquidity. In fact, this is one of the reasons that we discard the off-the-run TIPS and we explore how our regressions perform using only
on-the-run TIPS (see Table 7). A more complicated approach would be to derive a TIPS pricing model that accommodates liquidity directly. This type of pricing model could be estimated using both on-the-run and off-the-run TIPS, with the understanding that liquidity is captured by the model itself.
Second, although we conduct robustness checks using our variable ![]() , which is significant in Tables 10 and 12, we do not claim that our model in ( 1)-(2) is the best way to price a TIPS. Our motivation for using (1)-(2 ) is twofold - the model is parsimonious and we can solve the model in closed-form. Thus one avenue for future
research is to explore other pricing models and perhaps run a horse race between them to find the best pricing model. In the context of our paper, the best pricing model would be the one that provides the most information for forecasting future inflation. Lastly, we have shown that
, which is significant in Tables 10 and 12, we do not claim that our model in ( 1)-(2) is the best way to price a TIPS. Our motivation for using (1)-(2 ) is twofold - the model is parsimonious and we can solve the model in closed-form. Thus one avenue for future
research is to explore other pricing models and perhaps run a horse race between them to find the best pricing model. In the context of our paper, the best pricing model would be the one that provides the most information for forecasting future inflation. Lastly, we have shown that ![]() and
and ![]() are informationally relevant variables for explaining the inflation rate.
However, we do not examine higher-order moments of these variables, nor do we examine how the inflation probability density evolves over time. This latter topic is complicated since we estimate our model under the risk-adjusted probabilities. We leave these areas as ideas for future research.
are informationally relevant variables for explaining the inflation rate.
However, we do not examine higher-order moments of these variables, nor do we examine how the inflation probability density evolves over time. This latter topic is complicated since we estimate our model under the risk-adjusted probabilities. We leave these areas as ideas for future research.
Appendix
A. Pricing model for TIPS
We stack the nominal interest rate ![]() and the inflation rate
and the inflation rate ![]() into a vector
into a vector
![]() , where
, where ![]() denotes the transpose. Thus we can rewrite
(1)-(2 ) as
denotes the transpose. Thus we can rewrite
(1)-(2 ) as
where
![]() ,
,
![]() , and
, and ![]() and
and ![]() are the matrices
are the matrices
Since ![]() is not a diagonal matrix, (17) is a coupled system of equations. Changes in
is not a diagonal matrix, (17) is a coupled system of equations. Changes in ![]() depend on both
depend on both ![]() and
and ![]() , while changes in
, while changes in
![]() depend on both
depend on both ![]() and
and ![]() . Instead of working with
. Instead of working with ![]() directly, we work with a decoupled system that is related to (17). Define
directly, we work with a decoupled system that is related to (17). Define
![]() as
as
![\begin{displaymath} \Lambda =\left[ \begin{array}{cc} 1 & \frac{A_{12}}{\lambda _{2}-A_{11}} \ \frac{A_{21}}{\lambda _{1}-A_{22}} & 1 \end{array}\right] , \end{displaymath}](img131.gif)
where ![]() and
and ![]() are
are
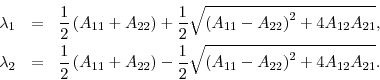
The constants ![]() and
and ![]() are the eigenvalues of
are the eigenvalues of ![]() , while the columns of
, while the columns of ![]() are the associated eigenvectors. It is easily verified that
are the associated eigenvectors. It is easily verified that
![]() , where
, where ![]() is the diagonal matrix
is the diagonal matrix
We now define a new set of variables
![]() , where
, where
![]() . Also define
. Also define
![]() and
and
![]() , where
, where
![]() and where
and where
Using Itô's lemma, the process for ![]() is
is
which is an uncoupled system since ![]() is diagonal. We solve (3) using the variables
is diagonal. We solve (3) using the variables ![]() and
and ![]() . We then recover the TIPS price in terms of
. We then recover the TIPS price in terms of ![]() and
and ![]() by noting that
by noting that
![]() , i.e.,
, i.e.,
To get the moments for ![]() and
and ![]() , we solve (18)
to get
, we solve (18)
to get
for ![]() . Taking expectations of (20)-(21) gives
. Taking expectations of (20)-(21) gives
To get the variance of ![]() , note that
, note that
A similar calculation gives
To get the covariance between ![]() and
and ![]() , note that
, note that
Given (18), ![]() and
and ![]() are bivariate normal with
conditional moments (22)-(23), (24)-(25), and (26). To evaluate the TIPS price, we need to know the joint distribution of
are bivariate normal with
conditional moments (22)-(23), (24)-(25), and (26). To evaluate the TIPS price, we need to know the joint distribution of
![]() and
and
![]() for
for
![]() . Using (19), note that
. Using (19), note that
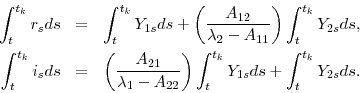
Thus to get the joint distribution of
![]() and
and
![]() , it is sufficient to characterize the joint distribution of
, it is sufficient to characterize the joint distribution of
![]() and
and
![]() . Since
. Since ![]() and
and ![]() are jointly normal,
are jointly normal,
![]() and
and
![]() are also jointly normal. This follows since the sum of normally distributed random variables is also normally distributed. Thus we only need to characterize the first
two moments of
are also jointly normal. This follows since the sum of normally distributed random variables is also normally distributed. Thus we only need to characterize the first
two moments of
![]() and
and
![]() .
.
Suppose ![]() and recall that
and recall that ![]() . We focus on the case of time
. We focus on the case of time ![]() , but our results apply for any
, but our results apply for any ![]() in the upper limit of integration. Using (20)-(21), we have
in the upper limit of integration. Using (20)-(21), we have
and
Thus
To get the variance of
![]() note that
note that
The last line of (31) includes two terms. The first term is
We need to calculate
![]() which is
which is
Substituting (33) into the right-hand side of (32), we get
which is easy to evaluate. The second term in the last line of ( 31) is
Using (27), note that
![\begin{eqnarray*} \int_{s}^{T}Y_{1u}du &=&\int_{s}^{T}e^{\lambda _{1}(u-s)}Y_{1s}du+\frac{b_{1} }{\lambda _{1}}\int_{s}^{T}\left[ e^{\lambda _{1}(u-s)}-1\right] du \ &&+\int_{s}^{T}e^{\lambda _{1}u}\int_{s}^{u}e^{-\lambda _{1}v}\left( \sigma _{11}dz_{1v}^{Q}+\sigma _{12}dz_{2v}^{Q}\right) du. \end{eqnarray*}](img197.gif)
The right hand side of the above expression has three terms, but only the first term on the right hand side has non-zero correlation with ![]() . Thus
. Thus
which can be evaluated using (24). Combining (34) and (35) gives the result
A similar calculation gives
To get the covariance between
![]() and
and
![]() , note that
, note that
Like equation (31), there are two terms in (36) that must be evaluated. The first term is
Since ![]() we have,
we have,
![\begin{eqnarray*} Cov_{t}^{Q}\left[ Y_{1s},Y_{2u}\right] &=&\mathbb{E}_{t}^{Q}\left[ \left( Y_{1s}-\mathbb{E}_{t}^{Q}\left[ Y_{1s}\right] \right) \left( Y_{2u}-\mathbb{E }_{t}^{Q}\left[ Y_{2u}\right] \right) \right] \ &=&e^{\lambda _{1}s}e^{\lambda _{1}u}\frac{\sigma _{11}\sigma _{21}+\sigma _{12}\sigma _{22}}{\lambda _{1}+\lambda _{2}}\left[ e^{-\left( \lambda _{1}+\lambda _{2}\right) t}-e^{-\left( \lambda _{1}+\lambda _{2}\right) u} \right] , \end{eqnarray*}](img210.gif)
and thus the right-hand side of (37) is easy to evaluate. The second term in (36) is
Using (28), we have
![\begin{eqnarray*} \int_{s}^{T}Y_{2u}du &=&\int_{s}^{T}e^{\lambda _{2}(u-s)}Y_{2s}du+\frac{b_{2} }{\lambda _{2}}\int_{s}^{T}\left[ e^{\lambda _{2}(u-s)}-1\right] du \ &&+\int_{s}^{T}e^{\lambda _{2}u}\int_{s}^{u}e^{-\lambda _{2}v}\left( \sigma _{21}dz_{1v}^{Q}+\sigma _{22}dz_{2v}^{Q}\right) du. \end{eqnarray*}](img212.gif)
The right hand side of the above expression has three terms, but only the first term on the right hand side has non-zero correlation with ![]() . Thus (38)
is
. Thus (38)
is
which can be evaluated using (26). Combining (37) and (39) gives the result
![\begin{displaymath} Cov_{t}^{Q}\left[ \int_{t}^{T}Y_{1s}ds,\int_{t}^{T}Y_{2u}du\... ...{1}+\lambda _{2}\right) (T-t)}-1\right] \end{array}\right\} . \end{displaymath}](img214.gif)
We now return to (3) to evaluate the TIPS price. The first term in (3) is
![\begin{displaymath} \sum_{k=1}^{n}cF \mathbb{E}_{t}^{Q}\left[ e^{\int_{u}^{t_{k}}i_{s}ds}e^{- \int_{t}^{t_{k}}r_{s}ds}\right] . \end{displaymath}](img215.gif)
Note that
where
![]() is
is
In (40), we have used the property that for any normally distributed random variable ![]() ,
,
![]() . The second term in (3) is
. The second term in (3) is
where ![]() is given in (41). The third term in (3 ) is
is given in (41). The third term in (3 ) is
where
![]() is the indicator function for the event in curly brackets. Equation (42) involves two expectations, where each expectation is of the
form
is the indicator function for the event in curly brackets. Equation (42) involves two expectations, where each expectation is of the
form
where ![]() and
and ![]() are bivariate normal random variables and
are bivariate normal random variables and ![]() is a constant. The joint distribution of
is a constant. The joint distribution of ![]() and
and ![]() is characterized by
is characterized by
![]() ,
,
![]() ,
, ![]() ,
, ![]() , and
, and
![]() . A direct calculation reveals that (43) is equal to
. A direct calculation reveals that (43) is equal to
where
![]() is the standard normal cumulative distribution function. To analyze the first expectation in (42 ), we use (44)
and we let
is the standard normal cumulative distribution function. To analyze the first expectation in (42 ), we use (44)
and we let
To analyze the second expectation in (42), we use ( 44) and we let
where ![]() and
and ![]() are given by (46) and (47),
respectively. Thus (42) depends on
are given by (46) and (47),
respectively. Thus (42) depends on
![]() ,
,
![]() ,
,
![]() ,
,
![]() , and
, and
![]() , which are given above. This completes the derivation of the TIPS price in (3).
, which are given above. This completes the derivation of the TIPS price in (3).
B. Pricing model for nominal Treasuries
We now derive the price of a nominal Treasury Note. Using equation (19), the first term in (5) can be written as
![\begin{displaymath} \sum_{k=1}^{n}\bar{c}F \mathbb{E}_{t}^{Q}\left[ e^{-\int_{t}^{t_{k}}r_{s}ds} \right] =\sum_{k=1}^{n}\bar{c}F \mathbb{E}_{t}^{Q}\left[ e^{- \int_{t}^{t_{k}}Y_{1s}ds -\left( \frac{A_{12}}{\lambda _{2}-A_{11}}\right) \int_{t}^{t_{k}}Y_{2s}ds}\right] \end{displaymath}](img254.gif)
Note that
where
![]() is
is
Like equation (41), (48) uses the property that for any normally distributed random variable ![]() ,
,
![]() . Similarly, the second term in (5) is
. Similarly, the second term in (5) is
where the function
![]() is obtained by substituting
is obtained by substituting ![]() for
for
![]() in (48). This completes the derivation of the nominal Treasury Note price in (5).
in (48). This completes the derivation of the nominal Treasury Note price in (5).
C. Long run means
In this section we show how to derive the long run means and the speeds of mean reversion for ![]() and
and ![]() . We can rewrite (17) as
. We can rewrite (17) as
![]() , where we define
, where we define ![]() and
and
![]() . Upon substituting we get
. Upon substituting we get
![]() , which is a more traditional form. The long run means are
, which is a more traditional form. The long run means are
Our empirical estimates for (49)-(50) are shown in Table 2.
Bibliography
|
ISIN |
Issue Date | Maturity Date | Coupon | Obs. |
| 10-year Treasury Inflation Protected Securities: 272M3 | 1/15/1997 | 1/15/2007 | 3.375 | 120 |
| 10-year Treasury Inflation Protected Securities:273T7 | 1/15/1998 | 1/15/2008 | 3.625 | 120 |
| 10-year Treasury Inflation Protected Securities:274Y5 | 1/15/1999 | 1/15/2009 | 3.875 | 120 |
| 10-year Treasury Inflation Protected Securities:275W8 | 1/15/2000 | 1/15/2010 | 4.25 | 120 |
| 10-year Treasury Inflation Protected Securities:276R8 | 1/15/2001 | 1/15/2011 | 3.5 | 113 |
| 10-year Treasury Inflation Protected Securities:277J5 | 1/15/2002 | 1/15/2012 | 3.375 | 101 |
| 10-year Treasury Inflation Protected Securities:28AF7 | 7/15/2002 | 7/15/2012 | 3 | 95 |
| 10-year Treasury Inflation Protected Securities:28BD1 | 7/15/2003 | 7/15/2013 | 1.875 | 83 |
| 10-year Treasury Inflation Protected Securities:28BW9 | 1/15/2004 | 1/15/2014 | 2 | 77 |
| 10-year Treasury Inflation Protected Securities:28CP3 | 7/15/2004 | 7/15/2014 | 2 | 71 |
| 10-year Treasury Inflation Protected Securities:28DH0 | 1/15/2005 | 1/15/2015 | 1.625 | 65 |
| 10-year Treasury Inflation Protected Securities:28EA4 | 7/15/2005 | 7/15/2015 | 1.875 | 59 |
| 10-year Treasury Inflation Protected Securities:28ET3 | 1/15/2006 | 1/15/2016 | 2 | 53 |
| 10-year Treasury Inflation Protected Securities:28FL9 | 7/15/2006 | 7/15/2016 | 2.5 | 47 |
| 10-year Treasury Inflation Protected Securities:28GD6 | 1/15/2007 | 1/15/2017 | 2.375 | 41 |
| 10-year Treasury Inflation Protected Securities:28GX2 | 7/15/2007 | 7/15/2017 | 2.625 | 35 |
| 10-year Treasury Inflation Protected Securities:28HN3 | 1/15/2008 | 1/15/2018 | 1.625 | 29 |
| 10-year Treasury Inflation Protected Securities:28JE1 | 7/15/2008 | 7/15/2018 | 1.375 | 23 |
| 10-year Treasury Inflation Protected Securities:28JX9 | 1/15/2009 | 1/15/2019 | 2.125 | 17 |
| 10-year Treasury Inflation Protected Securities:28LA6 | 7/15/2009 | 7/15/2019 | 1.875 | 11 |
| 10-year Treasury Inflation Protected Securities:28MF4 | 1/15/2010 | 1/15/2020 | 1.375 | 5 |
| 5-year Treasury Inflation Protected Securities: 273A8 | 7/15/1997 | 7/15/2002 | 3.625 | 60 |
| 5-year Treasury Inflation Protected Securities: 28CZ1 | 10/15/2004 | 4/15/2010 | 0.875 | 66 |
| 5-year Treasury Inflation Protected Securities:28FB1 | 4/15/2006 | 4/15/2011 | 2.375 | 50 |
| 5-year Treasury Inflation Protected Securities:28GN4 | 4/15/2007 | 4/15/2012 | 2 | 38 |
| 5-year Treasury Inflation Protected Securities: 28HW3 | 4/15/2008 | 4/15/2013 | 0.625 | 26 |
| 5-year Treasury Inflation Protected Securities: 28KM1 | 4/15/2009 | 4/15/2014 | 1.25 | 14 |
| 5-year Treasury Inflation Protected Securities: 28MY3 | 4/15/2010 | 4/15/2015 | 0.5 | 2 | 10-year matching nominal Treasury Notes: 272J0 | 2/15/1997 | 2/15/2007 | 6.25 | 120 |
| 10-year matching nominal Treasury Notes: 273X8 | 2/15/1998 | 2/15/2008 | 5.5 | 120 |
| 10-year matching nominal Treasury Notes:N/A | ||||
| 10-year matching nominal Treasury Notes:275Z1 | 2/15/2000 | 2/15/2010 | 6.5 | 120 |
| 10-year matching nominal Treasury Notes: 276T4 | 2/15/2001 | 2/15/2011 | 5 | 112 |
| 10-year matching nominal Treasury Notes:277L0 | 2/15/2002 | 2/15/2012 | 4.875 | 100 |
| 10-year matching nominal Treasury Notes:28AJ9 | 8/15/2002 | 8/15/2012 | 4.375 | 94 |
| 10-year matching nominal Treasury Notes:28BH2 | 8/15/2013 | 8/15/2013 | 4.25 | 82 |
| 10-year matching nominal Treasury Notes: 28CA6 | 2/15/2014 | 2/15/2014 | 4 | 76 |
| 10-year matching nominal Treasury Notes: 28CT5 | 8/15/2004 | 8/15/2014 | 4.25 | 70 |
| 10-year matching nominal Treasury Notes:28DM9 | 2/15/2005 | 2/15/2015 | 4 | 64 |
| 10-year matching nominal Treasury Notes:28EE6 | 8/15/2005 | 8/15/2015 | 4.25 | 58 |
| 10-year matching nominal Treasury Notes: 28EW6 | 2/15/2006 | 2/15/2016 | 4.5 | 52 |
| 10-year matching nominal Treasury Notes:28FQ8 | 8/15/2006 | 8/15/2016 | 4.875 | 46 |
| 10-year matching nominal Treasury Notes:28GH7 | 2/15/2007 | 2/15/2017 | 4.625 | 40 |
| 10-year matching nominal Treasury Notes:28HA1 | 8/15/2007 | 8/15/2017 | 4.75 | 34 |
| 10-year matching nominal Treasury Notes:28HR4 | 2/15/2008 | 2/15/2018 | 3.5 | 28 |
| 10-year matching nominal Treasury Notes:28JH4 | 8/15/2008 | 8/15/2018 | 4 | 22 |
| 10-year matching nominal Treasury Notes:28KD1 | 2/15/2009 | 2/15/2019 | 2.75 | 16 |
| 10-year matching nominal Treasury Notes:28LJ7 | 8/15/2009 | 8/15/2019 | 3.625 | 10 |
| 10-year matching nominal Treasury Notes:28MP2 | 2/15/2010 | 2/15/2020 | 3.625 | 4 |
| 5-year matching nominal Treasury Notes:273C4 | 7/31/1997 | 7/31/2002 | 6 | 61 |
| 5-year matching nominal Treasury Notes: 28CX6 | 10/15/2004 | 10/15/2009 | 3.375 | 60 |
| 5-year matching nominal Treasury Notes:28FD7 | 4/30/2006 | 4/30/2011 | 4.875 | 49 |
| 5-year matching nominal Treasury Notes:28GQ7 | 4/30/2007 | 4/30/2012 | 4.5 | 38 |
| 5-year matching nominal Treasury Notes:28HY9 | 4/30/2008 | 4/30/2013 | 3.125 | 26 |
| 5-year matching nominal Treasury Notes: 28KN9 | 4/30/2009 | 4/30/2014 | 1.875 | 14 |
| 5-year matching nominal Treasury Notes: 28MZ0 | 4/30/2010 | 4/30/2015 | 2.5 | 2 |
| Obs. | Option Value Range | ||||||||
| 5-year: | 506 | 0.0773 | 0.0294 | 1,826.4 | −$0.0270 | $1.4157 | 0.0003 | 0.0054 | $0.0000-$1.3134 |
| Standard Error: | (0.0085) | (0.0034) | |||||||
| 10-year: | 2,673 | 0.0534 | 0.0231 | 39,336.7 | $0.1775 | $2.9525 | −0.0003 | 0.0051 | $0.0000-$0.0615 |
| Standard Error: | (0.0006) | (0.0006) | |||||||
| 5&10-year: | 3,179 | 0.0537 | 0.0232 | 41,354.8 | $0.1559 | $2.7174 | -0.0002 | 0.0052 | $0.0000-$1.4447 |
| Standard Error: | (0.0006) | (0.0007) |
| Sample size | Wald test value | Degrees of freedom | p-value | |
| Panel A: Option values: 5-year: | 256 | 57,808.6 | 247 | <0.0001 |
| Panel A: Option values: 10-year: | 1,405 | 335.7 | 1,396 | 1 |
| Panel A: Option values: 5&10-year: | 1,661 | 73,766.1 | 1,652 | <0.0001 |
| Panel B: Option returns: 5-year: | 235 | 286,416.6 | 226 | <0.0001 |
| Panel B: Option returns: 10-year: | 741 | 7,223.4 | 732 | <0.0001 |
| Panel B: Option returns: 5&10-year: | 1,350 | 12,047.2 | 1,341 | <0.0001 |
| Variable | Obs. | Mean | Median | Std. Dev. | Minimum | Maximum |
| Option Val Index, 5-year | 119 | 0.0510 | 0.0107 | 0.1244 | 1.7967Ε−6 | 1.0685 |
| Option Val Index, 10-year | 160 | 0.0006 | 1.4964Ε−5 | 0.0038 | 8.1900Ε−8 | 0.0474 |
| Option Val Index, 5&10-year | 160 | 0.0300 | 0.0107 | 0.0830 | 0.0003 | 0.9093 |
| Option Ret Index, 5-year | 119 | 0.4743 | -0.0544 | 1.9018 | -0.9394 | 13.3280 |
| Option Ret Index, 10-year | 160 | 1.3545 | -0.0893 | 4.5093 | -0.9852 | 26.8252 |
| Option Ret Index, 5&10-year | 160 | 0.2500 | -0.0623 | 1.1400 | -0.9054 | 5.8962 |
| Yield Spread | 160 | 0.0172 | 0.0194 | 0.0099 | -0.0250 | 0.0345 |
| Gold Ret | 160 | 0.0089 | 0.0067 | 0.0471 | -0.1698 | 0.1797 |
| VIX Ret | 160 | 0.0187 | -0.0115 | 0.1918 | -0.3150 | 0.9075 |
| Bond Ret | 160 | 0.0027 | 0.0033 | 0.0142 | -0.0800 | 0.0449 |
| Inflation, lag1 | 160 | 0.0237 | 0.0236 | 0.0468 | -0.2321 | 0.1458 |
| Option Val | Option Ret | Yield Spread | Gold Ret | VIX Ret | Bond Ret | Inflation, Lag1 | |
| Panel A: Correlations for the 5-year sample: Option Val | 1.0000 | ||||||
| Panel A: Correlations for the 5-year sample: Option Ret | 0.1845 | 1.0000 | |||||
| P-value: | (0.0445) | ||||||
| Panel A: Correlations for the 5-year sample: Yield Spread | -0.6091 | -0.1196 | 1.0000 | ||||
| P-value: | (<0.0001) | (0.1950) | |||||
| Panel A: Correlations for the 5-year sample: Gold Ret | 0.1395 | -0.2775 | -0.0897 | 1.0000 | |||
| P-value: | (0.1304) | (0.0022) | (0.3322) | ||||
| Panel A: Correlations for the 5-year sample: VIX Ret | -0.0795 | 0.0603 | -0.0216 | -0.0992 | 1.0000 | ||
| P-value: | (0.3900) | (0.5149) | (0.8158) | (0.2833) | |||
| Panel A: Correlations for the 5-year sample: Bond Ret | -0.0309 | -0.2250 | 0.0836 | 0.3706 | -0.0893 | 1.0000 | |
| P-value: | (0.7390) | (0.0139) | (0.3659) | (<0.0001) | (0.3342) | ||
| Panel A: Correlations for the 5-year sample: Inflation, lag1 | -0.5608 | -0.4608 | 0.4013 | 0.0966 | 0.0439 | 0.1928 | 1.0000 |
| P-value | (<0.0001) | (<0.0001) | (<0.0001) | (0.2959) | (0.6358) | (0.0357) | |
| Panel B: Correlations for the 10-year sample: Option Val | 1.0000 | ||||||
| P-value | |||||||
| Panel B: Correlations for the 10-year sample: Option Ret | 0.2724 | 1.0000 | |||||
| P-value | (0.0005) | ||||||
| Panel B: Correlations for the 10-year sample: Yield Spread | -0.3768 | -0.1143 | 1.0000 | ||||
| P-value | (<0.0001) | (0.1503) | |||||
| Panel B: Correlations for the 10-year sample: Gold Ret | 0.1688 | -0.2454 | -0.0886 | 1.0000 | |||
| P-value | (0.0329) | (0.0018) | (0.2652) | ||||
| Panel B: Correlations for the 10-year sample: VIX Ret | -0.0553 | 0.0636 | -0.0574 | -0.0697 | 1.0000 | ||
| P-value | (0.4876) | (0.4243) | (0.4707) | (0.3812) | |||
| Panel B: Correlations for the 10-year sample: Bond Ret | -0.0402 | -0.2516 | 0.1166 | 0.3369 | -0.0293 | 1.0000 | |
| P-value | (0.6140) | (0.0013) | (0.1420) | (<0.0001) | (0.7131) | ||
| Panel B: Correlations for the 10-year sample:Inflation, lag1 | -0.5124 | -0.4916 | 0.2950 | 0.0637 | 0.0626 | 0.1532 | 1.0000 |
| P-value | (<0.0001) | (<0.0001) | (0.0002) | (0.4237) | (0.4319) | (0.0531) | |
| Panel C: Correlations for the 5&10-year sample: Option Val | 1.0000 | ||||||
| P-value | |||||||
| Panel C: Correlations for the 5&10-year sample: Option Ret | 0.3369 | 1.0000 | |||||
| P-value | (<0.0001) | ||||||
| Panel C: Correlations for the 5&10-year sample: Yield Spread | -0.4953 | -0.0989 | 1.0000 | ||||
| P-value | (<0.0001) | (0.2136) | |||||
| Panel C: Correlations for the 5&10-year sample: Gold Ret | 0.1271 | -0.2615 | -0.0933 | 1.0000 | |||
| P-value | (0.1092) | (0.0008) | (0.2417) | ||||
| Panel C: Correlations for the 5&10-year sample: VIX Ret | -0.0580 | 0.0342 | -0.0372 | -0.0697 | 1.0000 | ||
| P-value | (0.4665) | (0.6674) | (0.6408) | (0.3812) | |||
| Panel C: Correlations for the 5&10-year sample: Bond Ret | -0.0450 | -0.2261 | 0.1121 | 0.3444 | -0.0277 | 1.0000 | |
| P-value | (0.5723) | (0.0041) | (0.1583) | (<0.0001) | (0.7285) | ||
| Panel C: Correlations for the 5&10-year sample: Inflation, lag1 | -0.5769 | -0.5555 | 0.3413 | 0.0637 | 0.0626 | 0.1526 | 1.0000 |
| P-value | (<0.0001) | (<0.0001) | (<0.0001) | (0.4237) | (0.4319) | (0.0541) |
| 5-year | 5-year | 10-year | 10-year | 5&10-year | 5&10-year | |
| Panel A: Dependent variable is one-month ahead inflation, |
−0.011** | −0.0056** | −0.0052*** | −0.0031*** | −0.021*** | −0.013*** |
| t-statistics: | (-2.26) | (-2.08) | (-3.48) | (-2.97) | (-3.67) | (-2.90) |
| Panel A: Dependent variable is one-month ahead inflation, |
−0.027 | −0.43 | −0.0069 | |||
| t-statistics: | (-0.88) | (-0.89) | (-0.25) | |||
| Panel A: Dependent variable is one-month ahead inflation, |
0.31 | 0.39 | 0.58* | |||
| t-statistics: | (1.29) | (1.43) | (1.91) | |||
| Panel A: Dependent variable is one-month ahead inflation, |
0.28*** | 0.28*** | 0.24*** | |||
| t-statistics: | (3.10) | (3.39) | (2.67) | |||
| Panel A: Dependent variable is one-month ahead inflation, |
-0.0042 | 0.039 | 0.026 | |||
| t-statistics: | (-0.05) | (0.52) | (0.34) | |||
| Panel A: Dependent variable is one-month ahead inflation, |
-0.070*** | -0.053** | -0.054** | |||
| t-statistics: | (-2.93) | (-2.26) | (-2.31) | |||
| Panel A: Dependent variable is one-month ahead inflation, |
0.95* | 0.29 | 0.34 | |||
| t-statistics: | (1.84) | (0.93) | (1.06) | |||
| Panel A: Dependent variable is one-month ahead inflation, |
0.029*** | 0.016** | 0.031*** | 0.014** | 0.029*** | 0.011* |
| t-statistics | (6.05) | (2.39) | (8.43) | (2.41) | (8.50) | (1.75) |
| Panel A: Dependent variable is one-month ahead inflation, |
118 | 118 | 159 | 159 | 159 | 159 |
| Panel A: Dependent variable is one-month ahead inflation, |
0.175 | 0.375 | 0.245 | 0.353 | 0.250 | 0.356 |
| Panel B: Dependent variable is one-year ahead inflation, |
−0.0011* | −0.0014* | −0.00055** | −0.00066** | −0.0023*** | −0.0034*** |
| t-statistics: | (-1.69) | (-1.73) | (-2.59) | (-2.49) | (-2.63) | (-2.64) |
| Panel B: Dependent variable is one-year ahead inflation, |
-0.0033 | -0.27 | -0.015 | |||
| t-statistics: | (-0.22) | (-0.93) | (-0.90) | |||
| Panel B: Dependent variable is one-year ahead inflation, |
0.31^** | 0.090 | 0.15 | |||
| t-statistics: | (1.86) | (0.66) | (0.95) | |||
| Panel B: Dependent variable is one-year ahead inflation, |
-0.071 | -0.053 | -0.075 | |||
| t-statistics: | (-1.21) | (-1.07) | (-1.38) | |||
| Panel B: Dependent variable is one-year ahead inflation, |
0.018 | 0.020 | 0.015 | |||
| t-statistics: | (0.71) | (1.06) | (0.86) | |||
| Panel B: Dependent variable is one-year ahead inflation, |
-0.0074 | -0.0066 | -0.0068 | |||
| t-statistics: | (-1.02) | (-0.93) | (-0.97) | |||
| Panel B: Dependent variable is one-year ahead inflation, |
0.044 | 0.0062 | 0.0074 | |||
| t-statistics: | (0.45) | (0.12) | (0.15) | |||
| Panel B: Dependent variable is one-year ahead inflation, |
0.024*** | 0.021*** | 0.025*** | 0.025*** | 0.025*** | 0.025*** |
| t-statistics | (8.44) | (5.65) | (11.61) | (8.74) | (11.69) | (7.61) |
| Panel B: Dependent variable is one-year ahead inflation, |
107 | 107 | 148 | 148 | 148 | 148 |
| Panel B: Dependent variable is one-year ahead inflation, |
0.011 | 0.036 | 0.028 | 0.028 | 0.033 | 0.052 |
| 5-year | 5-year | 10-year | 10-year | 5&10-year | 5&10-year | |
| A: Dependent variable is one-month ahead inflation, |
−0.011** | −0.0061** | −0.0061*** | −0.0036*** | −0.020*** | −0.013*** |
| t-statistics: | (-2.21) | (-2.01) | (-3.53) | (-3.16) | (-3.44) | (-2.75) |
| Panel A: Dependent variable is one-month ahead inflation, |
-0.046 | -0.62 | -0.019 | |||
| t-statistics: | (-1.49) | (-1.40) | (-0.71) | |||
| Panel A: Dependent variable is one-month ahead inflation, |
0.41 | 0.68 | 0.71* | |||
| t-statistics | (0.67) | (1.05) | (1.67) | |||
| Panel A: Dependent variable is one-month ahead inflation, |
0.25*** | 0.28*** | 0.26*** | |||
| t-statistics: | (2.80) | (2.80) | (2.75) | |||
| Panel A: Dependent variable is one-month ahead inflation, |
0.025 | 0.058 | 0.033 | |||
| t-statistics: | (0.26) | (0.67) | (0.41) | |||
| Panel A: Dependent variable is one-month ahead inflation, |
-0.068*** | -0.052* | -0.060** | |||
| t-statistics: | (-2.65) | (-1.84) | (-2.32) | |||
| Panel A: Dependent variable is one-month ahead inflation, |
0.82 | 0.20 | 0.24 | |||
| t-statistics: | (1.50) | (0.71) | (0.76) | |||
| Panel A: Dependent variable is one-month ahead inflation, |
0.027*** | 0.014 | 0.030*** | 0.0067 | 0.028*** | 0.0066 |
| t-statistics: | (5.70) | (1.20) | (7.70) | (0.55) | (7.83) | (0.78) |
| Panel A: Dependent variable is one-month ahead inflation, |
113 | 113 | 139 | 139 | 153 | 153 |
| Panel A: Dependent variable is one-month ahead inflation, |
0.161 | 0.351 | 0.254 | 0.361 | 0.228 | 0.342 |
| Panel B: Dependent variable is one-year ahead inflation: Option Ret | -0.0010 | -0.0014* | -0.00055** | -0.00055** | -0.0024** | -0.0032** |
| t-statistics: | (-1.62) | (-1.72) | (-2.50) | (-2.03) | (-2.47) | (-2.54) |
| Panel B: Dependent variable is one-year ahead inflation: Option Val | -0.011 | -0.21 | -0.014 | |||
| t-statistics: | (-0.91) | (-1.05) | (-1.20) | |||
| Panel B: Dependent variable is one-year ahead inflation:Yield Spread | 0.28 | 0.16 | 0.17 | |||
| t-statistics: | (1.52) | (0.55) | (1.03) | |||
| Panel B: Dependent variable is one-year ahead inflation:Inflation, lag1 | -0.063 | -0.033 | -0.070 | |||
| t-statistics: | (-1.14) | (-0.77) | (-1.25) | |||
| Panel B: Dependent variable is one-year ahead inflation:Gold Ret | 0.011 | 0.028 | 0.0099 | |||
| t-statistics: | (0.40) | (1.44) | (0.53) | |||
| Panel B: Dependent variable is one-year ahead inflation:VIX Ret | -0.010 | -0.0096 | -0.0080 | |||
| t-statistics: | (-1.25) | (-1.36) | (-1.15) | |||
| Panel B: Dependent variable is one-year ahead inflation:Bond Ret | 0.0091 | 0.031 | 0.039 | |||
| t-statistics: | (0.07) | (0.80) | (0.79) | |||
| Panel B: Dependent variable is one-year ahead inflation:Constant | 0.024*** | 0.022*** | 0.025*** | 0.022*** | 0.025*** | 0.024*** |
| t-statistics: | (8.39) | (5.77) | (11.45) | (4.35) | (11.27) | (7.53) |
| Panel B: Dependent variable is one-year ahead inflation:Obs. | 103 | 103 | 130 | 130 | 142 | 142 |
| Panel B: Dependent variable is one-year ahead inflation:Adj- |
0.009 | 0.018 | 0.027 | 0.036 | 0.032 | 0.047 |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| Panel A: Dependent variable is one-month ahead inflation, |
−0.011*** | −0.0059** | ||||||
| t-statistics: | (-2.69) | (-2.39) | ||||||
| Panel A: Dependent variable is one-month ahead inflation, |
-0.017 | |||||||
| t-statistics: | (-0.35) | |||||||
| Panel A: Dependent variable is one-month ahead inflation, |
-0.0083** | -0.0040* | ||||||
| t-statistics: | (-2.57) | (-1.77) | ||||||
| Panel A: Dependent variable is one-month ahead inflation, |
-0.036 | |||||||
| t-statistics: | (-0.33) | |||||||
| Panel A: Dependent variable is one-month ahead inflation, |
−0.010*** | −0.0052** | ||||||
| t-statistics: | (-2.75) | (-2.21) | ||||||
| Panel A: Dependent variable is one-month ahead inflation, |
-0.017 | |||||||
| t-statistics: | (-0.26) | |||||||
| Panel A: Dependent variable is one-month ahead inflation, |
-0.0080** | -0.0036 | ||||||
| t-statistics: | (-2.25) | (-1.55) | ||||||
| Panel A: Dependent variable is one-month ahead inflation, |
-0.078 | |||||||
| t-statistics: | (-0.79) | |||||||
| Panel A: Dependent variable is one-month ahead inflation, |
0.33 | 0.28 | 0.31 | 0.26 | ||||
| t-statistics: | (1.37) | (1.26) | (1.32) | (1.24) | ||||
| Panel A: Dependent variable is one-month ahead inflation, |
0.27*** | 0.29*** | 0.28*** | 0.28*** | ||||
| t-statistics: | (3.07) | (3.19) | (3.13) | (2.94) | ||||
| Panel A: Dependent variable is one-month ahead inflation, |
-0.019 | -0.011 | -0.016 | -0.00023 | ||||
| t-statistics; | (-0.22) | (-0.12) | (-0.19) | (-0.00) | ||||
| Panel A: Dependent variable is one-month ahead inflation, |
-0.067*** | -0.067*** | -0.067*** | -0.069*** | ||||
| t-statistics: | (-2.85) | (-2.88) | (-2.86) | (-2.94) | ||||
| Panel A: Dependent variable is one-month ahead inflation, |
0.84* | 0.81* | 0.83* | 0.85* | ||||
| t-statistics: | (1.79) | (1.74) | (1.77) | (1.77) | ||||
| Panel A: Dependent variable is one-month ahead inflation, |
0.030*** | 0.016** | 0.030*** | 0.016** | 0.030*** | 0.016** | 0.030*** | 0.017** |
| t-statistics: | (6.70) | (2.32) | (6.80) | (2.09) | (6.79) | (2.20) | (6.57) | (2.40) |
| Panel A: Dependent variable is one-month ahead inflation, |
0.235 | 0.384 | 0.237 | 0.376 | 0.239 | 0.381 | 0.214 | 0.372 |
| Panel B: Dependent variable is one-year ahead inflation, |
-0.0012** | -0.0015* | ||||||
| t-statistics: | (-2.07) | (-1.87) | ||||||
| Panel B: Dependent variable is one-year ahead inflation, |
0.0039 | |||||||
| t-statistics: | (0.17) | |||||||
| Panel B: Dependent variable is one-year ahead inflation, |
−0.0011*** | −0.0015** | ||||||
| t-statistics: | (-3.02) | (-2.15) | ||||||
| Panel B: Dependent variable is one-year ahead inflation, |
0.047 | |||||||
| t-statistics: | (1.01) | |||||||
| Panel B: Dependent variable is one-year ahead inflation, |
-0.0012** | -0.0016* | ||||||
| t-statistics: | (-2.35) | (-1.97) | ||||||
| Panel B: Dependent variable is one-year ahead inflation, |
0.010 | |||||||
| t-statistics: | (0.36) | |||||||
| Panel B: Dependent variable is one-year ahead inflation, |
−0.0011*** | −0.0015** | ||||||
| t-statistics: | (-2.82) | (-2.14) | ||||||
| Panel B: Dependent variable is one-year ahead inflation, |
0.029 | |||||||
| t-statistics: | (0.68) | |||||||
| Panel B: Dependent variable is one-year ahead inflation, |
0.33** | 0.34** | 0.34** | 0.34** | ||||
| t-statistics: | (2.05) | (2.56) | (2.19) | (2.49) | ||||
| Panel B: Dependent variable is one-year ahead inflation, |
-0.073 | -0.068 | -0.073 | -0.072 | ||||
| t-statistics: | (-1.21) | (-1.11) | (-1.19) | (-1.12) | ||||
| Panel B: Dependent variable is one-year ahead inflation, |
0.013 | 0.0091 | 0.012 | 0.0086 | ||||
| t-statistics: | (0.53) | (0.39) | (0.47) | (0.35) | ||||
| Panel B: Dependent variable is one-year ahead inflation, |
-0.0065 | -0.0051 | -0.0061 | -0.0053 | ||||
| t-statistics: | (-0.91) | (-0.71) | (-0.85) | (-0.72) | ||||
| Panel B: Dependent variable is one-year ahead inflation, |
0.012 | -0.035 | -0.0043 | -0.020 | ||||
| t-statistics: | (0.12) | (-0.32) | (-0.04) | (-0.19) | ||||
| Panel B: Dependent variable is one-year ahead inflation, |
0.024*** | 0.021*** | 0.025*** | 0.020*** | 0.025*** | 0.021*** | 0.025*** | 0.021*** |
| t-statistics: | (8.60) | (5.61) | (8.68) | (5.91) | (8.64) | (5.70) | (8.64) | (6.23) |
| Panel B: Dependent variable is one-year ahead inflation, |
0.024 | 0.047 | 0.035 | 0.062 | 0.029 | 0.051 | 0.034 | 0.061 |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | OptRetlLT | -0.0022*** | -0.0013** |
| t-statistics | (-3.57) | (-2.23) | ||||||
| OptValLT | 1.17 | |||||||
| t-statistics | (0.56) | |||||||
| OptRetST | -0.0014*** | -0.00084** | ||||||
| t-statistics | (-3.69) | (-2.16) | ||||||
| OptValST | 7.18 | |||||||
| t-statistics | (0.90) | |||||||
| OptRetNTM | -0.0020*** | -0.0012** | ||||||
| t-statistics | (-3.53) | (-2.15) | ||||||
| OptValNTM | 1.54 | |||||||
| t-statistics | (0.61) | |||||||
| OptRetOTM | -0.0014*** | -0.00072 | ||||||
| t-statistics | (-2.90) | (-1.64) | ||||||
| OptValOTM | 0.67 | |||||||
| t-statistics | (0.08) | |||||||
| Yield Spread | 0.28 | 0.25 | 0.27 | 0.24 | ||||
| t-statistics | (1.05) | (0.96) | (1.03) | (0.90) | ||||
| Inflation, lag1 | 0.31*** | 0.32*** | 0.31*** | 0.32*** | ||||
| t-statistics | (3.91) | (4.17) | (3.99) | (4.25) | ||||
| Gold Ret | 0.042 | 0.045 | 0.044 | 0.059 | ||||
| t-statistics | (0.55) | (0.60) | (0.58) | (0.75) | ||||
| VIX Ret | -0.051** | -0.051** | -0.052** | -0.054** | ||||
| t-statistics | (-2.30) | (-2.32) | (-2.31) | (-2.34) | ||||
| Bond Ret | 0.24 | 0.23 | 0.24 | 0.27 | ||||
| t-statistics | (0.82) | (0.81) | (0.82) | (0.89) | ||||
| Constant | 0.030*** | 0.015** | 0.029*** | 0.014** | 0.030*** | 0.014** | 0.029*** | 0.014** |
| t-statistics | (8.17) | (2.43) | (8.13) | (2.37) | (8.15) | (2.41) | (8.00) | (2.34) |
| Adj- |
0.256 | 0.342 | 0.247 | 0.337 | 0.252 | 0.339 | 0.226 | 0.328 |
| OptRetlLT | -0.00024*** | -0.00031** | ||||||
| t-statistics | (-3.67) | (-2.39) | ||||||
| OptValLT | -0.19 | |||||||
| t-statistics | (-0.23) | |||||||
| OptRetST | -0.00015*** | -0.00021** | ||||||
| t-statistics | (-3.95) | (-2.37) | ||||||
| OptValST | 0.43 | |||||||
| t-statistics | (0.16) | |||||||
| OptRetNTM | -0.00022*** | -0.00029** | ||||||
| t-statistics | (-3.68) | (-2.34) | ||||||
| OptValNTM | -0.13 | |||||||
| t-statistics | (-0.14) | |||||||
| OptRetOTM | -0.00016*** | -0.00023** | ||||||
| t-statistics | (-3.79) | (-2.33) | ||||||
| OptValOTM | 0.36 | |||||||
| t-statistics | (0.16) | |||||||
| Yield Spread | 0.064 | 0.061 | 0.064 | 0.063 | ||||
| t-statistics | (0.50) | (0.48) | (0.49) | (0.50) | ||||
| Inflation, lag1 | -0.049 | -0.046 | -0.048 | -0.046 | ||||
| t-statistics | (-1.02) | (-0.98) | (-1.01) | (-0.98) | ||||
| Gold Ret | 0.019 | 0.019 | 0.019 | 0.019 | ||||
| t-statistics | (0.98) | (0.99) | (0.99) | (0.98) | ||||
| VIX Ret | -0.0061 | -0.0060 | -0.0061 | -0.0061 | ||||
| t-statistics | (-0.86) | (-0.85) | (-0.86) | (-0.86) | ||||
| Bond Ret | -0.0092 | -0.012 | -0.0091 | -0.010 | ||||
| t-statistics | (-0.17) | (-0.22) | (-0.17) | (-0.19) | ||||
| Constant | 0.025*** | 0.025*** | 0.025*** | 0.025*** | 0.025*** | 0.025*** | 0.025*** | 0.025*** |
| t-statistics | (11.46) | (8.88) | (11.40) | (8.92) | (11.44) | (8.87) | (11.40) | (8.99) |
| Adj- |
0.030 | 0.026 | 0.027 | 0.023 | 0.029 | 0.025 | 0.027 | 0.023 |
| 5&10-year | 5&10-year | 5&10-year,On-the-run | 5&10-year,On-the-run | |
| Panel A: Dependent variable is one-month ahead inflation, |
-0.029*** | -0.014** | -0.030*** | -0.014* |
| t-statistics: | (-3.70) | (-1.98) | (-3.63) | (-1.80) |
| Panel A: Dependent variable is one-month ahead inflation, |
-0.037 | -0.034 | ||
| t-statistics: | (-1.25) | (-1.20) | ||
| Panel A: Dependent variable is one-month ahead inflation, |
0.48 | 0.52 | ||
| t-statistics: | (1.61) | (1.16) | ||
| Panel A: Dependent variable is one-month ahead inflation, |
0.32*** | 0.34*** | ||
| t-statistics: | (3.96) | (3.86) | ||
| Panel A: Dependent variable is one-month ahead inflation, |
0.068 | 0.074 | ||
| t-statistics: | (0.92) | (0.96) | ||
| Panel A: Dependent variable is one-month ahead inflation, |
-0.060** | -0.064** | ||
| t-statistics: | (-2.34) | (-2.30) | ||
| Panel A: Dependent variable is one-month ahead inflation, |
0.44 | 0.32 | ||
| t-statistics: | (1.10) | (0.86) | ||
| Panel A: Dependent variable is one-month ahead inflation, |
0.037*** | 0.014* | 0.036*** | 0.011 |
| t-statistics: | (8.32) | (1.76) | (7.99) | (1.06) |
| Panel A: Dependent variable is one-month ahead inflation, |
159 | 159 | 153 | 153 |
| Panel A: Dependent variable is one-month ahead inflation, |
0.089 | 0.310 | 0.088 | 0.300 |
| Panel B: Dependent variable is one-year ahead inflation, |
-0.0031* | -0.0043* | -0.0035* | -0.0043* |
| t-statistics: | (-1.66) | (-1.66) | (-1.76) | (-1.66) |
| Panel B: Dependent variable is one-year ahead inflation, |
-0.023 | -0.018 | ||
| t-statistics: | (-1.25) | (-1.38) | ||
| Panel B: Dependent variable is one-year ahead inflation, |
0.12 | 0.12 | ||
| t-statistics: | (0.77) | (0.78) | ||
| Panel B: Dependent variable is one-year ahead inflation, |
-0.055 | -0.050 | ||
| t-statistics: | (-1.08) | (-0.96) | ||
| Panel B: Dependent variable is one-year ahead inflation, |
0.025 | 0.019 | ||
| t-statistics: | (1.20) | (0.84) | ||
| Panel B: Dependent variable is one-year ahead inflation, |
-0.0082 | -0.0091 | ||
| t-statistics: | (-1.10) | (-1.22) | ||
| Panel B: Dependent variable is one-year ahead inflation, |
0.033 | 0.060 | ||
| t-statistics: | (0.55) | (1.06) | ||
| Panel B: Dependent variable is one-year ahead inflation, |
0.026*** | 0.026*** | 0.026*** | 0.025*** |
| t-statistics: | (11.61) | (7.58) | (11.28) | (7.52) |
| Panel B: Dependent variable is one-year ahead inflation, |
148 | 148 | 142 | 142 |
| Panel B: Dependent variable is one-year ahead inflation, |
0.007 | 0.021 | 0.010 | 0.021 |
| 5-year | 10-year | 5&10-year | |
| Panel A: Dependent variable is one-month ahead inflation, |
-0.0040 | -0.0023** | -0.0094** |
| t-statistics: | (-1.59) | (-2.28) | (-2.13) |
| Panel A: Dependent variable is one-month ahead inflation, |
-0.023 | -0.19 | 0.0034 |
| t-statistics: | (-0.87) | (-0.39) | (0.12) |
| Panel A: Dependent variable is one-month ahead inflation, |
0.24 | 0.28 | 0.45* |
| t-statistics: | (1.10) | (1.16) | (1.71) |
| Panel A: Dependent variable is one-month ahead inflation, |
0.20** | 0.23*** | 0.21** |
| t-statistics: | (2.43) | (2.90) | (2.56) |
| Panel A: Dependent variable is one-month ahead inflation, |
-0.047 | -0.0041 | -0.011 |
| t-statistics: | (-0.63) | (-0.07) | (-0.16) |
| Panel A: Dependent variable is one-month ahead inflation, |
-0.055** | -0.042** | -0.043** |
| t-statistics: | (-2.59) | (-2.03) | (-2.07) |
| Panel A: Dependent variable is one-month ahead inflation, |
0.88* | 0.25 | 0.29 |
| t-statistics: | (1.86) | (0.81) | (0.90) |
| Panel A: Dependent variable is one-month ahead inflation, |
0.14*** | 0.14*** | 0.14*** |
| t-statistics: | (3.19) | (3.99) | (3.92) |
| Panel A: Dependent variable is one-month ahead inflation, |
0.016*** | 0.014** | 0.011* |
| t-statistics: | (2.67) | (2.52) | (1.89) |
| Panel A: Dependent variable is one-month ahead inflation, |
118 | 159 | 159 |
| Panel A: Dependent variable is one-month ahead inflation, |
0.469 | 0.455 | 0.454 |
| Panel B: Dependent variable is one-year ahead inflation, |
-0.0011 | -0.00052* | -0.0027** |
| t-statistics: | (-1.44) | (-1.97) | (-2.03) |
| Panel B: Dependent variable is one-year ahead inflation, |
-0.00082 | -0.22 | -0.013 |
| t-statistics: | (-0.05) | (-0.76) | (-0.74) |
| Panel B: Dependent variable is one-year ahead inflation, |
0.32* | 0.076 | 0.13 |
| t-statistics: | (1.97) | (0.58) | (0.88) |
| Panel B: Dependent variable is one-year ahead inflation, |
-0.083 | -0.060 | -0.079 |
| t-statistics: | (-1.41) | (-1.23) | (-1.44) |
| Panel B: Dependent variable is one-year ahead inflation, |
0.011 | 0.013 | 0.010 |
| t-statistics: | (0.45) | (0.69) | (0.57) |
| Panel B: Dependent variable is one-year ahead inflation, |
-0.0048 | -0.0048 | -0.0051 |
| t-statistics: | (-0.71) | (-0.74) | (-0.79) |
| Panel B: Dependent variable is one-year ahead inflation, |
0.030 | -0.00032 | -0.00046 |
| t-statistics: | (0.33) | (-0.01) | (-0.01) |
| Panel B: Dependent variable is one-year ahead inflation, |
0.023*** | 0.022*** | 0.020*** |
| t-statistics: | (2.71) | (3.18) | (2.89) |
| Panel B: Dependent variable is one-year ahead inflation, |
0.021*** | 0.025*** | 0.024*** |
| t-statistics: | (6.03) | (8.91) | (7.80) |
| Panel B: Dependent variable is one-year ahead inflation, |
107 | 148 | 148 |
| Adj- |
0.062 | 0.058 | 0.075 |
| Panel A: Dependent variable is one-month ahead inflation, |
-0.0055*** | -0.0025*** | ||
| t-statistics: | (-9.21) | (-3.40) | ||
| Panel A: Dependent variable is one-month ahead inflation, |
-0.037*** | -0.012 | ||
| t-statistics: | (-2.64) | (-0.98) | ||
| Panel A: Dependent variable is one-month ahead inflation, |
0.00010 | 0.000012 | ||
| t-statistics: | (0.47) | (0.06) | ||
| Panel A: Dependent variable is one-month ahead inflation, |
0.11 | 0.43 | ||
| t-statistics: | (0.31) | (1.39) | ||
| Panel A: Dependent variable is one-month ahead inflation, |
0.37*** | 0.42*** | ||
| t-statistics: | (5.24) | (4.59) | ||
| Panel A: Dependent variable is one-month ahead inflation, |
0.083 | 0.094 | ||
| t-statistics: | (0.96) | (0.97) | ||
| Panel A: Dependent variable is one-month ahead inflation, |
-0.059** | -0.071** | ||
| t-statistics: | (-2.06) | (-2.45) | ||
| Panel A: Dependent variable is one-month ahead inflation, |
0.25 | 0.47 | ||
| t-statistics: | (0.81) | (1.24) | ||
| Panel A: Dependent variable is one-month ahead inflation, |
0.028*** | 0.013* | 0.036*** | 0.0083 |
| t-statistics: | (5.46) | (1.97) | (6.47) | (0.94) |
| Panel A: Dependent variable is one-month ahead inflation, |
110 | 110 | 110 | 110 |
| Panel A: Dependent variable is one-month ahead inflation, : Adj- |
0.255 | 0.353 | 0.080 | 0.327 |
| Panel B: Dependent variable is one-year ahead inflation, |
-0.00049*** | -0.00059* | ||
| t-statistics: | (-4.83) | (-1.68) | ||
| Panel B: Dependent variable is one-year ahead inflation, |
-0.0065** | -0.0066* | ||
| t-statistics: | (-2.05) | (-1.82) | ||
| Panel B: Dependent variable is one-year ahead inflation, |
0.00036*** | 0.00032*** | ||
| t-statistics: | (3.61) | (2.87) | ||
| Panel B: Dependent variable is one-year ahead inflation, |
-0.018 | 0.086 | ||
| t-statistics: | (-0.15) | (0.60) | ||
| Panel B: Dependent variable is one-year ahead inflation, |
-0.042 | -0.045 | ||
| t-statistics: | (-0.94) | (-1.00) | ||
| Panel B: Dependent variable is one-year ahead inflation, |
0.030 | 0.030 | ||
| t-statistics: | (1.37) | (1.26) | ||
| Panel B: Dependent variable is one-year ahead inflation, |
-0.0047 | -0.0076 | ||
| t-statistics: | (-0.42) | (-0.73) | ||
| Panel B: Dependent variable is one-year ahead inflation, |
-0.0095 | 0.038 | ||
| t-statistics: | (-0.16) | (0.63) | ||
| Panel B: Dependent variable is one-year ahead inflation, |
0.025*** | 0.023*** | 0.026*** | 0.023*** |
| (8.12) | (6.57) | (7.15) | (5.67) | |
| Panel B: Dependent variable is one-year ahead inflation, |
99 | 99 | 99 | 99 |
| Panel B: Dependent variable is one-year ahead inflation, |
0.018 | 0.117 | 0.024 | 0.120 |
![\begin{displaymath} P_{t}=\mathbb{E}_{t}^{Q}\left[ \sum_{k=1}^{n}cFe^{ \int_{u}^{t_{k}}i_{s}ds}e^{-\int_{t}^{t_{k}}r_{s}ds}+e^{- \int_{t}^{t_{n}}r_{s}ds}\left[ Fe^{\int_{u}^{t_{n}}i_{s}ds}+\max \left( 0,F-Fe^{\int_{u}^{t_{n}}i_{s}ds}\right) \right] \right] \end{displaymath}](img33.gif)
![\begin{displaymath} \bar{P}_{t}=\mathbb{E}_{t}^{Q}\left[ \sum_{k=1}^{n}\bar{c} Fe^{-\int_{t}^{t_{k}}r_{s}ds}+Fe^{-\int_{t}^{t_{n}}r_{s}ds}\right] . \end{displaymath}](img46.gif)
![\begin{displaymath} \min\limits_{\Theta } SSE(\Theta )=\sum_{t=1}^{T}\left[ \sum_{n=1}^{N_{t}} \left( P_{nt}^{\ast }-P_{nt}\right) ^{2}+\sum_{n=1}^{\bar{N}_{t}}\left( \bar{ P}_{nt}^{\ast }-\bar{P}_{nt}\right) ^{2}\right] , \end{displaymath}](img52.gif)
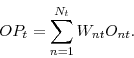
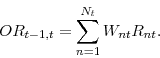
![\begin{displaymath} \left[ \begin{array}{c} r_{t} \ i_{t} \end{array}\right] =\left[ \begin{array}{cc} 1 & \frac{A_{12}}{\lambda _{2}-A_{11}} \ \frac{A_{21}}{\lambda _{1}-A_{22}} & 1 \end{array}\right] \left[ \begin{array}{c} Y_{1t} \ Y_{2t} \end{array}\right] =\left[ \begin{array}{c} Y_{1t}+\left( \frac{A_{12}}{\lambda _{2}-A_{11}}\right) Y_{2t} \ \left( \frac{A_{21}}{\lambda _{1}-A_{22}}\right) Y_{1t}+Y_{2t} \end{array}\right] . \end{displaymath}](img149.gif)
![\displaystyle e^{\lambda _{1}(s-t)}Y_{1t}+\frac{b_{1}}{\lambda _{1}}\left[ e^{\lambda _{1}(s-t)}-1\right] +e^{\lambda _{1}s}\int_{t}^{s}e^{-\lambda _{1}u}\left( \sigma _{11}dz_{1u}^{Q}+\sigma _{12}dz_{2u}^{Q}\right) ,](img151.gif)
![\displaystyle e^{\lambda _{2}(s-t)}Y_{2t}+\frac{b_{2}}{\lambda _{2}}\left[ e^{\lambda _{2}(s-t)}-1\right] +e^{\lambda _{2}s}\int_{t}^{s}e^{-\lambda _{2}u}\left( \sigma _{21}dz_{1u}^{Q}+\sigma _{22}dz_{2u}^{Q}\right) ,](img153.gif)
![\displaystyle e^{\lambda _{1}(s-t)}Y_{1t}+\frac{ b_{1}}{\lambda _{1}}\left[ e^{\lambda _{1}(s-t)}-1\right] ,](img156.gif)
![\displaystyle e^{\lambda _{2}(s-t)}Y_{2t}+\frac{ b_{2}}{\lambda _{2}}\left[ e^{\lambda _{2}(s-t)}-1\right] .](img158.gif)
![\displaystyle \mathbb{E}_{t}^{Q}\left[ \left( Y_{1s}- \mathbb{E}_{t}^{Q}\left[ Y_{1s}\right] \right) ^{2}\right] =e^{2\lambda _{1}s}\int_{t}^{s}e^{-2\lambda _{1}u}\left( \sigma _{11}^{2}+\sigma _{12}^{2}\right) du](img161.gif)
![\displaystyle \frac{\sigma _{11}^{2}+\sigma _{12}^{2}}{2\lambda _{1}}\left[ e^{2\lambda _{1}(s-t)}-1\right] .](img162.gif)
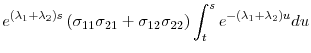
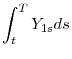
![\displaystyle \int_{t}^{T}e^{\lambda _{1}(s-t)}Y_{1t}ds+\frac{b_{1} }{\lambda _{1}}\int_{t}^{T}\left[ e^{\lambda _{1}(s-t)}-1\right] ds](img176.gif)
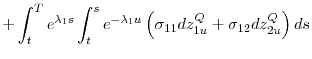
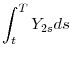
![\displaystyle \int_{t}^{T}e^{\lambda _{2}(s-t)}Y_{2t}ds+\frac{b_{2} }{\lambda _{2}}\int_{t}^{T}\left[ e^{\lambda _{2}(s-t)}-1\right] ds](img179.gif)
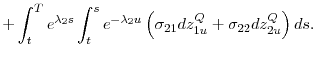
![\displaystyle \mathbb{E}_{t}^{Q}\left[ \int_{t}^{T}Y_{1s}ds\right]](img181.gif)
![\displaystyle \left( Y_{1t}+\frac{ b_{1}}{\lambda _{1}}\right) \frac{1}{\lambda _{1}}\left[ e^{\lambda _{1}(T-t)}-1\right] -\frac{b_{1}}{\lambda _{1}}\left( T-t\right) ,](img182.gif)
![\displaystyle \mathbb{E}_{t}^{Q}\left[ \int_{t}^{T}Y_{2s}ds\right]](img183.gif)
![\displaystyle \left( Y_{2t}+\frac{ b_{2}}{\lambda _{2}}\right) \frac{1}{\lambda _{2}}\left[ e^{\lambda _{2}(T-t)}-1\right] -\frac{b_{2}}{\lambda _{2}}\left( T-t\right) .](img184.gif)
![\displaystyle Var_{t}^{Q}\left[ \int_{t}^{T}Y_{1s}ds\right]](img186.gif)
![\displaystyle Cov_{t}^{Q}\left[ \int_{t}^{T}Y_{1s}ds,\int_{t}^{T}Y_{1u}du\right]](img187.gif)
![\displaystyle \int_{t}^{T}Cov_{t}^{Q}\left[ Y_{1s},\int_{t}^{s}Y_{1u}du\right] ds+\int_{t}^{T}Cov_{t}^{Q}\left[ Y_{1s},\int_{s}^{T}Y_{1u}du\right] ds.](img188.gif)
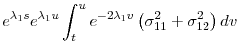
![\displaystyle e^{\lambda _{1}s}e^{\lambda _{1}u}\frac{\sigma _{11}^{2}+\sigma _{12}^{2} }{2\lambda _{1}}\left[ e^{-2\lambda _{1}t}-e^{-2\lambda _{1}u}\right] .](img194.gif)
![\displaystyle \int_{t}^{T}Cov_{t}^{Q}\left[ Y_{1s},\int_{s}^{T}Y_{1u}du\right] ds](img198.gif)
![\displaystyle \int_{t}^{T}Cov_{t}^{Q}\left[ Y_{1s},\int_{s}^{T}e^{\lambda _{1}(u-s)}Y_{1s}du\right] ds](img199.gif)
![\displaystyle \int_{t}^{T}Var_{t}^{Q}\left[ Y_{1s}\right] \left[ \int_{s}^{T}e^{\lambda _{1}(u-s)}du\right] ds](img200.gif)
![\displaystyle Cov_{t}^{Q}\left[ \int_{t}^{T}Y_{1s}ds,\int_{t}^{T}Y_{2u}du\right]](img204.gif)
![\displaystyle \int_{t}^{T}Cov_{t}^{Q}\left[ Y_{1s},\int_{t}^{T}Y_{2u}du\right] ds](img205.gif)
![\displaystyle \int_{t}^{T}Cov_{t}^{Q}\left[ Y_{1s},\int_{t}^{s}Y_{2u}du\right] ds](img206.gif)
![\displaystyle +\int_{t}^{T}Cov_{t}^{Q}\left[ Y_{1s},\int_{s}^{T}Y_{2u}du\right] ds.](img207.gif)
![\displaystyle e^{\int_{u}^{t}i_{s}ds}\mathbb{E}_{t}^{Q} \left[ e^{\left( \frac{A_{21}}{\lambda _{1}-A_{22}}-1\right) \int_{t}^{t_{k}}Y_{1s}ds+\left( 1-\frac{A_{12}}{\lambda _{2}-A_{11}}\right) \int_{t}^{t_{k}}Y_{2s}ds}\right]](img217.gif)
![\displaystyle \left( \frac{A_{21}}{\lambda _{1}-A_{22}}-1\right) \mathbb{E}_{t}^{Q} \left[ \int_{t}^{t_{k}}Y_{1s}ds\right] +\left( 1-\frac{A_{12}}{\lambda _{2}-A_{11}}\right) \mathbb{E}_{t}^{Q}\left[ \int_{t}^{t_{k}}Y_{2s}ds\right]](img221.gif)
![\displaystyle +\frac{1}{2}\left( \frac{A_{21}}{\lambda _{1}-A_{22}}-1\right) ^{2}Var_{t}^{Q}\left[ \int_{t}^{t_{k}}Y_{1s}ds\right] +\frac{1}{2}\left( 1- \frac{A_{12}}{\lambda _{2}-A_{11}}\right) ^{2}Var_{t}^{Q}\left[ \int_{t}^{t_{k}}Y_{2s}ds\right]](img222.gif)
![\displaystyle +\left( \frac{A_{21}}{\lambda _{1}-A_{22}}-1\right) \left( 1-\frac{A_{12}}{ \lambda _{2}-A_{11}}\right) Cov_{t}^{Q}\left[ \int_{t}^{t_{k}}Y_{1s}ds, \int_{t}^{t_{k}}Y_{2s}ds\right] .](img223.gif)
![\begin{displaymath} \mathbb{E}\left[ e^{Z_{1}}1_{\left\{ d>Z_{2}\right\} }\right] =e^{\mathbb{E} \left( Z_{1}\right) +\frac{1}{2}Var(Z_{1})} N\left( \frac{d-\mathbb{E} \left( Z_{2}\right) -Cov(Z_{1},Z_{2})}{\sqrt{Var(Z_{2})}}\right) , \end{displaymath}](img240.gif)
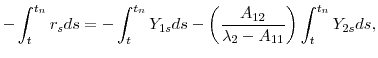
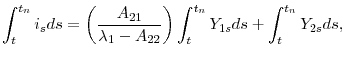
![\displaystyle -\mathbb{E}_{t}^{Q}\left[ \int_{t}^{t_{k}}Y_{1s}ds\right] -\left( \frac{ A_{12}}{\lambda _{2}-A_{11}}\right) \mathbb{E}_{t}^{Q}\left[ \int_{t}^{t_{k}}Y_{2s}ds\right]](img258.gif)
![\displaystyle +\frac{1}{2}Var_{t}^{Q}\left[ \int_{t}^{t_{k}}Y_{1s}ds\right] +\frac{1}{2} \left( \frac{A_{12}}{\lambda _{2}-A_{11}}\right) ^{2}Var_{t}^{Q}\left[ \int_{t}^{t_{k}}Y_{2s}ds\right]](img259.gif)
![\displaystyle +\left( \frac{A_{12}}{\lambda _{2}-A_{11}}\right) Cov_{t}^{Q}\left[ \int_{t}^{t_{k}}Y_{1s}ds,\int_{t}^{t_{k}}Y_{2s}ds\right] .](img260.gif)
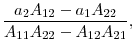
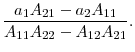
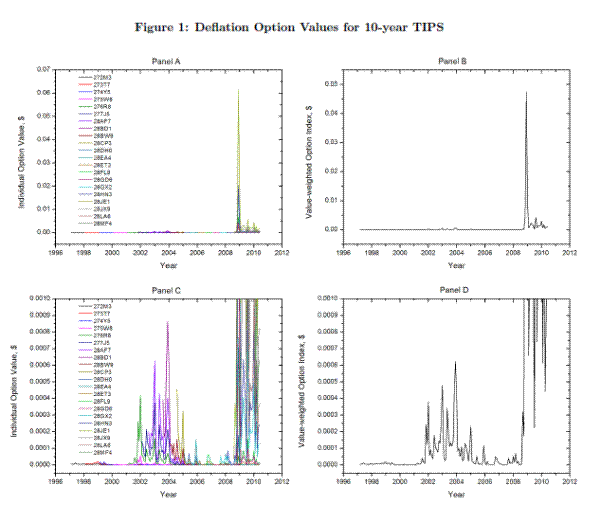
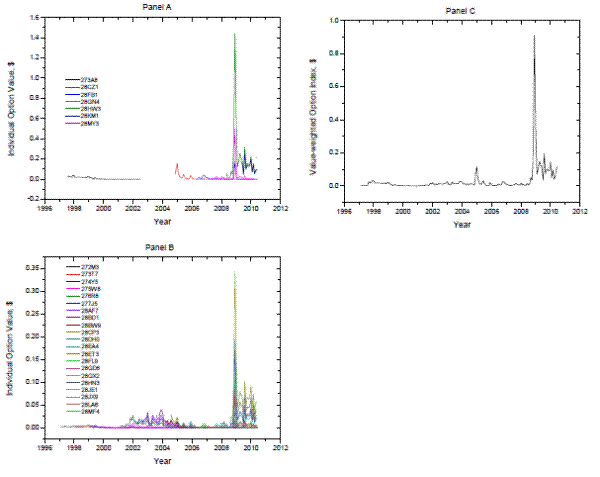
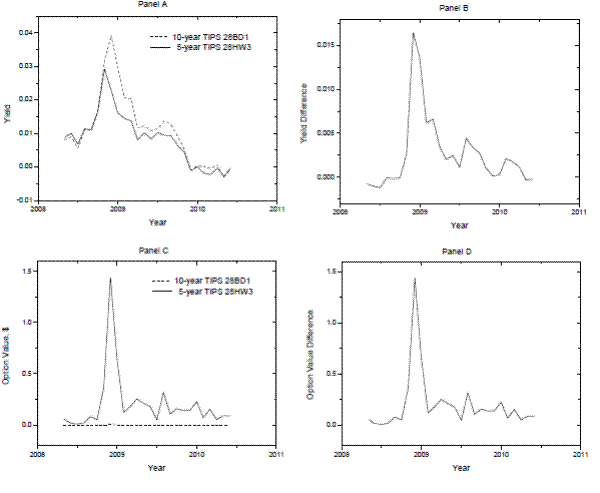
![\begin{eqnarray*} SSE(\Theta )=\sum_{t=1}^{T}\left[ \sum_{n=1}^{N_{t}}\left( P_{nt}^{\ast }-P_{nt}\right) ^{2}+\sum_{n=1}^{\bar{N}_{t}}\left( \bar{P}_{nt}^{\ast }-% \bar{P}_{nt}\right) ^{2}\right] , \end{eqnarray*}](table_img5.gif)