Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2013-53 Screen Reader version ^♣

Optimal Fiscal and Monetary Policy With
Occasionally Binding Zero Bound Constraints*

Taisuke Nakata*

Federal Reserve Board

First Draft: November 2011

This Draft: April 2013

Abstract

This paper studies optimal government spending and monetary policy when the nominal interest rate is subject to the zero lower bound constraint in a stochastic New Keynesian economy. I find that the government chooses to increase its spending when at the zero lower bound by a substantially larger amount in the stochastic environment than it would in the deterministic environment. The presence of uncertainty creates a unique time-consistency problem if the steady-state is inefficient. Although access to government spending policy increases welfare in the face of a large deflationary shock, it decreases welfare during normal times as the government reduces the nominal interest rate less aggressively before reaching the zero lower bound.

JEL: E32, E52, E61, E62, E63

Keywords: Fiscal Policy, Government Spending, Occasionally Binding Constraints, Liquidity Trap, Zero Lower Bound, Markov-Perfect Equilibria, Commitment, Welfare

1 Introduction

The short-term nominal interest rate, the conventional policy tool for macroeconomic stabilization, is subject to the constraint that it cannot go below zero. In late 2008, the Federal Reserve effectively lowered the federal funds rate to zero. The policy rate has been at the zero lower bound since then, and is expected to remain so for the near future. With the standard monetary policy tool constrained, the government has turned to alternative policy tools to stimulate the economy. One such policy tool was fiscal policy. In early 2009, Congress enacted the American Recovery and Reinvestment Act to provide fiscal stimulus to the U.S. economy in the hope that it would create jobs and promote economic recovery.

In light of this policy experience, many authors have recently examined positive and normative implications of fiscal policy when the nominal interest rate is constrained by the zero bound in the context of dynamic general equilibrium models. Some have shown that an exogenous increase in government spending leads to larger increases in consumption and output when the nominal interest rate is constrained at the zero lower bound.¹ Others have shown that it is even optimal to increase government spending when the nominal interest rate is zero.² These results support the active use of fiscal policy in the current economic environment.

Thus far, this body of work on fiscal policy has abstracted from uncertainty. It is typically assumed that an exogenous force that pushes the nominal interest rate to zero reverts back to its steady-state level in a deterministic manner, and fiscal multipliers and optimal fiscal policies are analyzed along a specific deterministic path.³ However, the current economic environment motivating these analyses is characterized by a high degree of uncertainty. Policymakers during any economic downturn are far from certain about the severity and duration of the recession, and this might be particularly true in the recent episode. There is anecdotal evidence suggesting that uncertainty has slowed investment and hiring by firms, and many believe that it has been a key factor contributing to the slow recovery. It would thus be useful to examine how the presence of uncertainty alters the assessment of fiscal policy when the nominal interest is at the zero lower bound.

Accordingly, this paper studies optimal fiscal and monetary policy when the nominal interest rate is subject to the zero lower bound constraint in a stochastic environment. The analysis is conducted in a standard New Keynesian economy. Following the framework of the previous literature, I use exogenous variation in the household's discount rate as the force that leads the government to lower the nominal interest rate to zero. However, unlike the previous literature that studied optimal fiscal policy along one specific path of the exogenous discount rate, the discount rate in this paper is stochastic. I then compare allocations, prices, and policy instruments in the deterministic economy with those in the stochastic economy to understand the effect of uncertainty. The available fiscal instrument is assumed to be the government spending financed by lump-sum taxation. The main analysis is conducted under the timing protocol in which the government makes decisions sequentially, taking as given the future policy functions of the government, household, and firms. I refer to the model with this timing protocol as the model without commitment. However, I also conduct the analysis under the alternative timing protocol in which the government decides a sequence of policy variables for all states for all time periods at the beginning of time one. I refer to the model with this timing protocol as the model with commitment.

In the model without commitment, the government increases its spending at the zero lower bound by a substantially larger amount in the stochastic environment than it would in the deterministic environment. When the nominal interest rate is constrained at the zero lower bound, a mean-preserving spread in the shock distribution increases the expected real interest rates and decreases the expected real marginal costs of production. Such changes in expectations lead forward-looking household and firms to consume less and set lower prices today. As a result, when the nominal interest rate is at the zero lower bound, the declines in consumption, output, and inflation in response to a given size of the shock are larger in the stochastic environment than in the deterministic environment. Faced with a more severe recession, the government chooses to increase its spending by a larger amount.

In the stochastic environment, access to the government spending policy not only affects allocations at the zero bound directly, but also affects allocations away from the zero bound indirectly through its effects on the expectations of the households and firms. When the nominal interest rate is at the zero lower bound, consumption, output, and inflation decline by a larger amount in the absence of fiscal instrument than in the presence of it. As a result, when the economy is away from the zero lower bound, not having access to government spending policy, even if the economy goes back to the zero lower bound in the future, leads the household and firms to reduce their expectations of future allocations and prices. Such shifts in expectations lead the forward-looking household and firms to lower consumption and prices today by more. Today's government tries to prevent such a reduction in consumption and inflation by lowering the nominal interest rate more aggressively. In equilibrium, the more aggressive nominal interest rate policy in the constrained economy without a fiscal instrument increases consumption and output when the nominal interest rate is near the zero lower bound constraint.

If imperfect competition in the product market leads steady-state consumption and output to be inefficiently low, such increases in consumption and output raise the conditional welfare away from the zero lower bound and increases the unconditional welfare as well. That is, the economy is better off without access to fiscal policy. This somewhat counterintuitive result--that welfare is larger without the fiscal policy instrument--arises because the constraint on the government spending policy has two aspects in the model without commitment. While it constrains the government's choice on its spending today, this constraint represents commitment not to rely on countercyclical fiscal policy in the future, which makes the nominal interest rate policy more aggressive and improves allocations today.⁴ On the other hand, if a production subsidy is available and the steady-state consumption and output are efficient, access to the government spending policy improves welfare. In such a case, having access to fiscal policy reduces the welfare costs of the zero lower bound roughly by half.

In the model with commitment, the government also increases its spending at the zero lower bound by a larger amount, and reduces the nominal interest rate more aggressively before reaching the zero lower bound constraint, in the presence of uncertainty than in the absence of it. However, unlike in the model without commitment, the additional increase in government spending due to uncertainty is quantitatively small. In the model with commitment, the more aggressive nominal interest rate policy goes a long way in mitigating the destabilizing effects of uncertainty, and the additional role for fiscal policy is limited.

This paper is the first to examine the consequences of an additional policy instrument in the model with occasionally binding zero bound constraints.⁵ Adam and Billi (2006), Adam (2007), and Nakov (2008) studied optimal policy with zero lower bound constraints in stochastic environments. However, in their models, the nominal interest rate is the only policy instrument and the government does not have any policy tool available once the nominal interest rate is at the zero lower bound. In principle, a variety of policy instruments are available to the government. While I focus on fiscal policy in this paper, it would be useful to consider the consequences of other policy tools as well. For example, one may want to examine the effect of financial policy in a similar environment. This paper can be seen as providing a framework within which one can conduct such analysis.

The rest of the paper is organized as follows. The next section describes the model and defines the private sector equilibrium, while section 3 formulates the government's problem. Section 4 discusses parametrization and the solution method. Sections 5 and 6 respectively discuss the results for the models without and with commitment. A final section concludes.

2 Model

This section describes the private sector of the model and defines the equilibrium. The model is given by a standard New Keynesian model, and is formulated in discrete time with an infinite horizon.

2.1 Household

The representative household chooses consumption, labor supply, and the holdings of one period risk free nominal bond to maximize the expected discounted sum of the future period utilities. The household likes consumption and dislikes labor. Following the setup of the previous work on fiscal policy at the zero bound, I assume that the household also values government spending. The period utility is assumed to be separable.⁶ The household problem is given by

$\displaystyle \operatorname*{max}_{C,N,B} E_{1} \sum_{t=1}^{\infty}\beta^{t-1} \Bigl[\prod_{s=0}^{t-1}\delta_{s}\Bigr] \Bigl[ \frac{C_{t}^{1-\chi_{c}}}{1-\chi_{c}} - \frac{N_{t}^{1+\chi_{n}}}{1+\chi_{n}} + \chi_{g,0}\frac{G_{t}^{1-\chi_{g,1}}}{1-\chi_{g,1}}\Bigr]$

subject to

$\displaystyle P_{t}C_{t} + R_{t}^{-1} B_{t} \leq W_{t}N_{t} + B_{t-1} - P_{t}T_{t} + P_{t}\Phi_{t}$

and $\delta_{1}$ is given. $C_{t}$ is consumption, $N_{t}$ is labor supply, and $G_{t}$ is government spending. $P_{t}$ is the price of consumption good, $W_{t}$ is nominal wage, $T_{t}$ is lump-sum taxation, and $\Phi_{t}$ is the profit from the intermediate goods producers. $B_{t}$ is a one-period risk-free bond that pays one unit of money at t+1, and $R_{t}$ is the return on the bond.

The discount rate at time t is given by $\beta\delta_{t}$ . $\delta_{t}$ is the discount factor shock that alters the weight of the future utility at time t+1 relative to the period utility at time t. $\delta_{t}$ follows an AR(1) process:

$\displaystyle (\delta_{t} - 1) = \rho(\delta_{t-1} - 1) + \epsilon_{t}\hspace{0.5em} \forall \hspace{0.5em} t\geq 2\\$

where $\epsilon_{t}$ is a shock to the discount factor shock and is distributed as normal with mean 0 and standard deviation $\sigma_{\epsilon}$ . One can think of $\delta_{t}$ as a measure of the household's patience. An increase in $\delta_{t}$ makes the household want to save more for tomorrow and spend less today. The main exercise of the paper will be to compare the case in which $\sigma_{\epsilon}>0$ with the case in which $\sigma_{\epsilon}=0$ .

2.2 Producers

There is a representative final-good producer and a continuum of intermediate-goods producers indexed by $i \in [0,1]$ . The representative final good producer purchases the intermediate goods, combines them into the final good using CES technology. It sells the final good to the household and the government. The optimization problem of the final good producer is given by

$\displaystyle \operatorname*{max}_{ Y_{i,t}, i \in [0,1] } \hspace{1em} P_{t}Y_{t} - \int_{0}^{1} P_{i,t}Y_{i,t} di$

subject to the CES production function, $Y_{t} = \Bigl[ \int_{0}^{1} Y_{i,t}^{\frac{\theta-1}{\theta}} di \Bigr]^{\frac{\theta}{\theta-1}}$ .

Intermediate-good producers use labor inputs and produce imperfectly substitutable intermediate goods according to a linear production function. Each firm sets the price of its own good to maximize the expected discounted sum of future profits. The optimization problem of the intermediate good producer is given by

$\displaystyle \operatorname*{max}_{ \{P_{i,t} \}_{t=1}^{\infty} } E_{1}\sum_{t=1}^{\infty} \beta^{t-1}\Bigl[\prod_{s=0}^{t-1}\delta_{s}\Bigr] \lambda_{t} \Bigl[ P_{i,t}Y_{i,t} - W_{t}N_{i,t} - P_{t}\frac{\varphi}{2}\bigl[ \frac{P_{i,t}}{P_{i,t-1}} - 1 \bigr]^{2} Y_{t} \Bigr]$

subject to $Y_{i,t} = \bigl[ \frac{P_{i,t}}{P_{t}} \bigr]^{-\theta}Y_{t}$ , and $Y_{i,t} = N_{i,t}$ . $\lambda_{t}$ is the Lagrangian multiplier on the household budget constraint at time t, and $\Bigl[\prod_{s=0}^{t-1}\delta_{s}\Bigr] \lambda_{t}$ measures the marginal value of an additional unit of profits to the household. Price changes are subject to quadratic adjustment costs. There is no heterogeneity in the time-zero prices across firms. That is, $P_{i,0} = P_{0}$ for some given constant $P_{0} > 0$ .

2.3 Government's Policy Instruments

The government's problem will be introduced in the next section. Here, I describe a set of restrictions on the government's policy instruments. Throughout the paper, I assume that lump-sum taxation is used to finance government spending and that the supply of the government bond is zero. Thus, the government budget constraint is given by $G_{t} = T_{t}$ .⁷

Finally, I impose that the nominal interest rate cannot fall below 1.

$\displaystyle R_{t} \geq 1$

2.4 Market Clearing Conditions

Market clearing conditions for the final good, labor, and the bond are given by

$\displaystyle Y_{t}$	$\displaystyle =$	$\displaystyle C_{t} + G_{t} + \int \frac{\varphi}{2}\bigl[\frac{P_{i,t}}{P_{i,t-1}} - 1\bigr]^{2}Y_{t} di$
$\displaystyle N_{t}$	$\displaystyle =$	$\displaystyle \int_{0}^{1}N_{i,t} di$
$\displaystyle B_{t}$	$\displaystyle =$	0

2.5 An Implementable Equilibrium

Given $P_{0}$ and $\{ \delta_{t} \}_{t=1}^{\infty}$ , an implementable equilibrium of this economy consists of allocations ( $\{C_{t},N_{t},N_{i,t},Y_{t},Y_{i,t} \}_{t=1}^{\infty}$ ), prices ( $\{ W_{t}, P_{t}, P_{i,t} \}_{t=1}^{\infty}$ ), and policy instruments ( $\{ R_{t}, G_{t}, T_{t}\}_{t=1}^{\infty}$ ) such that (i) allocations solve the problem of the household given prices and policies, (ii) $P_{i,t}$ solves the problem of firm i, (iii) $P_{i,t} = P_{j,t}$ for all $i \neq j$ , (iv) all markets clear.

It is straightforward to show that a set of implementable equilibria can be recursively characterized by $\{ C_{t},N_{t},Y_{t},w_{t},\Pi_{t},R_{t},G_{t}\}_{t=1}^{\infty}$ satisfying

		$\displaystyle C_{t}^{-\chi_{c}} = \beta \delta_{t}R_{t} E_{t}C_{t+1}^{-\chi_{c}}\Pi_{t+1}^{-1}$	(1)
		$\displaystyle w_{t} = N_{t}^{\chi_{n}}C_{t}^{\chi_{c}}$	(2)
		$\displaystyle \frac{N_{t}}{C_{t}^{\chi_{c}}}\bigl[ \varphi (\Pi_{t} - 1)\Pi_{t} - (1 - \theta) - \theta w_{t}\bigr] = \beta \delta_{t} E_{t}\frac{N_{t+1}}{C_{t+1}^{\chi_{c}}}\varphi (\Pi_{t+1} - 1)\Pi_{t+1}$	(3)
		$\displaystyle Y_{t} = C_{t} + G_{t} + \frac{\varphi}{2}\bigl[ \Pi_{t} - 1 \bigr]^{2}Y_{t}$	(4)
		$\displaystyle Y_{t} = N_{t}$	(5)
		$\displaystyle G_{t} = T_{t}$	(6)
		$\displaystyle R_{t} \geq 1$	(7)

Equation (1) is the consumption Euler Equation and equation (2) is the intratemporal optimality condition of the household. Equation (3) is the optimality condition of the intermediate good producing firms, often referred to as the forward-looking Phillips Curve. It relates today's inflation to the real marginal cost today and expected inflation tomorrow. Equation (4) is the aggregate resource constraint. The last term of equation (4) captures the resource cost of price adjustment. Equation (5) is the aggregate production function and equation (6) is the government budget constraint.

3 Government's Problem

This section formulates the government's problem. Previous studies have documented that the government's ability to commit makes stark differences in allocations when the nominal interest rate is constrained by the zero lower bound. Thus, I consider two alternative timing protocols. In the first protocol, the government sequentially makes decisions. Each period, the government maximizes the welfare of the household taking as given the policy functions of the government, the household, and firms in the future. I refer to this model as the model without commitment. In the second protocol, the government chooses a sequence of policy variables for all states for all time periods at the beginning of time one, announces it to agents in the private sector, and adheres to the announced policy in the future. I refer to this model as the model with commitment.

3.1 Model Without Commitment

For every period t, taking as given the next period value and policy functions ( $V_{t+1}(\cdot)$ , $C_{t+1}(\cdot)$ , $N_{t+1}(\cdot)$ , $Y_{t+1}(\cdot)$ , $\Pi_{t+1}(\cdot)$ , $w_{t+1}(\cdot)$ , $R_{t+1}(\cdot)$ , $G_{t+1}(\cdot)$ ), the government solves the following problem.

$\displaystyle V_{t}(\delta_{t}) =$ max $\displaystyle _{\{ d_{t} \}} \Bigl[ \frac{C_{t}^{1-\chi_{c}}}{1-\chi_{c}} - \frac{N_{t}^{1+\chi_{n}}}{1+\chi_{n}} + \chi_{g,0}\frac{G_{t}^{1-\chi_{g,1}}}{1-\chi_{g,1}}\Bigr] + \beta\delta_{t} E_{t} V_{t+1}(\delta_{t+1})$

where $d_{t}:=(C_{t}$ , $N_{t}$ , $Y_{t}$ , $w_{t}$ , $\Pi_{t}$ , $R_{t}$ , $G_{t})$ and the optimization is subject to the implementable equilibrium conditions stated above. A Markov-Perfect Equilibrium consists of a set of time-invariant value and policy functions $\{V(\cdot)$ , $C(\cdot)$ , $N(\cdot)$ , $Y(\cdot)$ , $w(\cdot)$ , $\Pi(\cdot)$ , $R(\cdot)$ , $G(\cdot)\}$ solving the Bellman equation above.⁸

3.2 Model With Commitment

The government with the ability to commit chooses a sequence of policy variables for all states for all time periods at the beginning of time one in order to maximize the expected discount sum of future utilities given by

$\displaystyle E_{1}\sum_{t=1}^{\infty} \beta^{t-1} \prod_{s=0}^{t-1}\delta_{s} \Bigl[ \frac{C_{t}^{1-\chi_{c}}}{1-\chi_{c}} - \frac{N_{t}^{1+\chi_{n}}}{1+\chi_{n}} + \chi_{g,0}\frac{G_{t}^{1-\chi_{g,1}}}{1-\chi_{g,1}}\Bigr]$

subject to the equations characterizing the implementable equilibria. A Ramsey equilibrium consists of $\{C(\delta^{t})$ , $N(\delta^{t})$ , $Y(\delta^{t})$ , $\Pi(\delta^{t})$ , $w(\delta^{t})$ , $G(\delta^{t})$ , $R(\delta^{t})\}$ satisfying the first order necessary conditions of the Ramsey planner's problem for all $\delta^{t}$ , where $\delta^{t} \equiv [\delta_{1},...,\delta_{t}]$ denotes the history of shocks. Following Marcet and Marimon (2011), I characterize the Ramsey equilibrium recursively. The government's problem can be written as

$\displaystyle W_{t}(\delta_{t},\phi_{1,t-1},\phi_{2,t-1}) =$ max $\displaystyle _{\{ d_{t} \}}$ min $\displaystyle _{\{ \phi_{t} \}}\Bigl[ \frac{C_{t}^{1-\chi_{c}}}{1-\chi_{c}} - \frac{N_{t}^{1+\chi_{n}}}{1+\chi_{n}} + \chi_{g,0}\frac{G_{t}^{1-\chi_{g,1}}}{1-\chi_{g,1}}\Bigr] + \beta\delta_{t} E_{t}W_{t+1}(\delta_{t+1},\phi_{1,t},\phi_{2,t})$

subject to the equations characterizing the implementable equilibria. $\phi_{t} = [\phi_{1,t},...,\phi_{7,t}]$ is a vector of Lagrangian multipliers for the seven equations characterizing the implementable equilibria. Let $s_{t} \equiv [\delta_{t}, \phi_{1,t-1},\phi_{3,t-1}]$ . A Ramsey equilibrium can be characterized by a set of time-invariant policy and value functions, [ $C(s_{t})$ , $N(s_{t})$ , $Y(s_{t})$ , $\Pi(s_{t})$ , $w(s_{t})$ , $G(s_{t})$ , $R(s_{t})$ , $\phi(s_{t})$ ], that solves the Bellman equation above.

4 Parametrization and Solution Method

4.1 Parametrization

Table 1 lists the parameter values selected. The values chosen for the household's preference parameters, the elasticity of substitution among intermediate goods, and the price adjustment cost are within the range considered in the literature. The value of the price adjustment cost, $\varphi$ , implies the slope of the Phillips curve that is equivalent to the one in the Calvo pricing model with 78 percent probability of price non adjustment. The steady-state discount rate, $\beta$ , is set to $\frac{1}{1+0.0075}$ , which implies an annualized steady state real interest rate of 3 percent. I follow Adam and Billi (2006), Adam and Billi (2007), and Nakov (2008) in setting the the persistence of the time-preference shock, $\rho$ , to 0.8. For the variance of shock, $\sigma_{\epsilon}$ , I choose a value of $\frac{0.445}{100}$ as a benchmark. This value makes the probability of being at the zero lower bound around 8 percent. The implied unconditional standard deviation of $\delta_{t}$ is 0.007, and is denoted by $\sigma_{\delta}$ . I consider the robustness of the results to alternative values of $\sigma_{\epsilon}$ in the Appendix.

4.2 Solution Method

The model is solved by the time-iteration method of Coleman (1991). The time-iteration method starts with a guess of the policy functions. Assuming that the guessed policy functions are in use for the next period, the first-order necessary conditions of the government problem is solved on a discrete number of grids to find the policy functions in the current period. This process is repeated until policy functions today become arbitrarily close to policy functions tomorrow. For the model without commitment, I use 1001 points on [ $1-4\sigma_{\delta},1+4\sigma_{\delta}$ ] for $\delta_{t}$ . For the model with commitment, I use 51 grid points on [ $1-4\sigma_{\delta},1+4\sigma_{\delta}$ ] for $\delta_{t}$ , 11 points on [0,0.05] for $\phi_{1,t}$ , and 11 points on [ $\bar{\phi}_{3}-0.02$ , $\bar{\phi}_{3}+0.02$ ] for $\phi_{3,t}$ where $\bar{\phi}_{3}$ is the Ramsey steady state of $\phi_{3,t}$ .

5 Results for the model without commitment

This section characterizes the equilibrium for the model without commitment. I first show how the presence of uncertainty affects allocations, prices, and policy instruments by comparing the stochastic economy with the deterministic economy. I then move on to study the effects of fiscal policy on allocations and welfare. To do so, I solve the model in which the government is constrained to keep its spending constant at the deterministic steady-state level for all states and for all time periods, and compare allocations and welfare in this constrained economy with those in the benchmark unconstrained economy.

5.1 Markov-Perfect Equilibrium With and Without Uncertainty

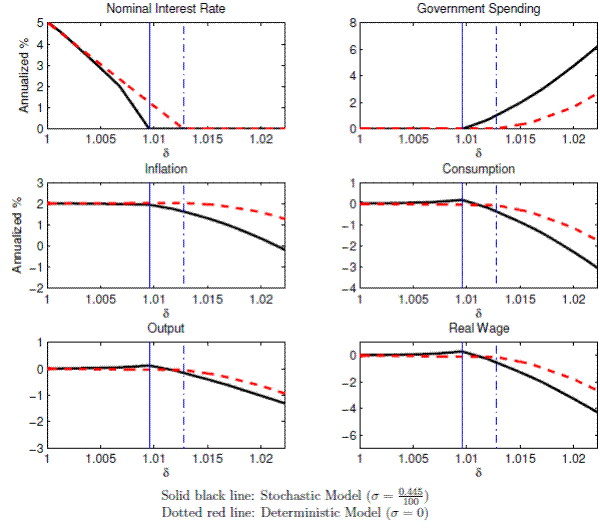
Solid black and dashed red lines in Figure 1 show the policy functions from the stochastic and deterministic economies ( $\sigma_{\epsilon}=\frac{0.445}{100}$ and $\sigma_{\epsilon}=0$ ).

In the deterministic economy, the government responds to an increase in the discount factor shock ( $\delta$ ) by reducing the nominal interest rate one-for-one, which can be seen in the dashed red line in the top left panel. An increase in the discount factor shock means that the household becomes more patient. As the household becomes more patient, s/he wants to save more for tomorrow and spend less today. The government chooses to offset this effect by offering lower nominal interest rates on the government bond. The government would like to completely neutralize the effect of an increase in $\delta$ because there is no capital or storage technology in the model and the allocations it wants to achieve do not depend on the household's discount rate. As a result, consumption, output, and inflation do not change from their deterministic steady-state levels as $\delta$ increases--as long as the government is able to reduce the nominal interest rate.⁹ The government also keeps its spending at its steady-state level as the nominal interest rate alone suffices to offset the shock.

For a sufficiently large discount factor shock, the government cannot reduce the nominal interest rate further to offset completely the increase in the discount factor shock due to the zero lower bound constraint, leading to a decline in the demand for goods by the household. In this model with nominal price rigidity, firms respond to the reduced demand for goods by shrinking their production, reducing the demand for labor and putting downward pressure on the real wage. The decline in the real wage in turn leads firms to set lower prices today. Lower inflation today increases the real interest rate in the previous period. Faced with a higher real interest rate, the household would like to reduce consumption even further. In equilibrium, consumption, output, and inflation all decline in response to the increase in the discount factor shock when the economy is at the zero lower bound. Faced with such declines in allocations and prices, the government chooses to increase its spending.

While consumption, output, and inflation decline at the zero lower bound both in the deterministic and stochastic economies, those declines are larger in the stochastic economy. While declines in the discount rate can be met by increases in the nominal interest rate, increases in the the discount rate cannot be met by interest rate cuts when the rate is already zero, as the nominal interest rate is truncated below by zero. As a consequence, when at the zero lower bound, a mean-preserving spread in the shock distribution increases the expected nominal interest rate, and thus the expected real rate, even though it does not alter the modal outcome. Faced with an increased real interest rate in the future, the forward-looking household reduces their consumption today. An increase in uncertainty similarly affects the firms' price-setting decisions. Since the government cannot prevent the real wage from falling when the nominal interest rate is constrained, but will not let the real wage rise above the steady-state level when it is not constrained, the policy function for the real wage is truncated from above. As a result, an increase in uncertainty reduces the expected real wages in the future, leading forward-looking firms to set lower prices today.¹⁰ Faced with larger declines in consumption, output, and inflation, the government chooses to increase its spending by a larger amount in the stochastic economy than in the deterministic economy. The differences in allocations between deterministic and stochastic economies are quantitatively important. For example, at $\delta=1+3\sigma_{\delta}$ , the declines in inflation and the increase in the government spending in the stochastic economy are more than twice as large as those in the deterministic economy.

Not only does the presence of uncertainty affect allocations and government spending policy at the zero lower bound, it also affects the conduct of nominal interest rate policy. Specifically, in the presence of uncertainty, the government reduces the nominal interest rate more aggressively in response to an increase in the discount factor shock before reaching the zero lower bound than it would in the deterministic economy. In the deterministic economy, once the economy is away from the zero lower bound, the economy never goes back to the zero bound state. However, in the stochastic economy, even if the economy is away from the zero bound, there is a positive probability that a future shock leads the economy back into the zero bound state. Thus, away from the zero lower bound, the expected real interest rate and the expected real wage are respectively higher and lower in the stochastic economy than in the deterministic economy. Forward-looking households and firms therefore would like to reduce consumption and set lower prices today. The government chooses to offset this effect by reducing the nominal interest rate further. In equilibrium, the more aggressive nominal interest rate policy creates temporary booms in output and consumption when the nominal interest rate is near the zero lower bound. This can be seen by the fact that solid black lines are above dashed red lines around the solid blue vertical lines for the policy functions for consumption and output.

Figure 2 gives us an alternative look at the effect of uncertainty by showing how differently the deterministic and stochastic economies respond to a one-time large increase in the discount rate shock. The solid black lines show the median response of the key variables in the economy with $\sigma_{\epsilon}=\frac{0.445}{100}$ and the dashed red lines show the evolution with $\sigma_{\epsilon}=0$ . In the stochastic environment, the declines in consumption, output, and inflation and the increase in government spending are substantially larger at the beginning of the recession. While consumption and inflation drop by about 1 and 0.5 percent in the deterministic economy, they drop by about 2 percent in the stochastic economy. While the government raises its spending by about 3 percent in the deterministic economy, the government in the stochastic economy does so by about 6 percent. The presence of uncertainty alters the monetary policy responses to the shock as well. As discussed earlier, the government reduces the nominal interest rate more aggressively before reaching the zero lower bound in the presence of uncertainty. The flip-side of this nominal interest rate policy is that the government is slower in increasing the nominal interest rate from zero out of a recession. While the government in the deterministic economy keeps the nominal interest rate at zero for 4 quarters, the government in the stochastic economy keeps the nominal interest rate at zero for 5 quarters.

5.2 Markov-Perfect Equilibrium With and Without Fiscal Policy

This subsection and the next compare equilibria with and without government spending policy in order to understand how access to fiscal policy alters allocations, prices, and welfare in the stochastic economy. Specifically, I solve the government's optimization problem described earlier with an additional constraint that government spending has to be fixed at its deterministic steady-state level for all states and all time periods. This constrained economy corresponds to the economy studied in Adam and Billi (2007) and Nakov (2008) in which the nominal interest rate is the only policy instrument.

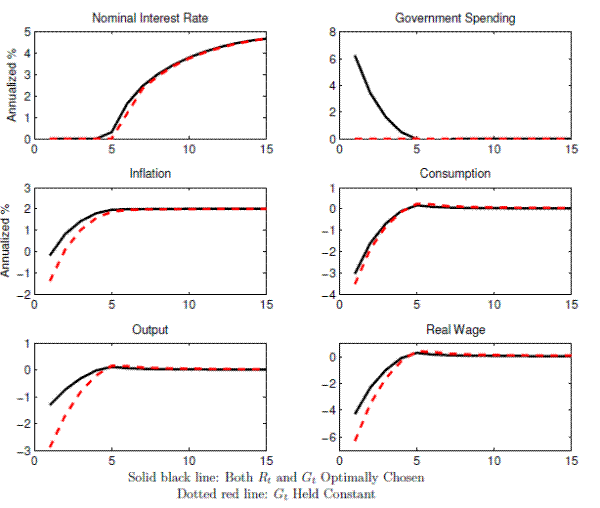
The solid black lines and dashed red lines in Figure 3 respectively show the policy functions from the economies with and without government spending policy in the stochastic environment. Not surprisingly, the declines in output and inflation are larger at the zero lower bound when the government is not allowed to use its spending tool. As a result of the reduced demand for goods, firms reduce the demand for labor, which puts downward pressures on the real wage. A reduction in the real wage is then translated into lower inflation due to nominal rigidities. Even though fewer resources are devoted to government spending, consumption is lower in the economy without government spending policy because output declines by more than one-for-one in response to a reduction in government spending.¹¹

The availability of a fiscal instrument also affects the conduct of nominal interest rate policy. The government without a fiscal policy instrument reduces the nominal interest rate more aggressively in response to an increase in the discount factor shock before reaching the zero lower bound. As discussed above, if the government is constrained to keep its spending constant, the declines in consumption, output, and inflation are larger at the zero lower bound. In the stochastic economy, even if the economy is away from the zero lower bound, the household and firms assign a positive probability to visiting those states in the future. Since the allocations are lower at the zero lower bound without fiscal policy than with it, the agents' expected consumption and inflation are lower, and forward-looking agents accordingly reduce consumption and lower prices by more in the economy without a fiscal instrument. The government without access to fiscal policy lowers the nominal interest rate by a larger amount to prevent such larger declines. In equilibrium, due to the more aggressive nominal interest rate policy, the temporary booms in output and consumption when the nominal interest rate is near the zero lower bound are larger in the economy without fiscal policy.

This difference in the nominal interest rate policy between the unconstrained and constrained economies manifests itself in the difference in the frequencies of the economy being at the zero lower bound. The first row of Table 2 shows that the frequencies of hitting the zero lower bound with and without fiscal policy in this model without commitment. The government without access to government spending policy lowers the nominal interest rate to zero about 9.7 percent of the time whereas the government with access to government spending policy reduces the policy rate to zero 8.0 percent of the time.

5.3 Welfare Implications of Fiscal Policy

The difference in the nominal interest rate policy described above has important implications for welfare. The first column of Table 3 shows the welfare costs of the zero lower bound in the economy with and without fiscal policy. The welfare costs are computed by the perpetual consumption transfer necessary to make the household in the economy with the zero lower bound constraint as well off as the agent in the hypothetical economy without the zero lower bound. In the table, the perpetual consumption transfer is expressed as a percentage of the deterministic steady-state consumption.

Negative numbers in the first column mean that, regardless of the availability of fiscal policy, welfare is larger in the economy with the zero lower bound constraint than in the economy without it. The fact that the number is lower in the economy with fiscal policy means that the economy is better off without the fiscal policy instrument. These somewhat counterintuitive results arise because of (i) the temporary consumption and output booms near the zero lower bound described above and (ii) the inefficient steady-state. In this model, the steady-state consumption and output are inefficiently low because of imperfect competition in the product market. As a result, the temporary increases in consumption and output near the zero lower bound are welfare-enhancing. Even though the consumption and output declines at the zero lower bound are welfare-reducing, this effect is dominated by the welfare enhancing effect of temporary output and consumption booms as the economy spends more time in the region of temporary booms than in the zero lower bound region. Unconditionally, welfare is larger in the economy with the zero lower bound than without it. As argued in the previous subsection, temporary booms in consumption and output are larger in the absence of fiscal policy, and therefore the welfare gains from the zero lower bound are larger in the constrained economy without fiscal policy. In other words, the access to fiscal policy decreases welfare.

Another way to understand this result--that the constraint on a policy instrument increases welfare--is to recognize that the constraint has two aspects in the model without commitment. While not having access to the fiscal instrument constrains the government's choice set today, it represents a form of commitment tomorrow. In this model, committing itself not to rely on fiscal policy in the future even if the nominal interest rate is zero makes today's government more aggressive in reducing the nominal interest rate, leading to better consumption and output outcomes today.¹²

These welfare results crucially depend on the inefficiency of the steady state. In the economy in which a production subsidy is available to offset the inefficiency arising from monopolistic competition, consumption and output are inefficiently high during the temporary booms in consumption and output near the zero lower bound. Thus, the zero lower bound is welfare-reducing near the zero lower bound as well as when at the zero lower bound. As a result, the welfare costs of the zero lower bound are positive, and the welfare costs of the zero bound are larger in the absence of the fiscal instrument than in the presence of it, as seen in the first column of Table 4. In this case, access to fiscal policy reduces the welfare costs arising from the zero lower bound constraint by about 40 percent ( $\frac{0.15}{100}$ percent with fiscal policy versus $\frac{0.26}{100}$ percent without fiscal policy).

6 Results for the model with commitment

This section characterizes allocations, prices, and welfare when the government can commit to a sequence of policy variables at time one. As in the previous section, I first study the implications of uncertainty on the conduct of fiscal and monetary policy by comparing the stochastic and deterministic economies. I then study the effect of having fiscal policy as an additional policy instrument on allocations and welfare by comparing the constrained and unconstrained economies.

Policy functions in the recursively formulated Ramsey equilibrium are functions of three state variables: the discount factor shock and two Lagrangian multipliers from the previous period. Instead of directly analyzing this high-dimensional object, I use the response of the economy to a large increase in the discount rate to discuss the key features of the model with commitment.

6.1 Ramsey Equilibrium With and Without Uncertainty

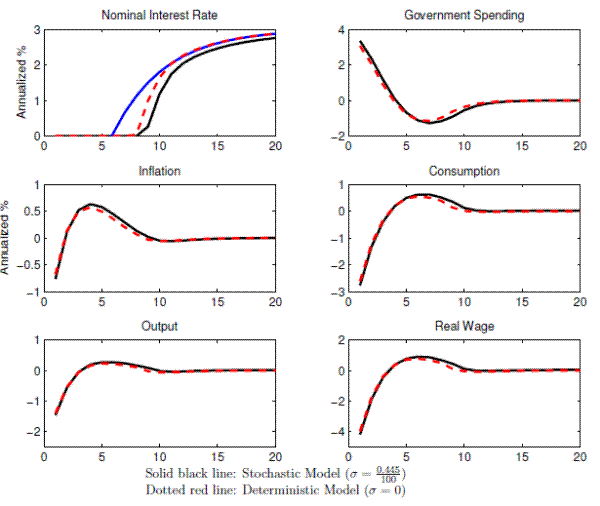
Figure 5 shows the Ramsey equilibria in response to the discount factor shock that pushes $\delta_{1}$ to $1 + 3\sigma_{\delta}$ . Solid black lines show the median responses of the key variables in the stochastic economy while dashed red lines plot the evolution of the key variables in the deterministic economy.

In the deterministic environment, the government promises to keep the nominal interest rate low for an extended period of time. While the natural real interest rate becomes positive at period 6 (see the blue line), the government keeps the nominal interest rate at zero until period 7 and keeps the rates substantially below the natural real interest rate until period 11. An extended period of low nominal interest rates, together with sustained above-trend inflation during the zero bound period, helps to mitigate the deflation that would otherwise occur at the beginning of the recession and creates temporary overshooting in consumption and output before the economy converges back to the steady state. Government spending policy is characterized by an initial increase followed by a gradual reduction below and an eventual return to the steady-state level. These features of optimal nominal interest rate and government spending policy in the deterministic environment are consistent with Eggertsson (2001) and Werning (2012).

In the stochastic economy, consumption, output, and inflation are stabilized less than in the deterministic economy: They initially decline by a larger amount and peak at higher levels before converging back to the steady-state. Under uncertainty, the government keeps nominal interest rates at zero for a longer period, as it does in the model without commitment. The government keeps the nominal interest rate at zero for 8 periods in the stochastic setting, as opposed to 7 periods in the deterministic setting, and keeps the rates below the natural real rate for an extended period. The presence of uncertainty also leads the government to increase its spending by more. The government increases its spending by 3.1 percent in the deterministic economy as opposed to 3.5 percent in the stochastic economy. Notice that the additional increase in government spending due to uncertainty is smaller than in the model without commitment. The effect of uncertainty on consumption, inflation, and output are smaller as well. Overall, the presence of uncertainty is less destabilizing to the economy in the model with commitment, and thus the role of fiscal policy is less affected by it.

6.2 Ramsey Equilibrium With and Without Fiscal Policy

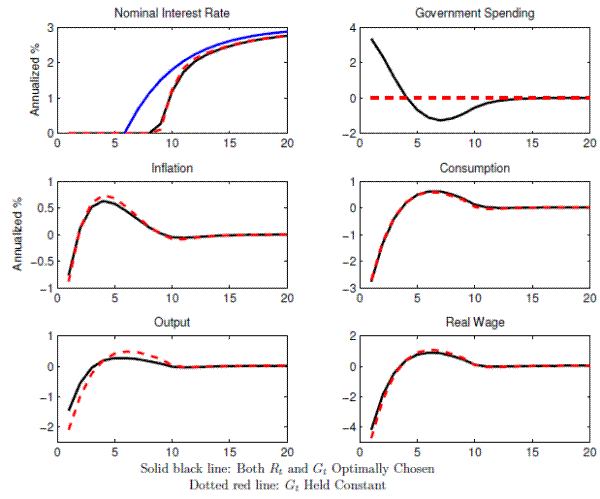
Figure 6 compares the Ramsey equilibria with and without government spending policy. The solid black lines show the median responses of the key variables in the unconstrained economy while dashed red lines show the evolution of the key variables in the constrained economy in which the government spending is held constant.

The availability of a fiscal instrument does not alter the nominal interest rate policy substantially. Both with and without fiscal policy, the government keeps the nominal interest rate at zero for 9 quarters before gradually raising it back to the steady-state level. The second row of Table 3 shows the frequencies of hitting the zero lower bound with and without fiscal policy. In contrast to the model without commitment, access to fiscal policy does not have material effects on the frequency. The access to fiscal policy leaves the consumption path essentially unchanged, and the variation in government spending leads to roughly one-for-one changes in output. As a result, the output path is more stabilized with government spending policy than without it. A smoother output path means smoother paths for the real wage and inflation. The real wage and inflation initially drops by 4.5 and 0.9 percent without government spending policy, while they declines by 4.0 and 0.8 percent with government spending policy. They peak at 1.2 and 0.7 percent in the constrained economy versus 0.9 and 0.6 percent in the unconstrained economy.

6.3 Welfare Implications of Fiscal Policy

The second column of Table 3 shows the welfare costs of the zero lower bound in the model with commitment. The welfare costs of the zero lower bound are about $\frac{0.11}{100}$ and $\frac{0.16}{100}$ in the unconstrained and constrained economies. Thus, the availability of fiscal policy reduces the welfare costs of the zero lower bound by about a third.

Since the steady-state nominal interest rate is lower in the economy with commitment, the same variance of shocks implies substantially more frequent zero-lower-bound episodes in the economy with commitment and the welfare costs are not directly comparable. To compare the welfare costs of the zero lower bound between the models with and without commitment, I solve the model in which the production subsidy is available to offset the steady-state inefficiency so that there is no inflation bias in the model without commitment and the steady-state nominal interest rates are the same in both economies. Table 4 shows the welfare costs of the zero lower bound in the economies with the production subsidy. The welfare costs of the zero lower bound are substantially smaller in the model with commitment than in the model without commitment. The finding that the welfare cost of the zero lower bound is small when the government can commit is consistent with the analyses of Adam and Billi (2007) and Nakov (2008). The additional welfare gain from fiscal policy is smaller in the model with commitment both in absolute and relative terms. The access to fiscal policy reduces the welfare cost of the zero lower bound by about 10 percent in the model with commitment ( $\frac{0.024}{100}$ percent with fiscal policy versus $\frac{0.026}{100}$ percent without fiscal policy), as opposed to by about 40 percent in the model without commitment.

7 Conclusion

This paper characterized optimal government spending and monetary policy when the nominal interest rate is subject to the zero lower bound constraint in a stochastic environment. In the model without commitment, the government increases its spending when at the zero lower bound by a substantially larger amount in the stochastic environment than it would in the deterministic environment. Access to government spending policy not only affects the allocations at the zero lower bound directly, but also affects the allocations away from the zero lower bound indirectly through its effect on the expectations of the household and firms. In particular, when the government does not have access to fiscal policy, it reduces the nominal interest rate more aggressively before reaching the zero lower bound. Such aggressive monetary policy increases consumption and output near the zero lower bound, which increases welfare if the steady-state consumption and output are inefficiently low. In the model with commitment, the government also increases its spending at the zero lower bound by a larger amount in the stochastic economy than in the deterministic economy, but the additional increase in the government spending due to uncertainty is small compared to that in the model without commitment.

References

Adam, K., and R. Billi (2006): "Optimal Monetary Policy Under Commitment with a Zero Bound on Nominal Interest Rates," Journal of Money, Credit, and Banking."

Adam, K., and R. Billi (2007): "Discretionary Monetary Policy and the Zero Lower Bound on Nominal Interest Rates," Journal of Monetary Economics.

Billi, R. (2011): "Optimal In ation for the US Economy," American Economic Journal: Macroeconomics.

Christiano, L., M. Eichenbaum, and S. Rebelo (2011): "When is the Government Spending Multiplier Large?," Journal of Political Economy."

Clarida, R., J. Gali, and M. Gertler (1999): "The Science of Monetary Policy: A New Keynesian Perspective," Journal of Economic Literature, 37, 1661-1707."

Coleman, W. J. (1991): "Equilibrium in a Production Economy with an Income Tax," Econometrica."

Eggertsson, G. (2001): "Real Government Spending in a Liquidity Trap," Working Paper."

Eggertsson, G. (2010): "What Fiscal Policy Is Eective At Zero Interest Rates?," NBER Macroeconomic Annual."

Eggertsson, G., and E. Swanson (2008): "Optimal Time-Consistent Monetary Policy in the New Key-nesian Model with Repeated Simultaneous Play,"Working Paper."

Eggertsson, G., and M. Woodford (2003): "The Zero Bound on Interest Rates and Optimal Monetary Policy," Brookings Papers on Economic Activity.

Erceg, C. J., and J. Linde (2010): "Is There a Fiscal Free Lunch in a Liquidity Trap?," Working Paper."

King, R. G., and A. L. Wolman (2004): "Monetary Discretion, Pricing Complementarity, and Dynamic Multiple Equilibria,"The Quarterly Journal of Economics.

Marcet, A., and R. Marimon (2011): "Recursive Contracts," Working Paper."

Martin, F. (2010): "Markov-Perfect Capital and Labor Taxes," Journal of Economic Dynamics and Control, 34, 503-521.

Nakata, T. (2012): "Uncertainty at the Zero Lower Bound," Working Paper.

Nakata, T. (2013): "Optimal Government Spending at the Zero Lower Bound: A Non-Ricardian Analysis,"Working Paper.

Nakov, A. (2008): "Optimal and Simple Monetary Policy Rules with Zero Floor on the Nominal Interest Rate," International Journal of Central Banking.

Ortigueira, S. (2006): "Markov-Perfect Optimal Taxation," Review of Economic Dynamics.

Schmidt, S. (2012): "Optimal Monetary and Fiscal Policy with a Zero Bound on Nominal Interest Rates," Working Paper.

van Zandweghe, W., and A. Wolman (2010): "Discretionary Monetary Policy in the Calvo model," Working Paper."

Werning, I.(2012): "Managing a Liquidity Trap: Monetary and Fiscal Policy," Working Paper.

Woodford, M.(2011): "Simple Analytics of the Government Expenditure Multiplier," American Economic Journal: Macroeconomics

Table 1: Parametrization

Parameter	Description	Parameter Value
$\beta$	Discount rate	$\frac{1}{1+0.0075} \approx 0.9925$
$\chi_{c}$	Inverse intertemporal elasticity of substitution for $C_{t}$	1.0
$\chi_{n}$	Inverse labor supply elasticity	1.0
$\chi _{g,0}$	Utility weight on $G_{t}$	0.25
$\chi _{g,1}$	Intertemporal elasticity of substitution for $G_{t}$	1.0
$\theta$	Elasticity of substitution among intermediate goods	10
$\varphi$	Price adjustment cost	175
$\rho$	AR(1) coefficient for the discount factor	0.8
$\sigma_{\epsilon}$	The standard deviation of shocks to the discount factor	[0, $\frac{0.445}{100}$ ]
$\sigma_{\delta}$	The implied unconditional standard deviation of $\delta$	0.007

Table 2: Probability of being at the Zero Lower Bound With and Without Fiscal Policy

	No Commitment	Commitment
With Fiscal Policy	8.0 %	19.7 %
Without Fiscal Policy	9.7 %	20.1 %

*The frequencies are computed based on 100,000 simulations.

Table 3:Welfare Costs of the Zero Lower Bound

	No Commitment	Commitment
With Fiscal Policy	- $\frac{1.3}{100}$ %	$\frac{0.11}{100}$ %
Without Fiscal Policy	- $\frac{2.0}{100}$ %	$\frac{0.16}{100}$ %

*The welfare costs are computed as the perpetual consumption transfer necessary to make the household in the economy with the zero lower bound as well-off as the household in the hypothetical economy without the zero lower bound. They are expressed as a percentage of the deterministic steady-state consumption.
**The welfare is computed based on 100,000 simulations.

Table 4: Welfare Costs of the Zero Lower Bound: Model with Production Subsidy
	No Commitment	Commitment
With Fiscal Policy	$\frac{0.15}{100}$ %	$\frac{0.024}{100}$ %
Without Fiscal Policy	$\frac{0.26}{100}$ %	$\frac{0.026}{100}$ %

*See the footnotes from Table 3.

Figure 1: Optimal Policy/Allocations Without Commitment:Deterministic vs. Stochastic Equilibria

*Policy functions are shown for the range of δ that covers its steady-state level (δ-1) to the level that is 3 standard deviations away from the steady-state (δ-021).

Figure 2: Recovery from a Recession Without Commitment:Deterministic vs. Stochastic Equilibria

* Solid black lines plot the median response.

Figure 3: Optimal Policy/Allocations Without Commitment:With and Without Fiscal Policy

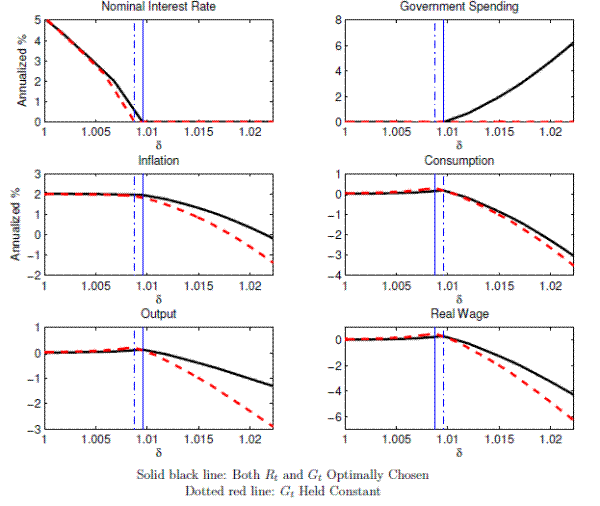
Policy functions are shown for the range of that covers its steady-state level (δ- 1) to the level that is 3 standard deviations away from the steady-state (δ- 1.021).

Figure 4: Recovery from a Recession Without Commitment:With and Without Fiscal Policy

* Solid black lines plot the median response.

Figure 5: Recovery from a Recession With Commitment:Deterministic vs. Stochastic Equilibria

* Solid black lines plot the median response.

** Solid blue line in the top left panel shows the natural real interest rate.

Figure 6: Recovery from a Recession With Commitment:With and Without Fiscal Policy

* Solid black lines plot the median response.

** Solid blue line in the top left panel shows the natural real interest rate.

figuresection tablesection

Appendix

Appendix A studies the sensitivity of the results in the main text to alternative values of key parameters. Appendix B discusses the implications of the zero lower bound constraint for the average inflation rate, with and without fiscal policy.

A. Sensitivity Analysis

An important result highlighted in the main text is that, in the model without commitment, the government chooses to increase its spending at the ZLB by a substantially larger amount in the stochastic environment than in the deterministic environment. With the baseline parameterization, the optimal increase in government spending is more than twice as large in the presence of uncertainty as in its absence. In this section, I document how the additional increase in the government spending due to uncertainty varies with (i) the variance of the shocks to the discount rate process and (ii) the valuation of the government spending by the household.

A.1 Alternative degrees of uncertainty

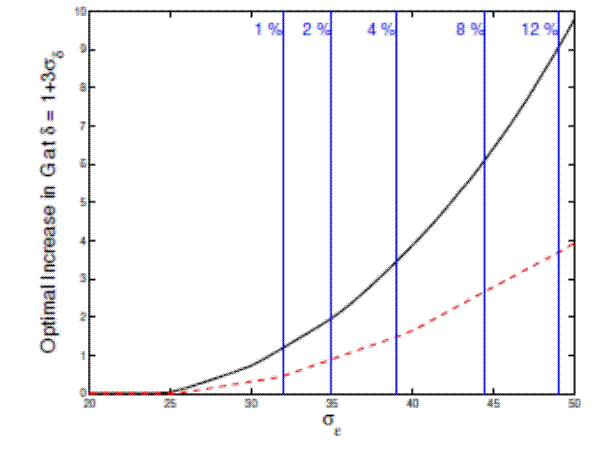
The additional increase in the government spending arising from the presence of uncertainty obviously depends on the magnitude of uncertainty. In the baseline parametrization, the standard deviation of the shock to the discount rate process is set so that the frequency of being at the ZLB is 8 percent in the model without commitment. Figure A.1 shows how the optimal increase in government spending varies with the variance of the shock to the discount rate process. The solid black and dashed red lines show the increase in the government spending (expressed as a percentage deviation from the steady-state) at $\delta=1+3\sigma_{\delta}$ in the stochastic and deterministic economies, while blue vertical lines show the levels of $\sigma_{\epsilon}$ at which the frequencies of being at the ZLB are 1, 2, 4, 8, and 12 percent.

Not surprisingly, the increases in the government spending are smaller in both deterministic and stochastic economies when $\sigma_{\epsilon}$ is smaller. The additional increase in government spending due to uncertainty is also smaller. However, relative to the increase in the deterministic economy, the additional increase is still sizable. For example, when $\sigma_{\epsilon}$ is such that the frequency of being at the zero bound is only one percent, the optimal spending increases are respectively 0.5 and 1.2 percent in the deterministic and stochastic economies. The increase in the government spending in the stochastic economy is typically two-to-three times as large as that in the deterministic economy, even when the degree of uncertainty is small. Thus, the presence of uncertainty has important implications for optimal government spending policy, regardless of the degree of uncertainty.

Figure A.1: Sensitivity Analysis: Alternative degrees of uncertainty

*The solid black and dashed red lines show the increase in the government spending (expressed as a percentage deviation from the steady-state) at δ -1 + 3σ_δ in the stochastic and deterministic economies,respectively.

**Blue vertical lines show the levels of σ _ε at which the frequencies of being at the ZLB are 1, 2, 4, 8, and 12 percent.

A.2 Alternative valuations of the government spending

As recently pointed out by Werning (2012), the government chooses to increase its spending when at the zero lower bound mainly for intra-temporal reasons. Specifically, the government increases its spending at the zero bound because, given the reduced level of consumption caused by the discount-rate shock, an increase in government spending better balances the marginal dis-utility of work and the marginal utility of the government spending. Thus, the magnitude of the optimal increase in government spending depends crucially on how much the household values the government spending.

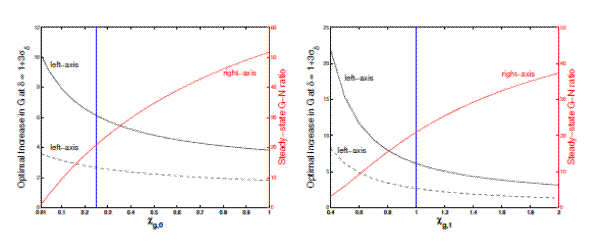
The left panel of Figure A.2 depicts how the optimal increase in government spending varies with $\chi _{g,0}$ , the weight on the government spending in the household's utility function. The solid and dashed black lines show the increases in the government spending at $\delta=1+3\sigma_{\delta}$ in the stochastic and deterministic economies, while the red line shows the deterministic steady-state level of the government spending-to-output ratio. The steady-state government spending-to-output ratio rises with $\chi _{g,0}$ as a larger $\chi _{g,0}$ means that the household values the government spending more. Both with and without uncertainty, the optimal increase in government spending decreases with $\chi _{g,0}$ in absolute terms, but increases with $\chi _{g,0}$ as the percentage deviation from the steady-state level. For a wide range of $\chi_{G,0}$ , the optimal government spending increase in the stochastic economy is roughly two-to-three times as large as that in the deterministic economy.

The right panel in figure A.2 depicts how the optimal increase in government spending and the steady-state government spending-to-output ratio vary with $\chi _{g,1}$ , the inverse intertemporal elasticity of substitution for government spending. As $\chi _{g,1}$ increases, the deterministic steady-state of the government spending-to-output ratio increases. Both with and without uncertainty, the increases in the government spending decline with $\chi _{g,1}$ as percentage deviation from the steady-state. The additional increases in the government spending due to uncertainty are large for a wide range of $\chi _{g,1}$ . Again, the optimal increase in the government spending in the stochastic economy is typically two-to-three times as large as that in the deterministic economy.

Figure A.2: Sensitivity Analysis: Alternative values for χ_g,0 and χ_g,1

The left panel of the figure depicts how the optimal increase in government spending varies with χ<sub>g,0</sub>, the weight on the government spending in the household's utility function. The solid and dashed black lines show the increases in the government spending at δ = 1+3σ <sub>α</sub> in the stochastic and deterministic economies, while the red line shows the deterministic steady-state level of the government spending-to-output ratio. The right panel of this Figure depicts how the optimal increase in government spending and the steady-state government spending-to-output ratio vary with χ <sub>g,0</sub>, the inverse intertemporal elasticity of substitution for government spending.

*In both panels, the solid and dashed black lines show the increase in the government spending, expressed as a percentage deviation from the steady-state, at δ − 1 +3σ _δ in the stochastic and deterministic economies. The red line shows the steady-state government spending-to-output ratio.

B. The average inflation rate

This section documents how the presence of government spending policy alters the average inflation rate in the stochastic New Keynesian economy. Table B.1 depicts the average inflation rates with and without government spending policy. The upper and lower sections of Table B.1 are respectively for the models with and without commitment. For each entry, the number on the top is the unconditional average inflation rate, while the second number in brackets is the conditional average inflation rate when the nominal interest rate is away from the zero bound.

Table B.1: Average Inflation Rates With and Without Fiscal Policy

	Without Zero Bound	With Zero Bound with $R_{t}$ only	With Zero Bound with $R_{t}$ and $G_{t}$
Unconditional Average: Without Commitment	2.031	1.950	1.984
Conditional Average: Without Commitment	(N/A)	(2.013)	(2.020)
Unconditional Average: With Commitment	0.0	0.022	0.018
Conditional Average: With Commitment	(N/A)	(0.005)	(0.004)

*The inflation rate is expressed as an annualized percentage. Unbracketed numbers are the unconditional averages from 100,000 simulations. The second numbers in the bracket are the averages conditional on the nominal interest rate strictly larger than zero.

In the model without commitment, the deterministic steady-state level of inflation, or equivalently the stochastic average rate of inflation that would prevail in the absence of the zero lower bound, is positive due to inflation bias. With occasionally binding zero bound constraints, the average inflation rate decreases as the economy experiences declines in inflation whenever the economy is at the zero lower bound. Since the expectation of visiting the zero lower bound also reduces inflation outside the zero lower bound, the conditional average inflation rate away from the zero bound is also lower than the deterministic level. As the decline in inflation is smaller at the zero lower bound if the government has the access to fiscal policy, the reduction in the average inflation rate is smaller with fiscal policy than without it.

In the model with commitment, the deterministic steady-state level of inflation is zero. The Ramsey planner chooses zero inflation rate in order to minimize the resource cost of non-zero inflation. Consistent with the findings in Adam and Billi (2006), Billi (2011), and Nakov (2008), the presence of the zero lower bound increases the average inflation rate to a positive value as the government generates positive inflation during much of the zero-bound episode by promising to maintain low nominal interest rates. Since the positive unconditional average inflation rate is mainly due to the positive average inflation during the zero-bound episode, the conditional average inflation rate away from the zero bound is very close to zero. When the government has fiscal policy as an additional policy instrument, the increase in inflation during the zero bound period is slightly lower, as discussed in the main text. Therefore, the average inflation rate is lower with fiscal policy than without it.

Overall, the analysis shows that access to fiscal policy partially unwinds the effect of the zero lower bound constraint on the average inflation rate. In the model without commitment, the presence of the zero lower bound reduces the average inflation rate, but the reduction is smaller if the fiscal instrument is available. In the economy with commitment, the zero lower bound increases the average inflation rate, but the increase is smaller if the fiscal instrument is available. Even without fiscal policy, the effects of the zero bound constraints on the average inflation rate tend to be very small. The active use of fiscal policy makes them even smaller.

Footnotes

* I would like to thank Tim Cogley, Mark Gertler, and Tom Sargent for their advice. I would also like to thank Jess Benhabib, Gauti Eggertsson, John Roberts, Christopher Tonetti, and seminar participants at 8th Annual DYNARE Conference, 18th International Conference on Computing in Economics and Finance, Bank of Canada, Boston Fed, Deutsche Bundesbank, Cleveland Fed, Federal Reserve Board, Kansas City Fed, New York University, NYU Stern, the 2012 North American Summer Meeting of the Econometric Society, and University of Oregon for their thoughtful comments. The views expressed in this paper, and all errors and omissions, should be regarded as those solely of the author, and are not necessarily those of the Federal Reserve Board of Governors or the Federal Reserve System. Return to Text

* Division of Research and Statistics, Federal Reserve Board, 20th Street and Constitution Avenue N.W. Washington, D.C. 20551; Email: [email protected]. Return to Text

1. For example, see Christiano, Eichenbam, and Rebelo (2011), Eggertsson (2010), Erceg and Linde (2010), and Woodford (2011). Return to Text

Return to Text

2. For example, see Eggertsson (2001), Nakata (2013), and Werning (2012) Return to Text

3. Eggertsson and Woodford (2003) and several other authors considered a two-state Markov process for the natural rate of interest with an absorbing state, and many subsequent authors have adopted that process. However, this setup is not well-suited for addressing the questions this paper is interested in, as the parameter of the Markov-process process governs both the degree of uncertainty and the persistence of the shock and one cannot isolate the effect of uncertainty from the effect of persistence. Return to Text

4. A similar observation--that the constraint on policy instruments increases welfare in the Markov-Perfect equilibrium--has been reported in other contexts. See Martin (2010) for an example. Return to Text

5. A recent independent work by Schmidt (2012) analyzes optimal fiscal and monetary policy in a stochastic New Keynesian model as well. Key differences between my work and his are that I (i) analyze a fully nonlinear economy, (ii) compare the deterministic versus stochastic economies, and (iii) do not always assume that the steady-state is efficient. Return to Text

6. See Appendix for the sensitivity analysis with respect to the parameters governing the value of the government spending to the household. Return to Text

7. The balanced budget assumption is made mainly to simplify the analysis. However, for economies with large deficits, fiscal policy might be constrained by pay-as-you-go rules that limit the extent of future borrowing, and this assumption may not be too restrictive. Return to Text

8. The within-period timing assumption that leads to this optimization problem is that the government and the agents in the private sector move simultaneously. See the discussion in Eggertsson and Swanson (2008). For alternative within-period timing assumptions, see King and Wolman (2004) and van Zandweghe and Wolman (2010). For a detailed discussion on the importance of the within-period timing assumption in Markov Perfect Equilibrium, see Ortigueira (2006). Return to Text

9. Notice that the steady-state inflation rate is positive in this model without commitment. Inflation bias arises because the steady-state output would be inefficiently low due to the monopolistic competition and the government has an incentive to increase output by creating a surprise inflation. See Nakata (2012) for a detailed exposition on inflation bias in the New Keynesian economy. Return to Text

10. See Nakata (2012) for a more detailed analysis of how a mean-preserving spread in the shock affects the decisions of the household and firms when the nominal interest rate is constrained. Return to Text

11. The consumption multiplier is about 0.3. Return to Text

12. See Martin (2010) for another example in which a constraint on policy instruments increases welfare in the Markov-Perfect equilibrium. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text

Optimal Fiscal and Monetary Policy With Occasionally Binding Zero Bound Constraints*

1 Introduction

2 Model

3 Government's Problem

4 Parametrization and Solution Method

5 Results for the model without commitment

6 Results for the model with commitment

Table 1: Parametrization

Table 2: Probability of being at the Zero Lower Bound With and Without Fiscal Policy

Table 3:Welfare Costs of the Zero Lower Bound

Figure 1: Optimal Policy/Allocations Without Commitment:Deterministic vs. Stochastic Equilibria

Figure 2: Recovery from a Recession Without Commitment:Deterministic vs. Stochastic Equilibria

Figure 3: Optimal Policy/Allocations Without Commitment:With and Without Fiscal Policy

Figure 4: Recovery from a Recession Without Commitment:With and Without Fiscal Policy

Figure 5: Recovery from a Recession With Commitment:Deterministic vs. Stochastic Equilibria

Figure 6: Recovery from a Recession With Commitment:With and Without Fiscal Policy

Appendix

A. Sensitivity Analysis

Figure A.1: Sensitivity Analysis: Alternative degrees of uncertainty

Figure A.2: Sensitivity Analysis: Alternative values for χg,0 and χg,1

B. The average inflation rate

Table B.1: Average Inflation Rates With and Without Fiscal Policy

Optimal Fiscal and Monetary Policy With
Occasionally Binding Zero Bound Constraints*

Figure A.2: Sensitivity Analysis: Alternative values for χ_g,0 and χ_g,1