
Credit-crunch dynamics with uninsured investment risk
Abstract:
Keywords: Incomplete markets, idiosyncratic risk, business cycles, risk-free rates
JEL codes: D52, E44, G11, O16
1 Introduction
This paper studies the short- and long-run effects of a shift from loose credit for firms to tight credit in an economy with uninsured investment risk. I focus on a general-equilibrium link between firms: financial claims issued by one firm can (directly or indirectly) be the asset of another firm. The debtor firm seeks to finance an investment. The creditor firm (which owns the debt perhaps in the form of a bank deposit) holds the other firm's debt in order to finance future investments or as a buffer against a bad shock to its own profitability.
When a firm faces tighter credit conditions, it seeks to decrease its borrowing: in part because it can no longer borrow as much against a given investment and in part because, with tighter credit, some investments are not worth pursuing and hence do not generate collateral. If many firms face tighter credit conditions, they will all seek to decrease their borrowing at the same time. Hence there will be fewer stores of value for other firms to hold.
To explore this linkage between firms and how it affects the economy's response to a credit crunch, I develop a tractable dynamic, general-equilibrium model in which collateral constraints limit the ability of entrepreneurs to hedge idiosyncratic risk. The model illustrates the interaction between idiosyncratic investment risk and limited commitment. In contrast, many papers on uninsured investment risk, including Angeletos (2007), Angeletos and Panousi (2009), Angeletos and Panousi (2011), and Panousi (2012), abstract from borrowing constraints, while many papers on shocks to collateral constraints, including Buera and Moll (2012) and Midrigan and Xu (2012), abstract from uninsured investment risk.
Thus, the paper's main contribution is to characterize the short- and long-run effects of credit tightening in a general-equilibrium model with uninsured investment risk. I emphasize the role of an endogenous decrease in the risk-free rate in determining the effects of credit tightening on capital accumulation, consumption riskiness, and the equity premium.
Preview of the model and results. In the model, firms are run by entrepreneurs and the output of each firm is subject to an idiosyncratic shock. Entrepreneurs can issue state-contingent assets of any maturity, but the set of financial contracts available to an entrepreneur is constrained because, in the event of default, creditors' recovery is limited. This limited-enforcement problem gives rise to collateral constraints. Due to these collateral constraints, taking advantage of investment opportunities requires forgoing insurance. Thus, entrepreneurs require a (private) equity premium.
The shock that I study takes the form of a decrease in creditors' recovery in the event of default. I begin by studying the economy's long-run response. When collateral constraints tighten, entrepreneurs are forced to retain a greater share of their profits. As each entrepreneur shifts to self-financing, he reduces the quantity of financial assets that can be owned by other entrepreneurs to insure against their bad idiosyncratic shocks. This has important general-equilibrium effects: the risk-free rate falls and consumption growth becomes riskier. The equity premium rises, for two reasons: first, credit tightening reduces the share of (risky) profits that entrepreneurs can sell to diversified investors; and, second, because the risk-free rate falls, hedging is more expensive. Correspondingly, the risk-adjusted return to saving falls. This gives rise to an income effect and a substitution effect, and thus aggregate capital decreases if and only if the elasticity of intertemporal substitution is sufficiently large.
I show that if the risk-free rate were constant, as in a small open economy, the economy's response would be qualitatively different. In particular, because the risk-free rate would not fall as entrepreneurs shift to self-financing, the decrease in firms' ability to borrow would lead entrepreneurs to scale back risk-taking. This endogenous decrease in risk-taking would be so large that, in the long run, the riskiness of consumption growth would be unchanged - even though credit tightening mechanically reduces the share of profits that entrepreneurs can sell to diversified investors. The equity premium would still rise, because, for a given investment, an entrepreneur has to bear more risk. However, because entrepreneurs would accumulate safe financial assets, they would be better hedged. Hence, the equity premium would not rise as much as it does when the risk-free rate is endogenous.
This highlights the general-equilibrium effects of the endogenous decrease in the risk-free rate after a shock to collateral constraints. In the long run, the increase in the equity premium is higher than it would be if the interest rate were constant. Moreover, the increase in the riskiness of consumption growth can be accounted for by the decrease in the risk-free rate.
This analysis of the long-run response to credit tightening begs the question of how the economy responds in the short run. I show that there is no "overshooting" in the equity premium: in response to a permanent decrease in firms' ability to pledge their future income, the equity premium immediately jumps to its new steady-state level and remains constant thereafter, even as aggregate capital adjusts over time. One corollary of this result is that if idiosyncratic uncertainty is sufficiently low, credit tightening has no short- or long-run effects on aggregate capital, the equity premium, or the riskiness of consumption. I also show that the absence of overshooting is a general-equilibrium effect. Finally, in the case where the elasticity of intertemporal substitution is equal to one, I show that, in the short run, the increase in the equity premium and the riskiness of consumption caused by credit tightening are larger than they would be if the risk-free rate were unaffected by credit tightening.
2 Related literature
My paper builds on the literature on uninsured investment risk, including Angeletos (2007), Angeletos and Panousi (2009), Angeletos and Panousi (2011), and Panousi (2012). These papers study how aggregate capital is affected by idiosyncratic investment risk using models in which entrepreneurs can trade only a risk-free bond. These papers ignore borrowing constraints (except for the "natural" borrowing constraint that consumption need always be positive) and, like Aiyagari (1994) and Guerrieri and Lorenzoni (2011), which use similar models of uninsured labor-income risk, ignore the micro-foundations for incomplete markets. In contrast, I explicitly incorporate a limited-enforcement problem that gives rise to collateral constraints.
Even though my paper features collateral constraints and state-contingent debt, some of the economic forces at work in Angeletos (2007) are similar and one of my results - that aggregate capital decreases when firms' ability to pledge their income decreases if and only if the elasticity of intertemporal substitution is greater than one - appears very similar to the main result of Angeletos (2007); in Angeletos (2007), aggregate capital is lower without state-contingent debt than with complete markets if and only if the elasticity of substitution is above a related threshold. However, it is not the case that my model nests Angeletos (2007), or vice versa. In my model, even when firms cannot pledge any future profits, the zero correlation between idiosyncratic productivity and the payment to outside investors is an endogenous, general-equilibrium outcome: in partial equilibrium, the entrepreneurs in my model could hedge, even when they cannot pledge any future income, by receiving, for example, a minimum salary from investors regardless of the realized shock. Thus, even when firms cannot pledge any future profits, the correlation between idiosyncratic productivity and the payment to outside investors is zero only because no entrepreneur can supply the assets that other entrepreneurs can use to hedge; that is, the risk-free rate must be sufficiently low such that entrepreneurs are willing to forgo insurance. In contrast, in Angeletos (2007), the correlation between idiosyncratic productivity and the payment to outside investors is exogenous. One advantage of my approach is that, in my paper, idiosyncratic productivity risk and the level of financial development can vary independently; in contrast, in Angeletos and Panousi (2011), idiosyncratic productivity risk and financial development are one and the same.
Two papers that emphasize idiosyncratic risk and borrowing constraints are Covas (2006) and Guerrieri and Lorenzoni (2011). Covas (2006) studies the effects of idiosyncratic investment risk on steady-state aggregate capital in a calibrated Bewley-type model of entrepreneurs with an ad-hoc (as opposed to "natural") borrowing constraint. In the paper's simulations, Covas (2006) often finds that, with uninsured investment risk and borrowing constraints, steady-state aggregate capital is higher than under complete markets. Covas (2006) attributes these results, in part, to precautionary saving. That is, uninsured investment risk and borrowing constraints increase the hedging demand for the safe asset, depressing the risk-free rate and thus making the risky entrepreneurial investment more attractive. However, as highlighted in my paper, this decrease in the risk-free rate also increases the cost of hedging, making risky entrepreneurial investment less attractive. In Covas (2006), it is not clear why the former effect tends to dominate the latter effect. Guerrieri and Lorenzoni (2011), like my paper, studies the short-run effects of a shock to borrowing constraints in the presence of idiosyncratic risk. Unlike my paper, Guerrieri and Lorenzoni (2011) focus on uninsured labor income risk in a Bewley-type model, rather than uninsured investment income risk in a model with collateral constraints on investment. In Guerrieri and Lorenzoni (2011), as in my paper, a credit crunch leads to a decrease in the risk-free rate, providing an example of a shock that can lead to a negative real risk-free rate and potentially a binding zero-lower-bound on the nominal risk-free rate. Eggertsson and Krugman (2012) explore a similar point in a simple, tractable model of consumers who borrow and lend due to heterogeneity in impatience to consume.
This paper also contributes to a growing literature that studies the short-run macroeconomic response to shocks that limit firms' ability to pledge their profits to outside investors. Some papers in this literature, including Jermann and Quadrini (2011), Kahn and Thomas (2010) and Buera and Moll (2012), study shocks to parameters, such as outside investors' recovery rate in bankruptcy, that directly enter into firms' collateral constraints. Other papers, including Christiano, Motto and Rostagno (2010), Gilchrist, Sim and Zakrajsek (2010), and Arellano, Bai and Kehoe (2010), study shocks to idiosyncratic and aggregate uncertainty in the presence of financial constraints.
Jermann and Quadrini (2011), like this paper, examines the short-run effects of credit tightening. However, their results rely on two particular assumptions: (i) an ad-hoc cost of changing the payout to equityholders; and (ii) tax benefits of debt. If there are no ad-hoc costs to changing dividends and no tax benefits of debt, shocks to firms' ability to borrow would not affect the real economy. In my paper, in contrast, there are no financial constraints beyond those that arise endogenously from the firms' limited enforcement problem, and entrepreneurs' financial decisions are driven by the investment risk they face. Kahn and Thomas (2011), in a calibrated DSGE model, study how fixed costs of capital adjustment affect the economy's response to a decrease in firms' ability to borrow. In Kahn and Thomas (2011), idiosyncratic investment risk is important, but for a different reason than in my paper. In Kahn and Thomas (2011), equityholders are fully diversified, and idiosyncratic uncertainty matters only because responding to shocks may trigger fixed costs of adjustment. In my paper, as in Angeletos (2007), idiosyncratic uncertainty matters because entrepreneurs are undiversified owners of the equity of their firms. Also, like Jermann and Quadrini (2011), Kahn and Thomas (2011) features ad-hoc financial frictions, such as the inability of widely held firms to issue equity.
Buera and Moll (2012), like this paper, analytically characterizes the short-run response to a collateral-constraints shock and emphasizes the effect of endogenous changes to the risk-free rate. However, the firm's problem and the economy's response to a credit crunch in Buera and Moll (2012) are different than in my paper. Buera and Moll (2012) assume that each firm's productivity is known with certainty at the time of investment and financial contracting; financial frictions limit the transfer of wealth from low-productivity firms to high-productivity firms and there is no uninsured investment risk. In contrast, in my model, each firm's productivity is unknown at the time of investment and financial contracting, but the distribution of next-period productivity is the same for each firm. As a result, in my model, financial frictions do not give rise to misallocation across firms, but there is uninsured investment risk.
Unsurprisingly, the economy's response to a collateral-constraints shock in my paper is qualitatively different than the economy's response in Buera and Moll (2012). For example, Buera and Moll (2012) focus on the investment wedge, defined as the tax on investment in a representative-agent economy that would make the Euler equation hold, as in Chari, Kehoe and McGrattan (2007).1 One of Buera and Moll (2012)'s main results is that, with idiosyncratic productivity shocks, the investment wedge is equal to zero and is unaffected by changes in firms' ability to borrow. Although Buera and Moll (2012)'s investment wedge is not the focus of my paper, I find that, comparing across steady states, Buera and Moll (2012)'s entrepreneurial investment wedge is generally non-zero, has a sign that depends on the elasticity of intertemporal substitution, and increases in absolute value when firms' ability to borrow decreases.
A number of calibration papers in this literature also abstract from uninsured idiosyncratic investment risk by assuming that tomorrow's productivity is revealed before today's investment and financial-contracting decisions. Midrigan and Xu (2012) study a shock to collateral constraints in a calibration that matches Korean establishment-level data. Buera and Shin (2010) study the effects of capital liberalization and a decrease in idiosyncratic taxes in a calibration that matches six emerging-market growth-acceleration episodes. Bassetto, Cagetti and DeNardi (2010) study a variety of financial shocks in a calibration that matches the U.S. firm-size distribution. Like my paper, these papers study both short-run dynamics and long-run effects.
It bears noting that, although my paper differs in important ways from these papers, many of these papers also emphasize the general-equilibrium effects of endogenous changes to the risk-free rate. For example, in the literature on collateral constraints, Midrigan and Xu (2012) find that steady-state TFP losses due to financial frictions are about 50 percent larger in a closed economy than in a small open economy. Similarly, Buera and Shin (2010) find that reducing idiosyncratic distortions leads to a much larger increase in TFP when accompanied by a capital-account liberalization that results in an exogenous increase in the interest rate. In the literature on uninsured investment risk, Panousi (2012) shows that the effect of capital taxation on capital accumulation is theoretically ambiguous, a surprising result that emerges because capital taxation leads to an increase in the risk-free rate and this in turn leads to a decrease in the equity premium.
3 Model
Time is discrete, indexed by
![]() There is a continuum of infinitely-lived entrepreneurs, indexed by
There is a continuum of infinitely-lived entrepreneurs, indexed by ![]() . Each entrepreneur runs a firm. There is only one good, used for both capital and consumption.
. Each entrepreneur runs a firm. There is only one good, used for both capital and consumption.
Technology. In period ![]() , firm
, firm ![]() has a history of
idiosyncratic productivity shocks
has a history of
idiosyncratic productivity shocks
![]() and invests
and invests ![]() in the
production technology. In period
in the
production technology. In period ![]() , the firm learns productivity
, the firm learns productivity
![]() . The firm then hires labor
. The firm then hires labor
![]() . The total output produced in period
. The total output produced in period ![]() is:
is:
Productivity ![]() is independently and identically distributed over
is independently and identically distributed over ![]() and
and
![]() .
.
Denote the cumulative distribution function over productivities ![]() by
by ![]() . I
normalize the expected productivity to be equal to one.
. I
normalize the expected productivity to be equal to one.
Financial markets. The firm can access financial markets by trading state-contingent promises that pay out conditional on the realization of productivity. At history ![]() , the firm sells a portfolio of Arrow-Debreu securities that represent a promise to pay
, the firm sells a portfolio of Arrow-Debreu securities that represent a promise to pay
![]() next period. Note that the promised payment
next period. Note that the promised payment
![]() may depend on the realization of
may depend on the realization of
![]() . Because the shocks are idiosyncratic, the proceeds from this sale, in equilibrium, are
. Because the shocks are idiosyncratic, the proceeds from this sale, in equilibrium, are
![]() , where
, where ![]() is the risk-free interest
rate between periods
is the risk-free interest
rate between periods ![]() and
and ![]() and the expectation is taken with respect to
productivity
and the expectation is taken with respect to
productivity
![]() .
.
Although the promises are state-contingent, markets are incomplete because entrepreneurs can renege on payment. In particular, if an entrepreneur reneges, the most that creditors can seize is a fraction
![]() of the firm's output net of labor costs. This setup nests no ability to borrow (
of the firm's output net of labor costs. This setup nests no ability to borrow (
![]() ) and complete financial markets (
) and complete financial markets (
![]() ). When a firm reneges, the unmet portion of the firm's debt is erased. (When the firm is allowed to issue promises due in more than one period, all future promises by the firm
are also erased). Given this, the firms repay in period
). When a firm reneges, the unmet portion of the firm's debt is erased. (When the firm is allowed to issue promises due in more than one period, all future promises by the firm
are also erased). Given this, the firms repay in period ![]() if and only if:
if and only if:
The path of
![]() is deterministic but potentially time varying. Moreover, there exists a
is deterministic but potentially time varying. Moreover, there exists a
![]() such that
such that
![]() if
if ![]() .
.
Preferences. I assume that entrepreneurs have Epstein-Zin preferences with constant elasticity of intertemporal substitution and constant relative risk aversion. That is, associated with a stochastic consumption stream
![]() is a stochastic utility stream that satisfies the following recursion:
is a stochastic utility stream that satisfies the following recursion:
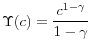 and
and 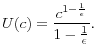
The supply of labor is inelastic and, in aggregate, equals ![]() . I normalize
. I normalize ![]()
Budgets. An entrepreneur's budget constraint at state ![]() is:
is:
I assume that workers are hand-to-mouth consumers, who live in financial autarky and each period consume their wage.
Equilibrium. The initial condition of the economy is given by the distribution of
![]() across firms. An equilibrium is a deterministic interest-rate and wage sequence
across firms. An equilibrium is a deterministic interest-rate and wage sequence
![]() , collections of state-contingent plans for entrepreneurs
, collections of state-contingent plans for entrepreneurs
![]() and paths for aggregate levels of debt
and paths for aggregate levels of debt ![]() consumption
consumption ![]() , capital
, capital ![]() , output
, output ![]() and labor
and labor ![]() such that:
such that:
- the plans
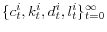 maximize the utility of each entrepreneur;
maximize the utility of each entrepreneur; - the bond-market clears:
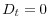 for all
for all 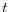 ;
; - the labor-market clears:
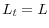 for all
for all 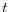 ;
; - aggregate quantities are determined by individual policies:
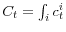 ,
,
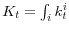 ,
,
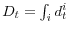 , and
, and
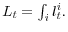
4.1 Partial equilibrium
In the model, profits and labor demand for each entrepreneur are linear in the physical capital owned by the entrepreneur, due to constant returns to scale in technology and the ability to adjust labor demand according to the realization of idiosyncratic productivity:
Thus, the firm's problem can be written recursively as:
subject to
and, for each
In period ![]() , the entrepreneur chooses how much to consume,
, the entrepreneur chooses how much to consume,
![]() , and its capital
, and its capital ![]() . These choices determine, through the
budget constraint (4.2), the expected value of next-period wealth. The firm also chooses a mapping from next-period productivity to next-period wealth,
. These choices determine, through the
budget constraint (4.2), the expected value of next-period wealth. The firm also chooses a mapping from next-period productivity to next-period wealth,
![]() , that must satisfy the budget constraint (4.2) and the limited-enforcement constraints (4.3).
, that must satisfy the budget constraint (4.2) and the limited-enforcement constraints (4.3).
The (private) equity premium is
![]() . When this equity premium is positive, the firm faces a three-way tradeoff between insurance, the timing of consumption, and
taking advantage of its investment opportunity. On the one hand, increasing capital
. When this equity premium is positive, the firm faces a three-way tradeoff between insurance, the timing of consumption, and
taking advantage of its investment opportunity. On the one hand, increasing capital ![]() increases expected next-period wealth, as shown in (4.2). On the other
hand, for any state of the world
increases expected next-period wealth, as shown in (4.2). On the other
hand, for any state of the world ![]() for which (4.3) is binding, an increase in capital requires an increase in the amount of next-period period wealth that
must be allocated to that state at the expense of either current consumption or the next-period wealth allocated to other states.
for which (4.3) is binding, an increase in capital requires an increase in the amount of next-period period wealth that
must be allocated to that state at the expense of either current consumption or the next-period wealth allocated to other states.
If ![]() is weakly concave, which I will verify below, then the period-
is weakly concave, which I will verify below, then the period-![]() wealth level
wealth level
![]() will feature some constant level of wealth for every state
will feature some constant level of wealth for every state
![]() below a threshold
below a threshold
![]() , and for every state
, and for every state
![]() greater than this threshold, wealth will be determined by (4.3). That is,
greater than this threshold, wealth will be determined by (4.3). That is,
![]() will be equal to the greater of a fixed salary or the minimum wealth level consistent with repayment. I denote the fixed salary by
will be equal to the greater of a fixed salary or the minimum wealth level consistent with repayment. I denote the fixed salary by ![]() , so that
, so that
Using this intuition, firms' optimal decisions for given prices can be characterized in closed form.
where
and
Equation (4.9) shows how the limited-enforcement problem interferes with insurance and the optimal timing of consumption. In period
In contrast, for productivity realizations for which the financial constraint does bind, insurance is limited: that is,
![]() is strictly increasing in
is strictly increasing in
![]() for
for
![]() . Moreover, for these high productivity realizations, the consumption growth rate is "too high": the entrepreneur would prefer
. Moreover, for these high productivity realizations, the consumption growth rate is "too high": the entrepreneur would prefer
![]() units of consumption in period
units of consumption in period ![]() rather than an additional unit of consumption next period in states with
rather than an additional unit of consumption next period in states with
![]() .
.
Correspondingly, when financial constraints bind with positive probability, entrepreneurs require an expected return on physical capital greater than the risk-free rate. The first-order conditions of (4.8) imply that the equity premium is:
Consider an entrepreneur in period
4.2 General equilibrium
Because shocks are i.i.d. across firms, the period-![]() market-clearing wage
market-clearing wage
![]() is determined by
is determined by
![]() . We can then define aggregate capital income in period
. We can then define aggregate capital income in period ![]() as
as
![]() By Lemma 1, an entrepreneur's consumption, investment and minimum
payoff are linear in his wealth, making the distribution of wealth irrelevant for calculating aggregates. This permits the following recursive characterization of general-equilibrium dynamics:
By Lemma 1, an entrepreneur's consumption, investment and minimum
payoff are linear in his wealth, making the distribution of wealth irrelevant for calculating aggregates. This permits the following recursive characterization of general-equilibrium dynamics:
where
Note that this system is recursive in
![]() In particular, given
In particular, given
![]() , the market-clearing condition (4.14) can be used to determine
, the market-clearing condition (4.14) can be used to determine
![]() . Next, equations (4.11) and (4.12) can be used to calculate
. Next, equations (4.11) and (4.12) can be used to calculate ![]() and
and ![]() . Then the first-order conditions of (4.8) determine
. Then the first-order conditions of (4.8) determine ![]() and
and ![]() , which in turn imply
, which in turn imply ![]() . Finally, (4.13) determines
. Finally, (4.13) determines
![]() .
.
A steady state is a fixed point
![]() of the dynamic system (4.11)-(4.14) with
of the dynamic system (4.11)-(4.14) with ![]() and
and
![]() .
.
5 Steady state analysis
I make the following assumption, as in Angeletos (2007).
Assumption 1.
![]()
Assumption 1 implies that
![]() . An example of technology that satisfies Assumption 1 is Cobb-Douglas technology.
. An example of technology that satisfies Assumption 1 is Cobb-Douglas technology.
(b) If a steady state exists, it is unique. In steady state
![]() where
where ![]() satisfies:
satisfies:
Aggregate capital is then determined by:
and the interest rate is determined by:
Also,
Hereafter, I will confine attention to economies which have a unique steady state. This is guaranteed by Assumption 2.
Assumption 2. If
![]() , then
, then
![]() , where
, where ![]() is determined by
is determined by
![]() .
.
The threshold
![]() in Assumption 2 is uniquely determined by preference parameters
in Assumption 2 is uniquely determined by preference parameters ![]() and
and ![]() , the distribution of idiosyncratic productivity
, the distribution of idiosyncratic productivity ![]() , and the ability of firms to borrow
, and the ability of firms to borrow ![]() . The threshold
. The threshold
![]() does not depend on the production function
does not depend on the production function ![]() . It can be shown
that
. It can be shown
that
![]() and that
and that
![]() is increasing in
is increasing in ![]() and
and ![]() and decreasing in
and decreasing in ![]() .
.
5.1 Effect of a credit crunch
The characterization of the economy's steady state in Proposition 3 immediately leads to the following result.
(a) a decrease in the minimum payoff ![]() and an increase in the riskiness of consumption; that is, the growth rate of idiosyncratic consumption with
and an increase in the riskiness of consumption; that is, the growth rate of idiosyncratic consumption with
![]() second-order stochastically dominates the growth rate of idiosyncratic consumption with
second-order stochastically dominates the growth rate of idiosyncratic consumption with
![]() if and only if
if and only if
![]() ;
;
(b) a decrease in the interest rate, R;
(c) an increase in the (private) equity premium,
![]() ;
;
(d) a decrease in aggregate capital if and only if the elasticity of intertemporal substitution is greater than one.
These changes will be strict if financial constraints bind in the new steady state.
More specifically, consider the steady states associated with
![]() and
and
![]() , with
, with
![]() , and suppose
, and suppose
![]() , so that financial constraints bind with positive probability in the
, so that financial constraints bind with positive probability in the
![]() steady state. Denote the productivity threshold above which financial constraints bind in the
steady state. Denote the productivity threshold above which financial constraints bind in the
![]() steady state by
steady state by
![]() . Then there will be a cutoff productivity
. Then there will be a cutoff productivity
![]() such that: for any productivity
such that: for any productivity
![]() , the consumption growth rate in the
, the consumption growth rate in the
![]() steady state is lower than the consumption growth rate in the
steady state is lower than the consumption growth rate in the
![]() steady state; for any productivity
steady state; for any productivity
![]() , the opposite holds. Hence, it follows that a decrease in
, the opposite holds. Hence, it follows that a decrease in ![]() leads to a simple increase in risk in the distribution of consumption growth.
leads to a simple increase in risk in the distribution of consumption growth.
According to (5.2), this increase in the riskiness of consumption leads to a decrease in aggregate capital if and only if the elasticity of intertemporal substitution is greater than one. This is because credit tightening leads to a decrease in the risk-adjusted return to saving, giving rise to opposing income and substitution effects; when the EIS is higher, the substitution effect is stronger.
Using Assumption 1 and (4.10), the equity premium can be written as:
Thus, in the general-equilibrium steady state:
With a shift from
In the remainder of this section, I will examine how the economy would react differently to a decrease in ![]() if the risk-free rate were held constant, as in a small open economy.
if the risk-free rate were held constant, as in a small open economy.
5.2 Understanding the endogenous decrease in the interest rate and its effects
To obtain a clearer understanding of Proposition 4, define a small-open-economy equilibrium as equivalent to the closed-economy equilibrium defined above, except that the bond-market clearing condition is replaced with an exogenously given interest rate.
Using the budget constraint (4.2) and Lemma 1, define the optimal debt policy as:
The aggregate dynamics in the small-open economy will satisfy:
as well as the optimality condition (4.13) and the first-order conditions of (4.8). A small-open-economy steady state is a fixed point of this system with
(a) There exists
![]() such that a small-open-economy steady state exists if and only if
such that a small-open-economy steady state exists if and only if
![]() .
.
(b) If a steady state exists, it is unique and entrepreneurs are not perfectly insured.
The next result shows how a small-open economy would respond to a decrease in ![]() .
.
(a) no change in the riskiness of consumption growth; the steady-state consumption growth rate
![]() is unchanged;
is unchanged;
(b) a decrease in net leverage,
![]() , and expected profits per unit wealth,
, and expected profits per unit wealth,
![]() ;
;
(c) an increase in the equity premium (and hence a decrease in aggregate capital).
Clearly, with a constant interest rate, no change in the riskiness of consumption after a decrease in firms' ability to pledge is consistent with (5.8): the certainty-equivalent of the wealth growth rate is unchanged; the interest rate is unchanged; and the minimum payoff
The response of the equity premium to a decrease in firms' ability to borrow, holding the interest rate constant, can then be seen from (5.4). Because the riskiness of consumption is unchanged,
![]() is unchanged: shifting one unit of consumption from low-productivity states to high-productivity states is equally unattractive before and
after the decrease in firms' ability to borrow. Nonetheless, mechanically, for each unit of physical capital that an entrepreneur holds, more consumption must be shifted from low-productivity states to high-productivity states. Correspondingly, the equity premium increases. Hence, aggregate capital
decreases unambiguously.
is unchanged: shifting one unit of consumption from low-productivity states to high-productivity states is equally unattractive before and
after the decrease in firms' ability to borrow. Nonetheless, mechanically, for each unit of physical capital that an entrepreneur holds, more consumption must be shifted from low-productivity states to high-productivity states. Correspondingly, the equity premium increases. Hence, aggregate capital
decreases unambiguously.
Proposition 6 explains why the risk-free rate falls in a closed economy in response to a decrease in ![]() . Consider a small, open economy with
. Consider a small, open economy with
![]() and suppose that, in the initial steady state, its current account was in balance. In this small open economy, a decrease in
and suppose that, in the initial steady state, its current account was in balance. In this small open economy, a decrease in ![]() leads to a persistent current-account surplus. The decrease in leverage,
leads to a persistent current-account surplus. The decrease in leverage,
![]() , has a mechanical component and an endogenous one. Mechanically, the decrease in
, has a mechanical component and an endogenous one. Mechanically, the decrease in ![]() means that, for high realizations of next-period productivity, the share of next-period profits pledged must decrease, in order to satisfy the limited-enforcement constraint. In addition, the decrease in
means that, for high realizations of next-period productivity, the share of next-period profits pledged must decrease, in order to satisfy the limited-enforcement constraint. In addition, the decrease in ![]() leads to an endogenous decrease in expected profits per unit wealth,
leads to an endogenous decrease in expected profits per unit wealth,
![]() . Thus, a decrease in
. Thus, a decrease in ![]() in the small open economy leads to a
decrease in net leverage, which explains why, in the closed economy, the interest rate must fall in response to a decrease in
in the small open economy leads to a
decrease in net leverage, which explains why, in the closed economy, the interest rate must fall in response to a decrease in ![]() .
.
The next proposition is the complement to Proposition 6: that is, Proposition 7 examines how a small-open economy is affected by changes in the risk-free rate.
(a) a decrease in the minimum payoff ![]() and an increase in the riskiness of consumption growth;
and an increase in the riskiness of consumption growth;
(b) an increase in net leverage,
![]() , and expected profits per unit wealth,
, and expected profits per unit wealth,
![]() ;
;
(c) an increase in the equity premium.
As before, the response of the equity premium to a decrease in the interest rate, holding all other exogenous variables constant, can be seen from (5.4). Because the riskiness of consumption increases,
![]() decreases: shifting one unit of consumption from low-productivity states to high-productivity states is more painful than before the
decrease in the interest rate. Thus, even though there is no change in the amount, per unit of physical capital, of wealth that must be shifted from low-productivity states to high-productivity states, reducing insurance is more painful because of the decrease in the risk-free rate.
decreases: shifting one unit of consumption from low-productivity states to high-productivity states is more painful than before the
decrease in the interest rate. Thus, even though there is no change in the amount, per unit of physical capital, of wealth that must be shifted from low-productivity states to high-productivity states, reducing insurance is more painful because of the decrease in the risk-free rate.
6 Transition dynamics
In this section, I study how the economy responds in the short run to the decrease in firms' ability to borrow. In the preceding analysis of the long-run response, I showed that a decrease in firms' ability to borrow leads to an increase in the equity premium and the riskiness of consumption. I also showed that steady-state aggregate capital may increase or decrease in response to a decrease in firms' ability to borrow, depending on the elasticity of intertemporal substitution. These results raise a number of questions about the short-run dynamics. For example, one might conjecture that if entrepreneurs accumulate wealth over time in response to credit tightening, then there will be overshooting in the equity premium: the equity premium would shoot up at first, but this initial increase would be partially reversed over time.
6.1 No overshooting of the equity premium
Thus, in this section, I fully characterize the transition dynamics of the equity premium and the riskiness of consumption for any path for
![]() . It turns out that, due to a general-equilibrium effect, the equity premium and one measure of consumption riskiness do not display any over- or under-shooting in response to
a decrease in firms' ability to borrow.
. It turns out that, due to a general-equilibrium effect, the equity premium and one measure of consumption riskiness do not display any over- or under-shooting in response to
a decrease in firms' ability to borrow.
In this section, I explicitly denote the dependence of steady-state variables on the share of profits that firms are able to pledge in the long run; for example, ![]() is steady state
aggregate capital when
is steady state
aggregate capital when
![]() .
.
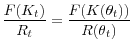
Another implication of Proposition 8 is that, at time ![]() , the future path for firms' ability to borrow,
, the future path for firms' ability to borrow,
![]() , does not affect the period-
, does not affect the period-![]() equity premium or the coefficient of variation of period-
equity premium or the coefficient of variation of period-![]() consumption, although it may affect period-
consumption, although it may affect period-![]() aggregate capital and consumption.
aggregate capital and consumption.
The absence of overshooting described in Proposition 8 is a general-equilibrium effect. The equity premium, given in (5.4), is greater when idiosyncratic consumption is riskier; that is, when
![]() is more risky. Thus, the equity premium can overshoot (or undershoot) after a permanent shock only if the riskiness of consumption varies
with aggregate capital. However, in the closed economy studied here, this is not possible. Consider a shock to aggregate capital, all else equal: if in response to the shock, entrepreneurs sought to take more risk by increasing leverage, this would lead to an increase in the supply of financial
assets, leading entrepreneurs to hedge more and thus contradicting the premise that the aggregate wealth shock leads to more risk taking.
is more risky. Thus, the equity premium can overshoot (or undershoot) after a permanent shock only if the riskiness of consumption varies
with aggregate capital. However, in the closed economy studied here, this is not possible. Consider a shock to aggregate capital, all else equal: if in response to the shock, entrepreneurs sought to take more risk by increasing leverage, this would lead to an increase in the supply of financial
assets, leading entrepreneurs to hedge more and thus contradicting the premise that the aggregate wealth shock leads to more risk taking.
6.2 Understanding the role of the interest rate in the short run
It is interesting to consider the short-run dynamics of the risk-free rate and whether the equity premium and consumption riskiness increase more in the short-run than they would if the interest-rate were fixed. I address this questions for the special case in which the elasticity of intertemporal substitution is equal to one. With an EIS equal to one, the path for aggregate capital is unaffected by the path for collateral constraints and idiosyncratic uncertainty.
(a) The path for aggregate quantities
![]() is unique and converges monotonically to the unique steady state, with
is unique and converges monotonically to the unique steady state, with
![]() and
and
![]() .
.
(b) Compare two economies, H and L, that are identical in their initial conditions and exogenous parameters, except that
![]() Then
Then
![]() and the period-
and the period-![]() equity premium in economy L is
greater than it would be if the period-
equity premium in economy L is
greater than it would be if the period-![]() risk-free rate in economy L were exogenous and equal to
risk-free rate in economy L were exogenous and equal to
![]() .
.
7 Conclusion
A number of recent papers have studied the short- and long-run effects of shocks to collateral constraints in models that abstract from uninsured investment risk. At the same time, other papers have studied uninsured investment risk while ignoring borrowing constraints. In this paper, I characterized the economy's response to a shock to collateral constraints in a model with uninsured risk. In the model, credit tightening leads to an increase in the equity premium and the riskiness of consumption. I showed that, both immediately after the shock and in the long run, the equity premium and the riskiness of consumption increase more than they would if the risk-free rate were constant. Indeed, the long-run increase in the riskiness of consumption growth was shown to be a purely general-equilibrium effect: if the risk-free rate were constant (as in a small open economy), an endogenous decrease in risk-taking by entrepreneurs would, in the long run, completely offset the decrease in their ability to diversify. I also showed that the credit shock leads to a decrease in aggregate capital if the elasticity of intertemporal substitution is sufficiently high. Finally, I demonstrated that, due to a general-equilibrium effect, there is no "overshooting" in the equity premium: in response to a permanent decrease in firms' ability to pledge their future income, the equity premium immediately jumps to its new steady-state level and remains constant thereafter, even as aggregate capital adjusts over time. Because the results highlight how changes in the risk-free rate affect risk-taking and the equity premium, it would be useful to extend the model to understand the implications of uninsured investment risk for monetary policy and the optimal level of government debt.
Appendix A: Proofs
Proof of Lemma 1
Define
subject to (4.2) and (4.3). Using (7.1), we can write (4.1) as:
Conjecture the following solution:
where
From (7.3), we have that
subject to
Dividing the first-order condition with respect to
where
This, together with the linearity of (7.5), implies that the solutions ![]() and
and ![]() to (7.4)-(7.5) are linear in
to (7.4)-(7.5) are linear in ![]() and that
and that
![]() is linear in
is linear in ![]() . In particular, we have
. In particular, we have
![]() , where
, where ![]() is given by (4.7). Moreover, re-arranging (7.6), one obtains (4.10).
is given by (4.7). Moreover, re-arranging (7.6), one obtains (4.10).
Substituting for
![]() into (7.2), one obtains:
into (7.2), one obtains:
The envelope condition is:
Taking the first-order condition, using the envelope condition, and rearranging, one obtains:
Forward iteration of (7.8) implies (4.6).
Finally, to verify (7.3), one must confirm that
Proof of Proposition 3
From assumption 1, one obtains
![]() Setting
Setting
![]() in (4.12), one obtains the steady-state condition:
in (4.12), one obtains the steady-state condition:
Hence, in steady state,
Using (4.7) and (7.8), one can write:
Then, setting
From (7.11), observe that
Using (4.14), (7.9) and (7.11), one obtains (5.2). Next, using (4.2) , (7.6) and (7.11) , one obtains (5.3). Note that
![]() . If
. If
![]() , then:
, then:
![]() ;
;
![]() ; and, from (5.3),
; and, from (5.3), ![]() . If
. If
![]() , then:
, then:
![]() ;
;
![]() ; and from, (5.3),
; and from, (5.3), ![]() .
.
![]()
Proof of Proposition 4
I will compare the steady states corresponding to two different values for firms' ability to borrow:
![]() and
and
![]() .
.
Suppose that
![]() . Denoting explicitly the dependence of steady-state policies on
. Denoting explicitly the dependence of steady-state policies on ![]() and using (5.1), one obtains that
and using (5.1), one obtains that
![]() This result, together with (5.5), implies that
This result, together with (5.5), implies that
![]() .
.
Next, I will show that a decrease in ![]() generates a mean-preserving spread in
generates a mean-preserving spread in ![]() . Note that, in steady state,
. Note that, in steady state, ![]() is the growth rate of idiosyncratic wealth and the growth rate of idiosyncratic consumption. Denote by
is the growth rate of idiosyncratic wealth and the growth rate of idiosyncratic consumption. Denote by ![]() the cumulative distribution function of
the cumulative distribution function of
![]() . Observe that
. Observe that
![]() . Furthermore,
. Furthermore,
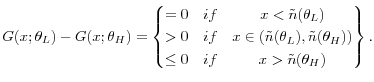
Proof of Lemma 5
In this proof, I will assume that ![]() is a continuous random variable and that
is a continuous random variable and that ![]() has positive support over
has positive support over
![]() . However, the more general proof is very similar.
. However, the more general proof is very similar.
In a small open economy, ![]() and
and
![]() are uniquely determined by the steady-state condition
are uniquely determined by the steady-state condition
![]() and (5.3), which is a partial-equilibrium steady-state condition. Define a function
and (5.3), which is a partial-equilibrium steady-state condition. Define a function ![]() by
by
![]() , where the domain of
, where the domain of ![]() is
is ![]() . Observe that:
. Observe that: ![]() ;
; ![]() ;
; ![]() is continuous; and
is continuous; and ![]() is
strictly decreasing in
is
strictly decreasing in ![]() . Write (5.3) as:
. Write (5.3) as:
Note that:
From (7.11), observe that
![]() if
if
![]() , where
, where
![]() .
.
![]()
Proof of Proposition 6
From (7.12), one observes that ![]() and
and ![]() do not
depend on
do not
depend on ![]() . Hence, a decrease in
. Hence, a decrease in ![]() leads to a decrease in
leads to a decrease in
![]() and has no effect on
and has no effect on ![]() . (5.4)
implies that a decrease in
. (5.4)
implies that a decrease in ![]() leads to an increase in
leads to an increase in
![]()
![]()
Proof of Proposition 7
From (7.12), we see that a decrease in ![]() leads to an increase in
leads to an increase in ![]() and thus a decrease in
and thus a decrease in ![]() . Hence, a decrease in
. Hence, a decrease in ![]() leads to an
increase in
leads to an
increase in
![]() and a decrease in
and a decrease in ![]() . (5.4)
implies that a decrease in
. (5.4)
implies that a decrease in ![]() leads to an increase in
leads to an increase in
![]() Because
Because ![]() decreases and
decreases and
![]() increases, one obtains that a decrease in
increases, one obtains that a decrease in ![]() leads to a simple
increase in risk in
leads to a simple
increase in risk in
![]() .
.
![]()
Proof of Proposition 8
As in the main text, I explicitly denote the dependence of steady-state variables on the share of profits that firms are able to pledge in the long run; for example, ![]() is steady
state aggregate capital when
is steady
state aggregate capital when
![]() .
.
Financial market clearing implies:
Next, observe that
![\displaystyle \frac{c_{t+1}^{i}}{E[c_{t+1}^{i}]}](img284.gif) |
|||
and hence the distribution of
Proof of Proposition 9
Proof of Part (a). From (4.6) and the assumption that
![]() , one observes that
, one observes that
![]() for all
for all ![]() . Then, from (4.14), one
obtains that
. Then, from (4.14), one
obtains that
![]() . Moreover, from (4.12), we have that steady state capital satisfies
. Moreover, from (4.12), we have that steady state capital satisfies
![]() and that the growth rate of aggregate capital is given by
and that the growth rate of aggregate capital is given by
![]() , so that convergence is monotonic.
, so that convergence is monotonic.
Proof of Part (b). Propositions 4 and 8 imply that
![]() . From part (a), we have that
. From part (a), we have that
![]() and hence
and hence
![]() .
.
Finally, consider an economy in which firms' ability to borrow is given by
![]() but the period-
but the period-![]() interest rate
is exogenous and equal to
interest rate
is exogenous and equal to
![]() . Suppose, by contradiction, that the period-
. Suppose, by contradiction, that the period-![]() equity premium in
this hypothetical economy were greater than the period-
equity premium in
this hypothetical economy were greater than the period-![]() equity premium in economy
equity premium in economy ![]() . Then, because
. Then, because
![]() , we have that period-
, we have that period-![]() aggregate capital in this
economy is less than period-
aggregate capital in this
economy is less than period-![]() aggregate capital in economy
aggregate capital in economy ![]() Because
aggregate capital in period-
Because
aggregate capital in period-![]() is identical in the hypothetical economy and in economy
is identical in the hypothetical economy and in economy ![]() , this implies that period-
, this implies that period-![]() net leverage in the hypothetical economy is less than period-
net leverage in the hypothetical economy is less than period-![]() net leverage in economy
net leverage in economy ![]() , which is given by
, which is given by
![]() . Equation (5.4) then implies that the period-
. Equation (5.4) then implies that the period-![]() equity premium in the hypothetical economy is greater than the period-
equity premium in the hypothetical economy is greater than the period-![]() equity premium in economy
equity premium in economy ![]() , a contradiction.
, a contradiction.
![]()
![\displaystyle \frac{1}{R_{t}}E_{t}[w_{t+1}^{i}]=\left(\frac{1}{R_{t}}E_{t}[\tilde{f}(s_{t+1}^{i},\omega_{t+1})]-1\right)k_{t}^{i}+x_{t}^{i}](img70.gif)
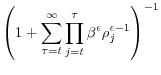
![\displaystyle \left(\frac{1}{R_{t}}E[\tilde{f}(s_{t+1},\omega_{t+1})]-1\right)\kappa+1.](img95.gif)
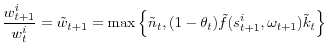
![\displaystyle \frac{1}{R_{t}}E_{t}[\tilde{f}(s_{t+1}^{i},\omega_{t+1})]-1=\frac{1}{R_{t}}E_{t}\left[(1-\theta_{t})\tilde{f}(s_{t+1}^{i},\omega_{t+1})\left(1-\Upsilon'\left(\frac{\tilde{w}_{t+1}}{\tilde{n}_{t}}\right)\right)\right]](img108.gif)
![\displaystyle \beta R=\frac{\left(\mathbb{CE}[\tilde{w}]\right)^{\frac{1}{\epsilon}}}{\left(\mathbb{CE}[\frac{\tilde{w}}{\tilde{n}}]\right)^{\gamma}}\leq1.](img143.gif)
![\displaystyle \frac{F_{K}(K_{t})}{R_{t}}=\left[1-E_{t}\left[(1-\theta_{t})s\left(1-\Upsilon'\left(\frac{\tilde{w}_{t+1}}{\tilde{n}_{t}}\right)\right)\right]\right]^{-1}](img172.gif)
![\displaystyle \frac{F_{K}}{R}=\left[1-E\left[\max\left\{ 0,(1-\theta)s\left(1-\Upsilon'\left(\frac{(1-\theta)s}{\tilde{n}}\right)\right)\right\} \right]\right]^{-1}](img173.gif)
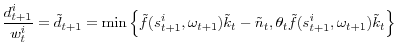
![\displaystyle \begin{bmatrix}C_{t}\\ K_{t}\\ D_{t+1} \end{bmatrix}=\begin{bmatrix}\tilde{c}_{t}\\ \tilde{k}_{t}\\ E_{t}[\tilde{d}_{t+1}] \end{bmatrix}\left(\Pi(K_{t-1})-D_{t}\right).](img175.gif)
![\displaystyle \frac{n_{t}^{i}}{k_{t}^{i}}=\left[\frac{E_{t}\left[\max\left\{ 0,(1-\theta_{t})\tilde{f}(s_{t+1}^{i};\omega_{t+1})\right\} \right]-\left(E_{t}[\tilde{f}(s_{t+1}^{i};\omega_{t+1})]-R_{t}\right)}{E_{t}\left[\max\left\{ 0,((1-\theta_{t})\tilde{f}(s_{t+1}^{i};\omega_{t+1}))^{1-\gamma}\right\} \right]}\right]^{1/\gamma}](img217.gif)
![\displaystyle \beta R=\frac{\left(\mathbb{CE}[\max\{z(x),sx\}]\right)^{\frac{1}{\epsilon}}}{\left(\mathbb{CE}[\max\{1,s\frac{x}{z(x)}\}]\right)^{\gamma}}\equiv H(x)](img271.gif)