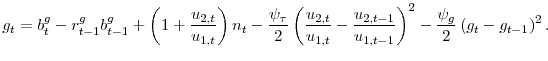Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2013-59 Screen Reader version ^♣

Cost of borrowing shocks and fiscal adjustment*

Oliver de Groot

Federal Reserve Board

Fédéric Holm-Hadulla

European Central Bank

Nadine Leiner-Killinger

European Central Bank

July 30, 2013

Abstract:

Do capital markets impose fiscal discipline on governments? We investigate the responses of fiscal variables to a change in the interest rate paid by governments on their debt in a panel of 14 European countries over four decades. To this end, we estimate a panel vector autoregressive (PVAR) model, using sign restrictions via the penalty function method of Mountford and Uhlig 2009 to identify structural cost of borrowing shocks. Our baseline estimation shows that a 1 percentage point rise in the cost of borrowing leads to a cumulative improvement of the primary balance-to-GDP ratio of approximately 2 percentage points over 10 years, with the fiscal response becoming significantly evident only two years after the shock. We also find that the bulk of fiscal adjustment takes place via a rise in government revenue rather than a cut in primary expenditure. The size of the total fiscal adjustment, however, is insufficient to avoid the gross government debt-to-GDP ratio from rising as a consequence of the shock. Sub-dividing our sample, we also find that for countries participating in Economic and Monetary Union (EMU) the primary balance response to a cost of borrowing shock was stronger in the period after 1992 (the year in which the Maastricht Treaty was signed) than prior to 1992.

Keywords: Fiscal policy, Long-term interest rates, VARs, Sign restrictions

JEL classifications: C33, E43, E62, H60

... The [Irish] Government has today decided that an overall [fiscal] adjustment of € 15 billion over the next four years is warranted $\ldots$ The key reasons for the significant increase from the figure announced in Budget 2010 are lower growth prospects ... and higher debt interest costs. (Statement by the Irish Government, 26 October 2010).¹

1 Introduction

During the European sovereign debt crisis, sharp rises in yields on government bonds have been met with promises from governments to accelerate and expand their fiscal consolidation plans. To the extent the promises are acted upon, this behaviour can be interpreted as a form of market-imposed fiscal discipline. Against this background, we examine empirically, over a long time series and across several European Union (EU) countries, the proposition that governments systematically respond to adverse shocks in their market borrowing rates by improving their fiscal positions.

This question is relevant for two reasons. First, by providing estimates of past patterns in the response of EU governments to changes in their cost of borrowing, the current analysis can inform views on how the medium-term fiscal stance is likely to evolve, in situations in which there is a re-pricing of government debt. Second, the paper provides a new perspective on the extent to which it may be appropriate to rely on financial markets to reinforce fiscal adjustment. To the extent that markets provide discipline, it may be less important to establish formal rules, such as those recently adapted in the Stability and Growth Pact.² The empirical analysis presented here may contribute to such an assessment by providing evidence on a critical link in the way financial markets can provide fiscal discipline--namely, whether market-induced changes in the cost of borrowing later affect the fiscal stance.

In doing so, the paper addresses an issue that, to date, has received little attention in academic research. As pointed out by Bayoumi, Goldstein, and Woglom 1995, analyses of whether fiscal authorities are subject to market discipline should address two questions. First, do markets adjust the terms at which they lend to governments when fiscal positions change? Second, do governments adjust their fiscal positions when their cost of borrowing changes? A great deal of research has investigated the first question in isolation.³ However, the hypothesis of market-induced fiscal discipline implies simultaneous responses of government bond market prices and fiscal policies, thus suggesting that the price and quantity of public debt are jointly determined. Yet, the causation from the cost of public debt service to fiscal policy decisions has received little attention in the empirical literature.⁴ This paper aims to bring some balance to the joint determination of fiscal variables and long-term interest rates by empirically assessing the response of fiscal policy to exogenous interest rate changes in a dynamic context.

To motivate our empirical analysis, we present a simple model, in which the government of a small open economy optimally commits to a state-contingent path of government spending, labour taxes, and debt. The government is able to issue debt on capital markets, paying the world interest rate plus a risk premium. In this set up, an exogenous rise in the risk premium demanded by international investors for holding this debt generates a tightening of the budgetary path. However, the optimal speed and composition for budget tightening is dependent on the structural features of the economy.

These model based simulations are then confronted with empirical estimates of the response of fiscal variables to changes in long-term interest rates. To this end, we use a vector autoregressive (VAR) model for a panel of 14 European countries and annual data from 1970 to 2011. The empirical analysis faces two important methodological challenges. First, because fiscal policy and the cost of borrowing are jointly determined, it is difficult to isolate exogenous movements in the cost of borrowing for governments. To overcome this challenge, we use the sign-restriction methodology of Mountford and Uhlig 2009 to identify several fundamental shocks that have been well documented in the macroeconometric literature. Having thus identified business cycle and fiscal policy shocks, we treat any additional unexpected movements in long-term interest rates, orthogonal to the business cycle and fiscal policy shocks, as truly exogenous shocks to the cost of borrowing.

Second, empirical estimates must respect the government's intertemporal budget constraint. We impose this restriction by keeping track of the nonlinear debt dynamics using the methodology of Favero and Giavazzi 2007. On this basis, it is possible to assess whether the fiscal response is sufficient to offset the dynamics of rising debt generated by an increase in the cost of borrowing.

We find a statistically significant fiscal policy response to exogenous changes in the cost of borrowing. In our baseline estimations, a 1 percentage point rise in the cost of borrowing leads to a cumulative increase in the primary balance-to-GDP ratio of 2 percentage points after 10 years. However, the debt-to-GDP ratio is 1 percentage point higher 10 years after the shock, i.e. the budgetary response is insufficient to compensate for the automatic debt-increasing effect of higher borrowing costs. The impulse responses reveal that the fiscal response is not immediate, with a significant consolidation appearing only two years after the shock. Almost all the adjustment takes place on the revenue side while primary expenditure remains broadly unchanged.

Given the wide-ranging changes in the European fiscal framework over recent decades and their potential effect on economic policy in EU member states, we separate our panel into EMU and non-EMU countries and the periods pre- and post-1992 (which marks the signing of the Maastricht Treaty). Our estimates reveal that the sub-sample including the post-1992 EMU countries show a significantly stronger fiscal consolidation response following a rise in the cost of borrowing than the pre-1992 EMU sample. A possible interpretation of this pattern is that those countries that eventually joined monetary union had an additional incentive to compensate for higher interest payments (which count against the Maastricht balance criterion) by tightening their stance with respect to other budget items.

The rest of the paper proceeds as follows. Section 2 provides a simple theoretical framework to clarify the responses predicted by standard macroeconomic theory. Section 3 outlines the empirical methodology, in particular the identification strategy. Section 4 presents the results while Section 5 discusses policy implications and concludes.

2 Theoretical motivation

In this section, we provide a stylized framework to analyze the responses of governments to an exogenous rise in the cost of borrowing. We use this model to illustrate the range of potential patterns of fiscal adjustment to shocks to the cost of borrowing. Based on these results, we test these implications in Section 4. The model is that of a small open economy populated by a large number of identical households and a benevolent government. Households have preferences over private and public consumption goods and hours worked and have access to incomplete international capital markets. The government can also borrow on international capital markets and has two fiscal instruments, distortionary taxes on labor income and public consumption expenditure. The government sets its two policy instruments optimally under commitment.

2.1 Model

The objective function of a representative household is

$\displaystyle \underset{c_{t},n_{t},b_{t}^{h}}{\max }E_{0}\sum\nolimits_{t=0}^{\infty}\beta ^{t}u_{t}$

(1)

subject to the intertemporal budget constraint

$\displaystyle c_{t}=b_{t}^{h}-r_{t}^{h}b_{t-1}^{h}+\left( 1-\tau _{t}\right) w_{t}n_{t}$

where $u_{t}\equiv u\left( c_{t},n_{t},g_{t}\right) \equiv v\left( c_{t},n_{t}\right) +w\left( g_{t}\right)$ are preferences over private consumption, $c_{t}$ , hours worked, $n_{t}$ , and public consumption, $g_{t}$ . The functional form for preferences over $c_{t}$ and $n_{t}$ follows Greenwood, Hercowitz, and Huffman 1988, eliminating wealth effect on labour supply. Public consumption is additively separable. $\beta \in \left( 0,1\right)$ is the subjective discount factor, $w_{t}$ is the real wage and $\tau _{t}$ is the tax rate on labor income. Households issue debt, denoted $b_{t}^{h}$ , on international capital markets. The interest rate households face is denoted $r_{t}^{h}$ and is assumed to be an increasing and convex function of both the aggregate debt-to-output ratio of the private sector, $\widetilde{b}^{h}/y$ (where a tilde denotes an aggregate quantity and

is output) and the government debt-to-GDP ratio, $% b^{g}/y$ :

$\displaystyle r_{t}^{h}\equiv r^{h}\left( \frac{\widetilde{b}_{t}^{h}}{y_{t}},\frac{% b_{t}^{g}}{y_{t}},\upsilon \xi _{t}\right)$

(2)

where $\upsilon$ captures the pass-through of the exogenous government cost of borrowing shock (to be described below) to the private sector's cost of borrowing. Production in the economy follows a linear technology, $% y_{t}=n_{t}$ , which implies that the real wage (before taxes) is constant and equal to one. The first-order conditions of the household problem are

$\displaystyle 1=\beta E_{t}\frac{u_{1,t+1}}{u_{1,t}}r_{t}^{h}$

(3)

and

$\displaystyle \left( 1-\tau _{t}\right) w_{t}=-\frac{u_{2,t}}{u_{1,t}}$

(4)

where $u_{1,t}$ , for example, denotes the first derivative of $u_{t}$ with respect to its first argument, $c_{t}$ . In equilibrium, $\widetilde{b}% _{t}^{h}=b_{t}^{h}$ .

The government can levy taxes on labour income and issue debt in international capital markets to finance public consumption, denoted $g_{t}$ . The government's intertemporal budget constraint is:

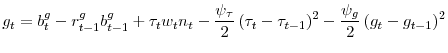$\displaystyle g_{t}=b_{t}^{g}-r_{t-1}^{g}b_{t-1}^{g}+\tau _{t}w_{t}n_{t}-\frac{\psi _{\tau }}{2}\left( \tau _{t}-\tau _{t-1}\right) ^{2}-\frac{\psi _{g}}{2}\left( g_{t}-g_{t-1}\right) ^{2}$

(5)

where $\frac{\psi _{\tau }}{2}\left( \tau _{t}-\tau _{t-1}\right) ^{2}$ and $% \frac{\psi _{g}}{2}\left( g_{t}-g_{t-1}\right) ^{2}$ are convex costs of adjusting tax rates and government expenditure, respectively. These reduced-form costs will play an important role in shaping the impulse responses to a cost of borrowing shock and generate paths for the primary balance that are able to match those in our empirical estimation in Section 4.

These costs can be interpreted in three ways. First, they can be interpreted as actual administrative and compliance costs of changing the tax code or devising well-targeted government spending programmes.⁵ Even when $\psi _{\tau }$ and $\psi _{g}$ are high, the equilibrium deadweight costs remain economically small as the government optimally adjusts its fiscal instruments more gradually.

Second, the adjustment costs can be thought of as capturing, in reduced form, the dynamics of distributional conflicts between different fiscal agents (or political parties) that have different preferences over the mix of fiscal instruments. [Tabellini 1986] showed that in this setting, the non-cooperative equilibrium would generate slower fiscal adjustment following shocks.

Third, and our preferred interpretation, is the analogy with the literature on optimal monetary-policy inertia. Aoki2006 and Woodford1999, for example, show that adjusting the monetary policy interest rate gradually is optimal without imposing any penalty on interest rate variations. As long as there is some friction due to which the policymaker cannot achieve its stabilization objectives independently in each period, optimal policy is history dependent. Providing a more fundamental model of this source of policy inertia, however, is left for future research.

The interest rate on government borrowing, like that of the households, is assumed to be an increasing and convex function of both the (aggregate) private sector and government debt-to-GDP ratio.

$\displaystyle r_{t}^{g}\equiv r^{g}\left( \frac{\widetilde{b}_{t}^{h}}{y_{t}},\frac{% b_{t}^{g}}{y_{t}},\xi _{t}\right)$

(6)

In addition, the interest rate faced by the government is assumed to be stochastic, with an exogenous cost of borrowing shock denoted by $\xi _{t}$ , which follows an $AR\left( 1\right)$ process, $\xi _{t}=\rho \xi _{t-1}+\zeta \varepsilon _{t}$ where $\varepsilon _{t}\sim NIID\left( 0,1\right)$ .

Closing the model requires two additional equations describing the behaviour of the government's two fiscal instruments. To do this, we assume that the government is benevolent and is able to commit to a time invariant (i.e. from the timeless perspective) optimal policy. The government therefore solves the following Lagrangian, which maximizes household utility subject to resource constraints and household's first order equilibrium conditions:

$\displaystyle \underset{c_{t},n_{t},b_{t}^{h},b_{t}^{g},g_{t},\mu _{1,t},\mu _{2,t}}{\max }% E_{0}\sum\nolimits_{t=0}^{\infty }\beta ^{t}\left( \begin{array}{c} u_{t}+\mu _{1,t}\left( b_{t}^{h}-r_{t-1}^{h}b_{t-1}^{h}-\frac{u_{2,t}}{% u_{1,t}}n_{t}-c_{t}\right) \\ +\mu _{2,t}\left( \begin{array}{c} b_{t}^{g}-r_{t-1}^{g}b_{t-1}^{g}+\left( 1+\frac{u_{2,t}}{u_{1,t}}\right) n_{t} \\ -\frac{\psi _{\tau }}{2}\left( \frac{u_{2,t}}{u_{1,t}}-\frac{u_{2,t-1}}{% u_{1,t-1}}\right) ^{2}-\frac{\psi _{g}}{2}\left( g_{t}-g_{t-1}\right) ^{2}-g_{t}% \end{array}% \right)% \end{array}% \right)$

(7)

where $\mu _{1,t}$ is the Lagrange multiplier on the household budget constraint and $\mu _{2,t}$ is the Lagrange multiplier on the government budget constraint, with equations (4) and (11) substituted in. We also assume that the government has the same subjective discount factor, $\beta$ as the private sector. The first-order conditions are given in Appendix A, as are the functional forms for the utility function and interest rate equations (2) and (6).

2.2 Calibration

Table 1 summarizes the calibration of the model and Table 2 summarizes the deterministic steady state around which a linear approximation of the model is taken. The calibration replicates several long-run averages in European data. For example, we achieve a debt-to-GDP ratio of both the private sector and the government of $50\%$ , broadly in line with the sample average of $51.3\%$ . Unlike small open economy models featuring a non-optimizing fiscal agent, the steady state debt-to-GDP ratio is uniquely pinned down in this model. In particular, it is pinned down in this model by the calibration of parameters $\phi ^{ij}$ and $\alpha ^{i}$ with $i,j\in \left\{ g,h\right\}$ , where $\phi ^{ij}$ defines the response of the interest rate faced by to a marginal change in the debt-to-GDP ratio of , and $\alpha ^{i}$ defines the wedge between the steady state interest rate faced by and the discount rate, $\beta ^{-1}$ . $\$ We set $% \phi ^{gg}=\phi ^{hh}=0.05$ , which implies that a 1 percentage point increase in the debt-to-GDP ratio increases the cost of borrowing by 5 basis points. There is very little evidence on the response of longer-term interest rates to fiscal shocks for European countries, so we chose a value that matched the finding in Laubach 2009 based on US data. The cross-elasticities $\phi ^{hg}=\phi ^{gh}$ are set to zero. The steady-state interest rate is set below the household's subjective discount rate in order to induce a positive holding of debt by both the private sector and the government. Given $\phi ^{gg}$ and $\phi ^{hh}$ , achieving the $50\%$ debt-to-GDP ratio required setting $\alpha ^{h}$ and $\alpha ^{g}$ at .0025 .

The preference parameters determine the number of hours worked. We therefore calibrate these parameters so that households work $25\%$ of their time endowment. The weight on public consumption in the utility function is chosen to achieve a government primary spending-to-GDP ratio of $40\%$ , which is consistent with the long-run average in our European data set. The adjustment cost parameters ${\footnotesize\psi }_{g}$ and $% {\footnotesize\psi }_{\tau }$ do not feature in the steady state. We will conduct sensitivity analysis with respect to these parameters, as well as $% \upsilon$ , the pass through of government cost of borrowing shocks to the private sector, when analyzing the impulse responses. The model is calibrated for annual data, which means we have $\beta =0.95$ and $\rho =0.8$ , which is approximately equal to a persistence oefficient of 0.95 in a quarterly model.

Table 1: Calibration

Symbol	Description	Value
$\beta$	Subjective discount factor	0.95
$\sigma$	Preference parameter	2
$\theta$	Preference parameter	1.8333
$\psi$	Preference parameter	1.0138
$\psi _{g}$	Government spending adjustment cost parameter	various
$\psi _{\tau }$	Tax adjustment cost parameter	various
$\alpha ^{h}$ , $\alpha ^{g}$	Steady state interest rate discount	0.025
$\phi ^{hh}$ , $\phi ^{gg}$	Interest rate sensitivity parameter	0.05
$\phi^{hg}$ , $\phi^{gh}$	Interest rate sensitivity parameter	0
$\rho$	Cost of borrowing shock persistence parameter	0.8

Table 2: Deterministic steady state

Symbol	Description	Value
$b^{h}/y$	Private sector debt-to-GDP ratio	50%
$b^{g}/y$	Government debt-to-GDP ratio	50%
	Proportion of hours worked	25%
	Government primary spending-to-GDP ratio	40%
$\tau$	Tax rate	41.4%
$r^{h}$ , $r^{g}$	Private sector and government cost of borrowing	2.76%

2.3 Impulse responses

When the government faces a higher path of borrowing costs, it must, at some point, generate a higher primary balance path to preserve solvency. The government, however, faces two important trade-offs in choosing the optimal path of its two fiscal policy instruments to a cost of borrowing shock. The first concerns the timing of adjustment. A sharp adjustment in the short-run can be costly due to the convex nature of the fiscal adjustment costs. However, a longer-term, more gradual adjustment means that the government will have to bear higher future interest rate payments. The second trade-off concerns the composition of adjustment. Cutting primary expenditures incurs both a deadweight cost of adjustment and a reduction in welfare due to the fall in public consumption, which directly enters households' utility. Raising taxes also incurs a deadweight adjustment cost as well as causing an increase in the distortion in the labour market. However, the social planner is able to use the tax rate to shift part of the economy's debt burden from the government (which is facing a relatively higher cost of borrowing) to the private sector.

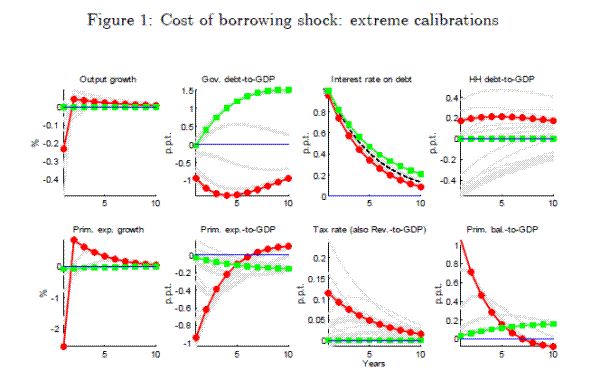
Figures 1-3 show the impulse responses to an exogenous, unexpected 1 percentage point rise in the government cost of borrowing, under various calibrations of the model. In each figure, the grey background lines show the dispersion of responses that the model is able to generate within a given parameter space. Figure 1 highlights two calibrations: one without fiscal instrument adjustment costs and one with extremely high adjustment costs. The shape of the responses are interesting for two reasons. First, the response of the government debt-to-GDP ratio is ambiguous. In the calibration without adjustment costs, the debt-to-GDP ratio immediately drops by 1 percentage point, while in the calibration with extremely high adjustment costs, the government debt-to-GDP ratio rises to 51.5 percentage points by the end of the 10 year horizon. Because the government makes only very gradual adjustments to its fiscal instruments in the second scenario, the rise in the debt-to-GDP ratio occurs largely because new debt issuance is used to cover higher interest payments. Without adjustment costs, the government cuts primary expenditure by 2 percentage points on impact, after which the level of primary expenditure is slowly rebuilt. This cut in primary expenditures translates into a fall in the primary expenditure-to-GDP ratio of almost 1 percentage point. The government also raises the tax rate on labour income by just over 0.1 percentage point. Since the real wage in this model is constant and equal to 1, the tax rate is always equal to the revenue-to-GDP ratio. The rise in the tax rates induces a reduction in labour supply and a consequent fall in output. The household smooths consumption by increasing borrowing.

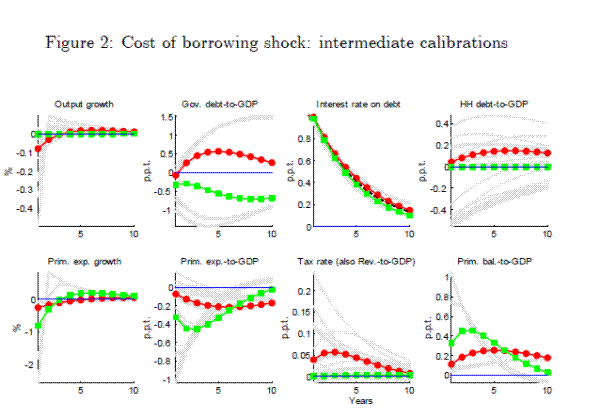
Figure 2 partly isolates the effect of the two fiscal instruments by varying the relative weight given to the two adjustment costs. In one of the highlighted responses, it is relatively more costly to adjust taxes, while in the other highlighted response it is more costly to adjust primary expenditure.⁶ With the intermediate calibration of the adjustment cost parameters in Figure 2 relative to Figure 1, the model generates hump-shaped responses of the fiscal instruments to cost of borrowing shocks, which is what we observe in our empirical analysis (see Section 4).

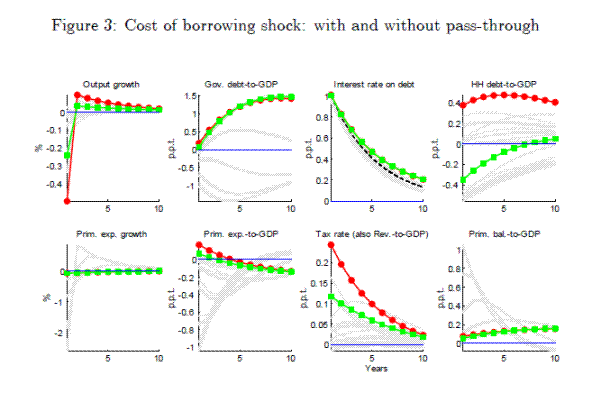
Figures 1 and 2 had assumed zero pass through from the cost of borrowing shock to the private sector. Figure 3, instead, assumes that the household cost of borrowing is shocked 1-for-1 with the government cost of borrowing, thus leaving the exogenous component of the spread between government and household cost of borrowing unchanged (that is, in equation (2), $\upsilon =1$ , rather than 0 ). This comparison highlights an adjustment mechanism that the social planner is able to exploit in the model. From a social planner's perspective, the debt of the household sector and the debt of the government are substitutes, and the social planner would like to shift the debt burden to the agent with the lowest cost of borrowing. The way the social planner is able to do this is by adjusting taxes. By increasing the tax rate, households reduce their supply of labour and smooth consumption by taking on more debt. Thus, raising

Figure 1: Cost of borrowing shock: extreme calibrations

Figure 1 Data

Note: The grey background lines show the dispersion of responses for parameter combinations in the set Φ ∈ {∨ ∈ (0,1), ψ _t ψ _g∈ (0, 5000) red dot: ∨ = 0, ψ _t = ψ _g=0, green square: ∨ =0, ψ _t=ψ _g=5000.

Figure 2: Cost of borrowing shock: intermediate calibrations

Figure 1: Cost of borrowing shock: intermediate calibrations.

Figure 2 Data

Note: The grey background lines show the dispersion of responses for parameter combinations in the set Φ ∈ {∨ ∈ (0,1), ψ _t ψ _g∈ (0, 5000) red dot: ∨ = 0, ψ _t =5, ψ _g=500, green square: ∨ =0, ψ _t= 500, ψ _g=50.

Figure 3: Cost of borrowing shock: with and without pass-through

Figure 3 Data

Note: The grey background lines show the dispersion of responses for parameter combinations in the set $\Phi \in \{v\in (0,1), \psi_{\tau }, \psi_{g} \in (0,5000)$ . red circle v = 0, $\psi _{\tau }$ = 0, $\psi _{g}$ = 5000, green square v = 1, $\psi _{\tau }$ = 0, $\psi _{g}$ = 5000.

taxes induces households to take on more debt. However, when the cost of borrowing for the household sector and the government rise proportionally, the social planner does not want the household to take on the higher burden of debt and it therefore does not increase the tax rate by as much. In Figure 3, the tax rate rises by only half as much when there is full pass through compared to when there is no pass through.

This stylized model yields a set of empirical hypotheses on the patterns of fiscal adjustment to cost of borrowing shocks. Based on this model, we test our main hypothesis empirically in the next section.

3 Empirical methodology

The subsequent subsections describe the data, estimation technique, and identification strategy we use to model the response of fiscal policy to cost of borrowing shocks.

3.1 Data

Our baseline empirical model is a VAR in five variables: The government primary expenditure-to-GDP ratio, government revenue-to-GDP ratio, GDP growth rate, inflation rate, and government nominal cost of borrowing. The government's intertemporal budget constraint (involving these five variables) is adhered to by keeping track of the government debt-to-GDP ratio, which enters the VAR as a lagged explanatory variable. The data covers an unbalanced panel of 14 European countries (Austria, Belgium, Germany, France, Finland, Greece, Ireland, Italy, Netherlands, Portugal, Spain, Denmark, UK and Sweden) at an annual frequency from 1970 to 2011.

All the endogenous variables in the VAR are stationary as they have either been expressed in terms of growth rates or relative to GDP. Measuring the two fiscal variables as a ratio to GDP has the added advantage that impulse responses for the primary balance-to-GDP ratio can be computed without approximation. A full description of the sources and construction of the data series can be found in Appendix B. For the government's nominal cost of borrowing, we calculate an implicit interest rate using a measure of the government's total interest payments in a given period and its outstanding debt stock:

$\displaystyle cob_{t}=100\times \frac{interest\text{ }payments_{t}}{debt\text{ }stock_{t-1}% }$

(8)

This measure for the cost of borrowing allows a direct mapping from the endogenous variables of the VAR to the government debt-to-GDP ratio that is the lagged explanatory variable in the VAR. We discuss this mapping in detail in the next subsection. The main drawback of this measure is that it represents the average cost of borrowing rather than the marginal cost of borrowing. The average and marginal cost of borrowing are only the same if the entire debt stock is refinanced every year. Since governments generally fund themselves at longer average maturities, a 1% rise in the marginal cost of borrowing will lead to a less than one-for-one rise in the average cost of borrowing.⁷ Yet, a temporary shock to the marginal cost of borrowing (assuming debt issuance patterns in terms of instruments, maturity etc. remain unchanged) has the same effect on the total cost of borrowing (i.e. the amount of tax revenue that is needed to service debt interest payments), independent of the maturity structure of the debt.⁸

While the marginal cost of borrowing may be conceptually preferable, finding a suitable measure is equally problematic. Since governments borrow using a large set of debt instruments, any single bond's yield would be a poor proxy of the marginal cost of borrowing. We also have less historical data for bond yields in our sample since several of the countries did not regularly access capital markets for funding in the early part of our sample. We do, however, test for robustness along this dimension by including the 10-year government bond yield in a larger-dimensioned VAR in Section 4.

3.2 Estimation

The panel VAR we estimate takes the form:

$\displaystyle Y_{i,t}=A\left( \ell \right) Y_{i,t-1}+F\left( \ell \right) W_{i,t-1}+u_{i,t}%$ $\displaystyle u_{i,t}\sim iid\left( 0,\Sigma _{u}\right)$

(9)

where $Y_{i,t}$ is a $G\times 1$ vector of endogenous variables, $W_{i,t}$ is an $H\times 1$ vector of predetermined variables, $A\left( \ell \right)$ and $F\left( \ell \right)$ are polynomials in the lag operator and

means identically and independently distributed. Time is denoted by the subscript

and the country unit is denoted by the subscript

. We estimate a homogenous panel VAR in the sense that the coefficient matrices $A_{j}$ and $F_{j}$ (where

denotes the lag) are independent of the country unit subscript

. We revisit this restrictive assumption in Section 4.

In our baseline estimation, and $Y=\left[ pe,v,g,\pi ,cob\right]$ where is the government primary expenditure-to-GDP ratio, is the revenue-to-GDP ratio, is the GDP growth rate, $\pi$ is the inflation rate and is the government nominal cost of borrowing. We have one predetermined variable: and where is the government debt-to-GDP ratio. All the variables are country- and time-demeaned to account for both country and time fixed effects. The panel VAR is estimated with two lags of the endogenous variables and one lag of the predetermined variable.⁹

The inclusion of the government debt-to-GDP ratio as a lagged explanatory variable follows the method of Favero and Giavazzi 2007. The rationale for its inclusion is that it imposes the government intertemporal budget constraint on fiscal responses to shocks. As long as the estimated coefficient vector, $\widehat{F}_{1}$ , is non-zero, all the endogenous variables are able to respond to the movements in the government debt-to-GDP ratio. Specifically, the government debt-to-GDP ratio evolves as follows:

$\displaystyle d_{t}=\frac{1+cob_{t}}{\left( 1+g_{t}\right) \left( 1+\pi _{t}\right) }% d_{t-1}+pe_{t}-v_{t}+s_{t}$

(10)

One of the advantages of the Favero and Giavazzi 2007 method is that the evolution of the debt-to-GDP ratio in equation (10) is calculated recursively using the VAR's endogenous variables. However, the method does give rise to two difficulties. First, the intertemporal budget constraint is a nonlinear function of the endogenous variables. Thus, when we generate impulse responses to shocks, the results will be sensitive to the initial debt-to-GDP ratio and the size of the shock. Second, in the fiscal accounts data the stocks and flows do not exactly tally and the residual is captured in the stock-flow adjustment variable,

. The inclusion of

in the endogenous vector,

, would ensure that the debt-to-GDP ratio holds as an identity but would also increase the number of coefficients we would need to estimate. Excluding

means that there is an additional source of uncertainty in the model coming from the debt equation. Nevertheless, since it is not necessary to identify all the shocks in our system, we treat $s_{t}$ as

. We reconsider this assumption when we conduct robustness exercises in Section 4.

To draw inferences about $\Phi =\left( A\left( \ell \right) ,F\left( \ell \right) \right)$ and $\Sigma _{u}$ , we employ a Bayesian approach, which combines information from sample and priors. We employ commonly used diffuse priors that allows us to benefit from Bayesian analysis without the difficulty of obtaining an informative prior. In particular, we employ a constant prior for $\Phi$ and the Jeffreys prior for $\Sigma$ , $% P_{J}\left( \Sigma \right) \propto \left\vert \Sigma \right\vert ^{-\left( G+1\right) /2}$ , which means that $P_{CJ}\left( \Phi ,\Sigma \right) \propto P_{J}\left( \Sigma \right)$ . The Bayes estimators are obtained via Monte Carlo (MC) simulations. By sampling $\left( \Phi ,\Sigma \right)$ from the joint posterior distribution, we generate the Bayes estimates numerically. Let the OLS estimates of $\left( \Phi ,\Sigma \right)$ be $% \left( B,S\right)$ . Under these assumptions, the posteriors are:

$\displaystyle \Sigma$	$\displaystyle \sim$	$\displaystyle IW\left[ \left( NTS\right) ^{-1},NT-GL_{Y}-HL_{W}\right]$
$\displaystyle vec\left( \Phi \right)$	$\displaystyle \sim$	$\displaystyle N\left[ vec\left( B\right) ,\Sigma \otimes \left( X^{\prime }X\right) ^{-1}\right]$

where the posteriors of $\Sigma$ are drawn from an inverse Wishart distribution, which takes as its arguments $\left( NTS\right) ^{-1}$ and degrees of freedom, $NT-GL_{Y}-HL_{W}$ where $L_{Y}$ and $L_{W}$ are the number of lags

and

respectively. The posteriors of $\Phi$ are drawn from a normal distribution, where

is the matrix containing the right-hand side variables. To generate the error bands around our impulse responses, we ran 5000 MC iterations.¹⁰

3.3 Identification

The estimated model, in its reduced form (equation (9)), lacks economic structure. This is because the errors, , that result from a one-step ahead forecast of the corresponding component of are unlikely to be orthogonal innovations since $\Sigma _{u}$ is unlikely to be diagonal. To give the model, and the shocks, economic structure, we must place some restrictions on the model that allow us to decompose the non-orthogonal innovations into orthogonal and economically interpretable shocks. We can do this by choosing a matrix such that $B\Sigma _{u}B^{\prime }=I$ since the new shocks, $\varepsilon =Bu$ will satisfy $E\left( \varepsilon \varepsilon ^{\prime }\right) =I$ . These orthogonalized innovations have the convenient property that they are uncorrelated across equations. There are many such factorizations of $\Sigma _{u}$ , so the choice of method of orthogonalizing is not innocuous. The aim is to choose such that the estimated model has a clear structural form with shocks, $\varepsilon$ that have a convincing economic interpretation.

There are several commonly used methods to recover the structural form (i.e. identify shocks) in the literature. In this paper, we identify cost of borrowing shocks by making use of a methodology which imposes sign restrictions (see Faust 1998, Uhlig 2005, and Canova and Nicoló 2002) upon impulse responses.¹¹

The central idea behind our identification strategy is that a cost-of-borrowing shock is a surprise change in the interest rate on government debt that is orthogonal to all other macroeconomic shocks. We do not want to impose any prior restrictions on the behaviour of the endogenous variables to a cost-of-borrowing shock. Instead, our identification strategy imposes sign restrictions that lead to the identification of a set of shocks that have been commonly studied in the macroeconomic literature. Any unexplained variation in our cost-of-borrowing variable that is orthogonal to these other macroeconomic shocks is then judged to be a cost-of-borrowing shock. If we were not to control for other macroeconomic shocks - fiscal policy shocks for example - it would be easy to end up confusing changes in the cost of borrowing due to supply shocks (surprise changes in the supply of government bonds) with changes in the level of government borrowing due to demand shocks (surprise changes in the demand for government bonds).

The theoretical model we presented in Section 2 is not rich enough to provide a robust set of sign restrictions to identify all the macroeconomic shocks that we wish to identify. The sign restrictions are therefore chosen from a wide reading of the macroeconomic literature to arrive at a set of sign restrictions that are as uncontroversial as possible. For two reasons, we also only impose sign restrictions on the responses of variables on impact. First, using impact sign restrictions in a model with annual data is analogous to the existing literature which usually imposes sign restriction for four quarters in a model with quarterly data. Second, the nonlinearity from the debt-to-GDP feedback severely complicates the identification strategy if sign restriction are imposed at further horizons.

Rather than simultaneously identifying all the shocks, subject to the orthogonality restrictions, we identify the shocks sequentially via a penalty function following the method of Mountford and Uhlig 2009. Conceptually, for the first shock to be identified, the penalty function method finds the set of parameter restrictions which minimize the sum of:

$\displaystyle pf\left( x_{j}\right) =\left\{ \begin{array}{ccc} -x_{j} & \text{if} & x_{j}>0 \\ -100x_{j} & \text{if} & x_{j}\leq 0\end{array}% \right.$ ,

(11)

across the sign restricted variables

where $x_{j}$ is the impact response of variable

(rescaled by the standard error of variable

). The function $pf\left( .\right)$ rewards large impulse responses with the right sign (we assume in equation (11) that we are looking for a positive response) more than small responses and punishes responses that go in the wrong direction. The second shock is then identified in the same way, with the additional restriction that it be orthogonal to the first shock. The rest of the shocks are identified similarly. The consequence of this sequential identification is that the penalty function ascribes as much movement as possible to the first shock, then the second shock and so on.

Table 3: Contemporaneous Identifying Sign Restrictions: Variables vs. Shocks

	Primary expenditure-to-GDP	Revenue-to-GDP	GDP growth rate	Inflation rate	Cost of borrowing
Aggregate demand	$\cdot$	$\left( +\right)$	$\left( +\right)$	$\left( +\right)$	$\cdot$
Cost-push	$\cdot$	$\cdot$	$\left( -\right)$	$\left( +\right)$	$\cdot$
Primary expenditure	$\left( +\right)$	$\cdot$	$\left( +\right)$	$\cdot$	$\cdot$
Revenue	$\cdot$	$\left( +\right)$	$\left( -\right)$	$\cdot$	$\cdot$
Cost of borrowing	$\cdot$	$\cdot$	$\cdot$	$\cdot$	$\left( +\right)$

Note:

or (-) mean that the response of variable

to shock

on year of impact is restricted to be positive or negative, respectively. A blank space means no restriction has been imposed.

An overview of our identifying sign restrictions on the impulse responses is provided in Table 3. First, we identify an aggregate demand shock (row 1 ). The $\left( +\right)$ symbols in the first row indicate that an aggregate demand shock is anything that generates, on impact, a positive comovement between the growth rate of GDP, the inflation rate and the government revenue-to-GDP ratio. The blank spaces in the first row says that we are agnostic about how the government primary expenditure-to-GDP ratio and the government cost of borrowing respond, on impact, to an aggregate demand shock. The restriction on the movement of government revenue-to-GDP is crucial for identifying the government revenue shock later. While there is debate in the literature on the numerical estimate of the income elasticity of tax revenue, imposing procyclicality is, we think, uncontroversial. Since we associate aggregate demand shocks with the predominant cause of business cycle fluctuations, we identify this shock first.

Second, we identify a cost-push shock. Our identifying assumption is that the growth rate of GDP and the inflation rate should negatively comove in response to a cost-push shock on impact. We also require the cost-push shock to be orthogonal to the aggregate demand shock. Third and fourth, we identify two fiscal policy shocks, a primary expenditure shock and a revenue shock. Both are identified by restricting the sign of the GDP growth rate response: GDP growth rate positively comoves with the government primary expenditure-to-GDP ratio for a primary expenditure shock and negatively comoves with the government revenue-to-GDP ratio for a revenue shock. The fiscal policy shocks are assumed to be orthogonal to the two, preceding, business cycle shocks but we do not require that the two fiscal policy shocks be orthogonal to each other. Again, without wanting to place any prior restrictions on the responses of endogenous variables to a cost of borrowing shock, we force ourselves to identify four common macroeconomic shocks in order to recover a cost of borrowing shock that is truly orthogonal to other fluctuations in the macroeconomy. A cost of borrowing shock, in our scheme, is therefore any unexpected movement in the cost of borrowing variable that induces a response of the other endogenous variables that is orthogonal to the response that the other four macroeconomic shocks generate.

A natural concern may arise regarding the ordering in which shocks are identified. How does the choice of ordering allow us, for example, to distinguish between shocks that are assumed to have the same effect on the same variables, such as the aggregate demand and primary expenditure shocks?¹² The nature of the penalty function means that the shocks identified earlier are likely to account for a larger share of total fluctuations. It seems reasonable therefore to order the business cycle shocks ahead of the fiscal policy shocks. More importantly, however, while switching the order is important for the identification of these two shocks, we find that the ordering of the first four shocks has almost no effect on the identification and impulse responses of the shock of interest, namely the cost of borrowing shock.

4 Results

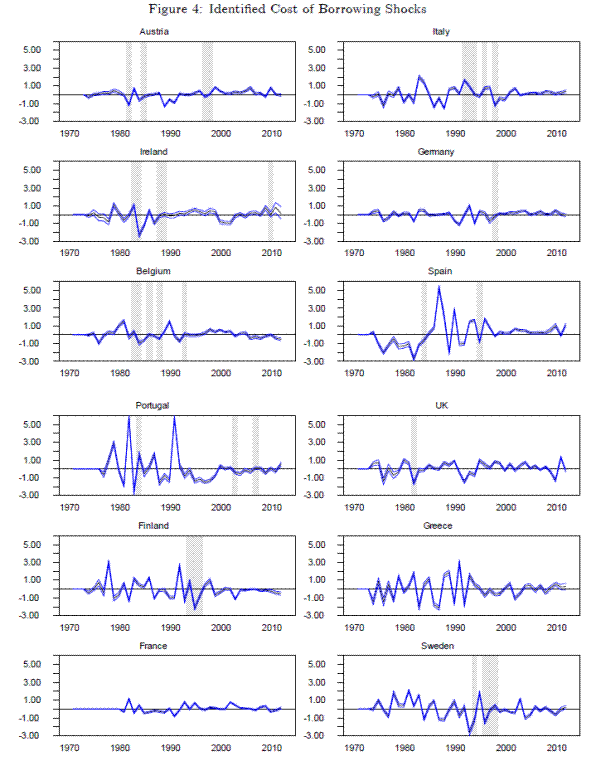
Figure 4 presents the identified cost of borrowing shocks, which are, by construction, orthogonal to the preceding four shocks.¹³ It suggests that the variance of cost-of-borrowing shocks was significantly higher in the 1980s and early 1990s than the late 1990s and early 2000s, across Europe.¹⁴

Before commencing the formal analysis, it is useful to graphically inspect if the identified shocks actually coincide or precede periods that have been identified as entailing strong fiscal efforts by certain governments. To this end, the shaded areas in Figure 4 denote periods of fiscal consolidation as identified by the narrative approach developed in Devries, Guajardo, Leigh, and Pescatori 2011. The two measures appear to be weakly correlated. Positive cost-of-borrowing shocks preceded the fiscal adjustment in Italy in the mid-1990s, Portugal in 1981, Finland in 1992 and Sweden in the end-1990s. The most striking omission is the apparent lack of fiscal adjustment following the cost of borrowing shocks in Portugal in 1990 and Spain in 1986. However, using an alternative measure of fiscal consolidations, Alesina and Perotti 1995 [Table 5. pp.218] record strong fiscal adjustments for Portugal in 1989 and Spain in 1986-87.

4.1 Baseline results

Figure 5 displays the impulse responses to a temporary cost of borrowing shock over a 10-year horizon. The responses have been normalized so that the cost of borrowing always rises by 1 percentage point. The initial level of the debt-to-GDP ratio will impact the impulse responses. In Figure 5, we initialize the debt-to-GDP ratio to 50% which is close to the sample mean. In Figure 6 below, we report sensitivity results to this choice of initial value. All the fiscal variables are measured in percentage points of GDP, while the interest rate and growth variables are measured in percent.

The impulse responses reveal four key results. First, the shock generates a relatively persistent effect on the nominal cost of borrowing, which takes 4 years to halve. Second, it is revenues rather than primary expenditures that react to the cost of borrowing shock, with the revenue-to-GDP ratio 0.2 percentage points higher at the end of the 10 year horizon and the response of the primary expenditure-to-GDP remaining insignificant throughout the 10 year horizon. Third, the fiscal policy adjustment is not immediate. The primary balance is unchanged on impact but still does not turn significantly positive until the second year following the shock. Fiscal adjustment between years 3 and 5 is fairly rapid before reaching peak adjustment in year 7. The cumulative change in the primary balance-to-GDP ratio reaches , 0.79 and 1.88 in years 2, 5 and 10 following the shock. Fourth, the fiscal adjustment is insufficient

Figure 4: Identified Cost of Borrowing Shocks

Note: The y-axis measures the identified cost of borrowing shock with a unit standard deviation, the x-axis measures time in years. The error bands are generated by Monte Carlo integration, showing the 14th, 50th and 86th percentiles. The shaded areas are periods of fiscal consolidation identified by the narrative approach in Devries, Guajardo, Leigh, and Pescatori .2011.

Figure 5: Responses to 1 p.p.t. increase in cost of borrowing

Figure 5 Data

Note: The cost of borrowing shock is ordered fifth and orthogonal to the business cycle and fiscal policy shocks. The y-axis is in percentage points, the x-axis is in years. The error bands are generated by Monte Carlo integration, showing the 14th, 50th and 86th percentiles. Responses have been normalized to a 1 percentage point rise in the cost of borrowing. The debt-to-GDP ratio is initially 0.5.

to counteract the debt-increasing effect from the cost-of-borrowing shock over this time horizon. The debt-to-GDP ratio has rises by 1.3 percentage points in year 6 and falls slightly to $1.1\%$ percentage points in year 10.

The inflation and growth adjusted cost of borrowing response follows closely that of the nominal cost of borrowing response. This is because the responses of output growth and inflation are both either economically or statically insignificant. The insignificant response of output growth suggests that shocks to the governments' cost of borrowing do not systematically affect private sector borrowing costs.

4.2 Initial conditions and debt feedback

The addition of the governments' budget constraint, in the form of the lagged debt-to-GDP ratio, generates a feedback mechanism in the vector autoregression model and potentially strong nonlinearities in the responses to shocks. In particular, we find that the fiscal adjustment to a cost of borrowing shock is sensitive to the level of the debt-to-GDP ratio at the time of the shock. Figure 6 plots the median impulse responses of the primary expenditure-, revenue-, primary balance- and debt-to-GDP ratios to a cost of borrowing shock with two different initial debt-to-GDP ratios, $20\%$ and $140\%$ respectively (and the baseline impulse responses plot in the background). Notice that this experiment is considering the response of our "representative" country being hit by cost of borrowing shocks when it's debt-to-GDP ratio is either cyclically high or cyclically low. Not until Figure 8 do we try and distinguish between the fiscal responses

Figure 6: Sensitivity to initial Debt-to-GDP ratio

Figure 6 Data

Note: Impulse responses to a cost of borrowing shock which raises the cost of borrowing by 1 percentage point. The y-axis is in percentage points, the x-axis is in years. The error bands are generated by Monte Carlo integration, showing the 14th, 50th and 86th percentiles.

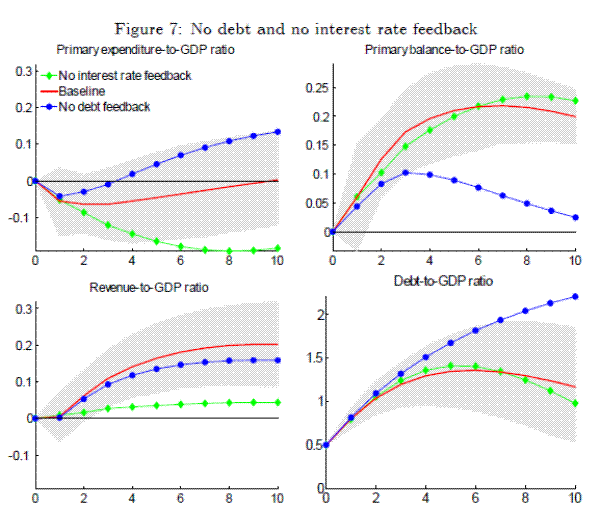
Since Bohn 1998, it has been common practice to describe the behavior of fiscal policy in terms of a fiscal reaction function, with the primary balance reacting to fluctuations in output and debt. How much of the response of the primary balance to a cost of borrowing shock is a direct response to a change in the debt-to-GDP ratio, and how much is a reaction to a change in the cost of borrowing? To investigate this, we conduct to experiments, presented in Figure 7. The first is to re-estimate the model, excluding the debt-to-GDP ratio as a lagged explanatory variable. The second is to restrict the coefficients on the cost of borrowing for the primary expenditure and revenue variables to zero. The impulse responses are presented in Figure 7.

of countries with historically high and historically low debt-to-GDP ratios.

This scenario analysis shows two interesting patterns. First, when a country's debt-to-GDP ratio is cyclically high at the onset of a cost of borrowing shock, it makes larger primary balance adjustments. The cumulative primary balance adjustment over 10 years is $3.6\%$ of GDP when the debt-to-GDP ratio is 140%, relative to an adjustment of $1.9\%$ when the debt-to-GDP ratio is 50%. Moreover, the median debt-to-GDP response peaks earlier in the 140% initial debt-to-GDP ratio scenario than in the 50% initial debt-to-GDP ratio scenario. However, the peak change in the debt-to-GDP ratio is larger when the initial debt-to-GDP ratio is higher. Second, with a high initial debt-to-GDP ratio the fiscal adjustment comes both via primary expenditure cuts and revenue increases. Using the median responses, for the 50% initial debt-to-GDP scenario, 12% of the fiscal adjustment is via cuts in primary expenditure. For the 140% initial debt-to-GDP ratio scenario, primary expenditure cuts account for 43% of the fiscal adjustment.

The impulse response functions reveal two interesting results. First, the response of the primary balance to a cost of borrowing shock is still significantly positive, even in the absence of debt feedback. Second, in the absence of interest rate feedback, the adjustment of the primary balance

Figure 7: No debt and no interest rate feedback

Figure 7 Data

Note: Impulse responses to a cost of borrowing shock. The

-axis is in percentage points, the

-axis is in years. The error bands are generated by Monte Carlo integration, showing the 14th, 50th and 86th percentiles.

to a cost of borrowing shock becomes significantly positive with a longer lag. This suggests a fiscal reaction function does not only respond to the current debt-to-GDP ratio, but also financial markets' expectations of future debt dynamics, as proxied by the cost of borrowing.

4.3 Heterogeneity across sub-samples

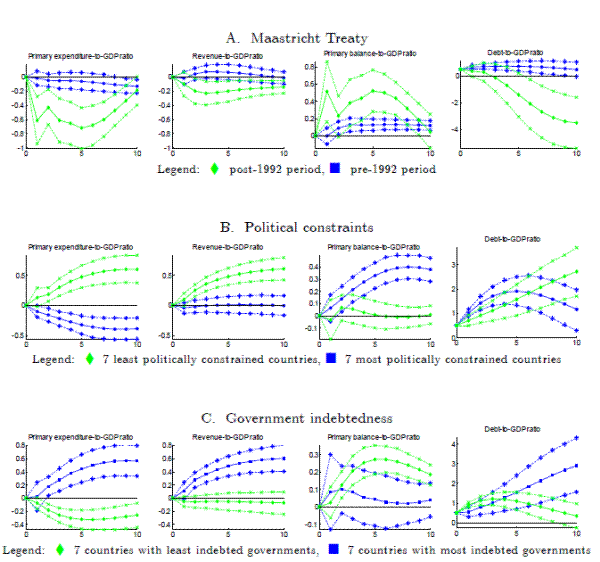
Thus far, we have considered the 14 countries as a homogenous block, restricting the responses to a cost of borrowing shock to be the same across the sample. While we lack sufficient degrees of freedom to estimate the model for each individual country, we can attempt to explain potential heterogeneity by sub-dividing our sample along several dimensions. The key results are reported in Figure 8. The countries which comprise each sub-group are reported in Table 4. It is important to emphasize that these results are based on somewhat ad hoc sorting of countries into sub-samples, which may reduce their robustness. However, we think they are sufficiently interesting to warrant future research.

Table 4: Country Groupings

	A. Maastricht Treaty	B. Political constraints $^{c}$	C. Government indebtedness $^{d}$
1 Austria	Yes	Most 0.78	Most 51%
2 Belgium	Yes	Most 0.87	Most 98%
3 Germany	Yes	Most 0.83	Least 45%
4 France	Yes	Most 0.79	Least 39%
5 Finland	Yes	Most 0.78	Least 28%
6 Greece	Yes $^{a}$	Least 0.36	Least 46%
7 Ireland	Yes	Least 0.75	Most 68%
8 Italy	Yes	Least 0.76	Most 67%
9 Netherlands	Yes	Most 0.83	Most 89%
10 Portugal	Yes	Least 0.62	Most 60%
11 Spain	Yes	Least 0.77	Least 50%
12 Denmark	No $^{b}$	Most 0.78	Least 48%
13 UK	No	Least 0.74	Most 51%
14 Sweden	No	Least 0.76	Least 49%

Note: $^{a}$ Greece adopted the Euro in 2001. $^{b}$ Denmark opted out of the Maastricht Treaty but remains in ERM II. $^{c}$ Average value of the POLCON index, Henisz 2000, for the period 1970-94. $^{d}$ Average government debt-to-GDP ratio for the period 1970-2011.

The first row of Figure 8 reports responses to a cost-of-borrowing shock for the 11 EMU countries, pre- and post-1992. We are interested in whether the signing of the Maastricht Treaty (in 1992) - which binds countries to adhere to the Maastricht criteria, restricting government deficits and debts - affected the fiscal response to cost of borrowing shocks. In the pre-Maastricht period, there is a relatively small positive primary balance response to a cost-of-borrowing shock. By contrast, in the post-Maastricht period, the response of the primary balance is significantly larger. In fact, the rise in the primary balance is sufficiently strong to generate a fall of the debt-to-GDP ratio to 46.5%, below its initial value of 50%, at the end of the 10 year horizon.

The second row of Figure 8 sub-divides the 14 countries based on a measure of political risk - the Political Constraint Index (POLCON) - developed by Henisz 2000. It attempts to measure "the ability of a government to craft a credible commitment to an existing policy regime" and prevent the "potential for arbitrary or capricious" policymaking, with a low score being more hazardous and a high score being more constrained. We take an average of the POLCON measure over the period 1970-1994 and split the sample of countries into a high and low grouping, using the median value in the sample as the threshold. The responses are robust to a 8-6 or 6-8 split of countries. The responses in Figure 8 for the two groups are supportive of the view that politically more constrained countries demonstrate more fiscal prudence. For example, the primary balance response of the low group is not significantly different from zero, while the response of the high group is significant and positive. Interestingly, the rise in the primary balance for the high group countries is the result of a fall in primary expenditure following a cost-of-borrowing shock.

Finally, the third row of Figure 8 sub-divides the 14 countries based on the historical indebtedness of the governments. Inference drawn from these impulse responses should be made with caution since there is a potential endogeneity problem, from the impulse responses, back to the groupings. The responses reveal that the primary balances of highly indebted countries do not respond to cost of borrowing shocks, while those for the less indebted countries do respond positively. The median debt-to-GDP ratio of a highly indebted country rises by percentage points, while the debt-to-GDP ratio of a less indebted country is insignificantly different from its initial level, at the 10 year horizon.

Note that this result is not in contradiction to the finding reported in Figure 6. The sub-sample estimation reveals that countries that have, on average, high debt-GDP ratios also display weak responses to cost of borrowing shocks. The results from Figure 6, in contrast, suggest that when a country experiences a cost of borrowing shock at a time when its debt-to-GDP ratio is high relative to what is normal for that country, the fiscal response to that cost of borrowing shock is also stronger relative to its normal response.

Figure 8: Heterogeneity across sub-samples

Figure 8 Data

Note: Impulse responses to a cost of borrowing shock. The

-axis is in percentage points, the

-axis is in years. The error bands are generated by Monte Carlo integration, showing the 14th, 50th and 86th percentiles.

4.4 Expanding the model

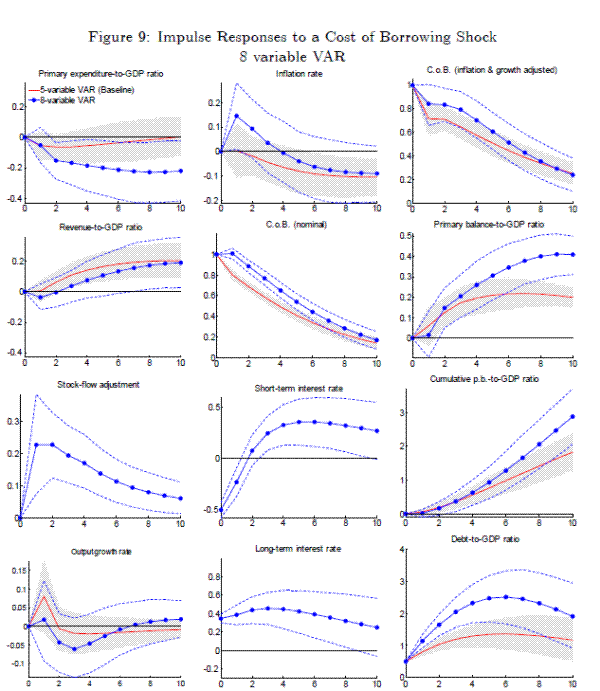
The results presented thus far are the product of a five-variable VAR. We next expand the model to include an additional three endogenous variables: the stock-flow adjustment in fiscal accounts, a short-term nominal interest rate, and a long-term nominal interest rate. The impulse responses following a cost of borrowing shock are presented in Figure 9.

As noted earlier, in the baseline analysis, we treated the stock-flow adjustment as an exogenous i.i.d. shock process.¹⁵ Here we include it as an additional endogenous variable. One of the notable omissions from the 5 variable VAR was any discussion of monetary policy. Unanticipated monetary policy shocks affect interest rates at both the short and the long end of the yield curve, Kuttner 2001. Including the short-term interest rate (3 month interbank rate) and a long-term interest rate (10 year government bond yield) allows us to identify a monetary policy shock, and ensure that the cost of borrowing shock we identify is orthogonal to the monetary policy shock.

The identifying assumptions for the expanded model are shown in Table 5. The first four shocks we identify are as before. The fifth shock we identify is the monetary policy shock. A monetary policy shock is identified by a contemporaneous increase in the short and long rates and a fall in the inflation rate, as well as by it being orthogonal to the preceding four shocks. Almost by construction though (due to the orthogonality restriction), the inflation rate is unchanged on impact. The sixth shock is the stock-flow adjustment, and the seventh is the cost of borrowing shock. While before we identified the cost of borrowing shock simply by the orthogonality requirements to the preceding shocks, and the cost of borrowing rising, in this VAR, we identify the cost of borrowing shock as simultaneously increasing both the long rate and the nominal cost of borrowing.

Table 5: 8-variable VAR sign restrictions: Variable vs. Shocks

	Primary expenditure-to-GDP	Revenue-to-GDP	Stock-flow adj.	GDP growth rate	Inflation rate	Cost of borrowing	Short interest rate	Long interest rate
Aggregate demand	$\cdot$	$\left( +\right)$	$\cdot$	$\left( +\right)$	$\left( +\right)$	$\cdot$	$\cdot$	$\cdot$
Cost-push	$\cdot$	$\cdot$	$\cdot$	$\left( -\right)$	$\left( +\right)$	$\cdot$	$\cdot$	$\cdot$
Primary expenditure	$\left( +\right)$	$\cdot$	$\cdot$	$\left( +\right)$	$\cdot$	$\cdot$	$\cdot$	$\cdot$
Revenue	$\cdot$	$\left( +\right)$	$\cdot$	$\left( -\right)$	$\cdot$	$\cdot$	$\cdot$	$\cdot$
Monetary policy	$\cdot$	$\cdot$	$\cdot$	$\cdot$	$\left( -\right)$	$\cdot$	$\left( +\right)$	$\left( +\right)$
Stock-flow adj.	$\cdot$	$\cdot$	$\left( +\right)$	$\cdot$	$\cdot$	$\cdot$	$\cdot$	$\cdot$
Cost of borrowing	$\cdot$	$\cdot$	$\cdot$	$\cdot$	$\cdot$	$\left( +\right)$	$\cdot$	$\left( +\right)$

Note:

or (-) mean that the response of variable

to shock

on year of impact is restricted to be positive or negative, respectively. A blank space means no restriction has been imposed.

The responses in this expanded VAR are broadly similar to the five variable VAR. The response of the primary balance is greater, rising to $0.5\%$ of GDP at the end of the 10 year horizon. However, the rise in the debt-to-GDP ratio is also greater, with the median response reaching a maximum of 2.8 percentage points of GDP above baseline in year 6 following the shock. This is, in part, because the rise in the inflation and growth adjusted cost of borrowing is more persistent.

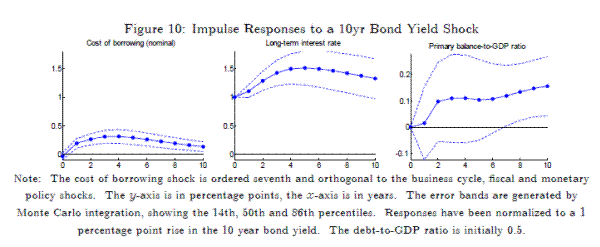
As one final experiment, we also test the robustness of our measure for the cost of borrowing. As discussed in Section 3, fiscal adjustment is likely to be a factor both of the marginal cost of borrowing and the average cost of borrowing, and we conjectured a relationship between these two measures. In practice, the 10 year bond yield measure is only a proxy for the marginal cost of borrowing as governments can borrow using various bonds of different maturities. Thus, an increase in the 10 year bond yield is likely to overstate the rise in the marginal cost of borrowing, unless there is a level shift in the entire yield curve. In any case, in Figure 10, we report the impulse responses to a cost of borrowing shock where we identify the cost of borrowing shock only as a rise in the long-term bond yield. It is clear that the true nominal cost of borrowing only increases with a lag, and that it increases by less than the increase in the long-term bond yield.¹⁶ The result is a more modest fiscal response, with the primary balance not turning significantly positive until 7 years following the shock.

We have applied several additional robustness checks to our estimates. These include altering the identifying sign restrictions for various shocks, altering the order in which some of the shocks are identified, and altering the definition of some of the variables used. These additional robustness checks are available in the online appendix.

5 Conclusions

This paper examines the response of fiscal variables to exogenous changes in the cost of public borrowing using a panel of European countries over four decades. Consistent with a simple theoretical model of fiscal behaviour, our results suggest that governments react to increases in the cost of borrowing by increasing their primary balances over several years. At the sample average, however, this response is not sufficiently strong to return the debt-to-GDP ratio to baseline over a 10-year horizon. The adjustment is found to only become statistically significant two years after the shock and to be generated mainly via the revenue side. At the same time, there is some tentative evidence that the magnitude of adjustment in response to a cost of borrowing shock is larger when the debt-to-GDP ratio is cyclically high. Also, the larger the adjustment, the more emphasis is placed on expenditure cuts relative to tax increases.

When subdividing our sample, we find that EMU countries in the period after the signing of the Maastricht Treaty show a significantly stronger budgetary response to cost-of-borrowing shocks than the same countries in the pre-Maastricht period. A possible interpretation of this pattern is that those countries that eventually joined monetary union had an additional incentive to compensate for higher interest payments (which count against the Maastricht deficit criterion) by tightening their stance with respect to other budget items.

Our results have important policy implications. The estimated average fiscal response suggests that market discipline can improve budgetary outcomes. Provided that financial market participants systematically and consistently sanction deteriorating fiscal positions through higher interest rates, they may deter governments from building up imbalances. At the same time, experience since the start of EMU shows that the relationship between the fiscal "health" of a country and its borrowing rates can be subject to abrupt shifts, which renders financial markets less reliable as an incentive mechanism for governments. Moreover, our estimates show that the budgetary response to market pressure tends to be delayed and alone is not sufficient to fully counteract its direct unfavourable effect on debt dynamics via rising interest payments. This in turn, suggests that further incentive mechanisms are needed to ensure that countries follow a fiscal reaction function aimed at restoring fiscal sustainability in a timely manner. Judging from our results, fiscal rules are an important complement to markets in this regard.

Figure 9: Impulse Responses to a Cost of Borrowing Shock

Figure 9 Data

Note: The cost of borrowing shock is ordered seventh and orthogonal to the business cycle, fiscal and monetary policy shocks. The

-axis is in percentage points, the

-axis is in years. The error bands are generated by Monte Carlo integration, showing the 14th, 50th and 86th percentiles. Responses have been normalized to a 1 percentage point rise in the cost of borrowing. The debt-to-GDP ratio is initially 0.5.

Figure 10: Impulse Responses to a 10yr Bond Yield Shock

Figure 10 Data

Note: The cost of borrowing shock is ordered seventh and orthogonal to the business cycle, fiscal and monetary policy shocks. The

-axis is in percentage points, the

-axis is in years. The error bands are generated by Monte Carlo integration, showing the 14th, 50th and 86th percentiles. Responses have been normalized to a 1 percentage point rise in the 10 year bond yield. The debt-to-GDP ratio is initially 0.5.

Bibliography

Afonso, A. and C. Rault, (2011)

.
Long-run determinants of sovereign yields.
Economics Bulletin 31(1).

Alesina, A. and R. Perotti, (1995)

.
Fiscal expansions and adjustments in OECD countries.
Economic Policy 10(21), 207-248.

Aoki, K., (2006)

.
Optimal commitment policy under noisy information.
Journal of Economic Dynamics and Control 30(1), 81 - 109.

Ardagna, S., F. Caselli, and T. Lane, (2007)

.
Fiscal discipline and the cost of public debt service: Some estimates for OECD countries.
The B.E. Journal of Macroeconomics 7(1), Article 28.

Attinasi, M., C. Checherita, and C. Nickel, (2009)

.
What explains the surge in euro area sovereign spreads during the financial crisis of 2007-09?
ECB Working Paper Series 1131.

Bayoumi, T., M. Goldstein, and G. Woglom, (1995)

.
Do credit markets discipline sovereign borrowers? Evidence from U.S. states.
Journal of Money, Credit and Banking 27(4), pp. 1046-1059.

Blanchard, O. and D. Quah, (1993)

.
The dynamic effects of aggregate demand and supply disturbances: Reply.
The American Economic Review 83(3), 653-658.

Blanchard, O. and M. Watson, (1986)

.
Are business cycles all alike?
In The American Business Cycle: Continuity and Change, pp. 123-180. University of Chicago Press.

Bohn, H., (1998)

.
The behavior of US public debt and deficits.
The Quarterly Journal of Economics 113(3), 949-963.

Browning, E. K., (1976)

.
The marginal cost of public funds.
Journal of Political Economy 84(2), pp. 283-298.

Canova, F. and G. Nicoló, (2002)

.
Monetary disturbances matter for business fluctuations in the G-7.
Journal of Monetary Economics 49(6), 1131-1159.

Christiano, L. J., M. Eichenbaum, and C. L. Evans, (1999)

.
Monetary policy shocks: What have we learned and to what end?
Volume 1, Part A of Handbook of Macroeconomics, pp. 65 - 148. Elsevier.

Devries, P., J. Guajardo, D. Leigh, and A. Pescatori, (2011)

.
A new action-based dataset of fiscal consolidation.
IMF Working Paper 11(128).

Evans, P., (1985)

.
Do large deficits produce high interest rates?
The American Economic Review 75(1), 68-87.

Faini, R., (2006)

.
Fiscal policy and interest rates in Europe.
Economic Policy 21(47), 443-489.

Faraglia, E., A. Marcet, and A. Scott, (2011)

.
Dealing with maturity: Optimal fiscal policy in the case of long bonds.
Unpublished manuscript.

Faust, J., (1998)

.
The robustness of identified VAR conclusions about money.
Carnegie-Rochester Conference Series on Public Policy 49(0), 207 - 244.

Favero, C. and F. Giavazzi, (2007)

.
Debt and the effects of fiscal policy.
Unpublished manuscript.

Greenwood, J., Z. Hercowitz, and G. W. Huffman, (1988)

.
Investment, capacity utilization, and the real business cycle.
The American Economic Review 78(3), pp. 402-417.

Henisz, W., (2000)

.
The institutional environment for economic growth.
Economics & Politics 12(1), 1-31.

King, R. G., C. I. Plosser, and S. T. Rebelo, (1988)

.
Production, growth and business cycles: I. The basic neoclassical model.
Journal of Monetary Economics 21(2–3), 195 - 232.

Kuttner, K., (2001)

.
Monetary policy surprises and interest rates: Evidence from the Fed funds futures market.
Journal of Monetary Economics 47(3), 523-544.

Laubach, T., (2009)

.
New evidence on the interest rate effects of budget deficits and debt.
Journal of the European Economic Association 7(4), 858-885.

Mayshar, J., (1991)

.
Taxation with costly administration.
The Scandinavian Journal of Economics 93(1), pp. 75-88.

Mertens, K. and M. Ravn, (2011)

.
The dynamic effects of personal and corporate income tax changes in the United States.
Unpublished manuscript.

Mountford, A. and H. Uhlig, (2009)

.
What are the effects of fiscal policy shocks?
Journal of Applied Econometrics 24(6), 960-992.

Romer, C. D. and D. H. Romer, (1989)

.
Does monetary policy matter? A new test in the spirit of Friedman and Schwartz.
NBER Macroeconomics Annual 4, pp. 121-170.

Schuknecht, L., P. Moutot, P. Rother, and J. Stark, (2011)

.
The Stability and Growth Pact: Crisis and reform.
ECB Occasional Paper Series 129, 1-21.

Schuknecht, L., J. Von Hagen, and G. Wolswijk, (2009)

.
Government risk premiums in the bond market: EMU and Canada.
European Journal of Political Economy 25(3), 371-384.

Sims, C., (1986)

.
Are forecasting models usable for policy analysis?
Quarterly Review 10(1), 2-16.

Sims, C. A., (1980)

.
Macroeconomics and reality.
Econometrica 48(1), pp. 1-48.

Tabellini, G., (1986)

.
Money, debt and deficits in a dynamic game.
Journal of Economic Dynamics and Control 10(4), 427-442.

Theofilakou, N. and Y. Stournaras, (2012)

.
Government solvency and financial markets: Dynamic panel estimates for the European Monetary Union.
Economics Letters 115(1), 130-133.

Uhlig, H., (2005)

.
What are the effects of monetary policy on output? Results from an agnostic identification procedure.
Journal of Monetary Economics 52(2), 381-419.

Woodford, M., (1999)

.
Optimal monetary policy inertia.
The Manchester School 67, 1-35.

A. Model appendix

The first-order conditions of the government's problem in equation (7) are:

		$\displaystyle 0=u_{1,t}+\mu _{1,t}\left( \left( \frac{u_{2,t}u_{11,t}}{u_{1,t}^{2}}-% \frac{u_{21,t}}{u_{1,t}}\right) n_{t}-1\right)$	(12)
		$\displaystyle +\mu _{2,t}\left( \left( \frac{u_{21,t}}{u_{1,t}}-\frac{u_{2,t}u_{11,t}}{% u_{1,t}^{2}}\right) n_{t}-\psi _{\tau }\left( \frac{u_{2,t}}{u_{1,t}}-\frac{% u_{2,t-1}}{u_{1,t-1}}\right) \left( \frac{u_{21,t}}{u_{1,t}}-\frac{% u_{2,t}u_{11,t}}{u_{1,t}^{2}}\right) \right)$
		$\displaystyle +\psi _{\tau }\beta E_{t}\mu _{2,t+1}\left( \frac{u_{2,t+1}}{u_{1,t+1}}-% \frac{u_{2,t}}{u_{1,t}}\right) \left( \frac{u_{21,t}}{u_{1,t}}-\frac{% u_{2,t}u_{11,t}}{u_{1,t}^{2}}\right) \text{,}$

		$\displaystyle 0=u_{2,t}+\mu _{1,t}\left( \left( \frac{u_{2,t}u_{12,t}}{u_{1,t}^{2}}-% \frac{u_{22,t}}{u_{1,t}}\right) n_{t}-\frac{u_{2,t}}{u_{1,t}}\right) +\beta E_{t}\mu _{1,t+1}\left( r_{1,t}^{h}\left( \frac{b_{t}^{h}}{n_{t}}\right) ^{2}+r_{2,t}^{h}\frac{b_{t}^{h}b_{t}^{g}}{n_{t}^{2}}\right)$	(13)
		$\displaystyle +\mu _{2,t}\left( \left( \frac{u_{22,t}}{u_{1,t}}-\frac{u_{2,t}u_{12,t}}{% u_{1,t}^{2}}\right) n_{t}+\left( 1+\frac{u_{2,t}}{u_{1,t}}\right) -\psi _{\tau }\left( \frac{u_{2,t}}{u_{1,t}}-\frac{u_{2,t-1}}{u_{1,t-1}}\right) \left( \frac{u_{22,t}}{u_{1,t}}-\frac{u_{2,t}u_{12,t}}{u_{1,t}^{2}}\right) \right)$
		$\displaystyle +\beta E_{t}\mu _{2,t+1}\left( r_{1,t}^{g}\frac{b_{t}^{g}b_{t}^{h}}{% n_{t}^{2}}+r_{2,t}^{g}\left( \frac{b_{t}^{g}}{n_{t}}\right) ^{2}+\psi _{\tau }\left( \frac{u_{2,t+1}}{u_{1,t+1}}-\frac{u_{2,t}}{u_{1,t}}\right) \left( \frac{u_{22,t}}{u_{1,t}}-\frac{u_{2,t}u_{12,t}}{u_{1,t}^{2}}\right) \right) \text{,}$

$\displaystyle u_{3,t}=\mu _{2,t}\left( 1+\psi _{g}\left( g_{t}-g_{t-1}\right) \right) -\beta \psi _{g}E_{t}\mu _{2,t+1}\left( g_{t+1}-g_{t}\right)$ ,

(14)

$\displaystyle \mu _{1,t}=\beta E_{t}\mu _{1,t+1}\left( r_{t}^{h}+r_{1,t}^{h}\frac{b_{t}^{h}% }{n_{t}}\right) +\beta E_{t}\mu _{2,t+1}r_{1,t}^{g}\frac{b_{t}^{g}}{n_{t}}% \text{,}$

(15)

$\displaystyle \mu _{2,t}=\beta E_{t}\mu _{1,t+1}r_{2,t}^{h}\frac{b_{t}^{h}}{n_{t}}+\beta E_{t}\mu _{2,t+1}\left( r_{t}^{g}+r_{2,t}^{g}\frac{b_{t}^{g}}{n_{t}}\right)$ ,

(16)

$\displaystyle c_{t}=b_{t}^{h}-r_{t-1}^{h}b_{t-1}^{h}-\frac{u_{2,t}}{u_{1,t}}n_{t}$ ,

(17)

and

$\displaystyle g_{t}=b_{t}^{g}-r_{t-1}^{g}b_{t-1}^{g}+\left( 1+\frac{u_{2,t}}{u_{1,t}}% \right) n_{t}-\frac{\psi _{\tau }}{2}\left( \frac{u_{2,t}}{u_{1,t}}-\frac{% u_{2,t-1}}{u_{1,t-1}}\right) ^{2}-\frac{\psi _{g}}{2}\left( g_{t}-g_{t-1}\right) ^{2}\text{.}$

(18)

The functional form for the utility function and the two interest rate equations (2) and (6) are as follows:

$\displaystyle u_{t}\equiv u\left( c_{t},n_{t},g_{t}\right) =\frac{\left( c_{t}-\psi n_{t}^{\theta }\right) ^{1-\sigma }-1}{1-\sigma }+\chi \log \left( g_{t}\right)$

(19)

$\displaystyle r_{t}^{h}$	$\displaystyle =$	$\displaystyle 1/\beta -\alpha ^{h}+\phi ^{hh}\left( \exp \left( \frac{% b_{t}^{h}}{n_{t}}-\frac{b^{h}}{n}\right) -1\right) +\phi ^{hg}\left( \exp \left( \frac{b_{t}^{g}}{n_{t}}-\frac{b^{g}}{n}\right) -1\right) +\upsilon \xi _{t}$	(20)
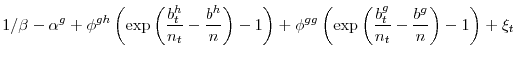$\displaystyle r_{t}^{g}$	$\displaystyle =$	$\displaystyle 1/\beta -\alpha ^{g}+\phi ^{gh}\left( \exp \left( \frac{% b_{t}^{h}}{n_{t}}-\frac{b^{h}}{n}\right) -1\right) +\phi ^{gg}\left( \exp \left( \frac{b_{t}^{g}}{n_{t}}-\frac{b^{g}}{n}\right) -1\right) +\xi _{t}$	(21)

B. Data appendix

All the data we use is publicly available. The majority of the data is taken from AMECO, which is the annual macro-economic database of the European Commission's Directorate General for Economic and Financial Affairs (DG ECFIN). Some of the interest rate series have been supplemented using data from the International Financial Statistics (IFS) database of the IMF. All variables used in the PVAR were year and country demeaned to account for country specific and time specific fixed effects (and the degrees of freedom in the estimated model appropriately adjusted). All AMECO codes are provided in brackets.

GDP growth rate is the growth rate of Gross Domestic Product at constant prices (OVGD).
Inflation rate is the growth rate of the GDP Deflator (PVGD).
Nominal short-term interest rate (ISN). This is usually a 3 month interbank rate. See the AMECO website for further details of the country specific interest rates used for this measure. For several countries, data from the IFS IMF Country Tables, row 60c (Treasury Bill Rate) has been used to supplement series for missing values in AMECO.
Cost of borrowing in the benchmark estimation is the Implicit Interest Rate (AYIGD), which is calculated as the ratio of total interest payments in year 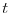to the debt stock in period 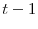. Alternatively we use the Nominal long-term interest rate (ILN). This is usually a 10 year government bond yield. See the AMECO website for further details of the country specific interest rates used for this measure. For several countries, data from the IFS IMF Country Tables, row 61 (Government Bond Yield) has been used to supplement series for missing values in AMECO.
Debt is General Government Consolidated Gross Debt (UDGG) as a ratio of GDP.
Revenue is the sum of Revenue from Indirect Taxes (UTVG), Revenue from Direct Taxes (UTYG) and Social Contributions Received (UTSG) as a ratio of GDP.
Primary expenditure is the sum of Expenditure on Benefits (UYTGH), Expenditure on Wages (UWCG) and Expenditure on Other (which is Total Current Expenditure excluding Interest (UUCGI) minus Expenditure on Benefits and Wages) as a ratio of GDP.

C. Preliminary results

This appendix contains the identified shocks and impulse responses of the 4 shocks of the 5 variable PVAR that we identify before the shock of interest - the cost of borrowing shock. Due to space constraints, we plot the identified shocks only for a sub-set of the countries in our sample. Further details are available from the authors on request. The error bands around the identified shocks and impulse responses are generated by Monte Carlo integration, and we plot the 14th, 50th and 86th percentiles. The identified shocks have, by construction a standard deviation of ${\normalsize 1}$ . We have included shaded areas to identify periods of recession. The impulse responses have been normalized so that a variable of interest (see notes on each graph) rises by 1% on impact of the shock, and have been drawn using an initial value of the debt-to-GDP ratio of $50\%$ .

C.1 Aggregate demand shock

The aggregate demand shock is identified first, requiring GDP growth, inflation and government revenue-to-GDP ratio to rise on impact. The identified aggregate demand shocks are plotted in Figure 11. Due to the use of both time- and country-fixed effects, the aggregate demand shocks correspond well with recessions which have been country specific, and corresponds less well with synchronized periods of recession. For example, if we look at the 2008-2011 period, countries that experienced relatively mild recessions appear to have experienced positive aggregate demand shocks.

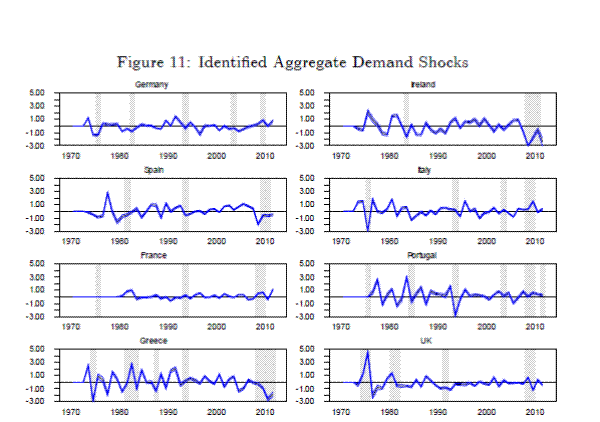
The impulse responses to an aggregate demand shock are plotted in Figure 12. A one percentage point increase in GDP growth increases the government revenue-to-GDP ratio by approximately 0.7 percentage points. With an average revenue-to-GDP ratio of , this means a $1\%$ rise in the GDP growth rate leads to an approximate $2.6\%$ increase in revenues.¹⁷ This elasticity is above the estimate used by the European Commission. However, Mertens and Ravn 2011 formulate an argument why the methodology used by the European Commission might generate a downwardly biased estimate (although they use US data in their example). While the effect on output growth is relatively short-lived, the rise in the government revenue-to-GDP ratio is more persistent. The aggregate demand shock leads to a strong decline in the debt-to-GDP ratio, because the primary balance improves, and because the shock generates a large fall in the growth and inflation adjusted cost of borrowing for the government. Two years following the shock, primary expenditure begins to rise, generating a reversal of the primary balance.

C.2 Cost-push shock

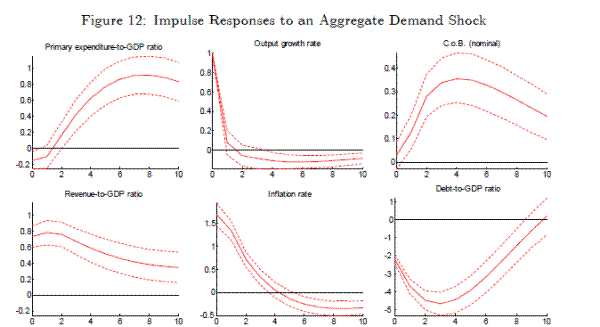
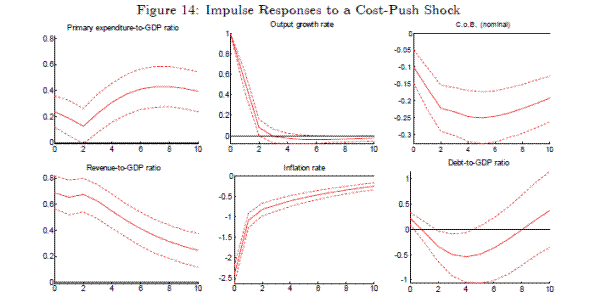
The (negative) cost-push shock is identified second, requiring inflation to fall on impact and GDP growth and revenues to rise, while also being orthogonal to the first shock. The identified cost-push shocks are plotted in Figure 13. These identified shocks correspond well with the existing literature, being more volatile for most countries in the pre-1990s part of the sample.

The impulse responses to a cost-push shock are plotted in Figure 14. We get a similar rise in the government revenue-to-GDP ratio on impact from a $1\%$ rise in the GDP growth rate, as under an aggregate demand shock. The improvement in the primary balance for debt-to-GDP dynamics is however offset by a sharp rise in the inflation and growth adjusted cost of borrowing. While the nominal cost of borrowing falls moderately, the fall in inflation is more than twice the rise in output growth.

Figure 11: Identified Aggregate Demand Shocks

Note: The

-axis measures the identified aggregate demand shock with a unit standard deviation, the

-axis measures time in years. The error bands are generated by Monte Carlo integration, showing the 14th, 50th and 86th percentiles. The shaded areas are periods of recession.

Figure 12:Impulse Responses to an Aggregate Demand Shock

Figure 12 Data

Note: The aggregate demand is ordered first. The

-axis is in percentage points, the

-axis is in years. The error bands are generated by Monte Carlo integration, showing the 14th, 50th and 86th percentiles. Responses have been normalized to a 1 percentage point rise in the GDP growth rate. The debt-to-GDP ratio is initially 0.5.

Figure 13: Identified Cost-Push Shocks

Note: The

-axis measures the identified cost-push shock with a unit standard deviation, the

-axis measures time in years. The error bands are generated by Monte Carlo integration, showing the 14th, 50th and 86th percentiles. The shaded areas are periods of recession.

Figure 14: Impulse Responses to a Cost-Push Shock

Figure 14 Data

Note: The cost-push shock is ordered second and orthogonal to the aggregate demand shock. The

-axis is in percentage points, the

-axis is in years. The error bands are generated by Monte Carlo integration, showing the 14th, 50th and 86th percentiles. Responses have been normalized to a 1 percentage point rise in the GDP growth rate. The debt-to-GDP ratio is initially 0.5.

Figure 15: Identified Primary Expenditure Shocks

Note: The

-axis measures the identified primary expenditure shock with a unit standard deviation, the

-axis measures time in years. The error bands are generated by Monte Carlo integration, showing the 14th, 50th and 86th percentiles. The shaded areas are periods of recession.

C.3 Primary expenditure shock

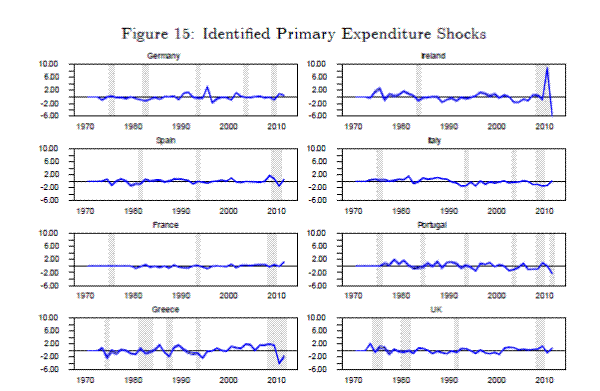
The primary expenditure shock is identified (joint) third, requiring the primary expenditure-to-GDP ratio and the GDP growth rate to rise on impact, while also being orthogonal to the two business cycle shocks. The identified primary expenditure shocks are plotted in Figure 15. The series of identified shocks is dominated by Ireland in 2010. Due to interventions in the banking system, the Irish government recorded a primary deficit-to-GDP ratio of $28\%$ . The results of the model are not sensitive to the inclusion of this single data point.

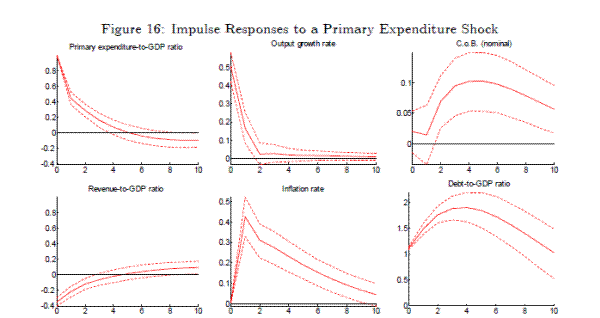
The impulse responses to a primary expenditure shock are plotted in Figure 16. The nominal cost of borrowing does not rise on impact, but does increase in the medium term, rising by a maximum of 10 basis points. This is broadly consistent with the findings of Ardagna, Caselli, and Lane 2007. The 0.5 percentage point increase in the GDP growth rate corresponds to a government spending multiplier of 0.2 , substantially below 1 .¹⁸ Assuming total revenues are unchanged, the expansion in output can explain the reduction in the revenue-to-GDP ratio on impact of the primary expenditure shock. This amplifies the deterioration of the primary balance. Expansionary government spending also generates a rise in inflation.

C.4 Government revenue shock

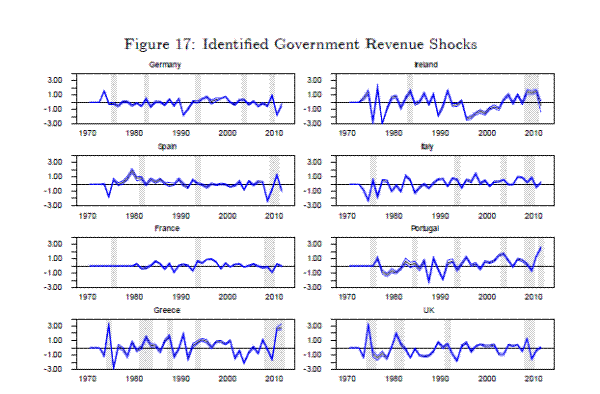
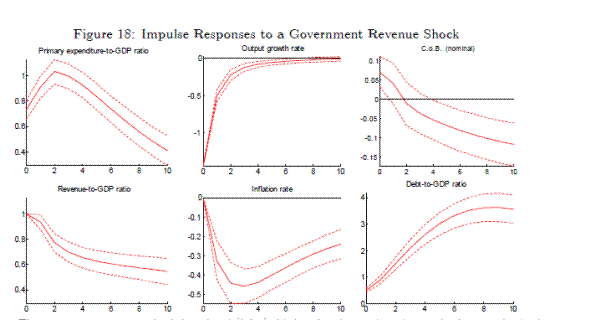
The government revenue shock is identified (joint) third, requiring the revenue-to-GDP ratio to rise and the GDP growth rate to fall on impact, while also being orthogonal to the two business cycle shocks. Note that we do not require the two fiscal policy shocks to be orthogonal, although adding this extra orthogonality restriction does not materially alter the results in the Section 4. The identified government revenue shocks are plotted in Figure 17.

The impulse responses to a government revenue shock are plotted in Figure 18. A 1 percentage point rise in the revenue-to-GDP ratio has a bigger impact on GDP growth than a 1

Figure 16: Impulse Responses to a Primary Expenditure Shock

Figure 16 Data

Note: The primary expenditure shock is ordered (joint) third and orthogonal to the two business cycle shocks. The

-axis is in percentage points, the

-axis is in years. The error bands are generated by Monte Carlo integration, showing the 14th, 50th and 86th percentiles. Responses have been normalized to a 1 percentage point rise in the primary expenditure-to-GDP ratio. The debt-to-GDP ratio is initially 0.5.

percentage point fall in the primary expenditure-to-GDP ratio. GDP growth falls by percentage points on impact, implying a impact tax revenue multiplier of -2.1 , which is substantially greater than -1 .¹⁹ Again, by assuming that primary expenditure is unchanged on impact due to a government revenue shock, the fall in the denominator of the primary expenditure-to-GDP ratio can account for its rise on impact of approximately 0.7 percentage points. The size of the revenue multiplier means that the rise in the primary-balance to GDP ratio is smaller than the rise in the revenue-to-GDP ratio. In addition, the fall in GDP growth (and subsequent fall in inflation) generate a rise in the inflation and growth adjusted cost of borrowing, causing the debt-to-GDP ratio to rise in the response to a positive revenue shock.

Figure 17: Identified Government Revenue Shocks

Note: The

-axis measures the identified government revenue shock with a unit standard deviation, the

-axis measures time in years. The error bands are generated by Monte Carlo integration, showing the 14th, 50th and 86th percentiles. The shaded areas are periods of recession.

Figure 18: Impulse Responses to a Government Revenue Shock

Figure 18 Data

Note: The government revenue shock is ordered (joint) third and orthogonal to the two business cycle shocks. The

-axis is in percentage points, the

-axis is in years. The error bands are generated by Monte Carlo integration, showing the 14th, 50th and 86th percentiles. Responses have been normalized to a 1 percentage point rise in the government revenue-to-GDP ratio. The debt-to-GDP ratio is initially 0.5.

Footnotes

* We would like to thank A. Afonso, K. Bankowski, G. Callegari, J. Cimadomo, C. Giannitsarou, E. de Groot, W. Lemke, J. Roberts, M. Slavik, M. Trabandt, A. Tudyka, participants at a joint LSE and BoE macroeconomic workshop, at an ECB seminar and at the RES annual conference for helpful discussions and suggestions during the writing of this paper. Oliver would particularly like to thank the hospitality of the Fiscal Policy Division of the European Central Bank during his visit. The dataset as well as MatLab and RATS code to reproduce the figures and tables in this paper are available at http://sites.google.com/site/oliverdegroot/research. Correspondence via [email protected]. Disclaimer: The views expressed are solely those of the authors and do not necessarily reflect those of the Federal Reserve Board or the European Central Bank. Return to Text

1. http://www.finance.gov.ie/viewdoc.asp?DocID=6552&CatID=1&StartDate=01+January+2010 Return to Text

2. For a discussion see, for example, Schuknecht, Moutot, Rother, and Stark et al.2011. Return to Text

3. Since the work of Evans 1985, there has been a large empirical literature on the effect of fiscal policy on long-term interest rates. Some of the more recent studies include Faini 2006, Ardagna, Caselli, and Lane 2007, Attinasi, Checherita, and Nickel 2009, Laubach 2009, Schuknecht, Von Hagen, and Wolswijk 2009 and Afonso and Rault 2011. Return to Text

4. The exception is Theofilakou and Stournaras 2012. They estimate a fiscal rule for a panel of European countries, and find evidence in favour of including government bond yields in governments' reaction functions. Their methodological approach is quite different to that used here, as they estimate a single equation model. Return to Text

5. Papers such as Browning 1976 and Mayshar 1991 attempt to model and estimate these types of administrative and compliance costs. They estimate such costs to be of the order of one percent of tax revenues. However, applying this estimates for calibrating the values of $% \psi _{\tau }$ and $\psi _{g}$ is not straightforward. Return to Text

6. The assumption of Greenwood, Hercowitz, and Huffman 1988 preferences implies that there is no government spending multiplier in this model. Had we used King, Plosser, and Rebelo 1988 preferences instead, the model would generate a positive government spending multiplier. However, we would also get a rise in output growth following a cost of borrowing shock. This is because a cost of borrowing shock acts like a wealth shock as it lowers the present value of future disposable income. Households will therefore react by supplying more labour which would generate a counterintuitive rise in output. Return to Text

7. Suppose we model the maturity structure of debt as a continuum of callable perpetuity bonds with stochastic call date arriving with probability

. The stock of debt evolves as $d_{t}=\left( 1-p\right) d_{t-1}+d_{t}^{n}$ , where $d_{t}^{n}$ is newly issued debt. The average cost of borrowing evolves as $i_{t}^{a}=\left( 1-p\right) i_{t-1}^{a}d_{t-1}/d_{t}+i_{t}^{m}d_{t}^{n}/d_{t}$ , where $i_{t}^{m}$ is the marginal cost of borrowing. The average maturity of the government's debt portfolio is $p^{-1}$ . The effect on the average cost of borrowing for a change in the marginal cost of borrowing (evaluated at the steady state) declines as the average maturity increases: $\left. \left( \partial i_{t}^{a}/\partial i_{t}^{m}\right) \right\vert _{d_{t}=d}=p$ . Return to Text

8. Using the model in the previous footnote and setting $d_{t}=d$ and $d_{t}^{n}=pd$ for $\forall t$ then $i_{t}^{a}=\left(1-p\right)i_{t-1}^{a}+pi_{t}^{m}$ . Let $\left\{ i_{t}^{m}\right\}_{t=0}^{\infty}=i+\sigma ,i,i,...$ . It is straight forward to show that $\sum\nolimits_{t=0}^{\infty }\left( i_{t}^{a}-i\right) =\sigma$ , which is independent of

, the average maturity of the debt. Return to Text

9. The choice of lag length is important due to the serial correlation in the maturity structure of government debt. As of 2010, the UK has the longest average maturity of debt of 13.7 years followed by Denmark with 7.9 years. Finland has the shortest average maturity with 4.3 years. The average maturity of debt across all the countries in our sample was 7 years (the data is from Faraglia, Marcet, and Scott 2011 who source the OECD and The Economist).

Our choice of a VAR with 2 lags came from the use of standard lag length selection criteria. We considered VAR specifications with lag lengths from 1 to 7 . The Schwarz Bayesian Criterion indicated a single lag, the Hannan-Quinn Criterion indicated two lags while the Akaike Information Criterion indicated 7 lags. Return to Text

10. Increasing the number of runs to 10,000 does not significantly alter inference. Return to Text

11. There are several alternative methods in the literature for identification in VAR models. Most of these methods use explicit (rather than implicit as in the case of sign restrictions) parameter restrictions. In general, the reduced-form model has more free parameters than the structural model. Parameter restrictions are therefore added to the reduced form model to enable the parameters of the structural model to be estimated. For early contributions to this literature, see Sims 1980, Blanchard and watson 1986 and Sims 1986. The literature has followed either the use of short-run identifying restrictions, see Christiano, Eichenbaum, and Evans 1999, or long-run identifying restrictions, see Blanchard and Quah 1993. An alternative approach to the structural VAR literature has been the narrative (or natural experiment) approach of Romer and Romer 1989. Return to Text

12. We are grateful to an anonymous referee for alerting us to this issue. Return to Text

13. We have relegated the identified aggregate demand, cost-push and fiscal policy shocks, as well as their corresponding impulse responses to Appendix C. Replication files for all the figures in this section, written in RATS code, is available from the corresponding author's homepage, http://sites.google.com/site/oliverdegroot/research Return to Text

14. In fact, the time series of identified cost-of-borrowing shocks in Figure 4 might not appear as one might expect, as we identify no large positive shocks for the countries struggling with the current sovereign debt crisis. In part, this relates to our discussion (in Section 3) of the marginal versus average cost of borrowing concepts. While the marginal cost of borrowing (proxied by 10 year government bond yields) for Greece, Ireland and Portugal etc. has increased sharply in recent years, their average cost of borrowing, which we use in this estimation, has moved by much less. The second explanation is that a considerable portion of the rise in governments' cost of borrowing in recent years may have been driven by changes in governments' primary deficits and debt, and have not been the consequence of unanticipated cost of borrowing shocks. Return to Text

15. This stock-flow adjustment captures, among other things, changes in the size of foreign-currency denominated debt associated with a change in the exchange rate, financial transactions in relation to government support to financial istitutions, privatization receipts and the purchase of assets. During financial crises, it can thus become an important determinant of government debt developments. Return to Text

16. If we use the response of the cost of borrowing in year 1 as our estimate of $di^{average}/di^{marginal}$ the we get an estimate of the average maturity of debt of $1/0.18\approx 5.6$ years. Return to Text

17. The elasticity of revenues with respect to output is $\xi =\frac{\Delta R/R}{% \Delta Y/Y}$ . The model provides the following information: $\Delta Y/Y=0.01$ , $\Delta \left( R/Y\right) \approx 0.007$ and $R/Y\approx 0.45$ . Using the approximation, $\Delta \left( R/Y\right) /\left( R/Y\right) \approx \Delta R/R-\Delta Y/Y$ we can rewrite the elasticity as $\xi \approx 1+\frac{\Delta \left( R/Y\right) /\left( R/Y\right) }{\Delta Y/Y}=1+\frac{% 0.007/0.45}{0.01}=2.6$ . Return to Text

18. The government spending multiplier is $\xi =\frac{\Delta Y/Y}{\Delta E/E}$ . The model provides the following information: $\Delta \left( E/Y\right) =0.01$ , $\Delta Y/Y\approx 0.005$ and $E/Y\approx 0.45$ . Using the approximation, $\Delta \left( E/Y\right) /\left( E/Y\right) \approx \Delta E/E-\Delta Y/Y$ we can rewrite the elasticity as $\xi \approx \frac{\Delta Y/Y}{\Delta Y/Y+\Delta \left( E/Y\right) /\left( E/Y\right) }=\frac{0.005}{% 0.005+0.01/0.45}=0.2$ . Return to Text

19. The tax revenue multiplier is $\xi =\frac{\Delta Y/Y}{\Delta R/R}$ . The model provides the following information: $\Delta \left( R/Y\right) =0.01$ , $% \Delta Y/Y\approx -0.015$ and $R/Y\approx 0.45$ . Using the approximation, $% \Delta \left( R/Y\right) /\left( R/Y\right) \approx \Delta R/R-\Delta Y/Y$ we can rewrite the elasticity as $\xi \approx \frac{\Delta Y/Y}{\Delta Y/Y+\Delta \left( R/Y\right) /\left( R/Y\right) }=\frac{-0.015}{% -0.015+0.01/0.45}=-2.1$ . Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text
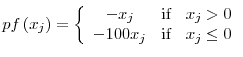
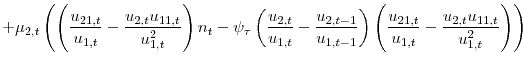
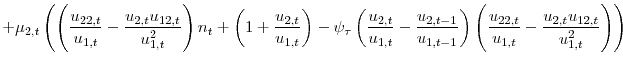
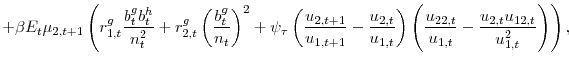
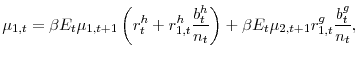
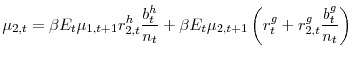