
Rising Intangible Capital, Shrinking Debt Capacity, and the US Corporate Savings Glut
Abstract:
JEL Classification: E22, E44, G31, G32
Keywords: Asset Intangibility; Debt Capacity; Risk Management; Corporate Cash Hoarding; (S,s) Adjustment
1 Introduction
Public corporations in the US have steadily increased their cash holdings over the last decades. This dramatic trend in corporate liquidity management is an actively debated issue that has attracted wide attention in the popular press, with commentators dubbing it the "corporate saving glut," expressing concerns it might hamper growth of the US economy, and even raising calls to heavily tax corporate savings. Yet, understanding which fundamental economic determinants drive the secular trend in corporate cash holdings and why corporations now hold almost three times as much cash as they used to in the 1970s1 represents a big outstanding challenge for both empirical and theoretical research in corporate finance.
In particular, on the empirical side, existing evidence on the determinants of the secular trend in corporate cash holdings is at best mixed. Several explanations have been put forth such as, for example, agency conflicts between managers and shareholders, or precautionary motives in the face of uncertainty (Bates, Kahle, and Stulz (2006)). However, these standard cross-sectional determinants of corporate cash holdings have been relatively stable over time and, thus, can offer at best only a partial explanation of why cash holdings have risen so much over time. On the theory side, the cash to asset ratios predicted by standard calibrations of existing models are much smaller than their empirical counterparts (Riddick and Whited (2009)). Thus, the current high levels of cash represent a quantitative puzzle for existing theories.
In this paper, we explore whether firms' growing reliance on intangible capital in their production technology can help address both the empirical and the theoretical challenges. Intangible capital cannot be easily verified or liquidated and, as such, cannot be pledged as collateral to raise debt financing. Under frictional capital markets where external funds command substantial premiums, we argue that its rising importance as an input of production may have boosted firms' precautionary demand for cash in order to insure that they have sufficient liquidity to weather adverse shocks and to exploit investment opportunities. We document a large number of new stylized facts which support this "collateral channel" and broadly suggest that there is a strong empirical link between the rise in intangible capital and the secular trend in corporate cash holdings. A structural model that can successfully replicate the facts suggests that the collateral channel is also quantitatively important, thus offering a potential resolution of the puzzle for existing theories. Overall, our results indicate that intangible capital is crucial to providing a satisfactory analytic account of the main stylized facts of corporate cash holdings.
Our focus on intangible capital builds on a vast body of evidence spanning several literatures, which shows that over the last decades there has been a shift away from physical capital investments. There is solid evidence at the aggregate level that investments in intangible capital by US firms have picked up substantially since the 1980s (Corrado, Hulten, and Sichel (2009) and Corrado and Hulten (2010)), especially in computerized information and private R&D. There is also evidence that organizational capital is becoming increasingly important (Lev (2001)). This well-documented shift in firms' mode of production is an economy-wide phenomenon, something that the literature has dubbed a general purpose technology (GPT) shock, or the third industrial revolution (Jovanovic and Rousseau (2005)). This body of evidence broadly suggests that fundamental technological changes in the 1980s and 1990s have had a pervasive effect on public corporations.
We start by documenting the stylized facts of the link between the rise in intangible capital and the secular trend in corporate cash holdings. To that end, we construct a new firm-level measure of intangible capital, which is challenging since intangible assets are not reported on firms' balance sheets. Existing attempts at measuring intangible capital have been mostly at the aggregate level. For example, one approach is to construct a proxy using aggregate stock market or accounting data (Hall (2001), McGrattan and Prescott (2007)). While these approaches measure intangibles as unexplained (by physical capital) residuals of stock market value or firm productivity, a more direct approach is to construct aggregate measures of the different components of intangible capital, which include the stock of assets created by R&D expenditures, brand equity, and human and organizational capital using NIPA accounts (Corrado, Hulten, and Sichel (2009) and Corrado and Hulten (2010)).
We build on this latter approach and use standard accounting data to construct a new comprehensive firm-level measure of intangible capital for all non-financial firms in Compustat between 1970 and 2010. Our measure is defined as the sum of three main components: the stock of information technology (IT) capital; the stock of innovative (R&D) capital; and the stock of human and organizational capital. The stock of innovative capital is constructed by capitalizing R&D expenditures using a standard perpetual inventory method (e.g., Hall (2001)), while the stock of human and organizational capital capitalizes SG&A expenditures.2 IT capital is constructed capitalizing expenditures in computer software from BEA.
Using this firm-level measure, we document several new empirical regularities on the link between intangible capital, firm financing, and corporate investment. In particular, there is a strong positive relation between intangible capital and corporate cash both in the cross-section and in the time-series, with intangible capital emerging as the most important firm-level determinant of cash holdings robustly across different specifications. Results of a simple out-of-sample forecasting exercise that follows the approach of Bates, Kahle, and Stulz (2006) show that an economically significant part of the overall increase in cash holdings over the last decades can be attributed to increases in intangible capital. Intangible capital does not affect only cash levels, but also the adjustment dynamics of cash and the relation between corporate investment and cash holdings. Finally, the link between cash and intangible capital is especially strong for firms that are financially constrained and those that belong to industries with greater investment inflexibility. Overall, our empirical results suggest that intangible capital has a pervasive impact on corporate cash holding decisions and that the impact is due to both financial and real frictions.
In order to better understand the economic forces that drive the empirical link between intangible capital, cash holdings, and corporate investment, we next develop a new dynamic model of the joint determination of firms' financing, risk management, and capital accumulation decisions. The model is cast in an infinite-horizon, discrete-time stochastic environment, where firms make value maximizing investment decisions in real (tangible and intangible) and financial (cash holdings, debt, and equity) assets. There are two key frictions: first, financial frictions arise since debt financing is subject to a collateral constraint, intangible capital cannot be pledged as collateral, and equity financing involves issuance costs; second, there are real frictions that arise since investment in real assets is subject to non-convex adjustment costs, which make it infrequent and lumpy (see Abel and Eberly (1994) for a standard treatment).
In this setting, we show that the interplay of external financing costs and non-convex adjustment costs of investment generates a quantitatively large precautionary demand for cash hoarding because it makes difficult for firms to generate funds by either divesting real assets or raising external
finance (see Bolton, Chen, and Wang (2009), and Riddick and Whited (2009) for related settings, which abstract from debt and capital heterogeneity; see also Froot, Scharfstein, and Stein (1993) for a seminal model
of corporate liquidity management). Intangible assets further boost this precautionary demand for cash by shrinking debt capacity through a tightening of the collateral debt constraint. As a result, firms with growth options tend to hold more cash in anticipation of (![]() ,
,![]() )-type adjustments in physical capital to avoid raising costly external finance. To assess the quantitative
importance of this "collateral channel" through which firms' debt capacity and asset tangibility are linked in our model, we develop a stationary general equilibrium analysis of net savings of corporations and households. All else equal, a technological transformation that increases firms' reliance
on intangible assets to levels that match their empirical counterparts in the US economy for the last decade leads to levels of corporate cash holdings that are roughly in line with their US averages for the same period. In addition, it endogenously generates a large shift of corporations' and
households' balance sheets toward switching their roles as net-savers, which is also in line with the data. Overall, these results suggest that technological change has contributed significantly to recent changes in US corporations' and households' private liquidity decisions.
)-type adjustments in physical capital to avoid raising costly external finance. To assess the quantitative
importance of this "collateral channel" through which firms' debt capacity and asset tangibility are linked in our model, we develop a stationary general equilibrium analysis of net savings of corporations and households. All else equal, a technological transformation that increases firms' reliance
on intangible assets to levels that match their empirical counterparts in the US economy for the last decade leads to levels of corporate cash holdings that are roughly in line with their US averages for the same period. In addition, it endogenously generates a large shift of corporations' and
households' balance sheets toward switching their roles as net-savers, which is also in line with the data. Overall, these results suggest that technological change has contributed significantly to recent changes in US corporations' and households' private liquidity decisions.
In addition to offering a potential resolution to important empirical and quantitative puzzles of corporate cash holdings, our results make two other important contributions. On the finance side, while it is well-established that more tangible capital assets support more debt (see Shleifer and Vishny (1992), and Hart and Moore (1994) for seminal contributions, and Rampini and Viswanathan (2010) for recent work), our contribution is to examine the quantitative implications of asset tangibility for liquidity management, which are relatively less well-understood. Our proposed rationale for the secular trend in corporate cash holdings based on technological change is complementary to recent work by Karabarbounis and Neiman (2012) who explore the link with the rise in the labor share.3 There are also recent studies by Bolton, Chen, and Wang (2013), Eisfeldt and Muir (2012) and Warusawitharana and Whited (2012), which focus on the short-run fluctuation of cash hoarding associated with equity market timing. Our contribution with respect to these studies is to offer a quantitative explanation of the long-run secular trend in corporate savings, which remains challenging even in a setting with equity market timing.4 On the macroeconomics side, we contribute to the financial accelerator literature (Kiyotaki and Moore (1997), Bernanke, Gertler, and Gilchrist (1999) and Cooley and Quadrini (2001)) by extending the analysis to the issue of dynamic risk management under financial market frictions in general equilibrium.
2 Intangible Capital and the Rise in Cash Holdings: The Evidence
We begin our analysis by summarizing the stylized facts of the evolution of intangible capital and corporate cash holdings over time, as well as a number of related empirical regularities on intangible capital, firm financing, and corporate investment. To that end, we retrieve standard accounting data from Compustat to assemble a large panel of 18,535 US corporations over the 1970 to 2010 period (176,877 firm-year observations).
2.1 Measuring Intangible Capital
We construct a measure of intangible capital for each firm-year,5 which is our empirical proxy for the amount of capital accumulated by past investments in intangible assets. The main hurdle with measuring intangible capital is that, since investments in intangible assets are expensed in the year in which they are incurred, the capital that is created by such investments is not reported on firm balance sheets.6 We use annual data on expenses in three broad categories of intangible investment whose importance has been emphasized in the literature on the economics of innovation (Corrado, Hulten, and Sichel (2009) and Corrado and Hulten (2010)): knowledge capital, organizational capabilities, and computerized information and software. Intangible capital is defined as the sum of the stocks of investments in these three categories divided by net book assets.
First, we construct the stock of knowledge capital from past R&D expenses using the perpetual inventory method:
where
Second, we construct the stock of organizational capital from past sales, general, and administrative (SG&A) expenses also using the same method with
![]() Lev and Radhakrishnan (2005), Eisfeldt and Papanikolaou (2013)). These investments enhance the
value of brand names and other knowledge embedded in firm-specific human and structural resources and include employee training costs, payments to management and strategy consultants, and distribution systems. Since SG&A expenditures include other expenses unrelated to investments in
organizational capabilities, we follow Corrado, Hulten, and Sichel (2009) and only weigh the stock of organizational capital by 0.2.8
Lev and Radhakrishnan (2005), Eisfeldt and Papanikolaou (2013)). These investments enhance the
value of brand names and other knowledge embedded in firm-specific human and structural resources and include employee training costs, payments to management and strategy consultants, and distribution systems. Since SG&A expenditures include other expenses unrelated to investments in
organizational capabilities, we follow Corrado, Hulten, and Sichel (2009) and only weigh the stock of organizational capital by 0.2.8
Third, we construct the stock of computerized information and software by applying again perpetual inventory method with a depreciation rate of ![]() as in the BEA data. Since these
expenses are not reported at the firm level, we use the annual (2-SIC) industry level BEA Fixed Reproducible Tangible Wealth (FRTW) data. We then construct a multiple of this stock to tangible capital stock at the industry level and apply the multiple to each firm's tangible capital stock (PPE) to
derive a firm-level stock.9 Our resulting estimate for average intangible to tangible capital over the last decade is close to 1, which is comparable to the
estimate in Corrado, Hulten, and Sichel (2009) based on aggregate NIPA accounts.
as in the BEA data. Since these
expenses are not reported at the firm level, we use the annual (2-SIC) industry level BEA Fixed Reproducible Tangible Wealth (FRTW) data. We then construct a multiple of this stock to tangible capital stock at the industry level and apply the multiple to each firm's tangible capital stock (PPE) to
derive a firm-level stock.9 Our resulting estimate for average intangible to tangible capital over the last decade is close to 1, which is comparable to the
estimate in Corrado, Hulten, and Sichel (2009) based on aggregate NIPA accounts.
2.2 Stylized Facts
We begin our analysis by considering the stylized facts of the evolution of corporate cash holdings over time. Figure 1 helps to visualize the main hypothesis of this paper: that the rising share of intangible capital in production is a fundamental driver of the secular downward trend in leverage and upward trend in corporate savings. The figure plots annual averages across firms of the ratio of intangible capital to book value of assets (left panel), of cash holdings to book assets (middle panel), and of net debt to book assets (net leverage ratio, right panel) over the last four decades. The intangible ratio rose tenfold from about 5% of net book assets in 1970 to about 60% in 2010. The share of liquid financial assets in the balance sheets of U.S. corporations has also grown from 8% to 22% over the same period, with cash holdings displaying a pronounced secular upward trend which was not concentrated in any particular decade, but rather has been steady; third, despite the cycles over medium-run, the net leverage ratio of U.S. corporations has trended down from 20% to 6% over the same period, and appears to be cointegrated with the cash ratio with a coefficient -1. Panels A and C of Table 2 show averages (and medians) by decades of the cash ratio and net leverage for the entire sample and for the sub-sample of firms that invest in R&D. The increase in cash holdings is even stronger for these firms, suggesting that the secular trend in average cash is not an artifact of these firms becoming more heavily represented. For instance, mean (median) cash holdings ratio for these firms have increased from 9% (5%) to 27 (19%) for the same period, which is 6ppt (8ppt) more than the total sample.
Next, we now turn to cross-industry and cross-firm univariate evidence. The left panel of Figure 2 plots the distribution of average industry cash and intangible ratios by decades. Intangible capital ratios have steadily risen in all broad industry categories (12-Fama and French) over the last four decades, consistent with an economy-wide shift in firms' mode of production that affected firms well beyond just high-tech sectors.10 While the increase has been more dramatic in some industries (e.g., by a factor of almost 40, from 0.13 to 5.07, in Healthcare), the intangible ratio went up by a factor of 10 (from 0.01 to 0.13) even in traditional industries such as retail (Shops). There is a strong correlation between intangible capital and cash ratios over time by industry, with a regression coefficient of about 0.13 and an R2 of more than 75%.
Moving on to cross-firm variation, we compute for each firm the change in average intangible capital ratio before and after 1990 and divide the sample into deciles according to these firm-level changes in intangible capital. The right panel of Figure 2 plots the corresponding average change in cash ratios before and after 1990 for each decile of the distribution of firm-level changes in intangible capital. Firms in the lower deciles have declines in intangible capital, while firms in the top deciles correspond to the largest increases. Changes in cash line up quite well along the diagonal, with firms that experienced a decline in intangible capital also seeing their cash ratios decline, while firms for which intangible capital rose the most also experiencing the greatest increases in cash.
Panels B and D of Table 1 show additional univariate evidence on cross-firm variation by stratifying the sample into four subsamples, based on quartiles of the empirical distribution of intangible capital and showing the average (and median) cash and net leverage ratios for each of these quartiles for the entire sample and for the sub-sample of firms that invest in R&D, respectively. Mean (median) cash ratios strongly and monotonically increase from about 8% (4%) in the bottom quartile of intangible capital to about 23% (12%) in the top quartile. The univariate relation between cash and intangible capital is even stronger when we restrict the sample to exclude firms that do not report R&D, with mean (median) cash ratios now going up to about 31% (23%) in the top quartile. Finally, the columns to the right show that firms in the top quartile of intangible capital are also those for which cash matters the most to finance growth opportunities, as especially in this top quartile cash rich firms have on average been investing relatively more and growing faster.
2.3 Panel Evidence
In the remainder of this section, we corroborate the stylized facts using panel data analysis. To that end, we regress cash holdings and net leverage ratios on our measure of intangible capital, while controlling for a set of standard determinants of cash holdings (e.g., Opler, Pinkowitz, Stulz, and Williamson (1999) and Bates, Kahle, and Stulz (2006)). In particular, we consider two specifications, OLS and fixed effects11, with firm-level controls such as industry cash flow volatility, market-to-book ratio, firm size, cash flow, capital expenditures, (cash) acquisitions expenditures, and a dummy for whether the firm pays dividend in any given year, as well as year effects to control for time variation in cash holdings.12 We evaluate statistical significance using robust clustered standard errors adjusted for non-independence of observations within firms.
The resulting estimates are reported in Panel A of Table 3 for the overall sample (Columns (1)-(4)) and for the subset of firms that report positive R&D (Columns (5)-(8)), to address the concern that the overall sample may reflect spurious differences in average cash holdings between non-innovative vs. innovative firms.13 The coefficient on intangible capital is robustly positive and statistically significant across the two samples and both specifications.14
Intangible capital is also economically significant. For example, for the baseline OLS specification in Column (1), one standard deviation increase in intangible capital is associated with about 8 and 1/2 % increase in the cash ratio, which is equal to about half the sample mean value of the cash ratio of 15%. In the specification with firm fixed effects (Column (2)), the estimates decline by only about 2 and 1/2%, suggesting that intangible capital is also an economically significant determinant of the within-firm time-series evolution of cash holdings. Finally, estimates for firms with positive R&D are even larger than those for the entire sample, which suggests that our baseline OLS result is not spurious and that intangible capital is an even more important economic determinant of cash holdings for innovative firms.
When we replicate our tests for net leverage, which is the ratio of total debt net of cash to book assets, the coefficient on intangible capital is robustly negative and statistically significant across both samples and specifications. It is also economically significant. For example, for the baseline OLS specification in Column (3), one standard deviation increase in intangible capital is associated with about 11 % decrease in net leverage ratio, which is almost as large as the sample mean value of net leverage of 14%. These results suggest that intangible capital is not only an important determinant of firms' cash holdings decisions, but also of their capital structure and net indebtedness.15
Quantifying the Contribution of Intangible Capital to the Rise in Cash
Figure 1 shows that cash holdings increased by about 10% over the last decades, from about 8% in 1970 to about 20% by 2010. To quantify the importance of intangible capital in explaining the secular trend in cash holdings, we investigate how changes in firm characteristics over time affect cash ratios.16 The intuition for this exercise is as follows: sample average intangible capital was 0.42 in 1980 and 0.75 in 2000. If the (unscaled) coefficient on intangible capital is 0.087, then we infer that, holding all other variables constant, the average cash ratio increased by 2.8 percentage points from 1980 to 2000 because of the increase in intangible capital, going from 3.7 percentage points (=0.087*0.42) in 1980 to 6.5 percentage points (=0.087*0.75) in 2000.
Panel A of Table 3 shows the results of this analysis that quantifies the contribution to the overall increase in the predicted cash ratio of changes in the firm-level determinants of that ratio. We first estimate the augmented OLS regression specification of Column (1) in the first half of the sample, i.e. the pre-1990 period. Using these coefficient estimates, we construct measures of the contributions of each of the explanatory variables in explaining changes in cash holdings between the 2000s and the pre-1990 period. Changes in intangible capital stand out as the most important driving factor of the rise in cash, with an increase in cash of about 3 (5) percentage points attributable to the increase in intangible capital in the overall sample (in the sub-sample of positive R&D firms). Changes in all other standard determinants have quite limited explanatory power for the rise in cash.
Intangible Capital and Cash Dynamics
We further probe the role of intangible capital in driving the time-series dynamics of corporate cash management by adding a lagged dependent variable to our baseline specification. This new ingredient allows us to do two things: first, though we do not report the coefficient estimates for brevity, we check that our results are robust to allowing for imperfections in cash rebalancing or partial adjustment in cash ratios (Lemmon, Roberts, and Zender (2008)); second, we gather additional evidence on the role of financing frictions. In particular, we examine the hypothesis that intangible capital lowers the speed of adjustment (SOA) of cash: if intangibles make it more difficult to raise external finance, then they should be expected to increase adjustment costs of cash, thus leading to lower SOA (see Faulkender, Flannery, Hankins, and Smith (2012) for more details on this intuition).
Because there is an ongoing debate in the literature about the proper estimation procedure of SOA, Panel B of Table 3 reports results for a wide battery of SOA estimators. The annual SOA of cash ranges between 0.27 and 0.54 (not shown), suggesting that cash is imperfectly adjusted toward its target. To provide economic intuition, we translate these SOAs into half-lives, the time that it takes a firm to adjust one-half the distance to its target cash after a one unit shock to the error term. The half-life ranges from about 1 to about 2 years. Robustly across the different estimation techniques, SOAs decline monotonically with intangible capital. For example, OLS estimates in Column (1) imply that the half-life of 3 years for firms in the top quartile of the distribution of intangible capital is almost three time larger than for firms in the bottom quartile. These results are consistent with the hypothesis that intangible capital increases adjustment costs of cash.
Corporate Investment and Firm Dynamics
Next, we detail the empirical regularities that pertain to the real side decisions of firms. We ask whether cash holdings are an important source of financing for firm investment and growth and, if so, whether their importance varies systematically with intangible capital. To that end, we regress total investment (the ratio of the sum of capex and R&D to net book assets) and sales growth on lagged cash holdings, while controlling for a set of standard determinants of investment (e.g., Gomes (2001)). We consider both OLS and firm fixed effects versions of this baseline model, with firm-level controls that include industry cash flow volatility, market-to-book ratio, firm size, cash flow, and a dummy for whether the firm pays dividend in any given year, as well as year effects. We evaluate statistical significance using robust clustered standard errors adjusted for non-independence of observations within firms.
The resulting estimates are reported in Panel A of Table 4 for the overall sample (Columns (1)-(4)) and for the subset of firms that report positive R&D (Columns (5)-(8)). The coefficient on lagged cash holdings is robustly positive and statistically significant across the two samples and both specifications, and is also economically significant. For example, for the baseline OLS specification in Column (1), an increase in lagged cash holdings from their lowest to their highest levels leads to about 7% increase in investment, which is almost as large as the sample mean value of investment of 10%. The estimate declines just a bit in the specification with firm fixed effects, and is even larger for firms with positive R&D, suggesting that cash holdings are an even more important source of financing growth opportunities for innovative firms.
Panel B of Table 4 shows that intangible capital strengthens the relation between cash holdings and firm investment and growth. In fact, when we run our investment and sales growth regressions separately for each of four bins of our sample depending on quartiles of the empirical distribution of intangible capital, the size of the coefficient on lagged cash holdings increases monotonically and about doubles as we move from the bottom to the top quartile. These findings hold robustly for both investment and sales growth, as well as for both the entire sample and the sub-sample of firms that are active in R&D.
The Role of Financial and Real Frictions
In our last set of panel results, we use sample-split analysis to better understand why intangible capital is an economically important determinant of corporate cash holdings. In particular, we examine both financial and real investment frictions, which are the key ingredients of our model. If firms with more intangible capital hold more cash because of financing frictions, we would expect that the relation between intangible and cash should be stronger among firms for which financing frictions are more severe. As for investment frictions, the basic insight of the vast literature on real options (e.g., Abel and Eberly (1994), Bertola and Caballero (1994)) is that fixed adjustment costs lead firms to make large, lumpy investments. Thus, if intangible capital makes it more difficult to raise external finance, these real frictions may lead firms with more intangible capital to accumulate even more cash to finance their large investments.
Panel A of Table 5 shows evidence supporting the role of financial frictions. We follow the standard approach in the literature (e.g., Hennessy and Whited (2007)) and in every year over the sample period we rank firms based on five ex-ante indicators of their financial constraint status, which include firm size, dividend payer status, the WW-Index by Whited and Wu (2006), a measure of asset liquidation value by Berger, Ofek, and Swary (1996), and an index of industry asset redeployability by Balasubramanian and Sivadasan (2009). We assign to the financially constrained (unconstrained) groups those firms in the bottom (top) quartile of the annual distribution of each of these measures in turn, except for the financial constraints index, for which the ordering is reversed. Consistently across specifications and irrespective of which indicator of ex-ante financing status is chosen, we find that the economic significance of the coefficient on intangible capital is much stronger in the sub-samples of firms that are more likely to face financial frictions. For example, the OLS coefficient in Column (1) more than triples when we go from the top to the bottom quartile of the firm size distribution (Rows [1] and [2]).
Panel B splits the sample between bottom and top quartiles of the following five (time-invariant) proxies of investment frictions: (4-SIC) industry frequency of investment inaction and an indicator for whether there are investment spikes in the industry, which are both defined following Cooper and Haltiwanger (2006); time-series skewness and kurtosis of annual aggregate industry investment, both based on Caballero (1999); and the time-series standard deviation of aggregate industry operating costs. The intuition underling these proxies is that, due to technological differences, the extent to which firms face fixed costs varies across industries. Thus, industries where fixed cost are higher are those where firms are more likely to adjust investment infrequently, and, conditional on adjusting, by a proportionally larger amount. In addition, in these industries fixed costs lead to a time-series distribution of aggregate investment that is sharply right-skewed and fat-tailed. Thus, we assign to the high (low) investment friction groups those firms in the top (bottom) quartile of the distribution of each of these measures in turn, except for the variability of operating costs, for which the ordering is reversed. Consistently across specifications and irrespective of the indicator chosen, the economic significance of the coefficient on intangible capital is much stronger in the sub-samples of firms that are more likely to face investment frictions. For example, the OLS coefficient in Column (1) about doubles for firms that are in industries with investment spikes compared to those without such spikes (Rows [3] and [4]).
In summary, the empirical regularities on intangible capital, firm financing, and corporate investment are:
- Firm cash holdings (net indebtedness) have increased (decreased) over time, and are positively (negatively) related with intangible capital both in the time series and in the cross section.
- Investment and growth are positively related to cash holdings, especially for firms with greater intangible capital.
- The adjustment dynamics of cash is more sluggish for firms with more intangible capital.
- The link between cash and intangible capital is stronger for the firms that are financially constrained and belong to industries with greater skewness and kurtosis in investment rates.
3 A Structural Model of Corporate Cash Management
This section develops a stationary general equilibrium model in which illiquidity of productive assets and financial market frictions interact with each other to determine firms' optimal liquidity management policies. Our general equilibrium approach has a number of advantages: it allows us to derive the ergodic joint distribution of capital stock, financial assets and liabilities and idiosyncratic technology of heterogeneous firms; it allows us to construct the exact moments of endogenous quantities in a simulation-free environment; it incorporates endogenous feedbacks of market prices in general equilibrium. To save space however, we focus on the description of firm problem in this section. A complete definition of stationary equilibrium and the numerical method can be found in the Appendix.
3.1 Technology
Firms combine labor and capital to produce and sell output in a competitive market. They use two different types of capital: tangible (![]() ) and intangible (
) and intangible (![]() ). In particular, the production technology takes the following Decreasing-Returns-to-Scale (DRS) Cobb-Douglas form:
). In particular, the production technology takes the following Decreasing-Returns-to-Scale (DRS) Cobb-Douglas form:
where
where
Note that we assume that capital service is given by a CRS-CES form with the elasticity of substitution given by
![]() . For the baseline specification, we specify
. For the baseline specification, we specify
![]() , implying Leontief,
, implying Leontief,
![]() . In this special case,
. In this special case,
![]() . It is then straightforward to verify that the profit function is simply given by
. It is then straightforward to verify that the profit function is simply given by
![]() . Since the two types of capital are held in a fixed proportion, the assumption preserves tractability by allowing us to essentially eliminate one
state variable. This reduces the size of problem considerably, especially in general equilibrium, thus allowing us to develop intuition about the main forces at work in the model. As a robustness check, we later consider the general CES case
. Since the two types of capital are held in a fixed proportion, the assumption preserves tractability by allowing us to essentially eliminate one
state variable. This reduces the size of problem considerably, especially in general equilibrium, thus allowing us to develop intuition about the main forces at work in the model. As a robustness check, we later consider the general CES case
![]() .
.
To motivate firms' cash holdings, it is necessary, although not sufficient, to introduce illiquidity of long-lived capital assets. For this reason, we assume that all capital expenditures are only partially reversible (Abel and Eberly (1996)). We denote initial
purchase prices and liquidation values by
![]() and
and ![]() for
for ![]() . The partial irreversibility can be formally expressed as
. The partial irreversibility can be formally expressed as
![]() for
for ![]() Since the desire to hold cash arise from
the imperfect resale value, we make a simplifying assumption,
Since the desire to hold cash arise from
the imperfect resale value, we make a simplifying assumption,
![]() for
for ![]() : the initial purchase prices are identical.
: the initial purchase prices are identical.
In addition, we also assume that adjustment of capital is costly in either direction because it involves fixed adjustment costs (interchangeably, non-convex adjustment). We assume that both types of capital are subject to the same amount of fixed costs, denoted by ![]() . Combining the two assumptions about the illiquidity of capital, we can express the adjustment cost as
. Combining the two assumptions about the illiquidity of capital, we can express the adjustment cost as
where
for
3.2 Financing Frictions
Firms have three financing options: (i) internal funds, including operating income and cash holdings; (ii) debt financing; and (iii) equity issuance. We consider capital market frictions that make the capital structure of the firm deviate from the Modigliani-Miller theorem. Next, we detail the debt and equity market frictions in turn.
3.2.1 Debt Market Friction
It is well-established in the literature that more tangible capital assets support more debt (see Shleifer and Vishny (1992), Hart and Moore (1994) and Rampini and Viswanathan (2010) for theoretical arguments, and Sibilkov (2009) for empirical evidence). This is because intangible capital, by its very own nature, is difficult to verify in quality or quantity. In fact, it often embodies the human capital of developers, which cannot be easily transferred to a third entity in its entirety. As a consequence, intangible capital is rarely pledged as collateral in debt contracts. To capture this feature, we assume that the firm cannot commit to transfer the technology embodied in the intangible capital stock to creditors upon default. Since embodied human capital cannot be transferred, intangible capital cannot be liquidated for a positive value by a third party.19
Furthermore, in the spirit of Hart and Moore (1994) we assume that the firm's output is observable, but not verifiable by a court. Hence, no debt contract can be written on the outcome of the firm's output. Under this circumstance, as shown by Kiyotaki and Moore (1997), the only possible form of debt contract is a risk-free debt contract collateralized by capital assets. We differ from Kiyotaki and Moore (1997) however in that only tangible capital assets constitute eligible collateral.20 The resulting risk-free debt contract is subject to the following borrowing constraint:
where
For later reference, we define the financial slack of the firm as
![]() . A natural interpretation of
. A natural interpretation of
![]() is collateralized line of credit arrangement. Note that the constraint is an occasionally binding one. Financial slack can be decomposed into two parts as follows:
is collateralized line of credit arrangement. Note that the constraint is an occasionally binding one. Financial slack can be decomposed into two parts as follows:
The second term on the right-hand side can be interpreted as debt while the last term as cash. The difference between the first and the second term is equivalent to the unused line of credit.
In our stylized setting, firms never hold debt and cash at the same time. In the case when a firm finds it optimal to have strictly positive cash balances, the firm's financial (liquidity) facility is composed of two terms: option to borrow up to the debt capacity given by
![]() and the cash holdings given by
and the cash holdings given by
![]() . When the firm finds it optimal to carry debt, the firm's remaining liquidity facility is given by
. When the firm finds it optimal to carry debt, the firm's remaining liquidity facility is given by
![]() , the unused line of credit.
, the unused line of credit.
3.2.2 Equity Market Friction
If there were no equity market frictions, the debt market friction would play no role since the firm could undo it at no cost by issuing new equity. Thus, to create scope for active risk management policies, we assume that equity finance is costly in that raising outside equity reduces the value
of existing shareholders more than the notional amount of equity issuance (See Myers and Majluf (1984) and Cooley and Quadrini (2001)). We capture the loss to existing shareholders using a "dilution" function,
![]() :
:
where
3.3 Value Maximization Problem
The flow of funds constraint facing the firm can be expressed as
where
Despite the tax advantage of debt, the firm may optimally choose to hold cash. In order to preserve tractability, we do not introduce frictions, such as transaction costs, that make frequent refinancing of debt costly. These frictions may lead the firm to simultaneously hold debt and liquid assets, an issue that is not central to the task of explaining the low frequency movement of cash.25
The firm problem can be defined recursively as the maximization of the value of equity,
where
The non-convexity of the value function with respect to capital due to the presence of fixed cost of adjustment makes the analysis of the efficiency condition for capital rather complicated. To detour this complexity, we redefine the firm problem as a discrete choice problem,
Following Abel and Eberly (1994), we proceed in two steps: first, find the optimal investment under the assumption that action (
Note that
- If
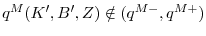 ,
,
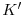 satisfies
satisfies
- If
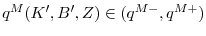 ,
,
 satisfies
satisfies
where
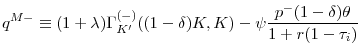 |
and
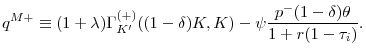 |
To build intution, consider the neoclassical case without financial frictions, i.e.,
![]() always. In this case, the optimality condition on action (13) reduces to
always. In this case, the optimality condition on action (13) reduces to
![]() , simply equalizing the marginal cost and benefit of investment. The difference brought about by the financial friction is that the marginal cost and benefit of
adjustment are no longer measured by
, simply equalizing the marginal cost and benefit of investment. The difference brought about by the financial friction is that the marginal cost and benefit of
adjustment are no longer measured by
![]() and
and ![]() , but by
, but by
![]() and
and
![]() as shown by (13).27 Since the shadow value of internal funds can go above 1 with financial frictions, we can see that these frictions increase the marginal cost of investment to
as shown by (13).27 Since the shadow value of internal funds can go above 1 with financial frictions, we can see that these frictions increase the marginal cost of investment to
![]() . However, they also increase the marginal benefit of investment, which is reflected in the fact that
. However, they also increase the marginal benefit of investment, which is reflected in the fact that
![]() . This last term measures the shadow value of the borrowing constraint: as the firm chooses a greater production capacity, it expands
its debt capacity as well. The second term of the marginal benefit of investment measures the marginal value of expanded debt capacity.
. This last term measures the shadow value of the borrowing constraint: as the firm chooses a greater production capacity, it expands
its debt capacity as well. The second term of the marginal benefit of investment measures the marginal value of expanded debt capacity.
The FOC (13) shows that the target capital level chosen by the firm when action is optimal is a function of the financial conditions of the firm. This is in contrast to the neoclassical benchmark in which the target capital stock is a function of investment fundamentals,
i.e., the current technology level. In particular, the tangibility of capital assets affects investment directly through the presence of ![]() in the efficiency condition: only to the
extent that the capital assets of the firm are pledgeable against debt financing, capacity expansion leads to the expansion of debt capacity. The secular downward trend in asset tangibility
in the efficiency condition: only to the
extent that the capital assets of the firm are pledgeable against debt financing, capacity expansion leads to the expansion of debt capacity. The secular downward trend in asset tangibility ![]() affects the trade-off involved in optimal investment decisions by making the marginal cost of investment weigh more than the marginal benefit of investment. One margin firms have to avoid this de facto strengthening of financial market frictions is
to reduce their dependence on debt financing by holding outright cash assets. Using a quantitative exercise we will provide a test of the strength of this "collateral channel."
affects the trade-off involved in optimal investment decisions by making the marginal cost of investment weigh more than the marginal benefit of investment. One margin firms have to avoid this de facto strengthening of financial market frictions is
to reduce their dependence on debt financing by holding outright cash assets. Using a quantitative exercise we will provide a test of the strength of this "collateral channel."
The efficiency condition for equity issuance can be derived in the same way. We start with the observation that
![]() is everywhere differentiable except at
is everywhere differentiable except at ![]() . Let
. Let
![]() denote the right hand side derivatie of
denote the right hand side derivatie of
![]() at
at ![]() .28 As in the case of investment problem, we derive an optimality condition based on
.28 As in the case of investment problem, we derive an optimality condition based on
![]() as follows:
as follows:
- If
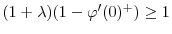 , equity issuance satisfies
, equity issuance satisfies
- If
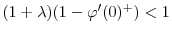 , equity issuance satisfies
, equity issuance satisfies
Note that (8) implies
![]() . Hence, the condition for equity issuance can also be stated as
. Hence, the condition for equity issuance can also be stated as
![]() . A few remarks are useful to characterize the equity issuance policy. First, (15) implies that equity
issuance is associated with
. A few remarks are useful to characterize the equity issuance policy. First, (15) implies that equity
issuance is associated with
![]() . Given the complementary slackness condition
. Given the complementary slackness condition
![]() , the condition implies that
, the condition implies that ![]() when equity issuance is strictly
positive, i.e., the firm never issues new shares and pays out dividends simultaneously. Second,
when equity issuance is strictly
positive, i.e., the firm never issues new shares and pays out dividends simultaneously. Second,
![]() in our parametric assumption of equity issuance cost. This means that (15) does not pin down the level of equity issuance. However,
since
in our parametric assumption of equity issuance cost. This means that (15) does not pin down the level of equity issuance. However,
since ![]() when
when ![]() ,
, ![]() should be determined by a financing gap,
should be determined by a financing gap,
![\displaystyle \frac{1}{1-\varphi _{1}}\left\{ \varphi _{0}+v_{K}\Gamma (K^{\prime },K)+(1+r_{B})B-[(1-\tau _{c})\Pi (K,Z;w)+\tau _{c}\delta K+B^{\prime }]\right\} ,](img118.gif) |
which is the amount of equity issuance required to satisfy the flow of funds constraint with
To analyze the efficiency condition for
![]() , we define, in an analogy to Tobin's Q, financial Q as
, we define, in an analogy to Tobin's Q, financial Q as
When
In the particular case of non-binding collateral constraint, one can merge (13) and (18) into a single expression,
This condition says that at the margin, the firm should be indifferent between physical investment and financial investment (either by investing in financial assets or by reducing debt). This suggests that the information contents of Tobin's marginal Q and financial Q (or corporate cash hoarding) are correlated along any equilibrium path, and more so if the collateral constraint is binding less frequently. In our quantitative exercise, we show that the secular downward trend in asset tangibility leads to a lower frequency of collateral constraint binding as the firms want to hold greater portions of line of credits unused. As a result, we predict that the decline in the asset tangibility leads to a greater correlation between Tobin's Q and cash hoarding, which is a new testable prediction of our theory.
3.4 Properties of Optimal Real and Financial Policies
In this section, before turning to the quantitative analysis we characterize the properties of the optimal policies of the individual firm in partial equilibrium by showing the marginal impact of each state variable. We denote a firm's real investment policy by
![]() , and net debt policy by
, and net debt policy by
![]()
3.4.1 Investment Options, Financial Frictions and Risk Management
The top panels of Figure 3 show how the net leverage policy (
![]() ) responds to the current capacity level (
) responds to the current capacity level (![]() , on the
horizontal axis). If the ratio is negative (positive), it means that the firm desires to hold net financial assets (liabilities) for the next period. The left panel shows the case when firms face both non-convex adjustment friction and partial irreversibility, whereas the right panel shows the case
with the irreversibility friction only (we follow the same order in subsequent figures).
, on the
horizontal axis). If the ratio is negative (positive), it means that the firm desires to hold net financial assets (liabilities) for the next period. The left panel shows the case when firms face both non-convex adjustment friction and partial irreversibility, whereas the right panel shows the case
with the irreversibility friction only (we follow the same order in subsequent figures).
The figures assume that the firm's current financial condition (![]() ) is held constant at its steady state level. The three lines for net leverage ratio correspond to the cases with a
normal technology level (blue, solid line), 30% above (black, dash-dotted line) and 30 % below (red, dashed line) the normal level. To highlight the properties of liquidity demand, we set
) is held constant at its steady state level. The three lines for net leverage ratio correspond to the cases with a
normal technology level (blue, solid line), 30% above (black, dash-dotted line) and 30 % below (red, dashed line) the normal level. To highlight the properties of liquidity demand, we set
![]() , a relatively low level of tangible capital ratio, which implies a low degree of pledgeability of production assets in borrowing contracts. In fact, as will be shown later,
this value of
, a relatively low level of tangible capital ratio, which implies a low degree of pledgeability of production assets in borrowing contracts. In fact, as will be shown later,
this value of ![]() is associated with a large accumulation of net financial assets by firms on average.
is associated with a large accumulation of net financial assets by firms on average.
Consider the case with the non-convex adjustment cost and irreversibility. The overall contour of the net leverage policy can be described in the following way: first, the liquidity demand is associated with relatively small firms while debt accumulation is associated with large firms on the scale of the horizontal axis; second, firms tend to accumulate liquid financial assets in anticipation of a large adjustment of production capacity, and then to disburse all liquid financial assets at the moment of exercising investment option (see the bottom left panel together with the top left panel to see the joint dynamics of capacity expansion and liquidity hoarding); third, the duration of cash hoarding tends to be longer with lower technology as the firms desire to keep their investment options alive given the mean reverting process of technology.
The general contour of the leverage policy for the pure irreversibility case is similar, but the overall level of cash hoarding is substantially smaller. The reason for this can be found in the difference in the nature of adjustments of physical capacity. In the bottom panels of the figure, one can see that the size of investment inaction region is greatly reduced without the non-convex adjustment.30 For example, when the technology level is at its steady state (the case of blue, solid line), the inaction region without the nonconvex adjustment cost is more than 80% smaller than with the non-convex cost, which explains the shorter duration of cash hoarding without the non-convex adjustment friction.
With the non-convex adjustment friction, the size of adjustment is much larger and lumpy. In the figure, the jumps up and down in capacity levels are on the order of 30% of existing capacity, which is what Cooper and Haltiwanger (2006) classify as (dis)investment " spikes" or "lumpy investment." Lumpy investment is what the firm wants to insure itself against by holding extra liquidity in frictional financial markets. Absent this friction, the optimal amount of liquidity insurance is substantially reduced in the top right panel. In fact, in this case, the financial policy can take an extreme form of never-to-invest in liquid financial assets, build up leverage to exploit tax benefits and to pay out the proceeds of debt issuance as dividends especially when the firm's current technology level is unusually high or the firm has a substantial degree of overcapacity as shown by black, dash-dotted line on the upper right panel.
As mentioned earlier in the discussion of FOCs, the financial friction modifies the properties of the (![]() ,
,![]() ) adjustment rule for production capacity. However, as shown in the bottom panels, under the financial friction, the investment targets are not independent of currently installed capital because the amount of financing that can be raised through internal funds and
borrowing may not be sufficient to cover investment expenditures if the gap between the target and currently installed capital is too large. As a result,
) adjustment rule for production capacity. However, as shown in the bottom panels, under the financial friction, the investment targets are not independent of currently installed capital because the amount of financing that can be raised through internal funds and
borrowing may not be sufficient to cover investment expenditures if the gap between the target and currently installed capital is too large. As a result,
![]() may positively respond to
may positively respond to ![]() even when firm's
investment mode is active despite the absence of convex adjustment cost.
even when firm's
investment mode is active despite the absence of convex adjustment cost.
3.4.2 Financial Frictions and Debt/Cash Dynamics
In this subsection, we show how past financial conditions affect the dynamics of risk management. To that end, we consider hypothetical firms with an identical level of technology (at its steady state), but with different net-debt position (![]() ). In the upper panels of Figure 4, we show how firms' liquidity demand changes as their initial financial condition changes. More specifically, we consider three levels of
). In the upper panels of Figure 4, we show how firms' liquidity demand changes as their initial financial condition changes. More specifically, we consider three levels of ![]() that would imply net debt ratios -0.3 (blue, solid line), 0.0 (black, dash-dotted line), and 0.30 (red, dashed line), relative to the steady state level of total assets (book value of capital plus cash,
that would imply net debt ratios -0.3 (blue, solid line), 0.0 (black, dash-dotted line), and 0.30 (red, dashed line), relative to the steady state level of total assets (book value of capital plus cash, ![]() ), respectively.
), respectively.
The first can be considered as the case of so called cash cow firm, a special case with ample financial slack that allows the firm to behave like a financially frictionless firm in most of the state space. The third can be thought of as the firm with weak balance
sheet condition, which are potentially subject to financial distress. Roughly, this case matches the net-debt structure of the firms in the 75 percentile of net-leverage distribution in 2012Q4 of Compustat. The second is an intermediate case. For each of these cases, we consider an identical level
of asset tangibility at
![]() .
.
The key takeaway here is that there is a tremendous amount of inertia in firm's financial position: firms that have net financial assets (positive net debt) today are more likely to hold net financial assets (positive net debt) tomorrow. In a frictionless world with no adjustment costs of financial assets/liabilities, there is no reason to expect such inertia since equity markets should provide perfect shock absorption. Equity frictions are responsible for making financial variables slow moving. Thus, the inertial dynamics of firms' balance sheet is an indicator of financial frictions.
This is also related to the phenomenon known as the sensitivity of cash to cash flow in the literature (see Almeida, Campello, and Weisbach (2004)). A poor balance sheet condition today is likely to lead to a poor cash flow today, which, in turn, is likely to lead to a poor balance sheet condition tomorrow under frictional financial markets. What is surprising in our results is that it is not only the firms with positive net debt position that exhibit sensitivity to cash flow in their cash/debt policy, but it is also the firms with ample financial slacks that show sensitivity to current financial conditions. This is because the seemingly unconstrained firms have obtained such financial slack to insure themselves against future financial constraints in a forward looking manner.
The lower panels show the same phenomenon from a different angle in (
![]() ) diagrams, where a purple, dashed line shows 45 degree line, which, when crossed by the policy functions, indicates fixed points
) diagrams, where a purple, dashed line shows 45 degree line, which, when crossed by the policy functions, indicates fixed points
![]() . To show the relationship between
. To show the relationship between ![]() and
and
![]() , we consider three fixed levels of production capacity. In all cases, we set the technology level equal to the steady state, 1.
, we consider three fixed levels of production capacity. In all cases, we set the technology level equal to the steady state, 1.
Consider the case with fixed cost and irreversibility, the lower left panel. The contour of the policy functions can be described as `S-shape' with two flat regions and an upward sloping region between them. Among the two flat regions, only one of them is the `target' level of net-debt position, as only the lower plateau crosses the 45 degree line from the above. The upward sloping region is responsible for the sluggish dynamics of cash. It indicates a positive serial correlation between today's and tomorrow's financial condition, which, in turn, is entirely due to the financial friction in our framework rather than to frictions in adjusting balance sheet condition.
Note that the upward sloping region is much smaller when the real adjustment friction is entirely due to irreversibility (the bottom right panel).31 The
inflexibility in the adjustment of physical capital interacts with financial friction to create a greater serial correlation in cash balances. The strength of the interaction crucially depends on the state of the firm, ![]() and
and ![]() .
.
3.4.3 Investment Predictability: Cash vs. Tobin's Q
Non-convex adjustment frictions imply that firms adjust their capital infrequently, and investment is lumpy when executed. When a firm anticipates an investment opportunity, but keeps the growth option alive, the value of equity grows due to the option value, but the current capacity shrinks at a constant rate of depreciation. This implies that a firm's Tobin's Q should be high when it nears the exercise of growth option. In contrast, Tobin's Q should be unusually low right after a large expansion of capacity. This pattern can be seen in Figure 5, which shows how Tobin's Q responds to changes in capital accumulation.32
If external financing is costly, the same dynamic pattern can be expected for the accumulation of liquid assets: a firm accumulates financial resources in anticipation of its investment opportunities, but decumulates its financial assets rather quickly or even accumulate debt after exercising the options. This suggests that the information contents of Tobin's Q and liquid asset holdings may be highly correlated under financial market friction and nonconvex adjustment friction.
To verify this possibility, the bottom panels reproduce the net debt-to-total capital ratios shown in Figure 3. By comparing the upper and lower panels together, one can easily see that Tobin's Q and cash accumulation are perfectly correlated when technology level
changes. For instance, in the left panels for the case with the fixed adjustment friction, black, dashed vertical lines indicate the places where the orderings of Tobin's Qs associated with different technology levels change. Tobin's Q for the case of low technology is higher (lower) than the one
of high technology exactly when net-debt policy
![]() is placed lower (higher) than
is placed lower (higher) than
![]() , suggesting that the ordering of Tobin's Q might be driven by the same mechanism behind the opposite ordering of net-debt policy. To put it more simply, Tobin's Q is
higher when the firm's liquidity demand, including unused line of credit, is higher. This confirms our conjecture that cash holdings and Tobin's Q may convey the same information regarding future investments.
, suggesting that the ordering of Tobin's Q might be driven by the same mechanism behind the opposite ordering of net-debt policy. To put it more simply, Tobin's Q is
higher when the firm's liquidity demand, including unused line of credit, is higher. This confirms our conjecture that cash holdings and Tobin's Q may convey the same information regarding future investments.
3.4.4 Asset Tangibility and Cash Accumulation
We now show the effect of changes in asset tangibility on the liquidity management strategy. Figure 6 considers three different values of the tangible capital ratio,
![]() , 0.5 and 0.3 for which we show the corresponding optimal
, 0.5 and 0.3 for which we show the corresponding optimal
![]() policies (upper panels).
policies (upper panels).
![]() is chosen to match the intangible-to-total tangible assets ratio, 0.25 (
is chosen to match the intangible-to-total tangible assets ratio, 0.25 (
![]() ) of early 1970s in the data, shown in the first panel of Figure 1.
) of early 1970s in the data, shown in the first panel of Figure 1.
![]() can be interpreted as implying the intangible ratio 1.0 (
can be interpreted as implying the intangible ratio 1.0 (
![]() ) around early 2000s in the data. We then consider one more hypothetical value
) around early 2000s in the data. We then consider one more hypothetical value
![]() , (or
, (or
![]() in terms of the intangible capital ratio) for a `projection'. This case also serves as an illustration of the liquidity management strategy for firms operating in
intangible intensive industries.33
in terms of the intangible capital ratio) for a `projection'. This case also serves as an illustration of the liquidity management strategy for firms operating in
intangible intensive industries.33
The dramatic increase in liquidity demand in reaction to the decline of asset tangibility is evident in the upper panels. For instance, when the real adjustment friction consists of fixed adjustment cost and irreversibility (the upper left panel), the maximum liquidity demand doubles from 0.25
to 0.5 relative to the book value of capital chosen for tomorrow when ![]() declines from 0.8 to 0.5. The liquidity demands also doubles to 1.0 relative to the book value of capital when
declines from 0.8 to 0.5. The liquidity demands also doubles to 1.0 relative to the book value of capital when
![]() further declines to 0.3.
further declines to 0.3.
The pure irreversibility case exhibits the same pattern, although in this case the magnitude of cash holdings becomes much smaller relative to the case with non-convex adjustment friction. It is not the fixed cost per se that increases the demand for liquidity. The lumpy investment friction makes it optimal to adjust physical capital only infrequently, increasing the average size of adjustment, which then requires a bulk of liquid financial resources.
Under the frictional financial market, the firm cannot pledge the capital against borrowing due to the reduced debt capacity with the decline in ![]() . As the growing reliance on
intangible capital in production reduces a firm's financial buffer, the firm compensates for the forgone financial flexibility by holding more liquid assets. The bottom panels of the figure show that the marginal gains from holding liquid assets can be quite substantial. To gauge the contribution
of the liquidity management strategy to equity value, we re-solve the equity problem after imposing a constraint that the firm cannot invest in liquid financial assets, i.e.
. As the growing reliance on
intangible capital in production reduces a firm's financial buffer, the firm compensates for the forgone financial flexibility by holding more liquid assets. The bottom panels of the figure show that the marginal gains from holding liquid assets can be quite substantial. To gauge the contribution
of the liquidity management strategy to equity value, we re-solve the equity problem after imposing a constraint that the firm cannot invest in liquid financial assets, i.e.
![]() . We denote this equity value by
. We denote this equity value by ![]() . The difference between
. The difference between ![]() and
and ![]() then measures the value
of option to invest in liquid assets. This is equivalent to the willingness to pay to obtain the option to invest in liquid assets. The bottom panels show that the option can increase the value of equity more than 5 percent, which can be considered a significant
improvement.
then measures the value
of option to invest in liquid assets. This is equivalent to the willingness to pay to obtain the option to invest in liquid assets. The bottom panels show that the option can increase the value of equity more than 5 percent, which can be considered a significant
improvement.
4.1 Calibration
Our key comparative statics consists in detailing the general equilibrium outcomes of our model for levels of asset tangibility that match their historical counterparts in the US economy over the last decades. The goal of the exercise is to assess whether the model can generate a good match for
the high average level of cash holdings we observe in US data for the last decade. The exercise relies on the following calibration. The elasticity of the profit function with respect to capital ![]() is set equal to 0.6 as in previous studies (for instance, see Hennessy and Whited (2007) for a structural estimate). We set the annual depreciation rate equal to 0.10. We choose the resale value of capital
is set equal to 0.6 as in previous studies (for instance, see Hennessy and Whited (2007) for a structural estimate). We set the annual depreciation rate equal to 0.10. We choose the resale value of capital
![]() . This is an upper bound with respect to the available evidence on the resale value of capital (see, for instance, Ramey and Shapiro
(2001)), which we choose to show that even a relatively small discount in resale value is sufficient to generate substantial amount of saving in liquid asset holdings.34 To parametrize the fixed cost of investment, we follow Cooper and Haltiwanger (2006), who estimate a fixed cost of investment of about 1% of installed capital. We set this value to be proportional to the steady state level of capital
accumulation in the frictionless benchmark. The fixed cost of operation (
. This is an upper bound with respect to the available evidence on the resale value of capital (see, for instance, Ramey and Shapiro
(2001)), which we choose to show that even a relatively small discount in resale value is sufficient to generate substantial amount of saving in liquid asset holdings.34 To parametrize the fixed cost of investment, we follow Cooper and Haltiwanger (2006), who estimate a fixed cost of investment of about 1% of installed capital. We set this value to be proportional to the steady state level of capital
accumulation in the frictionless benchmark. The fixed cost of operation (![]() ) is set to be equal to 5% of steady state profits following Gilchrist, Sim, and Zakrajsek
(2010). This value helps to match dividend payout ratio in the data. To calibrate the idiosyncratic technology shock process, we set
) is set to be equal to 5% of steady state profits following Gilchrist, Sim, and Zakrajsek
(2010). This value helps to match dividend payout ratio in the data. To calibrate the idiosyncratic technology shock process, we set
![]() and
and
![]() (equivalent to 0.15 in quarterly frequency), which is roughly in
line with the estimates of Gourio (2008) regarding the transitory part of idiosyncratic shock process based on Compustat data. As for the tangible-to-intangible capital ratio
(equivalent to 0.15 in quarterly frequency), which is roughly in
line with the estimates of Gourio (2008) regarding the transitory part of idiosyncratic shock process based on Compustat data. As for the tangible-to-intangible capital ratio ![]() , this is the key parameter for which we provide an extensive set of comparative statistics.
, this is the key parameter for which we provide an extensive set of comparative statistics.
The risk free rate is calibrated as 0.06, such that the after tax annual interest rate is about 0.04. We choose the fixed cost of equity issuance to be 1.5 percent of the steady state level of the frictionless capital stock. This is slightly higher than in Bolton, Chen, and Wang (2009), for example. For the linear cost of equity issuance, estimates and calibration choices in the literature range from 0.06 (Gomes (2001)) to 0.30 (Cooley and Quadrini (2001)). We choose a relatively conservative value of 0.15, which is roughly in the middle range. Finally, we set the corporate income tax and interest income tax rates as 0.35 and 0.30, respectively. As our results show, this difference is large enough to create a substantial incentive to accumulate debt without the need to make additional assumptions on firms' discounting factor or death probability. Finally, we specify a very small agency cost of cash holdings, 5bps.
4.2 Comparative Statistics in General Equilibrium
Tables 7 - 9 summarize our quantitative results on the effect of asset tangibility on real and financial decisions of individual firms and
macroeconomic aggregates in stationary equilibrium. We consider 3 different levels of asset tangibility (tangible-to-total capital ratio), starting from
![]() and going down to
and going down to
![]() , a range that roughly covers its empirical counterpart for the US economy since 1970s shown in Figure 1 and Table 2. For the sake of
comparison and to further highlight the quantitative implications of the model, we also report model-implied moments for an even lower hypothetical level of
, a range that roughly covers its empirical counterpart for the US economy since 1970s shown in Figure 1 and Table 2. For the sake of
comparison and to further highlight the quantitative implications of the model, we also report model-implied moments for an even lower hypothetical level of
![]() . We report the results for the non-convex adjustment cost and irreversibility case in the first three columns and the results for the irreversibility only case in the last three
columns of each table.
. We report the results for the non-convex adjustment cost and irreversibility case in the first three columns and the results for the irreversibility only case in the last three
columns of each table.
First, consider the economy with real frictions involving both non-convex adjustment and irreversibility in Table 7. The first row shows that as the tangible capital ratio declines from 0.8 to 0.5, the cash-to-tangible asset ratio (book value of tangible capital, profits and cash holdings) increases by 16ppt from 2% to 18%. This result shows that, in line with our reduced-form estimates, an increase in firms' precautionary demand for liquid assets in response to a decline in the pledgeability of production assets goes a long way toward explaining a substantial part of the observed secular trend in US cash holdings.
In fact, over the 1970-2010 period, the cash ratio in the data increased by 12ppt from 9% to 21% (the second row), suggesting that our model with non-convex adjustment frictions not only can resolve the quantitative puzzle in the literature, but if anything it actually overshoots the data. The third column of the table suggests that if asset tangibility had declined to 0.3, the model would have predicted that almost more than 40% of corporate balance sheets would consist of liquid financial assets, which represents a radical departure form the conventional notion of a public corporation which relies mostly on external finance. While this result may be surprising and the parameter choice is out of range when the benchmark is the entire US economy, it does have some relevance for firms operating in technology intensive industries.
In contrast, the right panel of Table 7 shows that the irreversibility friction by itself is not sufficient to match the magnitudes of liquid assets seen in the data: as the tangible capital ratio goes down from 0.8 to 0.5, cash-to-tangible asset ratio only goes up 5ppt from zero to 5% (the first row). While the hypothetical decline in the tangible ratio to 0.3 can generate 20% cash ratio, these results indicate that the interplay of both financial and real frictions is key to explaining the magnitude of liquidity hoardings we see in the data.35
The fourth row of the table shows that asset tangibility has a dramatic impact on net-leverage, a result that mirrors the rise in precautionary savings and further corroborates our "shrinking debt capacity" mechanism. The last row of the table shows that the decline in asset tangibility also greatly reduces the usage of debt capacity: the limited pledgeability not only reduces the debt capacity of firms, but leads them to hold greater slack in borrowing capacity. As we mentioned earlier, the model penalizes cash holding in two ways: tax disadvantage and agency costs. The precautionary saving motive in the face of rising intangible capital is potent enough to overcome these disadvantages. For instance, the economy with both non-convex cost and irreversible frictions is characterized by a reduction in net-leverage by 30ppt from 47% to 17% as asset tangibility declines from 0.8 to 0.5.
Figure 7 shows how the joint distribution of capital and net-debt positions also responds to the decline in the tangible capital ratio from
![]() (blue bars) to 0.5 (red bars) to 0.3 (light blue bars). As the tangible capital ratio declines, the distribution moves to the left in such a way that more probability mass is allocated to the negative portion of the support on the net-debt dimension. In
fact, with
(blue bars) to 0.5 (red bars) to 0.3 (light blue bars). As the tangible capital ratio declines, the distribution moves to the left in such a way that more probability mass is allocated to the negative portion of the support on the net-debt dimension. In
fact, with
![]() , the stationary distribution allocates more probability mass to the negative support than to the positive support, which means that the corporate sector moves toward becoming a
net creditor sector. The third column of the fourth row confirms this result. The flip side of this transformation is that households turn into a net borrowing sector, supplying liquid financial assets to the corporate sector.
, the stationary distribution allocates more probability mass to the negative support than to the positive support, which means that the corporate sector moves toward becoming a
net creditor sector. The third column of the fourth row confirms this result. The flip side of this transformation is that households turn into a net borrowing sector, supplying liquid financial assets to the corporate sector.
Table 8 shows several additional model-implied moments, including how asset tangibility affects the sensitivity of investment and cash holdings to cash flows (Rows [1]-[2]), and the comovement between investment, cash and Tobin's Q (Rows [3]-[4]), and the properties of
distribution of investment rates (Rows [5]-[6]). As predicted, asset tangibility generally increases the sensitivity of investment and cash to cash flow. This is another manifestation of the shrinking debt capacity. As shown in Row [3], the contemporaneous correlation between investment and Tobin's
Q is negative due to the nature of the (S,s) adjustment in capacity. Notably and in line with our earlier discussion of investment predictability, the contemporaneous correlation between cash and Tobin's Q is positive, and more importantly, increasing with the degree of intangibility. For instance,
consider the case with irreversibility friction only, shown in Row [3] of right panel. When
![]() , the correlation is essentially zero. However as
, the correlation is essentially zero. However as ![]() drops to
0.5, the correlation jumps to 0.83. The increase in the contemporaneous correlation is less dramatic when capacity adjustment involves non-convex adjustment cost as it jumps from 0.6 to 0.88. These results confirm our prediction that cash and Tobin's Q become more highly correlated as the share of
tangible assets declines and firms are led to rely increasingly on internal sources of funding.
drops to
0.5, the correlation jumps to 0.83. The increase in the contemporaneous correlation is less dramatic when capacity adjustment involves non-convex adjustment cost as it jumps from 0.6 to 0.88. These results confirm our prediction that cash and Tobin's Q become more highly correlated as the share of
tangible assets declines and firms are led to rely increasingly on internal sources of funding.
Finally, Table 9 shows that the decline in asset tangibility can have sizable, adverse consequences for the overall level of capital accumulation, output and consumption. Depending on the specification of the adjustment cost friction, a transition from
![]() to
to
![]() can have an impact on capital accumulation and consumption of an order of magnitude up to -2.3% and -1.2%, respectively. As the production technology shifts toward intangible
assets, capital assets lose a substantial part of their eligibility as collateral, which leads to a tightening of the debt constraint. Surprisingly, however, there is virtually no impact on total firm value, as shown in the last row. This result implies that firms are able to almost perfectly
neutralize the impact of declining asset tangibility by switching to liquidity management strategies that rely more heavily on cash. Nevertheless, the results on real economic activity point to an inefficiency in that the limited pledgeability of capital assets hinders efficient capital allocation,
a result that could have been avoided if the debt contracts had been fully enforceable.
can have an impact on capital accumulation and consumption of an order of magnitude up to -2.3% and -1.2%, respectively. As the production technology shifts toward intangible
assets, capital assets lose a substantial part of their eligibility as collateral, which leads to a tightening of the debt constraint. Surprisingly, however, there is virtually no impact on total firm value, as shown in the last row. This result implies that firms are able to almost perfectly
neutralize the impact of declining asset tangibility by switching to liquidity management strategies that rely more heavily on cash. Nevertheless, the results on real economic activity point to an inefficiency in that the limited pledgeability of capital assets hinders efficient capital allocation,
a result that could have been avoided if the debt contracts had been fully enforceable.
4.3 Alternative Specification: A General CES Case
Our baseline model uses the special case of CES capital aggregator when
![]() which implies no substitutability between tangible and intangible capital inputs. It is important to assess the extent to which our results owe to this specific
assumption. To address this question, we consider the case of a general CES capital aggregator. However, we have to face a classical curse of dimensionality issue that arises in this case due to the fact that with this more general technology we need to track the two types of capital as separate
state variables.
which implies no substitutability between tangible and intangible capital inputs. It is important to assess the extent to which our results owe to this specific
assumption. To address this question, we consider the case of a general CES capital aggregator. However, we have to face a classical curse of dimensionality issue that arises in this case due to the fact that with this more general technology we need to track the two types of capital as separate
state variables.
A final contribution of the paper is to show that one can overcome this problem and recover tractability by adopting the following setup: (i) the idiosyncratic technology follows a geometric random walk,
![]() ,
,
![]() ; (ii) the profit function is homogeneous of degree 1 in the technology and capital service, i.e.,
; (ii) the profit function is homogeneous of degree 1 in the technology and capital service, i.e.,
![]()
![]() ; (iii) the fixed costs of operation, the fixed costs of capital adjustment, and the fixed cost of equity issuance are
proportional to the current technology level. Under these assumptions, the equity value function is homogeneous of degree 1 in (
; (iii) the fixed costs of operation, the fixed costs of capital adjustment, and the fixed cost of equity issuance are
proportional to the current technology level. Under these assumptions, the equity value function is homogeneous of degree 1 in (
![]() ) as the capital aggregator is homogeneous of degree 1 in (
) as the capital aggregator is homogeneous of degree 1 in (
![]() ) and so is the profit function in
) and so is the profit function in ![]() and
and
![]() . Using this property, we can normalize the value function by the current technology level
. Using this property, we can normalize the value function by the current technology level ![]() , and solve the following 'normalized' value maximization problem:
, and solve the following 'normalized' value maximization problem:
where the normalized profit function is given by
![\displaystyle \pi (k_{T},k_{N})=\eta (w)\left[ (1-\theta )\left( \frac{k_{T}}{1-\theta }% \right) ^{-\rho }+\theta \left( \frac{k_{N}}{\theta }\right) ^{-\rho }\right] ^{-\gamma /\rho }](img180.gif) |
and
Even with the normalization, solving for
![]() requires tremendous computing resources. For this reason, we do not solve for a stationary general equilibrium, but solve for the individual firm problem, and then simulate
the model economy with a set random draws for idiosyncratic technology shocks in partial equilibrium with 250 periods and 10,000 firms.36 While not ideal,
our results indicate that we do not lose much insight by adopting this partial equilibrium setting.
requires tremendous computing resources. For this reason, we do not solve for a stationary general equilibrium, but solve for the individual firm problem, and then simulate
the model economy with a set random draws for idiosyncratic technology shocks in partial equilibrium with 250 periods and 10,000 firms.36 While not ideal,
our results indicate that we do not lose much insight by adopting this partial equilibrium setting.
Table 10 reports moments from this simulation exercise. In interpreting these results, it is important to keep in mind that the value of ![]() is no longer identical
to the tangible-to-total capital ratio since firms can now freely deviate from this value. The idea of the exercise is to see if firms still react to changes in
is no longer identical
to the tangible-to-total capital ratio since firms can now freely deviate from this value. The idea of the exercise is to see if firms still react to changes in ![]() in the same way they
did in our baseline results. With more flexible technology, firms may not have as strong an incentive to hoard liquid assets, since they now gain an extra margin from being able to substitute between the two types of real assets.
in the same way they
did in our baseline results. With more flexible technology, firms may not have as strong an incentive to hoard liquid assets, since they now gain an extra margin from being able to substitute between the two types of real assets.
The first and second rows show the impact of technological change on the ratios of cash-to-tangible assets and net debt-to-tangible assets. Firms do not hold liquid assets when
![]() . Relative to the Leontief case firms can now can use the more flexible technology as another risk management tool: when facing investment opportunities, firms can choose a
higher ratio of tangible-to-intangible capital ratio to expand their borrowing capacity despite lower technological efficiency.
. Relative to the Leontief case firms can now can use the more flexible technology as another risk management tool: when facing investment opportunities, firms can choose a
higher ratio of tangible-to-intangible capital ratio to expand their borrowing capacity despite lower technological efficiency.
![]() means that the marginal cost of deviating from the technologically efficient ratio is not big and, as a result, it reduces the amount of liquidity demand. However, as
means that the marginal cost of deviating from the technologically efficient ratio is not big and, as a result, it reduces the amount of liquidity demand. However, as
![]() decreases to 0.5 and to
decreases to 0.5 and to ![]() liquidity demand picks up significantly since the efficiency loss involved in the adoption of higher tangible capital ratios becomes higher and, as a result, firms are led to use their financial side for risk management and hold
more liquid assets. As in the baseline case, the net leverage ratio declines monotonically as
liquidity demand picks up significantly since the efficiency loss involved in the adoption of higher tangible capital ratios becomes higher and, as a result, firms are led to use their financial side for risk management and hold
more liquid assets. As in the baseline case, the net leverage ratio declines monotonically as ![]() goes down. This result, together with those on cash ratio, confirms that our baseline
conclusions are not driven by the Leontief assumption. The extended model also shows that the information content of Tobin's Q and cash holdings is almost identical as these variables are nearly perfectly correlated (row [3]).
goes down. This result, together with those on cash ratio, confirms that our baseline
conclusions are not driven by the Leontief assumption. The extended model also shows that the information content of Tobin's Q and cash holdings is almost identical as these variables are nearly perfectly correlated (row [3]).
The last row of the table reports the correlation between net leverage and tangible asset ratios. This correlation increases as ![]() goes down. This result shows that when firms find
it optimal to choose higher leverage ratios they tend to choose higher levels of tangible capital ratios. In the model, causation runs in both directions. Firms can borrow more because they have more tangible capital as collateral. However, at the same time, more vulnerable balance sheet conditions
also lead firms to hold more pledgeable assets in their balance sheet since these assets expand borrowing capacity for a long period of time and since it is costly to strengthen their balance sheet conditions by holding liquid assets in the short run.
goes down. This result shows that when firms find
it optimal to choose higher leverage ratios they tend to choose higher levels of tangible capital ratios. In the model, causation runs in both directions. Firms can borrow more because they have more tangible capital as collateral. However, at the same time, more vulnerable balance sheet conditions
also lead firms to hold more pledgeable assets in their balance sheet since these assets expand borrowing capacity for a long period of time and since it is costly to strengthen their balance sheet conditions by holding liquid assets in the short run.
Finally, an advantage of the CES extension is that it offers a setting that can be used to explore additional channels, over and above the collateral one that constitutes the main focus of our paper. For example, it would be interesting to explore whether lower asset tangibility also leads to higher cash holdings when intangible assets have lower depreciation rates or adjustment costs. However, these additional channels are beyond the scope of the present paper and constitute a potentially interesting avenue for future work.
5 Conclusion
We have presented new evidence and theory which support the hypothesis that the rise in intangible capital can explain the secular increase in US corporate cash holdings over the last four decades. Our empirical evidence shows that intangible capital is a key empirical determinant of cash holdings. In addition, the evidence suggests that both financial and real frictions contribute to explain why intangible capital matters so much. Next, we built a structural dynamic model where intangible capital matters for firms' cash management decisions through a "collateral channel" because of the interplay between financial and investment frictions. All else equal, our model generates an outsized increase in the demand for corporate cash in response to an increase in intangible capital. We conclude that intangible capital is a crucial ingredient to providing a satisfactory analytic account of key stylized facts in corporate finance and macroeconomics, which to date had eluded standard explanations.
References
"A Unified Model of Investment Under Uncertainty," The American Economic Review, 84(5), pp. 1369-1384.Note: Panel (a), (b) and (c) show intangible capital ratio relative to total (tangible) assets, cash-to-total (tangible) assets and net-debt-to-total (tangible) assets, respectively. The sample includes all Compustat firm-year observations from 1970 to 2010 with positive values for the book value of total assets and sales revenue for firms incorporated in the United States. Financial firms (SIC code 6000-6999) and utilities (SIC codes 4900-4999) are excluded from the sample, yielding a panel of 176,877 observations for 18,535 unique firms. Variable definitions are provided in the Appendix.
Note: The sample includes all Compustat firm-year observations from 1970 to 2010 with positive values for the book value of total assets and sales revenue for firms incorporated in the United States. Financial firms (SIC code 6000-6999) and utilities (SIC codes 4900-4999) are excluded from the sample, yielding a panel of 176,877 observations for 18,535 unique firms. Variable definitions are provided in the Appendix Table 1 also shows the levels of each combination of cash ratio and intangible ratio across time and industry.
Note: Blue, red and cyan bars are the cases with| 1970s Cash | 1970s Intgbl K | 1980s Cash | 1980s Intgbl K | 1990s Cash | 1990s Intgbl K | 2000s Cash | 2000s Intgbl K | |
| Hlth | 0.10 | 0.13 | 0.25 | 0.71 | 0.34 | 2.33 | 0.41 | 5.07 |
| BusEq | 0.10 | 0.18 | 0.18 | 0.47 | 0.27 | 0.89 | 0.31 | 1.75 |
| Durbl | 0.08 | 0.05 | 0.11 | 0.14 | 0.10 | 0.25 | 0.15 | 0.78 |
| Chems | 0.10 | 0.10 | 0.12 | 0.22 | 0.12 | 0.42 | 0.13 | 0.77 |
| Other | 0.11 | 0.02 | 0.15 | 0.13 | 0.15 | 0.35 | 0.21 | 0.59 |
| Manuf | 0.08 | 0.05 | 0.10 | 0.13 | 0.10 | 0.21 | 0.12 | 0.44 |
| Telcm | 0.06 | 0.02 | 0.08 | 0.07 | 0.13 | 0.13 | 0.14 | 0.35 |
| NonDur | 0.08 | 0.01 | 0.11 | 0.07 | 0.10 | 0.14 | 0.11 | 0.24 |
| Enrgy | 0.11 | 0.01 | 0.12 | 0.06 | 0.10 | 0.13 | 0.12 | 0.17 |
| Shops | 0.09 | 0.01 | 0.11 | 0.06 | 0.10 | 0.07 | 0.11 | 0.13 |
Note: Cash ratio is defined as cash and equivalents relative to total (tangible) assets and intangible ratio (Intgbl K) is defined as intangible-to-tangible asset ratio.
| Firm Financing: Cash: Mean | Firm Financing:Cash: Median | Firm Financing: Net Debt: Mean | Firm Financing: Net Debt: Median | Investment & Firm Dynamtics: Difference Between Cash Rich and Cash Strapped Firms: Investment: Mean | Investment & Firm Dynamtics: Difference Between Cash Rich and Cash Strapped Firms:Investment:Median | Investment & Firm Dynamtics: Difference Between Cash Rich and Cash Strapped Firms:Sales Growth: Mean | Investment & Firm Dynamtics: Difference Between Cash Rich and Cash Strapped Firms:Sales Growth:Median | |
| Panel A: Time-Series Stylized Facts, by Decade: 1970s | 0.09 | 0.05 | 0.18 | 0.19 | 0.04 | 0.02 | 0.03 | 0.02 |
| Panel A: Time-Series Stylized Facts, by Decade: 1980s | 0.13 | 0.06 | 0.15 | 0.17 | 0.07 | 0.04 | 0.07 | 0.06 |
| Panel A: Time-Series Stylized Facts, by Decade: 1990s | 0.17 | 0.07 | 0.11 | 0.14 | 0.08 | 0.05 | 0.08 | 0.08 |
| Panel A: Time-Series Stylized Facts, by Decade: 2000s | 0.21 | 0.11 | 0.05 | 0.06 | 0.06 | 0.03 | 0.05 | 0.05 |
| Panel B: Cross-sectional Stylized Facts, by Quartile of Intangible Capital:Intangible Capital, Q1 | 0.08 | 0.04 | 0.28 | 0.29 | 0.04 | 0.03 | 0.05 | 0.05 |
| Panel B: Cross-sectional Stylized Facts, by Quartile of Intangible Capital:Intangible Capital, Q2 | 0.10 | 0.05 | 0.20 | 0.21 | 0.04 | 0.03 | 0.07 | 0.06 |
| Panel B: Cross-sectional Stylized Facts, by Quartile of Intangible Capital:Intangible Capital, Q3 | 0.13 | 0.08 | 0.10 | 0.11 | 0.05 | 0.03 | 0.09 | 0.07 |
| Panel B: Cross-sectional Stylized Facts, by Quartile of Intangible Capital:Intangible Capital, Q4 | 0.23 | 0.12 | -0.07 | -0.10 | 0.13 | 0.06 | 0.11 | 0.08 |
| Panel C: Time-Series Stylized Facts for Innovative Firms (R&D > 0):1970s | 0.09 | 0.05 | 0.16 | 0.18 | 0.04 | 0.02 | 0.04 | 0.03 |
| Panel C: Time-Series Stylized Facts for Innovative Firms (R&D > 0):1980s | 0.15 | 0.07 | 0.10 | 0.12 | 0.08 | 0.04 | 0.08 | 0.07 |
| Panel C: Time-Series Stylized Facts for Innovative Firms (R&D > 0):1990s | 0.21 | 0.11 | 0.01 | 0.04 | 0.09 | 0.05 | 0.10 | 0.09 |
| Panel C: Time-Series Stylized Facts for Innovative Firms (R&D > 0):2000s | 0.27 | 0.19 | -0.06 | -0.06 | 0.07 | 0.03 | 0.06 | 0.05 |
| Panel D: Cross-sectional Stylized Facts for Innovative Firms (R&D > 0):Intangible Capital, Q1 | 0.08 | 0.04 | 0.26 | 0.27 | 0.03 | 0.02 | 0.06 | 0.06 |
| Panel D: Cross-sectional Stylized Facts for Innovative Firms (R&D > 0):Intangible Capital, Q2 | 0.10 | 0.05 | 0.18 | 0.20 | 0.04 | 0.02 | 0.08 | 0.07 |
| Panel D: Cross-sectional Stylized Facts for Innovative Firms (R&D > 0):Intangible Capital, Q3 | 0.14 | 0.08 | 0.08 | 0.10 | 0.05 | 0.03 | 0.10 | 0.08 |
| Panel D: Cross-sectional Stylized Facts for Innovative Firms (R&D > 0):Intangible Capital, Q4 | 0.31 | 0.23 | -0.10 | -0.14 | 0.14 | 0.06 | 0.12 | 0.09 |
| Whole Sample: Cash OLS (1) | Whole Sample: Cash FE (2) | Whole Sample: Net Debt: OLS (3) | Whole Sample: Net Debt: FE (4) | R&D>0: Firms Cash: OLS (5) | R&D>0:Cash: FE (6) | R&D>0:Net Debt: OLS (7) | R&D>0: Net Debt FE (8) | |
| Intangible Capital |
0.086*** | 0.061*** | 0.104*** | 0.067*** | -0.125*** | |||
| Intangible Capital |
(0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) |
| % Predicted Rise | 42.5% | 43.4% | ||||||
| Predicted Rise | 0.069 | 0.075 | ||||||
| Year fixed effects | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Firm Controls | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Adjusted R2 | 0.299 | 0.665 | 0.235 | 0.602 | 0.340 | 0.689 | 0.240 | 0.601 |
| OLS (1) | FE (2) | GMM (3) | OLS (4) | FE (5) | FE (6) | |
| Q1, SOA | 0.463*** | 0.721*** | 0.557*** | 0.527*** | 0.748*** | 0.729*** |
| Half-life | [1.1] | [0.5] | [0.9] | [0.9] | [0.5] | [0.5] |
| Q2, SOA | 0.350*** | 0.631*** | 0.512*** | 0.381*** | 0.643*** | 0.550*** |
| Half-life | [1.6] | [0.7] | [1.0] | [1.4] | [0.7] | [0.9] |
| Q3, SOA | 0.266*** | 0.526*** | 0.348*** | 0.300*** | 0.537*** | 0.331*** |
| Half-life | [2.2] | [0.9] | [1.6] | [1.9] | [0.9] | [1.7] |
| Q4, SOA | 0.210*** | 0.424*** | 0.294*** | 0.225*** | 0.431*** | 0.319*** |
| Half-life | [2.9] | [1.3] | [2.0] | [2.7] | [1.2] | [1.8] |
| Whole Sample: Investment OLS: (1) | Whole Sample: Investment FE: (2) | Whole Sample: Sales Growth OLS: (3) | Whole Sample: Sales Growth FE: (4) | R&D>0 Firms: Investment OLS: (5) | R&D>0 Firms:Investment FE: (6) | R&D>0 Firms:Sales Growth OLS: (7) | R&D>0 Firms:Sales Growth FE:(8) | |
| Panel A: Sensitivity to Cash Conditions: CDF(Cash |
0.071*** | 0.059*** | 0.145*** | 0.125*** | 0.076*** | 0.059*** | 0.166*** | 0.132*** |
| Panel A: Sensitivity to Cash Conditions: CDF(Cash |
(0.000) | (0.000) | (0.001) | (0.001) | (0.000) | (0.000) | (0.001) | (0.001) |
| Panel A: Sensitivity to Cash Conditions:Year fixed effects | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Panel A: Sensitivity to Cash Conditions:Firm Controls | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Panel A: Sensitivity to Cash Conditions:Adjusted R2 | 0.459 | 0.595 | 0.105 | 0.295 | 0.390 | 0.515 | 0.102 | 0.291 |
| Panel B: Sensitivity to Cash Conditions By Quartiles of Intangible Capital: Q1 | 0.049*** | 0.045*** | 0.145*** | 0.109*** | 0.054*** | 0.059*** | 0.145*** | 0.106*** |
| Panel B: Sensitivity to Cash Conditions By Quartiles of Intangible Capital: Q1 p-values | (0.001) | (0.001) | (0.001) | (0.001) | (0.001) | (0.001) | (0.001) | (0.001) |
| Panel B: Sensitivity to Cash Conditions By Quartiles of Intangible Capital: Q2 | 0.055*** | 0.053*** | 0.151*** | 0.118*** | 0.055*** | 0.061*** | 0.155*** | 0.148*** |
| Panel B: Sensitivity to Cash Conditions By Quartiles of Intangible Capital: Q2 p-values | (0.001) | (0.001) | (0.001) | (0.001) | (0.000) | (0.000) | (0.000) | (0.000) |
| Panel B: Sensitivity to Cash Conditions By Quartiles of Intangible Capital: Q3 | 0.062*** | 0.059*** | 0.165*** | 0.130*** | 0.062*** | 0.069*** | 0.190*** | 0.160*** |
| Panel B: Sensitivity to Cash Conditions By Quartiles of Intangible Capital: Q3 p-values | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) |
| Panel B: Sensitivity to Cash Conditions By Quartiles of Intangible Capital: Q4 | 0.096*** | 0.078*** | 0.280*** | 0.268*** | 0.106*** | 0.089*** | 0.303*** | 0.283*** |
| Panel B: Sensitivity to Cash Conditions By Quartiles of Intangible Capital: Q4 p-values | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) |
| Whole Sample OLS (1) Q1 | Whole Sample FE (2) Q4 | R& D > 0 Firms OLS (3) No | R& D > 0 Firms FE (4) Yes | |
| By Firm Size: [1] | 0.102 | 0.112 | 0.120 | 0.120 |
| By Firm Size: [1] P-values | (0.000) | (0.000) | (0.000) | (0.000) |
| By Firm Size: [2] | 0.030 | 0.028 | 0.037 | 0.039 |
| By Firm Size: [2]: p-values | (0.000) | (0.000) | (0.000) | (0.000) |
| By Dividend Payer Status: [3] | 0.100 | 0.075 | 0.124 | 0.090 |
| By Dividend Payer Status: [3] | (0.000) | (0.000) | (0.000) | (0.000) |
| By Dividend Payer Status [4] | 0.028 | 0.034 | 0.033 | 0.035 |
| By Dividend Payer Status [4] p-values | (0.000) | (0.000) | (0.000) | (0.000) |
| By WW-Index: [5] | 0.104 | 0.090 | 0.126 | 0.107 |
| By WW-Index: [5] p-values | (0.000) | (0.000) | (0.000) | (0.000) |
| By WW-Index [6] | 0.055 | 0.050 | 0.065 | 0.058 |
| By WW-Index [6] p-values | (0.000) | (0.000) | (0.000) | (0.000) |
| By Asset Liquidation Value [7] | 0.145 | 0.109 | 0.152 | 0.115 |
| By Asset Liquidation Value [7] p-values | (0.000) | (0.000) | (0.000) | (0.000) |
| By Asset Liquidation Value [8] | 0.051 | 0.049 | 0.059 | 0.054 |
| By Asset Liquidation Value [8] p-values | (0.000) | (0.000) | (0.000) | (0.000) |
| By Degree of Asset Redeployability [9] | 0.199 | 0.126 | 0.207 | 0.132 |
| By Degree of Asset Redeployability [9] : p-values | (0.000) | (0.000) | (0.000) | (0.000) |
| By Degree of Asset Redeployability [10] | 0.062 | 0.048 | 0.084 | 0.059 |
| By Degree of Asset Redeployability [10] p-values | (0.000) | (0.000) | (0.000) | (0.000) |
| Whole Sample OLS (5) Q1 | Whole Sample FE (6) Q4 | R& D > 0 Firms OLS (7) No | R& D > 0 Firms FE (8) Yes | |
| By Industry Frequency of Investment Inaction[1] | 0.024 | 0.031 | 0.030 | 0.036 |
| By Industry Frequency of Investment Inaction [1] p-values | (0.000) | (0.000) | (0.000) | (0.000) |
| By Industry Frequency of Investment Inaction [2] | 0.137 | 0.112 | 0.162 | 0.133 |
| By Industry Frequency of Investment Inaction: [2] p-values | (0.000) | (0.000) | (0.000) | (0.000) |
| By Investment Spikes in the Industry [3] | 0.049 | 0.048 | 0.061 | 0.049 |
| By Investment Spikes in the Industry: [3] p-values | (0.000) | (0.000) | (0.000) | (0.000) |
| By Investment Spikes in the Industry [4] | 0.095 | 0.079 | 0.120 | 0.081 |
| By Investment Spikes in the Industry [4] p-values | (0.000) | (0.000) | (0.000) | (0.000) |
| By Time-Series Skewness of Industry Investment [5] | 0.044 | 0.043 | 0.060 | 0.047 |
| By Time-Series Skewness of Industry Investmentt [5] p-values | (0.000) | (0.000) | (0.000) | (0.000) |
| By Time-Series Skewness of Industry Investment [6] | 0.100 | 0.079 | 0.145 | 0.104 |
| By Time-Series Skewness of Industry Investment [6] p-values | (0.000) | (0.000) | (0.000) | (0.000) |
| By Time-Series Kurtosis of Industry Investment [7] | 0.048 | 0.046 | 0.065 | 0.051 |
| By Time-Series Kurtosis of Industry Investment [7] p-values | (0.000) | (0.000) | (0.000) | (0.000) |
| By Time-Series Kurtosis of Industry Investmen [8] | 0.092 | 0.078 | 0.133 | 0.093 |
| By Time-Series Kurtosis of Industry Investmen [8] p-values | (0.000) | (0.000) | (0.000) | (0.000) |
| By Time-Series Variability of Operating Costs [9] | 0.038 | 0.040 | 0.054 | 0.050 | By Time-Series Variability of Operating Costs [9] p-values | (0.000) | (0.000) | (0.000) | (0.000) |
| By Time-Series Variability of Operating Cost [10] | 0.102 | 0.080 | 0.133 | 0.096 | By Time-Series Variability of Operating Cost [10]: p-values | (0.000) | (0.000) | (0.000) | (0.000) |
| Description | Calibration |
| Parameters of Technology and Preferences: Returns-to-scale | |
| Parameters of Technology and Preferences: Value-added share of capital | |
| Parameters of Technology and Preferences: Depreciation |
|
| Parameters of Technology and Preferences:Elasticity of substitution between capital inputs |
|
| Parameters of Technology and Preferences: Purchase price of capital |
|
| Parameters of Technology and Preferences: Partial irreversibility |
|
| Parameters of Technology and Preferences: Fixed cost of adjustment |
|
| Parameters of Technology and Preferences: Fixed cost of operation |
|
| Parameters of Technology and Preferences: Persistence of technology shock |
|
| Parameters of Technology and Preferences: Constant relative risk aversion |
|
| Parameters of Technology and Preferences: Volatility of technology shock |
|
| Parameters of Technology and Preferences: Inverse of Frisch elasticity of labor supply |
|
| Financial Parameters: Risk-free rate | |
| Financial Parameters: Agency Cost of Cash Holdings | |
| Financial Parameters: Fixed cost of issuance |
|
| Financial Parameters: Linear cost of issuance |
|
| Financial Parameters: Interest rate income tax rate |
|
| Financial Parameters: Corporate income tax
|
|
| FIX+IRR when the Technological parameter
|
FIX+IRR when the Technological parameter
|
FIX+IRR when the Technological parameter
|
IRR when the Technological parameter
|
IRR when the Technological parameter
|
IRR when the Technological parameter
|
|
| Cash-to-tangible assets (model) | 0.02 | 0.18 | 0.42 | 0.00 | 0.05 | 0.20 |
| Cash-to-tangible assets (data)
|
0.09 | 0.21 | - | 0.09 | 0.21 | - |
| Net debt-to-tangible assets (model)
|
0.47 | 0.17 | -0.24 | 0.60 | 0.43 | 0.13 |
| Net debt-to-tangible assets (data)
|
0.18 | 0.05 | - | 0.18 | 0.05 | - |
| 0.57 | 0.46 | 0.29 | 0.76 | 0.61 | 0.50 |
| FIX+IRR when the Technological parameter
|
FIX+IRR when the Technological parameter
|
FIX+IRR when the Technological parameter
|
IRR when the Technological parameter
|
IRR when the Technological parameter
|
IRR when the Technological parameter
|
|
| Corr (Investment, Cash flow) | 0.28 | 0.30 | 0.33 | 0.21 | 0.25 | 0.30 |
| Corr (Cash, Cash flow)
|
0.49 | 0.76 | 0.75 | 0.05 | 0.61 | 0.71 |
| Corr (Investment,Tobin's Q)
|
-0.20 | -0.21 | -0.20 | -0.31 | -0.32 | -0.31 |
| Corr (Cash, Tobin's Q)
|
0.60 | 0.88 | 0.91 | 0.05 | 0.83 | 0.86 |
| Skewness (Investment)
|
2.19 | 2.27 | 2.27 | 0.68 | 0.38 | 0.41 |
| Kurtosis (Investment)
|
8.10 | 8.47 | 8.22 | 5.23 | 4.69 | 5.11 |
| Tobin's
|
1.63 | 1.62 | 1.61 | 1.64 | 1.66 | 1.66 |
| FIX+IRR when the Technological parameter
|
FIX+IRR when the Technological parameter
|
FIX+IRR when the Technological parameter
|
IRR when the Technological parameter
|
IRR when the Technological parameter
|
IRR when the Technological parameter
|
|
| Technological parameter
|
0.80 | 0.50 | 0.30 | 0.80 | 0.50 | 0.30 |
Capital Accumulatio
 |
9.85 | 9.74 | 9.75 | 10.0 | 9.85 | 9.77 |
| Consumption ( |
5.57 | 5.54 | 5.55 | 5.64 | 5.59 | 5.57 |
| Output ( |
6.54 | 6.51 | 6.52 | 6.62 | 6.57 | 6.55 |
| Hours ( |
4.71 | 4.70 | 4.70 | 4.74 | 4.72 | 4.72 |
| 1.96 | 1.96 | 1.97 | 2.01 | 2.01 | 2.01 |
Note: The table shows the moments of endogenous variables in the economy with irreversibility and fixed adjustment cost, using stationary distribution. The stationary distribution
![]() is discretized on a space (50,50,5).
is discretized on a space (50,50,5).
| Technological parameter,
|
Technological parameter,
|
Technological parameter,
|
|
| Cash-to-tangible assets | 0.00 | 0.12 | 0.25 |
| Net debt-to-tangible assets | 0.46 | -0.04 | -0.23 |
| Corr (Cash, Tobin's |
n/a | 0.94 | 0.97 |
| Corr (Net leverage ratio, Tangible asset ratio
|
0.33 | 0.41 | 0.59 |
Note: The table shows the moments of endogenous variables in the economy with irreversibility and fixed adjustment cost, using actual simulation of size T=200 and N=10,000. The Markov Chain in the baseline is replaced with a Gauss-Hermite quadrature with same number of grids.
A. Stationary Equilibrium
The model economy consists of a continuum of firms that combine capital and labor to produce final outputs, and a continuum of households that provide labor hours to firms to earn market wages, consume final outputs and invest in firm's shares and debts to accumulate wealth. For the description of the firm problem, see the main text.
A.1 Stationary Distribution
The presence of persistent idiosyncratic shocks, DRS production technology and financial market friction imply a non-degenerate joint distribution of technology, capital accumulation and financial balances. We denote the joint distribution by
![]() . At any point in time, the joint distribution satisfies the following of motion37:
. At any point in time, the joint distribution satisfies the following of motion37:
where
A.2 Households
Since our focus is on firms' investment and financial policies, we assume the existence of a representative agent for the household sector. The household is assumed to maximize the expected present value of utility flows discounted at ![]() :
:
![]() . The utility flow is strictly increasing and concave in consumption, and is strictly decreasing and concave in labor hours.
For ease of interpretation of general equilibrium effects, we adopt a utility form that is nonseparable in consumption and hours following Greenwood, Hercowitz, and Huffman (1988). More specifically, we specify
. The utility flow is strictly increasing and concave in consumption, and is strictly decreasing and concave in labor hours.
For ease of interpretation of general equilibrium effects, we adopt a utility form that is nonseparable in consumption and hours following Greenwood, Hercowitz, and Huffman (1988). More specifically, we specify
Such specification abstracts from wealth effects on labor supply, thus making it straightforward to interpret the effects of technological changes on capital accumulation.
The household earns competitive market wage ![]() per work hour, and saves by investing in shares and debt issued by the firms. The budget constraint of the household is given by
per work hour, and saves by investing in shares and debt issued by the firms. The budget constraint of the household is given by
where
This identity simply says that the total value of equity today is the sum of the total value of shares outstanding yesterday and the value of new shares issued today. Substituting (25) in (24) and imposing stock market clearing condition
A few remarks are in order. First, by substituting (9) in (26), one can see that the term
![]() vanishes. This makes it clear that the costs of issuing equity take the form of discount sales of new shares such that the dilution costs to the old shareholders are exactly
offset by the gains of new shareholders in general equilibrium, thus leaving the resource constraint of the economy intact. Second, we use the same notation
vanishes. This makes it clear that the costs of issuing equity take the form of discount sales of new shares such that the dilution costs to the old shareholders are exactly
offset by the gains of new shareholders in general equilibrium, thus leaving the resource constraint of the economy intact. Second, we use the same notation ![]() to denote the debt issued by a
firm and held by the household. When
to denote the debt issued by a
firm and held by the household. When ![]() is positive, this means that the household has a financial claim on a firm. When
is positive, this means that the household has a financial claim on a firm. When ![]() is negative, this implies that the household owes money to a firm. Finally, we assume that the differential tax treatment of interest incomes and expenses applies only to the firms, but not to the household. This implies that the after-tax interest rate is
equalized to the time discount rate of the household in the stationary equilibrium,
is negative, this implies that the household owes money to a firm. Finally, we assume that the differential tax treatment of interest incomes and expenses applies only to the firms, but not to the household. This implies that the after-tax interest rate is
equalized to the time discount rate of the household in the stationary equilibrium,
![]() .
.
A.3 Government
The government follows a balanced budgeting rule, collecting taxes and then transferring them to the household. The budget constraint is given by
When a firm holds a strictly negative financial balance
A.4 Stationary Equilibrium
The stationary equilibrium consists of a constant market wage ![]() , the stationary distribution
, the stationary distribution
![]() , the individual policy rules of the firms,
, the individual policy rules of the firms,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() , the policy rules of the representative household,
, the policy rules of the representative household,
![]() , and
, and
![]() such that labor and goods markets clear39:
such that labor and goods markets clear39:
B. Investment with a Non-Convex Cost with Financial Friction
To analyze under what condition an active (dis)investment is warranted, we reformulate the program (11) as a discrete choice problem,
![]() where the two auxiliary value functions can be defined as
where the two auxiliary value functions can be defined as
The investment action is warranted if and only if
where we make distinctions between
Proposition 1 If (i) ![]() exists, (ii)
exists, (ii)
![]() , and (iii)
, and (iii)
![]() , then the capital stock tomorrow is determined by (13), i.e.,
, then the capital stock tomorrow is determined by (13), i.e.,
![]() ; if (i)
; if (i) ![]() exists, (ii)
exists, (ii)
![]() and (iii)
and (iii)
![]() , then the capital stock tomorrow is determined by (13), i.e.,
, then the capital stock tomorrow is determined by (13), i.e.,
![]() ; Otherwise, inaction is optimal, i.e.,
; Otherwise, inaction is optimal, i.e.,
![]() .
.
Note that in case where ![]() can be shown to be strictly concave with respect to
can be shown to be strictly concave with respect to
![]() in
in
![]() for a finite real number
for a finite real number
![]() , the third conditions,
, the third conditions,
![]() for the expansion problem, and
for the expansion problem, and
![]() for the contraction problem, are not required to establish the optimality of action.
for the contraction problem, are not required to establish the optimality of action.
To build intuition, it is useful to consider a neoclassical case without financial distortions. If
![]() for all
for all ![]() and
and
![]() , the value matching condition (32) is simplified into
, the value matching condition (32) is simplified into
The right hand side of the above, which measures the expected gain from adjustment, is strictly increasing in
Figure 8 illustrates the investment problem for a frictionless neoclassical firm. Solid blue line depicts the adjustment cost function
![]() . The horizontal axis measures
. The horizontal axis measures
![]() and the vertical axis shows the corresponding values of the left and right hand sides of (33). Due to the asymmetry of purchase and resale prices, the
function is kinked at
and the vertical axis shows the corresponding values of the left and right hand sides of (33). Due to the asymmetry of purchase and resale prices, the
function is kinked at
![]() . The fixed component of the adjustment cost places the function strictly above zero at
. The fixed component of the adjustment cost places the function strictly above zero at
![]() . Black, dash-dotted line and red, dash line depict two possible contours of the right hand side of (33). As noted before, the right hand
side is strictly increasing in
. Black, dash-dotted line and red, dash line depict two possible contours of the right hand side of (33). As noted before, the right hand
side is strictly increasing in
![]() and passes through the point, (
and passes through the point, (
![]() ).
).
Consider the case of black, dash-dotted line. The line intersects the adjustment cost at
![]()
![]() . Note that the slope of the black, dash-dotted line is
measured by
. Note that the slope of the black, dash-dotted line is
measured by ![]() . As the line cuts through the adjustment cost function from below, one can see that the second condition of Proposition 1,
. As the line cuts through the adjustment cost function from below, one can see that the second condition of Proposition 1,
![]() is satisfied. On the left side of the vertical line
is satisfied. On the left side of the vertical line
![]() , the expected gain from adjustment is strictly less than the cost of adjustment. On the right side of the vertical line, a strictly positive adjustment is warranted as
the gain dominates the cost. In the latter case, the optimal level of capital stock tomorrow
, the expected gain from adjustment is strictly less than the cost of adjustment. On the right side of the vertical line, a strictly positive adjustment is warranted as
the gain dominates the cost. In the latter case, the optimal level of capital stock tomorrow ![]() is determined such that the FOC
is determined such that the FOC
![]() is met. The green line segment located in the northeast corner of the figure depicts the slope of the gain from adjustment, the slope
of which coincides with
is met. The green line segment located in the northeast corner of the figure depicts the slope of the gain from adjustment, the slope
of which coincides with
![]() . Note that
. Note that
![]() is a necessary condition for adjustment, but not a sufficient condition as it may be satisfied with the expected gain from adjustment
stays below and never crosses the adjustment cost function. Using the same logic, one can see that
is a necessary condition for adjustment, but not a sufficient condition as it may be satisfied with the expected gain from adjustment
stays below and never crosses the adjustment cost function. Using the same logic, one can see that ![]() located at the southwest corner of the figure corresponds to the case of
contraction when the expected gain function is given by the red, dash line. It is important that the expected gain function (the right hand side of (33)) may never intersect the blue, solid line. In such a case, inaction, i.e.,
located at the southwest corner of the figure corresponds to the case of
contraction when the expected gain function is given by the red, dash line. It is important that the expected gain function (the right hand side of (33)) may never intersect the blue, solid line. In such a case, inaction, i.e.,
![]() is optimal.
is optimal.
C. Details of Variable Definition
The variables used in the analysis are defined as follows:
- Cash to book asset - our main dependent variable - is defined cash and marketable securities (data item #1) divided by book assets (#6)
- Other cash measures (robustness): Cash to Net Book Assets is cash and marketable securities (#1) divided by book assets (#6) minus cash and marketable securities (#1); Cash to Market Value of Assets is cash and marketable securities (#1) divided by long-term debt (#9) plus debt in current liabilities (#34) plus market value of equity.
- Net-Leverage is the ratio of long-term debt (#9) plus debt in current liabilities (#34) minus cash and marketable securities (data item #1) to book assets (#6).
- Industry sigma (cash flow risk) is the standard deviation of industry cash flow to book assets. Standard deviation of cash flow to book assets is computed for every firm-year using data over the previous ten years. We then average these cash flow standard deviations over 2SIC industries and each year.
- Market-to-book ratio is the ratio of the book value of assets (#6) minus the book value of equity (#60) plus the market value of equity (#199 * #25) to the book value of assets (#6).
- Firm size is the natural logarithm of book assets (#6) in 1990 dollars (using CPI).
- Cash flow is earnings after interest, dividends, and taxes before depreciation divided by book assets ((#13 - #15 - #16 - #21) / #6).
- Capital expenditures is the ratio of capital expenditures (#128) to book assets (#6).
- Dividend is a dummy variable equal to one in years in which a firm pays a common dividend (#21). Otherwise, the dummy equals zero.
- Acquisitions is the ratio of acquisitions (#129) to book assets (#6).
- Net working capital is the ratio of net working capital (#179) minus cash (#1) to book assets (#6).
- Leverage is the ratio of long-term debt (#9) plus debt in current liabilities (#34) to book assets (#6).
- Net debt (equity) issuance is annual total debt (equity issuance minus debt retirement (equity repurchases), divided by book assets.
- R&D (flow) is the ratio of R&D expenditures (#46) to book assets (#6).
- Asset Tangibility is the ratio of net PPE (#8) to book assets (#6) minus cash and marketable securities (#1).
- High-tech industries are defined following Loughran and Ritter (2004) as SIC codes 3571, 3572, 3575, 3577, 3578, 3661, 3663, 3669, 3674, 3812, 3823, 3825, 3826, 3827, 3829, 3841, 3845, 4812, 4813, 4899, 7370, 7371, 7372, 7373, 7374, 7375, 7378, and 7379.
- WW-Index is based on Whited and Wu (2006) and is as follows: WW-Index=-0.091*CashFlow -0.062*Dividend +0.021*Leverage -0.044*Size +0.102*Industry Growth -0.035*Growth
 where Industry
Growth is the 4-SIC industry sales growth, Growth is own-firm real sales growth, and the other variables are as defined above.
where Industry
Growth is the 4-SIC industry sales growth, Growth is own-firm real sales growth, and the other variables are as defined above. - Asset liquidation value is based on Berger et al. (1996) and is the sum of 0.715*Receivables(#2), 0.547*Inventory(#3), and 0.535*Capital(#8).
- Industry asset redeployability index is based on Balasubramanian and Sivadasan (2009) and is the fraction of total capital expenditures in an industry accounted for by purchases of used (as opposed to new) capital, computed at 4-digit SIC level and constructed using hand-collected US Census Bureau data. Since these data are available only once every 5 years and not for more recent years, we compute a time-invariant index by averaging the available quinquennial indices at the 4-SIC level. This measure is only available for a restricted sample of manufacturing firms.
- Investment inaction, small investments, and investment spikes are defined at the firm level based on Cooper and Haltiwanger (2006) as those firm-year observations corresponding to |Capex/book assets| < .01, | Capex/book assets|
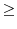 .01, and |Capex/book assets| > .2, respectively. Industry is 4-SIC. In each industry-year, we compute frequency as number of observations involving investment inaction (small investment) to total number of observations in the industry. This
procedure results in a time-invariant cross-sectional ranking of 4-SIC industries.
.01, and |Capex/book assets| > .2, respectively. Industry is 4-SIC. In each industry-year, we compute frequency as number of observations involving investment inaction (small investment) to total number of observations in the industry. This
procedure results in a time-invariant cross-sectional ranking of 4-SIC industries. - Time-series skewness and kurtosis of annual aggregate industry investment are based on Caballero (1999) and calculated as the skewness and kurtosis of average annual Capex to book assets ratios in each (4-SIC) industry. In every year, we calculate annual averages in each industry as industry-year means of individual firm-year Capex to book asset ratios.This procedure results in a time-invariant cross-sectional ranking of 4-SIC industries.
- Time-series standard deviation of aggregate industry operating costs is calculated after aggregating firm-level operating costs by taking annual means at the 4-SIC industry level. For each industry, the measure is the standard deviation of these annual industry means of operating costs. Operating costs are costs of good sold (#41). This measure gives a time-invariant cross-sectional ranking of 4-SIC industries.
D. Details of Regression Results in Panel A of Table 2
Table A-1: Details of Regression Analysis of Intangible Capital and Corporate Financing
| Whole Sample Cash OLS (1) | Whole Sample Cash FE (2) | Whole Sample Net Debt OLS (3) | Whole Sample Net Debt FE (4) | R&D >0 Firms only Cash OLS (5) | R&D >0 Firms only Cash FE (6) | R&D >0 Firms only Net Debt OLS (7) | R&D >0 Firms only Net Debt FE (8) | |
| Intangible Capital | 0.086 | 0.061 | -0.111 | -0.047 | 0.104 | 0.067 | -0.125 | -0.067 |
| Intangible Capital : p-values | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) |
| Industry sigma | 0.037 | -0.007 | -0.062 | 0.022 | 0.041 | -0.001 | -0.064 | 0.037 |
| Industry sigma: p-values | (0.000) | (0.190) | (0.000) | (0.000) | (0.000) | (0.739) | (0.000) | (0.000) |
| Market-to-book | 0.023 | 0.011 | -0.032 | -0.010 | 0.028 | 0.016 | -0.037 | -0.009 |
| Market-to-book: p-values | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) |
| Firm size | -0.024 | -0.039 | 0.025 | 0.011 | -0.022 | -0.032 | 0.005 | 0.067 |
| Firm size: p-values | (0.000) | (0.001) | (0.000) | (0.000) | (0.000) | (0.001) | (0.000) | (0.000) |
| Cash flow | 0.031 | 0.017 | -0.096 | -0.091 | 0.037 | 0.023 | -0.109 | -0.108 |
| Cash Flow: p-values | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) |
| Capex | -0.008 | -0.012 | 0.017 | 0.005 | -0.011 | -0.011 | 0.018 | 0.002 |
| Capex: p-values | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.038) |
| Dividend | -0.011 | 0.007 | -0.037 | -0.036 | -0.023 | 0.005 | -0.016 | -0.033 |
| Dividend: p-values | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.007) | (0.000) | (0.000) |
| Acquisitions | -0.010 | -0.008 | 0.034 | 0.018 | -0.012 | -0.009 | 0.036 | 0.023 |
| Acquisitions: p-values | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) | (0.000) |
| Year fixed effects | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Adjusted R2 | 0.299 | 0.665 | 0.235 | 0.602 | 0.340 | 0.689 | 0.240 | 0.601 |
The table reports detailed parameter estimates for the control variables included in the cash and net-debt regressions reported in Panel A of Table 2.
E. Numerical Method
The numerical procedure can be thought as an inner-outer loop iteration.
- Initiate the procedure assuming a uniform distribution for the joint distribution of technology, capital and net debt, denote by
 .
. - We then look for a market clearing wage
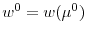 that solves (29) using a numerical root finder.
that solves (29) using a numerical root finder. - In the inner loop problem, an individual firm solves its value maximization problem taking as given the stationary joint distribution, and hence the market clearing wage. This procedure updates the policy functions,
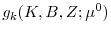 and
and
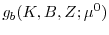 .
. - We then move to the outer loop where we iterate (22) until convergence to obtain
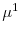 . We then look for a new market clearing wage
. We then look for a new market clearing wage
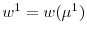 that solves (29) using a numerical root finder.
that solves (29) using a numerical root finder. - Check if
 . If yes, stop. If no, go back to step 3 and iterate the steps using
. If yes, stop. If no, go back to step 3 and iterate the steps using 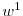 as a new initial guess.
as a new initial guess.
For the inner loop problem, we use an adaptive grid point method for value function iteration. We proceed in two stages. In the first stages, we specify 30![]() 40
40![]() 5 grid points in state dimension for (
5 grid points in state dimension for (![]() ). We use Markov chain process to
discretize the technology shock. In the choice dimension for (
). We use Markov chain process to
discretize the technology shock. In the choice dimension for (
![]() ), we use 300
), we use 300![]() 300 grid points. We then iterate on
Bellman equation to obtain the first stage value function. We denote the optimal choice of capital and net debt by (
300 grid points. We then iterate on
Bellman equation to obtain the first stage value function. We denote the optimal choice of capital and net debt by (
![]() ).
).
In the second stage, we allocate all grid points for (
![]() ) in ([
) in ([
![]() ]
]![]() [
[
![]() ]), i.e., in a rectangle around the optimal policies obtained in the first stage Bellman iteration. This way we allocate all computing resources
around the region where the optimal choices are mostly likely to exist. In each time we update the value function in the second stage, ([
]), i.e., in a rectangle around the optimal policies obtained in the first stage Bellman iteration. This way we allocate all computing resources
around the region where the optimal choices are mostly likely to exist. In each time we update the value function in the second stage, ([
![]() ]
]![]() [
[
![]() ]) is also updated with
]) is also updated with
![]() such that we focus on finer and finer grid points. This allow us to construct a fairly smooth policy functions. It is
important to make sure that for each grid point
such that we focus on finer and finer grid points. This allow us to construct a fairly smooth policy functions. It is
important to make sure that for each grid point ![]() in state dimension,
in state dimension,
![]() is always included in the choice dimension such that the program allows for inaction exactly.
is always included in the choice dimension such that the program allows for inaction exactly.
For the outer problem, we use a fixed (50![]() 50
50![]() 5) grid points for
5) grid points for
![]() . This means that we need to use interpolation to evaluate policy functions at points off the grid points used in the value function iteration. For speed, we use linear tensor
product interpolation.
. This means that we need to use interpolation to evaluate policy functions at points off the grid points used in the value function iteration. For speed, we use linear tensor
product interpolation.
![\displaystyle Y=Z^{1-(1-\alpha )\xi }N^{(1-\alpha )\xi }\left[ \theta \left( \frac{K_{T}}{% \theta }\right) ^{-\rho }+(1-\theta )\left( \frac{K_{N}}{1-\theta }\right) ^{-\rho }\right] ^{-\alpha \xi /\rho }-F_{O\text{ }}\text{, \ \ \ }0<\xi <1](img15.gif)
![\displaystyle \eta (w)Z\left[ \theta \left( \frac{K_{T}% }{\theta }\right) ^{-\rho }+(1-\theta )\left( \frac{K_{N}}{1-\theta }\right) ^{-\rho }\right] ^{-\gamma /\rho }](img25.gif)
![\displaystyle [1-(1-\alpha )\xi ]\left[ \dfrac{(1-\alpha )\xi }{w}\right] ^{\frac{(1-\alpha )\xi }{1-(1-\alpha )\xi }},\ \ \ \gamma \equiv \dfrac{% \alpha \xi }{1-(1-\alpha )\xi }.](img28.gif)
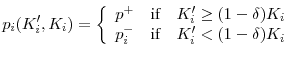
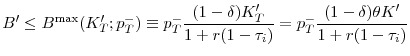
![\displaystyle \underset{% \text{Unused line of credit}}{\underbrace{B^{\max }(K_{T}^{\prime };p_{T}^{-})\text{ }-\text{ }\underset{\text{Debt}}{\underbrace{\max \{0,B^{\prime }\}}}}\text{ }}+\text{ }\underset{\text{Cash}}{\underbrace{% [-\min \{0,B^{\prime }\}]}}.](img55.gif)
![\displaystyle D=(1-\tau _{c})\left[ \Pi (K;\theta ,\rho )-F_{0}\right] -\sum_{i=T,N}[% \Gamma (K_{i}^{\prime },K_{i})-\tau _{c}\delta K_{i}]-[1+r(B)]B+B^{\prime }+E-\varphi (E)](img62.gif)
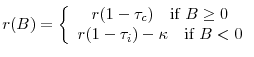
![\displaystyle \left. \min_{\lambda ,\psi }\max_{K^{\prime },B^{\prime },D,E}\right\{ (1+\lambda )D-E+\psi \left[ \frac{p_{T}^{-}(1-\delta )\theta }{1+r(1-\tau _{i})}K^{\prime }-B^{\prime }\right]](img72.gif)
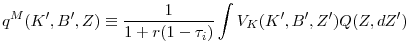


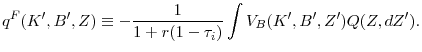

![\displaystyle \min_{\lambda ,\psi }\max_{\tilde{k}_{T}^{\prime },% \tilde{k}_{N}^{\prime },\tilde{b}^{\prime },d,e}\left\{ (1+\lambda )d-e+\psi % \left[ p_{T}^{-}\frac{(1-\delta _{T})\tilde{k}_{T}^{\prime }}{1+r(\tilde{b}% ^{\prime })}-\tilde{b}^{\prime }\right] \right.](img175.gif)
![\displaystyle (1-\tau _{c})[\pi (k_{T},k_{N})-F_{o}]-\sum_{i=T,N}[\Gamma (\tilde{k}% _{i}^{\prime },k_{i})-\tau _{c}\delta _{i}k_{i}]](img178.gif)
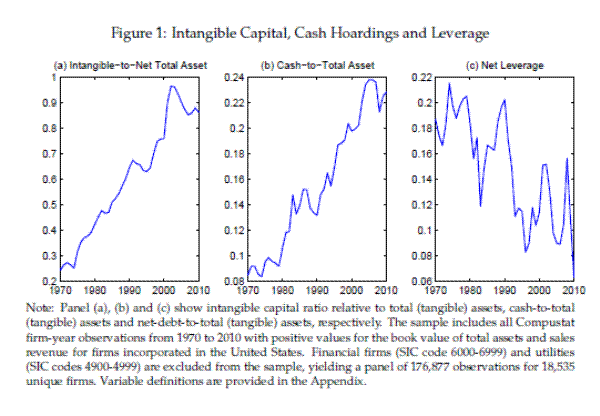
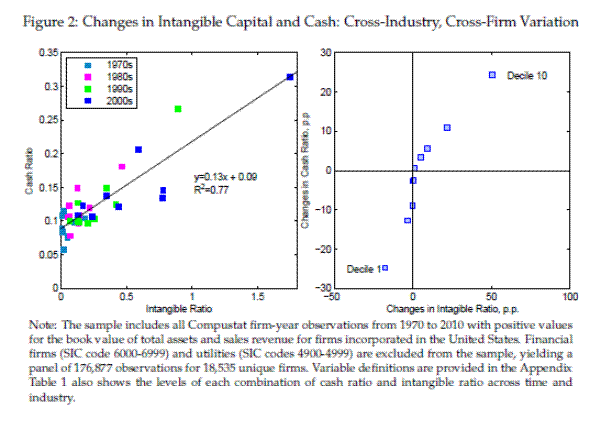
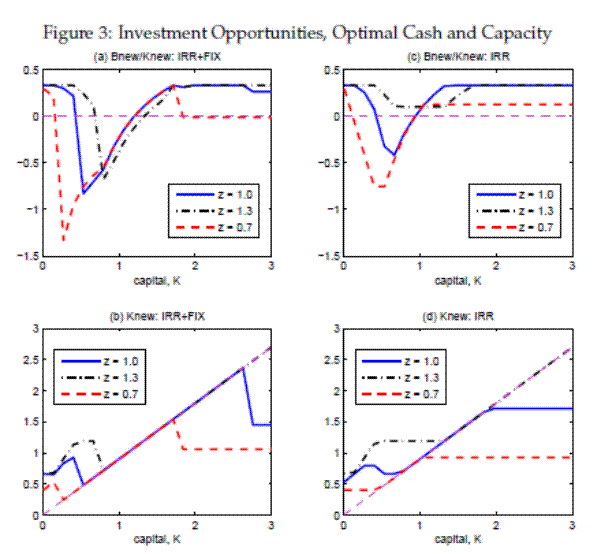
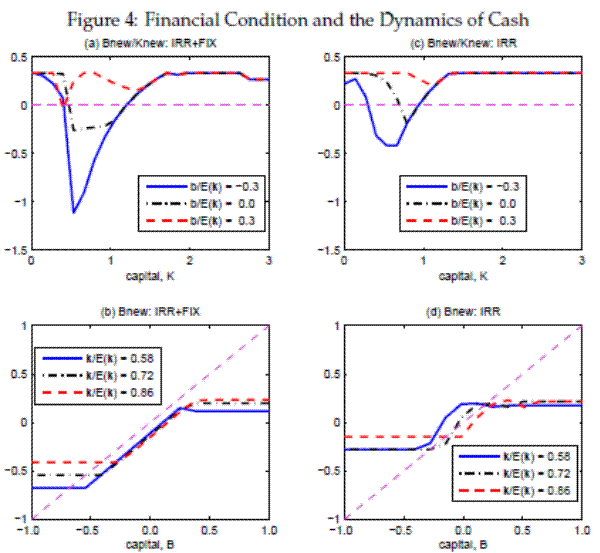
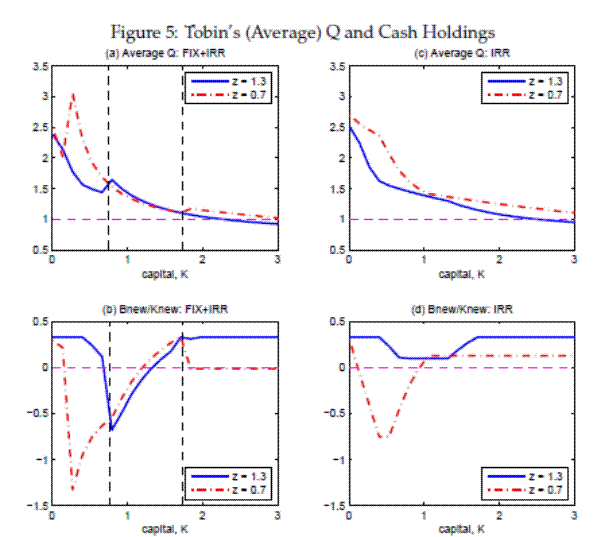
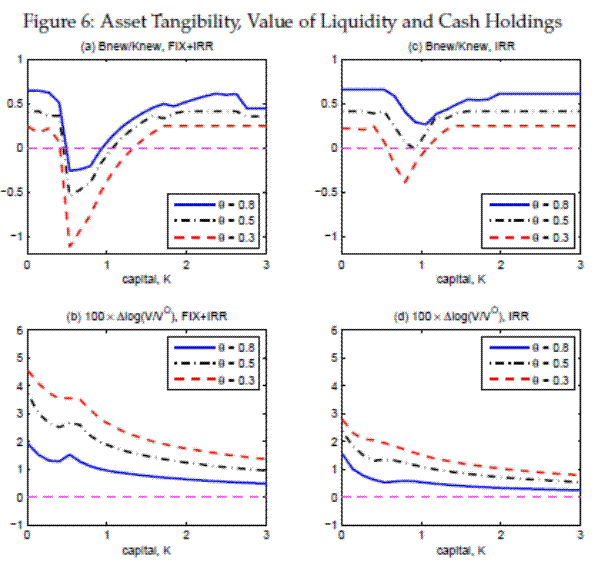
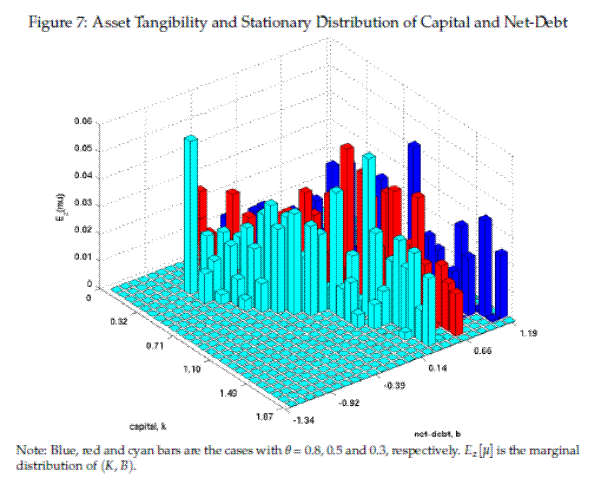
![\displaystyle u(C,N)=\frac{1}{1-\sigma }\left[ \left( C-\frac{\zeta }{1+\phi }N^{1+\phi }\right) ^{1-\sigma }-1\right] .](img255.gif)
![\displaystyle +\int \{(D+\tilde{P}_{S})S+[1+r(1-\tau _{i})]B\}\mu (dK,dB,dZ).](img258.gif)
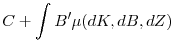
![\displaystyle +\int \{D-[E-\varphi (E)]+[1+r(1-\tau _{i})]B\}\mu (dK,dB,dZ).](img268.gif)
![\displaystyle T_{G}+T_{F}=\int \left[ \tau _{c}[\Pi (K,Z)-F_{0}]-\tau _{c}\delta K-(\tau _{c}-\tau _{i})\max \{0,B\}\right] \mu (dK,dB,dZ)](img271.gif)
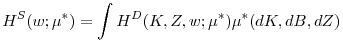
![\displaystyle C(w;\mu ^{\ast })=\int [Y(K,Z,w;\mu ^{\ast })-g_{I}(K,B,Z;\mu ^{\ast })+\kappa \min \{0,g_{B}(K,B,Z;\mu ^{\ast })\}]\mu ^{\ast }(dK,dB,dZ).](img283.gif)
![\displaystyle \min_{\lambda ,\psi }\max_{K^{\prime },B^{\prime },E,\nu _{E}}\left\{ (1+\lambda )D-E+\psi \left[ \frac{% p^{-}(1-\delta )\theta }{1+r(1-\tau _{i})}K^{\prime }-B^{\prime }\right] \right.](img286.gif)
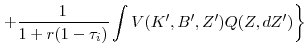
![\displaystyle \min_{\lambda ,\psi }\max_{B^{\prime },E,\nu _{E}}\left\{ (1+\lambda )D-E+\psi \left[ \frac{p^{-}(1-\delta )\theta }{1+r(1-\tau _{i})}(1-\delta )K-B^{\prime }\right] \right.](img291.gif)
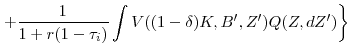
![\displaystyle +\frac{1}{1+r(1-\tau _{i})}\int [V(K^{\prime },B^{\prime },Z^{\prime })-V((1-\delta )K,B^{\prime (0)},Z^{\prime })]Q(Z,dZ^{\prime })](img298.gif)
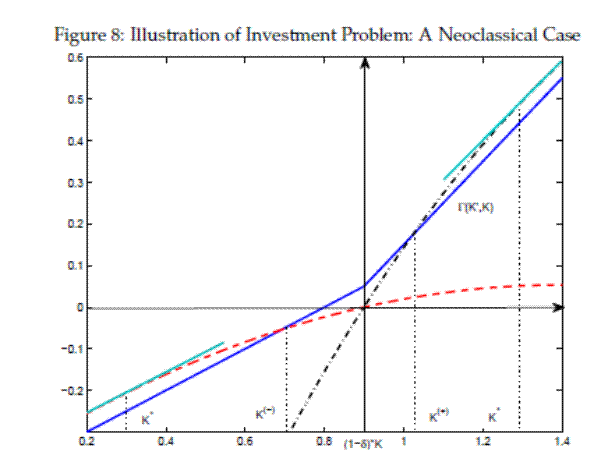
![\displaystyle \Gamma (\hat{K},K)=\frac{1}{1+r(1-\tau _{i})}\int [V(\hat{K},Z^{\prime })-V((1-\delta )K,Z^{\prime })]Q(Z,dZ^{\prime })](img321.gif)