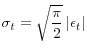Sectoral Allocation, Risk Efficiency and the Great Moderation
Abstract:
1 Introduction
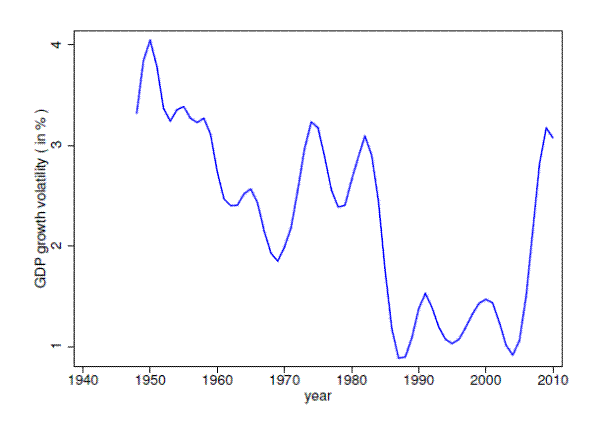
The decline in U.S. real GDP growth volatility after the early 1980s is well documented in the literature and it is coined as the Great Moderation by Stock and Watson (2003).1 The causes of the Great Moderation mentioned in the literature mostly include: better monetary policy, better inventory management and good luck.
In this paper, I use U.S. data for 22 sectors for the period 1947-2010 and I argue that the aggregate growth volatility has declined because of shifts in the production activity across different sectors. By taking a take a portfolio approach, I distinguish between the effect of changes in the
sectoral covariances and sectoral composition in the the decline in aggregate volatility. Representing the economy as a portfolio of ![]() sectors, the GDP growth volatility is given by:
sectors, the GDP growth volatility is given by:
where
To determine the effect of covariance and sectoral allocations, I present the growth and volatility in the economy in an efficient frontier framework. The growth-volatility efficient frontier is determined by the sectoral growth and covariances. The frontier is plotted in the GDP (volatility, growth) space and every point on the frontier represents a portfolio of sectors. The sectoral allocations on the frontier and the corresponding aggregate growth and volatility represent the maximum level of efficiency that the economy can achieve. An increase in the sectoral covariances or a decrease in the sectoral growth rates will shift the frontier and shrink the growth-volatility opportunity set. I define the shifts in the frontier due to changes in the sectoral covariances, as changes in the risk opportunity set.
The location of the economy relative to the frontier is determined by the actual sectoral allocation. I define the optimal allocation as the one that minimizes the distance of the economy from the frontier, where the distance is measured in the (volatility, growth) space. I measure the efficiency of the economy as the distance between the economy and the optimal allocation on the frontier. The closer the economy to the frontier, the higher the efficiency. The distance along the volatility dimension represents risk efficiency.
Using this setup, I can distinguish between the two sources for the decline in GDP volatility: 1) decrease in covariances represented by an expansion of the risk opportunity set and 2) changes in sectoral allocation represented by an increase in efficiency.
The set of 22 sectors used in this paper fully represents the U.S. economy. I use a one-sided 25-year rolling window to estimate the average sectoral growth rate and the sectoral covariances and to compute the frontier for each 25-year period between 1948 and 2010. I find that:
- The frontier has shifted down and the growth volatility opportunity set has shrunk. At least
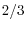 of the shrinkage is due to a lower sectoral growth, reflecting the productivity slowdown of
the 1970s. The rest is due to a doubling of the growth volatility in Agriculture (1980), Information (1997) and Finance and Insurance (1998). There is no change in the growth volatility of the other sectors or in the correlation across sectors. This implies that the Great Moderation was not the
outcome of a decline in sectoral covariances. As the GDP growth volatility is determined by the sectoral covariances and sectoral allocations, this suggests that the decline in GDP growth volatility was the outcome of changes in the sectoral allocations.
of the shrinkage is due to a lower sectoral growth, reflecting the productivity slowdown of
the 1970s. The rest is due to a doubling of the growth volatility in Agriculture (1980), Information (1997) and Finance and Insurance (1998). There is no change in the growth volatility of the other sectors or in the correlation across sectors. This implies that the Great Moderation was not the
outcome of a decline in sectoral covariances. As the GDP growth volatility is determined by the sectoral covariances and sectoral allocations, this suggests that the decline in GDP growth volatility was the outcome of changes in the sectoral allocations. - The distance of the economy from the frontier has decreased. The efficiency is estimated to have increased by 1.4 percentage points and it is interpreted as the decline in the growth volatility in the economy, if there were no changes in the sectoral covariances. This efficiency improvement is along the volatility dimension and is comparable to the 1.5 percentage points decline in GDP growth volatility in the data after the mid 1980s.
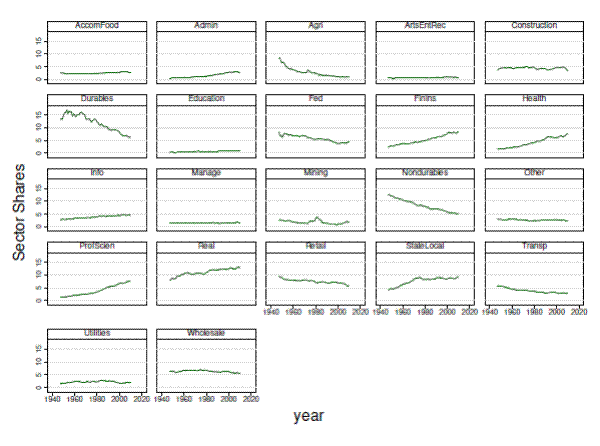
- The economy became more diversified after the early 1980s. The economic activity has become more equally spread across sectors, shifting away from Agriculture and Manufacturing towards services. Notably, the share of Finance and Insurance has increased steadily from 2.4% of GDP in 1947 to 8.4% in 2010. It became the third largest sector in the last decade, which coupled with the doubling of the growth volatility in this sector, contributed to the recent increase in GDP growth volatility.
To conclude, as a result of changes in the sectoral allocation, the economy has moved closer to the growth-volatility frontier. The Great Moderation was the outcome of more risk efficient and more diversified sectoral allocations.
There is a growing literature on the Great Moderation. The conclusion in this paper is closely related to Carvalho and Gabaix (2010). They define fundamental volatility as a weighted average of the variance of the total factor productivity of each sector, where the sectoral variance is constant over time. They derive GDP growth volatility to be proportional to the fundamental volatility. They conclude that the changes in fundamental volatility, therefore changes in GDP volatility, would come only from changes in the sectoral composition, corresponding to a more diversified economy.
Sectoral diversification captures one dimension of the changes in the sectoral allocation. This paper further contributes to the literature by introducing a measure of the efficiency of the sectoral allocations. Given the sectoral covariances, this measure converts the complexity of the changes in sectoral allocations into changes in efficiency.
Other explanations of the Great Moderation include: better monetary policy (Clarida, Gali and Gertler 2000, Cecchetti, Flores-Lagues and Krause 2006), and better inventory management (Kahn, McConnell, and Perez-Quiros 2002, McCarthy and Zakrajšek 2007, Irvine and Schuh 2005). This paper looks at the aggregate output from the production approach using the value added by sector and the role of inventory management is not explicit.2 However, the results in this paper do not reject the inventory hypothesis. They rather imply that the sectoral shift from manufacturing to services, especially finance, has decreased the contribution of a volatile inventory holding sector to aggregate volatility, hence lowering aggregate volatility.
Finally some have looked at the technology shocks. Galí and Gambetti (2009) show that the Great Moderation can be explained by the the change in the contribution of technology and non technology shocks. The findings in this paper do not explicitly exclude these factors, rather acknowledge that their impact might be channeled through the changes in the economic structure. Using counterfactual analysis, I show that the change in sectoral allocations is sufficient to explain the decline in GDP growth volatility. This paper weakens the case for the good luck hypothesis, as in smaller shocks, presented by Stock and Watson (2003).
In a broader perspective, this paper relates to the literature that uses sectoral data, an approach that has gained prominence in explaining cross-country differences in the level of production diversification and aggregate volatility. In cross-country studies, Imbs and Wacziarg (2003) find a U-shaped pattern of the sectoral diversification along different stages of development and Koren and Tenreyro (2007) find that sectoral diversification can explain the variation in aggregate volatility across countries.
This paper is organized as follows. Section 2 presents the sectoral allocation in a growth-volatility efficient frontier framework. Section 3 discusses the data. The results are presented in Section 4. Section 5 continues with some robustness checks and extensions and Section 6 concludes.
2 Sectoral Allocation in an Efficient Frontier Framework
In this section, I present a model of sectoral allocation in a growth-volatility efficient frontier framework. The efficient frontier is computed using the sectoral growth rates and sectoral covariances, and it provides the most risk efficient allocations that the economy can achieve. Given the sectoral growth rates and covariances, the observed growth and volatility in the economy will be determined by the observed sectoral shares. The closer the economy is to this efficient frontier, the more risk efficient the economy is. This set up allows for the identification of the two sources of changes in GDP volatility: 1) changes in the covariances, represented by an expansion of the growth-volatility opportunity set, and 2) changes in sectoral allocation resulting in changes in efficiency.
Efficient frontier: Given the sectoral growth rates and covariances, what is the sectoral allocation that yields the lowest GDP growth variance for a given value of GDP growth? This set of sectoral allocations and the corresponding GDP growth and volatility represent the efficient frontier.
The inputs in the computation of the efficient frontier are the vector of the expected sectoral growth rates and the covariance matrix of the sectoral growth rates. At any time ![]() , given
the vector of sectoral growth rates
, given
the vector of sectoral growth rates ![]() , the covariance matrix of the sectoral growth rates
, the covariance matrix of the sectoral growth rates ![]() and the vector of sectoral allocations
and the vector of sectoral allocations ![]() , the GDP growth rate is given by:
, the GDP growth rate is given by:
the expected GDP growth rate is given by:
and the variance of the GDP growth rate is given by:
where
![]() is an
is an
![]() covariance matrix of sectoral growth rates.
covariance matrix of sectoral growth rates.
A sectoral allocation is efficient, if for a given GDP growth rate, ![]() , it yields the lowest GDP growth volatility. The efficient allocation,
, it yields the lowest GDP growth volatility. The efficient allocation,
![]() , solves the following optimization problem:
, solves the following optimization problem:
Repeating ( 5) for every possible value of GDP growth, I compute the efficient frontier as a set of efficient sectoral allocations,
![]() , the corresponding GDP growth,
, the corresponding GDP growth,
![]() and volatility,
and volatility,
![]() .3 The efficient frontier is plotted in the (volatility, growth) space. A higher sectoral growth rate, a lower sectoral variance or a smaller correlation across sectors will shift the efficient frontier, expanding the growth-volatility opportunity set. The shifts in the
frontier, due to changes in the sectoral covariances, represent changes in the "risk opportunity".
.3 The efficient frontier is plotted in the (volatility, growth) space. A higher sectoral growth rate, a lower sectoral variance or a smaller correlation across sectors will shift the efficient frontier, expanding the growth-volatility opportunity set. The shifts in the
frontier, due to changes in the sectoral covariances, represent changes in the "risk opportunity".
Preferences: The economy likes GDP growth and dislikes GDP volatility.
Optimal allocation: Each of the sectoral allocations along the frontier is risk efficient. As the economy likes GDP growth and dislikes GDP volatility, the optimal risk efficient allocation is given by the portfolio on the frontier that is closest to the economy. The distance of the economy from the frontier is measured in the (volatility, growth) space.
The optimal sectoral allocation,
![]() at time t, is given by:
at time t, is given by:
where
I compute the distance of the economy from each of the sectoral allocations on the frontier as:
where, ![]() is time,
is time, ![]() indexes portfolios (sectoral allocations) on the efficient
frontier,
indexes portfolios (sectoral allocations) on the efficient
frontier, ![]() is the distance of the economy from the portfolio
is the distance of the economy from the portfolio ![]() on the
frontier for time
on the
frontier for time ![]() . The growth rate and the variance for the
. The growth rate and the variance for the ![]() portfolio on
the frontier is given by
portfolio on
the frontier is given by
![]() and
and
![]() , respectively, which represent the GDP growth and variance if the sectoral allocations in the economy were the same as the sectoral allocations of the
, respectively, which represent the GDP growth and variance if the sectoral allocations in the economy were the same as the sectoral allocations of the ![]() portfolio on the frontier. The observed GDP growth and volatility are denoted by
portfolio on the frontier. The observed GDP growth and volatility are denoted by ![]() and
and
![]() . Because the efficient frontier is concave and upward slopping, at
. Because the efficient frontier is concave and upward slopping, at
![]() , the GDP growth will be no less than the observed GDP growth and the GDP volatility will be no higher than the observed GDP volatility.
, the GDP growth will be no less than the observed GDP growth and the GDP volatility will be no higher than the observed GDP volatility.
The distance of the economy from the frontier, ![]() , is the distance from the optimal allocation on the frontier, as in:
, is the distance from the optimal allocation on the frontier, as in:
Efficiency: I define the efficiency of the economy as the distance of the economy from the optimal allocation, as in equation (8), where the distance is measured in the (growth, volatility) space. I define the risk efficiency as the distance attributed to the volatility dimension. In this efficient frontier framework of sectoral allocation, the two sources for a change in GDP volatility, changes in the sectoral covariances and sectoral allocations, are converted into changes in the risk opportunity set, and changes in the risk efficiency of the economy.
3 Data
The sectoral data is available from the Bureau for Economic Analysis. The data is available at an annual frequency, for the period 1947-2010 for 22 broad sectors of the economy. The list of sectors is given in Table 1 and they fully represent the economy. These
sectors correspond to the 2-digit level of the 2002 North American Industry Classification System (NAICS). The sectoral data for the period 1947-1987 is available only at the 2 digit level. The more disaggregated data (at a 3-digit level) is available starting from 1987. The data includes two
variables: chain-type quantity index for value added (![]() ) and value added as a percentage of GDP (
) and value added as a percentage of GDP (![]() ). The sectoral growth rate is given by
). The sectoral growth rate is given by
![]() . Let
. Let
![]() , then
, then
![]() ,
,
![]() , and
, and
![]() . Whelan (2000) shows that in the case of chain-type indices,
. Whelan (2000) shows that in the case of chain-type indices, ![]() as given in the National Income and Product Account (NIPA), would satisfy
as given in the National Income and Product Account (NIPA), would satisfy
![]() , if
, if
![]() represented contributions. As
represented contributions. As ![]() is defined as a nominal share, its
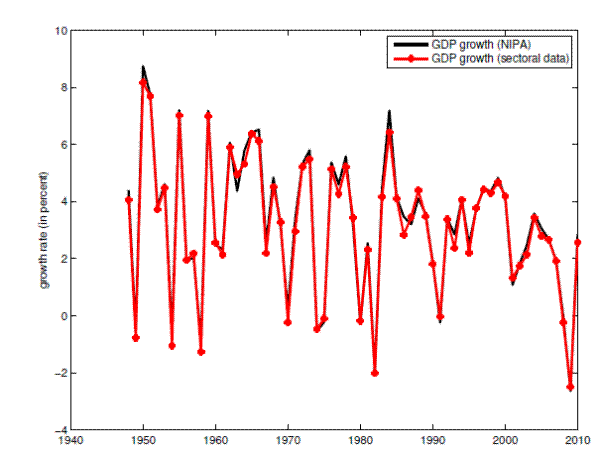
product with the sectoral growth rate represents growth contribitions. As shown in Figure 1, the GDP growth rate series from the NIPA and the GDP growth series using the sectors' growth rate and nominal shares match.
is defined as a nominal share, its
product with the sectoral growth rate represents growth contribitions. As shown in Figure 1, the GDP growth rate series from the NIPA and the GDP growth series using the sectors' growth rate and nominal shares match.
The existence, timing and magnitude of the Great Moderation using annual data. There is consensus in the literature on the start date of the Great Moderation as the first quarter of 1984. This break date is estimated using quarterly data for GDP growth. Since the sectoral data is available at an annual frequency, I test for the existence and the timing of the break in the GDP growth volatility using annual data. Following McConnell and Perez-Quiros (2000), and Stock and Watson (2002), I compute the instantaneous volatility as,
where
I test the null hypothesis of no breaks,
![]() , against the alternative of a single break, in the following regression:
, against the alternative of a single break, in the following regression:
where
Variance decomposition. As an initial diagnosis, Table 2 shows the variance decomposition of the GDP growth rate. The decomposition is based on the contribution of the sector's growth to GDP growth, which is defined
as the product of the sectoral growth rate with the sectoral share (
![]() ). By definition, the GDP growth volatility is the sum of the variance terms and the covariance terms of these contributions.
). By definition, the GDP growth volatility is the sum of the variance terms and the covariance terms of these contributions.
The variance decomposition of the contributions shows that the decline in the sum of the variance and covariance terms is comparable to the decline in the variance of the GDP growth rate. Similar to Irvine and Schuh (2005), the decline in the covariance of the contributions accounts for about 70 % of the decline of the aggregate volatility. Carvalho and Gabaix (2010) show that because of input linkages, there is comovement across sectors. The changes in the off-diagonal terms in the covariance matrix would simply reflect changes in their measure of fundamental volatility, which is defined as the weighted average of the sectoral volatilities. They also show that, while all the shocks in their model are idiosyncratic, even small measurement errors can create comovement in total factor productivity.
4 Results
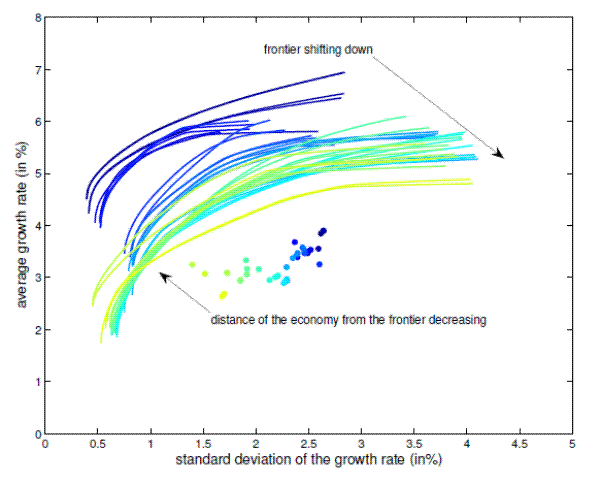
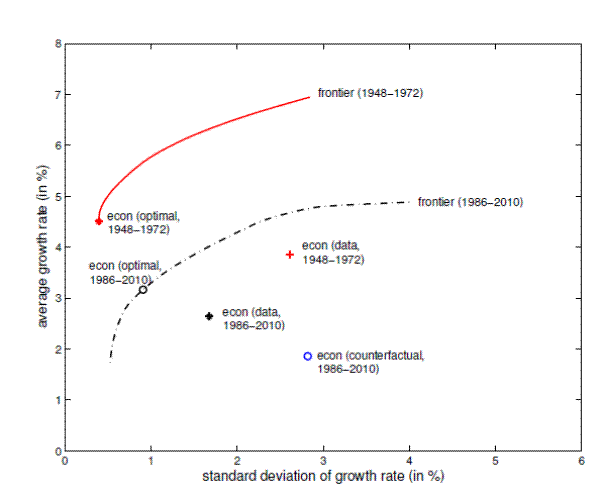
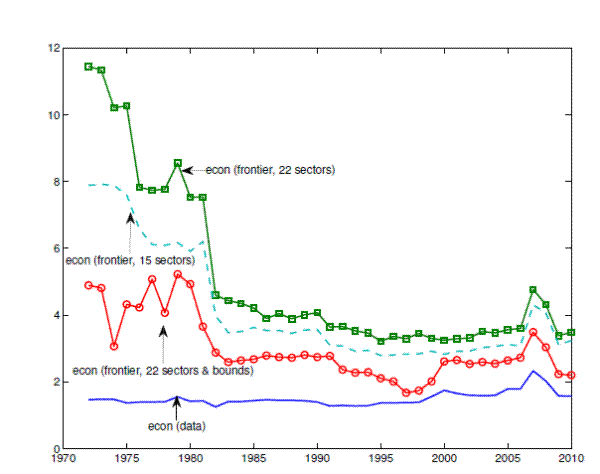
I use a one-sided 25-year rolling window to compute the frontier for each 25-year period between 1948 and 2010, where the first period starts in 1948 and the last periods ends in 2010. Figure 3 plots the efficient frontier for each 25-year period between 1948 and 2010. The first frontier is constructed for 1972 and it uses data on the sectoral growth rate for the period 1948-1972. The last frontier, the frontier for 2010, is constructed using data for the period 1986-2010. The color of the plots changes gradually, from dark blue to light green, where the dark blue corresponds to the earlier periods and the light green to the later ones.
I observe that:
- The efficient frontier has shifted down. This implies that over the period 1948-2010, if there were no changes in the sectoral allocation, the GDP volatility would have increased and the GDP growth would have decreased. Most of the shifts are along the growth dimension, suggesting that the shifts should be mainly due to a lower sectoral growth rate. The curvature of the frontiers is relatively unchanged, implying that there is no change in the correlation across sectors.
- The distance of the economy from the frontier has decreased. The decline in the sectoral growth rates, captured by the growth dimension of the shifts in the frontier, is higher than decline in the GDP growth in the data. Also the decline in the distance is mostly along the volatility dimension. That is, the economy became more risk efficient.
These observations are elaborated in the following subsections.
4.1 Efficient Frontier and Growth-Volatility Opportunity Set
To get a time series of the shifting down of the frontier, I compute the distance of the each frontier from the first frontier. The distance is measured in the (volatility, growth) space. Note that each frontier is computed by constructing ![]() portfolios which are equally spaced in the range of the growth rates for that frontier. For each frontier, I calculate the distance between the corresponding
portfolios which are equally spaced in the range of the growth rates for that frontier. For each frontier, I calculate the distance between the corresponding ![]() portfolios, where
portfolios, where ![]() 1 to N, as:
1 to N, as:
| (11) |
The distance of each frontier from the first one is given by the average distance between the corresponding portfolios as in equation ( 12).
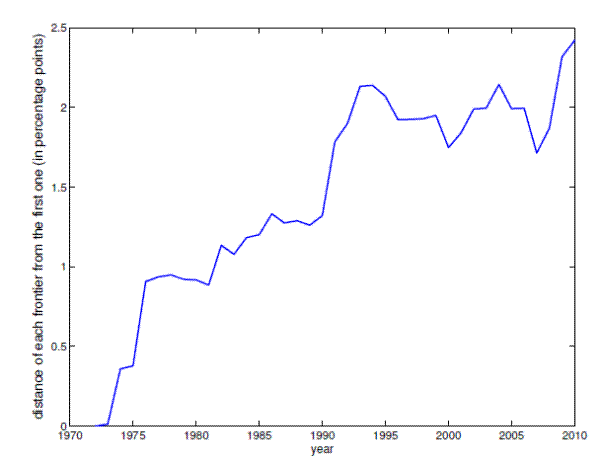
Figure 4 plots the distance of each frontier from the first frontier.
The distance is interpreted as the expected increase in GDP volatility or the expected decline in GDP growth in that period relative to the first one. For example, when comparing the last frontier (period 1986-2010) with the first one (period 1948-1972), a distance of 2.418 can be interpreted as: if there were no change in the efficiency of the economy, the growth GDP volatility would be up to 2.418 percentage points higher or the average growth rate would be up to 2.418 percentage points lower.
The shifting down of the frontier can be the outcome of a higher sectoral variance, a lower correlation across sectors or a lower sectoral growth. I compute the contribution of the changes in sectoral growth, volatility and correlation, by computing counterfactual frontiers where I allow for
only one of these three variables to change. To distinguish between the effect of a change in the sectoral growth and sectoral covariance, I compute a counterfactual frontier, using the sectoral growth from the first period, 1948-1972, and the covariance matrix from the period (1948+![]() ) to (1948+
) to (1948+![]() +25), where
+25), where ![]() takes values from 1 to 38. For example the counterfactual frontier for the last period, 1986-2010, is computed using the vector of sectoral growth rate from the period 1948-1972 and the covariance matrix from the period 1986-2010.
takes values from 1 to 38. For example the counterfactual frontier for the last period, 1986-2010, is computed using the vector of sectoral growth rate from the period 1948-1972 and the covariance matrix from the period 1986-2010.
I further decompose the change in the covariance matrix into a change in the sectoral variance and correlation across sectors. I compute a counterfactual covariance matrix as
where,
| (14) |
Figure 5 plots a time series decomposition of the frontier shifts due to changes in the sectoral growth rate, variance and correlation. The vertical axis measures the distance of each frontier from the first frontier. A non - zero slope represents a
shift in the frontier for the corresponding period. For example, the frontiers computed using data until the mid 80s, have shifted due to changes in the sectoral growth rates, variances and correlation. During this period, while the growth effect is larger, the magnitude of the shifts is comparable
across the three factors. However, the variance and the correlation effect for the latter frontiers is either unchanged or smaller, as the variance effect (the red line) is almost flat and the correlation effect (the blue line) is flat and slightly downward sloping in the latest period. The
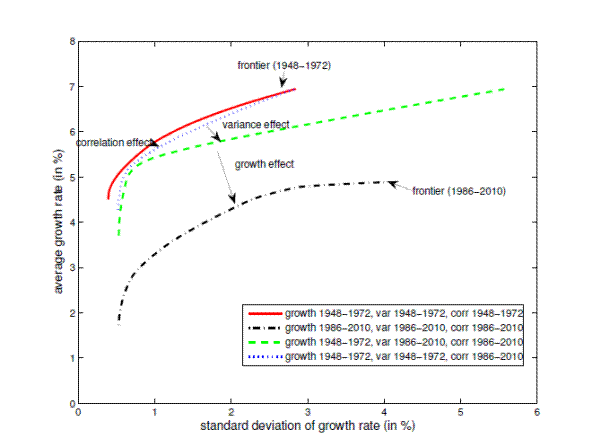
illustration of the decomposition of these effects for the latest frontier is shown in Figure 6. The latest frontier is computed using the data for the period 1986-2010 and as such it almost fully represents the period of the Great Moderation. It is evident that
the frontier has shifted down because of a lower sectoral growth rate, and a higher sectoral variance. A lower sectoral growth accounts for ![]() of the shift in the frontier, representing the
productivity slowdown in the 1970s.6
of the shift in the frontier, representing the
productivity slowdown in the 1970s.6
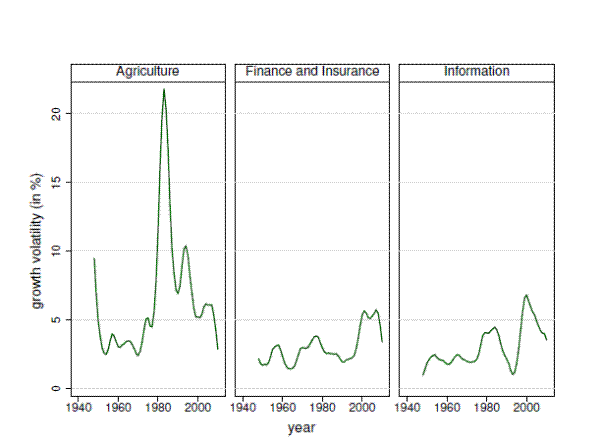
I test for breaks in growth volatility for each of the sectors. The Sup-F statistics, estimated break date and volatilities are given in Table 3. I find support for no change in the sectoral volatility for 19 sectors and an increase in sectoral volatility in 3 sectors: Agriculture, Information and Finance and Insurance. Figure 7 plots the sectoral volatility for these three sectors. As the sectoral variance has been higher and there has been no change in the correlation across sectors, we expect to observe a higher GDP volatility. Instead, the GDP volatility has decreased, implying that the decline in the GDP volatility was due to changes in the sectoral allocations.
4.2 Efficiency
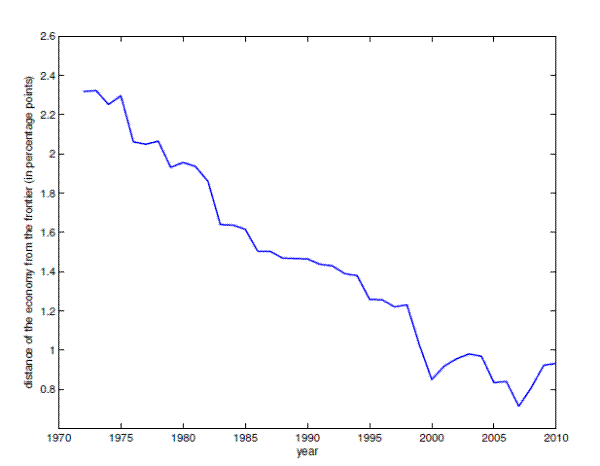
Figure 3 suggested that the economy has been getting closer to the frontier. I defined the efficiency of the economy as the distance of the economy from the frontier. Figure 8 shows that the distance of the economy from the frontier has been decreasing over time, i.e. the economy has become more efficient. The distance of the economy from the frontier was 2.32 in the period 1948-1972 and 0.93 in the period 1986-2010. The change in the efficiency of the economy from the period 1948-1972 to the period 1986-2010, given by the difference in distances, equals 1.39. Interpreted in terms of volatility, this implies that, if there were no change in the covariance matrix, the GDP growth volatility in the period 1986-2010 would be 1.39 percentage points lower than in the period 1948-1972. This improvement in efficiency is comparable to the 1.5 percentage points decline in the GDP growth volatility after 1984. To illustrate the effect of the increased efficiency of the economy in the decline of GDP volatility, I compute the counterfactual values for growth and volatility in the period 1986-2010, if there were no changes in the efficiency of the economy.
I set the efficiency at the period 1948-1972. In the (volatility, growth) space, I use the vector between the optimal portfolio and the economy in the period 1986-2010 and the distance of the economy from the frontier in the period 1948-1972 to locate the economy under this "what if" scenario. The results are plotted in Figure 9. If there were no change in the efficiency, the GDP volatility in the period 1986-2010, would be 2.82%, which is almost the same as the GDP volatility in the data during the period 1948-1972. The distance of the economy from the frontier has two dimentions: growth and volatility. As such, the increased efficiency can be attributed to a decrease in the distance along the growth or the volatility dimension.
A decrease in the distance along the growth (volatility) dimension implies a decline in the difference between the growth (volatility) observed in the data and the growth (volatility) at the optimal allocation. Figure 10 plots the growth rate and volatility at the optimal sectoral allocation, the GDP growth and volatility observed in the data, and the difference between the two. Figure 10 shows that the difference between the growth volatility in the data and the volatility at the optimal allocation has been decreasing over time. The increase in the efficiency occured along the volatility dimension, an increase in risk efficiency.
4.3 Sectoral Allocation
In the previous section, I showed that since the sectoral covariances have either increased or not changes, the Great Moderation was the outcome of changes in the sectoral allocations. Furthermore, the risk efficiency, as measured by the difference between the GDP volatility in the data vs.the model, has increased. These findings imply that the sectoral allocations were more risk efficient. From Finance, a lower volatility can be a benefit of diversification. To illustrate, I present a measure of sectoral diversification, which refers to the dispersion of the economic activity across sectors.
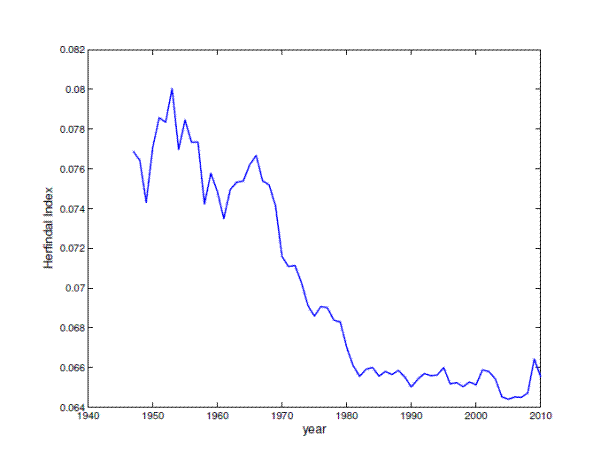
Figure 11 plots, the Herfindal Index, the most commonly used index of sectoral concentration.7 The Herfindal Index, (HI), is defined as,
where
Figure 11 suggests that there are two breaks (three regimes) in the HI series. I find strong evidence for the presence of two breaks.8 The estimated break dates are the 1970 and 1980, where the period 1970-1980 corresponds to the decline in the sectoral concentration and the period 1980 onwards corresponds to the period of a higher sectoral diversification. While the estimated date for the second break in the HI, 1980, occurs before the estimated break date in the GDP volatility, 1984, the 90% confidence interval for the second break in HI falls within the 90% confidence interval for a break in the GDP growth volatility.9
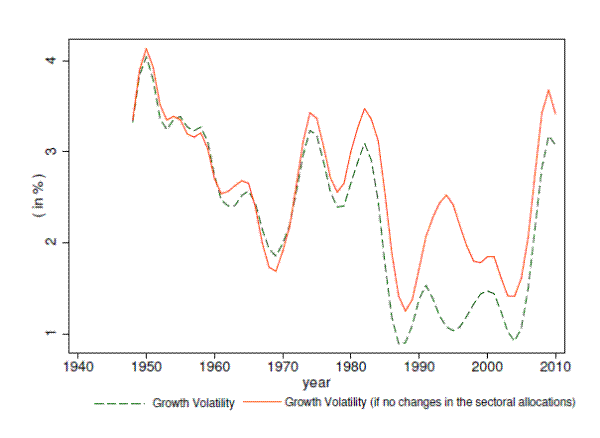
To further illustrate the effect of changes in the sectoral allocation in the decline of GDP growth volatility, I construct a counterfactual GDP growth series, using the sectoral growth rates in the data and setting the sectoral composition as in 1948:
I compute the instantaneous volatility of
![]() . Figure 13 plots the GDP volatility in the data and the GDP volatility for the counterfactual growth series.
. Figure 13 plots the GDP volatility in the data and the GDP volatility for the counterfactual growth series.
The only difference between these two series comes from the changes in the sectoral allocations over time. Figure 13 shows that the effect of the changes in the sectoral allocation occurs in the mid 1980s. I cannot reject the hypothesis of no break in the counterfactual GDP growth series. The change in sectoral allocations is sufficient to explain the decline in GDP growth volatility.
5.1 Robustness Checks
In this section, I test for the robustness of results using a less disaggregated classification and a more rigid frontier, where the sectoral shares are allowed to move within certain bounds.
Sectoral Classification. The selection of the 22 sectors, corresponding to the 2-digit NAICS, was dictated by the data availability. To test the robustness of the results with respect to the sectoral classification, I use 15 sectors corresponding to the sector level classification in the Input-Output Tables. The list of sectors is given in Table 4. I cannot test the robustness of the results for a less disaggregated classification as the data at a 3-digit level data is availabe starting from 1987, leaving out the period before the Great Moderation.
Bounds on Sectoral Shares. When computing the efficient frontier, the sectoral shares were just constrained to be between 0 and 1 and to sum up to 1, allowing for a very feasible structure of the economy. To introduce rigidities, I impose further constraints on the
sectoral shares. I set the lower (![]() ) and the upper bounds (
) and the upper bounds (![]() ) as:
) as:
| (17) |
| (18) |
Furthermore, I define 15 groups as in the sector level classification of the Input-Output Table. I impose bounds on the relative share of groups as follows:
![\displaystyle \left(\frac{\omega_{group_{i}}}{\omega_{group_{j}}}\right)_{L} = max \left\{0, \left[min\left(\frac{vapct_{group_{i}}}{vapct_{group_{j}}}\right)-3stdev\left((\frac{vapct_{group_{i}}}{vapct_{group_{j}}}\right)\right]\right\}](img95.gif) |
(19) |
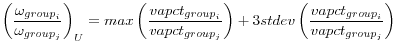 |
(20) |
The allocations along the efficient frontier are computed as in equation 21.
Table 5 shows the correlation coefficient for the measures of frontier shifts, efficiency and risk efficiency produced by these two specifications with the 22-sector baseline. I find that the results are robust to the less disaggregated classification and robust to the constraints on the sectoral shares: the growth-volatility opportunity set has shrunk, the economy has become more efficient and the improvement in efficiency is along the volatility dimension.
Table 6 shows the counterfactural GDP volatility for the period 1986-2010 if there were no changes in efficiency. The GDP volatility for the period 1948-1972 was 2.62 %. If the efficiency in 1986-2010 were the same as in the 1948-1972, the counterfactual GDP volatility produced by the 22-sector, 15-sector and 22-sector with sectoral share bounds would be 2.41%, 2.64% and 2.82% respectively. These results confirm that the decline the GDP volatility was the outcome of more risk efficient sectoral allocations.
The Herfindal Index, both in the 22-sector and 15-sector case, shows an increase in sectoral diversification, implying that the more diversified sectoral allocations were more risk efficient.10
5.2 Extensions
Preferences. The frontier is determined by the vector of the sectoral growth rate and the covariance matrix of the sectoral growth rates. Given the frontier, the actual sectoral allocations determine the location of the economy relative to the frontier. The preferences in terms of growth and volatility are represented in the distance of the economy from the frontier as in equation ( 7). The optimal allocation then corresponds to efficient allocation that minimizes the distance of the economy from the frontier in the (growth, volatility) space. I use the ratio of growth-to-volatility at the optimal allocation to capture the "revealed" preferences. Figure 14 plots the ratio of growth-to-volatility in the data and the optimal allocation on the frontier computed for three specifications: 22-sector and 15-sector classsification and the 22-sector with bounds on sectoral shares.
The growth-to-volatility ratio in the economy is stable at about 2. Across the three specifications, the growth-to-volatility ratio of the optimal allocation is higher and volatile in the period before the Great Moderation. During the Great Moderation, the ratio is in the range of 2 to 4, which is also the range usually used for the coefficient of risk aversion in the the mean-variance utility function.
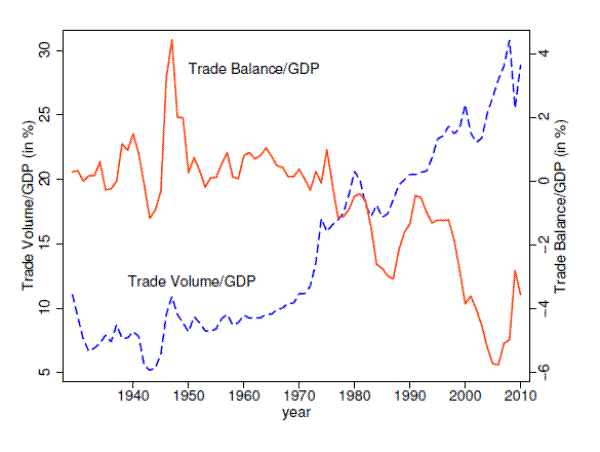
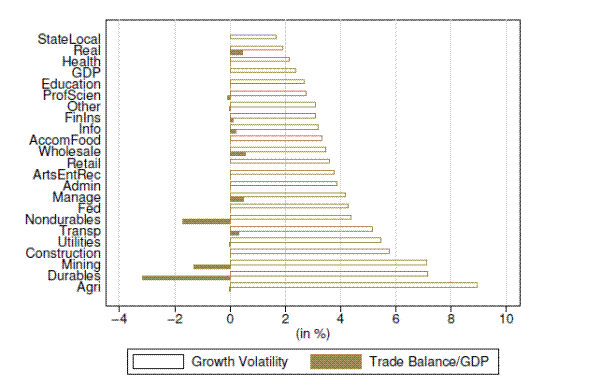
Sectoral Volatility and Trade Balance. While the trade volume has been increasing since the 1950s, the Great Moderation corresponds to a period of persistent trade deficits, as plotted in Figure 15. Figure 16 plots the trade balance and growth volatility for each sector. Figure 16 shows that the sectors with a trade deficit (Durables, Mining and Non durables) are among the more volatile sectors.
This suggests another point of view of the Great Moderation, as an outcome of "exporting volatility" by incurring a trade deficit in the more volatile sectors. It is not plausible to suggest that the increased trade openness led to an increase in growth volatility in these sectors, as I did not find support for a change in volatility in these sectors.
6 Concluding Remarks
Modeling the economy in the (growth, volatility) space, I can present the sectoral allocation in a growth-volatility efficient frontier and discuss the contribution of changes in sectoral covariances and sectoral allocations in explaining the Great Moderation. I convert the complexity of changes in the sectoral allocations into a measure of efficiency of the economy. I measure the efficiency as the distance of the economy from the growth-volatility efficient frontier. While the frontier has shifted down, shrinking the growth-volatility opportunity set, the efficiency has increased.
I conclude that the decline in GDP growth volatility after 1984, up until the last recession, can be sufficiently explalined by more efficient and more diversified sectoral allocations.
In addition, sectoral shifts have been proposed as an explanation for the slow increase in employement during the recoveries since the early 1990s. Risssman (2009) shows the structural changes were more prounounced in Finance, Insurance and Real Estate sector. These structural changes would contribute to the increase in the growth volatility in Finance and Insurance, which combined with the increase in the share of these sectors contributed to the recent increase in aggregate growth volatility.
Furthermore, the Great Moderation also concurs with a period of persistent trade deficits. These deficits were in the more volatile sectors. These facts suggest that the impact of the globalization on growth volatility is affected by the sectoral composition of the trade balance.
Table 1: List of Sectors. The selection of the sectors is dictated by the data availability, as to include observations before and after the Great Moderation. The data for the period 1947-1987 is available only at the 2-digit level, representing 22 sectors. The more disaggregated data is available only starting from 1987. I do a robustness test using the sector-level classification of the Input-Output table, representing 15 sectors, and I find that the results are robust to a less disaggregated data.
| Abbreviation | Sector | 2002 NAICS Code |
| Agri | Agriculture, Forestry, Fishing and Hunting | 11 |
| Mining | Mining | 21 |
| Utilities | Utilities | 22 |
| Construction | Construction | 23 |
| Durables | Durable goods | 33, 321, 327 |
| Nondurables | Nondurable goods | 31, 32 (except 321&327) |
| Wholesale | Wholesale trade | 42 |
| Retail | Retail trade | 44, 45 |
| Transp | Transportation and Warehousing | 48, 49 (except 491) |
| Info | Information | 51 |
| FinIns | Finance and Insurance | 52 |
| Real | Real estate, Rental, Leasing | 53 |
| ProfScien | Professional, Scientific and Technical Services | 54 |
| Manage | Management of Companies and Enterprises | 55 |
| Admin | Administrative and Waste Management Services | 56 |
| Education | Education services | 61 |
| Health | Health care and Social assistance | 62 |
| ArtsEntRec | Arts, Entertainment and Recreation | 71 |
| AccomFood | Accomodation and Food services | 72 |
| Other | Other Services, except Government | 81 |
| Fed | Federal Government | na |
| StateLocal | State and Local Government | na |
Table 2: Variance Decomposition. Sector's contribution to GDP growth is defined as the sector's growth rate weighted by the sector's share to GDP (
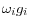 ). The sum of the variance terms is (
). The sum of the variance terms is (
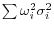 ) and the sum of the covariance terms is (
) and the sum of the covariance terms is (
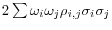 ).
).
| Early (1948-1983) | Late (1984-2010) | Late/Early | |
| Variance Real GDP growth | 7.32 | 3.07 | 0.42 |
| Sum of the variance terms | 2.05 | 0.77 | 0.38 |
| Sum of the covariance terms | 5.27 | 2.30 | 0.44 |
Table 3: Breaks in Sectoral Volatility. I find support for no change in the sectoral volatility for 19 sectors and an increase in sectoral volatility in 3 sectors: Agriculture, Information and Finance and Insurance. For these three sectors, Date, Before and After show the estimated break date, and the estimated volatility before and after the break date. The volatility in these three sectors has doubled. These results show that the decline in GDP growth volatility could have not been the outcome of a lower sectoral variance. Levels of significance: 1% (***), 5% (**).
| Sector | Sup-F | Date | Before | After |
| Agriculture, Forestry, Fishing and Hunting | 8.934** | 1980 | 3.8 | 9.5 |
| Mining | 6.341 | |||
| Utilities | 4.279 | |||
| Construction | 2.885 | |||
| Durable goods | 4.555 | |||
| Nondurable goods | 2.395 | |||
| Wholesale trade | 3.579 | |||
| Retail trade | 1.57 | |||
| Transportation and Warehousing | 6.327 | |||
| Information | 9.056** | 1997 | 2.4 | 5.4 |
| Finance and Insurance | 13.785*** | 1998 | 2.5 | 5.3 |
| Real estate, Rental, Leasing | 3.662 | |||
| Professional, Scientific and Technical Services | 1.87 | |||
| Management of Companies and Enterprises | 5.178 | |||
| Administrative and Waste Management Services | 4.178 | |||
| Education services | 2.24 | |||
| Health care and Social assistance | 5.759 | |||
| Arts, Entertainment and Recreation | 6.984 | |||
| Accomodation and Food services | 1.984 | |||
| Other Services, except Government | 2.36 | |||
| Federal Government | 2.043 | |||
| State and Local Government | 4.004 |
Table 4: Sector level Classification in the Input-Output Tables. The sector-level classification of the Input-Output Tables corresponds to 15 sectors. The results are robust to this level of aggregation. The 3-digit data is available starting from 1987
| Sector | I-O Codes | 2002 NAICS codes |
| Agriculture, forestry, fishing, and hunting | 11 | 11 |
| Mining | 21 | 21 |
| Utilities | 22 | 22 |
| Construction | 23 | 23 |
| Manufacturing | 31G | 31, 32, 33 |
| Wholesale trade | 42 | 42 |
| Retail trade | 44RT | 44, 45 |
| Transportation and warehousing | 48TW | |
| Information | 51 | 51 |
| Finance, insurance, real estate, rental, and leasing | FIRE | 52, 53 |
| Professional and business services | PROF | 54, 55, 56 |
| Educational services, health care, and social assistance | 6 | 6 |
| Arts, entertainment, recreation, accommodation, and food services | 7 | 7 |
| Other services, except government | 81 | 81 |
| Government | G | NA |
Table 5: Comparison of Different Specifications. "Frontier shifts" measures the distance of each frontier from the first one. "Efficiency" is measured by the distance of the economy from the efficient allocation, and "Risk Efficiency"
corresponds to the volatility dimension of "Efficiency". I test the robustness of the results to the level of dissagregation ("22 sectors" versus "15 sectors") and variability of sectoral shares ("22 sectors" versus "22 sectors & bounds"). In "22 sectors & bounds", the sector
shares and the ratio of sector shares are bounded to
![[min-3stdev, max+3stdev]](img4.gif) of the observed values. The results are robust to these changes. The growth-volatility opportunities set has been shrinking and the risk efficiency has been
increasing.
of the observed values. The results are robust to these changes. The growth-volatility opportunities set has been shrinking and the risk efficiency has been
increasing.
| Frontier Shifts (22 sectors) | Efficiency (22 sectors) | Risk Efficiency (22 sectors) | |
| Correlation coefficient for: 22 sectors | 1 | 1 | 1 |
| Correlation coefficient for: 15 sectors | 0.979 | 0.995 | 0.994 |
| Correlation coefficient for: 22 sectors & sectoral shares bounds | 0.965 | 0.974 | 0.866 |
Table 6: GDP volatility and Efficiency. The counterfactual GDP growth volatility is computed keeping the efficiency as in (1948-1972). Efficiency is measured by the distance of the economy from the frontier. The counterfactual GDP growth
volatility in the three specifications is almost the same as the volatility in the data in (1948-1972), reconfirming that the decline in GDP volatility was the outcome of more risk efficient sectoral allocations. "22 sectors" is the baseline, "15 sectors" corresponds to a more aggregated
datatset and "22 sectors & bounds" restricts the variability of the sector shares and the ratio of sector shares to
![[min-3stdev, max+3stdev]](img4.gif) .
.
| GDP growth volatility | |
| data (1948-1972) | 2.62 |
| data (1986-2010) | 1.68 |
| counterfactual (1986-2010) if efficiency as in (1948-2010)--22 sectors | 2.41 |
| counterfactual (1986-2010) if efficiency as in (1948-2010)--15 sectors | 2.64 |
| counterfactual (1986-2010) if efficiency as in (1948-2010)--22 sectors & sectoral shares bounds | 2.82 |
Figure 1: The GDP growth rate from the National Income and Product Accounts (NIPA) and as a weighted sum of the sectoral growth rates.
The instantaneous GDP volatility is defined as
![]() , where
, where
![]() is the error term from the AR(1) model of GDP growth. In the literature, the estimated start date of the decline in the GDP growth volatility is 1984:1. The estimated break date,
using annual data, is 1984.
is the error term from the AR(1) model of GDP growth. In the literature, the estimated start date of the decline in the GDP growth volatility is 1984:1. The estimated break date,
using annual data, is 1984.
Each line shows the efficient frontier for every 25-year rolling period between 1948 and 2010. The circles show the GDP growth and volatility observed in the data for every 25-year rolling period. There are 39 lines and 39 circles in this Figure. The distance of the economy from the frontier corresponds to distance of the circle from the line with the same color. The fontier has been shifting down to the right, implying that the opportunity set has shrunk. The distance of the economy from the frontier has decreased, implying that the efficiency of the economy has increased.
The distance is interpreted as the expected increase in GDP volatility or the expected decline in GDP growth in the corresponding period relative to the first one, if there were no change in efficiency. For example, the distance of the last frontier (1986-2010) from the first frontier (1948-1872) is 2.418. If there were no change in the distance of the economy from the frontier, i.e. no change in the efficiency, the GDP growth volatility in the last period would be up to 2.418 percentage point higher than in the first period.
Figure 5: Time Series of the Effect of Sectoral Growth, Variance and Correlation in Shifting the Frontier.
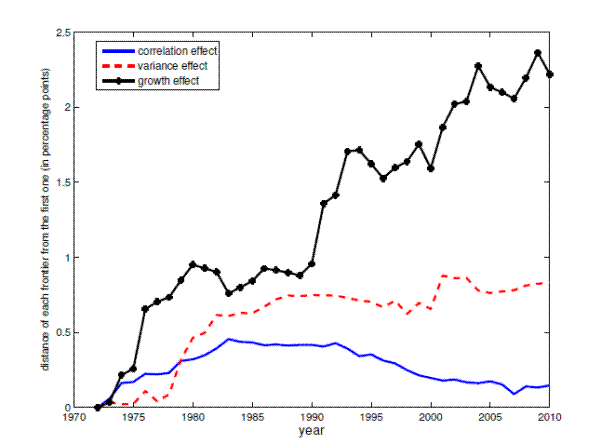
The vertical axis measures the distance of each frontier from the first frontier. A non - zero slope represents a shift in the frontier for the corresponding period.
The frontier for the first period (1948-19572) is given by the solid line and the frontier for the last period (1986-2010) is given by the dash-dot
line. The dash line and the dotted line represent counterfactual frontiers. The solid line and the dotted line are computed using the same vector of sectoral growth rate and the same sectoral variance. The distance between the solid line and the dotted line shows the effect of the change in the
correlation across sectors. The dotted line and the dash line are computed using the same vector of sectoral growth rate and the same correlation across sectors. The distance between the dotted line and the dash line shows the effect of a change in the variance. The dash line and the dash-dot line
are computed using the same covariance matrix. The distance between the dash line and the dash-dot line shows the effect of a change in the growth rate. A lower sectoral growth and a higher sectoral variance account for ![]() and
and ![]() of the shift in the frontier, respectively.
of the shift in the frontier, respectively.
The figure plots the growth volatility for the sectors that have a statistically significant break in volatility.
The efficiency is measured by the distance of the economy from the frontier. The distance of the economy from the frontier is measured as the minimum distance from each of the
portfolios from on the frontier, where the distance is measured in the (growth, volatility) space:
![]() , where
, where
![]() . The closer the economy to the frontier the higher the efficiency. A change in the
efficiency over time is interpreted as the expected increase in GDP growth, or decline in GDP volatility. For example, the efficiency between 1986-2010 and 1948-1972 increase by 1.39 (the distance of the economy from the frontier was 0.93 in 1986-2010 and 2.32 in 1948-1972). Interpreted along the
volatility dimension, if there were no change in the covariance matrix, the GDP volatility in the period 1986-2010 would be 1.39 percentage points lower than in the period 1948-1972.
. The closer the economy to the frontier the higher the efficiency. A change in the
efficiency over time is interpreted as the expected increase in GDP growth, or decline in GDP volatility. For example, the efficiency between 1986-2010 and 1948-1972 increase by 1.39 (the distance of the economy from the frontier was 0.93 in 1986-2010 and 2.32 in 1948-1972). Interpreted along the
volatility dimension, if there were no change in the covariance matrix, the GDP volatility in the period 1986-2010 would be 1.39 percentage points lower than in the period 1948-1972.
The efficiency of the economy is measured by the distance of the economy from the optimal allocation on the frontier. The distance of the economy from the frontier is given by the distance between the econ(data) and econ(optimal), where econ(optimal) is the optimal allocation on the frontier. As the economy likes GDP growth and dislikes GDP growth volatility, the optimal allocation is determined by the portfolio on the frontier closest to the corresponding econ(data), where the distance is measured in the (growth, volatility) space. The distance of the economy from the frontier has decreased, implying that the efficiency has increased. To illustrated the effect of the increased efficiency in the decline of GDP volatility, I compute a counterfactual economy: econ(counterfactual, 1986-2010) is computed such that the distance of econ(counterfactual, 1985-2010) from frontier(1986-2010) is the same as the distance of the economy from the frontier (1948-1972). If there were no changes in efficiency, there would be no decline in the growth volatility: the GDP volatility in the period 1986-2010, would be 2.82%, which is almost the same as the volatility during the period 1948-1972.
Figure 10: Risk Efficiency. This figure plots the improvements in efficiency along the growth and volatility dimension over time for the period 1970 to 2010.
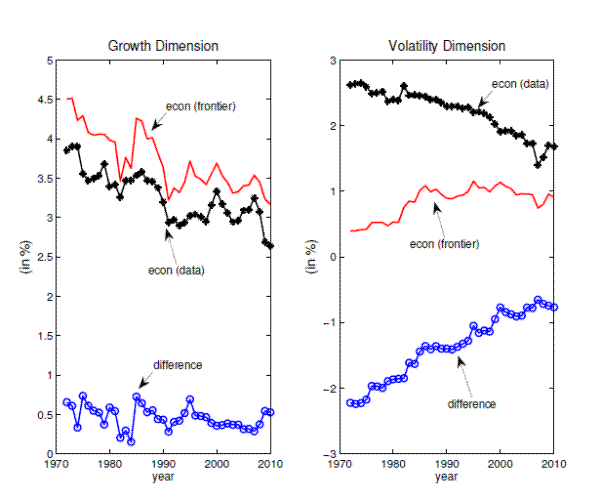
This figure plots the improvements in efficiency along the growth and volatility dimension. The distance of the economy from the frontier has been decreasing along the volatility dimension, implying an improvement in the risk efficiency. Efficiency is measured by the distance of the economy from the frontier in the (growth, volatility) space. The optimal allocation is defined as the allocation on frontier closest to the economy.
The sectoral concentration is measured by the Herfindal Index, as
![]() ,where
,where
![]() is the sector share to GDP. The Herfindal Index is calculated using the annual data for 22 broad sectors in the economy. The list of sectors is given in Table 1. The index takes values from 1/n (equal sectoral shares) to 1 (a single sector economy), where n=number of sectors. A decrease in the Herfindal Index corresponds to an increased in diversification. The economy was more diversified during the Great Moderation.
is the sector share to GDP. The Herfindal Index is calculated using the annual data for 22 broad sectors in the economy. The list of sectors is given in Table 1. The index takes values from 1/n (equal sectoral shares) to 1 (a single sector economy), where n=number of sectors. A decrease in the Herfindal Index corresponds to an increased in diversification. The economy was more diversified during the Great Moderation.
The economy has been shifting away from Agriculture and Manufacturing and moving toward services.
The dashed line plots the GDP growth volatility in the data. The solid line plots the growth volatility of a counterfactual GDP series, where the sectoral allocations are time invariant, and the sectoral growth rates vary as in the data. I cannot reject the hypothesis of no break in the counterfactual GDP growth series, providing further support that the decline in GDP growth volatility was the outcome of changes in the sectoral allocations.
It is assumed that the economy likes growth and dislikes volatility. The optimal allocation is defined as the allocation on the frontier that minimizes the distance of the economy from the frontier. Growth-to-Volatility Ratio produced by these allocations shows the same pattern across the three specifications. The ratio is lower and stable during the Great Moderation. It takes values from 2 to 4, which is also the range usually used for the coefficient of risk aversion in the the mean-variance utility function.
The trade volume has been increasing since the 1950s. Trade deficits have been persistent during the Great Moderation.
The more volatile sectors have a larger trade deficit. The trade data are from the 1998-2009 from the Input-Output Use Tables.