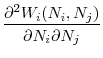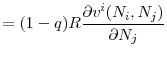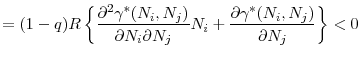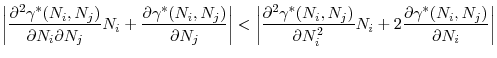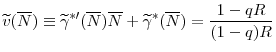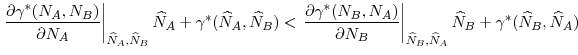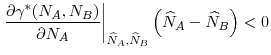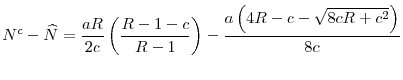Systemic Risk, International Regulation, and the Limits of Coordination*
Abstract:
1 Introduction
The underlying shocks that precipitated the financial crisis of 2007-2009 quickly spread across global financial markets and were amplified at an unprecedented scale. The strikingly global nature of the crisis has revived interest in the international coordination of financial regulation. Regulatory reforms and the strengthening of coordination between national financial regulators are prominent items on the international reform agenda. The Financial Stability Board (FSB) was set up by the G-20 countries during the crisis to create guidelines for regulatory coordination and the supervision of systemic risk in the international financial system.1
This paper, using a game-theoretic model, analyzes the incentives of national regulators towards international cooperation when there is systemic risk in global financial markets. In the model, systemic risk in financial markets is generated through asset fire sales. The model shows that in the absence of cooperation, independent regulators choose inefficiently low regulatory standards compared to regulation levels that would be chosen by a central regulator. A central regulator internalizes systemic risk and improves welfare in cooperating countries. The model also demonstrates that common central regulation will voluntarily emerge only between sufficiently similar countries.
Key features of a third generation of bank regulation principles, popularly known as Basel III, strengthen capital regulations and add new elements to Basel bank regulation principles such as liquidity and leverage ratio requirements. With Basel III, the objective of regulation aimed at creating a level playing field for internationally active banks is supported by an objective of creating sound regulatory practices that will contain systemic risk in national and international financial markets, and prevent pro-cyclical amplification of these risks over time. In this paper, I revisit the issue of coordinating international financial regulation in light of recent developments in the international regulatory infrastructure.
Acharya (2003, 2009) and Dell'Ariccia and Marquez (2006) are notable studies in the literature on international financial regulation. All three of these studies focus on the level playing field objective of financial regulation and examine the benefits to international coordination of financial regulation under externalities that operate through the competition in loan markets. This paper diverges from the previous literature by focusing on systemic externalities across financial markets generated by fire sales of assets. I examine the effects of systemic externalities on the nature of international financial regulation in the absence of cooperation between regulators, as well as its effects on the incentives of national regulators towards cooperation. The paper also contributes to the literature by examining the effects of structural differences across countries on the choice of regulatory standards when countries are linked through systemic externalities in international financial markets. I show herein that common central regulation voluntarily emerges only between sufficiently similar countries.
During times of distress, asset prices can move away from the fundamental values and assets can be traded at fire sale prices. When firms or financial intermediaries face liquidity shocks, and debt-overhang, collateral or commitment problems prevent them from borrowing or issuing new equity they may have to sell assets to generate the required resources. If the shocks are wide spread throughout an industry or an economy, then potentially deep-pocket outsiders will emerge as the buyers of the assets. However, some assets are industry-specific: when they are redeployed by outsiders, they will be less productive, and they will be sold to outsiders at a discount. This idea, which originated in Williamson (1988) and Shleifer and Vishny (1992), was later employed by fire sales models such as Lorenzoni (2008), Gai et al. (2008), Acharya et al. (2010) and Korinek (2011).
Industry-specific assets can be physical, or they can be portfolios of financial intermediaries because many of these contain exotic tailor-made financial assets (Gai et al., 2008). The asset specificity idea is captured in this paper through a decreasing returns to scale technology for outsiders, similar to the ones proposed by Kiyotaki and Moore (1997), Lorenzoni (2008), Gai et al. (2008), and Korinek (2011). The less efficient technology of outsiders makes the situation even worse for distressed intermediaries because they have to accept higher discounts to sell more assets. Empirical and anecdotal evidence suggests the existence of fire sales of physical as well as financial assets.2
These facts indicate that when numerous intermediaries concurrently face the same types of shocks and sell assets simultaneously, asset prices can fall, which forces the intermediaries to sell additional assets. Because an individual intermediary takes the market price as given and decides how much of its assets to sell to continue operating at an optimal scale, each intermediary ignores the negative externality of its asset sales on others. In a financially integrated world, intermediaries from different countries sell assets in a global market to potentially the same set of buyers. Therefore, initial shocks that hit individual countries can be amplified in globally integrated financial markets.
I consider this systemic externality in this paper, and also seek answers to the following questions: How do national regulators behave under this systemic externality if the regulators act non-cooperatively? Would an individual regulator tighten or relax regulation when regulation is tightened in another country? Would national regulators relinquish their authority to a central international regulator who would impose the same set of regulatory standards across countries? How do asymmetries across countries affect the nature of regulatory standards and the incentives of national regulators towards international cooperation?
Briefly, I propose a three-period, two-good model that features two countries with independent regulators. In each country there is a continuum of banks. Banks are protected by limited liability, and there is deposit insurance. Banks borrow consumption goods from local deposit markets, and invest in a productive asset in the first period.
All uncertainty in the model is resolved at the beginning of the second period and one of the two states of the world is realized: a good or a bad state. In the good state there are no shocks and banks' investments produce net positive returns in the last period. However, in the bad state, banks' investments are distressed and they have to be restructured to produce the normal positive returns that are obtained in good times.
A continuum of global investors with large resources in the second period can purchase productive assets in the second period to produce consumption goods in the third and final period. Assets in different countries are perfect substitutes for global investors. However, global investors are not as productive as the domestic banks in managing domestic assets and face decreasing returns to scale from these assets.
I solve the equilibrium of this model by backwards induction. Following the shocks in the interim period, banks need to sell some fraction of their assets in a global capital market to pay for the restructuring costs. An asset sale in the bad state is unavoidable because other domestic resources required to carry out the restructuring process are unavailable. The price of the productive asset is determined in a competitive market in which banks from the two countries and global investors meet.
I show that a higher initial investment by banks in either of these countries will lead to a lower price for the productive asset in this market. If the asset price falls below a minimum threshold, return to the assets that can be retained by the banks is lower than the value of the initial investment, and the banks become insolvent. I call this case a systemic failure. Depositors encounter real losses when a systemic failure occurs because returns to the remaining bank assets do not cover depositors' initial investment.
Regulation in this model can be interpreted as a minimum capital ratio requirement. Each regulator determines the initial regulatory standard by taking into account the equilibrium in the asset market in the interim period. Due to the systemic externality discussed above, banks always leverage up to the maximum by borrowing funds from the local deposit market. In other words, the minimum capital ratio always binds. Therefore, the initial investment level of banks in a given country is determined completely by the regulatory standard.
In the first period, regulators act simultaneously and choose the regulatory standard for their domestic banks by taking the regulatory standard in the other country as given. I show that when the countries are symmetric, there exists a unique symmetric Nash equilibrium of the game between the two regulators. Moreover, regulation levels in the two countries are strategic substitutes: if one regulator tightens the regulatory standard in its jurisdiction, the other regulator optimally loosens its regulatory standard. The intuition behind this result is as follows: When the first country reduces the maximum leverage level (i.e., tightens regulatory standards), the extent of the fire sale of assets in the bad state by banks in that country are reduced, and a higher price is realized for the assets sold by these banks. This increases the expected returns in the bad state, which allows the regulator in the other country to relax regulation levels.
I show that, due to this systemic risk, regulatory standards in equilibrium when regulators act non-cooperatively will be inefficiently lax compared to regulatory standards that would be chosen by a central regulator. A central regulator aims to maximize the total welfare of the two countries, and internalizes these externalities. I assume that, for political reasons, the central regulator has to choose the same regulation levels in both countries. If the two countries are symmetric, I show that forming a regulatory union will increase welfare in both. Therefore, it is incentive compatible for the independent regulators of symmetric countries to relinquish their authority to a central regulator.
I also consider the incentives of regulators when there are asymmetries between countries, with a focus on the asymmetries in the asset returns. In particular, I assume that banks in one country are uniformly more productive than the banks in the other country in terms of managing the long-term asset. I also show that cooperation would voluntarily emerge only between sufficiently similar countries. In particular, the regulator in the high-return country chooses lower regulatory standards in equilibrium and is less willing to compromise on stricter regulatory standards.
Interest in the international coordination of financial regulation is not an entirely recent phenomenon. Arguments in favor of coordination and harmonization of regulatory policies across countries were made in the 1988 Basel Accord (Basel I) which focused on credit risk and set minimum capital requirements for internationally active banks and was enforced in the G-10 countries in 1992.3
However, Basel I did not create an entirely level playing field for internationally active banks because countries retained a significant degree of discretion about different dimensions of regulation. Furthermore, rapid developments in financial markets, especially more complex financial products brought about by financial innovation, created significant differences about the stringency of capital regulations across countries in practice (Barth et al. ,2008). These developments created a challenge for regulators and paved the way for Basel II.4
While progress on the implementation of Basel II was slower than expected, the global financial crisis renewed urgency about increased cooperation and the better regulation of international financial markets, in part because insufficient policy coordination between countries and deficiencies in Basel II regulatory mechanisms were blamed for the severe contagion of the crisis. Most of the international regulatory mechanisms proposed prior to the crisis had emphasized the soundness of financial institutions individually (micro-prudential regulation), but had neglected regulatory standards that could enhance the stability of the financial system as a whole by considering systemic risks (macro-prudential regulation). The model in this paper focuses on macro-prudential regulation in the context of regulating systemic risk in the international banking system.
The paper proceeds as follows. Section 2 contains a brief summary of related literature. Section 3 provides the basics of the model and presents the main results of the paper without resorting to a particular functional form. International financial regulation between asymmetric countries is considered in Section 4. Section 5 investigates the robustness of the results obtained from the basic model to some changes in the model environment. Section 6 shows the set of parameter ranges for which systemic failures occur in the uncoordinated equilibrium when countries are symmetric. Conclusions are presented in Section 7. All proofs are provided in the Appendix.
2 Literature Review
This paper belongs to the international financial regulation theory that has developed in recent decades. This paper is closest to Acharya (2003), Dell'Ariccia and Marquez (2006), Acharya (2009), and Bengui (2011). In particular, Dell'Ariccia and Marquez (2006) investigate the incentives of national regulators to form a regulatory union in a two-country banking model, where a single bank from each country competes for loans in both markets in a Bertrand differentiated products setup. If one of the banks is allowed to expand its balance sheet, low average returns to bank loans will be realized in both markets. Banks in this model are also endowed with a costly monitoring technology. Low average returns reduce incentives of banks to monitor, and hence undermines their stability. The authors show that, under this externality, independent national regulators will implement lower capital requirements compared to capital requirements that would be implemented by a central regulator. They also show that symmetric countries always gain from cooperation, whereas a cooperation emerges voluntarily only between sufficiently similar asymmetric countries. The coordination problem for asymmetric countries as presented in this paper is similar to Dell'Ariccia and Marquez (2006) . However, in that model the asymmetry between countries was due to differences in regulators' exogenously specified tastes and preferences. In this paper I consider asymmetries that are due to structural differences across countries, such as differences in asset returns.
Acharya (2003) shows that convergence in international capital adequacy standards cannot be effective unless it is accompanied by convergence in other aspects of banking regulation, such as closure policies. Externalities in his model are in the form of cost of investment in the risky asset. He assumes that a bank in one country increases costs of investment for itself and for a bank in the other country as it invest more in the risky asset and thereby creates externalities for the bank in the neighboring country.
In the model considered by Acharya (2009), failure of a bank creates both negative and positive externalities for surviving banks. Negative externality is the increase in the cost of the deposits for surviving banks through a reduction in overall available funds. Positive externalities are strategic benefits that arise either through depositor migration from the failing banks to surviving banks, or through acquisition of the failed banks' assets and businesses by surviving banks. He shows that that if the negative externality dominates positive externalities, banks in different regions will choose their investments to be highly correlated compared to globally optimal correlation levels. Acharya calls this fact "systemic risk shifting".
This paper also differs from previously mentioned studies in terms of its source for the externalities between national financial markets. I focus on externalities between national financial markets that operate through asset markets and asset prices whereas the studies cited above considered externalities that operate through costs in the loan or deposit markets. In this paper, systemic risk in international financial markets arises as banks from two countries experience correlated liquidity shocks, and financial amplification effects are triggered due to fire sales. In that regard, this paper is closest to Bengui (2011) , but mainly differs from Bengui (2011) by considering the coordination problem under systemic risk for structurally different countries. On the other hand, Bengui (2011) considers the coordination problem for symmetric countries with risk averse individuals and imperfectly correlated shocks across countries. As this paper affirms, provision of macro-prudential regulation is insufficient when countries act independently, and regulatory standards are strategic substitutes across countries. He also shows that risk taking could be higher in nationally regulated economies compared to the competitive equilibrium, and that starting from a competitive equilibrium unilateral introduction of a (small) regulation could be welfare reducing for the country introducing the regulation.
Another branch of this literature considers regulation of a multi-national bank that operates across two countries. Two notable studies, Dalen and Olsen (2003) and Holthausen and Ronde (2004), focus on the tension between home and host country regulation of a multi-national bank where informational asymmetries are the driving force of regulatory competition. Unlike these studies, my paper focuses on a model in which banks invest in a single country and are therefore regulated only by their home country, but interact with each other in global asset markets. The tension between regulators in my model arises from the externalities that banks in different countries create for each other in global asset markets during times of distress.
This study can also be viewed as a part of the broader literature on macroeconomic policy coordination that was especially active especially from late 1970s through the 1990s. Cooper (1985) and Persson and Tabellini (1995) provide extensive reviews of this literature. Hamada (1974, 1976) are the pioneer studies in the application of the game-theoretic approach to strategic interactions among national governments.
Last, this paper is also related to the literature that features asset fire sales. The common theme across these studies is that, under certain conditions, asset prices can move away from the fundamental values and assets can be traded in markets at fire sale prices. One reason for fire sales is the combined effect of asset-specificity and correlated shocks that hit an entire industry or economy. Origins of this idea can be found in Williamson (1988) and Shleifer and Vishny (1992) which claim that fire sales are more likely when major players in an industry face correlated shocks and the assets of the indusry are not easily redeployable in other industries. In such a scenario, a firm needs to sell assets to restructure and continue operations at a smaller scale; however, it cannot sell its assets at full value because other firms in the same industry are experiencing similar problems. Outside investors would buy and manage these assets but they are not as sophisticated as the firms in the industry. Therefore, they would be willing to pay less than the full value of the assets to the distressed firms. Moreover, unsophisticated investors may face decreasing returns in the amounts of assets they employ. This possibility makes the situation even worse for distressed firms because if many of them try to sell assets to outside investors simultaneously, they will have to accept higher discounts.
The closest papers in this literature to mine are Lorenzoni (2008), Gai et al.(2008) and Korinek (2011) which essentially address the same question: how do privately optimal borrowing and investment levels of financial intermediaries compare to the socially optimal levels under pecuniary externalities in financial markets generated through asset fire sales? In these studies, the reasons for fire sales are limited commitment on financial contracts and the fact that asset prices are determined in a spot market. Lorenzoni (2008) and Gai et al. (2008) consider a single-country, three-period model with a continuum of banks. Banks borrow from consumers and offer them state-contingent contracts. In the interim period, banks are hit by shocks and need to sell assets in some states to restructure distressed investments. These papers show that there exists over-borrowing and hence over-investment in risky assets in a competitive setting compared to the socially optimal solution. Because in the competitive setting each bank treats the market price of assets as given when it makes borrowing and investment decisions in the initial period, it does not internalize the externalities created for other banks through fire sales. The planner considers the fact that a higher investment will translate into lower prices for capital sold by banks during the times of distress. The main difference between my paper and these papers is that they focus on issues in single-country cases to the exclusion of issues related to the international dimension of regulation.
Asset specificity is not the only reason for fire sales. In Allen and Gale (1994,1998) and Acharya and Yorulmazer (2008) the reason for fire sales is the limited available amount of cash in the market to buy long-term assets offered for sale by agents who need liquid resources immediately. The scarcity of liquid resources leads to necessary discounts in asset prices, a phenomenon known as "cash-in-the-market pricing".
3 Model
This model contains three periods, ![]() ; and two countries,
; and two countries, ![]() . In each
country there is a continuum of banks and a continuum of consumers each with a unit mass and a financial regulator. There is also a unit mass of global investors. All agents are risk-neutral.
. In each
country there is a continuum of banks and a continuum of consumers each with a unit mass and a financial regulator. There is also a unit mass of global investors. All agents are risk-neutral.
There are two goods in this economy: a consumption good and a capital good (i.e., the liquid and illiquid assets). Consumers are endowed with ![]() units of consumption goods at
units of consumption goods at ![]() , and none at later periods.5
, and none at later periods.5
Banks have a technology that converts consumption goods into capital goods one-to-one at ![]() . Capital goods that are managed by a bank until the last period yield
. Capital goods that are managed by a bank until the last period yield ![]() consumption goods per unit. Consumption goods are perishable, and the capital fully depreciates at
consumption goods per unit. Consumption goods are perishable, and the capital fully depreciates at ![]() Capital goods can never be converted into consumption goods.6
Capital goods can never be converted into consumption goods.6
Banks in each country ![]() choose the level of investment,
choose the level of investment, ![]() , in the capital
good at
, in the capital
good at ![]() , and borrow the necessary funds from domestic consumers. I consider deposit contracts that are in the form of simple debt contracts, and assume that there is a deposit insurance
fund operated by the regulator in each country. Therefore, banks can raise deposits from consumers at a constant and zero net interest rate. I also assume that banks are protected by limited liability.7
, and borrow the necessary funds from domestic consumers. I consider deposit contracts that are in the form of simple debt contracts, and assume that there is a deposit insurance
fund operated by the regulator in each country. Therefore, banks can raise deposits from consumers at a constant and zero net interest rate. I also assume that banks are protected by limited liability.7
All uncertainty is resolved at the beginning of ![]() : a country lands in good times with probability
: a country lands in good times with probability ![]() , and in bad times with probability
, and in bad times with probability ![]() . In order to simplify the analysis, I assume that the states of the world at
. In order to simplify the analysis, I assume that the states of the world at ![]() are perfectly correlated across countries. In good times no banks are hit with shocks, therefore no further actions are taken. Banks keep managing their capital goods and realize the full returns from their investment,
are perfectly correlated across countries. In good times no banks are hit with shocks, therefore no further actions are taken. Banks keep managing their capital goods and realize the full returns from their investment, ![]() , in the last period. They make the promised payment,
, in the last period. They make the promised payment, ![]() , to consumers, and hence
earn a net profit of
, to consumers, and hence
earn a net profit of
![]() However, in bad times, the investments of all banks in both countries are distressed. In case of distress, the investment has to be restructured in order to remain productive.
Restructuring costs are equal to
However, in bad times, the investments of all banks in both countries are distressed. In case of distress, the investment has to be restructured in order to remain productive.
Restructuring costs are equal to ![]() units of consumption goods per unit of capital. If
units of consumption goods per unit of capital. If ![]() is not paid, capital is scrapped (i.e., it fully depreciates).
is not paid, capital is scrapped (i.e., it fully depreciates).
There are no available domestic resources (i.e., consumption goods) with which to carry out the restructuring of distressed investment at ![]() . Only global investors are endowed with liquid
resources at this point. Due to a commitment problem, banks cannot borrow the required resources from global investors. My particular assumption is that individual banks cannot commit to pay their production to global investors in the last period.8 The only way for banks to raise necessary funds for restructuring is to sell some fraction of the investment to global investors in an exchange of consumption goods.
. Only global investors are endowed with liquid
resources at this point. Due to a commitment problem, banks cannot borrow the required resources from global investors. My particular assumption is that individual banks cannot commit to pay their production to global investors in the last period.8 The only way for banks to raise necessary funds for restructuring is to sell some fraction of the investment to global investors in an exchange of consumption goods.
These capital sales by banks will carry the features of a fire sale: the capital good will be traded below its fundamental value for banks, and the price will decrease as banks try to sell more capital. Banks in each country will retain only a fraction of their assets after fire sales. If the asset price falls below a threshold, the expected return on the assets that can be retained by banks will be lower than the value of the initial investment; hence, banks will become insolvent.9 I call this situation a "systemic failure".
Once it is known that banks are insolvent, deposit insurance requires the bank owners to manage their capital goods to realize the returns in the last period. The regulator then seizes banks' returns, and makes the promised payments to depositors. The deposit insurance fund runs a deficit. If fire sales are sufficiently mild, however, then banks will have enough assets to make the promised payments to the depositors. In this case banks remain solvent, but compared to good times they make smaller profits. This sequence of events is illustrated in Figure 1.
Banks are subject to regulation in the form of an upper limit on initial investment levels.10 Regulatory standards are set, independently, by the
individual national regulators at the beginning of ![]() . The regulator of country
. The regulator of country ![]() determines the maximum investment allowed for banks in its jurisdiction,
determines the maximum investment allowed for banks in its jurisdiction, ![]() , while taking into account the regulation in the other country,
, while taking into account the regulation in the other country, ![]() , as given. Investment levels of banks in country
, as given. Investment levels of banks in country ![]() have to satisfy
have to satisfy
![]() at
at ![]() The regulatory standard in a country is chosen to maximize
the net expected returns on risky investments.
The regulatory standard in a country is chosen to maximize
the net expected returns on risky investments.
3.1 Global Investors
Global investors are endowed with unlimited resources of consumption goods at ![]() 11 They can purchase capital,
11 They can purchase capital, ![]() , from banks in each country at
, from banks in each country at ![]() and employ this capital to produce
and employ this capital to produce ![]() units of consumption goods at
units of consumption goods at ![]() . For global investors capital supplied by the banks in these two countries are identical. 12 Let
. For global investors capital supplied by the banks in these two countries are identical. 12 Let
![]() denote the market price of the capital good at
denote the market price of the capital good at ![]() 13 Because we have a continuum of global investors, each investor treats the market price as given, and chooses the amount of capital to purchase,
13 Because we have a continuum of global investors, each investor treats the market price as given, and chooses the amount of capital to purchase, ![]() , to maximize net returns from investment at
, to maximize net returns from investment at ![]() .
.
| (1) |
The amount of assets they optimally buy satisfies the following first order conditions
| (2) |
The first order condition above determines global investors' (inverse) demand function for the capital good. Using this, we can define their demand function
We need to impose some structure on the return function of global investors and the model parameters in order to ensure that the equilibrium of this model is well-behaved.
3.2 Basic Assumptions
Assumption CONCAVITY says that although global investors' return is strictly increasing the amount of capital employed
![]() , they face decreasing returns to scale in the production of consumption goods
, they face decreasing returns to scale in the production of consumption goods
![]() , as opposed to banks that are endowed with a constant returns to scale technology as described above.
, as opposed to banks that are endowed with a constant returns to scale technology as described above.
![]() implies that global investors are less productive than banks at each level of capital employed.
implies that global investors are less productive than banks at each level of capital employed.
Concavity of the return function implies that the demand function of global investors for capital goods is downward sloping (see Figure 2). Global investors will require
higher discounts to absorb more capital from distressed banks at ![]() . This assumption intends to capture that distress selling of assets is associated with reduced prices. Using a large
sample of commercial aircraft transactions Pulvino (2002) shows that distressed airlines sell aircraft at a 14% discount from the average market price. This discount exists when the airline industry is depressed but not when it is booming. Coval and Stafford (2007) show that fire sales exist in equity markets when mutual funds engage in sales of similar stocks. Furthermore, Krugman (2000), Aguiar and Gopinath (2005), and Acharya et al. (2010) provide significant empirical and anecdotal evidence that during Asian and Latin
American crises, foreign acquisitions of troubled countries' assets were very widely spread across industries and assets were sold at sharp discounts. These evidence suggests that foreign investors took control of domestic enterprises mainly because they had liquid resources whereas the locals did
not, even though the locals had superior technology and know-how to run the domestic enterprises. Further support for this argument comes from the evidence in Acharya et al.
(2010) that many foreigners eventually flipped the assets they acquired during the Asian crisis to locals,
and usually made enormous profits from such trades.
. This assumption intends to capture that distress selling of assets is associated with reduced prices. Using a large
sample of commercial aircraft transactions Pulvino (2002) shows that distressed airlines sell aircraft at a 14% discount from the average market price. This discount exists when the airline industry is depressed but not when it is booming. Coval and Stafford (2007) show that fire sales exist in equity markets when mutual funds engage in sales of similar stocks. Furthermore, Krugman (2000), Aguiar and Gopinath (2005), and Acharya et al. (2010) provide significant empirical and anecdotal evidence that during Asian and Latin
American crises, foreign acquisitions of troubled countries' assets were very widely spread across industries and assets were sold at sharp discounts. These evidence suggests that foreign investors took control of domestic enterprises mainly because they had liquid resources whereas the locals did
not, even though the locals had superior technology and know-how to run the domestic enterprises. Further support for this argument comes from the evidence in Acharya et al.
(2010) that many foreigners eventually flipped the assets they acquired during the Asian crisis to locals,
and usually made enormous profits from such trades.
The idea that some assets are industry-specific, and hence less productive in the hands of outsiders, has its origins in Williamson (1988) and Shleifer and Vishny (1992). Examples of industry-specific assets include oil rigs and refineries, aircraft, copper mines, pharmaceutical patents, and steel plants. These studies have claimed that when major players in such industries face correlated liquidity shocks and cannot raise external finance due to debt overhang, agency, or commitment problems, they may have to sell assets to outsiders. Outsiders are willing to pay less than the value in best use for the assets of distressed enterprises because they do not have the specific know-how to manage these assets well and therefore face agency costs of hiring specialists to run these assets. The decreasing returns to scale technology assumption captures the inefficiency of outsiders, similar to Kiyotaki and Moore (1997), Lorenzoni (2008), Gai et al. (2008), and Korinek (2011). It is also a reduced way of modeling that global investors first purchase assets that are easy to manage, but as they purchase more assets they will need to buy ones that require sophisticated management and operation skills.
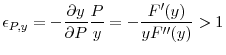 for all
for allAssumption ELASTICITY says that global investors' demand for the capital good is elastic. This assumption implies that the amount spent by global investors on asset purchases,
![]() , is strictly increasing in
, is strictly increasing in ![]() . Therefore we can also write
Assumption ELASTICITY as
. Therefore we can also write
Assumption ELASTICITY as
If this assumption was violated, multiple levels of asset sales would raise a given amount of liquidity, and multiple equilibria in the asset market at ![]() would be possible. This
assumption is imposed by Lorenzoni (2008) and Korinek (2011) in order to rule out multiple equilibria under fire sales.14
would be possible. This
assumption is imposed by Lorenzoni (2008) and Korinek (2011) in order to rule out multiple equilibria under fire sales.14
Assumption REGULARITY holds whenever the demand function of global investors is log-concave, but it is weaker than log-concavity.15 In order to see this, let
![]() denote the (inverse) demand function of global investors. We can rewrite Assumption REGULARITY as
denote the (inverse) demand function of global investors. We can rewrite Assumption REGULARITY as
We can show that the demand function is log-concave if and only if
![]() . Log-concavity of demand function is a common assumption used in the Cournot games literature (see Amir (1996));
it ensures the existence and uniqueness of equilibrium in a simple n-player Cournot game. Therefore, I call it a "regularity" assumption on
. Log-concavity of demand function is a common assumption used in the Cournot games literature (see Amir (1996));
it ensures the existence and uniqueness of equilibrium in a simple n-player Cournot game. Therefore, I call it a "regularity" assumption on ![]() Clearly
Assumption REGULARITY holds whenever the demand function is log-concave. However, Assumption REGULARITY is weaker than log-concavity and may also hold if the demand function is log-convex (i.e., if
Clearly
Assumption REGULARITY holds whenever the demand function is log-concave. However, Assumption REGULARITY is weaker than log-concavity and may also hold if the demand function is log-convex (i.e., if
![]() ).
).
Assumption REGULARITY will ensure that the objective functions of regulators are well-behaved. It will be crucial in showing that the equilibrium of this model exists and it is unique.
Many regular return functions satisfy conditions given by Assumptions CONCAVITY, ELASTICITY and REGULARITY. Here are two examples that satisfy all three of the above assumptions:
Example 1
![]()
Example 2
![]()
The following example satisfies Assumption CONCAVITY, but not Assumptions ELASTICITY and REGULARITY.
Example 3
![]() where
where
![]() for all
for all ![]()
Assumption RANGE says that the return on investment for banks must not be too low because if they are, equilibrium investment levels will be zero. Nor they must be too high; if they are, equilibrium investment levels will be infinite. This assumption, while not crucial for the results, allows us to focus on interesting cases in which equilibrium investment levels are neither zero nor infinite.
3.3 Equilibrium with Symmetric Countries
In this section I consider only symmetric countries and solve the model by backwards induction. First, I analyze the equilibrium at the interim period in each state of the world, for a given set of investment levels; then I solve the game between the regulators at ![]() Note that, if good times are realized
Note that, if good times are realized ![]() , no further actions need to be taken by any agent. Therefore, at
, no further actions need to be taken by any agent. Therefore, at
![]() we need only to analyze the equilibrium of the model for bad times.
we need only to analyze the equilibrium of the model for bad times.
I solve the model without resorting to some particular functional form. The results of this paper hold for any functional form that satisfy Assumptions CONCAVITY, ELASTICITY, and REGULARITY.
3.3.1 Crisis and fire sales
Consider the problem of a bank in country ![]() if bad times are realized at
if bad times are realized at ![]() .
The bank reaches
.
The bank reaches ![]() with a level of investment equal to
with a level of investment equal to ![]() which was chosen at
the initial period. The investment is distressed and must be restructured using liquid resources. The investment will not produce any returns in the last period if it is not restructured.16 The bank cannot raise external finance from global investors because it cannot commit to pay them in the last period. Therefore, the only way for the bank to raise the funds necessary for restructuring is to sell some fraction of
the investment to global investors and use the proceeds to pay for restructuring costs, whereby it can retain another fraction of the investment.
which was chosen at
the initial period. The investment is distressed and must be restructured using liquid resources. The investment will not produce any returns in the last period if it is not restructured.16 The bank cannot raise external finance from global investors because it cannot commit to pay them in the last period. Therefore, the only way for the bank to raise the funds necessary for restructuring is to sell some fraction of
the investment to global investors and use the proceeds to pay for restructuring costs, whereby it can retain another fraction of the investment.
At the beginning of ![]() in bad times, a bank in country
in bad times, a bank in country ![]() decides what fraction
of capital to restructure
decides what fraction
of capital to restructure
![]() and what fraction of restructured capital to sell
and what fraction of restructured capital to sell
![]() to generate the resources for restructuring. Note that
to generate the resources for restructuring. Note that
![]() will then represent the fraction of capital that a bank keeps after fire sales.17 Thus the bank takes the price of capital
will then represent the fraction of capital that a bank keeps after fire sales.17 Thus the bank takes the price of capital ![]() as given, and chooses
as given, and chooses ![]() and
and
![]() to maximize total returns from that point on
to maximize total returns from that point on
subject to the budget constraint
The first term in (4) is the (certain) total return that will be obtained from the unsold part of the restructured assets, which are
By Assumption CONCAVITY, the equilibrium price of capital must satisfy
![]() ,otherwise global investors will not purchase any capital. Later on, I will show that in equilibrium we must also have
,otherwise global investors will not purchase any capital. Later on, I will show that in equilibrium we must also have ![]() For the moment, we will assume that the equilibrium price of assets satisfies
For the moment, we will assume that the equilibrium price of assets satisfies
Now, consider the first order conditions of the maximization problem (4) while ignoring the constraints
From (8) it is obvious that
The fraction banks retain after fire sales
for
On the other hand, using (9) we can write the first order condition (7) as
Equation (11) shows that revenues are increasing in
Note that if the capital price is greater than ![]() , banks want to sell all the capital goods they have because they can get at most
, banks want to sell all the capital goods they have because they can get at most ![]() per unit by keeping and managing them. If the price is lower than
per unit by keeping and managing them. If the price is lower than ![]() , however, they will optimally scrap all of their capital (
, however, they will optimally scrap all of their capital (
![]() ). As discussed above, prices above
). As discussed above, prices above ![]() and below
and below ![]() will never arise in equilibrium. The total asset supply curve of banks from the two countries is plotted in Figure 2 for an initial total investment in the two countries of
will never arise in equilibrium. The total asset supply curve of banks from the two countries is plotted in Figure 2 for an initial total investment in the two countries of ![]() .
.
3.3.2 Equilibrium in the Capital Market at t=1
Equilibrium price of capital goods,
![]() will be determined by the market clearing condition
will be determined by the market clearing condition
The condition above says that the excess demand in the capital market, denoted by
by adding the individual supply of banks in each country given by (10).
This equilibrium is illustrated in Figure 2. Note that the equilibrium price of capital at ![]() will be a function of the initial investment level in the two countries. Therefore, from the perspective of the initial period I denote the equilibrium price as
will be a function of the initial investment level in the two countries. Therefore, from the perspective of the initial period I denote the equilibrium price as
![]() .
.
How does a change in the initial investment level in one of the countries affect the price of capital at ![]() ? Lemma 1 shows that if investment into the
risky asset in one country increases at
? Lemma 1 shows that if investment into the
risky asset in one country increases at ![]() , a lower price for capital will be realized in the fire sales state at
, a lower price for capital will be realized in the fire sales state at ![]()
Lemma 1 implies that higher investment in the risky asset in one country (i.e., a higher ![]() ) increases the severity of the financial crisis for both
countries by lowering the asset prices. This effect is illustrated in Figure 3. Suppose that initial investment level in country
) increases the severity of the financial crisis for both
countries by lowering the asset prices. This effect is illustrated in Figure 3. Suppose that initial investment level in country ![]() increases, increasing the total investment in the two countries from
increases, increasing the total investment in the two countries from ![]() to
to ![]() . In this case, banks in country A will have to sell more assets at each price, as can be seen from individual supply function given by (10). Graphically, the total supply curve will shift
to the right, as shown by the dotted-line supply curve in Figure 3, which will cause a decrease in the equilibrium price of capital goods. Lower asset prices, by contrast,
will induce more fire sales by banks in both countries in the bad state due to the downward-sloping supply curve. This additional result is formalized in Lemma 2.
. In this case, banks in country A will have to sell more assets at each price, as can be seen from individual supply function given by (10). Graphically, the total supply curve will shift
to the right, as shown by the dotted-line supply curve in Figure 3, which will cause a decrease in the equilibrium price of capital goods. Lower asset prices, by contrast,
will induce more fire sales by banks in both countries in the bad state due to the downward-sloping supply curve. This additional result is formalized in Lemma 2.
Together lemmas 1 and 2 imply that a higher initial investment in the risky investment in one country creates negative externalities for the other country by making financial crises more severe (i.e., via lower asset prices according to Lemma 1) and more costly (i.e., more fire sales according to Lemma 2).
3.3.3 Banks' Problem
Each bank in country ![]() at
at ![]() chooses the investment level,
chooses the investment level, ![]() , to maximize expected profits given by
, to maximize expected profits given by
where
Banks undoubtedly earn net positive returns in the good state since ![]() Moreover, due to the limited liability, they never receive negative profits in the bad state. Because
banks do not internalize the effect of their initial investment on the stability of the financial system at
Moreover, due to the limited liability, they never receive negative profits in the bad state. Because
banks do not internalize the effect of their initial investment on the stability of the financial system at ![]() there is no counter-effect that offsets the positive returns on investment.
Therefore, a bank's net expected return from risky investment at
there is no counter-effect that offsets the positive returns on investment.
Therefore, a bank's net expected return from risky investment at ![]() is always positive, and a bank always makes itself better off by investing more. Therefore, the regulatory upper limit on
the risky investment at
is always positive, and a bank always makes itself better off by investing more. Therefore, the regulatory upper limit on
the risky investment at ![]() will bind (i.e., banks will choose
will bind (i.e., banks will choose
![]() at
at ![]() ).
).
Fire sales will be severe for some parameters and banks may become insolvent in equilibrium, as analyzed in Section 5. I assume that when banks are insolvent after fire sales they are required by law to manage remaining assets until the last period and to transfer asset returns into the deposit insurance fund. This is a reasonable assumption because banks are the only sophisticated agents in our model domestic economy that can manage those assets. Furthermore, in practice, the dissolution process of insolvent banks usually does not happen immediately. It is a time-consuming process because, for example, loans have to be called-off or sold to third parties to make payments to debtors. This assumption also captures this time dimension of the dissolution process.
3.3.4 Regulators' Problem
Regulators of the two countries simultaneously determine the regulatory standards for the banks in their own jurisdictions before banks make their borrowing and investment decisions at ![]() . Regulation in each country
. Regulation in each country ![]() takes the form of an upper limit,
takes the form of an upper limit,
![]() , on the investment level allowed for domestic banks. Banks in country
, on the investment level allowed for domestic banks. Banks in country ![]() have to abide by the regulation by choosing their investment levels as
have to abide by the regulation by choosing their investment levels as
![]() . As they set the standards, regulators anticipate that banks will choose initial investment levels that are as high as possible, and incorporate this fact into their decision
problem.
. As they set the standards, regulators anticipate that banks will choose initial investment levels that are as high as possible, and incorporate this fact into their decision
problem.
The objective of an independent national financial regulator is to maximize the net expected social welfare of its own country. Social welfare is defined as the expected return to the risky investment minus the cost of the initial investment. Therefore, regulator ![]() chooses
chooses
![]() , to solve
, to solve
while taking the regulatory standard in the other country,
Social welfare given by (15) incorporates the fact that banks investment level, ![]() , equals
, equals ![]() , the regulatory upper limit. With probability
, the regulatory upper limit. With probability ![]() , the good state is realized when banks in country
, the good state is realized when banks in country ![]() obtain a total return of
obtain a total return of ![]() . With probability
. With probability ![]() both countries land in the bad state. In the bad state, banks perform asset sales as described previously, and manage the remaining assets,
both countries land in the bad state. In the bad state, banks perform asset sales as described previously, and manage the remaining assets,
![]() until
until ![]() , to obtain a gross return of
, to obtain a gross return of
![]() per unit. Therefore the return to the investment in the bad state in country
per unit. Therefore the return to the investment in the bad state in country ![]() is
is
![]() . The cost of the initial investment
. The cost of the initial investment ![]() is subtracted to obtain net returns to the investment. Each regulator takes into account the effect of both countries' regulatory standards on the price of capital in the bad state. This is why the fraction of assets that banks can keep after the fire sales,
is subtracted to obtain net returns to the investment. Each regulator takes into account the effect of both countries' regulatory standards on the price of capital in the bad state. This is why the fraction of assets that banks can keep after the fire sales,
![]() , is written as a function of the regulatory standards in the two countries.
, is written as a function of the regulatory standards in the two countries.
The following equation gives the first order conditions of regulator ![]() 's problem in (15)
's problem in (15)
By rearranging the terms, we can write this first order condition as a sum of the marginal benefit and marginal cost of increasing
When regulator
The second curly brackets in (17) give the expected marginal cost of increasing ![]() . Because
. Because
![]() is decreasing in
is decreasing in ![]() , as implied by Lemma 2, a smaller fraction of assets will be retained by banks if the bad state is realized for higher initial investment levels. The first term captures this fact: with probability
, as implied by Lemma 2, a smaller fraction of assets will be retained by banks if the bad state is realized for higher initial investment levels. The first term captures this fact: with probability ![]() the bad state is realized, and an additional unit of investment will decrease the fraction of capital that can be retained by banks of country
the bad state is realized, and an additional unit of investment will decrease the fraction of capital that can be retained by banks of country ![]() by
by
![]() , causing a total loss of
, causing a total loss of
![]() . Last, "-1" in the second curly brackets gives the marginal cost of funds required for the risky investment.
. Last, "-1" in the second curly brackets gives the marginal cost of funds required for the risky investment.
3.3.5 An alternative formulation of regulators' objective function
We can alternatively write the regulators' objective function in a way that explicitly shows the returns to the investment and costs of fire sales. Start by substituting ![]() for
for
![]() function, using the derivation obtained in (9) to write (15) as
function, using the derivation obtained in (9) to write (15) as
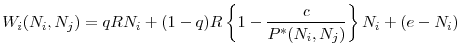 |
Add and subtract
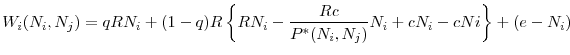 |
Last, rearranging the terms inside the curly brackets gives
Consider this alternative objective function in detail. It is composed of two main terms as in (15): net expected returns in both the good state and the bad state. Because the first term,
![]() , that gives the net expected return in the good state is clear, I focus on the latter. The first term inside the curly brackets gives the net total return that could be
obtained from the investment if there were no fire sales. The second term is the cost of fire sales:
, that gives the net expected return in the good state is clear, I focus on the latter. The first term inside the curly brackets gives the net total return that could be
obtained from the investment if there were no fire sales. The second term is the cost of fire sales:
![]() is the amount of assets sold in fire sales as given by (10), where banks receive
is the amount of assets sold in fire sales as given by (10), where banks receive ![]() from these assets instead of
from these assets instead of ![]() . The last term inside the curly brackets,
. The last term inside the curly brackets, ![]() , is the total cost of restructuring.
, is the total cost of restructuring.
Because the two versions of the regulators' objective function are the same, I will use the first formulation in the rest of the paper for the sake of analytical convenience, even though the alternative formulation could be more intuitive.
3.3.6 Regulatory Standards in the Uncoordinated Equilibrium
Having analyzed the problem of regulators, we can turn to investigating the equilibrium of the game between regulators at ![]() when they act independently. The aims are to show that there
exists a unique symmetric equilibrium of this game, and then to perform comparative statics. I start by analyzing the properties of the best response functions of regulators. The following lemma establishes that independent regulators have a unique best response to each regulatory standard choice
by the opponent country.
when they act independently. The aims are to show that there
exists a unique symmetric equilibrium of this game, and then to perform comparative statics. I start by analyzing the properties of the best response functions of regulators. The following lemma establishes that independent regulators have a unique best response to each regulatory standard choice
by the opponent country.
An interesting question in this setup concerns how that unique best response behaves as regulation in the opponent country changes. Suppose that the regulator of country B decides to tighten regulation (i.e., to reduce ![]() How would the regulator of country A optimally react? The next proposition shows that regulator A optimally chooses to relax its regulatory standard (i.e., increase
How would the regulator of country A optimally react? The next proposition shows that regulator A optimally chooses to relax its regulatory standard (i.e., increase ![]() ), as regulator B imposes stricter regulations. In other words, the optimal regulatory standards in the two countries are strategic substitutes.
), as regulator B imposes stricter regulations. In other words, the optimal regulatory standards in the two countries are strategic substitutes.
The intuition for this result is as follows: If regulator B tightens its regulatory standard by reducing the upper limit on the investment level for its banks, there will be less distressed assets at ![]() in the bad state; hence, a higher asset price will be realized. Therefore, fewer assets will be sold in equilibrium as shown by Lemma 2, which means that banks in both countries will be able to retain a higher fraction of their initial investment after fire sales. This retention
will increase the marginal return to investment and initially allow regulator A to optimally choose a higher upper limit on the investment level (i.e. relax its regulatory standard).
in the bad state; hence, a higher asset price will be realized. Therefore, fewer assets will be sold in equilibrium as shown by Lemma 2, which means that banks in both countries will be able to retain a higher fraction of their initial investment after fire sales. This retention
will increase the marginal return to investment and initially allow regulator A to optimally choose a higher upper limit on the investment level (i.e. relax its regulatory standard).
The next lemma shows that in order to have finite and strictly positive equilibrium investment levels in the two countries, banks' return from investment ![]() should not be too low or too
high. The exact condition on
should not be too low or too
high. The exact condition on ![]() is given by Assumption RANGE, which states that
is given by Assumption RANGE, which states that
![]()
![]() is the net expected cost of the investment: each unit of investment requires one unit of consumption good initially. With probability
is the net expected cost of the investment: each unit of investment requires one unit of consumption good initially. With probability ![]() bad times are realized, in which case banks have to incur an extra restructuring cost of
bad times are realized, in which case banks have to incur an extra restructuring cost of ![]() units of consumption goods per
unit of investment. If the return on the investment,
units of consumption goods per
unit of investment. If the return on the investment, ![]() , is less then this expected cost,
, is less then this expected cost, ![]() , booth countries' social welfare will be higher without any investment at all. Therefore, if
, booth countries' social welfare will be higher without any investment at all. Therefore, if
![]() , then equilibrium investment levels are zero in both countries. But if
, then equilibrium investment levels are zero in both countries. But if ![]() , then the expected return to the investment in the good state alone will be higher than initial cost of investment, which is 1. In this case, even when the entire initial investment is expected to be lost in the bad state, the net expected return to investment will always
be positive. For sufficiently high initial endowment levels, this case leads to a corner solution in which social welfare is maximized by having all endowments invested in the risky asset. I also impose
, then the expected return to the investment in the good state alone will be higher than initial cost of investment, which is 1. In this case, even when the entire initial investment is expected to be lost in the bad state, the net expected return to investment will always
be positive. For sufficiently high initial endowment levels, this case leads to a corner solution in which social welfare is maximized by having all endowments invested in the risky asset. I also impose ![]() in order to rule out these inconsequential details and focus on the interesting cases.
in order to rule out these inconsequential details and focus on the interesting cases.
Now we are ready to examine the existence of a Nash equilibrium in the game between regulators. The nice features of the objective functions of regulators established above help us to show that a Nash equilibrium exists.
The next natural question is whether there are multiple equilibria or there is a unique equilibrium. Fortunately, under the previously stated conditions there is a unique symmetric equilibrium of the game between the regulators, as shown by the following proposition.
3.3.7 Comparative Statics for the Uncoordinated Equilibrium
What happens to the unique regulatory standards of the uncoordinated equilibrium in the two countries as good state becomes more likely, or if bank's per unit return from investment, ![]() increases? The next proposition shows that in both cases, regulatory standards in the two countries are relaxed (i.e., regulators increase the upper limit on the risky investment).
increases? The next proposition shows that in both cases, regulatory standards in the two countries are relaxed (i.e., regulators increase the upper limit on the risky investment).
This result is quite intuitive because as the good state becomes more likely (i.e., as ![]() increases), regulators will face the cost of fire sales less often and will allow more investment in
equilibrium. But as
increases), regulators will face the cost of fire sales less often and will allow more investment in
equilibrium. But as ![]() increases, returns to investment in both good and bad states also increase, making the investment socially more profitable.
increases, returns to investment in both good and bad states also increase, making the investment socially more profitable.
I conclude this section by showing that in equilibrium, price of the capital good at ![]() in bad times must be greater than restructuring costs
in bad times must be greater than restructuring costs ![]() . I tentatively assumed this while discussing banks' optimal fire sales decisions at
. I tentatively assumed this while discussing banks' optimal fire sales decisions at ![]() after they receive bad shocks. Now it
is time to prove this claim formally. Under this result, as I have shown, banks optimally restructure all assets in equilibrium. In other words, as previously stated, scrapping of capital never arises in equilibrium.
after they receive bad shocks. Now it
is time to prove this claim formally. Under this result, as I have shown, banks optimally restructure all assets in equilibrium. In other words, as previously stated, scrapping of capital never arises in equilibrium.
Lemma 5 holds because if regulators allow the investment level in their country ![]() to be too high, they know that they will drive down the equilibrium
price below the cost of restructuring, in which case banks do not restructure any assets. Therefore, it is never optimal for any of the regulators to allow such high investment levels, independent of the choice of the competing regulator.
to be too high, they know that they will drive down the equilibrium
price below the cost of restructuring, in which case banks do not restructure any assets. Therefore, it is never optimal for any of the regulators to allow such high investment levels, independent of the choice of the competing regulator.
3.4 Internationally Coordinated Regulation
Suppose that there is a higher authority, call it the central regulator, that determines optimal regulatory standards in these two countries. In practice, the central regulator could be an international financial institution such as the International Monetary Fund or the Bank for International
Settlements, or it could be an institution created by a binding bilateral agreement between the two countries. I assume that, for political reasons, the central regulator must choose the same regulatory standards for both countries. The question that I address in this section is as follows: Suppose
that at the beginning of ![]() , national regulators can either set regulatory standards independently or simultaneously relinquish their authority to the central regulator. Would they choose
the latter?
, national regulators can either set regulatory standards independently or simultaneously relinquish their authority to the central regulator. Would they choose
the latter?
I define the central regulator's problem as follows: it chooses the regulatory standards in countries ![]() and
and ![]() ,
,
![]() , to maximize the sum of expected social welfare of these countries as given below
, to maximize the sum of expected social welfare of these countries as given below
In other words, the central regulator maximizes the sum of the objective functions of individual regulators. For symmetric countries, it is natural to assume that each country receives an equal weight in the central regulator's objective function.18 I denote the internationally optimal common regulatory standards by
![]() and compare them to the regulatory standards in the uncoordinated symmetric equilibrium,
and compare them to the regulatory standards in the uncoordinated symmetric equilibrium,
![]() .
.
Another way to state the central regulator's problem for symmetric countries involves thinking of the central regulator as choosing the total investment level across the two countries,
![]() , to maximize their overall welfare. After determining the optimal total investment level
, to maximize their overall welfare. After determining the optimal total investment level
![]() , it imposes
, it imposes
![]() for
for ![]() , where
, where
It is easy to see that the two alternative problems for the central regulator given by (19) and (20) are the same due to the countries' symmetry.
Now we can compare the internationally optimal regulatory standards to the standards that arise as a result of strategic interaction between regulators. The following proposition shows that a central regulator will impose tighter regulatory standards (i.e., a lower ![]() ) compared to what would have been chosen by independent regulators.
) compared to what would have been chosen by independent regulators.
Proposition 5 shows that due to the systemic risk caused by asset fire sales, standards chosen by independent national regulators are inefficiently lax compared to regulatory standards that would be chosen by a central regulator. A central regulator maximizes the total welfare in the two countries and hence internalizes the systemic externalities that arise from fire sales. A central regulator takes into account the fact that allowing more investment in the risky asset by relaxing regulatory standards in one country reduces the welfare of the other country due to higher numbers of fire sales during distress times.
3.4.1 Is voluntary cooperation possible?
We see that risky investment levels will be higher in both countries if regulators act strategically. But will countries ever benefit from relinquishing their regulatory authority to a central regulator that imposes tighter standards in both countries? The following proposition shows that symmetric countries always benefit from relinquishing their authority to a central regulator.
When regulators act independently, each allows investment into the risky asset up to the point where the expected marginal benefit from the risky investment is equal to the expected domestic marginal cost of the investment. However, at this level of investment, the marginal total cost across the two countries far exceeds the sum of the marginal benefits. This happens because neither regulator considers the adverse effect of increasing investment level on the welfare of the other country. Yet, the central regulator can choose a total investment level in the risky asset where the total marginal benefit is equal to the total marginal cost, and hence can improve the overall welfare of the two countries. Therefore, it is in the interest of the regulators of symmetric countries to simultaneously surrender their authority to a central regulator.
4 Asymmetric Countries
In the previous section, we saw that regulators of symmetric countries are always better off by relinquishing their authority to a central regulator. Can a similar argument be made for countries that are asymmetric in some dimensions? In other words, if there are differences across countries, would national regulators still benefit from relinquishing their authority to a central regulator? In this section, I answer this and the following questions that arise when there are asymmetries across countries: How would the asymmetries affect regulation levels in the two countries in equilibrium? How do central regulation levels compare to regulation levels chosen by national regulators independently? Which countries are more likely to accept a common central regulation?
I focus on differences in returns on the risky investment across countries. In particular, I assume that banks in country ![]() are uniformly more productive than banks in country
are uniformly more productive than banks in country
![]() . In terms of the parameters of the model, this assumption can be stated as
. In terms of the parameters of the model, this assumption can be stated as
![]() 19
19
Furthermore, to simplify the following analysis, I also assume that
![]() in this section.20 Under
this assumption, global investors will purchase capital only if the price of capital falls below one. This assumption also rules out possible multiple equilibria in the capital goods market at
in this section.20 Under
this assumption, global investors will purchase capital only if the price of capital falls below one. This assumption also rules out possible multiple equilibria in the capital goods market at ![]() when there are return differences between countries. Note that from global investors' perspectives, the capital goods in the two countries are still identical at
when there are return differences between countries. Note that from global investors' perspectives, the capital goods in the two countries are still identical at ![]()
The next proposition shows that when regulators act independently, the regulator of the high-return country chooses lower regulatory standards (i.e., a higher ![]() ) in equilibrium. This
result complies with Proposition 4 in the previous section where we have seen that equilibrium investment levels increase in the return to investments given by
) in equilibrium. This
result complies with Proposition 4 in the previous section where we have seen that equilibrium investment levels increase in the return to investments given by ![]()
Now we can compare common central regulatory standards to uncoordinated regulation levels when there are asymmetries between the countries. The next proposition shows that in order for a common central regulation to be acceptable to both regulators, it must require stricter regulatory standards in both countries compared to the uncoordinated regulatory standards.
The proof of Proposition 8 makes use of the envelope theorem to show that welfare of a country is decreasing in the investment level of the other country. In order to forego the authority to independently and optimally choose regulatory standards as a
response to the regulatory standards chosen by the other country, each regulator must be compensated by a stricter regulatory standard (i.e., a lower ![]() ) in the other country. Therefore, any
common regulation level above
) in the other country. Therefore, any
common regulation level above
![]() , which is the minimum of the two regulation levels given the assumption that
, which is the minimum of the two regulation levels given the assumption that
![]() will always be rejected by regulator
will always be rejected by regulator ![]() .
.
This discussion implies that if a common regulation level is accepted by the regulator of the high-return country, it will always be accepted by the regulator of the low-return country. This happens because common regulation reduces investment levels in both countries, as shown by Proposition 11. However, it reduces investment levels more in the high-return country compared to the low return country. Therefore, if the regulator of the high-return country is willing to accept a common regulation level, it will necessarily be accepted by the regulator of the low-return country, as shown by the following lemma.
Lemma 6 allows us to focus on the welfare of country ![]() in search of mutually acceptable common regulatory standards. We may define
in search of mutually acceptable common regulatory standards. We may define ![]() as the regulatory standard that maximizes the welfare of country A if it is uniformly imposed in both countries. Formally, I define
as the regulatory standard that maximizes the welfare of country A if it is uniformly imposed in both countries. Formally, I define ![]() as follows:
as follows:
Given this definition, we can write the net maximum benefit from common central regulation to country ![]() as
as
![]() . The next proposition shows that this net maximum benefit decreases as the differences between the countries become larger.
. The next proposition shows that this net maximum benefit decreases as the differences between the countries become larger.
Proposition 9 provides the main result of this section: if the return differences between the two countries are above a threshold, then at least the high-return country will be worse off if a common regulation level is imposed across the two countries, even if the common regulation is chosen such that it maximizes the welfare of the high-return country. Large return differences will imply that such a common regulation level is too strict compared to the regulatory standard that would be chosen by the high-return country in the uncoordinated equilibrium. Therefore, welfare of the high-return country will fall if it decides to accept common regulatory standards in the face of high return differences between countries. In other words, Proposition 9 shows that voluntary cooperation can exist only between sufficiently similar countries. If the differences across countries are sufficiently high, then at least one of them will be worse off by accepting common central regulation.
5 Extensions: Discussion of Assumptions
In this section I examine the robustness of the main results with regard to changes in some of the assumptions in the basic model. I revisit the assumptions of deposit insurance, limited liability for bank owners, and nonexistence of initial equity capital for bank owners, and show that the qualitative results do not change when these assumptions are relaxed.
5.1 Deposit Insurance
With a deposit insurance fund, banks are able to borrow at constant and zero net interest rate from consumers because consumers are guaranteed by the fund that they will always recover their initial investment. If banks do not have sufficient funds to make the promised payments to consumers following a bad state, the deposit insurance fund steps in and pays consumers the deficit between the promised payment and the resources available to a bank.
What happens if there is no deposit insurance? The answer depends on the competitive structure of the deposit market. I consider two polar cases: first, each bank is a local monopoly in the deposit market; and second, there is perfect competition between banks in the deposit market. I begin here with the local monopoly case and discuss the perfect competition case in Section 5.1.1. When each bank is a local monopoly as in the basic model, the interest on deposit contracts will be just enough to induce risk-neutral consumers to deposit their endowments with them. In technical terms, the individual rationality condition for consumers will bind. I restrict attention to deposit contracts that are in the form of simple debt contracts.21
A bank in country ![]() will choose the amount to borrow and invest in the risky asset,
will choose the amount to borrow and invest in the risky asset, ![]() , and the interest rate on the deposits,
, and the interest rate on the deposits, ![]() , to maximize the net expected profits:
, to maximize the net expected profits:
subject to
| (23) |
where
As before, the bank is also subject to the maximum investment regulation
![]() . Because the problem of a bank is still linear, it will yield a corner solution as before: there will be either a maximum investment (
. Because the problem of a bank is still linear, it will yield a corner solution as before: there will be either a maximum investment (
![]() ) or no investment at all (
) or no investment at all (![]() We can examine the choice of the
investment level
We can examine the choice of the
investment level ![]() and the choice of deposit rate
and the choice of deposit rate ![]() separately. First,
consider the choice of optimal
separately. First,
consider the choice of optimal ![]() for a given investment level. We can see from the problem of banks above that for a given
for a given investment level. We can see from the problem of banks above that for a given ![]() there are two cases to consider:
there are two cases to consider:
Case 1
![]() . In this case, banks have sufficient resources to cover the initial borrowing from depositors even in the bad state. Therefore, they will offer zero net interest to
consumers. Banks will set
. In this case, banks have sufficient resources to cover the initial borrowing from depositors even in the bad state. Therefore, they will offer zero net interest to
consumers. Banks will set ![]() , and the IR condition will be satisfied with equality. Because banks make net positive profits in both states of the world, they
want to invest as much as possible. Banks will borrow and invest in the risky asset until the regulatory requirement binds (
, and the IR condition will be satisfied with equality. Because banks make net positive profits in both states of the world, they
want to invest as much as possible. Banks will borrow and invest in the risky asset until the regulatory requirement binds (
![]() ). Given that banks invest as much as possible, regulators will choose the same standards in equilibrium as in the basic model. Therefore, the symmetric equilibrium of Section
3 and its qualitative results will prevail.
). Given that banks invest as much as possible, regulators will choose the same standards in equilibrium as in the basic model. Therefore, the symmetric equilibrium of Section
3 and its qualitative results will prevail.
Case 2
![]() . In this case, returns on the assets retained by banks after fire sales are not sufficient to cover the initial borrowing from depositors because
. In this case, returns on the assets retained by banks after fire sales are not sufficient to cover the initial borrowing from depositors because
![]() . Banks have to offer positive net interest rate to consumers in the good state to compensate for their losses in the bad state. For the IR condition of consumers to be satisfied,
. Banks have to offer positive net interest rate to consumers in the good state to compensate for their losses in the bad state. For the IR condition of consumers to be satisfied, ![]() has to be such that
has to be such that
This can be seen by rearranging the IR condition (22), and noting that
Because
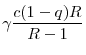 |
(26) |
In order to see that this is indeed the case in the symmetric equilibrium obtained in Section 3 (when
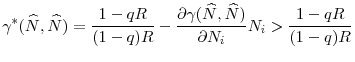 |
(27) |
since
5.1.1 No deposit insurance and perfectly competitive deposit markets
Now, instead of assuming that each bank is a local monopoly in the deposit market, I assume that the deposit market is perfectly competitive and analyze the robustness of the results to this change in the environment. If the deposit market is perfectly competitive banks will earn zero profits
because consumers will get all of the returns on the risky investment. Each bank in country ![]() will choose the amount of investment in the risky asset
will choose the amount of investment in the risky asset ![]() to maximize the expected utility of a representative depositor:
to maximize the expected utility of a representative depositor:
With probability
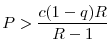 |
(29) |
This is the same condition as (25). We know from the analysis above that this condition is satisfied in the symmetric equilibrium of Section 3, i.e. when
5.2 Limited Liability
In the basic model, I assumed that banks are protected by limited liability. Limited liability assumption means that bank profits are (weakly) positive in each state of the world. If returns to the assets of a bank fall short of its liabilities, then the bank owners receive zero profits. Banks have always wanted to make unlimited investment in the risky asset under this assumption. Now instead, suppose that bank owners have some wealth or endowment at the last period that can be seized by depositors if the returns on assets are not enough to cover the promised payments to depositors.22
When there is no limited liability, a bank in country ![]() chooses
chooses
![]() to maximize the expected profits:
to maximize the expected profits:
where P is the price of capital in the fire sale market in the bad state at
The first order condition for the problem of banks is
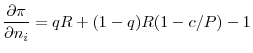 |
(31) |
The first order condition will be positive if and only if
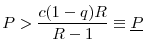 |
(32) |
In other words, as long as
5.3 Initial Bank Equity Capital
In the basic model, I also assumed that banks have no initial endowment of their own that they can invest in the risky asset. Because banks raised necessary funds for investment from the deposit market, the liability side of their balance sheets contained only debt and not any equity capital.23
In this section, I assume that banks have an initial endowment of ![]() units of consumption good which they have to invest in the risky asset. This equity is costly: the opportunity cost of
equity to bank owners,
units of consumption good which they have to invest in the risky asset. This equity is costly: the opportunity cost of
equity to bank owners, ![]() , is greater than one, the cost of insured deposits. These two assumptions are a common way of introducing equity capital to a banking model (see Dell'Ariccia and Marquez (2006), Hellmann et al. (2000), and Repullo (2004) among others). The assumption that the amount of equity capital is fixed captures the fact that it is difficult for banks to raise equity capital at short notice.
, is greater than one, the cost of insured deposits. These two assumptions are a common way of introducing equity capital to a banking model (see Dell'Ariccia and Marquez (2006), Hellmann et al. (2000), and Repullo (2004) among others). The assumption that the amount of equity capital is fixed captures the fact that it is difficult for banks to raise equity capital at short notice.
When there is bank equity capital, regulation will take the form of a minimum capital ratio requirement. Let
![]() be the actual capital ratio of a bank in country
be the actual capital ratio of a bank in country ![]() . In this case,
regulation will require banks to have
. In this case,
regulation will require banks to have
![]() , where
, where ![]() is the capital adequacy requirement in country
is the capital adequacy requirement in country
![]() .
.
Given its equity, and the price of capital goods in the bad state of ![]() , each bank chooses how much to invest in the risky asset (i.e.,
, each bank chooses how much to invest in the risky asset (i.e., ![]() as before) to maximize expected profits:
as before) to maximize expected profits:
subject to the capital regulation
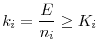 |
(34) |
Note that
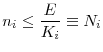 |
(35) |
This analysis shows that there is one-to-one mapping from capital regulations to the form of regulation used in the main text. The banks' problem does not change: they still want to invest in the risky asset as much as possible, as long as the net expected return is positive. The minimum capital requirement binds (i.e., banks will choose
Consider the regulators' problem after equity is introduced to the model. Regulators will anticipate that for a given capital ratio requirement, ![]() , banks will choose their total
investment level such that this requirement binds:
, banks will choose their total
investment level such that this requirement binds:
![]() . Because banks will raise
. Because banks will raise
![]() units of consumption goods from the local deposit market, we can write regulators' objective function as
units of consumption goods from the local deposit market, we can write regulators' objective function as
![\displaystyle W_{i}(K_{i},K_{j})= q\left[R\frac{E}{K_{i}}-\frac{E}{K_{i}}\right] +(1-q)\left[R \widehat{\gamma} \left( \frac{E}{K_{i}},\frac{E}{K_{j}}\right) \frac{E}{K_{i}}-\frac{E}{K_{i}}\right]](img218.gif) |
(36) |
The function
| (37) |
This objective function is exactly the same as the regulators' problem in the main text. Therefore, all qualitative results in the main section will carry on when we introduce costly bank equity and redefine regulation as a minimum capital ratio requirement.
Note that when we introduce costly equity, the net expected return on the risky investment must be sufficiently large to cover the opportunity cost of internal bank equity, ![]() , for
banks. Otherwise, banks will choose not to invest in the risky asset at all. For this reason, the set of parameters where we have strictly positive investment in equilibrium is smaller under costly equity.
, for
banks. Otherwise, banks will choose not to invest in the risky asset at all. For this reason, the set of parameters where we have strictly positive investment in equilibrium is smaller under costly equity.
6 Systemic Failures in Regulated Economies
In this section I examine systemic failures when the two countries are symmetric. By systemic failures I refer to the fact that all banks in the two countries become insolvent after fire sales. Systemic failures will occur if the asset prices in the crisis state are so low that the returns from investments that could be retained by banks after fire sales are not enough to cover the promised return to depositors, which is simply equal to the initial value of the investment. Systemic failures might occur even in regulated economies. Because countries are symmetric and we assume perfectly correlated shocks across countries, systemic failures, if they occur, will happen in both countries at the same time. We can write the systemic failure condition in equilibrium as
where
For the rest of the analysis I will work with a particular functional form for which I can obtain a closed-form solution for equilibrium investment levels. The technology of global investors is given by:
![]() . I solve the model for this particular functional form in Appendix A. Using this closed form solution, we can show that the systemic failure condition given by (38) above is
. I solve the model for this particular functional form in Appendix A. Using this closed form solution, we can show that the systemic failure condition given by (38) above is
where
By Proposition 4 we have already seen that equilibrium investment level is increasing in ![]() and
and ![]() Proposition 10 shows that if
Proposition 10 shows that if ![]() is sufficiently high, then systemic failures do not occur. In order to
prove this, I show that the difference
is sufficiently high, then systemic failures do not occur. In order to
prove this, I show that the difference
![]() is monotonically increasing in
is monotonically increasing in ![]() , and that this difference is
positive for any value of
, and that this difference is
positive for any value of ![]() if
if ![]() is sufficiently high. Remember that banks fail if
is sufficiently high. Remember that banks fail if
![]() , which means that they will not fail as long as the difference
, which means that they will not fail as long as the difference
![]() is positive. But if
is positive. But if ![]() has moderate values, given by
has moderate values, given by
![]() then banks fail in the bad state only if the probability of good state,
then banks fail in the bad state only if the probability of good state, ![]() , is sufficiently high. For moderate values of
, is sufficiently high. For moderate values of ![]() , a sufficiently high
, a sufficiently high ![]() leads to systemic failures because
leads to systemic failures because
![]() is increasing
is increasing ![]() whereas
whereas ![]() is independent of
is independent of ![]() as can be seen from (39). Hence, for any value of
as can be seen from (39). Hence, for any value of ![]() such that
such that
![]() there is a sufficiently high
there is a sufficiently high ![]() such that the difference
such that the difference
![]() is negative. Last, if
is negative. Last, if ![]() is sufficiently low, given by
is sufficiently low, given by
![]() then total return from maintained assets after fire sales is never enough to cover the initial value of the investment, because
then total return from maintained assets after fire sales is never enough to cover the initial value of the investment, because ![]() is the marginal cost of funds for the investment if the bad state is expected to occur with certainty. In order to prove this, I show that for these low values of
is the marginal cost of funds for the investment if the bad state is expected to occur with certainty. In order to prove this, I show that for these low values of ![]() , the difference
, the difference
![]() is negative for any value of
is negative for any value of ![]() . Therefore in this case,
systemic failures will surely happen in the bad state.
. Therefore in this case,
systemic failures will surely happen in the bad state.
The region of parameters for which systemic failures occur in the bad state is illustrated in the left panel of Figure 4. The horizontal axis in Figure 4 measures ![]() , the probability of success, from 0 to 1, and the
vertical axis measures
, the probability of success, from 0 to 1, and the
vertical axis measures ![]() , the return to investment, from 1 to 2. Since we assume that
, the return to investment, from 1 to 2. Since we assume that ![]() , we should ignore the region where
, we should ignore the region where ![]() in Figure 4. This region is shaded by grey. The blue region shows the set of
in Figure 4. This region is shaded by grey. The blue region shows the set of ![]() pairs for a given
pairs for a given ![]() , for which systemic failures occur in the bad state. Technically, in the blue region we have that
, for which systemic failures occur in the bad state. Technically, in the blue region we have that
![]() . There are two horizontal red lines in the left panel of Figure 4 . The lower one shows
. There are two horizontal red lines in the left panel of Figure 4 . The lower one shows ![]() , and it is clear from the graph that banks fail for any value of
, and it is clear from the graph that banks fail for any value of ![]() if
if ![]() . The higher red line shows
. The higher red line shows
![]() , and it is again clear from the graph that systemic failures never occur if
, and it is again clear from the graph that systemic failures never occur if
![]() . Last, if
. Last, if ![]() is between the two red lines (i.e., if
is between the two red lines (i.e., if
![]() ), then for any such
), then for any such ![]() there exists some
there exists some
![]() such that systemic failures occur if
such that systemic failures occur if
![]() , as claimed in Proposition 10.
, as claimed in Proposition 10.
It is clear from the analysis above that systemic failures are more likely when the initial investment level is high. Because central regulation reduces investment levels in both countries, we can claim that moving to a central regulation can eliminate systemic failures. This can be observed from the right panel in Figure 4 where the parameter values for which systemic crisis occurs under the common central regulation are shown in blue. The parameter set for which systemic crisis occurs in the uncoordinated equilibrium is the sum of the colored regions (the same area as in the left panel). It is clear from this right panel that when countries move to common central regulation, the parameter set for which systemic failures occur in the bad state shrinks. The following lemma shows the parameter values under which systemic crisis does occur in the bad state in the uncoordinated equilibrium and moving to a common central regulation eliminates the crisis. Therefore, a common central regulation improves not only the social welfare but also the financial stability of coordinating countries.
7 Conclusion
I have examined the incentives of national regulators to coordinate regulatory policies in the presence of systemic risk in global financial markets, using a two-country, three-period model. Banks borrow from local deposit markets and invest in risky long-term assets in the initial period. They may face negative shocks in the interim period that force them to sell assets. Asset sales of banks feature the characteristics of a fire sale: assets are sold at a discount, and the higher the number of assets sold, the lower the market price of assets is. The asset market in the interim period is competitive. Each bank treats the asset price as given, and therefore neglects the effects of its sales on other banks. Due to this externality, correlated asset fire sales by banks generate systemic risk across national financial markets.
If the regulatory standard is relaxed in one country, banks in this country invest more in the risky asset in the initial period. If the bad state arises in the interim period, these banks are forced to sell more assets, causing the asset price to fall further. A lower asset price will increase the cost of distress for the banks in the other country as well. Banks may even default in equilibrium if the asset prices fall below a threshold.
I have shown that, in the absence of cooperation, independent regulators choose inefficiently low regulation compared to regulatory standards that would be chosen by a central regulator. A central regulator takes the systemic risk into account and improves welfare in cooperating countries by imposing higher regulatory standards. Therefore, it is incentive compatible for national regulators of symmetric countries to relinquish their authority to a central regulator.
I have also considered the incentives of regulators when there are asymmetries between countries with a focus on the asymmetries in asset returns. In particular, I have assumed that banks in one country are uniformly more productive than the banks in the other country in terms of managing long-term assets. I have shown that cooperation would voluntarily emerge only between sufficiently similar countries. In particular, the regulator in the high-return country chooses lower regulatory standards in equilibrium and is less willing to compromise on stricter regulatory standards.
8.1 Functional Form Examples
Example 1
![]()
For this return function we obtain the (inverse) demand function as
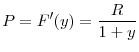 and hence and hence 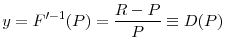 |
(8.1) |
This demand function is clearly downward slopping and convex as seen below
 and and 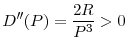 |
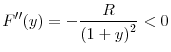 and since and since |
Let's check whether this functional form satisfies the conditions given by Assumption ELASTICITY and Assumption REGULARITY, respectively.
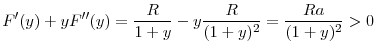 |
Clearly Assumption ELASTICITY is satisfied . Below we see that this function satisfies Assumption REGULARITY as well:
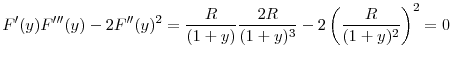 |
From above we can also see that this return function induces a log-convex demand function since we will have
Example 2
![]()
For this example the demand function will be obtained as
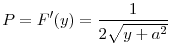 and hence and hence  |
This demand function is also downward slopping and convex as seen below
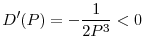 and and 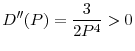 |
Assumption CONCAVITY is satisfied since
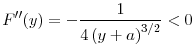 and and 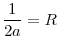 or or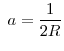 |
We can easily show that Assumption ELASTICITY is satisfied:
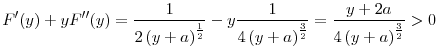 |
Likewise we can show that this function satisfies Assumption REGULARITY as well:
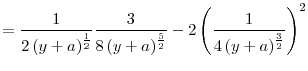 |
||
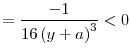 |
Note that in contrast to the first example this functional form induces a log-concave demand function since we can show that
8.2 Symmetric Countries: An example
In this section, I obtain closed form solutions for non-cooperative equilibrium regulation levels and regulation levels under cooperative benchmark for the particular functional form choice for the global investors' technology given by Example 1 above.
For analytical convenience suppose that the technology of global investors is given by the following logarithmic function as investigated by Example 1 above
| (8.2) |
where the amount of assets the global investors optimally buy satisfies the following first order conditions
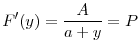 |
(8.3) |
which will induce a downward slopping demand function
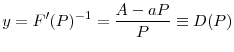 |
(8.4) |
Imposing Assumption CONCAVITY on this functional form gives
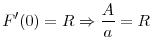 or or |
(8.5) |
It is shown in the previous section that this functional form satisfies the conditions given by Assumptions ELASTICITY and REGULARITY. Since this functional form satisfies all sufficient
conditions, we can proceed with solving for the equilibrium. We start solving the model backwards as in the previous section. Therefore we first find the equilibrium price at ![]() using the
market clearing condition.
using the
market clearing condition.
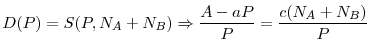 |
(8.6) |
Hence, we get the equilibrium price of assets at
which is clearly decreasing in the investment levels in both countries. Note also that equilibrium price is determined only by the total investment level in the two countries. Exact division of the total investment between the countries will not affect
We can also obtain equilibrium fraction of assets retained by banks after fire sales as a function of initial investment levels in each country by plugging the equilibrium price given by equation (8.7) into equation (9) that defines this fraction as a ratio of market price, which will give that
Remember that regulator
![]() s objective function is
s objective function is
| (8.9) |
Substituting for
![\displaystyle \underset{N_{i}\geq 0}{\max }W_{i}(N_{i},N_{j})=q(R-1)N_{i}+(1-q)\left[ R\left( 1-\frac{ac}{A-c(N_{i}+N_{j})}\right) N_{i}-N_{i}\right]](img290.gif) |
(8.10) |
where FOCs can be obtained as
Solving for
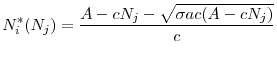 |
(8.12) |
where we define
We can use the best response functions to solve for the symmetric equilibrium investment level. After some algebra we can obtain that for ![]()
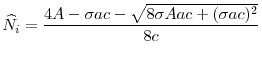 |
(8.14) |
Note that by Assumption CONCAVITY we impose that
8.2.1 Central Regulation
Let's consider the central regulator's problem where the central regulator chooses the total investment level in both countries.
| (8.16) |
Denote the solution to this global problem by
![]() Central regulator will impose maximum investment level in each country as
Central regulator will impose maximum investment level in each country as
![]()
![]() as discussed before.
as discussed before.
![]() will be characterized by the FOCs of the problem above which we could derive as
will be characterized by the FOCs of the problem above which we could derive as
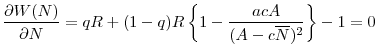 |
(8.17) |
Solving for
8.3.1 Proofs for the Symmetric Countries Case
First, note that using the expression for the total supply function given by (13) we obtain
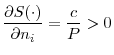 |
(8.20) |
Hence, we can write the derivative in (8.19) as
The following equivalence will help us to write this derivative using only return function of global investors' return function,
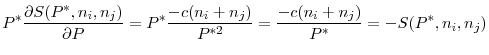 |
(8.22) |
Using this equivalence we can express the derivative given by (8.21) as
Let
![]() denote the total volume of equilibrium fire sales. In equilibrium we will have
denote the total volume of equilibrium fire sales. In equilibrium we will have
![]() from the demand curve. Therefore we can obtain
from the demand curve. Therefore we can obtain
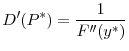 |
(8.24) |
where we make use of the fact that
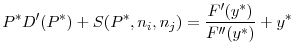 |
(8.25) |
which we can write equivalently as
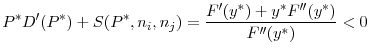 |
(8.26) |
This expression is negative since
| (8.27) |
by Assumption ELASTICITY.
Therefore we conclude that
![]()
![]()
| (8.28) |
Note that
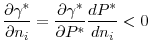 |
(8.29) |
since
Since equilibrium fraction of assets sold in each country is given by
![]() we obtain that this fraction is increasing in
we obtain that this fraction is increasing in ![]() for
for ![]() .
. ![]()
Let's reproduce regulators' objective function here for convenience
FOCs for regulator of country
 |
(8.31) |
Let's define the following function for convenience
Hence, we can write the FOCs simply as
We will show that Under Assumptions CONCAVITY, ELASTICITY and REGULARITY we have
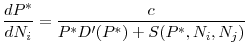 |
(8.34) |
which is negative as we have shown there. Since
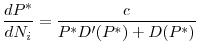 |
(8.35) |
We will use this expression in the derivative of
Hence we can obtain the second derivative as
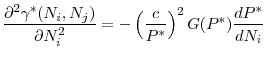 |
(8.37) |
where we define
Note that the derivative of
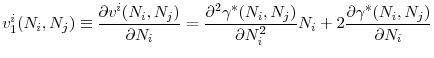 |
(8.39) |
Put the findings above together to get this derivative as
![\displaystyle v_{1}^{i}(\cdot )=-\left( \frac{c}{P^{\ast }}\right) ^{2}\left[ G(P^{\ast })N_{i}-\frac{2}{c}\right] \frac{dP^{\ast }}{dN_{i}}](img339.gif) |
(8.40) |
again where
Note that using
![]() and
and
![]() we can obtain
we can obtain
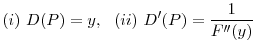 and and 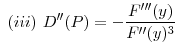 |
(8.41) |
Hence, we can write the expression in the numerator of
Re-arranging the RHS of (8.42), we obtain
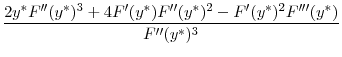 |
(8.43) |
Note that the denominator of the last expression is negative by Assumption CONCAVITY. Re-arrange the numerator to write it as
The expression in (8.44) is positive under Assumption ELASTICITY and REGULARITY as shown above. This implies that
| (8.45) |
i.e. the numerator of
The analysis above shows that FOCs of each regulator is monotone and decreasing. Therefore, we conclude that their best response functions are unique valued as desired.
If ![]() and
and ![]() are strategic substitutes we must have
are strategic substitutes we must have
![]() Remember that
Remember that
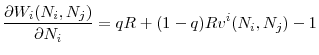 |
(8.46) |
where
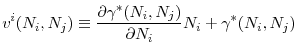 |
(8.47) |
hence
The sing of equation (8.48) is negative since
(i)
![]() as shown by eq (8.36) and
as shown by eq (8.36) and
(ii) for the cross derivative of
![]() we know that
we know that
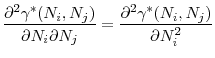 |
(8.49) |
since
![\displaystyle v_{2}^{i}(\cdot )\equiv \frac{\partial v^{i}(N_{i},N_{j})}{\partial N_{j}}=-\left( \frac{c}{P^{\ast }}\right) ^{2}\left[ G(P^{\ast })N_{i}-\frac{1}{c}\right] \frac{dP^{\ast }}{dN_{i}}](img358.gif) |
(8.50) |
which is negative under Assumptions 1 to 3 as shown in the proof of Lemma 3. Hence, the best response functions are downward slopping which implies that
Let's first define
Fix some
Case 1
![]()
Define
| (8.52) |
Consider regulators objective function as
| (8.53) |
Now note that
 |
(8.54) |
since
| (8.55) |
since
Case 2
![]()
By definition of ![]() this implies that
this implies that
![]() for any
for any
![]() In this case banks optimally discard all capital at
In this case banks optimally discard all capital at ![]() i.e.
i.e.
![]() which implies that
which implies that
![]() Hence social welfare in country
Hence social welfare in country ![]() will be given
by
will be given
by
| (8.56) |
since
Part 2 For the second part of the proof I will show that welfare in country ![]() is always decreasing in
is always decreasing in![]() when
when
![]() , and hence the best responses will be given by
, and hence the best responses will be given by
![]() Remember
Remember
| (8.57) |
Note that the highest value of
| If |
(8.58) |
Consider first
 |
(8.59) |
since
| (8.60) |
from which we can obtain
| (8.61) |
Re-arranging this inequality gives
| (8.62) |
where further simplification implies
Hence, we conclude that
![]() for
for ![]() as long as
as long as
![]()
![]()
I establish below that this game satisfies all three conditions stated in this theorem.
(i) Following Lemma 4 we can restrict strategy space for each regulator to ![]() which is compact and convex .
which is compact and convex .
(ii) Continuity of the objective function is obvious.
(iii) For concavity we evaluate the second derivative of the objective function with respect to the own action:
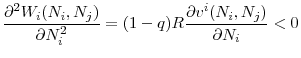 |
(8.63) |
as shown by Lemma 3 above. Hence Nash Equilibria equilibria exist. Existence of a symmetric Nash Equilibrium equilibrium is implied by the symmetry of the game.
In two-player games best response functions are contraction everywhere if the absolute value of their slopes are less than one everywhere. In order to show this, I make use of the nice feature of equilibrium price function that it is determined only by the sum of the investment levels in the two countries.
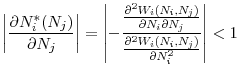 |
(8.64) |
which can be equivalently stated as
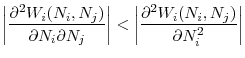 |
(8.65) |
Using the expressions for these derivatives given before this corresponds to
Note that derivative on the right hand side is negative by Lemma 3 and the derivative on the left hand side is negative by Proposition 1. Moreover,
![]() and its derivatives are determined only by the sum of the two investment levels, not by their individual values. This implies that
and its derivatives are determined only by the sum of the two investment levels, not by their individual values. This implies that
|
(8.67) |
which implies that
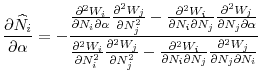
|
(8.68) |
where
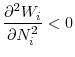 , and , and  for for |
(8.69) |
by Lemma 3 and Proposition 1. Moreover in the proof of Proposition 3 we have shown that
which implies that the sign of the denominator above is positive. Moreover, in a symmetric equilibrium we will have
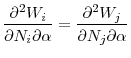 and and 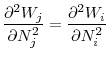 |
(8.71) |
which allows us to write the derivative as
![\displaystyle \frac{\partial \widehat{N}_{i}}{\partial \alpha }=-\frac{\frac{\partial ^{2}W_{i}}{\partial N_{i}\partial \alpha }\overset{(-)}{\overbrace{\left[ \frac{\partial ^{2}W_{i}}{\partial N_{i}^{2}}-\frac{\partial ^{2}W_{i}}{% \partial N_{i}\partial N_{j}}\right] }}}{\underset{(+)}{\underbrace{\frac{% \partial ^{2}W_{i}}{\partial N_{i}^{2}}\frac{\partial ^{2}W_{j}}{\partial N_{j}^{2}}-\frac{\partial ^{2}W_{i}}{\partial N_{i}\partial N_{j}}\frac{% \partial ^{2}W_{j}}{\partial N_{j}\partial N_{i}}}}}](img414.gif)
|
(8.72) |
the term inside the brackets in the numerator is again negative by the inequality (8.70). Therefore the sing of the derivative above will be equal to the sign of
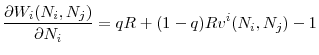 |
(8.73) |
which will imply that in equilibrium
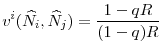 |
(8.74) |
Therefore we can obtain that
 |
(8.75) | |
 |
in equilibrium, using equation (8.33). Hence we conclude that
For comparative statics with respect to ![]() consider
consider
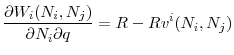 |
(8.76) |
which in equilibrium, using equation (8.33) we can write as
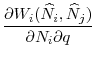 |
![\displaystyle =R\left[ 1-\frac{1-qR}{(1-q)R}\right]](img423.gif) |
(8.77) |
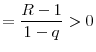 |
(8.78) |
hence we can also conclude that
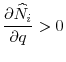 for for |
i.e. equilibrium investment levels in both countries are increasing as the probability of good state rises.
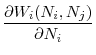 |
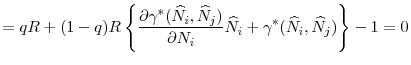 |
|
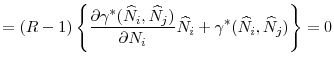 |
which implies that
 |
Lemma 3 has shown that
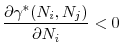 |
Therefore for the FOCs above to hold we need
| (8.79) |
which implies that
| (8.80) |
The FOCs for this problem will be given by
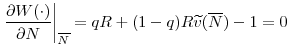 |
(8.81) |
where
where
| (8.83) |
Note that equilibrium fraction of rescued assets,
![]() , is determined by the sum of the investment levels in the two countries. In other words, exact division of global investment between the two countries do
not affect
, is determined by the sum of the investment levels in the two countries. In other words, exact division of global investment between the two countries do
not affect
![]() and hence its derivatives. This property allows us to write
and hence its derivatives. This property allows us to write
![]() as (with a slight abuse of notation)
as (with a slight abuse of notation)
On the other hand, remember that each independent regulator's FOCs will give us
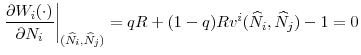 |
(8.85) |
from which we get that in equilibrium
Comparing (8.86) and (8.82) we see that
![]() where
where
![]() are the symmetric Nash equilibrium investment levels. Using this together with equality (8.84) we can write
are the symmetric Nash equilibrium investment levels. Using this together with equality (8.84) we can write
| (8.87) |
we have previously shown that
Since central regulation levels,
which implies that
8.3.2 Proofs for the Asymmetric Countries Case
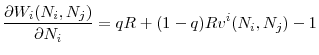 |
(8.88) |
which will imply that in equilibrium we have
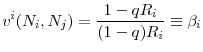 |
(8.89) |
Note that
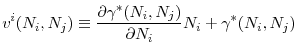 |
(8.90) |
![]() implies that
implies that
![]() . Using the expression above this is equivalent to
. Using the expression above this is equivalent to
Since
| (8.92) |
and
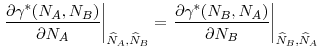 |
(8.93) |
Using these two equalities in (8.91) gives
From Lemma 3 we know that
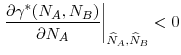 |
(8.95) |
Therefore, for inequality (8.94) to be true we need to have
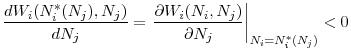 |
(8.96) |
By assumption we have
Moreover, by definition
| (8.98) |
Hence, any common regulation such that
| (8.99) |
where the first inequality is follows from Envelope Theorem given by (8.97), and the second is by definition of optimality. Remember that
| (8.100) |
Hence,
| (8.101) |
Which we can re-arrange and write as
Now consider
Now, let's compare (8.102) and (8.103). First note that the first terms are positive in both of them.
![\displaystyle \frac{d[W_{A}(N^{m},N^{m})-W_{A}(\widehat{N}_{A},\widehat{N}_{B})]}{ds}](img506.gif) |
(8.104) |
this derivative will be given by
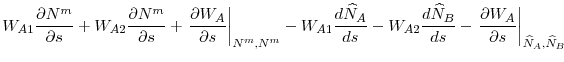
|
(8.105) |
Applying envelope theorem reduces this to
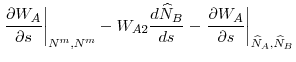 |
(8.106) |
Now note that since
| (8.107) |
we will have that
 and and  |
(8.108) |
Therefore
![\displaystyle \frac{d[W_{A}(N^{m},N^{m})-W_{A}(\widehat{N}_{A},\widehat{N}_{B})]}{ds}% =-W_{A2}\frac{d\widehat{N}_{B}}{ds}](img512.gif) |
(8.109) |
First note that
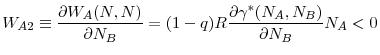 |
(8.110) |
Moreover, by Proposition 4 we have shown that
![\displaystyle \frac{d[W_{A}(N^{m},N^{m})-W_{A}(\widehat{N}_{A},\widehat{N}_{B})]}{ds}% =-W_{A2}\frac{d\widehat{N}_{B}}{ds}<0](img517.gif) |
(8.111) |
Hence, the benefit from cooperating is decreasing in the difference between the two countries. Therefore if
We will show that such an
![]() exists. It is clear that for
exists. It is clear that for ![]() we have
we have
![]() On the other hand, as
On the other hand, as
![]() , we can argue that
, we can argue that
![]() will necessarily become zero. From Proposition 11 we know that for central regulation be acceptable by regulator 1, we must have
will necessarily become zero. From Proposition 11 we know that for central regulation be acceptable by regulator 1, we must have ![]()
![]()
![]() However, as
However, as
![]() it won't be possible to reduce
it won't be possible to reduce
![]() sufficiently to compensate regulator 1. Therefore, we will have
sufficiently to compensate regulator 1. Therefore, we will have
![]() for sufficiently large
for sufficiently large ![]() By continuity an
By continuity an
![]() such that
such that
![]() must exist.
must exist. ![]()
8.3.3 Proof of the Systemic Failure Exercise
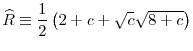 |
(8.112) |
I will first show that when ![]() the difference
the difference
![]() is monotonically increasing in
is monotonically increasing in ![]() Moreover, it is negative
when
Moreover, it is negative
when ![]() is small and positive for sufficiently high
is small and positive for sufficiently high ![]() Therefore, we will establish
using Intermediate Value Theorem that there exists some
Therefore, we will establish
using Intermediate Value Theorem that there exists some
![]() such that
such that
![]() Using definitions of
Using definitions of ![]() and
and
![]() we can write this difference as
we can write this difference as
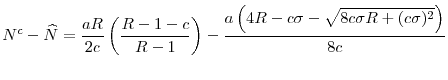 |
(8.113) |
where
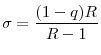 |
as defined before. Evaluating this difference at
We can determine the behavior of this difference as
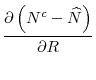 |
 |
(8.115) |
This derivative is clearly positive, which means that the difference is monotonically increasing in
| (8.116) |
This follows since
| (8.117) |
In order to see this we can expand the difference
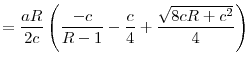 |
(8.118) |
Now, note that as
Case 1
![]()
The analysis above implies that for
![]() we have that
we have that
![]() Moreover, since for any given
Moreover, since for any given ![]() the highest value of
the highest value of
![]() is obtained when
is obtained when ![]() we will also have that for
we will also have that for
![]() we have
we have
![]() for all
for all
![]() In other words, if
In other words, if
![]() , banks never fail in the bad state for any value of
, banks never fail in the bad state for any value of
![]()
Case 2
![]()
In this case we can show that
Hence by the Intermediate Value Theorem we will conclude that there exists
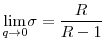 and and |
(8.121) |
Therefore let's consider
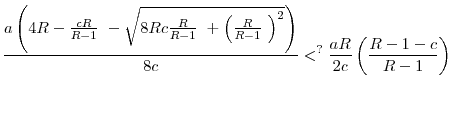 |
(8.122) |
where left hand side of the inequality is
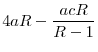 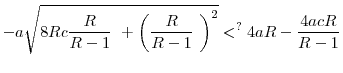 |
(8.123) |
simplifying further yields
| (8.124) |
which is true as long as
For the second part of the inequality (8.120) consider
![]() when
when ![]() and check when it is greater than
and check when it is greater than ![]()
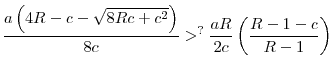 |
(8.125) |
where the left hand side of the inequality is
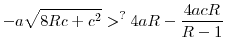 |
(8.126) |
Solving for
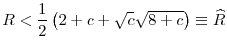 |
(8.127) |
Therefore we can conclude that if
![]()
Case 3
![]()
We know that when
![]() we will have
we will have
![]() by definition and
by definition and
![]() from Proposition 3. Therefore, we will have that
from Proposition 3. Therefore, we will have that
![]() whenever
whenever
![]() for all
for all
![]() . Therefore banks always fail in the bad state in this case.
. Therefore banks always fail in the bad state in this case. ![]()
We can follow the similar lines in the proof of Proposition 10, and show that if
![]() then there exists a
then there exists a
![]() such that for all
such that for all
![]() we have that
we have that
![]() In other words, for such
In other words, for such ![]() , if the probability of
the good state is higher than
, if the probability of
the good state is higher than
![]() banks fail in the bad state under common central regulation. If
banks fail in the bad state under common central regulation. If ![]() then banks always fail in the bad state, and if
then banks always fail in the bad state, and if
![]() then banks never fail in the bad state where
then banks never fail in the bad state where
It is clear that
![]() . We can also show that
. We can also show that
![]() which will complete the proof.
which will complete the proof. ![]()
References
Acharya, V. (2003). Is the international convergence of capital adequacy regulation desirable? The Journal of Finance 58(6), 2745-2782.
Acharya, V. (2009). A theory of systemic risk and design of prudential bank regulation. Journal of Financial Stability 5(3), 224-255.
Acharya, V., H. Shin, and T. Yorulmazer (2010). Fire-sale fdi.
Acharya, V. and T. Yorulmazer (2008). Cash-in-the-market pricing and optimal resolution of bank failures. Review of Financial Studies 21(6), 2705-2742.
Aguiar, M. and G. Gopinath (2005). Fire-sale foreign direct investment and liquidity crises. Review of Economics and Statistics 87(3), 439-452.
Allen, F. and D. Gale (1994). Limited market participation and volatility of asset prices. The American Economic Review, 933-955.
Allen, F. and D. Gale (1998). Optimal financial crises. The Journal of Finance 53(4), 1245-1284.
Amir, R. (1996). Cournot oligopoly and the theory of supermodular games. Games and Economic Behavior 15(2), 132-148.
Barth, J., G. Caprio, and R. Levine (2008). Bank regulations are changing: For better or worse? Comparative Economic Studies 50(4), 537-563.
Basel (1988). International convergence of capital measurement and capital standards. Bank for International Settlements.
Bengui, J. (2011). Macro-prudential policy coordination and global regulatory spillovers. University of Maryland, Manuscript.
Cooper, R. (1985). Economic interdependence and coordination of economic policies. Handbook of international economics 2, 1195-1234.
Coval, J. and E. Stafford (2007). Asset fire sales (and purchases) in equity markets. Journal of Financial Economics 86(2), 479-512.
Dalen, D. and T. Olsen (2003). Regulatory competition and multinational banking. CESifo Working Paper Series.
Dell'Ariccia, G. and R. Marquez (2006). Competition among regulators and credit market integration. Journal of Financial Economics 79(2), 401-430.
Gai, P., S. Kapadia, S. Millard, and A. Perez (2008). Financial innovation, macroeconomic stability and systemic crises. The Economic Journal 118 (527), 401-426.
Hamada, K. (1974). Alternative exchange rate systems and the interdependence of monetary policies. National Monetary Policies and the International Financial System, University of Chicago Press, Chicago, 13-33.
Hamada, K. (1976). A strategic analysis of monetary interdependence. The Journal of Political Economy, 677-700.
Hellmann, T., K. Murdock, and J. Stiglitz (2000). Liberalization, moral hazard in banking, and prudential regulation: Are capital requirements enough? American Economic Review , 147-165.
Holthausen, C. and T. Ronde (2004). Cooperation in international banking supervision. Working Paper Series.
Kiyotaki, N. and J. Moore (1997). Credit cycles. The Journal of Political Economy 105(2), 211-248.
Korinek, A. (2011). Systemic risk-taking: amplification effects, externalities, and regulatory responses. ECB Working Paper No. 1345.
Krugman, P. (2000). Fire-sale fdi. In Capital ows and the emerging economies: theory, evidence, and controversies, pp. 43{60. University of Chicago Press.
Lorenzoni, G. (2008). Inefficient credit booms. The Review of Economic Studies 75(3), 809-833.
Persson, T. and G. Tabellini (1995). Double-edged incentives: Institutions and policy coordination. Handbook of international economics 3, 1973-2030.
Pulvino, T. (2002). Do asset re sales exist? an empirical investigation of commercial aircraft transactions. The Journal of Finance 53(3), 939-978.
Repullo, R. (2004). Capital requirements, market power, and risk-taking in banking. Journal of financial Intermediation 13(2), 156-182.
Shleifer, A. and R. Vishny (1992). Liquidation values and debt capacity: A market equilibrium approach. The Journal of Finance, 1343-1366.
Townsend, R. (1979). Optimal contracts and competitive markets with costly state verification. Journal of Economic theory 21(2), 265-93.
Williamson, O. (1988). Corporate finance and corporate governance. The Journal of Finance, 567-591.
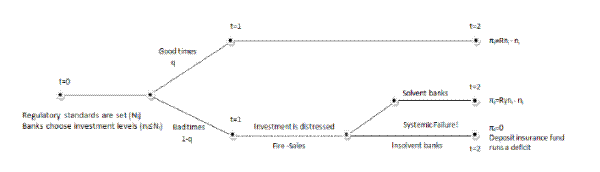
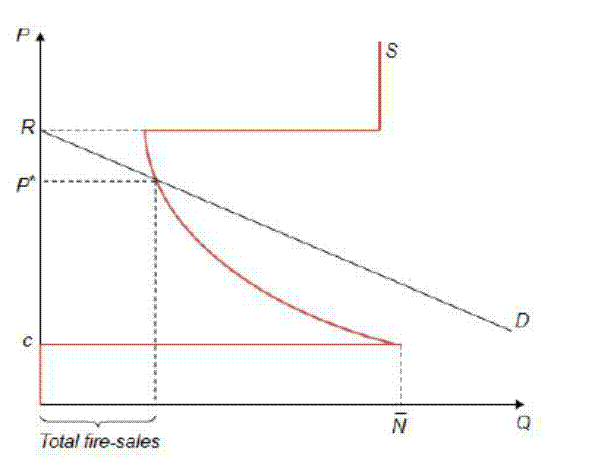
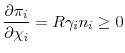
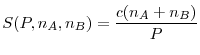
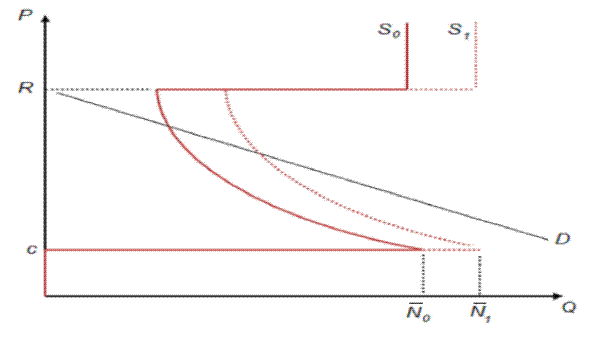
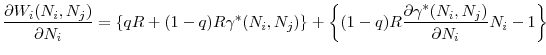
![\displaystyle W_{i}(N_{i},N_{j})=qRN_{i}+(1-q)\left\{RN_{i}-[R-P^{*}(N_{i},N_{j})]\frac{cN_{i}}{P^{*}(N_{i},N_{j})}-cN_{i}\right\}+(e-N_{i})](img120.gif)
![\displaystyle \underset{N_{A},N_{B}\geq 0}{\max } \ GW(N_{A},N_{B})=\underset{N_{A},N_{B}\geq 0}{\max } \ \sum_{i=A,B; j\neq i}% \{q(R-1)N_{i}+(1-q)[R\gamma ^{\ast }(N_{i},N_{j})N_{i}-N_{i}]\}](img139.gif)
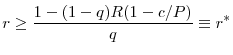
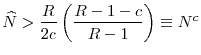

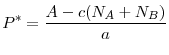
![\displaystyle \frac{\partial W_{i}(N_{i},N_{j})}{\partial N_{i}}=qR+(1-q)R\left\{ 1-\frac{% ac(A-cN_{j})}{[A-c(N_{i}+N_{j})]^{2}}\right\} -1=0](img291.gif)
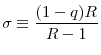
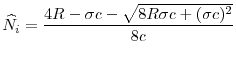
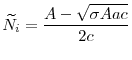

![\displaystyle \frac{dP^{\ast }}{dn_{i}}=\frac{c}{P^{\ast }D^{\prime }(P^{\ast })-P^{\ast }% \left[ \partial S(P^{\ast },n_{i},n_{j})/\partial P\right] }](img308.gif)
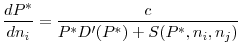
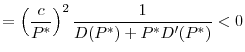
![\displaystyle G(P^{\ast })\equiv \frac{2D(P^{\ast })+4P^{\ast }D^{\prime }(P^{\ast })+P^{\ast 2}D^{\prime \prime }(P^{\ast })}{P^{\ast }[D(P^{\ast })+P^{\ast }D^{\prime }(P^{\ast })]^{2}}](img336.gif)
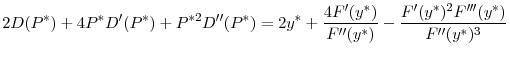
![\displaystyle 2F^{\prime \prime }(y^{\ast })^{2}\underset{(+)\textit{ by ELASTICITY}}{\underbrace{% \left[ y^{\ast }F^{\prime \prime }(y^{\ast })+F^{\prime }(y^{\ast })\right] }% }-F^{\prime }(y^{\ast })\underset{(-)\textit{ by REGULARITY}}{\underbrace{\left[ F^{\prime }(y^{\ast })F^{\prime \prime \prime }(y^{\ast })-2F^{\prime \prime }(y^{\ast })^{2}\right] }>0}](img349.gif)