How the Federal Reserve's Large-Scale Asset Purchases (LSAPs) Influence Mortgage-Backed Securities (MBS) Yields and U.S. Mortgage Rates
Abstract
We conduct an empirical analysis of the Federal Reserve's large-scale asset purchases (LSAPs) on MBS yields and mortgage rates. The Federal Reserve's accumulation of MBS and Treasury securities lowered MBS yields and mortgage rates by more than what would have been suggested by changes in market expectations alone, suggesting that portfolio rebalancing effects of LSAPs are an important consideration for monetary policy transmission. Our estimates also suggest that the Federal Reserve must hold a substantial market share of agency MBS or of Treasury securities to significantly lower MBS yields and in turn significantly lower mortgage rates.
JEL CODES: E52, E58, G01, G21
KEY WORDS: QE1, QE2, QE3, LSAP, mortgage-backed securities (MBS), mortgages, interest rates
1. Views on Large-Scale Asset Purchases (LSAPs)
Even before the recent financial crises, central bankers argued that monetary policy could retain its potency even when short-term rates are zero because central banks could also use open market operations, that is, purchases of a wide variety of assets, not just short-term government securities (King, 1999; Bernanke, 2002). Such operations, for example, could be used to enforce explicit ceilings for yields on longer-term securities, including longer-dated Treasury securities, agency debt, or agency mortgage-backed securities (Bernanke, 2002).2 If such a long-term asset purchase program were successful, not only would yields on such securities fall, but yields on private debt (such as mortgages) would likely fall as well. Moreover, with an increase in the monetary base, asset prices in general could rise and have an impact on spending (Mishkin, 1996; King, 1999). For these and other reasons, it was posited that even a central bank whose accustomed policy rate has been forced down to zero would not "run out of ammunition" (Bernanke, 2002).
In this study, we consider the effects of Federal Reserve large-scale asset purchases (LSAPs), commonly known as "quantitative easing" (QE) programs, on agency mortgage-backed securities (MBS) yields (and thereby on U.S. conforming mortgage rates). We focus on periods when financial markets are functioning fairly well, rather than on when MBS markets were in turmoil.3 During normal economic times, the prevailing view in the economics literature is that an LSAP by the central bank should have no effects on asset prices.4 Others, however, have argued that the Federal Reserve's LSAP programs can potentially work though three transmission channels: (1) signaling Federal Reserve intentions to financial markets (2) portfolio rebalancing effects, and (3) liquidity effects.5 All components of MBS yields are likely influenced somewhat through these transmission channels. Our study is unique in that we focus on MBS yields, rather than on Treasury security yields (as do D'Amico, English, Lopez-Salido, and Nelson, 2012) or across assets more broadly (as do Krishnamurthy and Vissing-Jorgensen, 2011), and because we are explicitly looking for evidence of portfolio rebalancing.
The most general effect of Federal Reserve LSAPs is derived from the signals provided by the FOMC that are sent to, and received by, all market participants. The signaling transmission channel operates principally via an impact on the expectations component of longer-term rates. Long-term asset purchases may increase the credibility of the Federal Reserve's commitment to keep interest rates lower than what the application of a Taylor rule would imply even after the economy recovers, particularly if the central bank weighs potential losses on its asset holdings in its objective function (Bauer and Rudebusch, 2012; Krishamurthy and Vissing-Jorgenson, 2011, Eggertson and Woodford, 2003; Clouse, Henderson, Orphanides, Small and Tinsley, 2000). This signaling transmission channel affects all bond market interest rates, since lower future federal funds rates can be expected to affect all interest rates. Note that market participants anticipate the announcement of Federal Reserve LSAPs, so the effects of a LSAP program can be reflected in market prices even before they are announced.
LSAPs by the Federal Reserve can also potentially affect MBS yields (and other asset prices) through a portfolio rebalancing transmission channel that works as follows: (1) the Federal Reserve purchases an asset and reduces the amount of the security that the private sector holds, while simultaneously increasing the amount of short-term, risk-free, bank deposits held by the private sector, (2) private sector investors hold more deposits than they desire because of the payments received to purchase their Treasury and agency securities, (3) the private sector investors desire to reduce their holdings of deposits and bid up the prices of the remaining longer-term securities and, as a result, there are lower yields on such securities.6 This "scarcity" effect is mainly focuses on the "current coupon yield" MBS, which will be described at length below.7
For longer-term securities, this portfolio rebalancing argument is often told in terms of duration and convexity risk: If the Federal Reserve withdraws MBS from the market, the institutions in the private sector that take these risks find themselves with too much cash on hand and cannot meet
their demands for duration and convexity without bidding more aggressively for MBS. The potential portfolio rebalancing adjustments made by these investors have two components: (1) a willingness to take less compensation for hedging the interest rate risks of financial assets, or a "duration
effect," that applies to both Treasury securities and MBS; and (2) a willingness to take less compensation for hedging the prepayment and volatility risks that are associated with holding MBS or a "convexity effect."
When purchasing Treasury securities, the Federal Reserve was quite aware of the duration effect and specifically targeted its purchases of Treasury securities toward those with a maturity of 4 to 7 years, so that it would withdraw more duration from the
market.8 MBS typically have a duration that is in the 4 to 7 year range.
At the same time, LSAPs by the Federal Reserve could potentially operate through a liquidity channel. Liquidity may be defined as the ease of reselling assets in the future.9 This definition is in line with Acharya and Pedersen (2005), who propose that liquidity is defined by how the security performs in a "bad" market.10 Investors are willing to pay a premium for a security that remains easy to sell when most other securities become illiquid or when market returns overall are low. The effect of Federal Reserve asset purchases on liquidity is unclear. On the one hand, the Federal Reserve's LSAPs may increase the ability of investors to sell their securities in the future, particularly during "bad" markets, because market participants believe the Federal Reserve will be a large and persistent buyer during any "bad" market. On the other hand, as the Federal Reserve's holdings of a security increases during "normal" times, the private sector holdings of the security may diminish, leading to a thinner market in the future with fewer opportunities to sell the security to other private market participants. Withdrawal of securities from the private sector by the Federal Reserve might diminish expected future liquidity if private market participants are uncertain about whether or not the Federal Reserve (or some other government entity) will be buying in a "bad" market in the future.11
2. A Review of Federal Reserve Actions
Table 1 updates the compilation of dates and announcements pertaining to monetary policy accommodation at the interest-rate lower bound that was developed by Woodford (2012).12 In addition, table 1 delineates the timing of the announcements for three separate rounds of QE--denoted using QE1, QE2, and QE3 in the fourth column--as well as when asset sales and purchases were taken to lengthen the maturities and to change the composition of the Federal Reserve's balance sheet--transactions that are sometimes described as an "Operation Twist," which is denoted by OT. The rightmost column of table 1 indicates whether each announcement is about an increase or a decrease in LSAPs, denoted by "increase" or "decrease," respectively; or is about the rationale for, or readiness of the Federal Reserve to engage in, accommodative monetary policy actions, described as a communication about asset purchases and denoted by "Com."
QE1 began in November 2008 when the Federal Reserve announced that it would initiate a program to purchase substantial quantities of MBS backed by Ginnie Mae, of agency debt, and of MBS backed by the housing-related government-sponsored enterprises (i.e., Fannie Mae and Freddie Mac) and ended in
March 31, 2010 when the previously announced asset purchases had been completed. 13
14 In contrast, QE2 involved purchases of Treasury securities: In August 2010, the Federal Reserve announced that it would redeploy into longer-term Treasury investments the principal payments from agency securities and in November 2010 it indicated that it would purchase
an additional $600 billion of longer-term Treasury securities by the end of the second-quarter of 2011. This second round of QE, the purpose of which was to end the de facto tightening of credit that occurred as the Federal Reserve portfolio shrank, ended on June 20,
2011.15
Operation twist, OT, began in September 2011 when the Federal Reserve initiated further adjustments to its portfolio, including an extension of the average maturity of its Treasury securities holdings and reinvestments of principal payments from agency securities into MBS, rather than into longer-term Treasury securities.
And on September 13, 2012, the third round of quantitative easing, QE3, began when the Federal Reserve announced that it would (1) increase policy accommodation by purchasing additional agency MBS at a pace of $40 billion per month,16 (2) continue through the end of 2012 its program to extend the average maturity of its holdings of securities, and (3) maintain its existing policy of reinvesting principal payments from its holdings of agency debt and agency mortgage-backed securities in agency mortgage-backed securities. These actions, which together increased the holdings of longer-term securities by about $85 billion each month at least through the end of 2012, were taken to "put downward pressure on longer-term interest rates, support mortgage markets, and help to make broader financial conditions more accommodative."17
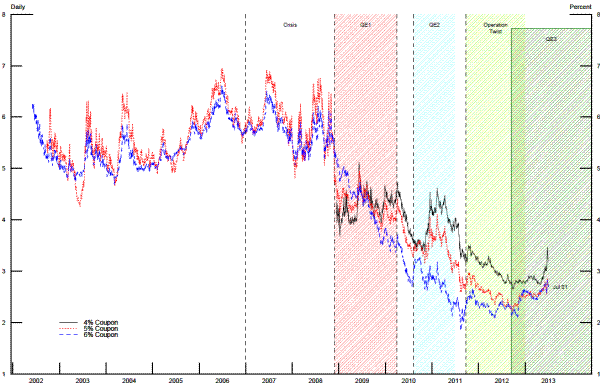
3. Finding the Par Value or Current Coupon for MBS
Fannie Mae and Freddie Mac issue MBS coupons in units of 50 basis points. For example, coupons exist with values of 2.5 percent, 3.0 percent, 3.5 percent, and so forth. As shown in figure 1, yields on MBS with different coupons tend to have similar time-series movements. The primary differences in the MBS yield is the prepayment risk associated with each MBS coupon in the coupon stack. Higher coupons are created using mortgages with higher mortgage rates, and these mortgages are more likely to prepay when mortgage rates fall.
When a mortgage is originated, the mortgage originator may subsequently exchange the mortgage for a Fannie Mae or Freddie Mac MBS. If the mortgage rate is, for example, 4.0 percent, a servicing fee of 25 basis points is deducted from the mortgage rate, as well as the Fannie Mae or Freddie guarantee fee. If the guarantee fee is, for example, 40 basis points, then the cash flow available to MBS investors will be 3.35 percent of the outstanding mortgage.
Mortgage pricing is often benchmarked by the current coupon MBS yield. This is the hypothetical coupon associated with an MBS pool that trades at par value (that is, the MBS trades at a price of $100 dollars for $100 of mortgages in the pool). In the example above, the current coupon is 3.35 percent. At this coupon, the mortgage originator can calculate the mortgage rate it needs to receive in order to breakeven when selling the mortgage in the secondary market.
However, 3.35 percent is not a coupon on an MBS that is available in the secondary market. MBS have either a coupon of 3.5 percent or of 3.0 percent. A mortgage pool with a 3.5 percent coupon has a price above 100 dollars for each 100 dollars of mortgage because MBS investor will be receiving a coupon that is above the prevailing current coupon mortgage rate. Similarly, if the mortgage pool has a coupon of 3.0 percent, the MBS security will likely sell for less than 100 dollars per dollar of mortgages with cash flows equal to 3.35 percent.
MBS with a range of coupons trade extensively every day in financial markets. A common way to determine the current coupon is to find the coupon that trades at a price slightly above $100 and find a different coupon that trades slightly below $100 and interpolate between the two coupons to find a coupon that has a hypothetical price of $100. This par-valued mortgage is of great interest to mortgage originators, who want calculate the breakeven mortgage rate for a new mortgage (that is they want to calculate which mortgage rate will yield a mortgage that can be traded into the secondary markets dollar-for-dollar.) However, when interest rates are volatile or when interest rates are moving decisively in one direction, then it is often not possible to find two coupons with prices that are just above and just below $100.
Indeed, since 2000, the downward general trend in interest rates has meant that there have been many periods when there was no MBS security that traded below par. During July 2000 to June 2013 a below par security did not exist on 672 of the 3388 trading days (20 percent). In particular, the current coupon mortgage was non-existent for long stretches of time in the post-financial crisis period.
When a below par security does not exist, two techniques are available for imputing a current coupon MBS yield value. First, one can extrapolate a curve from the existing coupons, and solve for the current coupon that equates to a price of $100. However, the extrapolation is often fragile, in the sense that small differences in the technique can lead to large differences in the estimated current coupon, when the drop in interest rates is substantial.
The second approach, which we employ, is to model the MBS bond pricing and to infer a current coupon rate from the model. Often, such a model incorporates mortgage prepayment functions. The valuation of the prepay options of homeowners is difficult and complex even in normal circumstances. But since the onset of the financial crisis, prepayment models have become even less reliable. Given that even the best prepayment option models often cannot reliably gauge prepayment risk over our estimation periods, particularly during a periods where interest rate are falling sharply, we use an empirically-based approach measure--the relationship between lowest-priced MBS security and its current-coupon yields.
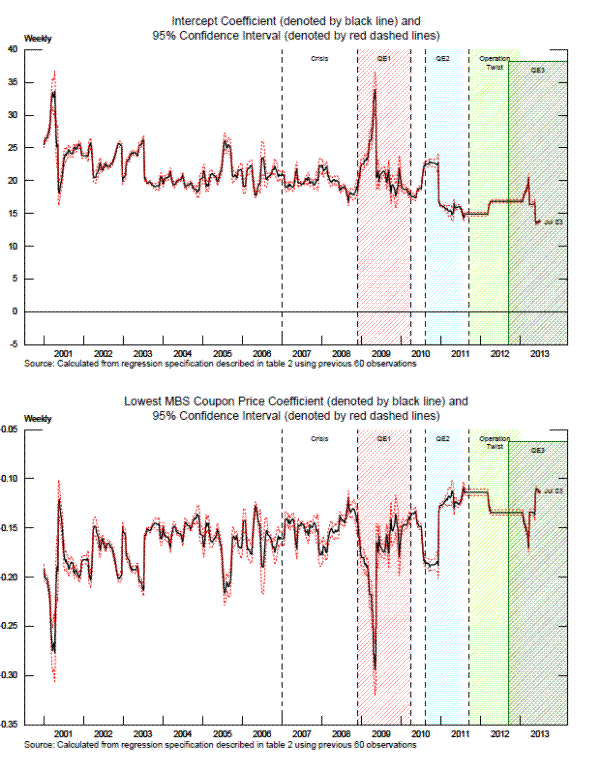
We regress the lowest current coupon for MBS against its price (table 2). The very close correlation is evident from the parameters being significant at the less than one percent level. We present the same regression specification for three periods: a pre-crisis period (i.e., July 5, 2000 through December 29, 2006), a crisis period (i.e., January 2, 2007 through May 28, 2009), and post-crisis period (June 1, 2009 through June 25, 2013). Looking across columns (1) through (4) in row 2, the relationship between the MBS yield and the price is fairly similar.
To "fill in" the missing current coupons, we use rolling 60 day regressions of the type described above using the lowest-coupon MBS that exists throughout this period. The coefficients on the lowest-coupon MBS price from these rolling regressions are shown in figure 2 (denoted by the solid black line), along with the 95 percent confidence interval for each coefficient estimate (denoted by red dotted lines). Overall, these estimates are fairly stable, with a couple of notable exceptions coinciding with steep falls in MBS yields.
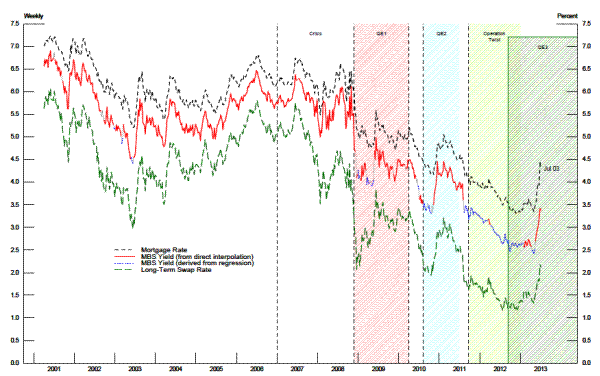
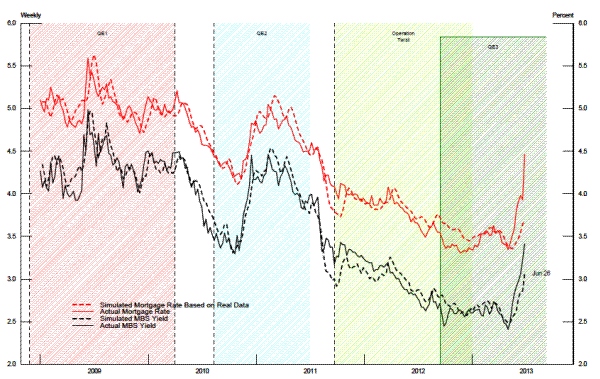
Using these rolling regression windows based on 60 observations, we create the current coupon series shown in figure 3. The MBS yields shown in solid red are current coupon MBS yields when trading prices existed both above and below par value, and the current coupon could be estimated by interpolating across the coupon stack. The MBS yields shown as blue dotted lines represent estimates that were generated from the rolling regression windows. The short-dashed black line is the current mortgage rate during the period. The "gaps" in the MBS yield curve, indicated by an absence of observations in red, are associated with vertical drops in the current coupon yield because of rapid declines in interest rates, when the market went quickly from having a traded price for an MBS priced at par value to not having such market information.
4. A Model of MBS Yields
A swap rate reflects the compensation to an investor from taking interest rate risk, but does not have the prepayment risk associated with an MBS. Most MBS investors use it as a benchmark return for MBS investing. Indeed, pairing an MBS with an interest rate swap may be the most common hedging transaction in financial markets, and thus is one reason that MBS and swap yields are tightly linked. Unlike MBS coupons, swaps are available at almost any yield and any maturity. More importantly, the quantity of swaps is not constrained by Federal Reserve LSAPs. As shown by the long-dashed green line in figure 3, the swap rate is continuously available.
As argued in Boudokh, Whitelaw, Richardson and Stanton (1997), there are good reasons to think that the level of longer-term interest rates and the slope of the yield curve are strongly related to the value of MBS. The level of a longer term rate is related to discounting the cash flows of a 30-year fixed rate MBS. Longer-term rates are also related to the incentive of a homeowner to refinance a mortgage; the homeowner compares past mortgage rates to the current mortgage rate, which reflects current longer-term rates. The slope of the Treasury yield curve is related to the market expectations about the future path of interest rates and the variation in the discount rate over long and short horizons. And, as our discussion above suggests, swap rates and the swap yield curve underpin much of the hedging against the risks of holding an MBS.
LSAPs can change the expectations held by market participants about future interest rates because they communicate the intentions of the Federal Reserve. To date, most other researchers have focused on event studies of Federal Reserve LSAPs (e.g., Gagnon et al., 2010 and Wright, 2011).18 Event studies attempt to isolate the effects of an accommodative policy by defining a brief period during which market participants become informed about a
Federal Reserve policy action and respond to it. For event studies, it is assumed that market participants quickly adjust expectations about the future consequences of the accommodative policy action and that these consequences are quickly reflected in the prices for financial assets. 19 However, information about the effects of new
quantitative easing programs, or about long-term asset purchases, is often learned over time; consequently asset prices may adjust more slowly.20 Moreover,
the liquidity effects associated with asset purchase programs, which are created as securities are withdrawn from the private market, may be difficult to understand, or to predict, at the time when asset purchase programs are announced. Finally, investors anticipate both the announcements and the
effects of LSAP programs, which may lead to underestimating the effect of a given announcement. Indeed, this is the premise of the many papers that have used event studies to capture MBS effects.
We attempt to measure whether LSAPs seem to influence MBS yields beyond simply by moving investor expectations. As argued above, investor expectations about secondary and primary mortgage markets, as well as the future course of both short- and long-term interest rates are strongly reflected in swap rates. Moreover, Federal Reserve purchases of MBS or Treasury securities do not influence the supply of swaps because swaps are simply a bilateral contractual commitment between investors to exchange cash flows. Thus, we can model the effect of changing market expectations on MBS yields using the swap yield and swap yield curve described above. We also incorporate into this MBS pricing model the typical announcement effects, as well as fixed-effects that describe the on-going shifts in expectations that are created during the time that respective Federal Reserve LSAPs are in place.
As shown earlier, the MBS yields trended downward during the post-crisis period. One possibility is that this downward trend simply reflected the responses to easier monetary policy by market participants. Indeed, the MBS yield is I(1). It is perhaps unusual for a market interest rate to be I(1), but the MBS yield along with many other interest rates are all influenced by expectations of future interest rates. Moreover, the Federal Reserve LSAPs were persistently in use over much of the post-crisis period, and may have created this downward trend through lowering market expectations about the future course of interest rates. However, during the same period, the Federal Reserve is persistently purchasing securities, and thus any portfolio rebalancing or liquidity effects are also in play. In this study, we attempt to distinguish the expectations effect and the portfolio rebalancing or liquidity effect.
Measuring Liquidity and Portfolio Rebalancing Effects
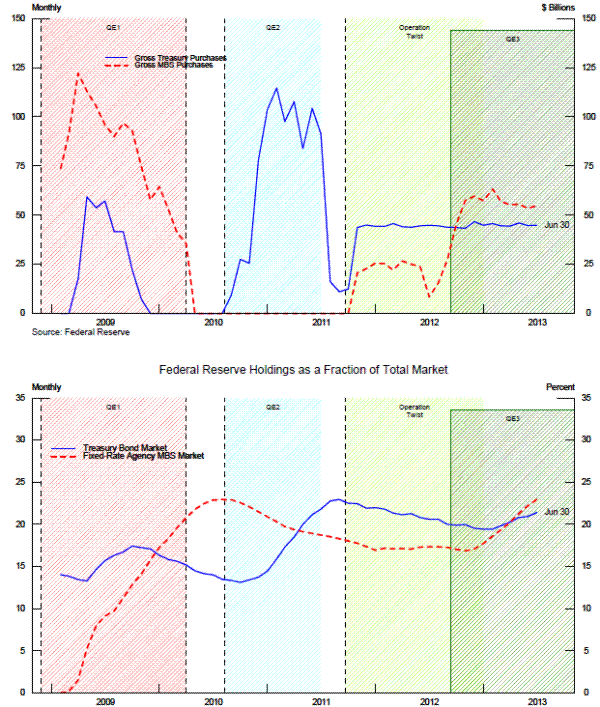
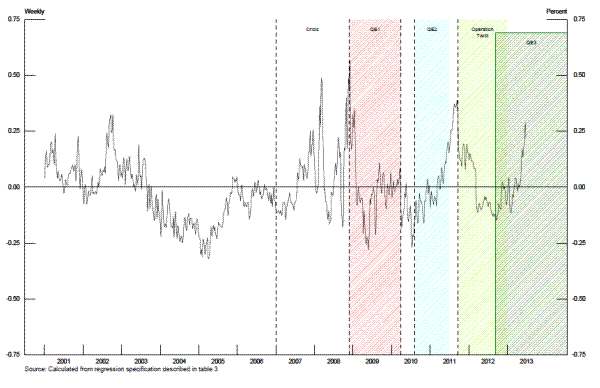
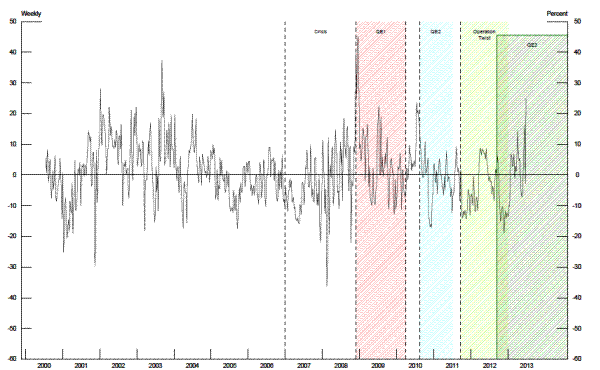
From the discussion of the liquidity channel and portfolio rebalancing channels above, a higher share of Federal Reserve security ownership could result in MBS yields either rising, falling, or remaining unchanged. The Federal Reserve's purchases of longer-term securities are shown in the top panel of figure 4. As shown by the red dashed line, Federal Reserve MBS purchases were greatest during QE1. Note that during QE2 (indicated by blue shading), MBS purchases were allowed to runoff and were replaced with longer-term Treasury securities. Thus, there are no MBS purchases during this period. To estimate the net result of these different channels, we use the Federal Reserve's share of MBS outstanding divided by total agency MBS outstanding that is backed by 30-year fixed rate mortgages (dashed red line, bottom panel, figure 4). We create a similar market share measure for the Federal Reserve's share of Treasury bonds and notes outstanding (solid blue line, bottom panel, figure 4). The cumulative stock of Treasury bond holdings (the solid blue line) and Federal Reserve agency MBS holdings (the red dashed line) eventually amounted to about one-fifth of all outstanding Treasury securities and fixed-rate agency MBS.21 The Federal Reserve's market share for each these securities declined throughout 2012. Only with the ongoing purchases under QE3, did the Federal Reserve's MBS share rise to its highest level in the sample period--23.8 percent on June 30, 2013. Despite a modest uptick in the Federal Reserve's market share of Treasury bonds in 2013, as of June 30, 2013, its market share of Treasury securities remained smaller than it was in 2011:Q4.
Our market share measures capture the idea that the Federal Reserve is withdrawing securities from the private sector. Suppose there are three liquid assets in the economy: bank deposits, Treasuries and government-backed MBS. All of these liquid assets are likely to maintain their value during a financial crisis or economic downturn. However, all have low risk-adjusted returns because of their substantial liquidity premiums. An investor who holds a "liquidity portfolio" might diversify across the three types of liquid assets because they each have different properties: the value of bank deposits depends the health of the bank and the government insurer; the value of Treasuries depends on the health of the government; and the value of MBS depends on the health of the government but is also backed by real estate collateral. Both Treasury and MBS securities, of course, can be subject to substantial interest rate risk, and MBS have prepayment risks. Supposedly, this investor has also invested in the significant fixed costs that are associated with managing the prepayment risks associated with MBS.
Denote the economy-wide aggregated private-investor liquidity portfolio as:
When the Federal Reserve purchases an MBS security (we assume that only MBS is purchased), bank deposits (BD) increase while mortgage-backed securities (MBS) decrease. Thus, the change in the private sector liquidity portfolio is:
The Federal Reserve purchase distorts the desired holdings of private-sector investors. It forces MBS prices to rise until some investors are willing to hold more deposits and fewer MBS than they would have held had the Federal Reserve not intervened.
We postulate that investors desire a certain amount of liquidity (perhaps as a proportion of economic activity or aggregated risky investments), and that they desire certain proportions of liquidity to be held in each of the three liquid assets. Deviations from equilibrium prices are driven by both temporary increases and decreases in flows of the securities, as well as persistent distortions from the quantities desired by investors.
When the Federal Reserve purchases either an MBS or a Treasury, it replaces the security with a bank deposit, which is an asset that investors do not want once their transaction demand is satisfied. The direct effect of Federal Reserve purchases is that yields fall and prices rise on MBS and Treasuries. An additional effect is that investors have a bank deposit they do not want, and thus a persistent, additional demand for MBS and/or Treasury securities is created.
We can measure the extent of this distortion from equilibrium holdings created by the Federal Reserve's LSAPs. Both the change in bank deposits and the change in MBS are equal to the purchase by the Federal Reserve (denoted as P). The sum of Federal Reserve purchases of MBS is by definition the Federal Reserve's holding of MBS in its portfolio (denoted by H). Thus, we measure the extent of distortion (D) in desired private-sector liquidity portfolios (LP) as the share of liquidity assets that are not invested in their desired security, or:
The distortions can be measured in particular markets (e.g,. MBS, Treasuries, or Deposits) or:
is the share of MBS held by the Federal Reserve.
As the distortion of private-sector liquidity portfolios increases, the price of MBS securities increases. We interpret this higher price as an additional liquidity premium for MBS, as investors seek to rebalance their liquidity portfolios. The higher MBS prices are reflected in lower MBS yields. Thus, the changes in the liquidity premium embedded in MBS are related to the change in the distortion of portfolios in the MBS market or:
![\displaystyle \frac{{\delta D}_{MBS}}{\delta t}=\left[\frac{P_t-s_{MBS}*\frac{\delta {MBS}_t}{\delta t}}{{MBS}_t}\right].](img9.gif)
are Federal Reserve purchases (which is the sum of both new MBS purchases and reinvestments, minus MBS prepayments).
Market participants, of course, expect the Federal Reserve's MBS purchases to alter its MBS holdings. The expected yield on MBS is the sum of the swap rate, the compensation for risks (e.g. interest rate risk, prepayment risk, and the other risks described above), and the liquidity premium. More generally, we can write this expectation as:
![\displaystyle E\left(y_{MBS}\right)=r_{swap}E\left[future\ rates\right]+LPrem\left[D,\frac{dD}{dt}\right]+Risks\left[E[future\ rates],\ D\right].](img11.gif)
As described above, we assume the swap rate, which is a generic benchmark rate for the MBS market, is only a function of expected future rates, where the liquidity premium (LPrem) is only a function of the Federal Reserve's holdings (or purchases). The compensation for the risks of holding MBS is a function of both expectation of future rates and the liquidity premium because of the influence of Federal Reserve purchase on other interest rates, particularly Treasury rates.
5. Estimating the MBS Yield Model
We estimate the effects of the Federal Reserve's LSAPs on the current-coupon MBS yield constructed using the techniques described earlier. The coefficients and t-statistics for the MBS yield regression, which is estimated using weekly data over July 7, 2000 to June 28, 2013, inclusive, are
presented in table 3.23 The MBS yield
regression includes both the swap-based measures that embed market expectations of future rates (rows 2 and 3) and the market shares of Federal Reserve securities holdings (rows 8 and 9). Consistent with a liquidity or portfolio rebalancing channel, an increase in either the Federal Reserve market
share of MBS (row 8), or its market share of US Treasury securities (row 9), significantly lowered MBS yields during the sample period. Using these estimates, the level of the MBS yields is about 55 basis points lower when the Federal Reserve holds 24 percent of the available MBS securities
compared with when it holds nothing at all (on June 30, 2013, this was equivalent to about a $1.21 trillion portfolio). The same estimate suggests that a $50 billion increase in the Federal Reserve's MBS holdings would result in an increase for the mean market share of Federal Reserve MBS holdings
(from 23.8 percent) to 24.8 percent and a decrease MBS yields by around 2 basis points. Finally, the regression suggests that MBS yields were, on average, lower during QE1 (row 4) and QE3 (row 6), when additional MBS purchases were taking place since dummy variables that equaled one throughout each
of these respective quantitative easing programs have coefficients that are significantly negative at the one percent level. In contrast, yields were on average higher during Operation Twist (row 7), when MBS purchases were made only to offset the run-off from the MBS portfolio.
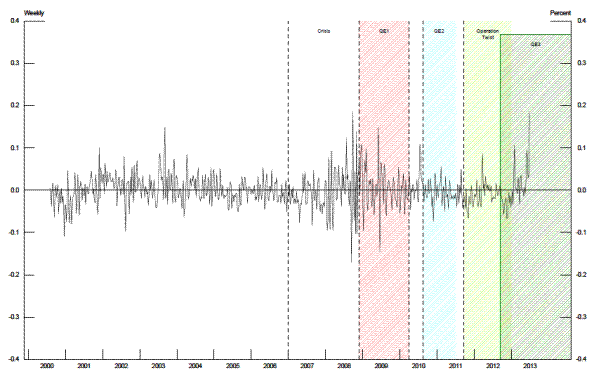
An increase in Federal Reserve holdings of Treasury securities also lowered the MBS yield (row 9, table 3). Using this estimate, the level of the MBS yield is about 76 basis points lower if the Federal Reserve holds 22 percent of the available Treasury securities (on June 30, 2013, this was equivalent to about a $1.93 trillion portfolio). At the mean market share for the Federal Reserve's Treasury security holdings, a $50 billion purchase of Treasury securities would lower the MBS yield by about 2 basis points. The residuals of the MBS yield equation are given in figure 5. There remain substantial periods when the residuals follow a trend or show a distinct jump. Regardless, the significance of the Federal Reserve's shares suggests that MBS yields are codetermined more than just from market expectations of future interest rates.
Robustness Tests
We present three variations of our MBS yield levels regression to get a sense of the robustness of our estimated long-run, co-determined equilibrium relationship. One concern is using a similar bond pricing model for both imputing the missing current coupon values and for estimating the effect of market expectations on MBS yields. Rather than use MBS yields directly, we can also estimate the model using MBS prices. Data for the price of MBS security that is 100 basis points above the current coupon, which we will refer to as the 100+ MBS price, always exists throughout our estimation period. With a fixed mark-up over the current coupon we hope to control for shifting prepayment incentives among households.
The regression results when using the 100+ MBS price as the dependent variable are similar to our MBS yield regression (table 4, column 1). The coefficient on the long swap rate is negative, so as the long swap rate increases, the price of MBS decreases (and the MBS yield increases). The coefficient on the slope of the yield curve is also negative; hence, as the yield curve steepens (our yield curve variable is the long swap rate minus the short swap rate), the price of MBS increases (and the MBS yield decreases). This coefficient is not consistent with our earlier model, but this inconsistency is perhaps not surprising because the changes in the yield curve (and thus the likelihood of prepayment) would be expected to be different for an MBS that is 100 basis points above the current coupon. Importantly, as the Federal Reserve increases its market share of MBS and Treasury securities, the price of MBS rises (and the MBS yield falls). We view this result as supporting evidence of an independent portfolio rebalancing or liquidity channel on MBS yields.
Another concern is that there may be an unspecified codetermining variable for the MBS yields and the swap rates. One possibility might be the European financial crisis, which is ongoing during the time of the LSAPs. We add to our regression a measure of continued market turbulence after 2008: the CDS spreads for sovereign debt of European countries (Italy, Ireland, Spain and Portugal). As shown in column 2 of table 4, European CDS spreads have a significant and positive effect on MBS current coupon yields over this period. This market turbulence variable may represent a risk that is fully accounted for by swap yields, although it is hard to articulate the nature of this risk. Regardless, the estimates of a portfolio rebalancing/ liquidity affect from Federal Reserve LSAPs (shown in rows 8 and 9) remains very strong.
Another possibility for an unspecified co-determining variable is the presence of an underlying rule used by the Federal Reserve for LSAPs that is not reflected in market expectations. We are hard pressed to describe such a rule, but we test the idea by using the following construct. The FOMC is concerned about inflation and unemployment and, at the zero lower-bound of the federal funds rate it uses asset purchases to put downward pressure on longer-term interest rates when the data indicates that the economy is performing at a "sub-par" level. By pushing down interest rates, it hopes to generate more employment, while maintaining inflation slightly above zero.
For the pre-crisis period, we estimate a simple model of the 10-year Treasury rate as a function of a lagged four-week moving average of inflation expectations (as measure by the inflation compensation embedded in the ten-year Treasury rate) and of the lagged twelve-week moving average of the unemployment rate. We emphasize the lagged structure of the right-hand side variables because we are trying to minimize the endogenous effects of Federal Reserve actions on our measure. We interpret this model as the prevailing relationship (the "normal" relationship) between long-term interest rate, inflation and unemployment before the persistent financial and economic stress during and after 2008.
The out-of-sample residual from this ten-year Treasury regression is used as a summary measure of how far the economy and the financial system are away from the pre-crisis "normal." When the actual ten-year Treasury rate is lower than the pre-crisis "normal" rate, the residual indicates the distance that ten-year yields are at levels that are lower and thereby inconsistent with fuller employment and/or higher expected inflation based on pre-crisis economic performance. This residual, denoted as the Treasury Gap, has a significant negative effect on MBS yields (table 4, column 3, row11) and is the expected sign. Again, however, its inclusion does not alter the conclusion that portfolio rebalancing/liquidity effects are an important determinant of MBS yields (rows 8 and 9).
6. A Dynamic Model of MBS Yields
We consider the MBS yield regression estimated above a codetermined relationship between the MBS yield and its risk components. To create a dynamic model of MBS yields, we estimate the first difference of this equation and use the residual of the codetermined relationship as a measure of market disequilibrium. The results from this cointegrated model are presented in table 5.
A larger change in the swap yield generates a larger change in the MBS yield, and a move toward a more steeply sloped swap yield curve increases the MBS yield (rows 2 and 3), but only the former effect is statistically significant. Any change in market expectations about future interest rates would likely be reflected through a change in swap rates, even during times when the MBS current coupon is not available in the market.
Purchases by the Federal Reserve of MBS that move the Federal Reserve's market share higher result in lower MBS yields (row 11), but the effect is not statistically significant. Similarly, purchases of Treasury securities (row 12) are also not statistically significant. Thus, our modeling suggests that it is Federal Reserve holdings, not purchases, which result in lower MBS yields. This result is consistent with the portfolio rebalancing view that investors must expect a persistent shortage of MBS securities to move MBS yields down, but they are not as influenced by day-to-day change in the Federal Reserve's MBS holdings.
Most importantly, when actual MBS yields exceed market equilibrium (row 12), MBS yields fall, suggesting that our equilibrium MBS equation does reflect a cointegrated relationship. Interestingly, none of the announcement effects for the beginning or ending of LSAP programs seem to change MBS yields beyond the change in market expectations, except for the beginning of QE1 and QE3. Perhaps only these announcements surprised market participants.
The residuals of this differenced equation are stationary (figure 6). During the financial crisis, the amplitude of the residuals rises, but they remain symmetrical and almost all of the trending of the residuals observed in the regression on the level of the MBS is absent.
7. The Tight Link between Mortgage Rates and MBS Yields
As suggested in figure 3, both agency MBS yields and fixed-rate mortgage rates were pushed down by QE1 and have subsequently remained relatively low compared to levels that were observed prior to the financial crisis.24 Ultimately, the goal of the Federal Reserve (in this context) is to lower mortgage rates. We argue that mortgage rates (r
) can be modeled as a mark-up over the MBS yield (r
). When banks and other providers originate a mortgage,
they compare the marginal return from holding a mortgage to the marginal return that arises from holding an MBS. Note that the MBS yield already reflects the financing and hedging costs incurred by an investor when holding a mortgage asset. Similarly, the MBS yield already embeds the capital cost
and the return on equity for bearing the interest rate risk associated with the mortgage.
We estimate a simple mark-up equation as our model of the mortgage rate. We posit that the bulk of the mark-up over MBS yields reflects an originator's credit risks and the capacity costs associated with refinancing mortgages. For example, higher FICO scores for homebuyers are expected to be associated with lower credit risks (as are many other such measures of credit risk). Our measure of credit risk is the FICO score of mortgage borrowers at the 50th percentile of the mortgage borrowers' FICO distribution; this measure is denoted by FICO. We expect that as credit risk increases (that is, the FICO scores decrease), the observed mortgage rates would increase.
The capacity of the mortgage system to process mortgage applications during a refinancing boom also plays a key role in mortgage rates. When refinancings are relatively high, banks and other mortgage originators raise their relative mortgage rates, as one method for managing their application "pipelines." Here, we measure the mortgage system's capacity utilization as a lagged, 4-week moving average of the ratio of mortgage refinancings (as measured by the MBS refinancing index) to the number of employees employed in the mortgage industry; this measure is denoted by Capacity. Therefore, we expect a positive relationship between capacity utilization and mortgage rates.
Other factors that influence credit risks, such as inflation and home prices, are only captured in this model to the extent that they are components of the factors listed above. Of course, there are strong correlations with these two factors and other macroeconomic variables, but we keep the model parsimonious so the regression results can be more clearly interpreted.
Finally, the intercept in the mortgage rate regression would represent any persistence in the spread between the mortgage rate and MBS yield, including servicing costs, guarantee fees, or excess servicing.
More specifically, our mortgage rate pricing model regression equation can be written as:
Our coefficient estimates for the mortgage rate regression are provided in table 6, where we present the regression for the entire sample period as well as for a pre-crisis, crisis, and post-crisis periods. The coefficients generally have the expected sign and most are statistically significant at the 99 percent confidence interval. Also note that the coefficient on the MBS yield is significantly less than one except in the post-crisis period, suggesting that for much of the sample a change in the MBS yields is never fully incorporated into the mortgage rate. Using the full-sample regression, a decline of 100 basis points in the MBS yield would translate to a decline of 91 basis points in the mortgage rate over a long period, all other things equal. Finally, as shown in figure 7, the residuals of the full-sample regression are stationary. Strikingly, there are large declines in the residuals from mortgage rate regression near announcements for LSAPs, suggesting that it takes some time for mortgage rates to adjust when MBS yields change.
As with the MBS yield regression, we examine a differenced mortgage rate regression (table 7). Because of the lagged adjustments in the residual of the mortgage rate regression, we considered this adjustment process, using the specification described in table 7. After some investigation, we settled on three lags of the change in MBS yields as being important in the determination of the mortgage rate 25 As shown in table 7, the first two lags are positive, and significant. In addition, when MBS yields rise, mortgage rates rise (rows 1-3). The change in FICO score is insignificant, whereas the change in capacity utilization (lagged by one week to reduce simultaneity with the mortgage rate) is significant and positive.
As shown in table 7, when the actual value of the mortgage rate exceeds the market equilibrium mortgage rate, the mortgage rate declines (row 6). Thus, the mortgage rate regression in table 6 represents a codetermined market equilibrium relationship, which makes sense because the originators of mortgages compare the return from holding a mortgage to the return from holding an MBS. The residuals of this differenced mortgage rate model, as shown in figure 8, are stationary.
8. Simulating the Effects of Federal Reserve Purchases
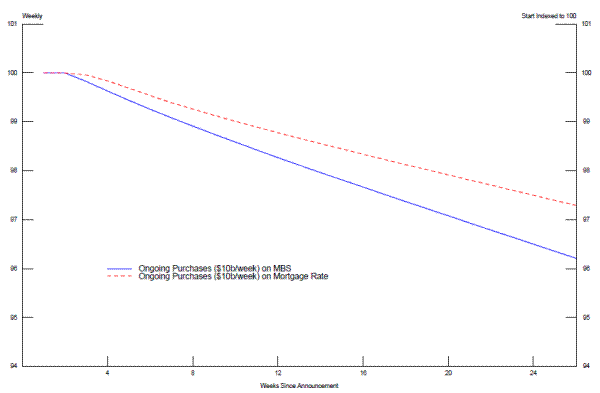
The MBS and mortgage rate market equilibrium equations, combined with the two change equations, form a four equation system that can be used to simulate the effects of a Federal Reserve MBS purchase on mortgages. To determine the market equilibrium, we use June 2013 values. With weekly purchases of $10 billion of MBS the ongoing purchases and the rising Federal Reserve MBS market share both work together to push MBS yields down 0.57 basis points per week (figure 9). Note that the figure shows the rates normalized to 100 and a 4.22.7 percent decline in the mortgage rate because of Federal Reserve purchases. The actual mortgage rate drops from 3.92 percentage points to 3.81 percentage points for a 11 basis point drop; since 3.81 is 97.3% of 3.92, the change is 2.78 percent.
We can also compare the results from our four equation system to the actual outcomes for the MBS yield and the mortgage rate. As shown in figure 10, we use the estimated model to calculate the "in-sample" simulated MBS yields and mortgage rates over the period of estimation. The "in-sample fit is very tight for both mortgage rates and MBS yields.
9. Conclusion
We provide an empirical analysis of the effects of the Federal Reserve's large-scale asset purchases (LSAPs) on MBS yields and on U.S. mortgage rates. Assessing the effects of these Federal Reserve open market operations is difficult because this type of monetary policy accommodation operates through many transmission channels, including a signaling channel that may alter expectations of market participants, as well as liquidity and portfolio rebalancing channels that may result from scarcities of long-term assets and the withdrawal of duration or of convexity from asset markets.
The decline in the MBS yields after the initial announcement of a large-scale asset program may generally reflect a shift of market expectations, but may not fully capture the actual effects of the large-scale security purchases as portfolio rebalancing actually commences. Our Federal Reserve market share variables were significant determinants of MBS yields, even after accounting for changes in expectations about future rates by market participants.
Our estimates also suggest that the Federal Reserve must hold a substantial market share of agency MBS or of Treasury securities to significantly lower MBS yields and in turn significantly lower mortgage rates. Our findings indicate that the liquidity or portfolio rebalancing effects of LSAPs, as well as markets' expectations of future interest rates, are important considerations for monetary policy. Finally, these findings suggest that such LSAPs achieved the FOMC's goal to "put downward pressure on longer-term interest rates, support mortgage markets, and help make broader financial conditions more accommodative."
References
Acharya, Viral V. and Lasse Heje Pedersen, 2005, "Asset Pricing with Liquidity Risk," Journal of Financial Economics, Vol. 77, pp.375-410.
Bauer, Michael D. and Glenn Rudebusch, 2012, "The Signaling Channel for Federal Reserve Bond Purchases," Federal Reserve Bank of San Francisco Working Paper Series, Working Paper 2011-21, August.
Bernanke, Ben S., 2002, "Deflation: Making Sure "It" Doesn't Happen Here," Remarks before the National Economists Club (Washington, DC), November 21.
Bernanke, Ben S., 2009, "The Crisis and the Policy Response," Remarks at the Stamp Lecture, London School of Economics (London, England), January 13 (available at: http:/www.federalreserve.go/newsevents/speech/bernanke20090113a.htm).
Bernanke, Ben S. and Vincent R. Reinhart, 2004, "Conducting Monetary Policy at Very Low Short-term Interest Rates," American Economic Review, vol. 94, no. 2, pp. 85-90, May.
Bernanke, Ben S, 2012, "Challenges in Housing and Mortgage Markets," Remarks at the Operation HOPE Global Financial Dignity Summit (Atlanta, Georgia), November 15.
Boudoukh, Jacob, Matthew Richardson, Richard Stanton, Robert Whitelaw, 1997, "Pricing Mortgage-Backed Securities in a Multifactor Interest Rate Environment: A Multivariate Density Estimation Approach," Review of Financial Studies, Vol. 10, No. 2, pp. 405-446.
Carpenter, Seth, Selva Demiralp, and Jens Eisenschmidt, 2013, "The Effectiveness of the Non-Standard Policy Measures during the Financial Crises: The Experiences of the Federal Reserve and the European Central Bank," Finance and Economics Discussion Series Working Paper, no. 2013-34, Board of Governors of the Federal Reserve System.
Clouse, James, Dale Henderson, Athanasios Orphanides, David Small, and Peter Tinsley, 2000, "Monetary Policy when the Nominal Short-term Interest Rate is Zero," Finance and Economics Discussion Series Working Paper, no. 2000-51, Board of Governors of the Federal Reserve System.
D'Amico, Stefania, William English, David Lopez-Salido, and Edward Nelson, 2012, "The Federal Reserve's Large-Scale Asset Purchase Programs: Rationale and Effects," Finance and Economics Discussion Series (FEDS) Working Paper, no. 2012-85, Board of Governors of the Federal Reserve System.
D'Amico, Stefania and Thomas B. King, 2010, "Flow and Stock Effects of Large-Scale Treasury Purchases," Finance and Economics Discussion Series (FEDS) Working Paper, no. 2010-52, Board of Governors of the Federal Reserve System.
Eggertson, Gauti B. and Michael Woodford, 2003, "The Zero Bound on Interest Rates and Optimal Monetary Policy," Brookings Papers on Economic Activity, Vol. 34 (1), pp. 139-211.
Fawley, Brett W. and Christopher J. Neely, 2013, "Four Stories of Quantitative Easing," Federal Reserve Bank of St. Louis Review, January/February, pp. 51-88.
Forester, Andrew and Guangye Cao (2013), "Expectations of Large-Scale Asset Purchases"Federal Reserve Bank of Kansas City Economic Review, Second Quarter 2013, pp. 5-29
Fuster Andreas and Paul S. Willen, 2010, "$1.25 Trillion is Still Real Money: Some Facts About the Effects of the Federal Reserve's Mortgage Market Investments," Federal Reserve Bank of Boston, Public Policy Discussion Papers, No. 10-4, November 18.
Gagnon, Joseph, Matthew Raskin, Julie Remache and Brian Sack, 2010, "Large Scale Asset Purchases by the Federal Reserve: Did They Work?," Federal Reserve Bank of New York Staff Reports, no. 441, March.
Hancock, Diana and Wayne Passmore, 2011, "Did the Federal Reserve's MBS Purchase Program Lower Mortgage Rates?" Journal of Monetary Economics, vol. 58, no. 5, pp. 498-514.
Hancock, Diana and Wayne Passmore., 2012, "The Federal Reserve's Portfolio and its Effects on Mortgage Markets, Finance and Economics Discussion Series (FEDS) Working Paper, no. 2012-22, Board of Governors of the Federal Reserve System.
Hoskins, Susan, Katie Jones, and Eric Weiss, 2013, "An Overview of the Housing Finance System in the United States," CRS Report for Congress 7-5700, Congressional Research Service, March 13.
Heuson, Andrea, S.W. Passmore, and Roger Sparks, 2001, "Credit Scoring and Mortgage Securitization: Implications for Mortgage Rates and Credit Availability," Journal of Real Estate Finance and Economics, vol. 23, November, pp. 337-363.
King, Mervyn, 1999, "Challenges for Monetary Policy: New and Old," in Federal Reserve Bank of Kansas City, New Challenges for Monetary Policy (Kansas City, MO) Federal Reserve Bank of Kansas City, pp. 11-57.
Kocherlakota, Narayana, 2013, 2012 Annual Report, Federal Reserve Bank or Minneapolis,: Federal Reserve Bank of Minneapolis, April.
Kiyotaki, Nobuhiro and John Moore, 2012, "Liquidity, Business Cycles, and Monetary Policy," NBER working paper 17934, National Bureau of Economic Research, March.
Krishnamurthy, Arvind and Annette Vissing-Jorgensen, 2011, "The Effects of Quantitative Easing on Interest Rates," Northwestern University Kellogg School of Management, Working Paper, February 10.
Krishnamurthy, Arvind and Annette Vissing-Jorgensen, 2013, "The Ins and Outs of LSAPs," paper delivered at "Global Dimensions of Unconventional Monetary Policy," a symposium sponsored by the Federal Reserve Bank of Kansas City, held in Jackson Hole, Wyo., August.
Lehnert, Andreas, Passmore S. Wayne and Shane Sherlund, 2008, "Mortgage Rates, and Secondary Market Activities," Journal of Real Estate Finance and Economics, vol. 36, no. 3, pp. 343-63.
Maddaloni, Angela and Jose-Luis Peydro, 2011, "Bank Risk-taking, Securitization, Supervision, and Low Interest Rates: Evidence from Euro-area and U.S. Lending Standards, Review of Financial Studies, vol. 24, no. 6, pp. 2121-2165.
Mishkin, Frederick S., 1996, "The Channels of Monetary Transmission: Lessons for Monetary Policy," NBER Working Paper Series Working Paper, no. 5464, February.
Passmore, S. Wayne, Shane Sherlund, and Gillian Burgess, 2005, "The Effect of Housing Government-Sponsored Enterprises on Mortgage Rates," Real Estate Economics, vol. 33, pp. 427-463.
Stroebel, Johannes and John Taylor, 2010, "Estimated Impact of the Fed's Mortgage-Backed Securities," Stanford University, mimeo, October.
Tobin, James, 1958, "Liquidity Preference as Behavior Towards Risk," Review of Economic Studies, 25, pp. 124-131.
Wallace, Neil, 1981, "A Modigliani-Miller Theorem for Open-Market Operations," American Economic Review, vol. 73, pp. 267-74.
Woodward, Michael, 2012, "Methods of Policy Accommodation at the Interest-Rate Lower Bound," Revised draft of paper presented at the Federal Reserve Bank of Kanas City Symposium on "The Changing Policy Landscape.", Jackson Hole, Wyoming, August 31.
Wright, Jonathan H., 2011, "What does Monetary Policy do to Long-Term Interest Rates at the Zero Lower Bound?" Johns Hopkins University Economics Department Working Paper, June 13.
Table 1: Annoncement Descriptions
| Order:Date | Announcement | Program | Type |
|---|---|---|---|
| 1:11/25/2008 | The Federal Reserve will purchase "up to $100 billion in GSE direct obligations" and "up to $500 billion in MBS." | QE1 | Increase(Increased Purchases) |
| 2:12/01/2008 | In a speech Chairman Bernanke states that the Federal Reserve "could purchase longer-term Treasury or agency securities...in substantial quantities." | QE1 | Com (Communication) |
| 3:12/16/2008 | The FOMC "anticipates...exceptionally low levels of the federal funds rate for some time." It also "stands ready to expand its purchases of agency debt and mortgage-backed securities...[and] is also evaluating the potential benefits of purchasing longer-term Treasury securities." | QE1 | Com |
| 4:01/28/2009 | The FOMC "is prepared to purchase longer-term Treasury securities." | QE1 | Com |
| 5:03/18/2009 | The FOMC "anticipates...exceptionally low levels of the federal funds rate for an extended period." It will also purchase "up to an additional $750 billion of agency mortgage-backed securities" "up to $100 billion" in agency debt and "up to $300 billion of longer-term Treasury securities over the next six months." | QE1 | Increase |
| 6:08/12/2009 | The FOMC "decided to gradually slow the pace" of Treasury purchases ("up to" language with reference to Treasury purchases is also removed). | QE1 | Decrease (Decreased Purchases) |
| 7:09/23/2009 | The FOMC "will gradually slow the pace of" of agency MBS purchases ("up to" language with reference to agency MBS purchases is also removed). | QE1 | Decrease |
| 8:11/04/2009 | The FOMC "will purchase...about $175 billion of agency debt" ("up to" language with reference to agency debt is also removed). | QE1 | Increase |
| 9:08/10/2010 | The FOMC will reinvest "principal payments from agency debt and agency mortgage-backed securities in longer-term Treasury securities." | QE2 | Increase |
| 10:08/27/2010 | In a speech Chairman Bernanke announces that "additional purchases of longer-term securities...would be effective in further easing financial conditions." | QE2 | Com |
| 11:09/21/2010 | The FOMC "is prepared to provide additional accommodation if needed." | QE2 | Com |
| 12:11/03/2010 | The FOMC "intends to purchase a further $600 billion of longerterm Treasury securities by the end of the second quarter of 2011 at a pace of about $75 billion per month." | QE2 | Increase |
| 13:09/21/2011 | The FOMC "intends to purchase by the end of June 2012 $400 billion of Treasury securities with remaining maturities of 6 years to 30 years and to sell an equal amount of Treasury securities with remaining maturities of 3 years or less." | OT | Increase |
| 14:06/20/2012 | The FOMC "decided to continue through the end of the year its program to extend the average maturity of its holdings of securities." An accompanying statement by the Federal Reserve Bank of New York clarifies that this continuation will "result in the purchase as well as the sale and redemption of about $267 billion in Treasury securities by the end of 2012." | OT | Increase |
| 15:09/13/2012 | The FOMC will increase the Committee's holdings of longer-term securities by about $85 billion each month through the end of the year" including "purchasing additional agency mortgage-backed securities at a pace of $40 billion per month." | QE3 | Increase |
| 16:12/12/2012 | The FOMC will continue purchasing at least as long as the unemployment rate remains above 6-1/2 percent inflation between one and two years ahead is projected to be no more than a half percentage point above the Committee's 2 percent longer-run goal and longer-term inflation expectations continue to be well anchored." | QE3 | Com |
Table 2: The Relationship Between MBS Current Coupon Yield and Prices
| Daily Data: Variable | Entire Period: Oct 16 2002 - Jun 25 2013 (1) | Pre-Crisis: Oct 16 2002 - Dec 29 2006 (2) | Crisis: Jan 2 2007 - May 28 2009 (3) | Post-Crisis: Jun 1 2009 - Jun 25 2013 (4) |
| (1) Intercept | 26.57707*** | 25.40187*** | 26.13503*** | 34.55308*** |
| (1) Intercept: std. errors | 0.102867 | 0.117009 | 0.231515 | 0.705106 |
| (2) Price of 5% Coupon MBS | -0.215894*** | -0.203827*** | -0.211557*** | -0.291607*** |
| (2) Price of 5% Coupon MBS: std. errors | 0.001037 | 0.001198 | 0.002396 | 0.006712 |
| Adjusted R-Squared | 0.961606 | 0.971454 | 0.944281 | 0.813692 |
| Number of Observations | 1732 | 851 | 461 | 420 |
Table 3: MBS Yields and Portfolio Rebalancing
| Variable | (1) Parameter Estimate | (2) Standard Error | (3) t Value |
| (1) Intercept | 2.53729*** | 0.057269 | 44.30463 |
| (2) Long Swap Rate | 0.816328*** | 0.007847 | 104.0326 |
| (3) Slope of Swap Yield Curve | 0.144894*** | 0.008359 | 17.33405 |
| (4) QE1 Indicator | -0.227952*** | 0.024783 | -9.197943 |
| (5) QE2 Indicator | 0.012911 | 0.029919 | 0.431528 |
| (6) QE3 Indicator | -0.162223*** | 0.028941 | -5.605231 |
| (7) Operation Twist Indicator | 0.128152*** | 0.02683 | 4.776397 |
| (8) Federal Reserve Market Share of MBS | -2.277377*** | 0.13107 | -17.37525 |
| (9) Federal Reserve Market Share of Treasury | -3.188897*** | 0.188383 | -16.92774 |
Adjusted R-Squared: 0.986521
Weekly Data from July 7 2000 to June 28 2013 (n = 678)
Source: Swaps -- Reuters; Announcement Dates -- Woodford (2012); Market Shares -- Federal Reserve, Treasury Dept, and eMBS Inc Asterisks *** represent significance at the 99% confidence level, ** at the 95% level, and * at the 90% percent level
Table 4: Variations of the MBS Regression
| Variable | (1) MBS Price | (2) Current Coupon | (3) Current Coupon |
| (1) Intercept | 4.635672*** | 2.488324*** | 2.235089*** |
| 0.855584*** | 0.839091*** | ||
| (3) Slope of Swap Yield Curve | 0.003522*** | 0.121833*** | 0.182563*** |
| (4) QE1 Indicator | -0.005816*** | -0.155302*** | -0.17876*** |
| (5) QE2 Indicator | 0.001487 | -0.042447 | 0.018457 |
| (6) QE3 Indicator | 0.004711*** | 0.012312 | -0.292352*** |
| (7) Operation Twist Indicator | 0.005092*** | -0.114988*** | 0.048902* |
| (8) Federal Reserve Market Share of MBS | 0.066485*** | -3.102625*** | -1.569363*** |
| (9) Federal Reserve Market Share of Treasury | 0.039755*** | -3.966629*** | -2.698299*** |
| (10) European CDS | NA | 0.089643*** | NA |
| (11) Treasury Gap | NA | NA | -0.101517*** |
| Adjusted R-Squared | 0.828416 | 0.987684 | 0.985589 |
Table 5: Differenced Regression for Current Coupon Yield
| Variable | (1) Parameter Estimate | (2) Standard Error | (3) t Value |
| (1) Change in Long Swap Rate | 0.778175*** | 0.027559 | 28.23693 |
| (2) Change in Swap Yield Slope | -0.049088 | 0.045054 | -1.089543 |
| (3) QE1 Start Dummy | -0.359527*** | 0.077677 | -4.62846 |
| (4) QE1 End Dummy | 0.022185 | 0.076531 | 0.289885 |
| (5) QE2 Start Dummy | -0.069487 | 0.076753 | -0.905326 |
| (6) QE2 End Dummy | -0.001441 | 0.076951 | -0.018732 |
| (7) QE3 Start Dummy | -0.150034* | 0.076568 | -1.959476 |
| (8) Operation Twist Start Dummy | -0.001863 | 0.077136 | -0.024152 |
| (9) Operation Twist End Dummy | -0.04967 | 0.076501 | -0.649268 |
| (10) Change in Fed MBS Shares | -2.781383 | 2.108055 | -1.319407 |
| (11) Change in Fed Treasury Shares | 3.861379 | 2.950033 | 1.308928 |
| (12) MBS Disequilibrium | -0.141949*** | 0.021277 | -6.671612 |
Table 6: Mortgage Rate Regression
| Daily Data: Variable | (1) Entire Period: Jul 14 2000 - Jun 28 2013 | (2) Pre-Crisis: Jul 14 2000 - Dec 29 2006 | (3) Crisis: Dec 29 2006 - May 29 2009 | (4) Post-Crisis: Jun 1 2009 - Jun 25 2013 |
| (1) Intercept | 2.017483*** | 10.40445*** | 0.188465 | -6.279775** |
| (1) Intercept: std. errors | 0.614523 | 2.278015 | 0.993674 | 2.74666 |
| (2) MBS Yield (Weekly Average) | 0.907456*** | 0.87332*** | 0.732621*** | 0.926323*** |
| (2) MBS Yield (Weekly Average): std. errors | 0.011592 | 0.011339 | 0.037205 | 0.022243 |
| FICO Score | -1.443349* | -12.64381*** | 2.562683** | 9.422248*** |
| FICO Score: std. errors | 0.769967 | 3.099339 | 1.18101 | 3.592438 |
| Capacity | 1.294622*** | 1.141098*** | -1.199764*** | 0.759748* |
| Capacity: std. errors | 0.202211 | 0.192958 | 0.42387 | 0.450476 |
| Adjusted R-Squared | 0.989424 | 0.974275 | 0.961533 | 0.977382 |
| Number of Observations | 677 | 338 | 127 | 214 |
Table 7: Differenced Mortgage Rate Regression
| Variable | (1) Parameter Estimate | (2) Standard Error | (3) t Value |
| (1) Change in MBS Yield | 0.320777*** | 0.014826 | 21.63553 |
| (2) Change in MBS Yield (1-Week Lag) | 0.350932*** | 0.021305 | 16.47174 |
| (3) Change in MBS Yield (2-Week Lag) | 0.019495 | 0.016269 | 1.198267 |
| (4) Change in FICO Score | 0.517887 | 5.381516 | 0.096234 |
| (5) Change in Capacity (1-Week Lag) | 0.67997*** | 0.259265 | 2.622687 |
| (6) Mortgage Rate Disequilibrium | -0.223024*** | 0.024853 | -8.973647 |
