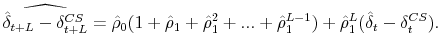Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2014-16 Screen Reader version ^♣

Using Data on Seller Behavior to Forecast Short-run House Price Changes*

Elliot Anenberg

Federal Reserve Board Federal Reserve Board

Steven Laufer

Federal Reserve Board Federal Reserve Board

January 29, 2014

Abstract:

We construct a new "list-price index" that accurately reveals trends in house prices several months before existing sales price indices like Case-Shiller. Our index is based on the repeat-sales approach but for recent months uses listings data, which are available essentially in real time, instead of transactions data, which become available with significant lags. Our index methodology is motivated by a simple model of the home-selling problem that shows how listings variables such as the list price and marketing time help predict the final sales price. In a sample of three large MSAs over the years 2008-2012, our index (i) accurately forecasts the Case-Shiller index several months in advance, (ii) outperforms forecasting models that do not use listings data, and (iii) outperforms the market's expectation as inferred from prices on Case-Shiller future contracts.

1 Introduction

Changes in house prices have important consequences for the real economy as they affect both households' wealth and their ability to borrow. Unlike the prices of other assets, such as stocks and bonds, which are available almost instantaneously, house price indices are reported with lags of several months. This delay is a significant information friction with measurable effects on important economic variables. We show, for example, that a release of the Case-Shiller house price index has an immediate effect on the stock prices of home building companies, despite the fact that this release contains information about housing market conditions from several months earlier.¹ If the stock market is not able to overcome the reporting delays associated with house prices, it seems likely that individual homeowners, policy makers, lenders, etc. are as well, suggesting that this information friction may have much broader effects on financial markets and real economic activity.

This delay in house price reporting emerges because once a buyer and seller have found each other and agreed on a sale price, there is little incentive for either party to publicize the negotiated price. Even once the sale price is disclosed (by law) at the closing, which is typically a couple months following the sale agreement, there is another delay of a couple additional months before the public record becomes available.² In contrast, before a contract is signed, the seller has a strong incentive to broadcast the current offering price, both as an advertisement that the house is for sale as well as a signal to potential buyers of the likely price at which the house can be purchased.³ Thus, information on listing prices is disseminated on internet platforms such as Multiple Listing Services (MLS) in essentially real time. On such forums, when a sale agreement is reached, the listing is removed immediately. By using information on the list prices of homes that are delisted, we can potentially learn about the level of sale prices well in advance of what is currently possible.

In this paper, we develop a new house price index that exploits the informational content of listings data. We construct our house price measure aiming to reproduce the Case-Shiller repeat-sales house price index. Our index is more timely than the Case-Shiller index because for months when sales prices are not yet observed, we substitute sales prices with an estimate based on the final list prices of all homes that are delisted. A key aspect of our methodology is that we associate each delisting with the most recent prior sale of that property. This creates a pair of observations analogous to a pair of repeat sales in the construction of the Case-Shiller index and other conventional repeat-sales indices. This is important because it allows us to provide a more timely index of house price trends without sacrificing the most attractive feature of the repeat-sales index: its ability to control for changes in the mix of homes sold over time by partialing out a house-specific fixed effect from each price.⁴

Our approach is complicated by the facts that the sale-to-list price ratio (i.e. the ratio of the actual sale price to the price at which the seller had listed the house) varies, both in the cross section and across time, and that many delistings do not ultimately result in transactions. However, a simple model of the home-selling problem shows how some of the variation in sale-to-list price ratios and the propensity to transact can by explained by other observable information on seller behavior, such as the time on market (TOM) and the history of list price changes. We show that the model's predictions are consistent with the data and we use this additional information to adjust the final list price up or down, and to weight delistings according to their predicted probabilities of becoming sales. These adjustments turn out to be quite helpful for performance, as 77% of the time series variation in the aggregate list sale-to-list price ratio and 71% of the time series variation in the share of delistings that transact is explained by observable information in our listings data.

We test the performance of our index using micro data from three large, diverse U.S. metropolitan areas over the 2008-2012 time period. During this sample period, our index (i) accurately forecasts the Case-Shiller index several months in advance; (ii) outperforms forecasting models that do not use listings data; and (iii) for the one MSA in which data on futures contracts are available, outperforms the market's expectation as inferred from prices on Case-Shiller futures contracts. We find that correcting for variation in sale-to-list price ratios and propensity to sell (the "adjusted list-price index") reduces our forecasting errors by approximately 20% relative to a simple model in which we neither adjust list prices nor weight delistings differently (the "simple list-price index"). Although the adjusted list-price index is more parametric than the simple list-price index, we present it as our preferred specification because the parametric assumptions are well-grounded in theory and hold in each of our cities individually and across different subsets of the sample period, and thus are likely to be valid out of sample. Nonetheless, the simple list-price index also performs quite well.

Our paper contributes to the large empirical and theoretical literature that studies various aspects of the home-selling process. (Anenberg, 2011b), (Carrillo, 2012), and (Merlo et al., 2013) estimate various extensions of the (Chen & Rosenthal, 1996) model of the home-selling problem, discussed above, using the type of micro data used in our paper. These empirical search models highlight how and why seller choice variables like the list price and marketing time relate to the sales price at a micro level. (Genesove & Mayer, 2001) and (Bucchianeri & Minson, 2013) study how behavioral factors such as loss aversion and anchoring influence seller behavior and ultimately sales prices. (Hendel et al., 2009) and (Levitt & Syverson, 2008) focus on how the seller's decision to use a realtor affects the selling process and selling outcomes. In the current paper, we exploit the relationships between seller behavior and sales prices highlighted by these existing papers to forecast the sales price.⁵

We also contribute to the literature on house price forecasting ((Gallin, 2008), (Malpezzi, 1999), (Rapach & Strauss, 2009), and (Case & Shiller, 1990), among others). The existing literature mostly focuses on the explanatory power of variables that measure macroeconomic conditions like rents, income, unemployment rates, mortgage rates, etc. An exception is a recent paper by (Carrillo et al., 2012), who show that including aggregate listings variables like average TOM in standard time-series forecasting models improves forecasting performance. In our paper, listings data provide predictive power for an entirely different but complementary reason. That is, we exploit the timeliness of listings data relative to transaction data. We are also unique in that we use the micro data on listings, rather than aggregates, to tie each individual list price to a previous sale price, as discussed above.⁶

This paper proceeds as follows. Section 2 presents a short motivating exercise. Section 3 describes our data sources and the particular sample we use to test the performance of our new index. Section 4 reviews the Case-Shiller sale price index methodology. Section 5 introduces our basic methodology with the simple list-price index, and discusses its advantages and potential issues. Section 6 presents theory and evidence on how and why we should use other available information on seller behavior to augment the simple list-price index and outlines our methodology for this adjusted list-price index. Section 7 characterizes the performance of our house price indices. Section 8 concludes the paper.

2 Motivating Empirical Exercise

In this section we conduct a brief empirical exercise that highlights the economic significance of the information lag associated with house prices. The Case-Shiller index is released in the last week of each month, with a two-month delay to the release (for example, the index summarizing January transactions is released the last week in March). From futures contracts traded on the Chicago Mercantile Exchange (CME), we can infer market expectations about the house price levels that will be reported in upcoming releases. Based on these expectations, we can measure the surprise in the Case-Shiller index, which we calculate as the percent change in the actual index value relative to the market's expectation of the index value on the day prior to its release. Figure 1 shows the results of an event study relating surprises in the 10-city Case-Shiller index to changes in the stock price of six different home building companies. For a sample of 25 Case-Shiller index release days for which data are available on futures prices, a one percent positive surprise is associated with a 0.35 percent increase in homebuilder stock prices and the effect is statistically significant. Additional details of this exercise are provided in the Appendix.

The key point of this exercise is that the Case-Shiller index release describes housing transactions that were negotiated up to four months earlier and the pricing information contained in these transactions appears to be important for valuing these companies. Yet during these intervening months, market participants were not fully able to incorporate this information. By using information that was available at the time of the contract negotiations, our list-price index is designed to mitigate this information friction.

3 Data

In this section we describe our data sources and the particular sample we use to test the performance of our new index.

Our first data requirement is the type of micro data on housing transactions used to produce the Case-Shiller index. These micro data are available for purchase from a few data vendors including Dataquick and CoreLogic. Essentially, these vendors collect data from local governments throughout the U.S. on home transactions (which in most cases are required to be publicly disclosed by law) and standardize the information into easy-to-use formats for industry professionals, investors, researchers, etc. For each home sale, these data include the sales price, the closing date, the precise address of the home, home characteristics, whether the home is single-family, as well as information about the lender, buyer, and seller. A point of emphasis for us is that these transaction data become available with a lag of several months because it takes time for a sale closing to be recorded in the public record. Furthermore, since sale agreements (i.e. when the sales price is agreed upon) typically precedes the sale closing date (i.e. when the agreement is finalized and the sales price is recorded in the public record) by one or two months, a new Case-Shiller release really summarizes price conditions from three or four months earlier.

Our second data requirement is micro data on home listings, which are available for purchase from Altos Research. For the universe of homes listed for sale on the Multiple Listing Service (MLS), the dominant platform through which homes for sale are advertised in the U.S., these data include the listing price of the home at a weekly frequency. Using the date of initial listing and the date of delisting - which occurs when there is a sale agreement or when the seller decides to withdraw the home from the market - we can infer the time-on-market (TOM). There is no variable that indicates why a property is delisted, and consequently, if it is delisted because of a sale agreement, we observe nothing about the terms of the agreement such as the sales price. In addition to the list price, the data include the precise address of the home and some house characteristics. The geographic coverage from Altos Research is expansive (it includes all 20 MSAs that comprise the Case-Shiller home price index), but they do not have listing data prior to 2008. Importantly and in contrast to sales data, the data from Altos Research can be purchased in real time.

To test the performance of our list-price index, we purchased sales data from Dataquick and listings data from Altos Research for three large and diverse MSAs: Los Angeles, Phoenix, and Seattle. The Dataquick data runs from 1988-2012 and the Altos Research data runs from 2008-2012. As we describe below, our list-price index requires linking each home in the listing data to its previous sales record in the transaction data. We do so using the address, which is common to both datasets. Our index also sometimes requires linking each delisting to a current sales record, which we also do using the address. We require a match of a delisting to a current sale to have a lag of less than nine months between delisting and closing. To be consistent with the sample of home sales used in the Case-Shiller index (which is described in more detail in the next section), we drop (i) delistings that do not merge to a previous transaction, (ii) delistings where the length of time since the last transaction is less than six months, (iii) delistings that are not single-family. In the end, we are left with a large micro dataset that includes the full history of list price changes for each listing, as well as the house's transaction history. We are aware of very few studies that have been able to compile such a rich dataset.⁷

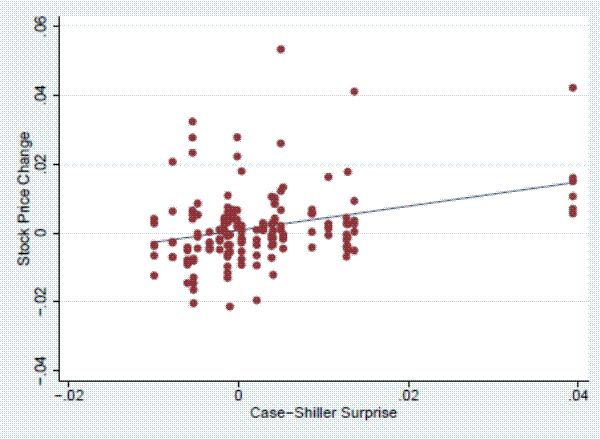
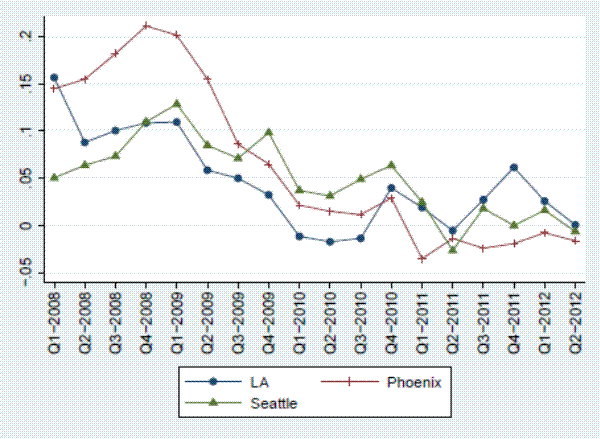
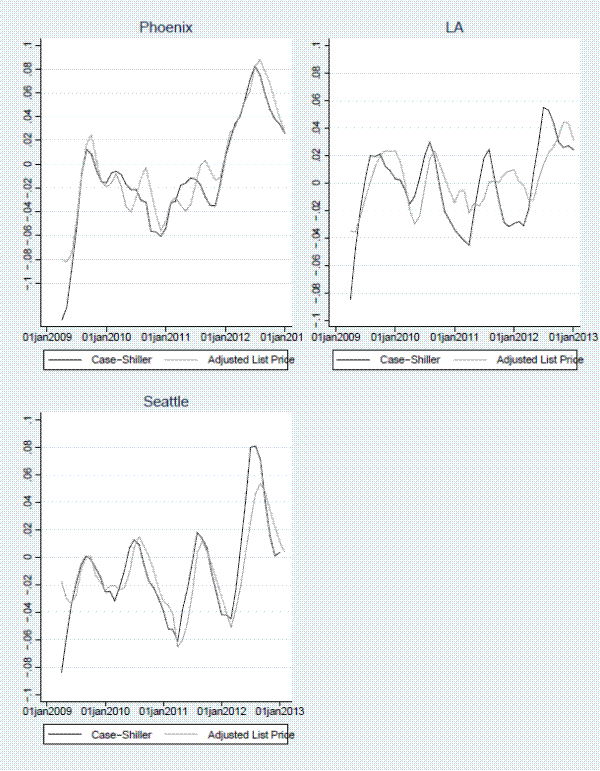
Figure 2 presents the Case-Shiller index for each of the MSAs over the time period in which our transactions data and listings data overlap (2008 - 2012). Like many US cities during this time period, all three cities in our sample experienced significant declines in house prices during the beginning of the sample period, although the magnitude of the decline varied considerably across cities, with Seattle experiencing a 29 percent decline and Phoenix experiencing a 45 percent decline. Our sample does not only include declining housing markets; prices rose by varying degrees in 2009 when the first-time home buyer tax credit was in effect and we have data from 2012, which is when the house price recovery started in many US cities, including the three in our sample. All three of the MSAs enter into the headline Case-Shiller 20-city composite index.

Table 1 presents summary statistics of the 978,000 single-family home listings that we can merge to a previous transaction record and that are delisted during our sample period. List prices in Los Angeles are the highest on average. A majority of listings are delisted without a list price change. The median TOM is between one and two months. Many delistings are relisted soon after delisting: 20 percent of delistings are relisted within less than a month and 17 percent of are relisted between 2 and 6 months later. Many of these relistings may be due to sales agreements that fall through because a mortgage contingency fails or an inspection fails. However, our listings data do not provide the specific reason.

4 Case-Shiller Sales Price Index

We begin with a stylized presentation of the Case-Shiller repeat sales methodology.⁸ Our list price indices will build off of the equations and notation introduced in this section.

The Case-Shiller regression equation is

$\displaystyle p_{it} = v_i + \delta_t + \varepsilon_{it}.$

(1)

where $p_{it}$ is the log sales price of house sold in month , is a house fixed effect, $\delta_t$ is a month effect that captures the citywide level of house prices at month , and $\varepsilon_{it}$ is the unexplained portion of the house price. (Case & Shiller, 1989) interpret $\varepsilon_{it}$ as a noise term due to randomness in the search process, the behavior of the real estate agent, or other imperfections in the market for housing. Estimates of $\delta_t$ , which we denote $\delta_t^{CS}$ , are the basis for the Case-Shiller index. For example, $\delta_t^{CS}-\delta_{t'}^{CS}$ is interpreted as the percent change in house prices in the city between months and .

To estimate equation (1), Case and Shiller employ a repeat sales approach. For each home sale, they use the previous home sale to difference out the house fixed effect, . This gives

$\displaystyle p_{it} - p_{i0} = \delta_t - \delta_0 + \varepsilon_{it} - \varepsilon_{i0}$

(2)

where 0 denotes the month of the previous sale of house

. The time effects can be estimated through weighted OLS on the pooled sample of sales pairs, where sales pairs with a longer interval between sales are downweighted to account for heteroskedasticity in $\varepsilon_{it} - \varepsilon_{i0}$ ("interval weighting"). Case and Shiller drop (i) homes that cannot be matched to previous sales (e.g. new construction) (ii) home pairs where the interval between sales is less than six months and (iii) all non single-family homes. In practice, Case and Shiller also weight each sale pair by the level of the first sale price, $p_{i0}$ , to ensure that the index tracks the aggregate value of the real estate market ("value weighting").⁹ They also use a three-month moving average index, which minimizes month-to-month noise in $\varepsilon_{it} - \varepsilon_{i0}$ . This is implemented by including a pair with a sale in month

as a pair in months

, and

It is important to emphasize that the time subscript in equation (1) reflects the month in which the sale officially closes. The closing date lags the date when the sale price was agreed upon by a month or two on average, as we show below. Furthermore, Case-Shiller do not release their price index for month until the last Tuesday of month because the sale prices become available with significant lags, as discussed above. Our list-price index, which we present next, is not subject to such significant information delays.

5 Simple List-Price Index

In this section we outline the methodology of the simple list-price index, which is the simplest way to use listings data to forecast the Case-Shiller index.¹⁰ Then, we will discuss the potential issues with the simple list-price index from a theoretical perspective, followed by an empirical investigation to determine which issues are important in practice. The empirical work will motivate the adjusted list-price index, which we present as our preferred index in the subsequent section.

5.1 Methodology

The simple list-price index is estimated off of the same regression equation as Case-Shiller (equation (2)), except for the months where the Case-Shiller index value is not yet available, we substitute sales prices with the final list prices of delistings that are expected to close in month .

One issue with our methodology is that even if we observe which delistings close, we do not know exactly when the closing date will be, as the lag between the delisting date and closing date is idiosyncratic. We assume that the lag is drawn from a discrete, known distribution and we estimate this distribution using the empirical distribution of .¹¹ Then for each delisting, we simulate a range of closing dates by drawing from this distribution. That is, for simulation of a house that is delisted at time , we generate a simulated closing at time $t_{ir}=t_i^d+l_{ir}$ , where $l_{ir}$ is the simulated value of drawn from the empirical distribution of lag times.

Define $\mu_{it}=p_{it}-p_{it}^L$ to be the log of the idiosyncratic sale-to-list price ratio for house that sells at time .¹² Then to obtain the month simple list-price index value, we substitute into equation (2) as follows

$\displaystyle p_{it_r}^L - p_{i0} = \delta_{t_r}-\delta_0 + \varepsilon_{it_r} - \varepsilon_{i0} - \mu_{it_r} = \delta_{t_r}-\delta_0 + \nu_{i{t_r}}$

(3)

where $p_{it_r}^L$ denotes the final list price of house

that closes in month

and $\nu_{i{t_r}}=\varepsilon_{it_r} - \varepsilon_{i0} - \mu_{it_r}$ .

Then, moving $\delta_0$ to the left-hand side, we arrive at our estimating equation

$\displaystyle p_{it_r}^L - p_{i0} + \delta_0 = \delta_{t_r} + \nu_{it_r}.$

(4)

Our estimate of $\delta_t$ , which we denote $\hat{\delta_t}$ , is the simple list-price index value for month . Note that equation (4) treats the previous sale price $p_{i0}$ and the time effect for the month of the previous sale, $\delta_0$ , as observable variables. We get $p_{i0}$ by linking each list price to its previous sale in the transaction data. We use $\delta_0^{CS}$ in place of $\delta_0$ , meaning that for the previous sale, we use the house price level calculated from the transaction data alone rather than re-estimating it using both transactions and listings data.¹³ Both of these pieces of information will always be available for the forecasting horizons we consider. In practice, when estimating equation (4), it will be important to account for the value and interval weighting done by Case-Shiller, as described above. We can do this since we observe the sale price and date of the previous transaction.

5.2 Discussion

The simple list-price index is attractive because it exploits the timely nature of listings data without compromising the key properties of the repeat sales index. In particular, like the Case-Shiller repeat sales index, the simple list-price index accounts for changes in the mix of homes sold over time. Furthermore, the simple list-price index is as simple to compute and transparent as the Case-Shiller index and can be similarly adjusted for heteroskedasticity and value weighting. This version of the list-price index, however, relies on several assumptions. In this section, we identify those assumptions and evaluate empirically the degree to which they actually hold in the data. In the following section, we will present an alternative list-price index where these assumptions are relaxed.

We start this discussion by noting that at the time of delisting, the researcher cannot observe which transactions will close and which will not. Our index therefore uses all delistings, some of which will not ultimately result in a transaction. We introduce the random variable $\tau_{it}$ and say that the delisting of house at time results in a transaction if $\tau_{it}>0$ , where the threshold 0 is chosen . With this notation in hand, we examine the assumptions necessary to estimate $\delta_t$ from equation (4). Suppose for now that there is no uncertainty over the lag between the agreement and closing date so that we do not need to simulate closing dates.

For the OLS estimator $\hat{\delta_t}$ to be consistent, it must be the case that

$\displaystyle E(\delta_{t},\nu_{it})=E(\delta_t,\varepsilon_{it} - \varepsilon_{i0} - \mu_{it})= 0.$

(5)

We can break up this expression into several terms:

$\displaystyle E(\delta_t,\varepsilon_{it} - \varepsilon_{i0} - \mu_{it})= E(\delta_t,\varepsilon_{it} - \varepsilon_{i0} \vert \tau_{it}>0)\cdot Pr(\tau_{it}>0) + E(\delta_t,\varepsilon_{it} - \varepsilon_{i0} \vert \tau_{it}<0)\cdot Pr(\tau_{it}<0) - E(\delta_t,\mu_{it})=0.$

(6)

Equation (6) will hold if (but not only if) each of the three expressions equals zero. We consider each term separately. First,

$\displaystyle E(\delta_t,\varepsilon_{it} - \varepsilon_{i0} \vert \tau_{it}>0)= 0,$

(7)

which says that among houses that sell, the error terms cannot be correlated with the time effects. This condition was already necessary for the consistent estimation of the standard repeat sales model in equation (2).

The next term,

$\displaystyle E(\delta_t,\varepsilon_{it} - \varepsilon_{i0} \vert \tau_{it}<0)= 0,$

(8)

requires that the error terms of listings that are withdrawn and do not result in transactions satisfy the same exogeneity restrictions as the error terms for the observations of houses that do sell (equation (7)). If delisted houses that do not sell have list prices that imply higher or lower values for the level of house prices, then including these observations will bias our estimates.

The final piece of equation (6) is

$\displaystyle E(\delta_t,\mu_{it})=0,$

(9)

which says that that the sale-to-list price ratio cannot co-vary with the time effects. A sufficient but not necessary condition would be that the sale-to-list price ratio be time invariant (i.e. $E_t(\mu_{it}) =\mu$ ), as the mean value of the sale-to-list price ratio would simply difference out when we look at changes across time periods. Intuitively, if variation in prices is caused by movements in the sale-to-list price ratio, we will not be able to identify this variation by looking only at list prices.

If these three conditions discussed above are satisfied, then $\delta_t$ can be consistently estimated from equation (4). Our list price model makes two additional assumptions that we abstracted from in the discussion above. First, it assumes that the lag between the delisting date and closing date has a constant, time-invariant distribution. If transactions implying different price levels differed systematically in the time between delisting and closing, this would create a problem for our estimates. Second, our methodology assumes that all completed transactions first appear as delistings in the MLS. In fact, not all homes that sell are listed on the MLS and if homes that are not sold via the MLS are a selected group of transactions, then the simple list-price index may be biased.

5.3 Descriptive Evidence

We next examine the empirical relevance of each potential issue with the simple list-price index in turn.

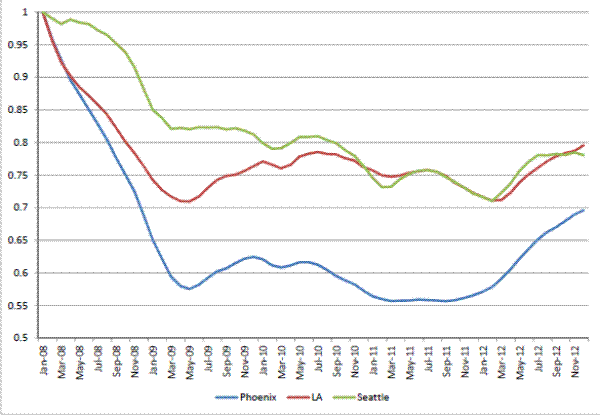
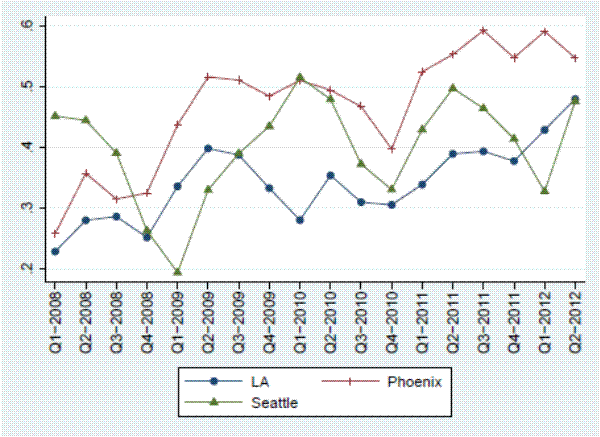
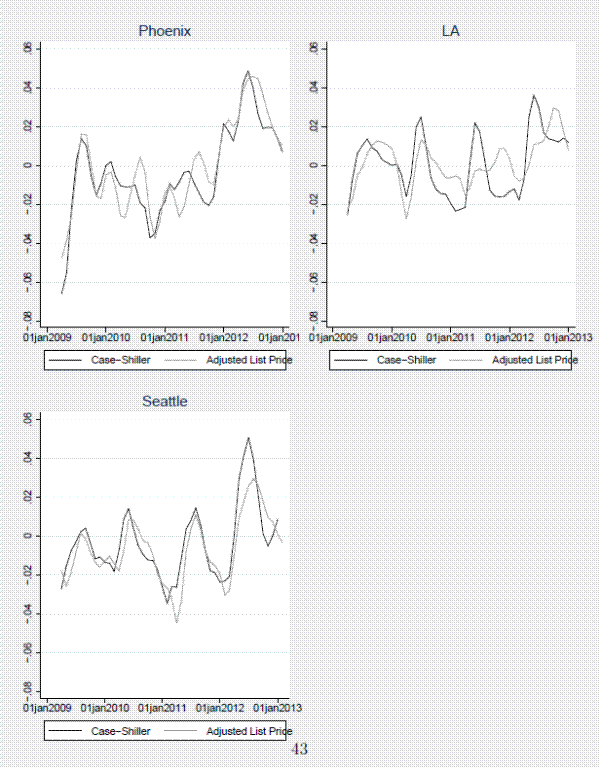
We first examine trends in the sale-to-list price ratio. Figure 3 summarizes the median sale-to-list price ratios for each city in our sample, as well as several other large cities for comparison, over time.¹⁴ Despite the extreme changes in housing market conditions over our sample period, the sale-to-list price ratio fluctuates within a band of only several percent. The variation does, however, appear to be correlated with the house price cycle, in violation of the assumptions of our simple list-price index. Periods of rising prices tend to have high sale-to-list price ratios, on average.

Another potential source of bias for the simple list-price index is the inclusion of all delistings rather than just those that lead to sales. Figure 4 shows that indeed, delistings that result in closings are a selected group of delistings that tend to have lower list prices¹⁵ relative to delistings that do not result in closings, and the magnitude of the list price difference is negatively correlated with the house price cycle. Figure 5 presents the share of delistings that result in a sale by quarter and city. This share is also volatile over time, with hotter markets being associated with a higher probability of sale. Figures 4 and 5 suggest that including all delistings, rather than only the ones that result in sales, will bias the index due to selection.

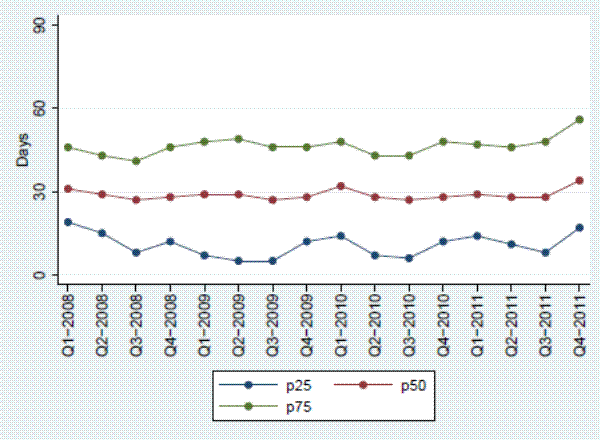
To investigate the assumption that the distribution of lags between the delisting dates is time-invariant, Figure 6 shows the percentiles of the distribution of Closing date - Delisting Date for delistings that result in sales over time. On average, there is a delay of about six weeks between delisting and closing. The distribution of delays does not change much over time. This suggests that the assumption of a time-invariant distribution seems very reasonable, especially since the index is calculated as a moving average of the previous three months.

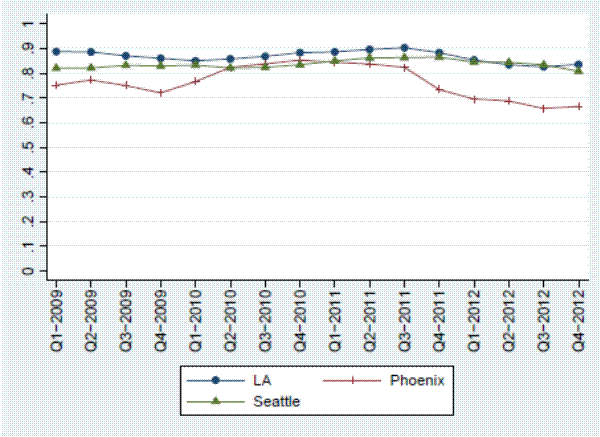
Finally, we investigate the potential for selection bias arising from the types of homes that are listed on the MLS. Figure 7 shows that the sales that do not appear in our listings data represent only a small minority of total sales, which is consistent with reports from the National Association of Realtors.¹⁶ This suggests that this type of selection should not have a large effect on the performance of the simple list-price index.¹⁷

To summarize, the empirical evidence suggests two problems with the simple list-price index. First, the price-to-list ratio varies with the housing cycle so that the final list price is a good, but not unbiased, predictor of the final sales price. Second, since this price index uses all delistings rather than only the ones that result in closed transactions, it is susceptible to selection bias. We next discuss an alternative specification meant to address these issues.

6 Adjusted List-Price Index

In our simple list-price index, the only elements of the listings data we use are the date at which the property is delisted and the final list price. This section examines whether we can use other information available at the time of delisting that the simple list-price index does not exploit - such as TOM and the list price history - to improve the performance of the simple list-price index.

6.1 Model

We first present a model of the home selling problem that generates variation in sale-to-list price ratios and the probability of sale conditional on delisting, which is precisely the variation that is an issue for the simple list-price index. The model delivers predictions for how these outcomes should vary with observable listings variables such as TOM and the list price history. This exercise therefore gives us a theoretical motivation for why such information should be useful in constructing an alternative list-price index meant to address the limitations of the simpler version.

The model is in the spirit of (Chen & Rosenthal, 1996) and describes the behavior of a homeowner trying to sell her house. The model generates variation in the outcomes of interest from two sources. The first is heterogeneity in the valuation that sellers place on not selling and staying in the home, which arises in practice from factors such as employment opportunities and changes in the seller's familial or financial situation. The second source is a finite selling horizon, which may be a good approximation of reality if things like the start of a school season or the closing date on a trade-up home purchase impose limits on the date by which the owner must sell.¹⁸ We keep the model simple enough so that we can analytically derive predictions that can be tested in the data.

There are two periods and in each period , the seller sets a list price and potential buyers arrive with a probability $\alpha_0 - \alpha_1p_t$ . We assume that $\alpha_1>0$ so that a higher list price discourages buyers from visiting the home.

We assume that all of the bargaining power rests with the seller so that when a potential buyer arrives, the negotiated price is equal to the buyer's reservation value. However, the list price functions as a commitment device so that if the buyer's reservation price is higher than the list price, the seller commits to selling the house at the list price, leaving the buyer with positive surplus. Thus, when setting the list price, the seller faces a trade-off: a high list price discourages buyers from visiting a home, but a high list price results in a higher sales price conditional on a buyer arriving. This result is consistent with the empirical evidence (e.g. (Merlo & Ortalo-Magne, 2004)).

There are two type of buyers in the market. A fraction $\beta$ are high types with sufficiently high valuation that the seller's commitment always binds and the negotiated sale price, equals the list price . A fraction $(1-\beta)$ are low types with valuation , which is sufficiently low that the commitment does not bind and the negotiated price equals . If the seller is unable to negotiate a sale with a perspective buyer by the end of the second period, she remains in the house, an outcome to which she assigns a value of $w_i \in [\underline{w},\bar{w}]$ . We assume $v>\bar{w}$ so that the negotiation with any buyer results in an acceptable sale price and the house goes unsold only if no buyer arrives.

Model Predictions

The theoretical results suggest that variables such as TOM, the history of list price changes, and indicators of the seller's reservation value may provide information about the heterogeneity among sellers and could therefore help us better predict variation in the sale-to-list price ratio and the probability of sale. These theoretical results are collected below. We provide proofs of these statements in the Appendix.

The model makes several predictions about how the sale-to-list price ratio and the probability of sale varies with TOM and the seller's reservation value:

1. The sale-to-list price ratio is increasing in the reservation value of the seller, .
2. The probability of sale conditional on delisting is increasing in the reservation value of the seller, .
3. The sale-to-list price ratio is decreasing in TOM, holding fixed the size of the list price change.
4. The probability of sale conditional on delisting is decreasing in TOM.

Over time, sellers tend to adjust their list prices downward and the model makes predictions about how the size of this reduction in list price is related to the sale-to-list price ratio and the probability of sale. These predictions depend on the values of the model parameters and in particular on how the sellers' reservation values compare to the valuation of an expected buyer. There are three possible cases.

Case 1: If $\underline{w} > (1-\beta)v$ , then the size of the reduction in the list price is decreasing in the reservation value of the seller, . In this case:
5a. The sale-to-list price ratio is increasing in the size of the list price reduction, holding fixed TOM.
6a. The probability of sale conditional on delisting is increasing in the size of the list price reduction, holding fixed TOM.
Case 2: If $\bar{w} < (1-\beta)v$ , then the size of the reduction in the list price is increasing in the reservation value of the seller, . In this case:
5b. The sale-to-list price ratio is decreasing in the size of the list price reduction, holding fixed TOM.
6b. The probability of sale conditional on delisting is decreasing in the size of the list price reduction, holding fixed TOM.
Case 3: If $(1-\beta)v$ falls within the support of the distribution of , then the size of the reduction in the list price is non-monotonic in the reservation value of the seller, . In this case:
5c. The sale-to-list price ratio is non-monotonic in the size of the list price reduction, holding fixed TOM.
6c. The probability of sale conditional on delisting is non-monotonic in the size of the list price reduction, holding fixed TOM.

Next, we test whether these predictions hold in our data.

6.2 Evidence

To summarize our empirical results, we find that that data do support the model's predictions and that they are most consistent with $\emph{Case 1}$ from above. That is, we show that predictions 1-4, 5a and 6a hold in our data.

Table 2 shows the results for a set of regressions with the sale-to-list price ratio as the dependent variable. We include monthly seasonal dummies and MSA fixed effects in all specifications. Consistent with the predictions of our model, homes that sell with shorter TOM have larger sale-to-list price ratios. Compared with properties that have been listed for more than six months, the sale-to-list price ratio for properties that sell within two weeks of listing is four percentage points higher according to column (1). Looking across the columns, we see that these estimates are consistent across the three MSAs and that the effects are somewhat larger before 2009.

Table 2 also shows that sellers who lower their list price have sale-to-list price ratios that are four percent larger than those who do not. Among those sellers who do lower their list prices, each percentage point decrease in the final list price relative to the initial list price is associated with a five percent increase in the sale-to-list price ratio. In the context of the model, this implies that it is sellers with lower reservation values who are making larger adjustments to their list prices, consistent with Case 1 from above.

In the regression, we also include dummy variables for whether the house is being sold by a bank that has foreclosed on the property and for whether the final listing price is lower than the home's previous sales price. Positive values for either of these variables predict a higher sales price relative to the final list price. According to the model under Case 1, this result suggests that these are sellers with lower reservation values. This interpretation is consistent with the findings in the literature on foreclosures and loss aversion, respectively.¹⁹

In our other main regression, we estimate the likelihood that a property is delisted because of a sale rather than because of a withdrawal by the seller for other reasons. We drop delistings in 2012 from the regression to avoid censoring issues. Results from a probit model are shown in Table 3. Properties that are taken off the market soon after they are first listed are much more likely to reflect sales compared with properties with longer TOM, consistent with prediction 1 from above. Sellers who have changed their list prices are more likely to delist their properties due to a sale, as are those who reduce prices by larger amounts relative to the initial list price. We interpret these results to mean that the sellers who make larger reductions in their list prices have lower reservation values. This is again consistent with Case 1. Foreclosure sales and sellers who list their properties for less than the previous sales price are also more likely to sell, again consistent with the idea that these sellers have lower reservation values. We also find that there is a discrete jump down in the probability of selling at a TOM of exactly six months, perhaps because many listing contracts with realtors expire after six months.

Ultimately, the effectiveness of using the listing history to augment the simple list-price index depends on the extent to which listing history can explain the time-series variation in the sale-to-list price ratio and sales rate. To examine this, Table 4 presents an aggregate version of the regressions in Tables 2 and 3. Each observation is a month-city combination, and the dependent variable and regressors are averages over all the delistings in a given month-city. The statistic of interest is R-squared. We find that our regressions can explain 76 percent of the variation in sale-to-list price ratio over time and 71 percent of the variation in the sales rate over time, suggesting that incorporating information on the listing history can significantly improve the performance of the simple price index.

In addition to the variation that can be captured by changes in the variables in the listing data, some variation in the sale-to-list price ratio and probability of sale is attributable to macroeconomic factors, which are likely to be persistent. As a result, we would expect that the errors in our list-price index are likely to be correlated over time. In Column 3 of Table 4, we include lagged dependent variables in the regression to test the possibility of serially correlated errors and present evidence that errors are in fact serially correlated. Taking advantage of these correlations allows us to explain an additional eight percent of the variation of the sale-to-list price ratio and 11 percent of the variation in the propensity to sell.²⁰

6.3 Adjusted List-Price Index: Methodology

In this section, we outline the methodology of our preferred list-price index, which takes advantage of the additional information in the listings data in a way that is consistent with the model and evidence presented in Sections 6.1 and 6.2.

Step 1: Estimate Expected Sale Dates and Prices

From earlier observations, we see which delistings resulted in transactions and, for those that did lead to sales, when the sale occurred and at what price. Based on this data, we estimate the empirical relationship between variables that are observable at the time of delisting, such as TOM and the list price history, and the variables related to the subsequent sale of the property (including whether or not the sale occurred).²¹

For the sample of delistings that sell, estimate the equation for the expected sale-to-list price ratio

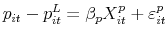
$\displaystyle p_{it} - p_{it}^L = \beta_p X_{it}^p + \varepsilon_{it}^p$ (10)

using OLS, where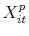 $X_{it}^p$ is the vector of observables that explain variation in the ratio.
For the entire sample, estimate the probability that a delisting results in a sale

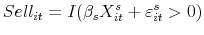
$\displaystyle Sell_{it} = I(\beta_s X_{it}^s + \varepsilon_{it}^s > 0)$ (11)

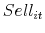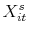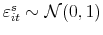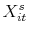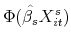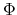where $Sell_{it}$ is an indictor that equals one when a sale is observed, $X_{it}^s$ is the vector of observables that explain variation in the propensity to sell and $\varepsilon_{it}^s \sim \mathcal{N}(0,1)$ . The estimated probability of sale conditional on $X_{it}^s$ is then $\Phi(\hat{\beta_s}X_{it}^s)$ where $\Phi$ is the standard normal c.d.f.
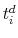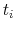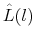For the sample of delistings that sell, calculate the empirical distribution of the time between delisting ( ) and closing ( ), . Denote this distribution $\hat{L}(l)$ .

Step 2: Simulate Transactions for Recent Delistings

Based on these estimates, we simulate many transactions for each observed delisting. These simulations use information that is available at the time of delisting to generate a distribution of possible transactions that will occur at future dates.

For each delisting 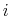at time 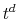, simulate 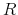outcomes indexed by .
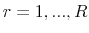1. For each observed delisting 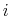, draw 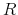random realizations of the error terms 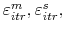$\varepsilon^m_{itr}, \varepsilon^s_{itr},$ and the time to closing $l_{itr}$ .
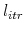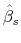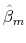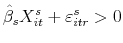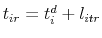2. Using the estimates $\hat{\beta}_s$ and $\hat{\beta}_m$ from the first stage, simulate a closing date and price for each random draw. If $\hat{\beta}_s X_{it}^s + \varepsilon_{itr}^s > 0$ , then then this simulated observation results in a sale. Otherwise, it is a withdrawal and is not included in the estimation of the price index. If there is a sale, the sale occurs at time $t_{ir}=t^d_i+l_{itr}$ and at closing price $p_{itr}= p_{it}^L +\hat{\beta}_p X_{it}^p + \varepsilon_{itr}^p$ .
3. To mimic the smoothing approach of Case-Shiller, generate three copies of each observation and add 0, 1, 2 to the time subscript on the sale price and previous sales price, respectively.
From the simulated transaction, estimate price levels 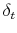$\delta_t$ from

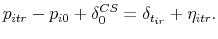
$\displaystyle p_{itr} - p_{i0}+\delta_0^{CS} = \delta_{t_{ir}} + \eta_{itr}.$ (12)

using weighted least squares, where the weighting depends on the elapsed time between the two transactions and the initial sales price, as described in Section 4.

Step 3: Correct for Serial Correlation

Finally, we calculate the amount of serial correlation in the errors generated by this process and use this information to adjust our predictions.

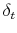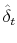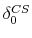Using the estimated values of $\delta_t$ from Step 2, estimate the serial correlation in the difference between the price level predicted by the list-price index $\hat{\delta}_{t}$ and the actual repeat-sales index $\delta_0^{CS}$ :

$\displaystyle \hat{\delta}_{t}-\delta_{t}^{CS}= \rho_0 + \rho_1( \hat{\delta}_{t-1}-\delta_{t-1}^{CS})+e_{t}$ (13)

using OLS where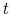 denotes the month. $\rho_1$ measures the degree of serial correlation in the estimation error. Note that nothing about the structure of our model implies that $\rho_1$ need be equal to zero.
Let 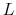denote the number of months ahead of the most recent available Case-Shiller index that we want to forecast. Then let 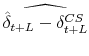$\widehat{\hat{\delta}_{t+L}-\delta_{t+L}^{CS}}$ denote the predicted estimation error for month 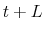, which we can express as

$\displaystyle \widehat{\hat{\delta}_{t+L}-\delta_{t+L}^{CS}}=\hat{\rho}_0(1+\hat{\rho}_1+\hat{\rho}_1^2+...+\hat{\rho}_1^{L-1})+\hat{\rho}_1^L(\hat{\delta}_{t}-\delta_{t}^{CS}).$ (14)

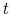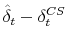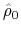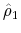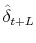This expression results from iteratively substituting into the right hand side of equation (13) until we get back to the observable (as of time ) error term $\hat{\delta}_t-\delta_{t}^{CS}$ . $\hat{\rho}_0$ and $\hat{\rho}_1$ denote the OLS estimates from (13). We correct for serial correlation in the estimation error by subtracting the right hand side of (14) from our estimate $\hat{\delta}_{t+L}$ .

7 Performance of the List-Price Index

In this section, we report the performance of both our simple and adjusted list price indices over the sample period. Recall that for the simple list price index, we assume that all delistings result in sales and we do not adjust the final list price depending on other listings variables (i.e. it skips the first two parts of Step 2). We consider the ability of both indexes to forecast the Case-Shiller HPI at various horizons, which we calculate as the number of weeks from the date of the last observed listings data until the end of the month we are trying to forecast. For example, at a horizon of one week, we observe all listings information for the first three weeks of the month and we are trying to forecast the HPI based on transactions that will close in that month. Given that closing dates lag agreement dates by several weeks, at this horizon we should observe close to the entire universe of delistings that would contribute to the Case-Shiller index for that month. At longer horizons, an increasing share of the the sales are from properties for which we have not yet observed delistings. However, even five months into the future, we find that our index still has significant predictive power. The ability of our index to predict prices so far into the future occurs because some transactions take a significant amount of time to close and also because the smoothing process causes sales that close in a given month to affect the price index for the two subsequent months as well.²²

For each forecasted index value of each MSA, we use the same estimates of the parameters $\beta_p$ , $\beta_s$ , , $\rho_0$ , and $\rho_1$ , which we estimate in a preliminary stage using our full sample of listings data. We use the regressors from the specifications presented in Tables 2 and 3 for and , respectively. The estimates of $\beta_p$ and $\beta_s$ are reported in Tables 2 and 3. $\rho_0$ and $\rho_1$ are estimated to be 0.004 and 0.92, respectively, for the simple list price index and 0 and 0.91 for the adjusted list price index, respectively.

7.1 Absolute Performance

Table 5 summarizes the absolute performance for both the simple list-price index and the adjusted list-price index at various horizons.²³ The number of months ahead of the Case-Shiller release of that month's HPI is reported in the second column. Since the Case-Shiller index level itself has no meaning, we forecast the change in the index level relative to the latest available index value associated with each forecasting horizon. Thus, a forecasting error of means that the list-price index under/over estimates the percent change in sales prices by percentage points.

The adjusted list-price index performs well, even at forecasting horizons of up to 12 weeks, which is five months in advance of the Case-Shiller release. The root mean square error (RMSE) associated with a forecasting horizon of 12 weeks is .031, the mean absolute error (MAE) is .023, and the adjusted list-price index explains over 50 percent of the variation in the five month percent change in the Case-Shiller index. Not surprisingly, performance improves as more listings information about the month we are trying to estimate becomes available. When the forecasting horizon is 0, the RMSE is .011 and the MAE is .009. Even the simple list-price index, despite its issues discussed in Section 5, performs well. When the forecasting horizon is zero weeks, the RMSE is .014 and the MAE is .012. Relative to the simple list-price index, the adjusted list-price index delivers improved performance of about 20 percent.

Figures 8-9 show additional detail for select forecasting horizons for the adjusted list-price index. The figures show that the index performs well (i) in each MSA individually, (ii) over the entire sample period, and (iii) during turning points. For example when sales prices started to come out of their multi-year slump in early 2012, list prices did so as well, albeit not to the same extent as sales prices in LA and Seattle. In addition, when sales prices ticked up in 2009 due to the Obama administration's first time home buyer tax credit, our list-price index moved up as well. The largest forecasting errors occur in LA during the house price slump in late 2011 and in Seattle when prices started appreciating rapidly in 2012.

7.1.1 Discussion

We want to make clear that our index achieves excellent performance at forecast horizons of four or five months even though we are not doing any forecasting in the usual sense.²⁴ In other words, we are not extrapolating any trends or projecting relationships forward. Rather, we are simply processing data on seller behavior in a novel way and exploiting the long lag between when seller behavior is observed and when the corresponding sales price index is released.

We should also emphasize that our sample period covers one of the most volatile time periods in U.S. housing market history, and one of the most volatile sub-markets (i.e. Phoenix). During such a period of heightened volatility, one might expect list prices to be the least informative about sales prices, as sellers may have difficulty assessing their home values when market conditions are changing so drastically. The fact that our index performs so well during this time period gives us confidence that performance would be as good, or possibly even better, out of sample.

7.2 Relative Performance

In this section we address two outstanding questions about performance. First, does listings information provide any explanatory power for short-run house price changes relative to a forecasting equation that does not using listings data? And a second, more challenging question: is the informational content of the listings data that we exploit already known to market participants?

To address the first question, we report the performance of an alternative short-run forecast calculated based on the following AR(3) specification:

$\displaystyle \delta_{j,t}^{CS} - \delta_{j,t-L}^{CS} = \rho_0+\rho_1 (\delta_{j,t-L}^{CS}-\delta_{j,t-2L}^{CS})+\rho_2 (\delta_{j,t-2L}^{CS}-\delta_{j,t-3L}^{CS})+\rho_3 (\delta_{j,t-3L}^{CS}-\delta_{j,t-4L}^{CS})+X_{j,t-L}+\varepsilon_{j,t}$

(15)

where

is the appropriate lag-length associated with the forecast horizon of interest,²⁵ $\delta_{j,t}^{CS}$ is the Case-Shiller index for city

in month

, and $X_{j,t-L}$ is a vector of controls including city dummies, seasonal dummies, national mortgage rates, and state level unemployment rates.²⁶

Table 6 presents the results, where equation (1) is estimated using the full sample of index values available for Los Angeles, Phoenix, and Seattle (i.e. 1988-2012). The gains in performance from the adjusted list-price index are large and statistically significant. The adjusted list-price index delivers 48 percent and 50 percent improved performance in terms of RMSE and MAE, respectively, for an estimate of Case-Shiller five months in advance. To evaluate statistical significance, we test the null hypothesis of forecast error equality against the one-sided alternative that the adjusted list-price index error is lower. Our test statistic is a panel version of the Diebold-Mariano test statistic with a bartlett kernel (see (Diebold & Mariano, 2002)).

To address the second question, we compare the performance of our index with the performance of the market's expectation as implied by the prices of futures contracts for the Case-Shiller index over our sample period. Futures contracts trade on the Chicago Mercantile Exchange for each individual city in the 10-city Case-Shiller composite, as well as for the composite as a whole. Contracts extending 18 months into the future are listed four times a year (February, May, August, November). Each of these contracts trades on a daily basis until the day preceding the release day of the Case-Shiller index value for the contract month, at which point there is a cash settlement. We interpret the price of the contract (i.e. the midpoint of the bid-ask spread) on day as the market's expectation of the house price index days into the future, where denotes the settlement day (i.e. the day that the index value is released). This interpretation is supported by the motivating exercise depicted in Figure 1, which shows that surprises in the index level measured relative to these futures prices shift around stock prices in the expected way.

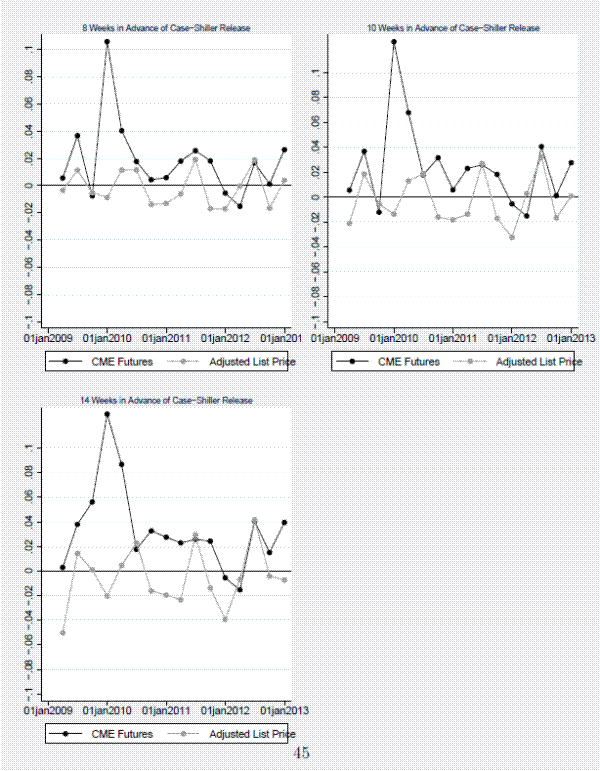
Of our three cities, only Los Angeles is contained in the 10-city composite and therefore has futures traded on the CME. We obtained daily price history for each of the 20 futures contracts for Los Angeles that expired during our sample period. Table 7 shows that the RMSE of the futures prices decline over time as the expiration date approaches. This is to be expected if traders are incorporating new information that arrives over time into their expectations. Table 7 also summarizes the performance of the adjusted list-price index for Los Angeles compared to the performance of the futures market for Los Angeles over our sample period. The detail for a few select forecasting horizons is presented in Figure 10. At a forecasting horizon of five weeks, the RMSE from our adjusted list-price index represents a 50 percent improvement over the forecast implied by the CME futures. For all of the forecast horizons considered in Table 7, we can reject the null hypothesis of no improvement in favor of the alternative hypothesis that the performance of the adjusted list-price index is superior.²⁷ This suggests that the information we exploit in our index is novel and not already known to the market.

8 Conclusion

In this paper, we have presented a new "list-price index," which attempts to fully use the information contained in listings data in order to predict house prices. Our approach has three main advantages. First, the listings data are available several months before the records of the actual transactions, allowing us to achieve a more timely measure of house prices. Second, we link each listing to its previous sale in a manner that is fully analogous to a standard repeat-sales index and accounts for the composition of houses that are sold each month. Third, we adjust for differences between the list prices and the expected transaction prices by exploiting other information in the listings data, such as time on market and the history of list-price changes. While the timely nature of our index is its primary advantage, the last two points are important because ultimately it is the transaction prices not the list prices that are the standard measure of house values.

Our methodology and combined sample of listings and sales are potentially useful for other interesting questions. For example, they could contribute to the preliminary but potentially influential literature that is investigating alternative indexes which address some of the limitations of the Case-Shiller index as a measure of fundamental valuation trends.²⁸ One such limitation is selection bias: only the prices of homes that turn over enter the Case-Shiller index. An index similar to the one we propose in this paper that uses all list prices, rather than just the ones that are delisted as part of a potential sale, could help to address this issue.

At a broader level, our approach is also potentially helpful for understanding how house prices respond to macroeconomic shocks. This is difficult to analyze just from looking at transactions because of the timing issues- it is not possible to tell from the recorded closing date whether the sale price was negotiated before or after the shock. On the other hand, looking just at movements in list prices solves the timing issue, as one can observe the immediate response of sellers to a macroeconomic shock, but doesn't have clear implications for how these changes will affect the sales prices. Our approach addresses both of these concerns and has potential to help us better understand the impact of economic developments on the housing market.

References

Elliot Anenberg. Loss aversion, equity constraints and seller behavior in the real estate market. Regional Science and Urban Economics, 41(1):67-76, 2011a.

Elliot Anenberg. Uncertainty, Learning, and the Value of Information in the Residential Real Estate Market'. mimeo Duke University, 2011b

Elliot Anenberg and Ed Kung. Estimates of the Size and Source of Price Declines Due to Nearby Foreclosures. Working Paper 84, Federal Reserve Board, December 2012.

Martin J. Bailey, Richard F. Muth, and Hugh O. Nourse. A Regression Method for Real Estate Price Index Construction'. Journal of the American Statistical Association 58(304):933-942, 1963

Tim Bollerslev, Andrew Patton, and Wenjing Wang. Daily House Price Indexes: Construction, Modeling, and Longer-Run Predictions'. mimeo Duke University, 2013

Grace Bucchianeri and Julia Minson. A Homeowner's Dilemma: Anchoring in Residential Real Estate Transactions. Technical report, mimeo, University of Pennsylvania, 2013

John Campbell, Stefano Giglio, and Parag Pathak. Forced Sales and House Prices. American Economic Review, 2011/

Andrew Caplin, Sumit Chopra, John V. Leahy, Yann LeCun, and Trivikraman Thampy. Machine Learning and the Spatial Structure of House Prices and Housing Returns mimeo New York University, 2008

Paul Carrillo, Erik De Wit, and William Larson. Can Tightness in the Housing Market Help Predict Subsequent Home Price Appreciation? Evidence from the U.S. and the Netherlands. mimeo George Washington University, 2012

P. E. Carrillo (2012). AN EMPIRICAL STATIONARY EQUILIBRIUM SEARCH MODEL OF THE HOUSING MARKET. International Economic Review 53(1):203-234, 2012

Karl. E. Case and Robert. J. Shiller. Prices of single-family homes since 1970: New indexes for four cities. New Eng. Econ. Rev.Sep/Oct:45-56, 1987

Karl E. Case and Robert J. Shiller. The Efficiency of the Market for Single-Family Homes. The American Economic Review 79(1):125-137, 1989.

Karl E. Case and Robert J. Shiller. Forecasting Prices and Excess Returns in the Housing Market. Real Estate Economics 18(3):253-273, 1990

Yongmin Chen and Robert W. Rosenthal. Asking Prices as Commitment Devices. International Economic Review 37(1):129-155, 1996

Francis X Diebold and Robert S Mariano. Comparing Predictive Accuracy. Journal of Business and Economic Statistics 20(1):134-144, 2002

Joshua Gallin. The Long-Run Relationship Between House Prices and Rents. Real Estate Economics 36(4):635-658, 2008

David Genesove and Christopher Mayer. Loss Aversion and Seller Behavior: Evidence from the Housing Market. The Quarterly Journal of Economics 116(4):1233-1260, 2001

David Genesove and Christopher J. Mayer. Equity and Time to Sale in the Real Estate Market The American Economic Review 87(3):255-269, 1997

Adam Guren. The Causes and Consequences of House Price Momentum.mimeo Harvard University, 2013

Lu Han and Will Strange. ''What is the Role of the Asking Price for a House? Technical report, mimeo, University of Toronto, 2013

Donald Haurin. ''The Duration of Marketing Time of Residential Housing. Real Estate Economics 16(4):396-410, 1988

Igal Hendel, Aviv Nevo, and Franois Ortalo-Magne. The Relative Performance of Real Estate Marketing Platforms: MLS versus FSBOMadison.com. American Economic Review 99(5):1878-98, 2009

Joel L. Horowitz. The role of the list price in housing markets: Theory and an econometric model. Journal of Applied Econometrics 7(2):115-129, 1992

John R. Knight. Listing Price, Time on Market, and Ultimate Selling Price: Causes and Effects of Listing Price Changes. Real Estate Economics 30(2):213-237.

Arthur Korteweg and Morten Sorensen. Estimating Loan-to-Value Distributions. mimeo Columbia University, 2013

Steven D. Levitt and Chad Syverson. Market Distortions When Agents Are Better Informed: The Value of Information in Real Estate Transactions'. Review of Economics and Statistics 90(4):599-611, 2008

Stephen Malpezzi. A simple error correction model of house prices. Journal of Housing Economics 8(1):27-62, 1999

Antonio Merlo and Francois Ortalo-Magne. ''Bargaining over residential real estate: evidence from England'' Journal of Urban Economics 56(2):192-216.

Antonio Merlo and Francois Ortalo-Magne and John Rust. The Home Selling Problem: Theory and Evidence. Technical report, mimeo, University of Pennsylvania, 2013

David E. Rapach and Jack K. Strauss. Differences in housing price forecastability across {US} states. International Journal of Forecasting 25(2):351 - 372, 2009

Stephen W. Salant. For sale by owner: When to use a broker and how to price the house. The Journal of Real Estate Finance and Economics 4(2):157-173, 1991

Robert J. Shiller. Arithmetic repeat sales price estimators. Journal of Housing Economics 1(1):110-126, 1991

A. Details on Motivating Empirical Exercise

This section provides additional details behind the construction of Figure 1, which we presented in Section 2. Changes in stock prices are measured as the opening price on the day of a Case-Shiller index release relative to the closing price on the day before, which is the appropriate comparison because the index is always released before the market opens. We difference off the overnight change in the S&P500 index from each homebuilder stock price change. We use the companies in the Google finance homebuilding sector. The stock tickers are TOL, RYL, BZH, PHM, DHI, KBH, WLH, HXM. We drop HXM from our analysis because it is a Mexican homebuilding company, although the result still holds if this company is included. Futures prices are available for four releases each year starting in August 2006 through August 2013. Section 7.2 provides more details about these future prices.

The statement about statistical significance is robust to clustering standard errors by each release date (the t-statistic is 3.84 in this case).

B. Model Derivations

This section provides proofs of the model predictions outlined in Section 6.1. We start with a series of propositions.

Proposition 1 In the second period, sellers with higher reservation values post higher prices than sellers with lower reservation values.

Proof. Working backwards, we consider the the second period problem of a seller with valuation . If she posts a list price , a buyer arrives with probability $\alpha_0 - \alpha_1p_2$ . Of these buyers, a fraction $\beta$ will be high types, resulting in a sale at price and a fraction $1-\beta$ will be low types, resulting in a sale at price . With probability $1-(\alpha_0 - \alpha_1p_2)$ , no buyer arrives and the seller is left with value .

The seller's problem

$\displaystyle V_2(w_i)=\max_{p_2} (1-\alpha_0 + \alpha_1p_2)w_i + (\alpha_0 - \alpha_1p_2)(\beta p_2 + (1-\beta)v)$

is solved by

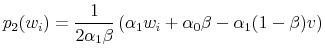$\displaystyle p_2(w_i)= \frac{1}{2 \alpha_1 \beta} \left(\alpha_1 w_i +\alpha_0 \beta - \alpha_1 (1-\beta)v \right)$

The derivative with respect to

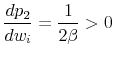$\displaystyle \frac{dp_2}{dw_i} = \frac{1}{2 \beta} > 0$

so that the posted list price

is higher for sellers with larger values of

Proposition 2 In the second period, sellers with higher valuations receive, on average, lower sale prices relative to their list prices compared to sellers with lower valuations.

Proof. Conditional on a buyer arriving, the expected sale price is

$\displaystyle Ep^*= \beta p_2 + (1-\beta)v$

The ratio of the expected sale price to the list price is given by

$\displaystyle \mu_2= Ep^*/p_2= \beta + (1-\beta)v/p_2,$

which is a decreasing function of the listing price. This happens simply because when the list price is not a binding constraint, the sale price is determined by the buyer's valuation. If listing price is higher, it will be higher relative to that valuation and the sale will occur at a smaller fraction of the list price. The derivative of this ratio of expected sale price to list price with respect to the seller's valuation,

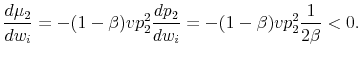$\displaystyle \frac {d \mu_2}{dw_i}= - (1-\beta)v p^2_2 \frac{dp_2}{dw_i}= - (1-\beta)v p^2_2 \frac{1}{2\beta}<0.$

Because they post higher list prices, sellers with higher valuations receive, on average, a lower sale price relative to that list price.

Proposition 3 In the second period, sellers with higher valuations are less likely to sell their homes than sellers with lower valuations.

Proof. The probability that the house is sold is equal to $\alpha_0 - \alpha_1p_t$ , which is a decreasing function of the listing price. Since $\frac{dp_2}{dw_i}<0$ , this implies that sellers with higher value of are less likely to sell their homes.

Proposition 4 The results in Propositions 1-3 hold in the first period as well.

Proof. Moving backwards to the first period, the seller faces the same problem except that if a buyer does not arrive in this period, the seller enters the second period so that the value of not selling is rather than . All of the above equations continue to hold with the substitution for .²⁹ Given the above solution for , we can write

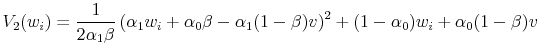$\displaystyle V_2(w_i)= \frac{1}{2\alpha_1 \beta} \left( \alpha_1 w_i + \alpha_0 \beta - \alpha_1(1-\beta)v \right)^2 + (1-\alpha_0)w_i + \alpha_0(1-\beta)v$

so that

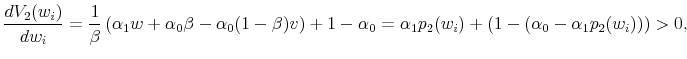$\displaystyle \frac{dV_2(w_i)}{dw_i}= \frac{1}{\beta} \left( \alpha_1 w + \alpha_0 \beta - \alpha_0(1-\beta)v \right) + 1 - \alpha_0 = \alpha_1 p_2(w_i) + (1-(\alpha_0-\alpha_1 p_2(w_i))) > 0,$

which means that

is a strictly increasing function and the results we derived for the second period also hold in the first period. That is, sellers with higher values of

have higher list prices, lower sale-to-list price ratios, and lower probability of sale in the first period as well.

Proposition 5 Sellers lower the list price in the second period, i.e. .

Proof. Consider the behavior of a seller who fails to attract a buyer in the first period and must now set a new list price in the second period. The change in list price from period one to period two is

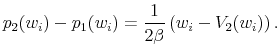$\displaystyle p_2(w_i)-p_1(w_i) = \frac{1}{2 \beta} \left( w_i - V_2(w_i) \right).$

In the second period, the seller receives value

if no buyer arrives but a strictly higher value if one does. This implies

so that from the above equation, the new list price is always lower than the original.

Proposition 6 If $\bar{w} < (1-\beta)v$ , then the decline in list prices, , is larger for sellers with higher reservation values. If $\underline{w} > (1-\beta)v$ , then it is the sellers with lower reservation values that decrease their list prices more.

Proof. The derivative of the change in list prices with respect to the seller's reservation value is given by:

$\displaystyle \frac{d}{dw_i} \left( p_1(w_i)-p_2(w_i) \right) = \frac{1}{2 \beta} \frac{d}{dw_i} \left(V_2(w_i) - w_i \right)= \frac{\alpha_1}{2 \beta} \left((1-\beta)v-w_i \right).$

If $\bar{w} < (1-\beta)v$ , then $(1-\beta)v>w_i$ , the derivative is positive, and the decline in list prices is larger for sellers with higher values of

. Alternatively, if $\underline{w} > (1-\beta)v$ , then $w_i>(1-\beta)v$ , the derivative is negative, and it is the sellers with lower reservation values that decrease their listing prices more.³⁰

In summary, the model characterizes differences in seller behavior as arising from differences in sellers' reservation value. Sellers with higher reservation values will have lower sale-to-list price ratios and lower probability of sale. The relationship between reservation values and the size of list price changes depends on the the sellers' reservation values relative to the expected value of matching with a buyer who is unwilling to pay the list price. If the range of sellers' reservation values is high compared to this expected value, then sellers with higher reservation values will lower their list prices more over time. If sellers' reservation values are lower, then it is sellers with relatively lower reservation values who will make larger reductions in list prices.

Generally, we will not observe the seller's reservation value and must rely on observable measures such as TOM and list price changes. First, we consider the effect of TOM. In the model, a longer TOM means we are considering a seller in the second period rather than the first. In the second period, some sellers are able to sell their homes and some withdraw, having not met a buyer. In the first period, sellers only delist their homes if there is a sale. This means that by construction, the probability that a delisting is a sale is higher in the first period. This is consistent with the data if we find that delistings with shorter TOM are more likely to result in sales. With regard to the sale-to-list price ratio, there are two changes in the second period relative to the first. The first change is that all sellers who are still in the market will lower their list prices. This increases the expected sale-to-list price ratio. The second change is a difference in composition. Sellers with higher reservation values will post higher prices and be less like to match with a buyer in the first period and will therefore make up a larger fraction of sellers in the second period. Because these sellers tend to have lower sale-to-list price ratios relative to sellers with lower valuations, this change in composition will have the opposite effect. Over-all, the effect of TOM is ambiguous. However, if we control for the size of the list-price change, differences in TOM should capture only this composition effect. In this case, the model predicts that, after controlling for the changes in list-price, sellers with greater TOM are more likely to have lower sale-to-list price ratios.

As described above, the model is ambiguous about which types of seller make larger changes to their list prices over time, and therefore it does not have clear predictions about whether sellers who have lowered their list prices more will have higher or lower sale-to-list price ratio and whether they will be more or less likely to sell. The model allows for several possible cases. As shown above, if sellers' reservation values are sufficiently bellow the valuation of the low-type buyers, then sellers with higher reservation values adjust their prices more. In this case, sellers with higher reservation values adjust their prices more and we would expect that larger list price changes are associated with both lower sale-to-list price ratios and lower probabilities of sale. Alternatively, if sellers' reservation values are closer to the valuations of buyers, then it is sellers with lower reservation values make the larger changes in list prices. In this case, we would expect that larger list price changes are associated with both higher sale-to-list price ratios and higher probabilities of sale.

Figure 1: Stock Price Response to Case-Shiller Index Release

Figure 1 Data

This figure shows the response of the stock prices of six different home-building companies to surprises in the Case-Shiller index upon its release. The surprise is measured as the difference between the released index value and market expectations based on futures contracts traded on the Chicago Mercantile Exchange. The figure shows a sample of 25 different Case-Shiller index release days for which data are available on futures prices. Changes in stock prices are measured as the opening price on the day of a Case-Shiller index release relative to the closing price on the day before. We difference off the overnight change in the S&P500 index from each homebuilder stock price change.

Figure 2: Case-Shiller House Price Index

Figure 2 Data

This figure shows the Case-Shiller House Price Index for Phoenix, Los Angeles and Seattle over the time period in which our transactions data and listings data overlap (2008 - 2012). The index in each city is normalized to 1 in January 2008.

Figure 3: Median Sale-to-List Price Ratio

Figure 3 Data

This figure shows median sale-to-list price ratios for each city in our sample, as well as several other large cities for comparison, over time. The data are from Zillow.

Figure 4: List Price of Withdrawals Relative to List Price of Sales

Figure 4 Data

This figure shows the difference between the median log list price of houses that are withdrawn in a given quarter-year relative to the median log list price of homes that are sold. Withdrawals are defined as delistings that do not result in closed transactions, while sales are delistings that do. An estimate of time-invariant house quality is partialed out of list prices, as discussed in the main text.

Figure 5: Share of Delistings that Result in Sales

Figure 5 Data

This figure shows the share of delistings that are observed to lead to sales in each quarter in each city.

Figure 6: Lag Between Delisting and Closing Dates

Figure 6 Data

This figure shows the 25th, 50th, and 75th percentiles of the distribution between closing dates and delisting dates for delistings that result in closed transactions. Closing date is when ownership of the house is transferred from the seller to the buyer, and the transaction is recorded in the public record.

Figure 7: Share of Sales Transactions Appearing in the Listings Data

Figure 7 Data

This figure shows the share of sales in each quarter and in each city that can be linked back to a listing in the MLS database.

Figure 8: Zero-weeks-ahead Forecast of List-Price Index

Figure 8 Data

The thick lines in the figure show the two-month change in house prices based on a repeat-sales index calculated following the Case-Shiller methodology. The thin lines show the forecast of this two-month change based on adjusted list-price index at a forecasting horizon of zero weeks, which is two months prior to the release of the Case-Shiller Index. Changes are calculated as the index value (which is the log of the price level) minus the index value two months before (which is the log of the price level from two months before).

Figure 9: Five-weeks-ahead Forecast of List-Price Index

Figure 9 Data

The thick lines in the figure shows the four-month change in house prices based on the repeat sales index calculated following the Case-Shiller methodology. The thin lines show the forecast of this four-month change based on adjusted list-price index at a forecasting horizon of five weeks. Changes are calculated as the index value (which is the log of the price level) minus the index value four months before (which is the log of the price level from four months before).

Figure 10: Forecast Errors of List-Price Index and CME Futures

Figure 10 Data

The thick lines in the figure show the forecast error associated with futures prices on the Chicago Mercantile Exchange (CME) 8, 10, 14 weeks ahead of the Case-Shiller release. The thin lines in the figure show the forecast error associated with the adjusted list-price index computed 8, 10, 14 weeks ahead of the Case-Shiller release. Forecast errors are calculated as the predicted index value (which is the predicted log of the price level) relative to true index value (which is the log of the price level). Results are for Los Angeles only.

Table 1: Summary Statistics for Delistings

	Percentile	Final List/ Initial List Price	Number of List Price Changes	List Price	Days on Market	I[House Relisted Within 1 Month]	I[House Relisted Within 2 to 6 Months]
LA	10	0.89	0	189000	0	0	0
LA	25	0.96	0	275000	14	0	0
LA	50	1.00	0	399999	49	0	0
LA	75	1.00	1	649000	106	0	0
LA	90	1.00	2	1100000	182	1	1
Phoenix	10	0.84	0	79900	0	0	0
Phoenix	25	0.93	0	114000	14	0	0
Phoenix	50	1.00	0	169900	42	0	0
Phoenix	75	1.00	1	274900	104	0	0
Phoenix	90	1.00	3	450000	176	1	1
Seattle	10	0.83	0	155700	14	0	0
Seattle	25	0.92	0	219900	36	0	0
Seattle	50	0.98	1	315000	83	0	0
Seattle	75	1.00	2	475000	154	0	0
Seattle	90	1.00	3	699950	246	1	1

This table shows summary statistics for houses that are delisted from the MLS databases between 2008-2012. The table describes 442,746 delistings in Los Angeles, 381,595 delistings in Phoenix and 154,050 delistings in Seattle. I[.] denotes the indicator function.

Table 2: Variation in Sale-to-List Price Ratio

Dependent Variable: Log (Sale Price) - Log (List Price) VARIABLES	(1)	(2)	(3)	(4)	(5)
I[Days on Market < 14]	0.0433***	0.0437***	0.0452***	0.0418***	0.0692***
I[Days on Market < 14]: Robust std. errors	(0.0008)	(0.0016)	(0.0013)	(0.0012)	(0.0014)
I[14 < Days on Market < 45]	0.0266***	0.0354***	0.0255***	0.0263***	0.0467***
I[14 < Days on Market < 45]: Robust std. errors	(0.0007)	(0.0015)	(0.0012)	(0.0012)	(0.0013)
I[45 < Days on Market < 90]	0.0166***	0.0207***	0.0182***	0.0147***	0.0305***
I[45 < Days on Market < 90]: Robust std. errrors	(0.0007)	(0.0015)	(0.0012)	(0.0011)	(0.0013)
I[90 < Days on Market < 180]	0.0057***	0.0090***	0.0085***	0.0033***	0.0109***
I[90 < Days on Market < 180]: Robust std. errors	(0.0007)	(0.0014)	(0.0012)	(0.0011)	(0.0012)
(Final List Price/Initial List Price)*I[Change List Price=1]	-0.0494***	-0.0809***	-0.0514***	-0.0463***	-0.0736***
(Final List Price/Initial List Price)*I[Change List Price=1]: Robust std. errors	(0.0038)	(0.0095)	(0.0052)	(0.0069)	(0.0058)
I[Final List Price > Initial List Price]	0.0192***	0.0121***	0.0222***	0.0186***	0.0153***
I[Final List Price > Initial List Price]: Robust std. errors	(0.0012)	(0.0040)	(0.0019)	(0.0017)	(0.0024)
I[Change List Price=1]	0.0381***	0.0770***	0.0411***	0.0323***	0.0660***
I[Change List Price=1]: Robust std. errors	(0.0035)	(0.0090)	(0.0049)	(0.0064)	(0.0054)
I[ Final List Price < Previous Sales Price ]	0.0225***	0.0139***	0.0312***	0.0164***	0.0193***
I[ Final List Price < Previous Sales Price ]: Robust std. errors	(0.0003)	(0.0007)	(0.0004)	(0.0005)	(0.0005)
Foreclosure Dummy	0.0058***	0.0050***	-0.0122***	0.0228***	0.0167***
Foreclosure Dummy: Robust std. errors	(0.0005)	(0.0013)	(0.0007)	(0.0007)	(0.0008)
Seasonal Dummies	X	X	X	X	X
MSA Dummies	X				X
LA sample	X			X	X
Phoenix sample	X		X		X
Seattle sample	X	X			X
Years less than 2010 only					X
Observations	384422	61785	170140	152497	142231
R-squared	0.051	0.041	0.061	0.053	0.079

Robust standard errors in parentheses *** p<0.01 ** p<0.05 * p<0.1

The sample is all delistings that sell. Change List Price equals one if the seller adjusted the list price at least once before delisting. I[.] denotes the indicator function.

Table 3: Variation in Probability of Sale

Dependent Variable: I[Sell] Marginal Effects from Probit VARIABLES	(1)	(2)	(3)	(4)	(5)
I[Days on Market < 14]	0.3467***	0.4739***	0.3803***	0.2569***	0.4136***
I[Days on Market < 14]: Robust std. errors	(0.0027)	(0.0050)	(0.0040)	(0.0045)	(0.0039)
I[14 < Days on Market < 45]	0.3080***	0.4089***	0.3059***	0.2613***	0.3502***
I[14 < Days on Market < 45]: Robust std. errors	(0.0028)	(0.0061)	(0.0042)	(0.0046)	(0.0043)
I[45 < Days on Market < 90]	0.2159***	0.2900***	0.2228***	0.1713***	0.2339***
I[45 < Days on Market < 90]: Robust std. errors	(0.0032)	(0.0074)	(0.0049)	(0.0048)	(0.0049)
I[90 < Days on Market < 180]	0.0683***	0.0731***	0.0771***	0.0504***	0.0691***
I[90 < Days on Market < 180]: Robust std. errors	(0.0024)	(0.0050)	(0.0038)	(0.0038)	(0.0036)
(Final List Price/Initial List Price)*I[Change List Price=1]	-0.1410***	-0.2862***	-0.1531***	-0.1083***	-0.2742***
(Final List Price/Initial List Price)*I[Change List Price=1]: Robust std. errors	(0.0117)	(0.0268)	(0.0173)	(0.0193)	(0.0167)
I[Final List Price > Initial List Price]	0.0027	-0.0493***	0.0043	-0.0098	-0.0117
I[Final List Price > Initial List Price]: Robust std. errors	(0.0054)	(0.0182)	(0.0089)	(0.0074)	(0.0090)
I[Change List Price=1]	0.1527***	0.2520***	0.1582***	0.1491***	0.2819***
I[Change List Price=1]: Robust std. errors	(0.0111)	(0.0248)	(0.0163)	(0.0185)	(0.0153)
I[ Final List Price < Previous Sales Price ]	0.0577***	0.0074**	0.1016***	0.0378***	0.0849***
I[ Final List Price < Previous Sales Price ]: Robust std. errors	(0.0014)	(0.0035)	(0.0022)	(0.0020)	(0.0020)
Foreclosure Dummy	0.1889***	0.1515***	0.1270***	0.2451***	0.2370***
Foreclosure Dummy: Robust std. errors	(0.0019)	(0.0056)	(0.0030)	(0.0028)	(0.0029)
I[90 < Days on Market ] * I[Change List Price]	0.1195***	0.1858***	0.1390***	0.0838***	0.1263***
I[90 < Days on Market ] * I[Change List Price]: Robust std. errors	(0.0035)	(0.0083)	(0.0054)	(0.0053)	(0.0052)
I[Days since last price change < 30]	0.0625***	0.0914***	0.0856***	0.0222***	0.0844***
I[Days since last price change < 30]: Robust std. errors	(0.0023)	(0.0048)	(0.0034)	(0.0039)	(0.0033)
I[Days on Market = 180]	-0.1131***	-0.1025***	-0.1203***	-0.1087***	-0.1227***
I[Days on Market = 180]: Robust std. errors	(0.0040)	(0.0086)	(0.0068)	(0.0057)	(0.0054)
Seasonal Dummies	X	X	X	X	X
MSA Dummies	X				X
LA sample	X			X	X
Phoenix sample	X		X		X
Seattle sample	X	X			X
Years less than 2009 only					X
Observations	624113	108736	246894	268483	294536

Robust standard errors in parentheses *** p<0.01 ** p<0.05 * p<0.1

The sample is all delistings. Change List Price equals one if the seller adjusted the list price at least once before delisting. The dependent variable, ''Sell'', equals one if the delisting results in a closed transaction. I[.] denotes the indicator function.

Table 4: Variation in Average Sale-to-List Price Ratio and Fraction of Sales

VARIABLES	(1) I[Sell]	(2) Log (Sale Price) - Log (List Price)	(3) I[Sell]	(4)Log (Sale Price) - Log (List Price)
I[Days on Market < 14]	-0.3817	0.0398	0.4001	-0.0157
I[Days on Market < 14]: std. errors	(0.5267)	(0.0286)	(0.4339)	(0.0237)
I[14 < Days on Market < 45]	-0.5224	-0.0384	0.4001	-0.0387
I[14 < Days on Market < 45]: std. errors	(0.5561)	(0.0322)	(0.4609)	(0.0258)
I[45 < Days on Market < 90]	-0.4494	-0.0534*	0.5233	-0.0451*
I[45 < Days on Market < 90]: std. errors	(0.5813)	(0.0294)	(0.4821)	(0.0235)
I[90 < Days on Market < 180]	-0.4437	-0.0575	-0.2384	-0.0494*
I[90 < Days on Market < 180]: std. errors	(0.2928)	(0.0351)	(0.2365)	(0.0281)
(Final List Price/Initial List Price)*I[Change List Price=1]	1.8978	-0.0148	0.7788	-0.0234
(Final List Price/Initial List Price)*I[Change List Price=1]: std. errors	(1.5354)	(0.0576)	(1.2410)	(0.0462)
I[Final List Price > Initial List Price]	2.0232	1.2296***	1.4844	0.1723
I[Final List Price > Initial List Price]: std. errors	(1.5438)	(0.1670)	(1.2418)	(0.1761)
I[Change List Price=1]	-2.9932	-0.0714	-1.5122	-0.0286
I[Change List Price=1]: std. errors	(1.8285)	(0.0537)	(1.4800)	(0.0433)
I[ Final List Price < Previous Sales Price ]	0.1016	0.0109	-0.0763	0.0022
I[ Final List Price < Previous Sales Price ]: std. errors	(0.1083)	(0.0156)	(0.0897)	(0.0125)
Foreclosure Dummy	1.0198***	0.1224**	0.9325***	0.0908**
Foreclosure Dummy: std. errors	(0.3038)	(0.0499)	(0.2443)	(0.0401)
I[90 < Days on Market ] * I[Change List Price]	0.4321		1.1767
I[90 < Days on Market ] * I[Change List Price]: std. errors	(0.8933)		(0.7234)
I[Days since last price change < 30]	1.2442***		0.5348
I[Days since last price change < 30]: std. errors	(0.4518)		(0.3733)
I[Days on Market = 180]	-1.0428		-0.7992
I[Days on Market = 180]: std. errors	(0.7314)		(0.5883)
Seasonal Dummies	X	X	X	X
MSA Dummies	X	X	X	X
2-month Lag of Dependent Variable			X	X
Observations	144	174	144	174
R-squared	0.715	0.759	0.818	0.846

Standard errors in parentheses *** p<0.01 ** p<0.05 * p<0.1

Each observation is a MSA-month. All variables are averages over all of the delistings in the MSA-month. Change List Price equals one if the seller adjusted the list price at least once before delisting. I[.] denotes the indicator function. For example, I[Sell] in MSA j in month t is the share of all delistings that result in sales in MSA j in month t.

Table 5: Forecasting Performance of Simple and Adjusted List-Price Indices

Forecast Horizon (Weeks)	# Months Ahead of Case Shiller	Adjusted Index RMSE	Adjusted Index MAE	Adjusted Index R-squared	Simple Index RMSE	Simple Index MAE	Simple Index R-squared	Adjusted Index/Simple Index RMSE	Adjusted Index/Simple Index MAE	Adjusted Index/Simple Index R-quared
-3	2	0.011	0.009	0.650	0.014	0.012	0.462	0.806	0.797	1.408
-2	2	0.011	0.009	0.649	0.014	0.012	0.463	0.808	0.798	1.404
-1	2	0.011	0.009	0.649	0.014	0.012	0.463	0.808	0.797	1.401
0	2	0.011	0.009	0.648	0.014	0.012	0.462	0.809	0.801	1.402
1	3	0.015	0.012	0.706	0.019	0.015	0.553	0.812	0.806	1.276
2	3	0.016	0.013	0.696	0.019	0.015	0.544	0.816	0.812	1.280
3	3	0.016	0.013	0.687	0.020	0.016	0.532	0.818	0.813	1.290
4	3	0.016	0.013	0.669	0.020	0.016	0.509	0.821	0.812	1.315
5	4	0.020	0.015	0.714	0.024	0.019	0.580	0.825	0.818	1.231
6	4	0.021	0.016	0.691	0.025	0.020	0.544	0.824	0.820	1.268
7	4	0.022	0.017	0.658	0.026	0.020	0.514	0.839	0.836	1.280
8	4	0.023	0.018	0.628	0.027	0.020	0.483	0.848	0.857	1.301
9	5	0.027	0.020	0.656	0.031	0.023	0.525	0.851	0.868	1.250
10	5	0.028	0.021	0.627	0.032	0.024	0.490	0.856	0.882	1.279
11	5	0.030	0.023	0.565	0.034	0.025	0.431	0.874	0.903	1.311
12	5	0.031	0.023	0.539	0.035	0.026	0.417	0.889	0.907	1.293
13	6	0.035	0.026	0.556	0.040	0.029	0.443	0.893	0.903	1.254
14	6	0.037	0.028	0.507	0.041	0.030	0.389	0.898	0.914	1.304
15	6	0.041	0.030	0.415	0.044	0.032	0.298	0.913	0.930	1.395
16	6	0.043	0.032	0.333	0.046	0.034	0.236	0.934	0.937	1.412
17	7	0.048	0.035	0.368	0.051	0.037	0.295	0.946	0.935	1.249
18	7	0.051	0.037	0.300	0.053	0.039	0.224	0.950	0.943	1.341
19	7	0.053	0.040	0.227	0.056	0.042	0.145	0.951	0.948	1.567
20	7	0.056	0.041	0.147	0.058	0.043	0.075	0.960	0.958	1.967
21	8	0.059	0.044	0.213	0.062	0.046	0.143	0.958	0.957	1.487
22	8	0.062	0.046	0.152	0.064	0.047	0.099	0.970	0.971	1.543
23	8	0.063	0.047	0.116	0.065	0.048	0.062	0.971	0.977	1.861
24	8	0.065	0.049	0.054	0.067	0.050	0.006	0.976	0.985	9.518

Table 6: Forecasting Performance of Adjusted List-Price Index Relative to Alternative Forecasts

# Months in advance of Case-Shiller	Root Mean Square Error: Forecasting Regression	Root Mean Square Error: Adjusted Index	Root Mean Square Error: Percent Improvement	Mean Absolute Error: Forecasting Regression	Mean Absolute Error: Adjusted Index	Mean Absolute Error: Percent Improvement
2	0.0151**	0.011	24%	0.0112883**	0.009	17%
3	0.0263**	0.015	41%	0.0197775**	0.016	37%
4	0.0379**	0.020	48%	0.0279057**	0.023	45%
5	0.0512**	0.027	48%	0.0399308**	0.030	50%
6	0.0557044**	0.035	37%	0.044	0.037	41%
7	0.072	0.048	34%	0.0569383**	0.042	39%
8	0.080	0.059	26%	0.063	0.045	31%

* ** *** denotes that we can reject the null of forecast error equality in favor of the alternative that the forecast error of the adjusted list-price index is lower at the 1 5 and 10 percent levels according to the Diebold-Mariano test.

Forecasting regression is an AR(3) with seasonal dummies, MSA dummies, controls for changes in national mortgage rates, and controls for changes in state level unemployment rates estimated on the entire history of Case-Shiller values for Los Angeles, Phoenix, and Seattle. Each observation is a MSA-month. The rst column shows the number of months until the release of the the Case-Shiller house price index for the month we are forecasting. The index is released with a two-month delay

Table 7: Forecasting Performance Relative to CME Futures

Forecast Horizon (Weeks)	# Months Ahead of Case Shiller	Root Mean Square Error: Adjusted Index	Root Mean Square Error: CME Futures	Root Mean Square Error: Percent Improvement	Mean Absolute Error: Adjusted Index	Mean Absolute Error: CME Futures	Mean Absolute Error: Percent Improvement
-3	2	0.013	0.022	44%	0.011	0.016	31%
-2	2	0.013	0.0230234*	46%	0.011	0.0173485*	35%
-1	2	0.013	0.0327717*	62%	0.011	0.0219181*	49%
0	2	0.012	0.0354012*	65%	0.011	0.0238356**	53%
1	3	0.019	0.0412213*	54%	0.017	0.0286714*	42%
2	3	0.019	0.041551*	55%	0.017	0.0289128*	42%
3	3	0.019	0.0427398*	56%	0.017	0.0296651*	43%
4	3	0.019	0.0446846*	57%	0.017	0.0320721**	48%
5	4	0.024	0.0474726*	49%	0.020	0.0361663*	46%
6	4	0.025	0.0572914**	57%	0.020	0.0432277**	54%
7	4	0.025	0.0576857**	56%	0.020	0.0439215**	55%
8	4	0.026	0.058152**	55%	0.021	0.0446137**	53%

The forecast horizon is measured from the date of the last observed listings data until the end of the month we are trying to forecast. The second column shows the number of months until the release of the the Case-Shiller house price index for the month we are forecasting. The index is released with a two-month delay. Performance for both the adjusted index and the Chicago Mercantile Exchange (CME) futures prices is for Los Angeles only. Futures contracts extending 18 months into the future are listed four times a year. Each of these contracts trades on a daily basis until the day preceding the Case-Shiller release day for the contract month. We use the price of the futures contract relative to the realized index value to calculate performance. Only the months in which a CME contract exists are used to calculate the performance of the adjusted list-price index/

Footnotes

* [email protected]. [email protected]. Both authors are members of the staff of the Board of Governors of the Federal Reserve System, Washington DC. We thank participants at the 2013 Annual Meeting of the Urban Economics Association, our Board colleagues, Pat Bayer, Moshe Buchinsky, Ingrid Ellen, Ed Kung, and Karen Pence for their helpful comments. All remaining errors are our own. The analysis and conclusions set forth are those of the authors and do not indicate concurrence by other members of the research staff or the Board of Governors. Return to Text

1. The Case-Shiller index, developed by (Bailey et al., 1963) and modified by (Case & Shiller, 1987) and (Case & Shiller, 1989), is the most widely followed measure of U.S. house price trends. The index is calculated using repeated transactions of the same house so as not to be distorted by changes in the mix of homes sold over time. Return to Text

2. For example, the Case-Shiller house price index summarizing sales prices that close in month

is not released until the end of month

. Return to Text

3. See (Chen & Rosenthal, 1996) for a discussion of the role of listing prices as a commitment device for sellers. Return to Text

4. Like the Case-Shiller index, our index can also account for (i) heteroskedastic errors (i.e. homes with a longer interval between sales should be downweighted because the likelihood of unobserved changes to house quality are higher) and (ii) value weighting (that more valuable homes comprise a larger share of a real-estate portfolio, and thus their appreciation/depreciation rates should be given more weight). Return to Text

5. Other related papers that study the home-selling problem include (Knight, 1996), (Genesove & Mayer, 1997), (Salant, 1991), (Anenberg, 2011a), (Merlo & Ortalo-Magne, 2004), (Horowitz, 1992), (Han & Strange, 2013), and (Haurin, 1988). Return to Text

6. Recently, several companies have starting using listings data to forecast house prices. For example, the Trulia Price Monitor is a measure of trends in current (not necessarily final) asking prices, adjusted for changes in several observable hedonic characteristics. CoreLogic incorporates new listing prices into a time series regression model to construct a "Pending HPI" (CoreLogic, 2012). Based on our reading of their published materials, neither of these measures fully exploits the informational content of the listings data as we do in the present study. Return to Text

7. See (Guren, 2013) and (Anenberg & Kung, 2012). Return to Text

8. For the full methodology, see (Shiller, 1991) and the Case-Shiller website. Return to Text

9. Value-weighted repeat sales indices are analogous to capitalization-weighted stock market indices. In both cases, if you hold a representative portfolio, both types of indices will track the aggregate value of that portfolio. Return to Text

10. We tailor our list price index methodology to track the Case-Shiller index specifically because the Case-Shiller index is currently the most widely followed measure of house price trends. Our approach could equally well be applied to track any other measures of house prices that are based on transactions data. We comment on the possibility of using listings data to generate a new house price index altogether in Section 8, but we leave that idea for future research. Return to Text

11. As described in Section 3, the support of

is 0,...,270 days. Return to Text

12. For notational convenience, we drop the

subscript from time variables when it appears elsewhere in the expression. Return to Text

13. Moving $\delta_0$ to the left hand side is a convenience that we can take because the Case-Shiller methodology uses a chain weighting procedure in which the estimate of $\delta_0$ is not affected by data after time 0 . If this were not the case, we could simply estimate $\delta_0$ along with $\delta_t$ . Return to Text

14. The source for Figure 3 is Zillow, which provides aggregate time series data (starting in late 2008) on sale-to-list price ratio by MSA. Results for LA, Phoenix, and Seattle are similar when we use our data. Return to Text

15. We normalize each list price by $(p_{i0}-\delta_0)$ to control for differences in house quality and we stop the sample in mid-2012 to avoid censoring issues. Return to Text

16. See for example the 2012 NAR Profile of Home Buyers and Sellers which reports that 88 percent of home sales are broker assisted. Return to Text

17. A common reason that a sale does not appear in our listings data is that the sale represents a transfer of a foreclosed property to an investor at a foreclosure auction. This is one explanation for the fact that we find that, on average, sales prices of homes that merge to a delisting are higher than the prices of homes that do not. Other potential reasons that a sale does not merge include 1) the home is sold without the assistance of a broker, 2) the address is coded with error, preventing a successful merge. Return to Text

18. See (Anenberg (2011b)) and (Merlo et al., 2013) for examples of structural search models that impose a finite selling horizon to provide a good fit to the micro data. Return to Text

19. See (Campbell et al., 2011) for evidence that banks are more motivated to sell than the typical non-bank seller. (Genesove & Mayer, 2001) argue that sellers are subject to loss aversion and are reluctant to re-sell their homes for less than they originally paid for it. Sellers who have posted list prices below the previous sales prices are essentially guaranteed to realize a nominal loss on the transaction. We might therefore expect that sellers would be less willing to do this unless they assigned a particularly low value to staying in the house. Return to Text

20. The following methodology section describes precisely how we correct for serial correlation in our list-price index. Return to Text

21. In practice, we estimate these relationships based on the entire sample. Alternatively, one could construct a separate estimate for each time period by only using transactions that would have been observed prior to that date. Return to Text

22. Recall that the Case-Shiller price index in month

actually reflects sales in months

and

. Return to Text

23. Performance is based on a comparison of our list-price index to a Case-Shiller HPI that we estimate using our transaction data from Dataquick. We do this rather than using the actual Case-Shiller index because Case-Shiller does not fully disclose how they deal with outliers and weighting to account for heteroskedasticity. In this way, forecasting error is due to the failure of the list price to predict the sales price, rather than any differences in the way we are handling outliers and weighting. Our computed Case-Shiller HPI is very close to the headline index, but not quite as smooth. Return to Text

24. Part of the reason for the success of our index at longer horizons of four or five months is that, as discussed above, the Case-Shiller index value is smoothed using the index value from the two

months. As discussed above, our methodology replicates this smoothing approach. Return to Text

25. For example, when the forecasting horizon is five weeks, we set

because our list-price index would be available two months before the Case-Shiller index. Return to Text

26. One might be concerned that we are omitting some key observable fundamental in equation (15). This seems unlikely because the fundamental would need to be available and to vary at a very high frequency given the short forecasting horizons we are considering. Furthermore, the explanatory power of any fundamental is weakened by the idiosyncratic lag between the agreement date and the closing date for a sale price. That is, house prices that close in period

actually reflect fundamentals from an unknown distribution of periods before

. Finally, we note that the literature has emphasized the role of search frictions and momentum in explaining house price dynamics, which may be best captured in the reduced form by the AR terms in equation (15). Return to Text

27. In evaluating statistical significance for a given forecasting horizon, here we ignore the possibility that forecast errors may be serially correlated and we thus test for significance using a differences in means test. We make this assumption because the futures contracts are spaced three months apart, and thus the data that contributes to the forecast of one observation is essentially orthogonal to the data that contributes to the forecast of another observation. Return to Text

28. See (Korteweg & Sorensen, 2013), (Bollerslev et al., 2013), and (Caplin et al., 2008). Return to Text

29. This requires a further assumption that

, i.e. that it is still optimal to accept an offer from a low-type buyer rather than reject that offer in hopes of matching with a high-type buyer in the second period. This assumption will hold if

is sufficiently low that the risk of not matching in the second period outweighs the potential gain of meeting a buyer willing to pay the second-period asking price. Return to Text

30. The intuition for this result is as follows. The seller in the first period is forward looking. A seller with a higher valuation knows that in the second period, she will set a higher list price in order to capture the higher benefit of matching with a potential buyer willing to pay that list price. A consequence of this higher list price is that it becomes less likely that she will attract a buyer in the second period. In particular, there is a lower probability that she will attract a low-type buyer and a higher probability that she will instead receive her reservation value

. If

is high compared with the expected benefit of matching with a low-type buyer ( $w_i>(1-\beta)v$ ), this increases the value of reaching the second period. This makes the seller with the higher valuation marginally raise her list price in the first period in order to increase the probability of reaching the second period. This higher price in the first period makes the size of the list price change larger. Conversely, if

is low compared with the expected benefit of matching with a low-type buyer ( $w_i>(1-\beta)v$ ), then a lower probability of matching with a low-type buyer decreases the value of reaching the second period. In this case, the seller with the relatively higher valuation will set a slightly lower list price in the first period in order to decrease the chance of reaching the second period. In this case, sellers with higher valuations will have smaller decline in list prices between the two periods. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text