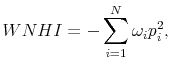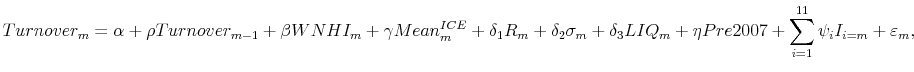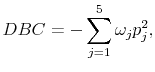Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2014-35 Screen Reader version ^♣

Are Household Investors Noise Traders? Evidence from Belief Dispersion and Stock Trading Volume

Dan Li

Federal Reserve Board

Geng Li *

Federal Reserve Board

February 2014

Abstract:

We document a robust positive relationship between the belief dispersion about macroeconomic conditions among household investors and the stock market trading volume, using more than 30 years of household survey data and a novel approach to measuring belief dispersions. Notably, such a relationship prevails even after various series of professional analysts' belief dispersions are controlled for. Consistent with a causal effect, such a relationship is most pronounced for belief dispersion among individuals who are most likely to own stocks and for trading volume of stocks that are most visible to household investors. Finally, we present suggestive evidence that the dispersion of changes in belief is also positively associated with the stock trading volume. On balance, our analysis implies that household investors, frequently believed to trade randomly as noise traders, appear to trade on their beliefs.

1 Introduction

Household investors directly own about 40% of outstanding equities in the U.S. and hold an additional 20% of outstanding equities through mutual funds.¹ Despite their substantial presence, we know little about the impact of household investors on the dynamics of the stock market. Much of the existing literature views household investors as less sophisticated, uninformed, trading randomly like noise traders (see, for example, Campbell (2007) and Barber, Odean, and Zhu (2006)). Some researchers argue that individual investors typically apply rules-of-thumb and are subject to psychological biases (Odean, 1998; Shefrin and Statman, 1985). Indeed, existing research largely focuses on household investors' suboptimal behaviors in the stock market, such as limited participation (Vissing-Jørgensen, 2002; Mankiw and Zeldes, 1991) and excessive trading (Odean, 1999; Agnew, Balduzzi, and Sundén, 2003).

This paper sheds light on the extent to which household investors trade based on their beliefs--as opposed to trading randomly--and the merit of the beliefs and information they have relative to those of the professional investors. We achieve this by studying how belief dispersion on macroeconomic conditions among household investors affects trading volume in the stock market.

In a standard representative agent model, no trading occurs because all investors are assumed to be identical. Trading may arise in models where investors have different beliefs (Basak, 2000,2005).² The theoretical significance of disagreement among investors on trading volume has been appreciated at least since Varian (1985) and Karpoff (1986), who show that trading arises if investors interpret signals differently or if they interpret signals in the same way but start with different prior beliefs.³ Empirical tests on these models have largely focused on how the trading of securities of individual firms is affected by disagreement among professional analysts, typically within a short period around earnings releases or other major corporate news announcements.

Our analysis brings household investors to the center of the stage and examines how disagreement among them about the macro economy affects the stock market. Because beliefs of household investors (and the dispersion therein) are potentially correlated with those of professional analysts, we run a horse race between household-based and analysts-based belief dispersion measures. To further challenge the household-based dispersion measure, we consider a wide range of professional analyst surveys--Survey of Professional Forecasters, Blue Chip Economic Indicator Survey, and I/B/E/S analyst forecasts of earnings. Our results suggest that, even after controlling for all three analyst-based dispersion measures, the positive correlation between household belief dispersion and stock market turnover rates remains substantial and significant. Specifically, a one-standard-deviation increase in household belief dispersion implies an increase in monthly market-wide turnover of about one quarter of its standard deviation. Interestingly, the effects of professional belief dispersion on trading volume diminish in the presence of household belief dispersion. This comparison is consistent with recent findings that some household investors are more sophisticated and may possess information beyond what is known to professional investors and the aggregate decisions of retail investors might contribute to market efficiency (Kelley and Tetlock, 2013; Campbell, 2007).

We also contribute to the literature by addressing the issue of causality between belief dispersion and trading volume, using split-sample analysis and event study. We first exploit the household socioeconomic and demographic information unique to our data and examine whether the sensitivity of trading volume to belief dispersion varies across subgroups of households with different propensities of investing in stocks. We find that trading volume is more sensitive to the belief dispersion among richer and more educated households, who are more likely to own stocks. In addition, belief dispersion has a larger impact on the trading volume of stocks that are more visible to household investors, such as those with larger market capitalization. Furthermore, an event study suggests firms recently added to the S&P 500 index experience an increase in the sensitivity of their firm-specific trading volume to household belief dispersion.

Our paper also makes a methodological innovation in measuring investor disagreements when beliefs are reported in categorical, instead of numerical, values. We introduce the weighted Herfindahl index to measure dispersion of ranked categorical variables. By giving more weight to responses that are different from the current status-quo, we are able to reduce noise from "lazy" answers.⁴ We show that our constructed series of household belief dispersion demonstrates significant counter-cyclicality. The pattern is more pronounced than what is demonstrated in the dispersion series of professional forecasts. Moreover, household belief dispersion tends to peak earlier in recessions compared to professional belief dispersion, revealing its potential merit as a leading indicator of macroeconomic conditions.

The baseline results hold in a number of robustness analysis. First, we adopt gross flow of equity mutual funds as an alternative measure of trading volume. We find that belief dispersion among households has a similar positive effect on fund flows, which represent indirect trading of stocks through mutual funds. Second, our results hold when we calculate trading volume from only two of the exchanges, NYSE and AMEX, to address the potential double counting problem with the NASDAQ trading volume (Anderson and Dyl, 2005). Third, we show that our results are not sensitive to the choice of detrending methods for the turnover series. Finally, we experiment with varying weights in constructing our belief dispersion measure--the weighted Herfindahl index--and with using standard deviations to measure belief dispersion.

We argue that households may possess information not available to professional analysts, as the population of consumers are sufficiently heterogeneous in terms of income level, geographic location, profession, personal financial and economic experience, and industry affiliation. The professional population, on the other hand, are much more homogeneous along these dimensions. Since these characteristics likely affect belief systematically, household surveys that use nationwide representative samples likely have an advantage in capturing the dispersion of opinions that are relevant for stock market trading. That said, it is important to note that we do not presume households necessarily have rational expectations. Neither does this paper test the rationality of household expectations. The focus of the paper is to link beliefs directly to trades, and furthermore, understand whose beliefs matter more for aggregate trading volume.

We complete our analysis by exploiting the short-panel structure of our data that allows us to directly measure investors' belief changes over time and to study how dispersion of belief changes affects trading activities--a question most of the earlier work has not addressed (with Barron (1995) and Bamber, Barron, and Stober (1997) being two notable exceptions).⁵ Our results confirm that greater dispersion in belief changes is also associated with greater trading volume.

The paper proceeds as follows. Section 2 summarizes the literature on the theory and empirics regarding the relationship between investor belief heterogeneity and trading volume. Section 3 describes the data. Section 4 introduces our measures of belief dispersion. Section 5 presents the main empirical results and robustness analysis. Section 6 addresses the identification strategy for establishing a potential causal relationship between belief dispersion and trading volume. Section 7 extends our analysis to the effect of dispersion of belief changes on stock trading volume. We conclude in Section 8.

2 Related Literature

One of the surprising and elegant pieces of economic theory is the No-Trade theorem (Milgrom and Stokey, 1982). The theorem states that in a speculative market composed of fully rational agents with identical prior beliefs, no trade will occur in equilibrium, even in the presence of asymmetric information. The prediction is obviously not meant to hold in reality, but it provides a starting point for any attempt to answer the question--why do people trade in financial markets?

Tirole (1982) describes the conditions under which the No-Trade theorem does not hold: (1) there exist irrational traders, or noise traders who trade for liquidity reasons; (2) some investors trade for hedging or diversification purposes; and (3) agents have different prior beliefs. Our focus in this paper is the third condition.⁶ This argument is, first and foremost, empirically sound. Considering "the glass is half full or half empty" argument, it speaks to the deep psychological roots of the dispersion of human optimism or pessimism. As Hong and Stein (2007) argue, "disagreement models uniquely hold the promise of being able to deliver a comprehensive joint account of stock prices and trading volume, which we consider to be one of the highest priorities for theoretical work in asset pricing."

Various theoretical papers have demonstrated how differences in beliefs can be linked to trading volume. Karpoff (1986) shows that both different interpretations of the same information and different prior beliefs can stimulate trading activities.⁷ Hence, two different aspects of belief heterogeneity--(1) dispersion of prior beliefs and (2) dispersion of belief changes--can stimulate trade, we address both in this paper. By no means is this paper the first attempt at providing empirical evidence for Karpoff's theory. Rather, we are motivated by the gaps in the existing, albeit vast, empirical literature. We highlight several major ways in which our paper improves upon and extends the previous empirical work.

First, most existing empirical studies focus on belief dispersions among financial analysts. However, Dinh and Gajewski (2007) point out that such proxies can be inaccurate since they represent only a distinct group of economic agents, who are often more informed and more sophisticated. In addition, analysts' forecasts can be biased by their private incentives. Such bias may render their belief dispersion an inefficient proxy for traders' disagreement. For example, analysts' desire to win investment banking clients may lead them to adjust their forecasts to avoid earnings disappointments (Chan, Karceski, and Lakonishok, 2003). Moreover, Hong, Kubik, and Solomon (2000) find that analysts, especially inexperienced ones, herd in their forecasts because of career concerns. These caution us in using and interpreting the forecasts made by professional analysts.

Effort has been made to characterize belief heterogeneity when beliefs are not measurable. Bessembinder, Chan, and Seguin (1996) consider the open interest of S&P 500 index futures a proxy for dispersion of traders' opinions regarding underlying values and find it positively related to trading volume. Goetzmann and Massa (2005) construct an indirect proxy of belief dispersion from age, income, and occupation information about 100,000 retail investors and find the proxy positively related to contemporaneous trading volume and stock return.

In addition, previous studies have largely focused on earnings forecasts of individual firms, instead of beliefs about future macroeconomic conditions. However, expectations on future macroeconomic and business conditions play a pivotal role in shaping investors' strategies and portfolio choices as these variables tend to influence the level and riskiness of future dividend flows of all firms and the interest rate at which future dividends are discounted.

Furthermore, most prior studies examine specific events, such as corporate earnings releases, and measure beliefs and trading volumes over a short period of time around such events (Lang and Litzenberger, 1989; Comiskey, Walkling, and Weeks, 1987; Ziebart, 1990). Nevertheless, agents do not trade only on their opinions about earnings releases. Investors' opinions about the economy and their perspectives on interest rates and employment should all be critical in forming their opinions about financial investment and trading strategies. In reality, agents receive new information on a continuous basis, especially information concerning the economy. As new information comes, investors update both their short- and long-term outlooks for the economy and financial markets. It is therefore an empirical question as to what extent each piece of information matters in generating trades. We address these concerns by constructing metrics of belief dispersion using data of self-reported expectations directly collected in a nationwide representative survey of consumers.

Finally, our paper is also related to the emerging literature that studies the financial decisions and trading behaviors of household or retail investors. For example, Amromin and Sharpe (forthcoming) examine stock market beliefs and portfolio choices of household investors. Kelley and Tetlock (2013) study the role of retail investors in stock pricing. In addition, using one year worth of data from a large discount broker from the Netherland, Hoffmann, Post, and Pennings (2013) present evidence that retail investors’ beliefs dynamics during the recent financial crisis appear to affect their trading activities.

3 Data Description

3.1 Surveys of Consumers

We use self-reported beliefs of households from the Thomson Reuters/University of Michigan Surveys of Consumers (SCA), which is the building block of the Consumer Sentiment Index. Introduced in the late 1940s, the Index has established itself as one of the most widely followed indicators of households' sentiments about current and future economic and business conditions.

The information content of the survey has long been recognized by the research community. Validation studies by the SCA staff show that the information collected in the SCA predicts the dynamics of the nationwide economy quite well. For example, the time series correlation between the index of consumer assessment of economic conditions and real GDP growth was 0.9. The correlation between the index of unemployment expectation and subsequent realized unemployment rate was 0.8.⁸ In addition, Carroll, Fuhrer, and Wilcox (1994) find the Index of Consumer Sentiment derived from the Survey and Consumers predicts future changes of household spending. More recently, Barsky and Sims (2012) document that the "Michigan Survey of Consumers have powerful predictive implications for the future paths of macroeconomic variables.’’ Moreover, Ang, Bekaert, and Wei (2007) find that the mean inflation projection of the same survey outperforms statistical time series or and term structure forecast models. These studies consistently demonstrate that, despite the substantial dispersion among household beliefs, their expectations on future macroeconomic conditions appear to be quite accurate on average.

Since 1978, the SCA has been conducting monthly surveys of a minimum of 500 consumers, the majority of whom were contacted within about two weeks.⁹ Our sample covers the period from 1978 to 2011, containing nearly 35 years' worth of monthly consumer-level data. The SCA survey data have a few notable advantages over various surveys of professional forecasters. The size of the SCA cross-section is more than 500, significantly larger than the sizes of professional forecasts, which typically have less than 50 respondents. Therefore, belief dispersion can be calculated more reliably in the household surveys. In addition, collecting all answers within a short window of 2 weeks ensures that forecasts are made based on a roughly similar information set across respondents. Another critical and unique feature of the SCA is that it collects key information about the demographic characteristics and the economic status of sampled consumers, which informs us of the respondens' propensity to own stocks. Finally, the SCA features a short longitudinal structure. About 40 percent of the respondents were surveyed again six months after their first interview.¹⁰ We exploit this feature later and study the effect of dispersion of belief changes on trading volume.

Each month, the SCA asks about 50 core questions broadly related to consumers' assessments of current economic conditions and their expectations about the future economic conditions of both their households and the country.¹¹ We focus on the dispersion of beliefs (and its changes) about future business conditions, personal financial conditions, unemployment, and interest rates. The upper panel of Table 1 lists the survey variables that our study focuses on. Four of the five questions are about consumers' expectations in the near term, typically within the next 12 months. The only question regarding long-term expectations is about consumers' expectations of business conditions during the next five years.

Most SCA questions have categorical, instead of numerical, answers.¹² For example, when asked about unemployment expectations, consumers choose from three answers--"more unemployment," "about the same," and "less unemployment". Similarly, when asked about future business conditions, consumers choose from "better off," "same," and "worse off." Categorical answers are likely easier for a typical household to respond. It is also less affected by "wild answers." However, constructing dispersion measures from categorical answers is less straightforward. We address this challenge by introducing a new measure of belief dispersion, which is explained in detail in Section 4.

3.2 Forecasts of Professionals

Earlier research has documented that dispersion of beliefs regarding corporate earnings among business analysts can influence trading activities of individual stocks (Lang and Litzenberger, 1989; Comiskey, Walkling, and Weeks, 1987; Ziebart, 1990). Conceivably, wider belief dispersion among professional forecasters regarding future macroeconomic conditions can also induce higher trading volume--a hypothesis we test. Should professional-based disagreement matter for stock trading volume, we are particularly interested in whether household-based belief dispersion has any net effects on trading volume beyond the extent to which their beliefs are correlated with those among professional forecasters. To study this, we collect professional forecasters' beliefs from the following three sources:

Survey of Professional Forecasters
The Survey of Professional Forecasters (SPF) is a survey of professional investors and analysts on their views about macroeconomic conditions.¹³ The SPF began in late 1960s, and we use the later portion of the SPF data that overlaps with the SCA data, from 1978 to 2011. The numbers of respondents for the SPF in recent years vary between 30 and 50. In addition to survey participants, the SPF differs from the SCA in a two other aspects. First, the SPF is conducted quarterly whereas the SCA is done monthly. We interpolate the SPF data to a monthly frequency to facilitate comparison. Moreover, the SPF answers are numerical, unlike the categorical answers in the household survey. The middle panel of Table 1 describes the SPF variables our study focuses on--growth of GDP, industrial production and corporate profit, and unemployment.¹⁴ The forecasters typically report to the SPF their level projections of an economic variable over the current and the next five quarters. We derived the implied annual growth forecast from the level forecast. For unemployment forecast, we use the annual averages.
Blue Chip Economic Indicator Survey
Blue Chip Economic Indicator Survey are survey data collected by a monthly newsletter published by Wolters Kluwer. Similar to the SPF, participants of the Blue Chip surveys are a mix of economists at large banks, consulting firms, or academic institutions. On average, the survey has around 50 participants each month. Our study focuses on the forecasts of the following variables--summarized in the lower panel of Table 1-- GDP growth, industrial production growth, nonresidential investment growth, unemployment rate, short-term interest rate, and longer-term interest rate.¹⁵Our sample of the Blue Chip survey data covers the period from 1984 to 2011.
I/B/E/S Analyst Forecasts of Corporate Earnings
The I/B/E/S database contains monthly updates of financial analyst forecasts of near-term levels of earnings-per-share (EPS) for the firms they cover. Pinto (2010) constructs a series of analysts' earning forecasts dispersion as the coefficient of variation of analysts' EPS estimates averaged across companies, which we use in this study. The series begin in 1976, and we use the period from 1978 to 2011 that overlaps with our main SCA data. The earnings forecasts are not exactly about macroeconomic conditions, which are the focus of the SCA, SPF and Blue Chip surveys. However, it is likely that the aggregate measure of forecasts' dispersion on earnings contains relevant information about the belief dispersion of macroeconomic variables that are particularly relevant for the stock market.

3.3 Trading Volume and Control Variables

Our measure of trading volume is the monthly turnover rate of the aggregate U.S. stock market (the total number of shares traded in a period divided by the average total number of shares outstanding during that period). Normalizing trading volume with shares outstanding allows us to abstract from increases in volume that are due mainly to the growth of the economy and the stock market. The turnover measure has been used in various studies, such as Campbell, Grossman, and Wang (1993). Data on both the number of shares traded and shares outstanding are from the Center for Research in Security Prices (CRSP). In our baseline analysis, we aggregate the monthly trading volume and shares outstanding of all securities traded on the New York Stock Exchange (NYSE), American Stock Exchange (AMEX), and NASDAQ.

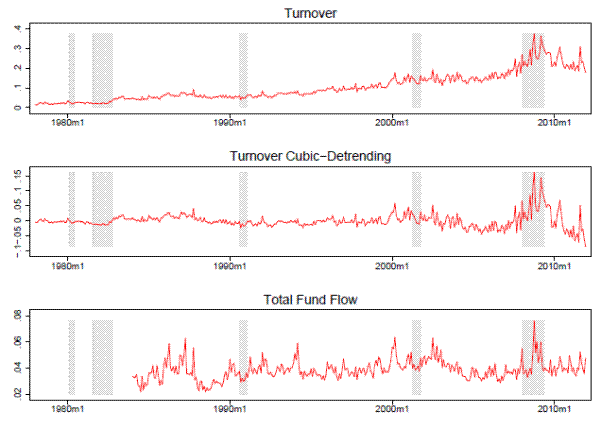
As shown in the upper panel of Figure 1, turnover rates in the U.S. stock market steadily increased during the SCA data sample period. Many explanations have been offered to explain this trend. For example, Smidt (1990) suggests that the long-run trend in equity turnover can be attributed to transaction cost changes. Some researchers also attribute this trend to the increasing importance of high-frequency trading. The Dickey-Fuller test we conduct suggests that the series is trend stationary. We then remove the trend using various detrending methods. The middle panel of Figure 1 shows the cubic detrended series of turnover, which is used in our baseline analysis. The cubic detrending method leaves smaller residual autocorrelation than linear, quadratic or fourth-order polynomial detrending method.¹⁶ The series has a zero mean and a standard deviation equal to 0.024.

As an alternative measure of market trading volume, we also use the gross flow of equity mutual funds. The data is from the Investment Company Institute. Monthly gross flows to the equity market are calculated as the sum of sales and redemption, normalized by total asset under management by equity mutual funds. The fund flow data start from January 1984 and are presented in the lower panel of Figure 1. Unlike the turnover rates, gross flows of equity mutual funds do not show any pronounced upward trend. One plausible explanation is that mutual fund flows reflect low-frequency trading that is not affected by the increasing importance of high-frequency trading, which likely contributed to the increase in stock turnovers.

We include the S&P 500 index return and the S&P 500 index volatility as control variables. Both variables are calculated from the CRSP data. In addition, we control for stock market liquidity, which is the Pastor-Stambaugh series (Pastor and Stambaugh, 2003) from WRDS. A higher value of the measure indicates more liquid market conditions.

4 Measures of Belief Dispersion

4.1 Dispersion Measures--Weighted Herfindahl Index

To measure belief dispersions from the SCA surveys, which have categorical answers, we introduce a weighted negative Herfindahl index (WNHI). Our measure is a variant of the widely used Herfindahl index, commonly used as a measure of market concentration in marketing and industrial organization research (see, for example, Neumark and Sharpe (1992)). We adapt it to measure the opposite of concentration--dispersion. Recall that the standard Herfindahl index is defined as

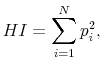$\displaystyle HI = \sum_{i=1}^{N}p_i^2,$

(1)

where

is the share of the

-th element among

elements. The Herfindahl index takes a value between

and 1. A lower value of the index indicates greater dispersion.

The standard Herfindahl index treats each of the elements symmetrically, without taking into account the ordering among the elements. In other words, the distances between elements are equal. However, one important aspect of the SCA data is that different answers are naturally ranked, and hence the distance between answers matters. For example, a sample consisting of 50 percent survey responses of "better off" and 50 percent "worse off" will yield the same value of standard Herfindahl index as a sample consisting of 50 percent "better off" and 50 percent "about the same" answers, although opinions in the first sample are more dispersed. To explicitly account for such relative distances, we construct (for each survey month) a weighted negative Herfindahl index as

$\displaystyle WNHI = -\sum_{i=1}^{N}\omega_i p_i^2,$

(2)

where $\omega_i$ is a weight assigned to element

. We take the negative value of the index for expositional convenience to make higher value of the index indicate greater dispersion. We give lower weights to elements closer to the polars and higher weights to elements in the middle so that we have less negative WNHI, or greater measured dispersion, for belief distributions with more polar responses. Specifically, in our baseline analysis, we let the weights on the answers of "better off" and "worse off" be equal to one and the weight on the answer of "about the same" be equal to two.

The weighting scheme of the measure not only allows us to preserve the rankings among categorical answers, but also provides flexibility in giving different importance to answers that are different in informational values. Answers of "about the same" are potentially "lazy answers" and reveal less information about the beliefs of the respondents.¹⁷ We can adjust for this by giving a high $\omega_i$ to these answers. That said, our results do not rely on any particular choice of weights; we alter the weights in the robustness analysis, and show that the results are qualitatively preserved.

4.2 Composite Dispersion Measure--A Principal Component Approach

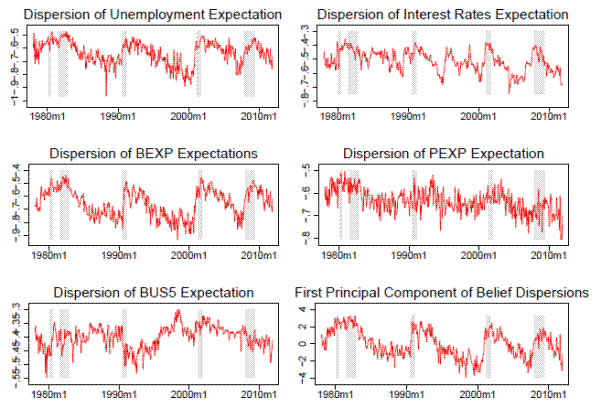
Figure 2 presents the time series of belief dispersion, measured using , for each SCA question we study. Recall that higher values of the (closer to zero) suggest more dispersed distribution of beliefs. Belief dispersions on different questions seem to follow a common pattern. In particular, consistent with Patton and Timmermann (2010), three of the five series of belief dispersion exhibit strong counter-cyclicality. The peaks in dispersion of expectations about near-term economic conditions (BEXP), interest rate, and unemployment largely coincide with recessions as defined by the National Bureau of Economic Research. However, the cyclical patterns in the belief dispersion for expectations about personal financial (PEXP) and longer-term business conditions (BUS5) are more muted. Moreover, it appears that beliefs about longer-term business conditions in the next five years (BUS5), are more dispersed than beliefs about shorter-term economic conditions in one year (BEXP).

Expectations on various macroeconomic indicators held by the same investor are likely correlated (people expecting lower unemployment also tend to expect better business conditions), potentially making dispersion of beliefs on these macroeconomic indicators also correlated. To summarize in a parsimonious manner the information contained in the five series of belief dispersion, following Buraschi and Whelan (2010), we compute the principal components of these series. Our subsequent analyses focus on the first principal component, which accounts for 50 percent of total variance. Each of the successive principal components explains no more than 20 percent of the total variance. As shown in the lower right panel of Figure 2, the first principal component exhibits pronounced counter-cyclicality. Heuristically, people may disagree more when greater uncertainty prevails. The cyclicality in our belief dispersion measures is broadly consistent with the cyclicality of economic uncertainty as documented in Bloom (2009).

The SPF and Blue Chip surveys provide numerical forecasts by professionals, which allow us to calculate belief dispersion as the cross-sectional standard deviation of the forecasts. As with the SCA, we compute the first principal components of the SPF and Blue Chip data, respectively. Finally, belief dispersion in the I/B/E/S data is summarized into a single series by taking a weighted average of firm-specific analysts' dispersion in their earnings forecasts (Pinto, 2010).

4.3 Visual Comparison of Various Dispersion Measures

Figure 3 contrasts the belief dispersion series derived from the four data sources. First, we notice that all four series demonstrate counter-cyclicality to some extent, with the cyclical pattern being particularly pronounced in the household belief dispersion series (SCA). A closer examination of the chart also reveals that household belief dispersions tend to rise sharply just before recessions (over the past twenty years in particular), whereas dispersions of professional forecasters tend to peak towards the end of recessions. This suggests that some household investors may have information predicting business cycles that is not possessed by professional analysts.¹⁸

It is too early to declare household investors a winner of the race, as each series shows some idiosyncratic dynamics that could be crucial for stock market trading volume. Indeed, as shown in the upper panel of Table 2, correlations among these series can be quite low, albeit positive. The SCA and SPF series have the highest correlation coefficient--0.63, while the SCA and the Blue Chip series have the lowest correlation coefficient--0.20, suggesting that the household belief dispersion series contain information orthogonal to what is reflected in the disagreement among professional analysts.

5 Baseline Results and Robustness Analysis

5.1 Baseline Analysis

We estimate the following model for stock market turnover:

$\displaystyle Turnover_m = \alpha + \rho Turnover_{m-1}+\beta WNHI_m + \gamma Mean^{ICE}_m + \delta_1 R_m +\delta_2 \sigma_m + \delta_3 LIQ_m \\ + \eta Pre2007+ \sum_{i=1}^{11}\psi_iI_{i=m} + \varepsilon_m,$

(3)

where

is the cubic polynomial-detrended turnover for month

. We include one lag, $Turnover_{m-1}$ , of the dependent variable as a control variable, taking into account the auto-correlations exhibited in the detrended turnover series. We control for the mean levels of the expectation index,

. The index is constructed by the SCA staff as a summary of investors' expectations about economic fundamentals and is therefore likely related to stock market trading activities.

is the contemporaneous gross return in the S&P 500 index. Many papers look at the relationship between stock returns and trading volume (see for example, Campbell, Grossman, and Wang (1993) and Llorente, Michaely, Saar, and Wang (2002)). We also control for stock market volatility $\sigma_m$ and stock market liquidity

, two additional factors potentially affecting market trading volume.¹⁹ In addition, considering the fact that market trading volume exploded during the financial crisis, and particularly so for stocks with the greatest level of institutional holdings (Chordia, Roll, and Subrahmanyam, 2011), we include a dummy,

, that indicates if the year is before 2007. The dummy controls for possible shifts in trading volume since the financial crisis that is not necessarily related to belief dispersion. Finally, we include a vector of monthly dummies to control for seasonal factors. Hong and Yu (2009) find that trading volume in summer vacation months is significantly lower than that in other months. In contrast, trading around year-end could be higher, partly driven by tax-related reasons. These seasonal fluctuations can be captured by the monthly dummies, denoted as $\sum_{i=1}^{11}\psi_iI_{i=m}$ in Equation (3).

In the above specification, the parameter of interest is $\beta$ . Recall that we construct the in such a way that higher (closer to zero) indicates greater belief dispersion. Should greater belief dispersion indeed induce larger trading volume, we will observe $\beta > 0$ in Equation (3). Column Model 1.a of Table 3 reports the baseline results of the relationship between stock trading volume and belief dispersion among household investors. All standard errors are adjusted for auto-correlations and heteroskadasticity using the Newey-West method.²⁰ Our estimates show that greater belief dispersion among household investors is indeed associated with higher stock turnover rates, and the estimated $\beta$ coefficient is positive, sizeable, and highly statistically significant. Putting the point-estimate in perspective, if the dispersion among household investors increases one standard deviation, the detrended monthly turnover rate will increase 0.56 percentage point, about one quarter of the standard deviation of the detrended turnover rate.

Regarding the effects of the control variables on stock turnover rate, we find that contemporaneous stock market returns are positively related to turnover rates, with a one-percent higher return inducing an approximately 0.4 percent higher detrended turnover rate. In addition, we find that the mean level of the household expectation index, , has a positive effect on turnover rates. Consistent with the literature, we find S&P 500 index volatility (annualized) to be significantly positively related to stock market trading volume. Somewhat surprisingly, stock market liquidity, as in Pastor and Stambaugh (2003), is negatively related to stock market trading volume, potentially due to the fact that episodes of high trading volume caused by fire sales tend to coincide with time of low market liquidity.

5.2 Horse Race Against Professional Analysts

Columns with heading Model 1.b through Model 1.d of Table 3 explore the relationships between stock market turnover and various belief dispersion measures for professional analysts. The models are almost identical to the one in Equation (3), except that the households' belief dispersion, , is replaced with those of professional analysts. Perhaps not surprisingly, estimated coefficients for belief dispersion in all three models are positive and statistically significant. An increase of one standard deviation in the belief dispersion among , Blue-Chip, and SPF analysts correspond to increase in detrended turnover rate of 9.5 percent, 12.1 percent and 10.9 percent, respectively. These numbers, though somewhat smaller than what is found for household belief dispersion, remain economically significant. To the best of our knowledge, this is the first exercise that documents a significant positive relationship between aggregate stock market trading volume and belief dispersion among professionals regarding macroeconomic conditions.

Since professional investors are typically deemed more sophisticated and informed than household investors, we are then interested in any incremental explanatory power of household belief dispersion over those among professional analysts. We do this by adding professional belief dispersions into our baseline model cumulatively. The results of the horse race are presented in columns Model 2 through Model 4 in Table 3. As shown in column Model 2, where the I/B/E/S dispersion series is added to Equation (3), the coefficient on household belief dispersion is little changed and remains statistically significant. Whereas the estimated coefficient for the I/B/E/S dispersion shrinks in magnitude compared to the result in Model 1.b and becomes statistically insignificant. In Model 3, we add Blue Chip dispersion to Model 2, and find that the size of the estimated coefficient for household belief dispersion somewhat increases and remains statistically significant. By contrast, the coefficient on Blue Chip dispersion series becomes smaller than in Model 1.c and less significant. Finally, when all four belief dispersion series are included, the coefficient on household belief dispersion (shown in the column Model 4) becomes the only one among four dispersion measures that is sizeable and significant at the 99-percent level. In contrast, statistical significance disappeared for the estimated coefficients on I/B/E/S and the SPF dispersion.²¹

The horse race results highlight the additional information in household belief dispersion that has a material effect on the dynamics in stock market trading volume. Our results thus sufficiently challenge the traditional view of households as noise traders, uninformed or insignificant participants in the stock market. To the extent that disagreement among such investors is significantly related to stock market trading volume, it is likely that, household investors collectively have information that professional analysts do not have and therefore contribute to price discovery and market efficiency.²²

5.3 Belief Dispersion and Mutual Fund Flow

A substantial portion of stocks are held by households through equity mutual funds. We therefore hypothesize that if household investors trade on their beliefs, greater disagreements among such investors may also leave footprints on equity mutual fund flows as they alter their exposures to market risks by changing their allocations to equity mutual funds. To test this hypothesis, we estimate Equation (3) with being replaced by the gross equity fund flow rate. The flow rate is calculated as the ratio between gross volume of equity mutual fund flows--the sum of new sales and redemption--and the total asset under management by stock mutual funds.²³The results, shown in Table 4, present several notable findings.

First, household belief dispersion is strongly positively related with gross equity fund flows. Model 1.a of Table 4 includes only the household belief dispersion variable. Professional dispersion series are added cumulatively in Model 2 through Model 4. Similar to the results for stock market turnover, we find equity fund flows to be positively related to household belief dispersion with a very high level of statistical significance. Second, the magnitude of household belief dispersion's effect on equity fund flows is significant across all models--a one-standard-deviation increase in household dispersion is associated with an increase in gross flow of one fifth of its standard deviation. Finally, disagreement among professional forecasters is either unrelated or negatively related to equity mutual fund flows. Somewhat surprisingly, most control variables, such as S&P return, stock market liquidity, and mean consumer expectation are unrelated to fund flows. Only the coefficient of S&P volatility is positively and statistically significant.

5.4 Robustness

Recall that in the baseline results presented above, we made specific choices on the method of detrending for our turnover rates, and on the weights used in constructing the dispersion measure . We now examine if our results are sensitive to these modeling choices. We implement a sequence of robustness analyses and show that the relationship presented between household belief dispersion and stock turnover rate is robust to various specification choices. The estimated $\beta$ coefficients in Equation (3) from alternative specifications are summarized in Table 5. The baseline results are presented in the top row of the table for comparison.

We first experiment with an alternative way of constructing the stock turnover rate. Specifically, we exclude trading in the NASDAQ exchange to address concerns that NASDAQ inter-dealer trades are double counted (Anderson and Dyl, 2005). We then experiment with various methods of detrending for the turnover rate time series. Specifically, we consider a linear trend, a quadratic trend, and a detrending algorithm used in Baker and Stein (2004).²⁴ All these results, presented in the upper panel of the table, suggest that variations in ways of constructing the dependent variable do not seem to materially change the results. The estimated $\beta$ coefficients remain sizeable with a very high level of statistical significance, with and without including in the model the series of belief dispersion among professional analysts.

We then experiment with giving different weights, $\omega_i$ in Equation (2), to survey answers of "about the same", when we compute the weighted Herfindahl index. In our baseline analysis, we give a weight of 2 to such answers. We now experiment with a smaller weight of 1.5 so that we down-weight such neutral answers to a less extent. Furthermore, we present the results where the ordering of the answers is not taken into account ( $\omega$ =(1,1,1)). Two observations stand out from the results. First, the estimated $\beta$ coefficient remains sizeable and statistically significant for both weighting options, regardless whether professional analysts' disagreement is controlled for, reassuring the robustness of our results. Second, the magnitude and statistical significance of $\beta$ estimates of $\omega$ =(1,1.5,1) are consistently smaller than in our baseline specification, and even more so for $\omega$ =(1,1,1), suggesting the extent to which we penalize central answers in constructing the belief dispersion series does matter regarding the explanatory power of the series with respect to trading activities. Indeed, we also experiment with assigning numerical values -1, 0, 1 to categorical answers of "worse," "same," and "better," respectively and compute the standard deviation as an alternative measure of belief dispersion. We find the estimated $\beta$ coefficients become less statistically significant, or even insignificant, as in Model 1.a and Model 2. Thus, we argue that, on balance, the we introduce serves as an informative and flexible way to better extract information regarding belief dispersion in categorical survey responses. That said, we also acknowledge that measuring household belief dispersion is tricky and the has its own potential limitations.

Finally, the bottom row of Table 5 shows that when we weight respondents' answers by their imputed likelihood of owning stocks before calculating the , our results become even more pronounced, suggesting that belief dispersion among households who are more likely investing in stocks matters more regarding stock market trading volume.²⁵

5.5 Why Household Beliefs Matters More?

What is the source of additional information possessed by households but not by professional analysts? We argue that the SCA panel is more heterogeneous and potentially captures information from a broad scope, as it consists of over 500 households that straddle different geographic locations, professions, personal financial and economic experience, and industry affiliations. Many studies document how economic shocks can vary among people across these dimensions. For example, Souleles (2004) finds household forecast errors in the SCA to be correlated to their demographic characteristics, as aggregate shocks do not hit all people equally. Favara and Song (2014) argue that dispersion of income shocks is a good proxy for information dispersion among city residents. The dispersion of income shocks also varies across cities, which helps explain cross-sectional differences in house price volatilities across US cities. In addition, two recent episodes of recessions affect specific industries, technology, and financial services disproportionately. Households who are directly linked to those industries likely form systematically different expectations from people linked to other industries. Finally, even with the same information set, people can form different expectations based on their different personal experience. Kaustia and Knüpfer (2008) find that people with more experience in IPO subscription make better return in future IPO investment. Choi, Laibson, Madrian, and Metrick (2009) find personal experience to affect saving decisions.

Compared to the SCA household data, the cross-section of professional forecasters in Blue-Chip, SPF, and I/B/E/S likely come from a more homogeneous pool. They typically work for the same industry (financial industry), live in a smaller set of metropolitan areas (likely financial center cities), and likely share similar personal financial experience. Thus, professional forecasters may possess an incomplete information set.

6 Identification Strategy and Evidence for A Causal Relationship

Thus far we have shown a pronounced positive correlation between belief dispersion among household investors and stock market trading volume. Such a relationship is robust to various model specifications and, in particular, to a horse race with belief dispersion among professional analysts. We now explore whether our results speak to a causal relationship between household disagreement and stock market trading.

Omitted variable bias is one obstacle we need to deal with before claiming causality. For example, one can potentially argue that household disagreement on macroeconomic conditions may be related to the amount of sunshine people have, which may also affect the amount of trading we observe. Although neither of such relationships has been documented, we cannot a priori rule them out. After all, Hirshleifer and Shumway (2003) find sunshine to be related to stock return. We address these concerns in two ways. The first method is a split-sample analysis. We split the sample of households in different ways and employ trading volume in different segments of the stock market to shed light on a causal effect. The premise of our test is that if household belief dispersion indeed affects trading volume, it should be true that belief dispersion among households who are more likely to own stocks has a stronger impact on trading volume. Similarly, household belief dispersion should have more impact on the volumes of stocks that are more visible to household investors.

An additional identification method we use is event study. We focus on events that increase visibility of individual stocks to household investors, and compare the sensitivity of the stock's turnover to household belief dispersion before and after such events. Specifically, the events we study are stock index inclusions and exclusions. We predict that post index inclusion, stocks' turnovers are more sensitive to household belief dispersion.

6.1 Analysis by Demographic Characteristics

To begin with, we study the effect on trading volume for belief dispersion among subgroups of households that have different demographic and socioeconomic characteristics and therefore have different propensities to own stocks. Existing studies, such as Hong, Kubik, and Stein (2004), document that prime-age, more educated, white, and higher-income investors are more likely to hold stocks. Consequently, we construct demographic-specific measures, as defined in Equation (2), using answers from subgroups of households that differ in dimensions such as age, educational attainment, race, and income, respectively. We then estimate Equation (3) with each of the demographic-specific s. We hypothesize that belief dispersion among prime-age, better educated, white, and higher-income consumers should have a more pronounced effect on stock trading volume.

The results, presented in Table 6, largely confirm our hypothesis. As in Table 5, we present the estimate of $\beta$ from the model that involves only household belief dispersion (Model 1.a) and the estimates from models that control for increasing number of analyst-based belief dispersion measures (Model 2, 3, 4). First, as shown in the top panel of the table, the $\beta$ coefficients corresponding to s calculated among consumers older than 35 are much larger and have a higher statistical significance than those for younger consumers. Second, belief dispersion among consumers without a high school diploma does not appear to affect stock trading volume. Third, the coefficients estimated for s derived among white investors are larger and more statistically significant than those estimated for belief dispersion among black investors. Similarly, the coefficients estimated for s derived from investors in the top quartile of income distribution are larger and more statistically significant than those estimated from investors in the bottom quartile. Finally, we divide the SCA sample by imputed stock ownership, which combines charateristics such as age, education, race, and income. The $\beta$ coefficients estimated for investors with an above-median likelihood to own stocks are larger and more statistically significant than the coefficients estimated for investors less likely to own stocks. To summarize, our results consistently show that belief dispersion among consumers more likely to own stocks has a greater effect on stock trading volume, which suggests that the relationship is likely causal.

6.2 Analysis by Market Capitalization

If dispersion of opinions drives households to trade stocks, and households are more drawn towards stocks of certain charateristics, we should observe the relationship between trading volume and household belief dispersion to be more pronounced for stocks more visible to households.

Unlike professional investors, who have the capacity to acquire and process information efficiently for a large set of stocks, household investors are more likely to focus their attention on a small subset of stocks that are more visible to them. Since stocks with larger market capitalization are more covered by media and analysts, these stocks should have greater visibility to retail investors. Indeed, Da, Engelberg, and Gao (2011) find that their direct measure of retail investors' attention to stocks--the Google search volume on the stock ticker--is significantly positively related to the size of the stock.

We thus hypothesize that trading volumes of large cap stocks are more sensitive to dispersion of opinions among household investors. We estimate Equation (3) with the detrended stock market turnover rates being replaced with turnover rates of companies in the top-, medium-, and bottom-terciles of market cap distribution, respectively. The results, controlling for all three belief dispersion series of professional analysts, are reported in Table 7, and they largely confirm our hypothesis. Indeed, the $\beta$ coefficient estimated for large-cap companies is similar to our baseline result (the left column), whereas household belief dispersion does not appear to materially affect trading volume of stocks of small- or medium-cap companies.

6.3 Evidence from S&P 500 Index Inclusion and Exclusion

One way for individual stocks to gain visibility among household investors is to be included in widely used indices, such as the S&P 500 index. We use events of index inclusion and exclusion to examine the changes in sensitivities of trading volume to household belief dispersion after changes in visibility. If household investors gravitate more towards highly visible stocks, such as those included in the S&P 500 index, we expect the sensitivity of trading volume to the belief dispersion among household investors to increase after index inclusion.

We use the S&P 500 index composition history file in CRSP to come up with a list of 728 index inclusion events, and 252 index exclusion events during the period of 1978-2011. The monthly turnover of these stocks around the index change events are calculated. The event window is chosen to be [-6,+6] months, and the event month, month 0, is removed. Since we are interested in time series variations, firm fixed-effects are included in the model. The panel setting in this exercise distinguishes itself from our baseline model where only aggregate stock market trading volume is studied.

We find that after being included in the S&P index, a stock's trading volume becomes more sensitive to household belief dispersion(Column 1 to 4 of Table 8), as suggested by the significantly positive coefficient for the term " $Post Event \times Household Disp$ ", which is an interaction term between the post event indicator and household belief dispersion. Trading volume's sensitivity to belief dispersion is not lowered immediately after index deletion (Column 5 to 8), where the interaction term becomes insignificant. The asymmetric results are consistent with similar asymmetric patterns of stock abnormal returns around index inclusion and exclusion events (Chen, Noronha, and Singal, 2004), which is explained by changes in investor awareness around index change events. Our results support the idea that stocks gain visibility to retail investors after being included in the index, but do not lose that visibility after being removed from the index. The event study results also suggest that our baseline results are not spurious; it holds true even in a panel setting, and is suggestive of a causal relationship between belief dispersion and trading volume.

7 Trading Volume and Dispersion of Belief Changes

Karpoff (1986) argues that, beside belief dispersion itself, dispersion in belief changes over a given period of time also affects trading activities. However, the theory has been tested far less frequently than the effect of the static belief dispersion dispersion. To test this hypothesis, similar to Bamber, Barron, and Stober (1997), we construct a measure of dispersion in belief changes that captures the differences in household belief dynamics.

In the SCA surveys, about 40 percent of the consumers are surveyed again six months after they were originally surveyed. We can thus track belief changes of the same household over a six-month interval.²⁶ When constructing a dispersion measure for belief changes, a similar problem arises. Recall that all of the SCA questions we study have categorical answers--whether the future of the economy will be better, worse, or about the same; whether an economic indicator, such as the interest rate and the unemployment rate, will go up, go down, or remain the same.

To measure dispersion of changes in categorial beliefs, in a similar way we measure dispersion in static beliefs, we first classify all possible belief changes into the following five types. For example, if a respondent's answer to a question six months ago was that "things will be worse", and the answer now is "things will be better", we consider the person having a "significantly improved outlook". Other changes of outlook are defined accordingly, as listed below. To reflect the fact that different types of belief changes are naturally ordered, we also assign different weights to them. The weights are chosen so that greater weights are assigned to no change in beliefs.

significantly improved outlook: "worse" $\rightarrow$ "better" $\omega = 1$
moderately improved outlook: "worse" $\rightarrow$ "the same" and "the same" $\rightarrow$ "better" $\omega = 1$
moderately deteriorated outlook: "the same" $\rightarrow$ "worse" and "better" $\rightarrow$ "the same" $\omega = 3$
significantly deteriorated outlook: "better" $\rightarrow$ "worse" $\omega = 3$
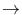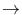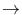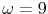
no change "better" $\rightarrow$ "better", "the same" $\rightarrow$ "the same" and "worse" $\rightarrow$ "worse" $\omega = 9$

The measure of dispersion of belief changes (DBC) is thus defined as below,

$\displaystyle DBC = -\sum_{j=1}^{5}\omega_j p_j^2,$

(4)

where corresponds to each of the five possible belief change outcomes.

To estimate the effects of dispersion of belief changes on trading volume, we replace the dispersion measure in Equation (3) with the measure of dispersion of belief changes, , defined above.²⁷ We study the effect of on stock turnover in month and in the six month period between and . All control variables are adjusted accordingly to be consistent with the time period for which the turnover rate refers to. The results are presented in Table 9 and are broadly consistent with the predictions of Karpoff (1986), that the extent to which people's belief revisions differ from each other also affects trading volume.²⁸ Indeed, $\beta$ -coefficients in both columns of Table 9 are sizeable and statistically significant.

8 Conclusion

This paper presents strong evidence that disagreement among household investors generates trades in the stock market. We find robust and pronounced evidence that stock turnovers and equity mutual fund flows are both positively related to the dispersion of household beliefs about the future macroeconomic outlook. Notably, household belief dispersions' effects on stock trading volume remain substantial and statistically significant even after controlling for up to three professional analyst-based dispersion measures, while those professional belief dispersion measures' impact on volume becomes statistically insignificant. Moreover, we find that the dispersion of belief changes ("belief jumbling") over a six-month period is also positively correlated with stock turnover rates during the same period--a relationship that has been tested only sparsely in the literature. In addition, our paper introduces the weighted Herfindahl index as a measure of belief dispersion for categorical responses provided in household surveys, a methodological innovation to the literature.

Exploiting some unique features of our consumers survey data, we present substantial evidence that greater belief dispersion may cause higher trading volume. In particular, we find that stock turnovers are more sensitive to belief dispersion among consumers who have greater propensities to own stocks. The impact of belief dispersion on trading activities is more prominent for stocks that are more visible to retail investors, such as stocks with larger capitalization and those that are recently included in the S&P 500 index.

Consistent with Campbell (2007) and Kelley and Tetlock (2013), our results indicate that household investors may have and trade on information not possessed by professional analysts. Household investors' collective involvement in the stock market contributes importantly to market efficiency and price discovery. More careful study of household stock trading activities presents a promising area of future research.

References

Agnew, Julie, Pieluigi Balduzzi, and Annika Sundén, 2003, Portfolio choice and trading in a large 401(k) plan, American Economic Review 93, 193-215.

Amromin, Gene, and Steven A. Sharpe, forthcoming, From the horse's mouth: How do investor expectations of risk and return vary with economic conditions?, Management Science.

Anderson, Anne-Marie, and Edward A. Dyl, 2005, Market structure and trading volume, Journal of Financial Research 28, 115-131.

Ang, Andrew, Geert Bekaert, and Min Wei, 2007, Do macro variables, asset markets, or surveys forecast inflation better?, Jounal of Monetary Economics 54, 1163-1212.

Baker, Malcolm, and Jeremy Stein, 2004, Market liquidity as a sentiment indicator, Journal of Financial Markets 7, 271-299.

Bamber, Linda Smith, Orie E. Barron, and Thomas L. Stober, 1997, Trading volume and different aspects of disagreement coincident with earnings announcements, The Accounting Review 72, 575-597.

Barber, Brad, Terrance Odean, and Ning Zhu, 2006, Do noise traders move markets, Working Paper.

Barberis, Nicholas, and Richard Thaler, 2003, A survey of behavioral finance, vol. 1 of Handbook of the Economics of Finance . pp. 1053-1128 (Elsevier).

Barron, Orie E., 1995, Trading volume and belief revisions that differ among individual analysts, Accounting Review 70, 581-597.

Barsky, Robert B., and Eric R. Sims, 2012, Information, animal spirits, and the meaning of innovations in consumer confidence, American Economic Review 102, 1343-1377.

Basak, Suleyman, 2000, A model of dynamic equilibrium asset pricing with heterogeneous beliefs and extraneous risk, Journal of Economic Dynamics and Control 24, 63-95.

____, 2005, Asset pricing with heterogeneous beliefs, Journal of Banking & Finance 29, 2849-2881.

Bessembinder, Hendrik, Kalok Chan, and Paul J. Seguin, 1996, An empirical examination of information, differences of opinion, and trading activity, Journal of Financial Economics 40, 105-134.

Bloom, Nick, 2009, The impact of uncertainty shocks, Econometrica 77, 623-685.

Buraschi, Andrea, and Paul Whelan, 2010, Term structure models with differences in beliefs, Working Paper.

Campbell, John, 2007, Who are the noise traders, Economist's View 61.

Campbell, John Y., Sanford J. Grossman, and Jiang Wang, 1993, Trading volume and serial correlation in stock returns, Quarterly Journal of Economics 108, 905-939.

Carroll, Christopher D, Jeffrey C Fuhrer, and David W Wilcox, 1994, Does consumer sentiment forecast household spending? if so, why?, American Economic Review 84, 1397-1408.

Chan, Louis K. C., Jason Karceski, and Josef Lakonishok, 2003, Analysts' conflict of interest and biases in earnings forecasts, Discussion paper National Bureau of Economic Research, Inc.

Chen, Honghui, Gregory Noronha, and Vijay Singal, 2004, The price response to s&p 500 index additions and deletions: Evidence of asymmetry and a new explanation, Journal of Finance 59, 1901-1930.

Choi, James J., David Laibson, Brigitte C. Madrian, and Andrew Metrick, 2009, Reinforcement learning and savings behavior, The Journal of Finance 64, 2515-2534.

Chordia, Tarun, Richard Roll, and Avanidhar Subrahmanyam, 2011, Recent trends in trading activity and market quality, Journal of Financial Economics 101, 243 - 263.

Comiskey, Eugene E., Ralph A. Walkling, and Michael A. Weeks, 1987, Dispersion of expectations and trading volume, Journal of Business Finance & Accounting 14, 229-239.

Da, Zhi, Joseph Engelberg, and Pengjie Gao, 2011, In search of attention, Journal of Finance 66, 1461-1499.

Detemple, Jerome, and Shashidhar Murthy, 1994, Intertemporal asset pricing with heterogeneous beliefs, Journal of Economic Theory 62, 294-320.

Dinh, Thanh Huong, and Jean-FranÃ§ois Gajewski, 2007, An experimental study of trading volume and divergence of expectations in relation to earnings announcement, CIRANO Working Papers 2007s-24 CIRANO.

Dumas, Bernard, 1989, Two-person dynamic equilibrium in the capital market, Review of Financial Studies pp. 157-188.

Favara, Giovanni, and Zheng Song, 2014, House price dynamics with dispersed information, Journal of Economic Theory 149, 350-382.

Goetzmann, William N., and Massimo Massa, 2005, Dispersion of opinion and stock returns, Journal of Financial Markets 8, 324-349.

Gollier, Christian, and Richard Zeckhauser, 2005, Aggregation of heterogeneous time preferences, Journal of Political Economy 113, 878-896.

Harris, M, and A Raviv, 1993, Differences of opinion make a horse race, Rev. Financ. Stud. 6, 473-506.

Hirshleifer, David, 2001, Investor psychology and asset pricing, Journal of Finance 56, 1533-1597.

Hoffmann, Arvid O.I., Thomas Post, and Joost M.E. Pennings, 2013, Individual investor perceptions and behavior during the financial crisis, Journal of Banking & Finance 37, 60-74.

Hong, Harrison, Jeffrey D. Kubik, and Amit Solomon, 2000, Security analysts' career concerns and herding of earnings forecasts, RAND Journal of Economics 31, 121-144.

Hong, Harrison, Jeffrey D. Kubik, and Jeremy C. Stein, 2004, Social interaction and Stock-Market participation, The Journal of Finance 59, 137-163.

Hong, Harrison, and Jeremy C. Stein, 2007, Disagreement and the stock market, Journal of Economic Perspectives 21, 109-128.

Hong, Harrison, and Jialin Yu, 2009, Gone fishin': Seasonality in trading activity and asset prices, Journal of Financial Markets 12, 672-702.

Jiang, Wang, 1996, The term structure of interest rates in a pure exchange economy with heterogeneous investors, Journal of Financial Economics 41, 75-110.

Kandel, Eugene, and Neil D Pearson, 1995, Differential interpretation of public signals and trade in speculative markets, Journal of Political Economy 103, 831-72.

Karpoff, Jonathan M, 1986, A theory of trading volume, Journal of Finance 41, 1069-87.

Kaustia, Markku, and Samuli Knüpfer, 2008, Do investors overweight personal experience? evidence from ipo subscriptions, The Journal of Finance 63, 2679-2702.

Kelley, Eric K., and Paul C. Tetlock, 2013, How wise are crowds? insights from retail orders and stock returns, Journal of Finance 68, 1229-1265.

Lang, Larry H.P., and Robert H. Litzenberger, 1989, Trading volume and changes in heterogeneous expectations, .

Llorente, Guillermo, Roni Michaely, Gideon Saar, and Jiang Wang, 2002, Dynamic volume-return relation of individual stocks, Review of Financial Studies 15, pp. 1005-1047.

Loh, Roger K., and René M. Stulz, 2014, Is sell-side research more valuable in bad times, NBER Working Paper 19778.

Mankiw, Gregory, and Steven Zeldes, 1991, The consumption of stockholders and nonstockholders, Journal of Financial Economics 29, 97-112.

Milgrom, Paul, and Nancy Stokey, 1982, Information, trade and common knowledge, Journal of Economic Theory 26, 17-27.

Neumark, David, and Steven A Sharpe, 1992, Market structure and the nature of price rigidity: Evidence from the market for consumer deposits, The Quarterly Journal of Economics 107, 657-80.

Odean, Terrance, 1998, Are investors reluctant to realize their losses?, Journal of Finance 53, 1775-1798.

____, 1999, Do investors trade too much?, American Economic Review 89, 1279-1298.

Pastor, Lubos, and Robert F. Stambaugh, 2003, Liquidity risk and expected stock returns, Journal of Political Economy 111, 642-685.

Patton, Andrew J., and Allan Timmermann, 2010, Why do forecasters disagree? lessons from the term structure of cross-sectional dispersion, Journal of Monetary Economics 57, 803 - 820.

Pinto, Eugenio, 2010, Forecasting investment with earnings expectations, unpublished memo.

Samuelson, William, and Richard Zeckhauser, 1988, Status quo bias in decision making, Journal of Risk and Uncertainty 1, 7-59.

Scheinkman, José, and Wei Xiong, 2002, Overconfidence, short-sale constraints, and bubbles, Princeton Economic Theory Working Papers.

Shefrin, Hersh, and Meir Statman, 1985, The disposition to sell winners too early and ride losers too long: Theory and evidence, Journal of Finance 40, 777-782.

Souleles, Nicholas S., 2004, Expectations, heterogeneous forecast errors, and consumption: Micro evidence from the michigan consumer sentiment surveys, Journal of Money, Credit and Banking 36, pp. 39-72.

Statman, Meir, Steven Thorley, and Keith Vorkink, 2006, Investor overconfidence and trading volume, Rev. Financ. Stud. 19, 1531-1565.

Tirole, Jean, 1982, On the possibility of speculation under rational expectations, Econometrica 50, 1163-81.

Varian, Hal R, 1985, Divergence of opinion in complete markets: A note, Journal of Finance 40, 309-17.

Vissing-Jørgensen, Annette, 2002, Limited stock market participation and the elasticity of intertemporal substitution, Journal of Political Economy 110, 825-853.

Wang, Jiang, 1994, A model of competitive stock trading volume, Journal of Political Economy 102, 127-168.

Warther, Vincent A., 1995, Aggregate mutual fund flows and security returns, Journal of Financial Economics 39, 209 - 235.

Ziebart, David A., 1990, The association between consensus of beliefs and trading activity surrounding earnings announcements., Accounting Review 65, 477-488.

Table 1: Description of Expectation Variables in SCA, SPF, and Bluechip

Variable	Description
Surveys of Consumers:	Now looking ahead--do you think that a year from now you (and your family living there) will be better off financially, or worse off, or just about the same as now?
Surveys of Consumers:	A year from now, do you expect that in the country as a whole business conditions will be better, or worse than they are at present, or just about the same?
Surveys of Consumers:	Looking ahead, which would you say is more likely--that in the country as a whole we’ll have continuous good times during the next five years or so, or that we will have periods of widespread unemployment or depression, or what?
Surveys of Consumers:	How about people out of work during the coming 12 months--do you think that there will be more unemployment than now, about the same, or less?
Surveys of Consumers:	Do you think will happen to interest rates for borrowing money during the next 12 months--will they go up, stay the same, or go down?
Survey of Professional Forecasters: GDP growth	log(ngdp5) - log(ngdp1), log difference between the GDP level projection of the quarter of the survey and the quarter one year later.
Survey of Professional Forecasters: Industrial production growth	log(indprod5) - log(indprod1), log difference between the industrial production level projection of the quarter of the survey and the quarter one year later.
Survey of Professional Forecasters: Corporate profit growth	log(cprof5) - log(cprof1), log difference between the corporate profit level projection of the quarter of the survey and the quarter one year later.
Survey of Professional Forecasters:Unemployment	(unemp2 + unemp3 + unemp4 + unemp5) / 4, average of the projected unemployment over the next four quarters.
Blue Chip Economic Indicator Survey: GDP growth	Projected annual GDP growth
Blue Chip Economic Indicator Survey:Industrial production growth	Projected annual industrial production growth
Blue Chip Economic Indicator Survey:Investment growth	Projected annual non-residential investment growth
Blue Chip Economic Indicator Survey: Unemployment	Projected unemployment
Blue Chip Economic Indicator Survey: Short-term interest rate	Projected 3-month Treasury bills rate
Blue Chip Economic Indicator Survey:Longer-term interest rate	Projected 10-year Treasury notes rate over the next year

Table 2: Overview of Dispersion Measures in Four Data Sources

Variables	SCA Household Disp	SPF Disp	IBES Analyst Disp	Blue-Chip Disp
SCA Household Disp	1.00
SPF Disp	0.63	1.00
IBES Analyst Disp	0.31	0.33	1.00
Blue-Chip Disp	0.20	0.55	0.56	1.00

	Std. Dev. (pcts)	Sample Period	N
SCA Household Disp	1.55	Jan. 1978-Dec. 2011	408
SPF Professional Disp	1.63	Jan. 1978-Dec. 2011	408
IBES Analyst Disp	1.42	Jan. 1978-Dec. 2011	408
Blue-Chip Disp	1.81	Jul. 1984-Dec. 2011	330

The upper panel presents pair-wise correlations for all four belief dispersion measures. The "SCA Household Disp" refers to belief dispersion among households surveyed in the Reuters/University of Michigan Surveys of Consumers. The "SPF Professional Disp" refers to belief dispersion among professional forecasters surveyed in the Survey of Professional Forecasters, "Blue-Chip Disp" refers to belief dispersion among respondents surveyed by the Blue Chip Economic Indicators, and "IBES Analyst Disp" refers to the series of corporate earnings belief dispersion among professional analysts that was constructed by Pinto (2010). All measures are monthly time series. The "SPF Professional Disp" is interpolated from quarterly surveys. The lower panel of the table presents standard deviations and sample period of the four series.

Table 3: Turnovers and Belief Dispersion

	Model 1.a	Model 1.b	Model 1.c	Model 1.d	Model 2	Model 3	Model 4
SCA Household Disp	0.359***				0.332***	0.417***	0.415***
SCA Household Disp (Standard error)	(0.075)				(0.078)	(0.096)	(0.097)
IBES Disp		0.164**			0.090	0.115	0.106
IBES Disp (Standard error)		(0.065)			(0.067)	(0.126)	(0.149)
Blue-Chip Disp			0.203***			0.136*	0.133*
Blue-Chip Disp (Standard error)			(0.062)			(0.078)	(0.081)
SPF Disp				0.172**			0.021
SPF Disp (Standard error)				(0.068)			(0.168)
Lag Turnover	0.489***	0.506***	0.482***	0.503***	0.477***	0.420***	0.420***
Lag Turnover (Standard error)	(0.040)	(0.041)	(0.046)	(0.042)	(0.041)	(0.048)	(0.048)
Mean Expectation	0.038***	0.011	0.014	0.021**	0.037***	0.054***	0.054***
Mean Expectation (Standard error)	(0.009)	(0.007)	(0.010)	(0.008)	(0.009)	(0.014)	(0.014)
S&P Return	0.384**	0.343**	0.315	0.334*	0.355**	0.321	0.320
S&P Return (Standard error)	(0.169)	(0.174)	(0.218)	(0.174)	(0.170)	(0.212)	(0.212)
S&P Volatility	7.543***	7.055***	7.557***	7.357***	7.290***	7.701***	7.675***
S&P Volatility (Standard error)	(1.220)	(1.250)	(1.412)	(1.239)	(1.233)	(1.383)	(1.396)
Stock Liquidity	-3.229**	-3.778**	-3.586**	-3.212**	-3.434**	-3.299**	-3.314**
Stock Liquidity (Standard error)	(1.448)	(1.485)	(1.665)	(1.482)	(1.450)	(1.603)	(1.608)
Pre 2007	-0.630**	0.050	-0.444	-0.252	-0.566*	-1.087***	-1.076***
Pre 2007 (Standard error)	(0.298)	(0.267)	(0.358)	(0.288)	(0.303)	(0.383)	(0.393)
Constant	-4.563***	-3.718***	-2.831***	-3.404***	-4.995***	-6.216***	-6.134***
Constant(Standard error)	(0.739)	(0.760)	(0.836)	(0.699)	(0.809)	(1.484)	(1.619)
Monthly Fixed-effects	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Adj. R-Squared	0.564	0.545	0.559	0.545	0.565	0.587	0.586
N	407	407	330	407	407	330	330

The table reports turnover's responses to the belief dispersion among households surveyed in SCA and among professional forecasters in SPF, Blue-Chip, and IBES. The model is described in Equation (3). The dependent variable is measured monthly and is quoted in percentage points. is also trend-adjusted using cubic detrending. Independent variables are described in Section 5.1. Model 1.a through Model 1.d include one of the four belief dispersion measures. Model 2 through Model 4 add professional dispersion measures to household dispersion measures cumulatively. Numbers in parentheses are Newey-West adjusted standard errors. ***, ** and * denote statistical significance at 1%, 5% and 10% levels, respectively.

Table 4: Mutual Fund Flow and Belief Dispersion

	Model 1.a	Model 1.b	Model 1.c	Model 1.d	Model 2	Model 3	Model 4
SCA Household Disp	0.060**				0.079***	0.086***	0.095***
SCA Household Disp (Standard error)	(0.024)				(0.025)	(0.026)	(0.026)
IBES Disp		-0.036			-0.060**	-0.029	0.013
IBES Disp(Standard error)		(0.024)			(0.025)	(0.033)	(0.040)
Blue-Chip Disp			-0.032**			-0.029	-0.020
Blue-Chip Disp(Standard error)			(0.016)			(0.021)	(0.022)
SPF Disp				-0.062**			-0.084*
SPF Disp(Standard error)				(0.028)			(0.045)
Lag Fund Flow	0.531***	0.547***	0.522***	0.536***	0.531***	0.504***	0.492***
Lag Fund Flow(Standard error)	(0.043)	(0.043)	(0.044)	(0.043)	(0.042)	(0.044)	(0.044)
Mean Expectation	0.006*	-0.001	0.001	-0.000	0.004	0.006*	0.007**
Mean Expectation(Standard error)	(0.003)	(0.003)	(0.003)	(0.003)	(0.003)	(0.003)	(0.004)
S&P Return	0.009	0.034	0.029	0.040	0.040	0.031	0.037
S&P Return(Standard error)	(0.056)	(0.058)	(0.058)	(0.057)	(0.057)	(0.057)	(0.057)
S&P Volatility	1.986***	2.170***	2.237***	2.317***	2.207***	2.274***	2.439***
S&P Volatility(Standard error)	(0.362)	(0.372)	(0.374)	(0.382)	(0.368)	(0.370)	(0.378)
Stock Liquidity	-0.453	-0.442	-0.418	-0.386	-0.381	-0.350	-0.276
Stock Liquidity(Standard error)	(0.443)	(0.447)	(0.446)	(0.446)	(0.440)	(0.439)	(0.438)
Pre 2007	-0.113	0.012	0.044	-0.003	-0.093	-0.074	-0.122
Pre 2007(Standard error)	(0.097)	(0.091)	(0.095)	(0.089)	(0.096)	(0.100)	(0.103)
Constant	1.509***	2.054***	1.753***	1.792***	1.948***	1.666***	1.335***
Constant(Standard error)	(0.274)	(0.328)	(0.258)	(0.257)	(0.327)	(0.377)	(0.414)
Month Effects	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Adj. R-Square	0.597	0.593	0.592	0.596	0.604	0.604	0.607
N	335	335	330	335	335	330	330

The table reports stock mutual fund flow's responses to the belief dispersion among households surveyed in SCA and among professional forecasters in SPF, Blue-Chip, and IBES. The model is described in Equation (3). The dependent variable is mutual fund gross flow as a percentage of total asset under management by stock mutual funds, and is quoted in percentage points. Independent variables are described in Section 5.1. Model 1.a through Model 1.d include one of the four belief dispersion measures. Model 2 through Model 4 add professional dispersion measures to household dispersion measures cumulatively. Numbers in parentheses are Newey-West adjusted standard errors. ***, ** and * denote statistical significance at 1%, 5% and 10% levels, respectively.

Table 5: Robustness of Baseline Results

Variation Type	Model 1.a	Model 2	Model 3	Model 4
Baseline	0.359***	0.332***	0.417***	0.415***
(cubic detrending, ) (Standard Error)	(0.105)	(0.109)	(0.134)	(0.134)
Variation in dependent variable ( ): Excluding NASDAQ	0.274**	0.247**	0.326**	0.332**
Variation in dependent variable ( ): Excluding NASDAQ (Standard Error)	(0.109)	(0.115)	(0.145)	(0.146)
Variation in dependent variable ( ): Linear Detrending	0.338***	0.343***	0.291**	0.256**
Variation in dependent variable ( ): Linear Detrending (Standard Error)	(0.104)	(0.111)	(0.121)	(0.119)
Variation in dependent variable ( ): Quadratic Detrending	0.351***	0.293***	0.361***	0.353***
Variation in dependent variable ( ): Quadratic Detrending (Standard Error)	(0.103)	(0.103)	(0.129)	(0.129)
Variation in dependent variable ( ): Baker-Stein Detrending	0.301***	0.314***	0.404***	0.420***
Variation in dependent variable ( ): Baker-Stein Detrending (Standard Error)	(0.105)	(0.114)	(0.143)	(0.144)
Variation in household dispersion measure calculation: Standard Deviation	0.122	0.082	0.259**	0.253**
Variation in household dispersion measure calculation: Standard Deviation (Standard Error )	(0.088)	(0.087)	(0.116)	(0.116)
Variation in household dispersion measure calculation:	0.295***	0.266***	0.346***	0.343***
Variation in household dispersion measure calculation: ( Standard Error)	(0.096)	(0.099)	(0.127)	(0.127)
Variation in household dispersion measure calculation:	0.261***	0.228**	0.270*	0.264*
Variation in household dispersion measure calculation: (Standard Error)	(0.092)	(0.098)	(0.143)	(0.144)
Variation in household dispersion measure calculation: Ownership Weighted	0.494***	0.540***	0.625***	0.637***
Variation in household dispersion measure calculation: Ownership Weighted (Standard Error)	(0.132)	(0.139)	(0.185)	(0.186)

This table reports coefficient $\beta$ as in Equation (3) estimated from variants of the baseline model. $\beta$ measures the sensitivity of stock market turnover to households' belief dispersion. Column titles "Model 1.a", "Model 2","Model 3","Model 4" correspond to model specifications in identically titled columns in Table 3. Where "Model 1.a" includes only "SCA Household Disp", and Model 2 through 4 add professional dispersion measures from SPF, Blue-Chip, and IBES cumulatively. The dependent variable is measured monthly and is quoted in percentage points. In the baseline model, the dependent variable is trend-adjusted using cubic detrending, and the household belief dispersion measure is calculated using the as defined in Equation (2) where the weights for answers of "better off", "about the same" and "worse off" are 1, 2 and 1, respectively. Details about the measure are described in Section 4.1. The upper part of this table deviates from the baseline model by changing the way the dependent variable ( ) is calculated. The lower part of the table deviates from the baseline model by changing the way household dispersion variable is calculated. Numbers in parentheses are Newey-West adjusted standard errors. ***, ** and * denote statistical significance at 1%, 5% and 10% levels, respectively.

Table 6: Turnover Sensitivities To Belief Dispersion Among Demographic Groups

Subgroups	Model 1.a	Model 2	Model 3	Model 4
by age: Age 35	0.171*	0.147	0.164	0.166
by age: Age 35 (Standard Error)	(0.098)	(0.099)	(0.112)	(0.113)
by age: Age $\ge$ 35	0.335***	0.307***	0.402***	0.405***
by age: Age $\ge$ 35 (Standard Error)	(0.095)	(0.099)	(0.123)	(0.124)
by education: Below high school	0.115	0.095	0.091	0.089
by education: Below high school (Standard Error)	(0.084)	(0.081)	(0.095)	(0.095)
by education: High school graduates	0.387***	0.361***	0.451***	0.452***
by education: High school graduates (Standard Error)	(0.108)	(0.113)	(0.140)	(0.141)
by race: Black	0.191***	0.180**	0.180*	0.177*
by race: Black (Standard Error)	(0.072)	(0.070)	(0.092)	(0.092)
by race: White	0.337***	0.305***	0.384***	0.382***
by race: White (Standard Error)	(0.102)	(0.108)	(0.132)	(0.132)
by income: Lowest income quintile	0.142*	0.124	0.190*	0.185*
by income: Lowest income quintile (Standard Error)	(0.084)	(0.082)	(0.107)	(0.108)
by income: Highest income quintile	0.260**	0.226*	0.252*	0.246*
by income: Highest income quintile (Standard Error)	(0.111)	(0.120)	(0.140)	(0.140)
by likelihood to hold stocks : Less likely to hold stocks	0.190**	0.173**	0.223**	0.219**
by likelihood to hold stocks : Less likely to hold stocks (Standard Error)	(0.084)	(0.082)	(0.104)	(0.105)
by likelihood to hold stocks : More likely to hold stocks	0.399***	0.372***	0.438***	0.439***
by likelihood to hold stocks : More likely to hold stocks (Standard Error)	(0.107)	(0.115)	(0.138)	(0.138)

This table reports coefficient $\beta$ as in Equation (3) estimated from different subsamples of the data based on demographic information. $\beta$ measures the sensitivity of stock market turnover to households' belief dispersion. Column titles "Model 1.a", "Model 2","Model 3","Model 4" correspond to model specifications in identically titled columns in Table 3. "Model 1.a" includes only "SCA Household Disp", and Model 2 through 4 add professional dispersion measures from SPF, Blue-Chip, and IBES cumulatively. The dependent variable is measured monthly and is quoted in percentage points. Numbers in parentheses are Newey-West adjusted standard errors. ***, ** and * denote statistical significance at 1%, 5% and 10% levels, respectively.

Table 7: Turnovers and Belief Dispersion, by Market Cap Tercile

	All	Large Cap	Medium Cap	Small Cap
SCA Household Disp	0.415***	0.404***	0.145	0.098
SCA Household Disp (Standard Error)	(0.097)	(0.125)	(0.099)	(0.088)
IBES Disp	0.106	0.138	0.240	0.185
IBES Disp (Standard Error)	(0.149)	(0.195)	(0.148)	(0.130)
Blue-Chip Disp	0.133*	0.200*	-0.060	-0.180**
Blue-Chip Disp (Standard Error)	(0.081)	(0.105)	(0.081)	(0.074)
SPF Disp	0.021	0.237	-0.047	0.098
SPF Disp (Standard Error)	(0.168)	(0.221)	(0.166)	(0.149)
Lag Turnover	0.420***	0.449***	0.611***	0.707***
Lag Turnover (Standard Error)	(0.048)	(0.047)	(0.041)	(0.034)
Mean Expectation	0.054***	0.040**	0.038***	0.039***
Mean Expectation (Standard Error)	(0.014)	(0.017)	(0.013)	(0.012)
S&P Return	0.320	0.108	0.910***	1.161***
S&P Return (Standard Error)	(0.212)	(0.275)	(0.233)	(0.220)
S&P Volatility	7.675***	10.774***	0.256	-0.778
S&P Volatility (Standard Error)	(1.396)	(1.832)	(1.364)	(1.264)
Stock liquidity	-3.314**	-4.331**	-3.093*	0.163
Stock liquidity (Standard Error)	(1.608)	(2.078)	(1.816)	(1.703)
Pre 2007	-1.076***	-2.319***	-1.223***	-0.366
Pre 2007 (Standard Error)	(0.393)	(0.536)	(0.397)	(0.338)
Constant	-6.134***	-4.446**	-4.093***	-3.437**
Constant (Standard Error)	(1.619)	(2.053)	(1.560)	(1.398)
Month Effects	Yes	Yes	Yes	Yes
Adj. R-Square	0.586	0.705	0.482	0.615
N	330	330	330	330

This table compares the sensitivity of turnover of different market cap terciles to the belief dispersion among households. The model is described in Equation (3). The dependent variable is measured monthly and is quoted in percentage points. It is also trend adjusted using cubic detrending. Independent variables are described in Section 5.1. Large, medium, and small cap are defined as the top 33%, 33%-66% and bottom 33% stocks in terms of market capitalization as of the end of the month. Numbers in parentheses are Newey-West adjusted standard errors. ***, ** and * denote statistical significance at 1%, 5% and 10% levels, respectively.

Table 8: Turnover Sensitivities To Belief Dispersion Before and After Index Addition and Deletion

	Addition: Model 1.a (1)	Addition:Model 2 (2)	Addition:Model 3 (3)	Addition:Model 4 (4)	Deletion: Model 1.a (5)	Deletion: Model 2 (6)	Deletion: Model 3 (7)	Deletion: Model 4 (8)
SCA Household Disp	0.077***	0.074***	0.078***	0.085***	0.120**	0.136***	0.136***	0.143***
SCA Household Disp (Standard Error)	(0.023)	(0.023)	(0.022)	(0.026)	(0.051)	(0.049)	(0.047)	(0.053)
Post Event	0.003	-0.004	0.001	0.044	-0.030	0.012	0.012	0.026
Post Event (Standard Error)	(0.032)	(0.033)	(0.031)	(0.042)	(0.133)	(0.131)	(0.131)	(0.162)
Post Event * Household Disp	0.044**	0.037**	0.039**	0.050*	0.020	0.056	0.056	0.058
Post Event * Household Disp (Standard Error)	(0.019)	(0.018)	(0.018)	(0.028)	(0.082)	(0.083)	(0.082)	(0.105)
IBES Analyst Disp		0.047*	0.074*	-0.017		-0.251***	-0.252***	-0.266**
IBES Analyst Disp (Standard Error)		(0.027)	(0.038)	(0.034)		(0.077)	(0.093)	(0.108)
SPF Professional Disp			-0.072	0.075*			0.003	0.048
SPF Professional Disp (Standard Error)			(0.056)	(0.041)			(0.101)	(0.146)
Blue-Chip Disp				-0.012				-0.046
Blue-Chip Disp (Standard Error)				(0.014)				(0.048)
Constant	1.283***	0.959**	0.876*	1.576***	1.063	2.800***	2.808***	2.926**
Constant (Standard error)	(0.333)	(0.431)	(0.452)	(0.431)	(0.844)	(1.017)	(0.998)	(1.152)
Month Effects	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Firm Effect	Yes	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Adj. R-Square	0.847	0.847	0.848	0.850	0.591	0.593	0.593	0.583
N	7,974	7,974	7,974	6,875	2,573	2,573	2,573	2,365

This table documents results from our event study of firm-specific stock turnover's sensitivity to aggregate household belief dispersion before and after the stock's inclusion into or deletion from the S&P 500 index. The "Event" is index addition for column (1) through (4), and index deletion for column (5) through (8). Stock turnover 6 months before and 6 months after index inclusion/deletion events are considered. The month of the event is removed from the sample. Column titles "Model 1.a", "Model 2","Model 3","Model 4" correspond to model specifications in identically titled columns in Table 3. Where "Model 1.a" includes only "SCA Household Disp", and Model 2 through 4 add professional dispersion measures to household dispersion measures cumulatively. equals one if the month of trading is after the month when the stock is either added into or deleted from the S&P 500 index, and zero otherwise. The index composition history file is from CRSP. Firm fixed effects are included in all regressions. The dependent variable is measured monthly and is quoted in percentage points. Numbers in parentheses are standard errors clustered at firm level. ***, ** and * denote statistical significance at 1%, 5% and 10% levels, respectively. Other control variables are not listed in the table.

Table 9: Turnovers and Dispersion of Household Belief Changes

	Turnover (1)	Turnover 6 month (2)
Disp of Belief Changes	0.167***	1.135***
Disp of Belief Changes (Standard error)	(0.062)	(0.359)
Lag Turnover	0.509***	0.520***
(Standard error)	(0.041)	(0.055)
Mean Expectation	0.016**	0.014*
Mean Expectation (Standard error)	(0.007)	(0.008)
S&P Return	0.388**	5.386**
S&P Return (Standard error)	(0.174)	(2.646)
S&P Volatility	7.698***	11.702***
S&P Volatility (Standard error)	(1.244)	(1.974)
Stock liquidity	-3.456**	-5.085
Stock liquidity (Standard error)	(1.490)	(3.719)
Pre 2007	-0.200	1.161
Pre 2007 (Standard error)	(0.278)	(1.859)
Constant	-3.189***	-28.088***
Constant (Standard error)	(0.664)	(5.102)
Month Effects	Yes	Yes
Adj. R-Square	0.546	0.657
N	401	396

The table reports turnover's responses to dispersion of changes in beliefs among SCA respondents. The model is similar to Equation (3), except that belief dispersion variable is replace with dispersion of belief change variable . The definition and calculation of is described in Section 4.2. The dependent variable is quoted in percentage points and trend-adjusted using cubic detrending. In column (1), the dependent variable is the turnover at the last month of the belief change window. In column (2), the dependent variable is the total turnover over the six months window when belief change happened. Other independent variables are described in Section 5.1. Numbers in parentheses are Newey-West adjusted standard errors. ***, ** and * denote statistical significance at 1%, 5% and 10% levels, respectively.

Figure 1:Stock Market Turnover and Aggregate Flows to Stock Market Mut ual Funds

Figure 1 Data

This figure plots monthly time series of our proxies for house hold trading activities in the US stock market. The top panel shows the turnover rates, the middle panel show s the turnover rates after cubic detrending and the bottom panel shows the aggregate flows to stock market mutual funds. All three variables are in fractions. Turnover rate is defined as the combined number of shares traded in NYSE, AMEX and NASDAQ in a given month divided by the average total number of shares outstanding during the same month. Mutual fund flow is defined as the sum of outflow and inflow as a fraction o f total asset under management by equity mutual funds in the same month. The date range is from 1978 to 2 011 for turnover rates and from 1984 to 2011 for total fund flow variable. Shaded areas correspond to NBER recessions.

Figure 2: Monthly Belief Dispersion from Household Surveys

Figure 2 Data

This figure plots time series of dispersion of beliefs on five e xpectation variables in the SCA. The five expectation variables are unemployment, interest rates, s hort-term business conditions (BEXP), personal financial conditions (PEXP), and long-term business condit ions (BUS5). The last panel plots the first principle component of the five dispersion series. Belief di spersion is measured using weighted negative Herfindahl index (WNHI) described in Equation (2). Larger va lues indicate higher dispersion. Shaded areas are NBER recession periods.

Figure 3: Comparison of Household Belief Dispersion Measure to Profes sional Belief Dispersion Measures

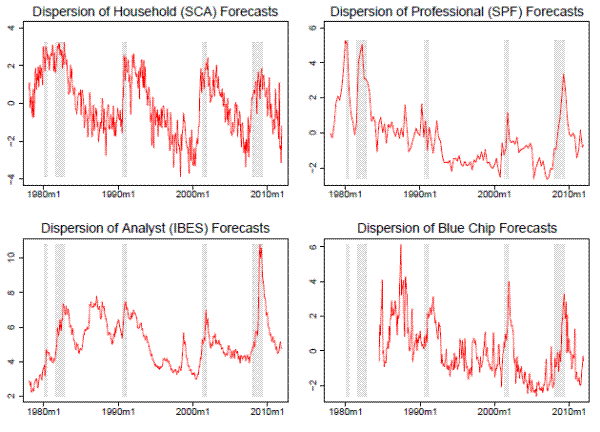Figure 3 Data

This figure compares belief dispersion among households in the SCA survey to the belief dispersions among professional forecasters in the SPF, IBES and Blue Chip surveys. Detailed description of the construction of these dispersion series is given in Section 4. Data frequency is monthly. The date range is from Jan. 1978 to Dec. 2011 for all time series except the Blue Chip time series, which is only available from Jul. 1984. Shaded areas correspond to NBER recessions.

Footnotes

* We thank Robert Barsky, Chris Carroll, Richard Green, Campbell Harvey, Harrison Hong, Frank de Jong, Stephen Sharpe, Nitish Sinha, Tyler Shumway, George Tauchen, Larry Wall, Wei Xiong, an anonymous editor, an anonymous referee, and conference and seminar participants for helpful discussions. We thank Patrick McCabe for his help on the ICI data, Eugenio Pinto for I/B/E/S data, and Min Wei and Scott Konzem for Blue Chip data. The views expressed herein are those of the authors and do not necessarily reflect the views of the Board of Governors of the Federal Reserve System or its staff. Return to Text

1. Flow of Funds Accounts published by the Federal Reserve Board. Return to Text

2. Other models have shown that trading arises among agents who have different endowment levels (Wang, 1994), discount rates (Gollier and Zeckhauser, 2005), and preferences (Dumas, 1989; Jiang, 1996). Return to Text

3. Throughout the paper, we will use "disagreement" and "belief dispersion" interchangeably. Return to Text

4. Survey respondents may simply check the modal answer "unchanged" to avoid taking a stand or being asked follow-up questions. Return to Text

5. Dispersion of belief changes is often dubbed "belief jumbling," a term introduced in Karpoff (1986) and Bamber, Barron, and Stober (1997). Return to Text

6. Regarding the first possibility, a rapidly growing literature in psychology and behavioral finance has documented the behavioral biases of human beings in making financial decisions. Hirshleifer (2001) and Barberis and Thaler (2003) provide thorough reviews of earlier contributions. Outside of the school of behavioral finance, a large body of the literature investigates trading volume under Tirole's second assumption, allowing agents to have different endowments or different preferences. For example, Wang (1994) introduces both heterogeneous investment opportunities (endowments) and asymmetric information in a competitive market, and identifies a link between the nature of heterogeneity among investors and the dynamics of trading volume. The challenge that the heterogeneous endowment argument faces is that it can generate only one round of trade, after which no further trade will take place. Return to Text

7. For subsequently developed models with different prior beliefs, see Detemple and Murthy (1994); for models in which investors have different ways of updating their posterior beliefs, see Harris and Raviv (1993) and Kandel and Pearson (1995). More recently, Scheinkman and Xiong (2002) suggest investor overconfidence as a potential source of heterogeneous beliefs, a hypothesis that finds empirical support in Statman, Thorley, and Vorkink (2006) Return to Text

8. The Index of Michigan Consumer Sentiment is included in the Leading Indicator Composite Index published by the Bureau of Economic Analysis because of its "economic significance" and "statistical adequacy." For more information about the SCA, see the documentation at the SCA webpage at www.sca.isr.umich.edu/. Return to Text

9. Although the survey started shortly after World War II, respondent-level data for the years before 1961 are not publicly available. For the period from 1961 to 1965, the respondent-level data are available only in February; for 1966, they are available in February and August; and for 1967 to 1977, the respondent-level data are available quarterly in February, May, August, and December. Return to Text

10. However, these consumers were not contacted again after the follow-up interview. Return to Text

11. From time to time, additional questions, known as the "riders", were added in special modules. These questions, though interesting and potentially closely related to stock market trading activities, are typically asked only for a limited number of months and are not asked at regular monthly frequency. Return to Text

12. The only exceptions are two questions about future inflation rates, for which consumers are asked to give numerical answers. We did not include inflation expectations in our study because, relative to dispersion of categorical responses, dispersion of numerical responses in consumer surveys are more prone to be influenced by "wild" answers. For example, some reported inflation expectations were as high as 50 percent per year. As a result, the cross-sectional standard deviations of inflation expectations in the SCA are much higher than those in the Survey of Professional Forecasters. Return to Text

13. The survey was conducted by the National Bureau of Economic Research before being transferred to the Federal Reserve Bank of Philadelphia in early 1990s. Return to Text

14. SPF began collecting forecasts of short- and longer-term interest rates in the third quarter of 1981. We do not include these forecasts in our baseline analysis to keep the sample period identical. Robustness tests that include the interest rates forecasts (using a shorter sample period) yields qualitatively similar results. Return to Text

15. Unlike the SPF, Blue Chip Economic Indicator Survey contains growth, instead of level, forecasts. Return to Text

16. In our robustness analysis, we experiment with different polynomial trends and a detrending technique due to Baker and Stein (2004). Return to Text

17. Choosing "about the same" answer is less cognitively consuming than answers that move away from the status quo. The so called "status quo bias" is extensively documented in the psycology and behavioral economics literature. See, for example, Samuelson and Zeckhauser (1988). Return to Text

18. In a recent working paper, Loh and Stulz (2014) also find that in bad times the accuracy of analysts' earnings forecasts is worse and that they disagree more. Return to Text

19. We also considered a specification with forward looking stock market volatility--the VIX, which measures the implied volatility of S&P 500 index options. The results are little changed. Return to Text

20. We use the Newey-West method with first-order autocorrelation. Allowing for higher orders of autocorrelation does not change the results qualitatively. Return to Text

21. Broadly speaking, the estimates of control variables are largely little changed across all columns in Table 3. There are only a few exceptions. First, the mean expectation coefficients are small and insignificant for Model 1.b (I/B/E/S) and Model 1.c (Blue Chip), and second, the coefficients of S&P return become less significant in columns Model 1.c, Model 3, and Model 4. The somewhat weaker effects of S&P returns on trading volume may be related to the lower sample frequencies (monthly) that our study uses, compared with the daily frequency used in the literature Return to Text

22. Examining market and limited orders placed by retail investors and the relationship between these orders and stock returns and firm news, (Kelley and Tetlock, 2013) also argue that retail investors potentially contribute to market efficiency. Return to Text

23. The mutual fund literature have been focusing on net flow, which is gross purchase minus gross redemption. Empirical studies on net flows to mutual funds largely establish a positive relationship between net flows and stock returns (see, for example, Warther (1995)). Return to Text

24. Baker and Stein (2004) propose a detrending technique of subtracting a lagged five-year mean from the current series. Return to Text

25. We impute the likelihood of owning stocks using a model estimated with the SCA data that include age, educational attainment, race, marital status, and income quartiles. Return to Text

26. One caveat of the data is that, for each consumer, only one observation of belief change is available because he will not be contacted again after the second interview. Return to Text

27. Assigning smaller weights to the status quo answers yields qualitatively similar but statistically less significant results. Return to Text

28. Because it is largely infeasible to construct belief revision measures using the surveys of professional analysts, we do not run a horse race as we do for belief dispersion. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text