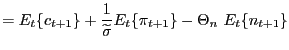Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 805, April 2004, Revised version: May 2006 --- Screen Reader Version*
This HTML version of this discussion paper is a revised and updated version of the same paper available as a PDF file at http://www.federalreserve.gov/pubs/ifdp/2004/805/ifdp805.pdf.
Understanding the Effects of Government Spending on Consumption*
International Finance Discussion Papers numbers 797-807 were presented on November 14-15, 2003 at the second conference sponsored by the International Research Forum on Monetary Policy sponsored by the European Central Bank, the Federal Reserve Board, the Center for German and European Studies at Georgetown University, and the Center for Financial Studies at the Goethe University in Frankfurt.
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. The views in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or any other person associated with the Federal Reserve System. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
Recent evidence suggests that consumption rises in response to an increase in government spending. That finding cannot be easily reconciled with existing optimizing business cycle models. We extend the standard new Keynesian model to allow for the presence of rule-of-thumb consumers. We show how the interaction of the latter with sticky prices and deficit financing can account for the existing evidence on the effects of government spending.
Keywords: rule-of-thumb consumers, non-Ricardian households, fiscal multiplier, government spending, Taylor rules rules
JEL Classification: E32, E62
1 Introduction
What are the effects of changes in government purchases on aggregate economic activity? How are those effects transmitted? Even though such questions are central to macroeconomics and its ability to inform economic policy, there is no widespread agreement on their answer. In particular, though most macroeconomic models predict that a rise in government purchases will have an expansionary effect on output, those models often differ regarding the implied effects on consumption. Since the latter variable is the largest component of aggregate demand, its response is a key determinant of the size of the government spending multiplier.
The standard RBC and the textbook IS-LM models provide a stark example of such differential qualitative predictions. The standard RBC model generally predicts a decline in consumption in response to a rise in government purchases of goods and services (henceforth, government spending, for short). In contrast, the IS-LM model predicts that consumption should rise, hence amplifying the effects of the expansion in government spending on output. Of course, the reason for the differential impact across those two models lies in how consumers are assumed to behave in each case. The RBC model features infinitely-lived Ricardian households, whose consumption decisions at any point in time are based on an intertemporal budget constraint. Ceteris paribus, an increase in government spending lowers the present value of after-tax income, thus generating a negative wealth effect that induces a cut in consumption.1By way of contrast, in the IS-LM model consumers behave in a non-Ricardian fashion, with their consumption being a function of their current disposable income and not of their lifetime resources. Accordingly, the implied effect of an increase in government spending will depend critically on how the latter is financed, with the multiplier increasing with the extent of deficit financing.2
What does the existing empirical evidence have to say regarding the consumption effects of changes in government spending? Can it help discriminate between the two paradigms mentioned above, on the grounds of the observed response of consumption? A number of recent empirical papers shed some light on those questions. They all apply multivariate time series methods in order to estimate the responses of consumption and a number of other variables to an exogenous increase in government spending. They differ, however, on the assumptions made in order to identify the exogenous component of that variable. In Section 2 we describe in some detail the findings from that literature that are most relevant to our purposes, and provide some additional empirical results of our own. In particular, and like several other authors that preceded us, we find that a positive government spending shock leads to a significant increase in consumption, while investment either falls or does not respond significantly. Thus, our evidence seems to be consistent with the predictions of models with non-Ricardian consumers, and hard to reconcile with those of the neoclassical paradigm.
After reviewing the evidence, we turn to our paper's main contribution: the development of a simple dynamic general equilibrium model that can potentially account for that evidence. Our framework shares many ingredients with recent dynamic optimizing sticky price models, though we modify the latter by allowing for the presence of rule-of-thumb behavior by some households.3 Following Campbell and Mankiw (1989), we assume that rule-of-thumb consumers do not borrow or save; instead, they are assumed to consume their current income fully. In our model, rule-of-thumb consumers coexist with conventional infinite-horizon Ricardian consumers.
The introduction of rule-of-thumb consumers in our model is motivated by an extensive empirical literature pointing to substantial deviations from the permanent income hypothesis. Much of that literature provides evidence of `` excessive'' dependence of consumption on current income. That evidence is based on the analysis of aggregate time series4, as well as natural experiments using micro data (e.g. response to anticipated tax refunds).5 That evidence also seems consistent with the observation that a significant fraction of households have near-zero net worth.6 On the basis of that evidence, Mankiw (2000) calls for the systematic incorporation of non-Ricardian households in macroeconomic models, and for an examination of the policy implications of their presence.
As further explained below, the existence of non-Ricardian households cannot in itself generate a positive response of consumption to a rise in government spending. To see this, consider the following equilibrium condition
Consider first an economy with a constant wedge,
![]() for all
for all
![]() . Notice that the
particular case of
. Notice that the
particular case of ![]() corresponds to the perfectly competitive case often assumed in the
RBC literature. According to both theory and evidence, an increase
in government purchases raises hours and, under standard
assumptions, lowers the marginal product of labor. Thus, it follows
that consumption must drop if the previous condition is to be
satisfied. Hence, a necessary condition for consumption to rise in
response to a fiscal expansion is the existence of a simultaneous
decline in the wedge
corresponds to the perfectly competitive case often assumed in the
RBC literature. According to both theory and evidence, an increase
in government purchases raises hours and, under standard
assumptions, lowers the marginal product of labor. Thus, it follows
that consumption must drop if the previous condition is to be
satisfied. Hence, a necessary condition for consumption to rise in
response to a fiscal expansion is the existence of a simultaneous
decline in the wedge ![]() .
This motivates the introduction in our framework of the assumption
of sticky prices in goods markets and, at least in one version of
our model, of imperfectly competitive labor markets. Those
complementary assumptions interact with the presence of
non-Ricardian consumers in a way that makes it possible to reverse
the sign of the response of consumption to changes in government
spending. As described below, our model predicts responses of
aggregate consumption and other variables that are in line with the
existing evidence, given plausible calibrations of the fraction of
rule-of-thumb consumers, the degree of price stickiness, and the
extent of deficit financing, .
.
This motivates the introduction in our framework of the assumption
of sticky prices in goods markets and, at least in one version of
our model, of imperfectly competitive labor markets. Those
complementary assumptions interact with the presence of
non-Ricardian consumers in a way that makes it possible to reverse
the sign of the response of consumption to changes in government
spending. As described below, our model predicts responses of
aggregate consumption and other variables that are in line with the
existing evidence, given plausible calibrations of the fraction of
rule-of-thumb consumers, the degree of price stickiness, and the
extent of deficit financing, .
Beyond the narrower focus of the present paper, a simple lesson emerges from our analysis: allowing for deviations from the strict Ricardian behavior assumed in the majority of existing macro models may be required in order to capture important aspects of the economy's workings.7 Our proposed framework, based on the simple model of rule-of-thumb consumers of Campbell and Mankiw (1989), while admittedly ad-hoc, provides in our view a good starting point.
The rest of the paper is organized as follows. Section 2 describes the existing empirical literature and provides some new evidence. Section 3 lays out the model and its different blocks. Section 4 contains an analysis of the model's equilibrium dynamics. Section 5 examines the equilibrium response to a government spending shock under alternative calibrations, focusing on the response of consumption and its consistency with the existing evidence. Section 6 summarizes the main findings of the paper and points to potential extensions and directions for further research.
2 An Overview of the Evidence
In the present section we start by summarizing the existing evidence on the response of consumption (and some other variables) to an exogenous increase in government spending, and provide some new evidence of our own. Most of the existing evidence relies on structural vector autoregressive models, with different papers using alternative identification schemes. Unfortunately, the data does not seem to speak with a single voice on this issue: while some papers uncover a large, positive and significant response of consumption, others find that such a response is small and often insignificant. As far as we know, however, there is no evidence in the literature pointing to the large and significant negative consumption response that would be consistent with the predictions of the neoclassical model.
Blanchard and Perotti (2002) and Fatás and Mihov (2001) identify exogenous shocks to government spending by assuming that the latter variable is predetermined relative to the other variables included in the VAR. Their most relevant findings for our purposes can be summarized as follows. First, a positive shock to government spending leads to a persistent rise in that variable. Second, the implied fiscal expansion generates a positive response in output, with the associated multiplier being greater than one in Fatás and Mihov (2001), but close to one in Blanchard and Perotti (2002). Third, in both papers the fiscal expansion leads to large (and significant) increases in consumption. Fourth, the response of investment to the spending shock is found to be insignificant in Fatás and Mihov (2001), but negative (and significant) in Blanchard and Perotti (2002).
Here we provide some complementary evidence using an identification strategy similar to the above mentioned papers. Using U.S. quarterly data, we estimate the responses of several macroeconomic variables to a government spending shock. The latter is identified by assuming that government purchases are not affected contemporaneously (i.e. within the quarter) by the innovations in the other variables contained in a VAR.8 Our VAR includes a measure of government spending, GDP, hours worked, consumption of nondurables and services, private nonresidential investment, the real wage, the budget deficit, and personal disposable income. In a way consistent with the model developed below, both government spending and the budget deficit enter the VAR as a ratio to trend GDP, where the latter is proxied by (lagged) potential output. The remaining variables are specified in logs, following convention.9.
Figure 1 displays the estimated impulse responses. Total government spending rises significantly and persistently, with a half-life of about four years. Output rises persistently in response to that shock, as predicted by the theory. Most interestingly, however, consumption is also shown to rise on impact and to remain persistently above zero. A similar pattern is displayed by disposable income; in fact, as shown in the bottom right graph, the response of consumption tracks, almost one-for-one, that of disposable income. With respect to the labor variables, our point estimates imply that both hours and the real wage rise persistently in response to the fiscal shock, although with some delay relative to government spending itself.10 By contrast investment falls slightly in the short run, though the response is not significant. Finally, the deficit rises significantly on impact, remaining positive for about two years.
Our point estimates in Figure 1 imply a government spending
multiplier on output,
![]() , of
, of ![]() on impact
on impact ![]() and of
and of ![]() at the end of the second year
(
at the end of the second year
(![]() ). Such estimated
multipliers are of a magnitude similar to the ones reported by
Blanchard and Perotti (2002). They are also roughly consistent with
the range of estimated short-run expenditure multipliers generated
by a variety of macroeconometric models.11 Most importantly for our purposes is
the observation that the multiplier on consumption is always
positive, going from
). Such estimated
multipliers are of a magnitude similar to the ones reported by
Blanchard and Perotti (2002). They are also roughly consistent with
the range of estimated short-run expenditure multipliers generated
by a variety of macroeconometric models.11 Most importantly for our purposes is
the observation that the multiplier on consumption is always
positive, going from ![]() on
impact to
on
impact to ![]() at the
end of the second year.
at the
end of the second year.
Table 1 illustrates the robustness of these findings to alternative specifications of the VAR, including number of variables (four vs. eight variable), sample period (full postwar, post Korean war, and post-1960), and definition of government spending (excluding and including military spending).12 The left panel of the table reports the size of the multipliers on output and consumption at different horizons (on impact, one-year, and two-year horizons, respectively).13 While the exact size of the estimated multipliers varies somewhat across specifications, the central finding of a positive response of consumption holds for the vast majority of cases.14
As mentioned above, some papers in the literature call into question (or at least qualify) the previous evidence. Perotti (2004) applies the methodology of Blanchard and Perotti (2002) to several OECD countries. He emphasizes the evidence of subsample instability in the effects of government spending shocks, with the responses in the 80s and 90s being more muted than in the earlier period. Nevertheless, the sign and magnitude of the response of private consumption in Perotti's estimates largely mimics that of GDP, both across countries and across sample periods. Hence, his findings support a positive comovement between consumption and income, conditional on government spending shocks, in a way consistent with the model developed below (though at odds with the neoclassical model).15
Mountford and Uhlig (2004) apply the agnostic identification procedure originally proposed in Uhlig (1997) to identify and estimate the effects of a `` balanced budget'' and a `` deficit spending'' shock.16 They find that government spending shocks crowd out both residential and non-residential investment, but they hardly change consumption (the response of the latter is small and insignificant).
Ramey and Shapiro (1998) use a narrative approach to identify shocks that raise military spending, and which they codify by means of a dummy variable (widely known as the "Ramey-Shapiro dummy"). They find that nondurable consumption displays a slight, though hardly significant decline, while durables consumption falls persistently, but only after a brief but quantitatively large rise on impact. They also find that the product wage decreases, even though the real wage remains pretty much unchanged.17
Several other papers have used subsequently the identification scheme proposed by Ramey and Shapiro in order to study the effects of exogenous changes in government spending on different variables. Thus, Edelberg, Eichenbaum and Fisher (1999) show that a Ramey-Shapiro episode triggers a fall in real wages, an increase in non-residential investment, and a mild and delayed fall in the consumption of nondurables and services, though durables consumption increases on impact. More recent work by Burnside, Eichenbaum and Fisher (2003) using a similar approach reports a flat response of aggregate consumption in the short run, followed by a small (and insignificant) rise in that variable several quarters after the Ramey-Shapiro episode is triggered.
Another branch of the literature, exemplified by the work of Giavazzi and Pagano (1990), has uncovered the presence of `` non-Keynesian effects'' (i.e. negative spending multipliers) during large fiscal consolidations, with output rising significantly despite large cuts in government spending. In particular, Perotti (1999) finds evidence of a negative comovement of consumption and government spending during such episodes of fiscal consolidation (and hence large spending cuts), but only in circumstances of `` fiscal stress'' (defined by unusually high debt/GDP ratios). In `` normal'' times, however, the estimated effects have the opposite sign, i.e. they imply a positive response of consumption to a rise in government purchases. Nevertheless, as shown in Alesina and Ardagna (1998), the evidence of non-Keynesian effects during fiscal consolidations can hardly be interpreted as favorable to the neoclassical model since, on average, cuts in government spending raise both output and consumption during those episodes.18
Overall, we view the evidence discussed above as tending to favor the predictions of the traditional Keynesian model over those of the neoclassical model. In particular, none of the evidence appears to support the kind of strong negative comovement between output and consumption predicted by the neoclassical model in response to changes in government spending. Furthermore, in trying to understand some of the empirical discrepancies discussed above it is worth emphasizing that the bulk of the papers focusing on the response to changes in government spending in "ordinary" times tend to support the traditional Keynesian hypothesis, in contrast with those that focus on "extraordinary" fiscal episodes (associated with wars or with large fiscal consolidations triggered by explosive debt dynamics).
In light of those considerations, we view the model developed below as an attempt to account for the effects of government spending shocks in `` normal'' times, as opposed to extraordinary episodes. Accordingly, we explore the conditions under which a dynamic general equilibrium model with nominal rigidities and rule-of-thumb consumers can account for the positive comovement of consumption and government purchases that arises in response to small exogenous variations in the latter variable.
3 A New Keynesian Model with Rule-of-Thumb Consumers
The economy consists of two types of households, a continuum of firms producing differentiated intermediate goods, a perfectly competitive firm producing a final good, a central bank in charge of monetary policy, and a fiscal authority. Next we describe the objectives and constraints of the different agents. Except for the presence of rule-of-thumb consumers, our framework consists of a standard dynamic stochastic general equilibrium model with staggered price setting à la Calvo.19
3.1 Households
We assume a continuum of infinitely-lived households, indexed by
![]() . A
fraction
. A
fraction ![]() of
households have access to capital markets where they can trade a
full set of contingent securities, and buy and sell physical
capital (which they accumulate and rent out to firms). We use the
term optimizing or Ricardian to refer to that subset of households.
The remaining fraction
of
households have access to capital markets where they can trade a
full set of contingent securities, and buy and sell physical
capital (which they accumulate and rent out to firms). We use the
term optimizing or Ricardian to refer to that subset of households.
The remaining fraction ![]() of households do not own any assets nor have
any liabilities, and just consume their current labor income. We
refer to them as rule of thumb
households. Different interpretations for that behavior include
myopia, lack of access to capital markets, fear of saving,
ignorance of intertemporal trading opportunities, etc. Our
assumptions imply an admittedly extreme form of non-Ricardian behavior among rule of thumb households, but one that captures in
a simple and parsimonious way some of the existing evidence,
without invoking a specific explanation. Campbell and Mankiw (1989)
provide some aggregate evidence, based on estimates of a modified
Euler equation, of the quantitative importance of such rule of
thumb consumers in the U.S. and other industrialized
economies.20
of households do not own any assets nor have
any liabilities, and just consume their current labor income. We
refer to them as rule of thumb
households. Different interpretations for that behavior include
myopia, lack of access to capital markets, fear of saving,
ignorance of intertemporal trading opportunities, etc. Our
assumptions imply an admittedly extreme form of non-Ricardian behavior among rule of thumb households, but one that captures in
a simple and parsimonious way some of the existing evidence,
without invoking a specific explanation. Campbell and Mankiw (1989)
provide some aggregate evidence, based on estimates of a modified
Euler equation, of the quantitative importance of such rule of
thumb consumers in the U.S. and other industrialized
economies.20
3.1.1 Optimizing Households
Let ![]() , and
, and
![]() represent
consumption and leisure for optimizing households. Preferences are
defined by the discount factor
represent
consumption and leisure for optimizing households. Preferences are
defined by the discount factor
![]() and the
period utility
and the
period utility
![]() .
A typical household of this type seeks to maximize
.
A typical household of this type seeks to maximize
subject to the sequence of budget constraints
and the capital accumulation equation
At the beginning of the period the consumer receives labor
income
![]() ,
where
,
where ![]() is the real wage,
is the real wage,
![]() is the price
level, and
is the price
level, and ![]() denotes hours of work. He also receives income from renting his
capital holdings
denotes hours of work. He also receives income from renting his
capital holdings ![]() to firms at the (real) rental cost
to firms at the (real) rental cost
![]() .
.
![]() is the
quantity of nominally riskless one-period bonds carried over from
period
is the
quantity of nominally riskless one-period bonds carried over from
period ![]() , and
paying one unit of the numéraire in period
, and
paying one unit of the numéraire in period ![]() .
. ![]() denotes the gross nominal return on bonds
purchased in period
denotes the gross nominal return on bonds
purchased in period ![]() .
.
![]() are dividends
from ownership of firms,
are dividends
from ownership of firms, ![]() denote lump-sum taxes (or transfers, if
negative) paid by these consumers.
denote lump-sum taxes (or transfers, if
negative) paid by these consumers. ![]() and
and ![]() denote, respectively, consumption and
investment expenditures, in real terms.
denote, respectively, consumption and
investment expenditures, in real terms. ![]() is the price of the final good.
Capital adjustment costs are introduced through the term
is the price of the final good.
Capital adjustment costs are introduced through the term
![]() ,
which determines the change in the capital stock induced by
investment spending
,
which determines the change in the capital stock induced by
investment spending ![]() . We assume
. We assume
![]() , and
, and
![]() , with
, with
![]() , and
, and
![]() .
.
In what follows we specialize the period utility-common to all households- to take the form:
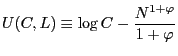
The first order conditions for the optimizing consumer's problem can be written as:
where
and where
We consider two alternative labor market structures. First we assume a competitive labor market, with each household choosing the quantity of hours supplied given the market wage. In that case the optimality conditions above must be supplemented with the first-order condition:
Under our second labor market structure wages are set in a centralized manner by an economy-wide union. In that case hours are assumed to be determined by firms (instead of being chosen optimally by households), given the wage set by the union. Households are willing to meet the demand from firms, under the assumption that wages always remain above all households' marginal rate of substitution. In that case condition (8) no longer applies. We refer the reader to section 3.6 below and Appendix 1 for a detailed description of the labor market under this alternative assumption.
3.1.2 Rule-of-Thumb Households
Rule-of-thumb households are assumed to behave in a "hand-to-mouth" fashion, fully consuming their current labor income. They do not smooth their consumption path in the face of fluctuations in labor income, nor do they intertemporally substitute in response to changes in interest rates. As noted above we do not take a stand on the sources of that behavior, though one may possibly attribute it to a combination of myopia, lack of access to financial markets, or (continuously) binding borrowing constraints.
Their period utility is given by
and they are subject to the budget constraint:
Accordingly, the level of consumption will equate labor income net of taxes:
Notice that we allow taxes paid by rule-of-thumb households
(![]() ) to differ
from those of the optimizing households (
) to differ
from those of the optimizing households (![]() ). Under the assumption of a
competitive labor market, the labor supply of rule-of-thumb
households must satisfy:
). Under the assumption of a
competitive labor market, the labor supply of rule-of-thumb
households must satisfy:
Alternatively, when the wage is set by a union, hours are determined by firms' labor demand, and (8) does not apply. Again we refer the reader to the discussion below.
3.1.4 Aggregation
Aggregate consumption and hours are given by a weighted average of the corresponding variables for each consumer type. Formally:
and
Similarly, aggregate investment and the capital stock are given by
3.2 Firms
We assume a continuum of monopolistically competitive firms producing differentiated intermediate goods. The latter are used as inputs by a (perfectly competitive) firm producing a single final good.
3.2.1 Final Goods Firm
The final good is produced by a representative, perfectly competitive firm with a constant returns technology:
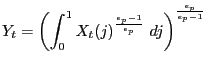
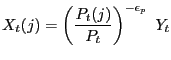
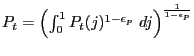 .
.
3.2.2 Intermediate Goods Firm
The production function for a typical intermediate goods firm
(say, the one producing good ![]() ) is given by:
) is given by:
where
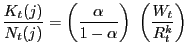
Real marginal cost is common to all firms and given by:
Price Setting. Intermediate firms are assumed to set nominal prices in a
staggered fashion, according to the stochastic time dependent rule
proposed by Calvo (1983). Each firm resets its price with
probability ![]() each
period, independently of the time elapsed since the last
adjustment. Thus, each period a measure
each
period, independently of the time elapsed since the last
adjustment. Thus, each period a measure ![]() of producers reset their
prices, while a fraction
of producers reset their
prices, while a fraction ![]() keep their prices unchanged.
keep their prices unchanged.
A firm resetting its price in period ![]() will seek to maximize
will seek to maximize
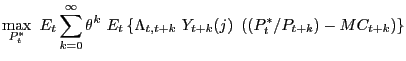
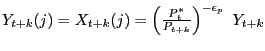 and where
and where
The first order condition for the above problem is:
where
3.3 Monetary Policy
In our baseline model the central bank is assumed to set the
nominal interest rate
![]() every period according to a simple linear interest rate rule:
every period according to a simple linear interest rate rule:
where
3.4 Fiscal Policy
The government budget constraint is
where
where
Finally, government purchases (in deviations from steady state, and normalized by steady state output) are assumed to evolve exogenously according to a first order autoregressive process:
where
3.5 Market Clearing
The clearing of factor and good markets requires that the
following conditions are satisfied for all ![]()
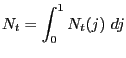
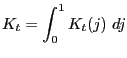
3.6 Linearized Equilibrium Conditions
In the present section we derive the log-linear versions of the
key optimality and market clearing conditions that will be used in
our analysis of the model's equilibrium dynamics. Some of these
conditions hold exactly, while others represent first-order
approximations around a zero-inflation steady state. Henceforth,
and unless otherwise noted, lower case letters denote
log-deviations with respect to the corresponding steady state
values (i.e.,
![]() ).
).
3.6.1 Households
Next we list the log-linearized versions of the above
households' optimality conditions, expressed in terms of the
aggregate variables. The log-linear equations describing the
dynamics of Tobin's ![]() and
its relationship with investment are given respectively by
and
its relationship with investment are given respectively by
and
The log-linearized capital accumulation equation is:
The log-linearized Euler equation for optimizing households is given by
Consumption for rule-of-thumb households is given, to a first order approximation by
where
As shown in the Appendix, the analysis is simplified by assuming
that steady state consumption is the
same across household types, i.e.
![]() , an
outcome that can always be guaranteed by an appropriate choice of
, an
outcome that can always be guaranteed by an appropriate choice of
![]() and
and ![]() . Since the focus of our paper
is on the differential responses to shocks, as opposed to steady
state differences across households, we view that assumption as
being largely innocuous, while simplifying the algebra
considerably.24 In
particular, under the above assumption, the log-linearized
expressions for aggregate consumption and hours take the following
simple form:
. Since the focus of our paper
is on the differential responses to shocks, as opposed to steady
state differences across households, we view that assumption as
being largely innocuous, while simplifying the algebra
considerably.24 In
particular, under the above assumption, the log-linearized
expressions for aggregate consumption and hours take the following
simple form:
and
Under perfectly competitive labor markets, we can log-linearize expressions (8), (12), and combine them with (28) and (29) to obtain:
Under the assumption of imperfectly competitive labor markets,
one can also interpret equation (30) as a
log-linear approximation to a generalized wage schedule of the form
![]() .
In that case, and under the assumption that each firm decides how
much labor to hire (given the wage), firms will allocate labor
demand uniformly across households, independently of their type.
Accordingly, we will have
.
In that case, and under the assumption that each firm decides how
much labor to hire (given the wage), firms will allocate labor
demand uniformly across households, independently of their type.
Accordingly, we will have
![]() for all
for all ![]() .25 In Appendix 1 we show how a wage
schedule of that form arises in an economy in which wages are set
by unions in order to maximize a weighted average of the utility of
both types of households.
.25 In Appendix 1 we show how a wage
schedule of that form arises in an economy in which wages are set
by unions in order to maximize a weighted average of the utility of
both types of households.
Independently of the assumed labor market structure we can derive an intertemporal equilibrium condition for aggregate consumption of the form:
In the case of perfectly competitive labor markets, the previous equation results from combining (8), (12), (26), (27), (28) and (29), the associated coefficients are given by:
where
By contrast, under the assumption of an imperfectly competitive
labor market, (31) can be derived from
combining (30), (26),
(27), (28), (29), as well as the assumption
![]() . In that case the
expressions for the coefficients in (31) are
given by:
. In that case the
expressions for the coefficients in (31) are
given by:
where
Notice that independently of the labor market structure assumed
we have
![]()
![]() ,
,
![]() , and
, and
![]()
![]() , i.e.,
as the fraction of rule-of-thumb consumers becomes negligible, the
aggregate Euler equation approaches its standard form given our
utility specification.
, i.e.,
as the fraction of rule-of-thumb consumers becomes negligible, the
aggregate Euler equation approaches its standard form given our
utility specification.
Discussion
A number of features of the above equilibrium conditions are
worth stressing. First, notice that the Euler equation (31) is the only log-linear equilibrium condition
involving aggregate variables which
displays a dependence on ![]() , the fraction of rule of thumb
households..
, the fraction of rule of thumb
households..
Second, the presence of rule-of-thumb households generates a direct effect of employment on the level of consumption (and, thus, on aggregate demand), beyond the effect of the long-term interest rate. This can be seen by "integrating" (31) to obtain the following expression in levels:
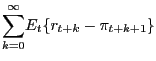
Thus, for any given path of real interest rates and taxes, an expansion in government purchases has the potential to raise aggregate consumption through its induced expansion in employment and the consequent rise in the real wage, labor income and, as a result, consumption of rule-of-thumb households. In turn, the resulting increase in consumption would raise aggregate demand, output and employment even further, thus triggering a multiplier effect analogous to the one found in traditional Keynesian models.
Third, the ultimate effect of government purchases on aggregate consumption depends on the response of taxes (accruing to rule-of-thumb households) and the expected long term real rate. Those responses will, in turn, be determined by the fiscal and monetary policy rules in place. Nevertheless, it is clear from the previous equation that in order for aggregate consumption to increase in response to a rise in government spending, the response of taxes and interest rates should be sufficiently muted. We return to this point below, when analyzing the sensitivity of our results to alternative calibrations of those policies.
3.6.2 Firms
Log-linearization of (16) and (17) around the zero inflation steady state yields the familiar equation describing the dynamics of inflation as a function of the log deviations of the average markup from its steady state level
where
or, equivalently,
Furthermore, as shown in Woodford (2003), the following "aggregate production function" holds, up to a first order approximation:
3.6.3 Market clearing
Log-linearization of the market clearing condition of the final good around the steady state yields:
where
3.6.4 Fiscal Policy
Linearization of the government budget constraint (19) around a steady state with zero debt and a balanced primary budget yields
Hence, under our assumptions, a necessary and sufficient
condition for non-explosive debt dynamics is given by
![]() , or equivalently
, or equivalently
4 Analysis of Equilibrium Dynamics
Combining all the equilibrium conditions and doing some straightforward, though tedious, substitutions we can obtain a system of stochastic difference equations describing the log-linearized equilibrium dynamics of the form
where
Each period is assumed to correspond to a quarter. We set the
discount factor ![]() equal to
equal to ![]() . We
assume a steady state price markup
. We
assume a steady state price markup ![]() equal to
equal to ![]() . The rate of depreciation
. The rate of depreciation ![]() is set to
is set to ![]() . The elasticity of output with
respect to capital,
. The elasticity of output with
respect to capital, ![]() ,
is assumed to be
,
is assumed to be
![]() , a value
roughly consistent with observed income shares, given the assumed
steady state price markup. All the previous parameter values remain
unchanged in the analysis below. Next we turn to the parameters for
which we conduct some sensitivity analysis, distinguishing between
the non-policy and the policy parameters.
, a value
roughly consistent with observed income shares, given the assumed
steady state price markup. All the previous parameter values remain
unchanged in the analysis below. Next we turn to the parameters for
which we conduct some sensitivity analysis, distinguishing between
the non-policy and the policy parameters.
Our baseline setting for the weight of rule-of-thumb households
![]() is
is
![]() . This is
within the range of estimated values in the literature of the
weight of the rule-of-thumb behavior (see Mankiw (2000)). The
fraction of firms that keep their prices unchanged,
. This is
within the range of estimated values in the literature of the
weight of the rule-of-thumb behavior (see Mankiw (2000)). The
fraction of firms that keep their prices unchanged, ![]() , is given a baseline value of
, is given a baseline value of
![]() , which
corresponds to an average price duration of one year. We set the
baseline value for the elasticity of wages with respect to hours
(
, which
corresponds to an average price duration of one year. We set the
baseline value for the elasticity of wages with respect to hours
(![]() ) equal to
) equal to
![]() . This is
consistent with Rotemberg and Woodford's (1997, 1999) calibration
of the elasticity of wages with respect to output of
. This is
consistent with Rotemberg and Woodford's (1997, 1999) calibration
of the elasticity of wages with respect to output of ![]() combined with an elasticity of
output with respect to hours of
combined with an elasticity of
output with respect to hours of
![]() . Finally,
we follow King and Watson (1996), and set
. Finally,
we follow King and Watson (1996), and set ![]() (the elasticity of investment
with respect to
(the elasticity of investment
with respect to ![]() )
equal to
)
equal to ![]() in our
baseline calibration.
in our
baseline calibration.
The baseline policy parameters are chosen as follows. We set the
size of the response of the monetary authority to inflation,
![]() , to
, to
![]() , a value commonly
used in empirical Taylor rules (and one that satisfies the
so-called Taylor principle). In order to calibrate the parameters
describing the fiscal policy rule (20) and
the government spending shock (21) (i.e.
, a value commonly
used in empirical Taylor rules (and one that satisfies the
so-called Taylor principle). In order to calibrate the parameters
describing the fiscal policy rule (20) and
the government spending shock (21) (i.e.
![]() ,
, ![]() , and
, and ![]() ) we use the VAR-based
estimates of the dynamic responses of government spending and
deficit (see Table 1 for details). In particular, we set the
baseline value of the parameter
) we use the VAR-based
estimates of the dynamic responses of government spending and
deficit (see Table 1 for details). In particular, we set the
baseline value of the parameter
![]() that
matches the half-life of the responses of government spending. The
latter value reflects the highly persistent response of government
spending to its own shock. We obtain the values of the parameter
that
matches the half-life of the responses of government spending. The
latter value reflects the highly persistent response of government
spending to its own shock. We obtain the values of the parameter
![]() from the
difference between the estimated impact responses of government
spending and deficit, respectively. As can be seen from Table 1,
our (average) estimates suggest a value for that parameter equal to
from the
difference between the estimated impact responses of government
spending and deficit, respectively. As can be seen from Table 1,
our (average) estimates suggest a value for that parameter equal to
![]() . Interestingly,
the estimates in Table IV of Blanchard and Perotti (2002) imply a
corresponding estimate of
. Interestingly,
the estimates in Table IV of Blanchard and Perotti (2002) imply a
corresponding estimate of ![]() , very much in line with our estimates and
baseline calibration. Finally, and given
, very much in line with our estimates and
baseline calibration. Finally, and given ![]() and
and ![]() , we calibrate parameter
, we calibrate parameter
![]() such that the
dynamics of government spending (21) and debt
(37) are consistent with the horizon at
which the deficit is back to zero in our estimates. Hence, in our
baseline calibration we set
such that the
dynamics of government spending (21) and debt
(37) are consistent with the horizon at
which the deficit is back to zero in our estimates. Hence, in our
baseline calibration we set
![]() , in line
with the estimated averages for different subsamples, as described
in Table 1. Finally, we set
, in line
with the estimated averages for different subsamples, as described
in Table 1. Finally, we set
![]() , which
roughly corresponds to the average share of government purchases in
GDP in postwar U.S. data.
, which
roughly corresponds to the average share of government purchases in
GDP in postwar U.S. data.
Much of the sensitivity analysis below focuses on the share of
rule-of-thumb households (![]() ) and its interaction with parameters
) and its interaction with parameters
![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and
![]() . Given the
importance of the fiscal rule parameters in the determination of
aggregate consumption (and, indirectly, of other variables) we will
also analyze the effect of alternative values for the policy
parameters
. Given the
importance of the fiscal rule parameters in the determination of
aggregate consumption (and, indirectly, of other variables) we will
also analyze the effect of alternative values for the policy
parameters ![]() and
and
![]() .
.
4.1 Rule-of-Thumb Consumers, Indeterminacy, and the Taylor Principle
Next we provide a brief analysis of the conditions that
guarantee the uniqueness of equilibrium. A more detailed analysis
of those conditions for an economy similar to the one considered
here (albeit without a fiscal block) can be found in Galí,
López-Salido and Vallés (2004). In that paper we show
how the presence of rule-of-thumb consumers can alter dramatically
the equilibrium properties of an otherwise standard dynamic sticky
price model. In particular, under certain parameter configurations
the economy's equilibrium may be indeterminate (and thus may
display stationary sunspot
fluctuations) even when the interest rate rule is one that
satisfies the Taylor principle (which corresponds to
![]() in our
model).
in our
model).
Figure 2 illustrates that phenomenon for the model developed in
the previous section. In particular the figure displays the regions
in ![]() ,
, ![]() space associated with either
a unique equilibrium or indeterminacy, when the remaining
parameters are kept at their baseline values. We see that
indeterminacy arises whenever a high degree of price stickiness
coexists with a sufficiently large weight of rule-of-thumb
households. Both frictions are thus seen to be necessary in order
for indeterminacy to emerge as a property of the equilibrium
dynamics. The figure also makes clear that the equilibrium is
unique under our baseline calibration (
space associated with either
a unique equilibrium or indeterminacy, when the remaining
parameters are kept at their baseline values. We see that
indeterminacy arises whenever a high degree of price stickiness
coexists with a sufficiently large weight of rule-of-thumb
households. Both frictions are thus seen to be necessary in order
for indeterminacy to emerge as a property of the equilibrium
dynamics. The figure also makes clear that the equilibrium is
unique under our baseline calibration (
![]() ,
,
![]() ). We
refer the reader to Galí, López-Salido and
Vallés (2004) for a discussion of the intuition underlying
that violation of the Taylor principle.26
). We
refer the reader to Galí, López-Salido and
Vallés (2004) for a discussion of the intuition underlying
that violation of the Taylor principle.26
5 The Effects of Government Spending Shocks
In the present section we analyze the effects of shocks to government spending in the model economy described above. In particular, we focus on the conditions under which an exogenous increase in government spending has a positive effect on consumption, as found in much of the existing evidence. Throughout we restrict ourselves to configurations of parameter values for which the equilibrium is unique.
Figure 3 shows the contemporaneous
response of output, consumption and investment (all normalized by
steady state output) to a positive government spending shock, as a
function of ![]() the
fraction of rule-of-thumb consumers. The size of the shock is
normalized to a one percent of steady state output. Given the above
normalizations, the plotted values can be interpreted as impact
multipliers. We restrict the range of
the
fraction of rule-of-thumb consumers. The size of the shock is
normalized to a one percent of steady state output. Given the above
normalizations, the plotted values can be interpreted as impact
multipliers. We restrict the range of ![]() values considered to those
consistent with a unique equilibrium. The remaining parameters are
kept at their baseline values. Figure 3.A corresponds to the
economy with competitive labor markets, Figure 3.B to its
imperfectly competitive counterpart. In the former case,
consumption declines for most values of
values considered to those
consistent with a unique equilibrium. The remaining parameters are
kept at their baseline values. Figure 3.A corresponds to the
economy with competitive labor markets, Figure 3.B to its
imperfectly competitive counterpart. In the former case,
consumption declines for most values of ![]() considered, except for
implausible large ones. The (absolute) size of the decline is,
however, decreasing in
considered, except for
implausible large ones. The (absolute) size of the decline is,
however, decreasing in ![]() , reflecting the offsetting role of
rule-of-thumb behavior on the conventional negative wealth and
intertemporal substitution effects triggered by the fiscal
expansion. When imperfect labor markets are assumed, the
possibility of crowding-in of consumption emerges for values of
, reflecting the offsetting role of
rule-of-thumb behavior on the conventional negative wealth and
intertemporal substitution effects triggered by the fiscal
expansion. When imperfect labor markets are assumed, the
possibility of crowding-in of consumption emerges for values of
![]() above a
threshold value of roughly
above a
threshold value of roughly
![]() , a more
plausible value. Notice also that the government spending
multiplier on inflation and output rises rapidly when
, a more
plausible value. Notice also that the government spending
multiplier on inflation and output rises rapidly when ![]() increases, attaining values
roughly in line with the empirical evidence reviewed in section
2.
increases, attaining values
roughly in line with the empirical evidence reviewed in section
2.
Figure 4 displays the dynamic responses of some key variables in
our model to a positive government spending shock under the
baseline calibration, and compares them to those generated by a
neoclassical economy. The latter corresponds to a particular
calibration of our model, with no price rigidities and no
rule-of-thumb consumers (
![]() ).
Again we consider two alternative labor market structures,
competitive and non-competitive. In each case the top-left graph
displays the pattern of the three fiscal variables (spending, taxes
and the deficit) in response to the shock considered. Notice that
the pattern of both variables is close to the one estimated in the
data (see Figure 1), consistently with our calibration of the
fiscal policy rule. The figure illustrates the amplifying effects
of the introduction of rule-of-thumb consumers and sticky prices:
the response of output and consumption is systematically above that
generated by the neoclassical model.27 Furthermore, in the baseline model,
and in contrast with the neoclassical model, the increase in
aggregate hours coexists with an increase in real wages. Overall we
view the model's predictions under the assumption of imperfectly
competitive labor markets as matching the empirical responses, at
least qualitatively.
).
Again we consider two alternative labor market structures,
competitive and non-competitive. In each case the top-left graph
displays the pattern of the three fiscal variables (spending, taxes
and the deficit) in response to the shock considered. Notice that
the pattern of both variables is close to the one estimated in the
data (see Figure 1), consistently with our calibration of the
fiscal policy rule. The figure illustrates the amplifying effects
of the introduction of rule-of-thumb consumers and sticky prices:
the response of output and consumption is systematically above that
generated by the neoclassical model.27 Furthermore, in the baseline model,
and in contrast with the neoclassical model, the increase in
aggregate hours coexists with an increase in real wages. Overall we
view the model's predictions under the assumption of imperfectly
competitive labor markets as matching the empirical responses, at
least qualitatively.
Figure 5 shows the government spending (impact) multipliers on
output, consumption, and investment, as a function of ![]() , the parameter measuring
the persistence of the spending process. In order to avoid
excessive dispersion, we henceforth report findings only for the
non-competitive labor market specification, which the analysis
above pointed to as the most promising one given our objectives.
Each of the four graphs in the Figure corresponds to a different
parameter configuration. The top-left graph is associated with our
baseline calibration. Notice that that in that case the crowding-in
effect on consumption (and the consequent enhancement of the output
multiplier) is decreasing in
, the parameter measuring
the persistence of the spending process. In order to avoid
excessive dispersion, we henceforth report findings only for the
non-competitive labor market specification, which the analysis
above pointed to as the most promising one given our objectives.
Each of the four graphs in the Figure corresponds to a different
parameter configuration. The top-left graph is associated with our
baseline calibration. Notice that that in that case the crowding-in
effect on consumption (and the consequent enhancement of the output
multiplier) is decreasing in ![]() . The intuition for that result is
straightforward: higher values of that parameter are associated
with stronger (negative) wealth effects lowering the consumption of
Ricardian households. Yet, we see that even for values of
. The intuition for that result is
straightforward: higher values of that parameter are associated
with stronger (negative) wealth effects lowering the consumption of
Ricardian households. Yet, we see that even for values of
![]() as high as
as high as
![]() a positive (though
relatively small) effect on aggregate consumption emerges. Notice
also that the response of investment to the same shock is negative
over the admissible range of
a positive (though
relatively small) effect on aggregate consumption emerges. Notice
also that the response of investment to the same shock is negative
over the admissible range of ![]() . Yet, for values of the latter parameter
close to unity (i.e., near-random walk processes for government
spending) that response becomes negligible.28
. Yet, for values of the latter parameter
close to unity (i.e., near-random walk processes for government
spending) that response becomes negligible.28
The other graphs in Figure 5 report analogous information for
three alternative "extreme" calibrations. Each calibration assumes
a limiting value for one (or two) parameters, while keeping the
rest at their baseline values. Thus, the flexible price scenario assumes ![]() , the no
rule-of-thumb economy assumes
, the no
rule-of-thumb economy assumes ![]() , whereas the neoclassical calibration combines both flexible
prices and lack of rule-of-thumb consumers (
, whereas the neoclassical calibration combines both flexible
prices and lack of rule-of-thumb consumers (
![]() ).
Notice that when prices are fully flexible, or when all consumers
are Ricardian (or when both features coexist, as under the
neoclassical calibration) consumption is always crowded-out in
response to a rise in government spending, independently of the
degree of persistence of the latter. This illustrates the
difficulty of reconciling the evidence with standard dynamic
general equilibrium models, as well as the role played by both
sticky prices and rule-of-thumb consumers to match that
evidence.
).
Notice that when prices are fully flexible, or when all consumers
are Ricardian (or when both features coexist, as under the
neoclassical calibration) consumption is always crowded-out in
response to a rise in government spending, independently of the
degree of persistence of the latter. This illustrates the
difficulty of reconciling the evidence with standard dynamic
general equilibrium models, as well as the role played by both
sticky prices and rule-of-thumb consumers to match that
evidence.
The graphs in Figure 6 summarize the sensitivity of the impact
multipliers to variations in three non-policy parameters to the
government spending shock. The first graph explores the sensitivity
of the impact multipliers to the degree of price stickiness, as
indexed by parameter ![]() .
Notice that the size of the response of output is increasing in the
degree of price rigidities, largely as a result of a stronger
multiplier effect on consumption. Given baseline values for the
remaining parameters, we see that values of
.
Notice that the size of the response of output is increasing in the
degree of price rigidities, largely as a result of a stronger
multiplier effect on consumption. Given baseline values for the
remaining parameters, we see that values of ![]() slightly higher than
slightly higher than
![]() are consistent
with a positive response of aggregate consumption. That range for
are consistent
with a positive response of aggregate consumption. That range for
![]() includes the
values generally viewed as consistent with the micro evidence and,
hence, used in most calibrations. The two middle and bottom graphs
show the impact multipliers when the degree of capital adjustment
costs,
includes the
values generally viewed as consistent with the micro evidence and,
hence, used in most calibrations. The two middle and bottom graphs
show the impact multipliers when the degree of capital adjustment
costs, ![]() , and the
wage elasticity parameter,
, and the
wage elasticity parameter, ![]() change. High capital adjustment costs (i.e.,
low
change. High capital adjustment costs (i.e.,
low ![]() ) tend to dampen
the fall in investment, but enhance the positive response of
consumption and output. Finally, we notice that the impact
multipliers are relatively insensitive to changes in
) tend to dampen
the fall in investment, but enhance the positive response of
consumption and output. Finally, we notice that the impact
multipliers are relatively insensitive to changes in ![]() .
.
Figure 7 illustrates the sensitivity of the model's predictions
to the three policy parameters (
![]() ,
,![]() ,
, ![]() ), each considered in turn. The top graph
shows an inverse relationship between the size of the impact
multipliers and the strength of the central bank's response to
inflation (
), each considered in turn. The top graph
shows an inverse relationship between the size of the impact
multipliers and the strength of the central bank's response to
inflation (
![]() ).
Intuitively, a large
).
Intuitively, a large
![]() leads to a
larger increase in the real rate in response to the higher
inflation induced by the fiscal expansion; as a result consumption
of Ricardian households declines further, dampening the total
effect on aggregate consumption. That finding should not be
surprising once we realize that in staggered price setting models
like ours the central bank can approximate arbitrarily well the
flexible price equilibrium allocation by following an interest rate
rule that responds with sufficient strength to changes in
inflation. Hence, an increase in
leads to a
larger increase in the real rate in response to the higher
inflation induced by the fiscal expansion; as a result consumption
of Ricardian households declines further, dampening the total
effect on aggregate consumption. That finding should not be
surprising once we realize that in staggered price setting models
like ours the central bank can approximate arbitrarily well the
flexible price equilibrium allocation by following an interest rate
rule that responds with sufficient strength to changes in
inflation. Hence, an increase in
![]() affects the
output and consumption multipliers in a way qualitatively similar
to an increase in price flexibility (i.e. a decline in
affects the
output and consumption multipliers in a way qualitatively similar
to an increase in price flexibility (i.e. a decline in ![]() ), as described above.
), as described above.
Finally, the second and third graphs show the sensitivity of the
multiplier to variations in the two parameters of the fiscal rule.
In particular, and of most interest given our objectives, we see
how a positive comovement of consumption and output in response to
government spending shocks requires a sufficiently high response of
taxes to debt (a high ![]() ), and a sufficiently low response of taxes to
current government spending (i.e. a low
), and a sufficiently low response of taxes to
current government spending (i.e. a low ![]() ). Such a configuration of
fiscal parameters will tend to imply a large but not-too-persistent
deficit in response to an increase in government spending, a
pattern largely consistent with the empirical evidence described in
Section 2.
). Such a configuration of
fiscal parameters will tend to imply a large but not-too-persistent
deficit in response to an increase in government spending, a
pattern largely consistent with the empirical evidence described in
Section 2.
6 Rule-of-Thumb Consumers vs. Non-Separable Preferences
In this section we discuss an alternative potential explanation for our evidence of a positive response of consumption to a rise in government spending: the presence of non-separable preferences in utility an leisure. In particular, Basu and Kimball (2002) bring up that possibility as an explanation for the significance of anticipated disposable income in the consumption Euler equation estimated by Campbell and Mankiw.(1989). We point to an aspect of the model with rule-of-thumb consumers which allows us to differentiate it, at least in principle, from one with non-separable preferences.
To see this formally consider the following specification of period utility:
where parameter
where
where
Notice also that (41) has a structure similar to
where
As stressed by Basu and Kimball (2002), however, Campbell and
Mankiw's interpretation of their results hinges on the assumption
of a utility that is separable in consumption. If preferences are
instead given by (39) (with
![]() ), a common
interpretation of their results as suggesting that a substantial
fraction of U.S consumers behave in a non-Ricardian fashion may not
be warranted. The reason is simple: given the high positive
correlation between changes in (log) disposable income and changes
in (log) hours, it is clear that a researcher estimating (42) would easily conclude that anticipated changes in
disposable income have predictive power for consumption growth
(i.e. a significant
), a common
interpretation of their results as suggesting that a substantial
fraction of U.S consumers behave in a non-Ricardian fashion may not
be warranted. The reason is simple: given the high positive
correlation between changes in (log) disposable income and changes
in (log) hours, it is clear that a researcher estimating (42) would easily conclude that anticipated changes in
disposable income have predictive power for consumption growth
(i.e. a significant ![]() ), even if all consumers were fully Ricardian
(as long as utility was non-separable). Furthermore, the positive
estimate for
), even if all consumers were fully Ricardian
(as long as utility was non-separable). Furthermore, the positive
estimate for ![]() obtained by Campbell and Mankiw would be consistent with a low
intertemporal elasticity of substitution (
obtained by Campbell and Mankiw would be consistent with a low
intertemporal elasticity of substitution (![]() ).
).
The problem of near-observational equivalence between the two
hypotheses, and the likely multicollinearity that the joint use of
changes in hours and disposable income would imply, led Basu and
Kimball (2002) to estimate a restricted version of (41). In particular, and using the fact that the
household's intratemporal optimality condition implies that
![]() , a ratio
which is in principle observable, they rewrite (41) as
, a ratio
which is in principle observable, they rewrite (41) as
where the choice of
Clearly, optimality condition (40) has some similarities with equation (31), reproduced here for convenience, which results in our model from combining the Euler equation of Ricardian households (endowed with separable preferences) with the budget constraint of rule-of-thumb households:
Notice however, one important difference between the two equations: in the model with rule-of-thumb consumers anticipated changes in taxes (minus transfers) accruing to those consumers should have predictive power for consumption growth, once we control for the influence of the interest rate and hours growth. That feature, on the other hand, is absent from the Euler equation in the Basu-Kimball model with Ricardian households and non-separable preferences.
We interpret the existing evidence on the response of consumption to anticipated changes in taxes as bearing directly on this issue. Thus, using household level data, Parker (1999) finds evidence of a large response of consumption to variations in after-tax income resulting from anticipated changes in Social Security taxes, with the estimated elasticity being close to one half. Similarly, Souleles (1999) finds evidence of excess sensitivity of households' consumption to predictable income tax refunds, with the implied marginal propensity to consume the tax refunds between 0.35 and 0.60. Similar results are uncovered by Johnson et al. (2005), focusing on the income tax rebate of 2001. None of those anticipated changes in taxes should have effect on consumption in a fully Ricardian model, independently of whether preferences are separable in consumption and labor or not.
Here we complement the evidence based on household data just discussed with our own evidence, using quarterly aggregate U.S. time series. To set the stage, we first re-estimate the Campbell-Mankiw Euler equation (42) using an updated data set, running from 1954:I to 2004:IV. We use as instruments second and third lags of the interest rate, changes in (log) consumption and changes in (log) hours. A detailed description of the data and sources can be found in the footnote to the Table.
Our estimates of the Campbell-Mankiw model, shown in the top
panel of Table 2, confirm the earlier findings of those authors.
Most importantly, (anticipated) change in (log) disposable income
are shown to have predictive power for consumption changes, with
the point estimate of ![]() being close to
being close to ![]() and, hence, of the same order of magnitude as the
original Campbell-Mankiw estimates. In addition, the estimates
uncover no evidence of any intertemporal substitution effects, as
reflected in the insignificant estimate of the interest rate
coefficient.
and, hence, of the same order of magnitude as the
original Campbell-Mankiw estimates. In addition, the estimates
uncover no evidence of any intertemporal substitution effects, as
reflected in the insignificant estimate of the interest rate
coefficient.
The second panel of Table 2 reports the IV estimates of
alternative versions of the Basu-Kimball Euler equation (43), imposing the steady state restrictions implied by
the theory. Row (1) shows the estimates of (43),
excluding changes in disposable income (![]() ). In contrast with the
findings based on the Campbell-Mankiw equation, the estimate of the
intertemporal elasticity of substitution (the coefficient on
interest rate) is now significantly different from zero, with a
point estimate close
). In contrast with the
findings based on the Campbell-Mankiw equation, the estimate of the
intertemporal elasticity of substitution (the coefficient on
interest rate) is now significantly different from zero, with a
point estimate close ![]() . In
addition, as shown in row (2) once changes in hours are properly
controlled for, (anticipated) changes in disposable income lose
their explanatory power for consumption changes, thus replicating
the main finding in Basu and Kimball (2002).
. In
addition, as shown in row (2) once changes in hours are properly
controlled for, (anticipated) changes in disposable income lose
their explanatory power for consumption changes, thus replicating
the main finding in Basu and Kimball (2002).
In row (3) we introduce changes in taxes as an explanatory
variable in the same IV equation, substituting disposable income,
and motivated by the predictions of the model with rule-of-thumb
consumers. Since we have no way to isolate taxes paid by
non-Ricardian households, we use instead a measure of overall net
taxes given by the difference between Government Current Tax
Receipts (GRCRT) and Government Current Transfer Payments (GETFP),
divided by (lagged) potential output (GDPPOTQ).29 Under the null implied by the
Ricardian model with non-separable utility, no variable other than
the (hours-adjusted) real interest rate should have predictive
power for (hours-adjusted) consumption changes, as implied by
(43) with ![]() . Yet, as shown in Table 2, anticipated
changes in (net) taxes enter the Euler equation significantly (and
with the expected sign). The estimated elasticity of intertemporal
substitution remains significant, though its point estimate has
been reduced to
. Yet, as shown in Table 2, anticipated
changes in (net) taxes enter the Euler equation significantly (and
with the expected sign). The estimated elasticity of intertemporal
substitution remains significant, though its point estimate has
been reduced to ![]() .
We interpret the evidence of the predictive power of tax changes on
consumption as a rejection of a fully Ricardian model with
non-separable preferences, and one that is at least suggestive of
the presence of non-Ricardian households, in accordance with the
micro evidence reviewed earlier.
.
We interpret the evidence of the predictive power of tax changes on
consumption as a rejection of a fully Ricardian model with
non-separable preferences, and one that is at least suggestive of
the presence of non-Ricardian households, in accordance with the
micro evidence reviewed earlier.
7 Concluding Comments and Further Research
The analysis above has shown how the interaction between rule-of-thumb behavior by some households (for which consumption equals labor income) and sticky prices (modeled as in the recent new Keynesian literature), make it possible to generate an increase in consumption in response to a rise in government spending, in a way consistent with much of the recent evidence. Rule-of-thumb consumers partly insulate aggregate demand from the negative wealth effects generated by the higher levels of (current and future) taxes needed to finance the fiscal expansion, while making it more sensitive to current disposable income. Sticky prices make it possible for real wages to increase (or, at least, to decline by a smaller amount) even in the face of a drop in the marginal product of labor, as the price markup may adjust sufficiently downward to absorb the resulting gap. The combined effect of a higher real wage and higher employment raises current labor income and hence stimulates the consumption of rule-of-thumb households. The possible presence of countercyclical wage markups (as in the version of the model with non-competitive labor markets developed above) provides additional room for a simultaneous increase in consumption and hours and, hence, in the marginal rate of substitution, without requiring a proportional increase in the real wage.
Perhaps most importantly, our framework generates a positive comovement of consumption and government spending under configurations of parameter values that are empirically plausible (and conventionally assumed in the business cycle literature). Thus, we view our results as providing a potential solution to the seeming conflict between empirical evidence and the predictions of existing DSGE models regarding the effects of government spending shocks.
In the present paper we kept both the model and its analysis as simple as possible, and focused on a single issue. As a result, we left out many possible extensions and avenues for further exploration. Thus, for instance, our theoretical analysis assumes that government spending is financed by means of lump-sum taxes (current or future). If only distortionary income taxes were available to the government, the response of the different macroeconomic variables to a government spending shock will generally differ from the one obtained in the economy with lump-sum taxes analyzed above, and will generally depend on the composition and timing of taxation.30 Allowing for staggered nominal wage setting or some form of real wage rigidity constitutes another potentially useful extension of our framework, one that is likely to have a significant effect on the response of real wages and, hence, of labor income and consumption to any fiscal shock.
Another avenue worth pursuing is the introduction of rule-of-thumb consumers in medium-scale DSGE models of the sort developed by Smets and Wouters (2003) and Christiano, Eichenbaum and Evans (2005). Those models incorporate many of the features that have been shown to be useful in accounting for different aspects of economic fluctuations, and which have been assumed away in the model developed above. Such a richer version of our model could be taken to the data, and generate estimates of the quantitative importance of rule of thumb consumers and their role in shaping historical economic fluctuations. Early examples of efforts in that direction can already be found in the work of Coenen and Straub (2005), Erceg, Guerrieri and Gust (2005), Forni, Liberatore and Sessa (2006), and López-Salido and Rabanal (2006).
A number of papers have documented a stronger interest rate response to changes in inflation during the past two decades, relative to the pre-Volcker era.31 There is also substantial evidence pointing to a rise in asset market participation over the postwar period, which in the context of our model could be interpreted as a decline in the fraction of rule of thumb consumers. The model developed above predicts a reduction in the government spending multiplier on consumption and output, in response to both developments. In that spirit, Bilbiie, Meier and Muller (2005) explore the implications of those changes in the context of a model similar to ours, and suggest that those developments may explain part of the observed decline in fiscal multipliers uncovered by Perotti (2004) and others.
Finally, one would want to consider some of the normative implications of our framework: in a model with the two types of consumers considered above, the monetary and fiscal policy responses to shocks of different nature can be expected to have distributional effects, which should be taken into account in the design of those policies. Exploring the implications of the present model for optimal monetary policy design constitutes an additional interesting avenue for future research.32
Appendix 1: Alternative Labor Market Structures
In the present Appendix we describe two alternative models of wage determination that generate a log-linear aggregate equilibrium condition corresponding to (30) in the text.
Perfectly Competitive Labor Markets
When households choose optimally their labor supply taking wages as given the intratemporal optimality condition takes the form,
for
Notice that under our assumption of equality of steady state consumption across household types, steady state hours will also be equated. Hence we can write
Wage-setting by Unions
Consider a model with a continuum of unions, each of which
represents workers of a certain type. Effective labor input hired
by firm ![]() is a CES
function of the quantities of the different labor types employed,
is a CES
function of the quantities of the different labor types employed,
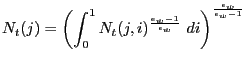
![$\displaystyle \lambda\left[ \frac{1}{C_{t}^{r}(z)}W_{t}(z)N_{t}(z)-\frac {N_{t}... ...1} {C_{t}^{o}(z)}W_{t}(z)N_{t}(z)-\frac{N_{t}^{1+\varphi}(z)}{1+\varphi}\right]$](img260.gif)
|
subject to a labor demand schedule
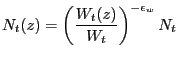
Since consumption will generally differ between the two types of
consumers, the union weighs labor income with their respective
marginal utility of consumption (i.e.
![]() and
and
![]() ).
Notice that, in writing down the problem above, we have assumed
that the union takes into account the fact that firms allocate
labor demand uniformly across different workers of type
).
Notice that, in writing down the problem above, we have assumed
that the union takes into account the fact that firms allocate
labor demand uniformly across different workers of type
![]() , independently of
their household type. It follows that, in the aggregate, we will
have
, independently of
their household type. It follows that, in the aggregate, we will
have
![]() for all
for all ![]() .
.
The first order condition of this problem can be written as
follows (after invoking symmetry, and thus dropping the
![]() index)
index)
where
Log-linearizing expression (45) and ignoring constant terms yields the wage schedule
where
Notice that, to the extent that tax policy equates steady state
consumption across household types (i.e.
![]() ) we will
have
) we will
have
![]() and,
hence,
and,
hence,
![]() and
and
![]() . We
can then rewrite the previous equilibrium condition as
. We
can then rewrite the previous equilibrium condition as
Under the present scenario we assume that the wage markup
![]() is
sufficiently large (and the shocks sufficiently small) so that the
conditions
is
sufficiently large (and the shocks sufficiently small) so that the
conditions ![]()
![]() for
for
![]() are satisfied
for all
are satisfied
for all ![]() . Both
conditions guarantee that both type of households will be willing
to meet firms' labor demand at the prevailing wage.
. Both
conditions guarantee that both type of households will be willing
to meet firms' labor demand at the prevailing wage.
Appendix 2. Steady State Analysis
In this short appendix we show that the steady state ratio of aggregate consumption to total output does not depend upon the fraction of rule-of-thumb consumers. In doing so, we just notice that the market clearing condition for final goods implies:
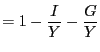 |
||
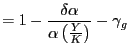
|
||
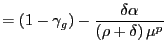
|
where the last equality follows from the fact that in the steady state
Appendix 3. Derivation of the Reduced Dynamical System
The equilibrium conditions describing the model dynamics are given by expressions (30)-(37). Now we reduce those conditions to the five variable system (38) in terms of hours, consumption, inflation, capital and government spending.
The first equation in the system (38)
corresponds to the linearized capital accumulation equation
(25), with ![]() substituted out using market clearing condition
(36) and replacing
substituted out using market clearing condition
(36) and replacing ![]() subsequently using the
production function (35):
subsequently using the
production function (35):
where
Substituting the previous expression (47) into (32), and making use of (35) yields the second equation in (38)
Aggregate Euler Equation: the Case of Perfectly Competitive Labor Markets
As noticed above, under the assumption of perfectly competitive labor markets, we can log-linearize expressions (8), (12), and combine them with (28) and (29) to yield expression (30). From log-linearizing expression (12) we obtain an expression for the evolution of the hours worked by the rule-of-thumb consumers
We now substitute the previous expression as well as (30) into expression (27). After
rearranging terms this yields ![]() as a function only of aggregate
variables,
as a function only of aggregate
variables,
As before noticed, we also apply the operator
![]() to
expression (28), which yields
to
expression (28), which yields
Finally, we substitute expressions (49) and (26) into the previous one, which after rearranging terms, yields the Euler equation for aggregate consumption presented in the main text
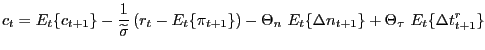
Aggregate Euler Equation: the Case of Imperfectly Competitive Labor Markets
We first substitute expression (30) into expression (27), this yields
![$\displaystyle =\left( \frac{WN}{C}\right) \ [c_{t}+(1+\varphi)n_{t}]-\left( \frac{Y}{C}\right) \ t_{t}^{r}$](img319.gif)
|
||
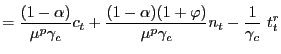
|
We proceed to use the operator
![]() into the
previous expression yielding
into the
previous expression yielding
We also apply the operator
![]() to
expression (28), which yields
to
expression (28), which yields
Finally, we substitute expressions (50) and (26) into the previous one, which after rearranging terms yields an Euler-like equation for aggregate consumption:
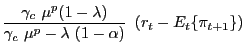
|
||
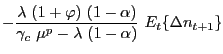
|
||
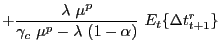
|
or, more compactly,
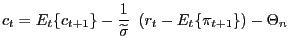
Plugging into the Euler equation the interest rate rule (18), the fiscal rule (20), and using the fact the government spending follows a first order autoregressive process (21) we obtain the third equation in (38):
In order to derive the fourth equation we first combine
(47) and (34) to obtain
![]() . The latter
expression and the interest rate rule (18),
allows us to rewrite the equations describing the dynamics of
Tobin's
. The latter
expression and the interest rate rule (18),
allows us to rewrite the equations describing the dynamics of
Tobin's ![]() and
investment as follows:
and
investment as follows:
Finally, substituting the relationship
![$\displaystyle i_{t}-k_{t}=\left( \frac{1}{1-\widetilde{\gamma}_{c}}\right) \lef... ...pha)n_{t}-\gamma_{c}c_{t}-g_{t}-(1-\widetilde{\gamma}_{c}-\alpha )k_{t}\right] $](img343.gif)
where
The last two equations of the system correspond to expression (37 ) describing the debt accumulation and the autoregressive process for government spending (21).
Hence the system of equations (46), (48), (51), (52), (37), and (21) can be written in a matrix form as follows
![\begin{displaymath}\mathbf{A}\equiv\left[ \begin{array}[c]{cccccc} 0 & 0 & 0 & 1... ...+\rho)(1-\phi_{g})\ 0 & 0 & 0 & 0 & 0 & 1 \end{array}\right] \end{displaymath}](img361.gif)
![\begin{displaymath}\mathbf{B}\equiv\left[ \begin{array}[c]{cccccc} \frac{\delta(... ...hi_{b}) & 0\ 0 & 0 & 0 & 0 & 0 & \rho_{g} \end{array}\right] \end{displaymath}](img362.gif)
References
Aiyagari, Rao, Lawrence Christiano and Martin Eichenbaum (1990): `` Output, Employment and Interest Rate Effects of Government Consumption'', Journal of Monetary Economics, 30, 73-86.
Alesina, Alberto, Silvia Ardagna, Roberto Perotti and Fabio Schiantarelli (2002): `` Fiscal Policy, Profits, and Investment,'' American Economic Review, 92 (3), 571-589.
Alesina, Alberto and Silvia Ardagna, (1998): `` Tales of Fiscal Adjustment'', Economic Policy, No. 27, October 1998, pp. 489-545.
Amato, Jeffery D., and Thomas Laubach (2003): `` Rule-of-Thumb Behavior and Monetary Policy,'' European Economic Review , vol. 47, 5, pages 791-831
Attanasio, O. and Martin Browning (1995) `` Consumption over the Life Cycle and Over the Business Cycle,'' American Economic Review, 85 (December),1118 -1137.
Basu, Susanto, and Miles Kimball (2002): `` Long-run Labor Supply and the Elasticity of Intertemporal Substitution for Consumption,'' University of Michigan, mimeo.
Basu, Susanto, and Miles Kimball (2003): `` Investment Planning Costs and the Effects of Monetary and Fiscal Policy,'' University of Michigan, mimeo.
Baxter, Marianne and Robert King (1993): `` Fiscal Policy in General Equilibrium'', American Economic Review, 83, 315-334.
Bilbiie, Florin O. (2005): `` Limited Asset Market Participation, Monetary Policy, and Inverted Keynesian Logic,'' mimeo, Nuffield College, Oxford U.
Bilbiie, Florin O. and Roland Straub (2005): `` Fiscal Policy, Business Cycles and Labor Market Fluctuations,'' European University Institute, mimeo.
Bilbiie, Florin O., André Maier, and Gernot J. Müller (2005): `` Asset Market Participation, Monetary Policy, and the Effects of U.S. Government Spending: What Accounts for the Declining Fiscal Mulitplier?,'' Goethe University, Frankfurt, mimeo.
Campbell, John Y. and N. Gregory Mankiw (1989): `` Consumption, Income, and Interest Rates: Reinterpreting the Time Series Evidence,'' in O.J. Blanchard and S. Fischer (eds.), NBER Macroeconomics Annual 1989, 185-216, MIT Press.
Clarida, Richard, Jordi Galí, and Mark Gertler (2000): `` Monetary Policy Rules and Macroeconomic Stability: Evidence and Some Theory,'' Quarterly Journal of Economics, vol. CXV, issue 1, 147-180.
Christiano, Lawrence and Martin Eichenbaum (1992): `` Current Real Business Cycles Theories and Aggregate Labor Market Fluctuations'', American Economic Review, 82, 430-450.
Blanchard, Olivier (2003): Macroeconomics, Third Edition, Prentice Hall
Blanchard, Olivier and Roberto Perotti (2002): ``An Empirical Characterization of the Dynamic Effects of Changes in Government Spending and Taxes on Output,'' Quarterly Journal of Economics,117, 4, 1329-1368.
Bohn, Henning (1998): ''The Behavior of Public Debt and Deficits'', The Quarterly Journal of Economics 113(3), 949-964.
Burnside, Craig, Martin Eichenbaum and Jonas Fisher (2003): ''Fiscal Shocks and their Consequences'', NBER WP 9772.
Campbell, John Y. and N. Gregory Mankiw (1989): ``Consumption, Income, and Interest Rates: Reinterpreting the Time Series Evidence,'' in O.J. Blanchard and S. Fischer (eds.), NBER Macroeconomics Annual 1989, 185-216, MIT Press
Calvo, Guillermo (1983): ``Staggered Prices in a Utility Maximizing Framework'', Journal of Monetary Economics, 12, 383-398.
Clarida, Richard, Jordi Galí and Mark Gertler (1999): '' The Science of Monetary Policy: A New Keynesian Perspective'', Journal of Economic Literature, 37, 1661-1707.
Coenen, G. and R. Straub (2005): `` Does Government Spending Crowd In Private Consumption: Theory and Empirical Evidence for the Euro Area,'' International Finance, 8 (3), 435-470.
Deaton, A. (1992), Understanding Consumption, Clarendon Lectures in Economics, Clarendon Press, Oxford, 1992.
Dotsey, Michael (1999): ``Structure from Shocks,'' Federal Reserve Bank of Richmond Working Paper 99-6.
Dupor, Bill (2002): ``Interest Rate Policy and Investment with Adjustment Costs,'' mimeo.
Edelberg, Wendy, Martin Eichenbaum, and Jonas Fisher (1999), `` Understanding the Effects of Shocks to Government Purchases,'' Review of Economic Dynamics, 2, 166-206.
Erceg, C.J., Guerrieri, L. and Gust, C. J., (2005): `` SIGMA A New Open Economy Model for Policy Analysis,'' Federal Reserve Board, International Finance Discussion Papers, no. 835.
Erceg, C.J., Guerrieri, L. and Gust, C. J., (2005): `` Expansionary Fiscal Shocks and the Trade Deficit'', FRB International Finance Discussion Paper No. 825.
Fatás, Antonio and Ilian Mihov (2001): `` The Effects of Fiscal Policy on Consumption and Employment: Theory and Evidence,'' INSEAD, mimeo.
Forni, Lorenzo, Libero Monteforte, and Luca Sessa (2006): "The Estimated General Equilibrium Effects of Fiscal Policy: the Case of the Euro Area," Banca d'Italia, mimeo.
Galí, Jordi, J.David López-Salido and Javier Vallés (2004): `` Rule-of- Thumb Consumers and the Design of Interest Rate Rules'', Journal of Money, Credit and Banking, Vol. 36 (4), August 2004, 739-764.
Giavazzi, Francesco, and Marco Pagano (1990): ``Can Severe Fiscal Contractions be Expansionary? Tales of Two Small European Countries'' in O.J. Blanchard and S. Fischer (eds.), NBER Macroeconomics Annual 1990, MIT Press
Hemming, Richard, Michael Kell and Selma Mahfouz (2002): `` The Effectiveness of Fiscal Policy in Stimulating Economic Activity-A Review of the Literature,'' IMF WP 02/208
IMF (2004), World Economic Outlook, 2004, IMF Washington D.C. April 2004.
Johnson, David S., Jonathan A. Parker, and Nicholas S. Souleles (2004): `` Household Expenditure and the Income Tax Rebates of 2001'', NBER Working Paper 1078.
Kim, Jinill (2000): ``Constructing and estimating a realistic optimizing model of monetary policy,'' Journal of Monetary Economics, 45, 2, 329-359
King, Robert, and Mark Watson (1996): `` Money, Prices, Interest Rates and the Business Cycle'' Review of Economics and Statistics, 78, 35-53
Lopez-Salido, J.David and Pau Rabanal (2006) `` Consumption, Hours Worked, and Fiscal Policy Shocks in an Estimated Business Cycle Model,'' mimeo Bank of Spain and IMF, March 2006.
Mankiw, N. Gregory (2000): ``The Savers-Spenders Theory of Fiscal Policy,'' American Economic Review, 90, 2, 120-125.
Mountford, Andrew and Harald Uhlig (2000): `` What are the Effects of Fiscal Policy Shocks?, mimeo, Humboldt University, Berlin, june 2004.
Parker, Jonathan (1999): "The Reaction of Household Consumption to Predictable Changes in Social Security Taxes," American Economic Review, 89(4), 959-973.
Perotti, Roberto (1999): `` Fiscal Policy in Good Times and Bad,'' Quarterly Journal of Economics, 114, 4, 1399-1436.
Perotti, Roberto (2004):`` Estimating the Effects of Fiscal Policy in OECD Countries, IGIER, March 2004.
Ramey, Valerie, and Matthew Shapiro (1998): ``Costly Capital Reallocation and the Effect of Government Spending,'' Carnegie-Rochester Conference Series on Public Policy, 48, 145-194.
Rotemberg, Julio and Michael Woodford (1992): `` Oligopolistic Pricing and the Effects of Aggregate Demand on Economic Activity'', Journal of Political Economy, 100, 1153-1297.
Rotemberg, Julio and Michael Woodford (1995): `` Dynamic General Equilibrium Models with Imperfectly Competitive Products Markets'', in Thomas F. Cooley (ed.), Frontiers in Business Cycle Research, Princeton University Press.
Rotemberg, Julio and Michael Woodford (1997): ''An Optimization Econometric Framework for the Evaluation of Monetary Policy'' in O.J. Blanchard and S. Fischer (eds.), NBER Macroeconomics Annual 1997, MIT Press.
Rotemberg, Julio and Michael Woodford (1999):''Interest Rate Rules in an Estimated Sticky Price Model'' in J.B. Taylor (ed.), Monetary Policy Rules, University of Chicago Press and NBER.
Souleles, Nicholas S. (1999): "The Response of Household Consumption to Income Tax Refunds," American Economic Review, 89(4), 947-958.
Taylor, John B. (1993): ``Discretion versus Policy Rules in Practice,'' Carnegie Rochester Conference Series on Public Policy , December 1993, 39, 195-214.
Wolff, Edward (1998): ''Recent Trends in the Size Distribution of Household Wealth'', Journal of Economic Perspectives 12, 131-150.
Woodford, Michael (2003) Interest and Prices, Chapter 4, Princeton University Press.
Yun, Tack (1996): `` Nominal Price Rigidity, Money Supply Endogeneity, and Business Cycles,'' Journal of Monetary Economics 37, 345-370.
Table 1. Estimated Effects of Government Spending Shocks
| Estimated Fiscal Multipliers: Output: 1stQ | Estimated Fiscal Multipliers: Output: 4thQ | Estimated Fiscal Multipliers: Output: 8thQ | Estimated Fiscal Multipliers: Consumption: 1stQ | Estimated Fiscal Multipliers: Consumption: 4thQ | Estimated Fiscal Multipliers: Consumption: 8thQ | Implied: Fiscal Parameters: |
Implied: Fiscal Parameters: |
Implied: Fiscal Parameters: |
|
| 1948:I-2003:IV | 1948:I-2003:IV | 1948:I-2003:IV | 1948:I-2003:IV | 1948:I-2003:IV | 1948:I-2003:IV | 1948:I-2003:IV | 1948:I-2003:IV | 1948:I-2003:IV | 1948:I-2003:IV |
| Baseline Spending: Small VAR | 0.51 | 0.31 | 0.28 | 0.04 | 0.09 | 0.19 | 0.85 | 0.10 | 0.10 |
| Baseline Spending: Larger VAR | 0.41 | 0.31 | 0.68 | 0.07 | 0.11 | 0.49 | 0.80 | 0.06 | 0.06 |
| Excluding Military: Small VAR | 0.15 | -0.12 | 0.34 | -0.11 | 0.24 | 0.32 | 0.95 | 0.005 | 0.60 |
| Excluding Military: Larger VAR | 0.36 | 0.62 | 1.53 | 0.03 | 0.51 | 0.68 | 0.94 | 0.005 | 0.60 |
| 1954:I-2003:IV | 1954:I-2003:IV | 1954:I-2003:IV | 1954:I-2003:IV | 1954:I-2003:IV | 1954:I-2003:IV | 1954:I-2003:IV | 1954:I-2003:IV | 1954:I-2003:IV | 1954:I-2003:IV |
| Baseline Spending: Small VAR | 0.74 | 0.75 | 1.22 | 0.14 | 0.46 | 0.73 | 0.95 | 0.13 | 0.20 |
| Baseline Spending: Larger VAR | 0.68 | 0.7 | 1.74 | 0.17 | 0.29 | 0.95 | 0.95 | 0.10 | 0.30 |
| Excluding Military: Small VAR | 0.63 | 1.95 | 2.60 | 0.25 | 1.41 | 1.12 | 0.95 | 0.05 | 0.50 |
| Excluding Military: Larger VAR | 0.74 | 2.37 | 3.50 | 0.37 | 1.39 | 1.76 | 0.95 | 0.01 | 0.50 |
| 1960:I-2003:IV | 1960:I-2003:IV | 1960:I-2003:IV | 1960:I-2003:IV | 1960:I-2003:IV | 1960:I-2003:IV | 1960:I-2003:IV | 1960:I-2003:IV | 1960:I-2003:IV | 1960:I-2003:IV |
| Baseline Spending: Small VAR | 0.91 | 1.05 | 1.32 | 0.19 | 0.59 | 0.84 | 0.95 | 0.13 | 0.20 |
| Baseline Spending: Larger VAR | 0.81 | 0.44 | 0.76 | 0.20 | 0.25 | 0.45 | 0.95 | 0.08 | 0.20 |
| Excluding Military: Small VAR | 0.72 | 1.14 | 1.19 | 0.17 | 0.78 | 0.68 | 0.94 | 0.03 | 0.50 |
| Excluding Military: Larger VAR | 1.13 | 1.89 | 2.08 | 0.40 | 1.14 | 1.07 | 0.98 | 0.01 | 0.55 |
Note: The "large" VAR corresponds to the
8-variable VAR described in the text; the "small" VAR estimates are
based on a 4-variable VAR including government spending, output,
consumption, and the deficit. Government spending excluding
military was obtained as GFNEH+GSEH+GFNIH+GSIH. For each
specification ![]() is the AR(1) coefficient
that matches the half-life of the estimated government spending
response. Parameter
is the AR(1) coefficient
that matches the half-life of the estimated government spending
response. Parameter ![]() is obtained as the
difference of the VAR-estimated impact effects of government
spending and deficit, respectively. Finally, given
is obtained as the
difference of the VAR-estimated impact effects of government
spending and deficit, respectively. Finally, given
![]() and
and ![]() , we calibrate the
parameter
, we calibrate the
parameter ![]() such that the dynamics of government spending
(21) and debt (37) are consistent
with the horizon at which the deficit is back to steady state,
matching our empirical VAR responses of the fiscal
deficit.
such that the dynamics of government spending
(21) and debt (37) are consistent
with the horizon at which the deficit is back to steady state,
matching our empirical VAR responses of the fiscal
deficit.
Table 2. Estimates of the Consumption Euler Equation
| Specification | Regressors: |
Regressors: |
Regressors: |
Regressors: |
| Campbell-Mankiw | .076 (.073) |
- | .477* (0.103) |
- |
| Basu-Kimball (1) | .314* (.066) |
.549* (.053) |
- | - |
| Basu-Kimball (2) | .317* (.076) |
.546* (.053) |
-.176 (.209) |
- |
| Basu-Kimball (3) | .201* (.051) |
.639* (.086) |
- | -.061* (.023) |
Note: Standard errors in brackets. A (*)
means that the variable is significant at 5% level. The instruments include the real
interest rate, (per capita) consumption growth and (per capita)
hours worked growth at ![]() and
and ![]() , and in the
last two columns the rate of growth of disposable income or taxes
between
, and in the
last two columns the rate of growth of disposable income or taxes
between ![]() and
and ![]() , respectively. Consumption
growth is defined as non-durable plus services (CNH+CSH), the real
interest rate (
, respectively. Consumption
growth is defined as non-durable plus services (CNH+CSH), the real
interest rate (![]() ) is constructed using the
3-month TBill rate (FTB3) minus the rate of growth of personal
consumption deflator -defined as the ratio between nominal and real
consumption ((CN+CS)/(CNH+CSH)). Per capita hours
(
) is constructed using the
3-month TBill rate (FTB3) minus the rate of growth of personal
consumption deflator -defined as the ratio between nominal and real
consumption ((CN+CS)/(CNH+CSH)). Per capita hours
(![]() ) correspond the Non-Farm Business Sector (LXNFH). The real
personal disposable income (
) correspond the Non-Farm Business Sector (LXNFH). The real
personal disposable income (![]() ) is from the FRED II, and
from the BEA we define the variable
) is from the FRED II, and
from the BEA we define the variable ![]() as the
difference between Government Current Tax Receipts (GRCRT) and
Government Current Transfer Payments (GETFP) divided by potential
output (GDPPOTQ) at
as the
difference between Government Current Tax Receipts (GRCRT) and
Government Current Transfer Payments (GETFP) divided by potential
output (GDPPOTQ) at ![]() .
.
Figure 1. The Dynamic Effects of a Government Spending Shock
![Figure 1 is a 3x3 panel of nine graphs of estimated impulse responses (IR) to a government spending shock. The x-axis range is [0,20] quarters for all graphs. Going left to right and top to bottom, the y-axis ranges are [0, 0.36] for government spending, [0, 0.5] for consumption, [-0.18, 0.27] for the deficit, [-0.16, 0.48] for hours, [-0.8, 1.2] for investment, [-0.12, 0.48] for disposable income, [0, 0.75] for gdp, [-0.1, 0.3] for the real wage, and [-0.05, 0.30] for consumption and income. Each of the first eight graphs includes +1/-1 standard error bands, which increase in the number of quarters. The IR for government spending rises from about 0.25 to 0.3 at 3 quarters out, then declines to about 0.15 at 20 quarters, The IR for consumption rises from 0.05 to about 0.3 at 10 quarters, then declines slightly. The IR for the deficit declines from 0.2 to around -0.05 at 10 quarters, then increases to around zero. The IR for hours increases from zero to around 0.3 at 10 quarters and declines back to zero. The IR for investment falls from zero to about -0.2 at 3 quarters, rises to around 0.6 at 11 quarters, then falls to zero. The IR for disposable income rises from zero to around 0.25 at 11 quarters, then falls slightly. The IR for gdp rises from 0.2 to 0.5 at 9 quarters, then falls back to around 0.3. The IR for the real wage rises from around zero to around 0.12 at 10 quarters, remaining virtually unchanged thereafter. The IRs for consumption and (disposable) income rise, level off, and fall together, with the IR for consumption always somewhat above that for income.](Figure1.gif)
Note: Estimated impulse responses to a government spending shock in the large VAR. Sample Period 1954:I-2003:IV. The horizontal axis represents quarters after the shock. Confidence intervals correspond +/- 1 standard deviations of empirical distributions, based on 1000 Monte Carlo replications. The right bottom panel plots the point estimates of both consumption (solid line) and disposable income (dashed line)
Figure 2. Determinacy Analysis
![Figure 2 plots a determinancy analysis. The x- and y-axes are $\theta$ and $\lambda$, both ranging over [0,1]. Most of the unit square is characterized by "uniqueness". "Indeterminancy" occupies a narrow wedge along the top of the unit square, widening from left to right.](Figure2.gif)
Note: Based on the model with competitive labor markets, remaining parameters at their baseline values.
Figure 3. Impact Multipliers: Sensitivity to 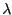
A. Competitive Labor Market
![Figure 3 has two panels. Panel A (Competitive Labor Market) plots the impact multipliers for output, investment, and consumption as a function of the rule-of-thumb share ($\lambda$). The rule-of-thumb share (x-axis) and the impact multipliers (y-axis) have ranges of [0,0.8] and [-0.5,2.0] respectively. The impact multiplier for output is about 0.8 for $\lambda = 0$, increasing gradually to 1.3 for $\lambda = 0.8$. The impact multiplier for investment is about zero and essentially invariant to $\lambda$. The impact multiplier for consumption is about -0.2 for $\lambda = 0$, increasing to zero for $\lambda = 0.6$ and up to about 0.4 for $\lambda = 0.8$. Panel B plots the same impact multipliers, but for a Non-Competitive Labor Market. The impact multipliers become more sensitive to $\lambda$, although the multiplier for investment remains nearly invariant.](Figure3a.gif)
B. Non-Competitive Labor Market
![Figure 3 has two panels. Panel A (Competitive Labor Market) plots the impact multipliers for output, investment, and consumption as a function of the rule-of-thumb share ($\lambda$). The rule-of-thumb share (x-axis) and the impact multipliers (y-axis) have ranges of [0,0.8] and [-0.5,2.0] respectively. The impact multiplier for output is about 0.8 for $\lambda = 0$, increasing gradually to 1.3 for $\lambda = 0.8$. The impact multiplier for investment is about zero and essentially invariant to $\lambda$. The impact multiplier for consumption is about -0.2 for $\lambda = 0$, increasing to zero for $\lambda = 0.6$ and up to about 0.4 for $\lambda = 0.8$. Panel B plots the same impact multipliers, but for a Non-Competitive Labor Market. The impact multipliers become more sensitive to $\lambda$, although the multiplier for investment remains nearly invariant.](Figure3b.gif)
Note: Baseline calibration for remaining parameters.
Figure 4. The Dynamic Effects of a Government Spending Shock: Baseline vs. Neoclassical Models
A. Competitive Labor Market
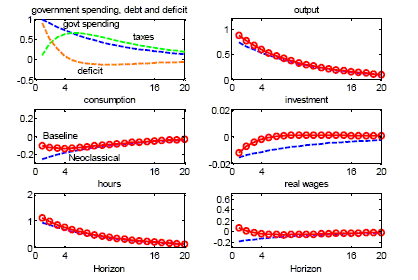
B. Non-Competitive Labor Market
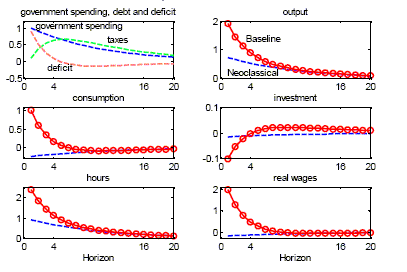
Note: Baseline calibration (circles), neoclassical calibration (dashes).
Figure 5. Impact Multipliers: Sensitivity to  --- Alternative Calibrations
--- Alternative Calibrations
(Non Competitive Labor Market)
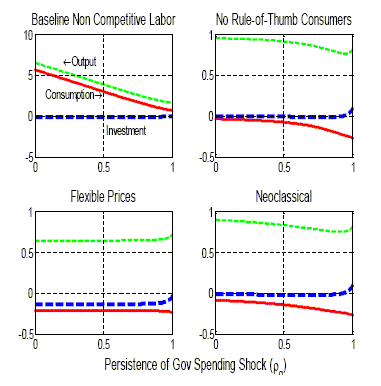
Figure 6. Impact Multipliers:
Sensitivity to Non-Policy Parameters ( 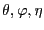 )
)
![Figure 6 is a 3x1 panel of graphs for output, consumption, and investment multipliers as a function of the non-policy parameters $\theta$ (over [0,0.8]), $\eta$ (over [0,10]), and $\phi$ (over [0,0.35]). In the first graph, the investment multiplier is slightly negative (about -0.1) and insensitive to $\theta$; the output multiplier increases in an accelerating manner from 0.6 to nearly 3; and the consumption multiplier likewise increases from about -0.2 to +1.9. In the second graph, all three multipliers gradually decline as $\eta$ increases: output from 2.2 to 1, consumption from 1.2 to 0.5, and investment from 0 to -0.5. In the third graph, all three multipliers appear insensitive to $\phi$, taking values of approximately 2 (output), 1 (consumption), and -0.1 (investment).](Figure6.gif)
Figure 7. Impact Multipliers: Sensitivity to Policy Parameters ( 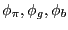 )
)
![Figure 7 is a 3x1 panel of graphs for output, consumption, and investment multipliers as a function of the policy parameters $\phi_\pi$ (over [1,2.5]), $\phi_g$ (over [0,1]), and $\phi_b$ (over [0,0.3]). In the first graph, the investment multiplier is slightly negative (about -0.1) and insensitive to $\phi_\pi$; the output multiplier decreases from 3.7, tending to around 1.3; and the consumption multiplier likewise decreases from about 2.8 to 0.4. In the second graph, the output and consumption multipliers decline approximately linearly from 2 to 0.8 and from 1.2 to -0.2 respectively as $\phi_g$ increases; the investment multiplier increases gradually from -0.2 to around zero. In the third graph, the output and consumption multipliers increase approximately linearly from 0.8 to 1.8 and from -0.1 to 0.8 respectively as $\phi_b$ increases; the investment multiplier is slightly negative (about -0.1) and insensitive to $\phi_b$.](Figure7.gif)
Footnotes
* We wish to thank Alberto Alesina, Javier Andrés, Florin Bilbiie, Günter Coenen, Gabriel Fagan, Eric Leeper, Ilian Mihov, Valery Ramey, Michael Reiter, Jaume Ventura, Lutz Weinke, co-editor Roberto Perotti, two anonymous referees, and seminar participants at the Bank of Spain, Bank of England, CREI-UPF, IGIER-Bocconi, INSEAD, York, Salamanca, NBER Summer Institute 2002, the 1st Workshop on Dynamic Macroeconomics at Hydra, the EEA Meetings in Stockholm and the 2nd International Research Forum on Monetary Policy for useful comments and suggestions. Galí acknowledges the financial support and hospitality of the Banco de España, and CREA-Barcelona Economics for research support. Anton Nakov provided excellent research assistance. This paper was written while the last author was working at the Research Department of the Banco de España. The opinions and analyses are the responsability of the authors and, therefore, do not necessarily coincide with those of the Banco de España or the Eurosystem. Return to text
† CREI and Universitat Pompeu Fabra Return to text
‡ Banco de España and CEPR Return to text
§ Economic Bureau of Spanish Prime Minister Return to text
1. The mechanisms underlying those effects are described in detail in Aiyagari et al. (1990), Baxter and King (1993), Christiano and Eichenbaum (1992), and Fatás and Mihov (2001), among others. In a nutshell, an increase in (non-productive) government purchases, financed by current or future lump-sum taxes, has a negative wealth effect which is reflected in lower consumption. It also induces a rise in the quantity of labor supplied at any given wage. The latter effect leads, in equilibrium, to a lower real wage, higher employment and higher output. The increase in employment leads, if sufficiently persistent, to a rise in the expected return to capital, and may trigger a rise in investment. In the latter case the size of the multiplier is greater or less than one, depending on parameter values. Return to text
2. See, e.g., Blanchard (2001). The total effect on output will also depend on the investment response. Under the assumption of a constant money supply, generally maintained in textbook versions of that model, the rise in consumption is accompanied by an investment decline (resulting from a higher interest rate). If instead the central bank holds the interest rate steady in the face of the increase in government spending, the implied effect on investment is nil. However, any `` intermediate'' response of the central bank (i.e., one that does not imply full accommodation of the higher money demand induced by the rise in output) will also induce a fall in investment in the IS-LM model. Return to text
3. See, e.g., Rotemberg and Woodford (1999), Clarida, Gali and Gertler (1999), or Woodford (2003) for a description of the standard new Keynesian model. Return to text
4. See, e.g. Campbell and Mankiw (1989), Deaton (1992) and references therein. Return to text
5. See, e.g., Souleles (1999), and Johnson, Parker and Souleles (2004). Return to text
6. See, e.g., Wolff (1998) Return to text
7. In a companion paper (Galí, López-Salido and Vallés (2005)), we study the implications of rule-of-thumb consumers for the stability properties of Taylor-type rules. Return to text
8. Qualitatively, the results below are robust to the use of military spending (instead of total government purchases) as a predetermined variable in the VAR, as in Rotemberg and Woodford (1992). Return to text
9. We use quarterly U.S. data over the period 1954:I-2003:IV. The series were drawn from Estima's USECON database (mnemonics reported in brackets below). These include government (Federal + State + Local) consumption and gross investment expenditures (GH), gross domestic product (GDPH), a measure of aggregate hours obtained by multiplying total civilian employment (LE) by weekly average hours in manufacturing (LRMANUA), nonfarm business hours (LXNFH), the real compensation per hour in the nonfarm business sector (LXNFR), consumption of nondurable and services (CNH+CSH), non-residential investment (FNH), and the CBO estimate of potential GDP (GDPPOTHQ). All quantity variables are in log levels, and normalized by the size of the civilian population over 16 years old (LNN). We included four lags of each variable in the VAR. Our deficit measure corresponds to gross government investment (GFDI+GFNI+GSI) minus gross government savings (obtained from the FRED-II database). The resulting variable, expressed in nominal terms was normalized by the lagged trend nominal GDP (GDPPOTQ). Finally, disposable income corresponds to real personal disposable income, also drawn from the FRED-II. Return to text
10. Fatas and Mihov (2001) also uncover a significant rise in the real wage in response to a spending shock, using compensation per hour in the non-farm business sector as a measure of the real wage. The positive comovement between hours and the real wage in response to a shock in military spending was originally emphasized by Rotemberg and Woodford (1992). See also Rotemberg and Woodford (1995). Return to text
11. See Hemming, Kell and Mahfouz (2002) and the survey of the evidence provided in IMF (2004, chapter 2). Return to text
12. See Table 1 for details. Return to text
13. The right panel is used below for the purposes of model calibration. Return to text
14. The only exception corresponds to the small VAR specification over the full sample period and excluding military spending. Yet, the underlying impulse responses (not shown) indicate that the slightly negative impact effect on consumption is quickly reversed in that case. Return to text
15. The response of private investment to the same shock tends to be negative, especially in the second sample period. Return to text
16. This method is based on sign and near-zero restrictions on impulse responses. Return to text
17. Ramey and Shapiro (1998) provide a potential explanation of the comovements of consumption and real wages in response to a change in military spending, based on a two-sector model with costly capital reallocation across sectors, and in which military expenditures are concentrated in one of the two sectors (manufacturing). Return to text
18. See Table 6 in Alesina and Ardagna (1998). Return to text
19. Most of the recent monetary models with nominal rigidities abstract from capital accumulation. A list of exceptions includes King and Watson (1996), Yun (1996), Dotsey (1999), Kim (2000) and Dupor (2002). In our framework, the existence of a mechanism to smooth consumption over time is important in order for the distinction between Ricardian and non-Ricardian consumers to be meaningful, thus justifying the need for introducing capital accumulation explicitly. Return to text
20. Mankiw (2000) reviews more recent microeconomic evidence consistent with that view. Return to text
21. See Basu and Kimball (2003) for a critical assessment of the predictions of new Keynesian models with endogenous capital accumulation and a proposal for reconciling those predictions with some of the evidence, based on the notion of costly investment planning. Return to text
22. Without loss of generality we normalize total factor productivity to unity. Return to text
23. The `` Taylor principle'' refers to a property of interest rate rules for which an increase in inflation eventually leads to a more than one-for-one rise in the nominal interest rate (see Woodford (2001)). Return to text
24. Notice that under perfectly
competitive labor markets marginal rates of substitution are
equalized across households. The assumption of equal consumption
levels in the steady state thus implies that
![]() as well.
As discussed below, under our alternative labor market structure
equality of hours across household types holds independently of
their relative level of consumption. See Appendix 1 for
details. Return to text
as well.
As discussed below, under our alternative labor market structure
equality of hours across household types holds independently of
their relative level of consumption. See Appendix 1 for
details. Return to text
25. We implicitly assume that the
resulting wage markup is sufficiently high (and fluctuations
sufficiently small) that the inequalities
![]()
![]() for
for
![]() are satisfied at
all times. Both conditions guarantee that both type of households
will be willing to meet firms' labor demand at the prevaling wage.
Notice also that consistency with balanced-growth requires that
are satisfied at
all times. Both conditions guarantee that both type of households
will be willing to meet firms' labor demand at the prevaling wage.
Notice also that consistency with balanced-growth requires that
![]() can be written as
can be written as
![]()
![]() (which happens to be
consistent with (30)). Return to text
(which happens to be
consistent with (30)). Return to text
26. See also Bilbiie (2005) for a subsequent analysis in a model without capital accumulation, and for a re-assessment of the evolution of Fed policies over the postwar period, in light of that analysis. Return to text
27. That monotonicity contrasts with some of the patterns observed in the data; we conjecture this is unrelated to the issue at hand and could be fixed by the introduction of habit formation and other mechanisms that generate inertia in aggregate demand. Return to text
28. As shown below the response of investment depend crucially upon the specification of capital adjustment costs. Lower capital adjustment costs tend to increase the (negative) response of investment (see middle panel of Figure 6). Return to text
29. See Table 2 for details on the definition of the variables. Tax data were drawn form the BEA web page. Return to text
30. An example of work in that direction is given by Bilbiie and Straub (2004), who study the interaction of distortionary taxes and rule of thumb households, albeit in a model without capital accumulation. Return to text
31. See, e.g. Clarida, Galí and Gertler (2000). Return to text
32. This is the road taken by Amato and Laubach (2003), albeit in the context of an alternative model of rule-of-thumb behavior. Return to text
This version is optimized for use by screen readers. A printable pdf version is available.
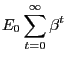
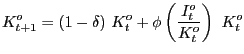
![$\displaystyle P_{t}Q_{t}=E_{t}\left\{ \Lambda_{t,t+1}\left[ R_{t+1}^{k}+Q_{t+1}... ...1}^{o}}{K_{t+1}^{o}}\right) \text{ }\phi_{t+1}^{\prime}\right) \right] \right\}$](img50.gif)
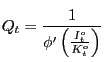
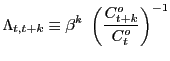
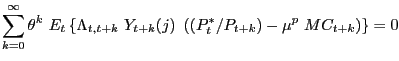
![$\displaystyle P_{t}=\left[ \theta\text{ }P_{t-1}^{1-\epsilon_{p}}+(1-\theta)\te... ...\left( P_{t}^{\ast}\right) ^{1-\epsilon_{p}}\right] ^{\frac{1}{1-\epsilon_{p}}}$](img96.gif)
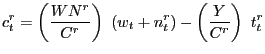
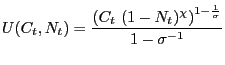
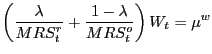
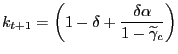
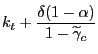
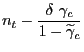
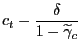
![$\displaystyle =\frac{(1-\alpha)}{\gamma_{c}\ \mu^{p} }[c_{t}-E_{t}\{c_{t+1}\}]+$](img322.gif)
![$\displaystyle \frac{(1-\alpha)(1+\varphi)}{\gamma_{c}\ \mu^{p}}[n_{t}-E_{t} \{n_{t+1}\}]-\frac{1}{\gamma_{c}}[t_{t}^{r}-E_{t}\{t_{t+1}^{r}\}]$](img323.gif)