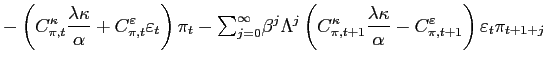Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 807, May 2004-Screen Reader Version*
Is Inflation Targeting Best-Practice Monetary Policy?
International Finance Discussion Papers numbers 797-807 were presented on November 14-15, 2003 at the second conference sponsored by the International Research Forum on Monetary Policy sponsored by the European Central Bank, the Federal Reserve Board, the Center for German and European Studies at Georgetown University, and the Center for Financial Studies at the Goethe University in Frankfurt.
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
We describe the inflation targeting framework (ITF) and compare it against hypothetical bestpractice based on optimization. The core requirements of the ITF are an explicit long-run inflation goal and a commitment to transparency in policymaking. Advocates and practitioners of the ITF have made many contributions to clear goal setting and communication by central banks. However, we contend that ITF communication policies both as advocated and practiced often have some elements that either obfuscate or, in some cases, explicitly contradict the dictates of optimization in a stabilization-policy paradigm. In this paradigm, the central bank has an objective function that places weight on both inflation and output-gap stabilization and faces a conventional (exploitable) Phillips-curve trade-off. We point out some problems that the ITF communication policy may generate in this setting. Our analysis leads us to make four suggestions for communication policy intended to help central banks avoid these problems.
Keywords: rules, discretion, commitment, transparency, communication, forecast, political economy, inflation bias, stabilization bias, trade off, expectations, fixed horizon, optimal policy, simple rule.
JEL classification: E50, E52, E58
*Faust is an Assistant Director and Henderson is a Special Adviser in the Division of International Finance at the Federal Reserve Board. We thank, without implicating, Michael Bordo, Matthew Canzoneri, Jinill Kim, Eric Leeper, Athanasios Orphanides, David Small, Lars Svensson, Peter Tinsley, Edwin Truman, Anders Vredin, and Alexander Wolman. We have benefitted greatly from the comments of Benjamin Friedman, our discussant at the conference. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting those of the Board of Governors of the Federal Reserve System or any other person associated with the Federal Reserve System. The email addresses of the authors are, respectively, [email protected] and [email protected]. Return to text
1 Introduction
The core requirements of inflation targeting are an explicit long-run inflation goal and a strong commitment to transparency. The framework built around these requirements has much to recommend it. Inflation and output performance in economies using the inflation-targeting framework (ITF) has been good by historical standards, and both governments and central banks claim to be pleased with the framework. Advocates and practitioners of the ITF have been leaders in shaping and exploiting the new consensus that central bank transparency can make policy more effective. Not only are ITF central banks among the most transparent in the world, they have experimented aggressively with ways to make communication with the public more effective. In the process, they have pioneered the use of various tools, such as fan charts, that make conveying essential, but difficult, concepts practical.
Economic performance in some non-ITF economies, such as the United States, has also been good in recent years. However, several ITFers (Mishkin (1999) and Bernanke, Laubach, Mishkin, and Posen (1999)) argue that this outcome has resulted in spite of the policymaking frameworks in those countries. Thus, they argue that the United States and others should `` fix the roof while the sun is shining.''
The recent hurricane in Washington has reminded many of us of the wisdom of this reasoning. It has also reminded us that even attractive new roofs--roofs that have weathered a few spring rains--might bear inspection. In that spirit, we examine whether the ITF constitutes best-practice monetary policy. We use the standard of some mythical best-practice policy to emphasize that we are not simply ranking the ITF relative to some set of ad hoc alternatives, such as the current practices at central banks around the world.
Of course, the ITF community is now large and varied. We focus mainly on the industrialized countries. One might say that we consider the role of the ITF in a low-inflation steady-state and do not address the important question of how it might help in reaching such a steady-state. In much of the paper we seek to highlight some generic issues. In doing so, we do not mean to suggest that there are not important differences among the practices of ITF central banks: our points will apply in varying degrees to ITF and other central banks.1
Our main message can be summarized succinctly. Common wisdom and conventional models suggest that best-practice policy can be summarized in terms of two goals: first, get mean inflation right; second, get the variance of inflation right. The ITF is of great help in achieving the first goal; whether it helps in achieving the second is more problematic. The argument goes as follows. Everyone now agrees that mean inflation should be modest. The ITF may be seen as a constructive attempt to cement the current consensus on this point. Unfortunately, agreement regarding the mean inflation rate has few practical implications at any finite horizon. Many of the most contentious debates over the conduct of policy in the postwar era are not about the mean but about the variance of inflation. That is, under what conditions should the central bank allow or promote movements of inflation around the mean in order to promote other goals such as real and financial stability? We argue that the ITF does not constitute best-practice in resolving this question. This claim is not new; it has also been made by both critics and supporters of the ITF, including Kohn (2003), Benjamin Friedman (2003), and Svensson (1999).
Of course, the ITF emerged near the end of a period of high inflation in the industrialized economies, when the most important challenge for policy was getting the mean right.2 As a period of generally low and stable inflation has emerged, more attention has been focused on the potential role of other goals in policy, and greater emphasis both in the academic literature and in ITF practice has been placed on the role of other goals. Our main critical point is not simply that there is more left to do. Rather, we argue that various features of the ITF--for example, the way the preeminence of the inflation goal is stated--obscure rather than facilitate the communication of best-practice policy.
Although we talk a great deal about the second goal of policy, getting the variance right, we emphasize that getting the mean right may be the goal of greatest importance. Arguably, the largest mistakes in the postwar era have been associated with failures to achieve this goal. Further, as a profession we are more certain about our advice regarding the mean of inflation and more confident that central banks can get it right. At a minimum, the best-practice policy framework should stress the goal that we are more clear about and that we are more confident central banks can achieve.
Finally, we raise many issues that are in principle subject to empirical investigation and, therefore, may one day be resolved. We focus on issues not currently amenable to clear empirical resolution. We do raise some questions for future empirical assessment.
In the next two sections we characterize the ITF in more detail and discuss some claims about the economy that underlie the approach. Our characterization, and our thinking more generally, rely heavily on such seminal work as Bernanke and Mishkin (1997), Bernanke, Laubach, Mishkin, and Posen (1999) and several contributions by Svensson including Svensson (1997a). The following three sections deal at a fairly abstract level with macroeconomic and political-economy aspects of the ITF. In the final two sections, we return to reality, discussing some complicating factors missing from the earlier analysis and then making some constructive suggestions.3
2 What is the inflation-targeting framework?
2.1 Central elements
One summary view of the ITF is provided by Bernanke, Laubach, Mishkin, and Posen (1999), hereafter BLMP:
Inflation targeting is a framework for monetary policy characterized by the public announcement of official quantitative targets (or ranges) for the inflation rate over one or more horizons, and by explicit acknowledgment that low and stable inflation is monetary policy's primary long-term goal. Among other important features of inflation targeting are vigorous efforts to communicate with the public about the plans and objectives of the monetary authorities, and, in many cases, mechanisms that strengthen the central bank's accountability for attaining those objectives. (p. 4, italics added)
We have italicized what we believe to be central elements. At the most general level, these elements can be summarized as follows: set an explicit, long-run inflation goal, give that goal a certain preeminence, and communicate vigorously about the conduct of policy relative to that goal. What may not be clear from the passage above is that ITF advocates also recommend taking into account goals other than inflation--for example, real and financial stability--and call for thorough communication about these goals. All major ITF banks have such goals.
We will regularly refer to two core requirements of the ITF: (i) set a long-run inflation goal and (ii) strive vigorously for transparency regarding all goals and aspects of policy.
These requirements might be viewed as innocuous. A long-run inflation target need have few finite-horizon implications. As Keynes (1923), (p.80) famously put it in discussing earlier monetary reforms,
But this long run is a misleading guide to current affairs. In the long run we are all dead.
The remaining core requirement is transparency. While how best to achieve transparency is a difficult question, that transparency is important seems uncontroversial; rather, it seems to be the new orthodoxy.
Based on these core requirements alone, it would be difficult to understand why the ITF has generated such strong sentiment for and against.
Going beyond the core requirements, advocates portray the full-blown ITF as a framework of ``constrained discretion'' and claim that it has great advantages over ``purely discretionary'' policy as practiced, say, at the Federal Reserve. In this paper, we attempt to identify which requirements of the ITF, beyond the core, give rise to such claims and then discuss whether these features should unambiguously be included among the requirements for best-practice.
2.2 Rules versus discretion
One definitional question that arises immediately is whether the ITF is best viewed as a ``rule'' or the exercise of ``discretion.'' Proponents such as BLMP and Svensson appear to differ on this matter, so it is important for us to make our view clear at the outset.
BLMP contend that the ITF is ``not a rule in the classical sense'' (p. 22); that is, it is not a forcing rule--a constraint on behavior that cannot be circumvented. They note that, ``an inflation-targeting framework will not directly prevent counterproductive attempts of a central bank to apply short-run stimulus. In this respect, inflation targeting is inferior to an ironclad rule...'' (p.24).
In contrast, Svensson (1999) argues that the ITF is a rule. We think that there is no contradiction here: Svensson is simply using a different definition. He mentions the standard definition, but provides an alternative under which advice to the central bank about how to use its discretion is a rule.4 For purposes of this discussion, the important point is that a Svensson-type rule does not represent even an approximation to a forcing rule. Any consequences of ignoring Svensson-type rules are contingent on the reaction of the public. Thus, in our view the ITF is a typical example of discretion in the classical sense, and we treat it as such in what follows.
2.3 What the ``discretion'' view implies for analyzing the ITF
Much standard policy advice comes in the form of concrete suggestions about how to pursue the goals of policy. Such advice often is either codified in the form of a reaction function or can reasonably be so codified for the purposes of study. In these cases, one can take some set of interesting macro models and run horse races among the implied reaction functions. One can also solve for the optimal rule and measure the inefficiency of the proposed rules relative to the optimum. Based on the results from several models, one can make statements about robustness and so on.
Many critics of the ITF have adopted a rules interpretation, but BLMP argue that these exercises completely miss the point (p.21).5 BLMP argue along the lines we have been discussing: the ITF does not place any constraints on the central bank that force it to deviate from the social optimum. Thus, it is not sensible to compare ITF outcomes to the optimum--the ITF can attain the optimum.6
It may seem like cheating to propose a framework and then simply to stipulate that it delivers optimal policy in model-based horse races. What role does this leave for policy research? We can distinguish two strands of the policy literature, which might be called institutional design and day-to-day implementation. If a forcing rule for central bank behavior is feasible and optimal, these two collapse to one: implement the forcing rule. If judgment must be exercised by the policymaker, these two interact but can be clearly distinguished. Research on institutional design seeks to define the optimal framework within which judgement will be exercised. Research on day-to-day implementation seeks to generate insights that will help policymakers exercise their judgement. The horse-race exercises may shed little direct light on the question of institutional design, but may be of great value in informing the ITF policymaking board regarding how best to use its discretion.
3 Conventional macroeconomics and the ITF
The reasoning supporting the ITF rests on several features of common ground in the macroeconomics profession and the policy community. Ultimately, some confusion about the ITF seems to arise because there are ITFers on both sides of a familiar dispute. In this section, we survey both the common ground and the disputed ground.
3.1 Macro common ground
3.1.1 Best-practice monetary policy would deliver low, stable inflation.
Inflation should be stationary, perhaps with infrequent, small mean shifts. Its mean should be low, certainly above zero and below 5 percent. Its variability should be sufficiently small that annual inflation is within 1 or 2 percentage points of the mean most of the time. Many technical issues may arise in giving this claim greater precision, but some version of it is now nearly universally accepted. This claim rests on three more basic claims.
First, there is no long-run Phillips-curve trade-off of the traditional variety. Failure to recognize this `` fact'' was surely behind some mistakes of the past, and Friedman (1968) and Phelps (1968) deserve great credit for pointing this out.7
Second, marginal positive expected inflation above some low rate is welfare-re-ducing. The profession can now list a multitude of channels through which expected inflation can affect welfare by reducing growth or in other ways. Widespread acceptance of the second claim rests neither on an appeal to a particular channel nor on incontrovertible econometric estimates of the costs of inflation. Nonetheless, in this paper we take for granted the common position that, above fairly low levels, raising mean inflation is bad.
Third, marginal decreases in expected inflation below some low, positive level are welfare-reducing. The recent experience of Japan and the return of low inflation in many countries has led economists to explore a number of channels through which deflation could be harmful. We will not focus much on deflation, but it is important to emphasize that inflation costs are two-sided.
3.1.2 There is a conventional short-run Phillips-curve trade-off
There may be many short-run trade-offs, but for concreteness we focus on the one that is most familiar to and relevant for many economists: the short-run Phillips-curve relation. We will take it as given that real activity is not always at the most efficient level and define the output gap as actual output minus efficient output. Policy actions that increase the gap are associated with a rise in inflation relative to steady-state inflation. As the next point makes clear, we do not mean to imply that best-practice policy can successfully exploit this trade-off.
3.1.3 The economy is complicated
Economic complications may include policy lags, changing relationships, the potential for self-fulfilling equilibria, and other nonlinearities. Finally, describing the state of the economy may require a high-dimensional state variable.
For a brief period, some leading members of the profession believed we were reaching the point where our understanding of economic dynamics allowed considerable range for beneficial intervention in business cycle dynamics. Friedman argued against this view, claiming that policy acted with long, variable, and unpredictable lags.8 Building on Friedman, Lucas famously added the Lucas critique to the list of complications.9 The general view that the economy is very complex is now widely accepted by academics and policymakers, for example, Greenspan (2003).
3.1.4 Due to political-economy problems, institutional design matters
There are various time-consistency, game theoretic, and institutional problems that might cause the government to set policy away from the social optimum.10 We lump all these under the title of political-economy problems. The profession still disagrees about the importance of, for example, time-consistency problems over the postwar era. But even those who feel that time consistency was not a big issue probably agree that institutional design is important. Some version of the claim that governments may have an incentive to exploit inflation surprises has been a common belief since the first time a government debased its currency.
3.2 Long-disputed ground
Whether monetary policy can beneficially exploit the short-run trade-off between inflation and the output gap is a long-standing dispute that is still at the center of monetary policy discussions.
3.2.1 No exploitable trade-offs
Friedman, and later Lucas, forcefully argue that given the
inherent complexity of the economy and our regrettably limited
knowledge of it, the ambitions of monetary policy should be limited
to achieving nominal stability. Their arguments are based on the
view that monetary policy has strong short-run real effects but
that there is no way monetary policy can beneficially exploit them.
They both suggest that a cautious response in the form of a
![]() -percent rule for money
growth is the best way to achieve nominal stability.
-percent rule for money
growth is the best way to achieve nominal stability.
Some ITFers hold the no exploitable trade-offs view (NET) and might well be called neo-Friedmanites. The NETers follow Friedman and Lucas in asserting that any trade-offs that exist cannot be successfully exploited, so that best-practice can only hope to achieve nominal stability. However, they argue that inflation stabilization is the best way to achieve nominal stability.11 They are at least as pessimistic as Lucas and Friedman about complications in the economy. Nevertheless, they argue that achieving inflation stability requires judgment and looking at a wide range of information variables (a ``look-at-everything'' strategy) and may require frequent changes in the instruments of policy.
Orphanides (2003b) provides support for the NET view and discusses its roots in Friedman. Ernst Welteke (2003), president of the Bundesbank and member of the governing council of the European Central Bank, has also clearly stated the NET view. Mishkin (2002) and BLMP both state the case for the NET view clearly, but, as we will explain, they belong in another camp.
What we will call the singular economy view is an alternative route to the NET position. In this view the economy is stochastically singular in a helpful way: stabilizing inflation automatically achieves any other goals of policy. For example, Rotemberg and Woodford (1997), King and Wolman (1999), and Goodfriend and King (2001a) produce simple models that exhibit a happy coincidence of the goals of stabilizing inflation and the output gap.12
Thus, either a vexing complexity or a fortuitous simplicity of the economy can get one to the view that there are no exploitable trade-offs.
3.2.2 Limited Exploitable Trade-offs
Fine-tuning the real and nominal economy is overly ambitious. In the limited exploitable trade-offs view (LET), there is some beneficially exploitable short-run trade-off between real activity and inflation, and best-practice policy exploits it. LETers, like NETers, contend that best-practice cannot be implemented using a rigid rule or by following a formal model. Studying optimal policy in formal models serves mainly to inform our collective wisdom, and this wisdom should be applied deftly in practice.
Many, if not most, advocates of the ITF are LETers. For example, Svensson and Woodford belong in the LET camp: in numerous papers, such as Svensson (1997a) and Svensson and Woodford (2003), they describe the ITF as involving optimal exploitation of the short-run trade off. BLMP also belong in this camp. Despite the claim of President Welteke of the Bundesbank cited above, we suspect that most central banks are in the LET camp, but this empirical claim need not detain us.
3.2.3 Comments
In both views, no rigid rule is appropriate, and policy must be based on a review of a wide variety of information. Neither camp takes an a priori stance on whether best-practice policy is ``activist'' in the sense of requiring frequent adjustment of instruments. Only in the LET camp is policy ``activist'' in the sense of attempting to manage the business cycle.
Because NETers argue that policy should only aim for inflation stability, they are open to the criticism that they are inflation nutters--which we take to mean that inflation is the only thing in the loss function. This criticism is misplaced: NETers are not nutters. The NETer argues from standard preferences that achieving nominal stability is the best we can hope for.
While the NET and LET views are distinct, in practice it is sometimes difficult to tell which view various parties take. Several problems emerge. First, some LETers believe that the degree of exploitability is quite low; thus, the views need not be that far apart.
Second, virtually everyone agrees that demand shocks push us toward the singular economy perspective. That is, in many standard models, demand shocks temporarily increase the output gap and raise inflation. Thus, smoothing inflation and the gap suggest roughly the same response. While limiting attention to demand shocks does not lead to exact singularity in most models, it certainly reduces the importance of the difference between the NET and LET views.
Supply shocks provide an interesting litmus test for deciding whether one is in the NET or LET camp. Consider a sharp increase in commodity prices. In many standard models, this shock tends to push inflation up and push output below the efficient level.13 Even if one leaves commodity prices out of the inflation measure, there will be indirect upward pressure on inflation. BLMP conclude that (p.35) `` a supply shock that is great enough or that arises from some unanticipated source may justify missing or changing a previously announced inflation target.'' In our view, this conclusion puts BLMP squarely in the LET camp. Mishkin (2002) makes similar arguments.
One might hope that empirical evidence would resolve this debate. The problem is that the distinction regards trade-offs along the efficient policy frontier. Informally, the LET view suggests that at the optimum the only way to reduce inflation variance is to raise gap variance. The NET view is that in the face of our profound ignorance, our best guess is that any deviation from the policy of smoothing inflation will increase both inflation and output variance. That is, policy injects variance into the economy with no expected benefit. Both sides agree that many of the significant policy changes we find in the data are movements toward the efficient frontier. Such moves may result in improvements in all aspects of performance.
In the remainder of the paper, we consider economies that have all the features of macro common ground and that are consistent with the LET view. Thus, much of our analysis will be of limited relevance for NETers.
4 Does the communication policy of the ITF maximize public understanding?
In this section, we begin our assessment of the ITF with the simplest case. We set aside political-economy problems and maintain the view that nothing in the ITF constrains the central bank from implementing the social optimum. Thus, there is no question of whether the ITF delivers good policy. That issue aside, the only remaining question is whether the communication policy of the ITF constitutes a good implementation of transparency. Our core requirements of the ITF give no details about how transparency is to be achieved, so this section also begins our filling in of the details of the ITF. We begin by presenting some arguments in favor of transparency, or as we put it, maximizing public understanding.
4.1 Why maximize public understanding?
In the recent past, few central banks would have placed heavy emphasis on maximizing public understanding. Moreover, there is no general presumption that increasing common knowledge in society improves welfare. The transparency literature is rife with examples where this is not the case, for example, Faust and Svensson (2001). Indeed, much of the transparency literature can be viewed as a study of when it is and is not optimal for the central bank to surprise the public deliberately. This conventional transparency literature does not address three arguments in favor of clear communication that are stressed by ITF advocates and many other commentators.
First, as Greenspan (2002) states, `` Openness is an obligation of a central bank in a free and democratic society.'' A great many conservative and liberal economists have supported this view. Deliberately surprising the public, even for its own good, is not the proper role of a central bank, in this view.
The second reason for clarity is that, as Lucas makes clear, what constitutes optimal policy is inextricably linked with public expectations about policy. The effects of a given policy action are not even defined without a treatment of policy expectations. More recently, discussions of the liquidity trap have reminded us of this point. The liquidity trap case drives the point home because, under certain assumptions, expanding the monetary base in a liquidity trap has no direct effects on the economy.14 Any effects result from changes in expectations.
Lucas argues that, even away from the liquidity trap, both the agent's problem and the central bank's problem in practice are intractable unless the public understands what the central bank is doing. An assumption about public understanding of the future course of policy is a precondition for coherent analysis of current policy.15
Accepting the role of expectations in the economy does not imply that central bank communication is important. Instead, Friedman and Lucas both argued for very simple policies that would largely obviate the need for communication. It is when we accept the view that best-practice cannot at this time be codified in a simply communicable way that continuing central bank explanation of actions becomes essential.
The third argument in favor of clear communication is that it may alter incentives in a beneficial way. Many variations of this idea have been studied in the political-economy literature. We argue that ITF advocates have a new channel in mind. This section focuses mainly on more direct benefits of clear communication; incentive effects are dealt with in section 6.
It is useful to note that none of these three reasons for clear communication has received much emphasis in the transparency literature. These may be the most important reasons for transparency in practice, however.
4.2 Our approach and model
Analyzing communication policy is complicated by the interaction between how policy is conducted and how it is communicated. If communication policy actually matters, then there is an interaction between what one should do and what one should say. Here we cut this knot by constructing an example in which we can unambiguously determine what one should do. In particular, we examine a simple model solved under the standard rational-expectations assumption that all agents fully understand the model and policy. We give the central bank the commitment technology to solve any political-economy problems. In this case, the socially optimal policy is unambiguous.
We then assess whether the ITF communication policy provides the most effective way to describe the conduct of policy. If we added an uninformed agent to the economy, would the ITF communication policy be the best approach to bringing that agent up to speed?
The model we employ has many standard features, and models like it have been used by supporters of the ITF, for example, Svensson (1997a). While it is exceedingly simple, it embodies the common ground described above. In our view, adding the complexity of reality would only tend to magnify the importance of the points we emphasize.
The model starts with the policymaker's loss function, which is the standard expected discounted sum of period losses conditional on available information:
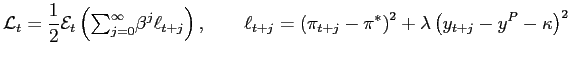
|
(1) |
where
The policymaker minimizes the loss function subject to the Phillips curve,16
| (2) |
where
The Phillips curve, (2), reflects two features of the common ground. First, there is no trade-off between mean inflation and any other mean or variance.17 This feature implies that the mean inflation rate can be set independent of other considerations in the model. In a more realistic model, there might be a link between, say, the mean and variance of inflation, but so long as the relation is generally positive this does not change the argument that low inflation can be chosen without regard to other goals.18
Second, there is a short-run trade-off between inflation and the output gap, and as we shall see, this trade-off is exploitable. The trade-off could be made fuzzier in various ways, but doing so would not alter the implications we emphasize.
4.3 Optimal policy in a backward-looking version
We use two special cases of the model to illustrate different
features of interest.19Here, we
consider a backward-looking version of the model in which there is
no wedge between potential and desired output (![]() ) and current inflation
depends on lagged inflation but not on expected future inflation
(
) and current inflation
depends on lagged inflation but not on expected future inflation
(![]() ). Under these
assumptions, the model generates no inflation bias and, under
optimal commitment policy, both the output gap and inflation follow
autoregressive processes:20
). Under these
assumptions, the model generates no inflation bias and, under
optimal commitment policy, both the output gap and inflation follow
autoregressive processes:20
| (3) | |
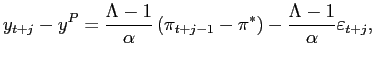
|
(4) |
where the parameter
These processes have the following implications that we will use in our discussion:
2. The unconditional expectation of inflation is the target
value,
![]() .
.
3. Conditional inflation expectations are described by
![]() .
.
4. There is an optimal balancing of output gap and inflation variance.
Implications like these are very general given the features of the common ground and the LET view.
4.4 Strengths of the ITF communication framework: transparency and anchoring
Under the assumption that the central bank implements the socially optimal policy as we have derived it, we can now ask whether several usual features of the ITF represent an effective way to communicate best-practice. As stated in the introduction, the first goal of best-practice is to get mean inflation right. In the model, we have that
| (5) |
so it is clearly appropriate to announce a long-run inflation target. Explanation of the behavior of inflation relative to the target is the centerpiece of ITF communication policy. A primary objective of the ITF is to anchor long-run inflation expectations, and the policy leaves little room for misunderstanding this objective. Thus, the ITF communication policy is arguably extremely successful in communicating about the first goal of monetary policy.
4.5 Room for improvement: the balance of multiple goals
In this section, we argue that the primary shortcoming of the ITF communication policy is that it does not explain clearly the roles and balance of multiple goals. Indeed, we argue that the ITF as implemented often involves elements that are literally inconsistent with best-practice policy and, in any case, obfuscates some basic issues.
To begin discussion, we list some usual features of the framework that we find problematic. It is often a feature of the ITF, as advocated and practiced, that one or more fixed horizons are associated with the inflation target. This practice is literally inconsistent with optimization. For example, the results above imply that
| (6) |
with probability 1, and that with certainty we will face times,
| (7) |
for any
Choosing a fixed horizon at which the inflation forecast must be
consistent with the target in some sense can be thought of as an
approximation to optimization. In particular, under full
optimization we can pick a horizon ![]() , a small probability
, a small probability
![]() , and a
margin of error
, and a
margin of error ![]() such that
such that
| (8) |
That is, at the horizon
Some central banks state target ranges for inflation. It is not clear how to interpret these ranges. Does a central bank aim to be inside its announced range all the time? Under best-practice, should it?
In our example, there is an interpretation of the term `` target
range'' that is consistent with best-practice. As is clear from
equation (8), the central bank can view the target range as a
confidence interval and relate the width of the range to the
probability that inflation (or its forecast at the relevant
horizon) will be in the range.21 Under
this interpretation , a target range is purely descriptive in that
it states that inflation will be within the range
![]() most of the time. This interpretation of the target range is
subtle, and we suspect not the predominant one.
most of the time. This interpretation of the target range is
subtle, and we suspect not the predominant one.
There is a contrasting interpretation that is not consistent
with best-practice. Under this interpretation, the central bank
wants inflation to be inside the range at all times, but control
errors might cause it to wander out at times. This interpretation
is not consistent with best-practice in the example. There is no
control error in our example--if there were, the ![]() associated with a given
associated with a given
![]() would be
larger. Under best-practice, the central bank deliberately sets
inflation outside any given interval at times. When evaluating
policy, no incident of inflation crossing the boundary is evidence
of central bank misbehavior; only excessive frequency of being
outside the interval constitutes such evidence.
would be
larger. Under best-practice, the central bank deliberately sets
inflation outside any given interval at times. When evaluating
policy, no incident of inflation crossing the boundary is evidence
of central bank misbehavior; only excessive frequency of being
outside the interval constitutes such evidence.
A key test as to whether the range is properly understood as a confidence interval is that under best-practice excessive frequency of being inside the range is also evidence of misbehavior. It should seem equally natural to punish the central bank for being inside the range too often as for being outside the range. In the LET view, no matter how limited one thinks the limited exploitability is, it remains the case that excessive smoothness and excessive volatility of inflation are equally costly at the margin in equilibrium. As BLMP document, some of the problems with target ranges we are pointing to have been observed in practice.
Next we note that the long-run inflation goal is often said to be preeminent in some sense in the ITF framework.22 While the intention here may seem clear enough, we do not understand what it means formally.
Given the common ground we are accepting, it is true that there
is no trade-off between setting the mean of inflation at
![]() and any
other goal of policy. There is no long-run trade-off; the mean of
inflation has no implications for other choices. Thus, the same
policy is obtained if inflation is the preeminent long-run goal or
if setting the gap equal to zero is the preeminent long-run
goal.
and any
other goal of policy. There is no long-run trade-off; the mean of
inflation has no implications for other choices. Thus, the same
policy is obtained if inflation is the preeminent long-run goal or
if setting the gap equal to zero is the preeminent long-run
goal.
Most crucially, we can arbitrarily rank the preeminence of long-run goals only if we are talking strictly about the mean of inflation. Generally, the preeminence statement is linked in some way to price stability. To the extent that stability is interpreted in a natural way as having something to do with the variability of prices and inflation, any statement of preeminence is the antithesis of the key feature of optimal policy--the notion that optimization implies an optimal marginal rate of exchange between stability of prices and stability of the gap.
Here is the essence of our argument so far. Monetary policy in the LET view involves conflicting goals. The mean inflation goal may reside outside this conflict, but any discussion of stability of prices or inflation must inevitably raise issues of other goals. We argue that several aspects of the ITF as practiced do not provide a natural and straightforward framework for communicating this fact. We now consider various ways other goals are accommodated.
One approach to balancing multiple goals is to state a target range for inflation that is assumed to give the central bank wiggle room to consider other goals. In practice, things have arguably worked this way. We return to the primary question of this section: is wiggle room the most effective way to communicate optimization with multiple conflicting goals? In our view, this way of communicating can clearly work, but is not the height of pedagogy.23
Escape clauses are another alternative. Every framework will surely need the equivalent of escape clauses. There will be events sufficiently peculiar from the standpoint of what was foreseeable at the time the framework was conceived that briefly abandoning the framework will be necessary. Still, taking account of the role of other goals through escape clauses is surely not fully transparent.
Finally, Svensson (1997a) has argued that in a quadratic
optimization framework like the one in our simple example, we can
view optimal policy as targeting the forecast of inflation, with
consideration of the gap incorporated by allowing it to affect the
horizon at which one wants the forecast to hit the target. Mishkin
(2002) argues for this approach and some ITF banks use this sort of
rhetoric. This approach is consistent with optimization. Formally,
it will be true under optimal policy that at each point in time,
![]() , there is a shortest
horizon,
, there is a shortest
horizon, ![]() , such
that
, such
that
| (9) |
for a given
If we were teaching this optimization process to an undergraduate or to the marginal agent added to the model, is this the most natural way? We have a linear-quadratic optimization with two conflicting goals and one instrument. The two goals of optimization are to get the mean right and to balance variability of inflation against variability of the gap. It seems strained, at best, to describe the optimization process in terms of a target for one variable and adjusting the horizon to take account of the other. This description fundamentally obfuscates the trade-off in question.
In this section, we have tried to make a simple point that many people find obvious. The ITF communication policy is tilted heavily toward emphasis on stabilizing inflation. Several usual features give inflation a role that is literally inconsistent with optimization in the LET perspective. Thus, in our view the communication policy of the ITF is not the best-practice way of maximizing public understanding.
5 Simplification and approximation
We have followed major advocates in interpreting the ITF as allowing the central bank to follow the socially optimal policy. Using this interpretation in a conventional LET-view model, we find that a dissonance arises between policy and the standard communication approach followed by the ITF. Perhaps we are being too literal: it may be that policy, or the communication of policy, is deliberately intended to be some sort of approximation of optimal behavior. These simplifications may be optimal in some broader perspective: perhaps there is some unmodelled simplicity constraint on either communication or policy itself that we have not captured. At some level, there surely are such constraints, so this possibility deserves serious treatment.
5.1 Simplicity constrained policy
Perhaps policy behavior is subject to a simplicity constraint that causes policymakers to follow rule-of-thumb-like policy. From where would such a constraint arise? The standard justification is that it arises from some need for ease of monitoring. Thus, a bank with a severe credibility problem might find that the credibility benefits of a rule that is trivial to monitor outweigh the costs. Fixed exchange rates are often justified in this way both in theory and practice (Atkeson and Kehoe (2002)).24 The arguments for a simplicity constraint in extreme cases are familiar.
Regarding the advanced economies that are the focus here, we make two points. First, if the ITF requires deviating from the optimal policy on economic grounds, then proper evaluation of the ITF requires a clear statement of the deviations required. In this case, we need to go back to the macromodel horse races to evaluate the costs of the deviations and attempt to weigh these costs against the benefits of simplicity. Second, as we argue next, even when banks assert that policy is constrained in this way, it often turns out that only communication is actually constrained.
5.2 Optimal policy/simplicity-constrained communication
We have generally treated the problematic elements of the ITF as constraining communication, not policy behavior. In practice, public communication requires some simplification, and as economists, we naturally think of simplification in terms of an approximation that is adequate so long as variables stay near some mean or steady-state values. The problems with ITF communication listed above will probably be minor so long as inflation and the gap stay near the steady-state values.
We believe that use of a communication policy simplified in this way is dangerous. As we get further from the steady state, the appropriateness of the simplified framework diminishes. Of course, since these conditions are observed infrequently, uncertainty on the part of the public about the central bank's policy is greatest at these times. Further, the conflict in society over the proper short-run policy becomes more intense as we move away from the steady state.25 Thus, the simplified communication works best when it is least needed and tends to break down when it is most needed.
If any ITF banks are following this course, they are on a well-trodden path. Central banks have regularly adopted rule-of-thumb communication devices that function well during normal times and then scrambled to wean the public from these rules (or adjust and qualify the rules) when times became more challenging.
Intermediate money targeting illustrates this claim. It provided a framework for the conduct and communication of policy. Although it was not necessarily presented this way at the outset, intermediate targeting was a simplifying approach that was viewed as ex ante suboptimal on stabilization grounds.26 Under such a system, there inevitably comes a time when the best judgments about how to run policy conflict with the direction dictated by the intermediate target.
The central bank must then choose between running policy it believes to be suboptimal or running policy inconsistent with the framework it typically uses in communication. In practice, banks generally chose the latter option. Thus, the Fed regularly redefined the target, redefined the target variable, and simply ignored the deviation of the target variable from target. Similarly, some have argued that the Bundesbank was an implicit inflation targeter and ignored the intermediate money target when it appeared inconsistent with inflation objectives.27 We are not at all critical of this solution: these banks probably made the right choice in deviating from the communication policy rather than from best policy.
This case illustrates that adopting simplified communication approaches need not actually simplify anything.28 Such communication works fine in easy times. In challenging times, a dissonance arises between the simple communication framework and the course of policy, generating a certain degree of turmoil and confusion.
5.3 Must the public have a simple yardstick?
One virtue of the problematic ITF features that we discuss is that they give the public a simple yardstick by which to judge policy. Given lexicographic preferences over inflation and other goals, an inflation target range, and a fixed horizon, inflation targeting becomes very easy to monitor. One simply checks whether the inflation forecast is at the target at the specified horizon.
The virtue of this yardstick is ease of use; the problem is that it is the wrong yardstick. From Heikensten and Vredin (2002), it seems that the Swedish National Bank (hereafter Riksbank) may have come closest to explicitly advocating that the public think of policy using such a simple rule of thumb. Recently policy pursued by the bank has deviated from this rule of thumb, perhaps illustrating to some extent the sort of communication problem we raise.29
Despite such examples, it is explicit or implicit in many discussions that ease of monitoring demands that the public be given a yardstick for measuring policy that is relatively straightforward to use. We believe that Fed policy over the past 15 years provides a counterexample. Arguably, one of the most notable aspects of Federal Reserve policy in the Greenspan era has been the fact that the Fed has resisted the temptation to characterize policy in terms of some simplified, and thereby inherently suboptimal, framework. The Fed has demonstrated that one can run policy with at least reasonable success without placing constraints on policy or communication that are thought ex ante to be suboptimal on economic grounds.
The Fed's approach in this period is at times viewed with alarm and/or suspicion. Svensson (2003a) argues that failure to adopt the ITF is a smokescreen that allows the FOMC freedom to secretly change its goals. Others argue that a concrete goal is essential for accountability.
These arguments may be correct, but they have been selectively applied. The second major goal of policy in the LET view is stabilizing the gap. It has become conventional wisdom that the gap is sufficiently difficult to measure that communicating a concrete goal for any particular measure of the gap would be problematic. This view is taken as adequate justification for not reporting a concrete goal for a gap measure. Let us set aside for a moment the factual question of whether difficulties in measuring the gap are different in kind or only in degree from those in measuring inflation.
Even acknowledging measurement problems, one must surely echo Svensson in asking whether these problems might be used as a smokescreen, allowing a central bank to shift its preferences about output stabilization.30 Further, one must ask how the central bank could possibly attain credibility and accountability on the gap goals without a concrete gap goal. These issues are no less pressing in the case of real stability than in the case of inflation stability.
In practice, we suspect that ITF advocates are comfortable with the view that credibility and accountability regarding real stability responsibilities can be attained through vigorous central bank communication. By the same token, we argue that it is, at the very least, an open question whether accountability and credibility regarding inflation necessitate adopting a simple yardstick that is suboptimal in the sense we have been describing.
6 Political-economy problems and the ITF communication policy
ITF advocates contend that central bank communication can solve political-economy problems. In our view, this is the least well analyzed claim of ITF advocates. In this section we describe the communication channel emphasized by ITFers and show how existing tools can be employed to analyze it. We ultimately conclude that use of this channel can play a role in getting the mean of inflation right, but seems as likely to complicate as to facilitate achieving the appropriate balance between inflation and output stability.
6.1 The communication channel
The basic idea behind the ITF communication channel is that people dislike exposure of their intentional trickery, honest mistakes, or incompetence. If this is so, then public promises carry their own enforcement mechanism based on policymaker aversion to criticism. The ITF is designed to make better use of this channel by requiring public statement of goals and then public reports about progress on the goals. As BLMP argue,
To the extent that the central bank governors dislike admitting publicly that they may miss their long-run inflation targets (or, alternatively, to the extent that they dislike having their inflation projections criticized as biased or manipulated), the existence of an inflation-targeting framework provides an incentive for the central bank to limit its short-run opportunism. (p.25)
Svensson (1999) is more emphatic:
I believe it fair to say that never before in monetary history has an incentive system been set up with such strong incentives for optimal monetary policy decisions. (p.663)
In more formal terms, the communication channel invokes terms in the central banker loss function--associated with, say, honesty and aversion to criticism--that have often been ignored.31
The ITFers' argument here seems consonant with two alternative views about political-economy problems. Blinder (1998) and McCallum (1997) argue that the time-consistency literature simply misses the point. According to McCallum, knowing about the commitment policy, central bankers would `` just do it.'' The ITF communication policy might be seen as an attempt to increase the probability of this outcome. Friedman has a different take on central bankers' loss functions:
From revealed preference [as revealed in central bank communication], I suspect that by far and away the two most important variables in their [Federal Reserve policymakers'] loss function are avoiding accountability on the one hand and achieving public prestige on the other... (quoted in Fischer (1990), footnote 52).
Whether or not one subscribes to such an uncomplimentary view, why not design a framework to constructively exploit motives such as a desire for prestige?
We readily accept the ITF premise that the threat of public criticism affects the incentives of the central bank and thereby the course of policy. We take the view (perhaps following Blinder and McCallum) that, in normal times and with first-rate policymakers, this channel may not be of great importance. These policymakers will ``just do'' the right thing, as they see it, largely independent of public accolade or criticism. In the spirit of preparing the roof for rainy days, however, we consider the case when a weaker or more political board is in place.
6.2 Solving political-economy problems using special loss functions
The communication channel involves terms in the loss function representing aversion to criticism that are usually neglected. Fortunately, the literature provides tools for studying solutions to political-economy problems using special loss functions. Rogoff (1985) considers simply picking a `` conservative'' central banker, one with a loss function that embodies greater aversion to inflation than the true social loss function. This approach generates a trade-off: excess aversion to inflation lowers mean inflation, but it causes inflation to be smoother and the output gap to be more variable than is optimal. Melitz (1988) and Obstfeld (1996) make use of terms in the loss function embodying `` political costs'' associated with breaking a pledge to keep the exchange rate fixed. They, too, generate a trade-off between reducing inflation bias and achieving stabilization objectives. Calling attention to this possible trade-off is one of the main contributions of the time-consistency literature.32 Canzoneri, Nolan, and Yates (1997) provide examples in which taking advantage of `` political cost'' terms generates more complicated trade-offs. These papers all consider intuitively appealing, but ad hoc, loss functions.
In contrast, Walsh (1995) and Persson and Tabellini (1993) show how one can derive a loss function that completely eliminates the inflation bias problem without introducing stabilization costs. They discuss how this structure of loss might be induced using performance contracts for policymakers. More recently Lockwood, Miller, and Zhang (1995), Svensson (1997b), and Svensson and Woodford (2003) construct loss functions that eliminate both inflation and stabilization biases in models like ours. The basic approach in all these studies is to amend the policymaker loss function in such a way that the implied first-order conditions under discretion give rise to the same policy as under commitment.
6.3 A formal example
Here we use a forward-looking version of our simple model to
illustrate how amending the loss function can eliminate inflation
bias and stabilization bias. In this version, we assume that
current inflation depends on expected future, but not lagged,
inflation (![]() ) and
that target output exceeds potential (
) and
that target output exceeds potential (![]() ). For simplicity, we
assume that there is a single random shock in period
). For simplicity, we
assume that there is a single random shock in period ![]() (
(
![]()
![]()
![]() ). Under
commitment, the policymaker can affect inflation at
). Under
commitment, the policymaker can affect inflation at ![]() and expected inflation in all future
periods. Therefore, it can smooth adjustment to the shock over
multiple periods. In future periods, the policymaker has an
incentive to renege but is locked in by commitment. However, under
discretion, when the shock hits at
and expected inflation in all future
periods. Therefore, it can smooth adjustment to the shock over
multiple periods. In future periods, the policymaker has an
incentive to renege but is locked in by commitment. However, under
discretion, when the shock hits at ![]() , the policymaker cannot have the desired effect on
inflation expectations in future periods because it cannot be
relied upon to ratify those expectations. Therefore, inflation
returns to its unconditional mean in period
, the policymaker cannot have the desired effect on
inflation expectations in future periods because it cannot be
relied upon to ratify those expectations. Therefore, inflation
returns to its unconditional mean in period ![]() and remains there, so adjustment
to the shock is smoothed less effectively. The formal solutions are
presented in Table 1.33 The
commitment policy we consider is commonly referred to as the
full-commitment policy (or the solution to the Ramsey problem): it
is the unconstrained optimum given that the policymaker can commit
to the chosen policy.
and remains there, so adjustment
to the shock is smoothed less effectively. The formal solutions are
presented in Table 1.33 The
commitment policy we consider is commonly referred to as the
full-commitment policy (or the solution to the Ramsey problem): it
is the unconstrained optimum given that the policymaker can commit
to the chosen policy.
Our model exhibits the classic inflation
bias under discretion. Ignoring any shocks, at the optimum
inflation rate of
![]() , the bank
has an incentive to surprise the public by increasing inflation in
an attempt to stimulate output. Inflation is increased to the point
at which the marginal cost of additional inflation just offsets the
marginal benefit of attempting to raise output above potential
toward the target. To see the inflation bias in this case, set
, the bank
has an incentive to surprise the public by increasing inflation in
an attempt to stimulate output. Inflation is increased to the point
at which the marginal cost of additional inflation just offsets the
marginal benefit of attempting to raise output above potential
toward the target. To see the inflation bias in this case, set
![]() equal
to zero in the discretion solutions in equations (
equal
to zero in the discretion solutions in equations (![]() ) and (
) and (![]() ) and assume that
) and assume that ![]() . Under discretion,
inflation is constant and exceeds
. Under discretion,
inflation is constant and exceeds
![]() by the
standard inflation bias,
by the
standard inflation bias,
![]() .
.
In contrast, under commitment, inflation is time varying. It
approaches
![]() from above
and is always less than the positive inflation under discretion.
Output is also time varying. It approaches
from above
and is always less than the positive inflation under discretion.
Output is also time varying. It approaches ![]() from above and is always below
from above and is always below
![]() . It is optimal
to have inflation above
. It is optimal
to have inflation above
![]() in order to
raise output above
in order to
raise output above ![]() for all finite
for all finite ![]() , but
optimal inflation and output must decline over time in order to be
consistent with the Phillips curve.
, but
optimal inflation and output must decline over time in order to be
consistent with the Phillips curve.
The model also exhibits stabilization
bias under discretion. A useful measure of stabilization
bias is the part of the extra loss from discretion relative to
commitment that results from the existence of the shock. To
consider stabilization bias, set ![]() equal to zero in all the solutions in Table 1
and assume that there is a positive cost shock in period
equal to zero in all the solutions in Table 1
and assume that there is a positive cost shock in period
![]() (
(
![]() )
and no shock in any other period. As might be expected, under
discretion the optimal response to the cost shock in period
)
and no shock in any other period. As might be expected, under
discretion the optimal response to the cost shock in period
![]() involves some increase
in inflation and some reduction in output in period
involves some increase
in inflation and some reduction in output in period ![]() and no response in any later period
because there are no shocks then.
and no response in any later period
because there are no shocks then.
Under commitment, the optimal responses of inflation and output
in period ![]() are damped
relative to those under discretion. There are reductions in both
inflation and output in period
are damped
relative to those under discretion. There are reductions in both
inflation and output in period ![]() and in every period thereafter with the responses
approaching zero from below as
and in every period thereafter with the responses
approaching zero from below as ![]() approaches infinity, in order to be consistent with
the Phillips curve. The Phillips curve in period
approaches infinity, in order to be consistent with
the Phillips curve. The Phillips curve in period ![]() implies that reducing inflation in
period
implies that reducing inflation in
period ![]() partially
offsets the upward pressure on inflation resulting from the shock.
Therefore, it is possible to damp the responses of both inflation
and output in period
partially
offsets the upward pressure on inflation resulting from the shock.
Therefore, it is possible to damp the responses of both inflation
and output in period ![]() . The
benefit in period
. The
benefit in period ![]() more
than offsets the losses in all future periods because, with a
quadratic loss function, the first small movements away from the
optimum in future periods cause negligible increases in loss.
more
than offsets the losses in all future periods because, with a
quadratic loss function, the first small movements away from the
optimum in future periods cause negligible increases in loss.
We can attain the full-commitment solution under discretion if the policymaker is given the amended loss function
Loosely speaking, one subtracts out terms in the discretion first-order condition that lead to the inflation bias and adds in terms relating to the time-varying and state-contingent optimal policy. In particular, stabilization bias can be eliminated only by subtracting terms that are time varying and depend on the size of the cost shock.
6.4 Likely effectiveness of the communication channel
Our example illustrates how political-economy problems can be avoided if only the policymaker's loss function differs from the social loss function in the proper way. It also shows that, even in a stripped down model, the required special terms are somewhat complicated and vary with the state of the economy. In this very simple model, we might, however, imagine writing an incentive contract to achieve optimality. Of course, it is a feature of the common ground that the actual economy is so complicated that it is impossible to codify such a contract.
ITFers argue that we can achieve much of the desired effect by exploiting policymaker aversion to criticism. However, to achieve this effect on the first-order conditions, these aversion-to-criticism terms would have to take a very particular, state-dependent form. We have seen no argument as to why aversion to criticism would work in the intended manner. Indeed, we have difficulty imagining how to form such an argument.
More generally, we know of no literature supporting the view that some combination of public promises, maximal scrutiny, and the threat of public criticism is an uncontroversial recipe for optimal public policy. Suppose we accept that weak policymakers will be swayed by criticism. Given the skewing of communication in the ITF, it strikes us that a weak policymaker may find it safest to excessively smooth inflation. That is, it might literally follow its pronouncements. Both this view and the contrary view, however, are highly speculative given the nature of the mechanism.
Despite our reticence to draw strong conclusions either way, we offer two comments. First, we find it plausible that stating a long-run inflation goal and communicating regularly about it will raise the chance that policy hits the long-run goal for the reasons cited by the ITF. Second, the ITF seems as likely to complicate as to facilitate achieving a proper balance of multiple goals by a weak policymaker.
7 Complicating factors largely missing from models
Up to now, we have been analyzing the ITF from a relatively abstract perspective. As preparation for making some constructive suggestions based on our analysis, we discuss some real-world complications that are largely missing from our analysis and most other formal work.
7.1 Strategic skewing and transparency
Beyond clarity, strategic skewing may be an essential component of effective public communication. One of the most famous principles of strategic skewing in the folk wisdom of central banking is that central banks should ``do what they do, but only talk about inflation.'' Alan Blinder contravened this principle, the story goes, in the famous Jackson Hole imbroglio, perhaps confirming its wisdom.
While most ITF advocates would vigorously dispute it, the ITF might be viewed as an application of this folk wisdom. Without the folk wisdom, it is difficult to imagine why a policy of optimization with multiple conflicting goals would be called ``inflation targeting.'' Calling reports on all aspects of policy ``inflation reports'' is an analogous misnomer. The folk wisdom would also justify discussing goals other than inflation only as they affect the horizon over which one intends to hit the inflation target.
The folk wisdom might actually be wisdom. If these topics are too sensitive to discuss, then we should stop praising the ITF and other central banks for their commitment to transparency; instead we should lament the fact that central banks cannot publicly discuss the pursuit of their multiple mandates. Further, the practical art of strategic skewing is well-studied, for example, by public relations experts. Economists have no special claim to expertise in optimal skewing.
7.2 Maximal transparency and deliberation
Unlimited transparency may be inconsistent with optimal deliberation. As Greenspan (2002) puts it,
The undeniable, though regrettable, fact is that the most effective policymaking is done outside the immediate glare of the press. (p. 5)
More generally, transparency could, depending on the social environment, generate inefficient dissension about policy. Goodfriend (1986) lays out various forms of this argument including the following:
In this view, secrecy could confer a social benefit because it makes consensus politics work more smoothly and with less cost.
The role of concerns like this in determining the current structure of the Federal Reserve is reviewed in Faust (1996).
We think it is almost certainly a grave error to trivialize such concerns. We cannot contribute much to their analysis, however. In our view proper treatment requires bringing in expertise from areas beyond economics. We stick to reviewing the more directly economic merits of transparency.
7.3 Multiple decisionmakers
In many countries a board is charged with making policy. In much of the theory we have been reviewing, the fact of multiple decisionmakers is inessential. The framers of the Federal Reserve, however, saw the composition of the board as an essential aspect of their response to political-economy problems. For example, Warburg (1930) argues that a
formula had to be found by means of which these two elements [big business and politicians] would be called upon to balance one another (p.773).
As is often the case with responses to difficult political design problems, the framers came up with a mish-mash solution.34 As a bottom line, they decided on a particular weighting of interests on the FOMC. Congressman Henry Steagall (1935) summarized the result:
[U]nder the bill embodied in the conference report the board [that is, the FOMC] will stand 5 to 7 giving the people of the country, as contradistinguished from private banking interest, control by a vote of 7 to 5 instead of by a vote of 3 to 2 [as proposed in the Senate].(p. 13706)
Multiple heterogeneous policymakers clearly pose a practical problem for transparent communication about the goals of policy, the rationale for policy, and the causes of past policy mistakes and successes. There seems to be disagreement about the magnitude of this problem, however. Some contend that there are not many differences of opinion about either the appropriate loss function for policy or about how the economy works. Others are not so sanguine.
If there are substantial disagreements over the loss function and/or the workings of the economy, one response would be to require multi-stage decisionmaking. First, the board agrees on goals of policy. Next, taking the goals as given, the board agrees on the model of the economy. Finally, the board makes policy taking the goals and model as given.
This approach has the convenient feature of making the policy process, for purposes of analysis, look rather like the simple single-decisionmaker problem. In some discussion, failure to agree first on goals of policy or the model sometimes seems to be taken as prima facia evidence of inefficient behavior by the policymaking board. This view trivializes the analysis of public decisionmaking.
There is no theorem of public decisionmaking stating that the multi-stage decisionmaking approach is good for society. One can write examples in which multi-stage decisionmaking is or is not efficient, but theoretical examples probably do not get to the heart of the matter. Imagine a monetary policy board populated by astute, public-spirited, policy-oriented economists--epitomized perhaps by James Tobin and Milton Friedman. The multi-stage approach would require that they agree first on goals, next on the model, and only then consider policy options, given those goals and model. In an alternative approach, we could simply charge them with agreeing on and implementing policy. One suspects that the multi-stage approach may not even be feasible in practice. There is at least room to differ regarding which approach would lead to better policy.
7.4 Measurement of inflation and the gap
Choosing a measure of inflation and an appropriate long-run inflation goal presents practical problems that may not have been fully appreciated during periods of high inflation. In 1980, any low number seemed like a good thing. Fortunately, gone are days when proponents of low inflation could simply assert, ``Zero is a nice round number.''
There is now general agreement that most, if not all, price indices exhibit non-negligible quality biases. Further, for various reasons to do with quality bias and composition, different indices often behave quite differently for substantial periods of time. Thus, the issue of which index to focus on may be of some importance.35
Many economists inside and outside the ITF camp have also concluded that the inflation goal should be set high enough to limit the probability of hitting the zero lower bound on nominal interest rates. Thus, they argue for allowing a non-negligible stabilization buffer that exceeds proposed allowances for quality bias.36 Exactly how large a buffer to allow is a technical question involving the costs of moderate inflation, the costs of being mired in a recession, and the responsiveness of the economy to changes in the policy rate. The answer may change over time as the economy changes.37 In our view, the fact that choosing the appropriate target is a technical question and the possibility that a good initial answer may not be found argue strongly for keeping the choice of the inflation target in the hands of central banks and for revisiting it periodically.
Obviously, ITF banks believe that the benefits of a concrete target outweigh any costs that might be generated by these measurement issues. Some current and past U.S. policymakers agree--for example, Bernanke (BLMP) and Meyer (2002). Gramlich (2003a) speculates that announcing a long-run range for inflation might increase transparency without unduly limiting flexibility. In contrast, Greenspan (2002) argues that
For all these conceptual uncertainties and measurement problems, a specific numerical inflation target would represent an unhelpful and false precision. (p.6)
Greenspan argues, loosely speaking, that the Fed is striving for price stability properly measured and that achieving this goal does not correspond reliably to hitting a long-run target for any particular index. We do not attempt to resolve this empirical dispute in this paper, but discuss some of its implications in the final section.
It is generally believed that the measurement issues regarding the gap are much more serious. Here, in discussing the real world, we are moving beyond our model and using gap as a short-hand for the relevant measure of economic slack. In practice, there may be many relevant gaps, and none is easy to measure. Indeed, one version of the NET view is that these problems are so overwhelming that the gap should not be part of policymaking.38
In the LET view, these measurement issues may be immense and, hence, exploitability may be minimal. By definition, however, the LETer believes that we can monitor the economy sufficiently well to attain some beneficial exploitation of the short-run trade-off. If this is so, there is also some way to communicate this information to the public. That is, there should be a heavy presumption against the view caricatured by Karl Brunner that central banking is an inaccessible art, and that the
...esoteric nature of the art is moreover revealed by an inherent impossibility to articulate its insights in explicit and intelligible words and sentences (as quoted in Goodfriend (1986))
Arguably, to the extent that there is less controversy regarding the measurement of inflation than the gap, careful and thorough communication about the gap is more essential. Under this view, the emphasis in the communication strategy of the ITF is misplaced.
8 Conclusions
In Section 2, we state that two core requirements of the ITF are a long-run inflation target, and transparency. The first only constrains central bank policy in the long run; the second constrains talk, not actions. Based on these requirements alone, it would be difficult to understand the passionate debate over the ITF.
In filling out the description of the ITF, we have come to believe that some of the passion comes from the following characterization. Inflation targeting has been portrayed as a snug-fitting garment that is a great improvement over pure discretion. The latter is caricatured as a seat of the pants approach. Less colorfully, inflation targeting is depicted as constrained discretion.39
From one perspective, this characterization is quite reassuring. Purely discretionary, seat-of-the-pants policymaking sounds a bit risky. Given that monetary policy is made in a complicated world and is subject to conflicting pressures in society over what policy is best, there is rightfully something comforting about the notion of a snug-fitting garment.
From another perspective the characterization is distressing. Central banks have often put on snug-fitting garments--for example, fixed exchange rates and money targeting. Historically, these garments have proven uncomfortable; they have regularly split at the seams.
Which perspective is correct? ITF advocates tell us there is nothing to fear from the snug-fitting garment: the constraints in constrained discretion do not constrain the central bank from pursuing optimal behavior. While there is nothing, in principle, wrong with this claim,40 we remain uncertain about the basis of this claim. Going beyond the core requirements, in practice ITF imposes many requirements--for example, fixed horizons, target ranges, lexicographic preferences regarding price stability. These requirements might be viewed as constraining policy, but they are inconsistent with optimization under conventional views about the economy. We have treated them not as constraints on policy behavior, but merely as features of the ITF communication policy that generate dissonance between how the banks talk and how they act. We have not identified requirements of the ITF that constrain use of policymaking discretion, while remaining consistent with optimization.
We acknowledge that, despite their costs, central banks might find simple yardsticks or rules of thumb useful in guiding the communication of and/or conduct of policy. It is an open question whether such simplifications yield net benefits in any particular context. Until such constraints are better justified, they are not, in our view, clearly part of best-practice monetary policy.
8.1 Constructive Suggestions
Our review of the ITF leads to several constructive suggestions regarding best-practice, whether inside or outside the ITF. In short form, these amount to a guide for implementing the core requirements.
Suggestion 1: Central banks should state a clear long-run inflation goal. No range or fixed horizon should be given.41 If no numeric target is given, clear countervailing interests should be stated, and effort should be made to reduce uncertainty regarding the long-run goal. The value of this goal in meeting all long-run goals of policy should be stressed.
In order to be consistent with this suggestion, ITF central banks would have to modify the characterization of their long-run inflation goals in many cases. The Fed regularly communicates its strong commitment to the principle of price stability but has not stated an explicit target. As justification for not stating an explicit target, various policymakers have cited problems due to measurement issues, political-economy considerations, and the existence of multiple decisionmakers. A key question facing the Fed is whether with careful statement and qualification, it might obtain some of the benefits of a more concrete goal while minimizing the costs.
Suggestion 2: Central banks should communicate in a balanced way about the objectives driving short-run policy. If these objectives are seen as conflicting due to the structure of the economy, this viewpoint should be made clear. To the extent that other goals are more difficult to quantify than the inflation stability goal, the need for clear reporting is heightened and banks should strive to find ways to communicate about these goals effectively.
For ITF central banks, adopting suggestion 2 would involve changing some language that is literally inconsistent with optimization in the LET view. It would also require providing more complete communication about the role of goals other than inflation in policy. It is a matter of perspective whether these are viewed as small or large changes. They may well be minor tweaks on the idealized ITF framework defined by Svensson.
If transparency is truly a goal in central banking, then the area with the greatest room left for improvement at most central banks is communicating the roles of goals other than inflation. For ITF banks and others, it would greatly clarify issues if three questions were answered: Is some notion of real stability an objective of the central bank? Does the bank take the NET or LET view? If it is a LETer, how will the trade-off be managed? At a general level, ITF central banks and others have done quite well in answering the first of these questions but less well in answering the latter two.
Answering the second question--are you a NETer or LETer?--is relatively straightforward. Answering the third question requires successfully characterizing how the trade-off will be managed. This is a complex task that all LET central banks must face. We have no special insights on this topic. We believe, however, that clarity on goals and the NET/LET distinction is an important first step. It brings real stability into the conversation in its proper role. The focus on inflation has led to valuable innovation in communication; putting real stability on the table can promote similar innovation on the real side. The Reserve Bank of New Zealand and the Bank of Norway have begun this experimentation process.42
Suggestion 3: If best-practice policy is complicated, the totality of central bank communication should reflect that complexity.
This suggestion is based on the distinction between two dictionary senses of transparent. The first, and the one generally applied throughout the central banking literature, is that transparent means ``frank, open, candid.'' However, sometimes the idea surfaces that central bank communication should be transparent in the sense of being, ``easily seen through, recognized, [or] understood.''43 If best-practice dictates complicated policy, then communication that is frank, open, and candid will probably not be easily understood.
In practice, central banks probably need to have a multi-layered approach to communication with differing levels of complexity. However, there should be readily available information that makes it possible for a reasonably tenacious and intelligent person to understand policy in its complexity.
A review of the material on the web sites of several ITF banks suggests several useful examples of this multi-layered approach. Setting aside our particular criticisms about overemphasis of inflation, the monetary policy reports of ITF banks represent an extremely valuable aid in understanding the function of policy. These banks generally commission and publish outside reviews of the reports; for this and other reasons, their content is steadily improving.
Assessing the communication of the Fed is more difficult. It is certainly true that there is no one source of information that brings together the information represented in the best of the ITF monetary policy reports. Due to the sheer bulk of reports to Congress, testimony and speeches by FOMC members, and publications by the Board and 12 member banks, it would be a daunting (and unenviable) task to confirm reliably which topics are covered and which are not. A key issue facing the Fed in vigorously pursuing effective transparency is whether this material can be more concisely packaged and delivered, while respecting the diverse committee structure of the FOMC.
Suggestion 4: Central banks should strive to communicate clearly the likely course of policy. If forecasts are part of this process, the relationship between the forecasts and the future course of policy should be explained.
If policy cannot be codified in a simple rule, as we have assumed, then helping the public understand the likely course of policy is an essential part of effective policymaking. Central bank forecasts are a central feature of the monetary policy reports of ITF banks. While such forecasts can and do play many roles,44 determining the proper role of forecasts in shaping policy expectations is more complex than usually recognized.45 Under standard practice, the forecasts are of unclear value in understanding the course of policy.
For example, it is standard practice to report a forecast for output and inflation conditioned on some counterfactual path for policy such as a constant policy rate. These forecasts are generally depicted as judgmental, and the reader cannot know the model in more than general terms. It is very difficult to see how such a forecast has any marginal value in predicting the course of policy, beyond the predictive power of the standard data available to the public. For example, if the central bank optimizes in the LET view, then the public certainly cannot deduce that a conditional forecast of inflation above target means policy will be tightened. Further, releasing a forecast for output growth (which is only tenuously related to the gap or other relevant notions of slack) provides little help. Only if there is a known mapping from the conditional forecast to policy is that forecast of clear use.46
In contrast, an unconditional forecast of goal variables and the policy rate would shed a good deal of light on policy. Given that the public already has its own unconditional forecast of the economy and policy, the public can see if the two forecasts differ and, by comparing the policy rate forecasts, make an attempt to deduce whether those differences stem from different views of the future path of policy or from different views of other aspects of the economy.47
Of course, central banks have historically been very wary of providing direct information about the future course of policy. The political countervailing interests may be overwhelming. Absent direct information about the future course of policy, a more thorough discussion of the link between the forecast and future policy would be useful.48
8.2 Summing up
Overall, our four suggestions for best-practice reflect the views that central banks should have clear, though possibly conflicting, goals and should aspire to maximize public understanding of policy. Advocates and practitioners of the ITF deserve great credit for their many contributions to clear goal setting and communication by central banks. Our suggested approach differs from the standard ITF approach in that we more strongly reject the folk wisdom of central banking that all communication should be couched in terms of inflation. Further, we do not favor the use of concrete but inherently suboptimal yardsticks for measuring central bank performance. We advocate a more ``candid and open'' approach to transparency.
Table 1
Discretion Solutions
|
( |
|
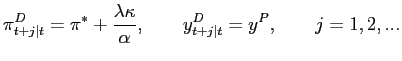
|
( |
Commitment Solutions
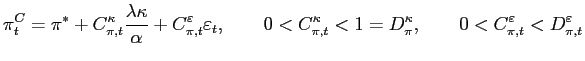
|
( |
|
| ( |
||
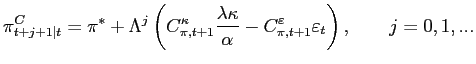
|
( |
|
| ( |
||
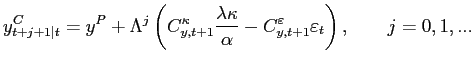
|
( |
|
| ( |
Appendix
Backward-Looking Version
In the backward-looking version, ![]() and
and ![]() . Therefore, the loss function with the output
gap eliminated using the Phillips curve is
. Therefore, the loss function with the output
gap eliminated using the Phillips curve is
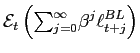
|
(A.1) |
![$\displaystyle \ell_{t+j}^{BL}=\left( \pi_{t+j}-\pi^{\ast}\right) ^{2}+\frac{\la... ...right) -\beta\left( \pi_{t+j-1}-\bar{\pi}\right) -\varepsilon_{t+j}\right] ^{2}$](img77.gif)
|
The first-order condition for
![$\displaystyle \pi_{t+j}-\pi^{\ast}+\frac{\lambda}{\alpha^{2}}\left\{ \left[ \le... ...\right) -\left( \pi_{t+j-1}-\bar{\pi}\right) \right] -\varepsilon_{t+j}\right\}$](img78.gif)
|
(A.2) |
![$\displaystyle -\frac {\lambda\beta}{\alpha^{2}}\left\{ \left[ \left( \pi_{t+j+1\mid t+j} -\bar{\pi}\right) -\left( \pi_{t+j}-\bar{\pi}\right) \right] \right\} =0$](img79.gif)
|
Taking the unconditional expectation of equation (A.2) yields
the result that
![]() Using this result, collecting terms, and multiplying through by
Using this result, collecting terms, and multiplying through by
![]() yields
yields
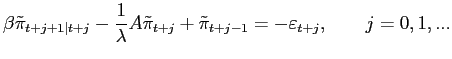
|
(A.3) |
The roots represented by
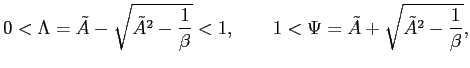
|
(A.4) |
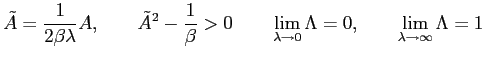
|
Using standard methods we obtain the solutions:
| (A.5) | ||
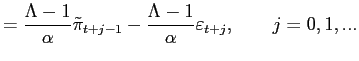
|
where
Taking expectations conditioned on information at time
![]() yields the
forecasts
yields the
forecasts
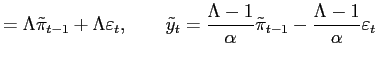
|
||
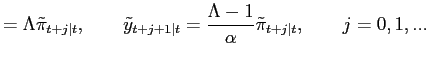
|
(A.6) |
as stated in the text. By repeated substitution
![$\displaystyle =y^{P}+\frac{\Lambda-1}{\alpha}\left( \Lambda\right) ^{j}\pi^{\as... ...alpha} \pi_{t-1}-\frac{\Lambda-1}{\alpha}\varepsilon_{t}\right] \quad j=0,1,...$](img99.gif)
|
(A.7) |
Now we derive the unconditional efficient policy frontier
implied by the optimal commitment rule. We begin by finding the
unconditional variances of
![]() and
and
![]() :
:
|
(A.8) |
where
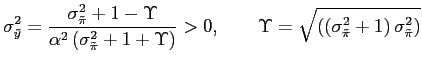
|
(A.9) |
The policy frontier has a negative slope and is convex to the origin since
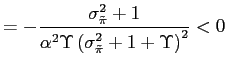
|
(A.10) | |
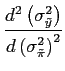
|
![$\displaystyle =\frac{1}{2}\left[ \frac{2\sigma _{\tilde{\pi}}^{2}+1+2\Upsilon}{... ...}^{2} \Upsilon\left( \sigma_{\tilde{\pi}}^{2}+1+\Upsilon\right) ^{2}}\right] >0$](img110.gif)
|
(A.11) |
An increase in
Forward-Looking Version
In the forward-looking version, ![]() and
and ![]() . The loss function with the output gap
eliminated using the Phillips curve is
. The loss function with the output gap
eliminated using the Phillips curve is
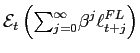
|
||
| (A.12) | ||
![$\displaystyle =\left( \pi_{t+j}-\pi^{\ast}\right) ^{2}+\frac{\lambda }{\alpha^{... ...\left( \pi_{t+j-1}-\bar{\pi}\right) -\varepsilon_{t+j}-\alpha\kappa\right] ^{2}$](img116.gif)
|
To simplify the analysis, we assume that the only shock occurs in period
Discretion
Under discretion, the first-order condition for ![]() holding
holding
![]() constant
is
constant
is
![$\displaystyle \pi_{t+j}-\pi^{\ast}+\frac{\lambda}{\alpha^{2}}\left[ \left( \pi_... ...a\left( \pi_{t+j+1}-\bar{\pi}\right) -\varepsilon _{t+j}-\alpha\kappa\right] =0$](img118.gif)
|
(A.13) |
Taking the unconditional expectation yields the familiar inflation bias result
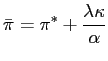
|
(A.14) |
so that the first-order condition for deviations from the unconditional mean is
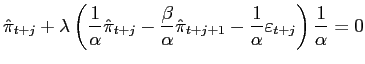
|
(A.15) |
It will be optimal to have no deviations from period
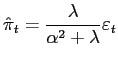
|
(A.16) |
and the full solutions for inflation in period
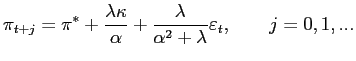
|
(A.17) |
Commitment
Under commitment, the first-order condition for any period
except period ![]() is
is
![$\displaystyle -\frac{\lambda\beta}{\alpha^{2}}\left[ \left( \pi_{t+j}-\bar{\pi}... ...arepsilon_{t+j}-\alpha \kappa\right] +\beta\left( \pi_{t+j+1}-\pi^{\ast}\right)$](img124.gif)
|
(A.18) |
![$\displaystyle +\frac{\lambda\beta}{\alpha^{2}}\left[ \left( \pi_{t+j+1}-\bar{\p... ...left( \pi_{t+j+2}-\bar{\pi}\right) -\varepsilon_{t+j+1}-\alpha \kappa\right] =0$](img125.gif)
|
Taking unconditional expectations yields the familiar commitment result that
| (A.19) |
Multiplying through by
![]() and collecting terms,
the first-order conditions can be rewritten in deviation form
as
and collecting terms,
the first-order conditions can be rewritten in deviation form
as
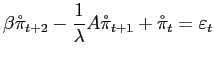
|
(A.20) |
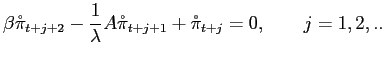
|
(A.21) |
| (A.22) |
where the condition (A.20) for
| (A.23) |
The first-order condition for period
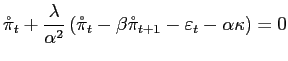
|
(A.24) |
Multiplying through by
| (A.25) |
The first-order conditions for
| (A.26) | |
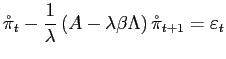
|
(A.27) |
where
The solutions are
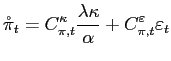
|
(A.28) |
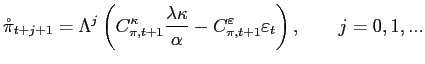
|
(A.29) |
|
(A.30) |
|
(A.31) |
|
(A.32) |
where all of the
References
Alesina, A., and H. Rosenthal (1996) Partisan Politics, Divided Government and the Economy, Cambridge University Press, New York.
Aoki, K. (2001) `` Optimal Monetary Policy Responses to Relative Price Changes'', Journal of Monetary Economics, 48, 55--80.
Atkeson, A., and P. Kehoe (2002) `` Exchange-rate Based vs. Money-based Monetary Policy: The Advantage of Transparency'', processed, Federal Reserve Bank of Minneapolis.
Barro, R., and D. Gordon (1983) `` A Positive Theory of Monetary Policy in a Natural Rate Model'', Journal of Political Economy, 91, 589--610.
Bernanke, B. S., T. Laubach, F. S. Mishkin, and A. S. Posen (1999) Inflation Targeting: Lessons from the International Experience, Princeton University Press, Princeton.
Bernanke, B. S., and F. S. Mishkin (1997) `` Inflation Targeting: A New Framework for Monetary Policy?'', Journal of Economic Perspectives, 11, 97--116.
Blinder, A. S. (1998) Central Banking in Theory and Practice, MIT Press, Cambridge MA.
Canzoneri, M. (1985) `` Monetary Policy Games and the Role of Private Information'', American Economic Review, 75, 1056--1070.
Canzoneri, M., C. Nolan, and A. Yates (1997) `` Mechanisms for Achieving Monetary Stability: Inflation Targeting versus the ERM'', Journal of Money Credit and Banking, 29, 46--60.
Clarida, R., J. Gali, and M. Gertler (1999) `` The Science of Monetary Policy: A New Keynesian Perspective'', Journal of Economic Literature, 37, 1661--1707.
Clouse, J., D. Henderson, A. Orphanides, D. Small, and P. Tinsley (2003) `` Monetary Policy When the Nomical Short-Term Interest Rate Is Zero'', Topics in Macroeconomics, 3, 1, Article 12 (www.bepress.com/bejm/topics/vol3/iss1/art12).
Debelle, G. (2003) `` The Australian Approach to Inflation Targeting'', processed, Reserve Bank of Australia.
Erceg, C. J., D. W. Henderson, and A. T. Levin (2000) `` Optimal Monetary Policy with Staggered Wage and Price Contracts'', Journal of Monetary Economics, 46, 281--313.
Faust, J. (1996) `` Whom Can We Trust to Run the Fed? Theoretical Support for the Founders' Views'', Journal of Monetary Economics, 37, 267--283. 36
Faust, J., and L. E. Svensson (2001) `` Transparency and Credibility: Monetary Policy with Unobservable Goals'', International Economic Review, 42, 369--97.
Fischer, S. (1990) `` Rules Versus Discretion in Monetary Policy'', in B. M. Friedman and F. H. Hahn (eds.) Handbook of Monetary Economics, North Holland, Amsterdam and New York, 1155--1184.
Friedman, B.M. (2003) `` The Use andMeaning ofWords in Central Banking: Inflation Targeting, Credibility, and Transparency'', in P. Mizen (ed.) Central Banking, Monetary Theory, and Practice: Essays in Honor of Charles Goodhart, Volume 1, Edward Elgar, Northamption, MA, 111--24.
Friedman, B. M., and K. Kuttner (1996) `` A Price Target for U.S. Monetary Policy? Lessons from the Experience with Money Growth Targets'', Brookings Papers on Economic Activity, 77--125.
Friedman, M. (1948) `` A Monetary and Fiscal Program for Economic Stability'', American Economic Review, 38, 245--64.
Friedman, M. (1959) A Program for Monetary Stability, Fordham University Press, New York.
Friedman, M. (1968) `` The Role of Monetary Policy'', American Economic Review, 58, 1--17.
Gavin, W. T. (2003) `` Inflation Targeting: How It Works and How To Make It Work Better'', processed, Federal Reserve Bank of St. Louis.
Goodfriend, M. (1986) `` Monetary Mystique: Secrecy and Central Banking'', Journal of Monetary Economics, 17, 63--92.
Goodfriend, M., and R. King (2001) `` The Case for Price Stability'', in A. G. Herrero, V. Gaspar, L. Hoogduin, J. Morgan, and B. Winkler (eds.) Why Price Stablity? European Central Bank, Frankfurt, 53--94 (First European Central Banking Conference www.ecb.int/pub/pdf/whypricestability.pdf).
Gramlich, E. M. (2003) `` Maintaining Price Stability'', (www.federalreserve.gov/boarddocs/speeches/2003/20031001/default.htm).
Greenspan, A. (2002) `` Chairman's Remarks'' , Federal Reserve Bank of St. Louis Review, 84, 4, 928--56.
Greenspan, A. (2003) `` Opening Remarks'', in Monetary Policy and Uncertainty: Adapting to a Changing Economy, Federal Reserve Bank of Kansas City Symposium Series.
Heikensten, L., and A. Vredin (2002) `` The Art of Targeting Inflation'', Swedish Riksbank Economic Review, 4, 5--34. 37
Henderson, D.W. (2004) `` What ShouldMonetary Policy Be Targeting'', in P.Minford (ed.) Money Matters, Edward Elgar Publishing, Cheltenham, 312--322.
HMTreasury (2003) Remit for the Monetary Policy Committee of the Bank of England and the New Inflation Target, HM Treasury, London (including annex).
Jensen, H. (2002) `` Targeting Nominal Income Growth or Inflation?'', American Economic Review, 92, 928--56.
Keynes, J. M. (1923) A Tract on Monetary Reform, Macmillan, London.
Kiley, M. T. (1998) `` Monetary Policy under Neoclassical and New-Keynesian Phillips Curves, with an Application to Price Level and Inflation Targeting'', Finance and Economics Discussion Series No. 1998-27, Federal Reserve Board.
Kim, J., and D. W. Henderson (2002) `` Inflation Targeting and Nominal Income Growth Targeting: When and Why Are They Suboptimal?'', International Finance Discussion Paper 719, Federal Reserve Board.
King, R. G., and A. L. Wolman (1999) `` What Should the Monetary Authority Do When Prices Are Sticky?'', in J. Taylor (ed.) Monetary Policy Rules, The University of Chicago Press, Chicago, 349--398.
Kohn, D. L. (2004) `` Comment on ``Inflation Targeting in the United States?'''', in B. S. Bernanke andM.Woodford (eds.) The Inflation Targeting Debate, University of Chicago Press, Chicago, forthcoming.
Kohn, D. L., and B. P. Sack (2003) `` Central Bank Talk: Does It Matter and Why?'', www.federalreserve.gov/BoardDocs/ Speeches/2003/20030620/default.htm).
Kydland, F., and E. Prescott (1977) `` Rules Rather than Discretion: The Inconsistency of Optimal Plans'', Journal of Political Economy, 85, 473--491.
Leeper, E. M. (2003) `` An ``Inflation Report'' Report'', Sveriges Riksbank Economic Review, 3, 94--118.
Levin, A., and J. Williams (2003) `` Robust Monetary Policy with Competing Reference Models'', FRBSF Working Paper 2003-10, Federal Reserve Bank of San Francisco.
Lockwood, B., M. Miller, and L. Zhang (1995) `` Designing Monetary Policy When Unemployment Persists'', processed, University of Exeter.
Lucas, R. E. (1976) `` Econometric Policy Evaluation: A Critique'', in K. Brunner and A. H. Meltzer (eds.) The Phillips Curve and Labor Markets, Volume 1 of Carnegie Rochester Conference Series on Public Policy, NorthHolland, Amsterdam, 19--46.
Lucas, R. E. (1980) `` Rules, Discretion and the Role of Economic Adviser'', in S. Fischer (ed.) Rational Expectations and Economic Policy, University of Chicago Press, Chicago, 199--210. 38
McCallum, B. T. (1997) `` Crucial Issues Concerning Central Bank Independence'', Journal of Monetary Economics, 39, 99--112.
McCallum, B. T., and E. Nelson (1999) `` Performance of Operational Policy Rules in an Estimated Semiclassical Structural Model'', in J. Taylor (ed.) Monetary Policy Rules, The University of Chicago Press, Chicago, 349--398.
Melitz, J. (1988) `` Monetary Discipline, Germany and the European Monetary System'', Kredit and Kapital, 481--511.
Meyer, L. H. (2002) `` Inflation Targets and Inflation Targeting'', The North American Journal of Economics and Finance, 13, 147--162.
Mishkin, F. S. (1999) `` International Experiences with Different Monetary Policy Regimes'', Journal of Monetary Economics, 43, 579--605.
Mishkin, F. S. (2002) `` Overview'', in Rethinking Stabilization Policy, Federal Reserve Bank of Kansas City Symposium Series.
Obstfeld, M. (1996) `` Models of Currency Crises with Self-Fulfilling Features'', European Economic Review, 40, 1037--47.
Orphanides, A. (2003a) `` Monetary Policy Evaluation with Noisy Information'', Journal of Monetary Economics, 50, 605--631.
Orphanides, A. (2003b) `` The Quest for Prosperity Without Inflation'', Journal of
Monetary Economics, 50, 633--663.
Persson, T., and G. Tabellini (1993) `` Designing Institutions for Monetary Stability'', Carnegie-Rochester Conference Series on Public Policy, 39, 53--84.
Persson, T., and G. Tabellini (2002) Macroeconomic Policy, Credibility and Politics, Routledge, New York.
Phelps, E. S. (1968) `` Money-Wage Dynamics and Labor-Market Equilibrium'', Journalof Political Economy, 76, 678--711.
Phelps, E. S. (1972) Inflation Policy and Unemployment Theory, Macmillan, London.
Rogoff, K. (1985) `` The Optimal Degree of Commitment to an Intermediate Monetary Target'', Quarterly Journal of Economics, 100, 1169--1189.
Romer, C. D., and D. H. Romer (2000) `` Federal Reserve Information and the Behavior of Interest Rates'', American Economic Review, 90, 3, 429--57.
Rotemberg, J. J., and M. Woodford (1997) `` An Optimization-Based Econometric Framework for the Evaluation of Monetary Policy'', in NBER Macroeconomics Annual 1997, MIT Press, Cambridge, 297--346.
Steagall, H. (1935) `` Remarks'', Congressional Record. 39
Stein, J. C. (1989) `` Cheap Talk and the Fed: A Theory of Imprecise Policy Announcements'', American Economic Review, 79, 32--42.
Svensson, L. E. O. (1997a) `` Inflation Forecast Targeting: Implementing and Monitoring Inflation Targets'', European Economic Review, 41, 1111--46.
Svensson, L. E. O. (1997b) `` Optimal Inflation Targets, `` Conservative'' Central Banks, and Linear Inflation Contracts'', American Economic Review, 87, 98--114.
Svensson, L. E. O. (1999) `` Inflation Targeting As a Monetary Policy Rule?'', Journal of Monetary Economics, 43, 607--54.
Svensson, L. E. O. (2001) `` Independent Review of the Operation of Monetary Policy in New Zealand'', (www.treasury.govt.nz/monpolreview/).
Svensson, L. E. O. (2003) `` What Is Wrong With Tayor Rules? Using Judgment in Monetary Policy through Targeting Rules'', Journal of Economic Literature, forthcoming.
Svensson, L. E. O., and M. Woodford (2004) `` Implementing Optimal Policy through Inflation Forecast Targeting'', in B. S. Bernanke and M. Woodford (eds.) The Inflation Targeting Debate, University of Chicago Press, Chicago, forthcoming.
Sveriges Riksbank (2003) Inflation Report 2003:4, Sveriges Riksbank, Stockholm.
Truman, E. M. (2003) Inflation Targeting in the World Economy, Institute for International Economics, Washington.
Walsh, C. E. (1995) `` Optimal Contracts for Independent Central Bankers'', American Economic Review, 85, 167.
Warburg, P. M. (1930) The Federal Reserve System, Volume 2, Macmillan, New York.
Welteke, E. (2003) `` Reforming Europe'', (www.bis.org/review/r031202b.pdf), (closing remarks at the European Banking Congress, Frankfurt, 21 November 2003).
Wolman, A. L. (2001) `` A Primer on Optimal Monetary Policy with Staggered Price-Setting'', Federal Reserve Bank of Richmond Economic Quarterly, 87, 4, 1--14.
Footnotes
1. There are excellent taxonomies of the approaches used by different ITF central banks. See, e.g., Bernanke, Laubach, Mishkin, and Posen (1999), Debelle (2003), and Truman (2003). Return to text
2. Truman (2003) emphasizes the important distinction between actual or potential inflation targeters that have essentially achieved their desired mean inflation rates and those that have not. He provides a thorough analysis of the experience with inflation targeting and argues that mutual understanding among the major central banks would be significantly increased if they all adopted inflation targeting. Return to text
3. Gavin (2003) also makes useful suggestions for improving the ITF framework. Return to text
4. In simple models, there is a multitude of formally equivalent ways of recommending that the central bank optimize; an example is `` satisfy your first-order conditions''. Svensson (1999) examines several interesting exact and approximate ways to recommend optimization in the linear-quadratic framework. Return to text
5. Examples are Friedman and Kuttner (1996), Jensen (2002), and Kim and Henderson(2002). Return to text
6. This statement is correct, so long as the social optimum is consistent with hitting a long-run inflation objective, as it is in virtually all horse-race models. There are many possible optima given by various discretion and commitment solutions. Exactly which one is reached depends on considerations (communication policy, etc.) that are generally left out of horse-race models. As we will explain, it is these considerations that are supposed to insure that the ITF yields the right optimum. Return to text
7. This first claim is sometimes stated as the claim that expected inflation does not affect real variables in the long run. When stated this way, the myriad ways that expected inflation leads to welfare losses are presented as exceptions. Recently, considerable attention has been focused on the possibility that expected inflation might affect output because wages and prices are set in staggered contracts that are not fully indexed. See, for example, Wolman (2001). Return to text
8. See Friedman (1948, 1959) . Return to text
9. See Lucas (1976, 1980) . Return to text
10. Kydland and Prescott (1977) and Barro and Gordon (1983) initiated a large literature on time consistency. There are many good treatments of the political-economy issues, e.g., Alesina and Rosenthal (1996) and Persson and Tabellini (2002). Return to text
11. One might also imagine a neo-Friedmanite view centered on other notions of nominal stability, such as nominal income stability. Given the topic of the paper, we do not develop this idea. Return to text
12. In these models, only the price of the single composite good is affected by staggered contracts. There are at least two standard modifications that imply trade-offs. The first is adding a cost shock to the price-setting equation for the single good as in, for example, Kiley (1998), McCallum and Nelson (1999b), and Clarida, Gali, and Gertler (1999). This modification is incorporated into the simple model we will present here. The second modification is to assume that the wage of composite labor (or the price of a second composite good) is affected by staggered contracts, as in, for example, Erceg, Henderson, and Levin (2000). Return to text
13. Included are models with explicit microeconomic foundations, such as the one used by Aoki (2001). Return to text
14. For one discussion of the liquidity trap situation and references to many more, see Clouseetal (2003) . Return to text
15. A recent confirmation that central bank talk matters is provided by Kohn and Sack (2003). Return to text
16. Using Phillips curves that include both lagged and expected future inflation is common practice; the exact specification in equation (2) is used in Clarida, Gali, and Gertler (1999). One way of arriving at this Phillips curve (2) is to assume that inflation rates are set in Calvo-type contracts and that the inflation rates of agents who do not get to reset prices in the current period are indexed to the unconditional mean of inflation. Return to text
17. This property can be confirmed by taking the unconditional expectation of the Phillips curve. Return to text
18. Of course, there could be conflict among various low rates, as the bliss points for the mean and variance need not coincide. Return to text
19. Analyzing the general model might be nicer in some respects, but would be unduly complicated given our very limited ambitions. Return to text
20. All derivations are in the Appendix. Return to text
21. The central bank can choose a
probability,
![]() , and derive
the width of the range,
, and derive
the width of the range, ![]() , or pick a width and derive the
probability. Return to text
, or pick a width and derive the
probability. Return to text
22. For example, the Reserve Bank of New Zealand's 2002 Policy Targets Agreement states that ``[i]n pursuing its price stability objective, the Bank shall seek to avoid unnecessary instability in output, interest rates and the exchange rate.'' The Bank of England Act charges the bank ``(a) to maintain price stability, and (b) subject to that, to support the economic policy of Her Majesty's Government, including its objectives for growth and employment.'' There is similar language for the Swedish National Bank, as confirmed by Heikensten and Vredin (2002). Return to text
23. Faust and Svensson (2001) present an example in which inflation fluctuates narrowly around the optimum value, but due to lack of transparency about the nature of other goals the economy is significantly more volatile than under full transparency. Return to text
24. We are dealing here with the
case in which the simplicity constraint binds in the sense that the
central bank deviates from the policy that is best on standard
macro-stabilization grounds. Thus, we are distinguishing this case
from the one in which simple rules are best, even from a pure
stabilization standpoint. For example, Friedman argued that a
![]() percent rule is
optimal due to our profound ignorance. Others have argued that
simple rules may be optimal, or nearly so, from the standpoint of
robustness (Levin and Williams (2003)). Return to text
percent rule is
optimal due to our profound ignorance. Others have argued that
simple rules may be optimal, or nearly so, from the standpoint of
robustness (Levin and Williams (2003)). Return to text
25. For example, for the quadratic
loss function used in the model,
![]() and
and
![]() both rise as
both rise as
![]() and
and
![]() move from the
steady state. Return to text
move from the
steady state. Return to text
26. Intermediate targeting is inherently suboptimal so long as the word intermediate is not superfluous. Svensson (1999) has derived the conditions under which an intermediate target is ``ideal,'' and this, by definition, is when there is no (observable implication of the) distinction between the intermediate and ultimate goal. When intermediate money targeting was adopted, no one claimed that money was ``ideal.'' Return to text
27. See, for example, Svensson (1999) and Romer and Romer (2000). Return to text
28. The Fed's recent experience with the bias in the directive arguably provides another example. Return to text
29. For a discussion of the Riksbank's policy during this period, see Sveriges and Riksbank (2003). Return to text
30. Faust and Svensson (2001) show that even modest variations in this regard can be costly. Return to text
31. The conventional literature has examined several channels through which talk by the central bank could alter equilibrium outcomes. For example, it could lead to the cheap-talk equilibrium of Stein (1989), facilitate coordination on the best of the many equilibria of a monetary policy game as shown by Barro and Gordon (1983), or beneficially expand the set of equilibria as illustrated by Atkeson and Kehoe (2002). ITF advocates have in mind something much simpler--although formalization could involve elements like those discussed above. The communication channel as described here has a family resemblance to what Barro and Gordon called reputational equilibria in which the public might raise its expectation of future inflation in order to ``punish'' the misdeeds of the central bank. Technically, the important distinctions here are that the disutility from the punishment falls directly on the central bankers, involves no costs to the public, and is automatically attached to failure to deliver on ``promises.'' Return to text
32. Canzoneri (1985) also calls attention to such a trade-off. In his paper, the trade-off arises because of the imposition of an additional constraint on the policymaker, a requirement to achieve an average value for the money supply, not because of a special policymaker loss function. Return to text
33. As before, all derivations are in the Appendix. Return to text
34. For example, there are 12 votes on the FOMC; five presidents vote; the president of the New York Fed and either the Chicago or Cleveland Fed president always vote. The Reserve Bank presidents are nominated by the boards of their respective banks and confirmed by the Federal Reserve Board. The nominating boards are composed of nine directors, six chosen by district bankers (three representing district bankers and three representing general district interests), and three chosen by the Federal Reserve Board. The seven governors are nominated by the President of the United States with due regard to a fair representation of the financial, agricultural, industrial, and commercial interests. Return to text
35. Recent discussion of the issues regarding changing the relevant index in the United Kingdom (HMTreasury (2003)) and of the role of energy prices in Sweden (Sveriges and Riksbank (2003)) are a reminder that the choice of price index can have important implications. Return to text
36. For a particularly eloquent statement of the case for a stabilization buffer, see Phelps (1972), p. 210. Return to text
37. Henderson (2004) puts forward views similar to those expressed here. Return to text
38. See, for example, Orphanides (2003a). Return to text
39. This characterization can be found in many places, including BLMP. Return to text
40. For example, `attain the social optimum' could be viewed as a constraint that imposes no costs. More generally, of course, constraints on behavior off the desired equilibrium path have no cost of the sort we are discussing and may help in selecting from among equilibria. Return to text
41. Certainly no fixed horizon shorter than a business cycle. Return to text
42. For example, both include a forecast for the gap in their inflation reports. Return to text
43. These definitions come from the Oxford English Dictionary, definitions 2a and 2b of transparent, respectively. Return to text
44. We note that there may be public good benefits from releasing a central bank forecast that are independent of whether the forecast reveals something about central bank intentions. We are setting those aside. Any such benefits may be substantially reduced if the forecast is a conditional one, however. Return to text
45. Anyone who doubts this claim is referred to the excellent work of Svensson and Woodford (2003) on this relationship. Return to text
46. Leeper (2003) makes these and several other points about the use of forecasts. Return to text
47. In addition to its inflation forecast, the Reserve Bank of New Zealand releases forecasts of both the policy rate and the gap. To our knowledge it is the only major ITF central bank that follows this practice. Svensson (2001) has praised this practice and argued that others should follow it. Return to text
48. As discussed in subsection 5.3, the Riksbank has provided a rule of thumb linking their forecast to future policy. This rule, if followed, would make the forecast more useful, but is inconsistent with optimization. Return to text
This version is optimized for use by screen readers. A printable pdf version is available.
![$\displaystyle {\textstyle\sum_{j=0}^{\infty}} \beta^{j}\left[ \left( \pi_{t+j}-... ...\left( \alpha^{2}+\lambda-\frac {\lambda\kappa}{\alpha}\right) \pi_{t+j}\right]$](img56.gif)