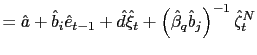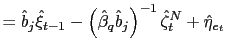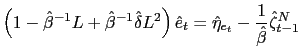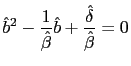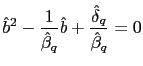Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 814, August 2004--Screen Reader Version*
PPP Rules, Macroeconomic (In)stability and Learning
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
Governments in emerging economies have pursued real exchange rate targeting through Purchasing Power Parity (PPP) rules that link the nominal depreciation rate to either the deviation of the real exchange rate from its long run level or to the difference between the domestic and the foreign CPI-inflation rates. In this paper we disentangle the conditions under which these rules may lead to endogenous fluctuations due to self-fulfilling expectations in a small open economy that faces nominal rigidities. We find that besides the specification of the rule, structural parameters such as the share of traded goods (that measures the degree of openness of the economy) and the degrees of imperfect competition and price stickiness in the non-traded sector play a crucial role in the determinacy of equilibrium. To evaluate the relevance of the real (in)determinacy results we pursue a learnability (E-stability) analysis for the aforementioned PPP rules. We show that for rules that guarantee a unique equilibrium, the fundamental solution that represents this equilibrium is learnable in the E-stability sense. Similarly we show that for PPP rules that open the possibility of sunspot equilibria, a common factor representation that describes these equilibria is also E-stable. In this sense sunspot equilibria and therefore aggregate instability are more likely to occur due to PPP rules than previously recognized.
Keywords: Small Open Economy, PPP rules, Multiple Equilibria, Sunspot Equilibria, Indeterminacy, Expectational Stability and Learning
JEL Classification: C62, D83, E32, F41
*Email address: [email protected]. This paper is based on a chapter of my Ph.D. dissertation at the University of Pennsylvania. I am grateful to Martín Uribe, Stephanie Schmitt-Grohé and Frank Schorfheide for comments on early versions of this paper. I also thank David Bowman, George Evans and Dale Henderson for comments and suggestions. All errors remain mine. The views in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
1 Introduction
It has been claimed that the real exchange rate is perhaps the most popular real target in developing economies. The reason is that policy makers in these economies are always concerned about avoiding losses in competitiveness in foreign markets, or similarly, about maintaining purchasing power parity (PPP). In order to achieve the real exchange target policy makers often follow PPP rules. Such rules link the nominal rate of devaluation of the domestic currency to the deviation of the real exchange rate from its long run level or to the difference between the domestic inflation rate and the foreign inflation rate. For instance, Calvo et al. (1995) argued that Brazil, Chile and Colombia followed such rules in the past.
The characterization of the channels through which real exchange rate targeting affects the business cycles in emerging economies is a central issue in the design and implementation of the PPP rules. The theoretical literature about PPP rules has tried to disentangle these channels.1 One of these important attempts is made by Uribe (2003) who analyzes a PPP rule whereby the government increases the devaluation rate when the real exchange rate is below its steady-state level. He pursues a determinacy of equilibrium analysis and argues that PPP rules may lead to aggregate instability in the economy by inducing endogenous fluctuations due to self-fulfilling expectations.
From the economic policy-design perspective, this result has important implications. It states that the aforementioned rules may open the possibility of sunspot equilibria and lead the economy to equilibria with undesirable properties such as a large degree of volatility. This implication in turn suggests that a determinacy of equilibrium analysis can be used to differentiate among rules favoring those that at least avoid sunspot equilibria by guaranteeing a unique equilibrium with a lower degree of volatility.2 Although appealing this argument is still far from complete and may suffer from some drawbacks. The reason is that in the typical determinacy of equilibrium analysis, it is implicitly assumed that agents can coordinate their actions and learn the equilibria (unique or multiple) induced by the rule. But relaxing this assumption may have interesting consequences for the design of PPP rules. On one hand, if agents cannot learn the unique equilibrium targeted by the rule then the economy may end up diverging from this equilibrium. But if this is the case then it is clear that there are some rules that although guaranteeing a unique equilibrium, do not insure that the economy will reach it.3 On the other hand, if agents cannot learn sunspot equilibria then one may doubt about the relevance of characterizing rules that lead to multiple equilibria as ``bad'' ones. After all, if agents cannot learn sunspot equilibria then they are less likely to occur.
Therefore, it seems clear that a determinacy of equilibrium analysis of PPP rules should in principle be accompanied by a learnability of equilibrium analysis. Both analyses would help policy makers to distinguish and design PPP rules satisfying two requirements: uniqueness and learnability of the equilibrium. The first requirement would prevent the economy from achieving sunspot equilibria with undesirable properties such as a large degree of volatility. Whereas, the second requirement would guarantee that agents can indeed coordinate their actions on the equilibrium the policy makers are targeting.
The present paper is motivated by the interest of studying if particular representations of the equilibria (unique or multiple) induced by PPP rules are learnable in the Expectational - Stability (E-Stability) sense proposed by Evans and Honkapohja (1999, 2001).4 5 In fact our purpose in the present paper is three-fold. First we study and disentangle the structural conditions of an open economy under which an Uribe-type PPP rule may generate multiple equilibria (real indeterminacy).6 We use a small open economy model with traded and non-traded goods. We assume flexible prices for the former and sticky prices for the latter. Under this set-up we show how the aforementioned conditions depend not only on the responsiveness of the rule to the real exchange rate but also on some important structural parameters of the economy. For instance we find that ceteris paribus, given the sensitivity of the rule to the real exchange rate, the lower the degree of openness of the economy (the lower the share of traded goods), the more likely that the rule will induce aggregate instability in the economy by generating multiple equilibria. In addition, keeping the rest constant, the lower (the higher) the degree of price stickiness (the degree of monopolistic competition) in the non-traded sector, the more likely that the rule will lead to real indeterminacy.
The second goal of this paper consists of showing that under real determinacy the fundamental solution that describes the unique equilibrium induced by the PPP rule is learnable in the E-stability sense.7 In addition we use the recent work by Evans and McGough (2003) to prove that under real indeterminacy some common factor representations of stationary sunspot equilibria are also E-stable.8 This result suggests that under some reasonable assumptions agents can learn and coordinate their actions to achieve sunspot equilibria, making them ``more likely'' to occur under PPP rules. In this sense these equilibria should not be perceived as mere mathematical and theoretical curiosities.
The natural question that arises from these results is whether under a different timing of the PPP rule, it is possible for policy makers to design a simple rule that avoids sunspot equilibria but still induces a unique equilibrium whose characterization is learnable. In accord with the findings in the interest rate rule literature, we find that a PPP rule that is backward-looking in the sense of being defined in terms of the (deviation of the) past real exchange rate (from its long run level) satisfies these two requirements.
Finally the third goal of this paper is associated with the original work by Dornbusch (1980, 1982) that studies how a PPP rule whereby the nominal exchange rate is linked to the (deviation of the) current domestic price level (from its long-run level), may affect the output price-level stability trade-off by playing a role as an absorber of fundamental shocks.9 We analyze a rule motivated by Dorbunsch's works assuming that the nominal devaluation rate is positively linked to the difference between the domestic and foreign CPI-inflation rates. In fact this specification tries to capture the previously mentioned stylized facts about PPP rules in Brazil, Colombia and Chile. As before we state the conditions under which this rule leads to real indeterminacy. We also show that the common factor representation of stationary sunspot equilibria as well as the fundamental solution that describes the unique equilibrium induced by the rule are learnable in the E-stability sense.
The remainder of this paper is organized as follows. Section 2 presents the set-up of a sticky-price model with its main assumptions. Section 3 pursues the determinacy of equilibrium analysis for a PPP rule defined in terms of the current real exchange rate. Section 4 deals with the learnability analysis for the aforementioned rule. Section 5 pursues all the previous analyses for a PPP rule defined in terms of the CPI-inflation rate. Finally Section 6 concludes.
2 A Sticky-Price Model
2.1 The Household-Firm Unit
Consider a small open economy inhabited by a large number of
identical household-firm units indexed by
![]() . The
household-firms live infinitely and the preferences of the
representative agent
. The
household-firms live infinitely and the preferences of the
representative agent ![]() can be
described by the intertemporal utility function10
can be
described by the intertemporal utility function10
where
We assume that the non-traded good is a composite good. We
introduce monopolistic competition in the model by assuming that
the household-firm unit ![]() can choose the price of the non-traded good it supplies,
can choose the price of the non-traded good it supplies,
![]() , subject
to a particular demand constraint described by
, subject
to a particular demand constraint described by
where
We also assume that there are sticky prices in the production of
the non-traded good. This assumption is useful to understand the
last term of the intertemporal utility function (1). Following Rotemberg (1982) we suppose that the
household-unit dislikes having its price of non-traded goods grow
at a rate different from
![]() , the
steady-state level of the non-traded goods inflation rate.12 We introduce sluggish adjustment in
prices not only because this will enrich our analysis, but also
because, as Uribe (2003) points out, one of the main reasons that
explains and motivates the real exchange targeting through PPP
rules, is that policy makers believe in eliminating the real
rigidities imposed by a fixed exchange rate system in an
environment with nominal rigidities.
, the
steady-state level of the non-traded goods inflation rate.12 We introduce sluggish adjustment in
prices not only because this will enrich our analysis, but also
because, as Uribe (2003) points out, one of the main reasons that
explains and motivates the real exchange targeting through PPP
rules, is that policy makers believe in eliminating the real
rigidities imposed by a fixed exchange rate system in an
environment with nominal rigidities.
The production of traded and non-traded goods only requires labor and uses the following technologies
where
where
The law of one price holds for the traded good and to simplify
the analysis we normalize the foreign price of the traded good to
one. Therefore, the domestic currency price of traded goods
(![]() ) is equal to
the nominal exchange rate (
) is equal to
the nominal exchange rate (
![]() ). This
simplification in tandem with (1) and
(2) can be used to derive the consumer price
index (CPI)
). This
simplification in tandem with (1) and
(2) can be used to derive the consumer price
index (CPI)
Using equation (6) and defining the nominal devaluation rate as
it is straightforward to derive the CPI-inflation rate,
We define the real exchange rate (![]() ) as the ratio between the price of traded goods
and the aggregate price of non-traded goods
) as the ratio between the price of traded goods
and the aggregate price of non-traded goods
From this definition of the real exchange rate we deduce that
We assume that in each period ![]() the representative agent can purchase two types
of financial assets: fiat money
the representative agent can purchase two types
of financial assets: fiat money
![]() and
nominal state contingent claims,
and
nominal state contingent claims,
![]() that pay
one unit of currency in a specified state of period
that pay
one unit of currency in a specified state of period ![]() and that are traded
internationally. There exists a set of these state contingent
claims that completely spans the fundamental (intrinsic)
uncertainty associated with productivity shocks. Moreover following
Kimbrough (1986), we suppose that money reduces the transaction
costs in goods markets. These costs measured in terms of the traded
good can be described by
and that are traded
internationally. There exists a set of these state contingent
claims that completely spans the fundamental (intrinsic)
uncertainty associated with productivity shocks. Moreover following
Kimbrough (1986), we suppose that money reduces the transaction
costs in goods markets. These costs measured in terms of the traded
good can be described by
where
Using the previous assumptions the representative agent's flow constraint each period can be written as13
where
To derive the period-by-period budget constraint of the representative agent, it is important to notice that total beginning-of-period wealth in the following period is given by
and that
Then we can use equations (12), (13) and (14) to derive the budget constraint of the representative agent as
The agent is also subject to a Non-Ponzi game condition described by
at all dates and under all contingencies, where
with
Under this sticky-price set-up the problem of the representative
agent is reduced to choose the sequences {
![]() in order to maximize (1) subject to
(2), (3), (4), (11), (15) and (16), and given
in order to maximize (1) subject to
(2), (3), (4), (11), (15) and (16), and given
![]() and
and
![]() and the
time paths for
and the
time paths for ![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
, ![]() and
and ![]() and
and
![]() Note that
the utility function specified in (1) and
(2) implies that the preferences of the agent
display non-sasiation. This means that constraints (15) and (16) both hold with
equality.
Note that
the utility function specified in (1) and
(2) implies that the preferences of the agent
display non-sasiation. This means that constraints (15) and (16) both hold with
equality.
The first order conditions correspond to (15) and (16) both with equality and
where
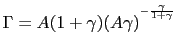 .
The interpretation of the first order conditions is
straightforward. In particular, equation (18)
is the usual intertemporal envelope condition that makes the
marginal utility of consumption of traded goods equal to the
marginal utility of wealth (
.
The interpretation of the first order conditions is
straightforward. In particular, equation (18)
is the usual intertemporal envelope condition that makes the
marginal utility of consumption of traded goods equal to the
marginal utility of wealth (
Finally we postpone the explanation of condition (23). The reason is that it will be used to derive the augmented Phillips curve for non-traded goods, that is actually one of the relevant equations for the determinacy and learnability of equilibrium analyses.
2.2 The Government
The government issues two nominal liabilities: money,
![]() , and state
contingent debt
, and state
contingent debt
![]() It also
levies taxes,
It also
levies taxes, ![]() pays
interest on its debt, and receives revenues from
seigniorage
pays
interest on its debt, and receives revenues from
seigniorage![]() Thus we can
write the government budget constraint as
Thus we can
write the government budget constraint as
where
Finally we define the monetary policy as in Uribe (2003). The
government follows a PPP rule whereby the government sets the
nominal devaluation rate as a function of the deviation of the
current real exchange rate (![]() ) with respect to its long-run level
(
) with respect to its long-run level
(![]() ). That is
). That is
where
2.3 The Equilibrium
We will focus on a symmetric
equilibrium in which all the household-firm units choose the
same price for the good they produce. Therefore in equilibrium all
agents are identical and we can drop the index ![]() . In equilibrium the money market and
the non-traded goods market clear. Thus
. In equilibrium the money market and
the non-traded goods market clear. Thus
and
We also assume free capital mobility. This implies that the following non-arbitrage condition must hold
where
where
But this result of a constant marginal utility and conditions (14 ) and (22) imply that
where
Utilizing (20), (23),
![]() the symmetry in
equilibrium, the equilibrium condition in the non-traded sector (
the symmetry in
equilibrium, the equilibrium condition in the non-traded sector (
![]() )
and (30), we obtain
)
and (30), we obtain
that corresponds to the augmented Phillips curve for the non-traded goods inflation.16
Furthermore applying the symmetry in equilibrium and recalling (30), we can rewrite (18), (19) and (21) as
We proceed giving the definition of a symmetric equilibrium for a government that pursues a Ricardian fiscal policy and follows a PPP rule that responds to the current real exchange rate as described by (26).
Definition 1 Given, ![]()
![]()
![]() and
and ![]() and the exogenous
stochastic processes
and the exogenous
stochastic processes
![]() a Symmetric Equilibrium under a Ricardian
fiscal policy is defined as a set of stochastic processes
a Symmetric Equilibrium under a Ricardian
fiscal policy is defined as a set of stochastic processes
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() satisfying conditions (32),
(33), (34), (35), the intertemporal version of (24) together with (25), the PPP
rule defined by (26), the money market
clearing condition (27), definitions (7), (17) and equations (10), (14), and (31).
satisfying conditions (32),
(33), (34), (35), the intertemporal version of (24) together with (25), the PPP
rule defined by (26), the money market
clearing condition (27), definitions (7), (17) and equations (10), (14), and (31).
3 The Determinacy of Equilibrium Analysis
To pursue the determinacy of equilibrium analysis we reduce the model further. To do so we can use conditions (33) and (34) to obtain
that together with the PPP rule (26) and equations (5), (10), (31) and (32), are the only equations necessary to pursue the determinacy of equilibrium analysis in our model. They help us to find the stochastic processes
![$\displaystyle \bar{\pi}^{N}=\bar{\epsilon}\qquad\qquad\left( 1+\bar{\imath}\rig... ...rac{\bar{\imath}}{1+\bar{\imath} }\right) ^{\frac{\gamma}{1+\gamma}}\right] >0 $](img138.gif)
![$ \left( \bar{c}^{N}\right) ^{\frac{1}{\theta_{N}}}=\frac {(1-\alpha)(\mu-1)\the... ...\frac{\bar {\imath}}{1+\bar{\imath}}\right) ^{\frac{\gamma}{1+\gamma}}\right] }$](img139.gif) and
and
We point out that we do not need to consider in the determinacy
analysis equations (24) and (25). The reason is that under a Ricardian fiscal
policy, the intertemporal version of the government's budget
constraint in conjunction with its transversality condition will be
always satisfied. Moreover the stochastic processes
![]()
![]()
![]()
![]() can be recovered
using (7), (14),
(17), (27), (34) and (35).17
can be recovered
using (7), (14),
(17), (27), (34) and (35).17
We can go further reducing and log-linearizing the model. Using equations (5), (10), (26), (31), (32), and (36) yields18
where
and
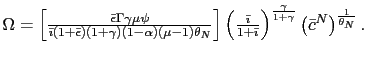 For our future analyses it is important to observe that
For our future analyses it is important to observe that
As we mentioned before in this analysis we only study the possibilities of real indeterminacy or real determinacy of the equilibrium. By real indeterminacy we mean a situation in which the behavior of one or more (real) variables of the model are not pinned down by the model. This situation implies that there are multiple equilibria and opens the possibility of the existence of sunspot equilibria.
Before we analyze the conditions under which PPP rules may lead to real indeterminacy, it is worth constructing some intuition using the model of why these rules may induce equilibria in which expectations are self-fulfilled. In order to accomplish this task we can assume perfect foresight (no uncertainty). Then we rewrite equations (37) and (38) as
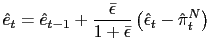
Equation (43) implies that current inflation of non-traded goods is determined by the discounted sum of the expected future real exchange rates and nominal depreciation rates. The first term inside of the parenthesis is associated with future real exchange rates. It captures the fact that higher expected future real exchange rates make non-traded goods become relatively cheaper than traded goods. This leads to a higher expected future excesses of demand for non-traded goods to which the firm-unit responds raising the current price of non-traded goods up and therefore increasing the current non-traded goods inflation rate. On the other hand, the second term in (43) that is associated with future nominal depreciation rates captures the effect of the intertemporal price of consumption on the determination of the current non-traded goods inflation. In essence, expectations of nominal appreciation (negative nominal depreciation rates) decrease the nominal interest rate provided that the uncovered interest parity condition holds under perfect foresight. But a decrease in the nominal interest rate pushes the liquidity transaction costs down, which in turn expands consumption of non-traded (and traded) goods. This increase in consumption lead to a positive excess of demand for non-traded goods and therefore to a higher current inflation.
Equation (44) simply describes the depreciation (or appreciation) of the real exchange rate as a difference between the nominal depreciation rate and the non-traded goods inflation rate.
With these two last equations, equation (42) and the PPP rule,
![]() we can show that multiple equilibria are possible by
constructing a self-fulfilling equilibrium. Assume that at time
we can show that multiple equilibria are possible by
constructing a self-fulfilling equilibrium. Assume that at time
![]() when the economy
is in its steady state, private agents expect a real appreciation
after time
when the economy
is in its steady state, private agents expect a real appreciation
after time ![]() . More
explicitly they expect the following path for the (deviation of
the) real exchange rate.20 At time
. More
explicitly they expect the following path for the (deviation of
the) real exchange rate.20 At time
![]() the real exchange
rate is at the steady state level (
the real exchange
rate is at the steady state level (
![]() ). At
times
). At
times ![]() and
and ![]() the real exchange rate is above
its steady state level (
the real exchange rate is above
its steady state level (
![]() and
and
![]() )
and satisfies
)
and satisfies
![]() showing a real
appreciation and convergence to the steady state level over
time
showing a real
appreciation and convergence to the steady state level over
time![]() Given this path of
the real exchange rate and given the PPP rule, the government will
induce a nominal appreciation (
Given this path of
the real exchange rate and given the PPP rule, the government will
induce a nominal appreciation (
![]() with
with
![]() and
and
![]() ) over time
after time
) over time
after time ![]() . Then using
our interpretation of (43) we can infer that
the expected path for the real exchange rate and the expected
nominal appreciation will motivate the household-firm unit to raise
the price of non traded goods in period
. Then using
our interpretation of (43) we can infer that
the expected path for the real exchange rate and the expected
nominal appreciation will motivate the household-firm unit to raise
the price of non traded goods in period ![]() . In other words inflation at time
. In other words inflation at time
![]() will go up (
will go up (
![]() ). By equation (42) this effect will increase inflation of non
traded goods in period
). By equation (42) this effect will increase inflation of non
traded goods in period ![]() (
(
![]() ), if it is strong enough to
overcome the opposite effects that the assumed path for the real
exchange rate (
), if it is strong enough to
overcome the opposite effects that the assumed path for the real
exchange rate (
![]() ) and
the rule-induced path for the nominal depreciation rate (
) and
the rule-induced path for the nominal depreciation rate (
![]() ) have over inflation of
non-traded goods at period
) have over inflation of
non-traded goods at period ![]() (
(
![]() ).
Observe that this possibility is determined by the values of the
structural parameters of the model that affect
).
Observe that this possibility is determined by the values of the
structural parameters of the model that affect ![]() and
and ![]() , and by the value of the nominal depreciation
response coefficient to the real exchange rate (
, and by the value of the nominal depreciation
response coefficient to the real exchange rate (![]() ). But if inflation of
non-traded goods goes up (
). But if inflation of
non-traded goods goes up (
![]() ) and people expect a nominal
appreciation (
) and people expect a nominal
appreciation (
![]() ) in period
) in period ![]() accordingly with equation
(44), we conclude that the real exchange
rate will appreciate over time ((
accordingly with equation
(44), we conclude that the real exchange
rate will appreciate over time ((
![]() ). Since all the
variables of the system, including the real exchange rate, converge
to their steady state level over time then the original
expectations of a future real appreciation will be
self-fulfilled.
). Since all the
variables of the system, including the real exchange rate, converge
to their steady state level over time then the original
expectations of a future real appreciation will be
self-fulfilled.
Although this intuitive argument points out the possibility of self-fulfilling equilibria induced by a PPP rule, it is important to disentangle the conditions under which these equilibria are possible. The following proposition achieves this goal characterizing locally the equilibrium for the model described by equations (37)-(40).
![$\displaystyle \tilde{\rho}_{e}=\frac{\left[ 2(1+\bar{\epsilon})\left( 1+\frac{1... ...{\epsilon}\right] }{\left[ \bar{e}\left( 1+\frac{1}{\beta }-H\right) \right] } $](img183.gif)
- a) If
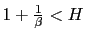 and
and
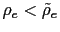 then there is real indeterminacy.
then there is real indeterminacy. - b) If
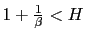 and
and
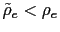 then there is real determinacy.
then there is real determinacy. - c) If
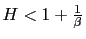 then there is real determinacy for any
then there is real determinacy for any
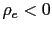 .
.
From Proposition 1 it is clear that conditions under which PPP
rules lead to multiple equilibria do not simply depend on the
response coefficient
![]() On the
contrary some of the structural parameters of the model play a
fundamental role in the determinacy of equilibrium. In essence all
the parameters that affect
On the
contrary some of the structural parameters of the model play a
fundamental role in the determinacy of equilibrium. In essence all
the parameters that affect ![]() and
and ![]() are
relevant for the analysis. In order for the PPP rule to induce
multiple equilibria two conditions must be satisfied. The first one
constrains the possible values that the structural parameters may
take (
are
relevant for the analysis. In order for the PPP rule to induce
multiple equilibria two conditions must be satisfied. The first one
constrains the possible values that the structural parameters may
take (
![]() ); the second one points out the
importance of the PPP rule on inducing real indeterminacy. It sets
a threshold for the nominal depreciation response coefficient that
depends on the structural parameters of the model (
); the second one points out the
importance of the PPP rule on inducing real indeterminacy. It sets
a threshold for the nominal depreciation response coefficient that
depends on the structural parameters of the model (
![]() ). Even more interesting
is the result of part c) in the
proposition. It says that for some values that the structural
parameters may take and regardless of the value of the nominal
devaluation response coefficient (
). Even more interesting
is the result of part c) in the
proposition. It says that for some values that the structural
parameters may take and regardless of the value of the nominal
devaluation response coefficient (![]() , the model displays real determinacy. This
result contrasts with the results of Uribe (2003) that claims that
if the elasticity of the PPP rule is sufficiently large then a
model with sticky-prices always displays real indeterminacy.
, the model displays real determinacy. This
result contrasts with the results of Uribe (2003) that claims that
if the elasticity of the PPP rule is sufficiently large then a
model with sticky-prices always displays real indeterminacy.
To understand the important role that some of the structural
parameters of the model may play in the determinacy of equilibrium
analysis, we study how the aforementioned threshold (
![]() )
varies with respect to some of these structural parameters.
Specifically we consider the share of traded goods (
)
varies with respect to some of these structural parameters.
Specifically we consider the share of traded goods (![]() ), the degree of monopolistic
competition in the non-traded sector (
), the degree of monopolistic
competition in the non-traded sector (![]() ) and the degree of price
stickiness in the non-traded sector (
) and the degree of price
stickiness in the non-traded sector (![]() ).21 Note
that the share of traded goods can be considered a measure of the
degree of openness of the economy with
).21 Note
that the share of traded goods can be considered a measure of the
degree of openness of the economy with
![]() describing a very closed economy. The following corollary
summarizes the main results.
describing a very closed economy. The following corollary
summarizes the main results.
Corollary 1 Suppose the government follows a PPP rule given by
![]() with
with
![]() . Let
. Let
![]() be defined as in Proposition 1 and
assume
be defined as in Proposition 1 and
assume
![]() ,
then a)
,
then a)
![]() ; b)
; b)
![]() and c)
and c)
![]() .
.
Using Proposition 1 and Corollary 1 we can understand the
effects of varying some of the structural parameters and the
semi-elasticity of the rule (
![]() on
the determinacy of equilibrium. In fact when
on
the determinacy of equilibrium. In fact when
![]() we can conclude that given the semi-elasticity of the PPP rule, the
less open the economy is (the lower
we can conclude that given the semi-elasticity of the PPP rule, the
less open the economy is (the lower ![]() is), the more likely that the PPP rule will
induce aggregate instability in the economy by generating multiple
equilibria. In addition, given the semi-elasticity of the PPP rule
and keeping the rest constant, the higher the degree of
monopolistic competition in the non-traded sector (the higher
is), the more likely that the PPP rule will
induce aggregate instability in the economy by generating multiple
equilibria. In addition, given the semi-elasticity of the PPP rule
and keeping the rest constant, the higher the degree of
monopolistic competition in the non-traded sector (the higher
![]() ), the more likely
that the rule will lead to real indeterminacy. Finally under
ceteris paribus and given the semi-elasticity of the rule we find
that the lower the degree of price stickiness in the non-traded
sector (the lower
), the more likely
that the rule will lead to real indeterminacy. Finally under
ceteris paribus and given the semi-elasticity of the rule we find
that the lower the degree of price stickiness in the non-traded
sector (the lower ![]() ),
the more feasible that the rule will induce multiple
equilibria.
),
the more feasible that the rule will induce multiple
equilibria.
Notwithstanding the relevance of these analytical results, it is
crucial to investigate their quantitative importance. To accomplish
this we rely on a specific parametrization of the model. Since this
exercise is merely indicative we borrow some values of the
parameters from previous studies about emerging and small open
economies.22
Following Schmitt-Grohé and Uribe's (2001) study about
Mexico we assign the following values to some of the relevant
structural parameters of the model:
![]() per
quarter,
per
quarter,
![]() per quarter,
per quarter,
![]() ,
,
![]()
![]() and
and
![]() . We
set
. We
set
![]() that
corresponds roughly to the imports to GDP share in Mexico during
the 90's. Finally we set
that
corresponds roughly to the imports to GDP share in Mexico during
the 90's. Finally we set ![]() , that corresponds to Dib's (2001) estimate
of
, that corresponds to Dib's (2001) estimate
of ![]() for Canada in a
model with only nominal rigidities.23 With these values, we will perform
four exercises characterizing locally the equilibrium. We will vary
the semi-elasticity of the rule,
for Canada in a
model with only nominal rigidities.23 With these values, we will perform
four exercises characterizing locally the equilibrium. We will vary
the semi-elasticity of the rule,
![]() and
one and only one of the following structural and policy parameters:
and
one and only one of the following structural and policy parameters:
![]() ,
, ![]()
![]() and
and
![]() We
summarize the parametrization in the following table.
We
summarize the parametrization in the following table.
Table 1
|
|
|
||||||
|---|---|---|---|---|---|---|---|
The results of our exercises are presented in Figure 1, where ``I'' stands for real indeterminacy and ``D'' stands for real determinacy. As can be observed, this figure confirms the results in Proposition 1 and Corollary 1 showing how significant these results are in quantitative terms. Consider the top left panel. From this panel we can infer the following. Suppose that the government in response to a 1 per cent appreciation of the real exchange rate, devalues the nominal exchange rate by 2 percent. In other words, assume that the semi-elasticity of the PPP rule is -2. Whereas this PPP rule may induce multiple equilibria in an economy whose degree of openness is 0.2, the same rule leads to a unique equilibrium in an economy whose degree of openness is 0.6.
Similar inferences can be pursued from the top right and bottom left panels of Figure 1. That is although a rule with semi-elasticity of -2 guarantees a unique equilibrium in an economy with a degree of monopolistic competition of 5 (a degree of price stickiness of 5), the same rule induces multiple equilibria when the aforementioned degree corresponds to 15 (2).
Although it is not possible to derive an analytical result to
see how varying the implied nominal depreciation target (
![]() ) and
the semi-elasticity of the rule (
) and
the semi-elasticity of the rule (
![]() ) affects the determinacy of
equilibrium, it is possible to evaluate this quantitatively as
presented in the bottom right panel of Figure 1. This panel
illustrates that given the semi-elasticity of the rule the lower
the implied nominal depreciation target the more likely is that the
PPP rule will induce real indeterminacy. In addition, it is
important to observe that in all four panels of Figure 1 there are
regions for which the model always displays real determinacy
regardless of the semi-elasticity of the rule. This agrees with
part c) of Proposition 1.
) affects the determinacy of
equilibrium, it is possible to evaluate this quantitatively as
presented in the bottom right panel of Figure 1. This panel
illustrates that given the semi-elasticity of the rule the lower
the implied nominal depreciation target the more likely is that the
PPP rule will induce real indeterminacy. In addition, it is
important to observe that in all four panels of Figure 1 there are
regions for which the model always displays real determinacy
regardless of the semi-elasticity of the rule. This agrees with
part c) of Proposition 1.
To finalize this section we want to point out that similar
qualitative results to the ones presented in this section can be
obtained if the PPP rule is defined in terms of the real
depreciation rate. That is
![]() where
where
![]() 24
24
4 The Learnability Analysis
The importance of the result from the previous section, that a PPP rule may induce aggregate instability by generating multiple equilibria in the economy, stems from the fact that such rule opens the possibility of expectations driven fluctuations in economic activity. In particular, the model may admit self-fulfilling rational expectations equilibria driven by extraneous processes known as sunspots.25
However the previous results, as the ones in Uribe (2003), do not discuss the attainability of these PPP rule induced sunspot equilibria. They do not even mention how attainable the unique equilibrium is. Strictly speaking, and regardless of real determinacy or real indeterminacy, it is not clear whether and how agents may coordinate their actions in order to achieve a particular equilibrium in the model. The purpose of this section is to address this issue. We want to study the potential of agents to learn the unique equilibrium characterized by the fundamental solution and sunspot equilibria described by a common factor solution.
Figure 1: This figure shows
how the local determinacy of equilibrium varies with respect to the
semi-elasticity of the rule (
![]() ), the
share of traded goods (
), the
share of traded goods (![]() ), the degree of monopolistic competition in
the non-traded sector (
), the degree of monopolistic competition in
the non-traded sector (![]() ), the degree of price stickiness in the
non-traded sector (
), the degree of price stickiness in the
non-traded sector (![]() )
and the implied nominal depreciation rate target (
)
and the implied nominal depreciation rate target (
![]() ). ``I''
stands for real indeterminacy (multiple equilibria) and ``D''
stands for real determinacy (a unique equilibrium). ``ES''
corresponds to E-Stability.
). ``I''
stands for real indeterminacy (multiple equilibria) and ``D''
stands for real determinacy (a unique equilibrium). ``ES''
corresponds to E-Stability.
Description of Figure 1
Figure 1 shows the combinations of the
semi-elasticity of the rule and other structural parameters of the
model under which there is a unique equilibrium (real determinacy)
whose Minimal State Variable (MSV) representation is learnable in
the E-stability sense. These combinations are denoted by `` D-ES''.
The figure also shows the combinations of these parameters under
which there are multiple equilibria (real indeterminacy) and
sunspot equilibria whose Common Factor (CF) representation is
learnable in the E-stability sense. We denote these combinations by
`` I-ES''. Figure 1 has four panels. We proceed to describe each
panel. The top-left panel shows the combinations for the
semi-elasticity of the rule (
![]() ) and the
share of traded goods (
) and the
share of traded goods (![]() ) under which there is `` D-ES'' or `` I-ES''.
The panel measures
) under which there is `` D-ES'' or `` I-ES''.
The panel measures
![]() on the
vertical axis with
on the
vertical axis with
![]() and
and ![]() on the horizontal axis with
on the horizontal axis with
![]() For
For
![]() and
regardless of
and
regardless of
![]() there is
always `` D-ES''. For
there is
always `` D-ES''. For
![]() there is a
frontier of combinations of
there is a
frontier of combinations of
![]() and
and
![]() that separates
the combinations of `` D-ES'' from `` I-ES''. This frontier is
concave and has a negative slope. It crosses the
that separates
the combinations of `` D-ES'' from `` I-ES''. This frontier is
concave and has a negative slope. It crosses the
![]() -axis at
-1.5 and the
-axis at
-1.5 and the ![]() -axis at
0.7 approximately.(`` approximately'' since
-axis at
0.7 approximately.(`` approximately'' since ![]() cannot be zero.) To the
north-east of this frontier we have the combinations for
cannot be zero.) To the
north-east of this frontier we have the combinations for
![]() and
and
![]() under which there
is `` D-ES''. To the south-west of this frontier we have the
combinations for
under which there
is `` D-ES''. To the south-west of this frontier we have the
combinations for
![]() and
and
![]() under which there
is `` I-ES''.
under which there
is `` I-ES''.
The top-right panel shows the combinations for the
semi-elasticity of the rule (
![]() ) and the
degree of monopolistic competition (
) and the
degree of monopolistic competition (![]() ) under which there is `` D-ES'' or `` I-ES''. This
panel measures
) under which there is `` D-ES'' or `` I-ES''. This
panel measures
![]() on the
vertical axis with
on the
vertical axis with
![]() and
and ![]() on the horizontal axis with
on the horizontal axis with
![]() For
For
![]() and
regardless of
and
regardless of
![]() there is
always `` D-ES''. For
there is
always `` D-ES''. For ![]() there is a frontier of combinations of
there is a frontier of combinations of
![]() and
and
![]() that separates the
combinations of `` D-ES'' from `` I-ES''. This frontier is concave
and has a positive slope. It crosses the
that separates the
combinations of `` D-ES'' from `` I-ES''. This frontier is concave
and has a positive slope. It crosses the ![]() -axis.at 6 approximately. To the
north-west of this frontier we have the combinations for
-axis.at 6 approximately. To the
north-west of this frontier we have the combinations for
![]() and
and
![]() under which there is
`` D-ES''. To the south-east of this frontier we have the
combinations for
under which there is
`` D-ES''. To the south-east of this frontier we have the
combinations for
![]() and
and
![]() under which there is
`` I-ES''.
under which there is
`` I-ES''.
The bottom-left panel shows the combinations for the
semi-elasticity of the rule (
![]() ) and the
degree of price stickiness (
) and the
degree of price stickiness (![]() ) under which there is `` D-ES'' or `` I-ES''.
This panel measures
) under which there is `` D-ES'' or `` I-ES''.
This panel measures
![]() on the
vertical axis with
on the
vertical axis with
![]() and
and ![]() on the horizontal axis with
For
on the horizontal axis with
For
![]() and
regardless of
and
regardless of
![]() there is
always `` D-ES''. For
there is
always `` D-ES''. For ![]() there is a frontier of combinations of
there is a frontier of combinations of
![]() and
and
![]() that separates the
combinations o
that separates the
combinations o![]() f `` D-ES'' from `` I-ES''. This frontier is concave
and has a negative slope. It crosses the
f `` D-ES'' from `` I-ES''. This frontier is concave
and has a negative slope. It crosses the
![]() -axis at
-0.8 and the
-axis at
-0.8 and the ![]() -axis.at
4.75 approximately.(`` approximately'' since
-axis.at
4.75 approximately.(`` approximately'' since ![]() cannot be zero.) To the
north-east of this frontier we have the combinations for
cannot be zero.) To the
north-east of this frontier we have the combinations for
![]() and
and
![]() under which there
is `` D-ES''. To the south-west of this frontier we have the
combinations for
under which there
is `` D-ES''. To the south-west of this frontier we have the
combinations for
![]() and
and
![]() under which there
is `` I-ES''.
under which there
is `` I-ES''.
The bottom-right panel shows the combinations for the
semi-elasticity of the rule (
![]() ) and the
depreciation target (
) and the
depreciation target (
![]() ) under
which there is `` D-ES'' or `` I-ES''. This panel measures
) under
which there is `` D-ES'' or `` I-ES''. This panel measures
![]() on the
vertical axis with
on the
vertical axis with
![]() and
and
![]() on the
horizontal axis with
on the
horizontal axis with
![]() For
For
![]() and regardless of
and regardless of
![]() there is
always `` D-ES''. For
there is
always `` D-ES''. For
![]() there is a frontier of combinations of
there is a frontier of combinations of
![]() and
and
![]() that
separates the combinations of `` D-ES'' from `` I-ES''. This
frontier is concave and has a negative slope. It crosses the
that
separates the combinations of `` D-ES'' from `` I-ES''. This
frontier is concave and has a negative slope. It crosses the
![]() -axis at
0 and the
-axis at
0 and the
![]() -axis at
0.022 approximately. To the north-east of this frontier we have the
combinations for
-axis at
0.022 approximately. To the north-east of this frontier we have the
combinations for
![]() and
and
![]() under
which there is `` D-ES''. To the south-west of this frontier we
have the combinations for
under
which there is `` D-ES''. To the south-west of this frontier we
have the combinations for
![]() and
and
![]() under
which there is `` I-ES''.
under
which there is `` I-ES''.
As a criterion of ``learnability'' of an equilibrium we will use the concept of ``E-stability'' proposed by Evans and Honkapohja (1999, 2001). That is, an equilibrium is ``learnable'' if it is ``E-Stable''.26 Consequently we start by assuming that agents in our model no longer are endowed with rational expectations. Instead they have adaptive rules whereby agents form expectations using recursive least squares updating and data from the system. Then we derive the conditions for expectational stability (E-stability).
In our analysis we will focus on the expectational stability concept for the following reasons. First, in models that display a unique equilibrium (real determinacy models), Marcet and Sargent (1989) and Evans and Honkapohja (1999, 2001) have shown that under some general conditions, the notional time concept of expectational stability of a rational expectation equilibrium governs the local convergence of real time adaptive learning algorithms. Specifically they have shown that under E-stability, recursive least-squares learning is locally convergent to the rational expectations equilibrium. Second, Evans and McGough (2003) have numerically argued that under some assumptions about the parameters of a linear stochastic univariate model, with a predetermined variable, the same argument applies when this model displays sunspot equilibria. Formally they have stated that under a strict subset of the structural parameter space, there exist stationary sunspot equilibria that are locally stable under least square learning provided that agents use a common factor representation for their estimated law of motion.
We adapt the methodology of Evans and Honkapohja (1999, 2001) and Evans and McGough (2003) to pursue the learnability (E-stability) analysis. Accordingly we need to define the concept of E-stability. In order to define it we give an idea of the methodology we apply for the case of real determinacy.
To grasp the methodology, it becomes useful to reduce our model to the following linear stochastic difference equations system. Use (37), (38), (39) and (40) to rewrite the model as
where
Iterating forward this law of motion and using it to eliminate all the forecasts in the model we can derive the implied actual law of motion (ALM)
Then we obtain the T-mapping
![]() whose fixed points correspond to the rational expectations
equilibria. An equilibrium is said to be E-stable if this mapping
is stable at the equilibrium in question. More formally a fixed
point of the T-mapping is E-stable provided that the differential
equation
whose fixed points correspond to the rational expectations
equilibria. An equilibrium is said to be E-stable if this mapping
is stable at the equilibrium in question. More formally a fixed
point of the T-mapping is E-stable provided that the differential
equation
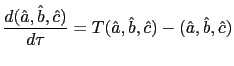
For the case of sunspot equilibria we apply the same methodology but in that case the PLM is augmented by the sunspot and its particular structure. In particular we will focus on the common factor representation proposed by Evans and McGough (2003). Due to space constraint we refer the readers to the aforementioned references for a detailed explanation.29
It is important to observe that a fundamental part in the
learnability analysis consists of making explicit what agents know
when they form their forecasts. In the E-stability analysis
literature it is common to assume that when agents form their
expectations
![]() they
do not know
they
do not know
![]() In this
paper this assumption may be inconsistent with the assumptions that
we use to derive the equations of the model. In particular notice
that for the derivation of the first order conditions of the
representative agent we assume that
In this
paper this assumption may be inconsistent with the assumptions that
we use to derive the equations of the model. In particular notice
that for the derivation of the first order conditions of the
representative agent we assume that
![]() (or in a symmetric
equilibrium
(or in a symmetric
equilibrium
![]() ) and
) and
![]() Therefore assuming in the learnability analysis that the agents do
not know
Therefore assuming in the learnability analysis that the agents do
not know ![]() when
forming expectations would have some implications for the
specification of the model. Specifically it would require to
replace
when
forming expectations would have some implications for the
specification of the model. Specifically it would require to
replace
![]() and
and
![]() in
equations (37), (38)
and (40) with the expectations of
in
equations (37), (38)
and (40) with the expectations of
![]() and
and
![]() given
current information (
given
current information (
![]()
![]() and
exogenous shocks). Henceforth for the learnability analysis of the
model (45) we will assume that when
forming expectations agents know
and
exogenous shocks). Henceforth for the learnability analysis of the
model (45) we will assume that when
forming expectations agents know
![]()
We proceed to present the results of the learnability analysis for the fundamental solution of the model (45) in the following Proposition.
where
Proposition 2 points out that when the model displays a unique equilibrium (real determinacy) then the fundamental solution is E-stable. This is the reason of denoting as ``D-ES'' the regions of the four panels of Figure 1 for which the model displays not only real determinacy but also E-stability. The importance of this result stems from the fact that policy makers will face less difficulties in implementing PPP rules that lead to a unique equilibrium since they know that agents will coordinate on that equilibrium and the macroeconomic system will not diverge away from the targeted equilibrium.
It is also possible to show that under real indeterminacy the fundamental solution or MSV solution can be E-stable. However in this case policy makers will face other difficulties. In particular under multiple equilibria there might be self-fulfilling rational expectations equilibria driven by extraneous processes known as sunspot. These equilibria may be characterized by undesirable features such as larger volatility of macroeconomic variables suggesting that policy makers should avoid rules that in principle may induce multiple equilibria.
Although the previous argument may sound appealing, it may
suffer from some drawbacks. For instance, it is not clear whether
agents are able to coordinate their actions on a particular sunspot
equilibria. To clarify this issue the next proposition illustrates
that some particular representations of stationary sunspot
equilibria can be E-stable. To simplify the analysis and to be able
to derive analytical results we assume that
![]()
where
- a) Under the
real indeterminacy conditions specified in Proposition 1, there are
stationary sunspot equilibria of (45)
characterized by the common factor representation (48) and (49), where
 and
and
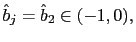 and this representation is learnable in the E-stability
sense.
and this representation is learnable in the E-stability
sense. - b) Under the
real indeterminacy conditions specified in Proposition 1, there are
stationary sunspot equilibria of (45)
characterized by the common factor representation (48) and (49), where
 and
and
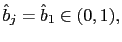 and this representation is NOT learnable in the
E-stability sense.31
and this representation is NOT learnable in the
E-stability sense.31
Proposition 3 demonstrates that some common factor
representations of sunspot equilibria induced by PPP rules are
learnable in the sense of E-stability. We would like to emphasize
the important role that the common factor representations proposed
by Evans and McGough (2003) play in the learnability analysis. To
see this, observe that the typical stationary sunspot equilibrium
representation,
![]() where
where
![]() denotes
the sunspot, is never E-stable. The reason is that such perceived
law of motion leads to an actual law of motion
denotes
the sunspot, is never E-stable. The reason is that such perceived
law of motion leads to an actual law of motion
![]() that implies that
that implies that
![]() But this
suggests that the typical sunspot representation is not
learnable
But this
suggests that the typical sunspot representation is not
learnable![]() This
argument in tandem with Proposition 3 reveal that common factor
representations make stationary sunspot equilibria more likely to
arise under private learning than previously recognized.
This
argument in tandem with Proposition 3 reveal that common factor
representations make stationary sunspot equilibria more likely to
arise under private learning than previously recognized.
Our results from the real determinacy and learnability of
equilibrium analyses pose the question of whether changing the
timing of the PPP rule avoids sunspot equilibria and still induces
a unique equilibrium that is E-stable. Similarly to the findings in
the interest rate rule literature, we find that a PPP rule that is
backward-looking in the sense of being defined in terms of the past
real exchange rate satisfies these two requirements.32 A backward-looking PPP rule can be
described as
![]() and using this
specification and equations (37), (38) and (39), we can reduce
the model to
and using this
specification and equations (37), (38) and (39), we can reduce
the model to
where
and
The following proposition summarizes the aforementioned result.
where
- a) If
either
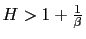 and
and
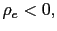 or
or
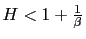 and
and
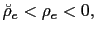 with
with
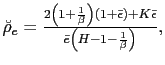 then the model (50) displays a unique equilibrium (real
determinacy) that can be represented by the fundamental solution
(52) with
then the model (50) displays a unique equilibrium (real
determinacy) that can be represented by the fundamental solution
(52) with
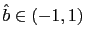 . Moreover this
solution is E-stable.
. Moreover this
solution is E-stable. - b) If
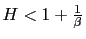 and
and
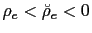 then there exists no equilibrium.
then there exists no equilibrium.
5 PPP Rules Defined in Terms of The CPI-Inflation
In this section we analyze a different type of PPP rule. We study rules whereby the government in response to an increase in the CPI-inflation, increases the nominal depreciation rate. The motivation to consider this type of rule is twofold. First, from an empirical point of view, Calvo et al. (1995) mention that starting in 1968, Brazil's government implemented a rule by which the exchange rate was adjusted as a function of the difference between domestic and U.S. inflation. In addition, between 1985 and 1992, Chile used an exchange rate band whose trend was determined by the difference between the domestic inflation rate and a measure of the average inflation in the rest of the world. Second, from a theoretical point of view, Dornbusch (1980, 1982) conceives PPP rules as a means to introduce the necessary real flexibility to cope with intrinsic (fundamental) uncertainty in a world that faces nominal rigidities. He defines a PPP rule as a function whereby the nominal exchange rate is positively linked to the domestic price index.
We try to capture the aforementioned stylized facts and some of
the flavor of Dornbusch's work by defining a rule whereby the
nominal depreciation rate is positively linked to the difference
between the domestic CPI inflation (![]() ) and the foreign CPI-inflation.33 However note that since in our
analysis the foreign variables are considered exogenous and
constant, then the specification of the PPP rule reduces to
) and the foreign CPI-inflation.33 However note that since in our
analysis the foreign variables are considered exogenous and
constant, then the specification of the PPP rule reduces to
where
As before we proceed in the following way. First we will prove that such rule may induce aggregate instability in the economy by generating multiple equilibria and opening the possibility of sunspot equilibria. Specifically we will study and disentangle the conditions under which this rule leads to real indeterminacy or to real determinacy. Second, we will study the ``learnability'' properties not only of the fundamental solution but also of the common factor representation of stationary sunspot equilibria.
The following proposition summarizes the conditions under which the aforementioned PPP rule induces either real determinacy or real indeterminacy in the model.
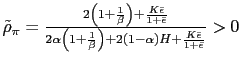 .
.- a) If
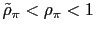 then there is real indeterminacy.
then there is real indeterminacy. - b) If
either
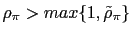 or
or
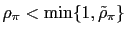 then there is real determinacy.
then there is real determinacy. - c) If
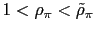 then there exists no equilibrium.
then there exists no equilibrium.
Proposition 5 suggests that multiple equilibria are also
possible for PPP rules that depend on the current CPI-inflation. In
particular it points out that a necessary condition for these rules to cause real
indeterminacy is that the response coefficient to the CPI-
inflation be less than one. That means that in response to a one
percent increase in the CPI-inflation rate, the government raises
the nominal devaluation rate in less than one percent.
Interestingly such response seems to be feasible in the practice of
economic policy. However in order to generate real indeterminacy
the nominal depreciation response coefficient,
![]() must be
above a threshold,
must be
above a threshold,
![]() which in turn depends on the structural parameters that affect
which in turn depends on the structural parameters that affect
![]() and
and ![]() Therefore, as before, we proceed
studying analytically and numerically how varying some structural
parameters of the model affects the previously mentioned threshold.
In particular we focus our analysis on the degree of openness of
the economy,
Therefore, as before, we proceed
studying analytically and numerically how varying some structural
parameters of the model affects the previously mentioned threshold.
In particular we focus our analysis on the degree of openness of
the economy, ![]() , and
the degrees of monopolistic competition,
, and
the degrees of monopolistic competition, ![]() and price stickiness,
and price stickiness,
![]() , in the non-traded
sector. The results are presented in Corollary 2.
, in the non-traded
sector. The results are presented in Corollary 2.
Corollary 2 Suppose the government follows a PPP rule given by
![]() with
with
![]() . Let
. Let
![]() be defined as in Proposition 5 and
satisfy
be defined as in Proposition 5 and
satisfy
![]() then a)
then a)
![]() ,
b)
,
b)
![]() and c)
and c)
![]() .
.
Using Proposition 5 and Corollary 2 we can breakdown the effects
of varying some of the structural parameters of the model and the
PPP rule response coefficient to CPI-inflation
![]() on the
determinacy of equilibrium analysis. In fact, when
on the
determinacy of equilibrium analysis. In fact, when
![]() we can
conclude the following. Given the PPP rule response coefficient to
CPI-inflation, the less open the economy is (the lower
we can
conclude the following. Given the PPP rule response coefficient to
CPI-inflation, the less open the economy is (the lower ![]() is), the more likely that the
PPP rule will induce aggregate instability in the economy by
generating multiple equilibria. In addition, given the rule
response coefficient to CPI-inflation and keeping the rest
constant, the higher the degree of monopolistic competition in the
non-traded sector (the higher
is), the more likely that the
PPP rule will induce aggregate instability in the economy by
generating multiple equilibria. In addition, given the rule
response coefficient to CPI-inflation and keeping the rest
constant, the higher the degree of monopolistic competition in the
non-traded sector (the higher ![]() , the more likely that the rule will lead to real
indeterminacy. Finally under ceteris paribus and given the rule
response coefficient to CPI-inflation, the lower the degree of
price stickiness in the non-traded sector (the lower
, the more likely that the rule will lead to real
indeterminacy. Finally under ceteris paribus and given the rule
response coefficient to CPI-inflation, the lower the degree of
price stickiness in the non-traded sector (the lower ![]() ), the more feasible that the rule
will induce multiple equilibria.
), the more feasible that the rule
will induce multiple equilibria.
Under the parametrization of Table 1 we construct Figure 2 that
corroborates these results quantitatively. To some extent it also
validates numerically how likely is that the aforementioned PPP
rule may destabilize the economy by generating multiple equilibria.
Moreover although it is not possible to derive an analytical result
to see how varying the implied nominal depreciation target (
![]() ) and
the response coefficient to the CPI-inflation (
) and
the response coefficient to the CPI-inflation (
![]() ) affect the
determinacy of equilibrium, it is possible to evaluate this
quantitatively. In short the bottom right panel of Figure 2
illustrates that given the response coefficient of the rule the
lower the nominal depreciation target is, the more likely is that
the PPP rule will induce real indeterminacy.
) affect the
determinacy of equilibrium, it is possible to evaluate this
quantitatively. In short the bottom right panel of Figure 2
illustrates that given the response coefficient of the rule the
lower the nominal depreciation target is, the more likely is that
the PPP rule will induce real indeterminacy.
It is also important to observe that similar qualitative results
to the ones described in Proposition 5 and Corollary 2 can be
obtained if the PPP rule is defined in terms of the non-traded
goods inflation rate. That is
![]() with
with
![]() Furthermore it is also possible to prove that a backward-looking
rule defined in terms of the past CPI-inflation rate will avoid
multiple equilibria.34
Furthermore it is also possible to prove that a backward-looking
rule defined in terms of the past CPI-inflation rate will avoid
multiple equilibria.34
Description of Figure 2
Figure 2 shows the combinations of the PPP rule response coefficient to the CPI-inflation and other structural parameters of the model under which there is a unique equilibrium (real determinacy) whose Minimal State Variable (MSV) representation is learnable in the E-stability sense. These combinations are denoted by `` D-ES''. The figure also shows the combinations of these parameters under which there are multiple equilibria (real indeterminacy) and sunspot equilibria whose Common Factor (CF) representation is learnable in the E-stability sense. We denote these combinations by `` I-ES''. In addition the figure shows the combinations that imply the non-existence of an equilibrium denoted by `` N''. Figure 2 has four panels. We proceed to describe each panel.
The top-left panel shows the combinations for the PPP rule
response coefficient to the CPI-inflation (
![]() ) and the
share of traded goods (
) and the
share of traded goods (![]() ) under which there is `` D-ES'' or `` I-ES''.
The panel measures
) under which there is `` D-ES'' or `` I-ES''.
The panel measures
![]() on the
vertical axis with
on the
vertical axis with
![]() and
and ![]() on the horizontal axis with
on the horizontal axis with
![]() For
For
![]() there
is `` D-ES'' or `` N''. For
there
is `` D-ES'' or `` N''. For
![]() there
is a frontier of combinations of
there
is a frontier of combinations of
![]() andthat separates
the combinations of `` D-ES'' from `` I-ES''. This frontier is
convex and has a positive slope. It crosses the
andthat separates
the combinations of `` D-ES'' from `` I-ES''. This frontier is
convex and has a positive slope. It crosses the
![]() -axis at 0.45
appr
-axis at 0.45
appr![]() oximately.(`` approximately'' since
oximately.(`` approximately'' since ![]() cannot be zero.) To the
north-west of this frontier we have the combinations for
cannot be zero.) To the
north-west of this frontier we have the combinations for
![]() and
and
![]() under which there
is `` I-ES''. To the south-east of this frontier we have the
combinations for
under which there
is `` I-ES''. To the south-east of this frontier we have the
combinations for
![]() and
and
![]() under which there
is `` D-ES''.
under which there
is `` D-ES''.
The top-right panel shows the combinations for the PPP rule
response coefficient to the CPI-inflation (
![]() ) and the
degree of monopolistic competition (
) and the
degree of monopolistic competition (![]() ) under which there is `` D-ES'', `` I-ES'' or ``
N''. This panel measures
) under which there is `` D-ES'', `` I-ES'' or ``
N''. This panel measures
![]() on the
vertical axis with
on the
vertical axis with
![]() and
and ![]() on the horizontal axis with
on the horizontal axis with
![]() For
For
![]() and
and
![]() there is ``
D-ES'' or `` N''. For
there is ``
D-ES'' or `` N''. For
![]() and
and
![]() there is ``
D-ES''. For
there is ``
D-ES''. For
![]() there
is a frontier of combinations of
there
is a frontier of combinations of
![]() and
and
![]() that separates the
combinations of `` D-ES'' from `` I-ES''. This frontier is convex,
has a negative slope and goes through
that separates the
combinations of `` D-ES'' from `` I-ES''. This frontier is convex,
has a negative slope and goes through
![]() To the north-east of this
frontier we have the combinations for
To the north-east of this
frontier we have the combinations for
![]() and
and
![]() under which there is
`` I-ES''. To the south-west of this frontier we have the
combinations for
under which there is
`` I-ES''. To the south-west of this frontier we have the
combinations for
![]() and
and
![]() under which there is
`` D-ES''.
under which there is
`` D-ES''.
The bottom-left panel shows the combinations for the PPP rule
response coefficient to the CPI-inflation (
![]() ) and the
degree of price stickiness (
) and the
degree of price stickiness (![]() ) under which there is `` D-ES'', `` I-ES'' or ``
N''. This panel measures
) under which there is `` D-ES'', `` I-ES'' or ``
N''. This panel measures
![]() on the
vertical axis with
on the
vertical axis with
![]() and
and ![]() on the horizontal axis with
on the horizontal axis with
![]() For
For
![]() and
and
![]() there is ``
D-ES'' or `` N''. For
there is ``
D-ES'' or `` N''. For
![]() and
and
![]() there is ``
D-ES''. For
there is ``
D-ES''. For
![]() there
is a frontier of combinations of
there
is a frontier of combinations of
![]() and
and
![]() that separates the
combinations of `` D-ES'' from `` I-ES''. This frontier is concave,
has a positive slope and goes through
that separates the
combinations of `` D-ES'' from `` I-ES''. This frontier is concave,
has a positive slope and goes through
![]() and
and
![]() approximately.(``
approximately'' since
approximately.(``
approximately'' since ![]() cannot be zero.) To the north-west of this
frontier we have the combinations for
cannot be zero.) To the north-west of this
frontier we have the combinations for
![]() and
and
![]() under which there
is `` I-ES''. To the south-east of this frontier we have the
combinations for
under which there
is `` I-ES''. To the south-east of this frontier we have the
combinations for
![]() and
and
![]() under which there
is `` D-ES''.
under which there
is `` D-ES''.
The bottom-right panel shows the combinations for the PPP rule
response coefficient to the CPI-inflation (
![]() ) and the
depreciation target (
) and the
depreciation target (
![]() ) under
which there is `` D-ES'', `` I-ES'' or `` N''. This panel measures
) under
which there is `` D-ES'', `` I-ES'' or `` N''. This panel measures
![]() on the
vertical axis with
on the
vertical axis with
![]() and
and
![]() on the
horizontal axis with
on the
horizontal axis with
![]() For
For
![]() and
and
![]() there is `` D-ES'' or `` N''. For
there is `` D-ES'' or `` N''. For
![]() and
and
![]() there is `` D-ES''. For
there is `` D-ES''. For
![]() there
is a frontier of combinations of
there
is a frontier of combinations of
![]() and
and
![]() that
separates the combinations of `` D-ES'' from `` I-ES''. This
frontier is concave, has a positive slope and goes through
that
separates the combinations of `` D-ES'' from `` I-ES''. This
frontier is concave, has a positive slope and goes through
![]() and
and
![]() approximately.
To the north-west of this frontier we have the combinations for
approximately.
To the north-west of this frontier we have the combinations for
![]() and
and
![]() under
which there is `` I-ES''. To the south-east of this frontier we
have the combinations for
under
which there is `` I-ES''. To the south-east of this frontier we
have the combinations for
![]() and
and
![]() under
which there is `` D-ES''.
under
which there is `` D-ES''.
We proceed by pursuing the learnability analysis. As argued
before this analysis is useful to evaluate the attainability of the
possible unique equilibrium and multiple equilibria induced by the
PPP rule. We use equations (37), (38), (39) and the
log-linearized versions of (8) and
![]() to reduce the model to
to reduce the model to
where
As before in order to pursue the learnability analysis we use the methodology proposed by Evans and Honkapohja (1999, 2001). We derive some E-stability conditions and check whether a particular representation of the equilibrium under analysis satisfies or violates them.
The following proposition summarizes the results.
- a) Under the
real determinacy conditions specified in Proposition 5 there exists
a unique equilibrium characterized by the fundamental
solution
where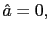
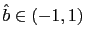 is uniquely defined by the quadratic
equation
is uniquely defined by the quadratic
equation
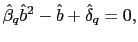 and
and 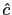 is also uniquely defined
by
is also uniquely defined
by
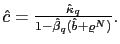 This solution is learnable in the
E-stability sense.35
This solution is learnable in the
E-stability sense.35 - b) Assume
that
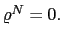 Under the real indeterminacy conditions
specified in Proposition 5 there are stationary sunspot equilibria
described by the common factor representation
Under the real indeterminacy conditions
specified in Proposition 5 there are stationary sunspot equilibria
described by the common factor representation
where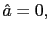
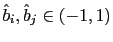 are unique and correspond to the roots of the quadratic
equation
are unique and correspond to the roots of the quadratic
equation
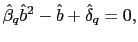
 is arbitrary,
is arbitrary,
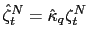 and
and
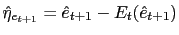 is a martingale difference sequence.
In particular, the common factor
representation (57) and (58) with
is a martingale difference sequence.
In particular, the common factor
representation (57) and (58) with
 and
and
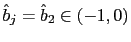 is learnable in the E-stability sense.36
is learnable in the E-stability sense.36
Proposition 6 states that when the PPP rule under study induces a unique equilibrium then this equilibrium represented by the fundamental solution, also known as the MSV solution, is learnable in the E-stability sense. This result is important since it means that given that the rule induces a unique equilibrium then agents will be able to coordinate on that particular equilibrium and therefore the economy will converge towards it over time. In addition as was demonstrated in Proposition 2, it is also possible to prove for PPP rules defined in terms of the CPI-inflation, that even under real indeterminacy the fundamental solution is still E-stable. However under real indeterminacy there are other equilibria such as stationary sunspot equilibria whose feasibility is worth evaluating in terms of learnabiliy. Accordingly, the second part of Proposition 6 shows that a common factor representation of stationary sunspot equilibria is learnable in the sense of E-stability. This result is interesting for two reasons. First, as mentioned before, it suggests that sunspot equilibria induced by PPP rules are more likely to occur. Second, it warns policy makers about some of the negative consequences of implementing PPP rules that respond to inflation. Dornbusch (1980, 1982) conceived PPP rules as a means to introduce the necessary real flexibility to cope with intrinsic (fundamental) uncertainty in an economy with nominal rigidities. In contrast our result points out that such PPP rules may open the possibility of learnable representations of sunspot equilibria aggravating the effects of extrinsic (non-fundamental) uncertainty in an economy with nominal rigidities.
6 Conclusions
In this paper we establish and disentangle the conditions under which PPP rules lead to real (in)determinacy in a small open economy that faces nominal rigidities. We find that besides the specification of the rule, structural parameters such as the share of traded goods (that measures the degree of openness of the economy) and the degrees of imperfect competition and price stickiness in the non-traded sector play a crucial role in the determinacy of equilibrium.
More importantly to evaluate the relevance of the determinacy results we also pursue a learnability (E-stability) analysis. We show that for rules that guarantee a unique equilibrium the fundamental solution that describes this equilibrium is learnable in the E-stability sense. Similarly we show that for PPP rules that open the possibility of sunspot equilibria, some common factor representations of these equilibria are also E-stable. That is, agents can coordinate their actions and learn some representations of stationary sunspot equilibria. In this sense these equilibria are more likely to occur under PPP rules than previously recognized and therefore these rules are more prone to cause aggregate instability in the economy.
Dornbusch (1980, 1982) conceived PPP rules as a means of introducing the real flexibility necessary to cope with intrinsic (fundamental) uncertainty in an economy with nominal rigidities. Our results indicate that PPP rules must be chosen with care in order to avoid the possibility of ``learnable'' sunspot equilibria and the associated aggravation of the effects of extrinsic (non-fundamental) uncertainty. In other words, PPP rules should satisfy two stability requirements: uniqueness and learnability. On one hand, the rule should avoid sunspot equilibria that are usually associated with undesirable properties such as a large degree of volatility. On the other hand, the rule should guarantee that agents can indeed coordinate their actions on the equilibrium the policy makers are targeting and that the economy will not in fact diverge away from this target.
There are some possible extensions of the analysis presented in this paper. First, one may consider extending the model to have two traded goods: a domestic one and a foreign one. This will enrich the analysis making the model more similar to the ones in Dornbusch (1980, 1982). Under this set-up one can explore how our results may vary when the government responds to different measures of inflation in the PPP rule. Second one may study how our determinacy and learnability of equilibrium results may be affected by following the approach by Preston (2003). That is, instead of imposing the assumption of non-rational expectations on the derived log-linearized model, we may impose this assumption as a primitive one of the model. This assumption implies that agents do not have a complete economic model with which to derive true probability laws since they do not know other agents' tastes and beliefs. In this case agents solve multi-period decision problems whereby their actions depend on forecasts of macroeconomic conditions many periods into the future. We leave these extensions for further research.
7 Appendix
Lemma 1 In
a ![]() linearized system of difference equations
whose matrix is denoted by
linearized system of difference equations
whose matrix is denoted by ![]() and whose characteristic
equation corresponds to
and whose characteristic
equation corresponds to
![]() (
( ![]() )=
)=
![]() if
either a)
if
either a)
![]() , or b)
, or b)
![]() or c)
or c) ![]() then the system
displays real eigenvalues.
then the system
displays real eigenvalues.
To prove b) we start by noting that
![]() means that
means that
![]() But this
implies that
But this
implies that
![]() that with the aforementioned sufficient condition in turn leads to
that with the aforementioned sufficient condition in turn leads to
![]() . Hence the eigenvalues are real.
. Hence the eigenvalues are real.
To prove c) we point out that
![]() means that
means that
![]() But this
implies that
But this
implies that
![]() that in turn leads to
that in turn leads to
![]() . Hence the eigenvalues are real.
. Hence the eigenvalues are real. ![]()
7.1 Proof of Proposition 1
![\begin{displaymath} \left( \begin{array}[c]{c} \hat{\pi}_{t}^{N}\ \hat{e}_{t-1... ...\end{array}\right) +U\hat{\eta}_{\pi_{t+1}}+V\hat{z}_{t+1}^{N} \end{displaymath}](img354.gif)
![$\displaystyle =\beta\left[ 1+\frac{H\rho_{e}\bar{e}}{\Delta}\right] \qquad J_{1... ...left[ K-\frac{H\rho_{e}\bar{e}(1+\bar{\epsilon})}{\bar{\epsilon }\Delta}\right]$](img356.gif)
|
||
![$\displaystyle =\beta\frac{\bar{\epsilon}}{1+\bar{\epsilon}}\left[ 1+\frac {H\rh... ...silon}}-\frac{H\rho_{e}\bar{e}}{\Delta}\right] +\frac{\Delta}{1+\bar{\epsilon}}$](img358.gif)
|
![$\displaystyle =\beta\left[ 1+\frac{K\bar{\epsilon}}{1+\bar{\epsilon}}\right] +\frac{1+\bar{\epsilon}-\rho_{e}\bar{e}}{1+\bar{\epsilon}}>0$](img372.gif)
|
||
![$\displaystyle =\beta\left[ \frac{1+\bar{\epsilon}-(1-H)\rho_{e} \bar{e}}{1+\bar{\epsilon}}\right]$](img374.gif)
|
||
respectively. Using these expressions we obtain
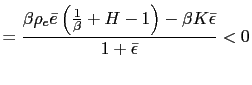
|
||
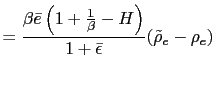
|
where
![$ \tilde{\rho}_{e}=\frac{\left[ 2(1+\bar{\epsilon})\left( 1+\frac {1}{\beta}\rig... ...r{\epsilon}\right] }{\left[ \bar{e}\left( 1+\frac{1}{\beta}-H\right) \right] }.$](img381.gif)
All these expressions together with
![]()
![]() and
and
![]() and the
assumptions about the structural parameters allows us to observe
that
and the
assumptions about the structural parameters allows us to observe
that
![]() and
and
![]() By Lemma 1, this last inequality implies that the eigenvalues are
real.
By Lemma 1, this last inequality implies that the eigenvalues are
real.
To prove part a) we proceed as follows. Observe that since
![]() then
then
![]() .
Hence from
.
Hence from
![]() and
and
![]() we can conclude that
we can conclude that
![]() This in conjunction with
This in conjunction with
![]() and
and
![]() imply
that the system has two explosive eigenvalues
imply
that the system has two explosive eigenvalues
![]() and
and
![]() (which means
that
(which means
that
![]() and
and
![]() Thus the steady state is a source (See Azariadis, 1993). Since
Thus the steady state is a source (See Azariadis, 1993). Since
![]() is
the only non-predetermined variable of the system then by Blanchard
and Kahn (1980) we conclude that the model displays real
indeterminacy.
is
the only non-predetermined variable of the system then by Blanchard
and Kahn (1980) we conclude that the model displays real
indeterminacy.
To prove b) we note that from
![]() and
and
![]() we can conclude
that
we can conclude
that
![]() This in tandem with
This in tandem with
![]() and
and
![]() imply
that the system has one explosive eigenvalue
imply
that the system has one explosive eigenvalue
![]() and one
non-explosive eigenvalue
and one
non-explosive eigenvalue
![]() Hence the
steady state is a saddle path (See Azariadis, 1993). Since
Hence the
steady state is a saddle path (See Azariadis, 1993). Since
![]() is
the only non-predetermined variable of the system then by Blanchard
and Kahn (1980) we conclude that the model displays real
determinacy.
is
the only non-predetermined variable of the system then by Blanchard
and Kahn (1980) we conclude that the model displays real
determinacy.
Finally to prove c) we use the fact that
![]() implies that
implies that
![]() and therefore
and therefore
![]() Then the analysis pursued to prove part b) follows.
Then the analysis pursued to prove part b) follows. ![]()
7.2 Proof of Corollary 1
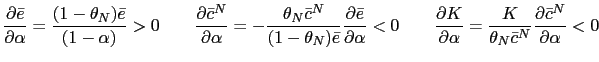
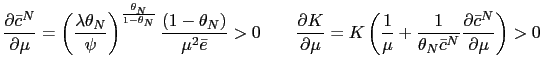

![$ \Xi=\frac{\left( 1+\frac{1}{\beta}\right) \left[ \bar{\epsilon }+2\frac{H}{K}(1+\bar{\epsilon})\right] }{\left( 1+\frac{1}{\beta}-H\right) ^{2}}>0.$](img400.gif)
7.3 Proof of Proposition 2
where
whose roots are denoted by
where
Third, using these relationships and the proof in Proposition 1,
it is trivial to show that under real determinacy, the unique
equilibrium of the model (45)
characterized by the fundamental solution (47)
with
![]() is in
fact a solution of the model (45).
is in
fact a solution of the model (45).
Fourth, we derive the E-stability conditions. Consider the model (45) and assume that the agents follow a perceived law of motion (PLM) that in this case of real determinacy corresponds to the fundamental solution
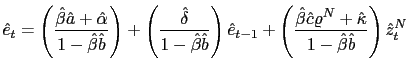
![$ T(\hat{a},\hat{b},\hat{c})=\left[ T_{1} ,T_{2},T_{3}\right] ^{\prime}=\left[ \... ...eta}\hat{c}\varrho^{N}+\hat{\kappa}}{1-\hat{\beta}\hat{b}}\right] ^{^{\prime}},$](img410.gif) whose fixed points correspond to the rational expectations
equilibrium with
whose fixed points correspond to the rational expectations
equilibrium with 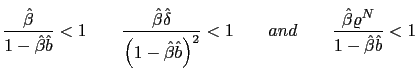
Moreover using (60) we can rewrite these conditions as
Finally recall that in the proof of Proposition 1 we derived
that real determinacy is associated with one explosive eigenvalue
![]() and one
non-explosive eigenvalue
and one
non-explosive eigenvalue
![]() Then using
this and
Then using
this and
![]() we can infer that
we can infer that
![]() and either
and either
![]() or
or
![]() Moreover using (61) we can rewrite the conditions (62) as
Moreover using (61) we can rewrite the conditions (62) as
For
![]() we
have that the E-stability conditions (63)
become
we
have that the E-stability conditions (63)
become
Then defining
![]() Proposition 2 follows since it is simple to see that the
E-stability conditions are satisfied given
Proposition 2 follows since it is simple to see that the
E-stability conditions are satisfied given
![]() ,
,
![]() and either
and either
![]() or
or
![]()
![]()
7.4 Proof of Proposition 3
where
whose roots are denoted by
Second, we point out that following Propositions 3 and 4 in
Evans and McGough (2003), it is simple to prove that the process
![]() is a
rational expectations equilibrium in (45)
with
is a
rational expectations equilibrium in (45)
with
![]() , if and
only if there is a martingale difference sequence
, if and
only if there is a martingale difference sequence
![]() such that
such that
![]() solves
(48) with (49).
solves
(48) with (49).
Third, we derive the E-stability conditions adapting the
analysis of Evans and McGough (2003). In particular, note that we
assume that agents knows
![]() when
making the forecast
when
making the forecast
![]() Consider the stochastic model (45) and
suppose that the agents follow a perceived law of motion (PLM) such
as
Consider the stochastic model (45) and
suppose that the agents follow a perceived law of motion (PLM) such
as
where
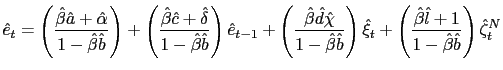
![$\displaystyle T(\hat{a},\hat{b},\hat{c},\hat{d},\hat{k},\hat{l})=\left[ T_{1},T... ...at{b}},\frac{\hat{\beta}\hat{l}+1}{1-\hat{\beta}\hat{b}},0\right] ^{^{\prime}} $](img446.gif)
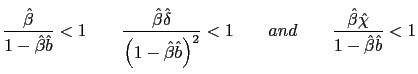
Moreover using (66) and noting that
![]() and
and
![]() we can
rewrite these conditions as
we can
rewrite these conditions as
However note that for the last E-stability condition, it is
always true that for the common factor representation we have that
either
![]() and therefore
and therefore
![]() implying
implying
![]() or,
or,
![]() and therefore
and therefore
![]() implying
implying
![]() Hence the differential equation for
Hence the differential equation for
![]() is
is
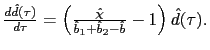 Using a similar argument to the one developed in Evans and
Honkapohja (1992) it is possible to show that as either
Using a similar argument to the one developed in Evans and
Honkapohja (1992) it is possible to show that as either
![]() or
or
![]() then
then
![]() converges to a finite value. This means that the only stability
conditions that are required to be checked are
converges to a finite value. This means that the only stability
conditions that are required to be checked are
![]() and
and
![]()
Fourth, we recall our result from the beginning of this proof
that states that under real indeterminacy the roots are
![]() and
and
![]()
To prove part a) we use the fact that for
![]() we
have that the E-stability conditions
we
have that the E-stability conditions
![]() and
and
![]() become
become
![]() and
and
![]() Since
Since
![]() and
and
![]() it is clear that these E-stability conditions are satisfied. Hence
the common factor representation (48) and
(49) with
it is clear that these E-stability conditions are satisfied. Hence
the common factor representation (48) and
(49) with
![]() and
and
![]() is learnable in the
E-stability sense.
is learnable in the
E-stability sense.
To prove part b) we utilize the fact that for
![]() we
have that the E-stability condition
we
have that the E-stability condition
![]() is
clearly not satisfied for
is
clearly not satisfied for
![]() given that
given that
![]() implies
implies
![]()
![]()
7.5 Proof of Proposition 4
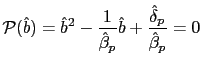
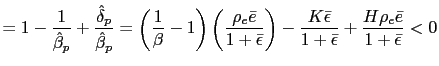
|
||
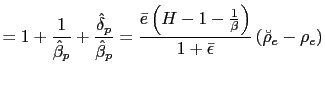
|
where
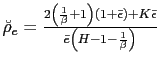 . Observe that since
. Observe that since
Third note that if either
![]() and
and
![]() or
or
![]() and
and
![]() then
then
![]() Using this and the previous results that
Using this and the previous results that
![]() and that the eigenvalues are real we may infer that the steady
state is a saddle with one of the eigenvalues falling in
(
and that the eigenvalues are real we may infer that the steady
state is a saddle with one of the eigenvalues falling in
(![]() ) and the other
one falling in (
) and the other
one falling in (![]() ) as explained in Azariadis (1993). Given that
) as explained in Azariadis (1993). Given that
![]() is the
only predetermined variable then by Blanchard and Kahn (1980) we
conclude that the model displays real determinacy.
is the
only predetermined variable then by Blanchard and Kahn (1980) we
conclude that the model displays real determinacy.
Fourth it is straightforward to prove that the fundamental
solution
![]() is in fact a solution of (50).
Fifth we prove that this fundamental solution is E-stable. In order
to do so we need to derive the E-stability conditions. The
procedure to derive them is exactly the same as the procedure
followed in the proof of Proposition 2. In fact the conditions are
the same as the ones previously derived. Here we present only the
conditions. The E-stability conditions are
is in fact a solution of (50).
Fifth we prove that this fundamental solution is E-stable. In order
to do so we need to derive the E-stability conditions. The
procedure to derive them is exactly the same as the procedure
followed in the proof of Proposition 2. In fact the conditions are
the same as the ones previously derived. Here we present only the
conditions. The E-stability conditions are
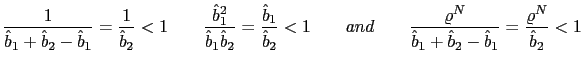
It is simple to see that the E-stability conditions are
satisfied given
![]() ,
,
![]() and
and
![]() Then the fundamental
solution is learnable in the E-stability sense and statement a) of
this proposition follows.
Then the fundamental
solution is learnable in the E-stability sense and statement a) of
this proposition follows.
To prove b) it is enough to note that if
![]() and
and
![]() then we can derive
that
then we can derive
that
![]() .
Using this and the previous results that
.
Using this and the previous results that
![]() and that the eigenvalues are real we may infer from Azariadis
(1993) that the steady state is a source with one eigenvalue
falling in (
and that the eigenvalues are real we may infer from Azariadis
(1993) that the steady state is a source with one eigenvalue
falling in (
![]() ) and the
other in (
) and the
other in (![]() ).
Since
).
Since
![]() is the
only predetermined variable then by Blanchard and Kahn (1980) we
conclude that the model displays no equilibrium for this case.
is the
only predetermined variable then by Blanchard and Kahn (1980) we
conclude that the model displays no equilibrium for this case.
![]()
7.6 Proof of Proposition 5
![\begin{displaymath} \left( \begin{array}[c]{c} \hat{\pi}_{t}^{N}\ \hat{e}_{t-1... ...\end{array}\right) +U\hat{\eta}_{\pi_{t+1}}+V\hat{z}_{t+1}^{N} \end{displaymath}](img354.gif)
![$\displaystyle =\frac{\beta\left\{ 1-\left[ \alpha+(1-\alpha)H\right] \rho_{\pi }\right\} }{1-\alpha\rho_{\pi}}\qquad\qquad\qquad J_{12}=\beta K$](img489.gif)
|
||
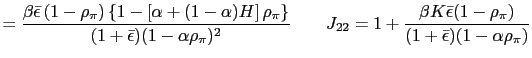
|
![$\displaystyle =1+\frac{\beta K\bar{\epsilon}(1-\rho_{\pi})}{(1+\bar{\epsilon })... ...\{ 1-\left[ \alpha+(1-\alpha )H\right] \rho_{\pi}\right\} }{1-\alpha\rho_{\pi}}$](img491.gif)
|
||
![$\displaystyle =\frac{\beta\left\{ 1-\left[ \alpha+(1-\alpha )H\right] \rho_{\pi}\right\} }{1-\alpha\rho_{\pi}}$](img492.gif)
|
||
respectively. Using these expressions we obtain
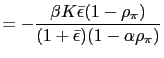
|
||
![$\displaystyle =\frac{\beta\left[ 2\alpha\left( 1+\frac{1}{\beta }\right) +2(1-\... ...}{1+\bar{\epsilon}}\right] }{1-\alpha\rho_{\pi}}(\tilde{\rho}_{\pi}-\rho_{\pi})$](img494.gif)
|
where
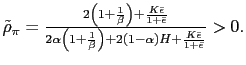 In this proof we will use the facts that
In this proof we will use the facts that To prove part a) we proceed as follows. Observe that since
![]() and
and
![]() then
then
![]() and therefore
and therefore
![]() By Lemma 1, this last inequality implies that the eigenvalues are
real. In addition since by assumption
By Lemma 1, this last inequality implies that the eigenvalues are
real. In addition since by assumption
![]() (and
(and
![]() ), then we can infer
that
), then we can infer
that
![]() It is straightforward to show that
It is straightforward to show that
![]() and
and
![]() imply that
imply that
![]() a result we will use
later
a result we will use
later![]() Hence
Hence
![]() in tandem with
in tandem with
![]() help us to conclude that the system has two explosive eigenvalues
help us to conclude that the system has two explosive eigenvalues
![]() and
and
![]() and that the
steady state is a source as explained in Azariadis (1993). This
means that
and that the
steady state is a source as explained in Azariadis (1993). This
means that
![]() and
and
![]() Since
Since
![]() is
the only non-predetermined variable of the system then by Blanchard
and Kahn (1980) we conclude that the model displays real
indeterminacy.
is
the only non-predetermined variable of the system then by Blanchard
and Kahn (1980) we conclude that the model displays real
indeterminacy.
To prove b) consider the assumption
![]() We have to take into account two cases:
We have to take into account two cases:
![]() and
and
![]() For
For
![]() we have that since by
assumption
we have that since by
assumption
![]() then
then
![]() By Lemma 1, this last inequality implies that the eigenvalues are
real. In addition since by assumption
By Lemma 1, this last inequality implies that the eigenvalues are
real. In addition since by assumption
![]() then we can infer
that
then we can infer
that
![]() This in tandem with
This in tandem with
![]() imply that the steady state is a saddle point with one explosive
eigenvalue
imply that the steady state is a saddle point with one explosive
eigenvalue
![]() and one non-explosive
eigenvalue
and one non-explosive
eigenvalue
![]() as shown in Azariadis (1993).
as shown in Azariadis (1993).
For
![]() we have that since by
assumption
we have that since by
assumption
![]() then
then
![]() In addition since by assumption
In addition since by assumption
![]() then we can infer
that
then we can infer
that
![]() which in turn implies, by Lemma 1, that the eigenvalues are real.
Since
which in turn implies, by Lemma 1, that the eigenvalues are real.
Since
![]() and
and
![]() then the steady state is a saddle point and the system has one
explosive eigenvalue
then the steady state is a saddle point and the system has one
explosive eigenvalue
![]() and one non-explosive
eigenvalue
and one non-explosive
eigenvalue
![]() as explained in Azariadis (1993).
as explained in Azariadis (1993).
Now consider the assumption
![]() Using this we can infer that in any case we have that since
Using this we can infer that in any case we have that since
![]() then
then
![]() But this implies
that
But this implies
that
![]() By Lemma 1, we derive that the eigenvalues are real. In addition
since by assumption
By Lemma 1, we derive that the eigenvalues are real. In addition
since by assumption
![]() then we can infer
that
then we can infer
that
![]() This in tandem with
This in tandem with
![]() imply that the steady state is a saddle point with one explosive
eigenvalue
imply that the steady state is a saddle point with one explosive
eigenvalue
![]() and one non-explosive
eigenvalue
and one non-explosive
eigenvalue
![]() as shown in Azariadis (1993)
as shown in Azariadis (1993)![]()
Therefore under either
![]() or
or
![]() the steady state is a saddle path. Since
the steady state is a saddle path. Since
![]() is
the only non-predetermined variable of the system then by Blanchard
and Kahn (1980) we conclude that the model displays real
determinacy.
is
the only non-predetermined variable of the system then by Blanchard
and Kahn (1980) we conclude that the model displays real
determinacy.
Finally to prove c) we start by observing that
![]() Hence
Hence
![]() .
These inequalities imply that
.
These inequalities imply that
![]() and
and
![]() Then we have to consider two cases:
Then we have to consider two cases:
![]() and
and
![]() For the
first case if
For the
first case if
![]() then since
then since
![]() we have that
we have that
![]() By Lemma 1 this implies that
the roots are real. Moreover utilizing this and
By Lemma 1 this implies that
the roots are real. Moreover utilizing this and
![]() and
and
![]() we can infer that the steady state is a sink with two non explosive
eigenvalues
we can infer that the steady state is a sink with two non explosive
eigenvalues
![]() and
and
![]() as explained in Azariadis(1993)
as explained in Azariadis(1993)![]()
On the other hand, for the second case we have that since
![]() and
and
![]() then
then
![]() (provided that
(provided that
![]() Using
this and
Using
this and
![]() and
and
![]() we can conclude from Azariadis (1993) that regardless of whether
the eigenvalues are real or complex the steady state is a source
with two non explosive eigenvalues
we can conclude from Azariadis (1993) that regardless of whether
the eigenvalues are real or complex the steady state is a source
with two non explosive eigenvalues
![]() and
and
![]()
Therefore in both cases we have concluded that the steady-state
is a source. Hence
![]() and
and
![]() Since
Since
![]() is
the only non-predetermined variable of the system then by Blanchard
and Kahn (1980) we conclude that the model displays no equilibrium.
is
the only non-predetermined variable of the system then by Blanchard
and Kahn (1980) we conclude that the model displays no equilibrium.
![]()
7.7 Proof of Corollary 2
![$\displaystyle =\frac{2\left( H-1-\frac{1}{\beta}\right) \left[ 2\left( 1+\frac{... ...}}{1+\bar{\epsilon}}\right] -\Theta\frac{\partial K}{\partial\alpha}}{\Phi^{2}}$](img539.gif)
|
||
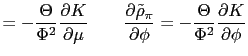
|
where
7.8 Proof of Proposition 6
whose roots are denoted by
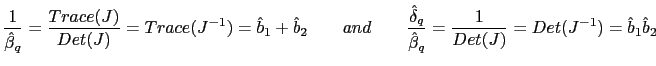
Third we use these relationships to prove a). Since under real
determinacy in the proof of Proposition 5 we have that either
![]() and
and
![]() or
or
![]() and
and
![]() then we can conclude that
then we can conclude that
![]() and either
and either
![]() or
or
![]()
Fourth, it is simple to show that under real determinacy, the
unique equilibrium of the model (54)
characterized by the fundamental solution (56)
with
![]() is in
fact a solution of the model (54).
is in
fact a solution of the model (54).
Fifth, we derive the E-stability conditions. However the
procedure is the same as the one explained in the proof of
Proposition 2. We only rename
![]() and
and
![]() as
as
![]() and
and
![]() respectively. Then following the proof of Proposition 2, it is
straightforward to prove that the unique equilibrium of the model
(54) characterized by the fundamental
solution (56) with
respectively. Then following the proof of Proposition 2, it is
straightforward to prove that the unique equilibrium of the model
(54) characterized by the fundamental
solution (56) with
![]() and
either
and
either
![]() or
or
![]() is E-stable.
is E-stable.
Sixth to prove b) we start by noting that in (68) we have that
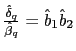 . Next we recall that in the proof of a) in Proposition 5 we
argued that real indeterminacy is associated with two non-explosive
eigenvalues
. Next we recall that in the proof of a) in Proposition 5 we
argued that real indeterminacy is associated with two non-explosive
eigenvalues
![]() and
and
![]() Then using
this and
Then using
this and
![]() help us to infer
that
help us to infer
that
![]() and
and
![]() Furthermore under real indeterminacy it is easy to show that
Furthermore under real indeterminacy it is easy to show that
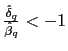 . Hence
. Hence
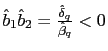 which in turn means that the roots are real
which in turn means that the roots are real![]() Then without loss of generality we
can assume that the roots are
Then without loss of generality we
can assume that the roots are
![]() and
and
![]()
Seventh, we point out that following Propositions 3 and 4 in
Evans and McGough (2003), it is simple to prove that the process
![]() is a
rational expectations equilibrium of (54)
with
is a
rational expectations equilibrium of (54)
with
![]() , if and
only if there is a martingale difference sequence
, if and
only if there is a martingale difference sequence
![]() such that
such that
![]() solves
(57) with (58).
Henceforth we focus on proving the learnability of the common
factor representation. However the proof is similar to the proof
for Proposition 3. We just have to rename
solves
(57) with (58).
Henceforth we focus on proving the learnability of the common
factor representation. However the proof is similar to the proof
for Proposition 3. We just have to rename
![]() and
and
![]() as
as
![]() and
and
![]() respectively, and follow the steps. Then statement b) follows.
respectively, and follow the steps. Then statement b) follows.
![]()
8 References
Adams, C. and D. Gros (1986), ``The Consequences of Real Exchange Rate Rules for Inflation: Some Illustrative Examples, IMF Staff Papers, 33, 439-476.
Azariadis, C. (1993), Intertemporal Macroeconomics, Blackwell, Cambridge, Massachusetts.
Benhabib, J., S. Schmitt-Grohé and M. Uribe (2001), ``Monetary Policy Rules and Multiple Equilibria,'' American Economic Review, 91, 167-184.
Blanchard, O. and C. Kahn (1980), ``The Solution of Linear Difference Models Under Rational Expectations,'' Econometrica, 48, 1305-1312.
Bullard, J. and K. Mitra, (2002), ``Learning About Monetary Policy Rules,'' Journal of Monetary Economics, 49, 1105-1129.
Calvo, G. (1983), ``Staggering Prices in a Utility-Maximizing Framework,'' Journal of Monetary Economics, 12, 383-398.
Calvo, G., Reinhart, C. and C. Vegh (1995), ``Targeting the Real Exchange Rate: Theory and Evidence,'' Journal of Development Economics, 47:1, 97-134.
Carlstrom, C. and T. Fuerst (2001), ``Timing and Real Indeterminacy in Monetary Models,'' Journal of Monetary Economics, 47:2, 285-298.
Clarida, J., J. Gali and M. Gertler (2000), ``Monetary Policy Rules and Macroeconomic Stability: Evidence and Some Theory,'' Quarterly Journal of Economics, 115, 147-180.
Clarida, J., J. Gali and M. Gertler (2001), ''Optimal Monetary Policy in Open Versus Closed Economies: An Integrated Approach,'' American Economic Review, 91 (2), 253-257.
Dornbusch, R.(1980), Open Economy Macroeconomics, New York: Basic.
Dornbusch, R.(1982), ``PPP Exchange Rate Rules and Macroeconomic Stability,'' Journal of Political Economy, 90:3, 158-165.
Dib, A. (2001), ``An Estimated Canadian DSGE Model with Nominal and Real Rigidities,'' Bank of Canada, Working Paper, 26.
Dupor, B. (2001), ``Investment and Interest Rate Policy,'' Journal of Economic Theory, 98, 85-113.
Evans, G, and S. Honkapohja (1986), ``A Complete Characterization of ARMA Solutions to Linear Rational Expectations Models,'' Review of Economic Studies, 53, 227-239.
Evans, G, and S. Honkapohja (1992), ``On theRobustness of Bubbles in Linear RE Models,'' International of Economic Review, 33, 1-14.
Evans, G, and S. Honkapohja (1999), ``Learning Dynamics,'' in Handbook of Macroeconomics, eds. J. Taylor and M. Woodford, Elsevier, Amsterdam, Vol. 1, 449-542.
Evans, G, and S. Honkapohja (2001), Learning and Expectations, Princeton University Press, New Jersey.
Evans, G, and B. McGough (2003), ``Stable Sunspot Solutions in Model with Predetermined Variables,'' Manuscript, University of Oregon, Forthcoming Journal of Economic Dynamics and Control.
Gali, J. and T. Monacelli (2004), ``Monetary Policy and Exchange Rate Volatility in a Small Open Economy,'' CREI, Manuscript.
Keynes, J. M. (1936), The General Theory of Employment, Interest and Money, Macmillan, London.
Kimbrough, K. (1986), ``The Optimal Quantity of Money Rule in the Theory of Public Finance,'' Journal of Monetary Economics, 18, 277-284.
Lizondo, J. (1991), ``Real Exchange Rate Targets, Nominal Exchange Rate Policies, and Inflation,'' Revista de Análisis Económico, 6, 5-22.
Marcet, A., and T. Sargent (1989), ``Convergence of Least-Square Learning Mechanisms in Self-Referential Linear Stochastic Models,'' Journal of Economic Theory, 48, 337-368.
McCallum, B. (1983), ``On Nonuniqueness in Linear Rational Expectations Moldels: An Attempt at Perspective,'' Journal of Monetary Economics, 11, 134-168.
Montiel, A. and J. Ostry (1991), ``Macroeconomic Consequences of Real Exchange Rate Targeting in Developing Economies,'' IMF Staff Papers, 38, 872-900.
Preston, B. (2003), ``Learning About Monetary Policy Rules when Long-Horizon Expectations Matter,'' Manuscript, Columbia University.
Rotemberg, J. (1982), ''Sticky Prices in the United States,``Journal of Political Economy, 90(6), 1187-1211.
Rotemberg, J. and M. Woodford (1999), ``Interest-Rate Rules in an Estimated Sticky-Price Model,'' in Monetary Policy Rules, edited by John B. Taylor, Chicago, National Bureau of Economic Research.
Schmitt-Grohé, S. and M. Uribe (2001), ``Stabilization Policy and the Costs of Dollarization,'' Journal of Money, Credit and Banking, 33, 482-509.
Uribe, M. (2003), ``Real Exchange Rate Targeting and Macroeconomic Instability,'' University of Pennsylvania, Manuscript, Journal of International Economics, Forthcoming.
Woodford, M. (2003), Interest and Prices: Foundations of a Theory of Monetary Policy, Princeton University Press, New Jersey.
Zanna, L. F. (2003a), ``Interest Rate Rules and Multiple Equilibria in the Small Open Economy: The Role of Non-Traded Goods,'' IFDP #785, Board of Governors of the Federal Reserve System.
Zanna, L. F. (2003b), ``International Economics, Monetary Rules and Multiple Equilibria'' Ph.D. Dissertation, University of Pennsylvania.
Footnotes
1. See Dornbusch (1980,1982), Adams and Gros (1986), Lizondo (1991), Montiel and Ostry (1991) and Calvo et al. (1995), among others. Return to text
2. This idea is not specific to PPP rules. In fact the idea that a rule that leads to indeterminacy of equilibrium may be seen as undesiderable has been emphasized by recent studies about interest rate rules. See Benhabib, Schmitt-Grohé and Uribe (2001), Carlstrom and Fuerst (2001), Clarida, Gali and Gertler (2000), Rotemberg and Woodford (1999) and Woodford (2003) among others. Return to text
3. Bullard and Mitra (2002) have emphasized the importance of this point in the interest rate rule literature. Return to text
4. Henceforth we will use the terms `` learnability'', `` E-stability'' and `` expectational stability'' interchangeably in this paper. Return to text
5. Evans and Honkapoja (1999, 2001) have argued that a unique equilibrium and sunspot equilibria are not `` fragile'' if they are learnable in the sense of E-stability. Technically what they propose is to assume that agents in the model initially do not have rational expectations but are endowed with a mechanism to form forecasts using recursive learning algorithms and previous data from the economy. Then they develop some E-stability conditions which govern whether or not a given rational expectations equilibrium is aymptotically stable under least squares learning. Return to text
6. From now on we will use the terms `` multiple equilibria'' and `` real indeterminacy'' (a `` unique equilibrium'' and `` real determinacy'') interchangeably. By real indeterminacy we mean a situation in which the behavior of one or more (real) variables of the model is not pinned down by the model. This situation implies that there are multiple equilibria and opens the possibility of the existence of sunspot equilibria. Return to text
7. This fundamental solution is also well-known as the Minimal State Variable solution. See McCallum (1983). Return to text
8. The common factor representation is an alternative representation of a Rational Expectations Equilibria. See Evans and Honkapoja (1986). Return to text
9. Dornbusch (1980,1982) uses a Mundell and Fleming small open economy model with sticky wages á la Taylor and finds that the aformentioned PPP rule affects the output price-level stability trade-off through two different channels. On one hand, it tries to maintain constant the real exchange rate stabilizing net exports and therefore the demand side. On the other hand, it affects the supply side by its effect on the price of imported intermediate goods. Dornbusch shows that in such a model if the economy is hit by supply shocks then the price volatility always increases with tighter PPP rules. If the demand channel dominates the supply channel then the PPP rule reduces the volatility of output. But if the supply channel dominates the demand channel then the volatility of output is increased. Return to text
10. The set-up of this model is very similar to Uribe (2003) and Zanna (2003a). However we endogenize labor in both sectors and introduce technology shocks. Moreover we use specific functional forms to be able to convey the main message of this paper. In particular we assume separability in terms of both types of consumption. A CES utility function will not affect the qualitative results of this paper but will make the derivation of our analytical results cumbersome. Return to text
11. For the first part of the paper we will assume that agents have rational expectations. However for the E-stability analysis we will relax this assumption. Return to text
12. Benhabib et al. (2001a,b) and Dupor (2001) also follow this approach to model price stickiness. An alternative approach follows Calvo (1983). Our results are invariant to this approach. Return to text
13. We follow Woodford (2003) to construct the budget constraint of the representative agent. Return to text
14. This price is equal to its output cost (=1) plus a term that is a function of the opportunity cost of holding wealth in monetary form. Return to text
15. Note that as a consequence of the aforementioned contingent claims that completely span the uncertainty about productivity shocks the model abstracts from wealth effects due to current account imbalances. In this respect the model is similar to the ones in Clarida, Gali and Gertler (2001) and Gali and Monacelli (2004). Return to text
16. We would have derived a similar augmented Phillips curve if we had follow Calvo's (1983) approach. Return to text
17. Note that the spirit of the PPP
rule and the assumption that ![]() is sticky imply that
is sticky imply that ![]() is a predetermined variable. As
a consequence assuming that
is a predetermined variable. As
a consequence assuming that ![]() and
and ![]() are given corresponds to assume that
are given corresponds to assume that
![]() is
given which in turn avoids the possibility of nominal
indeterminacy. Return to
text
is
given which in turn avoids the possibility of nominal
indeterminacy. Return to
text
18. Observe that we have not
included equation
![]() .
The reason is that
.
The reason is that
![]() does
not affect the other equations. It may affect the current account.
But as in Clarida et al. (2001) and Gali and Monacelli (2004) we
are abtracting from wealth effects due to current account
imbalances. Return to text
does
not affect the other equations. It may affect the current account.
But as in Clarida et al. (2001) and Gali and Monacelli (2004) we
are abtracting from wealth effects due to current account
imbalances. Return to text
19. Here we assume that
![]() is a
bounded sequence and that
is a
bounded sequence and that
![]()
![]() Return to text
Return to text
20. It is important to remember that in the log-linearized set-up all the variables are expressed as deviations from their steady state level. Return to text
21. It is possible to do the same
exercise with respect to other structural parameters such as the
share of labor in the production function (
![]() ). These
results are available upon request. We focus our analyzis on the
share of traded goods (
). These
results are available upon request. We focus our analyzis on the
share of traded goods (![]() ) because this is a particular feature of open
economies. We also concentrate the analysis on the degrees of
monopolistic competition (
) because this is a particular feature of open
economies. We also concentrate the analysis on the degrees of
monopolistic competition (![]() ) and price stickiness (
) and price stickiness (![]() ) in the non-traded sector because
these parameters capture an important asymmetry between the traded
and non-traded sectors. Return to
text
) in the non-traded sector because
these parameters capture an important asymmetry between the traded
and non-traded sectors. Return to
text
22. Note that for this exercise we do not need to assign values to all the parameters. We only present the parametrization of the relevant parameters. Return to text
23. There is no clear consensus about the value that this parameter must take in emerging economies. One of the reasons is the lack of studies that have tried to estimate Phillips curves for these economies and that may give information about possible values for this parameter. Even for an industrialized economy such as Canada, this parameter varies between 2.80 and 44.07, depending on the model specification (type of nominal and real rigidities). See Dib (2001). Return to text
24. See Zanna (2003b). Return to text
25. The idea of expectation driven fluctuations dates back to Keynes (1936). Return to text
26. It is important to observe that for models with multiple stationary equilibria this statement lacks of technical formality. As pointed out by Evans and McGough (2003) for a model with multiple equilibria, a rational expectations equilibrium may have different representations. Therefore one should not strictly speak of learnable rational expectations equilibrium, but whether a rational expectations equilibrium representation is learnable (E-stable). Return to text
27. The Minimal State Variable (MSV) solution according to McCallum (1983). Return to text
28. Observe that this definition
suggests that to prove E-stability of a fixed point corresponds to
prove that all the eigenvalues of the matrix of derivatives
![]() are less than 1. Return to text
are less than 1. Return to text
29. The proof of learnability of common factor representations of sunspot equilibria in this paper also goes over this methodology. Return to text
30. Note that strictly speaking
since we are assuming that the economy starts at ![]() and we have an initial condition
for
and we have an initial condition
for
![]() then in
the common factor representation of a rational expectations
equilibrium
then in
the common factor representation of a rational expectations
equilibrium
![]() equation
(48) should be written as
equation
(48) should be written as
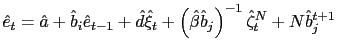
31. Note that
NOT introducing the constant ![]() in the perceived law of motion, such that
in the perceived law of motion, such that
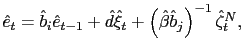 is not innocuous for statement b) of the proposition. In
this case the common factor representation with
is not innocuous for statement b) of the proposition. In
this case the common factor representation with
![]() and
and
![]() becomes
E-stable. Return to
text
becomes
E-stable. Return to
text
32. Forward-looking PPP rules defined in terms of the expected future real exchange rate still open the possibility of sunspot equilibria as shown in Zanna (2003b). Return to text
33. This is also the specification in Montiel and Ostry (1991). Return to text
34. See Zanna (2003b). Return to text
35. Under real indeterminacy it is
also possible to prove that there is an equilibrium characterized
by fundamental solution (56) with
![]() which
is E-stable
which
is E-stable![]() Return to text
Return to text
36. Excluding a constant
![]() in the
perceived law of motion such that
in the
perceived law of motion such that
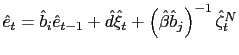 is not innocuous for this part of the proposition. In this
case the common factor representation with
is not innocuous for this part of the proposition. In this
case the common factor representation with
![]() and
and
![]() is also
E-stable. Return to text
is also
E-stable. Return to text
37. One can analyze either of the
forms because the eigenvalues of ![]() correspond to
correspond to
![]() where
where
![]() are the
eigenvalues of
are the
eigenvalues of ![]() Return to
text
Return to
text
38. Note that
![]() since
since
![]() Return
to text
Return
to text
39. One can analyze either of the
forms because the eigenvalues of ![]() correspond to
correspond to
![]() where
where
![]() are the
eigenvalues of
are the
eigenvalues of ![]() Return to
text
Return to
text
This version is optimized for use by screen readers. A printable pdf version is available.
![$\displaystyle E_{0}\underset{t=0}{\overset{\infty}{\sum}}\beta^{t}\left[ A(c_{t... ...2}\left( \frac{P_{t}^{N}(j)}{P_{t-1}^{N}(j)}-1-\bar{\pi}^{N}\right) ^{2}\right]$](img9.gif)
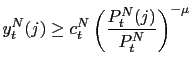

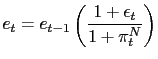
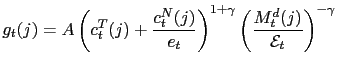
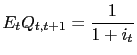
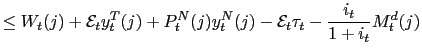
![$\displaystyle \frac{\alpha}{c_{t}^{T}(j)}=\lambda_{t}(j)\left[ 1+\Gamma\left( \frac{i_{t} }{1+i_{t}}\right) ^{\frac{\gamma}{1+\gamma}}\right]$](img76.gif)
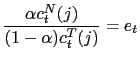
![$\displaystyle \left( \frac{P_{t}^{N}(j)}{P_{t}^{N}}-\frac{\delta_{t}(j)e_{t}}{\... ...a_{N}-1)}}{e_{t}}=z_{t}^{T}\theta_{T}\left[ h_{t}^{T}(j)\right] ^{\theta_{T}-1}$](img78.gif)
![$\displaystyle \frac{M_{t}^{d}(j)}{\mathcal{E}_{t}}=\left[ (A\gamma)\left( 1+\fr... ...ht] ^{\frac{1}{1+\gamma}}\left( c_{t}^{T}(j)+\frac {c_{t}^{N}(j)}{e_{t}}\right)$](img79.gif)
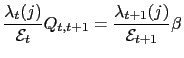
![$\displaystyle \beta\phi E_{t}\left\{ \left[ \frac{P_{t+1}^{N}(j)}{P_{t}^{N}(j)}... ...\pi}^{N}\right] \frac{P_{t+1}^{N}(j)}{\left[ P_{t}^{N}(j)\right] ^{2} }\right\}$](img81.gif)
![$\displaystyle =\phi\left[ \frac{P_{t}^{N}(j)}{P_{t-1}^{N}(j)}-1-\bar{\pi} ^{N}\right] \frac{1}{P_{t-1}^{N}(j)}+$](img82.gif)
![$\displaystyle \frac{\lambda_{t}(j)z_{t}^{N}\left[ h_{t}^{N}(j)\right] ^{\theta_... ...u c_{t}^{N}}{P_{t}^{N}}\left[ \frac{P_{t}^{N}(j)}{P_{t}^{N}}\right] ^{-(1+\mu)}$](img83.gif)
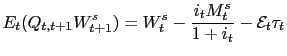
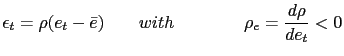
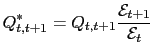
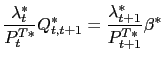
![$\displaystyle 1+i_{t}=\beta^{-1}\left[ E_{t}\left( \frac{1}{1+\epsilon_{t+1}}\right) \right] ^{-1}$](img117.gif)
![$\displaystyle E_{t}\left[ (\pi_{t+1}^{N}-\bar{\pi}^{N})(1+\pi_{t+1}^{N})\right]... ...eta\theta_{N}}\left( \frac{c_{t}^{N}}{z_{t}^{N}}\right) ^{\frac{1}{\theta_{N}}}$](img121.gif)
![$\displaystyle \frac{\alpha}{c_{t}^{T}}=\lambda\left[ 1+\Gamma\left( \frac{i_{t}}{1+i_{t} }\right) ^{\frac{\gamma}{1+\gamma}}\right]$](img122.gif)
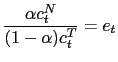
![$\displaystyle \frac{M_{t}^{d}}{\mathcal{E}_{t}}=\left[ (A\gamma)\left( 1+\frac{... ...) \right] ^{\frac{1}{1+\gamma}}\left( c_{t}^{T}+\frac{c_{t}^{N} }{e_{t}}\right)$](img124.gif)
![$\displaystyle \frac{1-\alpha}{c_{t}^{N}}=\frac{\lambda}{e_{t}}\left[ 1+\Gamma\left( \frac{i_{t}}{1+i_{t}}\right) ^{\frac{\gamma}{1+\gamma}}\right]$](img135.gif)
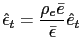
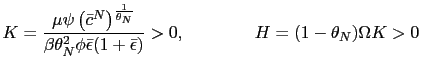
![$\displaystyle \hat{\pi}_{t}^{N}=\sum\limits_{k=0}^{\infty}\beta^{k}\left[ K\hat{e} _{t+k}-H\hat{\epsilon}_{t+1+k}\right]$](img162.gif)
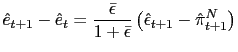
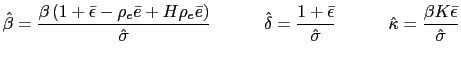
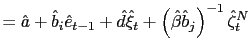
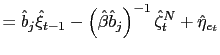
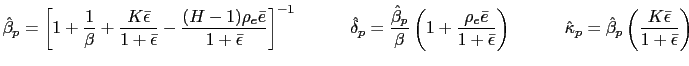
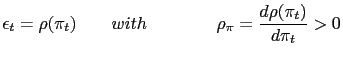
![$\displaystyle \hat{\beta}_{q}=\frac{1-\left[ \alpha+(1-\alpha)H\right] \rho_{\p... ...}\left( 1-\rho_{\pi}\right) }{\left( 1+\bar{\epsilon}\right) \hat{\sigma }_{q}}$](img322.gif)