
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 832, April 2005, revised September 2005 --- Screen Reader
Version*
A Flexible Finite-Horizon Identification of Technology Shocks*
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
Recent empirical studies using infinite horizon long-run restrictions question the validity of the technology-driven real business cycle hypothesis. These results have met with their own controversy, stemming from their sensitivity to changes in model specification and the general poor performance of long-run restrictions in Monte Carlo experiments. We propose an alternative identification that maximizes the contribution of technology shocks to the forecast-error variance of labor productivity at a long, but finite horizon. In small samples, our identification outperforms its infinite horizon counterpart by producing less biased impulse responses and technology shocks that are more highly correlated with the technology shocks from the underlying model. We apply our identification to post-war U.S. data and find that the negative hours response is not robust to allowing a slightly greater role for non-technology shocks in the variance of productivity at long horizons. We conclude that restrictions aimed at isolating the dynamics of productivity beyond business cycle frequencies do not provide information sufficient to robustly predict short-run movements in labor hours.
Keywords: Productivity, structural VAR, long-run restrictions
JEL classification: C32, C50, E32
1 Introduction
The notion that technological innovations are the pre-eminent force behind business cycle fluctuations has circulated in the macroeconomic literature for some time. This view has recently come under fire in empirical studies, notably Galí (1999), that identify technology shocks in VARs using long-run restrictions.1 Identification in these models is based on the assumption that technology shocks are the sole impetus behind the persistence in labor productivity. Specifically, identification requires that the unit root in labor productivity arise exclusively from technological innovation. Applied to the data, this assumption predicts a decline in labor hours following a positive innovation in technology, apparently contradicting the theoretical predictions of a broad class of real business cycle (RBC) models.2
This result has initiated some controversy, with a number of studies offering conflicting evidence based on alternative specifications of the non-productivity component of Galí's empirical model. Much of this debate has arisen around the assumption regarding the stationarity of hours and its relation to the short-run negative response to technology shock.3 This paper focuses instead on the identifying assumption regarding the estimated long-run productivity process. We propose an alternative identification which addresses some of the econometric shortcomings of existing long-run VAR models of technology. Our approach also allows us to perform an exhaustive robustness analysis of the hours prediction in a general class models. We find that although our identification has better small sample properties in Monte Carlo exercises, Galí's original finding that hours decline following a technology shock is nonetheless upheld in the data. However, we also find that modest allowance for the effect of non-technology shocks on long-run productivity can qualitatively alter this short-run hours response.
By their nature, long-run restricted structural vector autoregression (LR-SVAR) models are subject to the generic criticism that restrictions on infinite-order lag polynomials are ill suited to estimation in samples of realistic proportions [see, for example, Sims (1972), Faust (1996), Faust and Leeper (1997)]. The intuition is that finite samples generate imprecise measures of the VAR moving-average parameters at very long horizons, which when relied on for identification purposes, translate into imprecise and potentially spurious inference. Using Monte Carlo methods, Erceg, Guerrieri, and Gust (EGG, 2004) and Chari, Kehoe, and McGrattan (CKM, 2005) assess the extent of these small sample estimation problems. These papers simulate repeated small samples from variations of the standard RBC model and apply the long-run restriction from Galí (1999) to obtain hypothetical small-sample distributions of the LR-SVAR impulse responses. Both CKM and EGG conclude that LR-SVAR impulse responses can be substantially biased, either in sign or magnitude.
In addition to these econometric shortcomings, there may be a practical argument against the theoretical assumption that technology is the only process influencing the long-run behavior of labor productivity. Francis and Ramey (forthcoming) and Uhlig (2003) incorporate capital tax shocks, which may also contribute to the variance of long-run labor productivity. In this case, long-run exclusivity restrictions may be inappropriate to obtain a proper measure of the technology shock from the data.
We offer an alternative identification approach that aims at these and other shortcomings, while maintaining the association between technology and productivity at frequencies beyond typical business cycles. Specifically, we identify the technology shock as that which produces the maximum forecast-error variance (MFEV) share in labor productivity at a long, finite horizon. This approach has several potential advantages over the conventional long-run approach. First, by focusing on a finite horizon, we hope to gain estimation precision over the long-run restriction which relies on much longer horizon parameter estimates. Second, in place of the restriction that there is a unit root in productivity driven exclusively by technology, our approach imposes a weaker restriction that the long-run forecast-error variance in productivity at long horizons is dominated by the technology shock. Thus, we allow other shocks to influence labor productivity at all horizons. Lastly, inference based on our MFEV specification is robust to near-unit root behavior in productivity. A known shortcoming of LR-SVAR approach to technology shocks is that it does not appropriately account for uncertainty regarding near-unit root alternatives.4 In small samples, it is difficult to rule out the possibility that the observed persistence in productivity is not due to a sequence of shocks to a highly persistent, but stationary technology process.
In the next section, we present the MFEV identification approach analytically and discuss its similarities and differences with the LR-SVAR approach in more detail. We then compare the small sample performances of the MFEV and LR-SVAR approaches using Monte Carlo methods and a standard RBC model. We also compute the correlations of the estimated technology shocks with the realized shocks from the RBC model. Although the performance of the two identification approaches depends on the parameterization of the theoretical model, we find that the MFEV often performs significantly better and never performs worse than the LR-SVAR.
In the remainder of the paper, we apply the MFEV approach to postwar U.S. data and examine the robustness of the LR-SVAR findings to our relaxation of the original identifying assumption. Estimating the MFEV model directly predicts a negative short-run response in hours to a technology shock, supporting Gali's original finding, albeit with greater statistical precision than in that and similar models.
An important additional finding, however, is that the negative hours response is not robust to a general class of models that allow a greater role for non-technology shocks. To test for this possibility, we incorporate into the estimation an additional restriction that hours respond positively to a technology shock, and examine whether this causes a significant shift in the associated MFEV value. We find that the additional restriction on hours lowers the MFEV value at ten years from between 6 to 25 percent. However, our robustness analysis shows that, interpreted broadly, the generic long-run identification approach does not provide sufficient information structure to predict short-run movements in hours. In all of MFEV cases, as in the LR-SVAR models, the identifying restriction is aimed at isolating the variance in productivity that occurs beyond business cycle frequencies, yet very different predictions for hours are attainable within this group.
2 Identification
In this section, we review the method of using long-run restrictions for
identifying technology shocks and introduce an alternative identifying
restriction on the share of productivity's long-horizon forecast-error
variance due to technology. The identifying assumption in technology LR-SVARs
comes from a class of RBC models in which log labor productivity xt can
be decomposed into two orthogonal components, technology, zt , and
non-technology,
![]() , in the following manner:
, in the following manner:
| (1) |
Since all processes but technology are assumed stationary, the unit root in productivity must arise from zt.5 This condition provides the foundation for both the standard long-run identification and our finite-horizon identification.
2.1 Infinite-Order Long-Run Identification
We assume that the data generating process can approximated by the following linear model:
| (2) |
where yt is an n × 1 vector of macroeconomic time series,
![]()
![]() is a matrix polynomial in the lag operator,
L, εt is a structural innovation, and
is a matrix polynomial in the lag operator,
L, εt is a structural innovation, and
![]() . To estimate this model using data, we begin
with the reduced-form VAR:
. To estimate this model using data, we begin
with the reduced-form VAR:
| (3) |
where ![]()
![]()
![]() ,
, ![]() , and
, and
![]() . The goal is to find a rotation of the moving-average
representation of this VAR,
. The goal is to find a rotation of the moving-average
representation of this VAR,
(C(L) = B(L)-1) which identifies the i.i.d. structural shocks of model:
where A0 is the contemporaneous parameter matrix. Identification is
accomplished by imposing a sufficient number of restrictions on the system;
![]() restrictions are required to fully identify the structural
form (fewer less restrictions are necessary to identify a single shock).
Short-run restrictions often take the form of recursive or non-recursive
zero restrictions on A0. Long-run restrictions place constraints on the
effect of the jth shock on the ith variable at an infinite horizon, given
by
restrictions are required to fully identify the structural
form (fewer less restrictions are necessary to identify a single shock).
Short-run restrictions often take the form of recursive or non-recursive
zero restrictions on A0. Long-run restrictions place constraints on the
effect of the jth shock on the ith variable at an infinite horizon, given
by
![]() , where neutrality implies the
restriction
, where neutrality implies the
restriction
![]() .
.
The key identifying assumption in Galí (1999) is that the technology shocks are the only influence on long-run labor productivity. With productivity entering in differences and ordered first in the VAR, this assumption is implemented by restricting the long-run responses to all non-technology shocks to be zero.
Assumption A.1 The unit root in productivity is solely attributable to the technology shock z. That is,
| (4) |
where i = 1 represents labor productivity ordered first and j ≠ i indicates all non-technology shocks.
One can simply express the effect of the structural shocks on y at any horizon in terms of the h-step ahead forecast error for y:
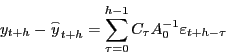 |
(5) |
The h-step ahead forecast-error variance share for a particular variable i, attributable to a particular shock j is
![\begin{displaymath} \omega _{ij} (h)=\frac{{e}'_i \left[ {\sum\limits_{\tau =0}^{h-1} {C_\tau A_0^{-1} e_j {e}'_j A_0^{-1} ^\prime {C}'_\tau } } \right]e_i }{{e}'_i \left[ {\sum\limits_{\tau =0}^{h-1} {C_\tau \Omega _\mu {C}'_\tau } } \right]e_i } \end{displaymath}](img6eq.gif) |
(6) |
where ei and ej are, respectively, column vectors with the ith and jth elements equal to one and zero everywhere else. With this in mind, one can see that equation (4) implies the following:
If productivity is ordered first, the assumption that the long-run response of labor productivity to all non-technology shocks are negligible drives, for i > 1, the numerator in equation (6) to zero for large τ. In the following section, we propose an alternative identification scheme based on equation 6 with a large, but finite, h.
2.2 Finite-Order Long-Run Identification
As in Galí (1999), we aim at isolating technology shocks by their effect on productivity at horizons longer than business cycles. However, we differ from conventional long-run identification by relaxing the requirement that labor productivity has a unit root or that its unit root be fully characterized by the technology process. Instead, we identify the technology shock as belonging to the set of rotations that obtains the maximum forecast-error variance share in productivity at long horizons. We impose our long-horizon restriction via methods first introduced in Faust (1998). Appendix 1 contains a more detailed exposition of the solution algorithm.
We choose a large, finite h such that the technology shock yields the maximum h-step ahead forecast error variance share for productivity6:
![\begin{displaymath} \mathop {\max }\limits_\alpha \frac{{e}'_i \left[ {\sum\limits_{\tau =0}^{h-1} {\tilde {C}_\tau \alpha {\alpha }'\tilde {{C}'}_\tau } } \right]e_i }{{e}'_i \left[ {\sum\limits_{\tau =0}^{h-1} {C_\tau \Omega _\mu {C}'_\tau } } \right]e_i } \end{displaymath}](imgeq7.gif) |
(7) |
where α is an n × 1 vector, and ![]() is obtained by post multiplying Cτ by any orthogonal decomposition of Ωμ.7
is obtained by post multiplying Cτ by any orthogonal decomposition of Ωμ.7
Allowing for parameter uncertainty emphasizes several important differences between the two approaches. First, as demonstrated in EGG and CKM, LR-SVARs have been shown to perform poorly in simulated data from standard RBC models when the sample size is set similar to that of postwar U.S. data. Second, there may be cause for relaxing the assumption that there is a unit root in productivity. In particular, differencing productivity in the VAR on the basis of unit root pretests may result in misspecification error because of the low power of these tests [Sims (1989)]. Finally, Uhlig (2003), Fisher (2003), and others argue that factors other than technology (e.g., capital tax shocks) can affect the long-run variance of productivity . By maximizing the forecast error variance in productivity due to technology at a finite horizon, our approach implicitly accounts for these considerations, while not precluding a unit root in productivity.
While the MFEV approach has some advantages in small samples, the fact that the identification is data dependent may introduce an additional source of error. In small samples, regardless of whether or not the unit root assumption holds in the population, it is possible to attribute too much of the forecast-error variance in productivity to technology due to errors in estimating CτA0-1. Given this trade-off, whether the MFEV identification yields a net advantage in small samples must be determined. In the next section, we measure the net effect of employing the MFEV identification by comparing the small-sample performance of the LR-SVAR and MFEV identifications against a known data-generating process.
3 Monte Carlo Experiments
Following recent studies (EGG, CKM), we employ Monte Carlo methods to gauge the ability of the MFEV and LR-SVAR approaches to appropriately identify technology shocks in small samples.8 We calibrate the neoclassical growth model presented in Francis and Ramey (forthcoming) in which (4) holds to obtain both theoretical impulse responses to a technology shock and repeated small samples of simulated data.9 From these data, we compute small-sample distributions of estimated impulse responses obtained under the MFEV and LR-SVAR identification approaches. We compare the methods in terms of their ability to match (mimic) the theoretical impulse responses and ability to uncover the realized technology shocks.
We next compare the approaches under alternative calibrations of the theoretical model. First we check the performance of both identifications when relaxing the assumption of a unit root in technology. This latter specification may be especially important in the face of the low power of standard unit root tests in finite samples. It could be, for example, that the observed persistence in productivity is due to repeated shocks to a highly persistent, but stationary technology process. Second, we compared both methods under different assumptions on the importance of non-technology shocks. Persistent non-technology components in productivity - e.g., persistent capital taxes - may contaminate the identified technology process if not properly isolated. Our analyses compare the ability of the LR-SVAR and MFEV to isolate technology from any such persistent non-technology component(s). Lastly, we examine the role that our finite horizon assumption plays in obtaining better small sample performance versus the infinite horizon assumption of the LR-SVAR approach. Our model follows.10
3.1 Our Baseline Theoretical Model
For our baseline model, households choose consumption, Ct , labor, Nt , and investment, It , to maximize the expected present-discounted value of utility:
![$\ U(C_{t},N_{t})=\sum_{t=1}^{\infty}\beta^{t-1}\left[ \ln(C_{t})+\Phi_{t}<tex2html_comment_mark>37 \ln(1-N_{t})\right] ,$](img58.gif)
subject to a standard budget constraint:
![]()
The equation characterizing the evolution of capital, Kt,
![]()
and an economy-wide resource constraint:
![]()
and a government spending constraint:
![]()
where rt is the pre-tax return on capital, Wt is the real
wage rate, δt is the depreciation rate, β is the discount
factor, Ψt is a lump-sum tax, τit is the tax on labor, and
ςkt is the tax on capital income. Consumers own the capital and
rent it to firms. The government balances its budget each period and
finances its spending through a combination of lump-sum taxes and
distortionary labor and capital income taxes. Tax growth rates on labor
income and capital are stochastically determined by
![]() ,
, ![]() (where
(where
![]() and
and
![]() are the steady-state values). The preference growth process,
φt , and the growth rate for government purchases, gt , have
similar first-order autoregressive processes. Finally, output is determined
by a Cobb-Douglas production technology:
are the steady-state values). The preference growth process,
φt , and the growth rate for government purchases, gt , have
similar first-order autoregressive processes. Finally, output is determined
by a Cobb-Douglas production technology:
![]()
where ![]() is an exogenous process for labor-augmenting technological
innovation,
is an exogenous process for labor-augmenting technological
innovation, ![]()
![]() is the
log of technology, and
is the
log of technology, and
![]() .
.
We can then generate impulse responses and simulated data for a variety of parameterizations.11, 12 Table 1 presents the sets of parameter values used to simulate the model. We experiment with several values of the shocks' persistence in order to determine whether the LR-SVAR and/or the MFEV approaches come close to the theoretical responses under different parameterizations.13
The steady state value for the ratio of government to output deserves special mention. We follow Uhilg (2003) and treat the difference between private output and the sum of private consumption and investment as exogenous government consumption (see Figure 8 and the accompanying text of Uhlig (2003b)). This simplifying assumption means that we do not explicitly model an international sector or government investment, although these sectors may in fact be relevant in the actual transmission of technology.
3.2 Results
Similar to CKM and EGG, we estimate a four-variable VAR of productivity, hours, the consumption-output ratio, and the investment-output ratio. The VAR reduced-form parameters are estimated via maximum likelihood in the following Monte Carlo exercises and in the data section below. Productivity enters the VAR in first differences for the LR-SVAR but enters in levels for the MFEV approach.14 The benchmark case has the AR(1) coefficient of technology, ρz, set to one with all other stochastic processes having AR(1) coefficients of 0.6. Subsequent specifications test near unit root technology processes and more persistent non-technology shocks. All other parameter values are held constant across specifications. In this exercise, we exogenously assume a maximization horizon for the MFEV approach of 10 years (i.e., the technology shock is chosen to be that which maximizes the forecast-error variance share at a horizon of 10 years); we later examine alternative horizons.
3.2.1 Impulse Responses
Figures 1 to 4 present the impulse responses to a one-percent shock to technology for various model parameterizations. The thick solid line depict the theoretical impulse responses, while the dotted lines show the median responses and 68 percent error bands from from the LR-SVAR. The MFEV median responses are shown by the thick dashed lines and the shaded areas are 68 percent probability intervals from the MFEV model. The model generated responses reveal that, in response to a positive technology shock, labor productivity rises and converges to a higher steady state, hours rise on impact and gradually return to zero, the consumption-output ratio falls on impact and also slowly returns to zero, and investment-output ratio rises before eventually returning to its original steady state.
Figure 1 depicts our benchmark case, in which technology has a unit root and the non-technology shocks have first-order coefficients of 0.6. At first glance, the qualitative results for the two approaches are encouraging although they display some obvious biases. The LR-SVAR responses corroborate EGG's findings that the LR-SVAR biases the median responses but preserves their qualitative nature. The MFEV responses, while still biased, perform considerably better. Although the theoretical impulse response for productivity is near the upper tail of the 68% probability interval for both methods, the median productivity response of the MFEV demonstrates less bias and the error bands associated with the MFEV are much narrower. The MFEV bias for the response of the other variables is also generally smaller for the first 4 quarters and the MFEV intervals are somewhat narrower.
Figure 2 shows the response in the case in which technology has a unit root and all other stochastic processes have AR(1) coefficients of 0.98. The relative performance of the two approaches is similar to Figure 1 with respect to the productivity response. However, for the non-productivity variables, the LR-SVAR error bands contain zero as an impact response while the error bands for the MFEV are bounded away from zero in the same direction as the data generating process. This suggests that, in small samples, the MFEV is better able to isolate all of the variable responses regardless of the persistence of the other shocks.
Now consider the case in which the technology shock is persistent yet stationary. Figures 3 and 4 depict the cases when the AR(1) coefficient on technology is 0.98 and non-technology shocks have first-order coefficients of 0.6 and 0.98, respectively. Biases caused by the LR-SVAR may now be due to both small sample error and misspecification resulting from differencing (stationary) productivity, and in the case of Figure 4, the presence of other persistent shocks. Obvious from these graphs is that, regardless of the persistence of the non-technology components, the MFEV approach outperforms the long-run restriction approach when identifying a persistent yet stationary technology shock. When the non-technology components are less persistent (Figure 3), the median responses for all variables predicted by the MFEV lie closer to the theoretical responses in the first year. Indeed, the LR-SVAR error bands do not contain the theoretical impulse responses for the first few periods, whereas the MFEV do. When the non-technology components are even more persistent (Figure 4), the 68 percent probability intervals for the MFEV are significantly narrower than for the LR-SVAR. In both of these cases, as in Figure 2 above, the LR-SVAR error bands for the non-productivity variables contain zero while the MFEV bands do not. This suggests that the LR-SVAR has more difficulty differentiating the technology from the non-technology shocks.
3.2.2 Correlation of Shocks
To further differentiate the two empirical approaches, we present the correlations between the technology shocks from the data generating process and their estimates from the LR-SVAR and the MFEV identifications. Table 2 presents the median and the 16th and 84th quantiles of the correlations taken from the simulations.
As expected, the LR-SVAR identification performs best when technology is a unit root. Under the specifications with ρz = 1, the correlations between the technology shocks from the model and the LR-SVAR approach are 0.79 and 0.64, respectively, versus values of about 0.60 when technology is a near unit root (ρz = 0.98). However in every case, the technology shocks identified by the MFEV approach are much more highly correlated with the realized shocks from the model. When the model parameterization accords most closely with the key LR-SVAR assumptions -technology follows a unit root and the non-technology shocks are not important at long horizons - the LR-SVAR performs at its best, but the MFEV still performs better. When the technology shock coefficient is 0.98 is no longer a unit root, the LR-SVAR correlations decline significantly (to about 0.6) whereas the MFEV correlations increase slightly. Indeed, when the technology shock is a near unit root and other shocks are persistent, the distribution for the MFEV is far to the right of and has little overlap with the LR-SVAR distribution.
3.3 Quantifying the Role of the Finite-Horizon Assumption
The above results are based on an exogenously chosen MFEV horizon, h, of ten years. Figure 5 presents results summarizing the bias properties of the MFEV approach when h varies between 5 to 80 quarters (1.25 to 16 years) in the case where ρz = 1 and ρ = 0.6. For each h, we generate 5000 draws of simulated data and obtain the median variable impulse responses predicted by MFEV(h) and LR-SVAR. The solid line in Figure 5 shows the bias in the median impulse responses for MFEV(h), measured as the average absolute deviation of the median response from the model response over the first 4 quarters, expressed in percent of the model response. The dashed line shows a similar measure for LR-SVAR, which assumes a long run of 80 quarters throughout.
For all variables and all horizons, the bias shown by the MFEV line is smaller than that of the LR-SVAR. The productivity bias of MFEV is relatively stable for horizons greater than 30 quarters. As expected, this bias increases with h but at a surprisingly slow rate; the productivity bias associated with MFEV(80) is well below that associated with LR-SVAR. Thus, the finite estimation horizon in MFEV is only one of several factors contributing to the smaller bias in our MFEV(h) simulations.
4 Max FEV Share Identification in the Data
Having evaluated the performance of our identification scheme through Monte Carlo experiments, we turn to the data. We estimate a four-variable, four-lag VAR with and without the Sims-Zha (1998) prior.15 The data are quarterly series from 1959:1 to 2002:4 for private business productivity, private business hours, real consumption as a share of output, and real investment as a share of output. All variables enter as log levels. Raw data are taken from the BEA and BLS. The error bands are computed using methods described in Sims and Zha (1999).
The shaded areas in Figure 6 show 68 percent probability intervals for the impulse responses in the case of no prior and the shaded areas in Figure 7 shows similar results estimated with the Sims-Zha prior. Except for hours, the responses are in the same direction as those from the theoretically generated responses in the previous section. In response to a positive technology shock, the consumption share of output decreases and the investment share increases; however, labor hours fall for the first few quarters and then eventually rise above zero.
As some variation exists in the data, we estimate versions of this model including nonstandard constructions for consumption and investment as well as hours and productivity measures that are adjusted for demographically-persistent components (see Francis and Ramey 2004b).16 The variable responses to a technology shock were qualitatively similar across these models. In the results that follow, the benchmark model shown in Figures 6 and 7 is labeled model A and models C-D incorporate various combinations of the different series.
Table 3 shows the share of output and hours forecast-error variance attributable to technology shocks under the two identification approaches. The share of output variance is large at most horizons under both identifications; however, technology shocks typically explain only a minority share of the variance in hours. These results are consistent with results found in CEV (2004) and suggest that technology shocks are not an important driver of the positive correlation in output and hours at a business cycle frequency.
While the finding that hours respond negatively to a positive technology shock corroborates Galí's original finding, one might reasonably wonder about the robustness of this conclusion. It is not hard to imagine other plausible modifications to the identifying assumption that yield a different qualitative prediction for hours. We can imagine, for example, that a small shift in the specification of long-run productivity might yield a positive hours response by allowing for more accommodative monetary policy or greater influence of non-technology factors. Taking all such possibilities into account, a more complete robustness test asks does there exists a reasonable specification of technology shocks that yields a positive response in hours?
A salient advantage of the MFEV approach is that it provides a means to address this larger question. Specifically, we reestimate the MFEV model conditional on an additional restriction that hours respond positively on impact to a positive technology shock and then examine whether this has a discernible effect on the forecast-error variance share attributable to technology.17
The thick solid lines in Figures 6 and 7 show the point estimates of the impulse responses to a positive technology shock when the models are estimated with an additional restriction that hours respond positively on impact. Examination of the productivity responses shows that they are indeed similar to the unrestricted cases. However, the responses of the other variables have changed considerably. The addition of the short-run restriction shifts the point estimate of the impulse response of hours upward. Estimated without a prior (Figure 6), the restricted hours response is now just outside the upper band of the 68 interval from the less restricted model during the first four quarters. Estimated with the Sims-Zha prior, the additional short-run restriction pushes the point estimate for the impulse response of hours well above the 68% interval. The responses of the consumption and investment shares are also magnified when hours are restricted to be positive.
Tables 4 and 5 show the MFEV share values obtained for models A-D estimated with and without a prior as well as the corresponding 68% error bands. The fourth and fifth columns in these tables present MFEVs from the same models estimated with an additional restriction that hours responds positively on impact. In every case, the maximum attainable forecast-error variance share in labor productivity declines when we require that hours respond positively to the technology shock. Moreover, there is little overlap in the probability intervals for the MFEV in the two cases. This shows that a positive hours response is attainable, but only if we are willing to relax the importance of technology shocks at the ten-year horizon, implying a larger role for non-technology shocks.18 This suggests that the negative hours finding in LR-SVAR model depends importantly on the assumption that technology shocks have exclusive influence on productivity at long horizons.19
At the same time, the difference in the MFEV shares are not large. The additional restriction lowers MFEV share by as little as 6 percent and by no more than 25 percent and technology remains by far the dominant influence in all of the cases. Thus, in our view, it makes sense to think of these cases as part of a general class of models that require a dominant (possibly exclusive) role for technology in labor productivity at either a very long but finite or infinite horizon. Seen from this perspective our results indicate that long-run restrictions as a class appear to contain only limited information about short-run movements in hours. While similar in an economic sense in their specification of technology, individually, these models have potentially very different implications for the effect of technology shocks on labor hours.20
4.1 MFEV versus LR-SVAR
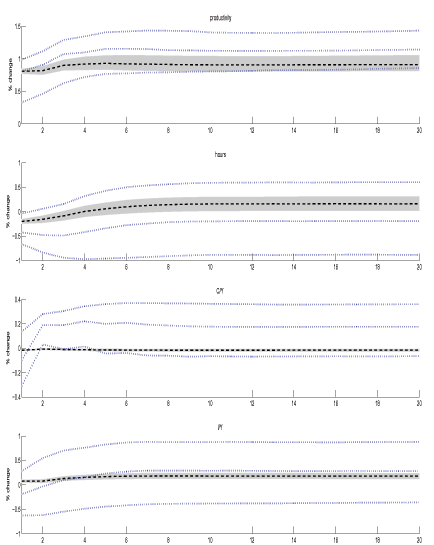
Figures 8 (no prior) and Figure 9 (Sims-Zha prior) show the empirical responses to a technology shock identified by the LR-SVAR (thin-dotted lines) and MFEV (thick-dashed and shaded areas) approaches in model A with their associated 68% error bands. The two approaches clearly obtain important differences. Most obviously, the error bands associated with the MFEV are everywhere much narrower. Further, the short-run responses in the non-productivity variables are much smaller in the MFEV estimates for the same sized technology shock. These differences were also present in comparisons based on models B-D.
Comparison of the sign prediction for hours Figures 8 and 9 is also interesting. The LR-SVAR estimates in Figure 8 mirror the finding in CEV (2004) that hours respond positively to a technology shock when the series enters the VAR in levels.21 However, when we estimate the LR-SVAR model with the Sims-Zha prior (Figure 9), the sign on the hours response turns negative, even when hours are in levels. This suggests that the low frequency movements in hours and/or its low frequency co-movement with consumption and investment are relevant in determining the sign on the hours response in LR-SVAR estimates (since the non-stationarity and co-integration assumptions in the Sims Zha prior matter). When we perform the same exercise on the demographically-detrended hours series in model B, we find that hours respond negatively when estimated with or without a prior. In contrast, hours respond negatively under the MFEV approach whether or not the estimation includes a prior and whether or not the data is demographically adjusted.22
5 Conclusion
We propose an alternative method for identifying technology shocks that is robust to relaxing key assumptions about the data-generating process. While maintaining the spirit of long-run restrictions on labor productivity, our proposed method identifies the technology shock as that which yields the maximum forecast-error variance share in productivity at some predetermined, yet finite, horizon.
Applied to artificial small samples generated from an off-the-shelf neoclassical growth model, our identification technique more closely replicates the model generated impulse responses. In addition, the identified impulse responses provide more precise coverage than the standard long-run restrictions first proposed by Galí (1999). We also find that the technology shocks implied by our MFEV methodology are more highly correlated with the shocks underlying the data processes than the shocks identified by the long-run approach. These results evince a clear improvement over LR-SVAR estimates in small samples. This improvement is even greater in the presence of highly persistent but stationary technology shocks or potentially confounding persistent non-technology shocks.
When taken to actual data, the MFEV model predicts a negative short-run response in hours, confirming the original LR-SVAR hypothesis. However our robustness analysis finds that a positive hours response is attainable if we allow for an increased (albeit modest) role for non-technology shocks. Although we are unable to measure which model has higher probability, our results suggest that the rejection of the RBC framework on the basis of the qualitative response in hours depends critically on whether one is willing to assume that technology has exclusive influence on long run productivity.
Viewing our model and the infinite horizon models as a class, however, our results can also be interpreted negatively as a demonstration of the limitations of long- run restrictions in predicting short-run movements in hours. It takes only a very modest, and likely empirically reasonable, adjustment in the long-run assumption regarding the importance of non-technology factors to obtain a very different prediction for the sign on hours. With this lesson in mind, we nonetheless believe that long-run restrictions add relevant information structure to the data. Indeed, our work suggests that augmenting long-run restriction models with additional structural information is a promising direction for future research.
Table 1: Parameter Values Used in Model Simulation
| Parameter | Description | Value |
|---|---|---|
| capital share | 0.36 | |
| quarterly depreciation rate | 0.02 | |
| discount factor | 1/1.03 | |
| autocorrelation of technology shock | 0.98 & 1 | |
| autocorrelation of capital tax shock | 0.6 & 0.98 | |
| autocorrelation of labor tax shock | 0.6 & 0.98 | |
| autocorrelation of government spending shock | 0.6 & 0.98 | |
|
|
autocorrelation of preference shock | 0.6 & 0.98 |
|
|
steady state ratio of government to output | 0.03 |
|
|
steady state labor | 1/3 |
|
|
steady state capital tax rate | 0.38 |
|
|
steady state labor tax rate | 0.22 |
Notes: The parameters are for a standard RBC model augmented with preference shocks, capital and labor income taxes. The setup abstracts from international markets (imports and exports) and variable capital utilization.
Table 2: Correlation Between Estimated and Model Technology Shocks
Parameterization: ρz | Parameterization: ρnon-z | Model | 16th percentile | Median | 84th percentile |
|---|---|---|---|---|---|
1 |
0.6 |
LR-SVAR |
0.29057 |
0.79503 |
0.91648 |
1 |
0.6 |
MFEV |
0.84106 |
0.90234 |
0.93721 |
1 |
0.98 |
LR-SVAR |
0.32088 |
0.63779 |
0.84105 |
1 |
0.98 |
MFEV |
0.67098 |
0.83063 |
0.91003 |
0.98 |
0.98 |
LR-SVAR |
0.30701 |
0.60688 |
0.82965 |
0.98 |
0.98 |
MFEV |
0.68372 |
0.84119 |
0.91851 |
0.98 |
0.6 |
LR-SVAR |
0.22422 |
0.59424 |
0.86757 |
0.98 |
0.6 |
MFEV |
0.84669 |
0.90581 |
0.94094 |
Notes: We generate artificial data from the RBC model using the AR(1) values for technology and non-technology shocks in column 1. For each parameterization we employ our empirical identification techniques (LR-SVAR and MFEV) and back out implied technology shocks for each of 5000 draws of the simulated data. The correlations are then calculated for each of the 5000 draws from which we obtain the median, 16th and 84th percentiles.
Table 3: Contribution of Technology to Forecast Error Variance
| Model | Horizon | Output: MFEV | Output: LR-SVAR | Hours: MFEV | Hours: LR-SVAR |
|---|---|---|---|---|---|
| A | 1 year | 0.90 | 0.73 | 0.03 | 0.34 |
| A | 5 years | 0.95 | 0.86 | 0.21 | 0.51 |
| A | 10 years | 0.96 | 0.93 | 0.29 | 0.51 |
| A | 20 years | 0.95 | 0.52 | 0.42 | 0.52 |
| B* | 1 year | 0.89 | 0.96 | 0.02 | 0.02 |
| B* | 5 years | 0.93 | 0.98 | 0.10 | 0.08 |
| B* | 10 years | 0.94 | 0.99 | 0.10 | 0.08 |
| B* | 20 years | 0.86 | 0.99 | 0.11 | 0.08 |
| CT | 1 year | 0.72 | 0.28 | 0.04 | 0.33 |
| CT | 5 years | 0.80 | 0.62 | 0.29 | 0.26 |
| CT | 10 years | 0.85 | 0.90 | 0.32 | 0.41 |
| CT | 20 years | 0.81 | 0.97 | 0.38 | 0.66 |
| D*T | 1 year | 0.59 | 0.09 | 0.09 | 0.03 |
| D*T | 5 years | 0.73 | 0.59 | 0.73 | 0.14 |
| D*T | 10 years | 0.93 | 0.93 | 0.80 | 0.02 |
| D*T | 20 years | 0.89 | 0.98 | 0.16 | 0.10 |
Notes: Table 3 shows the shares of the forecast error variance of output and hours due to technology shocks at several horizons using LR-SVAR and MFEV. The numbers for MFEV are calculated with maximization at an horizon of 10 years. * Demographically adjusted productivity and hours. T Durable consumption excluded from consumption and included in investment; government consumption included in consumption.
Table 4. MFEV10 Share of Productivity without Sims-Zha Prior
| Model | Pt. Est. - Hours Unrestricted | 68% interval - Hours Unrestricted | Pt. Est. - Hours0 > 0 | 68% interval Hours0 > 0 |
|---|---|---|---|---|
| A | .9512 | (.9506, .9929) | .8757 | (.8452, .9674) |
| B* | .9343 | (.9448, .9825) | .8572 | (.8194, .9628) |
| CT | .8243 | (.8876, .9669) | .7751 | (.8067, .9359) |
| D*T | .9484 | (.9635, .9922) | .7373 | (.7963, .9482) |
Notes: Table 4 shows the forecast error variance attributed to technology shocks in the MFEV models, estimated with an uniformative prior. Left panel has results for hours unrestricted, while right panel has results for hours restricted to be non-negative on impact. MFEV10 is the maximum forecast error variance at 10 year horizon. * Demographically adjusted productivity and hours. T Durable consumption excluded from consumption and included in investment; government consumption included in consumption.
Table 5. MFEV10 Share of Productivity with Sims-Zha prior
| Model | Pt. Est. - Hours Unrestricted | 68% interval - Hours Unrestricted | Pt. Est. - Hours0 > 0 | 68% interval Hours0 > 0 |
|---|---|---|---|---|
| A | .9957 | (.9969, .9997) | .9086 | (.8933, .9875) |
| B* | .9958 | (.9948, .9994) | .9318 | (.8980, .9916) |
| CT | .9944 | (.9972, .9996) | .9262 | (.9069, .9931) |
| D*T | .9962 | (.9947, .9993) | .9508 | (.9099, .9941) |
Notes: Table 5 shows the forecast error variance attributed to technology shocks in the MFEV models, estimated with the Sims-Zha prior. Left panel has results for hours unrestricted, while right panel has results for hours restricted to be non-negative on impact. MFEV10 is the maximum forecast error variance at 10 year horizon. * Demographically adjusted productivity and hours; T Durable consumption excluded from consumption and included in investment; government consumption included in consumption.
Figure 1: Impulse Responses to a Technology Shock
Theoretical responses (with AR(1) technology coefficient ρz = 1.0 and non-technology AR(1) coefficients ρ = 0.6) are shown by thick solid lines. Median and 68% probability intervals for MFEV from Monte Carlo experiments are shown with dashed lines and shaded areas. LR-SVAR median responses and 68% probability intervals are shown by dotted lines. Monte Carlo estimates based on 5000 draws of samples with 174 observations.
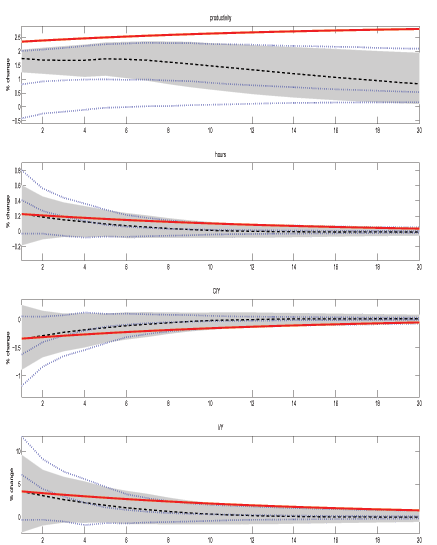
Figure 2: Impulse Responses to a Technology Shock
Theoretical responses (with AR(1) technology coefficient ρz = 1.0 and non-technology AR(1) coefficients ρ = 0.98) are shown by thick solid lines. Median and 68% probability intervals for MFEV from Monte Carlo experiments are shown with dashed lines and shaded areas. LR-SVAR median responses and 68% probability intervals are shown by dotted lines. Monte Carlo estimates based on 5000 draws of samples with 174 observations.
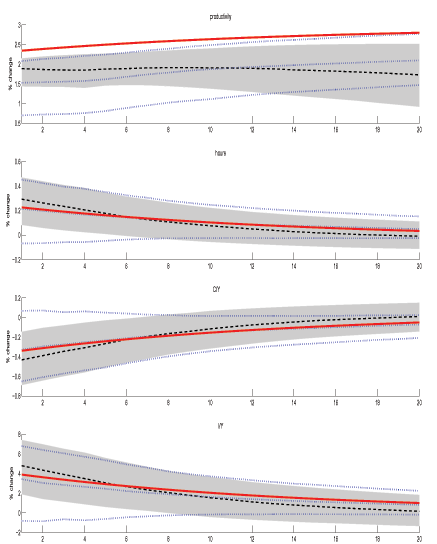
Figure 3: Impulse Responses to a Technology Shock
Theoretical responses (with AR(1) technology coefficient ρz = 0.98 and non-technology AR(1) coefficients ρ = 0.6) are shown by thick solid lines. Median and 68% probability intervals for MFEV from Monte Carlo experiments are shown with dashed lines and shaded areas. LR-SVAR median responses and 68% probability intervals are shown by dotted lines. Monte Carlo estimates based on 5000 draws of samples with 174 observations.
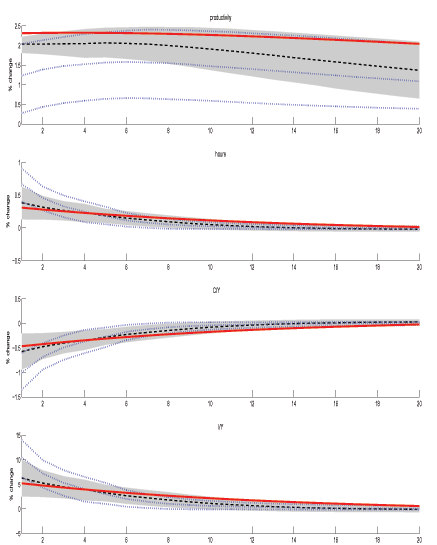
Figure 4: Impulse Responses to a Technology Shock
Theoretical responses (with AR(1) technology coefficient ρz = 0.98 and non-technology AR(1) coefficients ρ = 0.98) are shown by thick solid lines. Median and 68% probability intervals for MFEV from Monte Carlo experiments are shown with dashed lines and shaded areas. LR-SVAR median responses and 68% probability intervals are shown by dotted lines. Monte Carlo estimates based on 5000 draws of samples with 174 observations.
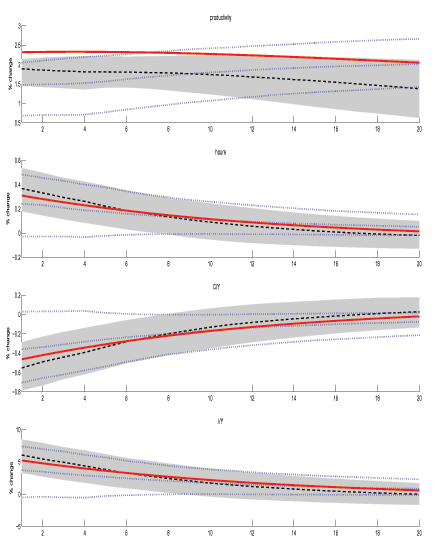
Figure 5: Comparison of Average Absolute Bias in MFEV (dotted) vs. LR-SVAR (solid), as function of MFEV Maximization Horizon
Bias is measured as the absolute difference between the median MFEV (or LR-SVAR) and theoretical responses, averaged over the first four quarters. The theoretical model in each case is specified with technology AR(1) coefficient ρz = 1.0 and non-technology AR(1) coefficients ρ = 0.6). The median MFEV and LR-SVAR responses are based on 5000 draws of simulated data samples (n=174).
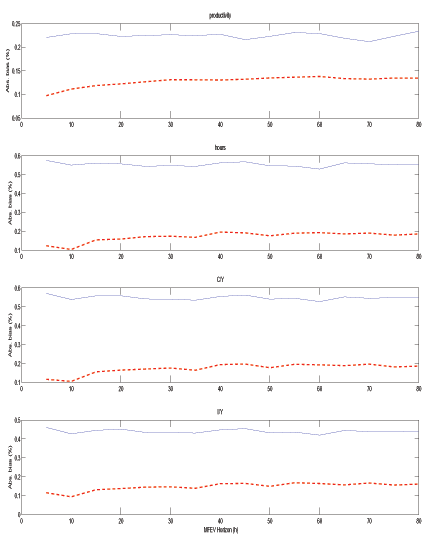
Figure 6: Impulse Responses to a Technology Shock in MFEV estimated without prior using U.S. Quarterly Data 1959:1 - 2002:4
MFEV estimated without prior (shaded area is 68 percent probability interval) vs. predicted responses when hours restricted to be positive on impact (thick solid line).
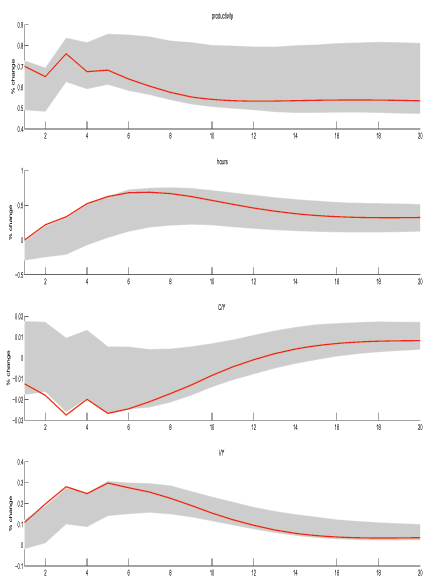
Figure 7: Impulse Responses to a Technology Shock in MFEV estimated with Sims-Zha prior using U.S. Quarterly Data 1959:1 - 2002:4
MFEV estimated without prior (shaded area is 68 percent probability interval) vs. predicted responses when hours restricted to be positive on impact (thick solid line).
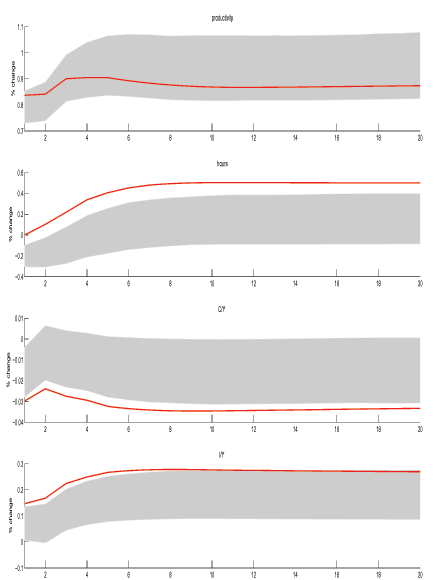
Figure 8: Impulse Responses to a Technology Shock
Using US quarterly data for Model A, estimated in MFEV (thick dashed lines and shaded areas) vs. LR-SVAR (thin dotted lines). Error bands are 68% intervals from posterior probability distributions estimated with flat prior.
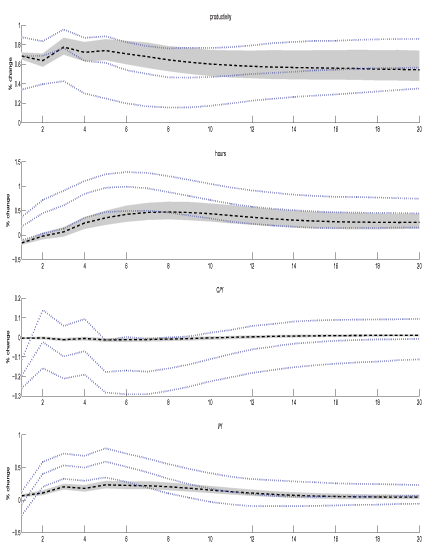
Figure 9: Impulse Responses to a Technology Shock
Using US quarterly data for Model A, estimated with Sims-Zha prior in MFEV (thick dashed lines and shaded areas) vs. LR-SVAR (thin dotted lines). Error bands are 68% intervals from posterior probability distributions.
Appendix 1: The Max Forecast-Error Variance Identification Algorithm
This appendix formalizes the optimization problem in our MFEV identification, the solution algorithm is the same as that described in the appendix of Faust (1998). We begin by forming a generic orthogonalized moving-average representation of the estimated reduced form VAR:
yt = C (L) HH-1 μt |
(8) |
where Et(H -1μt )(H -1μt )′ = I. Next, consider the space of identifications, which can be expressed as linear rotations of (8), each formed according to an orthonormal matrix D:
yt = |
(9) |
where now
![]() and
and
![]() . We then denote dynamic response of yt to the jth shock as
. We then denote dynamic response of yt to the jth shock as
![]() , where α is the jth column of D. The jth shock is then
, where α is the jth column of D. The jth shock is then ![]() .
.
Following Faust (1998), we identify
α* as the vector associated with the maximum forecast-error variance share for productivity due to the shock
![]() :
:
![\begin{displaymath} \alpha ^\ast =\arg \max \left[ {\frac{{e}'_i \left[ {\sum\limits_{t=0}^{h-1} {\left( {\tilde {C}_\tau \alpha {\alpha }'\tilde {{C}'}_\tau } \right)} } \right]e_i }{{e}'_i \left[ {\sum\limits_{t=0}^h {\left( {C_\tau \Omega _\mu C_\tau } \right)} } \right]e_i }} \right] \end{displaymath}](imgeq10.gif)
| (10) |
| s.t. α′α = 1 |
The restriction that α has unit length obtains the normalization of structural error variance to unity. In addition, we can easily incorporate linear sign and shape restrictions on the impulse responses by subjecting the optimization to restrictions of the form ![]() .
.
Appendix 2: Existence of the VAR Representation
Given the recursive solution
| (11) |
| (12) |
where xt is a vector of endogenous state variables (in our case, capital, k, is the lone endogenous state variable), zt is a vector of exogenous state variables (e.g., technology, A, preference/taste shock, Φ, government growth shock, g, and capital and labor tax shocks, τk and τn), and yt is a vector of other endogenous variables (e.g., output, consumption, investment, labor, and the interest rate). The vectors p, Q, W, and S are determined by simulating the model, conditional on the parameter values from Table 1.
Substituting (11) into (12) yields
| (13) |
Realize that
| (14) |
and substitute (14) into (13). Collecting terms yields:
| (15) |
We can rewrite this in its VARMA form:
| (16) | |
Finally, given the parameterizations from Table 1, we ensured that the roots of C(L) = I + [S-1(WQ - pS)]L lie outside the unit circle as required for invertibility.
References
Basu, Susanto; Fernald, John and Kimball, Miles. "Are Technology Improvements Contractionary?" Working Paper 2004-20, Federal Reserve Bank of Chicago, June 2004.
Blough, Stephen R. "The Relationship Between Power and Level for Generic Unit Root Tests in Finite Samples."Journal of Applied Econometrics, July-September 1992, 7(3), pp. 295-308.
Chari, V.V.; Kehoe, Patrick J. and McGrattan, Ellen R. "A Critique of Structural VARs Using Real Business Cycle Theory." Working Paper 631, Federal Reserve Bank of Minneapolis, February 2005.
Christiano, Lawrence J. and Eichenbaum, Martin. "Unit Roots in Real GNP: Do We Know, and Do We Care?" Carnegie-Rochester Conference Series on Public Policy, Spring 1990, 32(0), pp. 7-61.
Christiano, Lawrence J.; Eichenbaum, Martin and Vigfusson, Robert. "What Happens After a Technology Shock?" Manuscript, August 2004.
Cochrane, John H. "A Critique of the Application of Unit Root Tests." Journal of Economic Dynamics and Control, April 1991, 15(2), pp. 275-84.
Cooley, Thomas F. and Dwyer, Mark. "Business Cycle Analysis Without Much Theory: A Look at Structural VARs." Journal of Econometrics, March/April 1998, 83(1/2), pp. 57-88.
Erceg, Christopher J.; Guerrieri, Luca and Gust, Christopher. "Can Long-Run Restrictions Identify Technology Shocks?" International Finance Discussion Paper No. 792, Board of Governors of the Federal Reserve System, October 2004.
Faust, Jon. "Theoretical Confidence Level Problems with Confidence Intervals for the Spectrum of a Time Series." International Finance Discussion Paper No. 575, Board of Governors of the Federal Reserve System, December 1996.
Faust, Jon. "The Robustness of Identified VAR Conclusions about Money." Carnegie-Rochester Conference Series on Public Policy, December 1998, 49(0), pp. 207-44.
Faust, Jon and Leeper, Eric M. "When Do Long-Run Identifying Restrictions Give Reliable Results?" Journal of Business and Economic Statistics, July 1997, 15(3), pp. 345-53.
Fernald, John. "Trend Breaks, Long Run Restrictions, and the Contractionary Effects of Technology Shocks." Manuscript, 2004.
Fisher, Jonas D.M. "Technology Shocks Matter." Working Paper 2002-14, Federal Reserve Bank of Chicago, December 2003.
Francis, Neville; Owyang, Michael T.; and Theodorou, Athena. ""What Explains the Varying Monetary Response to Technology Shocks in G-7 Countries?" Working Paper 2004-002C, Federal Reserve Bank of St. Louis, December 2004.
Francis, Neville and Ramey, Valerie A. "Is the Technology-Driven Real Business Cycle Hypothesis Dead? Shocks and Aggregate Fluctuations Revisited." Journal of Monetary Economics, forthcoming.
Francis, Neville and Ramey, Valerie A. "The Source of Historical Economic Fluctuations: An Analysis Using Long-Run Restrictions." Working Paper No. 10631, National Bureau of Economic Research, July 2004a.
Francis, Neville and Ramey, Valerie A. "A New Measure of Hours Per Capita." Manuscript, November 2004b.
Galí, Jordi. "Technology, Employment, and the Business Cycle: Do Technology Shocks Explain Aggregate Fluctuations?" American Economic Review, March 1999, 89(1), pp. 249-71.
Owyang, Michael T. "On the Robustness of Monetary Policy Asymmetries." Working Paper 2002-18, Federal Reserve Bank of St. Louis, 2004.
Pesavento, Elena and Rossi, Barbara. "Do Technology Shocks Drive Hours Up or Down? A Little Evidence from an Agnostic Procedure." Macroeconomic Dynamics, forthcoming.
Shea, John. "What Do Technology Shocks Do?" NBER/Macroeconomics Annual, 1998, 13(1), pp. 275-310.
Sims, Christopher A. "The Role of Approximate Prior Restrictions in Distributed Lag Estimation." Journal of the American Statistical Association, March 1972, 67(337), pp. 169-75.
Sims, Christopher A. "Bayesian Skepticism on Unit Root Econometrics." Journal of Economic Dynamics and Control, June/September 1988, 12(2/3), pp. 463-74.
Sims, Christopher A. "Modeling Trends." Mimeo, Yale University, 1989.
Sims, Christopher A. and Uhlig, Harald. " Understanding Unit Rooters: A Helicopter Tour." Econometrica, November 1991, 59(6), pp. 1591-9.
Sims, Christopher A. and Zha, Tao. "Bayesian Methods for Dynamic Multivariate Models." International Economic Review, November 1998, 39(4), pp. 949-68.
Sims, Christopher A. and Zha, Tao. "Error Bands for Impulse Responses." Econometrica, September 1999, 67(5), pp. 1113-55.
Stock, James H. "Unit Roots in Real GNP: Do We Know, and Do We Care?: A Comment." Carnegie-Rochester Conference Series on Public Policy, Spring 1990, 32(0), pp. 63-82.
Uhlig, Harald. "What Are the Effects of Monetary Policy on Output? Results from an Agnostic Identification Procedure." Discussion Paper 2137, Center for Economic Policy Research, May 1999.
Uhlig, Harald. "How Well do we Understand Business Cycles and Growth? Examining the Data with a Real Business Cycle Model" Manuscript, January 2003(b).
Uhlig, Harald. "Do Technology Shocks Lead to a Fall in Total Hours Worked?" Manuscript, December 2003.
Watson, Mark W. "Measures of Fit for Calibrated Models." Journal of Political Economy, December 1993, 101(6), pp. 1011-41.
Footnotes
* The authors thank Kristie M. Engemann for research assistance. This paper benefited from conversations with David Bowman, Jon Faust, Jonas Fisher, Oscar Jorda, Dale Henderson, Marco Del Negro, Valerie Ramey, Barbara Rossi, Chris Sims, Martin Sola, and Jonathan Wright. Views expressed here are the authors' alone and do not reflect the opinions of the Federal Reserve Bank of St. Louis, the Federal Reserve Board of Governors, or the Federal Reserve System. All remaining errors are our own. Return to text
† Department of Economics. University of North Carolina. Gardener Hall CB#3305. Chapel Hill, NC 27599. [email protected]. Return to text
‡ Research Department. Federal Reserve Bank of St. Louis. 411 Locust Street, St. Louis, MO 63102. [email protected]. Return to text
§ Corresponding author. Board of Governors of the Federal Reserve System, Mailstop 74, 20th Street and C St., NW, Washington, DC 20551. [email protected]. Return to text
1. Others have criticized the so-called real business cycle models on the grounds of not fitting the data well [Watson (1993)]. Return to text
2. Basu, Fernald, and Kimball (2004) and Shea (1998) used different techniques to identify technology. These studies also find that hours contract on impact in response to a positive technology shock. Return to text
3. Christiano, Eichenbaum, and Vigfusson (CEV, 2004) argue that labor, if assumed stationary, responds to a technology shock positively on impact. They contend that per capita labor is bounded and cannot have a unit root. In a related paper, Francis and Ramey (2004a, 2004b) reject a unit root in per capita hours after accounting for demographic components. However, this resulting demographically-adjusted per capita labor series responds negatively to a technology shock. Further, Pesavento and Rossi (forthcoming) employ near-unity approximations to construct robust confidence intervals for the impulse responses. They find that hours respond negatively on impact. Return to text
4. Unit root tests are well understood to have low power in finite samples [Blough (1992), Cochrane (1991), Christiano and Eichenbaum (1990), Stock (1990), Sims (1989)]. Also, classical confidence intervals are inappropriate in the presence of uncertainty about unit roots [Sims and Zha (1999) and Sims and Uhlig (1991)]. Return to text
5. This arises from the steady-state condition
![]() relating labor productivity X to wages W, where k is the ratio of capital to technology, N is labor, α is the marginal productivity of labor, and Z is the level of technology. The relation (1) resembles the Beveridge-Nelson decomposition, where
εtnon-tech can be thought of as a composite non-technology shock including fiscal, monetary, and tax shocks. Return to text
relating labor productivity X to wages W, where k is the ratio of capital to technology, N is labor, α is the marginal productivity of labor, and Z is the level of technology. The relation (1) resembles the Beveridge-Nelson decomposition, where
εtnon-tech can be thought of as a composite non-technology shock including fiscal, monetary, and tax shocks. Return to text
6. Our identification is similar in flavor to that proposed in Uhlig (2003) in that we also focus on the conditional variance in productivity at a finite (in Uhlig's case, medium term) forecast horizon. The primary difference is that we allow the data to determine the value of the FEV share attributable to technology at a finite horizon at which productivity is exclusively driven by technology. Return to text
7. The orthogonalization ensures that technology shocks identified by α* are independent of the non-technology shocks in the system. Return to text
8. Comparisons of theoretical impulse responses and those obtained from LR-SVARs using model-generated data have revealed a number of qualitative differences. Cooley and Dwyer (1998) and CKM find that LR-SVARs can reverse the signs of model-generated impulse responses. Based on this finding, they conclude that LR-SVARs introduce sufficient bias that the estimated impulse responses cannot be considered reliable. However, EGG find that Galí-type restrictions do not reverse the qualitative responses but tend to bias their magnitude. Return to text
9. Our model roughly corresponds to the fixed capital utilization simulation EGG (2004); however, we do not include adjustment costs in capital accumulation. Return to text
10. As in the other Monte Carlo work of this nature mentioned above, it is important to caution that conclusions drawn from this approach cannot be generalized beyond the underlying model. That is, our method may be able to replicate the true impulse responses generated by this particular model but fail to do so with another model. Return to text
11. The model is solved by first eliminating nonstationarities arising from technology by dividing Yt, Kt-1, It, Ct, Gt, Wt, and Ψt by Zt. Next, the necessary first-order and steady-state conditions are computed based on selected parameter values. We then log-linearize the model around the steady-state growth paths and solve for the recursive equilibrium law of motion using the method of undetermined coefficients. A more detailed explanation of this procedure for solving dynamic stochastic models can be found in Uhlig (1999). Return to text
12. The model produces data that are a deviation around the steady-state growth path. To facilitate comparison with existing empirical work, we need to reverse this transformation. This avoids overdifferencing productivity using the transformed data. We also restrict the simulated data to be of length 174 sample points in order to match the typical length of postwar U.S. quarterly data; we make 5000 draws of sample size of 174. Return to text
13. We ensure that VAR representation exists under each parameterization. Writing the model in its VARMA form, we can verify that the MA portion is invertible. Appendix 2 presents the derivation of the VARMA representation. Numerical calculations confirm that each parameterization has a VAR representation. Return to text
14. We also experimented with entering productivity in differences and then backing out the levels before maximizing the FEV share. This specification, which is not robust to near-unit behavior in productivity in small or large samples, resulted in larger median biases for the responses compared with the cases presented here. Return to text
15. The estimates based on the informative prior account for cointegration and non-stationarity in the underlying series and a belief about the decay of lag parameters. We show below that our results are robust to inclusion or exclusion of the prior, although the conclusions are, in some cases, statistically more distinct when the prior is included. Return to text
16. Models A and B use the standard real consumption and investment series. Models C and D employ alternative constructions for these series, where consumption is composed of nondurables, services, and government spending and investment is composed of private investment plus durables. In addition, models A and C use a standard measure of private business productivity and hours, while models B and D use hours and productivity measures that are adjusted for demographically-persistent components. All findings in this section are invariant to correcting productivity and hours for demographic persistence and to the chosen measures of consumption and investment unless otherwise noted. Return to text
17. Appendix 1 details how marginal sign restrictions are incorporated into the MFEV identification approach. Note that an additional restriction on hours is not an overidentifying restriction that would lend itself to a likelihood ratio test. The identifying assumption on productivity is sufficient to identify technology but the system as a whole is underidentified with or without the additional sign restriction. Return to text
18. Note that it does not necessarily follow that there are, in fact, other influences on long-run productivity. Odds ratios for the restricted and unrestricted models were indistinguishable, preventing us from drawing such a conclusion. Return to text
19. We consider this interpretation reasonable since we think ten years is long enough to capture dynamics beyond business cycle frequencies. Return to text
20. Similar differences are attainable from alternative calibrations of our simple theoretical model presented in the Monte Carlo sections of the paper. Return to text
21. Recall that hours enters in log levels in all models presented in this paper whereas they enter in differences in the LR-SVARs presented in Galí (1999) and Francis and Ramey (forthcoming). Return to text
22. Results available upon request. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text