Skip to: [Printable Version (PDF)]

Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 842, October 2005--- Screen Reader Version*

Alternative Procedures for Estimating Vector Autoregressions Identified with Long-Run Restrictions^*

Lawrence J. Christiano, Martin Eichenbaum, and Robert Vigfusson^†

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

We show that the standard procedure for estimating long-run identified vector autoregressions uses a particular estimator of the zero-frequency spectral density matrix of the data. We develop alternatives to the standard procedure and evaluate the properties of these alternative procedures using Monte Carlo experiments in which data are generated from estimated real business cycle models. We focus on the properties of estimated impulse response functions. In our examples, the alternative procedures have better small sample properties than the standard procedure, with smaller bias, smaller mean square error and better coverage rates for estimated confidence intervals.

Keywords: Technology shocks, hours worked, frequency domain, spectral density matrix

JEL classification: E24, E32, O3

1  Introduction

There is a large literature in which researchers impose long-run identifying restrictions on vector autoregressions (VARs) to identify the dynamic effects of shocks to the economy. These restrictions are motivated by the implications that many economic models have for the long-run effects of shocks. We show that the standard procedure for estimating long-run-identified vector autoregressions uses a particular estimator of the zero-frequency spectral density matrix of the data. This estimator is derived from the estimated coefficients of a finite order VAR. When the actual VAR of the data contains more lags of the variables than the econometrician uses, this estimator of the zero-frequency spectral density matrix can have poor properties. These poor properties stem from the difficulties involved in estimating the sum of the coefficients in a VAR. We develop alternative procedures that combine different zero-frequency spectral density matrix estimators with VARs. The specific estimators that we consider are the Bartlett estimator and the estimator proposed by Andrews and Monahan (1992). We evaluate the properties of our alternative procedures using Monte Carlo experiments in which data are generated from estimated Real Business Cycle (RBC) models. We focus on the properties of estimated impulse response functions. In our examples, the alternative procedures have better small sample properties than the standard procedure: they are associated with smaller bias, smaller mean square error and better coverage rates for confidence intervals.

The small sample properties of spectral density estimators can depend on the properties of the underlying data generating mechanism. Therefore some caution must be taken in extrapolating from our results. At a minimum our results suggest that applied econometricians should consider alternative procedures for estimating long-run identified vector autoregressions.

2  Long-Run Identifying Restrictions and VARs

There is an important literature in which researchers impose long-run identifying restrictions on VAR. For example, Galí (1999) imposes the identifying assumption that the only shock that affects the log of labor productivity, a_t, in the long run is a technology shock $$\varepsilon_{t}^{z}$$. Galí's identifying assumption corresponds to the exclusion restriction:

$$\mathop {\lim }\limits_{j\to\infty} \left[ {E_{t} a_{t+j} -E_{t-1} a_{t+j} } \right] =f(\varepsilon_{t}^{z} only)$$ (1)

In addition Galí imposes the sign restriction that f is an increasing function of $$\varepsilon_{t}^{z}$$.

Galí imposes the exclusion and sign restrictions on a VAR to compute $$\varepsilon_{t}^{z}$$ and identify its dynamic effects on macroeconomic variables. Denote the N variables in a VAR by Y_t:

$$Y_{t+1} =B(L)Y_{t} +u_{t+1} ,Eu_{t+1} {u}^{\prime}_{t+1} =V$$ (2)

$$B(L)\equiv B_{1} +B_{2} L+...+B_{q} L^{q-1}$$

$$Y_{t} =\left( {{\begin{array}{*{20}c} {\Delta \log a_t } \hfill \ {\log l_t } \hfill \ {x_t } \hfill \ \end{array} }} \right)$$

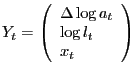
Here l_t denotes per capita hours worked and x_t is an additional vector of variables that may be included in the VAR. In all of our applications we assume that q =4. Suppose that the fundamental economic shocks are related to u_t via the relationship:

$$u_{t} =C\varepsilon_{t} ,E\varepsilon_{t} {\varepsilon}^{\prime}_{t} =I,C{C}^{\prime}=V$$ (3)

where the first element in ε_t is $$\varepsilon_{t}^{z}$$. It is easy to verify that:

$$\mathop {\lim }\limits_{j\to\infty} E\left[ {a_{t+j} \vert\Omega_{t} } \right] -E_{t-1} [a_{t+j} \vert\Omega_{t-1} ]=\tau[I-B(1)]^{-1}C\varepsilon _{t}$$ (4)

Here $\tau$ is a row vector with all zeros, except unity in the first location and B(1) is the sum, B₁ + ... + B_q. Also, E is the expectation operator and is $\Omega$ = {Y_t, ... , Y_t-q+1} is the information set.

To compute the dynamic effects of $\varepsilon^{z}_{t }$on the elements of Y_t we need to know B₁, ..., B_q and C₁, the first column of C. The matrix, V, and the B_i's can be estimated by an ordinary least squares regression. The requirement that CC´ = V is insufficient to determine a unique value of C₁. Adding the exclusion and sign restrictions does uniquely determines C₁. The exclusion restriction implies that:

$$[I-B(1)]^{-1}C=\left[ {{\begin{array}{*{20}c} {number} \hfill & {\mathop 0\limits_{1\times (N-1)} } \hfill \ {numbers} \hfill & {numbers} \hfill \ \end{array} }} \right]$$

The 0 matrix reflects the assumption that only a technology shock can have along run effect on a_t. The sign restriction implies that the (1,1) element of [I - B(1)]^-1C is positive.

The standard algorithm for computing C₁ requires the matrix

Although we cannot directly estimate D, we can estimate DD´:

$$D{D}^{\prime}=[I-B(1)]^{-1}V[I-B(1{)}^{\prime}]^{-1}$$ (5)

The right hand side of (5) can be computed directly from the VAR coefficients and the variance-covariance matrix of the u_t. There are many D matrices consistent with (5) as well as the sign and exclusion restrictions. However, these matrices all have the same first column, D₁ (see Christiano, Eichenbaum, and Vigfusson CEV (2005)). This unique D₁ implies a unique value for C₁:

The right hand side of (5) is the estimate of the zero-frequency spectral density matrix of Y_t, S_Y (0), that is implicit to the VAR of order q. When the true value of q is larger than the one used by the econometrician, there is reason to be concerned about the statistical properties of this estimator. A mismatch between the true value of q and the value that the econometrician assumes can arise when the data generating process is a dynamic stochastic general equilibrium model. For these types of models, Y_t may have an infinite-ordered VAR, i.e. q = $\infty$.

To understand the nature of the problem when q is misspecified, it is useful to consider a simple analytic expression closely related to results in Sims (1972). Equation (7) approximates what an econometrician who fits a misspecified VAR will find. The expression is an approximation because it assumes a large sample of data. Let $$\hat{B}_{1} ,...,\hat{B}_{q}$$ and $$\hat{V}$$ denote the estimated parameters of a VAR with q lags. Then,

$$\hat{V}=V+\mathop {\min }\limits_{\hat{B}_{1} ,...,\hat{B}_{q} } \frac{1} {2\pi}\int_{-\pi}^{\pi}{\left[ {B\left( {e^{-i\omega}} \right) -\hat {B}\left( {e^{-i\omega}} \right) } \right] } S_{Y} (\omega)\left[ {B\left( {e^{i\omega}} \right) -\hat{B}\left( {e^{i\omega}} \right) } \right] ^{\prime}d\omega$$ (7)

where B(e^-iω) is B(L) with L replaced by e^-iω.¹ Here, B and V are the parameters of the actual VAR representation of the data, and S_Y ($\omega)$ is the associated spectral density at frequency $\omega$.

According to (7), estimating an unconstrained VAR approximately involves choosing parameters to minimize a quadratic form in the difference between the estimated and true lag matrices. The quadratic form assigns greatest weight to the frequencies where the spectral density is the greatest. If the econometrician's VAR is correctly specified, then $$\hat{B}$$ = B and $$\hat{V}$$ = V. If the econometrician estimates a VAR with too few lags relative to the true VAR, then this specification error implies that $$\hat{B}$$ ≠ B and $$\hat{V}$$ > V.² Equation (7) indicates that $$\hat{B}$$(1) will be a good approximation for B(1) only if S_Y ($\omega)$ happens to be relatively large in a neighborhood of $\omega$ =0. This is not something we can rely on.

Our alternative procedure for estimating long-run identified VARs involves replacing the zero-frequency spectral density estimator in (5) by other estimators specifically designed for the task. There is a very large literature that analyzes the properties of alternative estimators of zero-frequency spectral density matrices. One alternative is to use the Bartlett estimator:

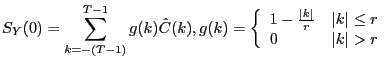
$$S_{Y} (0)=\sum\limits_{k=-(T-1)}^{T-1} {g(k)\hat{C}(k),g(k)=\left\{ {{\begin{array}{*{20}c} {1-\frac{\vert k\vert }{r}} \hfill & {\vert k\vert \le r} \hfill \ 0 \hfill & {\vert k\vert >r} \hfill \ \end{array} }} \right. }$$ (8)

where, after removing the sample mean from Y_t,

$$\hat{C}(k)=\frac{1}{T}\sum\limits_{t=k+1}^{T} {Y_{t} {Y}^{\prime}_{t-k} }$$

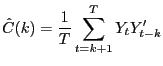
Another alternative is to use the Andrews-Monahan (1992) estimator:

$$S_{Y} (0)=\left[ {I-\left( {B_{1} +...+B_{p} } \right) } \right] ^{-1}F_{u} (0)\left[ {I-\left( {B_{1} +...+B_{p} } \right) ^{\prime}} \right] ^{-1}$$ (9)

$$F_{u} (0)=\sum\limits_{k=-r}^{r} {\vert1-\frac{k}{r}\vert G(k),} G(k)=\frac{1}{T}\sum\limits_{t=k}^{T} {u_{t} {u}^{\prime}_{t-k} }$$

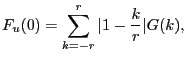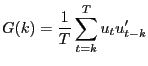In our alternative procedure for estimating the dynamic effect of a technology shock, we replace the estimate of S_Y (0) , used to construct DD´ and D₁ in the standard procedure, with the estimator of S_Y (0) given by either (8) or (9). We refer to these procedures as the Bartlett and Andrews-Monahan procedures, respectively. We then construct C₁ using (6).³ In the alternative procedures C₁ still depends on the sum of the VAR coefficients even though D₁ does not. To implement (8) or (9) we use essentially all possible covariances in the data by choosing a large value of r, r = 150.⁴ In addition, we examine the properties of our alternative procedures when we use smaller values of r.

3  The Data Generating Process

CEV (2005) show that a standard RBC model with a permanent technology shock and a labor supply shock implies the following reduced form model for Y_t = [Δlog a_t, log l_t]´:

$$Y_{t} =\left[ {\Delta\log a_{t} ,\log l_{t} } \right] ^{\prime}: Y_{t} =\phi_{1} Y_{t-1} +\phi_{2} Y_{t-2} +\varepsilon_{t} +\theta_{1} \varepsilon_{t-1} +\theta_{2} \varepsilon_{t-2}$$ 10

where $\phi_{1 }$and $\phi_{2 }$are scalars, θ_i is two by two matrix and ε_t is a normally distributed vector with variance-covariance matrix $\Psi$. The sign and exclusion restrictions are satisfied by the RBC model that CEV(2005) consider. Equation (10) implies that Y_t has an infinite-order VAR. Therefore, any finite-order VAR is misspecified.

In the benchmark version of the model, we use values for the exogenous shock processes obtained by CEV (2005) who maximize the Gaussian log likelihood function for Y_t using postwar U.S. data over the sample 1959QIII to 2001QIV. We summarize their results as follows:

$$\phi_{1} =1.9439,\phi_{2} =-0.9445, \Psi=\frac{1}{1000}\left( {{\begin{array}{*{20}c} {0.039137} \hfill & {-0.0095548} \hfill \ {-0.0095548} \hfill & {0.073729} \hfill \ \end{array} }} \right)$$

$$\theta_{1} =\left( {{\begin{array}{*{20}c} {-1.926} \hfill & {0.027834} \hfill \ {-0.0066342} \hfill & {-0.97012} \hfill \ \end{array} }} \right) , \theta_{2} =\left( {{\begin{array}{*{20}c} {0.92682} \hfill & {-0.027548} \hfill \ 0 \hfill & 0 \hfill \ \end{array} }} \right)$$

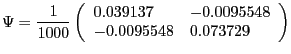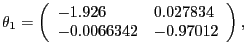
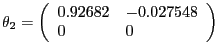In the CKM version of the model, we assume values for the parameters equal to those used by Chari, Kehoe, and McGrattan's (CKM) (2005) in their benchmark model. CKM obtain these values using a Kalman filter framework to estimate the model. CKM impose the highly questionable identifying assumption that, up to a small measurement error, the change in government spending and net exports is a good measure of the change in technology. CEV (2005) show that there is overwhelming empirical evidence against the restrictions imposed by CKM. Despite the empirical implausibility of the CKM model, we use it as a data generating process because it provides us with an additional example to assess our alternative procedures. CKM's estimated parameter values are given by:

$$\phi_{1} =1.9093,\phi_{2} =-0.9114, \Psi=\frac{1}{1000}\left( {{\begin{array}{*{20}c} {0.11604} \hfill & {-0.14605} \hfill \ {-0.14605} \hfill & {0.52697} \hfill \ \end{array} }} \right)$$

$$\theta_{1} =\left( {{\begin{array}{*{20}c} {-1.8967} \hfill & {0.041277} \hfill \ {-0.0064704} \hfill & {-0.96777} \hfill \ \end{array} }} \right) , \theta_{2} =\left( {{\begin{array}{*{20}c} {0.89971} \hfill & {-0.040268} \hfill \ 0 \hfill & 0 \hfill \ \end{array} }} \right)$$

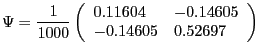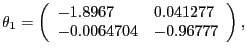
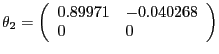4  Results

To analyze the properties of our different procedures we generate multiple data sets, each of length 180 observations. We generate 1000 data sets using the benchmark model and 1000 data sets using the CKM model as the data generating mechanism. For each data set, we estimate a four-lag VAR and we estimate S_Y (0) using the standard VAR-based estimator, the Bartlett estimator, and the Andrews-Monahan estimator. We then calculate three different estimates of the dynamic response of hours worked to a technology shock, as described in Section 2.

Figure 1 reports the average estimated response across all simulations (the solid line) and the true model response (the starred line). In addition, Figure 1 reports the true degree of sampling uncertainty, measured by the standard deviation of the estimated impulse response functions across the 1000 synthetic data sets (the dashed interval). To assess whether an econometrician would correctly estimate the true degree of sampling uncertainty, we proceed as follows. For each synthetic data set, and corresponding estimated impulse response function, we calculate the bootstrap standard deviation of each point in the impulse response function. Specifically, we estimate a VAR on each of the 1000 data sets that we simulate from the economic model. We use the VAR coefficients and fitted disturbances in a bootstrap procedure to generate 200 synthetic data sets, each of length 180 observations. For each of these 200 synthetic data sets, we estimate a new VAR and impulse response function. We then calculate the standard deviation of the coefficients in the impulse response functions across the 200 data sets. We use this standard deviation to construct a two standard deviation confidence interval around the estimated responses. We also calculate coverage rates for the first coefficient in the impulse response function. Specifically, we report how often, across the 1000 data sets simulated from the economic model, the econometrician's confidence intervals contain the first coefficient of the true impulse response function. In addition, Figure 1 reports the average confidence interval (the circles) that an econometrician would construct.

To help quantify the statistical properties of the different procedures Table 1 reports summary statistics for X, the estimated contemporaneous response of l_t to a technology shock.: median, mean and standard deviation of X across the 1000 synthetic data sets for each model. A different metric for assessing the different procedures is to focus on the mean square error (MSE) of X. The MSE combines information about bias and sampling uncertainty. We calculate the square root of the MSE, $$\left[ {(1000)^{-1}\sum\nolimits_{i=1}^{1000} {\left( {X_{i} -\xi} \right) ^{2}} } \right] ^{1/2}$$ , for our different procedures. Here X_i denotes the value of X obtained in the i^th synthetic data set and $\xi$ is the true response. Table 1 reports the value of this statistic for the different procedures relative to the MSE associated with the standard procedure. Finally we report coverage rates for X.

Consider first the results obtained using the CKM model as the data generating process. Figure 1 indicates that there is substantial upward bias associated with the standard procedure, although the bias is small relative to sampling uncertainty. Figure 1 indicates that the size of the bias associated with the Andrews-Monahan procedure is substantially smaller than the bias associated with the standard procedure. The bias associated with the Bartlett procedure is smaller still. Table 1 indicates that the bias for X falls from 0.63 using the standard procedure to 0.31 for the Andrews-Monahan procedure and to 0.08 for the Bartlett procedure. The square root of the MSE for X also falls with the modified procedures: the ratio of the MSE for the Andrews-Monahan and Bartlett procedures relative to the standard procedure is 0.91 and 0.77, respectively.

Table 1 indicates that the coverage rate for X of our alternative procedures improves relative to the standard procedure. For the standard procedure, the coverage rate for X is only 74 percent which is substantially below the nominal size of 95 percent. For the Andrews-Monahan procedure, the coverage rate is 91 percent and the coverage rate is 94 percent for the Bartlett procedure. Finally, Table 1 indicates that for both alternative procedures, setting r to 150 leads to better properties than setting r to 25 or 50.

Taken together, our results indicate that for data generated by the CKM model, our alternative procedures perform better than the standard procedure with smaller bias, smaller mean square error, and coverage rates that are closer to the nominal size. In this particular application, the Bartlett procedure outperforms the Andrews-Monahan procedure.

We now briefly discuss results when the data generating mechanism is our benchmark model. Figure 1 shows that the bias associated with the standard procedure is much smaller than when the data are generated using the CKM model. Even so, both modified procedures outperform the standard procedure. Again the bias is smaller, the MSE is reduced and coverage rates are closer to nominal sizes. Judging between the Andrews-Monahan and Bartlett procedures is more difficult. Bias is larger for the Bartlett procedure but the MSE is smaller and the coverage rate is closer to the nominal size.

5  Conclusion

We develop alternative procedures for estimating long-run identified vector autoregressions. We assess their properties relative to the standard procedure used in the literature. We evaluate the properties of the different procedures using Monte Carlo experiments where we generate data from estimated RBC models. Focusing on estimated response functions, we find that our alternative procedures have better small sample properties than the standard procedure: they are associated with smaller bias, smaller mean square error and better coverage rates for confidence intervals.

References

Andrews, D.W.K., and J.C. Monahan, 1992, An improved heteroskedasticity and autocorrelation consistent covariance matrix estimator, Econometrica 60, pp.953-966.

Chari, V.V., Patrick Kehoe, and Ellen McGrattan, 2005, 'A Critique of Structural VARs Using Real Business Cycle Theory,' Federal Reserve Bank of Minneapolis Staff Report 364 July.

Christiano, Lawerence J., Martin Eichenbaum and Robert Vigfusson, 2005, 'Assessing Structural VARs', manuscript, Northwestern University.

Galí, Jordi, 1999, 'Technology, Employment, and the Business Cycle: Do Technology Shocks Explain Aggregate Fluctuations?' American Economic Review, 89(1), 249-271.

Sims, Christopher, 1972, 'The Role of Approximate Prior Restrictions in Distributed Lag Estimation,' Journal of the American Statistical Association, 67(337), 169-175.

Table 1:  The Contemporaneous Response of Hours Worked to a Positive Technology Shock

Panel A:  CKM Model (Hours Response 0.32)

Procedure	r	Median	Mean	Standard Deviation	MSE*	Coverage
Standard	-	1.03	0.95	0.68	-	0.74
Andrews-Monahan	25	1.16	1.04	0.81	1.17	0.76
Andrews-Monahan	50	0.98	0.85	0.92	1.14	0.87
Andrews-Monahan	150	0.74	0.63	0.79	0.91	0.91
Bartlett	25	0.53	0.48	0.52	0.58	0.90
Bartlett	50	0.60	0.51	0.78	0.86	0.92
Bartlett	150	0.44	0.40	0.71	0.77	0.94

Panel B:  Our Benchmark Model (Hours Response 0.28)

Procedure	r	Median	Mean	Standard Deviation	MSE*	Coverage
Standard	-	0.43	0.33	0.42	-	0.84
Andrews-Monahan	25	0.44	0.34	0.48	1.13	0.86
Andrews-Monahan	50	0.39	0.29	0.53	1.25	0.88
Andrews-Monahan	150	0.28	0.21	0.44	1.06	0.87
Bartlett	25	0.16	0.14	0.22	0.63	0.89
Bartlett	50	0.19	0.15	0.35	0.89	0.92
Bartlett	150	0.15	0.12	0.33	0.87	0.91

Notes:  Results from Monte Carlo experiments with data simulated from two parameterizations of a RBC model.
*  MSE represents the ratio of the square root of the mean squared error relative to the standard procedure.

Figure 1:  The Response of Hours Worked to a Positive Technology Shock

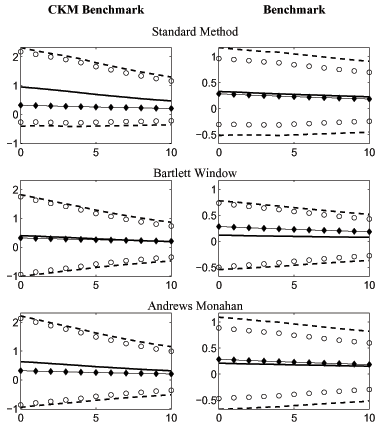
Data for Figure 1: The Response of Hours Worked to a Positive Technology Shock: Panel A: CKM Benchmark

Period	True	Standard Method: Average	Standard Method: 2 Std. Deviation Interval, Lower Bound	Standard Method: 2 Std. Deviation Interval, Upper Bound	Standard Method: Average Confidence Interval, Upper Bound	Standard Method: Average Confidence Interval, Lower Bound	Bartlett Window: Average	Bartlett Window: 2 Std. Deviation Interval, Lower Bound	Bartlett Window: 2 Std. Deviation Interval, Upper Bound	Bartlett Window: Average Confidence Interval, Upper Bound	Bartlett Window: Average Confidence Interval, Lower Bound	Andrews Monhan: Average	Andrews Monhan: 2 Std. Deviation Interval, Lower Bound	Andrews Monhan: 2 Std. Deviation Interval, Upper Bound	Andrews Monhan: Average Confidence Interval, Upper Bound	Andrews Monhan: Average Confidence Interval, Lower Bound
0	0.3173	0.9504	-0.4170	2.3179	2.1712	-0.2703	0.3994	-1.0181	1.8169	1.7476	-0.9488	0.6319	-0.9528	2.2166	2.1338	-0.8700
1	0.3037	0.9078	-0.3902	2.2057	2.0816	-0.2661	0.3816	-0.9507	1.7140	1.6261	-0.8628	0.6018	-0.8975	2.1012	2.0039	-0.8002
2	0.2908	0.8582	-0.3949	2.1113	1.9940	-0.2776	0.3569	-0.8898	1.6036	1.5118	-0.7981	0.5657	-0.8498	1.9813	1.8802	-0.7488
3	0.2784	0.8051	-0.4170	2.0273	1.9020	-0.2917	0.3376	-0.8245	1.4996	1.4088	-0.7336	0.5331	-0.8039	1.8701	1.7620	-0.6959
4	0.2665	0.7497	-0.4235	1.9229	1.7923	-0.2929	0.3140	-0.7712	1.3991	1.2941	-0.6662	0.4959	-0.7639	1.7558	1.6346	-0.6427
5	0.2551	0.6909	-0.4080	1.7899	1.6553	-0.2735	0.2881	-0.7061	1.2823	1.1642	-0.5879	0.4587	-0.7071	1.6246	1.4891	-0.5716
6	0.2442	0.6419	-0.3965	1.6803	1.5459	-0.2621	0.2667	-0.6527	1.1860	1.0628	-0.5295	0.4278	-0.6614	1.5171	1.3761	-0.5204
7	0.2338	0.5926	-0.3868	1.5720	1.4332	-0.2480	0.2453	-0.6013	1.0918	0.9611	-0.4706	0.3963	-0.6187	1.4113	1.2602	-0.4675
8	0.2239	0.5447	-0.3813	1.4707	1.3335	-0.2441	0.2235	-0.5608	1.0077	0.8751	-0.4282	0.3658	-0.5852	1.3168	1.1627	-0.4310
9	0.2143	0.5040	-0.3709	1.3789	1.2411	-0.2331	0.2064	-0.5182	0.9310	0.7971	-0.3843	0.3399	-0.5492	1.2291	1.0721	-0.3923
10	0.2052	0.4670	-0.3617	1.2957	1.1591	-0.2251	0.1910	-0.4807	0.8627	0.7304	-0.3484	0.3163	-0.5181	1.1507	0.9939	-0.3613

Data for Figure 1: The Response of Hours Worked to a Positive Technology Shock: Panel B: Benchmark

Period	True	Standard Method: Average	Standard Method: 2 Std. Deviation Interval, Lower Bound	Standard Method: 2 Std. Deviation Interval, Upper Bound	Standard Method: Average Confidence Interval, Upper Bound	Standard Method: Average Confidence Interval, Lower Bound	Bartlett Window: Average	Bartlett Window: 2 Std. Deviation Interval, Lower Bound	Bartlett Window: 2 Std. Deviation Interval, Upper Bound	Bartlett Window: Average Confidence Interval, Upper Bound	Bartlett Window: Average Confidence Interval, Lower Bound	Andrews Monhan: Average	Andrews Monhan: 2 Std. Deviation Interval, Lower Bound	Andrews Monhan: 2 Std. Deviation Interval, Upper Bound	Andrews Monhan: Average Confidence Interval, Upper Bound	Andrews Monhan: Average Confidence Interval, Lower Bound
0	0.2844	0.3281	-0.5167	1.1730	0.9611	-0.3048	0.1185	-0.5424	0.7794	0.7356	-0.4986	0.2086	-0.6747	1.0919	0.8872	-0.4701
1	0.2724	0.3190	-0.5071	1.1451	0.9422	-0.3042	0.1145	-0.5279	0.7570	0.7025	-0.4734	0.2032	-0.6649	1.0714	0.8614	-0.4549
2	0.2608	0.3056	-0.5079	1.1191	0.9210	-0.3098	0.1074	-0.5157	0.7304	0.6696	-0.4549	0.1949	-0.6543	1.0442	0.8349	-0.4451
3	0.2498	0.2928	-0.5086	1.0942	0.8981	-0.3124	0.1026	-0.4958	0.7010	0.6396	-0.4343	0.1900	-0.6362	1.0161	0.8100	-0.4300
4	0.2392	0.2833	-0.5165	1.0831	0.8800	-0.3134	0.0991	-0.4816	0.6797	0.6111	-0.4129	0.1847	-0.6277	0.9971	0.7856	-0.4162
5	0.2291	0.2723	-0.5036	1.0481	0.8425	-0.2980	0.0948	-0.4584	0.6479	0.5725	-0.3830	0.1783	-0.6051	0.9617	0.7464	-0.3898
6	0.2194	0.2637	-0.4938	1.0212	0.8147	-0.2873	0.0911	-0.4382	0.6204	0.5427	-0.3605	0.1732	-0.5880	0.9344	0.7170	-0.3706
7	0.2101	0.2538	-0.4828	0.9905	0.7818	-0.2741	0.0872	-0.4183	0.5927	0.5098	-0.3354	0.1673	-0.5693	0.9040	0.6831	-0.3484
8	0.2012	0.2439	-0.4734	0.9612	0.7511	-0.2634	0.0832	-0.4001	0.5664	0.4800	-0.3137	0.1614	-0.5524	0.8751	0.6523	-0.3295
9	0.1927	0.2350	-0.4638	0.9338	0.7229	-0.2528	0.0797	-0.3827	0.5421	0.4529	-0.2935	0.1560	-0.5364	0.8485	0.6240	-0.3119
10	0.1845	0.2267	-0.4550	0.9084	0.6973	-0.2439	0.0765	-0.3666	0.5196	0.4289	-0.2759	0.1510	-0.5219	0.8239	0.5986	-0.2966

Footnotes

*  The first two authors are grateful for the financial support of grants from the NSF to the National Bureau of Economic Research. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any person associated with the Federal Reserve System. Return to text

†  Christiano: Northwestern University, email [email protected], Eichenbaum: Northwestern University, email: [email protected], Vigfusson: Board of Governors of the Federal Reserve System, email: [email protected] Return to text

1.  The minimization is over the trace of the indicated integral. Return to text

2.  By $$\hat{V}$$ > V we mean that $$\hat{V}$$ - V is a positive definite matrix. Return to text

3.  The C matrix constructed with this C₁ will not have the property that CC´ = V. Return to text

4.  The rule of always setting the bandwidth, r, equal to sample size does not yield a consistent estimator of the spectral density at frequency zero. We assume that as the sample size increases the bandwidth is increased sufficiently slowly to obtain a consistent estimator. Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

Home | Economic research and data | Publications and education resources
Accessibility | Contact us
Last update: September 29, 2008