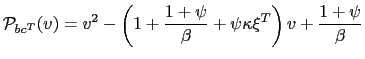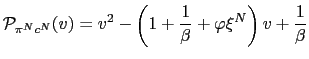Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 848, This Draft April 2006 --- Screen Reader
Version*
Fighting Against Currency Depreciation, Macroeconomic Instability and Sudden Stops1
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
In this paper we show that, in the aftermath of a currency crisis, a government that adjusts the nominal interest rate in response to domestic currency depreciation can induce aggregate instability in the economy by generating self-fulfilling endogenous cycles. We find that, if a government raises the interest rate proportionally more than an increase in currency depreciation, then it induces self-fulfilling cycles that, driven by people's expectations about depreciation, replicate several of the salient stylized facts of the "Sudden Stop" phenomenon. These facts include a decline in domestic production and aggregate demand, a collapse in asset prices, a sharp correction in the price of traded goods relative to non-traded goods, an improvement in the current account deficit, a moderately higher CPI-inflation, more rapid currency depreciation, and higher nominal interest rates. In this sense, an interest rate policy that responds to depreciation may have contributed to generating the dynamic cycles experienced by some economies in the aftermath of a currency crisis.
Keywords: Small Open Economy, Interest Rate Policies, Currency Depreciation, Self-fulfilling Cycles, Sudden Stops, Collateral Constraints.
JEL classification: E32, E52, E58, F41.
1 Introduction
One of the policy debates that emerged out of the Asian Crisis of 1997 was that of the appropriate interest rate policy to fight domestic currency depreciation. On one hand, the IMF advocated for higher interest rates to prevent excessive depreciation. It claimed that such a policy would reduce capital outflows by raising the cost of currency speculation and induce capital inflows by making domestic assets more attractive.3 On the other hand, some critics of the IMF policy prescription recommended lowering interest rates in the face of depreciation.4 These critics argued that lower rates would alleviate the subsequent recessions in the Asian economies, and improve the banks' and corporations' balance sheets, which had weakened significantly as a result of the negative effects of rapid currency depreciation on their dollarized liabilities.
These two views had something in common. They both advocated for changes in interest rates in response to some macroeconomic indicators, in this case the currency depreciation rate. They both implied a feedback mechanism, positive or negative, from the current depreciation rate to the nominal interest rate.5 In this paper, we study some of the possible macroeconomic consequences of these interest rate feedback policies in countries that have been hit by a currency crisis. Our main result is that in the aftermath of a crisis, an interest rate policy that calls for changing the nominal interest rate, positively or negatively, in response to currency depreciation can induce aggregate instability in the economy by generating self-fulfilling endogenous cycles. That is, this policy can cause cycles in the economy that are driven exclusively by people's self-fulfilling beliefs rather than fundamentals, and regardless of whether the response to depreciation is positive or negative.
We find that if a government raises the interest rate proportionally more than an increase in currency depreciation, then it induces self-fulfilling cycles that replicate several of the salient empirical regularities of emerging market crises. In particular, we build a model in which these cycles, which are driven exclusively by people's expectations about currency depreciation, replicate many of the stylized facts following a currency crisis. These facts, labeled by Calvo (1998) as the "Sudden Stop" phenomenon, include a decline in domestic production and aggregate demand, a collapse in asset prices, a sharp correction in the price of traded goods relative to non-traded goods, an improvement in the current account deficit, a moderately higher CPI-inflation, more rapid currency depreciation and higher nominal interest rates. In this sense, interest rate policies that respond to depreciation may have contributed to generating the dynamic cycles experienced by some economies in the aftermath of a currency crisis.
As a building block to our full model, we first construct a simple environment of a small open economy in which we are able to derive analytical results. We show that interest rate policies that respond only to currency depreciation can induce real indeterminacy or multiple equilibria, which in turn opens the possibility of self-fulfilling equilibria.6 The intuition for this result is the following. Suppose that in response to a "sunspot," agents in the economy expect a higher inflation rate. Because the interest rate policy responds only to currency depreciation - and not to inflation - the real interest rate can fall, boosting aggregate demand. As firms see aggregate demand rising, they raise prices, thus validating the original expectations of a higher inflation.7
Our full model is a sticky-price small open economy with traded and non-traded goods with two important features: an interest rate policy that responds to currency depreciation, and a collateral constraint which captures the fact that international loans must be guaranteed by physical assets such as capital. Loosely speaking, the crisis is modelled as a time when this constraint is unexpectedly binding.8 The model also includes other features that have become very useful to match quantitatively some of the stylized facts of the aftermath of a crisis. In particular, we consider non-traded distribution services, and domestic and international loan requirements to hire labor and to purchase an imported intermediate input.9
In this full model, an interest rate policy that responds only to depreciation also induces multiple equilibria. However, the interaction of this policy with the collateral constraint induces self-fulfilling cycles. This result is related to, but differs from, the seminal work by Kiyotaki and Moore (1997). They show that a binding collateral constraint induces credit cycles that may amplify business cycles driven by fundamentals. In our work this constraint creates cycles, but the interest rate policy makes them self-fulfilling to the extent that they are driven by people's expectations about the economy.
We think our results have at least three important implications. First, they do not support any of the views of the previously mentioned debate. In fact we unveil a peril that may be present in both policy recommendations. What seems crucial is not whether the government increases or decreases the interest rate, but instead the feedback response of the nominal interest rate to currency depreciation that most of the previous studies have ignored.
Second, our results provide a possible explanation of why the empirical literature has not been able to obtain conclusive evidence about whether higher interest rates can cause nominal currency depreciation or, instead, appreciation in the aftermath of a crisis.10 This literature has tried to control for the variables that influence the nominal exchange rate. But our results suggest that there can be potential influences that may depend on "sunspots," which in turn can induce self-fulfilling cycles in the nominal exchange rate (or the nominal depreciation rate) as well as in other variables. Clearly these influences do not depend on fundamentals, and their effect should be taken into account by this literature.
Third, since interest rate policies that respond to currency depreciation can induce expectations-driven fluctuations, then they can destabilize the economy. Therefore they can be costly in terms of macroeconomic instability and welfare.11 This has not been studied in the previous literature and deserves further research. For instance, Lahiri and Vegh (2002, 2003) and Flood and Jeanne (2000) focus on the fiscal and output costs of higher interest rates before and after a crisis. In addition Lahiri and Vegh (2003) claim that there is a non-monotonic relationship between welfare and the increase in interest rates. Christiano, Gust and Roldos (2004) explore conditions under which a cut (rise) in the interest rate in the midst of a crisis will stimulate output and improve welfare. Aghion, Bacchetta and Banerjee (2000) find that it might not be optimal to raise interest rates either when the proportion of foreign currency debt is not too large, or when credit provision, domestic investment and production are highly sensitive to changes in nominal interest rates; whereas Braggion, Christiano and Roldos (2005) build a model where, in response to a financial crisis, it is optimal to raise the interest rate immediately, and then reduce it sharply.
The remainder of this paper is organized as follows. In Section 2, we consider a simple economy in "good" times and characterize analytically the equilibrium under interest rate policies that respond only to currency depreciation. In Section 3, we build our full model, which includes, among other things, a collateral constraint. Here we study the determinacy of equilibrium analysis through numerical simulations. In addition, we show that even if the interest rate policy responds to past CPI-inflation, it can still induce multiple equilibria as long as it responds to currency depreciation.12 In Section 4, we use our full model to construct a self-fulfilling equilibrium that captures the stylized facts of a "Sudden Stop." Section 5 concludes.
2 The Simple Model
In this section we develop a simple infinite-horizon small open economy model. The economy is populated by a continuum of identical household-firm units and a government who are blessed with perfect foresight. Before we describe in detail the behavior of these agents we state a few general assumptions and definitions.
There are two consumption goods: a traded good and a composite
non-traded good whose prices are denoted by ![]() and
and ![]() respectively. We assume that the
law of one price holds for the traded good. Then
respectively. We assume that the
law of one price holds for the traded good. Then
![]() where
where
![]() is the nominal exchange rate,
and
is the nominal exchange rate,
and
![]() is the foreign price of the
traded good. Below we will relax this assumption. We also set
is the foreign price of the
traded good. Below we will relax this assumption. We also set
![]() implying that
implying that
![]() .
.
The real exchange rate (![]() ) is defined as
the ratio between the price of traded goods and the aggregate price
of non-traded goods,
) is defined as
the ratio between the price of traded goods and the aggregate price
of non-traded goods,
![]() . From this
definition we deduce that
. From this
definition we deduce that
where
3 The Government
The government issues two nominal
liabilities: money, ![]() , and a domestic
bond,
, and a domestic
bond,
![]() that pays a gross nominal interest
rate
that pays a gross nominal interest
rate ![]() . It does not have access to foreign
debt and makes lump-sum transfers to the household-firm units,
. It does not have access to foreign
debt and makes lump-sum transfers to the household-firm units,
![]() pays interest on its domestic debt,
(
pays interest on its domestic debt,
(
![]() , and receives revenues from
seigniorage
, and receives revenues from
seigniorage![]() Its budget constraint is described by
Its budget constraint is described by
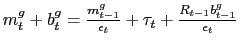 where
where
![]() and
and
![]() It follows a Ricardian fiscal policy by setting the lump-sum
transfers in order to satisfy the intertemporal version of its
budget constraint and its transversality condition
It follows a Ricardian fiscal policy by setting the lump-sum
transfers in order to satisfy the intertemporal version of its
budget constraint and its transversality condition
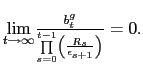
The description of monetary policy is motivated by the debate that emerged after the Asian crisis about the appropriate interest rate policy to fight against currency depreciation. We assume the government implements an interest rate policy that responds to the deviation of the current depreciation rate from a depreciation target.13 That is,
where ![]() is a continuous, differentiable, and
strictly positive function in its argument with
is a continuous, differentiable, and
strictly positive function in its argument with
![]() and
and
![]() ; and
; and
![]() and
and
![]() are the targets of the
nominal interest rate and the nominal depreciation rate that the
government wants to achieve.14
are the targets of the
nominal interest rate and the nominal depreciation rate that the
government wants to achieve.14
This policy can respond positively to the deviation of the
nominal depreciation rate from its target,
![]() , capturing the policy
recommendation of the IMF; or it can react negatively,
, capturing the policy
recommendation of the IMF; or it can react negatively,
![]() , describing, to some
extent, the policy recommendation of the opposite view.
Nevertheless we exclude the cases
, describing, to some
extent, the policy recommendation of the opposite view.
Nevertheless we exclude the cases
![]() 15 In other words,
the interest rate policy corresponds to (2)
with
15 In other words,
the interest rate policy corresponds to (2)
with
![]() and
either
and
either
![]() or
or
![]()
2.2 The Household-Firm Unit
There is a large number of identical household-firm units. They have perfect foresight, live infinitely and derive utility from consuming, not working, and liquidity services of money. The intertemporal utility function of the representative unit is described by
where
![]() corresponds to the subjective
discount rate,
corresponds to the subjective
discount rate, ![]() and
and ![]() denote the consumption of traded and non-traded goods respectively,
denote the consumption of traded and non-traded goods respectively,
![]() and
and
![]() are the labor allocated to the
production of the traded good and the non-traded good, and
are the labor allocated to the
production of the traded good and the non-traded good, and
![]() refers to real money holdings measured
with respect to foreign currency. The specification in (3) assumes separability in the single period utility
function among consumption, labor, and real money balances. Hence
there are no distortionary effects of transactions money
demand.16 Moreover the utility function is
separable in
refers to real money holdings measured
with respect to foreign currency. The specification in (3) assumes separability in the single period utility
function among consumption, labor, and real money balances. Hence
there are no distortionary effects of transactions money
demand.16 Moreover the utility function is
separable in
![]()
![]()
![]() and
and
![]() This allows us to derive
analytical results in the determinacy of equilibrium
analysis. To complete the characterization we also make the
following assumption.
This allows us to derive
analytical results in the determinacy of equilibrium
analysis. To complete the characterization we also make the
following assumption.
Assumption 1. a)![]()
![]()
![]()
![]() and
and
![]() are twice continuously
differentiable; and b)
are twice continuously
differentiable; and b) ![]()
![]() and
and ![]() are strictly
increasing (
are strictly
increasing (
![]()
![]()
![]() ) and
strictly concave (
) and
strictly concave (![]()
![]()
![]() ), whereas
), whereas
![]() and
and ![]() are
strictly decreasing (
are
strictly decreasing (
![]()
![]() ) and strictly concave
(
) and strictly concave
(![]()
![]() ).
).
The household-firm unit produces a flexible-price traded good and a sticky-price non-traded intermediate differentiated good by employing labor from perfectly competitive markets. For simplicity we assume that there is zero labor mobility.17 The technologies are described by
where
![]() and
and
![]() denote the labor hired by
the household-firm unit for the production of the traded good and
the non-traded good, respectively. The technologies satisfy the
following assumption.
denote the labor hired by
the household-firm unit for the production of the traded good and
the non-traded good, respectively. The technologies satisfy the
following assumption.
Assumption 2.
![]() and
and
![]() are twice continuously
differentiable, strictly increasing (
are twice continuously
differentiable, strictly increasing (
![]()
![]() ), and strictly concave
(
), and strictly concave
(![]()
![]() )
)![]()
Consumption of the non-traded good,
![]() is a composite good made of a
continuum of intermediate differentiated goods. The aggregator
function is of the Dixit-Stiglitz type. Each household-firm unit is
the monopolistic producer of one variety of non-traded intermediate
goods. The demand for the intermediate good is of the form
is a composite good made of a
continuum of intermediate differentiated goods. The aggregator
function is of the Dixit-Stiglitz type. Each household-firm unit is
the monopolistic producer of one variety of non-traded intermediate
goods. The demand for the intermediate good is of the form
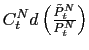 satisfying
satisfying
![]() and
and
![]() with
with
![]() where
where ![]() denotes the level of aggregate demand for the non-traded good,
denotes the level of aggregate demand for the non-traded good,
![]() is the nominal price of
the intermediate non-traded good produced by the household-firm
unit, and
is the nominal price of
the intermediate non-traded good produced by the household-firm
unit, and ![]() is the price of the composite
non-traded good. The unit sets the price of the good it supplies,
is the price of the composite
non-traded good. The unit sets the price of the good it supplies,
![]() , taking the level of
aggregate demand for the good as given. Specifically, the
monopolist is constrained to satisfy demand at that price. That
is,
, taking the level of
aggregate demand for the good as given. Specifically, the
monopolist is constrained to satisfy demand at that price. That
is,
Following Rotemberg (1982), we introduce nominal price
rigidities for the intermediate non-traded good. The household-firm
unit faces a resource cost of the type
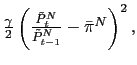 where
where
![]() is the steady-state level of
the gross non-traded goods inflation.
is the steady-state level of
the gross non-traded goods inflation.
There are incomplete markets. The representative household-firm
unit has access to the following two risk free bonds: a government
domestic bond, ![]() , that pays a gross nominal
interest rate
, that pays a gross nominal
interest rate ![]() and a foreign bond,
and a foreign bond,
![]() that pays a gross foreign
interest rate
that pays a gross foreign
interest rate
![]() In addition, the unit receives
income from working,
In addition, the unit receives
income from working,
![]() ,
transfers from the government,
,
transfers from the government, ![]() , and
dividends. Then the flow budget constraint in units of the traded
good can be written as
, and
dividends. Then the flow budget constraint in units of the traded
good can be written as
where
![]()
![]() with
with ![]() and
and
Equation (5) says that the end-of-period real
financial domestic assets (money plus domestic bond) can be worth
no more than the real value of financial domestic wealth, brought
into the period, plus the sum of wage income, transfers, and
dividends (
![]() ) net of consumption. The
dividends described in (6) correspond to the
difference between sale revenues and costs, taking into account
that through the firm-side the representative unit can hold foreign
debt,
) net of consumption. The
dividends described in (6) correspond to the
difference between sale revenues and costs, taking into account
that through the firm-side the representative unit can hold foreign
debt,
![]() . For holdings of foreign debt
the unit pays interests (
. For holdings of foreign debt
the unit pays interests (
![]() Moreover
the unit is subject to a Non-Ponzi game condition
Moreover
the unit is subject to a Non-Ponzi game condition
where
![]()
The problem of the household-firm unit consists of choosing the
set of sequences
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() in order to maximize
(3) subject to (4),
(5), (6) and (7), given the initial condition
in order to maximize
(3) subject to (4),
(5), (6) and (7), given the initial condition ![]() and the set of sequences {
and the set of sequences {
![]() ,
, ![]() ,
,
![]()
![]()
![]()
![]()
![]() ,
, ![]() ,
,
![]() Note that since the utility
function specified in (3) implies that the
preferences of the agent display non-sasiation, then both
constraints (5) and (7) hold
with equality. The Appendix contains a detailed derivation of the
necessary conditions for optimization. Imposing these conditions
along with the market clearing conditions in the labor markets, the
equilibrium symmetry (
Note that since the utility
function specified in (3) implies that the
preferences of the agent display non-sasiation, then both
constraints (5) and (7) hold
with equality. The Appendix contains a detailed derivation of the
necessary conditions for optimization. Imposing these conditions
along with the market clearing conditions in the labor markets, the
equilibrium symmetry (
![]() and
and
![]() the market
clearing condition for the non-traded good
the market
clearing condition for the non-traded good
and the definitions
![]()
![]() and
and
![]() we obtain
we obtain
where
![]() corresponds to the marginal cost of producing the non-traded good.
In addition equilibrium in the traded good market implies that
corresponds to the marginal cost of producing the non-traded good.
In addition equilibrium in the traded good market implies that
The interpretation of these equations is straightforward. Condition (9) corresponds to an Uncovered Interest Parity condition (UIP) that equalizes the returns of the foreign and domestic bonds. Equation (10) makes the marginal rate of substitution between labor, assigned to the production of the traded good, and consumption of the traded good equal to the marginal product of labor in the production of the traded good. Equations (11) and (12) are the standard Euler equations for consumption of the traded good and consumption of the non-traded good. Equation (13) corresponds to the augmented Phillips curve for the sticky-price non-traded goods inflation. And (14) describes the dynamics of the current account deficit.
2.3 Capital Markets
We introduce imperfect international capital markets using the following ad-hoc supply curve of funds
and where
![]() corresponds to the country-specific risk premium, and
corresponds to the country-specific risk premium, and ![]() is the risk free international interest rate. This
specification captures the idea that the small borrowing economy
faces a world interest rate,
is the risk free international interest rate. This
specification captures the idea that the small borrowing economy
faces a world interest rate,
![]() , that increases when the stock
of foreign debt,
, that increases when the stock
of foreign debt,
![]() , is above its long run level,
, is above its long run level,
![]() . Then as the external debt
grows, so does the risk of default, and in order to compensate the
lenders for this risk, the economy has to pay them a premium over
the risk free international interest rate. We also assume that the
long-run level of foreign stock of debt is positive.
. Then as the external debt
grows, so does the risk of default, and in order to compensate the
lenders for this risk, the economy has to pay them a premium over
the risk free international interest rate. We also assume that the
long-run level of foreign stock of debt is positive.
Assumption 3. The long-run level of the foreign stock
of debt is positive:
![]()
By introducing (15), we "close the small open economy" and avoid the unit root problem, as discussed in Schmitt-Grohé and Uribe (2003). This will allow us to pursue a meaningful analysis of the dynamics of the non-linear equations that describe the economy, using a log-linear approximation.18
2.4 A Perfect Foresight Equilibrium
We are ready to provide a definition of a perfect foresight equilibrium in this economy.
Since fiscal policy is Ricardian, this definition ignores the
budget constraint of the government and its transversality
condition. The definition also ignores real money balances. This is
because monetary policy is described as an interest rate policy in
(2),and real balances enter in the utility
function in a separable way. In addition, note that once we solve
for
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() it is
possible to retrieve the set of sequences
it is
possible to retrieve the set of sequences
![]()
![]()
![]()
![]()
![]()
![]()
![]() using (1), (5), and equations (41)-(44), (46), and (48) that are
presented in the Appendix.
using (1), (5), and equations (41)-(44), (46), and (48) that are
presented in the Appendix.
2.5 The Determinacy of Equilibrium Analysis
In order to pursue the determinacy of
equilibrium analysis, we log-linearize the system of equations that
describe the dynamics of this economy around a steady state
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . In the Appendix we
characterize this steady state.
. In the Appendix we
characterize this steady state.
Log-linearizing the equations of Definition 1 around the steady-state yields
where
![]() and
and
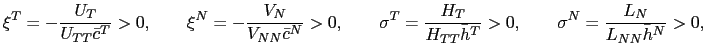
![$\displaystyle \kappa=\frac{1}{\bar{b}^{\ast}}\left[ \bar{c}^{T}+\frac{F_{T}\bar{h} ^{T}\sigma^{T}\omega^{T}}{\left( \sigma^{T}+\omega^{T}\right) \xi^{T} }\right] >0,\text{ \ and \ \ }\varphi=\left[ \frac{(\mu-1)\bar{c}^{N}} {\beta\gamma\bar{\epsilon}^{2}}\right] \left[ \frac{\bar{c}^{N}(\sigma ^{N}+\omega^{N})}{G_{N}\bar{h}^{N}\sigma^{N}\omega^{N}}+\frac{1}{\xi^{N} }\right] >0, $](img220.gif)
whose signs are derived using Assumptions 1, 2 and 3. Equations (16 )-(21) correspond to the reduced log-linear representations of the interest rate policy, the UIP condition, the Euler equation for consumption of the non-traded good, the augmented Phillips curve, the current account equation, and the Euler equation for consumption of the traded good, respectively.
Our main goal is to show that the policy in (16) is prone to induce multiple equilibria in the
economy described by equations (17
)-(21). Proving this implies that this
policy can cause fluctuations in the economy that are driven by
people's self-fulfilling beliefs rather than fundamentals. In fact,
before we provide a formal proof, it is worth developing a simple
intuition. To do so, it is sufficient to concentrate on equations
(16)-(19). Note
that given the international interest rate,
![]() then the policy
(16) and the UIP condition (17) determine the dynamics of the depreciation rate,
then the policy
(16) and the UIP condition (17) determine the dynamics of the depreciation rate,
![]() and the nominal interest
rate,
and the nominal interest
rate,
![]() Moreover, the nominal interest
rate,
Moreover, the nominal interest
rate,
![]() is not affected by either the
non-traded good inflation,
is not affected by either the
non-traded good inflation,
![]() or the consumption of
the non-traded good,
or the consumption of
the non-traded good, ![]() . Taking this into
account, we can construct the following self-fulfilling
equilibrium.
. Taking this into
account, we can construct the following self-fulfilling
equilibrium.
Assume that agents, in response to a "sunspot," expect
a higher non-traded good inflation in the next period. Since the
interest rate policy does not react to these expectations, then the
real interest rate measured with respect to the expected non-traded
good inflation,
![]() declines.19 In response, households increase
consumption of non-traded goods - see (18) - which leads firms to raise their prices,
inducing a higher non-traded inflation - see (19). But by doing this, firms end validating the
original non-traded inflation expectations.
declines.19 In response, households increase
consumption of non-traded goods - see (18) - which leads firms to raise their prices,
inducing a higher non-traded inflation - see (19). But by doing this, firms end validating the
original non-traded inflation expectations.
This simple intuition is appealing but incomplete, unless we show that all the equilibrium conditions (16)-(21) are satisfied on the entire equilibrium path. In other words, we need to characterize formally the equilibrium of this economy. To accomplish this, we start by writing equations (16)-(21) as
Then, we use this system to find and to compare the dimension of its unstable subspace with the number of non-predetermined variables.20 If the dimension of this subspace is smaller than the number of non-predetermined variables, then, from the results by Blanchard and Kahn (1980), we can infer that there exist multiple perfect foresight equilibria. This forms the basis for the existence of self-fulfilling fluctuations.
The following Proposition states the main result of the determinacy of equilibrium analysis: an interest rate policy that raises or lowers the nominal interest rate in response to current currency depreciation leads to multiple perfect foresight equilibria or, equivalently, to real indeterminacy.
- a) if
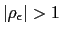 then the degree of indeterminacy is of order 1.21
then the degree of indeterminacy is of order 1.21 - b) if
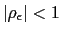 then the degree of indeterminacy is of order 2.
then the degree of indeterminacy is of order 2.
Proof. The eigenvalues of the matrix ![]() in (23) correspond to
the roots of the characteristic equation
in (23) correspond to
the roots of the characteristic equation
![]() Using
the definition of
Using
the definition of ![]() in (23), this equation can be written as
in (23), this equation can be written as
where
![$\displaystyle \mathcal{P}^{f}(v)=\left[ v^{2}-\left( 1+\frac{1+\psi}{\beta}+\psi\kappa \xi^{T}\right) v+\frac{1+\psi}{\beta}\right] \left[ v^{2}-\left( 1+\frac{1}{\beta}+\varphi\xi^{N}\right) v+\frac{1}{\beta}\right] . $](img244.gif)
By Lemma 4 in the Appendix,
![]() has real roots
satisfying
has real roots
satisfying
![]()
![]() ,
,
![]() and
and
![]() The fifth
root of
The fifth
root of
![]() is
is
![]() Clearly, if
Clearly, if
![]() then
then
![]() whereas
if
whereas
if
![]() then
then
![]() Therefore, using this, the characterization of the roots of
Therefore, using this, the characterization of the roots of
![]() and (24), we can conclude the following. If
and (24), we can conclude the following. If
![]() then
then
![]() has three explosive
roots, namely
has three explosive
roots, namely
![]() ,
,
![]() and
and
![]() While if
While if
![]() then
then
![]() has two explosive
roots, namely
has two explosive
roots, namely
![]() and
and
![]() Hence,
regardless of whether
Hence,
regardless of whether
![]() or
or
![]() there are at most three explosive roots. Given that there are four
non-predetermined variables,
there are at most three explosive roots. Given that there are four
non-predetermined variables,
![]() ,
,
![]() ,
,
![]() and
and
![]() , then the number of
non-predetermined variables is greater than the number of explosive
roots. Applying the results of Blanchard and Kahn (1980), it
follows that there exists an infinite number of perfect foresight
equilibria converging to the steady state. Finally, parts a) and b)
follow from the difference between the number of non-predetermined
variables and the number of explosive roots, when
, then the number of
non-predetermined variables is greater than the number of explosive
roots. Applying the results of Blanchard and Kahn (1980), it
follows that there exists an infinite number of perfect foresight
equilibria converging to the steady state. Finally, parts a) and b)
follow from the difference between the number of non-predetermined
variables and the number of explosive roots, when
![]() and
and
![]() respectively.
respectively. ![]()
Proposition 1 has two important implications. First, provided that the fiscal policy is Ricardian, then the interest rate policy induces not only real indeterminacy but also nominal indeterminacy. That is, the nominal exchange rate is not pinned-down.22 This follows from the definition of the nominal depreciation rate, and the fact that the nominal exchange rate is also a non-predetermined variable. Second, and in contrast to the intuition provided above, Proposition 1 suggests that it is possible to construct self-fulfilling equilibria that are based on expectations of a different variable from the non-traded inflation. For instance, we can construct a self-fulfilling equilibrium driven by people's beliefs about currency depreciation. We will pursue this exercise in Section 4.
Table 1. Determinacy of Equilibrium Analysis - Degree of Responsiveness of Interest Rate Policy
|
The Simple Model - |
The Simple Model - |
The Full Model - |
The Full Model - |
|
|---|---|---|---|---|
Forward-Looking
|
M |
M |
M |
M |
|
Contemporaneous
|
M |
M |
M |
M |
|
Backward-Looking
|
M |
U |
M |
M or U |
Note: ![]() refers to multiple equilibria and
refers to multiple equilibria and ![]() refers to a unique equilibrium.
refers to a unique equilibrium.
The results of Proposition 1 also pose the
question of whether policies that respond exclusively to either the
future depreciation rate, a forward-looking policy
![]() or to the
past depreciation rate, a backward-looking policy
or to the
past depreciation rate, a backward-looking policy
![]() , can induce
multiple equilibria. The answer is yes and the analysis is provided
in the Appendix. In particular, we find that forward-looking
policies can still lead to multiple equilibria when the interest
rate response coefficient to future depreciation satisfies either
, can induce
multiple equilibria. The answer is yes and the analysis is provided
in the Appendix. In particular, we find that forward-looking
policies can still lead to multiple equilibria when the interest
rate response coefficient to future depreciation satisfies either
![]() or
or
![]() On the
contrary, backward-looking policies that are very aggressive with
respect to past depreciation, and satisfy
On the
contrary, backward-looking policies that are very aggressive with
respect to past depreciation, and satisfy
![]() will guarantee a unique equilibrium; whereas timid policies that
satisfy
will guarantee a unique equilibrium; whereas timid policies that
satisfy
![]() can lead to real indeterminacy. These results, as well as the
results from Proposition 1, are presented in
Table 1 in the columns labeled as "The Simple Model." 23
can lead to real indeterminacy. These results, as well as the
results from Proposition 1, are presented in
Table 1 in the columns labeled as "The Simple Model." 23
Note that the assumption of zero labor mobility is not crucial for the results of Proposition 1. In fact, it is possible to obtain similar analytical results under perfect labor mobility and some extra assumptions about the disutility of working.24 Then, what are the features of the model that drive these results? The crucial features are the following: the description of monetary policy as an interest rate feedback rule, non-traded goods price-stickiness, and the exclusive dependence of the policy on currency depreciation. By Sargent and Wallace (1975), we know that the first feature by itself leads to nominal indeterminacy of the exchange rate level (price level), in a flexible price model under a Ricardian fiscal policy. The second characteristic together with the policy elucidate why nominal indeterminacy turns into real indeterminacy. And finally, the first two features, in tandem with the exclusive response of the policy to depreciation, are what explains why multiple equilibria arise, to some extent, regardless of the degree of responsiveness of the policy.25
This simple model suffers from at least two drawbacks. On one hand, there is no feature that captures the fact that the economy is in a crisis. On the other hand, the dynamics of non-traded consumption and inflation, that are supported as a self-fulfilling equilibrium, are completely at odds with the stylized facts of a "Sudden Stop." In particular, the self-fulfilling equilibrium that we constructed above implies that non-traded consumption and inflation are positively correlated. In contrast, the stylized facts suggest that there was a strong decline in consumption accompanied by an increase in inflation. To improve the model, in the next section, we will add some extra features.
3 The Full Model
In this section we enrich the simple model in several dimensions. First, in accord with Burnstein, Eichenbaum, and Rebelo (2005a,b), we introduce non-traded distribution services. This together with price stickiness are crucial to explain the large movements in real exchange rates after large devaluations. Second, following Lahiri and Vegh (2002) and Christiano, Gust, and Roldos (2004) we assume that the household-firm unit requires domestic and international loans to hire labor and to purchase an imported intermediate input, respectively. This is important to obtain a decline in output and demand in the midst of the crisis, when interest rates rise. Third, as in the new literature about currency crises, we introduce a collateral constraint. That is, international loans must be guaranteed by physical assets such as capital. This will help to provide a definition of a crisis. Fourth, we consider a utility function that is not separable in the two types of consumption. We proceed to explain how we introduce these features and their influence in the previous equations.
3.1 The Additional Features
As in Burnstein et al. (2003), we
assume that the traded good needs to be combined with some
non-traded distribution services before it is consumed. In order to
consume one unit of the traded good, it is required ![]() units of the basket of differentiated non-traded goods.
Let
units of the basket of differentiated non-traded goods.
Let
![]()
![]() and
and ![]() be the producer's price of the
traded good, the consumer's price of the traded good, and the
general price level of the basket of differentiated non-traded
goods, respectively. All of them are expressed in domestic
currency. Hence the consumer's price is simply
be the producer's price of the
traded good, the consumer's price of the traded good, and the
general price level of the basket of differentiated non-traded
goods, respectively. All of them are expressed in domestic
currency. Hence the consumer's price is simply
![]() And since PPP holds at the production level of the traded good (
And since PPP holds at the production level of the traded good (
![]() ), and
the foreign price of the traded good is normalized to one (
), and
the foreign price of the traded good is normalized to one (
![]() ), we have that
), we have that
![]()
The production of the differentiated non-traded good is still demand determined by
where
![]()
![]()
![]() denotes the level of aggregate
demand for the non-traded good,
denotes the level of aggregate
demand for the non-traded good,
![]() is the price of the
intermediate non-traded good set by the household-firm unit, and
is the price of the
intermediate non-traded good set by the household-firm unit, and
![]() corresponds to the level of
aggregate consumption of the traded good. But now the demand
requirements come from two sources.26They come from
consumption of non-traded goods
corresponds to the level of
aggregate consumption of the traded good. But now the demand
requirements come from two sources.26They come from
consumption of non-traded goods
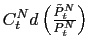 that provide utility, and from non-traded distribution services
that provide utility, and from non-traded distribution services
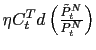 that are necessary to bring one unit of the traded good to the
household-firm unit. Note that there is no difference between
non-traded consumption goods and non-traded distribution services.
As a consequence, in equilibrium the basket of non-traded goods
required to distribute traded goods will have the same composition
as the non-traded basket consumed by the household-firm unit.
that are necessary to bring one unit of the traded good to the
household-firm unit. Note that there is no difference between
non-traded consumption goods and non-traded distribution services.
As a consequence, in equilibrium the basket of non-traded goods
required to distribute traded goods will have the same composition
as the non-traded basket consumed by the household-firm unit.
The introduction of the loan requirements and the collateral
constraint in the model follows Christiano et al. (2004). The
household-firm unit requires domestic loans to hire labor (
![]() and
and
![]() ), and international loans
to buy an imported input (
), and international loans
to buy an imported input (![]() ), that will be
used in the production of the traded good. These loans are obtained
at the beginning of the period and repaid at the end of the period.
In this sense, they represent short-term debt and differ from
long-term foreign debt
), that will be
used in the production of the traded good. These loans are obtained
at the beginning of the period and repaid at the end of the period.
In this sense, they represent short-term debt and differ from
long-term foreign debt
![]() We do not model, however,
the financial institutions that provide these loans. Instead, we
assume that the domestic loans are provided by the government,
whereas foreign loans are supplied by foreign creditors.27 For
these loans the unit pays interests
We do not model, however,
the financial institutions that provide these loans. Instead, we
assume that the domestic loans are provided by the government,
whereas foreign loans are supplied by foreign creditors.27 For
these loans the unit pays interests
![]() and (
and (
![]() that
are accrued between periods, where
that
are accrued between periods, where ![]() is the
domestic nominal interest rate, and
is the
domestic nominal interest rate, and ![]() is
the international interest rate. The latter is assumed to be
constant and equal to
is
the international interest rate. The latter is assumed to be
constant and equal to
![]() .
.
The production technology of the traded good uses labor (
![]() ), an imported input
(
), an imported input
(![]() ), and capital (
), and capital (![]() );
whereas the technology for the non-traded intermediate
differentiated goods only requires labor (
);
whereas the technology for the non-traded intermediate
differentiated goods only requires labor (
![]() ) and capital (
) and capital (![]() ). That is,
). That is,
Furthermore, as in Christiano et al. (2004) and Mendoza and Smith (2002), among others, capital is assumed to be time-invariant, does not depreciate, and there is no technology to making it bigger. Under these new features, the dividends that the household-firm unit receives can be written as
where
![]() with
with ![]() and
and
![]()
To model the crisis, we follow Christiano et al. (2004) by imposing the following collateral constraint:
where ![]() and
and ![]() represent the real value, in units of foreign currency, of one unit
of capital for the production of the non-traded and traded goods,
respectively, and
represent the real value, in units of foreign currency, of one unit
of capital for the production of the non-traded and traded goods,
respectively, and ![]() is the fraction of these
stocks that foreign creditors accept as collateral. The constraint
(27) says that the total value of foreign
and domestic debt, that the representative household-firm unit has
to pay to completely eliminate the debt of the firm by the end of
period
is the fraction of these
stocks that foreign creditors accept as collateral. The constraint
(27) says that the total value of foreign
and domestic debt, that the representative household-firm unit has
to pay to completely eliminate the debt of the firm by the end of
period ![]() cannot exceed the value of the
collateral. The crisis makes this constraint unexpectedly binding
in every period henceforth without the possibility of being
removed.
cannot exceed the value of the
collateral. The crisis makes this constraint unexpectedly binding
in every period henceforth without the possibility of being
removed.
Finally, we relax the assumption in (3) of a
separable utility function between the two types of consumption,
![]() . But we will still
assume separability among consumption, labor, and real money
balances. We proceed to study how all these features influence the
previous optimal conditions.
. But we will still
assume separability among consumption, labor, and real money
balances. We proceed to study how all these features influence the
previous optimal conditions.
3.2 The New Equilibrium Conditions
The problem that the household firm
unit has to solve is similar to the one presented in the simple
model. The agent chooses the set of sequences
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() in order to maximize
in order to maximize
![$\displaystyle \overset{\infty}{\sum_{t=0}}\beta^{t}\left[ \tilde{U}(c_{t}^{T},c_{t} ^{N})+H(h_{t}^{T})+L(h_{t}^{N})+J(m_{t})\right] $](img362.gif)
subject to the budget constraint
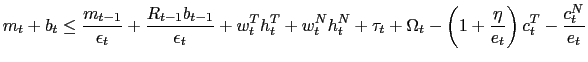
and the constraints (7), (25), (26), and (27), given the initial conditions
![]()
![]() and
and
![]() and the set of sequences {
and the set of sequences {
![]() ,
, ![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]() The optimization conditions
together with symmetry and market clearing conditions can be used
to find the laws of motion of the economy. They correspond to
(1), (2), (27) with equality,
The optimization conditions
together with symmetry and market clearing conditions can be used
to find the laws of motion of the economy. They correspond to
(1), (2), (27) with equality,
where
![]() and
and
![]() are the Lagrange multipliers of
the collateral constraint and the budget constraint. The latter
multiplier evolves according to the asset pricing equation
are the Lagrange multipliers of
the collateral constraint and the budget constraint. The latter
multiplier evolves according to the asset pricing equation
Equations (28)-(34) are equivalent to equations (8)-(14) in the simple model.28 Therefore they have a similar interpretation. Equations (35)-(37) correspond to the optimal conditions that determine the demands for labor (for the production of the traded and non-traded good) and for the imported input; and (38) is the intratemporal condition that makes the marginal rate of substitution between labor, assigned to the production of the non-traded good, and consumption of the non-traded good equal to the real salary measured in units of the non-traded good.
The new laws of motion reveal that the additional features have
some important consequences. On one hand, distribution services
affect the relative price of the traded good at the consumer level
with respect to the nominal exchange rate. In the simple model this
relative price was equal to one. In the full model this price is
![]() which depends on the
distribution costs parameter
which depends on the
distribution costs parameter ![]() From (30) and (31), it is clear
that through this price, distribution costs affect, in equilibrium,
the optimal intratemporal decisions between labor and consumption
of the traded good, as well as the optimal intertemporal choices
for consumption of the traded good. On the other hand, distribution
services generate an extra demand of non-traded goods, as is
captured by the last term,
From (30) and (31), it is clear
that through this price, distribution costs affect, in equilibrium,
the optimal intratemporal decisions between labor and consumption
of the traded good, as well as the optimal intertemporal choices
for consumption of the traded good. On the other hand, distribution
services generate an extra demand of non-traded goods, as is
captured by the last term,
![]() , of the right hand side of
(28). This extra demand also influences
the dynamics of non-traded goods inflation, as can be seen in
(33).
, of the right hand side of
(28). This extra demand also influences
the dynamics of non-traded goods inflation, as can be seen in
(33).
The binding collateral constraint generates an endogenous risk
premium, as reflected by the modified UIP condition in (29). In fact, because of this constraint, the
effective international interest rate that domestic agents pay
becomes
![]() Thus, raising
external debt
Thus, raising
external debt
![]() not only requires the payment
of interests (
not only requires the payment
of interests (
![]() ), but also tightens
the binding constraint (
), but also tightens
the binding constraint (
![]() ). This generates an
additional interest cost.29
). This generates an
additional interest cost.29
The requirement of loans to hire labor and the binding
collateral constraint affect the labor demand decisions, as can be
inferred from (35) and (36). Keeping the rest constant, these two features and
the fact that in the short run
![]() imply the following.
Increases in the effective interest rate,
imply the following.
Increases in the effective interest rate,
![]() push the cost of hiring
labor up, which in turn discourages the demands for labor for the
production of the traded and non-traded goods.
push the cost of hiring
labor up, which in turn discourages the demands for labor for the
production of the traded and non-traded goods.
The optimal condition for demand of the imported input, equation
(37), equalizes the marginal product of this
input to the effective cost of foreign working capital,
![]() that is necessary to
import it. As the constraint tightens and
that is necessary to
import it. As the constraint tightens and ![]() goes up, the effective cost raises and the demand for the imported
input decreases. Furthermore, the purchases of this input influence
the current account equation (34). A decrease
in the imported input can cause an improvement in the current
account deficit. This improvement is almost immediate, given the
assumption that external short term loans to finance the
intermediate input have to be repaid at the end of the period, and
not at the beginning of next period.
goes up, the effective cost raises and the demand for the imported
input decreases. Furthermore, the purchases of this input influence
the current account equation (34). A decrease
in the imported input can cause an improvement in the current
account deficit. This improvement is almost immediate, given the
assumption that external short term loans to finance the
intermediate input have to be repaid at the end of the period, and
not at the beginning of next period.
Finally, it is possible to derive the equilibrium value of the prices of capital. The equilibrium value of these asset prices are described by
where ![]() and
and ![]() are the
marginal products of capital in the production of the traded and
non-traded goods, respectively.
are the
marginal products of capital in the production of the traded and
non-traded goods, respectively.
3.3 The Determinacy of Equilibrium Analysis
Using this set-up, the definition of equilibrium under a currency crisis is the following.
Note that, as in Christiano et al. (2004) among others, we model
the crisis as a collateral constraint that binds in every period.
Nevertheless, at the steady state, the shadow price of the
collateral constraint is equal to zero. To see this use (39) in tandem with
![]() to obtain
to obtain
![]() This implies that the
collateral constraint is marginally not binding at the
steady state. Hence the credit restrictions disappear marginally.
In contrast, in the short run the shadow price of the collateral
constraint may vary as
This implies that the
collateral constraint is marginally not binding at the
steady state. Hence the credit restrictions disappear marginally.
In contrast, in the short run the shadow price of the collateral
constraint may vary as ![]() changes. When
changes. When
![]() is high then the collateral
constraint tightens.
is high then the collateral
constraint tightens.
As before, to pursue the determinacy of equilibrium analysis, we log-linearize the system of equations around the perfect-foresight steady state. Then we characterize the dimension of the unstable subspace of the system and compare it to the number of non-predetermined variables. By log-linearizing the system, we are following the same approach that Kiyotaki and Moore (1997) adopt to solve for an equilibrium of a model with a binding collateral constraint. This precludes the possibility of exploring non-linear equilibrium dynamics.30Moreover, since it is not possible to derive analytical results, we have to rely on numerical simulations. We use the following functional forms. For consumption and labor preferences we use
![$\displaystyle \tilde{U}(c_{t}^{T},c_{t}^{N})=\frac{\left[ (\alpha)^{\frac{1}{\text{a}} }\left( c_{t}^{T}\right) ^{\frac{\text{a}-1}{\text{a}}}+(1-\alpha)^{\frac {1}{\text{a}}}\left( c_{t}^{N}\right) ^{\frac{\text{a}-1}{\text{a}}}\right] ^{\left( \frac{\text{a}}{\text{a}-1}\right) (1-\sigma)}-1}{1-\sigma} $](img434.gif)
and
where
![]() ,
,
![]() a
a![]() and
and
![]() whereas for technologies we
utilize
whereas for technologies we
utilize
![$\displaystyle F\left( h_{t}^{T},K^{T},I_{t}\right) =\left\{ \varpi\left[ \vartheta _{1}(h_{t}^{T})^{\theta^{T}}(K^{T})^{1-\theta^{T}}\right] ^{\frac{\chi -1}{\chi}}+(1-\varpi)\left[ \vartheta_{2}I_{t}\right] ^{\frac{\chi-1}{\chi} }\right\} ^{\frac{\chi}{\chi-1}} $](img440.gif)
and
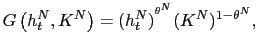
where
![]() and
and
![]()
Table 2.
| 1.06 | |
| 0.943 | |
| 1.16 | |
| 17.5 | |
| 6 | |
| 0.85 | |
| 0.185 | |
| 0.7 | |
| a | 0.4 |
| 2 | |
| 4.59 | |
| 5 | |
| 0.6 | |
| 1.4 | |
| 3.5 | |
| 0.5 | |
| 0.7 | |
| 0.64 | |
| 1 | |
| 2 |
The values of the parameters are mainly borrowed from the
calibration by Christiano et al. (2004), except for the
intratemporal elasticity of substitution ![]() a)
a)![]() the parameter related to distribution
services (
the parameter related to distribution
services (![]() , the parameter that governs the
degree of price stickiness (
, the parameter that governs the
degree of price stickiness (![]() and the
parameter associated with the degree of imperfect competition
(
and the
parameter associated with the degree of imperfect competition
(![]() 31 We do not pick any particular
value for the interest rate response coefficient to currency
depreciation (
31 We do not pick any particular
value for the interest rate response coefficient to currency
depreciation (
![]() ), since we will study how
this parameter affects the determinacy of equilibrium. We choose
values for "a" and
), since we will study how
this parameter affects the determinacy of equilibrium. We choose
values for "a" and ![]() that
are in line with similar values used in the distribution services
literature.32 Since there are no robust estimates
of a New-Keynesian Phillips curve for emerging economies, we choose
values for
that
are in line with similar values used in the distribution services
literature.32 Since there are no robust estimates
of a New-Keynesian Phillips curve for emerging economies, we choose
values for ![]() and
and ![]() that are
consistent with the values used in the closed economy literature
about nominal price rigidities.33 Table 2 summarizes
the parametrization.
that are
consistent with the values used in the closed economy literature
about nominal price rigidities.33 Table 2 summarizes
the parametrization.
Using this parametrization, we study how the determinacy of
equilibrium varies with respect to the response coefficient to
depreciation (
![]() ) of the policy (2) and other structural parameters. As an illustrative
case, we focus on the experiment of varying the intratemporal
elasticity of substitution (a), while keeping the other structural
parameters constant. The results are presented in Figure 1, where a
cross "x" denotes combinations of
) of the policy (2) and other structural parameters. As an illustrative
case, we focus on the experiment of varying the intratemporal
elasticity of substitution (a), while keeping the other structural
parameters constant. The results are presented in Figure 1, where a
cross "x" denotes combinations of
![]() and "a" under which the
policy induces multiple cyclical equilibria, whose degree of
indeterminacy is of order one; and a dot "." represents parameter
combinations under which the policy induces multiple cyclical
equilibria, whose degree of indeterminacy is of order two.34 As
can be seen in this figure, a policy that responds to current
currency depreciation, by raising (
and "a" under which the
policy induces multiple cyclical equilibria, whose degree of
indeterminacy is of order one; and a dot "." represents parameter
combinations under which the policy induces multiple cyclical
equilibria, whose degree of indeterminacy is of order two.34 As
can be seen in this figure, a policy that responds to current
currency depreciation, by raising (
![]() with
with
![]() ) or lowering (
) or lowering (
![]() with
with
![]() ) the nominal interest
rate, can induce multiple equilibria regardless of the
intratemporal elasticity of substitution "a."
) the nominal interest
rate, can induce multiple equilibria regardless of the
intratemporal elasticity of substitution "a."
Figure 1. Contemporaneous Policies

Figure 1: Characterization of the equilibrium for interest rate
policies
![]() varying the degree of responsiveness to currency
depreciation (
varying the degree of responsiveness to currency
depreciation (
![]() ) and
the intratemporal elasticity of substitution (a). It is assumed
that
) and
the intratemporal elasticity of substitution (a). It is assumed
that
![]() . A cross "x" denotes parameter combinations under which
the policy induces multiple cyclical equilibria whose degree of
indeterminacy is of order one. A dot "." represents parameter
combinations under which the policy induces multiple cyclical
equilibria whose degree of indeterminacy is of order
two.
. A cross "x" denotes parameter combinations under which
the policy induces multiple cyclical equilibria whose degree of
indeterminacy is of order one. A dot "." represents parameter
combinations under which the policy induces multiple cyclical
equilibria whose degree of indeterminacy is of order
two.
Figure 1 - Detailed Description: Figure 1 shows the characterization of
the equilibrium for contemporaneous interest rate policies
-.5in0pt-.5in0pt-.5in0pt-.5in0pt-.5in0pt-.5in0pt-.5in1046pt-.5in1396pt varying
the degree of responsiveness to currency depreciation (
![]() ) and the
intratemporal elasticity of substitution (a). The figure measures
) and the
intratemporal elasticity of substitution (a). The figure measures
![]() on the
vertical axis with
on the
vertical axis with
![]() and "a" on the horizontal axis with a
and "a" on the horizontal axis with a
![]() The figure
shows that for a
The figure
shows that for a
![]() , any interest
policy that satisfies
, any interest
policy that satisfies
![]() will induce multiple cyclical equilibria whose degree of
indeterminacy is of order one. In addition for a
will induce multiple cyclical equilibria whose degree of
indeterminacy is of order one. In addition for a
![]() , any interest
policy that satisfies
, any interest
policy that satisfies
![]() will induce multiple
cyclical equilibria whose degree of indeterminacy is of order two.
For
will induce multiple
cyclical equilibria whose degree of indeterminacy is of order two.
For
![]() and a
and a
![]() the interest
rate policy will lead to multiple equilibria, but depending on the
value of "a" the order of indeterminacy could be either one or
two.
the interest
rate policy will lead to multiple equilibria, but depending on the
value of "a" the order of indeterminacy could be either one or
two.
Experiments with respect to other structural parameters lead to similar results.35 This suggests that the results in the full set-up are similar to the ones in the simple set-up. But there is an important distinction. Now because of the binding collateral constraint, there exist self-fulfilling cycles or, equivalently, multiple cyclical equilibria. This is just a consequence of two mechanisms working together. On one hand, from the results in the simple model we have that this policy can induce self-fulfilling "non-cyclical" fluctuations. On the other hand, from Kiyotaki and Moore (1997) we know that the introduction of a binding collateral constraint can cause credit cycles. Hence the combination of the two mechanisms can lead to self-fulfilling cyclical equilibria. The following Proposition summarizes these results.
These results are not specific to the particular policy that we
consider. In the Appendix we study forward-looking policies,
![]() and
backward-looking policies,
and
backward-looking policies,
![]() . We find
that forward-looking policies always induce multiple cyclical
equilibria, as long as the response coefficient to future
depreciation satisfies either
. We find
that forward-looking policies always induce multiple cyclical
equilibria, as long as the response coefficient to future
depreciation satisfies either
![]() or
or
![]() .
Except for the presence of cycles these results coincide, to some
extent, with the ones from the simple model. On the other hand, for
backward-looking policies the coefficient of response to past
depreciation plays an important role in the characterization of the
equilibrium. That is, timid rules satisfying
.
Except for the presence of cycles these results coincide, to some
extent, with the ones from the simple model. On the other hand, for
backward-looking policies the coefficient of response to past
depreciation plays an important role in the characterization of the
equilibrium. That is, timid rules satisfying
![]() always induce multiple equilibria, while aggressive rules with
always induce multiple equilibria, while aggressive rules with
![]() can guarantee a unique equilibrium. Nevertheless, being aggressive
with respect to past depreciation (
can guarantee a unique equilibrium. Nevertheless, being aggressive
with respect to past depreciation (
![]() )
is a necessary but not a sufficient condition to guarantee a unique
equilibrium. Therefore, backward-looking policies can still
destabilize the economy by inducing self-fulfilling cyclical
fluctuations.
)
is a necessary but not a sufficient condition to guarantee a unique
equilibrium. Therefore, backward-looking policies can still
destabilize the economy by inducing self-fulfilling cyclical
fluctuations.
These results, as well as the results for a contemporaneous
policy
![]() are
summarized in Table 1 in the columns labeled as "The Full
Model." Note that our results do not support any of the views of
the debate about the right interest rate policy in the aftermath of
the Asian crisis. In fact, we unveil a peril that may be present in
both policy recommendations. What is crucial in our analysis is not
whether the government increases or decreases the interest rate;
instead, it is the feedback response of the nominal interest rate
to current, future, or past currency depreciation, that most of the
previous studies have ignored.
are
summarized in Table 1 in the columns labeled as "The Full
Model." Note that our results do not support any of the views of
the debate about the right interest rate policy in the aftermath of
the Asian crisis. In fact, we unveil a peril that may be present in
both policy recommendations. What is crucial in our analysis is not
whether the government increases or decreases the interest rate;
instead, it is the feedback response of the nominal interest rate
to current, future, or past currency depreciation, that most of the
previous studies have ignored.
It is possible to argue that, in the aftermath of a crisis, governments may also adjust the nominal interest rate in response to inflation. This raises the question of whether a policy that reacts to both the CPI-inflation and the depreciation rate can still induce aggregate instability in the economy. The answer to this question is affirmative making our previous results stronger. To some extent, the response to currency depreciation is crucial to explain the possibility of multiple equilibria. To see this, we can study the following interest rate policy
that reacts, positively or negatively, to current currency depreciation and, aggressively and positively, to past CPI-inflation.36
Figure 2. Responding to Past CPI Inflation and Current Depreciation

Figure 2: Characterization of the equilibrium for the rule
![]() varying the degrees of responsiveness to past
CPI-inflation (
varying the degrees of responsiveness to past
CPI-inflation (
![]() ) and to
current currency depreciation (
) and to
current currency depreciation (
![]() ). It is
assumed that
). It is
assumed that
![]() . A cross "x" denotes parameter combinations associated
with multiple equilibria whose degree of indeterminacy is of order
one. These equilibria can be cyclical or non-cyclical. A dot "."
represents parameter combinations associated with multiple
equilibria whose degree of indeterminacy is of order two. These
equilibria are cyclical and we name these combinations as "MCE(2)". The white regions represent parameter combinations under
which there exists a unique equilibrium.
. A cross "x" denotes parameter combinations associated
with multiple equilibria whose degree of indeterminacy is of order
one. These equilibria can be cyclical or non-cyclical. A dot "."
represents parameter combinations associated with multiple
equilibria whose degree of indeterminacy is of order two. These
equilibria are cyclical and we name these combinations as "MCE(2)". The white regions represent parameter combinations under
which there exists a unique equilibrium.
Figure 2 - Detailed Description:
Figure 2 shows the characterization of
the equilibrium for the rule
![]() varying the degrees of responsiveness to past CPI-inflation
(
varying the degrees of responsiveness to past CPI-inflation
(
![]() ) and to
current currency depreciation (
) and to
current currency depreciation (
![]() ). The
figure measures
). The
figure measures
![]() on the
vertical axis with
on the
vertical axis with
![]() and
and
![]() on the
horizontal axis with
on the
horizontal axis with
![]() The figure shows that for
The figure shows that for
![]() ,
any interest policy that satisfies
,
any interest policy that satisfies
![]() will induce multiple equilibria (cyclical and non-cyclical) whose
degree of indeterminacy is of order one. For the region within the
coordinates (
will induce multiple equilibria (cyclical and non-cyclical) whose
degree of indeterminacy is of order one. For the region within the
coordinates (
![]()
![]()
![]()
![]()
![]() and
and ![]() approximately, the rule will
induce multiple equilibria (cyclical and non-cyclical) whose degree
of indeterminacy is either of order one or two. For the region
within the coordinates (
approximately, the rule will
induce multiple equilibria (cyclical and non-cyclical) whose degree
of indeterminacy is either of order one or two. For the region
within the coordinates (
![]()
![]()
![]() and
and ![]() approximately, the rule will
lead to a unique equilibrium.
approximately, the rule will
lead to a unique equilibrium.
The results of the analysis are shown in Figure 2. We study how
variations of the degrees of responsiveness to past CPI-inflation
and current depreciation,
![]() and
and
![]() , affect the characterization
of the equilibrium. We observe that policies that respond to both
past CPI-inflation and currency depreciation can still
induce multiple equilibria. In fact, using the parametrization in
Table 2 and under the celebrated "Taylor coefficient",
, affect the characterization
of the equilibrium. We observe that policies that respond to both
past CPI-inflation and currency depreciation can still
induce multiple equilibria. In fact, using the parametrization in
Table 2 and under the celebrated "Taylor coefficient",
![]() any policy that responds to
currency depreciation will lead to real indeterminacy. Note also
that if the policy is positively aggressive with respect to current
depreciation,
any policy that responds to
currency depreciation will lead to real indeterminacy. Note also
that if the policy is positively aggressive with respect to current
depreciation,
![]() , then excessively
aggressive policies with respect to inflation, say any
, then excessively
aggressive policies with respect to inflation, say any
![]() will continue to
induce self-fulfilling equilibria. Nevertheless, this analysis also
highlights the importance of reacting aggressively to past
CPI-inflation in order to avoid destabilizing the economy.
will continue to
induce self-fulfilling equilibria. Nevertheless, this analysis also
highlights the importance of reacting aggressively to past
CPI-inflation in order to avoid destabilizing the economy.
There is still a relevant question that has not been answered. If the governments of the Asian economies followed these interest rate policies, then would it be possible to support the stylized facts of the aftermath of the crisis, the "Sudden Stop" phenomenon, as one of these self-fulfilling equilibria? An affirmative answer to this question would make our previous results more credible. This defines the goal of the next section.
4 Constructing a Self-fulfilling Cyclical Equilibrium
In this section, we use the full model in tandem with an interest rate policy that responds to currency depreciation, in order to construct a self-fulfilling cyclical equilibrium that replicates some of the stylized facts of the "Sudden Stop" phenomenon. In this equilibrium, the only source of cyclical fluctuations is the self-validation of people's beliefs about currency depreciation.
We assume the government follows an interest rate policy,
![]() , that responds
aggressively,
, that responds
aggressively,
![]() ,
to current depreciation,
,
to current depreciation,
![]() .37 This policy
captures the immediate reaction to currency depreciation.
Unfortunately, in the empirical literature that emerged after the
Asian crisis, there are no robust estimates for the
parameter
.37 This policy
captures the immediate reaction to currency depreciation.
Unfortunately, in the empirical literature that emerged after the
Asian crisis, there are no robust estimates for the
parameter
![]() . For illustrative purposes
we set
. For illustrative purposes
we set
![]() implying that the
government increases the interest rate proportionally more than the
increase in depreciation.
implying that the
government increases the interest rate proportionally more than the
increase in depreciation.
From Proposition 2 we know that varying
![]() will not preclude the
possibility of multiple equilibria. This, however, changes the
degree of indeterminacy. For
will not preclude the
possibility of multiple equilibria. This, however, changes the
degree of indeterminacy. For
![]() the degree of
indeterminacy is one.38 Then we can construct a
self-fulfilling cyclical equilibrium in which a "sunspot"
affects people's expectations of only one variable of the
economy, such as currency depreciation
the degree of
indeterminacy is one.38 Then we can construct a
self-fulfilling cyclical equilibrium in which a "sunspot"
affects people's expectations of only one variable of the
economy, such as currency depreciation![]() 39
Moreover, as long as
39
Moreover, as long as
![]() , increasing or reducing
, increasing or reducing
![]() will not change the
qualitative results that we will present, and that capture some of
the stylized facts of the "Sudden Stops."
will not change the
qualitative results that we will present, and that capture some of
the stylized facts of the "Sudden Stops."
We assume the crisis occurs exogenously. That is, the binding
collateral constraint is exogenously imposed at time ![]() as in Christiano et al. (2004). In this sense, we are
only interested in studying what happens in the economy at and in
the aftermath of the crisis. In what follows, therefore, we
concentrate exclusively in the equilibrium dynamics of the economy
at and after
as in Christiano et al. (2004). In this sense, we are
only interested in studying what happens in the economy at and in
the aftermath of the crisis. In what follows, therefore, we
concentrate exclusively in the equilibrium dynamics of the economy
at and after ![]()
Imagine that when the crisis hits the economy at time
![]() people develop expectations, in
response to a "sunspot", of a 10% higher domestic currency
nominal depreciation. By the determinacy of equilibrium analysis,
we know that these expectations will be self-validated. In
addition, they induce cycles as described by the impulse response
functions presented in Figures 3 and 4. In these figures, all the
variables but the multiplier of the collateral constraint are
measured as percentage deviations from the steady state. A quick
inspection reveals that at time
people develop expectations, in
response to a "sunspot", of a 10% higher domestic currency
nominal depreciation. By the determinacy of equilibrium analysis,
we know that these expectations will be self-validated. In
addition, they induce cycles as described by the impulse response
functions presented in Figures 3 and 4. In these figures, all the
variables but the multiplier of the collateral constraint are
measured as percentage deviations from the steady state. A quick
inspection reveals that at time ![]() and for some
subsequent periods, the self-fulfilling equilibrium captures the
following stylized facts of the "Sudden Stops": a decline in the
aggregate demand (consumptions of traded and non-traded goods and
aggregate consumption), a collapse in the domestic production
(traded output and non-traded output), a collapse in asset prices
(prices of traded and non-traded capital), a sharp correction in
the price of traded goods relative to non-traded goods, an
improvement in the current account deficit, a moderately higher
CPI-inflation, a more rapid currency depreciation, and higher
nominal interest rates. After some periods, domestic output and
aggregate demand increase, the current account deficit
deteriorates, and CPI-inflation, currency depreciation and interest
rates decrease. Then, the cycles are quickly dampened, and the
economy converges to the steady state.
and for some
subsequent periods, the self-fulfilling equilibrium captures the
following stylized facts of the "Sudden Stops": a decline in the
aggregate demand (consumptions of traded and non-traded goods and
aggregate consumption), a collapse in the domestic production
(traded output and non-traded output), a collapse in asset prices
(prices of traded and non-traded capital), a sharp correction in
the price of traded goods relative to non-traded goods, an
improvement in the current account deficit, a moderately higher
CPI-inflation, a more rapid currency depreciation, and higher
nominal interest rates. After some periods, domestic output and
aggregate demand increase, the current account deficit
deteriorates, and CPI-inflation, currency depreciation and interest
rates decrease. Then, the cycles are quickly dampened, and the
economy converges to the steady state. ![]()
We proceed to explain these results. The self-validated increase
in the nominal depreciation rate implies an increase in the nominal
exchange rate and, by the policy, leads to an increase in the
nominal interest rate at ![]() . Since the rule is
aggressive, the nominal interest rate rises by more than both the
expected non-traded good inflation rate and the expected traded
good inflation rate at time
. Since the rule is
aggressive, the nominal interest rate rises by more than both the
expected non-traded good inflation rate and the expected traded
good inflation rate at time ![]() .40
Hence, the real interest rate at
.40
Hence, the real interest rate at ![]() measured in
terms of either the expected traded inflation or the non-traded
inflation at
measured in
terms of either the expected traded inflation or the non-traded
inflation at ![]() goes up. Provided that this induces
an intertemporal substitution effect in consumption that more than
offsets any intratemporal substitution effect, then consumption of
the traded good and consumption of the non-traded good decline at
goes up. Provided that this induces
an intertemporal substitution effect in consumption that more than
offsets any intratemporal substitution effect, then consumption of
the traded good and consumption of the non-traded good decline at
![]() . This can be inferred from (31) and (32). As a result of
this, aggregate consumption also decreases implying that the model
is able to capture the initial decline in aggregate demand present
in the "Sudden Stops."
. This can be inferred from (31) and (32). As a result of
this, aggregate consumption also decreases implying that the model
is able to capture the initial decline in aggregate demand present
in the "Sudden Stops."
Figure 3. Impulse Responses
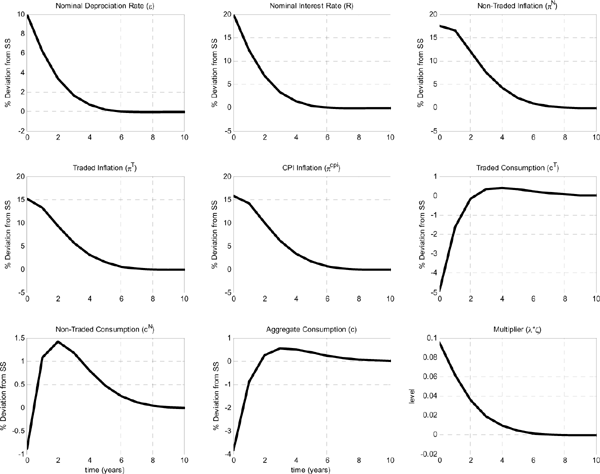
Figure 3: Impulse responses of a self-fulfilling equilibrium, when at
time ![]() people expect a
higher nominal depreciation rate (
people expect a
higher nominal depreciation rate (
![]() This equilibrium replicates some of the "Sudden Stops"
stylized facts: a decline of consumption of traded and non-traded
goods, a relatively moderate increase in CPI-inflation, a higher
depreciation rate, and a higher nominal interest rate. All the
variables are measured as percentage deviations from the steady
state except for the multiplier.
This equilibrium replicates some of the "Sudden Stops"
stylized facts: a decline of consumption of traded and non-traded
goods, a relatively moderate increase in CPI-inflation, a higher
depreciation rate, and a higher nominal interest rate. All the
variables are measured as percentage deviations from the steady
state except for the multiplier.
Figure 3 - Detailed Description:
Figure 3 presents the impulse responses
of a self-fulfilling equilibrium, when at time (5.1, -3) people expect a higher nominal
depreciation rate (t = 0). The figure has 9 panels that
correspond to the impulse responses for the nominal depreciation
rate (
![]() ), the
nominal interest rate (
), the
nominal interest rate (![]() ), the non-traded inflation rate (
), the non-traded inflation rate (
![]() ), the
traded inflation rate (
), the
traded inflation rate (
![]() ), the
CPI-inflation rate (
), the
CPI-inflation rate (![]() ), the traded good consumption (
), the traded good consumption (![]() ), the non-traded good
consumption (
), the non-traded good
consumption (![]() ),
the aggregate consumption (
),
the aggregate consumption (![]() ), and the multiplier (
), and the multiplier (
![]() ).
All the variables are measured as percentage deviations from the
steady state except for the multiplier. In general the impulse
responses replicate some of the "Sudden Stops" stylized facts: a
decline of consumption of traded and non-traded goods, a relatively
moderate increase in CPI-inflation, a higher depreciation rate, and
a higher nominal interest rate. We proceed to describe these
responses individually.
).
All the variables are measured as percentage deviations from the
steady state except for the multiplier. In general the impulse
responses replicate some of the "Sudden Stops" stylized facts: a
decline of consumption of traded and non-traded goods, a relatively
moderate increase in CPI-inflation, a higher depreciation rate, and
a higher nominal interest rate. We proceed to describe these
responses individually.
- At (5.1, -3) the
percentage deviation of the nominal depreciation rate jumps to
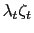 . After this, it
declines and converges to zero over time. It reaches the value of
zero when 10% approximately.
. After this, it
declines and converges to zero over time. It reaches the value of
zero when 10% approximately. - At (5.1, -3) the percentage deviation of the nominal interest rate jumps to t = 5. After this, it declines and converges to zero over time. It reaches the value of zero when 10% approximately.
- At (5.1, -3) the percentage deviation of the non-traded inflation rate jumps to 20% approximately. After this, it declines and converges to zero over time. It reaches the value of zero when 17.5% approximately.
- At (5.1, -3) the percentage deviation of the traded inflation rate jumps to t=7 approximately. After this, it declines and converges to zero over time. It reaches the value of zero when 17.5% approximately.
- At (5.1, -3) the percentage deviation of the CPI-inflation rate jumps to 15% approximately. After this, it declines and converges to zero over time. It reaches the value of zero when 17.5% approximately.
- At (5.1, -3) the percentage deviation of the traded good consumption reaches the value of 16% approximately. At -5% it attains a maximum of t = 4 approximately and then it converges to zero over time. It reaches the value of zero when 0.4% approximately.
- At (5.1, -3) the percentage deviation of the non-traded good consumption reaches the value of t = 9 approximately. At -0.9% it attains a maximum of t = 2 approximately and then it converges to zero over time. It reaches the value of zero when 1.4% approximately.
- At (5.1, -3) the percentage deviation of the aggregate consumption reaches the value of t = 8 approximately. At -3.8 it attains a maximum of t = 3 approximately and then it converges to zero over time. It reaches the value of zero when 1.4 % approximately.
- At (5.1, -3) the multiplier reaches the value of 0.5% and then declines and converges to zero over time. It reaches the value of zero when 0.095 approximately.
Figure 4. Impulse Responses
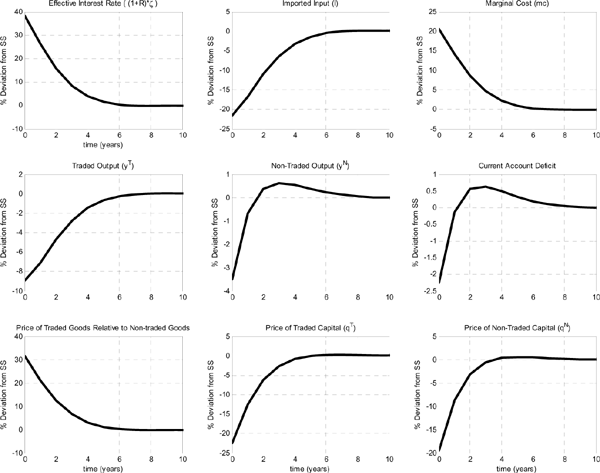
Figure 4: Impulse responses of a self-fulfilling equilibrium, when at
time ![]() people expect a
higher nominal depreciation rate (
people expect a
higher nominal depreciation rate (
![]() This equilibrium replicates some of the "Sudden Stops"
stylized facts: a collapse in the domestic production (of the
traded and non-traded good), a collapse in asset prices (prices of
capital), a sharp correction in the price of traded goods relative
to non-traded goods, and an improvement in the current account
deficit. All the variables are measured as percentage deviations
from the steady state.
This equilibrium replicates some of the "Sudden Stops"
stylized facts: a collapse in the domestic production (of the
traded and non-traded good), a collapse in asset prices (prices of
capital), a sharp correction in the price of traded goods relative
to non-traded goods, and an improvement in the current account
deficit. All the variables are measured as percentage deviations
from the steady state.
Figure 4 - Detailed Description:
Figure 4 presents the impulse responses
of a self-fulfilling equilibrium, when at time (5.1, -3) people expect a higher nominal
depreciation rate t = 0. The figure has 9 panels that
correspond to the impulse responses for the effective nominal
interest rate (t = 6),
the imported input (![]() ),
the marginal cost of producing the non-traded good (
),
the marginal cost of producing the non-traded good (![]() ), the traded output
(
), the traded output
(![]() ), the
non-traded output (
), the
non-traded output (![]() ), the current account deficit, the price of
traded goods relative to non-traded goods, the price of capital
allocated to the production of the traded good (
), the current account deficit, the price of
traded goods relative to non-traded goods, the price of capital
allocated to the production of the traded good (
![]() ) and the
price of capital allocated to the production of the non-traded good
(
) and the
price of capital allocated to the production of the non-traded good
(
![]() .
.
All the variables are measured as percentage deviations from the steady state. In general the impulse responses replicate some of the "Sudden Stops" stylized facts: a collapse in the domestic production (of the traded and non-traded good), a collapse in asset prices (prices of capital), a sharp correction in the price of traded goods relative to non-traded goods, and an improvement in the current account deficit. We proceed to describe the impulse responses individually.
- At (5.1, -3) the percentage deviation of the effective interest rate jumps to 17.5% approximately. After this, it declines and converges to zero over time. It reaches the value of zero when 0.095 approximately.
- At (5.1, -3) the percentage deviation of the imported input jumps to 38%. After this, it converges to zero over time reaching the value of zero when 0.095 approximately.
- At (5.1, -3) the percentage deviation of the marginal cost jumps to -21% approximately. After this, it declines and converges to zero over time. It reaches the value of zero when 0.095 approximately.
- At (5.1, -3) the percentage deviation of the traded output jumps down to 21% approximately. After this, it converges to zero over time, reaching the value of zero when 17.5% approximately.
- At (5.1, -3) the percentage deviation of the non-traded output jumps down to -9% approximately 17.5%. At -3.8% it attains a maximum of -3.5% approximately and then it converges to zero over time. It reaches the value of zero when 1.4% approximately.
- At (5.1, -3) the percentage deviation of the current account reaches the value of 0.7% approximately. At -3.8% it attains a maximum of -2.3% approximately and then it converges to zero over time. It reaches the value of zero when 1.4% approximately.
- At (5.1, -3) the percentage deviation of the price of traded goods relative to non-traded goods jumps to 0.6% approximately. After this, it converges to zero over time reaching the value of zero when 0.095 approximately.
- At (5.1, -3) the percentage deviation of the price of capital allocated to the production of the traded good jumps down to 32% approximately. After this, it converges to zero over time reaching the value of zero when 10% approximately.
- At (5.1, -3) the percentage deviation of the price of capital allocated to the production of the non-traded good reaches the value of -23% approximately. At 10% it attains a maximum of -18% approximately and then it converges to zero over time. It reaches the value of zero when 1.4% approximately.
Since the real value of capital as a collateral is expressed in
terms of foreign currency, then the previously mentioned increase
of the nominal exchange rate at t = 0 reduces this
value. Thus, there is an incentive to reduce the demand for the
imported input at t = 0, as can be deduced from
(27) as an equality, and taking into
account that
![]() is a predetermined variable.
At the same time, a higher interest rate in response to
depreciation also pushes up the costs of loans to hire labor
utilized in the production of traded goods. This creates an
incentive for the household-firm unit to cut back labor in the
production of the traded good.41 The simulations show that in fact
these incentives are materialized leading to a decrease in traded
output at t = 0.
is a predetermined variable.
At the same time, a higher interest rate in response to
depreciation also pushes up the costs of loans to hire labor
utilized in the production of traded goods. This creates an
incentive for the household-firm unit to cut back labor in the
production of the traded good.41 The simulations show that in fact
these incentives are materialized leading to a decrease in traded
output at t = 0.
On the other hand, the supply of the non-traded good is demand determined. This supply satisfies both consumption of non-traded goods and distribution services for traded goods. Consequently, the previously mentioned decrease in demand of both goods causes a decrease in non-traded output (labor) at t = 0. Thus the model is able to capture the decline in output of both non-traded and traded goods. Provided that the decrease in traded output is smaller than the contractions in consumption of the traded good and the imports of the intermediate input, then the current account improves, as can be seen in (34).
As the collateral constraint tightens and the nominal interest
rate rises, the "effective" nominal interest rate
![]() increases. As a result of
this, marginal costs of producing the non-traded good go up,
forcing the household-firm unit to raise the price of this good.
This, in turn, leads to a higher non-traded goods inflation rate,
as can be deduced from (33) and (36). Higher currency depreciation rates and non-traded
inflation rates induce higher CPI-inflation rates.
increases. As a result of
this, marginal costs of producing the non-traded good go up,
forcing the household-firm unit to raise the price of this good.
This, in turn, leads to a higher non-traded goods inflation rate,
as can be deduced from (33) and (36). Higher currency depreciation rates and non-traded
inflation rates induce higher CPI-inflation rates.
In addition, the presence of price-stickiness and distribution
services implies that, as a consequence of large depreciations,
there is a sharp correction in the price of the traded good
relative to the price of non-traded good at the consumer level
![]() .
This captures another empirical regularity of the aftermath of a
crisis.
.
This captures another empirical regularity of the aftermath of a
crisis.
The real value of a unit of capital for traded output (respectively, non-traded output), in terms of foreign currency, is determined by the net present value of the flows of the marginal product of capital in the production of the traded good (respectively, non-traded good). This can be seen by iterating forward equations (40). Provided that capital is constant in the analysis, the decreases in labor and in the intermediate input cause a decline in the marginal product of capital, reducing the real value of capital. A similar mechanism reduces the real value of capital for non-traded output. Therefore, asset prices fall capturing another stylized fact of the "Sudden Stops."
5 Concluding Remarks
In this paper we study interest rate policies that, in the aftermath of a currency crisis, call for adjusting the nominal interest rate in response to domestic currency depreciation. We show that these policies can induce macroeconomic instability by generating self-fulfilling cycles. We find that, if a government raises the interest rate proportionally more than an increase in currency depreciation, then it induces self-fulfilling cycles that, driven by people's expectations about depreciation, replicate several of the salient stylized facts of the "Sudden Stop" phenomenon. In this sense, interest rate policies that respond to depreciation may have contributed to generating the dynamic cycles experienced by some economies in the aftermath of a currency crisis.
Our results have the following implications. Previous works have emphasized that these interest rate policies can cause fiscal and output costs. We suggest that these policies can be also costly to the extent that they can induce macroeconomic instability in the economy by opening the possibility of "sunspot" equilibria. These equilibria, that are not driven by fundamentals, can be associated with a large degree of volatility for some macroeconomic aggregates such as consumption. Provided that agents are risk averse, then volatile consumption can be costly in terms of welfare.
Our results also provide a possible explanation of why the empirical literature has not been able to disentangle the relationship between interest rates and the nominal exchange (depreciation) rate in the aftermath of a crisis. This literature has tried to control for the variables that influence the nominal exchange rate. But our results suggest that there can be potential influences that may depend on "sunspots", which in turn can induce self-fulfilling cycles in the nominal exchange rate (or the nominal depreciation rate) as well as in other variables. Clearly, these influences do not depend on fundamentals, and their effect is something that the empirical literature should take into account.
An issue that we have not addressed is whether the "sunspot" equilibria are learnable by the agents of the economy. It was implicitly assumed that agents could learn and coordinate their actions on any particular equilibrium. In future research, we plan to relax this assumption and use the Expectational Stability concept developed in Evans and Honkapojha (2001) to pursue a learnability analysis.
A Appendix
This Appendix has two parts. The first part includes material that supports the analysis for the simple model of Section 2. The second part includes the simulations of the determinacy of equilibrium analysis for forward-looking and backward-looking rules for the full model of Section 3.
A.1 The Simple Model
A.1.1 The First Order Conditions of the Household-Firm Unit Problem in the Simple Model
The representative household-firm unit
chooses the set of sequences
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() in order to maximize
(3) subject to (4),
(5), (6) and (7), given the initial condition
in order to maximize
(3) subject to (4),
(5), (6) and (7), given the initial condition ![]() and the set of sequences {
and the set of sequences {
![]() ,
, ![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]() The first order conditions
correspond to (5) and (7)
with equality and
The first order conditions
correspond to (5) and (7)
with equality and
| 0 | 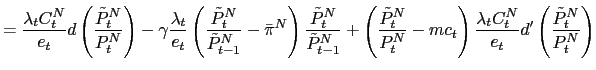
|
(47) |
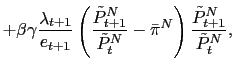
|
where
We will focus on a symmetric equilibrium in which all the
monopolistic producers of sticky-price non-traded goods pick the
same price. Hence
![]() Since all the
monopolists face the same wage rate,
Since all the
monopolists face the same wage rate,
![]() and the same production function,
and the same production function,
![]() then they will
demand the same amount of labor
then they will
demand the same amount of labor
![]() In equilibrium
the money market, the domestic bond market, the labor markets, the
non-traded goods market, and the traded good market clear. In
particular, for the non-traded good market and traded good market
we have
In equilibrium
the money market, the domestic bond market, the labor markets, the
non-traded goods market, and the traded good market clear. In
particular, for the non-traded good market and traded good market
we have
and
Combining (49) and (50) yields the uncovered interest parity condition
(9). From (43) and
(45) we can derive equation (10). Using conditions (41)
and (49) we obtain the Euler equation for
consumption of the traded good that corresponds to (11). Utilizing (1), (41), (42), and (50) we derive the Euler equation (12 ) for consumption of the non-traded good. And
finally using the notion of a symmetric equilibrium, conditions
(4), (42), (44), (46), (47), the labor market equilibrium conditions, and
the definitions
![]()
![]() and
and
![]() we can derive the
augmented Phillips curve described by equation (13).
we can derive the
augmented Phillips curve described by equation (13).
A.1.2 Characterization of the Steady State in the Simple Model
We use
![]() , (1),
(8 )-(15), and the
condition that at the steady state
, (1),
(8 )-(15), and the
condition that at the steady state
![]() for all the variables to
derive
for all the variables to
derive
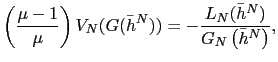
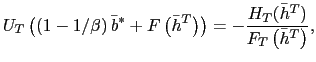
Then it is simple to prove that under some assumptions that include
Assumptions 1, 2, and 3, and given ![]()
![]() and
and
![]() there exists a steady
state
there exists a steady
state
![]()
![]()
![]()
![]()
![]()
![]() for the economy that
provided a particular
for the economy that
provided a particular
![]() satisfies these equations
with
satisfies these equations
with
![]() and
and
![]() In particular to guarantee that there exist
In particular to guarantee that there exist
![]() we need
some Inada-type assumptions such as
we need
some Inada-type assumptions such as
![]()
![]()
![]() and
and
![]() 42
42
A.1.3 Forward-Looking and Backward-Looking Policies in the Simple Model
In order to pursue the determinacy of
equilibrium analysis for a forward-looking policy,
![]() we use this
and equations (17)-(21) to obtain
we use this
and equations (17)-(21) to obtain
Then the determinacy of equilibrium analysis delivers the results stated in the following proposition.
To derive the results for a backward-looking policy we use the
log-linearized version of this policy,
![]() together with
equations (20)-(17) to
obtain the log-linearized system
together with
equations (20)-(17) to
obtain the log-linearized system
Then the determinacy of equilibrium analysis delivers the results stated in the following proposition.
- a) if
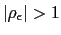 then there exists a unique perfect foresight equilibria in which
the sequences
then there exists a unique perfect foresight equilibria in which
the sequences
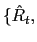
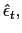
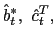
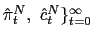 converge to the steady state.
converge to the steady state. - b) if
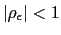 then there exists a continuum of perfect foresight equilibria
(indeterminacy) in which the sequences
then there exists a continuum of perfect foresight equilibria
(indeterminacy) in which the sequences
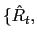
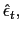
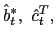
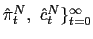 converge
asymptotically to the steady state. In addition, the degree of
indeterminacy is of order 2.
converge
asymptotically to the steady state. In addition, the degree of
indeterminacy is of order 2.
where
On the contrary, by the previous analysis, if
![]() then the number of explosive roots, 2, is less than the number of
non-predetermined variables (
then the number of explosive roots, 2, is less than the number of
non-predetermined variables (
![]() ,
,
![]() ,
,
![]() and
and
![]()
![]() Applying the results of Blanchard and Kahn (1980), it follows that
there exists an infinite number of perfect foresight equilibria
converging to the steady state. The degree of indeterminacy is the
difference between the number of non-predetermined variables and
the number of explosive roots. This completes the proof for b).
Applying the results of Blanchard and Kahn (1980), it follows that
there exists an infinite number of perfect foresight equilibria
converging to the steady state. The degree of indeterminacy is the
difference between the number of non-predetermined variables and
the number of explosive roots. This completes the proof for b).
![]()
A.1.4 Lemmata and Proofs for the Results in the Simple Model
A.2 The Full Model
A.2.1 Forward-Looking and Backward-Looking Policies in the Full Model
We characterize the equilibrium for
forward-looking policies (
![]() ) and backward
looking policies (
) and backward
looking policies (
![]() ), using the
parametrization of Table 2. As an illustrative case, we focus on
the experiment of varying the degree of responsiveness to future
(past) currency depreciation (
), using the
parametrization of Table 2. As an illustrative case, we focus on
the experiment of varying the degree of responsiveness to future
(past) currency depreciation (
![]() ) and the intratemporal
elasticity of substitution (a), keeping the rest constant. The
results are presented in Figure 5. The top panel shows the results
for a forward-looking policy. The bottom panel presents the results
for a backward-looking policy.
) and the intratemporal
elasticity of substitution (a), keeping the rest constant. The
results are presented in Figure 5. The top panel shows the results
for a forward-looking policy. The bottom panel presents the results
for a backward-looking policy.
Figure 5. Forward-Looking Policies
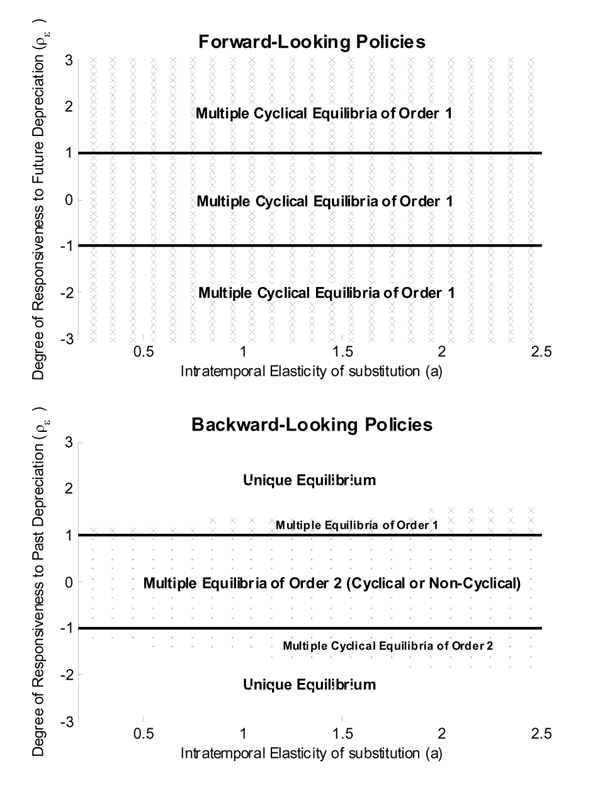
Figure 5: Characterization of the equilibrium for forward-looking
(top-panel) and backward-looking (bottom-panel) policies varying
the degree of responsiveness to currency depreciation (
![]() ) and
the intratemporal elasticity of substitution (a). It is assumed
that
) and
the intratemporal elasticity of substitution (a). It is assumed
that
![]() . A cross "x" denotes parameter combinations under which
the policy induces multiple equilibria whose degree of
indeterminacy is of order one. A dot "." represents parameter
combinations under which the policy induces multiple equilibria
whose degree of indeterminacy is of order two. The white regions
represent parameter combinations under which there exists a unique
equilibrium.
. A cross "x" denotes parameter combinations under which
the policy induces multiple equilibria whose degree of
indeterminacy is of order one. A dot "." represents parameter
combinations under which the policy induces multiple equilibria
whose degree of indeterminacy is of order two. The white regions
represent parameter combinations under which there exists a unique
equilibrium.
Figure 5 - Detailed Description: Figure 5 shows the characterization of
the equilibrium for forward-looking (top-panel) and
backward-looking (bottom-panel) policies varying the degree of
responsiveness to currency depreciation (
![]() ) and the
intratemporal elasticity of substitution (a).
) and the
intratemporal elasticity of substitution (a).
The top panel (forward-looking policies) measures
0.9% the
response coefficient to future depreciation, on the vertical axis
with
![]() and "a" on the horizontal axis with a
and "a" on the horizontal axis with a
![]() The panel
shows that for a
The panel
shows that for a
![]() , any
interest policy that satisfies
, any
interest policy that satisfies
![]() will induce multiple cyclical equilibria whose degree of
indeterminacy is of order one.
will induce multiple cyclical equilibria whose degree of
indeterminacy is of order one.
The bottom panel (backward-looking policies) measures
0.9% the
response coefficient to past depreciation, on the vertical axis
with
![]() and "a" on the horizontal axis with a
and "a" on the horizontal axis with a
![]() The panel
shows that for a
The panel
shows that for a
![]() , any
interest policy that satisfies
, any
interest policy that satisfies
![]() will induce multiple
equilibria (cyclical or non-cyclical) whose degree of indeterminacy
is of order two. For
will induce multiple
equilibria (cyclical or non-cyclical) whose degree of indeterminacy
is of order two. For
![]() then depending on a
then depending on a
![]() the
backward-looking policy can induce either a unique equilibrium or
multiple cyclical equilibria whose degree of indeterminacy is of
order one. In particular in the region within the coordinates
the
backward-looking policy can induce either a unique equilibrium or
multiple cyclical equilibria whose degree of indeterminacy is of
order one. In particular in the region within the coordinates ![]() a,
a,
![]()
![]() (0, 3) and (2.5, 3), approximately the policy
always induces a unique equilibrium. In addition for
(0, 3) and (2.5, 3), approximately the policy
always induces a unique equilibrium. In addition for
![]() then depending on a
then depending on a
![]() the
backward-looking policy can induce either a unique equilibrium or
multiple cyclical equilibria whose degree of indeterminacy is of
order two. In particular in the region within the coordinates
the
backward-looking policy can induce either a unique equilibrium or
multiple cyclical equilibria whose degree of indeterminacy is of
order two. In particular in the region within the coordinates ![]() a,
a,
![]()
![]() (0, 3), and (2.5, -3), approximately the policy always induces a unique equilibrium.
(0, 3), and (2.5, -3), approximately the policy always induces a unique equilibrium.
From the top-panel, we can infer that forward-looking policies
always induce multiple cyclical equilibria, as long as
![]() and either
and either
![]() or
or
![]() . On the other
hand, for backward-looking rules, the coefficient of response to
past depreciation,
. On the other
hand, for backward-looking rules, the coefficient of response to
past depreciation,
![]() plays an important role. In
particular, timid rules with respect to past depreciation (
plays an important role. In
particular, timid rules with respect to past depreciation (
![]() )
always induce multiple equilibria, regardless of the intratemporal
elasticity of substitution (a). In contrast, aggressive rules (
)
always induce multiple equilibria, regardless of the intratemporal
elasticity of substitution (a). In contrast, aggressive rules (
![]() )
can guarantee a unique equilibrium. Nevertheless, being aggressive
with respect to past depreciation (
)
can guarantee a unique equilibrium. Nevertheless, being aggressive
with respect to past depreciation (
![]() )
is not a sufficient condition to guarantee a unique equilibrium. It
is only a necessary condition.
)
is not a sufficient condition to guarantee a unique equilibrium. It
is only a necessary condition.
Varying other structural parameters different from the
intratemporal elasticity of substitution (a), in tandem with
![]() lead to similar
results.44 The following proposition summarizes
these results.
lead to similar
results.44 The following proposition summarizes
these results.
- If the government follows a forward-looking policy such as
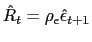 with
with
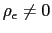 and either
and either
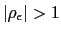 or
or
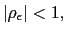 then there exists a continuum of perfect foresight "cyclical"
equilibria (indeterminacy), in which the sequences
then there exists a continuum of perfect foresight "cyclical"
equilibria (indeterminacy), in which the sequences
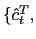
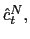
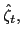
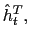
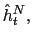
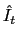 ,
,
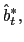
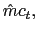
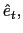
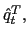
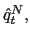
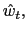
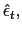
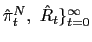 converge to
the steady state.
converge to
the steady state. - If the government follows a backward-looking policy such as
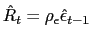 with
with
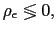 then
then
- a)
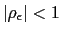 is a sufficient condition for the existence of a continuum of
perfect foresight equilibria, possibly "cyclical", in which the
sequences
is a sufficient condition for the existence of a continuum of
perfect foresight equilibria, possibly "cyclical", in which the
sequences
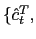
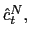
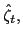
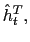
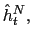
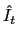 ,
,
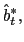
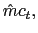
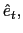
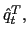

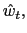
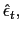
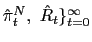 converge to
the steady state.
converge to
the steady state. - b)
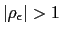 is a necessary but not a sufficient condition for the existence of
a unique perfect foresight equilibrium, where the sequences
is a necessary but not a sufficient condition for the existence of
a unique perfect foresight equilibrium, where the sequences
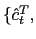
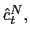
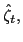
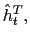
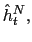
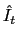 ,
,
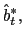
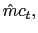
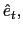
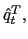
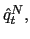
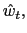
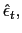
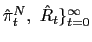 converge to
the steady state.
converge to
the steady state.
References
[1] Aghion, P., P Bacchetta and A. Banerjee (2000), "A Simple Model of Monetary Policy and Currency Crises," European Economic Review, 44:728-738.
[2] Azariadis, C. (1993), Intertemporal Macroeconomics (Blackwell, Cambridge, Massachussetts).
[3] Benhabib, J., S. Schmitt-Grohé and M. Uribe (2001), "Monetary Policy Rules and Multiple Equilibria", American Economic Review 91(1):167-184.
[4] Blanchard, O. and C. Kahn (1980), "The Solution of Linear Difference Models Under Rational Expectations", Econometrica 48(5):1305-1312.
[5] Braggion, F., Christiano L. and J. Roldos (2005), "The Optimal Monetary Response to a Financial Crisis," Northwestern Univesrity, Manuscript.
[6] Burnstein, A., Neves J. and S. Rebelo (2003), "Distribution Costs and Real Exchange Rate Dynamics," Journal of Monetary Economics, 50:1189-1214.
[7] Burnstein, A., Eichenbaum M. and S. Rebelo (2005a), "Large Devaluations and the Real Exchange Rate," forthcoming Journal of Political Economy.
[8] Burnstein, A., Eichenbaum M. and S. Rebelo (2005b), "Modeling Exchange Rate Passthrough After Large Devaluations," forthcoming Journal of Monetary Economics.
[9] Caballero, R. and A. Krishnamurthy (2001), "International and Domestic Collateral Constraints in a Model of Emerging Market Crises," Journal of Monetary Economics, 48:513-548.
[10] Calvo, G. (1998), "Capital Flows and Capital-Market Crises: The Simple Economics of Sudden Stops," Journal of Applied Economics, 1:35-54.
[11] Cass, D. and K. Shell (1980), "Do Sunspots Matter?," Journal of Political Economy, 91:103-227.
[12] Cho, D. and K. West (2003), "Interest Rates and Exchange Rates in the Korean, Phillipine and Thai Exchange Rate Crises," in: M. Dooley abd J. Frankel eds., Managing Currency Crises in Emerging Markets, University of Chicago Press, 11-30.
[13] Christiano L., C. Gust and J. Roldos (2004), "Monetary Policy in a Financial Crisis," Journal of Economic Theory, 119:64-103.
[14] Corsetti, G., L. Dedola and S. Leduc (2005), "DSGE Models of High Exchange-Rate Volatility and Low Pass-Through," Manuscript, Federal Reserve Board.
[15] Evans, G, and S. Honkapohja (2001), Learning and Expectations, Princeton University Press, New Jersey.
[16] Fischer, S. (1998), "In Defense of the IMF: Specialized Tools for a Specialized Task", Foreign Affairs 77(2).
[17] Flood, R. and O. Jeanne (2000), "An Interest Rate Defense of a Fixed Exchange Rate", Working Paper No. 00/159, International Monetary Fund.
[18] Furman, J. and J. Stiglitz (1998), "Economic Crises: Evidence and Insight from East Asia", Brookings Papers on Economic Activity 2:1 -114.
[19] Goldfajn, I. and T. Baig (1998), "Monetary Policy in the Aftermath of Currency Crises: The Case of Asia", Working Paper No. 98/170, International Monetary Fund.
[20] Gould, D. and S. Kamin (2000), "The Impact of Monetary Policy on Exchange Rates During Financial Crises", IFDP No.699, Board of Governors of the Federal Reserve System.
[21] Guckenheimer J. and P. Holmes (1983), Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Field, Springer-Verlag, New York.
[22] Kiyotaki, N. and J. Moore (1997), "Credit Cycles," The Journal of Political Economy, 105(2):211-348.
[23] Krugman, P. (1999) "Balance Sheets, the Transfer Problem and Financial Crises", in: P. Isard, A. Razin and A. Rose, eds., International Finance and Financial Crises (Kluwer Academic Publishers).
[24] Lahiri, A. and C. Vegh (2002), "Output Costs, BOP Crises and Optimal Interest Rate Policy", Manuscript, UCLA.
[25] Lahiri, A. and C. Vegh (2003), "Delaying the Inevitable: Interest Rate Defense and Balance of Payment Crises", Journal of Political Economy, 111(2), 404-424.
[26] Mendoza, E. and K. Smith (2002), "Margin Calls, Trading Costs, and Asset Prices in Emerging Markets: The Financial Mechanics of The 'Sudden Stop' Phenomenon," NBER Working Paper No. 9286.
[27] Montiel, P. (2003), "Tight Money in a Post-Crisis Defense of the Exchange Rate: What Have We Learned?," The World Bank Research Observer, 18(1), 1-23.
[28] Paasche, B. (2001), "Credit Constraints and International Financial Crises," Journal of Monetary Economics, 28:623-650.
[29] Radelet, S. and J. Sachs (1998), "The East Asian Financial Crisis: Diagnosis, Remedies, Prospects", Brookings Papers on Economic Activity 1:1-90.
[30] Rotemberg, J. (1982), "Sticky Prices in the United States", Journal of Political Economy 90(6):1187-1211.
[31] Sargent, T. and N. Wallace, (1975), "Rational Expectations, the Optimal Monetary Instrument, amd the Optimal Money Supply Rule," Journal of Political Economy 83(2):241-254.
[32] Schmitt-Grohé, S. and M. Uribe (2003), "Closing Small Open Economy Models," Journal of International Economics, 61, 163-185.
[33] Schmitt-Grohé, S. and M. Uribe (2004), "Optimal Fiscal and Monetary Policy under Sticky Prices," Journal of Economic Theory, 114, 198-230.
[34] Taylor, J. B.(1999), Monetary Policy Rules, Chicago, National Bureau of Economic Research.
[35] Woodford, M. (2003), Interest and Prices: Foundations of a Theory of Monetary Policy, Princeton,Princeton University Press.
[36] Zanna, L. F. (2003), "Interest Rate Rules and Multiple Equilibria in the Small Open Economy," IFPD No. 785, Board of Governors of the Federal Reserve System.
Footnotes
1. This paper is based on chapter 3 of my dissertation at the University of Pennsylvania. I am grateful to Martín Uribe, Stephanie Schmitt-Grohé and Frank Schorfheide for their guidance and teaching. I also received helpful suggestions and benefitted from conversations with Roc Armenter, Martin Bodenstein, David Bowman, Sanjay Chugh, Bill Dupor, Bora Durdu, Fabio Ghironi, Chris Gust, Dale Henderson, Sylvain Leduc, Gustavo Suárez and seminar participants at the International Economics Brown Bag Lunch at the University of Pennsylvania, the International Finance Workshop at the Federal Reserve Board and the fall 2005 SCIEA Meetings. All errors remain mine. Previous versions of this paper circulated under the title: "Interest Rate Rules and Multiple Equilibria in the Aftermath of BOP Crises". The views expressed in this paper are solely the responsibility of the author and should not be interpreted as reflecting the view of the Board of Governors of the Federal Reserve System or of any other person associated to the Federal Reserve System. Return to text
2. Board of Governors of the Federal Reserve System, 20th Street and Constitution Avenue, NW, Washington, D.C., 20551. Tel.: (202)452-2337. Fax: (202)736-5638. Email: [email protected]. Return to text
3. See Fischer (1998) among others. Return to text
4. See for instance Furman and Stiglitz (1998) and Radelet and Sachs (1998) among others. Return to text
5. In fact some works motivated by the debate describe, implicitly or explicitly, the interest rate policy as a feedback rule responding to some measure of nominal depreciation. See for instance Cho and West (2001), Goldfajn and Baig (1998), and Lahiri and Vegh (2003), among others. Return to text
6. From now on we will use the terms "multiple equilibria" and "real indeterminacy" (a "unique equilibrium" and "real determinacy") interchangeably. By real indeterminacy we mean that the behavior of one or more (real) variables of the economy is not pinned down by the model. This implies that there are multiple equilibria, which in turn opens the possibility of having fluctuations in the economy generated by endogenous beliefs that are of the "sunspot" type; i.e., they are based on stochastic variables that are extrinsic in Cass and Shell's (1983) terminology. Return to text
7. An interest rate policy that responds to inflation does not necessarily preclude the possibility of self-fulfilling equilibria. But as we discuss below, the response to currency depreciation makes the interest rate policy more prone to induce self-fulfilling equilibria. Return to text
8. This idea of modelling the crisis as an unexpected binding collateral constraint captures the essence of a "Sudden Stop." Other works that introduce such collateral constraints include Caballero and Krishnamurthy (2001), Christiano, Gust and Roldos (2004), Krugman (1999), Mendoza and Smith (2002), and Paasche (2001) among others. Return to text
9. See Burnstein, Eichenbaum and Rebelo (2005a,b) and Christiano, Gust and Roldos (2004), among others. Return to text
10. See the review of this literature by Montiel (2003). Return to text
11. These policies can lead to "sunspot" equilibria that are characterized by a large degree of volatility of some macroeconomic aggregates such as consumption. Provided that agents are risk averse, then these policies can induce equilibria where agents are worse-off. Return to text
12. The new interest rate rules literature argues that aggressive rules with respect to past inflation are more likely to guarantee a unique equilibrium. See for instance Benhabib, Schmitt-Grohé, and Uribe (2001), Taylor (1999), and Woodford (2003) among others. See also Zanna (2003) for an analysis of interest rate rules in small open economies. Return to text
13. Some of the works inspired by this debate, such as Cho and West (2001), Goldfajn and Baig (1998), and Lahiri and Vegh (2003) among others, also describe the interest rate policy, implicitly or explicitly, as a rule that reacts to some measure of nominal depreciation. Return to text
14. For simplicity we also assume that these targets correspond to the steady-state levels of these variables. Return to text
15. As we will see below, the cases of
![]() or
or
![]() introduce a unit root in
the log-linearized system of the economy, precluding the
possibility of using the "Theorem of Hartman and Grobman" to
derive meaningful conclusions about the dynamics of the non-linear
system. See Guckenheimer and Holmes (1985). Return to text
introduce a unit root in
the log-linearized system of the economy, precluding the
possibility of using the "Theorem of Hartman and Grobman" to
derive meaningful conclusions about the dynamics of the non-linear
system. See Guckenheimer and Holmes (1985). Return to text
16. Because of this, we can write the
real money balances that enter the utility function in terms of
foreign currency,
![]() without consequences for our results. Return to text
without consequences for our results. Return to text
17. As we discuss below, our results do not depend on this assumption. Return to text
18. The "unit-root problem" that is
commonly present in small open economy models arises because of
assuming that
![]() To see why,
use this assumption together with condition (49) to deduce that
To see why,
use this assumption together with condition (49) to deduce that
![]() This is an
equation that has a unit root and that introduces a unit root in
the entire dynamical system of the simple set-up. See
Schmitt-Grohé and Uribe (2003). Return to text
This is an
equation that has a unit root and that introduces a unit root in
the entire dynamical system of the simple set-up. See
Schmitt-Grohé and Uribe (2003). Return to text
19. Because of perfect foresight
![]() Return to text
Return to text
20. The dimension of the unstable subspace is given by the number of roots of the system that are outside the unit circle. See Blanchard and Kahn (1980). Return to text
21. The degree of indeterminacy is defined as the difference between the number of non-predetermined variables and the dimension of the unstable subspace of the log-linearized system. Return to text
22. A Non-Ricardian fiscal policy
combined with the monetary policy under study will determine the
level of the nominal exchange rate if
![]() but not if
but not if
![]() . Return to text
. Return to text
23. Our general results still hold if we
describe monetary policy as
![]() with
with ![]() and
and
![]() This resembles the implicit
descriptions in some of the empirical works mentioned in Montiel
(2003). Return to text
This resembles the implicit
descriptions in some of the empirical works mentioned in Montiel
(2003). Return to text
24. When labor is mobile across sectors
then
![]() and the equilibrium in
the labor market becomes
and the equilibrium in
the labor market becomes
![]() In
addition, if we assume that
In
addition, if we assume that ![]() and
and
![]() and keep the rest of Assumptions
1, 2, and 3, then the log-linearized system of equations that
describes the economy is still (16)-(21 ). But in this
case,
and keep the rest of Assumptions
1, 2, and 3, then the log-linearized system of equations that
describes the economy is still (16)-(21 ). But in this
case,
![]() and
and
![]() Return to text
Return to text
25. In Zanna (2003), we show that in order to guarantee a unique equilibrium, a rule must respond aggressively to the non-traded inflation but timidly to depreciation. A rule that responds aggressively to currency depreciation still opens the possibility of multiple equilibria, regardless of its response to non-traded inflation. Return to text
26. See Corsetti, Dedola, and Leduc. (2005). Return to text
27. To formalize this point, we could introduce financial institutions in the model that behave in a perfectly competitive way and supply the aforementioned loans. This would not change our main results. Return to text
28. In the simple model
![]() Return to text
Return to text
29. Note also that in contrast to the
simple model, we have assumed that
![]() . Nevertheless, in
this context, this typical assumption of the small open economy
literature does not cause the unit-root problem. Under this
assumption and with the binding constraint, condition (39) becomes
. Nevertheless, in
this context, this typical assumption of the small open economy
literature does not cause the unit-root problem. Under this
assumption and with the binding constraint, condition (39) becomes
![]() which does not introduce a unit root in the system of equations
that describes the economy. Return to
text
which does not introduce a unit root in the system of equations
that describes the economy. Return to
text
30. To pursue a determinacy of equilibrium analysis in the augmented non-linear model is a very challenging task. Most of the works, that include a collateral constraint and that simulate equilibrium dynamics for the non-linear system, do not characterize the equilibrium. They assume that the equilibrium that is found computationally is the relevant one, whose properties must be studied. See Mendoza and Smith (2002) and Christiano et al. (2004), among others. Return to text
31. Note that target nominal depreciation
rate,
![]() can be found by evaluating
(29) at the steady state. That is,
can be found by evaluating
(29) at the steady state. That is,
![]() The
value of
The
value of ![]() that we take is close to the one in
Christiano et al. (2004). Return to
text
that we take is close to the one in
Christiano et al. (2004). Return to
text
32. See Burnstein et al. (2005a,b). Return to text
33. See Schmitt-Grohé and Uribe (2004), among others. Return to text
34. Cyclical equilibria are associated with the existence of non-explosive complex roots of the log-linearized system. Return to text
35. The results are available from the author upon request. Return to text
36. The literature of interest rate rules claims that an aggressive backward-looking rule with respect to inflation is more prone to guarantee a unique equilibrium than forward-looking and contemporaneous policies. See Woodford (2003). Return to text
37. It is also possible to construct self-fulfilling equilibria with the forward-looking and backward-looking policies that, in principle, replicate most of the stylized facts. Return to text
38. That is, in this case the dynamic log-linearized system that describes the economy has complex and non-explosive eigenvalues, and the number of non-predetermined variables exceeds the number of explosive eigenvalues by one. Return to text
39. If the degree of indeterminacy were 2, then we would have an extra degree of freedom. We could assume that a "sunspot" affects the expectations of an additional variable different from the depreciation rate. In this sense, we are being conservative. Return to text
40. This is probably the case because there is sluggish price adjustment for the price of the non-traded good that, in turn, affects the price of the traded good through the existence of non-traded distribution services. Return to text
41. This can be deduced from (35) and the production technology of the traded
good. Labor costs increase not only because the nominal interest
rate increases but also because the collateral constraint tightens.
That is, there is an increase in the "effective" nominal
interest rate
![]() . Return to text
. Return to text
42. Details are available from the author upon request. Return to text
43. The degree of indeterminacy is defined as the difference between the number of non-predetermined variables and the dimension of the unstable subspace of the log-linearized system. Return to text
44. The results are available from the author upon request. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text
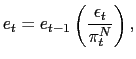
![$\displaystyle \overset{\infty}{\sum_{t=0}}\beta^{t}\left[ U(c_{t}^{T})+V(c_{t}^{N} )+H(h_{t}^{T})+L(h_{t}^{N})+J(m_{t})\right] ,$](img51.gif)
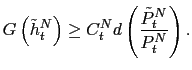
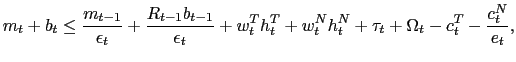
![$\displaystyle \Omega_{t}=\left[ F\left( \check{h}_{t}^{T}\right) -w_{t}^{T}\check{h} _{t}^{T}\right] -\frac{1}{e_{t}}\left[ \frac{\tilde{P}_{t}^{N}}{P_{t}^{N} }C_{t}^{N}d\left( \frac{\tilde{P}_{t}^{N}}{P_{t}^{N}}\right) -e_{t}w_{t} ^{N}\tilde{h}_{t}^{N}-\frac{\gamma}{2}\left( \frac{\tilde{P}_{t}^{N}} {\tilde{P}_{t-1}^{N}}-\bar{\pi}\right) ^{2}\right] -R_{t-1}^{\ast} b_{t-1}^{\ast}+b_{t}^{\ast}.$](img116.gif)
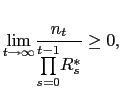

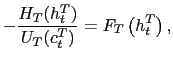
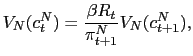
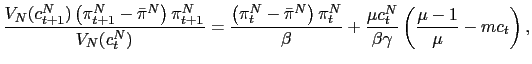
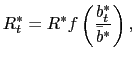 with
with 
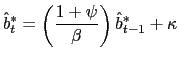
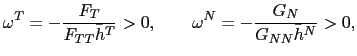
![$\displaystyle \left( \begin{array}[c]{c} \hat{\epsilon}_{t+1}\\ \hat{b}_{t}^{\ast}\\ \text{$\hat{c}_{t+1}^{T}$}\\ \hat{\pi}_{t+1}^{N}\\ \text{$\hat{c}_{t+1}^{N}$} \end{array} \right) =\underset{J^{c}}{\underbrace{\left( \begin{array}[c]{ccccc} \rho_{\epsilon} & -\frac{\psi\left( 1+\psi\right) }{\beta} & -\psi\kappa & 0 & 0\\ 0 & \frac{1+\psi}{\beta} & \kappa & 0 & 0\\ 0 & \frac{\psi\left( 1+\psi\right) \xi^{T}}{\beta} & \left( 1+\psi\kappa \xi^{T}\right) & 0 & 0\\ 0 & 0 & 0 & \frac{1}{\beta} & -\varphi\\ \rho_{\epsilon}\xi^{N} & 0 & 0 & -\frac{\xi^{N}}{\beta} & \left( 1+\varphi \xi^{N}\right) \end{array} \right) }}\left( \begin{array}[c]{c} \hat{\epsilon}_{t}\\ \hat{b}_{t-1}^{\ast}\\ \text{$\hat{c}_{t}^{T}$}\\ \hat{\pi}_{t}^{N}\\ \text{$\hat{c}_{t}^{N}$} \end{array} \right) .$](img229.gif)

![$\displaystyle =F\left( \breve{h}_{t}^{T},I_{t},K^{T}\right) +\frac{1} {e_{t}}\left[ \frac{\tilde{P}_{t}^{N}}{P_{t}^{N}}G\left( \tilde{h}_{t} ^{N},K^{N}\right) -\frac{\gamma}{2}\left( \frac{\tilde{P}_{t}^{N}}{\tilde {P}_{t-1}^{N}}-\bar{\pi}\right) ^{2}\right]$](img340.gif)
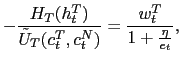
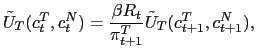 where
where 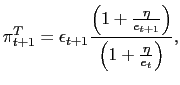
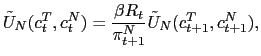
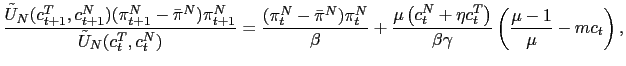
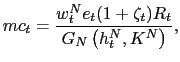
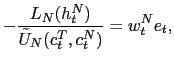
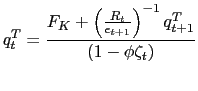 and
and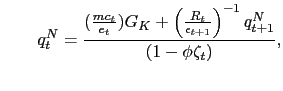
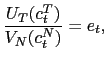
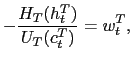
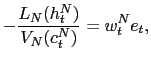
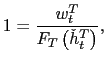
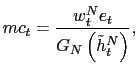
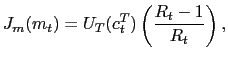
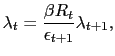
![$\displaystyle \left( \begin{array}[c]{c} \hat{b}_{t}^{\ast}\\ \text{$\hat{c}_{t+1}^{T}$}\\ \hat{\pi}_{t+1}^{N}\\ \text{$\hat{c}_{t+1}^{N}$} \end{array} \right) =\underset{J^{f}}{\underbrace{\left( \begin{array}[c]{cccc} \frac{1+\psi}{\beta} & \kappa & 0 & 0\\ \frac{\psi\left( 1+\psi\right) \xi^{T}}{\beta} & \left( 1+\psi\kappa\xi ^{T}\right) & 0 & 0\\ 0 & 0 & \frac{1}{\beta} & -\varphi\\ \frac{\rho_{\epsilon}\psi\left( 1+\psi\right) \xi^{N}}{\beta(\rho_{\epsilon }-1)} & \frac{\rho_{\epsilon}\psi\kappa\xi^{N}}{(\rho_{\epsilon}-1)} & -\frac{\xi^{N}}{\beta} & \left( 1+\varphi\xi^{N}\right) \end{array} \right) }}\left( \begin{array}[c]{c} \hat{b}_{t-1}^{\ast}\\ \text{$\hat{c}_{t}^{T}$}\\ \hat{\pi}_{t}^{N}\\ \text{$\hat{c}_{t}^{N}$} \end{array} \right) .$](img658.gif)
![$\displaystyle \left( \begin{array}[c]{c} \hat{R}_{t+1}\\ \hat{\epsilon}_{t+1}\\ \hat{b}_{t}^{\ast}\\ \text{$\hat{c}_{t+1}^{T}$}\\ \hat{\pi}_{t+1}^{N}\\ \text{$\hat{c}_{t+1}^{N}$} \end{array} \right) =\underset{J^{b}}{\underbrace{\left( \begin{array}[c]{cccccc} 0 & \rho_{\epsilon} & 0 & 0 & 0 & 0\\ 1 & 0 & -\frac{\psi\left( 1+\psi\right) }{\beta} & -\psi\kappa & 0 & 0\\ 0 & 0 & \frac{1+\psi}{\beta} & \kappa & 0 & 0\\ 0 & 0 & \frac{\psi\left( 1+\psi\right) \xi^{T}}{\beta} & \left( 1+\psi\kappa\xi^{T}\right) & 0 & 0\\ 0 & 0 & 0 & 0 & \frac{1}{\beta} & -\varphi\\ \xi^{N} & 0 & 0 & 0 & -\frac{\xi^{N}}{\beta} & \left( 1+\varphi\xi ^{N}\right) \end{array} \right) }}\left( \begin{array}[c]{c} \hat{R}_{t}\\ \hat{\epsilon}_{t}\\ \hat{b}_{t-1}^{\ast}\\ \text{$\hat{c}_{t}^{T}$}\\ \hat{\pi}_{t}^{N}\\ \text{$\hat{c}_{t}^{N}$} \end{array} \right) .$](img679.gif)