
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 865, August 2006-Screen Reader Version*
Does The Time Inconsistency Problem Make Flexible Exchange Rates Look Worse Than You Think?*
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
The Barro-Gordon inflation bias has provided an influential argument for fixed exchange rate regimes. However, with low inflation rates now widespread, credibility concerns seem no longer relevant. Why give up independent monetary policy to contain an inflation bias that is already under control? We argue that credibility problems do not end with the inflation bias and they are a larger drawback for flexible exchange rates than usually thought. Absent commitment, independent monetary policy can induce expectation traps--that is, welfare ranked multiple equilibria--and perverse policy responses to real shocks, i.e., an equilibrium policy response that is welfare inferior to policy inaction. Both possibilities imply that flexible exchange rates feature unnecessary macroeconomic volatility.
Keywords: Time inconsistency, independent monetary policy, exchange rate regimes
JEL Classification: E61, E33, F41
1 Introduction
The most influential argument in favor of fixed exchange rates is based on the celebrated inflation bias of Barro and Gordon (1983). A monetary authority that lacks the credibility to commit to a policy, the logic goes, can peg its currency, import the monetary policy of another country with more credible institutions and achieve lower average inflation. Of course, the fixed exchange rate regime has to be credible for this argument to go through--a premise we adopt in this paper. The textbook case against fixed exchange rates follows the lines of the classic Mundell-Fleming analysis. A fixed exchange rate implies no independent monetary policy and therefore no ability to ease real macroeconomic volatility.1
With low inflation rates widespread these days, the case for fixed exchange rates appears less appealing. For example, Chang and Velasco (2000) concludes that `` the credibility consideration seems to be less compelling than it once was for emerging markets.'' Rogoff (2003) has argued that globalization has enhanced the central bank's credibility in fighting inflation.
However, the problems arising from the lack of credibility do not end with the inflation bias. We argue that a flexible exchange rate regime additionally suffers from two independent phenomena associated with the time inconsistency problem: expectation traps and perverse policy responses. Both have been overlooked in the exchange rate regime debate but constitute key drawbacks of flexible exchange rates.
First, the lack of credibility can induce expectation traps, i.e., welfare-ranked multiple equilibria.2 High inflation expectations force the monetary authority to accommodate and the economy can be caught in long spells of high inflation. Moreover, undesirable macroeconomic volatility can arise from spurious shifts in private sector expectations.
Second, we show that the monetary authority overreacts to persistent real shocks. As a result, the equilibrium policy response to these shocks can be worse than policy inaction--we refer to this as a perverse policy response. In a fully specified model, real shocks are bound to affect the monetary authority's incentives to inflate beyond expectations--for example, shocks can change the slope of the `` Phillips curve.'' The private sector responds to the changed incentives by updating inflation expectations. In equilibrium, the monetary authority has to react both to the shock and the induced change in inflation expectations. There is no guarantee then that the policy response is close to the optimal one. The lesson from perverse policy responses is that the Mundell-Fleming argument does not carry over to the case of policy without commitment: contrary to the standard view, flexible exchange rates may feature excessive macroeconomic volatility.
We show that expectation traps can be ruled out by a soft exchange rate peg with appropriately chosen bands, without hindering the ability of the monetary authority to respond to macroeconomic shocks. However, a hard peg is required in order to avoid perverse policy responses.
To illustrate both phenomena we present a tractable model of a small open economy that builds upon Armenter and Bodenstein (2004). Nominal rigidities introduce a role for active monetary policy. Combined with monopoly distortions, nominal rigidities also set the stage for optimal monetary policy to be time inconsistent. Furthermore, in order to introduce a cost of inflation we assume that some firms have to borrow the wage bill in advance. We define two policy equilibrium concepts, where monetary policy is endogenously determined as the outcome of a benevolent policymaker. In the analysis of flexible exchange rates, we work with Markov equilibria where the monetary authority has full discretion in setting monetary policy.3 We define policy equilibria under the constraint of an arbitrary exchange rate regime. The policymaker takes the exchange rate regime as given and it therefore constitutes an exogenously sustained commitment.
Expectation traps arise naturally in the context of monetary policy discretion and lack of credibility.4 There is a low inflation equilibrium where the monopoly and financial distortions are balanced. The monetary authority has little to gain from further inflation: any sticky price firms' output expansion is nearly offset by the output loss in the financially constrained sector. It is a different scenario when the private sector believes inflation will be high. Since sticky prices are set according to expectations, low actual inflation would imply very high real prices. On the other hand, if high inflation expectations are validated, then the financially constrained firms will be severely distorted.
We find two Markov equilibria in an economy calibrated to match several stylized facts about inflation and openness. The low inflation equilibrium features an inflation rate around 2%, in line with what is an acceptable level of inflation for many countries. However, the second equilibrium features costly high inflation. In our loosely calibrated economy, the high inflation equilibrium raises the costs of the lack of commitment by a factor of three.
We illustrate the perverse policy response phenomenon with a persistent negative terms of trade shock. The shock contracts the sector of tradeables, which makes the whole economy less competitive and therefore it increases the time inconsistency problem. The heightened monopoly distortion raises the incentives of the monetary authority to inflate. In equilibrium, private sector inflation expectations rise, shifting monetary policy away from the optimal response to the shock. In our calibrated economy, the policy response in a Markov equilibrium overshoots the optimal response by a factor of ten. Households prefer no policy response--the outcome under a fixed exchange rate regime--to the Markov equilibrium policy response. Hence, a flexible exchange rate fails to provide the macroeconomic stability which is presumed to be its main virtue.
To the best of our knowledge, the possibility of a perverse policy response has not been discussed in the literature. Our finding, though, is related to the stabilization bias. Clarida, Gali, and Gertler (1999) and Svensson (1997), among others, point out that credibility is needed to implement the optimal policy response. However, the literature has not pursued the analysis of stabilization policy in the absence of credibility.
We do not claim, theoretically or empirically, that fixed exchange rates are always welfare superior. First and foremost, fixed exchange rates are not exogenously credible.5 Nevertheless, the lack of a credible monetary policy is a larger drawback for flexible exchange rates than usually thought. No previous research work has considered the possibility of expectation traps and perverse policy responses. Their omission renders any welfare analysis of exchange rate regimes incomplete.6
Our analysis implies that we should treat with caution some of the arguments made lately in favor of flexible exchange rates. For example, the observed fall of inflation rates worldwide should not be taken as conclusive evidence that the credibility problem in monetary policy has been solved. All that is needed to be back to high inflation is a shift in inflation expectations. Moreover, larger real volatility does not necessarily make a stronger case for flexible exchange rate regimes either. Summarizing the state of the debate, Frankel (1998) asserts that `` if the country is subject to many external disturbances, [...] then it is more likely to want to float its currency.'' Chang and Velasco (2000) also concludes that the case for exchange-rate flexibility is `` especially strong for countries that are often hit by large real shocks from abroad.'' It is necessary to check that the relevant real shocks do not induce perverse policy responses. If they do, larger real volatility actually makes the case for flexible exchange rates weaker.
The remainder of the paper is organized as follows. In Section 2 we present our model and define the equilibrium concepts. Section 3 discusses expectation traps and Section 4 takes upon the possibility of perverse policy responses. Section 5 concludes. An Appendix, containing several proofs as well as calibration details, is included.
2 The Economy
First, we characterize the private sector equilibrium, which includes a detailed description of the economy. Then we define the different policy equilibrium concepts considered: Markov equilibrium, Ramsey equilibrium and Exchange Rate policy equilibrium.
2.1 Private Sector Equilibrium
This infinite-horizon small open economy is populated by a representative household, a representative final good firm, a continuum of intermediate good firms and a monetary authority.
Figure 1: Timing of Relevant Decisions for Period
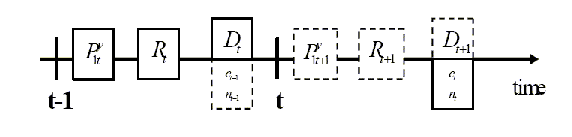
Figure 1 illustrates the timing of the
model. Several of the decisions relevant for period ![]() are made one period in advance.
First, a fraction of the intermediate good firms--the sticky price
firms indexed by
are made one period in advance.
First, a fraction of the intermediate good firms--the sticky price
firms indexed by ![]() --set
their nominal price for period
--set
their nominal price for period ![]() ,
,
![]() , at the start
of period
, at the start
of period ![]() . Second,
the monetary authority chooses the policy instrument to maximize
the representative household's welfare taking
. Second,
the monetary authority chooses the policy instrument to maximize
the representative household's welfare taking
![]() as given.
Then households choose nominal deposits
as given.
Then households choose nominal deposits ![]() along with consumption
along with consumption
![]() and labor
and labor
![]() . On the demand
side of the market for nominal deposits, a subset of financially
constrained firms borrow their wage bill for date
. On the demand
side of the market for nominal deposits, a subset of financially
constrained firms borrow their wage bill for date ![]() . As indicated in Figure 1, date
. As indicated in Figure 1, date ![]() consumption and labor decisions are made at the end of period
consumption and labor decisions are made at the end of period
![]() .
.
We assume that the monetary policy instrument is the nominal
interest rate, ![]() ,
that is paid at date
,
that is paid at date ![]() on
nominal deposits carried from period
on
nominal deposits carried from period ![]() . The nominal interest rate is implemented by
intervening in the market for nominal deposits. As shown below,
there is a one-to-one relationship between the nominal interest
rate and the inflation rate at date
. The nominal interest rate is implemented by
intervening in the market for nominal deposits. As shown below,
there is a one-to-one relationship between the nominal interest
rate and the inflation rate at date ![]() ,
,
![]() Hence, we can
think of the inflation rate as the policy instrument.
Hence, we can
think of the inflation rate as the policy instrument.
Before the monetary policy decision, the sticky price firms must
form a belief about inflation in period ![]() , denoted
, denoted
![]() , in order
to set their nominal price
, in order
to set their nominal price
![]() . Following
the literature, we commonly refer to
. Following
the literature, we commonly refer to
![]() as private
sector inflation expectations, although `` beliefs'' would be more
accurate.
as private
sector inflation expectations, although `` beliefs'' would be more
accurate.
We show that real prices and allocations in a private sector
equilibrium at date ![]() are
fully determined by the state of the economy
are
fully determined by the state of the economy
![]() . Neither past
nor future policy decisions are relevant and there is no physical
state variable in the economy. By focusing on Markov perfect
equilibria, we can study the monetary authority's decision as a
sequence of static problems.
. Neither past
nor future policy decisions are relevant and there is no physical
state variable in the economy. By focusing on Markov perfect
equilibria, we can study the monetary authority's decision as a
sequence of static problems.
We do not model money directly. Implicitly, nominal deposits are as good as cash balances. This feature of the model allows us to abstract from money demand considerations and to focus on nominal frictions on the supply side of the economy.7
2.1.1 Households
Household preferences at date ![]() are given by
are given by
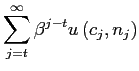
The household's problem at date ![]() is
is
subject to
| 0 |
and
for all
The intertemporal Euler equation associated with the household's
problem (1) at date ![]() is
is
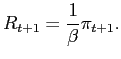
Labor supply is characterized by the first order condition
Neither the level of deposits ![]() nor the price level
nor the price level ![]() appear in the intertemporal
Euler equation and the labor supply condition. Therefore we write
both equilibrium conditions in terms of the economy wide state
appear in the intertemporal
Euler equation and the labor supply condition. Therefore we write
both equilibrium conditions in terms of the economy wide state
![]() .8 First the labor supply condition
is
.8 First the labor supply condition
is
As the policy choice for period
We will drop the time subscripts for the remainder of the paper
and normalize the last period's aggregate price index to
![]() .
.
2.1.2 Firms
There is a continuum
![]() of
intermediate goods. There is a representative final good firm which
combines a continuum
of
intermediate goods. There is a representative final good firm which
combines a continuum
![]() of intermediate inputs
of intermediate inputs
![]() to produce the final good
to produce the final good
![]() according to
according to
with
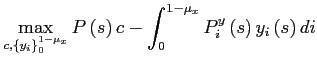
where
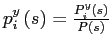 .
.
There is a fraction ![]() of non-tradeable intermediate goods and a
fraction
of non-tradeable intermediate goods and a
fraction
![]() of tradeable intermediate goods.
of tradeable intermediate goods.
There is monopolistic competition in the non-tradeable
intermediate good sector. Each good is produced by a single firm
![]() according to a linear
technology on labor,
according to a linear
technology on labor,
There are three types of intermediate good firms in the
non-tradeable input sector. Let ![]() denote the measure of firms of type
denote the measure of firms of type
![]() , with
, with
![]() . We assume symmetry
within each firm type.
. We assume symmetry
within each firm type.
Firms of type ![]() --the
sticky price firms--set their nominal prices before the monetary
authority's policy choice. As a consequence, their nominal price,
--the
sticky price firms--set their nominal prices before the monetary
authority's policy choice. As a consequence, their nominal price,
![]() , is a function of
the private sector inflation expectations
, is a function of
the private sector inflation expectations ![]() but not of the actual
inflation
but not of the actual
inflation ![]() . As all
intermediate good firms, the sticky price firms take in account the
demand function for its own good,
. As all
intermediate good firms, the sticky price firms take in account the
demand function for its own good,
![]() .
Given our specification for the demand of each good
.
Given our specification for the demand of each good ![]() , (6), profit
maximization implies that the nominal price equals a constant
markup over the expected marginal cost
, (6), profit
maximization implies that the nominal price equals a constant
markup over the expected marginal cost
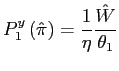
where
Firms of type ![]() are
flexible price setters, i.e.,they set the nominal price,
are
flexible price setters, i.e.,they set the nominal price,
![]() , after the monetary
authority's decision. Hence it is a function of both
, after the monetary
authority's decision. Hence it is a function of both ![]() and
and ![]() . We assume that firms of type
. We assume that firms of type ![]() are financially constrained and they
must borrow the nominal wage bill
are financially constrained and they
must borrow the nominal wage bill ![]() one period in advance at the nominal interest rate
one period in advance at the nominal interest rate
![]() .9 Their
optimal pricing rule is
.9 Their
optimal pricing rule is
The fact that their marginal cost is augmented by
Finally, firms of type ![]() are flexible price setters and financially
unconstrained. Therefore we have
are flexible price setters and financially
unconstrained. Therefore we have
Note that if the expectation and the actual inflation rate are
the same,
![]() ,
(7) and (9) imply that prices
and output are the same across sticky and non-financially
constrained flexible price firms, i.e.,
,
(7) and (9) imply that prices
and output are the same across sticky and non-financially
constrained flexible price firms, i.e.,
![]() and
and
![]() . Moreover,
if
. Moreover,
if
![]() , all firms' prices and
production are identical. Since the production function for the
final good (5) is convex, symmetry across firm
types is a necessary condition for production efficiency. In other
words,
, all firms' prices and
production are identical. Since the production function for the
final good (5) is convex, symmetry across firm
types is a necessary condition for production efficiency. In other
words,
![]() and
and
![]() introduce costly price distortions.
introduce costly price distortions.
The tradeable intermediate good
sector is composed of export and import firms. There is a
measure ![]() of
export firms, which produce domestically and they supply
exclusively to the world markets. We assume that the country's
export goods are not differentiated so the export price is
determined in the world markets.10 Hence, export firms take the price as
given.
of
export firms, which produce domestically and they supply
exclusively to the world markets. We assume that the country's
export goods are not differentiated so the export price is
determined in the world markets.10 Hence, export firms take the price as
given.
The production function for export firms is
In addition the law of one price equates the domestic price, in nominal terms, to the world market price for
where
where
Import firms do not produce domestically: they simply buy
![]() from the world markets. Import prices are determined in the world
market and taken as given by firms. Hence
from the world markets. Import prices are determined in the world
market and taken as given by firms. Hence
Imports constitute a measure
Because there is no trade in intertemporal assets with the rest of the world, the value of imports and exports must be equated every period,
where
2.1.3 Market Clearing Conditions and Private Sector Equilibrium Definition
The aggregate resource constraint is
where (5) has been combined with each intermediate good production technology. The market clearing condition for the labor market is
Equations (3)-(16)
are sufficient to solve for all real prices and allocations as
function of expected and actual inflation. This confirms our
conjecture that
![]() fully characterizes all
allocations. We proceed now to define a Private Sector Equilibrium
(PSE) given
fully characterizes all
allocations. We proceed now to define a Private Sector Equilibrium
(PSE) given ![]() as a
collection of allocation and price functions defined over
as a
collection of allocation and price functions defined over
![]() and a sticky
nominal price
and a sticky
nominal price
![]() .
.
- The household optimal conditions, (3) and (4), are satisfied.
- Firm maximize profits, (7)-(10) are satisfied.
- Markets clear, (5), (6) and (12)-(16) hold.
A Private Sector Equilibrium
outcome in state
![]() is the collection of
allocations and prices which occur at a PSE given
is the collection of
allocations and prices which occur at a PSE given ![]() evaluated at
evaluated at ![]() .
.
Our definition of the PSE is sufficient to characterize the monetary authority's problem. Note that nominal prices, deposits and monetary transfers are not included in the PSE. Now we show how to characterize these variables and why they are not relevant for the monetary authority's problem.
It is straightforward to recover all nominal prices, as under
our normalization,
![]() .
The nominal deposit market clearing condition is
.
The nominal deposit market clearing condition is
where
Finally, the household budget constraint (2)
gives a law of motion for nominal deposits,
![]() . Since
. Since
![]() , the path for nominal deposits
is strictly positive given
, the path for nominal deposits
is strictly positive given ![]() .
.
2.1.4 Solving for the PSE
In our model, the PSE can be solved for analytically. We start
by taking ![]() , a
number, as given. Then we solve for the PSE functions that map the
actual inflation rate
, a
number, as given. Then we solve for the PSE functions that map the
actual inflation rate ![]() into allocations and prices. Using these PSE functions, we can
characterize the sticky price firms decision as function of the
expected inflation rate,
into allocations and prices. Using these PSE functions, we can
characterize the sticky price firms decision as function of the
expected inflation rate,
![]() .
.
From the Fisher equation (4), the nominal interest rate and inflation are simply linked by
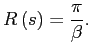
The relative price of sticky price firm's goods is given by
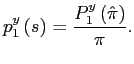
![$\displaystyle \frac{y_{i}\left( s\right) }{y_{j}\left( s\right) }=\left[ \frac ... ...j}^{y}\left( s\right) }{p_{i}^{y}\left( s\right) }\right] ^{\frac {1}{1-\eta}} $](img112.gif)
Using the pricing formulas (7)-(13),
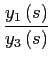
|
![$\displaystyle =\left[ \frac {1}{\eta\theta_{3}}\frac{w\left( s\right) }{p_{1}^{y}\left( s\right) }\right] ^{\frac{1}{1-\eta}}$](img115.gif)
|
|

|
![$\displaystyle =\left[ \frac{\theta_{2}}{\theta_{3}}R\left( s\right) ^{-1}\right] ^{\frac {1}{1-\eta}}$](img117.gif)
|
|
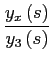
|
![$\displaystyle =\left[ \frac{\theta_{x}}{\eta\theta_{3}}\right] ^{\frac{1}{1-\eta}}$](img119.gif)
|
|
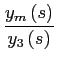
|
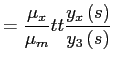
|
where the latest equality is derived using (14). We combine these expressions with (5) to obtain
Next, we use the pricing formula and demand for the intermediate
good ![]() ,
,
![$\displaystyle \left[ \frac{w\left( s\right) }{\eta\theta_{3}}\right] ^{\frac{\e... ... ^{\eta}\left[ \frac{\theta_{x}}{\eta\theta_{3}}\right] ^{\frac{\eta}{1-\eta}} $](img124.gif)
where

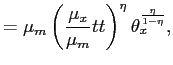
|
||
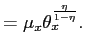 |
This expression is the key to solve for the PSE. With knowledge
of the real wage rate
![]() , the
rest of equilibrium allocations and prices follow. Labor
, the
rest of equilibrium allocations and prices follow. Labor
![]() is
given by (3). To pin down output, use
(16) to derive
is
given by (3). To pin down output, use
(16) to derive
![$\displaystyle \frac{n\left( s\right) }{y_{3}\left( s\right) }=\frac{\mu_{3}}{\t... ...theta_{x}}\left[ \frac{\theta_{x}} {\eta\theta_{3}}\right] ^{\frac{1}{1-\eta}} $](img132.gif)
![$\displaystyle \varphi\left( s\right) =\frac{\left[ \tilde{\mu}_{3}+\tilde{\mu} ... ...\right) }\right] ^{\frac{1}{1-\eta}}+\tilde{\mu}_{x}\eta ^{\frac{1}{\eta-1}}}. $](img134.gif)
![$ \left[ \frac{w\left( s\right) }{\eta }\right] ^{\frac{1}{1-\eta}}$](img135.gif) .
.
To close the PSE, it is still needed to solve for
![]() . Given expectations
. Given expectations
![]() , (7) implies that
, (7) implies that
![]() will satisfy
will satisfy
![]() . This allows to write the real wage rate when
. This allows to write the real wage rate when
![]() as
as
and hence, using (7) again,
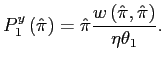
2.2 Policy Equilibria
We view the policy decision as an equilibrium object. We consider three different policy equilibrium concepts: the Markov equilibrium, the Ramsey equilibrium and the Exchange Rate Policy equilibrium.
In the Markov equilibrium, the monetary authority's problem is
to choose the inflation rate which maximizes household welfare
taking nominal prices ![]() as given. Hence the monetary authority has
no ability to manipulate the private sector inflation
expectations.
as given. Hence the monetary authority has
no ability to manipulate the private sector inflation
expectations.
The Ramsey equilibrium characterizes the optimal monetary policy with commitment. A formal definition is given below but the reader can think of the Ramsey equilibrium as the result of an alternative timing where the monetary policy is determined once and for all before sticky price are set.
Finally, the Exchange Rate Policy (ERP) equilibrium captures the possibility that the monetary authority's decision is constrained by an exchange rate policy.
2.2.1 The Markov Equilibrium
The monetary authority's problem is to choose the inflation rate
that maximizes household welfare. The monetary authority takes the
nominal price
![]() as given.
as given.
The choice of the inflation rate is constrained as follows.
First, the nominal interest rate is bounded below by one, i.e.,
![]() . This bound is implied by the
arbitrage condition between nominal bonds and cash balances. The
latter are not explicitly modelled here, yet we can use (4) to establish that the lower bound for inflation
equals the intertemporal discount rate,
. This bound is implied by the
arbitrage condition between nominal bonds and cash balances. The
latter are not explicitly modelled here, yet we can use (4) to establish that the lower bound for inflation
equals the intertemporal discount rate,
![]() .
.
Second, the existence of a PSE outcome also imposes an upper
bound,
![]() , on the inflation
rate. This upper bound is an increasing function of the private
sector inflation expectations. As
, on the inflation
rate. This upper bound is an increasing function of the private
sector inflation expectations. As ![]() approaches the upper bound
approaches the upper bound ![]() , the sticky price firms
have unbounded losses.11
, the sticky price firms
have unbounded losses.11
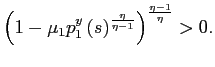
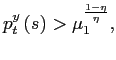

![]()
In Armenter and Brodenstein (2004), we show that the policy choice set can be defined without any loss of generality as
Because a PSE outcome fully determines the household period welfare, we can state the monetary authority's problem as an intratemporal optimization problem
where
All is set for the definition of a Markov equilibrium. The nomenclature emphasizes that equilibria based on trigger strategies are ruled out.
We will say that a policy ![]() is time consistent if there exists a Markov
equilibrium with
is time consistent if there exists a Markov
equilibrium with
![]() . The
definition is for an one-period economy. The corresponding
definition for the infinite horizon economy is not problematic but
it requires some additional formalization. We have decided then to
skip it for the sake of expositional clarity.
. The
definition is for an one-period economy. The corresponding
definition for the infinite horizon economy is not problematic but
it requires some additional formalization. We have decided then to
skip it for the sake of expositional clarity.
2.2.2 The Ramsey Equilibrium
In the Ramsey equilibrium, the monetary authority pins down private sector expectations with its policy decision. The Ramsey equilibrium policy also characterizes the optimal monetary policy with commitment.
Not surprisingly, the optimal monetary policy with commitment
turns out to be the Friedman rule. All distortions associated with
price dispersion are zeroed by setting the nominal interest rate to
zero,
![]() .
The distortion that arises from monopoly pricing remains. However,
there is nothing monetary policy can do to curtail the market power
of the intermediate good firms.13 Hence, labor remains
undersupplied.
.
The distortion that arises from monopoly pricing remains. However,
there is nothing monetary policy can do to curtail the market power
of the intermediate good firms.13 Hence, labor remains
undersupplied.
Does the Friedman Rule constitute a Markov Equilibrium? Assume
private sector expectations are such that
![]() , i.e., sticky
nominal prices are set under the belief that the Friedman Rule will
be chosen by the monetary authority. Ex-post, the monetary
authority can choose to inflate
, i.e., sticky
nominal prices are set under the belief that the Friedman Rule will
be chosen by the monetary authority. Ex-post, the monetary
authority can choose to inflate ![]() and cut the markup of the sticky price
firms. However, such a move creates price distortions. The price
difference between the sticky and flexible price firm goods is
welcome as it reflects the improved efficiency in the sticky price
firms' good production. However, there is an additional price
distortion. The marginal cost of financially constrained firms are
augmented by
and cut the markup of the sticky price
firms. However, such a move creates price distortions. The price
difference between the sticky and flexible price firm goods is
welcome as it reflects the improved efficiency in the sticky price
firms' good production. However, there is an additional price
distortion. The marginal cost of financially constrained firms are
augmented by
![]() . This
implies lower efficiency in the production of financially
constrained firms. Hence, at least on the margin, whether the
Friedman Rule is time consistent depends on the relative weight of
each distortion which, in our model, are closely linked to each
firm type.
. This
implies lower efficiency in the production of financially
constrained firms. Hence, at least on the margin, whether the
Friedman Rule is time consistent depends on the relative weight of
each distortion which, in our model, are closely linked to each
firm type.
2.2.3 The Exchange Rate Policy Equilibrium
In the exchange rate policy equilibrium (ERP), the monetary authority takes the private sector expectations as given and maximizes household welfare--as in the Markov equilibrium. However, its policy choice is exogenously constrained by the exchange rate policy.
We formalize the exchange rate policy as a set of acceptable
nominal exchange rates, ![]() . A fixed exchange rate regime reduces
. A fixed exchange rate regime reduces
![]() to a singleton
to a singleton
![]() ,
,
![]() . A soft
exchange rate peg, which specifies some bands
. A soft
exchange rate peg, which specifies some bands
![]() , would be formalized as
, would be formalized as
![]() . As we focus our analysis in commonly observed exchange
rate regimes, we do not consider the possibility that the set
. As we focus our analysis in commonly observed exchange
rate regimes, we do not consider the possibility that the set
![]() is history
dependent.
is history
dependent.
The monetary authority's problem in a ERP is
subject to
We have assumed implicitly that it is not possible to review the exchange rate policy. In other words, the policymaker is able to commit to an exchange rate regime but not to a given monetary policy.
3 Expectation Traps
In this section we show that the absence of commitment can lead to costly volatility due to self-fulfilling private sector expectations. The multiplicity of Markov equilibria is a robust property of this economy.14
3.1 Understanding Expectation Traps
To understand expectation traps, we first discuss the monetary authority's decision for given private sector expectations. In this economy, the costs and benefits of inflation are driven by the heterogeneous impact of inflation across firm types. Inflation reduces overall efficiency by distorting relative prices and by increasing the cost of working capital for financially constrained firms. On the other hand, unexpected inflation erodes the markup of sticky price firms thereby improving efficiency. In a Markov equilibrium, the costs and benefits from unexpected inflation are balanced.
Expectations traps arise because expected inflation changes the composition of the intermediate good sector. While the measure of each firm type is constant, inflation alters the relative output of sticky price firms and financially constrained firms.
Sector composition is the key determinant of the monetary authority's decision. When expected inflation is low, each type of firm operates at similar scale. Efficiency gains from unexpected inflation are almost zero: any cut in the markup of the sticky price firms is roughly offset by an increase in the marginal cost of the financially constrained firms. As a result, there are little net efficiency gains to outweigh the costs of price distortion. A low inflation equilibrium exists where the marginal costs of price distortion are low.
When the private sector expects high inflation, financially constrained firms operate at reduced scale because of the large costs of nominal working capital. There are considerable net efficiency gains from unexpected inflation because the sticky price sector is relatively large compared to the financially constrained sector. These large efficiency gains can exceed the higher marginal cost of price distortion. Hence, the monetary authority will find it optimal to validate the high inflation expectations.
Figure 2: Expectation Traps in a Calibrated Economy
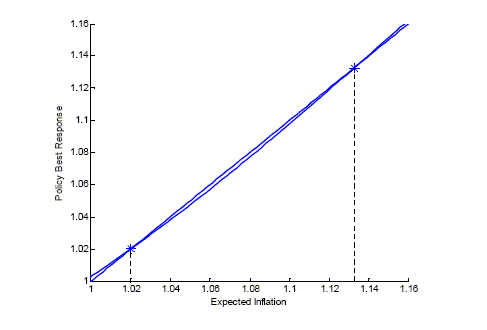
Figure 2 displays the policy best response
![]() as a
function of private sector expectations
as a
function of private sector expectations ![]() . The 45-degree line is the set of points where actual inflation equals expected
inflation,
. The 45-degree line is the set of points where actual inflation equals expected
inflation,
![]() . This is
the rational expectation locus. Crossings of the policy best
response function with the 45-degree line indicate Markov
equilibria. We calibrated the economy displayed in Figure 2 to match two Markov equilibria with inflation rates
of
. This is
the rational expectation locus. Crossings of the policy best
response function with the 45-degree line indicate Markov
equilibria. We calibrated the economy displayed in Figure 2 to match two Markov equilibria with inflation rates
of ![]() and
and ![]() .15 An additional feature to note is that
each Markov equilibrium is locally unique.
.15 An additional feature to note is that
each Markov equilibrium is locally unique.
We have argued that the changes in the composition of the
intermediate good sector are behind the expectation traps. This is
illustrated in Figure 3. Output for sticky
price firms and financially constrained firms is plotted along the
rational expectations locus, i.e.,
![]() , for
different values of inflation
, for
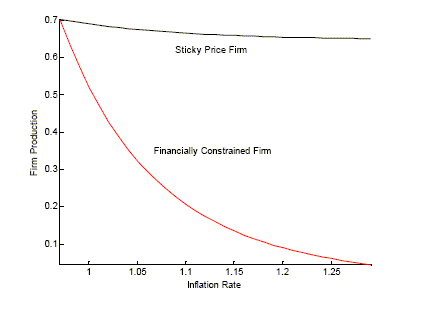
different values of inflation ![]() . Firms' output is similar across firm types when
inflation is low.16 High
inflation disproportionately reduces the production of financially
constrained firms. Sticky price firm production also falls because
aggregate demand is reduced by the price distortion.
. Firms' output is similar across firm types when
inflation is low.16 High
inflation disproportionately reduces the production of financially
constrained firms. Sticky price firm production also falls because
aggregate demand is reduced by the price distortion.
Figure 3: Intermediate Good Output for Firms 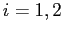 .
.
The welfare implications of expectation traps dwarf the classic inflation bias analyzed by Barro and Gordon (1983). Table 1 documents this claim for several economies calibrated to match different equilibrium inflation rates. This is achieved by varying the measure of sticky price firms and financially constrained firms in the economy.
Table 1: Welfare Implications: Several Calibrations
Welfare changes computed as percentage points of consumption at equilibrium inflation
|
For each economy we compute the welfare implications of several
experiments. First, we reduce inflation from the low inflation,
![]() , to the Ramsey
equilibrium,
, to the Ramsey
equilibrium, ![]() . This
is equivalent to correcting the classic inflation bias in an
economy with a single equilibrium. Second, we evaluate the shift
from the high inflation,
. This
is equivalent to correcting the classic inflation bias in an
economy with a single equilibrium. Second, we evaluate the shift
from the high inflation, ![]() , to the low inflation equilibrium,
, to the low inflation equilibrium,
![]() . The last two
columns report the welfare change per period as given by the
equivalent consumption change in percentage points evaluated at the
low inflation equilibrium
. The last two
columns report the welfare change per period as given by the
equivalent consumption change in percentage points evaluated at the
low inflation equilibrium ![]() .
.
In our baseline calibration, with a low inflation of
![]() , the welfare
impact of an equilibrium shift is about three times the welfare
gains of removing the classic inflation bias. The overall magnitude
of welfare losses is significant but not large. The situation is
similar for alternative calibrations.17
, the welfare
impact of an equilibrium shift is about three times the welfare
gains of removing the classic inflation bias. The overall magnitude
of welfare losses is significant but not large. The situation is
similar for alternative calibrations.17
How common are expectations traps? Several papers find multiple equilibria in a variety of monetary economies. All of them focus on Markov perfect equilibria and so none of the equilibrium multiplicity results hinge on trigger strategies. Albanesi (2003) explores a cash/credit good model and show that monetary policy discretion may lead to expectation traps. King and Wolman (2004) also finds multiple equilibria in a simple new Keynesian model with two-period staggered pricing. Siu (2004) allows firms to set their degree of price stickiness and shows that, once again, equilibrium multiplicity arises. Finally, Armenter (2004) argues that the necessary conditions for the existence of expectation traps are very general.
Armenter and Brodenstein (2004) perform a thorough characterization
of expectation traps in a closed economy version. The main finding
is that for all parametrizations with an equilibrium inflation rate
between ![]() and
and
![]() , there is an
additional Markov equilibrium with higher inflation. This property
of the model is robust and it does not rely upon large nominal
frictions.
, there is an
additional Markov equilibrium with higher inflation. This property
of the model is robust and it does not rely upon large nominal
frictions.
3.2 The Case for Soft Exchange Rate Pegs
Expectation traps do not conflict with monetary policy flexibility. With respect to exchange rate policy, a soft peg with appropriately chosen bands is sufficient to rule out expectation traps, yet it allows to the monetary authority to react to real shocks.
To see this, consider an inflation cap ![]() strictly below the high
inflation equilibrium,
strictly below the high
inflation equilibrium,
![]() ,
but strictly above the low inflation equilibrium rate,
,
but strictly above the low inflation equilibrium rate,
![]() .
Such a cap exists because the Markov equilibria are locally unique.
Assume the cap is an exogenous constraint: the monetary authority
cannot validate high inflation expectations even if it would like
to. Therefore the low inflation equilibrium
.
Such a cap exists because the Markov equilibria are locally unique.
Assume the cap is an exogenous constraint: the monetary authority
cannot validate high inflation expectations even if it would like
to. Therefore the low inflation equilibrium ![]() becomes the unique Markov
equilibrium of the economy.18
becomes the unique Markov
equilibrium of the economy.18
Next we show how to implement a given inflation cap ![]() with an exchange rate
policy
with an exchange rate
policy ![]() .
Combining (10) with (12), we
obtain
.
Combining (10) with (12), we
obtain
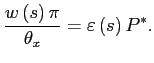
where we use the normalization that
![$\displaystyle \bar{\varepsilon}=\frac{\eta}{\pi^{\ast}\theta_{x}}\left[ \left( ... ...ta}}+\tilde{\mu}_{2}\beta^{\frac{\eta}{1-\eta} }\right] ^{\frac{1-\eta}{\eta}} $](img200.gif)
A soft exchange rate regime improves welfare even if it does not correct the classic inflation bias, i.e.,it does not implement the optimal monetary policy. First, the monetary authority cannot be caught in the high inflation equilibrium. Second, there will be no volatility arising from expectation shifts.
Moreover, the exchange rate bands can be wide enough so they allow considerable monetary policy flexibility. In our calibration, the difference between the low and high equilibrium inflation rates is about ten percentage points. This leaves plenty of room for policy responses to plausible real shocks. Hence, absent any other considerations and leaving the inflation bias unchanged, the classic textbook argument a la Mundell-Fleming favours broad bands to a hard exchange rate pegs. We challenge this view in the next section.
4 Perverse Policy Responses
The textbook argument against fixed exchange rates builds on the classic Mundell-Fleming analysis. A fixed exchange rate regime means no independent monetary policy. The monetary authority loses its ability to react to real shocks and ends up `` importing'' the foreign monetary policy. The loss of flexibility is often seen as the downside of the gains that the commitment to a fixed exchange rate can provide.
We argue that the Mundell-Fleming argument does not hold for the case of monetary policy without commitment. We show that the policy response to certain real shocks can be perverse, i.e.,worse than inaction, as shocks exacerbate the time inconsistency problem. Independent monetary policy is no guarantee for lower macroeconomic volatility.
The intuition behind a perverse policy response is quite general. A real shock can increase the welfare gains from unexpected inflation. Consequently, firms anticipate higher inflation. The monetary authority reacts, rightfully, to the real shock but also reacts, unnecessarily, to the induced change in private sector expectations. If the latter dominates, the equilibrium policy response leads to a worsening of the inflation bias and to welfare inferior allocations.
We focus on a negative terms of trade shock because of its appeal for developing economies, where the case for fixed exchange rates is often built upon time inconsistency issues.19 A negative terms of trade shock contracts the open intermediate sector, which is characterized by perfect competition. As a result, the economy is less competitive, the distortion from monopolistic competition is larger and so is the temptation to cut markups with unexpected inflation.
To see this, we compute an `` aggregate'' markup ![]() by dividing the final good
price by the aggregate marginal cost of production. In the
Appendix, we detail the construction of the aggregate markup and
show that
by dividing the final good
price by the aggregate marginal cost of production. In the
Appendix, we detail the construction of the aggregate markup and
show that
![$\displaystyle \kappa=\frac{\left[ \left( \frac{\mu_{1}y_{1}}{y}+\frac{\mu_{2}y_... ...eta}}+\frac{\mu_{3}y_{3}}{y}\right) +\frac{\mu_{m}y_{m}}{y}\right] ^{1-\eta}}. $](img203.gif)
In response to a negative terms of trade shock, imports contract
in relative terms, i.e.,
![]() falls
as the relative price of imports goes up.20 The aggregate markup increases as the
competitive sector is weighted less. In the Appendix we show that
the markup is decreasing in
falls
as the relative price of imports goes up.20 The aggregate markup increases as the
competitive sector is weighted less. In the Appendix we show that
the markup is decreasing in
![]() .
.
The assumption that the tradeable sector is competitive is
important. One possible motivation is that the country's exports
are not differentiated and hence export prices ![]() are set in the world markets.
This particularly suits a developing economy framework.
are set in the world markets.
This particularly suits a developing economy framework.
We illustrate the perverse policy phenomenon in the calibrated
version of our model. We compare a fixed and flexible exchange rate
regime in the event of a unanticipated and permanent negative terms
of trade shock. The fixed exchange rate regime is modelled as an
Exchange Rate Policy equilibrium with
![]() . For the
flexible exchange rate regime, we use our concept of Markov
equilibrium. Since there are usually multiple Markov equilibria, we
pick the one with lowest inflation.21
. For the
flexible exchange rate regime, we use our concept of Markov
equilibrium. Since there are usually multiple Markov equilibria, we
pick the one with lowest inflation.21
In order to abstract from the classic inflation bias, we set the
world inflation rate
![]() such that
the flexible and the fixed exchange rate regime deliver the same
allocations in the pre-shock economy. In other words, there are no
`` level'' gains in terms of inflation under a fixed exchange rate
regime as the world inflation rate is set equal to the inflation
rate
such that
the flexible and the fixed exchange rate regime deliver the same
allocations in the pre-shock economy. In other words, there are no
`` level'' gains in terms of inflation under a fixed exchange rate
regime as the world inflation rate is set equal to the inflation
rate ![]() in the low
inflation Markov equilibrium.
in the low
inflation Markov equilibrium.
We model the terms of trade shock as unforeseen. This is the best scenario for active monetary policy. By adjusting inflation, the monetary authority can ease the impact of a real shock. The stabilization role ends after one period once all firms have had a chance to re-set their prices.
We also assume that the shock is permanent. We then report all welfare computations per period. Hence the assumption that the shock is permanent has no impact beyond providing us with at least one period where the shock is unanticipated and one period where the shock is anticipated by the sticky price firms.
The timing of the shock is as follows. At date ![]() , the economy is in the original
steady state. The terms of trade deteriorate by
, the economy is in the original
steady state. The terms of trade deteriorate by ![]() after firms of type
after firms of type ![]() have set their sticky price for date
have set their sticky price for date
![]() but before the
monetary authority policy decision. Hence, there is a stabilization
role for monetary policy. At date
but before the
monetary authority policy decision. Hence, there is a stabilization
role for monetary policy. At date ![]() , sticky price firms are aware that the shock is
permanent and they set their prices accordingly. Prices and
allocations reach the new steady state at date
, sticky price firms are aware that the shock is
permanent and they set their prices accordingly. Prices and
allocations reach the new steady state at date ![]() .22
.22
Figure 4: Equilibrium Response to a Negative Terms of Trade Shock. Solid line correspond to the low inflation Markov equilibrium. Dashed line corresponds to a fixed exchange rate regime. See text for details.
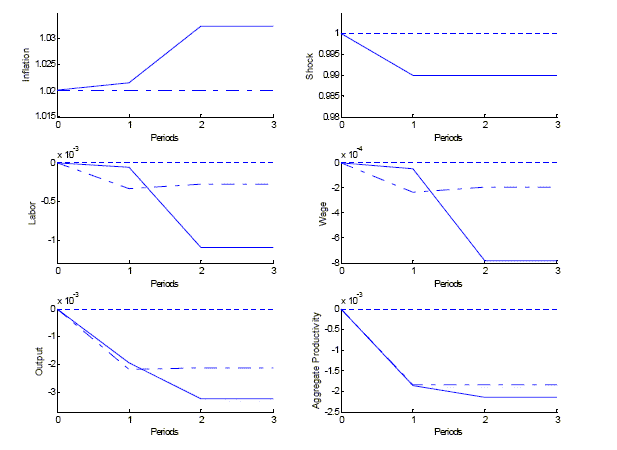
Description for Figure 4:
Figure 4 is titled �Equilibrium Response to a Negative Terms of Trade Shock�. It contains six graphs. In each of the graphs, the x-axis is labeled �Periods� and runs from 0 to 3 in increments of 1. In the top left graph, the y-axis is labeled �Inflation� and runs form 1.015 to 1.035. A dashed horizontal line runs where inflation is 1.02. The curve in the graph is not smooth; it connects the points given at the integer time periods. At period 0, inflation has a value of 1.02. At period 1, inflation has a value of about 1.021. At periods 2 and 3, inflation has a value of 1.0325. In the top right graph, the y-axis is labeled �Shock� and runs form 0.98 to 1.005. A dashed horizontal line runs where the shock is 1. The curve in the graph is not smooth; it connects the points given at the integer time periods. At period 0, shock has a value of 1. At periods 1, 2 and 3, the shock has a value of 0.99. In the middle left graph, the y-axis is labeled �Labor� and runs from -0.0015 to 0 in increments of 0.0005. A dashed horizontal line runs where labor is 0. There are two curves in this graph; neither is smooth. The curves connect the points given at integer time periods. The first curve has a labor value of 0 at period 0. At period 1, the curve has a labor value of -0.0001. At periods 2 and 3, the curve has a labor value of -0.0011. The second curve has a labor value of 0 at period 0. At period 1, the curve has a labor value of -0.0003. At periods 2 and 3, the curve has a labor value of -0.00025. In the middle right graph, the y-axis is labeled �Wage� and runs from -0.0008 to 0 in increments of 0.0002. A dashed horizontal line runs where wage is 0. There are two curves in this graph; neither is smooth. The curves connect the point given at integer time periods. The first curve has a wage value of 0 at period 0. At period 1, the curve has a wage value of -0.00005. At periods 2 and 3, the curve has a wage value of -0.00079. The second curve has a wage value of 0 at period 0. At period 1, the curve has a wage value of -0.00022. At period 2 and 3, the curve has a wage value of -0.0002. In the bottom left graph, the y-axis is labeled �Output� and runs from -0.004 to 0 in increments of 0.001. A dashed horizontal line runs where output is 0. There are two curves in the graph; neither is smooth. The curves connect the point given at integer time periods. The first curve has an output value of 0 at period 0. At period 1, the curve has an output value of -0.002. At periods 2 and 3, the curve has an output value of -0.0035. The second curve has an output value of 0 at period 0. At periods 1, 2, and 3, the curve has an output value of -0.0022. In the bottom right graph, the y-axis is labeled �Aggregate Productivity� and runs from -0.0025 to 0 in increments of 0.0005. A dashed horizontal line runs where aggregate productivity is 0. There are two curves in the graph; neither is smooth. The curves connect the point given at integer time periods. The first curve has an aggregate productivity value of 0 at period 0. At period 1, the curve has a value of -0.0018. At periods 2 and 3, the curve has a value of -0.0022. The second curve has an aggregate productivity of 0 at period 0. At periods 1, 2, and 3, the curve has a value of -0.0018.
Figure 4 displays the response of selected
prices and allocations. The solid line corresponds to the Markov
equilibrium and the dashed line to the ERP equilibrium with
![]() . The most
important graph is in the upper left corner and it displays the
inflation rate. Under the fixed exchange rate inflation is
constant. Under independent monetary policy, inflation increases in
two steps. At date
. The most
important graph is in the upper left corner and it displays the
inflation rate. Under the fixed exchange rate inflation is
constant. Under independent monetary policy, inflation increases in
two steps. At date ![]() ,
there is a small inflation increase. This is the optimal response
induced by the presence of nominal frictions.23However, at date
,
there is a small inflation increase. This is the optimal response
induced by the presence of nominal frictions.23However, at date ![]() inflation jumps by a large amount
in the Markov equilibrium, when there is no longer a role for
monetary policy to ease the real shock. From date
inflation jumps by a large amount
in the Markov equilibrium, when there is no longer a role for
monetary policy to ease the real shock. From date ![]() onwards, high inflation only
reflects higher sticky prices.24This
response is clearly welfare reducing.
onwards, high inflation only
reflects higher sticky prices.24This
response is clearly welfare reducing.
Prices and allocations tell the same story. At date ![]() , the policy response in the
Markov equilibrium keeps the wage and labor close to their steady
state values despite the shock, while under the fixed exchange rate
there is no smoothing. However, from date
, the policy response in the
Markov equilibrium keeps the wage and labor close to their steady
state values despite the shock, while under the fixed exchange rate
there is no smoothing. However, from date ![]() onwards, the impact is more
pronounced under flexible exchange rate regime. Higher expected
inflation brings wage, labor and output below their counterparts
under the fixed exchange rate regime.
onwards, the impact is more
pronounced under flexible exchange rate regime. Higher expected
inflation brings wage, labor and output below their counterparts
under the fixed exchange rate regime.
Table 2: Welfare Comparison: Markov equilibrium versus fixed exchange rate in the event of a terms of trade shock.
| Period | Date
|
Date
|
Date
|
|---|---|---|---|
| Date |
0 | 0 | 0 |
Negative Shock: Date |
0.00015 | 0.00016 | 0.00017 |
Negative Shock: Date |
-0.0393 | -0.0597 | -0.0912 |
Positive Shock: Date |
0.00014 | 0.00016 | 0.00017 |
Positive Shock: Date |
0.0241 | 0.0296 | 0.0348 |
Welfare changes reported as percentage points of consumption under non-stochastic economy. Values per period.
Table 2 compares the welfare properties of both exchange rate regimes. We report the per period consumption compensation, in percentage points, for a shift from the fixed exchange rate regime to the Markov equilibrium. A negative number means that households are willing to pay to keep the fixed exchange rate regime for the given period. We include several calibrations: we report the corresponding Markov equilibrium inflation rate in the pre-shock economy. In each calibration, the world inflation rate is set such that the flexible and the fixed exchange rate have the same welfare properties in the pre-shock economy.
At date ![]() , right
after the negative terms of trade shock, the Markov equilibrium
dominates the fixed exchange rate. The welfare difference, though,
is quite small. From date
, right
after the negative terms of trade shock, the Markov equilibrium
dominates the fixed exchange rate. The welfare difference, though,
is quite small. From date ![]() onwards, the fixed exchange rate equilibrium is
welfare dominant. The welfare gains from a fixed exchange rate at
date
onwards, the fixed exchange rate equilibrium is
welfare dominant. The welfare gains from a fixed exchange rate at
date ![]() are about three
times the welfare losses at date
are about three
times the welfare losses at date ![]() . These are per period welfare changes. So even if
the shock lasted only two periods, the fixed exchange rate would be
preferred. Under the assumption of a permanent shock, we should
multiply the welfare change at date
. These are per period welfare changes. So even if
the shock lasted only two periods, the fixed exchange rate would be
preferred. Under the assumption of a permanent shock, we should
multiply the welfare change at date ![]() by
by
![]() .
.
The impact of a positive terms of trade shock is not symmetric.
Table 2 also reports the welfare ranking in
the aftermath of a positive shock to the terms of trade. In this
event, the flexible exchange rate is welfare superior both at date
![]() and
and ![]() . However, the welfare
implications under positive and negative shocks do not cancel each
other. As shown in Table 2, a positive
terms of trade shock brings welfare gains which are about half the
welfare loss under a negative terms of trade shock. This is a
direct consequence of the concavity of the policy problem.
. However, the welfare
implications under positive and negative shocks do not cancel each
other. As shown in Table 2, a positive
terms of trade shock brings welfare gains which are about half the
welfare loss under a negative terms of trade shock. This is a
direct consequence of the concavity of the policy problem.
To summarize, Table 2 clearly speaks in favour of fixed exchange rates in the event of a real shock--a scenario usually associated with the costs of losing monetary independence.
4.1 Other Shocks
A terms of trade shock is not the sole instance of a perverse policy response. Consider a negative shock to the financially constrained firm's sector. We have in mind an exogenous tightening of financial constraints, perhaps due to a banking crisis.
Figure 5: Equilibrium Response to a Negative Productivity Shock in Financially Constrained Firms. Solid line correspond to the low inflationMarkov equilibrium. Dashed line corresponds to a fixed exchange rate regime. See text for details.
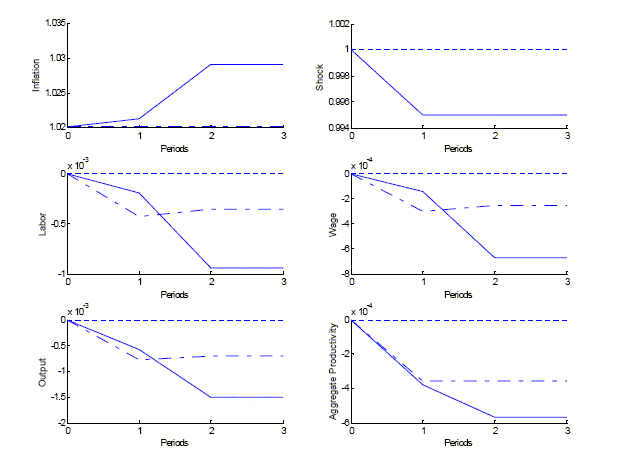
Figure 5 shows the response of
selected prices and allocations to a unexpected fall in the
productivity of financially constrained firms of ![]() . The monetary response in date
. The monetary response in date
![]() , right after the
shock, eases the impact on the wage rate and output. However, once
sticky price firms adjust their prices, the resulting policy
response leads to further, unnecessary inflation. Wage rate and
output are significantly lower then.
, right after the
shock, eases the impact on the wage rate and output. However, once
sticky price firms adjust their prices, the resulting policy
response leads to further, unnecessary inflation. Wage rate and
output are significantly lower then.
Table 3: Welfare Comparison: Markov equilibrium versus fixed exchange rate in the event of a shock to financially constrained firms.
| Period | Date |
|---|---|
| Date |
0 |
Negative Shock: Date |
0.00041 |
Negative Shock: Date |
-0.0705 |
Positive Shock: Date |
0.00047 |
Positive Shock: Date |
0.0388 |
Welfare changes reported as percentage points of consumption under non-stochastic economy. Values per period.
The welfare properties of the two exchange rate regimes--shown
in Table 3--are not surprising. In the
event of a negative shock, a fixed exchange rate shock is clearly
preferred: the welfare loss associated with independent monetary
policy from date ![]() onwards is much larger than any welfare gains from stabilization.
Due to concavity, the fixed exchange rate retains its welfare
dominance even if positive and negative shocks are
equiprobable.
onwards is much larger than any welfare gains from stabilization.
Due to concavity, the fixed exchange rate retains its welfare
dominance even if positive and negative shocks are
equiprobable.
We do not claim that a fixed exchange rate is welfare superior in the event of any shock. In some cases, stabilization is very important or the shock leaves the monetary authority's incentives unchanged. However, our robustness exercises suggest that it is the persistence of shocks that triggers the perverse policy response. Estimated real shocks typically have a half-life of over two years, which leaves no doubt that these shocks are highly persistent.
5 Conclusion
This paper contributes to the exchange rate regime debate but by no means settles it. A definitive welfare ranking of exchange rate regimes is more elusive than ever. Expectation traps and perverse policy responses increase the complexity of any welfare evaluation of exchange rate regimes--yet any such evaluation is incomplete without considering both phenomena.
The world-wide downward trend in inflation does not mean that the credibility problems are a thing of the past--and so is the case for a fixed exchange rate regime. A low inflation country may be only a shift in expectations away from high inflation. Moreover, large real volatility does not necessarily make a stronger case for a flexible exchange rate. We have to ask first what is the impact of the relevant real shocks on the time inconsistency problem and how likely is it that independent monetary policy reacts perversely.
We have abstracted from the time consistency of the exchange rate policy itself in order to highlight the credibility problems under a flexible exchange rates. Certainly, we do not think that an exchange rate regime is free of credibility problems. Trying to sustain a fixed exchange rate absent commitment can lead to self-fulfilling currency crises, as discussed in Obstfeld (1996)--although, as our paper points out, a flexible exchange rate can lead to self-fulfilling currency crises, too. Hence, a country may be left only with an extreme solution such as dollarization.
Yet, it is often the case that fixed exchange rates are brought down by fiscal rather than monetary crises. We do not view fixed exchange rates as a solution to fiscal problems. The ongoing skepticism about fixed exchange rate credibility arises very much from using the wrong tool for the wrong problem.
References
Albanesi, S., Chari, V. and Christiano, L. J.: 2003, Expectation traps and monetary policy, The Review of Economic Studies 70(4), 715�742.
Armenter, R.: 2004, A general theory (and some evidence) of expectation traps in monetary policy. Working Paper, Federal Reserve Bank of New York.
Armenter, R. and Bodenstein, M.: 2004, Can the U.S. monetary policy fall (again) in an expectation trap? Working Paper, Federal Reserve Bank of New York.
Barro, R. J. and Gordon, D.: 1983, A positive theory of monetary policy in a natural rate model, Journal of Political Economy 91(4), 589�610.
Calvo, G. A. and Reinhart, C. M.: 2002, Fear of floating, Quarterly Journal of Economics 117(2), 379�408.
Chang, R. and Velasco, A.: 2000, Exchange-rate policy for developing countries, The American Economic Review 90(2), 71�75.
Chang, R. and Velasco, A.: 2003, Dollarization: Analytical issues, in E. Levy Yeyati and F. Sturzenegger (eds), Dollarization, MIT Press, Cambridge, Mass. and London, pp. 53� 75.
Chari, V., Christiano, L. J. and Eichenbaum, M.: 1998, Expectation traps and discretion, Journal of Economic Theory 81(2), 462�492.
Clarida, R., Gali, J. and Gertler, M.: 1999, The science of monetary policy: A new Keynesian perspective, Journal of Economic Literature 37(4), 1661�1707.
Cooley, T. F. and Quadrini, V.: 2001, The costs of losing monetary independence: The case of Mexico, Journal of Money, Credit and Banking 33(2), 370�397.
Devereux, M. B. and Engel, C.: 2003,Monetary policy in the open economy revisited: Price setting and exchange rate-flexibility, Review of Economic Studies 70, 765�783.
Duarte, M. and Obstfeld, M.: 2005, Monetary policy in the open economy revisited: The case for exchange-rate flexibility restored. mimeo, Federal Reserva Bank of Richmond.
Dupor, B.: 2003, Optimal random monetary policy with nominal rigidity, Journal of Economic Theory 112(1), 66�78.
Frankel, J. A.: 1998, No Single Currency Regime is Right for All Countries or at All Times, number 215, Princeton University Press, Princeton. Essays in International Finance.
King, R. G. and Wolman, A. L.: 2004, Monetary discretion, pricing complementarity and dynamic multiple equilibria, Quarterly Journal of Economics 119(4), 1513�1553.
Mendoza, E. G.: 2001, The benefits of dollarization when stabilization policy lacks credibility and financial markets are imperfect, Journal of Money, Credit and Banking 33(2), 440�474.
Obstfeld, M.: 1996, Models of currency crises with self-fulfilling features, European Economic Review 40, 1037�48.
Obstfeld, M. and Rogoff, K.: 1996, Foundations of International Macroeconomics, TheMIT Press, Cambridge, Massachusetts.
Rogoff, K. S.: 2003, Globalization and global disinflation, Monetary Policy and Uncertainty: Adapting to a Changing Economy, Federal Reserve Bank of Kansas City.
Romer, D.: 1993, Openness and inflation: Theory and evidence, The Quarterly Journal of Economics 108(4), 869�903.
Siu, H. E.: 2004, Time consistent monetary policy with endogenous price rigidity. Working Paper, University of British Columbia.
Svensson, L. E. O.: 1997, Optimal inflation targets, "conservative" central banks, and linear inflation contracts, The American Economic Review 87(1), 98�114.
Woodford, M.: 2003, Interest and Prices, Princeton University Press, Princeton.
A Appendix
A.1 Calibration
We start by setting the preference parameters to standard
values. The inverse of ![]() is the real interest rate in our economy: we set
it equal to
is the real interest rate in our economy: we set
it equal to ![]() ,
,
![]() , which
means evaluating the model at the annual frequency.
, which
means evaluating the model at the annual frequency.
Our choice for leisure preferences is
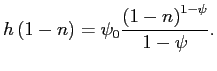
We set the share of nontradeable goods at ![]() and the share of export firms at
and the share of export firms at
![]() . The last of the
pre-set parameters is
. The last of the
pre-set parameters is ![]() , which is set to replicate a
, which is set to replicate a ![]() markup.
markup.
We calibrate the measure of firms of type ![]() and
and ![]() to match a
to match a ![]() range in the low inflation equilibrium. In
every case we find a second equilibrium with inflation in the range
of
range in the low inflation equilibrium. In
every case we find a second equilibrium with inflation in the range
of ![]() . We find
that we can match these numbers with reasonable parameter values.
The share of firms with sticky prices is about
. We find
that we can match these numbers with reasonable parameter values.
The share of firms with sticky prices is about ![]() , and the measure of financially
constrained firms is just above
, and the measure of financially
constrained firms is just above ![]() .
.
Our parameter choices are summarized in Table 4.
Table 4: Baseline Calibration.
| Parameter | Notation | Value |
|---|---|---|
| Intertemporal Discount Rate | .9709 | |
| Leisure-Consumption | .5 | |
| Inverse Frisch Labor Elasticity | 1 | |
| Share of Non Tradeables | .6 | |
| Inverse Markup | ||
| Measure of Firms |
.12 | |
| Measure of Firms |
.0552 | |
| Measure of Firms |
.12 |
A.2 The Aggregate Markup
In order to provide some insight on the perverse policy response phenomenon, we compute an aggregate markup. From the final good firm's profit maximization problem, we write the corresponding cost minimization problem:
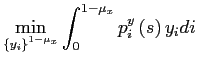
![$\displaystyle y\leq\left[ \int_{0}^{1-\mu_{x}}y_{i}^{\eta}di\right] ^{\frac{1}{\eta}}. $](img238.gif)
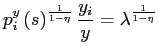
![$\displaystyle \left[ \int_{0}^{1-\mu_{x}}p_{i}^{y}\left( s\right) ^{\frac{1}{1-\eta} }\frac{y_{i}}{y}di\right] ^{1-\eta}=\lambda $](img242.gif)
We compute the markup in a Markov equilibrium. We substitute the pricing formula for each price to obtain:
![$\displaystyle \lambda=\left[ \mu_{1}\frac{y_{1}}{y}\left( \frac{w}{\eta\theta_{... ...ft( q\left( s\right) p_{m}^{\ast}\right) ^{\frac{1}{1-\eta}}\right] ^{1-\eta}. $](img243.gif)
![$\displaystyle \lambda=w\left[ \left( \mu_{1}\frac{y_{1}}{y}+\mu_{2}\frac{y_{2}}... ...{1}{\eta }\right) ^{\frac{1}{1-\eta}}+\mu_{x}\frac{y_{m}}{y}\right] ^{1-\eta}. $](img245.gif)
![$\displaystyle \tilde{\lambda}=w\left[ \left( \mu_{1}\frac{y_{1}}{y}+\mu_{2}\fra... ...eta}}+\mu_{3}\frac{y_{3}}{y}\right) +\mu_{x}\frac{y_{m}} {y}\right] ^{1-\eta}. $](img246.gif)
To see that ![]() is decreasing with
is decreasing with ![]() , note that
, note that
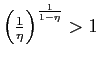 and apply simple differential calculus.
and apply simple differential calculus.
Footnotes
* The authors are grateful to Gadi Barlevy, Christian Broda, Lawrence Christiano, Martin Eichenbaum, Sergio Rebelo, Alexander Wolman, Sevin Yeltekin, and Kei Mu Yi for discussions. In addition, the authors thank seminar participants at the 2002 SED Meeting in New York, the 2002 CEPALES Conference, Northwestern University, the Federal Reserve Bank of New York, the SCIEA meetings at the Board of Governors, Universitat Pompeu i Fabra, University of British Columbia, the 2nd Annual Meeting of German Economists Abroad and the Federal Reserve Bank of Philadelphia. The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or any other person associated with the Federal Reserve System, or the Federal Reserve Bank of New York. Return to text
† Armenter: Federal Reserve Bank of New York, e-mail: [email protected]; Bodenstein: Board of Governors of the Federal Reserve System, e-mail: [email protected]. Return to text
1. Of course there are other persuasive macroeconomic arguments in favor of fixed exchange rates, such as the well known `` fear of floating'' of Calvo and Reinhart (2002). See also Devereux and Engel (2003) who argue that an optimal policy with commitment features a fixed exchange rate in the presence of a large degree of local-currency pricing. However, this claim has been recently disputed by Duarte and Obstfeld (2005). See Obstfeld and Rogoff (1996) and references therein for a general discussion. Return to text
2. Chari, Christiano and Eichenbaum (1998) originally introduced the term. Return to text
3. We label this equilibrium Markov because we focus on equilibria sustainable in finite horizon economies. This rules out equilibria based in trigger strategies. Return to text
4. There is a growing literature on multiple equilibria with discretionary monetary policy, e.g., Albanesi, Chari, and Christiano (2003), King and Wolman (2004), Armenter and Brodenstein (2004) and Siu (2004). Armenter (2004) characterizes the necessary conditions for the existence of expectation traps and argues that they are very general. Return to text
5. There are mechanisms to embody a fixed exchange rate regime with some credibility, such as dollarization. Return to text
6. See, for example, the recent literature on dollarization considering the time inconsistency problem. A small sample are Chang and Velasco (2003), Cooley and Quadrini (2001) and Mendoza (2001). Return to text
7. This in the spirit of the cashless economies discussed in Woodford (2003). Return to text
8. We can do this because we restrict our analysis to Markov equilibrium. Return to text
9. These firms provide the demand
side for the household deposits. Note that the deposit demand is
also determined with knowledge of the actual policy choice
![]() . Return to text
. Return to text
10. This assumption suits developing economies particularly well. Return to text
11. It is possible to allow firms to
shut down or re-set nominal prices if profits fall below some
arbitrary level. A PSE would then exist for all
![]() . Whether
we allow for negative profits or not does not affect our
results. Return to text
. Whether
we allow for negative profits or not does not affect our
results. Return to text
12. Existence of
![]() follows from
follows from
![]() being bounded above and the closure of the policy choice set
previously discussed. However, the solution of (21) can be a correspondence. Armenter and
Bodenstein (2005) carefully explores this rare
possibility. Return to text
being bounded above and the closure of the policy choice set
previously discussed. However, the solution of (21) can be a correspondence. Armenter and
Bodenstein (2005) carefully explores this rare
possibility. Return to text
13. Dupor03 (2003) shows that optimal monetary policy with commitment may have a random component which can alleviate the monopoly distortion. This is not the case in this economy. Return to text
14. See Armenter and Bodenstein (2004) for an in depth exploration of expectation traps in a closed economy version of the model. Return to text
15. In the Appendix we provide the details of our calibration. Return to text
16. Indeed, firm production is
identical when inflation is equal to ![]() , the optimal monetary policy, as firms do not
differ in productivity in this numerical
illustration. Return to text
, the optimal monetary policy, as firms do not
differ in productivity in this numerical
illustration. Return to text
17. We also mentioned the possibility of expectation shifts. Rigorously speaking, this possibility is ruled out by our definition of Markov equilibrium. However, it is possible to relax the Markov restriction to allow for sunspots equilibria without allowing trigger strategies. Return to text
18. The inflation cap does not
constitute a Markov equilibrium by itself because, for all
![]() ,
,
![]() ,
i.e., the policy best response is always below inflation
expectations. This property is specific to a two Markov equilibria
economy. Return to text
,
i.e., the policy best response is always below inflation
expectations. This property is specific to a two Markov equilibria
economy. Return to text
19. We spare the reader of a re-formulation of the private sector equilibrium with uncertainty. The extension is trivial. The shock is treated as a zero-probability event, which emphasizes the positive role of stabilization policy. Return to text
20. The measure of firms
![]() is an exogenous
parameter and stays constant. However, production
is an exogenous
parameter and stays constant. However, production ![]() is endogenous and it adjusts to
the shock. Return to text
is endogenous and it adjusts to
the shock. Return to text
21. Alternatively, the reader can think of a comparison between a soft and a hard exchange rate regime. The former would be characterized by exchange rate bands chosen to rule out the high inflation equilibrium and to allow enough flexibility, as documented in the previous section. Return to text
22. We need to be more precise about our terms of trade shock. Given a change in the relative price of exports and imports, there are many possible changes in the price levels. We pick the change in the price levels such that, given a constant monetary policy, the ratio of domestic to world inflation remains constant. In other words, we abstract from non-policy induced real exchange rate movements which may occur simultaneously with a terms of trade shock. Return to text
23. This is the ex-post optimal response: the monetary authority is a benevolent policymaker. The Ramsey policy in a stochastic economy would not necessarily look alike. First, the response would be evaluated around the Friedman rule, which is the optimal level of inflation. Second, if the terms of trade shock had a positive probability of occurring, the Ramsey policy would have ex-ante considerations. Return to text
24. Date ![]() and
and ![]() are, effectively, two steady
states. Hence, the model implies a negative relationship between
inflation and openness. Romer (1993) finds
cross-country evidence of this relationship. Return to text
are, effectively, two steady
states. Hence, the model implies a negative relationship between
inflation and openness. Romer (1993) finds
cross-country evidence of this relationship. Return to text
This version is optimized for use by screen readers. A printable pdf version is available.
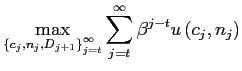
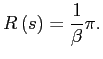
![$\displaystyle y\left( s\right) =\left[ \int_{0}^{1-\mu_{x}}y_{i}\left( s\right) ^{\eta }di\right] ^{\frac{1}{\eta}}$](img42.gif)

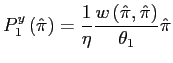
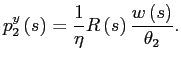
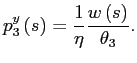
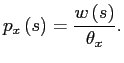
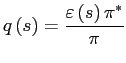
![$\displaystyle c\left( s\right) =\left[ \sum_{i=1}^{3}\mu_{i}\left( \theta_{i} n... ...}\left( \theta_{m}n_{m}\left( s\right) \right) ^{\eta}\right] ^{\frac{1}{\eta}}$](img93.gif)
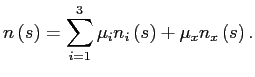
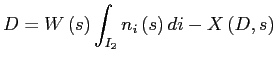
![$\displaystyle \frac{y\left( s\right) }{y_{3}\left( s\right) }=\left[ \mu_{3}+\m... ..._{x} }{\eta\theta_{3}}\right] ^{\frac{\eta}{1-\eta}}\right] ^{\frac{1}{\eta} }.$](img122.gif)
![$\displaystyle w\left( s\right) =\eta\left[ \frac{\tilde{\mu}_{3}+\tilde{\mu}_{2... ...}p_{1}^{y}\left( s\right) ^{\frac{\eta}{\eta-1}}}\right] ^{\frac{1-\eta}{\eta}}$](img125.gif)
![$\displaystyle w\left( \hat{\pi},\hat{\pi}\right) =\eta\left[ \tilde{\mu}_{3}+\t... ...u}_{1}+\tilde{\mu} _{m}\eta^{\frac{\eta}{\eta-1}}\right] ^{\frac{1-\eta}{\eta}}$](img138.gif)
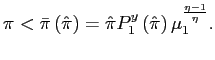
![$\displaystyle \frac{\eta}{\theta_{x}}\left[ \left( \tilde{\mu}_{1}+\tilde{\mu}_... ...}{1-\eta}}\right] ^{\frac{1-\eta}{\eta} }=\varepsilon\left( s\right) \pi^{\ast}$](img197.gif)