
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 900, July 2007--- Screen Reader
Version*
Bargaining, Fairness, and Price Rigidity in a DSGE Environment *
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
A growing body of evidence suggests that an important reason why firms do not change prices nearly as much as standard theory predicts is out of concern for disrupting ongoing customer relationships because price changes may be viewed as "unfair". Existing models that try to capture this concern regarding price-setting are all based on goods markets that are fundamentally Walrasian. In Walrasian goods markets, transactions are spot, making the idea of ongoing customer relationships somewhat difficult to understand. We develop a simple dynamic general equilibrium model of a search-based goods market to make precise the notion of a customer as a repeat buyer at a particular location. In this environment, the transactions price plays a distributive role as well as an allocative role. We exploit this distributive role of prices to explore how concerns for fairness influence price dynamics. Using pricing schemes with bargaining-theoretic foundations, we show that the particular way in which a "fair" outcome is determined matters for price dynamics. The most stark result we find is that complete price stability can arise endogenously. There are issues about which models based on standard Walrasian goods markets are silent.
Keywords: Sticky prices, fair pricing, customer markets, search models
JEL classification: E20, E30, E31, E32
1. Introduction
A growing body of evidence suggests that an important reason why firms do not change prices nearly as much as standard theory predicts is out of concern for disrupting ongoing customer relationships because price changes may be viewed as "unfair." Several recently-developed models try to capture this concern regarding price-setting, but in all of them the underlying model of the goods market is Walrasian. In Walrasian goods markets, transactions are spot, making the idea of ongoing customer relationships somewhat difficult to understand. Instead, models that feature explicit bilateral relationships between customers and firms seem to be called for in order to study the interactions between customer relationships and price rigidities. We develop a simple model that embeds a search-based goods market in an otherwise-standard dynamic general equilibrium model, making the notion of a customer as a repeat buyer at a particular location well-defined. In this framework, the transactions price (the terms of trade) plays a distributive role as well as an allocative role. We exploit this distributive role of prices to explore how concerns for fairness influence price dynamics. The most stark result we find is that if pricing is guided by a "fairness norm," complete price stability can arise endogenously. More generally, the consequences of menu costs of price adjustment on the dynamics of prices and allocations depend crucially on the manner in which price and quantity in specific relationships are determined, something about which standard models based on Walrasian goods markets are silent.
The two foundations of our model are a specific notion of customer relationships and menu costs of changing prices in those customer markets. In our model, customer relationships are valuable to both consumers and firms because of search frictions that each must overcome before goods trade can occur. The presence of search frictions leads to a surplus when a customer and a firm meet, and the parties must decide how to share the local monopoly rents. Regarding menu costs, we do not claim we have an explanation any deeper than existing ones for why there may be costs of changing prices; for convenience, such costs can be thought of in the typical fashion of costs associated with recording, reporting, and implementing new prices. By situating menu costs in a clearly-defined concept of a customer relationship, however, we are able to show that the consequences of price rigidities as typically formulated may depend critically on how prices and quantities traded are determined in specific relationships.
We focus on bargaining schemes as the mechanism by which prices and quantities are determined in customer markets. Despite using the formalisms of bargaining theory, we do not need to take literally the idea that customers and firms haggle over prices in every meeting. Rather, it seems to us that the idea that customers wield some "bargaining power" accords with the evidence of Blinder et al (1998) and others that firms often try to avoid upsetting their existing customers.
Given this interpretation, we adopt three bargaining protocols to pin down terms of trade between customers and firms: Nash bargaining, proportional bargaining, and a pricing system that we refer to as fair bargaining. We adopt Nash bargaining as a benchmark because of its familiarity: it has recently become relatively well-understood in macroeconomics due to the ongoing explosion of quantitative labor search models that employ it. Both proportional bargaining and fair bargaining implement an idea of a fairness norm under which parties always split the surplus in a fixed proportion, a feature that Nash bargaining does not always respect. The main difference between proportional bargaining and fair bargaining is the manner in which parties arrive at the fair outcome. Proportional bargaining assumes that the fair outcome is achieved through a mechanical sharing rule. In contrast, our notion of fair bargaining, although not axiomatic like the Nash and proportional outcomes, attempts to retain Nash bargaining's strategic foundation by imposing fairness as a constraint on the standard Nash optimization problem.
Akerlof (2007) makes the case that incorporating norms in macroeconomic models may be an evolutionary step for the field. We view our fairness norm, whether captured through proportional bargaining or fair bargaining, as in this spirit. We also view our idea as complementary to Rotemberg (2005, 2006), who has also stressed the notion that modeling fairness in pricing may be important. The crucial way in which our models of fair-pricing differ from Rotemberg (2005, 2006) is that we embed fairness as a feature of the trading structure of the environment, rather than altering preferences to account for it.
In our model, if there are no menu costs, the Nash-bargaining outcome, the proportional-bargaining outcome, and the fair-bargaining outcome all coincide. In the presence of menu costs, however, the three bargaining protocols imply quite different dynamics of prices and allocations. Under proportional bargaining, menu costs turn out to be completely irrelevant for both quantity and price dynamics, which seems to accord with survey evidence, such as Blinder et al (1998) and Fabiani et al (2006), that menu costs are not a very important friction in practice. Under fair bargaining, prices always remain at their steady-state values and dynamic allocations are completely unaffected by price rigidity. The key to understanding the dynamics under both proportional bargaining and fair bargaining is the fact that under Nash bargaining, price movements cause a time-varying wedge between short-run and long-run shares of the surplus accruing to customers and firms. With a fairness norm, parties eliminate such wedges, but the way in which the wedges are eliminated matters. If the wedges are eliminated according to proportional bargaining's mechanical sharing rule, customers and firms efficiently and equally share the consequences of menu costs and are able to engineer the zero-menu-cost Nash outcome. On the other hand, if the wedges are eliminated with the strategic considerations of fair bargaining in the background, menu costs are borne entirely by firms and eliminating the wedges requires complete price stability.
Due to the presence of local monopoly rents, our model also has something to say about markup behavior irrespective of menu costs. There lately has been a surge of interest in developing models in which markups are endogenously time-varying for reasons other than the presence of price rigidities.1 Our flexible-price models deliver a time-varying markup; moreover, the flexible-price markup is countercyclical with respect to demand shocks, which seems to accord with empirical evidence and which has been the attention of much modeling effort. However, with fair bargaining and the presence of menu costs, the markup is constant, which is simply a reflection of the fact that both prices and marginal cost are time-invariant under fair bargaining.
In terms of bringing to bear data on our model, we exploit a central idea captured by our model: firms and consumers expend resources looking for trading partners. In our model, firms direct resources towards advertising in order to attract customers, and shoppers spend time looking for and purchasing goods from firms. Empirical evidence shows that the resources expended in such search activities are not negligible. Firm expenditures on advertising constitute over two percent of GDP, and time-use surveys show that individuals spend an average of about one hour per day shopping. Using such evidence, we can calibrate two deep features of our model. A by-product of our structure is that our model reproduces remarkably well the cyclical dynamics of aggregate advertising behavior in U.S. data.
We articulate our ideas in a non-monetary model, meaning the price dynamics on which we focus are those of real (relative) prices. It is apparent that much interest would lie in whether and to what extent our results carry over to monetary environments. We have reason to believe that the crucial aspects of our results -- namely, that the consequences of menu costs depend critically on how customers and firms determine prices and quantities and, in particular, the conclusion that some trading arrangements would lead to the endogenous emergence of price stability -- would carry over to monetary economies because the core mechanisms at work in our environment do not depend on things being cast in nominal or real terms. However, adding a monetary dimension to our model may not be as straightforward as imposing an ad-hoc cash-in-advance constraint or other typical monetary formulation used in the literature because once customer relationships are modeled explicitly, we may have to be careful about issues such as which consumers carry cash, which firms require payment in cash, etc. A monetary extension seems a logical next step; here, though, we concentrate on understanding some basic principles of the interactions between price rigidity and customer relationships.
Hall (2007) takes a very similar view of product markets as we take here and does use it to think about monetary policy issues. As in our model, the price at which goods change hands in Hall's (2007) model plays a distributive role in additional to the standard allocational role. Different prices inside a customer relationship achieve different distributions of the surplus between the consumer and the firm, but this does not affect the underlying efficiency of a trade. This admits the possibility of, in Hall's (2007) language, equilibrium sticky prices in customer markets. Given what we perceive as a growing sense of frustration with pricing models currently used in macroeconomic models, stemming from the growing body of micro pricing facts that challenge standard time-dependent or state-dependent pricing rules, allowing a distributional role for prices, as both our model and Hall's (2007) model do, may be a useful new direction for macroeconomic models. It seems to us that allowing this additional role for prices accords better with the idea that firms do not re-set prices out of worry for upsetting customers than do standard views of price rigidity. Besides the difference in focus on monetary versus non-monetary issues, we think another aspect of our model that sets it apart from Hall's (2007) is that we embed it from the start in a fully-articulated, quantitative DSGE environment, making comparisons with predictions of existing DSGE models straightforward.
Indeed, there lately has been a general surge of interest in developing simple structures of customer-firm interactions that can be tractably incorporated into state-of-the-art quantitative macroeconomic models. Our work here also falls into this broad category. A few recent examples of work in this broadly-defined area are the deep habits models of Ravn, Schmitt-Grohe, and Uribe (2006) and Nakamura and Steinsson (2007) and the switching-cost model of Kleschelski and Vincent (2007). As we mentioned, in terms of some basic motivation -- the idea that fairness norms may interact with or may lead to price rigidity -- the studies by Rotemberg (2005, 2006) are the closest in spirit to what we set out to achieve here. We view our work as complementary to all these recent efforts because we model customer relationships and fairness concerns through trading arrangements rather than essentially just through preferences. One could of course go back much further and tie ideas to the rich customer-markets literature, which includes studies by, among many others, Diamond (1971) and Klemperer (1995). Okun (1981) voices some of the ideas -- namely, that search frictions in goods markets may have important consequences for aggregate phenomena -- that we formalize through a modern search and matching framework. We certainly cannot do justice to the rich history of thought on these topics.
The rest of our paper is organized as follows. In Section 2, we lay out our baseline model with standard Nash bargaining, proportional bargaining, and fair bargaining. In the baseline model, only an extensive margin of consumption exists, and bargaining occurs just over the price paid by the customer. We provide some partial equilibrium analytics in Section 3, which illustrate the core forces at work in our environment. We examine the fully general equilibrium baseline model's numerical properties in Section 4, including a discussion of how and why fair bargaining leads to complete price rigidity in the face of arbitrarily small menu costs of price adjustment. In Section 5, we enrich our environment to allow for bargaining over both price and quantity in a given customer relationship, thus allowing for extensive and intensive margins of consumption. Finally, in Section 6, we briefly extend our model to include exogenous government purchases to demonstrate that our basic results carry over to an environment with demand shocks. Section 7 concludes and offers some ideas for continuing work. Most of the derivations of key relationships in our model are relegated to the appendices.
2. Baseline Model
Our key point of departure from standard macro models is that, for some goods trades, households and firms each have to expend resources finding individuals on the other side of the market with whom to trade. A fraction of goods market exchange is thus explicitly bilateral, in contrast to all trades happening against the anonymous Walrasian auctioneer. Our model also does feature standard Walrasian goods for which search frictions are absent. We believe this view of goods markets is quite natural -- some goods require effort to find and some goods do not. For search goods, households spend time looking for firms from which to purchase goods, while firms direct part of their revenues towards trying to attract customers. We think of these two search activities as shopping and advertising, respectively.
Because we want to avoid taking a specific stand on the details of why it is that goods-market trading is costly -- there are probably a great many reasons -- we adopt the modeling device of an aggregate matching function from the labor search literature. Hall (2007) also takes this route. We describe more fully this matching mechanism below.2 For our purposes, the important consequence of these search and matching frictions is that once a customer relationship is formed, each party has an incentive to keep the match intact because dissolving the relationship would mean each has to re-enter the costly search process. The existence of a surplus to be shared in a customer relationship means that we must think beyond standard Walrasian marginal pricing conditions because prices play both distributional and allocative roles. In the rest of this section, we describe in detail the households and firms in our model as well as the rest of the economic environment.
2.1 Households
There is a measure one of identical households, with a measure
one of individuals that live within each household. In a given
period, an individual member of the representative household can be
engaged in one of four activities: purchasing goods (shopping) at a
firm, working, searching for goods, or leisure. More specifically,
![]() members
members
There is a measure one of identical households, with a measure
one of individuals that live within each household. In a given
period, an individual member of the representative household can be
engaged in one of four activities: purchasing goods (shopping) at a
firm, working, searching for goods, or leisure. More specifically,
![]() members of the household are working in
a given period;
members of the household are working in
a given period; ![]() members are searching
for firms from which to buy goods;
members are searching
for firms from which to buy goods; ![]() members are shopping at firms with which they previously
formed relationships; and
members are shopping at firms with which they previously
formed relationships; and
![]() members are
enjoying leisure. Note our distinction between shopping and
searching for goods. Individuals who are searching are looking to
form relationships with firms, which takes time. Individuals who
are shopping were previously successful in forming customer
relationships, but the act of acquiring and bringing home goods
itself takes time.3 We assume that the members of a
household share equally the consumption that shoppers acquire.
members are
enjoying leisure. Note our distinction between shopping and
searching for goods. Individuals who are searching are looking to
form relationships with firms, which takes time. Individuals who
are shopping were previously successful in forming customer
relationships, but the act of acquiring and bringing home goods
itself takes time.3 We assume that the members of a
household share equally the consumption that shoppers acquire.
With this atomistic structure, we assume that lifetime discounted household utility is
![$\displaystyle E_{0} \sum_{t=0}^{\infty} \beta^{t} \left[ u(x_{t}) + \vartheta v\left( \int_{0}^{N^{h}_{t}} c_{it} di \right) + g(1-l_{t} -s_{t}-N^{h}_{t}) \right]$](img24.gif)
|
(1) |
where
Note that consumption of the search good potentially has two
dimensions in our model: an extensive margin (the number of
shoppers who buy goods) and an intensive margin (the number of
goods each shopper buys). For the results in this section, we shut
down adjustment at the intensive margin by setting
![]() . We begin by closing down the
intensive margin for two reasons: doing so emphasizes the extensive
margin, which is the most novel aspect of our model, and it also
allows us some flexibility in calibrating our model. We discuss
this issue further below when we present the calibration of the
baseline model. In Section 5, we
endogenize adjustment at the intensive margin of consumption. In
the remainder of this section, then, we specialize to the case
. We begin by closing down the
intensive margin for two reasons: doing so emphasizes the extensive
margin, which is the most novel aspect of our model, and it also
allows us some flexibility in calibrating our model. We discuss
this issue further below when we present the calibration of the
baseline model. In Section 5, we
endogenize adjustment at the intensive margin of consumption. In
the remainder of this section, then, we specialize to the case
![]() , and our notation reflects
this. Finally, we point out that searching and shopping each
detract from household leisure in the same, linear, manner.4
, and our notation reflects
this. Finally, we point out that searching and shopping each
detract from household leisure in the same, linear, manner.4
Whether or not we allow intensive adjustment, note that the
aggregator inside ![]() is linear in the total
amount of search goods, meaning what we have in mind is a world in
which all search goods are perfect substitutes in utility. Our
baseline model focuses on this polar case because it means that any
"monopoly markups" that arise in our model are due solely to
search and matching frictions that create temporary bilateral
monopolies, rather than to any ex-ante differentiation of products
that create pure monopolies. That is, beginning with this
assumption again allows us to isolate effects stemming from the
search frictions in goods markets. As we will see in
Section 5, in order to endogenize
the intensive quantity traded, we must add some curvature to the
consumption aggregator inside
is linear in the total
amount of search goods, meaning what we have in mind is a world in
which all search goods are perfect substitutes in utility. Our
baseline model focuses on this polar case because it means that any
"monopoly markups" that arise in our model are due solely to
search and matching frictions that create temporary bilateral
monopolies, rather than to any ex-ante differentiation of products
that create pure monopolies. That is, beginning with this
assumption again allows us to isolate effects stemming from the
search frictions in goods markets. As we will see in
Section 5, in order to endogenize
the intensive quantity traded, we must add some curvature to the
consumption aggregator inside ![]() . The economic
content of such curvature is that goods obtained from distinct
matches are imperfect substitutes. We defer further discussion on
this point until we encounter the full model in
Section 5.
. The economic
content of such curvature is that goods obtained from distinct
matches are imperfect substitutes. We defer further discussion on
this point until we encounter the full model in
Section 5.
Using
![]() for now, then, the flow
budget constraint the household faces is
for now, then, the flow
budget constraint the household faces is
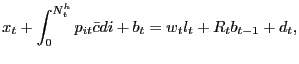
|
(2) |
where
| (3) |
| (4) |
| (5) |
where
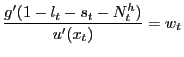
|
(6) |
and consumption-savings optimality condition
| (7) |
The household must also choose how much effort to devote to
searching and a desired number of future shoppers; ![]() is not free to be chosen at the beginning of period
is not free to be chosen at the beginning of period
![]() because that depends on how many searchers
were previously successful in forming customer relationships. The
household faces a perceived law of motion for the number of active
customer relationships in which it is engaged,
because that depends on how many searchers
were previously successful in forming customer relationships. The
household faces a perceived law of motion for the number of active
customer relationships in which it is engaged,
| (8) |
where
Finally, then, the household first-order conditions with respect
to ![]() and
and
![]() are
are
| (9) |
and
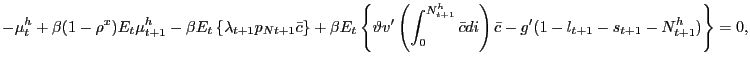
|
(10) |
where
Having taken first-order conditions and given that we restrict
attention to symmetric equilibria in which
![]() for all
for all ![]() ,
the first-order condition on
,
the first-order condition on
![]() becomes
becomes
| (11) |
where ![]() now stands for the real (measured in
units of
now stands for the real (measured in
units of ![]() ) price of any given good for which there
exists a customer-firm relationship. Condensing this expression
with the household first-order condition on
) price of any given good for which there
exists a customer-firm relationship. Condensing this expression
with the household first-order condition on ![]() , we have
, we have
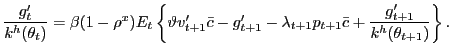
|
(12) |
Using (3) and re-grouping terms, we have
![$\displaystyle \frac{g^{\prime}_{t}}{ k^{h}(\theta_{t})} = \beta (1-\rho^{x}) E_{t} \left\{ \bar{c} \left[ \vartheta v^{\prime}_{t+1} - p_{t+1} u^{\prime}(x_{t+1}) \right] - g^{\prime}_{t+1} + \frac{g^{\prime }_{t+1}}{k^{h}(\theta_{t+1})} \right\} ,$](img97.gif)
|
(13) |
which we refer to as the household's shopping condition. The
shopping condition simply states that at the optimum, the household
should send a number of individuals out to search for goods such
that the expected marginal cost of shopping (the left-hand-side
of (13)) equals the expected
marginal benefit of shopping (the right-hand-side of (13)). The expected marginal benefit of
shopping is composed of two parts: the utility gain from obtaining
![]() more goods via the search market
rather than via the Walrasian market (net of the direct disutility
more goods via the search market
rather than via the Walrasian market (net of the direct disutility
![]() of shopping) and the benefit to
the household of having one additional pre-existing customer
relationship entering period
of shopping) and the benefit to
the household of having one additional pre-existing customer
relationship entering period ![]() . If all trades
were frictionless, household optimal choices would imply
. If all trades
were frictionless, household optimal choices would imply
![]() . With
frictions, in order to engage in costly search, it must be that on
the margin, the household expects
. With
frictions, in order to engage in costly search, it must be that on
the margin, the household expects
![]() .5 This positive flow
return ensures that the household finds it worthwhile to send some
of its members shopping.
.5 This positive flow
return ensures that the household finds it worthwhile to send some
of its members shopping.
2.2 Walrasian Firms
To make pricing labor simple, we assume that there is a
representative firm that buys labor in and sells the Walrasian good
![]() in competitive spot markets. The firm
operates a linear production technology that is subject to
aggregate TFP fluctuations,
in competitive spot markets. The firm
operates a linear production technology that is subject to
aggregate TFP fluctuations,
![]() , where
, where ![]() denotes the labor hired by Walrasian firms.
Profit-maximization yields the standard result that
denotes the labor hired by Walrasian firms.
Profit-maximization yields the standard result that
| (14) |
which all participants in the economy, including the non-Walrasian firms described next, take as given.6
2.3 Non-Walrasian Firms
We also assume that there is a representative firm that sells a large number of goods in bilateral trades. For each good that it sells, the representative search firm must first attract customers. To attract customers, the firm must advertise, and how any given level of advertisements it posts maps into how many customers it finds is governed by a matching technology to be described below. Owing to frictions associated with finding customers, the firm views existing customers as assets. Its total stock of customers evolves according to the perceived law of motion
| (15) |
where ![]() is the number of advertisements the
firm posts in period
is the number of advertisements the
firm posts in period ![]() , and
, and ![]() is the probability that one of the firm's
advertisements attracts a customer, which depends on goods market
tightness
is the probability that one of the firm's
advertisements attracts a customer, which depends on goods market
tightness ![]() ;
; ![]() is
taken as given by the firm.
is
taken as given by the firm.
As with competitive firms, the production technology is linear
in labor and subject to an exogenous aggregate productivity shock.
Total output of the non-Walrasian firm is thus
![]() , where
, where ![]() denotes the labor hired by the non-Walrasian firm.
Because we assume a constant-returns production technology with no
fixed costs of production (there is a fixed cost of advertising,
but no fixed cost of producing), its real marginal cost of
production is constant and coincides with average cost.7
Denoting marginal production cost by
denotes the labor hired by the non-Walrasian firm.
Because we assume a constant-returns production technology with no
fixed costs of production (there is a fixed cost of advertising,
but no fixed cost of producing), its real marginal cost of
production is constant and coincides with average cost.7
Denoting marginal production cost by ![]() in
period
in
period ![]() , we can express the firm's total
production costs as the sum of production costs across all of its
customer relationships,
, we can express the firm's total
production costs as the sum of production costs across all of its
customer relationships,
![]() .
.
The firm also faces a menu cost of adjusting the per-unit price of each good it sells to a given customer. Specifically, we use a Rotemberg-type quadratic cost of price adjustment, which is a fairly conventional way of modeling menu costs. As we mentioned earlier, our goal is not to provide a compelling micro-foundation for why price adjustment may entail costs; rather, adopting a typical reduced-form specification is just a tractable way to get at our ultimate objective.
With this structure in place, total profits of the
representative search firm in a given period ![]() are
are
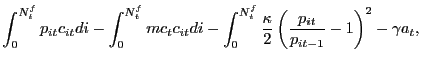
|
(16) |
where ![]() is the relative price (which is,
recall again, measured in units of
is the relative price (which is,
recall again, measured in units of ![]() ) of good
) of good
![]() ,
, ![]() is the flow
cost of an advertisement, thus
is the flow
cost of an advertisement, thus
![]() is the total flow advertising
cost the firm incurs. We again specialize right away to the case
is the total flow advertising
cost the firm incurs. We again specialize right away to the case
![]() and, as we have already
mentioned, defer considering intensive adjustment until
Section 5. The parameter
and, as we have already
mentioned, defer considering intensive adjustment until
Section 5. The parameter
![]() measures how large menu costs are;
setting
measures how large menu costs are;
setting ![]() of course means there are no menu
costs. The firm's customer base
of course means there are no menu
costs. The firm's customer base ![]() is
pre-determined entering period
is
pre-determined entering period ![]() . Discounted
lifetime profits of the firm are thus
. Discounted
lifetime profits of the firm are thus
![$\displaystyle E_{0} \sum_{t=0}^{\infty} \Xi_{t\vert}\left[ \int _{0}^{N^{f}_{t}} p_{it} \bar{c} di - \int_{0}^{N^{f}_{t}} mc_{t} \bar{c} di - \int_{0}^{N^{f}_{t}} \frac{\kappa}{2} \left( \frac{p_{it}}{p_{it-1}<tex2html_comment_mark>138 }-1\right) ^{2} - \gamma a_{t} \right] ,$](img133.gif)
|
(17) |
where ![]() is the period-0 value to the
household of period-
is the period-0 value to the
household of period-![]() goods, which we assume the
firm uses to discount profit flows because the households are the
ultimate owners of firms.8
goods, which we assume the
firm uses to discount profit flows because the households are the
ultimate owners of firms.8
The problem of the firm is thus to maximize (17) subject to the evolution of its customer
base (15) by choosing
![]() . In the firm's
pursuit of customers, it takes
. In the firm's
pursuit of customers, it takes ![]() and
and
![]() as given because those will be
determined in the trading protocols to be described below. Note an
important point of departure from standard macro models of goods
markets: the firm is not a unilateral price-setter
here.9 The first-order conditions with
respect to
as given because those will be
determined in the trading protocols to be described below. Note an
important point of departure from standard macro models of goods
markets: the firm is not a unilateral price-setter
here.9 The first-order conditions with
respect to
![]() thus are
thus are
| (18) |
and
![$\displaystyle - \Xi_{t\vert} \mu^{f}_{t} + (1-\rho^{x}) E_{t} \left\{ \Xi_{t+1\vert} \mu ^{f}_{t+1} \right\} + E_{t} \left\{ \Xi_{t+1\vert} \left[ p_{N,t+1} \bar{c} - mc_{t+1} \bar{c} - \frac{\kappa}{2} \left( \frac{p_{N,t+1}}{p_{N,t}} - 1\right) ^{2} \right] \right\} = 0,$](img143.gif)
|
(19) |
where
![]() is the Lagrange multiplier on
the firm's customer constraint. Condensing these first-order
conditions, we arrive at the firm's optimal advertising condition,
is the Lagrange multiplier on
the firm's customer constraint. Condensing these first-order
conditions, we arrive at the firm's optimal advertising condition,
![$\displaystyle \frac{\gamma}{k^{f}(\theta_{t})} = (1-\rho ^{x}) E_{t} \left\{ \Xi_{t+1\vert t} \left[ p_{t+1} \bar{c} - mc_{t+1} \bar{c} - \frac{\kappa}{2} \left( \frac{p_{N,t+1}}{p_{N,t}} - 1\right) ^{2} + \frac{\gamma}{k^{f}(\theta_{t+1})} \right] \right\} ,$](img145.gif)
|
(20) |
where
![]() is the
household discount factor (again, technically, the real interest
rate) between period
is the
household discount factor (again, technically, the real interest
rate) between period ![]() and
and ![]() . In
equilibrium,
. In
equilibrium,
![]() ,
which in turn, by the household optimality condition (3), is
,
which in turn, by the household optimality condition (3), is
![]() . In writing (20), we
have also imposed symmetric equilibrium, in which
. In writing (20), we
have also imposed symmetric equilibrium, in which
![]() for any
for any ![]() .
.
The advertising condition states that at the optimum, the
expected marginal cost of posting an ad (the left-hand-side
of (20)) equals the
expected marginal benefit of forming a relationship with a new
customer (the right-hand-side of (20)). The expected marginal benefit
takes into account the revenue from selling to one extra customer,
the production costs incurred for producing to sell those extra
units, future menu costs in that customer relationship, and the
cost savings of finding another customer in the future due to the
pre-existing (in time ![]() ) customer relationship.
Condition (20) is a
free-entry condition in advertising. The fact that an entry
decision must be made before a firm can enjoy any profit flows
means that profit flows from sales of goods are not pure rents as
they are in commonly-employed formulations of goods markets.
) customer relationship.
Condition (20) is a
free-entry condition in advertising. The fact that an entry
decision must be made before a firm can enjoy any profit flows
means that profit flows from sales of goods are not pure rents as
they are in commonly-employed formulations of goods markets.
2.4 Price Determination
With bilateral relationships between customers and firms, there is an array of ways to think about how prices are determined. We focus on three bargaining schemes, two that are axiomatic and one that, although it is not axiomatic, seems to us to capture important intuitive elements underlying each of the two axiomatic schemes. In considering bargaining, we do not need to take literally the idea that customers and firms haggle over prices in every meeting, even though that is the formalism we use. Rather, it seems to us that the idea that customers wield some "bargaining power" accords with the evidence that firms often try to avoid "upsetting their existing customers."
To make progress with this idea, then, we consider three bargaining protocols. The first protocol is Nash bargaining, the second is proportional bargaining, and the third is a modified Nash problem in which the two parties always divide the match surplus in a fixed proportion. We refer to this third trading protocol as fair bargaining, although we recognize that bargaining theorists would not accord this trading protocol "bargaining" status. Conceding this point, we nonetheless use the term fair bargaining to make the discussions symmetric.
Proportional bargaining and fair bargaining implement the idea of "fairness" in trading outcomes in similar, but distinct, ways. Our specific notion of fairness is one in which the surplus accruing to customers is always a fixed ratio of the surplus accruing to firms. Clearly, as discussed by Binmore (2007) and many others, there are a great many ways to operationalize the concept of fairness. Given our environment of explicit relationships between consumers and firms, we think ours is at least one natural definition. As we show below, and is well-known in bargaining applications (see Aruoba, Rocheteau, and Waller (2007) for a particularly recent application), the Nash solution does not generally satisfy this definition of fairness.
It is well-understood that Nash bargaining has explicit strategic foundations. Specifically, Rubinstein (1982) shows that the Nash bargaining solution is the limiting solution of a strategic alternating-offers bargaining environment. In contrast, proportional bargaining, while it does, as we show below, capture our definition of fairness, does not have as clear a strategic foundation. Instead, it accords better with the concept of a focal-point equilibrium, an outcome that, perhaps for some evolutionary reason, simply is the accepted social norm. Experimental evidence on bilateral games people play, summarized by, among others, Binmore (2007, Chapter 6), suggests that both strategic and focal-point elements are typically at work. This motivates us to construct our fair-bargaining scheme in an attempt to retain the strategic element inherent in Nash bargaining as well as the fairness/focal-point element inherent in proportional bargaining.
2.4.1 Nash Bargaining
In Nash bargaining over the ![]() -th product, the
firm and the customer jointly choose
-th product, the
firm and the customer jointly choose ![]() to
maximize the Nash product
to
maximize the Nash product
| (21) |
where
![]() is the value to a household
of having a member engaged in a relationship with a firm,
is the value to a household
of having a member engaged in a relationship with a firm,
![]() is the value to a household
of having a member searching for goods,
is the value to a household
of having a member searching for goods,
![]() is the value to a firm of
being engaged in a relationship with a customer, and
is the value to a firm of
being engaged in a relationship with a customer, and ![]() is a standard time-invariant Nash bargaining weight. The
value to a firm of an advertisement that failed to attract any
customers is normalized to zero. As we show in
Appendix B (where we
present the definitions of
is a standard time-invariant Nash bargaining weight. The
value to a firm of an advertisement that failed to attract any
customers is normalized to zero. As we show in
Appendix B (where we
present the definitions of
![]() ,
,
![]() , and
, and
![]() ), the price
), the price ![]() that emerges from Nash bargaining in any particular
customer-firm relationship satisfies the sharing rule
that emerges from Nash bargaining in any particular
customer-firm relationship satisfies the sharing rule
| (22) |
in which
![]() is the effective bargaining power
of the customer and
is the effective bargaining power
of the customer and
![]() is the effective bargaining
power of the firm. Specifically,
is the effective bargaining
power of the firm. Specifically,
| (23) |
where
![]() and
and
![]() measure marginal changes in
the value of a customer relationship for the firm and the
household, respectively.
measure marginal changes in
the value of a customer relationship for the firm and the
household, respectively.
We provide more details in Appendix B, but three
points are worth mentioning here. First, time-variation in
![]() means that the household's
surplus
means that the household's
surplus
![]() from an
active customer relationship is not a fixed ratio of the firm's
surplus
from an
active customer relationship is not a fixed ratio of the firm's
surplus
![]() . The Nash solution thus does
not generally satisfy our definition of fairness. Second, with zero
costs of price adjustment in period
. The Nash solution thus does
not generally satisfy our definition of fairness. Second, with zero
costs of price adjustment in period ![]() (which may
arise for two reasons: either
(which may
arise for two reasons: either ![]() or
or
![]() but
but
![]() ),
),
![]() (because in that case
(because in that case
![]() ). It is
thus variation in prices coupled with the presence of menu
costs that drives a time-varying wedge between effective
bargaining power and the Nash bargaining weights. Indeed, if the
Nash product the customer and firm maximized were
). It is
thus variation in prices coupled with the presence of menu
costs that drives a time-varying wedge between effective
bargaining power and the Nash bargaining weights. Indeed, if the
Nash product the customer and firm maximized were
![]() rather than (21), the outcome
would be the sharing rule (22).
Third, in the long run (i.e., the deterministic steady state),
rather than (21), the outcome
would be the sharing rule (22).
Third, in the long run (i.e., the deterministic steady state),
![]() because
because
![]() (recall
these are real prices). Thus, the wedge between
(recall
these are real prices). Thus, the wedge between ![]() and
and
![]() is a business-cycle
phenomenon.
is a business-cycle
phenomenon.
With time-varying effective bargaining power, the price solves
![$\displaystyle \lefteqn{\frac{\omega_{t}}{1-\omega_{t}} \left[ p_{it} \bar{c} - mc_{t} \bar{c} - \frac{\kappa}{2} \left( \frac{p_{it}}{p_{it-1} }-1\right) ^{2} + \frac{\gamma}{k^{f}(\theta_{t})}\right] = \frac{\tilde {u}(\bar{c})}{\lambda_{t}} - p_{it} \bar{c} + }$](img185.gif)
|
|
![$\displaystyle + (1-\theta_{t} k^{f}(\theta_{t})) E_{t}\left[ \Xi_{t+1\vert t} \left( \frac{\omega_{t+1}}{1-\omega_{t+1}}\right) (1-\rho^{x}) \left[ p_{it+1} \bar{c} - mc_{t+1} \bar{c} - \frac{\kappa}{2}\left( \frac{p_{it+1}}{p_{it} }-1\right) ^{2} + \frac{\gamma}{k^{f}(\theta_{t})} \right] \right] .$](img188.gif)
|
(24) |
where
![]() is the utility function
defined over the quantity consumed of a good obtained from a given
customer relationship (rather than the utility
is the utility function
defined over the quantity consumed of a good obtained from a given
customer relationship (rather than the utility ![]() defined over the household's aggregate consumption of
search goods
defined over the household's aggregate consumption of
search goods
![]() .).10 The
pricing condition (24) shows that
price-setting is forward-looking for two distinct reasons. One
reason is a standard sticky-price reason: with costs of price
adjustment, a setting for
.).10 The
pricing condition (24) shows that
price-setting is forward-looking for two distinct reasons. One
reason is a standard sticky-price reason: with costs of price
adjustment, a setting for ![]() has
ramifications for future setting of
has
ramifications for future setting of ![]() . But
note that even with
. But
note that even with ![]() ,
, ![]() is affected by expectations regarding
is affected by expectations regarding ![]() . This forward-looking aspect of pricing has to do
with the long-lived customer relationship: with probability
. This forward-looking aspect of pricing has to do
with the long-lived customer relationship: with probability
![]() , the customer and firm will
bargain over the same good again in the future. In typical models,
price-setting is static in the absence of menu costs; in our
framework, it is dynamic even in the absence of menu costs.11
, the customer and firm will
bargain over the same good again in the future. In typical models,
price-setting is static in the absence of menu costs; in our
framework, it is dynamic even in the absence of menu costs.11
Finally, we note that with ![]() , the Nash
sharing rule (22) reduces to
the more standard
, the Nash
sharing rule (22) reduces to
the more standard
![]() ,
and the pricing equation (24)
simplifies dramatically to
,
and the pricing equation (24)
simplifies dramatically to
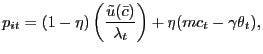
|
(25) |
which one can obtain by working through the derivations in Appendix B.
2.4.2 Proportional Bargaining
Condition (22) shows that in
the presence of menu costs, the surplus is split between consumers
and firms according to time-varying shares. Suppose instead that
some fairness norm in pricing were in place in which the customer
and firm ensure that they always split the total surplus in a
time-invariant ratio. An axiomatic solution (see Kalai (1977) for
the original exposition) that guarantees constant splits is the
proportional bargaining solution. Under proportional bargaining,
the price ![]() solves
solves
| (26) |
without any reference to an underlying maximization
problem.12 Substituting the definitions of
![]() ,
,
![]() , and
, and
![]() presented in
Appendix B, the
proportional-bargaining price solves
presented in
Appendix B, the
proportional-bargaining price solves
![$\displaystyle \lefteqn{\frac{\eta}{1-\eta} \left[ p_{it} \bar{c} - mc_{t} \bar{c} - \frac{\kappa}{2} \left( \frac{p_{it} }{p_{it-1}}-1\right) ^{2} + \frac{\gamma}{k^{f}(\theta_{t})}\right] = \frac{\tilde{u}(\bar{c})}{\lambda_{t}} - p_{it} \bar{c} + }$](img207.gif)
|
|
![$\displaystyle + (1-\theta_{t} k^{f}(\theta_{t})) \left( \frac{\eta}{1-\eta}\right) E_{t}\left[ \Xi_{t+1\vert t} (1-\rho^{x}) \left[ p_{it+1} \bar{c} - mc_{t+1} \bar{c} - \frac{\kappa}{2}\left( \frac{p_{it+1}}{p_{it}}-1\right) ^{2} + \frac{\gamma}{k^{f}(\theta_{t})} \right] \right] ,$](img210.gif)
|
(27) |
which differs from (24) only in
that
![]() replaces
replaces
![]() .
.
2.4.3 Fair Bargaining
As we discussed above, Nash bargaining has clear strategic foundations, while those underlying proportional bargaining are less clear. To try to capture both the strategic element underlying Nash bargaining and the focal-point element underlying proportional bargaining -- both elements that the evidence of Binmore (2007) suggests are important for understanding bilateral interactions -- we construct a pricing scheme that draws on both.
The way in which we implement this idea is to continue using the
Nash product as the objective the parties seek to maximize;
however, constant shares are now enforced. Specifically,
![]() is chosen to maximize
is chosen to maximize
| (28) |
subject to a constant-split rule
| (29) |
The most straightforward constant-split rule to understand is the
case
![]() , which amounts to enforcing
the standard Nash sharing condition despite the presence of menu
costs. We focus just on this case.13
, which amounts to enforcing
the standard Nash sharing condition despite the presence of menu
costs. We focus just on this case.13
We provide the details behind this problem in Appendix C, but the outcome of fair bargaining over price is
| (30) |
in which ![]() is defined as the gross rate of
price change between period
is defined as the gross rate of
price change between period ![]() and
and ![]() ,
,
![]() . If this
were a monetary model, we would of course call
. If this
were a monetary model, we would of course call ![]() inflation and thus may be tempted to refer to
condition (30) as a
modern Phillips curve because it links period-
inflation and thus may be tempted to refer to
condition (30) as a
modern Phillips curve because it links period-![]() price growth (inflation) to expected future price growth
(inflation).
price growth (inflation) to expected future price growth
(inflation).
What prevents condition (30) from being a Phillips curve (aside from the fact that our model is not cast in nominal terms) is that it contains nothing at all about allocations. To show how tantalizingly close (30) is to a standard New Keynesian Phillips curve, compare it with the standard pricing equation that emerges from New Keynesian models; for example, the analogous condition in Chugh (2006, equation 7) is
| (31) |
where ![]() is some function that depends on the
marginal cost of production.14 The fact that marginal cost,
which reflects something about allocations, appears in a standard
New Keynesian Phillips curve of course provides the linkage between
real activity and price movements in that class of models.
is some function that depends on the
marginal cost of production.14 The fact that marginal cost,
which reflects something about allocations, appears in a standard
New Keynesian Phillips curve of course provides the linkage between
real activity and price movements in that class of models.
Our fair-pricing condition (30), missing marginal costs, is thus of course not a Phillips curve because it does not link price changes to real activity. Indeed, it is quite the opposite of the spirit of a Phillips Curve: condition (30) describes only the dynamics of prices and demonstrates that the dynamics of allocations are divorced from the dynamics of prices. Thus, price rigidity coupled with a fairness norm in bargaining effectively decouples prices from quantities in our model.
Finally, we point out that our notion of fairness in pricing is an assertion about the bargaining protocol. We are not modeling deeper-rooted reasons that may underlie why fair bargaining (or proportional bargaining, for that matter) may be adopted in the first place. One potential candidate explanation is the recent model of Rotemberg (2006), in which customer "anger" over prices that are perceived to be exploitative may lead to a fairness norm. More broadly, Akerlof (2007), in his overture to macroeconomics to adopt more "norm-based" behavior into standard models, discusses why incorporating norms and, at least as a first step, ignoring endogeneity of norm adoption may be an important evolutionary step for the field. Such issues are quite interesting to consider, and if our model proves to be useful in thinking about some aspects of goods-market relationships, one may want to embed such mechanisms in our model in future work. For now, our focus is on the consequences of menu costs of price adjustment given a fairness norm in pricing.
2.5 Goods Market Matching
The number of new customer-firm relationships that are formed in
any period ![]() is described by an aggregate matching
function
is described by an aggregate matching
function
![]() . We assume the matching
technology is Cobb-Douglas,
. We assume the matching
technology is Cobb-Douglas,
![]() . With Cobb-Douglas matching,
the probabilities that shoppers and firms, respectively, find
partners is
. With Cobb-Douglas matching,
the probabilities that shoppers and firms, respectively, find
partners is
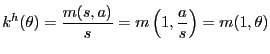
|
(32) |
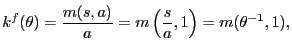
|
(33) |
with
![]() a measure of how thick (the
ratio of firms searching for customers to individuals searching for
goods) the goods market is.
a measure of how thick (the
ratio of firms searching for customers to individuals searching for
goods) the goods market is.
As in the labor search literature, the matching function is meant to be a reduced-form way of capturing the idea that it takes time for parties on opposite sides of the market to meet. Rogerson, Shimer, and Wright (2005, p. 968) note that the ability to be agnostic about the actual mechanics of the process by which parties make contact with each other may be a virtue. Our modeling motivation is very much in line with this idea.
With the matching function describing the flow of new customer relationships, the aggregate number of active customer relationships evolves according to
| (34) |
2.6 Resource Constraint
Total output of the economy is absorbed by Walrasian consumption, non-Walrasian consumption, price adjustment costs, and advertising costs. The resource constraint is thus
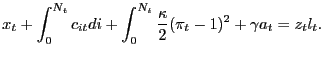
|
(35) |
2.7 Equilibrium
We restrict attention to a symmetric equilibrium in which the
price ![]() is identical across all active customer
relationships. Because (part of) goods trade is carried out in
non-Walrasian markets, the core notion of equilibrium in our model
is that of a search equilibrium, rather than a competitive
equilibrium. This motivates the definition of a symmetric search
equilibrium for our model.
is identical across all active customer
relationships. Because (part of) goods trade is carried out in
non-Walrasian markets, the core notion of equilibrium in our model
is that of a search equilibrium, rather than a competitive
equilibrium. This motivates the definition of a symmetric search
equilibrium for our model.
A symmetric search equilibrium is endogenous processes for the
household's choice
![]() ,
the Walrasian firm's choice
,
the Walrasian firm's choice
![]() , the
non-Walrasian firm's choice
, the
non-Walrasian firm's choice
![]() , the real
wage
, the real
wage
![]() , bond returns
, bond returns
![]() , dividends
, dividends
![]() , prices in the
non-Walrasian goods market
, prices in the
non-Walrasian goods market
![]() , and matching
probabilities
, and matching
probabilities
![]() such that
such that
- given
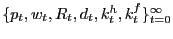 , the household maximizes (1) subject to (2) and (8);
, the household maximizes (1) subject to (2) and (8); - given
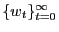 , the Walrasian firm
chooses labor to maximize profit;
, the Walrasian firm
chooses labor to maximize profit; - given
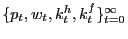 , the
non-Walrasian firm maximizes (17) subject to (15);
, the
non-Walrasian firm maximizes (17) subject to (15); -
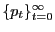 satisfies
either (24) (Nash bargaining)
or (30) (fair
bargaining);
satisfies
either (24) (Nash bargaining)
or (30) (fair
bargaining); - the resource constraint (35)
holds for
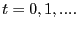 ;
; - the labor market clears,
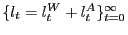 ;
; - the customer market clears,
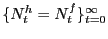 ;
; - the aggregate law of motion for active customer relationships
is given by (34) for
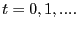 ;
; - the bond market clears,
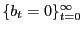 ;
; - dividends
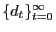 are determined
residually from the non-Walrasian firm's profit function;
are determined
residually from the non-Walrasian firm's profit function; -
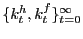 are
given by (32) and (33).
are
given by (32) and (33).
Collecting conditions that summarize the equilibrium,
equilibrium is endogenous processes
![]() that satisfy (6), (7), (13), (14), (20), either (24) or (30), (34), and (35), for
given exogenous process
that satisfy (6), (7), (13), (14), (20), either (24) or (30), (34), and (35), for
given exogenous process
![]() .
.
3. Partial Equilibrium Analytics
Our main interest lies in some general equilibrium business
cycle consequences of search frictions in goods trade and price
rigidity. However, we can gain a lot of intuition for the economic
forces at work in our model by examining both analytically and
numerically its steady-state equilibrium. The triple
![]() are the most important
endogenous variables describing our frictional goods
market.15 Features such as the intensive
quantity
are the most important
endogenous variables describing our frictional goods
market.15 Features such as the intensive
quantity ![]() , presence of a production technology, and
endogenous labor force participation are all present to make our
model quantitatively realistic and readily comparable to other
quantitative macroeconomic models. We again emphasize that the
fundamental notion of goods-market equilibrium here is that of a
search equilibrium, not a Walrasian (or Walrasian-based)
equilibrium.16
, presence of a production technology, and
endogenous labor force participation are all present to make our
model quantitatively realistic and readily comparable to other
quantitative macroeconomic models. We again emphasize that the
fundamental notion of goods-market equilibrium here is that of a
search equilibrium, not a Walrasian (or Walrasian-based)
equilibrium.16
To make some analytical progress, then, for the moment suppose
the general equilibrium features of our model were shut down.
Specifically, suppose ![]() and labor is not needed
(
and labor is not needed
(![]() ).17 In this partial equilibrium
version of our model, then, imposing steady-state on the firm
advertising condition gives us
).17 In this partial equilibrium
version of our model, then, imposing steady-state on the firm
advertising condition gives us
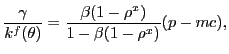
|
(36) |
in which we have used the fact that in the deterministic steady
state, prices do not change (remember, these are real prices),
hence there are no menu costs of price adjustment. With
Cobb-Douglas matching, the probability a firm that has advertised
matches with a customer is
![]() . Imposing this
and rearranging, we have
. Imposing this
and rearranging, we have
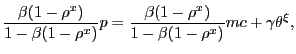
|
(37) |
which shows that the markup of price over marginal cost of
production is governed by the advertising cost ![]() and customer market tightness
and customer market tightness ![]() .
If
.
If ![]() , we have
, we have ![]() ,
which makes perfect sense because in that case it is costless for
firms to find customers and we have assumed that goods are ex-ante
perfect substitutes; in other words, the goods market is (nearly)
Walrasian with
,
which makes perfect sense because in that case it is costless for
firms to find customers and we have assumed that goods are ex-ante
perfect substitutes; in other words, the goods market is (nearly)
Walrasian with ![]() . With
. With ![]() , firms make normal profits by charging simply their
marginal production cost as in a textbook model. Clearly, then, it
is the search friction embodied in
, firms make normal profits by charging simply their
marginal production cost as in a textbook model. Clearly, then, it
is the search friction embodied in
![]() that drives a wedge
between price and marginal production cost. Indeed, because
that drives a wedge
between price and marginal production cost. Indeed, because
![]() ,
, ![]() . Figure 1 shows that the advertising
condition is upward-sloping in
. Figure 1 shows that the advertising
condition is upward-sloping in
![]() space.18 To preview some of
the intuition behind the dynamics of markups we present soon:
because
space.18 To preview some of
the intuition behind the dynamics of markups we present soon:
because ![]() in general will vary over time as
part of business cycle fluctuations, the markup of price over
marginal production cost should be expected to be time-varying, and
this markup is endogenous. Time-variation in search costs drives
time-variation in markups in our framework.19
in general will vary over time as
part of business cycle fluctuations, the markup of price over
marginal production cost should be expected to be time-varying, and
this markup is endogenous. Time-variation in search costs drives
time-variation in markups in our framework.19
To determine the steady-state
![]() , we must also examine (the
steady-state version of) the pricing condition (24), which is the relevant pricing condition
for both Nash and fair bargaining (because, recall again, both
bargaining schemes deliver the same outcome when there is no cost
of price adjustment, which is true in the steady-state of all our
models). Again assuming
, we must also examine (the
steady-state version of) the pricing condition (24), which is the relevant pricing condition
for both Nash and fair bargaining (because, recall again, both
bargaining schemes deliver the same outcome when there is no cost
of price adjustment, which is true in the steady-state of all our
models). Again assuming ![]() and after also using the
steady-state version of the advertising condition, we can express
the steady-state pricing condition as
and after also using the
steady-state version of the advertising condition, we can express
the steady-state pricing condition as
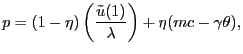
|
(38) |
where we have used the fact that in steady state,
![]() . The first term on the
right-hand-side of this expression, because it itself depends on
. The first term on the
right-hand-side of this expression, because it itself depends on
![]() in general equilibrium (because the
marginal utility of wealth
in general equilibrium (because the
marginal utility of wealth ![]() is a general
equilibrium object), makes analyzing this expression prohibitively
more complicated than analyzing the steady-state advertising
condition. To focus ideas, though, suppose it were simply a
constant,
is a general
equilibrium object), makes analyzing this expression prohibitively
more complicated than analyzing the steady-state advertising
condition. To focus ideas, though, suppose it were simply a
constant, ![]() . In that case, we have the very simple
pricing equation
. In that case, we have the very simple
pricing equation
| (39) |
which states that the price lies inside an interval bounded above
by the firm's production cost net of savings on search costs and
bounded below by the household's utility of consumption ![]() . The convex weights are simply the Nash bargaining
weights.20 The locus (39) is downward-sloping in
. The convex weights are simply the Nash bargaining
weights.20 The locus (39) is downward-sloping in
![]() space, as illustrated in
Figure 1; the
steady-state equilibrium
space, as illustrated in
Figure 1; the
steady-state equilibrium
![]() is determined where it and the
pricing condition cross in Figure 1.
is determined where it and the
pricing condition cross in Figure 1.
Conditions (37)
and (39) characterize
![]() in terms of deep parameters. It
is fairly straightforward to show (we provide the details in
Appendix D) that the
steady-state price is strictly decreasing in customer bargaining
power
in terms of deep parameters. It
is fairly straightforward to show (we provide the details in
Appendix D) that the
steady-state price is strictly decreasing in customer bargaining
power ![]() . This result makes a lot of intuitive
sense: the more bargaining power customers wield, the less rents
the firm can extract out of the match surplus, meaning the smaller
is the markup of unit price over unit marginal production cost.
. This result makes a lot of intuitive
sense: the more bargaining power customers wield, the less rents
the firm can extract out of the match surplus, meaning the smaller
is the markup of unit price over unit marginal production cost.
So far, we have characterized the equilibrium pair
![]() . To complete the description of
the steady-state equilibrium core of our model, it remains to
characterize
. To complete the description of
the steady-state equilibrium core of our model, it remains to
characterize ![]() (or, equivalently,
(or, equivalently, ![]() ,
because
,
because
![]() ) for a given
) for a given
![]() . To do this, we begin by noting
that in a steady-state equilibrium, the flow of individuals from
search into customer relationships equals the flow of individuals
from customer relationships (gone sour) back into search. Equating
these flows,
. To do this, we begin by noting
that in a steady-state equilibrium, the flow of individuals from
search into customer relationships equals the flow of individuals
from customer relationships (gone sour) back into search. Equating
these flows,
![]() .21
Rearranging,
.21
Rearranging,
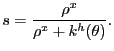 |
(40) |
Cobb-Douglas matching implies
![]() . In
. In
![]() space, then, the flow
condition (40), which
characterizes activity on the household side of the goods market,
defines the downward-sloping locus shown in Figure 2.
space, then, the flow
condition (40), which
characterizes activity on the household side of the goods market,
defines the downward-sloping locus shown in Figure 2.
Finally, to describe equilibrium in ![]() space,
we need a description of activity on the firm side of the goods
market; such a description comes from combining (37)
and (39). Specifically,
solving (37) for
space,
we need a description of activity on the firm side of the goods
market; such a description comes from combining (37)
and (39). Specifically,
solving (37) for ![]() , substituting in (39),
and using the implicit function theorem to compute the slope of
, substituting in (39),
and using the implicit function theorem to compute the slope of
![]() with respect to
with respect to ![]() (we
again relegate the details to Appendix D), we can show
that the resulting form of the advertising condition is the
upward-sloping ray in
(we
again relegate the details to Appendix D), we can show
that the resulting form of the advertising condition is the
upward-sloping ray in ![]() space shown in
Figure 2;
the steady-state equilibrium
space shown in
Figure 2;
the steady-state equilibrium ![]() is determined
where it and the locus (40)
cross in Figure 2. In combination, then,
Figures 1
and 2 fully
characterize the steady-state (partial) equilibrium triple
is determined
where it and the locus (40)
cross in Figure 2. In combination, then,
Figures 1
and 2 fully
characterize the steady-state (partial) equilibrium triple
![]() that describes goods-market
trade.
that describes goods-market
trade.
4. Quantitative Results in Baseline Model
With these analytics in mind, we turn to characterizing the full
deterministic steady state of our model numerically (i.e., fully
endogenizing
![]() by re-introducing
elastic labor supply). We begin by describing the calibration we
use.
by re-introducing
elastic labor supply). We begin by describing the calibration we
use.
4.1 Calibration
For instantaneous utility, we choose the common functional forms
| (41) |
| (42) |
and
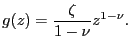 |
(43) |
The time unit of our model is meant to be one quarter, so we set
![]() , in line with an average annual
real interest rate of about four percent. We fix the curvature
parameter for the subutility function over leisure to
, in line with an average annual
real interest rate of about four percent. We fix the curvature
parameter for the subutility function over leisure to ![]() . We set the preference parameter
. We set the preference parameter
![]() as a baseline. With this
baseline setting and given the rest of the calibration described
below, the fraction of equilibrium total consumption that is
comprised of consumption obtained through search is 43 percent.
That is,
as a baseline. With this
baseline setting and given the rest of the calibration described
below, the fraction of equilibrium total consumption that is
comprised of consumption obtained through search is 43 percent.
That is,
![]() delivers
delivers
![]() , which does not
seem unreasonable. Varying
, which does not
seem unreasonable. Varying ![]() varies
this share; in the limit, of course,
varies
this share; in the limit, of course,
![]() collapses our model to one in
which all goods are exchanged via Walrasian trade.
collapses our model to one in
which all goods are exchanged via Walrasian trade.
As we mentioned earlier, we choose a Cobb-Douglas specification for the matching function,
| (44) |
and set the elasticity to
![]() . We choose Cobb-Douglas
because of its convenient properties -- in particular, the fact
that matching probabilities depend only on goods-market tightness
. We choose Cobb-Douglas
because of its convenient properties -- in particular, the fact
that matching probabilities depend only on goods-market tightness
![]() , as we already mentioned --
but recognize that it would be desirable to test how empirically
useful the Cobb-Douglas description is for goods-market
frictions.22 For the Nash bargaining weight
, as we already mentioned --
but recognize that it would be desirable to test how empirically
useful the Cobb-Douglas description is for goods-market
frictions.22 For the Nash bargaining weight
![]() , we choose a middle-of-the-road
calibration
, we choose a middle-of-the-road
calibration
![]() for most of the results we
report, but do vary it in some of our experiments. One virtue of
setting
for most of the results we
report, but do vary it in some of our experiments. One virtue of
setting
![]() , well-known to search
theorists, is that, as Hosios (1990) first showed in the context of
labor search models, the underlying search equilibrium is socially
efficient. We of course do not know if an efficient search
equilibrium in the goods market is the best description of the
data, but it seems useful as a starting point.
, well-known to search
theorists, is that, as Hosios (1990) first showed in the context of
labor search models, the underlying search equilibrium is socially
efficient. We of course do not know if an efficient search
equilibrium in the goods market is the best description of the
data, but it seems useful as a starting point.
We calibrate a number of other parameters in the version of our
model in which there are zero costs of price adjustment
(![]() ). In this flexible-price version of
our model, we set
). In this flexible-price version of
our model, we set
![]() so that the household spends 30
percent of its time working (equivalently, the household sends 30
percent of its family members to work) and then hold this value
fixed as we move to other versions of our model. We also calibrate
so that the household spends 30
percent of its time working (equivalently, the household sends 30
percent of its family members to work) and then hold this value
fixed as we move to other versions of our model. We also calibrate
![]() ,
, ![]() , and
, and
![]() , all of which we discuss in more detail
immediately below, in the zero-menu-cost version of our model and
hold the resulting values constant throughout all versions of our
model.
, all of which we discuss in more detail
immediately below, in the zero-menu-cost version of our model and
hold the resulting values constant throughout all versions of our
model.
Two novel properties of our model about which we can obtain some
empirical evidence are the amount of time consumers spend shopping
and firms' expenditures on advertising. According to the American
Time Use Survey (ATUS), conducted annually by the U.S. Bureau of
Labor Statistics, the average American consumer spends just under
one hour per day shopping, which is roughly one-fourth as much time
spent working.23 The questionnaire that is the basis
for the survey does not distinguish between, in the terminology of
our model, "searching" for goods and "shopping" for goods. Thus,
we calibrate our model so that, in the deterministic steady state,
![]() and allow the model to
endogenously determine
and allow the model to
endogenously determine ![]() and
and ![]() separately. Hitting this target requires setting the intensive
quantity traded in a customer relationship to
separately. Hitting this target requires setting the intensive
quantity traded in a customer relationship to
![]() .
.
Regarding advertising expenditures, we use data from the BLS and
Universal McCann, an advertising agency that tracks and projects
developments in the industry.24 According to these data, total
nominal advertising expenditures in the U.S. in 2005 were about
$276 billion and are estimated to have been about $290 billion in
2006, putting the share of advertising in total nominal GDP around
2.25 percent. This figure strikes us as non-neglible: firm spend
quite a lot attracting and retaining customers. Going back to 1950,
this share has generally fluctuated within the range 2 percent to
2.5 percent. Because the notion of advertising in our model is
likely a bit more general than activities typically expensed as
advertising, we use the upper limit of 2.5 percent as our
guidepost.25 We thus calibrate ![]() so that
so that ![]() in our model is 2.5
percent of GDP in steady state. In Appendix F, we provide
for interested researchers annual aggregate advertising data.
in our model is 2.5
percent of GDP in steady state. In Appendix F, we provide
for interested researchers annual aggregate advertising data.
Unfortunately, neither the shopping data nor the advertising
data gives us any guidance (at least not that we have been able to
discern) about how to calibrate our model's matching and separation
probabilities. Lacking solid evidence, we calibrate the matching
function parameter ![]() in the flexible-price
version of our model so that
in the flexible-price
version of our model so that
![]() . The resulting value is
. The resulting value is
![]() , which we hold fixed as we move
to other versions of our model. We simply set the parameter that
governs the breakup of a customer relationship at
, which we hold fixed as we move
to other versions of our model. We simply set the parameter that
governs the breakup of a customer relationship at
![]() , which states that a firm
loses ten percent of its existing customers in any given period.
Equivalently, this parameter setting means that a newly-formed
customer-firm relationship is expected to last for
, which states that a firm
loses ten percent of its existing customers in any given period.
Equivalently, this parameter setting means that a newly-formed
customer-firm relationship is expected to last for
![]() periods (quarters), which we
think does not seem implausible.
periods (quarters), which we
think does not seem implausible.
We also face a problem in terms of calibrating the
price-adjustment parameter ![]() . Ideally, we
would like to set it so that in the deterministic steady state,
resources devoted to price adjustment absorb some
empirically-relevant portion of output. However, because all prices
are real in our model, price-adjustment costs are always zero in
any deterministic steady state, making
. Ideally, we
would like to set it so that in the deterministic steady state,
resources devoted to price adjustment absorb some
empirically-relevant portion of output. However, because all prices
are real in our model, price-adjustment costs are always zero in
any deterministic steady state, making ![]() irrelevant for the steady state. Hence, we report results for
several values of
irrelevant for the steady state. Hence, we report results for
several values of ![]() , corresponding to no,
small, moderate, and large menu costs. We think this strategy is
sufficient because the main results we wish to convey are
conceptual rather than quantitative.
, corresponding to no,
small, moderate, and large menu costs. We think this strategy is
sufficient because the main results we wish to convey are
conceptual rather than quantitative.
Finally, the exogenous TFP process follows an AR(1) in logs,
| (45) |
with
![]() . We
choose
. We
choose
![]() and
and
![]() in keeping with the RBC
literature -- see, for example, King and Rebelo (1999, p. 955). As
our results show, this setting for the volatility of the shock to
TFP delivers volatility of total output in our model of about 1.6
percent, in line with empirical evidence. Thus, the amplification
of TFP shocks to GDP fluctuations in our model is no different than
in a standard RBC model.
in keeping with the RBC
literature -- see, for example, King and Rebelo (1999, p. 955). As
our results show, this setting for the volatility of the shock to
TFP delivers volatility of total output in our model of about 1.6
percent, in line with empirical evidence. Thus, the amplification
of TFP shocks to GDP fluctuations in our model is no different than
in a standard RBC model.
4.2 Steady State Numerical Results
Steady-state prices and quantities are reported in
Table 1 for our
baseline calibration. At our benchmark value
![]() , the markup in the search goods
sector is just above eight percent, in line with empirical evidence
and with the settings for product-market markups employed by many
quantitative macroeconomic models.
, the markup in the search goods
sector is just above eight percent, in line with empirical evidence
and with the settings for product-market markups employed by many
quantitative macroeconomic models.
The basic motivation of our work is that customer bargaining
power may be important in pricing (and other) decisions. As such,
one would want to know the predictions of our framework regarding
key endogenous variables as customer bargaining power changes.
Figure 4 illustrates how
a number of steady-state variables vary with customer bargaining
power ![]() regardless of whether or not there are
menu costs of price adjustment. The results in Figure 4 are invariant to both the menu cost
parameter
regardless of whether or not there are
menu costs of price adjustment. The results in Figure 4 are invariant to both the menu cost
parameter ![]() and the specific bargaining
protocol because in the steady state,
and the specific bargaining
protocol because in the steady state, ![]() (i.e.,
prices are unchanging) because the interesting price in our model
is a real price -- in the steady state, real prices are of course
constant.
(i.e.,
prices are unchanging) because the interesting price in our model
is a real price -- in the steady state, real prices are of course
constant.
As shown in Figure 4,
an increase in consumer bargaining power depresses the bargained
price (the top left panel), confirming our analytical results.
Because marginal production cost is constant at unity by
construction, the markup declines as ![]() rises, as
well. A lower price leaves the household with a larger gain
rises, as
well. A lower price leaves the household with a larger gain
![]() from forming a match
(the top right panel), which also induces it to put more effort
into search. The firm, on the other hand, loses from a rise in
from forming a match
(the top right panel), which also induces it to put more effort
into search. The firm, on the other hand, loses from a rise in
![]() , as the fall in
, as the fall in
![]() shows. The firm reduces its
advertising because lower prices eat directly into profits, making
customer relationships less valuable to it. With lower
shows. The firm reduces its
advertising because lower prices eat directly into profits, making
customer relationships less valuable to it. With lower ![]() and higher
and higher ![]() , market thickness
, market thickness
![]()
![]() unambiguously falls.
unambiguously falls.
Regarding the flow of new relationships formed, the reduction in
advertising expenditures dominates the increase in search activity,
and the number of customer-firm relationships (![]() )
falls. For our calibration, even though
)
falls. For our calibration, even though ![]() rises, the
total amount of time that households spend engaged in
shopping-related activities (
rises, the
total amount of time that households spend engaged in
shopping-related activities (![]() ) declines.
Households optimally reallocate this additional time between labor
and leisure according to the consumption-leisure optimality
condition (expression (6)), and
it turns out that total labor declines, which, in turn, leads to
lower total output.
) declines.
Households optimally reallocate this additional time between labor
and leisure according to the consumption-leisure optimality
condition (expression (6)), and
it turns out that total labor declines, which, in turn, leads to
lower total output.
The latter result highlights an interesting point of contrast with the standard Dixit-Stiglitz model of monopolistic competition. In the standard model, reducing the degree of firms' pricing power (in the form of a higher elasticity of demand for its output) pushes price closer to marginal cost, causing output to rise. Figure 4 shows that in our model, reducing firms' pricing power (here, in the form of lower bargaining power for the firm) causes households to devote less time to production activities and enjoy more leisure, causing output to decline.
The reason for the difference in the response of output as the markup of price over marginal cost falls is of course a direct result of the non-Walrasian features of our model. Advertising activities open up a supply-side channel missing in a standard model. When the firm has less to gain from trading in the non-Walrasian market, it simply chooses to reduce its activity there by cutting back on advertising. The resulting number of transactions in the non-Walrasian market declines. Shopping becomes less of a burden for households, who enjoy more leisure and devote less time to production activities.26
4.3 Dynamics
To study dynamics, we approximate our model by linearizing in
levels the equilibrium conditions of the model around the
non-stochastic steady-state. Our numerical method is our own
implementation of the perturbation algorithm described by
Schmitt-Grohe and Uribe (2004b). We conduct 5000 simulations, each
100 periods long. For each simulation, we compute first and second
moments and report the medians of these moments across the 5000
simulations. To make the comparisons meaningful as we vary model
parameters, the same realizations for productivity shocks are used
across versions of our model. Because by construction marginal
production cost is always
![]() in our model, we will speak
interchangeably about the dynamics of prices and markups. Depending
on the issue at hand, one or the other language will typically be
more convenient to use, which we think is clear in the ensuing
discussion.
in our model, we will speak
interchangeably about the dynamics of prices and markups. Depending
on the issue at hand, one or the other language will typically be
more convenient to use, which we think is clear in the ensuing
discussion.
4.3.1. Nash Bargaining with No Menu Costs
Table 2
presents simulation-based first and second moments for key
variables under Nash bargaining and zero menu costs. Examining
basic business cycle statistics reveals that the search goods
market is a source of consumption smoothing, in the sense that the
volatility of total consumption is lower than the volatility of
GDP.27 In our model, total consumption is
![]() . The volatility of total search
consumption
. The volatility of total search
consumption ![]() , at 1.13 percentage points, is
noticeably lower than the volatility of Walrasian consumption
, at 1.13 percentage points, is
noticeably lower than the volatility of Walrasian consumption
![]() . In our baseline calibration, search
consumption makes up 43 percent of total consumption in the
steady-state
. In our baseline calibration, search
consumption makes up 43 percent of total consumption in the
steady-state ![]() . The volatility of total
consumption, at 1.55 percent (not shown in the table), is thus a
bit lower than volatility of total output. The consumption
smoothing, although obviously not as quantitatively strong as in an
RBC model with capital, arises because active customer-firm
relationships are a state variable in our environment, making part
of total consumption pre-determined. At roughly 0.94% ( =
1.55/1.66), the relative volatility of aggregate consumption in our
model is clearly not as low as that which obtains in an RBC model
with capital (see, for example, Table 3 in King and Rebelo (1999,
p. 957)). Thus, we are clearly not claiming that search consumption
induces as quantitatively strong a smoothing effect as does
capital. The fact that consumption smoothing can arise in a
model with completely perishable goods and no capital, though, is
novel.
. The volatility of total
consumption, at 1.55 percent (not shown in the table), is thus a
bit lower than volatility of total output. The consumption
smoothing, although obviously not as quantitatively strong as in an
RBC model with capital, arises because active customer-firm
relationships are a state variable in our environment, making part
of total consumption pre-determined. At roughly 0.94% ( =
1.55/1.66), the relative volatility of aggregate consumption in our
model is clearly not as low as that which obtains in an RBC model
with capital (see, for example, Table 3 in King and Rebelo (1999,
p. 957)). Thus, we are clearly not claiming that search consumption
induces as quantitatively strong a smoothing effect as does
capital. The fact that consumption smoothing can arise in a
model with completely perishable goods and no capital, though, is
novel.
Nevertheless, in terms of developing intuition for the basic dynamics of the model, we find it useful to think of the formation of customer-firm relationships as an investment decision for participants on both sides of the market. Households invest time searching for retailers, and firms invest advertising dollars in order to attract shoppers. A comparison of the volatility of advertising expenditures in our model to the volatility of investment in a standard RBC model with capital supports this analogy. We have more to say about the business cycle properties of advertising expenditures below.
The final point worth emphasizing is that even with flexible prices, our model delivers a time-varying markup, a result that is of some interest on its own. Our baseline model predicts that markups are procyclical, as the fifth column in Table 2 documents. However, most empirical evidence -- for example, Rotemberg and Woodford (1999) or, more recently, Jaimovich (2006) -- suggests that markups are countercyclical. We do not view this as a shortcoming of our model for two reasons. First, our basic goal was not to model markup behavior per se. Second, our baseline model features only TFP shocks. Our reading of the empirical evidence is that it is not even clear whether countercyclicality of markups observed in the data is due to demand shocks or supply shocks. In Section 6, we briefly extend our model to include demand shocks and demonstrate that our model is in fact capable of delivering countercyclical markups.
4.3.2 Nash Bargaining with Menu Costs
We now turn on menu costs. Table 3 presents
simulation-based first and second moments for key variables under
Nash bargaining and for several values of ![]() .
Comparing results across models, one feature that stands out is
that the volatility and correlation properties of the typical
quantity variables GDP, (Walrasian) consumption
.
Comparing results across models, one feature that stands out is
that the volatility and correlation properties of the typical
quantity variables GDP, (Walrasian) consumption ![]() ,
and time spent working
,
and time spent working ![]() are virtually invariant to
the size of the menu cost
are virtually invariant to
the size of the menu cost ![]() . The same is
true of the correlation and volatility properties of time spent
shopping
. The same is
true of the correlation and volatility properties of time spent
shopping ![]() and time spent searching
and time spent searching ![]() .
Quantity variables as a whole are thus largely unaffected by the
magnitude of menu costs. An exception is goods-market tightness
.
Quantity variables as a whole are thus largely unaffected by the
magnitude of menu costs. An exception is goods-market tightness
![]() , which becomes a bit less volatile as
, which becomes a bit less volatile as
![]() rises. Because, as we just noted, the
volatility of
rises. Because, as we just noted, the
volatility of ![]() changes little with
changes little with ![]() , changes in the volatility of
, changes in the volatility of ![]() are driven by fluctuations in firms' incentives to advertise. We
document and discuss this latter feature of our model further at
the close of this section.
are driven by fluctuations in firms' incentives to advertise. We
document and discuss this latter feature of our model further at
the close of this section.
With most quantity variables largely unaffected by the degree of
price rigidity, then, we focus most of the rest of our discussion
on the dynamics of prices (equivalently, markups) and effective
bargaining power. As Table 2 shows, with zero costs
of price adjustment, effective bargaining power is constant over
the business cycle at
![]() . We pointed out in
Section 2.4.1 that this must be
the case with no costs of price adjustment, and
Appendix B proves this.
Nevertheless, prices, and hence markups, do vary. Recall that for
the case
. We pointed out in
Section 2.4.1 that this must be
the case with no costs of price adjustment, and
Appendix B proves this.
Nevertheless, prices, and hence markups, do vary. Recall that for
the case ![]() , the Nash pricing condition can be
expressed as in (25),
which makes clear that in general prices vary over time despite
constant effective bargaining power because the marginal utility of
wealth
, the Nash pricing condition can be
expressed as in (25),
which makes clear that in general prices vary over time despite
constant effective bargaining power because the marginal utility of
wealth
![]() and aggregate goods-market
tightness
and aggregate goods-market
tightness
![]() are both time-varying.
are both time-varying.
As Table 3
shows, prices (markups) become more volatile and more persistent as
![]() rises, mirroring what happens to
customers' effective bargaining power
rises, mirroring what happens to
customers' effective bargaining power
![]() . In fact,
. In fact,
![]() and
and ![]() are
negatively correlated over the business cycle: their mean
correlation across simulations is -0.11 with
are
negatively correlated over the business cycle: their mean
correlation across simulations is -0.11 with ![]() , -0.64 with
, -0.64 with
![]() , -0.79 with
, -0.79 with
![]() , and -0.81 with
, and -0.81 with
![]() . Figure 5 provides more evidence of this
phenomenon. We think this result is quite easy to understand: at
times when consumers' effective bargaining power is low, firms are
more likely to be to able to push through higher prices. The
relationship holds in the opposite direction as well, of course: at
times when consumers' effective bargaining power is high, firms
must lower their profit margins. Our model predicts that such
phenomena hold at a business-cycle frequency, perhaps opening a new
way to empirically thinking about how and why markups change over
time. Regardless of the ability to empirically test this idea with
currently available data, eliminating the phenomenon that prices
are higher the lower is consumers' bargaining power (and
vice-versa) is precisely the goal of the fair-bargaining norm that
we examine below.
. Figure 5 provides more evidence of this
phenomenon. We think this result is quite easy to understand: at
times when consumers' effective bargaining power is low, firms are
more likely to be to able to push through higher prices. The
relationship holds in the opposite direction as well, of course: at
times when consumers' effective bargaining power is high, firms
must lower their profit margins. Our model predicts that such
phenomena hold at a business-cycle frequency, perhaps opening a new
way to empirically thinking about how and why markups change over
time. Regardless of the ability to empirically test this idea with
currently available data, eliminating the phenomenon that prices
are higher the lower is consumers' bargaining power (and
vice-versa) is precisely the goal of the fair-bargaining norm that
we examine below.
Finally, we noted above that firms' incentives to advertise
fluctuate over time. Changes in these incentives are reflected in
shifts of the firm advertising condition, the steady-state version
of which, recall, is the downward-sloping locus in
Figure 1. In
Figure 6, we scatter
the dynamic realizations of
![]() for a representative simulation
with
for a representative simulation
with ![]() . Comparing the results with
Figure 1, clearly
both the advertising condition and the Nash pricing condition shift
over the business cycle, but shifts in the advertising condition
dominate because the resulting scatter is upward-sloping. This
result carries over to the environment with positive menu costs, as
the comparable results presented in Figure 7 show. For brevity, we
omit plotting the dynamic realizations of
. Comparing the results with
Figure 1, clearly
both the advertising condition and the Nash pricing condition shift
over the business cycle, but shifts in the advertising condition
dominate because the resulting scatter is upward-sloping. This
result carries over to the environment with positive menu costs, as
the comparable results presented in Figure 7 show. For brevity, we
omit plotting the dynamic realizations of ![]() in
the space of Figure 2, which all show that
it is dynamic shifts in the flow condition (40) that dominate. The reason that
in
the space of Figure 2, which all show that
it is dynamic shifts in the flow condition (40) that dominate. The reason that
![]() fluctuates so much more than
fluctuates so much more than ![]() is that firm profits are linear in
is that firm profits are linear in ![]() , while
household utility displays diminishing returns in leisure (which
depends on
, while
household utility displays diminishing returns in leisure (which
depends on ![]() ). All else equal, the household has an
incentive to limit fluctuations in its search activity in a way
that firms do not.
). All else equal, the household has an
incentive to limit fluctuations in its search activity in a way
that firms do not.
Whether in the face of zero menu costs (Table 2) or positive menu costs (Table 3), the standard deviation of advertising, at over 4 percent, lines up well with the cyclical volatility of advertising behavior in the U.S. economy. In Appendix F, we present data and summary statistics for U.S. aggregate advertising. The cyclical volatility of advertising over the past 50 years is 4.2 percent, and its contemporaneous correlation with GDP is 0.73; our model predictions are quite close to these. We did not set out to match advertising dynamics per se, but the fact that our basic model matches quite well the volatility and correlation of advertising behavior means that it is not subject to the same critique Shimer (2005) leveled at labor search models.28
In summary, regardless of the presence of menu costs, the
dynamics of prices and quantities are largely divorced from each
other in the search goods market. The price ![]() plays
much more of a distributive role (determining how the surplus in a
customer relationship is split) than the purely allocative role it
plays in standard Walrasian views of goods markets. This point is
made quite clearly in Figure 8,
which shows impulse responses to a one-time, persistent TFP shock
for
plays
much more of a distributive role (determining how the surplus in a
customer relationship is split) than the purely allocative role it
plays in standard Walrasian views of goods markets. This point is
made quite clearly in Figure 8,
which shows impulse responses to a one-time, persistent TFP shock
for ![]() and
and
![]() . Output dynamics are essentially
identical (the two responses in the top panel of
Figure 8 lie virtually on top of
each other) despite large differences in price dynamics.
. Output dynamics are essentially
identical (the two responses in the top panel of
Figure 8 lie virtually on top of
each other) despite large differences in price dynamics.
Because the price plays a distributive role, our model seems
ideally suited to study notions of fairness in pricing. With some
understanding of the dynamic results under Nash bargaining in hand,
we thus turn next to dynamics under our two fairness schemes,
proportional bargaining and fair bargaining. We again point out
that these fairness schemes are only relevant in the presence of
menu costs (![]() ) because, as we discussed
in Section 2.4, all three
bargaining schemes collapse to standard Nash bargaining, both in
steady state and dynamically, if
) because, as we discussed
in Section 2.4, all three
bargaining schemes collapse to standard Nash bargaining, both in
steady state and dynamically, if ![]() .
.
4.3.3 Proportional Bargaining
The proportional-bargaining price always solves (27), which is identical to
the Nash sharing condition (22)
when
![]() , which occurs, recall, if
, which occurs, recall, if
![]() . Thus, no matter the magnitude of
. Thus, no matter the magnitude of
![]() , all dynamics under proportional
bargaining, both those of prices and quantities, are identical to
the dynamics under Nash bargaining and
, all dynamics under proportional
bargaining, both those of prices and quantities, are identical to
the dynamics under Nash bargaining and ![]() reported in Table 2. The way in which
fairness is captured by proportional bargaining thus renders menu
costs completely irrelevant.
reported in Table 2. The way in which
fairness is captured by proportional bargaining thus renders menu
costs completely irrelevant.
To understand this, recall from the analysis of the results
under Nash bargaining and positive menu costs that the primary
channel through which menu costs affected price dynamics was
through time-variation in effective bargaining power
![]() . In proportional bargaining, in
contrast, there is no notion of "bargaining power" -- indeed, this
is what we mean when we say that proportional bargaining lacks
clear strategic foundations. In proportional bargaining, parties'
adherence to the ad-hoc rule that splits the surplus according to
fixed shares no matter what shuts down the transmission of menu
costs to prices intermediated through effective bargaining power.
As a consequence, price dynamics are governed entirely by the
dynamics of the underlying surplus, and any price adjustment is
simply an efficient response to a shock and neutralizes the
distributive role of prices.
. In proportional bargaining, in
contrast, there is no notion of "bargaining power" -- indeed, this
is what we mean when we say that proportional bargaining lacks
clear strategic foundations. In proportional bargaining, parties'
adherence to the ad-hoc rule that splits the surplus according to
fixed shares no matter what shuts down the transmission of menu
costs to prices intermediated through effective bargaining power.
As a consequence, price dynamics are governed entirely by the
dynamics of the underlying surplus, and any price adjustment is
simply an efficient response to a shock and neutralizes the
distributive role of prices.
Finally, to square proportional bargaining with Nash bargaining
in a different way and to motivate fair bargaining from a
quantitative perspective, we conduct the following thought
experiment. For a given value of ![]() and using
Nash bargaining, we can construct the sequence
and using
Nash bargaining, we can construct the sequence
![]() of effective
bargaining power that would make the Nash outcome coincide with the
proportional-bargaining outcome. In other words,
of effective
bargaining power that would make the Nash outcome coincide with the
proportional-bargaining outcome. In other words,
![]() is a series we can
construct residually to make the Nash dynamics for a given
is a series we can
construct residually to make the Nash dynamics for a given
![]() identical to the Nash dynamics for
identical to the Nash dynamics for
![]() . Using
. Using ![]() , the
last row of Table 2 reports the dynamics of
this counterfactual effective bargaining power series. This
residual measure of effective bargaining power is much more
volatile than any of the actual effective bargaining power series
reported in Table 3. In proportional
bargaining,
, the
last row of Table 2 reports the dynamics of
this counterfactual effective bargaining power series. This
residual measure of effective bargaining power is much more
volatile than any of the actual effective bargaining power series
reported in Table 3. In proportional
bargaining,
![]() is indeed nothing but a
residual; there is no notion of bargaining power at all in
proportional bargaining. This fact, coupled with the observation
that if there were a notion of bargaining power behind
fairness it would apparently fluctuate a great deal, is part of our
motivation for constructing our fair-bargaining protocol, the
results of which we now turn to.
is indeed nothing but a
residual; there is no notion of bargaining power at all in
proportional bargaining. This fact, coupled with the observation
that if there were a notion of bargaining power behind
fairness it would apparently fluctuate a great deal, is part of our
motivation for constructing our fair-bargaining protocol, the
results of which we now turn to.
4.3.4 Fair Bargaining
Table 4 compiles results
using fair bargaining for the same set of experiments as in
Table 3. The
central result here is that the presence of menu costs makes the
price of the search good completely rigid. In the discussion
surrounding expression (23), we noted
that
![]() if and only if the cost of
price adjustment in period
if and only if the cost of
price adjustment in period ![]() is zero. The menu
cost can be zero either because
is zero. The menu
cost can be zero either because ![]() or because
or because
![]() . Under fair bargaining, the
customer and firm are constrained to share the surplus according to
. Under fair bargaining, the
customer and firm are constrained to share the surplus according to
![]()
![]() . With
. With ![]() , the only way
this sharing norm can be achieved is if prices never vary. One way
of understanding this result is that the "fairness constraint" on
the Nash bargaining problem effectively eliminates the efficient
adjustment of the price that obtains under proportional bargaining.
Echoing the result under proportional bargaining, however, the
magnitude of menu costs (here, as long as they are positive) is
irrelevant for price, as well as quantity, dynamics.
, the only way
this sharing norm can be achieved is if prices never vary. One way
of understanding this result is that the "fairness constraint" on
the Nash bargaining problem effectively eliminates the efficient
adjustment of the price that obtains under proportional bargaining.
Echoing the result under proportional bargaining, however, the
magnitude of menu costs (here, as long as they are positive) is
irrelevant for price, as well as quantity, dynamics.
However, it is not a theorem that would hold in any
goods-search model of the type we propose that fair bargaining
necessarily requires complete price stability. With the features
present in our model, it is only time-variation of prices that
create a wedge between ![]() and
and
![]() . One can easily extend our model
to include other features that would affect this wedge. For
example, in Arseneau and Chugh (2007), time-varying labor taxes
also induce such a wedge (albeit in a model of wage bargaining, but
we think the idea would translate readily to our environment).
Suppose exogenous tax movements and (endogenous) price movements
were both present in our model. In such an environment, there may
be situations in which variations in the two offset each other in
such a way as to leave no wedge at all between
. One can easily extend our model
to include other features that would affect this wedge. For
example, in Arseneau and Chugh (2007), time-varying labor taxes
also induce such a wedge (albeit in a model of wage bargaining, but
we think the idea would translate readily to our environment).
Suppose exogenous tax movements and (endogenous) price movements
were both present in our model. In such an environment, there may
be situations in which variations in the two offset each other in
such a way as to leave no wedge at all between ![]() and
and
![]() . Indeed, the fair-bargaining norm
may require customers and firms to engineer price movements
in precisely the right way to offset exogenous tax shifts. We have
not conducted such experiments with our model and so cannot assert
this definitively, but based on our work here and the results and
intuition in Arseneau and Chugh (2007), this hypothesis seems
sound.
. Indeed, the fair-bargaining norm
may require customers and firms to engineer price movements
in precisely the right way to offset exogenous tax shifts. We have
not conducted such experiments with our model and so cannot assert
this definitively, but based on our work here and the results and
intuition in Arseneau and Chugh (2007), this hypothesis seems
sound.
Quantity dynamics, which are also invariant to ![]() , are very nearly, but not completely, identical to the
flexible-price Nash baseline. The most obvious difference is in the
volatility of goods-market tightness
, are very nearly, but not completely, identical to the
flexible-price Nash baseline. The most obvious difference is in the
volatility of goods-market tightness ![]() . Its
standard deviation of about 1.2 percent in Table 4 is roughly half
that of all the results under Nash bargaining displayed in
Tables 2
and 3.
Because the volatility of
. Its
standard deviation of about 1.2 percent in Table 4 is roughly half
that of all the results under Nash bargaining displayed in
Tables 2
and 3.
Because the volatility of ![]() is virtually the
same across models, the smaller fluctuations in
is virtually the
same across models, the smaller fluctuations in ![]() under fair bargaining must be due to smaller
fluctuations in
under fair bargaining must be due to smaller
fluctuations in ![]() . To verify this conjecture, we
plot in Figure 9 the dynamic realizations
of the pairs
. To verify this conjecture, we
plot in Figure 9 the dynamic realizations
of the pairs
![]() and
and ![]() for a
representative simulation.29 The reason that advertising does not
fluctuate as much under fair bargaining is simple: because
for a
representative simulation.29 The reason that advertising does not
fluctuate as much under fair bargaining is simple: because
![]() does not fluctuate, a firm's incentives to
advertise do not vary nearly as much as they do under Nash
bargaining. With the return to advertising thus much less variable
over time, actual advertising is less variable as well.
does not fluctuate, a firm's incentives to
advertise do not vary nearly as much as they do under Nash
bargaining. With the return to advertising thus much less variable
over time, actual advertising is less variable as well.
Related to a point we made earlier, we do not need to take
literally the idea that customers and firms calculate deviations of
![]() from
from ![]() and use
that to inform what prices they consider acceptable. Our model is
obviously a metaphor for more subjective forces underlying the
kinds of evidence that Blinder et al (1998) and others tabulate
that suggest that avoiding customer anger is often a major concern
of firms when determining prices.
and use
that to inform what prices they consider acceptable. Our model is
obviously a metaphor for more subjective forces underlying the
kinds of evidence that Blinder et al (1998) and others tabulate
that suggest that avoiding customer anger is often a major concern
of firms when determining prices.
4.3.5 Customer Bargaining Power and Price Volatility
In the dynamic results so far, we have focused on the case
![]() , which corresponds to the
Hosios (1990) parameterization. In our model with Nash bargaining,
even though effective bargaining power
, which corresponds to the
Hosios (1990) parameterization. In our model with Nash bargaining,
even though effective bargaining power
![]() generally is different from
generally is different from
![]() along the business cycle, in the
long-run (i.e., in steady-state),
along the business cycle, in the
long-run (i.e., in steady-state),
![]() . Thus, using the Hosios setting
implies that customers' long-run bargaining power is such that the
underlying search equilibrium is efficient, which is a useful
benchmark.
. Thus, using the Hosios setting
implies that customers' long-run bargaining power is such that the
underlying search equilibrium is efficient, which is a useful
benchmark.
Of course, long-run bargaining power may not satisfy the Hosios
condition. A basic goal of our study is to shed some light on the
consequences of bargaining and bargaining power for pricing
outcomes. We need not limit ourselves to short-run changes in
bargaining power; we can also easily investigate how changes in
long-run bargaining power affect pricing. We thus repeat our basic
experiments for alternative values of long-run customer bargaining
power ![]() . Table 5 reports results for
Nash bargaining (the issue at hand here is moot with fair
bargaining because fair bargaining renders prices constant), fixing
. Table 5 reports results for
Nash bargaining (the issue at hand here is moot with fair
bargaining because fair bargaining renders prices constant), fixing
![]() , using a lower setting for
customer bargaining power (
, using a lower setting for
customer bargaining power (
![]() ) and a higher setting for
customer bargaining power (
) and a higher setting for
customer bargaining power (
![]() ) (the middle panel repeats
results from the top panel of Table 2).
) (the middle panel repeats
results from the top panel of Table 2).
As the results make apparent, the means, volatilities, and
correlations of almost all variables change little as we vary
long-run bargaining power. The exception, though, is prices
(equivalently, the markup): the standard deviation of prices in the
search goods sector falls about four-fold as long-run customer
bargaining power rises from ![]() to
to
![]() . Thus, not only does higher
average customer bargaining power lower the average markup (from 15
percent to less than 5 percent in Table 5), it lowers its
volatility as well. To demonstrate this point a bit further, we
plot in Figure 10
the mean volatility of prices across simulations for a wide range
of values of
. Thus, not only does higher
average customer bargaining power lower the average markup (from 15
percent to less than 5 percent in Table 5), it lowers its
volatility as well. To demonstrate this point a bit further, we
plot in Figure 10
the mean volatility of prices across simulations for a wide range
of values of ![]() and for several values of
and for several values of
![]() .30 The rate at which price
volatility declines as long-run customer bargaining power rises is
larger the higher is
.30 The rate at which price
volatility declines as long-run customer bargaining power rises is
larger the higher is ![]() . Figure 10 thus illustrates two
implications of our model that may be testable using time-series
data on, say, sectoral-level prices: the relationship between
volatility of prices and the fraction of repeat customers (which
may serve as a proxy for average customer bargaining power), and
how this relationship changes with the importance of pure menu
costs in that sector. Such empirical investigation is left for
future work. The main point that emerges from our experiments here,
though, is that average bargaining power has implications not only
for average prices (as illustrated in Figure 4) but also for price volatility.
. Figure 10 thus illustrates two
implications of our model that may be testable using time-series
data on, say, sectoral-level prices: the relationship between
volatility of prices and the fraction of repeat customers (which
may serve as a proxy for average customer bargaining power), and
how this relationship changes with the importance of pure menu
costs in that sector. Such empirical investigation is left for
future work. The main point that emerges from our experiments here,
though, is that average bargaining power has implications not only
for average prices (as illustrated in Figure 4) but also for price volatility.
5. Intensive Quantity Adjustment
In order to highlight the consequences of the formation and
dissolution of customer relationships, we have so far limited
fluctuations in consumption of search goods to fluctuations at the
extensive margin (fluctuations in ![]() ). In goods
markets, it is natural to think that fluctuations also occur at the
intensive margin, the quantity traded per transaction; indeed, this
is the only margin at which fluctuations occur in standard models.
We now relax the assumption in our baseline model that
). In goods
markets, it is natural to think that fluctuations also occur at the
intensive margin, the quantity traded per transaction; indeed, this
is the only margin at which fluctuations occur in standard models.
We now relax the assumption in our baseline model that
![]() in every trade
in every trade ![]() and instead endogenize
and instead endogenize ![]() .
.
In order to open up the intensive margin of adjustment, we
modify one feature of our baseline model. In our baseline model,
the aggregator over search goods over which subutility ![]() is defined is linear in the number of goods obtained,
is defined is linear in the number of goods obtained,
![]() . In a symmetric
equilibrium,
. In a symmetric
equilibrium, ![]() , which makes clear that from the
point of view of just preferences, the household does not care
whether a given amount of total search consumption comes from many
matches, each with a small per-match quantity, or a small number of
matches, each with a large per-match quantity. From a cost
perspective, however, the latter is cheaper than the former because
finding and engaging in many customer relationships takes time.
Thus, were we to stick with the formulation of
, which makes clear that from the
point of view of just preferences, the household does not care
whether a given amount of total search consumption comes from many
matches, each with a small per-match quantity, or a small number of
matches, each with a large per-match quantity. From a cost
perspective, however, the latter is cheaper than the former because
finding and engaging in many customer relationships takes time.
Thus, were we to stick with the formulation of ![]() we have used thus far as we endogenize
we have used thus far as we endogenize ![]() , the number
of matches would be driven very low and quantity traded per match
would be very large. This poses both a conceptual and a
quantitative problem. Conceptually, our model is meant to be one in
which consumers "must" engage in search and shopping to obtain
goods; a model in which
, the number
of matches would be driven very low and quantity traded per match
would be very large. This poses both a conceptual and a
quantitative problem. Conceptually, our model is meant to be one in
which consumers "must" engage in search and shopping to obtain
goods; a model in which ![]() and
and ![]() are
extremely small and
are
extremely small and ![]() extremely large goes
against this spirit. The agents in our model would cleverly
circumvent the frictions we have placed in their way.
Quantitatively, it could easily be the case that we would need to
employ an incentive-compatibility constraint in the baseline model
to ensure that firms would actually want to participate in such an
equilibrium because if a given customer is able to bargain a large
extremely large goes
against this spirit. The agents in our model would cleverly
circumvent the frictions we have placed in their way.
Quantitatively, it could easily be the case that we would need to
employ an incentive-compatibility constraint in the baseline model
to ensure that firms would actually want to participate in such an
equilibrium because if a given customer is able to bargain a large
![]() , price could easily be driven below
marginal production cost, in which case it of course does not make
sense for firms to want to engage in advertising to find customers
in the first place.31
, price could easily be driven below
marginal production cost, in which case it of course does not make
sense for firms to want to engage in advertising to find customers
in the first place.31
To sidestep such conceptual and quantitative issues, we modify
the aggregator inside ![]() to be a CES composite of
the goods obtained from distinct matches,
to be a CES composite of
the goods obtained from distinct matches,
![$\displaystyle y_{t} = \left[ \int_{0}^{N_{t}} c_{it}^{\rho} \right] ^{1/\rho},$](img469.gif)
|
(46) |
with ![]() , which indicates that households
have a preference for obtaining consumption from different matches.
With sufficiently diminishing returns to consumption at the
intensive margin,
, which indicates that households
have a preference for obtaining consumption from different matches.
With sufficiently diminishing returns to consumption at the
intensive margin, ![]() will not be driven too low.
Aside from the reasons we have already mentioned, introducing such
diminishing returns to intensive consumption may be natural in its
own right. For example, were sweaters to never carry labels, two
sweaters from Banana Republic may be completely indistinguishable
from two sweaters from JCrew. With labels, however, it is plausible
that a household may desire one sweater from Banana Republic
and one sweater from JCrew. This type of preference idea
often goes under the name "preference for variety," and the label,
so to speak, applies well enough to our idea here, as well.32
Finally, note that in a symmetric equilibrium,
will not be driven too low.
Aside from the reasons we have already mentioned, introducing such
diminishing returns to intensive consumption may be natural in its
own right. For example, were sweaters to never carry labels, two
sweaters from Banana Republic may be completely indistinguishable
from two sweaters from JCrew. With labels, however, it is plausible
that a household may desire one sweater from Banana Republic
and one sweater from JCrew. This type of preference idea
often goes under the name "preference for variety," and the label,
so to speak, applies well enough to our idea here, as well.32
Finally, note that in a symmetric equilibrium,
![]() .
.
We briefly describe the main modifications to the baseline model
of Section 2 and leave most
details to Appendix B
and C. In principle,
the modifications to the model are simple: in addition to the
introduction of curvature in the consumption aggregator,
![]() from the baseline model is replaced
by
from the baseline model is replaced
by ![]() in all equilibrium conditions, and we
must describe the protocol by which quantity traded in a customer
relationship is determined. We assume that the customer and firm
bargain (either Nash-bargain or fair-bargain) simultaneously over
price and quantity.
in all equilibrium conditions, and we
must describe the protocol by which quantity traded in a customer
relationship is determined. We assume that the customer and firm
bargain (either Nash-bargain or fair-bargain) simultaneously over
price and quantity.
5.1 Households
Discounted household utility is now
![$\displaystyle E_{0} \sum_{t=0}^{\infty} \beta^{t} \left[ u(x_{t}) + \vartheta v\left( \left[ \int_{0}^{N^{h}_{t}} c_{it}^{\rho} di\right] ^{\frac{1}{\rho}} \right) + g(1-l_{t}-s_{t}-N^{h}_{t}) \right] ,$](img475.gif)
|
(47) |
and in the flow budget constraint (2),
we simply replace ![]() by
by ![]() . Because the household takes as given
. Because the household takes as given ![]() in its unilateral utility maximization problem, all
household first-order conditions are identical to those in the
baseline model, with appropriate replacement of
in its unilateral utility maximization problem, all
household first-order conditions are identical to those in the
baseline model, with appropriate replacement of ![]() by
by ![]() . For example, in a symmetric
equilibrium, the shopping condition is now
. For example, in a symmetric
equilibrium, the shopping condition is now
![$\displaystyle \frac{g^{\prime}_{t}}{k^{h}(\theta_{t})} = \beta(1-\rho^{x}) E_{t} \left\{ c_{t+1} \left[ \vartheta v^{\prime}_{t+1} - p_{t+1} u^{\prime}(x_{t+1}) \right] - g^{\prime}_{t+1} + \frac{g^{\prime}_{t+1}}{k^{h}(\theta_{t+1})} \right\} .$](img481.gif)
|
(48) |
5.2 Firms
Walrasian firms are no different than in our baseline model.
Search firms are also no different, except that in the
profit-maximization problem ![]() is replaced
by
is replaced
by ![]() , which has the consequence that
, which has the consequence that
![]() appears in the period-
appears in the period-![]() advertising condition,
advertising condition,
![$\displaystyle \frac{\gamma}{k^{f}(\theta_{t})} = (1-\rho_{x}) E_{t} \left\{ \Xi_{t+1\vert t} \left[ p_{t+1} c_{t+1} - mc_{t+1} c_{t+1} - \frac{\kappa}{2}\left( \frac{p_{t+1}}{p_{t}} - 1 \right) ^{2} + \frac{\gamma}{k^{f}(\theta_{t+1})} \right] \right\} .$](img486.gif)
|
(49) |
Just as households do, search firms take ![]() as
given in their unilateral optimzation problem.
as
given in their unilateral optimzation problem.
5.3 Price and Quantity Determination
We extend both Nash bargaining and fair bargaining to now
include simulataneous bargaining over
![]() .
.
5.3.1 Nash Bargaining
In simultaneous Nash bargaining over
![]() , the customer and firm
continue to maximize the Nash product (21). The bargained price continues to
satisfy condition (24), with
appropriate replacement of
, the customer and firm
continue to maximize the Nash product (21). The bargained price continues to
satisfy condition (24), with
appropriate replacement of ![]() by
by
![]() . The bargained quantity
. The bargained quantity ![]() solves a condition that takes a similar form,
solves a condition that takes a similar form,
![$\displaystyle \lefteqn{\frac{\o_{t}}{1-\o_{t}} \left[ p_{it} c_{it} - mc_{t} c_{it} - \frac{\kappa}{2} \left( \frac{p_{it}}{p_{it-1} }-1\right) ^{2} + \frac{\gamma}{k^{f}(\theta_{t})}\right] = \frac{\tilde {u}(c_{it})}{\lambda_{t}} - p_{it} c_{it} + }$](img493.gif)
|
|
![$\displaystyle + (1-\theta_{t} k^{f}(\theta_{t})) E_{t}\left[ \Xi_{t+1\vert t} \left( \frac{\o _{t+1}}{1-\o _{t+1}}\right) (1-\rho^{x}) \left[ p_{it+1} c_{it+1} - mc_{t+1} c_{it+1} - \frac{\kappa}{2}\left( \frac{p_{it+1}}{p_{it}}-1\right) ^{2} + \frac{\gamma}{k^{f}(\theta_{t})} \right] \right] ,$](img496.gif)
|
(50) |
except with bargaining weights ![]() and
and
![]() , and
, and
![]() . The main conceptual
difference between
. The main conceptual
difference between ![]() and
and
![]() is that the former depends on
is that the former depends on
![]() whereas the
latter does not. If
whereas the
latter does not. If ![]() , a more convenient
characterization of the solution for the quantity traded is
available. With
, a more convenient
characterization of the solution for the quantity traded is
available. With ![]() ,
, ![]() satisfies
satisfies
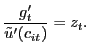
|
(51) |
Further details are provided in Appendix B and Appendix E.
5.3.2 Proportional Bargaining
As we know from the presentation and discussion of proportional
bargaining in the baseline model, the outcome replicates that of
Nash bargaining with ![]() . The irrelevance of
menu costs under proportional bargaining thus readily extends to
simultaneous bargaining over price and quantity.
. The irrelevance of
menu costs under proportional bargaining thus readily extends to
simultaneous bargaining over price and quantity.
5.3.3 Fair Bargaining
Simultaneous fair bargaining over price and quantity means that
the customer and firm choose
![]() to maximize
to maximize
![]() subject to the constant-split rule
subject to the constant-split rule
![]() .
Price continues to be characterized by (30), while the quantity satisfies
.
Price continues to be characterized by (30), while the quantity satisfies
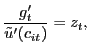
|
(52) |
exactly as in the Nash case with ![]() . Thus,
fair bargaining, in eliminating the wedge in price-bargaining, also
eliminates the wedge in quantity-bargaining. Further details appear
in Appendix C
and Appendix E.
. Thus,
fair bargaining, in eliminating the wedge in price-bargaining, also
eliminates the wedge in quantity-bargaining. Further details appear
in Appendix C
and Appendix E.
5.4 Equilibrium
The variables and conditions defining a symmetric search
equilibrium are the same as in Section 2.7 (with appropriate replacement of
![]() by
by ![]() ), with
the addition of
), with
the addition of ![]() as an endogenous stochastic
process and, depending on whether we are using Nash bargaining or
fair bargaining, either condition (50) or (52) to
pin down quantity traded.
as an endogenous stochastic
process and, depending on whether we are using Nash bargaining or
fair bargaining, either condition (50) or (52) to
pin down quantity traded.
5.5 Quantitative Results
5.5.1 Parameterization
The functional forms we use are the same as in the baseline
model, and, as we already discussed, we use the aggregator
![$ \left[ \int_{0}^{N_{t}} c_{it} ^{\rho} \right] ^{\frac{1}{\rho}}$](img516.gif) inside the subutility function
inside the subutility function ![]() . We keep all
parameter settings fixed at their values in the baseline model to
try to achieve some comparability. However, the models are not
readily comparable because we also must choose
. We keep all
parameter settings fixed at their values in the baseline model to
try to achieve some comparability. However, the models are not
readily comparable because we also must choose ![]() ; by thus changing a structural parameter of the
economy relative to the baseline economy, cross-model comparisons
inherently become difficult to interpret. In our setting for
; by thus changing a structural parameter of the
economy relative to the baseline economy, cross-model comparisons
inherently become difficult to interpret. In our setting for
![]() , we choose to make the steady-state
markup the same as in the baseline model when
, we choose to make the steady-state
markup the same as in the baseline model when
![]() . Setting
. Setting
![]() delivers a gross markup of 1.0835
here, identical to that in the baseline calibration of the model of
Section 2.
delivers a gross markup of 1.0835
here, identical to that in the baseline calibration of the model of
Section 2.
5.5.2 Steady State
Steady-state prices and quantities are reported in
Table 6 for the
model with intensive adjustment. Comparing with Table 1, the main difference is that
the fraction of time spent in shopping-related activities is much
higher. Both the number of active customer relationships and time
spent searching are much higher. Larger ![]() reflects the
curvature we introduced in the search goods aggregator, which, as
we discussed at the start of this section, gives households a
preference for obtaining consumption from many matches. Absent some
other counteracting feature of the environment, this version of our
model thus cannot account for the time-use evidence that shows
reflects the
curvature we introduced in the search goods aggregator, which, as
we discussed at the start of this section, gives households a
preference for obtaining consumption from many matches. Absent some
other counteracting feature of the environment, this version of our
model thus cannot account for the time-use evidence that shows
![]() . Because relationships
occasionally dissolve, households must also search more in order to
maintain the larger
. Because relationships
occasionally dissolve, households must also search more in order to
maintain the larger ![]() , explaining the higher
level of
, explaining the higher
level of ![]() in the model here compared to the baseline
model.
in the model here compared to the baseline
model.
Figure 11 illustrates how
key steady-state variables change with customer bargaining power
![]() . As the middle left panel shows, the
extensive quantity
. As the middle left panel shows, the
extensive quantity ![]() falls, as it did in
Figure 4; the difference
here is that the intensive quantity
falls, as it did in
Figure 4; the difference
here is that the intensive quantity ![]() simultaneously rises the larger is
simultaneously rises the larger is ![]() . This
substitution reflects the fact that with higher
. This
substitution reflects the fact that with higher ![]() , households know they can leverage a higher quantity out
of each customer relationship. Given that match formation is
costly, it makes sense for the household to essentially substitute
out of extensive consumption and into intensive consumption. The
levels and responses of all other variables are very similar to
those in Figure 4, so we
do not discuss them further.
, households know they can leverage a higher quantity out
of each customer relationship. Given that match formation is
costly, it makes sense for the household to essentially substitute
out of extensive consumption and into intensive consumption. The
levels and responses of all other variables are very similar to
those in Figure 4, so we
do not discuss them further.
5.5.3 Dynamics
Tables 7
and 8 catalog results
for the same set of dynamic experiments we conducted in
Section 4.3;
endogenizing the intensive quantity does not change the main
quantitative results presented there. A few new notable results do
arise, though. First, endogenizing the intensive quantity imparts
more persistence to household search behavior. Second, as shown in
Tables 2
, 3,
and 4,
with fixed ![]() , search activity is weakly
procyclical no matter the bargaining protocol. In contrast, with
endogenous intensive quantity, the cyclicality of
, search activity is weakly
procyclical no matter the bargaining protocol. In contrast, with
endogenous intensive quantity, the cyclicality of ![]() depends crucially on the bargaining protocol in place. In turn, the
cyclicality of search mirrors the cyclicality of the intensive
quantity
depends crucially on the bargaining protocol in place. In turn, the
cyclicality of search mirrors the cyclicality of the intensive
quantity ![]() .
.
With Nash bargaining, ![]() is always countercyclical
with respect to total GDP. This result is the dynamic manifestation
of the substitution between
is always countercyclical
with respect to total GDP. This result is the dynamic manifestation
of the substitution between ![]() and
and ![]() just discussed above: because of the "preference for
variety" in this version of the model, all else equal, the
household prefers that expansions in search consumption come at the
extensive margin rather than at the intensive margin. It is also
striking how much less volatile
just discussed above: because of the "preference for
variety" in this version of the model, all else equal, the
household prefers that expansions in search consumption come at the
extensive margin rather than at the intensive margin. It is also
striking how much less volatile ![]() is than
is than
![]() is: between five- and six-fold less
volatile depending on the value of
is: between five- and six-fold less
volatile depending on the value of ![]() . A
standard model's notion of consumption-smoothing is thus pushed
down to the level of intensive consumption in this version of our
model. We think this makes sense because it is intensive
consumption that is essentially governed by a MRS-type of
optimality condition; this can be seen most clearly in
condition (51), which is also
the core of condition (50).
. A
standard model's notion of consumption-smoothing is thus pushed
down to the level of intensive consumption in this version of our
model. We think this makes sense because it is intensive
consumption that is essentially governed by a MRS-type of
optimality condition; this can be seen most clearly in
condition (51), which is also
the core of condition (50).
As in the baseline model without intensive adjustment, the
proportional bargaining outcome, no matter the value of ![]() , is identical to the Nash outcome with
, is identical to the Nash outcome with ![]() , so this notion of fairness leaves
, so this notion of fairness leaves ![]() countercyclical. In contrast, under fair bargaining,
countercyclical. In contrast, under fair bargaining, ![]() is procyclical with respect to total GDP. This seems to be
related to the result that the volatility of
is procyclical with respect to total GDP. This seems to be
related to the result that the volatility of ![]() relative to the volatility of
relative to the volatility of ![]() is not nearly as
small under fair bargaining as it is under Nash bargaining. As in
the baseline model, fair bargaining mutes the volatility of
is not nearly as
small under fair bargaining as it is under Nash bargaining. As in
the baseline model, fair bargaining mutes the volatility of
![]() , which in turn governs the incentives of
firms to cyclically alter their advertising behavior. With
advertising not nearly as volatile as under Nash bargaining, the
equilibrium stock of active customer relationships does not
fluctuate nearly as much, which in turn means that the scope for
substitution between
, which in turn governs the incentives of
firms to cyclically alter their advertising behavior. With
advertising not nearly as volatile as under Nash bargaining, the
equilibrium stock of active customer relationships does not
fluctuate nearly as much, which in turn means that the scope for
substitution between ![]() and
and ![]() is
dramatically reduced. Thus, despite the primitive "preference for
variety," households must accept procyclical movements of
is
dramatically reduced. Thus, despite the primitive "preference for
variety," households must accept procyclical movements of
![]() to vary their consumption of search
goods.
to vary their consumption of search
goods.
6. Demand Shocks
We noted in Section 4.3 that, although our basic model driven by only TFP shocks does not deliver countercyclical markups, extending our model to allow for demand shocks can overturn this prediction. To the extent that it is not clear whether the countercyclicality of markups observed in the data is due predominately to demand shocks or supply shocks, we think it is useful to at least know that our model is capable of matching this stylized fact for some shocks.
We introduce demand shocks by allowing exogenous government
purchases. For the sake of simplicity, we only conduct the
experiments in this section in the baseline model with fixed
![]() . Total output is now absorbed by
consumption (of both Walrasian and search goods), advertising
costs, price adjustment costs, and government spending, so the
resource constraint is
. Total output is now absorbed by
consumption (of both Walrasian and search goods), advertising
costs, price adjustment costs, and government spending, so the
resource constraint is
| (53) |
No other features of the baseline model of Section 2 change, hence all equilibrium conditions, with the obvious exception of the resource constraint, are unchanged. Government spending is assumed to follow an AR(1) in logs,
| (54) |
with
![]() , and
the shock to government spending is uncorrelated with the shock to
TFP. We set
, and
the shock to government spending is uncorrelated with the shock to
TFP. We set
![]() so that government spending
makes up about 19 percent of total output, set
so that government spending
makes up about 19 percent of total output, set
![]() , in line with Schmitt-Grohe
and Uribe (2004a), and set
, in line with Schmitt-Grohe
and Uribe (2004a), and set
![]() so that the standard deviation of
government purchases is 6 percent of the mean level
so that the standard deviation of
government purchases is 6 percent of the mean level ![]() -- the resulting value is
-- the resulting value is
![]() .
.
We examine the dynamics of this model in the face of just shocks
to government spending. The upper panel of Table 9
shows that with ![]() and Nash bargaining as the
pricing mechanism, the contemporaneous correlation of the markup
with GDP is -0.32. As
and Nash bargaining as the
pricing mechanism, the contemporaneous correlation of the markup
with GDP is -0.32. As ![]() increases, however,
the correlation turns positive. So our claim is not that our model
with demand shocks always predicts a countercyclical markup, just
that it can. Finally, we do not need to consider fair bargaining
here because markups are time-invariant under that protocol. We
leave to future work a full investigation of the cyclicality
properties of the markup in our model.
increases, however,
the correlation turns positive. So our claim is not that our model
with demand shocks always predicts a countercyclical markup, just
that it can. Finally, we do not need to consider fair bargaining
here because markups are time-invariant under that protocol. We
leave to future work a full investigation of the cyclicality
properties of the markup in our model.
7. Conclusion
We constructed a model in which long-lived customer relationships allow one to think about an array of pricing schemes in goods-market transactions. Our focus here was on bargaining arrangements between firms and customers in which fairness was of paramount concern. Depending on exactly how our concept of fairness is operationalized, menu costs may be either completely irrelevant for dynamics (proportional bargaining) or may lead endogenously to complete price stability (fair bargaining). Under proportional bargaining, consumers and firms effectively share the menu costs efficiently, making them irrelevant. Under fair bargaining, price changes are the only source of time-variation in effective bargaining power between a firm and a customer. Avoiding this time-variation in effective bargaining power requires ensuring price stability. As we noted, in a richer model (one that includes, for example, labor or consumption taxes), stabilizing surplus shares need not require complete price stability.
Understanding how pricing decisions are affected by bargaining power is an understudied topic, at least in the context of modern quantitative macroeconomic models. Survey evidence seems to repeatedly support the view that firms often avoid changing prices out of concern for upsetting their existing customers. It is difficult to articulate very precisely such views in standard models of goods markets because in the basic Walrasian framework, of course, there simply are no clear notions of customers and bargaining. We think we have made some progress in at least pointing out a potentially useful direction, one that is immediately tractable in modern quantitative macroeconomic models. An even deeper bargaining-theoretic explanation for price rigidity is provided by Menzio (2007), but the tension there is that his framework seems likely not readily tractable in standard DSGE models.
More broadly than the fair-bargaining result around which we centered much of our analysis, we think the general framework we developed of search-based frictions in goods markets holds the promise of being usefully incorporated into standard quantitative macroeconomic models. Such a line of research immediately allows one to think beyond the standard marginal pricing conditions present in most models and therefore is likely to be useful in bringing to bear new ideas about a host of issues in macroeconomics. As we have admitted, more work needs to be done in thinking about the empirical counterparts of and calibration of some elements of our model. But at least these are testable parts of our model.
It is well-understood from standard macro models that wedges between consumption-leisure marginal rates of substitution and marginal rates of transformation must stem from frictions in goods markets or from frictions in labor markets or both. Chari, Kehoe, and McGrattan (2006), among others, have emphasized that understanding this (to use their terminology) "labor wedge" is quite important for macro modeling efforts. Our model posits search frictions in product markets alongside a perfectly-competitive labor market, so the wedge between the MRS and the consumption-leisure MRT stems from goods market frictions. Labor search models, especially their recent DSGE incarnations, have made clear that such wedges arise from primitive labor matching frictions as well. A model featuring labor search and goods search frictions may have even more to offer in terms of explaining labor wedges. In addition, a nominal version of such a model, in which it is nominal prices and nominal wages over which parties bargain, would have some potentially very interesting things to say regarding dynamics of real wages. Hall's (2007) model does incorporate both goods search and labor search frictions and points out some interesting tradeoffs regarding stabilizing goods markets versus stabilizing labor markets that monetary policy may face.
We see a great many other possible applications of our framework. One application is to asset pricing: the fact that marginal utility of consumption is tied to consumer search frictions opens up a new mechanism for thinking about asset prices. Another possible use for our framework is to provide a micro-foundation behind habit-based consumption models: part of consumption is a state variable in our model, as it is in habit-based models, because it directly reflects the number of pre-existing customer relationships. Our framework, sufficiently enriched on the pricing/bargaining side of the model, may also provide a different way to think about time-varying markups in goods markets, an issue we only scratched the surface of here.
Finally, another important motivation behind the construction of our model is the eventual design of optimal macroeconomic policy in such an environment. Arseneau and Chugh (2006, 2007) study optimal policy in the presence of deep-rooted frictions in labor markets, with all other macro markets quite standard. Aruoba and Chugh (2006) study optimal policy in the presence of deep-rooted frictions in money markets, with all other macro markets quite standard. Both of these studies uncover policy channels and implications about which standard models used to study dynamic optimal policy are silent, and several of the policy prescriptions obtained in these studies are indeed opposite those reached using standard frameworks. However, each of these studies considers goods trade in more or less standard Walrasian fashion. We conjecture that thinking about deep-rooted frictions in goods markets is likely to also yield new insights about how macroeconomic policy ought to be conducted, a topic rising on our research horizon.
Appendix A. Tables and Figures
Figure 1: Steady-state firm advertising condition and Nash pricing condition.
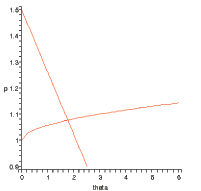
Figure 2: Steady-state flow condition and firm advertising condition.
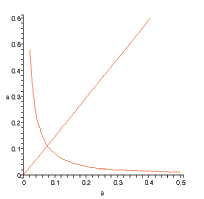
Table 1: Steady-state prices and quantities under benchmark calibration.
| 1.0835 | 0.0151 | 0.0189 | 0.8000 | 0.0680 | 0.0952 | 0.1919 | 0.2943 |
Figure 3: Steady-state allocation as function of customer bargaining power ![]() .
.
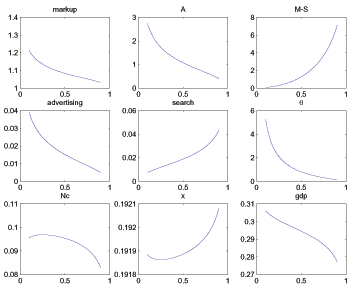
Table 2: Simulation-based moments in baseline model with Nash bargaining, zero menu costs, and TFP shocks as driving force.
No menu
cost, ![]()
| Variable | Mean | Std. Dev. | SD % | Auto corr. | Corr | Corr |
|---|---|---|---|---|---|---|
| 1.0835 | 0.0036 | 0.0033 | 0.1751 | 0.5557 | 0.5850 | |
| 0.2945 | 0.0049 | 0.0166 | 0.9342 | 1.0000 | 0.9993 | |
| 0.1918 | 0.0036 | 0.0190 | 0.9246 | 0.9996 | 1.0000 | |
| 1.4000 | 0 | 0 | -- | -- | -- | |
| 0.0681 | 0.0008 | 0.0113 | 0.9274 | 0.9345 | 0.9212 | |
| 0.0954 | 0.0011 | 0.0113 | 0.9274 | 0.9345 | 0.9212 | |
| 0.2945 | 0.0007 | 0.0025 | 0.7866 | -0.9626 | -0.9718 | |
| 0.9997 | 0.0190 | 0.0190 | 0.9216 | 0.9993 | 1.0000 | |
| 1.0835 | 0.0036 | 0.0033 | 0.1751 | 0.5557 | 0.5850 | |
| 0.0189 | 0.0007 | 0.0360 | 0.0187 | 0.0885 | 0.1237 | |
| 0.7996 | 0.0233 | 0.0292 | 0.9209 | 0.9992 | 1.0000 | |
| 0.5000 | 0.0000 | 0.0000 | -- | -- | -- | |
| 0.0152 | 0.0007 | 0.0494 | 0.2868 | 0.6624 | 0.6878 |
Addendum
| Variable | Mean | Std. Dev. | SD % | Auto corr. | Corr | Corr |
|---|---|---|---|---|---|---|
| | 0.5000 | 0.0138 | 0.0277 | -0.3752 | -0.2030 | -0.1776 |
Table 3: Simulation-based moments in baseline model with Nash bargaining, positive menu costs, and TFP shocks as driving force.
Menu
cost, ![]()
| Variable | Mean | Std. Dev. | SD % | Auto corr. | Corr | Corr |
|---|---|---|---|---|---|---|
| 1.0835 | 0.0032 | 0.0030 | 0.8008 | 0.9387 | 0.9488 | |
| 0.2945 | 0.0049 | 0.0166 | 0.9344 | 1.0000 | 0.9993 | |
| 0.1918 | 0.0036 | 0.0190 | 0.9245 | 0.9995 | 1.0000 | |
| 1.4000 | 0 | 0 | -- | -- | -- | |
| 0.0681 | 0.0008 | 0.0113 | 0.9285 | 0.9346 | 0.9211 | |
| 0.0954 | 0.0011 | 0.0113 | 0.9285 | 0.9346 | 0.9211 | |
| 0.2945 | 0.0007 | 0.0025 | 0.7864 | -0.9623 | -0.9716 | |
| 0.9997 | 0.0190 | 0.0190 | 0.9216 | 0.9993 | 1.0000 | |
| 1.0835 | 0.0032 | 0.0030 | 0.8008 | 0.9387 | 0.9488 | |
| 0.0189 | 0.0007 | 0.0356 | 0.0256 | 0.0940 | 0.1295 | |
| 0.7996 | 0.0230 | 0.0287 | 0.9227 | 0.9994 | 1.0000 | |
| 0.5000 | 0.0015 | 0.0031 | 0.1087 | -0.3572 | -0.3246 | |
| 0.0152 | 0.0007 | 0.0488 | 0.2934 | 0.6642 | 0.6898 |
Menu
cost,
![]()
| Variable | Mean | Std. Dev. | SD % | Auto corr. | Corr | Corr |
|---|---|---|---|---|---|---|
| 1.0834 | 0.0050 | 0.0047 | 0.9775 | 0.9533 | 0.9467 | |
| 0.2945 | 0.0049 | 0.0165 | 0.9344 | 1.0000 | 0.9993 | |
| 0.1918 | 0.0036 | 0.0190 | 0.9244 | 0.9995 | 1.0000 | |
| 1.4000 | 0 | 0 | -- | -- | -- | |
| 0.0681 | 0.0008 | 0.0113 | 0.9293 | 0.9346 | 0.9211 | |
| 0.0954 | 0.0011 | 0.0113 | 0.9293 | 0.9346 | 0.9211 | |
| 0.2945 | 0.0007 | 0.0025 | 0.7882 | -0.9627 | -0.9720 | |
| 0.9997 | 0.0190 | 0.0190 | 0.9216 | 0.9993 | 1.0000 | |
| 1.0834 | 0.0050 | 0.0047 | 0.9775 | 0.9533 | 0.9467 | |
| 0.0189 | 0.0007 | 0.0353 | 0.0296 | 0.1076 | 0.1432 | |
| 0.7996 | 0.0221 | 0.0277 | 0.9242 | 0.9995 | 1.0000 | |
| 0.5000 | 0.0031 | 0.0061 | 0.5501 | -0.4542 | -0.4233 | |
| 0.0152 | 0.0007 | 0.0481 | 0.2940 | 0.6618 | 0.6876 |
Menu
cost,
![]()
| Variable | Mean | Std. Dev. | SD % | Auto corr. | Corr | Corr |
|---|---|---|---|---|---|---|
| 1.0833 | 0.0093 | 0.0086 | 0.9967 | 0.5995 | 0.5909 | |
| 0.2945 | 0.0048 | 0.0164 | 0.9344 | 1.0000 | 0.9993 | |
| 0.1918 | 0.0036 | 0.0190 | 0.9244 | 0.9995 | 1.0000 | |
| 1.4000 | 0 | 0 | -- | -- | -- | |
| 0.0681 | 0.0008 | 0.0111 | 0.9298 | 0.9345 | 0.9210 | |
| 0.0954 | 0.0011 | 0.0111 | 0.9298 | 0.9345 | 0.9210 | |
| 0.2945 | 0.0008 | 0.0026 | 0.7967 | -0.9658 | -0.9747 | |
| 0.9997 | 0.0190 | 0.0190 | 0.9216 | 0.9993 | 1.0000 | |
| 1.0833 | 0.0093 | 0.0086 | 0.9967 | 0.5995 | 0.5909 | |
| 0.0189 | 0.0007 | 0.0349 | 0.0293 | 0.1570 | 0.1922 | |
| 0.7997 | 0.0190 | 0.0237 | 0.9256 | 0.9996 | 0.9999 | |
| 0.5001 | 0.0058 | 0.0117 | 0.8008 | -0.1332 | -0.1113 | |
| 0.0152 | 0.0007 | 0.0459 | 0.2750 | 0.6429 | 0.6691 |
Table 4: Simulation-based moments in baseline model with fair bargaining and TFP shocks as driving force.
Menu
cost, ![]()
| Variable | Mean | Std. Dev. | SD % | Auto corr. | Corr | Corr |
|---|---|---|---|---|---|---|
| 1.0835 | 0 | 0 | -- | -- | -- | |
| 0.2945 | 0.0048 | 0.0161 | 0.9341 | 1.0000 | 0.9993 | |
| 0.1918 | 0.0036 | 0.0190 | 0.9242 | 0.9995 | 1.0000 | |
| 1.4000 | 0 | 0 | -- | -- | -- | |
| 0.0681 | 0.0007 | 0.0106 | 0.9299 | 0.9342 | 0.9210 | |
| 0.0954 | 0.0010 | 0.0106 | 0.9299 | 0.9342 | 0.9210 | |
| 0.2945 | 0.0009 | 0.0029 | 0.8184 | -0.9737 | -0.9812 | |
| 0.9997 | 0.0190 | 0.0190 | 0.9216 | 0.9993 | 1.0000 | |
| 1.0835 | 0 | 0 | -- | -- | -- | |
| 0.0189 | 0.0007 | 0.0346 | 0.0474 | 0.3010 | 0.3341 | |
| 0.7998 | 0.0098 | 0.0123 | 0.9294 | 0.9999 | 0.9998 | |
| 0.5000 | 0 | 0 | -- | -- | -- |
Menu
cost,
![]()
| Variable | Mean | Std. Dev. | SD % | Auto corr. | Corr | Corr |
|---|---|---|---|---|---|---|
| 1.0835 | 0 | 0 | -- | -- | -- | |
| 0.2945 | 0.0048 | 0.0161 | 0.9341 | 1.0000 | 0.9993 | |
| 0.1918 | 0.0036 | 0.0190 | 0.9242 | 0.9995 | 1.0000 | |
| 1.4000 | 0 | 0 | -- | -- | -- | |
| 0.0681 | 0.0007 | 0.0106 | 0.9299 | 0.9342 | 0.9210 | |
| 0.0954 | 0.0010 | 0.0106 | 0.9299 | 0.9342 | 0.9210 | |
| 0.2945 | 0.0009 | 0.0029 | 0.8184 | -0.9737 | -0.9812 | |
| 0.9997 | 0.0190 | 0.0190 | 0.9216 | 0.9993 | 1.0000 | |
| 1.0835 | 0 | 0 | -- | -- | -- | |
| 0.0189 | 0.0007 | 0.0346 | 0.0474 | 0.3010 | 0.3341 | |
| 0.7998 | 0.0098 | 0.0123 | 0.9294 | 0.9999 | 0.9998 | |
| 0.5000 | 0 | 0 | -- | -- | -- |
Menu
cost,
![]()
| Variable | Mean | Std. Dev. | SD % | Auto corr. | Corr | Corr |
|---|---|---|---|---|---|---|
| 1.0835 | 0 | 0 | -- | -- | -- | |
| 0.2945 | 0.0048 | 0.0161 | 0.9341 | 1.0000 | 0.9993 | |
| 0.1918 | 0.0036 | 0.0190 | 0.9242 | 0.9995 | 1.0000 | |
| 1.4000 | 0 | 0 | -- | -- | -- | |
| 0.0681 | 0.0007 | 0.0106 | 0.9299 | 0.9342 | 0.9210 | |
| 0.0954 | 0.0010 | 0.0106 | 0.9299 | 0.9342 | 0.9210 | |
| 0.2945 | 0.0009 | 0.0029 | 0.8184 | -0.9737 | -0.9812 | |
| 0.9997 | 0.0190 | 0.0190 | 0.9216 | 0.9993 | 1.0000 | |
| 1.0835 | 0 | 0 | -- | -- | -- | |
| 0.0189 | 0.0007 | 0.0346 | 0.0474 | 0.3010 | 0.3341 | |
| 0.7998 | 0.0098 | 0.0123 | 0.9294 | 0.9999 | 0.9998 | |
| 0.5000 | 0 | 0 | -- | -- | -- |
Menu
cost,
![]()
| Variable | Mean | Std. Dev. | SD % | Auto corr. | Corr | Corr |
|---|---|---|---|---|---|---|
| 1.0835 | 0 | 0 | -- | -- | -- | |
| 0.2945 | 0.0048 | 0.0161 | 0.9341 | 1.0000 | 0.9993 | |
| 0.1918 | 0.0036 | 0.0190 | 0.9242 | 0.9995 | 1.0000 | |
| 1.4000 | 0 | 0 | -- | -- | -- | |
| 0.0681 | 0.0007 | 0.0106 | 0.9299 | 0.9342 | 0.9210 | |
| 0.0954 | 0.0010 | 0.0106 | 0.9299 | 0.9342 | 0.9210 | |
| 0.2945 | 0.0009 | 0.0029 | 0.8184 | -0.9737 | -0.9812 | |
| 0.9997 | 0.0190 | 0.0190 | 0.9216 | 0.9993 | 1.0000 | |
| 1.0835 | 0 | 0 | -- | -- | -- | |
| 0.0189 | 0.0007 | 0.0346 | 0.0474 | 0.3010 | 0.3341 | |
| 0.7998 | 0.0098 | 0.0123 | 0.9294 | 0.9999 | 0.9998 | |
| 0.5000 | 0 | 0 | -- | -- | -- |
Table 5: Simulation-based moments, for various values of ![]() , in basic model with Nash bargaining,
, in basic model with Nash bargaining, ![]() , and TFP shocks as driving force.
, and TFP shocks as driving force.
Low customer bargaining power (![]() )
)
| Variable | Mean | Std. Dev. | SD % | Auto corr. | Corr | Corr |
|---|---|---|---|---|---|---|
| 1.1526 | 0.0059 | 0.0052 | 0.2616 | 0.6868 | 0.6778 | |
| 0.3021 | 0.0051 | 0.0168 | 0.9167 | 1.0000 | 0.9999 | |
| 0.1918 | 0.0036 | 0.0190 | 0.9236 | 0.9998 | 1.0000 | |
| 1.4000 | 0 | 0 | -- | -- | -- | |
| 0.0691 | 0.0007 | 0.0107 | 0.9256 | 0.9163 | 0.9213 | |
| 0.0968 | 0.0010 | 0.0107 | 0.9256 | 0.9163 | 0.9213 | |
| 0.3021 | 0.0007 | 0.0022 | 0.9498 | -0.9942 | -0.9955 | |
| 0.9997 | 0.0190 | 0.0190 | 0.9216 | 0.9999 | 1.0000 | |
| 1.1526 | 0.0059 | 0.0052 | 0.2616 | 0.6868 | 0.6778 | |
| 0.0105 | 0.0004 | 0.0342 | 0.0311 | 0.0357 | 0.0235 | |
| 2.6707 | 0.0916 | 0.0343 | 0.9215 | 0.9999 | 1.0000 | |
| 0.2000 | 0 | 0 | -- | -- | -- | |
| 0.0281 | 0.0014 | 0.0494 | 0.3186 | 0.7270 | 0.7188 |
Equal bargaining power (![]() )
)
| Variable | Mean | Std. Dev. | SD % | Auto corr. | Corr | Corr |
|---|---|---|---|---|---|---|
| 1.0835 | 0.0036 | 0.0033 | 0.1751 | 0.5557 | 0.5850 | |
| 0.2945 | 0.0049 | 0.0166 | 0.9342 | 1.0000 | 0.9993 | |
| 0.1918 | 0.0036 | 0.0190 | 0.9246 | 0.9996 | 1.0000 | |
| 1.4000 | 0 | 0 | -- | -- | -- | |
| 0.0681 | 0.0008 | 0.0113 | 0.9274 | 0.9345 | 0.9212 | |
| 0.0954 | 0.0011 | 0.0113 | 0.9274 | 0.9345 | 0.9212 | |
| 0.2945 | 0.0007 | 0.0025 | 0.7866 | -0.9626 | -0.9718 | |
| 0.9997 | 0.0190 | 0.0190 | 0.9216 | 0.9993 | 1.0000 | |
| 1.0835 | 0.0036 | 0.0033 | 0.1751 | 0.5557 | 0.5850 | |
| 0.0189 | 0.0007 | 0.0360 | 0.0187 | 0.0885 | 0.1237 | |
| 0.7996 | 0.0233 | 0.0292 | 0.9209 | 0.9992 | 1.0000 | |
| 0.5000 | 0 | 0 | -- | -- | -- | |
| 0.0152 | 0.0007 | 0.0494 | 0.2868 | 0.6624 | 0.6878 |
High customer bargaining power (![]() )
)
| Variable | Mean | Std. Dev. | SD % | Auto corr. | Corr | Corr |
|---|---|---|---|---|---|---|
| 1.0452 | 0.0015 | 0.0015 | 0.2316 | 0.5364 | 0.5951 | |
| 0.2846 | 0.0047 | 0.0165 | 0.9448 | 1.0000 | 0.9974 | |
| 0.1919 | 0.0036 | 0.0189 | 0.9282 | 0.9985 | 0.9998 | |
| 1.4000 | 0 | 0 | -- | -- | -- | |
| 0.0635 | 0.0007 | 0.0116 | 0.9368 | 0.9459 | 0.9202 | |
| 0.0889 | 0.0010 | 0.0116 | 0.9368 | 0.9459 | 0.9202 | |
| 0.2846 | 0.0008 | 0.0027 | 0.6392 | -0.8747 | -0.9072 | |
| 0.9997 | 0.0190 | 0.0190 | 0.9216 | 0.9974 | 1.0000 | |
| 1.0452 | 0.0015 | 0.0015 | 0.2316 | 0.5364 | 0.5951 | |
| 0.0326 | 0.0011 | 0.0343 | 0.0824 | 0.1325 | 0.2022 | |
| 0.2338 | 0.0059 | 0.0251 | 0.9196 | 0.9970 | 1.0000 | |
| 0.8000 | 0 | 0 | -- | -- | -- | |
| 0.0076 | 0.0004 | 0.0468 | 0.3301 | 0.6403 | 0.6914 |
Figure 4: Steady-state allocation as function of customer bargaining power ![]() .
.
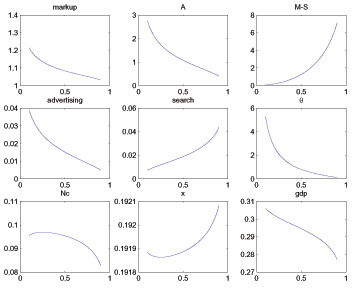
Table 6: Steady-state prices and quantities with intensive adjustment.
| 1.0835 | 0.0267 | 0.1851 | 0.1443 | 0.2830 | 0.5951 | 0.1684 | 0.1276 | 0.3088 |
Figure 5: Dynamic relationship between customer effective bargaining power ![]() and Nash price for various degrees of price rigidity.
and Nash price for various degrees of price rigidity.
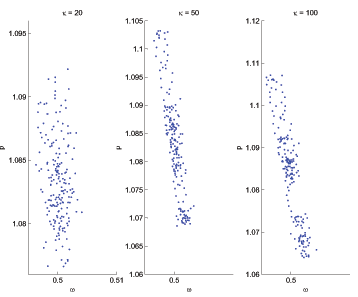
Table 7: Simulation-based moments in model with intensive adjustment, Nash bargaining, and TFP shocks as driving force.
Flexible prices, ![]()
| Variable | Mean | Std. Dev. | SD % | Auto corr. | Corr | Corr |
|---|---|---|---|---|---|---|
| 1.0834 | 0.0030 | 0.0027 | 0.8317 | 0.9196 | 0.9701 | |
| 0.3088 | 0.0044 | 0.0143 | 0.9613 | 1.0000 | 0.9874 | |
| 0.1276 | 0.0022 | 0.0173 | 0.9484 | 0.9982 | 0.9952 | |
| 0.5951 | 0.0012 | 0.0020 | 0.8868 | -0.7597 | -0.6487 | |
| 0.2829 | 0.0035 | 0.0123 | 0.9783 | 0.9466 | 0.8840 | |
| 0.1684 | 0.0018 | 0.0105 | 0.9827 | 0.9672 | 0.9151 | |
| 0.3088 | 0.0016 | 0.0053 | 0.7549 | -0.8355 | -0.9115 | |
| 0.9997 | 0.0190 | 0.0190 | 0.9216 | 0.9874 | 1.0000 | |
| 1.0834 | 0.0030 | 0.0027 | 0.8317 | 0.9196 | 0.9701 | |
| 0.1851 | 0.0032 | 0.0173 | 0.6639 | -0.3275 | -0.1772 | |
| 0.1442 | 0.0067 | 0.0466 | 0.9224 | 0.9878 | 1.0000 | |
| 0.5000 | 0.0000 | -- | -- | -- | -- | |
| 0.0267 | 0.0013 | 0.0473 | 0.7884 | 0.8672 | 0.9329 |
Menu
cost, ![]()
| Variable | Mean | Std. Dev. | SD % | Auto corr. | Corr | Corr |
|---|---|---|---|---|---|---|
| 1.0833 | 0.0084 | 0.0078 | 0.9802 | 0.9892 | 0.9553 | |
| 0.3088 | 0.0044 | 0.0141 | 0.9601 | 1.0000 | 0.9882 | |
| 0.1276 | 0.0022 | 0.0174 | 0.9459 | 0.9979 | 0.9960 | |
| 0.5951 | 0.0012 | 0.0020 | 0.8827 | -0.7379 | -0.6274 | |
| 0.2829 | 0.0034 | 0.0120 | 0.9791 | 0.9432 | 0.8816 | |
| 0.1684 | 0.0017 | 0.0101 | 0.9834 | 0.9668 | 0.9165 | |
| 0.3088 | 0.0017 | 0.0054 | 0.7710 | -0.8540 | -0.9233 | |
| 0.9997 | 0.0190 | 0.0190 | 0.9216 | 0.9882 | 1.0000 | |
| 1.0833 | 0.0084 | 0.0078 | 0.9802 | 0.9892 | 0.9553 | |
| 0.1851 | 0.0031 | 0.0165 | 0.6694 | -0.3077 | -0.1616 | |
| 0.1442 | 0.0064 | 0.0447 | 0.9258 | 0.9903 | 0.9999 | |
| 0.5000 | 0.0034 | 0.0068 | 0.9397 | -0.8392 | -0.7470 | |
| 0.0267 | 0.0012 | 0.0454 | 0.7967 | 0.8759 | 0.9375 |
Menu
cost,
![]()
| Variable | Mean | Std. Dev. | SD % | Auto corr. | Corr | Corr |
|---|---|---|---|---|---|---|
| 1.0832 | 0.0173 | 0.0160 | 0.9947 | 0.8147 | 0.7554 | |
| 0.3088 | 0.0043 | 0.0138 | 0.9580 | 1.0000 | 0.9898 | |
| 0.1276 | 0.0022 | 0.0176 | 0.9428 | 0.9978 | 0.9970 | |
| 0.5951 | 0.0012 | 0.0020 | 0.8750 | -0.6628 | -0.5526 | |
| 0.2829 | 0.0032 | 0.0112 | 0.9799 | 0.9375 | 0.8788 | |
| 0.1684 | 0.0016 | 0.0095 | 0.9836 | 0.9676 | 0.9220 | |
| 0.3088 | 0.0018 | 0.0057 | 0.7932 | -0.8851 | -0.9423 | |
| 0.9997 | 0.0190 | 0.0190 | 0.9216 | 0.9898 | 1.0000 | |
| 1.0832 | 0.0173 | 0.0160 | 0.9947 | 0.8147 | 0.7554 | |
| 0.1851 | 0.0028 | 0.0151 | 0.6623 | -0.2531 | -0.1158 | |
| 0.1442 | 0.0058 | 0.0404 | 0.9294 | 0.9933 | 0.9996 | |
| 0.5001 | 0.0089 | 0.0178 | 0.9685 | -0.5538 | -0.4626 | |
| 0.0267 | 0.0011 | 0.0416 | 0.8032 | 0.8857 | 0.9410 |
Menu
cost, ![]()
| Variable | Mean | Std. Dev. | SD % | Auto corr. | Corr | Corr |
|---|---|---|---|---|---|---|
| 1.0830 | 0.0225 | 0.0208 | 0.9973 | 0.5805 | 0.5337 | |
| 0.3088 | 0.0041 | 0.0134 | 0.9559 | 1.0000 | 0.9912 | |
| 0.1276 | 0.0023 | 0.0178 | 0.9401 | 0.9978 | 0.9977 | |
| 0.5951 | 0.0011 | 0.0018 | 0.8415 | -0.5144 | -0.4056 | |
| 0.2829 | 0.0029 | 0.0103 | 0.9803 | 0.9324 | 0.8771 | |
| 0.1684 | 0.0015 | 0.0089 | 0.9837 | 0.9689 | 0.9277 | |
| 0.3088 | 0.0018 | 0.0060 | 0.8133 | -0.9109 | -0.9574 | |
| 0.9997 | 0.0190 | 0.0190 | 0.9216 | 0.9912 | 1.0000 | |
| 1.0830 | 0.0225 | 0.0208 | 0.9973 | 0.5805 | 0.5337 | |
| 0.1851 | 0.0025 | 0.0136 | 0.6410 | -0.1672 | -0.0388 | |
| 0.1442 | 0.0050 | 0.0347 | 0.9318 | 0.9953 | 0.9993 | |
| 0.5002 | 0.0126 | 0.0252 | 0.9681 | -0.1732 | -0.1076 | |
| 0.0267 | 0.0010 | 0.0368 | 0.8038 | 0.8900 | 0.9407 |
Table 8: Simulation-based moments in model with intensive adjustment, fair bargaining, and TFP shocks as driving force.
Flexible prices, ![]()
| Variable | Mean | Std. Dev. | SD % | Auto corr. | Corr | Corr |
|---|---|---|---|---|---|---|
| 1.0835 | 0 | 0 | -- | -- | -- | |
| 0.3088 | 0.0037 | 0.0120 | 0.9475 | 1.0000 | 0.9952 | |
| 0.1276 | 0.0024 | 0.0186 | 0.9325 | 0.9982 | 0.9993 | |
| 0.5951 | 0.0007 | 0.0012 | 0.6530 | 0.6820 | 0.7494 | |
| 0.2829 | 0.0018 | 0.0064 | 0.9805 | 0.9193 | 0.8768 | |
| 0.1684 | 0.0012 | 0.0070 | 0.9821 | 0.9743 | 0.9477 | |
| 0.3088 | 0.0022 | 0.0071 | 0.8677 | -0.9664 | -0.9869 | |
| 0.9997 | 0.0190 | 0.0190 | 0.9216 | 0.9952 | 1.0000 | |
| 1.0835 | 0 | 0 | -- | -- | -- | |
| 0.1851 | 0.0018 | 0.0095 | 0.5763 | 0.3775 | 0.4645 | |
| 0.1443 | 0.0017 | 0.0121 | 0.9428 | 0.9998 | 0.9969 | |
| 0.5000 | 0 | 0 | -- | -- | -- | |
| 0.0267 | 0.0005 | 0.0181 | 0.7691 | 0.8605 | 0.9062 |
Menu
cost,
![]()
| Variable | Mean | Std. Dev. | SD % | Auto corr. | Corr | Corr |
|---|---|---|---|---|---|---|
| 1.0835 | 0 | 0 | -- | -- | -- | |
| 0.3088 | 0.0037 | 0.0120 | 0.9475 | 1.0000 | 0.9952 | |
| 0.1276 | 0.0024 | 0.0186 | 0.9325 | 0.9982 | 0.9993 | |
| 0.5951 | 0.0007 | 0.0012 | 0.6530 | 0.6820 | 0.7494 | |
| 0.2829 | 0.0018 | 0.0064 | 0.9805 | 0.9193 | 0.8768 | |
| 0.1684 | 0.0012 | 0.0070 | 0.9821 | 0.9743 | 0.9477 | |
| 0.3088 | 0.0022 | 0.0071 | 0.8677 | -0.9664 | -0.9869 | |
| 0.9997 | 0.0190 | 0.0190 | 0.9216 | 0.9952 | 1.0000 | |
| 1.0835 | 0 | 0 | -- | -- | -- | |
| 0.1851 | 0.0018 | 0.0095 | 0.5763 | 0.3775 | 0.4645 | |
| 0.1443 | 0.0017 | 0.0121 | 0.9428 | 0.9998 | 0.9969 | |
| 0.5000 | 0 | 0 | -- | -- | -- | |
| 0.0267 | 0.0005 | 0.0181 | 0.7691 | 0.8605 | 0.9062 |
Menu
cost,
![]()
| Variable | Mean | Std. Dev. | SD % | Auto corr. | Corr | Corr |
|---|---|---|---|---|---|---|
| 1.0835 | 0 | 0 | -- | -- | -- | |
| 0.3088 | 0.0037 | 0.0120 | 0.9475 | 1.0000 | 0.9952 | |
| 0.1276 | 0.0024 | 0.0186 | 0.9325 | 0.9982 | 0.9993 | |
| 0.5951 | 0.0007 | 0.0012 | 0.6530 | 0.6820 | 0.7494 | |
| 0.2829 | 0.0018 | 0.0064 | 0.9805 | 0.9193 | 0.8768 | |
| 0.1684 | 0.0012 | 0.0070 | 0.9821 | 0.9743 | 0.9477 | |
| 0.3088 | 0.0022 | 0.0071 | 0.8677 | -0.9664 | -0.9869 | |
| 0.9997 | 0.0190 | 0.0190 | 0.9216 | 0.9952 | 1.0000 | |
| 1.0835 | 0 | 0 | -- | -- | -- | |
| 0.1851 | 0.0018 | 0.0095 | 0.5763 | 0.3775 | 0.4645 | |
| 0.1443 | 0.0017 | 0.0121 | 0.9428 | 0.9998 | 0.9969 | |
| 0.5000 | 0 | 0 | -- | -- | -- | |
| 0.0267 | 0.0005 | 0.0181 | 0.7691 | 0.8605 | 0.9062 |
Menu
cost,
![]()
| Variable | Mean | Std. Dev. | SD % | Auto corr. | Corr | Corr |
|---|---|---|---|---|---|---|
| 1.0835 | 0 | 0 | -- | -- | -- | |
| 0.3088 | 0.0037 | 0.0120 | 0.9475 | 1.0000 | 0.9952 | |
| 0.1276 | 0.0024 | 0.0186 | 0.9325 | 0.9982 | 0.9993 | |
| 0.5951 | 0.0007 | 0.0012 | 0.6530 | 0.6820 | 0.7494 | |
| 0.2829 | 0.0018 | 0.0064 | 0.9805 | 0.9193 | 0.8768 | |
| 0.1684 | 0.0012 | 0.0070 | 0.9821 | 0.9743 | 0.9477 | |
| 0.3088 | 0.0022 | 0.0071 | 0.8677 | -0.9664 | -0.9869 | |
| 0.9997 | 0.0190 | 0.0190 | 0.9216 | 0.9952 | 1.0000 | |
| 1.0835 | 0 | 0 | -- | -- | -- | |
| 0.1851 | 0.0018 | 0.0095 | 0.5763 | 0.3775 | 0.4645 | |
| 0.1443 | 0.0017 | 0.0121 | 0.9428 | 0.9998 | 0.9969 | |
| 0.5000 | 0 | 0 | -- | -- | -- | |
| 0.0267 | 0.0005 | 0.0181 | 0.7691 | 0.8605 | 0.9062 |
Figure 6: Dynamic relationship between goods market tightness
![]() and Nash price
and Nash price ![]() in baseline model with
in baseline model with ![]() .
.
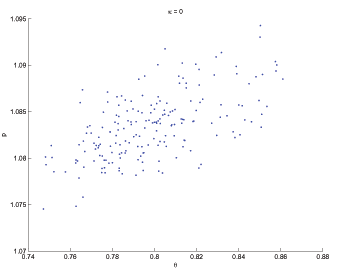
Figure 7: Dynamic relationship between goods market tightness
![]() and Nash price
and Nash price ![]() in baseline model with
in baseline model with ![]() .
.
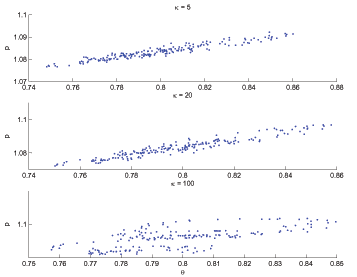
Figure 8: Impulse Response in baseline model.
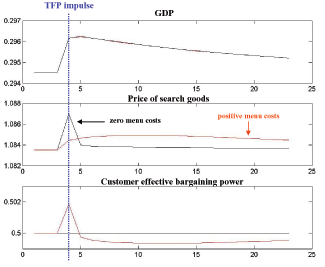
Figure 9: Dynamic relationship between goods market tightness
![]() and Nash price
and Nash price ![]() (left panel) and advertisements
(left panel) and advertisements ![]() and consumer
search activity
and consumer
search activity ![]() in baseline model with fair
bargaining.
in baseline model with fair
bargaining.
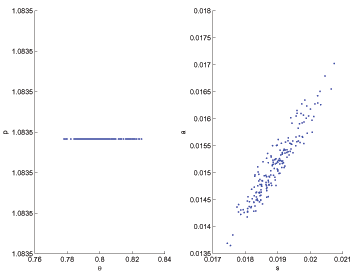
Figure 10: Volatility of price (expressed in standard deviation
percentage points) as function of customer bargaining power
![]() in baseline model with Nash bargaining
for various values of
in baseline model with Nash bargaining
for various values of ![]() .
.
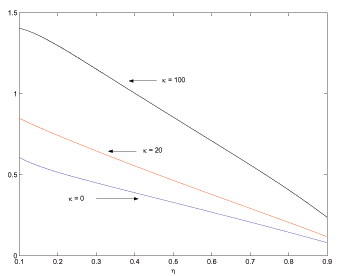
Figure 11: Steady-state allocation as function of customer bargaining
power ![]() in model with intensive
adjustment.
in model with intensive
adjustment.
Table 9: Simulation-based moments in basic model with government spending, Nash bargaining, and government purchase shocks as driving force.
Zero menu cost
| Variable | Mean | Std. Dev. | SD % | Auto corr. | Corr | Corr | Corr |
|---|---|---|---|---|---|---|---|
| 1.0835 | 0.0006 | 0.0006 | -0.0650 | -0.3222 | -- | -0.3065 | |
| 0.3368 | 0.0020 | 0.0061 | 0.7678 | 1.0000 | -- | 0.9999 | |
| 0.1868 | 0.0002 | 0.0013 | 0.7927 | -0.9992 | -- | -0.9997 | |
| 1.4000 | 0 | 0 | -- | -- | -- | -- | |
| 0.0663 | 0.0001 | 0.0014 | 0.7949 | -0.7672 | -- | -0.7777 | |
| 0.0929 | 0.0001 | 0.0014 | 0.7949 | -0.7672 | -- | -0.7777 | |
| 0.3368 | 0.0020 | 0.0061 | 0.7678 | 1.0000 | -- | 0.9999 | |
| 1.0000 | 0 | 0 | -- | -- | -- | -- | |
| 1.0835 | 0.0006 | 0.0006 | -0.0650 | -0.3222 | -- | -0.3065 | |
| 0.0184 | 0.0002 | 0.0084 | -0.0386 | -0.5131 | -- | -0.4988 | |
| 0.8000 | 0.0002 | 0.0002 | 0.8108 | 0.9974 | -- | 0.9984 | |
| 0.5000 | 0 | 0 | -- | -- | -- | -- | |
| 0.0147 | 0.0001 | 0.0084 | -0.0354 | -0.4917 | -- | -0.4773 |
Menu
cost, ![]()
| Variable | Mean | Std. Dev. | SD % | Auto corr. | Corr | Corr | Corr |
|---|---|---|---|---|---|---|---|
| 1.0835 | 0.0004 | 0.0003 | 0.6454 | 0.1137 | -- | 0.1277 | |
| 0.3368 | 0.0020 | 0.0061 | 0.7676 | 1.0000 | -- | 0.9999 | |
| 0.1868 | 0.0002 | 0.0013 | 0.7923 | -0.9992 | -- | -0.9997 | |
| 1.4000 | 0 | 0 | -- | -- | -- | -- | |
| 0.0663 | 0.0001 | 0.0014 | 0.7978 | -0.7669 | -- | -0.7776 | |
| 0.0929 | 0.0001 | 0.0014 | 0.7978 | -0.7669 | -- | -0.7776 | |
| 0.3368 | 0.0020 | 0.0061 | 0.7676 | 1.0000 | -- | 0.9999 | |
| 1.0000 | 0 | 0 | -- | -- | -- | -- | |
| 1.0835 | 0.0004 | 0.0003 | 0.6454 | 0.1137 | -- | 0.1277 | |
| 0.0184 | 0.0002 | 0.0084 | -0.0334 | -0.5106 | -- | -0.4961 | |
| 0.8000 | 0.0001 | 0.0001 | 0.6178 | 0.9807 | -- | 0.9773 | |
| 0.5000 | 0.0003 | 0.0005 | -0.1895 | -0.4863 | -- | -0.4741 | |
| 0.0147 | 0.0001 | 0.0084 | -0.0259 | -0.5016 | -- | -0.4871 |
Menu
cost,
![]()
| Variable | Mean | Std. Dev. | SD % | Auto corr. | Corr | Corr | Corr |
|---|---|---|---|---|---|---|---|
| 1.0835 | 0.0006 | 0.0006 | 0.9711 | 0.5143 | -- | 0.5230 | |
| 0.3368 | 0.0020 | 0.0061 | 0.7674 | 1.0000 | -- | 0.9998 | |
| 0.1868 | 0.0002 | 0.0013 | 0.7922 | -0.9992 | -- | -0.9997 | |
| 1.4000 | 0 | 0 | -- | -- | -- | -- | |
| 0.0663 | 0.0001 | 0.0014 | 0.8000 | -0.7664 | -- | -0.7774 | |
| 0.0929 | 0.0001 | 0.0014 | 0.8000 | -0.7664 | -- | -0.7774 | |
| 0.3368 | 0.0020 | 0.0061 | 0.7674 | 1.0000 | -- | 0.9998 | |
| 1.0000 | 0 | 0 | -- | -- | -- | -- | |
| 1.0835 | 0.0006 | 0.0006 | 0.9711 | 0.5143 | -- | 0.5230 | |
| 0.0184 | 0.0002 | 0.0084 | -0.0329 | -0.4990 | -- | -0.4840 | |
| 0.8000 | 0.0002 | 0.0002 | 0.8626 | -0.9820 | -- | -0.9851 | |
| 0.5000 | 0.0004 | 0.0008 | 0.2115 | -0.5358 | -- | -0.5267 | |
| 0.0147 | 0.0001 | 0.0085 | -0.0150 | -0.5191 | -- | -0.5044 |
Menu
cost,
![]()
| Variable | Mean | Std. Dev. | SD % | Auto corr. | Corr | Corr | Corr |
|---|---|---|---|---|---|---|---|
| 1.0835 | 0.0008 | 0.0007 | 0.9923 | 0.3406 | -- | 0.3461 | |
| 0.3368 | 0.0020 | 0.0060 | 0.7668 | 1.0000 | -- | 0.9998 | |
| 0.1868 | 0.0002 | 0.0013 | 0.7926 | -0.9991 | -- | -0.9997 | |
| 1.4000 | 0 | 0 | -- | -- | -- | -- | |
| 0.0663 | 0.0001 | 0.0015 | 0.8012 | -0.7658 | -- | -0.7774 | |
| 0.0929 | 0.0001 | 0.0015 | 0.8012 | -0.7658 | -- | -0.7774 | |
| 0.3368 | 0.0020 | 0.0060 | 0.7668 | 1.0000 | -- | 0.9998 | |
| 1.0000 | 0 | 0 | -- | -- | -- | -- | |
| 1.0835 | 0.0008 | 0.0007 | 0.9923 | 0.3406 | -- | 0.3461 | |
| 0.0184 | 0.0002 | 0.0086 | -0.0390 | -0.4679 | -- | -0.4518 | |
| 0.8000 | 0.0008 | 0.0010 | 0.8114 | -0.9972 | -- | -0.9984 | |
| 0.5000 | 0.0005 | 0.0011 | 0.5698 | 0.0485 | -- | 0.0582 | |
| 0.0147 | 0.0001 | 0.0090 | 0.0013 | -0.5519 | -- | -0.5368 |
Appendix B. Nash Bargaining
Here we derive the Nash-bargaining solution between an
individual customer and the firm. We present the most general case
in which bargaining occurs over both price and quantity, and at the
end of the section we show how to simplify things if the quantity
is fixed and bargaining occurs only over price. For notational
simplicity, we omit the conditional expectations operator
![]() where it is understood.
where it is understood.
The marginal value to the household of a family member who is already engaged in a relationship (a shopper) with a firm is
![$\displaystyle \mathbf{M_{t}} = \frac{\tilde{u}(c_{it})}{\lambda_{t}} - \frac{g^{\prime}(1-l_{t}-s_{t}-N_{t})}{\lambda_{t}} - p_{it} c_{it} + E_{t} \left[ \Xi_{t+1\vert t} \left( (1-\rho^{x}) \mathbf{M_{t+1}} + \rho^{x} \mathbf{S_{t+1}} \right) \right] .$](img959.gif)
|
(55) |
Here, ![]() denotes the price of the consumption
good traded between a firm and a customer, and
denotes the price of the consumption
good traded between a firm and a customer, and ![]() denotes its quantity. The function
denotes its quantity. The function ![]() is the marginal utility to the household of
obtaining consumption from the
is the marginal utility to the household of
obtaining consumption from the ![]() -th match. The
precise expression for
-th match. The
precise expression for ![]() depends on whether
the household's aggregator over search consumption goods is linear
(as in the baseline model) or displays curvature (as in the model
with intensive adjustment). For simplicity, here we assume that the
aggregator is linear, and the expression for
depends on whether
the household's aggregator over search consumption goods is linear
(as in the baseline model) or displays curvature (as in the model
with intensive adjustment). For simplicity, here we assume that the
aggregator is linear, and the expression for ![]() for the case with curvature is derived in
Appendix E. Thus, let
for the case with curvature is derived in
Appendix E. Thus, let
![]() be defined as simply the sum of the
be defined as simply the sum of the
![]() 's,
's,
![]() , in which case
, in which case
![]() is defined as
is defined as
![]() ,
which reduces to
,
which reduces to
![]() . Because the
units of
. Because the
units of ![]() are utils, we convert it into
units of the final composite by dividing by the period-
are utils, we convert it into
units of the final composite by dividing by the period-![]() marginal utility of wealth for the household,
marginal utility of wealth for the household,
![]() , which has units of utils per
final good.
, which has units of utils per
final good.
The marginal value to the household of an individual who is searching for goods is
![$\displaystyle \mathbf{S_{t}} = -\frac{g^{\prime}(1-l_{t}-s_{t}-N_{t} )}{\lambda_{t}} + E_{t} \left[ \Xi_{t+1\vert t} \left( \theta_{t} k^{f} (\theta_{t}) (1-\rho^{x}) \mathbf{M_{t+1}} + (1-\theta_{t} k^{f}(\theta_{t}) (1-\rho^{x}) ) \mathbf{S_{t+1}} \right) \right] .$](img975.gif)
|
(56) |
The only instantaneous components of
![]() is the marginal reduction in
utility due to the marginal reduction in total household leisure
time because of searching.
is the marginal reduction in
utility due to the marginal reduction in total household leisure
time because of searching.
The value to a firm of an existing customer is
![$\displaystyle \mathbf{A_{t}} = p_{it} c_{it} - mc_{t} c_{it} - \frac{\kappa}{2}\left( \frac{p_{it}}{p_{it-1}} - 1\right) ^{2} + E_{t} \left[ \Xi_{t+1\vert t} (1-\rho^{x}) \mathbf{A_{t+1}} \right] ,$](img977.gif)
|
(57) |
where the instantaneous components takes into account the revenue from sales to the customer, the total cost of production, and the cost of price adjustment.
Bargaining occurs every period over the price ![]() and quantity
and quantity ![]() . The firm and
customer maximize the Nash product
. The firm and
customer maximize the Nash product
| (58) |
where
![]() is the fixed weight given to
the customer's individual surplus. The first-order condition of the
Nash product with respect to
is the fixed weight given to
the customer's individual surplus. The first-order condition of the
Nash product with respect to ![]() is
is
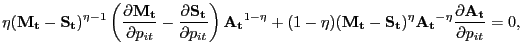
|
(59) |
which can be condensed as usual to
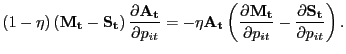
|
(60) |
We have
![]() ,
,
![]() , and
, and
![$\displaystyle \frac{\partial\mathbf{A_{t}}}{\partial p_{it}} = c_{it} - \kappa\left( \frac{p_{it}}{p_{it-1}} - 1\right) \frac{1}{p_{it-1}} + (1-\rho^{x}) E_{t} \left[ \Xi_{t+1\vert t} \kappa\left( \frac{p_{it+1}}{p_{it}} - 1\right) \frac{p_{it+1}}{p_{it}} \frac{1}{p_{it}} \right] ,$](img987.gif)
|
(61) |
which reveals a second forward-looking element to pricing, independent of the forward-looking element that arises due to the long-lived customer relationship.
Defining
![]() as the gross
growth rate of the price of the
as the gross
growth rate of the price of the ![]() -th good,
-th good,
![$\displaystyle \frac{\partial\mathbf{A_{t}}}{\partial p_{it}} = c_{it} - \kappa(\pi_{it} - 1)\frac{1}{p_{it-1}} + (1-\rho^{x}) \kappa E_{t} \left[ \Xi_{t+1\vert t} (\pi_{it+1}-1) \frac{\pi_{it+1}}{p_{it}} \right] .$](img990.gif)
|
(62) |
Next, define
![]() ,
,
![]() ,
and thus
,
and thus
| (63) |
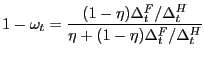
|
(64) |
as time-varying bargaining weights. With these definitions, the
sharing rule that determines ![]() is
is
| (65) |
The surplus is split proportionally according to time-varying
weights, which is a generalization of the usual Nash-sharing rule.
Note that if ![]() (i.e., there are no menu
costs),
(i.e., there are no menu
costs),
![]() , in which case the typical
Nash sharing rule
, in which case the typical
Nash sharing rule
![]() emerges.
emerges.
Using the Bellman equation for the value to a firm of an
existing customer along with the advertising condition, we have
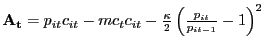 . Using this along with the definitions of
. Using this along with the definitions of
![]() and
and
![]() and going through several
algebraic rearrangements, we can, after some tedious algebra, show
that the price
and going through several
algebraic rearrangements, we can, after some tedious algebra, show
that the price ![]() is characterized by
is characterized by
![$\displaystyle \lefteqn{\frac{\omega_{t}}{1-\omega_{t}} \left[ p_{it} c_{it} - mc_{t} c_{it} - \frac{\kappa}{2} \left( \frac{p_{it}} {p_{it-1}}-1\right) ^{2} + \frac{\gamma}{k^{f}(\theta_{t})}\right] = \frac{\tilde{u}(c_{it})}{\lambda_{t}} - p_{it} c_{it} + }$](img1004.gif)
|
|
![$\displaystyle + (1-\theta_{t} k^{f}(\theta_{t})) E_{t}\left[ \Xi_{t+1\vert t} \left( \frac{\omega_{t+1}}{1-\omega_{t+1}}\right) (1-\rho^{x}) \left[ p_{it+1} c_{it+1} - mc_{t+1} c_{it+1} - \frac{\kappa}{2}\left( \frac{p_{it+1}}{p_{it} }-1\right) ^{2} + \frac{\gamma}{k^{f}(\theta_{t})} \right] \right] .$](img1007.gif)
|
(66) |
Note there are two reasons why price-setting is forward-looking.
One reason is a standard sticky-price reason: with costs of price
adjustment, a setting for ![]() has
ramifications for future setting of
has
ramifications for future setting of ![]() . But
note that even with
. But
note that even with ![]() ,
, ![]() is affected by expectations regarding
is affected by expectations regarding ![]() . This has to do with the long-lived customer
relationship: with probability
. This has to do with the long-lived customer
relationship: with probability
![]() , the customer and firm will
bargain over the same good again in the future. If
, the customer and firm will
bargain over the same good again in the future. If ![]() , we have that
, we have that
![]() , and the
bargaining weight collapses to
, and the
bargaining weight collapses to
![]() .
.
Bargaining over the quantity ![]() traded
yields
traded
yields
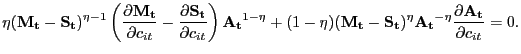
|
(67) |
We have
![]() ,
,
![]() (because
of our maintained assumption that
(because
of our maintained assumption that ![]() is
separable in its two arguments), and
is
separable in its two arguments), and
![]() . Thus, the sharing rule that determines
. Thus, the sharing rule that determines ![]() is
is
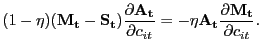
|
(68) |
Similar to how we proceeded above in Nash bargaining over the
price, we can define the following:
![]() ,
,
![]() ,
and thus
,
and thus
| (69) |
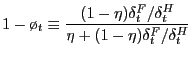
|
(70) |
as time-varying bargaining weights. Note that
![]() . Proceeding
completely analogously as above (i.e., using the Bellam equations
for the value to a firm of an existing customer along with the
advertising condition and going through several tedious steps of
algebra), we can show that the quantity
. Proceeding
completely analogously as above (i.e., using the Bellam equations
for the value to a firm of an existing customer along with the
advertising condition and going through several tedious steps of
algebra), we can show that the quantity ![]() is
characterized by
is
characterized by
![$\displaystyle \lefteqn{\frac{\o_{t}}{1-\o_{t}} \left[ p_{it} c_{it} - mc_{t} c_{it} - \frac{\kappa}{2} \left( \frac{p_{it}}{p_{it-1} }-1\right) ^{2} + \frac{\gamma}{k^{f}(\theta_{t})}\right] = \frac{\tilde {u}(c_{it})}{\lambda_{t}} - p_{it} c_{it} + }$](img1031.gif)
|
|
![$\displaystyle + (1-\theta_{t} k^{f}(\theta_{t})) E_{t}\left[ \Xi_{t+1\vert t} \left( \frac{\o _{t+1}}{1-\o _{t+1}}\right) (1-\rho^{x}) \left[ p_{it+1} c_{it+1} - mc_{t+1} c_{it+1} - \frac{\kappa}{2}\left( \frac{p_{it+1}}{p_{it}}-1\right) ^{2} + \frac{\gamma}{k^{f}(\theta_{t})} \right] \right] ,$](img1034.gif)
|
(71) |
which is expression (50) in
the text. Clearly, the only difference between (66)
and (71) is in the
relevant bargaining weights. In particular, note that ![]() depends on
depends on
![]() through
through
![]() ,
whereas
,
whereas
![]() does not. With curvature in the
aggregator over search consumption goods, deriving the expression
for
does not. With curvature in the
aggregator over search consumption goods, deriving the expression
for
![]() requires some
tedious algebra, the details of which are provided in
Appendix E.
requires some
tedious algebra, the details of which are provided in
Appendix E.
If ![]() , a more convenient representation
of the solution for the quantity traded is available. Using the
derivatives of
, a more convenient representation
of the solution for the quantity traded is available. Using the
derivatives of
![]() and
and
![]() , (68)
becomes
, (68)
becomes
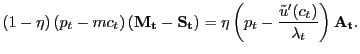
|
(72) |
Next, recognize that, with ![]() , the Nash
solution for the price satisfies
, the Nash
solution for the price satisfies
![]() . Imposing this on the previous expression, we have that the
quantity
. Imposing this on the previous expression, we have that the
quantity ![]() traded solves
traded solves
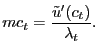
|
(73) |
Recall that households' optimal choice of labor implied
![]() ,
meaning
,
meaning
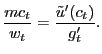
|
(74) |
Finally, because marginal cost is identically equal to the ratio of
the real wage to the marginal product of labor
![]() , in equilibrium, the quantity
traded in any given customer-firm relationship satisfies
, in equilibrium, the quantity
traded in any given customer-firm relationship satisfies
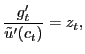
|
(75) |
which is a goods-market efficiency condition stating that the household's MRS between leisure and consumption of a particular good equals the marginal product of labor. Thus, with simultaneous bargaining over price and quantity traded of any given good, quantity (the intensive margin of consumption) is privately efficient, which is a standard outcome of Nash bargaining. One implication of this result is that if consumption were subject to proportional taxation, the intensive margin of trade would be unaffected by the consumption tax, given a number of customer-firm relationships (which in general would be distorted by a consumption tax).
In our baseline model without the intensive margin, the customer
and firm asset values
![]() and
and
![]() simplify to
simplify to
![$\displaystyle \mathbf{M_{t}} = \frac{\tilde{u}(\bar{c})}{\lambda_{t}} - \frac{g^{\prime }(1-l_{t}-s_{t}-N_{t})}{\lambda_{t}} - p_{it} \bar{c} + E_{t} \left[ \Xi_{t+1\vert t} \left( (1-\rho^{x}) \mathbf{M_{t+1}} + \rho^{x} \mathbf{S_{t+1}} \right) \right]$](img1054.gif)
|
(76) |
and
![$\displaystyle \mathbf{A_{t}} = p_{it} \bar{c} - mc_{t} \bar{c} - \frac{\kappa}{2}\left( \frac{p_{it}}{p_{it-1}} - 1\right) ^{2} + E_{t} \left[ \Xi_{t+1\vert t} (1-\rho^{x}) \mathbf{A_{t+1}} \right] .$](img1055.gif)
|
(77) |
That is, quantity exchanged in a customer match is fixed at
![]() . Maximization of the Nash product
is now with respect to only
. Maximization of the Nash product
is now with respect to only ![]() . Proceeding
similarly as above,
. Proceeding
similarly as above,
![$\displaystyle \lefteqn{\frac{\omega_{t}}{1-\omega_{t}} \left[ p_{it} \bar{c} - mc_{t} \bar{c} - \frac{\kappa}{2} \left( \frac{p_{it} }{p_{it-1}}-1\right) ^{2} + \frac{\gamma}{k^{f}(\theta_{t})}\right] = \frac{\tilde{u}(\bar{c})}{\lambda_{t}} - p_{it} \bar{c} + }$](img1058.gif)
|
|
![$\displaystyle + (1-\theta_{t} k^{f}(\theta_{t})) E_{t}\left[ \Xi_{t+1\vert t} \left( \frac{\omega_{t+1}}{1-\omega_{t+1}}\right) (1-\rho^{x}) \left[ p_{it+1} \bar{c} - mc_{t+1} \bar{c} - \frac{\kappa}{2}\left( \frac{p_{it+1}}{p_{it} }-1\right) ^{2} + \frac{\gamma}{k^{f}(\theta_{t})} \right] \right] ,$](img1061.gif)
|
(78) |
which is expression (24) in the text.
Appendix C. Fair Bargaining
Rather than the surplus being split according the time-varying
rule
![]() , here we impose fair bargaining, in which it is required that
, here we impose fair bargaining, in which it is required that
![]() . That is, suppose that the customer and firm arrange the effects
of inflation so that the shares of the surplus each gets are not
time-varying.
. That is, suppose that the customer and firm arrange the effects
of inflation so that the shares of the surplus each gets are not
time-varying.
In fair bargaining, the customer and firm jointly choose
![]() to maximize the Nash
product
to maximize the Nash
product
| (79) |
subject to the constraint
| (80) |
Letting ![]() be the Lagrange multiplier on the
constraint, the first-order conditions of the bargaining problem
are
be the Lagrange multiplier on the
constraint, the first-order conditions of the bargaining problem
are
![$\displaystyle \eta\mathbf{A_{t}} \left[ \frac{\partial\mathbf{M_{t}}}{\partial p_{it}} - \frac{\partial\mathbf{S_{t}}}{\partial p_{it}} + \frac{\partial\mathbf{A_{t}} }{\partial p_{it}} \right] + \eta\iota_{t} \frac{\partial\mathbf{A_{t}} }{\partial p_{it}} \frac{\mathbf{A_{t}}^{\eta}}{(\mathbf{M_{t}}-\mathbf{S_{t} })^{1-\eta}} = (1-\eta) \iota_{t} \left[ \frac{\partial\mathbf{M_{t}} }{\partial p_{it}} - \frac{\partial\mathbf{S_{t}}}{\partial p_{it}} \right] \frac{\mathbf{A_{t}}^{\eta}}{(\mathbf{M_{t}}-\mathbf{S_{t}})^{1-\eta}}% $](img1068.gif)
|
(81) |
and
![$\displaystyle \eta\mathbf{A_{t}} \left[ \frac{\partial\mathbf{M_{t}}}{\partial c_{it}} - \frac{\partial\mathbf{S_{t}}}{\partial c_{it}} + \frac{\partial\mathbf{A_{t}} }{\partial c_{it}} \right] + \eta\iota_{t} \frac{\partial\mathbf{A_{t}} }{\partial c_{it}} \frac{\mathbf{A_{t}}^{\eta}}{(\mathbf{M_{t}}-\mathbf{S_{t} })^{1-\eta}} = (1-\eta) \iota_{t} \left[ \frac{\partial\mathbf{M_{t}} }{\partial c_{it}} - \frac{\partial\mathbf{S_{t}}}{\partial c_{it}} \right] \frac{\mathbf{A_{t}}^{\eta}}{(\mathbf{M_{t}}-\mathbf{S_{t}})^{1-\eta}}.$](img1069.gif)
|
(82) |
In obtaining these, we used the constraint to make the substitution
![]() .
Next, because
.
Next, because
![]() ,
clearly
,
clearly
![]() , and similarly for derivatives with respect to
, and similarly for derivatives with respect to ![]() . The two first-order conditions thus reduce to
. The two first-order conditions thus reduce to
![$\displaystyle \eta\mathbf{A_{t}} \left[ \frac{\partial\mathbf{M_{t}}}{\partial p_{it}} - \frac{\partial\mathbf{S_{t}}}{\partial p_{it}} + \frac{\partial\mathbf{A_{t}} }{\partial p_{it}} \right] = 0$](img1074.gif)
|
(83) |
and
![$\displaystyle \eta\mathbf{A_{t}} \left[ \frac{\partial\mathbf{M_{t}}}{\partial c_{it}} - \frac{\partial\mathbf{S_{t}}}{\partial c_{it}} + \frac{\partial\mathbf{A_{t}} }{\partial c_{it}} \right] = 0.$](img1075.gif)
|
(84) |
Because
![]() , the terms in
brackets characterize the fair bargaining solutions for
, the terms in
brackets characterize the fair bargaining solutions for ![]() and
and ![]() .
.
With the definitions of
![]() ,
,
![]() , and
, and
![]() ,
,
![]() ,
,
![]() (because
of our maintained assumption that
(because
of our maintained assumption that ![]() is
separable in its two arguments), and
is
separable in its two arguments), and
![]() . Inserting these in the latter FOC,
. Inserting these in the latter FOC,
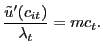
|
(85) |
Once again, using the equilibrium condition
![]() and
the fact that
and
the fact that
![]() ,
,
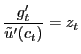
|
(86) |
characterizes the solution for the quantity traded, just as in the
Nash case with ![]() . Thus, in fair
bargaining, eliminating the wedge in price-bargaining has the
associated effect of eliminating the wedge in quantity-bargaining
as well. As was the case in Nash bargaining, the derivation of
. Thus, in fair
bargaining, eliminating the wedge in price-bargaining has the
associated effect of eliminating the wedge in quantity-bargaining
as well. As was the case in Nash bargaining, the derivation of
![]() is presented in
Appendix E.
is presented in
Appendix E.
Proceeding similarly, the price is characterized by
| (87) |
which reveals something very interesting. If this were a monetary
model and thus ![]() were the rate of change of the
nominal price level, this condition would be identical to a
standard New Keynesian Phillips curve except for the fact that
nothing at all about allocations appears.
were the rate of change of the
nominal price level, this condition would be identical to a
standard New Keynesian Phillips curve except for the fact that
nothing at all about allocations appears.
Appendix D. Steady-State Analytics
Using conditions (37)
and (39), we first prove our
claim in Section 4.2 that
the steady-state price (and hence the steady-state markup)
decreases as customer bargaining power ![]() rises.
Using the fact that Cobb-Douglas matching implies the probability a
firm finds a customer is
rises.
Using the fact that Cobb-Douglas matching implies the probability a
firm finds a customer is
![]() ,
from (37) we can solve
for
,
from (37) we can solve
for ![]() :
:
![$\displaystyle \theta= \left[ \frac{\beta(1-\rho^{x})}{1-\beta(1-\rho^{x})} \frac {p-mc}{\gamma} \right] ^{\frac{1}{\xi}}.$](img1097.gif)
|
(88) |
Inserting this in (39):
![$\displaystyle p = (1-\eta) A + \eta\left[ mc - \gamma\left( \frac{\beta(1-\rho^{x})} {1-\beta(1-\rho^{x})} \frac{p-mc}{\gamma} \right) \right] .$](img1098.gif)
|
(89) |
Defining an implicit function
![]() using this last expression,
we can compute the partials
using this last expression,
we can compute the partials
![$\displaystyle F_{p} = 1 + \frac{\eta\gamma}{\xi} \left( \frac{\beta(1-\rho^{x})} {\gamma[1-\beta(1-\rho^{x})]} \right) \left( \frac{\beta(1-\rho^{x} )}{1-\beta(1-\rho^{x})} \frac{p-mc}{\gamma} \right) ^{\frac{1}{\xi} - 1}% $](img1100.gif)
|
(90) |
and
![$\displaystyle F_{\eta} = A - \left[ mc - \gamma\left( \frac{\beta(1-\rho^{x})} {1-\beta(1-\rho^{x})} \frac{p-mc}{\gamma} \right) ^{\frac{1}{\xi}} \right] .$](img1101.gif)
|
(91) |
With search frictions,
![]() ; the advertising
condition then guarantees that
; the advertising
condition then guarantees that ![]() . Hence,
given that all other parameters are of appropriate sign and
magnitude (i.e.,
. Hence,
given that all other parameters are of appropriate sign and
magnitude (i.e.,
![]() ,
,
![]() ,
,
![]() ,
,
![]() , and
, and ![]() ),
), ![]() . Next, note
that we can write
. Next, note
that we can write ![]() compactly as
compactly as
![]() . If
. If
![]() , forming
customer relationships would not even be socially beneficial
because the social marginal benefit (the utility
, forming
customer relationships would not even be socially beneficial
because the social marginal benefit (the utility ![]() of consuming) would not cover the social marginal cost of forming
relationships and producing. Thus, we simply assume that
of consuming) would not cover the social marginal cost of forming
relationships and producing. Thus, we simply assume that
![]() , implying
, implying
![]() , Finally, then, we have by
the implicit function theorem that the bargained price decreases
the higher is customer bargaining power,
, Finally, then, we have by
the implicit function theorem that the bargained price decreases
the higher is customer bargaining power,
![]() .
.
Next, to characterize the firm advertising condition in
![]() space, first solve for
space, first solve for ![]() from (37):
from (37):
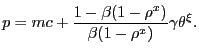
|
(92) |
Inserting this in (39) gives us a version of the advertising condition that embeds the pricing condition:
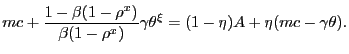
|
(93) |
Replacing ![]() by
by ![]() , we can
define an implicit function
, we can
define an implicit function
![]() using this last expression and
compute the partials
using this last expression and
compute the partials
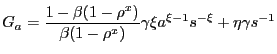
|
(94) |
and
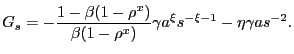
|
(95) |
By the implicit function theorem, the slope of the advertising
condition in ![]() space is thus
space is thus
![]() .
With a couple of steps of algebra, it is not difficult to show that
.
With a couple of steps of algebra, it is not difficult to show that
![]() , meaning that in
, meaning that in
![]() space, the advertising condition is a
ray through the origin with angle
space, the advertising condition is a
ray through the origin with angle ![]() to the
to the
![]() axis, as illustrated in
Figure 2.
axis, as illustrated in
Figure 2.
Appendix E. Intensive Quantity Adjustment
For use in the Nash-bargaining and fair-bargaining solutions for
quantity, we require an expression for
![]() . Recall that
with curvature, the household subutility function over search
consumption goods is
. Recall that
with curvature, the household subutility function over search
consumption goods is
![$\displaystyle v\left( \left[ \int_{0}^{N_{t}}c_{jt}^{\rho}dj\right] ^{1/\rho}\right) .$](img1133.gif)
|
(96) |
With
![]() defined as the
marginal utility to the household of obtaining consumption
from the
defined as the
marginal utility to the household of obtaining consumption
from the ![]() -th match, we have
-th match, we have
![$\displaystyle \widetilde{u}(c_{it})=v^{\prime}\left( \left[ \int _{0}^{N_{t}}c_{jt}^{\rho}di\right] ^{1/\rho}\right) \frac{1}{\rho}\left[ \int_{0}^{N_{t}}c_{jt}^{\rho}dj\right] ^{\frac{1}{\rho}-1}\rho c_{it} ^{\rho-1}.$](img1136.gif)
|
(97) |
Note the distinction between the indices ![]() and
and
![]() :
: ![]() is a dummy index
of integration, while
is a dummy index
of integration, while ![]() denotes a good obtained
from the
denotes a good obtained
from the ![]() -th customer relationship.
-th customer relationship.
For use in the bargaining solutions for the intensive quantity,
what requires some work is obtaining
![]() because, note,
because, note,
![]() appears three times in
expression (97): as one of the
consumption terms in the argument to
appears three times in
expression (97): as one of the
consumption terms in the argument to ![]() , as one
of the consumption terms in the integral
, as one
of the consumption terms in the integral
![]() , and by itself
in the last term on the right-hand-side. To make the problem
manageable, define
, and by itself
in the last term on the right-hand-side. To make the problem
manageable, define
![$\displaystyle f(c_{it}) \equiv v^{\prime}\left( \left[ \int_{0}^{N_{t}} c_{jt}^{\rho} dj \right] ^{1/\rho} \right) ,$](img1146.gif)
|
(98) |
![$\displaystyle g(c_{it}) \equiv\frac{1}{\rho} \left[ \int_{0}^{N_{t}} c_{jt}^{\rho} dj\right] ^{\frac{1}{\rho} - 1},$](img1147.gif)
|
(99) |
| (100) |
Letting
![]() , what we are
interested in deriving is
, what we are
interested in deriving is
![]() . Proceeding,
. Proceeding,
![$\displaystyle f^{\prime}= v^{\prime\prime}\left( \left[ \int_{0}^{N_{t}} c_{jt}^{\rho} dj \right] ^{1/\rho} \right) \frac{1}{\rho} \left[ \int_{0}^{N_{t}} c_{jt} ^{\rho} dj \right] ^{\frac{1}{\rho}-1} \rho c_{it}^{\rho-1},$](img1151.gif)
|
(101) |
![$\displaystyle g^{\prime}= \frac{1}{\rho} \left( \frac{1}{\rho} - 1\right) \left[ \int _{0}^{N_{t}} c_{jt}^{\rho} dj \right] ^{\frac{1}{\rho}-2} \rho c_{it}<tex2html_comment_mark>279 ^{\rho-1},$](img1152.gif)
|
(102) |
| (103) |
We limit attention to symmetric equilibria, so having computed
derivatives, we can impose symmetry, ![]() , on
, on
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
![]() , and
, and
![]() , yielding
, yielding
| (104) |
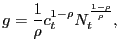
|
(105) |
| (106) |
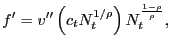
|
(107) |
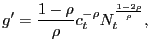
|
(108) |
| (109) |
Constructing the symmetric version of
![]() and rearranging,
and rearranging,
![$\displaystyle \tilde{u}^{\prime}(c_{t}) = N_{t}^{\frac{1-\rho}{\rho}} \left[ v^{\prime \prime}\left( c_{t} N_{t}^{1/\rho}\right) N_{t}^{\frac{1-\rho}{\rho}} + v^{\prime}\left( c_{t} N_{t}^{1/\rho}\right) (1-\rho) c_{t}^{-1} \left( \frac{1}{N_{t}} - 1\right) \right] ,$](img1168.gif)
|
(110) |
which goes into the Nash- and fair-bargaining solutions for the
intensive quantity traded. Note that if we we were to remove
curvature by setting ![]() , this collapses to
, this collapses to
![]() .
.
Appendix F. Advertising Data
The aggregate advertising data are from two separate sources. The data for 1951 to 1999 are obtained from an updated version of Robert J. Coen's (McCann-Erikson, Inc.) original data published in Historical Statistics of the United States, Colonial Times to 1970. The data for 2000 to 2005 are obtained from the Newspaper Association of America (NAA). The aggregate data include spending for advertising in newspapers, magazines, radio, broadcast television, cable television, direct mail, billboards and displays, Internet, and other forms. The GDP figures are from the US Bureau of Economic Analysis (BEA).
Using the nominal data in Table 10, we construct a real advertising series by deflating by the all-items Consumer Price Index (results were quite similar deflating by the GDP deflator). Logging and HP-filtering the resulting series, we find that over the entire sample the cyclical volatility of real advertising is 4.2 percent, the contemporaneous correlation with GDP is 0.73, and its first-order serial correlation is 0.6.
Table 10: Advertising Data
| Year | Aggregate nominal advertising expenditure ($B) | Nominal GDP ($B) | Share of GDP (%) |
|---|---|---|---|
| 1950 | 5.7 | 293.8 | 1.9 |
| 1951 | 6.4 | 339.3 | 1.9 |
| 1952 | 7.1 | 358.3 | 2.0 |
| 1953 | 7.7 | 379.4 | 2.0 |
| 1954 | 8.2 | 380.4 | 2.1 |
| 1955 | 9.2 | 414.8 | 2.2 |
| 1956 | 9.9 | 437.5 | 2.3 |
| 1957 | 10.3 | 461.1 | 2.2 |
| 1958 | 10.3 | 467.2 | 2.2 |
| 1959 | 11.3 | 506.6 | 2.2 |
| 1960 | 12.0 | 526.4 | 2.3 |
| 1961 | 11.9 | 544.7 | 2.2 |
| 1962 | 12.4 | 585.6 | 2.1 |
| 1963 | 13.1 | 617.7 | 2.1 |
| 1964 | 14.2 | 663.6 | 2.1 |
| 1965 | 15.3 | 719.1 | 2.1 |
| 1966 | 16.6 | 787.8 | 2.1 |
| 1967 | 16.9 | 832.6 | 2.0 |
| 1968 | 18.1 | 910.0 | 2.0 |
| 1969 | 19.4 | 984.6 | 2.0 |
| 1970 | 19.6 | 1,038.5 | 1.9 |
| 1971 | 20.7 | 1,127.1 | 1.8 |
| 1972 | 23.2 | 1,238.3 | 1.9 |
| 1973 | 25.0 | 1,382.7 | 1.8 |
| 1974 | 26.6 | 1,500.0 | 1.8 |
| 1975 | 27.0 | 1,638.3 | 1.7 |
| 1976 | 33.3 | 1,825.3 | 1.8 |
| 1977 | 37.4 | 2,030.9 | 1.8 |
| 1978 | 43.3 | 2,294.7 | 1.9 |
| 1979 | 48.8 | 2,563.3 | 1.9 |
| 1980 | 53.6 | 2,789.5 | 1.9 |
| 1981 | 60.5 | 3,128.4 | 1.9 |
| 1982 | 66.7 | 3,255.0 | 2.0 |
| 1983 | 76.0 | 3,536.7 | 2.1 |
| 1984 | 88.0 | 3,933.2 | 2.2 |
| 1985 | 94.9 | 4,220.3 | 2.2 |
| 1986 | 102.4 | 4,462.8 | 2.3 |
| 1987 | 110.3 | 4,739.5 | 2.3 |
| 1988 | 118.8 | 5,103.8 | 2.3 |
| 1989 | 124.8 | 5,484.4 | 2.3 |
| 1990 | 129.6 | 5,803.1 | 2.2 |
| 1991 | 127.6 | 5,995.9 | 2.1 |
| 1992 | 132.7 | 6,337.7 | 2.1 |
| 1993 | 139.5 | 6,657.4 | 2.1 |
| 1994 | 151.7 | 7,072.2 | 2.1 |
| 1995 | 162.9 | 7,397.7 | 2.2 |
| 1996 | 175.2 | 7,816.9 | 2.2 |
| 1997 | 187.5 | 8,304.3 | 2.3 |
| 1998 | 201.6 | 8,747.0 | 2.3 |
| 1999 | 215.3 | 9,268.4 | 2.3 |
| 2000 | 243.3 | 9,817.0 | 2.5 |
| 2001 | 231.3 | 10,128.0 | 2.3 |
| 2002 | 236.9 | 10,469.6 | 2.3 |
| 2003 | 245.6 | 10,960.8 | 2.2 |
| 2004 | 263.8 | 11,712.5 | 2.3 |
| 2005 | 271.1 | 12,455.8 | 2.2 |
References
Akerlof, George A., (2007). "The Missing Motivation in Macroeconomics", American Economic Review, Vol. 97, pp. 5-36.
Alessandria, George, (2005). "Consumer Search, Price Dispersion, and International Relative Price Volatility", Federal Reserve Bank of Philadelphia Working Paper No. 05-9.
Arseneau, David M. and Sanjay K. Chugh, (2006). "Ramsey Meets Hosios: The Optimal Capital Tax and Labor Market Efficiency", International Finance Discussion Paper no. 870, Board of Governors of the Federal Reserve System.
Arseneau, David M. and Sanjay K. Chugh, (2007). "Optimal Fiscal and Monetary Policy with Costly Wage Bargaining", International Finance Discussion Paper no. 891, Board of Governors of the Federal Reserve System.
Aruoba, S. Boragan and Sanjay K. Chugh, (2006). "Optimal Fiscal and Monetary Policy When Money is Essential", International Finance Discussion Paper no. 880, Board of Governors of the Federal Reserve System.
Aruoba, S. Boragan, Guillaume Rocheteau, and Christoper J. Waller, (2007). "Bargaining and the Value of Money", Journal of Monetary Economics. Forthcoming.
Binmore, Ken, (2007). Does Game Theory Work? The Bargaining Challenge, MIT Press.
Blinder, Alan S., Elier D. Canetti, David E. Lebow, and Jeremy B. Rudd, (1998). Asking About Prices: A New Approach to Understanding Price Stickiness, Russell Sage Foundation.
Chari, V.V., Patrick J. Kehoe, and Ellen R. McGrattan, (2006). "Business Cycle Accounting", Econometrica. Forthcoming.
Chugh, Sanjay K., (2006). "Optimal Fiscal and Monetary Policy with Sticky Wages and Sticky Prices", Review of Economic Dynamics, Vol. 9, pp. 683-714.
Diamond, Peter A., (1971). " A Model of Price Adjustment", Journal of Economic Theory, Vol. 3, pp. 156-168.
Gust, Christopher, Sylvain Leduc, and Robert J. Vigfusson, (2006). "Trade Integration, Competition, and the Decline in Exchange-Rate Pass-Through", International Finance Discussion Paper no. 864, Board of Governors of the Federal Reserve System.
Fabiani, Silvia, Martine Druant, Ignacio Hernando, Claudia Kwapil, Bettina Landau, Claire Loupias, Fernando Martins, Thomas Matha, Roberto Sabbatini, Harald Stahl, and Ad Stokman, (2006). "What Firms' Surveys Tell Us About Price-Setting Behavior in the Euro Area", International Journal of Central Banking, Vol. 2, pp. 3-47.
Hall, Robert E., (2005), "Equilibrium Wage Stickiness", American Economic Review, Vo. 95, pp. 50-65.
Hall, Robert E., (2007), "Equilibrium Sticky Prices", Stanford University.
Hosios, Arthur J., (1990). "On the Efficiency of Matching and Related Models of Search and Unemployment", Review of Economic Studies, Vol. 57, pp. 279-298.
Jaimovich, Nir, (2006). "Firm Dynamics, Markup Variations, and the Business Cycle", Stanford University.
Kalai, Ehud, (1977). "Proportional Solutions to Bargaining Situations: Interpersonal Utility Comparisons", Econometrica, Vol. 45, pp. 1623-1630.
King, Robert G. and Sergio T. Rebelo, (1999). "Resuscitating Real Business Cycles". In Handbook of Macroeconomics, edited by John B. Taylor and Michael Woodford, Vol. 1B, Elsevier.
Klemperer, Paul, (1995). "Competition When Consumers Have Switching Costs: An Overview with Applications to Industrial Organization, Macroeconomics, and International Trade", Review of Economic Studies, Vol. 62, pp. 515-539.
Kleshchelski, Isaac and Nicolas Vincent, (2007). "Market Share and Price Rigidity", Northwestern University.
Menzio, Guido, (2007). "A Search Theory of Rigid Prices", University of Pennsylvania.
Nakamura, Emi and Jon Steinsson, (2007), "Price Setting in Forward-Looking Customer Markets", Harvard University.
Okun, Arthur M., (1981), "Prices and Quantities", The Brookings Institution.
Petrongolo, Barbara and Christopher A. Pissarides, (2001). "Looking into the Black Box: A Survey of the Matching Function", Journal of Economic Literature, Vol. 39, pp. 390-431.
Pissarides, Christopher A., (2000). "Equilibrium Unemployment Theory", MIT Press.
Ravn, Morten, Stephanie Schmitt-Grohe, and Martin Uribe, (2006). "Deep Habits", Review of Economic Studies, Vol. 73, pp. 195-218.
Rogerson, Richard, Robert Shimer, and Randall Wright, (2005). "Search-Theoretic Models of the Labor Market: A Survey", Journal of Economic Literature, Vol. 43, pp. 959-988.
Rotemberg, Julio J., (2005). "Customer Anger at Price Increases, Changes in the Frequency of Price Adjustment, and Monetary Policy", Journal of Monetary Economics, Vol. 52, pp. 829-852.
Rotemberg, Julio J., (2006). "Fair Pricing", Harvard University.
Rotemberg, Julio J. and Michael Woodford, (1999). "The Cyclical Behavior of Prices and Costs". In Handbook of Macroeconomics, edited by John B. Taylor and Michael Woodford, Vol. 1B, Elsevier.
Rubinstein, Ariel, (1982). "Perfect Equilibrium in a Bargaining Model", Econometrica, Vol. 50, pp. 97-109.
Schmitt-Grohe, Stephanie and Martin Uribe, (2004a). "Optimal Fiscal and Monetary Policy Under Imperfect Competition", Journal of Macroeconomics, Vol. 26, pp. 183-209.
Schmitt-Grohe, Stephanie and Martin Uribe, (2004b). "Solving Dynamic General Equilibrium Models Using a Second-Order Approximation to the Policy Function", Journal of Economic Dynamics and Control, Vol. 28, pp. 755-775.
Shimer, Robert, (2005). "The Cyclical Behavior of Equilibrium Unemployment and Vacancies", American Economic Review, Vol. 95, pp. 25-49.
Footnotes
*The views expressed here are solely those of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Email addresses: [email protected] and [email protected]. Return to text
1. Some examples are Jaimovich (2006), Ravn, Schmitt-Grohe, and Uribe (2006), and Gust, Leduc, and Vigfusson (2006). Return to text
2. Those familiar with the basic labor search model as described by Pissarides (2000, chapter 1), will find close analogies in several of our modeling choices. Return to text
3. For example, even if one knows exactly where to go to buy certain goods, one may still have to walk around the aisles, stand in the checkout line, etc. Return to text
4. We recognize that in making
![]() and
and ![]() perfect substitutes
in how they detract from utility -- each unit of
perfect substitutes
in how they detract from utility -- each unit of ![]() or
or ![]() is equivalent to forgoing one unit of
leisure -- we are taking a particular stand on the relative
disutility of what we term searching versus shopping.
A more general specification that allows for finer distinction
between the disutility from shopping versus from searching would be
is equivalent to forgoing one unit of
leisure -- we are taking a particular stand on the relative
disutility of what we term searching versus shopping.
A more general specification that allows for finer distinction
between the disutility from shopping versus from searching would be
![]() Because we think we would not
have sufficient guidance from data or existing models on how to
calibrate, let alone construct, such a function, we adopt the
formulation that we do. Despite limitations imposed by data and the
lack of previous such modeling efforts, it has been suggested to us
that perhaps shopping does not entail disutility at all and
that it is only searching that is associated with
disutility. In that case, we may consider writing
Because we think we would not
have sufficient guidance from data or existing models on how to
calibrate, let alone construct, such a function, we adopt the
formulation that we do. Despite limitations imposed by data and the
lack of previous such modeling efforts, it has been suggested to us
that perhaps shopping does not entail disutility at all and
that it is only searching that is associated with
disutility. In that case, we may consider writing
![]() , in which
, in which ![]() continues to detract from leisure, which has some precedent from
"shopping-time" models, but
continues to detract from leisure, which has some precedent from
"shopping-time" models, but ![]() does not. We do not
have a strong prior regarding this latter view that shopping and
searching are sufficiently distinct activities. Thus, rather than
present a dizzying array of alternative preference specifications,
our approach is to simply lump shopping and searching together in
terms of utils and see how much progress we can make on our core
ideas. If the primitive trading arrangements our model emphasizes
(which are independent of how we wish to write preferences) are
deemed sufficiently useful, one may want to consider alternative
preference specifications. Return to
text
does not. We do not
have a strong prior regarding this latter view that shopping and
searching are sufficiently distinct activities. Thus, rather than
present a dizzying array of alternative preference specifications,
our approach is to simply lump shopping and searching together in
terms of utils and see how much progress we can make on our core
ideas. If the primitive trading arrangements our model emphasizes
(which are independent of how we wish to write preferences) are
deemed sufficiently useful, one may want to consider alternative
preference specifications. Return to
text
5. In the calibrated version of the model, this condition does indeed hold, but it is likely not a theorem that this condition must hold. For some parameterizations, it is likely that the condition fails, in which case a participation constraint would be needed to ensure an equilibrium in which search goods are desirable. We echo and expand on this point in the context of firm incentives in this environment when we discuss the model with intensive adjustment in section 5. Return to text
6. A structure isomorphic to our division into Walrasian firms and non-Walrasian firms described next is to suppose that there is a single representative firm that hires labor to produce output, some of which it sells directly to consumers via Walrasian markets and some of which it sells via search-based channels. One could labels these two channels of sales to consumers as "wholesale" and "retail" channels, which would make the environment look more similar to that of Hall (2007). Return to text
7. To preview the equilibrium,
![]()
![]() in
our model because we have
in
our model because we have
![]() . Return to text
. Return to text
8. Technically, of course, it is the real
interest rate with which firms discount profits, and in equilibrium
the real interest rate between time zero and time ![]() is measured by
is measured by ![]() . Because there will be
no confusion using this equilibrium result "too early," we skip
this intermediate level of notation and structure. Return to text
. Because there will be
no confusion using this equilibrium result "too early," we skip
this intermediate level of notation and structure. Return to text
9. The fact that price is "taken as given" as the firm optimally chooses its level of advertising might lead some to interpret this model as one in which firms have a primitive concern for maximizing their market share, an objective that some models of customer relations do posit. While this is somewhat a semantic point, we note that it is in fact profits that the firms in our environment maximize. It is just that firms are not free to unilaterally set prices to achieve maximum profits, rather they must form relationships before determining prices jointly with customers. Return to text
10. With intensive adjustment not allowed
here in our basic model, we could just as well use the notation
![]() rather than
the structure we present. Looking forward to our full model in
section 5, though, the additional
notation here will prove useful in comparing features across
models. Return to text
rather than
the structure we present. Looking forward to our full model in
section 5, though, the additional
notation here will prove useful in comparing features across
models. Return to text
11. In Ravn, Schmitt-Grohe, and Uribe's (2006) and Nakamura and Steinnson's (2007) models, pricing is also forward-looking despite the absence of menu costs. In their setups, "deep habits," which are long-lived preference relationships consumers have with particular goods, are the source of forward-looking pricing. At the core of their models, though, is still the typical Walrasian goods market, making, in our view, relationships perhaps a more tenuous idea than in our framework. No matter the relative merits of our approach versus others, a broader idea that emerges is that one can model long-lived customer relationships through preferences, as Ravn, Schmitt-Grohe and Uribe (2006) and Nakamura and Steinsson (2007) both do, or through trading arrangements, as we do here. Return to text
12. Technically, one could write an underlying maximization problem that gives rise to this sharing rule, as well, but for most practical applications, one does not need to do so. For more on the relationship between Nash bargaining and proportional bargaining, see Kalai (1977). Return to text
13. Although Nash bargaining is ostensibly at the core of this pricing protocol, we point out that while Nash bargaining, due to its axiomatic nature, is a cooperative equilibrium concept, fair bargaining is a non-cooperative equilibrium concept. In particular, because by construction Nash bargaining places the bargaining parties on the Pareto frontier, the fact that the fair-bargaining solution differs necessarily means that it does not place the parties on the Pareto frontier. Return to text
14. In New Keynesian models, the Phillips curve is essentially just the first-order condition of firms facing rigidities in their price-setting choices and of course has nothing to do with bargaining. Return to text
15. In this regard, there is a very tight analogy with the basic static labor search model, as described by Pissarides (2000, chapter 1), as we mentioned earlier. Those familiar with the textbook labor search model will find the analytical exposition here extremely familiar; because there are a couple of details that do not carry over completely (but, admittedly, nearly completely) identically, we think it worthwhile to explain the basics. Return to text
16. As is apparent, what we discuss in
this section is equilibrium in the search-goods market; Walrasian
equilibrium is of course the relevant equilibrium concept for the
good ![]() . Return to
text
. Return to
text
17. Really all we require for this
partial equilibrium steady-state analysis is just that labor is
fixed at
![]() . Going all the way to
essentially an endowment model -- in which when a firm finds a
customer to whom to sell, product magically appears -- in which
. Going all the way to
essentially an endowment model -- in which when a firm finds a
customer to whom to sell, product magically appears -- in which
![]() just eases the ensuing exposition a
bit. Return to text
just eases the ensuing exposition a
bit. Return to text
18. In constructing Figures 1 and 2, we use the parameter values described in Section 4.1. Return to text
19. In a different notion of "consumer search" (one in which search means that consumers explicitly face a distribution of prices from which to choose), Alessandria (2005) makes the very similar point that search costs are reflected in prices. Return to text
20. Once again, to those familiar with the modern theory of labor markets, this is all very familiar. Indeed, as we pointed out at the outset, our steady-state analysis is parallel to the analysis of the basic labor search model in Pissarides (2000, Chapter 1). Return to text
21. Here it is critical that it is only
searching and shopping that are the two possible activities for
individuals, meaning ![]() . If individuals could
also work/take leisure and work/leisure were a possible state to
transit to after a failed customer experience, it would be much
more difficult to conduct the ensuing analysis. Return to text
. If individuals could
also work/take leisure and work/leisure were a possible state to
transit to after a failed customer experience, it would be much
more difficult to conduct the ensuing analysis. Return to text
22. Petrongolo and Pissarides (2001) survey the empirical usefulness of Cobb-Douglas matching for labor markets. Return to text
23. Data on the American Time Use Survey, which began in 2003, can be accessed at http://www.bls.gov/tus/. Return to text
24. A summary of the data through 2005 can be found in the BLS's 2007 Statistical Abstract of the United States, Table 1261. Return to text
25. In our model, any activity that potentially helps a firm attract customers is "advertising." Return to text
26. One way to interpret this is that firms can indirectly manage labor demand through the non-Walrasian market. By changing advertising behavior, the firm can influence the number of long-term relationships in the economy and, hence the amount of time households spend in shopping activities. Shopping time, in turn, is closely linked to the household labor supply decision. Return to text
27. Trivially, in a model with no search markets and in which labor is the only production input, the volatility of GDP would be identical to the volatility of consumption simply because all output is absorbed by consumption. Return to text
28. Specifically, in work that has
sparked much subsequent modeling effort, Shimer (2005) demonstrated
that the standard Mortensen-Pissarides structure coupled with Nash
bargaining fails to match the volatilities of unemployment and
vacancies, the two inputs to the aggregate matching function,
observed in the data. Our model employs a Mortensen-Pissarides
structure coupled with Nash bargaining, yet at least one of the
inputs to the aggregate matching function -- advertising -- is as
volatile as observed in the data. Regarding the volatility of the
other input to the matching function -- household search behavior
-- the American Time Use Survey only began in 2003, so we cannot
compute meaningful time-series summary statistics for it. We can
only note that over the four years of its survey, household time
spent shopping has been remarkably stable, which also qualitatively
matches our model's prediction regarding the volatility of
![]() and
and ![]() . Return to text
. Return to text
29. The setting for ![]() does not matter here because equilibrium dynamics are
invariant to
does not matter here because equilibrium dynamics are
invariant to ![]() . Return to text
. Return to text
30. The experiments we conduct in this section of course would be trivial under fair bargaining because prices never change under fair bargaining. Return to text
31. A bit more precisely, we tried,
holding fixed the calibration in our baseline model, endogenizing
![]() (using the mechanisms described below)
with the linear aggregator and indeed found that firms need to be
subsidized (i.e.,
(using the mechanisms described below)
with the linear aggregator and indeed found that firms need to be
subsidized (i.e., ![]() ) to be induced
to advertise and produce for customers (and the resulting
equilibrium featured
) to be induced
to advertise and produce for customers (and the resulting
equilibrium featured ![]() ). It could be the
case that for some other constellation of parameters of our
baseline model, this would not occur, but we did not find one.
Assuming that such a parameter constellation does not exist or that
such a parameter constellation is unrealistic on other grounds, one
would need to impose a constraint that would guarantee that firms
enjoy non-negative profits from paying for advertising.
Because this entry decision occurs every period, such a constraint
would in principle be an occasionally-binding constraint, which
would require quite different numerical tools than we use to solve
the model and would likely be difficult to implement in any case
due to the size of our model. Return to
text
). It could be the
case that for some other constellation of parameters of our
baseline model, this would not occur, but we did not find one.
Assuming that such a parameter constellation does not exist or that
such a parameter constellation is unrealistic on other grounds, one
would need to impose a constraint that would guarantee that firms
enjoy non-negative profits from paying for advertising.
Because this entry decision occurs every period, such a constraint
would in principle be an occasionally-binding constraint, which
would require quite different numerical tools than we use to solve
the model and would likely be difficult to implement in any case
due to the size of our model. Return to
text
32. We could also call this formulation "differentiation" of products, as is typical in models that use this type of consumption aggregator. We hesitate to use this terminology, though, because what we have in mind is not an ex-ante notion of differentiation, but rather an ex-post notion of differentiation. To continue with the example, what we have in mind is that at a primitive level the household does not care whether it finds sweaters at Banana Republic or JCrew or does not even care whether it obtains either at all. More subtly, given that one sweater has been purchased from Banana Republic, in our formulation the household would prefer if the second sweater were purchased from JCrew. In the end, however, this is a somewhat semantic point, and if one wants to call this formulation of our model one in which there is differentiation of goods, we do not strongly object. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text