The Federal Reserve Board eagle logo links to home page

Frequency of Observation and the Estimation of Integrated Volatility in Deep and Liquid Financial Markets1

Alain P. Chaboud2, Benjamin Chiquoine3, Erik Hjalmarsson4, and Mico Loretan5

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

Using two newly available ultrahigh-frequency datasets, we investigate empirically how frequently one can sample certain foreign exchange and U.S. Treasury security returns without contaminating estimates of their integrated volatility with market microstructure noise. Using the standard realized volatility estimator, we find that one can sample dollar/euro returns as frequently as once every 15 to 20 seconds without contaminating estimates of integrated volatility; 10-year Treasury note returns may be sampled as frequently as once every 2 to 3 minutes on days without U.S. macroeconomic announcements, and as frequently as once every 40 seconds on announcement days. Using a simple realized kernel estimator, this sampling frequency can be increased to once every 2 to 5 seconds for dollar/euro returns and to about once every 30 to 40 seconds for T-note returns. These sampling frequencies, especially in the case of dollar/euro returns, are much higher than those that are generally recommended in the empirical literature on realized volatility in equity markets. The higher sampling frequencies for dollar/euro and T-note returns likely reflect the superior depth and liquidity of these markets.

Keywords: Realized volatility, integrated volatility, critical sampling frequency, market microstructure noise, government bond markets, foreign exchange markets, liquidity, kernel estimator, robust estimator, jumps

JEL classification: C22, F31, G12

1  Introduction

Estimating the volatility of asset returns is important for many economic and financial applications, including risk management, derivative pricing, and analyzing investment choices and policy alternatives. As Mandelbrot (1963, p. 418) noted, volatility estimation is complicated by the fact that "large [price] changes tend to be followed by large changes--of either sign--and small changes tend to be followed by small changes," i.e., that volatility tends to cluster. One approach to estimating volatility is to use a parametric framework, such as the class of ARCH, GARCH, and stochastic volatility models. If data on returns are available at sufficiently high frequencies, one can also estimate volatility nonparametrically by computing the realized volatility, which is the natural estimator of the ex post integrated volatility. This nonparametric method is appealing both because it is computationally simple and because it is a valid estimator under fairly mild statistical assumptions.

The higher the sampling frequency and thus the larger the sample size of intraday returns, the more precise the estimates of daily integrated volatility should become. In practice, however, the presence of so-called market microstructure features, which arise especially if the data are sampled at very high frequencies, creates important complications. The finance literature has identified many such features. Among them are the facts that financial transactions--and hence price changes and non-zero returns--arrive discretely rather than continuously over time, that buyers and sellers usually face different prices (separated by the bid-ask spread), that returns to successive transactions tend to be negatively serially correlated (due to, for instance, the so-called bid-ask bounce), and that the initial impact of trades on prices is often at least partially reversed.6

The first aim of our paper is to study, for two specific financial assets, how the standard estimator of integrated volatility is affected by the choice of sampling frequency and, as a result, by the bias caused by market microstructure features. The two asset price series we study are obtained from some of the deepest and most liquid financial markets in existence today. They are the spot exchange rate of the dollar/euro currency pair, provided by Electronic Broking Systems (EBS), and the price of the on-the-run 10-year U.S. Treasury note, which is traded on BrokerTec. Both of these markets are electronic order book systems, which quite likely represent the future of wholesale financial trading systems. Both markets are strictly inter-dealer. These markets are far larger in terms of total trading volume than markets for individual stocks, even the handful of most liquid stocks traded on the New York Stock Exchange, and bid-ask spreads in these markets are narrower than in typical stock markets. In 2005, the time period considered in this paper, bid-ask spreads averaged 1.04 basis points for dollar/euro spot transactions on EBS and 1.68 basis points for 10-year Treasury note transactions on BrokerTec. Prices for both time series are available at ultra-high sampling frequencies--up to the second-by-second frequency.

Our main hypothesis is that in such deep and liquid markets, microstructure-induced noise should pose less of a concern for volatility estimation, in the sense that it should be possible to sample returns more frequently than, say, returns on individual stocks before estimates of integrated volatility encounter significant bias caused by the markets' microstructure features. We label this sampling frequency (provided, of course, that it exists) the critical sampling frequency. This thesis is indeed borne out by our empirical results. Using volatility signature plots, we find that the critical sampling interval lengths for dollar/euro returns are as short as 15 to 20 seconds. The corresponding critical sampling interval lengths for returns on 10-year Treasury notes are between 2 and 3 minutes. These intervals are considerably shorter than the sampling intervals of several minutes--usually five or more minutes--that have often been recommended in the empirical literature on estimating integrated volatility for a number of other financial markets. The shorter critical sampling intervals and the associated larger sample sizes afford a considerable gain in the precision with which the integrated volatility of returns may be estimated. We conclude that in very deep and liquid markets, microstructure-induced frictions may be much less of an issue for integrated volatility estimation than was previously thought.

We also analyze whether the presence or absence of scheduled U.S. macroeconomic news announcements influences the precision with which the integrated volatility of asset returns may be estimated. While confirming the results of several previous empirical studies that integrated volatility is systematically higher on announcement days than on non-announcement days, we find that the critical sampling frequency is also systematically higher on announcement days. We interpret this finding as an indication that the higher trading volumes that occur on announcement days, an especially prominent feature in the U.S. Treasury bills and notes markets, help reduce some of the frictions caused by market microstructure features, raising the critical sampling frequencies and hence allowing greater estimation precision.

Although the critical sampling frequencies are already very high for both time series we consider in this paper, we find that it is possible to further increase these critical sampling frequencies by using so-called kernel estimators, which are designed explicitly to control for the effects of market microstructure noise. We find that by using a very simple version of a kernel estimator, it is possible to sample dollar/euro returns at frequencies as high as once every 2 to 5 seconds, and that T-note returns can be sampled as frequently as once every 30 to 40 seconds without incurring noticeable bias generated by market microstructure noise. This kernel estimator, which is almost as easy to compute as the standard realized volatility estimator, therefore offers substantial additional gains in terms of both how frequently one can sample on an intraday basis and the accuracy with which integrated volatility may be estimated.

Finally, we also examine how certain robust estimators of integrated volatility perform for the two time series at hand. These alternative estimators are not based on functions of the standard quadratic variation process, but instead on functions of absolute variation and bipower variation processes. A reason for considering such methods is that they are, by construction, more robust than the standard estimator to outlier activity (heavy tails) in the data; such "outliers" are frequently generated by discontinuities or jumps in the time series of financial asset prices. In general, these estimators measure somewhat different (but highly relevant) aspects of daily variation than does the standard realized volatility estimator. We find empirically that these alternative methods are indeed more robust than the standard estimator to the presence of jumps. For instance, the volatility estimates show less dispersion across announcement and non-announcement days than do estimates that are based on squared variation. However, we find no evidence that these robust methods are also less sensitive than the standard estimator to bias imparted by market microstructure noise. To the contrary, our results indicate that one should typically sample less frequently when using the absolute-variation base estimator, relative to the critical sampling frequency we found for the standard volatility estimator.

The remainder of our paper is organized as follows. Section 2 provides some motivation for the use of the standard estimator of integrated volatility, which is based on the quadratic variation of returns. The section also details how market microstructure noise may cause bias in the standard estimator, provides an introduction to kernel-based estimators designed to circumvent this problem, and sets out the use of estimators based on absolute and bipower variation processes. Section 3 provides an overview of the characteristics of the foreign exchange (FX) and bond market data used in our empirical work. Section 4 provides the empirical results for the standard estimator of realized volatility, using both volatility signature plots and the Aït-Sahalia, Mykland, and Zhang (2005) and Bandi and Russell (2006) rule for choosing sampling frequencies. Section 5 shows the results from the realized kernel estimators. Section 6 provides the estimation results for the robust estimators of realized volatility, such as the one that is based on the absolute variation process. Section 7 provides a discussion of some broader issues raised by our empirical findings, and Section 8 concludes.

2  Motivation and Estimation Techniques

2.1  Motivation

The fundamental idea behind the use of realized volatility is that quadratic variation can be used as a measure of ex-post variance in a diffusion process. The quadratic variation $ QV_{t}$ of a process $ X_{t}$ is defined as

$\displaystyle QV_{t}=\left[ X,X\right] _{t}=\plim_{n\to\infty}\sum_{j=1}^{n} \left( X_{t_{j}}-X_{t_{j-1}}\right) ^{2},$ (1)

for any sequence of deterministic partitions $ 0=t_{0}<t_{1}<\dots<t_{n}=t$ with $ \sup_{j} \abs {t_j-t_{j-1} } \downarrow0$ as $ n \to\infty$; see, for instance, Andersen, Bollerslev, Diebold, and Labys (2003) and Barndorff-Nielsen and Shephard (2004a). If $ X_{t}$ follows a standard diffusion process, such as
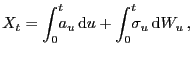$\displaystyle X_{t}=\int_{0}^{t} \!\!\! a_{u} \dee u+\int_{0}^{t} \!\!\!\sigma_{u} \dee W_{u}\,,$ (2)

where $ W_{u}$ is standard-scale Brownian motion, and if $ a_{u}$ and $ \sigma_{u}$ satisfy certain regularity conditions, then
$\displaystyle \left[ X,X\right] _{t}=\int_{0}^{t} \!\!\!\sigma_{u}^{2} \dee u\,.$ (3)

In this model, which is frequently used in financial economics, the quadratic variation measures the integrated variance over some time interval and is thus a natural way of measuring the ex-post variance. For most of the discussion, and unless otherwise noted, we will maintain the assumption that the logarithm of the price process follows the diffusion process in equation (2). This is not crucial to the analysis in the paper, but it facilitates the exposition of the theoretical concepts outlined below. In Section 2.5 below, we discuss the effects of adding a jump component to equation (2). Suppose the log-price process $ X_{t}$ is sampled at fixed intervals $ \delta$ over some time period $ [0,t]$. Let $ n=\floor {t/\delta}$. The realized variance, given by
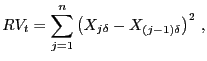$\displaystyle RV_{t}=\sum_{j=1}^{n} \left( X_{j \delta}-X_{(j-1)\delta} \right) ^{2}\, ,$ (4)

is a natural estimator of the quadratic variation over the interval $ [0,t]$. In practice, we usually consider the integrated volatility, which is the square root of the integrated variance, and the corresponding realized volatility, which is obtained by taking the square root of $ RV_{t}$.

The properties of $ RV_{t}$ have been analyzed extensively in the econometrics literature.7 In particular, it has been shown that under very weak conditions realized variance is a consistent estimator of quadratic variation. That is, for a fixed time interval $ [0,t]$, $ RV_{t}\to_{p} QV_{t}$ as $ \delta \downarrow0$. In addition, if $ X_{t}$ satisfies equation (2), the limiting distribution of $ RV_{t}$ is mixed normal and is centered on $ QV_{t} $:

$\displaystyle \sqrt{n}(RV_{t}-QV_{t}) \Rightarrow MN(0, 2 Q_{t})\,,$ (5)

where $ Q_{t}=\int_{0}^{t}\! \sigma_{u}^{4} \dee u$ is called the quarticity of $ X_{t} $.

2.2  Market Microstructure Noise

According to the asymptotic result in equation (5), it is preferable to sample $ X_{t}$ as frequently as possible in order to achieve more precise estimates of the quadratic variation. In practice, however, price changes in financial assets sampled at very high frequencies are subject to market frictions--such as the bid-ask bounce and the price impact of trades--in addition to reacting to more fundamental changes in the value of the asset.

Suppose the observed price $ X_{t}$ can be decomposed as

$\displaystyle X_{t}=Y_{t}+U_{t},$ (6)

where $ Y_{t}$ is the so-called latent price process and $ U_{t}$ represents market microstructure noise. The object of interest is now the quadratic variation of the unobserved process $ Y_{t}$, which is assumed to satisfy the diffusion process given by equation (2). A standard assumption is that $ U_{t}$ is a white noise process, independent of $ Y_{t}$, with mean zero and constant variance  $ \omega^{2}$. Now, as $ \delta$, the length of sampling intervals, goes to zero, the squared increments in $ X_{t}$ will be dominated by the changes in $ U_{t}$. This follows because the increments in $ Y_{t}$ are of order $ O_{p}(\sqrt{\delta})$ under equation (2), whereas the increments in $ U_{t}$ are of order $ O_{p}(1)$ regardless of sampling frequency. Calculating the realized variance using extremely high frequency (such as second-by-second) returns from the observed price process $ X_{t}$ will therefore result in a biased and inconsistent estimate of the quadratic variation of the latent price process $ Y_{t}$.

2.3  Optimal Choice of Sampling Frequency

The initial reaction to this problem was simply to sample at frequencies for which market frictions are believed not to play a significant role. Even with this limitation, daily volatility estimates can be obtained with some precision. In particular, sampling prices and returns at the five-minute frequency appears to have emerged as a popular choice to compute daily-frequency estimates of volatility. In order to formalize this line of reasoning, Bandi and Russell (2006) derive an optimal sampling frequency rule for the standard realized variance estimator.8 Their rule is based on a function of the signal-to-noise ratio between the innovations to the latent price process and the noise process. Their key assumption is that by sampling at the highest possible frequency, it may be possible to obtain a consistent estimate of the variance of the noise, $ \omega^{2}$. For example, let $ \delta^{\onesec }$ denote the one-second sampling frequency, which is the highest possible in our data, and let $ n^{\onesec }$ denote the number of non-zero one-second returns during the day; i.e., $ n^{\onesec }$ counts the number of one-second periods during the whole day for which there is actual market activity that moves the price. An estimator of  $ \omega^{2}$ is now given by

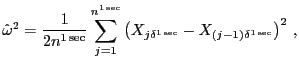$\displaystyle \hat{\omega}^{2}=\frac1{2n^{\onesec }}\sum_{j=1} ^{n^{\onesec }} \left( X_{j\delta^{\onesec }} -X_{(j-1)\delta^{\onesec }} \right) ^{2}\,,$ (7)

where the summation is carried out over the $ n^{\onesec }$ intervals with nonzero returns.

By estimating $ \omega^{2}$, the strength of the noise in the returns data can thus be measured. The strength of the signal, i.e., variations in $ X_{t}$ which come from the latent price process $ Y_{t}$, can be measured by the quarticity of that process. By relying on data sampled at a lower frequency, such as once every ten minutes, where the market microstructure noise should not be an issue, the quarticity of $ Y_{t}$ can be estimated consistently (though not efficiently) by

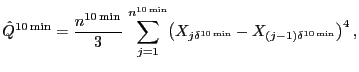$\displaystyle \hat{Q}^{\tenmin }=\frac{n^{\tenmin }}{3}\,\sum_{j=1}^{n^{\tenmin }} \bigl( X_{j\delta^{\tenmin }}-X_{(j-1)\delta^{\tenmin }} \bigr)^{4} \,,$ (8)

where $ n^{\tenmin }$ is the number of 10-minute intervals with non-zero returns in a day. Thus, by using returns obtained by sampling at different frequencies, it is possible to assess the relative importance of the signal $ Y_{t}$ and the noise $ U_{t}$. Bandi and Russell (2006) show that an approximate rule of thumb for the optimal sampling frequency, $ \delta^{\opt } =1/n^{\opt }$, is given by
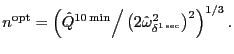$\displaystyle n^{\opt }=\Bigl( \hat{Q}^{\tenmin } \Big/ \left( 2 \hat{\omega }_{\delta^{\onesec }}^{2} \right) ^{2} \Bigr)^{1/3}\,.$ (9)

2.4  Estimators of Integrated Volatility That are Robust to the Presence of High-Frequency Market Microstructure Noise

The other approach to dealing with the microstructure noise issue is to design estimators that explicitly control for and potentially even eliminate its effects on volatility estimates. At the cost of some loss of simplicity, this approach has the potential of extracting useful information that would otherwise be discarded if a coarser sampling scheme is employed. A number of estimators have been proposed recently to deal with market microstructure noise in this manner; see, for instance, Aït-Sahalia, Mykland, and Zhang (2008, 2005), Hansen and Lunde 2006), Oomen (2006, 2005), Zhang (2006), and Zhang, Mykland, and Aït-Sahalia (2005).9 While these recently-proposed estimators possess several desirable properties, such as asymptotic consistency under their respective maintained assumptions and (in some cases) asymptotic efficiency as well, the actual performance of these estimators in empirical practice remains a topic of ongoing research.

Here, we focus on a kernel-based estimator proposed by Barndorff-Nielsen, Hansen, Lunde, and Shephard (2008), hereafter BNHLS . Although BNHLS were not the first to consider kernel estimators--earlier contributions include Zhou (1996) and Hansen and Lunde (2006)--they were the first to provide a comprehensive analysis, including results on consistency and efficiency. We therefore focus on their approach when analyzing estimators that are robust to market microstructure noise. Define the realized autocovariation process

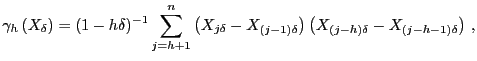$\displaystyle \gamma_{h} \left( X_{\delta}\right) =(1-h\delta)^{-1} \sum_{j=h+1}^{n} \left( X_{j\delta}- X_{(j-1)\delta} \right) \left( X_{(j-h)\delta}- X_{(j-h-1)\delta}\right) \,,$ (10)

for $ h\geq0$, where the term $ (1-h\delta)^{-1}$ is a small-sample correction factor. The realized kernel estimator in BNHLS is given by

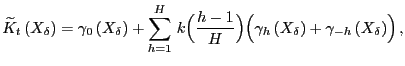$\displaystyle \widetilde{K}_{t}\left( X_{\delta}\right) = \gamma_{0} \left( X_{\delta}\right) + \sum_{h=1}^{H} \, k\Bigl( \frac{h-1}{H} \Bigr) \Bigl( \gamma_{h} \left( X_{\delta}\right) +\gamma_{-h} \left( X_{\delta}\right) \Bigr)\,,$ (11)

for some kernel function $ k(\cdot)$ that satisfies $ k(0)=1$ and $ k(1)=0$ and for a suitably chosen lag truncation or bandwidth parameter $ H$.10 The first term in equation (11), $ \gamma_{0} \left( X_{\delta}\right) $, is identical to the standard realized variance estimator. The second term is a weighted sum of autocovariances up to order $ H$ and can be viewed as a correction term that aims to eliminate the serial dependence in returns induced by market microstructure noise. The estimator given in equation (11) is obviously a natural analogue of the well-known heteroskedasticity and autocorrelation consistent (HAC) estimators of long-run variances in more typical econometric settings.

Apart from realized kernel estimators, so-called subsampling estimators (e.g., Zhang, Mykland, and Aït-Sahalia 2005) have also been proposed to correct for the effects of market microstructure noise. Subsampling estimators are, in fact, very closely related to realized kernel estimators; see Aït-Sahalia, Mykland, and Zhang (2008), BNHLS, as well as the discussion of the quadratic form representation in Andersen, Bollerslev, and Meddahi (2006). Since the initial version of this paper was written, several studies that analyze the so-called pre-averaging approach to estimating realized volatility have been published; see Jacod, Li, Mykland, Podolskij, and Vetter (2009). To keep the exposition of our empirical results manageable in this paper, we focus only on the realized kernel approach.

2.5  Absolute power and bipower variation methods

Any estimator of volatility which is based on squared values of observations will, to some extent, be sensitive to the occurrence of outliers in the data in general, and, within the framework of financial models, to jumps in asset prices.11 To examine how the presence of jumps affects the properties of the realized variance estimator (4), it is necessary to consider generalizations of the data generating process (2). Barndorff-Nielsen and Shephard (2006b) do so by replacing the Brownian motion component of (2), $ \int_{0}^{t}\! \sigma_{u} \dee W_{u}$, with a Lévy process. Lévy processes have independent and stationary increments but need not have continuous sample paths. All non-Brownian Lévy processes have jumps, and they may be classified according to whether the number of jumps in any finite period of time is finite or infinite; the resulting classes are labeled finite-activity and infinite-activity Lévy processes, respectively.12

To simplify the exposition of how the presence of jumps affects the estimation of integrated volatility, we shall restrict our attention to the case of finite-activity Lévy processes which contain a diffusive component.13Suppose that the log price process $ X_{t}$ is given by

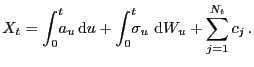$\displaystyle X_{t}=\int_{0}^{t}\!\!\!a_{u}\dee u+\int_{0}^{t}\!\!\!\sigma _{u}\, \dee W_{u}+\sum_{j=1}^{N_{t}}c_{j}\,.$ (12)

The process $ N_{t}$ is a finite jump counting process, and the coefficients $ c_{j}$ are the sizes of the associated jumps.14 The total quadratic variation of $ X_{t}$ is now given by

$\displaystyle \left[ X,X\right] _{t}=\int_{0}^{t} \!\!\! \sigma_{u}^{2} \dee u + \sum_{j=1}^{N_{t}} c_{j}^{2}\,,$ (13)

and it is straightforward to show that the realized variance (4) converges to this term as $ \delta\downarrow0$.

In the tradition of robust econometric estimation, absolute-value versions of the realized variance estimator have been introduced. Barndorff-Nielsen and Shephard (2004b) consider the following normalized versions of realized absolute variation and realized bipower variation. They set

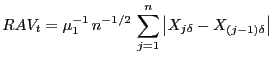$\displaystyle RAV_{t}=\mu_{1}^{-1}\,n^{-1/2}\,\sum_{j=1}^{n} \abs {X_{j\delta} - X_{(j-1)\delta} }$ (14)

and

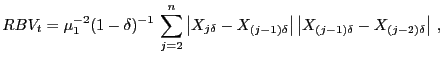$\displaystyle RBV_{t}=\mu_{1}^{-2}(1-\delta)^{-1}\,\sum_{j=2}^{n} \abs { X_{ j\delta}-X_{(j-1)\delta}}\abs { X_{(j-1)\delta}- X_{(j-2)\delta}}\,,$ (15)

where $ \mu_{1}=\E {\abs {Z}}=\sqrt{2/\pi}\approx0.798$ and $ Z$ is a standard normal random variable. Because a diffusion process has unbounded absolute variation, scaling by $ n^{-1/2}$ is required in equation (14) in order to obtain an estimator that converges to a proper limit as the sample size, $ n$, increases to infinity; this contrasts with the definitions of the realized variance and realized bipower estimators, where no such adjustment term is required. The term $ (1-\delta)^{-1}$ in equation (15) is a small-sample correction factor. In the absence of market microstructure noise and assuming that equation (2) holds, Barndorff-Nielsen and Shephard (2004b) show that $ RAV_{t}$ and $ RBV_{t}$, respectively, are consistent estimators of the quantities $ \int_{0}^{t}\! \sigma_{u} \dee u$ and $ \int_{0}^{t}\! \sigma _{u}^{2}\dee u$. Hence, realized bipower variation provides an alternative estimator of the integrated variance of $ X_{t}$ when the data do not contain a jump component.

Of primary interest for the discussion of the effects of jumps on volatility estimation is that it has been shown that bipower variation is a consistent estimator of $ \int_{0}^{t}\! \sigma_{u}^{2}\dee u$ under much more general conditions than (2). For instance, under (12) the realized absolute variation and the realized bipower variation are still consistent estimators of $ \int_{0}^{t}\! \sigma_{u} \dee u$ and $ \int_{0} ^{t}\! \sigma_{u}^{2} \dee u$, respectively. By calculating both the realized (quadratic) variation and the realized bipower variation of $ X_{t}$, one can separate the total quadratic variation into its diffusive and jump components. This is useful, for instance, in volatility forecasting, because the jump component of the total quadratic variation is, in general, far less persistent than the diffusive component (Andersen, Bollerslev, and Diebold 2007). Even though the limit of the realized absolute variation, $ \int_{0}^{t}\! \sigma_{u} \dee u$, has no direct use in most financial applications, such as the pricing of options, Forsberg and Ghysels (2007) and Ghysels, Santa-Clara, and Valkanov (2006) report that it is, empirically, a very useful predictor of future quadratic variation.

Since predicting future volatility is often the ultimate goal, we therefore also discuss in our paper how often to sample when estimating the absolute variation of the returns to a financial time series that is obtained from deep and liquid markets. In particular, we examine how estimates of realized absolute variation may be affected by market microstructure noise in such markets. So far, there has been little work aimed at dealing with the presence of market microstructure noise when calculating realized absolute and bipower variation. The only attempt that we are aware of is a paper by Andersen, Bollerslev, and Diebold (2007). They suggest using staggered, or skip-one, returns to mitigate spurious autocorrelations in the returns that may occur due to microstructure-induced noise. That is, they suggest using the following modified version of equation (15),

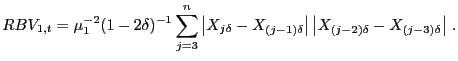$\displaystyle RBV_{1,t}=\mu_{1}^{-2}(1-2\delta)^{-1}\sum_{j=3} ^{n} \abs { X_{j\delta}-X_{(j-1)\delta }}\abs {X_{(j-2)\delta}- X_{(j-3)\delta }}\,.$ (16)

3  The Data

3.1  The Foreign Exchange Data

We analyze high-frequency spot dollar/euro exchange rate data from EBS (Electronic Broking System) spanning January through December 2005. EBS operates an electronic limit order book system used by virtually all FX dealers across the globe to trade in several major currency pairs. Since the late 1990s, inter-dealer trading in the spot dollar/euro exchange rate, the most-traded currency pair, has, on a global basis, become heavily concentrated on EBS . As a result, over our sample period EBS processed a clear majority of the world's inter-dealer transactions in spot dollar/euro. Publicly available estimates of EBS's share of global trading volume in 2005 range from 60 to 90%, and prices on the EBS system were the reference prices used by all dealers to generate dollar/euro derivatives prices and spot prices for their customers. Further details on the EBS trading system and the data can be found in Chaboud, Chernenko, and Wright (2008) and Berger, Chaboud, Chernenko, Howorka, and Wright (2008).

The exchange rate data we use are the midpoints of the highest bid and lowest ask quotes in the EBS limit-order book at the top of each second. The exchange rate is expressed as dollars per euro, the market convention. The source of the data is the EBS second-by-second ticker, which is provided to EBS's clients to generate customer quotes and as input for algorithmic trading. These quotes are executable, not just indicative, and they therefore represent a true price series. We consider 5 full 24-hour trading days per week, each one beginning at 17:00 (5 p.m.) New York time.15 Trading occurs around the clock on EBS on those days. We exclude all data collected from Friday 17:00 New York time to Sunday 17:00 New York time from our sample, as trading activity during weekend hours is minimal and is not encouraged by the FX trading community.

We chose to drop several market holidays and days of unusually light trading activity near these holidays in 2005: January 3, March 25 and 28 (Good Friday and Easter Monday), May 31 (Memorial Day), July 4, September 5 (Labor Day), November 24 and 25 (Thanksgiving and the following day), December 23 and 26, and December 30. Similar conventions on holidays have been used in other research on FX markets, such as by Andersen, Bollerslev, Diebold, and Vega (2003). The resulting number of business days is 250. In the analysis undertaken for this paper, we drop an additional 4 days in order to line up the FX trading days with those in the U.S. bond market, in which several additional business days are treated as market holidays, as described below.

The upper half of Table 1 presents some summary statistics for dollar/euro returns sampled at 24-hour and 5-minute intervals, where returns are calculated as log-differences of the dollar/euro exchange rate. In 2005, the average 24-hour return was about -2 basis points (= -0.02 percent)--here, a negative return implies an appreciation of the dollar versus the euro--and its standard deviation was about 50 basis points (0.5 percent). At the 5-minute frequency, the mean return is, of course, very near zero. At the 5-minute frequency, returns were extremely leptokurtic, and their standard deviation was about 3 basis points.

Table 1.  Summary Statistics

 
Sampling Interval Length: 24 Hours
Sampling Interval Length: 5 Minutes
(i) FX Returns: Mean
-4.94
-0.014
(i) FX Returns: Absolute Mean
43.31
2.16
(i) FX Returns: Standard Deviation
55.71
3.30
(i) FX Returns: Skewness
0.23
-0.14
(i) FX Returns: Kurtosis
3.27
22.17
(i) FX Returns: Minimum
-139.1
-61.19
(i) FX Returns: Maximum
169.8
76.26
(ii) 10-Year T-Note Returns: Mean
-0.68
0.001
(ii) 10-Year T-Note Returns: Absolute Mean
30.20
2.05
(ii) 10-Year T-Note Returns: Standard Deviation
37.91
3.15
(ii) 10-Year T-Note Returns: Skewness

-0.24
-0.57
(ii) 10-Year T-Note Returns: Kurtosis
2.87
24.09
(ii) 10-Year T-Note Returns: Minimum
-109.04
-55.14
(ii) 10-Year T-Note Returns: Maximum
80.66
38.84

All numbers are expressed as basis point of the price.

3.2  The Bond Market Data

We analyze high-frequency 10-year on-the-run Treasury cash market data from BrokerTec, also spanning January through December 2005. In the last few years, BrokerTec has become one of the two leading electronic brokers for inter-dealer trading in Treasury securities.16 Estimates of BrokerTec's share of trading in on-the-run Treasury securities in 2005 range from 40 percent to 70 percent. BrokerTec operates an electronic limit order book in which traders can enter bid or offer limit orders (or both) and can also place market orders, similar to EBS .17 Fleming and Mizrach (2008) provide an overview and an analysis of the market microstructure features inherent in the BrokerTec platform.

The 10-year Treasury price data that we use are the midpoint of the highest bid and lowest ask quotes at the top of each second. As in the EBS data, the BrokerTec quotes are executable, not just indicative, and they therefore constitute a true price series. Unlike the EBS data, however, we focus on five 8-hour-long trading days per week, from 08:00 New York time to 16:00 New York time. BrokerTec operates (nearly) continuously on five days each week, from 19:00 New York time to 17:30 New York time, with Monday trading actually beginning on Sunday evening New York time. However, unlike trading in dollar/euro, the vast majority of trading in Treasury securities occurs during New York business hours (Fleming 1997), and for this reason we limit our analysis to the 08:00 to 16:00 New York time frame. We excluded the same holidays and days of extremely light activity from our sample that we excluded from our EBS data. We also dropped a few additional days, which the U.S. Bond Market Association declared to be market holidays, from the sample.18 The total number of business days retained for both datasets is 246.

The lower half of Table 1 presents summary statistics for T-note returns sampled at 24-hour and 5-minute intervals, where the T-note returns are calculated as log differences of the price of the 10-year on-the-run Treasury note. Daily returns are measured from 16:00 New York time readings. The mean daily price return is about $ 2$ basis point (0.02 percent) and the standard deviation of daily T-note returns was about 44 basis points in 2005.19 Returns at the five-minute frequency have a standard deviation of about 3 basis points, and they are also very leptokurtic.

3.3  Prevalence of Zero-Return Intervals Across Sampling Frequencies

The highest available sampling frequency in our datasets is once every second, by construction. In order to have a reasonably large number of within-day samples within each trading day for each frequency we consider, we set the longest sampling interval equal to 30 minutes (1,800 seconds) for the dollar/euro returns and to 15 minutes (900 seconds) for T-note returns, resulting in within-day sample sizes of 48 and 32, respectively, at the lowest sampling frequencies.

A large fraction of the observed high-frequency returns in both markets under study is equal to zero. A zero return during a given sampling interval can occur either because the price changes during the sampling interval but then returns to its initial level before the interval ends or--much more commonly--because the price does not change at all. Table 2 presents the fraction of sampling intervals with zero returns in both markets, for sampling interval lengths ranging from 1 second to 10 minutes. At the 1-second sampling frequency, about 90 percent of all returns are zero in both series, although the fraction of zero returns is slightly higher for the T-note data. At the 1-minute sampling frequency, 45 percent of all T-note returns are zero and 26 percent of all exchange rate returns are zero. In Section 6 we consider in detail the consequences of the prevalence of sampling intervals with zero returns on the optimal selection of the sampling frequency and on the estimation of integrated volatility using absolute and bipower variation methods.

Table 2. Frequencies of Zero Returns in Foreign Exchange and Treasury Note Data - Sampling Interval Length (in seconds)

 
1
5
15
30
60
300
600
FX
0.861
0.652
0.478
0.365
0.263
0.108
0.070
10-Year T-Note
0.924
0.789
0.652
0.549
0.450
0.239
0.174

4.3  U.S. Macroeconomic Data Releases

The impact of scheduled U.S. macroeconomic data releases on the level and volatility of exchange rates and government bond prices has been well documented; see, e.g., Andersen, Bollerslev, Diebold, and Vega (2003) for foreign exchange and Fleming and Remolona (1999) and Balduzzi, Elton, and Green (2001) for Treasury securities. In the empirical analysis below, we split the full sample into days with scheduled U.S. macroeconomic announcements, selected because of their apparent impact on asset prices, and days without announcements. The monthly announcements we select are the employment report (non-farm payrolls and the rate of unemployment), the consumer price index, the producer price index, retail sales, and orders for durable goods. We also select the three quarterly GDP releases (advance, preliminary, final), each released quarterly, and the eight FOMC announcements. With the exception of the FOMC announcements, which are released at about 14:15 New York time, all announcements considered here are released at 8:30 New York time. We treat these days as announcement days irrespective of whether the actual data released differed from published market expectations or not. Accounting for days with multiple announcements, this gives us a subsample size of 58 days; the number of non-announcement days is 188.

4  Results for the Standard Estimator of Integrated Volatility

4.1  Overview

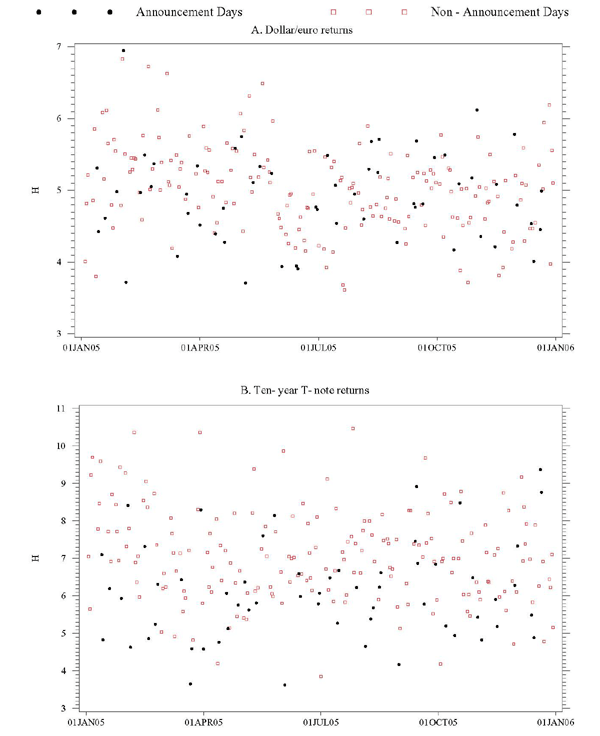
Figure 1 shows the 2005 time series of daily estimates of the integrated volatility of dollar/euro returns and T-note returns, based on the standard realized volatility estimator and a sampling frequency of once every five minutes. Several conclusions may readily be drawn from these plots. First, for both series there is considerable dispersion in volatility across adjacent days. Second, in 2005 neither volatility series displays a discernible time trend or any seasonality patterns, indicating that it may be meaningful to compute (suitably defined) averages in order to study general relationships between sampling frequency and realized volatility. Third, volatility is clearly higher, on average, on days with scheduled major U.S. macroeconomic news announcements, depicted by solid circles in both plots, than on non-announcement days, shown as open squares. This is particularly--but certainly not surprisingly--true for the T-note return volatility estimates shown in Panel B of Figure 1.

Figure 1.  Point Estimates of Realized Volatility in 2005, Dollar/Euro and T-Note Returns

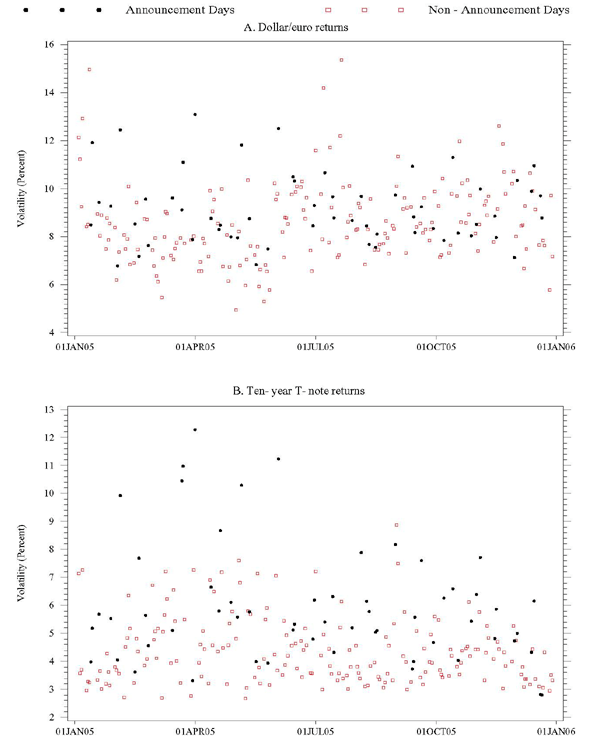
Figure 1 has two panels. The upper panel shows daily realized volatility for foreign exchange (FX) returns. The lower panel shows daily realized volatility for ten-year Treasury note returns. In each panel, the x-axis is time, daily, from January 1, 2005, through December 30, 2005. The y-axis is volatility, expressed in percent (one standard deviation as a percent of the price, annualized). Volatility on days with U.S. macro announcements is shown as dots, volatility on days without announcements is shown as little squares. Volatility ranges from 5 to 16 percent for FX returns, from 8 to 12 percent for T-note returns. Volatility tends to be higher on days with macro announcements, but not always so.

Note: Realized volatility estimates are based on returns sampled at 5-minute intervals.

A volatility signature plot, by common convention, graphs sampling frequencies on the horizontal axis and the associated estimates of realized volatility on the vertical axis. Such plots, which appear to have been first used in the context of realized volatility estimation by Andersen, Bollerslev, Diebold, and Labys (2000, p. 106), are now used frequently in empirical research on this subject because they provide an intuitive visual tool for the analysis of the relationships between these two variables. Quite often, it is possible to discern from a volatility signature plot a sampling frequency, which we will call the critical sampling frequency, that serves to separate sufficiently-low frequencies, for which market microstructure noise does not seem to affect estimates of realized volatility, from the higher frequencies, for which market microstructure noise does appear to have an effect. We make extensive use of volatility signature plots in our paper.

Because we need to display volatility estimates over very wide ranges of sampling interval lengths--from 1 second to nearly 210 seconds--and because our focus is on the empirical effects of market microstructure noise--which is generally thought to be present in returns mainly at the highest sampling frequencies--we display all signature plots using a base-2 logarithmic scale on the horizontal axis. A logarithmic scale, by design, gives greater visual prominence to the relationship between sampling frequency and volatility at shorter sampling intervals (higher sampling frequencies).

The shapes of the daily volatility signature plots can vary considerably across days. Figure 2 shows signature plots for dollar/euro volatility for two days in 2005: October 3, a day of average volatility, and July 21, the day in 2005 with the highest realized volatility using sampling intervals of 5 minutes.20 The two signature plots differ not only in their vertical scales but also in their shapes. On October 3 (Figure 2A), realized volatility decreases at first as the sampling interval lengths increase from 1 second to about 15 seconds, then shows no further trend and roughly constant dispersion as the sample intervals lengthen to about 120 seconds, and exhibits a rapidly increasing dispersion as the lengths of the sampling intervals increase further to 30 minutes (1,800 seconds). On July 21, realized volatility declines, though only slightly, as the sampling interval length rises from 1 second to 3 seconds; volatility then increases modestly on average and also is slightly more dispersed as the interval lengths rise to about 120 seconds, and it becomes much more dispersed (but without apparent trend) as the interval lengths increase further.

Figure 2. Realized Volatility Signature Plots for Dollar/Euro Returns on 2 Specific Dates

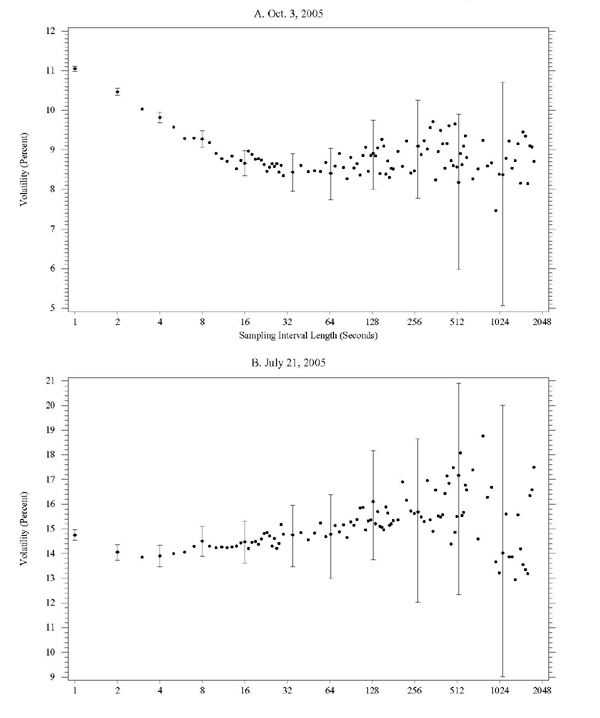
Figure 2 has 2 panels, corresponding to specific days in 2005 (October 3 and July 21). In each panel, the x-axis is sampling interval length, ranging from 1 to 2048 seconds, the y-axis is realized volatility for the euro-dollar, expressed in percent. For the October 3 sample, realized volatility based on long sampling intervals is about 9 percent, but it rises towards 11 percent at sampling intervals below 15 seconds. For the July 21 sample, the volatility based on long sampling intervals is about 15 percent. It declines towards 14 percent as sampling intervals decline.

Notes: Horizontal axes use logarithmic scale. Vertical lines represent 95% confidence intervals. The confidence interval in Panel B for the 1024-second interval is truncated below to conserve vertical space.

Ninety-five percent confidence intervals, based on the asymptotic result stated in equation (5), are also shown in Figure 2 for selected sampling frequencies.21 These confidence intervals clearly illustrate the potential benefits of sampling more frequently, as they show that sampling uncertainty regarding volatility declines rapidly as the number of intra-daily observations increases. Of course, the confidence intervals are only unbiased if the realized volatilities that they are constructed around are unbiased estimates of the true integrated volatility. As the sampling frequency increases, this assumption becomes increasingly less likely. However, if one could sample dollar/euro returns at, say, the 30-second frequency without inducing bias, the increase in precision compared with the conventional 5-minute sampling frequency is clearly considerable.

Considerable heterogeneity in the shapes of the dependence of realized volatility on the sampling frequency also applies to T-note returns; cf. Figure 3. On October 3, realized volatility at first decreases steadily, up to a sample length of about 15 seconds, and then becomes increasingly dispersed without an apparent trend as the sampling intervals lengthen further. On July 21, in contrast, the point estimates of realized volatility decline on average as the sample length increases, while their dispersion, even across adjacent sample lengths, becomes rapidly very pronounced. 95 confidence intervals are shown for selected frequencies.

The signature plots in Figures 2 and 3 thus illustrate a distinct advantage of computing realized volatility at higher rather than at lower intraday frequencies--as long as, of course, the sampling frequency does not exceed the critical sampling frequency. The signature plots show that the range of realized volatility estimates across adjacent sampling frequencies is considerably lower if dollar/euro and T-note returns are sampled at sample interval lengths between 15 and 120 seconds than if they are sampled at longer intervals. Sampling at higher frequencies therefore makes it less likely that the choice of the sampling frequency introduces an undesirable degree of arbitrariness into the process of estimating realized volatility.22

4.2  The Dependence of Realized Volatility on the Sampling Frequency

As we noted in the discussion of Figure 1, the realized volatility of dollar/euro and T-note returns is higher, on average, on days with scheduled major U.S. macroeconomic news announcements. This result is especially evident when one averages the daily volatility estimates over time, i.e., if the volatility signature curves are averaged separately for announcement days and non-announcement days.

Figure 3. Realized Volatility Signature Plots for T-Note Returns on 2 Specific Dates

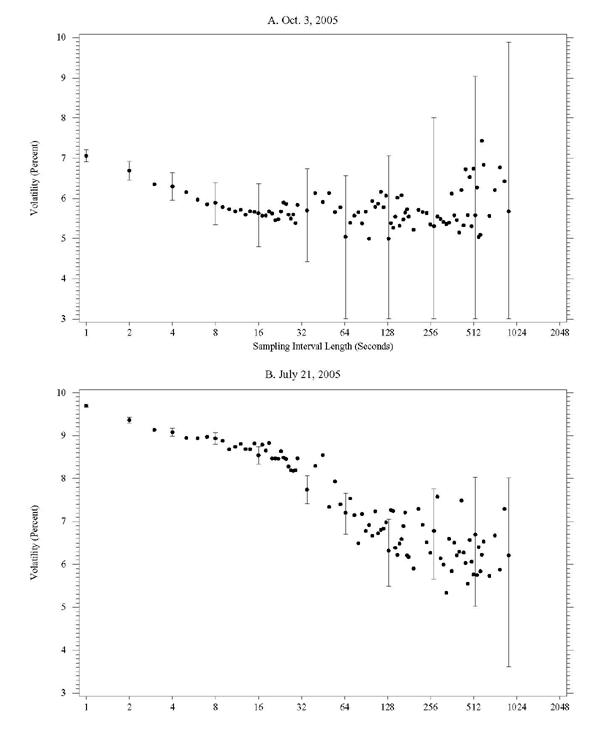
Figure 3 is similar to figure 2, but the volatility is based on T-note returns. The figure has 2 panels, corresponding to specific days in 2005 (October 3 and July 21). In each panel, the x-axis is sampling interval length, ranging from 1 to 2048 seconds, the y-axis is volatility, expressed in percent. On the 2 dates, the volatility increases as the sampling intervals decrease. For October 3, the volatility starts rising as the sampling interval goes below 16 seconds. For the July 21 date, the volatility rises below sampling intervals of 128 seconds.

Notes: Horizontal axes use logarithmic scale. Vertical lines represent 95% confidence intervals. The confidence intervals in Panel A for the 64-second to 1024-second intervfals are truncated below to conserve vertical space.

Figure 4A shows the effect of averaging within each of these two types of days on the relationship between sampling frequency and realized volatility for dollar/euro returns. The plot highlights the stylized fact that if a day falls into the subset of announcement days, realized volatility is elevated relative to the subset of non-announcement days. In addition, the figure also shows that, on average, estimates of realized volatility on non-announcement days are quite insensitive to the choice of sampling interval length, at least as long as it falls into a range from about 20 seconds to about 10 minutes. In contrast, for sampling intervals shorter than 20 seconds, the estimates of integrated volatility are noticeably higher, and they increase progressively as the interval lengths decrease. This suggests that whereas market microstructure noise is present and affects realized volatility at the very highest sampling frequencies, it does not have a noticeable effect on realized volatility for sampling frequencies lower than once every 20 seconds. This same general finding also applies for the subset of days with major scheduled economic announcements: realized volatility increases markedly if returns are sampled more often than once every 15 seconds.23 For the case of dollar/euro returns, the critical sampling frequencies, i.e., the frequencies above which market microstructure noise has an increasingly important influence on realized volatility, are thus roughly the same in the two subsamples.

Figure 4B shows the time-averaged signature plots of T-note returns for announcement days and for non-announcement days. One notes immediately that, for any given sampling frequency, integrated volatility is much higher on announcement days than it is on non-announcement days. In addition, it appears that, on average, the contribution of market microstructure noise to realized volatility is considerably larger for T-note returns, as the slopes of the (time-averaged) signature plots are steeper at the very highest sampling frequencies than was the case for dollar/euro returns. Third, and of the most relevance for the purposes of our paper, the critical sampling frequency is rather different from the dollar/euro case, for both announcement and non-announcement days. It is in the range of once every 120 to 180 seconds on days without scheduled major macroeconomic announcements, and about once every 40 seconds on announcement days. We infer that even though volatility is higher on announcements days, the critical sampling frequency is at least three times higher on announcement days than on non-announcement days. This finding clearly suggests that it is preferable to sample T-note returns more frequently on announcement days than on non-announcement days, in order to obtain volatility estimates that are more precise yet not affected noticeably by market microstructure noise.

Figure 4. Time-Averaged Realized Volatility Signature Plots and Announcement Effects

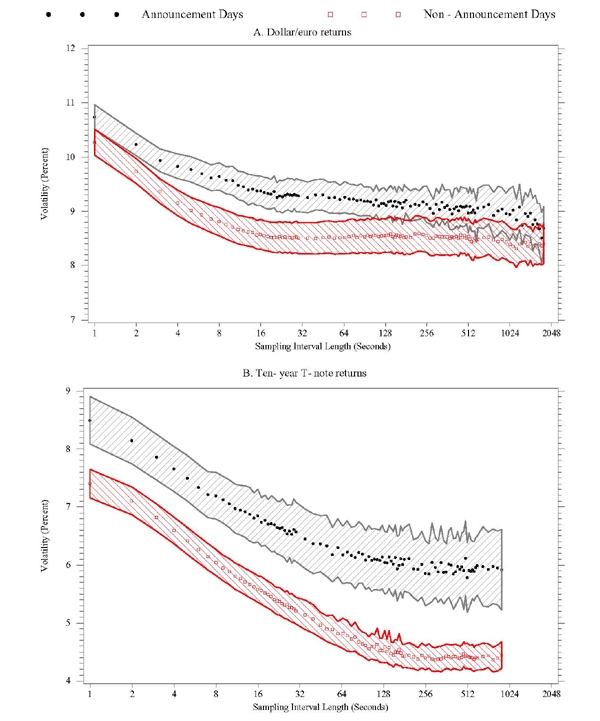
Figure 4 has two panels, the top for FX, the bottom for T-notes. In each panel, the x-axis is sampling interval length, ranging from 1 to 2048 seconds, the y-axis is volatility, expressed in percent. There are two set of points in each panel, on for announcement days, one for days without announcements. Shaded areas show 95% confidence intervals. In both panels, average realized volatility is higher for announcement days, and it rises as the sampling interval gets smaller.

Notes: Horizontal axes use log scale. Shaded areas represent 95% confidence intervals for average volatility.

The shaded areas in the graphs in Figure 4 represent 95% confidence intervals for the average daily volatilities, on announcement and non-announcement days, for each sampling frequency.24 These confidence intervals further highlight the difference in the average volatility on announcement and non-announcement days.

To sum up, when using the standard realized volatility estimator, the volatility signature plots suggest that it is possible to sample dollar/euro returns as frequently as once every 20 seconds on non-announcement days (15 seconds on announcement days), and to sample T-note returns as often as once every 2 to 3 minutes on non-announcement days (once every 40 seconds on announcement days), without incurring a significant penalty in the form of an upward bias to estimated volatility. Our estimated critical sampling frequencies--especially for the case of dollar/euro returns--are considerably higher than those published by other researchers, who typically focused on returns to individual equities and suggested that one should not sample more often than once every 5 minutes or so if one wishes to avoid bias caused by market microstructure dynamics (e.g., Andersen, Bollerslev, Diebold, and Ebens 2001).25

4.3  A Formal Rule for Choosing the Optimal Sampling Frequency

In addition to examining volatility signature plots, one may wish to have a more formal method for establishing the critical sampling frequency. One such method is the optimal sampling rule of Bandi and Russell (2006), which was introduced in Section 2 and is also very similar to the rule developed by Aït-Sahalia, Mykland, and Zhang (2005). The optimal sampling frequencies for dollar/euro and T-note returns are shown in Figure 5 for each day of the sample. The average sample interval lengths across all days in the full sample are 170 and 327 seconds, respectively, for dollar/euro returns and T-note returns. Although there is a fair degree of variation from day to day, these averages are nevertheless considerably above those we deduced from the volatility signature plots shown in the previous section. This is especially true for dollar/euro returns; according to the signature plots, it may be possible to sample as often as once every 15 to 20 seconds in the dollar/euro market without incurring a significant bias caused by market microstructure features.

Signature plots are, of course, informal graphical tools which cannot by themselves deliver unambiguous answers. Nevertheless, signature plots are essentially model-free and they rely on much less stringent assumptions about the nature of the data generating process than formal sampling rules do. For example, the method of Bandi and Russell (2006) assumes that there are no jumps in the price process. Even more important, in our view, is the possibility that the variance  $ \omega^{2}$ of the noise term cannot be estimated properly from the returns sampled at the second-by-second frequency, which is the highest-available frequency in both datasets. If the time series are generated in deep and liquid markets, returns sampled even at the second-by-second frequency may still contain too much signal, and hence not enough noise, in order to be able to estimate  $ \omega^{2}$ consistently. (Hansen and Lunde (2006) make a similar point.) This issue may be less of a concern for the T-note returns, where the signature plots indicated critical sampling intervals in the 2 to 3 minute range. This may explain why the results from the signature plots and the Bandi-Russell sampling rule are somewhat closer to each other for T-note returns than they are for dollar/euro returns.

Figure 5. Optimal Samplling Interval Lengths Suggested by Bandi and Russell (2006) Method

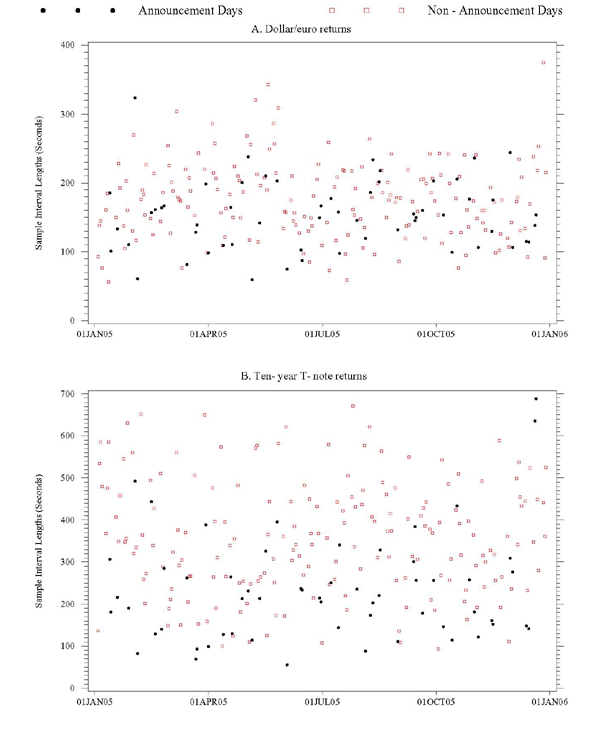
Figure 5 has two panels, the top for FX, the bottom for T-notes. In each panel, the x-axis is the date, ranging from January 1, 2005 to December 30, 2005. The y-axis shows, for each day, the optimal sampling interval length suggested by Bandi and Russell (2006). It ranges from 0 to 400 seconds for FX and 0 to 700 seconds for T-notes. The optimal sampling intervals are usually lower for announcement days.

The optimal sampling frequencies we obtain using the Bandi and Russell rule are higher, and the associated sampling interval lengths are shorter, on days with scheduled U.S. macro announcements. This confirms one of the findings we obtained from the signature plots, which is that even though market microstructure noise is likely to be greater on announcement days (for instance, in terms of a larger bid-ask spread), the signal is even stronger on such days, implying that the critical sampling frequency is higher on announcement days.

As we noted in Section 3.3, when returns are sampled at very high frequencies, many of the dollar/euro and T-note returns are zero because there is no price change over many of the short time intervals. Phillips and Yu (2006, 2008) observe that the prevalence of flat pricing over short time intervals implies that the market microstructure noise and the unobserved efficient price components of the observed price process are negatively correlated over these periods, and that these two components may become perfectly negatively correlated as $ \delta\downarrow0$. In addition, the maintained assumption that the market microstructure noise is independent of the latent price process, which underlies the derivation of the Bandi and Russell rule, cannot be strictly valid if the observed price process is discrete rather than continuous. In such a framework, sampling at ever-higher frequencies ultimately does not even produce a consistent estimator of the variance of the market microstructure noise. If this feature of the data is not taken into account, the Bandi and Russell rule will tend to lead to choices of the optimal sampling interval lengths that are too large. We interpret our empirical results as being fully consistent with this theoretical observation.

5  Kernel-Based Methods

5.1  Autocorrelations in High-Frequency Returns

The use of the realized kernel estimator of integrated volatility, described in Section 2.4 above, is motivated along lines similar to those for heteroskedasticity and autocorrelation consistent (HAC) estimators of the long-run variance of a time series in traditional econometrics (e.g., Newey and West 1987). That is, by adding autocovariance terms, an estimator is constructed which better captures the relevant long-run variance in the data. Before showing our empirical results for the performance of the BNHLS realized kernel estimator, it is therefore instructive to study the autocorrelation patterns in the high-frequency intraday returns data to build up some intuition that will help guide the interpretation of our empirical results.

Figure 6 shows the average autocorrelation across all days in the sample, out to 30 lags, for data sampled at the 1, 10, 30, and 60-second sampling frequencies. That is, for a given lag and sampling frequency, the within-day autocorrelation in high-frequency returns is calculated for each day and is then averaged across all days in the sample. When sampling at the 1-second frequency, it is evident that there is some negative autocorrelation in both dollar/euro and T-note returns, and that this correlation stretches out for about 10 to 15 lags, i.e., that non-zero serial dependence in 1-second returns persists for about 10 to 15 seconds. For returns sampled at the 10-second frequency, there is still some evidence of nonzero autocorrelation in the first 4 to 5 lags. For returns sampled at the 30- and 60-second frequencies, there is little evidence of any systematic pattern in the autocorrelations of the dollar/euro returns; for the T-note returns, only the first two serial correlation coefficients are nonzero for these two sampling frequencies.

The autocorrelation patterns shown in Figure 6 correspond well to the findings using signature plots of how often one can sample returns when using the standard realized volatility estimator. In particular, there is little evidence of any autocorrelation in the dollar/euro data for returns sampled at frequencies lower than once every ten seconds. The conclusion from the volatility signature plots shown above was that the critical sampling frequency for dollar/euro returns is in the 15 to 20 second range. This finding corresponds very well to the fact that dollar/euro return autocorrelations are insignificant for time spans beyond about 20 seconds. Similarly, because there is still a large amount of negative first-order autocorrelation in the one-minute T-note returns, it is not surprising that we also obtained a much lower critical sampling frequency for this asset using the signature plot method.

Overall, the results in Figure 6 suggest that in the case of dollar/euro returns and for sampling intervals shorter than 30 seconds, using kernel estimators should help reduce any bias in realized volatility estimates. For T-note returns, this results holds for returns sampled at frequencies higher than once every 2 minutes.

5.2  Optimal Bandwidth Choice

The graphs in Figure 6 give some indication of how many lags one may want to include in the realized kernel estimator in equation (11). However, they do not, by themselves, provide a simple prescription for action. BNHLS also propose a rule for an optimal choice of the bandwidth or lag truncation parameter. They show that, in their framework, the optimal bandwidth is a function of both the sampling frequency and a scale parameter, $ \hat{c}$, which is independent of the sampling frequency; $ \hat{c}$ must be estimated, and the details are given in BNHLS . The optimal bandwidth is then given by $ H=\hat{c}\,n^{1/2}$.

Figure 6.  Autocorrelation Functions of Returns Sampled at Selected Frequencies

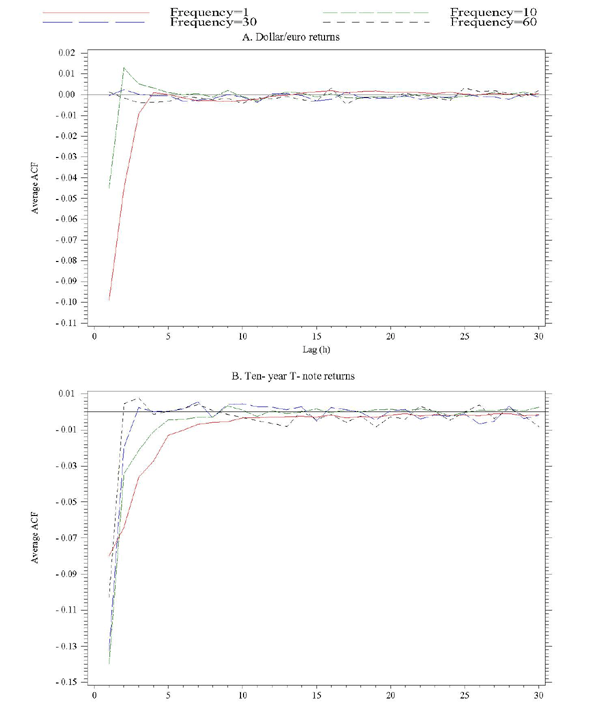
Figure 6 has two panels, the top for FX, the bottom for T-notes. In each panel, the x-axis is the lag used in calculating autocorrelation, ranging from 0 to 30. The y-axis is the average autocorrelation coefficient, centered at 0. In each panel, we show lines for autocorrelations calculated at 4 sampling frequencies, corresponding to intervals of 1,10, 30 and 60 seconds. For lags of 5 and above, autocorrelations are all near zero. At shorter lags, particularly one, returns tend to be negatively autocorrelated, more so in T-notes.

Note: Sampling frequencies are expressed in seconds.

The time series of optimal bandwidths in 2005 for returns sampled at the 1-second frequency are shown in Figure 7. For dollar/euro data (Figure 7A), the optimal bandwidths range between 4 and 7, and for T-note returns (Figure 7B), the optimal bandwidths are typically between 5 and 10. The optimal bandwidths are roughly similar to, but usually somewhat smaller, than the number of lags for which there seems to be a non-zero autocorrelation in the 1-second returns (Figure 6). As with any kernel estimator, the choice of the value for the bandwidth parameter involves a bias-variance trade-off, with a larger value leading to a smaller bias but also a higher variance. The optimal bandwidth choice incorporates this bias-variance trade-off. It is, in general, not optimal to control for all of the autocorrelation in the data by using a very large value for the bandwidth parameter, as doing so may induce a lot of variance into the estimator.

Calculating the optimal bandwidth parameter $ H$ for returns sampled at the 1-minute and lower frequencies, we find that the result is always a number between 0 and 1 for the dollar/euro returns series and between 0 and 2 for the T-note series, for all days in the sample. Depending on whether one rounds the results up or down--recall that the bandwidth has to be an integer--the result is thus always an optimal bandwidth of either 0 or 1 for the dollar/euro data or 0, 1, or 2 for the T-note data, at these lower sampling frequencies. Throughout the rest of the analysis reported in this section, the estimate for the optimal bandwidth is always rounded up, so that at least one lag is always included in the realized kernel estimator that incorporates the optimally chosen bandwidth for each sampling frequency.

In summary, for the very highest sampling frequencies available in our dataset, the bandwidth selection rules of BNHLS suggest that a moderate number of lags should be included, but for lower sampling frequencies the rule indicates that at most two lags should be included.

5.3  Signature Plots for Realized Kernel Estimates

In this section we display signature plots for 6 different choices of $ H$: the standard realized volatility estimator (which corresponds to the realized kernel estimator with bandwidth zero), the realized kernel estimator with fixed bandwidths of 1, 5, 10, and 30, and the realized kernel estimator that uses a bandwidth optimally chosen for each sampling frequency.

As we did in Section 4 for the standard realized volatility estimator, we begin by studying the volatility signature plots for two specific business days in 2005. Signature plots for dollar/euro returns on these days are displayed in Figure 8, while signature plots for T-note returns are shown in Figure 9.26 Figure 8A shows the signature plot of dollar/euro returns on October 3, 2005, which was a day of average volatility. For this day, we easily observe the pattern that one would expect as a result of changing the bandwidth parameter. The standard estimator, which is obtained by setting $ H=0$, yields nearly constant estimates of realized volatility (of about 8.5 percent at an annualized rate) for all sampling interval lengths between about 15 seconds and about 4 minutes. In contrast, for sampling frequencies higher than about once every 15 seconds the standard estimator is biased upwards, and it becomes increasingly more biased as the sampling frequency increases. For bandwidths greater than 0, the influence of market microstructure noise on realized volatility becomes increasingly less pronounced, especially at the highest-available sampling frequencies. For $ H=1$ (the blue short-dashed line), we find that one can sample as frequently as once every 5 seconds without incurring any apparent bias in estimated volatility; setting $ H=10$ would allow us to sample as frequently as once every 2 seconds; and if one were to use 30 lags in the kernel estimator, there is no apparent bias even at the 1-second sampling frequency. Using the optimal bandwidth produces a signature plot that is quite similar to the one that results from using a fixed bandwidth equal to 1.

Figure 7. Optimal Choices of Bandwidth Parameter H Using the BNHLS Method, for 1-Second Returns

Figure 7 has two panels, the top for FX, the bottom for T-notes. In each panel, the x-axis is time, daily, from January 1, 2005, through December 30, 2005. The y-axis is the optimal bandwith parameter H, ranging from 3 to 7 for FX and from 3 to 11 for T-notes. Both announcement and non-annoucement days are shown. The optimal H, which varies in both panels from day to day, is greater on average for T-notes than for FX, and there is little obvious difference between announcement and non-announcement days.

Note: Bandwidth parameter H isnot constrained to be integer-valued.

In contrast, for the high-volatility day of July 21, 2005, shown in Figure 8B, it is harder to draw any firm conclusions. On that day, using a value of $ H>1$ would result in estimates of realized volatility that are actually slightly larger than those obtained with the standard estimator, except when the sampling interval lengths are as short as 1 or 2 seconds. It is worth noting that volatility and trading volume were both exceptionally high on that day, and hence it may not even be necessary to employ a kernel-based correction for this specific day in order to obtain a low-bias estimate of volatility.

The results for the T-note returns on the same two dates are overall quite similar to those for dollar/euro returns, but there are also some striking differences. In Figure 9A, for the medium-volatility day of October 3, 2005, we see a pattern that is fairly similar to the one we observed in Figure 8A for dollar/euro returns: setting $ H=1$ already achieves important gains in terms of the usable critical sampling frequency, from about once every 20 seconds to once every 4 seconds; by $ H=10$, one can sample as frequently as once every second; and increasing the bandwidth further to $ H=30$ produces little additional gain for any of the higher sampling frequencies of interest.27 For the high-volatility day of July 21, 2005, setting $ H=1$ shortens the critical sampling interval length from about 2 minutes to about 30 seconds, and setting $ H=10$ or $ H=30$ reduces the length of this interval further, to about 15 seconds.

Figure 10 shows the signature plots of dollar/euro returns averaged separately for non-announcement days and announcement days in 2005. As was discussed in Section 4, when using the standard realized volatility estimator the critical sampling interval length for dollar/euro returns on non-announcement days and announcement days, respectively, was between 15 and 20 seconds in 2005. By including just one lag in the realized kernel estimator, the critical sampling interval length for dollar/euro returns drops to about 4 seconds (on average) on non-announcement days. Using the optimal bandwidth selection rule of BHNLS results in a similar critical sampling interval length. If one sets $ H=10$ or $ H=30$, even sampling at the 1-second frequency seems admissible for the purpose of calculating realized volatility. On the subset of announcement days, shown in the lower panel of Figure 10, setting $ H=1$ shortens the critical sampling interval length to about 8 seconds, and setting $ H=5$ shortens this interval still further, to about 4 seconds.

Figure 8. Kernel-Based Realized Volatility Signature Plots, DOllar/Euro Returns, 2 Specific Dates

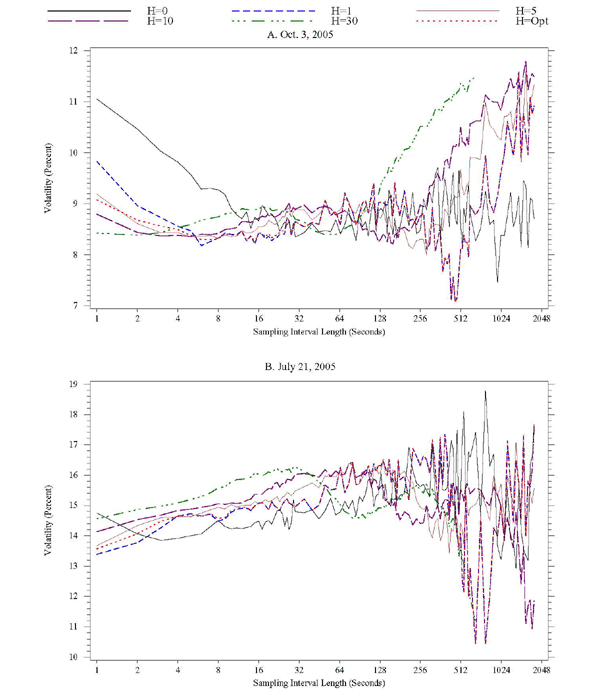
Figure 8 has 2 panels, corresponding to specific days in 2005 (October 3 and July 21). In each panel, the x-axis is sampling interval length, ranging from 1 to 2048 seconds, the y-axis is volatility, expressed in percent. In each panel, six lines are show, corresponding to kernel-based realized volatility estimates calculated with bandwidth parameters H equal to 0, 1, 5, 10, 30, and the optimal H. For the October 3 date, the kernel-based estimates are lower at short sampling intervals than the bandwidth-zero estimate, but that is not the case for the July 21 estimates.

Note: For the case of H=30, volatility estimates were computed only for sampling interval lengths up 600 seconds, as small-sample issues made calculating realized volatility unreliable at longer sampling intervals.

Figure 9. Kernel-Based Realized Volatility Signature Plots, T-Note Returns, 2 Specific Dates

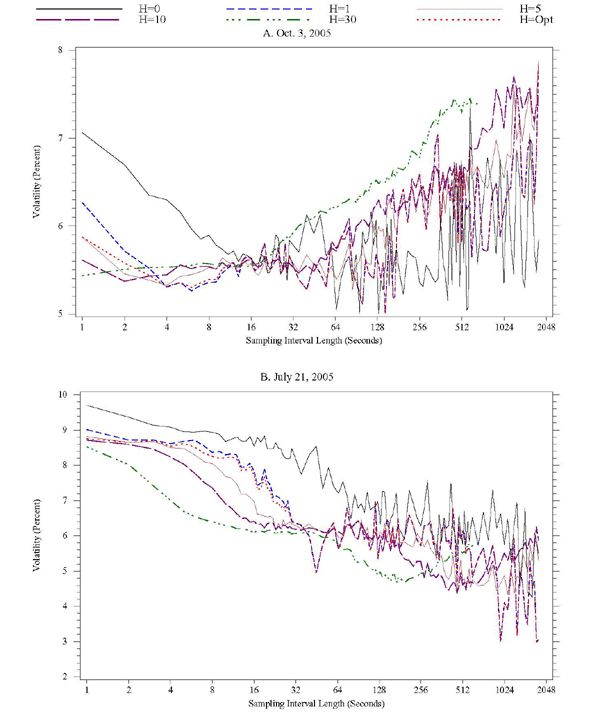
Figure 9 has 2 panels, corresponding to specific days in 2005 (October 3 and July 2). In each panel, the x-axis is sampling interval length, ranging from 1 to 2048 seconds, the y-axis is volatility, expressed in percent. In each panel, six lines are show, corresponding to kernel-based realized volatility estimates calculated with bandwidth parameters H equal to 0, 1, 5, 10, 30, and the optimal H. On both days, kernel-based estimates are lower at short sampling intervals than the bandwidth-zero estimate. In most cases, the lowest estimates are the ones with the highest bandwidth, although not at all sampling intervals.

Note: See explanation given in Figure 8

The results for the T-note returns, shown in Figure 11, are similar in nature to those for dollar/euro returns: including just 1 lag in the realized kernel estimator increases the critical sampling frequency to about once every 40 seconds on non-announcement days and to once every 30 seconds on announcement days. Using 30 lags, this frequency climbs to about once every 8 seconds, on both types of days in 2005.

5.4  Implications for Practical use of Realized Kernel Estimators

The results just presented indicate that there is considerable scope for achieving much higher critical sampling frequencies, for dollar/euro and T-note returns, by using a kernel estimator rather than the standard estimator of realized volatility, and thereby also achieving greater precision in the estimates of volatility. There is, however, a bias-variance trade off for the number of lags included in the realized kernel estimator. Thus, even though we find that using 30 lags would allow us to sample at the 1-second frequency in the case of dollar/euro returns and the 8-second frequency for T-note returns, it may not be optimal to do so. Indeed, according to the BNHLS rule, the (time-averaged) optimal bandwidth at the 1-second frequency is always much smaller than 30. Using the optimal bandwidth, the critical sampling frequency appears to be about once every 2 to 5 seconds for dollar/euro returns, while for T-note returns it is about once every 30 to 40 seconds.

Unfortunately, calculating the optimal bandwidth is fairly involved. However, judging by the results shown in Figures 8 through 11, our empirical results for the kernel-based realized volatility estimator using the optimally chosen bandwidth are very similar for those we found using the kernel estimator with a fixed lag length of 1. Note that for $ H=1$ the kernel estimator has a very simple functional form, viz.,

$\displaystyle \widetilde{K}_{t}\left( X_{\delta}\right) = \gamma_{0} \left( X_{\delta }\right) + 2\gamma_{1} \left( X_{\delta}\right) \,,$ (17)

because if $ H=1$ we have $ k(0)=1$ in equation (11). Therefore, at least for the two financial returns series studied in this paper, we find that by augmenting the standard realized volatility estimator with just one additional term, the critical sampling frequency can be increased considerably without giving up much in terms of the simplicity of the calculations. This estimator is, incidentally, also identical to the noise-corrected estimator proposed in the seminal paper of Zhou (1996).

Figure 10. Time-Averaged Kernel-Based Volatility Signature Plots, Dollar/Euro Returns

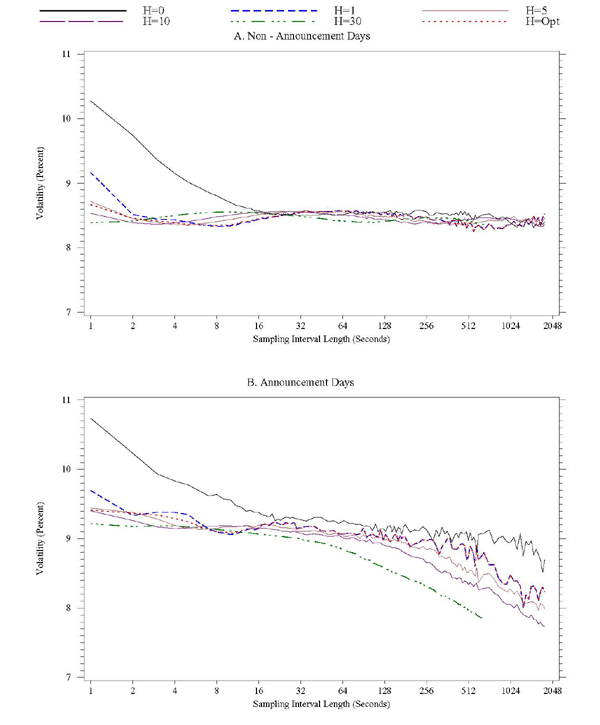
Figure 10, for FX, has two panels, the upper for non-announcement days, the lower for announcement days. In each panel, the x-axis is sampling interval length, ranging from 1 to 2048 seconds, the y-axis is volatility, expressed in percent. In each panel, six lines are show, corresponding to kernel-based realized volatility estimates calculated with bandwidth parameters H equal to 0, 1, 5, 10, 30, and the optimal H. Realized volatility is higher on announcement days. Kernel-based volatilities are lower than bandwith-zero estimates at lower sampling intervals.

Note: See explanation given in Figure 8

Figure 11. Time-Averaged Kernel-Based Volatility Signature Plots, T-Note Returns

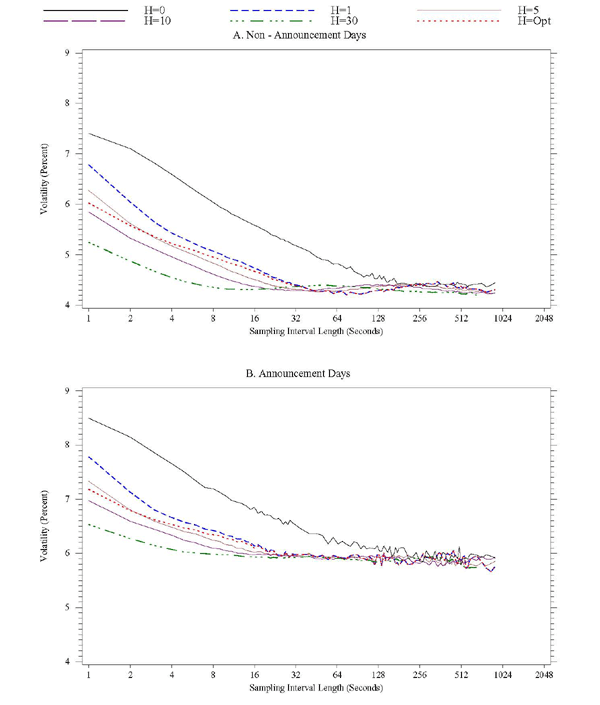
Figure 11, for T-notes, has two panels, the upper for non-announcement days, the lower for announcement days. In each panel, the x-axis is sampling interval length, ranging from 1 to 2048 seconds, the y-axis is volatility, expressed in percent. In each panel, six lines are show, corresponding to kernel-based realized volatility estimates calculated with bandwidth parameters H equal to 0, 1, 5, 10, 30, and the optimal H. Realized volatility is higher on announcement days. Kernel-based volatilities are lower than bandwith-zero estimates at lower sampling intervals. The estimates begin to increase at higher sampling intervals than for FX.

Note: See explanation given in Figure 8


6  Estimation of Integrated Volatility Using Absolute Power and Bipower Variation Methods

The standard estimator of integrated volatility is potentially quite sensitive to outliers, as it is computed from squared returns. This raises the issue of how robust estimators of volatility, which are functions of absolute rather than squared returns, perform in practice. As discussed before, these estimators converge to measures of the daily variation of the diffusive , or non-jump, part of the returns process. Since much of the difference in daily volatility that was seen for announcement days relative to non-announcement days (Figure 4), may very well stem from jumps rather than diffusive moves in returns, it is particularly interesting to examine how estimates of volatility differ between announcement and non-announcement days when the two robust methods are used. In addition, we also study the degree to which market microstructure noise affects estimates of volatility across sampling frequencies when robust estimators are employed.

6.1  Volatility Estimation Using Absolute Variation Methods

The realized absolute variation of a continuous time diffusion process $ X$, sampled over $ [0,t]$ at intervals $ \delta$, was introduced earlier as

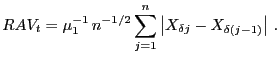$\displaystyle RAV_{t}=\mu_{1}^{-1}\,n^{-1/2}\sum_{j=1}^{n} \abs { X_{\delta j} - X_{\delta (j-1)}}\,.$ (18)

The factor $ \mu_{1}^{-1}=\sqrt{\pi/2}\approx1.253$ is needed to obtain an estimate of the mean absolute variation of $ X_{t}$ over $ [0,t]$, $ \int_{0} ^{t}\!\sigma_{u}\dee u$, under the diffusion model (2), rather than of the mean absolute return of $ X_{t}$ over that period.28

Because real data are generated discretely and not continuously, the term $ n$, the sample size, in equation (18) needs to be interpreted carefully in empirical work. When data are generated discretely, there will be time intervals during which no new data arrive and hence returns are zero. Furthermore, because trading activity is not distributed uniformly during the day, the relative frequency of zero-return intervals increases as the intraday sampling frequency rises.29 With discretely-generated data, then, one must take care not to use the theoretical sample size, $ \floor {t/\delta}$, that corresponds to a given sampling interval length $ \delta$, because more and more of the sample periods would be characterized by zero returns as $ \delta\downarrow0$. Instead, one should use the effective sample size, i.e., the number of intervals within a day during which a transaction occurred.

We compute estimates of the daily variation based on the realized absolute variation of dollar/euro and T-note returns using the same range of sampling frequencies as in the preceding section, and we also average separately across announcement and non-announcement days. The resulting signature plots are shown in Figure 12. These plots share certain similarities with the ones shown in Figure 4, but they also exhibit some important differences. First, we find that the estimates of daily variation that are based on absolute returns differ by less, on average, across announcement and non-announcement days than is the case for the volatility estimates that are based on squared returns. This suggests that the jump components of returns, which presumably are both more frequent and more pronounced on announcements days, indeed affect the standard realized volatility estimator disproportionately, just as the asymptotic theory for this estimator would predict. This effect is particularly strong for dollar/euro returns (Figure 12A): volatility estimates show little difference across the two subsamples when they are computed using absolute returns. The 95% confidence intervals for the average daily variation in the dollar/euro returns further re-enforce this finding, with a fairly large overlap between the announcement and non-announcement days, especially at lower sampling frequencies.30

A second important difference between the signature plots for the robust estimator in Figure 12 and those for the standard estimator in Figure 4 lies in their response to changes in the sampling frequency. For both dollar/euro and T-note returns, and both on announcement days and on non-announcement days, realized volatility increases faster with the sampling frequency if it is computed as a function of absolute returns. While we can not offer a full explanation for this finding, we conjecture that this difference may offer important clues to the nature of the market microstructure noise process that affects returns at the very highest frequencies.

Judging from the signature plots shown in Figure 12, the critical sampling frequency equals about 4 to 5 minutes for both dollar/euro and T-note returns, and both on announcement and on non-announcement days. These estimates of the critical sampling frequencies are substantially lower, and the associated sampling interval lengths are therefore substantially longer, than those we found when computing realized volatility using squared returns. Exploring the causes of this pronounced difference is left to future research.

6.2  Integrated Volatility Estimated From Bipower Variation

As set out in Section 2, bipower variation is calculated from the products of adjacent absolute returns, rather than simple squared returns, and it is therefore more robust to large outliers such as non-diffusive jumps. For a sample interval length of 300 seconds, for which neither market microstructure noise effects nor small-sample effects should be relevant for our two series, Table 3 shows that the ratio of bipower-based volatility to total realized volatility averages about 0.94 for dollar/euro returns, on both announcement days and non-announcement days. For T-note returns, this ratio comes to 0.90 and 0.94, respectively, on announcement and non-announcement days.31 Thus, in 2005 only about 5 to 10 percent of the total volatility was contributed by the jump component of returns of either series, while the remainder stemmed from the diffusive component. The approximate equality of these proportions across the two subsamples is intriguing, but this finding may well be specific to our sample period. For more volatile periods than 2005--when volatility in many markets was among the lowest recorded in years--the relative contributions of diffusive and jump shocks to the total variation may well be very different.

Figure 12. Time-Averaged Absolute Variation Volatility Signature Plots

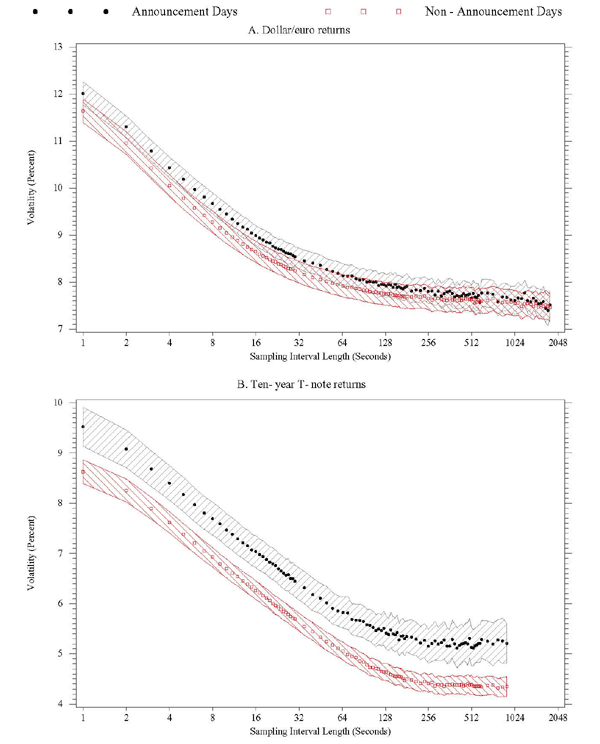
Figure 12 has two panels, the top for FX, the bottom for T-notes. In each panel, the x-axis is sampling interval length, ranging from 1 to 2048 seconds, the y-axis is volatility, expressed in percent. There are two set of points in each panel, on for announcement days, one for days without announcements. Shaded areas show 95% confidence intervals. For FX and T-notes, so in both panels, average realized volatility is higher for announcement days, and it rises as the sampling interval gets smaller. The signature plots begin increasing at about 128 seconds for T-notes, at shorter sampling intervals for FX.

Notes: Horizontal axes use log scale. Shaded areas represent 95% confidence intervals for average volatility.

Table 3. Fraction of Total Realized Volatility Contributed by Bipower Volatility - Sample Interval Length (in seconds)

 
1
5
15
30
60
300
600
(i) FX Returns: Full Sample - Mean Total Realized Volatility
10.42
9.22
8.78
8.71
8.70
8.70
8.61
(i) FX Returns: Full Sample - Mean Bipower Volatility
6.62
7.90
8.04
8.04
8.16
8.17
8.12
(i) FX Returns: Full Sample - Ratio
0.64
0.86
0.92
0.92
0.94
0.94
0.94
(i) FX Returns: Non-Announcement Days - Mean Total Realized Volatility
10.31
9.05
8.53
8.53
8.54
8.58
8.49
(i) FX Returns: Non-Announcement Days - Mean Bipower Volatility
6.43
7.65
7.82
7.82
7.95
8.02
7.95
(i) FX Returns: Non-Announcement Days - Ratio
0.62
0.85
0.92
0.92
0.93
0.94
0.94
(i) FX Returns: Announcement Days - Mean Total Realized Volatility
10.79
9.81
9.33
9.33
9.28
9.16
9.09
(i) FX Returns: Announcement Days - Mean Bipower Volatility
7.16
8.64
8.70
8.70
8.77
8.60
8.59
(i) FX Returns: Announcement Days - Ratio
0.66
0.88
0.93
0.93
0.94
0.94
0.95
(ii) 10-Year T-Note Returns: Full Sample - Mean Total Realized Volatility
7.55
6.56
5.43
5.43
5.09
4.69
4.72
(ii) 10-Year T-Note Returns: Full Sample - Mean Bipower Volatility
3.78
4.83
4.69
4.69
4.53
4.40
4.46
(ii) 10-Year T-Note Returns: Full Sample - Ratio
0.50
0.74
0.86
0.86
0.89
0.94
0.95
(ii) 10-Year T-Note Returns: Non-Announcement Days - Mean Total Realized Volatility
7.26
6.27
5.07
5.07
4.71
4.30
4.33
(ii) 10-Year T-Note Returns: Non-Announcement Days - Mean Bipower Volatility
3.61
4.58
4.35
4.35
4.19
4.06
4.14
(ii) 10-Year T-Note Returns: Non-Announcement Days - Ratio
0.50
0.73
0.86
0.86
0.89
0.94
0.96
(i) FX Returns: Announcement Days - Mean Total Realized Volatility
8.49
7.50
6.57
6.57
6.30
5.96
5.99
(i) FX Returns: Announcement Days - Mean Bipower Volatility
4.29
5.60
5.67
5.67
5.56
5.40
5.43
(i) FX Returns: Announcement Days - Ratio
0.51
0.75
0.86
0.86
0.88
0.91
0.91

Figure 13 shows the signature plots for dollar/euro and T-note returns using the realized bipower variation estimator defined in equation (15).32 These signature are quite different from those shown that are based on squared returns (Figure 4) or absolute returns (Figure 12). Most notably, at the very highest sampling frequencies available, the bipower-based signature plots are downward sloping as a function of the sampling frequency. Although we cannot rule out that market microstructure noise could account for a part of this feature, its most likely determinant is the fact that, as the sampling frequency increases, the fraction of sampling intervals with zero returns increases as well. Because the bipower variation estimator is calculated from the sum of the products of adjacent absolute returns, two consecutive non-zero returns are required to obtain a non-zero increment to the estimate of volatility. As zero returns are especially prevalent at the highest sampling frequencies, the result is a decline in estimated volatility at those frequencies.33

The critical frequency thus depends both on the actual properties of the microstructure noise process as well as on the relative scarcity of non-zero observations at various sampling frequencies. For the bipower-based volatility of dollar/euro returns, this frequency appears to be around 15 to 30 seconds on announcement days and around 1 minute on non-announcement days. For T-note returns, the critical frequencies are around 1 and 2 minutes, respectively, on announcement and non-announcement days.

Figure 14 shows the signature plots for the realized bipower variation using the skip-one returns defined in equation (16). This estimator relies on products of absolute returns with one sample period left out in between the terms. The intuition for this method is that by skipping over one term one may be able to eliminate some of the serial correlation in returns that could be caused by market microstructure features. Unfortunately, the volatility estimates we obtain using the skip-one method are not straightforward to interpret. Across most sampling frequencies and for both dollar/euro and T-note returns, estimated volatility using the skip-one bipower method tends to be lower than if it is computed on the basis of the standard bipower estimator. This result could be due to a more thorough elimination of bias imparted by market microstructure noise. However, we note that this result is also present at longer sampling interval lengths, for which microstructure noise is thought to play a less significant role. Hence, the lower volatility estimates using the skip-one method almost certainly also reflect patterns in the latent efficient-price component of the observed returns process. For instance, if large returns (of either sign) tend to cluster, the skip-one estimator is likely to be biased downward in practice irrespective of the chosen sampling frequency.

In summary, we find that it is hard to assess the impact of market microstructure noise on volatility estimated from the realized bipower variation of a process. The primary cause of this difficulty appears to be the issue of zero returns in samples that are drawn from discretely generated data. Nevertheless, it is evident that the choice of sampling frequency is important for this class of volatility estimators as well. There is some evidence that using the skip-one estimator may help eliminate some of the noise, as suggested by the fairly flat signature plots for T-note returns in Figure 14B, but this estimator may also induce a downward bias that depends on the conditional distribution of the efficient-price component of the returns process. Given the increasing popularity of the bipower volatility estimator, an important topic for future research is the development of formal rules for choosing the critical or optimal sampling frequency. In addition, it would appear to be useful to develop kernel-based or subsampling-based extensions to volatility estimators that are based on the absolute power variation and bipower variation of the returns process.

Figure 13. Time-Averaged Bipower Variation Volatility Signature Plots

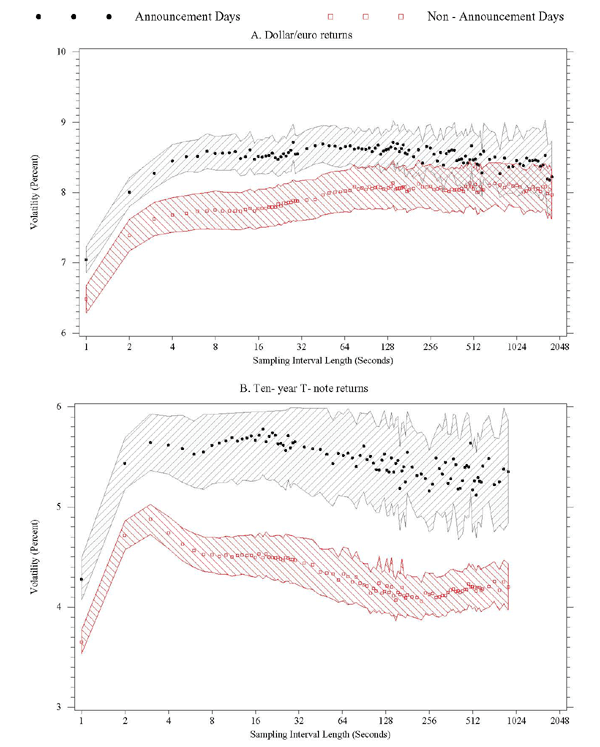
Figure 13 has two panels, the top for FX, the bottom for T-notes. In each panel, the x-axis is sampling interval length, ranging from 1 to 2048 seconds, the y-axis is volatility, expressed in percent. There are two set of points in each panel, on for announcement days, one for days without announcements. Shaded areas show 95% confidence intervals. For FX and T-notes, so in both panels, average realized volatility is higher for announcement days. Realized volatility tends to be higher on announcement days. At the very lowest sampling intervals (1 and 2 seconds), the realized bipower variation declines.

Notes: Horizontal axes use log scale. Shaded areas represent 95% confidence intervals for average volatility.

Figure 14. Time-Averaged Bipower Variation Volatility Signature Plots, using Skip-One Returns

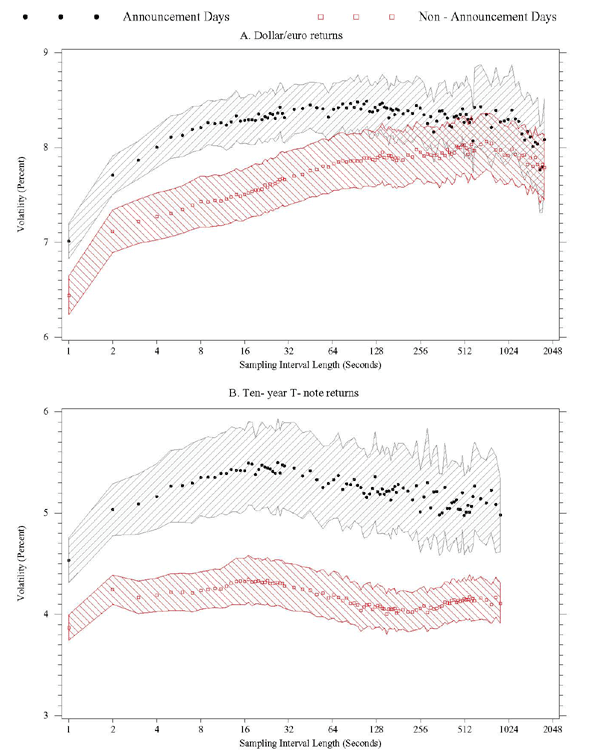
Figure 14 has two panels, the top for FX, the bottom for T-notes. In each panel, the x-axis is sampling interval length, ranging from 1 to 2048 seconds, the y-axis is volatility, expressed in percent. There are two set of points in each panel, one for announcement days, one for days without announcements. For FX and T-notes, so in both panels, average realized volatility is higher for announcement days. At shorter sampling intervals, the realized skip-one bipower variation declines.

Notes: Horizontal axes use log scale. Shaded areas represent 95% confidence intervals for average volatility.


7  Discussion

Using volatility signature plots, we have found that the critical sampling frequency is considerably higher (by a factor of 6 or more) and the resulting intraday sample lengths are considerably lower for dollar/euro returns than for T-note returns. What are some of the--not necessarily independent--factors that may explain this striking difference? Both markets are based on electronic order book systems, and both have achieved large market shares in their respective fields. However, the number of active trading terminals is considerably larger on EBS than on BrokerTec, as is the number of transactions per day. In contrast, the average size of each transaction is lower on EBS than it is on BrokerTec, suggesting that the price impact of EBS transactions may also be lower on average. In addition, the bid-ask spread in the dollar/euro exchange rate pair is, on average, only about sixty percent the size of that of the 10-year Treasury note. All of these factors may explain the observed differences in the critical sampling frequencies.

Judging from the volatility signature plots, the critical sampling frequencies for estimating the realized volatility of the returns to the 10-year Treasury securities and, even more so, of the returns to the dollar/euro pair are much higher, and the associated critical sampling interval lengths are therefore shorter, than those reported in the empirical literature for all but the most liquid of exchange-traded shares (e.g., Bandi and Russell 2006). Lower bid-ask spreads and other lower transaction costs, a smaller price impact of trades, and the fact that the number of distinct assets traded on these two systems is quite small--which, ceteris paribus, should raise their liquidity--are all good candidates for explaining why their critical sampling frequencies are so much higher than those in some other financial markets.

Two additional findings reported in this paper are that there is, in general, substantial heterogeneity in the shapes of the daily volatility signature plots and that, on any given day, the realized volatilities computed from adjacent sampling frequencies can differ considerably from each other at lower sampling frequencies. A related finding, we believe, is that the sampling interval lengths chosen by the rules proposed by Bandi and Russell (2006) and Aït-Sahalia, Mykland, and Zhang (2005) are generally considerably longer than those that would be chosen visually, i.e., on the basis of the signature plots. We conjecture that a key to interpreting these findings is to recall that financial returns--and especially those sampled at very high frequencies--tend to be very leptokurtic. Returns that occur during possibly just a handful of intraday periods may make disproportionate contributions to estimates of realized volatility, and these contributions can depend strongly on the precise choice of sampling frequency. The heterogeneity in the shapes of the daily volatility signature plots may also be a by-product of the leptokurtosis of high-frequency data. We suggest that one of the practical uses of computing realized volatility via robust methods--such as those that are based on the absolute power, bipower, and multipower variation of returns--may be to shed more light on the role leptokurtosis of returns plays in driving the heterogeneity present in the shapes of the daily realized volatility signature plots.

The extent to which these findings carry over to other time series is obviously of great interest from an applied perspective. First, because heavy tails are a fairly prevalent feature in most return series, it would seem likely that the aspects of the above findings that can be related to the leptokurtosis of returns apply to many other assets and markets as well. In particular, the heterogeneity in the shapes of the daily volatility signature plots seems unlikely to be specific to the two series that we study here.

Second, regarding the systematic differences we find between the sampling frequencies chosen by the formal rules and those based on the signature plots, it also seems likely that these differences should be most serious for the most liquid financial time series. When returns sampled even at the highest-available frequency still contain too much signal and not enough noise to consistently estimate the noise-to-signal ratio that enters into the formula for the optimal sampling rule, we would expect that these rules would understate the optimal sampling frequency and overstate the optimal sampling interval lengths.

This "problem," such as it is, should be most acute in the most liquid markets; conversely, it should be less severe, e.g., in markets for thinly traded stocks. The dollar/euro spot market studied in this paper is, by several measures, the most liquid market in the world, and it therefore seems plausible that the differences in the conclusions regarding the optimal sampling frequency stemming from the use of signature plots and formal decision rules could be considerable. This conjecture is supported by our finding that even for the T-note market, which is also very liquid but not as liquid as the dollar/euro spot FX market, the differences between the optimal sampling frequencies indicated by the signature plots and the formal sampling rules are smaller, even though they are still significant.

We caution that as many markets tend to become deeper and more liquid over time, it will likely become increasingly difficult to obtain good estimates of the noise variance parameter that are needed to formally calculate the optimal sampling frequency. Finally, since major liquid markets often tend to be the ones that are studied most frequently in applied finance and econometrics, this issue is likely to be a relevant concern in many situations.

8  Conclusion

In this paper, we use various methods to examine the dependence of estimates of realized volatility on the sampling frequency and to determine if one can determine empirically a critical sampling frequency, beyond which estimates of integrated volatility become increasingly contaminated by market microstructure noise. We study returns on the dollar/euro exchange rate pair and on the on-the-run 10-year U.S. Treasury security in 2005, at intraday sampling frequencies as high as once every second. We detect strong evidence of an upward bias in realized volatility at the very highest sampling frequencies. Time-averaged volatility signature plots suggest that dollar/euro returns may be sampled as frequently as once every 15 to 20 seconds without the standard realized volatility estimator incurring market microstructure-induced bias. In contrast, returns on the 10-year Treasury security should be sampled no more frequently than once every 2 to 3 minutes on non-announcement days, and about once every 40 seconds on announcement days, in order to avoid obtaining upwardly-biased estimates of realized volatility.

If one uses realized kernel estimators, which eliminate some of the serial correlation in the returns that is induced by market microstructure noise, the critical sampling frequencies increase even further. By using the simplest possible realized kernel estimator, which merely adds the first-order autocovariance term to the standard estimator, the critical sampling frequency rises to about once every 2 to 5 seconds for dollar/euro returns and to about once every 30 to 40 seconds for T-note returns. The resulting high degree of precision with which integrated volatility may be estimated suggests that the economic benefits for risk-averse investors who employ these methods to guide their portfolio choices should be substantial, in comparison with approaches that estimate volatility using either daily-frequency data or more sparsely sampled intraday data.

References

Ait-Sahalia, Y., and J. Jacod, 2009, "Testing for jumps in a discretely observed process," Annals of Statistics, 37(1), 184-222.

Ait-Sahalia, Y., P.A. Mykland, and L. Zhang, 2005, "How often to sample a continuous-time process in the presence of market microstructure noise," Review of Financial Studies, 18(2), 351-416.

-----, 2008, "Ultra high frequency volatility estimation with dependent market microstructure noise," Manuscript, Department of Statistics, University of Chicago.

Andersen, T.G., T. Bollerslev, and F.X. Diebold, 2007, "Roughing it up: Including jump components in the measurement, modeling and forecasting of return volatility," Review of Economics and Statistics, 89(4), 701-720.

Andersen, T.G., T. Bollerslev, F.X. Diebold, and H. Ebens, 2001, "The distribution of realized stock return volatility," Journal of Financial Economics, 61(1), 43-76.

Andersen, T.G., T. Bollerslev, F.X. Diebold, and P. Labys, 2000,"Great realisations," Risk, 13, 105-108.

-----, 2001, "The distribution of realized exchange rate volatility," Journal of the American Statistical Association, 96(453), 42-55.

-----, 2003, "Modeling and forecasting realized volatility," Econometrica, 71(2), 579-625.

Andersen, T. G., T. Bollerslev, F. X. Diebold, and C. Vega, 2003, "Micro effects of macro announcements: Real-time price discovery in foreign exchange," American Economic Review, 93(1), 38-62.

Andersen, T. G., T. Bollerslev, and N. Meddahi, 2006, "Realized volatility forecasting and market microstructure noise," Manuscript, Department of Economics, Duke University, Durham NC.

Balduzzi, P., E. J. Elton, and T. C. Green, 2001, "Economic news and bond prices: Evidence from the U.S. Treasury market," Journal of Financial and Quantitative Analysis, 36(4), 523-543.

Bandi, F. M., and J.  R. Russell, 2006, "Separating microstructure noise from volatility," Journal of Financial Economics, 79(3), 655-692.

-----, 2007, "Volatility estimation," in Handbooks in Operations Research and Management Science, Volume 15: Financial Engineering, ed. by J. R. Birge, and V. Linetsky. Elsevier Science, Amsterdam, chap. 5, pp. 183-222.

-----, 2008, "Microstructure noise, realized variance, and optimal sampling," Review of Economic Studies, 75(2), 339-369.

Barndorff-Nielsen, O. E., 1997a,"Normal inverse Gaussian distributions and stochastic volatility modelling," Scandinavian Journal of Statistics, 24(1), 1-13.

-----, 1997b, "Processes of normal inverse Gaussian type," Finance and Stochastics, 2(1), 41-68.

Barndorff-Nielsen, O. E., P. R. Hansen, A. Lunde, and N. Shephard, 2008, "Designing realized kernels to measure the ex-post variation of equity prices in the presence of noise," Econometrica, 76(6), 1481-1536.

Barndorff-Nielsen, O. E., and N. Shephard, 2001, "Non-Gaussian Ornstein-Uhlenbeck based models and some of their uses in financial economics (with discussion)," Journal of the Royal Statistical Society, Series B, 63(2), 167-241.

-----, 2002a, "Econometric analysis of realized volatility and its use in estimating stochastic volatility models," Journal of the Royal Statistical Society, Series B, 64(2), 253-280.

-----, 2002b, "Estimating quadratic variation using realized variance," Journal of Applied Econometrics, 17(5), 457-477.

-----, 2003, "Realized power variation and stochastic volatility models," Bernoulli, 9(2), 243-265.

-----, 2004a, "Econometric analysis of realized covariation: High frequency based covariance, regression, and correlation in financial economics," Econometrica, 72(3), 885-925.

-----, 2004b, "Power and bipower variation with stochastic volatility and jumps (with discussion)," Journal of Financial Econometrics, 2(1), 1-48.

-----, 2006a, "Econometrics of testing for jumps in financial economics using bipower variation," Journal of Financial Econometrics, 4(1), 1-30.

-----, 2006b, "Impact of jumps on returns and realised variances: Econometric analysis of time-deformed Lévy processes," Journal of Econometrics, 131(1-2), 217-252.

-----, 2007, "Variation, jumps, market frictions and high frequency data in financial econometrics," in Advances in Economics and Econometrics, Theory and Applications, Ninth World Congress; Volume 3 (Econometric Society Monographs 43), ed. by R. Blundell, W. K. Newey, and T. Persson. Cambridge University Press, Cambridge, chap. 10, pp. 328-372.

Berger, D. W., A. P. Chaboud, S. V. Chernenko, E. Howorka, and J. H. Wright, 2008, "Order flow and exchange rate dynamics in Electronic Brokerage System data," Journal of International Economics, 75(1), 93-109.

Calvet, L. E., and A. J. Fisher, 2008, Multifractal Volatility: Theory, Forecasting, and Pricing. Academic Press, San Diego.

Campbell, J. Y., A. W. Lo, and A. C. MacKinlay, 1997, The Econometrics of Financial Markets. Princeton University Press, Princeton, NJ.

Chaboud, A. P., S. V. Chernenko, and J. H. Wright, 2008, "Trading activity and macroeconomic announcements in high-frequency exchange rate data," Journal of the European Economic Association, 6(2-3), 589-596.

Fleming, M. J., 1997, "The round-the-clock market for U.S. Treasury securities," Federal Reserve Bank of New York Economic Policy Review, 3(2), 9-32.

Fleming, M. J., and B. Mizrach, 2008, "The microstructure of a U.S. Treasury ECN: The BrokerTec platform," Manuscript, Department of Economics, Rutgers University.

Fleming, M. J., and E. M. Remolona, 1999, "Price formation and liquidity in the U.S. Treasury market: The response to public information," Journal of Finance, 54(5), 1901-1915.

Forsberg, L., and E. Ghysels, 2007, "Why do absolute returns predict volatility so well?," Journal of Financial Econometrics, 5(1), 31-67.

French, K. R., and R. Roll, 1986, "Stock return variances: The arrival of information and the reaction of traders," Journal of Financial Economics, 17(1), 5-26.

Ghysels, E., P. Santa-Clara, and R. I. Valkanov, 2006, "Predicting volatility: Getting the most out of return data sampled at different frequencies," Journal of Econometrics, 131(1-2), 59-95.

Hansen, P. R., and G. Horel, 2009, "Quadratic Variation by Markov Chains," Research Paper 2009-13, Center for Research in Econometric Analysis of Time Series (CREATES), School of Economics and Management, University of Aarhus, Denmark.

Hansen, P. R., and A. Lunde, 2006, "Realized variance and market microstructure noise (with discussion)," Journal of Business and Economic Statistics, 24(2), 127-218.

Harris, L., 1990, "Estimation of stock variance and serial covariance from discrete observations," Journal of Financial and Quantitative Analysis, 25(3), 291-306.

-----, 1991, "Stock price clustering and discreteness," Review of Financial Studies, 4(3), 389-415.

Hasbrouck, J., 1991, "Measuring the information content of stock trades," Journal of Finance, 46(1), 179-207.

-----, 2006, Empirical Market Microstructure. The Institutions, Economics, and Econometrics of Securities Trading. Oxford University Press, New York.

Jacod, J., Y. Li, P. A. Mykland, M. Podolskij, and M. Vetter, 2009, "Microstructure noise in the continuous case: The pre-averaging approach," Stochastic Processes and Their Applications, 119(7), 2249-2276.

Lee, S. S., and P. A. Mykland, 2008, "Jumps in financial markets: A new nonparametric test and jump dynamics," Review of Financial Studies, 21(6), 2535-2563.

Lee, T., and W. Ploberger, 2009, "Optimal test for jump detection," Manuscript, Department of Economics, Washington University in St. Louis.

Mandelbrot, B. B., 1963, "The variation of certain speculative prices," Journal of Business, 36(4), 394-429.

McAleer, M., and M. C. Medeiros, 2008, "Realized volatility: A review," Econometric Reviews, 27(1-3), 10-45.

Merton, R. C., 1976, "Option pricing when underlying stock returns are discontinuous," Journal of Financial Economics, 3(1-2), 125-144.

Newey, W. K., and K. D. West, 1987, "A simple, positive semi-definite, heteroskedasticity and autocorrelation consistent covariance matrix," Econometrica, 55(3), 703-708.

O'Hara, M., 1995, Market Microstructure Theory. Blackwell, Cambridge.

Oomen, R. C., 2005, "Properties of bias-corrected realized variance under alternative sampling schemes," Journal of Financial Econometrics, 3(4), 555-577.

-----, 2006, "Properties of realized variance under alternative sampling schemes," Journal of Business and Economic Statistics, 24(2), 219-237.

Phillips, P. C. B., and J. Yu, 2006, "Comment [on Hansen and Lunde]," Journal of Business and Economic Statistics, 26(2), 202-208.

-----, 2008, "Information loss in volatility measurement with flat price trading," Manuscript, School of Economic and Social Sciences, Singapore Management University.

Roll, R., 1984, "A simple implicit measure of the effective bid-ask spread in an efficient market," Journal of Finance, 39(4), 1127-1139.

Woerner, J. H. C., 2005, "Estimation of integrated volatility in stochastic volatility models," Applied Stochastic Models in Business and Industry, 21, 27-44.

-----, 2007, "Inference in Lévy type stochastic volatility models," Annals of Applied Probability, 39(2), 531-549.

Zhang, L., 2006, "Efficient estimation of stochastic volatility using noisy observations: A multi-scale approach," Bernoulli, 12(6), 1019-1043.

Zhang, L., P. A. Mykland, and Y. Ait-Sahalia, 2005, "A tale of two time scales: Determining integrated volatility with noisy high-frequency data," Journal of the American Statistical Association, 100(472), 1394-1411.

Zhou, B., 1996, "High-frequency data and volatility in foreign-exchange rates," Journal of Business and Economic Statistics, 14(1), 45-52.

Footnotes

1.  Chaboud and Hjalmarsson are with the Division of International Finance, Federal Reserve Board, Washington DC 20551, USA . Chiquoine is with the Investment Fund for Foundations, 97 Mount Auburn Street, Cambridge MA 02138, USA . Loretan is with the Asian Division of the IMF Institute, Washington DC 20006, USA . The initial version of this paper was written while Chiquoine and Loretan were employed in the Division of International Finance of the Federal Reserve Board. The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System, of any other person associated with the Federal Reserve System, or of any persons associated with the International Monetary Fund. Joshua K. Hausman provided excellent research assistance on the initial version of this paper, and Kai Steverson provided outstanding assistance for the most recent version. We thank EBS (now part of ICAP) for the high-frequency foreign exchange data, and we are grateful to Jennifer Roush and Michael Fleming for providing access to the BrokerTec data. Claudio Borio, Celso Brunetti, Dobrislav Dobrev, Paul Embrechts, Jacob Gyntelberg, Lennart Hjalmarsson, Sam Ouliaris, Frank Packer, Eli Remolona, Ryan Stever, Jun Yu, and seminar participants at Singapore Management University, National University of Singapore, the Reserve Bank of New Zealand, the 2008 Far Eastern Meetings of the Econometric Society (FEMES) in Singapore, and the Eidgenössische Technische Hochschule Zürich provided helpful comments and discussions. Any remaining errors are obviously our own. Return to text

2.  Email: [email protected] Return to text

3.  Email: [email protected] Return to text

4.  Email: [email protected] Return to text

5.  Corresponding author. Email: [email protected] Return to text

6.  For an overview of many of these market microstructure issues and their importance for financial theory and practice, we refer the reader to Hasbrouck (2006), O'Hara (1995), Campbell, Lo, and MacKinlay (1997, ch. 3), as well as to Roll (1984), Harris (1991, 1990), and Hasbrouck (1991). Return to text

7.  The asymptotic properties of realized volatility and other related estimators have been primarily developed in a series of papers by Barndorff-Nielsen and Shephard (e.g., 2004b, 2002a, 2002a, 2006a, 2003, 2002b, 2001). Other important contributions include Andersen, Bollerslev, Diebold, and Labys (2001, 2003) and, more recently, Bandi and Russell (2008). Surveys of this literature are given in Barndorff-Nielsen and Shephard (2007) and McAleer and Medeiros (2008). Hansen and Horel (2009) have recently proposed a novel estimator of quadratic variation that does not rely on the continuous-time semimartingale assumption for its justification or derivation. Return to text

8.  Aït-Sahalia, Mykland, and Zhang (2005) study optimal sampling frequency rules that are similar to that given by Bandi and Russell (2006). Based on the model originally proposed by Roll (1984) and extended by French and Roll (1986), they suggest that the variance of the market microstructure noise can be calculated from the bid-ask spread in the data. In particular, if $ s$ is the bid-ask spread in the market (expressed in percent of the price), then $ \omega ^{2}=s^{2}/4$. However, as Aït-Sahalia, Mykland, and Zhang (2005) point out, by estimating  $ \omega^{2}$ strictly from the bid-ask spread, the contributions of any other sources to microstructure noise are ignored. The resulting estimate of  $ \omega^{2}$ should therefore be interpreted as a lower bound on the actual variance of the noise. Return to text

9.  Related studies include Andersen, Bollerslev, Diebold, and Ebens (2001) and Zhou (1996). Bandi and Russell (2007) and Barndorff-Nielsen and Shephard (2007) provide surveys. Return to text

10.  In our empirical work, we rely exclusively on the Modified Tukey-Hanning$ _{p}$ kernel, which is defined on p. 1496 of BNHLS as $ k(x)=\sin^{2} \bigl((\pi /2)(1-x)^{p} \bigr)$ for $ x\in[0,1]$ and for some positive integer $ p$. This kernel function additionally satisfies $ k^{\prime}(0)= k^{\prime}(1)=0$, and it is asymptotically the most efficient of the kernels considered by BNHLS . In this paper, we set $ p=2$ and $ H=\hat{c} \cdot n^{1/2}$, where $ \hat{c}$ is a constant given in equation (16) on p. 1494 of BNHLS. Return to text

11.  Barndorff-Nielsen and Shephard (2006a), Lee and Mykland (2008), Aït-Sahalia and Jacod (2009), and Lee and Ploberger (2009) propose formal tests of the hypothesis that a series has a jump component. Return to text

12.  An example of the former class are jump diffusion processes; jump diffusions are the sum of Brownian motion and a compound Poisson jump process with Gaussian jump sizes (see, e.g., Merton1976). Two examples of infinite-activity Lévy processes are the normal inverse Gaussian process (Barndorff-Nielsen 1997b, a) and the multifractal model of asset returns (MMAR); see Calvet and Fisher (2008) for an overview of the theory and empirical evidence for the MMAR. Return to text

13.  Because financial data are invariably generated discretely and because prices are reported with only a finite degree of precision, distinguishing between finite- and infinite-activity processes may not be possible in practice. Furthermore, as Barndorff-Nielsen and Shephard (2006b) and Woerner (2005, 2007) have shown, several robust estimators of integrated volatility share the same statistical properties for either type of jump process as long as certain regularity conditions are met, including the assumption that the increments of the process have finite second moments. Return to text

14.  Hence, equation (2) is a special case of (12), with $ N_{t} \equiv0$ or, equivalently, $ c_{j}\equiv0$ for all $ j$. Return to text

15.  In the FX market, by global convention, the value date changes at 17:00 New York time (whether or not Daylight Saving time is in effect). This cutoff thus represents the threshold between two trading days. Return to text

16.  The other leading electronic communication network (ECN) for trading in U.S. Treasuries is eSpeed. Return to text

17.  BrokerTec and EBS have both been acquired by ICAP in recent years. BrokerTec was acquired in 2003, EBS in 2006. Return to text

18.  In 2005, these days were January 17 (Martin Luther King, Jr. Day), February 21 (Presidents Day), October 10 (Columbus Day), and November 11 (Veterans Day). There were also several days in the sample for which the Bond Market Association recommended a 14:00 closing time. We account for these days in our calculations by limiting the day to 08:00 to 14:00 New York time and scaling the estimated volatilities appropriately. Return to text

19.  As a rule of thumb, in the present case a 1-percent change in the price of the T-note corresponds to about a 13 basis point change in the yield. Return to text

20.  On July 21, 2005, after close of business in China but before the start of the business day in North America, the Chinese authorities announced a revaluation of their currency, the renminbi, by 2.1 percent against the U.S. dollar. On that day, FX market volatility was quite elevated in most major currency pairs. Return to text

21.  The confidence intervals shown in Figures 2 and 3 are constructed using equation (5). The widths of the confidence intervals are determined by the number of observations, which is proportional to the inverse of the sampling frequency, and the quarticity $ Q_{t}$ of the process. The quarticity is estimated using equation (8), with returns sampled at the 10-minute frequency in all cases. That is, the same estimate of the quarticity, based on 10-minute returns, is used in the calculation of the confidence intervals for the realized volatility at all sampling frequencies. We follow this convention in order to cleanly identify the effects of the increasing sample size as the sampling frequency increases, while avoiding the effects of potential biases and differences in the point estimates of the quarticity calculated for different sampling frequencies. i.e., the quarticity estimate based on the 10-minute data should be unbiased, and the widths of the confidence intervals should therefore be unbiased as well, even though the volatility estimates around which the intervals are formed could obviously be biased, especially at the highest sampling frequencies. Return to text

22.  To be sure, this drawback of using sampling frequencies that are too low could be attenuated by computing the realized volatilities for several, staggered starting points and then averaging across these estimates. It seems more straightforward, however, to estimate the volatility directly from returns sampled at the higher frequency, while ensuring that one does not exceed the critical sampling frequency. Return to text

23.  We also observe that, in contrast to the case of non-announcement days, where the plot line is virtually flat for frequencies lower than the critical frequency, the plot line declines steadily (though only slightly) as the sampling interval length increases beyond 15 seconds. This suggests that FX trading dynamics on announcement days in 2005 may also have been characterized by a small amount of mean reversion at medium frequencies rather than just at the highest frequencies (as would be the case if the dynamics were purely of the microstructure variety). Return to text

24.  The confidence intervals are calculated in a standard manner from the standard deviation of the daily realized volatilities; this standard deviation is obtained using Newey and West (1987) standard errors to control for serial correlation in the daily realized volatilities.
Alternatively, by noting that realized volatility tends to be distributed log-normally rather than normally (e.g., Andersen, Bollerslev, Diebold, and Labys2003), one could attempt to improve upon the precision of these confidence intervals in the manner described by Hansen and Lunde (2006, Appendix B, pp. 159-160). We applied their method, but found that the resulting confidence intervals are virtually identical to the ones shown here.  Return to text

25.  Some of the differences in the critical sampling frequencies also owe to a reported general increase in market liquidity and depth common to many financial markets between the late 1990s and 2005, the year used in this study. Return to text

26.  Given the large number of lines already shown in Figures 8-11, no confidence intervals are presented. Return to text

27.  For the T-note returns, kernel estimates with $ H=30$ are not reported for the lowest sampling frequencies, i.e. the longest sampling intervals, since there are not enough observations available at these frequencies to form an estimate when using $ 30$ lags. Return to text

28.  The justification for using the quantity $ \mu_{1}^{-1}$ in empirical work is mainly asymptotic. According to the summary statistics shown in Table 1, for the case of 24-hour returns, the empirical ratio of the standard deviation of returns to the mean absolute return is equal to 1.29 and 1.32, respectively, for dollar/euro and T-note returns, fairly close to the value of $ \mu_{1}^{-1}$. However, for 5-minute returns, which are considerably more leptokurtic than 24-hour returns, this ratio equals 1.52 and 1.54, respectively, for dollar/euro and T-note returns. We leave to future research to establish in more detail how the conversion factor $ \mu_{1}^{-1}$ should be adjusted to take into account that the data generating process is subject to jumps. Return to text

29.  As is shown in Table 2, on an average trading day in 2005 the effective sample size for dollar/euro and T-note returns at the 1-second frequency was only 14 percent and 8 percent, respectively, as large as the theoretical sample size. We note that these numbers represent averages across all trading days in 2005. The fraction of 1-second intervals with non-zero returns within a day can vary considerably across days. Return to text

30.  The confidence intervals in Figures 12 to 14 are calculated in an analogous manner to those presented in Figure 4; see the first paragraph in footnote 19 for details. Return to text

31.  Similar ratios obtain for slightly shorter sample interval lengths. Return to text

32.  The volatility, rather than variance, estimates are shown, i.e., results for $ \sqrt{RBV_{t}}$ are displayed. Return to text

33.  Note that in the case of the absolute power variation method, a natural way for adjusting the estimator for changes in the prevalence of intervals with zero returns is to adjust the sample size, i.e., to set the sample size equal to the number of intervals with non-zero returns. No such simple adjustment is available for the estimator that is based on the bipower variation of returns. Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

Home | Economic research and data | Publications and education resources
Accessibility | Contact us
Last update: October 20, 2009