Skip to: [Printable Version (PDF)]

Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 909, November 2007 --- Screen Reader Version*

Quantitative Implications of Indexed Bonds in Small Open Economies^*

Ceyhun Bora Durdu^**

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

This paper analyzes the macroeconomic implications of real-indexed bonds, indexed to the terms of trade or GDP, using a general equilibrium model of a small open economy with financial frictions. Although indexed bonds provide a hedge to income fluctuations and can thereby mitigate the effects of financial frictions, they introduce interest rate fluctuations. Because of this tradeoff, there exists a nonmonotonic relation between the "degree of indexation" (i.e., the percentage of the shock reflected in the return) and the benefits that these bonds introduce. When the nonindexed bond market is shut down and only indexed bonds are available, indexation strengthens the precautionary savings motive, increases consumption volatility and deepens the impact of Sudden Stops for degrees of indexation higher than a certain threshold. When the nonindexed bond market is retained, nonmonotonic relationship between the degree of indexation and the benefits of indexed bonds still remain. Degrees of indexation higher than a certain threshold lead to more volatile consumption than lower degrees of indexation. The threshold degree of indexation depends on the volatility and persistence of income shocks as well as on the relative openness of the economy.

Keywords: Indexed bonds, degree of indexation, financial frictions, sudden stops

JEL classification: F41, F32, E44

1  Introduction

Liability dollarization¹ and frictions in world capital markets have played a key role in the emerging-market crises or Sudden Stops. Typically, these crises are triggered by sudden reversals of capital inflows that result in sharp real exchange rate (RER) depreciations and collapses in consumption. Figures 1 and 2 and Table 4 document the Sudden Stops observed in Argentina, Chile, Mexico, and Turkey in the last decade and a half. For example in 1994, Turkey experienced a Sudden Stop characterized by the following: a 10 percent current account-GDP reversal, 10 percent consumption and GDP drops relative to their trends, and a 31 percent RER depreciation.²

In an effort to remedy Sudden Stops and smooth macroeconomic fluctuations, Caballero (2002) and Borensztein and Mauro (2004) propose the issuance of state-contingent debt instruments by emerging-market economies. Caballero (2002) argues that crises in some emerging economies are driven by external shocks (e.g., terms of trade shocks) and that, contrary to their developed counterparts, these economies have difficulty absorbing the shocks as a result of imperfections in world capital markets. He argues that most emerging countries could reduce aggregate volatility in their economies and cut precautionary savings if they possessed debt instruments for which returns are contingent on the external shocks that trigger crises.³ He suggests creating an indexed bonds market in which bonds' returns are contingent on terms of trade shocks or commodity prices. Borensztein and Mauro (2004) argue that GDP-indexed bonds could reduce aggregate volatility and the likelihood of unsustainable debt-to-GDP levels in emerging economies. Hence, they argue that such bonds can help these countries avoid procyclical fiscal policies.

Despite the debates in the academic literature and policy circles regarding the merits of indexation, the existing literature lacks quantitative studies investigating the implications of indexed bonds and understanding their key features. This paper aims to fill this gap by introducing indexed bonds into quantitative models of small open economies to analyze the implications of those bonds for macroeconomic fluctuations and Sudden Stops. Can indexed bonds smooth macroeconomic fluctuations or help emerging countries mitigate detrimental effects of Sudden Stops? Under what type of conditions are their benefits maximized? What type of frictions can those bonds introduce? Does the return structure affect their overall implications? I aim to provide answers to those questions in this paper.

The analysis consists of two steps. First, I start with a canonical quantitative one-sector economy in which infinitely lived agents receive persistent endowment shocks, credit markets are perfect but insurance markets are incomplete (henceforth, the frictionless one-sector model), and analyze the implications of indexed bonds on precautionary savings motive, consumption volatility, co-movement of consumption with income. Second, I move to a two-sector model, which incorporates financial frictions proposed in the Sudden Stops literature (Calvo, 1998; Mendoza, 2002; Mendoza and Smith, 2005; Caballero and Krishnamurthy, 2001; among others). This model (henceforth, the two-sector model with financial frictions) can produce Sudden Stops endogenously through a debt-deflation mechanism similar to Mendoza (2002). Using this framework, I explore the implications of indexed bonds on Sudden Stops and RER fluctuations.

The analyses establish that there exists a nonmonotonic relation between the "degree of indexation" of the bonds (i.e., the percentage of the shock that is passed on to the bonds' return) and the overall benefits of the bonds on macroeconomic variables. When the nonindexed bonds market is shut down and only indexed bonds are available, indexation improves welfare and reduces precautionary savings, volatility of consumption, and correlation of consumption with income or smooths Sudden Stops only if the degree of indexation is lower than a critical value. If it is higher than that threshold (as with full-indexation), indexed bonds worsen those macroeconomic variables. When the indexed bonds market is retained, the nonmonotonic relationship between the degree of indexation and the benefits of indexed bonds remains, i.e., degrees of indexation higher than a certain threshold lead to higher consumption volatility than lower degrees of indexation. The threshold degree of indexation depends on the volatility and persistence of income shocks, as well as relative openness of the economy.

The quantitative analysis starts with exploring the frictionless one-sector model. In this model, when the only available instruments are nonindexed bonds with constant exogenous returns, agents try to insure away income fluctuations with trade balance adjustments. Because insurance markets are incomplete, agents are not able to attain full consumption smoothing, consumption is volatile, and the correlation of consumption with income is positive. Moreover, agents try to self-insure by engaging in precautionary savings. If the returns of the bonds are indexed to the exogenous income shock only, the insurance markets are only partially complete. To achieve complete markets, either the full set of state-contingent assets, such as Arrow securities, must be available (i.e., there are as many assets as the states of nature) or the returns of the bonds must be state contingent (i.e., contingent on both the exogenous shock and the debt levels; see Section 2.1 for further discussion). Although indexed bonds partially complete the market, the hedge they provide is imperfect because they introduce interest rate fluctuations. The quantitative analysis establishes that the interaction of these two effects implies a nonmonotonic relation between the degree of indexation of the bonds and the overall benefits that indexation introduces. Therefore, as mentioned above, indexed bonds can reduce precautionary savings, the volatility of consumption, and the correlation of consumption with income only if the degree of indexation is lower than a critical value.⁴

The changes in precautionary savings are driven by changes in the "catastrophic level of income." Risk-averse agents have strong incentives to avoid attaining levels of debt that the economy cannot support when income is at catastrophic level.⁵ Otherwise, agents would have non-positive consumption in the worst state of the economy which in turn would lead to infinitely negative utility. The degree of indexation has a significant effect on the state of nature that defines catastrophic levels of income and whether these income levels are higher or lower than what they would be without indexation. With higher degrees of indexation, these income levels can be determined at a positive shock; for example, if agents receive positive income shocks forever, they will receive higher endowment income but will also pay higher interest rates. My analysis shows that for higher values of the degree of indexation, the latter effect is stronger, leading to lower catastrophic income levels. This effect in turn creates stronger incentives for agents to build up buffer stock savings.

The effect of indexation on consumption volatility can be analyzed by decomposing the variance of consumption. (Consider the budget constraint of such an economy: $c_{t}=(1+\varepsilon_{t})y-b_{t+1}+(1+r+\varepsilon _{t})b_{t}$ .⁶ Using this budget constraint, $var(c_{t} )=var(y_{t})+var(tb_{t})-2cov(tb_{t},y_{t})$). On one hand, for a given income volatility, indexation increases the covariance of trade balance with income (since in good (or bad) times indexation commands higher (or lower) repayments to the rest of the world), which lowers the volatility of consumption. On the other hand, indexation increases the volatility of the trade balance (because of introduction of interest rate fluctuations), which increases the volatility of consumption. My analysis suggests that at high levels of indexation, the increase in the variance of the trade balance dominates the increase in the covariance of the trade balance with income, which in turn increases consumption volatility.⁷

To understand the implications of indexed bonds on Sudden Stops, I introduce them into a two-sector economy, which incorporates financial frictions that can account for the key features of Sudden Stops. In particular, the economy suffers from liability dollarization, and international debt markets impose a borrowing constraint on the small open economy. This constraint limits debt to a fraction of the economy's total income valued at tradable goods prices. As established in Mendoza (2002), when the only available instrument is nonindexed bonds, an exogenous shock to productivity or to the terms of trade that renders the borrowing constraint binding triggers a Fisherian debt deflation mechanism.⁸ A binding borrowing constraint leads to a decline in tradables consumption relative to nontradables consumption, inducing a fall in the relative price of nontradables as well as a depreciation of the RER. The decline in RER makes the constraint even more binding, because it creates a feedback mechanism that induces collapses in consumption and the RER as well as a reversal in capital inflows.

The tradeoffs mentioned in the frictionless one-sector model are preserved in the two-sector model with financial frictions. Moreover, in the two-sector model, the interaction of the indexed bonds with the financial frictions leads to additional benefits and costs. Specifically, when indexed bonds are in place, negative shocks can result in a relatively small decline in tradable consumption; as a result, the initial capital outflow is milder and the RER depreciation is weaker than in a case with nonindexed bonds. The cushioning in the RER can help contain the Fisherian debt deflation process. Although the indexed bonds help relax the borrowing constraint in case of negative shocks, this time, an increase in debt repayment following a positive shock can lead to a larger need for borrowing, which can make the borrowing constraint suddenly binding, triggering a debt deflation. Quantitative analysis of this model suggests, once again, that the degree of indexation needs to be lower than a critical value to smooth Sudden Stops. When indexation is higher than this critical value, the latter effect dominates the former, hence leading to more detrimental effects of Sudden Stops. The degree of indexation that minimizes macroeconomic fluctuations and the impact effect of Sudden Stops depends on the persistence and volatility of the exogenous shock triggering Sudden Stops as well as the size of the nontradables sector relative to its tradables sector; this finding suggests that the indexation level that maximizes benefit of indexed bonds needs to be country-specific. An indexation level that is appropriate for one country in terms of its effectiveness at preventing Sudden Stops may not be effective for another and may even expose that country to higher risk of facing Sudden Stops.

Debt instruments indexed to real variables (i.e., GDP, commodity prices, etc.) have not been widely employed in international capital markets.⁹ As Table 3 shows, only a few countries have issued this type of instrument in the past, where Argentina is the most recent issuer of GDP-linked securities.¹⁰ Moreover, most of those countries stopped issuing them: for example, Bulgaria swapped its GDP-indexed bonds for nonindexed bonds. Although the literature has emphasized the problems on the demand side as the primary reason for the limited issuance of indexed bonds, the supply of such bonds has always been thin, because countries have exhibited little interest in issuing them. Although answering as to why those countries may have had little interest issuing indexed bonds is beyond the scope of this paper, my results may help to illuminate why that has been the case: countries may have been reluctant because of the imperfect hedge that those bonds provide.¹¹

Several studies have explored the costs and benefits of indexed debt instruments in the context of public finance and optimal debt management.¹² As mentioned above, Borensztein and Mauro (2004) and Caballero (2002) drew attention to such instruments as possible vehicles to provide insurance benefits to emerging countries. Moreover, Caballero and Panageas (2003) quantified the potential welfare effects of credit lines offered to emerging countries. They used a one-sector model with collateral constraints in which Sudden Stops are exogenous to explore the benefits of such credit lines in smoothing Sudden Stops, interpreting them as akin to indexed bonds. This paper contributes to this literature by modeling indexed bonds explicitly in a dynamic stochastic general equilibrium model in which Sudden Stops are endogenous. Endogenizing Sudden Stops reveals that, depending on the structure of indexation, indexed bonds may amplify the effects of Sudden Stops.¹³

This paper is related to studies in several strands of macroeconomics and international finance literature. The model has several features common to the literature on precautionary saving and macroeconomic fluctuations (e.g., Aiyagari, 1994; Hugget, 1993). The paper is also related to studies exploring business cycle fluctuations in small open economies (e.g., Mendoza, 1991; Neumeyer and Perri, 2005; Kose, 2002; Oviedo, 2005; Uribe and Yue, 2005) from the perspective of analyzing how interest rate fluctuations affect macroeconomic variables. In addition to the papers in the Sudden Stops literature, this paper is also related to follow-up studies to this literature, including Calvo et. al. (2003); Durdu and Mendoza (2006); Durdu, Mendoza and Terrones (2007); and Caballero and Panageas (2003), which investigate the role of relevant policies in preventing Sudden Stops. Durdu and Mendoza (2006) explore the quantitative implications of price guarantees offered by international financial organizations on emerging-market assets. They find that these guarantees may induce moral hazard among global investors and conclude that the effectiveness of price guarantees depends on the elasticity of investors' demand as well as on whether the guarantees are contingent on debt levels. Similarly, in this paper, I explore the potential imperfections that indexation can introduce and derive the conditions under which such a policy could be effective in preventing Sudden Stops. Durdu et. al. (2007) uses a similar framework to this one to understand the rationale behind the recent surge in foreign reserve holdings of emerging economies.

Earlier seminal studies in the financial innovation literature, such as Shiller (1993) and Allen and Gale (1994), analyze how creation of a new class of "macro markets" can help manage economic risks such as real estate bubbles, inflation, and recessions and discuss what sorts of frictions can prevent the creation of such markets. This paper emphasizes possible imperfections in global markets and points out under which conditions issuance of indexed bonds may not improve macroeconomic conditions for a given emerging-market.

The next section starts with description of the models used for analyses and presents quantitative results. Section 3 provides conclusions and offers extensions for further research.

2  Quantitative models of Small Open Economies

2.1  The frictionless one-sector model

I start my analysis with a standard quantitative one-sector small open economy model, of which the benchmark model with nonindexed bonds is an endowment economy version of the model described in Mendoza (1991).¹⁴ This model has some features similar to Huggett (1993) and Aiyagari (1994). Unlike Huggett's and Aiyagari's works with uninsurable idiosyncratic risk in a closed economy, this model features a small open economy with uninsurable aggregate risk. But in both those models and my model, uninsurable risk derives precautionary savings in the economy. As I describe later, natural debt limits self-imposed by agents in the economy due to uninsurable risk plays a crucial role in determining the equilibrium amount of savings in my framework as well as Huggett's and Aiyagari's works.

Representative households receive a stochastic endowment of tradables, which is denoted as $(1+\varepsilon_{t})y^{T}$. $\varepsilon_{t}$ is a shock to the world value of the mean tradables endowment that could represent either a productivity shock or a terms-of-trade shock. $\varepsilon\in\mathcal{E} =[\varepsilon_{1}<...<\varepsilon_{m}]$ (where $\varepsilon_{1}=-\varepsilon _{m}$) evolves according to an $m$-state symmetric Markov chain with transition matrix $\mathcal{P}$. Households derive utility from aggregate consumption ($c$, which equals to tradable consumption, $c^{T}$, in this frictionless one-sector model), and they maximize Epstein's (1983) stationary cardinal utility function:

$$U=E_{0}\left\{ \sum_{t=0}^{\infty}\exp\left[ -\sum_{\tau =0}^{t-1}\gamma\log(1+c_{t})\right] u(c_{t})\right\} .$$ (1)

where

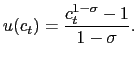$$u(c_{t})=\frac{c_{t}^{1-\sigma}-1}{1-\sigma}.$$ (2)

The instantaneous utility function (2) is in CRRA form and has an intertemporal elasticity of substitution $1/\sigma$. $\exp\left[ -\sum _{\tau=0}^{t-1}\gamma\log(1+c_{t})\right]$ is an endogenous discount factor that is introduced to induce stationarity in consumption and asset dynamics. $\gamma$ is the elasticity of the subjective discount factor with respect to consumption. Mendoza (1991) introduced preferences with endogenous discounting to quantitative small open economy models, and such preferences have since been widely used.¹⁵

The households' budget constraint is

$$c_{t}^{T}=(1+\varepsilon_{t})y^{T}-b_{t+1}+(1+r+\phi \varepsilon_{t})b_{t},$$ (3)

where $b_{t}$ is current bond holdings, and $(1+r+\phi\varepsilon_{t})$ is the gross return on bonds.¹⁶ The indexation mechanism works as follows: the returns of the indexed bonds are low in the low state of nature and high in the high one, but the mean of the returns remains unchanged and equal to $R=1+r$. When households' current bond holdings are negative (i.e., when households are debtors) they pay less (more) in the event of a negative (positive) endowment shock. I introduce the degree of indexation, $\phi\in[0, 1]$, to have flexibility to analyze the cases with no indexation, full-indexation and the cases in between. Notice that $\phi$ affects the variance of the bonds' returns (since $var(1+r+\phi\varepsilon_{t})=\phi^{2}var(\varepsilon_{t} )$).¹⁷ As $\phi$ increases, the bonds provide a better hedge against negative income shocks, but at the same time they introduce additional volatility by increasing the returns' variance.¹⁸

Implicit in this formulation is that the agents can issue either nonindexed bonds or indexed bonds at a given time. I relax this assumption later in Section 2.3. In our baseline analysis, I focus on one-asset case because of its tractability and robustness of its solution.

The optimality conditions of the problem facing households can be reduced to the following standard Euler Equation:

$$U_{c}(t)=\exp\left[ -\gamma\log(1+c_{t})\right] E_{t}\left\{ (1+r+\phi\varepsilon_{t})U_{c}(t+1)\right\}$$ (4)

along with the budget constraint (3), and the standard Kuhn-Tucker conditions. $U_{c}$ is the derivative of lifetime utility with respect to consumption.

As discussed before, indexed bonds with returns indexed to the exogenous shock are not able to complete the market; they just partially complete it by providing the agents with the means to hedge against fluctuations in endowment income. If I call $(1+r+\phi\varepsilon)b_{t}$ financial income, the underlying goal to complete the market would be to keep the sum of endowment and financial incomes constant and equal to the mean endowment income (i.e., $(1+\varepsilon_{t})y^{T}+(1+r+\phi\varepsilon)b_{t}=y^{T}$). Clearly, one can keep this sum constant only if the bonds' returns are state-contingent (i.e., contingent on both the exogenous shock and the debt stock, which requires $R_{t}(b,\varepsilon)=-\frac{\varepsilon_{t}y^{T}}{b_{t}}$) or if agents can trade Arrow securities (i.e., there are as many assets as the number of state of nature). Moreover, indexed bonds introduce a tradeoff: on one the hand, they hedge income fluctuations but on the other hand, they introduce interest rate fluctuations.

Given the income uncertainty, and the incompleteness of the insurance market, households' engage in precautionary savings to hedge away the risk of attaining "catastrophic" levels of income. They accomplish this task by imposing on themselves a debt limit (i.e., the natural debt limit), given by the annuity value of the worst income realizations. Indexation of the return reduces the incentives for precautionary savings against low realizations of income shocks but it might introduce incentives to save against high realizations of income shocks if the degree of indexation is such that the repayments to the rest of the world outweigh the additional income received in those states. (I provide a formal analysis of this point below).

Exploring the overall implications of indexation in different dimensions requires a detailed analysis of the model economy presented above. For this purpose, I perform a series of numerical exercises presented below.

2.1.1  Dynamic programming representation

The dynamic programming representation of the household's problem is as follows:

$$\begin{split}V(b,\varepsilon)=\max_{b^{\prime}}\left\{ u(c)+(1+c)^{-\gamma} E\left[ V(b^{\prime},\varepsilon^{\prime})\right] \right\} \quad s.t.\\ c^{T}=(1+\varepsilon)y^{T}-b^{\prime}+(1+r+\phi\varepsilon)b. \end{split}$$ (5)

Here, the endogenous state-space is given by $\mathcal{B}=\{b_{1} <...<b_{NB}\}$, which is constructed using $NB=1,000$ equidistant grid points. The exogenous Markov process is assumed to have two states for simplicity: $\mathcal{E}=\{\varepsilon_{L}<\varepsilon_{H}\}$. Optimal decision rules, $b^{\prime}(b,\varepsilon):\mathcal{E}\times\mathcal{B}\rightarrow\mathcal{R}$ , are obtained by solving the above problem via a value-function iteration algorithm.

2.1.2  Calibration

The parameter values used to calibrate the model are summarized in Table 1. The CRRA parameter $\sigma$ is set to 2, the mean endowment $y^{T}$ is normalized to one, and the gross interest rate is set to the quarterly equivalent of 6.5 percent, following values used in the small open economy RBC literature (see, for example, Mendoza, 1991). The steady state debt-to-GDP ratio is set to 35 percent, which is in line with the estimate for the net asset positions of Turkey (see Lane and Milesi-Ferretti, 1999). The elasticity of the subjective discount factor follows from the Euler Equation for consumption evaluated in steady state:

$$(1+\overline{c})^{-\gamma}(1+r)=1\Rightarrow\gamma =\log(1+r)/\log(1+\bar{c}).$$ (6)

The standard deviation of the endowment shock is set to 3.51 percent and the autocorrelation is set to 0.524; those values are the standard deviation and the autocorrelation of tradable output for Turkey given in Table 4.

Table 1:  Parameter Values

σ	2	Relative risk-aversion	RBC parameterization
yT	1	Tradable endowment	Normalization
σε	0.0351	Tradable output volatility	Turkish data
ρε	0.524	Tradable output autocorrelation	Turkish data
R	1.0159	Gross interest rate	RBC parameterization
γ	0.0228	Elasticity of discount factor	Steady state condition

Using the "simple persistence" rule, I construct a Markovian representation of the time series process of output. The transition probability matrix $\mathcal{P}$ of the shocks follows:

$$\mathcal{P}(i,j)=(1-\rho_{\varepsilon})\Pi_{i}+\rho_{\varepsilon} \mathcal{I}_{i,j}$$ (7)

where $i,j=1,2$; $\Pi_{i}$ is the long-run probability of state $i$; and $\mathcal{I}_{i,j}$ is an indicator function, which equals 1 if $i=j$ and 0 otherwise, $\rho_{\varepsilon}$ is the first-order serial autocorrelation of the shocks. I set $\Pi_{i}$ to 0.5, assuming a symmetric markov chain. This assumption along with autocorrelation of output process, estimated from data implies the following values for the transition probability matrix:

$$\mathcal{P}=\left[ \begin{array}[c]{cc} 0.762 & 0.238\\ 0.238 & 0.762\\ & \end{array} \right] .$$ (8)

2.1.3  Simulation results

To show the effect of indexation on consumption smoothing, I report long-run values of the key macroeconomic variables, such as mean bond holdings (a measure of precautionary savings), volatility of consumption, correlation of consumption with income (which measures the extent to which income fluctuations affect consumption fluctuations) and serial autocorrelation of consumption (which measures the persistence of consumption, see Table 5). Without indexation ($\phi=0$), mean bond holdings are higher than the case with perfect foresight (-0.35) (a value that implies precautionary savings); volatility of consumption is positive; and consumption is correlated with income.

When the degree of indexation is in the [0.015, 0.25) range, households engage in less precautionary savings (as measured by the long-run average of $b$) and the standard deviation of consumption declines relative to the case without indexation. Moreover, in this range, correlation of consumption with GDP falls slightly and its serial autocorrelation increases slightly. The results suggest that when the degree of indexation is in this range, indexation improves these macroeconomic variables from the consumption-smoothing perspective. When the degree of indexation is greater than 0.25, however, the improvements reverse. In the full-indexation ($\phi =1$) case, for example, the standard deviation of consumption is 4.8 percent, four times the standard deviation in the no-indexation case. The persistence of consumption also declines at higher degrees of indexation. The autocorrelation of consumption in the full-indexation case is 0.886, compared with 0.978 in the no-indexation case and the high of 0.984 when $\phi=0.10$. Not surprisingly, the ranking of welfare (calculated as compensating variations in consumption) is in line with the ranking of consumption volatility, as the last row of Table 5 reveals. However, the absolute values of the differences in welfare are quite small.¹⁹

The above results are driven by the changes in the ability to hedge income fluctuations with indexed bonds. This hedging ability is affected by the degree of indexation because indexation alters the incentives for precautionary savings. In particular, it has a significant effect on determining the state of nature that defines the catastrophic level of income at which household reach their natural debt limit. The natural debt limit ($\psi$) is the largest debt that the economy can support to guarantee non-negative consumption in the event that income remains at its catastrophic level almost surely; that is,

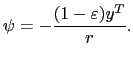$$\psi=-\frac{(1-\varepsilon)y^{T}}{r}.$$ (9)

With nonindexed bonds, the catastrophic level of income is realized with a negative endowment shock. When the bond holdings approach the natural debt limit, consumption approaches zero, which leads to infinitely negative utility. Hence, agents have strong incentives to avoid holding levels of bonds lower than the natural debt limit. To guarantee positive consumption almost surely in the event that income remains at its catastrophic level, agents engage in strong precautionary savings. An increase (or decrease) in this debt limit strengthens (or weakens) the incentive to save, because the level of bond holdings that agents would try to avoid would be higher (or lower). With indexation, the natural debt limit can be determined at either negative or positive realization of the endowment shock, depending on which yields the lower income (i.e., determines the catastrophic level of income). To see this effect, notice that using the budget constraint, when the shock is negative,

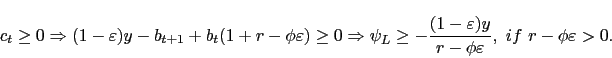
$$\begin{split}c_{t}\geq0 \Rightarrow(1-\varepsilon)y-b_{t+1}+b_{t} (1+r-\phi\varepsilon) \geq0 \Rightarrow\psi_{L}\geq-\frac{(1-\varepsilon)y}{r-\phi\varepsilon },\ if\ r-\phi\varepsilon>0. \end{split}$$ (10)

For the ranges of values of $\phi$ where $r-\phi\varepsilon<0$, Equation 10 yields an upper bound for the bond holdings; i.e., $\psi_{L} \leq-(1-\varepsilon)y/(r-\phi\varepsilon)$. Hence, in this range, negative shock will not play any role in determining the natural debt limit. Again using the budget constraint, positive endowment shock implies the following natural debt limit:

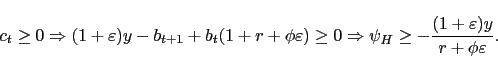
$$\begin{split}c_{t}\geq0 \Rightarrow(1+\varepsilon)y-b_{t+1}+b_{t} (1+r+\phi\varepsilon) \geq0 \Rightarrow\psi_{H}\geq-\frac{(1+\varepsilon)y}{r+\phi\varepsilon}. \end{split}$$ (11)

Combining the two equations yields the following formula:

$$\psi=\{ \begin{array}[c]{c} \max{\{-\frac{(1-\varepsilon)y}{r-\phi\varepsilon},-\frac{(1+\varepsilon )y}{r+\phi\varepsilon}\}},\ if \ \phi<r/\varepsilon\\ -\frac{(1+\varepsilon)y}{r+\phi\varepsilon}, \; if \; \phi>r/ \varepsilon. \end{array}$$ (12)

Further algebra suggests that when $\frac{1-\varepsilon}{1+\varepsilon} <\frac{r-\phi\varepsilon}{r+\phi\varepsilon}$ or $\phi<r$, the natural debt limit is sound in the state of nature with a negative endowment shock. In this case, $\partial\psi/ \partial\phi<0$; that is, increasing the degree of indexation decreases the natural debt limit or weakens the precautionary savings incentive. However, if $\frac{1-\varepsilon}{1+\varepsilon} >\frac{r-\phi\varepsilon}{r+\phi\varepsilon}$ or $\phi>r$, then $\partial\psi/ \partial\phi>0$, that is, increasing the degree of indexation increases the natural debt limit or strengthens the precautionary savings incentive.

Table 6 shows calculations for these natural debt limits as functions of the degrees of indexation, along with the corresponding returns in both states ( $R_{t}^{i}=1+r+\phi\varepsilon_{t}$), and confirms the analytical results derived above. When the degree of indexation is less than 0.0159, the natural debt limit is determined by the negative shock; and it decreases (i.e., becomes looser) as $\phi$ increases. When $\phi$ is greater than 0.0159, the debt limit is determined by the positive shock, and it increases (i.e., becomes tighter) as $\phi$ increases (the corresponding limits are shown in bold in Table 6). In the full-indexation case, for example, this debt limit is -20.09, whereas the corresponding value is -61.49 in the nonindexed case (since, the endowment is normalized to 1, those nominal values of debt limit are in units of GDP). In other words, in the full-indexation case, positive endowment shocks decrease the catastrophic level of income to one third of the value in the nonindexed case. This decrease, in turn, sharply strengthens the precautionary savings motive.

To understand the role of indexation on volatility of consumption, I perform a variance decomposition analysis. Higher indexation provides a better hedge to income fluctuations by increasing the covariance of the trade balance ($tb$ = $b^{\prime}-R_{t}^{i}$b) with income (because in good (or bad) times agents pay more (or less) to the rest of the world). Higher indexation, however, also increases the volatility of the trade balance because it introduces interest rate fluctuations. To pin down the effect of indexation on these variables, I perform a variance decomposition using the following identity:

$$var(c^{T})=var((1+\varepsilon)y^{T})+var(tb)-2cov(tb,y^{T}).$$

Table 7 presents the corresponding values for the last two terms in the above equation for each of the indexation levels.²⁰ Clearly, both the variance of the trade balance and the covariance of the trade balance with income monotonically increase with the level of indexation. However, the term $var(tb)-2cov(tb,(1+\varepsilon)y^{T})$ fluctuates in the same direction as the volatility of consumption, suggesting that at high levels of indexation, the rise in the variance of the trade balance offsets the improvement in the co-movement of the trade balance with income (i.e., the effect of increased fluctuation in interest rate dominates the effect of hedging provided by indexation). Hence, consumption becomes more volatile for higher degrees of indexation.

In summary, when the degree of indexation is higher than a critical value (as with full-indexation), the precautionary savings motive is stronger and the volatility of consumption is higher than in the nonindexed case. These results arise because the natural debt limit is higher at higher levels of indexation and because the increased volatility in the trade balance far outweighs the improvement in the co-movement of the trade balance with income.

The results suggest that to improve macroeconomic variables, the indexation level should be low. When $\phi$ is lower than 0.25, agents can better hedge against fluctuations in endowment income than when $\phi$ is at higher levels. In this case, the precautionary savings motive is weaker, the volatility of consumption is smaller, and consumption is more persistent. When $\phi$ is in the [0.10,0.25] range, the correlation of consumption with income approaches zero and the autocorrelation of consumption nears unity. These values resemble the results that could be attained in the full-insurance scenario, and they suggest that partial indexation is optimal.

The results using a frictionless one-sector model shed light on the implications of indexed bonds. The findings in this section suggest that the hedge provided by indexed bonds is imperfect and that the implications of indexed bonds depend on the degree of indexation of the bonds. The implications of indexation could be a nonmonotonic function of the degree of indexation. For values of this variable that are higher than a certain threshold, households may end up being worse off with indexation than without it.

2.2  The two-sector model with financial frictions

I build on the previous frictionless one-sector model by introducing a non-tradable sector and a borrowing constraint. Foreign debt is denominated in units of tradables, and imperfect credit markets impose a borrowing constraint that limits external debt to a share of the value of total income in units of tradables (this constraint therefore reflects changes in the relative price of nontradables that is the model's RER). With these new features, the model with nonindexed bonds is the same as described in Mendoza (2005) (an endowment economy version of Mendoza, 2002).

Representative households receive a stochastic endowment of tradables and a nonstochastic endowment of nontradables, which are denoted $(1+\varepsilon _{t})y^{T}$ and $y^{N}$, respectively. As in the previous model, $\varepsilon_{t}$ is a shock to the world value of the mean tradables endowment, which could represent a productivity shock or a terms-of-trade shock, $\varepsilon\in\mathcal{E}=[\varepsilon_{1}<...<\varepsilon_{m}]$ (where $\varepsilon_{1}=-\varepsilon_{m}$) evolves according to an $m$-state symmetric Markov chain with transition matrix $\mathcal{P}$. Households derive utility from aggregate consumption ($c$), and they maximize Epstein's (1983) stationary cardinal utility function (see Equation (1), where the utility function (2) is in CRRA form). The consumption aggregator is represented in constant elasticity of substitution (CES) form as follows:

$$c_{t}(c_{t}^{T},c_{t}^{N})=\left[ \omega(c_{t}^{T})^{-\mu }+(1-\omega)(c_{t}^{N})^{-\mu}\right] ^{-\frac{1}{\mu}}.$$ (13)

where $1/(1+\mu)$ is the elasticity of substitution between consumption of tradables and nontradables and where $\omega$ is the CES weighting factor.

The households' budget constraint is

$$c_{t}^{T}+p_{t}^{N}c_{t}^{N}=(1+\varepsilon_{t})y^{T}+p_{t}^{N} y^{N}-b_{t+1}+(1+r+\phi\varepsilon_{t})b_{t}$$ (14)

where $p_{t}^{N}$ is relative price of nontradables. (The rest of the variables are defined as in the frictionless one-sector model). Here, the returns of the bonds are indexed to the terms of trade shock.²¹

In addition to the budget constraint, foreign creditors impose the following borrowing constraint, which limits debt issuance as a share of total income at period $t$ not to exceed $\kappa$:

$$b_{t+1}\geq-\kappa\left[ (1+\varepsilon_{t})y^{T}+p_{t} ^{N}y^{N}\right] .$$ (15)

The borrowing constraint takes a similar form to those used in the Sudden Stops literature to mimic the tightening of the available credit to emerging countries (see, for example, Caballero and Krishnamurthy, 2001; Mendoza, 2002; Mendoza and Smith, 2005; Caballero and Panageas, 2003). As Mendoza and Smith (2005) explain, even though these types of borrowing constraints are not based on a contracting problem between lenders and borrowers, they are realistic in the sense that they resemble the risk management tools used in international capital markets, such as the Value-at-Risk models that investment banks use.

The optimality conditions are:

$$U_{c}(t)\left( 1-\frac{\nu_{t}}{\lambda_{t}}\right) =\exp\left[ -\gamma\log(1+c_{t})\right] E_{t}\left\{ \frac{(1+r+\phi\varepsilon_{t} )p_{t}^{c}}{p_{t+1}^{c}}U_{c}(t+1)\right\} ,$$ (16)

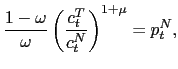
$$\frac{1-\omega}{\omega}\left( \frac{c_{t}^{T}}{c_{t}^{N}}\right) ^{1+\mu}=p_{t}^{N},$$ (17)

the budget constraint (14), the borrowing constraint (Equation 15), and the standard Kuhn-Tucker conditions. $\nu$ and $\lambda$ are the Lagrange multipliers of the borrowing constraint and the budget constraint, respectively. $U_{c}$ is the derivative of lifetime utility with respect to aggregate consumption. $p_{t}^{c}$ is the CES price index of aggregate consumption in units of tradable consumption, which equals $\left[ \omega^{\frac{1}{\mu+1}}+(1-\omega)^{\frac{1}{\mu+1}} (p^{N})^{\frac{\mu} {\mu+1}}\right] ^{\frac{1+\mu}{\mu}}$ . Equation 16 is the standard Euler equation equating marginal utility at date $t$ to that of date $t+1$. Equation 17 equates the marginal rate of substitution between tradables consumption and nontradables consumption to the relative price of nontradables.

I conduct a series of numerical exercises to explore the implications of indexed bonds on Sudden Stops. Those results are presented in the next section.

2.2.1  Dynamic programming representation

With introduction of liability dollarization and the borrowing constraint, the dynamic programming of the households' problem is updated as follows:

$$\begin{split}V(b,\varepsilon) & =\max_{b^{\prime}}\left\{ u(c)+(1+c)^{-\gamma} E\left[ V(b^{\prime},\varepsilon^{\prime})\right] \right\} \quad s.t.\\ c^{T} & =(1+\varepsilon)y^{T}-b^{\prime}+(1+r+\phi\varepsilon)b\\ c^{N} & =y^{N}\\ b^{\prime} & \geq-\kappa\left[ (1+\varepsilon)y^{T}+p^{N}y^{N}\right] . \end{split}$$ (18)

As in the previous one-sector model, the endogenous state-space is given by $\mathcal{B}=\{b_{1}<...<b_{NB}\}$, and the exogenous Markov process is assumed to have two states: $\mathcal{E}=\{\varepsilon_{L}<\varepsilon_{H}\}$. Optimal decision rules, $b^{\prime}(b,\varepsilon):\mathcal{E}\times \mathcal{B}\rightarrow\mathcal{R}$ , are obtained by solving the above dynamic programming problem (DPP).

2.2.2  Solving the model

I solve the stochastic simulations using value-function iteration over a discrete state-space in the [-2.5, 5.5] interval with 1,000 evenly spaced grid points. I derive this interval by solving the model repeatedly until the solution captures the ergodic distribution of bond holdings. The endowment shock has the same Markov properties described in the previous section. The solution procedure is similar to that described in Mendoza (2002). I start with an initial conjecture for the value-function and solve the model without imposing the borrowing constraint for each coordinate ($b$, $\varepsilon$) in the state-space, I then check whether the implied $b^{\prime}$ satisfies the borrowing constraint. If so, the solution is found and I calculate the implied value-function, which is then used as a conjecture for the next iteration. If not, I impose the borrowing constraint with equality and solve a system of non-linear equations defined by the three constraints given in the DPP (Equation 18) as well as the optimality condition given in Equation (17). Then, I calculate the implied value-function using the optimal $b^{\prime}$ and iterate to convergence.

2.2.3  Calibration

I calibrate the model such that aggregates in the non-binding case match certain aggregates of Turkish data. In addition to the parameters used in the frictionless one-sector model, I introduce the following parameters, the values of which I summarize in Table 2.: $y^{N}$ is set to 1.3418, which implies a share of nontradables output in line with the average ratio of the non-tradable output to tradable output between 1987 and 2004 for Turkey; $\mu$ is set to 0.316, which is the value Ostry and Reinhart (1992) estimate for emerging countries; the steady-state relative price of nontradables is normalized to unity, which implies a value of 0.4027 for the CES share of tradable consumption ($\omega$), calculated using the condition that equates the marginal rate of substitution between tradables and nontradables consumption to the relative price of nontradables (Equation 17). The elasticity of the subjective discount factor ($\gamma$) is recalculated to include the new variables in the solution of the non-linear system of equations implied by the steady-state equilibrium conditions of the model given in Equation 6. $\kappa$ is set to 0.3 (i.e., households can borrow up to 30 percent of their current income), which is found by solving the model repeatedly until the model matches the empirical regularities of a typical Sudden Stop episode at a state where the borrowing constraint binds with a positive probability in the long-run.

Table 2:  Parameter Values

μ	0.316	Elasticity of substitution	Ostry and Reinhart (1992)
yN/yT	1.3418	Share of NT output	Turkish data
pN	1	Relative price of NT	Normalization
κ	0.3	Constraint coefficient	Set to match SS dynamics
ω	0.4027	CES weight	Calibration
γ	0.0201	Elasticity of discount factor	Calibration

2.2.4  Simulation results

The stochastic simulation results are divided into three sets. In the first set, which I refer to as the frictionless economy, the borrowing constraint never binds. In the second set of results, which I refer to as the constrained economy, the borrowing constraint occasionally binds and households can issue only nonindexed bonds. In the last set, which I refer to as the indexed economy, borrowing constraint occasionally binds but households can issue indexed bonds.

My results, which compare the frictionless and constrained economies are analogous of those presented by Mendoza (2002). Hence, I emphasize the results that are specific and crucial to the analysis of indexed bonds and refer the interested reader to Mendoza (2002) for further details. Because at equilibrium, the relative price of nontradables is a convex function of the ratio of tradables consumption to nontradables consumption, a decline in tradables consumption relative to nontradables consumption as the result of a binding borrowing constraint leads to a decline in the relative price of nontradables, which makes the constraint more binding and leads to a further decline in tradables consumption.

Figure 3 shows the ergodic distributions of bond holdings. The distribution in the frictionless economy is close to normal and symmetric around its mean. The mean bond holding is -0.299, higher than the steady state bond holding of -0.35; this level reflects the precautionary savings motive that arises as a result of uncertainty and the incompleteness of financial markets. The distribution of bond holdings in the constrained economy is shifted right relative to that of the frictionless economy. Mean bond holdings in the constrained economy are 0.244, which reflects a sharp strengthening in the precautionary savings motive due to the borrowing constraint.

Table 8 presents the long-run business cycle statistics for the simulations. Relative to the frictionless economy, the correlation of consumption with the tradables endowment is higher in the constrained economy. In line with this strong co-movement, the persistence (autocorrelation) of consumption is lower in the constrained economy.

Behavior of the model can be divided into three ranges. In the first range, debt is sufficiently low that the constraint is not binding. In this case, the response of the constrained economy to a negative endowment shock is similar to that of the frictionless economy, and a negative endowment shock is smoothed by a widening in the current account deficit as a share of GDP. In addition debt levels are too high in a range of bond holdings. In this range, the constraint always binds regardless of the endowment shock. At more realistic debt levels, however, where the constraint only binds when the economy suffers a negative shock, the model with nonindexed bonds roughly matches the empirical regularities of Sudden Stops. This range, which I call the "Sudden Stop region" following Mendoza and Smith (2005), corresponds to grid points 218 to 230 (bond holdings on those grid points are -76.2 percent and -66.61 percent, which correspond to respective debt-to-GDP ratios of 32.28 percent and 28.56 percent).

In Figure 4, I plot the conditional forecasting functions of the frictionless and constrained economies for tradables consumption, aggregate consumption, the relative prices of nontradables, and the current account-GDP ratios, in response to an endowment shock of one-standard deviation. These forecasting functions are conditional on the 229th bond grid, which is one of the Sudden Stop states and has a long-run probability of 0.47 percent, and they are calculated as percentage deviations from the long-run means of their frictionless counterparts.²²

As the graphs suggest, the response of the constrained economy is dramatic. The endowment shock results in a 4.1 percent decline in tradable consumption, compared with a decline of only 0.9 percent in the frictionless economy. In line with the larger collapse in the tradables consumption, the responses of aggregate consumption and the relative price of nontradables are more dramatic in the constrained economy than in the frictionless economy. Whereas households in the frictionless economy are able to absorb the shock via adjustments in the current account (the current account deficit slips to 1.4 percent of GDP), households in the constrained economy cannot because of the binding borrowing constraint (the current account shows a surplus of 0.02 percent of GDP). These figures also suggest that the effects of Sudden Stops are persistent. It takes more than 40 quarters for these variables to converge back to their long-run means.

Figures 5, 6, and 7 compare the detrended conditional forecasting functions of the constrained economy with that of the indexed economy to illustrate how indexed bonds can help smooth Sudden Stop dynamics (the degrees of indexation are provided on the graphs).²³ As Figure 5 suggests, when the degree of indexation is 0.05, indexed bonds provide little improvement over the constrained case; indeed, the difference in the forecasting functions is not visible. When indexation reaches 0.10, however, the improvements are minor yet noticeable. At this degree of indexation, aggregate consumption rises 0.11 percent, tradables consumption rises 0.24 percent, and the relative price of nontradables increases 0.30 percent.

With increases in the degree of indexation to 0.25 and 0.45, the initial effects are relatively small. Figure 6 suggests that the improvements in tradables consumption are close to 1 percent and 1.8 percent when the degrees of indexation are 0.25 and 0.45, respectively. Figure 7 suggests that when the degree of indexation becomes higher, 0.7 and 1.0, for example, tradables consumption and aggregate consumption fall below the constrained case after the fourth quarter and stay below for more than 30 quarters, despite the initially small effects of a negative endowment shock. In other words, degrees of indexation higher than 0.45 in an indexed economy imply more pronounced detrimental Sudden Stop effects than in a constrained economy.

Table 9 summarizes the initial effects of both a negative and a positive shock conditional on the same grid points used in the forecasting functions. When indexed bonds are in place, my results suggest that if the degree of indexation is within [0.05, 0.25], indexed bonds help to smooth the effects of Sudden Stops. As Table 9 suggests, when the degree of indexation is 0.05, indexed bonds provide little improvement. As the degree of indexation increases, the initial impact of a negative endowment shock on key variables decreases. In this case, debt relief accompanies a negative endowment shock, and that relief helps reduce the initial impact of a binding borrowing constraint. Hence, the depreciation in the relative price of nontradables is milder, an effect that, in turn, prevents Fisherian debt deflation.

Table 9 also suggests that although the smallest initial impact of a negative endowment shock occurs when the degree of indexation is unity (full-indexation), this level of indexation has significant adverse effects if a positive shock occurs. In this case, households must pay a significantly higher interest rate over and above the risk-free rate. Although the constrained economy is not vulnerable to a Sudden Stop when a positive endowment shock occurs, agents in such an economy face a Sudden Stop from a sudden jump in debt-servicing costs.

Hence, my analysis suggests that households face a tradeoff when they engage in debt contracts with high degrees of indexation. If the households are hit by a negative endowment shock, highly indexed bonds can allow them to absorb the shock without suffering severely in terms of consumption. Such a shock might trigger a Sudden Stop if households were to borrow instead using nonindexed bonds (the initial effects are closest to the frictionless case when the degree of indexation is 1). If households receive a positive endowment shock, however, the initial effects are larger in the indexed economy (where the degree of indexation equals 1) than in the constrained economy (e.g., the impact on tradable consumption jumps from -1.1 percent to -6.7 percent). Analyzing the results in columns 3-9 of Table 9 shows that degrees of indexation in the [0.45, 1.0] interval lead to stronger Sudden Stop effects. If one takes the average of initial responses across the high and the low states in this range of values, one finds that the minimum of those averages is attained when the degree of indexation is 0.25, a result suggesting that households with concave utility functions would attain a higher utility with this consumption profile than ones achieved with indexation levels higher than 0.25.

In Figure 8, I plot the time-series simulations of the frictionless, constrained, and indexed economies. The simulations are derived first by generating a random, exogenous endowment-shock process using the transition matrix, $\mathcal{P}$, and then by feeding these series into each of the respective economies. As the graphs reveal, although patterns of consumption in each economy mostly move together, in some cases (around periods 2000, 3600, 6500, and 8800), sharp declines in constrained economy are seen. Those declines correspond to Sudden Stop episodes. In those cases, a consecutive series of negative endowment shocks makes the constraint binding, which in turn triggers a debt deflation that leads to a collapse in consumption.

When the return is indexed and the degree of indexation is 0.05 (top right graph), the volatility of consumption is noticeably lower than in the constrained case, and collapses in consumption during Sudden Stop episodes are milder. When the degree of indexation increases to 0.45, however, the volatility of consumption significantly increases, and more frequent collapses occur than the constrained case. When the degree of indexation is 1.0, a spike in volatility and much more frequent and sizeable collapses in consumption occur than the economies with lower degrees of indexation. The simulations illustrate that when indexation is full, the effect on consumption can be significantly negative, and moreover that indexation can yield benefits for consumption volatility only if the degree of indexation is quite low.

Table 8 suggests that in addition to the tradeoff of gains in the low state for losses in the high state, a short-run versus long-run tradeoff exists with respect to issuing indexed bonds with high degrees of indexation. With higher indexation levels, indexed bonds can generate substantial short-run benefits, but higher indexation levels also introduce more severe adverse effects in the long-run (i.e., consumption volatility and its co-movement with income increase with greater degrees of indexation). Consistent with my findings in the frictionless one-sector model, the value of indexation that minimizes the co-movement of consumption with GDP and yields more persistent consumption is low (in the range of [0.05, 0.1] for this calibration). These results also suggest that, depending on the objectives, the optimal degree of indexation level may vary. As illustrated earlier, the level of indexation that would minimize the effect of Sudden Stops is in the [0.25, 0.45] interval, whereas the level that minimizes long-run fluctuations is in the [0.05, 0.1] range. Regardless of whether one would like to smooth Sudden Stops or long-run fluctuations, full-indexation is undesirable.

2.3  Discussions, Extensions and Sensitivity Analysis

This section presents the results of analysis aimed at evaluating the robustness of my results to several variations in model parameterization. Due to space limitations, I only provide results for some of the extensions. For the other possible extensions, I provide discussions on their potential implications.

Number of States in Markov Chain. I first analyze the robustness of the results to changes in the number of states in the markov chain that approximates the endowment process using the one-sector model. For this analysis, I use a seven-state Markov chain that maintains the same autocorrelation and standard deviation of the shock as in the previous framework. Note that the simple persistence rule can be applied only if the number of exogenous-state variables is two. To create the transition matrix with seven exogenous states, I employ the method described in Tauchen and Hussey (1991).²⁴ The first block in Table 10 presents key long-run statistics, which are nearly identical to the ones presented in Table 5; in fact, for a given indexation level, the statistics are the same out to two decimal points. Hence, the results are robust to the number of state variables used in the Markov process.

Standard Deviation of the Endowment Shock. Next, I increase the standard deviation of the exogenous endowment shock to 4.5 percent. As Table 10 suggests, when bonds are not indexed, the precautionary savings motive is stronger, and consumption is more volatile; consumption displays greater correlation with income when variation in the magnitude of the exogenous endowment shock increases. Comparing Table 10 with Table 5 for the indexed case, I conclude that the optimal indexation level that minimizes long-run macroeconomic fluctuations is in the [0.05, 0.1] interval in the high-volatility case, whereas it is in the [0.1, 0.25] interval in the low-volatility case. In other words, the optimal degree of indexation decreases with increases in the volatility of the exogenous endowment shock.

Persistence of the Endowment Shock. Next, I evaluate the changes in results that arise when one lowers the autocorrelation of the endowment shock using the one-sector model. Compared with the baseline results given in Table 5, with an endowment shock autocorrelation of 0.4, agents engage in less precautionary savings. Moreover, consumption volatility and its co-movement with income are lower. When indexed bonds are in place, the lower the persistence of the shock, the higher the degree of indexation that would minimize the co-movement of consumption with income. For instance, when the indexation is 0.1, the correlation of consumption with income is 0.07 when the autocorrelation of the shock is 0.4. By comparison, at the same indexation level, the correlation of consumption with income is 0.017 when the autocorrelation is 0.524.

Interest Rate on Net Factor Payments. In my baseline results, I assumed that the small open economy can borrow or lend at the world interest rate following some of the studies in the literature such as Mendoza (2002), among others. Alternatively, one can assume that the economy pays a premium on top of the world interest rate that captures the spread that emerging countries pay when they borrow in world capital markets as in Uribe and Yue (2006). I conjecture that higher interest rate on net factor payments would not affect the nonmonotonicity results qualitatively, but would surely affect in which range the threshold degree of indexation falls, as the interest rate affects the natural debt limits. I leave out this analysis due to space limitation.

Two-asset Case. In my baseline analysis, I focused on the one-asset case, i.e., assumed that agents can issue either indexed bonds or nonindexed bonds at a given time. Providing the opportunity to the agents to choose a portfolio of bonds poses a nontrivial portfolio allocation problem, which severely reduces the tractability of the solution. Thus, I analyzed the merits of indexation in detail in a tractable and robust setup with one-asset in my benchmark analysis. Here, I relax this assumption and explore the implications of indexation when both indexed and nonindexed bonds are present.

Recent studies in the literature such as Devereux and Sutherland (2006), Evans and Hnatkovska (2006), and Tille and van Wincoop (2007) developed solution methods to solve such difficult portfolio allocation problems in open-economy macroeconomics models. Those techniques, however, can be applied only to local approximation methods such as perturbation or linearization. Judd, Kruber and Schmedders (2000) review the methods that can ease the portfolio allocation problems when using global approximation methods.²⁵ One of the methods heavily employed in the literature and thoroughly discussed in Judd et. al. is the introduction of transaction costs to trading one of the assets. Those transaction costs, which are quantitatively small in the stochastic steady state, help to differentiate between the two assets. Without those costs, it is impossible to get a well defined portfolio allocation of assets as the differences of higher order moments of assets are not sufficient to differentiate between the two assets in the equilibrium at the machine precision. I also use transaction costs while solving the two-asset case.

The modified dynamic programming problem with the two-assets and transaction costs in the one-sector model can be summarized as follows:

$$\begin{split}V(b,\varepsilon)=\max_{b^{\prime}}\left\{ u(c)+(1+c)^{-\gamma} E\left[ V(b^{\prime},\varepsilon^{\prime})\right] \right\} \quad s.t.\\ c^{T}=(1+\varepsilon)y^{T}-{b^{i}}^{\prime}-b^{\prime}+(1+r+\phi \varepsilon)b^{i}+(1+r)b+\frac{\delta}{2}({b^{i}}^{\prime}-b^{i})^{2}. \end{split}$$ (19)

where $\delta$ is the transaction cost of trading indexed bonds. I set this transaction cost to a small value of 0.08.²⁶ Rest of the parameter values remains the same. I solve the stochastic steady state simulations discretizing the [-10.0 5.0] interval with 100 nodes in both nonindexed and indexed bonds direction.

Table 11 summarizes the moments of key macroeconomic variables in the stochastic steady state. I compare those moments for degrees of indexation values in [0.1 1.0] interval, as well as with $\phi$ equals 0. I generate the results with $\phi$ set to 0 using the benchmark model with one-asset solved in the interval [-10.0 5.0] with 100 grid points. I cannot simply solve the model with two assets by setting the degree of indexation to zero, because, it makes both assets nonindexed, i.e., indistinguishable or solution becomes degenerate. The main result that arises in this exercise is that volatility of consumption, first, declines as the degree of indexation increases in [0.1, 0.4) interval; it takes its lowest value with 0.4; and lastly, in (0.4, 1.0] interval, volatility of consumption increases as the degree of indexation increases. As those results illustrate, although agents try to adjust their asset holdings to changes in the degree of indexation, they cannot simply attain a constant level of consumption volatility for various degrees of indexation. This result confirms that the nonmonotonic relationship between the degree of indexation and the benefits that indexation introduces also arise in this case with two-assets.

Next, I plot the limiting distributions of indexed and nonindexed bonds in the stochastic steady state to illustrate the nondegeneracy of the solution. As Figure 9 shows, distributions are well-defined for all cases. The only exceptions seem to be with $\phi$ equals 0.1 and 0.2. In those cases, distributions do not look as dispersed as in the other cases. However, even excluding the corresponding moments with those levels of indexation, the nonmonotonicity result still holds.

Investors' preferences towards risk. Through out my analysis, I assumed that investors are risk-neutral and that as long as the expected returns are the same for indexed and nonindexed bonds, they are indifferent holding either type of assets. It is reasonable to argue that investors may me risk-averse. I conjecture that in such a case, investors would charge a premium for indexed bonds, which would then increase the cost of indexation and that the threshold degree of indexation would be lower. I leave out this analysis due to space limitation.

Relative Openness of the Economy. As a final robustness check, I examine the effect of increasing the size of nontradables sector. The results are summarized in Table 12. I set the $y^{N}/y^{T}$ ratio to 1.6, implying that the degree of openness of the country is lower than in the baseline case. Not surprisingly, the model in this case captures the empirical regularities of an economy with less financial integration than the baseline case. In particular, consumption is more volatile than in the baseline case (for instance, the volatility of the tradables consumption in the frictionless economy increases to 1.6 percent, compared to the baseline value of 1.5 percent), and the co-movement of consumption with income is stronger (the correlation of tradables consumption with income in the frictionless economy increases to 0.75 from the baseline value of 0.69). Comparing the initial responses of each of these economies to a 1-standard-deviation endowment shock, one finds that the response of the constrained economy with a higher share of nontradable output is stronger than that of the one with baseline parameters, an outcome that suggests that the debt-deflation process is more severe in the economy with higher share of nontradable output. This result is consistent with the empirical evidence on the relationship between the degree of openness and the severity of Sudden Stops (see Calvo et al., 2003). To compare the optimal indexation levels across different parameterizations, I compare the average responses of the economies in the high and the low states to a 1-standard-deviation endowment shock. The results suggest that the minimum average response is attained when the degree of indexation is 0.25, which is the same degree of indexation in the baseline results. This result, however, depends on the coarseness of the indexation intervals with which one is solving the problem. Economic intuition suggests that lower financial integration would require higher indexation levels to smooth exogenous shocks better.

The sensitivity analysis presented in this section suggests that the optimal indexation level depends on country-specific characteristics such as the properties of the exogenous shock, including its persistence and its volatility as well as relative openness of the country. Hence, the optimal degree of indexation must be country specific, because it is highly likely that each emerging country receives shocks with different statistical properties or each country has different levels of integration with the rest of the world. The findings of this paper suggest that although indexed bonds might aid many countries in averting or at least mitigating the effects of Sudden Stops in emerging markets, an indexation level appropriate for one country might not be optimal for another.

3  Conclusion

Recent policy proposals argue that indexing the debt of emerging markets could help prevent the sudden reversals of capital inflows accompanied by RER devaluations that were typical of the emerging-market crises of the past decade. This paper explores the quantitative implications of this policy in various quantitative models of small open economies.

I conducted quantitative experiments to evaluate the effects of indexed bonds in two steps. First, I studied the effects of bonds indexed to output in a canonical one-sector infinite-horizon small open economy model with varying degrees of indexation. The introduction of indexed bonds partially completes the insurance market in such an economy When the nonindexed bond market is shut down and only indexed bonds are available, indexation improves welfare and reduces precautionary savings, volatility of consumption, and correlation of consumption when the degree of indexation is lower than a critical value. When this degree is higher than that threshold (as with full-indexation, for example), indexation can, in fact, make agents worse off. Increase in the variance of trade balance (resulting from higher interest rate fluctuations) outweighed the improvement in the covariance of trade balance with income, which then led to higher volatility of consumption; catastrophic income levels decreased, which in turn led to an increase in precautionary savings. When the indexed bonds market is retained, the nonmonotonic relationship between the degree of indexation and the benefits of indexed bonds still remains.

In the second step, I analyzed the role of indexed bonds in smoothing Sudden Stops and RER fluctuations. Indexed bonds can reduce the initial capital outflow in the event of an exogenous shock that otherwise triggers a Sudden Stop in an economy with only nonindexed bonds. Indexed bonds can, in turn, reduce the depreciation in the RER and break the Fisherian debt deflation mechanism. Once again, however, the benefit of those bonds depends critically on the degree of indexation. When the level of indexation is lower than a critical value, indexed bonds weaken Sudden Stops. If indexation is higher than this critical value, indexed bonds can provide some temporary relief in the event of a negative shock, but the initial improvement is short lived. Moreover, in the event of a positive shock, the economy is vulnerable to a Sudden Stop even though such a shock would never trigger a Sudden Stop in an economy in which household facing borrowing constraints could issue only nonindexed bonds. In this case, a positive shock commands higher repayment, which increases the need for larger amount of borrowing, this shift can make the borrowing constraint suddenly binding, and trigger a debt-deflation.

To conclude, the degree of indexation is a critical variable that determines the overall benefits that indexation introduces, and that a critical value of this variable, which maximizes the benefit of indexation (i.e., optimal degree of indexation) exists. This optimal value depends on the persistence and the volatility of the exogenous shocks a given country experiences as well as on the size of the country's nontradables sector relative to its tradables sector (i.e., the openness of the country). Hence, in terms of policy implications, my analysis reveals that the degree of indexation is a key variable that should optimally be chosen to smooth Sudden Stops; moreover this value should be country specific.

In my analysis, I assumed that investors are risk neutral and that indexing debt repayments would not require them to obtain country specific information. Indexed returns, however, may affect investors' incentives to collect country specific information. The implications of introducing risk-averse investors or informational costs in a dynamic framework are left for future research. The model also can be used to explore the implications of indexation to the relative price of nontradables, or to the CPI, but that is also left for further research.

References

Aiyagari, S. R. (1994). "Uninsured Idiosyncratic Risk and Aggregate Saving." Quarterly Journal of Economics, v. 109, No. 3, pp. 17-31.

Allen, F. and D. Gale (1994). Financial Innovation and Risk Sharing. Cambridge, MA:MIT Press.

Barro, R. J. (1995). "Optimal Debt Management." Working Paper, NBER, 5327.

Borensztein, E., and P. Mauro (2004). "GDP-Indexed Bond." Economic Policy, pp. 165-216.

Caballero, R. J. (2002). "Coping with Chile's External Vulnerability: A Financial Problem." Draft, MIT.

Caballero, R. J., A. Krishnamurthy (2001). "International and Domestic Collateral Constraints in a Model of Emerging Market Crises." Journal of Monetary Economics, v. 48, No.3, pp. 513-548.

Caballero, R. J., S. Panageas. "Hedging Sudden Stops and Precautionary Recessions: A Quantitative Framework." Journal of Development Economics, forthcoming.

Calvo, G. A. (1988). "Servicing the Public Debt: The Role of Expectations." American Economic Review, v. 78, No. 4, 647-661, September.

Calvo, G. A. (1998). "Capital Flows and Capital-Market Crises: The Simple Economics of Sudden Stops." Journal of Applied Economics, v.1, pp. 35-54.

Calvo, G. A., A. Izquierdo, and E. Talvi (2003). "Sudden Stops, The Real Exchange Rate, and Fiscal Sustainability: Argentina's Lessons." Working Paper, NBER, 9828.

Devereux, M. B. and A. Sutherland (2006). "A Dynamic Equilibrium Model of Imperfectly Integrated Financial Markets." Draft, University of British Columbia.

Durdu, C. B., E. G. Mendoza (2006). "Are Asset Price Guarantees Useful for Preventing Sudden Stops?: The Globalization Hazard-Moral Hazard Tradeoff of Asset Price Guarantees." Journal of International Economics, v. 69, pp. 84-119.

Durdu, C. B., E. G. Mendoza, M. Terrones (2007). "Precatuionary Demand for Foreign Assets in Sudden Stop Economies: An Assessment of New Merchantalism." Working Paper, NBER, 13123.

Epstein, L. G. (1983). "Stationary Cardinal Utility and Optimal Growth under Uncertainty." Journal of Economic Theory, v. 31, pp. 133-152.

Evans, M. and V. Hnatkovska (2006). "Solving General Equilibrium Models with Incomplete Markets and Many Assets." Draft, Georgetown University.

Fischer, Stanley (1975). "The Demand for Indexed Bonds." The Journal of Political Economy, v. 83, No. 3, 509-534, June.

Froot, K., M. J. Keen, and J. Stein (1989) "LDC Debt: Forgiveness, Indexation, and Investment Incentives." Journal of Finance, v. 44, No. 5, pp. 1335-50

Huggett, M. (1993) "The Risk Free Rate in Heterogenous-Agent, Incomplete-Insurance Economies." Journal of Economics Dynamics and Control, v. 17, No. 5-6, pp. 953-969.

Judd, K. L., F. Kubler and K. Schmedders (2000). "Computational Methods for Dynamic Equilibria with Heterogenous Agents." Draft, Stanford University.

Kehoe, P. and F. Perri (2000). "International Business Cycles with Endogenous Incomplete Markets." Econometrica, v. 70, No. 3, pp. 907-928.

Kim, S. H. and M. A. Kose (2003). "Dynamics of Open-Economy Business-Cycle Models: Role of the Discount Factor." Macroeconomic Dynamics, Cambridge University Press, vol. 7(2), pages 263-90.

Kose, M. Ayhan (2002). "Explaining business cycles in small open economies: 'How much do world prices matter?'." Journal of International Economics, v. 56(2), pp. 299-327.

Krugman, P. (1988). "Financing vs. Forgiving a Debt Overhang." Journal of Development Economics, v.29, pp. 253-68.

Lane, P., G. M. Milesi-Ferretti (2001). "The External Wealth of Nations: Measures of Foreign Assets and Liabilities for Industrial and Developing Countries." Journal of International Economics, v. 55, pp. 263-294.

Lucas, Robert E. Jr. (1987). Models of Business Cycles, New York: Basil Blackwell.

Magil, M., M. Quinzil (1995). "Which Improves Welfare More: A Nominal or an Indexed Bond?," Economic Theory, v. 10, pp. 1-37.

Mendoza, E. G. (1991). "Real Business Cycles in a Small Open Economy," American Economic Review, v. 81, 797-818, September.

Mendoza, E. G. (2002). "Credit, Prices, and Crashes: Business Cycles with a Sudden Stop" in Preventing Currency Crisis in Emerging Markets, ed. by S. Edwards and J. Frankel, University of Chicago Press.

Mendoza, E. G. and K. A. Smith (2005). "Margin Calls, Trading Costs, and Asset Prices in Emerging Markets: The Financial Mechanics of the 'Sudden Stop' Phenomenon," Working paper, NBER, 9286.

Mendoza, E. G. (2005). "Real Exchange Rate Volatility and the Price of Nontradables in Sudden-Stop Prone Economies" Economia, fall, pp. 103-148.

Neumeyer, P. A., F. Perri (2005). "Business Cycles in Emerging Economies: the Role of Interest Rates." Journal of Monetary Economics, v. 52, pp. 345-380.

Ostry, J. D., C. Reinhart (1992). "Private Saving and Terms of Trade Shocks." IMF Staff Papers, v. 39, pp 495-517.

Oviedo, P. Marcelo (2005). "World Interest Rates, Business Cycles, and Financial Intermediation in Small Open Economies." mimeo, Iowa State University.

Shiller, R.J. (1993). Macro Markets: Creating Institutions for Managing Society's Largest Economic Risks. Oxford: Clarendon Pres.

Tauchen, G., R. Hussey (1991). "Quadrature-Based Methods for Obtaining Approximate Solutions to Nonlinear Asset Pricing Models." Econometrica, v. 59, no. 2, pp. 371-396.

Tille, C. and E. van Wincoop (2007). "International Capital Flows." Draft, University of Virginia.

Schmitt-Grohé, S., M. Uribe (2003). "Closing Small Open Economy Models." Journal of Inernational Economics, v. 61, pp. 163-185.

Uribe, M., V. Yue (2006). "Country Spreads and Emerging Countries: Who Drives Whom?," Journal of Inernational Economics, Vol. 69, pp. 6-36.

Table 3:  Previous Attempts with Indexed Bonds

Country	Date Issued	Indexation Clause	Note
Argentina	1972 - 1989, 2002	CPI, GDP	GDP-indexed payments are granted to the investors as part of debt restructuring.
Australia	1985 - 1988	CPI	-
Bosnia and Herzegovina	1990s	GDP	Issued as part of Brady Plan, VRRs.
Brazil	1964-	CPI	-
Bulgaria	1990s	GDP	Issued as part of Brady Plan, VRRs.
Colombia	1967-	CPI	-
Costa Rica	1990s	GDP	Issued as part of Brady Plan, VRRs.
Chile	1956-	CPI	-
Israel	1955-	CPI	-
France	1973	Gold	Debt servicing cost increased significantly from depreciation of French franc against gold.
France	1970s	Oil	Issued as petro-bonos.
Mexico	1990s	Oil	Issued as part of Brady Plan, VRRs.
Mexico	1989-	CPI	-
Turkey	1994-	CPI	-
United Kingdom	1975-	CPI	-
Venezuela	1990s	Oil	Issued as part of Brady Plan, VRRs.

Table 4:  Business Cycle Facts for Emerging Countries

Variable: x	σ(x)	σ(x) / σ(Y)	ρ(x)	ρ(x,Y)	Sudden Stop	Sudden Stop relative to std.
Argentina 2002:1-2 GDP (Y)	4.022	1.000	0.865	1.000	-12.952	3.220
Argentina 2002:1-2 tradables GDP	4.560	1.134	0.667	0.923	-15.100	3.311
Argentina 2002:1-2 nontradables GDP	3.977	0.989	0.894	0.990	-12.169	3.060
Argentina 2002:1-2 consumption	4.475	1.113	0.830	0.975	-17.063	3.813
Argentina 2002:1-2 real exchange rate	15.189	3.777	0.754	0.454	-48.177	3.172
Argentina 2002:1-2 CA/Y	0.916	0.228	0.837	-0.802	1.353	1.476
Chile 1998:4-1999:1 GDP (Y)	2.093	1.000	0.731	1.000	-4.492	2.147
Chile 1998:4-1999:1 tradables GDP	1.833	0.876	0.473	0.762	-5.068	2.764
Chile 1998:4-1999:1 nontradables GDP	2.520	1.204	0.796	0.961	-4.840	1.921
Chile 1998:4-1999:1 consumption	4.184	1.999	0.748	0.898	-8.410	2.010
Chile 1998:4-1999:1 real exchange rate	0.007	0.003	0.649	0.372	-0.019	2.578
Chile 1998:4-1999:1 CA/Y	3.302	1.578	0.352	-0.512	10.932	3.311
Mexico 1994:4-1995:1 GDP (Y)	2.261	1.000	0.799	1.000	-7.440	3.290
Mexico 1994:4-1995:1 tradables GDP	2.682	1.186	0.712	0.921	-8.976	3.347
Mexico 1994:4-1995:1 nontradables GDP	2.189	0.968	0.832	0.978	-6.178	2.822
Mexico 1994:4-1995:1 consumption	4.222	1.867	0.841	0.973	-11.200	2.653
Mexico 1994:4-1995:1 real exchange rate	8.627	3.816	0.726	0.599	-32.844	3.807
Mexico 1994:4-1995:1 CA/Y	0.698	0.309	0.831	-0.475	2.220	3.180
Turkey 1994:1-2 GDP (Y)	3.695	1.000	0.667	1.000	-10.383	2.001
Turkey 1994:1-2 tradables GDP	3.511	0.950	0.524	0.962	-10.925	3.112
Turkey 1994:1-2 nontradables GDP	4.021	1.088	0.680	0.982	-10.007	2.489
Turkey 1994:1-2 consumption	4.134	1.119	0.746	0.919	-10.098	2.443
Turkey 1994:1-2 real exchange rate	9.110	2.465	0.675	0.602	-31.630	3.472
Turkey 1994:1-2 CA/Y	2.744	0.743	0.633	-0.591	9.704	3.375

Source:  Argentinean Ministry of Finance (MECON), Bank of Chile, Bank of Mexico, Central Bank of Turkey, International Financial Statistics. The data cover periods 1993:Q1-2004:Q4 for Argentina, 1986:Q1-2001Q3 for Chile, 1987:Q1-2004:Q4 for Mexico, 1987:Q1-2004:Q4 for Turkey. Data are quarterly seasonally adjusted real series. GDP and consumption data are logged and filtered using an HP filter with a smoothing parameter 1600. Real exchange rates are calculated using the IMF definition (RER_i = NER_i x CPI_i / CPI_US for country i).

Table 5:  Long-Run Business Cycle Statistics of the One-Sector Model

Degree of Indexation (Φ)	0.00	0.015	0.02	0.05	0.10	0.25	0.45	0.70	1.0
E(b)	-0.328	-0.349	-0.355	-0.385	-0.428	-0.042	0.522	1.458	2.026
σ(cons)	1.243	1.242	1.240	1.236	1.209	1.474	2.119	3.291	4.731
σ(tb/y)	3.486	3.516	3.527	3.590	3.674	4.211	4.820	5.724	6.755
ρ(cons, y)	0.186	0.160	0.151	0.097	0.017	-0.311	-0.409	-0.381	-0.304
ρ(tb/y, y)	0.936	0.937	0.937	0.939	0.945	0.943	0.916	0.849	0.752
ρ(cons)	0.978	0.980	0.980	0.981	0.984	0.909	0.870	0.876	0.886
ρ(tb/y)	0.549	0.549	0.548	0.546	0.541	0.542	0.562	0.601	0.646
welfare	n.a.	0.0025	0.0034	0.0090	0.0146	-0.0032	-0.0092	-0.0120	-0.0136

Notes:  Standard deviations are percentages of the mean. Welfare gains are percentages relative to the nonindexed model. n.a. refers to not applicable.

Table 6:  Returns and Natural Debt Limits in Units of GDP

Degree of Indexation (Φ)	0.00	0.01	0.015	0.05	0.10	0.25	0.45	0.70	1.0
Ri(L)	1.016	1.016	1.015	1.014	0.012	1.007	1.000	0.991	0.981
Ri(H)	1.016	1.016	1.016	1.018	1.019	1.025	1.032	1.040	1.051
NDL(L)	-61.487	-62.182	-62.894	-68.503	-78.431	-138.754	5440.508	106.131	48.760
NDL(H)	-64.517	-63.819	-63.136	-58.642	-53.262	-41.767	-32.434	-25.353	-20.089

Notes:  The first two rows are the corresponding gross returns in each states. In the last two rows, the implied natural debt limits are in bold.

Table 7:  Variance Decomposition Analysis for Consumption

Degree of Indexation (Φ)	0.00	0.015	0.02	0.05	0.10	0.25	0.45	0.70	1.0
σ(cons)	1.243	1.242	1.240	1.236	1.209	1.474	2.119	3.291	4.731
var(tb)	12.241	12.463	12.540	13.008	13.638	17.707	22.903	31.959	44.788
cov(tb, y)	11.508	11.620	11.660	11.897	12.248	13.929	15.365	16.724	17.364
var(tb)-2cov(tb, y )	-10.775	-10.777	-10.781	-10.792	-10.857	-10.147	-7.827	-1.488	10.061

Table 8:  Long-Run Business Cycle Statistics of the Two-Sector Model

Degree of Indexation (Φ)	F	C	0.05	0.10	0.25	0.45	0.70	1.0
E(b)	-0.299	0.244	0.122	0.276	0.594	1.599	2.328	2.516
σ(cT)	1.530	1.268	1.251	1.389	1.851	2.835	3.914	5.266
σ(c)	0.775	0.638	0.631	0.697	0.923	1.392	1.889	2.508
σ(pN)	2.026	1.682	1.660	1.845	2.467	3.804	5.291	7.162
σ(tb/y)	1.534	1.467	1.491	1.610	1.799	2.113	2.398	2.755
ρ(cT, y)	0.687	0.663	0.636	0.567	0.609	0.773	0.875	0.930
ρ(c, y)	0.687	0.664	0.637	0.567	0.608	0.770	0.870	0.924
ρ(pN, y)	0.687	0.663	0.636	0.567	0.609	0.774	0.877	0.933
ρ(tb/y, y)	0.512	0.648	0.646	0.548	0.290	-0.141	-0.404	-0.580
ρ(cT)	0.986	0.971	0.976	0.967	0.953	0.926	0.911	0.907
ρ(c)	0.986	0.971	0.976	0.967	0.953	0.925	0.909	0.903
ρ(pN)	0.986	0.971	0.976	0.967	0.953	0.927	0.912	0.909
ρ(tb/y)	0.581	0.546	0.540	0.546	0.572	0.609	0.631	0.661

Notes:  The first column is the frictionless economy, the second column is the constrained economy, and the rest of the columns are for the economy with borrowing constraints and indexed bonds (with given degrees of indexation). Standard deviations are percentages.

Table 9:  Initial Responses to a 1-Standard-Deviation Endowment Shock

Degree of Indexation (Φ)	F (non-indexed)	C (non-indexed)	0.05	0.10	0.25	0.45	0.70	1.0
Negative shock: tradable consumption	-0.907	-4.126	-4.007	-3.888	-3.531	-3.056	-1.657	-1.748
Negative shock: aggregate consumption	-0.384	-1.780	-1.728	-1.676	-1.520	-1.312	-0.706	-0.745
Negative shock: relative price of nontradables	-1.197	-5.398	-5.244	-5.090	-4.626	-4.007	-2.179	-2.299
Positive shock: tradable consumption	-0.291	-1.095	-2.019	-2.138	-2.494	-2.970	-4.369	-6.691
Positive shock: aggregate consumption	-0.120	-0.464	-0.862	-0.913	-1.068	-1.275	-1.887	-2.919
Positive shock: relative price of nontradables	-0.387	-1.444	-2.653	-2.808	-3.274	-3.895	-5.714	-8.716

Notes:  The first column is the frictionless economy, the second column is the constrained economy, and the rest of the columns are for the economy with borrowing constraints and indexed bonds (with given degrees of indexation). Initial responses are calculated as percentage deviations relative to the long-run mean of the frictionless economy.

Table 10:  Sensitivity Analysis of the One-Sector Model

Degree of Indexation (Φ)	0.00	0.015	0.02	0.05	0.10	0.25	0.45	0.70	1.0
1. seven-state markov chain: E(b)	-0.320	-0.345	-0.351	-0.369	-0.371	-0.083	0.548	1.459	1.968
1. seven-state markov chain: σ(cons)	1.246	1.245	1.244	1.243	1.258	1.487	2.147	3.319	4.776
1. seven-state markov chain: ρ(cons, y)	0.182	0.154	0.144	0.079	0.031	-0.301	-0.410	-0.378	-0.293
1. seven-state markov chain: ρ(cons)	0.970	0.971	0.971	0.974	0.982	0.906	0.869	0.870	0.869
2. σε=0.045: E(b)	-0.315	-0.335	-0.343	-0.359	-0.295	-0.017	0.908	1.741	2.064
2. σε=0.045: σ(cons)	1.567	1.566	1.566	1.560	1.576	1.919	2.899	4.272	6.226
2. σε=0.045: ρ(cons, y)	0.208	0.173	0.160	0.085	-0.046	-0.270	-0.357	-0.307	-0.230
2. σε=0.045: ρ(cons)	0.983	0.987	0.988	0.991	0.974	0.927	0.892	0.893	0.898
3. ρε=0.4: E(b)	-0.335	-0.357	-0.361	-0.398	-0.477	-0.300	0.180	0.918	1.637
3. ρε=0.4: σ(cons)	1.074	1.069	1.068	1.060	1.034	1.202	1.462	2.229	3.351
3. ρε=0.4: ρ(cons, y)	0.178	0.157	0.152	0.112	0.070	-0.167	-0.361	-0.367	-0.301
3. ρε=0.4: ρ(cons)	0.966	0.968	0.969	0.970	0.975	0.944	0.865	0.865	0.885

Note:  Resulting transition matrix for seven-state markov chain is approximated using the method described in Tauchen and Hussey (1991). Standard deviations are percentages.

Table 11:  Sensitivity Analysis of the One-Sector Model: Two-Asset Case

Degree of Indexation (Φ)	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
E(b)	4.98	5.74	6.32	6.26	3.92	3.05	1.79	0.31	0.59	0.56
E(bi)	-5.47	-5.48	-5.26	-5.66	-4.65	-4.34	-1.99	-0.45	-1.05	-1.06
σ(cons)	6.30	5.10	2.44	2.26	2.39	3.39	3.90	4.31	4.31	4.38
ρ(cons, y)	0.25	0.14	0.15	0.16	0.09	0.03	-0.02	-0.04	-0.03	-0.01
ρ(cons)	0.96	0.96	0.89	0.73	0.74	0.84	0.81	0.80	0.80	0.78

Table 12:  Sensitivity Analysis of the Two-Sector Model: Higher Share of Non-tradable Output

Degree of Indexation (Φ)	F	C	0.05	0.10	0.25	0.45	0.70	1.0
1. Long run statistics: E(b)	-0.290	0.258	0.084	0.682	0.667	1.739	2.399	2.551
1. Long run statistics: σ(cT)	1.590	1.306	1.261	1.639	1.957	2.919	3.956	5.300
1. Long run statistics: σ(c)	0.822	0.671	0.649	0.836	0.994	1.457	1.941	2.565
1. Long run statistics: σ(pN)	2.105	1.734	1.672	2.182	2.609	3.920	5.351	7.211
1. Long run statistics: ρ(cT, y)	0.749	0.716	0.691	0.664	0.714	0.844	0.913	0.951
1. Long run statistics: ρ(c, y)	0.750	0.718	0.692	0.664	0.713	0.841	0.908	0.945
1. Long run statistics: ρ(pN, y)	0.749	0.716	0.691	0.664	0.714	0.845	0.915	0.953
1. Long run statistics: ρ(cT)	0.987	0.975	0.975	0.973	0.956	0.931	0.914	0.909
1. Long run statistics: ρ(c)	0.987	0.976	0.976	0.974	0.956	0.930	0.911	0.905
1. Long run statistics: ρ(pN)	0.987	0.975	0.975	0.973	0.957	0.932	0.915	0.911
2. Initial Responses: Negative shock: tradable consumption	-1.036	-4.254	-4.122	-3.991	-3.596	-3.070	-1.608	-1.623
2. Initial Responses: Negative shock: aggregate consumption	-0.395	-1.655	-1.603	-1.551	-1.395	-1.187	-0.616	-0.622
2. Initial Responses: Negative shock: relative price of nontradables	-1.366	-5.565	-5.395	-5.224	-4.711	-4.025	-2.115	-2.135
2. Initial Responses: Positive shock: tradable consumption	-0.420	-2.029	-2.156	-2.292	-2.686	-3.213	-4.675	-7.074
2. Initial Responses: Positive shock: aggregate consumption	-0.157	-0.780	-0.818	-0.883	-1.037	-1.244	-1.823	-2.788
2. Initial Responses: Positive shock: relative price of nontradables	-0.557	-2.666	-2.985	-3.010	-3.525	-4.211	-6.111	-9.208

Notes:  y^N/y^T ratio is set to 1.6 in this analysis. Standard deviations are percentages of the mean. The first column is the frictionless economy, the second column is the constrained economy, and the rest of the columns are for the economy with borrowing constraints and indexed bonds (with given degrees of indexation).

Figure 1.  Sudden Stops in Emerging Markets
Panel A: Current Account-GDP Ratio

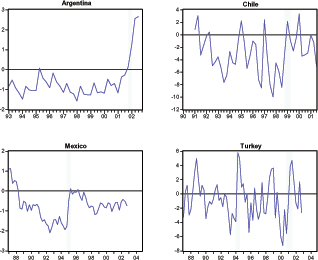
Figure 1.  Sudden Stops in Emerging Markets
Panel B: Real Exchange Rate

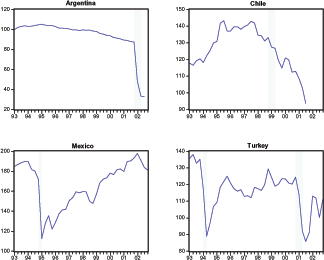
Figure 2.  Deviations from Trend in Consumption and Output
Panel A: Consumption

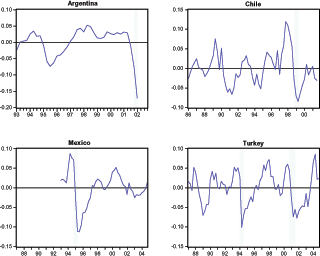
Figure 2.  Deviations from Trend in Consumption and Output
Panel B: Output

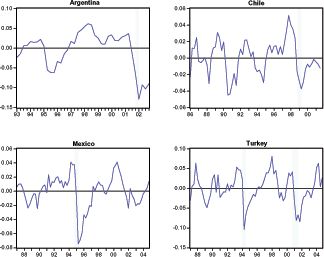
Figure 3:  Long-Run Distributions of Bond Holdings in Nonindexed Economies

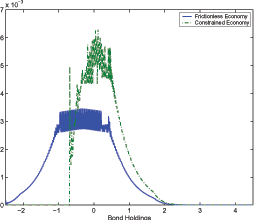
Figure 4:  Conditional Forecasting Functions in Response to a 1-Standard-Deviation Negative Endowment Shock

Notes:  Forecasting functions are conditional on the 229th grid point of the bond holdings, which implies a debt-to-GDP ratio of 30 percent. Solid and dashed lines are forecasting functions of the frictionless and constrained economies, respectively. NT refers to nontradable goods.

Figure 5:  Conditional Forecasting Functions in Response to a 1-Standard-Deviation Negative Endowment Shock

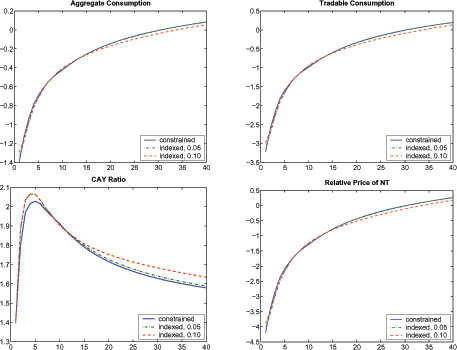
Notes:  Forecasting functions are conditional on the 229th grid point of the bond holdings, which implies a debt-to-GDP ratio of 30 percent. NT refers to nontradable goods.

Figure 6:  Conditional Forecasting Functions in Response to a 1-Standard-Deviation Negative Endowment Shock

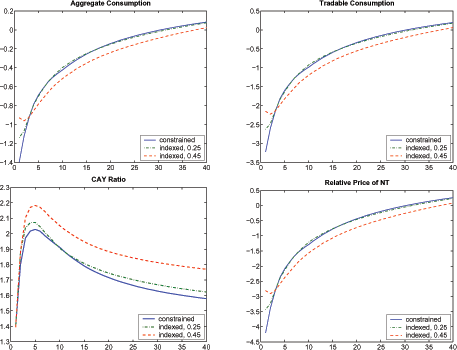
Notes:  Forecasting functions are conditional on the 229th grid point of the bond holdings, which implies a debt-to-GDP ratio of 30 percent. NT refers to nontradable goods.

Figure 7:  Conditional Forecasting Functions in Response to a 1-Standard-Deviation Negative Endowment Shock

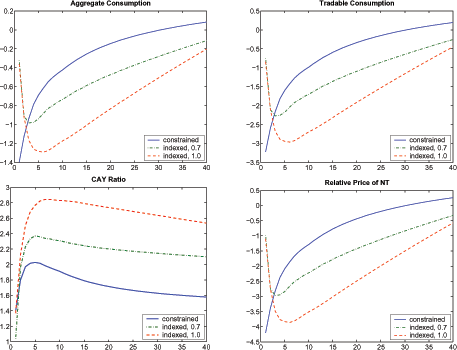
Notes:  Forecasting functions are conditional on the 229th grid point of the bond holdings, which implies a debt-to-GDP ratio of 30 percent. NT refers to nontradable goods.

Figure 8:  Time Series Simulation

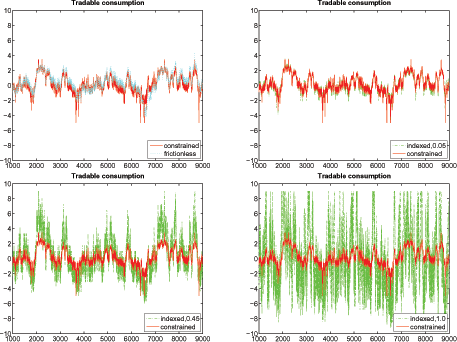
Notes:  On the top left graph, the dotted line is the tradable consumption series for the frictionless economy. The solid line is the series for the constrained economy. Consumptions are in percentage deviations from their corresponding means. The first 1,000 periods have been excluded from the graphs to focus on the data which are independent of initial conditions. Space limitations require us to leave out the figures associated with other degrees of indexation.

Figure 9:  Limiting Distribution in Two-Asset Case

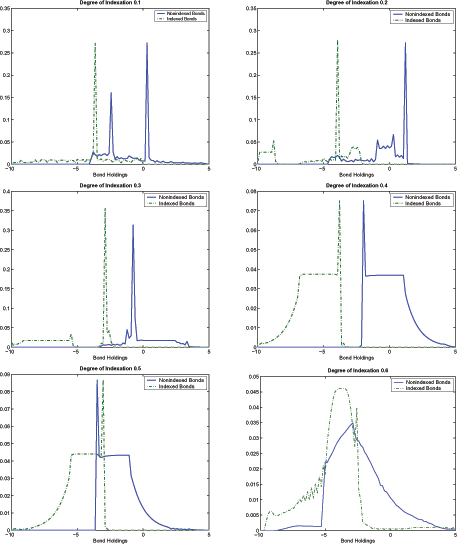
Figure 9:  Limiting Distribution in Two-Asset Case Continued

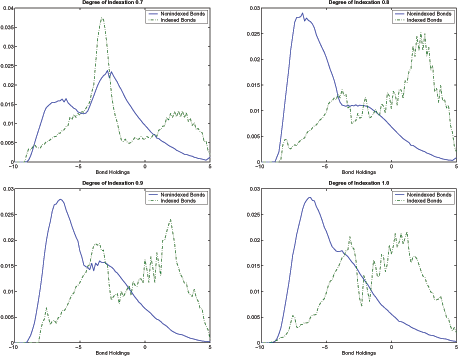
Footnotes

*  I am greatly indebted to Enrique Mendoza for his guidance and advice. Boragan Aruoba, Guillermo Calvo and John Rust also provided invaluable suggestions, and I thank them here. I would also like to thank David Bowman, Emine Boz, Christian Daude, Jon Faust, Dale Henderson, Ayhan Köse, Sylvain Leduc, Marcelo Oviedo, John Rogers, Harald Uhlig, Carlos Vegh, Mark Wright and the seminar participants at the Federal Reserve Board, the Congressional Budget Office, the Dallas FED, the Bank of England, the Bank of Hungary, Koç University, Sabanci University, Bilkent University, TOBB ETU University, the Central Bank of Turkey, the University of Maryland, 2005 Inter-University Student Conference at Princeton University, 2006 SCE Meetings in Cyprus, and 2007 SED Meetings in Prague for their useful comments. All errors are my own. The ideas expressed herein are those of the author and should not be interpreted as those of the Board of Governors of the Federal Reserve System. An earlier version of this paper has been circulated with the title "Are Indexed Bonds a Remedy for Sudden Stops?" Return to text

**  Address: Federal Reserve Board, the Division of International Finance, Washington, D.C. 20551. E-mail: [email protected]. Tel: (202)452-3755  Return to text

1.  Liability dollarization refers to the denomination of debt in units of tradables (i.e., hard currencies). Liability dollarization is common in emerging markets, where debt is denominated in units of tradables but partially leveraged on large nontradables sectors. Return to text

2.  See Figures 1 and 2 and Table 4 for further documentation of these empirical regularities (see Calvo et al., 2003, among others for a more detailed empirical analysis). Return to text

3.  Precautionary savings refers to extra savings caused by financial markets being incomplete. Caballero (2002) points out that precautionary savings in emerging countries arise as excessive accumulation of foreign reserves. Return to text

4.  The nonmonotonic relation with the degree of indexation and the benefits that indexation introduce still goes through if the nonindexed bond market is retained. See Section 2.3 for details. Return to text

5.  The largest debt that the economy can support to guarantee non-negative consumption in the event that income is almost surely at its catastrophic level is referred to as natural debt limit. Return to text

6.  Here, $b$ is bond holdings, $r$ is risk-free net interest rate, $y$ is endowment income, $\varepsilon_{t}$ is the income shock, and $c$ is consumption. Return to text

7.  I explain my motivation as to why I focus on the case where agents can issue only indexed or only nonindexed bonds at a given time and as to why I use this specific functional form for the bonds return in Section 2.1. Return to text

8.  See Mendoza and Smith (2005), and Mendoza (2005) for further analysis on Fisherian debt deflation. Return to text

9.  CPI-indexed bonds may not provide a hedge against income risks, because inflation is procyclical. Return to text

10.  Argentina granted GDP-linked payments to international investors as part of debt-restructuring of its 2001 default. Return to text

11.  I should emphasize, once again, that my motivation is not to understand why those countries do not issue indexed bonds. I rather investigate if those countries were to use indexed bonds, how those bonds would affect macroeconomic fluctuations and Sudden Stops. Return to text

12.  See, for instance, Barro, 1995; Calvo, 1988; Fischer, 1975; Magill and Quinzil, 1995; among others. Return to text

13.  Krugman (1988) and Froot et al. (1989) emphasize moral hazard problems that GDP indexation can introduce. Here, I point out other adverse effects that indexation can cause, even in the absence of moral hazard. Return to text

14.  A companion paper, Durdu et. al. (2007), uses this model with nonindexed bonds to account for the surge in foreign reserves holdings of emerging economies driven by precautionary savings incentives. Return to text

15.  See Schmitt-Grohé and Uribe (2003) for other specifications used for this purpose. See Kim and Kose (2003) for a comparison of quantitative implications of endogenous discounting with that of constant discounting. Return to text

16.  Note that I make an exogenous market incompleteness assumption. Modeling endogenous market incompleteness à la Perri and Kehoe (2000), among others, is beyond the scope of this paper. Return to text

17.  Note that with this functional form, the return is indexed to coupon payments. I also analyzed the case in which the return is indexed to the principal as well as the coupon payments. Such an indexation scheme requires the gross return to be $(1+r)(1+\phi\varepsilon_{t})$. I found that the results with this specification are very close to the ones in this paper. I present the results with indexation to coupon payments, because that is how countries issued indexed bonds including Argentina. Return to text

18.  I do not claim that there is any theoretical or practical reason for the households to choose this specific functional form for indexed bonds return. I use this functional form, because it simply allows us to analyze how macroeconomic fluctuations are affected for various levels of bonds return that imply higher volatility in return but at the same time better hedge to income fluctuations. Return to text

19.  As pointed out by Lucas (1987), the welfare implications of altering consumption fluctuations in this type of model are quite low. Return to text

20.  Because the endowment is not affected by changes in the indexation level, its variance is constant. Return to text

21.  Although returns are indexed to terms of trade shock, my modeling approach potentially sheds light on the implications of RER indexation as well. In this model, the aggregate price index (i.e., the RER) is an increasing function of the relative price of nontradables ($p^{N}$), which is determined at equilibrium in response to endowment shocks. Return to text

22.  Bond holdings on that grid point are equal to -0.674, which implies a debt-to-GDP ratio of 30 percent. Return to text

23.  These forecasting functions are detrended by taking the differences relative to the frictionless case. Return to text

24.  Original Tauchen (1981) approach can also be used for this purpose. Return to text

25.  I chose to use global approximation, since methods that rely on local approximation cannot capture the large deviations of net foreign asset holdings from their steady state values that can arise due to indexation. Return to text

26.  I also used other values. Qualitative results are robust to various values of those transaction costs. Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

Home | Economic research and data | Publications and education resources
Accessibility | Contact us
Last update: November 28, 2007