
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 917, January 2008 --- Screen Reader
Version*
Measuring U.S. International Relative Prices: A WARP View of the World
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
In this paper we construct a new measure of U.S. prices relative to those of its trading partners and use it to reexamine the behavior of U.S. net exports. Our measure differs from existing measures of the dollar's real effective exchange rate (REER) in that it explicitly incorporates both the difference in price levels between the United States and developing economies and the growing importance of these developing economies in world trade. Unlike existing REERs, our measure shows that relative U.S. prices have increased significantly over the past 15 years. In terms of simple correlations, the relationship between our measure of relative prices and U.S. net exports is much more coherent than that between existing REERs and net exports. To explore this relationship further, we use our measure to construct an index of foreign prices relevant for U.S. export volumes and reexamine several export equations. We find that export equations with the new index dominate those with previous measures in terms of in-sample fit, out-of-sample fit, and parameter constancy. In addition, we find that with the new index of foreign prices the estimated elasticity of U.S. exports with respect to foreign income is a good bit higher than the unitary elasticity found in previous studies using other price measures. This has implications for U.S. current account adjustment.
Keywords: Automated model specification, China, competitiveness, IMF, FRB, geometric aggregation, Penn World Tables, real effective exchange rates, trade elasticities
JEL classification: C82, F41, C22
1 Introduction
In this paper we assemble a new measure of international relative prices to gauge the average amount by which U.S. prices differ from foreign prices. Interest in developing such measures in international economics is not new.1 What is new in this paper is the focus on the interactions between the dispersion of prices across countries and the increased trade with emerging economies. Recognition of these interactions yields a picture of U.S. international relative prices that is fundamentally different from the one given by existing measures of the real effective exchange rate. Indeed, unlike existing measures of relative prices, we find a significant increase in U.S. prices relative to its trading partners over the past 15 years. Further, most of this increase owes to greater trade with developing economies rather than increases in U.S. prices relative to individual countries.
Our measure differs from those currently available for two reasons. First, we measure bilateral relative price levels, as opposed to bilateral relative price indexes. Second, we use an aggregation method that retains the information embodied in those levels. In contrast, existing measures of relative prices are constructed by either chaining or averaging indexes - that is, they begin with price and exchange rate indexes constructed to have a value of 100 in a base year so that the value of the index in a given period indicates how much prices have changed since the base year. Thus, multi-country aggregates of these indexes measure the average change relative to the base year. Such methods are ideal if the purpose is to measure average changes in bilateral real exchange rates but not for measuring the level of U.S. prices relative to prices elsewhere.
Of course, others have recognized the importance of differentiating price indexes from price levels.2 But the implications of combining that distinction with the increased role of developing countries in world trade has not received attention. In particular, the fact that prices in some developing economies are systematically below those in developed economies, combined with the fact that emerging economies' share of world trade has been increasing, has led to a decline in the average world price of traded goods even though prices in individual countries have not fallen. Aggregates based on price indexes cannot capture this interaction between price levels and trade shares. Our weighted average relative price (WARP) is designed specifically to capture this interaction and does so by using a geometric aggregate where the weights capture the change in the structure of U.S. external trade.
Section 2 reviews the evolution of several well known real effective exchange rate indexes. Although these indexes differ in source data and aggregation scheme, they generally paint a similar picture: U.S. prices relative to foreign prices have risen and fallen since 1975 but, on balance, they show no trend. Section 3 presents the WARP, discusses a few of its properties, and compares it to other measures. According to WARP, U.S. prices have risen significantly relative to its trading partners' prices since 1975 with most of the increase occurring since 1990.
This upward trend in U.S. international relative prices constitutes the main result of this paper. Section 4 examines several factors responsible for this upward trend: choice of price data, aggregation method, and currency basket. We find that the upward trend owes to the aggregation of relative price levels as such and to the shift in U.S. trade patterns away from the relatively high-price industrial countries toward the lower-price developing economies. Section 5 examines the sensitivity of this upward trend to both parametric structures and measurement errors; we find that the upward trend of U.S. international relative prices is robust.
Section 6 addresses whether WARP can be thought of as a measure of competitiveness. A point that comes clearly from the analysis is that any reasonable measure of competitiveness will necessarily incorporate the prices of non-traded goods and services as well as the prices of traded goods and services. Indeed, with analytical examples we show why the suitability of a measure of competitiveness to a particular application is largely an empirical question. With this in mind, Section 6 also looks at the relationship between WARP and the U.S. trade balance. We find that in terms of simple correlations, the relationship between relative prices and the U.S. trade balance (as a share of GDP) is much tighter when one uses WARP than when using conventional measures of real effective exchange rates. To explore why this might be the case, we examine several econometric specifications for the volume of U.S. exports. The focus is on assessing the implications for parameter estimates of using WARP-based and other measures of foreign prices to construct a relative price of exports. Our goal is not to offer detailed specifications for exports but, rather, to see if the WARP passes the "proof of concept" test. The evidence suggests that it does.
2 Existing Measures of Relative Prices
Existing measures of the dollar's real effective exchange rate (REER) are designed to reflect how much, on average, U.S. prices have changed relative to the prices of its trading partners.3 The top panel of figure 1 shows the measures constructed by the Federal Reserve, the OECD, and the IMF, all of which are based on relative CPIs.4 Though they differ from one another in many important methodological respects, they all show two common features. First, over the past thirty years, U.S. relative prices have changed little on average, a property that is at odds with the growing U.S. current-account deficit. Second, over shorter periods, U.S. international relative prices deviate substantially from their long-term mean and indeed these prices reached a historical peak in 1985.5
These three measures are constructed by aggregating bilateral real exchange rate indexes. That is, they begin with bilateral nominal exchange rate indexes and adjust them by relative movements in U.S. and foreign consumer price indexes. These bilateral real exchange rates (indexed to 1973=100) are shown in the middle panels of figure 1. The left panel plots the indexes vis-a-vis selected industrial countries; the right panel plots the indexes vis-a-vis selected emerging economies.6 There is clearly a good deal of dispersion among these bilateral indexes, indicating that the CPI-adjusted value of the dollar has risen relative to some countries' currencies and fallen relative to others. On a bilateral basis, these real exchange rates can be interpreted as changes in relative prices.
Given the dispersion of bilateral real exchange rates across countries, it is hard to tell if there is a general pattern to the movements. This is the point of a REER: to distill these various movements into a single measure. To do so requires a weighting scheme. The aggregates shown in the top panels use weights based on trade shares. The weights used by the Federal Reserve Board in its Broad Real Index are representative; a selection of these is given in the bottom panels of figure 1.7 We note the increasing weight given to developing economies, especially China and Mexico, since 1990.
Figure 1: Real Exchange Rate Indexes: Effective and Bilateral - Selected Institutions
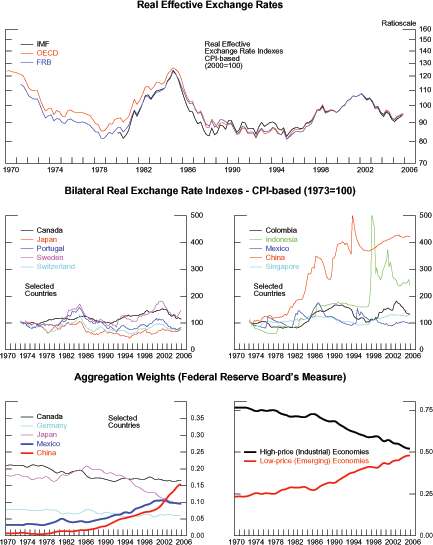
How has the increased weight of the developing economies affected the REERs? If one looks at both the increase (depreciation) in China's bilateral real exchange rate since 1973 (middle right panel) and the increase in China's weight in U.S. trade since 1990 (bottom left) one might conclude that China's real exchange rate has had a significant impact on the dollar's REER. However, in fact, China's real exchange rate has had a relatively small effect on the dollar's REER. The mechanics for this result vary with the particular REER used but, in general, the reason is that most of the increase in the dollar real bilateral exchange rate vis-a-vis China occurred prior to 1990, a time when China's weight in U.S. trade was relatively small. REERs designed to show average changes do not get much of a boost from the Yuan's real depreciation prior to 1990 because China's weight in the index was small during that period. Conversely, despite the increase in the weight of China after 1990, there has not been much real depreciation of the Yuan during the period when the weight was large, so, again, the REERs do not get much of a boost. In general, what matters for existing measures of real effective exchange rates is whether the bilateral exchange rates are changing and, if they are not changing much, then increasing the weights on these countries does not cause the REER to change.
If the sole objective is to measure changes in the real effective exchange rates, then one can hardly improve upon existing measures. What we argue is that an exclusive focus on such changes carries a loss of information, that this loss is more than a theoretical possibility, and that the increased participation of low-cost producers in the world economy gives it economic significance.
3 The WARP
3.1 Intuition
The basic idea behind our aggregate is simple. Suppose, for
expository ease only, that we have the foreign-currency price of a
basket of goods in a foreign country ![]() (call it
(call it
![]() ), and that we also have the dollar price
of the same basket in the United States (call it
), and that we also have the dollar price
of the same basket in the United States (call it ![]() ). As shown in equation (1), by multiplying the ratio
of these prices by the market exchange rate we can define a
bilateral relative price
). As shown in equation (1), by multiplying the ratio
of these prices by the market exchange rate we can define a
bilateral relative price ![]() as
as
 |
(1) |
This relative price is unitless and easy to interpret: A value of 2
means that the basket is twice as expensive in the United States as
it is in country ![]() .
.
To combine these bilateral relative prices into an aggregate measure for the United States, we use a weighted geometric mean where the weights vary over time and reflect each country's importance in U.S. trade. Specifically,
| (2) |
where ![]() is the time-varying weight associated
with the
is the time-varying weight associated
with the ![]() country.8 Two features of
country.8 Two features of
![]() are worth noting. First, the level of
the aggregate has meaning: a value of 1.5 means that U.S. prices
are on average fifty percent above foreign prices and this value is
not arbitrarily determined by the choice of base year. Second, the
aggregate can change even if all bilateral relative prices are
fixed.
are worth noting. First, the level of
the aggregate has meaning: a value of 1.5 means that U.S. prices
are on average fifty percent above foreign prices and this value is
not arbitrarily determined by the choice of base year. Second, the
aggregate can change even if all bilateral relative prices are
fixed.
An obvious alternative to ![]() is the commonly
used chained aggregate, which is a weighted average of the growth
rates of bilateral relative prices:
is the commonly
used chained aggregate, which is a weighted average of the growth
rates of bilateral relative prices:
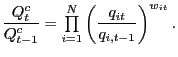
|
(3) |
By convention,
![]() is set equal to 100 in a given
base period and the level of the index for all other periods is
defined recursively. Chained aggregation has two important features
to recommend it. First, the index is independent of the levels of
its constituent
is set equal to 100 in a given
base period and the level of the index for all other periods is
defined recursively. Chained aggregation has two important features
to recommend it. First, the index is independent of the levels of
its constituent ![]() 's, implying that we do not have to
choose a meaningful base period for them. Second, changes in the
aggregate index only reflect changes in the underlying relative
prices. That is, if these rates do not change over a given period,
then the aggregate index will not change, even if the weights do.
Thus,
's, implying that we do not have to
choose a meaningful base period for them. Second, changes in the
aggregate index only reflect changes in the underlying relative
prices. That is, if these rates do not change over a given period,
then the aggregate index will not change, even if the weights do.
Thus, ![]() may be ideal for measuring the
average change in the dollar's bilateral relative prices.9
may be ideal for measuring the
average change in the dollar's bilateral relative prices.9
Given these aggregation formulas, how can, in the aggregate, U.S. prices rise relative to foreign prices? Holding all else equal, there are four channels:
- The nominal dollar exchange rate can appreciate.
- U.S. prices can rise.
- Foreign prices can fall.
- The weight of relatively low-price foreign economies can increase.
The first three channels operate through their impact on the
bilateral relative prices - the ![]() 's - and they are
fully captured in both the geometric and chained aggregates.
However, the chained index does not attempt to capture the fourth
channel whereas the geometric aggregate does so explicitly.
Specifically, logarithmic differentiation of equations (2) and (3) with respect to
time yields
's - and they are
fully captured in both the geometric and chained aggregates.
However, the chained index does not attempt to capture the fourth
channel whereas the geometric aggregate does so explicitly.
Specifically, logarithmic differentiation of equations (2) and (3) with respect to
time yields
which implies that
Thus the difference in growth rates between the geometric and the
chained aggregate is
![]() This term captures the interaction between each period's
distribution of the level of bilateral relative prices and the
evolution of the weights; if the weights are constant, then the two
growth rates are identical.
This term captures the interaction between each period's
distribution of the level of bilateral relative prices and the
evolution of the weights; if the weights are constant, then the two
growth rates are identical.
3.2 Implementation
The previous discussion assumed, for expository convenience, the
availability of data for the price levels of the foreign and
domestic baskets. Thus the first step in implementing our measure
is to obtain the bilateral relative prices-the ![]() 's. Data for bilateral relative prices are particularly
difficult to obtain because they require comparability of products
across countries.10 To this end we use the Penn World
Tables, which offer data on purchasing power parties.11
's. Data for bilateral relative prices are particularly
difficult to obtain because they require comparability of products
across countries.10 To this end we use the Penn World
Tables, which offer data on purchasing power parties.11
Greatly simplified, Penn collects data on spending and prices
for products that are comparable across countries to estimate
bilateral purchasing power parities. To avoid the calculations
being sensitive to the choice of base country, Penn introduces the
concept of "international dollars." This strategy generates a
system of simultaneous equations-the Geary-Khamis system-in which
the PPP estimates depend on the international dollar and vice
versa.12 Specifically, given the
international-dollar price of the ![]() product,
product,
![]() , the purchasing power parity for the
, the purchasing power parity for the
![]() country is
country is
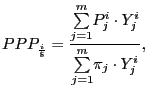
|
(4) |
where ![]() is the price of the
is the price of the ![]() product in the
product in the ![]() country,
country, ![]() is the amount produced of the
is the amount produced of the ![]() product in the
product in the
![]() country, and the
country, and the ![]() index
runs over the list of goods and services included in GDP.13 The
numerator equals the nominal GDP of the
index
runs over the list of goods and services included in GDP.13 The
numerator equals the nominal GDP of the ![]() country
expressed in local-currency terms whereas the denominator is the
value of
country
expressed in local-currency terms whereas the denominator is the
value of ![]() country's GDP expressed in international
dollars. Given
country's GDP expressed in international
dollars. Given
![]() the international dollar
price for the
the international dollar
price for the ![]() product is computed as
product is computed as
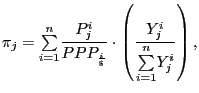
|
(5) |
where the first term is the price of the ![]() product in the
product in the ![]() country expressed in
international dollars and the second term is the
country expressed in
international dollars and the second term is the ![]() 's country share in world output of the
's country share in world output of the ![]() product.
product.
The system given by (4) and (5) consists of
![]() equations, of which only
equations, of which only ![]() are linearly independent. To address the
over-determined character of the system, Penn uses the United
States as the numeraire country meaning that the international
dollar has the same purchasing power over total U.S. GDP as the
U.S. dollar. Thus the average U.S. price relative to the average
price of the
are linearly independent. To address the
over-determined character of the system, Penn uses the United
States as the numeraire country meaning that the international
dollar has the same purchasing power over total U.S. GDP as the
U.S. dollar. Thus the average U.S. price relative to the average
price of the ![]() country can be estimated as the
market exchange rate divided by Penn's PPP:
country can be estimated as the
market exchange rate divided by Penn's PPP:
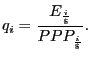
|
(6) |
There are several drawbacks to the Penn data for studying the open-economy implications of movements of U.S. international relative prices. First, the data are released with long delays: the most recent release (release 6.2 in 2006) has data ending in 2004.14 Second, the data are annual. To address these two limitations, the paper develops a method to extend Penn's annual parities and to estimate the associated quarterly observations.15 Finally, the data are subject to errors and section 5 examines the implications of these errors for our measure of U.S. international relative prices.
With these considerations in mind, the top panels of figure 2 show the evolution of the levels of bilateral relative prices for selected countries.16 Among the industrial countries (left panel), U.S. prices are highest relative to Portugal and lowest relative to Switzerland with most measures near or a little below one. As shown to the right, among emerging economies, there is a good deal more dispersion with relative prices ranging between 1.5 and 6.
Figure 2: U.S. International Relative Prices: Bilateral and Aggregate
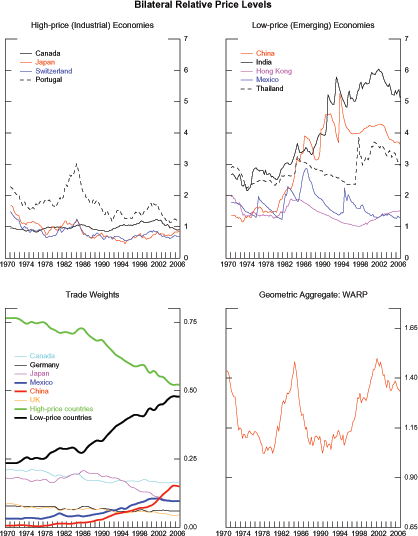
For aggregation we use the same trade weights as those in the Federal Reserve's Broad Real Dollar index (shown in lower left panel). Note that between 1980 and 1990 the total weight of emerging economies held steady near 25 percent, but since 1990 it has doubled to near 50 percent, reflecting rising weights for China and Mexico. The weight for industrial countries has declined, with Japan's weight declining the most. The weighted average of the 34 bilateral relative prices is constructed using equation (2) and shown in the lower right panel. The aggregate of U.S. international relative prices shows an upward trend since the end of the Bretton-Woods period. Indeed, by this measure, U.S. prices are roughly 40 percent above those of its trading partners.
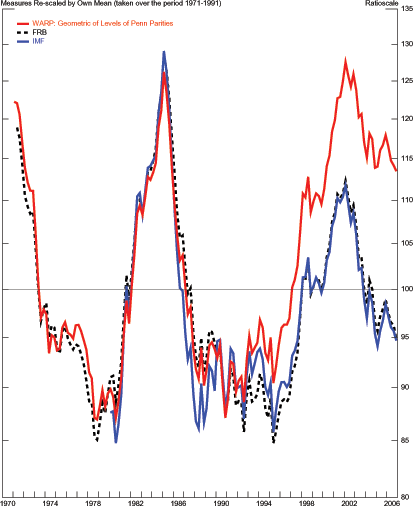
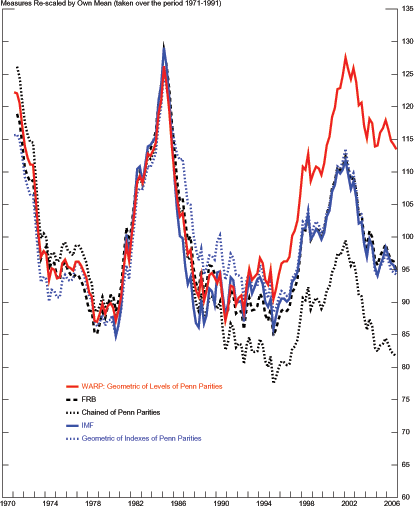
Figure 3 compares the evolution of this measure to the real effective exchange rates from the Federal Reserve and the IMF, rescaled by their own 1971-1991 sample means. The three measures move in near lockstep between 1971 and 1986. As such, neither the choice of aggregation method nor the measure of bilateral price has a noticeable effect on the aggregate measure of U.S. international relative prices through 1986. Since then, however, the aggregates tend to diverge. Specifically, the WARP shows a sustained increase and by 2002 it reaches the same value it had in 1985. In contrast, the other measures remain well below their 1985 peaks. This more recent divergence of U.S. international relative prices might be of interest in assessing the likelihood of a dollar depreciation large enough to address the U.S. external imbalance. Specifically, if one were to apply the 1985-1987 dollar depreciation to the 2006 values of the aggregates based on bilateral price indexes, then these aggregates would fall to levels not recorded in history. In contrast, applying the same depreciation to WARP would bring it to its 1986 value and, by this historical standard, such a depreciation would be consistent with previous experience.
Figure 3: Alternative Measures of International Relative Prices
4 Explaining the Rise in U.S. International Relative Prices
We now look at why our WARP has risen much more than the other measures since the late 1980s. To ease the exposition, we abstract from differences involving country coverage and weighting scheme to focus on the measurement of bilateral prices and aggregation methods.
4.1 Aggregation Methods and Price Measures
WARP differs from existing measures in both the choice of
aggregation formula and the measure of bilateral prices, raising
the question of which of these two factors explains the different
trends in the aggregates. To address this question, we construct
similar aggregates to those reported by other institutions where
their bilateral relative prices are replaced with ours![]() This strategy ensures that any difference can be
interpreted as due to the choice of aggregation method.
This strategy ensures that any difference can be
interpreted as due to the choice of aggregation method.
The Federal Reserve reports chained aggregates of bilateral CPI-adjusted exchange-rate indexes:
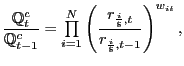
|
(7) |
where
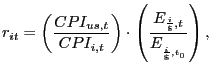
![]() represents the base period,
represents the base period, ![]() is the U.S. consumer price index, and
is the U.S. consumer price index, and ![]() is the consumer price index for the
is the consumer price index for the ![]() country. The IMF reports a fixed-weight geometric aggregate of
bilateral CPI-adjusted exchange rates:
country. The IMF reports a fixed-weight geometric aggregate of
bilateral CPI-adjusted exchange rates:
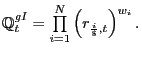
|
(8) |
There are several differences between ![]() and
and
![]() that are potentially relevant for
explaining differences between WARP and existing measures of real
effective exchange rates. First,
that are potentially relevant for
explaining differences between WARP and existing measures of real
effective exchange rates. First, ![]() measures the
level of bilateral relative prices whereas
measures the
level of bilateral relative prices whereas ![]() measures the percent change in bilateral relative prices. Second,
the basket used for
measures the percent change in bilateral relative prices. Second,
the basket used for ![]() refers to GDP items and
thus includes consumption, investment, government purchases, and
exports. The basket used for
refers to GDP items and
thus includes consumption, investment, government purchases, and
exports. The basket used for ![]() is limited to
consumption items both from domestic and foreign sources. Finally,
the baskets embodied in
is limited to
consumption items both from domestic and foreign sources. Finally,
the baskets embodied in ![]() are the same for U.S.
and foreign prices whereas the baskets embodied in
are the same for U.S.
and foreign prices whereas the baskets embodied in ![]() are not the same for U.S. and foreign prices.
are not the same for U.S. and foreign prices.
To examine whether the upward trend in our WARP is due to
differences between ![]() and
and ![]() we construct the same aggregates reported by other
institutions while using
we construct the same aggregates reported by other
institutions while using ![]() instead of
instead of ![]() Following the FRB's methodology, we construct a
chained aggregate of bilateral relative prices
Following the FRB's methodology, we construct a
chained aggregate of bilateral relative prices![]()
![]() substituting the Penn parities
(the
substituting the Penn parities
(the
![]() into equation (7). We also report
the geometric average of indexes of bilateral relative
prices, similar to the IMF's methodology:
into equation (7). We also report
the geometric average of indexes of bilateral relative
prices, similar to the IMF's methodology:
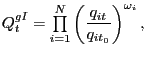
where, following the IMF, we set
![]() as the mean of the values of
as the mean of the values of
![]() in 2000 and
in 2000 and
![]() as the sample mean from 1989 to
1991.
as the sample mean from 1989 to
1991.
Figure 4 shows
the evolution of the real effective exchange rates from the Federal
Reserve and the IMF along with
![]()
![]() and
and
![]() for comparison purposes, we
rescale these measures by their own 1971-1991 sample means. The
results indicate that aggregates based on Penn's bilateral relative
price indexes,
for comparison purposes, we
rescale these measures by their own 1971-1991 sample means. The
results indicate that aggregates based on Penn's bilateral relative
price indexes, ![]() and
and
![]() , show a downward trend
meaning that the upward trend in WARP is not due to differences
between
, show a downward trend
meaning that the upward trend in WARP is not due to differences
between ![]() and
and ![]() but, rather,
to the choice of aggregation method.
but, rather,
to the choice of aggregation method.
Figure 4: U.S. International Relative Price - Sensitivity to Price Data and Aggregation Method
4.2 Currency Baskets and Weighting Schemes
We now ask what factors in our aggregation method are
responsible for the upward trend in ![]() Is this
trend due to the composition of the currency basket or to our
weighting scheme? To address these questions, figure 5 reports separate
geometric sub-aggregates for industrial countries and for emerging
economies; the
Is this
trend due to the composition of the currency basket or to our
weighting scheme? To address these questions, figure 5 reports separate
geometric sub-aggregates for industrial countries and for emerging
economies; the
![]() for each group are
renormalized to add up to one. The thick blue line is the aggregate
of U.S. prices relative to other industrial countries alone. It has
been trending down slowly, and it indicates that in 2006 U.S.
prices were on average 10 percent below those in other industrial
countries. The thick black line plots U.S. prices relative to the
prices of emerging economies alone. It has been trending up
sharply. These calculations suggest that a key factor accounting
for the upward trend in our WARP, the thick red line, is the shift
in U.S. trade patterns. Specifically, within the overall aggregate,
trade has shifted away from the relatively high-price industrial
countries toward the lower-price emerging economies, which tends to
raise the overall measure of U.S. prices relative to our trading
partners. Within the emerging economies sub-aggregate (the black
line), trade has shifted toward the lowest-price economies, such as
China; this shift tends to raise U.S. prices relative to the
group.
for each group are
renormalized to add up to one. The thick blue line is the aggregate
of U.S. prices relative to other industrial countries alone. It has
been trending down slowly, and it indicates that in 2006 U.S.
prices were on average 10 percent below those in other industrial
countries. The thick black line plots U.S. prices relative to the
prices of emerging economies alone. It has been trending up
sharply. These calculations suggest that a key factor accounting
for the upward trend in our WARP, the thick red line, is the shift
in U.S. trade patterns. Specifically, within the overall aggregate,
trade has shifted away from the relatively high-price industrial
countries toward the lower-price emerging economies, which tends to
raise the overall measure of U.S. prices relative to our trading
partners. Within the emerging economies sub-aggregate (the black
line), trade has shifted toward the lowest-price economies, such as
China; this shift tends to raise U.S. prices relative to the
group.
Figure 5: U.S. International Relative Price - Sensitivity to Currency Basket and Weighting Scheme.
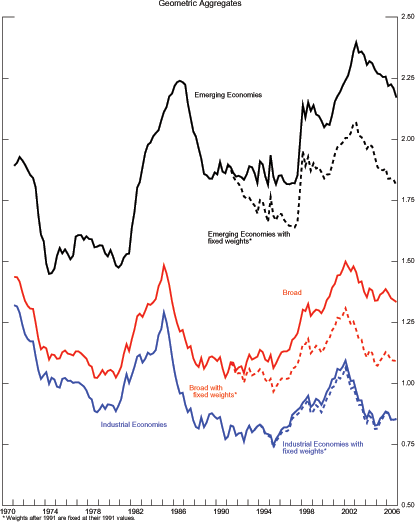
* Weights after 1991 are fixed at their 1991 values for the Emerging and Industrial Economies and the Broad with fixed weights series.
To illustrate the importance of the increased weight of the low-price economies, we construct a counterfactual where we ask what would have happened if the weights after 1991 were fixed at their 1991 values. As shown by the dashed red line, in this world, our measure would have U.S. prices only about 10 percent above those of our trading partners--roughly unchanged since 1975 and near the 30-year average. Further, this fixed-weight aggregate has a downward trend with a historical peak in 1985, quite similar to the pattern of the standard aggregates shown earlier. The key question, however, is whose weights exert the strongest influence. To address that question, the figure reports the fixed-weight aggregate for the industrial countries. Appearing as the dashed blue line, this aggregate exhibits a downward trend with a historical peak in 1985, similar to the case of variable weights and to the associated aggregates reported by other institutions. This result implies that fixing industrial-country weights does not change the evolution of that sub-aggregate. In contrast, fixing the weights of each emerging economy induces a downward trend in the associated sub-aggregate (dashed black line), which leaves the historical peak back in 1985, unlike its variable-weight version which peaks in 2003. Therefore, the upward trend in our measure of U.S. international relative prices is due to the increased weight of the low-price economies in the U.S. basket.
5 Sensitivity Analysis
5.1 Sensitivity to Parameterization
A well known result is that our ![]() is a
particular case of the CES function
is a
particular case of the CES function
![$\displaystyle Q_{t}^{ces}=\left[ {\textstyle\sum\limits_{i=1}^{n}} w_{it}\cdot\left( q_{it}\right) ^{\sigma-1}\right] ^{\frac{1}{\sigma-1}}, $](img93.gif)
where ![]() is the elasticity of substitution
among purchases of foreign products and
is the elasticity of substitution
among purchases of foreign products and
![]() .
In the absence of econometric evidence supporting
.
In the absence of econometric evidence supporting ![]() a relevant question to pose is how sensitive is the
upward trend in U.S. international relative prices to alternative
values of σ.17
a relevant question to pose is how sensitive is the
upward trend in U.S. international relative prices to alternative
values of σ.17
Figure 6 shows
the sensitivity of
![]() to values of
to values of ![]() ranging from high substitutability (
ranging from high substitutability (
![]() ) to near complementarity (
) to near complementarity (
![]() ). The calculations reveal three
findings. First, there is a direct association between the value of
). The calculations reveal three
findings. First, there is a direct association between the value of
![]() and the slope of the trend of U.S.
relative prices. Second, the 2006 level of WARP is sensitive to
extreme values of
and the slope of the trend of U.S.
relative prices. Second, the 2006 level of WARP is sensitive to
extreme values of ![]() (2.5 and 0.05); using
using less extreme values of
(2.5 and 0.05); using
using less extreme values of ![]() (1.1 and 0.9)
yields values of
(1.1 and 0.9)
yields values of
![]() quite close to the values taken
by
quite close to the values taken
by ![]() . Finally, if one interprets the large
swings in U.S. bilateral trade shares as suggesting high
substitutability among foreign products (
. Finally, if one interprets the large
swings in U.S. bilateral trade shares as suggesting high
substitutability among foreign products (![]() ), then the upward trend in
), then the upward trend in ![]() understates the extent to which U.S. international
relative prices have been increasing.
understates the extent to which U.S. international
relative prices have been increasing.
Figure 6: U.S. International Relative Prices - CES Aggregates with Alternative Values of σ
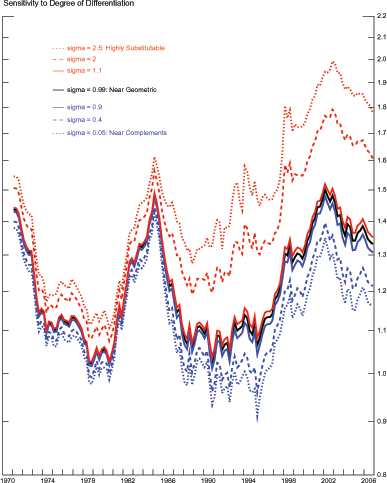
Overall, we interpret these results as suggesting that the upward trend in U.S. international relative prices associated with WARP is not due to our reliance on a unitary elasticity of substitution among foreign products. This conclusion, however, abstracts from the quality of the data of relative prices, an issue that we examine next.
5.2 Sensitivity to Measurement Errors
We now ask how sensitive is the upward trend of WARP to
measurement errors. Other things equal, a lower estimate of
![]() raises
raises ![]() our measure of U.S. prices relative to country
our measure of U.S. prices relative to country ![]() Thus a relevant question is whether we are over-estimating
Thus a relevant question is whether we are over-estimating
![]() and hence WARP, because Penn is
underestimating
and hence WARP, because Penn is
underestimating
![]() for emerging economies. We
consider three approaches to address this question: examining
alternative measures of purchasing power parity for China;
adjusting our measures of relative prices by imputing correction
factors larger than those of Kravis and Lipsey (1990); and
comparing the WARP to calculations based on the price data for the
Big Mac.
for emerging economies. We
consider three approaches to address this question: examining
alternative measures of purchasing power parity for China;
adjusting our measures of relative prices by imputing correction
factors larger than those of Kravis and Lipsey (1990); and
comparing the WARP to calculations based on the price data for the
Big Mac.
5.2.1 Alternative Estimates of PPP for China
A focus on China's purchasing power parity can be motivated in
two ways. First, the weight for China has experienced the largest
increase and it now has the second largest value in our weighting
scheme. Second, the price data for China are of questionable
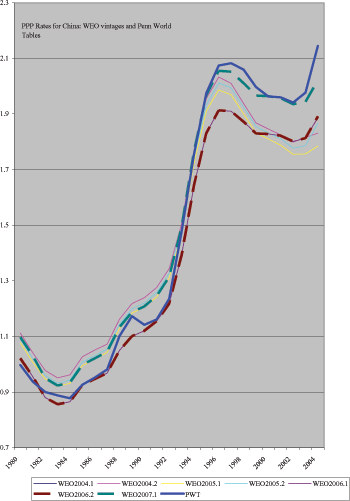
reliability. Figure 7 compares the
estimates for China's
![]() from Penn (solid dark-blue line)
to the IMF's estimates from seven recent vintages.18
Prior to 1994, Penn's estimate is never more than eight percent
below the IMF estimates. For all the post-1994 period, Penn's
estimate is at least as large as any of the estimates from the IMF.
Thus there does not seem to be a systematic undervaluation of
Penn's parities relative to those of the IMF. The one estimate we
could find that is above that of Penn is that of the OECD.19 For
2004, the OECD estimate for China is 2.3, compared to Penn's
estimate of 2.1. Thus the OECD estimate is roughly 10 percent above
the Penn estimate.
from Penn (solid dark-blue line)
to the IMF's estimates from seven recent vintages.18
Prior to 1994, Penn's estimate is never more than eight percent
below the IMF estimates. For all the post-1994 period, Penn's
estimate is at least as large as any of the estimates from the IMF.
Thus there does not seem to be a systematic undervaluation of
Penn's parities relative to those of the IMF. The one estimate we
could find that is above that of Penn is that of the OECD.19 For
2004, the OECD estimate for China is 2.3, compared to Penn's
estimate of 2.1. Thus the OECD estimate is roughly 10 percent above
the Penn estimate.
Figure 7: IMF PPP $ Rates for China - Sensitivity to Data Vintage
We do not interpret this scant evidence as suggesting that Penn's estimates are relatively error free but that, perhaps, comparing inaccurate measures across institutions is not informative. Thus we examine below the implications of imputing large measurement errors to the relative prices of emerging economies. Indeed, we find that even if the relative prices for all emerging economies were 20 percent below what Penn estimates, this is still not enough to overturn the basic upward trend of WARP.
5.2.2 Imputation of Correction Factors
We now impute measurement errors to the relative prices of
emerging economies to examine the sensitivity of WARP to such
mismeasurement. Specifically, we denote
![]() as the error-free but
unobserved bilateral relative price and postulate that
as the error-free but
unobserved bilateral relative price and postulate that
![]() where
where
![]() is the imputed correction factor. We
could impute the value of
is the imputed correction factor. We
could impute the value of ![]() using either
the 13 percent estimated by Kravis and Lipsey (1990) or the 10
percent wedge implied by the OECD estimate for China. To encompass
these sources and to allow for even larger errors, we apply
using either
the 13 percent estimated by Kravis and Lipsey (1990) or the 10
percent wedge implied by the OECD estimate for China. To encompass
these sources and to allow for even larger errors, we apply
![]() to the relative prices of China,
of Latin American countries, of all emerging economies excluding
both China and Latin America countries, and of all emerging
economies. Note that the magnitude of the error is directly related
to the value of
to the relative prices of China,
of Latin American countries, of all emerging economies excluding
both China and Latin America countries, and of all emerging
economies. Note that the magnitude of the error is directly related
to the value of ![]() If
If ![]() and
and
![]() then
then
![]() implying an error of 19
percent.
implying an error of 19
percent.
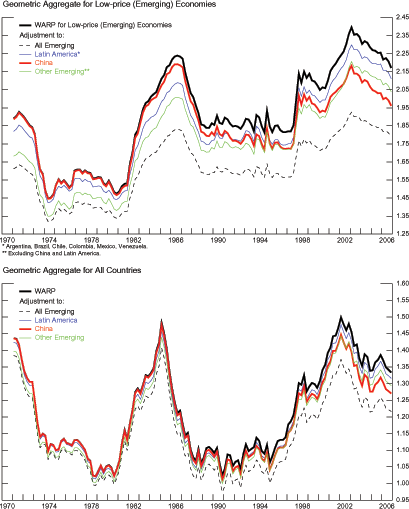
The top panel of figure 8 shows how U.S.
prices relative to those of emerging economies respond to the
imputed correction factor. We find that if
![]() is applied to all developing
countries, then reliance on Penn data overstates U.S. relative
prices vis-a-vis this countries by about 20 percent. The bottom
panel of figure 8 shows how these
measurement errors affect WARP.20 When the correction
is applied only to China, the upward trend in U.S. international
relative prices remains in place. Applying the correction factor to
either Latin America or other emerging economies (except China and
Latin American countries), leaves the trend rate of WARP largely
unchanged. Finally, applying the correction factor to all of
the emerging economies dampens the upward trend of WARP but by no
means eliminates it.
is applied to all developing
countries, then reliance on Penn data overstates U.S. relative
prices vis-a-vis this countries by about 20 percent. The bottom
panel of figure 8 shows how these
measurement errors affect WARP.20 When the correction
is applied only to China, the upward trend in U.S. international
relative prices remains in place. Applying the correction factor to
either Latin America or other emerging economies (except China and
Latin American countries), leaves the trend rate of WARP largely
unchanged. Finally, applying the correction factor to all of
the emerging economies dampens the upward trend of WARP but by no
means eliminates it.
Figure 8: U.S. International Relative Prices - Sensitivity to Measurement Error
5.2.3 Consistency with Big Mac Prices
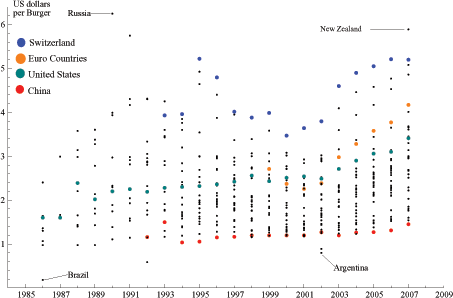
We now evaluate whether the results from using Penn's parities are unique by comparing them to the prices of McDonald's Big Mac reported by The Economist. This alternative is of interest because The Economist reports the absolute dollar-price levels for the Big Mac. Figure 9 shows the cross-country dispersion of dollar prices for the Big Mac from 1986 to 2007 for 31 countries.21 The data reveal that the number of countries with prices below the U.S. price has increased markedly over the years. As for the range of prices, Switzerland tends to have the highest price whereas China generally has the lowest price.
Figure 9: Cross-country Dispersion of Big Mac Prices - 1986-2007
Given these prices, we construct the U.S. bilateral relative
price of a Big Mac, ![]() as
as
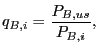
where ![]() is the dollar price of a Big Mac in
the United States and
is the dollar price of a Big Mac in
the United States and ![]() is dollar price of a
Big Mac in the
is dollar price of a
Big Mac in the ![]() country. Given
country. Given ![]() , the associated geometric aggregate is
, the associated geometric aggregate is
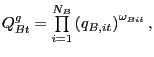
|
(9) |
where ![]() is the number of countries included in
the aggregate and
is the number of countries included in
the aggregate and
![]() is the trade weight for the
is the trade weight for the
![]() country; we construct this aggregate for
countries that are included in the Federal Reserve's Broad Real
Dollar index.
country; we construct this aggregate for
countries that are included in the Federal Reserve's Broad Real
Dollar index.
Because the list of countries reported by the Economist
varies across time, we construct
![]() for two groups that differ in the
span of continuous data: group A with data since 1994 and group B
with data since 1999; the list of countries in group B includes the
countries of group A along with the euro area and other emerging
economies. For comparison purposes, we also compute the chained
aggregate of relative CPIs and the geometric aggregate of Penn's
parities for each country group. Figure 10 shows that the
aggregate of Big Mac relative prices and the WARP for group B
increase from 1999 to 2006. In contrast, the chained aggregate of
relative CPIs for group B declines between these two dates;
comparisons based on group A give the same result. Thus we
interpret these features as corroborating the evidence embodied in
the WARP: U.S. international relative prices have increased.
for two groups that differ in the
span of continuous data: group A with data since 1994 and group B
with data since 1999; the list of countries in group B includes the
countries of group A along with the euro area and other emerging
economies. For comparison purposes, we also compute the chained
aggregate of relative CPIs and the geometric aggregate of Penn's
parities for each country group. Figure 10 shows that the
aggregate of Big Mac relative prices and the WARP for group B
increase from 1999 to 2006. In contrast, the chained aggregate of
relative CPIs for group B declines between these two dates;
comparisons based on group A give the same result. Thus we
interpret these features as corroborating the evidence embodied in
the WARP: U.S. international relative prices have increased.
Figure 10: U.S. International Relative Prices: WARP and Big Mac
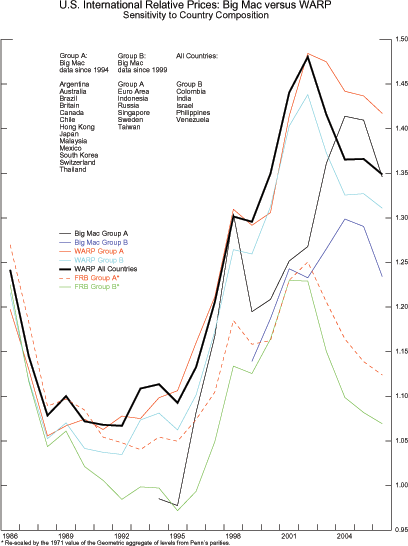
* The FRB Group A and B series are re-scaled by the 1971 value of the Geometric aggregate of levels from Penn's parities.
6 Applications
6.1 WARP and Competitiveness
One question of interest is whether our WARP is informative for issues involving international competitiveness. A priori, one could argue that the WARP is not informative because it depends importantly on the prices of non-tradeables. There are, however, developments related to relative prices across countries that are not well reflected in standard measures of real exchange rates and yet have important influences on trade and other macro variables. In particular, our aim is to assess whether the WARP captures some aspects of what people have in mind when they use the term 'competitiveness' in a macro context.
It is common practice to consider competitiveness in terms of the prices of tradeable products at home and abroad:
A change in the relative price of a manufactured product (tradable good) between any two suppliers is defined as a change in price competitiveness. (McGuirk, 1986, page 3)
However, this view is somewhat sharpened by recognizing that prices of competing goods influence each other and that differences in competitiveness are determined by differences in costs that manifest themselves as differences in margins in the tradeable sector:
One might say that an industry is internationally competitive if it produces tradables and is profitable. A reduction in competitiveness is then a reduction in profitability in some or all tradables industries. (Corden 1994, page 267)
This latter view is a return to Keynes' view in 1925 when he wrote
My own guess is that, compared with 1913, sheltered [non-tradeable] prices here are, at the present rates of sterling exchange, perhaps as much as ten per cent. too high in comparison with the unsheltered [tradeable] prices, and that the injury thus caused to the competitive position of our exports in the international market is aggravated by the fact that in Germany, France, Belgium and Italy the sheltered prices are fully ten per cent. too low. (Keynes, 1925, page 301). Emphasis and bracketed entries added.
Keynes recognized that the prices of "unsheltered" (traded) products would be nearly equalized in the world market and that competitiveness would be determined by, and reflected in, the relative prices of sheltered (non-traded) goods.
One way to illustrate Keynes' point is to show that conventional
measures of competitiveness are not invariant to developments in
the non-tradeable sector. Specifically, following Corden, we
express competitiveness for the ![]() product as the
ratio of producers' markups
product as the
ratio of producers' markups

where we assume that the law of one price holds with
![]() being the associated price;
being the associated price;
![]() is the marginal cost of the
is the marginal cost of the
![]() product in country 1 and
product in country 1 and ![]() is the U.S. counterpart. If
is the U.S. counterpart. If
![]() then "Country 1 is said to be
more competitive than the United States in the
then "Country 1 is said to be
more competitive than the United States in the ![]() industry."
industry."
To determine marginal costs, appendix A.4 develops a
simple, three country model in which production takes place with a
Leontieff technology using labor and both tradeable and
non-tradeable intermediate inputs. With these assumptions, marginal
costs are linear functions of factor prices and input requirements.
Thus, as detailed in equation (31) in appendix
A.4, the
effect on ![]() of a one percent decrease in
U.S. productivity of the non-tradeable input is
of a one percent decrease in
U.S. productivity of the non-tradeable input is
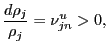
where
![]() is the share of the
non-tradeable input in
is the share of the
non-tradeable input in ![]() . This dependency of
. This dependency of
![]() on non-tradeables embodies Keynes'
point: questions of competitiveness cannot be usefully examined by
abstracting from the prices of non-tradeables.
on non-tradeables embodies Keynes'
point: questions of competitiveness cannot be usefully examined by
abstracting from the prices of non-tradeables.
Overall, this example shows that if the essence of a measure of competitiveness is invariance to developments in the non-tradeable sector, then a popular measure offered in the literature is as deficient as our WARP. This difficulty, which arises independently of any compounding issues related to data availability, is simply an example of where it makes sense to tailor one's tool to address the question at hand. Thus the suitability of a given measure to a particular application is largely an empirical question which we now examine using WARP.
6.2 WARP and U.S. External Imbalances
A central tenet of macroeconomic theory for open economies is
that, other things equal, an increase in a country's prices
relative to prices abroad will result in a deterioration in net
exports. There is less agreement, however, on how to measure
relative prices, and the empirical validity of the tenet clearly
depends on how prices are measured. To examine this idea, figure
11 shows scatter
diagrams between U.S. non-oil net exports, as a share of GDP, and
the contemporaneous value of U.S. international relative prices
using three measures: chained aggregate of Penn parities
(![]() ), chained aggregate of relative
CPIs (
), chained aggregate of relative
CPIs (
![]() ), and the geometric
aggregate of levels of Penn parities (
), and the geometric
aggregate of levels of Penn parities (![]() ). For
1971 to 2006 (left panels), the data indicate that whether net
exports are inversely related to the U.S. international relative
price depends on how one measures that price. Indeed, the
association is absent if one uses
). For
1971 to 2006 (left panels), the data indicate that whether net
exports are inversely related to the U.S. international relative
price depends on how one measures that price. Indeed, the
association is absent if one uses ![]() where it is present if one uses
where it is present if one uses
![]() and strongest if one uses
and strongest if one uses
![]() .
.
Figure 11: U.S. Non-oil Net Exports and U.S. International Relative Prices
A full understating of these disparate correlations involves recognizing that the character of bivariate associations is influenced by the level of aggregation and by omitted factors, such as foreign income and dynamic adjustments, the role of which could depend on the measure of relative prices. We will examine the role of these factors below but, in the meantime, closer inspection of the scatter plots reveals clusters of observations in which net exports and relative prices are inversely related. These clusters are most distinct for the plots using the chained aggregates of either CPIs or Penn's parities. Thus the panels on the right re-examine the relationship using the clusters formed with data from 1971-1986 and from 1987-2006; this dating is motivated by the evidence of figure 3 showing a break in the trends of international relative prices in 1987. For each of these subsamples, there is an inverse relationship between external balances and the U.S. international relative price. For the first sample, the strength of the relationship is comparable across the three measures of international relative prices. For the second sample, the association strengthens only for the geometric aggregate.
Overall, reliance on ![]() offers the greatest
empirical support for the textbook proposition that net exports and
relative prices are inversely related. Nevertheless, the evidence
raises several questions that need to be addressed before declaring
that
offers the greatest
empirical support for the textbook proposition that net exports and
relative prices are inversely related. Nevertheless, the evidence
raises several questions that need to be addressed before declaring
that ![]() passes the "proof of concept" test.
Specifically, as indicated earlier, how can one be sure that these
correlations are not unduly influenced by the absence of other key
factors such as foreign economic activity?
passes the "proof of concept" test.
Specifically, as indicated earlier, how can one be sure that these
correlations are not unduly influenced by the absence of other key
factors such as foreign economic activity?
6.3 WARP and Trade Modeling: The Case of Exports
To address these questions, we examine whether the alternative
measures of international relative prices have implications for
characterizing the behavior of aggregate U.S. exports. We focus on
exports because they are directly related to foreign prices, the
objective of WARP. Indeed, if one postulates that exports respond
to foreign economic activity and to the price of exports
(![]() relative to the foreign price
(
relative to the foreign price
(![]() ,
,
![]() then one needs to
construct a measure for
then one needs to
construct a measure for
![]() The current practice is
to use official statistics for
The current practice is
to use official statistics for ![]() and to measure
and to measure
![]() as a chained aggregate of foreign
CPIs, expressed in U.S. dollars. In contrast, our approach is to
measure
as a chained aggregate of foreign
CPIs, expressed in U.S. dollars. In contrast, our approach is to
measure ![]() so as to ensure consistency with the
evolution of U.S. international relative prices. For example, if
one adopts
so as to ensure consistency with the
evolution of U.S. international relative prices. For example, if
one adopts ![]() as the relevant measure of
international relative prices, then
as the relevant measure of
international relative prices, then
![]() where
where
![]() is the U.S. GDP deflator.22
Alternatively, if one adopts
is the U.S. GDP deflator.22
Alternatively, if one adopts ![]() , then the
aggregate measure of foreign prices is
, then the
aggregate measure of foreign prices is
![]() where
where
![]() is either the U.S. GDP deflator or
the U.S. CPI, depending on how
is either the U.S. GDP deflator or
the U.S. CPI, depending on how ![]() is
constructed.
is
constructed.
We do not focus on modeling imports because the advantage of our
measure of international relative prices is less obvious given the
availability of official statistics for the components of the
relative price of imports![]() 23
23
Measuring the Relative Price of
Exports To measure the relative price of exports we first tailor the
weighting scheme to exports and re-compute our three measures of
U.S. international relative prices using weights that exclude the
contribution of imports and include the role of bilateral exports
and third-country markets; figure 12 shows that the
choice of weights has a relatively minor effect on our three
measures of international relative prices. Second, we solve for the
implied ![]()
 geometric of levels of
Penn parities geometric of levels of
Penn parities |
(10) | |
 chained of levels of
Penn parities chained of levels of
Penn parities |
||
 chained
of CPIs, chained
of CPIs, |
where a sub-script 'x' denotes the use of
export weights and
![]() is the chained aggregate of
foreign CPIs, expressed in U.S. dollars. Third, given
is the chained aggregate of
foreign CPIs, expressed in U.S. dollars. Third, given ![]() we obtain the three measures of relative export prices as
we obtain the three measures of relative export prices as
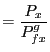 |
(11) | |
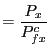 |
||
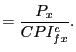 |
Figure 12: U.S. International Relative Prices - Sensitivity to Weighting Scheme
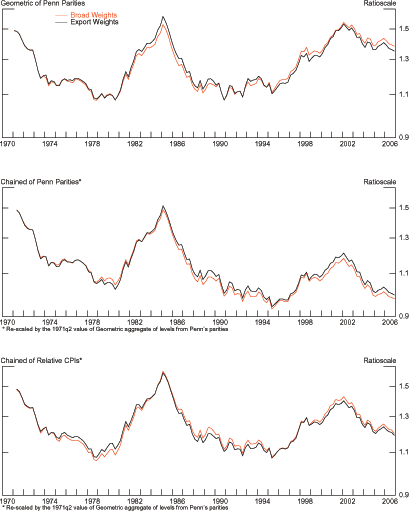
* The Chained of Penn Parities and Chained of Relative CPIs series are re-scaled by the 1971q2 value of Geometric aggregate of levels from Penn's parities.
How important are differences in international relative prices
for the profile of the relative price of exports? Figure 13 documents the
data and the steps taken to arrive at the three measures of
![]() . The top-left panel shows the
(export-weighted) measures of international relative prices; the
right panel shows the three U.S. price indexes:
. The top-left panel shows the
(export-weighted) measures of international relative prices; the
right panel shows the three U.S. price indexes: ![]()
![]() and
and ![]() The bottom-left panel shows the implied measures of
aggregate foreign prices (equation 10); the series
have upward trends and move together through 1987 but diverge
afterwards with
The bottom-left panel shows the implied measures of
aggregate foreign prices (equation 10); the series
have upward trends and move together through 1987 but diverge
afterwards with
![]() flattening while the other two
series continue their upward trends, albeit at a lower rate. The
flattening of
flattening while the other two
series continue their upward trends, albeit at a lower rate. The
flattening of
![]() reflects the increasing
importance of low-price economies, a phenomenon captured only by
reflects the increasing
importance of low-price economies, a phenomenon captured only by
![]() . The bottom-right panel shows the
three measures for
. The bottom-right panel shows the
three measures for ![]() (equation 11);
(equation 11);
![]() and
and
![]() move together and have
downward trends reflecting the upward trend in their measures of
foreign prices. In contrast,
move together and have
downward trends reflecting the upward trend in their measures of
foreign prices. In contrast,
![]() trends down through 1990 and
flattens afterwards, reflecting the flattening of
trends down through 1990 and
flattens afterwards, reflecting the flattening of
![]() . Overall, aggregation schemes
that recognize interactions between price levels and the increased
trade with emerging economies, as captured by
. Overall, aggregation schemes
that recognize interactions between price levels and the increased
trade with emerging economies, as captured by
![]() yield a picture of U.S. relative
export prices that is fundamentally different from the one given by
existing aggregation methods. We now examine whether this
difference matters for characterizing the response of U.S. exports
to income and relative prices.
yield a picture of U.S. relative
export prices that is fundamentally different from the one given by
existing aggregation methods. We now examine whether this
difference matters for characterizing the response of U.S. exports
to income and relative prices.
Figure 13: Derivation of U.S. Relative Export Price
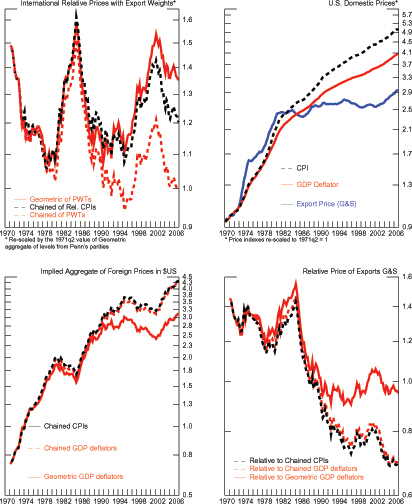
* International Relative Prices with Export Weights are re-scaled by the 1971q2 value of Geometric aggregate of levels from Penn's parities. The U.S. Domestic Price indexes are re-scaled to 1971q2 = 1.
Econometric Formulation To model U.S. exports, we assume that foreign and domestic products are imperfect substitutes for each other (see Goldstein and Khan, 1985) and postulate an error-correction formulation:
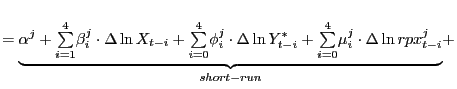
|
(12) | |
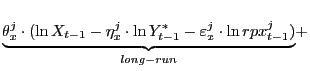
|
||
where ![]() is the volume of exports of goods and
services;
is the volume of exports of goods and
services; ![]() is the foreign real GDP;
is the foreign real GDP;
![]() is the long-run income
elasticity; and
is the long-run income
elasticity; and
![]() is the long-run
price elasticity.24 Equation (12) assumes that
the growth rate of exports responds to short- and long-run factors.
Specifically, movements in income and relative prices induce
cyclical swings in exports. But, even if income and relative prices
were fixed, exports could be changing as they adjust to their long
run level given by
is the long-run
price elasticity.24 Equation (12) assumes that
the growth rate of exports responds to short- and long-run factors.
Specifically, movements in income and relative prices induce
cyclical swings in exports. But, even if income and relative prices
were fixed, exports could be changing as they adjust to their long
run level given by
![]() This gradual adjustment is captured by the term in parentheses
where
This gradual adjustment is captured by the term in parentheses
where
![]() represents the speed of
adjustment. Finally, finding that
represents the speed of
adjustment. Finally, finding that
![]() means that exports would
automatically change over time regardless of the evolution of
income and relative prices and thus we interpret a significant
means that exports would
automatically change over time regardless of the evolution of
income and relative prices and thus we interpret a significant
![]() as evidence of misspecification.
as evidence of misspecification.
As formulated, equation (12) is non-linear in the parameters. To avoid the associated estimation difficulties, we re-express this equation as linear in the parameters:
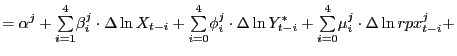
|
(13) | |
| |
Using a '^' to denote an estimated value,
we use the least squares values of
![]() ,
,
![]() , and
, and
![]() to compute the
implied elasticities as
to compute the
implied elasticities as
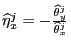 and
and
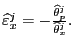 Note that these elasticity estimates are ratios of normal
variables and thus the associated distributions are not known in
advance.25 Thus the associated confidence
intervals are constructed using Monte Carlo simulations
Note that these elasticity estimates are ratios of normal
variables and thus the associated distributions are not known in
advance.25 Thus the associated confidence
intervals are constructed using Monte Carlo simulations![]() appendix A.5 has the details.
appendix A.5 has the details.
Estimation Strategy For parameter estimation we apply least squares to equation (13) using observations from 1972Q3 to 2004Q4 with data from 1971Q2 to 1972Q2 reserved for lags and data from 2005Q1 to 2006Q4 reserved for evaluating out-of-sample predictive accuracy. One may argue that there are gains in precision of the estimates if one were to exclude insignificant variables from the model. To avoid the statistical pitfalls associated with the joint nature of model specification and parameter estimation, we rely on a computer-automated algorithm, developed by Hendry and Krolzig (2001).26 Their algorithm combines least squares with a selection criteria that excludes insignificant coefficients and tests for both parameter constancy and white-noise residuals; the critical values for rejection are not fixed in advance but, rather, are calculated sequentially. We report results for equation (13), labeled the General formulation, and for the simplified formulation, labeled the Specific formulation.
To examine the potential for simultaneity bias, we postulate a vector-autoregressive model explaining exports, income, and relative prices and then apply Johansen's cointegration method to estimate the cointegration vector; this approach treats income and prices as endogenous.27
Econometric Results Table 1 shows estimation and test results for all three measures
of relative export prices. The signs for
![]()
![]() and
and
![]() are consistent with
expectations and their magnitudes are roughly comparable across
measures of relative export prices. In terms of in-sample fit, the
standard error of the regression has a narrow range of variation:
from 1.89% for
are consistent with
expectations and their magnitudes are roughly comparable across
measures of relative export prices. In terms of in-sample fit, the
standard error of the regression has a narrow range of variation:
from 1.89% for
![]() to 1.93% for
to 1.93% for
![]() Furthermore, the Chow tests
cannot reject the hypothesis of parameter stability, and the
residuals exhibit normality, serial independence, and
homoskedasticity.
Furthermore, the Chow tests
cannot reject the hypothesis of parameter stability, and the
residuals exhibit normality, serial independence, and
homoskedasticity.
Table 1: Parameter Estimates for Model of U.S. Exports of Goods and Services: Sensitivity to Measure of Foreign Prices - OLS, 1971Q2-2004Q4
| Measures of Sensitivity | Geometric Foreign PGDP: General (1) | Geometric Foreign PGDP: Specific (2) | Chained Foreign PGDP: General (3) | Chained Foreign PGDP: Specific (4) | Chained Foreign CPIs: General (5) | Chained Foreign CPIs: Specific (6) | Chained Foreign CPIs: ex. Intercept (7) |
|---|---|---|---|---|---|---|---|
| Parameter Estimate: Intercept α | 0.0392 | 0e | 0.1618 | 0e | 0.1966 | 0.1574 | set to zero |
| Parameter Estimate: Intercept α - se | 0.0474 | - | 0.0664 | - | 0.0725 | 0.0657 | - |
| Parameter Estimate: Sum of coefficients for ∆lnX | -0.3157 | 0e | -0.1478 | 0e | -0.1448 | 0e | 0e |
| Parameter Estimate: Sum of coefficients for ∆lnX - se | 0.192 | - | 0.186 | - | 0.1829 | - | - |
| Parameter Estimate: Sum of coefficients for ∆lnY | 4.3777 | 2.899 | 3.8885 | 3.1748 | 4.0375 | 2.8246 | 3.2633 |
| Parameter Estimate: Sum of coefficients for ∆lnY - se | 0.79 | 0.4267 | 0.7885 | 0.4247 | 0.786 | 0.4571 | 0.4267 |
| Parameter Estimate: Sum of coefficients for ∆lnRP | 0.088 | 0e | 0.1178 | 0e | 0.1661 | 0e | 0e |
| Parameter Estimate: Sum of coefficients for ∆lnRP - se | 0.1885 | - | 0.2109 | - | 0.1954 | - | - |
| Parameter Estimate: Lagged Exports: θx | -0.1244 | -0.1157 | -0.1547 | -0.1249 | -0.1534 | -0.1295 | -0.1138 |
| Parameter Estimate: Lagged Exports: θx - se | 0.0368 | 0.0260 | 0.0448 | 0.0299 | 0.0404 | 0.0292 | 0.0289 |
| Parameter Estimate: Lagged Foreign Income: θy | 0.1735 | 0.1709 | 0.1860 | 0.1813 | 0.1748 | 0.1508 | 0.1644 |
| Parameter Estimate: Lagged Foreign Income: θy - se | 0.0579 | 0.0391 | 0.0626 | 0.0443 | 0.0552 | 0.0423 | 0.0427 |
| Parameter Estimate: Lagged Relative Price: θp | -0.1314 | -0.0982 | -0.1439 | -0.0755 | -0.1503 | -0.1195 | -0.0675 |
| Parameter Estimate: Lagged Relative Price: θp - se | 0.0315 | 0.0203 | 0.0368 | 0.0171 | 0.0358 | 0.0269 | 0.0162 |
| Measures of Fit: SER | 1.807% | 1.890% | 1.812% | 1.917% | 1.809% | 1.895% | 1.930% |
| Measures of Fit: Adj Rqrd | 0.459 | 0.408 | 0.455 | 0.391 | 0.457 | 0.405 | 0.382 |
| Measures of Fit: No. of Parameters | 18 | 5 | 18 | 5 | 18 | 6 | 5 |
| Hypotheses (p-values)(a): Parameter Stability: Half Sample | 0.999 | 0.998 | 0.996 | 0.996 | 0.998 | 0.995 | 0.998 |
| Hypotheses (p-values)(a): Parameter Stability: Last 8 quarters | 0.973 | 0.858 | 0.835 | 0.589 | 0.908 | 0.788 | 0.700 |
| Hypotheses (p-values)(a): Properties of residuals: Normality | 0.020 | 0.108 | 0.039 | 0.175 | 0.026 | 0.153 | 0.170 |
| Hypotheses (p-values)(a): Properties of residuals: Serial Independence | 0.841 | 0.093 | 0.578 | 0.417 | 0.174 | 0.174 | 0.299 |
| Hypotheses (p-values)(a): Properties of residuals: Homoskedasticity | 0.009 | 0.137 | 0.016 | 0.188 | 0.150 | 0.150 | 0.140 |
| Implied Elasticities: Income = -θy / θx | 1.39 | 1.48 | 1.20 | 1.45 | 1.14 | 1.16 | 1.44 |
| Implied Elasticities: Price= -θp / θx | -1.06 | -0.85 | -0.93 | -0.60 | -0.98 | -0.92 | -0.59 |
0e: Algorithm finds the variable to be statistically irrelevant and sets the coefficient to zero.
(a) An entry less that 0.01 means that the associated hypothesis can be rejected at the 1% significance level.
The sole dissonant note in these results is the presence of a
positive and statistically significant intercept in the specific
formulation using the chained of relative CPIs (column 6). Finding
that
![]() means that exports would
expand even if income and relative prices were fixed. We do not see
an economic justification for such a result and treat this finding
as an instance in which an algorithm delivering an otherwise
statistically reliable model is not delivering an economically
meaningful model. Thus we also re-estimate the parameters of the
model constraining the intercept to zero and find (column 7) that
the constrained model exhibits a slight deterioration of fit, which
is not surprising, and that the values for the remaining parameter
estimates based on
means that exports would
expand even if income and relative prices were fixed. We do not see
an economic justification for such a result and treat this finding
as an instance in which an algorithm delivering an otherwise
statistically reliable model is not delivering an economically
meaningful model. Thus we also re-estimate the parameters of the
model constraining the intercept to zero and find (column 7) that
the constrained model exhibits a slight deterioration of fit, which
is not surprising, and that the values for the remaining parameter
estimates based on
![]() are close to the estimates
based on
are close to the estimates
based on
![]() (This finding is reassuring
given the similarity in the data for these two relative prices.) In
terms of the elasticities, the implied income elasticity is
positive and ranges from 1.4 for
(This finding is reassuring
given the similarity in the data for these two relative prices.) In
terms of the elasticities, the implied income elasticity is
positive and ranges from 1.4 for
![]() to 1.5 for
to 1.5 for
![]() ; the implied price elasticity
is negative and ranges from -0.6 for
; the implied price elasticity
is negative and ranges from -0.6 for
![]() to -0.9 for
to -0.9 for
![]() .
.
To assess the statistical properties of these estimates, figure
14 shows the 95%
(Monte Carlo) confidence intervals for the estimated income
elasticity along with the confidence bands for estimates from the
Johansen method; figure 18 in appendix
A.5 shows the
densities for all income elasticities. The results indicate that
the median income elasticity is positive; greater than one;
significantly greater than zero; and quite similar to the implied
income elasticity of table 1. Furthermore, the median elasticity
based on
![]() exceeds the median elasticity
for the other measures of relative prices, a result robust to
estimation method. Note that the proximity of the median to the 95%
bound means that the empirical distribution is not symmetrical.
Finally, the estimates from the Johansen method are quite close to
the estimates from the General formulation; this finding suggests
that simultaneity biases, if present, are not affecting the income
elasticity.
exceeds the median elasticity
for the other measures of relative prices, a result robust to
estimation method. Note that the proximity of the median to the 95%
bound means that the empirical distribution is not symmetrical.
Finally, the estimates from the Johansen method are quite close to
the estimates from the General formulation; this finding suggests
that simultaneity biases, if present, are not affecting the income
elasticity.
Figure 14: Long-run Income Elasticity for U.S. Exports
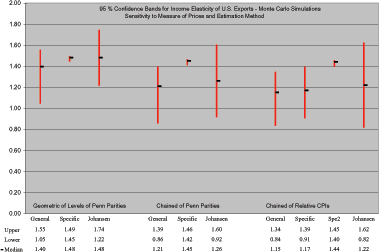
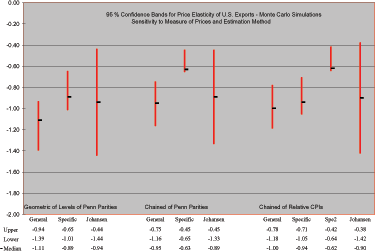
Figure 15 reports the
95% (Monte Carlo) confidence intervals for the estimated price
elasticity; figure 19 in appendix
A.5 shows the
densities for all price elasticities. The results indicate that the
median price elasticity is negative, significantly below zero, and
quite close to the implied price elasticity of table 1.
Furthermore, the median elasticity based on
![]() exceeds (in absolute value)
the median elasticity for the other measures of relative prices, a
result robust to estimation method. Finally, the estimates from the
Johansen method are quite close to the estimates from the General
formulation.
exceeds (in absolute value)
the median elasticity for the other measures of relative prices, a
result robust to estimation method. Finally, the estimates from the
Johansen method are quite close to the estimates from the General
formulation.
Figure 15: Long-run Price Elasticity for U.S. Exports
We find that, unless one has strong priors about the values of
income and price elasticities, the results do not allow us to
select one measure of relative prices over another. To that end, we
assess whether forecast accuracy is sensitive to the measure of
relative prices. Specifically, we generate one-step ahead
predictions for the growth rate of exports from 2005Q1 to 2006Q4.
Table 2 reports that the root mean squared error for the specific
formulations varies from 0.60 percent for
![]() to 1.25% for
to 1.25% for
![]() the mean forecast error varies
from -0.14 for
the mean forecast error varies
from -0.14 for
![]() to -1.12% for
to -1.12% for
![]() Overall, the formulation using
Overall, the formulation using
![]() has the lowest mean forecast
error and the lowest RMSE.
has the lowest mean forecast
error and the lowest RMSE.
Table 2: Forecast Accuracy for U.S. Exports of Goods and Services: Alternative Measures, 2005Q1-2006Q4
| Measure of Accuracy | Geometric Foreign PGDP: General (1) | Geometric Foreign PGDP: Specific (2) | Chained Foreign PGDP: General (3) | Chained Foreign PGDP: Specific (4) | Chained Foreign CPIs: General (5) | Chained Foreign CPIs: Specific (6) | Chained Foreign CPIs: ex. Intercept (7) |
|---|---|---|---|---|---|---|---|
| Root Mean Squared Error | 0.558% | 0.595% | 1.232% | 1.248% | 0.889% | 0.749% | 1.004% |
| Mean Forecast Error(a) | 0.033% | -0.140% | -1.098% | -1.123% | -0.695% | -0.461% | -0.844% |
(a) Actual minus predicted.
Finally, we implement an encompassing test to establish which measure of relative prices offers the best statistical characterization of U.S. exports. The approach involves two steps. First, we postulate a general model that encompasses the three formulations examined so far as special cases:
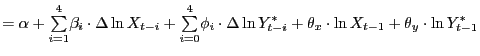
|
||

|
||
Second, we apply the automated specification algorithm to estimate the parameters of the above model. The possible outcomes are
- only one measure of relative prices matters and all others are redundant;
- one needs more than one measure of relative prices to explain U.S. exports;
- relative prices do not matter for explaining U.S. exports.
Table 3 reports the estimation results for both the general and
the specific formulations. We find that reliance on
![]() makes redundant the
alternative measures of relative prices. In other words, the
geometric measure of relative export prices encompasses the other
two measures of relative prices. Further, the resulting specific
formulation of table 3 is the same as the specific formulation for
the model using
makes redundant the
alternative measures of relative prices. In other words, the
geometric measure of relative export prices encompasses the other
two measures of relative prices. Further, the resulting specific
formulation of table 3 is the same as the specific formulation for
the model using
![]() of table 1 (column 2).
of table 1 (column 2).
Table 3: Encompassing Test for Model of U.S. Exports - 1971Q2-2004Q4
| Encompassing Test Measures | General (1) | Specific (2) |
|---|---|---|
| Intercept α | 0.19066 | 0e |
| Intercept α - se | 0.11642 | - |
| Sum of coefficients for ΔlnX | -0.4146 | 0e |
| Sum of coefficients for ΔlnX - se | 0.2261 | - |
| Sum of coefficients for ΔlnY | 4.1348 | 2.899 |
| Sum of coefficients for ΔlnY - se | 0.8351 | 0.4267 |
| Sum of coefficients for ΔlnRP-Geo | -2.1863 | 0e |
| Sum of coefficients for ΔlnRP-Geo - se | 0.9996 | - |
| Sum of coefficients for ΔlnRP-c | -0.0426 | 0e |
| Sum of coefficients for ΔlnRP-c - se | 1.6391 | - |
| Sum of coefficients for ΔlnRP-CPI | 2.4899 | 0e |
| Sum of coefficients for ΔlnRP-CPI - se | 1.2075 | - |
| Lagged Exports: θx | -0.1493 | -0.116 |
| Lagged Exports: θx - se | 0.0538 | 0.026 |
| Lagged Foreign Income: θy | 0.17535 | 0.1709 |
| Lagged Foreign Income: θy - se | 0.07861 | 0.0391 |
| Lagged Relative Price: θp: Geometric of Levels of Penn Parities | -0.1113 | -0.0982 |
| Lagged Relative Price: θp: Geometric of Levels of Penn Parities - se | 0.07789 | 0.0203 |
| Lagged Relative Price: θp: Chained of Levels of Penn Parities | 0.04414 | 0e |
| Lagged Relative Price: θp: Chained of Levels of Penn Parities - se | 0.19017 | - |
| Lagged Relative Price: θp: Chained of Relative CPIs | -0.1245 | 0e |
| Lagged Relative Price: θp: Chained of Relative CPIs - se | 0.2085 | - |
| Measures of Fit: SER | 0.01771 | 0.0189 |
| Measures of Fit: Adj. R2 | 0.47991 | 0.4076 |
| Measures of Fit: No. of Parameters | 30 | 5 |
| Hypotheses (p-values)(a): Parameter Stability: Half Sample | 0.9878 | 0.998 |
| Hypotheses (p-values)(a): Parameter Stability: Last 8 quarters | 0.9593 | 0.858 |
| Hypotheses (p-values)(a): Properties of residuals: Normality | 0.2516 | 0.108 |
| Hypotheses (p-values)(a): Properties of residuals: Serial Independence | 0.1003 | 0.093 |
| Hypotheses (p-values)(a): Properties of residuals: Homoskedasticity | 0.1123 | 0.137 |
0e: Algorithm finds the variable to be statistically irrelevant and sets the coefficient to zero.
(a) An entry less that 0.01 means that the associated hypothesis can be rejected at the 1% significance level.
This finding is of interest for two reasons. First, the measure
of relative prices that has the strongest association with net
exports in figure 11 above is also
the measure of relative prices that offers the best explanation of
exports. Second, the choice of measure of relative prices matters
for characterizing the response of U.S. exports to changes in
income and prices. Specifically, the estimated income elasticity
based on
![]() is higher than estimates based
on other measures of relative prices and higher than the unitary
elasticity previously reported in the literature.28 This
finding is potentially relevant for addressing general questions
involving the sustainability of the U.S. current account and more
pointedly whether the Houthakker-Magee asymmetry of income
elasticities is being influenced by the measure of relative
prices.
is higher than estimates based
on other measures of relative prices and higher than the unitary
elasticity previously reported in the literature.28 This
finding is potentially relevant for addressing general questions
involving the sustainability of the U.S. current account and more
pointedly whether the Houthakker-Magee asymmetry of income
elasticities is being influenced by the measure of relative
prices.
7 Conclusions
This paper identifies an aspect of international price developments--the interaction of differences in price levels with changing trade shares--that is not captured in conventional real exchange rate indexes and constructs a new weighted average relative price (WARP) to capture this interaction. The WARP indicates that over the past 20 years there has been a secular rise in U.S. prices relative to prices in the rest of the world when these prices are weighted by U.S. trade shares. This is in sharp contrast to what conventional measures indicate--that there has been no change in U.S. prices relative to the rest of the world. We use WARP to take a fresh look at on ongoing puzzle: how could U.S. prices relative to the rest of the world show no trend and yet U.S. net exports, as a share of GDP, have declined? We find that our WARP shows the strongest inverse association between net exports and relative prices. In other words, WARP restores the usefulness of that theoretical prediction. To examine whether this resolution is the result of a statistical artifact, we characterize the response of U.S. exports to income and relative prices and examine its sensitivity to the measure of relative price of exports used. Unless one has strong priors about the values of income and price elasticities, the results do not allow us to select one measure of relative prices over another. Thus we examine the forecast accuracy of the different models and find that the formulation based on WARP has the lowest forecast errors. Furthermore, encompassing tests indicate that the inclusion of the WARP-based measure of export's relative prices in the specification makes redundant the alternative measures of relative prices.
A Appendixes
A.1 Data for Bilateral Relative Prices
Extending Parities from Penn World Tables Through 2006 For most countries, the annual data for bilateral relative prices from the Penn World Tables end in 2004. We extrapolate the data through 2006 by assuming that the Penn purchasing power parities grow from 2004 to 2006 at the same rate as the ratio of U.S. to foreign-currency GDP deflators. For Brazil, Colombia, India, Malaysia, Thailand, and Russia, the extrapolation process starts in 2003 because that is when the data end for these countries. The rationale for using the GDP deflator series in the extrapolation is that they use a GDP basket of goods similar, in theory, to the basket used by the Penn parities. The data for GDP deflators are available from the International Monetary Fund's International Financial Statistics (IFS) database and HAVER databases.
Quarterly Parities from Penn World Tables The procedure uses an annual "target" series,
![]() and a quarterly "pattern"
series,
and a quarterly "pattern"
series,
![]() where the superscripts
1 and 4 refer to the
frequency, either annual or quarterly. The annual target series is
the series that we wish to have on a quarterly basis; the quarterly
pattern series is used to guide the interpolation between values of
the annual target series. For the annual target series of the
where the superscripts
1 and 4 refer to the
frequency, either annual or quarterly. The annual target series is
the series that we wish to have on a quarterly basis; the quarterly
pattern series is used to guide the interpolation between values of
the annual target series. For the annual target series of the
![]() country, we use the annual bilateral
relative price from the Penn World Tables-namely,
country, we use the annual bilateral
relative price from the Penn World Tables-namely,
![]() For the quarterly pattern
series, we use the CPI-adjusted bilateral exchange rate corrected
for the systematic gap in inflation rates between the U.S. CPI and
the U.S. GDP deflator:
For the quarterly pattern
series, we use the CPI-adjusted bilateral exchange rate corrected
for the systematic gap in inflation rates between the U.S. CPI and
the U.S. GDP deflator:
where
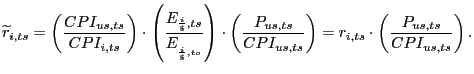
Our choice of
![]() is based on two
considerations. First, quarterly GDP deflators (the ideal series)
are not available for several emerging economies. Second, one
avoids the biases induced by the well-known wedge between the trend
growth rate of the U.S. CPI and the trend growth rate of the U.S.
GDP deflator; such a wedge is minimal for other countries. This
wedge is relevant because the bilateral relative prices from the
Penn World Tables are based on GDP prices and thus, ignoring this
wedge, would bias the quarterly growth rates.
is based on two
considerations. First, quarterly GDP deflators (the ideal series)
are not available for several emerging economies. Second, one
avoids the biases induced by the well-known wedge between the trend
growth rate of the U.S. CPI and the trend growth rate of the U.S.
GDP deflator; such a wedge is minimal for other countries. This
wedge is relevant because the bilateral relative prices from the
Penn World Tables are based on GDP prices and thus, ignoring this
wedge, would bias the quarterly growth rates.
We want to emphasize that we are not relying on a quarterly
bilateral exchange-rate index to serve as a suitable proxy
to estimate quarterly data for the level of the bilateral
relative price. Rather, we use
![]() to obtain the quarterly
pattern within a year of the growth rates of the bilateral relative
prices. With these considerations in mind, there are 10 steps to
construct quarterly data:
to obtain the quarterly
pattern within a year of the growth rates of the bilateral relative
prices. With these considerations in mind, there are 10 steps to
construct quarterly data:
- Estimate quarterly weights using a cubic spline subject to two constraints: (1) the average of the quarterly weights for a given year be the same as the annual weight for that year and (2), the sum of the weights across currencies for a given quarter be equal to one.
- Compute the annual counterpart of the quarterly pattern series
as
- Compute the ratio of the annual target series to the newly
created annual pattern series:

- Extend
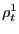 backwards through 1970 with its
1971 value; extend
backwards through 1970 with its
1971 value; extend
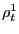 forward through 2006 with its
2005 value
forward through 2006 with its
2005 value
 and
and
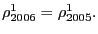
- Apply a cubic spline to
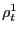 using
using
 and
and
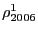 as terminal conditions. This
step yields a quarterly ratio series,
as terminal conditions. This
step yields a quarterly ratio series,
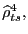
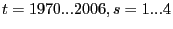 .
. - Obtain a first-round estimate of the quarterly target series as
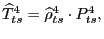

- Compute the annual value implied by
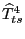 as
as
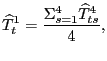
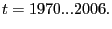
- Calculate the error between
 and
and
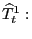
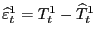 ,
,
 with
with
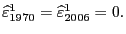
- Construct a quarterly series of errors,
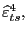 where the
value of the error in each quarter of a given year
where the
value of the error in each quarter of a given year  is equal to
is equal to
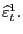 Thus
Thus
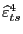 has the same
value in all the quarters of a given year:
has the same
value in all the quarters of a given year:
![\begin{displaymath} \left( \begin{array}[c]{c} \widehat{\varepsilon}_{t,1}^{4}\ \widehat{\varepsilon}_{t,2}^{4}\ \widehat{\varepsilon}_{t,3}^{4}\ \widehat{\varepsilon}_{t,4}^{4} \end{array}\right) =\left( \begin{array}[c]{c} \widehat{\varepsilon}_{t}^{1}\ \widehat{\varepsilon}_{t}^{1}\ \widehat{\varepsilon}_{t}^{1}\ \widehat{\varepsilon}_{t}^{1} \end{array}\right) ,\text{ }t=1970...2006. \end{displaymath}](img303.gif)
- Add
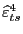 to
to
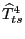 to obtain a
second-round estimate of the quarterly target series:
The last two steps ensure that the second-round estimate (
to obtain a
second-round estimate of the quarterly target series:
The last two steps ensure that the second-round estimate (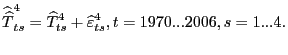
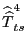 ), when
converted into an annual series, has the same values as our
original target series (
), when
converted into an annual series, has the same values as our
original target series (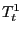 ). Specifically,
Figure 16 shows that the profiles for the annual and quarterly values for WARP are identical.
). Specifically,
Figure 16 shows that the profiles for the annual and quarterly values for WARP are identical.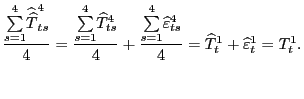
Figure 16: Geometric Aggregate of Bilateral PWT Relative Prices: Annual versus Quarterly
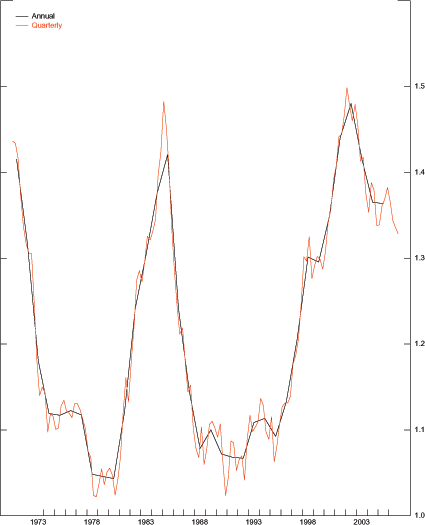
A.2 Chained and Geometric Aggregates: A Numerical Example
To illustrate the properties of these aggregates, we use a
hypothetical numerical example in which there are three countries:
the United States and two foreign countries: A high-price country,
![]() , and a low-price country,
, and a low-price country, ![]() and their bilateral relative prices are denoted as
and their bilateral relative prices are denoted as ![]() and
and
![]() With this information, we compute
the chained and geometric aggregates as
With this information, we compute
the chained and geometric aggregates as

The initial level of the chained aggregate is arbitrary and thus,
to ease the comparison between the aggregates, we set the first
period level of the chained equal to the first period level of the
Geometric-that is,
![]() . The values for the
weights are those of the Broad Real index where we group industrial
countries as the High-price country and emerging economies as the
Low-price country. With this classification, the top panel of
figure 17 shows
the evolution of the weights. Notice that the data for the weight
of the low-price country shows a relatively low starting value that
has grown significantly over time.
. The values for the
weights are those of the Broad Real index where we group industrial
countries as the High-price country and emerging economies as the
Low-price country. With this classification, the top panel of
figure 17 shows
the evolution of the weights. Notice that the data for the weight
of the low-price country shows a relatively low starting value that
has grown significantly over time.
Figure 17: Hypothetical Measures of U.S. International Relative Price
To focus on the role of the interaction between changing weights and differentials in relative prices, we assume both nominal exchange rates against the dollar are set to one. With these assumptions, we consider two cases: fixed and changing bilateral relative prices.
Case 1: Fixed Bilateral Relative
Prices We start out in period one with prices in country ![]() , expressed in dollars, being 10 percent above those in the
United States. Thus the bilateral relative price against
, expressed in dollars, being 10 percent above those in the
United States. Thus the bilateral relative price against
![]() , denoted by
, denoted by ![]() is 1
over 1.1 or 0.91:
is 1
over 1.1 or 0.91:
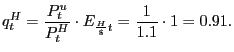
For prices in country ![]() we assume they start out
at one half those in the Untied States, so the dollar's bilateral
relative price against
we assume they start out
at one half those in the Untied States, so the dollar's bilateral
relative price against ![]() is 1 over 0.5 or 2:
is 1 over 0.5 or 2:
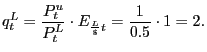
The middle panel of figure 17 shows what
happens if the individual bilateral relative prices remain fixed,
but we let the weight of country ![]() rise. Because
bilateral relative prices are fixed, the chained index (shown in
black) remains flat at its initial value. However, the geometric
aggregate (in red) rises because the weight applied to the
low-price country,
rise. Because
bilateral relative prices are fixed, the chained index (shown in
black) remains flat at its initial value. However, the geometric
aggregate (in red) rises because the weight applied to the
low-price country,
![]() is rising over time.
is rising over time.
Case 2: Changing Bilateral Relative Prices Given the many ways in which once can assume hypothetical
changes in relative prices, we impose several assumptions that are
neutral with respect to aggregation. First, we assume that the
fluctuations, in percent, of
![]() and
and ![]() are
the same and that each bilateral relative price ends at its
starting level. For the pattern of fluctuations, we use the ones
registered by the Federal Reserve Board's broad real exchange rate.
The bottom panel shows what happens if we let the bilateral
relative prices move along with the weights. Both the chained and
the geometric track the general movements in the bilateral relative
prices; and in this rather special case, the chained aggregate
returns to its initial value. The geometric, however, has an upward
trend reflecting the increasing weight of the low price country.
This is the main idea behind the geometric aggregate.
are
the same and that each bilateral relative price ends at its
starting level. For the pattern of fluctuations, we use the ones
registered by the Federal Reserve Board's broad real exchange rate.
The bottom panel shows what happens if we let the bilateral
relative prices move along with the weights. Both the chained and
the geometric track the general movements in the bilateral relative
prices; and in this rather special case, the chained aggregate
returns to its initial value. The geometric, however, has an upward
trend reflecting the increasing weight of the low price country.
This is the main idea behind the geometric aggregate.
The main lesson from these graphs is that if we want to construct a measure of aggregate relative prices that reflects the evolving importance of countries with differing prices, then we need an aggregator that is sensitive to these differences.
A.3 WARP and Substitutability Among Foreign Products
As noted in the text, the geometric aggregate ![]() is a particular case of
is a particular case of
![$\displaystyle Q_{t}^{ces}=\left[ {\textstyle\sum\limits_{i=1}^{n}} \omega_{it}\cdot\left( q_{it}\right) ^{\sigma-1}\right] ^{\frac{1} {\sigma-1}}, $](img329.gif)
with
![]() Evaluating the sensitivity of
Evaluating the sensitivity of
![]() to alternative values of
to alternative values of
![]() is simple but interpreting the
results requires an economic interpretation of
is simple but interpreting the
results requires an economic interpretation of ![]() To that end, we rely on Varian (1984, p. 33) and
assume that the bundle of foreign products
To that end, we rely on Varian (1984, p. 33) and
assume that the bundle of foreign products![]()
![]() can be expressed as
can be expressed as
![$\displaystyle F=\left[ {\textstyle\sum\limits_{i=1}^{n}} \left( a_{i}\cdot F_{i}\right) ^{-\left( \frac{1-\sigma}{\sigma}\right) }\right] ^{-1/\left( \frac{1-\sigma}{\sigma}\right) }, $](img336.gif)
where ![]() represents purchases of products from
the
represents purchases of products from
the ![]() country;
country;
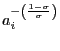 is the
distribution parameter that translates units of
is the
distribution parameter that translates units of ![]() into units of
into units of ![]() and
and ![]() is the elasticity of substitution among foreign
products
is the elasticity of substitution among foreign
products![]() a large value of
a large value of ![]() means that foreign products are highly substitutable whereas a
small value of
means that foreign products are highly substitutable whereas a
small value of ![]() means the opposite.
means the opposite.
To get from an assumption about the aggregate of purchases of
foreign products to a measure of the U.S. international relative
price, we follow Varian (1984, p. 33) and assume that ![]() is determined so as to minimize the cost of attaining a
given level of
is determined so as to minimize the cost of attaining a
given level of ![]() the resulting price of the
cost-minimizing bundle of foreign products
the resulting price of the
cost-minimizing bundle of foreign products![]()
![]() is
is
![$\displaystyle P_{f}=\left[ {\textstyle\sum\limits_{i=1}^{n}} \left( \frac{P_{fi}}{a_{i}}\right) ^{1-\sigma}\right] ^{\frac{1}{1-\sigma} },$](img350.gif)
|
(14) |
where ![]() is the (dollar) price of products
from the
is the (dollar) price of products
from the ![]() country. Note that, in Varian's
derivation, the distribution parameter,
country. Note that, in Varian's
derivation, the distribution parameter,
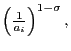 depends on
depends on ![]() Thus the familiar application of
L'H
Thus the familiar application of
L'H
![]() pital's rule to equation
(14) will not yield
pital's rule to equation
(14) will not yield
![]() as a geometric aggregate of purchases
of foreign products as
as a geometric aggregate of purchases
of foreign products as
![]() . To get that convergence
one needs to assume that
. To get that convergence
one needs to assume that
![]() where
where
![]() is the
is the ![]() country's weight in the Federal Reserve's Broad measure of the
dollar. Thus, with this assumption, the resulting aggregate of
foreign prices purchased by U.S. residents is given by
country's weight in the Federal Reserve's Broad measure of the
dollar. Thus, with this assumption, the resulting aggregate of
foreign prices purchased by U.S. residents is given by
![$\displaystyle P_{f}=\left[ {\textstyle\sum\limits_{i=1}^{n}} \omega_{i}\cdot\left( P_{fi}\right) ^{1-\sigma}\right] ^{\frac{1}{1-\sigma }}.$](img361.gif)
|
(15) |
However, as written, equation (15) is not suitable
for numerical analysis because data for ![]() are not
available
are not
available![]() To bypass this limitation, we develop an
equivalent expression in terms of
To bypass this limitation, we develop an
equivalent expression in terms of
![]() for which data
are available from the Penn World Tables
for which data
are available from the Penn World Tables![]() Thus,
equation (15) can be
re-expressed as
Thus,
equation (15) can be
re-expressed as
![$\displaystyle P_{f}=\left[ {\textstyle\sum\limits_{i=1}^{n}} \omega_{i}\cdot\left( P_{u}\cdot\frac{P_{fi}}{P_{u}}\right) ^{1-\sigma }\right] ^{\frac{1}{1-\sigma}}=\left[ {\textstyle\sum\limits_{i=1}^{n}} \omega_{i}\cdot\left( P_{u}\right) ^{1-\sigma}\cdot\left( q_{i}\right) ^{\sigma-1}\right] ^{\frac{1}{1-\sigma}}=P_{u}\cdot\left[ {\textstyle\sum\limits_{i=1}^{n}} \omega_{i}\cdot\left( q_{i}\right) ^{\sigma-1}\right] ^{\frac{1}{1-\sigma} }. $](img366.gif)
The resulting international relative price of U.S. products is
![$\displaystyle \frac{P_{u}}{P_{f}}=\frac{P_{u}}{P_{u}\cdot\left[ {\textstyle\sum\limits_{i=1}^{n}} \omega_{i}\cdot\left( q_{i}\right) ^{\sigma-1}\right] ^{\frac{-1}{\sigma -1}}}=\left[ {\textstyle\sum\limits_{i=1}^{n}} \omega_{i}\cdot\left( q_{i}\right) ^{\sigma-1}\right] ^{\frac{1}{\sigma-1} }\equiv Q^{ces}.$](img367.gif)
|
(16) |
A.4 Theoretical Measures of Competitiveness
This lengthy appendix constructs analytical analogues to the measures of competitiveness offered in the literature. Our goal is to show that they are just as subject to the influence of the prices of non-tradeables as WARP.
A.4.1 Structure of Production and Trade
We assume that the world economy is divided into three country
blocs: A foreign country of interest (country 1), the United
States, and the Rest of the World (ROW). There are five goods,
denoted as
![]() that can be used
either as intermediate inputs or as a final consumption: goods
that can be used
either as intermediate inputs or as a final consumption: goods
![]() and
and
![]() are non-traded whereas
goods
are non-traded whereas
goods
![]()
![]() ,
,
![]() are traded. Country 1
and the United States produce
are traded. Country 1
and the United States produce
![]() and
and
![]() production is
undertaken with labor and intermediates. The endowment of labor
production is
undertaken with labor and intermediates. The endowment of labor
![]() is given and intermediates can be locally
produced or imported. Product
is given and intermediates can be locally
produced or imported. Product
![]() is not produced by
these two countries because the marginal cost of production is
assumed to exceed the world price. For the pattern of trade, we
assume that country 1 exports
is not produced by
these two countries because the marginal cost of production is
assumed to exceed the world price. For the pattern of trade, we
assume that country 1 exports
![]() and imports
and imports
![]() ,
,
![]() that the United States
exports
that the United States
exports
![]() and imports
and imports
![]() ,
,
![]() and that ROW exports
and that ROW exports
![]() and imports
and imports
![]() and
and
![]()
We denote
![]() as the total supply
of the product delivered from the
as the total supply
of the product delivered from the ![]() industry
to the
industry
to the ![]() productive sector. This supply can be
made up of domestic production or imports- that is,
productive sector. This supply can be
made up of domestic production or imports- that is,
![]() where
where
![]() represents domestic production of
the
represents domestic production of
the ![]() product purchased by the
product purchased by the ![]() productive sector and
productive sector and ![]() represents
imports of the
represents
imports of the ![]() product purchased by the
product purchased by the
![]() productive sector.
productive sector.
We denote ![]() as purchases of the
as purchases of the ![]() product for final consumption. These purchases might be
met by domestic production or by imports - that is,
product for final consumption. These purchases might be
met by domestic production or by imports - that is,
![]() where
where ![]() represents purchases of domestic production of the
represents purchases of domestic production of the
![]() product for final consumption and
product for final consumption and
![]() represents imports of the
represents imports of the ![]() product for final consumption. Note that
product for final consumption. Note that
![]() and
and ![]() treat domestic production and imports of the
treat domestic production and imports of the
![]() product as perfect substitutes for each
other. Thus, we expect the law of one price to hold. Finally,
denoting
product as perfect substitutes for each
other. Thus, we expect the law of one price to hold. Finally,
denoting ![]() as exports of the
as exports of the ![]() product, the tableau of economic transactions is
product, the tableau of economic transactions is
| Input Suppliers (i) | Users: Productive Sector (j): Π1 | Users: Productive Sector (j): Π2 | Users: Productive Sector (j): Π3 | Users: Productive Sector (j): Π4 | Users: Final Demand: C | Users: Final Demand: X | Users: Final Demand: M |
|---|---|---|---|---|---|---|---|
| Labor: L | L1 | L1 | L1 | L1 | - | - | - |
| Industry 1: | C1 | 0 | 0 | ||||
| Industry 2: | C2 | 0 | 0 | ||||
| Industry 3: | C3 | X3 | 0 | ||||
| Industry 4: | C4 | 0 | m4c | ||||
| Non-Substitutable Imports: | C5 | 0 | m5c |
Entries along the first row denote deliveries of labor services
to the ![]() productive sector. Deliveries by
industries 1 and 2 are used as intermediate inputs and as final
consumption. Deliveries by industry 3 are used as an intermediate
input, as final consumption, and as exports; by assumption, good 3
is not imported. Deliveries by industry 4 are used as an
intermediate input and as final consumption; these deliveries are
augmented by imports of good 4. Deliveries of non-substitutable
imports, good 5, are used as an intermediate input in all
industries and in final consumption.
productive sector. Deliveries by
industries 1 and 2 are used as intermediate inputs and as final
consumption. Deliveries by industry 3 are used as an intermediate
input, as final consumption, and as exports; by assumption, good 3
is not imported. Deliveries by industry 4 are used as an
intermediate input and as final consumption; these deliveries are
augmented by imports of good 4. Deliveries of non-substitutable
imports, good 5, are used as an intermediate input in all
industries and in final consumption.
Entries along a column for the ![]() productive
sector (
productive
sector (![]() ) represent purchases of this
sector of labor services and of products from the
) represent purchases of this
sector of labor services and of products from the ![]() supplier of inputs (
supplier of inputs (
![]() . Entries in column
. Entries in column ![]() and
and ![]() represents purchases for final
consumption and for exports. Column
represents purchases for final
consumption and for exports. Column ![]() is not
included in conventional presentations but we use it here to record
imports for final consumption.
is not
included in conventional presentations but we use it here to record
imports for final consumption.
We use this tableau to establish the identity between uses and
sources of the ![]() product. Specifically, the gross
supply of the
product. Specifically, the gross
supply of the ![]() product facing substitutable
imports,
product facing substitutable
imports,
![]() is
is
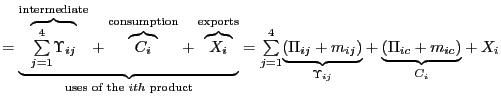
|
||
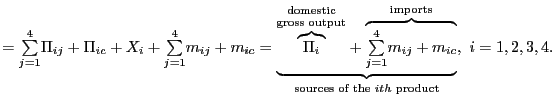
|
Thus, domestic gross output is
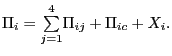
|
(17) |
The gross supply of non-substitutable imports (![]() ) is
) is
|
Technology We assume a Leontieff production function for the ![]() productive sector (
productive sector (![]() ).
Specifically, the labor requirement for producing one unit of the
).
Specifically, the labor requirement for producing one unit of the
![]() product is
product is
![]() where
where
![]() is determined by equation (17). The direct
requirement of the
is determined by equation (17). The direct
requirement of the ![]() intermediate product
needed for producing one unit of the
intermediate product
needed for producing one unit of the ![]() product is
product is
![]() The tableau in
terms of technological coefficients is
The tableau in
terms of technological coefficients is
| Coefficients | Productive Sector (j): Π1 | Productive Sector (j): Π2 | Productive Sector (j): Π3 | Productive Sector (j): Π4 | Final Demand: C | Final Demand: X | Final Demand: M |
|---|---|---|---|---|---|---|---|
| Labor: L | - | - | - | ||||
| Industry 1: | |||||||
| Industry 2: | |||||||
| Industry 3: | |||||||
| Industry 4: | |||||||
| Non-substitutable Imports: |
Marginal Costs Because we assume constant returns to scale, we express marginal costs in terms of prices and technological requirements. For example, the marginal cost in productive sector 3 is
where ![]() is the wage rate,
is the wage rate, ![]() (
(![]() is the price of the
is the price of the ![]() product, and a bar denotes the world price. Note that the
industry's use of its own output is valued not at the market price
but at the industry's own marginal cost. We now solve for marginal
costs in terms of market prices and technology:
product, and a bar denotes the world price. Note that the
industry's use of its own output is valued not at the market price
but at the industry's own marginal cost. We now solve for marginal
costs in terms of market prices and technology:
| (18) | ||
| (19) | ||
| (20) | ||
| (21) |
The generic expression for the marginal cost of the ![]() industry (
industry (![]() ) is
) is
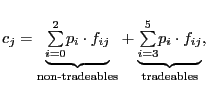
|
(22) |
where
![]() for
for
![]() is the total amount of the
is the total amount of the
![]() product required to produce one unit of
the
product required to produce one unit of
the ![]() product
product![]() The difference
between total and direct requirements is the allowance of the
The difference
between total and direct requirements is the allowance of the
![]() product to serve as an input in the
production of the
product to serve as an input in the
production of the ![]() product. Using equations
(18)-(21), we compute the
matrix of responses of marginal costs to changes in technological
coefficients:
product. Using equations
(18)-(21), we compute the
matrix of responses of marginal costs to changes in technological
coefficients:
![$\displaystyle \left[ \frac{\partial c_{j}}{\partial a_{ij}}\right] =\left[ \begin{array}[c]{cccc} \frac{\partial c_{1}}{\partial a_{01}} & \frac{\partial c_{2}}{\partial a_{02}} & \frac{\partial c_{3}}{\partial a_{03}} & \frac{\partial c_{4} }{\partial a_{04}}\\ \frac{\partial c_{1}}{\partial a_{11}} & \frac{\partial c_{2}}{\partial a_{12}} & \frac{\partial c_{3}}{\partial a_{13}} & \frac{\partial c_{4} }{\partial a_{14}}\\ \frac{\partial c_{1}}{\partial a_{21}} & \frac{\partial c_{2}}{\partial a_{22}} & \frac{\partial c_{3}}{\partial a_{23}} & \frac{\partial c_{4} }{\partial a_{24}}\\ \frac{\partial c_{1}}{\partial a_{31}} & \frac{\partial c_{2}}{\partial a_{32}} & \frac{\partial c_{3}}{\partial a_{33}} & \frac{\partial c_{4} }{\partial a_{34}}\\ \frac{\partial c_{1}}{\partial a_{41}} & \frac{\partial c_{2}}{\partial a_{42}} & \frac{\partial c_{3}}{\partial a_{43}} & \frac{\partial c_{4} }{\partial a_{44}}\\ \frac{\partial c_{1}}{\partial a_{51}} & \frac{\partial c_{2}}{\partial a_{52}} & \frac{\partial c_{3}}{\partial a_{53}} & \frac{\partial c_{4} }{\partial a_{54}} \end{array} \right] =\left[ \begin{array}[c]{cccc} \frac{p_{0}}{(1-a_{11})} & \frac{p_{0}}{(1-a_{22})} & \frac{p_{0}}{(1-a_{33})} & \frac{p_{0}}{(1-a_{44})}\\ \frac{c_{1}}{(1-a_{11})} & \frac{p_{1}}{(1-a_{22})} & \frac{p_{1}}{(1-a_{33})} & \frac{p_{1}}{(1-a_{44})}\\ \frac{p_{2}}{(1-a_{11})} & \frac{c_{2}}{(1-a_{22})} & \frac{p_{2}}{(1-a_{33})} & \frac{p_{2}}{(1-a_{44})}\\ \frac{\overline{p}_{3}}{(1-a_{11})} & \frac{\overline{p}_{3}}{(1-a_{22})} & \frac{c_{3}}{(1-a_{33})} & \frac{\overline{p}_{3}}{(1-a_{44})}\\ \frac{\overline{p}_{4}}{(1-a_{11})} & \frac{\overline{p}_{4}}{(1-a_{22})} & \frac{\overline{p}_{4}}{(1-a_{33})} & \frac{c_{4}}{(1-a_{44})}\\ \frac{\overline{p}_{5}}{(1-a_{11})} & \frac{\overline{p}_{5}}{(1-a_{22})} & \frac{\overline{p}_{5}}{(1-a_{33})} & \frac{\overline{p}_{5}}{(1-a_{44})} \end{array} \right] .$](img567.gif)
|
(23) |
Producer's Markup The producer markup of the ![]() productive
sector is defined as
productive
sector is defined as
![$\displaystyle \mu_{j}=\left\{ \begin{array}[c]{c} \frac{p_{j}}{c_{j}}\text{ for }j=1,2\\ \\ \frac{\overline{p}_{j}}{c_{j}}\text{ for }j=3,4 \end{array} \right. .$](img569.gif)
|
(24) |
Sectoral Final Demand Final demand for the ![]() product,
product, ![]() , is derived as
, is derived as
![$\displaystyle =\overset{{\small\Upsilon}_{i}}{\overbrace{\left[ {\textstyle\sum\limits_{j=1}^{4}} a_{ij}\cdot\Pi_{j}+C_{i}+X_{i}\right] }}-\left[ {\textstyle\sum\limits_{j=1}^{4}} a_{ij}\cdot\Pi_{j}+m_{ic}\right]$](img573.gif)
|
(25) | |
Nominal GDP GDP is the value of final demands valued at prices that exclude indirect taxes:
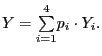
|
(26) |
A.4.2 Measures of Competitiveness
The structure developed above allows us to examine formally how
the measures of competitiveness offered in the literature respond
to technology shocks. To this end, we denote U.S. variables with a
superscript ![]() and Country 1 variables with a
superscript 1.
and Country 1 variables with a
superscript 1.
Ratio of Marginal Costs of tradeable Products The ratio of marginal costs of tradeable products is
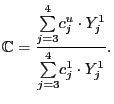
|
(27) |
The denominator of
![]() is the value of tradeables in
country 1 valued using that country's marginal costs; the numerator
of
is the value of tradeables in
country 1 valued using that country's marginal costs; the numerator
of
![]() is the value of the same bundle
valued with U.S. marginal cost. Thus if
is the value of the same bundle
valued with U.S. marginal cost. Thus if
![]() then "Country 1 is said to
be more competitive than the United States." The effect on
then "Country 1 is said to
be more competitive than the United States." The effect on
![]() of a decrease in U.S.
productivity of non-tradeable product 1 (
of a decrease in U.S.
productivity of non-tradeable product 1 (
![]() is
is
![$\displaystyle d \mathbb{C} =\frac{1}{ {\textstyle\sum\limits_{j=3}^{4}} c_{j}^{1}\cdot Y_{j}^{1}}\cdot\left[ {\textstyle\sum\limits_{j=3}^{4}} \frac{\partial c_{j}^{u}}{\partial a_{1j}^{u}}\cdot Y_{j}^{1}\cdot da_{1j} ^{u}\right] .$](img586.gif)
|
(28) |
Using the partial derivatives shown in equation (23),
![]() can be re-expressed as
can be re-expressed as
![$\displaystyle d \mathbb{C} =\frac{p_{1}^{u}}{ {\textstyle\sum\limits_{j=3}^{4}} c_{j}^{1}\cdot Y_{j}^{1}}\cdot\left[ \frac{Y_{3}^{1}}{(1-a_{33}^{u})}\cdot da_{13}^{u}+\frac{Y_{4}^{1}}{(1-a_{44}^{u})}\cdot da_{14}^{u}\right] >0. $](img588.gif)
This expression indicates that a decline in U.S. productivity of
non-tradeables raises U.S. marginal costs relative to marginal
costs in country 1. Thus,
![]() is not invariant to developments
in the non-tradeable sector.
is not invariant to developments
in the non-tradeable sector.
Sectoral Ratio of Producers' Markups
of Tradeables Corden's measure of competitiveness for the ![]() tradeable product is the ratio of producers' markups:
tradeable product is the ratio of producers' markups:

This equation can be expressed as the U.S. marginal cost for the
![]() tradeable product relative to that in
country 1:
tradeable product relative to that in
country 1:
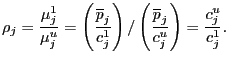
|
(29) |
The effect of a decrease in the productivity of U.S. non-tradeable
good 1 (
![]() on
on ![]() is
is
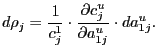
Using equation (23) yields
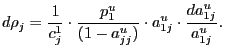
Recalling that
![]() implies that
implies that
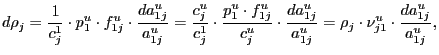
|
(30) |
where
![]() is
the fraction of
is
the fraction of ![]() accounted by cost of
intermediate input 1. For the special case of
accounted by cost of
intermediate input 1. For the special case of
![]() we get
we get
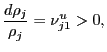 |
(31) |
This expression indicates that a decrease in U.S. productivity of
non-tradeable product 1 raises ![]() , even if
, even if
![]() were an ideal measure of
competitiveness for a given product.
were an ideal measure of
competitiveness for a given product.
A.5 Empirical Implementation
Computer-Automated Specification Algorithm The computer-automated algorithm used here (PcGets), developed by Hendry and Krolzig (2001) and Krolzig and Hendry (2001),combines ordinary least squares with a selection strategy that is implemented in four stages:
- Estimate the parameters of a general formulation-equation (13) for example-and test for congruency (e.g., white-noise residuals and parameter constancy).
- Implement multiple "simplification paths" simultaneously. One simplification path could get started by excluding the least significant variable whereas another simplification path could get initiated by excluding a block of variables that are jointly insignificant.
- Test whether the specification from a simplification path is congruent. If it is, then implement another round of simplifications and re-test for congruency; continue this process until the specification violates congruency. In that case, the algorithm selects the immediately prior specification and labels it Final model.
- Collect the Final models from all simplification paths and apply encompassing tests to them. The specification that encompasses all others becomes the Specific model. If there is no single encompassing model, then the algorithm forms a "union" model using the variables from all of the Final models and re-starts the specification search from step (2). If this strategy fails to yield a single Specific model, then the algorithm applies three information criteria (Akaike, Schwarz, and Hannan-Quinn) to the Final models and selects the one that minimizes all these criteria; that model becomes the Specific model. There is no guarantee that reliance on these three criteria will yield a unique model. In that event, the user specifies a criteria ranking to settle the conflict; this paper uses the Akaike Information Criterion. Otherwise, the algorithm fails to find a Specific model.
Monte-Carlo Distributions of Long-run Elasticities The distributions of
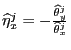 and
and
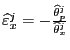 are not known in advance because they are the ratios of normal
variables which lack a well known distribution. Thus we generate
the distributions of these elasticities in three steps:
are not known in advance because they are the ratios of normal
variables which lack a well known distribution. Thus we generate
the distributions of these elasticities in three steps:
- Generate the
 drawing of
drawing of
 (
(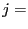 geo, c, cpi) as
where
geo, c, cpi) as
where and
and![\begin{displaymath} \widehat{\theta}^{j}\equiv\left( \begin{array}[c]{c} \widehat{\theta}_{x}^{j}\ \widehat{\theta}_{y}^{j}\ \widehat{\theta}_{p}^{j} \end{array}\right) ,\text{ }\widehat{\Omega}^{j}=\left[ \begin{array}[c]{ccc} v\widehat{a}r(\widehat{\theta}_{x}^{j}) & c\widehat{o}v(\widehat{\theta} _{x}^{j},\widehat{\theta}_{y}^{j}) & c\widehat{o}v(\widehat{\theta}_{x} ^{j},\widehat{\theta}_{p}^{j})\ c\widehat{o}v(\widehat{\theta}_{x}^{j},\widehat{\theta}_{y}^{j}) & v\widehat{a}r(\widehat{\theta}_{y}^{j}) & c\widehat{o}v(\widehat{\theta} _{p}^{j},\widehat{\theta}_{y}^{j})\ c\widehat{o}v(\widehat{\theta}_{x}^{j},\widehat{\theta}_{p}^{j}) & c\widehat{o}v(\widehat{\theta}_{p}^{j},\widehat{\theta}_{y}^{j}) & v\widehat{a}r(\widehat{\theta}_{p}^{j}) \end{array}\right] , \end{displaymath}](img614.gif)
 is the lower-triangular
Cholesky decomposition of
is the lower-triangular
Cholesky decomposition of
 We use the same seeds
of the random-number generator across the various measures of
relative export prices to ensure comparability of the results.
We use the same seeds
of the random-number generator across the various measures of
relative export prices to ensure comparability of the results. - Compute the long-run elasticities associated with the
 drawing as
drawing as
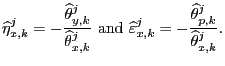
- Use the 1000 drawings for each elasticity to generate the associated empirical densities.
Figures 18 and 19 show the densities for income and price elasticities associated with the Specific formulations of table 1. The results show the median and the bounds associated with 95 confidence interval; note the lack of symmetry in the underlying distributions.
Figure 18: Monte Carlo Densities of Long-run Income Elasticity
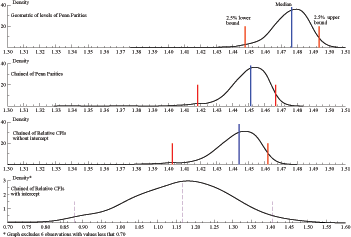
* Chained of Relative CPIs with intercept graph excludes 6 observations with values less that 0.70.
Figure 19: Monte Carlo Densities of Long-run Price Elasticity
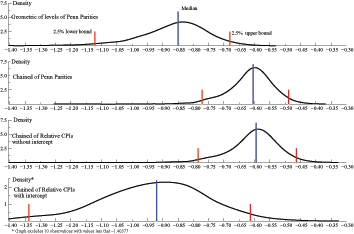
* Chained of Relative CPIs with intercept graph excludes 10 observations with values less that -1.40377.
Table A1: Augmented Dickey-Fuller Tests for Stationarity
| Variable | D-lag | t-adf | coefficient on level of Dep. Variable | SER | AIC |
|---|---|---|---|---|---|
| ln Y* | 3 | -1.1250 | 0.9987 | 0.0041 | -10.9800 |
| ln Y* | 2 | -1.1260 | 0.9987 | 0.0040 | -10.9900 |
| ln Y* | 1 | -1.1720 | 0.9987 | 0.0040 | -11.0100 |
| ln Y* | 0 | -2.0480 | 0.9973 | 0.0048 | - |
| ln X | 3 | -0.7305 | 0.9974 | 0.0240 | -7.4250 |
| ln X | 2 | -0.7337 | 0.9974 | 0.0239 | -7.4380 |
| ln X | 1 | -0.7605 | 0.9972 | 0.0245 | -7.3940 |
| ln X | 0 | -0.9199 | 0.9966 | 0.0248 | - |
| ln rpxg | 3 | -1.0770 | 0.9861 | 0.0235 | -7.4630 |
| ln rpxg | 2 | -0.9250 | 0.9880 | 0.0238 | -7.4480 |
| ln rpxg | 1 | -0.9347 | 0.9880 | 0.0237 | -7.4630 |
| ln rpxg | 0 | -0.7859 | 0.9898 | 0.0240 | - |
| ln rpxc | 3 | -0.2692 | 0.9976 | 0.0232 | -7.4880 |
| ln rpxc | 2 | -0.1053 | 0.9991 | 0.0235 | -7.4690 |
| ln rpxc | 1 | -0.1198 | 0.9989 | 0.0234 | -7.4840 |
| ln rpxc | 0 | 0.0302 | 1.0003 | 0.0236 | - |
| ln rxpcpi | 3 | -0.3818 | 0.9968 | 0.0228 | -7.5210 |
| ln rxpcpi | 2 | -0.2412 | 0.9980 | 0.0231 | -7.5060 |
| ln rxpcpi | 1 | -0.2596 | 0.9978 | 0.0230 | -7.5210 |
| ln rxpcpi | 0 | -0.1221 | 0.9990 | 0.0233 | - |
Notes: Sample is 1972Q2 to 2004Q4 (NOBS = 131). ADF regression includes a constant. The 5% rejection value is -2.88; the 1% rejection value is -3.48.
Data for Modeling Aggregate U.S. Exports
Data for U.S. exports of goods and services (![]() ), measured in chained 2000 dollar and on a NIPA-basis, come
from Bureau of Economic Analysis, Survey of Current
Business, table 4.2.6.
), measured in chained 2000 dollar and on a NIPA-basis, come
from Bureau of Economic Analysis, Survey of Current
Business, table 4.2.6.
Data for the deflator of U.S. exports of goods and services
(![]() ), come from Bureau of Economic
Analysis, Survey of Current Business, table 4.2.4.
), come from Bureau of Economic
Analysis, Survey of Current Business, table 4.2.4.
We measure economic activity outside the United States as a
geometric weighted average of the real GDP indexes for all the
countries included in the Federal Reserve's Broad measure of the
effective value of the dollar-that is,
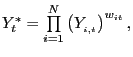 where
where
![]() is the index of real GDP of the
is the index of real GDP of the
![]() country;
country; ![]() is the
bilateral trade weight that excludes the contribution of imports
and includes the role of bilateral export and third-country
markets. Data for each country's real GDP come from national
sources and from the IMF.
is the
bilateral trade weight that excludes the contribution of imports
and includes the role of bilateral export and third-country
markets. Data for each country's real GDP come from national
sources and from the IMF.
Data for the weights come from the Federal Reserve's statistical release H10: http://www.federalreserve.gov/releases/h10/Weights/
References
Anderson, R. and J. Thursby, 1986, "Confidence Intervals for Elasticity Estimators in Translog Models," The Review of Economics and Statistics, 68, 647-656.
Bayoumi, T., J. lee, and S. Jayanthi, 2005, "New Rates from New Heights," IMF Working paper WP/05/99.
Chinn, M., 2005, "A Primer on Real Effective Exchange Rates: Determinants, Overvaluation, Trade Flows and Competitive Devaluation," NBER Working Paper No. 11521.
Corden, M., 1994, Economic Policy, Exchange Rates, and the International System, Chicago: University of Chicago Press.
Duran, M., J. Simon, and C. Webb, 1992, "OECD's Indicators of International Trade and Competitiveness," OECD Economic Papers, No. 120.
Duran, M., C. Madaschi, and F. Terribile, 1998, "Trends in OECD Countries' International Competitiveness: The Influence of Emerging Market Economies," OECD Economic Papers, No. 195.
Feenstra, R., 1994, "New Product Varieties and the Measurement of International Prices," The American Economic Review, 84, 157-177.
Feenstra, R., A. Heston, M. Timmer, and H. Deng, 2005, "Estimating Real Production and Expenditures Across Nations: A Proposal for Improving the Penn World Tables," University of California, Davis, manuscript.
Froot, K. and K. Rogoff, 1995, "Perspectives on PPP and Long-run Real Exchange Rates," in G. Grossman and K. Rogoff (eds.), Handbook of International Economics, vol 3., Amsterdam: North-Holland.
Goldstein, M. and M. Khan, 1985, "Income and Price Effects in Foreign Trade," in R. Jones and P. Kenen (eds.), Handbook of International Economics, vol 2., Amsterdam: North-Holland.
Granger, C. and D. F. Hendry, 2004, "A Dialogue Concerning a New Instrument for Econometric Modeling," Econometric Theory, 21, 278-297.
Gulde, A. M. and M. Schulze-Ghattas, 1993, "Purchasing Power Parity Based Weights for the World Economic Outlook," World Economic Outlook-December 1993, Washington DC: International Monetary Fund.
Hendry, D. F. and J. Doornik, 1999, Empirical Econometric Modelling Using PcGive, London: Timberlake.
Hendry, D. F. and H. Krolzig, 2001, Automatic Econometric Model Selection Using PcGets, London: Timberlake.
Hendry, D. F. and H. Krolzig, 2003, "New Developments in Automatic General-to-Specific Modeling," in B. Stigum (ed.), Econometrics and the Philosophy of Economics, Princeton: Princeton University Press.
Heston, A., R. Summers and B. Aten, 2006, Penn World Table Version 6.2, Center for International Comparisons of Production, Income and Prices at the University of Pennsylvania.
Hollinger, P., 2007, TROLL Reference Manual for Release 2.0, Needham: Intex Solutions.
Hooper, P. and J. Morton, 1978, "Summary Measures of the Dollar's Foreign Exchange Value," Federal Reserve Bulletin, 783-89.
Hooper, P. and J. Richardson (eds.), 1991, International Economic Transactions: Issues in Measurement and Empirical Research, Chicago: University of Chicago Press.
Hooper, P., K. Johnson, and J. Marquez, 2000, "Trade elasticities for the G-7 countries," Princeton Studies in International Economics, No. 87, Princeton: Princeton University.
Houthakker, H. and S. Magee, 1969, "Income and Price Elasticities in World Trade," Review of Economics and Statistics, 51, 111-125.
Keynes, J., 1925, "The Committee on the Currency," The Economic Journal, 138, 299-304.
Klau, M. and S. Fung, 2006, "The New BIS Effective Exchange Rate Indices," BIS Quarterly Review, March, 51-65.
Kravis, I. and M. Gilbert, 1954, An International Comparison of National Products and the Purchasing Power of Currencies: A Study of the United States, the United Kingdom, France, Germany, and Italy, Paris: OECD.
Kravis, I. and R. Lipsey, 1971, Price Competitiveness in World Trade, New York: Columbia University Press.
Kravis, I. and R. Lipsey, 1990, "The International Comparison Program: Current Status and Problems," NBER Working Paper no. 3304.
Kravis, I., A. Heston, and R. Summers, 1978, International Comparisons of Real Product and Purchasing Power, Baltimore: Johns Hopkins University Press.
Kravis, I., A. Heston, and R. Summers, 1982, World Product and Income: International Comparisons of Real Gross Product, Baltimore: Johns Hopkins University Press.
Krolzig, H. and D.F. Hendry, 2001, "Computer Automation of General-to-Specific Model Selection Procedures," Journal of Economic Dynamics & Control, 25, 831-866.
Leahy, M., 1998, "New Summary Measures of the Foreign Exchange Value of the Dollar," Federal Reserve Bulletin, 811-18.
Lipsey, R., L. Molinary, and I. Kravis, 1990, "Measures of Prices and Price Competitiveness in International Trade in Manufactured Goods," NBER Working Paper, No. 3442.
Loretan, M., 2005, "Indexes of the Foreign Exchange Value of the Dollar," Federal Reserve Bulletin, Vol. 91, No.1 (Winter), 1-8.
McGuirk, A., 1986, "Measuring Price Competitiveness for Industrial Country Trade in Manufactures," IMF Working paper WP/87/34.
Maciejewski, E., 1983, " `Real' Effective Exchange Rate Indices," IMF Staff Papers, 30, 491-541.
Mann, C., 1999, Is the U.S. Trade Deficit Sustainable? Washington DC: Institute for International Economics.
Marsaglia, G., 1965, "Ratios of Normal Variables and Ratios of Sums of Uniform Variables," Journal of the American Statistical Association, 60, 193-204.
Pauls, B. D., 1987, "Measuring the Foreign Exchange Value of the Dollar," Federal Reserve Bulletin, 411-22.
Phillips, P., 2004, "Automated Discovery in Econometrics," Cowles Foundation Discussion Paper No. 1469, Yale University.
Summers, R. and A. Heston, 1991, "The Penn World Table (Mark 5): An expanded Set of International Comparisons, 1950-1988," Quarterly Journal of Economics, 106, 327-368.
Thomas, C. and J. Marquez, 2006, "Measurement Matters for Modeling U.S. Import Prices," Federal Reserve Board International Finance Discussion Papers, No. 883.
Turner, A. and S. Golub, 1997, "Towards a System of Multilateral Unit Labor Cost-Based Competitiveness Indicators for Advanced, Developing, and Transition Economies," IMF Working paper WP/97/151.
Turner, P. and J. Van't dack, 1993, "Measuring International Price and Cost Competitiveness," BIS Economic Papers, No. 39.
Vachris, M. and J. Thomas, 1999, "International Price Comparisons Based on Purchasing Power Parities," BLS Monthly Labor Review, October, 3-12.
Varian, H., 1984, Microeconomic Analysis, New York: Norton.
Zanello, A. and D. Desruelle, 1997, "A Primer on the IMF's Information Notice System," IMF Working paper WP/97/71.
Footnotes
* We are grateful to George Alessandria, Tam Bayoumi, Menzie Chinn, Judith Dean, Neil Ericsson, Robert Feenstra, Michael Ferrantino, Joe Gagnon, Dale Henderson, Karen Johnson, Michael Leahy, Jaewoo Lee, Gian Maria Milessi-Ferreti, Alessandro Prati, Trevor Reeve, Luca Ricci, Nathan Sheets, Antonio Spilimbergo, and Eric van Wincoop for their detailed comments. A previous version of this paper was presented in the workshop series of the Federal Reserve, the International Monetary Fund, the U.S. International Trade Commission, and the Fall 2005 and 2007 meetings of the Midwest International Economics Group. The calculations use TROLL: Hollinger (2007), PcGive: Hendry and Doornik (1999), and PcGets: Hendry and Krolzig (2001). The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
1. For a recent review, see Froot and Rogoff (1995). For early work on the importance of measuring relative prices, see Keynes (1925), Kravis and Gilbert (1954), and Kravis and Lipsey (1971). Other relevant papers include Lipsey, Molinari, and Kravis (1990), Hooper and Richardson (1991), and Turner and Van't dac (1993). Return to text
2. For example, Turner and Van't dac (1993) examine this distinction using cross-sectional data. Return to text
3. The theoretical underpinnings of the REERs date back to work by Armington who, as McGuirk (1986, p. 3) points out, showed that an ideal weighting system is one in which an equiproportionate change in the product prices of all countries would leave the demand for any one country's product unchanged. Return to text
4. Both the OECD and the IMF also report real effective exchange rates that are based on unit-labor costs; these measures show pronounced secular declines. Return to text
5. Chinn (2005) reviews these measures. For the IMF, see Bayoumi et al. (2005), Zanello and Desruelle (1997), Turner and Golub (1997), Maciejewski (1983); for the Federal Reserve, see Hooper and Morton (1978), Pauls (1987), Leahy (1998), Loretan (2005); for the OECD, see Durand, Simon, and Webb (1992), Durand, Madaschi, and Terribile (1998). The BIS also constructs a real effective exchange rate comparable to that of the OECD and the Federal Reserve but the series starts in 1994 and so it is not suitable for our analysis; see Klau and Fung (2006). Return to text
6. The countries for each group were selected so as to encompass (form an envelope around) all the bilateral real exchange rates in our sample of 34 countries. The group of industrial countries corresponds to the Federal Reserve's classification of countries with major currencies; the group of emerging economies corresponds to the Federal Reserve's list of currencies of Other Important Trading Partners (OITP). These country groupings coincide, respectively, with the "High-price" and "Low-price" countries. Return to text
7. The FRB's weight for a given country consists of trade shares for bilateral non-oil imports, bilateral exports, and a measure of the importance of the competition between that country and the United States in third-country markets. For further details on the construction of these weights, see Leahy (1998). Return to text
8. Because ![]() is a
limiting case of the more general CES function, section 5.1 below examines
the sensitivity of our results to alternative
parameterization. Return to text
is a
limiting case of the more general CES function, section 5.1 below examines
the sensitivity of our results to alternative
parameterization. Return to text
9. Appendix A.2 documents the
properties of ![]() and
and ![]() using
numerical examples. Return to
text
using
numerical examples. Return to
text
10. See Vachris and Thomas (1999) for the importance of comparability. Return to text
11. Penn's purchasing power parties have been used extensively in empirical analyses for the last three decades. See Heston, Summers and Aten (2006). For an introduction to the Penn World Tables, see Summers and Heston (1991) and Gulde and Schulze-Ghattas (1993). For the associated details, see Kravis, Heston, and Summers (1978, 1982). Other institutions also report purchasing power parities, but we use those from Penn because they include a relatively long time series. For recent efforts to improve the Penn World Tables, see Feenstra et al. (2005). Return to text
12. Our presentation follows closely that of Gulde and Schulze-Ghattas (1993); see Kravis, Heston, Summers (1978, 1982) for additional details. Return to text
13. Note that the weights (the ![]() ) are the same for the international dollar and for the
prices of the
) are the same for the international dollar and for the
prices of the ![]() country. We want to emphasize that
these
country. We want to emphasize that
these ![]() are not physical measures of output but
notional quantities; see Kravis, Heston, and Summers (1978, 1982)
for details of this concept. Return to
text
are not physical measures of output but
notional quantities; see Kravis, Heston, and Summers (1978, 1982)
for details of this concept. Return to
text
14. An earlier version of this paper used data from the 6.1 release and the results are quite comparable to the ones reported here. Nevertheless, recent data from the World Bank's International Comparison Program (December 2007) point to data revisions for recent years. Section 5.2 below examines the implications of measurement errors. Further, in personal communication, Alan Heston informed us that there will be a new release of the PWT. Once the new data are available, we will update our calculations. Return to text
15. Appendix A.1 documents these methods; for estimating quarterly parities we impose the constraint that the average of quarterly parities for a given year must be equal to the annual Penn parity for that year. Return to text
16. The countries for each group were selected so as to encompass all the bilateral relative prices in our sample. Return to text
17. Appendix A.3 shows the derivation of Qces. Return to text
18. The data come from the World Economic Outlook. The IMF's calculation starts with the PPP exchange rate in year 2000 from the World Bank; this value is then extended forwards and backwards by the growth in relative GDP deflators. See http://www.imf.org/external/pubs/ft/weo/faq.htm#q21 Return to text
19. See OECD Economic Surveys China Volume 2005/13 September 2005, page 9. Return to text
20. Assuming that the measurement error
is concentrated in countries
![]() the WARP is constructed
as
the WARP is constructed
as
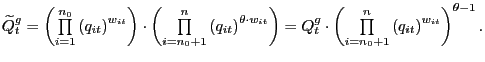 Return to text
Return to text
21. The data for this section was collected by Jeffrey Traczynski. Note that for countries that adopted the euro, The Economist reports prices beginning in 1999. Return to text
22. Note that we back out the foreign price with the standard U.S. GDP deflator which does not have, exactly, the same basket as that used by the Penn World Tables. Return to text
23. Preliminary work (available on
request) indicates that ![]() helps in correcting the
estimation bias associated with how new products are measured in
official import prices,
helps in correcting the
estimation bias associated with how new products are measured in
official import prices, ![]() see Hooper and
Richardson (1991) and Feenstra (1994). Furthermore, our measures of
see Hooper and
Richardson (1991) and Feenstra (1994). Furthermore, our measures of
![]() are relevant for explaining
are relevant for explaining
![]() which is normally modeled as a
function of foreign prices; see Thomas and Marquez (2006) for
further details on the modeling of
which is normally modeled as a
function of foreign prices; see Thomas and Marquez (2006) for
further details on the modeling of ![]() . Return to text
. Return to text
24. Based on the results from the Augmented Dickey-Fuller test, one cannot reject a unit-root for the level of exports, foreign income, and the three measures of relative prices. See table A.1 in the data appendix. Return to text
25. See Marsaglia (1965) and Anderson and Thursby (1986) for details. Return to text
26. For a discussion of the issues raised by automated specification, see Hendry and Krolzig (2003), Granger and Hendry (2004), and Phillips (2004). Return to text
27. Results from the Johansen method are sensitive to the number of lags included in the VAR. To recognize this feature, we estimate VARs with alternative lags: from 12 quarters to 3 quarters. The estimates reported here correspond to the number of lags that maximizes the probability of having one cointegrating vector. Return to text
28. See Houthakker and Magee (1969), Mann (1999), and Hooper, Johnson, and Marquez (2000). Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text