The Federal Reserve Board eagle logo links to home page

Emerging Market Business Cycles Revisited: Learning about the Trend*

Emine Boz, International Monetary Fund
Christian Daude, Inter-American Development Bank
Ceyhun Bora Durdu, Federal Reserve Board†

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

The data reveal that emerging markets do not differ from developed countries with regards to the variance of permanent TFP shocks relative to transitory. They do differ, however, in the degree of uncertainty agents face when formulating expectations. Based on these observations, we build an equilibrium business cycle model in which the agents cannot perfectly distinguish between the permanent and transitory components of TFP shocks. When formulating expectations, they assign some probability to TFP shocks being permanent even when they are purely transitory. This is sufficient for the model to produce "permanent-like" effects in response to transitory shocks. The imperfect information model calibrated to Mexico predicts a higher variability of consumption relative to output and a strongly negative correlation between the trade balance and output, without the predominance of trend shocks. The same model assuming perfect information and calibrated to Canada accounts for developed country business cycle regularities. The estimated relative variance of trend shocks in these two models is similar.

Keywords: Emerging markets, business cycles, learning, Kalman filter

JEL classification: F41, E44, D82


1  Introduction

Some of the key stylized facts regarding economic fluctuations in emerging market economies seem at odds with the neoclassical theory of business cycle fluctuations for small open economies. In particular, it has been a challenge for these models to generate a higher variability of consumption relative to output along with a negative correlation between the cyclical components of the trade balance and output as observed in the data. The present paper analyzes the importance of imperfect information and learning about trend shocks hitting the economy in explaining these features of emerging market business cycles.

To do so, we build a small open economy model in which the agent in an emerging market economy observes all the past and current realizations of TFP shocks and knows the stochastic properties of the distributions of trend growth and transitory components, but does not observe the realizations of these components. Using the available information, she forms expectations about trend growth (or permanent) and transitory (or cycle) components of total factor productivity (TFP, henceforth) shocks using the Kalman Filter.1 The agent in the developed economy, however, is fully informed about the decomposition of TFP. The two economies are identical otherwise.

Our motivation for differentiating these two types of countries (i.e., emerging market vs. developed) based on available information relies on the following empirical observation. We find that the average standard deviation of GDP growth forecasting errors for emerging markets is more than twice that of developed economies suggesting that an additional layer of uncertainty regarding the decomposition of TFP into its components is relevant. In the emerging market economy model, the agent can react to a transitory shock as if it were permanent, amplifying business cycle fluctuations.

The model features production with endogenous capital and labor, where there are costs associated with adjusting capital. The agent can borrow and lend in international capital markets. Capital markets are incomplete, because the only financial instrument available is a one-period non-contingent bond. This bond pays an interest rate that increases with the debt level to account for possible risk premia charged due to a higher default risk when debt increases.

This paper shows that the imperfect information model calibrated to Mexico, can closely match the data. In particular, it generates a higher variability of consumption relative to output and a strong negative correlation between the trade balance and output for a wide range of relative variance of trend shocks. A standard deviation of trend shocks relative to cyclical shocks in the interval $ [0.5,5]$ allows the model to match key features of emerging market moments reasonably well.

The main mechanism driving our results is based on the learning dynamics. Under imperfect information, the agent assigns some probability to the TFP shocks being permanent even when they are purely transitory. When the signals are modeled as trend plus cycle (as opposed to trend plus noise or cycle plus noise), the agent's beliefs about the contemporaneous trend shocks relative to the cycle are amplified. In this setting, the agent optimally decomposes signals into trend growth shocks and cyclical level shocks. An important implication of this formulation is that when updating the beliefs about the changes in the cyclical shocks, the agent updates her beliefs not only about the contemporaneous cyclical shocks but also their first lag. Although this backward revision has no implications for the already executed decisions in the previous period, it implies, for example, that in response to a positive signal, the agent may improve her beliefs about the change in level of cyclical shocks by not only improving her beliefs about the contemporaneous cyclical shock but also by lowering the one about the previous period's cyclical shock. Therefore, she improves her beliefs about contemporaneous cyclical shock by less than she would otherwise, leading to a dampening of the cyclical shocks relative to the trend growth. Hence, when the agent observes a signal, her beliefs are biased towards the trend growth component. Moreover, the policy functions react more to the trend growth shocks compared to cyclical; therefore, a slightly higher probability assigned to the trend growth component relative to the contemporaneous cyclical component is sufficient for the model to produce "permanent-like" responses.

The perfect information model calibrated to Canada is also successful in accounting for business cycle regularities in developed countries as shown by Aguiar and Gopinath (2007) (AG, henceforth). The relative variance of trend shocks estimated using Canadian data in the perfect information model is very close to that estimated using Mexican data with the imperfect information model confirming that these two models do not rely on differences in relative variance of trend shocks. Consistently, when we feed the Mexico parameters estimated using imperfect information model into the perfect information model, we find that the resulting business cycle moments are similar to those of developed countries.

Our paper relates mainly to AG and Garcia-Cicco, Pancrazzi and Uribe (2006) (GPU, henceforth).2 AG made a significant contribution to the literature by showing that introducing trend shocks to an otherwise standard small open economy real business cycle model can account for the aforementioned features of economic fluctuations in emerging market economies.3 Our perfect information setup is identical to AG's model.

In order for AG's model to account for the two key features of emerging market cycles mentioned above, a high variability of trend shocks relative to the transitory shocks is necessary.4 Empirical evidence regarding the predominance of trend shocks, however, is inconclusive. AG present evidence suggesting that the relative variance of trend shocks to transitory shocks in Mexico might be higher than in Canada, but caution that this result is statistically insignificant in a univariate analysis.5 In a more recent study, GPU present estimates for Argentina that suggest otherwise. GPU argue that the assumption of highly dominant trend shocks is not robust to considering longer time series data. In this study, instead of focusing on one country, we calculate the relative variance of trend shocks using TFP data for 21 developed and 25 emerging market countries and show that developed and emerging market countries are not significantly different in this regard. Therefore, explanations of the differences between these two types of countries should not hinge on the relative variance of trend growth shocks.

Our paper differs from the existing literature mainly with regards to modelling of imperfect information and learning. The existing literature assumes that the agents are fully-informed about the types of shocks, that is, when they observe a high realization of output, they know for sure if it is permanent or transitory. If TFP would measure primarily idiosyncratic technological shocks at the firm level, one could argue that at the micro level, agents could have perfect information about the type of shocks they receive and that imperfect information is just a statistical problem for the econometrician. However, the main intuition proposed in the literature for why trend shocks could be more dominant in emerging markets is the importance of regime changes (monetary, fiscal, and trade policies) which most certainly are not perfectly distinguishable at the firm or household level. Thus, it appears to be rather a strong assumption especially for emerging market economies. The empirical evidence presented in this paper shows that the degree of uncertainty faced by agents for emerging markets when formulating expectations differs significantly compared to those formulated for developed economies as discussed above.

Our findings do not imply that trend shocks are unimportant. On the contrary, our study confirms the importance of these shocks in explaining emerging market regularities in a setting where agents are imperfectly informed about the types of shocks. By modelling this informational friction explicitly, we eliminate the need for higher variability of trend shocks which does not appear to be supported by the data.

Other papers that our study is related to include Mendoza and Smith (2006), who build an equilibrium model with collateral constraints that amplifies negative productivity shocks to explain excess volatility movements nested in regular business cycles such as Sudden Stops. In a related paper, Neumeyer and Perri (2005) show that real interest rates including default risk are volatile in emerging markets and argue that they lead the business cycles.6

Our paper also relates to the literature on macro models with learning.7 To our knowledge, ours is the first paper to incorporate a learning problem with permanent shocks as well as persistent AR(1) transitory shocks using Kalman filtering techniques into a dynamic stochastic general equilibrium growth model. In this literature, Nieuwerburgh and Veldkamp (2004) study U.S. business cycle asymmetries in an RBC framework with asymmetric learning. Their analysis focuses on whether learning regarding transitory TFP shocks can induce asymmetries in output growth over the business cycle. Also, Boz (2007) investigates the business cycle implications of learning about persistent productivity shocks. Again, this model does not allow simultaneously for both, permanent and transitory shocks. In a related paper, Edge, Laubach and Williams (2004) show that uncertainty with respect to the nature of productivity shocks (permanent shifts versus transitory shocks) helps explain some of the U.S. business cycle characteristics. Their model, however, differs from ours in that the focus of their paper is to understand the U.S. economy in the presence of the alleged TFP acceleration that took place in the early 1990's.8 In addition, in their setup, signals are modelled as trend plus iid shocks, whereas we model signals as trend plus AR(1) cycle shocks which leads to the amplification of trend shocks. Last but not the least Jaimovich and Rebelo (2006) and Lorenzoni (2006) also model informational frictions in the context of news driven business cycles.

The rest of the paper is structured as follows. The next section presents our empirical findings. Section 3 introduces the model as well as the information structure and the consequent learning process. Section 4 presents the results of our quantitative analysis and compares those results with existing studies. Section 5 concludes and discusses extensions for further research.

2  Empirical Evidence

2.1  Comparison of Solow Residuals

In this subsection, we explore whether there are any systematic differences in the dominance of permanent shocks between emerging market economies and developed economies. In order to analyze this issue, we apply the methodology of Cochrane (1988) to calculate the variance of the random walk components relative to transitory ones for Solow residuals using annual data for 1960-2003 for a set of developed (21) and emerging market (25) countries.9

The decomposition of shocks into permanent and transitory components proposed by Cochrane (1988) relies on the following intuition. Suppose that TFP ($ A_t$) follows a random walk with drift, such that:

$\displaystyle \ln A_t = \mu + \ln A_{t-1} + \varepsilon_t,$ (1)

where $ \varepsilon$ is assumed to be a white noise process with mean 0 and standard deviation $ \sigma^2_{\varepsilon}$.

In this case, the variance of the k-differences defined as $ \Delta_k = \ln A_t - \ln A_{t-k}$ would increase linearly in $ k$, given that:

$\displaystyle \sigma^2_k = var(\Delta_k) = k \sigma^2_{\varepsilon}.$ (2)

However, if the TFP process is dominated by a stationary process - potentially following an ARMA process around a deterministic trend (e.g. $ \ln A_t = \mu + \alpha t + \eta_t$ with $ \eta_t = \Theta(L)\varepsilon_t$) this variance would converge to a constant, independent of k. This implies that as k increases, the following variance ratio: $ \frac{\sigma^2_{k}}{k \sigma^2_{\varepsilon}}$, converges either to 1 - if the permanent component of shocks dominates - or to 0 if transitory perturbations around a deterministic trend dominates. As Cochrane (1988) argues, this test has the advantage of not imposing too much structure on the underlying process and remains valid for any $ I(1)$ time series that allows a Beveridge-Nelson representation into a stochastic trend and a transitory component.

In order to analyze whether there is any systematic evidence of trend shocks being more dominant in emerging market countries compared to developed economies, we compute the sample variances for the log-differences of the Solow residuals for $ k \in \{1,...,20\}$ for each country from Blyde, Daude and Fernandez-Arias (2007).10 This is the same procedure AG use to analyze the cases of Canada and Mexico. However, our sample period is almost twice as long as AG's and we use a large sample of countries.

Figure 1 displays average random walk components of Solow residuals for both groups of countries. For lags less than 15, developed countries' point estimates appear to be larger than those of emerging market countries. This finding, however, depends on the lag specification and is not statistically significant. Moreover, there is considerable dispersion across countries within each group as suggested by the estimated kernel densities reported in Figure 2. For lag specifications of 5 and 10, the distributions for developed countries are to the right of those of emerging market countries suggesting higher dominance of the random walk component, but again these differences are not statistically significant. We conclude that developed and emerging market countries do not significantly differ in the importance of permanent shocks to TFP.11

2.2  Comparison of Forecast Errors

To explore if there are any differences in the uncertainty faced in emerging markets compared to developed economies, we calculate the standard deviations of forecast errors, check the efficiency of these errors, and also examine their autocorrelation structure.

Let the forecast for period $ t+1$ based on information available at time $ t$ be defined by $ \hat{y}_{t+1,t}$ and actual GDP growth be $ y_{t+1}$. Then, the one-step-ahead forecast error can be defined as:

$\displaystyle e_{t+1,t} = y_{t+1} - \hat{y}_{t+1,t}$ (3)

First, we investigate the standard deviations of forecast errors based on Consensus Forecasts, IMF's World Economic Outlook forecasts, and finally by estimating an ARMA model using TFP data. Table 1 summarizes the standard deviations of Consensus Forecasts' forecast errors ($ e_{t+1,t}$) for quarterly GDP growth (at annualized rates) for a set of developed and emerging market countries until the third quarter of 2007 since - at most - the last quarter of 1998.12 This table suggests that the standard deviations of forecast errors for emerging markets are systematically higher than those of developed economies. On average, the standard deviation of these errors are 1.04 percentage points for emerging markets and 0.46 percentage points for developed countries, less than half that of emerging markets. The same result holds if we consider the median standard deviation of forecast errors for both groups. In this case, emerging markets median value is 0.81 versus 0.38 for developed countries. Thus, forecasts are subject to more uncertainty in emerging markets than in developed countries. Similar evidence is reported by Timmermann (2006) regarding the World Economic Outlook forecast errors. For example, for Western Hemisphere the standard deviation of forecast errors is 2.41%, Asia (2.22%), Middle East (6.38%), Africa (3.19%), and Central and Eastern Europe (3.49%), while for advanced economies it is 1.36%. Finally, estimating a simple country-specific ARMA model including or not a time trend for our TFP yields standard deviations of forecast errors for the emerging market sample that are on average 78% larger than for developed countries.13

Second, in emerging market economies forecast errors are more likely to be inefficient, in the sense that the sample mean of forecasting errors differs significantly from zero which would imply that forecasters make systematic errors when projecting GDP growth. While in the case of developed countries there are just two cases out of ten where the forecast errors are biased, for emerging markets in more than 40% of the cases (8 out of 18) the sample mean of forecast errors differs significantly from zero at a 10% level of significance. This result suggests again that there are serious difficulties in forecasting the relevant economic variables for emerging markets.

Finally, we also examine first order AR of forecast errors. These autocorrelations are positive and significant for the cases of Argentina and Mexico, however, there is no developed country with a significant autocorrelation. This positive autocorrelation implies that if e.g. the current GDP growth forecast is below the actual realization, next period it will probably underestimate growth again. This type of errors are likely to occur if a trend shock hits and agents are uncertain about it. In the case of a positive (negative) trend shock, they would underestimate (overestimate) until they learn that a structural break took place.14

3  Model

We consider a standard small open economy real business cycle model with trend shocks similar to that utilized by AG and GPU. Unlike these two studies, in our emerging market economy model, the representative agent is imperfectly informed about the trend-cycle decomposition of the TFP shocks and, thereby, solves a learning problem as explained in detail below. When for comparison we consider a developed economy model, we assume perfect information. Therefore, the model for the developed economy is identical to those considered previously in the literature.

The model features production with endogenous capital and labor. There are costs associated with adjusting capital which are typically introduced in the literature to match the variability and the persistence in investment. The agent can borrow and lend in international capital markets. We assume incomplete asset markets, such that the only financial instrument available is a one-period non-contingent bond that pays an interest rate that increases with the debt level to account for possible risk premia charged due to a higher default risk when debt increases.15 At the beginning of every period, the agent observes the realization of TFP shock, updates expectations regarding the components of TFP, makes investment, labor, level of debt, and consumption decisions.

The production function takes a standard Cobb-Douglas form,

$\displaystyle Y_t=e^{z_t}K_t^{1-\alpha}(\Gamma_tL_t)^\alpha,$ (4)

where $ \alpha\in(0,1)$ is the labor's share of output. $ z_t$ is the transitory shock that follows an AR(1) process

$\displaystyle z_t=\rho_z z_{t-1}+\varepsilon_t^z$ (5)

with $ \vert\rho_z\vert<1$, and $ \varepsilon_t^z$ is independently and identically and normally distributed, $ \varepsilon_t^z\sim N(0, \sigma_z^2)$. $ \Gamma_t$ represents the cumulative product of growth shocks and is defined by

$\displaystyle \Gamma_t=e^{g_t}\Gamma_{t-1}=\prod_{s=0}^t e^{g_s},$    

and

$\displaystyle g_t=(1-\rho_g)\mu_g+\rho_g g_{t-1}+\varepsilon^g_t,$    

where $ \vert\rho_g\vert<1$, and $ \varepsilon_t^g$ is independently and identically and normally distributed with $ \varepsilon_t^g\sim N(0, \sigma_g^2)$. The term $ \mu_g$ represents the long run mean growth rate. Combining trend growth and transitory shocks, we define a single productivity shock $ A$:16

$\displaystyle \ln (A_t)\equiv z_t+\alpha\ln (\Gamma_t).$ (6)

and growth rate of $ A$ as $ g^A$:

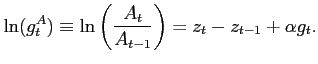
$\displaystyle \ln (g^A_t)\equiv \ln \left(\frac{A_t}{A_{t-1}}\right)=z_t-z_{t-1}+\alpha g_t.$ (7)

The representative agent's utility function is in Cobb-Douglas form:

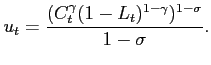
$\displaystyle u_t=\frac{(C_t^\gamma(1- L_t)^{1-\gamma})^{1-\sigma}}{1-\sigma}.$ (8)

The agent maximizes expected present discounted value of utility subject to the following resource constraint:

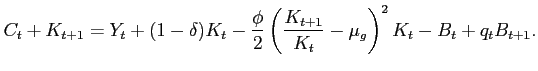
$\displaystyle C_t+K_{t+1}=Y_t+(1-\delta)K_t-\frac{\phi}{2}\left(\frac{K_{t+1}}{K_t}-\mu_g \right)^2K_t-B_t+q_tB_{t+1}.$ (9)

$ C_t$, $ K_t$, $ q_t$, and $ B_t$ denote consumption, the capital stock, price of debt and the level of debt, respectively. We assume that capital depreciates at the rate $ \delta$, and adjustments to capital stock requires quadratic adjustment cost where $ \phi$ is adjustment cost parameter. $ \mu_g$ denotes the unconditional mean of the growth rate of $ A$.

We assume that the small open economy faces a debt-elastic interest-rate premium, such that the interest rate paid is given by:

$\displaystyle \frac{1}{q_t}=1+r_t=1+r^*+\psi\left[e^{\frac{B_{t+1}}{A_t}-b}-1\right],$ (10)

where $ b$ is the aggregate level of debt that the representative agent takes as given.17

Since realizations of shock $ g_t$ permanently affect $ \Gamma_t$, output is nonstationary. To induce stationarity, we normalize all the variables by $ A_{t-1}$.18 We use the notation that a variable with a hat denotes its detrended counterpart. After detrending, the resource constraint becomes:

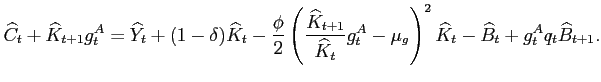
$\displaystyle \widehat{C}_t+\widehat{K}_{t+1}g_t^A=\widehat{Y}_t+(1-\delta) \widehat{K}_t-\frac{\phi}{2}\left(\frac{\widehat{K}_{t+1}}{\widehat{K}_t}g_t^A-\mu_g \right)^2\widehat{K}_t-\widehat{B}_t+g_t^Aq_t\widehat{B}_{t+1}.$ (11)

The recursive representation of the representative agent's problem can be formulated as follows:

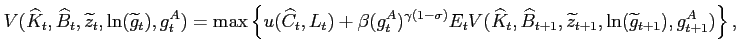
$\displaystyle V(\widehat{K}_t,\widehat{B}_t,\widetilde{z}_t,\ln(\widetilde{g}_t), g_t^A)=\max \left\{u(\widehat{C}_t,L_t)+\beta (g^A_t)^{\gamma(1-\sigma)}E_tV(\widehat{K}_t,\widehat{B}_{t+1}, \widetilde{z}_{t+1},\ln(\widetilde{g}_{t+1}),g_{t+1}^A)\right\},$ (12)

where $ \widetilde{z}_t$ and $ \ln(\widetilde{g}_t)$ are the beliefs regarding the transitory and permanent shock, respectively.

subject to the budget constraint:

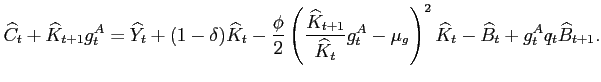
$\displaystyle \widehat{C}_t+\widehat{K}_{t+1}g_t^A=\widehat{Y}_t+(1-\delta) \widehat{K}_t-\frac{\phi}{2}\left(\frac{\widehat{K}_{t+1}}{\widehat{K}_t}g_t^A-\mu_g \right)^2\widehat{K}_t-\widehat{B}_t+g_t^Aq_t\widehat{B}_{t+1}.$ (13)

Defining investment as $ X_t$, we can summarize the evolution of the capital stock as follows:

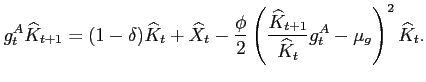
$\displaystyle g_t^A\widehat{K}_{t+1}=(1-\delta)\widehat{K}_t+\widehat{X}_t- \frac{\phi}{2}\left(\frac{\widehat{K}_{t+1}}{\widehat{K}_t}g_t^A-\mu_g\right)^2\widehat{K}_t.$ (14)

The first order conditions for the competitive equilibrium are:

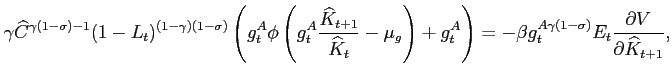
$\displaystyle \gamma \widehat{C}^{\gamma(1-\sigma)-1}(1-L_t)^{(1-\gamma)(1-\sigma)} \left(g_t^A\phi\left(g_t^A\frac{\widehat{K}_{t+1}}{\widehat{K}_t}-\mu_g\right)+g_t^A\right)=-\beta g_t^{A\gamma(1-\sigma)}E_t\frac{\partial V}{\partial \widehat{K}_{t+1}},$ (15)


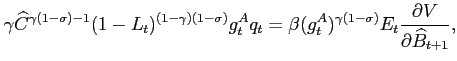
$\displaystyle \gamma \widehat{C}^{\gamma(1-\sigma)-1}(1-L_t)^{(1-\gamma)(1-\sigma)}g_t^Aq_t=\beta (g^A_t)^{\gamma(1-\sigma)}E_t\frac{\partial V}{\partial \widehat{B}_{t+1}},$ (16)

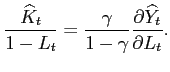
$\displaystyle \frac{\widehat{K}_t}{1-L_t}=\frac{\gamma}{1-\gamma}\frac{\partial \widehat{Y}_t}{\partial L_t}.$ (17)

Equation (15) is the Euler Equation that relates the marginal benefit of investing an additional unit of resource in capital to marginal cost of not consuming that unit. Equation (16) is the Euler Equation related to the level of debt and equation (17) is the first order condition concerning the labor-leisure choice.

3.1  Filtering Problem

In our emerging market economy model, we assume that the representative agent is imperfectly informed about the true decomposition of the TFP shocks into its trend growth and cycle components and forms expectations about this decomposition using the Kalman filter. Her information set as of time $ t$ includes the entire history of TFP shocks; $ I_t\equiv\{A_t, A_{t-1},...\}$. We also assume that underlying probabilistic distributions of $ \Gamma$ and $ z$ are known to the agent. Thus, we abstract from any consideration regarding model uncertainty to concentrate exclusively on the implications of learning under imperfect information about the nature of the shocks.

In order to use the Kalman filter, we express the filtering problem in state space form as described in Harvey (1989). This form is composed of a measurement equation and a transition equation. The measurement equation describes the relationship between the observed variable $ g^A$, and the unobserved variables $ z$ and $ g$, and is given by:

$\displaystyle \ln(g_t^A)=\underbrace{\left[ \begin{array}{c c c} 1& -1 &\alpha\end{array}\right]}_{\textbf{Z}} \underbrace{\left[ \begin{array}{c} z_t \\ z_{t-1}\\ g_t \end{array}\right]}_{\boldsymbol{\alpha}_t}.$ (18)

The measurement equation is in fact just a restatement of Equation (7). The transition equation summarizes the evolution of unobserved variables and is given by:

$\displaystyle \underbrace{\left[ \begin{array}{c} z_t \\ z_{t-1}\\ g_t \end{array}\right]}_{\boldsymbol{\alpha}_t}= \underbrace{\left[ \begin{array}{c c c} \rho_z& 0 &0 \\ 1&0&0 \\ 0&0&\rho_g \end{array}\right]}_{\textbf{T}} \underbrace{\left[ \begin{array}{c} z_{t-1} \\ z_{t-2} \\ g_{t-1} \end{array}\right]}_{\boldsymbol{\alpha}_{t-1}}+ \underbrace{\left[ \begin{array}{c} 0 \\ 0\\ (1-\rho_g) \mu_g \end{array}\right]}_{\textbf{c}}+ \underbrace{\left[ \begin{array}{c c} 1 &0 \\ 0 & 0\\ 0&1\end{array}\right]}_{\textbf{R}} \underbrace{\left[ \begin{array}{c} \epsilon_t^z \\ \epsilon_t^g \end{array}\right]}_{\boldsymbol{\eta}_t}$ (19)

where $ \boldsymbol{\eta}_t\sim N(0,\textbf{Q})$ and $ \textbf{Q}\equiv\left[ \begin{array}{c c} \sigma^2_z & 0\\ 0 & \sigma^2_g \end{array}\right]$ . Equation (19) simply summarizes the autoregressive processes of trend growth and transitory components of TFP in matrix notation. Given the normality of the disturbances, the optimal estimator that minimizes the mean squared error is linear. The matrices Z, d, T, c, R and Q are the system matrices. Following the notation of Harvey (1989), we denote the optimal estimator of $ \boldsymbol{\alpha}_{t}$ based on information set, $ I_{t}$ by $ \textbf{a}_{t}$:

$\displaystyle \textbf{a}_{t}\equiv E[\boldsymbol{\alpha}_{t}\vert I_{t}].$ (20)

The covariance matrix of the estimation error is given by $ \textbf{P}_{t}$:

$\displaystyle \textbf{P}_{t} \equiv E[(\boldsymbol{\alpha}_{t}-\textbf{a}_{t})(\boldsymbol{\alpha}_{t}-\textbf{a}_{t})'].$ (21)

In this setting, the updating rule converges monotonically to the steady state and the error covariance matrix becomes time-invariant.19 In addition, the steady state error covariance matrix can be calculated as a solution to the following algebraic Riccati equation:

$\displaystyle \textbf{P}=\textbf{T}\textbf{P}\textbf{T}'-\textbf{T}\textbf{P}\textbf{Z}'(\textbf{Z}\textbf{P}\textbf{Z}')^{-1} \textbf{Z}\textbf{P}\textbf{T}'+\textbf{R}\textbf{Q}\textbf{R}'.$ (22)

Finally, based on $ I_{t-1}$ and the transition equation, we have:

$\displaystyle \textbf{a}_{t\vert t-1}=\textbf{T} \textbf{a}_{t-1}+\textbf{c}.$ (23)

The updating rule sets the posteriors $ \textbf{a}_t$ to be a convex combination of prior beliefs $ \textbf{a}_{t\vert t-1}$ and the new signal $ \ln(g_t^A)$:

$\displaystyle \textbf{a}_t=\underbrace{[\textbf{I}-\textbf{P}\textbf{Z}'(\textbf{Z}\textbf{P}\textbf{Z}')^{-1} \textbf{Z}]}_{k^1}\textbf{a}_{t\vert t-1}+\underbrace{[\textbf{P}\textbf{Z}'(\textbf{Z}\textbf{P}\textbf{Z}')^{-1}]}_{k^2}\ln(g_t^A)$ (24)

where $ \textbf{I}$ is an identity matrix of size 3 $ \times$ 1. Equations (23) and (24) fully characterize learning.

Equation (24) deserves a closer look. This equation consists of two parts. The first part is priors, $ \textbf{a}_{t\vert t-1}$ or $ E[\boldsymbol{\alpha}\vert I_{t-1}]=E[z_t, z_{t-1},g_{t}\vert I_{t-1}]$ , multiplied by their corresponding weights summarized in the matrix $ k^1_{3 \times 3}$. The second part is the new signal, $ y_t$ or $ g^A_t$, multiplied by the Kalman gain $ k^2_{3 \times 1}$. Weights assigned to priors and new signals ($ k^1$ and $ k^2$) depend mainly on the relative variance of trend to cycle, $ \sigma_g/\sigma_z$. For example, in an extreme case where $ \sigma_z\approx 0$, the agent would optimally attribute all of the fluctuations in the signal $ y_t$ to trend shocks. This would imply that posterior beliefs of $ z_t$ and $ z_{t-1}$ (the first two elements of $ \textbf{a}_t$) would be inelastic with respect to fluctuations in $ y_t$. In other words, $ k^2_{1}$ and $ k^2_{2}$ would be small, whereas $ k^2_3$ and the weights assigned to the priors of $ z_t$ and $ z_{t-1}$ ($ k^1_{11}$ and $ k^1_{22}$) would be large.20

4  Quantitative Analysis

This section explains the calibration and estimation procedure of the parameters, documents the estimated parameters, and business cycle moments for both Mexico and Canada. In addition, for Mexico, it plots impulse response functions and explains in detail the implications of introducing imperfect information.

4.1  Emerging Market Business Cycles: Application to Mexico

We calibrate our model to quarterly Mexican data. We use a combination of calibrated and estimated parameters. For $ \beta$, $ \gamma$, $ b$, $ \psi$, $ \alpha$, $ \sigma$, and $ \delta$, we use values that are standard in the literature (see e.g., Mendoza, 1991; AG; Schmitt-Grohé and Uribe, 2003; Neumeyer and Perri, 2005). The parameter $ \gamma$ is set to 0.36 which implies that around one-third of agent's time is devoted to labor in the steady-state. Note that the coefficient on the interest rate premium is set to a small value, 0.001. The full set of calibrated parameters is summarized in Table 2.

We set $ \mu_g$ to the average growth rate of output from the data and estimate the remaining structural parameters, $ \sigma_g$, $ \sigma_z$, $ \rho_g$, $ \rho_z$, and $ \phi$ using a GMM estimation applied to the imperfect information model.21 Our estimation, reported in Table 3, yields a standard deviation of transitory component higher than the standard deviation of the trend growth component. The autocorrelation coefficients for both the trend growth and the transitory components are close to 0.6. Next, we summarize our findings and relate them to those in the literature.

4.1.1  Business Cycle Moments

We solve our model using a first order approximation around the deterministic steady state following the "brute-force iterative procedure" proposed by Binder and Pesaran (1997).22 Table 4 compares the business cycle moments of the imperfect information model with Mexican data as well as with those of the benchmark perfect information model calibrated to AG's Mexico parameters. For comparison, we also calculate the moments of the perfect information model using the imperfect information model's parameters. We calculate all moments using simulated data series. Simulated data is HP-filtered with a smoothing parameter of 1600, the standard value for quarterly data.

Before examining the model with imperfect information, it is worth revisiting the dynamics of the benchmark model with perfect information. In the perfect information model, when there is a positive transitory shock to output, the representative agent increases her consumption but this increase is lower than the increase in output. Because the agent knows that the output will gradually decline back to its previous level, she saves a portion of the increase in output. This is the standard consumption-smoothing effect in the presence of transitory shocks. When the shock is permanent, however, i.e., there is a positive shock to trend growth rate, the agent observes an increase in output today but she also realizes that future output will be even higher. The agent's optimal response to such positive permanent shocks is to increase her consumption more than the increase in current output. When both shocks are present in such an environment with perfect information, whether the effects of trend growth shocks dominate the transitory shocks depends on the relative variance of each shock. With imperfect information, however, the model can generate permanent-like responses even with lower relative variability of permanent components as agents can assign certain probability of transitory shocks being permanent or vice versa.

The imperfect information model matches the key moments of the Mexican data very closely (Table 4). The ratio of consumption variability to income variability is 1.17, compared to 1.26 in the data. The correlation of net-export with output is -0.69, which compares quite well with the value of -0.75 in the data. The model also matches the other moments closely as illustrated in Table 4. The GMM estimation reveals a relative variability of 0.78 suggesting that the imperfect information model matches the data without a predominance of trend growth shocks. With this parametrization, the detrended output is less volatile than in the data, which also implies a higher relative variability of investment and the trade balance compared to the data. This latter result might be due to the dampening of the shocks in models with imperfect information, also found by Boz (2007), among others.

The imperfect information model performs well with AG parameters, too. When those parameters are fed into the imperfect information model, the model can match key moments reasonably well as illustrated in the fourth column of Table 4. Therefore, the imperfect information model does not hinge on a specific value for relative variability of trend shocks as we explain further below.

In contrast, the perfect information model requires strong predominance of permanent shocks. AG estimate a variability for trend growth shocks of 2.55 percent and a variability for transitory shocks of 0.54 percent, which implies a relative variance of trend shock, $ \sigma_g/\sigma_z$, of 4.02. To illustrate the resulting implications of the perfect information model when permanent shocks are not predominant, we also report in the last column of Table 4 the moments of this model using the imperfect information model's parametrization. When permanent shocks are not predominant, the perfect information model implies a consumption variability less than that of output and procyclical net-exports, which is clearly at odds with the empirical moments. Also, the correlation of output with consumption and investment is significantly smaller than in the data.

4.1.2  Impulse Response Functions

Figure 3 plots the impulse response functions to 1-percent shocks to transitory as well as permanent components of TFP in the perfect information model. With a 1-percent transitory shock, as illustrated by the first panel, the model displays consumption smoothing: taking into account that output would gradually move back to its initial value, the agent saves a portion of the current increase in output; hence, consumption increases less than output and net exports becomes positive. When the economy is hit by a 1-percent permanent shock as illustrated in the second panel, however, consumption increases more than output and net export becomes significantly negative.

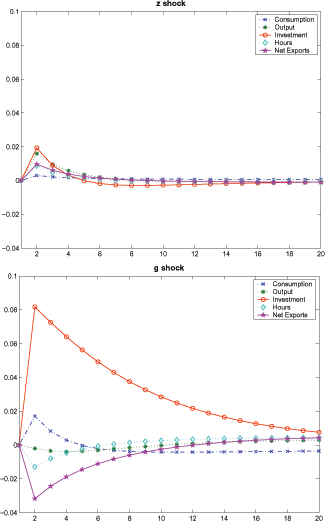
Figure 4 plots the response of the imperfect information model to transitory and permanent shocks. In response to a 1-percent transitory shock (top panel), the model displays "permanent-like" responses: consumption increases more than output; net export declines significantly. In response to a 1-percent permanent shock (bottom panel), the model again displays permanent-like responses: consumption responds more than output; net-export declines significantly. Even though imperfect information dampens the response of all variables, for the case of transitory shocks, there is an amplification effect, driven by the fact that the agent assigns a positive probability to the event that the shock might be permanent and, therefore, increases investment and consumption by more than in the perfect information case. In addition, comparing the perfect information model impulse responses depicted in Figure 3 to those of imperfect information model, learning introduces persistence.

To illustrate the learning dynamics implied by the model, we plot beliefs for permanent and transitory components along with TFP in Figure 5. The crossed solid line depicts TFP, the diamond-dashed line plots the evolution of the belief about the permanent component, while the star-dashed line represents the evolution of the belief for the transitory component. In the top panel, the source of fluctuations in TFP is a 1-percent transitory component shock, whereas in the bottom panel, it is a trend shock of the same magnitude. In the first panel, interestingly, TFP shock turns negative after the initial positive shock. This is in fact intuitive. Rewriting Equation (7), we have: $ \ln (g^A_t)=z_t-z_{t-1}+\alpha g_t$. Thus, $ g_t$ is zero as only the transitory component is shocked in the first panel, while $ z_t$ increases by 1-percent on impact and $ z_{t-1}=0$ because we start from the steady state. As the shock dies out after the first period, $ z_t=\rho_z z_{t-1}$ becomes smaller than $ z_{t-1}$ implying a negative value for $ z_t-z_{t-1}$. With $ z_t-z_{t-1}<0$ and $ g_t=0$, we have $ \ln (g^A_t)$ turning negative after the initial period as depicted in the top panel of Figure 5.

The Kalman Filter assigns slightly higher probability to trend component. This appears counterintuitive considering that the cycle component is more volatile than trend according to our GMM estimations of the imperfect information model. However, the experiment explained next clarifies the intuition for this finding.

We simulate a case where both 1% permanent shock and 1% transitory shock are given at the same time to perfect and imperfect information economies. Table 5 documents the true values of shocks in perfect information case and the beliefs calculated by the agent in imperfect information case. As expected, under perfect information, the shocks are 1 % each for $ g_t$ and $ z_t$ leading to 1.68 % growth in TFP, given that $ \alpha=0.68$. Under imperfect information, however, while decomposing TFP between $ g_t$ and $ \Delta z_t$, the agent assigns $ 0.65 \%$ to $ \widetilde{g}_t$, $ 0.60 \%$ to $ \widetilde{z}_t$, and $ -0.63 \%$ to $ \widetilde{z}_{t-1}$. In other words, the agent, using the Kalman filter, increases $ \widetilde{z}_t$ while decreasing $ \widetilde{z}_{t-1}$, part of the increase in $ \Delta \widetilde{z}_t$ coming from an update of $ \widetilde{z}_{t-1}$. This leads to the increase in $ \widetilde{g}_t$ to be larger than $ \widetilde{z}_t$ inducing a dampening of the contemporaneous cyclical component in imperfect information model. Considering that the policy decisions of time $ t-1$ are already executed at the time when the signal $ \ln(g_t^A)$ arrives, the reduction in $ \widetilde{z}_{t-1}$ does not impact the imperfect information model's long run moments directly. However, as mentioned earlier, the reduction in $ \widetilde{z}_{t-1}$ allows the agent to increase $ \Delta \widetilde{z}_t$ by increasing $ \widetilde{z}_t$ by a smaller amount than she would otherwise under perfect information scenario. This has a significant impact on the long run moments because it induces the agent to give more weight to permanent shocks relative to transitory in the imperfect information model. Moreover, note that both $ \widetilde{g}_t$ and $ \widetilde{z}_t$ under imperfect information are lower than $ g_t$ and $ z_t$ under perfect information. This leads to a dampening in the overall volatilities in imperfect information setting as evident in perfect information setting predicting higher output variability (3.21 vs 2.18, Table 4) compared to imperfect information scenario using GMM estimated parameters of the imperfect information model.

The revision of $ \widetilde{z}_{t-1}$ in case of a positive shock at time $ t$ is downwards. This is because the agent assigns positive probability to a scenario with a negative transitory shock in period $ t-1$. A close investigation of the top panel of Figure 5 reveals that for example in the case of a positive transitory shock in period 1, $ g_t^A=\alpha g_t+z_t-z_{t-1}$ increases in period 1 with unchanged $ z_{t-1}$ and $ g_t$. However, starting with the second period, $ g_t^A$ turns negative with $ z_t<z_{t-1}$ as the shock dies out gradually. The mirror image of these dynamics occur in the case of a negative shock. Going back to Table 5, observing a positive signal in period $ t$, the agent realizes that a positive transitory or permanent shock might have hit at time $ t$, or a negative transitory shock might have hit in period $ t-1$ and $ g^A$ went up in period $ t$ as this negative shock dies out. Assigning some probability to each of these scenarios, the agent increases her belief about $ g_t$, $ z_t$, and reduces the one about $ z_{t-1}$.

4.1.3  Sensitivity Analysis on the Relative Variability of Trend Shocks

Figure 6 shows how key moments change as we change the relative variability of the trend shocks, $ \sigma_g/\sigma_z$, while keeping the other parameters constant. As the first panel illustrates, as long as the relative variability of the permanent component relative to the transitory component is higher than approximately 0.7, the model can generate a higher consumption variability relative to output variability. In order for the model to match counter-cyclicality of the trade balance, the relative variability of trend shocks needs to be less than 2. Hence, the imperfect information model can match these two key moments with $ \sigma_g/\sigma_z$ in 0.7 to 2 range, considering $ \rho_g=0.61$. However, this does not imply that the imperfect information model requires a $ \sigma_g/\sigma_z$ in the range of $ [0.7,2]$. Our analysis suggests that once we allow the other estimated parameters ($ \rho_z$, $ \rho_g$, $ \phi$) to change, the imperfect information model is able to match the data fairly closely for a wide range of values for $ \sigma_g/\sigma_z$.23

The ability of the imperfect information model to match the key moments ( $ \sigma(c)/\sigma(y)$ and $ \rho(nx,y)$) for a wide range of relative variability of trend shocks is evident in Figure 7. The top panel of this figure plots $ \sigma(c)/\sigma(y)$ for different values of relative variability of trend shocks (y-axis) and $ \rho_g$ (x-axis).24 We keep the remaining parameters ( $ \rho_z, \mu, \phi$) at their original values from the baseline parametrization of imperfect information model. Similarly, the bottom panel shows $ \rho(nx,y)$ for the same sets of parameters. The top panel suggests that, in general, $ \sigma(c)/\sigma(y)$ increases with the relative variability of trend shocks and $ \rho_g$. $ \sigma(c)/\sigma(y)$ of 1.26 observed in the data can be matched with $ (\sigma_g/\sigma_z,\rho_g) \in \{(5,0),(3,0.2),(2,0.4),(1,0.61),(2.2,0.8)\}$ . That is, the model can match this moment with higher relative variability of trend shocks if one allows for lower $ \rho_g$. Similarly, the correlation between output and net exports, $ \rho(nx,y)$ of $ -0.75$, in the data is implied by the imperfect information model for $ (\sigma_g/\sigma_z,\rho_g) \in$ $ \{(4.5,0),(2.2,0.2),(1.1,0.4)$, $ (0.7,0.61),(0.5,0.8)\}$. Likewise, the model can match this moment with several values for relative variability of trend shocks and $ \rho_g$ combinations if lower $ \rho_g$'s are combined with higher relative variability of trend shocks.

Figure 8 displays the results of the same exercise for the perfect information model with AG parametrization. The perfect information model is able to generate $ \sigma(c)/\sigma(y)$ and $ \rho(nx,y)$ that are similar to those in the data only with high variability for trend component and low $ \rho_g$. In this model, $ \sigma(c)/\sigma(y)$ monotonically increases with relative variability of trend shocks. However, with respect to $ \rho_g$, it does not display a monotonic relationship. It generates $ \sigma(c)/\sigma(y)>1$ when relative variability of trend shocks is greater than 3.5 with $ \rho_g=0$, and when relative variability of trend shocks is greater than around 2 for higher values of $ \rho_g$. For the perfect information model to predict $ \rho(nx,y)<0$, $ \rho_g$ needs to be lower than 0.6, and for it to reach the levels of countercyclicality in the data (lower than $ -0.50$), $ \rho_g$ has to be in the close neighborhood of zero and relative variability of trend shocks needs to be higher than 2.5.

Summing up, so far our results show the ability of the imperfect information model to match the business cycle fluctuations in emerging market countries for a large range of key parameter values. Motivated by the observation that there is greater degree of uncertainty faced in emerging markets compared to developed economies, a model that incorporates learning problem regarding the decomposition of TFP to its components performs remarkably well. To illustrate the importance of this layer of uncertainty that distinguishes emerging market economies from their developed counterparts, we next revisit the implications of the perfect information model for an developed economy business cycles, Canada.

4.2  Developed Economy Business Cycles: Application to Canada

Next, we revisit the perfect information model calibrated to match Canadian business cycles. Calibrated parameters, estimation and solution methods are the same as those used for Mexico. Estimated parameters are summarized in Table 6. These parameters are similar to those documented by AG. Notice that the implied relative variability of the trend shock is 0.78, which is similar to the corresponding value in the imperfect information model calibrated to match Mexican business cycles. As Table 7 illustrates, with these estimated parameters, perfect information model matches Canadian business cycles closely. Thus, an important result that our analysis conveys is that simply introducing an additional layer of uncertainty can explain the observed differences in the business cycles of developed and emerging market economies remarkably well without reliance on differences in relative variance of trend shocks.

5  Conclusion

In this paper, we explained the differences in key business cycle characteristics of developed and emerging market economies based on differences in the information available to the agents. In the emerging market economy, agents are imperfectly informed about the trend-cycle decomposition of productivity shocks, and they solve a learning problem using the Kalman Filter to estimate the components of the TFP. In the developed economy, however, we assume that agents are fully informed about this decomposition based on our empirical findings. In particular, large errors in Consensus Forecasts for real GDP growth in emerging markets relative to their developed counterparts suggest that emerging market countries differ significantly in the degree of uncertainty faced by agents when formulating expectations.

We estimated both models using GMM and showed that the imperfect information model can generate higher volatility of consumption relative to output and strongly counter-cyclical trade balance without reliance on higher variability of trend shocks. In fact, the implied relative variability of trend shocks across these models are similar. This result is consistent with our empirical analysis based on data from 21 developed and 25 emerging market countries which suggests that emerging market countries do not differ from their developed counterparts in this respect confirming the relevance of our theoretical findings.

The mechanism that drives the results in the imperfect information model relies on the learning dynamics. While formulating expectations, the Kalman Filter decomposes the beliefs into trend growth shocks and changes in level of cyclical shocks. For example, considering a positive signal, while updating the beliefs about the changes in the level of the cyclical shock, agents increase the value of their beliefs about the contemporaneous component whereas revising their beliefs about the first lag downward (i.e., part of the increase in changes comes from an increase in contemporaneous component and the remaining part is due to a backward revision of the first lag). Therefore, the learning mechanism dampens the effect of cycle shocks relative to the trend. In addition, permanent shocks have stronger effects on policy decisions compared to the transitory ones. Hence, a slightly higher probability assigned to the trend component relative to the contemporaneous cycle component is sufficient for the imperfect information model to produce "permanent-like" responses. Our results also showed that the imperfect information model can account for stylized facts for a wide range of relative variability of trend shocks to transitory, including those less than one.

Our analysis underscores the uncertainty regarding the decomposition of TFP into its trend-cycle components in explaining the differences between emerging market and developed economy real business cycles. We showed that explicitly modeling this friction improves business cycle models' ability to explain fluctuations in emerging markets significantly. In particular, with those frictions in place, the model can generate the key features of emerging market business cycles for a wide range of relative variability of trend shocks.


Appendix

A.1  TFP computation

Assume that output ($ Y_t$) can be represented by the following Cobb-Douglas production function:

$\displaystyle Y_t = K_t^\alpha (h_tL_t)^{1-\alpha} A_t,$    

where $ K_t$ is the capital stock, $ L_t$ is labor which is augmented its relative efficiency due to schooling ($ h_t$), and $ A_t$ is TFP.

For capital, we use annual investment data from the Penn World Tables, version 6.2. The capital stock series are constructed via the perpetual inventory approach following Easterly and Levine (2001). In particular, the law of motion for the capital stock is given by:

$\displaystyle K_{t+1} = K_t (1-\delta) + I_t,$    

where $ I_t$ denotes investment and the rate of depreciation of the capital stock which is set to 0.07. In steady state, the initial capital-output ratio is:

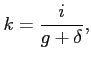$\displaystyle k = \frac{i}{g+\delta},$    

where $ i$ is the steady state investment-output ratio and $ g$ the steady state growth rate. In order to calibrate $ k$, we approximate $ i$ by the country's average investment-output ratio in the first ten years of the sample and $ g$ by a weighted average between world growth (75%) and the country's average growth in the first ten years of the sample. The initial capital level $ K_0$ is obtained by multiplying the three-year average output at the beginning of the sample.

For labor, we use the labor force implied by the real GDP per worker and real GDP (chain) series from the Penn World Tables. To calibrate human capital $ h_t$, we follow Hall and Jones (1999) and consider $ h$ to be the relative efficiency of a unit of labor with $ E$ years of schooling. In particular, $ h$ is constructed by:

$\displaystyle h = e^{\varphi(E)},$    

where $ \varphi(\cdot)$ is a function that maps the years of schooling into efficiency of labor with $ \varphi(0)=0$ and $ \varphi'(E)$ equal to the Mincerian return to schooling. We assume the same rates of return to schooling for all countries: 13.4% for the first four years, 10.1% for the next four, and 6.8% for all years of schooling above eight years (following Psacharopoulos, 1994). The data on years of schooling is obtained from the Barro-Lee database and linear extrapolations are used to complete the five-year data.

Output per worker is given by:

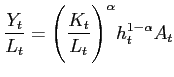
$\displaystyle \frac{Y_t}{L_t} = \Bigg( \frac{K_t}{L_t} \Bigg )^\alpha h_t^{1-\alpha} A_t$    

Taking logs and reorganizing terms yields:

$\displaystyle \ln(A_t) = \ln(Y_t)-\ln(L_t) + \alpha \big ( \ln(k_t)+\ln(L_t)\big ) + (1-\alpha)\ln(h_t).$    

A.2  GMM Estimation

This subsection presents the GMM moment conditions and procedures used in our estimations. The estimated structural parameters are $ b\equiv (\sigma_g,\sigma_z,\rho_g,\rho_z,\phi)$. In terms of notation, all lower-case variables are in logs and $ \tilde{x}$ refers to the Hodrick-Prescott filtered series of $ x$. Net exports, $ nx$, is expressed as a fraction of output. Furthermore, $ \sigma$ refers to the theoretical variance-covariance terms, while $ S$ refers to the moments in the data. The moments conditions are given by:

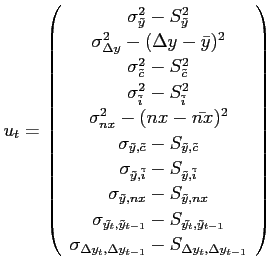
$\displaystyle u_t= \left( \begin{array}{c} \sigma_{\tilde{y}}^2 - S_{\tilde{y}}^2 \\ \sigma_{\Delta y}^2 - (\Delta y - \bar{y})^2 \\ \sigma_{\tilde{c}}^2 - S_{\tilde{c}}^2 \\ \sigma_{\tilde{i}}^2 - S_{\tilde{i}}^2 \\ \sigma_{nx}^2 - (nx - \bar{nx})^2 \\ \sigma_{\tilde{y},\tilde{c}} - S_{\tilde{y},\tilde{c}} \\ \sigma_{\tilde{y},\tilde{i}} - S_{\tilde{y},\tilde{i}} \\ \sigma_{\tilde{y},nx} - S_{\tilde{y},nx} \\ \sigma_{\tilde{y_t},\tilde{y}_{t-1}} - S_{\tilde{y_t},\tilde{y}_{t-1}} \\ \sigma_{\Delta y_t,\Delta y_{t-1}} - S_{\Delta y_t,\Delta y_{t-1}} \\ \end{array} \right )$    

Let $ \bar{u}$ be the sample mean of $ u_t$ and $ J(b,W)=\bar{u}'W\bar{u}$, with $ W$ being a symmetric positive definite weighting matrix. The GMM estimate of $ b$ is given by the vector that minimizes $ J(b,W)$. The matrix $ W$ is estimated using the two-step procedure outlined by Burnside (1999).


References

Aguiar, Mark and Gita Gopinath, 2007, "Emerging Market Business Cycles: The Cycle is the Trend," Journal of Political Economy, Vol. 115(1), pp. 69-102.

Binder, Michael and M. Hashem Pesaran, 1997, "Multivariate Linear Rational Expectations Models: Characterization of the Nature of the Solution and Their Fully Recursive Computation," Econometric Theory, Vol. 13, pp. 877-888.

Blyde, Juan, Christian Daude and Eduardo Fernandez-Arias, 2007. "Output Collapses and Total Factor Productivity Destruction," mimeo, Inter-American Development Bank.

Boz, Emine, 2007, "Can Miracles Lead to Crises? The Role of Optimism in Emerging Market Crises," IMF Working Paper No. 07/223.

Burnside, Craig, 1999, "Real Business Cycle Models: Linear Approximation and GMM Estimation," manuscript, The World Bank, May.

Cochrane, John, 1988, "How Big is the Random Walk in GNP?,"Journal of Political Economy, 96, pp. 893-920.

Easterly, William and Ross Levine, 2001, "It's Not Factor Accumulation: Stylized Facts and Growth Models," World Bank Economic Review, Vol. 15, No. 2.

Edge, Rochelle M., Thomas Laubach, and John C. Williams, 2007, "Learning and Shifts in Long-Run Productivity Growth," Journal of Monetary Economics, forthcoming.

Evans, George W. and Seppo Honkapohja, 1999. "Chapter 7 Learning Dynamics" in Kenneth J. Arrow and Michael D. Intriligator (editors), Handbook of Marcoeconomics, North-Holland, pp. 449-542.

Garcia-Cicco, Javier, Roberto Pancrazzi and Martin Uribe, 2006, "Real Business Cycles in Emerging Countries?," NBER Working paper No. 12629.

Guerrieri, Luca, Dale Henderson, and Jinill Kim, 2005. "Investment-Specific and Multifactor Productivity in Multi-sector Open Economies: Data and Analysis," International Finance Discussion Papers No. 828, Board of Governors of the Federal Reserve System.

Hall, Robert E. and Charles I. Jones, 1999, "Why Do Some Countries Produce So Much More Output Per Worker Than Others?," Quarterly Journal of Economics, Vol. 114, No. 1, pp. 83-116.

Harvey, Andrew C., 1989, Forecasting, Structural Time Series Models and the Kalman Filter, Cambridge: Cambridge University Press.

Jaimovich, Nir and Sergio Rebelo, 2006, "Can News About the Future Drive the Business Cycle?," NBER Working paper No. 12537.

Kalman, R. E., 1960, "A New Approach to Linear Filtering and Prediction Problems," Journal of Basic Engineering, Transactions ASME Series D, Vol. 82, pp. 35-45.

Lorenzoni, Guido, 2006,"A Theory of Demand Shocks," NBER Working paper No. 12477.

Mendoza, Enrique G., 1991, "Real Business Cycles in a Small Open Economy," American Economic Review, Vol. 81, pp. 797-818, September.

Mendoza, Enrique and Katherine A. Smith, 2006, "Quantitative Implications of a Debt-Deflation Theory of Sudden Stops and Asset Prices," Journal of International Economics.

Neumeyer, Pablo A. and Fabrizio Perri, 2005, "Business Cycles in Emerging Economies: the Role of Interest Rates," Journal of Monetary Economics, Vol. 52, pp. 345-380.

Nieuwerburgh, Stijn and Laura Veldkamp, 2006, "Learning Asymmetries in Real Business Cycles," Journal of Monetary Economics, Vol.53(4) pp. 753-772.

Obstfeld, Maurice and Kenneth Rogoff, 1996, Foundations of International Macroeconomics, Cambridge: MIT University Press.

Oviedo, Marcelo, 2005, "The World Interest Rate, Business Cycles, and Financial Intermediation in Small Open Economies," mimeo.

Psacharopoulos, George, 1994, "Returns to Investment in Education: A Global Update," World Development, Vol. 22, pp. 1325-1343.

Schmitt-Grohé, Stephanie and Martin Uribe, 2003, "Closing Small Open Economy Models," Journal of International Economics, Vol. 61, pp. 163-185.

Timmermann, Allan, 2006, "An Evaluation of the World Economic Outlook Forecasts," IMF Working Paper WP/06/59.

Uribe, Martin and Vivian Z. Yue, 2006. "Country Spreads and Emerging Countries: Who Drives Whom?," Journal of International Economics, Vol. 69, pp. 6-36.

Figure 1:  Relative Variance of Random Walk Component

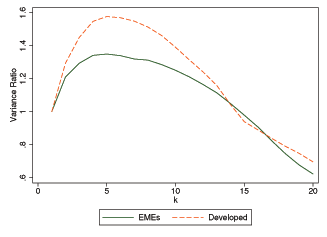
Figure 1 displays average random walk components of Solow residuals for both emerging market economies and developed countries. For lags less than 15, developed countries' point estimates appear to be larger than those of emerging market countries. This finding, however, depends on the lag specification and is not statistically significant.

Figure 2:  Densities of the Relative Variances of the Random Walk Component

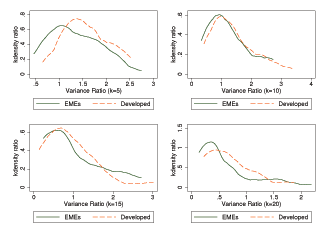
Figure 2 displays estimated kernel densities for emerging market economies and developed countries. For lag specifications of 5 and 10, the distributions for developed countries are to the right of those of emerging market countries suggesting higher dominance of the random walk component, but these differences are not statistically significant. This figure shows that developed and emerging market countries do not significantly differ in the importance of permanent shocks to TFP.

Figure 3:  Impulse Responses in the Perfect Information Model

Figure 3 plots the impulse response functions to 1-percent shocks to transitory as well as permanent components of TFP in the perfect information model. With a 1-percent transitory shock, as illustrated by the first panel, the model displays consumption smoothing: taking into account that output would gradually move back to its initial value, the agent saves a portion of the current increase in output; hence, consumption increases less than output and net exports becomes positive. When the economy is hit by a 1-percent permanent shock as illustrated in the second panel, however, consumption increases more than output and net export becomes significantly negative.

Note:  This figure illustrates the response of the endogenous variables to a 1-percent shock to the transitory (top panel) vs. trend growth component (bottom panel) of the TFP.


Figure 4:  Impulse Responses in the Imperfect Information Model

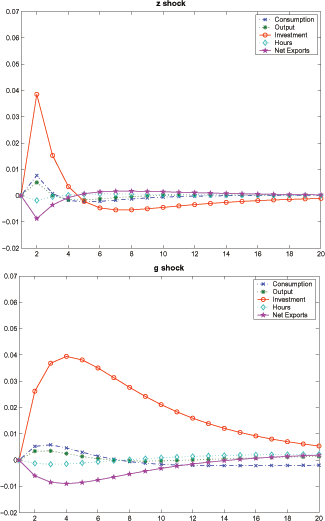
Figure 4 plots the response of the imperfect information model to transitory and permanent shocks. In response to a 1-percent transitory shock (top panel), the model displays permanent-like responses: consumption increases more than output; net export declines significantly. In response to a 1-percent permanent shock (bottom panel), the model again displays permanent-like responses: consumption responds more than output; net-export declines significantly.

Note:  This figure illustrates the response of the endogenous variables to a 1-percent shock to the transitory (top panel) vs. trend growth component (bottom panel) of the TFP.


Figure 5:  Beliefs Attached to TFP Components

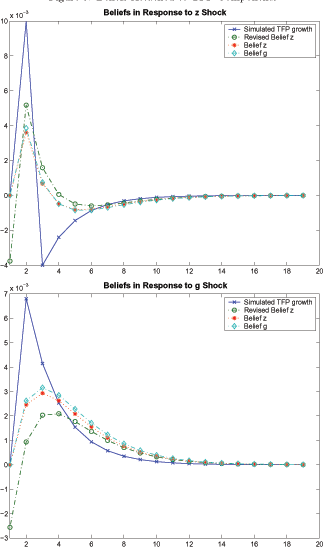
Figure 5 plots the beliefs attached to the permanent and transitory components. The crossed solid line depicts TFP, the diamond-dashed line plots the evolution of the belief about the permanent component, while the star-dashed line represents the evolution of the belief for the transitory component. In the top panel, the source of fluctuations in TFP is a 1-percent transitory component shock, whereas in the bottom panel, it is a trend shock of the same magnitude. In this exercise, the Kalman Filter assigns slightly higher probability to trend component.

Figure 6:  Sensitivity of Moments to the Relative Variability of Trend Shocks Ratios

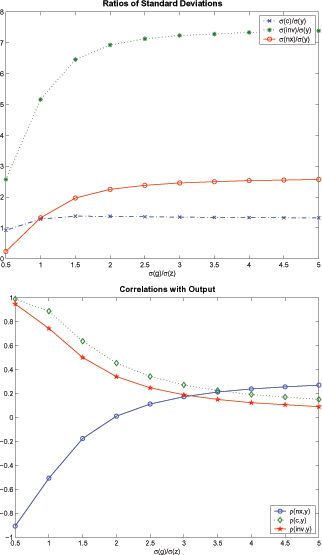
Figure 6 shows how key moments change as we change the relative variability of the trend shocks while keeping the other parameters constant. As the first panel illustrates, as long as the relative variability of the permanent component relative to the transitory component is higher than approximately 0.7, the model can generate a higher consumption variability relative to output variability. In order for the model to match counter-cyclicality of the trade balance, the relative variability of trend shocks needs to be less than 2.

Figure 7:  Imperfect Information Model Moments with Different $ \sigma_g/\sigma_z$ and $ \rho_g$'s

Figure 7 plots the relative variability of consumption relative to output as well as the correlation of trade balance with output in the imperfect information model. This figure shows that imperfect information model can match those moments for a wide range of values.

Figure 8:  Perfect Information Model Moments with Different $ \sigma_g/\sigma_z$ and $ \rho_g$'s

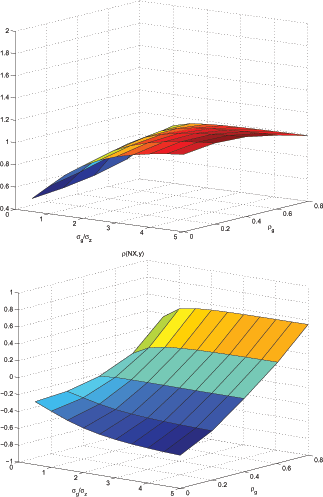
Figure 8 plots the relative variability of consumption relative to output as well as the correlation of trade balance with output in the perfect information model. This figure shows that perfect information model can match those moments only with high variability for trend component and low persistence of the trend shock.

Table 1:   Moments of Forecast Errors in EMEs vs. Developed Economies - Panel A:  Developed Countries

Country
No. of observations
Mean
Std
corr (et + 1, t , et, t - 1)
Australia
33
-0.01
0.87
0.27
Denmark
23
0.11
0.94
0.22
Finland
11
0.35*
0.60
-0.41
France
25
-0.02
0.30
-0.35
Italy
18
-0.11
0.38
-0.02
Netherlands
16
-0.02
0.36
0.32
Spain
20
0.04
0.15
-0.13
Switzerland
14
0.14
0.44
0.08
United Kingdom
36
0.05*
0.13
0.01
Average
21.78
0.06
0.46
0.00

Table 1:   Moments of Forecast Errors in EMEs vs. Developed Economies - Panel B:  EMEs

Country
No. of observations
Mean
Std
corr (et + 1, t , et, t - 1)
Argentina
26
-0.57
2.23
0.57*
Brazil
28
-0.28*
0.83
0.06
Chile
14
0.10
0.28
0.21
China
21
0.30*
0.55
-0.33
Colombia
17
0.23
0.87
0.03
India
21
0.30
0.85
0.06
Indonesia
20
0.18*
0.43
0.18
Hong Kong
26
0.70*
0.80
-0.16
Korea
23
0.23
0.86
-0.10
Malaysia
28
0.44
2.74
0.04
Mexico
33
0.05
0.59
0.31*
Peru
61
0.43*
1.45
-0.13
Philippines
17
-0.35*
0.65
-0.13
Singapore
18
-0.37*
0.46
-0.21
South Africa
23
-0.01
0.80
0.28
Taiwan
22
-0.16
0.86
0.21
Thailand
18
-0.19*
0.42
0.16
Turkey
28
-0.13
3.12
0.10
Average
24.67
0.05
1.04
0.06

Source:  Bloomberg. * Significantly different from 0 at 10% level.

Table 2:  Calibrated Parameters

β
 Discount factor
0.98
γ
 Consumption exponent of utility
0.36
b
 Steady state normalized debt
10
ψ
 Coefficient on interest rate premium
0.001
α
 Labor exponent
0.68
σ
 Risk aversion
2
δ
 Depreciation rate
0.05

Table 3:  Estimated Parameters of the Imperfect Information Model for Mexico

σg
 Stdev of permanent component noise
1.06 (0.00)
σz
 Stdev of transitory component noise
1.35 (0.00)
ρg
 Persistence of permanent component
0.61 (0.02)
ρz
 Persistence of transitory component
0.60 (0.03)
$ \phi$
 Capital adjustment cost
1.27 (0.03)
μg
 Growth rate
0.66
σg / σz
 Relative variance of trend shocks
0.78

Note:  This table summarizes the parameter estimates calculated using generalized method of moments. The moment conditions are provided in the Appendix. The numbers in parentheses are standard errors in percent.

Table 4:  Business Cycle Moments for Mexico

Moments
Data
AG
GMM with II
II with AG
PI with II param
σ(y)
2.40
2.13
2.18
1.46
3.21
σ(Δy)
1.52
1.42
1.55
1.33
2.68
σ(c) / σ(y)
1.26
1.10
1.17
1.17
0.75
σ(I) / σ(y)
4.15
3.83
4.17
6.74
3.71
σ(NX) / σ(y)
0.90
0.95
0.89
1.44
1.31
ρ(y)
0.83
0.82
0.77
0.66
0.68
ρ(Δy)
0.27
0.18
0.27
0.04
0.10
ρ(y, NX)
-0.75
-0.50
-0.69
-0.69
0.38
ρ(y, c)
0.92
0.91
0.97
0.95
0.44
ρ(y, I)
0.91
0.80
0.85
0.83
0.31

Notes:  Moments are calculated using the simulated and HP-filtered data generated by the corresponding model. AG refers to the perfect information model using the parameter values from Aguiar and Gopinath (2007), II refers to the imperfect information model. The column "II with AG param" refers to the imperfect information model using AG parameters, while the column 'PI with II param' reports the moments of the perfect information setup generated using the estimated parameters of the imperfect information setup.

Table 5:  Perfect vs Imperfect Information

Model
$ \ln(g_t^A)$=αgt+ $ \Delta z_t$
$ \widetilde{g}_t$
$ \widetilde{z}_t$
$ \widetilde{z}_{t-1}$
PI
1.68 %
1 %
1 %
0 %
II
1.68 %
0.65 %
0.60 %
-0.63 %

Note:   $ \widetilde{g}_t$, $ \widetilde{z}_t$, and $ \widetilde{z}_{t-1}$ are equal to their true values in the perfect information case.

Table 6:  Estimated Parameters of the Perfect Information Model for Canada

σg
 Stdev of permanent component noise
0.52 (0.00)
σz
 Stdev of transitory component noise

0.67 (0.00)
ρg
 Persistence of permanent component
0.33 (0.01)
ρz
 Persistence of transitory component
0.96 (0.02)
$ \phi$
 Capital adjustment cost
2.15 (0.03)
μg
 Growth rate
0.73
σg / σz
 Relative variance of trend shocks
0.78

Notes:  This table summarizes the parameter estimates calculated using generalized method of moments to match Canadian business cycles. The numbers in parentheses are standard errors in percent.

Table 7:  Business Cycle Moments for Canada

Moments
Data
Model
σ(y)
1.55
1.29
σ(Δy)
0.80
0.92
σ(c) / σ(y)
0.74
0.71
σ(I) / σ(y)
2.67
3.72
σ(NX) / σ(y)
0.57
0.68
ρ(y)
0.93
0.76
ρ(Δy)
0.55
0.23
ρ(y, NX)
-0.12
-0.13
ρ(y, c)
0.87
0.83
ρ(y, I)
0.74
0.83

Footnotes

*  We would like to thank Eduardo Fernandez-Arias, Luca Guerrieri, Dale Handerson, Nan Li, Ben Malin, Enrique Mendoza, Marcelo Oviedo, Andrea Raffo, Stephanie Schmitt-Grohè, Martín Uribe, Laura Veldkamp, and Rob Vigfusson, as well as the seminar participants of Duke, the Federal Reserve Board, Ohio State, and the Society for Computational Economics Meetings in Montreal. Paul S. Eitelman provided excellent research assistance. All remaining errors are exclusively our responsibility. Correspondence: EBoz@imf.org, ChristianD@iadb.org, Bora.Durdu@frb.gov. Return to text

†  The views expressed in this paper are those of the authors and should not be attributed to the International Monetary Fund, the Inter-American Development Bank, or the Board of Governors of the Federal Reserve System. Return to text

1.  It has been shown by Kalman (1960) that this filter is the optimal linear predictor in our setup, which resembles the assumption of rationality in the sense that the agent makes the most efficient use of the information available. Return to text

2.  An early contribution in this literature includes Mendoza (1991), who provides a workhorse real business cycle model for small open economies. Mendoza's model calibrated to Canada proves successful in explaining the observed persistence and variability of output fluctuations as well as counter-cyclicality of trade balance. Return to text

3.   The intuition for this result relies on the response of the current account to permanent changes in income, (see e.g., Chapter 2 in Obstfeld and Rogoff, 1996) which, has its roots in the permanent-income theory of consumption. If faced with a positive trend growth shock to output, the agent increases her consumption by more than the increase in current output since she expects an even higher output in the following period. This mechanism generates a consumption profile that is more volatile than output and also a trade balance deficit in response to a positive trend growth shock for the agent to finance a consumption level above output. Return to text

4.  Throughout the paper, we loosely use the terms "trend shocks" and "cycle shocks" to refer to the trend growth shocks and the transitory shocks, respectively. Return to text

5.  See AG page 84: "...Furthermore, the standard errors are large, and accordingly there is limited power in distinguishing between the random walk components of the two series. In short, a univariate approach to this issue is bound to be inconclusive..." Return to text

6.  See also Uribe and Yue (2006), and Oviedo (2005) on this issue. Return to text

7.  See Evans and Honkapohja (1999) for a comprehensive survey on the role of learning dynamics in macroeconomic models. Return to text

8.  See also Guerrieri et. al., 2005 for an analysis of importance of learning in a multisector open economy model. Return to text

9.  Developed countries include Australia, Austria, Belgium, Canada, Denmark, Finland, France, Greece, Ireland, Iceland, Italy, Japan, Netherlands, Norway, New Zealand, Portugal, Spain, Sweden, Switzerland, UK, USA. Emerging market countries include Algeria, Argentina, Brazil, Chile, Colombia, Costa Rica, Dominican Republic, Ecuador, El Salvador, India, Indonesia, Israel, Korea, Malaysia, Mexico, Pakistan, Panama, Peru, Philippines, South Africa, Thailand, Trinidad and Tobago, Turkey, Uruguay, and Venezuela. Return to text

10.  See Appendix for more details on the construction of the TFP series. Return to text

11.  While not reported here, using GDP data instead of TFP yield qualitatively similar results which are available upon request. Return to text

12.  The GDP growth data are taken from Bloomberg and refer to quarterly year-on-year growth rates. We report only those countries for which we have at least 10 quarters of forecasts available. Return to text

13.  More detailed results on the ARMA estimations are available upon request. Return to text

14.  For both Argentina and Mexico, quarters of extreme collapses in output are not included due to lack of Consensus Forecast data. We conjecture the results would be much stronger in the case of Argentina, if the two quarters of 2002 where output collapsed at year-on-year rates greater than -10% were included in our sample. Consensus Forecasts are unavailable for these particular quarters, which per se is an indicative of the degree of uncertainty surrounding this kind of episodes. Return to text

15.  Schmitt-Grohé and Uribe (2003) show that this is a useful way, although somewhat mechanical, to induce a well-defined stationary distribution of net foreign assets in small open economy models. Return to text

16.  This follows directly from the fact that the production function could be written alternatively as $ Y_t=A_tK_t^{1-\alpha}(L_t)^\alpha$, where $ A_t=e^{z_t}\Gamma_t^\alpha$. Return to text

17.  The debt elastic interest rate premium is introduced so as to induce stationarity to the asset holdings in the stochastic steady state. Other formulations used in the literature for this purpose include Mendoza (1991)'s endogenous discounting, and Aiyagari (1994)'s preferences with the rate of time preference higher than the interest rate. Schmitt-Grohé and Uribe (2003) survey some of the alternative methods used for this purpose and concludes that quantitative differences among the approaches applied to linearized systems are negligible. Return to text

18.  Note that AG normalize by $ \Gamma_{t-1}$. In our imperfect information setting, $ \Gamma_{t-1}$ is not in the information set of the agent. $ Y_{t-1}$ and $ A_{t-1}$ are other plausible candidates for normalization as they grow at the same rate as $ A$ and are in emerging market representative agent's information set. We choose to normalize by $ A_{t-1}$, but normalizing by $ Y_{t-1}$ would yield identical results. Return to text

19.  See Harvey (1989) pp. 123 for a proof of this statement. Return to text

20.  $ k_{ij}$ refers to $ i^{th}$ row and $ j^{th}$ column of matrix $ k$. Return to text

21.  See the appendix for more details, as well as Burnside (1999) for the description and application of the GMM methodology. Return to text

22.  The log-linearized system is provided in an Appendix available upon request. See Binder and Pesaran (1997) for a detailed description of the solution method. Return to text

23.  Comparing Figure 6 with Figure 4 of AG, in both setups, $ \sigma(c)/\sigma(y)$ increases with $ \sigma_g/\sigma_z$. However, $ \rho(nx,y)$ increases with $ \sigma_g/\sigma_z$ in the imperfect information setup, whereas it decreases in the perfect information model with AG parameters. Return to text

24.  We conducted similar analysis by allowing $ \rho_z$ and $ \phi$ to vary along with the relative variability of trend shocks and found that variation in those parameters do not change the relationship between $ \sigma(c)/\sigma(y)$, $ \rho(nx,y)$, and the relative variability of trend shocks. In other words, regardless of $ \rho_z$ and $ \phi$, $ \sigma(c)/\sigma(y)$ and $ \rho(nx,y)$ increase with relative variability of trend shocks. Simulations are available upon request. Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

Home | Economic research and data | Publications and education resources
Accessibility | Contact us
Last update: April 11, 2008