Interpreting Long-Horizon Estimates in Predictive Regressions

Erik Hjalmarsson^*

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

This paper analyzes the asymptotic properties of long-horizon estimators under both the null hypothesis and an alternative of predictability. Asymptotically, under the null of no predictability, the long-run estimator is an increasing deterministic function of the short-run estimate and the forecasting horizon. Under the alternative of predictability, the conditional distribution of the long-run estimator, given the short-run estimate, is no longer degenerate and the expected pattern of coefficient estimates across horizons differs from that under the null. Importantly, however, under the alternative, highly endogenous regressors, such as the dividend-price ratio, tend to deviate much less than exogenous regressors, such as the short interest rate, from the pattern expected under the null, making it more difficult to distinguish between the null and the alternative.

Keywords: Predictive regressions, long-horizon regressions, stock return predictability

JEL classification: C22, G1

1 Introduction

Long-run regressions were made popular by influential articles such as Fama and French (1988) and Campbell and Shiller (1988). When attempting to predict stock returns over longer horizons, often covering several years, rather than on a month-to-month basis, the evidence in favour of predictability generally appears much stronger. For instance, the estimated regression coefficients tend to increase almost linearly with the forecasting horizon. However, in a recent paper, Boudoukh, Richardson, and Whitelaw (2006) (BRW hereafter) show that this pattern is exactly the one to be expected in the absence of predictability. Although it is well known that the estimated slope coefficient will increase with the horizon when there is predictability, BRW appear to be the first ones to observe that the same is also true under the null hypothesis. They interpret their findings as a strong critique of the widespread belief that long-horizon regressions provide solid evidence of predictability (e.g. Cochrane, 2001).¹

The aim of the current paper is to understand in more detail the properties of long-horizon estimates under an alternative of predictability. The practical purpose of this is to establish the pattern of estimated coefficients that may be expected both under the null and the alternative, across different forecasting horizons. Although the generally increasing pattern of coefficients in long-horizon regressions is well established, the exact asymptotic sampling properties of long-run estimators under an alternative of predictability are not previously well understood.

I derive the asymptotic distribution of the long-run OLS estimator, with overlapping observations, under the assumptions that the true data generating process is given by the standard linear predictive regression model and that the regressors are highly persistent variables. Under the alternative of predictability, the sampling properties of the long-run estimator are fundamentally different than under the null hypothesis, and the limiting distribution is highly non-standard. From a practical perspective, this result is of individual interest. It shows that confidence intervals for long-run estimates, based on inverting a test statistic that is valid under the null hypothesis, will not be correctly sized under the alternative, given the non-standard distribution.

The theoretical results allow for an exact characterization of the conditional distribution of the long-run estimator, given the short-run estimate. Under the null hypothesis, the long-run estimator is, asymptotically, completely determined once the short-run estimate is given. Importantly, however, this is not true under the alternative of predictability. In fact, the degree to which the long-run estimate can vary independently of the short-run estimate is determined by the degree of endogeneity of the regressors.² Long-run estimates for highly endogenous regressors, such as the dividend-price ratio, are also almost completely pinned down by the short-run estimate under the alternative hypothesis. On the other hand, for near exogenous regressors such as the short interest rate, the long-run estimator has a relatively large independent component given the short-run estimate.³ Given the short-run estimate, under the alternative of predictability, the implications are that: (i) the highly endogenous regressor will have a more predictable pattern for long-horizons than the near exogenous one, and (ii) this pattern will closely resemble that under the null hypothesis.

These results provide an alternative interpretation of the empirical findings in BRW. BRW interpret the findings that the dividend-price ratio has a pattern very similar to that predicted under the null, whereas the short interest rate does not, as evidence against the predictive ability of the dividend-price ratio and in favor of the predictive ability of the short rate. Given the results in this paper, however, their findings could merely reflect the fact that there is more independent variation in the long-run estimates for fairly exogenous regressors.

2 Model and assumptions

Let $r_{t+1}$ denote the one period stock return from to and let $r_{t+q}\left( q\right) =\sum_{j=1}^{q}r_{t+j}$ be the corresponding period return from to . The standard long-run forecasting regression is specified as follows,

$\displaystyle r_{t+q}\left( q\right) =\alpha_{q}+\beta_{q}x_{t}+u_{t+q}\left( q\right) ,$

(1)

where long-run future returns are regressed onto a one period predictor, $x_{t}$ . Let the OLS estimator of $\beta_{q}$ in equation (1), using overlapping observations, be denoted by $\hat{\beta}_{q}$ . The primary focus of interest will be the properties of $\hat{\beta}_{q}$ for different values of , and in particular the relationship between $\hat{\beta}_{1}$ and $\hat{\beta}_{q}$ for .

In order to formally analyze the sampling properties of $\hat{\beta}_{q}$ , the data generating process for $r_{t}$ and $x_{t}$ need to be explicitly specified. Following Nelson and Kim (1993) and Campbell (2001), I assume that $r_{t}$ and $x_{t}$ satisfy:

$\displaystyle r_{t+1}$	$\displaystyle =\alpha+\beta x_{t}+u_{t+1},$	(2)
$\displaystyle x_{t+1}$	$\displaystyle =\gamma+\rho x_{t}+v_{t+1}.$	(3)

Thus, the one-period regression in equation (1) coincides with the true data generating process and for any horizon, $x_{t}$ will be the optimal forecaster of returns given current information at time .⁴ To capture the near persistence found in most forecasting variables, such as interest rates or valuation ratios, it is further assumed that the auto-regressive root, $\rho$ , is close to one in a local sense. In particular, it is assumed that $\rho=1+c/T$ , where is some finite parameter and is the sample size with . This captures the near unit-root, or highly persistent, behavior of many predictor variables, but is less restrictive than a pure unit-root assumption. The near unit-root construction, where the autoregressive root drifts closer to unity as the sample size increases, is used as a tool to enable an asymptotic analysis where the persistence in the data remains large relative to the sample size, also as the sample size increases to infinity. That is, if $\rho$ is treated as fixed and strictly less than unity, then as the sample size grows, the process $x_{t}$ will behave as a strictly stationary process asymptotically and the standard first order asymptotic results will not provide a good guide to the actual small sample properties of the model. For $\rho=1$ , the usual unit-root asymptotics apply to the model, but this is clearly a restrictive assumption for most potential predictor variables. Instead, by letting $\rho=1+c/T$ , the effects from the high persistence in the regressor will appear also in the asymptotic results, but without imposing the strict assumption of a unit root. Cavanagh et al. (1995), Lanne (2002), Valkanov (2003), Torous et al. (2004), and Campbell and Yogo (2006) all use similar models, with a near unit-root construct, to analyze the predictability of stock returns.

The error processes are assumed to satisfy a martingale difference sequence with finite fourth order moments. That is, let $w_{t}=\left( u_{t} ,v_{t}\right) ^{\prime}$ and $\mathcal{F}_{t}=\left\{ \left. w_{s} \right\vert s\leq t\right\}$ be the filtration generated by $w_{t}$ . Then $E\left[ \left. w_{t}\right\vert \mathcal{F}_{t-1}\right] =0$ , $E\left[ w_{t}w_{t}^{\prime}\right] =\Sigma=\left[ \left( \sigma_{11},\sigma _{12}\right) ,\left( \sigma_{21},\sigma_{22}\right) \right]$ , $\sup _{t}E\left[ u_{t}^{4}\right] <\infty$ , and $\sup_{t}E\left[ v_{t} ^{4}\right] <\infty.$

By standard arguments, $T^{-1/2}\sum_{t=1}^{\left[ Tr\right] } w_{t}\Rightarrow B\left( r\right) =BM\left( \Sigma\right) \left( r\right) ,$ where $B\left( \cdot\right) =\left( B_{1}\left( \cdot\right) ,B_{2}\left( \cdot\right) \right) ^{\prime}$ denotes a two dimensional Brownian motion and $\Rightarrow$ denotes weak convergence of the associated probability measures. Further, as $T\rightarrow\infty$ , $T^{-1/2}x_{\left[ Tr\right] }\Rightarrow J_{c}\left( r\right) =\int _{0}^{r}e^{\left( r-s\right) c}dB_{2}\left( s\right)$ and an analogous result holds for the demeaned variables $\underline{x}_{t}=x_{t}-T^{-1} \sum_{t=1}^{n}x_{t}$ , with the limiting process $J_{c}$ replaced by $\underline{J}_{c}=J_{c}-\int_{0}^{1}J_{c}$ (Phillips, 1987, 1988). Let $W_{1}\left( \cdot\right)$ and $W_{2}\left( \cdot\right)$ be the standardized Brownian motions, with unit variance and correlation $\delta=\sigma_{12}\left( \sigma_{11}\sigma_{22}\right) ^{-1/2}$ , that correspond to $B_{1}\left( \cdot\right)$ and $B_{2}\left( \cdot\right)$ , respectively. By the properties of conditional normal distributions, $W_{2}=\sqrt{1-\delta^{2}}W_{2\cdot1}+\delta W_{1}$ , where $W_{2\cdot1}$ is a Brownian motion with unit variance and orthogonal to $W_{1}$ . Further, let $J_{c}^{W}$ be the standardized version of $J_{c}$ .

To ease the notation, define

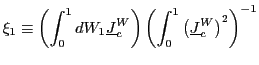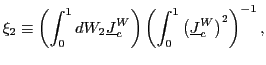
$\displaystyle \xi_{1}\equiv\left( \int_{0}^{1}dW_{1}\underline{J}_{c}^{W}\right) \left( \int_{0}^{1}\left( \underline{J}_{c}^{W}\right) ^{2}\right) ^{-1}$ and $\displaystyle \xi_{2}\equiv\left( \int_{0}^{1}dW_{2}\underline{J}_{c}^{W}\right) \left( \int_{0}^{1}\left( \underline{J}_{c}^{W}\right) ^{2}\right) ^{-1},$

(4)

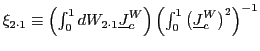and write $\xi_{2}=\sqrt{1-\delta^{2}}\xi_{2\cdot1}+\delta\xi_{1},$ where $\xi_{2\cdot1}\equiv\left( \int_{0}^{1}dW_{2\cdot1}\underline{J}_{c} ^{W}\right) \left( \int_{0}^{1}\left( \underline{J}_{c}^{W}\right) ^{2}\right) ^{-1}$ .

3 Asymptotic distributions under the null and the alternative

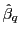
3.1 The limiting distribution of $\hat{\beta}_{q}$

The foundations for the subsequent analysis is given in the following theorem, which outlines the asymptotic properties of $\hat{\beta}_{q}$ under both the null hypothesis of no predictability and the alternative of predictability.

Theorem 1 Suppose the data are generated by equations (2) and (3).

1. Under the null hypothesis that $\beta=0$ , as $T\rightarrow\infty$ ,

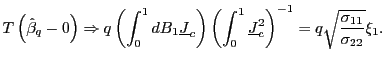
$\displaystyle T\left( \hat{\beta}_{q}-0\right) \Rightarrow q\left( \int_{0}^{1} dB_{1}\underline{J}_{c}\right) \left( \int_{0}^{1}\underline{J}_{c} ^{2}\right) ^{-1}=q\sqrt{\frac{\sigma_{11}}{\sigma_{22}}}\xi_{1}.$

(5)

2. Under the alternative hypothesis that $\beta\neq0$ , as $T\rightarrow\infty$ ,

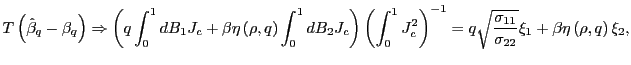
$\displaystyle T\left( \hat{\beta}_{q}-\beta_{q}\right) \Rightarrow\left( q\int_{0} ^{1}dB_{1}J_{c}+\beta\eta\left( \rho,q\right) \int_{0}^{1}dB_{2} J_{c}\right) \left( \int_{0}^{1}J_{c}^{2}\right) ^{-1}=q\sqrt{\frac {\sigma_{11}}{\sigma_{22}}}\xi_{1}+\beta\eta\left( \rho,q\right) \xi _{2},$

(6)

where $\beta_{q}\equiv\beta\nu\left( \rho,q\right)$ with $\nu\left( \rho,q\right) =\left( 1+\rho+...+\rho^{q-1}\right) =q+O\left( T^{-1}\right)$ , and $\eta\left( \rho,q\right) \equiv\sum_{h=1}^{q-1} \sum_{p=h}^{q-1}\rho^{p-h}=\frac{q\left( q-1\right) }{2}+O\left( T^{-1}\right)$ . For $\rho=1$ , it holds exactly that $\nu\left( \rho,q\right) =q$ , and $\eta\left( \rho,q\right) =\frac{q\left( q-1\right) }{2}$ .

Remark 1.1 Note that the asymptotic distribution of $\hat{\beta}_{1}$ is identical under the null and the alternative. That is, for any value of $\beta$ ,

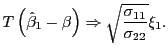
$\displaystyle T\left( \hat{\beta}_{1}-\beta\right) \Rightarrow\sqrt{\frac{\sigma_{11} }{\sigma_{22}}}\xi_{1}.$

(7)

This follows both from standard asymptotic theory applied to the one-period OLS estimator, but also from plugging in in equations (5) and (6).

Remark 1.2 Under the null hypothesis, the asymptotic distribution of $\hat{\beta}_{q}$ is identical to that of $\hat{\beta}_{1}$ , apart from a scaling factor. This result follows from the persistent nature of the regressors; the intuition behind it is discussed in more detail in Hjalmarsson (2007). For the purposes of this paper, the implications are that the short-run and long-run estimators are perfectly correlated asymptotically. In fact, from equation (5) it follows that,

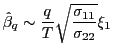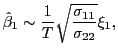
$\displaystyle \hat{\beta}_{q}\sim\frac{q}{T}\sqrt{\frac{\sigma_{11}}{\sigma_{22}}}\xi _{1}$ and $\displaystyle \hat{\beta}_{1}\sim\frac{1}{T}\sqrt{\frac{\sigma_{11}} {\sigma_{22}}}\xi_{1},$

(8)

where $\sim$ is used to denote an approximate distributional equivalence. Asymptotically, therefore, the conditional distribution of $\hat{\beta}_{q}$ given $\hat{\beta}_{1}$ satisfies $\left. \hat{\beta}_{q}\right\vert \hat{\beta}_{1}=q\hat{\beta}_{1}$ . Given $\hat{\beta}_{1}$ , the estimator $\hat{\beta}_{q}$ is thus asymptotically a deterministic linear function of the forecasting horizon. This is similar to the result in BRW, which is derived under the assumption of a fixed autoregressive root $\rho$ that is strictly less than unity.

Remark 1.3 Under the alternative hypothesis, the long-run estimator converges to the parameter $\beta_{q}=\beta\nu\left( \rho,q\right)$ , which for $\rho=1+c/T$ implies that $\beta_{q}=q\beta+O\left( T^{-1}\right)$ . That is, the 'true' parameter value, $\beta_{q}$ , as well as the estimator $\hat{\beta}_{q}$ , grows approximately one-to-one with the forecasting horizon.

Remark 1.4 Under the alternative hypothesis of predictability, the distribution of $\hat{\beta}_{q}$ is quite different than under the null hypothesis. To understand the intuition behind this result, note first that the true model is given by equations (2) and (3). The long-run regression equation is thus a fitted regression, rather than the data generating process. As shown in Appendix A, the long-run returns $r_{t+q}\left( q\right)$ actually satisfy the following relationship when ignoring the constant, derived from equations (2) and (3):

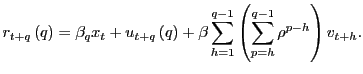
$\displaystyle r_{t+q}\left( q\right) =\beta_{q}x_{t}+u_{t+q}\left( q\right) +\beta \sum_{h=1}^{q-1}\left( \sum_{p=h}^{q-1}\rho^{p-h}\right) v_{t+h}.$

(9)

There are now two error terms, the usual $u_{t+q}\left( q\right)$ plus the additional term $\beta\sum_{h=1}^{q-1}\left( \sum_{p=h}^{q-1}\rho ^{p-h}\right) v_{t+h}$ , which stems from the fact that at time there is uncertainty regarding the path of $x_{t+j}$ for . That is, since the true model is given by equations (2) and (3), there is uncertainty regarding both the future realizations of the returns as well as of the predictor variable when forming period ahead forecasts. The first error term, $u_{t+q}\left( q\right)$ , corresponds to the asymptotic $\xi_{1}$ term in the limiting distribution and the second error term, $\beta\sum_{h=1}^{q-1}\left( \sum_{p=h}^{q-1}\rho^{p-h}\right) v_{t+h}$ , corresponds to the $\xi_{2}$ term. For large , the second error term in (9) will clearly dominate the asymptotic properties since it is of an order of magnitude larger than the first one, a result reflected in the weights on $\xi_{1}$ and $\xi_{2}$ in equation (6). However, the weight on $\xi_{2}$ in (6) also depends on $\beta$ . Thus for $\beta$ close to zero, $\xi_{1}$ will still be important for relatively large .

Remark 1.5 Following the analysis in BRW, the results are derived under the assumption that is fixed as $T\rightarrow\infty$ . However, it is easy to show that the results remain similar if increases with the sample size , but at a slower pace, such that $q/T\rightarrow0$ , as $q,T\rightarrow\infty$ . Under this assumption, it follows easily under the null hypothesis that $\frac{T} {q}\left( \hat{\beta}_{q}-0\right) \Rightarrow\sqrt{\frac{\sigma_{11} }{\sigma_{22}}}\xi_{1}$ . Under the alternative hypothesis, $\frac{T} {\eta\left( \rho,q\right) }\left( \hat{\beta}_{q}-\beta_{q}\right) =\frac{T}{q}\left( \frac{\hat{\beta}_{q}}{q}-\frac{\beta_{q}}{q}\right) +o_{p}\left( 1\right) \Rightarrow\beta\xi_{2}$ , where the first term in (6) now disappears asymptotically. As discussed in the previous remark, however, the first term in (6) will still be important for relatively large , provided $\beta$ is small; this can be achieved also for asymptotically large by treating $\beta$ as small in a local sense. All the results in this paper therefore hold also under the general assumption that grows with the sample size but at a slower pace. As shown in Hjalmarsson (2007), asymptotic results derived under this assumption seem to provide good approximations of the finite sample properties of $\hat{\beta }_{q}$ for forecasting horizons spanning upwards of to percent of the sample size. For completeness, however, Appendix B presents the results for the case where is asymptotically large relative to , in a manner such that $q/T=\lambda\in\left( 0,1\right)$ , as $T\rightarrow\infty$ ; i.e. when grows at the same pace as the sample size.

3.2 Finite sample adjustments

In the analysis of BRW, it follows that under the null hypothesis, $\hat {\beta}_{q}\sim\nu\left( \rho,q\right) \hat{\beta}_{1}$ (see equation 6 in BRW), rather than $\hat{\beta}_{q}\sim q\hat{\beta}_{1}$ , as found here, where $\nu\left( \rho,q\right)$ is defined in Theorem 1.⁵ However, under the current assumption of $\rho=1+c/T$ , it follows that $\nu\left( \rho,q\right) =q+O\left( T^{-1}\right)$ . Thus, for the local-to-unity specification of $\rho$ that is used here, $\nu\left( \rho,q\right)$ and are asymptotically indistinguishable, and replacing by $\nu\left( \rho,q\right)$ does not affect the asymptotic arguments but merely provides a finite sample adjustment. As the analysis of BRW implies, along with simulation results that are not reported here, the rate of growth of $\hat{\beta}_{q}$ under the null hypothesis seems to correspond best to $\nu\left( \rho,q\right)$ , rather than , in finite samples.

Likewise, in Part 2 of Theorem 1, the factor in front of $\xi _{1}$ can be replaced by $\nu\left( \rho,q\right)$ , since this multiplier arises in an identical manner to the one in Part 1. That is, under the alternative hypothesis, one can write,

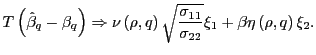
$\displaystyle T\left( \hat{\beta}_{q}-\beta_{q}\right) \Rightarrow\nu\left( \rho,q\right) \sqrt{\frac{\sigma_{11}}{\sigma_{22}}}\xi_{1}+\beta\eta\left( \rho,q\right) \xi_{2}.$

(10)

In the analysis in the next section, I use these finite sample adjusted results. This does not qualitatively change any of the results, and for $\rho=1$ it holds exactly that $q=\nu\left( \rho,q\right)$ .

4 The relationship between the long-run and the short-run

The results in the previous section provide the necessary building blocks for understanding the properties of, and relationship between, the long- and short-run estimators both under the null hypothesis and under the alternative of predictability. In this section, I consider the implications of these results through an informal analysis. For ease of notation, it is assumed that $\sigma_{11}=\sigma_{22}=1$ .

Under both the null and the alternative, the short-run estimator satisfies, $T\left( \hat{\beta}_{1}-\beta_{1}\right) \Rightarrow\xi_{1}$ , and one can write informally,

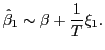$\displaystyle \hat{\beta}_{1}\sim\beta+\frac{1}{T}\xi_{1}.$

(11)

Similarly, under the null with $\beta=0$ , the long-run estimator satisfies

$\displaystyle \hat{\beta}_{q}\sim\nu\left( \rho,q\right) \frac{1}{T}\xi_{1}=\nu\left( \rho,q\right) \hat{\beta}_{1}.$

(12)

Thus, as noted above, under the null-hypothesis, $\hat{\beta}_{1}$ and $\hat{\beta}_{q}$ are perfectly asymptotically correlated.

Under the alternative of predictability,

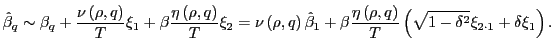
$\displaystyle \hat{\beta}_{q}\sim\beta_{q}+\frac{\nu\left( \rho,q\right) }{T}\xi_{1} +\beta\frac{\eta\left( \rho,q\right) }{T}\xi_{2}=\nu\left( \rho,q\right) \hat{\beta}_{1}+\beta\frac{\eta\left( \rho,q\right) }{T}\left( \sqrt{1-\delta^{2}}\xi_{2\cdot1}+\delta\xi_{1}\right) .$

(13)

The distribution of $\hat{\beta}_{q}$ is now a function of $\hat{\beta}_{1}$ , as well as an additional term. Note, however, that given $\hat{\beta}_{1}$ , the random variable $\xi_{1}$ is fixed, and the only independent information in $\hat{\beta}_{q}$ , given $\hat{\beta}_{1}$ , derives from the $\xi_{2\cdot 1}$ variable.

To better understand the properties of $\hat{\beta}_{q}$ under the alternative hypothesis, it is useful to consider the two special cases of $\delta=0$ and $\delta$ close to . The case of $\delta$ close to will be symmetrical to that of $\delta$ close to , but the latter is much more common in stock return applications. To more easily understand the variation in $\hat{\beta }_{q}$ , Figure 1 shows the density plots for $\xi_{1}$ , for different values of $\delta$ , and $\xi_{2}$ for the case of $\left( \rho=1\right)$ ; the density of $\xi_{2\cdot1}$ is identical to that of $\xi_{2}$ .

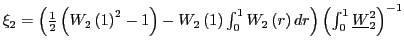As is seen in Figure 1, $\xi_{2}$ , and hence $\xi_{2\cdot1}$ , is almost always negative, a fact which will be used in the discussion below. To see this analytically, consider the case when and note that one can then write $\xi_{2}=\left( \frac{1}{2}\left( W_{2}\left( 1\right) ^{2}-1\right) -W_{2}\left( 1\right) \int_{0}^{1}W_{2}\left( r\right) dr\right) \left( \int_{0}^{1}\underline{W}_{2}^{2}\right) ^{-1}$ . Since $W_{2}\left( 1\right) ^{2}$ is distributed as a $\chi_{1}^{2}$ variable, there is an approximately two-thirds probability that the first term in the numerator will be negative. The second term will also tend to be negative, since the correlation between $W_{2}\left( 1\right)$ and $W_{2}\left( r\right)$ is positive. Further, when $W_{2}\left( 1\right) ^{2}$ is large, the denominator will also be large, skewing the distribution further to the left. The ratio will therefore be negative most of the time and have a negative mean. A similar argument can be made for $c\neq0$ .

4.1 The case of $\delta=0$

When $\delta=0$ ,

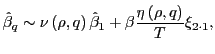
$\displaystyle \hat{\beta}_{q}\sim\nu\left( \rho,q\right) \hat{\beta}_{1}+\beta\frac {\eta\left( \rho,q\right) }{T}\xi_{2\cdot1},$

(14)

where the second term is stochastically independent of $\hat{\beta}_{1}$ . Since $E\left[ \xi_{2\cdot1}\right] <0$ , as is apparent from Figure 1 and the discussion above, $\hat{\beta}_{q}$ will tend to be below the curve $\hat{\beta}_{1}\nu\left( \rho,q\right)$ ; the 5th, 50th and 95th percentile of $\xi_{2\cdot1}$ , for , are given by , , and , respectively. To further understand the relationship between $\hat{\beta}_{1}$ and $\hat{\beta}_{q}$ in this case, consider a simple example. Suppose , , and $\hat{\beta}_{1}=0.015$ , which is a typical estimate of the short-run slope parameter in a regression with monthly standardized data such that $\sigma_{11}=\sigma_{22}=1$ (e.g. Campbell and Yogo, 2006). If the true value of $\beta$ is equal to zero, then asymptotically, $\hat{\beta}_{q}=\nu\left( \rho,q\right) \hat{\beta} _{1}=0.75$ . On the other hand, if $\beta=0.015$ , so that the short-run estimate is equal to the true value, then conditional on $\hat{\beta}_{1}$ , the 5th, 50th and 95th percentiles of $\hat{\beta}_{q}$ are equal to , , and , respectively, based on equation (14) and the percentiles of $\xi_{2\cdot1}$ .

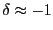
4.2 The case of $\delta\approx-1$

As $\delta\downarrow-1,$

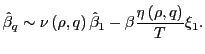
$\displaystyle \hat{\beta}_{q}\sim\nu\left( \rho,q\right) \hat{\beta}_{1}-\beta\frac {\eta\left( \rho,q\right) }{T}\xi_{1}.$

(15)

For $\delta$ close to minus one, $\xi_{1}$ is almost always positive, and $\hat{\beta}_{q}$ will tend to be smaller than $\nu\left( \rho,q\right) \hat{\beta}_{1}$ . Note also, that once $\hat{\beta}_{1}$ is determined, there is no additional variance left in the estimator $\hat{\beta}_{q}$ . That is, since $\hat{\beta}_{1}\sim\beta+\xi_{1}/T$ , for a given $\hat{\beta}_{1}$ and $\beta$ , $\xi_{1}$ is pinned down, and hence $\hat{\beta}_{q}$ as well.

Consider a similar thought experiment to that above. Again, suppose , , and $\hat{\beta}_{1}=0.015$ . If $\beta=0$ , then $\hat{\beta }_{1}=\xi_{1}/T$ , which implies that $\xi_{1}=7.5$ and $\hat{\beta}_{q} =q\hat{\beta}_{1}=0.75.$ Now, if $\beta=0.01$ , then $\hat{\beta}_{1}=\beta +\xi_{1}/T$ implies that $\xi_{1}=2.5$ , and $\hat{\beta}_{q}=0.689$ . If $\beta=0.015$ , then $\xi_{1}=0$ , and $\hat{\beta}_{q}=0.75.$ To the extent that $\beta$ is greater than or equal to zero, a large negative correlation $\delta\,$ severely limits the range of probable values that $\hat{\beta}_{q}$ can attain once $\hat{\beta}_{1}$ is fixed. (The 5th, 50th and 95th percentile of $\xi_{1}$ for $\delta=-0.99$ and , are given by , , and , respectively.)

4.3 Implied long-horizon estimates

Thus, when the predictor is exogenous, so that $\delta=0$ , somewhat substantial deviations in $\hat{\beta}_{q}$ from that predicted under the null are possible and to some extent expected. When the regressors are highly endogenous, and $\delta$ is close to minus one, the range of possibilities also under the alternative is more restricted and large deviations from that predicted under the null are not likely.⁶

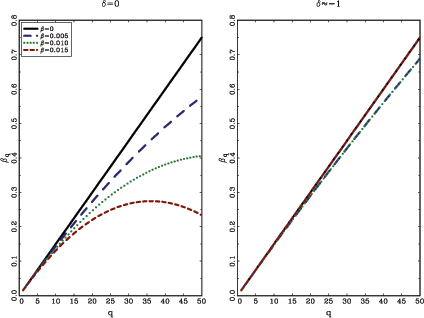
Figure 2 further illustrates this last point. Using equations (14) and (15), it plots potential outcomes of $\hat{\beta}_{q}$ , given $\hat{\beta}_{1}=0.015$ , for four different values of the true $\beta =0,0.005,0.010,0.015$ . The same parameters as in the examples above are used, with and . For $\delta\approx-1$ , once $\hat{\beta} _{1}$ and $\beta$ are fixed, the outcome of $\hat{\beta}_{q}$ is fully determined and there is thus no range of possibilities. For $\delta=0$ , there is independent variation left in $\hat{\beta}_{q}$ , given $\hat{\beta}_{1}$ and $\beta$ , in the form of $\xi_{2\cdot1}$ . The graphs for $\delta=0$ show the lower bound of $\hat{\beta}_{q}$ , based on the 5th percentile of $\xi_{2\cdot1}$ . The upper bound, based on the 95th percentile of $\xi _{2\cdot1}$ is virtually identical to $\nu\left( \rho,q\right) \hat{\beta }_{1}$ , since the 95th percentile of $\xi_{2\cdot1}$ is almost equal to zero.

The graphs clearly demonstrate the limited range of plausible outcomes for $\hat{\beta}_{q}$ given a typical one-period estimate of $\hat{\beta}_{1}$ , when the regressor is highly endogenous. Indeed, when the estimate $\hat {\beta}_{1}$ is in fact identical to the true $\beta$ , the outcome is observationally equivalent to that under the null hypothesis. When the predictor is exogenous, the range of outcomes is obviously much larger, and there is a fair chance of detecting patterns that deviate substantially from those expected under the null.

In their empirical analysis, BRW show that the coefficients for the dividend-price ratio, which is highly endogenous, are nearly linear in the forecasting horizon whereas those for the short interest rate, which is nearly exogenous, grow at a much slower pace. In light of Figure 2, these findings are suggestive of predictive ability in the short interest rate, but can say little or nothing regarding the predictive ability of the dividend-price ratio.⁷

5 Summary and conclusion

To sum up, under the null hypothesis, the long-run estimator is asymptotically completely determined by the one-period estimate and the persistence in the regressor. Under the alternative hypothesis, the degree to which the long-run estimates can vary independently of the one period ones is determined by the degree of endogeneity in the regressors. Nearly exogenous predictors, such as the short interest rate, allow for more independent variation than highly endogenous predictors such as the earnings-price ratio. Unfortunately, long-run estimates therefore provide additional information in cases where short-run inference is relatively straightforward but adds little in the case of endogenous regressors where short-run inference is fraught with difficulties (i.e. Stambaugh, 1999, and Campbell and Yogo, 2006).

Finally, it is worth pointing out, that the asymptotic framework used in this paper delivers an asymptotically degenerate distribution of $\hat{\beta}_{q}$ given $\hat{\beta}_{1}$ , under the null hypothesis. This prevents the construction of formal, and asymptotically meaningful, tests on the joint distribution of $\hat{\beta}_{1}$ and $\hat{\beta}_{q}$ under the null. BRW devise a joint test of $\beta_{1}=\beta_{2}=...=\beta_{q}=0$ under the assumption of a fixed $\rho$ strictly less than one. However, under these assumptions, the standard asymptotic distribution of the test is not likely to be well satisfied due to the standard complications in inference with endogenous and persistent variables. Monte Carlo simulations not reported in this paper confirm that for a large negative $\delta$ , the BRW test will tend to severely over reject. It is also interesting to note that the Wald statistic of BRW is scaled by $\left( 1-\rho\right) ^{-1}$ , which diverges to infinity as $\rho\rightarrow1$ . The degenerate case encountered in the current asymptotics thus follows as a limiting case in their analysis. The construction of an asymptotically valid and correctly sized joint test of $\beta_{1}$ and $\beta_{q}$ for $\rho$ close to unity is thus left unresolved.

Appendix A Proof of Theorem 1

Proof. For ease of notation the case with no intercept is treated. The results generalize immediately to regressions with fitted intercepts by replacing all variables by their demeaned versions. Part 1 is proved in Hjalmarsson (2007), but is repeated here for completeness.

1. Under the null hypothesis,

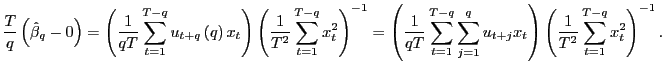
$\displaystyle \frac{T}{q}\left( \hat{\beta}_{q}-0\right) =\left( \frac{1}{qT}\sum _{t=1}^{T-q}u_{t+q}\left( q\right) x_{t}\right) \left( \frac{1}{T^{2}} \sum_{t=1}^{T-q}x_{t}^{2}\right) ^{-1}=\left( \frac{1}{qT}\sum_{t=1} ^{T-q}\sum_{j=1}^{q}u_{t+j}x_{t}\right) \left( \frac{1}{T^{2}}\sum _{t=1}^{T-q}x_{t}^{2}\right) ^{-1}.$

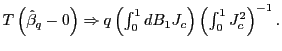
By standard arguments, $\frac{1}{qT}\sum_{t=1}^{T-q}\sum_{j=1}^{q}u_{t+j} x_{t}=\frac{1}{qT}\sum_{t=1}^{T-q}\left( u_{t+1}x_{t}+...+u_{t+q} x_{t}\right) \Rightarrow\int_{0}^{1}dB_{1}J_{c},$ as $T\rightarrow\infty$ , since for any , $\frac{1}{T}\sum_{t=1}^{T}u_{t+h}x_{t}\Rightarrow\int _{0}^{1}dB_{1}J_{c}$ . Therefore, $T\left( \hat{\beta}_{q}-0\right) \Rightarrow q\left( \int_{0}^{1}dB_{1}J_{c}\right) \left( \int_{0}^{1} J_{c}^{2}\right) ^{-1}.$

2. By summing up on both sides in equation (2),

	$\displaystyle r_{t+q}\left( q\right) =\beta\left( x_{t}+x_{t+1}+...+x_{t+q-1}\right) +u_{t+q}\left( q\right)$
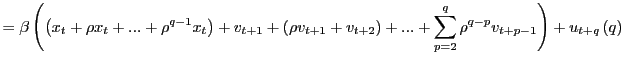
	$\displaystyle =\beta\left( \left( x_{t}+\rho x_{t}+...+\rho^{q-1}x_{t}\right) +v_{t+1}+\left( \rho v_{t+1}+v_{t+2}\right) +...+\sum_{p=2}^{q}\rho ^{q-p}v_{t+p-1}\right) +u_{t+q}\left( q\right)$
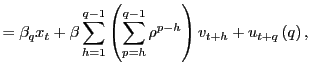
	$\displaystyle =\beta_{q}x_{t}+\beta\sum_{h=1}^{q-1}\left( \sum_{p=h}^{q-1}\rho ^{p-h}\right) v_{t+h}+u_{t+q}\left( q\right) ,$

where $\beta_{q}=\beta\left( 1+\rho+...+\rho^{q-1}\right) =\beta\nu\left( \rho,q\right)$ . Thus,

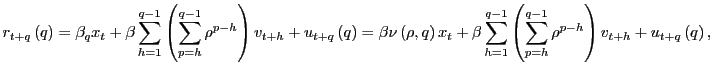
$\displaystyle r_{t+q}\left( q\right) =\beta_{q}x_{t}+\beta\sum_{h=1}^{q-1}\left( \sum_{p=h}^{q-1}\rho^{p-h}\right) v_{t+h}+u_{t+q}\left( q\right) =\beta \nu\left( \rho,q\right) x_{t}+\beta\sum_{h=1}^{q-1}\left( \sum_{p=h} ^{q-1}\rho^{p-h}\right) v_{t+h}+u_{t+q}\left( q\right) ,$

and

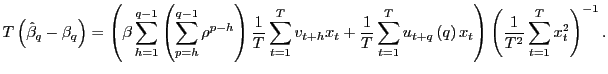
$\displaystyle T\left( \hat{\beta}_{q}-\beta_{q}\right) =\left( \beta\sum_{h=1} ^{q-1}\left( \sum_{p=h}^{q-1}\rho^{p-h}\right) \frac{1}{T}\sum_{t=1} ^{T}v_{t+h}x_{t}+\frac{1}{T}\sum_{t=1}^{T}u_{t+q}\left( q\right) x_{t}\right) \left( \frac{1}{T^{2}}\sum_{t=1}^{T}x_{t}^{2}\right) ^{-1}.$

Observe that $\frac{1}{T}\sum_{t=1}^{T}v_{t+h}x_{t}\Rightarrow\int_{0} ^{1}dB_{2}J_{c}$ for all . Let $\eta\left( \rho,q\right) =\sum _{h=1}^{q-1}\sum_{p=h}^{q-1}\rho^{p-h}$ and it follows that, as $T\rightarrow \infty$ , $\sum_{h=1}^{q-1}\left( \sum_{p=h}^{q-1}\rho^{p-h}\right) \frac {1}{T}\sum_{t=1}^{T}v_{t+h}x_{t}\Rightarrow\eta\left( \rho,q\right) \int _{0}^{1}dB_{2}J_{c}$ . By the results in Part 1., $\frac{1}{T}\sum_{t=1} ^{T}u_{t+q}\left( q\right) x_{t}\Rightarrow q\int_{0}^{1}dB_{1}J_{c}$ , as $T\rightarrow\infty$ , and the desired result follows. Note that,

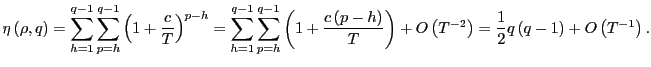
$\displaystyle \eta\left( \rho,q\right) =\sum_{h=1}^{q-1}\sum_{p=h}^{q-1}\left( 1+\frac {c}{T}\right) ^{p-h}=\sum_{h=1}^{q-1}\sum_{p=h}^{q-1}\left( 1+\frac{c\left( p-h\right) }{T}\right) +O\left( T^{-2}\right) =\frac{1}{2}q\left( q-1\right) +O\left( T^{-1}\right) .$

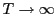
Appendix B Results for the case when $q/T=\lambda\in\left( 0,1\right)$ as $T\rightarrow\infty$

Some of the literature on long-horizon regressions has analyzed the case where is asymptotically large relative to , such that $q/T=\lambda\in\left( 0,1\right)$ , as $T\rightarrow\infty$ . In the context of this study, such asymptotics are less useful because the long-run OLS estimator will not converge to a properly defined long-run coefficient. Since the current focus is on the distribution of the long-run estimator conditional on the short-run estimator, it makes more sense to consider the case when the long-run estimator does converge. Nevertheless, it is still interesting to see if any of the results derived in the main text continue to hold under this assumption.

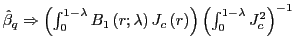Again treating the case without an intercept, Valkanov (2003) shows that under the null hypothesis, with $q/T=\lambda$ as $T\rightarrow\infty,$ $\hat{\beta }_{q}\Rightarrow\left( \int_{0}^{1-\lambda}B_{1}\left( r;\lambda\right) J_{c}\left( r\right) \right) \left( \int_{0}^{1-\lambda}J_{c}^{2}\right) ^{-1}$ , where $B_{1}\left( r;\lambda\right) \equiv B_{1}\left( r+\lambda\right) -B_{1}\left( r\right)$ . 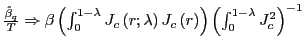Under the alternative, $\frac{\hat{\beta}_{q}}{T}\Rightarrow\beta\left( \int_{0}^{1-\lambda} J_{c}\left( r;\lambda\right) J_{c}\left( r\right) \right) \left( \int_{0}^{1-\lambda}J_{c}^{2}\right) ^{-1}$ , where $J_{c}\left( r;\lambda\right) \equiv\int_{r}^{r+\lambda}J_{c}\left( r\right) .$ Thus, $\hat{\beta}_{q}$ no longer converges to a constant and it is therefore not surprising that the strong connection between the asymptotic distributions for the short-run and long-run estimators is no longer apparent. Indeed, given the highly non-standard limiting distributions, it is difficult to get a grasp of the properties of $\hat{\beta}_{q}$ . A very rough approximation, however, can provide some guidelines.

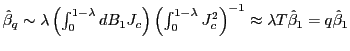Note that $B_{1}\left( r+\lambda\right) -B_{1}\left( r\right) =\int _{r}^{r+\lambda}dB_{1}\left( s\right) \approx\lambda dB_{1}\left( r\right)$ and $\int_{r}^{r+\lambda}J_{c}\left( r\right) \approx\lambda J_{c}\left( r\right)$ . Under the null hypothesis, it follows that $\hat{\beta}_{q} \sim\lambda\left( \int_{0}^{1-\lambda}dB_{1}J_{c}\right) \left( \int _{0}^{1-\lambda}J_{c}^{2}\right) ^{-1}\approx\lambda T\hat{\beta}_{1} =q\hat{\beta}_{1}$ , and under the alternative hypothesis, $\hat{\beta}_{q}\sim T\lambda\beta=q\beta$ . Thus, also for $q/T=\lambda$ , it would appear that $\hat{\beta}_{q}$ will grow with the forecasting horizon. Under the null hypothesis, there is still some indication of the relationship between $\hat{\beta}_{q}$ and $\hat{\beta}_{1}$ , but under the alternative hypothesis the more subtle connections between the short-run and the long-run estimator are no longer evident, as might be expected given the lack of a consistent long-run estimator.

Appendix C Asymptotic properties of R²

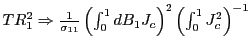Let $R_{q}^{2}$ be the coefficient of determination from the period regression in equation (1). Using the same arguments as in the proof of Theorem 1, it follows that under the null hypothesis, $TR_{1} ^{2}\Rightarrow\frac{1}{\sigma_{11}}\left( \int_{0}^{1}dB_{1}J_{c}\right) ^{2}\left( \int_{0}^{1}J_{c}^{2}\right) ^{-1}$ . Similarly, 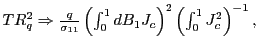$TR_{q} ^{2}\Rightarrow\frac{q}{\sigma_{11}}\left( \int_{0}^{1}dB_{1}J_{c}\right) ^{2}\left( \int_{0}^{1}J_{c}^{2}\right) ^{-1},$ using the result that $\frac{1}{qT}\sum_{t=1}^{T}u_{t+q}^{2}\left( q\right) \rightarrow_{p} \sigma_{11}$ , which is derived in Hjalmarsson (2007). Thus, asymptotically, under the null hypothesis, $\left. R_{q}^{2}\right\vert R_{1}^{2}=qR_{1}^{2}$ .

Because $x_{t}$ is a near-integrated regressor, it follows easily that $R_{q}^{2}\rightarrow_{p}1$ as $T\rightarrow\infty$ . This is not very useful from a practical perspective and it is more interesting to analyze the properties under a local alternative, $\beta=b/\sqrt{T}$ . Under this alternative, using similar arguments as before, $R_{1}^{2}\Rightarrow 1-\frac{\sigma_{11}}{\sigma_{11}+b^{2}\left( \int_{0}^{1}J_{c}^{2}\right) },$ and $R_{q}^{2}\Rightarrow1-\frac{\sigma_{11}}{\sigma_{11}+qb^{2}\left( \int_{0}^{1}J_{c}^{2}\right) }.$ Standardizing so that $\sigma_{11}=1$ , and using the approximation that $\left( 1+x\right) ^{-1}\approx1-x$ , it follows that $R_{1}^{2}\approx b^{2}\left( \int_{0}^{1}J_{c}^{2}\right)$ and $R_{q}^{2}\approx qb^{2}\left( \int_{0}^{1}J_{c}^{2}\right) \approx qR_{1}^{2}$ .

References

Boudoukh J., M. Richardson, and R.F. Whitelaw, 2006. The myth of long-horizon predictability, Review of Financial Studies, forthcoming.

Campbell, J.Y., 2001. Why long horizons? A study of power against persistent alternatives, Journal of Empirical Finance 8, 459-491.

Campbell, J.Y., and R. Shiller, 1988. Stock prices, earnings, and expected dividends, Journal of Finance 43, 661-676.

Campbell, J.Y., and M. Yogo, 2006. Efficient Tests of Stock Return Predictability, Journal of Financial Economics 81, 27-60.

Cavanagh, C., G. Elliot, and J. Stock, 1995. Inference in models with nearly integrated regressors, Econometric Theory 11, 1131-1147.

Cochrane, J., 2001. Asset Pricing, Princeton, Princeton University Press.

Fama, E.F., and K.R. French, 1988. Dividend yields and expected stock returns, Journal of Financial Economics 22, 3-25.

Goetzman W.N., and P. Jorion, 1993. Testing the Predictive Power of Dividend Yields, Journal of Finance 48, 663-679.

Hansen, L.P., and R.J. Hodrick, 1980. Forward Exchange Rates as Optimal Predictors of Future Spot Rates: An Econometric Analysis, Journal of Political Economy 88, 829-853.

Hjalmarsson, E., 2007. Inference in Long-Horizon Regressions, Working Paper, Federal Reserve Board.

Hodrick, R.J., 1992. Dividend Yields and Expected Stock Returns: Alternative Procedures for Inference and Measurement, Review of Financial Studies 5, 357-386.

Lanne, M., 2002. Testing the Predictability of Stock Returns, Review of Economics and Statistics 84, 407-415.

Kirby, C., 1997. Measuring the Predictable Variation in Stock and Bond Returns, Review of Financial Studies 10, 579-630.

Nelson, C.R., and M.J. Kim, 1993. Predictable Stock Returns: The Role of Small Sample Bias, Journal of Finance 48, 641-661.

Phillips, P.C.B, 1987. Towards a Unified Asymptotic Theory of Autoregression, Biometrika 74, 535-547.

Phillips, P.C.B, 1988. Regression Theory for Near-Integrated Time Series, Econometrica 56, 1021-1043.

Richardson, M., 1993. Temporary Components of Stock Prices: A Skeptic's View, Journal of Business and Economics Statistics 11, 199-207.

Richardson, M., and T. Smith, 1991. Tests of Financial Models in the Presence of Overlapping Observations, Review of Financial Studies 4, 227-254.

Richardson, M., and T. Smith, 1994. A Unified Approach to Testing for Serial Correlation in Stock Returns, Journal of Business 67, 371-399.

Richardson, M., and J.H. Stock, 1989. Drawing Inferences from Statistics Based on Multiyear Asset Returns, Journal of Financial Economics 25, 323-348.

Stambaugh, R., 1999. Predictive regressions, Journal of Financial Economics 54, 375-421.

Torous, W., R. Valkanov, and S. Yan, 2004. On Predicting Stock Returns with Nearly Integrated Explanatory Variables, Journal of Business 77, 937-966.

Valkanov, R., 2003. Long-horizon regressions: theoretical results and applications, Journal of Financial Economics 68, 201-232.

Figure 1: Density plots of $\xi_{1}$ and $\xi_{2}$ for c = 0.

The graphs show the densities for the Brownian functionals $\xi_{1}$ , for different values of $\delta$ , and $\xi_{2}$ , obtained by kernel estimation of simulated data using repetitions and a sample size of in each repetition. The shape of the density of $\xi_{2\cdot1}$ is identical to that of $\xi_{2}.$

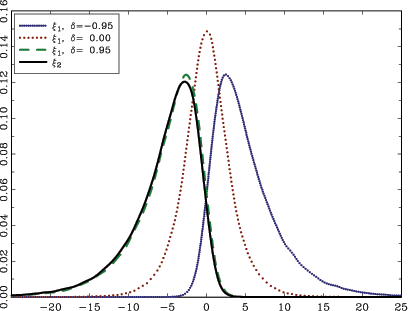
Figure 2: Possible outcomes of $\hat{\beta}_{q}$ given $\hat{\beta}_{1}$ and $\beta$ .

The graphs show potential outcomes of $\hat{\beta}_{q}$ , given that $\hat{\beta}_{1}=0.015$ , for $\beta=0,0.005,0.01,0.015$ . The left hand side panel shows the case for exogenous regressors with $\delta=0$ and the right hand side shows the case with highly endogenous regressors. The plots are formed using equations (14) and (15), letting and . For $\delta\approx-1$ , once $\hat{\beta}_{1}$ and $\beta$ are fixed, the outcome of $\hat{\beta}_{q}$ is fully determined and there is thus no range of possibilities. The graphs for $\delta=0$ show the lower bound of $\hat{\beta }_{q}$ , based on the 5th percentile of $\xi_{2\cdot1}$ . The upper bound, based on the 95th percentile of $\xi_{2\cdot1}$ , is virtually identical to $\nu\left( \rho,q\right) \hat{\beta}_{1}$ ; i.e. the line for $\beta=0$ .

Footnotes

* This paper has benefitted from comments by Lennart Hjalmarsson, Randi Hjalmarsson and Jonathan Wright, as well as an anonymous referee. Tel.: +1-202-452-2426; fax: +1-202-263-4850; email: erik.hjalmarsson@frb.gov. The views in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text

1. Earlier studies discussing other inferential issues in long-horizon regressions include Hansen and Hodrick (1980), Richardson and Stock (1989), Richardson and Smith (1991, 1994), Hodrick (1992), Goetzman and Jorion (1993), Nelson and Kim (1993), Richardson (1993), Kirby (1997), and Valkanov (2003). Return to text

2. A predictive regressor is generally referred to as endogenous if the innovations to the returns are contemporaneously correlated with the innovations to the regressor. When the regressor is strictly stationary, such endogeneity has no impact on the properties of the estimator, but when the regressor is persistent in some manner, the properties of the estimator will be affected (e.g. Stambaugh, 1999). Return to text

3. The contemporaneous correlation between the innovations to the returns and the innovations to the regressor determines the endogeneity of a predictive regressor (see previous footnote). Campbell and Yogo (2006) show that for valuation ratios, such as the dividend-price ratio, this correlation is large and often greater than in absolute magnitude. For interest rate variables, however, the correlation is close to zero and, from the perspective of a predictive regression, these variables are thus nearly exogenous. Return to text

4. There are two primary reasons why the analysis of the long-run regression in equation (1) is of interest under the assumption that the true model is given by the short-run equation (2). First, there is the long standing popular belief that predictability is more evident in the long run, and that there may therefore be power gains to analyzing the long-horizon regression, even if the short-run specification given by equation (2) is correct; for instance, Campbell (2001) analyzes the power of long-run tests under the same specification that is used in this paper. Alternatively, since there appears to be no other data generating processes that are widely used for modeling return predictability, in the short- or long-run, the results derived under the data generating process given by equations (2) and (3) can be viewed as a benchmark against which to compare results from other specifications. Return to text

5. I use the ' $\sim$ ' sign here because in the framework of BRW, the asymptotic distribution of $\hat{\beta}_{q}$ is not entirely pinned down by $\hat{\beta }_{1}$ . Return to text

6. Apart from increasing slope coefficients, increasing $R^{2}s$ have also been used as an argument in favor of long-run predictability. In Appendix C, I first replicate BRW's finding that $R^{2}$ increases with the forecast horizon under the null hypothesis. In addition, I show that the asymptotic properties of $R^{2}$ under the alternative hypothesis are not a function of the degree of endogeneity of the regressor and that $R^{2}$ still increases almost linearly with the forecasting horizon. Thus, unlike for $\hat{\beta}_{q}$ , there is no systematic difference in the asymptotic properties of $R^{2}$ for exogenous and endogenous regressors under the alternative hypothesis. Return to text

7. The results in this paper are all based on the assumption that the regressor follows a near unit-root process. For a fixed autoregressive root $\rho$ strictly less than unity, the effects arising from endogeneity would not appear in the asymptotic analysis, although one could perhaps obtain some similar results using the finite sample bias derived in Stambaugh (1999). In practice, of course, the near unit-root construction is designed to asymptotically capture the finite sample bias that arises from highly persistent and endogenous regressors, which are not necessarily unit-root processes. For regressors with very low persistence, i.e. $\rho<<1$ , there will be no effects from endogeneity and there should thus be no systematic difference between endogenous and exogenous regressors in the behavior of either the short-run or the long-run estimators. However, most relevant predictors of stock returns tend to be highly persistent. Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text