
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 933, June 2008 --- Screen Reader
Version*
Predicting Global Stock Returns*
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
I test for stock return predictability in the largest and most comprehensive data set analyzed so far, using four common forecasting variables: the dividend- and earnings-price ratios, the short interest rate, and the term spread. The data contain over 20,000 monthly observations from 40 international markets, including 24 developed and 16 emerging economies. In addition, I develop new methods for predictive regressions with panel data. Inference based on the standard fixed effects estimator is shown to suffer from severe size distortions in the typical stock return regression, and an alternative robust estimator is proposed. The empirical results indicate that the short interest rate and the term spread are fairly robust predictors of stock returns in developed markets. In contrast, no strong or consistent evidence of predictability is found when considering the earnings- and dividend-price ratios as predictors.
Keywords: Cross-sectional dependence, panel data, pooled regression, predictive regression, stock return predictability
JEL classification: C22, C23, G12, G15
1 Introduction
Our empirical knowledge regarding the predictability of stock returns by variables such as the dividend-price ratio has been subject to constant updating over time. Early work by Fama and French (1988, 1989) and Campbell and Shiller (1988) concluded that there is generally strong evidence of predictability. Recent studies that use more robust econometric methods, such as Campbell and Yogo (2006) and Lewellen (2004), still find evidence of predictability, but their results are much less conclusive than the earlier studies.
Despite the mixed evidence and uncertainty regarding stock return predictability, there have been surprisingly few attempts at furthering our understanding by using data other than that of the U.S. stock-market. Since the predictable component of stock returns must be small, if indeed one does exist, there seems to be little chance of reaching a decisive conclusion using U.S. data alone, which effectively provides only one time-series at the market level. There has, of course, been some analysis of predictability in international stock returns, but many of the results are based on relatively small data sets and non-robust econometric methods.1 In addition, most international results are based only on individual time-series regressions and very little analysis has been conducted with pooled panel data regressions. Yet, it is well known that pooling the data may lead to more powerful methods, which is particularly relevant when studying stock return predictability since any predictable component will always be small relative to the overall variance in the returns process.
The aim of this paper is twofold. First, by considering a large global data set, I provide the most comprehensive picture of stock return predictability to date. The data contain over 20,000 monthly observations from 40 countries, including markets in 24 developed economies.2 The longest data series is for the U.K. stock-market and dates back to 1836 while data for eight other markets date back to before 1935. Second, I develop and apply new results for pooled forecasting regressions, utilizing the panel structure of the data.
Since an international data set of stock returns and forecasting variables provides a panel, the theory part of this paper analyzes econometric inference in predictive regressions in a panel data setting, when the regressors are nearly persistent and endogenous.3 As is well known (Stambaugh (1999)), OLS inference in the corresponding time-series predictive regressions is generally biased and various bias and size correction procedures have been proposed.
In the panel case, it turns out that the pooled estimator is unbiased as long as no fixed effects are included. The intuition behind this is that when pooling the data, independent cross-sectional information dilutes the endogeneity effects that cause the Stambaugh bias in the time-series case. That is, the Stambaugh bias only arises when the predictors are both persistent and endogenous; by pooling the data, the endogeneity is, in a sense, removed, and hence also the bias. Furthermore, the standard pooled estimator has an asymptotically normal distribution and normal inference can therefore be performed.
The intuition just described for the standard pooled estimator
no longer holds when fixed effects are allowed for, and the
asymptotic properties of the pooled estimator with fixed effects
are very different from those of the pooled estimator with a common
intercept. The time-series demeaning of the data, which is implicit
in a fixed effects estimation, causes the fixed effects estimator
to suffer from a second order bias that invalidates inference from
standard test statistics. When demeaning each time-series in the
panel, information after time t is used to form the
time t regressor, and information before time
t is used to form the time t
returns. This induces a correlation between the lagged value of the
demeaned regressor and the error term in the forecasting equation,
which gives rise to the second order bias in the fixed effects
estimator. Thus, in contrast to the case with a common intercept,
the regressors no longer act as if they were exogenous. To correct
for this bias, I develop an estimator based on the idea of
recursive demeaning (e.g. Moon and Phillips (2000), and Sul et al.
(2005)). By using information only after time ![]() in
the demeaning of the returns and the non-demeaned regressor as an
instrument, the distortive effects arising from standard demeaning
are eliminated.
in
the demeaning of the returns and the non-demeaned regressor as an
instrument, the distortive effects arising from standard demeaning
are eliminated.
The overall conclusion from the theoretical results and the supporting Monte Carlo simulations is that, in the typical panel data case with fixed effects, persistent and endogenous regressors will cause standard inference to be biased. While this result is well established in the time-series case (e.g. Stambaugh (1999)), the results in this paper show that equal caution is required when working with panel data.
In the empirical analysis, I conduct time-series regressions for individual countries as well as pooled regressions. In both types of analyses, I estimate regressions for four of the most commonly used forecasting variables: the dividend- and earnings-price ratios, the short interest rate, and the term spread. In the pooled regressions, countries are either all grouped together in a global panel or split up into groups of developed and emerging markets.
The results indicate that the short interest rate and the term spread are both fairly robust predictors of (excess) stock returns in developed markets. The null of no predictability is clearly rejected in the pooled regressions for developed markets as well as in a number of individual time-series regressions. These results are generally in line with those found by Campbell and Yogo (2006) with U.S. data and with the limited international results of Ang and Bekaert (2007). In contrast to the interest rate variables, no strong or consistent evidence of predictability is found when considering the earnings- and dividend-price ratios as predictors. In particular, neither predictor yields any consistent predictive power for the developed markets and, as seen in plots of the regression coefficient over time, this is especially true for the dividend-price ratio.
The rest of the paper is organized as follows. Sections II and III describe the empirical model and derive the main asymptotic properties of the pooled estimators. The finite sample properties of the procedures developed in this paper are analyzed through Monte Carlo experiments in Section IV. The data are described in Section V and the empirical results, including out-of-sample exercises, are provided in Section VI. Section VII concludes and technical assumptions and proofs are found in the Appendix.
II Pooled Estimation in Predictive Regressions
II.A Model and Assumptions
Consider a panel model with dependent variables ![]() ,
, ![]() ,
, ![]() , and
the corresponding vector of regressors,
, and
the corresponding vector of regressors, ![]() , where
, where
![]() is an
is an ![]() vector. In this paper,
vector. In this paper, ![]() is the stock return in
country
is the stock return in
country ![]() , and
, and ![]() are the
corresponding predictor variables. The behavior of
are the
corresponding predictor variables. The behavior of ![]() and
and ![]() are modelled as
follows:
are modelled as
follows:
| (1) | ||
| (2) | ||
| (3) | ||
| (4) |
That is, stock returns ![]() are a function of the
past values of the predictor variables plus two factors
representing country specific
are a function of the
past values of the predictor variables plus two factors
representing country specific
![]() and global
and global
![]() innovations. In the
typical time-series predictive regression using, for instance,
aggregate U.S. data, these two error terms are generally not
distinguishable, and in terms of econometric inference, it makes no
difference whether the shocks are U.S. specific or global in some
sense. However, when pooling data from several countries, it
becomes important to control for whether innovations to returns are
due to country specific shocks or shocks that are common to all
countries in the sample. Intuitively, if one ignores the presence
of common factors in the error terms, the total amount of
(independent) variation in the pooled data is overstated, and the
econometric inference will be biased.
innovations. In the
typical time-series predictive regression using, for instance,
aggregate U.S. data, these two error terms are generally not
distinguishable, and in terms of econometric inference, it makes no
difference whether the shocks are U.S. specific or global in some
sense. However, when pooling data from several countries, it
becomes important to control for whether innovations to returns are
due to country specific shocks or shocks that are common to all
countries in the sample. Intuitively, if one ignores the presence
of common factors in the error terms, the total amount of
(independent) variation in the pooled data is overstated, and the
econometric inference will be biased.
The vector of predictor variables, ![]() , is
also assumed to be the sum of country specific
, is
also assumed to be the sum of country specific
![]() and global
and global
![]() terms. Both
terms. Both
![]() and
and ![]() follow
follow
![]() processes. More precisely,
the auto-regressive roots of both of these processes are
parameterized as being local-to-unity, such that
processes. More precisely,
the auto-regressive roots of both of these processes are
parameterized as being local-to-unity, such that
![]() and
and
![]() , where both
, where both ![]() and
and ![]() are
are ![]() matrices. This captures the near unit-root, or highly persistent,
behavior of many predictor variables, but is less restrictive than
a pure unit-root assumption. The near unit-root construction, where
the autoregressive root drifts closer to unity as the sample size
increases, is used as a tool to enable an asymptotic analysis where
the persistence in the data remains large relative to the sample
size, even when the sample size increases to infinity. That is, if
the auto-regressive roots are treated as fixed and strictly less
than unity, then as the sample size grows, the regressors will
behave as strictly stationary processes asymptotically, and the
standard first order asymptotic results will not provide a good
guide to the actual small sample properties of the model. If the
roots are exactly equal to unity, the usual unit-root asymptotics
apply to the model, but this is clearly a restrictive assumption
for most potential predictor variables. Instead, by using the near
unit-root construction, the effects from the high persistence in
the regressor will appear also in the asymptotic results, but
without imposing the strict assumption of a unit root.
matrices. This captures the near unit-root, or highly persistent,
behavior of many predictor variables, but is less restrictive than
a pure unit-root assumption. The near unit-root construction, where
the autoregressive root drifts closer to unity as the sample size
increases, is used as a tool to enable an asymptotic analysis where
the persistence in the data remains large relative to the sample
size, even when the sample size increases to infinity. That is, if
the auto-regressive roots are treated as fixed and strictly less
than unity, then as the sample size grows, the regressors will
behave as strictly stationary processes asymptotically, and the
standard first order asymptotic results will not provide a good
guide to the actual small sample properties of the model. If the
roots are exactly equal to unity, the usual unit-root asymptotics
apply to the model, but this is clearly a restrictive assumption
for most potential predictor variables. Instead, by using the near
unit-root construction, the effects from the high persistence in
the regressor will appear also in the asymptotic results, but
without imposing the strict assumption of a unit root.
Finally, the regressors ![]() can be
endogenous in the sense that
can be
endogenous in the sense that ![]() and
and
![]() are contemporaneously correlated;
are contemporaneously correlated;
![]() and
and ![]() may be
contemporaneously correlated as well, and can, in fact, be
identical. The model specification is completed in Appendix
A with some
additional formal assumptions. Unless otherwise noted, all
variables appearing in the asymptotic distributions derived below
are defined in Appendix A.
may be
contemporaneously correlated as well, and can, in fact, be
identical. The model specification is completed in Appendix
A with some
additional formal assumptions. Unless otherwise noted, all
variables appearing in the asymptotic distributions derived below
are defined in Appendix A.
II.B Motivations for Pooling
II.B.1 Practical and Econometric Considerations
The theoretical part of this paper analyzes the pooled
estimation of the slope coefficient in equation (1). That is, by
pooling data from several countries, an estimate of a joint slope
coefficient ![]() is obtained. If the individual
slope coefficients are all identical, such that
is obtained. If the individual
slope coefficients are all identical, such that
![]() for all
for all ![]() , the pooled estimator will converge to this common
parameter. In addition, the pooled estimator can either impose a
common intercept
, the pooled estimator will converge to this common
parameter. In addition, the pooled estimator can either impose a
common intercept ![]() , or allow for individual
intercepts, or fixed effects,
, or allow for individual
intercepts, or fixed effects,
![]() . When the restrictions
. When the restrictions
![]() , and potentially
, and potentially
![]() , hold for all
, hold for all ![]() , pooling the data should lead to more precise estimates
than time-series estimation of each individual
, pooling the data should lead to more precise estimates
than time-series estimation of each individual ![]() .
.
When the slope coefficients ![]() are not all
identical, pooled estimation may still be useful. In this case, the
pooled estimator will converge to a well-defined average slope
coefficient. The pooled estimate, and related tests, thus makes a
statement about the average predictive relationship in the
panel, which provides a useful tool for interpreting and
understanding the empirical results, especially if the individual
time-series regressions deliver mixed results. Furthermore, and as
importantly, the pooled estimate may in some respects provide at
least as good an estimate of
are not all
identical, pooled estimation may still be useful. In this case, the
pooled estimator will converge to a well-defined average slope
coefficient. The pooled estimate, and related tests, thus makes a
statement about the average predictive relationship in the
panel, which provides a useful tool for interpreting and
understanding the empirical results, especially if the individual
time-series regressions deliver mixed results. Furthermore, and as
importantly, the pooled estimate may in some respects provide at
least as good an estimate of ![]() for a given
for a given
![]() , by providing a possibly less noisy
estimate than the time-series one. That is, if the
, by providing a possibly less noisy
estimate than the time-series one. That is, if the
![]() are not identical, the pooled
estimator will generally not provide an unbiased estimate for a
given
are not identical, the pooled
estimator will generally not provide an unbiased estimate for a
given ![]() , but in a bias-variance trade-off
it may still dominate the time-series estimate of
, but in a bias-variance trade-off
it may still dominate the time-series estimate of ![]() . This bias-variance trade-off is illustrated by
out-of-sample forecasts at the end of this paper where it is shown
that the forecasts based on the pooled estimator often dominate
those based on the time-series estimates.
. This bias-variance trade-off is illustrated by
out-of-sample forecasts at the end of this paper where it is shown
that the forecasts based on the pooled estimator often dominate
those based on the time-series estimates.
II.B.2 Economic Rationale
Is it likely, from the perspective of economic theory, that the
![]() and
and
![]() are identical across
are identical across ![]() ? That is, can one justify pooling the data from an economic
perspective, and if so, should fixed effects be included?
? That is, can one justify pooling the data from an economic
perspective, and if so, should fixed effects be included?
Consider first the question of fixed effects. Under the null of
no predictability, such that
![]() for all
for all ![]() , the
restriction of
, the
restriction of
![]() for all
for all ![]() imposes the same expected excess return in all countries. Although
it is very difficult to obtain precise estimates of average
returns, detailed empirical studies such as Jorion and Goetzman
(1999) strongly suggest that the equity premium varies across
countries. In addition, if an international world CAPM applies,
identical
imposes the same expected excess return in all countries. Although
it is very difficult to obtain precise estimates of average
returns, detailed empirical studies such as Jorion and Goetzman
(1999) strongly suggest that the equity premium varies across
countries. In addition, if an international world CAPM applies,
identical
![]() in the absence of predictability
imply that the world CAPM beta for each country is identical. The
restriction of identical CAPM betas is strongly rejected in
previous studies such as Ferson and Harvey (1994), who report
international CAPM betas in the range from
in the absence of predictability
imply that the world CAPM beta for each country is identical. The
restriction of identical CAPM betas is strongly rejected in
previous studies such as Ferson and Harvey (1994), who report
international CAPM betas in the range from ![]() to
1.3, and Harvey (1995), who shows that the
world CAPM betas for some emerging markets are negative. Although
the world CAPM does not offer a complete model of stock returns, it
does capture a sizeable amount of the variation in international
stock returns (Ferson and Harvey, 1994). Model predictions that
strongly contradict it, such as identical CAPM betas for all
countries, should thus be seen as a warning sign of
misspecification. Therefore, given the importance of having a model
that is correctly specified under the null hypothesis, fixed
effects should generally be included.4
to
1.3, and Harvey (1995), who shows that the
world CAPM betas for some emerging markets are negative. Although
the world CAPM does not offer a complete model of stock returns, it
does capture a sizeable amount of the variation in international
stock returns (Ferson and Harvey, 1994). Model predictions that
strongly contradict it, such as identical CAPM betas for all
countries, should thus be seen as a warning sign of
misspecification. Therefore, given the importance of having a model
that is correctly specified under the null hypothesis, fixed
effects should generally be included.4
In order to understand the economic constraints that are imposed
by identical
![]() , one needs to analyze a model that
implies predictability in stock returns. Menzly et al. (2004)
explicitly analyze cross-sectional differences in time-series
return predictability. They use an external habit model similar to
Campbell and Cochrane (1999) and show that the dividend-price ratio
predicts excess stock returns. The slope coefficient in this
predictive regression varies across assets as a function of the
properties of the assets' cash-flow share of overall income; in an
international asset pricing framework, with integrated markets,
each country portfolio can be viewed as an individual asset, as in
the international CAPM. The model in Menzly et al. (2004) thus
implies that, in general, the slope coefficients
, one needs to analyze a model that
implies predictability in stock returns. Menzly et al. (2004)
explicitly analyze cross-sectional differences in time-series
return predictability. They use an external habit model similar to
Campbell and Cochrane (1999) and show that the dividend-price ratio
predicts excess stock returns. The slope coefficient in this
predictive regression varies across assets as a function of the
properties of the assets' cash-flow share of overall income; in an
international asset pricing framework, with integrated markets,
each country portfolio can be viewed as an individual asset, as in
the international CAPM. The model in Menzly et al. (2004) thus
implies that, in general, the slope coefficients ![]() in the predictive regression in equation (1) may not be
identical across
in the predictive regression in equation (1) may not be
identical across ![]() . However, the model says little
about how disperse the slope coefficients actually are in practice.
That is, even though it is unlikely that the
. However, the model says little
about how disperse the slope coefficients actually are in practice.
That is, even though it is unlikely that the
![]() are identical across
countries or assets, as is true for most parameters that may be
estimated in economics or finance, what is of primary importance
for the empirical scope of this paper is whether they are similar
enough that it may be beneficial from an econometric point of view
to treat them as equal.5 From this empirical perspective, the
implications of the Menzly et al. (2004) model are essentially
silent, and it is unlikely that other models of return
predictability would deliver any stronger practical
implications.
are identical across
countries or assets, as is true for most parameters that may be
estimated in economics or finance, what is of primary importance
for the empirical scope of this paper is whether they are similar
enough that it may be beneficial from an econometric point of view
to treat them as equal.5 From this empirical perspective, the
implications of the Menzly et al. (2004) model are essentially
silent, and it is unlikely that other models of return
predictability would deliver any stronger practical
implications.
The results in the current paper suggest that pooling the data,
and thus imposing a common slope coefficient, is in fact quite
often empirically justified in the sense that the null hypothesis
of a common slope coefficient can often not be rejected in formal
statistical tests and the forecasts based on the pooled estimates
often tend to outperform those based on the individual time-series
estimates in out-of-sample exercises. Thus, even though economic
theory does not generally predict that the
![]() are all identical, it cannot be
a priori rejected that they are similar enough for there to
be benefits from pooling the data, which ties back to the
discussion on the practical motivations in the section above.
are all identical, it cannot be
a priori rejected that they are similar enough for there to
be benefits from pooling the data, which ties back to the
discussion on the practical motivations in the section above.
In general, it is quite reasonable to conjecture that countries that share many common characteristics are more likely to have similar predictability patterns than those that do not. One of the most natural splits along these lines in international data is to distinguish between developed and emerging markets. Previous literature, such as Harvey (1995), also shows that emerging markets tend to have different return characteristics than developed markets, and different patterns of predictability. To the extent that stock markets in different countries are more likely to have similar predictability if they are priced globally in integrated financial markets, rather than locally in segregated markets, the group of developed markets is also likely to better satisfy this requirement. The empirical analysis separately analyzes developed and emerging market panels, and includes a test of slope homogeneity that shows that these two groups of countries appear more homogenous than all countries combined.
II.C Pooled Estimation
To understand the basic properties of pooled estimators of a
common slope coefficient ![]() in equation (1), it is
instructive to start with analyzing the case when there are no
common factors in the data. That is, let
in equation (1), it is
instructive to start with analyzing the case when there are no
common factors in the data. That is, let
![]() and
and
![]() , for all
, for all ![]() .
This assumption will be maintained throughout the remainder of
Section II and the
effects of common factors are analyzed in Section III. Unless
otherwise noted, it is assumed that the slope coefficients
.
This assumption will be maintained throughout the remainder of
Section II and the
effects of common factors are analyzed in Section III. Unless
otherwise noted, it is assumed that the slope coefficients
![]() are identical and equal to
are identical and equal to
![]() for all
for all ![]() .
.
II.C.1 The Standard Pooled Estimator without Fixed Effects
To estimate the parameter ![]() , consider first
the traditional pooled estimator when there are no individual
effects, i.e. when
, consider first
the traditional pooled estimator when there are no individual
effects, i.e. when
![]() for all
for all ![]() . Although the previous discussion strongly suggested the
use of individual intercepts in the international analysis
performed in the current paper, there may be other cases when a
common intercept can be justified. In addition, a comparison of the
pooled estimator with and without fixed effects highlights some
important differences and helps form an understanding of the
effects of pooling the data. The pooled estimator with a common
intercept is given by
. Although the previous discussion strongly suggested the
use of individual intercepts in the international analysis
performed in the current paper, there may be other cases when a
common intercept can be justified. In addition, a comparison of the
pooled estimator with and without fixed effects highlights some
important differences and helps form an understanding of the
effects of pooling the data. The pooled estimator with a common
intercept is given by
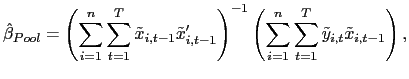
| (5) |
where
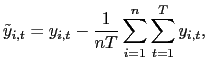 and
and 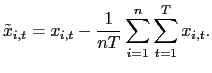
| (6) |
Following the work of Phillips and Moon (1999), asymptotic results
for the panel estimators are derived using sequential limits, which
implies first keeping the cross-sectional dimension, ![]() , fixed and letting the time-series dimension,
, fixed and letting the time-series dimension, ![]() , go to infinity, and then letting
, go to infinity, and then letting ![]() go to
infinity. Such sequential convergence is denoted
go to
infinity. Such sequential convergence is denoted
![]() .6 As mentioned
before, the definitions of the variables that appear in the
theorems and derivations below are all found in Appendix A, unless
otherwise noted.
.6 As mentioned
before, the definitions of the variables that appear in the
theorems and derivations below are all found in Appendix A, unless
otherwise noted.
| (7) |
The pooled estimator of ![]() is thus
asymptotically normally distributed; summing up over the
cross-section eliminates the usual near unit-root asymptotic
distributions found in the time-series case. The rate of
convergence is also faster in the pooled case
is thus
asymptotically normally distributed; summing up over the
cross-section eliminates the usual near unit-root asymptotic
distributions found in the time-series case. The rate of
convergence is also faster in the pooled case
![]() compared to the
time-series case
compared to the
time-series case
![]() , which again is a result of
the additional cross-sectional information. The limiting
distribution depends on
, which again is a result of
the additional cross-sectional information. The limiting
distribution depends on
![]() and
and ![]() and,
in order to perform inference, estimates of these parameters are
required. Let
and,
in order to perform inference, estimates of these parameters are
required. Let
![]() ,
,
![]() , and
, and
![]() . The estimator
. The estimator
![]() is thus the panel equivalent
of HAC (heteroskedasticty and auto-correlation consistent)
estimators for long-run variances.
is thus the panel equivalent
of HAC (heteroskedasticty and auto-correlation consistent)
estimators for long-run variances.
Standard tests can now be performed. For instance, the null
hypothesis
![]() , for
some
, for
some ![]() , where
, where
![]() , can be tested using a
, can be tested using a ![]() test. Let
test. Let
![]() . Using the results derived above, it follows easily that under the
null-hypothesis,
. Using the results derived above, it follows easily that under the
null-hypothesis,
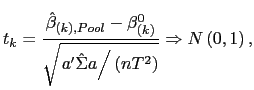
| (8) |
as
![]() ,
where
,
where ![]() is an
is an ![]() vector with
the
vector with
the ![]() 'th component equal to one and zero
elsewhere, and
'th component equal to one and zero
elsewhere, and
![]() is the
is the
![]() 'th component of
'th component of
![]() . More general linear
hypotheses can be evaluated using a Wald test.
. More general linear
hypotheses can be evaluated using a Wald test.
II.C.2 Fixed Effects
Let
![]() and
and
![]() denote the time-series
demeaned data. That is,
denote the time-series
demeaned data. That is,
![]() and
and
![]() .
The fixed effects pooled estimator, which allows for individual
intercepts, is then given by
.
The fixed effects pooled estimator, which allows for individual
intercepts, is then given by
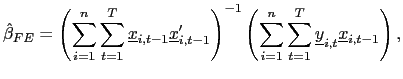
| (9) |
and
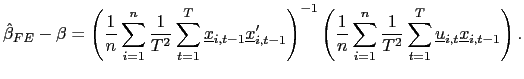
| (10) |
Clearly, the estimator is still consistent. Its asymptotic
distribution, however, will be affected by the demeaning. For fixed
![]() , as
, as
![]() ,
,
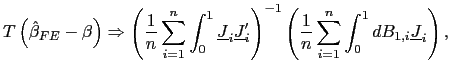
| (11) |
where
![]() and
and ![]() are the limiting processes of
are the limiting processes of
![]() and
and ![]() , respectively, as defined in Appendix A; the limiting
process for
, respectively, as defined in Appendix A; the limiting
process for ![]() is denoted
is denoted ![]() . Let
. Let
![]() denote the average covariance vector between
denote the average covariance vector between ![]() and
and ![]() , and observe that
, and observe that
![$\displaystyle E\left[ \int_{0}^{1}dB_{1,i}\underline{J}_{i}\right]$](img145.gif)
|
![$\displaystyle =E\left[ \int _{0}^{1}dB_{1,i}\left( r\right) J_{i}\left( r\right) -\int_{0}^{1} dB_{1,i}\left( s\right) \int_{0}^{1}J_{i}\left( r\right) dr\right]$](img146.gif)
| |
![$\displaystyle =-\int_{0}^{1}\int_{0}^{1}\int_{0}^{r}E\left[ e^{\left( r-s\right) C_{i} }\right] E\left[ dB_{1,i}\left( s\right) dB_{2,i}\left( q\right) \right] dsdr$](img147.gif)
| ||
![$\displaystyle =-\left( \int_{0}^{1}\int_{0}^{r}E\left[ e^{\left( r-s\right) C_{i} }\right] dsdr\right) \omega_{21},$](img148.gif)
| (12) |
which is different from zero whenever
![]() . Thus, as
. Thus, as
![]() ,
,
![$\displaystyle T\left( \hat{\beta}_{FE}-\beta\right) \rightarrow_{p}-\underline{\Omega }_{xx}^{-1}\left( \int_{0}^{1}\int_{0}^{r}E\left[ e^{\left( r-s\right) C_{i}}\right] dsdr\right) \omega_{21},$](img151.gif)
| (13) |
and the estimator suffers from a second order bias from the demeaning process.7
The differences in sample properties between the standard pooled
estimator with a common intercept and the fixed effects estimator
are rather striking. Mechanically, the standard pooled estimator
works well because for each ![]() , the terms in the
numerator of the estimator have mean zero and are independently
distributed across
, the terms in the
numerator of the estimator have mean zero and are independently
distributed across ![]() . As they are summed up over
. As they are summed up over
![]() , the central limit theorem applies and an
asymptotically normally distributed estimator is obtained. More
intuitively, when pooling the data, independent cross-sectional
information dilutes the endogeneity effects that cause the
Stambaugh (1999) bias in the time-series case. The same result does
not hold for the fixed effects estimator because the numerator
terms no longer have a zero mean as a consequence of the
time-series demeaning of the data, which leads to a correlation
between the innovation processes
, the central limit theorem applies and an
asymptotically normally distributed estimator is obtained. More
intuitively, when pooling the data, independent cross-sectional
information dilutes the endogeneity effects that cause the
Stambaugh (1999) bias in the time-series case. The same result does
not hold for the fixed effects estimator because the numerator
terms no longer have a zero mean as a consequence of the
time-series demeaning of the data, which leads to a correlation
between the innovation processes ![]() and the
demeaned regressors
and the
demeaned regressors
![]() whenever the regressor
is endogenous. Thus, unlike in the case with a common intercept,
the pooling does not remove the endogeneity effects and the
estimator suffers from a second order bias.
whenever the regressor
is endogenous. Thus, unlike in the case with a common intercept,
the pooling does not remove the endogeneity effects and the
estimator suffers from a second order bias.
More generally, from the perspective of panel data econometrics,
the natural way of understanding the detrimental impact of fixed
effects is to view them as an instance of the incidental parameter
problem, which was originally raised by Neyman and Scott (1948) and
discussed in a panel data context by Nickell (1981). That is, as
the panel grows larger asymptotically, the number of (incidental)
fixed effects that need to be estimated also goes to infinity, as
the cross-sectional dimension grows. Thus, although more and more
data becomes available asymptotically, the number of parameters to
estimate also increases. In the traditional (dynamic) panel setup
studied by Nickell (1981), where ![]() is fixed as
is fixed as
![]() , inclusion of fixed
effects causes the standard estimator of the slope coefficient to
become inconsistent. Here, where both
, inclusion of fixed
effects causes the standard estimator of the slope coefficient to
become inconsistent. Here, where both ![]() and
and
![]() tend to infinity, the fixed effects
estimator remains consistent but with a second order bias.
tend to infinity, the fixed effects
estimator remains consistent but with a second order bias.
II.D Recursive Demeaning
The second order bias in the fixed effects estimator arises
because the demeaning process induces a correlation between the
innovation processes ![]() and the demeaned
regressors
and the demeaned
regressors
![]() . Intuitively,
. Intuitively,
![]() and
and
![]() are correlated
because, in the demeaning of
are correlated
because, in the demeaning of ![]() ,
information available after time
,
information available after time ![]() is used. Or,
equivalently, because in the demeaning of the dependent variable,
is used. Or,
equivalently, because in the demeaning of the dependent variable,
![]() , information before time
, information before time ![]() is used. One solution is therefore to use recursive
demeaning of
is used. One solution is therefore to use recursive
demeaning of ![]() and
and ![]() (e.g.
Moon and Phillips, (2000), and Sul et al. (2005)). In particular, I
will consider a `forward demeaned' equation. That is, define
(e.g.
Moon and Phillips, (2000), and Sul et al. (2005)). In particular, I
will consider a `forward demeaned' equation. That is, define
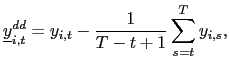 and
and 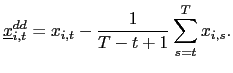
| (14) |
Observe that
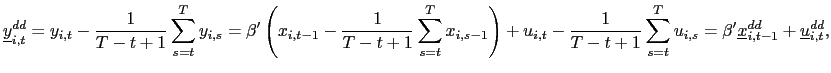
and consider the following pooled estimator, using the recursively demeaned data,
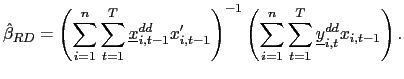
| (15) |
In
![]() , the non-demeaned
regressors
, the non-demeaned
regressors ![]() are used as instruments, and
the dependent variable,
are used as instruments, and
the dependent variable,
![]() , is formed using
data dated only after time
, is formed using
data dated only after time ![]() . Since
. Since
![]() and
and ![]() are now independent of each other, unlike
are now independent of each other, unlike
![]() and
and
![]() , the estimator
, the estimator
![]() will not suffer from the
same second order bias as the standard fixed effects estimator.
This is stated formally in the following theorem.
will not suffer from the
same second order bias as the standard fixed effects estimator.
This is stated formally in the following theorem.
| (16) |
To perform inference, let
![]() ,
,
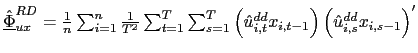 , and
, and
![]() . The
. The ![]() test and Wald test based on
test and Wald test based on
![]() and
and
![]() will
satisfy the usual properties. Observe that the forward demeaning of
the data introduces a moving average component in the returns
process, which is reflected in the limiting distribution derived in
the proof of Theorem 2. The
variance-covariance matrix estimator that was just proposed
automatically accounts for this by calculating the long-run
variance using the forward demeaned residuals and the panel
equivalent of a HAC estimator.
will
satisfy the usual properties. Observe that the forward demeaning of
the data introduces a moving average component in the returns
process, which is reflected in the limiting distribution derived in
the proof of Theorem 2. The
variance-covariance matrix estimator that was just proposed
automatically accounts for this by calculating the long-run
variance using the forward demeaned residuals and the panel
equivalent of a HAC estimator.
The recursive demeaning procedure gives up some efficiency by
relying on a somewhat inefficient method for demeaning the data.
However, there are no clear-cut alternatives in the general case
when the autoregressive roots ![]() (or
equivalently,
(or
equivalently, ![]() ) are unknown. If the
) are unknown. If the ![]() were known, the bias term in equation (13) could be
directly estimated and a bias-corrected fixed effects estimator
could be constructed. More ambitiously, for known
were known, the bias term in equation (13) could be
directly estimated and a bias-corrected fixed effects estimator
could be constructed. More ambitiously, for known ![]() , a panel version of fully modified estimation could be
considered, as suggested by Phillips and Moon (1999) in the pure
unit-root case. However, although such procedures are likely more
efficient than the recursive demeaning proposed here, they are not
feasible in practice since the
, a panel version of fully modified estimation could be
considered, as suggested by Phillips and Moon (1999) in the pure
unit-root case. However, although such procedures are likely more
efficient than the recursive demeaning proposed here, they are not
feasible in practice since the ![]() are
unknown.8
are
unknown.8
II.E Relaxing the Pooling Assumption
II.E.1 Properties of the Pooled Estimators
when the
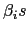 Are Not Identical
Are Not Identical
So far, the focus has been on the problems raised by fixed
effects. However, it is also possible that the slope coefficients
![]() may vary across
may vary across ![]() .
In this section, I therefore discuss the properties of the pooled
estimator when the
.
In this section, I therefore discuss the properties of the pooled
estimator when the
![]() are not identical.9 To
start with, suppose
are not identical.9 To
start with, suppose
![]() , where
, where
![]() is
is
![]() with mean zero.
with mean zero.
(a) If
| (17) |
(b) If
![$\displaystyle \hat{\beta}_{FE}\rightarrow_{p}\beta+\underline{\Omega}_{xx}^{-1}E\left[ \left( \int_{0}^{1}\underline{J}_{i}\underline{J}_{i}^{\prime}\right) \theta_{i}\right] .$](img233.gif)
| (18) |
In the case where the distribution of the slope coefficients is
independent of the regressors, it follows that the pooled estimator
converges to the average parameter
![]() . The
rate of convergence is much slower than in the homogenous case,
however, and the fixed effects estimator no longer suffers from a
small sample bias. These results stem from the fact that when the
. The
rate of convergence is much slower than in the homogenous case,
however, and the fixed effects estimator no longer suffers from a
small sample bias. These results stem from the fact that when the
![]() are non-identical, the residuals
in the regression are now given by
are non-identical, the residuals
in the regression are now given by
![]() . Since
. Since
![]() is a near integrated process, it
will dominate the asymptotic properties of the residuals, and will
therefore slow down the rate of convergence and also render the
second order bias term in the fixed effects estimator irrelevant.
However, when the deviations
is a near integrated process, it
will dominate the asymptotic properties of the residuals, and will
therefore slow down the rate of convergence and also render the
second order bias term in the fixed effects estimator irrelevant.
However, when the deviations
![]() are small, the second order bias
term is still a concern. Results from Monte Carlo simulations,
which are not presented here, show that for most potentially
relevant values of
are small, the second order bias
term is still a concern. Results from Monte Carlo simulations,
which are not presented here, show that for most potentially
relevant values of ![]() and
and
![]() in a stock return predictability
context, the bias in the fixed effects estimator is still highly
relevant. Likewise, when the deviations
in a stock return predictability
context, the bias in the fixed effects estimator is still highly
relevant. Likewise, when the deviations
![]() are small, the slow-down in the
rate of convergence will not be as drastic as in Theorem 3.10
are small, the slow-down in the
rate of convergence will not be as drastic as in Theorem 3.10
If the
![]() are correlated with the
regressors, the pooled estimator does not converge to the average
slope coefficient
are correlated with the
regressors, the pooled estimator does not converge to the average
slope coefficient ![]() . However, as discussed
at length in Phillips and Moon (1999, 2000), the average of the
individual parameters
. However, as discussed
at length in Phillips and Moon (1999, 2000), the average of the
individual parameters ![]() is not necessarily
the natural way of defining an average relationship between
is not necessarily
the natural way of defining an average relationship between
![]() and
and ![]() .
Phillips and Moon note that in a framework with persistent
variables, one can define the individual regression coefficients
.
Phillips and Moon note that in a framework with persistent
variables, one can define the individual regression coefficients
![]() as
as
![]() ,
where
,
where
![]() is the long-run variance for
is the long-run variance for
![]() and
and
![]() is the long-run covariance
between
is the long-run covariance
between ![]() and
and ![]() .
They then define the long-run average relationship between
.
They then define the long-run average relationship between
![]() and
and ![]() as
as
![]() , rather than
, rather than
![]() , and
show that the pooled estimator, with or without fixed effects, will
converge to
, and
show that the pooled estimator, with or without fixed effects, will
converge to
![]() under very general conditions;
in the special case when
under very general conditions;
in the special case when
![]() and
and
![]() is independent of
is independent of ![]() , it follows that
, it follows that
![]() . Thus,
. Thus,
![]() and
and
![]() converge to a well
defined average relationship under very general circumstances,
although not necessarily to
converge to a well
defined average relationship under very general circumstances,
although not necessarily to
![]() .
.
II.E.2 A Test of Slope Homogeneity
The analysis above shows that the pooled estimators are robust
to deviations from the assumption of homogenous slope coefficients,
and will converge to a well-defined average coefficient when the
![]() are non-identical. In many cases,
it is still of interest, however, to evaluate whether the slope
coefficients are in fact all equal.
are non-identical. In many cases,
it is still of interest, however, to evaluate whether the slope
coefficients are in fact all equal.
I adopt a version of a test originally proposed by Swamy (1970)
and further developed by Pesaran (2007). The basic idea is to
analyze a weighted sum of squared differences between the
unrestricted time-series estimates of the individual
![]() and the fixed effects pooled
estimate, which imposes a common slope coefficient.
and the fixed effects pooled
estimate, which imposes a common slope coefficient.
Define the following weighted fixed effects estimator,
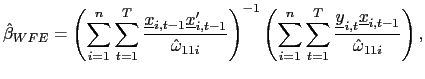
| (19) |
where
![]() is an estimate of the
variance of
is an estimate of the
variance of ![]()
![]() ; the
standardization by
; the
standardization by
![]() leads to a natural reduction in
nuisance parameters in the asymptotic distribution of the below
test statistic. Further, let
leads to a natural reduction in
nuisance parameters in the asymptotic distribution of the below
test statistic. Further, let
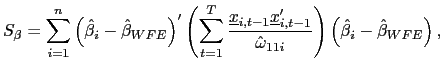
| (20) |
where
![]() is the OLS estimate of the
slope coefficient for country
is the OLS estimate of the
slope coefficient for country ![]() .
.
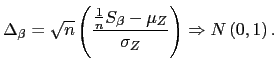
| (21) |
Given ![]() and
and
![]() ,
,
![]() provides an asymptotically
normally distributed test of slope homogeneity. Unfortunately,
provides an asymptotically
normally distributed test of slope homogeneity. Unfortunately,
![]() and
and
![]() are functions of the unknown
nuisance parameters
are functions of the unknown
nuisance parameters
![]() ; they are
also functions of the average correlation
; they are
also functions of the average correlation
![]() between the
innovations
between the
innovations ![]() and
and ![]() , but
this value can easily be estimated.
, but
this value can easily be estimated.
Through simulations, it easy to show that ![]() changes fairly slowly with the values of the
changes fairly slowly with the values of the
![]() , whereas
, whereas
![]() can vary substantially from small
changes in the
can vary substantially from small
changes in the ![]() . In order to obtain a
feasible test with approximately correct size, I therefore propose
to use
. In order to obtain a
feasible test with approximately correct size, I therefore propose
to use ![]() , evaluated for a common value of
, evaluated for a common value of
![]() for all
for all ![]() ,
where
,
where ![]() is given by the average of the
median unbiased estimates of each
is given by the average of the
median unbiased estimates of each ![]() . As
originally shown by Stock (1991), median unbiased, although
inconsistent, estimates of each
. As
originally shown by Stock (1991), median unbiased, although
inconsistent, estimates of each ![]() can be
obtained by inverting a unit-root test statistic. Further,
can be
obtained by inverting a unit-root test statistic. Further,
![]() is replaced by an empirical
estimate that is consistent under the null hypothesis of
is replaced by an empirical
estimate that is consistent under the null hypothesis of
![]() for all
for all ![]() .
Write
.
Write
![]() where
where
![]() represents the expression in
(20). From the proof
of Theorem 4, an estimate of
represents the expression in
(20). From the proof
of Theorem 4, an estimate of
![]() is obtained by calculating the
sample standard deviation of
is obtained by calculating the
sample standard deviation of ![]() . Under the
alternative, when the
. Under the
alternative, when the
![]() are not all identical, this
estimate will be upward biased for
are not all identical, this
estimate will be upward biased for
![]() , and some power will therefore be
lost. However, given a lack of knowledge of the
, and some power will therefore be
lost. However, given a lack of knowledge of the ![]() , and the strong dependence of
, and the strong dependence of
![]() on the values of the
on the values of the ![]() , this seems like a preferable approach.
, this seems like a preferable approach.
In terms of practical implementation, the median unbiased
estimates for ![]() are obtained by inverting the
DF-GLS unit-root test statistic, as described in detail in Campbell
and Yogo (2006). In the case when
are obtained by inverting the
DF-GLS unit-root test statistic, as described in detail in Campbell
and Yogo (2006). In the case when ![]() is a
vector, the same procedure can be applied to each of the component
processes of
is a
vector, the same procedure can be applied to each of the component
processes of ![]() and, with the extra restriction
that
and, with the extra restriction
that ![]() is a diagonal matrix, one can proceed
exactly as in the scalar case. The variances
is a diagonal matrix, one can proceed
exactly as in the scalar case. The variances
![]() of
of ![]() and the average correlation
and the average correlation
![]() between
between ![]() and
and ![]() are estimated from
the residuals of the time-series regressions of equations (1) and (2). The values for
are estimated from
the residuals of the time-series regressions of equations (1) and (2). The values for
![]() are obtained by direct simulation of
the asymptotic expression given in the proof of Theorem 4; these
values are available from the author upon request. The null
hypothesis is rejected for large positive values of
are obtained by direct simulation of
the asymptotic expression given in the proof of Theorem 4; these
values are available from the author upon request. The null
hypothesis is rejected for large positive values of
![]() ; e.g. a five percent test
would reject for values larger than 1.65.
; e.g. a five percent test
would reject for values larger than 1.65.
III Cross-Sectional Dependence
III.A The Effects of Common Factors
I now return to the general setup with common factors in the
data. The following theorem summarizes the asymptotic properties of
both the standard pooled estimator and the fixed effects estimator
when there are common factors. Again, the
![]() are assumed to be identical
unless otherwise noted.
are assumed to be identical
unless otherwise noted.
![$\displaystyle T\left( \hat{\beta}_{Pool}-\beta\right) \Rightarrow\left( \Omega _{xx}+\Omega_{zz}\right) ^{-1}\left[ \int_{0}^{1}\left( \gamma^{\prime }dB_{f}\right) \left( \Gamma^{\prime}J_{g}\right) \right] .$](img336.gif)
| (22) |
![$\displaystyle T\left( \hat{\beta}_{FE}-\beta\right) \Rightarrow\left( \underline{\Omega }_{xx}+\underline{\Omega}_{zz}\right) ^{-1}\left[ \int_{0}^{1}\left( \gamma^{\prime}dB_{f}\right) \left( \Gamma^{\prime}\underline{J}_{g}\right) -\left( \int_{0}^{1}\int_{0}^{r}E\left[ e^{\left( r-s\right) C_{i} }\right] dsdr\right) \omega_{21}\right] .$](img340.gif)
| (23) |
Thus, in the presence of the general factor structure outlined
in Section II, the
standard pooled estimator exhibits a non-standard limiting
distribution, although it is still consistent; standard tests can
therefore not be used. Similarly, the limiting behavior of the
fixed effects estimator is determined by the bias term arising from
the time-series demeaning of the data, as well as an additional
term that stems from the common factors in the data. Note that the
term
![]() is random and can take on both negative and positive values. Thus,
correcting for it will have an ambiguous effect on the outcome of
the estimation and test results.
is random and can take on both negative and positive values. Thus,
correcting for it will have an ambiguous effect on the outcome of
the estimation and test results.
III.B Robust Estimators
Based on the methods of Pesaran (2006), I propose an estimator
that is more robust to cross-sectional dependence in the data.
Pesaran's (2006) idea is to project the data onto the space
orthogonal to the common factors, thereby removing the
cross-sectional dependence from the data used in the estimation.
However, since the factors are not observed in practice, an
indirect approach is required. Pesaran suggests using the
cross-sectional means of the dependent and independent variable as
proxies for the common factors. A similar approach is adopted
below, but only the cross-sectional means of the regressors are
used to control for the common factors. This is done because of the
different orders of integration between the error terms and the
regressors. For
![]() , the stochastic behavior of
, the stochastic behavior of
![]() is dominated by that of
is dominated by that of ![]() , and the matrix
, and the matrix
![]() would be asymptotically singular.
would be asymptotically singular.
Thus, consider the following estimator of ![]() ,
,
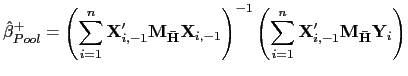
| (24) |
where
![]() denotes the
denotes the ![]() matrix of the observations for the dependent
variable and
matrix of the observations for the dependent
variable and
![]() the
the ![]() matrix of regressor observations.
matrix of regressor observations.
![]() is a
is a ![]() matrix and
matrix and
![]() is the
is the ![]() matrix of observations of
matrix of observations of
![]()
The estimator
![]() is obtained by
applying the pooled estimator to the residuals from a projection of
the original data onto the cross-sectional averages of the
regressors. The intuition behind this is that the cross-sectional
average of
is obtained by
applying the pooled estimator to the residuals from a projection of
the original data onto the cross-sectional averages of the
regressors. The intuition behind this is that the cross-sectional
average of ![]() is close to the common
stochastic trend
is close to the common
stochastic trend ![]() , since the cross-sectional
averages of the cross-sectionally independent data may be expected
to be close to zero; the projection onto the compliment of the
cross-sectional means will therefore remove the effects of the
common factors in the regressors. As is shown in the proof of the
following theorem, it is sufficient to remove the factors from the
regressors (and not from the innovations to the regressand) in
order to achieve a mixed normal distribution.
, since the cross-sectional
averages of the cross-sectionally independent data may be expected
to be close to zero; the projection onto the compliment of the
cross-sectional means will therefore remove the effects of the
common factors in the regressors. As is shown in the proof of the
following theorem, it is sufficient to remove the factors from the
regressors (and not from the innovations to the regressand) in
order to achieve a mixed normal distribution.
| (25) |
The estimator
![]() thus achieves a
thus achieves a
![]() convergence rate and an asymptotic
mixed normal distribution. The mixed normality in this case arises
from the common factors, which leads to a mixed normal distribution
rather than the normal distribution seen above in the no common
factors case. That is, the limiting distribution is effectively a
normal distribution with a random variance-covariance matrix that
is a function of the common shocks; conditional on the realization
of the common factors, the distribution is thus normal. For
practical purposes, the mixed normal distribution allows for
standard inference in that the
convergence rate and an asymptotic
mixed normal distribution. The mixed normality in this case arises
from the common factors, which leads to a mixed normal distribution
rather than the normal distribution seen above in the no common
factors case. That is, the limiting distribution is effectively a
normal distribution with a random variance-covariance matrix that
is a function of the common shocks; conditional on the realization
of the common factors, the distribution is thus normal. For
practical purposes, the mixed normal distribution allows for
standard inference in that the ![]() tests and Wald
tests will have asymptotically standard distributions. Allowing for
fixed effects in the arguments, it is easy to show the following
result.
tests and Wald
tests will have asymptotically standard distributions. Allowing for
fixed effects in the arguments, it is easy to show the following
result.
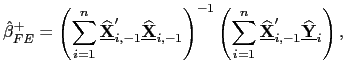
| (26) |
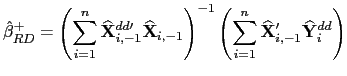
| (27) |
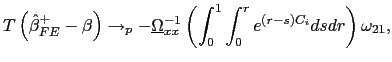
| (28) |
| (29) |
![]() and
and
![]() thus provide pooled
estimators for predictive regressions that are asymptotically mixed
normally distributed in the presence of common factors and with the
allowance for fixed effects in the latter. Standard
thus provide pooled
estimators for predictive regressions that are asymptotically mixed
normally distributed in the presence of common factors and with the
allowance for fixed effects in the latter. Standard ![]() tests and Wald tests can therefore be used; by simply using
the defactored data, the variance-covariance matrix can be
estimated in a manner analogous to that described above for the no
common factors case. The practical implementation of these
estimators is thus very simple: Premultiply the data by
tests and Wald tests can therefore be used; by simply using
the defactored data, the variance-covariance matrix can be
estimated in a manner analogous to that described above for the no
common factors case. The practical implementation of these
estimators is thus very simple: Premultiply the data by
![]() , and use the
resulting variables in the original estimation procedures.
, and use the
resulting variables in the original estimation procedures.
As shown in the simulations below, the
![]() test of slope homogeneity
appears robust to the presence of factors -unlike the pooled
test of slope homogeneity
appears robust to the presence of factors -unlike the pooled
![]() tests- and I do not attempt to modify it
to control for common factors.
tests- and I do not attempt to modify it
to control for common factors.
IV Finite Sample Evidence
IV.A No Cross-Sectional Dependence
To evaluate the small sample properties of the panel data
estimators proposed in this paper, a Monte Carlo study is
performed. In particular, I focus on the size and power properties
of the pooled ttests. Equations (1) and (3) are simulated
for the case with a single regressor. The innovations
![]() are drawn
from normal distributions with mean zero, unit variance, and
correlations δ = 0, -0.4, -0.7, and -0.95; there is no cross-sectional dependence. The
local-to-unity parameters
are drawn
from normal distributions with mean zero, unit variance, and
correlations δ = 0, -0.4, -0.7, and -0.95; there is no cross-sectional dependence. The
local-to-unity parameters ![]() are drawn from
a uniform distribution with support [-20, -2]. In analyzing the
power properties, the slope coefficient β varies
between -0.05 and 0.05, and is
identical for all i. The sample size is given
by T = 100, n = 20. The intercepts
are drawn from
a uniform distribution with support [-20, -2]. In analyzing the
power properties, the slope coefficient β varies
between -0.05 and 0.05, and is
identical for all i. The sample size is given
by T = 100, n = 20. The intercepts
![]() are normally distributed with
mean and standard deviation equal to 0.005. All
results are based on 10,000 repetitions. The
are normally distributed with
mean and standard deviation equal to 0.005. All
results are based on 10,000 repetitions. The ![]() test based on the fixed effects estimator using standard
demeaning,
test based on the fixed effects estimator using standard
demeaning, ![]() , and that based on the
recursively demeaned pooled estimator,
, and that based on the
recursively demeaned pooled estimator, ![]() , are considered. Throughout
the simulation study, the normal distribution is used to determine
significance; i.e. the null is rejected for absolute test values
greater than 1.96.
, are considered. Throughout
the simulation study, the normal distribution is used to determine
significance; i.e. the null is rejected for absolute test values
greater than 1.96.
Panel A in Table 1 shows the average rejection rates for the nominal five percent two sided t-tests under the null hypothesis of β = 0. Panels A1 and A2 in Figure 1 show the corresponding power curves of the tests for the cases of δ = 0 and δ = -0.95. Table 1 and the power curves in Figure 1 clearly show the effects of the second-order bias in the fixed effects estimator; the test based on the standard fixed effects estimator severely over rejects under the null hypothesis for δ = -0.95. The test based on the recursively demeaned estimator has rejection rates close to the nominal size under the null, while maintaining decent power properties.11
IV.B Common Factors
In this section, I repeat the Monte Carlo experiment above for
the case when there is a common factor in the innovations. In
particular, equations (1)-(4) are now
simulated with a single regressor and a single common factor
![]() , drawn from a standard normal
distribution. The factor loadings,
, drawn from a standard normal
distribution. The factor loadings,
![]() and
and
![]() , are also normally distributed
with means of minus one and plus one, respectively, and standard
deviations equal to 2-1/2 in both cases. The
innovations in the returns and regressor processes are formed as
, are also normally distributed
with means of minus one and plus one, respectively, and standard
deviations equal to 2-1/2 in both cases. The
innovations in the returns and regressor processes are formed as
![]() and
and
![]() ,
respectively, where
,
respectively, where
![]() are drawn
from standard normal distributions; the scaling by 2-1/2 is performed in order to achieve an approximate unit
variance in the innovations, which enables easier comparison with
the cross-sectionally independent case. As before, the correlation
between
are drawn
from standard normal distributions; the scaling by 2-1/2 is performed in order to achieve an approximate unit
variance in the innovations, which enables easier comparison with
the cross-sectionally independent case. As before, the correlation
between ![]() and
and ![]() is set δ = 0, -0.4, -0.7 and -0.95.
is set δ = 0, -0.4, -0.7 and -0.95.
The results are shown in Panels B and C of Table 1 and in Panels
B1, B2, C1, and C2 in Figure 1. Panel B in
Table 1 and Panels B1
and B2 in Figure 1
show the outcomes of the Monte Carlo experiments when the model
generated with common factors is estimated using the estimators
![]() and
and
![]() , which do not control for
cross-sectional dependence. It is clear that when the common
factors are ignored in the estimation process, the actual size of
the corresponding
, which do not control for
cross-sectional dependence. It is clear that when the common
factors are ignored in the estimation process, the actual size of
the corresponding ![]() tests is very far from the
nominal size of
tests is very far from the
nominal size of ![]() percent, with rejection rates
above
percent, with rejection rates
above ![]() percent under the null.
percent under the null.
Panel C in Table 1
and Panels C1 and C2 in Figure 1 show the same
results for the estimators
![]() and
and
![]() , which do control for
the common factors. The
, which do control for
the common factors. The ![]() test based on the
recursively demeaned data,
test based on the
recursively demeaned data,
![]() , now possesses good
size and power properties. As before, the standard fixed effects
estimator exhibits a finite sample bias and extremely poor size
properties.
, now possesses good
size and power properties. As before, the standard fixed effects
estimator exhibits a finite sample bias and extremely poor size
properties.
IV.C Test of Slope Homogeneity
The final set of simulations analyzes the finite sample
properties of the
![]() test of slope homogeneity.
The setup is identical to that used above, with the exception of
the slope coefficients. Three different scenarios are considered.
In the first, the null hypothesis is imposed and
test of slope homogeneity.
The setup is identical to that used above, with the exception of
the slope coefficients. Three different scenarios are considered.
In the first, the null hypothesis is imposed and
![]() . In the two other cases,
the slope coefficients exhibit heterogeneity and are generated as
. In the two other cases,
the slope coefficients exhibit heterogeneity and are generated as
![]() , where
, where
![]() is a standard normal random
variable, independently distributed across
is a standard normal random
variable, independently distributed across ![]() , and
, and
![]() is equal to
is equal to ![]() and
and
![]() , respectively. The cases with and
without common factors are considered, although, as described
previously, no adjustment to the test is made when there are common
factors. The test is evaluated as a one-sided test with a nominal
size of five percent; i.e. the null is rejected when
, respectively. The cases with and
without common factors are considered, although, as described
previously, no adjustment to the test is made when there are common
factors. The test is evaluated as a one-sided test with a nominal
size of five percent; i.e. the null is rejected when
![]() is greater than 1.65.
is greater than 1.65.
Panel A of Table 2 shows the
results without any common factors and Panel B shows the results
with common factors. Under the null, the test is somewhat under
sized, and marginally more so when there are common factors. Unlike
the ![]() tests analyzed above, the test of slope
homogeneity is thus not particularly sensitive to common factors in
the data. Under the first alternative, with
tests analyzed above, the test of slope
homogeneity is thus not particularly sensitive to common factors in
the data. Under the first alternative, with
![]() , the power of the test is around
45 percent without common factors, and
around 35 percent with common factors. Under the
second alternative, with
, the power of the test is around
45 percent without common factors, and
around 35 percent with common factors. Under the
second alternative, with ![]() , the power rises to
above 90 percent in both cases. The relatively low
power under the first alternative reflects the fact that it is
difficult to distinguish between such small absolute
differences between the
, the power rises to
above 90 percent in both cases. The relatively low
power under the first alternative reflects the fact that it is
difficult to distinguish between such small absolute
differences between the
![]() , even though the relative
differences are reasonably large; one should keep in mind that the
test compares across the cross-section of the data, which in the
simulations only amounts to
, even though the relative
differences are reasonably large; one should keep in mind that the
test compares across the cross-section of the data, which in the
simulations only amounts to ![]() observations.
Nevertheless, the test can serve as a useful diagnostic of panel
homogeneity.
observations.
Nevertheless, the test can serve as a useful diagnostic of panel
homogeneity.
V Data Description
All of the data come from the Global Financial Data database and are on a monthly frequency. Total returns, including direct returns from dividends, on market wide indices in 40 countries were obtained, as well as the corresponding dividend- and earnings-price ratios and measures of the short and long interest rates.
With the exception of Spain, the dividend-price ratio data is available over the same sample period as the total stock returns. But, the other predictor variables are typically not available during the whole sample of total stock returns. Due to the two world wars, France, Germany, Japan, and the U.K. have some years during which no observations are available. Further, Spain's total returns data start in 1940, but no dividends data is available during 1968-1983. Thus, in the time-series analysis, separate regressions are fitted for each sample period for these five countries, and in the pooled estimation separate intercepts are estimated. In Table 3, which presents the pooled results, the row listing the number of 'countries' in each panel can therefore include more than one count of some countries.
As is conventional in the literature, the dividend-price ratio is defined as the sum of dividends during the past year divided by the current price and the earnings-price ratio is defined as the current price divided by the latest 12 months of available earnings. Short interest rate measures come from Global Financial Data and use rates on 3-month T-bills when available or, otherwise, private discount rates or interbank rates. The long rate is measured by the yield on long-term government bonds. When available, a 10-year bond is used; otherwise, I use that with the closest maturity to 10 years. The term spread is defined as the log difference between the long and short rates. Excess stock returns are defined as the return on stocks, in the local currency, over the local short rate. This provides the international analogue of the typical forecasting regressions estimated for U.S. data. All regressions are run at the one-month frequency using log-transformed variables with the log excess returns over the domestic short rate as the dependent variable.
Countries are pooled into a global panel, as well as developed and emerging stock market panels, according to the MSCI classifications.12
VI Empirical Results
In the empirical analysis, I conduct pooled regressions as well
as time-series regressions for individual countries. The results
from the pooled regressions and summaries of the time-series
results are presented in Table 3. The time-series
results for individual countries are given in Table 4. Each table
contains multiple panels, which correspond to the different
forecasting variables. For the pooled regressions, results from
both the standard fixed effects estimator,
![]() , and the corresponding
, and the corresponding
![]() statistic,
statistic, ![]() , as
well as the estimator using recursively demeaned data,
, as
well as the estimator using recursively demeaned data,
![]() and
and ![]() ,
are documented. Separate results are shown for the case when common
factors are controlled for and when they are not. As discussed at
length above, the
,
are documented. Separate results are shown for the case when common
factors are controlled for and when they are not. As discussed at
length above, the ![]() test is not robust to
the endogeneity and persistence of the regressors, but provides an
interesting illustration of the potential pitfalls of not
addressing these issues. The short interest rate and the term
spread are generally less endogenous and inference based on the
fixed effects estimator for these two variables will be fairly
accurate (see also the discussion on this topic in Campbell and
Yogo (2006)); however, the fixed effects
test is not robust to
the endogeneity and persistence of the regressors, but provides an
interesting illustration of the potential pitfalls of not
addressing these issues. The short interest rate and the term
spread are generally less endogenous and inference based on the
fixed effects estimator for these two variables will be fairly
accurate (see also the discussion on this topic in Campbell and
Yogo (2006)); however, the fixed effects ![]() test
will tend to greatly over reject the null for the dividend- and
earnings-price ratio. In Table 3, significant
results at the one-sided five percent level based on robust
test-statistics from which proper inference can be drawn, i.e. the
test
will tend to greatly over reject the null for the dividend- and
earnings-price ratio. In Table 3, significant
results at the one-sided five percent level based on robust
test-statistics from which proper inference can be drawn, i.e. the
![]() statistic corresponding to
statistic corresponding to
![]() , are indicated with a
, are indicated with a
![]() .13
.13
The results from the individual time-series regressions, shown
in Table 4, are
presented in a similar manner to the pooled regressions. Since
normal inference based on the OLS ![]() statistic
will generally be biased, inference based on a robust 90 percent confidence interval for
statistic
will generally be biased, inference based on a robust 90 percent confidence interval for ![]() , using the methods of Campbell and Yogo (2006), are
also provided. If viewed as a test, this confidence interval can be
seen as a five percent one-sided test and a rejection of the null
hypothesis of no predictability is indicated with a
, using the methods of Campbell and Yogo (2006), are
also provided. If viewed as a test, this confidence interval can be
seen as a five percent one-sided test and a rejection of the null
hypothesis of no predictability is indicated with a ![]() next to the coefficient estimate; for brevity, the
actual confidence intervals are not shown. In Table 3, the number of
individual time-series regressions that yield significant
coefficients according to the Campbell and Yogo test is indicated
in the column labeled CY
next to the coefficient estimate; for brevity, the
actual confidence intervals are not shown. In Table 3, the number of
individual time-series regressions that yield significant
coefficients according to the Campbell and Yogo test is indicated
in the column labeled CY
![]() .
.
VI.A Testing for Slope Homogeneity
Before considering the empirical results for the different
predictor variables, it is useful to briefly analyze the
homogeneity of the slope coefficients in the pooled predictive
regressions. Table 3
shows the outcome of the
![]() test of slope homogeneity; it
is a one-sided test, and a value greater than 1.65 indicates that the null hypothesis of
test of slope homogeneity; it
is a one-sided test, and a value greater than 1.65 indicates that the null hypothesis of
![]() for all
for all ![]() is rejected at the five percent level. As is seen, slope
homogeneity can always be rejected for the global panel. For the
developed panel, homogeneity is only rejected in the dividend-price
ratio regression using the full sample, which spans a much larger
range of time than the other panels since the dividend-price ratio
is available further back than any of the other predictor
variables; when data before 1950 is dropped, slope homogeneity can
no longer be rejected. For the emerging market panels, the null of
slope homogeneity is only rejected in the regression with the short
interest rate. These results thus support the notion that countries
within the groups of developed and emerging markets tend to be more
homogenous in terms of predictability than countries across these
groups.
is rejected at the five percent level. As is seen, slope
homogeneity can always be rejected for the global panel. For the
developed panel, homogeneity is only rejected in the dividend-price
ratio regression using the full sample, which spans a much larger
range of time than the other panels since the dividend-price ratio
is available further back than any of the other predictor
variables; when data before 1950 is dropped, slope homogeneity can
no longer be rejected. For the emerging market panels, the null of
slope homogeneity is only rejected in the regression with the short
interest rate. These results thus support the notion that countries
within the groups of developed and emerging markets tend to be more
homogenous in terms of predictability than countries across these
groups.
As shown previously, the pooled analysis is valid also when the slope coefficients are not homogenous. However, the estimates from the global panels, and in a couple of instances from the developed and emerging panels, are best interpreted as average relationships, and the corresponding tests as tests of whether there is predictability on average in the data.
VI.B The Earnings-Price Ratio
The results for the earnings-price ratio are presented in Panel A of Tables 3 and 4. There is minimal evidence of a positive predictive relationship. Specifically, pooling the data at either the global or developed market levels does not yield a significant coefficient, regardless of whether one controls for common factors; however, there is evidence of a predictive relationship when pooling at the emerging market level and controlling for common factors. To ensure that the developed market results are not driven by the longer earnings-price ratio time-series available for the U.K. and the U.S., I also estimate these pooled regressions when restricting the sample to observations after 1950. The individual country time-series results confirm the lack of evidence of a predictive relationship in the pooled regressions. In particular, in the post-1950 sample, only four of the 38 time-series regressions (Argentina, Jordan, South Africa, and the U.K.) yield any significant coefficients.
There is thus rather weak evidence that the earnings-price ratio predicts stock returns; the majority of evidence that does exist is for emerging economies. It is noteworthy that the null of no predictability would have been rejected in all of the pooled regressions if one relied on non-robust methods that fail to control for the endogeneity and persistence of the regressors, as well as common factors in the data. Controlling for common factors appears to be of potentially great importance. It is interesting to note that doing so does not necessarily weaken the results.
VI.C The Dividend-Price Ratio
Panel B in Table 3 shows the results from pooled regressions with the dividend-price ratio as the regressor. The results are generally somewhat stronger than for the earnings-price ratio. Specifically, when controlling for common factors, the coefficient is significant when pooling both at the post-1950 global level and the developed market level, as well as in the full sample emerging panel. The overall picture depicted by the individual time-series regressions shown in Panel B of Table 4, however, is still fairly weak, although evidence of predictability is observed for post-1950 Australia, Chile, post-WWII Japan, Jordan, Mexico, Taiwan, the U.K., and post-1950 U.S. The time-series evidence thus presents no clear pattern of predictability and the evidence that exists is distributed fairly equally between developed and emerging markets. As in the case of the earnings-price ratio, the null of no predictability would have been often rejected when using non-robust tests.
VI.D The Short Interest Rate
In light of the empirical evidence of a predictive relationship seen in U.S. data, one would expect there to be a negative relationship between the current short rate and future stock returns. The data used in all interest rate regressions are restricted to start in 1952 or after, following the convention used in studies with U.S. data.14 The pooled results for the short interest rate are presented in Panel C of Table 3.
The null of no predictability is strongly rejected in the pooled sample of developed markets. In contrast to this strongly significant negative relationship, the pooled relationship in the emerging markets is not significant. Given the rather capricious character of interest rates in many emerging economies (e.g. Argentina), I focus strictly on the developed market results. As seen in Panel C of Table 4, this finding of predictability is supported by the results of the individual time-series regressions for the developed markets. In particular, a significant predictive relationship is found in eight out of 23 developed markets, including: Canada, Germany, the Netherlands, New Zealand, Portugal, Spain, Switzerland, and the U.S.. In addition, a closer look at the individual country level results further strengthens this pattern; in particular, it reveals that the estimates for 15 of the developed markets are more than one standard deviation away from zero while the slope coefficient estimate is negative for 20 of the 23 countries.
VI.E The Term Spread
Based on the U.S. experience, one would expect there to be a positive predictive relationship, if any, between the term spread and stock returns. As in the case of the short interest rate, I find a positive significant predictive relationship only in developed markets. As shown in Panel D of Table 3, there is strong evidence of a predictive relationship when pooling the developed economies. As this relationship is not evident for the emerging markets, I once again focus on the results for the developed markets. As seen in Panel D of Table 4, this finding of predictability is supported strongly by the results of the individual time-series regressions for the developed markets. For 10 of 23 individual time-series regressions, there is a positive and significant predictive relationship: Canada, France, Germany, Italy, the Netherlands, New Zealand, Norway, Spain, Switzerland, and the U.S.. Furthermore, 14 countries have a coefficient that is more than one standard deviation from zero.
VI.F Stability over Time
How robust are these patterns of predictability to different sample periods? To analyze this, I consider pooled regressions with expanding windows of observations for the developed markets. I focus on the developed panel since the time-series in that panel typically have longer samples available. A new country is added to the expanding window regression when there are five years of observations available; no 'old' observations are ever dropped from the estimation window and the estimates at each point in time are thus based on all observations available up to that date.15 Confidence intervals, with a nominal 90 percent coverage rate, are calculated in a manner analogous to the test statistics shown in Table 3, based on the normal distribution. The left column of Figure 2 shows the results from using the standard fixed effects estimator, without controlling for common factors. The right column shows the results from the estimator using recursively demeaned data and controlling for common factors. The confidence intervals in the left column are thus typically biased and will generally not have an actual coverage rate of 90 percent; however, these results further illustrate the importance of controlling for endogeneity and common factors.
The results presented in Figure 2 mostly reflect
those discussed above based on the complete sample. However, the
results for the dividend-price ratio
![]() , which generally appeared
somewhat stronger than those for the earnings-price ratio
, which generally appeared
somewhat stronger than those for the earnings-price ratio
![]() , now appear very weak
when viewed over time. Overall, the support of any stable
predictive ability in either of these two variables is very weak.
The term spread
, now appear very weak
when viewed over time. Overall, the support of any stable
predictive ability in either of these two variables is very weak.
The term spread
![]() coefficient
fluctuates around zero until the late 1970s, after which the lower
bound of the confidence interval typically hovers above zero,
although the coefficient is only consistently significant after
1993. It is only for the short rate
coefficient
fluctuates around zero until the late 1970s, after which the lower
bound of the confidence interval typically hovers above zero,
although the coefficient is only consistently significant after
1993. It is only for the short rate
![]() that the coefficient is
significantly different from zero during the whole sample period
that is analyzed. The overall instability of the regression
coefficients over time is in line with the results of the formal
test procedures of Pettenuzzo and Timmermann (2005) and Paye and
Timmermann (2006).
that the coefficient is
significantly different from zero during the whole sample period
that is analyzed. The overall instability of the regression
coefficients over time is in line with the results of the formal
test procedures of Pettenuzzo and Timmermann (2005) and Paye and
Timmermann (2006).
Given the relative strength of the findings for the short interest rate and the term spread found so far, I also present expanding window regression estimates for individual country time-series regressions for these two variables. The time-series OLS estimates for the short interest rate, with corresponding robust 90 percent confidence intervals calculated using the Campbell and Yogo method, are shown in Figure 3, for the twelve developed markets with the longest sample periods.16 For all of the countries considered, except Japan, a very similar pattern is evident. After around 1980, the estimated coefficients and confidence intervals stabilize; in most cases, this occurs on or below zero, indicating a significant or near significant negative relationship. The analogous results for the term spread are shown in Figure 4. These show a similar pattern to that found for the short interest rate, but overall the results are perhaps somewhat weaker.
VI.G Out-of-Sample Evidence
Finally, the out-of-sample predictability of stock returns is
considered, using the forecasting variables discussed above. To
allow for a sufficient sample size in the out-of-sample analysis,
which requires an initial 'training-sample' to obtain the estimates
on which the first round of forecasts is based, I exclude all
countries with less than 40 years of data; this allows for a
20-year training period and a minimum of a 20-year forecasting
period. In each period following the first twenty years, the
coefficients are re-estimated, with the latest observations
included. Next period's returns are forecasted based on the
estimated regression equation. These `conditional' forecasts, based
on the regression model, are compared to the `unconditional'
forecasts, which in each period are identical to the sample mean of
the then available past returns. To compare the conditional and
unconditional forecasts, an out-of-sample ![]() is
calculated,
is
calculated,
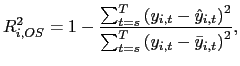
| (30) |
where
![]() and
and
![]() are the conditional and
unconditional forecasts, respectively, and
are the conditional and
unconditional forecasts, respectively, and ![]() is the
length of the training sample. The
is the
length of the training sample. The
![]() statistic will be positive when
the conditional forecast outperforms the unconditional one. I
consider out-of-sample forecasts that are based on both the
time-series and pooled fixed effects estimates of the slope
coefficients in the forecasting regressions. It is possible that
the pooled estimate yields better out-of-sample performance if the
time-series estimate is imprecise due to fewer available
observations, even though the fitting of individual coefficients
for each country allows for more freedom.
statistic will be positive when
the conditional forecast outperforms the unconditional one. I
consider out-of-sample forecasts that are based on both the
time-series and pooled fixed effects estimates of the slope
coefficients in the forecasting regressions. It is possible that
the pooled estimate yields better out-of-sample performance if the
time-series estimate is imprecise due to fewer available
observations, even though the fitting of individual coefficients
for each country allows for more freedom.
The forward demeaning used in the recursively demeaned estimator makes it less suitable for out-of-sample exercises. The standard fixed effects estimator is therefore used, even though it will tend to produce biased estimates for the valuation ratios, which may limit the benefits of using pooled estimates for these variables when forming forecasts.
Although the strongest in-sample results were found for the
interest rate variables, it is still worth briefly considering the
out-of-sample performance of the valuation ratios. As seen in
Panels A and B of Table 5, there are three
countries where the earnings-price ratio is a significant predictor
according to the Campbell and Yogo test, and two countries where
the dividend-price ratio is significant. For each of the
regressions, which delivered significant in-sample results with the
earnings-price ratio as a predictor, the out-of-sample ![]() is positive when the forecasts are based on either the
time-series estimates or the pooled estimates. The results for the
dividend-price ratio are overall weaker, with the out-of-sample
is positive when the forecasts are based on either the
time-series estimates or the pooled estimates. The results for the
dividend-price ratio are overall weaker, with the out-of-sample
![]() most often negative.
most often negative.
As seen in Panel C of Table 5, there are five
countries for which the domestic short rate has a significant
negative predictive relationship. For these five countries, the
out-of-sample ![]() are positive in three cases when
using the conditional forecasts that are based on the pooled
estimates; using the time-series based forecasts, the out-of-sample
are positive in three cases when
using the conditional forecasts that are based on the pooled
estimates; using the time-series based forecasts, the out-of-sample
![]() for Spain alone is positive. In total,
there are 10 countries for which the estimated coefficients are
more than one standard deviation away from zero (with the right
sign), and for six of these the out-of-sample
for Spain alone is positive. In total,
there are 10 countries for which the estimated coefficients are
more than one standard deviation away from zero (with the right
sign), and for six of these the out-of-sample ![]() are positive when using the pooled forecasts, but only
for one when using the time-series based forecasts.
are positive when using the pooled forecasts, but only
for one when using the time-series based forecasts.
Panel D of Table 5
presents the results for the term spread. In this case, a
significant in-sample predictive relationship is seen in seven
countries, according to the Campbell and Yogo test, and ten
countries have (positive) coefficients that are more than one
standard deviation away from zero. When basing the forecasts on the
pooled estimates, the conditional forecast beats the unconditional
one in all seven of the countries with significant in-sample
results, and in nine out of ten of the countries with a ![]() statistic greater than one. For the time-series based
forecasts, the unconditional forecast is beaten only in four out of
the seven significant countries and in five out of ten of the
countries with a
statistic greater than one. For the time-series based
forecasts, the unconditional forecast is beaten only in four out of
the seven significant countries and in five out of ten of the
countries with a ![]() statistic greater than one.
statistic greater than one.
Overall, the results in Table 5 provide some evidence that a significant in-sample relationship also tends to be associated with out-of-sample predictive power, particularly for the term spread.17 In addition, forecasts based on the pooled estimates typically out-perform forecasts based on the time-series estimates. Thus, it is possible that pooled methods could be useful in reducing risk when using conditional forecasts in portfolio choice.
VII Conclusion
I analyze stock return predictability in a large global data set with 40 different markets and develop new econometric methods for predictive regressions with panel data. The theoretical results provide an important extension to the existing literature on time-series methods for predictive regressions and show that a careful analysis of the impact of nearly persistent and endogenous regressors is required also in the panel data case.
The empirical analysis delivers two main findings: (i) Traditional valuation measures such as the dividend- and earnings-price ratios have very limited predictive ability in international data. It is evident, however, that using methods that do not account for the persistence and endogeneity of these variables would lead one to vastly misjudge their predictive powers. (ii) Interest rate variables are more robust predictors of stock returns, although their predictive power is mostly evident in developed markets.
The international results for the interest rate variables are similar to those of the U.S. while the overall findings for the earnings- and dividend-price ratios are substantially weaker. In summary, the results presented in this paper provide strong evidence that there is a predictable component in stock returns, which is captured at least partially by interest rate variables.
Appendix
A Formal Assumptions
1. The factor loadings
2. Rank
The rank condition on ![]() is required for
identification in the estimation procedures that control for the
common factors. It essentially states that all information
regarding the common factors in the regressors can potentially be
recovered from the data on the regressors.
is required for
identification in the estimation procedures that control for the
common factors. It essentially states that all information
regarding the common factors in the regressors can potentially be
recovered from the data on the regressors.
1.
2. The innovations to the regressor,
3. The long-run variance-covariance matrix of
4.
5.
The innovations to the dependent variable, ![]() and
and ![]() , satisfy martingale
difference sequences (mds) and the innovations to the regressor,
, satisfy martingale
difference sequences (mds) and the innovations to the regressor,
![]() and
and ![]() , are
assumed to follow general linear processes. The idiosyncratic
innovations
, are
assumed to follow general linear processes. The idiosyncratic
innovations
![]() are
independent of the common factors
are
independent of the common factors
![]() , and
cross-sectionally independent.
, and
cross-sectionally independent.
By standard arguments,
![]() , where
, where
![]() denote a
denote a ![]() dimensional Brownian motion.
Further, by the results in Phillips (1987, 1988), it follows that
as
dimensional Brownian motion.
Further, by the results in Phillips (1987, 1988), it follows that
as
![]() ,
,
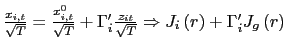 , where
, where
![]() and
and
![]() . Analogous results hold for the time-series demeaned data,
. Analogous results hold for the time-series demeaned data,
![]() ,
with
,
with ![]() replaced by
replaced by
![]() ;
when there is no risk of confusion, the dependence of
;
when there is no risk of confusion, the dependence of
![]() and
and ![]() on
on
![]() will be suppressed. Finally, the following
two lemmas summarize the key asymptotic results that are used to
prove the main results in the paper.
will be suppressed. Finally, the following
two lemmas summarize the key asymptotic results that are used to
prove the main results in the paper.
(a)
![$ \Phi_{ux}\equiv E\left[ \left( \int_{0}^{1}dB_{1,i}J_{i}\right) \left( \int_{0}^{1}dB_{1,i} J_{i}\right) ^{\prime}\right] $](img559.gif) ,
,
![$ \Phi_{uz}\equiv\Gamma^{\prime}\left( E\left[ \left. \left( \int_{0}^{1}dB_{1,i}J_{g}\right) \left( \int _{0}^{1}dB_{1,i}J_{g}\right) ^{\prime}\right\vert \mathcal{C}\right] \right) \Gamma$](img560.gif) , and
, and
(b)
![$ \Phi _{fx}=\gamma^{\prime}E\left[ \left. \left( \int_{0}^{1}dB_{f}J_{i}\right) \left( \int_{0}^{1}dB_{f}J_{i}\right) ^{\prime}\right\vert \mathcal{C} \right] \gamma$](img566.gif) .
.(d)
(e)
(f)
(g)
1.
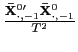 is of order
is of order
2.
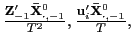
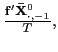 and
and
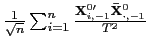 are of order
are of order
B Technical Proofs
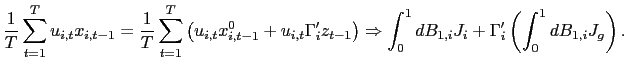
![$\displaystyle \frac{1}{\sqrt{n}}\sum_{i=1}^{n}\int_{0}^{1}dB_{1,i}J_{i}\Rightarrow N\left( 0,E\left[ \left( \int_{0}^{1}dB_{1,i}J_{i}\right) \left( \int_{0} ^{1}dB_{1,i}J_{i}\right) ^{\prime}\right] \right) . $](img588.gif)
![$\displaystyle \frac{1}{\sqrt{n}}\sum_{i=1}^{n}\Gamma_{i}^{\prime}\left( \int_{0} ^{1}dB_{1,i}J_{g}\right) \Rightarrow MN\left( 0,E\left[ \left. \Gamma _{i}^{\prime}\left( \int_{0}^{1}dB_{1,i}J_{g}\right) \left( \int_{0} ^{1}dB_{1,i}J_{g}\right) ^{\prime}\Gamma_{i}\right\vert \mathcal{C}\right] \right) . $](img593.gif)
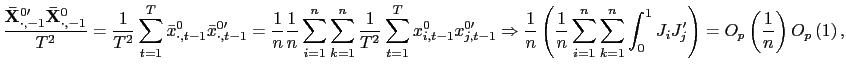
![$\displaystyle \frac{\tilde{x}_{i,t=\left[ Tr\right] }}{\sqrt{T}}=\frac{x_{i,t}}{\sqrt{T} }-\frac{1}{n}\sum_{i=1}^{n}\frac{1}{T^{3/2}}\sum_{t=1}^{T}x_{i,t} =\frac{x_{i,t}}{\sqrt{T}}+O_{p}\left( \frac{1}{\sqrt{n}}\right) \Rightarrow J_{i}\left( r\right) , $](img601.gif)
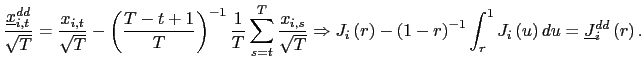
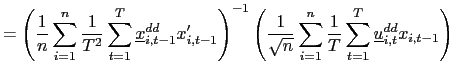
|
|
![$\displaystyle \Rightarrow\left( \frac{1}{n}\sum_{i=1}^{n}\int_{0}^{1}\underline{J} _{i}^{dd}J_{i}^{\prime}\right) ^{-1}\left( \frac{1}{\sqrt{n}}\sum_{i=1} ^{n}\int_{0}^{1}\left[ dB_{1,i}\left( r\right) -\left( 1-r\right) ^{-1}\Delta_{r}B_{1,i}\left( 1\right) dr\right] J_{i}\right) ,$](img612.gif)
|
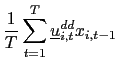
|
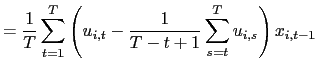
|
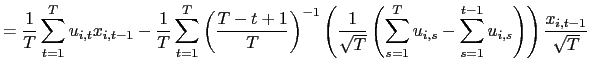
|
|
| (31) | 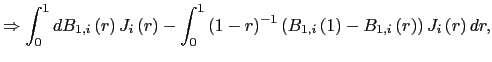
|
![$\displaystyle \equiv\int_{0}^{1}\left[ dB_{1,i}\left( r\right) -\left( 1-r\right) ^{-1}\Delta_{r}B_{1,i}\left( 1\right) dr\right] J_{i}\left( r\right)$](img618.gif)
|
by standard arguments. By the independent increments property of the Brownian motion, it follows that the expectation of (31) is equal to zero. Denote
![$\displaystyle \underline{\Phi}_{ux}^{RD}=E\left[ \left( \int_{0}^{1}J_{i}\left( r\right) \left[ dB_{1,i}\left( r\right) -\left( 1-r\right) ^{-1}\Delta_{r} B_{1,i}\left( 1\right) dr\right] \right) \left( \int_{0}^{1}J_{i}\left( r\right) \left[ dB_{1,i}\left( r\right) -\left( 1-r\right) ^{-1} \Delta_{r}B_{1,i}\left( 1\right) dr\right] \right) ^{\prime}\right] , $](img620.gif)
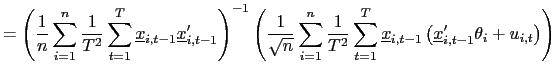
|
|
![$\displaystyle \Rightarrow N\left( 0,\underline{\Omega}_{xx}^{-1}E\left[ \left( \int _{0}^{1}\underline{J}_{i}\underline{J}_{i}^{\prime}\right) \theta_{i}\left( \left( \int_{0}^{1}\underline{J}_{i}\underline{J}_{i}^{\prime}\right) \theta_{i}\right) ^{\prime}\right] \underline{\Omega}_{xx}^{-1}\right) \equiv N\left( 0,\underline{\Omega}_{xx}^{-1}\underline{\Phi}_{xx}^{\theta }\underline{\Omega}_{xx}^{-1}\right) ,$](img626.gif)
|
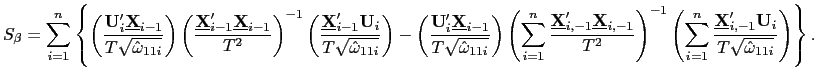
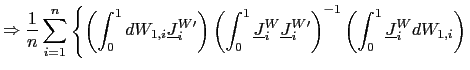
|
|
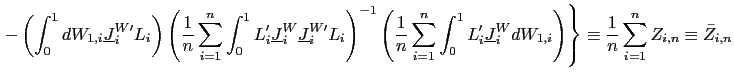
|
![$\displaystyle \rightarrow_{p}E\left[ \left( \int_{0} ^{1}dW_{1\cdot2,i}\underline{J}_{i}^{W\prime}\right) \left( \int_{0} ^{1}\underline{J}_{i}^{W}\underline{J}_{i}^{W\prime}\right) ^{-1}\left( \int_{0}^{1}\underline{J}_{i}^{W}dW_{1\cdot2,i}\right) \right]$](img657.gif)
|
|
![$\displaystyle +\delta^{\prime}E\left[ \left( \int_{0}^{1}dW_{2,i}\underline{J} _{i}^{W\prime}\right) \left( \int_{0}^{1}\underline{J}_{i}^{W}\underline {J}_{i}^{W\prime}\right) ^{-1}\left( \int_{0}^{1}\underline{J}_{i} ^{W}dW_{2,i}^{\prime}\right) \right] \delta$](img658.gif)
|
|
![$\displaystyle -\delta^{\prime}E\left[ \int_{0}^{1}dW_{2,i}\underline{J}_{i}^{W\prime }\right] E\left[ \int_{0}^{1}\underline{J}_{i}^{W}\underline{J}_{i} ^{W\prime}\right] ^{-1}E\left[ \int_{0}^{1}\underline{J}_{i}^{W} dW_{2,i}^{\prime}\right] \delta.$](img659.gif)
|
![$\displaystyle \sqrt{n}T\left( \hat{\beta}_{Pool}^{+}-\beta\right) =\left( \frac{1}{n} \sum_{i=1}^{n}\frac{\mathbf{X}_{i,-1}^{\prime}\mathbf{M}_{\mathbf{\bar{H}} }\mathbf{X}_{i,-1}}{T^{2}}\right) ^{-1}\left[ \left( \frac{1}{\sqrt{n}} \sum_{i=1}^{n}\frac{\mathbf{X}_{i,-1}^{\prime}\mathbf{M}_{\mathbf{\bar{H}} }\mathbf{f}\gamma_{i}}{T}\right) +\left( \frac{1}{\sqrt{n}}\sum_{i=1} ^{n}\frac{\mathbf{X}_{i,-1}^{\prime}\mathbf{M}_{\mathbf{\bar{H}}} \mathbf{u}_{i}}{T}\right) \right] . $](img662.gif)
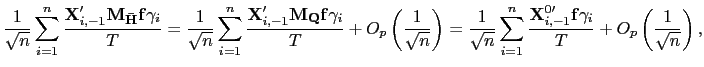
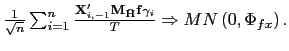 Similarly,
Similarly,
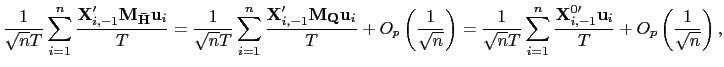
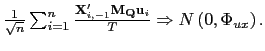 Finally,
Finally,
![$\displaystyle \frac{1}{n}\sum_{i=1}^{n}\frac{\mathbf{X}_{i,-1}^{\prime}\mathbf{M} _{\mathbf{\bar{H}}}\mathbf{X}_{i,-1}}{T^{2}}=\frac{1}{n}\sum_{i=1}^{n} \frac{\mathbf{X}_{i,-1}^{\prime}\mathbf{M}_{\mathbf{Q}}\mathbf{X}_{i,-1} }{T^{2}}+O_{p}\left( \frac{1}{\sqrt{n}}\right) =\frac{1}{n}\sum_{i=1} ^{n}\frac{\mathbf{X}_{i,-1}^{0\prime}\mathbf{X}_{i,-1}^{0}}{T^{2}} +O_{p}\left( \frac{1}{\sqrt{n}}\right) \rightarrow_{p}E\left[ \int_{0} ^{1}J_{i}J_{i}^{\prime}\right] , $](img672.gif)
References
Amihud, Y., and C. Hurvich. "Predictive Regressions: A Reduced-Bias Estimation Method." Journal of Financial and Quantitative Analysis, 39 (2004), 813-841.
Andrews, D.W.K., 2005. "Cross-section Regression with Common Shocks", Econometrica 73, 1551-1585.
Ang, A., and G. Bekaert. "Stock Return Predictability: Is it There?" Review of Financial Studies, 20 (2007), 651-707.
Campbell, J.Y. "Consumption-Based Asset Pricing." In Handbook of the Economics of Finance, Vol. 1B, Constantinides, G.M., Harris M., and Stulz R. eds. Amsterdam: North-Holland (2003).
Campbell, J.Y., and J.H. Cochrane. "By Force of Habit: A Consumption-Based Explanation of Aggregate Stock Market Behavior." Journal of Political Economy, 107 (1999), 205-251.
Campbell, J.Y., and R. Shiller. "Stock Prices, Earnings, and Expected Dividends." Journal of Finance, 43 (1988), 661-676.
Campbell., J.Y., and S.B. Thompson. "Predicting the Equity Premium Out of Sample: Can Anything Beat the Historical Average?" Working Paper, Harvard University (2004).
Campbell, J.Y., and M. Yogo. "Efficient Tests of Stock Return Predictability." Journal of Financial Economics, 81 (2006), 27-60.
Cavanagh, C., G. Elliot, and J. Stock. "Inference in Models with Nearly Integrated Regressors." Econometric Theory, 11 (1995), 1131-1147.
Fama, E.F., and K.R. French. "Dividend Yields and Expected Stock Returns." Journal of Financial Economics, 22 (1988), 3-25.
Fama, E.F., and K.R. French. "Business Conditions and Expected Returns on Stocks and Bonds." Journal of Financial Economics, 25 (1989), 23-49.
Ferson, W.E., and C.R. Harvey. "The Risk and Predictability of International Equity Returns." Review of Financial Studies, 6 (1993), 527-566.
Ferson, W.E., and C.R. Harvey. "Sources of Risk and Expected Returns in Global Equity Markets." Journal of Banking and Finance, 18 (1994), 775-803.
Harvey C.R. "The World Price of Covariance Risk." Journal of Finance, 46 (1991), 111-157.
Harvey C.R. "Predictable Risk and Returns in Emerging Markets." Review of Financial Studies, 8 (1995), 773-816.
Jansson, M., and M.J. Moreira. "Optimal Inference in Regression Models with Nearly Integrated Regressors." Econometrica, 74 (2006), 681-714.
Jorion, P., and W.N. Goetzmann. "Global Stock Markets in the Twentieth Century." Journal of Finance, 54 (1999), 953-980.
Kaminsky G.L., and S.L. Schmukler. "Short-Run Pain, Long-Run Gain: The Effects of Financial Liberalization." Working Paper, George Washington University (2002).
Lewellen, J. "Predicting Returns with Financial Ratios." Journal of Financial Economics, 74 (2004), 209-235.
Mankiw, N.G., and M.D. Shapiro. "Do We Reject Too Often? Small Sample Properties of Tests of Rational Expectations Models." Economics Letters, 20 (1986), 139-145.
Menzly, L.; T. Santos; and P. Veronesi. "Understanding Predictability." Journal of Political Economy, 112 (2004), 1-47.
Moon, H.R., and P.C.B. Phillips. "Estimation of Autoregressive Roots near Unity using Panel Data." Econometric Theory, 16 (2000), 927-998.
Neyman, J., and E.L. Scott. "Consistent Estimates Based on Partially Consistent Observations." Econometrica, 16 (1948), 1-32.
Nickell, S. "Biases in Dynamic Models with Fixed Effects." Econometrica, 49 (1981), 1417-1426.
Paye, B.S., and A. Timmermann. "Instability of Return Prediction Models." Journal of Empirical Finance, 13 (2006), 274-315.
Pesaran, M.H. "Estimation and Inference in Large Heterogeneous Panels with a Multifactor Error Structure." Econometrica, (2006), forthcoming.
Pesaran, M.H. " Testing Slope Homogeneity in Large Panels." Journal of Econometrics, (2007), forthcoming.
Pettenuzzo, D., and A. Timmermann. "Predictability of Stock Returns and Asset Allocation under Structural Breaks." Working paper, UCSD (2005).
Phillips, P.C.B. "Towards a Unified Asymptotic Theory of Autoregression." Biometrika, 74 (1987), 535-547.
Phillips, P.C.B. "Regression Theory for Near-Integrated Time Series." Econometrica, 56 (1988), 1021-1043.
Phillips, P.C.B., and H.R. Moon. "Linear Regression Limit Theory for Nonstationary Panel Data." Econometrica, 67 (1999), 1057-1111.
Phillips, P.C.B., and H.R. Moon. "Nonstationary Panel Data Analysis: An Overview of Some Recent Developments." Econometric Reviews, 19 (2000), 263-286.
Polk, C., S. Thompson, and T. Vuolteenaho. "Cross-sectional Forecasts of the Equity Premium." Working Paper, Department of Economics, Harvard University (2004).
Stambaugh, R. "Predictive Regressions." Journal of Financial Economics, 54 (1999), 375-421.
Stock, J.H. "Confidence Intervals for the Largest Autoregressive Root in U.S. Economic Time-Series." Journal of Monetary Economics, 28 (1991), 435-460.
Sul, D.; P.C.B. Phillips; and C.Y. Choi. "Prewhitening Bias in HAC Estimation." Oxford Bulletin of Economics and Statistics, 67 (2005), 517-546.
Swamy, P.A.V.B. "Efficient Inference in a Random Coefficient Regression Model." Econometrica, 38 (1970), 311-323.
Table 1: Size Results from the Monte Carlo Study - Panel A: No Common Factor
The table shows the average rejection rates under the null of β = 0, for the t-tests corresponding to the respective estimators; the nominal size of the tests are 5 percent. The differing values of δ are given in the top row of the table and the results are based on 10,000 repetitions. The sample size used is T = 100 and n = 20. Panel A shows the results when no common factors are included in the data generating process, Panel B shows the effects of including common factors in the data but ignoring them in the estimation, and Panel C shows the results when common factors are included and accounted for in the estimation.
| Estimator | δ = 0.0 | δ = -0.4 | δ = -0.7 | δ = -0.95 |
|---|---|---|---|---|
| | 0.078 | 0.177 | 0.379 | 0.563 |
| | 0.069 | 0.071 | 0.071 | 0.074 |
Table 1: Size Results from the Monte Carlo Study - Panel B: Common Factor with no Correction
| Estimator | δ = 0.0 | δ = -0.4 | δ = -0.7 | δ = -0.95 |
|---|---|---|---|---|
| | 0.430 | 0.503 | 0.559 | 0.604 |
| | 0.353 | 0.348 | 0.356 | 0.347 |
Table 1: Size Results from the Monte Carlo Study - Panel C: Common Factor Using Correction
| Estimator | δ = 0.0 | δ = -0.4 | δ = -0.7 | δ = -0.95 |
|---|---|---|---|---|
| | 0.026 | 0.065 | 0.157 | 0.284 |
| | 0.029 | 0.031 | 0.039 | 0.052 |
Table 2: Size and Power for the Test of Slope Homogeneity - Panel A: No Common Factor
The table shows the average rejection rates for the Δβ-test of slope homogeneity under the null of βi = β = 0 for all i, as well as under two different alternative hypotheses; the nominal size of the test is 5 percent. The alternative hypotheses are given by βi = β + βθi , where θi is a standard normal random variable, independent across i and β is equal to 0.05 and 0.1 under Alternative 1 and Alternative 2, respectively. The differing values of δ are given in the top row of the table and the results are based on 10,000 repetitions. The sample size used is T = 100 and N = 20. Panel A shows the results when no common factors are included in the data generating process and Panel B shows the effects of including common factors in the data.
| Hypothesis | δ = 0.0 | δ = -0.4 | δ = -0.7 | δ = -0.95 |
|---|---|---|---|---|
| Null | 0.014 | 0.015 | 0.014 | 0.016 |
| Alternative 1 | 0.453 | 0.450 | 0.445 | 0.439 |
| Alternative 2 | 0.958 | 0.955 | 0.956 | 0.951 |
Table 2: Size and Power for the Test of Slope Homogeneity - Panel B: Common Factor
| Hypothesis | δ = 0.0 | δ = -0.4 | δ = -0.7 | δ = -0.95 |
|---|---|---|---|---|
| Null | 0.007 | 0.008 | 0.007 | 0.009 |
| Alternative 1 | 0.367 | 0.347 | 0.346 | 0.324 |
| Alternative 2 | 0.923 | 0.922 | 0.916 | 0.913 |
Table 3: Pooled Results - Panel A: The Earnings-Price Ratio
The first column indicates which panel is being used, with (1950.1-) denoting
that all observations before 1950 are dropped from that panel. The next two columns give the number of
individual time series and total number of observations in the panel. The column labeled Δβ shows the outcome of the test of slope homogeneity.
The following four columns report the
results from the estimation procedures that do not control for common factors.
The pooled estimate based on recursive demeaning of the data, the standard fixed effects estimate,
and the two corresponding t-statistics are shown. The next four columns give the corresponding results
when controlling for common factors. The last column gives the number of significant coefficients in
the individual time-series regressions performed on each of the time-series in the panel,
based on the Campbell and Yogo methods. The ![]() -statistics and the Δβ-statistics that are significant
at the one-sided five percent level (i.e. greater than 1.65) are shown with a * next to them.
-statistics and the Δβ-statistics that are significant
at the one-sided five percent level (i.e. greater than 1.65) are shown with a * next to them.
| Panel | n | # obs | Δβ | No Control for Common Factors: | No Control for Common Factors: | No Control for Common Factors: tRD | No Control for Common Factors: tFE | Controlling for Common Factors: | Controlling for Common Factors: | Controlling for Common Factors: | Controlling for Common Factors: | CYsig |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Global | 38 | 13,610 | 2.234* | 0.020 | 0.010 | 0.334 | 4.079 | 0.002 | 0.001 | 1.126 | 1.518 | 5 |
| Global (1950.1-) | 38 | 12,400 | 1.984* | 0.035 | 0.010 | 0.391 | 3.905 | 0.002 | 0.001 | 1.172 | 1.817 | 4 |
| Developed | 23 | 10,151 | 1.399 | -0.008 | 0.005 | -0.751 | 2.866 | -0.001 | 0.000 | -0.802 | -0.805 | 2 |
| Developed (1950.1-) | 23 | 8,941 | 1.030 | -0.003 | 0.004 | -0.353 | 2.637 | -0.001 | 0.000 | -0.688 | -0.029 | 1 |
| Emerging | 16 | 3,518 | -1.638 | -0.018 | 0.024 | -1.441 | 6.252 | 0.011 | 0.007 | 2.438* | 2.415 | 4 |
Table 3: Pooled Results - Panel B: The Dividend-Price Ratio
| Panel | n | # obs | Δβ | No Control for Common Factors: | No Control for Common Factors: | No Control for Common Factors: tRD | No Control for Common Factors: tFE | Controlling for Common Factors: | Controlling for Common Factors: | Controlling for Common Factors: | Controlling for Common Factors: | CYsig |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Global | 46 | 20,594 | 2.485* | 0.006 | 0.006 | 1.216 | 3.352 | 0.001 | 0.000 | 0.628 | 0.953 | 6 |
| Global (1950.1-) | 41 | 14,947 | 1.905* | 0.007 | 0.009 | 1.354 | 4.742 | 0.002 | 0.001 | 2.334* | 3.318 | 7 |
| Developed | 30 | 17,001 | 1.733* | 0.001 | 0.004 | 0.556 | 2.149 | 0.000 | 0.000 | -0.344 | -0.142 | 2 |
| Developed (1950.1-) | 25 | 11,354 | 1.263 | 0.001 | 0.007 | 0.679 | 4.583 | 0.002 | 0.001 | 2.402* | 4.307 | 3 |
| Emerging | 16 | 3,593 | 1.156 | -0.108 | 0.013 | -0.371 | 2.814 | 0.005 | 0.004 | 1.658* | 2.238 | 4 |
Table 3: Pooled Results - Panel C: The Short Rate
| Panel | n | # obs | Δβ | No Control for Common Factors: | No Control for Common Factors: | No Control for Common Factors: tRD | No Control for Common Factors: tFE | Controlling for Common Factors: | Controlling for Common Factors: | Controlling for Common Factors: | Controlling for Common Factors: | CYsig |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Global | 39 | 15,260 | 2.666* | 0.224 | 0.100 | 1.103 | 0.494 | 0.098 | 0.086 | 0.476 | 0.462 | 11 |
| Developed | 23 | 11,468 | 1.341 | -0.525 | -0.980 | -1.858 | -4.164 | -0.958 | -0.687 | -4.494* | -3.958 | 8 |
| Emerging | 16 | 3,792 | 1.846* | 0.250 | 0.137 | 1.115 | 0.604 | 0.107 | 0.087 | 0.484 | 0.434 | 3 |
Table 3: Pooled Results - Panel D: The Term Spread
| Panel | n | # obs | Δβ | No Control for Common Factors: | No Control for Common Factors: | No Control for Common Factors: tRD | No Control for Common Factors: tFE | Controlling for Common Factors: | Controlling for Common Factors: | Controlling for Common Factors: | Controlling for Common Factors: | CYsig |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Global | 35 | 13,048 | 2.310* | 0.223 | 0.902 | 0.736 | 1.247 | 0.051 | 0.113 | 0.185 | 0.423 | 12 |
| Developed | 23 | 10,784 | 1.368 | 2.133 | 1.957 | 3.906 | 3.869 | 1.685 | 1.794 | 2.809* | 3.318 | 10 |
| Emerging | 12 | 2,264 | 0.612 | 0.028 | 0.318 | 0.147 | 0.353 | -0.159 | -0.089 | -0.712 | -0.469 | 2 |
Table 4: Country Level Results - Panel A: The Earnings-Price Ratio
The first and second columns indicate the country and sample period, respectively, on which the estimates are based. The third and fourth columns show the OLS estimates and corresponding t-statistics, respectively. A * next to the coefficient estimate indicates that the coefficient is significantly different from zero, with the expected sign, according to the robust 90 percent confidence interval obtained from the Campbell and Yogo procedure; this is equivalent to a one-sided rejection of the null hypothesis at the five percent level.
Country | Sample | ||
|---|---|---|---|
Argentina | 1988.1 - 2004.6 | 0.041* | 2.277 |
Australia | 1962.1 - 2004.6 | 0.010 | 1.468 |
Austria | 1981.11 - 2004.6 | 0.002 | 0.423 |
Belgium | 1969.9 - 2004.6 | 0.012 | 1.305 |
Brazil | 1988.3 - 2004.5 | 0.022 | 1.632 |
Canada | 1956.3 - 2004.6 | 0.000 | 0.064 |
Chile | 1988.3 - 2004.6 | 0.024 | 2.324 |
Denmark | 1970.1 - 2004.6 | 0.001 | 0.165 |
Finland | 1988.3 - 2004.6 | -0.005 | -0.615 |
France | 1971.11 - 2004.6 | -0.001 | -0.112 |
Germany | 1969.9 - 2004.6 | 0.008 | 1.359 |
Greece | 1977.3 - 2004.6 | -0.003 | -0.302 |
Hong Kong | 1973.1 - 2004.6 | 0.060 | 3.610 |
Hungary | 1993.3 - 2004.6 | 0.001 | 0.088 |
India | 1988.3 - 2003.12 | 0.025 | 1.640 |
Ireland | 1990.7 - 2004.6 | 0.034 | 1.731 |
Italy | 1981.3 - 2004.6 | 0.005 | 0.959 |
Japan | 1956.3 - 2004.6 | 0.006 | 1.864 |
Jordan | 1988.3 - 2003.2 | 0.025* | 1.787 |
Malaysia | 1973.1 - 2004.6 | 0.022 | 1.553 |
Mauritius | 1996.3 - 2002.12 | 0.003 | 0.225 |
Mexico | 1988.1 - 2004.6 | 0.017 | 0.959 |
Netherlands | 1969.9 - 2004.6 | 0.002 | 0.439 |
New Zealand | 1988.3 - 2004.6 | -0.007 | -0.979 |
Norway | 1970.1 - 2001.9 | -0.004 | -0.764 |
Philippines | 1982.3 - 2004.5 | 0.011 | 0.837 |
Poland | 1992.3 - 2004.5 | 0.025 | 1.398 |
Portugal | 1988.3 - 2004.6 | 0.010 | 0.832 |
Singapore | 1973.1 - 2004.6 | 0.041 | 2.821 |
South Africa | 1960.3 - 2004.6 | 0.020* | 2.277 |
Spain | 1980.1 - 2004.6 | 0.018 | 1.405 |
Sweden | 1969.9 - 2004.6 | 0.002 | 0.343 |
Switzerland | 1969.9 - 2004.6 | -0.006 | -0.879 |
Taiwan | 1988.3 - 2004.1 | 0.043 | 1.761 |
Thailand | 1975.6 - 2004.6 | 0.013 | 1.300 |
Turkey | 1986.3 - 2004.6 | 0.035 | 2.706 |
UK | 1928.1 - 2004.6 | 0.010* | 2.471 |
UK | 1950.1 - 2004.6 | 0.011* | 2.513 |
USA | 1871.3 - 2004.6 | 0.011* | 3.398 |
USA | 1950.1 - 2004.6 | 0.007 | 1.874 |
Table 4: Country Level Results - Panel B: The Dividend-Price Ratio
Country | Sample | ||
|---|---|---|---|
Argentina | 1988.3 - 2004.6 | -0.003 | -0.224 |
Australia | 1882.12 - 2004.6 | 0.005 | 1.416 |
Australia | 1950.1 - 2004.6 | 0.013* | 1.916 |
Austria | 1970.2 - 2004.6 | 0.001 | 0.196 |
Belgium | 1952.1 - 2004.6 | 0.003 | 0.694 |
Brazil | 1988.3 - 2004.5 | 0.000 | -0.016 |
Canada | 1934.3 - 2004.6 | 0.006 | 1.592 |
Canada | 1950.1 - 2004.6 | 0.007 | 1.483 |
Chile | 1983.3 - 2004.6 | 0.019* | 2.234 |
Denmark | 1970.2 - 2004.6 | 0.000 | 0.071 |
Finland | 1962.3 - 2004.6 | -0.004 | -0.742 |
France | 1898.1 - 1914.7 | 0.048 | 1.681 |
France | 1919.2 - 1940.3 | 0.018 | 0.813 |
France | 1941.5 - 2004.6 | -0.001 | -0.353 |
France | 1950.1 - 2004.6 | 0.004 | 0.836 |
Germany | 1872.9 - 1942.3 | 0.035 | 2.123 |
Germany | 1953.2 - 2004.6 | 0.003 | 0.451 |
Greece | 1977.3 - 2004.6 | 0.003 | 0.505 |
Hong Kong | 1973.1 - 2004.6 | 0.070 | 4.108 |
Hungary | 1993.12 - 2004.6 | 0.017 | 0.874 |
India | 1988.3 - 2003.12 | 0.036 | 2.213 |
Ireland | 1990.7 - 2004.6 | 0.047 | 2.775 |
Israel | 1994.1 - 2004.6 | 0.018 | 1.139 |
Italy | 1925.3 - 2004.6 | -0.006 | -1.623 |
Italy | 1950.1 - 2004.6 | 0.006 | 0.988 |
Japan | 1922.1 - 1942.1 | -0.008 | -0.665 |
Japan | 1949.7 - 2004.6 | 0.006* | 2.474 |
Jordan | 1988.2 - 2003.2 | 0.013* | 1.802 |
Luxembourg | 1985.2 - 1994.12 | -0.007 | -0.512 |
Malaysia | 1973.1 - 2004.6 | 0.042 | 2.776 |
Mauritius | 1997.1 - 2002.12 | 0.004 | 0.515 |
Mexico | 1988.3 - 2004.6 | 0.037* | 2.273 |
Netherlands | 1969.9 - 2004.6 | 0.004 | 0.720 |
New Zealand | 1987.1 - 2004.6 | 0.039 | 2.290 |
Norway | 1970.2 - 2001.9 | 0.008 | 0.937 |
Philippines | 1982.3 - 2004.5 | 0.003 | 0.635 |
Poland | 1993.12 - 2004.5 | 0.045 | 2.451 |
Portugal | 1988.4 - 2004.6 | -0.004 | -0.367 |
Singapore | 1973.1 - 2004.6 | 0.034 | 2.714 |
South Africa | 1960.4 - 2004.6 | 0.018 | 2.063 |
Spain | 1940.6 - 1968.12 | 0.002 | 0.230 |
Spain | 1981.3 - 2004.6 | 0.003 | 0.638 |
Sweden | 1919.2 - 2004.6 | -0.002 | -0.532 |
Sweden | 1950.1 - 2004.6 | 0.006 | 1.140 |
Switzerland | 1966.4 - 2004.6 | 0.001 | 0.091 |
Taiwan | 1988.3 - 2004.1 | 0.024* | 2.188 |
Thailand | 1976.1 - 2004.6 | 0.004 | 0.620 |
Turkey | 1986.4 - 2004.6 | 0.041 | 2.687 |
UK | 1836.1 - 1916.12 | 0.006 | 1.585 |
UK | 1924.2 - 2004.6 | 0.018* | 2.970 |
UK | 1950.1 - 2004.6 | 0.026* | 3.550 |
USA | 1871.3 - 2004.6 | 0.004 | 1.105 |
USA | 1950.1 - 2004.6 | 0.009* | 2.294 |
Table 4: Country Level Results - Panel C: The Short Interest Rate
Country | Sample | ||
|---|---|---|---|
Argentina | 1988.1 - 2004.5 | 2.034 | 5.349 |
Australia | 1952.1 - 2004.3 | -0.711 | -1.260 |
Austria | 1970.1 - 2004.5 | -1.739 | -1.179 |
Belgium | 1952.1 - 2004.6 | -0.514 | -0.682 |
Brazil | 1988.1 - 2004.5 | -0.042 | -0.417 |
Canada | 1952.1 - 2004.5 | -1.489* | -2.540 |
Chile | 1983.1 - 2004.5 | 0.770 | 1.418 |
Denmark | 1970.1 - 2004.5 | -0.528 | -0.917 |
Finland | 1962.1 - 2004.5 | -1.369 | -1.541 |
France | 1952.1 - 2004.5 | -1.022 | -1.399 |
Germany | 1953.1 - 2004.5 | -3.201* | -2.572 |
Greece | 1977.1 - 2004.5 | 1.689 | 1.440 |
Hong Kong | 1970.1 - 2004.5 | -3.076 | -1.355 |
Hungary | 1991.3 - 2004.5 | -0.922 | -0.698 |
India | 1988.1 - 2003.12 | -1.368 | -0.794 |
Ireland | 1988.3 - 2004.5 | -0.338 | -0.292 |
Israel | 1993.1 - 2004.5 | 2.489 | 1.219 |
Italy | 1952.1 - 2004.5 | -0.886 | -1.512 |
Japan | 1952.1 - 2004.5 | 1.182 | 1.178 |
Jordan | 1988.1 - 2003.2 | -6.669* | -3.393 |
Malaysia | 1972.12 - 2004.5 | -4.135 | -1.091 |
Mauritius | 1989.9 - 2004.5 | -7.398* | -3.635 |
Mexico | 1988.1 - 2004.6 | -0.011 | -0.030 |
Netherlands | 1952.1 - 2004.5 | -1.932* | -2.213 |
New Zealand | 1986.8 - 2004.3 | -4.346* | -3.915 |
Norway | 1970.1 - 2001.9 | -1.589 | -1.223 |
Philippines | 1982.1 - 2004.5 | -0.173 | -0.175 |
Poland | 1991.6 - 2004.5 | 0.039 | 0.033 |
Portugal | 1988.3 - 2004.5 | -2.221* | -1.986 |
Singapore | 1970.1 - 2004.5 | -0.308 | -0.153 |
South Africa | 1960.3 - 2004.5 | -0.991 | -1.354 |
Spain | 1952.1 - 2004.5 | -1.609* | -3.045 |
Sweden | 1952.1 - 2004.5 | 0.475 | 0.651 |
Switzerland | 1966.3 - 2004.6 | -2.492* | -2.010 |
Taiwan | 1988.1 - 2004.1 | -4.339 | -0.798 |
Thailand | 1975.6 - 2004.6 | -5.321* | -3.540 |
Turkey | 1986.3 - 2004.6 | 0.518 | 0.595 |
UK | 1952.1 - 2004.5 | -0.475 | -0.629 |
USA | 1952.1 - 2004.5 | -1.825* | -2.558 |
Table 4: Country Level Results - Panel D: The Term Spread
Country | Sample | ||
|---|---|---|---|
Argentina | 1997.1-2004.6 | 2.682* | 2.169 |
Australia | 1952.1 - 2004.6 | 1.428 | 1.056 |
Austria | 1970.1 - 2004.6 | -0.976 | -0.345 |
Belgium | 1952.1 - 2004.6 | 0.822 | 0.366 |
Brazil | 1994.1 - 2004.5 | 0.006 | 0.005 |
Canada | 1952.1 - 2004.6 | 3.387* | 2.467 |
Denmark | 1970.1 - 2004.6 | 0.591 | 0.520 |
Finland | 1962.1 - 2004.6 | 2.559 | 1.345 |
France | 1952.1 - 2004.6 | 2.902* | 1.646 |
Germany | 1953.1 - 2004.6 | 3.402* | 1.780 |
Greece | 1993.3 - 2004.6 | -4.889 | -1.212 |
Hong Kong | 1994.11 - 2004.6 | 0.271 | 0.029 |
Hungary | 1997.4 - 2004.6 | 3.692 | 0.308 |
India | 1988.1 - 2003.12 | 1.813 | 0.936 |
Ireland | 1988.3 - 2004.6 | 0.111 | 0.069 |
Italy | 1952.1 - 2004.6 | 2.656* | 1.659 |
Japan | 1952.1 - 2004.6 | -3.154 | -1.997 |
Malaysia | 1972.12 - 2004.6 | 3.579 | 0.911 |
Mexico | 1995.3 - 2004.6 | -0.488 | -0.227 |
Netherlands | 1952.1 - 2004.6 | 2.922* | 1.824 |
New Zealand | 1986.8 - 2004.6 | 10.240* | 4.099 |
Norway | 1970.1 - 2001.9 | 3.022* | 1.497 |
Philippines | 1994.11 - 2004.5 | -0.966 | -0.331 |
Poland | 1994.4 - 2004.5 | 3.553 | 0.529 |
Portugal | 1988.3 - 2004.6 | 5.605 | 1.142 |
Singapore | 1988.1 - 2004.6 | 11.227 | 1.415 |
South Africa | 1960.3 - 2004.6 | 2.240 | 1.425 |
Spain | 1952.1 - 2004.6 | 3.678* | 3.555 |
Sweden | 1952.1 - 2004.6 | -0.106 | -0.061 |
Switzerland | 1966.3 - 2004.6 | 3.234* | 1.769 |
Taiwan | 1995.3 - 2004.1 | -4.869 | -0.388 |
Thailand | 1977.2 - 2004.6 | 6.253* | 2.275 |
Turkey | 1997.11 - 2004.6 | -1.474 | -1.065 |
UK | 1952.1 - 2004.6 | 0.941 | 0.711 |
USA | 1952.1 - 2004.6 | 4.946* | 2.826 |
Table 5: Out-of-Sample Results - Panel A: The Earnings-Price Ratio
The first and second columns indicate the country and the sample period that are used, respectively. The next three columns show the in-sample standard t-statistic, the full sample R2 expressed in percent, and whether the in-sample coefficient estimate is found signficant according to the Campbell and Yogo test. The following two columns show the out-of-sample R2 expressed in percent, based on the time-series estimates and the pooled estimates, respectively.
| Country | Sample | In-Sample: | In-Sample: | In-Sample: CYsig | Time-Series: | Pooled: |
|---|---|---|---|---|---|---|
| Australia | 1962.1 - 2004.6 | 1.468 | 0.423 | NO | -0.910 | -0.138 |
| Canada | 1956.3 - 2004.6 | 0.064 | 0.001 | NO | -0.529 | -1.719 |
| Japan | 1956.3 - 2004.6 | 1.864 | 0.598 | NO | 0.289 | 0.606 |
| South Africa | 1960.3 - 2004.6 | 2.277 | 0.969 | YES | 0.899 | 0.644 |
| UK | 1928.1 - 2004.6 | 2.471 | 0.662 | YES | 0.396 | 0.627 |
| USA | 1871.3 - 2004.6 | 3.398 | 0.718 | YES | 0.435 | 0.570 |
Table 5: Out-of-Sample Results - Panel B: The Dividend-Price Ratio
| Country | Sample | In-Sample: | In-Sample: | In-Sample: CYsig | Time-Series: | Pooled: |
|---|---|---|---|---|---|---|
| Australia | 1882.12 - 2004.6 | 1.416 | 0.138 | NO | -0.328 | 0.012 |
| Belgium | 1952.1 - 2004.6 | 0.694 | 0.077 | NO | -0.493 | -0.047 |
| Canada | 1934.3 - 2004.6 | 1.592 | 0.300 | NO | -0.160 | -0.294 |
| Finland | 1962.3 - 2004.6 | -0.742 | 0.109 | NO | -0.584 | -0.097 |
| France | 1941.5 - 2004.6 | -0.353 | 0.016 | NO | -0.186 | 0.151 |
| Germany | 1953.2 - 2004.6 | 0.451 | 0.033 | NO | -0.268 | -0.032 |
| Italy | 1925.3 - 2004.6 | -1.623 | 0.276 | NO | -1.280 | -0.661 |
| Japan | 1949.7 - 2004.6 | 2.474 | 0.921 | YES | -0.355 | 0.247 |
| South Africa | 1960.4 - 2004.6 | 2.063 | 0.798 | NO | 0.808 | 0.052 |
| Sweden | 1919.2 - 2004.6 | -0.532 | 0.028 | NO | -0.530 | -0.044 |
| UK | 1924.2 - 2004.6 | 2.970 | 0.908 | YES | 0.203 | -0.241 |
| USA | 1871.3 - 2004.6 | 1.105 | 0.076 | NO | -0.310 | -0.571 |
Table 5: Out-of-Sample Results - Panel C: The Short Interest Rate
| Country | Sample | In-Sample: | In-Sample: | In-Sample: CYsig | Time-Series: | Pooled: |
|---|---|---|---|---|---|---|
| Australia | 1952.1 - 2004.3 | -1.260 | 0.254 | NO | -0.990 | -0.828 |
| Belgium | 1952.1 - 2004.6 | -0.682 | 0.074 | NO | -0.812 | -0.569 |
| Canada | 1952.1 - 2004.5 | -2.540 | 1.019 | YES | -0.286 | -0.383 |
| Finland | 1962.1 - 2004.5 | -1.541 | 0.466 | NO | -0.024 | 0.278 |
| France | 1952.1 - 2004.5 | -1.399 | 0.311 | NO | -0.375 | 0.048 |
| Germany | 1953.1 - 2004.5 | -2.572 | 1.064 | YES | -0.141 | 0.702 |
| Italy | 1952.1 - 2004.5 | -1.512 | 0.363 | NO | -1.881 | -0.548 |
| Japan | 1952.1 - 2004.5 | 1.178 | 0.221 | NO | -0.355 | -0.948 |
| Netherlands | 1952.1 - 2004.5 | -2.213 | 0.775 | YES | -0.777 | -0.033 |
| South Africa | 1960.3 - 2004.5 | -1.354 | 0.345 | NO | -0.890 | 0.382 |
| Spain | 1952.1 - 2004.5 | -3.045 | 1.457 | YES | 0.093 | 2.970 |
| Sweden | 1952.1 - 2004.5 | 0.651 | 0.068 | NO | -0.894 | -1.898 |
| UK | 1952.1 - 2004.5 | -0.629 | 0.063 | NO | -1.705 | -1.855 |
| USA | 1952.1 - 2004.5 | -2.558 | 1.032 | YES | -1.134 | 0.902 |
Table 5: Out-of-Sample Results - Panel D: The Term Spread
| Country | Sample | In-Sample: | In-Sample: | In-Sample: CYsig | Time-Series: | Pooled: |
|---|---|---|---|---|---|---|
| Australia | 1952.1 - 2004.6 | 1.056 | 0.177 | NO | -0.404 | -0.158 |
| Belgium | 1952.1 - 2004.6 | 0.366 | 0.021 | NO | -0.870 | 0.020 |
| Canada | 1952.1 - 2004.6 | 2.467 | 0.960 | YES | 0.229 | 0.459 |
| Finland | 1962.1 - 2004.6 | 1.345 | 0.355 | NO | 0.199 | 0.511 |
| France | 1952.1 - 2004.6 | 1.646 | 0.430 | YES | 0.244 | 0.266 |
| Germany | 1953.1 - 2004.6 | 1.780 | 0.512 | YES | 0.342 | 0.503 |
| Italy | 1952.1 - 2004.6 | 1.659 | 0.436 | YES | -0.213 | 0.546 |
| Japan | 1952.1 - 2004.6 | -1.997 | 0.631 | NO | -0.599 | -0.110 |
| Netherlands | 1952.1 - 2004.6 | 1.824 | 0.527 | YES | -0.242 | 0.349 |
| South Africa | 1960.3 - 2004.6 | 1.425 | 0.382 | NO | -0.753 | 0.476 |
| Spain | 1952.1 - 2004.6 | 3.555 | 1.973 | YES | 1.939 | 1.775 |
| Sweden | 1952.1 - 2004.6 | -0.061 | 0.001 | NO | -0.616 | -0.495 |
| UK | 1952.1 - 2004.6 | 0.711 | 0.081 | NO | -1.176 | -0.264 |
| USA | 1952.1 - 2004.6 | 2.826 | 1.256 | YES | -0.544 | 0.557 |
Figure 1: Power Results from the Monte Carlo Study
The graphs show the average rejection rates
for a two-sided 5 percent t-test
of the null hypothesis of β = 0, for
samples with T = 100, and n = 20. The
x-axis shows the true value of the
parameter β, and the y-axis
indicates the average rejection rate. The left-hand column gives
the results for the case of exogenous regressors (δ = 0), and the right-hand
column gives the results for the case of highly endogenous
regressors (δ = -0.95). In the top two
panels, A1 and A2, there are no common factors in the data, and the
results for the t-tests corresponding to the
standard fixed effects estimator, ![]() , and the estimator based
on recursive demeaning,
, and the estimator based
on recursive demeaning,![]() , are given by the long
dashed lines and the short dotted lines, respectively. In the
middle panels, B1 and B2, there is a common factor in the data but
the estimators
, are given by the long
dashed lines and the short dotted lines, respectively. In the
middle panels, B1 and B2, there is a common factor in the data but
the estimators ![]() and
and ![]() that do not control for
common factors, are still used. In the bottom panels, C1 and C2,
the common factor is controlled for by using the estimators
that do not control for
common factors, are still used. In the bottom panels, C1 and C2,
the common factor is controlled for by using the estimators ![]() and
and ![]() , and the results for
the corresponding t-tests are shown. The flat
lines indicate the 5% rejection rate. All
results are based on 10,000 repetitions.
, and the results for
the corresponding t-tests are shown. The flat
lines indicate the 5% rejection rate. All
results are based on 10,000 repetitions.
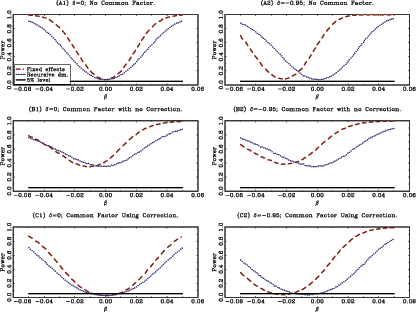
Figure 2: Expanding Window Regression Estimates for the Developed Panel
The left hand graphs
depict the fixed effects estimates without controlling for common
factors (i.e.
![]() ), and the corresponding
confidence bounds with a nominal coverage rate of 90% that are
obtained when pooling at the developed market level all
observations available up until the year in the plot. The right
hand graphs depict the corresponding results for the recursive
demeaning estimator, when also controlling for common factors (i.e.
), and the corresponding
confidence bounds with a nominal coverage rate of 90% that are
obtained when pooling at the developed market level all
observations available up until the year in the plot. The right
hand graphs depict the corresponding results for the recursive
demeaning estimator, when also controlling for common factors (i.e.
![]() ). A time-series is
added to the panel when five years of observations become
available. The flat solid lines indicate a value of zero.
). A time-series is
added to the panel when five years of observations become
available. The flat solid lines indicate a value of zero.
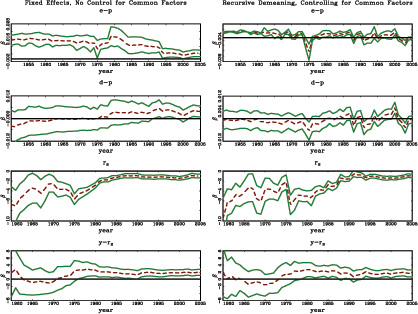
Figure 3: Expanding Window Regression Estimates for the Short Interest Rate
Each graph depicts the point estimate and the Campbell and Yogo 90 percent confidence interval that result from regressing excess returns, in the country indicated, on the lagged value of the short interest rate. The samples used in the estimation include data up till the year shown in the graph. The flat solid lines indicate a value of zero.
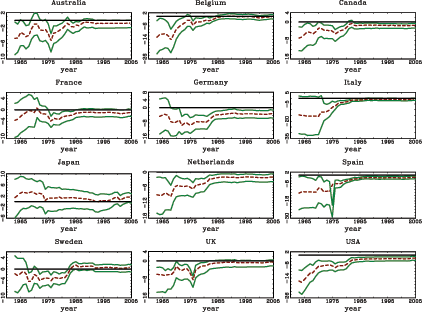
Figure 4: Expanding Window Regression Estimates for the Term Spread
Each graph depicts the point estimate and the Campbell and Yogo 90 percent confidence interval that result from regressing excess returns, in the country indicated, on the lagged value of the term spread. The samples used in the estimation include data up till the year shown in the graph. The flat solid lines indicate a value of zero.
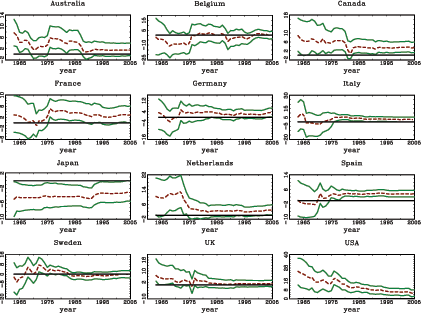
Footnotes
* This paper is forthcoming in the Journal of Financial and Quantitative Analysis. The current working paper version contains some additional technical material that will not appear in the published article. Return to text
† I am very grateful to Peter Phillips and Robert Shiller for providing much useful advice. Other helpful comments have been provided by Don Andrews, Jon Faust, Lennart Hjalmarsson, Randi Hjalmarsson, Yuichi Kitamura, George Korniotis, Ugur Lel, Edith Liu, Vadim Marmer, Alex Maynard, Taisuke Otsu, Kevin Song, Jon Wongswan, Jonathan Wright, Pär Österholm, as well as participants in the summer workshop and econometrics seminar at Yale University, the international finance seminar at the Federal Reserve Board, the finance seminar at Göteborg University, and the European Summer Meeting of the Econometric Society in Vienna. Tel.: +1-202-452-2426; fax: +1-202-263-4850; email: [email protected]. The views in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
1. See, for instance, Harvey (1991, 1995), Ferson and Harvey (1993), Campbell (2003), Polk et al. (2004), Paye and Timmermann (2006), and Ang and Bekaert (2007). Return to text
2. Included in the sample are the stock-markets in Hong Kong and Taiwan. Since Hong Kong is part of China and Taiwan is not a formally recognized sovereign state, the use of the term country for these markets is not entirely correct, but is used for convenience throughout the paper. Return to text
3. A predictive regressor is generally referred to as endogenous if the innovations to the returns are contemporaneously correlated with the innovations to the regressor. When the regressor is strictly stationary, such endogeneity has no impact on the properties of the estimator, but when the regressor is persistent in some manner, the properties of the estimator will be affected; see, for instance, Mankiw and Shapiro (1986), Cavanagh et al. (1995), Stambaugh (1999), Amihud and Hurvich (2004), Lewellen (2004), Campbell and Yogo (2006), and Jansson and Moreira (2006). Return to text
4. By imposing a common intercept α, it is also implicitly assumed that the mean of xi,t is the same for all i. In the international data used in this paper, this is often a very restrictive assumption. For instance, the nominal short interest rate will on average be much higher in countries that have experienced high inflation over the sample period, but it is typically too strong an assumption to assume that the stock returns in these countries therefore have been below their long-run average for most of the sample period, as a predictive regression with a common intercept and negative slope coefficient would imply. Return to text
5. One could make a similar argument for the treatment of fixed effects, although the observed differences in equity premia across countries immediately makes the argument rather weak. Importantly, however, omitting fixed effects in the analysis will lead to estimates and test statistics that are only consistent when the assumption of a common intercept holds. In contrast, the pooled estimator is robust to heterogeneity in the βis as mentioned in the previous section, and tests on the slope coefficient will provide valid inference on the (average) predictability in the panel. Return to text
6. Subject to potential rate restrictions, such as n/T → 0, these results can generally be shown to hold as n and T go to infinity jointly; technical proofs of such joint convergence is not pursued in the current study, however. Return to text
7. In the special case of ω12 = 0, it follows easily that
![]() is also asymptotically
normally distributed with convergence rate
is also asymptotically
normally distributed with convergence rate ![]() , and inference can proceed in a manner analogous to
the pooled case with a common intercept. Return to text
, and inference can proceed in a manner analogous to
the pooled case with a common intercept. Return to text
8. The test of slope homogeneity developed below does rely on knowledge of the Cis, and an approximate solution is proposed. However, such an approach, which is not proven to be asymptotically correct, seems more justified in a test of slope homogeneity, which is of a more diagnostic nature and of second order importance, as compared to the actual test of return predictability. Return to text
9. Note that this section focuses on estimating a common parameter (β), when the individual βis are not identical. This is in contrast to the fixed effects αi, which are in fact estimated for each i. However, estimating individual βis as well would simply reduce the problem to individual time-series regressions. Return to text
10. Although the asymptotic distributions
for ![]() (and
(and
![]() ) differ depending on
whether the βis are identical or not, it is easy
to show that inference based on standard test statistics will be
self-standardizing. Thus, no prior knowledge on the homogeneity of
the βis is required to perform inference
on the pooled estimate. Return to
text
) differ depending on
whether the βis are identical or not, it is easy
to show that inference based on standard test statistics will be
self-standardizing. Thus, no prior knowledge on the homogeneity of
the βis is required to perform inference
on the pooled estimate. Return to
text
11. Although not shown here, additional simulations also illustrate the asymptotic normality and unbiased nature of the standard pooled estimator when αi = α for all i, as predicted by Theorem 1. Return to text
12. According to the MSCI classification scheme, there are actually three different groups of markets: developed, emerging, and frontier markets. Here, I group together the emerging and frontier markets and refer to them as simply emerging markets. The MSCI classifictions can be found at http://www.mscibarra.com/products/indices/intl.jsp; the classifications used in this paper are as of February 2008. The group of emerging markets includes Argentina, Brazil, Chile, Hungary, India, Israel, Jordan, Malaysia, Mauritius, Mexico, the Philippines, Poland, South Africa, Taiwan, Thailand, and Turkey; the other countries shown in Table 4 are classified as developed. Return to text
13. Since the panels used in the estimation are typically unbalanced, i.e. not all time-series are of the same length, the estimation procedures are modified in a straightforward manner to allow for this; details are available upon request. Return to text
14. In the U.S., the interest rate was pegged by the Federal Reserve before this date. Of course, in other countries, deregulation of the interest rate markets occurred at different times, most of which are later than 1952. As seen in the international finance literature (e.g. Kaminsky and Schmukler (2002)), however, it is often difficult to determine the exact date of deregulation. And, if one follows classification schemes, such as those in Kaminsky and Schmukler (2002), then most markets are not considered to be fully deregulated until the 1980s, resulting in a very small sample period to study. Thus, the extent to which observed interest rates reflect actual market rates is hard to determine and one should keep this caveat in mind when interpreting the results. Return to text
15. The term 'expanding window regression' is used instead of 'recursive regression' as to avoid confusion with the pooled estimator using recursive demeaning. Return to text
16. Since the confidence intervals are not based directly on the OLS estimate, they are not necessarily symmetric around the point estimate. In fact, the OLS point estimate need not be inside the confidence interval, as is the case for Spain in Figure 3. Return to text
17. Campbell and Thompson (2004) argue that by imposing some weak restrictions on stock return forecasts, their performance can be greatly improved. Results not presented in this paper show that by imposing the sign restrictions proposed by Campbell and Thompson, the out-of-sample results provided here can be substantially strengthened. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text