
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 937, July 2008--- Screen Reader
Version*
Simple Monetary Rules Under Fiscal Dominance*
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
This paper asks whether an aggressive monetary policy response to inflation is feasible in countries that suffer from fiscal dominance, as long as monetary policy also responds to fiscal variables. We find that if nominal interest rates are allowed to respond to government debt, even aggressive rules that satisfy the Taylor principle can produce unique equilibria. But following such rules results in extremely volatile inflation. This leads to very frequent violations of the zero lower bound on nominal interest rates that make such rules infeasible. Even within the set of feasible rules the optimal response to inflation is highly negative, and more aggressive inflation fighting is inferior from a welfare point of view. The welfare gain from responding to fiscal variables is minimal compared to the gain from eliminating fiscal dominance.
Keywords: Optimal simple policy rules, fiscal dominance
JEL classification: E61, E62
"... A central bank charged with maintaining price stability cannot be indifferent as to how fiscal policy is determined" (Woodford, 2001) "Ideally, where fiscal policy that undermines central bank control of inflation is a real possibility, this should be accounted for, discussed in inflation reports, and reflected in central bank projections" (Sims, 2005)
1 Introduction
Is a monetary authority's commitment to fighting inflation aggressively a sufficient condition for ensuring price stability? It has long been held that the answer to this question should be negative. The reason is that the central bank's inflation objective may collide with an inflexible, or dominant, stance of fiscal policy that is unable or unwilling to adjust primary surpluses to stabilize government debt. Fiscal dominance was analyzed by Sargent and Wallace (1981) in an economy with real debt, where an unrealistic inflation objective leads to insufficient seigniorage revenue in the short run that has to be made up by higher seigniorage, and therefore inflation, in the long run. The fiscal theory of the price level of Woodford (1996, 1998, 2001)1 considers an economy with nominal debt, and shows that non-explosive government debt in the face of dominant fiscal policy can only be guaranteed by ensuring that real interest rates fall when inflation rises.2 This is the opposite of the Taylor (1993) principle for stabilizing inflation, which requires higher real interest rates in response to higher inflation, and which is generally taken to represent the notion of fighting inflation aggressively. The Taylor principle is derived in a standard New Keynesian setup for monetary policy analysis by assuming that the fiscal authority sets lump sum taxes that satisfy a balanced budget requirement.
In this paper we focus on inflation targeting under fiscal dominance as in Woodford (2001), motivated by the belief that this framework may be appropriate to describe the pressures facing at least some of the developing countries that have recently started to adopt inflation targeting. The reasons for fiscal dominance include some combination of a weak fiscal revenue base, a rudimentary tax collection system that encourages tax evasion, the contingent bailout liabilities attached to weak banking systems, and simple overspending at the federal or regional level. Under such conditions, if the government has issued nominal debt denominated in local currency, fiscal difficulties are often resolved not through an increase in tax revenues but instead through high inflation that erodes the real value of government liabilities.3 The assumptions underlying the policy recommendations of the inflation targeting literature are therefore clearly not satisfied.
But the recent literature has shown that this alone does not settle the question of whether fiscal dominance unambiguously prevents a central bank from fighting inflation. On the one hand, Loyo (1999) and Sims (2005) hold that a lack of fiscal adjustment could make inflation targeting completely infeasible. But on the other hand, Benigno and Woodford (2006) argue that while inflation volatility is higher under fiscal dominance, it need not be excessively high as long as medium term inflation expectations are anchored. To show this they compute a Ramsey optimal policy where the monetary authority implicitly responds to fiscal variables.
The result of a Ramsey optimal policy is a set of implied laws of motion for the main macroeconomic variables, but unfortunately there is no obvious mapping from such a policy to an implementable policy rule, which for a modern central bank would invariably take the form of an interest rate rule. It is therefore not immediately obvious whether the results of Benigno and Woodford (2006) should be interpreted as fighting inflation aggressively in the sense of the Taylor principle. Moreover, the Ramsey policymaker is assumed to formulate policies in response to a great deal of information that includes private agents' behavioral rules and expectations, while in practice policymakers have to set interest rates in response to observable economic variables and subject to practical constraints. The question of what constitutes an optimal policy therefore needs to be narrowed even further, and we attempt to do so in this paper. Specifically, we ask whether a benevolent monetary authority can substitute for fiscal adjustment if its only available policy instrument is the nominal interest rate, if that interest rate is restricted to respond in a linear fashion to observed macroeconomic variables, and if that interest rate may not hit its zero lower bound excessively often. The spirit of the exercise is similar to Schmitt-Grohe and Uribe's (2006) analysis of simple and implementable rules.
But we add one key innovation. It is based on the observation that, under fiscal dominance, the monetary authority must be clearly aware that it is the only entity capable of ensuring not only price stability but also fiscal solvency. It is therefore natural to suppose that it would take fiscal variables such as government debt into account in formulating its policy, and that this would increase its ability to react aggressively to inflation. We therefore allow the nominal interest rate to respond not only to inflation and output, but also to government spending or to government debt.
We then analyze the feasibility and desirability of an aggressive response of the interest rate to inflation by applying three successive criteria. First, we check for determinacy of equilibria. Second, we rule out determinate equilibria that violate the zero lower bound on nominal interest rates too frequently. Third, we rank the remaining equilibria by computing their welfare implications.
Equilibrium determinacy under different monetary and fiscal rules was the subject of Leeper's (1991) seminal contribution that will also form the benchmark of our study. Under a passive fiscal policy the fiscal authority adjusts taxes in order to meet the government budget constraint. In this case determinacy requires an active monetary policy that reacts strongly to inflation to achieve price stability. Under an active fiscal policy the primary surplus does not respond to the level of government debt. Determinacy then requires a passive monetary policy so that inflation can balance the budget, and this prevents price stability from being achieved. All other combinations of fiscal and monetary policies do not lead to a unique equilibrium. Since the New Keynesian literature has assumed that the fiscal authority adjusts taxes appropriately, the usual policy recommendation is to have the monetary authority fight inflation aggressively. More recently Schmitt-Grohe and Uribe (2006) have analyzed the combinations of fiscal and monetary rules that lead to a unique equilibrium when allowing for the more realistic case of distortionary taxation. They also add the zero lower bound criterion in checking for the implementability of different rules. Their paper broadly confirms Leeper's results.
Our results first restate the case for the Taylor principle in the absence of fiscal dominance. We then show that under fiscal dominance it is indeed beneficial to include government spending or government debt as an argument in the central bank's interest rate rule, because doing so entails an improvement, albeit very small, in welfare. But the optimal rules have highly negative coefficients on inflation, and an inflation coefficient greater than one is practically impossible even when monetary policy responds to fiscal variables. Government spending in the policy rule does not even expand the range of determinate equilibria to include inflation coefficients greater than one. When government debt enters the policy rule, part of the determinacy region does include an inflation feedback coefficient greater than one. But that region displays extremely high inflation volatility, and it is ruled out by the zero lower bound constraint on nominal interest rates. Furthermore, inflation volatility and welfare losses are much higher than under a Ricardian policy, and increase dramatically as the coefficient on inflation is increased away from its optimal value.
Our conclusion contains an important message for developing countries' central banks. This is that fiscal discipline must absolutely be established before committing to inflation targeting. Monetary policy alone cannot engineer a rescue.
The paper is organized as follows. Section 2 describes the model. Section 3 analyzes optimal monetary and fiscal policy when fiscal policy is not dominant. Section 4 determines optimal policy under fiscal dominance. Section 5 concludes.
2 The Model
We take as our baseline case the model described in Schmitt-Grohe and Uribe (2004a). This model is simple but retains the necessary ingredients to evaluate fiscal and monetary policy interactions. Namely, monetary policy is non-neutral due to a transactions cost technology and due to sticky goods prices in a world of monopolistic competition. Financial markets are incomplete in that the government can only issue one period nominal bonds.4 The presence of nominal bonds gives the government an incentive to use inflation to make real returns state contingent as described in Chari and Kehoe (1999). In fact, if prices were fully flexible then the real allocations would be the same as if markets were complete. In this model, market incompleteness does matter because there are price adjustment costs. The costs of changing prices can be motivated by costs of acquiring and processing information (Zbaracki et al. (2005)). For the sake of realism the government can only use distortionary forms of taxation.
Households are indexed by
![]() , and have the utility
function
, and have the utility
function
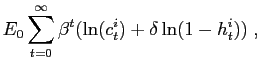
|
(1) |
where ![]() is consumption of the composite good
and
is consumption of the composite good
and ![]() is labor effort. Consumption is in
turn an aggregate of imperfectly substitutable varieties
is labor effort. Consumption is in
turn an aggregate of imperfectly substitutable varieties
![]() ,
,
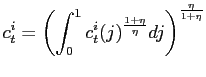 ,
, |
(2) |
so that cost minimization implies the set of goods demands
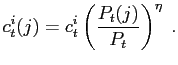
|
(3) |
Money facilitates consumption purchases, which are subject to a proportional transactions cost
| (4) |
where
![]() is money
velocity,
is money
velocity, ![]() is the aggregate price level of the
composite consumption good, and
is the aggregate price level of the
composite consumption good, and ![]() is nominal
money holdings.
is nominal
money holdings.
Producers are indexed by
![]() and are identical to the set
of households because each household is the sole producer of a
single variety
and are identical to the set
of households because each household is the sole producer of a
single variety ![]() of the composite good. These
goods are produced with a linear technology
of the composite good. These
goods are produced with a linear technology
| (5) |
where ![]() is productivity and
is productivity and ![]() is labor hired in a competitive labor market. The
output market is monopolistically competitive, and each producer
sets the price of the good it supplies subject to quadratic price
adjustment costs of the form
is labor hired in a competitive labor market. The
output market is monopolistically competitive, and each producer
sets the price of the good it supplies subject to quadratic price
adjustment costs of the form
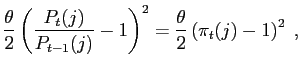
|
(6) |
and taking the level of aggregate demand for its good as given.
Aggregate demand consists of private consumption demand ![]() and government demand
and government demand ![]() , with
, with
| (7) |
Aggregate consumption demand is given by (3) aggregated over
all demands ![]() :
:
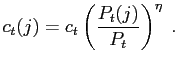
|
(8) |
Government demands a composite ![]() that consists
of the same varieties as the consumption good, with the same
elasticity of substitution, so that government demand for variety
that consists
of the same varieties as the consumption good, with the same
elasticity of substitution, so that government demand for variety
![]() is given by
is given by
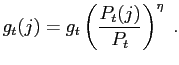
|
(9) |
Aggregate output is then naturally given by

|
(10) |
Financial assets include money and non-state contingent
one period nominal government bonds held from period ![]() to
to ![]() , denoted by
, denoted by ![]() , with gross nominal interest rate
, with gross nominal interest rate ![]() . A borrowing constraint is imposed to prevent
households from engaging in Ponzi schemes.
. A borrowing constraint is imposed to prevent
households from engaging in Ponzi schemes.
Non-financial income accrues to households in the form of
net cash flows from their activity as producers and from wage
income. The former is given by
![]() , and the latter by
, and the latter by
![]() , where
, where ![]() is the nominal wage (the real wage is denoted by
is the nominal wage (the real wage is denoted by
![]() ) and
) and ![]() is the labor
income tax rate.
is the labor
income tax rate.
The household budget constraint, combining the previous features, is given by
| (11) | ||
![$\displaystyle +P_{t}\left[ \left( \frac{P_{t}(i)}{P_{t}}\right) y_{t}(i)-w_{t} h_{t}(i)-\frac{\theta}{2}\left( \frac{P_{t}(i)}{P_{t-1}(i)}-1\right) ^{2}\right] +(1-\tau_{t})P_{t}w_{t}h_{t}^{i}\;.$](img37.gif)
|
The household maximizes (1) subject to (11), (4), (5) and (6). The first-order conditions for this problem are shown in Appendix A. Note that household superscripts and producer indices can be dropped in these conditions as all agents face identical decision problems and therefore obtain identical solutions in equilibrium.
The government budget constraint is given by
| (12) |
The monetary and fiscal authorities decide on the nominal interest
rate and on the labor tax rate
![]() . The precise form of the
rules that determine these two policy instruments is of course
critical for the presence and implications of fiscal dominance.
Those rules will therefore be discussed in detail in the subsequent
sections of the paper.
. The precise form of the
rules that determine these two policy instruments is of course
critical for the presence and implications of fiscal dominance.
Those rules will therefore be discussed in detail in the subsequent
sections of the paper.
Shock processes are given by the following laws of motion
for productivity and government spending:
| (13) |
| (14) |
Calibration follows Schmitt-Grohé and Uribe (2004) and is summarized in Table 1. A bar over a variable indicates its steady state value. The time unit is one year.
| β | 0.96 |
| 1.042 | |
| 0.2 | |
|
|
0.2 |
|
|
0.44 |
|
|
1.2 |
| 17.5/4 | |
| A | 0.0111 |
| B | 0.07524 |
| 0.9 | |
| 0.0302 | |
| 0.82 | |
| 0.0229 |
3 Monetary Policy in a Ricardian World
In this section we specify how the monetary authority can
implement a desired equilibrium in a world of endogenous taxation
that ensures budget balance. The monetary authority is assumed to
specify an interest rate rule that responds to deviations of
current inflation and output from their target values, while the
fiscal authority is assumed to raise or lower labor tax rates in
response to deviations - lagged by one year - of government
liabilities from a target value.5 This second, fiscal part of the
rule ensures long-run government solvency. In particular, we
consider the rule:6![]() 7
7
| (15) | ||
where
![]() are
total lagged government liabilities,
are
total lagged government liabilities,
![]() and
and ![]() are
inflation and output target values of the monetary authority, and
are
inflation and output target values of the monetary authority, and
![]() and
and ![]() are
tax and asset target values of the fiscal authority. As in
Schmitt-Grohe and Uribe (2006), we set the target values to be
equal to the non-stochastic steady state of the associated Ramsey
optimal policy problem. Note that we are departing from the most
conventional monetary policy analysis because taxation is
distortionary and is also an object of optimization.
are
tax and asset target values of the fiscal authority. As in
Schmitt-Grohe and Uribe (2006), we set the target values to be
equal to the non-stochastic steady state of the associated Ramsey
optimal policy problem. Note that we are departing from the most
conventional monetary policy analysis because taxation is
distortionary and is also an object of optimization.
We find that the parameter
![]() does not affect most of our key
results in an important way, and we therefore show most results for
the case
does not affect most of our key
results in an important way, and we therefore show most results for
the case
![]() . Where it does have some
effect we comment accordingly.8 The first panel of Figure 1,
labelled "Determinacy", shows the equilibrium determinacy
analysis. The vertical axis considers different values of the
feedback coefficient on government liabilities
. Where it does have some
effect we comment accordingly.8 The first panel of Figure 1,
labelled "Determinacy", shows the equilibrium determinacy
analysis. The vertical axis considers different values of the
feedback coefficient on government liabilities
![]() while the horizontal axis
considers different values of the inflation feedback coefficient
while the horizontal axis
considers different values of the inflation feedback coefficient
![]() . White areas signal that the
equilibrium exists and is unique. The figure displays two white
regions. One area is associated with a sufficiently large tax
response (significantly greater than zero) and a strong response of
interest rates to inflation
. White areas signal that the
equilibrium exists and is unique. The figure displays two white
regions. One area is associated with a sufficiently large tax
response (significantly greater than zero) and a strong response of
interest rates to inflation
![]() (greater than one, the Taylor
principle). In this constellation of parameters the fiscal rule
guarantees government solvency while the monetary rule fights
inflation aggressively in order to pin down the price level. This
confirms the results known from the New Keynesian literature with
lump sum taxation. The second area corresponds to an active fiscal
and passive monetary policy.
(greater than one, the Taylor
principle). In this constellation of parameters the fiscal rule
guarantees government solvency while the monetary rule fights
inflation aggressively in order to pin down the price level. This
confirms the results known from the New Keynesian literature with
lump sum taxation. The second area corresponds to an active fiscal
and passive monetary policy.
In the next panel of Figure 1, labelled "Zero Bound", we plot
in black all rules that are not consistent with either equilibrium
determinacy or with the zero lower bound on nominal interest
rates.9 As in Schmitt-Grohe and Uribe (2006),
the zero lower bound constraint is imposed by requiring that
![]() . By comparing the
first and second panel one can see that the zero bound does not
eliminate many rules. Both in the top left and bottom right regions
there are many rules that can lead to an implementable
equilibrium.
. By comparing the
first and second panel one can see that the zero bound does not
eliminate many rules. Both in the top left and bottom right regions
there are many rules that can lead to an implementable
equilibrium.
The next panel "Welfare" plots welfare contours for combinations of coefficients that satisfy the determinacy and zero lower bound conditions. We compute welfare using a second order approximation, as explained in detail in Schmitt-Grohe and Uribe (2004b).10 Consider two policy regimes, a reference regime denoted by r, and an alternative regime denoted by a. The welfare loss is defined as the fraction of regime r's mean consumption that the household would be willing to forego while still being as well off as under regime a. We consider the Ramsey allocation to be the reference regime and the allocations induced by the simple rule to be the alternative regime. We observe that the welfare results for an active monetary and passive fiscal policy are generally superior to those for active fiscal and passive monetary policy. Furthermore, welfare increases in the direction of a more aggressive monetary response to inflation. The welfare loss of the best rule is 0.02%, and that rule is given by11
| (16) | ||
The final panel of Figure 1, labelled "Inflation Volatility", shows that the welfare results are closely related to the volatility of inflation implied by the chosen policy mix. It shows that an active monetary policy response to inflation stabilizes inflation volatility far better than an active fiscal policy. Furthermore this effect, which works through agents' inflation expectations, is stronger for a more aggressive response to inflation.
For later comparison with fiscal dominance, Figures 2a and 2b show impulse responses for one standard deviation shocks to productivity and government spending. We observe that in a Ricardian world monetary policy responds to inflation in the short run, while tax rates are adjusted very gradually to stabilize debt in the long run. The critical feature of fiscal dominance is that tax rates are not available for this task.
4 Monetary Policy under Fiscal Dominance
We model fiscal dominance by assuming that the tax rate is exogenous and constant. With government spending specified as an exogenous stochastic process (13), fiscal instruments are therefore not being used to ensure that the intertemporal budget constraint of the government holds. In such a world the central bank has no choice but to accommodate fiscal shocks. An important question is whether it can still fight inflation aggressively while doing so. The conventional answer is that it cannot, and this is based on using a monetary rule identical to (15) combined with exogenous taxes. But we suggest that a monetary authority that knows it is the only institution capable of ensuring fiscal solvency (in addition to price stability) would not ignore fiscal variables in setting its policy. We therefore allow for monetary rules that may respond not only to inflation and output but also to fiscal variables. We establish whether this improves the performance of interest rate rules under fiscal dominance, and whether such rules may make it possible to respond aggressively to inflation.
Specifically, the interest rate rules we consider continue to react to inflation and output. But in addition we consider a response to deviations of either government spending or of government liabilities from their desired levels. Stability and welfare analysis of the same type as in Figure 1 is shown for these two cases in Figures 3 and 4.
4.1 Government Spending in the Interest Rate Rule
We first consider an interest rate rule that takes into account
deviations of government spending from a constant value ![]() :
:
| (17) |
Rule (17) posits that
if government spending is 1% above its steady state level then the
interest rate will be changed by
![]() basis points. This case is
presented in Figure 3. The main result is that responding to
government expenditures does not increase the determinacy region
for
basis points. This case is
presented in Figure 3. The main result is that responding to
government expenditures does not increase the determinacy region
for
![]() compared to the conventional
case of
compared to the conventional
case of
![]() , as monetary policy still has
to be passive,
, as monetary policy still has
to be passive,
![]() . The zero lower bound
restriction on nominal interest rates imposes further restrictions
on the implementable range of feedback coefficients, specifically
the coefficient on government spending cannot be too large in
absolute value. The best rule in the class (17) is described by
. The zero lower bound
restriction on nominal interest rates imposes further restrictions
on the implementable range of feedback coefficients, specifically
the coefficient on government spending cannot be too large in
absolute value. The best rule in the class (17) is described by
| (18) |
We find that the welfare losses associated with this rule are very
much larger than for the Ricardian case, at 0.202% versus 0.02%.
Allowing for a non-zero coefficient on government spending is
beneficial, but only slightly so, as under the restriction
![]() welfare losses can be shown to
rise to 0.210%. The third panel of Figure 3 shows that maximizing
welfare calls for a highly negative coefficient on inflation, and
that attempting a more aggressive inflation response leads to lower
welfare. The reason can be seen in the final panel of Figure 3,
which shows that inflation volatility increases as
welfare losses can be shown to
rise to 0.210%. The third panel of Figure 3 shows that maximizing
welfare calls for a highly negative coefficient on inflation, and
that attempting a more aggressive inflation response leads to lower
welfare. The reason can be seen in the final panel of Figure 3,
which shows that inflation volatility increases as
![]() is raised above its optimal
value. This not only leads to more volatile nominal interest rates
and therefore violations of the zero lower bound constraint, but
also to more variable real interest rates and output, which causes
welfare losses. The Taylor principle in this case is not even
consistent with determinacy, not to mention the zero lower bound or
welfare considerations. We now turn to another argument of the
policy rule that holds more promise in expanding the monetary
authority's options, government liabilities.
is raised above its optimal
value. This not only leads to more volatile nominal interest rates
and therefore violations of the zero lower bound constraint, but
also to more variable real interest rates and output, which causes
welfare losses. The Taylor principle in this case is not even
consistent with determinacy, not to mention the zero lower bound or
welfare considerations. We now turn to another argument of the
policy rule that holds more promise in expanding the monetary
authority's options, government liabilities.
4.2 Government Liabilities in the Interest Rate Rule
We consider an interest rate rule that responds to deviations of inflation and output from their target values, as before, and to deviations of government debt (scaled by steady state GDP) from its target value. Since the monetary authority faces no policy implementation lags, we will assume that the interest rate rule reacts to the current level of government liabilities:
| (19) |
The rule (19)
assumes that if the ratio of government liabilities to output is 1
percentage point higher than target, then the interest rate will be
raised by
![]() basis points. Does this rule,
which is considered in Figure 4, allow for an aggressive response
to inflation? At first sight it looks a lot more promising than
Figure 3. Most strikingly, as long as solvency is guaranteed by
lowering interest rates sufficiently in response to excessive
government liabilities, it is now possible to reach the region of
determinacy even with an aggressive response to inflation. But this
is an illusion, as the analysis of the zero lower bound condition
on nominal interest rates shows. All coefficient combinations that
include an aggressive response to inflation violate the lower
bound, which makes this rule impossible to implement in practice.
For instance, if the coefficient on inflation were 1.5 and that on
liabilities were -0.2, then the standard deviation of interest
rates would be 4.1. Such volatility implies that interest rates
would have to be higher than 8.2% on average to satisfy the lower
bound condition, while in our economy the average interest rate is
3.8%. It is true that many developing economies experience high
inflation and consequently high nominal interest rates. However, if
a successful inflation targeting regime were to be implemented in
developing countries then inflation and nominal interest rates
would be lower. The best rule in this class is
basis points. Does this rule,
which is considered in Figure 4, allow for an aggressive response
to inflation? At first sight it looks a lot more promising than
Figure 3. Most strikingly, as long as solvency is guaranteed by
lowering interest rates sufficiently in response to excessive
government liabilities, it is now possible to reach the region of
determinacy even with an aggressive response to inflation. But this
is an illusion, as the analysis of the zero lower bound condition
on nominal interest rates shows. All coefficient combinations that
include an aggressive response to inflation violate the lower
bound, which makes this rule impossible to implement in practice.
For instance, if the coefficient on inflation were 1.5 and that on
liabilities were -0.2, then the standard deviation of interest
rates would be 4.1. Such volatility implies that interest rates
would have to be higher than 8.2% on average to satisfy the lower
bound condition, while in our economy the average interest rate is
3.8%. It is true that many developing economies experience high
inflation and consequently high nominal interest rates. However, if
a successful inflation targeting regime were to be implemented in
developing countries then inflation and nominal interest rates
would be lower. The best rule in this class is
| (20) |
Similar to (17), we
find that including government liabilities in the rule does lead to
a slightly better performance, with welfare losses dropping from
0.210% under the restriction
![]() to 0.204% for (20).12Maximizing welfare again calls for a
highly negative coefficient on inflation, and even pushing in the
direction of a rule satisfying the Taylor principle, without
actually getting there, is detrimental. These welfare results are
closely related to the implied inflation volatilities of each
regime, shown in the last panel of Figure 4. Under a Ricardian
regime inflation volatility is 0.08 for the optimal rule (16). Under
fiscal dominance inflation volatility is very much higher, about
1.5 when the optimal rule is implemented. Moreover, the volatility
of inflation increases dramatically as a more aggressive inflation
response is attempted. The implied volatility of the real interest
rate and therefore of real variables explains why welfare
deteriorates in this attempt.
to 0.204% for (20).12Maximizing welfare again calls for a
highly negative coefficient on inflation, and even pushing in the
direction of a rule satisfying the Taylor principle, without
actually getting there, is detrimental. These welfare results are
closely related to the implied inflation volatilities of each
regime, shown in the last panel of Figure 4. Under a Ricardian
regime inflation volatility is 0.08 for the optimal rule (16). Under
fiscal dominance inflation volatility is very much higher, about
1.5 when the optimal rule is implemented. Moreover, the volatility
of inflation increases dramatically as a more aggressive inflation
response is attempted. The implied volatility of the real interest
rate and therefore of real variables explains why welfare
deteriorates in this attempt.
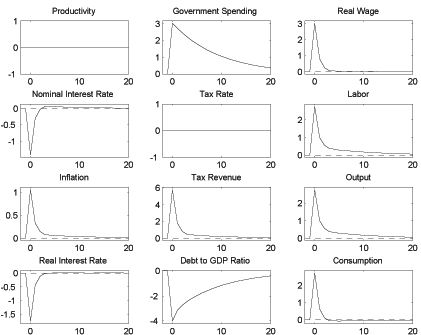
Finally, Figures 5a and 5b present the impulse responses for technology and government spending shocks under rule (20). The crucial difference to the Ricardian case is that under fiscal dominance the interest rate rather than the tax rate has to be used to stabilize debt, and this stabilization takes place over a much shorter time horizon. As a result nominal and real interest rates are much more volatile. The response of the debt to GDP ratio in each example is the opposite of the Ricardian case.
Figure 5a shows that a positive productivity shock leads to an increase in the public debt, rather than a fall as in Figure 2a. Under a Ricardian policy debt is used as a shock absorber. This means that higher productivity, which reduces marginal cost and therefore inflation, is allowed to reduce the real interest rate, thereby boosting demand and reinforcing the direct effect of higher productivity on the real wage. The result is an increase in tax revenue that, combined with the lower real interest rate, reduces debt. The economy subsequently benefits from this debt reduction through a reduction of the distortionary labor tax rate, which gradually returns debt to its long run value. But under fiscal dominance tax rates cannot fall to pass on the beneficial tax revenue effects of higher productivity. If there is an unexpected increase in productivity, debt must therefore increase immediately through a surprise decrease in the rate of inflation that is about five times larger than under a Ricardian policy. The reason is that lower inflation leads to an increase in the real interest rate that further reduces demand and therefore marginal cost. The higher real interest rate causes debt to rise for two interrelated reasons. First, it directly increases the real cost of servicing the debt. Second, it reduces demand for output and thus for labor, which reduces tax revenue and leads to a primary deficit. But the real interest rate drop is quickly reversed while higher productivity continues for some time, thereby turning the primary deficit into a primary surplus. At that point government debt starts to approach its long run level from above.
Figure 5b shows that an increase in government spending leads to a fall in the public debt, rather than an increase as in Figure 2b. Under a Ricardian policy higher government spending is translated, without any increase in inflation, into higher debt that is subsequently repaid very gradually through higher taxes. But under fiscal dominance tax rates cannot rise to deal with a higher debt level. If there is an unexpected increase in spending, debt must therefore be eroded immediately with surprise and very sizeable inflation that is allowed to reduce the real interest rate, thereby lowering the real cost of servicing the debt. In addition, the combination of higher government spending and a lower real interest rate boosts demand for output and thus for labor, which in turn increases tax revenue and leads to a primary surplus. But because the real interest rate drop is quickly reversed while elevated government spending continues for some time, this almost immediately turns into a primary deficit. At that point government debt starts to approach its long run level from below.
The impulse responses for a government spending shock in Figure 5b look qualitatively similar to those reported in Benigno and Woodford (2006) in their discussion of the exogenous taxation case. Our policy rule (20) may therefore be one simple way to implement the target criterion they have in mind. It implements their prescription that inflation expectations must be firmly anchored, in the sense that while inflation is much more volatile than in the Ricardian case, it also quickly returns to its long run value. The importance of this prescription stems from the fact that it requires less inflation to maintain intertemporal solvency, because with rapid but anchored movements in inflation the endogenous response of output and therefore of tax revenue is stronger and moves debt in the same direction as inflation.
But in practice, as shown in a large empirical literature covering many different countries, a firm anchoring of inflation expectations has only been successfully implemented in cases where monetary policy responds aggressively to inflation. Yet as we have seen, this is neither a feasible nor a desirable alternative in a world of fiscal dominance. This poses a severe problem for policymakers, because it seems very doubtful that the public would interpret a monetary rule with a very negative inflation coefficient as providing a firm anchor for inflation. The inclusion of fiscal variables in the monetary rule makes very little difference to these results, either in terms of the optimal inflation coefficient or in terms of welfare outcomes. The welfare gains from removing fiscal dominance altogether are an order of magnitude greater than the gains from targeting fiscal variables through nominal interest rates.
5 Conclusions
This paper has considered optimal monetary policy when the fiscal authority is unable, or unwilling, to control tax revenues and spending. Weak taxation systems, tax evasion, banking crises or overspending are some of the factors that can undermine the control of fiscal deficits in developing economies. The paper shows that under such circumstances the usual prescription of the inflation targeting literature, a more than proportional interest rate response to inflation innovations known as the Taylor principle, becomes impractical and undesirable. The optimal coefficient on inflation is invariably highly negative.
It has not been clear from the literature whether this situation can be rescued by a central bank that adapts itself to fiscal dominance by conditioning its actions on fiscal variables such as government spending or government debt. This paper directly addresses that question. It finds that responding to government spending does not even expand the set of inflation coefficients that give rise to unique equilibria. Responding to debt is more promising because the set of unique equilibria is expanded and allows for an aggressive response to inflation. However, an interest rate rule that tackles fiscal dominance by responding to debt and that simultaneously satisfies the Taylor principle is not a robust solution. First, volatility of all variables is extremely high when an aggressive response to inflation is attempted. Second, and as a direct consequence, policies that follow the Taylor principle always violate the zero lower bound on nominal interest rates. Third, and also as a direct consequence of volatility, welfare considerations call for a highly negative coefficient on inflation.
There is one positive result, which is that under fiscal dominance it does make sense for the central bank to include fiscal variables in its policy rule, because doing so improves welfare. But that improvement is trivial compared to what could be accomplished by removing fiscal dominance altogether. Only solid fiscal fundamentals allow for both a benign outcome in terms of welfare and for the ability to fight inflation aggressively. Fiscal reform in developing countries is therefore an indispensable step before implementing inflation targeting regimes.
Appendix
A First Order Conditions
Let the multiplier of the budget constraint (11) be given by
![]() , and let
, and let
![]() . Denote real
money balances by
. Denote real
money balances by
![]() . Finally, use the fact that
the equilibrium is symmetric, with
. Finally, use the fact that
the equilibrium is symmetric, with
![]() . Then we have the
following conditions for government debt, consumption, labor
supply, money demand, and price setting:
. Then we have the
following conditions for government debt, consumption, labor
supply, money demand, and price setting:

|
(A.1) |
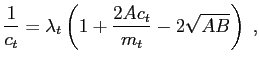
|
(A.2) |
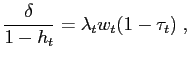
|
(A.3) |
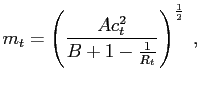
|
(A.4) |
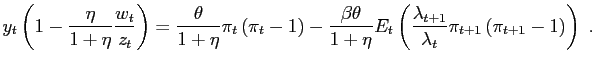
|
(A.5) |
B Determinacy and Zero Lower Bound Computations
The pictures in Figures 1, 3 and 4 are computed using 101 points
both for the coefficients on the horizontal and on the vertical
axis. The coefficient
![]() is assumed to belong to the set {-0.5, 0, 0.5}. Hence, for each rule we
consider a grid of 30603 points. The welfare evaluations may be
inaccurate for points near the indeterminacy regions. To overcome
this problem we only compute welfare for points lying in the
interior of the unique equilibrium area. The statistics referred to
in the paper were computed through 500 simulations of 100 periods.
All computations have been done with the DYNARE toolkit.
is assumed to belong to the set {-0.5, 0, 0.5}. Hence, for each rule we
consider a grid of 30603 points. The welfare evaluations may be
inaccurate for points near the indeterminacy regions. To overcome
this problem we only compute welfare for points lying in the
interior of the unique equilibrium area. The statistics referred to
in the paper were computed through 500 simulations of 100 periods.
All computations have been done with the DYNARE toolkit.
C Welfare Computations
Following the Bellman equation one can define:
| (21) |
where ![]() is period utility and
is period utility and ![]() is life-time utility. Conditional welfare is the value
of life-time utility taking into account that the initial starting
point is a predetermined level. This value can be obtained from the
a second order approximation to the policy function of
is life-time utility. Conditional welfare is the value
of life-time utility taking into account that the initial starting
point is a predetermined level. This value can be obtained from the
a second order approximation to the policy function of ![]() . With the policy function at hand, conditional welfare
can be obtained by plugging the initial steady state into the
policy function of
. With the policy function at hand, conditional welfare
can be obtained by plugging the initial steady state into the
policy function of ![]() . It is common to
consider the initial steady state to be the non-stochastic steady
state.
. It is common to
consider the initial steady state to be the non-stochastic steady
state.
We conduct welfare comparisons of different rules. Consider the reference policy, denoted by r, and an alternative policy denoted by a. We have taken the reference policy to be the Ramsey policy. The conditional welfare of the reference regime is
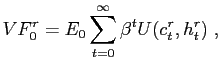
|
(22) |
where ![]() and
and ![]() denote consumption and hours of work in the reference regime.
Similarly, conditional welfare in the alternative regime is
denote consumption and hours of work in the reference regime.
Similarly, conditional welfare in the alternative regime is
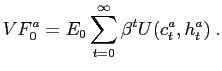
|
(23) |
We denote by ![]() the welfare cost of following
the alternative regime. It is defined as the fraction of regime
r's consumption that the household would be willing to lose
to be as well off under regime a as regime r:
the welfare cost of following
the alternative regime. It is defined as the fraction of regime
r's consumption that the household would be willing to lose
to be as well off under regime a as regime r:

|
(24) |
For the specific utility function considered, the expression can be rearranged as
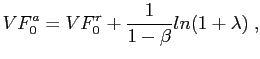
|
(25) |
where ![]() is defined as an implicit function,
which we will approximate up to second order. Following
Schmitt-Grohe and Uribe (2004b), we introduce a parameter
is defined as an implicit function,
which we will approximate up to second order. Following
Schmitt-Grohe and Uribe (2004b), we introduce a parameter
![]() that scales the variance of the
exogenous stochastic processes
that scales the variance of the
exogenous stochastic processes ![]() and
and
![]() . Totally differentiating equation
(25) twice with
respect to
. Totally differentiating equation
(25) twice with
respect to ![]() we can obtain
we can obtain
![]() , which is the only
term different from zero in the second order approximation around
the non-stochastic steady state. It easily follows that
, which is the only
term different from zero in the second order approximation around
the non-stochastic steady state. It easily follows that
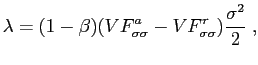
|
(26) |
or equivalently
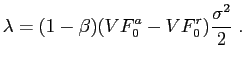
|
(27) |
References
Benigno, P. and Woodford, M. (2006), "Optimal Inflation Targeting under Alternative Fiscal Regimes", NBER Working Papers, Number 12158.
Chari, V.V. and Kehoe, P.J. (1999), "Optimal Fiscal and Monetary Policy", Chapter 26 in Taylor, J.B. and Woodford, M., eds., Handbook of Macroeconomics, Volume 1C, Elsevier.
Cochrane, J.H. (1998), "A Frictionless View of US Inflation", NBER Macroeconomics Annual, 13, 323-384.
Cochrane, J.H. (2000), "Money as Stock: Price Level Determination with No Money Demand", NBER Working Papers, Number 7498.
Collard, F. and Juillard, M. (2001), "Accuracy of Stochastic Perturbation Methods: The Case of Asset Pricing Models", Journal of Economic Dynamics and Control, 25(6-7), 979-999.
Daniel, Betty (2001), "A Fiscal Theory of Currency Crises," International Economic Review, vol. 42(4), pages 969-88.
Kumhof, M., Li, S. and Yan, I. (2007), "Balance of Payments Crises under Inflation Targeting", Journal of International Economics, 72(1), 242-264.
Kumhof, M. and Tanner, E. (2007), "Government Debt: A Key Role in Financial Intermediation", in A. Velasco (ed.), Festschrift in Honor of Guillermo A. Calvo (forthcoming).
Leeper, E. (1991), "Equilibrium under Active and Passive Monetary and Fiscal Policies", Journal of Monetary Economics, 27(2), 129-147.
Loyo, E. (1999), "Tight Money Paradox on the Loose: A Fiscalist Hyperinflation", Manuscript, Kennedy School of Government.
Marcet, A. and Scott, A. (2001), "Debt and Deficit Fluctuations and the Structure of Bond Markets", C.E.P.R. Discussion Papers, Number 3029.
Nunes, R.C. (2005), "Inflation Dynamics: The Role of Expectations", Manuscript, Universitat Pompeu Fabra.
Sargent, T.J. and Wallace, N. (1981), Some Unpleasant Monetary Arithmetic, Fedreal Researve Bank of Minneapolis Quaterly Review, Fall, 1-17.
Schmitt-Grohe, S. and Uribe, M. (2004a), "Optimal Fiscal and Monetary Policy Under Sticky Prices", Journal of Economic Theory, 114, 198-230.
Schmitt-Grohe, S. and Uribe, M. (2004b), "Solving Dynamic General Equilibrium Models Using a Second-Order Approximation to the Policy Function", Journal of Economic Dynamics and Control, 28(4), 755-775.
Schmitt-Grohe, S. and Uribe, M. (2006), "Optimal Simple and Implementable Monetary and Fiscal Rules", Journal of Monetary Economics (forthcoming).
Sims, C.A. (1994), "A Simple Model for the Study of the Determination of the Price Level and the Interaction of Monetary and Fiscal Policy", Economic Theory, 4, 381-399.
Sims, C. (2005), "Limits to Inflation Targeting", in: B. Bernanke and M. Woodford, eds., The Inflation Targeting Debate, Chicago: University of Chicago Press.
Woodford, M. (1996), "Control of the Public Debt: A Requirement for Price Stability?", NBER Working Paper, Number 5684.
Woodford, M. (1998), "Public Debt and the Price Level", Manuscript, Princeton University.
Woodford, M. (2001), "Fiscal Requirements for Price Stability", NBER Working Paper, Number 8072.
Figure 1: Ricardian Fiscal Policy and the Taylor Rule
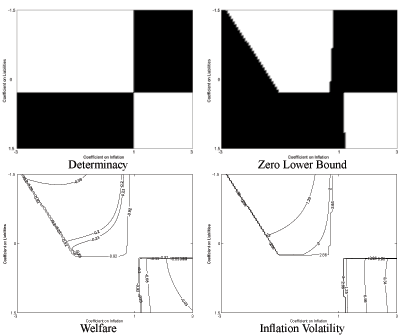
Figure 2a: Productivity Shock under Ricardian Fiscal Policy
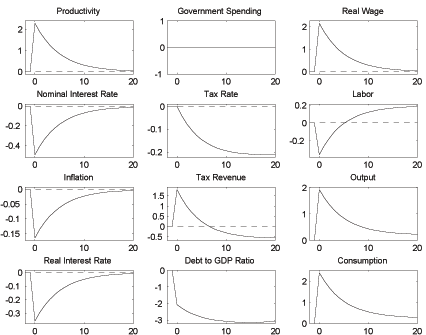
Figure 2b: Government Spending Shock under Ricardian Fiscal Policy
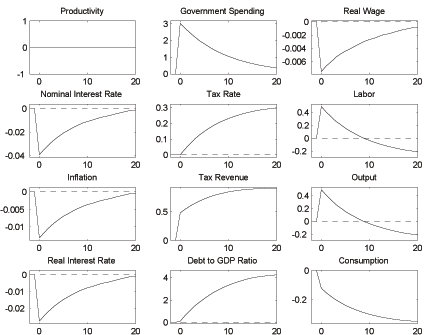
Figure 3: Fiscal Dominance and Interest Rate Feedback to Government Spending

Figure 4: Fiscal Dominance and Interest Rate Feedback to Government Liabilities
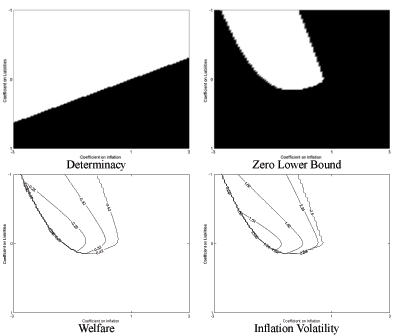
Figure 5a: Productivity Shock under Fiscal Dominance
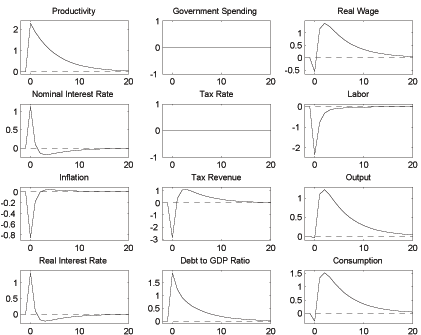
Figure 5b: Government Spending Shock under Fiscal Dominance
Footnotes
* The authors thank Jordi Gali, Michel Juillard Albert Marcet and seminar participants at Universitat Pompeu Fabra and the IMF for helpful comments. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the IMF, the IMF Executive Board, IMF management, the Board of Governors of the Federal Reserve System or any other person associated with the Federal Reserve System. Return to text
1. Other key contributions to this literature are Cochrane (1998) and Sims (1994). A long list of additional references is contained in Cochrane (1998, 2000) and Woodford (2001). Return to text
2. This assumption implies that the out of equilibrium present value of budget supluses is not equal to the real value of debt. This does not mean that the government does not care about satisfying the intertemporal budget constraint. It is that the level of surplus is set before the price level is determined. Return to text
3. If all of an inflation targeting government's debt is denominated in foreign currency, the same circumstances would result in a balance of payments crisis, as shown by Kumhof, Li and Yan (2007). Kumhof and Tanner (2007) presents evidence on the size of local currency government debt markets in developing countries. Daniel (2001) presents a detailed examination of the fiscal determinants of currency crisis. Return to text
4. Marcet and Scott (2001) provide arguments to support the assumption of incomplete markets. Return to text
5. This is based on the realistic premise that fiscal decisions occur with a one year lag. Return to text
6. Another Ricardian rule is sometimes
considered in the literature, namely
![]() . This may be easier to implement, as the monetary authority does
not need information on the steady state levels of the interest
rate and output. However, we have found qualitatively very similar
results between this rule and (15), and therefore
concentrate our discussion on the latter. Return to text
. This may be easier to implement, as the monetary authority does
not need information on the steady state levels of the interest
rate and output. However, we have found qualitatively very similar
results between this rule and (15), and therefore
concentrate our discussion on the latter. Return to text
7. Inflation forecast based rules would replace current inflation by expectations of inflation, but this presumes that the monetary authority can perfectly observe private agents' expectations. In practice this could either mean extracting them from surveys or applying econometric techniques to extract them from financial data. As for the former, Nunes (2005) shows why survey expectations may not reflect actual expectations. As for the latter, in the developing countries that motivated this study the data required to use these techniques are generally not available. Return to text
8. We found it sufficient to consider only
three values of
![]() to characterize the solutions,
namely
to characterize the solutions,
namely
![]() . Return to text
. Return to text
9. The reader is refered to Appendix B for details on these computations. Return to text
10. See also Collard and Juillard (2001). The reader is referred to Appendix C for a description of the welfare computations. Return to text
11. We limit our search to inflation
coefficients
![]() . A further small welfare
improvement would be attainable with even higher
. A further small welfare
improvement would be attainable with even higher
![]() . Return to text
. Return to text
12. This makes little difference to the
optimal behavior of monetary policy. Under the restriction
![]() the optimal coefficient on
inflation changes to
the optimal coefficient on
inflation changes to
![]() . Return to text
. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text