
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 948, September 2008 --- Screen Reader
Version*
Exchange Rates and Fundamentals: A Generalization*
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
Exchange rates have raised the ire of economists for more than 20 years. The problem is that few, if any, exchange rate models are known to systematically beat a naive random walk in out of sample forecasts. Engel and West (2005) show that these failures can be explained by the standard-present value model (PVM) because it predicts random walk exchange rate dynamics if the discount factor approaches one and fundamentals have a unit root. This paper generalizes the Engel and West (EW) hypothesis to the larger class of open economy dynamic stochastic general equilibrium (DSGE) models. The EW hypothesis is shown to hold for a canonical open economy DSGE model. We show that all the predictions of the standard-PVM carry over to the DSGE-PVM. The DSGE-PVM also yields an unobserved components (UC) models that we estimate using Bayesian methods and a quarterly Canadian-U.S. sample. Bayesian model evaluation reveals that the data support a UC model that calibrates the discount factor to one implying the Canadian dollar-U.S. dollar exchange rate is a random walk dominated by permanent cross-country monetary and productivity shocks.
Keywords: Exchange rates, present-value model and fundamentals, random walk, DSGE model, unobserved components model, Bayesian model comparison
JEL classification: E31, E37, F41
1 Introduction
The search for satisfactory exchange rate models continues to be elusive. This paper studies a workhorse theory of currency market equilibrium determination, the present-value model (PVM) of exchange rates, in the spirit of Engel and West (2005). Starting with the PVM and using uncontroversial assumptions about fundamentals and the discount factor, Engel and West (EW) hypothesize that the PVM generates an approximate random walk in exchange rates if the PVM discount factor approaches one and fundamentals are I(1). An important implication of the EW hypothesis is that fundamentals have no power to forecast future exchange rates, even with the PVM dictating equilibrium in the currency market. EW support their hypothesis with a key theorem and empirical and simulation evidence.
This paper complements Engel and West (2005) by generalizing their main hypothesis in two ways. First, the EW hypothesis is generalized using a canonical two-country monetary dynamic stochastic general equilibrium (DSGE) model. Its linearized uncovered interest parity (UIP) and money demand equations yield the DSGE-PVM that coincides with the standard PVM of the exchange rate. Second, we show the standard- and DSGE-PVMs make equivalent predictions for exchange rates. The predictions are summarized in five propositions: (1) the exchange rate and fundamental cointegrate [Campbell and Shiller (1987)], (2) the PVM yields an error correction model (ECM) for currency returns in which the lagged cointegrating relation is the only regressor, (3) the PVM predicts a limiting economy (i.e., the PVM discount factor approaches one from below) in which the exchange rate is a martingale, (4) given fundamental growth depends only on the lagged cointegrating relation, the exchange rate and fundamental have a common trend-common cycle decomposition [Vahid and Engle (1993)], and (5) the EW hypothesis is also satisfied when the exchange rate and fundamental share a common feature and the PVM discount factor approaches one. A corollary to (5) is that the exchange rate is unpredictable when the PVM discount factor goes to one.
We report evidence from vector autoregression (VARs) about the propositions using quarterly floating rate Canadian-, Japanese-, and U.K.-U.S. samples. The VAR evidence rejects cointegration and reveals substantial serial correlation for the exchange rate and the fundamental. There is also evidence that a common feature exists between the Canadian dollar-, Yen-, and Pound-U.S. dollar exchange rates and the relevant fundamentals. Nonetheless, the VAR approach is unable to address the EW hypothesis question of whether the PVM discount factor approaches one.1
The DSGE-PVM possesses a deep structure tied to the primitives of the underlying open economy unlike the standard-PVM. Rather than rely on the entire set of DSGE optimality and equilibrium condition, we give empirical content to the DSGE-PVM by placing restrictions on its fundamentals (cross-country money and consumption). We restrict these fundamentals with permanent-transitory decompositions. This decomposition allows us to cast the DSGE-PVM as a tri-variate unobserved components (UC) model in the exchange rate and observed fundamentals. The UC model also incorporates DSGE-PVM cross-equation restrictions conditional on whether the discount factor is calibrated or estimated. Three UC models calibrate the discount factor to one, which disconnects the exchange rate from the transitory component(s) of fundamentals. Transitory fundamentals restrict the exchange rate in three other UC models in which the DSGE-PVM discount factor is estimated.
We estimate six UC models on a Canadian-U.S. sample running from 1976Q1 to 2004Q4. The UC models yield state space systems for the DSGE-PVM, which allows us to recruit the Kalman filter to evaluate likelihoods. We compute likelihoods of the UC models using the Metropolis-Hastings (MH) simulator described by Rabanal and Rubio-Ramírez (2005) to draw Markov chain Monte Carlo (MCMC) replications from posteriors. We conduct model comparisons using marginal posterior likelihoods of the six UC models to find which is favored by the data. We find that the data favors the UC model that calibrates the discount factor to one and in which cyclical fluctuations are driven only with the transitory shock to cross-country consumption. Favored next is the UC model with the same transitory shock and in which the estimated posterior mean of the DSGE-PVM discount factor is 0.9962. The posterior of this UC model reveals that permanent shocks to fundamentals dominate exchange rate fluctuations. Thus, the data prefer UC models that are consistent with the EW hypothesis. Moreover, we find that the data fail to support UC models that tie the exchange rate to the transitory monetary shock. Rogoff (2007) also notes that exchange rates appear disconnected from 'mean reverting monetary fundamentals'. These results stand in contrast to those of open economy DSGE models which assign key roles to nominal rigidities, UIP shock persistence, and monetary disturbances.2
The next section constructs the standard- and DSGE-PVMs of the exchange rate. Section 3 presents five propositions that generalize the EW hypothesis. Our Bayesian econometric strategy is discussed in section 4. Section 5 reports estimates of six UC models. We conclude in section 6.
2 Two Present-Value Models of Exchange Rates
This section fleshes out the standard PVM, in which the equilibrium exchange rate is determined by melding a liquidity-money demand function, UIP condition, purchasing power parity (PPP), and flexible prices. This is a workhorse exchange rate model used by, among others, Dornbusch (1976), Bilson (1978), Frankel (1979), Meese (1986), Mark (1995), and Engel and West (2005). This section also develops a PVM of the exchange rate derived from a canonical optimizing two-country monetary DSGE model. We show that the EW hypothesis generalizes to this wider class of models.
2.A The Standard Present-Value Model of Exchange Rates
The standard-PVM of the exchange rate starts with the liquidity-money demand function
| (1) |
where ![]()
![]() ,
,
![]() , and
, and ![]() denote
the home country's natural logarithm of money stock, price level,
output, and the level of the nominal interest rate. The parameter
denote
the home country's natural logarithm of money stock, price level,
output, and the level of the nominal interest rate. The parameter
![]() measures the income elasticity of money
demand. Since the nominal interest rate is in its level,
measures the income elasticity of money
demand. Since the nominal interest rate is in its level,
![]() is the interest rate semi-elasticity of
money demand. Define cross-country differentials
is the interest rate semi-elasticity of
money demand. Define cross-country differentials ![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]() , and
, and
![]()
![]()
![]()
![]()
![]() , where
, where
![]() denotes the foreign country. Assuming PPP
holds,
denotes the foreign country. Assuming PPP
holds, ![]()
![]()
![]() , where
, where ![]() is the log of the
(nominal) exchange rate in which the U.S dollar is the home
country's currency.
is the log of the
(nominal) exchange rate in which the U.S dollar is the home
country's currency.
Under UIP, the law of motion of the exchange rate is approximately
| (2) |
Substitute for ![]() in the law of motion of
the exchange rate
(2)
with the money demand function
(1) and
impose PPP to produce the Euler equation
in the law of motion of
the exchange rate
(2)
with the money demand function
(1) and
impose PPP to produce the Euler equation
![]() , where the standard-PVM discount factor is
, where the standard-PVM discount factor is
![]() and
and
![]() is the standard-PVM
fundamental, which nets cross-country money with its income demand.
Iterate on the Euler equation through date T and
recognize that the transversality condition
is the standard-PVM
fundamental, which nets cross-country money with its income demand.
Iterate on the Euler equation through date T and
recognize that the transversality condition
![]() to obtain the standard PVM relation
to obtain the standard PVM relation
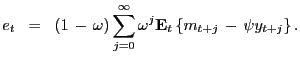
|
(3) |
The standard PVM
(3)
sets the log exchange rate equal to the annuity value of the
fundamental
![]() at the standard-PVM
discount factor
at the standard-PVM
discount factor ![]() .3
.3
2.B The DSGE Model
The optimizing monetary DSGE model consists of the preferences of domestic and foreign economies and their resource constraints. For the home (h) and foreign (f) countries, the former objects take the form
![$\displaystyle \mathcal{U}\left( C_{i,t}, \, \, \frac{M_{i,t}}{P_{i,t}} \right) \; \; = \; \; \frac{\left[ C_{i,t}^{ \displaystyle \nu}\left( \frac {\displaystyle M_{i,t} }{\displaystyle P_{i,t}} \right) ^{\displaystyle (1 - \nu)}\right] ^{ \displaystyle (1 - \varphi)}}{1 - \varphi}, \; \; \; \; 0 \, < \, \nu\, < 1, \; \; \; 0 \, < \, \varphi,$](img69.gif)
|
(4) |
where ![]() and
and ![]() represent the
represent the ![]() th country's consumption and the
th country's consumption and the
![]() th country's holdings of its money stock.
The resource constraint of the home country is
th country's holdings of its money stock.
The resource constraint of the home country is
| (5) |
where
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() , and
, and
![]() denote the ith country's
nominal holding of its own bonds at the end of date t,
the ith country's nominal holding of the
denote the ith country's
nominal holding of its own bonds at the end of date t,
the ith country's nominal holding of the
![]() th country's bonds at the end of date
t, the return on the ith
country's bond, the return on the
th country's bonds at the end of date
t, the return on the ith
country's bond, the return on the ![]() th
country's bond, the output level of the ith country,
and the level of the exchange rate. The two-country DSGE model is
closed with
th
country's bond, the output level of the ith country,
and the level of the exchange rate. The two-country DSGE model is
closed with
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . This
condition forces the world stock of nominal debt to be in zero net
supply, period-by-period, along the equilibrium path.
. This
condition forces the world stock of nominal debt to be in zero net
supply, period-by-period, along the equilibrium path.
In section 2, analysis of the standard-PVM relies on I(1) fundamentals. Likewise, we assume that the processes for
labor-augmenting total factor productivity (TFP), ![]() , and
, and ![]() satisfy
satisfy
ASSUMPTION 1:
![]() and
and
![]()
![]() .
.
ASSUMPTION 2: Cross-country TFP and money stock differentials are I(1) and do not cointegrate.
Assumptions 1 and 2 impose stochastic trends on the two-country DSGE model.
2.C Optimizing UIP and Money Demand
The home country maximizes its expected discounted lifetime utility over uncertain streams of consumption and real balances,
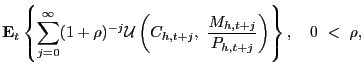
|
subject to (5). The first-order necessary conditions of economy i yield optimality conditions that describe UIP and money demand. The utility-based UIP condition of the home country is
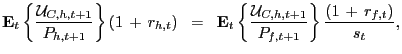
|
(6) |
where
![]() is the marginal utility
of consumption of the home country at date t. Given
the utility specification
(4),
the exact money demand function of country i is
is the marginal utility
of consumption of the home country at date t. Given
the utility specification
(4),
the exact money demand function of country i is
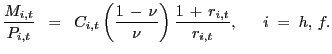
|
(7) |
The consumption elasticity of money demand is unity, while the interest elasticity of money demand is a nonlinear function of the steady state bond return.
The UIP condition (6) and money demand equation (7) can be stochastically detrended and then linearized to produce an equilibrium DSGE-law of motion for the exchange rate. Begin by combining the utility function (4) and the UIP condition (6) to obtain
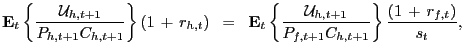
|
where
![]() is the utility level of
country i at date t. Prior to
stochastically detrending the previous expression, define
is the utility level of
country i at date t. Prior to
stochastically detrending the previous expression, define
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() , and
, and
![]() . Note that
. Note that
![]() is the transitory
component of consumption of the
is the transitory
component of consumption of the ![]() th economy,
th economy,
![]() is the TFP
(money) growth rate of country
is the TFP
(money) growth rate of country ![]() , and the
cross-country TFP (money stock) differential
, and the
cross-country TFP (money stock) differential
![]() are I(1).
Applying the definitions, the stochastically detrended UIP
condition becomes
are I(1).
Applying the definitions, the stochastically detrended UIP
condition becomes
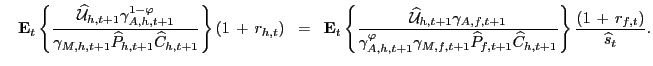
|
A log linear approximation of the stochastically detrended UIP condition yields
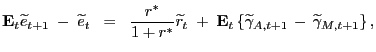
|
(8) |
where, for example,
![]() and
and
![]() denotes the steady state world real rate.
denotes the steady state world real rate.
2.D A DSGE-PVM of the Exchange Rate
We use the linear approximate law of motion of the exchange rate
(8), and a
stochastically detrended version of the money demand equation
(7)
to produce the DSGE-PVM. When linearized, the unit consumption
elasticity-money demand equation
(7)
produces
![]()
![]()
![]() . Impose PPP on the stochastically detrended version of the money
demand equation and combine it with the law of motion
(8) of the
transitory component of the exchange rate to find
. Impose PPP on the stochastically detrended version of the money
demand equation and combine it with the law of motion
(8) of the
transitory component of the exchange rate to find
![$\displaystyle \left[ 1 \; - \; \frac{1 \; \;}{1 + r^{\ast}} \mathbf{E}_{t} \mathbf{L}^{-1} \right] \widetilde{e}_{t} \; \; = \; \; \frac{1 \; \;}{1 + r^{\ast}} \mathbf{\ E}_{t} \left\{ \widetilde{\gamma}_{M,t+1} \, - \, \widetilde {\gamma}_{A,t+1} \right\} \; \; - \; \; \frac{r^{\ast}}{1 + r^{\ast}} \widetilde{c}_{t}.$](img148.gif)
|
Solving this stochastic difference equation forward gives a present value relation for the transitory component of the exchange rate
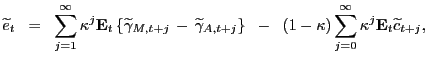
|
(9) |
where the relevant tranversality conditions are invoked and the
DSGE-PVM discount factor ![]()
![]()
![]() . Note
that the DSGE-PVM and permanent income hypothesis discount factors
are equivalent.
. Note
that the DSGE-PVM and permanent income hypothesis discount factors
are equivalent.
The DSGE-PVM relation (9) is the equilibrium law of motion of the cyclical component of the exchange rate. Transitory movements in the exchange rate are equated with the future discounted expected path of cross-country money and TFP growth and the (negative of the) annuity-value of the transitory component of cross-country consumption. The DSGE model identifies the exchange rate's unobserved time-varying risk premium with the expected path of cross-country TFP growth and transitory consumption, which suggest additional sources of exchange rate fluctuations.
The DSGE model produces a present value relation that resembles the standard-PVM (3). The DSGE-PVM follows from unwinding the stochastic detrending of the present value (9)
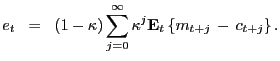
|
(10) |
Thus, the standard-PVM
(3)
and DSGE-PVM
(10) are identical
up to differences in their discount factors and real fundamentals.
The standard-PVM discount factor ![]() is tied to
the interest rate semi-elasticity of money demand,
is tied to
the interest rate semi-elasticity of money demand, ![]() , while the DSGE-PVM sets
, while the DSGE-PVM sets ![]() to the
inverse of the gross steady state real world interest rate,
to the
inverse of the gross steady state real world interest rate,
![]() . For the standard-PVM
(DSGE-PVM), the real fundamental is cross-country output
. For the standard-PVM
(DSGE-PVM), the real fundamental is cross-country output
![]() (consumption
(consumption ![]() ).
Table 1 summarizes the notable elements of the standard- and
DSGE-PVMs.
).
Table 1 summarizes the notable elements of the standard- and
DSGE-PVMs.
3 Generalizing the Engel-West Hypothesis
This section presents five propositions that generalize the EW hypothesis. This allows a broader empirical analysis of the EW hypothesis, and does so using standard time series tools. The propositions apply to the standard-PVM and the DSGE-PVM because their present value relations coincide. Thus, we generalize the EW hypothesis to the large class of two-country monetary DSGE models.
We collapse the differences in the discount factor and real
fundamental of the standard-PVM
(3)
and DSGE-PVM
(10) to stress
their mutual predictions in this section. These differences are put
aside by defining a PVM discount factor
![]() equal to either
equal to either ![]() or
or ![]() , while the fundamental
, while the fundamental
![]() is equivalent to either
is equivalent to either ![]()
![]()
![]() or
or ![]()
![]()
![]() . With these
assumptions, the focus is on the PVM
. With these
assumptions, the focus is on the PVM
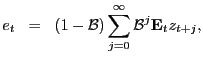
|
(11) |
which subsumes the standard- and DSGE-PVMs. The PVM (11) provides several predictions given
ASSUMPTION 3:
![]() .
.
ASSUMPTION 4:
![]() has a Wold
representation,
has a Wold
representation,
![]() , where
, where
![]() .4
.4
Engel and West (2005) employ Assumption 3, but they do not require restrictions as strong as Assumption 4. However, Assumption 4 is standard for linear rational expectation models; see Hansen, Roberds, and Sargent (1991). Assumption 4 is also an implication of a linear approximate solution of the open economy DSGE model, while Assumption 3 is consistent with Assumptions 1 and 2.
3.A Cointegration Restrictions
The first prediction is that ![]() and
and
![]() share a common trend. This follows
from subtracting the latter from both sides of the equality of the
present-value relation
(11) and combining
terms to produce the exchange rate-fundamental cointegrating
relation
share a common trend. This follows
from subtracting the latter from both sides of the equality of the
present-value relation
(11) and combining
terms to produce the exchange rate-fundamental cointegrating
relation
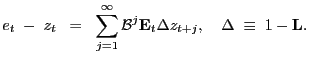
|
(12) |
Equation (12) reflects the forces - expected discounted value of fundamental growth - that push the exchange rate toward long-run PPP. The explanation is
PROPOSITION 1: If ![]() satisfies Assumptions 3 and 4,
satisfies Assumptions 3 and 4,
![]() forms
a cointegrating relation with cointegrating vector
forms
a cointegrating relation with cointegrating vector
![]() , where
, where
![]() .
.
The proposition is a variation of results found in Campbell and
Shiller (1987). We interpret the
cointegration relation
![]() as the 'adjusted' exchange
rate because movements in fundamentals are eliminated from it.
According to the cointegration present value relation
(12), the
'adjusted' exchange rate is stationary and forward-looking in
fundamental growth. Moreover, the cointegration relation
as the 'adjusted' exchange
rate because movements in fundamentals are eliminated from it.
According to the cointegration present value relation
(12), the
'adjusted' exchange rate is stationary and forward-looking in
fundamental growth. Moreover, the cointegration relation
![]() is an infinite-order moving
average, MA
is an infinite-order moving
average, MA![]() equal to
equal to
![]()
![]() , where
, where
![]()
![]()
![]() and
and
![]()
![]()
![]() under Assumptions 3 and 4 (i.e.,
under Assumptions 3 and 4 (i.e., ![]() is
is
![]() and its growth rate has a Wold
representation). Thus, the 'adjusted' exchange rate is a "cycle
generator" - as defined by Engle and Issler (1995) - because shocks to serially
correlated fundamental growth create persistent PPP deviations.
and its growth rate has a Wold
representation). Thus, the 'adjusted' exchange rate is a "cycle
generator" - as defined by Engle and Issler (1995) - because shocks to serially
correlated fundamental growth create persistent PPP deviations.
The standard- and DSGE-PVM require Assumptions 3 and 4 to
satisfy Proposition 1. Rather than these assumptions, we can
construct a cointegration relation from the DSGE model using
Assumptions 1 and 2 because
![]() is implied by the balanced
growth restriction,
is implied by the balanced
growth restriction,
![]() ,
where
,
where
![]() and
and
![]() . In this case, PPP
deviations arise from the DSGE-PVM because of restrictions the
present-value relation
(9) places on the
transitory component of the exchange rate,
. In this case, PPP
deviations arise from the DSGE-PVM because of restrictions the
present-value relation
(9) places on the
transitory component of the exchange rate,
![]() .
.
3.B Equilibrium Currency Return Dynamics
The second PVM prediction is that currency returns depend only
on the lagged 'adjusted' exchange rate and fundamental forecast
innovation. We show this by first rewriting the PVM of
(11)
as ![]()
![]()
![]()
![]() . Differencing this equation produces,
. Differencing this equation produces,
![$ \Delta e_{t} - (1 - \mathcal{B}) \Delta z_{t} = (1 - \mathcal{B}) \displaystyle \sum^{\infty}_{j=1} \mathcal{B}^{j} \left[ \mathbf{E}_{t} z_{t+j} - \mathbf{E}_{t-1} z_{t+j-1} \right] $](img226.gif) . Next, add and subtract
. Next, add and subtract
![]() inside the
brackets, and substitute with the cointegration-present-value
relation
(12) to obtain
inside the
brackets, and substitute with the cointegration-present-value
relation
(12) to obtain
![$\displaystyle \Delta e_{t} \; - \; \frac{1 - \mathcal{B}}{\mathcal{B}} \mathcal{X}_{t-1} \; \; = \; \; (1 - \mathcal{B}) \sum^{\infty}_{j=0} \mathcal{B}^{j} \bigl[ \mathbf{E}_{t} \, - \, \mathbf{E}_{t-1} \bigr] z_{t+j} .$](img229.gif)
|
(13) |
In equilibrium, currency return are generated by the lagged
cointegration relation,
![]() , and the expected annuity
value of the forecast innovations of the fundamental. The lagged
cointegration relation is the error correction mechanism of
(13) that reflects
the only force that restores currency returns to equilibrium and
PPP in response to the shock innovation
, and the expected annuity
value of the forecast innovations of the fundamental. The lagged
cointegration relation is the error correction mechanism of
(13) that reflects
the only force that restores currency returns to equilibrium and
PPP in response to the shock innovation
![]() . These ideas are summarized
by
. These ideas are summarized
by
PROPOSITION 2: Under Proposition 1, the PVM predicts that the equilibrium currency return is an error correction mechanism in which the lagged 'adjusted' exchange rate (or cointegration relation) is the only factor that drives the exchange rate to PPP in response to fundamental shock innovations.
Equation
(13) is an ECM
that regresses currency returns only on the lagged `adjusted'
exchange rate. The regression is
![]()
![]()
![]()
![]()
![]() with factor loading
with factor loading
![]()
![]()
![]() and currency return forecast error
and currency return forecast error
![]()
![]()
![]() .5
.5
3.C A Limiting Model of Exchange Rate Determination
Proposition 2 relies on
![]() < 1 to define short- to
medium-run currency return dynamics. This raises the question of
the impact of relaxing this bound.
< 1 to define short- to
medium-run currency return dynamics. This raises the question of
the impact of relaxing this bound.
PROPOSITION 3: The exchange rate
approaches a martingale (in the strict sense) as
![]() ,
according to the present-value relation
(13) assuming
Proposition 1.
,
according to the present-value relation
(13) assuming
Proposition 1.
Proposition 3 relies on
![]() to produce the
martingale
to produce the
martingale
![]()
![]()
![]() and random walk behavior in the
exchange rate.6 This behavior suggests an equilibrium
path for
and random walk behavior in the
exchange rate.6 This behavior suggests an equilibrium
path for ![]() in which its best forecast is
in which its best forecast is
![]() , given relevant information, because
the source of serial correlation,
, given relevant information, because
the source of serial correlation,
![]() disappears as
disappears as
![]() .7
.7
3.D PVM Exchange Rate Dynamics Redux
Engel and West (2005) show that
the PVM of the exchange rate yields an approximate random walk as
![]() approaches one. This section
affirms the EW hypothesis, but unlike Proposition 3 does not rely
on Proposition 2. Rather than follow the EW proof exactly, we
invoke Assumptions 3 and 4, the present-value relation
(3), the
Weiner-Kolmogorov prediction formula, and the conjecture
approaches one. This section
affirms the EW hypothesis, but unlike Proposition 3 does not rely
on Proposition 2. Rather than follow the EW proof exactly, we
invoke Assumptions 3 and 4, the present-value relation
(3), the
Weiner-Kolmogorov prediction formula, and the conjecture
![]() a
a![]() to find that currency returns are unpredictable.
to find that currency returns are unpredictable.
The EW hypothesis is
![]() . Its hypothesis test begins by noting
. Its hypothesis test begins by noting ![]()
![]()
![]()
![]()
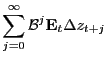 , which is obtained from the present-value relation
(3). Use this
equation to construct
, which is obtained from the present-value relation
(3). Use this
equation to construct
![]()
![]()
![]() , given
Assumptions 3 and 4 and the Weiner-Kolmogorov prediction formula.
The PVM of
(11)
also sets currency returns equal to the annuity value of
fundamental growth,
, given
Assumptions 3 and 4 and the Weiner-Kolmogorov prediction formula.
The PVM of
(11)
also sets currency returns equal to the annuity value of
fundamental growth,
![]()
![]()
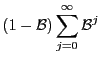
![]() . The last two
equations yield
. The last two
equations yield
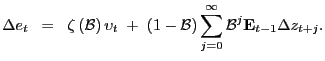
|
(14) |
By letting
![]() , the random
walk hypothesis of EW is verified independent of the ECM of
Proposition 2 (and cointegration prediction of Proposition
1).8
, the random
walk hypothesis of EW is verified independent of the ECM of
Proposition 2 (and cointegration prediction of Proposition
1).8
The ECM
(13) and
Proposition 2 maps into the EW currency return generating equation
(14).
First, apply the change of index ![]() to the
present value of
(14)
to obtain the present-value cointegration relation
(12) lagged once.
For the ECM
(13), its present
value
to the
present value of
(14)
to obtain the present-value cointegration relation
(12) lagged once.
For the ECM
(13), its present
value
![]() equals
equals
![]()
![]() subsequent to
evoking Assumptions 3 and 4 and the Weiner-Kolmogorov prediction
formula. Thus, when the PVM discount factor
subsequent to
evoking Assumptions 3 and 4 and the Weiner-Kolmogorov prediction
formula. Thus, when the PVM discount factor
![]() is arbitrarily close to one, the
EW hypothesis predicts
is arbitrarily close to one, the
EW hypothesis predicts
![]()
![]()
![]()
![]() which is
consistent with currency returns following an ECM with no own lags
or lags of fundamental growth. Since the standard- and DSGE-PVMs
produce the ECM, the EW hypothesis is generalized to the larger
class of two-country monetary DSGE models.
which is
consistent with currency returns following an ECM with no own lags
or lags of fundamental growth. Since the standard- and DSGE-PVMs
produce the ECM, the EW hypothesis is generalized to the larger
class of two-country monetary DSGE models.
3.E A Common Trend-Common Cycle Model of Exchange Rates and Fundamentals
Proposition 2 predicts an ECM for currency returns that is consistent with the EW currency return generating equation (14). These results rely, at most, on assumptions 3 and 4 under which fundamentals are I(1) and have a Wold representation in growth rates. However, empirical work on exchange rates often employ multivariate time series models (i.e., VARs) instead of the deeper notion of a Wold representation.
This section studies the impact on the bivariate exchange
rate-fundamental process,
![]() of endowing
an ECM on fundamental growth. In this case,
of endowing
an ECM on fundamental growth. In this case,
![]() forms a VECM(0)
forms a VECM(0)
![$\displaystyle \Delta q_{t} \; \; = \; \; \left[ \begin{array}[c]{c} \vartheta\\ \eta \end{array} \right] \mathcal{X}_{t-1} \; + \; \left[ \begin{array}[c]{c} u_{\Delta e,t}\\ u_{\Delta z,t} \end{array} \right] ,$](img300.gif)
|
(15) |
where ![]() is the factor loading on
is the factor loading on
![]() for
for
![]() and
and
![]() is its forecast innovation.
Pre-multiplying the VECM(0) by
is its forecast innovation.
Pre-multiplying the VECM(0) by
![]() creates the common feature
creates the common feature
| (16) |
The vector
![]() satisfies the
Engle and Kozicki (1993) notion of a
common feature because it creates a linear combination of
satisfies the
Engle and Kozicki (1993) notion of a
common feature because it creates a linear combination of
![]() and
and
![]() that is unpredictable
conditional on their history. Given this common feature restriction
and the cointegration relation of Proposition 1, Vahid and Engle
(1993) provide a method to construct
a Stock and Watson (1988)
multivariate Beveridge and Nelson (1981) common trend-common cycle
decomposition. We summarize these results with
that is unpredictable
conditional on their history. Given this common feature restriction
and the cointegration relation of Proposition 1, Vahid and Engle
(1993) provide a method to construct
a Stock and Watson (1988)
multivariate Beveridge and Nelson (1981) common trend-common cycle
decomposition. We summarize these results with
PROPOSITION 4: Assume fundamental
growth is the ECM process
![]()
![]()
![]()
![]()
![]() , where the forecast
innovation
, where the forecast
innovation
![]() is Gaussian. When Proposition
2 holds,
is Gaussian. When Proposition
2 holds, ![]() has a common feature,
has a common feature,
![]() ,
in the sense of Engle and Kozicki (1993), where
,
in the sense of Engle and Kozicki (1993), where
![]() . The cointegrating and common feature vectors
. The cointegrating and common feature vectors ![]() and
and
![]() restrict the trend-cycle
decomposition of
restrict the trend-cycle
decomposition of ![]() , as described by Vahid and
Engle (1993).
, as described by Vahid and
Engle (1993).
The common feature of Proposition 4 endows
![]() with a
common trend and a common cycle Beveridge-Nelson-Stock-Watson
(BNSW) decomposition. Vahid and Engle (1993) provide an example in which the
cointegration and common feature vectors restrict the trend of
with a
common trend and a common cycle Beveridge-Nelson-Stock-Watson
(BNSW) decomposition. Vahid and Engle (1993) provide an example in which the
cointegration and common feature vectors restrict the trend of
![]() to
to
![]()
![]()
![]() , which gives trend and cycle components
, which gives trend and cycle components
![]() and
and
![]() , respectively.9 The BNSW decomposition imposes a
common cycle on
, respectively.9 The BNSW decomposition imposes a
common cycle on ![]() and
and ![]() in
the short-, medium-, and long-run, which restricts the exchange
rate to be unpredictable at all forecast horizons. This prediction
is at odds with the empirical evidence of Mark (1995).
in
the short-, medium-, and long-run, which restricts the exchange
rate to be unpredictable at all forecast horizons. This prediction
is at odds with the empirical evidence of Mark (1995).
The common feature relation (16) also provides another approach to verify the EW hypothesis,
![]() .
.
PROPOSITION 5: Let the exchange rate
and fundamental have the VECM(0)
(15).
Then, the EW hypothesis requires currency returns and fundamental
growth to share a common feature defined by
![]() and that
and that ![]()
![]() 0 or
0 or
![]() .
.
Proposition 5 differs from other approaches to the EW
hypothesis. First, the common feature relation
(16)
imposes cross-equation restrictions on
![]() because its cycle generator,
the lagged cointegrating relation
because its cycle generator,
the lagged cointegrating relation
![]() , is annihilated by
, is annihilated by
![]() . Having
eliminated
. Having
eliminated
![]() , the EW hypothesis
decouples the exchange rate from fundamental growth and its
forecast innovation
, the EW hypothesis
decouples the exchange rate from fundamental growth and its
forecast innovation
![]() (
(![]()
![]() ). Finally,
observe that when
). Finally,
observe that when ![]()
![]() 0 (or
0 (or
![]() ,
,
![]()
![]()
![]() . This leaves only the forecast
innovation
. This leaves only the forecast
innovation
![]() to generate movements in
to generate movements in
![]() . Thus, the EW hypothesis is
affirmed by Proposition 5.10
. Thus, the EW hypothesis is
affirmed by Proposition 5.10
A corollary of Proposition 5 is that changes in fundamentals do
not Granger cause currency returns as
![]() . Only if
. Only if
![]() , do movements in
fundamentals have predictive power for currency returns according
to the PVM. However, currency returns Granger cause growth in the
fundamental as long as it is predicted by its own lagged forecast
innovations. The equilibrium currency return generating equation
(13) and
Proposition 2 shows that this holds even if
, do movements in
fundamentals have predictive power for currency returns according
to the PVM. However, currency returns Granger cause growth in the
fundamental as long as it is predicted by its own lagged forecast
innovations. The equilibrium currency return generating equation
(13) and
Proposition 2 shows that this holds even if
![]() .
.
3.F Reduced Form Evidence
The propositions suggest testable restrictions on exchange rates and fundamentals. Table 3 describes details of the tests and summarizes results. Fisrt, if the lag length of the levels VAR of the exchange rate and fundamental exceeds one, the VECM (15) is rejected. Second, cointegration tests are sufficient to examine Proposition 1. Finally, common feature tests are used, following Vahid and Engel (1993) and Engel and Issler (1995), that yield information about Proposition 4.
We estimate VARs of foreign currency-U.S. dollar exchange rates
and fundamentals using Canadian, Japanese, U.K., and U.S. data on a
1976Q1 - 2004Q4 sample.11 VAR
lag lengths are chosen using likelihood ratio (LR) statistics,
given a VAR(8), ![]() , VAR(1).12 As
described in Table 3, the Canadian-, Japanese-, and U.K.-U.S.
samples yield a VAR(8), VAR(5), and VAR(4), respectively.13
Thus, the Canadian, Japanese, U.K., and U.S. data reject the VECM
(15)
because
, VAR(1).12 As
described in Table 3, the Canadian-, Japanese-, and U.K.-U.S.
samples yield a VAR(8), VAR(5), and VAR(4), respectively.13
Thus, the Canadian, Japanese, U.K., and U.S. data reject the VECM
(15)
because
![]() has more serial correlation
than explained by the lagged cointegration relation
has more serial correlation
than explained by the lagged cointegration relation
![]() .
.
Table 3 also presents Johansen (1991,
1994) trace and ![]() max test statistics
that fail to confirm the cointegration prediction of Proposition 1
for the Canadian-, Japanese-, and U.K.-U.S. samples. This finding
is consistent with Engel and West (2005), who argue there is little evidence
that exchange rates and fundamentals cointegrate.
max test statistics
that fail to confirm the cointegration prediction of Proposition 1
for the Canadian-, Japanese-, and U.K.-U.S. samples. This finding
is consistent with Engel and West (2005), who argue there is little evidence
that exchange rates and fundamentals cointegrate.
Finally, the common feature test is described in Table 3. This
uses squared canonical correlations of currency returns and
fundamental growth. The common feature null is that the smallest
correlation equals zero. We use a ![]() statistic of Vahid and Engle (1993)
and a F-statistic developed by Rao (1973) to test this null. The tests reject
the null for the largest canonical correlation, but not for the
smaller one in the three samples. This is evidence that currency
returns and fundamental share a common feature in the Canadian-,
Japanese-, and U.K.-U.S. samples. Given a common feature, the
exchange rate approximates a random walk when
statistic of Vahid and Engle (1993)
and a F-statistic developed by Rao (1973) to test this null. The tests reject
the null for the largest canonical correlation, but not for the
smaller one in the three samples. This is evidence that currency
returns and fundamental share a common feature in the Canadian-,
Japanese-, and U.K.-U.S. samples. Given a common feature, the
exchange rate approximates a random walk when
![]() . The next
section explores the empirical content of this hypothesis in the
Canadian-U.S. data.
. The next
section explores the empirical content of this hypothesis in the
Canadian-U.S. data.
4 Econometric Models and Methods
Propositions 1-5 broaden our understanding of the EW hypothesis, which is also generalized to hold for the DSGE-PVM. Although the previous section discusses VAR methods that yield evidence about the joint behavior of the exchange rate and standard-PVM fundamentals, this approach is not informative about estimates of the PVM discount factor.
This section presents methods to estimate a PVM discount factor
and test the EW hypothesis. Instead of relying on VARs, we employ
unobserved components (UC) models to estimate the DSGE-PVM and test
the EW hypothesis using Bayesian methods. A brief example motivates
our approach. Consider the PVM
(11)
where the fundamental ![]() has the
permanent-transitory decomposition
has the
permanent-transitory decomposition ![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]()
![]() 0,
0,
![]()
![]()
![]() ,
,
![]()
![]()
![]() , and
, and
![]()
![]() 0 for all
0 for all ![]() and
and
![]() .14 Combining the PVM
(11)
and the permanent-transitory decomposition of
.14 Combining the PVM
(11)
and the permanent-transitory decomposition of ![]() gives an equilibrium permanent-transitory decomposition
of the exchange rate,
gives an equilibrium permanent-transitory decomposition
of the exchange rate,
![]() , where
, where
![]() is a 1
is a 1 ![]()
![]() row vector with a first element of
one and zeros elsewhere and
row vector with a first element of
one and zeros elsewhere and
![]() is the companion
matrix of the AR of
is the companion
matrix of the AR of
![]() . The exchange rate trend
is identified with the random walk of
. The exchange rate trend
is identified with the random walk of ![]() under
its permanent-transitory decomposition. Transitory exchange rate
fluctuations are driven by the fundamental cyclical component,
under
its permanent-transitory decomposition. Transitory exchange rate
fluctuations are driven by the fundamental cyclical component,
![]() , which is the common
dynamic factor of the exchange rate and observed fundamental. The
permanent-transitory decomposition of the exchange rate is useful
for the EW hypothesis because it becomes possible to estimate
, which is the common
dynamic factor of the exchange rate and observed fundamental. The
permanent-transitory decomposition of the exchange rate is useful
for the EW hypothesis because it becomes possible to estimate
![]() , along with the coefficients of
the permanent-transitory decomposition of
, along with the coefficients of
the permanent-transitory decomposition of ![]() .
Note also that as
.
Note also that as
![]() approaches one, the permanent
component
approaches one, the permanent
component ![]() comes to dominate exchange rate
fluctuations as predicted by the EW hypothesis.
comes to dominate exchange rate
fluctuations as predicted by the EW hypothesis.
We use Bayesian methods to estimate multivariate UC models of
the DSGE-PVM. The models represent different combinations of
restrictions imposed by the DSGE-PVM on the exchange rate,
cross-country money, and cross-country consumption. For example,
![]() is estimated for three UC models,
which ties the exchange rate to the transitory component(s) of
fundamentals. The exchange rate is disconnected from transitory
shocks in remaining three UC models because
is estimated for three UC models,
which ties the exchange rate to the transitory component(s) of
fundamentals. The exchange rate is disconnected from transitory
shocks in remaining three UC models because ![]() is
calibrated to one. We cast the UC models in state space form to
evaluate numerically the likelihoods. We use a sample of the
Canadian dollar-U.S. dollar
(CDN$/US$) exchange rate and the
Canadian-U.S. money and consumption differentials from
1976Q1-2004Q4. The random walk
MH simulator is used to generate MCMC draws from the UC model
posterior distributions conditional on this sample. We compute
model moments, such as parameter means, unconditional variance
ratios, permanent-transitory decompositions, and forecast error
variance decompositions (FEVDs), from the posterior distributions.
Model comparisons are based on marginal likelihoods, which we
construct by integrating the likelihood function of each model
across its parameter space where the weighting function is the
model prior.
is
calibrated to one. We cast the UC models in state space form to
evaluate numerically the likelihoods. We use a sample of the
Canadian dollar-U.S. dollar
(CDN$/US$) exchange rate and the
Canadian-U.S. money and consumption differentials from
1976Q1-2004Q4. The random walk
MH simulator is used to generate MCMC draws from the UC model
posterior distributions conditional on this sample. We compute
model moments, such as parameter means, unconditional variance
ratios, permanent-transitory decompositions, and forecast error
variance decompositions (FEVDs), from the posterior distributions.
Model comparisons are based on marginal likelihoods, which we
construct by integrating the likelihood function of each model
across its parameter space where the weighting function is the
model prior.
4.A State Space Systems of the UC Models
The state space systems of the six UC models begin with the
balanced growth restriction the DSGE model imposes on the exchange
rate. This restriction is equivalent to the permanent-transitory
decomposition
![]() .
The DSGE-PVM
(9) places
cross-equation restrictions on the stationary component of the
exchange rate,
.
The DSGE-PVM
(9) places
cross-equation restrictions on the stationary component of the
exchange rate,
![]() .
.
Cross-equation restrictions are conditioned on the permanent and
transitory components of cross-country money and cross-country
consumption. The permanent components of money and consumption are
![]() ,
,
![]() , and
, and
![]() ,
,
![]() , respectively. Note that
, respectively. Note that
![]() and
and ![]() are
the deterministic trend growth rates of cross-country money and
TFP. We assume
are
the deterministic trend growth rates of cross-country money and
TFP. We assume
![]() is a MA
is a MA
![]() ,
,
![]() , where
, where
![]() and
and
![]() . For
. For
![]() , we employ a AR
, we employ a AR
![]() ,
,
![]() , where
, where
![]() . Put these elements together to form the balanced growth version
of the DSGE-PVM
. Put these elements together to form the balanced growth version
of the DSGE-PVM
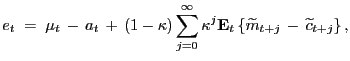
|
(17) |
which satisfies the DSGE balanced growth path restrictions. The
balanced growth DSGE-PVM
(17) implies the
cointegrating relation of Proposition 1. Thus, the exchange rate
responds only to trends in cross-country money, ![]() , and TFP,
, and TFP, ![]() , in the long-run.
Serial correlation in the exchange rate is produced by the
transitory components of cross-country money and consumption,
, in the long-run.
Serial correlation in the exchange rate is produced by the
transitory components of cross-country money and consumption,
![]() and
and
![]() . Also, if a common cycle
generates these transitory components, the exchange also shares the
restriction. Thus, the permanent and transitory components of
cross-country money and consumption drive exchange rate
fluctuations, which give rise to cross-equation restrictions in the
UC models.
. Also, if a common cycle
generates these transitory components, the exchange also shares the
restriction. Thus, the permanent and transitory components of
cross-country money and consumption drive exchange rate
fluctuations, which give rise to cross-equation restrictions in the
UC models.
The UC models are classified according to whether there are two
cycles or a common cycle and whether ![]() is
calibrated to one or estimated. Three UC models follow from solving
the DSGE-PVM
(17) given
is
calibrated to one or estimated. Three UC models follow from solving
the DSGE-PVM
(17) given
![]() MA
MA
![]() and
and
![]() AR
AR
![]() or a common cycle is
imposed using either the MA
or a common cycle is
imposed using either the MA
![]() or AR
or AR
![]() . The three UC models are
estimated when
. The three UC models are
estimated when ![]() is calibrated to one. We also
use the UC models to estimate
is calibrated to one. We also
use the UC models to estimate ![]() . The six UC
models have in common the cross-country money trend,
. The six UC
models have in common the cross-country money trend, ![]() , and TFP trend,
, and TFP trend, ![]() .
.
A rich set of cross-equation restrictions arises in the 2-trend,
2-cycle UC model with
![]() . In part, its state space
system consists of the observation equations
. In part, its state space
system consists of the observation equations
![$\displaystyle \qquad\left[ \begin{array}[c]{c} e_{t}\\ m_{t}\\ c_{t} \end{array} \right] \; \; = \; \; \left[ \begin{array}[c]{cccccccccc} 1 & -1 & \delta_{\widetilde{m},0} & \delta_{\widetilde{m},1} & \ldots & \delta_{\widetilde{m},k_{\widetilde{m}}} & \delta_{\widetilde{c},0} & \delta_{\widetilde{c},1} & \ldots & \delta_{\widetilde{c},k_{\widetilde{c}} -1}\\ 1 & 0 & 1 & \alpha_{1} & \ldots & \alpha_{k_{\widetilde{m}}} & 0 & 0 & \ldots & 0\\ 0 & 1 & 0 & 0 & \ldots & 0 & 1 & 0 & \ldots & 0\\ & & & & & & & & & \end{array} \right] \mathcal{S}_{\widetilde{m},c,t},$](img479.gif)
|
(18) |
where
![]() , factor loadings on
, factor loadings on
![]() and its lags
are
and its lags
are
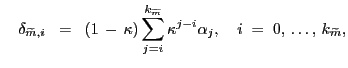
|
(19) |
factor loadings on
![]() ,
, ![]() ,
,
![]() are
elements of the row vector
are
elements of the row vector
![$\displaystyle \delta_{\widetilde{c}} \; \; = \; \; -s_{\widetilde{c}} (1 \, - \, \kappa) \biggl [\mathbf{I}_{k_{\widetilde{c}}} \, \, - \, \, \kappa\Theta\biggr]^{-1}, \quad s_{\widetilde{c}} \; = \; [1 \; \; \, \mathbf{0}_{1 \times k_{\widetilde{c}}-1}],$](img486.gif)
|
(20) |
and ![]() is the companion matrix of the AR
is the companion matrix of the AR
![]() of
of
![]() . The system of first-order
state equations is
. The system of first-order
state equations is
![$\displaystyle \mathcal{S}_{\widetilde{m},c,t+1} \; \; = \; \; \left[ \begin{array}[c]{c} \mu^{\ast}\\ a^{\ast}\\ 0\\ \vdots\\ 0\\ \vdots \end{array} \right] \; \; + \; \; \left[ \begin{array}[c]{ccccccc} 1 & 0 & \ldots & 0 & 0 & \ldots & 0\\ 0 & 1 & \ldots & 0 & 0 & \ldots & 0\\ 0 & 0 & \ldots & 0 & 0 & \ldots & 0\\ \vdots & \vdots & \mathbf{I}_{k_{\widetilde{m}}} & \vdots & \vdots & & \vdots\\ 0 & 0 & \ldots & 0 & \theta_{1} & \ldots & \theta_{k_{\widetilde{c}}}\\ \vdots & \vdots & & \vdots & & \mathbf{I}_{k_{\widetilde{c}}-1} & \mathbf{0}_{(k_{\widetilde{c}}-1) \times1}\\ & & & & & & \end{array} \right] \, \mathcal{S}_{\widetilde{m},c,t} \; \; + \; \; \left[ \begin{array}[c]{c} \varepsilon_{\mu,t+1}\\ \varepsilon_{a,t+1}\\ \varepsilon_{\widetilde{m},t+1}\\ \mathbf{0}_{k_{\widetilde{m}} \times1}\\ \varepsilon_{\widetilde{c},t+1}\\ \mathbf{0}_{(k_{\widetilde{c}}-1) \times1}\\ \end{array} \right] ,$](img490.gif)
|
(21) |
with covariance matrix
![]() , where
, where
![]() .
.
We also study UC models that impose one common transitory factor
on ![]() and
and ![]() . When the
common component is
. When the
common component is
![]() , the response of
, the response of
![]() to
to
![]() is denoted
is denoted
![]() . This implies
. This implies
![]()
![]()
![]() and
gives rise to the 2-trend, money cycle UC model. Identifying the
common transitory component with
and
gives rise to the 2-trend, money cycle UC model. Identifying the
common transitory component with
![]() defines
defines
![]()
![]()
![]() which restricts the 2-trend, consumption cycle UC model. The
appendix describes the state space systems of the 2-trend, money
cycle and 2-trend, consumption cycle UC models.
which restricts the 2-trend, consumption cycle UC model. The
appendix describes the state space systems of the 2-trend, money
cycle and 2-trend, consumption cycle UC models.
The three remaining UC models set ![]() . The
restriction on the state space of the 2-trend, 2-cycle UC model is
that the exchange rate is decoupled from transitory cross-country
money and consumption shocks. Similar restrictions arise in the
observer equation of the 2-trend, money cycle and 2-trend,
consumption cycle UC models. Thus, we are able to compare DSGE-PVMs
in which
. The
restriction on the state space of the 2-trend, 2-cycle UC model is
that the exchange rate is decoupled from transitory cross-country
money and consumption shocks. Similar restrictions arise in the
observer equation of the 2-trend, money cycle and 2-trend,
consumption cycle UC models. Thus, we are able to compare DSGE-PVMs
in which ![]() is estimated to those in which
is estimated to those in which
![]() is calibrated to one. This provides
an empirical appraisal of the EW hypothesis.
is calibrated to one. This provides
an empirical appraisal of the EW hypothesis.
4.B The UC Model and Its Likelihood Function
We label the 2-trend, 2-cycle UC model with
![]()
![]() . Likewise,
. Likewise,
![]() and
and
![]() denote the
2-trend, money cycle and 2-trend, consumption cycle,
denote the
2-trend, money cycle and 2-trend, consumption cycle,
![]() UC models. The state
space system of
UC models. The state
space system of
![]() is
(18)
and
(21), while the
appendix presents these systems for
is
(18)
and
(21), while the
appendix presents these systems for
![]() and
and
![]() . These state
space systems represent the dynamics of
. These state
space systems represent the dynamics of
![]() restricted by the DSGE-PVM and permanent-transitory specifications
of
restricted by the DSGE-PVM and permanent-transitory specifications
of ![]() and
and ![]() . We calibrate
. We calibrate
![]() in
in
![]() ,
,
![]() , and
, and
![]() . The state
space systems are mapped into the Kalman filter to evaluate
likelihood functions as proposed by Harvey (1989) and Hamilton (1994).15 Denote the likelihood
. The state
space systems are mapped into the Kalman filter to evaluate
likelihood functions as proposed by Harvey (1989) and Hamilton (1994).15 Denote the likelihood
![]() , where
, where ![]()
![]() 2,
2,
![]() ,
,
![]() is either calibrated to one or
estimated, and
is either calibrated to one or
estimated, and
![]() is the parameter vector
of
is the parameter vector
of
![]() .
.
The largest parameter vector is
![]() . It contains
. It contains
![]() elements,
elements,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . We add the parameters
. We add the parameters
![]() ,
,
![]() ,
,
![]() , and
, and ![]() to
to
![]() to better fit
to better fit
![]() to the data. For example,
the Canadian-U.S. TFP differential exhibits more variation than
to the data. For example,
the Canadian-U.S. TFP differential exhibits more variation than
![]() if the correlation coefficient of
innovations to
if the correlation coefficient of
innovations to ![]() and
and
![]() ,
,
![]() , is negative.16 The remaining three parameters allow
for an unrestricted exchange rate intercept,
, is negative.16 The remaining three parameters allow
for an unrestricted exchange rate intercept, ![]() , a linear exchange rate trend,
, a linear exchange rate trend, ![]() , and a factor loading on the Canadian-U.S. TFP
differential,
, and a factor loading on the Canadian-U.S. TFP
differential, ![]() , rather than set the
(1, 2) element in the matrix of the
observation system
(18)
to negative one.17 We estimate
, rather than set the
(1, 2) element in the matrix of the
observation system
(18)
to negative one.17 We estimate ![]() to ask if the data supports the cointegration-balanced growth path
restriction imposed on the DSGE-PVM
(17).
to ask if the data supports the cointegration-balanced growth path
restriction imposed on the DSGE-PVM
(17).
The parameter vectors of the other five UC models are smaller.
The
![]() model drops two
plus
model drops two
plus
![]() parameters from
parameters from
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , while adding the factor loading on
, while adding the factor loading on
![]() for
for ![]() ,
,
![]() . The factor loading
. The factor loading
![]() enters the parameter
vector of
enters the parameter
vector of
![]() , while
, while
![]()
![]() and
and
![]() are dropped from
are dropped from
![]()
![]()
![]()
![]()
![]()
![]() . The parameter vectors of the UC models
. The parameter vectors of the UC models
![]() ,
,
![]() , and
, and
![]() are identical
to
are identical
to
![]() ,
,
![]() , and
, and
![]() except that
except that
![]() .
.
4.C The Data
The sample runs from 1976Q1 to 2004Q4, T = 116. We have observations on the Canadian dollar-U.S. dollar exchange rate (average of period). The Canadian monetary aggregate is M1 in current Canadian dollars, while for the U.S. it is the Board of Governors monetary base (adjusted for changes in reserve requirements) in current U.S. dollars. Consumption is the sum of non-durable and services expenditures in constant local currency units.18 The aggregate quantity data is converted to per capita units. The data is logged and multiplied by 100, but is neither demeaned nor detrended.
4.D Estimation Methods
The likelihood functions of the UC models do not have analytic
solutions. We approximate the likelihoods
![]() and
and
![]() with posterior distributions of
with posterior distributions of
![]() and
and
![]() , generated by the
MCMC replications of the random walk MH simulator. Our estimates of
, generated by the
MCMC replications of the random walk MH simulator. Our estimates of
![]() and
and
![]() and marginal
likelihoods build on the Bayesian estimation tools of
Fernández-Villaverde and Rubio-Ramírez (2004), Rabanal and Rubio-Ramírez
(2005), Geweke (1999, 2005), An and
Schorfheide (2007), and Gelman,
Carlin, Stern, and Rubin (2004).
The MH simulator creates 1.5 million MCMC draws from the posterior.
The initial 750,000 draws are treated as a burn-in sample and
therefore discarded. We base our estimates on the remaining 750,000
draws from the posteriors of the
and marginal
likelihoods build on the Bayesian estimation tools of
Fernández-Villaverde and Rubio-Ramírez (2004), Rabanal and Rubio-Ramírez
(2005), Geweke (1999, 2005), An and
Schorfheide (2007), and Gelman,
Carlin, Stern, and Rubin (2004).
The MH simulator creates 1.5 million MCMC draws from the posterior.
The initial 750,000 draws are treated as a burn-in sample and
therefore discarded. We base our estimates on the remaining 750,000
draws from the posteriors of the
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() , and
, and
![]() models.19
models.19
4.E Priors
The second column of table 4 (5) list the priors of
![]()
![]() ,
, ![]()
![]() 2,
2,
![]() ,
,
![]() . Under a normal prior, the
first element is the degenerate mean and second its standard
deviation. The inverse-gamma priors are parameterized by its
degrees of freedom, the first element, and its mean, the second
element. The left and right end points of a uniform prior is
denoted by its first and second elements.
. Under a normal prior, the
first element is the degenerate mean and second its standard
deviation. The inverse-gamma priors are parameterized by its
degrees of freedom, the first element, and its mean, the second
element. The left and right end points of a uniform prior is
denoted by its first and second elements.
We choose degenerate priors for the lag lengths of the MA
![]() of
of
![]() and AR
and AR
![]() of
of
![]() that set
that set
![]() .
Normal priors for the MA (
.
Normal priors for the MA (
![]() and
and
![]() ) and AR (
) and AR (
![]() and
and
![]() ) coefficients allow for disparate
transitory behavior in
) coefficients allow for disparate
transitory behavior in
![]() and
and
![]() . The prior means of
. The prior means of
![]() ,
,
![]() ,
,
![]() , and
, and
![]() guarantee that the relevant
eigenvalues are strictly less than one. The eigenvalues of the
MA(2) (AR(2)) of
guarantee that the relevant
eigenvalues are strictly less than one. The eigenvalues of the
MA(2) (AR(2)) of
![]() (
(
![]() ) are 0.60 ± 0.20i (0.95 and -0.10). The standard
deviation of the normal priors of the MA and AR coefficients
provide for a wide set of realizations for
) are 0.60 ± 0.20i (0.95 and -0.10). The standard
deviation of the normal priors of the MA and AR coefficients
provide for a wide set of realizations for
![]() ,
,
![]() ,
,
![]() , and
, and
![]() . However, when a draw generates
an eigenvalue greater than one (in absolute value) for either the
MA or AR coefficients, the draw is discarded. Nonetheless, the MA
and AR priors admit transitory cycles in cross-country money and
consumption that allow for power at the business cycle frequencies,
if the data wants.
. However, when a draw generates
an eigenvalue greater than one (in absolute value) for either the
MA or AR coefficients, the draw is discarded. Nonetheless, the MA
and AR priors admit transitory cycles in cross-country money and
consumption that allow for power at the business cycle frequencies,
if the data wants.
We opt for priors of
![]() and
and ![]() that
rely on the Canadian-U.S. money stock and consumption differentials
samples. Since
that
rely on the Canadian-U.S. money stock and consumption differentials
samples. Since
![]() and
and ![]() represent deterministic trend growth, we ground the priors on
normal distributions. The prior standard deviations of
represent deterministic trend growth, we ground the priors on
normal distributions. The prior standard deviations of
![]() and
and ![]() match
sample moments.
match
sample moments.
Priors on the standard deviations of the shock innovations
reflect standard practice for estimating DSGE models with Bayesian
methods. For example, Adolfson, Laséen, Lindé, and
Villani (2007) employ
inverse-gamma priors for the standard deviations of the shock
innovations of their sticky price open economy DSGE model. However,
there is a lack of good information about
![]() ,
,
![]() ,
,
![]() , and
, and
![]() . This explains why we
impose a prior with two degrees of freedom, which forces these
standard deviations to be positive. On the other hand, we attach a
normally distributed prior to the correlation of innovations to
. This explains why we
impose a prior with two degrees of freedom, which forces these
standard deviations to be positive. On the other hand, we attach a
normally distributed prior to the correlation of innovations to
![]() and
and
![]() ,
,
![]() . Its mean is
negative to capture our prior that the TFP differential,
. Its mean is
negative to capture our prior that the TFP differential,
![]() , is smoother than cross-country
consumption,
, is smoother than cross-country
consumption, ![]() . Since we have no information
about the extent of the smoothness, the mean is -0.5 with a standard deviation of 0.2 that places draws close
to negative one or zero in the 95 percent coverage interval of the
prior. Draws greater than one or less than negative one are
ignored. The correlation of innovations to
. Since we have no information
about the extent of the smoothness, the mean is -0.5 with a standard deviation of 0.2 that places draws close
to negative one or zero in the 95 percent coverage interval of the
prior. Draws greater than one or less than negative one are
ignored. The correlation of innovations to ![]() and
and
![]() is fixed at zero,
reflecting our assumption that the sources and causes of permanent
and transitory monetary shocks are orthogonal.
is fixed at zero,
reflecting our assumption that the sources and causes of permanent
and transitory monetary shocks are orthogonal.
The exchange rate intercept and linear time trend priors are set
according to a linear regression of the exchange rate on these
objects. This motivates our choice of normally distributed priors
for
![]() and
and ![]() and
of their degenerate means and standard deviations.
and
of their degenerate means and standard deviations.
The remaining factor loadings have priors that reflect a dearth
of information on our part. The uniform priors of
![]() ,
,
![]() , and
, and
![]() are wide and include
zero. If, for example,
are wide and include
zero. If, for example, ![]() is small it
indicates the inadequacy of the balanced growth restriction and the
impact of permanent fluctuations in Canadian-U.S. TFP differentials
on the exchange rate. The same holds for the response of
is small it
indicates the inadequacy of the balanced growth restriction and the
impact of permanent fluctuations in Canadian-U.S. TFP differentials
on the exchange rate. The same holds for the response of
![]() to transitory movements in
the Canadian-U.S. money stock (consumption) differential.
to transitory movements in
the Canadian-U.S. money stock (consumption) differential.
The
![]() models have only one
'economic' parameter, the DSGE-PVM discount factor
models have only one
'economic' parameter, the DSGE-PVM discount factor
![]() , in common. We adopt the Engel and West (2005) prior for
, in common. We adopt the Engel and West (2005) prior for ![]() . They
argue that it is necessary for
. They
argue that it is necessary for
![]() to generate an
approximate random walk exchange rate from the standard-PVM. Hence,
our prior on
to generate an
approximate random walk exchange rate from the standard-PVM. Hence,
our prior on ![]() is constructed to provide
information about the EW hypothesis from the posteriors of the
is constructed to provide
information about the EW hypothesis from the posteriors of the
![]() models. We impose an
inverse-gamma prior on the DSGE-PVM discount factor
models. We impose an
inverse-gamma prior on the DSGE-PVM discount factor ![]() , which follows Del Negro and Schorfheide (2006). The degenerate prior means of
, which follows Del Negro and Schorfheide (2006). The degenerate prior means of
![]() and
exp([a* = 0.158]/400) imply an annual
average real world interest rate of about five percent. Although a
five percent real world interest rate is large for the floating
rate period, the standard deviation of 0.038 guarantees draws for
and
exp([a* = 0.158]/400) imply an annual
average real world interest rate of about five percent. Although a
five percent real world interest rate is large for the floating
rate period, the standard deviation of 0.038 guarantees draws for
![]() that cover a wide interval. However,
MCMC draws from the random walk MH simulator of the
that cover a wide interval. However,
MCMC draws from the random walk MH simulator of the
![]() models obey the EW prior
because we ignore draws for which
models obey the EW prior
because we ignore draws for which
![]() .
.
5 Results
This section presents the results of implementing our empirical
strategy. Tables 4 and 5 provide the posterior means and standard
deviations of
![]() and
and
![]() vectors, i
vectors, i ![]() 2,
2,
![]() ,
,
![]() , for the six UC models. We
include marginal likelihoods of the six UC models, using methods
described by Fernández-Villaverde and Rubio-Ramírez
(2004), Rabanal and
Rubio-Ramírez (2005), and
Geweke (1999), to conduct inference
across these models. We present densities of the prior and
posteriors of
, for the six UC models. We
include marginal likelihoods of the six UC models, using methods
described by Fernández-Villaverde and Rubio-Ramírez
(2004), Rabanal and
Rubio-Ramírez (2005), and
Geweke (1999), to conduct inference
across these models. We present densities of the prior and
posteriors of ![]() for
for
![]() ,
,
![]() , and
, and
![]() in figure 1.
Tables 6, 7, 8, and 9 report factor loadings on the exchange rate
of the transitory components of money and consumption
differentials, unconditional variance ratios of the present
discounted value of the shock innovations to the exchange rate,
FEVDs of the trend-cycle decomposition of the exchange rate with
respect to these shocks, and summary statistics of trend-cycle
decompositions, respectively. Figures 2, 3, and 4 plot the
trend-cycle decomposition of the
CDN$/US$ exchange rate.
in figure 1.
Tables 6, 7, 8, and 9 report factor loadings on the exchange rate
of the transitory components of money and consumption
differentials, unconditional variance ratios of the present
discounted value of the shock innovations to the exchange rate,
FEVDs of the trend-cycle decomposition of the exchange rate with
respect to these shocks, and summary statistics of trend-cycle
decompositions, respectively. Figures 2, 3, and 4 plot the
trend-cycle decomposition of the
CDN$/US$ exchange rate.
5.A Parameter Estimates
Tables 4 and 5 list the posterior means and standard deviations
of the parameters of the six UC models. Estimates of
![]() ,
,
![]() ,
,
![]() appear in
table 4. These three models exhibit persistence in the transitory
components of the money and consumption differentials,
appear in
table 4. These three models exhibit persistence in the transitory
components of the money and consumption differentials,
![]() and
and
![]() . For example, the
. For example, the
![]()
![]() model
yields AR (MA) estimates that imply the half life of a shock to
model
yields AR (MA) estimates that imply the half life of a shock to
![]() is 17 (7) years.20 However, only
is 17 (7) years.20 However, only
![]() is persistent in the
is persistent in the
![]() model. The half life of
a shock to
model. The half life of
a shock to
![]() is less than two quarters,
while for
is less than two quarters,
while for
![]() it is between nine and ten
years. Note also that the priors and posterior means of the MA
coefficients,
it is between nine and ten
years. Note also that the priors and posterior means of the MA
coefficients,
![]() and
and
![]() , only differ for the
, only differ for the
![]() model.
Although the posterior means of the AR coefficients have moved away
from the prior means, a one standard deviation of the posterior of
model.
Although the posterior means of the AR coefficients have moved away
from the prior means, a one standard deviation of the posterior of
![]() covers zero for the
covers zero for the
![]() and
and
![]() models.
models.
The posterior means of
![]() and
and ![]() show
that Canada experiences slower (faster) trend money (TFP) growth
than the U.S. over the sample. Trend U.S. money growth is on
average about 0.05 percent higher annually according to the
posteriors of the
show
that Canada experiences slower (faster) trend money (TFP) growth
than the U.S. over the sample. Trend U.S. money growth is on
average about 0.05 percent higher annually according to the
posteriors of the
![]() ,
,
![]() , and
, and
![]() models. Across
these models,
models. Across
these models,
![]() indicates Canadian
deterministic trend TFP growth dominates its U.S. counterpart by
about 0.06 percent at an annual rate.
indicates Canadian
deterministic trend TFP growth dominates its U.S. counterpart by
about 0.06 percent at an annual rate.
The
![]() ,
,
![]() , and
, and
![]() models show
differences across estimates of the posterior means of the shock
innovation standard deviations. Only the estimated impulse
structure of the
models show
differences across estimates of the posterior means of the shock
innovation standard deviations. Only the estimated impulse
structure of the
![]() model is
dominated by movements in the permanent innovations of the money
shock,
model is
dominated by movements in the permanent innovations of the money
shock,
![]() . The converse is that this
model yields the smallest posterior means of the standard deviation
of the TFP differential shock and
. The converse is that this
model yields the smallest posterior means of the standard deviation
of the TFP differential shock and
![]() shock innovations,
shock innovations,
![]() and
and
![]() . The
. The
![]() model yields
the largest estimates of
model yields
the largest estimates of
![]() and
and
![]() , but these posterior
means are about the same magnitude. Note also that the correlation
of the innovations to the TFP shock and
, but these posterior
means are about the same magnitude. Note also that the correlation
of the innovations to the TFP shock and
![]() shock is estimated to be
shock is estimated to be
![]() and
and
![]() by the
by the
![]() and
and
![]() models,
respectively. Thus, these models are consistent with the TFP trend
being more volatile than observed Canadian-U.S. consumption.
models,
respectively. Thus, these models are consistent with the TFP trend
being more volatile than observed Canadian-U.S. consumption.
Estimates of the exchange rate intercept and linear time trend
indicate that the
![]() model provides
the largest value for the US$ in steady state
and the largest deterministic growth rate for the
CDN$/US$ exchange rate. The posterior
means of
model provides
the largest value for the US$ in steady state
and the largest deterministic growth rate for the
CDN$/US$ exchange rate. The posterior
means of ![]() and
and ![]() imply that the steady state
CDN$/US$ exchange rate is 1.23 with a
deterministic annual growth rate of about 0.8 percent. For the
imply that the steady state
CDN$/US$ exchange rate is 1.23 with a
deterministic annual growth rate of about 0.8 percent. For the
![]() model,
the analogous values are 1.10 (1.03) and 0.3 (0.2) percent per
annum. Thus, the
model,
the analogous values are 1.10 (1.03) and 0.3 (0.2) percent per
annum. Thus, the
![]() model places
more emphasis on deterministic elements to fit the data compared to
the other two UC models that calibrate
model places
more emphasis on deterministic elements to fit the data compared to
the other two UC models that calibrate ![]() to
one.
to
one.
The remaining coefficients are the factor loadings ![]() ,
,
![]() , and
, and
![]() . Posterior mean
estimates of
. Posterior mean
estimates of ![]()
![]() and
-9.02 reveal that there are statistically
and economically large deviations from the balanced growth path by
the
and
-9.02 reveal that there are statistically
and economically large deviations from the balanced growth path by
the
![]() and
and
![]() models. The
models. The
![]() model is
closer to satisfying the balanced growth hypothesis that
model is
closer to satisfying the balanced growth hypothesis that
![]() . This UC model has a
posterior mean of -0.72 for
. This UC model has a
posterior mean of -0.72 for
![]() whose two standard
deviation interval contains the balanced growth restriction. The
response of the Canadian-U.S. money stock differential to
whose two standard
deviation interval contains the balanced growth restriction. The
response of the Canadian-U.S. money stock differential to
![]() is also close to negative
one for the
is also close to negative
one for the
![]() model because
the posterior mean of
model because
the posterior mean of
![]() with a
standard deviation of 0.21. The
with a
standard deviation of 0.21. The
![]() model reveals
that a one percent rise in
model reveals
that a one percent rise in
![]() results in a 4.4 percent
rise in the Canadian-U.S. consumption differential.
results in a 4.4 percent
rise in the Canadian-U.S. consumption differential.
The key economic parameter of the DSGE-PVM is its discount
factor ![]() . Table 5 lists the posterior means
and standard deviations of the
. Table 5 lists the posterior means
and standard deviations of the
![]() and
and
![]() , and
, and
![]() vectors
that include estimates of
vectors
that include estimates of ![]() . Aside from
the inclusion of the prior, posterior mean, and standard deviation
. Aside from
the inclusion of the prior, posterior mean, and standard deviation
![]() at the top of table 5, the posterior
means and standard deviations of the remaining coefficients
resemble those reported in table 4. The only notable exceptions are
that the posterior means of
at the top of table 5, the posterior
means and standard deviations of the remaining coefficients
resemble those reported in table 4. The only notable exceptions are
that the posterior means of
![]() ,
,
![]() ,
,
![]() , and
, and
![]() are smaller for the
are smaller for the
![]() model compared
to its cousin with the calibration
model compared
to its cousin with the calibration ![]() . The
result is that
. The
result is that
![]() is the largest innovation shock
standard deviation of the
is the largest innovation shock
standard deviation of the
![]() model. Also,
this UC model and the data produce an estimate of
model. Also,
this UC model and the data produce an estimate of ![]() whose one standard deviation coverage interval
contains negative one. Thus, the
whose one standard deviation coverage interval
contains negative one. Thus, the
![]() model is closer
to the balanced growth hypothesis and relies to a greater extent on
permanent shocks to the Canadian-U.S. money stock differential.
model is closer
to the balanced growth hypothesis and relies to a greater extent on
permanent shocks to the Canadian-U.S. money stock differential.
The posterior means of ![]() range from
0.966 for the
range from
0.966 for the
![]() model, to 0.974 for the
model, to 0.974 for the
![]() model, to the
largest estimate of 0.9962 for the
model, to the
largest estimate of 0.9962 for the
![]() model. These
estimates are consistent with annual world real interest rates of
15.1, 11.4, and 1.7 percent given the posteriors of the
model. These
estimates are consistent with annual world real interest rates of
15.1, 11.4, and 1.7 percent given the posteriors of the
![]() ,
,
![]() and
and
![]() models,
respectively. Although the
models,
respectively. Although the
![]() ,
,
![]() models have
posteriors that suggest unreasonably large world real interest
rates, these UC models yield 95 percent coverage intervals whose
upper end is 0.999. The
models have
posteriors that suggest unreasonably large world real interest
rates, these UC models yield 95 percent coverage intervals whose
upper end is 0.999. The
![]() model produces a
posterior of
model produces a
posterior of ![]() with a 95 percent coverage
interval whose lower end equals 0.987. This value of
with a 95 percent coverage
interval whose lower end equals 0.987. This value of ![]() is greater than the posterior means of
is greater than the posterior means of ![]() for the
for the
![]() and
and
![]() models. Thus,
the
models. Thus,
the
![]() model generates
a posterior distribution of
model generates
a posterior distribution of ![]() that is to
the right of those produced by the
that is to
the right of those produced by the
![]() and
and
![]() models.
models.
Figure 1 reinforces the view that the
![]() model posteriors
yield estimates of
model posteriors
yield estimates of ![]() that are to the right
of those of the
that are to the right
of those of the
![]() and
and
![]() models.
Posterior densities of
models.
Posterior densities of ![]() appear in figure 1 for
these UC models, along with the density of the inverse-gamma prior
restricted to the EW prior of
appear in figure 1 for
these UC models, along with the density of the inverse-gamma prior
restricted to the EW prior of
![]() . The solid (black)
line is the
. The solid (black)
line is the ![]() prior density. It is close to the
posterior density of
prior density. It is close to the
posterior density of ![]() derived from the
derived from the
![]() model, which is the dashed
(blue) line. The
model, which is the dashed
(blue) line. The
![]() model generates
a posterior density of
model generates
a posterior density of ![]() , the dot-dash (green)
plot, that moves off the prior by placing less weight on
, the dot-dash (green)
plot, that moves off the prior by placing less weight on
![]() s less than 0.97 and more weight above
it. The dot-dot (red) plot is the density of
s less than 0.97 and more weight above
it. The dot-dot (red) plot is the density of ![]() from the
from the
![]() model posterior.
This density is deflated by ten percent to ease comparison to the
other densities. A striking feature of figure 1 is that the
model posterior.
This density is deflated by ten percent to ease comparison to the
other densities. A striking feature of figure 1 is that the
![]() model posterior
pushes
model posterior
pushes ![]() off of its prior because its mass
lays between 0.98 and 0.999.
off of its prior because its mass
lays between 0.98 and 0.999.
Table 6 contains the posterior means of the exchange rate factor
loadings with respect to
![]() and
and
![]() , the
, the
![]() s and
s and
![]() s.21 A
striking aspect of the estimates of
s.21 A
striking aspect of the estimates of
![]() ,
,
![]() , and
, and
![]() is that the
response of the
CDN$/US$ exchange rate to innovations in
is that the
response of the
CDN$/US$ exchange rate to innovations in
![]() is economically small for
either the
is economically small for
either the
![]() or
or
![]() models. The
large posterior standard errors on these factor loading also
indicate the imprecision the Canadian-U.S. data give to these
estimates. The data yield a more precise estimate of
models. The
large posterior standard errors on these factor loading also
indicate the imprecision the Canadian-U.S. data give to these
estimates. The data yield a more precise estimate of
![]() for the
for the
![]() model. The posterior mean of
this factor loading shows that the exchange rate falls by 0.6
percent given a one percent increase in
model. The posterior mean of
this factor loading shows that the exchange rate falls by 0.6
percent given a one percent increase in
![]() . These estimates drop to
-0.33 for the
. These estimates drop to
-0.33 for the
![]() model. Also, the
associated 95 percent coverage interval contains zero. In summary,
the
model. Also, the
associated 95 percent coverage interval contains zero. In summary,
the
![]() ,
,
![]() , and
, and
![]() models have
posteriors in which there is either a negligible exchange rate
response to
models have
posteriors in which there is either a negligible exchange rate
response to
![]() shocks or an economically
large negative reaction by the
CDN$/US$ exchange rate to
shocks or an economically
large negative reaction by the
CDN$/US$ exchange rate to
![]() fluctuations. However, the
latter exchange rate response is sometimes estimated
imprecisely.
fluctuations. However, the
latter exchange rate response is sometimes estimated
imprecisely.
5.B Unconditional Variance Ratios and FEVDs of the Exchange Rate
Tables 7 and 8 present unconditional variance ratios and FEVDs
computed using the posteriors of the
![]() ,
,
![]() , and
, and
![]() models. We
calculate the variances of the present discounted values (PDVs) of
the money, TFP, and consumption shock innovations using the
DSGE-PVM version of the equilibrium currency return generating
equation
(14)
and UC model restrictions when
models. We
calculate the variances of the present discounted values (PDVs) of
the money, TFP, and consumption shock innovations using the
DSGE-PVM version of the equilibrium currency return generating
equation
(14)
and UC model restrictions when ![]() is estimated.
The variance ratios are these values divided by the sample variance
of the
CDN$/US$ exchange rate (
is estimated.
The variance ratios are these values divided by the sample variance
of the
CDN$/US$ exchange rate (![]() 2.04). According to the unconditional variance ratios, only
permanent shocks to the Canadian-US money differential,
2.04). According to the unconditional variance ratios, only
permanent shocks to the Canadian-US money differential,
![]() , and the TFP
differential,
, and the TFP
differential,
![]() , explain variation in the
CDN$/US$ exchange rate. The variances
of the PDVs of shock innovations to
, explain variation in the
CDN$/US$ exchange rate. The variances
of the PDVs of shock innovations to
![]() and
and
![]() are small and lack
precision. Note that except for the
are small and lack
precision. Note that except for the
![]() model, the
variance of the PDV of
model, the
variance of the PDV of
![]() is larger than that of
is larger than that of
![]() .
.
We report FEVDs in table 8 with implications similar to the
unconditional variance ratios.22 The top panel of figure 8 shows
that the posterior of the
![]() model yields a FEVD in which
the TFP shock
model yields a FEVD in which
the TFP shock
![]() makes a large and
increasing contribution to exchange rate fluctuations at longer
horizons. The money shock
makes a large and
increasing contribution to exchange rate fluctuations at longer
horizons. The money shock
![]() remains economically
important for exchange rate movements out to a three to five year
horizon, but shocks to
remains economically
important for exchange rate movements out to a three to five year
horizon, but shocks to
![]() and
and
![]() are unimportant at any
horizon. Much the same is true for the FEVDs found using the
are unimportant at any
horizon. Much the same is true for the FEVDs found using the
![]() model posterior.
However, the relative shares of the
model posterior.
However, the relative shares of the
![]() and
and
![]() shocks are unchanged at a
two-thirds/one-third split from the one quarter to ten year
horizons.
shocks are unchanged at a
two-thirds/one-third split from the one quarter to ten year
horizons.
The posterior of the
![]() model imbues a
sluggish dynamic to the exchange rate FEVDs found in the bottom
panel of table 8. The
model imbues a
sluggish dynamic to the exchange rate FEVDs found in the bottom
panel of table 8. The
![]() and
and
![]() shocks are responsible for
about 60 and 40 percent, respectively, of fluctuations in the
exchange rate at short horizons. At a 10 year horizon, the
contribution of
shocks are responsible for
about 60 and 40 percent, respectively, of fluctuations in the
exchange rate at short horizons. At a 10 year horizon, the
contribution of
![]() (
(
![]() ) only falls (rises) to 55
(45) percent. Thus, only the posterior of the
) only falls (rises) to 55
(45) percent. Thus, only the posterior of the
![]() model predicts
that permanent shocks to money dominate exchange rate movements at
longer horizons.
model predicts
that permanent shocks to money dominate exchange rate movements at
longer horizons.
5.C Trend-Cycle Decompositions
Trend-cycle decompositions of the
CDN$/US$ exchange rate and
Canadian-U.S. money and consumption differentials are plotted in
figures 2 and 3 with summary statistics given in table 9. We run
![]() ,
,
![]() , and
, and
![]() model
posteriors through the Kalman smoother to create trend-cycle
decompositions and summary statistics. Figures 2 and 3 and table 9
contain moments that are averages over 750,000 draws from UC model
posteriors. Trend exchange rate growth is labeled
model
posteriors through the Kalman smoother to create trend-cycle
decompositions and summary statistics. Figures 2 and 3 and table 9
contain moments that are averages over 750,000 draws from UC model
posteriors. Trend exchange rate growth is labeled
![]() in table 9.
in table 9.
The top window of figure 2 contains plots of the exchange rate
and smoothed trends taken from the posteriors of the
![]() and
and
![]() models.23 The
solid (black) line is
models.23 The
solid (black) line is ![]() , the log of the actual
exchange rate. The smoothed trends of the
, the log of the actual
exchange rate. The smoothed trends of the
![]() and
and
![]() models are the
dashed (blue) and dotted (red) plots, respectively. Note that these
UC models generate smoothed exchange rate trends that are more
volatile than the actual exchange rate. The top row of table 9
indicate that the posteriors of the
models are the
dashed (blue) and dotted (red) plots, respectively. Note that these
UC models generate smoothed exchange rate trends that are more
volatile than the actual exchange rate. The top row of table 9
indicate that the posteriors of the
![]() and
and
![]() models generate
standard deviations of
models generate
standard deviations of
![]() equal to 2.66 and 2.44,
respectively. The standard deviation of
equal to 2.66 and 2.44,
respectively. The standard deviation of
![]() equals 2.04.
equals 2.04.
The smoothed exchange rate cycles appear in the bottom window of
figure 2. The dotted (blue) line is the smoothed exchange rate
cycle,
![]() , based on the posterior of
the
, based on the posterior of
the
![]() model, while the dotted
(red) line is associated with the
model, while the dotted
(red) line is associated with the
![]() model. Although
the former
model. Although
the former
![]() exhibits more variability
than the latter (the standard deviations are 3.68 and 2.44), these
exhibits more variability
than the latter (the standard deviations are 3.68 and 2.44), these
![]() s are persistent with AR1
correlation statistics of 0.97 and 0.98. Note that only the
posterior of the
s are persistent with AR1
correlation statistics of 0.97 and 0.98. Note that only the
posterior of the
![]() model yields a
(close to) non-zero correlation for
model yields a
(close to) non-zero correlation for
![]() and
and
![]() , according to table 9.
, according to table 9.
Figure 3 depicts smoothed permanent-transitory decompositions of
the Canadian-U.S. money and consumption differentials. The actual
differentials and smoothed trends appear in the top row of windows,
while smoothed cycles are found in the bottom row of windows. The
money (consumption) differentials are the right (left) side
windows. The posterior of the
![]() model produces a money
trend,
model produces a money
trend, ![]() that almost perfectly mimics the
actual Canadian-U.S. money differentials, as shown in the top left
window of figure 3. The result is that smoothed
that almost perfectly mimics the
actual Canadian-U.S. money differentials, as shown in the top left
window of figure 3. The result is that smoothed
![]() is much less volatile,
with a standard deviation of 0.68 compared to a standard deviation
of 1.62 for
is much less volatile,
with a standard deviation of 0.68 compared to a standard deviation
of 1.62 for ![]() . The bottom left window of
figure 3 shows a saw-toothed pattern in
. The bottom left window of
figure 3 shows a saw-toothed pattern in
![]() , conditional on the
posterior of the
, conditional on the
posterior of the
![]() model. This explains the AR1
correlation statistic of -0.68 for
model. This explains the AR1
correlation statistic of -0.68 for
![]() (middle of the second
column of table 9).
(middle of the second
column of table 9).
Table 9 reveals that the posterior of
![]() model produces a
smoothed money trend,
model produces a
smoothed money trend, ![]() , that is about as
volatile as in the
, that is about as
volatile as in the
![]() model. The relevant standard
deviations are 1.62 and 1.71 (second and fourth columns of table
9). However, the smoothed
model. The relevant standard
deviations are 1.62 and 1.71 (second and fourth columns of table
9). However, the smoothed ![]() and
and
![]() have a positive correlation
of 0.62 only in the posterior of the
have a positive correlation
of 0.62 only in the posterior of the
![]() model (bottom
half of the fourth column of table 9).
model (bottom
half of the fourth column of table 9).
The posteriors of the
![]() and
and
![]() models yield
qualitatively similar plots for the smoothed TFP trend
differential,
models yield
qualitatively similar plots for the smoothed TFP trend
differential, ![]() . These plots appear in the top
right window of figure 3 as dashed (blue) and dotted (red) lines
for the
. These plots appear in the top
right window of figure 3 as dashed (blue) and dotted (red) lines
for the
![]() and
and
![]() models,
respectively, where observed cross country consumption is the solid
(black) line. The smoothed TFP growth differential,
models,
respectively, where observed cross country consumption is the solid
(black) line. The smoothed TFP growth differential, ![]() , is 50 percent more volatile for the
, is 50 percent more volatile for the
![]() model than it is
for the
model than it is
for the
![]() model. The posteriors of
these two UC models also produce correlations of -0.71 and -0.85 between
model. The posteriors of
these two UC models also produce correlations of -0.71 and -0.85 between
![]() and
and ![]() .
Thus, a rising U.S. TFP is associated with an appreciation of the
U.S. dollar. The late 1970s is one such period because Canada
experienced a greater relative productivity slowdown. By the 1980s,
Canadian TFP is growing more rapidly than in the U.S., which
continues into the early 1990s. Subsequently, U.S. TFP recovers
relative to Canadian TFP. At the end of the sample, the
Canadian-U.S. TFP differential is expanding once more.
.
Thus, a rising U.S. TFP is associated with an appreciation of the
U.S. dollar. The late 1970s is one such period because Canada
experienced a greater relative productivity slowdown. By the 1980s,
Canadian TFP is growing more rapidly than in the U.S., which
continues into the early 1990s. Subsequently, U.S. TFP recovers
relative to Canadian TFP. At the end of the sample, the
Canadian-U.S. TFP differential is expanding once more.
The bottom right window of figure 3 presents the smoothed
![]() of the
of the
![]() and
and
![]() models. The
former cycle is the dashed (blue) line and the latter is the dotted
(red) plot. These cycles are persistent, with AR1 correlation
statistics of 0.97 and 0.98, but the
models. The
former cycle is the dashed (blue) line and the latter is the dotted
(red) plot. These cycles are persistent, with AR1 correlation
statistics of 0.97 and 0.98, but the
![]() model generates a third less
volatility in smoothed
model generates a third less
volatility in smoothed
![]() than found for the
than found for the
![]() model.
model.
The smoothed
![]() has peaks and troughs that
coincide with several U.S.-Canadian business cycle dates. For
example, troughs in the posterior mean of
has peaks and troughs that
coincide with several U.S.-Canadian business cycle dates. For
example, troughs in the posterior mean of
![]() appear in 1981 and 1990,
which also represent recessions dates in the U.S. and Canada. Since
the end of the 1990-1991 recession, the rise in
appear in 1981 and 1990,
which also represent recessions dates in the U.S. and Canada. Since
the end of the 1990-1991 recession, the rise in
![]() points to a persistent,
but transitory, rise in U.S. consumption relative to Canada.
Nonetheless,
points to a persistent,
but transitory, rise in U.S. consumption relative to Canada.
Nonetheless,
![]() has been falling rapidly
since a peak in late 2001, which corresponds to the end of the last
U.S. recession.
has been falling rapidly
since a peak in late 2001, which corresponds to the end of the last
U.S. recession.
The bottom row of table 9 shows that
![]() and
and
![]() are perfectly negatively
correlated in the posteriors of the
are perfectly negatively
correlated in the posteriors of the
![]() and
and
![]() models. The
negative correlation of the transitory component of the exchange
rate with
models. The
negative correlation of the transitory component of the exchange
rate with
![]() helps to interpret
exchange rate fluctuations. Peaks in the transitory component of
the exchange rate occur either at or shortly after the end of
recessions. For example, the smoothed exchange rate cycles have a
tendency to peak and trough around dates usually associated with
U.S. and Canadian business cycle dates (i.e., the late
1970s, early 1990s, and 2001). A specific case is the peak in
helps to interpret
exchange rate fluctuations. Peaks in the transitory component of
the exchange rate occur either at or shortly after the end of
recessions. For example, the smoothed exchange rate cycles have a
tendency to peak and trough around dates usually associated with
U.S. and Canadian business cycle dates (i.e., the late
1970s, early 1990s, and 2001). A specific case is the peak in
![]() during the 1990-1991
recession in the U.S., which is a moment at which the Canadian
dollar approached par against the U.S. dollar. An exception is the
end of the 2001 recession when the Canadian dollar reached a low of
nearly 0.62 to the U.S. dollar.
during the 1990-1991
recession in the U.S., which is a moment at which the Canadian
dollar approached par against the U.S. dollar. An exception is the
end of the 2001 recession when the Canadian dollar reached a low of
nearly 0.62 to the U.S. dollar.
5.D Comparing the UC models
The bottom row of table 4 reports the log marginal likelihoods,
![]() , of the
, of the
![]() ,
,
![]() , and
, and
![]() models. These
marginal likelihoods show that our Canadian-U.S. sample gives most
support to the
models. These
marginal likelihoods show that our Canadian-U.S. sample gives most
support to the
![]() model. The
difference between this model and the
model. The
difference between this model and the
![]() model is about 29, so that
the Bayes factor prefers the UC model with only transitory
consumption. For the data to give more credence to the latter
model, its prior probability must be raised by the prior
probability of the
model is about 29, so that
the Bayes factor prefers the UC model with only transitory
consumption. For the data to give more credence to the latter
model, its prior probability must be raised by the prior
probability of the
![]() model
multiplied by 4.7 × 1012[=exp(29.18)]. Since
the magnitude of this factor is large, it seems unreasonable to
include the transitory money shock in the UC model when
model
multiplied by 4.7 × 1012[=exp(29.18)]. Since
the magnitude of this factor is large, it seems unreasonable to
include the transitory money shock in the UC model when ![]() is calibrated to one.
is calibrated to one.
The last row of table 5 contains the log marginal likelihoods of
the
![]() ,
,
![]() , and
, and
![]() models. The
ranking of these models matches that of the UC models with the
models. The
ranking of these models matches that of the UC models with the
![]() calibration. The
calibration. The
![]() model dominates
the
model dominates
the
![]() and
and
![]() models. A
key reason is that the posteriors of these models yield
economically implausible estimates of the DGSE-PVM discount factor
models. A
key reason is that the posteriors of these models yield
economically implausible estimates of the DGSE-PVM discount factor
![]() .
.
This raises the question of whether it is difficult to choose
between the
![]() and
and
![]() models. Our
sample favors the
models. Our
sample favors the
![]() and
and
![]() models compared
to the other four. The
models compared
to the other four. The
![]() model has the
largest marginal likelihood, which suggests that the data support
it over the
model has the
largest marginal likelihood, which suggests that the data support
it over the
![]() model. This
choice relies on the belief that scaling up the prior probability
of the
model. This
choice relies on the belief that scaling up the prior probability
of the
![]() model by 167.3 = exp(5.12)
is too large to be
justified. If, on the other hand, this factor is regarded as
inconclusive in rejecting the
model by 167.3 = exp(5.12)
is too large to be
justified. If, on the other hand, this factor is regarded as
inconclusive in rejecting the
![]() model, it could
be argued that our Canadian-U.S. sample cannot pick between the
model, it could
be argued that our Canadian-U.S. sample cannot pick between the
![]() and
and
![]() models.24
Nonetheless, these UC models support for the EW hypothesis.
models.24
Nonetheless, these UC models support for the EW hypothesis.
5.E Exchange Rate
Dynamics as
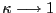
Engel and West (2005) argue that
the exchange rate will approximate a random walk when the discount
factor is close to one and fundamentals have a unit root.
Propositions 3 and 5 also predict that
![]() will collapse to random
walk as
will collapse to random
walk as
![]() .
.
We extract evidence about the EW hypothesis from the
![]() and
and
![]() model
posteriors. The focus is on these UC models rather than the
model
posteriors. The focus is on these UC models rather than the
![]() model because
it attributes all exchange rate movements to permanent shocks. We
conduct this comparison with
model because
it attributes all exchange rate movements to permanent shocks. We
conduct this comparison with ![]() s at the 16th
and 84th percentiles, along with the largest
s at the 16th
and 84th percentiles, along with the largest ![]() s, from the
s, from the
![]() and
and
![]() vectors. For
the
vectors. For
the
![]() (
(
![]() ) model, the 16th
percentile, 84th percentile, and largest
) model, the 16th
percentile, 84th percentile, and largest ![]() s
are 0.9425, 0.9883, and 0.9990 (0.9943, 0.9987, and 0.9990),
respectively. Fixing
s
are 0.9425, 0.9883, and 0.9990 (0.9943, 0.9987, and 0.9990),
respectively. Fixing ![]() at these values, we
simulate the
at these values, we
simulate the
![]() and
and
![]() models
extracting 2000 draws from the posteriors, discard the first 1000,
run the Kalman smoother on the remaining 1000, and average the
ensemble to generate exchange rate cycles that respect the rational
expectations hypothesis.
models
extracting 2000 draws from the posteriors, discard the first 1000,
run the Kalman smoother on the remaining 1000, and average the
ensemble to generate exchange rate cycles that respect the rational
expectations hypothesis.
Figure 4 plots the smoothed exchange rate cycles. The top
(bottom) window contains the
![]() created from the posterior
of the
created from the posterior
of the
![]() (
(
![]() ) model. The
dot-dash (blue), dotted (green), and dotted (red) lines are
conditional on the 16th percentile, 84th percentile, and largest
) model. The
dot-dash (blue), dotted (green), and dotted (red) lines are
conditional on the 16th percentile, 84th percentile, and largest
![]() s, respectively. Across the top and
bottom windows, the volatility of
s, respectively. Across the top and
bottom windows, the volatility of
![]() is compressed as
is compressed as
![]() approaches 0.999. This is reflected
in the standard deviations of
approaches 0.999. This is reflected
in the standard deviations of
![]() that equal 4.44, 2.84, and
0.57 moving from the smallest to largest
that equal 4.44, 2.84, and
0.57 moving from the smallest to largest ![]() for the
for the
![]() model. The equivalent
standard deviations are 3.74, 1.64, and 1.30 for the
model. The equivalent
standard deviations are 3.74, 1.64, and 1.30 for the
![]() model. Although
the
model. Although
the
![]() model generates exchange
rate cycles that are smoother than at its posterior mean only for
the largest
model generates exchange
rate cycles that are smoother than at its posterior mean only for
the largest ![]() s, this UC model is able to
produce smoother exchange rate cycles at the 84th percentile and
largest
s, this UC model is able to
produce smoother exchange rate cycles at the 84th percentile and
largest ![]() s. Thus, pushing
s. Thus, pushing ![]() increases the smoothness of the exchange rate cycle.
This is evidence that lends credence to the EW hypothesis.
increases the smoothness of the exchange rate cycle.
This is evidence that lends credence to the EW hypothesis.
6 Conclusion
Economists have little to say about the impact of policy on currency markets without an equilibrium theory of exchange rate determination that is empirically relevant. According to Engel and West (2005), the near random walk behavior of exchange rates explains the failure of equilibrium models to fit the data or to find any model that systematically beats it at out-of-sample forecasting. They conjecture that the standard-present value model (PVM) of exchange rates yields the random walk prediction when fundamentals are persistent and the discount factor is close to one.
This paper generalizes the Engel and West (EW) hypothesis by constructing a PVM from a two-country monetary dynamic stochastic general equilibrium (DSGE) model. The standard- and DSGE-PVMs yield identical predictions for the exchange rate. These predictions are summarized by five propositions. Thus, we generalize the EW hypothesis to the larger class of open economy DSGE models.
Our empirical results support the view that the Canadian-U.S. data prefer a random walk exchange rate and a DSGE-PVM with a discount factor calibrated to one. At the same time we obtain evidence on the nature of the shocks driving exchange rates. Bayesian estimates of the DSGE-PVM indicate that the Canadian dollar-U.S. dollar exchange rate is dominated by permanent shocks, whether the discount factor is estimated or calibrated to one, which supports the EW hypothesis. Our evidence is also consistent with the recent VAR literature suggesting that monetary policy shocks have only a minor impact on exchange rate fluctuations. Monetary policy shocks are also found to be unimportant for exchange rate movements by Lubik and Schorfheide (2006) within the context of an estimated open economy DSGE model. Whether this result holds across a wider set of open economy DSGE models is a worthy goal of future research.
References
Adolfson, M., S. Laséen, J. Lindé, and M. Villani. 2007. Bayesian Estimation of an Open Economy DSGE Model with Incomplete Pass-Through. Journal of International Economics 72, 481-511.
An, S., F. Schorfheide. 2007. Bayesian analysis of DSGE models. Econometric Reviews 26, 113-172.
Beveridge, S., C.R. Nelson. 1981. A New Approach to Decomposition of Economic Time Series into Perman- ent and Transitory Components with Particular Attention to Measurement of the Business Cycle. Journal of Monetary Economics 7, 151-174.
Bilson, J.F.O. 1978. Rational Expectations and the Exchange Rate. in Frenkel, J.A., H.G. Johnson, THE ECONOMICS OF EXCHANGE RATES: SELECTED STUDIES, Addison-Wesley, Reading, MA.
Campbell, J.Y., R. Shiller. 1987. Cointegration and Tests of Present Value Models. Journal of Political Economy 93, 1062-1088.
Del Negro, M., F. Schorfheide. 2006. Forming Priors for DSGE Models (and How it Affects the Assessment of Nominal Rigidites). Working Paper 2006-16, Federal Reserve Bank of Atlanta.
Dornbusch, R. 1976. Expectations and Exchange Rate Dynamics. Journal of Political Economy 84, 1161-1176.
Eichenbaum, M., C. Evans, 1995. Some Empirical Evidence on the Effects of Monetary Policy Shocks on Exchange Rates. Quarterly Journal of Economics 110, 975-1010.
Engel, C., K.D. West, 2005. Exchange Rates and Fundamentals. Journal of Political Economy 113, 485-517.
Engle, R.F., J.V. Issler, 1995. Estimating Common Sectoral Cycles. Journal of Monetary Economics 35, 83-113.
Engle, R.F., S. Kozicki, 1993. Testing for Common Features. Journal of Business and Economics Statistics 11, 369-395.
Faust, J., J. Rogers, 2003.
Monetary Policy's Role in Exchange Rate Behavior. ![]() Journal of Monetary Economics 50, 1403-1424.
Journal of Monetary Economics 50, 1403-1424.
Fernández-Villaverde, J., J.F. Rubio-Ramírez. 2004. Comparing Dynamic Equilibrium Models to Data: A Bayesian Approach. Journal of Econometrics 123, 153-187.
Frankel, J.A., 1979. On the Mark: A Theory of Floating Exchange Rates Basedon Real Interest Rate Differentials. American Economics Review 69, 610-622.
Gelman, A., J.B. Carlin, H.S. Stern, D.B. Rubin, 2004, BAYESIAN DATA ANALYSIS, SECOND EDITION, Chapman and Hall, New York, NY.
Geweke, J., 1999. Using Simulation Methods for Bayesian Econometric Models: Inference, Development and Communication. Econometric Reviews 18, 1-126.
Geweke, J., 2005. CONTEMPORARY BAYESIAN ECONOMETRICS AND STATISTICS, J. Wiley and Sons, Inc., Hoboken, NJ.
Hamilton, J.D., 1994, TIME SERIES ANALYSIS, Princeton University Press, Princeton, NJ.
Hansen, L.P., W. Roberds, T.J. Sargent. 1991. Time Series Implications of Present Value Budget Balance and of Martingale Models and Consumption and Taxes. in Hansen, L.P., T.J. Sargent (eds.), RATIONAL EXPECTATIONS ECONOMETRICS, Westview Press, Boulder, CO.
Harvey, A.C., FORECASTING, STRUCTURAL TIME SERIES MODELS AND THE KALMAN FILTER, Cambridge University Press, Cambridge, England.
Harvey, A.C., T.M. Trimbur, H.K. van Dijk. 2007. Trends and Cycles in Economic Time Series: A Bayesian Approach. Journal of Econometrics 140, 618-649.
Hecq, A., F.C. Palm, J-P. Urbain. 2000. Permanent-Transitory Decomposition in VAR Models with Cointegration and Common Cycles. Oxford Bulletin of Economics and Statistics 62, 511-532.
Jeffreys, H., 1998. THEORY OF PROBABILITY, Oxford University Press, Oxford, UK.
Johansen, S. 1991. Estimation and Hypothesis Testing of Cointegration Vectors in Gaussian Vector Auto- regressive Models. Econometrica 59, 1551-1580.
Johansen, S. 1994. The Role of the Constant and Linear Terms in Cointegration Analysis and Nonstationary Variables. Econometric Reviews 13, 205-229.
Kim, S., N. Roubini. 2000. Exchange Rate Anomalies in the Industrial Countries: A Solution with a Structural VAR Approach. Journal of Monetary Economics 45, 561-586.
Lubik, T., F. Schorfheide. 2006. A Bayesian Look at New Open Economy Macroeconomics. in Gertler, M., K. Rogoff (eds.), NBER MACROECONOMICS ANNUAL 2005. MIT Press, Cambrigde, MA.
MacKinnon, J.G., A.A. Haug, L. Michelis. 1999. Numerical Distributions of Likelihood Ratio Tests of Cointegration. Journal of Applied Econometrics 14, 563-577.
Maheswaran, S., C.A. Sims. 1993. Empirical Implications of Arbitrage-Free Asset Markets. in Phillips, P.C.B. (ed.), MODELS, METHODS AND APPLICATIONS OF ECONOMETRICS, Blackwell Publishing, Oxford, UK.
Mark, N. 1995. Exchange Rates and Fundamentals: Evidence on Long-Horizon Predictability. American Economics Review 85, 201-218.
Mark, N., D. Sul, 2003. Cointegration Vector Estimation by Panel DOLS and Long-Run Money Demand. Oxford Bulletin of Economics and Statistics 65, 665-680.
Meese, R.A., 1986. Testing for Bubbles in Exchange Markets: A Case of Sparkling Rates. Journal of Political Economy 94, 345-373.
Morley, J.C., C.R. Nelson, E. Zivot. 2003. Why Are Beveridge-Nelson and Unobserved Component Decompositions of GDP So Different? Review of Economics and Statistics 85, 235-234.
Osterwald-Lenum, M. 1992. Quantiles of the Asymptotic Distribution of the Maximum Likelihood Cointegration Rank Test Statistics, Oxford Bulletin of Economics and Statistics 54, 461-472.
Rabanal, P., J.F. Rubio-Ramírez. 2005. Comparing New Keynesian Models of the Business Cycle: A Bayesian Approach. Journal of Monetary Economics 52, 1151-1166.
Rao, C.S. 1973. LINEAR STATISTICAL INFERENCE, Wiley, Ltd., New York, NY.
Rogers, J.H., 2000. Monetary Shocks and Real Exchange Rates. Journal of International Economics 49, 269-288.
Rogoff, K. 2007. Comments on: Engel, Mark, and West's Exchange Rate Models Are Not as Bad as You Think. in Acemoglu, D., K. Rogoff, M. Woodford (eds.), NBER MACROECONOMICS ANNUAL 2007, VOL. 22, MIT Press, Cambridge, MA.
Rossi, B. 2007. Comments on: Engel, Mark, and West's Exchange Rate Models Are Not as Bad as You Think. in Acemoglu, D., K. Rogoff, M. Woodford (eds.), NBER MACROECONOMICS ANNUAL 2007, VOL. 22, MIT Press, Cambridge, MA.
Scholl, A., Uhlig, H., 2005. New Evidence on the Puzzles. Results from Agnostic Identification on Monetary Policy and Exchange Rates. SFB 649 Discussion Paper No. 2005-037.
Sims, C.A. 1980. Macroeconomics and Reality. Econometrica 48, 1-48.
Sims, C.A., Stock, J.H., M.W. Watson. 1990. Inference in Linear Time Series Models with Some Unit Roots. Econometrica 58, 113-144.
Stock, J.H., M.W. Watson. 1988. Testing for Common Trends. Journal of the American Statistical Association 83, 1097-1107.
Vahid, F., R.F. Engle. 1993. Common Trends and Common Cycles. Journal of Applied Econometrics 8, 341-360.
Table 1: Summary of Standard PVM and DSGE-PVM: Panel A: Standard-PVM
| ECM(0): |
(13)
|
|---|---|
| EW Equation: |
(14)
|
| Parameters: |
|
| Fundamentals: |
|
Table 1: Summary of Standard PVM and DSGE-PVM: Panel B: DSGE-PVM
| ECM(0): |
(13)
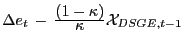 |
|---|---|
| EW Equation: |
(14)
|
| Parameters: |
|
| Fundamentals: |
|
Table 2: Summary of Propositions for Standard- and DSGE-PVMs
| Proposition 1: | PVM Predicts Exchange Rate and Fundamentals Cointegrate; Campbell and Shiller (1987). |
|---|---|
| Proposition 2: | Currency Returns Are an ECM(0). |
| Proposition 3: | Exchange Rate Approximates a
Martingale as
|
| Proposition 4: | VECM(0) Imply Common Trend and Common Cycle for Exchange Rate and Fundamental. |
| Proposition 5: | EW's (2005) Hypothesis Needs
Currency Returns and Fundamental Growth Share a
Co-Feature and
|
Table 3: Tests of Propositions 1, 3, and 5: Sample 1976Q1 - 2004Q4: Panel A: Proposition 3: VECM(0)
| Statistic | Canada & U.S. | Japan & U.S. | U.K. & U.S. |
|---|---|---|---|
| Levels VAR Lag Length | 8 | 5 | 4 |
| LR statistic p-value | (0.02) | (0.01) | (0.09) |
Table 3: Tests of Propositions 1, 3, and 5: Sample 1976Q1 - 2004Q4: Panel B: Proposition 1: Common Trend Cointegration Tests
| Model | Canada & U.S. Case 2* | Japan & U.S. Case 1 | U.K. & U.S. Case 1 |
|---|---|---|---|
| λ-Max statistic: Two Unit Root | 0.20 | 2.27 | |
| λ-Max statistic: One Unit Root | 17.28 | 4.64 | 12.32 |
| Trace statistic: Two Unit Root | 0.20 | 2.27 | |
| Trace statistic: One Unit Root | 12.42 | 4.43 | 10.04 |
Table 3: Tests of Propositions 1, 3, and 5: Sample 1976Q1 - 2004Q4: Panel C: Proposition 5: Common Cycle
| Statistic | Canada & U.S. | Japan & U.S. | U.K. & U.S. |
|---|---|---|---|
| Sq. Canonical Correlations | 0.30, 0.09 | 0.44, 0.08 | 0.19, 0.07 |
| χ2-statistic p-value | (0.01), (0.69) | (0.00), (0.21) | (0.00), (0.12) |
| F-statistic p-value | (0.00), (0.61) | (0.00), (0.19) | (0.00), (0.11) |
The level of fundamentals equals cross-country money netted with cross-country output calibrated to a unitary income elasticity of money demand. The money stocks (outputs) are measured in current (constant) local currency units and per capita terms. A constant and linear time trend are included in the level VARs. The LR statistics employ the Sims (1980) correction and have standard asymptotic distribution according to results in Sims, Stock, and Watson (1990). The case 2* and case 1 model definitions are based on Osterwald-Lenum (1992). MacKinnon, Haug, and Michelis (1999) provide five percent critical values of 8.19 (8.19) and 18.11 (15.02) for the case 2* model λ-max (trace) tests and 3.84 (3.84) and 15.49 (14.26) for the case 1 model. The common feature tests compute the canonical correlations of Δet and Δmt - Δyt. The common feature null is all or a subset of the canonical correlations are zero. See Engle and Issler (1995) and Vahid and Engle (1993) for details.
Table 4: UC Model Posterior Means, κ = 1
| Parameter | Priors | 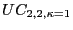 | ||
|---|---|---|---|---|
| | Normal | -1.1906 | -0.8691 | - |
[-1.2, 0.10] | (0.0613) | (0.0470) | - | |
| | Normal | 0.4133 | 0.9501 | - |
[0.40, 0.17] | (0.1092) | (0.0528) | - | |
| | Normal | 0.9407 | - | 0.9830 |
[0.85, 0.10] | (0.0491) | - | (0.0296) | |
| | Normal | 0.0403 | - | 0.0069 |
[0.10, 0.15] | (0.0488) | - | (0.0291) | |
| | Normal | -0.1260 | -0.1258 | -0.1258 |
[-0.126, 0.015] | (0.0150) | (0.0150) | (0.0120) | |
Normal | 0.1615 | 0.1645 | 0.1571 | |
[0.158, 0.025] | (0.0229) | (0.0213) | (0.0199) | |
| | Inv-Gamma | 1.8838 | 2.4629 | 1.6784 |
[2.0, 1.5] | (0.1436) | (0.1507) | (0.1264) | |
| | Inv-Gamma | 1.0471 | 0.3971 | 1.9461 |
[2.0, 0.4] | (0.2206) | (0.0345) | (0.3831) | |
| | Inv-Gamma | 0.6002 | 0.4728 | - |
[2.0, 0.6] | (0.0899) | (0.1168) | - | |
| | Inv-Gamma | 1.2874 | - | 2.0135 |
[2.0, 0.7] | (0.2354) | - | (0.3823) | |
| | Normal | -0.8758 | - | -0.9475 |
[-0.5, 0.2] | (0.0462) | - | (0.0234) | |
Normal | 80.1528 | 138.8984 | 62.9442 | |
[100.0, 15.0] | (6.8283) | (5.7281) | (2.9991) | |
Normal | 0.7038 | 1.9366 | 0.3831 | |
[1.0, 0.5] | (0.1710) | (0.1106) | (0.1306) | |
Uniform | -2.6822 | -9.0223 | -0.7208 | |
[-10.0, 0.0] | (0.6316) | (0.5377) | (0.1886) | |
| | Uniform | - | 4.3973 | - |
[-2.0, 7.5] | - | (1.1057) | - | |
| | Uniform | - | - | -0.8985 |
[-7.5, 2.0] | - | - | (0.2099) | |
| | - | -53.95 | -226.76 | -24.76 |
Table 5: UC Model Posterior Means, κ ∈ [0.9, 0.999]
| Parameter | Priors | |||
|---|---|---|---|---|
Inv-Gamma | 0.9658 | 0.9738 | 0.9962 | |
[0.988, 0.038] | (0.0219) | (0.0196) | (0.0046) | |
| | Normal | -1.1892 | -0.8828 | - |
[-1.20, 0.10] | (0.0673) | (0.0369) | - | |
| | Normal | 0.4131 | 0.8465 | - |
[0.40, 0.17] | (0.1179) | (0.0223) | - | |
| | Normal | 0.9396 | - | 0.9799 |
[0.85, 0.10] | (0.0431) | - | (0.0315) | |
| | Normal | 0.0421 | - | 0.0018 |
[0.10, 0.15] | (0.0422) | - | (0.0314) | |
| | Normal | -0.1256 | -0.1260 | -0.1260 |
[-0.126, 0.015] | (0.0148) | (0.0149) | (0.0147) | |
Normal | 0.1621 | 0.1630 | 0.1578 | |
[0.158, 0.025] | (0.0227) | (0.0205) | (0.0243) | |
| | Inv-Gamma | 1.8914 | 2.4241 | 1.7188 |
[2.0, 1.5] | (0.1484) | (0.1663) | (0.1112) | |
| | Inv-Gamma | 1.0842 | 0.4043 | 1.5738 |
[2.0, 0.4] | (0.2477) | (0.0378) | (0.2727) | |
| | Inv-Gamma | 0.6068 | 0.5752 | - |
[2.0, 0.6] | (0.0865) | (0.0975) | - | |
| | Inv-Gamma | 1.3828 | - | 1.6742 |
[2.0, 0.7] | (0.2346) | - | (0.2772) | |
| | Normal | -0.8990 | - | -0.9256 |
[-0.5, 0.2] | (0.0409) | - | (0.0291) | |
Normal | 85.2271 | 135.7241 | 67.8714 | |
[100.0, 15.0] | (6.7620) | (6.3363) | (3.7506) | |
Normal | 0.7955 | 1.9076 | 0.4526 | |
[1.0, 0.5] | (0.1774) | (0.1211) | (0.1112) | |
Uniform | -3.2825 | -8.8023 | -1.2605 | |
[-10.0, 0.0] | (0.6426) | (0.5900) | (0.3087) | |
| | Uniform | - | 4.4186 | - |
[-2.0, 7.5] | - | (0.7952) | - | |
| | Uniform | - | - | -1.0380 |
[-7.5, 2.0] | - | - | (0.2179) | |
| | - | -53.94 | -253.03 | -29.88 |
Table 6: UC Model Posterior Means, κ ∈ [0.9, 0.999], Factor Loadings on Money and Consumption Cycles
| Parameter | |||
|---|---|---|---|
| | 0.0086 | -0.0841 | - |
(0.0096) | (0.0676) | - | |
| | -0.0269 | 0.0064 | - |
(0.0188) | (0.0082) | - | |
| | 0.0143 | -0.0762 | - |
(0.0108) | (0.0624) | - | |
| | -0.0040 | -0.1542 | - |
(0.0202) | (0.1237) | - | |
| | -0.6044 | - | -0.3252 |
(0.2042) | - | (0.2052) | |
| | -0.0238 | - | -0.0004 |
(0.0261) | - | (0.0111) | |
| | -0.6283 | - | -0.3256 |
(0.2117) | - | (0.2053) |
† The factor loadings
![]() and
and
![]() equal zero for the
equal zero for the
![]() model.
model.
Table 7: US Model Posterior Means, κ ∈ [0.9, 0.999], Variance(PDV-ε) / Variance(Δe)
| Parameter | |||
|---|---|---|---|
| | 0.92 | 1.48 | 0.71 |
(0.15) | (0.22) | (0.09) | |
| | 3.04 | 0.36 | 0.96 |
(0.73) | (0.06) | (0.53) | |
| | 0.00 | 0.00 | - |
(0.00) | (0.00) | - | |
| | 0.22 | - | 0.12 |
(0.16) | - | (0.22) |
Table 8: UC-Models, κ ∈ [0.9, 0.999], Exchange Rate FEVDs†: Panel A: ![]() Model
Model
Forecast Horizon | |||
|---|---|---|---|
1 | 0.23 | 0.77 | 0.00 |
4 | 0.23 | 0.77 | 0.00 |
12 | 0.21 | 0.79 | 0.00 |
20 | 0.19 | 0.80 | 0.01 |
40 | 0.15 | 0.82 | 0.03 |
Table 8: UC-Models, κ ∈ [0.9, 0.999], Exchange Rate FEVDs†: Panel B: ![]() Model
Model
Forecast Horizon | |||
|---|---|---|---|
1 | 0.32 | 0.68 | - |
4 | 0.32 | 0.68 | - |
12 | 0.32 | 0.68 | - |
20 | 0.32 | 0.68 | - |
40 | 0.32 | 0.68 | - |
Table 8: UC-Models, κ ∈ [0.9, 0.999], Exchange Rate FEVDs†: Panel C: ![]() Model
Model
Forecast Horizon | |||
|---|---|---|---|
1 | 0.59 | 0.40 | 0.01 |
4 | 0.58 | 0.41 | 0.01 |
12 | 0.57 | 0.42 | 0.01 |
20 | 0.57 | 0.43 | 0.01 |
40 | 0.55 | 0.45 | 0.01 |
† The summary statistics are the
means of the ensemble of FEVDs with respect to permanent and
transitory Canadian-U.S. money differential and Canadian-U.S.
consumption differential shocks generated from the
![]() ,
,
![]() , and
, and
![]() model
posterior distributions.
model
posterior distributions.
Table 9: UC-Models, κ ∈ [0.9, 0.999], Summary of the Trend-Cycle Decomposition†
| Parameter | |||
|---|---|---|---|
| | 2.66 | 104.28 | 2.44 |
| | 3.68 | 106.84 | 2.55 |
| | 0.97 | 0.55 | 0.98 |
| | -0.06 | -0.37 | -0.02 |
| | 1.62 | 4.54 | 1.71 |
| | 0.68 | 3.03 | - |
| | -0.68 | 0.13 | - |
| | 0.26 | -0.24 | - |
| | 0.99 | 12.18 | 1.56 |
| | 5.73 | - | 7.73 |
| | 0.97 | - | 0.98 |
| | -0.16 | - | -0.14 |
| | 0.01 | -0.40 | 0.62 |
| | -0.85 | -0.93 | -0.71 |
| | 0.52 | 0.55 | 0.10 |
| | 0.04 | -0.73 | - |
| | -1.00 | - | -1.00 |
† The summary statistics are the
means of the ensemble of
CDN$/US$ exchange rate,
Canadian-U.S. money differential, and Canadian-U.S. consumption
differential trends and cycles generated from the
![]() ,
,
![]() , and
, and
![]() model
posterior distributions.
model
posterior distributions.
Figure 1: Prior and Posterior PDFs of DSGE-PVM Discount Factor
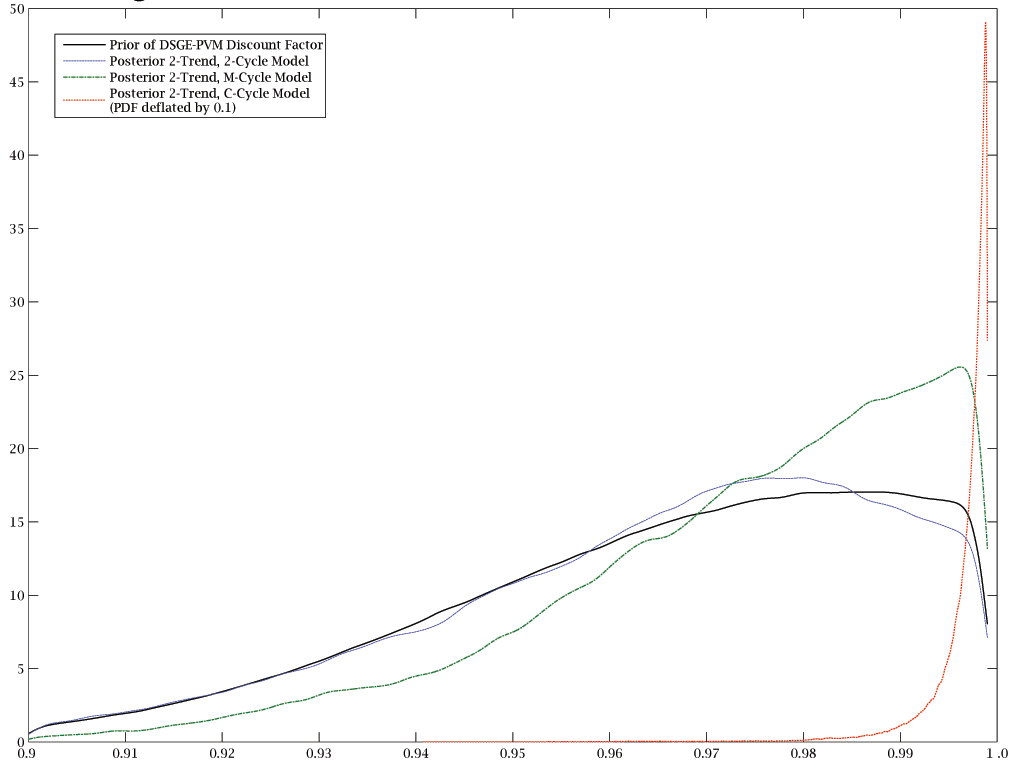
Figure 2: CDN$/US$ Exchange Rate Trend and Cycle, 1976Q1 - 2004Q4
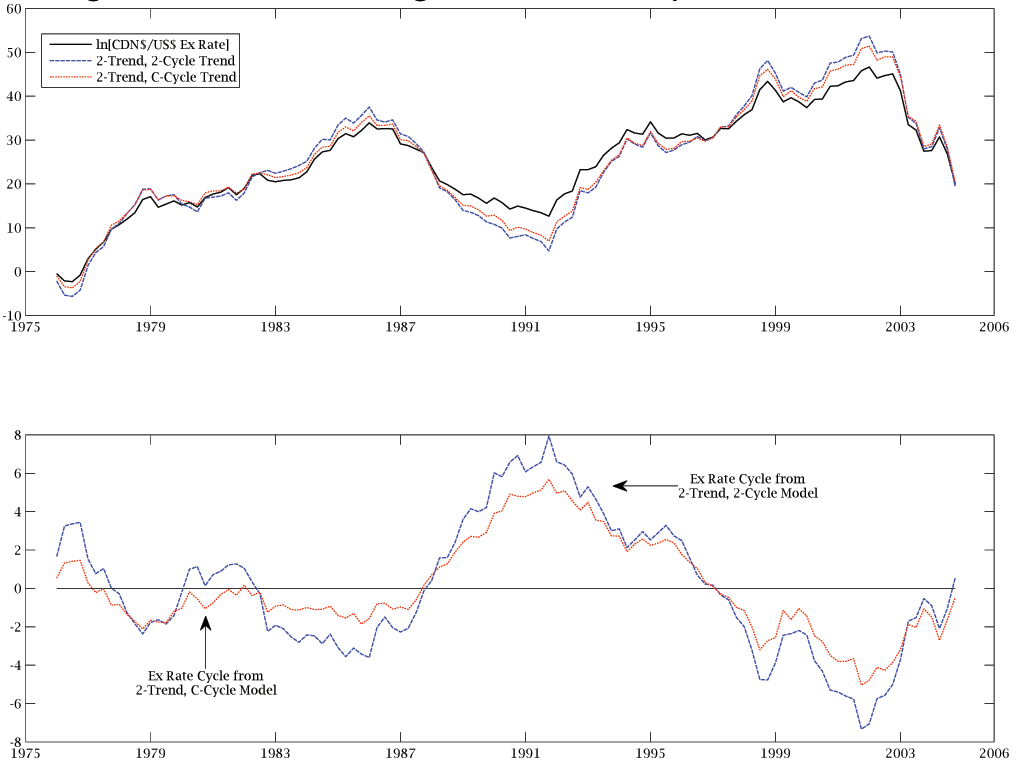
Figure 3: CDN-US Money, Consumption Trends and Cycles, 1976Q1 - 2004Q4
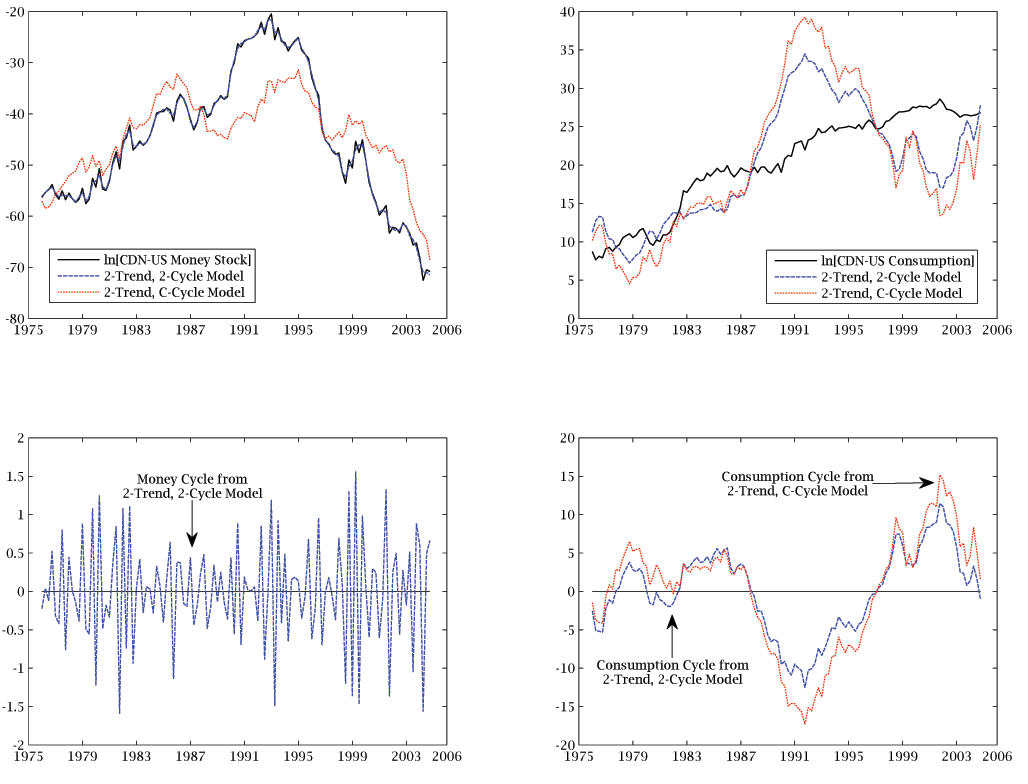
Figure 4: CDN$/US$ Ex Rate Cycles at Different DSGE-PVM Discount Factors
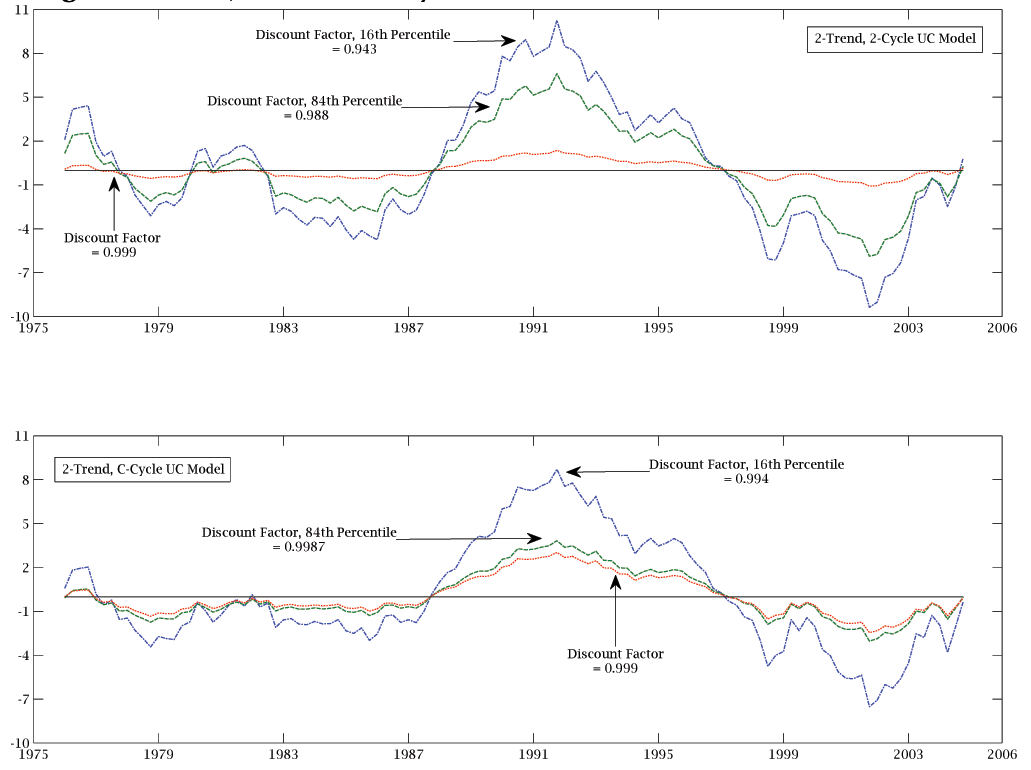
Footnotes
* We wish to thank Toni Braun, Fabio Canova, Menzie Chinn, Frank Diebold, John Geweke, Fumio Hayashi, Sharon Kozicki, Adrian Pagan, Juan F. Rubio-Ramírez, Tom Sargent, Pedro Silos, Ellis Tallman, Noah Williams, Farshid Vahid, Kenji Wada, Ken West, Tao Zha, the Federal Reserve Bank of Atlanta macro lunch study group, and seminar participants at the 2006 NBER Summer Institute Working Group on Forecasting and Empirical Methods in Macroeconomics and Finance, the 2007 Norges Bank Workshop on, "Prediction and Monetary Policy in the Presence of Model Uncertainty", the 2007 Bank of Canada-European Central Bank Exchange Rate Modeling Workshop, the 2007 Reserve Bank of Australia Research Workshop, "Monetary Policy in Open Economies", Ohio State, Houston, Tokyo, and Washington University for useful comments. The views in this paper represent those of the authors and are not those of either the Federal Reserve Bank of Atlanta, the Board of Governors of the Federal Reserve System, or any of its staff. Errors in this paper are the responsibility of the authors. Return to text
† Authors' contact details: James M. Nason, Research Department, Federal Reserve Bank of Atlanta, 1000 Peachtree St., N.E., Atlanta, GA 30309, email: [email protected]. John H. Rogers, International Finance Division, Board of Governors of the Federal Reserve System, Washington, D.C. 20551, email: [email protected]. Return to text
1. Actual data most often rejects the standard-PVM. Typical are tests Meese (1986) reported that employed the first ten years of the floating rate regime. He finds that exchange rates are infected with persistent deviations from fundamentals, which reject the standard-PVM and its cross-equation restrictions. However, Meese is unable to uncover the source of the rejections. Instead of a condemnation of the standard-PVM, we view results such as Meese's as a challenge to update and deepen its analysis. Return to text
2. The open economy VAR literature offers mixed evidence on the importance of various shocks for the exchange rate. Early papers including Eichenbaum and Evans (1995), Rogers (2000) and Kim and Roubini (2000) found some significance for identified monetary shocks. Recent contributions, however, suggest that monetary policy shocks have only a minor impact on exchange rate fluctuations, consistent with Rogoff's view, for example, see Faust and Rogers, (2003) and Scholl and Uhlig (2005). Return to text
3. The present-value relation
(3)
yields the weak prediction that ![]() Granger-causes
Granger-causes
![]() . Engel and West (2005) and Rossi (2007) report that this prediction is often
not rejected in G -7 data. Return to
text
. Engel and West (2005) and Rossi (2007) report that this prediction is often
not rejected in G -7 data. Return to
text
4. The restrictions on the moving
average are
![]() is linearly deterministic,
is linearly deterministic,
![]() ,
,
![]() is an infinite order lag
polynominal with roots outside the unit circle, the
is an infinite order lag
polynominal with roots outside the unit circle, the ![]() s are square summable, and
s are square summable, and
![]() is mean zero, homoskedastic,
linearly independent given history and is serially uncorrelated
with itself and the past of
is mean zero, homoskedastic,
linearly independent given history and is serially uncorrelated
with itself and the past of
![]() . Return to text
. Return to text
5. The error
![]() is also justified if the
econometrician's information set is strictly within that of
currency traders. Return to text
is also justified if the
econometrician's information set is strictly within that of
currency traders. Return to text
6. Maheswaran and Sims (1993) show that the martingale restriction has little empirical content for tests of asset pricing models when data is sampled at discrete moments in time. Return to text
7. Hansen, Roberds, and Sargent (1991) study linear rational expectations models that anticipate Proposition 3. Return to text
8. This analysis matches equations A.3 - A.11 and the surrounding discussion of Engel and West (2005). Return to text
9. Vahid and Engle show a n-dimension VAR(1) with d cointegrating relations has n - d common feature relations. Return to text
10. Proposition 5 can also be cast as an
implication of the BNSW representation of
![]() . In this case,
. In this case,
![]() removes the
vector MA
removes the
vector MA![]() in
in
![]() and
and
![]() from the BNSW representation
of
from the BNSW representation
of
![]() . Only a linear combination of
pure forecast innovations,
. Only a linear combination of
pure forecast innovations,
![]() and
and
![]() , are left to drive
, are left to drive
![]() . Let
. Let ![]()
![]() 0 to obtain the random walk
exchange rate with innovation
0 to obtain the random walk
exchange rate with innovation
![]()
![]()
![]() . Return to text
. Return to text
11. Fundamentals equal cross-country
money minus cross-country output, which implies an income
elasticity of money demand, ![]() , calibrated to
one. This calibration is consistent with estimates reported by Mark
and Sul (2003). The money stocks
(outputs) are measured in current (constant) local currency units
and per capita terms. Return to
text
, calibrated to
one. This calibration is consistent with estimates reported by Mark
and Sul (2003). The money stocks
(outputs) are measured in current (constant) local currency units
and per capita terms. Return to
text
12. The VARs include a constant and linear time trend. The LR statistics employ the Sims (1980) correction and have standard asymptotic distribution according to results in Sims, Stock, and Watson (1990). Return to text
13. The Canadian-U.S. and Japanese-U.S. VARs are selected when the p-value of the LR test is five percent or less. Since the U.K.-U.S. VAR offers ambiguous results, we settle on a VAR(4). Return to text
14. We thank Farshid Vahid for suggesting this example. Return to text
15. A related example is Harvey, Trimbur, and van Dijk (2007) who use Bayesian methods to estimate permanent-transitory decompositions of aggregate time series, but without rational expectations cross-equation restrictions. Return to text
16. Morley, Nelson, and Zivot (2003) show that this restriction applied to an univariate UC model resolves its differences with the Beverage and Nelson (1981) decomposition. Return to text
17. The factor loading on the permanent
component of ![]() remains (normalized to)
one. Return to text
remains (normalized to)
one. Return to text
18. The appendix discusses the data and explains, for example, that Canadian consumption includes semi-durable expenditures. Return to text
19. The posterior distributions are
based on acceptance rates of between 25 and 36 percent. Besides the
750,000 MCMC draws used to compute the moments reported below, four
more sequences of 750,000 MCMCs are generated from disparate
starting values to assess across chain and within chain
convergence. We compute the
![]() statistic of Gelman, Carlin,
Stern, and Rubin (2004) to
evaluate across chain across and the separated partial means test
of Geweke (2005) convergence, which
is distributed asymptotically
statistic of Gelman, Carlin,
Stern, and Rubin (2004) to
evaluate across chain across and the separated partial means test
of Geweke (2005) convergence, which
is distributed asymptotically ![]() . Across the
77 parameters of the six UC models, the two largest
. Across the
77 parameters of the six UC models, the two largest
![]() s are 1.20 and 1.04, while
Gelman, et al suggest a
s are 1.20 and 1.04, while
Gelman, et al suggest a
![]() of about 1.10. On five
subsamples, the Geweke separated partial means test has no
p-value smaller than 0.21 across the six UC
models and five MCMC simulation sequences. Return to text
of about 1.10. On five
subsamples, the Geweke separated partial means test has no
p-value smaller than 0.21 across the six UC
models and five MCMC simulation sequences. Return to text
20. The half life equals log[0.5]/log[q], where q is the largest modulus of the companion matrix of the AR or MA coefficients. Return to text
21. For the
![]() and
and
![]() models, the
relevant factor loadings are multiplied by
models, the
relevant factor loadings are multiplied by
![]() or
or
![]() . Return to text
. Return to text
22. The FEVDs are computed using the VECM implied by equation (13). The VECM is placed in state space form as outlined by Heqc, Palm, and Urbain (2000) and iterated to create the FEVDs of table 8. Return to text
23. We do not present the trend-cycle
decompositions based on the posterior of the
![]() model because
its log marginal likelihood is far below those of the other UC
models. Table 9 includes standard deviations of
model because
its log marginal likelihood is far below those of the other UC
models. Table 9 includes standard deviations of
![]() and
and
![]() from the posterior of the
from the posterior of the
![]() model that are
larger by a factor of 30 or compared to these statistics from the
model that are
larger by a factor of 30 or compared to these statistics from the
![]() and
and
![]() models. This
signals the lack of acceptance of the
models. This
signals the lack of acceptance of the
![]() model by our
Canadian-U.S. sample. Return to
text
model by our
Canadian-U.S. sample. Return to
text
24. Jeffreys (1998, p. 432) contends that Bayes factors differing by 3.16 is evidence about the two models just between 'not worth more than a bare mention' and substantially in favor of the model with the larger marginal likelihood. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text