
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 953, October 2008 --- Screen Reader
Version*
Testing the Expectations Hypothesis When Interest Rates are Near Integrated
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
Nominal interest rates are unlikely to be generated by unit-root processes. Using data on short and long interest rates from eight developed and six emerging economies, we test the expectations hypothesis using cointegration methods under the assumption that interest rates are near integrated. If the null hypothesis of no cointegration is rejected, we then test whether the estimated cointegrating vector is consistent with that suggested by the expectations hypothesis. The results show support for cointegration in ten of the fourteen countries we consider, and the cointegrating vector is similar across countries. However, the parameters differ from those suggested by theory. We relate our findings to existing literature on the failure of the expectations hypothesis and to the role of term premia.
Keywords: Bonferroni tests, cointegration, expectations hypothesis, near integration, term premium
JEL classification: C22, G12
1. Introduction
Empirical tests of the expectations hypothesis of the term structure often fail to find support for the theory. The logic underlying the theory, that expectations of future short interest rates shape the term structure of longer interest rates, is intuitive, appealing, and a common assumption in macroeconomic modelling. However, the predictability of excess returns shown by Fama and Bliss (1987), Campbell and Shiller (1991) and more recently by Cochrane and Piazzesi (2005) undermines the premise that long interest rates are rational expectations of future short rates up to a constant term premium. Rather, such evidence points strongly toward time-varying risk premia. Indeed, Dai and Singleton (2002) demonstrate that interest rates adjusted for time-varying risk premia estimated from dynamic term structure models meet the predictions of the expectations hypothesis in traditional excess-return regressions.
One strand of the empirical literature on interest rates has sought to test the expectations hypothesis using the techniques of cointegration. As pointed out by Engle and Granger (1987) in their seminal paper on cointegration, if nominal interest rates are generated by a unit-root process, cointegration between yields of different maturities is a necessary condition for the validity of the expectations hypothesis. Intuitively, if interest rates are integrated of order one, the expectations hypothesis implies that the spread between any pair of yields is stationary. Following Engle and Granger's early work, several studies have taken a similar path and have found only mixed evidence for the expectations hypothesis; see, for example, Campbell and Shiller (1987), Boothe (1991), Hall et al. (1992), Zhang (1993) and Lardic and Mignon (2004).
It is an empirical fact that nominal interest rates are highly persistent and the poor power of traditional univariate Dicky-Fuller type tests against the null of a unit root (Stock, 1994) has led many researchers to conclude that interest rates are integrated of order one. Moreover, the convenience of working with established results for integrated processes has made it attractive to assume the presence of a unit root for empirical purposes. As such, nominal interest rates have been treated as integrated of order one in numerous empirical papers, including Karfakis and Moschos (1990), Bremnes et al. (2001), Chong et al. (2006), Kleimeier and Sander (2006), De Graeve et al. (2007) and Liu et al. (2008). For theoretical purposes, the unit-root assumption can also be a useful modelling device to capture stylistically the highly persistent nature of interest rates in finite samples, exemplified by Cogley and Sargent's (2001) approach to modelling the dynamics of a system of macroeconomic variables.
However, the exact unit-root assumption for nominal interest rates can be questioned on both empirical and theoretical grounds. Empirically, standard tests for unit roots have difficulty discriminating true integration from highly-persistent dynamics but panel unit-root tests - which tend to be more powerful than univariate tests - tend to find support for mean reversion in nominal interest rates (Wu and Chen, 2001). Theoretically, it might be unsatisfactory to model interest rates as unbounded in the limit.1 More importantly though, most economic models predict that real interest rates possess a long-run equilibrium value, determined by the long-run rate of potential output growth and population growth, and agents' rate of time preference and risk aversion. Similarly, consumption growth is typically viewed as stationary - albeit slowly mean-reverting (Bansal and Yaron, 2004). The standard consumption Euler equation thus implies stationary real interest rates. Nominal interest rates have varied substantially in recent decades, partly reflecting the undulations of inflation expectations, but over the long-run, have wandered within reasonable bounds. Indeed, from an historical perspective, short-term nominal interest rates were in the range of four to eight percent during the years of the Roman Empire, and western European commercial and mortgage borrowing rates moved in the four-to-eight percent range from the 13th to 17th century (Homer and Sylla, 1996). Private nominal interest rates are in a similar range today, an outcome that would be virtually impossible if interest rates possessed a unit root but consistent with a highly-persistent data generating process.
Unfortunately, standard cointegration-based inference designed for unit-root data is typically not robust to even small deviations from the unit-root assumption. Results will generally be biased when the autoregressive roots in the data are close, but not identical, to unity; this is true both for actual tests of the cointegrating rank (Hjalmarsson and Österholm, 2007a,b) as well as for inference on the cointegrating vector (Elliott, 1998). Conclusions of empirical tests of the expectations hypothesis that rely on traditional cointegration are therefore called into question. As such, empirical analysis within a framework that acknowledges the high persistence in nominal interest rates but that does not impose the strict assumption of a unit root is desirable but very few examples exist in the literature. To our knowledge, exceptions include one study of the Fisher effect (Lanne, 2001) and one on the term structure of interest rates (Lanne, 2000).
In this paper, we revisit the question of cointegration between yields of different maturities using methods that allow for valid inference when data are near integrated. That is, we assume that interest rates are highly persistent with autoregressive roots that are close to unity. The empirical framework nests the standard unit-root assumption used in the traditional cointegration studies mentioned above, but also permits interest rates to be (slowly) mean reverting. We test for cointegration using the recently developed methods of Hjalmarsson and Österholm (2007a) that are robust to deviations from the pure unit-root assumption and apply the tests to monthly data of the term structure of interest rates in several developed and emerging economies, namely Australia, Canada, Hungary, India, Japan, Mexico, New Zealand, Poland, Singapore, South Africa, Sweden, Switzerland, the United Kingdom and the United States. The results provide strong support for cointegration between long and short interest rates in ten of these countries. Among the developed countries, results show support for cointegration in Australia, Canada, New Zealand, Sweden, Switzerland and the United States. Among the emerging economies, a similar result is returned for Hungary, Mexico, Poland and Singapore.
Cointegration is only one of two necessary conditions for the validity of the expectations hypothesis; the theory also contains strong predictions about the parameters of the cointegrating vector. However, earlier work has largely overlooked the interpretation of the parameters of the cointegrating vector. We test whether the parameters are consistent with the theoretically-suggested values using an extension of fully-modified estimation that is again robust to deviations from the pure unit-root assumption. Fully modified estimation of cointegrated systems was initially developed by Phillips and Hansen (1990) and discussed by Hjalmarsson (2007) in the context of predictive regressions with near unit-root variables; in the current paper, we extend those ideas further to accommodate inference in a general bivariate cointegrating relationship with nearly integrated variables.2 For the ten countries in which cointegration is detected, the cointegrating vector does not coincide with that suggested by theory. In each case, long rates move by less than short rates, with the similarity of the estimated vectors across countries hinting at a common explanation. Indeed, the estimated cointegrating vectors suggest that another near-integrated variable that covaries inversely with the short rate also affect the term structure of longer interest rates. This is consistent with time-varying bond risk premia put forward by Campbell and Shiller (1991) and Dai and Singleton (2002) to explain the puzzling patterns of coefficients from yield-spread regressions, and with the countercyclical pattern of excess returns noted by Fama and Bliss (1987) and Cochrane and Piazzesi (2005). We conjecture that the phenomenon underlying the rejection of the expectations hypothesis in excess-return regressions may also be responsible for the failure of the expectations hypothesis in cointegration methods.
The remainder of the paper is organized as follows. Section 2 presents the theoretical framework regarding the term structure of interest rates and the econometric methodology. In Section 3, the empirical analysis is conducted and the results discussed and Section 4 concludes. Some sensitivity analysis is presented in the Appendix.
2. Theoretical framework
This section presents the theoretical motivation for our empirical tests. We briefly lay out the expectations hypothesis of the term structure then move on to the econometric methodology of testing for cointegration between near-integrated processes.
2.1 The term structure of interest rates
We begin with a statement of the expectations hypothesis of the term structure similar to that found in Campbell and Shiller (1991):
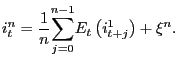 |
(1) |
Simply put, the expectations hypothesis posits that the interest
rate on a longer-term ![]() -period bond,
-period bond, ![]() , is equal to the average of the expected path of
future one-period interest rates over the life of the bond,
, is equal to the average of the expected path of
future one-period interest rates over the life of the bond,
![]()
![]() , plus a constant term premium,
, plus a constant term premium,
![]() , that may differ across maturities,
, that may differ across maturities,
![]() . Expectations of future short interest rates
are assumed to be rational.
. Expectations of future short interest rates
are assumed to be rational.
Subtracting ![]() from both sides of equation
(1) and
rearranging terms, the expectations hypothesis states that the
yield spread between an
from both sides of equation
(1) and
rearranging terms, the expectations hypothesis states that the
yield spread between an ![]() -period bond and the current
one-period rate can be viewed as the weighted average of expected
changes in short interest rates over the life of the bond:
-period bond and the current
one-period rate can be viewed as the weighted average of expected
changes in short interest rates over the life of the bond:
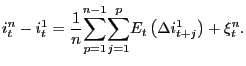
|
(2) |
Paired with the assumption that one-period nominal interest rates
are integrated or near integrated, the sum of first differences on
the right hand side of equation (2) must
be stationary. This in turn implies that any ![]() -period yield should be cointegrated with the one-period
interest rate and that the cointegrating vector will be
(1, -1). Note that the term
premium in equation (2) has
been generalised to include a time subscript,
-period yield should be cointegrated with the one-period
interest rate and that the cointegrating vector will be
(1, -1). Note that the term
premium in equation (2) has
been generalised to include a time subscript,
![]() . This has been done deliberately,
acknowledging that testing for cointegration between the
left-hand-side variables cannot discriminate between theories of
the term structure in which term premia are constant versus
theories in which term premia are time-varying but stationary, as
noted by Miron (1991) and Lanne (2000). As such, evidence for
cointegration does not speak to the strict form of the expectations
hypothesis shown in equation (1) but does
substantially narrow the class of models that fit the data. For
example, it rules out market segmentation and preferred habitat
models of the term structure.
. This has been done deliberately,
acknowledging that testing for cointegration between the
left-hand-side variables cannot discriminate between theories of
the term structure in which term premia are constant versus
theories in which term premia are time-varying but stationary, as
noted by Miron (1991) and Lanne (2000). As such, evidence for
cointegration does not speak to the strict form of the expectations
hypothesis shown in equation (1) but does
substantially narrow the class of models that fit the data. For
example, it rules out market segmentation and preferred habitat
models of the term structure.
Cointegration alone is insufficient to conclude that the expectations hypothesis fits the data. If the cointegrating vector differs from the theoretically suggested value of (1, -1), the requirements of the theory have not been met.3 However, this has quite different implications from an outright rejection of cointegration in the data. A vector that differs from (1, -1) is compatible, for example, with the presence of additional near-integrated processes driving the term structure, which systematically covary with the spread or the short interest rate.
2.2 Econometric methodology
The main starting point of our empirical analysis is the
assumption that both the long and short interest rates follow near
unit-root processes with local-to-unity roots
![]() and
and
![]() , respectively, where
, respectively, where
![]() is the sample size; there is no requirement
that
is the sample size; there is no requirement
that
![]() . Thus, if
. Thus, if
![]() , it is
assumed that
, it is
assumed that
| (3) |
where ![]() is a
is a ![]() matrix
with
matrix
with
![]() , and
, and
![]() . The
innovations
. The
innovations ![]() are assumed to satisfy a general
linear, or infinite moving average, process. Although not necessary
for the formal econometric procedures that are used, we will
maintain the assumption throughout the paper that
are assumed to satisfy a general
linear, or infinite moving average, process. Although not necessary
for the formal econometric procedures that are used, we will
maintain the assumption throughout the paper that
![]() , which rules out explosive
processes. Since we are analysing interest rates, this is clearly a
weak assumption.
, which rules out explosive
processes. Since we are analysing interest rates, this is clearly a
weak assumption.
This specification of the data-generating process for the interest rates at different horizons is a generalisation of a pure unit-root model where interest rates at all maturities contain a unit root. Compared to a pure unit-root process, equation (3) offers considerably more flexibility. First, the model allows for deviations from the strict unit-root assumption while still preserving, also asymptotically, the empirically observed feature that interest rates are highly persistent. Second, the model above also allows for different degrees of persistence in interest rates with different maturities. Although it is natural to believe that interest rates at different horizons share the same persistence if the expectations hypothesis is true, this does not necessarily hold under an alternative hypothesis.
As shown in the empirical analysis below, the near unit-root
model suggested here finds more support in the data than the pure
unit-root model. For several series, the null of a unit root can be
rejected and unbiased estimates of ![]() and
and
![]() are typically negative, suggesting some
mean reversion in the data.
are typically negative, suggesting some
mean reversion in the data.
While the concept of cointegration readily carries over to variables with near unit roots, as discussed in Phillips (1998), traditional cointegration tests based on a unit-root assumption are biased (Hjalmarsson and Österholm, 2007a,b). Furthermore, if the presence of cointegration between near unit-root variables is established, subsequent tests on the cointegrating vector will be biased if performed under the assumption of unit roots in the data (Elliott, 1998). Moreover, even if the null of a unit root in the variables cannot be rejected, there is no guarantee that the data contain an exact unit root, as unit-root tests have low power against alternatives close to a unit root. Thus, unless there are very strong a priori reasons to believe that there is an exact unit root in the data, based on some theoretical argument for instance, any cointegration test based on the unit-root assumption is subject to a potential bias.
In the next two sections, we outline methods for dealing with an unknown local deviation from the pure unit-root assumption, both for actual tests of cointegration as well as for inference on the cointegrating vector.
2.2.1 Robust tests for cointegration
We focus on residual-based tests of cointegration and rely on the methods proposed by Hjalmarsson and Österholm (2007a) to deal with the issues raised by near unit-root variables. In effect, a residual-based cointegration test evaluates whether the residuals from the empirical regression contain a unit root. However, if the original data are in fact near integrated, with a root less than unity, the test will over-reject as the residuals will not contain a unit root even if there is no cointegration.
The idea behind Hjalmarsson and Österholm's test is therefore to replace the critical values of the test under the unit-root assumption with critical values based on a conservative estimate of the local-to-unity root in the original data. Intuitively, if one views a residual-based test of cointegration as a test of whether there is less persistence in the residuals than in the original data, this test is only valid if the persistence of the original data is not overstated.
In particular, we will use a modified version of the traditional Engle-Granger (EG) test for cointegration. Consider the cointegrating regression
| (4) |
where the fitted residuals
![]() are tested for a unit root
according to
are tested for a unit root
according to
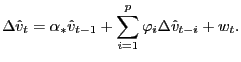
|
(5) |
The EG test is defined as the ![]() statistic on
statistic on
![]() from equation (5).
from equation (5).
As shown by Hjalmarsson and Österholm (2007a), under the
near unit-root assumption, the limiting distribution of the
EG test statistic depends on the unknown matrix of
local-to-unity parameters
![]() , and the
critical values of the EG test are thus unknown in the near
unit-root case. In order to obtain a practically feasible
procedure, Hjalmarsson and Österholm first show that the
relevant critical values of this limiting distribution are
primarily a function of
, and the
critical values of the EG test are thus unknown in the near
unit-root case. In order to obtain a practically feasible
procedure, Hjalmarsson and Österholm first show that the
relevant critical values of this limiting distribution are
primarily a function of ![]() , the persistence of the
`` dependent'' variable, and are almost invariant to the value of
, the persistence of the
`` dependent'' variable, and are almost invariant to the value of
![]() , the persistence of the regressor
variable. They therefore suggest using critical values based on
, the persistence of the regressor
variable. They therefore suggest using critical values based on
![]() , rather
than
, rather
than
![]() , which
greatly simplifies the feasible implementation.
, which
greatly simplifies the feasible implementation.
Furthermore, the critical values for the EG testare
increasing in ![]() . Therefore, in order to form a
correctly sized test, all that is needed is a `` sufficiently''
conservative estimate of
. Therefore, in order to form a
correctly sized test, all that is needed is a `` sufficiently''
conservative estimate of ![]() . As shown by Stock
(1991), a confidence interval for
. As shown by Stock
(1991), a confidence interval for ![]() can be
obtained by inverting a unit-root test-statistic for
can be
obtained by inverting a unit-root test-statistic for ![]() ; since only the lower bound matters here, a
one-sided confidence interval is appropriate. According to
Bonferroni's inequality, if the confidence level of this one-sided
confidence interval is 95 percent and the nominal
size of the EG test, evaluated using the critical values
based on the lower bound for
; since only the lower bound matters here, a
one-sided confidence interval is appropriate. According to
Bonferroni's inequality, if the confidence level of this one-sided
confidence interval is 95 percent and the nominal
size of the EG test, evaluated using the critical values
based on the lower bound for ![]() , is five
percent, then the actual size of the cointegration test is less
than or equal to ten percent.
, is five
percent, then the actual size of the cointegration test is less
than or equal to ten percent.
As shown by Hjalmarsson and Österholm, however,
Bonferroni's inequality tends to be strict and the actual size of
the test procedure just described is, in fact, very close to zero.
Instead, they find that if the EG test is evaluated at the
five percent level and the critical values are based on the lower
bound of a one-sided confidence interval for ![]() with confidence level of
with confidence level of ![]() percent, the
overall test of cointegration will have an actual size of
approximately five percent. Thus, the median unbiased estimate of
percent, the
overall test of cointegration will have an actual size of
approximately five percent. Thus, the median unbiased estimate of
![]() can be used to form the critical
values.
can be used to form the critical
values.
In summary, the following procedure to test the null of no cointegration for near-integrated variables will thus be used in the analysis here:
- (i) Obtain the value of the test statistic from a standard implementation of the EG test.
- (ii) Invert the test statistic from the Dickey-Fuller test with GLS
detrending (ADF-GLS) of Elliott et al. (1996) and
obtain the median unbiased estimate of
 ; denote
this estimate
; denote
this estimate
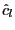 . For a given value of the
ADF-GLS test statistic, the corresponding median unbiased
estimate can be found in Table A1 of Hjalmarsson and Österholm
(2007a).
. For a given value of the
ADF-GLS test statistic, the corresponding median unbiased
estimate can be found in Table A1 of Hjalmarsson and Österholm
(2007a). - (iii) Compare the EG test statistic to the critical value in
Table A3 in Hjalmarsson and Österholm (2007a), corresponding
to the distribution under
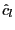 if
if
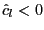 . If
. If
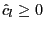 , use the critical values
from the traditional EG test, that is, for
, use the critical values
from the traditional EG test, that is, for 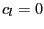 .
.
We will refer to the test of cointegration constructed in the above manner as the Bonferroni EG test.
2.2.2 Tests of restrictions on the cointegrating vector
If one does establish that variables are cointegrated, it is often of interest to perform inference on the cointegrating vector. In the current application, we are interested in whether the cointegrating vector is (1, -1), since this is an additional condition for the expectations hypothesis to hold once cointegration between the short and long interest rates has been established.
In the case with unit-root regressors, inference on the cointegrating vector is typically performed using standard tests based on the estimates from some efficient estimation procedure of the cointegrating vector, such as the dynamic OLS of Saikkonen (1991) and Stock and Watson (1993) or the fully modified OLS (FM-OLS) of Phillips and Hansen (1990). Using these efficient estimation methods, which are asymptotically equivalent, the resulting test statistics have standard distributions. However, as shown by Elliott (1998), this is no longer true when the data are nearly integrated, and tests based on the unit-root assumption can be highly misleading.
In this paper, we therefore apply an extension of the FM-OLS
procedure for nearly integrated regressors. The idea was developed
by Hjalmarsson (2007) for predictive regressions with nearly
integrated regressors. Given the predictive nature of that model,
the FM-OLS estimator needs to be slightly modified to fit the
standard (contemporaneous) cointegration regression studied here.
The following results are derived under the assumption of
cointegration, such that equation (4) represents a
true relationship, with a stationary error term ![]() .
.
To fix notation, let ![]() be the innovations
to the short interest rate variable; that is,
be the innovations
to the short interest rate variable; that is,
| (6) |
where
![]() . The model is now given by
equations (4) and (6). Denote the
joint innovations
. The model is now given by
equations (4) and (6). Denote the
joint innovations
![]() and suppose that
and suppose that ![]() satisfy a functional law such
that
satisfy a functional law such
that
![]() , where
, where
![]() denotes a two-dimensional Brownian motion with variance-covariance
matrix
denotes a two-dimensional Brownian motion with variance-covariance
matrix
![]() ; that is,
; that is, ![]() is the long-run two-sided
variance-covariance matrix for
is the long-run two-sided
variance-covariance matrix for ![]() . Further, let
. Further, let
![]() and
and
![]() be the one-sided long-run covariance and variance, respectively.
be the one-sided long-run covariance and variance, respectively.
In general, the OLS estimator of ![]() in
equation (4) is not
efficient, and the resulting test statistics have non-standard
asymptotic distributions whenever there is a non-zero correlation
between
in
equation (4) is not
efficient, and the resulting test statistics have non-standard
asymptotic distributions whenever there is a non-zero correlation
between ![]() and
and ![]() . In the
pure unit-root case, Phillips and Hansen (1990) therefore suggest
that the OLS estimator be `` fully modified''. As shown in
Hjalmarsson (2007), in the near unit-root case, a similar method
can also be considered. However, the modification makes use of the
innovations
. In the
pure unit-root case, Phillips and Hansen (1990) therefore suggest
that the OLS estimator be `` fully modified''. As shown in
Hjalmarsson (2007), in the near unit-root case, a similar method
can also be considered. However, the modification makes use of the
innovations ![]() , which can only be obtained by
knowledge of
, which can only be obtained by
knowledge of ![]() , which is unknown.4 We
therefore first derive the estimator under the assumption that
, which is unknown.4 We
therefore first derive the estimator under the assumption that
![]() is known, and then discuss feasible
methods to deal with an unknown
is known, and then discuss feasible
methods to deal with an unknown ![]() . Define
. Define
| (7) |
and let
![]() and
and
![]() where
where
![]() and
and
![]() are consistent estimates
of the respective parameters and
are consistent estimates
of the respective parameters and
![]() and
and
![]() denote the demeaned
data. The fully modified OLS estimator is given by
denote the demeaned
data. The fully modified OLS estimator is given by
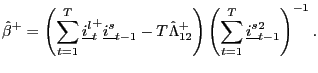
|
(8) |
Define
![]() and as shown in Hjalmarsson (2007), as
and as shown in Hjalmarsson (2007), as
![]() ,
,

|
(9) |
where
![]() ,
,
![]() and
and
![]() denotes a mixed normal
distribution. The mixed normality implies that the asymptotic
distribution is normal with a random variance. For practical
purposes, the main implication is that corresponding tests will
have asymptotically standard distributions; in particular, the
corresponding
denotes a mixed normal
distribution. The mixed normality implies that the asymptotic
distribution is normal with a random variance. For practical
purposes, the main implication is that corresponding tests will
have asymptotically standard distributions; in particular, the
corresponding ![]() statistic is normally distributed and
confidence intervals for
statistic is normally distributed and
confidence intervals for ![]() can be constructed in a
standard manner. The parameters
can be constructed in a
standard manner. The parameters
![]() and
and
![]() can be consistently
estimated from the residuals of first stage OLS regressions, using
standard long-run covariance estimation methods such as those of
Newey and West (1987).5 In fact, for a given
can be consistently
estimated from the residuals of first stage OLS regressions, using
standard long-run covariance estimation methods such as those of
Newey and West (1987).5 In fact, for a given
![]() , once the innovations
, once the innovations
![]() are
obtained, the FM-OLS procedure for near unit-root variables is
identical to the standard one used in the unit-root case.
are
obtained, the FM-OLS procedure for near unit-root variables is
identical to the standard one used in the unit-root case.
For a given value of ![]() , a confidence interval
for
, a confidence interval
for ![]() at the
at the ![]() confidence level is given by
confidence level is given by
![]() , where
, where
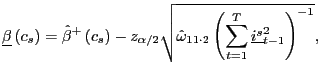
|
(10) |
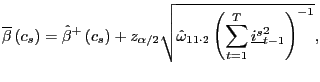
|
(11) |
and
![]() denotes the
denotes the
![]() quantile of the standard normal
distribution. Here
quantile of the standard normal
distribution. Here
![]() is explicitly written as a
function of
is explicitly written as a
function of ![]() to facilitate the discussion below
when
to facilitate the discussion below
when ![]() is unknown. The estimate of
is unknown. The estimate of
![]() is simply given by
is simply given by
![]() .
.
In order to get around the issue of an unknown ![]() parameter, we rely on similar methods to those used for
the cointegration test. That is, given a confidence interval for
parameter, we rely on similar methods to those used for
the cointegration test. That is, given a confidence interval for
![]() , we can calculate
, we can calculate
![]() for
all values
for
all values ![]() in this confidence interval.
It is easy to show that
in this confidence interval.
It is easy to show that
![]() will
be a monotone function of
will
be a monotone function of ![]() and it is
sufficient to calculate the values at the endpoints of the
interval. In fact, if the long-run correlation between
and it is
sufficient to calculate the values at the endpoints of the
interval. In fact, if the long-run correlation between ![]() and
and ![]() is negative (positive),
then
is negative (positive),
then
![]() will
be decreasing (increasing) in
will
be decreasing (increasing) in ![]() . Suppose
the confidence level of the lower bound of
. Suppose
the confidence level of the lower bound of ![]() is
such that
is
such that
![]() and that of the upper bound such that
and that of the upper bound such that
![]() , with
, with
![]() . If
. If
![]() , a robust confidence
interval for
, a robust confidence
interval for ![]() , with a confidence level of at
least
, with a confidence level of at
least
![]() is then
given by
is then
given by
| (12) |
and if
![]() by
by
| (13) |
Thus, if
![]() and
and
![]() , a
, a ![]() percent confidence interval for
percent confidence interval for ![]() is obtained.
As in the case of the cointegration test in the previous section,
the actual confidence level may be higher, and for a given
is obtained.
As in the case of the cointegration test in the previous section,
the actual confidence level may be higher, and for a given
![]() ,
,
![]() and
and
![]() can be chosen to
achieve a desired actual confidence level. Campbell and Yogo (2006)
discuss in detail the methods for adjusting
can be chosen to
achieve a desired actual confidence level. Campbell and Yogo (2006)
discuss in detail the methods for adjusting
![]() and
and
![]() . In fact, as shown by
Hjalmarsson (2007), the methods in Campbell and Yogo (2006) can be
interpreted as a special case of the FM-OLS framework adapted to
. In fact, as shown by
Hjalmarsson (2007), the methods in Campbell and Yogo (2006) can be
interpreted as a special case of the FM-OLS framework adapted to
![]() processes, with the same
asymptotic properties under this more restrictive assumption. We
can therefore rely on their values for
processes, with the same
asymptotic properties under this more restrictive assumption. We
can therefore rely on their values for
![]() and
and
![]() as given in Table 2 of
Campbell and Yogo (2006).6 Setting
as given in Table 2 of
Campbell and Yogo (2006).6 Setting
![]() , and using these values of
, and using these values of
![]() and
and
![]() result in a confidence
interval for
result in a confidence
interval for ![]() with confidence level of
with confidence level of
![]() percent. For completeness, in the
empirical section we also show the plain non-size-adjusted 90
percent confidence interval that is obtained by setting
percent. For completeness, in the
empirical section we also show the plain non-size-adjusted 90
percent confidence interval that is obtained by setting
![]() and
and
![]() .
.
In terms of practical implementation, we obtain a confidence
interval for ![]() by inverting the ADF-GLS
unit-root test statistic, and use the Newey-West estimator to
calculate all long-run variances and covariances.
by inverting the ADF-GLS
unit-root test statistic, and use the Newey-West estimator to
calculate all long-run variances and covariances.
3. Empirical results
3.1 The data and their univariate properties
We use monthly data on short and long nominal interest rates in Australia, Canada, Hungary, India, Japan, Mexico, New Zealand, Poland, Singapore, South Africa, Sweden, Switzerland, the United Kingdom and the United States. For all countries, the long interest rate is the yield on a benchmark government bond and the short interest rate is a representative three-month rate. Details of the data for each country are given in the Appendix. Sample starting dates vary from 1955 to 1997, with the sample for the emerging economies generally shorter owing to poorer market functioning and data keeping. Country-specific samples are shown in Table 1.
We begin by documenting the univariate properties of the data
series, applying the ADF-GLS test to all variables. Results
are shown in Table 1. The table also shows median unbiased
estimates of ![]() and
and ![]() , and
their 90 percent confidence intervals which are computed by
inverting the ADF-GLS test statistic following the
methodology suggested by Stock (1991).7 The estimate of
, and
their 90 percent confidence intervals which are computed by
inverting the ADF-GLS test statistic following the
methodology suggested by Stock (1991).7 The estimate of
![]() is used in the Bonferroni EG
test if it is smaller than zero.
is used in the Bonferroni EG
test if it is smaller than zero.
Two important features stand out in Table 1; all of the interest
rate series are highly persistent, but the pure unit-root
assumption is likely to be too restrictive. Unbiased estimates of
![]() are in most cases negative, suggesting
mean reversion in the data. Moreover, the null hypothesis of a unit
root is rejected at the five percent level for the three-month
interest rate in Canada, New Zealand, Singapore and Switzerland.
The benefits of the Bonferroni EG test are evident in these
cases. Most researchers would - rightly so - be reluctant to use
traditional cointegration analysis after having detected evidence
of stationarity. The Bonferroni EG test, on the other hand,
provides a tool for valid inference also in the near-integrated
case.
are in most cases negative, suggesting
mean reversion in the data. Moreover, the null hypothesis of a unit
root is rejected at the five percent level for the three-month
interest rate in Canada, New Zealand, Singapore and Switzerland.
The benefits of the Bonferroni EG test are evident in these
cases. Most researchers would - rightly so - be reluctant to use
traditional cointegration analysis after having detected evidence
of stationarity. The Bonferroni EG test, on the other hand,
provides a tool for valid inference also in the near-integrated
case.
3.2 Cointegration
Having investigated the univariate time-series properties of the data, we now turn to the issue of cointegration between long and short interest rates. As described in Section 2.2.1, cointegration is tested by calculating the EG test statistic for the residuals of the following regression,
| (14) |
where
![]() and
and
![]() are the long and short nominal
interest rates, respectively, for each country
are the long and short nominal
interest rates, respectively, for each country ![]() .
The five percent critical value for the traditional EG test,
based on a pure unit-root assumption, is -3.341. For the Bonferroni
EG test, however, the critical value depends on
.
The five percent critical value for the traditional EG test,
based on a pure unit-root assumption, is -3.341. For the Bonferroni
EG test, however, the critical value depends on ![]() and is given for each country in Table 2.
and is given for each country in Table 2.
Among the developed countries, the null of no cointegration is rejected for Australia, Canada, New Zealand, Sweden, Switzerland and the United States at the five percent level. The null can similarly be rejected for Hungary, Mexico, Poland and Singapore. These countries thus satisfy the first of the two necessary conditions for the expectations hypothesis to be a valid description of their term structures. The null of no cointegration cannot be rejected for Japan and the United Kingdom, nor India and South Africa. For Japan, this finding is not surprising given the complex zero-nominal-bound problem that disrupted the Japanese economy for much of the sample.8 It is more surprising that cointegration does not hold for the United Kingdom. Nonetheless, the finding is in line with evidence from previous studies, such as Cuthbertson (1996). The failure to detect a cointegrating relationship between long and short rates in the United Kingdom may owe to the substantial and long-lived decline in long rates midway through the sample. Following the shift to inflation targeting in the mid 1990s, long-run inflation expectations declined and the risk premia embedded in long-horizon bond yields likely compressed, perhaps mimicking a structural break in the cointegrating relationship between short rates and long rates. However, this is only one of several factors that may have been at work; other countries in our panel also shifted to inflation targeting without detracting from the cointegration result.
Given the relative immaturity of financial markets in emerging economies, it is noteworthy that the null hypothesis of no cointegration is rejected in four of our six emerging economies. Only India and South Africa fail the test, with structural change the likely reason in both cases. In 1998, the Reserve Bank of India adopted a multiple-indicator approach, a departure from earlier monetary policy that appeared to foster a permanent reduction in long and short interest rates. The relatively long sample available for South Africa clearly makes structural breaks a potential problem. Following the end of apartheid in the early 1990s, international interest in South Africa resumed, accompanied by strong inflows of foreign financial capital, and like several other countries, South Africa adopted inflation targeting in early 2000, with a concomitant reduction in long interest rates.
An important feature of Table 2 is that the critical values of the Bonferroni EG test are to the left of the standard unit-root EG critical value, once uncertainty regarding the exact value of the largest autoregressive root in the data has been taken into account. This adjustment of critical values is crucial, as it is key to valid inference when variables do not have exact unit roots. Failing to make this adjustment tends to make traditional tests of cointegration over-sized. As seen here, the standard EG cointegration test, based on the unit-root assumption, and the robust Bonferroni test lead to similar conclusions. However, the Bonferroni test, which is correctly sized under more general conditions than the standard test, gives us greater confidence in rejections of the null hypothesis of no cointegration. That is, by performing inference with the Bonferroni test, one no longer needs to condition on the auxiliary assumption that the data were generated by a pure unit-root process when interpreting the cointegration results. The evidence in favour of cointegration is valid also if the data were generated by a weakly mean-reverting process.
3.3 The cointegrating vector
Having found evidence for cointegration in several countries, we
turn to testing whether the cointegrating vector matches the
theoretically-suggested value
(1, -1). As mentioned in the
introduction, researchers have typically overlooked interpretation
of the estimated vector, either because of a lack of suitable
econometric tools in the case of earlier research, or because it
has not been the focus. With the methods developed in this paper,
we are able to conduct valid inference about the parameter values.
Our focus is the 90 percent confidence interval for ![]() ; if this does not cover unity, the null hypothesis of
; if this does not cover unity, the null hypothesis of
![]() is rejected, which is equivalent to
rejecting the cointegrating vector
(1, -1). Point estimates of
is rejected, which is equivalent to
rejecting the cointegrating vector
(1, -1). Point estimates of
![]() are shown in Table 3, both
are shown in Table 3, both
![]() based on OLS estimation
and
based on OLS estimation
and
![]() based on standard
unit-root FM-OLS. Confidence intervals are also shown. As discussed
in Section 2.2.2, two
Bonferroni confidence intervals are presented: (i) the
size-adjusted interval and (ii) the non-size-adjusted interval.
Both methods lead to qualitatively similar results, and it is
evident that the size adjustment is not crucial in this particular
application.
based on standard
unit-root FM-OLS. Confidence intervals are also shown. As discussed
in Section 2.2.2, two
Bonferroni confidence intervals are presented: (i) the
size-adjusted interval and (ii) the non-size-adjusted interval.
Both methods lead to qualitatively similar results, and it is
evident that the size adjustment is not crucial in this particular
application.
For all ten countries in which cointegration was detected using
the Bonferroni EG test, the cointegrating vector differs
significantly from the values predicted by theory. That is, despite
the presence of cointegration, the expectations hypothesis is
rejected as a description of the term structure. Interestingly, the
values are similar across countries, with ![]() significantly smaller than one and clustered between
significantly smaller than one and clustered between ![]() and
and ![]() . The confidence intervals also
overlap substantially. The finding of a slope coefficient less than
one is not unique to this paper; for example, Engle and Granger
(1987), Boothe (1991) and MacDonald and Speight (1991) report
similar coefficients using data from different countries and sample
periods. Unlike previous studies, however, we have the tools to
reliably conclude that the deviations from the
theoretically-implied relationship are statistically
significant.
. The confidence intervals also
overlap substantially. The finding of a slope coefficient less than
one is not unique to this paper; for example, Engle and Granger
(1987), Boothe (1991) and MacDonald and Speight (1991) report
similar coefficients using data from different countries and sample
periods. Unlike previous studies, however, we have the tools to
reliably conclude that the deviations from the
theoretically-implied relationship are statistically
significant.
3.4 Interpretation and discussion
The joint finding of cointegration with a slope coefficient less than one is intriguing, as it suggests that the term structures of many countries are driven not just by expectations of future short interest rates and stationary term premia but by an additional near-integrated component that covaries systematically with the short interest rate. Rather than an outright rejection of the expectations hypothesis, it suggests that something more is at work. One candidate for this additional component is a time-varying but persistent risk premium linked to the state of the term structure. Campbell and Shiller (1991) propose exactly this to explain why coefficients in their yield-spread regressions deviate from theory. Specifically, they suggest time-varying risk premia as a rationale for why ``long rates underreact to short-term interest rates'' (p. 513). Dai and Singleton (2002) go further, showing that yield-spread regressions using risk-premium adjusted yields from a broad class of affine term structure models recover expectations-hypothesis predicted coefficients. To match the empirical findings of Fama and Bliss (1987) and Campbell and Shiller (1991), Dai and Singleton's model-estimated risk premia are negatively correlated with the short interest rate.
To see how this explanation fits into the present application, consider a generalisation of equation (2) that retains the basic structure of the expectations hypothesis but generalises the term premium:
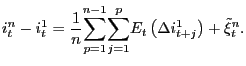
|
(15) |
The new term premium
![]() , is the sum of two
components, the stationary component posited earlier,
, is the sum of two
components, the stationary component posited earlier,
![]() , plus a new component,
, plus a new component,
![]() , that is near-integrated
and covaries with the short interest rate. Specifically, assume
that
, that is near-integrated
and covaries with the short interest rate. Specifically, assume
that
![]() such that
if
such that
if ![]() is near integrated, so too is
is near integrated, so too is
![]() and they will in fact be
cointegrated. Moving this term to the left hand side,
and they will in fact be
cointegrated. Moving this term to the left hand side,
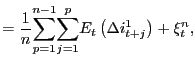
|
(16) |
our empirical finding of a slope coefficient of less than unity
leads us to infer that ![]() is also negative. That
is, the near-integrated element of
is also negative. That
is, the near-integrated element of
![]() appears to covary
inversely with the short interest rate, consistent with the
existing literature on the term structure for the United States
described above. While the empirical analysis in this paper has by
no means identified such risk premia, it is a plausible explanation
for the results in Table 3, as it is likely to be a common
characteristic of the behaviour of investors across countries and
markets. Naturally, other explanations for the failure of the
expectations hypothesis abound, such as departures from rational
expectations or sluggish adjustment of expectations about
persistent changes in short rates. For some countries in our
sample, gradual adjustment of long-run inflation expectations
during the shift to a lower-inflation environment may have delayed
adjustment of long interest rates, as suggested by Kozicki and
Tinsley (2005) for the United States during the 1980s. However,
given the similar results we find across countries and time
periods, an explanation based on the failure of expectations to
adjust quickly or rationally seems less likely to be the common
explanation.
appears to covary
inversely with the short interest rate, consistent with the
existing literature on the term structure for the United States
described above. While the empirical analysis in this paper has by
no means identified such risk premia, it is a plausible explanation
for the results in Table 3, as it is likely to be a common
characteristic of the behaviour of investors across countries and
markets. Naturally, other explanations for the failure of the
expectations hypothesis abound, such as departures from rational
expectations or sluggish adjustment of expectations about
persistent changes in short rates. For some countries in our
sample, gradual adjustment of long-run inflation expectations
during the shift to a lower-inflation environment may have delayed
adjustment of long interest rates, as suggested by Kozicki and
Tinsley (2005) for the United States during the 1980s. However,
given the similar results we find across countries and time
periods, an explanation based on the failure of expectations to
adjust quickly or rationally seems less likely to be the common
explanation.
4. Conclusion
Nominal interest rates are likely to be stationary, albeit slowly mean reverting. The theoretical determinants of interest rates, such as agents' risk aversion and long-run growth rates of the macroeconomy, imply that real interest rates possess a long-run equilibrium value. Historically, nominal interest rates have fluctuated for many centuries within a fairly narrow band that encompasses values common today. However, their typically slow rate of mean reversion poses a problem for traditional unit-root tests, and confronted with series that behave as integrated in finite samples, many researchers have proceeded to apply cointegration methods based on the unit-root assumption. Unfortunately, empirical analysis based on this assumption can be misleading. Even small deviations from the unit-root assumption can lead to large size distortions and thus mistaken inference.
This paper illustrates the application of near-integration methods of cointegration by testing the expectations hypothesis on term-structure data from numerous countries. The econometric framework is robust to deviations from the unit-root hypothesis by nesting the high-persistence and unit-root cases. The empirical results strongly support cointegration between long and short interest rates in several developed and emerging economies, a necessary condition for the expectations hypothesis to hold. However, for all ten countries in which cointegration is present, the theoretically-predicted vector (1, -1) is rejected. Moreover, the estimated vectors are similar across countries, with long rates moving by less than short rates, on average. While the causes for this are far from obvious, our empirical findings are consistent with the presence of time-varying bond term premia that are themselves highly persistent and covary inversely with the short rate. Such reasoning is in a similar spirit to explanations put forward for the failure of the expectations hypothesis in the excess-returns literature, and with the stylised fact that risk premia are countercyclical. Our empirical analysis is not sufficiently structural to test this hypothesis, and looking deeper requires reliable estimates of risk premia, a complex issue in itself. We nevertheless believe it to be an interesting direction for future research.
Appendix
This appendix details the data types and sources used in the analysis. For Australia, Canada, India, Japan, New Zealand, Sweden, Switzerland, the United Kingdom and the United States, the long interest rate is the yield on the benchmark ten-year government bond, for Hungary, Poland and Singapore, the yield on the five-year government bond, for Mexico, the yield on the three-year government bond and, finally, for South Africa, the yield on the twenty-year government bond. The long interest rates are measured as yields on coupon securities. Turning to short interest rates, these are the three month bank bill rate for Australia and New Zealand, the three month corporate paper rate for Canada, the three month certificate of deposit rate for India and Japan, the three month interbank rate for Switzerland and the United Kingdom, and the three month treasury bill rate for Hungary, Mexico, Poland, Singapore, South Africa, Sweden and the United States. The data were sourced from the Board of Governors of the Federal Reserve System, the International Monetary Fund, and Global Financial Data.
Following Campbell and Shiller (1987), the long interest rates in our sample are the yields on specific coupon securities, as synthetic, constant-maturity, zero-coupon yields are not readily available for all countries. As pointed out by Shea (1992), conducting our analysis using yields from coupon securities relies on approximations that could distort inference. For the United Kingdom and the United States, we are able to check whether our choice materially affects our conclusions by performing our analysis on synthetic constant-maturity yields provided by the respective central banks.
The results of this exercise (reported below) indicate that our
findings are not sensitive to the choice of how the long interest
rate is measured. Denote the ten-year zero-coupon yield as
![]() and
and
![]() for the United Kingdom and
United States respectively - as the long interest rate. The sample
period for the United Kingdom is the same as for the main data. For
the United States, the sample period is considerably shorter than
originally, namely January 1973 to October 2006; in order to be to
able make direct comparisons for the U.S. data, we therefore also
redo the analysis using the coupon-bearing bond rate over this
shorter sample.
for the United Kingdom and
United States respectively - as the long interest rate. The sample
period for the United Kingdom is the same as for the main data. For
the United States, the sample period is considerably shorter than
originally, namely January 1973 to October 2006; in order to be to
able make direct comparisons for the U.S. data, we therefore also
redo the analysis using the coupon-bearing bond rate over this
shorter sample.
Table A1 shows the results from unit-root tests and provides estimates of the local-to-unity parameters for the different series. In Table A2, results from the cointegration tests are presented. As can be seen from the tables, the results are qualitatively the same as when we use the original data - cointegration is supported in the United States but not in the United Kingdom. As we found no evidence of cointegration for the United Kingdom, inference regarding the cointegrating vector can only be carried out for the United States. Results from this exercise are shown in Table A3. While there are some minor quantitative differences, the two datasets still communicate a message very similar to that seen previously. The cointegrating vector (1, -1) is clearly rejected and estimates suggest a value of around (1, -0.7).
Table 1: Results From Unit-Root Tests
Sample | ||||
|---|---|---|---|---|
| | -1.841 |
-6.231 |
[-13.211, 0.426] |
1970M01 - 2006M10 |
| | -1.043 |
-1.663 |
[-6.341, 2.826] |
|
| | -2.300 |
-9.968 |
[-18.345, -1.982] |
1956M01 - 2006M10 |
| | -0.952 |
-1.281 |
[-5.748, 3.001] |
|
| | -0.576 |
-0.178 |
[-3.378, 3.426] |
1997M03 - 2004M05 |
| | -0.582 |
-0.190 |
[-3.762, 3.419] |
|
| | -0.403 |
0.171 |
[-3.058, 3.567] |
1995M01 - 2006M10 |
| | 0.279 |
0.974 |
[-1.293, 3.942] |
|
| | 0.377 |
1.055 |
[-1.113, 3.992] |
1989M01 - 2006M10 |
| | -0.296 |
0.342 |
[-2.708, 3.630] |
|
| | -0.506 |
-0.030 |
[-3.479, 3.505] |
1995M02 - 2004M05 |
| | -0.938 |
-1.231 |
[-5.671, 3.015] |
|
| | -2.145 |
-8.612 |
[-16.479, -1.105] |
1974M01 - 2006M10 |
| | -1.447 |
-3.662 |
[-9.402, 1.884] |
|
| | 0.759 |
1.329 |
[-0.888, 4.046] |
1994M03 - 2004M0 |
| | 0.516 |
1.163 |
[-0.556, 4.138] |
|
| | -2.009 |
-7.517 |
[-14.998, -0.364] |
1988M01 - 2004M05 |
| | -0.227 |
0.438 |
[-2.479, 3.672] |
|
| | -1.552 |
-4.313 |
[-10.365, 1.525] |
1976M01 - 2004M05 |
| | -1.536 |
-4.213 |
[-10.212, 1.592] |
|
| | -0.877 |
-1.018 |
[-5.263, 3.082] |
1987M01 - 2006M10 |
| | 0.041 |
0.744 |
[-1.793, 3.819] |
|
| | -2.059 |
-7.901 |
[-15.518, -0.634] |
1975M10 - 2006M10 |
| | -0.480 |
0.023 |
[-3.366, 3.521] |
|
| | -0.880 |
-1.030 |
[-5.289, 3.079] |
1978M01 - 2006M10 |
| | 0.097 |
0.799 |
[-1.670, 3.848] |
|
| | -1.087 |
-1.852 |
[-6.640, 2.740] |
1955M01 - 2006M10 |
| | -0.841 |
-0.895 |
[-5.069, 3.122] |
Notes:*indicates significance at the five percent significance level.
Table 2: Results From Cointegration Tests
![\begin{displaymath} \begin{array}[c]{c} \text{Critical value for}\ \text{Bonferroni \textit{EG} test} \end{array}\end{displaymath}](img38t.gif) | Sample | ||
|---|---|---|---|
| Australia | -4.231 | -3.387 | 1970M01 - 2006M10 |
| Canada | -4.789 | -3.375 | 1956M01 - 2006M10 |
| Hungary | -4.991 | -3.346 | 1997M03 - 2004M05 |
| India | -2.493 | -3.341 | 1995M01 - 2006M10 |
| Japan | -2.220 | -3.341 | 1989M01 - 2006M10 |
| Mexico | -5.757 | -3.374 | 1995M02 - 2004M05 |
| New Zealand | -6.278 | -3.485 | 1974M01 - 2006M10 |
| Poland | -5.275 | -3.341 | 1994M03 - 2004M05 |
| Singapore | -4.358 | -3.341 | 1988M01 - 2004M05 |
| South Africa | -2.374 | -3.516 | 1976M01 - 2004M05 |
| Sweden | -4.243 | -3.341 | 1987M01 - 2006M10 |
| Switzerland | -4.186 | -3.341 | 1975M10 - 2006M10 |
| United Kingdom | -2.913 | -3.341 | 1978M01 - 2006M10 |
| United States | -4.034 | -3.364 | 1955M01 - 2006M10 |
Notes: Critical values are for a test with a nominal size of five percent. The five percent critical value of the standard EG test under a unit-root assumption is equal to -3.341.
Table 3: Estimates of the Cointegrating Vector
Sample | |||||
|---|---|---|---|---|---|
| Australia | 0.680 |
0.651 |
1970M01 - 2006M10 |
||
| Canada | 0.715 |
0.696 |
1956M01 - 2006M10 |
||
| Hungary | 0.798 |
0.799 |
1997M03 - 2004M05 |
||
| India | - |
- |
- |
- |
1995M01 - 2006M10 |
| Japan | - |
- |
- |
- |
1989M01 - 2006M10 |
| Mexico | 0.788 |
0.802 |
1995M02 - 2004M05 |
||
| New Zealand | 0.647 |
0.624 |
1974M01 - 2006M10 |
||
| Poland | 0.794 |
0.786 |
1994M03 - 2004M0 |
||
| Singapore | 0.677 |
0.636 |
1988M01 - 2004M05 |
||
| South Africa | - |
- |
- |
- |
1976M01 - 2004M05 |
| Sweden | 0.727 |
0.704 |
1987M01 - 2006M10 |
||
| Switzerland | 0.385 |
0.378 |
1975M10 - 2006M10 |
||
| United Kingdom | - |
- |
- |
- |
1978M01 - 2006M10 |
| United States | 0.859 |
0.836 |
1955M01 - 2006M10 |
Notes: The 90 percent coinfidence interval (i) has been size adjusted, whereas (ii) has not.
Table A1: Results from Unit-Root Tests
Sample | ||||
|---|---|---|---|---|
| | -0.880 |
-1.030 |
[-5.289, 3.079] |
1978M01 - 2006M10 |
| | 0.349 |
1.034 |
[-1.162, 3.978] |
|
| | -0.880 |
-1.030 |
[-5.289, 3.079] |
1978M01 - 2006M10 |
| | 0.097 |
0.799 |
[-1.670, 3.848] |
|
| | -1.176 |
-2.225 |
[-7.269, 2.541] |
1973M01 - 2006M10 |
| | -1.215 |
-2.412 |
[-7.562, 2.461] |
|
| | -1.176 |
-2.225 |
[-7.269, 2.541] |
1973M01 - 2006M10 |
| | -1.121 |
-2.387 |
[-7.520, 2.472] |
Notes: * indicates significance at the five percent significance level.
Table A2: Results From Cointegration Tests
EG | ![\begin{displaymath} \begin{array}[c]{c} \text{Critical value for}\ \text{Bonferroni \textit{EG} test} \end{array}\end{displaymath}](img77t.gif) | Sample | |
|---|---|---|---|
| United Kingdom, zero coupon yield | -2.832 | -3.341 | 1978M01 - 2006M10 |
| United Kingdom | -2.913 | -3.341 | 1978M01 - 2006M10 |
| United States, zero coupon yield | -3.601 | -3.419 | 1973M01 - 2006M10 |
| United States | -3.553 | -3.418 | 1973M01 - 2006M10 |
Notes: Critical values are for a test with a nominal size of five percent. The five percent cirtical value of the standard EG test under a unit-root assumption is equal to -3.341.
Table A3: Estimates of the Cointegrating Vector
Sample | |||||
|---|---|---|---|---|---|
| United Kingdom, zero coupon yield | - |
- |
- |
- |
1978M01 - 2006M10 |
| United Kingdom | - |
- |
- |
- |
1978M01 - 2006M10 |
| United States, zero coupon yield | 0.697 |
0.677 |
1973M01 - 2006M10 |
||
| United States | 0.773 |
0.755 |
1973M01 - 2006M10 |
Notes: The 90 percent coinfidence interval (i) has been size adjusted, whereas (ii) has not.
References
Bansal, R., Yaron, A., 2004. Risks for the long run: A potential resolution of asset pricing puzzles. Journal of Finance 59, 1481-1509.
Boothe, P, 1991. Interest parity, cointegration, and the term structure in Canada and the United States. Canadian Journal of Economics 24, 595-603.
Bremnes, H., Gjerde, Ø., Sættem, F, 2001. Linkages among interest rates in the United States, Germany and Norway. Scandinavian Journal of Economics 103, 27-145.
Campbell, J. Y., Shiller, R. J., 1987. Cointegration and tests of present value models. Journal of Political Economy 95, 1062-1088.
Campbell, J. Y., Shiller, R. J., 1991. Yield spreads and interest rate movements: A bird's eye view. Review of Economic Studies 58, 495-514.
Campbell, J. Y., Yogo, M., 2006. Efficient tests of stock return predictability. Journal of Financial Economics 81, 27-60.
Chong, B. S., Liu, M.-H., Shrestha, K., 2006. Monetary transmission via the administered interest rate channels, Journal of Banking and Finance 30, 1467-1484.
Cochrane, J. H., Piazzesi, M., 2005. Bond risk premia. American Economic Review 95, 138-160.
Cogley, T., Sargent, T. J., 2001. Evolving post-World war II U.S. inflation dynamics, NBER Macroeconomics Annual 16, 331-373.
Cuthbertson, K., 1996. The expectations hypothesis of the term structure: The UK interbank market. Economic Journal 106, 578-592.
Dai, Q., Singleton, K., 2002. Expectations puzzles, time-varying risk premia, and affine models of the term structure. Journal of Financial Economics 63, 415-441.
De Graeve, F., De Jonghe, O. and Vander Vennet, R., 2007. Competition, transmission and bank pricing policies: Evidence from Belgian loan and deposit markets. Journal of Banking and Finance 31, 259-278.
Elliott, G., 1998. On the robustness of cointegration methods when regressors almost have unit roots. Econometrica 66, 149-158.
Elliott, G., Rothenberg, T. J., Stock, J. H., 1996. Efficient tests for an autoregressive unit root. Econometrica 64, 813-836.
Engle, R., Granger C. W. J., 1987. Co-integration and error correction: Representation, estimation, and testing. Econometrica 55, 251-276.
Fama, E. F., Bliss, R. R., 1987. The information in long-maturity forward rates. American Economic Review 77, 680-692.
Hall, A. D., Anderson, H. D., Granger, C. W. J., 1992. A cointegration analysis of treasury bill yields. Review of Economics and Statistics 74, 116-126.
Hjalmarsson, E., 2007. Fully modified estimation with nearly integrated regressors. Finance Research Letters 4, 92-94.
Hjalmarsson, E., Österholm, P., 2007a. A residual-based cointegration test for near unit root variables. International Finance Discussion Papers 907, Board of Governors of the Federal Reserve System.
Hjalmarsson, E., Österholm, P., 2007b. Testing for cointegration using the Johansen methodology when variables are near-integrated. IMF Working Paper 07/141, International Monetary Fund.
Homer, S., Sylla, R., 1996. A history of interest rates. Rutgers University Press: New Brunswick.
Karfakis, C. J., Moschos, D. M., 1990. Interest rate linkages within the European monetary system: A time series analysis. Journal of Money, Credit and Banking 22, 388-394.
Kleimeier, S., Sander, H., 2006. Expected versus unexpected monetary policy impulses and interest rate pass-through in euro-zone retail banking, Journal of Banking and Finance 30, 1839-1870.
Kozicki, S., Tinsley, P., 2005. What do you expect? Imperfect policy credibility and tests of the expectations hypothesis. Journal of Monetary Economics 52, 421-447.
Lanne, M., 2000. Near unit roots, cointegration, and the term structure of interest rates. Journal of Applied Econometrics 15, 513-529.
Lanne, M., 2001. Near unit root and the relationship between inflation and interest Rates: A reexamination of the Fisher effect. Empirical Economics 26, 357-366.
Lardic, S., Mignon, V., 2004. Fractional cointegration and the term structure. Empirical Economics 29, 723-736.
Liu, M.-H., Margaritis, D., Tourani-Rad, A., 2008. Monetary policy transparency and pass-through of retail interest rates. Journal of Banking and Finance 32, 501-511.
MacDonald, R., Speight, A. E. H., 1991. The term structure of interest rates under rational expectations: Some international evidence. Applied Financial Economics 1, 211-221.
Miron, J. A., 1991. Pitfalls and opportunities: What macroeconomists should know about unit roots: Comment. NBER Macroeconomics Annual 6, 211-218.
Newey, W. K., West, K. D., 1987. A simple, positive semi-definite, heteroskedasticity and autocorrelation consistent covariance matrix. Econometrica 55, 703-708.
Nicolau, J., 2002. Stationary processes that look like random walks - The bounded random walk process in discrete and continuos time. Econometric Theory 18, 99-118.
Phillips, P. C. B., 1988. Regression theory for near-integrated time series. Econometrica 56, 1021-1043.
Phillips, P. C. B., Hansen, B., 1990. Statistical inference in instrumental variables regression with I(1) processes. Review of Economic Studies 57, 99-125.
Ruge-Murcia, F. J., 2006. The expectations hypothesis of the term structure when interest rates are close to zero. Journal of Monetary Economics 53, 1409-1424.
Saikkonen, P., 1991. Asymptotically efficient estimation of cointegrating regressions. Econometric Theory 7, 1-21.
Shea, G. S., 1992. Benchmarking the expectations hypothesis of the interest-rate term structure: An analysis of cointegration vectors. Journal of Business and Economic Statistics 10, 347-366.
Stock, J. H., 1991. Confidence intervals for the largest autoregressive root in U.S. economic time-series. Journal of Monetary Economics 28, 435-460.
Stock, J. H., 1994. Unit roots and trend breaks. In Engle, R., McFadden, D. (Eds.), Handbook of Econometrics, Vol. 4. North Holland: Amsterdam.
Stock, J. H., Watson, M. W., 1993. A simple estimator of the cointegrating vectors in higher order integrated systems. Econometrica 61, 783-820.
Svensson, L. E. O., 2003. Escaping from a liquidity trap and deflation: The foolproof way and others. Journal of Economic Perspectives 17, 145-166.
Ueda, K., 2005. The Bank of Japan's struggle with the zero lower bound on nominal interest rates: Exercises in expectations management. International Finance 8, 329-350.
Wallis, K., 1987. Time series analysis of bounded economic variables. Journal of Time Series Analysis 8, 115-123.
Wu, J.-L., Chen, S.-L., 2001. Mean reversion of interest rates in the eurocurrency market. Oxford Bulletin of Economics and Statistics 63, 459-474.
Zhang, H.,1993. Treasury yield curves and cointegration. Applied Economics 25, 361-367.
Footnotes
a Divison of Monetary Affairs, Board of Governors of the Federal Reserve System, 20th and C Streets, Washington, DC 20551, USA Return to text
b Divison of International Finance, Board of Governors of the Federal Reserve System, 20th and C Streets, Washington, DC 20551, USA Return to text
c Department of Economics, Uppsala University, Box 513, 751 20 Uppsala, Sweden Return to text
1. Because nominal interest rates are bounded downward, they cannot strictly be a linear unit-root process with an additive error term fulfilling standard assumptions (Nicolau, 2002). However, the approximation error from making such an assumption is likely to be negligible, and other bounded variables, such as unemployment rates, are often treated as possessing a unit root for this reason. Moreover, the problem of boundedness can be overcome by transforming the series, for example, by taking the natural logarithm of nominal interest rates. A discussion of such transformations can be found in Wallis (1987). Return to text
2. As mentioned above, Lanne (2000) also analyses the term structure of interest rates within a framework of near-integrated processes but takes quite a different approach to that in this paper. He applies a joint test of cointegration and the value of the cointegrating vector(s) to U.S. term structure data, whereas we sequentially test for the presence of cointegration and for specific values of the cointegrating vector in a larger international data set. The different approaches have different benefits. Our approach enables us to detect departures of the cointegrating vector from theory in the presence of cointegration. This could provide insight into how and why the expecations hypothesis fails to describe the dynamic behaviour of the term structure. Return to text
3. As pointed out by Miron (1991), even if
cointegration with the vector
![]() is supported, this is
still not sufficient for the validity of the expectations
hypothesis, but merely another necessary condition. For example, a
weighting scheme other than
is supported, this is
still not sufficient for the validity of the expectations
hypothesis, but merely another necessary condition. For example, a
weighting scheme other than ![]() would be
consistent with the same vector. However, in practice, very few
reasonable hypotheses would remain to compete with the expectations
hypothesis. Return to text
would be
consistent with the same vector. However, in practice, very few
reasonable hypotheses would remain to compete with the expectations
hypothesis. Return to text
4. Note that it is possible to estimate
![]() consistently, but not precisely
enough to consistently identify
consistently, but not precisely
enough to consistently identify
![]() ; median
unbiased estimates can also be obtained, as presented in the
empirical section, but these are again not consistent
estimates. Using an estimate of
; median
unbiased estimates can also be obtained, as presented in the
empirical section, but these are again not consistent
estimates. Using an estimate of ![]() to obtain
estimates of the innovations
to obtain
estimates of the innovations ![]() in the
FM-OLS procedure discussed here will lead to biased
tests. Return to text
in the
FM-OLS procedure discussed here will lead to biased
tests. Return to text
5. Since ![]() is
consistently estimable, it follows that
is
consistently estimable, it follows that ![]() ,
,
![]() , and
, and
![]() are consistently estimable,
even though
are consistently estimable,
even though ![]() is not. Return to text
is not. Return to text
6. The relevant `` endogeneity'' parameter
that determines the choice of
![]() and
and
![]() (
(![]() in Table 2 of Campbell and Yogo, 2006) is now given by
the long-run correlation
in Table 2 of Campbell and Yogo, 2006) is now given by
the long-run correlation
![]() . Return to text
. Return to text
7. Lag length in the ADF-GLS and
EG tests was determined using the Schwarz information
criterion. Using the Akaike information criterion instead in both
tests does affect the lag length chosen and the estimate of
![]() in quite a few cases. However, it
typically does not affect our qualitative conclusion regarding the
presence of cointegration. In fact, only for Poland and the United
States is the qualitative conclusion different, as we find no
support for cointegration when using the Akaike information
criterion. Results are not reported but are available upon
request. Return to text
in quite a few cases. However, it
typically does not affect our qualitative conclusion regarding the
presence of cointegration. In fact, only for Poland and the United
States is the qualitative conclusion different, as we find no
support for cointegration when using the Akaike information
criterion. Results are not reported but are available upon
request. Return to text
8. Since the mid-1990's, nominal interest rates in Japan have been extremely low. This problematic fact has received substantial attention in the monetary policy literature; see Svensson (2003) and Ueda (2005). For a discussion of some aspects of the expectations hypothesis and the zero-bound problem, see Ruge-Murcia (2006). Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text