
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 955, November 2008 --- Screen Reader
Version*
Estimating the Parameters of a Small Open Economy DSGE Model: Identifiability and Inferential Validity
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
This paper estimates the parameters of a stylized dynamic stochastic general equilibrium model using maximum likelihood and Bayesian methods, paying special attention to the issue of weak parameter identification. Given the model and the available data, the posterior estimates of the weakly identified parameters are very sensitive to the choice of priors. We provide a set of tools to diagnose weak identification, which include surface plots of the log-likelihood as a function of two parameters, heat plots of the log-likelihood as a function of three parameters, Monte Carlo simulations using artificial data, and Bayesian estimation using three sets of priors. We find that the policy coefficients and the parameter governing the elasticity of labor supply are weakly identified by the data, and posterior predictive distributions remind us that DSGE models may make poor forecasts even when they fit the data well. Although parameter identification is model- and data-specific, the lack of identification of some key structural parameters in a small-scale DSGE model such as the one we examine should raise a red flag to researchers trying to estimate -- and draw valid inferences from -- large-scale models featuring many more parameters.
Keywords: Bayesian estimation, forecasting, identification, MCMC, Switzerland
JEL classification: C11, C15, F41
1. Introduction
In the last decade, the monetary and fiscal policy literature has taken a great leap from calibrating dynamic stochastic general equilibrium (DSGE) models to estimating them, often using Bayesian techniques. Models were calibrated mainly because researchers were interested in examining their dynamics and how closely they resembled those of the data, and in evaluating policy implications under reasonable assumptions about the parameter values. However, as these models grew in complexity to address misspecification issues and incorporate more realistic features found in the data, it became less obvious how to calibrate many of the new deep parameters which emerged. Furthermore, analyses of calibrated DSGE models are not always robust to alternative calibrations. Bayesian techniques are well suited to address this calibration problem, since they provide a formal way to estimate the parameters by combining prior information about them with the data as viewed through the lens of the model being analyzed. This seems to provide hope that calibration may no longer be necessary, as long as the data do indeed have something to say about plausible parameter values. Another useful feature of the Bayesian approach is that it provides a framework for designing policies that are robust to the estimated uncertainty surrounding the parameters.1
Calibration can thus be viewed as a means to an end: researchers calibrate models because they want to analyze them in order to address interesting economic questions. In this case, Bayesian or maximum likelihood estimation can and should replace calibration, since they constitute a potentially more accurate way to derive reasonable parameter values. When maximum likelihood techniques are used to estimate DSGE models (e.g., Ireland (2003) ), the estimates are coming purely from the data2 and without controversy over the role of priors. But even if Bayesian techniques are used, if one has confidence in one's priors, there is no need to be concerned about whether the posterior estimates are mainly driven by the prior distribution or the data; it is only important that the posterior estimates are reasonable, which they will be if the priors and data are reasonable. So far, most studies featuring Bayesian estimates of DSGE models have focused more on economics (e.g., using the model to explain interesting features in the data, or studying the implications of alternative policies) and less on the estimation itself.3 A few studies, such as Lubik and Schorfheide (2005) and Onatski and Stock (200), do perform sensitivity checks of their baseline estimates to those obtained using diffuse priors and find that, for some parameters, the two estimates are substantially different.4 In these studies, Bayesian estimation can therefore be viewed as a more comprehensive way to calibrate a model, by taking into account both the data and the researcher's prior information and beliefs about the parameters.
However, estimating the parameters can also be viewed as an end in itself. In other words, the ultimate goal may be to make inference about the parameters, given the model and the data. For example, a researcher may be interested in assessing how aggressively the central bank is fighting inflation; this can be judged by estimating the parameter governing the interest rate response to inflation. However, obtaining an accurate parameter estimate from the data crucially depends on whether or not the parameter is identified. Specifically, if the likelihood function is nearly flat along the dimension of a given parameter of interest, the marginal posterior for this parameter would simply resemble its prior distribution. For example, using a normally distributed prior centered at 1.70, Smets and Wouters (2003) obtain an estimated posterior mean of 1.69, and the plot of the estimated marginal posterior is practically identical to that of the assumed prior distribution. They conclude that their estimation "delivers plausible parameters for the long- and short-run reaction function of the monetary authorities, broadly in line with those proposed by Taylor (1993)," and "in agreement with the large literature on estimated interest rate rules" (p.1148). Given that the data have almost nothing to say along this dimension of the likelihood function (since the prior and posterior coincide), the claim that this parameter was estimated is misleading. As stated by Canova and Sala (2006), when models are under-identified "reasonable estimates are obtained not because the data [are] informative but because of a priori or auxiliary restrictions, which make the likelihood of the data (or a portion of it) informative. ... In these situations, structural parameter estimation amounts to sophisticated calibration (p. 34)."
If the ultimate goal is to actually learn something about the parameters from the data, then parameter identification has to be taken seriously. Only a few studies examine the issue of identification explicitly. Beyer and Farmer (2004) consider identification issues in a class of three-equation monetary models. The results from their experiments suggest the policy rule, the Phillips curve and the IS curve are generally not identified unless arbitrary decisions are made about which variables enter these equations. In another important contribution, Canova and Sala (2006) examine identifiability issues using an estimation technique known as impulse response matching. This limited information technique involves minimizing the distance between the model and the estimated impulse response functions. They conclude that DSGE models generally appear to be under-identified. However, the authors also recognize that identification problems detected in limited information techniques do not necessarily carry over to full information methods. Canova and Sala (2006) suggest using a sequence of prior distributions with increasing variances to help detect potential identification problems, which is one of the diagnostics used in this paper. Ruge-Murcia (2007) uses Monte Carlo simulations to compare standard econometric techniques for estimating DSGE models. The techniques are evaluated based on their ability to deliver consistent parameter estimates in the presence of weak identification, stochastic singularity, and model misspecification. The techniques studied are maximum likelihood (also incorporating priors), generalized method of moments (GMM), simulated methods of moments (SMM), and indirect inference. The moment-based methods (GMM and SMM) are shown to be more robust to misspecification and are less affected by stochastic singularity. However, achieving identification in these limited information methods requires choosing the right moments to match when estimating the model. When using Bayesian techniques, Ruge-Murcia (2007) finds that having good priors and allowing for measurement errors can improve the estimates in the presence of these challenges.
The original goal of this study was to use the estimated parameter uncertainty to design optimal monetary policies for a small open economy. As in Levin, Onatski, Williams and Williams (2005) and Batini, Justiniano, Levine and Perlman (2004), Bayesian estimation techniques were chosen as a means to an end, since we initially wanted policy makers in our model to respond optimally to uncertainty that was estimated, not assumed. However, we learned that some of the parameter estimates were highly sensitive to the choice of priors, making economic inference difficult. Further examination of the likelihood function revealed ridge lines along some dimensions of the parameter space and regions with little curvature. For these parameters there is a dramatic interaction between the prior and the likelihood. Therefore, their posterior estimates should be interpreted differently because the prior swamped the data.
In the next section we discuss a stylized small open economy model that is subsequently estimated. Section 3 describes the data used to estimate the model. In section 4 we examine the properties of the likelihood function and use several techniques to diagnose identification problems. In section 5 we estimate the model using three sets of priors; Section 6 employs posterior predictive distributions to examine forecast accuracy. The last section concludes with a brief discussion.
2. Small Open Economy Model With Habit Formation
The model estimated in this study is essentially Monacelli's (2003) small open economy model which features deviations from the law of one price. The difference is that we introduce external habit formation in consumption to better fit the data (Fuhrer (2000); Chistiano, Eichenbaum, and Evans (2005)).
The domestic small open economy is populated by a continuum of infinitely-lived households whose preferences are given by
| (1) | ![$\displaystyle E_{0}\sum_{t=0}^{\infty}\beta^{t}\biggl[\frac{(C_{t} -H_{t})^{1-\sigma}}{ 1-\sigma}-\frac{N_{t}^{1+\varphi}}{1+\varphi}\biggr] \ ,$](img1.gif)
|
where
| (2) | ![$\displaystyle C_{t}\equiv\biggl[(1-\gamma)^{\frac{1}{\eta}}C_{H,t}^{\frac {\eta-1}{\eta}}+\gamma^{\frac{1}{\eta}}C_{F,t}^{\frac{\eta-1}{\eta} }\biggr]^{\frac{ \eta-1}{\eta}} \ ,$](img8.gif)
|
where
| (3) | ![$\displaystyle \int_{0}^{1}\left[ P_{H,t}(i)C_{H,t}(i)+P_{F,t}(i)C_{F,t}(i)\right] di+E_{t} \left[ Q_{t,t+1}D_{t+1}\right] \leq W_{t}N_{t}+D_{t} \ ,$](img13.gif)
|
where
Optimal allocation of expenditures between domestic and foreign goods implies
| (4) | 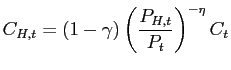 and
and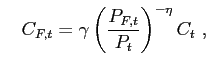
|
where the consumer price index is defined as
| (5) | ![$\displaystyle P_{t}\equiv\left[ (1-\gamma)P_{H,t}^{1-\eta}+\gamma P_{F,t}^{1-\eta} \right] ^{\frac{1}{1-\eta}} \ .$](img22.gif)
|
The first order condition of the consumer's problem gives us the intratemporal labor/ leisure choice
| (6) | 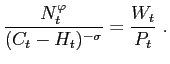
|
The intertemporal first order condition is given by
| (7) | 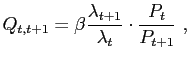
|
where
| (8) | ![$\displaystyle E_{t}Q_{t,t+1}=\beta E_{t}\left[ \frac{\lambda_{t+1}}{\lambda_{t}}\cdot \frac{P_{t}}{P_{t+1}}\right] \ .$](img26.gif)
|
Since the nominal interest rate
| (9) | ![$\displaystyle \frac{1}{1+i_{t}}=\beta E_{t}\left[ \frac{\lambda_{t+1}} {\lambda_{t}}\cdot\frac{P_{t}}{P_{t+1}}\right] \ .$](img29.gif)
|
The representative household in the rest of the world is assumed to face an identical optimization problem, making the optimality conditions for the world economy analogous to the ones described above. Also, following Gali and Monacelli (2005), the small open economy is assumed to be of negligible size relative to the rest of the world. This makes the world economy equivalent to a closed economy, since the weight of home goods in the foreign CES aggregator is zero. So for the foreign economy, output equals domestic consumption, and CPI inflation equals domestic inflation.
Domestic goods indexed by ![]() are
produced by a continuum of monopolistic competitive firms, owned by
consumers and subject to Calvo-style price setting behavior. Their
constant returns-to-scale production function is given by
are
produced by a continuum of monopolistic competitive firms, owned by
consumers and subject to Calvo-style price setting behavior. Their
constant returns-to-scale production function is given by
![]() , where
, where ![]() is an exogenous productivity shock.
is an exogenous productivity shock.
Firms choose the optimal price for good ![]() by
maximizing the expected discounted value of profits
by
maximizing the expected discounted value of profits
| (10) | ![$\displaystyle E_{t}\sum_{T=t}^{\infty}\theta_{H}^{T-t}Q_{t,T}Y_{H,T}(i)\left[ P_{H,t}(i)-P_{H,T}MC_{H,T}\right]$](img34.gif)
|
subject to the demand function
| (11) | 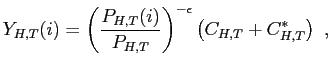
|
where
| (12) | ![$\displaystyle E_{t}\sum_{T=t}^{\infty}\theta_{H}^{T-t}Q_{t,T}Y_{H,T}(i)\left[ P_{H,T}(i)- \frac{ \theta_{H}}{\theta_{H}-1}P_{H,T}MC_{H,T}\right] =0 \ ,$](img40.gif)
|
where
For simplicity, assume that the export price of the domestic
good,
![]() , is flexible and subject to the
law of one price.
, is flexible and subject to the
law of one price.
The novelty of Monacelli's (2003) model is that retail firms
importing foreign differentiated goods are assumed to have a small
degree of pricing power. That is, although the law of one price
holds at "the docks," when selling imported goods to domestic
consumers these retail firms will charge a mark-up over their cost
since they are assumed to be monopolistically competitive. This
creates a wedge between the world market price of foreign goods
paid by importing firms (
![]() , where
, where ![]() is the level of the nominal exchange rate) and the
domestic currency price of these goods when they are sold to
consumers (
is the level of the nominal exchange rate) and the
domestic currency price of these goods when they are sold to
consumers (![]() ). Monacelli's (2003)
calls this wedge the law of one price gap, defined as
). Monacelli's (2003)
calls this wedge the law of one price gap, defined as
| (13) | 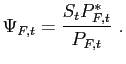 |
Retail firms also operate under Calvo-style price setting, with
![]() as the fraction of firms not
allowed to set prices optimally in any period
as the fraction of firms not
allowed to set prices optimally in any period ![]() .
Their problem is to maximize the expected stream of discounted
profits
.
Their problem is to maximize the expected stream of discounted
profits
| (14) | ![$\displaystyle E_{t}\sum_{T=t}^{\infty}\theta_{F}^{T-t}Q_{t,T}C_{F,T}(i)\left[ P_{F,t}(i)-S_{T}P_{F,T}^{*}\right]$](img50.gif)
|
subject to the demand curve
| (15) | 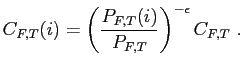
|
The first order condition associated with this problem yields
| (16) | ![$\displaystyle E_{t}\sum_{T=t}^{\infty}\theta_{F}^{T-t}Q_{t,T}C_{F,T}(i)\left[ P_{F,T}(i)- \frac{ \theta_{F}}{\theta_{F}-1}S_{T}P_{F,T}^{*}\right] =0 \ .$](img52.gif)
|
Since imports from the small open economy are negligibly small
in the large foreign economy's consumption bundle, they have no
effect on the foreign price index ![]() and
are thus ignored in the analysis.
and
are thus ignored in the analysis.
The stochastic discount factors in the two economies have to be equalized under complete international asset markets, since households will engage in perfect risk-sharing:
| (17) | ![$\displaystyle \beta\left[ \frac{\lambda_{t+1}}{\lambda_{t}}\cdot\frac{P_{t} }{P_{t+1}}\right] = Q_{t,t+1}=\beta\left[ \frac{\lambda_{t+1}^{*}}{\lambda _{t}^{*}}\cdot\frac{P_{t}^{*}S_{t}} {P_{t+1}^{*}S_{t+1}}\right] \ .$](img54.gif)
|
Equation (17) allows us to derive the uncovered interest rate parity condition
| (18) | ![$\displaystyle (1+i_{t})=(1+i_{t}^{*})E_{t}\left[ \frac{S_{t+1}}{S_{t}}\right] \ .$](img55.gif)
|
Finally, goods market clearing in the domestic and foreign economies requires that
| (19) |
The model is log-linearized around a deterministic steady state
so that it can be estimated empirically. The log-linear equations
are listed in Appendix A. The model assumes that the foreign
economy shares the same preferences and technology as the domestic
economy. However, we could also estimate the foreign block as an
unrestricted vector autoregression (VAR) since it is exogenous to
the domestic economy (recall that the small open economy is assumed
to be infinitely small relative to the large foreign economy). In
addition to relaxing the assumption of common preferences and
technology, estimating the foreign block as a VAR gives more
flexibility to the reduced form dynamics of these variables. Under
this specification, the foreign observables are generated by the
process
![]() where
where
![]() ,
,
![]() is a
is a
![]() coefficient matrix, and
coefficient matrix, and
![]() is a vector of independent
and identically-distributed (IID) random errors. We estimated the
model under both specifications for the foreign block, but we
obtained implausible parameter estimates under the literal
interpretation of the model.5 Therefore, only the results from
treating the foreign block as an exogenous VAR process are
reported.
is a vector of independent
and identically-distributed (IID) random errors. We estimated the
model under both specifications for the foreign block, but we
obtained implausible parameter estimates under the literal
interpretation of the model.5 Therefore, only the results from
treating the foreign block as an exogenous VAR process are
reported.
3. Data
The model is estimated using quarterly data from Switzerland and the European Union. The sample period is 1970:Q1-2005:Q2.6 For Switzerland the data consist of the discount rate (International Financial Statistics), import price inflation (Swiss National Bank), log detrended real per capita GDP (IFS and WDI), annualized CPI inflation (IFS), and log detrended real exchange rate (OECD). For the Euro-Area, the observed variables are annualized CPI inflation (OECD), log detrended real GDP per capita (OECD), and short term interest rate (Area Wide Model updated by Euro Area Business Cycle Network). The log real exchange rate and log real GDP per capita series are demeaned. Inflation and interest rates are expressed as decimals.
4. Exploring the Likelihood Function
To determine how informative the data are we first try to
estimate the parameters using maximum likelihood. The sample log
likelihood function is derived using the Kalman filter.7 Since
we cannot analytically derive the likelihood as a function of the
model's structural parameters, the maximization has to be performed
numerically. We found that numerical gradient methods are unable to
find the maximum when the likelihood function is nearly flat along
several dimensions (as shown later).8 Another complication
arises from the presence of "cliffs" in the likelihood function
at extreme parameter values, as well as regions in which the
likelihood function is undefined because the model's solution is
indeterminate for certain parameter combinations. After
experimenting with many different algorithms, we developed our own,
which proved to be extremely reliable in our experiments. This
algorithm is described in Appendix C. After finding the global
maximum, we use Metropolis-Hastings Markov Chain Monte Carlo (MCMC)
simulations to determine the 95 percent likelihood intervals. The
estimates are shown in Table I. The relatively wide confidence
bounds for the parameters ![]() ,
, ![]() ,
,
![]() , and
, and
![]() suggest that the data
are not very informative about them.
suggest that the data
are not very informative about them.
Figure 1 plots the marginal likelihood densities for the key
structural parameters. The plots suggest that the inverse
elasticity of labor supply (![]() ), the
elasticity of substitution between domestic and foreign goods
(
), the
elasticity of substitution between domestic and foreign goods
(![]() ), the persistence of the productivity
shocks (
), the persistence of the productivity
shocks (![]() ), and the interest rate response to
inflation and the output gap (
), and the interest rate response to
inflation and the output gap (
![]() , and
, and
![]() ) are weakly identified
by the data. The parameter
) are weakly identified
by the data. The parameter ![]() also
appears to have a bimodal distribution. We can also examine the properties of the likelihood function
along several dimensions. In what follows we examine surface plots
of the sample log-likelihood as a function of a given parameter
pair. In generating these plots, all other parameters are fixed at
their estimated likelihood means shown in Table I.
also
appears to have a bimodal distribution. We can also examine the properties of the likelihood function
along several dimensions. In what follows we examine surface plots
of the sample log-likelihood as a function of a given parameter
pair. In generating these plots, all other parameters are fixed at
their estimated likelihood means shown in Table I.
The top-left panel of Figure 2 depicts the sample log-likelihood
as a function of the parameters ![]() (degree of
openness), and
(degree of
openness), and ![]() (coefficient of relative risk
aversion). The likelihood function displays a prominent and
well-defined peak around
(coefficient of relative risk
aversion). The likelihood function displays a prominent and
well-defined peak around
![]() and
and
![]() , consistent with the estimates
reported in Table I. In contrast, the top-right panel of Figure 2
illustrates that the sample log likelihood function displays little
curvature along the dimensions of
, consistent with the estimates
reported in Table I. In contrast, the top-right panel of Figure 2
illustrates that the sample log likelihood function displays little
curvature along the dimensions of
![]() and
and
![]() , which explains why the
Monte Carlo likelihood intervals are wide for them. The bottom
panel of Figure 2 shows the log likelihood as a function of the
inverse elasticity of labor supply (
, which explains why the
Monte Carlo likelihood intervals are wide for them. The bottom
panel of Figure 2 shows the log likelihood as a function of the
inverse elasticity of labor supply (![]() ) and
the persistence of the productivity shock (
) and
the persistence of the productivity shock (![]() ). This plot confirms that
). This plot confirms that ![]() indeed has a bimodal distribution when
indeed has a bimodal distribution when ![]() is low
enough, and that the slope along
is low
enough, and that the slope along ![]() is fairly
flat.
is fairly
flat.
Another way to visualize weak parameter identification is to
plot the likelihood as a function of three parameters, holding the
others fixed at their estimated means. The left panel of Figure 3
shows a heat plot of the sample log-likelihood as a function
of the parameters ![]() ,
,
![]() , and
, and
![]() , which are well identified by the
data. The volume depicts parameter combinations which yield
log-likelihood values in the top 1%. For well identified
parameters, we would expect to see the top 1% of likelihood values
to be restricted to a narrow range of parameter combinations, as is
the case for
, which are well identified by the
data. The volume depicts parameter combinations which yield
log-likelihood values in the top 1%. For well identified
parameters, we would expect to see the top 1% of likelihood values
to be restricted to a narrow range of parameter combinations, as is
the case for ![]() ,
,
![]() , and
, and
![]() . The right panel of Figure 3
shows a heat plot of the log likelihood as a function of
. The right panel of Figure 3
shows a heat plot of the log likelihood as a function of
![]() ,
, ![]() , and
, and
![]() , with the other
parameters fixed at their estimated likelihood means. The maximum
log-likelihood value occurs at
, with the other
parameters fixed at their estimated likelihood means. The maximum
log-likelihood value occurs at
![]() ,
,
![]() , and
, and
![]() . However, the dark
region (in red) spanning log-likelihood values close to the global
maximum is large, demonstrating that the maximum is not
well-defined along these dimensions.
. However, the dark
region (in red) spanning log-likelihood values close to the global
maximum is large, demonstrating that the maximum is not
well-defined along these dimensions.
Is the lack of identification coming from model
misspecification, a small time period sampled in the data, or a
small number of state variables observed? To answer this question,
we conducted a series of Monte Carlo simulations that estimated the
parameters of the model using artificial data. Since the artificial
data are generated by the model, this allows us to check if the
model could be identified even in the absence of model
misspecification. For the data generating process (DGP) we choose a
particular calibration of the model parameters, denoted by
![]() . The artificial data were
then generated by simulating the random draws for the IID shocks
and feeding them into the state space representation of the model
equations. Using this artificial data, we then found the parameter
vector
. The artificial data were
then generated by simulating the random draws for the IID shocks
and feeding them into the state space representation of the model
equations. Using this artificial data, we then found the parameter
vector
![]() that maximized the sample
log-likelihood. If
that maximized the sample
log-likelihood. If
![]()
![]()
![]() , then we are confident that
the parameters are locally identified by the model
structure.9
, then we are confident that
the parameters are locally identified by the model
structure.9
The first artificial data set consisted of 142 simulated
observations for the same eight state variables observed in the
actual data (i.e., domestic and foreign interest rates, real
output, CPI inflation, import price inflation and the real exchange
rate). Can we accurately estimate all the parameters using this
artificial data set? Unfortunately, the answer is no. As shown in
Table II, when we try to jointly estimate all 29 parameters,
![]() is very far from its "true" value
(in
is very far from its "true" value
(in
![]() ), while
), while ![]() ,
, ![]() ,
,
![]() , and
, and
![]() are somewhat far from
their "true" values. If the sample size of the artificial data is
increased to 1000 observations, then, as shown in the last column
of Table 2, all the estimates become quite accurate. These tests
reveal that even if our model was perfectly specified, we would
still need many more observations than are actually available to
obtain accurate estimates of
are somewhat far from
their "true" values. If the sample size of the artificial data is
increased to 1000 observations, then, as shown in the last column
of Table 2, all the estimates become quite accurate. These tests
reveal that even if our model was perfectly specified, we would
still need many more observations than are actually available to
obtain accurate estimates of ![]() ,
, ![]() ,
, ![]() and
and
![]() .
.
5. Bayesian Estimates
Fortunately, Bayesian analysis can help identify these parameters, since we can incorporate prior information on plausible values for the parameters based on past studies. However, the benefit comes at a cost. As noted by Poirier (1998)
A Bayesian analysis of a nonidentified model is always possible if a proper prior on all the parameters is specified. There is, however, no Bayesian free lunch. The price is that there exist quantities about which the data are uninformative, i.e., their marginal prior and posterior distributions are identical (p. 483).
If our goal is to learn about these parameters from the data, then at the very least we should know which parameters are accurately estimated by the data.
For most parameters in our model, the priors are based on past empirical studies using both micro and macro data. One should not place too much confidence in the prior means obtained from previous studies since these estimates crucially depend on the model assumptions, the econometric techniques and the data that are used. For example, there is a large empirical literature on estimating the coefficients of interest rate rules. The coefficients from single-equation estimates will vary for different countries, sample periods, and functional forms assumed for the interest rate rule (e.g., to which variables the interest rate is allowed to respond). When the interest rate rule coefficients are estimated in the context of a general equilibrium model, the estimates will depend on the equations and lag structure of that model. Different estimates will also result from the use of real-time data versus ex-post revised data in the estimation. For other parameters such as the coefficient of relative risk aversion or the elasticity of labor supply, economists are still trying to reconcile estimates obtained using micro data with those obtained using aggregate macro data.
The only parameter in our model which is not estimated is the
discount factor ![]() . As shown in previous studies,
the discount factor is not well-identified from the cyclical
dynamics of the data. We calibrate
. As shown in previous studies,
the discount factor is not well-identified from the cyclical
dynamics of the data. We calibrate
![]() , which corresponds to an annual
steady-state real interest rate of about 4 percent. For the other
29 parameters, we estimate the model under three sets of priors:
uniform, somewhat informative, and informative. The prior
distributions and 95% prior intervals are specified in Table III.
Details on prior specification are given in Appendix D.
, which corresponds to an annual
steady-state real interest rate of about 4 percent. For the other
29 parameters, we estimate the model under three sets of priors:
uniform, somewhat informative, and informative. The prior
distributions and 95% prior intervals are specified in Table III.
Details on prior specification are given in Appendix D.
Table IV and Figure 4 examine the posterior means and Bayesian 95% intervals for the estimated parameters under the three sets of priors. As we would expect, the results using the uniform priors are virtually identical to the likelihood estimates reported in Table I. For most of the parameters, the results look remarkably consistent across the three sets of priors, suggesting they are well informed by the data.
The parameter that is least informed by the data is
![]() . The range of its 95%
posterior interval is very wide when the uniform priors are used
(1.4 to 9.5). When the informative priors are used, the range
narrows sharply to just (0.5 to 1.1). The common practice of
inferring that the data is informative about a given parameter by
just checking that the prior and posterior means differ from one
another would be misleading in this case. Even though the
informative prior mean of 0.5 is different than the posterior mean
estimate of 0.75, this tells us little about how informative the
data truly are. As evidenced by the likelihood estimates, the
estimates under the uniform priors, the Monte Carlo tests and the
surface and heat plots shown in the previous section, the data have
little to say about
. The range of its 95%
posterior interval is very wide when the uniform priors are used
(1.4 to 9.5). When the informative priors are used, the range
narrows sharply to just (0.5 to 1.1). The common practice of
inferring that the data is informative about a given parameter by
just checking that the prior and posterior means differ from one
another would be misleading in this case. Even though the
informative prior mean of 0.5 is different than the posterior mean
estimate of 0.75, this tells us little about how informative the
data truly are. As evidenced by the likelihood estimates, the
estimates under the uniform priors, the Monte Carlo tests and the
surface and heat plots shown in the previous section, the data have
little to say about
![]() . The lack of
identification is perhaps due to the fact that we do not observe
the output gap. To conclude, using the informative prior for
. The lack of
identification is perhaps due to the fact that we do not observe
the output gap. To conclude, using the informative prior for
![]() amounts to a
complicated way of calibrating it; the data have virtually nothing
to say about this parameter, and the posterior estimate is
therefore mainly driven by the prior.
amounts to a
complicated way of calibrating it; the data have virtually nothing
to say about this parameter, and the posterior estimate is
therefore mainly driven by the prior.
Similarly, the policy response to inflation (
![]() ), the inverse elasticity of labor
supply (
), the inverse elasticity of labor
supply (![]() ), and the persistence of the
productivity shocks (
), and the persistence of the
productivity shocks (![]() ) have fairly wide
posterior intervals when the uniform priors are used. These
estimates vary moderately when the somewhat informative and
informative priors are used in the estimation. It is perhaps fair
to say the data are only moderately informative about these
parameters.
) have fairly wide
posterior intervals when the uniform priors are used. These
estimates vary moderately when the somewhat informative and
informative priors are used in the estimation. It is perhaps fair
to say the data are only moderately informative about these
parameters.
Finally, the data are informative about the other 25 parameters in our model, so we can safely claim that their estimates were mainly determined by the data and not the priors.
6. Posterior Predictive Distributions
One way to assess the ability of a time series model to fit the
data is to compute posterior predictive distributions for
future data values given past data Gelman, Carlin, Stern, and Rubin (2004b).
That is, after observing the data
![]() , we can predict an unknown observable
, we can predict an unknown observable
![]() for any forecast horizon
for any forecast horizon
![]() according to
according to
| (20) | 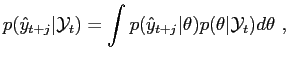
|
where
is the
likelihood of the ![]() -period ahead forecast
computed with the Kalman Filter (Hamilton(1994)
)10.
-period ahead forecast
computed with the Kalman Filter (Hamilton(1994)
)10.
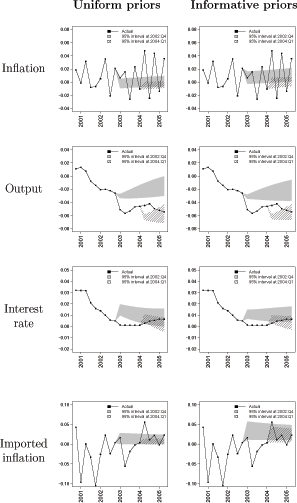
Figure 5 compares the out-of-sample forecasts under the informative priors and the uniform priors. The shaded regions denote the 95% intervals from the posterior predictive distributions, and the solid lines denote the ex-post realizations of the data. The choice of prior has little influence over the model's forecasts. As we would expect, our highly stylized model generates rather poor out-of-sample forecasts. The model cannot generate the volatility found in the inflation data, nor can it explain the persistent deviations of output from its trend. The poor forecasting ability of micro-founded macro models is well known, and is a result of model misspecification (i.e., the rigid cross-equation restrictions and lag structure in the dynamic equations) and overparametrization. Even though our model fits the data quite well11, it does a rather poor job of forecasting the data into the future, particularly at short horizons.
Smets and Wouters (2007) compare the forecasting performance of their DSGE model to that of a VAR and Bayesian VAR (BVAR) and find that overall the DSGE model does a better job at forecasting. As pointed out by Litterman (1986), both VAR and BVAR are overparametrized, yielding good in-sample fit but poor out-of-sample forecast performance. But one may also argue that our DSGE model, featuring 29 parameters, is overparametrized. Although comparing forecasting performance of alternative models is useful, it is still important to be able to judge whether the model does a good job at forecasting the data or not. A DSGE model may forecast better than a VAR or BVAR, but it still may be a poor forecasting model. Comparing the posterior predictive plots to the ex-post realizations of the data is a useful way to assess the model's out-of-sample forecast performance.
7. Conclusions
In attempting to estimate the parameters of a small open economy model, we find that several of the key structural parameters are weakly identified by the data. Some of these parameters, such as the interest rate response to inflation and the output gap, are of considerable interest to economists performing policy analysis. We find that the posterior intervals for the policy parameters are narrow when an informative prior is used, but extremely wide when the prior distribution is diffuse. Thus, the final estimates for these parameters are mainly being driven by the assumed prior distributions, and not the data, and it would be misleading to claim that they can be estimated. Our Monte Carlo simulations demonstrate that having more observations would fix the identification problem in our model. Posterior predictive distributions of future data given the past provide valuable information about out-of-sample performance of econometric models, which is not at all the same thing as in-sample fit of such models. Finally, our diagnostic tools -- including surface plots, heat plots, likelihood estimates, and Bayesian estimates under three sets of priors -- provide an easy way to verify which parameters are poorly informed by the data.
Appendix A. Log Linear Equations
After log-linearization, the variables will be interpreted in
terms of their log deviations from their respective steady-state
values. There are 8 exogenous IID shocks:
![]() (shock to domestic
inflation),
(shock to domestic
inflation),
![]() (shock to imported
goods inflation),
(shock to imported
goods inflation),
![]() (risk premium shock),
(risk premium shock),
![]() (domestic monetary policy
shock),
(domestic monetary policy
shock),
![]() (shock to foreign
inflation),
(shock to foreign
inflation),
![]() (foreign monetary
policy shock),
(foreign monetary
policy shock),
![]() (domestic productivity
shock), and
(domestic productivity
shock), and
![]() (foreign
productivity shock). The log-linearized equations that fully
characterize the domestic and foreign economies are listed
below.12
(foreign
productivity shock). The log-linearized equations that fully
characterize the domestic and foreign economies are listed
below.12
| (1′) Domestic Inflation |
where ![]()
| (2′)Imported Inflation |
| (3′) CPI Inflation |
| (4′) Marginal Cost |
| (5′) Real Exchange Rate |
| (6′) Law of one price gap |
| (7′) Terms of trade |
| (8′) "Link" equation |
| (9′) UIP condition |
| (10′) Market clearing |
| (11′) Monetary policy |
| (12′) Output gap |
where
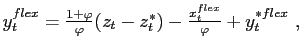 and
and ![]() and
and ![]()
![]()
| (13′) Productivity shock |
| (14′) Foreign output |
| (15′) Foreign inflation |
| (16′) Foreign marginal cost |
| (17′) Foreign monetary policy |
| (18′) Foreign output gap |
![]()
and ![]() and
and ![]()
| (19′) Foreign productivity shock |
In estimating the model, the foreign block is treated as
exogenous, and equations
![]() above are
replaced with the following VAR process:
above are
replaced with the following VAR process:
![]() ,
where
,
where
![]() ,
,
![]() is a
is a
![]() coefficient matrix, and
coefficient matrix, and
![]() is a vector of normally
distributed IID errors. The elements of the coefficient matrix
is a vector of normally
distributed IID errors. The elements of the coefficient matrix
![]() are the parameters
are the parameters
![]() ,
, ![]() .
.
Appendix B. Likelihood Funcation and Posterior Distribution
The linear model is solved using the algorithm of Sims (2002), which relies on matrix eigenvalue decompositions. Then, in order to derive the likelihood for the data, the model's solution is written in state-space form,
| (21) | ![$\displaystyle \left\{ \begin{array}[c]{l} x_{t}=Fx_{t-1}+Qz_{t}\\ y_{t}=Hx_{t}+Rv_{t} \end{array} \right\} \ ,$](img460.gif)
|
where
| (22) |
|
where
Having specified a prior density for the model parameters,
![]() , where
, where ![]() is the
parameter vector, the posterior distribution of the parameters is
given by
is the
parameter vector, the posterior distribution of the parameters is
given by
| (23) | 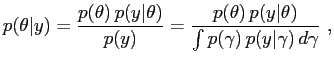
|
where ![]() is the observed data and
is the observed data and
![]() is the likelihood function
derived above. With fixed
is the likelihood function
derived above. With fixed ![]() , the denominator
in (23) does not depend
on
, the denominator
in (23) does not depend
on ![]() and can therefore be treated as a
constant; thus the unnormalized posterior density can be
expressed as
and can therefore be treated as a
constant; thus the unnormalized posterior density can be
expressed as
| (24) |
The likelihood function can only be evaluated if we have at
least as many structural shocks as observable variables13. As
described in Appendix A, the 8 exogenous shocks are: domestic and
foreign productivity shock, domestic and foreign monetary policy
shocks, domestic and imported inflation shocks, a shock to the
uncovered interest parity condition, and a shock to the large
foreign economy's inflation equation. To allow for model
misspecification, we include measurement errors in all of the 8
observables. These measurement errors are meant to capture
movements in the data that the model cannot explain. They are
characterized by the ![]() matrix in equation
(21). The variance
of the measurement errors
matrix in equation
(21). The variance
of the measurement errors
![]() is estimated from the
data.
is estimated from the
data.
Appendix C. Numerical Maximization Algorithm
The following algorithm is used to find the maximum of the likelihood function and the posterior mode. First, an initial guess for the parameter vector is chosen from 1,000 function evaluations using random values chosen from a uniform distribution with very wide bounds for each parameter. Of these 1,000 random draws, the parameter vector which generated the highest function value is chosen as the starting value for the algorithm.
The algorithm then loops through the following gradient-based and non-gradient based optimization routines: simulated annealing Belisle (1992), quasi-Newton "BFGS" method (Broyden (1970), Fletcher (1970), Goldfarb (1970), and Shanno (1970)), the Nelder and Mead (1965) simplex method, and the conjugate-gradient method of Reeves (1964). The optimized end value from one method is used as the starting value for the next method, and the entire loop is repeated until the improvement is less than 0.1.
Finally, the entire process is repeated 20 times using 20 different starting values. Although this algorithm provides a good guess for the likelihood mode or posterior mode, convergence to the true mode is achieved by using an adaptive Markov Chain Monte Carlo (MCMC) simulation, similar to that suggested by Browne and Draper (2006). Appendix E discusses the adaptive MCMC algorithm in detail.
Appendix D. Priors
In this appendix we examine the background literature used in designing the priors for each parameter. The exact prior specifications are reported in Table III of the paper.
Many economists prefer to use a CRRA value of unity as suggested
by Arrow (1971), implying that a
constant-relative-risk-aversion utility depends on the log of
income, thus keeping the utility function bounded. Most Bayesian
studies estimating DSGE models use a prior for ![]() which is centered at this theoretically-based value of
1, with varying degrees of uncertainty. By doing this, they are
ignoring a plethora of empirical studies which have estimated this
parameter. In specifying a prior for
which is centered at this theoretically-based value of
1, with varying degrees of uncertainty. By doing this, they are
ignoring a plethora of empirical studies which have estimated this
parameter. In specifying a prior for ![]() , we
considered empirical estimates from the financial economics
literature, as well as estimates of the income elasticity of the
value of statistical life (VSL) derived from labor and product
markets14. As reviewed in Kaplow (2005), VSL estimates are typically below 1, whereas
more recent CRRA estimates from the financial economics literature
often exceed 10. Since the two estimates should in theory be
roughly the same15, the prior is specified to allow for
the possibility of a low CRRA consistent with the VSL literature,
and a high CRRA consistent with the financial economics
literature.
, we
considered empirical estimates from the financial economics
literature, as well as estimates of the income elasticity of the
value of statistical life (VSL) derived from labor and product
markets14. As reviewed in Kaplow (2005), VSL estimates are typically below 1, whereas
more recent CRRA estimates from the financial economics literature
often exceed 10. Since the two estimates should in theory be
roughly the same15, the prior is specified to allow for
the possibility of a low CRRA consistent with the VSL literature,
and a high CRRA consistent with the financial economics
literature.
The degree of habit persistence is bounded between 0 and 1. Most
empirical studies have found ![]() to be greater than
0.6. Christiano, Eichenbaum, and Evans (2005) estimate an
to be greater than
0.6. Christiano, Eichenbaum, and Evans (2005) estimate an ![]() of 0.63
for the United States. Fuhrer (2000) finds somewhat
higher estimates of 0.8 and 0.9, and the highest estimates found in
the literature are those of Bouakez, Cardia, and Ruge-Murcia (2005), who estimate
a value of 0.98.
of 0.63
for the United States. Fuhrer (2000) finds somewhat
higher estimates of 0.8 and 0.9, and the highest estimates found in
the literature are those of Bouakez, Cardia, and Ruge-Murcia (2005), who estimate
a value of 0.98.
Economists have devoted a great amount of effort to estimating the intertemporal elasticity of labor supply, which plays an important role in explaining business cycles. However, the estimates are still much lower than required by Real Business Cycle models to match certain "stylized facts" in the economy. In a meta-analysis of 32 micro-based empirical estimates of labor supply elasticities covering 7 European countries and the United States, Evers, de Mooij, and van Vuuren (2006) find a mean of 0.24 (with a standard deviation of 0.42) for the elasticity of labor supply. Using a contract model, Ham and Reilly (2006) obtain much higher estimates ranging from 0.9 to 1.3.
The elasticity of substitution between domestic and foreign-produced goods is a key parameter in all open-economy macro models, since it governs the trade balance and terms of trade relationships, and affects the degree to which shocks can be transmitted across countries. Once again, the micro- and macro-based empirical studies provide quite different estimates for this parameter. The micro-econometric studies using sector-level trade data usually report higher estimates, ranging from 5 to 12, whereas the several available macro studies report estimates of 1-2 for the United States, and slightly lower estimates for Europe and Japan16.
Using monthly CPI databases from 9 European countries, Dhyne, Alvarez, Bihan, Veronese, Dias, and Hof (2005) estimate a median price duration of 10.6 months
in Europe, compared to only 4.6 months in the U.S. Similarly, a
study by Angeloni, Aucremanne, Ehrmann, Gali, Levin, and Smets (2004) finds that European firms on
average change prices once a year. This translates into a
![]() coefficient of 0.75. These
empirical estimates of price durations do not distinguish between
domestic firms and importing firms, so the priors for both
coefficient of 0.75. These
empirical estimates of price durations do not distinguish between
domestic firms and importing firms, so the priors for both
![]() and
and
![]() are the same. Since there are no
studies estimating this parameter for Switzerland, it is assumed
that Swiss firms change prices on average with the same frequency
as European firms.
are the same. Since there are no
studies estimating this parameter for Switzerland, it is assumed
that Swiss firms change prices on average with the same frequency
as European firms.
Ever since Taylor (1993) published his celebrated paper "Discretion Versus Monetary Policy Rules in Practice," in which he showed that actual monetary policy in the United States can be characterized by a simple interest rate feedback rule, economists and central bankers have estimated similar reaction functions for many countries and time-periods. Even though the original Taylor rule does not include a lagged interest rate term, most empirical studies of monetary policy rules have found a large degree of interest rate smoothing. For example, Clarida, Gali, and Gertler (1998) estimate lagged interest rate coefficients ranging from 0.91 to 0.95 for Germany, Japan, U.S., France, Italy and the United Kingdom. For the case of Switzerland, Neumann and von Hagen (2002) also find a very strong and statistically significant reaction of the interest rate to its own lag.
Empirical studies have shown that the conduct of monetary policy in Europe (as described by the coefficients of an interest rate feedback rule) is not much different than in the United States. For example, Gerlach and Schnabel (1999) estimate the coefficient on the output gap to be 0.45 and the coefficient on inflation to be 1.58, values that are statistically indistinguishable from those suggested by Taylor for the United States. For Switzerland, Nuemann and von Hagen (2002) do not find that overnight interest rates react to the output gap, but they do find a strong and significant reaction to inflation, similar in magnitude to that of Germany. Similarly, Cecchetti and Ehrmann (2000) find evidence of a high aversion to inflation variability in Switzerland, similar in magnitude to Germany's17. In 1999, the Swiss National Bank (SNB) abandoned monetary targeting and instead decided to target a forecast of inflation. Kugler and Rich (2000) find evidence that even during the monetary targeting period, the path of short-term interest rates frequently agreed with that derived from a Taylor rule. To summarize, there is some evidence that the SNB's behavior can be characterized by a Taylor rule with a higher response to inflation than to the output gap, and a strong degree of interest rate smoothing.
The existing literature provides little information on the magnitude of the standard deviation of the IID shocks, so in general we allow for a wide range of values in all prior specifications.
There is ample evidence in the literature that productivity
shocks are highly persistent in both Europe and the United States.
For example, Gruber (2002) conducts augmented
Dickey-Fuller tests to the productivity series of each of the G7
countries and in all cases fails to reject the hypothesis of a unit
root at conventional significance levels18. Backus, Kehoe, and Kydland (1992) estimate autoregressive coefficients of
0.904(0.073) and 0.908(0.036) for the U.S. and Europe,
respectively. This suggests that ![]() and
and
![]() are either 1 or close to
1.
are either 1 or close to
1.
The parameter ![]() could in principle be
calibrated directly from the data as the average ratio of imported
goods to Switzerland's GDP over the entire sample period. Using
data from the Swiss National Bank, we find that this ratio is
approximately 0.3, and is fairly constant over the entire sample
period. To allow for some flexibility when estimating this
parameter, we use a Beta distribution with mean 0.3 for the
somewhat and informative priors. The less informative uniform prior
is bounded by the unit interval.
could in principle be
calibrated directly from the data as the average ratio of imported
goods to Switzerland's GDP over the entire sample period. Using
data from the Swiss National Bank, we find that this ratio is
approximately 0.3, and is fairly constant over the entire sample
period. To allow for some flexibility when estimating this
parameter, we use a Beta distribution with mean 0.3 for the
somewhat and informative priors. The less informative uniform prior
is bounded by the unit interval.
Appendix E. Adaptive MCMC Algorithm
When using Bayesian simulation to summarize the posterior density, one must be careful to ensure that the target distribution is well represented by the simulated draws, and that the results are not influenced by the chosen starting values of the MCMC chain. Convergence of each chain was first checked by calculating the diagnostics of Geweke and Heidelberger and Welch, available in the R-CODA package. After verifying that the individual chains converged with 200,000 draws, Gelman and Rubin's convergence diagnostic was calculated using four parallel chains with dispersed starting values19. These diagnostics are discussed in Cowles and Carlin (1996) and Brooks and Gelman (1998).
Following Browne and Draper (2006), the MCMC algorithm has three stages: adaptation, burn-in, and monitoring. The adaptation stage begins at our estimate of the posterior mode, and adjusts the covariance matrix of the jumping distribution every 2,500 iterations to be proportional to the covariance matrix estimated from these iterations, with the scale factor adapted to achieve a target acceptance rate of 0.25 Gelman, Roberts, and Gilks (1995). The adaptation stage consists of 300,000 iterations, after which we fix the covariance matrix of the jumping distribution to that of the estimated covariance of the last 150,000 draws20. The scale factor is then re-calibrated and fixed to achieve a target acceptance rate of 0.25. Following a burn-in period of 100,000 iterations, we then monitor the chain for 200,000 iterations. All of the inferences we make about the parameters come from this last chain of 200,000 iterations from the monitoring phase.
References
Angeloni, I., L. Aucremanne, M. Ehrmann, J. Gali, A. Levin, and F. Smets (2004): "Inflation Persistence in the Euro Area: Preliminary Summary of Findings," Working paper, European Central Bank, National Bank of Belgium, CREI and Universitat Pompeu Fabra, Federal Reserve Board.
Arrow, K. J. (1971): Essays in the Theory of Risk Bearing. chap. 3. Chicago: Markham Publishing Co.
Backus, D. K., P. J. Kehoe, and F. E. Kydland (1992): "International Real Business Cycles," Journal of Political Economy, 100(4), 745–75.
Baier, S. L., and J. H. Bergstrand (2001): "The growth of world trade: tariffs, transport costs, and income similarity," Journal of International Economics, 53(1), 1–27.
Batini, N., A. Justiniano, P. Levine, and J. Pearlman (2004): "Robust Inflation- Forecast-Based Rules to Shield against Indeterminacy," Working paper 0804, Department of Economics, University of Surrey.
Baxter, M., and M. J. Crucini (1995): "Business Cycles and the Asset Structure of Foreign Trade," International Economic Review, 36(4), 821–54.
Belisle, C. J. (1992): "Convergence Theorems for a Class of Simulated Annealing Algorithms on Rd," Journal of Applied Probability, 29(4), 885–895.
Beltran, D. O. (2007): “Model uncertainty and the design of robust monetary policy rules in a small open economy: A Bayesian approach,” Ph.D. thesis, University of California, Santa Cruz.
Beyer, A., and R. E. A. Farmer (2004): "On the Indeterminacy of New-Keynesian Economics," Computing in Economics and Finance 2004 152, Society for Computational Economics.
Bouakez, H., E. Cardia, and F. Ruge-Murcia (2005): "The Transmission of Monetary Policy in a Multi-Sector Economy," Cahiers de recherche 2005-16, Universite de Montreal, Departement de sciences economiques.
Brooks, S., and A. Gelman (1998): "General Methods for Monitoring Convergence of Iterative Simulations," Journal of Computational and Graphical Statistics, 7, 434–455.
Browne, W. J., and D. Draper (2006): “A comparison of Bayesian and likelihoodbased methods for fitting multilevel models,” Bayesian Analysis, 1(3), 473–550.
Broyden, C. (1970): "The Convergence of a Class of Double-Rank Minimization Algorithms," IMA Journal fo Applied Mathematics, 6(1), 76–90.
Canova, F., and L. Sala (2006): "Back to square one: identification issues in DSGE models," Computing in Economics and Finance 2006 196, Society for Computational Economics.
Cecchetti, S., and M. Ehrmann (2000): "Does Inflation Targeting Increase Output volatility? An International Comparison of Policy Maker’s Preferences and Outcomes," Working Papers Central Bank of Chile 69, Central Bank of Chile.
Christiano, L. J., M. Eichenbaum, and C. L. Evans (2005): "Nominal Rigidities and the Dynamic Effects of a Shock to Monetary Policy," Journal of Political Economy, 113(1), 1–45.
Clarida, R., J. Gali, and M. Gertler (1998): "Monetary policy rules in practice: Some international evidence," European Economic Review, 42(6), 1033–1067.
Cowles, M. K., and B. P. Carlin (1996): "Markov Chain Monte Carlo Convergence Diagnostics: A Comparative Review," Journal of the American Statistical Association, 91(434), 883–904.
Deardorff, A. V., and R. M. Stern (1990): Computational Analysis of Global Trading Arrangements. chap. 3. Ann Arbor, MI: The University of Michigan Press.
Dhyne, E., L. J. Alvarez, H. L. Bihan, G. Veronese, D. Dias, and J. Hof (2005): "Price setting in the Euro area: some stylized facts from individual consumer price data," Working Paper Series 524, European Central Bank.
Draper, D. (2007): "Bayesian multilevel analysis and MCMC," in Handbook of Multilevel Analysis, ed. by J. de Leeuw, and E. Meijer, pp. 77–140. Springer, New York.
Epstein, L. G., and S. E. Zin (1989): "Substitution, Risk Aversion, and the Temporal Behavior of Consumption and Asset Returns: A Theoretical Framework," Econometrica, 57(4), 937–69.
Evers, M., R. A. de Mooij, and D. J. van Vuuren (2006): "What explains the Variation in Estimates of Labour Supply Elasticities?," Tinbergen Institute Discussion Papers 06-017/3, Tinbergen Institute.
Fletcher, R. (1970): "A New Approach to Variable Metric Algorithms," The Computer Journal, 13(3), 317–322.
Fletcher, R., and C. Reeves (1964): "Function minimization by conjugate gradients," Computer Journal, 7(2), 149–154.
Fuhrer, J. C. (2000): "Habit Formation in Consumption and Its Implications for Monetary-Policy Models," American Economic Review, 90(3), 367–390.
Gali, J., and T. Monacelli (2005): "Monetary Policy and Exchange Rate Volatility in a Small Open Economy," Review of Economic Studies, 72(3), 707–734.
Gelman, A., J. B. Carlin, H. S. Stern, and D. B. Rubin (2004a): Bayesian Data Analysis. Chapman & Hall/CRC.
Gelman, A., J. B. Carlin, H. S. Stern, and D. B. Rubin(2004b): Bayesian Data Analysis. p. 8. Chapman & Hall/CRC.
Gelman, A., G. Roberts, and W. Gilks (1995): "Efficient Metropolis Jumping Rules," in Bayesian Statistics 5, ed. by J.M.Bernardo, J.O.Berger, A.P.Dawid, and A.F.M.Smith. Oxford University Press, Oxford.
Gerlach, S., and G. Schnabel (1999): "The Taylor Rule and Interest Rates in the EMU Area," CEPR Discussion Papers 2271, C.E.P.R. Discussion Papers.
Goldfarb, D. (1970): "A Family of Variable-Metric Methods Derived by Variational Means," Mathematics of Computation, 24(109), 23–26.
Gruber, J. W. (2002): "Productivity shocks, habits, and the current account," International Finance Discussion Papers 733, Board of Governors of the Federal Reserve System (U.S.).
Ham, J. C., and K. T. Reilly (2006): "Using Micro Data to Estimate the Intertemporal Substitution Elasticity for Labor Supply in an Implicit Contract Model," IEPR Working Papers 06.54, Institute of Economic Policy Research (IEPR).
Hamilton, J. D. (1994): Time Series Analysis. chap. 13. New Jersey: Princeton University Press.
Harrigan, J. (1993): "OECD imports and trade barriers in 1983," Journal of International Economics, 35(1-2), 91–111.
Hummels, D. (2001): "Toward a Geography of Trade Costs," Working paper, Purdue University.
Ireland, P. N. (2003): "Endogenous money or sticky prices?," Journal of Monetary Economics, 50(8), 1623–1648.
Justiniano, A., and B. Preston (2004): "Small Open Economy DSGE Models: Specification, Estimation, and Model Fit," Working paper, IMF and Columbia University.
Kaplow, L. (2005): "The Value of a Statistical Life and the Coefficient of Relative Risk Aversion," Journal of Risk and Uncertainty, 31(1), 23–34.
Kugler, P., and G. Rich (2002): "Monetary Policy under Low Interest Rates: The Experience of Switzerland in the late 1970’s," Schweizerische Zeitschrift fr Volkswirtschaft und Statistik, 138(3), 241–269.
Levin, A. T., A. Onatski, J. C. Williams, and N. Williams (2005): "Monetary Policy Under Uncertainty in Micro-Founded Macroeconometric Models," NBER Working Papers 11523, National Bureau of Economic Research, Inc.
Lubik, T., and F. Schorfheide (2005): "A Bayesian Look at New Open Economy Macroeconomics," Economics Working Paper Archive 521, The Johns Hopkins University, Department of Economics.
Monacelli, T. (2003): "Monetary policy in a low pass-through environment," Working Paper Series 227, European Central Bank.
Nelder, J., and R. Mead (1965): "A simplex algorithm for function minimization," Computer Journal, 7(4), 308–313.
Neumann, M. J., and J. von Hagen (2002): "Does inflation targeting matter?," Federal Reserve Bank of St.Louis Review, July, 127–148.
Onatski, A., and J. H. Stock (2000): "Robust Monetary Policy Under Model Uncertainty in a Small Model of the U.S. Economy," NBER Working Papers 7490, National Bureau of Economic Research, Inc.
Poirier, D. J. (1998): "Revising Beliefs In Nonidentified Models," Econometric Theory, 14(04), 483–509.
Ruge-Murcia, F. J. (2007): "Methods to estimate dynamic stochastic general equilibrium models," Journal of Economic Dynamics and Control, 31(8), 2599–2636.
Shanno, D. (1970): "Conditioning of Quasi-Newton Methods for Function Minimization," Mathematics of Computation, 24(111), 647–656.
Sims, C. A. (2002): "Solving Linear Rational Expectations Models," Computational Economics, 20(1-2), 1–20.
Smets, F., and R. Wouters (2003): "An Estimated Dynamic Stochastic General Equilibrium Model of the Euro Area," Journal of the European Economic Association, 1(5), 1123–1175.
Smets, F., and R. Wouters (2007): "Shocks and Frictions in US Business Cycles: A Bayesian DSGE Approach," American Economic Review, 97(3), 586–606.
Stern, R. M., J. Francis, and B. Schumacher (1976): Price Elasticities in International Trade: An Annotated Bibliography. London: Macmillan Press LTD.
Taylor, J. B. (1993): "Discretion versus policy rules in practice," Carnegie-Rochester Conference Series on Public Policy, 39, 195–214.
West, M., and J. Harrison (1999): Bayesian Forecasting and Dynamic Models. New York: Springer-Verlag, Inc.
Whalley, J. (1985): Trade Liberalization Among Major World Trading Areas. chap. 5. MIT Press.
Table 1. Maximum Likelihood Estimates
| Parameter | Description | 2.5% | 97.5% | Mean | MCSE |
|---|---|---|---|---|---|
| Degree of openness | 0.1387 | 0.2497 | 0.1906 | 0.00090 | |
| Relative risk aversion | 0.0439 | 0.1476 | 0.0915 | 0.00082 | |
| External habit | 0.9927 | 0.9975 | 0.9951 | 0.00004 | |
| Inverse elast. of labor supply | 0.0545 | 6.0019 | 1.4420 | 0.08333 | |
| Elast. domestic vs. foreign goods | 0.3301 | 0.7184 | 0.4964 | 0.00309 | |
| | Calvo domestic prices | 0.9326 | 0.9659 | 0.9506 | 0.00027 |
| | Calvo imported prices | 0.9857 | 0.9988 | 0.9947 | 0.00010 |
| Productivity persistence | 0.6089 | 0.9897 | 0.8403 | 0.00310 | |
| Policy, lagged interest rate | 0.9391 | 0.9930 | 0.9781 | 0.00064 | |
| | Policy, inflation | 1.0141 | 3.2129 | 1.5318 | 0.02206 |
| | Policy, output gap | 1.1989 | 9.4666 | 4.6244 | 0.08520 |
| | VAR, | 0.8967 | 0.9958 | 0.9496 | 0.00087 |
| | VAR, | -0.0445 | 0.0413 | -0.0012 | 0.00064 |
| | VAR, | -0.0558 | 0.0500 | -0.0041 | 0.00078 |
| | VAR, | 0.0184 | 0.0776 | 0.0474 | 0.00048 |
| | VAR, | -0.0146 | 0.0453 | 0.0112 | 0.00048 |
| | VAR, | 0.9438 | 1.0153 | 0.9846 | 0.00059 |
| | VAR, | 0.0457 | 0.1135 | 0.0796 | 0.00053 |
| | VAR, | 0.9071 | 0.9745 | 0.9439 | 0.00052 |
| | VAR, | 0.0224 | 0.1053 | 0.0601 | 0.00063 |
| | St.dev. policy shock | 0.0011 | 0.0032 | 0.0019 | 0.00002 |
| | St.dev. productivity shock | 0.0093 | 0.0509 | 0.0242 | 0.00033 |
| | VAR, shock to | 0.0046 | 0.0074 | 0.0058 | 0.00002 |
| | VAR, shock to | 0.0061 | 0.0088 | 0.0074 | 0.00002 |
| | St.dev. domestic inflation shock | 0.0273 | 0.0391 | 0.0326 | 0.00009 |
| | St.dev. imported inflation shock | 0.0766 | 0.0987 | 0.0867 | 0.00017 |
| | St.dev. U.I.P. shock | 0.0011 | 0.0081 | 0.0037 | 0.00006 |
| | VAR, shock to | 0.0029 | 0.0060 | 0.0043 | 0.00002 |
| | St.dev. measurement error | 0.0104 | 0.0119 | 0.0112 | 0.00001 |
For a given parameter
![]() , the Monte Carlo standard error
of the mean (MCSE) is calculated as:
, the Monte Carlo standard error
of the mean (MCSE) is calculated as:
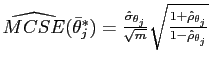 , where
, where ![]() is the number of iterations in the chain,
is the number of iterations in the chain,
![]() is the estimated
standard deviation, and
is the estimated
standard deviation, and
![]() is the estimated
first order autocorrelation Draper (2007).
is the estimated
first order autocorrelation Draper (2007).
Table 2. Monte Carlo Test Using Artificial Data
| Parameter | | | |
|---|---|---|---|
| 0.300 | 0.332 | 0.291 | |
| 1.500 | 1.336 | 1.513 | |
| 0.850 | 0.854 | 0.844 | |
| 0.700 | 0.183 | 0.660 | |
| 0.500 | 0.430 | 0.520 | |
| | 0.750 | 0.688 | 0.754 |
| | 0.650 | 0.684 | 0.661 |
| 0.970 | 0.954 | 0.966 | |
| 0.860 | 0.852 | 0.865 | |
| | 1.450 | 1.396 | 1.503 |
| | 0.120 | 0.184 | 0.129 |
| | 0.400 | 0.435 | 0.428 |
| | -0.100 | -0.098 | -0.061 |
| | -0.010 | -0.053 | -0.052 |
| | 0.100 | -0.057 | 0.097 |
| | 0.500 | 0.439 | 0.496 |
| | -0.020 | -0.045 | -0.020 |
| | 0.100 | 0.098 | 0.092 |
| | 0.500 | 0.513 | 0.505 |
| | 0.800 | 0.808 | 0.796 |
| | 0.001 | 0.001 | 0.001 |
| | 0.020 | 0.034 | 0.023 |
| | 0.050 | 0.041 | 0.053 |
| | 0.020 | 0.021 | 0.021 |
| | 0.040 | 0.034 | 0.037 |
| | 0.050 | 0.052 | 0.049 |
| | 0.020 | 0.001 | 0.018 |
| | 0.010 | 0.008 | 0.011 |
| | 0.010 | 0.010 | 0.010 |
The artificial data set consists of 1,000 observations generated by the model equations using random draws for the IID shocks. The log likelihood function is maximized using the algorithm described in Appendix C.
Table 3. Prior Distributions
| Uniform, | Uniform, | Uniform, | Somewhat informative, | Somewhat informative, | Somewhat informative, 2.5 percentile | Somewhat informative, 97.5 percentile | Informative, | Informative, | Informative, 2.5 percentile | Informative, 97.5 percentile | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| U | 0.001 | 0.999 | B | 0.3 | 0.06 | 0.63 | B | 0.3 | 0.13 | 0.51 | |
| U | 0.001 | 50 | W | 10 | 0.25 | 36.9 | G | 1 | 0.03 | 3.69 | |
| U | 0.001 | 0.999 | B | 0.6 | 0.09 | 0.98 | B | 0.8 | 0.44 | 0.99 | |
| U | 0.001 | 10 | G | 2 | 0.5 | 5.83 | G | 3 | 1.37 | 5.25 | |
| U | 0.001 | 10 | G | 3 | 0.43 | 8 | G | 3 | 1.02 | 6.03 | |
| | U | 0.001 | 0.999 | B | 0.75 | 0.3 | 0.99 | B | 0.75 | 0.53 | 0.92 |
| | U | 0.001 | 0.999 | B | 0.75 | 0.3 | 0.99 | B | 0.75 | 0.53 | 0.92 |
| U | 0.001 | 0.999 | B | 0.9 | 0.67 | 1 | B | 0.9 | 0.78 | 0.98 | |
| U | 0.001 | 0.999 | B | 0.7 | 0.23 | 0.99 | B | 0.7 | 0.44 | 0.9 | |
| | U | 1.001 | 10 | IG | 2 | 1.06 | 3.73 | IG | 1.5 | 1.09 | 2.06 |
| | U | 0.001 | 10 | E | 0.5 | 0 | 1.82 | G | 0.5 | 0.25 | 0.83 |
| | U | -1 | 2 | N | 0.4 | -2.54 | 3.34 | N | 0.4 | -1.56 | 2.36 |
| | U | -2 | 2 | N | 0 | -2.94 | 2.94 | N | 0 | -1.96 | 1.96 |
| | U | -2 | 2 | N | 0 | -2.94 | 2.94 | N | 0 | -1.96 | 1.96 |
| | U | -2 | 2 | N | 0 | -2.94 | 2.94 | N | 0 | -1.96 | 1.96 |
| | U | -1 | 2 | N | 0.4 | -2.54 | 3.34 | N | 0.4 | -1.56 | 2.36 |
| | U | -2 | 2 | N | 0 | -2.94 | 2.94 | N | 0 | -1.96 | 1.96 |
| | U | -2 | 2 | N | 0 | -2.94 | 2.94 | N | 0 | -1.96 | 1.96 |
| | U | -2 | 2 | N | 0 | -2.94 | 2.94 | N | 0 | -1.96 | 1.96 |
| | U | -1 | 2 | N | 0.4 | -2.54 | 3.34 | N | 0.4 | -1.56 | 2.36 |
| | U | 0.001 | 3 | E | 0.5 | 0 | 1.85 | E | 0.13 | 0 | 0.46 |
| | U | 0.001 | 3 | E | 0.5 | 0 | 1.85 | E | 0.13 | 0 | 0.46 |
| | U | 0.001 | 3 | E | 0.5 | 0 | 1.85 | E | 0.13 | 0 | 0.46 |
| | U | 0.001 | 3 | E | 0.5 | 0 | 1.85 | E | 0.13 | 0 | 0.46 |
| | U | 0.001 | 3 | E | 0.5 | 0 | 1.85 | E | 0.13 | 0 | 0.46 |
| | U | 0.001 | 3 | E | 0.5 | 0 | 1.85 | E | 0.13 | 0 | 0.46 |
| | U | 0.001 | 3 | E | 0.5 | 0 | 1.85 | E | 0.13 | 0 | 0.46 |
| | U | 0.001 | 3 | E | 0.5 | 0 | 1.85 | E | 0.13 | 0 | 0.46 |
| | U | 0.001 | 1 | E | 0.5 | 0 | 1.85 | E | 0.13 | 0 | 0.46 |
For the density functions, U represents the uniform distribution, with lower and upper bounds shown under the column headings lb and ub, respectively. The other distributions are: W=Weibull, B=Beta, G=Gamma, IG=Inverse-gamma, N=Normal, and E=Exponential. The analytical forms for these distributions are outlined in the appendix of Gelman, Carlin, Stern, and Rubin (2004a).
Table 4. Posterior Estimates
| Uniform, 2.5 percentile | Uniform, 97.5 percentile | Uniform, Mean | Somewhat informative, 2.5 percentile | Somewhat informative, 97.5 percentile | Somewhat informative, Mean | Informative, 2.5 percentile | Informative, 97.5 percentile | Informative, Mean | |
|---|---|---|---|---|---|---|---|---|---|
| 0.135 | 0.251 | 0.192 | 0.122 | 0.245 | 0.183 | 0.079 | 0.173 | 0.124 | |
| 0.043 | 0.145 | 0.091 | 0.045 | 0.148 | 0.092 | 0.03 | 0.17 | 0.09 | |
| 0.9927 | 0.9976 | 0.9951 | 0.9929 | 0.9975 | 0.9952 | 0.9922 | 0.9985 | 0.9956 | |
| 0.1 | 5.4 | 1.3 | 0.1 | 3.7 | 1.3 | 1.5 | 5.0 | 3.0 | |
| 0.33 | 0.74 | 0.49 | 0.35 | 0.82 | 0.53 | 0.54 | 1.28 | 0.83 | |
| | 0.932 | 0.966 | 0.951 | 0.933 | 0.968 | 0.953 | 0.917 | 0.955 | 0.937 |
| | 0.985 | 0.999 | 0.995 | 0.986 | 0.999 | 0.995 | 0.957 | 0.989 | 0.975 |
| 0.57 | 0.99 | 0.84 | 0.72 | 0.99 | 0.90 | 0.79 | 0.98 | 0.92 | |
| 0.949 | 0.993 | 0.980 | 0.922 | 0.980 | 0.956 | 0.887 | 0.947 | 0.921 | |
| | 1.0 | 3.6 | 1.6 | 1.01 | 1.72 | 1.22 | 1.01 | 1.25 | 1.08 |
| | 1.4 | 9.5 | 5.0 | 0.8 | 3.3 | 1.7 | 0.48 | 1.09 | 0.75 |
| | 0.897 | 0.994 | 0.948 | 0.900 | 0.995 | 0.953 | 0.940 | 1.008 | 0.981 |
| | -0.047 | 0.039 | -0.002 | -0.042 | 0.047 | 0.004 | -0.024 | 0.055 | 0.017 |
| | -0.055 | 0.051 | -0.004 | -0.062 | 0.045 | -0.010 | -0.064 | 0.027 | -0.021 |
| | 0.019 | 0.075 | 0.046 | 0.022 | 0.080 | 0.051 | 0.040 | 0.106 | 0.071 |
| | -0.015 | 0.044 | 0.011 | -0.010 | 0.058 | 0.018 | -0.006 | 0.076 | 0.028 |
| | 0.946 | 1.015 | 0.985 | 0.929 | 1.010 | 0.977 | 0.914 | 1.011 | 0.972 |
| | 0.047 | 0.114 | 0.080 | 0.042 | 0.108 | 0.075 | 0.020 | 0.083 | 0.053 |
| | 0.906 | 0.976 | 0.944 | 0.899 | 0.968 | 0.936 | 0.899 | 0.962 | 0.933 |
| | 0.021 | 0.104 | 0.060 | 0.028 | 0.112 | 0.068 | 0.043 | 0.122 | 0.079 |
| | 0.0011 | 0.0033 | 0.0020 | 0.0011 | 0.0035 | 0.0021 | 0.0011 | 0.0044 | 0.0026 |
| | 0.009 | 0.053 | 0.024 | 0.010 | 0.044 | 0.021 | 0.009 | 0.026 | 0.015 |
| | 0.0046 | 0.0073 | 0.0059 | 0.0047 | 0.0076 | 0.0060 | 0.0043 | 0.0071 | 0.0056 |
| | 0.0061 | 0.0088 | 0.0074 | 0.0061 | 0.0090 | 0.0074 | 0.0061 | 0.0089 | 0.0074 |
| | 0.0271 | 0.0386 | 0.0323 | 0.0265 | 0.0382 | 0.0318 | 0.0229 | 0.0329 | 0.0273 |
| | 0.077 | 0.099 | 0.087 | 0.077 | 0.099 | 0.087 | 0.077 | 0.100 | 0.088 |
| | 0.0012 | 0.0087 | 0.0037 | 0.0012 | 0.0090 | 0.0037 | 0.0012 | 0.0083 | 0.0036 |
| | 0.0029 | 0.0060 | 0.0043 | 0.0030 | 0.0064 | 0.0045 | 0.0034 | 0.0077 | 0.0051 |
| | 0.0105 | 0.0120 | 0.0112 | 0.0104 | 0.0119 | 0.0111 | 0.0105 | 0.0120 | 0.0113 |
Due to space limitations, Monte Carlo standard errors (MCSE) are not reported in this table. In general, they are of the same order of magnitude as those presented in Table I. The actual MCSEs are used in an approximate manner to determine the level of accuracy with which the estimates are displayed.
Figure 1. Density plots of likelihood function using 200,000 draws of the MCMC sampler.
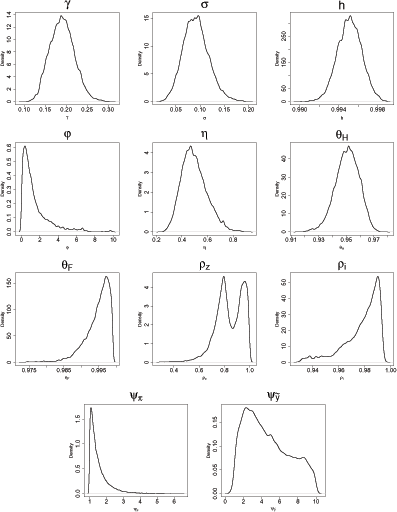
Figure 2. Log likelihood
expressed as a function of ![]() and
and
![]() (top left);
(top left);
![]() and
and
![]() (top right);
(top right);
![]() and
and ![]() (bottom).
(bottom).
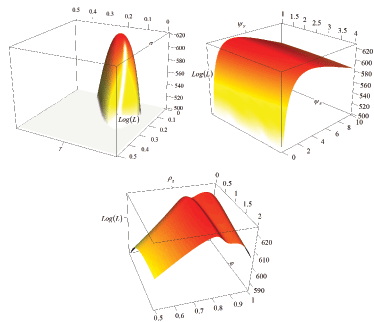
Figure 3. "Heat" plots
of log-likelihood as a function of
![]() ,
,
![]() , and
, and ![]() (left
panel); as a function of
(left
panel); as a function of ![]() ,
,![]() , and
, and
![]() (right panel). Only the
top 1% of likelihood values are made visible, with darker regions
(in red) denoting the values closest to the maximum.
(right panel). Only the
top 1% of likelihood values are made visible, with darker regions
(in red) denoting the values closest to the maximum.
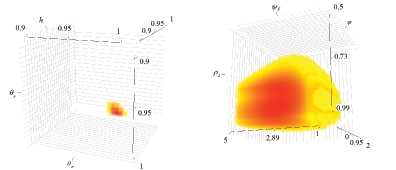
Figure 4. Parameters weakly identified by the data. Solid lines represent estimated kernel densities using 200,000 draws from the posterior distribution. Shaded regions are histograms using 200,000 draws from the uniform, somewhat informative, and informative prior distributions.
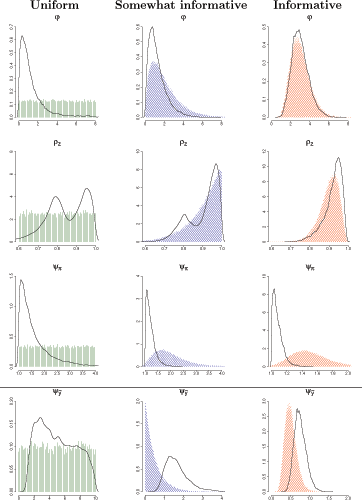
Figure 5. Posterior predictive distributions for the data. Output is expressed as percent deviation from its linear trend. Inflation, the nominal interest rate, and imported inflation are expressed as decimals.
Footnotes
* We would like to thank Federico Ravenna, Carl Walsh, Andrew Levin, Alejandro Justiniano, Doireann Fitzgerald, Luca Guerrieri, Dale Henderson, and seminar participants at the Federal Reserve Board, the Bureau of Economic Analysis, and the Small Open Economies in a Globalized World conference for their valuable feedback. Grant Long and Zachary Kurtz provided excellent research assistance. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
1. See, for example, Levin, Onatski, Williams, and Williams (2005) and Batini, Justiniano, Levine, and Perlman (2004). Return to text
2. Although, as will be discussed below, if the likelihood function is essentially flat for a parameter, the precise "maximum" found by numerical maximization may be largely arbitrary. Return to text
3. For example, Smets and Wouters (2007) estimate a DSGE model of the U.S. economy in order to examine the sources of business cycle fluctuations, and to explain the "Great Moderation" phenomenon that began in the mid 1980s. Return to text
4. Since parameter estimation was not the ultimate goal of these studies, no further attention was given to the issue of widely varying posterior estimates when more diffuse priors were used. Return to text
5. Justiniano and Perlman (2004) also obtain implausible results when estimating the literal interpretation of this model for Canada, New Zealand, and Australia. Return to text
6. The first 12 out of 142 observations (corresponding to three years of data) are used to initialize the Kalman filter. Return to text
7. More details on how to derive the likelihood function can be found in Appendix B. Return to text
8. In other words, the inverse of the Hessian is very large and the direction of the search gets blurred. Return to text
9. The goal here to is determine which parameters do not pass the local identification test. Testing for global identification is not feasible given the number of parameters and the wide range of possible values they can take. Return to text
10. We first thin Gelman, Carlin, Stern, and Rubin (2004a) the posterior distribution, by selecting every twentieth draw from the chain of 200,000 draws (for a total of 10,000 draws). Return to text
11. The Kalman filtered variables track the data closely; see Beltran (2007) for details. Return to text
12. For more details on deriving the log-linearized model and the expression for the output gap, see Beltran (2007). Return to text
13. If there are more observable
variables than structural shocks, it is as if some of the shocks
are perfectly correlated, and the matrix
![]() in the likelihood
function is singular. Return to
text
in the likelihood
function is singular. Return to
text
14. By not using Epstein-Zin preferences Epstein and Zin (1989), which disentangle the elasticity of intertemporal substitution from the degree of risk aversion in the utility function, some of the CRRA estimates from the finance literature are probably biased. Return to text
15. As explained in Kaplow (2005), the income elasticity of VSL depends on how the marginal utility cost of expenditures to protect one's life changes with income, or the rate at which marginal utility of income falls as income rises, which is essentially the same as the CRRA. In theory, though, since the value of preserving one's life increases with income, the income elasticity of VSL should exceed CRRA, making the discrepancy in the empirical estimates even more puzzling. Return to text
16. For examples of micro-based studies, see Harrigan (1993), Hummels (2001) and Baier and Bergstrand (2001). Some macro studies include Stern, Francis, and Shumacher (1976), and Deardorff and Stern (1990) and Whalley (1985). Return to text
17. They do not however, estimate Taylor rules directly. Return to text
18. Baxter and Crucini (1995) find the same results for the U.S. and Europe. Return to text
19. If the starting value is too far away from the mode, convergence may be impaired because of cliffs in the likelihood function or regions of indeterminacy. Return to text
20. During the first 150,000 iterations of the adaptive stage, the chain is still converging. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text
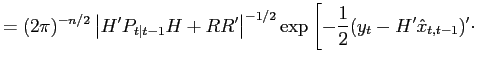
![$\displaystyle \hspace*{0.15in} \left. \left[ ( H^{ \prime} P_{ t \vert t - 1 } H + RR )^{ \prime} \right] ^{ - 1 } ( y_{t} - H^{ \prime} \hat{ x }_{ t , t - 1 } ) \right] \ ,$](img476.gif)