
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 962, First version December 2008, current version September 2009 --- Screen Reader
Version*
Uncertainty Over Models and Data: The Rise and Fall of American Inflation1
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
An economic agent who is uncertain of her economic model learns, and this learning is sensitive to the presence of data measurement error. I investigate this idea in an existing framework that describes the Federal Reserve's role in U.S. inflation. This framework successfully fits the observed inflation to optimal policy, but fails to motivate the optimal policy by the perceived Philips curve trade-off between inflation and unemployment. I modify the framework to account for data uncertainty calibrated to the actual size of data revisions. The modified framework ameliorates the existing problems by adding sluggishness to the Federal Reserve's learning: the key point is that the data uncertainty is amplified by the nonlinearity induced by learning. Consequently there is an explanation for the rise and fall in inflation: the concurrent rise and fall in the perceived Philips curve trade-off.
Keywords: Data uncertainty, data revisions, real time data, optimal control, parameter uncertainty, learning, extended Kalman filter, Markov-chain Monte Carlo
JEL classification: E01, E58
1. Introduction
A great deal of research has gone towards identifying the causes of the large swings in inflation in the United States between 1970 and 1985. One strand of literature advances the view that evolving government behavior had an important role in these events. Clarida, Gali, and Gertler (2000) and Boivin (2006), among others, provides evidence of time-varying U.S. monetary policy responses over different parts of the postwar era. Romer and Romer (1990) and Owyang and Ramey (2004) suggest that the changing response might be explained by changing Federal Reserve objectives. Alternatively, Sargent (1999) suggests that evolving Federal Reserve beliefs about the economic environment can explain the rise and fall of inflation.3
This last explanation relies on the idea that agents learn about their economic environment, as advocated by learning and expectations. In such a framework, agents' prediction errors update their beliefs, represented as the parameters to their own economic model. These prediction errors are based on the data actually observed, which may contain measurement error. The point of this paper is that agents' data uncertainty, engendered by measurement errors, affects the evolution of their beliefs. Similar to Brainard (1997), we see that this uncertainty tempers policy-makers' behavior: their learning is made more sluggish by data uncertainty.
To investigate the importance of this observation in practice, I modify the framework in Sargent, Williams, and Zha (2006) that itself extends Sargent (1999). The Federal Reserve optimally controls inflation in light of constant unemployment and inflation targets, but is unconvinced that its economic model is correct and hence changes its beliefs in response to new data. Thus the great American inflation is explained as optimal policy given changing estimates of the Federal Reserve's economic model, the Philips curve. However, those existing results suffer from three key problems. One, the Federal Reserve's unemployment rate forecasts, the basis for setting inflation, are very inaccurate, much more so than the Greenbook forecasts they should mimic. Second, the amount of estimated model uncertainty is very large, which undermines the plausibility that the Federal Reserve believed in its estimated Philips curve enough to use it as the basis for policy. Third, the framework explains the rise in inflation between 1973 and 1975, but does not give a good reason for the drastic fall in inflation between 1980 and 1984. The recent Carboni and Ellison (forthcoming) modifies Sargent, Williams, and Zha's (2006) optimal control problem to target actual Greenbook forecasts, which successfully addresses the first two problems.4 However, an explanation for the rise and fall of inflation remains missing. The results here address all three problems.
I modify the optimal control framework by assuming the Federal Reserve recognizes that data may be measured with error, the size of which I calibrate to existing evidence. In line with this, and following the general suggestion of Orphanides (2001), I differ from Sargent, Williams, and Zha (2006) and Carboni and Ellison (forthcoming) by fitting the model to real-time data. Since at least as far back as Zellner (1958) - who admonished readers to be "careful'' with "provisional'' data - the reality of data uncertainty has been clearly recognized.5 What has been less clear is the impact this data uncertainty may hold for the purposes of economic research, and this paper suggests that data uncertainty can have a sizeable effect in frameworks where agents are learning.6 Data uncertainty introduces sluggishness into Federal Reserve's learning process, and the ensuing framework is able to avoid the aforementioned problems. The Federal Reserve's model uncertainty drop significantly and the framework predicts unemployment forecasts that resemble Greenbook forecasts. Importantly, the results show a sharp drop in the perceived Philips trade-off between 1980 and 1984 that explains the concomitant fall of inflation.
The paper is organized as follows. Section 2 introduces the theory of the paper: Section 2.1 briefly analyzes the interaction of model uncertainty and data uncertainty, and Section 2.2 describes and extends Sargent, Williams, and Zha (2006) framework. Section 3 presents the estimation results both without- and including data uncertainty, and discusses how data uncertainty matters to this exercise. Section 4 concludes.
2. Theory
I briefly discuss the meanings of the terms data uncertainty and model uncertainty and explain how they may be related. Then I introduce a basic optimal control framework following Sargent, Williams, and Zha (2006) that is meant to describe Federal Reserve behavior during the 1970s-1980s. Finally, I modify the framework to explicitly account for the Federal Reserve's data uncertainty.
2.1 Why Data Uncertainty Matters
Generally speaking, the simple point made in this section is that the estimated size of modeled random shocks is positively biased by other sources of variation that are unmodeled. Moreover, the agent's learning process is nonlinear in the latent variables (that is, latent parameters multiply latent economic variables), which amplifies bias.
Suppose an agent forms a forecast of an economic quantity
![]() . The agent's model maps data and parameters
into this prediction. Model uncertainty is the situation
where past predictions and realized data might change the agent's
parameter vector going forward. Data uncertainty is the
situation where data is measured with error, maybe but not
necessarily observed after the fact. The main question here is, if
the agent is uncertain both of the model and the data, what is the
impact of the researcher ignoring the agent's data uncertainty?
. The agent's model maps data and parameters
into this prediction. Model uncertainty is the situation
where past predictions and realized data might change the agent's
parameter vector going forward. Data uncertainty is the
situation where data is measured with error, maybe but not
necessarily observed after the fact. The main question here is, if
the agent is uncertain both of the model and the data, what is the
impact of the researcher ignoring the agent's data uncertainty?
The intuition is straightforward that when the agent's forecast is correct there is nothing to change about her beliefs (her model).7 When such is the case, the agent has nothing to learn since her model's performance cannot be improved. When the forecast error is nonzero, suppose the agent has an incentive to evaluate her model and learn from the error. At this point, the agent needs to understand why the forecast error is nonzero: to answer this, let us consider the forecast error decomposition, which is the machinery that answers the question why. In the case of linear forecasters, the forecast error decomposition is a function of the modeled errors' variances. To sketch out why the ignored data uncertainty biases up the researcher's estimate of the agent's model uncertainty, we turn to a simple example.
Let
![]() be a normal error associated with the
agent-predicted parameter vector
be a normal error associated with the
agent-predicted parameter vector ![]() ,
,
![]() be a normal error associated
with the agent-predicted data vector
be a normal error associated
with the agent-predicted data vector ![]() ,
,
![]() be a normal error, all errors be mean
zero, and each error be uncorrelated with the others.8
Suppose that the true data generating process is
be a normal error, all errors be mean
zero, and each error be uncorrelated with the others.8
Suppose that the true data generating process is
![]() . The agent knows this specification of the data generating process
and makes a linear forecast
. The agent knows this specification of the data generating process
and makes a linear forecast
![]() . Finally, the
agent knows that
. Finally, the
agent knows that
![]() is given by
is given by
where
![]() ,
,
![]() , and
, and
![]() , and these three quantities are known
to the agent.9
, and these three quantities are known
to the agent.9
However the researcher ignores the agent's data uncertainty,
which means he assumes that
![]() . So the researcher
decomposes the forecast error variance as
. So the researcher
decomposes the forecast error variance as
![]() . But
. But
and it becomes clear that there will be a positive bias to his
estimates due to the presence of the ignored ![]() and
and ![]() .
.
A function relating Var![]() to
to
![]() and
and ![]() requires some knowledge about how these quantities are related.
Writing the matrix
requires some knowledge about how these quantities are related.
Writing the matrix
![\begin{displaymath}\left( \begin{array}[c]{cc} \mbs{P} & \mbs{0}\ \mbs{0} & \sigma^{2} \end{array}\right) = \delta\mbs{D}\end{displaymath}](img28.gif) , assume that the researcher knows the true
, assume that the researcher knows the true ![]() (determining the correlation structure and relative proportions of
the variances), but must estimate the scalar
(determining the correlation structure and relative proportions of
the variances), but must estimate the scalar ![]() (determining the scale of the variances). It is easy
to see the researcher's estimate is related to the truth by
(determining the scale of the variances). It is easy
to see the researcher's estimate is related to the truth by
This algebra is directly related to frameworks that specify that economic agents are learning, and thus involve filtering. At each point in time the filter delivers conditional means (the data and parameter predictions) and conditional covariance matrices (the errors' covariance structure). The forecast is a function of the means, and the forecast error is decomposed by a gain matrix that is a function of the covariance matrices. Obviously, the gain matrix can only decompose the observed forecast error to sources that are modeled, and so those sources are inferred to have taken on a larger realization than they actually did.
The key idea is that this bias is a nonlinear function of the covariance matrix of the data errors, and so amplification of small (in terms of variance) data uncertainty is possible. It is a different matter to say whether or not this amplification happens in practice, and to investigate that possibility we turn to the next section.
2.2 The Federal Reserve's Optimal Control Problem
Why did inflation rise and fall so dramatically in the United States between 1973 and 1984? Sargent, Williams, and Zha (2006) reverse engineer Federal Reserve Philips curve beliefs that explain inflation as an optimal policy. The Federal Reserve's model evolves because we assume the Federal Reserve is learning about the Philips curve. In light of the previous section, it is worth asking if the exclusion of data uncertainty significantly affects the framework's predictions. We will see in Section 3 that the answer to this question is, yes. But first we describe Sargent, Williams, and Zha's (2006) framework, and then modify it to explicitly account for Federal Reserve data uncertainty.
The Federal Reserve has a dual mandate to keep both the unemployment rate and the inflation rate at target. Directly following Sargent, Williams, and Zha (2006), the Federal Reserve's objective function is written
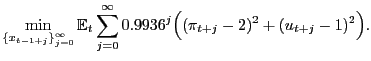 |
(2.1) |
Setting the inflation and unemployment targets to Sargent, Williams, and Zha's (2006) values delivers the attractive message that the Federal Reserve has always tried to lower inflation and unemployment while retaining the tractable quadratic objective function. The important message of this equation is that the Federal Reserve has always had the same inflation and unemployment targets.
To achieve this objective, the Federal Reserve controls the rate
of inflation up to an exogenous shock. Therefore the annualized
inflation rate ![]() is
is
| (2.2) |
where ![]() is the part of inflation controllable
by the Federal Reserve using information through time
is the part of inflation controllable
by the Federal Reserve using information through time ![]() , and
, and
![]() is an exogenous
shock.
is an exogenous
shock.
In order to understand the relationship between inflation (which can be somewhat directly controlled) and the unemployment rate (which cannot be directly controlled), the Federal Reserve uses a Philips curve model. However, at any point in time the Federal Reserve is uncertain that its estimated model is correct, and so is constantly learning and updating its model estimate. We accomplish this by assuming the parameters follow a random walk, which introduces model uncertainty (and a motivation for learning) following the basic idea of Cooley and Prescott (1976):
![$\displaystyle = \boldsymbol{\alpha}^{\prime}_{t-1} \left( \begin{array}[c]{c} \pi_{t}\\ \pi_{t-1}\\ u_{t-1}\\ \pi_{t-2}\\ u_{t-2}\\ 1 \end{array} \right) + \zeta_{2} \epsilon_{2t} \equiv\boldsymbol{\alpha}^{\prime}_{t-1} \boldsymbol{\Phi}_{t} + \zeta_{2} \epsilon_{2t}$](img39.gif) |
(2.3) |
| (2.4) |
Because the parameters follow a random walk whose steps are
independent of everything else, the Federal Reserve's estimate of
![]() is also its
estimate of
is also its
estimate of
![]() ;
thus we solve the problem for each period
;
thus we solve the problem for each period ![]() using
"anticipated utility'', following conquestamericaninflation and
Sargent, Williams, and Zha (2006). Hence, the time
using
"anticipated utility'', following conquestamericaninflation and
Sargent, Williams, and Zha (2006). Hence, the time ![]() solution to the
dynamic programming problem is found by using the Philips curve
estimate
solution to the
dynamic programming problem is found by using the Philips curve
estimate
![]() as the law
of motion for all
as the law
of motion for all ![]() ; the time
; the time ![]() plugs in the estimate
plugs in the estimate
![]() ; and so
forth.
; and so
forth.
Without Data Uncertainty If we assume the Federal Reserve ignores data measurement error, and therefore has no data uncertainty, then the Federal Reserve's Philips curve estimates are the solution to a linear filtering problem:10
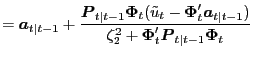 |
(2.5) |
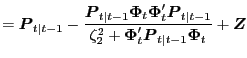 |
(2.6) |
where
![]() . The information actually available to the Federal Reserve at time
. The information actually available to the Federal Reserve at time
![]() is
is
![]() , which are the available real-time data on inflation and
unemployment rates (cf. ?). When the Federal Reserve
ignores measurement error, it assumes that the real-time data are
the true values of the economic variables; that is,
, which are the available real-time data on inflation and
unemployment rates (cf. ?). When the Federal Reserve
ignores measurement error, it assumes that the real-time data are
the true values of the economic variables; that is,
![]() and
and
![]() .
.
Including Data Uncertainty On the other hand, there is evidence that data, particularly real-time, is subject to measurement error. Macroeconomic data get revised (cf. Croushore and Stark (2001)), and data collection agencies document and publicly analyze collection errors. It is reasonable to suppose a well-informed policy-maker, such as the Federal Reserve, associates some uncertainty to the observed real-time data.
This modification makes latent both the true values of economic
variables and the true values of economic model parameters.
Therefore the state-space will be nonlinear in the state variables
due to the Philips curve, where latent data multiply latent
parameters. This nonlinearity in the transition equation for the
optimal control problem spreads also to the optimal policy rule
equation delivering the Federal Reserve's inflation control
variable ![]() (which, due to the unpredictability
of
(which, due to the unpredictability
of
![]() , is also the forecast of
, is also the forecast of
![]() ). I choose to put both of these
nonlinear equations in the state equation and leave the observation
equation linear.11 The interesting state equations
are
). I choose to put both of these
nonlinear equations in the state equation and leave the observation
equation linear.11 The interesting state equations
are
| (2.7) |
| (2.8) |
| (2.9) |
(2.7), (2.8), and (2.9) repeat (2.2),
(2.3), and (2.4),
respectively, and ![]() is written explicitly
as the optimal policy function depending on latent state variables.
is written explicitly
as the optimal policy function depending on latent state variables.
Turning to the observation equations, we have
| (2.10) |
| (2.11) |
where
![\begin{displaymath}\left( \begin{array}[c]{c} \varepsilon_{4 t}\ \varepsilon_{5t} \end{array}\right) \sim iid\left( \left[ \begin{array}[c]{c} \mu_{4}\ \mu_{5} \end{array}\right] , \left[ \begin{array}[c]{cc} \zeta_{4}^{2} & 0\ 0 & \zeta_{5}^{2} \end{array}\right] \right) \end{displaymath}](img73.gif) , a distribution that is calibrated to evidence presented in
Section 3.3.
, a distribution that is calibrated to evidence presented in
Section 3.3.
3. Empirical Results
In this section we estimate the two frameworks described above. The results without data uncertainty in Section 3.2 are similar to the Sargent, Williams, and Zha's (2006) results. I describe three problems that emerge from these results and propose to address them by modifying the model so as to allow the Federal Reserve to explicitly account for data measurement error. Then Section 3.3 calibrates the amount of data uncertainty to existing evidence and presents estimated results that ameliorates the three fore mentioned problems. The final section discusses how the problems were ameliorated.
3.1 Estimation
The Extended Kalman filter approximates the state space model using a Taylor-expansion about the linear prediction of the state, as suggested by Anderson and Moore (1979) and following Tanizaki (1996). I have found little difference in practice between the first-order and second-order expansions and use the former to computational simplicity. In the interest of exposition, discussion of the Extended Kalman filter and the likelihood is put in Appendix A.I.
The parameter estimated is
where
Chol![]() is the Cholesky factor of positive
definite matrix.12 Because of
is the Cholesky factor of positive
definite matrix.12 Because of
![]() 's large dimension, I follow
Sargent, Williams, and Zha (2006) and use a Bayesian empirical method discussed in
Appendix A.III: a Markov-Chain
Monte Carlo algorithm using the Metropolis-Hastings algorithm with
random walk proposals to draw from the posterior
distribution13
's large dimension, I follow
Sargent, Williams, and Zha (2006) and use a Bayesian empirical method discussed in
Appendix A.III: a Markov-Chain
Monte Carlo algorithm using the Metropolis-Hastings algorithm with
random walk proposals to draw from the posterior
distribution13
| (3.1) |
where
![]() is the prior and
is the prior and
![]() is the
likelihood (in Appendix A.I). From the
simulated posterior distribution I report medians as my point
estimates and quantiles as probability intervals for the
parameters. Following Sargent, Williams, and Zha (2006),
is the
likelihood (in Appendix A.I). From the
simulated posterior distribution I report medians as my point
estimates and quantiles as probability intervals for the
parameters. Following Sargent, Williams, and Zha (2006),
![]() is set to a
regression estimate from presample data.
is set to a
regression estimate from presample data.
Here we must note a distinction between the framework with and
without data uncertainty. Without data uncertainty, the parameters
![]() and
and
![]() can be scaled
together with no effect on the likelihood - there is an
unidentification problem. Sargent, Williams, and Zha (2006) note this problem and
overcome it by assuming that
can be scaled
together with no effect on the likelihood - there is an
unidentification problem. Sargent, Williams, and Zha (2006) note this problem and
overcome it by assuming that ![]() is
one-tenth the size of the standard deviation of a structural
equation for the unemployment rate that they additionally
estimate.14 Because this structural equation has
nothing to do with the Federal Reserve's belief-generating
mechanism, I refrain from specifying it at all, just as
Carboni and Ellison (forthcoming) refrain during the analysis of their third and
fourth sections.
is
one-tenth the size of the standard deviation of a structural
equation for the unemployment rate that they additionally
estimate.14 Because this structural equation has
nothing to do with the Federal Reserve's belief-generating
mechanism, I refrain from specifying it at all, just as
Carboni and Ellison (forthcoming) refrain during the analysis of their third and
fourth sections.
Table 1: Parameter Estimates without Data Uncertainty - ![]() : Standard Deviations and Correlations
: Standard Deviations and Correlations
| 0.2959 | -0.9854 | 0.1539 | 0.8839 | -0.1088 | -0.2848 |
| 0.2796 | -0.0762 | -0.8792 | 0.1675 | 0.3918 | |
| 0.1611 | 0.3821 | 0.8009 | 0.7949 | ||
| 0.1901 | 0.2922 | -0.0387 | |||
| 0.3224 | 0.7471 | ||||
| 5.0793 |
![]() :0.21, (0.20, 0.22)
:0.21, (0.20, 0.22)
![]() : 0.23
: 0.23
Notes on table 1: median of posterior distribution. ![]() is the standard deviation of
is the standard deviation of
![]() , the additive shock to the
Federal Reserve's inflation control;
, the additive shock to the
Federal Reserve's inflation control; ![]() is the
standard deviation of the additive shock in the Federal Reserve's
Philips curve, and is imposed as the value estimated in the model
including data uncertainty (Table 2). 95%
probability intervals in parentheses. The bottom array is comprised
as follows: the main diagonal are the square roots of the main
diagonal of
is the
standard deviation of the additive shock in the Federal Reserve's
Philips curve, and is imposed as the value estimated in the model
including data uncertainty (Table 2). 95%
probability intervals in parentheses. The bottom array is comprised
as follows: the main diagonal are the square roots of the main
diagonal of ![]() ; the off-diagonal elements are
the correlations derived from
; the off-diagonal elements are
the correlations derived from ![]() ;
; ![]() is the covariance matrix of the
is the covariance matrix of the
![]() shock to the
time-varying Philips curve parameters
shock to the
time-varying Philips curve parameters
![]() . The vector
. The vector
![]() multiplies
multiplies
![]() .
.
Instead, we note that in the framework including data
uncertainty ![]() is separately identified from
is separately identified from
![]() and
and
![]() . This identification
follows from the fact that changes in
. This identification
follows from the fact that changes in
![]() and
and
![]() affect the optimal
control policy rule while changes in
affect the optimal
control policy rule while changes in ![]() have
no such effect. The inflation equation (2.7)
will therefore respond differently to
have
no such effect. The inflation equation (2.7)
will therefore respond differently to
![]() and
and
![]() than to
than to ![]() , and therefore the likelihood will respond
differently, and thus
, and therefore the likelihood will respond
differently, and thus
![]() and
and
![]() are separately
identified. Of course, since the effect of
are separately
identified. Of course, since the effect of
![]() dies out rapidly,
the evolution of beliefs is almost solely directed by the estimate
of
dies out rapidly,
the evolution of beliefs is almost solely directed by the estimate
of
![]() , which allows for
identification between
, which allows for
identification between
![]() and
and
![]() . Therefore, I impose that the
value for
. Therefore, I impose that the
value for ![]() in the framework without data
uncertainty is equal to the estimate from the framework including
data uncertainty. Moreover, I place the estimates of
in the framework without data
uncertainty is equal to the estimate from the framework including
data uncertainty. Moreover, I place the estimates of
![]() in Appendix A.I because this
parameter is far less important to the story and point of the paper
than are
in Appendix A.I because this
parameter is far less important to the story and point of the paper
than are ![]() ,
, ![]() , and
, and ![]() .
.
3.2 Without Data Uncertainty
Data on inflation and the civilian unemployment rate for ages 16
and older comes from the ALFRED, a real-time data archive
established by the St. Louis Federal Reserve Bank. Table 1
displays the estimates for the framework without data uncertainty
as the posterior median of 700,000 MCMC iterations from two
separate runs of 400,000 with different initial conditions where
the first 50,000 of each run is burned.15 The estimates in
Table 1, and the
following figures, are qualitatively similar to those of
Sargent, Williams, and Zha (2006). However, they are not identical since I use
real-time data and calibrate ![]() to a
different value.
to a
different value.
Figure 1: Real-Time Inflation vs. Federal Reserve Control, Without Data Uncertainty
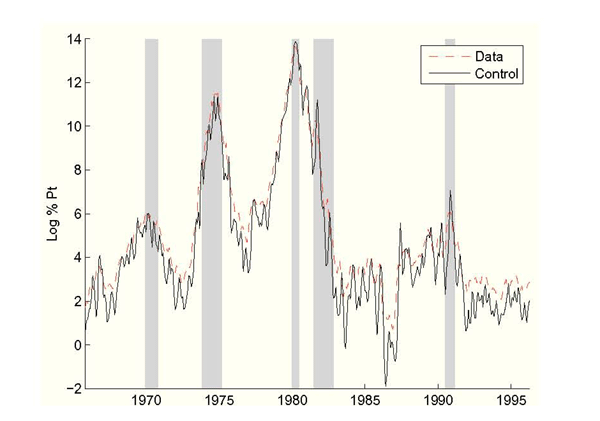
Figure 1 shows the predicted inflation control choices. Figure 1 shows the
Federal Reserve choosing to set inflation high in the two
high-inflation episodes of the mid 1970s and early 1980s. With ![]() estimated at about
1/5 the Federal Reserve believes
that it has rather tight control of inflation.
estimated at about
1/5 the Federal Reserve believes
that it has rather tight control of inflation.
The Philips curve beliefs
![]() are used to forecast the
next month's unemployment rate for any inflation control setting.
According to the model, the Federal Reserve sets inflation with
this forecast in mind. Therefore an important aspect of the model-predicted Federal
Reserve beliefs are what they deliver in terms of unemployment
forecasts: these are plotted in Figure 2. These
forecasts have a bias of -2.13 percentage points and a
root mean squared error of 2.71 percentage points. Both the bias
and the volatility are due to the estimated Philips curve
parameters. A volatile estimated evolution for the natural rate of
unemployment, plotted in Figure 3,
accounts for the large fluctuations.16 Meanwhile, the bias is due to a persistent and large estimated
Philips curve trade-off, a point to which I return in Section
3.4.17
are used to forecast the
next month's unemployment rate for any inflation control setting.
According to the model, the Federal Reserve sets inflation with
this forecast in mind. Therefore an important aspect of the model-predicted Federal
Reserve beliefs are what they deliver in terms of unemployment
forecasts: these are plotted in Figure 2. These
forecasts have a bias of -2.13 percentage points and a
root mean squared error of 2.71 percentage points. Both the bias
and the volatility are due to the estimated Philips curve
parameters. A volatile estimated evolution for the natural rate of
unemployment, plotted in Figure 3,
accounts for the large fluctuations.16 Meanwhile, the bias is due to a persistent and large estimated
Philips curve trade-off, a point to which I return in Section
3.4.17
Figure 2: Real-Time Unemployment vs. Federal Reserve Forecasts, Without Data Uncertainty
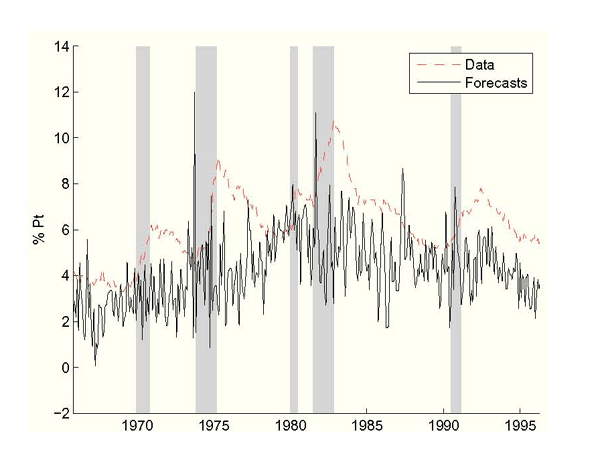
Notes: Step-Ahead unemployment forecasts come from Phillips curve (2.3) using the Federal Reserve's inflation setting and real-time unemployment and inflation data. NBER recessions shaded.
Figure 3: Natural Rate of Unemployment, Without Data Uncertainty
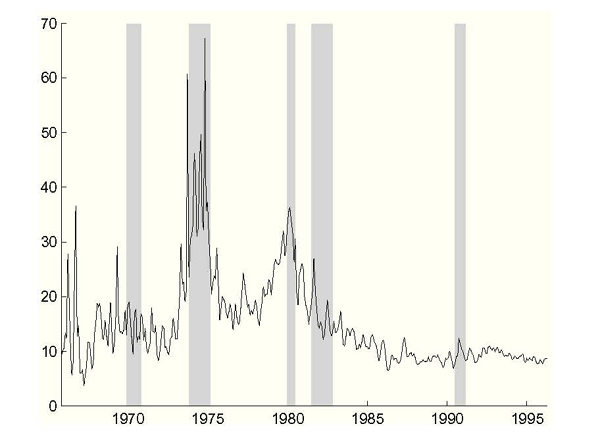
Notes: Estimated natural rate of unemployment from the Philips curve (2.3) using the Federal Reserve's inflation setting and real-time unemployment and inflation data. NBER recessions shaded.
These unemployment rate forecasts should explain actual Federal
Reserve unemployment rate forecasts because this framework explains
high inflation as Federal Reserve policy that attempts to bring
down unemployment. Therefore, it is informative to compare the
predicted forecasts to actual Greenbook forecasts over this time
span.18 A simple test of similarity between
these forecasts is Diebold and Mariano's (1995). Their statistic ![]() is a two-sided test of the null hypothesis that the
predicted unemployment forecasts have accuracy equal to the
Greenbook forecasts and
is a two-sided test of the null hypothesis that the
predicted unemployment forecasts have accuracy equal to the
Greenbook forecasts and ![]() has an asymptotic
standard normal distribution. Here
has an asymptotic
standard normal distribution. Here
![]() , so we can
reject the null of equal forecasting accuracy at the 99% level.
This suggests that the predicted forecasts are unlike the Greenbook
forecasts they should mimic.
, so we can
reject the null of equal forecasting accuracy at the 99% level.
This suggests that the predicted forecasts are unlike the Greenbook
forecasts they should mimic.
The large unemployment forecast errors drive up the estimated
standard deviation of the time-varying Philips curve. Notice that
the estimated ![]() implies that the Federal
Reserve believes that every month the constant parameter is very
volatile. Since this parameter drives the natural rate of
unemployment, this result can be interpreted as saying the Federal
Reserve believed there was on any given month about a 30% chance
that the natural rate of unemployment would jump by 5 percentage
points!19 This is borne out in the volatility
of the Federal Reserve's estimated natural rate of inflation
plotted in Figure 3. In addition,
the estimated natural rate of unemployment shoots up to
unreasonable values during the early 1970s as inflation rose, the
Federal Reserve tried to exploit a large perceived Philips
trade-off, but unemployment continued to rise. In other words, the
Federal Reserve has several reasons to disbelieve this Philips
curve model.
implies that the Federal
Reserve believes that every month the constant parameter is very
volatile. Since this parameter drives the natural rate of
unemployment, this result can be interpreted as saying the Federal
Reserve believed there was on any given month about a 30% chance
that the natural rate of unemployment would jump by 5 percentage
points!19 This is borne out in the volatility
of the Federal Reserve's estimated natural rate of inflation
plotted in Figure 3. In addition,
the estimated natural rate of unemployment shoots up to
unreasonable values during the early 1970s as inflation rose, the
Federal Reserve tried to exploit a large perceived Philips
trade-off, but unemployment continued to rise. In other words, the
Federal Reserve has several reasons to disbelieve this Philips
curve model.
These results cast doubt on the economic story that the Federal
Reserve's Philips curve beliefs motivated high inflation. The
estimates imply the Federal Reserve perceived its Philips curve
model as unstable, and the model delivers implausible estimates of
the natural rate of unemployment and poor forecasts. Given the
large estimate of
![]() and
and ![]() and the poor forecasting performance, it seems implausible that the
Federal Reserve would have tried to exploit a Philips curve
trade-off by letting inflation achieve the heights it did.
Moreover, even if the Federal Reserve did believe its estimated
Philips curve enough to use it as a basis for policy, we will see
below that this framework's estimated Philips curve trade-off does
not explain inflation's rise and fall.
and the poor forecasting performance, it seems implausible that the
Federal Reserve would have tried to exploit a Philips curve
trade-off by letting inflation achieve the heights it did.
Moreover, even if the Federal Reserve did believe its estimated
Philips curve enough to use it as a basis for policy, we will see
below that this framework's estimated Philips curve trade-off does
not explain inflation's rise and fall.
3.3 Including Data Uncertainty
I propose to modify the framework by allowing the Federal Reserve to explicitly account for measurement error in the data it observes, and argue that so doing is natural for two reasons. First and most importantly, we have data on measurement errors. Much macroeconomic data is revised and this issue is common knowledge in policy and forecasting discussions (e.g. Cunningham, Jeffery, Keptanios, and Labhard (2007), Pesaran and Timmermann (2005). Secondly, Section 2.1's analysis suggested that unmodeled data uncertainty could increase the estimated volatility of an agent's beliefs, which apparently is a problem for the optimal control framework as it now stands.
I introduce data uncertainty through the measurement errors
![]() in (2.10)-(2.11) whose
distribution I calibrate. To do this, I look at the revision
between the first-reported value of the data and the recent vintage
(circa 2008). Making the assumption - ubiquitous in macroeconomics
- that the recent data vintage is more accurate than the real-time
data, I define the measurement error as the observed revision.
These revisions' statistical properties (c.f. Aruoba (2005) calibrate
the measurement error stochastic process:
in (2.10)-(2.11) whose
distribution I calibrate. To do this, I look at the revision
between the first-reported value of the data and the recent vintage
(circa 2008). Making the assumption - ubiquitous in macroeconomics
- that the recent data vintage is more accurate than the real-time
data, I define the measurement error as the observed revision.
These revisions' statistical properties (c.f. Aruoba (2005) calibrate
the measurement error stochastic process:
![\begin{displaymath} \left( \begin{array}[c]{c} \mu_{4}\ \mu_{5} \end{array}\right) = \left( \begin{array}[c]{c} \-0.005\ 0 \end{array}\right) , \left( \begin{array}[c]{cc} \zeta_{4}^{2} & 0\ 0 & \zeta_{5}^{2} \end{array}\right) = \left( \begin{array}[c]{cc} 0.106^{2} & 0\ 0 & 0.112^{2} \end{array}\right) . \end{displaymath}](img140.gif)
Obviously, the amount of data uncertainty is small.
Table 2 reports
estimates for the framework including data uncertainty from the
posterior median of 700,000 MCMC iterations from two separate runs
of 400,000 with different initial conditions where the first 50,000
of each run is burned. Figure 4 shows that
the Federal Reserve's inflation control explains the rise and fall
of American inflation.
Once again the estimate of ![]() implies
the Federal Reserve believes its inflation control is quite good.
Turning now to the Federal Reserve's unemployment rate forecasts in
Figure 4, we find a far
different picture than in the framework without data uncertainty.
The Federal Reserve's forecasts are considerably more accurate than
before, with insignificant bias and a RMSE of 0.30 percentage
points.20
implies
the Federal Reserve believes its inflation control is quite good.
Turning now to the Federal Reserve's unemployment rate forecasts in
Figure 4, we find a far
different picture than in the framework without data uncertainty.
The Federal Reserve's forecasts are considerably more accurate than
before, with insignificant bias and a RMSE of 0.30 percentage
points.20
Again, seeing as the model forecasts are intended to predict the
Federal Reserve's actual forecasts, we can directly compare them to
Greenbook unemployment rate forecasts. Again using Diebold and Mariano's (1995) test
we find
![]() and we accept
the hypothesis that the model forecasts and Greenbook forecasts are
equally accurate: by this measure the predicted unemployment rate
forecasts are statistically indistinguishable from actual Greenbook
forecasts.
and we accept
the hypothesis that the model forecasts and Greenbook forecasts are
equally accurate: by this measure the predicted unemployment rate
forecasts are statistically indistinguishable from actual Greenbook
forecasts.
Table 2: Parameter Estimates, Including Data Uncertainty -
![]() : Standard Deviations and Correlations
: Standard Deviations and Correlations
| 0.0106 | 0.9665 | -0.9746 | -0.8234 | 0.9520 | -0.1226 |
| 0.0211 | -0.9894 | -0.9395 | 0.9541 | 0.0005 | |
| 0.0566 | 0.8950 | -0.9870 | 0.1251 | ||
| 0.0128 | -0.8334 | -0.2346 | |||
| 0.0475 | -0.2685 | ||||
| 0.2351 | |||||
![]() : 0.22, (0.20, 0.25)
: 0.22, (0.20, 0.25)
![]() : 0.23, (0.21, 0.26)
: 0.23, (0.21, 0.26)
Notes: median of posterior distribution. ![]() is the standard deviation of
is the standard deviation of
![]() , the additive shock to the
Federal Reserve's inflation control;
, the additive shock to the
Federal Reserve's inflation control; ![]() is the
standard deviation of the additive shock in the Federal Reserve's
Philips curve. 95% probability intervals in parentheses. The bottom
array is comprised as follows: the main diagonal are the square
roots of the main diagonal of
is the
standard deviation of the additive shock in the Federal Reserve's
Philips curve. 95% probability intervals in parentheses. The bottom
array is comprised as follows: the main diagonal are the square
roots of the main diagonal of ![]() ; the
off-diagonal elements are the correlations derived from
; the
off-diagonal elements are the correlations derived from ![]() ;
; ![]() is the covariance matrix of
the
is the covariance matrix of
the
![]() shock to the
time-varying Philips curve parameters
shock to the
time-varying Philips curve parameters
![]() . The vector
. The vector
![]() multiplies
multiplies
![]() .
.
Figure 4: Real-Time CPI Inflation vs. Federal Reserve Control, Including Data Uncertainty
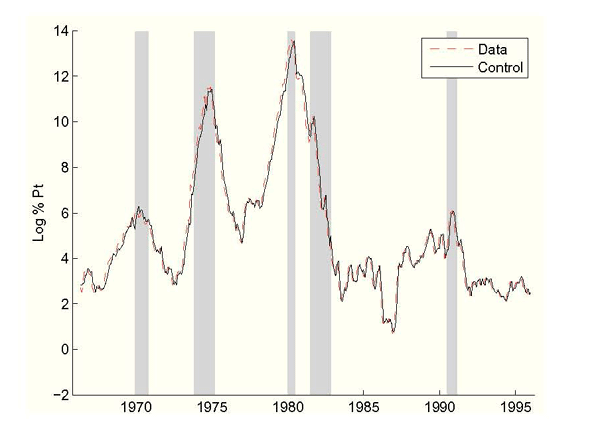
Notes: Real-time CPI inflation and model predicted Federal Reserve inflation control. NBER recessions shaded.
The estimate of
![]() in Table 2 is
much smaller than before. For instance, the estimated
in Table 2 is
much smaller than before. For instance, the estimated ![]() implies that the Philips curve's intercept has a
monthly shock with a standard deviation of about 20 unemployment
rate basis points as opposed to the 500 basis points we saw before.
Roughly speaking, the shocks are smaller by a factor of 8 for
inflation parameters, a factor of 5 for unemployment parameters,
and a factor of 20 for the constant parameter. Now the estimated
natural rate of unemployment, plotted in Figure 6, is
much less volatile and does not shoot off to the ethereal levels it
attain before, although still it elevates implausibly high.
implies that the Philips curve's intercept has a
monthly shock with a standard deviation of about 20 unemployment
rate basis points as opposed to the 500 basis points we saw before.
Roughly speaking, the shocks are smaller by a factor of 8 for
inflation parameters, a factor of 5 for unemployment parameters,
and a factor of 20 for the constant parameter. Now the estimated
natural rate of unemployment, plotted in Figure 6, is
much less volatile and does not shoot off to the ethereal levels it
attain before, although still it elevates implausibly high.
Figure 5: Real-Time Unemployment vs. Federal Reserve Forecast, Including Data Uncertainty
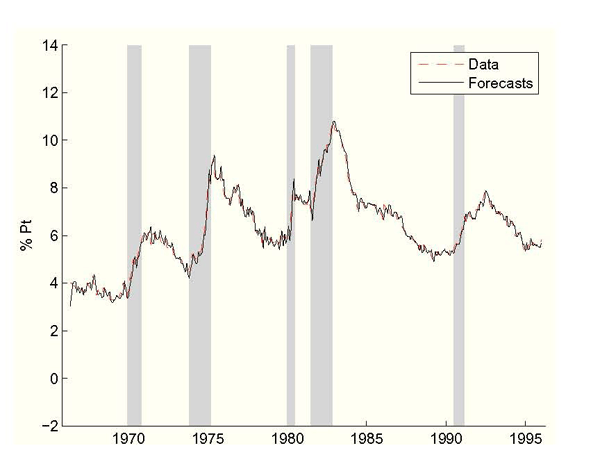
Notes: Step-ahead unemployment forecasts come from the Philips curve (2.3) using the Federal Reserve's inflation setting and real-time unemployment and inflation data. NBER recessions shaded.
Figure 6: Natural Rate of Unemployment, Including Data Uncertainty
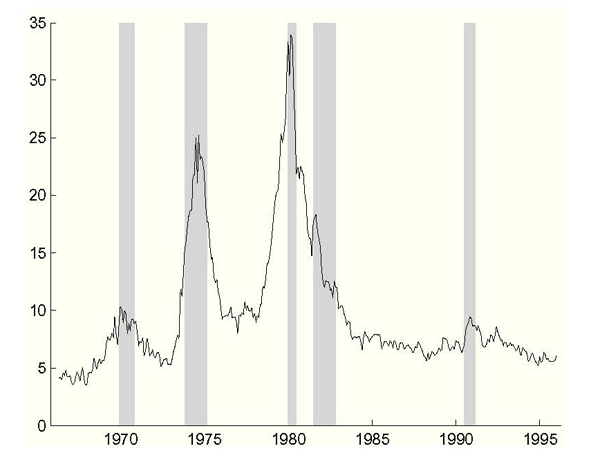
Notes: Estimated natural rate of unemployment from the Philips curve (2.3) using the Federal Reserve's inflation setting and estimated values of past values of the unemployment and inflation rates. NBER recessions shaded.
Figure 7: Evolution of the Philips Curve Trade-Off
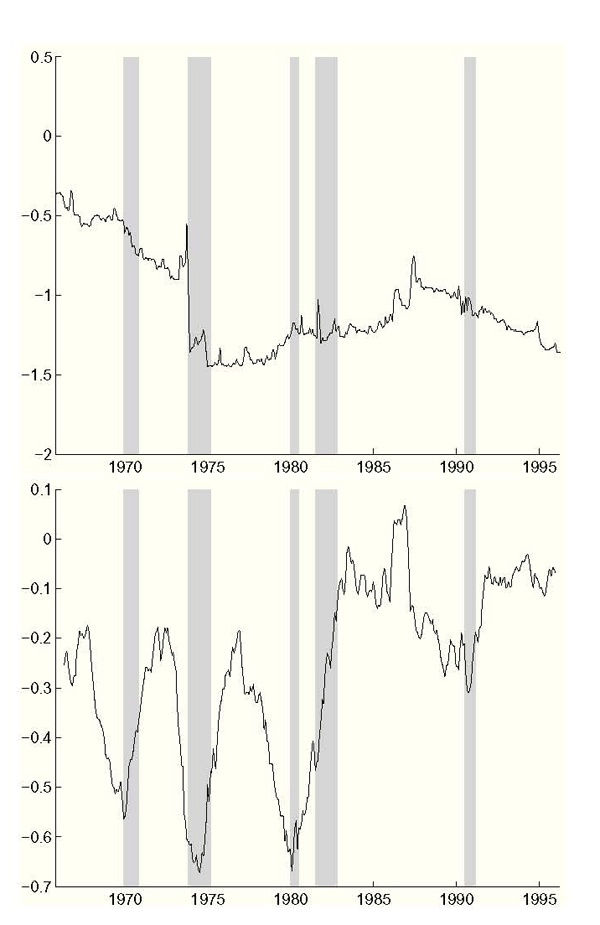
Notes: Top Panel: From framework without data uncertainty, sum of Philips curve inflation coefficient estimates. Bottom Panel: From framework including data uncertainty, sum of Philips curve inflation coefficient estiamtes. NBER recessions are shaded.
Let us turn now to the predicted evolution of the Federal Reserve's beliefs about the Philips curve trade-off, which is the sum of the coefficients on inflation in the Philips curve. As seen in the top panel of Figure 7, the trade-off in the framework without data uncertainty experiences a large jump between 1973 and 1975 which explains the great rise in inflation over those years. Thereafter the trade-off stays high, with no sharp activity around the disinflation of the early 1980s. But this does not bear out the main story, which is that the evolution of the Philips curve trade-off led to the rise and fall of inflation. In the framework without data uncertainty, the dramatic fall of inflation from 14.4 to 2.2% between 1980 and 1984 occurs without any sharp change in the Federal Reserve's beliefs.21
On the other hand, consider the trade-off in the framework including data uncertainty, depicted in the bottom panel of Figure 7. Here the we predict a drastic drop in the Philips curve trade-off starting around 1980. As this perceived trade-off diminishes, inflation falls by than 80% off its peak going into 1984.22 Thus, the framework including data uncertainty describes a consistent connection between the Federal Reserve's inflation control and the Federal Reserve's beliefs about the Philips curve trade-off.
3.4 Discussion
How can such a small amount of data uncertainty change the results? There are two parts to the answer. Firstly, introducing measurement error into the learning framework creates a nonlinearity (recall Section 2.1) that amplifies the modest amount of data uncertainty into a largely biased estimate of model uncertainty. Secondly, the evident data uncertainty is actually a fair bit larger than the Federal Reserve's model uncertainty (particularly the variances of the parameters on inflation and unemployment in the Philips curve) to begin with.
By ignoring the Federal Reserve's data uncertainty, we overestimate the size of the shocks to the Philips curve coefficients on inflation and unemployment. Therefore, these parameters shift a lot from period to period in response to the large unemployment rate forecast errors; hence, there are shifts in the optimal policy rule's dependence on past inflation and unemployment. But inflation over this period is rather persistent: so each period ceteris paribus the current optimal policy should be somewhat near last period's policy in order to fit the data. So the constant in the Philips curve adjusts to offset the change in the policy rule engendered by the shifting Philips curve coefficients on inflation and unemployment.
These measurement errors work differently than do the shocks
![]() appearing in
the inflation control and Philips curve equation: they make the
values of past inflation and unemployment latent. Therefore, their
presence helps to explain forecast errors for several periods
because past (true) values of inflation and unemployment enter the
forecast rule. Therefore the Federal Reserve is more sluggish to
change its Philips curve estimate on the basis of the observed
forecast errors, inferring that some of this forecast error may be
due to measurement error in past values of inflation and
unemployment on which the forecast is based. The important
characteristic of data uncertainty is that these past economic
variables remain latent to the agent for some time.
appearing in
the inflation control and Philips curve equation: they make the
values of past inflation and unemployment latent. Therefore, their
presence helps to explain forecast errors for several periods
because past (true) values of inflation and unemployment enter the
forecast rule. Therefore the Federal Reserve is more sluggish to
change its Philips curve estimate on the basis of the observed
forecast errors, inferring that some of this forecast error may be
due to measurement error in past values of inflation and
unemployment on which the forecast is based. The important
characteristic of data uncertainty is that these past economic
variables remain latent to the agent for some time.
These results highlight two main points in favor of explicitly including data uncertainty in economic frameworks that specify agents' model uncertainty. Firstly, the nonlinearity of a framework with learning amplifies small amounts of data uncertainty. By explicitly accounting for the data uncertainty, we obtain an intuitive message that is similar to Brainard's (1967) point that a policy-maker's model uncertainty leads to an optimal "dampening'' of her policies: here the point is that a policy-maker's data uncertainty leads to an optimal "dampening'' of her learning. As we have just seen, an economic researcher may make substantially different inferences depending on whether or not data uncertainty is accounted for, even if the amount of uncertainty they would ignore is small.
Second and perhaps more importantly, we are able to discipline this "dampening'' with the facts. We have evidence, one form of which are data revisions, to point to when discussing data uncertainty and ascertaining how large it may be. The role of data uncertainty can be disciplined by observables, and this makes it a potentially constructive part of learning frameworks. In fact, this quality positively distinguishes the concept of data uncertainty from the concept of model uncertainty, which has little if any such evidence to discipline its role.23
4. Conclusion
This paper analyzes the effects of data uncertainty in frameworks with agents who learn. Ignoring data uncertainty can bias estimates of agents' model uncertainty. I investigate the importance of this point by extending the framework of Sargent, Williams, and Zha (2006) and showing that the explicit modeling of data uncertainty remedies some well-known issues with that paper's results. The mechanism by which data uncertainty matters is through introducing sluggishness into the Federal Reserve's learning. Once this is the case, the framework predicts that the inflation of the 1970s and 1980s can be explained by evolving beliefs about the Philips curve trade-off between inflation and unemployment.
References
Anderson, B. D. O., and J. B. Moore (1979): Optimal Filtering. Prentice-Hall.
Andrews, D. W. K. (1991): "Heteroskedasticity and Autocorrelation Consistent Covariance Matrix Estimation," Econometrica, 59(2), 817-58.
Aruoba, S. B. (2004): "Data Uncertainty in General Equilibium," Computing in Economics and Finance 2004 131, Society for Computational Economics
--------- (2005): "Data Revisions are not Well-Behaved," Discussion Paper, University of Maryland.
Boivin, J. (2006): "Has US Monetary Policy Changed? Evidence from Drifting Coefficients and Real-Time Data," Journal of Money, Credit, and Banking, 38(5), 1149-1173
Brainard, W. (1967): "Uncertainty and the Effectiveness of Policy," The American Economic Review: Papers and Proceedings, 57, 411-435.
Carboni, G., and M. Ellison (forthcoming): "The Great Inflation and the Greenbook," Journal of Monetary Economics.
Clarida, R., J. Gali, and M. Gertler (2000): "Monetary Policy Rules and Macroeconomic Stability: Evidence and Some Theory," The Quarterly Journal of Economics, 115(1), 147-180.
Cooley, T.F., and E.C. Prescott (1976): "Estimation in the Presence of Stochastic Parameter Variation," Econometrica, 44(1), 167-84.
Croushore, D., and T. Stark(2001): "A real-time data set for macroeconomists," Journal of Econometrics, 105(1), 111-130.
Cunningham, A., C. Jeffery, G. Kapetanios, and V. Labhard (2007): "A State Space Approach to the Policymaker's Data Uncertainty Problem," Money Macro and Finance (MMF) Research Group Conference 2006 168, Money Macro and Finance Research Group.
Diebold, F. X., and R. S. Mariano (1995): "Comparing Predictive Accuracy," Journal of Business & Economic Statistics, 13(3), 253-63.
Elliott, G., I. Komunjer, and A. Timmermann (2005): "Estimation and Testing of Forecast Rationality under Flexible Loss," Review of Economic Studies, 72(4), 1107-1125.
Evans, G. W., and S. Honkapohja (2001): Learning and Expectations in Macroeconomics.Princeton University Press.
Harvey, A. C. (1989): Forecasting, Structural Time Series Models and the Kalman Filter. Cambridge University Press.
Howrey, E. P. (1978): "The Use of Preliminary Data in Econometric Forecasting," The Review of Economics and Statistics, 60(2), 193-200.
Kan, R. (2008): "From moments of sum to moments of product," Journal of Multivariate Analysis, 99(3), 543-554.
Nason, J. M., and G. W. Smith (forthcoming): "The New Keynesian Phillips Curve: Lessons from Single-Equation Econometric Estimation," Economic Quarterly.
Orphanides, A. (2001): "Monetary Policy Rules Based on Real-Time Data," American Economic Review, 91(4), 964-985.
Orphanides, A., and J. C. Williams (2006): "Monetary Policy with Imperfect Knowledge," Journal of the European Economic Association, 4(2-3), 366-375.
Owyang, M. T., and G. Ramey (2004): "Regime switching and monetary policy measurements," Journal of Monetary Economics, 51(8), 1577-1597.
Pesaran, H., and A. Timmermann (2005): "Real-Time Econometrics," Econometric Theory, 21, 212-231.
Raftery, A., and S. Lewis (1992): "How Many Iterations in the Gibbs Sampler,".
Robert, C. P., and G. Casella (2004): Monte Carlo Statistical Methods. Springer, 2 edn.
Romer, C. D., and D. H. Romer (1990): "Does Monetary Policy Matter? A New Test in the Spirit of Friedman and Schwartz," NBER Working Papers 2966, National Bureau of Economic Research, Inc.
Sargent, T. J. (1999): The Conquest of American Inflation. Princeton University Press.
Sargent, T. J., N. Williams, and T. Zha (2006): "Shocks and Goverment Beliefs: The Rise and Fall of American Inflation," American Economic Review, 96(4), 1193-1224.
Sims, C. A. (2006): "Improving Monetary Models," Discussion paper.
Tanizaki, H. (1996): Nonlinear Filters: Estimation and Applications. Springer-Verlag, 2 edn.
Watson, M. W., and R. F. Engle (1983): "Alternative Algorithms for the Estimation of Dynamic Factor, MIMIC, and Varying Coefficient Regression Models," Journal of Econometrics, 23, 385-400.
Zellner, A. (1958): "A Statistical Analysis of Provisional Estimates of Gross National Product and Its Components, of Selected National Income Components, and of Personal Saving," Journal of the American Statistical Association, 53(281), 54-65.
A Appendix
Sargent, Williams, and Zha (2006).
A.I Extended Kalman Filter and Likelihood
Extended Kalman Filter We first discuss the state space model more generally, and then
relate this algebra to the notation used in the paper. Let
![]() and
and
![]() for
for
![]() . The "expansion" about
. The "expansion" about ![]() is in fact exact:
is in fact exact:
| (A.1) |
The "expansion" about
![]() is approximate:
is approximate:
| (A.2) |
where
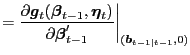 |
||
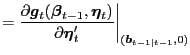 |
I motivate the derivation of optimal prediction and updating for the approximating system (A.1) and (A.2) by assuming Gaussian shocks, as in Howrey (1987), Watson and Engle (1983), and Harvey (1989).24 In this case, the relevant conditional expectations have the known forms given below. In particular, I assume
![]()
The Extended Kalman Filtering equations are
| (A.3) | ||
Conditional on the data
![]() , parameters
, parameters
![]() , and initial conditions
, and initial conditions
![]() , the
sequences of left hand side variables (A.3)-(A.4) are found by
matrix multiplication.
, the
sequences of left hand side variables (A.3)-(A.4) are found by
matrix multiplication.
Table A.1.a: Remaining Parameter Estimates: Framework Without Data Uncertainty - P1|0: Standard Deviations and Correlations
| 0.3273 | 0.9875 | 0.9187 | -0.9953 | -0.6626 | -0.9959 |
| 0.4412 | 0.9237 | -0.9978 | -0.6624 | -0.9972 | |
| 0.0748 | -0.9182 | -0.9134 | -0.9191 | ||
| 0.7743 | 0.6545 |
0.9996 | |||
| 0.0424 | 0.6515 | ||||
| 0.3111 |
Table A.1.b: Remaining Parameter Estimates: Framework Including Data Uncertainty - P1|0: Standard Deviations and Correlations
| 0.3273 | 0.9875 | 0.9187 | -0.9953 | -0.6626 | -0.9959 |
| 0.4412 | 0.9237 | -0.9978 | -0.6624 | -0.9972 | |
| 0.0748 | -0.9182 | -0.9134 | -0.9191 | ||
| 0.7743 | 0.6545 | 0.9996 | |||
| 0.0424 | 0.6515 | ||||
| 0.3111 |
Notes: The arrays are comprised as follows: The main diagonal is the square roots of the main diagonal of P1|0; the off-diagonal elements are the correlations derived from P1|0; P1|0 is the Federal Reserve's initial step-ahead uncertainty over the initial Philips curve parameter estimate a1|0.
Referring back to the paper's notation,
Likelihood The likelihood is
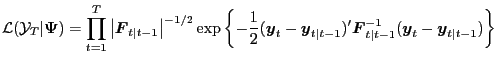
where the
![]() come from
(A.3).
come from
(A.3).
The estimates of
![]() from both models are
displayed in Table A.1.
from both models are
displayed in Table A.1.
A.II Greenbook Forecasts
The main issue with comparing the model predicted unemployment forecasts to Greenbook forecasts is the difference in the frequency of observation. The model forecasts the monthly unemployment rate one month into the future. The Greenbook forecasts quarterly unemployment rates and are released without rigid frequency. For example, there are Greenbook forecasts published monthly through the 1970s, but into the 1980s and 1990s these forecasts are published almost at a bimonthly frequency. I take the following steps to make the comparison.
First, I form a quarterly unemployment rate series as the average of unemployment rate for the three underlying months. It is against these series that the forecasts produce forecast errors.
Second, I form a quarterly model-forecast series as the average
of the step-ahead forecasts for the three underlying months. That
is, the model's quarterly unemployment forecast for quarter ![]() composed of months
composed of months
![]() is
is
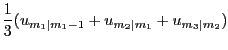
where ![]() is the forecast made at time
is the forecast made at time ![]() pertaining to time
pertaining to time ![]()
Third, I form the quarterly Greenbook-forecast series as an
average of all the forecasts made the month before or anytime
during a quarter. That is, the Greenbook quarterly forecast for ![]() composed of months
composed of months
![]() and immediately preceded
by month
and immediately preceded
by month ![]() is
is
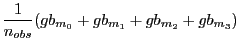
where ![]() is the Greenbook forecast for quarter
is the Greenbook forecast for quarter ![]() published in month
published in month ![]() . It
should be noted that all four of these forecasts do not exist for
every quarter, in which case only those observed are summed and
. It
should be noted that all four of these forecasts do not exist for
every quarter, in which case only those observed are summed and ![]() adjusts to however many forecasts are observed.
adjusts to however many forecasts are observed.
The Diebold and Mariano (1995) statistic ![]() takes forecast
error series
takes forecast
error series
![]() and
and
![]()
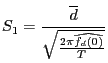
where
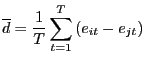
and I take
![]() to be Andrews (1991)
quadratic-spectral HAC estimator. The errors under consideration
run from 1970 through 1995 so that
to be Andrews (1991)
quadratic-spectral HAC estimator. The errors under consideration
run from 1970 through 1995 so that ![]() .
.
A.III MCMC Implementation and Robustness
Priors The prior for
![]() is multivariate normal
with a non-zero mean and a diagonal covariance matrix - so
equivalently, the priors for each parameter are independent
normals. The exact specifications are listed below where
is multivariate normal
with a non-zero mean and a diagonal covariance matrix - so
equivalently, the priors for each parameter are independent
normals. The exact specifications are listed below where
![]() following the notation of Sargent, Williams, and Zha (2006):
following the notation of Sargent, Williams, and Zha (2006):
-
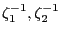 :
:
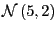
-
Chol
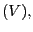 Chol
Chol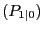 : Follows Sargent, Williams, and Zha (2006). For each element
on the diagonal of
Chol
: Follows Sargent, Williams, and Zha (2006). For each element
on the diagonal of
Chol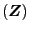 or
Chol
or
Chol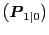 the
prior is
the
prior is
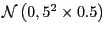 ;
for those elements off the diagonal, it is
;
for those elements off the diagonal, it is
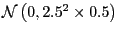
Convergence of the MCMC To address the convergence of the MCMC algorithm to its
posterior distribution, I computed the number of iterations
required to estimate the 0.025 quantile with a precision of 0.02
and probability level of 0.950 using the method of rafteryle92. For
each chain (with different initial conditions) the max of these
across
![]() was below the
was below the ![]() iterations taken from each chain, suggesting that
mixing the two chains (after burn-in) yields satisfactory
precision.
iterations taken from each chain, suggesting that
mixing the two chains (after burn-in) yields satisfactory
precision.
Metropolis Algorithm An important part of the MCMC algorithm sampling from the posterior in a reasonable number of iterations is the covariance matrix of the proposal random step in the Metropolis algorithm. The Metropolis algorithm is
1. Given
![]() , propose
a new value
, propose
a new value
![]()
where
![]() is normal with mean zero
and covariance matrix
is normal with mean zero
and covariance matrix
![]()
2. Compute
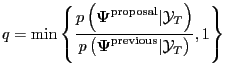
3. Randomly draw
![]()
4. If ![]() , accept
, accept
![]() as
current draw; otherwise, set
as
current draw; otherwise, set
![]() as the
current draw
as the
current draw
Given the manner in which all parameters affect the optimal
policy, I arrived at this proposal covariance matrix
![]() by doing the
following. Using the covariance matrix for
by doing the
following. Using the covariance matrix for
![]() numerically solved for
as described in Sargent, Williams, and Zha (2006)'s Appendix D and the prior covariance
terms for all other elements of
numerically solved for
as described in Sargent, Williams, and Zha (2006)'s Appendix D and the prior covariance
terms for all other elements of
![]() given above, the MCMC was
started. For tens of thousands of iterations based on one initial
condition, I considered only elements of the MCMC chain where a
proposal had been accepted. From these chain elements I calculated
the sample covariance matrix of the successful proposal shocks and
set
given above, the MCMC was
started. For tens of thousands of iterations based on one initial
condition, I considered only elements of the MCMC chain where a
proposal had been accepted. From these chain elements I calculated
the sample covariance matrix of the successful proposal shocks and
set
![]() equal to this. I
tried different initial conditions and took the weighted average of
the Cholesky factors of these sample covariance matrices. The
tuning parameter
equal to this. I
tried different initial conditions and took the weighted average of
the Cholesky factors of these sample covariance matrices. The
tuning parameter ![]() was adjusted to achieve an
acceptance rate of around 25-35% during the first 20,000
iterations: after this, it was unadjusted, as continual
chain-dependent adjustment of Metropolis step-size can negate the
ergodicity upon which MCMC methods are based (see Robert and Casella (2004)).
was adjusted to achieve an
acceptance rate of around 25-35% during the first 20,000
iterations: after this, it was unadjusted, as continual
chain-dependent adjustment of Metropolis step-size can negate the
ergodicity upon which MCMC methods are based (see Robert and Casella (2004)).
Footnotes
1. First version: February 2007. I thank Jim Hamilton for his insightful advice. Thanks also to Alina Barnett, Gray Calhoun, Martin Ellison, Margie Flavin, Nir Jaimovich, Garey Ramey, Valerie Ramey, Chris Sims, Allan Timmermann, Harald Uhlig, Chris Wignall, and Tao Zha for helpful discussions; to an anonymous referee for extensive comments; and to seminar participants at UCSD, Georgetown, HEC Montreal, Texas A&M, Penn State, UCSC, Cambridge University Learning and Macroeconomic Policy Conference, the Philadelphia, Kansas City, and Atlanta Federal Reserve Banks, and the Federal Reserve Board. Return to text
2. Division of International Finance, mail to: [email protected]. This paper reflects the views and opinions of the author and does not reflect on the views or opinions of the Federal Reserve Board, the Federal Reserve System, or their respective staffs. Return to text
3. Orphanides and Williams (2006) and Sims (2006) also argue that policy is sensitive to model uncertainty, and Nason and Smith (forthcoming) finds instability in the Philips curve relationship since the 1950s. Return to text
4. In contrast, this paper produces unemployment forecasts that are statistically indistinguishable from the Greenbook forecasts without using those Greenbook forecasts as data. Return to text
5. In fact, data uncertainty was recognized by Burns and Mitchell, who revised their business cycle indicators as data revisions came in, and considered many macroeconomic variables for that reason. Return to text
6. Recent related work is in Aruoba (2004) who analyzes the welfare effects of more accurate data collection, and Aruoba (2005) who analyzed the statistical features of data revision processes. Return to text
7. This naturally follows from usual assumptions: the agent has an economic loss function, the agent's prediction is rational with respect to that loss function, and the loss function is minimized when the prediction error is zero. See Elliott, Komunjer, and Timmerman (2005) for more extensive discussion. Return to text
8. That is
![]() ,
etc. Return to text
,
etc. Return to text
9. The value ![]() is the sum of
expectations of fourth-order products of the elements of
is the sum of
expectations of fourth-order products of the elements of
![]() and
and
![]() . Kan's (2008) Proposition 1
ensures that this
. Kan's (2008) Proposition 1
ensures that this ![]() is positive, as well as that
expectation of the terms involving
is positive, as well as that
expectation of the terms involving ![]() drop
out. Return to text
drop
out. Return to text
10. Given initial conditions
![]() and
and
![]() . Return to text
. Return to text
11. One could rewrite the state space in other equivalent ways. Return to text
12. I estimate the reciprocals of
![]() because it is easy to
draw them as normals and avoid nonnegativity
constraints. Return to text
because it is easy to
draw them as normals and avoid nonnegativity
constraints. Return to text
13. I must use a accept/reject simulation
technique because, due to the effects of
![]() on the whole sequence of
forecasts, the form of (3.1) is not known.
Further details are in Appendix A.III. Return to text
on the whole sequence of
forecasts, the form of (3.1) is not known.
Further details are in Appendix A.III. Return to text
14. This has the effect of lowering the
estimated values for
![]() and
and
![]() . We will see later
that high values of
. We will see later
that high values of
![]() imply a difficult economic
story (namely that the Federal Reserve's model of the economy was
extremely unstable), and so to some extent the calibration of
imply a difficult economic
story (namely that the Federal Reserve's model of the economy was
extremely unstable), and so to some extent the calibration of ![]() to one-tenth (as opposed to,
say, one-half or two times) is an assumption that
drives favorable results for Sargent, Williams, and Zha (2006). Return to text
to one-tenth (as opposed to,
say, one-half or two times) is an assumption that
drives favorable results for Sargent, Williams, and Zha (2006). Return to text
15. Sargent, Williams, and Zha's (2006) results come from a sequence of 50,000 draws with an unspecified burn-in interval. Return to text
16. The natural rate at time ![]() is the steady-state rate of unemployment with inflation set
at target, defined as
is the steady-state rate of unemployment with inflation set
at target, defined as
![]() , following Sargent, Williams, and Zha (2006) and Carboni and Ellison (forthcoming). The natural rate
essentially follows the estimated constant parameter: a plot of the
constant parameter time series is available from the author upon
request. Return to text
, following Sargent, Williams, and Zha (2006) and Carboni and Ellison (forthcoming). The natural rate
essentially follows the estimated constant parameter: a plot of the
constant parameter time series is available from the author upon
request. Return to text
17. See Figure 7 Return to text
18. Appendix A.II discusses these forecasts and provides more details on the test statistic. Return to text
19. The probability that a normal random variable is at least one standard deviation away from its mean is around 30%. Return to text
20. The other measurement equation forecasts are pictured in Appendix A.III. Return to text
21. Sargent, Williams, and Zha (2006) and Carboni and Ellison's (forthcoming) estimated trade-offs are similar to each other but a little different from the one here. Theirs' experiences the large jump between 1973 and 1975, but no sharp fall between 1980 and 1984. Return to text
22. One manner of seeing this is to
compute the coherence between the Philips curve trade-off and
inflation at low-frequencies. This coherence is ![]() for fluctuations with a period between 1 and 10 years.
For the model without uncertainty this coherence is
for fluctuations with a period between 1 and 10 years.
For the model without uncertainty this coherence is ![]() . Return to text
. Return to text
23. This last point is disputable. Research on disagreement between policy-makers, and related evidence, may be useful in this regard (c.f. Romer (2009)). Return to text
24. Technically, I must assume that the
vector
![]() appearing in the first-order expansion iis
Gaussian; assuming a Gaussian
appearing in the first-order expansion iis
Gaussian; assuming a Gaussian
![]() for the general
nonlinear case does not assure
that the shock in the first-order expansion would be
Gaussian. Return to text
for the general
nonlinear case does not assure
that the shock in the first-order expansion would be
Gaussian. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text