Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 971, May 2009 --- Screen Reader
Version*
Consumption Response to Expected Future Income
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
This paper shows empirical evidence in favor of forward-looking household consumption--that consumption today depends directly on household-specific ex-ante expectations of future income. This analysis is unique in using a direct consumption measure combined with an ex-ante household-specific measure of expected future income, constructed from detailed survey and administrative data on Social Security, pensions, and retirement plans. Households with high expected future income spend more today than households that have lower future income but identical current income and net worth. Omitting household-specific future income can cause mis-estimation of key consumption questions. Furthermore, when all three resources for consumption (current income, net worth, and future income) are accounted for, the average propensity to spend out of current income is similar to predictions of optimal consumption under uncertainty in a dynamic stochastic model, although the propensities to spend out of accumulated net worth and expected future income are notably lower in the data than the optimal model. Finally, these data also provide evidence on the effect of risk on consumption while controlling for all three resources. Households with high measured risk aversion consume less out of future income. All households, on average, consume more out of the more predictable sources of future income, such as future Social Security benefits.
Keywords: Consumption, permanent income hypothesis
JEL classification: D12, D13, D91
1. Introduction
More than forty years after the first debates over the permanent income hypothesis (PIH) and the lifecycle model, economists still disagree over how forward-looking households are in their consumption and savings decisions. Euler equation orthogonality tests, which do not require full specification of the income process or households' expectations, have generated mixed results. The general conclusion from the Euler equation literature is that consumption responds to some types of predictable income, contrary to a basic lifecycle or PIH model (see Browning & Lusardi, 1996). While these results suggest that households do not fully re-optimize consumption over short periods and relatively small amounts of money, they do not provide significant evidence against long-horizon forward-looking behavior of the magnitude posited by the lifecycle model or permanent income hypothesis.
Some macroeconomic studies have found evidence linking scaled consumption to future income or asset returns, which could be interpreted as households consuming in anticipation of future income growth (Campbell, 1987 & 1993, Lettau & Ludvigson, 2001, 2002). At the household level, many empirical challenges to the PIH have been at least partially, if not conclusively, addressed by enhancements to a forward-looking model, keeping the main lifecycle/PIH element intact (for example precautionary savings, demographic changes, bequests, and home production).
Nonetheless, most household-level studies that test a direct link between current consumption and future income have shown no convincing evidence of this fundamental PIH relationship (Carroll, 1994, Deaton, 1992, 1997 and Alessie & Lusardi, 1997). A recent exception is Nalewaik (2006), who used a synthetic cohort approach to find micro-data support for a forward-looking relationship between consumption growth and income growth. This paper uses direct panel observations of consumption and ex-ante household-specific expected future income to provide more conclusive evidence of that relationship.
Of course, precautionary savings makes simple tests of the lifecycle model more difficult, moving optimal consumption away from the certainty-equivalent (CEQ) lifecycle path. But even under uncertainty, consumption should still reflect differences in mean expected future resources if consumers are forward-looking consumption-smoothers. The primary difficulty of directly testing this feature of the model is measuring the household's expectations of future income ex-ante. As has long been recognized, ex-ante income uncertainty makes the use of ex-post income data for individual households, or even for groups, highly problematic. Instead, more recent studies specify an income process that varies by education group, if at all, and these income profiles substitute for households' expected future income.
This paper ameliorates these issues with recent data and some convenient facts. First, several recent studies support the conclusion that precautionary saving motives dominate consumption behavior in early to middle working years, but lifecycle retirement savings become predominant by late working years (Carroll & Samwick 1998; Gourinchas & Parker 2002; Cagetti 2003). Furthermore, the future income of older households, composed mainly of Social Security and pensions, is more stable and more predictable to both the household and econometrician. This suggests that older households are the ideal group for testing the lifecycle model. Accurately modeling this age group is also important to address questions of aggregate saving and wealth accumulation, since households between ages 50 and 74 account for a disproportionate share of saving and wealth in the economy.1 However, few tests of the lifecycle model focus on households over age 50, with the exception of the retirement consumption puzzle literature, which focuses on the few years surrounding retirement, and the literature on end-of-life spend-down. Prominent exceptions that do focus on older households include Hurd (1989,1999), Hubbard, Skinner, Zeldes (1994), Palumbo (1999), Dynan, Skinner, Zeldes (2002), and Scholz, Seshadri, and Khitatrakun (2006).2 None of these, however, test the PIH directly using data on both total consumption and comprehensive measures of income and wealth for the same households.
This paper uses older households (ages 53-73) from the Health and Retirement Study (HRS). The identification strategy is this age group's predictable heterogeneity of retirement income among households with similar current income. For example, households with similar employment status in terms of education, industry, and occupation may have heterogeneity in the generosity of their retirement pensions. This heterogeneity would likely be known in advance by the household. The availability of administrative Social Security data, both respondent-provided and employer-provided details of pension plans, and extensive survey data on households' histories and retirement plans in the HRS allow high-quality estimation of expected retirement income for each household. The HRS also contains a more comprehensive consumption measure than is available in most surveys (other than the Consumer Expenditure Survey (CEX)). Therefore, an extremely simple test for forward-looking consumption behavior is possible: is expected future income a significant predictor of current consumption, controlling for current income and current net worth?
The results of this simple test are affirmative. Households with higher than average expected future income, such as high retirement income, spend more today than other households with identical current income and net worth. In a simple OLS, omitting future income would cause overestimation of the propensity to consume out of current income, underestimation of the ability to explain consumption with lifetime income, and possible mis-estimation of the effects of other variables on consumption.
With income uncertainty, the propensity to consume out of each of the different components of total wealth, or lifetime resources (current income, accumulated net worth, and future income), are not predicted to be equal, as they would be in a CEQ model. Because future income is less certain than current income, and net worth acts as a "buffer stock" against future shocks, there are different optimal consumption propensities for the different components of total wealth.3Therefore, this paper compares the average propensities to consume out of each of the three components observed in the data to the optimal propensities from a dynamic stochastic model simulated for a similar demographic sample.
The average propensity to spend out of current income in the data is similar to that of the simulated sample. However, the propensity to consume out of accumulated net worth and expected future income is notably lower in the data than the simulated model predicts. Consistent with precautionary savings, households have the highest rate of consumption out of the relatively certain and predictable present value of future Social Security benefits, relative to other sources of future income. In contrast, the rate of consumption out of future pensions is similar to that of net worth. Finally, the rate of consumption out of total future income is lower for households with high aversion to risk. Additional factors for explaining consumption heterogeneity across households, including life expectancy and expected returns on risky assets, are addressed in Pounder (2007).
2. Model
Using a standard stochastic model, taking the specification and notation from Carroll (2001), households maximize utility as follows:
![\begin{displaymath} \begin{array}[c]{l} Max\quad\sum\limits_{s=t}^{T}{\beta^{s-t}U(C_{s})}\quad s.t.\quad\quad \quad\quad\quad\quad\quad\ W_{s+1}=R_{s+1}(X_{s}-C_{s})\quad\quad\quad\quad\quad\quad\quad\ Y_{s+1}=P_{s+1}\varepsilon_{s}\quad\quad\quad\quad\quad\quad\quad\ P_{s+1}=GP_{s}N_{s+1}\quad\quad\quad\quad\quad\quad\quad\ X_{s+1}=W_{s+1}+Y_{s+1}\quad\quad\quad\quad\quad\quad\quad\quad \end{array}\end{displaymath}](img1.gif)
where C is consumption, W is net worth, X is " cash on hand" as
defined by Deaton (1991), R is the gross return on savings
(equivalent to 1+r), Y is current income, P is permanent income,
is a log-normal, mean one
transitory shock to income, N is a log-normal mean one permanent
shock to income, and G is the one period deterministic growth rate
of income. In this model, death, or terminal date T, is fixed and
known. Utility is assumed to be CRRA:
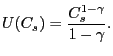
Define future income, or human wealth, H, as the present discounted value of expected future income (in this case human wealth includes retirement assets such as Social Security and pensions as well as other expected income such as veterans benefits or SSI payments):4
![$\displaystyle H_{t}=E_{t}\left[ {\sum\limits_{i=t+1}^{T}{\frac{Y_{i}}{(1+r)^{(i-t)}}} }\right] $](img7.gif)
Therefore total wealth, or remaining lifetime resources, equals Y+W+H or, equivalently, X+H each period.
This paper simulates the model to create a sample of optimizing consumers. This sample is constructed to have demographic composition and income histories similar to the actual HRS data. The simulations are described in section IV.
3. HRS Data
The HRS is a nationally representative panel survey of households over the age of 50. This paper primarily uses two cohorts, the original HRS cohort that began the survey in 1992 at ages 50-60, and later entrants, the "war baby" cohort, that entered the sample in 1998, then ages 50-56. This study uses the 2000, 2002, and 2004 waves of the HRS, including 2001 and 2003 calendar year income data (asked in the 2002 and 2004 waves, respectively) to match to the consumption data described below.
Although income observations are only directly available in the survey starting in calendar year 1991, both cohorts were merged with their W-2 earnings reports starting in 1980, and with their entire Social Security earnings records. Combined, these sources give complete information for calculating expected Social Security benefits, as well as reliable lifetime earnings histories for most workers, with earnings histories back to 1980 for high earners and non-covered workers.5
The HRS also includes both respondent-reported and employer-reported information about defined benefit and defined contribution pension plans (including payout formulas, employment tenure, matching rates, etc.) which allows high-quality calculation of expected pension benefits. Described fully in the appendix, the measure of future income is the present value of expected cash flows from Social Security, pensions, self-reported remaining years of work, and assorted other income sources such as veterans' benefits, disability, and poverty programs like SSI.6 Unlike most analyses of consumption and permanent or future income, this measure of expected future income is truly ex-ante, constructed independently from education, and household-specific. The error normally introduced into future income by current or past income shocks is largely mitigated, because neither of these income measures is used as the primary basis for future income. Some summary statistics are provided in Table 1.
Finally, this paper also relies on the 2001 and 2003 waves of the Consumption and Activities Mailout Survey (CAMS), which are the first two waves of this HRS supplement. CAMS is sent to a random subset of the HRS sample and asks about 26 categories of expenditure on housing and nondurable goods.7 The categories included on CAMS cover well over 90% of household expenditure judging by the much more detailed Consumer Expenditure Survey. Expenditures on housing and vehicles are replaced with consumption flows based on household-specific rental equivalence and vehicle values. The calculation of total consumption is described in the appendix. Using CAMS, however, limits the sample for this exercise to those HRS households that are in the 2001 CAMS sample and have matching Social Security records, resulting in 1,962 observations. Of these observations, 1,811 have a head of household in the age range from 53 to 73.8
4. Simulations
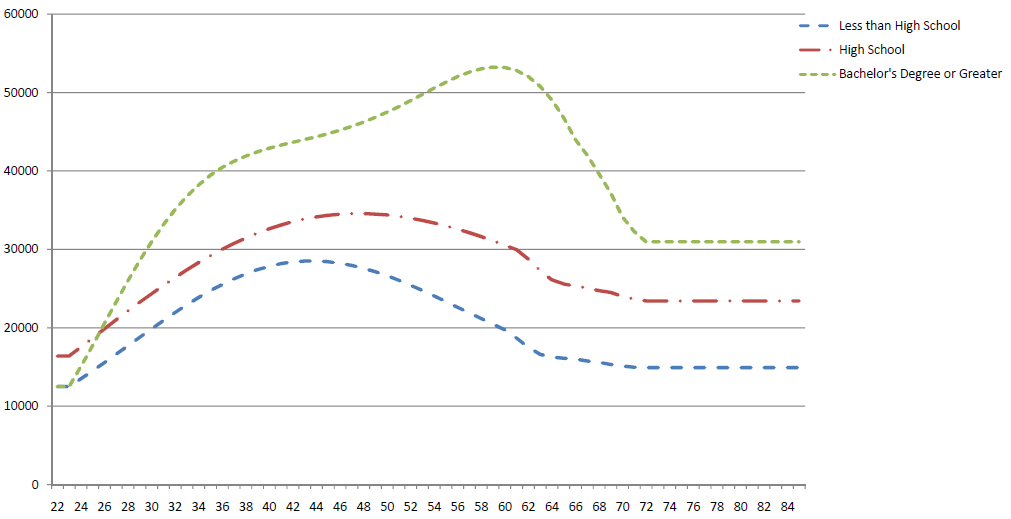
Using the earnings histories described above along with the constructed expected future income flows, the lifetime income profiles for all HRS households in this age range were averaged for each of three education groups: less than high school degree, high school degree, and more than high school degree. These profiles determine income growth, G, for the simulated households in the model. The starting income for each education group is also taken from the income histories (adjusted for inflation to be in terms of year 2000 dollars). Figure 1 shows the average profiles for the three education groups. Table 2 shows the frequency by age cohort and education group in the HRS data (note that the education composition varies by age cohort). Although this exercise is similar to what some authors have used to estimate expected future income, in this case the profiles are not imposed on the households in the HRS data as a proxy for expected income. Instead, they are only used within the simulation to generate broad differences in level and timing of income between education groups.9
The parameters of the model were set to: 
=2;
=0.98; R=1.02; 
=0.2
for transitory shocks; and 
=0.0075 for
permanent shocks.
The model was solved for each of the education groups, simulating 4,000 observations in each case. A random sample of simulated households (their consumption, current income, net worth, and mean expected future income) was collected from each education group's simulation outcomes that represent ages 53 to 73. The sample size and age distribution of each selection was chosen to match the age and educational composition of the HRS data. The result was a sample of 2,000 randomly chosen simulated households, similar in size, income profile, and age distribution to the HRS dataset. Since optimal consumption propensities should vary by age, this composition matching prevents the need to adjust for the effects of changing education composition by age when comparing the HRS consumption to the simulated sample consumption.
This simulation exercise was repeated ten times, giving a total of 20,000 random simulated observations. This exercise is a monte carlo-type experiment that generates sufficient observations to converge on true coefficients, but also allows testing of each simulated sample individually to give a range of possible coefficients that would be consistent with the model when observing a sample size as small as the HRS data. Table 3 compares some basic statistics of the HRS and simulated samples. The HRS sample has higher income and, particularly, higher net worth. This may be in part because of cyclically high asset values, of both stocks and housing, in the 2001 to 2003 period.
5. Future Income and Current Consumption
The simple test for forward-looking behavior is whether current consumption is correlated with ex-ante expected future income, controlling for the level of current income and accumulated net worth. In other words, do households that are otherwise identical consume differently today based on their expectations of retirement income? This can be tested with the following OLS specification.
Table 4 shows that expected future income is highly significant for each of two separate observations of the consumption-resources relationship in the HRS.10 The first uses 2001 total consumption and 2001 resources (income, net worth, and future income) and the second uses consumption and resources as of 2003. Although the same households are sampled in those two years, the consumption, current income, and net worth variables are new survey observations. The two separate observations yield very similar coefficients--the small differences between the 2001 and 2003 coefficients for the income and wealth variables are not statistically significant.
Age is included in these regressions because the rate at which households consume out of total wealth should increase slightly with age.11 Marital status is included to make the results more comparable to the simulated data since the HRS data includes both singles and married couples, whereas the simulated data is implicitly single person households. About half of the HRS sample is retired in 2001, but controlling for retirement status does not change the coefficients on the resource measures.12
Rather than comparing the coefficients of the various components of total wealth to each other, as one would if they had a CEQ model in mind, this paper compares the HRS coefficients to those obtained from the simulated optimal consumers who face income uncertainty. The far right columns of Table 4 show the coefficients for the simulated sample of 20,000 observations. Table 5 shows the range of coefficients when running separate regressions on each random sample of 2,000, as well as the extreme range of the 95% confidence intervals.
First, controlling for other sources of total wealth, the coefficient on after-tax current income, which represents the cross-sectional average rate of spending attributable to variation in current income, is 10 or 11 percent.13 This is not far from the 9 percent coefficient from the simulated sample, which is within the 95 percent confidence interval of the HRS results for both 2001 and 2003. Furthermore, Table 5 shows that the 10 percent coefficient from the 2001 regression is within the 95 percent confidence interval on the income coefficient from some of the small samples of simulated households. This result suggests that it is not impossible for the HRS data to have been drawn from a model like the one specified.
In contrast, the coefficients on net worth and future income in the HRS are not nearly so close to the model. With income uncertainty, the propensity to consume out of net worth and future income should be lower than out of current income. The simulated sample has a coefficient on net worth of 8 percent and on future income of 5 percent. However, the coefficients on net worth and future income are each around 1 percent in both of the HRS data samples. The variation around the point estimates in the simulated sample is also much narrower for net worth and future income than it was for current income, as Table 5 shows. Therefore, the HRS households clearly under-consume out of these sources of wealth relative to the specified model. This could imply that households are only partially forward-looking. Alternatively, it may indicate that uncertainty surrounding both retirement income and returns on net worth (which are treated as certain in the model) are perceived by households as more risky than the model represents.
6. Future Income Matters
Even though current income and future income are highly
co-linear, especially for older households, future income variation
across households has an effect on consumption independent of
current income variation. Therefore, omitting variation in future
income from consumption analyses could, in some cases, bias the
conclusions. Although the consumption literature certainly does not
rely on simple OLS regressions of the levels of current income and
consumption, nonetheless, Table 6 shows that such a naïve
regression omitting future income would be misleading. The
co-linearity of the two income measures is apparent in the fact
that the coefficient on current income increases when future income
is omitted, dramatically so for the simulated data. As the
R
measure falls modestly, the current
income variable absorbs much of the variation in consumption that
is more accurately attributed to variation in future income. This
somewhat overstates the relationship between consumption and
current income and slightly understates the ability of total wealth
to explain variation in consumption.
Perhaps more interestingly, Table 7 shows that changes in consumption, although quite noisy in the HRS data and not well explained by any of the regressors, are more readily explained by changes in future income than by changes in current income.14 Finally, Table 8 shows that simple test of whether households undertake less precautionary saving if they have long-term care (LTC) insurance would be biased if expected future income were omitted. If nursing home or similar late-life medical expenditures were a significant motive for precautionary savings by older households, then those with insurance should need less precautionary savings and consume more, all else equal. The regression uses a dummy variable for LTC insurance, and is run with and without future income as a control variable. Omitting future income substantially overestimates the association of LTC insurance and consumption.
7. Precautionary Saving in Older Households
The results from section V show that household consumption is related to the mean, or expected value, of future income. The low coefficient on future income, however, may suggest that households also respond to the perceived variance of future income. Tables 9 and 10 indicate that older households consume less out of riskier streams of future income and that highly risk-averse households also have lower consumption, regardless of how uncertain their labor income is.
Table 9 shows that households have the highest propensity to consume out of expected Social Security benefits, just over 2%. Intuitively, Social Security represents the most certain resources for retired households, at least for the generation already at or near retirement by 2001. The propensity to consume out of future labor earnings, which are all fairly near-term, and therefore more certain compared to retirement benefits, is also just over 2%. The propensities for both defined benefit and defined contribution pensions are notably lower at or under 1.0%, similar to the propensity to consume out of net worth. In contrast, households show no propensity or negative propensity to spend in anticipation of "other income", which primarily contains benefits from anti-poverty programs such as SSI, modeled by the author to represent an income floor for households whose expected future income is below the poverty line.15 This variable may be acting as an indicator for the poorest households.
These results suggest that households perceive Social Security and near-term labor earnings as more certain than pensions. Alternatively, since the latter, pensions, are likely to be measured with more error than the former, there may simply be more attenuation bias in the coefficients for pensions.
Table 10a is reminiscent of the evidence for precautionary savings shown in Carroll (1994) and derived from those tests. Certain education and occupation groups, such as those without a high school degree and farmers, have particularly high income uncertainty. The results show that these groups spend less after controlling for total wealth. The coefficient on farmer is large but insignificant, likely because of the small sample size for farmers.
Finally, Table 10b shows that households with high measured risk aversion have lower total consumption, controlling for total wealth. This risk aversion measure is solicited by asking respondents income gamble questions (see Barsky, Juster, Kimball, Shapiro 1997). These risk-averse households could be engaging in precautionary saving for reasons other than the typical earnings variance that dominates uncertainty scenarios for younger households. Instead, they could worry about outliving their expected lifespan, lower than expected returns on their net worth, or high late-life medical expenses.
8. Conclusions
This paper has presented empirical evidence in favor of a lifecycle, or forward-looking, consumption model for older households. The combination of lower income variance of retired households with high-quality household-specific data enables a meaningful analysis of levels of consumption and total wealth, including ex-ante expected future income. The HRS data confirms a strong empirical relationship between observed consumption and expected future income. Omitting this relationship can bias consumption analysis. However, older households also exhibit precautionary savings in response to riskier income streams and to higher risk aversion.
References
Alessie, Rob and Lusardi, Annamaria, "Saving and Income Smoothing: Evidence from Panel Data", European Economic Review, vol. 41, pages 1251-1279, 1997.
Ando, A. and F. Modigliani, "The `Life-Cycle' Hypothesis of Saving: Aggregate Implications and Tests", American Economic Review, 53, pp.55-84.
Barsky, B., F.T. Juster, M. Kimball, and M. Shapiro, M., "Preference Parameters and Be-
havioral Heterogeneity: An Experimental Approach in the Health and Retirement Study,"
Quarterly Journal of Economics 112 (2), May 1997, 537-579.
Browning, Martin, and Annamaria Lusardi, "Household Savings: Micro Theories and Micro Facts," Journal of Economic Literature, Dec. 1996 Vol. 34, pp. 1797-1855.
Cagetti, Marco, "Wealth Accumulation Over the Lifecycle and Precautionary Savings," Journal of Business and Economic Statistics, Vol. 21, 2003.
Campbell, John Y., "Does Saving Anticipate Declining Labor Income? An Alternative Test of the Permanent Income Hypothesis", Econometrica, vol. 55, 1987, pages 1797-1855.
Campbell, John Y., "Understanding risk and return," Journal of Political Economy 104, 1996, 298-345.
Campbell, John Y., "Intertemporal Asset Pricing without Consumption Data", American Economic Review, vol. 83, 1993, pages 487-512.
Campbell, John Y. and N. Gregory Mankiw, "Permanent Income, Current Income, and
Consumption," Journal of Business and Economic Statistics, 1990, pp. 265-279.
Carroll, C. D. and M. Kimball, "Liquidity Constraints and Precautionary Saving", NBER Working Paper W8496, Oct. 2001.
Carroll, Christopher D. and Andrew A. Samwick, "The Nature of Precautionary Wealth", Journal of Monetary Economics, vol. 40, 1997 pp41-71.
Cutler, David and Lawrence Katz (1991) "Macroeconomic Performance and the Disadvantaged" Brookings Papers on Economic Activity Vol. 1991 No.2.
Deaton, Angus, "Saving and Liquidity Constraints," Econometrica, 59, 1991, pages 1221-1248.
Deaton, Angus, Understanding Consumption, Oxford: Clarendon Press, 1992.
Deaton, Angus, The Analysis of Household Surveys, The World Bank, Johns Hopkins University Press, 1997.
Dynan, Karen E. & Jonathan Skinner & Stephen P. Zeldes, 2000. "Do the Rich Save More?," NBER Working Papers 7906.
Gourinchas, Pierre-Olivier and Jonathan A. Parker, "Consumption Over the Life Cycle", Econometrica vol. 70(1), 2002, pp47-89.
Gustman, Alan and Thomas Steinmeier, "The Social Security Early Entitlement Age in a Structural Model of Retirement and Wealth" NBER Working Paper 9183, September 2002.
Hubbard, R. Glenn, J. Skinner, S. P. Zeldes, "Expanding the Life-Cycle Model: Precautionary Saving and Public Policy", The American Economic Review, vol. 84(2), Papers and Proceedings, May 1994, pp174-179.
Hubbard, R. Glenn, J. Skinner, S. P. Zeldes, "The Importance of Precautionary Motives in Explaining Individual and Aggregate Saving", NBER Working Paper 4516, 1994.
Hurd, M. D., "Mortality Risk and Bequests", Econometrica Vol 57(4) July 1989, pp.779-813.
Hurd, Michael D., and Kathleen McGarry, "The Predictive Validity
of Subjective Probabilities of Survival", Economic
Journal
Royal Economic Society, vol. 112(482),
pages 966-985, October 2002.
Hurd, M.D. and Smith, J.P., "Expected Bequests and their Distribution," NBER Working Paper W9142, 2002.
Johnson, David, Stephanie Shipp, and Thesia Garner (1997) "Developing Poverty Thresholds Using Expenditure Data" in Proceedings of the Government and Social Statistics Section, American Statistical Association, August 1997.
Laitner, J. "Estimating Life-Cycle Parameters from Consumption Behavior at Retirement", NBER Working Paper W11163, March 2005.
Lettau, Matrin and Ludvigson, Sydney, "Consumption, Aggregate Wealth, and Expected Stock Returns", Journal of Finance, vol. 56, 2001, pages 815-849.
Lettau, Matrin and Ludvigson, Sydney, "Time-varying Risk Premia and the Cost of Capital: An Alternative Implication og the Q Theory of Investment", Journal of Monetary Economics, vol. 49, 2002, pages 31-66.
Lusardi, Annamaria, "On the Importance of the Precautionary Saving Motive", The American Economic Review, vol. 88(2), Papers and Proceedings, May 1998, pages 449-453.
Lusardi, Annamaria, "Planning and Saving for Retirement", Dartmouth College Working Paper, December 2003.
Mayer, Thomas, Permanent Income, Wealth, and Consumption: A Critique of the Permanent Income Theory, the Life-Cycle Hypothesis, and Related Theories, Berkeley:
Univ. California Press, 1972.
Merton, Robert C. "Lifetime Portfolio Selection Under Uncertainty: The Continuous-Time Case," Review of Economics and Statistics, 51 (August): 247-57.
Merton, Robert C. "Optimum Consumption and Portfolio Rules in a Continous-Time Model," Journal of Economic Theory, 3 (December): 373-413.
Merton, Robert C. Continuous-Time Finance. Basil Blackwell Inc., Cambridge Massachusetts, 1990.
Modigliani, F. and Brumberg, R., "Utility Analysis and the Consumption Function: An Interpretation of Cross-Section Data", in Kurihara, K. (ed), Post-Keynesian Economics, New Brunswick: Rutgers University Press, 1954.
Nalewaik, Jeremy J., "Current Consumption and Future Income Growth," Journal of Monetary Economics, vol. 53, pages 2239-2266, November 2006.
Palumbo, M. G., "Uncertain Medical Expenses and Precautionary Saving Near the End of the Life Cycle", The Review of Economic Studies Vol 66(2) April 1999, pp.395-421.
Perozak, Maria, "Using subjective expectations to forecast longevity: do survey respondents know something we don't know?" Finance and Economics Discussion Series 2005-68. Board of Governors of the Federal Reserve, 2005.
Pounder, Laurie, "Examining Consumption", University of Michigan Dissertation, 2007.
Samwick, Andrew A., "Discount rate heterogeneity and social security reform," Journal of Development Economics, vol. 57(1), pages 117-146, October 1998.
Scholz, John K., Ananth Seshadri, and Surachai Khitatrakun, "Are Americans Saving Optimally for Retirement?" NBER Working Paper 10260, Feb 2004.
Table 1. Characteristics of Consumption and Total Wealth - Panel A. Future Income and Total Wealth in 2000
| 25th% | 50th% | 75th% | Mean | |
|---|---|---|---|---|
| Consumption | $25,000 | $35,100 | $49,200 | $40,330 |
| Future Income: Earnings | $101,500 | $81,600 | ||
| Future Income: Social Security | $104,300 | $184,300 | $288,100 | $192,800 |
| Future Income: DB Pension | $15,400 | $150,000 | $125,500 | |
| Future Income: DC Pension | $9,000 | $72,000 | $69,500 | |
| Future Income: Other (Poverty, Veterans, Disability) | $20,300 | |||
| Total Future Income | $174,900 | $362,400 | $678,300 | $494,000 |
| Net Worth Excluding Housing | $40,000 | $208,000 | $220,000 | |
| House Equity | $33,000 | $90,000 | $160,000 | $122,000 |
| Total Net Worth | $33,000 | $130,000 | $368,000 | $342,000 |
| Current Income | $20,000 | $40,600 | $76,500 | $63,600 |
| Total Wealth | $227,900 | $533,000 | $1,122,800 | $899,000 |
Table 1. Characteristics of Consumption and Total Wealth - Panel B. Mean Values by Quartile of Future Income
| 0-25% | 25-50% | 50-75% | 75-100% | |
|---|---|---|---|---|
| Earnings | $4,500 | $31,300 | $74,300 | $217,800 |
| Social Security | $67,800 | $173,600 | $245,200 | $285,300 |
| DB Pension | $7,100 | $30,500 | $107,300 | $356,900 |
| DC Pension | $6,000 | $19,000 | $55,200 | $195,800 |
| Other | $23,100 | $8,400 | $16,500 | $29,800 |
Table 1. Characteristics of Consumption and Total Wealth - Panel C. Values for Individual Households Who Fall at the Quartiles of Future Income
| 25th% | 50th% | 75th% | |
|---|---|---|---|
| Earnings | $364,600 | ||
| Social Security | $174,900 | $119,400 | $313,700 |
| DB Pension | $131,000 | ||
| DC Pension | $112,000 | ||
| Other | |||
| Total Future Income | $174,900 | $326,400 | $678,300 |
| Net Worth Excluding Housing | $117,500 | $172,000 | $2,057,000 |
| House Equity | $80,000 | $225,000 | $300,000 |
| Earned Income 2001 | $27,000 | $42,000 | $91,000 |
| Unearned Income 2001 | $12,000 | $6,000 | |
| Total Wealth | $411,400 | $807,400 | $3,126,300 |
| Consumption | $33,100 | $45,700 | $68,200 |
| Age in 2001 | 69 | 71 | 55 |
Table 2. Frequency by Age and Education Group in the HRS
| Age: 53-59 | Age: 60-65 | Age: 66-73 | Total | |
|---|---|---|---|---|
| Less Than High School | 4% | 7% | 8% | 20% |
| High School and Some College | 17% | 19% | 17% | 54% |
| College Degree | 9% | 8% | 8% | 26% |
| Total | 31% | 35% | 34% |
Table 3. Summary Statistics for HRS and Simulation
| Simulation Year 2007 | HRS 2001: Unrestricted | HRS 2001: Head & Spouse Only | HRS 2003: Unrestricted | HRS 2003: Head & Spouse Only | |
|---|---|---|---|---|---|
| N | 20000 | 1710 | 1151 | 1241 | 823 |
| Age* | 62.8 | 62.7 | 63.4 | 64.7 | 65.3 |
| Gross Income | N.A. | $63,550 | $64,456 | $58,380 | $57,847 |
| After Tax Income | $32,557 | $50,070 | $50,795 | $46,859 | $46,624 |
| Net Worth | $115,489 | $342,290 | $366,205 | $372,025 | $388,966 |
| Future Income | $475,618 | $494,410 | $512,439 | $470,281 | $488,267 |
| Consumption | $33,246 | $40,070 | $39,448 | $39,671 | $38,399 |
Note: * For HRS sample, age is age of head of household
Table 4. Regressions of Consumption on Components of Total Wealth
| Consumption HRS 2001: Estimated Coefficient | Consumption HRS 2001: t-statistic | Consumption HRS 2003*: Estimated Coefficient | Consumption HRS 2003*: t-statistic | Consumption Simulated Sample: Estimated Coefficient | Consumption Simulated Sample: t-statistic | |
|---|---|---|---|---|---|---|
| Independent Variable: After-Tax Current Income | 0.104 (0.013) | 7.8 | 0.110 (0.017) | 6.3 | 0.089 (0.002) | 52.8 |
| Independent Variable: Net Worth (Including Housing) | 0.011 (0.001) | 11.0 | 0.010 (0.001) | 8.3 | 0.075 (0.0003) | 225.9 |
| Independent Variable: Present Value of Expected Future Income (after tax) | 0.010 (0.001) | 6.9 | 0.009 (0.002) | 5.7 | 0.046 (0.001) | 314.6 |
| Independent Variable: Age | 128 (122) | 1.0 | 278 (169) | 1.6 | 1,025 (3.2) | 315.8 |
| Independent Variable: Married (dummy) | 8,039 (1,380) | 5.8 | 8,112 (1,814) | 4.5 | N.A. | N.A. |
| Intercept | 11,810 (7,895) | 1.5 | 3,276 (10,906) | 0.3 | -64,375 (240) | -268.3 |
| Number of Observations | 1029 | 665 | 19120 | |||
| Adjusted R-squared | 0.42 | 0.37 | 0.96 |
Note: * The 2003 regression exludes 3 outlier households whose stock holdings, and total net worth, increased by between $9 million and $65 million over the 2002 to 2004 period. Numbers in parenthesis are the standard errors.
Table 5. Range of Simulated Sample Coefficients for Components of Total Wealth
| Over 10 Simulated Samples: Range of Coefficients | Over 10 Simulated Samples: Extremes of 95% confidence intervals | |
|---|---|---|
| After-Tax Current Income | 0.082-0.095 | 0.072-0.105 |
| Net Worth (Including Housing) | 0.0744-0.0768 | 0.072-0.079 |
| Present Value of Expected Future Income (after tax) | 0.0451-0.0462 | 0.044-0.047 |
Table 6. Regressions Omitting Future Income
| Consumption HRS 2001: Estimated Coefficient | Consumption HRS 2001: t-statistic | Consumption HRS 2003*: Estimated Coefficient | Consumption HRS 2003*: t-statistic | Consumption Simulated Sample: Estimated Coefficient | Consumption Simulated Sample: t-statistic | |
|---|---|---|---|---|---|---|
| Independent Variable: After-Tax Current Income | 0.135 (0.013) | 10.6 | 0.136 (0.017) | 8.0 | 0.519 (0.002) | 214.0 |
| Independent Variable: Net Worth (Including Housing) | 0.010 (0.001) | 10.5 | 0.010 (0.001) | 8.2 | 0.049 (0.001) | 61.3 |
| Independent Variable: Age | -69 (121) | -0.6 | 15 (167) | 0.1 | 296 (5.7) | 52.4 |
| Independent Variable: Married (dummy) | 10,035 (1,368) | 7.3 | 10,583 (1,802) | 5.9 | N.A. | N.A. |
| Intercept | 26,493 (7,728) | 3.4 | 22,104 (10,632) | 2.1 | -7,825 (395) | -19.8 |
| Number of Observations | 1029 | 665 | 19120 | |||
| Adjusted R-squared | 0.39 | 0.34 | 0.74 |
Note: * The 2003 regression exludes 3 outlier households whose stock holdings, and total net worth, increased by between $9 million and $65 million over the 2002 to 2004 period. Numbers in parenthesis are the standard errors.
Table 7. Changes in Consumption and Components of Total Wealth
| Mean Regression - Change in Consumption, HRS 2001 & 2003: Estimated Coefficient | Mean Regression - Change in Consumption, HRS 2001 & 2003: t-statistic | Median Regression - Change in Consumption, HRS 2001 & 2003: Estimated Coefficient | Median Regression - Change in Consumption, HRS 2001 & 2003: t-statistic | |
|---|---|---|---|---|
| Independent Variable: Change in After-Tax Income | -0.0001 (0.0131) | -0.01 | -0.0018 (0.0058) | -0.3 |
| Independent Variable: Change in Net Worth | -0.0019 (0.0017) | -1.0 | 0.0030 (0.0006) | 5.2 |
| Independent Variable: Change in Present Value of Expected Future Income | 0.0062 (0.0037) | 1.7 | 0.0049 (0.0017) | 2.8 |
| Intercept | 1,662 (702) | 2.4 | 259 (342) | 0.8 |
| Number of Observations | 661 | 661 | ||
| Adjusted R-squared | 0.001 | 0.01 |
Note: Numbers in parenthesis are the standard errors.
Table 8. Regressions of Consumption on Long-Term Care Insurance, Omitting Future Income
| HRS Consumption 2001: Estimated Coefficient | HRS Consumption 2001: t-statistic | HRS Consumption 2001: Estimated Coefficient | HRS Consumption 2001: t-statistic | HRS Consumption 2003: Estimated Coefficient | HRS Consumption 2003: t-statistic | HRS Consumption 2003: Estimated Coefficient | HRS Consumption 2003: t-statistic | |
|---|---|---|---|---|---|---|---|---|
| Independent Variable: After-Tax Current Income | 0.138 (0.013) | 10.7 | 0.109 (0.013) | 8.1 | 0.128 (0.017) | 7.5 | 0.098 (0.018) | 5.6 |
| Independent Variable: Net Worth (Including Housing) | 0.010 (0.001) | 10.4 | 0.011 (0.001) | 11.0 | 0.009 (0.001) | 7.4 | 0.009 (0.001) | 7.7 |
| Independent Variable: Present Value of Expected Future Income (after tax) | 0.009 (0.001) | 6.4 | 0.0110 (0.002) | 6.0 | ||||
| Independent Variable: Long-Term Care Insurance | 5,835 (1,749) | 3.3 | 3,830 (1,745) | 2.2 | 4,963 (2,546) | 2.0 | 3,082 (2,502) | 1.2 |
| Independent Variable: Age | -85 (121) | -0.7 | 106 (123) | 0.9 | 8 (165) | 0.1 | 256 (166) | 1.5 |
| Independent Variable: Married (dummy) | 9,567 (1,372) | 7.0 | 7,749 (1,387) | 5.6 | 12,284 (1,766) | 7.0 | 9,655 (1,776) | 5.4 |
| Intercept | 26,889 (7,740) | 3.5 | 12,908 (7,940) | 1.6 | 21,563 (10,513) | 2.1 | 3,646 (10,674) | 0.3 |
| Number of Observations | 1029 | 1029 | 686 | 686 | ||||
| Adjusted R-squared | 0.39 | 0.42 | 0.33 | 0.37 |
Note: Numbers in parenthesis are the standard errors.
Table 9. Regressions of Total Consumption and Sources of Income
| Total Consumption 2001: Estimated Coefficient | Total Consumption 2001: t-statistic | |
| Independent Variable: After-Tax Current Income | 0.099 (0.013) | 7.4 |
| Independent Variable: Net Worth (Including Housing) | 0.011 (0.001) | 10.8 |
| Independent Variable: Future Income: Social Security | 0.022 (0.007) | 3.2 |
| Independent Variable: Future Income: Defined Benefit Pension | 0.007 (0.002) | 3.7 |
| Independent Variable: Future Income: Defined Contribution Pension | 0.010 (0.004) | 2.7 |
| Independent Variable: Future Income: Labor Earnings | 0.022 (0.005) | 4.6 |
| Independent Variable: Future Income: Other Income | -0.010 (0.007) | -1.5 |
| Age | 227 (127) | 1.8 |
| Married (dummy) | 6,348 (1,568) | 4.1 |
| Intercept | 4,460 (8,232) | 0.5 |
| Number of Observations | 1029 | |
| Adjusted R-squared | 0.43 |
Note: Numbers in parenthesis are the standard errors.
Table 10a. Regressions of Consumption on Current Income and Future Income
| HRS Consumption 2001: Estimated Coefficient | HRS Consumption 2001: t-statistic | |
|---|---|---|
| Independent Variable: After-Tax Current Income | 0.101 (0.013) | 7.6 |
| Independent Variable: Net Worth (Including Housing) | 0.010 (0.001) | 10.5 |
| Independent Variable: Present Value of Expected Future Income (after tax) | 0.008 (0.001) | 5.9 |
| Independent Variable: Less Than High School Education | -7,765 (1,764) | -4.4 |
| Independent Variable: Farmer | -4,753 (3,420) | -1.4 |
| Independent Variable: Age | 177 (125) | 1.4 |
| Independent Variable: Married (dummy) | 8,257 (1,413) | 5.8 |
| Intercept | 10,927 (8,057) | 1..4 |
| Number of Observations | 991 | |
| Adjusted R-squared | 0.42 |
Note: Numbers in parenthesis are the standard errors.
Table 10b. Regressions of Consumption on Current Income and Future Income - Subsample with Risk Aversion Measure (Retired & Non-retired)
| HRS Consumption 2001: Estimated Coefficient | HRS Consumption 2001: t-statistic | |
|---|---|---|
| Independent Variable: After-Tax Current Income | 0.117 (0.014) | 8.1 |
| Independent Variable: Net Worth (Including Housing) | 0.011 (0.001) | 10.5 |
| Independent Variable: Present Value of Expected Future Income (after tax) | 0.010 (0.002) | 5.9 |
| Independent Variable: High Measured Risk Aversion | -3,619 (1,385) | -2.6 |
| Independent Variable: Age | 303 (138) | 2.2 |
| Independent Variable: Married (dummy) | 7,834 (1,493) | 5.3 |
| Intercept | 2,352 (8,836) | 0.3 |
| Number of Observations | 729 | |
| Adjusted R-squared | 0.47 |
Note: Some households are missing the risk aversion measure, resulting in a smaller sample size. Numbers in parenthesis are the standard errors.
Figure 1. HRS Historical Income Profiles by Education
| Less Than High School | High School | Bachelor's Degree or Greater | |
|---|---|---|---|
| 22 | 12500 | 16400 | 12500 |
| 23 | 12500 | 16400 | 12500 |
| 24 | 13487.5 | 17548 | 15062.5 |
| 25 | 14512.55 | 18706.17 | 17758.69 |
| 26 | 15557.45 | 19865.95 | 20529.04 |
| 27 | 16630.92 | 21018.18 | 23300.46 |
| 28 | 17711.93 | 22153.16 | 26003.32 |
| 29 | 18792.36 | 23260.81 | 28577.65 |
| 30 | 19863.52 | 24354.07 | 30978.17 |
| 31 | 20916.29 | 25401.3 | 33146.64 |
| 32 | 21941.18 | 26417.35 | 35102.29 |
| 33 | 22928.54 | 27394.79 | 36787.2 |
| 34 | 23868.61 | 28326.22 | 38221.9 |
| 35 | 24727.88 | 29204.33 | 39445 |
| 36 | 25519.17 | 30022.05 | 40431.13 |
| 37 | 26233.71 | 30772.6 | 41239.75 |
| 38 | 26863.31 | 31449.6 | 41899.59 |
| 39 | 27400.58 | 32078.59 | 42444.28 |
| 40 | 27838.99 | 32623.93 | 42911.17 |
| 41 | 28173.06 | 33113.28 | 43297.37 |
| 42 | 28398.44 | 33543.76 | 43643.75 |
| 43 | 28512.04 | 33879.19 | 43992.9 |
| 44 | 28512.04 | 34150.23 | 44344.84 |
| 45 | 28426.5 | 34355.13 | 44743.94 |
| 46 | 28227.51 | 34492.55 | 45191.38 |
| 47 | 27945.24 | 34561.54 | 45688.49 |
| 48 | 27581.95 | 34561.54 | 46236.75 |
| 49 | 27140.64 | 34492.41 | 46837.83 |
| 50 | 26624.97 | 34388.93 | 47493.56 |
| 51 | 26039.22 | 34216.99 | 48205.96 |
| 52 | 25414.28 | 33977.47 | 48977.26 |
| 53 | 24753.51 | 33705.65 | 49760.89 |
| 54 | 24060.41 | 33368.59 | 50557.07 |
| 55 | 23338.6 | 33001.54 | 51315.42 |
| 56 | 22615.1 | 32572.52 | 52033.84 |
| 57 | 21891.42 | 32116.51 | 52606.21 |
| 58 | 21169 | 31634.76 | 53027.06 |
| 59 | 20449.25 | 31096.97 | 53239.17 |
| 60 | 19753.98 | 30537.22 | 53185.93 |
| 61 | 18687.26 | 29957.01 | 52813.63 |
| 62 | 17509.97 | 28758.73 | 52021.42 |
| 63 | 16599.45 | 27263.28 | 50772.91 |
| 64 | 16250.86 | 26090.96 | 49046.63 |
| 65 | 16104.6 | 25595.23 | 46790.49 |
| 66 | 15991.87 | 25339.28 | 43983.06 |
| 67 | 15767.98 | 25060.55 | 42003.82 |
| 68 | 15594.54 | 24734.76 | 39609.6 |
| 69 | 15313.83 | 24512.15 | 37193.42 |
| 70 | 15099.44 | 24021.9 | 34143.56 |
| 71 | 14963.55 | 23661.57 | 32265.66 |
| 72 | 14903.69 | 23424.96 | 30975.03 |
| 73 | 14903.69 | 23424.96 | 30975.03 |
| 74 | 14903.69 | 23424.96 | 30975.03 |
| 75 | 14903.69 | 23424.96 | 30975.03 |
| 76 | 14903.69 | 23424.96 | 30975.03 |
| 77 | 14903.69 | 23424.96 | 30975.03 |
| 78 | 14903.69 | 23424.96 | 30975.03 |
| 79 | 14903.69 | 23424.96 | 30975.03 |
| 80 | 14903.69 | 23424.96 | 30975.03 |
| 81 | 14903.69 | 23424.96 | 30975.03 |
| 82 | 14903.69 | 23424.96 | 30975.03 |
| 83 | 14903.69 | 23424.96 | 30975.03 |
| 84 | 14903.69 | 23424.96 | 30975.03 |
| 85 | 14903.69 | 23424.96 | 30975.03 |
Data Appendices
Appendix A: Constructing Future Income (Human Wealth) and Total Wealth
Total wealth is estimated in the HRS by summing financial and housing assets with human wealth, or the present value of future income streams. Net worth comes from the RAND user-contribution variables which include some imputations for assets. Net worth is defined as the value of primary residence, vehicles, owned businesses, other real estate, IRAs, stocks/mutual funds, investment trusts, bonds, Treasury securities, CDs, "other assets", and money market, savings, and checking accounts less the value of all mortgages, home loans, and other debt (such as unpaid medical bills, loans, or credit card debt). Due to the multiple categories and the extensive use of brackets plus limited imputations to reduce non-response, these data are generally considered high quality.
1. Earnings
As stated above, human wealth, or future income, has four components. First, for non-retired households, earnings income is estimated deterministically based on current wages incremented each year for tenure and experience.16 Wages from 2002 until assumed retirement were forecast deterministically using the method of Gustman and Steinmeier (2002) that increments wages from the existing wage base for each additional year of experience and tenure using experience and tenure coefficients from a wage regression.17. Earnings are accrued until the estimated retirement age, which itself is based on survey responses to questions about planned retirement.18
2. Social Security
Future Social Security benefits are estimated by calculating the
AIME and PIA using each respondent's record of covered Social
Security earnings since 1951 (as well as forecasted earnings up to
age retirement). If retirement age is 
=62 the
household is assumed to take reduced benefits at age 62. For
retirement ages from 63 to 68, households are assumed to begin
receiving Social Security (with actuarial adjustment) at retirement
age. For retirement ages 68 and over, Social Security benefits
(actuarially adjusted) are assumed to begin at age 68. The
calculation then generates the present value of after-tax household
expected Social Security benefits up to age 100. The present value
calculation includes discounts for actual mortality probabilities
from age 65 to 100 based on life tables.19
3. Pensions
Third, the cash flow and present value of defined benefit pensions are estimated using the HRS Pension Calculator and using actual earnings histories rather than projecting earnings from one base year. The cash flow value is only used in the calculation of tax brackets but the present value provided by the Calculator is included in M. The present value of defined contribution plans provided by the Calculator is also added to M. Imputations based on self-reports where used when either a defined benefit or defined contribution pension was missing or zero and the respondent self-reported a value.
4. Permanent Benefits
Households already receiving other government income in 2002 that is not poverty-based, such as veteran benefits or Social Security disability, are assumed to continue receiving those benefits until death. The present value of after-tax benefits from these sources is included in wealth. The present value calculation includes discounts for actual mortality probabilities from age 65 to 100 based on life tables.
5. Poverty Benefits
SSI is a federal welfare program for the elderly and disabled that essentially sets a floor on elderly income in the vicinity of $6,000-10,000 per year (varies by state and marital status). Any household whose final present value of wealth by the described calculations ends up below the approximate present value (mortality discounted) of receiving this income floor for the rest of their lives, is assumed to receive this income floor as a government benefit.20
6. Taxes
Annual tax rates are estimated based on projected income from: earnings; the annual cash flow of pension annuities (from the pension calculator); a rough fraction of interest, dividend, or rent producing financial assets for high-financial-wealth households (to represent taxable interest or rental income); veterans and SSDI benefits; and the portion of Social Security benefits that are taxable (determined explicitly on a year to year basis). These tax rates, specific to each household each year, are applied to annual earnings and Social Security before the present value calculation. The tax rate applied to the present value of pension annuities (generated by the pension calculator) is the average of the household's tax rates from ages 65-85.
Appendix B: Imputation of Housing and Vehicle Consumption
For homeowners, spending on mortgage, property tax, and homeowners insurance is replaced by an imputed rental equivalence value for their home. Rental equivalence values were estimated using the relationship between housing characteristics and reported rental equivalence for owned homes in the 2001 CEX. To impute the flow of consumption from housing, housing characteristics including property value, census district, urban/rural, number of rooms, and type of housing (such as single family, apartment, or trailer) were regressed on reported rental equivalence in the 2001 CEX for the sample of homeowners with household head aged 53 or over (see Table A2). The coefficients were then applied to each household's housing characteristics as reported in the 2002 HRS. This regression has an adjusted r-square of .40, very similar to that for the hedonic regression in Johnson, Shipp, and Garner (1997) that regresses actual rent paid by renters on factors such as location, rooms, and housing type.
A value for vehicle consumption is imputed based on the relationship between household characteristics and net outlays on new and used cars and trucks in the 2001 CEX, as described in the Appendix B. As in Cutler and Katz (1991), the household characteristics used to impute vehicle consumption include income, family size, education of head, total household expenditures (less vehicle expenditures), and total expenditures squared, as well as number of cars owned (see Table A1). This imputation is applied to households that either report owning a vehicle in the 2000 HRS or report paying vehicle insurance in the CAMS.
Table A1. Regression to Impute Vehicle Consumption Using Consumer Expenditure Survey. Dependent Variable: Vehicle Consumption
| Coefficient | Standard Error | |
|---|---|---|
| Total Non-Vehicle Expenditures | 0.052** | 0.0086 |
| Total Non-Vehicle Expenditures squared | -1.76xE-9 | 5.18xE-9 |
| Pretax Income | 0.005 | 0.0039 |
| Age of Reference Person | -43** | 14 |
| Family Size | 386** | 126 |
| Male | -11 | 267 |
| Education: Less Than High School | 249 | 416 |
| Education: High School | 953** | 342 |
| Education: Some College | 332 | 400 |
| Education: College (omitted group) | ||
| Intercept | 2287 | 1106 |
| R-Squared | 0.215 |
Notes: * Denotes significant at the 90% level while ** denotes significance at the 95% level.
Table A2. Regression to Impute Housing Consumption Using Consumer Expenditure Survey. Dependent Variable: Rental Equivalence
| Coefficient | Standard Error | |
|---|---|---|
| Property Value | 0.0037** | 0.0001 |
| Property Value Squared | -1.7xE-9** | 9.4xE-11 |
| Census Division: Mid-Atlantic | -408** | 60 |
| Census Division: South Atlantic | -247** | 29 |
| Census Division: East North Central | -505** | 47 |
| Census Division: West North Central | -122** | 29 |
| Census Division: East South Central | -459** | 35 |
| Census Division: West South Central | -267** | 32 |
| Census Division: Mountain | -467** | 59 |
| Census Division: Pacific | -22 | 31 |
| Urban | 16 | 31 |
| Urban*Mid-Atlantic | 300** | 57 |
| Urban*West North Central | 261** | 47 |
| Urban*Mountain | 259** | 58 |
| Number of rooms in house | 28** | 3 |
| Housing Type: Duplex | -144** | 46 |
| Housing Type: Apartment | 114** | 39 |
| Housing Type: Mobile Home | -31 | 30 |
| Housing Type: Other Housing | 53 | 81 |
| Housing Type: Single Family Home | ||
| Intercept | 542** | 46 |
| R-Squared | 0.397 |
Notes: * Denotes significant at the 90% level while ** denotes significance at the 95% level.
Footnotes
* The author is a staff economist in the Division of International Finance, Board of Governors of the Federal Reserve System, Washington, D.C. 20551 U.S.A. The views in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. The author thanks Grant Long for valuable research assistance and Marco Cagetti, Miles Kimball, Bob Willis, Claudia Sahm, and seminar participants at the Federal Reserve Board of Governors, the University of Michigan, and the Eastern Economics Conference for helpful comments and discussion. Return to text
1. Rough calculations based on the 2004 Survey of Consumer Finances show that households aged 55-74 hold almost 50% of U.S. household net worth; more than 70% of net worth for households aged 45-74. Return to text
2. Hurd (1989, 1999) laid groundwork for the role of mortality in the consumption decision for older households. Other works by Hurd, Smith, Laitner, and Kotlikoff as well as Dynan, Skinner, Zeldes (2002) debate the role of intended bequests, while Palumbo (1999) and Dynan, Skinner, and Zeldes (2002) highlight the potential importance of late-life medical costs. Return to text
3. This was the primary point of Carroll (1994), with which this paper is in complete agreement. Furthermore, using HRS data, such measures of income uncertainty as Carroll (1994) used produce qualitatively similar results of significantly reduced consumption. Return to text
4. Note that if there were no shocks (i.e.
and N are 1) and utility is CRRA,
then this standard consumption problem would have the familiar
certainty-equivalent solution that is linear in total
resources.
![$ C_{t}=k_{t}\ast\lbrack Y_{t}+H_{t}+W_{t}]$](img5.gif){kind=small}
In this certainty equivalent solution, k
is a
function of the interest rate, time remaining (T-(t+1)), the
discount rate, and the preference parameters of the utility
function. Pounder (2007) adds time-varying mortality hazards,
stochastic risky asset returns, bequests, and separation of the
risk aversion and inter-temporal substitution parameters to the
model in an attempt to match the heterogeneity of consumption in
the HRS. Return to text
5. These data are used only with strictly restricted access for purposes of protecting respondent privacy. Return to text
6. Earnings for future years of work are projected by tenure and age from current wages, but these make up only a small portion of future income. IRAs, or similar non-employer-sponsored lump-sum retirement assets, are included in net worth not in future income. However, employer-sponsored defined contribution plans are considered future income. Return to text
7. The mailout was sent to 5,000 households from the 2000 HRS survey and had a simple response rate of 77%. The responding sample is not significantly different from the HRS sample as a whole on most basic economic and demographic characteristics such as age, marital status, race, and income, although any small differences in race and age are compensated for by a special set of weights created for the CAMS. Return to text
8. Since the sampling design chose individuals in the relevant age range but then incorporated both spouses into the survey, and since household age is taken from the age of the male for a married couple, it is possible that the household age is out of the official sampling age range. For example, take a 59 year old woman selected into the original HRS cohort in 1992 that was married to a then 63 year old man. In 2001 the woman would be 68 but the household would be 72. Most households that are out of the official range are older than that range, due to older husbands. Therefore, this analysis includes households up to age 73 in order to not artificially exclude the households with women who are in the sampling age range and whose husbands are not too far outside the range to expect significantly different behavior. Return to text
9. Even so, this method does make the assumption that the simulated households expect the average income growth that the cohort actually received, on average by education group. A better assumption would be to take the average income profile by education and occupation group for households that are about five to fifteen years older than the households of interest, using fine gradations of age, such as two- or three- year age groups. This would, for example, assume that a twenty-five year-old forms his expectations about income growth by observing the incomes of thirty to forty year-olds. However, although the combined HRS sources provide full income series for certain cohorts, small sample sizes limit the reasonable amount of disaggregation that can be done by age, education, and occupation while still obtaining robust means. Alternatively, other sources of historical income growth, such as the CPS, may not be available consistently as far back as when most of these households began work, the 1940s and 1950s. Return to text
10. These regressions restrict the analysis to households that only include a head or head and spouse. Households with children or other family members at home are excluded, since these households will likely spend more for temporary demographic reasons. In addition, households who added or lost a member between 2000 and 2002 (for the 2001 analysis) or between 2002 and 2004 (for the 2003 analysis) were also excluded. This reduces the sample size by about 750 observations. Return to text
11. Think of consumption as an annuity flow with total wealth as the principal, the shorter the annuitization period, the higher the portion of the principal that gets paid out each year. Furthermore, with stochastic income, uncertainty over total remaining income declines each year as income is realized, reducing the incentive for precautionary saving incrementally with age. Return to text
12. The retired variable itself is negative but insignificant. Return to text
13. In a CEQ model, where relationships are linear, this would be interpreted as both an average and marginal propensity to consume out of additional current income. Return to text
14. These consumption data are clearly too noisy to perform meaningful Euler equation analyses, which is why this paper focuses on levels of consumption. First differencing always exacerbates measurement error and the sample size, 663, may be too small to generate precise estimates. The fact that the data is too noisy to get a strong signal after first differencing does not invalidate the strong signal obtained from the cross-sectional analysis of the levels. Return to text
15. "Other income" also includes a projection forward of veterans benefits currently received by the household. Since this component of "other income" is a linear projection of an element of current income, it is not expected to have an independent effect on consumption since current income is already in the regression. Return to text
16. Work assignment and labor earnings were calculated separately for each respondent. Respondents with a zero or missing 2002 wage and designated "not in the labor force" (as opposed to retired), were not assigned a wage and were assumed not to work. Respondents with a zero or missing 2002 wage who self-report that they are fully retired (even if they have not reached their pre-determined retirement age) are assumed to not work or receive any labor earnings for the remainder of their lives. All others with a zero or missing 2002 wage (due to unemployment or any reason other than self-report of full retirement) were assumed to be working full time and assigned their wage from 2000 Return to text
17. The wage regression, using the same covariates as Gustman and Steinmeier, returned almost identical coefficients for tenure and experience as their paper, which is not surprising since they also use a subset of the HRS sample. Return to text
18. Retirement ages are set based on self-reports of expected retirement age or year (taking the most recent previous wave's report when multiple reports are available). Only about half of workers report a specific age or year of expected retirement. However, a majority of the rest does report at least one of the following: a "normal retirement age" for their job/occupation, an age at which they expect to change jobs (presumably leave a primary job for a slower-paced job), or an age at which they expect to reduce work hours. These responses were used as benchmarks to estimate an expected retirement age for each household. For example, someone reporting that the normal retirement age for their job is 62 and they expect to reduce hours at age 60 would be assigned a retirement age of 62. About 10% of workers responded to none of these questions and were arbitrarily assigned a retirement age of 65. Expected retirement ages are bounded at 50 and 70. Return to text
19. For married couples, household benefits are the maximum of each spouse receiving Social Security based on their own work history or 1.5 times the Social Security for the higher earning spouse. The present value calculation for married couples also incorporates the different mortality risks for different age spouses. The expected value for each year is the sum of three values, the couple's SS benefit multiplied by the probability of both being alive, the head's benefit multiplied by the probability that only the head is alive, and the survivor's benefit multiplied by the probability of only the spouse being alive. Return to text
20. The discounted present value of this income floor is approximately $100,000 for a 65 year-old couple. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text