
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 982, October 2009 --- Screen Reader Version*
The Market-Perceived Monetary Policy Rule1
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
We introduce a novel method for estimating a monetary policy rule using macroeconomic news. Market forecasts of both economic conditions and monetary policy are affected by news, and our estimation links the two effects. This enables us to estimate directly the policy rule agents use to form their expectations, and in so doing flexibly capture the particular dynamics of policy response. We find evidence that between 1994 and 2007 the market-perceived Federal Reserve policy rule changed: the output response vanished, and the inflation response path became more gradual but larger in long-run magnitude. In a standard model we show that output smoothing caused by a larger inflation response magnitude is offset by the more measured pace of response. Our response coefficient estimates are robust to measurement and theoretical issues with both potential output and the inflation target.
Keywords: Monetary policy rule, market perceptions, Taylor Rule, Fed funds futures
JEL classification: E43, E52, E58
1. Introduction
A large literature estimates monetary policy rules of the form proposed by Taylor (1993) that relate the realized fed funds rate to past or expected future indicators of output and inflation. Examples include Evans (1998), Clarida, Gali, and Gertler (2000), Rudebusch (2002), Owyang and Ramey (2004), Boivin (2006), Ang, Dong, and Piazzesi (2007), and Smith and Taylor (forthcoming). That kind of estimation is well suited to describe what policy rule the Fed has actually followed.
However, there is also considerable interest in what market participants expect the Fed to do. Expectations of future monetary policy are a key part of the monetary transmission mechanism in virtually any macroeconomic model. The Federal Reserve's expected future policy rate influences current interest rates immediately upon the market learning about the Federal Reserve's intentions to stimulate or curtail economic behavior (Hamilton (2008)). Moreover, Federal Open Market Committee (FOMC) statements provide guidance for the direction of future policy rates and are responded to instantaneously by the market upon their public release (Kohn and Sack (2004)).
This paper proposes a novel method that enables us to uncover the market's perceived monetary policy rule. Like many previous researchers (e.g., Gürkaynak, Sack, and Swanson (2005), Faust, Rogers, Wang, and Wright (2007), and Bartolini, Goldberg, and Sacarny (2008)), we identify news by the difference between a macroeconomic data release value and the value expected beforehand by the market. On this news day, we measure the news' effects on economic fundamentals' forecasts and monetary policy forecasts, the latter coming from the change in market prices for fed funds futures contracts. Our contribution is to use a Taylor-Rule structure to link the fundamentals forecast updates with the policy forecast updates in order to estimate the market-perceived parameters for a Taylor Rule.
Our methodology opens up to researchers the use of daily data, which offers three advantages we highlight. First, by looking at the response of fed funds futures prices for contracts of different horizons to a new data release, we are able to measure how long the market believes it will take the Fed to adjust interest rates in response to changing fundamentals. We can thereby obtain new measures of the nature of monetary policy inertia, something that is difficult for traditional methods to estimate.5 We document a change in the market's perception of the Fed's policy rule in terms of both the magnitude of the ultimate response and in the degree of inertia. Since 2000, the market-perceived monetary policy rule involves an eventual response to inflation that is bigger than that associated with perceived pre-2000 behavior. On the other hand, the market also believes that the Fed is more sluggish in making its intended adjustments. We show in simulations with a simple new-Keynesian model that the first feature would tend to stabilize output, whereas the second feature would be destabilizing. These simulations suggest that the "measured pace" of monetary tightening during 2004-2006 may have been counterproductive.
Second, our approach offers a cleaner answer for how to handle real-time versus revised data sets, by focusing on market expectations formed on the basis of the information as it had actually been publicly released as of a particular calendar date.
Third, our approach is robust to estimation problems engendered by potential output and the inflation target. Potential output is tricky to define and measure in real time (Orphanides and van Norden (2002)), and Orphanides (2001) argues that this can confound policy rule estimation. On the other hand, the Fed's inflation target is unobservable, and moreover a growing literature, including Ireland (2007) and Cogley and Sbordone (2008) among others, has postulated an important historical role for low-frequency variation in the Fed's inflation target. The latency of potential output and the inflation target poses a problem for standard policy rule estimation methods because their values are necessary for measuring the explanatory variables. Our method uses daily data to difference out these slowly moving latent variables from the estimation equations.
The remainder of the paper is structured as follows: Section 2 introduces our framework and its testable implications. Section 3 discusses the empirical strategy based on these implications and describes the data. Section 4 presents our baseline full sample results, and then shows evidence of time variation in perceived policy response and estimates parameters on subsamples. Section 5 generalizes the approach to estimation of a Taylor Rule with lagged adjustment dynamics and discusses the economic significance of those dynamics. We investigate the sensitivity of our conclusions to various assumptions and variable decisions in Section 6. Section 7 concludes.
2. Framework
We begin with a standard Taylor Rule that is assumed by the market to
characterize Federal Reserve decisions. Let ![]() represent a particular month
and
represent a particular month
and ![]() the average daily effective fed funds rate for that month. The
market assumes that the Fed sets the funds rate in response to the Taylor Rule
variables
the average daily effective fed funds rate for that month. The
market assumes that the Fed sets the funds rate in response to the Taylor Rule
variables
![]() , the deviation from target of cumulative
inflation between
, the deviation from target of cumulative
inflation between ![]() and
and ![]() , and
, and
![]() , a measure of the real
output gap in
, a measure of the real
output gap in ![]() :
:
| (2.1) |
where ![]() is real output growth and
is real output growth and ![]() is potential real output growth.
is potential real output growth.
We will be keeping careful track in this analysis of exactly when data of
different sorts arrives. Let
![]() denote the information set that is
actually available to market participants as of the
denote the information set that is
actually available to market participants as of the ![]() th day of month
th day of month ![]() ;
let
;
let
![]() denote the Fed's information set at that time. The
formulation (2.1) assumes that the Fed knows the values of
denote the Fed's information set at that time. The
formulation (2.1) assumes that the Fed knows the values of
![]() and
and
![]() at the time it sets
at the time it sets ![]() even
though
even
though ![]() and
and ![]() would not be known to market participants until
some later time. The framework is readily generalizable to a case where the
Fed instead sets
would not be known to market participants until
some later time. The framework is readily generalizable to a case where the
Fed instead sets ![]() on the basis of information available as of some day
on the basis of information available as of some day
![]() within month
within month ![]() :
:
| (2.2) |
Consider the expectation of (2.1) conditional on information
available to the market as of the ![]() th day of an earlier month
th day of an earlier month ![]() :
:
| (2.3) |
Alternatively, if we take expectations of (2.2) conditional on the information set
![]() , the identical equation (2.3) follows due to the Law of Iterated Expectations.6 In either case, we obtain the
following expression for the change in expectations between the
, the identical equation (2.3) follows due to the Law of Iterated Expectations.6 In either case, we obtain the
following expression for the change in expectations between the ![]() th day and
the previous day
th day and
the previous day ![]() of month
of month ![]() :
:
| (2.4) | ||
Equation (2.4) is the key to what follows, stating that updates to the market forecast of future policy are linked to updates to the market forecast of future economic conditions via the market-perceived monetary policy rule.
We will consider a set of
![]() different days within month
different days within month ![]() on
which particular information becomes available. Consider first
on
which particular information becomes available. Consider first ![]() which we
associate with the release of, say, the CPI. Let
which we
associate with the release of, say, the CPI. Let ![]() denote the day in
month
denote the day in
month ![]() on which a new inflation number (namely, the value of
on which a new inflation number (namely, the value of
![]() is released. For example, for
is released. For example, for ![]() December 2008, the CPI data
reported on December 16 (
December 2008, the CPI data
reported on December 16 (
![]() was the value for November 2008 (so
that
was the value for November 2008 (so
that
![]() became known on
became known on
![]() Consider then the initial
report of the value of
Consider then the initial
report of the value of
![]() on day
on day ![]() . We will proxy the
news content of this report by comparing the actual value
. We will proxy the
news content of this report by comparing the actual value
![]() with
the value expected by the market, which we denote
with
the value expected by the market, which we denote
![]() :
:
The CPI announcement of
![]() (arriving on
(arriving on ![]() ) has an
implication for what market participants would have expected
) has an
implication for what market participants would have expected ![]() to turn
out to be. We propose to model this implication by a linear equation
forecasting
to turn
out to be. We propose to model this implication by a linear equation
forecasting ![]() on the basis of
on the basis of
![]()
![]() ,
and
,
and
![]() , where
, where
![]() denotes a vector of
other variables that would have been known to market participants prior to the
day
denotes a vector of
other variables that would have been known to market participants prior to the
day ![]() of month
of month ![]() :
:
| (2.5) |
The first subscript (![]() on the coefficients indicates that this is a
coefficient used to forecast subsequent inflation, and the second subscript
(1) indicates that the forecast is formed on the day on which the first
information variable (the CPI) is released. Note that the coefficients in
equation (2.5) are defined as linear projection
coefficients, so that
on the coefficients indicates that this is a
coefficient used to forecast subsequent inflation, and the second subscript
(1) indicates that the forecast is formed on the day on which the first
information variable (the CPI) is released. Note that the coefficients in
equation (2.5) are defined as linear projection
coefficients, so that
![]() is uncorrelated with
is uncorrelated with
![]() ,
,
![]() , and
, and
![]() by the definition of
by the definition of
![]() ,
,
![]() , and
, and
![]() . The
consequences of the month
. The
consequences of the month ![]() day
day ![]() news release about
news release about
![]() for market expectations of
for market expectations of ![]() are then given by
are then given by
| (2.6) |
where we will subsume the dependence of ![]() on
on ![]() when it is clear
from the context.
when it is clear
from the context.
The announcement of
![]() may also hold implications for market
expectations about real output
may also hold implications for market
expectations about real output ![]() , which we proxy analogously as
, which we proxy analogously as
| (2.7) |
Note that certain elements of
![]() and
and
![]() may be set to zero, depending on what elements
of
may be set to zero, depending on what elements
of
![]() forecast
forecast ![]() or
or ![]() .
.
Let
![]() denote the futures interest rate on day
denote the futures interest rate on day ![]() of month
of month
![]() for a fed funds futures contract based on
for a fed funds futures contract based on ![]() the effective fed
funds rate
the effective fed
funds rate ![]() months ahead. We propose that these fed funds futures offer us
a direct observation on how the market expectation of
months ahead. We propose that these fed funds futures offer us
a direct observation on how the market expectation of ![]() changed on day
changed on day
![]() :
:
| (2.8) |
Here
![]() captures the average change in the risk premium on fed funds
futures contracts and
captures the average change in the risk premium on fed funds
futures contracts and
![]() any change in the risk premium relative
to that average. In the absence of risk aversion in the fed funds futures
markets, the terms
any change in the risk premium relative
to that average. In the absence of risk aversion in the fed funds futures
markets, the terms
![]() and
and
![]() would be identically zero.
There is certainly good evidence for supposing the contribution of risk
aversion to daily changes in fed funds prices to be small; see
Piazzesi and Swanson (2008) and Hamilton (2009).7 In the
estimation strategy adopted here, any changes in the risk premium, along with
changes in the market's expectation of the residual in the Taylor Rule,
changes in the market's expectation of the inflation target, and changes in
the market's expectation of potential output growth, are incorporated into a
specification error
would be identically zero.
There is certainly good evidence for supposing the contribution of risk
aversion to daily changes in fed funds prices to be small; see
Piazzesi and Swanson (2008) and Hamilton (2009).7 In the
estimation strategy adopted here, any changes in the risk premium, along with
changes in the market's expectation of the residual in the Taylor Rule,
changes in the market's expectation of the inflation target, and changes in
the market's expectation of potential output growth, are incorporated into a
specification error
![]() ,
,
| (2.9) | ||
Substituting (2.6), (2.7), (2.8), and (2.9) into (2.4), we have
Consider next a second news release in month ![]() , namely the real activity
indicator
, namely the real activity
indicator
![]() released on day
released on day ![]() . For these days we employ the
auxiliary forecasting equations
. For these days we employ the
auxiliary forecasting equations
where
![]() is known prior to day
is known prior to day ![]() . From these we
derive
. From these we
derive
In general, if some indicator
![]() is released on day
is released on day
![]() we have the following three equations:
we have the following three equations:
| (2.10) |
| (2.11) |
| (2.12) |
Let
![]() denote the vector including the day
denote the vector including the day ![]() release of
release of
![]() and the information available as of the day before,
where we assume that
and the information available as of the day before,
where we assume that
![]() is uncorrelated with
is uncorrelated with
![]() ,
,
![]() and
and
![]() . Similarly, we take
. Similarly, we take
![]() to be uncorrelated with
to be uncorrelated with
![]()
![]() and
and
![]() , for
, for
![]() . Thus our identifying assumption is that the following vector
has expectation zero:
. Thus our identifying assumption is that the following vector
has expectation zero:
![$\displaystyle \left[ \begin{array}[c]{c} \left( \pi_{t}-\gamma_{\pi,1}w_{1,\tau-1}-\xi_{\pi,1}\tilde{w}_{1,\tau -1}-\mathbf{\zeta}_{\pi,1}^{\prime}\mathbf{x}_{1,\tau}\right) \mathbf{z} _{1,\tau}\\ \left( y_{t}-\gamma_{y,1}w_{1,\tau-1}-\xi_{y,1}\tilde{w}_{1,\tau -1}-\mathbf{\zeta}_{y,1}^{\prime}\mathbf{x}_{1,\tau}\right) \mathbf{z} _{1,\tau}\\ \left[ f_{i(1),\tau}^{(h)}-f_{i(1)-1,\tau}^{(h)}-\eta_{r,1}-(\beta\gamma _{\pi,1}+\delta\gamma_{y,1})(w_{1,\tau-1}-\tilde{w}_{1,\tau-1})\right] \mathbf{z}_{1,\tau}\\ \vdots\\ \left( \pi_{t}-\gamma_{\pi,K}w_{K,\tau-1}-\xi_{\pi,K}\tilde{w}_{K,\tau -1}-\mathbf{\zeta}_{\pi,K}^{\prime}\mathbf{x}_{K,\tau}\right) \mathbf{z} _{K,\tau}\\ \left( y_{t}-\gamma_{y,K}w_{K,\tau-1}-\xi_{y,K}\tilde{w}_{K,\tau -1}-\mathbf{\zeta}_{y,K}^{\prime}\mathbf{x}_{K,\tau}\right) \mathbf{z} _{K,\tau}\\ \left[ f_{i(K),\tau}^{(h)}-f_{i(K)-1,\tau}^{(h)}-\eta_{r,k}-(\beta\gamma _{\pi,K}+\delta\gamma_{y,K})(w_{K,\tau-1}-\tilde{w}_{K,\tau-1})\right] \mathbf{z}_{K,\tau} \end{array} \right] .$](img128.gif) |
(2.13) |
Note that the ability to distinguish ![]() from
from ![]() results from using
at least
results from using
at least ![]() different news releases during month
different news releases during month ![]() . A single
release such as the inflation number could in principle have implications both
for future inflation (as captured by
. A single
release such as the inflation number could in principle have implications both
for future inflation (as captured by
![]() ) and future output (as
captured by
) and future output (as
captured by
![]() Hence any response of the fed funds futures
prices to that news could come from either the policy rule inflation
coefficient (
Hence any response of the fed funds futures
prices to that news could come from either the policy rule inflation
coefficient (![]() or output coefficient (
or output coefficient (![]() However,
However,
![]() and
and
![]() are each separately observable (from the
differing responses of
are each separately observable (from the
differing responses of ![]() and
and ![]() to
to
![]() ), so the change
in the futures price on
), so the change
in the futures price on ![]() tells us one linear combination (namely
tells us one linear combination (namely
![]() of the policy rule parameters
of the policy rule parameters
![]() and
and ![]() But the separate response to the output release on day
But the separate response to the output release on day
![]() gives us a second linear combination (
gives us a second linear combination (
![]() . Thus, the
. Thus, the ![]() equations above are sufficient to identify
equations above are sufficient to identify
![]() and
and ![]() separately.
separately.
For each month ![]() there are
there are ![]() days of interest, for
days of interest, for ![]() the number of
economic indicators under consideration. Identification of this system is
achieved so long as it is not the case that any one indicator always arrives
on the same day as another indicator.8 Of course, it is all right for any two
indicators occasionally to arrive on the same day.
the number of
economic indicators under consideration. Identification of this system is
achieved so long as it is not the case that any one indicator always arrives
on the same day as another indicator.8 Of course, it is all right for any two
indicators occasionally to arrive on the same day.
3. Estimation
We begin this section by describing the formal estimation strategy, which is Hansen's (1982)generalized method of moments. Then we describe the data used.
3.1 Method
Recall that ![]() . Denoting
. Denoting
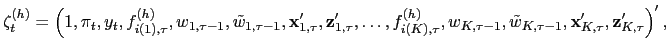
we rephrase (2.13) as the following population
orthogonality condition for each
![]() ,
,
![]()
| (3.1) |
where
![]() collects the auxiliary forecasting parameters
collects the auxiliary forecasting parameters
![]() along with the main parameters of interest, the policy rule
coefficients
along with the main parameters of interest, the policy rule
coefficients
![]() . Let
. Let
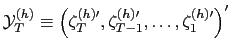 be the vector of all observations for each choice of
horizon
be the vector of all observations for each choice of
horizon ![]() . Then we have the sample average
. Then we have the sample average
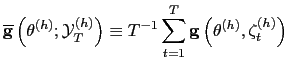
and the GMM estimator (Hansen (1982)) for each horizon
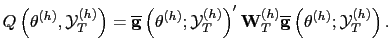 |
(3.2) |
As usual, the optimal weighting matrix
![]() is given by the
inverse of the asymptotic variance of the sample mean of
is given by the
inverse of the asymptotic variance of the sample mean of
![]() . In turn, we
calculate a heteroskedasticity and autocorrelation robust estimate
. In turn, we
calculate a heteroskedasticity and autocorrelation robust estimate
![]() of this asymptotic variance, and the efficient
GMM estimator uses the inverse of this HAC estimate as the weighting matrix,
with the following asymptotic approximations:
of this asymptotic variance, and the efficient
GMM estimator uses the inverse of this HAC estimate as the weighting matrix,
with the following asymptotic approximations:
![$\displaystyle , \hat{\mathbf{V}} _{T}^{(h)}=\left( [\hat{\mathbf{D}}_{T}^{(h)}][\hat{\mathbf{S}}_{T} ^{(h)}]^{-1}[\hat{\mathbf{D}}_{T}^{(h)}]^{\prime}\right) ^{-1}$](img171.gif) |
|
| and |
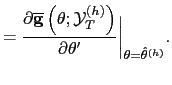 |
Since
![]() is nonlinear in
is nonlinear in
![]() , the
minimization of (3.2) is achieved numerically. Our
results are calculated by two-step GMM starting from an initial guess provided
by a simple two-stage OLS procedure and with other initial conditions
considered to obtain some assurance that the global optimum has been
found.9 The inconsistent two-stage
OLS procedure would instead first estimate the auxiliary forecasting equations
independently, then use these forecast parameter estimates to generate
regressors for the Taylor Rule regression.10 Joint estimation by (nonlinear) two-step GMM is
consistent and efficient - see Newey and McFadden (1994).11 We estimate each
horizon
, the
minimization of (3.2) is achieved numerically. Our
results are calculated by two-step GMM starting from an initial guess provided
by a simple two-stage OLS procedure and with other initial conditions
considered to obtain some assurance that the global optimum has been
found.9 The inconsistent two-stage
OLS procedure would instead first estimate the auxiliary forecasting equations
independently, then use these forecast parameter estimates to generate
regressors for the Taylor Rule regression.10 Joint estimation by (nonlinear) two-step GMM is
consistent and efficient - see Newey and McFadden (1994).11 We estimate each
horizon ![]() independently from the others so that nothing other than the
original data links these estimates to one another.
independently from the others so that nothing other than the
original data links these estimates to one another.
As mentioned, identification is achieved by considering at least two
indicators ![]() , in which case the system (3.2) in general
is just-identified. When we use more than two indicators, the system naturally
delivers overidentifying restrictions. Additionally, we can impose
cross-equation restrictions that create overidentification. Our baseline
specification is overidentified for both reasons.
, in which case the system (3.2) in general
is just-identified. When we use more than two indicators, the system naturally
delivers overidentifying restrictions. Additionally, we can impose
cross-equation restrictions that create overidentification. Our baseline
specification is overidentified for both reasons.
3.2 Data
Our data set consists of ![]() particular days for each month over the period
1994:M1 through 2007:M6. Data on fed funds futures contracts come from the
Chicago Board of Trade. Fed funds futures are accurate predictors of the
effective fed funds rate, as documented in numerous studies including
Evans (1998), Gürkaynak, Sack, and Swanson (2007), Piazzesi and Swanson (2008),
and Hamilton (2009). We restrict our attention to fed funds futures
traded after 1994. One reason, as noted by Gürkaynak, Sack, and Swanson (2007), is
that the Federal Open Market Committee began announcing the fed funds target
in 1994, and this change in procedure could cause changes in the forecasting
relations. In addition, the trading volumes pick up noticeably during this
year.12 At the other end of
the sample period, we end our data at 2007:M7 in order to avoid the period of
major financial disruptions that started in the late summer of 2007 following
the fund freezes by BNP Paribas in early August.
particular days for each month over the period
1994:M1 through 2007:M6. Data on fed funds futures contracts come from the
Chicago Board of Trade. Fed funds futures are accurate predictors of the
effective fed funds rate, as documented in numerous studies including
Evans (1998), Gürkaynak, Sack, and Swanson (2007), Piazzesi and Swanson (2008),
and Hamilton (2009). We restrict our attention to fed funds futures
traded after 1994. One reason, as noted by Gürkaynak, Sack, and Swanson (2007), is
that the Federal Open Market Committee began announcing the fed funds target
in 1994, and this change in procedure could cause changes in the forecasting
relations. In addition, the trading volumes pick up noticeably during this
year.12 At the other end of
the sample period, we end our data at 2007:M7 in order to avoid the period of
major financial disruptions that started in the late summer of 2007 following
the fund freezes by BNP Paribas in early August.
We measure inflation by the year-over-year growth rate of the Core-PCE price index from the BEA. This has been the Federal Reserve's key inflation indicator over the sample we consider. We measure output growth by the year-over-year growth rate of industrial production from the Federal Reserve Board. To use as much data as possible we stay at the monthly frequency and therefore require a monthly output growth series. Industrial production growth has been used by previous studies to proxy for overall output growth (e.g. Stock and Watson (2002)) and is a natural candidate for our baseline. As a robustness check we will consider another measure for output growth, Macroeconomic Advisers' monthly GDP.
The economic indicators we consider are data releases from various government agencies that are followed by the Money Market Survey (MMS). Following Gürkaynak, Sack, and Swanson (2005), the median forecast provides a proxy for each variable's market expectation. MMS provides market expectations for several candidate economic indicators. Our choice is guided by asking which economic variables might be most helpful for forecasting output growth and core PCE inflation. It is natural for this purpose to use core CPI inflation (CPIXFE) and industrial production (INDPRD) themselves.13 In addition, the macroeconomic announcement literature has noted that market participants scrutinize and respond to nonfarm payroll employment (Gürkaynak, Sack, and Swanson (2005), Bartolini, Goldberg, and Sacarny (2008)), and so we will consider that indicator (NFPAY) as well. It is worth noting that NFPAY and the unemployment rate are released on the same day each month, in the BLS Employment Situation report. As mentioned above, this implies that either one of these, but not both, can be used in estimation. Given the importance of NFPAY found by prior studies, this steers us away from the unemployment rate as an indicator. This in turn makes the unemployment rate less attractive a proxy for output growth, since we would naturally then use it as an indicator.
In terms of the variables entering the auxiliary forecasting equations, we set

The lagged values of inflation and output growth are included to control for
their autoregressive nature. For parsimony, we set to zero the first element
of
![]() , the coefficient on
, the coefficient on
![]() in indicator
in indicator
![]() 's auxiliary forecasting equation for
's auxiliary forecasting equation for ![]() ; likewise, we zero out the
second element of
; likewise, we zero out the
second element of
![]() , the coefficient on
, the coefficient on
![]() in
indicator
in
indicator ![]() 's auxiliary forecasting equation for
's auxiliary forecasting equation for ![]() . The fed funds
futures prediction for the day before
. The fed funds
futures prediction for the day before ![]() is included to control for the
predictive content (vis-a-vis each Taylor Rule variable) of the futures price
that has already been priced into the contract.
is included to control for the
predictive content (vis-a-vis each Taylor Rule variable) of the futures price
that has already been priced into the contract.
4. Results
First we present our baseline full-sample results using three indicators. We then show that statistical tests of our overidentifying restrictions fail to reject our baseline model, along with other specifications considered for robustness. Motivated by related literature, we run tests for breaks in the policy rule parameters and find evidence of their variation over time. Placing the break around the beginning of the year 2000, we present subsample estimates suggesting the market-perceived monetary policy rule has changed over time, and repeat the overidentification tests on the separate subsamples.
4.1 Baseline
Our baseline results use three indicators - CPIXFE, INDPRD, and NFPAY - and impose the cross-equation restriction that the average risk premium change is identical across indicators:
| (4.1) |
This cross-equation restriction embodies the assumption that the different economic indicators systematically affect the forecasted policy rate only through changes to forecasted inflation and output, and it adds statistical precision to our estimates; we further discuss and test this restriction in Section 6. The policy rule response coefficient estimates are presented in Table 1, and we note a few features deserving mention.14
Table 1. Market-Perceived Monetary Policy Rule Estimates, Baseline
h=1 | h=2 | h=3 | h=4 | h=5 | h=6 | |
|---|---|---|---|---|---|---|
| | 0.3423 0.2046 |
0.8723** 0.1496 |
1.3487 0.7757 |
1.1114** 0.4305 |
1.1068* 0.5118 |
1.3733 0.7252 |
| | 0.0510** 0.0092 |
0.0279 0.0204 |
0.1603** 0.0361 |
0.1258** 0.0306 |
0.1429** 0.0438 |
0.1938** 0.0702 |
Notes: The policy rule coefficient on inflation is ![]() and on the output gap is
and on the output gap is ![]() . HAC standard errors in italics. The markers * and ** denote significance at 5% and 1% levels, respectively.
There are 160 observations for
. HAC standard errors in italics. The markers * and ** denote significance at 5% and 1% levels, respectively.
There are 160 observations for ![]() , 159 for
, 159 for ![]() , etc. The indicators are CPIXFE, INDPRD, and NFPAY. Point estimates and standard errors from two-step nonlinear GMM. Data run over 1994:M1-2007:M7.
, etc. The indicators are CPIXFE, INDPRD, and NFPAY. Point estimates and standard errors from two-step nonlinear GMM. Data run over 1994:M1-2007:M7.
First, we obtain reasonably precise estimates of the market-perceived policy response to inflation. Horizons two, four, and five all exhibit inflation response coefficients that are significant at the 5% level, and coefficients for the remaining horizons are significant at the 10% level. The output response coefficient is statistically significant and positive at the 1 level for all horizons except the second. These results suggest that our empirical methodology effectively extracts information from market forecast updates that occur in response to macroeconomic news.
Second, the market does not expect the Fed to implement changes immediately.
The response coefficients at longer horizons tend to be larger than the
response coefficients at shorter horizons, and 95% confidence intervals for
![]() or
or ![]() often exclude the point estimates obtained for different
often exclude the point estimates obtained for different
![]() . Recall that the units of the inflation response coefficients are
identical across horizons, as are the coefficients on output. These parameters
answer the question: looking
. Recall that the units of the inflation response coefficients are
identical across horizons, as are the coefficients on output. These parameters
answer the question: looking ![]() months ahead, what is the response of the
forecasted policy rate to a one unit increase in the forecasted rate of
inflation or output growth? This feature of the results strongly suggests that
the market believes the Fed gradually adjusts policy in response to economic
fundamentals, a point we explore further in Section 5.
months ahead, what is the response of the
forecasted policy rate to a one unit increase in the forecasted rate of
inflation or output growth? This feature of the results strongly suggests that
the market believes the Fed gradually adjusts policy in response to economic
fundamentals, a point we explore further in Section 5.
4.2 Overidentification and Break Tests
We next evaluate the appropriateness of the assumptions behind these
estimates. We first investigate Hansen's (1982) ![]() -tests of
overidentifying restrictions given by
-tests of
overidentifying restrictions given by
| (4.2) |
for ![]() the number of overidentifying restrictions. The
the number of overidentifying restrictions. The ![]() -values for this
test are presented in Table 2. Recall that our baseline specification overidentifies the model
both by using three indicators and by imposing that the policy rule
specification error means are identical for these indicators (equation (4.1)). Row 1 displays the
-values for this
test are presented in Table 2. Recall that our baseline specification overidentifies the model
both by using three indicators and by imposing that the policy rule
specification error means are identical for these indicators (equation (4.1)). Row 1 displays the ![]() -values associated with
the
-values associated with
the ![]() -statistics for the baseline specification. We fail to reject at the
5% level the overidentifying restrictions for every horizon
-statistics for the baseline specification. We fail to reject at the
5% level the overidentifying restrictions for every horizon ![]() , offering
some confirmation that our basic framework is consistent with the data.
, offering
some confirmation that our basic framework is consistent with the data.
Papers including Clarida, Gali, and Gertler (2000), Primiceri (2006), and Boivin (2006) have argued that U.S. monetary policy has changed over time. Unfortunately, our data are not available for the period over which those papers find the most dramatic policy changes. Nonetheless, if monetary policy changed once, then it could change again - and market participants are aware of this possibility. We therefore ask whether market participants' perception of the monetary policy rule have changed over time.
Table 2. Overidentification Tests, Baseline
h=1 | h=2 | h=3 | h=4 | h=5 | h=6 | |
|---|---|---|---|---|---|---|
| (1) BASELINE | 0.1176 | 0.1172 | 0.1099 | 0.1006 | 0.1222 | 0.1044 |
| (2) BASELINE, PRE | 0.3657 | 0.4600 | 0.3881 | 0.3827 | 0.4038 | 0.4068 |
| (3) BASELINE, POST | 0.2790 | 0.2879 | 0.2756 | 0.2963 | 0.3018 | 0.3045 |
Notes: ![]() -values from Hansen's (1982)
-values from Hansen's (1982) ![]() -test of overidentifying restrictions, for the baseline specifications. BASELINE is the baseline specification estimated over the full sample. BASELINE, PRE and BASELINE, POST are the baseline specifications estimated over the pre-2000 and post-2000 subsamples, respectively.
-test of overidentifying restrictions, for the baseline specifications. BASELINE is the baseline specification estimated over the full sample. BASELINE, PRE and BASELINE, POST are the baseline specifications estimated over the pre-2000 and post-2000 subsamples, respectively.
To answer this question, we test for a break in the parameters of interest.
Using Andrews's (1993) break test, we test the null hypothesis that
all parameters are constant against the alternative that the policy rule
coefficients ![]() ,
, ![]() , and
, and ![]() experienced a
break.15 Letting the policy rule coefficient vector be
experienced a
break.15 Letting the policy rule coefficient vector be
![]() , we test:
, we test:
![\begin{displaymath}
H_{1}(\varpi): \mathbf{b}_{t} = \left\{
\begin{array}[c]{l}
\mathbf{b}_{1}(\varpi) \quad\text{for } t=1,\ldots,T\varpi\\
\mathbf{b}_{2}(\varpi) \quad\text{for } t=T\varpi+1,\ldots,T
\end{array}\right\} \text{ for some constants } \mathbf{b}_{1}(\varpi),\mathbf{b}
_{2}(\varpi) \in\mathbb{R}^{3}
\end{displaymath}](img216.gif)
for values of ![]() in (0.25,0.75). We use the sup-Wald statistic and
tabulated critical values in Andrews (1993).
in (0.25,0.75). We use the sup-Wald statistic and
tabulated critical values in Andrews (1993).
For each horizon considered, there is strong evidence of a break in the policy
rule coefficients
![]() . In particular, for our application the 1 critical value is 16.6: the sup-Wald statistic is estimated to be 204.3,
190.2, 170.6, 168.4, 142.0, and 123.1 for horizons 1 through 6, respectively.
Moreover, these maximal statistics occur at nearly the same time for every
horizon, at the beginning of the year 2000. In light of this evidence, we
re-estimate our baseline model on the pre-2000 and post-2000 subsamples.
. In particular, for our application the 1 critical value is 16.6: the sup-Wald statistic is estimated to be 204.3,
190.2, 170.6, 168.4, 142.0, and 123.1 for horizons 1 through 6, respectively.
Moreover, these maximal statistics occur at nearly the same time for every
horizon, at the beginning of the year 2000. In light of this evidence, we
re-estimate our baseline model on the pre-2000 and post-2000 subsamples.
Returning to the overidentification test results of Table 2,
rows 2 and 3 display the ![]() -values for the model estimated across horizons on
each subsample. We now find that the model is readily accepted for each
subsample. Evidently, the break in the policy parameters was a factor in the
lower full sample
-values for the model estimated across horizons on
each subsample. We now find that the model is readily accepted for each
subsample. Evidently, the break in the policy parameters was a factor in the
lower full sample ![]() -values in row 1. Once the parameters are allowed to
differ by sub-period, we find no evidence against our framework.
-values in row 1. Once the parameters are allowed to
differ by sub-period, we find no evidence against our framework.
Table 3. Market-Perceived Monetary Policy Rule Estimates, Baseline Pre-2000 and Post-2000
h=1 | h=2 | h=3 | h=4 | h=5 | h=6 | |
|---|---|---|---|---|---|---|
| PRE-2000 - | 0.3611 0.2173 |
0.8309* 0.3717 |
1.2049* 0.4708 |
1.2125 0.7954 |
1.1116* 0.4630 |
1.3821 0.7610 |
| PRE-2000 - | 0.1550** 0.0349 |
0.1284** 0.0314 |
0.2641** 0.0670 |
0.3968** 0.1142 |
0.3844** 0.1364 |
0.5744** 0.1436 |
| POST-2000 - | 0.1465** 0.0537 |
0.3797** 0.0673 |
0.4292* 0.2110 |
0.5913** 0.1318 |
0.8237** 0.1694 |
2.2240* 0.9529 |
| POST-2000 - | 0.0366** 0.0127 |
0.0034 0.0071 |
-0.0474 0.0248 |
-0.0544* 0.0277 |
0.0401 0.0297 |
-0.0777 0.0834 |
Notes: The policy rule coefficient on inflation is ![]() and on the output gap is
and on the output gap is ![]() . HAC standard errors in italics. The markers * and ** denote significance at 5% and 1% levels, respectively. pre-2000, there are 69 observations for
. HAC standard errors in italics. The markers * and ** denote significance at 5% and 1% levels, respectively. pre-2000, there are 69 observations for ![]() , 68 for
, 68 for ![]() , etc.; post-2000, there are 88 observations for
, etc.; post-2000, there are 88 observations for ![]() , etc. The indicators are CPIXFE, INDPRD, and NFPAY. Point estimates and standard errors from two-step nonlinear GMM. Data run over 1994:M1-2007:M7
, etc. The indicators are CPIXFE, INDPRD, and NFPAY. Point estimates and standard errors from two-step nonlinear GMM. Data run over 1994:M1-2007:M7
4.3 Time Variation
Table 3 displays the estimation results for the two subsamples. We now discuss the output and inflation response coefficients estimated in each subsample and how they differ from one another.
Looking at the output response coefficients, the output response during the 1990s is moderate but tightly estimated. At all horizons the point estimates are positive and significant at the 1% level. The response is around 0.15 in the first month, rising to 0.57 by the sixth month, and hence the policy response exhibits gradual adjustment. However, during the 2000s the response to output changes dramatically. For half of the horizons the output response is a tightly estimated zero, while for the remaining horizons the response is small and insignificant. Taken together, this evidence suggests that during the 1990s the market perceived a moderate output gap response that essentially vanished during the 2000s.
Looking now at the inflation responses, we see two noteworthy differences across the subsamples. First, the pre-2000 estimates are not as precisely estimated as the post-2000 estimates. Prior to the year 2000 none are significant at 1% level. On the other hand, post-2000 all horizons are statistically significant at the 5% level, with four horizons significant at the 1% level. This suggests that the more recent period has seen greater signal, relative to noise, in the market forecast updates to policy and fundamentals.
Second, the post-2000 inflation response is lower at short horizons and higher at the long horizon. For the first four months after an inflation forecast increase, the forecasted policy response during the 2000s is half what it was during the 1990s. For these early horizons we can reject at the 1% level that the post-2000 inflation responses are equal to their pre-2000 estimated values. At the long horizon, the post-2000 six-month horizon response (2.22) is about 50% greater than the pre-2000 six-month horizon response (1.38). During the 1990s, policy followed the Taylor Principle (a more-than one-for-one response of nominal rates to inflation) by the third month after a shock to forecasted inflation; during the 2000s, policy has met this principle only by the sixth month.
Together, these observations suggest that the market-perceived policy response to inflation changed over time in two distinct ways: during the 1990s the response adjusted at a quicker pace with a moderate long-run magnitude, while during the 2000s the response adjusted at a slower pace with a larger long-run magnitude.
5. Dynamic Analysis of the Policy Response
Up to this point in the paper we have been investigating a static Taylor Rule
of the form of equation (2.1). We found that the implied market
expectations of how the Fed would respond to news turned out to be a function
of the time horizon ![]() , meaning that the Fed is implicitly assumed by the
market to implement the policy changes warranted by the news only gradually.
We next formulate a more detailed specification of the nature of that lagged
response that is consistent with the observed market behavior, developing and
calibrating a dynamic Taylor rule. Section 5.3 then explores the implications of
these changed dynamics using a simple new-Keynesian model.
, meaning that the Fed is implicitly assumed by the
market to implement the policy changes warranted by the news only gradually.
We next formulate a more detailed specification of the nature of that lagged
response that is consistent with the observed market behavior, developing and
calibrating a dynamic Taylor rule. Section 5.3 then explores the implications of
these changed dynamics using a simple new-Keynesian model.
5.1 Dynamic Forecasting Equations
We first modify the earlier notation to make the dependence on the horizon ![]() explicit, rewriting the
explicit, rewriting the ![]() -period-ahead forecasting equations (2.11) and (2.10) as
-period-ahead forecasting equations (2.11) and (2.10) as
| (5.1) |
| (5.2) |
We will also now need a version of equations (5.1) and (5.2) for the case ![]() , in order to keep track of the
implication of the release of one indicator for the values of other indicators
to be released later that month. Suppose that the first indicator released in
month
, in order to keep track of the
implication of the release of one indicator for the values of other indicators
to be released later that month. Suppose that the first indicator released in
month ![]() is NFPAY, denoted here as
is NFPAY, denoted here as ![]() . That release could
cause us to update our expectation of the values for INDPRD
(
. That release could
cause us to update our expectation of the values for INDPRD
(
![]() ) and CPIXFE (
) and CPIXFE (
![]() ) that will be
reported later that same month
) that will be
reported later that same month ![]() according to
according to
| (5.3) |
| (5.4) |
Thus for example estimates of
![]() and
and
![]() could be obtained by OLS estimation of (5.3) and (5.4). Later in month
could be obtained by OLS estimation of (5.3) and (5.4). Later in month ![]() when the output indicator
when the output indicator
![]() is released, that allows us to know the value of
is released, that allows us to know the value of ![]() with
certainty, which to preserve the general notation we would represent by
with
certainty, which to preserve the general notation we would represent by
![]() , and would also induce an update to the forecast for
, and would also induce an update to the forecast for
![]() ,
,
| (5.5) |
When ![]() is finally released, it has no implications for
is finally released, it has no implications for ![]() which is already known (
which is already known (
![]() ) and changes our forecast of
inflation one-for-one (
) and changes our forecast of
inflation one-for-one (
![]() ).
).
5.2 A Dynamic Taylor Rule
Consider now the following dynamic generalization of (2.1):
| (5.6) |
Unlike our earlier expression (2.2),
equation (5.6) is strictly a backward-looking
formulation, presuming that the Fed responds dynamically to the history of
available information; note that ![]() and
and ![]() are the most
recent values available as of the end of month
are the most
recent values available as of the end of month ![]() .
.
Recall that the value of
![]() is released on day
is released on day ![]() , and let
, and let
![]() denote the interest rate implied by a futures contract
for settlement based on the value of
denote the interest rate implied by a futures contract
for settlement based on the value of ![]() , and quoted as of the end of
trading on day
, and quoted as of the end of
trading on day ![]() . For example,
. For example,
![]() would reflect an
expectation of the current month's fed funds rate on the day that the
indicator
would reflect an
expectation of the current month's fed funds rate on the day that the
indicator
![]() is released. Take the expectation of (5.6) conditional on market information available on day
is released. Take the expectation of (5.6) conditional on market information available on day
![]() and subtract from it the expectation formed the day before:
and subtract from it the expectation formed the day before:
| (5.7) | ||
For comparison, recalling that ![]() , we can rewrite equation (2.12) as
, we can rewrite equation (2.12) as
| (5.8) |
where
![]() and
and
![]() denote the original parameters whose
estimates we reported in column
denote the original parameters whose
estimates we reported in column ![]() of Tables 1 or 3. Comparing equations (5.7) and (5.8), the
values of the dynamic parameters
of Tables 1 or 3. Comparing equations (5.7) and (5.8), the
values of the dynamic parameters
![]() in (5.6) are related to our baseline estimates
in (5.6) are related to our baseline estimates
![]() according to
according to
| (5.9) |
To arrive at estimates of the dynamic parameters, we chose
![]() so as to minimize the equally-weighted sum of squared
differences between the LHS and RHS of (5.9) across indicators
so as to minimize the equally-weighted sum of squared
differences between the LHS and RHS of (5.9) across indicators
![]() and horizons
and horizons
![]() . On the RHS, the values for
. On the RHS, the values for
![]() for
for
![]() were taken from the earlier split-sample GMM estimation reported
in Table 3, while values for
were taken from the earlier split-sample GMM estimation reported
in Table 3, while values for ![]() were obtained from GMM estimation of
were obtained from GMM estimation of
![]() ,
,
![]() ,
,
![]() ,
,
![]() , and
, and
![]() based
on the moment conditions
based
on the moment conditions
![$\displaystyle \left[ \begin{array}[c]{c} \left( y_{t}-\gamma_{y,1}^{(0)}w_{1,t}-\xi_{y,1}^{(0)}\tilde{w} _{1,t}-\mathbf{\zeta}_{y,1}^{(0)\prime}\mathbf{x}_{1,t+1}\right) \mathbf{z}_{1,t+1}\\ \left( \pi_{t}-\gamma_{\pi,1}^{(0)}w_{1,t}-\xi_{\pi,1}^{(0)}\tilde{w} _{1,t}-\mathbf{\zeta}_{\pi,1}^{(0)\prime}\mathbf{x}_{1,t+1}\right) \mathbf{z}_{1,t+1}\\ \left[ f_{i(1),t+1 }^{(0)}-f_{i(1)-1,t+1 }^{(0)}-\eta^{(0)}-(\beta ^{(0)}\gamma_{\pi,1}^{(0)}+\delta^{(0)}\gamma_{y,1}^{(0)})(w_{1,t}-\tilde {w}_{1,t})\right] \mathbf{z}_{1,t+1}\\ \left( \pi_{t}-\gamma_{\pi,2}^{(0)}w_{2,t}-\xi_{\pi,2}^{(0)}\tilde{w} _{2,t}-\mathbf{\zeta}_{\pi,2}^{(0)\prime}\mathbf{x}_{2,t+1}\right) \mathbf{z}_{2,t+1}\\ \left[ f_{i(2),t+1 }^{(0)}-f_{i(2)-1,t+1 }^{(0)}-\eta^{(0)}-(\beta ^{(0)}\gamma_{\pi,2}^{(0)}+\delta^{(0)}\gamma_{y,2}^{(0)})(w_{2,t}-\tilde {w}_{2,t})\right] \mathbf{z}_{2,t+1}\\ \left[ f_{i(3),t+1 }^{(0)}-f_{i(3)-1,t+1 }^{(0)}-\eta^{(0)}-(\beta ^{(0)}\gamma_{\pi,3}^{(0)}+\delta^{(0)}\gamma_{y,3}^{(0)})(w_{3,t}-\tilde {w}_{3,t})\right] \mathbf{z}_{3,t+1}\\ \end{array} \right]$](img288.gif) |
(5.10) |
where as before
![]() denotes information available the day
prior to release of
denotes information available the day
prior to release of ![]() . This last GMM estimation resulted in the
estimates
. This last GMM estimation resulted in the
estimates
![]() for the
pre-2000 subsample, and
for the
pre-2000 subsample, and
![]() after 2000. For all the above calculations, the values
after 2000. For all the above calculations, the values
![]() ,
,
![]() , and
, and
![]() were imposed throughout.
were imposed throughout.
The resulting values of ![]() and
and
![]() are reported in Table 4. In the last column is the sum of the parameter values across all
are reported in Table 4. In the last column is the sum of the parameter values across all
![]() , which gives the long-run response to the inflation or output pressure.
, which gives the long-run response to the inflation or output pressure.
Table 4. Dynamic Taylor Rule Parameters
j=1 | j=2 | j=3 | j=4 | j=5 | j=6 | j=7 | sum | |
|---|---|---|---|---|---|---|---|---|
| PRE-2000 - | 0.3629 | -0.0009 | 0.8859 | -0.0994 | 0.2395 | -0.0542 | -0.0464 | 1.2874 |
| PRE-2000 - | 0.1760 | -0.0102 | -0.0147 | 0.0399 | 0.1692 | -0.0674 | -0.0343 | 0.2585 |
| POST-2000 - | 0.0848 | 0.0830 | 0.3642 | 0.2760 | 0.4918 | -0.1552 | 0.4330 | 1.5780 |
| POST-2000 - | 0.0060 | 0.0140 | -0.0040 | -0.0414 | 0.0442 | 0.0302 | 0.0102 | 0.0592 |
Notes: from minimum-distance method described in text, using subsample parameter estimates across all horizons.
Recall from Section 3.1 that the parameter
vector
![]() for horizon
for horizon ![]() was estimated completely
independently from any other horizon. This approach of leaving the dynamics
implied by
was estimated completely
independently from any other horizon. This approach of leaving the dynamics
implied by
![]() completely unrestricted
offers at least two benefits. First, nothing in our procedure requires that
the long-horizon responses should be bigger than the short-horizon responses.
The fact that we nonetheless find them to be increasing in
completely unrestricted
offers at least two benefits. First, nothing in our procedure requires that
the long-horizon responses should be bigger than the short-horizon responses.
The fact that we nonetheless find them to be increasing in ![]() is strong
evidence that the market perceives policy to respond only gradually to
changing conditions. Second, our procedure allows the adjustment to
inflationary pressures to differ from the adjustment to real activity, similar
to the policy rules of Christiano, Eichenbaum, and Evans (1996,
2005). Table 4 implies different paths in the response of policy
to inflation and output. For example, the pre-2000 response to inflation jumps
up at the three-month lag (
is strong
evidence that the market perceives policy to respond only gradually to
changing conditions. Second, our procedure allows the adjustment to
inflationary pressures to differ from the adjustment to real activity, similar
to the policy rules of Christiano, Eichenbaum, and Evans (1996,
2005). Table 4 implies different paths in the response of policy
to inflation and output. For example, the pre-2000 response to inflation jumps
up at the three-month lag (![]() ) while the response to output stays
relatively steady until the 5-month lag (
) while the response to output stays
relatively steady until the 5-month lag (![]() ). This flexibility in the
rule's process is greater than that permitted by including only lags of the
policy rate itself, and our estimates suggest this greater flexibility is
warranted by the data.
). This flexibility in the
rule's process is greater than that permitted by including only lags of the
policy rate itself, and our estimates suggest this greater flexibility is
warranted by the data.
5.3 Implications of changes in the dynamics
We now explore the implications of the estimated changes in the Taylor Rule for the consequences of monetary policy. Following Clarida, Gali, and Gertler (2000), we use a standard sticky-price, rational expectations model whose equilibrium conditions, log-linearized around a zero inflation steady state, are
| (5.11) | ||
| (5.12) | ||
| (5.13) |
The first equation (5.11) says that inflation today is a function of
the output gap and the expectation of next period's inflation, which in turn
can be derived from an underlying Calvo pricing structure. With relative risk
aversion measured by
![]() , equation (5.12) is an IS schedule
where today's output depends on the ex ante real rate and the expectation of
next period's output gap. Equation (5.13) is a dynamic Taylor Rule
that closes the model. The model is driven by autocorrelated demand shocks
, equation (5.12) is an IS schedule
where today's output depends on the ex ante real rate and the expectation of
next period's output gap. Equation (5.13) is a dynamic Taylor Rule
that closes the model. The model is driven by autocorrelated demand shocks
![]() and supply shocks
and supply shocks ![]() with the same unconditional variance. We
take parameter values from Clarida, Gali, and Gertler (2000) and set
with the same unconditional variance. We
take parameter values from Clarida, Gali, and Gertler (2000) and set
![]() ,
,
![]() ,
,
![]() , and the shocks'
autocorrelation to 0.9655 in our monthly model.
, and the shocks'
autocorrelation to 0.9655 in our monthly model.
Our goal is to characterize what difference the inflation-response parameters
![]() might make for the volatility of macro variables according to this
model. To do so, we fix
might make for the volatility of macro variables according to this
model. To do so, we fix ![]() at the pre-2000 values, and calculate the
difference in volatilities using pre-2000 and post-2000 values for
at the pre-2000 values, and calculate the
difference in volatilities using pre-2000 and post-2000 values for ![]() .
We find that the post-2000 dynamics imply a 41.2% reduction in the variance
of inflation, a 0.2% reduction in the variance of output, and a 33.5 reduction in the variance of the fed funds rate. Alternatively, we fixed the
output dynamics
.
We find that the post-2000 dynamics imply a 41.2% reduction in the variance
of inflation, a 0.2% reduction in the variance of output, and a 33.5 reduction in the variance of the fed funds rate. Alternatively, we fixed the
output dynamics ![]() at the post-2000 values, and calculated how much
difference the change in inflation dynamics
at the post-2000 values, and calculated how much
difference the change in inflation dynamics ![]() made for that
specification, with very similar results. These comparisons are reported in
the last column of Table 5.
made for that
specification, with very similar results. These comparisons are reported in
the last column of Table 5.
We next wanted to see what it was about the post-2000 inflation response that
helped stabilize inflation. Was it the overall magnitude of the inflation
response, as reflected in the sum of the ![]() coefficients, or was it
the more gradual post-2000 response, as reflected in the shape of the dynamic
response? To find out, we explored the consequences of changing just one of
these two elements at a time. Let
coefficients, or was it
the more gradual post-2000 response, as reflected in the shape of the dynamic
response? To find out, we explored the consequences of changing just one of
these two elements at a time. Let
![]() denote the
pre-2000 inflation responses and
denote the
pre-2000 inflation responses and
![]() the post-2000
responses. We calculated what would happen if the inflation responses were
given by
the post-2000
responses. We calculated what would happen if the inflation responses were
given by
![$\displaystyle \beta_{j}=\beta_{j}^{POST}\frac{[\beta_{0}^{PRE}+\beta_{1}^{PRE}+...+\beta _{6}^{PRE}]}{[\beta_{0}^{POST}+\beta_{1}^{POST}+...+\beta_{6}^{POST}]} $](img3a.gif)
so that the sum of the coefficients ![]() was restricted to be the same
as for the pre-2000 estimates, while the shape of
was restricted to be the same
as for the pre-2000 estimates, while the shape of ![]() was that for the
post-2000 estimates. These results are reported in the column labeled
"post-path, pre-LR" in Table 5. Such a change
would have only modestly improved the variance of inflation, and would have
resulted in a significant deterioration in the variability of output.
was that for the
post-2000 estimates. These results are reported in the column labeled
"post-path, pre-LR" in Table 5. Such a change
would have only modestly improved the variance of inflation, and would have
resulted in a significant deterioration in the variability of output.
Table 5. Effects of Changing Inflation Policy Response - Percentage Change in Volatility from Benchmark
| Variable | Output Coefficients | Inflation Coefficient - PRE PATH PRE LR | Inflation Coefficient - POST PATH PRE LR | Inflation Coefficient - PRE PATH POST LR | Inflation Coefficient - POST PATH POST LR |
|---|---|---|---|---|---|
PRE |
0 |
-8.7 |
-39.3 |
-41.2 |
|
POST |
0 |
-7.9 |
-40.6 |
-41.4 |
|
PRE |
0 |
+24.2 |
-17.4 |
-0.2 |
|
POST |
0 |
+30.9 |
-21.0 |
+0.7 |
|
PRE |
0 |
-14.0 |
-26.3 |
-33.5 |
|
POST |
0 |
-15.7 |
-27.6 |
-35.6 |
Notes: volatilities of endogenous variables of the sticky-price model described in text. Dynamic Taylor Rule coefficients in Table 4. PRE PATH, PRE LR is benchmark using the dynamic Taylor Rule derived from pre-2000 estimates. POST PATH, PRE LR uses the dynamic Taylor Rule derived from post-2000 estimates, with inflation coefficients multiplied by the ratio of the pre-2000 long-run inflation response to the post-2000 long-run inflation response. PRE PATH, POST LR uses the dynamic Taylor Rule derived from pre-2000 estimates, with inflation coefficients multiplied by the ratio of the post-2000 long-run inflation response to the pre-2000 long-run inflation response. POST PATH, POST LR uses the dynamic Taylor Rule derived from the post-2000 estimates. These inflation coefficient modifications are considered holding constant the output coefficients at the pre-2000 values in rows marked PRE, and at the post-2000 values in rows marked POST.
On the other hand, if we change just the long-run response, but leave the dynamics the same as for the pre-2000 rule,
![$\displaystyle \beta_{j}=\beta_{j}^{POST}\frac{[\beta_{0}^{PRE}+\beta_{1}^{PRE}+...+\beta _{6}^{PRE}]}{[\beta_{0}^{POST}+\beta_{1}^{POST}+...+\beta_{6}^{POST}]} $](img3a.gif)
as reported in the "pre-path, post-LR" column of Table 5, we would have achieved the full benefits of inflation stabilization as well as additional benefits of output stabilization.
Thus the key improvement in perceived monetary policy was a stronger long-run response to inflation. The fact that the market also perceives these responses to come more slowly in the post-2000 data has in fact been counterproductive.
A lesson from this basic New Keynesian analysis is the following. Increasing the long-run magnitude of inflation response, as the market perceives the Fed to have done, had a stabilizing effect both on inflation and output. Implementing the response more slowly, as the market also perceives the Fed to have done, counteracted what otherwise would have been a benefit for output volatility of the stronger eventual inflation response. The "measured pace" of monetary tightening during 2004-2006 could thus have been a factor contributing to unnecessary volatility of output - doing the same thing more quickly might have produced a better result.
Table 6. Specification Tests
h=1 | h=2 | h=3 | h=4 | h=5 | h=6 | |
|---|---|---|---|---|---|---|
| (4) K=2, PRE | 0.0939 | 0.1061 | 0.1113 | 0.0975 | 0.0957 | 0.0956 |
| (5) K=2, POST | 0.0781 | 0.0707 | 0.0721 | 0.0649 | 0.0650 | 0.0705 |
| (6) MGDP, PRE | 0.3422 | 0.3681 | 0.3723 | 0.3725 | 0.3765 | 0.3974 |
| (7) MGDP, POST | 0.3015 | 0.2816 | 0.2719 | 0.2850 | 0.2857 | 0.2859 |
| (8) CROSS, PRE | 0.9878 | 0.9668 | 0.9185 | 0.9961 | 0.9829 | 0.9985 |
| (9) CROSS, POST | 0.9999 | 0.9869 | 0.9488 | 0.9999 | 0.9999 | 0.9999 |
Notes: -values from Hansen's (1982) -test of overidentifying restrictions, for various alternate specifications. K=2, PRE and K=2, POST use only two indicators (CPIXFE and INDPRD). MGDP, PRE, and MGDP, POST use monthly GDP instead of Industrial Production as the output variable. CROSS, PRE and CROSS, POST tests the cross-equation restriction that the average risk premium change is identical across indicators.
6. Sensitivity Analysis
We next investigate the sensitivity of our results to using alternative economic indicators, test the cross-equation restrictions imposed, and look for corroboration of the identifying assumptions from other data sources.
6.1 Results for Alternative Economic Indicators
Here we analyze the sensitivity of our baseline results to the data used. First, we report results using only two indicators. Second, we report results using monthly GDP, as calculated by Macroeconomic Advisers, instead of industrial production to measure monthly output. Given the strong evidence of a parameter break, we consider these alternate specifications estimated separately over the two subsamples. Table 6 displays the overidentification test results while Table 7 presents the response coefficient estimates.
Specifications (4) and (5) of Table 7 suggest that the nonfarm payrolls indicator provides useful variation to the estimation. In its absence, the parameter estimates are less precisely estimated at several horizons. We still estimate a pre-2000 steeply adjusting inflation response, nearly identical to the baseline pre-2000 estimates. And again the pre-2000 output response, when statistically significant, looks to be modest. However, the longer horizon estimates are accompanied by large standard errors, rendering them statistical insignificant. Still, the overidentifying tests in Table 6 fail to reject at the 5% level.
Table 7. Market-Perceived Monetary Policy Rule Estimates, ALternate Specifications
h=1 | h=2 | h=3 | h=4 | h=5 | h=6 | |
|---|---|---|---|---|---|---|
| (4) K=2, PRE - | 0.3655* 0.1451 |
0.8756** 0.2245 |
1.1693** 0.3877 |
1.1302* 0.4897 |
1.0811 3.6476 |
1.3718 1.9668 |
| (4) K=2, PRE - | 0.0628** 0.0136 |
0.0487** 0.0166 |
0.1386 0.0762 |
0.1338 0.1227 |
0.1875 0.6804 |
0.1984 0.3485 |
| (5) K=2, POST - | -0.0737** 0.0255 |
4.7939 60.3866 |
0.9579 1.5374 |
-0.0881 0.1503 |
1.0009 1.5029 |
2.6046 18.1027 |
| (5) K=2, POST - | 0.0111** 0.0038 |
0.1660 2.0437 |
-0.0357 0.1054 |
0.0253 0.0208 |
0.0643 0.0329 |
0.2120 1.2092 |
| (6) MGDP, PRE - | 0.4059 0.2170 |
0.9063** 0.1916 |
1.1353** 0.2419 |
1.1681** 0.2716 |
1.1832* 0.4921 |
1.4515 0.9977 |
| (6) MGDP, PRE - | 0.2140** 0.0615 |
0.0848** 0.0197 |
0.2163** 0.0418 |
0.3608** 0.0593 |
0.3795** 0.1101 |
0.5833** 0.1910 |
| (7) MGDP, POST - | 0.0012 0.2929 |
0.3985** 0.0818 |
0.3923** 0.0984 |
0.1520* 0.0667 |
0.9583** 0.1467 |
1.8190** 0.5357 |
| (7) MGDP, POST - | 0.2986 0.1678 |
0.0063 0.0448 |
-0.1860** 0.0706 |
-0.1570* 0.0721 |
0.0923 0.0752 |
0.0533 0.1134 |
| (8) NO CROSS, PRE - | 0.3606 0.2435 |
0.8534* 0.4101 |
1.2100* 0.5341 |
1.2124 0.8613 |
1.1126 0.5899 |
1.3821 0.9823 |
| (8) NO CROSS, PRE - | 0.1548** 0.0369 |
0.1316** 0.0364 |
0.2615** 0.0841 |
0.3970** 0.1220 |
0.3857* 0.1509 |
0.5746** 0.2012 |
| (9) NO CROSS, POST - | 0.1425** 0.0542 |
0.3656* 0.1455 |
-1.1842 0.6257 |
0.5738** 0.1802 |
0.8037** 0.2048 |
2.0393 1.0932 |
| (9) NO CROSS, POST - | 0.0368** 0.0126 |
0.0037 0.0091 |
0.1361* 0.0621 |
-0.0559 0.0337 |
0.0409 0.0306 |
-0.0691 0.0793 |
Notes: The policy rule coefficient on inflation is and on the output gap is . HAC standard errors in italics. The markers * and ** denote significance at 5% and 1% levels, respectively. See the notes for Table 6 or the text of Section 6 for descriptions of the alternate specifications. Point estimates and standard errors from two-step nonlinear GMM. Data run over 1994:M1-2007:M7
Specifications (6) and (7) of Table 7 give evidence that our baseline results are robust to other measures of output. The pre-2000 output response coefficients are very similar to the baseline, with a slightly larger 0.21 response at the one-month horizon and virtually unchanged 0.58 response at the six-month horizon. The profile for the post-2000 response is similar to the baseline results, again with the three- and four-month horizon responses wrongly signed. Tests of the overidentifying restrictions in Table 6 are quite supportive of the assumptions.
6.2 Tests of Cross-Equation Restrictions
In addition to the average change in the risk premium on fed funds futures
contracts, the constant term
![]() in equation (2.12) would incorporate any non-zero mean for the
specification error that represented day-to-day changes in the market
forecasts of potential output, the inflation target, and the policy rule
residual (see expression (2.9)). If this
constant terms turned out to be different for different indicators
in equation (2.12) would incorporate any non-zero mean for the
specification error that represented day-to-day changes in the market
forecasts of potential output, the inflation target, and the policy rule
residual (see expression (2.9)). If this
constant terms turned out to be different for different indicators ![]() , that
could be evidence of general mis-specification. For example, if the indicators
were in part providing signals about changes in potential output, and if the
value of this signal differed across indicators, that might show up as
differences in
, that
could be evidence of general mis-specification. For example, if the indicators
were in part providing signals about changes in potential output, and if the
value of this signal differed across indicators, that might show up as
differences in
![]() across different
across different ![]() .
.
It is easy to conduct tests of the restriction (4.1) that the policy rule constant is identical across indicators based again on
Hansen's ![]() -statistic
-statistic
where
![]() is the GMM parameter estimate subject to the
cross-equation restriction
is the GMM parameter estimate subject to the
cross-equation restriction
![]() and
and
![]() is the unrestricted estimate. The
is the unrestricted estimate. The ![]() -values for
this test are reported in rows 8 and 9 of Table 6.
The restrictions are quite consistent with the data.
-values for
this test are reported in rows 8 and 9 of Table 6.
The restrictions are quite consistent with the data.
The unrestricted policy parameter estimates from
![]() are reported in rows 8 and 9 of Table 7. Nothing substantive is lost, and statistical precision is noticeably gained,
by imposing the cross-equation restriction that the policy rule constant is
identical across economic indicators. Comparing rows 8 and 9 of Table 7 to Table 3, one sees that estimating separate
policy rule constants reduces the statistical precision with which we estimate
the policy rule response coefficients, in particular the inflation response
coefficients at longer horizons.
are reported in rows 8 and 9 of Table 7. Nothing substantive is lost, and statistical precision is noticeably gained,
by imposing the cross-equation restriction that the policy rule constant is
identical across economic indicators. Comparing rows 8 and 9 of Table 7 to Table 3, one sees that estimating separate
policy rule constants reduces the statistical precision with which we estimate
the policy rule response coefficients, in particular the inflation response
coefficients at longer horizons.
6.3 Potential Output and the Inflation Target
A challenge for standard methods of estimating monetary policy rules is the
difficulty in measuring potential output ![]() and the inflation target
and the inflation target
![]() . We have argued that our approach can avoid these problems to
the extent that the daily news items of which we make use have negligible
consequences for
. We have argued that our approach can avoid these problems to
the extent that the daily news items of which we make use have negligible
consequences for ![]() or
or ![]() . Here we provide additional evidence on
why we believe that is a reasonable assumption.
. Here we provide additional evidence on
why we believe that is a reasonable assumption.
To explore this issue empirically, we will be looking at the properties of the
Congressional Budget Office's series for quarterly potential real GDP growth,
denoted ![]() where
where ![]() indexes quarters. If one looks at the historical
values of this series as reported in the January 2009 vintage,
indexes quarters. If one looks at the historical
values of this series as reported in the January 2009 vintage, ![]() is
an extremely smooth and highly predictable series. However, over time the CBO
will make many revisions to its estimate of the value of
is
an extremely smooth and highly predictable series. However, over time the CBO
will make many revisions to its estimate of the value of ![]() for a
given historical quarter
for a
given historical quarter ![]() . For example, on April 17, 1996, CBO estimated
the growth rate of potential GDP for
. For example, on April 17, 1996, CBO estimated
the growth rate of potential GDP for ![]() 1995:Q4 to be 1.98% (at an annual
rate), whereas by January 8, 2009, they had revised the estimate for
1995:Q4 to be 1.98% (at an annual
rate), whereas by January 8, 2009, they had revised the estimate for
![]() up to 2.76%. Orphanides (2001) and
Orphanides and van Norden (2002) demonstrated that such revisions can pose a big
problem for traditional Taylor Rule estimates. Is it reasonable to assert that
the daily news events exploited in our analysis had negligible implications
for these subsequent revisions of potential GDP?
up to 2.76%. Orphanides (2001) and
Orphanides and van Norden (2002) demonstrated that such revisions can pose a big
problem for traditional Taylor Rule estimates. Is it reasonable to assert that
the daily news events exploited in our analysis had negligible implications
for these subsequent revisions of potential GDP?
Let ![]() denote the information set available to the public as of the
20th calendar day of the first month of quarter
denote the information set available to the public as of the
20th calendar day of the first month of quarter ![]() . For example, for
. For example, for ![]() 1995:Q4,
1995:Q4, ![]() would represent information publicly reported as of
January 20, 1996. By this date, values for the percentage growth in nonfarm
payrolls for each month of quarter
would represent information publicly reported as of
January 20, 1996. By this date, values for the percentage growth in nonfarm
payrolls for each month of quarter ![]() would have been reported, denoted
would have been reported, denoted
![]()
![]() and
and
![]() though the
actual GDP growth rate for quarter
though the
actual GDP growth rate for quarter ![]() would not yet be known. Thus for
example for
would not yet be known. Thus for
example for ![]() 1995:Q4,
1995:Q4,
![]() would be the growth rate of
seasonally adjusted nonfarm payroll employment during the month of October
1995 as reported by the Bureau of Labor Statistics on January 6, 1996, while
would be the growth rate of
seasonally adjusted nonfarm payroll employment during the month of October
1995 as reported by the Bureau of Labor Statistics on January 6, 1996, while
![]() would be the November 1995 growth rate as reported on
January 6. Let
would be the November 1995 growth rate as reported on
January 6. Let
![]() denote
the four most recent quarterly growth rates for potential GDP as they would
have been reported by CBO prior to date
denote
the four most recent quarterly growth rates for potential GDP as they would
have been reported by CBO prior to date ![]() ; for example, for
; for example, for ![]() 1995:Q4,
1995:Q4,
![]() is the potential growth rate for 1995:Q3 as
estimated by CBO on February 1, 1995 (the most recent CBO estimate released
prior to January 20, 1996). Finally, let
is the potential growth rate for 1995:Q3 as
estimated by CBO on February 1, 1995 (the most recent CBO estimate released
prior to January 20, 1996). Finally, let
![]() denote the potential
GDP growth rate for quarter
denote the potential
GDP growth rate for quarter ![]() as reported on January 8, 2009. Vintage values
for
as reported on January 8, 2009. Vintage values
for
![]() and
and
![]() were obtained from ALFRED,
the real-time archived data set maintained by the Federal Reserve Bank of St. Louis.
were obtained from ALFRED,
the real-time archived data set maintained by the Federal Reserve Bank of St. Louis.
We then estimated the following regression by OLS for ![]() 1994:Q1 to
2007:Q3:
1994:Q1 to
2007:Q3:
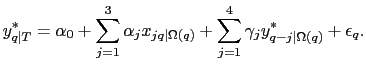
The coefficients
![]() can tell us the extent to which the values of
nonfarm payroll growth that arrive during quarter
can tell us the extent to which the values of
nonfarm payroll growth that arrive during quarter ![]() could help predict the
potential GDP growth rate for quarter
could help predict the
potential GDP growth rate for quarter ![]() as it would ultimately be reported,
relative to information about potential GDP that had arrived prior to the
quarter's actual GDP report. We fail to reject the null hypothesis that
as it would ultimately be reported,
relative to information about potential GDP that had arrived prior to the
quarter's actual GDP report. We fail to reject the null hypothesis that
![]() (
(
![]() ). On
the other hand, a parallel regression for predicting the actual real GDP
growth rates as eventually reported,
). On
the other hand, a parallel regression for predicting the actual real GDP
growth rates as eventually reported,
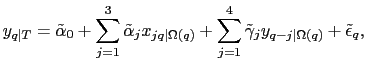
leads to rejection of
![]() (
(
![]() ). Nonfarm payrolls contain
useful information about the current quarter's actual GDP growth but little
information about the current quarter's potential GDP growth.
). Nonfarm payrolls contain
useful information about the current quarter's actual GDP growth but little
information about the current quarter's potential GDP growth.
We repeated the same calculations using monthly industrial production growth
rates in place of nonfarm payroll employment growth.16 We again found
that industrial production is of no use in predicting potential GDP (
![]() ), but is helpful for predicting actual GDP (
), but is helpful for predicting actual GDP (
![]() ). Our maintained assumption that markets are responding to news
about near-term economic conditions
). Our maintained assumption that markets are responding to news
about near-term economic conditions ![]() and not potential output
and not potential output
![]() is thus fully consistent with these hypothesis tests.
is thus fully consistent with these hypothesis tests.
As far as the inflation target is concerned, the validity of our identifying assumption seems even more compelling. Although there may be changes in the Fed's inflation objectives over time, the suggestion that the FOMC is changing its long-run inflation target on a daily basis in response to the latest economic news would seem quite strange to those who actually implement monetary policy. Apart from the discrete effects of personnel changes, the Fed's long-run inflation target should be by definition an even smoother series than potential GDP.
7. Conclusion
It is important to be able to measure market participants' beliefs, manifest through their behavior, about how monetary policy is conducted. Previous work has identified futures contract prices as powerful predictors of their underlying; in particular, fed funds futures contracts are good predictors of future Federal Reserve policy. This paper proposed that market participants forecast future policy along with future economic conditions, and linked the two by the Taylor Rule. This enabled us to measure the market's beliefs about how the Federal Reserve responds to inflation and the output gap. Additionally, by focusing on daily forecast updates, we are able to nearly eliminate the impact of potential output and the inflation target on our main focus: the market-perceived monetary policy response to inflation and output.
Our baseline results for the 1994-2007 sample suggest the market perceives that the Federal Reserve gradually responds to inflation and real activity. Similar to previous literature working on post-Volcker data, we find the Federal Reserve follows the Taylor Principle, a greater than one-for-one response to inflation. We also find evidence that the market-perceived monetary policy rule changed over our sample. During the 1990s market-perceived policy responded robustly to output and quickly to inflation; during the 2000s market-perceived policy doesn't respond to output and responds at a more measured pace to inflation, though its long-run inflation response is greater than before. We quantify the importance of the inflation response path and long-run magnitude in a standard model, and find that raising the long-run magnitude is effective at lowering inflation volatility while making the path more gradual is counterproductive. Our baseline results were found to be robust to alternative possible specifications.
References
Andrews, D.W.K. (1993): "Tests for Parameter Instability and Structural Change with Unknown Change Point," Econometrica, 61, 821-856.
Ang, A., S. Dong, and M. Piazzesi (2007): "No-Arbitrage Taylor Rules," NBER Working Papers 13448, National Bureau of Economic Research, Inc.
Bartolini, L., L. Goldberg, and A. Scarny (2008): "How Economic News Moves Markets," Current Issues in Economics and Finance, 14(6), 1-7, Federal Reserve Bank of New York.
Boivin, J. (2006): "Has US Monetary Policy Changed? Evidence from Drifting Coefficients and Real-Time Data," Journal of Money, Credit, and Banking, 38(5), 1149-1173.
Christiano, L., M. Eichenbaum, and C. Evans (2005): "Nominal Rigidities and the Dynamic Effects of a Shock to Monetary Policy," Journal of Political Economy, 113(1), 1-45.
Christiano, L.J., M. Eichenbaum, and C. Evans (1996): "The Effects of Monetary Policy Shocks: Evidence from the Flow of Funds," The Review of Economics and Statistics, 78(1), 16-34.
Clarida, R., J. Gali, and M. Gertler (2000): "Monetary Policy Rules And Macroeconomic Stability: Evidence And Some Theory," The Quarterly Journal of Economics, 115(1), 147-180.
Cogley, T., and A. M. Sbordone (2008): "Trend Inflation, Indexation, and Inflation Persistence in the New Keynesian Phillips Curve," American Economic Review, 98(5), 2101-26.
Evans, C.L. (1998): "Real-time Taylor rules and the federal funds futures market," Economic Perspectives, pp. 44-55.
Faust, J., J. H. Rogers, S.-Y.B. Wang, and J.H. Wright (2007): "The High-Frequency Response of Exchange Rates and Interest Rates to Macroeconomic Announcements," Journal of Monetary Economics, 54(4), 1051-68.
Gurkaynak, R.S., B. Sack, and E. Swanson (2005): "The Sensitivity of Long-Term Interest Rates to Economic News: Evidence and Implications for Macroeconomic Models," American Economic Review, 95(1), 425-436.
Gurkaynak, R. S., B. T. Sack, and E.P. Swanson (2007): "Market-Based Measures of Monetary Policy Expectations," Journal of Business & Economic Statistics, 25, 201-212.
Hamilton, J. D. (2008): "Daily monetary policy shocks and new home sales," Journal of Monetary Economics, 55, 1171-1190.
----- (2009): "Daily Changes in Fed Funds Futures Prices," Journal of Money, Credit, and Banking, 41, 567-582.
Hansen, L. P. (1982): "Large Sample Properties of Generalized Method of Moments Estimators," Econometrica, 50, 1029-1054.
Ireland, P. N. (2007): "Changes in the Federal Reserve's Inflation Target: Causes and Consequences," Journal of Money, Credit and Banking, 39(8), 1851-1882.
Kohn, D. L., and B. P. Sack (2004): "Central bank talk: does it matter and why?," in Macroeconomics, Monetary Policy, and Financial Stability, pp. 175-206. Bank of Canada.
Newey, W. K., and D. McFadden (1994): "Large sample estimation and hypothesis testing," in Handbook of Econometrics, ed. by R. F. Engle, and D. McFadden, vol. 4 of Handbook of Econometrics, chap. 36, pp. 2111-2245. Elsevier.
Newey, W. K., and K. D. West (1987): "A Simple, Positive Semi-Definite, Heteroskedasticity and Autocorrelation Consistent Covariance Matrix," Econometrica, 55(3), 703-708.
Orphanides, A. (2001): "Monetary Policy Rules Based on Real-Time Data," American Economic Review, 91(4), 964-985.
Orphanides, A., and S. Van Norden (2002): "The Unreliability of Output-Gap Estimates in Real Time," Review of Economics and Statistics, 84(4), 569-583.
Owyang, M. T., and G. Ramey (2004): "Regime switching and monetary policy measurement," Journal of Monetary Economics, 51(8), 1577-1597.
Pagan, A. (1986): "Two Stage and Related Estimators and Their Applications," Review of Economic Studies, 53(4), 517-38.
Piazzesi, M., and E. T. Swanson (2008): "Futures prices as risk-adjusted forecasts of monetary policy," Journal of Monetary Economics, 55(4), 677-691.
Primiceri, G. E. (2006): "Why Inflation Rose and Fell: Policy-Makers' Beliefs and U.S. Postwar Stabilization Policy," Quarterly Journal of Economics, 121(3), 867-901.
Rudebusch, G. D. (2002): "Term structure evidence on interest rate smoothing and monetary policy inertia," Journal of Monetary Economics, 49(6), 1161-1187.
----- (2006): "Monetary Policy Inertia: Fact or Fiction?," International Journal of Central Banking, 2(4), 85-135.
Smith, J., and J. B. Taylor (forthcoming): "The Long and Short End of the Term Structure of Policy Rules," Journal of Monetary Economics.
Stock, J. H., and M. W. Watson (2002): "Macroeconomic Forecasting Using Diffusion Indexes," Journal of Business & Economic Statistics, 20(2), 147-62.
Taylor, J. B. (1993): "Discretion versus Policy Rules in Practice," Carnegie-Rochester Conference Series on Public Policy, XXXIX, 195-214.
A. Appendix
Tables and Figures
Table A1. Policy Rule Constant Estimates
h=1 | h=2 | h=3 | h=4 | h=5 | h=6 | |
|---|---|---|---|---|---|---|
| BASELINE | -0.4024** 0.0787 |
-0.4750** 0.1031 |
-0.6223** 0.1351 |
-0.5060** 0.1223 |
-0.6844** 0.1041 |
-0.6056** 0.1046 |
| BASELINE, PRE | -0.4085** 0.0897 |
-0.4744** 0.0693 |
-0.6187** 0.1050 |
-0.5288** 0.1459 |
-0.7056** 0.2027 |
-0.6310* 0.2691 |
| BASELINE, POST | -0.4228** 0.1174 |
-0.5163** 0.1545 |
-0.6179** 0.0924 |
-0.5194** 0.1440 |
-0.6075** 0.1945 |
-0.6850** 0.1587 |
Notes: is the average risk premium change. HAC standard errors in italics. The markers * and ** denote significance at 5% and 1% levels, respectively. Point estimates and standard errors from two-step nonlinear GMM. Data run over 1994:M1-2007:M7.
Figure A1. Trading Volume on Fed Funds Futures Contracts
Notes: Data from Chicago Board of Trade. As quarterly average.
Footnotes
1. First version: January, 2009. We thank Michele Cavallo, Joseph Gruber, Elmar Mertens, Ricardo Nunes, Robert Vigfusson, and participants of the International Finance Workshop, Midwest Macro Meetings 2009, and North American Econometric Society Meetings 2009 for helpful comments, and Michael Reynolds for research assistance. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
2. [email protected] Return to text
3. [email protected] Return to text
4. [email protected] Return to text
5. See Rudebusch (2002) and Rudebusch (2006) for alternative approaches. Return to text
6. We assume that
![]() . Return to text
. Return to text
7. Our method works if either the risk premium is constant, as implied by the common "expectations hypothesis" or under the implication of consumption-based asset pricing models that the risk premium would change little on a daily basis. Piazzesi and Swanson's (2008) results indicate that "[these] risk premia seem to change primarily at business-cycle frequencies." Return to text
8. We make sure this is the case with the indicators we choose below. Return to text
9. We have tried Continually-Updated GMM, but have found this makes little difference to our baseline results. Return to text
10. Since our framework introduces a generated-regressor, the two-stage OLS procedure is inconsistent - see Pagan (1986). Return to text
11. Our HAC estimator is that of Newey and West (1987) with 13 lags. Return to text
12. See Figure A1 for a plot of these data. Return to text
13. MMS does not survey forecasts for Core-PCE inflation, hence our reliance on Core-CPI inflation. Fortunately, Core-CPI forecasts Core-PCE inflation well - further details are available from the authors upon request. Return to text
14. Estimates of the constant are reported in Table A1 of Appendix A.1. Return to text
15. The vector of parameters taken to be constant under both the
null and the alternative is the vector of auxilliary forecasting parameters
![]() . Return to text
. Return to text
16. Release of the
December 1995 value for industrial production was delayed until January 24,
1996. We used this January 24, 1996 release for ![]() 1995:Q4. Return to text
1995:Q4. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text