Skip to: [Printable Version (PDF)]

Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1007, September 2010 --- Screen Reader Version*

Offshoring Bias in U.S. Manufacturing: Implications for Productivity and Value Added^**

Susan Houseman,⁺ Christopher Kurz,^*** Paul Lengermann,^*** and Benjamin Mandel^***

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

The rapid growth of offshoring has sparked a contentious debate over its impact on the U.S. manufacturing sector, which has recorded steep employment declines yet strong output growth--a fact reconciled by the notable gains in manufacturing productivity. We maintain, however, that the dramatic acceleration of imports from developing countries has imparted a significant bias to the official statistics. In particular, the price declines associated with the shift to low-cost foreign suppliers are generally not captured in input cost and import price indexes. Although cost savings are a primary driver of the shift in sourcing to foreign suppliers, the price declines associated with offshoring are not systematically observed; this is the essence of the measurement problem. To gauge the magnitude of these discounts, we draw on a variety of evidence from import price microdata from the Bureau of Labor Statistics, industry case studies, and the business press. To assess the implications of offshoring bias for manufacturing productivity and value added, we implement the bias correction developed by Diewert and Nakamura (2009) to the input price index in a growth accounting framework, using a variety of assumptions about the magnitude of the discounts from offshoring. We find that from 1997 to 2007 average annual multifactor productivity growth in manufacturing was overstated by 0.1 to 0.2 percentage point and real value added growth by 0.2 to 0.5 percentage point. Furthermore, although the bias from offshoring represents a relatively small share of real value added growth in the computer and electronic products industry, it may have accounted for a fifth to a half of the growth in real value added in the rest of manufacturing.

Keywords: Foreign outsourcing, TFP, price measurement, growth accounting

JEL classification: O47, F40, L60

1.  Introduction

Developing economies have become the new, low-cost suppliers of a wide range of products purchased by consumers and used as intermediate inputs by producers, with China--now the largest exporter to the United States--accounting for about a third of the growth in commodity imports over the last decade.¹ The rapid growth of offshoring--defined as the substitution of imported for domestically produced goods and services--has sparked a contentious debate over its impact on the U.S. manufacturing sector, which shed 20 percent of its employment, or roughly 3.5 million jobs, from 1997 to 2007. Concerns over employment losses and the trade deficit have prompted a recent spate of government and private sector proposals to revitalize manufacturing.²

In spite of the steep employment declines and numerous plant closures, official statistics indicate that output growth in the U.S. manufacturing sector was robust: real value added grew at an annual rate of 3 percent, only slightly less than the 3.1 percent rate for all nonfarm business, from 1997 to 2007.³ These disparate trends--steep employment declines and strong output growth--can be reconciled by the notable gains in manufacturing productivity.

Our paper highlights the dramatic growth of offshoring and the structural changes occurring in manufacturing in the decade prior to the current recession. During this time, more than 40 percent of imported manufactured goods were used as intermediate inputs, primarily by domestic manufacturers. We examine the contributions to the real growth in domestic shipments in manufacturing from the inputs to production and from multifactor productivity and find substantial evidence of offshoring. The contribution from imported materials to the growth in real manufacturing shipments was larger than that of any other factor input and was more than twice the contribution from capital. At the same time, contributions from domestic materials and from labor were negative.

We maintain that the dramatic acceleration of imports from developing countries is imparting a significant bias to official statistics.⁴ Price declines associated with the shift to low-cost foreign suppliers generally are not captured in price indexes. The problem is analogous to the widely discussed problem of outlet substitution bias in the literature on the Consumer Price Index (CPI).⁵ Just as the CPI fails to capture lower prices for consumers brought by the entry and expansion of big-box retailers like Wal-Mart, import price indexes and the intermediate input price indexes based on them generally do not capture the price drops associated with a shift to new suppliers in China and other developing countries. The bias to the input price index will be proportional to the growth in share captured by the low-cost supplier and the percentage discount offered by the low-cost supplier (Diewert and Nakamura, 2009). If growth in the input price index is overstated, productivity and real value-added will also be overstated.

The necessary conditions for this bias, a substantial shift towards foreign sources and the existence of significant discounts on intermediate inputs, were both present in the decade preceding the recent recession. Moreover, the shift in the import composition towards developing countries, especially China, accelerated during the downturn as consumers and businesses have become increasingly price sensitive.⁶ Using confidential microdata on foreign non-oil materials intermediates, we present estimates of substantial offshoring by manufacturers.⁷ We find that non-energy materials inputs from domestic sources actually fellwhile foreign non-energy materials inputs to manufacturing expanded nearly fifty percent--to 25 percent of all materials inputs--from 1997 to 2007. Moreover, developing- and intermediate-income countries accounted for almost all of this growth in import market share, with developing countries, mainly China, accounting for over half of the pick-up.

Although cost savings are a primary driver of the shift in sourcing to foreign suppliers, the price declines associated with offshoring are not systematically observed; this is the essence of the measurement problem.⁸ To gauge the magnitude of these discounts, we draw on a variety of evidence from import price microdata (IPP) from the Bureau of Labor Statistics (BLS) , industry case studies, and the business press. Industry case studies and the business press generally put the magnitude of the discount from offshoring general manufactured products to developing countries, such as China, at about 30 to 50 percent, and the discount to intermediate countries, such as Mexico, at 20 to 30 percent for auto parts.

Using BLS import price microdata, we examine differences in prices for detailed commodities from advanced versus developing countries and from advanced versus intermediate countries, as a proxy for the discounts between the United States and developing and intermediate countries. As an alternative approach, we employ a structural model that endeavors to control for any systematic differences in product quality among countries.⁹ We also examine price differentials from observations where importers appear to have shifted sourcing of a specific product from a supplier in an advanced country to one in a developing or intermediate country. Overall, our estimates of price differentials from the import price microdata are quite consistent with evidence from case studies and the business press.

As shown in Figure 1, differences in the growth rates of the price indexes used by the Bureau of Economic Analysis (BEA) to deflate intermediate materials inputs are indicative of a possible measurement problem. If price indexes were accurately capturing the cost savings to businesses that presumably underlie the recent share growth of imported intermediates, markets clear, and elasticities of substitution between foreign and domestic intermediate inputs are greater than one, then the growth of the import price index should be slower than the domestic price index, indicating a fall in the price of imported relative to domestic inputs.¹⁰ Instead, the foreign price deflator for intermediate materials rose faster than the domestic deflator.¹¹ The differential between foreign and domestic materials price deflators is especially apparent beginning in 2002, coincident with the rapid rise of imports from China.

To assess the implications of biases to the input price deflator for manufacturing productivity and output measures, we implement the bias correction to the input price index developed by Diewert and Nakamura (2009), using a variety of assumptions about the magnitude of the discounts from offshoring. We then incorporate the alternative measures of real intermediates into a growth accounting framework and estimate the bias to multifactor productivity and value added.

We provide estimates not only for the aggregate manufacturing sector but also for the 19 three-digit NAICS manufacturing industries. The disaggregate results highlight the fact that one industry--computers and electronic equipment (NAICS 334)--accounted for most of the growth in productivity and real value added in manufacturing over the decade, although that industry accounted for less than 10 percent of manufacturing's employment and nominal value added.¹² Moreover, if the evidence from industry case studies, the business press, and the micro import data is representative of the actual discounts manufacturers realized from offshoring, our work implies that from 1997 to 2007 multifactor productivity growth in manufacturing was overstated by 0.1 to 0.2 percentage point and real value added growth was overstated by 0.2 to 0.5 percentage point. Furthermore, although the bias from offshoring represents a relatively small share of real value added growth in the computer and electronic products industry, it may have accounted for a fifth to a half of the growth in real value added in the rest of manufacturing.

We also implement an alternative bias correction to the import price index that only accounts for shifts in sourcing of non-energy materials inputs from advanced to developing and intermediate countries (i.e. the shifts from domestic to foreign suppliers is ignored). This more limited examination of biases suggests that shifts in sourcing among foreign suppliers could have resulted in up to a 22 percent bias in multifactor productivity growth over the decade.

Our paper is closest in spirit to recent work by Feenstra, Mandel, Reinsdorf and Slaughter (2009), who document the effect of various biases in published statistics for aggregate output and productivity and find that that measurement problems, which are tantamount to under-reported terms of trade gains, create a significant upward bias to measured output and multi-factor productivity growth in the United States. In this paper, which focuses on the manufacturing sector at a detailed level, we capture an additional source of bias via the level changes in input prices that are realized by U.S. producers when they offshore intermediate inputs or shift sourcing among foreign countries.

The paper proceeds as follows. The next section presents additional background on the current state of manufacturing in the United States. Section 3 reviews data sources and our growth accounting framework and presents a baseline set of growth accounting estimates. Section 4 provides an overview of BLS prices and discusses the biases that may arise from offshoring, while section 5 provides evidence on the import discount from IPP microdata and case studies. Sections 6 and 7 present our results on offshoring bias to manufacturing productivity and value added, respectively. Section 8 concludes.

2.  Background: International Trade and the State of American Manufacturing

One of the most important developments in the U.S. economy in recent years has been the rapid growth of trade.¹³ After being little changed in the early 1990s, the total value of imports and exports of goods and services jumped from roughly 20 percent of U.S. GDP to 28 percent prior to the recent downturn. Importantly, roughly 80 percent of the increase was attributable to a run up in the value of imports. The growth of non-oil imports was the most important contributor to the increase during this period, and non-oil goods imports--largely manufactured goods--accounted for almost half of total import growth, while oil accounted for about a third and services for the remainder of the growth.¹⁴

The surge in the imports of manufactured goods--more than 100 percent from 1997 to 2007--reflects both an increase in the import share of goods for final consumption and the import share of intermediate inputs, which is our focus in this paper. According to BEA, the share of intermediate material inputs used by manufacturers that was imported increased from under 17 percent in 1997 to 25 percent in 2007. Figure 2 plots this substantial shift in the sourcing of intermediates from domestic to foreign suppliers.¹⁵

Low-wage countries accounted for the most of the growth in imported intermediate inputs. In figure 2, we categorize countries into one of three groups--developing, intermediate, and advanced--based on the country's per capita GDP in 2008.¹⁶ Developing countries accounted for half of the growth in foreign materials inputs, with much of that growth coming from China. Intermediate countries, such as Mexico, accounted for about a third of the growth.

How has the U.S. manufacturing sector performed given the growth of imports from low-wage countries? In particular, has the substantial shift in sourcing "hollowed out" manufacturing or instead contributed to the emergence of a leaner, more efficient industrial sector? On the one hand, dramatic drops in employment and plant closures portray a sector in decline. The precipitous decline in manufacturing employment since the late 1990s is evident in figure 3A, and is coincident with the rise in foreign sourcing. Employment never rebounded after the 2001-2002 recession as it had following previous downturns. Indeed, in the decade leading up to the current recession, manufacturing employment declined by 20 percent, while manufacturing's share of employment in the economy fell from 14 percent in 1997 to 10 percent in 2007 (figure 3B). Naturally, plant closures accompanied the employment declines, and for more recent data, the net number of manufacturing establishments fell by 10 percent from 1998 to 2007 (Table 1).¹⁷ At the same time, the nominal share of manufacturing value added in GDP fell from 15.4 percent in 1997 to 11.7 percent in 2007.

Statistics on manufacturing production, however, paint a much more favorable picture of the sector. From 1960 to 2009, the average annual rate of change in real nonfarm business output was 3.5 percent, only slightly higher than the 3.2 percent annual change for manufacturing.¹⁸ More recently, from 1997 to 2007, the annual growth rate of real value added in manufacturing was 3.0 percent, almost the same as the 3.1 percent growth for all private industry. Moreover, cross-country comparisons show larger output gains in U.S. manufacturing relative to other advanced industrial countries, according to OECD data.

The divergent trends of employment declines and plant closures, on the one hand, and rapid growth in real value added, on the other, are primarily reconciled through the lens of productivity. The steadily increasing series in Figure 3B shows the ratio of output per hour in manufacturing to output per hour in all nonfarm business since 1960; the series indicates that labor productivity grew considerably faster in manufacturing throughout the period. From 1997 to 2007, the average annual growth rate of labor productivity in manufacturing was 4.1 percent compared to 2.7 percent for all nonfarm business. Manufacturing labor productivity also grew substantially faster in the United States than in most other major industrialized countries during this decade.¹⁹ The rapid growth in labor productivity has more than offset the declines in labor input and has permitted firms to sustain robust growth in real value added.

Analysts have pointed to the robust output and productivity growth to argue that the manufacturing sector is healthy.²⁰ Our work, however, suggests that the story is more complex. The aggregate numbers are unrepresentative of the trends in most of manufacturing. Moreover, we find that the performance of U.S. manufacturing has been overstated to some extent in the official statistics because of offshoring.

3.  The Role of Imported Intermediate Materials in U.S. Manufacturing: Baseline Growth Accounting Results, 1997-2007

3.1  Data for the Growth Accounting Framework

Data from multiple sources are required to estimate industry-level multifactor productivity and the contribution of foreign intermediates to growth. The BEA's GDP-by-industry accounts, part of their Annual Industry Accounts, provide estimates of gross output, intermediate inputs, value added, and their respective chain-type price indexes for 61 private industries and 4 government classifications.²¹ For our analysis, we focus on the 19 manufacturing industries contained in the GDP-by-industry accounts. To further decompose intermediate inputs, we use the BEA's industry-level KLEMS account, which decompose intermediate inputs into estimates of energy, materials, and purchased-services. ²² The KLEMS data contain estimates in current dollars along with their corresponding quantity and price indexes.

Industry-level capital input was derived from BEA's detailed Fixed Assets Accounts. In order to measure the productive services of an industry's capital stock, asset-by-industry capital stocks are aggregated using ex-post rental prices following the Jorgenson-Griliches (1967) approach used by BLS. Instead of simply chain aggregating the value of capital stocks, this approach aggregates with the goal of appropriately weighting various stocks with respect to their productive capabilities. The detailed capital asset types are aggregated into two components, information technology (IT) and other capital (equipment, structures, and inventories).²³

Labor input is measured as the change in hours worked by all persons (employees and self employed) at the GDP-by-industry level with no explicit differentiation by characteristics of workers. As discussed in Corrado, et al (2007), the underlying source data on employment and hours contain serious breaks and inconsistencies due to the introduction of NAICS. We adopt their methods for deriving industry level labor input series whose changes are both consistent over time and appropriate for calculating productivity.²⁴ To better control for the effects of worker heterogeneity on labor input and productivity, we also differentiate hours worked implicitly using the very detailed information on industry-level employment and payrolls from the Census Bureau's County Business Patterns (CBP) file.

Lastly, we employ data on imported intermediates and their respective prices, which we obtain from a combination of published and unpublished BEA sources.²⁵ The values and prices are available at the six-digit Input-Output (I-O) commodity level.²⁶ The BEA calculates the value of imported commodities used by each industry by assuming that each industry uses imports of a commodity in the same proportion as the overall ratio of imports-to-domestic supply of the same commodity.²⁷ This assumption, known as the "import comparability assumption," has been used in numerous studies, starting with Feenstra and Hanson's outsourcing work (1996, 1998).²⁸

The BEA also provided us with detailed imported commodity price indexes, which it constructs using a concordance between BLS's SITC import price indexes and BEA's commodity (item) codes. When there is not a concordance between the BLS price measures and the BEA commodity codes, the BEA constructs its own end-use import price index. Taken altogether, we have data on 272 imported commodities, representing more than half of the approximately 500 detailed BEA commodity codes.²⁹

3.2  The Growth Accounting Framework

The traditional neoclassical growth accounting framework provides a useful tool to measure the effects of import price mismeasurement on multifactor productivity (MFP). Growth accounting decomposes the sources of growth among the factors that drive economic activity, i.e., capital, labor, both domestic and imported intermediate inputs, and MFP--which is estimated residually and represents the returns to all factors of production.³⁰ Growth accounting is a useful mechanism not only for measuring the contribution of imported intermediates , but also for assessing the extent to which mismeasured import and input prices affect MFP. Specifically, by adjusting published estimates of import and input prices to account for the bias from offshoring, we can derive alternative estimates of the contribution to output growth from intermediate inputs, and hence re-estimate MFP. In what follows, we employ a gross output approach to measure the contribution of imported intermediates to economic growth which, as opposed to the sectoral output approach favored by BLS, more fully accounts for the substitution between intermediate inputs at the detailed industry level.³¹

Growth rates are denoted with hat-notation, where $\mathop{y}\limits^{\wedge }$ denotes the real growth rate of y. Let k denote an industry, sector, or any other aggregation over industries. In order to estimate industry-level multifactor productivity we use industry-level growth rates for gross output, $\mathop{Q}\limits^{\wedge } k$, and industry-level growth rates for the production inputs, i.e. labor $\mathop{L}\limits^{\wedge } k$ , capital $\mathop{K}\limits^{\wedge } k$, and intermediate inputs $\mathop{M}\limits^{\wedge } k$.³²

Total intermediate inputs at the industry level, Mk, are decomposed into domestically supplied materials, imported materials, and purchases of energy and services,

$${{{M_k=M}^D_k+M}^F_k+E_k+S}_k,$$

where $M^D_k$ and $M^F_k$ denote domestic and foreign materials, and Ek and Sk are energy and services, respectively.³³ For this decomposition of total intermediate materials use, ${M^D_k+M}^F_k$, is the total value of materials inputs, MATk, for industry k. As mentioned previously, data on total materials use, purchased energy, and services comes from BEA's industry-level KLEMS accounts. We then split total materials inputs into domestic and foreign components using BEA's imported commodities matrix.

We also define the cost shares for each input for industry k ($s^L_k$,$\ s^K_k$, $\ s^{m^D}_k$, $s^{m^F}_k,s^S_k,s^E_k$), as the factor cost to the total cost for all input factors for industry k. We use these cost shares to construct weights for our growth accounting model, where an input's weight for industry k is a two-period average of the input's cost share in industry k. As the labor input used for our MFP estimates is the hours worked of all persons in the industry, we adjust the labor cost ${{\rm L}}_{{\rm k}}$ by the ratio of all hours to employee hours, i.e., the adjusted labor share is: $s^L_k=\left(\frac{L_k}{Q_k}\right)\left(\frac{{Hours\ all\ persons}_k}{{Hours\ of\ employees}_k}\right)$ .³⁴ The share of intermediates, $s^M_k=\frac{{MAT}_k}{Q_k}$, can be further decomposed using the KLEMS categories and the value of imported intermediates into the shares of imported materials domestic materials, energy and services, $s^M_k=s^{M^D}_k+s^{M^F}_k+s^S_k+s^E_k$. Lastly, the share of capital is calculated as a residual, $s^K_k=1-(s^L_k+s^M_k)$.

Chained price indexes for gross output, value added, intermediate inputs (materials, energy, and services) are available from BEA's annual industry accounts at the GDP-by-industry level. To calculate the real growth of domestic materials inputs, we derive a domestic materials price index using total materials prices from the industry accounts and commodity-level data on imports and import prices provided to us by the BEA. Given prices and nominal values for total materials and imported materials, the price index and nominal values for domestic materials purchases ($M^D_k$) are calculated by chain stripping the real value of imported intermediates from the real value of total materials.³⁵

Given the aforementioned definitions, we define productivity growth as:

$${M\hat{F}P}_k=\widehat{Q_k}-\left(s^L_k{\hat{L}}_k+s^K_k{\hat{K}}_k+s^{m^D}_k\widehat{M^D_k}{\rm ,+}s^{m^F}_k\widehat{M^F_k}+s^S_k\widehat{E_k}+s^E_k\widehat{S_k}\right)$$ (1)

We generate estimates for each of the 19 GDP-by-industry manufacturing industries, and then aggregate these results to obtain estimates for the entire manufacturing sector, for the durable and nondurable manufacturing subsectors, and for several aggregates excluding computer and electronic products.

3.3  Baseline Results, 1997-2007

The baseline estimates presented in this section are derived from unadjusted data and are intended to serve as a reference for the alternative estimates we derive in section 6, which adjust the official input and import price series for offshoring bias.³⁶ As shown in figure 2, the import share of materials intermediates jumped over the 10-year period we analyze and reached 25 percent of materials use in 2007. In addition, the value of total materials--both domestic and foreign--used by the manufacturing sector expanded over this period. In other words, not only did the total amount of purchased materials used by U.S. manufacturers increase during this period but the composition of these inputs changed substantially as well. The shift towards materials, particularly imported materials, suggests there have been substantial changes in the relative importance of the various factors of production in terms of their contributions to output growth. We discuss below how imported materials appear to have contributed substantially to the growth of most manufacturing industries. In contrast, domestic materials appear to have made consistently negative contributions.

Table 2 provides our baseline growth accounting results.³⁷ The first column presents the average annual rate of growth for real gross output from 1997 to 2007. The sources of growth- including MFP, capital, labor, energy, services, and domestic and foreign materials-appear in columns 2 though 8. The contributions from MFP and each factor input sum to the growth in gross output. The first row in Table 2 reports the decomposition for manufacturing as a whole, while the subsequent rows show decompositions for manufacturing excluding computers and electronic products,³⁸ durable and nondurable manufacturing, durable goods excluding computers and electronic products, and the 19 individual GDP-by-industry manufacturing sectors.

We estimate that real output growth in the manufacturing sector averaged 1.2 percent between 1997 and 2007, with most of the output gains driven by the durable goods producing sector, and, in particular, the computer and electronic products industry. Although contributions from MFP, capital, services, and foreign materials all played important roles over the time period of interest, the sources-of-growth notably vary across industries. In particular, while MFP growth is a primary contributor to output gains in all industries, the contributions from capital and services inputs, though on balance positive, were negative in a number of industries. . On the other hand, the contribution to growth from labor, energy, and domestic materials were negative were negative for manufacturing overall and for almost all industries.

Columns 7 and 8 in Table 2, which show the contributions to growth from intermediate materials, provide a clear picture of the rapid pace of structural change currently underway in U.S. manufacturing. During the period, the contribution of domestically supplied materials inputs fell, while that of imported materials inputs greatly expanded, reflecting the substitution of foreign for domestic intermediate inputs.³⁹ For all manufacturing, the contribution of imported materials inputs to output growth was greater than that of any other factor of production and was more than double the contribution from capital. For manufacturing excluding the computer industry, imported materials account for 60 percent of the growth during this period.

Looking across the individual industries, many appear to have cut back on domestic intermediates while simultaneously boosting their use of foreign intermediates. More specifically, domestically purchased materials contributed positively to output growth in only 7 of the 19 manufacturing industries, with a substantial contribution found in nonmetallic minerals, miscellaneous manufacturing, petroleum and coal products, and plastics and rubber products. By contrast, the purchases of foreign intermediate materials contributed positively in all but two manufacturing sectors (textiles and apparel).

Nevertheless, our baseline growth accounting results present a picture in which MFP is the predominant contributor to output growth in the U.S. manufacturing sector; MFP growth averages 1.3 percent for all manufacturing, more than 2 percent for durables, and about 0.5 percent for nondurables producing industries. For all manufacturing, the contribution to real output growth from MFP actually exceeds real gross output growth, indicating that MFP can account for all of the growth in real gross output over the decade. Capital, purchased services, and materials all play important, albeit more modest, roles, while the contribution of labor is negative and large, reflecting the steep employment declines during the period.

Another striking result in Table 2 is that computer and electronic products manufacturing--which includes computers, semiconductors, and telecommunications equipment--accounts for most of the output and productivity growth in manufacturing over the period.⁴⁰ Output and productivity growth in the computer industry averaged 7.4 and 6.8 percent per year, respectively, compared to growth of only about 0.5 percent for output and 0.7 percent for MFP in the rest of manufacturing.⁴¹ The extraordinary productivity and output growth in computers reflects, to a large degree, technological improvements of the products produced and output price deflators that, when properly adjusted for product improvements, are often falling rapidly.⁴²

Because statistics on labor productivity, defined as output per hour worked, are widely used in research and policy analyses, it is also of interest to consider the relationship between labor productivity growth and offshoring. In the official BLS labor productivity release, manufacturing output includes imported intermediates but excludes intermediates sourced from within the domestic manufacturing sector. As a result, shifts in sourcing from a domestic to a foreign supplier do not offset each other, mechanically increasing labor productivity.⁴³ To this point, Eldridge and Harper (2009) find that imported intermediate materials explain 20 percent of the growth in manufacturing labor productivity from 1997 to 2006. We find that the contribution to manufacturing labor productivity from imported materials inputs significantly accelerated over the period.

Although Table 2 documents the substantial growth in offshoring during the period, it nevertheless likely understates the true magnitude of the phenomenon. Our focus below concerns the systematic upward bias in the price indexes used to deflate intermediate materials. We could not account for the measurement of two additional factors which likely also impart an upward bias: (i) imported capital inputs, such as computers and machinery, have exhibited substantial gains in import penetration and (ii) imported services inputs (i.e. services offshoring) have accelerated in recent years, albeit from a very low level.⁴⁴

4.  BLS Prices Programs and Price Measurement Problems

4.1  Background on prices programs

Understanding why offshoring results in biases to price statistics requires some background on the relevant price programs. The Bureau of Labor Statistics (BLS) constructs separate price indexes for imports and domestically produced goods. In the International Price Program (IPP), BLS surveys a sample of importing establishments on the prices they pay for imports of a detailed product. To construct the Producer Prices Index (PPI), the BLS surveys domestic producers on the prices they receive for a sample of products.⁴⁵ The Bureau of Economic Analysis (BEA) then estimates price indexes for industries' intermediate inputs using the domestic and import price indexes and using information on each industry's input structure from the input-output tables. We will now visit each of these three pricing programs in more detail.

The BLS's IPP program aims to calculate broad and consistent Laspeyres import and export price indexes. In order to compute import price indexes, the IPP program selects a sample of importing establishments and products to be followed in overlapping 5-year periods. The IPP collects `at-the-dock' prices per unit of imports on a monthly basis for approximately 20,000 items.⁴⁶ Importers report characteristics of the imported items of interest and their transaction prices. The unit of observation used to construct the import price index is the period-to-period change in the purchase price of a specific item imported by a specific establishment. ⁴⁷ Therefore, the first time a product is sampled at a reporting establishment, its price change is missing and cannot be used in the construction of the index. If a change is made to the description of a sampled item or to its trade factors, which include country of origin, BLS attempts to adjust for the value of new characteristic. If changes are too large and adjustments are not feasible, the item is added to the group and the new series is "linked in" to the index. This means that the price change between the old product and the new item that replaces it is dropped when computing the price index, and it is assumed that the price movements of newly sampled products are the same as the average price changes of on-going products at the time of its introduction. Nakamura and Steinsson (2009) note that because performing hedonic adjustments is extremely expensive, the procedure is rarely done, and the overwhelming majority of product replacements in the import prices sample are "linked in". The IPP uses a modified Laspeyres formula to aggregate across establishments and detailed product categories, using product import sales volumes as weights.⁴⁸

The producer price indexes measure average changes in prices received by domestic producers for their products. The PPI is a transaction based pricing metric, with price-determining variables, such as color, defining different products. The BLS performs quality adjustment over time, as characteristics change. If there is a physical change in the product that can be assigned a value, then the BLS uses various methods to adjust for quality changes. As with the IPP, the use of hedonic techniques to adjust for quality changes is rare. If no price is reported by the survey respondent, the change is imputed as the average change for other items in the same cell. The PPI is a modified Laspeyres formula, with aggregation weights constructed from the latest Census of Manufactures.

The BEA integrates information from the annual and benchmark I-O accounts, from the GDP-by-industry accounts, and from various price indexes constructed by BLS to create the National Income and Product Accounts (NIPAs). An important part of that exercise involves deflating intermediate purchases in order to properly measure value added at the industry and sector level. Using the I-O accounts, BEA estimates the amount of each commodity used in the creation of each industry's gross output. The I-O accounts do not distinguish whether intermediate inputs are of foreign or domestic origin. Therefore, as discussed above, when constructing a price index to deflate intermediate inputs, BEA assumes that the fraction of a particular intermediate input that is foreign is the same across all user industries and that it equals the import share of all domestic consumption of that commodity--the import comparability or constant industry assumption.

BEA generally uses the PPI to deflate the value of domestically produced intermediate inputs and the import price index from the International Prices Program to deflate imported intermediate inputs. In 1996, BEA introduced its own hedonic index to adjust for quality changes in semiconductors. In addition, BEA further corrects BLS PPI prices for telecommunications equipment based on hedonic methods. The resulting commodity quantity indexes are aggregated up to the industry level via a Fisher index-number formula and used to calculate a price index at that same level (Strassner and Moyer 2002).⁴⁹

4.2  Problems with the price indexes programs

The BLS takes great care to ensure that it is pricing the same item over time, and thus that price indexes are based on "apples to apples" comparisons. Conceptually, each observation used in the construction of a particular price index represents the period-to-period price change of an item as defined by very specific attributes and reported by a specific establishment. Efforts to carefully control for product attributes when collecting data on price changes lead to two classes of problems in pricing at the elemental level, both of which have been widely discussed in the literature on the CPI:⁵⁰

1) New goods and quality changes. If a new product is introduced or the attributes of an ongoing product change significantly, then a price change for the product is missing or difficult to construct.

2) New supplier. Because the unit of observation is the price change reported for a specific item by a specific establishment, price indexes often fail to capture price declines consumers and businesses experience when they shift purchases to a new, low-cost supplier. In the literature on the CPI, this problem was termed outlet substitution bias.

A third class of problems widely discussed in the price index literature concern the proper aggregation of the sampled observations of price changes. Composite price indexes must be constructed, and even if all price changes are accurately measured, the problem of how to add up "apples and oranges" remains. In particular, the Laspeyres index, which computes the price change for a fixed basket of goods, does not allow for substitution by purchasers among goods over time as relative prices change, and thus in some cases superlative indexes are preferred. However, when the price changes themselves are missing or mismeasured, as in the case of new goods or new suppliers, reweighting the sampled price changes does not correct this more fundamental problem.⁵¹ Although an extensive literature on the implications of these measurement problems exists for the CPI, their implications for other price indexes and economic statistics have, until recently, received relatively little attention. As mentioned earlier, Feenstra, Mandel, Reinsdorf and Slaughter (2009) estimate biases to the import price index resulting from the growth in new goods or product varieties, from the exclusion of tariffs in IPP prices, and to the fact that the import price index is constructed using a Laspeyres rather than a superlative index formula. They find that each of these factors contributes to an index of U.S. terms of trade being underestimated. That is, similar in spirit to our results below but for different reasons, official price measures ascribe what are actually mismeasured terms of trade gains to productivity growth.

In addition, Nakamura and Steinsson (2009) consider biases to import and export price indexes as a result of model changes, which constitute the introduction of new goods or varieties, in imported and exported commodities--what they term "product replacement bias." They argue that because price changes associated with model changes are generally missing, the responsiveness of import and export prices to exchange rate changes has been much greater than previously estimated.

Our paper, along with several recent studies, focuses on biases to price indexes resulting from the shift in sourcing to low-cost overseas producers.⁵² We turn now to a fuller examination of this bias.

4.3  Price biases arising from offshoring and other shifts in sourcing of inputs

Consider first the problem of measuring the drop in an input price when an organization shifts its sourcing from a domestic supplier to a new, low-cost foreign supplier. There may be considerable lag before a new item is included in the import price sample, and, as noted above, because indexes are constructed from observations of price changes of specific items sampled in a reporting establishment, the price change will be missing when the item is first sampled. Moreover, to correctly measure the input price change at the elemental level, the BLS should measure the price difference between the imported item and the domestic item it replaces (Alterman 2009, Diewert and Nakamura 2009, Houseman 2008).⁵³

Figure 4 presents a stylized depiction of the problem in the context of offshoring. The IPP measures the price change from period t to t+1 of a specific imported product from a particular importer, and the IPP measures the price change from period t to t+1 of a specific product produced by a specific domestic producer. Neither the IPP nor the PPI captures the price drop (d) that occurs when businesses shift from a high-cost domestic to a low-cost foreign supplier. The input price index, as computed by the statistical agencies, is essentially a weighted average of period-to-period changes measured in the IPP and the PPI, and thus the price drop from offshoring is missed. The correct index, however, would capture the period-to-period change of the average price that U.S. companies pay for each intermediate input. More rapid introduction of new suppliers into the BLS sampling frame or more frequent sampling of prices--common suggestions for improving price statistics--will not address this particular problem.

Bias in price indexes arising from a shift in sourcing to a new, low-cost domestic or foreign supplier is analogous to outlet substitution bias in the CPI literature (Houseman 2008, Diewert and Nakamura 2009). Building upon Diewert (1998), which characterizes outlet substitution bias to the CPI, Diewert and Nakamura (2009) characterize the bias to the input price index from outsourcing and offshoring. Consider the rate of price increase for an item used as an input in production. The ratio of the price of that item reported by a specific producer (or importer) in periods t and t-1accurately characterizes the rate of price increase facing purchasers of that input in the absence of shifts in sourcing of that input. However, if the producer shifts all or some of its sourcing of the input to a lower-cost provider, the measured rate of price increase will be upward biased. Following Diewert and Nakamura (2009, pp. 17-18), the true rate of price increase at the elemental level may be characterized as follows:

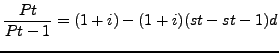$$\frac{Pt}{Pt-1} =(1+i)-(1+i)(st-st-1)d$$ (2)

where P represents the unit value of a homogeneous input, s is the physical share of the input sourced from the low-cost supplier, d is the percentage discount offered by the low-cost supplier, and 1+i is the rate of price increase from period t-1 to 1 for the high cost supplier (assumed the same for the low-cost supplier).⁵⁴

It is commonly believed that biases to price indexes from the introduction of new goods or--what is observationally equivalent in the data--the entry of a new supplier of existing goods, are not large, because at any point in time the number of new goods or new suppliers is small, and because the market share of new products or new entrants is small.⁵⁵ With respect to the first point, however, recent research points to extraordinarily high product turnover in the import data (Broda and Weinstein 2006; Nakamura and Steinsson 2009).⁵⁶

The second point--that biases to price indexes are small because market shares of new products or new entrants are small-also may not hold in the case of offshoring, given, as we have shown earlier, the large and growing magnitude of international sourcing. Moreover, the likely presence of sizable information and other short-run adjustment costs that decline with time implies that low cost suppliers may continue to expand market share following the initial entry, even if their prices relative to competing products do not change. For instance, to explain the existence of large and persistent cross-country differences in the price of observationally identical semiconductor wafers, Byrne, Kovak, and Michaels (2010) hypothesize that firms may respond to new opportunities to produce semiconductor wafers at lower average cost overseas with a lag because they have large sunk costs in existing facilities. More generally, although the dynamic by which low-cost producers enter and capture market share from incumbents is an important mechanism by which prices change, it is a dynamic largely missed in price indexes.⁵⁷

Recent studies based on the microdata from the IPP also show considerable rigidity in import prices. In particular, Nakamura and Steinsson report that 45 percent of items in the IPP register no price changes during the entire period they are in the sample, and more than 70 percent have two price changes or less. Whatever the underlying reason for the rigidity in prices, the stylized fact is important because if the import price for a particular product registers most of its relative price change after entering the U.S. market, such a dynamic, in theory, might be picked up by the IPP. The growth in market share of low-cost imports from developing economies no doubt reflects continual productivity gains in those countries, quality improvements, and declines in quality-adjusted product prices. Yet the combination of high rates of product replacement and price rigidity in ongoing products suggests that the import price index will not pick up this dynamic.

Widespread shifts in sourcing have occurred not only from domestic to low-cost foreign suppliers, but also from relatively high-cost foreign suppliers toward new, low-cost foreign entrants, as evidenced by the growth in the share of imported inputs from developing and intermediate countries. Unlike the PPI, the import prices program surveys the purchaser, rather than the seller, of the items sampled. Thus, it is possible that a price change associated with such shifts in sourcing among foreign suppliers will be captured in the import price index.

The key to capturing the price change is that, when the shift to the new source occurs, the imported item from the new source is not treated as a new series but rather as a continuation of the old item. Suppose, for example, that a manufacturer purchases a specific part from a wholesale importer that, in turn, shifts its sourcing of the part to a lower-cost provider in a different country. A shift in sourcing the item from one country to another will be flagged as a change in a trade factor, which may trigger the discontinuation of one series, the introduction of a new series, and hence a break in the price series. If, however, the importer confirms that the item from the new source country is identical to the one it replaces or if it can adjust for any quality differences, the series will be continued and the price change from the shift in sourcing will be recorded. If, instead, it is a different wholesale importer that purchases the item from the new, low-cost foreign supplier and, in shifting source countries for its imported parts, the manufacturer simultaneously changes import wholesalers, the price change will be missed.

5.  Empirical Evidence on Offshoring of Intermediate Materials and "Offshoring Bias"

5.1  Evidence on share shifts for commodities used as intermediate materials

In this section we document patterns of changing market share among domestic and international sources for intermediate inputs at the level of detailed commodities. As depicted in figure 2, the aggregate share of imported intermediate goods has increased from 17 to 25 percent over the period 1997-2007, driven largely by increases in developing and intermediate countries' shares. The detailed product data underlying these aggregate shares tell a richer, more intricate story of domestic-international and intra-foreign share dynamics and permit us to identify country-product shares that are increasing at the expense of other country-product shares. In other words, we can determine to which countries share is accruing and at which countries' expense.

To begin, we consider the shifts in shares among U.S. import sources. As mentioned, we categorize countries into one of three groups--developing, intermediate, and advanced. Figure 5 shows the long differences, i.e., differences calculated over the entire sample period, in market share of developing- and intermediate-income countries for 344 manufactured commodities over the period 1997-2007. ⁵⁸ It is immediately apparent that most observations lie to the right of the vertical axis, denoting an increase in developing country shares; for over 90 percent of products, developing country shares increased. It is also notable that in the majority of those cases, developing country gains outpaced both the gains and losses of the intermediate countries: observations in the bottom-right quadrant above the downward-sloping 45 degree line are instances in which developing country share growth exceeded intermediate share declines, implying that the share of advanced countries also registered a decline. Observations in the top-right quadrant below the upward-sloping 45 degree line are instances in which developing country share growth exceeded intermediate share increases, implying not only that the share of advanced countries declined but that the developing share increased relative to intermediate. In the top-left quadrant there are a few instances in which intermediate share increased at the expense of developing, and in the bottom-left virtually none in which advanced increased share at the expense of both intermediate and developing.

For our implementation of the input price bias correction below we require a measure of the share of imported inputs. We thus combine the import shares with information on domestically produced inputs to compute the input share coming from developing and intermediate countries. Figure 6 shows the long differences in the domestically sourced input share as they relate to the combined growth of developing and intermediate share at the commodity level.⁵⁹ Here the vast majority of observations are in the bottom-right quadrant, denoting a gain in developing and intermediate share at the expense of a loss of domestic share. The 45-degree line in this diagram informs us of the extent to which advanced foreign countries are gaining share from domestic sources: observations above that line are those in which developing/intermediate share is growing faster than domestic share is falling, implying that the advanced input share is falling as well. Since the share changes line up well with the 45-degree line, there does not seem to be any large net changes in the share of inputs sourced from advanced countries. Most of the action involves the shifting from domestic sources to developing and intermediate foreign sources.

5.2  Evidence on the Import Discount from IPP Microdata

5.2.1  Overview

As described in equation 2, the formula to correct for import price bias due to offshoring requires a measure of the discount ('d') offered by foreign input producers relative to domestic ones. Since there are no direct data sources for this discount spanning the large number of industries we examine, we consider three alternatives using microdata collected by the IPP. First, we examine the relative prices of U.S. imports coming from low- and intermediate-income source countries compared to those of advanced countries. Second, recognizing that the composition of traded varieties across income groups can vary substantially even within narrowly defined products (which could be driving some of the price differences observed),⁶⁰ we examine price-switching behavior at the more detailed level of U.S. importing firms. Specifically, we compute the price change when a given firm switches providers to a new source country, which likely controls for item specification changes to a greater extent. Finally, we take a structural approach to adjusting relative prices for compositional quality differences, using recently developed methods from the international trade literature. We then compare our empirical measures of the offshoring discount with evidence from industry-specific case studies of cross-country cost differentials in the next section.

5.2.2  Full Sample, Unadjusted Estimates

For our first empirical proxy for d we define the relative import price from low-wage source countries. These relatives are constructed at the level of transactions within narrowly defined product groups over the period September 1993 to May 2007. When an item enters the IPP sample, a detailed description is collected and the reporting importer is asked to update the price for that specifically defined item (i) over time (t). Items are identified by an array of transaction and product characteristics, including: country of origin (c), Harmonized System 10-digit (HS10) product code (j) and the unit of measure (e.g., pound, kg, container, etc.) in which the sale took place (u). ⁶¹,⁶²

As described above, we separate countries into three groups: advanced, developing, and intermediate, based on each country's per capita GDP in 2008 relative to the U.S.: c $\in$ A denotes the set of advanced countries; c $\in$ I denotes the set of intermediate-income countries; and c $\in$ D denotes the set of developing countries. The import price discount for an individual item in the developing set, and analogously for items from intermediates, is measured as:

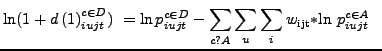$${\ln (1+{d\left(1\right)}^{c\in D}_{iujt})\ }={\ln p^{c\in D}_{iujt}-\sum_{c?A}{\sum_u{\sum_i{{w_{{\rm ijt}}{\rm *} {\rm ln}{\ p}^{c\in A}_{iujt}\ }}}}\ }$$ (3)

where each d(1) is the percent difference in price between an import transaction from a developing country and a geometric mean of advanced country transaction prices in the same HS10 group, unit of sale and month.⁶³ The weights in the geometric mean are wijt is the item-level probability weight used by the IPP in aggregating to the HS10 product-level. The discount from (3) can then be aggregated further using IPP item- and establishment level weights; for instance, $d(1)_{jt}^{c\epsilon D}$ is the average discount for developing country c in product j at time t. Aggregation of $d(1)_{jt}^{c\epsilon D}$ across time periods and products uses fixed weights; for example, China's growing market share and compositional shifts into new and larger product groups do not feed back into a greater weight to China's differentials.⁶⁴

The top two panels of figure 7 illustrate the magnitude of d(1) for developing and intermediate-income exporters by NAICS 4-digit product code in the manufacturing sector. The vast majority of relative prices are negative with an average price difference of 63 percent for the developing group and 58 percent for the intermediate group. There is a substantial amount of heterogeneity in the import discount across products: both the left (i.e., food, beverage, textiles, apparel) and middle (i.e., wood, fuel, chemicals, plastics, minerals) portions of the product spectrum are characterized by significant dispersion in both discount magnitude as well as the difference between developing and intermediate, whereas the right (i.e., machinery, electronics, semiconductors, transportation) is characterized by large cross-product variation but smaller differences between developing and intermediate prices. In the top-left panel, the size of each bubble is weighted by the change in input share of developing or intermediate countries. This weighting shows where the bulk of mass resides for each discount in our implementation of the price index correction formula. To the right of the figure, there is a large concentration of developing country discounts of between 60 and 80 percent and lying systematically below the intermediate export prices for the same products. The top-right panel uses the average size (in dollars) of each industry's imported intermediate input as weights, showing even greater emphasis on machinery, electronics, semiconductors and transportation products.

The relative price (HS10) columns of table 3 break out the import discount of selected countries. For the developing countries, with the exception of Argentina and some smaller exporters, all price differences are negative, with notably low price source countries including Bangladesh, Bolivia, China, India, Nicaragua, Pakistan and Sri Lanka. For the intermediate countries, all price differences, save Croatia and Venezuela, are negative, with notably low price source countries including Hong Kong, Hungary, Poland and Taiwan.

5.2.3  Switching Estimates

A closer empirical counterpart to the decision of U.S. producers to switch to input sources from abroad is the decision of U.S. importing firms to switch among foreign source countries. For instance, one would expect that trends toward U.S. sourcing in China would not only correspond to switches away from U.S. producers but away from Japanese and European producers as well. We thus identify firms in the IPP sample that have added new source countries to existing import product categories and measure the product prices from those sources relative to incumbents. Despite focusing on a significantly smaller portion of the IPP sample than the previous discount measure, the firm switching relative price confers the significant benefit of controlling for cross-firm variation in import composition. It stands to reason that heterogeneity in this composition within firms will be lower than the corresponding measure at the HS10 product level.

A country switch is defined as a new import item in a firm-HS10-month cell from a country other than where incumbent items are sourced. In the full sample, in many cases a new item is observed at the same time that a firm enters the IPP sample; since these are uninformative about switching behavior they were discarded, leaving 9,676 instances of new items in incumbent firms over the course of the sample. Of those, 7,609 new items were from the same country as an incumbent item.⁶⁵ The relative prices of these new items did not vary greatly relative to incumbents, and were on average 2 percent higher in the developing country set, 3 percent for the intermediate countries and 4 percent for advanced countries. The remaining 2,067 observations are instances in which new items came from a new country source. The relative price of a country switch from an advanced to a developing country is defined as:

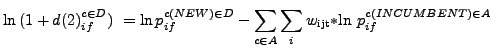$${\ln {(1+d(2)}^{c\in D}_{if})\ }={\ln p^{c(NEW)\in D}_{if}-\sum_{c\in A}{\sum_i{{w_{{\rm ijt}}{\rm *} {\rm ln}{\ p}^{c(INCUMBENT)\in A}_{if}\ }}}\ }$$ (4)

where the subscript f indexes a specific importing firm and the product, unit of sale and month subscripts are suppressed for clarity. Again, w denotes the item-specific weight constructed by the IPP.

Table 4 shows the average relative prices of these switches in percent, broken down according to our country classification. For instance, when a new item sourced from a developing country appears in a cell containing an advanced country incumbent (the top-right entry of panel (a)), the average discount is 44 percent; switching from an advanced to intermediate source confers a discount of 28 percent. To see how these discounts have evolved over time, we compute the same statistics for the first seven years of the sample (panel (b)) and the last seven years (panel (c)). Interestingly, the developing country discount is fairly stable over those periods while the intermediate-advanced discount is much more pronounced in the early period.⁶⁶

Moving back to table 3, the second column displays the developing and intermediate switching discounts by country, alongside the average (unadjusted) cross-country price differences for all imports within an HS10.⁶⁷ For the larger U.S. trading partners, the discounts are still significantly negative, though less so than the unadjusted measures. China's discount drops from 75 percent to 62 percent, India's discount drops from 76 percent to 46 percent, Brazil drops from 45 percent to 12 percent, and Mexico drops from 54 percent to 15 percent. Overall, the discounts at the HS10- and HS10-firm-level are correlated positively, however consistent with the narrative that compositional differences across items are smaller within importing firms, firm-level switching discounts tend to be smaller.

5.2.4  Structurally Adjusted Estimates

Finally, we implement a structural estimation to infer the degree of unobserved compositional differences driving the relative prices. The objective is to convert observed price differences across countries into common units of quality, where the remaining heterogeneity in prices is a `pure' measure of production cost advantage. For instance, if China has lower average quality embedded in its products then the unadjusted relative prices will overstate the benefits to outsourcing to China. In order to discern quality from cost drivers of price differences, we regress the cross-country variance of unadjusted prices on estimates of quality ladder length at the detailed product level. The residual of that estimation is the component of price variance not due to variance in quality characteristics.

Our measures of quality ladder length for U.S. imports use the same method as described in Mandel (2010), which proposes a simple theory to discern whether firms within a given industry are competing in price versus quality space. The theory introduces costs to producing quality characteristics, such that productive firms endogenously choose to produce higher quality outputs. What relative price those highly productive firms charge depends on the balance of: (i) lower prices due to lower costs, and (ii) higher prices due to producing a good that consumers value more. Ultimately, this balance depends on the nature of the good; a product group with little quality differentiation will have productive (larger) firms selling at lower prices, while a product type with more scope for quality differentiation will have productive (larger) firms selling at higher prices.

The identification of quality scope uses IPP micro-data as described above. A structural equation is derived for the skewness of U.S. import prices at the product level as a function of the skewness of source country wages and the skewness of the firm size distribution. It is the size-price correlation that is informative about the scope for quality differentiation; the observation of higher sales at higher prices suggests that there is a significant degree of heterogeneity in quality characteristics across product varieties. The price skewness at the HS10 level is measured directly using IPP import prices while the firm size skewness uses the export sales size distribution of U.S. exporting firms within the same category.⁶⁸ The result is a classification scheme of products; those with a high correlation of price skewness and size skewness are classified as high quality scope industries, while those with a low correlation of price skewness and size skewness are classified as low quality scope (i.e., more homogeneous).⁶⁹

Given quality scope measures, the assumption used to identify quality differences in relative prices across sources is that the dispersion in observed item prices is proportional to the underlying dispersion in quality composition. To be concrete, let us define a quality-adjusted item price, qi, and some measure of that item's quality, zi. The quality-adjusted price is the observed price, pi, normalized by quality to obtain a comparable measure of price across items: pi=qi*zi. The variance of (the log of) observed prices within an HS10 group can then be rewritten as a function of the variance of ln(z) and ln(q), as follows:

$${var}_j\left({\ln p_i\ }\right)=\sum_i{{\left({\ln p_i\ }-\overline{{\ln p_i\ }}\right)}^2}$$

$$=\sum_i{{\left(\left({\ln q_i\ }-\overline{{\ln q_i\ }}\right)+\left({\ln z_i\ }-\overline{{\ln z_i\ }}\right)\right)}^2}$$ (5)

$$={var}_j\left({\ln q_i\ }\right)+{var}_j\left({\ln z_i\ }\right)+2{cov}_j\left({\ln q_i\ },{\ln z_i\ }\right)$$

where $\overline{{\ln x_i\ }}$ is a geometric mean of variable x across items within an HS10 group. It is immediate that if the covariance of quality and quality-adjusted price were to be zero, then the variance of observed prices would vary one-for-one with the variance of quality.⁷⁰ Since no reliable measures exist for this covariance, and since there are offsetting theoretical rationale for its sign, we proceed by employing the simplifying assumption that it is zero. The variance of quality-adjusted prices from (5) is then approximated by the difference in the variance of observed prices and unobserved quality:

$${var}_j\left({\ln q_i\ }\right){\cong var}_j\left({\ln p_i\ }\right)-{var}_j\left({\ln z_i\ }\right)$$ (6)

This relationship is implemented in the data by regressing the relative price of developing and intermediate-income exporters on a measure of product-level quality variance described above and a quadratic term for quality variance:

$$\left\vert{d(1)}_{kjt}\right\vert={\alpha }_0+{\alpha }_1*{var}_j\left({\ln z_i\ }\right)+{\alpha }_2*{{var}_j\left({\ln z_i\ }\right)}^2+{\varepsilon }_{kjt}$$ (7)

where the size of the country relative price, |d(1)_kjt|, measures the degree of intra-product price dispersion.⁷¹ The residual of this expression is our measure of the variance of quality-adjusted price: ${var}_j\left({\ln q_i\ }\right)$. Table 5 displays regression results for (7) for two sets of U.S. import product groups.⁷² For our purposes, the most conservative estimates to use are those which ascribe the most observed price variance to quality. With this in mind, we apply estimates from specification (7) to the construction of quality-adjusted relative prices as follows:

$${\hat{d}(3)}_{kjt}=\left\{ \begin{array}{c} {d(1)}_{kjt}-{\widehat{\alpha }}_0-{\widehat{\alpha }}_1*{var}_j\left({\ln z_i\ }\right){\alpha }_0-{\widehat{\alpha }}_2*{{var}_j\left({\ln z_i\ }\right)}^2,\ \ \ \ \ {d(1)}_{kjt}>0\ \\ {d(1)}_{kjt}+{\widehat{\alpha }}_0+{\widehat{\alpha }}_1*{var}_j\left({\ln z_i\ }\right){\alpha }_0+{\widehat{\alpha }}_2*{{var}_j\left({\ln z_i\ }\right)}^2,\ \ \ \ \ {d(1)}_{kjt}<0 \end{array} \right.$$ (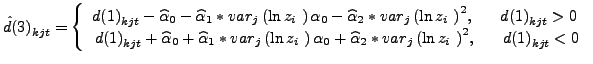8)

The resulting product-level relative prices are illustrated in the bottom two panels of figure 7. As expected given the positive relationship between price and quality variance, there is a pronounced compression of the variance of quality-adjusted prices relative to the unadjusted set in the top two panels, with developing and intermediate country relative prices increasing to about 30 and 15 percent below their advanced country counterparts, respectively. This large adjustment is driven by low-priced varieties in long quality ladder industries being given a correspondingly large boost upwards to account for differences in specification. For example if China has a relatively low price in a highly quality differentiated industry, that is indicative in the model of both low quality and low productivity. In that case, China's quality-adjusted price would be higher than its unadjusted price. In most instances, after the quality-adjustment the ordering of developing versus intermediate country groups is preserved.

The third column in table 3 shows the quality-adjusted relative price measures by source country. Overall, the developing country discount is 25 percent and the intermediate country discount is 14 percent. Notably large increases in relative price due to quality differences occurred in Bangladesh, Bolivia, Costa Rica, China, India, Kenya, Nicaragua, Pakistan and Sri Lanka. Under the assumptions of the structural model, this implies that a significant portion of their discount may be accounted for by quality differences. For the intermediate set of countries, there are instances in which the relative price flipped signs due to the quality-adjustment (i.e., became a premium). The fact that South Korea is pricing at a premium of 13 percent in quality-adjusted terms may suggest that our adjustment is conservative in some cases.⁷³

5.3  Case Study Evidence on the Import Discount

As a means of checking the validity of our three discount measures, we have compiled several examples of industry case studies and press articles documenting cross-country input cost differences (see table 6). These studies often have richer data on particular product specifications, albeit for a single industry classification, and can therefore control for quality differences directly for that industry.

For the developing country set, case study evidence is most widely available for high-tech products imported from China. A McKinsey (2006) study cites cost savings from production of electronic equipment in China of between 20 and 60 percent; for the narrower product category of semiconductors, Byrne, Kovak and Michaels (2009) find the savings to be roughly 40 percent, while a Business Week (2004) article cites 40-50 percent for circuit boards. All of these estimates are in line with our measures, with the developing country price differences in the NAICS category 334 (Computer and Electronic Product Manufacturing) bounding the case study estimates. For general manufactured goods, Business Week (2004) pins the China discount at 30-50 percent, in line with our range of 35-60 percent between the firm-level source switches and the unadjusted estimates.

For intermediate countries, case studies have focused on auto parts exported from Mexico. Klier and Rubenstein (2009) estimate a cost discount for aluminum wheels, a highly homogeneous product category, of 19 percent, while Kennedy (2004) finds the Mexican discount for auto parts in general to be 20-30 percent.⁷⁴ Both of these studies are line with our median firm-level switching measure of 26 percent. Of note, the quality-adjusted Mexican premium of 60 percent is an instance in which our structural quality adjustment is out of line with the industry estimates, and may have been overly punitive. On the other hand, our quality-adjusted estimate of the intermediate country semiconductor discount of 34 percent is closest to that of 24 percent estimated by Byrne, Kovak and Michaels (2009) for Singapore.

5.4  Implementation of the Diewert & Nakamura (2009) formula

As discussed above in Section 4, with measures of changing import shares and the price discount of low-cost foreign suppliers in hand, Diewert and Nakamura's (2009) formula-based approach can be implemented to estimate the size of the upward bias in input prices due to offshoring. Commodity-level input prices were derived using the price index for high-cost (i.e. domestic) suppliers in conjunction with information on the import discount and share in domestic supply of each commodity.⁷⁵ We implement this correction at the NAICS 4-digit product (commodity) level to adjust the materials deflators used for our baseline growth accounting framework in Section 3.⁷⁶

For illustrative purposes, let us examine the correction for a specific industry and year. In 2006, the deflator for the agriculture, construction, and mining machinery industry (NAICS 3331) increased by 3.5 percent. Concurrently the share of inputs sourced from developing countries increased by almost 3.5 percent, priced at an unadjusted discount of roughly 40 percent. Plugging these numbers into the bias correction formula results in a (1.035)*(0.035)*(0.4) = 1.4 percent overstatement of input cost growth, over a third of the measured change in the deflator. It is the corrected deflator change of about 2.1 percent for that commodity and period, and subsequently aggregated to the industry level, that we use to estimate bias-corrected real output and MFP in the following sections.

From the commodity level, the shipment deflators are aggregated by industry using each industry's use of the commodity (i.e., its share in total manufactured materials use) as its weight. The industry deflator is then combined with the deflator for non-manufactured components to obtain a measure of the intermediate materials price deflator (Section 6 provides more detail on this approach).

In figure 8, we compare the published data to one of our bias-corrected measures. The vertical distance between each point and the 45 degree line represents the size of the offshoring bias. For all manufacturing, we find that cumulative price growth of 20 percent⁷⁷ over the period 1997 to 2007 overstates the bias-corrected inflation rate by 9 percent when we adjust input costs with our full sample (unadjusted) estimates of the foreign price discount. That is, nearly half of the growth in input costs over that period may be attributable to international source switching. Also shown are commodity specific cumulative price changes. Given similar input cost inflation, it is interesting to note the industry-specific differences in the bias. For example, electrical equipment had a larger bias than nonmetallic minerals even though they both had unadjusted deflators that rose by about 30 percent over the sample period. Similarly, furniture and primary metals had larger biases relative to printing and chemicals, respectively. An important category not shown in the figure, but included in our calculations below, is that of computers and equipment. That industry had unadjusted price declines of 35 percent over the ten year period, 51 percent after adjusting for the offshoring bias.

6.  Offshoring Bias and Measured Productivity in U.S. Manufacturing

6.1  Overview

As discussed in Section 5, we apply our offshoring correction at the commodity level to construct a range of alternative input price indexes for U.S. manufacturers. We use these adjusted input prices to construct industry-level purchased materials deflators, adopting essentially the same approach as the BEA. In this section, we update the growth accounting exercise initially performed in Section 3 using these alternative industry-level materials deflators to investigate the extent to which offshoring may have distorted measures of manufacturing productivity. Industry output, and the contributions of capital, labor, energy, and services are all unchanged from Section 2. As such, all of the revisions to multifactor productivity presented below stem from our adjustments to purchased materials.

6.2  Constructing industry-level materials deflators from our adjusted commodity-level input prices

To derive our industry-level materials deflators, we first aggregate over the real values of commodities to obtain the total real materials use for each of the 19 manufacturing industries in the GDP-by-industry accounts. Fisher-ideal chained dollar indexes are constructed in which the weights are each commodity's share of each industry's total materials use. We then aggregate across industries to derive Fisher chained dollar materials indexes for durable and non-durable manufacturing and for all of manufacturing.

For our baseline estimates, and following the BEA, imported and domestic commodities are treated as separate inputs (Strassner and Moyer, 2002). Real values for each imported commodity are calculated using the confidential data provided to us by BEA. Domestic commodity values are derived residually based upon BEA's KLEMS Intermediate Use Estimates, which show the total use of each commodity by each industry and the values of imported commodities.⁷⁸ The deflators for domestic commodities were provided to the Federal Reserve Board by the BEA. As discussed in Section 4, although the BEA mostly uses PPIs to deflate domestic materials, there are a handful of commodities for which they develop their own price indexes using hedonic methods.

For our adjusted estimates, as discussed in Section 5, commodity level input prices were constructed using the price index for high-cost (i.e. domestic) suppliers in conjunction with information on the import discount and on import shares. Thus, under this approach, we no longer distinguish between imported and domestic commodities when aggregating across commodities to construct industry level materials deflators. Instead, the real value for each commodity is derived by deflating the total use of the commodity (i.e. both imported and domestic) with its corresponding bias-adjusted input price. Our adjusted approach is otherwise identical to our baseline approach. In other words, real industry-level materials use is derived as a Fisher-ideal chained dollar aggregate derived from real commodity values and using the commodity shares of total materials use as weights.

6.3  Distinguishing manufactured materials from non-manufactured materials

Although the majority of purchased materials used by manufacturers are "manufactured" materials, some purchased materials are sourced from outside the manufacturing sector (for example, mining materials and agricultural products).⁷⁹ For durable goods manufacturers, the total use of these so-called "non-manufactured" materials is typically quite small. However, the use of non-manufactured materials is more significant for several nondurable manufacturing industries, in particular food product and petroleum and chemicals manufacturing.

Unfortunately, we do not presently have price deflators for most non-manufactured commodities at a sufficiently detailed level (either imported or domestic). As such, we were forced to restrict the estimation approach described in Section 6.2 to manufactured materials. More specifically, although the BEA does not publish industry-level manufactured materials price deflators, we construct them following BEA's methodology for all purchased materials. Given published values for total purchased materials and our estimate of total manufactured materials, the implied values for non-manufactured materials (nominal and real values) are then backed out residually (via chains-stripping). As with capital, labor, energy, and services, the implied contribution of non-manufactured materials to economic growth is held fixed in the growth accounting simulations discussed below.⁸⁰

6.4  Offshoring and the Bias to MFP

Table 7 presents our alternative estimates of multifactor productivity growth in U.S. manufacturing for the period 1997-2007. The first column restates our baseline MFP results from Section 3, while column (2) presents estimates in which all commodities - both domestic and imported - have been deflated with the unadjusted domestic deflators provided to us by BEA. Because BEA's domestic deflators are mostly PPIs, column (2) is labeled "IPP=PPI". Since our alternative materials deflators are derived by adjusting domestic commodity prices, the estimates in column (2) should be interpreted as the appropriate reference or "jumping-off" point for gauging the incremental effect of offshoring. In other words, they show what MFP would be if the rate of price inflation for imported commodities was the same as for their domestic counterparts. This assumption is maintained in equation (2) in order to hone in on the impact of the level difference in prices between imported and domestic commodities.

For the entire manufacturing sector (row 1), deflating imported materials with domestic prices serves to reduce MFP growth by a bit less than 0.1 percentage point, from 1.30 percent in our baseline scenario, to 1.23 percent. Almost all of this revision stems from the differences in the deflators for imported and domestic semiconductors. ⁸¹ In other words, prices for imported semiconductors--a product used heavily by the computer and electronic products industry--fell less rapidly than their domestic counterparts. The discrepancies are especially evident in the early years of our data and appear to be the result of inconsistent adjustment of imported and domestic semiconductor prices for quality improvements. Although not the focus of our paper, the drop in MFP between columns (1) and (2) likely represents an additional modest bias.⁸²

In terms of the industry-level contributions to overall manufacturing MFP, almost all of the "IPP=PPI" effect is concentrated within the computer and electronic products industry, which is not surprising given it is the largest consumer of high tech materials: average annual MFP growth in the industry falls from 6.8 to 6.3 percent after we deflate imported high-tech materials with their corresponding domestic prices. Moreover, once we exclude the contribution of the computer and electronic products industry, overall manufacturing MFP is essentially unchanged from our baseline estimate under the "IPP=PPI" scenario at 0.67 percent (row 2, column 1 versus column 2).

Columns (4) - (11) present MFP estimates that have been further adjusted to account for offshoring bias. The differences across these columns are driven entirely by the assumptions we make about the size of the import discount as discussed in Section 5. In columns (4) - (9), our estimates of the import discount are informed by our analysis of IPP microdata, while in columns (10) and (11) we apply discounts that are roughly consistent with the available case study evidence.

On balance, for the entire manufacturing sector (row 1), we find that correcting for offshoring bias lowers MFP growth by an additional 0.1 to 0.2 percentage point during the 1997-2007 period. In other words, average annual productivity growth is between 5 and 15 percent less than in column (2) and between 10-20 percent less than our original, baseline estimate in column (1). These numbers are fairly significant, as a 0.1 percent average annual growth rate for multifactor productivity roughly equals the average annual contribution of the capital stock to manufacturing growth during this period.

MFP growth is reduced in all 19 manufacturing industries, with revisions of more than 20 percent occurring for wood products, nonmetallic mineral products, machinery, motor vehicles, other transportation equipment, furniture, food products, textiles and apparel, paper products, and plastic and rubber products.

The disaggregate results also highlight the fact that one industry--computers and electronic equipment (NAICS 334)--account for most of the growth in productivity in manufacturing over the decade, although that industry accounted for about 10 percent of manufacturing's employment and nominal value added. Indeed, baseline multifactor productivity grew at an annual rate of only 0.69 for manufacturing excluding the computer industry (column 1, line 2).

Moreover, if we exclude the contribution of the computer and electronic products industry, correcting for offshoring results in larger percentage adjustments to MFP which falls from 0.67 percent in column (2) to between 0.52 percent (column 4) and 0.63 percent (column 5); in other words the reduction in MFP widens to as much as 22 percent.

As expected, MFP growth falls the most under the unadjusted import discount scenario (column 4) and the least under the structurally adjusted discount scenario (column 5). However, the differences between these estimates--and also those associated with our median switching results (columns 6 - 9) are relatively small, with MFP falling by roughly 0.1 percentage point for both the structurally adjusted import discount (column 5) and the pooled and within product switching discounts that control for outliers (columns 6 and 8), and by about 0.2 percentage point under the unadjusted discount scenario and the median switching scenarios that excludes both outliers and rules out positive discounts.

Finally, columns (10) and (11) present MFP estimates associated with a blanket discount of either 50 or 30 percent for commodities from developing countries and either 30 or 15 percent for commodities from intermediate countries. These represent discounts on the high and low end, respectively, of those found in the case study and business literature presented in Section 5. The results for both of these scenarios remain broadly consistent with our results based on IPP microdata, with manufacturing MFP (overall and excluding computers) falling between 0.2 and 0.1 percentage point. Interestingly, after excluding the contribution of computers and electronic products, the estimates for our 50/30 scenario in column (11) align quite closely with those for our unadjusted import discount in column (4).

6.5  Substitution Bias from Within the Import Price Index

Although the primary focus of our paper is on offshoring, in this section we briefly examine whether import price mismeasurement may also have distorted manufacturing productivity. Just as input prices fail to fully account for the savings realized by domestic producers from offshoring, so too may import prices be overstated if they fail to fully account for shifts among importing countries (i.e. from advanced to intermediate countries, intermediate to developing, etc.). If import price growth has been overstated, then domestic input prices will be also, along with MFP.⁸³

To investigate this, we adjust for the substitution within the import price index before passing alternative import price series through our growth accounting framework. We correct IPP commodity prices following an analogous approach to our adjustment for input prices: IPP prices are simply substituted for domestic prices for the price inflation term in equation (1), and changes in import shares replace changes in domestic supply.⁸⁴ Two alternative import price series were constructed based upon our unadjusted and adjusted import discounts. Following the same approach as described in Section 3, we then fold the adjusted import prices into our baseline growth accounting procedure for building industry-level intermediate input prices.

More specifically, Fisher-ideal chained index values for imported materials are computed for each manufacturing industry, for durable and non-durable manufacturing, and for all of manufacturing. Real domestic materials values are then derived residually via chain stripping based on published estimates for total purchased materials. For our growth accounting estimates, we then hold the domestic materials prices fixed at the values estimated in the baseline scenario. Thus, MFP will increase or decrease directly as a result of changes in the valuation of imported materials.

The results for import price measurement and its effect on manufacturing productivity during 1997-2007 are shown in Table 8. Unlike our correction for offshoring, the effect of import price mismeasurment on MFP does not "jump off" from the IPP=PPI scenario. Rather, the appropriate reference points are the unadjusted, baseline MFP estimates presented in Table 2 (column 2) and in Table 7 (column 1). These are restated in the first column of Table 8, while columns (2) and (3) present the MFP estimates associated with our correction to import prices.

The effect of import price mismeasurement on MFP is considerably more varied--and therefore less conclusive--than for offshoring. Using the unadjusted discount, import price mismeasurement would appear to impart a substantial bias to manufacturing productivity, with average annual MFP growth falling from 1.30 percent in our baseline scenario to 1.02 percent. Under this scenario, the bias from import price mismeasurement is actually somewhat greater than even our largest estimates of the bias from offshoring. In contrast, under the adjusted discount scenario, MFP growth is little changed from the baseline estimates.

Clearly more work on this topic is warranted. However, the limited evidence we bring to bear on import price mismeasurement suggests it may provide an important additional source of upward bias to manufacturing MFP.

7.  Offshoring and the Bias to Real Value Added

7.1  Overview and Methodology for Value Added Simulations

In this section, we present a range of alternative estimates for real value added growth with the goal of ascertaining the extent to which offshoring bias may have caused the official estimates to be overstated. The BEA derives indexes for industry-level value added using the double-deflation method in which real value added is computed as the difference between real gross output and real intermediate inputs (i.e. energy, services, and materials). More specifically, separate estimates of real gross output and intermediate inputs are combined in a Fisher index-number formula in order to generate indexes for value added (see Kim et al, 2008). Thus, if real intermediate input growth is understated as a result of offshoring bias then real value added growth will be overstated.

In what follows, we replicate this double-deflation procedure using our adjusted measures of real purchased materials in place of the official one. In other words, we derive the implied value of real value added associated with published measures of real gross output, energy, and services and our adjusted measures for purchased materials inputs.⁸⁵ This was done for all of the private sector industries in the GDP-by-industry accounts, and for several aggregates of interest. Our alternative measures of real value added can then be compared with the published estimates.

7.2  Value added results

The results of this procedure can be found in Table 9, which is structured nearly identically to Table 7. Estimates of real average value added growth for 1997-2007 are presented under the same alternative scenarios we used for MFP. In addition to showing results for manufacturing, the bottom three rows of Table 9 also contain estimates for private goods producing industries, private service producing industries, and all private industries.

Before turning to our adjusted estimates, we first discuss the baseline results in column (1). These were derived using our unadjusted materials deflators, the construction of which was described in Section 6. Because our unadjusted materials measures uses the imported and domestic commodity values (nominal and real) provided to us by the BEA--values which feed directly into their official estimates--it is not surprising that our baseline estimates are very close to the published figures.⁸⁶

Under our baseline scenario, manufacturing value added growth averaged a robust 3.04 percent per year during 1997-2007 (line 1), a rate of growth nearly 1.25 percentage point larger than for the entire goods producing sector (line 24), and roughly on par with the private sector as a whole (line 26). Value added growth for private service providing industries averaged a somewhat larger 3.5 percent per year.

Nearly two-thirds of the value added growth in manufacturing originated in the computer and electronics product industry. Once we exclude this industry, which grew at a whopping 23 percent average annual rate (line 8), value added growth for the rest of the manufacturing sector falls to a much less remarkable 0.94 percent (line 2).

As was the case in Section 6, in order to quantify the effect of offshoring bias on value added, we first need an appropriate jumping off, or reference, point. Because our offshoring adjustment involves building input cost measures from domestic commodity prices (along with import discounts and shifts in the imported share of domestic supply), this reference point is a set of estimates in which all manufactured materials--both imported and domestic--are deflated with domestic deflators. The results of this adjustment are shown in column (2). The scenario is once again labeled "IPP=PPI" because most of the domestic commodity deflators used by BEA are in fact PPIs. Real value added growth falls from 3.04 percent to 2.82 percent for the entire manufacturing sector and from 0.94 percent to 0.86 percent for manufacturing excluding the computer and electronic products industry.

As with our results for MFP, nearly all of the differences between the baseline estimates and the "IPP=PPI" estimates reflect the fact that import prices for high-tech commodities fell less rapidly than their domestic counterparts. Indeed, we see in column (3) that resetting the prices just for these high-tech commodities yields value added estimates that are virtually identical to those in column (2). As such, the industry-level differences between column (1) and column (2) primarily reflect differences in the intensity of use of high-tech commodities. The largest adjustments are seen within durable goods manufacturing industries, while smaller adjustments occur for nondurable manufacturing industries and for service producing industries.

The value added estimates associated with our correction for offshoring bias are presented in columns (4) - (11). The differences across these columns--which are driven entirely by our assumptions about the import discount--are slightly more pronounced than for our results on MFP; our results indicate that offshoring bias has significantly distorted real value added during this period. For the entire manufacturing sector (line 1), our offshoring correction reduces value added growth from 2.82 percent per year to between 2.31 and 2.65 percent per year. In other words, correcting for offshoring bias lowers manufacturing value added growth by 7 to 18 percent.

If we exclude the contribution of the computer and electronic products industry, however, correcting for offshoring bias results in larger percentage adjustments to value added: average annual value added growth falls from 0.86 percent in column (2) to between 0.44 percent and 0.75 percent, a significant reduction of between 13 and 49 percent.

As with our results for MFP, value added growth falls the most if we apply our unadjusted import discount, (column 4) and the least if we apply the adjusted discount (column 5). The (50/30) discount simulation (column 11) informed by our case study evidence yields estimates that are again quite close to the unadjusted estimates, while a smaller discount of 30 percent for developing country commodities and 15 percent for intermediate country commodities yields adjusted value added estimates that are somewhat closer to the structurally adjusted ones. Among the four sets of estimates derived with the import discounts from our median switching results, manufacturing value added excluding the computer industry is reduced by a substantial 30 to 48 percent.

A final point to note is that, after correcting for offshoring bias, it appears that the value added growth in the U.S. manufacturing sector lagged considerably behind that of the private sector as a whole. Moreover, the wedge between service sector value added growth and manufacturing sector value added growth now appears wider, increasing from three-quarters of a percentage point in column (2) to between 1 and 1¼ percentage points in columns (4) - (11).

8.  Conclusion

This paper brings a variety of data to bear on the question: are our measures of import prices, input costs, and hence value added and productivity systematically biased by the increased incidence of offshoring? Taken as a whole, our findings suggest that both productivity and value added have indeed been overstated due to the failure of statistical agencies to capture level differences in prices associated with shifts in sourcing from domestic to foreign suppliers. In other words, multifactor productivity has been a somewhat less important driver of manufacturing output growth, while trade liberalization has played a larger role. Our application of a formula-based correction to this offshoring bias extends the empirical literature on outlet substitution in the CPI to both input and international prices, and confirms evidence by Reinsdorf and Yuskavage (2009) and Nakamura and Steinsson (2009) that the IPP is missing important information at the point of item substitution.⁸⁷ Our results imply that the concurrent rise in output and fall in employment at U.S. manufacturing establishments are not entirely at odds; rather an important portion of value added growth simply reflects price declines in imported intermediate inputs not captured by official statistics.

Similar biases, however, may also arise from the offshoring of other inputs and affect statistics for other sectors and for the aggregate economy. For instance, in the 2000s, sizable import penetration by developing countries occurred in computers and machinery products, which are largely treated as capital inputs in the industry accounts. Price drops accompanying the substitution of imported for domestic capital equipment would not be captured in capital price deflators, possibly leading to an understatement of the growth of capital services and an overstatement of growth in multifactor productivity.⁸⁸ The same problem arises from services offshoring. Collecting accurate price information on services trade is complicated by the fact that the level of detail in services sector data is quite limited (Sturgeon et al. 2006, Norwood et al. 2006, Jensen 2009) and that the BLS international prices program does not cover business services imports and exports. Identifying incremental sources of offshoring bias in productivity measures is a promising area for future research.

There may also be some overlap in the offshoring effect we identify empirically and the impact of new traded varieties measured in Feenstra, Mandel, Reinsdorf and Slaughter (2009). In principle, new traded varieties and those specifically due to offshoring are observationally equivalent, so while the two sources of bias in prices are largely complimentary in the way that they are measured, we do not view our results and those in Feenstra et al. as strictly additive.

Finally, in principle it is possible to correct for this bias directly without resorting to a formula-based approximation as we do here. Alterman (2009) has proposed the construction of an input price index based on a survey of purchasers, which if implemented by BLS, would address the biases to the industry statistics from all shifts in sourcing. The proposed index, which would not distinguish source country, would capture price changes from shifts in sourcing among domestic suppliers, among domestic and international suppliers, and among international suppliers.

References

Abraham, Katharine G. and Susan K. Taylor. 1996. "Firm's Use of Outside Contractors: Theory and Evidence." Journal of Labor Economics, 14(3): 394-424.

Alterman, William. 2009. "Producing an Input Price Index." Paper prepared for the conference on Measurement Issues Arising from the Growth of Globalization, Washington, DC.

Baldwin, Richard E. and Tadashi Ito. 2008. "Quality competition versus price competition goods: An empirical classification." HEID Working Paper No. 7/2008.

Bergsten, C. Fred. 2010. "Beijing Is Key to Creating More U.S. Jobs." Foreignpolicy.com: http://www.foreignpolicy.com/articles/2010/04/14/china_the_job_killer?print=yes&hidecomments=yes&page=full

Bils, Mark. 2009. "Do Higher Prices for New Goods Reflect Quality Growth or Inflation?," The Quarterly Journal of Economics, MIT Press, vol. 124(2), pages 637-675.

Broda, Christian. and David Weinstein. 2006. "Globalization and the Gains from Variety," Quarterly Journal of Economics, 121(2): 541-585.

Brown, Clair, and Greg Linden. 2005. "Offshoring in the Semiconductor Industry: A Historical Perspective." In Brookings Trade Forum: 2005: Offshoring White-Collar Work, ed. Lael Brainard and Susan M. Collins, 279-333. Washington, DC: Brookings Institution Press.

Byrne, David, Brian Kovak, and Ryan Michaels. 2009. "Offshoring and Price Measurement in the Semiconductor Industry." Paper prepared for the conference on Measurement Issues Arising from the Growth of Globalization, Washington, DC.

Campa, Jose and Linda S. Goldberg. 1997. "The Evolving External Orientation of

Manufacturing: A Profile of Four Countries." FRBNY Economic Policy Review, July: 53-81.

Cavallo, Michele, and Anthony Landry. 2010. "The Quantitative Role of Capital Goods Imports in US Growth." American Economic Review, 100(2): 78-82.

Cline, William R., and John Williamson. 2010. "Notes on Equilibrium Exchange Rates: January 2010." Peterson Institute for International Economics, Number PB10-2. Washington, DC: Peterson Institute for International Economics.

Corrado, Carol, and Joe Mattey. 1997. "Capacity Utilization." Journal of Economic Perspectives, 11(1): 151-167.

Corrado, Carol, Paul Lengermann, Eric Bartelsman, and Joe Beaulieu. 2006. "Modeling Aggregate Productivity at a Disaggregate Level" draft presented at NBER/CRIW Summer Institute, July 2006.

Corrado, Carol, Paul Lengermann, Eric Bartelsman, and Joe Beaulieu. 2007. "Sectoral Productivity in the United States: Recent Developments and the Role of IT" German Economic Review, 8(May).

Diewert, W. Erwin. 1998. "Index Number Issues in the Consumer Price Index." Journal of Economic Perspectives, 12(1): 47-58.

Diewert, W. Erwin, and Alice Nakamura. 2009. "Bias in the Import Price Index Due to Outsourcing: Can it be Measured?" Paper prepared for the conference on Measurement Issues Arising from the Growth of Globalization, Washington, DC.

Eldridge, Lucy P., and Michael J. Harper. 2010. "Effects of Imported Intermediate Inputs on Productivity." Monthly Labor Review, June: 3-15.

Executive Office of the President of the United States. 2009. "A Framework for Revitalizing American Manufacturing." Washington, D.C.: U.S. Government Printing Office.

Feenstra, Robert C. 1994. "New Product Varieties and the Measurement of International Prices," American Economic Review, 84(1), 157-177.

Feenstra, Robert C. 1998. "Integration of Trade and Disintegration of Production in the Global Economy." Journal of Economic Perspectives, 12(April): 31-50.

Feenstra, Robert and Robert Lipsey. 2010. Report on the State of Available Data for the Study of International Trade and Investment. Report prepared for the Committee on Economics Statistics of the American Economic Association.

Feenstra, Robert C. and J. Bradford Jensen. 2009. "Evaluating Estimates of Materials Offshoring from U.S. Manufacturing." Paper prepared for the conference on Measurement Issues Arising from the Growth of Globalization, Washington, DC.

Feenstra, Robert C., Benjamin R. Mandel, Marshall B. Reinsdorf, and Matthew Slaughter. 2009. "Effects of Terms of Trade Gains and Tariff Changes on the Measurement of U.S. Productivity Growth." National Bureau of Economic Research Working Paper, Number 15592.

Foster, Lucia, John Haltiwanger, and Chad Syverson. 2008. "Reallocation, Firm Turnover and Efficiency: Selection on Productivity or Profitability?" American Economic Review, 98(1): 394-425.

Grimm, Bruce T. 1998. "Price Indexes for Selected Semiconductors." Survey of Current Business, 78(2): 8-24.

Hallak, Juan Carlos and Peter K. Schott. 2008. "Estimating Cross-Country Differences in Product Quality." NBER Working Paper No. W13807.

Hausman, Jerry. 2003. "Sources of Bias and Solutions to Bias in the Consumer Price Index." Journal of Economic Perspectives, 17(1): 23-44.

Helper, Susan. 2008. "Renewing U.S. Manufacturing: Promoting a High-Road Strategy." EPI Briefing Paper 212. Washington, DC: Economic Policy Institute.

Houseman, Susan, and Kenneth Ryder. 2010. "Measurement Issues Arising from the Growth of Globalization." Report prepared for the U.S. Bureau of Economic Affairs.

Hulten, Charles R. 2009. "Growth Accounting." National Bureau of Economic Research Working Paper, No. 15341.

Hummels, David and Peter J. Klenow. 2005. "The Variety and Quality of a Nation's Exports."American Economic Review, 95(3): 704-723.

Hummels, David, Jun Ishii, and Kei-Mu Yi. 2001. "The Nature and Growth of Vertical Specialization in World Trade." Journal of International Economics, 54 (June): 75-86.Jensen, J. Bradford. 2009. "Measuring the Impact of Trade in Services: Prospects and Challenges." Paper prepared for the conference on Measurement Issues Arising from the Growth of Globalization, Washington, DC.

Jorgenson, Dale W., Frank M. Gollop, and Barbara M. Fraumeni. 1987. Productivity and U.S. Economic Growth. Cambridge, Mass: Harvard University Press.

Jorgenson, Dale W., Mun S. Ho, and Kevin J. Stiroh. 2005. "Information Technology, Education, and the Sources of Economic Growth across U.S. Industries." In Measuring Capital in the New Economy, C. Corrado, J. Haltiwanger, and D. Sichel, eds. Chicago: The University of Chicago Press.

Jorgenson, Dale W., Mun S. Ho, and Kevin J. Stiroh. 2008. "A Retrospective Look at the U.S. Productivity Growth Resurgence." Journal of Economic Perspectives, 22(1): 3-24.

Khandelwal, Amit. 2009. "The Long and Short (of) Quality Ladders." forthcoming in Review of Economic Studies.

Klier, Thomas H., and James M. Rubenstein. 2009. "Imports of Intermediate Parts in the Auto Industry--A Case Study." Paper prepared for the conference on Measurement Issues Arising from the Growth of Globalization, Washington, DC.

Kurz, Christopher and Paul Lengermann. 2008. "Outsourcing and U.S. Economic Growth: The Role of Imported Intermediate Inputs." Paper presented for the 2008 World Congress on National Accounts and Economic Performance Measures for Nations.

Leonard, Jeremy A. 2008. "The Tide is Turning: An Update on Structural Cost Pressures Facing U.S. Manufacturers." Published jointly by the Manufacturers Alliance/MAPI and The Manufacturing Institute. http://institute.nam.org/view/2001005065073451188/info

Linden, Greg, Jason Dedrick, and Kenneth L. Kraemer. 2009. "What the iPod Tells Us." http://delong.typepad.com/egregious_moderation/2009/12/greg-linden-jason-dedrick-and-kenneth-l-kraemer-what-the-ipod-tells-us.html

Mandel, Benjamin R. 2010. "Heterogeneous Firms and Import Quality: Evidence from Transaction-Level Prices." Board of Governors of the Federal Reserve System, International Finance Discussion Papers, Number 991.

McKinsey & Company. 2006. "China and India as Global Supply Points: A Business Opportunity!" Consensor Results. Presentation Pudong Shangri-La Hotel, Shanghai, May 22-24.

Nakamura, Emi, and Jón Steinsson. 2009. "Lost in Transit: Product Replacement Bias and Pricing to Market." http://www.columbia.edu/~en2198/papers/ippsubs.pdf.

New America Foundation. 2010. "America Needs a Manufacturing Strategy." (February 3). http://www.newamerica.net/publications/policy/america_needs_a_manufacturing_ strategy.

Norwood, Janet L., Carol Carson, Manuel Deese, Norman J. Johnson, Franklin S. Reeder, and John E. Rolph. 2006. "Offshoring: How Big Is It?" Report of the Panel of the National Academy of Public Administration for the U.S. Congress and the Bureau of Economic Analysis. Washington, DC: National Academy of Public Administration.

Oliner, Stephen D., and Daniel E. Sichel. 2000. "The Resurgence of Growth in the Late 1990s: Is Information Technology the Story?" The Journal of Economic Perspectives, 14(4): 3-22.

Oliner, Stephen D., Kevin J. Stiroh, and Daniel E. Sichel. 2007. "Explaining a Productive Decade." Brookings Papers on Economic Activity, 1: 81-137.

O'Rourke, Kevin H. and Jeffrey.G. Williamson. 1999. Globalization and History, The MIT Press, Cambridge, Massachusetts.

Pisano, Gary P., and Willy C. Shih. 2009. "Restoring American Competitiveness." Harvard Business Review, July-August: 114-125.

Pollin, Robert, and Dean Baker. 2010. "Reindustrializing America:A Proposal for Reviving U.S. Manufacturing and Creating Millions of Good Jobs." New Labor Forum, 19(2): 17-34.

Reinsdorf, Marshall. 1993. "The Effect of Outlet Price Differentials in the U.S. Consumer Price Index." In Price Measurements and Their Use, ed. Murray F. Foss, Marylin E. Manser, and Allan H.Young, 227-254. Chicago: University of Chicago Press.

Reinsdorf, Marshall, and Robert Yuskavage. 2009. "Are there Unmeasured Declines in Prices of Imported Final Consumption Goods?" Paper prepared for the conference on Measurement Issues Arising from the Growth of Globalization, Washington, DC.

Schott, Peter K. 2004. "Across-product Versus Within-product Specialization in International Trade." Quarterly Journal of Economics, MIT Press, 119(2): 646-677.

Strassner, Erich H. And Brian C. Moyer. 2002. "An Analysis of the Composition of Intermediate Inputs by Industry," Bureau of Economic Analysis Working Paper, 2002-05.

Sturgeon, Timothy J., Frank Levy, Clair Brown, J. Bradford Jensen, and David Weil. 2006. "Why We Can't Measure the Economic Effects of Services Offshoring: The Data Gaps and How to Fill Them." Services Offshoring Working Group Final Report. Cambridge, MA: Massachusetts Institute of Technology, Industrial Performance Center. http://web.mit.edu/ipc/publications/pdf/IPC_Offshoring_Report.pdf.

Surdna Foundation. 2010. "Revitalizing America's Manufacturing Sector." http://www.surdna.org/what-we-fund/sustainable-environments/sustainable-environments-whats-new/203-revitalizing-americas-manufacturing-sector-summary-of-surdna-roundtable.html.

Syverson, Chad. 2010. "What Determines Productivity?" NBER Working Paper, No. 15712.

U.S. Department of Labor, Bureau of Labor Statistics. 1997. "International Price Indexes." BLS Handbook of Methods, 154-159. Washington, D.C.: U.S. Government Printing Office.

U.S. Department of Labor, Bureau of Labor Statistics, 2008. "Producer Prices." BLS Handbook of Methods, 1-12. Washington, D.C.: U.S. Government Printing Office.

U.S. Department of Labor, Bureau of Labor Statistics, 2009. "International Comparisons of Manufacturing Productivity and Unit Labor Cost Trends, 2008." News Release. http://www.bls.gov/news.release/pdf/prod4.pdf

Wasshausen, David B., and Brent R. Moulton. 2006. "The Role of Hedonic Methods in Measuring Real GDP in the United States. Prepared for the 31st Committee on Statistical Information in the Economic and Social Sphere (CEIES Seminar) Are We Measuring Productivity Correctly?

Yeats, A.J. 2001. "Just How Big Is Global Production Sharing?" in: Arndt, S. and H.Kierzkowski (Eds.), Fragmentation: New Production Patterns in theWorld Economy. Oxford University Press, Oxford, pp. 108-43.

Yuskavage, Robert E., Erich H. Strassner, and Gabriel W. Medeiros. 2008. "Outsourcing and Imported Services in BEA's Industry Accounts." In International Flows of Invisibles: Trade in Services and Intangibles in the Era of Globalization, ed. Marshall Reinsdorf and Matthew Slaughter, 247-288. Chicago: University of Chicago Press.

Appendix 1.  Comparability of Baseline MFP Results with Published Values

This section provides a comparison of our baseline MFP results to the manufacturing productivity estimates published by BLS.⁸⁹ Appendix table 2 and appendix figure 1 display our estimates of MFP growth for manufacturing along with the contributions to growth of the various factor inputs (i.e. capital, labor, materials, energy, and services). The columns in appendix table 2 present average annual growth rates for the entire 1997-2007 period, as well as several different sub-periods, while the first three rows of the table present, respectively, the MFP measure used in this paper, the BLS MFP measure, and the difference between the two measures.

According to BLS, manufacturing MFP growth averaged 2.2 percent per year for the 1997 to 2007 period, while our measure of MFP expanded at more moderate, 1.3 percent pace. As described below, roughly one-third of the 0.9 percentage point discrepancy between the two MFP measures appears to be driven by different vintages of source data. Methodological differences, both with respect to the measurement of output and the measurement of factor inputs, appear to explain most of the remaining discrepancy.

As discussed in Section 3, BLS estimates manufacturing MFP annually using the concept of sectoral output, which is defined as sales to final users plus deliveries to other industries outside the manufacturing sector.⁹⁰ The BLS measure of intermediate inputs also differs from our measure in that it excludes intermediates inputs sourced from within the manufacturing sector. In other words, while an imported auto part would be included in the both our measure of intermediate inputs and the BLS measure, the BLS measure would not include an identical, domestically-sourced part. However, it is important to note that although these methodological differences should result in substantial level differences in output and intermediate inputs, because BLS uses fixed adjustment factors to convert gross output to sectoral output and to net out intra-sector intermediates, the growth of our series and the BLS should, in principle, be approximately equal.⁹¹

Line 4 in appendix table 2 shows the difference between the two output measures. For the entire period, BLS output grew 0.37 percentage point faster per year, on average, than our output measure. As can be seen in the upper panels of appendix figure 1, most of this discrepancy is due to the substantial difference in output growth in 2007. As of this writing, BEA has yet to fold the 2007 Census of Manufactures (CM) into the annual industry accounts data which we use for our analysis. In contrast, BLS have incorporated the 2007 CM data into their output measures, although given the Census Bureau has not fully released all the accompanying detail for the 2007 CM, this may lead to future revisions in the BLS measure.

If we exclude 2007 from our comparison, the difference between the two output measures becomes much smaller as we would expect, and stands at just 0.1 percentage point. This in turn leads to smaller gap between the BLS MFP measure and our own measure, which shrinks from 0.9 percentage point to 0.6 percentage point.

Excluding 2007, most of the difference in average MFP growth therefore appears to be driven by differences in input measurement. Line 5 and lines 5a through 5e present the differences between the contributions of the various factor input measures (i.e. the growth rates weighted by their cost shares). For 1997 to 2006, the total factor input differential is 0.57 percentage point (line 5). Among the various factor inputs, the labor and materials contributions differ consistently across sub-periods and combine to explain most of total input difference.⁹²

In terms of the labor contribution, although we attempt to control for changes in labor quality, the BLS do not, a fact which likely explains entire difference shown in line 5a.⁹³ As can be seen in appendix figure 1, although both series exhibit a very similar contour, our labor contribution measure falls less than the BLS measure during the 2000-2001 recession, consistent with the observation that labor quality tends to move counter-cyclically.

For the materials contribution, the 0.35 stronger growth we observe for our measure in line 5e likely owes to differences in the weight used to compute the contribution of materials to output growth. Because the level of our materials measure exceeds the level of the BLS materials measure (again, the growth rates should be roughly equivalent), the resulting cost share for materials should also be greater. That said, as can be seen in appendix figure 1, the general contour of our purchased materials contribution is very similar to the BLS one between 1997 and 2007.

Line 6 presents the remaining difference between the two MFP measures after accounting for differences in output and input measurement. This residual is quite small, averaging roughly 0.1 percentage point in each of the sub-periods. As a final robustness check, we also calculated MFP estimates based on a sectoral output concept (i.e. excluding intra-sector shipments from our output and intermediate inputs measures). As shown in line 7, if we ignore the data vintage issue for 2007, the resulting MFP estimate is also quite close to the BLS measure, with the average annual growth differing by less than 0.1 percentage point during 1997 and 2006.

Appendix 2: Implementation of the Diewert-Nakamura (2009) Offshoring Correction and Derivation of Physical Share Terms

Diewert and Nakumra (2009) develop a three-sector, two-period model to demonstrate the bias imparted to an input price index from outsourcing (see pp. 15-18 of their work). They define the "true" index for period 1 as the ratio of the correct (unit) price in period 1 to the price in period 0 in the case where a domestic producer (sector 3) has switched all or part of its sourcing of inputs from a high-cost supplier (sector 1) to a low-cost supplier (sector 2):

(A1) $P_{T}^{\eqref{GrindEQ__3_}} =u_{3}^{1} /p_{13}^{0}$

Diewert and Nakamura show (pp. 18) that the true period 1 price index can be restated as follows:

(A2) $P_{T}^{\eqref{GrindEQ__3_}} =(1+i)-(1+i)dS_{23}^{1} ;$

where d and $S_{23}^{1}$are price discount for the low-cost supplier (relative to sector 1) and the gain in market share (previously zero), and i+i is the underlying rate of inflation for the high-cost supplier (sector 1):

(A3) $1+i=p_{13}^{1} /p_{13}^{o} =P_{I}^{\eqref{GrindEQ__3_}}$

The rate of inflation faced by sector 3 is assumed equal to the underlying rate of inflation in the high-cost producer (which is assumed equal to the rate of inflation for the low-cost producer), or the ratio of the high cost supplier's prices in period 1 and period 0.

Substituting, the correct price in period 1, $u_{3}^{1}$, may therefore be expressed as:

(A3') $u_{3}^{1} =[(1+i)-(1+i)dS_{23}^{1} ]p_{13}^{0}$$$

We modified the above expression to account for the base period indexes and multiple time periods in our data. Importantly, the rate of inflation for the high cost producer between any two periods is defined as the ratio of the unadjusted (biased) index, I, in period t to the index in period t-1: $I_{t}^{} /I_{t-1} =(1+i)_{t}$. In the absence of any outsourcing/offshoring bias, one can express the index in period t, It, as the product of last period's index and the rate of inflation (1+i):$_{}^{}$

(A4) $I_{t}^{} =(1+i)I_{\begin{array}{l} {t-1} \\ {} \end{array}}$

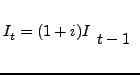
Applying the same logic as in equation A3', one can therefore approximate the "true" input price index, IT, as:

(A5) $I_{T,t}^{} =[(1+i)_{t} -(1+i)_{t} d(s_{t} -s_{t-1} )]I_{T,t-1}^{}$

Finally, we adapt equation A5 to our three-country classification framework as follows:

(A6) $$\begin{array}{l} {I_{T,t}^{} =[(1+pctchng)_{t} -(1+pctchng)_{t} (1-ppreli\_ d)(share\_ qd_{t} -share\_ qd_{t-1} )-} \\ {(1+pctchng)_{t} (1-ppreli\_ i)(share\_ qi_{t} -share\_ qi_{t-1} )]I_{T,t-1}^{} } \end{array}$$

Where ppreli_d and ppreli_i are the price relatives for developing and intermediate countries respectively (relative to advanced countries), share_qd and share_qi are the shares of developing and intermediate imports in total domestic consumption, and 1+pctchng is the rate of inflation for the high cost (i.e. domestic) intermediate producer. The price relative for advanced countries is assumed equal to one, i.e. we assume there is no discount associated shifts in sourcing from a domestic supplier to a supplier from an advanced country.

Consider the following numerical example: Suppose the rate of inflation is 2 percent, so 1+i = 1.02. Developing countries gain market share (quantity terms) of 1 percent (.01) and the discount is 50 percent (.5). For simplicity, assume also that the intermediate countries' share is constant. Then the true rate of inflation is 1.02 - 0.0051= 1.0149. Last period's corrected index would be multiplied by 1.0149 to generate this period's corrected index.

Finally, although the share terms in the Diewert and Nakamura (2009) correction are explicitly defined as quantity (or physical) shares, we lack specific information on these variables. However, these quantity shares can in fact be expressed as a function of their corresponding expenditure shares and price discounts, variables for which data are available. Define the price relative for developing countries as $dd=\frac{Pd}{Pa}$, and the price relative for intermediate countries as $di=\frac{Pi}{Pa}$. These are just the ppreli_d and ppreli_i terms in equation (A6). Rearranging terms, we have $\frac{Pa}{Pd} =\frac{1}{dd}$and $\frac{Pa}{Pi} =\frac{1}{di}$.

Omitting time subscripts, expenditure shares for advanced, developing, and intermediate countries (sea, sed, sei) at any point in time are:

$$sea=\frac{PaQa}{PaQa+PdQd+PiQi}$$

$$sei=\frac{PiQi}{PaQa+PdQd+PiQi}$$

$$sed=\frac{PdQd}{PaQa+PdQd+PiQi}$$

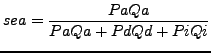
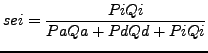
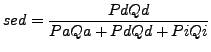
It is straightforward to show that the quantity shares may then be expressed as functions of dd, di, sea, sei, and sed:

$$sa=\frac{Qa}{Qa+Qd+Qi} =\frac{sea}{sea+sed\left({\raise0.7ex\hbox{$ 1 $}\!\mathord{\left/ {\vphantom {1 dd}} \right. \kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$ dd $}} \right)+sei\left({\raise0.7ex\hbox{$ 1 $}\!\mathord{\left/ {\vphantom {1 di}} \right. \kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$ di $}} \right)}$$

$$sd=\frac{Qd}{Qa+Qd+Qi} =\left[\frac{1}{dd} \right]\frac{sed}{sea+sed\left({\raise0.7ex\hbox{$ 1 $}\!\mathord{\left/ {\vphantom {1 dd}} \right. \kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$ dd $}} \right)+sei\left({\raise0.7ex\hbox{$ 1 $}\!\mathord{\left/ {\vphantom {1 di}} \right. \kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$ di $}} \right)}$$

$$si=\frac{Qi}{Qa+Qd+Qi} =\left[\frac{1}{di} \right]\frac{sei}{sea+sed\left({\raise0.7ex\hbox{$ 1 $}\!\mathord{\left/ {\vphantom {1 dd}} \right. \kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$ dd $}} \right)+sei\left({\raise0.7ex\hbox{$ 1 $}\!\mathord{\left/ {\vphantom {1 di}} \right. \kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$ di $}} \right)}$$

This is the approach we follow when estimating equation A6 in the paper.

Footnotes

**  This research was supported with funding from the Bureau of Economic Analysis and the Alfred P. Sloan Foundation and was conducted with restricted access to Bureau of Labor Statistics (BLS) import price data as well as unpublished detail on imported materials provided to us by the Bureau of Economic Analysis (BEA). The analysis and conclusions set forth are those of the authors and do not indicate concurrence by other members of the research staff of the Board of Governors, the BLS, or the BEA. We thank Jonathan Collins and Lillian Vesic-Petrovic for research assistance and the participants of the NBER-CRIW 2010 Summer Institute, the conference on Measurement Issues Arising from the Growth of Globalization, Washington, DC, November 2009 for comments and suggestions. We are especially grateful to Bill Alterman, Erwin Diewert, Nicole Mayerhauser, Emi Nakamura, Alice Nakamura, Marshall Reinsdorf, Erich Strassner, Steve Rosenthal, and Rozi Ulics for their invaluable feedback and assistance on this project. Return to text

+  Upjohn Institute Return to text

***  Federal Reserve Board Return to text

1.   Expressed as a percent of GDP, imports rose by roughly 5 percentage points from 12½ percent of GDP in 1997 to 17½ percent in 2008, while exports as a share of GDP increased only marginally. In 2007, China became the largest exporter of goods to the United States, surpassing Canada. Return to text

2.   See, for example, Executive Office of the President (2009), Pisano and Shih (2009), New America Foundation (2010), Helper (2008), Pollin and Baker (2010), and the Surdna Foundation (2010). Return to text

3.   With the Bureau of Economic Analysis's May 2010 comprehensive revision to the Annual Industry Accounts, manufacturing output now expands at a slightly faster rate during this period. The analysis throughout this paper is based upon the previous vintage of these data published in 2009. Return to text

4.   Michael Mandel makes note of this phenomenon in his June 3rd, 2009 Business Week article, "Growth: Why the Stats are Misleading." Return to text

5.   See Diewert (1998), Hausman (2003), and Reinsdorf (1993) on biases to the CPI arising from outlet substitution bias and Houseman (2008) and Diewert and Nakamura (2009) on the relationship between outlet substitution bias and biases to input price indexes arising from shifts in the sourcing of inputs.  Return to text

6.   See "In Recession, placecountry-regionChina Solidifies its Lead in Global Trade," The New York Times, October 14, 2009. Return to text

7.   Similarly, see Kurz and Lengermann (2008) and Yuskavage, Strassner, and Medeiros (2008) for empirical evidence on the increased foreign sourcing of intermediate inputs. Hummels, Ishii, and Yi (2001), Feenstra (1998), Yeats (2001), and Campa and Goldberg (1997) also discuss the issue. Return to text

8.   In addition to cost savings, risk sharing and specialization are also factors that play a role in a firm's decision to outsource or offshore. See Abraham and Taylor (1996). Return to text

9.   Bils (2009) finds evidence in the CPI that two-thirds of the price increases for new-model substitution can be attributed to quality upgrading. The objective of our structural approach is to adjust for possible level differences in quality across countries. Return to text

10.   Reinsdorf and Yuskavage (2009) reach a similar conclusion. Moreover, results from Feenstra (1994) and Broda and Weinstein (2006) indicate the demand between imported varieties tends to be elastic. Return to text

11.   The dynamics contained in Figure 1--where import prices rise faster that domestic prices--could also reflect a lagged response to a lower level of import prices owing to adjustment costs, transaction costs, or supply shocks.  Return to text

12.   The extraordinary growth in the computer industry, in turn, largely reflects rapidly dropping prices, which for several component industries have been adjusted using hedonic methods to account for rapid technological improvements to products. Return to text

13.   That said, the late 19th century witnessed a level of global integration that in some ways remains unsurpassed. See O'Rourke and Williamson (1999). Return to text

14.   In terms of services trade, in 2008, BEA data on the trade in services indicates that 59 percent was travel, transport, royalties, and education-related, while the remaining 41 percent was business services. Return to text

15.   See Hummels, Ishii, and Yi (2001) for the seminal work that measures the increase vertical integration using input-output tables from the OECD and emerging market countries. The authors estimate that vertical specialization accounts for up to 30 percent of world exports, and has grown as much as 40 percent in the last twenty-five years. Return to text

16.   We classify countries with less than 20 percent of U.S. per capita GDP as developing, and, with a few exceptions, countries with per capita GDP equal to or exceeding two-thirds that of that in the United States as advanced. The remaining countries are classified as intermediate. We classify the Middle East oil-producing countries as intermediate, although per capita GDP exceeds two-thirds of U.S. per capita GDP on account of their oil revenues. In addition, we classify Singapore, Hong Kong and Brunei as intermediate although in recent years their per capita GDP has been at or somewhat higher than our cut-off level. Below we report evidence of large differences in observed price levels of imports from these countries and those from advanced countries within detailed product categories, which provide a justification for classifying these borderline countries as intermediate. A comprehensive list of countries by category is provided in Appendix Table 1. Return to text

17.   The data in Table 1 portray the number of plants in a particular size class at two points in time and represent net changes: plant openings, plant closures, and changes in plant size that result in a particular plant being reclassified into a different size category.  Return to text

18.   Although the average growth of manufacturing has been fairly close to that of the economy as a whole, the sector has typically exhibited greater cyclical swings. As a result, the sector tends to make outsized contributions to changes in GDP growth during economic turning points (Corrado and Mattey, 1997). In addition, the relatively faster gains in manufacturing productivity have resulted in lower relative goods prices which, in combination with inelastic demand for goods (on average), has led to a decline in manufacturing's share of nominal output. Return to text

19.   See "International Comparisons of Manufacturing Productivity and Unit Labor Cost Trends," BLS (2009). Return to text

20.   This perspective is illustrated by Executive Office of the President (2009), which emphasizes the strength of output and productivity growth of U.S. manufacturers vis-à-vis the aggregate economy and manufacturers in other industrialized countries and which largely attributes the employment declines to productivity growth. Recent articles in the popular press also have advanced this view (e.g. Sara Murray, 2009. "U.S. Manufacturing Productivity Jumps." Wall Street Journal, October 23, pp A2 and "Industrial Metamorphosis" The Economist, September 29, 2005).  Return to text

21.   Gross output is defined as sales or receipts and other operating income, commodity taxes, and inventory change; intermediate inputs is defined as energy, raw materials, semi-finished goods, and purchased services. Return to text

22.   Materials inputs consist of agricultural, mining, manufactured, wholesale trade, and transportation. In 2007, 63 percent of all materials inputs used by the manufacturing sector consisted of manufactured materials. The KLEMS intermediate use estimates are published for 1998-2007. We impute the 1997 estimates for the decomposition of intermediate inputs. Return to text

23.   Information technology is defined as computers, communications equipment, and software. The tabulated results do not include the decomposition of capital between IT and other capital as the focus of this paper is on the contribution from foreign intermediates.  Return to text

24.   See Appendix B of Corrado, et al. (2006) for more details. Pre-1998 unpublished data on hours worked at the detailed SIC level are controlled to be consistent with recent NIPA releases and concorded to a NAICS basis. The levels of the BEA/BLS NAICS employment series are then adjusted in all years to conform to the industry composition in the Census Bureau's County Business Patterns data. Next, hours worked at the industry level are derived which embody the adjusted employment levels but preserve the implied workweek in published series. Finally, all adjusted data are controlled so that they sum to the published BEA/BLS estimates for employment and hours worked in total private industries. Return to text

25.   We extend our gratitude to Erich Strassner, George Smith, Sue Okubo, and others at BEA for providing us with the confidential microdata on imported intermediates. The 1997 and 2002 imported intermediate values (import matrices) are publically available.  Return to text

26.   The imported values we employ are I-O based, or after redefinitions. Redefinitions occur when secondary products have an input structure that differs substantially from the primary product input structure. The BEA "redefines" by moving secondary products from the industry in which it is produced to the industry in which it is primary. Redefinitions allow the resulting input-output tables to conform to the "commodity-technology assumption," consistent with a homogeneous input-output structure. In addition, outside of benchmark years, the detailed import values are derived from annual industry accounts, which rely on the "constant industry technology" assumption, or that the real use of total intermediates relative to an industry's gross output has not changed from the prior year. Return to text

27.   Domestic supply represents the total amount of a commodity available for consumption, i.e., domestic output plus imports less exports. Using this assumption to calculate the industry-level estimates implies that all variability of import usage across industries reflects the assumption and is not based on industry-specific information. Return to text

28.   The import comparability assumption is described further in Yuskavage, et al (2008) and critiqued in Feenstra and Jensen (2009). Return to text

29.   It is important to note that not all commodities are imported. Return to text

30.   See Jorgenson, Gollop, and Fraumeni (1987) and Hulten (2009) for more on growth accounting methodology, its early development, and current applications. Return to text

31.   Sectoral output is defined as the gross output of an industry or sector less the amount produced and consumed within that industry or sector. While the sectoral output approach is useful for measuring the contribution of foreign intermediates to overall growth, in this framework the contribution from imported intermediates and other intermediates are not comparable, as domestic intermediates only contain inputs purchased from outside of the sector (see Domar, 1961 and Hulten, 1978). Similarly, Jorgenson et al. (2005) favor a gross-output approach over a value-added one so that the contribution of intermediate inputs to output growth may be identified. Return to text

32.   The definitions and notation presented here are similar to those presented in Corrado, et al. (2007). Return to text

33.   We do not decompose purchased services into domestic and foreign components. Services imports as a share of total imports remained constant over the time period 1997 to 2007. Return to text

34.   This adjustment is necessary because the compensation measure in the GDP-by-industry accounts only includes employees whereas our hours measure includes both employees and self-employed workers. Return to text

35.   Chain stripping (or chain disaggregation) involves solving for the index residual (i.e. the price index for domestic materials) when an aggregate exists (the price index of total purchased materials), and one "child" exists (the price index for imported materials). Return to text

36.   The presentation of the baseline results closely follows previous work by Kurz and Lengermann (2008). Return to text

37.   As noted, the growth accounting results in Table 2 reflect the authors' calculations and rely on a differentmethodology than what is used by BLS. However, many of the salient features of the data are also observed in the BLS estimates. See Appendix 1 for a comparison and reconciliation of our baseline results with those published by BLS.  Return to text

38.   i.e., NAICS 334 which includes the production of computers, semiconductors, and communications equipment. Return to text

39.   The growth of imported intermediate inputs, to some degree, will also reflect the direct substitution of imported goods for domestic labor and capital. To see this, consider the case in which a firm previously produced an intermediate input and final product internally, but now sources that input from a foreign supplier. In this instance, gross output will not change, but imported materials inputs will rise and the labor and capital previously used to produce the input will fall. Return to text

40.   Similar findings have been reported in other studies. See, for example, Oliner and Sichel (2000) and Jorgenson, Ho and Stiroh (2008). See also Oliner, Stiroh, and Sichel (2007) and Syverson (2010) for in-depth reviews of recent research on U.S. productivity growth.  Return to text

41.   Throughout the decade, the computer industry's share of manufacturing value added remained relatively constant at around 10 percent. In spite of the rapid value added and MFP growth in this sector, the trade deficit within this product group greatly widened during the decade and substantial offshoring of components of the industry occurred (Brown and Linden 2005, Linden, Dedrick and Kraemer 2009). Return to text

42.   BLS uses hedonic methods to adjust prices in the computer industry. For a review of these, see Wasshausen and Moulton (2006). Return to text

43.   This could also occur if a firm imports an intermediate input it previously produced internally. In this case, output will not change but the labor input used to produce that intermediate input will fall. Return to text

44.   See Cavallo and Landry (2010) for a discussion of imported capital goods, and Yuskavage, Strassner, and Maderios (2008) and Eldridge and Harper (2009) for estimates of services offshoring. Return to text

45.   For more information on the BLS price index computations see Chapters 14 and 15 in the BLS Handbook of Methods (2009). Return to text

46.   For imports, the preferred price basis for the BLS is f.o.b., or the price "free on board" at the foreign port of exportation. Return to text

47.   More precisely, the unit of observation is the ratio of a relative item price in a given period (relative to the item's price in a base year) to the item's relative price in the previous month. Return to text

48.   The weights for the upper-level indexes have changed annually since 2001. Prior to the annual updating, the weights changed infrequently. For instance the 1997 index used 1995 weights, and the 1993-1996 indexes used 1990 weights. Return to text

49.   By definition, an industry's value added equals its gross output minus its consumption of intermediates. The chain-type quantity index for an industry's value added is prepared by deflating the current-dollar commodity measures of gross output and intermediate inputs with the corresponding commodity price indexes and combining the resulting commodity quantity indexes of gross output and intermediate inputs by industry in a Fisher index-number formula Return to text

50.   See, for example, Diewert (1998) and Hausman (2003) for expositions of the categories of price measurement problems in the CPI.  Return to text

51.   Hausman (2003) points out that the biases from new goods or varieties and from new suppliers or outlets are first order effects, while substitution bias arising from the incorrect weighting of price observations is a second order effect.  Return to text

52.   These studies, include Alterman (2009), Diewert and Nakamura (2009), Reinsdorf and Yuskavage (2009), Byrne, Kovak, and Michaels (2010), and Klier and Rubenstein (2009). Return to text

53.   Because of the rapid entry and market share expansion of low-cost suppliers from developing countries in recent years, the empirical focus of this paper is on price biases arising from offshoring. However, it should be noted that the producer price index and the input price index also would be biased with the entry of a new, low-cost domestic suppliers of intermediate inputs. The relevant price change is the discount the new supplier offers, which will not be measured even when the new entrant is introduced into PPI sample because the index is constructed from observations on period-to-period changes in the sales price received by individual suppliers. Return to text

54.   A complete derivation of equation 2 can be found in the Appendix 2. Return to text

55.   See Aizcorbe, Corrado, and Doms (2003) for an exposition of this argument.  Return to text

56.   Similarly, Besedes and Prusa (2006) analyze publicly available import data at the product level and show that the median spell of imports lasts only about 1 year, while 70 percent of import trade spells last roughly 2 years.  Return to text

57.   Although we have focused on the substitution of low cost foreign for domestic inputs because of the recent empirical importance of offshoring, the entrance and market share expansion of low-cost domestic suppliers is an important aspect of firm dynamics in the United States and also would impart biases to price indexes. See Foster, Haltiwager, and Syverson (2008) for evidence that entrants, on average, have higher physical productivity and offer lower prices than incumbent firms. Return to text

58.   Manufactured commodities are defined as 6-digit NAICS codes. Return to text

59.   Since the international and domestic data are merged at a slightly higher level of aggregation, here commodities are defined as 4-digit NAICS codes. Return to text

60.   The narrowly defined groups in this instance are Harmonized System 10-digit codes, which we assume contain varieties that are substitutable. This classification is widely viewed as the most similar, observable categorization among traded products. As mentioned above, existing estimates of elasticity of substitution among varieties within HS10 groups are typically found to be elastic. Return to text

61.   The IPP has its own internal classification scheme called classification groups, which are slightly more aggregate than the HS10 codes. The purpose of those groups is to combine related categories where sampling is relatively sparse to form an appropriate mass of imports. In the majority of cases classification groups map uniquely to HS10 codes, and in the majority of the remainder to only two HS10 codes, and so we use HS10 to describe both types of category. Return to text

62.   Other item fields include shipping information, price collection details as well as flags for transfer prices and missing value imputations. In certain instances where comparability is feasible, instead of starting a new series for a new item, IPP staff will replace an item and make an adjustment to the price. These types of adjustment account for about 1 percent of the price observations and are treated as real prices.  Return to text

63.   Missing price relatives are set equal to 1, implying an import price discount of zero.  Return to text

64.   The assumption of fixed weights across time does not significantly alter our qualitative or quantitative results below. Return to text

65.   These items could either be newly consumed varieties or simply newly sampled items in the IPP survey.  Return to text

66.   Table 4 also contains information on the number of country source switches per income level pair. Notably, there is a lot of within group switching (e.g. developing to developing, advanced to advanced, etc.), accounting for 42 percent of all switches. The other 58 percent have more high to low income switches than the other way around, with the ratio of observations in the upper triangle of the cross tab (i.e., high to low switches) to the lower triangle (i.e., low to high switches) equal to 1.24. That is, there are 24 percent more high to low income switches. That ratio is more pronounced in the second half of the sample with 32 percent more high to low switches than low to high. Return to text

67.   Since the cell sizes for the country switches are small, we compute the median discount for each country and NAICS product group. Return to text

68.   In order to use this richer measure of product-level firm size which is only available for the U.S., it is assumed that the curvature of the firm size distribution is the same in the rest of the world. If the underlying size distribution is the same function from the power law family of distributions, this assumption is satisfied even if productivity and size levels are very different across countries. Moreover, this measure of firm size is exogenous to the price distribution of U.S. imports. Return to text

69.   See Mandel (2010) for descriptive statistics on the classification scheme and for additional detail on the estimation technique. For other variations on this identification strategy, see: Hallak and Schott (2008), Khandelwal (2009) and Baldwin and Ito (2009). The resulting product classification scheme covers approximately 1,100 HS6 codes for U.S. imports. Return to text

70.   Recent empirical studies suggest that this covariance may be negative due to the positive links between exporter income and export prices (see, for instance, Schott (2004) or Hummels and Klenow (2005)); the implication is that richer, more productive countries export higher quality items, but with lower marginal costs per unit of quality. On the other hand, theoretical frameworks in which markups vary across producers suggest that this covariance may be positive. Under general specifications of industry demand such as the translog expenditure function, higher productivity exporters obtain a higher market share, and hence charge a higher markup over marginal cost. The partial effect of markups would be to increase quality-adjusted prices of the higher productivity, higher quality exporters, offsetting at least in part the marginal cost effect. Return to text

71.   Since quality variance measures are only available at the HS 6-digit level of aggregation, we estimate robust standard errors clustering HS10-country groups within HS6 categories. Return to text

72.   In the left panel, for all exporters the relationship is significant and positive, and particularly strong for the quadratic term; the variance of prices increases at an increasing rate with the variance of quality. Given that the relative prices are in reference to the advanced set by construction, product variance is better described by the relative prices of only the developing and advanced countries. The right panel shows results for that specification and, indeed, the estimates are larger for both the linear and quadratic terms. Return to text

73.   Though we find the quality-adjusted discount to remain negative in most cases, the discount could be positive (i.e., a premium) for several reasons. On the one hand, for an identical good we would expect to find that developing and intermediate countries have higher prices relative to advanced countries in industries where advanced countries have a productivity advantage. Moreover, the premia may be partly attributable to the way IPP collects its prices; IPP aims to collect prices 'at the dock' and net of tariffs. Therefore, if tariffs have been going down for developing countries (note that China's accession to the WTO as well as the expiry of the MFA are contained in the sample period), we might not observe a change in their IPP price even if imports increase. Return to text

74.   See "Exporting Work: Outsourcing That Once Sent Low-Skill Jobs to Mexico Is Now Sending Some of San Diego's High-Skilled, High-Wage Jobs to India, China and Elsewhere." San Diego Tribune, April 4, 2004. Return to text

75.   Thus, we are again assuming here that the price discounts for products from developing and intermediate countries relative to their U.S. counterparts are the same as for advanced foreign economies. Return to text

76.   While this is slightly more aggregate than the BEA product codes described in Section 3, which are NAICS 6-digit classification codes, the concordance between the Harmonized System categories used by the BLS at the micro-level and NAICS was greatly simplified by aggregating slightly. Moreover, given the sampling frame of the IPP, certain products have relatively sparse data giving rise to noisy estimates of the import discount. Aggregating to the NAICS 4-digit level also serves to smooth through the product-level volatility in the discount estimates. Return to text

77.   Cumulative input cost inflation is computed as the percent change between the index values in 2007 and 1997. Commodity level inflation is computed in similar fashion at the NAICS 3-digit level. Included in the overall manufacturing number but excluded from the chart are the following commodities: petroleum products, computer and electronic components. Petroleum products had cumulative input cost inflation of 137 percent and bias-corrected inflation of 134 percent. Computer and peripherals had input costs decline by 35 percent, 51 percent adjusted. Return to text

78.   These tables show the use of four digit commodities by each of the 65 industries in the GDP-by-Industry accounts, with commodities categorized as energy, materials, or services. These data are available for download at http://www.bea.gov/industry/xls/KLEMS_intermediate_use_1998_2007.xls.  Return to text

79.   Manufactured materials comprise roughly 60 percent of total materials and exclude farming, mining, wholesale and retail trade, and transportation. In durable manufacturing industries, the manufactured materials share of total purchased materials is approximately 80 percent, while in nondurable industries it is approximately 50 percent. The share for nondurable manufacturing industries is held down primarily because of two industries: food products manufacturers are heavy users of agricultural commodities, while petroleum and chemicals industries consume large quantities of mining materials.  Return to text

80.   We therefore likely continue to overstate MFP in industries where the offshoring of non-manufactured material inputs has been pervasive. Return to text

81.   Indeed, the estimates in column (3)--where we only reset import prices for commodities in this category--are virtually identical to those in column (2). Resetting import prices for all commodities except high-tech yields MFP estimates that are very close to the baseline estimates in column 1.  Return to text

82.   Because of the high import penetration in semiconductors and other high-tech products, consistently adjusting domestic and import prices for product improvements is important for the accuracy of industry and national income statistics, though difficult owing to lack of product detail, particularly for imports. Addressing this problem has resulted in substantial revisions to the national accounts statistics in the past (Grimm, 1998). Return to text

83.   As discussed above, when constructing their published, industry-level materials deflators the BEA uses IPP prices to deflate imported commodities, along with domestic deflators (largely PPIs) to deflate domestic commodities. Return to text

84.   In addition, the correction was applied to IPP prices at the NAICS 6-digit product (commodity) level rather than at the 4-digit level that was used for our input price adjustment. Return to text

85.   As discussed in Section 6.2, in practice we were only able to adjust our baseline measure of manufactured material inputs. Our baseline estimate of non-manufactured materials was held fixed in all of the value added simulations along with the published values for gross output, energy, and services. Return to text

86.   This was not the case for our baseline estimates of MFP. As discussed in section 3, our approach to estimating productivity differs somewhat from that of the BLS. Return to text

87.   Reinsdorf and Yuskavage (2009) examine pricing in selected consumer goods and provide preliminary evidence of biases to GDP from import growth. Biases to price indexes from offshoring and their implied biases to GDP growth also have been covered in the business press. (See Michael Mandel, "The Real Costs of Offshoring," Business Week, June 18, 2007, and Michael Mandel, "Growth: Why the Stats Are Misleading," Business Week, June 3, 2009.) Return to text

88.   On the other hand, real value added--by definition--would not be affected by the mismeasurement of the imported price of capital equipment. Return to text

89.   See, for instance, the February 2010 BLS News Release "Multifactor Trends in Manufacturing."  Return to text

90.   For more information on the BLS methodology see Chapters 10 and 11 in the BLS Handbook of Methods (2009). Return to text

91.   We thank Steve Rosenthal at BLS for pointing this out. Return to text

92.   Over the full 1997-2006 period, our capital contribution is about 0.1 percentage point smaller than the BLS one. Although we adopt a very similar approach to the BLS for estimating capital services, BLS include land in their measure, along with equipment, structures, and inventories, while we do not. The differences for energy and services are trivial.  Return to text

93.   Indeed, our unadjusted hours growth measure, which is not shown in appendix table 2, is identical to the BLS one. Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

Home | Economic research and data | Publications and education resources
Accessibility | Contact us
Last update: October 18, 2010