The Federal Reserve Board eagle logo links to home page

Oil Shocks and the Zero Bound on Nominal Interest Rates**

Martin Bodenstein, Luca Guerrieri***, and Christopher Gust

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

Beginning in 2009, in many advanced economies, policy rates reached their zero lower bound (ZLB). Almost at the same time, oil prices started rising again. We analyze how the ZLB affects the propagation of oil shocks. As these shocks move inflation and output in opposite directions, their effects on economic activity are cushioned when monetary policy is constrained. The burst of inflation from an oil price increase lowers real interest rates at the ZLB and stimulates the interest-sensitive component of GDP, offsetting the usual contractionary effects. In fact, if the increase in oil prices is gradual, the persistent rise in inflation can cause a GDP expansion.

Keywords: Oil Shocks, zero lower bound, DSGE models

JEL classification: F32, F41

1  Introduction

An important, ongoing debate in macroeconomics concerns the influence of oil shocks on aggregate activity. One view is that oil shocks are a principal source of business cycle fluctuations. In this vein, Hamilton (2009) argued that most of the global recession that began in 2008 reflects the preceding run-up in oil prices. In contrast, Blanchard and Galí (2007) attributed a small role to oil shocks as drivers of economic fluctuations in the 1980s and 1990s, and suggested an even smaller role in more recent years.

Within this debate, the systematic response of monetary policy to oil shocks plays a prominent role.1 Bernanke, Gertler, and Watson (1997), for instance, argued that a large part of the effect of increases in oil prices in the 1970s can be attributed to tighter monetary policy in response to these shocks. Beginning in 2009, there has been another important systematic change in monetary policy. Namely, in many advanced economies, policy rates reached their zero lower bound (ZLB) inhibiting their stabilization role. At the same time, the spot price of West Texas Intermediate crude doubled from a trough of a little less than $40 per barrel in February of 2009 to a peak of $80 in July 2010. In light of these events, we address how the zero lower bound constraint on policy rates affects the transmission of oil shocks on the macroeconomy.

In our analysis, we extend the two-country DSGE model in Bodenstein, Erceg, and Guerrieri (2010) with price and wage rigidities and by introducing a monetary policy rule that explicitly recognizes the ZLB constraint on nominal interest rates. A key finding of our analysis is that oil price shocks propagate differently when policy rates in the oil importing country are at the zero lower bound. In particular, we show that the zero lower bound constraint tends to diminish rather than amplify the fall in GDP that occurs in response to higher oil prices in normal times when monetary policy is unconstrained by the zero lower bound.

To understand this result, consider the effects of a shock that raises the demand for oil by foreigners, pushing up the price of oil in the home, oil-importing country. When monetary policy is unconstrained, this shock tends to push up inflation and reduce output in the home country. When policy rates are at the zero lower bound, the higher inflation induced by the shock can lead to lower real rates, stimulating the interest-sensitive sectors of the economy, and offsetting the usual contractionary effects of the shock. In fact, if the increase in oil prices occurs gradually, it can induce a persistent rise in inflation that might even cause GDP to expand temporarily.

To put these results in context, it is useful to contrast them with recent work on the zero lower bound that has emphasized that the effects of demand shocks, such as government spending shocks, are amplified at the zero lower bound. The amplification of these shocks reflects that they tend to move output and inflation in the same direction. For instance, a rise in government spending induces increased resource utilization and higher inflation. In normal times, monetary policy offsets the stimulative effects of the shock by raising interest rates. However, if the ZLB has been reached because the economy is mired in a deep recession, policy rates remain unvaried and the higher inflation induces a fall in real rates. These lower real rates in turn crowd in investment, amplifying the effects of the government spending shock.2 In contrast, the ZLB constraint on policy rates tends to cushion the effects of oil shocks on activity, since these shocks move output and inflation in opposite directions.

We consider sensitivity of our results along several dimensions, including the specification of monetary policy, the economy's interest rate sensitivity, the degree of exchange-rate pass-through, and the inclusion of financial frictions. We show that the interest rate reaction function plays an important role in cushioning the effects of oil shocks. In the benchmark simulation, we use an interest rate rule that responds to inflation and the output gap and give a prominent role to interest rate smoothing through the inclusion of the lagged policy rate. Relative to this benchmark rule, we show that a rule with no interest-rate smoothing term further cushions the effects at the zero lower bound.

The particular inflation measure included in the rule can also affect the extent to which the ZLB cushions the economy from oil shocks. Our benchmark rule responds to current core inflation; however, some central banks appear to have a focus on headline inflation.3 We find that rules responding to a forecast of headline inflation can be less effective in stabilizing inflation in response to oil shocks. As a result, they can lead to larger movements in real rates at the zero lower bound and a greater cushioning of the effects of oil shocks.

In line with recent empirical evidence by Kilian (2009) and Kilian, Rebucci, and Spatafora (2009), we also examine the robustness of our results to alternative shocks that generate fluctuations in oil prices. Apart from the benchmark oil demand shock, we consider the effects of oil price changes that stem from changes in oil supply and aggregate technology shocks. We find that, if oil supply shocks are close to unit-root processes as argued in Bodenstein, Erceg, and Guerrieri (2010), then there is a one-time increase in the price of oil which does not have a protracted effect on inflation. Thus, the real interest rate is little changed at the zero bound and the shock has similar effects at the zero bound and in normal times.

The oil price response implied by a 1% temporary decline in the level of productivity is not large enough to substantially affect the transmission of technology shocks. However, as such shocks increase firms' marginal costs directly and lead to a rise in inflation made persistent by the real rigidities in our model (adjustment costs for investment, consumption habits, and lagged price and wage indexation), their effects are also cushioned at the zero bound relative to normal times.

The rest of this paper proceeds as follows. Section 2 describes the model, while its calibration and solution method are discussed in Section 3. Our results for oil demand shocks are presented in Section 4, while Section 5 discusses the effects of alternative shocks. Finally, Section 6 concludes.


2  Model Description

The model follows closely Bodenstein, Erceg, and Guerrieri (2010) with the addition of nominal rigidities in price and wage setting.4 There are two countries, a home country (calibrated based on U.S. data) and a foreign country (rest-of-the-world). Because the structure of the country blocs is symmetric, we focus on the home country, although our calibration allows for differences in population size, oil intensities, the per capita oil endowments, and nonoil trade flows. In each country a continuum of firms produces differentiated varieties of an intermediate good under monopolistic competition. These firms use capital, labor, and oil as factor inputs. Goods prices are determined by Calvo-Yun staggered contracts. Trade occurs at the level of intermediate goods and within each country the varieties are aggregated into a (nonoil) consumption and an investment goods. Households consume oil, the nonoil consumption good, save and invest, and supply differentiated labor services under monopolistic competition. For ease of presentation, we assume competitive bundlers whose technology mimics the preferences of the households over oil and the nonoil consumption good. While asset markets are complete at the country level, asset markets are incomplete internationally. Finally, both the home and foreign country are endowed with a non-storable supply of oil each period with the home country assumed to be an oil importer.

2.1  Households

A continuum of monopolistically competitive households (indexed on the unit interval) supplies a differentiated labor service to the intermediate goods-producing sector. A representative labor aggregator combines the households' labor hours in the same proportions as firms would choose. This labor index $L_{t}$ has the Dixit-Stiglitz form

\begin{displaymath} L_{t}=\left[ \int_{0}^{1}N_{t}\left( h\right)^{\frac{ 1}{1+\theta _{w}}}dh\right] ^{1+\theta_{w}}, \end{displaymath} (1)

where $\theta _{w}>0$ and $N_{t}(h)$ is hours worked by a typical member of household $h$. The aggregator minimizes the cost of producing a given amount of the aggregate labor index, taking each household's wage rate $W_{t}\left( h\right) $ as given. One unit of the labor index sells at the unit cost $W_{t}$

\begin{displaymath} W_{t}=\left[ \int_{0}^{1}W_{t}{}\left( h\right) ^{\frac{-1}{\theta _{w}}}dh \right] ^{-\theta _{w}}. \end{displaymath} (2)

$W_{t}$ is referred to as the aggregate wage index. The aggregator's demand for the labor services of household $ h$ satisfies

\begin{displaymath} N_{t}\left( h\right) =\left[ \frac{W_{t}\left( h\right) }{W_{t}}\right] ^{- \frac{1+\theta _{w}}{\theta _{w}}}L_{t}. \end{displaymath} (3)

The utility functional of a representative household $h$ is

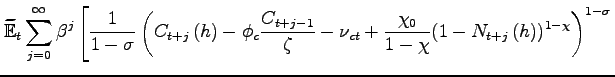$\displaystyle \widetilde{\mathbb{E}}_{t}\sum_{j=0}^{\infty }\beta ^{j}\left[ \frac{1}{ 1-\sigma }\left( C_{t+j}\left( h\right) -\phi_{c} \frac{C_{t+j-1}}{\zeta } -\nu _{ct} + \frac{\chi _{0}}{1-\chi }(1-N_{t+j}\left( h\right) )^{1-\chi }\right) ^{1-\sigma }\right.$  
$\displaystyle \left. +V\left( \frac{MB_{t+j+1}\left( h\right) }{P_{t+j}}\right) \right] ,$ (4)

where the discount factor $\beta $ satisfies$\ 0<\beta <1.$ Our benchmark preference specification follows Greenwood, Hercowitz, and Hoffman (1988) but we also consider additively separable preferences over consumption and leisure. As in Smets and Wouters (2003), we allow for the possibility of external habits. At date $t$ household $h$ cares about consumption relative to lagged per capita consumption, $C_{t-1}$. The preference shock $\nu _{ct}$ follows an exogenous first order process with a persistence parameter of $\rho _{\nu }$. The parameter $\zeta $ controls for population size. The household's period utility function depends on current leisure $1-N_{t}\left( h\right) $, the end-of-period real money balances, $\frac{MB_{t+1}\left( h\right) }{P_{t}}$. The liquidity-service function $V\left( \cdot \right) $ is increasing in real money balances at a decreasing rate up to a satiation level. Beyond the satiation level, utility from liquidity services is constant. With this specification of the utility function, the demand for real money balances is always positive regardless of the level of the nominal interest rate.5

Each member of household $h$ faces a budget constraint in period $t$ which states that the combined expenditure on goods and the net accumulation of financial assets must equal disposable income

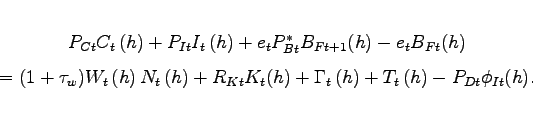\begin{displaymath} \begin{array}{c} P_{Ct}C_{t}\left( h\right) +P_{It}I_{t}\left( h\right) +e_{t}P_{Bt}^{\ast }B_{Ft+1}(h)-e_{t}B_{Ft}(h) \ =(1+\tau_{w})W_{t}\left( h\right) N_{t}\left( h\right) +R_{Kt}K_{t}(h)+\Gamma _{t}\left( h\right) +T_{t}\left( h\right)-P_{Dt}\phi_{It}(h) . \end{array}\end{displaymath} (5)

Final consumption goods are purchased at the price $P_{Ct},$ and final investment goods at the price $P_{It}.$ Investment in physical capital augments the per capita capital stock $K_{t+1}(h)$ according to a linear transition law of the form

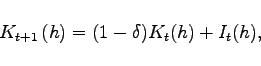\begin{displaymath} K_{t+1}\left( h\right) =(1-\delta )K_{t}(h)+I_{t}(h), \end{displaymath} (6)

where $\delta $ is the depreciation rate of capital.

Individuals accumulate financial assets by purchasing state-contingent domestic bonds, and a non state-contingent foreign bond. Given the representative agent structure at the country level, we omit terms involving the former from the budget constraint. The term $ B_{Ft+1}(h)$ in the budget constraint represents the quantity of the non state-contingent bond purchased by a typical member of household $h$ at time $t$ that pays one unit of foreign currency in the subsequent period, $ P_{Bt}^{\ast }$ is the foreign currency price of the bond, and $e_t$ is the exchange rate expressed in units of home currency per unit of foreign currency. To ensure that net foreign assets are stationary, we follow Turnovsky (1985) and assume there is an intermediation cost $\phi_{Bt}$ paid by households in the home country for purchases of foreign bonds. Specifically, the intermediation costs depend on the ratio of economy-wide holdings of net foreign assets to nominal output ($P_{Dt} Y_t$, defined below)

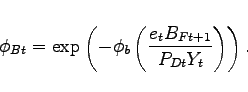\begin{displaymath} \phi_{Bt} = \exp\left(-\phi_b \left(\frac{e_t B_{Ft+1}}{P_{Dt} Y_t} \right)\right). \end{displaymath} (7)

If the home economy has an overall net lender position, a household will earn a lower return on any holdings of foreign bonds. By contrast, if the economy has a net debtor position, a household will pay a higher return on any foreign debt.

Each member of household $h$ earns labor income $(1+\tau_{w})W_{t}\left( h\right) N_{t}\left( h\right) $ and capital income $R_{Kt}K_{t}(h)$. The employment subsidy $\tau_{w}$ exactly offsets the monopolistic distortion, so that the household's marginal rate of substitution would equal the consumption real wage in the absence of nominal wage rigidities. The member also receives an aliquot share $\Gamma _{t}\left( h\right) $ of the sum of firm profits and the sale of oil services, and receives net transfers of $T_{t}(h)$. Finally, as in Christiano, Eichenbaum, and Evans (2005), it is costly to change the level of gross investment from the previous period, so that the acceleration in the capital stock is penalized

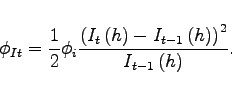\begin{displaymath} \phi _{It}=\frac{1}{2}\phi _{i}\frac{\left( I_{t}\left( h\right) -I_{t-1}\left( h\right) \right) ^{2}}{I_{t-1}\left( h\right)}. \end{displaymath} (8)

In every period $t$, a typical member of household $h$ maximizes the utility functional (26) with respect to consumption, labor supply, investment, end-of-period capital stock, and holdings of foreign bonds, subject to its budget constraint (5), and the transition equation for capital (6). In doing so, prices, wages, and net transfers are taken as given.

2.2  Firms and Production

The production of goods involves several layers. Monopolistic competitors produce a continuum of intermediate good varieties. Perfectly competitive distributors in each country purchase the varieties and create an aggregate over the varieties for each origin of intermediates, i.e., an aggregate of domestic and foreign varieties, respectively. Using the home and foreign aggregates as inputs, competitive bundlers produce a nonoil consumption good, government consumption good and an investment good. In order to produce the final consumption good, a last set of firms combines the nonoil consumption good with oil.

Production of Domestic Intermediate Goods. There is a continuum of differentiated intermediate goods (indexed by $i\in[0,1]$) in the home country, each of which is produced by a single monopolistically competitive firm. Firms charge different prices at home and abroad, i.e., they practice pricing-to-market. In the home market, firm $i$ faces a demand function that varies inversely with its output price $P_{Dt}(i)$ and directly with aggregate demand at home $Y_{Dt}$

\begin{displaymath} Y_{Dt}(i) =\left[ \frac{P_{Dt}(i) }{P_{Dt}}\right] ^{\frac{-\left( 1+\theta _{p}\right) }{\theta _{p}}}Y_{Dt}, \end{displaymath} (9)

where $\theta_p > 0$, and $P_{Dt}$ is an aggregate price index defined below. Similarly, in the foreign market, firm $i$ faces the demand function

\begin{displaymath} X_{t}(i) =\left[ \frac{P^{*}_{Mt}(i)}{P^{*}_{Mt}}\right] ^{\frac{-\left( 1+\theta _{p}\right) }{\theta _{p}}}M^{*}_{t}, \end{displaymath} (10)

where $X_{t}(i)$ denotes the foreign quantity demanded of home good $i$, $P^{*}_{Mt}(i)$ denotes the price, denominated in foreign currency, that firm $i$ sets in the foreign market, $P^{*}_{Mt}$ is the foreign import price index, and $M^{*}_{t}$ is aggregate foreign imports.

Each producer utilizes capital services $K_{t}\left( i\right) $, a labor index $L_{t}\left( i\right) $, and oil $O_{t}\left( i\right) $ to produce its respective output good. The representative firm's technology can be characterized as a nested constant-elasticity of substitution specification of the form

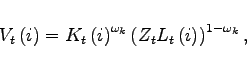\begin{displaymath} V_{t}\left( i\right)=K_{t}\left( i\right)^{\omega _{k}} \left( Z_{t}L_{t}\left( i\right)\right) ^{1-\omega _{k}}, \end{displaymath} (11)
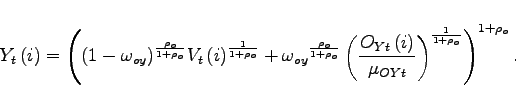\begin{displaymath} Y_{t}\left( i\right)=\left( (1-\omega _{oy})^{\frac{\rho _{o}}{1+\rho _{o}}}V_{t}\left( i\right)^{\frac{1 }{1+\rho _{o}}}+\omega _{oy}{}^{\frac{\rho _{o}}{1+\rho _{o}}}\left(\frac{O_{Yt}\left( i\right)}{\mu _{OYt}}\right)^{\frac{1}{1+\rho _{o}}}\right) ^{1+\rho _{o}}. \end{displaymath} (12)

Each producer utilizes capital and labor services, $K_{t}\left( i\right)$ and $ L_{t}\left( i\right)$, to make a "value-added" input $V_{t}$. This composite input is combined with oil services $O_{Yt}\left( i\right)$ to produce the domestic nonoil good $Y_{t}\left( i\right)$. The term $Z_{t}$ represents a stochastic process for the evolution of technology. The term $\mu _{OYt}$ represents a stochastic process for the oil intensity in production, which might capture a switch in the composition of capital towards machines with different energy intensities.

The prices of intermediate goods are determined by Calvo-style staggered contracts, see Calvo (1983) and Yun (1996). Each period, a firm faces a constant probability, $1-\xi_p$, to reoptimize its price at home $P_{Dt}(i)$ and probability of $1-\xi_{px}$ to reoptimize the price that it sets in the foreign country of $P^{*}_{Mt}(i)$. These probabilities are independent across firms, time, and countries. To offset the distortion due to monopolistic competition, firms receive a production subsidy. Together with the wage subsidy, the allocations under flexible prices and wages are Pareto-optimal.

Production of Domestic Goods Indices

A representative aggregator combines the differentiated intermediate products into a composite home-produced good $Y_{Dt}$ according to

\begin{displaymath} Y_{Dt}=\left[ \int_{0}^{1}Y_{Dt}\left( i\right) ^{\frac{1}{1+\theta _{p}}}di \right] ^{1+\theta _{p}}. \end{displaymath} (13)

The optimal bundle of goods minimizes the cost of producing $Y_{Dt}$ taking the price of each intermediate good as given. The bundle $Y_{Dt}$ is used as input in producing the domestic nonoil consumption good and investment good. A unit of the sectoral output index sells at the price

\begin{displaymath} P_{Dt}=\left[ \int_{0}^{1}P_{Dt}\left( i\right) ^{\frac{-1\,\,}{\theta _{p}\, }}di\right] ^{-\theta _{p}} . \end{displaymath} (14)

Similarly, a representative aggregator in the foreign economy combines the differentiated home products $X_t(i)$ into a single index for foreign imports

\begin{displaymath} M^{*}_{t}=\left[ \int_{0}^{1}X_{t}\left( i\right) ^{\frac{1}{1+\theta _{p}}}di \right] ^{1+\theta _{p}}, \end{displaymath} (15)

and sells $M^{*}_t$ at price $P^{*}_{Mt}$

\begin{displaymath} P^{*}_{Mt}=\left[ \int_{0}^{1}P^{*}_{Mt}\left( i\right) ^{\frac{-1\,\,}{\theta _{p}\, }}di\right] ^{-\theta _{p}}. \end{displaymath} (16)

The bundle $M^{*}_{t}$ is used as input into the production of the foreign nonoil consumption good and investment good.

Production of Nonoil Consumption, Government and Investment Goods

The nonoil consumption good $C_{Nt}$, the government consumption good $G_{t}$, and the investment good $I_{t}$ are produced by perfectly competitive distributors using both aggregates over home and foreign varieties. The production function for the nonoil consumption good $C_{Nt}$ is given by

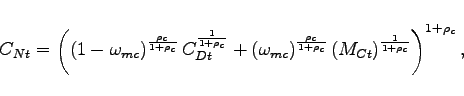\begin{displaymath} C_{Nt}=\left( \left( 1-\omega _{mc}\right) ^{\frac{\rho _{c}}{1+\rho _{c}} }C_{Dt}^{\frac{1}{1+\rho _{c}}}+\left( \omega _{mc}\right) ^{ \frac{\rho _{c}}{1+\rho _{c}}}(M_{Ct})^{\frac{1}{1+\rho _{c}}}\right) ^{1+\rho _{c}}, \end{displaymath} (17)

where $C_{Dt}$ denotes the quantity of the aggregate over domestically-produced varieties purchased at a price of $P_{Dt}$, and used as an input by the representative nonoil consumption distributor. The term $M_{Ct}$ denotes imports of the aggregate over foreign varieties purchased at a price of $P_{Mt}$. The Lagrangian multiplier from the cost minimization problem for the distributors determines the price of the nonoil consumption good, $P_{CNt}$.

The production of the government consumption good $G_{t}$ is identical to the production of the nonoil consumption good with the inputs. Thus, its price is $P_{CNt}$.

Finally, the production function for investment goods is isomorphic to that given in equation (17), though allowing for possible differences in the import intensity of investment goods (determined by $\omega_{mi}$, akin to $\omega_{mc}$ in equation (17)), and the degree of substitutability between nonoil imports and domestically-produced goods in producing investment goods (determined by $\rho_{i}$). The inputs are denoted by $I_{Dt}$ and $M_{It}$. Thus,

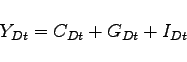\begin{displaymath} Y_{Dt}=C_{Dt}+G_{Dt}+I_{Dt} \end{displaymath} (18)
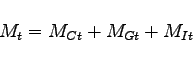\begin{displaymath} M_{t}=M_{Ct}+M_{Gt}+M_{It} \end{displaymath} (19)

The Lagrangian from the problem that investment distributors face determines the price of new investment goods, $P_{It}$, that appears in the household's budget constraint.6

Production of Final Consumption Good

The consumption basket $C_{t}$ that enters the household's budget constraint is produced by perfectly competitive consumption distributors. The form of the production function mirrors the preferences of households over consumption of nonoil goods and oil. These distributors purchase a nonoil consumption good $C_{Nt}$ and oil services $O_{Ct}$ as inputs in perfectly competitive input markets, and produce a composite consumption good according to a CES production function

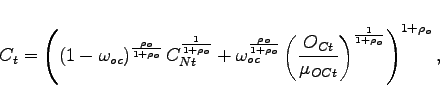\begin{displaymath} C_{t}=\left( \left( 1-\omega _{oc}\right) ^{\frac{\rho _{o}}{1+\rho _{o}} }C_{Nt}^{\frac{1}{1+\rho _{o}}}+\omega _{oc}^{\frac{\rho _{o}}{1+\rho _{o} }}\left(\frac{O_{Ct}}{\mu _{OCt}}\right)^{\frac{1}{1+\rho _{o}}}\right) ^{1+\rho _{o}}, \end{displaymath} (20)

where the quasi-share parameter $\omega _{oc}$ determines the importance of oil purchases in the household's composite consumption bundle, and the parameter $\rho _{o}$ determines the long-run price elasticity of demand for oil. This shock could capture changes in oil demand coming from external factors, such as unusually cold winters, or a shift towards consuming goods that are more energy intensive.

Consumption distributors choose a contingency path for their inputs $C_{Nt}$ and $O_{Ct}$ to minimize the costs of producing the consumption bundle, taking as given input prices $P_{CNt}$ and $P_{Ot}$, respectively. The Lagrangian multiplier from this cost-minimization problem determines the price of the consumption bundle charged to households, i.e., $P_{Ct}$ in the household's budget constraint given in equation (5).

2.3  The Oil Market

Each period the home and foreign countries are endowed with exogenous supplies of oil $Y_{Ot}$ and $Y^{*}_{Ot}$, respectively. The two endowments are governed by distinct stochastic processes.

With both domestic and foreign oil supply determined exogenously, the oil price $P_{Ot}$ adjusts endogenously to clear the world oil market

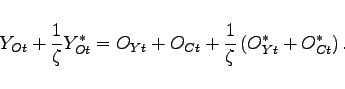\begin{displaymath} Y_{Ot} + \frac{1}{\zeta} Y^{*}_{Ot} = O_{Yt} + O_{Ct} + \frac{1}{\zeta}\left(O^{*}_{Yt} + O^{*}_{Ct}\right). \end{displaymath} (21)

To clear the oil market, the sum of home and foreign oil production must equal the sum of home and foreign oil consumption by firms and households. Because all variables are expressed in per capita terms, foreign variables are scaled by the relative population size of the home country $\frac{1}{\zeta}$, in equation 21.

2.4  Monetary and Fiscal Policy

Monetary policy follows an interest rate reaction function as suggested by Taylor (1993). However, when policy rates reach zero, we assume that no further actions are taken by the central bank. The notional rate that would be dictated by the interest rate reaction function barring the zero lower bound is denoted by $i_{t}^{not}$, whereas the policy rate that can actually be implemented is denoted by $i_{t}$. The two differ only if the notional rate turns negative

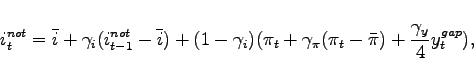\begin{displaymath} i_{t}^{not}= \bar{i} + \gamma _{i} (i_{t-1}^{not} - \bar{i}) +(1-\gamma _{i})(\pi_t + \gamma_{\pi }(\pi _{t}-\bar{\pi})+\frac{\gamma _{y}}{4}y_{t}^{gap}), \end{displaymath} (22)
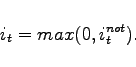\begin{displaymath} i_{t} = max(0,i_{t}^{not}). \end{displaymath} (23)

The terms $\bar{i}$ and $\bar{\pi}$ are the steady-state values for the nominal interest rate and inflation, respectively. The inflation rate $\pi _{t}$ is expressed as the logarithmic percentage change of the domestic price level, $\pi_t = log(P_{Dt}/P_{Dt-1})$. The term $y_{t}^{gap}$ denotes the output gap, given by the log difference between actual and potential output, where the latter is the level of output that would prevail in the absence of nominal rigidities. Notice that the coefficient $\gamma_y$ is divided by four as the rule is expressed in terms of quarterly inflation and interest rates. The parameter $\gamma_i$ allows for interest rate smoothing.7

Government purchases are a constant fraction of output $\bar{g}$ and they fall exclusively on the domestically-produced varieties. These purchases make no direct contribution to household utility. To finance its purchases, the government imposes a lump-sum tax on households that is adjusted so that the government's budget is balanced every period.

The government finances its purchases $P_{Ct}G_{t}$, and the subsidies to firms and households through lump-sum taxes. Given the Ricardian structure of the model, we assume that the government budget is balanced each period.

2.5  Resource Constraints for Nonoil Goods, and Net Foreign Assets

The resource constraint for the nonoil goods sector of the home economy can be written as

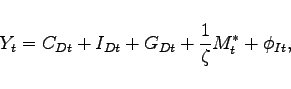\begin{displaymath} Y_{t} = C_{Dt}+I_{Dt}+G_{Dt} + \frac{1}{\zeta} M^{*}_{t} + \phi_{It}, \end{displaymath} (24)

where $M^{*}_t$ denotes foreign imports - again expressed in per capita terms, which accounts for the population scaling factor $\frac{1}{\zeta}$. The term $\phi_{It}$ denotes the resources that are lost due to costs of adjusting investment.

The evolution of net foreign assets can be expressed as

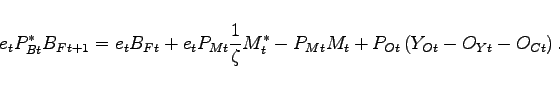\begin{displaymath} e_{t}P_{Bt}^{\ast }B_{Ft+1}=e_{t}B_{Ft}+e_{t}P_{Mt}\frac{1}{\zeta } M_{t}^{\ast }-P_{Mt}M_{t}+P_{Ot}\left( Y_{Ot}-O_{Yt}-O_{Ct}\right) . \end{displaymath} (25)

This expression can be derived by combining the budget constraint for households, the government budget constraint, and the definition of firm profits.


3  Solution Method and Calibration

The model is log-linearized around its steady state.8 To obtain the reduced-form solution of the model, we use the numerical algorithm of Anderson and Moore (1985), which provides an efficient implementation of the method proposed by Blanchard and Kahn (1980).9 Adapting the ideas in Svensson and Laséen (2009), as Hebden, Lindé, and Svensson (2010), we implement the zero bound constraint on the nominal interest rate through a series of anticipated monetary policy shocks. These anticipated policy shocks raise the nominal interest rate to zero relative to the a simulation in which the zero bound constraint is ignored. Thus, under the zero bound constraint, monetary policy can be interpreted as being too tight. Appendix A outlines the computational procedure.10

The model is calibrated at a quarterly frequency. The parameter values for the home economy under our benchmark calibration are listed in Table 1. Parameters for the foreign economy are identical except for the parameters determining the intensity of oil use, the capital share of production, and the trade shares. The latter are determined by the assumption that trade is balanced in the steady state and that the relative population size, $\zeta$, is scaled so that the home economy accounts for one third of world GDP.

The parameter $\sigma$ is set equal to 1. We set $\chi = 10$, implying a Frisch elasticity of labor supply of 0.2. The utility parameter $\chi _{0}$ is set so that employment comprises one-third of the household's time endowment. In line with Smets and Wouters (2007), the real rigidities affecting consumption, $\phi_{c}$, and investment, $\phi_{i}$, are 0.8 and 3, respectively.

The depreciation rate of capital $\delta =0.03$ is consistent with an annual depreciation rate of 12 percent. We set the government share of output to 18 percent, and adjust the capital share parameter $\omega _{k} = 0.28$, so that the investment share of output equals an empirically-realistic value of 20 percent.

Nominal rigidities in prices and wages have an average duration of four quarters, determined by the parameters $\xi_p=0.75$ and $\xi_w=0.75$. Export price rigidities have a shorter duration of 2 quarters, as implied by the parameter $\xi_{px}=0.5$. As noted above, monetary policy follows the Taylor rule, aside from allowing for interest rate smoothing and taking account of the zero lower bound constraint. Thus, the parameter $\gamma_{\pi}$ on the inflation gap is 0.5 and the parameter $\gamma_y$ on the output gap is also 0.5; we set the smoothing parameter $\gamma_i$ to 0.8. The steady state real interest rate is set to 2% per year ($\beta = 0.995$). Given steady state inflation $\bar{\pi}$ equal to zero, the implied steady state nominal interest rate is two percent.

The calibration of the parameters $\omega_{oy}$ and $\omega_{oc}$ is informed by the overall oil share of output, and the end-use ratios of oil in consumption and production. Based on data from the Energy Information Administration of the U.S. Department of Energy for 2008, the overall oil share of the domestic economy is set to 4.2 percent, with one-third of total oil usage accounted for by households, and two-thirds by firms. The oil imports of the home country are set to 70 percent of total demand in the steady state, implying that one third of oil demand is satisfied by domestic production. This estimate is based on 2008 data from the National Income and Product Accounts. In the foreign block, the overall oil share is set to 8.2 percent. The oil endowment abroad is 9.5 percent of foreign GDP, based on oil supply data from the Energy Information Administration.

Turning to the parameters determining trade flows, $\omega_{mc}$ is chosen to match the estimated average share of imports in total U.S. consumption of about 7 percent using NIPA data, while the parameter $\omega_{mi}$ is chosen to match the average share of imports in total U.S. investment of about 40 percent. This calibration implies a ratio of nonoil goods imports relative to GDP for the home country of about 12 percent. Given that trade is balanced in steady state, and that the oil import share for the home country is 3 percent of GDP, the goods export share is 15 percent of GDP.

The parameters governing the elasticity of substitution for oil, $\rho_{o}$, the elasticity of substitution between domestic and foreign goods, $\rho_c=\rho_i$ are chosen in line with those obtained from the moment matching exercise in Bodenstein, Erceg, and Guerrieri (2010). More specifically, we set $\rho_{o}$ to obtain an oil price elasticity of 0.4, and $\rho_c=\rho_i$ to obtain a trade elasticity of 1.1.

The model in Bodenstein, Erceg, and Guerrieri (2010) differs from ours only with respect to the presence of nominal rigidities. However, in their moment matching exercise Bodenstein, Erceg, and Guerrieri (2010) focus on medium term frequencies rather than business cycle frequencies implying little bearing of nominal rigidities for their estimates.


4  Oil Demand Shocks

Our analysis focuses on the effects of oil shocks against the backdrop of an initial severe recession in the home country. The initial recession is generated by a preference shock, $\nu _{ct}$, that follows an autoregressive process with persistence parameter equal to 0.9. The shock reduces the home country's marginal utility of consumption. As a result of the shock, monetary policy attempts to stimulate the economy by lowering rates, but the policy rate reaches the zero lower bound, which is expected to bind for 10 quarters at the point in which the additional oil shock strikes. As the initial consumption shock occurs exclusively in the home country, the foreign economy has latitude to offset much of the contractionary spillover impact by reducing its policy rate.11

Figures 1 and 2 consider the effect of an oil demand shock abroad against the severe domestic recession. Following Bodenstein, Erceg, and Guerrieri (2010), the oil demand shock has a persistent growth component and a level error correction component. The process governing the shock is:

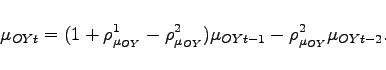
\begin{displaymath} \mu_{OYt} = (1+\rho^1_{\mu_{OY}}-\rho^2_{\mu_{OY}}) \mu_{OYt-1} - \rho^2_{\mu_{OY}} \mu_{OYt-2}. \end{displaymath}

We set $\rho^1_{\mu_{OY}}=0.5$ and $\rho^2_{\mu_{OY}}=0.02$. Furthermore, there is perfect correlation between $\mu_{OYt}$ and $\mu_{OCt}$, respectively the demand shock for oil in production, and the demand shock for oil in consumption.12 As shown in Figure 1, the price of oil deflated by the price of the domestic nonoil good rises for one year, then slowly declines. All the responses shown are presented in deviation from the path implied by the initial severe recession. Each panel in the figure shows three lines: the response to the shock against the background of the severe recession, the solid lines; the response to the shocks in normal times when the zero lower bound does not bind, the dashed lines; and the response to the shock in an economy with flexible prices and wages, the dotted lines. The shock is unchanged for the three cases shown and the relative price of oil shows negligible differences across the cases.

The form of our modified Taylor rule, was chosen so that there would only be quantitatively small differences between the effects of the shock with and without nominal rigidities, as long as the zero lower bound is not enforced, or equivalently in a linear setting, as long as zero lower bound does not bind. We interpret the proximity of such responses, the dashed and the dotted lines in Figure 1, as heuristic evidence that the monetary policy rule is nearly optimal, at least in the case of an oil demand shock.13

In all of the cases shown, the persistent rise in the price of oil induces a fall in home oil demand. Both households and firms substitute away from the more costly oil input. The decline in oil use has effects on gross nonoil output, the expenditure components, and the real interest rate that resemble those of a highly persistent decline in productivity. Lower oil use leads to a fall in the current and future marginal product of capital, causing investment and gross output to fall. In the long term the capital stock also falls. Consumption contracts due to a reduction in household income.

Strikingly, the imposition of the zero lower bound can generate persistent qualitative differences in the response of real GDP. GDP temporarily rises at the zero lower bound, while it falls uniformly when the zero bound is not binding. Morevor, at the zero bound, the eventual fall of GDP is cushioned persistently. In the simulation that enforces the zero bound, GDP remains above its unconstrained level for years past the end of the liquidity trap.

As policy rates are constrained, and as the oil shock generates a persistent increase in inflation, the short-term real interest rate falls more, cushioning the fall of investment. The cushioning of the investment props up the capital stock in such a way as to introduce a persistent wedge between real (nonoil) gross output at the zero bound relative to its counterpart in normal times. Due to the presence of consumption habits and investment adjustment costs, as well as to the phasing in of the oil shock, gross output only falls gradually. In this setting, the difference between gross output and GDP is a wedge implied by the presence of imported oil inputs in production. The initial fall is gross output happens to be small enough that the contraction in oil imports brought about by higher oil prices translates into a boost to GDP.

Turning to the implications for the external sector, while the responses of investment and gross output to the oil supply shock resemble those of a persistent contraction in technology, the exchange rate response does not.14 Since the rational expectations solution requires that the net foreign asset position is bounded away from infinity (conditional on current information), the home country's nonoil balance must improve enough to offset the long-run deterioration in the oil balance, as well as to finance interest payments on the stock of debt accumulated along the transition path. Thus, as the home economy faces the burden of a larger oil deficit, the exchange rate depreciates, which stimulates home nonoil net exports (the terms of trade track the real exchange rate closely in this setting). As the shock to oil supply leads to a very persistent rise in oil prices, consumption smoothing dictates a quick offset of the deficit from the oil side of the trade balance by a surplus in the nonoil balance. If the offset were delayed, a greater accumulation of debt and related interest rate payments would reduce future consumption inefficiently. The imposition of the zero bound does not change the response of the external sector qualitatively. Quantitatively, however, lower real rates at home imply a larger depreciation of the real exchange rate (shown as an upward movement in Figure 2). Consequently real net exports expand more, but the trade balance expressed as a nominal share of GDP is little changed.

4.1  Alternative Policy Rules and Interest Rate Sensitivity

We consider sensitivity analysis for the specification of monetary policy with respect to two important dimensions: the interest rate smoothing and the measure of inflation included in the rule. The panels in the left column of Figure 3 reports responses to the same foreign demand shock as considered in the benchmark experiment described. However, the monetary policy rule used in this case excludes the lagged interest rate term by setting $\gamma_i$ to zero, (see Equation 22). For ease of comparison, the panels in the right column of Figure 3 reproduce the benchmark results.15

Away from the lower bound, the rule that excludes the smoothing term induces a less persistent rise in real rates in response to the same oil shock, enhancing the inflation response and further cushioning the effects at the zero lower bound. On impact, with the less aggressive rule, the initial rise in GDP is almost doubled relative to the benchmark case. Moreover, the the wedge between the response of GDP at the zero bound and its counterpart away from the zero bound is also enhanced quantitatively.

The particular inflation measure included in the rule is also important. Our benchmark rule responds to current core inflation (the inflation for the price of the consumption basket with the oil component stripped out). A number of central banks characterize their policies as focusing on a forecast of future headline inflation. As discussed by Bodenstein, Erceg, and Guerrieri (2008), such rules can be less effective in controlling inflation. When faced with temporary increases in the price of oil, rules that incorporate a forecast of headline inflation can look past the peak inflation response and lower rates in anticipation of the expected decline in oil prices.

The responses shown in the left panels of Figure 4 build on the previous sensitivity exercise by not only doing away with the smoothing term in the monetary policy rule, but also substituting the current core inflation measure with the forecast of next period headline inflation rate. For ease of comparison the panels in the right column of the figure report the effects of the same foreign oil demand shock for the case in which the only modification to the rule involves the exclusion of the smoothing term and the rule responds to current core inflation.

As shown in the bottom panels of Figure 4, the rule that responds to headline inflation implies a larger inflation response. At the zero bound, more inflation translates into a bigger fall in the real interest rate. Investment and consumption still fall, but are propped up relative to their response under the rules considered previously. Moreover, the fall in net real rates enhances the exchange rate depreciation. The consequent boost to net exports leads to a temporary expansion in gross output. Under this alternative rule, at the zero bound real GDP rises close to 0.3 percent on impact, while it drops almost 0.1 percent in normal times.

The wedge between the responses to the oil demand shock at the zero bound relative to normal times stem from the lowering the profile of real rates. By incorporating consumption habits, the benchmark calibration constrains the economy's interest sensitivity. The left panels of Figure 5 report the response to the foreign oil demand shock for a calibration of the model that excludes consumption habits. The panels in the right column replicate the responses for the baseline calibration with consumption habits.

As in normal times the benchmark policy rule implies a rise in the longer-term real interest rates such as the 5-year rate shown in the figure, the decline in private absorption is amplified by the exclusion of habits. However, a higher degree of interest rate sensitivity implies that at the zero lower bound lower real rates relative to the unconstrained case can generate a larger wedge relative to the unconstrained responses.

4.2  Sensitivity: Alternative Preferences and Additional Rigidities of a Policy Model

Figure 6 compares the effects of an oil demand shock under two preference specifications. The left panels in the figure reproduce the results from the benchmark model with preferences that follow those in Greenwood, Hercowitz, and Hoffman (1988). The right panels in Figure 6 show responses from a model with the commonly used specification of additively separable preferences over consumption and leisure. Under this alternative, the utility functional of a typical member of household $h$ is

\begin{eqnarray*} \mathbb{E}_{t}\sum_{j=0}^{\infty }\beta ^{j} && \left[ \frac{1}{1-\sigma }\left( C_{t+j}\left( h\right)-\phi_c \frac{ C_{t+j-1}}{\zeta }\right) ^{1-\sigma} + \right. \\ && \left. \frac{ \chi _{0}}{1-\chi }(1-N_{t+j}\left( h\right) )^{1-\chi } + V\left( \frac{MB_{t+j+1}\left( h\right) }{P_{t+j}}\right)\right]. \end{eqnarray*}

Under the alternative, we left the function $V$ unchanged relative to the benchmark specification. Also unchanged are the values chosen for the parameters $\sigma, \phi_c, \zeta,$ and $\chi$. We calibrated the value for the parameter $\chi_0$ so that employment comprises one-third of the household's time endowment as for the benchmark preferences.

The additively separable preferences let the marginal utility of consumption influence labor supply. As shocks that push up the price of oil compress consumption for the home oil-importing country, the marginal utility of consumption increases and stimulates labor supply. Figure 6 shows an expansion in labor supply both in normal times and at the zero lower bound for the alternative preferences. Under additively separable preferences, an increase in the price of oil can lead to such an increase in labor supply that gross output and GDP expand even when the economy is not in a liquidity trap. By contrast, in the benchmark model it is the liquidity trap that initially reverses the sign for the response of GDP. However, under both types of preference, the zero lower bound cushions the eventual contraction of economic activity.16

Figure 7 compares the effects of an oil demand shock in the benchmark model with an extension that incorporates financial frictions as in Bernanke, Gertler, and Gilchrist (1999) and Christiano, Motto, and Rostagno (2003) and limited exchange rate pass-through to import prices as in Gust, Leduc, and Sheets (2009). Both of these features could potentially diminish the expansionary effects that oil price shocks have at the zero lower bound. With financial frictions, the relevant real interest rate that affects investment demand is no longer the risk-free rate but one that takes into account an asymmetric information problem between borrowers and lenders. If this asymmetric problem worsens in response to higher oil prices, there can be a more severe contraction in investment, which all else equal induces deflationary pressure. Accordingly, at the zero lower bound, real policy rates may not fall as much, reducing the stimulative effects of higher oil prices at the zero lower bound. Similarly, lower exchange rate pass-through can potentially reduce the inflationary effects that occur when the home currency depreciates in response to the rise in oil prices.

The panels in the first column of Figure 7 show the response of key variables in the extended model to the oil demand shock when monetary policy is constrained by the zero lower bound and when its unconstrained. For purposes of comparison, the panels on the right show the analogous responses in the benchmark model. In both the benchmark and extended models, GDP falls when monetary policy is unconstrained and rises when the zero lower bound constraint binds. Relative to the benchmark model, the stimulative effects of the oil price shock at the zero lower bound are only marginally smaller in the extended model. These smaller effects mainly reflect the reduction in pass-through, which mitigates the rise in inflation associated with higher oil prices. The rise in inflation is smaller in the extended model, because exchange rate pass-through is lower, which implies that import prices do not rise as much when the home currency depreciates. As a consequence, there is less monetary stimulus in the extended model at the zero lower bound than in the benchmark model. However, as shown in Figure 7, the difference in the response of headline inflation and in long-term rates across the two models is very small. This small difference in part reflects that the exchange rate tends to depreciate by more in the extended model, as lower pass-through tends to amplify exchange rate movements, which all else equal increases the inflationary consequences of the oil demand shock.

To understand why the financial accelerator mechanism of Bernanke, Gertler, and Gilchrist (1999) does not reduce the stimulative effects of oil shocks at the zero lower bound, recall that the asymmetric information problem between borrowers/enterpreneurs and lenders gives rise to a spread between interest rates used to finance capital purchases and the risk-free rate. This spread varies with the total demand for funds by borrowers (i.e., their capital purchases) less their net worth. Because higher oil prices reduce the demand for capital somewhat more than a borrower's net worth, the spread actually falls slightly, and there is little change in the results once financial frictions are incorporated into the model. Moreover, we find that there is little change in results across a broad range of parameter values characterizing this financial friction.


5  Alternative Shocks

In addition to oil demand shocks, we consider shocks to oil supply and technology as possible determinants of the price of oil.

Oil supply shocks Following Bodenstein, Erceg, and Guerrieri (2010), we assume that the oil supply in each country follows a process close to a unit-root.17 Figure 8 shows the domestic response to a foreign oil supply shock both when the economy is mired in a liquidity trap and in normal times. For ease of comparison, we also show the responses to an oil demand shock. The contraction in foreign oil supply is sized to match the peak of the oil demand shock discussed earlier. However, in contrast to the oil demand shock, the supply shock does not lead to a protracted rise in inflation. Apart from the initial period, headline inflation is close to zero. Thus, the real interest rate is little changed at the zero bound and the shock has similar effects at the zero bound and in normal times.

Abstracting from monetary policy consideration at the zero lower bound, our model with nominal rigidities displays responses similar to the flexible price economy in Bodenstein, Erceg, and Guerrieri (2010). The nearly permanent foreign supply contraction leads to a persistent fall in domestic activity, and a persistent deterioration of the home country's oil balance that is mostly offset by an improvement in the nonoil trade balance. The latter is brought about by a persistent depreciation of the home country's real exchange rate.

If the oil supply shock lead to a period of increasing oil prices similar to the oil demand shock and thus to protracted inflation, the oil supply shock would be compressed in the same manner. However, as argued in Bodenstein, Erceg, and Guerrieri (2010) oil supply and demand shocks differ along exactly this dimension: oil supply shocks are near unit-root processes, but oil demand shocks are best described as AR(2) processes. 18

Technology shocks Figure 9 shows the effects of a 1% temporary decline in the level of the home country's productivity.19 In line with Bodenstein, Erceg, and Guerrieri (2010), the oil price response implied by the technology shocks is not large enough to substantially affect the transmission of technology shocks. However, as such shocks lead to a rise in inflation made persistent by the real rigidities in our model (adjustment costs for investment, consumption habits, and lagged price and wage indexation), their effects are also cushioned at the zero bound relative to normal times.

In contrast to the oil demand shocks, the technology shock primarily affects output rather than inflation. With gross output falling sharply on impact, the stimulating effect of lower real interest rates caused by positive inflation at the zero bound cannot reverse the sign of the GDP response on impact.20


6  Conclusion

When monetary policy has latitude to adjust policy rates, the incorporation of nominal rigidities into a model that allows for trade in oil and nonoil is not sufficient to imply large departures in the transmission of oil shocks from a model with flexible prices and wages. However, even for rules that come close to replicating the flexible-price equilibrium, at the zero lower bound the transmission of oil shocks can be substantially different.

The discussion of the consequences of a liquidity trap has recently focused on the amplification of demand shocks. Such shocks typically move inflation and output in the same direction. By contrast, oil shocks move inflation and output in opposite directions so that their effects on activity are cushioned in a liquidity trap. The cushioning is larger for shocks that imply a persistent bout of inflation especially under policy rules that do not imply an aggressive response to inflation away from the zero lower bound. Extensions of the model that refine the trade linkages in the model and that limit the passthrough of exchange rate movements to import prices and inflation do not change the results qualitatively. Similarly, extensions of the model that incorporate financial frictions and endogenous risk premia on corporate interest rates do little to change our benchmark results.

References

Adam, K. and R. M. Billi (2006). Optimal Monetary Policy under Commitment with a Zero Bound on Nominal Interest Rates. Journal of Money, Credit, and Banking 7, 1877-1905.

Adam, K. and R. M. Billi (2007). Discretionary Monetary Policy and the Zero Lower Bound on Nominal Interest Rates. Journal of Monetary Economics 3, 728-752.

Anderson, G. and G. Moore (1985). A Linear Algebraic Procedure for Solving Linear Perfect Foresight Models. Economic Letters 17, 247-52.

Bernanke, B., M. Gertler, and M. Watson (1997). Systematic Monetary Policy and the Effects of Oil Price Shocks. Brookings Papers on Economics Activity (1), 91-142.

Bernanke, B. S., M. Gertler, and S. Gilchrist (1999). The Financial Accelerator in a Quantitative Business Cycle Framework. In J. B. Taylor and M. Woodford (Eds.), Hanbook of Macroeconomics, pp. 1341-1393. Elsevier Science.

Blanchard, O. J. and J. Galí (2007, April). The Macroeconomic Effects of Oil Price Shocks: Why are the 2000s so different from the 1970s? In International Dimensions of Monetary Policy, NBER Chapters, pp. 373-421. National Bureau of Economic Research, Inc.

Blanchard, O. J. and C. M. Kahn (1980). The Solution of Linear Difference Models under Rational Expectations. Econometrica 48 (5), 1305-1312.

Bodenstein, M., C. Erceg, and L. Guerrieri (2008). Optimal Monetary Policy with Distinct Core and Headline In°ation Rates. Journal of Monetary Economics 55, S18-S33.

Bodenstein, M., C. Erceg, and L. Guerrieri (2009). The Effects of Foreign Shocks when Interest Rates are at Zero. International Finance Discussion Paper 983.

Bodenstein, M., C. Erceg, and L. Guerrieri (2010). Oil Shocks and External Adjustment. International Finance Discussion Paper 897.

Calvo, G. A. (1983, September). Staggered Prices in a Utility-Maximizing Framework. Journal of Monetary Economics 12, 383-398.

Christiano, L., M. Eichenbaum, and S. Rebelo (2009). When is the Government Spending Multiplier Large?

Christiano, L. J., M. Eichenbaum, and C. L. Evans (2005). Nominal Rigidities and the Dynamic Effects of a Shock to Monetary Policy. Journal of Political Economy 113 (1), 1-45.

Christiano, L. J., R. Motto, and M. Rostagno (2003). The Great Depression and the Friedman-Schwartz Hypothesis. Journal of Money, Credit, and Banking 35, 1119-1198.

Eggertsson, G. (2006). Was the New Deal Contractionary? Federal Reserve Bank of New York, Staff Report 264.

Eggertsson, G. B. and M. Woodford (2003). The Zero Bound on Interest Rates and Optimal Monetary Policy. Brookings Papers on Economic Activity (1), 139-233.

Engel, C. and J. Wang (2008). International Trade in Durable Good: Understanding, Volatility, Cyclicality, and Elasticities. NBER Working Paper No. 13814.

Erceg, C., L. Guerrieri, and C. Gust (2006). SIGMA: A New Open Economy Model for Policy Analysis. International Journal of Central Banking, 1-50.

Fair, R. and J. B. Taylor (1983). Solution and Maximum Likelihood Estimation of Dynamic Nonlinear Rational Expectations Models. Economectrica 51, 1169-1185.

Greenwood, J., Z. Hercowitz, and G. W. Ho®man (1988). Investment, Capacity Utilization, and the Real Business Cycle. American Economic Review 78 (3), 402-417.

Gust, C., S. Leduc, and N. Sheets (2009). The Adjustment of Global External Imbalances: Does Partial Exchange-Rate Pass-Through to Trade Prices Matter? Journal of International Economics 79, 173-185.

Hamilton, J. (2009). Causes and Consequences of the Oil Shock of 2007-08. Mimeo, U.C. San Diego.

Hamilton, J. and C. Herrera (2004). Oil Shocks and Aggregate Macroeconomic Behavior: The Role of Monetary Policy: Comment. Journal of Money, Credit, Banking 36 (2), 265-86.

Hebden, J., J. Lindé, and L. Svensson (2010). Optimal Monetay Policy in the Hybrid New Keynesian Model under the Zero Lower Bound. Working Paper, Federal Reserve Board.

Jaimovich, N. and S. Rebelo (2009, September). Can News about the Future Drive the Business Cycle? American Economic Review 99 (4), 1097-1118.

Jeanne, O. and L. E. Svensson (2007). Credible Commitment to Optimal Escape from a Liquidity Trap: The Role of the Balance Sheet of an Independent Central Bank. American Economic Review 97, 474-490.

Jung, T., Y. Teranishi, and T. Watanabe (2005). Zero Bound on Nominal Interest Rates and Optimal Monetary Policy. Journal of Money, Credit, and Banking 37, 813-836.

Kilian, L. (2009). Not All Price Shocks Are Alike: Disentangling Demand and Supply Shocks in the Crude Oil Market. American Economic Review 99 (3), 1053-69.

Kilian, L., A. Rebucci, and N. Spatafora (2009). Oil Shocks and External Balances.

Kilian, L. and R. Vigfusson (2009). Pitfalls in Estimating Asymmetric Effects of Energy Price Shocks. Manuscript, University of Michigan.

Leduc, S. and K. Sill (2004). A Quantitative Analysis of Oil-Price Shocks, Systematic Monetary Policy, and Economic Downturns. Journal of Monetary Economics 51, 781-808.

Smets, F. and R. Wouters (2003). An Estimated Dynamic Stochastic General Equilibrium Model of the Euro Area. Journal of the European Economic Association 1, 1124-1175.

Smets, F. and R. Wouters (2007). Shocks and Frictions in US Business Cycles: A Bayesian DSGE Approach. American Economic Review 97 (3), 586-606.

Svensson, L. E. and S. Laséen (2009). Anticipated Alternative Instrument-Rate Paths in Policy Simulations.

Taylor, J. B. (1993). Discretion versus Policy Rules in Practice. Carnegie-Rochester Conference Series on Public Policy 39, 195-214.

Turnovsky, S. J. (1985). Domestic and Foreign Disturbances in an Optimizing Model of Exchange-Rate Determination. Journal of International Money and Finance 4 (1), 151-71.

Yun, T. (1996). Nominal price rigidity, money supply endogeneity, and business cycles. Journal of Monetary Economics 37, 345-370.

Table 1a. Benchmark Calibration: Parameters Common Across Countries

Parameter Used to Determine Parameter Used to Determine
$\beta = 0.99 $ discount factor $\sigma = 1.5$ intertemporal consumption elasticity
$\chi = 10$ labor supply elasticity (0.2) $N_{ss} = 0.33$ steady state labor share to fix $\chi_{0}$
$\kappa = 0.8$ habit persistence $\phi_i = 3$ investment adj. cost
$\delta = 0.025$ depreciation rate of capital $g = 0.18 $ steady state gov. cons. share of GDP
$\rho_o = -1.6$ oil sub. elasticity (0.38) $\rho_c=\rho_i = 13$ cons./ inv. import sub. elasticity (1.1)
$\xi_p = 0.75$ prob. of not adjusting price $\xi_w = 0.75$ prob. of not adjusting wage
$\xi_{px} = 0.05$ prob. of not adjusting export price    

Table 1b. Benchmark Calibration: Parameters Not Common Across Countries

Parameter Used to Determine Parameter Used to Determine
$\omega_k = 1.54 $ parameter on K in value added (home) $\omega_k^* = 1.60 $ parameter on K in value added (foreign)
$\omega_{oy} = 0.028 $ weight on oil in production (home) $\omega_{oy}^* = 0.057 $ weight on oil in production (foreign)
$\omega_{oc} = 0.023 $ weight on oil in consumption (home) $\omega_{oc}^* = 0.041 $ weight on oil in consumption (foreign)
$\omega_{mc} = 0.068 $ weight on imports in consumption (home) $\omega_{mc}^* = 0.039 $ weight on imports in consumption (foreign)
$\omega_{mi} = 0.40 $ weight on imports in investment (home) $\omega_{mi}^* = 0.25 $ weight on imports in investment (foreign)

Table 1c. Benchmark Calibration: Parameters Specific to Home Country

Parameter Used to Determine Parameter Used to Determine
$\zeta = 1/2$ relative size of home country 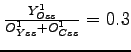$\frac{Y_{Oss}^1}{O_{Yss}^1+O_{Css}^1} = 0.3 $ steady state ratio oil prod. to cons. (home)
$\phi_b = 0.0001$ curvature of bond intermed. cost    

*Values determined using simulated method of moments. See also Table 2.

Figure 1. An Oil Demand Shock at the Zero Lower Bound

Figure 1: Our analysis focuses on the effects of oil shocks against the backdrop of an initial severe recession in the home country. The initial recession is generated by a preference shock, $\nu _{ct}$, that follows an autoregressive process with persistence parameter equal to 0.9. The shock reduces the home country's marginal utility of consumption. As a result of the shock, monetary policy attempts to stimulate the economy by lowering rates, but the policy rate reaches the zero lower bound, which is expected to bind for 10 quarters at the point in which the additional oil shock strikes. As the initial consumption shock occurs exclusively in the home country, the foreign economy has latitude to offset much of the contractionary spillover impact by reducing its policy rate. Figures 1 and 2 consider the effect of an oil demand shock abroad against the severe domestic recession. The oil demand shock has a persistent growth component and a level error correction component. The process governing the shock is: \[ \mu_{OYt} = (1+\rho^1_{\mu_{OY}}+\rho^2_{\mu_{OY}}) \mu_{OYt-1} - \rho^2_{\mu_{OY}} \mu_{OYt-2}. \] We set $\rho^1_{\mu_{OY}}=0.5$ and $\rho^2_{\mu_{OY}}=0.02$. Furthermore, there is perfect correlation between $\mu_{OYt}$ and $\mu_{OCt}$, respectively the demand shock for oil in production, and the demand shock for oil in consumption.\footnoteSS{In our model the unconditional behavior of oil prices reflects a variety of shocks and their propagation mechanisms. Accordingly, the finding that a simple unit root process provides a good fit for the behavior of oil prices in the postwar period does not imply that all structural shocks affecting the oil market should themselves be governed by unit root processes.} As shown in Figure 1, the price of oil deflated by the price of the domestic nonoil good rises for one year, then slowly declines. All the responses shown are presented in deviation from the path implied by the initial severe recession. Each panel in the figure shows three lines: the response to the shock against the background of the severe recession, the solid lines; the response to the shocks in normal times when the zero lower bound does not bind, the dashed lines; and the response to the shock in an economy with flexible prices and wages, the dotted lines. The shock is unchanged for the three cases shown and the relative price of oil shows negligible differences across the cases. The form of the interest rate reaction function, our modified Taylor rule, was chosen so that there would only be quantitatively small differences between the effects of the shock with and without nominal rigidities, as long as the zero lower bound is not enforced, or equivalently in a linear setting, as long as zero lower bound does not bind. We interpret the proximity of such responses, the dashed and the dotted lines in Figure 1, as heuristic evidence that the monetary policy rule is nearly optimal, at least in the case of an oil demand shock.\footnoteSS{Characterizing the optimal response exactly is no small task in the presence of the zero lower bound. The task is made more difficult by the open economy nature of the model.} In all of the cases shown, the persistent rise in the price of oil induces a fall in home oil demand. Both households and firms substitute away from the more costly oil input. The decline in oil use has effects on gross nonoil output, the expenditure components, and the real interest rate that resemble those of a highly persistent decline in productivity. Lower oil use leads to a fall in the current and future marginal product of capital, causing investment and gross output to fall. In the long term the capital stock also falls. Consumption contracts due to a reduction in household income. Strikingly, the imposition of the zero lower bound can generate persistent qualitative differences in the response of real GDP. GDP temporarily \emph{rises} at the zero lower bound, while it falls uniformly when the zero bound is not binding. Morevor, at the zero bound, the eventual fall of GDP is cushioned persistently. In the simulation that enforces the zero bound, GDP remains above its unconstrained level for years past the end of the liquidity trap. As policy rates are constrained, and as the oil shock generates a persistent increase in inflation, the short-term real interest rate falls more, cushioning the fall of investment. The cushioning of the investment props up the capital stock in such a way as to introduce a persistent wedge between real (nonoil) gross output at the zero bound relative to its counterpart in normal times. Due to the presence of consumption habits and investment adjustment costs, as well as to the phasing in of the oil shock, gross output only falls gradually. In this setting, the difference between gross output and GDP is a wedge implied by the presence of imported oil inputs in production. The initial fall is gross output happens to be small enough that the contraction in oil imports brought about by higher oil prices translates into a boost to GDP. Turning to the implications for the external sector, while the responses of investment and gross output to the oil supply shock resemble those of a persistent contraction in technology, the exchange rate response does not.\footnoteSS{The benchmark calibration of the trade elasticity around unity implies an appreciation of the real exchange rate in reaction to a persistent contraction in technology.} Since the rational expectations solution requires that the net foreign asset position is bounded away from infinity (conditional on current information), the home country's nonoil balance must improve enough to offset the long-run deterioration in the oil balance, as well as to finance interest payments on the stock of debt accumulated along the transition path. Thus, as the home economy faces the burden of a larger oil deficit, the exchange rate depreciates, which stimulates home nonoil net exports (the terms of trade track the real exchange rate closely in this setting). As the shock to oil supply leads to a very persistent rise in oil prices, consumption smoothing dictates a quick offset of the deficit from the oil side of the trade balance by a surplus in the nonoil balance. If the offset were delayed, a greater accumulation of debt and related interest rate payments would reduce future consumption inefficiently. The imposition of the zero bound does not change the response of the external sector qualitatively. Quantitatively, however, lower real rates at home imply a larger depreciation of the real exchange rate (shown as an upward movement in Figure 2). Consequently real net exports expand more, but the trade balance expressed as a nominal share of GDP is little changed.

Figure 2. An Oil Demand Shock at the Zero Lower Bound: Trade Flows

Figure 2: Our analysis focuses on the effects of oil shocks against the backdrop of an initial severe recession in the home country. The initial recession is generated by a preference shock, $\nu _{ct}$, that follows an autoregressive process with persistence parameter equal to 0.9. The shock reduces the home country's marginal utility of consumption. As a result of the shock, monetary policy attempts to stimulate the economy by lowering rates, but the policy rate reaches the zero lower bound, which is expected to bind for 10 quarters at the point in which the additional oil shock strikes. As the initial consumption shock occurs exclusively in the home country, the foreign economy has latitude to offset much of the contractionary spillover impact by reducing its policy rate. Figures 1 and 2 consider the effect of an oil demand shock abroad against the severe domestic recession. The oil demand shock has a persistent growth component and a level error correction component. The process governing the shock is: \[ \mu_{OYt} = (1+\rho^1_{\mu_{OY}}+\rho^2_{\mu_{OY}}) \mu_{OYt-1} - \rho^2_{\mu_{OY}} \mu_{OYt-2}. \] We set $\rho^1_{\mu_{OY}}=0.5$ and $\rho^2_{\mu_{OY}}=0.02$. Furthermore, there is perfect correlation between $\mu_{OYt}$ and $\mu_{OCt}$, respectively the demand shock for oil in production, and the demand shock for oil in consumption.\footnoteSS{In our model the unconditional behavior of oil prices reflects a variety of shocks and their propagation mechanisms. Accordingly, the finding that a simple unit root process provides a good fit for the behavior of oil prices in the postwar period does not imply that all structural shocks affecting the oil market should themselves be governed by unit root processes.} As shown in Figure 1, the price of oil deflated by the price of the domestic nonoil good rises for one year, then slowly declines. All the responses shown are presented in deviation from the path implied by the initial severe recession. Each panel in the figure shows three lines: the response to the shock against the background of the severe recession, the solid lines; the response to the shocks in normal times when the zero lower bound does not bind, the dashed lines; and the response to the shock in an economy with flexible prices and wages, the dotted lines. The shock is unchanged for the three cases shown and the relative price of oil shows negligible differences across the cases. The form of the interest rate reaction function, our modified Taylor rule, was chosen so that there would only be quantitatively small differences between the effects of the shock with and without nominal rigidities, as long as the zero lower bound is not enforced, or equivalently in a linear setting, as long as zero lower bound does not bind. We interpret the proximity of such responses, the dashed and the dotted lines in Figure 1, as heuristic evidence that the monetary policy rule is nearly optimal, at least in the case of an oil demand shock.\footnoteSS{Characterizing the optimal response exactly is no small task in the presence of the zero lower bound. The task is made more difficult by the open economy nature of the model.} In all of the cases shown, the persistent rise in the price of oil induces a fall in home oil demand. Both households and firms substitute away from the more costly oil input. The decline in oil use has effects on gross nonoil output, the expenditure components, and the real interest rate that resemble those of a highly persistent decline in productivity. Lower oil use leads to a fall in the current and future marginal product of capital, causing investment and gross output to fall. In the long term the capital stock also falls. Consumption contracts due to a reduction in household income. Strikingly, the imposition of the zero lower bound can generate persistent qualitative differences in the response of real GDP. GDP temporarily \emph{rises} at the zero lower bound, while it falls uniformly when the zero bound is not binding. Morevor, at the zero bound, the eventual fall of GDP is cushioned persistently. In the simulation that enforces the zero bound, GDP remains above its unconstrained level for years past the end of the liquidity trap. As policy rates are constrained, and as the oil shock generates a persistent increase in inflation, the short-term real interest rate falls more, cushioning the fall of investment. The cushioning of the investment props up the capital stock in such a way as to introduce a persistent wedge between real (nonoil) gross output at the zero bound relative to its counterpart in normal times. Due to the presence of consumption habits and investment adjustment costs, as well as to the phasing in of the oil shock, gross output only falls gradually. In this setting, the difference between gross output and GDP is a wedge implied by the presence of imported oil inputs in production. The initial fall is gross output happens to be small enough that the contraction in oil imports brought about by higher oil prices translates into a boost to GDP. Turning to the implications for the external sector, while the responses of investment and gross output to the oil supply shock resemble those of a persistent contraction in technology, the exchange rate response does not.\footnoteSS{The benchmark calibration of the trade elasticity around unity implies an appreciation of the real exchange rate in reaction to a persistent contraction in technology.} Since the rational expectations solution requires that the net foreign asset position is bounded away from infinity (conditional on current information), the home country's nonoil balance must improve enough to offset the long-run deterioration in the oil balance, as well as to finance interest payments on the stock of debt accumulated along the transition path. Thus, as the home economy faces the burden of a larger oil deficit, the exchange rate depreciates, which stimulates home nonoil net exports (the terms of trade track the real exchange rate closely in this setting). As the shock to oil supply leads to a very persistent rise in oil prices, consumption smoothing dictates a quick offset of the deficit from the oil side of the trade balance by a surplus in the nonoil balance. If the offset were delayed, a greater accumulation of debt and related interest rate payments would reduce future consumption inefficiently. The imposition of the zero bound does not change the response of the external sector qualitatively. Quantitatively, however, lower real rates at home imply a larger depreciation of the real exchange rate (shown as an upward movement in Figure 2). Consequently real net exports expand more, but the trade balance expressed as a nominal share of GDP is little changed.

Figure 3. An Oil Demand Shock at the Zero Lower Bound: Monetary Policy Rule with No Smoothing

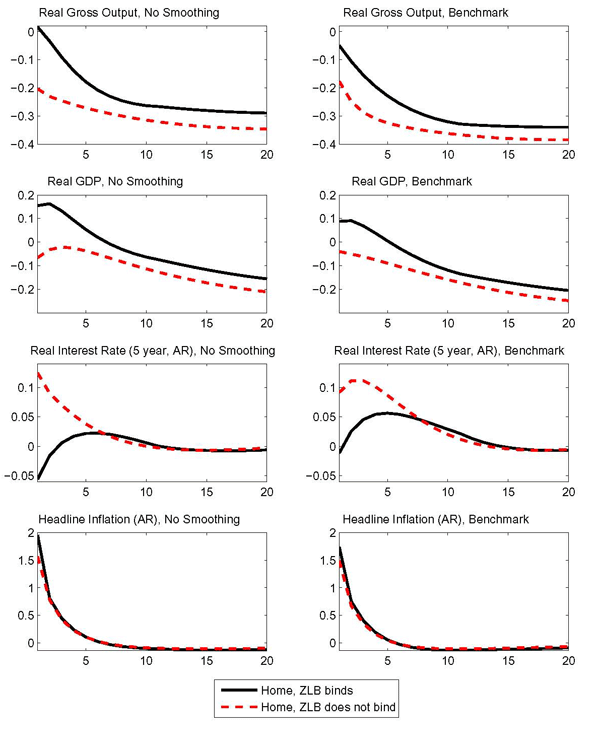
Figure 3: We consider sensitivity analysis for the specification of monetary policy with respect to two important dimensions: the interest rate smoothing and the measure of inflation included in the rule. The panels in the left column of Figure 3 reports responses to the same foreign demand shock as considered in the benchmark experiment described. However, the monetary policy rule used in this case excludes the lagged interest rate term by setting $\gamma_i$ to zero. For ease of comparison, the panels in the right column of Figure 3 reproduce the benchmark results. Away from the lower bound, the rule that excludes the smoothing term induces a less persistent rise in real rates in response to the same oil shock, enhancing the inflation response and further cushioning the effects at the zero lower bound. On impact, with the less aggressive rule, the initial rise in GDP is almost doubled relative to the benchmark case. Moreover, the the wedge between the response of GDP at the zero bound and its counterpart away from the zero bound is also enhanced quantitatively. The particular inflation measure included in the rule is also important. Our benchmark rule responds to current core inflation (the inflation for the price of the consumption basket with the oil component stripped out). A number of central banks characterize their policies as focusing on a forecast of future headline inflation. When faced with temporary increases in the price of oil, rules that incorporate a forecast of headline inflation can look past the peak inflation response and lower rates in anticipation of the expected decline in oil prices.

Figure 4. An Oil Demand Shock at the Zero Lower Bound: Monetary Policy Rule Responds to a Forecast of Headline Inflation

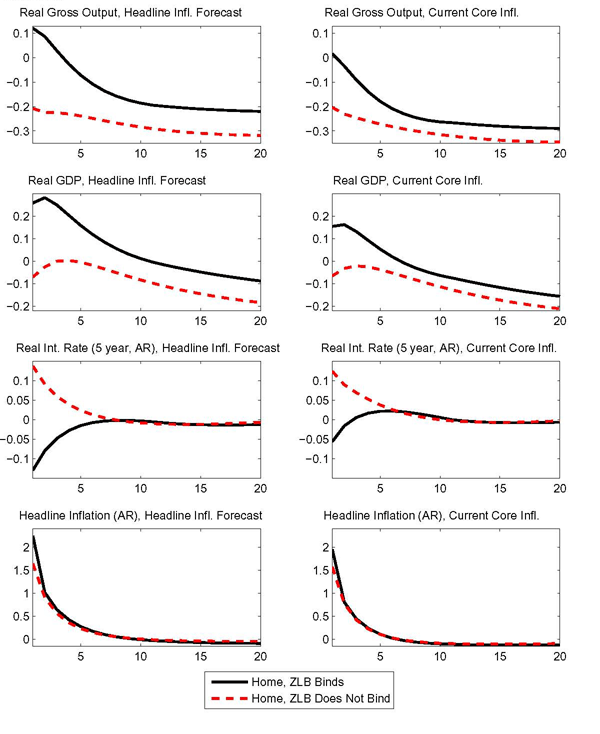
Figure 4: The responses shown in the left panels of Figure 4 build on the previous sensitivity exercise by not only doing away with the smoothing term in the monetary policy rule, but also substituting the current core inflation measure with the forecast of next period headline inflation rate. For ease of comparison the panels in the right column of the figure report the effects of the same foreign oil demand shock for the case in which the only modification to the rule involves the exclusion of the smoothing term and the rule responds to current core inflation. As shown in the bottom panels of Figure 4, the rule that responds to headline inflation implies a larger inflation response. At the zero bound, more inflation translates into a bigger fall in the real interest rate. Investment and consumption still fall, but are propped up relative to their response under the rules considered previously. Moreover, the fall in net real rates enhances the exchange rate depreciation. The consequent boost to net exports leads to a temporary expansion in gross output. Under this alternative rule, at the zero bound real GDP rises close to 0.3 percent on impact, while it drops almost 0.1 percent in normal times.

Figure 5. An Oil Demand Shock at the Zero Lower Bound: No Habit Persistence

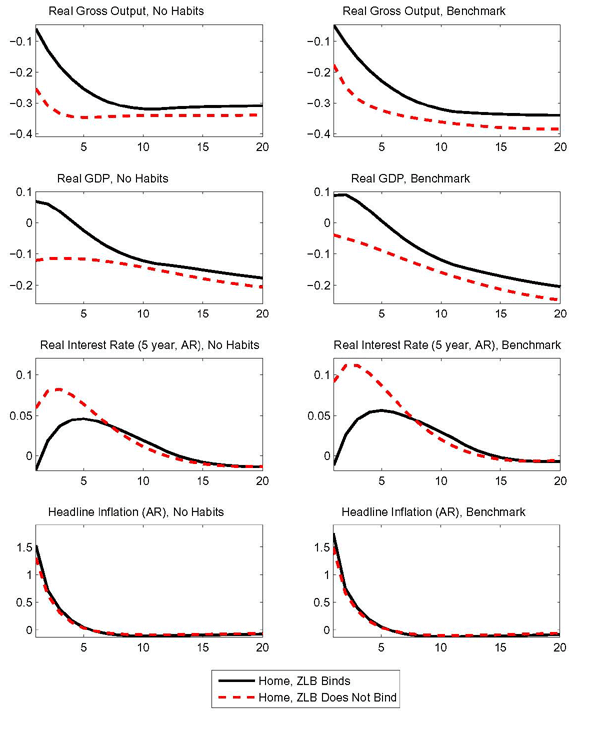
Figure 5: The wedge between the responses to the oil demand shock at the zero bound relative to normal times stem from the lowering the profile of real rates. By incorporating consumption habits, the benchmark calibration constrains the economy's interest sensitivity. The left panels of Figure 5 report the response to the foreign oil demand shock for a calibration of the model that excludes consumption habits. The panels in the right column replicate the responses for the baseline calibration with consumption habits. As in normal times the benchmark policy rule implies a rise in the longer-term real interest rates such as the 5-year rate shown in the figure, the decline in private absorption is amplified by the exclusion of habits. However, a higher degree of interest rate sensitivity implies that at the zero lower bound lower real rates relative to the unconstrained case can generate a larger wedge relative to the unconstrained responses.

Figure 6. An Oil Demand Shock at the Zero Lower Bound: Alternative Preferences

Figure 6 compares the effects of an oil demand shock under two preference specifications. The left panels in the figure reproduce the results from the benchmark model with preferences that follow those in Greenwood and Hercowitz and Huffman (1988). The right panels in Figure \ref{figure_noghh} show responses from a model with the commonly used specification of additively separable preferences over consumption and leisure. Under this alternative, the utility functional of a typical member of household $h$ is \begin{eqnarray*} \mathbb{E}_{t}\sum_{j=0}^{\infty }\beta ^{j} && \left[ \frac{1}{1-\sigma }\left( C_{t+j}\left( h\right)-\phi_c \frac{% C_{t+j-1}}{\zeta }\right) ^{1-\sigma} + \right. \\ && \left. \frac{% \chi _{0}}{1-\chi }(1-N_{t+j}\left( h\right) )^{1-\chi } + V\left( \frac{MB_{t+j+1}\left( h\right) }{P_{t+j}}\right)\right]. \label{utilityfunctional} \end{eqnarray*} Under the alternative, we left the function $V$ unchanged relative to the benchmark specification. Also unchanged are the values chosen for the parameters $\sigma, \phi_c, \zeta,$ and $\chi$. We calibrated the value for the parameter $\chi_0$ so that employment comprises one-third of the household's time endowment as for the benchmark preferences. The additively separable preferences let the marginal utility of consumption influence labor supply. As shocks that push up the price of oil compress consumption for the home oil-importing country, the marginal utility of consumption increases and stimulates labor supply. Figure 6 shows an expansion in labor supply both in normal times and at the zero lower bound for the alternative preferences. Under additively separable preferences, an increase in the price of oil can lead to such an increase in labor supply that gross output and GDP expand even when the economy is not in a liquidity trap. By contrast, in the benchmark model it is the liquidity trap that initially reverses the sign for the response of GDP. However, under both types of preference, the zero lower bound cushions the eventual contraction of economic activity.

Figure 7. An Oil Demand Shock at the Zero Lower Bound: Comparison with a Policy Model

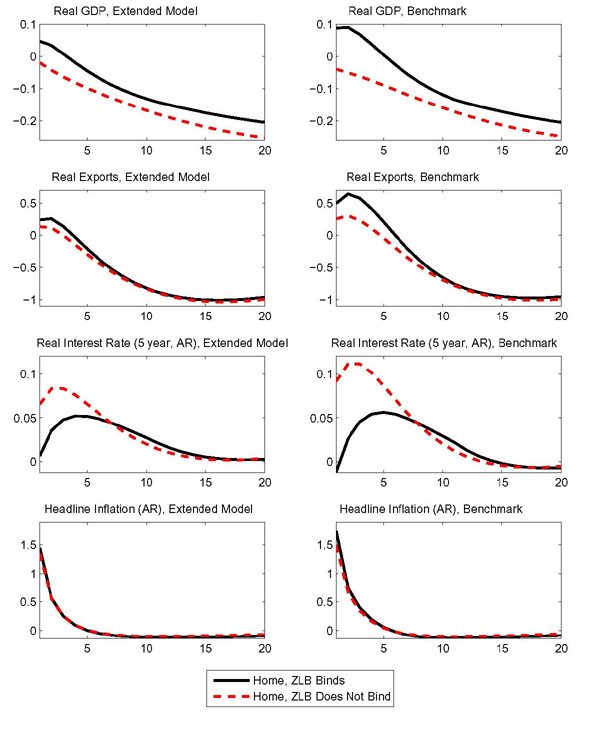
Figure 7 compares the effects of an oil demand shock in the benchmark model with an extension that incorporates financial frictions and limited exchange rate pass-through to import prices. Both of these features could potentially diminish the expansionary effects that oil price shocks have at the zero lower bound. With financial frictions, the relevant real interest rate that affects investment demand is no longer the risk-free rate but one that takes into account an asymmetric information problem between borrowers and lenders. If this asymmetric problem worsens in response to higher oil prices, there can be a more severe contraction in investment, which all else equal induces deflationary pressure. Accordingly, at the zero lower bound, real policy rates may not fall as much, reducing the stimulative effects of higher oil prices at the zero lower bound. Similarly, lower exchange rate pass-through can potentially reduce the inflationary effects that occur when the home currency depreciates in response to the rise in oil prices. The panels in the first column of Figure 7 show the response of key variables in the extended model to the oil demand shock when monetary policy is constrained by the zero lower bound and when its unconstrained. For purposes of comparison, the panels on the right show the analogous responses in the benchmark model. In both the benchmark and extended models, GDP falls when monetary policy is unconstrained and rises when the zero lower bound constraint binds. Relative to the benchmark model, the stimulative effects of the oil price shock at the zero lower bound are only marginally smaller in the extended model. These smaller effects mainly reflect the reduction in pass-through, which mitigates the rise in inflation associated with higher oil prices. The rise in inflation is smaller in the extended model, because exchange rate pass-through is lower, which implies that import prices do not rise as much when the home currency depreciates. As a consequence, there is less monetary stimulus in the extended model at the zero lower bound than in the benchmark model. However, as shown in Figure 7, the difference in the response of headline inflation and in long-term rates across the two models is very small. This small difference in part reflects that the exchange rate tends to depreciate by more in the extended model, as lower pass-through tends to amplify exchange rate movements, which all else equal increases the inflationary consequences of the oil demand shock. To understand why the financial accelerator mechanism does not reduce the stimulative effects of oil shocks at the zero lower bound, recall that the asymmetric information problem between borrowers/enterpreneurs and lenders gives rise to a spread between interest rates used to finance capital purchases and the risk-free rate. This spread varies with the total demand for funds by borrowers (i.e., their capital purchases) less their net worth. Because higher oil prices reduce the demand for capital somewhat more than a borrower's net worth, the spread actually falls slightly, and there is little change in the results once financial frictions are incorporated into the model. Moreover, we find that there is little change in results across a broad range of parameter values characterizing this financial friction.

Figure 8. An Oil Supply Shock at the Zero Lower Bound

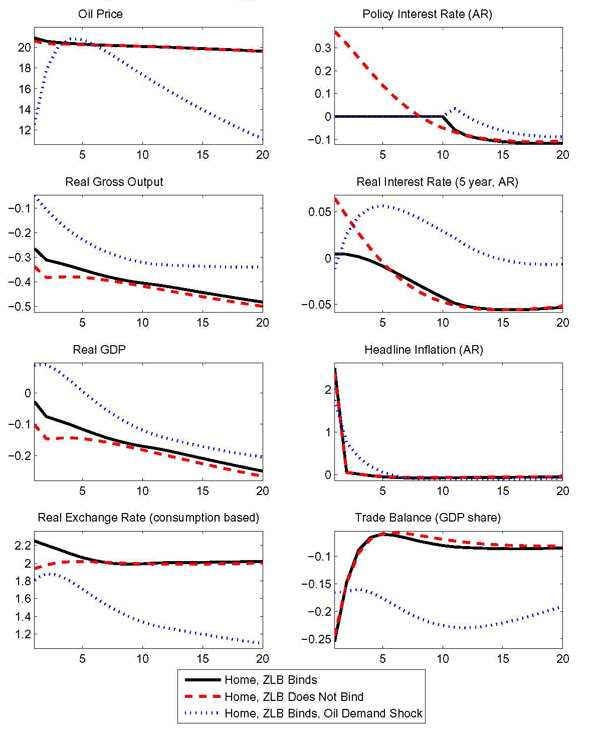
Figure 8 shows the domestic response to a foreign oil supply shock both when the economy is mired in a liquidity trap and in normal times. For ease of comparison, we also show the responses to an oil demand shock. The contraction in foreign oil supply is sized to match the peak of the oil demand shock discussed earlier. However, in contrast to the oil demand shock, the supply shock does not lead to a protracted rise in inflation. Apart from the initial period, headline inflation is close to zero. Thus, the real interest rate is little changed at the zero bound and the shock has similar effects at the zero bound and in normal times. The nearly permanent foreign supply contraction leads to a persistent fall in domestic activity, and a persistent deterioration of the home country's oil balance that is mostly offset by an improvement in the nonoil trade balance. The latter is brought about by a persistent depreciation of the home country's real exchange rate. If the oil supply shock lead to a period of increasing oil prices similar to the oil demand shock and thus to protracted inflation, the oil supply shock would be compressed in the same manner. However, oil supply and demand shocks differ along exactly this dimension: oil supply shocks are near unit-root processes, but oil demand shocks are best described as AR(2) processes. \footnoteSS{Our finding, that the transmission of highly persistent oil shocks hardly differs when they occur against the backdrop of a large recession compared to normal times does not depend on our assumption of incomplete financial markets. If international financial markets were complete, the domestic country could smooth the effects of the oil shock by running a persistent trade deficit. However, a near unit-root shock to oil supply would still imply a very short-lived increase in inflation.

Figure 9. A Technology Shock at the Zero Lower Bound

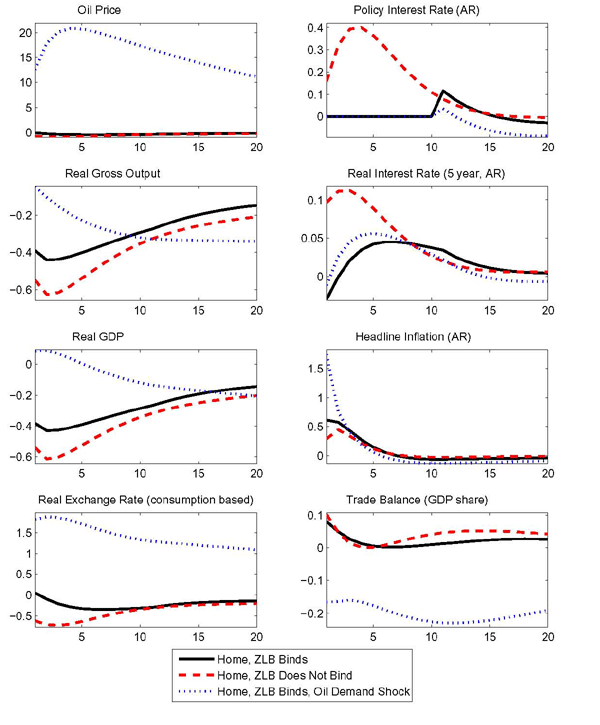
Figure 9 shows the effects of a 1\% temporary decline in the level of the home country's productivity. The oil price response implied by the technology shocks is not large enough to substantially affect the transmission of technology shocks. However, as such shocks lead to a rise in inflation made persistent by the real rigidities in our model (adjustment costs for investment, consumption habits, and lagged price and wage indexation), their effects are also cushioned at the zero bound relative to normal times. In contrast to the oil demand shocks, the technology shock primarily affects output rather than inflation. With gross output falling sharply on impact, the stimulating effect of lower real interest rates caused by positive inflation at the zero bound cannot reverse the sign of the GDP response on impact.

A  Numerical Implementation

Svensson and Laséen (2009) suggested a method for obtaining simulations with arbitrary restrictions on the path of the nominal interest rate in a linear model with perfect foresight. A desired path for the nominal interest rate can be implemented through a sequence of anticipated monetary policy shocks in the interest rate reaction function of the policy maker.

Consider the policy rule for the notional policy rate and the definition of the effective interest rate in equations (22) and (23), which we repeat below for convenience:

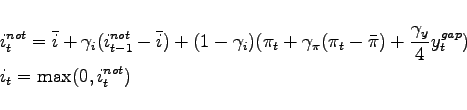
\begin{eqnarray*} && i_{t}^{not}= \bar{i} + \gamma _{i} (i_{t-1}^{not} - \bar{i}) +(1-\gamma _{i})(\pi_t + \gamma_{\pi }(\pi _{t}-\bar{\pi})+\frac{\gamma _{y}}{4}y_{t}^{gap}) \ && i_{t} = \max(0,i_{t}^{not}) \end{eqnarray*}

Repurposing the method outlined in Svensson and Laséen (2009) to implement the zero lower bound constraint implies replacing the $\max$ operator in the definition of the effective rate with:

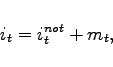\begin{displaymath} i_t = i_t^{not} + m_t, \end{displaymath} (26)

where $m_t$ is the current monetary policy shock. The current shock is itself linked to past shocks in the following fashion:

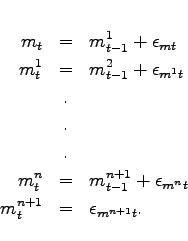
\begin{eqnarray*} m_t &=& m^1_{t-1} + \epsilon_{mt} \ m^1_{t} &=& m^2_{t-1} + \epsilon_{m^1t} \ & . & \ & . & \ & . & \ m^{n}_{t} & = & m^{n+1}_{t-1} + \epsilon_{m^{n}t} \ m^{n+1}_t & = & \epsilon_{m^{n+1}t}. \end{eqnarray*}

Notice that this shock structure has the convenient property that $E_t m_{t+i} = m^i_t$.

Following Anderson and Moore (1985), the linear approximation to the decision rule for our model in the neighborhood of its non-stochastic steady state can be represented as:

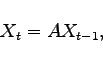
\begin{displaymath} X_t = A X_{t-1}, \end{displaymath}

where $X_t$ is a vector of all the variables in the model expressed in deviation from the steady state. Equation (A) implies that

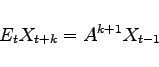
\begin{displaymath} E_t X_{t+k} = A^{k+1} X_{t-1} \end{displaymath}

for all $k \in \mathbb{N}$. Let $A^{k+1}_{[i]}$ denote the row of the matrix $A^{k+1}$ that corresponds to the effective policy interest rate $i$. We can then trace the expected path for the notional interest rate using the following equation:

\begin{displaymath}\left( \begin{array}{c} i_t \ E_t i_{t+1} \ . \ . \ . \ E_t i_{t+n} \end{array} \right) = \left[ \begin{array}{c} A_{[i]}\ A^2_{[i]} \ . \ . \ . \ A^{n+1}_{[i]} \end{array} \right] X_{t-1}. \end{displaymath} (27)

The last equation suggests that we can use the predetermined values for the monetary policy shocks described above, $m^1_{t-1}, ..., m^{n+1}_{t-1}$, to achieve any desired expected path for the effective interest rate. Denoting $A^{k+1[m]}_{[i]}$ the columns of row vector $A^{k+1}_{[i]}$ that correspond to the shocks $m^1_{t-1}, ..., m^{n+1}_{t-1}$ we can obtain:

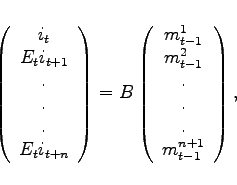\begin{displaymath} \left(\begin{array}{c} i_t \ E_t i_{t+1} \ . \ . \ . \ E_t i_{t+n} \end{array} \right) = B \left( \begin{array}{c} m^1_{t-1} \ m^2_{t-1} \ . \ . \ . \ m^{n+1}_{t-1} \end{array} \right), \end{displaymath} (28)

and where $B$ is a square matrix given by

\begin{displaymath}B = \left[ \begin{array}{c} A^[m]_{[i]}\ A^{2[m]}_{[i]} \ . \ . \ . \ A^{n+1[m]}_{[i]} \end{array} \right] \end{displaymath} (29)

Accordingly, we can invert the system of equation above to find the predetermined values for $m^1_{t-1}, ..., m^{n+1}_{t-1}$ that will achieve a desired expected path for the effective interest rate (equivalently, we could back out the relevant innovations $\epsilon_{mt},...,\epsilon_{m^nt}$).

Implementing the zero lower bound involves constraining the effective rate to remain at zero in those periods when the notional interest rate falls below zero and otherwise equating the effective and notional rates. We can endogenize the duration of the liquidity trap contingent on the realization of particular shocks with the following algorithm:

  1. Guess duration of the liquidity trap based on periods in which the ``unconstrained'' decision rule in equation (A) implies a negative value for the potential interest rate 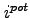$i^{pot}$ in response to the shocks.
  2. Based on equation (28), choose a sequence of foreseen monetary policy shocks to enforce the zero lower bound constraint. Only those periods for which the constraint is enforced need to be considered in (28).
  3. Revise the duration of liquidity trap given the sequence of monetary policy shocks; if in any period $i^{not} > i$ do not enforce the zero lower bound for that period.
  4. Repeat steps 2 and 3 above until no revision to the periods in which to enforce the zero lower bound constraint is necessary.

Relative to the algorithm described by Jung, Teranishi, and Watanabe (2005), this algorithm has several advantages: 1) it deals naturally with cases in which the zero lower bound constraint binds only after a number of periods from the shock's impact; 2) the extension to multicountry models simply requires stacking the paths for the effective policy rates across countries in equation (28); 3) for models with a large number of state variables, the inversion equation (28) is faster than the inversion of the entire decision rule required by the method in Jung, Teranishi, and Watanabe (2005). Relative to the implementation suggested by Hebden, Lindé, and Svensson (2010), our algorithm involves fewer iterations.


B  Baseline Simulation

Figure 10 shows the response to the consumption shock that generates the initial conditions for the benchmark simulation of an oil demand shock, shown in Figures 1 and 2, and for the oil supply and technology shocks shown in Figures 8 and 9. As parameter changes can affect the expected duration of the zero lower bound, to make the simulations comparable, we changed the size of the underlying preference shock so as to keep the duration of the liquidity trap unchanged.

In all cases, the preference shock $\nu_{ct}$ affects the home country only. Home consumption declines sharply, as does inflation. The economy's output falls below its potential level in the absence of sticky prices and wages. Home policy rates are cut gradually because of the smoothing term in the benchmark rule. However, after one quarter, the nominal policy rate reaches its lower bound indicated by a fall to -4 % in the figure. The drop in inflation and the size of the output gap shown in Figure 10 might seem outsize relative to the recent U.S. experience.

Our benchmark model implies little inflation persistence, but the addition of real rigidities such as variable price markups considered as sensitivity analysis, and lagged indexation would reduce the drop in inflation in Figure 10 to a magnitude in line with the recent experience. These features would also cushion the movement in the output gap. However, these additional complications would imply little change in our simulation results for the effects of oil shocks. The increased inflation persistence would compensate for the smaller initial change in influencing longer term real interest rates that affect the response of consumption and investment in our model. Accordingly, we decided to omit such features from the discussion.

All of the simulations presented in the main body of the paper start in the first period of the liquidity trap, so that agents expect the trap to last 10 quarters in the absence of additional shocks, but are surprised by one more shock.

Figure 10. A Severe Domestic Recession that Takes the Home Economy to the Zero Lower Bound on Policy Rates

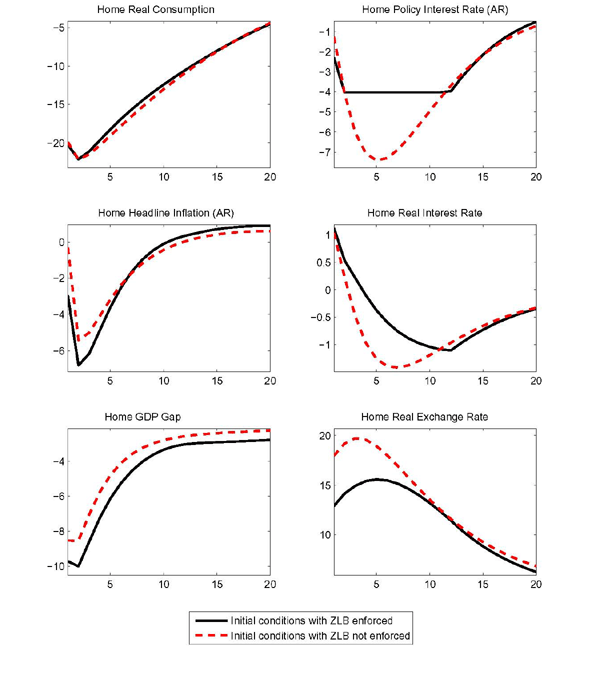
Figure 10 shows the response to the consumption shock that generates the initial conditions for the benchmark simulation of an oil demand shock. As parameter changes can affect the expected duration of the zero lower bound, to make the simulations comparable, we changed the size of the underlying preference shock so as to keep the duration of the liquidity trap unchanged. In all cases, the preference shock $\nu_{ct}$ affects the home country only. Home consumption declines sharply, as does inflation. The economy's output falls below its potential level in the absence of sticky prices and wages. Home policy rates are cut gradually because of the smoothing term in the benchmark rule. However, after one quarter, the nominal policy rate reaches its lower bound indicated by a fall to -4 \% in the figure. The drop in inflation and the size of the output gap shown in Figure 10 might seem outsize relative to the recent U.S. experience. Our benchmark model implies little inflation persistence, but the addition of real rigidities such as variable price markups considered as sensitivity analysis, and lagged indexation would reduce the drop in inflation in Figure 10 to a magnitude in line with the recent experience. These features would also cushion the movement in the output gap. However, these additional complications would imply little change in our simulation results for the effects of oil shocks. The increased inflation persistence would compensate for the smaller initial change in influencing longer term real interest rates that affect the response of consumption and investment in our model. Accordingly, we decided to omit such features from the discussion. All of the simulations presented in the main body of the paper start in the first period of the liquidity trap, so that agents expect the trap to last 10 quarters in the absence of additional shocks, but are surprised by one more shock.


Footnotes

**  The views expressed in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text

***  Corresponding author. Telephone (202) 452 2550. E-mail Luca.Guerrieri@frb.gov. Return to text

1.  See Bernanke, Gertler, and Watson (1997), Hamilton and Herrera (2004), and Leduc and Sill (2004). Return to text

2.  See, for example, Eggertsson (2006), Christiano, Eichenbaum, and Rebelo (2009). Return to text

3.   The Bank of England and the European Central Bank, for example, focus on headline inflation both in framing objectives, and as an operational guide to policy; while others appear relatively more concerned with the behavior of core inflation, at least in describing the basis for policy decisions. For example, the Bank of England has a target of 2% that is expressed in terms of headline inflation. It describes operational policy as adjusting interest rates so that its forecast of headline inflation reverts to target within a reasonable time frame without inducing undue instability in real activity (see http://www.bankofengland.co.uk/monetarypolicy/framework.htm).  Return to text

4.   Relative to the work of Christiano, Eichenbaum, and Evans (2005) and Smets and Wouters (2003), our model is extended to a two-country setting that incorporates trade in oil and nonoil goods, as well as incomplete financial markets across countries. Return to text

5.   More formally, we follow Jeanne and Svensson (2007) in assuming that $ V\left( MB_{t+1}/P_{t}\right) <V_{0}$, $V^{\prime }\left( MB_{t+1}/P_{t}\right) >0$, $V^{\prime \prime }\left( MB_{t+1}/P_{t}\right) <0$ for $MB_{t+1}<\bar{m}$, the satiation level of real money. And $V\left( MB_{t+1}/P_{t}\right) =V_{0}$ for $MB_{t+1}\geq \bar{m}$, and $V^{\prime }\left( MB_{t+1}/P_{t}\right) \rightarrow \infty $ for $MB_{t+1}/P_{t}\rightarrow 0.$ Return to text

6.   As discussed in Erceg, Guerrieri,a nd Gust (2006), our trade specification implies that the activity variable driving (nonoil) import and export demand can be regarded as a weighted average of consumption and investment, with the latter receiving a large weight consistent with the high weight of investment goods in U.S. trade. The paper also provides empirical support in favor of this specification over a specification in which the real activity variable driving trade is total absorption. See also Engel and Wang (2008). Return to text

7.   Jung, Teranishi, and Watanabe (2005), Eggertsson and Woodford (2003), Adam and Billi (2006), and Adam and Billi (2007) derive the optimal policy under the zero bound constraint in a closed economy. In the face of contractionary shocks, optimal monetary policy calls for keeping interest rates lower for an extended period in a liquidity trap relative to normal times. This feature is captured by interest rate smoothing in our model. Return to text

8.   A linear framework might appear at odds with the empirical work that has stressed asymmetries in the propagation of oil shocks to the macroeconomy. However, more recently, Kilian and Vigfusson (2009) found very little, if any, evidence of asymmetries in the response of U.S. GDP, unemployment, and gasoline consumption to energy price shocks. Return to text

9.   The steady state around which we linearize depends on the relative level of technology in each country, which we initialize to unity. Return to text

10.   Bodenstein, Erceg, adn Guerrieri (2009) discuss two alternative approaches for implementing the zero bound constraint. The first approach uses a shooting algorithm that builds on Fair and Taylor (1983) and is suitable even for fully nonlinear models under the assumption of perfect foresight. The second approach presented in Bodenstein, Erceg, and Guerrieri (2009) exploits the piecewise linearity of the model. All model equations are linear when the zero bound constraint binds, and they are also linear, albeit modified, when the zero bound constraint does not bind. However, the time period for which the economy is at the zero bound is a non-linear function of the exogenous disturbances. In particular for large-scale DSGE models, implementing the zero bound through a sequence of anticipated monetary policy shocks turns out to be computationally expedient relative to the methods described in Bodenstein, Erceg, adn Guerrieri (2009) as discussed in more detail in Appendix A.  Return to text

11.   The appendix provides further details about the initial recession that generates the predetermined conditions for the subsequent oil shock. Return to text

12.   In our model the unconditional behavior of oil prices reflects a variety of shocks and their propagation mechanisms. Accordingly, the finding that a simple unit root process provides a good fit for the behavior of oil prices in the postwar period does not imply that all structural shocks affecting the oil market should themselves be governed by unit root processes. Return to text

13.   Characterizing the optimal response exactly is no small task in the presence of the zero lower bound. The task is made more difficult by the open economy nature of the model. Return to text

14.   The benchmark calibration of the trade elasticity around unity implies an appreciation of the real exchange rate in reaction to a persistent contraction in technology. Return to text

15.   As changes in calibration affect the expected duration of the liquidity trap, we varied the size of the consumption shock that generates the initial severe recession in order to equalize the expected duration of the liquidity trap across calibrations. Return to text

16.   The large influence of wealth effect on labor supply with additively separable preferences is well understood. For instance, see Jaimovich and Rebelo (2009). Return to text

17.   To be specific, the AR(1) coefficient for home and foreign oil supply is set at 0.99. Return to text

18.   Our finding, that the transmission of highly persistent oil shocks hardly differs when they occur against the backdrop of a large recession compared to normal times does not depend on our assumption of incomplete financial markets. If international financial markets were complete, the domestic country could smooth the effects of the oil shock by running a persistent trade deficit. However, a near unit-root shock to oil supply would still imply a very short-lived increase in inflation. Return to text

19.   The AR(1) coefficient is set to 0.9. Return to text

20.   The mapping between oil shocks and technology shocks that is often asserted in the closed economy literature, e.g. Blanchard and Galí (2007), does not apply in our open economy model. Trade in oil and a long-run price elasticity of oil demand below unity are the key ingredients that make the mapping between oil and technology shocks inapplicable. Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

Home | Economic research and data | Publications and education resources
Accessibility | Contact us
Last update: October 25, 2010