
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 991, January 2010 --- Screen Reader
Version*
Heterogeneous Firms and Import Quality: Evidence from Transaction-Level Prices
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
A key emerging insight in international economics is that the scope for quality differentiation can help to explain patterns in export prices at the level of products or firms. In this paper, a unified theoretical framework of firm heterogeneity in cost and quality is brought to bear on an expansive data set of U.S. import transaction prices collected by the Bureau of Labor Statistics (BLS). The higher moments of the price distribution are used to identify the scope for quality differentiation at the detailed product level; highly differentiated products account for about half of U.S. import value. The product classification is then used to evaluate two claims in the nascent firm-level trade quality literature. First, the positive link between exporter capability and price is found to depend on the nature of the product: productive exporters simultaneously specialize in high-priced varieties in quality differentiated goods and low-priced varieties in more homogeneous goods. Second, a novel time series test documents firm sorting into export markets according to output quality.
Keywords: Quality differentiation, heterogeneous firms, firm sorting
JEL classification: F12, F41
Introduction
The price levels of internationally traded goods are largely driven by marginal costs of production, reflecting the underlying productivity differences across exporting firms, and product quality, the heterogeneity in desirable characteristics across competing varieties. A key emerging insight in international economics is that the scope for quality differentiation can help to explain observed patterns in average export prices at the level of products or firms.1 That is, in contrast to industry models of firm heterogeneity in which high productivity firms set lower prices,2 a theory in which higher productivity firms set higher prices for higher quality goods helps to match broad empirical facts. The tension between the lack of comprehensive measures of unobserved product quality and their usefulness in describing trade patterns has given rise to two common assertions, that: (i) firms sort into export markets according to their output quality, and (ii) capable exporters set high prices for high quality outputs. This paper evaluates these claims using newly developed methods and finds support for (i) and a modified version of (ii).
In addition to improving our understanding of trade patterns, quality's role in price setting has important implications for how we actually measure prices. Mis-measured or ignored compositional changes create bias in prices, as discussed at length in the index number literature,3 and there is mounting evidence that the dynamics of quality differentiated goods prices are different relative to those of more homogeneous goods.4 Therefore, there is strong impetus to be able to quantify the scope of quality differentiation across products and exporting countries, and to account for their respective dynamics. In this paper, a straightforward departure from existing 'cost' models of firm heterogeneity is modeled to allow for an endogenous array of quality types, and this unified framework is brought to bear on an expansive data set of transaction-level U.S. import and export prices collected by the International Price Program (IPP) of the Bureau of Labor Statistics (BLS). The focus is on the distribution of transactions prices and firm productivity within narrowly defined product groups to make inference as to the scope of unobserved product quality for the majority of U.S. trade, and to explore the higher moments of the price distribution. Indexes of exporter capability and quality are then constructed to measure their sensitivity to changes in the macroeconomy, across countries and over time.
The point of departure for these empirical exercises is a classification scheme of products according to their scope for quality differentiation5 which, in turn, is derived from the upper moments of the U.S. import price distribution. In section 1, I provide a descriptive analysis of U.S. import prices within detailed harmonized system 10-digit categories. I find significant clustering of prices within products and skewness that is highly industry-specific. I then extend a benchmark model of heterogeneous firms to show that these patterns are consistent with a theoretical framework in which firms endogenously choose their level of quality and sort into export markets accordingly. In section 2, I use the theoretical setup's sharp predictions about the higher moments of the price level distribution to identify differences in the scope for quality differentiation across product groups. This contrasts with prior studies of product or sectoral quality measurement, such as Hallak and Schott (2009), Khandelwal (2009), Baldwin and Ito (2008), Johnson (2008), Harrigan & Barrows (2006), Feenstra (1988) and Aw and Roberts (1986) in that it directly exploits intra-product pricing patterns without relying on inference from average prices at any level of aggregation. Moreover, it is argued that the identification of quality ladder length is robust to more general model specifications with variable markups across firms. Employing measured import price skewness, and controlling for other factors affecting the distribution of prices, 'cost' industries with low scope for quality differentiation are distinguished from 'quality' industries with a high scope for quality differentiation. I find that quality industries account for roughly half of U.S. import value.
Given the model and resulting classification scheme, it is possible to discern from price data alone the high productivity/high quality exporters from the low. The theory suggests that within an industry, each exporting country's productivity level and specialization in quality characteristics can be ascertained by its location in the U.S. import price distribution (i.e., a relatively high price in a long-quality ladder industry denotes both high quality and capability). In section 3, I use quantile regression techniques to identify country export productivity and find that, within a given sector, more productive countries tend to sell 'quality' products at higher prices and 'cost' products at lower prices on world markets. This result refines the income-quality nexus suggested by Schott (2004), Hummels and Klenow (2005) Hallak (2006) and Choi, Hummels and Xiang (2006), in that country export quality is not a monolith: high unit value prices in wealthier (more productive) countries belie specialization in low priced varieties in less-quality-differentiated sectors.
Finally, the paper provides a novel time series test of firm sorting by output quality. The model has stark implications for the average prices of imports in response to any shock that alters the composition of firms participating in trade. I describe and measure the implications of quality sorting for real-exchange rate pass-through; index number techniques are used to identify the relative price and quality of entering and exiting firms, and hence changes in composition due to the extensive margin. Consistent with the predicted ordering of firms in the model, I find that pass-through is systematically higher in unit values (i.e., not controlling for composition) than in constant-quality prices.
The remaining sections are organized as follows. The next section describes patterns in the price distribution of U.S. imports, which motivate the model of endogenous firm quality choice presented in section 2. Then, the cross-section and time series of the price and quality distributions in U.S. imports are detailed in sections 3 and 4, respectively. Section 5 concludes.
1 The IPP Import Price Data
The IPP data, which consist of transaction-level 'at-the-dock' prices for approximately 40,000 imported and exported items per month,6 provides a large breadth of coverage for roughly the entire range of U.S. goods import industries over the period 1994-2006. Transaction prices are surveyed from U.S. importers for uniquely defined items; IPP staff take a detailed description of each item and respondents are asked to provide its unit price on a monthly basis going forward. A panel of this size and diversity makes it an extremely useful tool in the investigation of international price-setting.7
Previously, studies have used national micro-data to investigate the quality composition of aggregate price deflators. For example, for the micro-data underlying the CPI, Bils (2004) quantifies the difference between price and quality growth by examining the point at which one product is substituted for another and the explicit quality adjustment made by the BLS. Bils's work is motivated by earlier estimates of quality bias in the CPI by the Boskin Commission (1996) and by Moulton and Moses (1997). Since the IPP constructs a matched model index for imports, which is quality-adjusted by construction,8 the empirical methods used by Bils are not applicable and new means of inference must be devised to obtain information about aggregate quality from individual prices. I begin by analyzing the price distribution for very disaggregate product groups, which offers some clues to that end.
In terms of classification, we consider the disaggregate, 'narrowly-defined' product group as a Harmonized System 10-digit (HS10) category. The IPP uses a similar definition called 'classification', which groups together smaller, similar HS10 products;9 since in roughly half of cases, classification groups are identical to HS10 groups (with the majority of the remainder containing two HS10 groups), I will refer to them synonymously. Examples of HS10 groups in U.S. imports are:
- Portable digital automatic data processing machine, not more than 10 kg, w/ CPU, keyboard & display
- Cucumbers, gherkins; Entry 12/1-end of February; fresh or chilled
The first example is simply the description ascribed to laptop computers, which composes the majority of the more aggregate HS6 category: handheld computers. In the IPP sample, a laptop price observation would be for a particular, precisely defined model and brand imported in a particular unit of measure, from a given country in a given month.10 For laptops, it is clear that most differentiation across laptops takes place within the HS10 group; that is, differentiation in screen size, memory and processor speed will all be reflected in price differences at the item level. In contrast, the category of winter cucumbers and gherkins is relatively homogeneous, and there are only six sub-categories defined by the USDA denoting cucumber coloration, formation and size. I will show that the price distribution is indeed quite different between these types of products, which can be used to distinguish their scope of quality differentiation.
The general contours of the sample of import prices at the HS10 level are as follows. The entire 12 year sample contains over 66,000 items (specific varieties) categorized into over 7,000 classification groups.11 Certain product groups (e.g. HS84 and HS85 which contain the sizable machinery and electric equipment categories) are relatively large, though the average number of items per classification group does not vary wildly across categories. Figure 1 shows an illustrative example of (log) import prices within a particular classification group over time. Each blue dot is a monthly import price for a specifically defined item,12 and the long, straight series of dots reflect the fact that most items do not change prices very frequently. For the product in Figure 1, the item prices tend to diminish over time, but the distribution in any given month looks fairly similar at any given point along the horizontal axis.
Generally, within HS10 groups (and in a given month) there is a clear distinction between the high and low priced goods, typically manifested in a tight group of prices around the median and a few outlying higher or lower priced items. The clustering of prices is consistent with what we would expect from a power law-type distribution of firm productivity in that the large mass of firms with similar (relatively low) productivity sets prices which are similar. Studies of detailed firm-level data, as in Bernard and Jensen (1999) and related works, have shown that the size distribution of firms, which moves in tandem with firm-level productivity in most models, looks something of this sort with a tight cluster of small firms and fewer, much larger firms. That right skewed shape has motivated the calibration assumption in quantitative trade models that the productivity distribution of firms is Pareto. Returning to our example in Figure 1, the high price outliers are exactly the opposite of what we would expect from a Pareto distribution of firm productivity since the large, high productivity firms should be setting prices that are low reflecting their cost advantages. One potential explanation is that more productive firms elect to produce higher quality, more costly goods whose prices are high outliers.
Aggregating across HS10 products and time within 16 broad sectors,13 Table 1 presents some of the moments of the import and export price distributions. The statistics are calculated monthly by HS10 group and then averaged over months and HS10 groups within a sector using sales weights. For U.S. imports, we confirm the significant clustering of prices across sectors, with the average kurtosis found to be greater than 3 (i.e., leptokurtic, with a more acute peak than a standard normally distributed variable). The skewness statistic, on the other hand, appears to have a large product- or industry-specific component. For industries we might imagine to have a lower degree of product differentiation, such as wood and mineral products, skewness is negative (i.e., skewed left; with low outliers). For industries with a higher degree of product differentiation and value added, such as textiles, electric machinery and computers, skewness is positive (i.e., skewed right; with high outliers). For U.S. exports, the skewness of prices tends to be lower overall but the ordering of sectors is remarkably similar, with primary goods and commodities more negatively skewed and higher value added manufacturing and technology sectors more positively skewed.14
Based on the observed distribution of price levels in the data, the skewness statistic is indicative of the type of differentiation in each industry. In the less quality-differentiated industries, one might expect a higher degree of cost and price competition, as goods are less defined by their characteristics. With more competition in cost, only the high productivity firm outliers are able to break from the cluster of median prices in each category to offer lower prices, thus skewness is negative. On the other hand, with a higher degree of differentiation in characteristics, it is only those firms that are productive enough to bear the costs of innovation and more intricate processes that are able to produce high quality, high priced goods, causing skewness to be positive.
The overall skewness of prices is positive, which is reflected in the higher incidence of high outliers relative to low outliers.15 This is consistent with empirical work such as Baldwin and Harrigan (2007), which suggests that on average, unit value prices are biased upward by quality. Here the data suggest that underlying the average positive skewness of U.S. import prices is an array of industries whose price distribution (and hence unit values) reflect the cost advantages of high productivity firms in two distinct ways. Also of interest is the observation that variable skewness across industries is caused not only by an increase in high priced outliers, but a decrease in low priced outliers. Aside from quality, another interpretation of low-price outliers is the new entry onto world markets of low cost producers, sometimes referred to as a 'Wal-mart effect.' In the following sections, I attempt to (jointly) quantify these effects for U.S. imports and find that there are very important product- and country-specific components that determine a good's likelihood of being a high or low outlier in the IPP sample. To guide those empirical exercises, in the next section I specify a model of firm heterogeneity in productivity and quality.
2 A Model of Endogenous Quality Choice
The model uses the probabilistic framework of firm heterogeneity
with monopolistically competitive firms distinguished in their
productivity, as in Melitz (2003) and several subsequent works.
Firms are differentiated along an array of productivities (indexed
by
![]() ) where each firm produces a
unique variety
) where each firm produces a
unique variety ![]() . Production of each variety in
every HS10 product group is subject to positive consumer demand
which, in turn, is based on a constant elasticity of substitution
sub-utility function:
. Production of each variety in
every HS10 product group is subject to positive consumer demand
which, in turn, is based on a constant elasticity of substitution
sub-utility function:
![$\displaystyle X=\left\{ \int_{\omega\in\Omega}\left[ x(\omega)z(\omega)\right] ^{\frac{\sigma-1}{\sigma}}d\omega\right\} ^{\frac{\sigma}{\sigma-1}} $](img3.gif)
where ![]() is the quantity of variety
is the quantity of variety
![]() , and
, and ![]() is the
'weight' attributed to the unique characteristics of that variety.
Of course, consumers only care about the composite good
is the
'weight' attributed to the unique characteristics of that variety.
Of course, consumers only care about the composite good
![]() , which defines the
'quality-adjusted' quantity
, which defines the
'quality-adjusted' quantity
![]() . Consumers
compare quality-adjusted varieties and their respective
quality-adjusted prices in deciding their purchase allocation,
where quality-adjusted price
. Consumers
compare quality-adjusted varieties and their respective
quality-adjusted prices in deciding their purchase allocation,
where quality-adjusted price ![]() is defined
as the sticker price
is defined
as the sticker price
![]() normalized by quality:
normalized by quality:
![]() . This
specification of utility gives rise to the standard demand and
expenditure (
. This
specification of utility gives rise to the standard demand and
expenditure (![]() ) functions in quality-adjusted
terms:
) functions in quality-adjusted
terms:
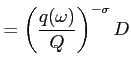 |
(1) | |
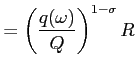 |
(2) |
where ![]() is a composite quantity of the
differentiated product and
is a composite quantity of the
differentiated product and ![]() aggregate
expenditure on that product. The aggregate quality-adjusted price
index is:
aggregate
expenditure on that product. The aggregate quality-adjusted price
index is:
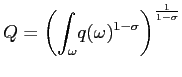 |
(3) |
Production accounts explicitly for the costs of quality, and
each firm employs labor inputs ![]() :
:
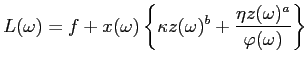 |
(4) |
Labor consists of a fixed cost ![]() and two variable
costs which are increasing in the level of quality. In order to
have an interior solution for quality level, the average cost of
quality must have a well-defined minimum. As I will show, a
sufficient condition for a non-degenerate distribution of quality
is
and two variable
costs which are increasing in the level of quality. In order to
have an interior solution for quality level, the average cost of
quality must have a well-defined minimum. As I will show, a
sufficient condition for a non-degenerate distribution of quality
is ![]() . What these unit cost curvature
assumptions imply is that there are increasing returns to quality
in
. What these unit cost curvature
assumptions imply is that there are increasing returns to quality
in
![]() , and decreasing returns to
quality in
, and decreasing returns to
quality in
![]() . For intuition, consider
. For intuition, consider
![]() to be a 'process'
component and
to be a 'process'
component and
![]() to be a 'monitoring'
component. Process costs, in addition to increasing in quality at
an increasing rate, are lower for more productive (higher
to be a 'monitoring'
component. Process costs, in addition to increasing in quality at
an increasing rate, are lower for more productive (higher
![]() ) firms. These can be understood as
something analogous to an input material cost: a graphite tennis
racquet costs more to produce than a wooden one, and a more
productive firm requires fewer people to assemble it. Units of
monitoring cost, on the other hand, increase in quality at a
decreasing rate and are the same across firms. One might imagine
this as quality control infrastructure: adding a supervisor to
inspect the tennis racquets for visible flaws decreases the
incidence of defects (i.e., increases quality), though his or her
cost is no greater for a graphite racquet than a wooden
one.16 This monitoring aspect of production
can alternatively be interpreted as a reduced form of the O-ring
production function proposed by Kremer (1993).17 In this case,
firms that choose to produce more complex/ higher quality products
have an incrementally higher wage bill due to monitoring costs.
) firms. These can be understood as
something analogous to an input material cost: a graphite tennis
racquet costs more to produce than a wooden one, and a more
productive firm requires fewer people to assemble it. Units of
monitoring cost, on the other hand, increase in quality at a
decreasing rate and are the same across firms. One might imagine
this as quality control infrastructure: adding a supervisor to
inspect the tennis racquets for visible flaws decreases the
incidence of defects (i.e., increases quality), though his or her
cost is no greater for a graphite racquet than a wooden
one.16 This monitoring aspect of production
can alternatively be interpreted as a reduced form of the O-ring
production function proposed by Kremer (1993).17 In this case,
firms that choose to produce more complex/ higher quality products
have an incrementally higher wage bill due to monitoring costs.
Given this technology, the Home firm's profit function is:
![$\displaystyle =x(\omega)\left\{ p(\omega)-w\left[ \kappa z(\omega)^{b}+\frac{\eta z(\omega)^{a}}{\varphi(\omega)}\right] \right\} -wf$](img31.gif)
|
where ![]() is the wage rate, considered exogenous by
the firm. The expression for profit can also be written in the
quality-adjusted notation described above:
is the wage rate, considered exogenous by
the firm. The expression for profit can also be written in the
quality-adjusted notation described above:
![$\displaystyle \pi(\omega)=d(\omega)\left\{ q(\omega)-w\left[ \kappa z(\omega)^{b-1} +\frac{\eta z(\omega)^{a-1}}{\varphi(\omega)}\right] \right\} -wf$](img33.gif) |
(5) |
Quality and quality-adjusted prices are chosen simultaneously by
the firm, which allows us to separate the firm problem into two
parts. For the quality component, (5) is
maximized by the firm with respect to ![]() (
(![]() ); given that the expression for profit is in terms
of quality-adjusted quantity and price, it is immediately clear
that maximizing profits is equivalent to minimizing the term in
square brackets, the average cost of quality:
); given that the expression for profit is in terms
of quality-adjusted quantity and price, it is immediately clear
that maximizing profits is equivalent to minimizing the term in
square brackets, the average cost of quality:
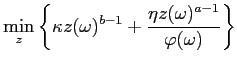
|
||
| (6) |
where
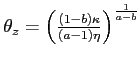 is a positive constant. The result is an expression for the
quality characteristics chosen by each firm as a function of its
productivity draw, where the quality of each variety is increasing
in the level of firm productivity.
is a positive constant. The result is an expression for the
quality characteristics chosen by each firm as a function of its
productivity draw, where the quality of each variety is increasing
in the level of firm productivity.
The pricing rule is derived by maximizing profits (5) with respect to the quality-adjusted price,
subject to the consumer demand relation (1).
This setup leads to the standard constant markup pricing rule for
the firm, only now the marginal cost term contains a measure of the
good's quality. Quality-adjusted price ![]() is expressed
in terms of
is expressed
in terms of ![]() ,
, ![]() and the
firm-specific productivity parameter:
and the
firm-specific productivity parameter:
![$\displaystyle q[z(\varphi),\varphi]=\left( \frac{\sigma}{\sigma-1}\right) w\left[ \kappa z(\omega)^{b-1}+\frac{\eta z(\omega)^{a-1}}{\varphi(\omega)}\right]$](img42.gif) |
(7) |
Substituting (6) into (7), the quality-adjusted price can be expressed purely as a function of the wage and productivity parameter:
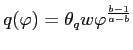 |
(8) |
where
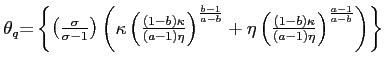 is a positive constant. The quality-adjusted price diminishes in
productivity, similar to the prices in Melitz (2003), which are a
CES markup of
is a positive constant. The quality-adjusted price diminishes in
productivity, similar to the prices in Melitz (2003), which are a
CES markup of ![]() .
.
Quality-inclusive prices can be reconstituted by multiplying quality-adjusted prices by quality:
| (9) |
where
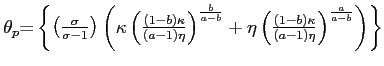 is a positive constant.
is a positive constant.
Equation (9) is particularly
interesting since prices are not constrained to be a negative
function of firm productivity. If
![]() , more productive firms
choose quality that is sufficiently high so as to increase price
relative to low productivity firms: this is what will be referred
to as a quality industry. If
, more productive firms
choose quality that is sufficiently high so as to increase price
relative to low productivity firms: this is what will be referred
to as a quality industry. If
![]() , more productive firms
choose higher quality, but cost advantages still lead them to set
lower prices relative to low productivity firms: this is what will
be referred to as a cost industry.
, more productive firms
choose higher quality, but cost advantages still lead them to set
lower prices relative to low productivity firms: this is what will
be referred to as a cost industry.
2.1 Distinguishing Cost vs. Quality Industries: U.S. Imports
In this section, the observed IPP import price moments are
matched with those predicted by the model in order to estimate the
parameters underlying the scope of quality differentiation across
products. The intuition behind this identification is that the
productivity (![]() ) distribution of firms, usually
assumed to be skewed right (i.e., with high outliers), maps very
differently into prices depending on the level of sectoral quality
differentiation. As in standard models, in more homogeneous sectors
high productivity maps directly into low costs and price, so the
distribution is skewed left (i.e., with low outliers). In contrast,
one might expect high productivity firms to be more adept at
producing quality characteristics, as demonstrated by the
equilibrium levels of quality in the model, so in quality
differentiated sectors high productivity maps into higher quality,
cost and prices; thus, the price distribution is also skewed
right.
) distribution of firms, usually
assumed to be skewed right (i.e., with high outliers), maps very
differently into prices depending on the level of sectoral quality
differentiation. As in standard models, in more homogeneous sectors
high productivity maps directly into low costs and price, so the
distribution is skewed left (i.e., with low outliers). In contrast,
one might expect high productivity firms to be more adept at
producing quality characteristics, as demonstrated by the
equilibrium levels of quality in the model, so in quality
differentiated sectors high productivity maps into higher quality,
cost and prices; thus, the price distribution is also skewed
right.
Switching to discrete notation, we have expressions for quality,
quality-adjusted price and quality-inclusive price by item
![]() , HS-10 product
, HS-10 product ![]() , country
, country
![]() , and month
, and month ![]() :
:
| Quality: | (10) | |
| Adjusted Price | : |
(11) |
| Inclusive Price | : |
(12) |
where
![]() ,
,
![]() and
and
![]() are positive
product-specific constants.
are positive
product-specific constants.
Taking logs of the quality-inclusive price (12) yields:
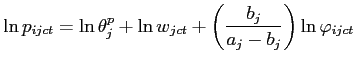
|
(13) |
As noted above,
![]() is the slope of the
productivity-price schedule, which I assume is HS10-specific: for
positive values, the costs of producing (a higher number of)
quality characteristics outweigh the cost savings of being farther
right along the productivity distribution. Since firm-level
productivity data are not available across a broad array of
products and countries to estimate (13)
directly, I proceed by using approximations of the
distribution of firm productivity and wage to try to
identify the sign and magnitude of
is the slope of the
productivity-price schedule, which I assume is HS10-specific: for
positive values, the costs of producing (a higher number of)
quality characteristics outweigh the cost savings of being farther
right along the productivity distribution. Since firm-level
productivity data are not available across a broad array of
products and countries to estimate (13)
directly, I proceed by using approximations of the
distribution of firm productivity and wage to try to
identify the sign and magnitude of
![]() . From (13), the second and third moments of the price
distribution can also be expressed as the following, derived in the
Appendix:
. From (13), the second and third moments of the price
distribution can also be expressed as the following, derived in the
Appendix:
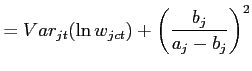
|
(14) | |
![$\displaystyle \frac{Skew_{jt}(\ln p_{ijct})}{\left[ Var_{jt}(\ln p_{ijct})\right] ^{-\frac{3}{2}}}$](img72.gif)
|
![$\displaystyle =\frac{Skew_{jt}(\ln w_{jct})}{[Var_{jt}(\ln w_{jct})]^{-\frac{3}{2}}}+\left( \frac{b_{j}}{a_{j}-b_{j}}\right) ^{3} \frac{Skew_{jt}(\ln\varphi_{ijct})}{[Var_{jt}(\ln\varphi_{ijct})]^{-\frac {3}{2}}}$](img73.gif)
|
(15) |
The left-hand side variables of (15) can be measured at the HS10 level using the IPP data, and the distribution of industry-level wage across countries is calculated using annual industry data from the ILO Yearbook of Labor Statistics.18 Since firm productivity measures are not available by product and source country, as a proxy for the firm productivity distribution I exploit another statistic used by the BLS in the construction of its aggregate international prices. Specifically, the IPP uses firm-level export sales weights to aggregate within HS10 groups for its U.S. export price indexes. To the extent that the size distribution of firm-level sales corresponds to firm productivity, these weights provide a handy approximation of the U.S. export productivity for thousands of disaggregate products, and I apply these weights uniformly to foreign exporters.19
Figure 2 portrays selected percentiles for the product-level skewness of transaction prices, exporter wages and firm export size. In the top-left panel, the import price skewness of the median HS10 product is roughly zero (i.e., prices for that HS10 are symmetrically distributed), with a substantial number of both positive and negative skewness products, This is consistent with the wide range of skewness statistics by sector in Table 1. Wages, on the other hand, shown in the top-left panel, are almost all left skewed, likely reflecting the high incidence of trade among high income countries, with low-wage exceptions. Finally, in accord with prior firm-level studies, U.S. export sales skewness by product shown in the bottom panel is predominantly positive.20
Denoting the dollar export weights ![]() , the
estimating equation for (15) is:
, the
estimating equation for (15) is:
| (16) |
where
![]() is the point estimate for
is the point estimate for
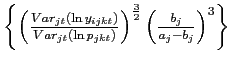 within a given HS6 category.21
within a given HS6 category.21
2.1.1 Variable Markups and (16)
What would be the implication for (16) if the firm's competitive environment also factored into its price-setting decision? For instance, if the underlying consumer demand for imports was of the translog functional form instead of CES, then the markup charged by firms of differing productivity would no longer be the same proportion of marginal cost. As a result, the pricing equation (9) would be different and observed skewness of prices would reflect variable markups in addition to quality differences. For the identification of the quality scope, this is a problem if the price distribution interacts with variable markups distinctly in low versus high scope industries.
Consider the relationship between markups and productivity when
consumers allocate consumption across varieties according to the
translog expenditure function. In that setting, more productive
firms are not only larger, with higher market share, they also
charge a higher percentage markup over their marginal cost. In an
industry with high scope for quality differentiation, indeed the
high-priced, high-quality varieties also have higher markups; part
of the observed price skewness in the industry is potentially
driven by markups. On the other hand, in an industry with low
scope, the productive firms with relatively high share and high
markups have relatively low prices. In those industries, the
observed price skewness is attenuated by variable markups
and is less negative as a result. In sum, variable markups of the
type described introduce an upward level-shift in measured
skewness. The fact that skewness is higher in both high and low
scope industries suggests that the bias in
![]() due to variable markups is of the
second-order: it depends not on the degree of markups but on the
difference of that degree across industries.
due to variable markups is of the
second-order: it depends not on the degree of markups but on the
difference of that degree across industries.
2.1.2 Results
The OLS regression of (16) is pooled
across all product categories for which price, wage and size data
are available: 41,633 product-time pair observations. Also included
are year dummy variables, to control for secular trends in the
respective distributions.22 This specification yields estimates
for approximately 1,100 HS6 categories, approximately 450 of which
are statistically distinguishable from zero.23 The resulting
estimates for the largest products by volume in cost industries
![]() and quality
industries
and quality
industries
![]() are shown
in Table 2. At first glance, the quality industries in the top
panel seem to conform to our prior notions of products with a high
degree of quality differentiation (e.g., passengers cars, clothing
and wine). Likewise, the bottom panel includes goods with a 'cost
story' such as machine parts and accessories, and metal furniture.
On the other hand, both panels contain products that are not so
intuitively categorized, such as transport motor vehicles and
parlour games in the cost panel, and liquefied butane in the
quality panel.
are shown
in Table 2. At first glance, the quality industries in the top
panel seem to conform to our prior notions of products with a high
degree of quality differentiation (e.g., passengers cars, clothing
and wine). Likewise, the bottom panel includes goods with a 'cost
story' such as machine parts and accessories, and metal furniture.
On the other hand, both panels contain products that are not so
intuitively categorized, such as transport motor vehicles and
parlour games in the cost panel, and liquefied butane in the
quality panel.
There are several reasons not to get bogged down in constructing stories to explain the level of quality differentiation across product groups. First, category definitions at the HS6 or HS10 level are somewhat arbitrary. For example, liquefied butane's largest HS category encompasses grades of the hydrocarbon between zero and 80 percent purity, which by definition is highly differentiated. Alternatively, if a new categorization scheme emerges including a separate group for a particular laptop brand with 2GB SD RAM and 80GB hard disk drive, we would not observe much quality differentiation within that product despite the fact that the broader product class has a lot of quality heterogeneity. What is important is that there is a consistent way to characterize what is going on within each product group, however defined. Second, the estimates should be interpreted in the context of U.S. import demand. A narrow scope for quality differentiation in transport vehicles reflects the fact that the U.S. imports a narrow range of these goods; therefore the measure should be interpreted as the scope of quality within an HS6 category conditional on an international transaction taking place.
Third, we must be careful to discern between horizontal and
vertical (quality) differentiation, where the former is
differentiation that occurs across product features that cannot be
ordered. For example it would be difficult to place ice cream as
either a cost or a quality industry; while there is a lot of
horizontal differentiation in flavors, it is not clear whether
there is a broad array of quality differences among similar flavors
coming from different producers. To check the extent that the
measured quality scope corresponds to product-level horizontal
differentiation, I compare
![]() with previous estimates by
Broda and Weinstein (2006) of intra-product elasticity of
substitution (
with previous estimates by
Broda and Weinstein (2006) of intra-product elasticity of
substitution (![]() ). In the CES framework above,
). In the CES framework above,
![]() indexes consumers' willingness to
substitute among quality-adjusted varieties, so in this context it
can be strictly interpreted as an index of horizontal
differentiation. In Table 2, there is no clear pattern between
indexes consumers' willingness to
substitute among quality-adjusted varieties, so in this context it
can be strictly interpreted as an index of horizontal
differentiation. In Table 2, there is no clear pattern between
![]() and
and ![]() , and on
average a slight negative relationship (i.e., cost industries have
a low
, and on
average a slight negative relationship (i.e., cost industries have
a low ![]() while quality industries have a high
while quality industries have a high
![]() ). Taking the model of vertical
differentiation very seriously, one might expect producers in a
horizontally differentiated sector (low
). Taking the model of vertical
differentiation very seriously, one might expect producers in a
horizontally differentiated sector (low ![]() ) to not
need to distinguish themselves as much vertically, however I find
that over all estimates the correlation between
) to not
need to distinguish themselves as much vertically, however I find
that over all estimates the correlation between
![]() and
and ![]() , albeit
measured with a large degree of error from both sets of parameter
estimates, is only 0.01.
, albeit
measured with a large degree of error from both sets of parameter
estimates, is only 0.01.
A more subtle point is that the sign of
![]() in (16)
could reflect the magnitude of the skewness of productivity rather
than its sign. That is, considering a product where both prices and
firm export size are positively skewed, a negative sign could still
arise for
in (16)
could reflect the magnitude of the skewness of productivity rather
than its sign. That is, considering a product where both prices and
firm export size are positively skewed, a negative sign could still
arise for
![]() if the prices are simply less
positively skewed relative to other product groups of equal
productivity skewness. Thus positive skew prices can still be cost
industries, which is less intuitive. As an indirect way of
decomposing how much of the scope estimates are due to sign versus
magnitude, the estimates are rerun for only the set of products
with both positively skewed prices and productivity.24 I
find that even though there are still quite a number of significant
negative estimates for
if the prices are simply less
positively skewed relative to other product groups of equal
productivity skewness. Thus positive skew prices can still be cost
industries, which is less intuitive. As an indirect way of
decomposing how much of the scope estimates are due to sign versus
magnitude, the estimates are rerun for only the set of products
with both positively skewed prices and productivity.24 I
find that even though there are still quite a number of significant
negative estimates for
![]() , the average magnitude of the
estimates changes substantially. For products with a significant
negative estimate (indicating that they are a cost industry) in the
unrestricted sample, the average size of
, the average magnitude of the
estimates changes substantially. For products with a significant
negative estimate (indicating that they are a cost industry) in the
unrestricted sample, the average size of
![]() is -1.70, compared to 22.30
for the identical set of products in the restricted sample. The
estimates for quality industries remain roughly unchanged at 4.82
in the unrestricted sample versus 3.42 in the restricted sample.
This suggests that the sign of price skewness plays a very
important role in determining cost versus quality industries.
is -1.70, compared to 22.30
for the identical set of products in the restricted sample. The
estimates for quality industries remain roughly unchanged at 4.82
in the unrestricted sample versus 3.42 in the restricted sample.
This suggests that the sign of price skewness plays a very
important role in determining cost versus quality industries.
Finally, applying the quality scope estimates, the share of U.S. import trade accounted for by cost and quality industries is illustrated in Figure 3. In panel (a), approximately 50-60 percent of total import value is categorized as either cost or quality, with the asterisk superscript denoting quality scope estimates that are significantly different from zero.25 Between 1993 and 2006, the share of cost industries declined from 40 percent to about 25 percent with quality industries growing from 20 percent to about 25 percent. Thus, the current proportion of imports with a large scope for quality differentiation is roughly 50 percent. Within a balanced panel of products in panel (b), the shares of cost and quality imports are more stable at 50 percent.26 In the sections that follow, the distinction between cost and quality products will be applied to further explore the cross-section and dynamic features of the import price distribution.
2.2 Distinguishing Cost vs. Quality Industries: U.S. Exports
Given the availability of U.S. export transaction prices, the quality ladder measures for imports in the preceding section can be compared with those for exports. The use of export prices leads to several simplifications in the empirical implementation. First, the measure of the firm size skewness for U.S. exporters has a direct measure. Second, given a single source country, the wage skewness term from (16) drops out, leaving the following regression of HS10 export price skewness on the HS10 firm size distribution:
| (17) |
As discussed in the appendix, the interpretation of
![]() in this specification does not
contain information on the magnitude of
in this specification does not
contain information on the magnitude of
![]() but, rather, only its sign.
Running (17) across the array of U.S.
exports yields estimates for
but, rather, only its sign.
Running (17) across the array of U.S.
exports yields estimates for
![]() in 439 HS6 industries, 324 of
which are distinguishable from zero as either quality or cost
industries. Table 3 displays the largest quality and cost products
by sales volume. Again, with a few exceptions, we see a more or
less intuitive categorization scheme, with semiconductors and
automobiles among the most quality differentiated and more
commoditized goods such as parts and accessories among the least
quality differentiated. Based on industries where estimates are
available, representing $422 billion dollars (or 53 percent) of
U.S. exports in 2005, quality industries account for approximately
48 percent of trade volume.
in 439 HS6 industries, 324 of
which are distinguishable from zero as either quality or cost
industries. Table 3 displays the largest quality and cost products
by sales volume. Again, with a few exceptions, we see a more or
less intuitive categorization scheme, with semiconductors and
automobiles among the most quality differentiated and more
commoditized goods such as parts and accessories among the least
quality differentiated. Based on industries where estimates are
available, representing $422 billion dollars (or 53 percent) of
U.S. exports in 2005, quality industries account for approximately
48 percent of trade volume.
It is not obvious a priori what the relationship between
import and export quality scope measures should be. First, product
level specialization is reflected in the relatively limited overlap
of very large import and export HS6 categories. Of the 1,098 import
and 439 export scope estimates, only 215 match. Of those,
intra-product specialization may, in theory, lead to vastly
different scope estimates. In the U.S. data, the sign of the import
and export quality scope measures (i.e., the sign of the
price-productivity schedule) correlate positively and
significantly, with a logit regression coefficient of 0.68 (0.27)
between sign dummies for
![]() in (16)
and (17).
in (16)
and (17).
3 Quality Specialization by Country
In the previous section, the correlation of price and productivity skewness identified the scope for quality differentiation of products. In this section, quality scope measures and import price levels are employed to rank exporting countries according to their productivity and quality levels. Relative quality is identified by picking a product and observing which countries inhabit the tails of its price distribution. Countries consistently selling in a quality industry's right tail are considered to be specialized in quality, with the converse holding for cost industries. In this section, quantile regression techniques are used to discern countries' propensity to sell in the tails of the price distribution and, indeed, similar sets of countries populate the tails; a country exporting at a high price in a quality industry tends to export at a low price in a more homogeneous cost industry. In other words, the price distribution and the underlying productivity-price mapping reveals the productivity of exporting countries; given a monotone link between productivity and quality, relative quality levels are also identified. Previous studies find that average prices vary systematically with country characteristics such as wealth and distance, and so this exercise can be interpreted as additionally documenting inter-product heterogeneity in country pricing patterns consistent with the model of quality choice.
Once again the first order conditions of the firm problem offer a convenient starting point. The item pricing equation (13) is a simple relationship between quality-inclusive price, wage and firm productivity. Controlling for wage, the residual of item price contains information about the exporting firm's location within the productivity distribution as well as any other country- or firm-specific factor. Conditioning by country (as opposed to firm productivity in the previous section) allows for analysis in levels:
| (18) |
where
![]() estimates a country-specific
relative price, controlling for product composition with HS10 dummy
variables
estimates a country-specific
relative price, controlling for product composition with HS10 dummy
variables ![]() and for time variation with year
dummy variables
and for time variation with year
dummy variables ![]() . Given the observation above
of asymmetric price distributions, and the implication that quality
levels differ substantially across the spectrum of observations
within a product, least squares estimates of the conditional mean
country elasticities confound effects in the tightly clustered body
of the price distribution with those in the more disperse tail. To
additionally condition on location within the distribution, we
separate positively and negatively skewed classification groups and
then estimate quantile regressions at the 15th and 85th quantiles
of each set.27 Each regression pools across
products within a sector, so each sector has four estimates for
each active country: the 15th quantile of the positively skewed
products (i.e. the 'body' of the distribution), the 85th quantile
of the positively skewed products (i.e. the 'tail' of the
distribution), the 15th quantile (tail) of the negatively skewed
products and the 85th quantile (body) of the negatively skewed
products. Again, using ILO Yearbook data to construct
country-product-year wage measures, monthly transaction prices are
regressed on wage and fixed effects within each of seven sectors.
The country coefficients can be interpreted as relative to Canada,
the omitted country dummy.
. Given the observation above
of asymmetric price distributions, and the implication that quality
levels differ substantially across the spectrum of observations
within a product, least squares estimates of the conditional mean
country elasticities confound effects in the tightly clustered body
of the price distribution with those in the more disperse tail. To
additionally condition on location within the distribution, we
separate positively and negatively skewed classification groups and
then estimate quantile regressions at the 15th and 85th quantiles
of each set.27 Each regression pools across
products within a sector, so each sector has four estimates for
each active country: the 15th quantile of the positively skewed
products (i.e. the 'body' of the distribution), the 85th quantile
of the positively skewed products (i.e. the 'tail' of the
distribution), the 15th quantile (tail) of the negatively skewed
products and the 85th quantile (body) of the negatively skewed
products. Again, using ILO Yearbook data to construct
country-product-year wage measures, monthly transaction prices are
regressed on wage and fixed effects within each of seven sectors.
The country coefficients can be interpreted as relative to Canada,
the omitted country dummy.
Table 4(a) displays the wage coefficients of (18) by sector. Recall from (13) that the simple model predicts a wage
elasticity of one. While not always precisely estimated, all but
one of the significant coefficients (denoted by an asterisk for p
![]() .1) are positive, some with
coefficients quite close to one. Each sectoral regression produces
four lists of country relative prices. Comparing these prices for
the same country across products of different quality scope reveals
an interesting pattern. As an illustration, Table 5 presents the
results for the textiles sector.28 To begin, consider the
fitted regression lines running through the tails of the price
distribution: the 85th quantile (high prices) of the quality
products and the 15th quantile (low prices) of the cost products.
We observe that the relatively high prices in the quality products
correspond with relatively lower prices in the cost products;
Pakistan and Bangladesh are farther out in the tails while Korea,
Macao and Hong Kong reside closer to the dense cluster of prices in
the body. A theory of quality sorting like the one above suggests
that firms in Pakistan and Bangladesh are more productive in
textiles exports for the products included in (18), while those in East Asian countries are less
so. In contrast, there is not a clearly discernible pattern, or
perhaps even the opposite pattern, for the regression lines fitted
through the body of the price distribution (i.e., 15th quantile of
quality products and 85th quantile of cost products) where a
producer like Korea tends to have relatively low prices and a
producer like Turkey tends to have relatively high prices in both
types of product.
.1) are positive, some with
coefficients quite close to one. Each sectoral regression produces
four lists of country relative prices. Comparing these prices for
the same country across products of different quality scope reveals
an interesting pattern. As an illustration, Table 5 presents the
results for the textiles sector.28 To begin, consider the
fitted regression lines running through the tails of the price
distribution: the 85th quantile (high prices) of the quality
products and the 15th quantile (low prices) of the cost products.
We observe that the relatively high prices in the quality products
correspond with relatively lower prices in the cost products;
Pakistan and Bangladesh are farther out in the tails while Korea,
Macao and Hong Kong reside closer to the dense cluster of prices in
the body. A theory of quality sorting like the one above suggests
that firms in Pakistan and Bangladesh are more productive in
textiles exports for the products included in (18), while those in East Asian countries are less
so. In contrast, there is not a clearly discernible pattern, or
perhaps even the opposite pattern, for the regression lines fitted
through the body of the price distribution (i.e., 15th quantile of
quality products and 85th quantile of cost products) where a
producer like Korea tends to have relatively low prices and a
producer like Turkey tends to have relatively high prices in both
types of product.
Figure 4 illustrates the 'tail' prices across all sectors,29 where each point in the scatter plot is a pair of relative price estimates for a particular country-sector combination, based on quantile regressions of the 85th quantile of the quality products and 15th quantile of the cost products (i.e., including estimates for textiles in columns 2 and 3 of Table 5). On the horizontal axis is a given country's relative price for its quality products in a given sector, and on the vertical axis is that country's relative price in cost industries for that sector. Across all sectors, the pattern in textiles is preserved, with the majority of estimates falling in the top-left or bottom-right quadrants of the grid, tracing out a downward linear trend. On one end of the spectrum, UK plastics exports have relatively high prices in quality products and relatively low prices in cost products. The quality choice theory would suggest that this reflects UK firms' position on the tail of the productivity distribution. On the other end of the spectrum, Mexican metals exports are low-priced in quality products and high-priced in cost products, denoting lower average productivity. The high incidence of estimates in the top-left and bottom-right quadrants indicates that such sign-switching in relative prices across products occurs frequently, and the general pattern across countries and sectors is a negative relationship, with a one percent higher relative price in quality industries corresponding to a 0.28 percent lower relative price in cost industries.
Figure 5 shows the analogous illustration for the body of the price distribution. In contrast to the tail estimates, the resulting price mapping across cost and quality industries actually has a positive upward trend, with a one percent higher relative price in quality industries corresponding to a 0.45 percent higher relative price in cost industries. The incidence of relative prices of like sign is much higher than in the tail of the distribution, as illustrated by the greater number of estimates in the top-right and bottom-left quadrants. Assuming firms in a country-sector cell have similar productivity, the pattern in Figure 4 is consistent with the price-setting behavior outlined in the model of quality choice; productivity maps into price inversely for quality and cost industries. How can we then explain the pattern in Figure 5? One possibility is that it is simply harder to precisely measure a negative relationship between relative prices across products with different skewness in the body of the price distribution versus the tail. This, in turn, may suggest that it is beneficial to use transactions prices instead of unit value average prices for this exercise, where unit values confound the within-distribution pricing behavior of exporters. Alternatively, firm sorting in prices might not be as strong for firms that are not productivity outliers. We also cannot neglect the possibility that firms in a country-sector do not have similar productivity. For example, if Japan has high productivity in the production of engines (positive skewness) and low productivity in the production of office machine parts (negative skewness), then we would observe a positive relationship among Japanese export prices in the machinery sector. However, if that were the case, we would also expect that pattern to be generated by the same sector-countries in the tail of the price distribution, which we do not observe.
The robustness of this pattern is checked by conditioning on additional features of the price observations. The IPP collects an array of characteristics for each price in its sample, including whether it is a market or transfer price, what its unit of measure is and when it was discontinued.30 Additional dummy variables are added to (18) for market-based transfer price, cost-based transfer price, the various units of measure and irregular discontinuation. The last variable denotes an item that was discontinued due to reasons other than regular sample rotation, the price of which may reflect the idiosyncrasies of an item at the end of its life cycle. The control estimates are shown in Table 4(b) for sectors with enough observations. As above, the coefficient on wage is generally positive. The estimates for transfer prices do not show a clear pattern, though it is interesting to note that 'market-based' transfer prices are often significantly different from prices at arms-length. For the most part, and particularly for quality industries, items discontinued irregularly had lower prices than those which were not discontinued over the course of the sample. Based on the ordering of firms by quality level, this implies that it is the low quality varieties that tend to exit the export market. For cost industries, the relationship is somewhat ambiguous with the exiting varieties having either lower or higher prices. The resulting country estimates for the distribution tail and body are shown in Figure 6 and Figure 7, respectively. Similar to Figure 4, Figure 6 illustrates a negative relationship between the tail relative prices in cost and quality industries, with a one percent higher price in quality industries corresponding to a 0.47 percent lower price in cost industries. In Figure 7, on the other hand, the positive relationship between the body relative prices in Figure 5 disappears.
In sum, these relative price patterns suggest that the nature of specialization is particular to where producers reside in the exporter productivity distribution. The firms in the tail of the distribution specialize in high quality products in quality industries and low price products in cost industries. This observation is broadly consistent with sectoral comparative advantage translating into price distinctly, depending on the scope for quality differentiation of the export. As such, it is both supportive of the theory of quality sorting and revealing of the heterogeneous pattern of specialization in quality and cost industries.
4 A Time Series Test of Quality Sorting
Since the composition of quality characteristics is conditional on an export transaction taking place, patterns in composition will depend on any factor that affect the firm's export participation decision. In this section, patterns in quality composition are predicted and measured in response to real exchange rate changes. In the model, firms endogenously sort into foreign export markets if they are above some threshold productivity (and hence profit) level.31 It is the firms on the extensive margin of firm entry, at the low end of the productivity distribution of active firms, whose survival in the market is predicated upon any change that affects the location of the threshold firm. For the measurement of average prices in the wake of such a change, key considerations are: who are the marginal firms, and do they have relatively high or low prices? In a cost industry, the marginal, least productive, firms have the highest price and so firm entry will put upward pressure on the average price of remaining firms. In a quality industry, the marginal, least productive, firms have the lowest price, and so entry will put downward pressure on the average price. I test these predictions across a wide array of disaggregate products by comparing two types of import price index: one that controls completely for import composition, a 'constant-quality' index, and a second that allows for changes in the extensive margin, a 'quality-inclusive' index.
Exchange rate pass-through is incomplete in this simple framework due to firm entry and exit. With CES preferences, changes in costs pass through on a 1-for-1 basis into prices at the firm level; thus pass-through is complete for each individual variety. To be concrete, an adverse, exogenous change in firm marginal cost is reflected as a proportional increase in price. Accounting for the changing mass of firms, however, average prices reflect the changing composition of the import bundle. For example, a real appreciation in the foreign country causes the least productive firms in each industry to drop out of the market, such that in a quality industry the lowest price firms exit and the average price of the remaining firms increases. These extensive margin effects are above and beyond any other price change the firm will undertake in response to the shock. In a cost industry, the least productive, highest price firms exit the market and the average price of the remaining firms decreases. These compositional effects will be manifested in a quality-inclusive price index, which is constructed from unit values average prices. In contrast, aggregating transaction-level IPP prices for exactly the same items from period to period allows for the construction of an index that is bereft of quality changes by definition, a constant-quality index. Since the extensive margin is shut down and aggregation weights are fixed in each period in the constant-quality index, the changes in average prices due to composition, as are observed in unit values, are absent. Thus, the sharpest predictions of the model due to quality sorting are that: (i) in quality industries, firms will pass through exchange rate shocks to quality-inclusive prices by more than to constant-quality prices, and (ii) in cost industries, firms will pass through exchange rate shocks to quality-inclusive prices by less than to constant-quality prices.
To explore these predictions for the U.S., I run pass-through regressions for both constant-quality prices and quality-inclusive prices of the form:
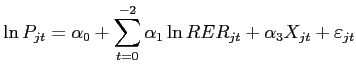
|
(19) |
where
![]() is the annual import price index
level for each classification group,
is the annual import price index
level for each classification group, ![]() , in year
, in year
![]() . For the measure of quality-inclusive
price, I construct Tornqvist indices of annual unit value price
changes using HS10-country export quantity (
. For the measure of quality-inclusive
price, I construct Tornqvist indices of annual unit value price
changes using HS10-country export quantity (
![]() ), sales (
), sales (
![]() ) and trade
weights (
) and trade
weights (
![]() ) data provided by Feenstra
et al. (2002):32
) data provided by Feenstra
et al. (2002):32
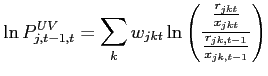
|
(20) |
For the measure of constant-quality price, I aggregate the
Tornqvist indices directly from the individual variety prices
(![]() ) in the IPP sample, using annual
country weights to approximate item sales weights (
) in the IPP sample, using annual
country weights to approximate item sales weights (
![]() ):
):
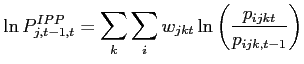
|
(21) |
Cumulating (20) and (21) yields the cumulative import index levels
for quality-inclusive (
![]() ) and constant-quality (
) and constant-quality (
![]() ) import prices,
respectively, by classification group.33 Additionally, I
compute an annual index of the real exchange rate by classification
group using IFS country data for real exchange rates, and aggregate
using the Tornqvist formula and import sales weights, as above.
Included in (19) are current and two lags of the
exchange rate index. Finally, I include a vector of controls (
) import prices,
respectively, by classification group.33 Additionally, I
compute an annual index of the real exchange rate by classification
group using IFS country data for real exchange rates, and aggregate
using the Tornqvist formula and import sales weights, as above.
Included in (19) are current and two lags of the
exchange rate index. Finally, I include a vector of controls (
![]() ) containing an annual index of
competing export prices (published by the BLS at the HS4 level), an
index of tariffs, a measure of the Chinese import share in each
classification group and a full set of classification group fixed
effects. Since the import price indexes are both 'at-the-dock'
(i.e., net of tariff), we expect either a zero or negative
coefficient on the tariff control.34 Bergin and Feenstra
(2007) demonstrate that increasing export competition by countries
with fixed exchange rates may be lessening exchange rate
pass-through in flexible exchange rate exporter prices, so I
include the share of Chinese and Hong Kong exports in each
classification group as a proxy for fixed exchange rate export
competition.
) containing an annual index of
competing export prices (published by the BLS at the HS4 level), an
index of tariffs, a measure of the Chinese import share in each
classification group and a full set of classification group fixed
effects. Since the import price indexes are both 'at-the-dock'
(i.e., net of tariff), we expect either a zero or negative
coefficient on the tariff control.34 Bergin and Feenstra
(2007) demonstrate that increasing export competition by countries
with fixed exchange rates may be lessening exchange rate
pass-through in flexible exchange rate exporter prices, so I
include the share of Chinese and Hong Kong exports in each
classification group as a proxy for fixed exchange rate export
competition.
Table 6 shows the results for the fixed effects OLS regression of (19), run annually (1994-2004) over all classification groups for which data are available.35 Additionally, the data are split by cost and quality groups based on the estimates in the method of moments exercise above.36 The results are supportive of: (i) the existence of quality sorting in the data, and (ii) the notion that quality differentiated products have higher pass-through. For sorting, the theory suggests that in cost industries quality-inclusive prices pass through currency appreciation by less than constant-quality prices. The results are consistent with this prediction, as pass-through of the real exchange rate is positive and significant at approximately 7 percent37in columns (I) and (II), and indistinguishable from zero in quality-inclusive prices in columns (III) and (IV). Though suggestive, large standard errors make it impossible to distinguish between the two coefficients.
The theory also suggests that in quality industries quality-inclusive prices pass through currency appreciation by more than constant-quality prices, reflecting the exit of the low-priced marginal firms in the wake of a real exchange rate appreciation. The results in columns (IX)-(XII) strongly support this hypothesis with estimates of pass through more than doubling in quality-inclusive prices relative to constant-quality prices, with estimates statistically distinguishable from one another at the 5 percent level. Finally, analyzing both cost and quality products jointly in columns (V)-(VIII), we see that overall quality-inclusive prices have higher pass-through than the corresponding constant-quality indexes (also significantly different from one another). This suggests that U.S. import prices behave, on average, like a quality industry. The second interesting pattern in Table 6 is that, within import price measures, quality industries have higher pass-through coefficients than cost industries. This is suggested by the monotone increase in estimates from left to right in the sets of columns: {(I),(V),(IX)}, {(II),(VI),(X)}, etc. In quality-inclusive prices, the degree of pass-through in quality industries is significantly greater than that in cost industries.
One might expect a more pronounced impact of quality differentiation on price dynamics in sectors with longer quality ladders and a greater diversity of products, such as mechanical devices and electric machinery: HS84 and HS85. These sectors compose approximately one third of the classification groups for which quality scope estimates exist and (due to their sheer size of import value) tend to have more products sampled by the IPP per classification group than others, augmenting confidence in the measures of sample skewness and quality scope. Indeed, the left panel in Table 7 presents stronger support of quality sorting than Table 6: in cost industries, constant-quality prices are 11 percent while quality inclusive prices are approximately zero and in quality industries constant quality prices are 6 percent compared to 43 percent in quality-inclusive industries.
Finally, in the right panel of Table 7, we apply the
cost/quality classification derived from U.S. exports in order to
expand the range of products for which pass-through elasticities
can be computed. Above, the quality range of U.S. imports as
measured by the sign of
![]() , was shown to be positively
correlated with the sign of the quality range for U.S. exports. As
such, I use the export classification as an additional gauge of the
quality differentiation of certain import products. The pattern of
pass-through coefficients is similar to to the estimates using the
import-based classification: the pass-through estimate is
insignificant in the cost industry quality inclusive index and very
high in the quality industries.
, was shown to be positively
correlated with the sign of the quality range for U.S. exports. As
such, I use the export classification as an additional gauge of the
quality differentiation of certain import products. The pattern of
pass-through coefficients is similar to to the estimates using the
import-based classification: the pass-through estimate is
insignificant in the cost industry quality inclusive index and very
high in the quality industries.
Comparing pass-through in 'matched model' prices (in which the composition of varieties is held constant) to unit values is not in itself novel. Alterman (1991) argues that compositional effects have a large effect on pass-through estimation due to the unit value's imperfect measurement of price. Here, these large difference are shown to be systematic in the way that firms sort into export markets in quality and cost industries.
5 Conclusions
It has long been recognized that average prices are imperfect measures of both price and quality. This paper takes a step forward in overcoming the difficulties of quality inference from average prices by disentangling their relationship transaction by transaction. Exploring the distribution of transaction prices within narrow product groups introduces a new dimension to our understanding of firm pricing behavior and adds texture to our observations of average trade patterns.
In particular, the higher moments in prices reveal not only the scope for differentiation across products, but the countries that specialize in quality and the dynamics of pricing due to compositional changes. I find evidence that an average relation between output price and exporter capability nets out highly disparate patterns of specialization: productive exporters simultaneously set high prices in quality differentiated industries and low prices in more homogeneous industries. This relationship between productivity, quality and price also emerges in the time series of average prices. Index number techniques identify firm entry and exit along the extensive margin after a change in the real exchange rate and the relative quality of marginal firms. The exit of low productivity, low quality, low price firms in a quality differentiated industry pushes up the average price of the surviving firms. Both sets of results bolster the positive relationship between productivity and quality typically asserted in models of quality choice.
Finally, it is important to view the results herein in context. Perhaps the future of trade price data promises a global census of transaction quantities and prices and perfect information about product specifications. In such a world, it would be feasible and straightforward to estimate the marginal value of product characteristics and there would be no need to infer quality from composition-contaminated average prices. In the meantime, this paper presents an intermediate rung on the data quality ladder.
Bibliography
Alterman, William (1991) "Price Trends in U.S. Trade: New Data, New Insights,'' in Peter Hooper and J. David Richardson, eds. International Economic Transactions. Studies in Income and Wealth, no. 55. Chicago: Univ. of Chicago Press and NBER, 109-139.
Auer, Raphael and Thomas Chaney (2009): "Exchange Rate Pass-Through in a Competitive Model of Pricing-to-Market," Journal of Money, Credit and Banking, vol. 41(s1): 151-175.
Aw, Bee Yan & Roberts, Mark J. (1986): "Measuring Quality Change in Quota-Constrained Import Markets: The Case of U.S. Footwear," Journal of International Economics, Elsevier, vol. 21(1-2), pages 45-60, August.
Baldwin, Richard E. and James Harrigan (2007): "Zeros, Quality and Space: Trade Theory and Trade Evidence," NBER Working Papers 13214, National Bureau of Economic Research, Inc.
Baldwin, Richard E. and Tadashi Ito (2008): "Quality competition versus price competition goods: An empirical classification," HEID Working Paper No7/2008.
Bergin, Paul R. and Robert C. Feenstra (2007): "Pass-through of Exchange Rates and Competition Between Floaters and Fixers," NBER Working Papers 13620, National Bureau of Economic Research.
Bernard, Andrew B. and J. Bradford Jensen (1999): "Exceptional Exporter Performance: Cause, Effect, or Both?," Journal of International Economics, 47(1), 1-25.
Bils, Mark (2004): "Measuring the Growth from Better and Better Goods." NBER Working Papers 10606, National Bureau of Economic Research.
Bureau of Labor Statistics (2009): BLS Handbook of Methods, Chapter 15.
Boskin M.J., E.R. Dulberger, R.J. Gordon, Z. Griliches and D.W. Jorgenson (1997): "The CPI Commission: Findings and Recommendations" American Economic Review, Vol. 87, No. 2, Papers and Proceedings of the Hundred and Fourth Annual Meeting of the American Economic Association (May), pp. 78-83.
Broda, Christian. & David E. Weinstein (2006): "Globalization and the Gains from Variety," Quarterly Journal of Economics, MIT Press, vol. 121(2), pages 541-585, May.
Campa, José Manuel and Linda S. Goldberg (2005): "Exchange Rate Pass-Through into Import Prices," Review of Economics and Statistics, 87(4): 679-690.
Choi, Yo Chul, David Hummels and Chong Xiang (2006): "Explaining Import Variety and Quality: The Role of the Income Distribution," NBER Working Papers 12531, National Bureau of Economic Research.
Crozet, M., K. Head and T. Mayer (2009): "Quality sorting and trade: Firm-level evidence for French wine" CEPR Discussion Paper 7295.
Feenstra, Robert C. (1996): "U.S. Imports, 1972-1994: Data and Concordances," NBER Working Paper 5515.
Feenstra, Robert C. (1988): "Quality Change under Trade Restraints in Japanese Autos," Quarterly Journal of Economics, 103(1): 131-46.
Feenstra, Robert C., Romalis, John and Peter K. Schott (2002): "U.S. Imports, Exports and Tariff Data, 1989-2001," NBER Working Paper 9387, National Bureau of Economic Research.
Goldberg, Pinelope and Michael Knetter (1997): "Goods Prices and Exchange Rates: What Have We Learned?'' Journal of Economic Literature, 35, 1243-1272.
Gopinath, Gita and Roberto Rigobon (2008): "Sticky Borders," Quarterly Journal of Economics, 123(2): 531-575.
Gopinath, Gita, Oleg Itskhoki and Roberto Rigobon (2007): "Currency Choice and Exchange Rate Pass-Through," manuscript.
Gust, Christopher, Sylvain Leduc and Robert J. Vigfusson (2006): "Trade Integration, Competition, and the Decline in Exchange-Rate Pass-Through,'' Board of Governors of the Federal Reserve System International Finance Discussion Paper #864.
Hallak, Juan Carlos (2006): "Product Quality and the Direction of Trade," Journal of International Economics, 68, 238-265.
Hallak, Juan Carlos and Peter K. Schott (2009): "Estimating Cross-Country Differences in Product Quality," Working paper.
Hallak, Juan Carlos and Jagadeesh Sivadasan (2008): "Productivity, Quality and Exporting Behavior Under Minimum Quality Requirements'', mimeo.
Harrigan, James and Geoffrey Barrows (2006): "Testing the Theory of Trade Policy: Evidence from the Abrupt End of the Multifibre Arrangement," NBER Working Papers 12579, National Bureau of Economic Research.
Hummels, David and Peter J. Klenow (2005): "The Variety and Quality of a Nation's Exports," American Economic Review, 95(3): 704-723.
Johnson, Robert C. (2008): "Trade and Prices with Heterogeneous Firms," mimeo.
Khandelwal, Amit (2009): "The Long and Short (of) Quality Ladders," forthcoming in Review of Economic Studies.
Kremer, Michael R. (1993): "The O-ring Theory of Economic Development." The Quarterly Journal of Economics, Vol. 108, No. 3, pg. 551-575, August.
Kugler, Maurice and Eric A. Verhoogen (2008): "The Quality-Complementarity Hypothesis: Theory and Evidence from Colombia.'' NBER working paper #14418, Oct. 2008.
Manova, Kalina B. and Zhiwei Zhang (2009): "Export Prices and Heterogeneous Firm Models", mimeo, Stanford University.
Marazzi, Mario, Nathan Sheets, Robert J. Vigfusson, Jon Faust, Joseph E. Gagnon, Jaime Marquez, Robert F. Martin, Trevor A. Reeve and John H. Rogers (2005): "Exchange Rate Pass-through to U.S. Import Prices: Some New Evidence,'' Board of Governors of the Federal Reserve System International Finance Discussion Paper #833.
Melitz, Marc J. (2003): "The Impact of Trade on Intra-Industry Reallocations and Aggregate Industry Productivity." Econometrica, Vol. 71, No. 6., pp. 1695-1725, November.
Moulton, Brent R. & Moses, Karin E. (1997): "Addressing the Quality Change Issue in the Consumer Price Index" Brookings Papers on Economic Activity 1, 305-349.
Olivei, G. (2002): "Exchange Rates and the Prices of Manufacturing Products Imported into the United States,'' New England Economic Review, First Quarter, 3-18.
Schott, Peter K. (2004): "Across-product Versus Within-product Specialization in International Trade," Quarterly Journal of Economics, MIT Press, 119(2): 646-677.
Schott, Peter K. (2008): "The Relative Sophistication of Chinese Exports," Economic Policy, 53:5-49.
Verhoogen, Eric A. (2008): "Trade, Quality Upgrading, and Wage Inequality in the Mexican Manufacturing Sector," Quarterly Journal of Economics, 123(2): 489-530.
Theoretical Moments
- Mean:
- Variance:
Within country
 , the variance of quality-inclusive
prices for product
, the variance of quality-inclusive
prices for product 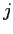 at time
at time 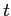 is:
is: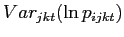
![$\displaystyle = {\textstyle\int\limits_{i\in\omega_{kt}}} \left[ \ln p_{ijkt}-\overline{\ln p_{jkt}}\right] ^{2}$](img145.gif)
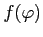
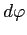
![$\displaystyle =\left( \frac{b}{a-b}\right) {\textstyle\int\limits_{i\in\omega_{kt}}} \left[ \ln\varphi_{ijkt}-\overline{\ln\varphi_{jkt}}\right] ^{2}$](img148.gif)
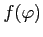
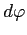
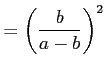
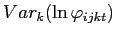
For product
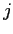 (all export countries), the variance
of quality-inclusive prices additionally depends on the variance of
wages across countries:
(all export countries), the variance
of quality-inclusive prices additionally depends on the variance of
wages across countries: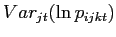
![$\displaystyle = {\displaystyle\sum\limits_{k}} \frac{1}{k}\left\{ {\textstyle\int\limits_{i\in\omega_{kt}}} \left[ \ln p_{ijkt}-\overline{\ln p_{jt}}\right] ^{2}\text{ }f(\varphi )\text{ }d\varphi\right\}$](img155.gif)
![$\displaystyle = {\displaystyle\sum\limits_{k}} \frac{1}{k}\left\{ {\textstyle\int\limits_{i\in\omega_{kt}}} \left[ \begin{array}[c]{c} (\ln w_{jkt}-\overline{\ln w_{jt}})+\\ \left( \frac{b}{a-b}\right) (\ln\varphi_{ijkt}-\overline{\ln\varphi_{jt}}) \end{array} \right] ^{2}\text{ }f(\varphi)\text{ }d\varphi\right\}$](img156.gif)
![$\displaystyle = {\displaystyle\sum\limits_{k}} \frac{1}{k}\left\{ {\displaystyle\int\limits_{i\in\omega_{kt}}} \left[ \begin{array}[c]{c} (\ln w_{jkt}-\overline{\ln w_{jt}})^{2}+\\ \left( \frac{b}{a-b}\right) ^{2}(\ln\varphi_{ijkt}-\overline{\ln\varphi _{jt}})^{2}\\ +2\left( \frac{b}{a-b}\right) (\ln w_{jkt}-\overline{\ln w_{jt}})\\ (\ln\varphi_{ijkt}-\overline{\ln\varphi_{jt}}) \end{array} \right] \text{ }f(\varphi)\text{ }d\varphi\right\}$](img157.gif)
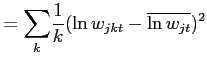
![$\displaystyle +\left( \frac{b}{a-b}\right) ^{2} {\displaystyle\sum\limits_{k}} \frac{1}{k}\left[ {\textstyle\int\limits_{i\in\omega_{kt}}} (\ln\varphi_{ijkt}-\overline{\ln\varphi_{jt}})^{2}\text{ }f(\varphi)\text{ }d\varphi\right]$](img159.gif)
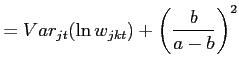
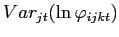
(22) In the fourth line, the covariance between item productivity and country wage is assumed to be zero.
- Skewness:
Assuming uniform wage across countries, the skewness of quality-inclusive prices for product
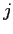 is:
is: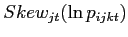
![$\displaystyle =\frac{ {\displaystyle\sum\limits_{k}} \frac{1}{k}\left\{ {\textstyle\int\limits_{i\in\omega_{kt}}} \left[ \ln p_{ijkt}-\overline{\ln p_{jt}}\right] ^{3}\text{ }f(\varphi )\text{ }d\varphi\right\} }{ {\displaystyle\sum\limits_{k}} \frac{1}{k}\left\{ {\textstyle\int\limits_{i\in\omega_{kt}}} \left[ \ln p_{ijkt}-\overline{\ln p_{jt}}\right] ^{2}\text{ }f(\varphi )\text{ }d\varphi\right\} ^{\frac{3}{2}}}$](img164.gif)
![$\displaystyle =\left( \frac{\frac{b}{a-b}}{\left\vert \frac{b}{a-b}\right\vert }\right) ^{3}\frac{ {\displaystyle\sum\limits_{k}} \frac{1}{k}\left\{ {\textstyle\int\limits_{i\in\omega_{kt}}} \left[ \ln\varphi_{ijkt}-\overline{\ln\varphi_{jt}}\right] ^{3}\text{ }f(\varphi)\text{ }d\varphi\right\} }{ {\displaystyle\sum\limits_{k}} \frac{1}{k}\left\{ {\textstyle\int\limits_{i\in\omega_{kt}}} \left[ \ln\varphi_{ijkt}-\overline{\ln\varphi_{jt}}\right] ^{2}\text{ }f(\varphi)\text{ }d\varphi\right\} ^{\frac{3}{2}}}$](img165.gif)
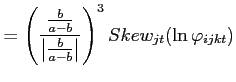
This means that the skewness of prices has the same sign as the skewness of firm productivity if
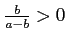 . That is, if prices are
increasing in firm productivity and productivity has positive
skewness (high outliers), then price skewness will be positive; if
prices are decreasing in productivity and productivity has positive
skewness, then price skewness will be negative. Interestingly, the
skewness of prices always has the same magnitude as the skewness of
productivity.
. That is, if prices are
increasing in firm productivity and productivity has positive
skewness (high outliers), then price skewness will be positive; if
prices are decreasing in productivity and productivity has positive
skewness, then price skewness will be negative. Interestingly, the
skewness of prices always has the same magnitude as the skewness of
productivity.Allowing wages to differ across countries, the skewness of quality-inclusive prices for product
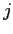 is:
is: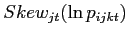
![$\displaystyle =\frac{ {\displaystyle\sum\limits_{k}} \frac{1}{k}\left\{ {\textstyle\int\limits_{i\in\omega_{kt}}} \left[ \ln p_{ijkt}-\overline{\ln p_{jkt}}\right] ^{3}\text{ } f(\varphi)\text{ }d\varphi\right\} }{\left[ Var_{j}(\ln p_{ijkt})\right] ^{\frac{3}{2}}}$](img170.gif)
![$\displaystyle \frac{Skew_{jt}(\ln p_{ijkt})}{\left[ Var_{jt}(\ln p_{ijkt})\right] ^{-\frac{3}{2}}}$](img171.gif)
![$\displaystyle = {\displaystyle\sum\limits_{k}} \frac{1}{k}\left\{ {\textstyle\int\limits_{i\in\omega_{kt}}} \left[ \ln p_{ijkt}-\overline{\ln p_{jkt}}\right] ^{3}\text{ } f(\varphi)\text{ }d\varphi\right\}$](img172.gif)
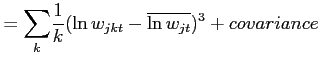
![$\displaystyle +\left( \frac{b}{a-b}\right) ^{3} {\displaystyle\sum\limits_{k}} \frac{1}{k}\left[ {\textstyle\int\limits_{i\in\omega_{kt}}} (\ln\varphi_{ijkt}-\overline{\ln\varphi_{jt}})^{3}\text{ }f(\varphi)\text{ }d\varphi\right]$](img175.gif)
(23) ![$\displaystyle =\frac{Skew_{jt}(\ln w_{jkt})}{[Var_{jt}(\ln w_{jkt})]^{-\frac{3}{2}} }+\left( \frac{b}{a-b}\right) ^{3}\frac{Skew_{jt}(\ln\varphi_{ijkt} )}{[Var_{jt}(\ln\varphi_{ijkt})]^{-\frac{3}{2}}}$](img176.gif)
(24) Again, assuming that the covariance terms of industry productivity and country wage are zero, (23) reduces to an expression which states that quality-inclusive price skewness (non-standardized) is a function of cross-country wage skewness and average industry productivity skewness.
Within exporting country ![]() ,
the average quality-inclusive price of product
,
the average quality-inclusive price of product ![]() at time
at time ![]() is:
is:
|
||
![$\displaystyle = {\textstyle\int\limits_{i}} \left[ \ln\theta_{j}^{p}+\ln w_{jkt}+\left( \frac{b}{a-b}\right) \ln \varphi_{ijkt}\right] f(\varphi\vert\varphi\in\omega_{jkt})d\varphi$](img130.gif)
|
||
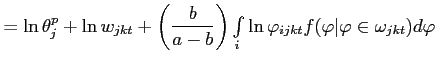
|
||
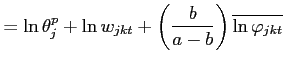
|
where
![]() is the range of active firms
and
is the range of active firms
and
![]() is their
average productivity level. For product
is their
average productivity level. For product ![]() in year
in year
![]() , the average quality-inclusive price is a
simple average across countries:
, the average quality-inclusive price is a
simple average across countries:
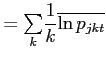
|
||
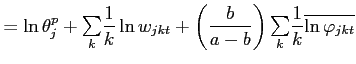
|
||
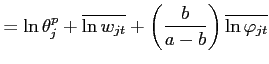
|
Figure 1. Monthly Transaction Price Levels Within and Illustrative HS10 Category
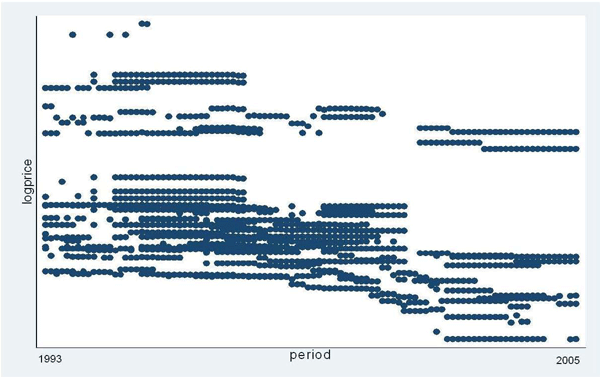
Figure 2a. Cross-HS10 Distributions on U.S. Import Price Skewness, Foreign Wage Skewness and U.S. Firm-Level Export Size Skewness (U.S. Import Price Skewness vs. Percentile)
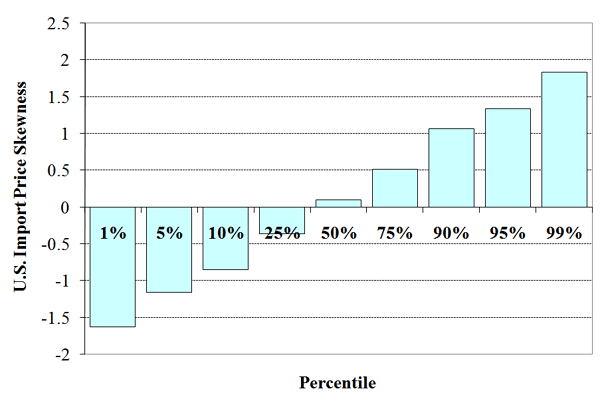
Data for Figure 2a
| Percentile | U.S. Import Price Skewness |
|---|---|
| 1% | -1.630635 |
| 5% | -1.155385 |
| 10% | -0.8507763 |
| 25% | -0.3611532 |
| 50% | 0.095959 |
| 75% | 0.5095435 |
| 90% | 1.063205 |
| 95% | 1.336499 |
| 99% | 1.828139 |
Figure 2b. Cross-HS10 Distributions on U.S. Import Price Skewness, Foreign Wage Skewness and U.S. Firm-Level Export Size Skewness (Foreign Exporter Wage Skewness vs. Percentile)
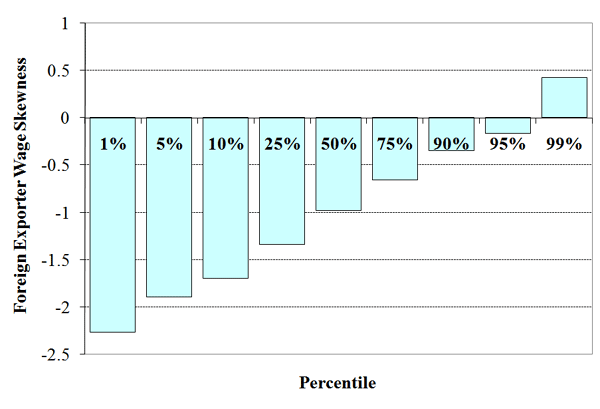
Data for Figure 2b
| Percentile | Foreign Exporter Wage Skewness |
|---|---|
| 1% | -2.266686 |
| 5% | -1.895942 |
| 10% | -1.698316 |
| 25% | -1.342487 |
| 50% | -0.9831445 |
| 75% | -0.657082 |
| 90% | -0.3509376 |
| 95% | -0.1657747 |
| 99% | 0.4209203 |
Figure 2c. Cross-HS10 Distributions on U.S. Import Price Skewness, Foreign Wage Skewness and U.S. Firm-Level Export Size Skewness (U.S. Exporter Firm Size Skewness vs. Percentile)
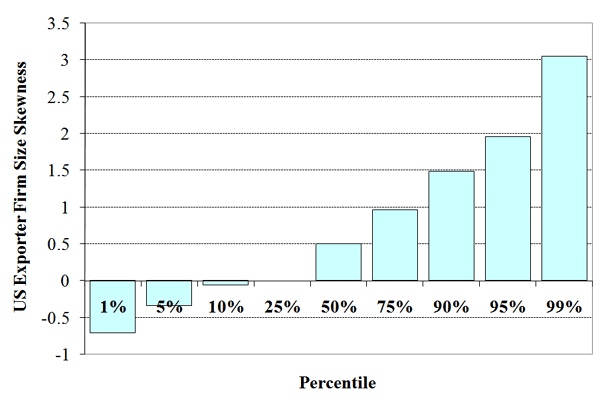
Notes: Skewness is measured at the HS10 level for a given month and then averaged over products and time using import sales weights.
Data for Figure 2c
| Percentile | U.S. Exporter Firm Size Skewness |
|---|---|
| 1% | -0.7071068 |
| 5% | -0.3371869 |
| 10% | -0.0567487 |
| 25% | 0 |
| 50% | 0.5008844 |
| 75% | 0.9629322 |
| 90% | 1.486405 |
| 95% | 1.952562 |
| 99% | 3.046526 |
Figure 3a. Estimated Value Share of Cost and Quality Imports Over Time - Aggregate Imports; Unbalanced
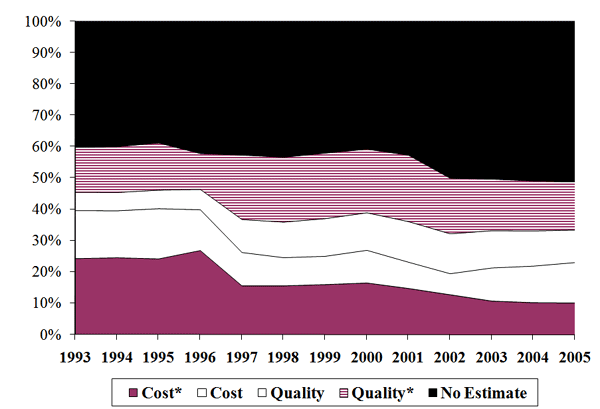
Data for Figure 3a
| Year | Cost | Cost* | Quality | Quality* | No Estimate |
|---|---|---|---|---|---|
| 1993 | 8.62E+10 | 1.36E+11 | 3.28E+10 | 8.05E+10 | 2.24E+11 |
| 1994 | 9.67E+10 | 1.58E+11 | 3.77E+10 | 9.42E+10 | 2.56E+11 |
| 1995 | 1.16E+11 | 1.75E+11 | 4.30E+10 | 1.09E+11 | 2.79E+11 |
| 1996 | 8.90E+10 | 1.83E+11 | 4.44E+10 | 7.82E+10 | 2.86E+11 |
| 1997 | 8.82E+10 | 1.28E+11 | 8.66E+10 | 1.69E+11 | 3.49E+11 |
| 1998 | 7.81E+10 | 1.34E+11 | 9.77E+10 | 1.78E+11 | 3.71E+11 |
| 1999 | 8.70E+10 | 1.53E+11 | 1.15E+11 | 2.00E+11 | 4.00E+11 |
| 2000 | 1.19E+11 | 1.87E+11 | 1.36E+11 | 2.30E+11 | 4.60E+11 |
| 2001 | 8.53E+10 | 1.49E+11 | 1.31E+11 | 2.14E+11 | 4.29E+11 |
| 2002 | 6.40E+10 | 1.20E+11 | 1.20E+11 | 1.67E+11 | 4.69E+11 |
| 2003 | 1.26E+11 | 1.27E+11 | 1.41E+11 | 1.95E+11 | 5.93E+11 |
| 2004 | 1.62E+11 | 1.41E+11 | 1.55E+11 | 2.20E+11 | 6.99E+11 |
| 2005 | 2.06E+11 | 1.60E+11 | 1.65E+11 | 2.43E+11 | 8.08E+11 |
Figure 3b. Estimated Value Share of Cost and Quality Imports Over Time - Subset of Imports; Balanced
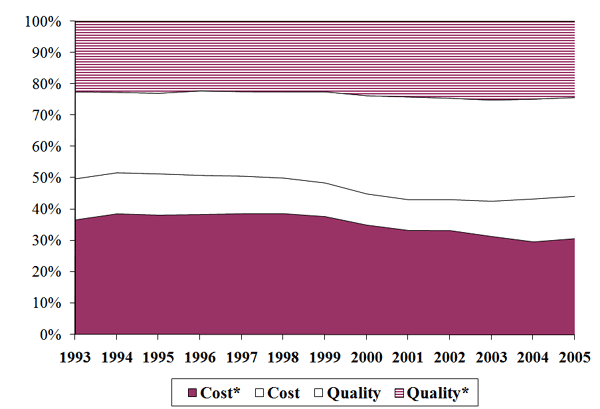
Data for Figure 3b
| Year | Cost | Cost* | Quality | Quality* |
|---|---|---|---|---|
| 1993 | 4.43E+09 | 1.24E+10 | 9.33E+09 | 7.56E+09 |
| 1994 | 5.06E+09 | 1.49E+10 | 9.86E+09 | 8.68E+09 |
| 1995 | 5.76E+09 | 1.67E+10 | 1.12E+10 | 9.96E+09 |
| 1996 | 5.96E+09 | 1.83E+10 | 1.28E+10 | 1.05E+10 |
| 1997 | 6.30E+09 | 2.03E+10 | 1.41E+10 | 1.17E+10 |
| 1998 | 6.47E+09 | 2.20E+10 | 1.56E+10 | 1.27E+10 |
| 1999 | 6.98E+09 | 2.45E+10 | 1.88E+10 | 1.45E+10 |
| 2000 | 7.58E+09 | 2.66E+10 | 2.37E+10 | 1.79E+10 |
| 2001 | 7.24E+09 | 2.45E+10 | 2.40E+10 | 1.76E+10 |
| 2002 | 7.57E+09 | 2.54E+10 | 2.46E+10 | 1.86E+10 |
| 2003 | 9.31E+09 | 2.59E+10 | 2.65E+10 | 2.06E+10 |
| 2004 | 1.28E+10 | 2.77E+10 | 2.96E+10 | 2.30E+10 |
| 2005 | 1.38E+10 | 3.13E+10 | 3.20E+10 | 2.46E+10 |
Figure 4. Estimated Mean Relative Prices in the Tail of the Price Distribution
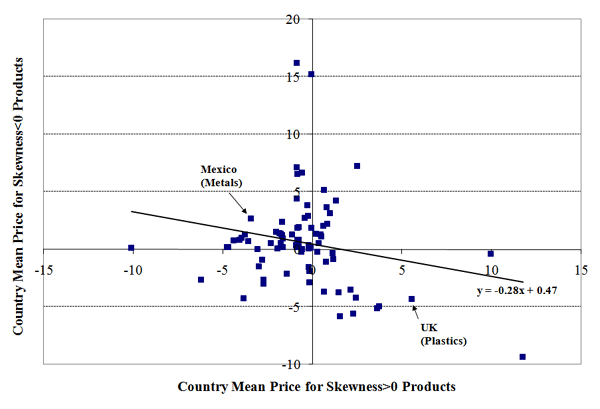
Data for Figure 4
| Country Mean Price for Skewness>0 Products | Country Mean Price for Skewness<0 Products |
|---|---|
| -10.11444 | 0.153171 |
| -4.782756 | 0.2052139 |
| -4.71394 | 0.2152985 |
| -3.582234 | 0.7490403 |
| -4.065117 | 0.8090972 |
| -0.639707 | -0.2274928 |
| -0.5799576 | 0.0060176 |
| -0.1994466 | 0.1063334 |
| -0.1184715 | 0.1642229 |
| 11.72568 | -9.349154 |
| 1.53091 | -5.817983 |
| 2.2608 | -5.59527 |
| 3.623451 | -5.138698 |
| 3.728769 | -4.955288 |
| 5.518045 | -4.313876 |
| 2.426349 | -4.199431 |
| 1.447247 | -3.721534 |
| 2.103632 | -3.507814 |
| 9.953273 | -0.3673959 |
| -0.2247853 | -1.517359 |
| 1.146522 | -0.8228443 |
| 1.114611 | -0.3218352 |
| 0.2607556 | -0.1980343 |
| -0.8833787 | 0.1722269 |
| -0.78822 | 0.334959 |
| -0.901993 | 0.3486976 |
| 0.3358116 | 0.5727592 |
| -0.7737846 | 0.8401546 |
| -1.675096 | 0.9756155 |
| 0.474345 | 1.128554 |
| -1.152189 | 1.280672 |
| -1.756256 | 1.334413 |
| -1.833015 | 1.402323 |
| -0.778387 | 1.957658 |
| -3.839179 | -4.258099 |
| -2.73615 | -2.654394 |
| -3.086861 | 0.0412235 |
| -3.956799 | 1.037744 |
| 0.4557409 | 1.274498 |
| 0.2076585 | 1.33233 |
| 0.6035393 | 2.0496 |
| -3.447118 | 2.674378 |
| -0.8716277 | 4.43208 |
| 0.6259792 | 5.200751 |
| -0.5816155 | 6.708881 |
| -2.735316 | -2.965466 |
| -6.23677 | -2.650788 |
| -1.437093 | -2.093869 |
| -0.1790623 | -1.877002 |
| -2.982831 | -1.485673 |
| -2.803877 | -0.8848576 |
| -1.940236 | 0.0706112 |
| -1.649451 | 0.207007 |
| -2.315316 | 0.519621 |
| -1.765553 | 0.5585735 |
| -4.394921 | 0.7623545 |
| -0.8265831 | 0.8566853 |
| -1.678855 | 1.213771 |
| -3.79113 | 1.314711 |
| -0.0691737 | 1.87958 |
| -1.712989 | 2.374948 |
| -0.4415287 | 2.738531 |
| -0.2550793 | 2.932352 |
| 0.9541885 | 3.134134 |
| 0.769422 | 3.67442 |
| 0.6440994 | -3.650882 |
| -0.1784252 | -2.854464 |
| 0.7565701 | -1.066402 |
| -0.2158611 | 0.3590142 |
| -2.033778 | 1.535422 |
| -0.8416017 | 1.868131 |
| 0.8393441 | 2.222082 |
| -0.2771971 | 3.855709 |
| 1.290968 | 4.251696 |
| -0.82676 | 6.55023 |
| -0.8710443 | 7.16599 |
| 2.479824 | 7.263012 |
| -0.0515303 | 15.22865 |
| -0.8727452 | 16.23221 |
Figure 5. Estimated Mean Relative Prices in the Body of the Price Distribution
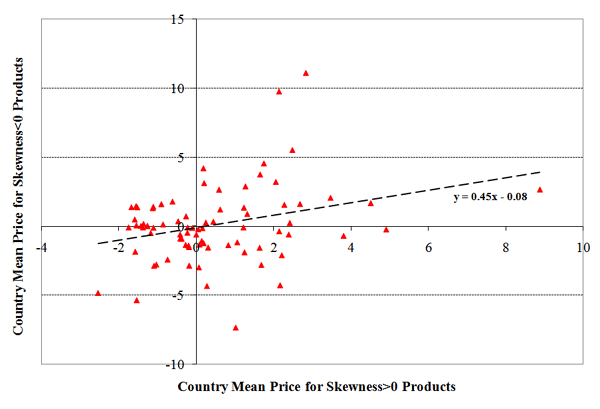
Data for Figure 5
| Country Mean Price for Skewness>0 Products | Country Mean Price for Skewness<0 Products |
|---|---|
| 1.211662 | -0.0642513 |
| -0.2303636 | -0.0673111 |
| -0.1072958 | -0.104288 |
| 0.4342728 | 0.3509969 |
| 0.2387114 | 0.2890435 |
| -0.3870456 | -0.8795604 |
| -0.0082582 | -0.5799576 |
| 0.0417432 | -0.1994466 |
| 0.1527304 | -0.1184715 |
| 0.1949874 | 3.139247 |
| -0.6217048 | 1.804978 |
| 1.22343 | 1.367941 |
| 0.1767835 | 4.216126 |
| 0.1321326 | -1.043826 |
| 8.873891 | 2.671988 |
| 2.15916 | -4.24415 |
| 0.6092577 | 1.228038 |
| 3.799033 | -0.6743028 |
| 3.463405 | 2.081322 |
| -1.184522 | -0.4710454 |
| -1.684931 | 1.394498 |
| -1.531067 | 1.387677 |
| -1.119483 | 1.433453 |
| -1.269094 | 0.0353993 |
| -1.56321 | 1.474358 |
| -1.372703 | 0.1962806 |
| -1.556102 | 0.0800682 |
| -1.272423 | 0.0517785 |
| -1.757401 | -0.0601634 |
| -1.133154 | 1.325465 |
| -0.4758098 | 0.3770594 |
| -1.383624 | -0.0600614 |
| -1.43781 | 0.0372182 |
| -0.9102964 | 1.620091 |
| -2.547158 | -4.798788 |
| 0.298005 | -1.514893 |
| 0.2673651 | -4.298798 |
| 1.674151 | -2.772949 |
| 2.67343 | 1.629715 |
| -0.1964543 | -1.481343 |
| 2.380946 | -0.5820705 |
| -0.2072578 | -1.370588 |
| 4.901645 | -0.2043063 |
| 0.0754055 | -1.302928 |
| 0.819689 | -1.344286 |
| 0.1822023 | -1.204628 |
| -1.548112 | -5.32539 |
| -0.4219023 | -0.8702205 |
| 1.010778 | -7.304376 |
| -0.867112 | 0.1503713 |
| -1.039727 | -2.745634 |
| -1.585169 | -1.819566 |
| -0.2715584 | 0.7446443 |
| -0.749746 | -2.388735 |
| -1.114863 | -0.0814989 |
| -0.1910081 | -2.82543 |
| -0.2828111 | -1.323559 |
| -0.4244107 | -0.5758441 |
| 0.0600955 | -2.954971 |
| 1.264466 | 2.903331 |
| 1.051651 | -1.139473 |
| 1.628646 | -1.533682 |
| 1.31032 | 0.9099249 |
| 2.409009 | 0.2577803 |
| 2.135491 | -0.3440759 |
| 2.202709 | -2.077771 |
| -1.09959 | -2.836397 |
| 1.237845 | -1.863368 |
| -0.2374539 | -0.4502838 |
| 2.269219 | 1.56875 |
| -1.597545 | 0.5091571 |
| 2.048803 | 3.227532 |
| 0.5808608 | 2.66271 |
| 1.740055 | 4.557546 |
| 1.641416 | 3.762842 |
| 2.476018 | 5.534033 |
| 4.501459 | 1.693295 |
| 2.130895 | 9.762493 |
| 2.824802 | 11.10184 |
Figure 6. Estimated Mean Relative Prices in the Tail of the Price Distribution
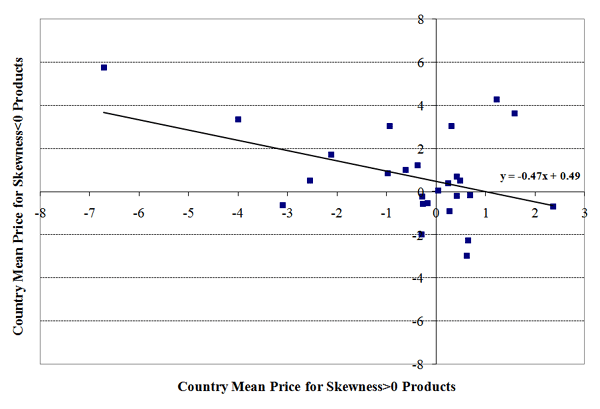
Data for Figure 6
| Country Mean Price for Skewness>0 Products | Country Mean Price for Skewness<0 Products |
|---|---|
| -0.9773338 | 0.8660071 |
| 0.043604 | 0.0599405 |
| -0.2848843 | -0.2232344 |
| -4.002689 | 3.361159 |
| 1.580434 | 3.644843 |
| -0.6260032 | 1.017278 |
| -3.10988 | -0.6320824 |
| -6.719578 | 5.774083 |
| -2.548709 | 0.52073 |
| -0.2737784 | -0.5700209 |
| -0.9455292 | 3.057484 |
| 0.6456147 | -2.246524 |
| 0.6123197 | -2.972801 |
| 2.361789 | -0.6778565 |
| 0.4074908 | 0.6948807 |
| -0.3008427 | -1.99259 |
| -2.12396 | 1.737596 |
| 1.213401 | 4.287158 |
| 0.3025998 | 3.043957 |
| -0.3735099 | 1.216197 |
| 0.271241 | -0.9046901 |
| 0.4844016 | 0.5116533 |
| 0.4124107 | -0.1787722 |
| 0.2415011 | 0.395026 |
| 0.6805309 | -0.1585916 |
| -0.1723394 | -0.5371525 |
Figure 7. Estimated Mean Relative Prices in the Body of the Price Distribution
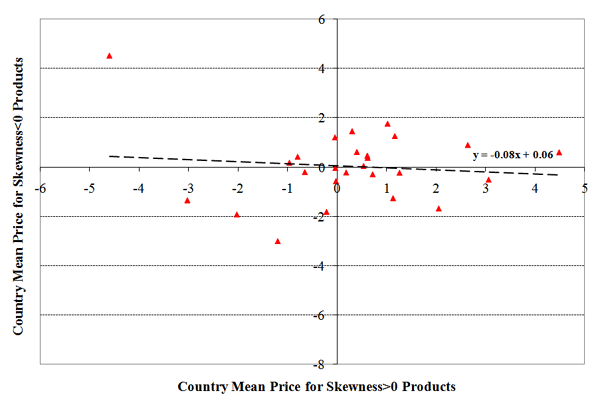
Data for Figure 7
| Country Mean Price for Skewness>0 Products | Country Mean Price for Skewness<0 Products |
|---|---|
| -0.801167 | 0.430791 |
| -0.0375248 | -0.0229663 |
| -0.654767 | -0.1917363 |
| -3.02928 | -1.331576 |
| 2.637777 | 0.9077079 |
| -0.0456816 | 1.217611 |
| -0.9676863 | 0.1894145 |
| -4.605075 | 4.525943 |
| -2.029626 | -1.904782 |
| -1.202777 | -2.987114 |
| 1.016615 | 1.769821 |
| 1.126951 | -1.245277 |
| 3.058576 | -0.4956317 |
| 4.483743 | 0.6142358 |
| -0.0269655 | -0.5575173 |
| -0.2167907 | -1.798918 |
| 2.049781 | -1.663903 |
| 1.163156 | 1.268846 |
| 0.3007753 | 1.466926 |
| 1.257632 | -0.2155802 |
| 0.7161143 | -0.2794122 |
| 0.607142 | 0.474896 |
| 0.6123449 | 0.3908289 |
| 0.3955428 | 0.6228089 |
| 0.5316172 | 0.0604997 |
| 0.1795166 | -0.2051397 |
Table 1a. The Intra-HS10 Distribution Properties of U.S. Import Prices, by Sector (U.S. Imports)
| Standard Deviation | Skewness | Kurtosis | Freq. of High Outliers | Freq. of Low Outliers | |
|---|---|---|---|---|---|
| Wood & Wood Products | 0.32 | -0.37 | 4.57 | 0.14 | 0.12 |
| Mineral Products | 0.25 | -0.33 | 4.98 | 0.16 | 0.10 |
| Animal & Animal Products | 0.43 | -0.11 | 4.48 | 0.10 | 0.14 |
| Raw Hides, Skins, Leather | 1.03 | -0.10 | 3.04 | 0.18 | 0.13 |
| Stone / Glass | 1.01 | -0.01 | 2.79 | 0.17 | 0.13 |
| Metals | 0.83 | 0.01 | 3.46 | 0.16 | 0.14 |
| Footwear / Headgear | 0.61 | 0.03 | 3.43 | 0.18 | 0.14 |
| Miscellaneous | 1.40 | 0.03 | 2.94 | 0.16 | 0.15 |
| Vegetable Products | 0.29 | 0.05 | 3.42 | 0.17 | 0.13 |
| Transportation | 1.06 | 0.13 | 2.93 | 0.16 | 0.16 |
| Foodstuffs | 0.52 | 0.16 | 3.28 | 0.17 | 0.15 |
| Electric Machinery | 1.58 | 0.28 | 3.29 | 0.17 | 0.12 |
| Mechanical & Computers | 1.60 | 0.29 | 3.71 | 0.18 | 0.12 |
| Chemicals & Allied Ind. | 2.08 | 0.35 | 2.79 | 0.19 | 0.12 |
| Textiles | 0.56 | 0.38 | 4.15 | 0.17 | 0.11 |
| Plastics / Rubber | 1.35 | 0.73 | 3.99 | 0.18 | 0.10 |
| 1.18 | 0.15 | 3.43 | 0.17 | 0.13 |
Table 1b. The Intra-HS10 Distribution Properties of U.S. Import Prices, by Sector (U.S. Exports)
| Standard Deviation | Skewness | |
|---|---|---|
| Raw Hides, Skins, Leather | 0.40 | -1.25 |
| Miscellaneous | 1.92 | -0.28 |
| Foodstuffs | 0.61 | -0.20 |
| Vegetable Products | 0.28 | -0.19 |
| Mineral Products | 0.21 | -0.18 |
| Animal & Animal Products | 0.48 | -0.10 |
| Chemicals & Allied Ind. | 0.85 | -0.05 |
| Transportation | 1.33 | -0.03 |
| Mechanical & Computers | 1.88 | -0.02 |
| Metals | 1.14 | -0.01 |
| Footwear / Headgear | 0.59 | 0.00 |
| Wood & Wood Products | 0.49 | 0.02 |
| Electric Machinery | 1.81 | 0.09 |
| Stone / Glass | 0.90 | 0.18 |
| Plastics / Rubber | 1.04 | 0.27 |
| Textiles | 0.36 | 0.64 |
| 1.49 | 0.00 |
Notes: Sample includes those classification groups with greater than 10 item price observations in a given monthly period. All statistics are calculated within a classification group and then aggregated over classifications and time, weighted by the dollar sales value of imports. The frequency of high price outliers is the number of products with prices greater than one standard deviation above the median price. An analogous defintion holds for the frequency of low price outliers.
Table 2a. Quality Scope Estimates, ((b/(a-b))), and a Measure of Horizontal Differentiation, σ, for Selected Import Products (Top 20 Largest Quality Products by Value)
| HS6 | 2005 Import Value ($bn) | b/(a-b) | sigma | Description |
|---|---|---|---|---|
| 870323 | 46.50 | 2.02 | 27.08 | Passenger Vehicles, Spark-Ignition, Engine >1500 CC |
| 852520 | 24.90 | 2.30 | 3.08 | Transmission Apparatus Incorporating Reception Apparatus |
| 300490 | 24.00 | 0.44 | 11.03 | Medicaments NESOI, Measured Doses, Retail, NESOI |
| 852990 | 5.14 | 0.36 | 2.97 | Parts For Transmission, Radar, Radio,TV, NESOI |
| 620342 | 5.11 | 1.65 | 4.57 | Men'S Or Boys' Trousers, Not Knit, Cotton |
| 901890 | 4.86 | 0.29 | 2.07 | Instruments & Appliances For Medical Surgical Dental Vet., NESOI |
| 850440 | 4.81 | 0.29 | 8.91 | Static Converters; Automated Data Processor Power Supplies |
| 848180 | 4.39 | 1.03 | 2.38 | Other Valves And Other Appliances For Pipes, Tanks, Vats Or The Like |
| 271112 | 4.24 | 1.11 | 6.25 | Propane, Liquefied |
| 852190 | 3.97 | 1.73 | 2.20 | Video Recording/Reproduction Appliances |
| 853710 | 3.81 | 0.82 | 3.82 | Bases For Electric Control Or Distribution, Not Exceeding 1,000V |
| 401110 | 3.74 | 2.44 | 4.88 | New Pneumatic Tires Of Rubber, For Motor Cars |
| 760110 | 3.73 | 1.20 | 27.85 | Unwrought Aluminum, Not Alloyed |
| 760120 | 3.47 | 4.34 | 9.16 | Unwrought Aluminum Alloys |
| 740311 | 3.24 | 8.28 | 33.70 | Refined Copper Cathodes And Sections Of Cathodes |
| 220421 | 3.05 | 1.35 | 4.07 | Wine, From Grapes, NESOI, <2 Liters |
| 271114 | 2.87 | 2.28 | 29.76 | Ethylene, Propylene, Butylene |
| 842952 | 2.51 | 1.58 | 18.00 | Mechanical Shovels & Excavators |
| 271113 | 2.34 | 2.74 | 9.55 | Butanes, Liquefied |
| 853400 | 2.12 | 0.29 | 9.71 | Printed Circuits |
Table 2b. Quality Scope Estimates, ((b/(a-b))), and a Measure of Horizontal Differentiation, σ, for Selected Import Products (Top 20 Largest Cost Products by Value)
| HS6 | 2005 Import Value ($bn) | b/(a-b) | sigma | Description |
|---|---|---|---|---|
| 847330 | 27.60 | -0.19 | Parts & Accessories For Automated Data Processor Machines & Units | |
| 870431 | 10.80 | -3.06 | 42.90 | Motor Vehicles For The Transport Of Goods, Not Over 5 Metric Tons |
| 851790 | 8.59 | -0.28 | Parts Of Electrical Apparatus For Line Telephony Or Line Telegraphy | |
| 840734 | 6.66 | -2.77 | 26.62 | Reciprocating Piston Engines For Vehicles, Exceeding 1, 000CC |
| 854430 | 5.78 | -0.23 | Insulated Wiring Sets For Vehicles, Ships, Aircraft | |
| 940190 | 5.74 | -0.32 | Parts Of Seats (Excl. Medical, Barber, Dental Etc) | |
| 950490 | 3.58 | -0.90 | 1.20 | Other Articles For Funfair, Table Or Parlour Games |
| 610910 | 3.42 | -2.44 | 5.61 | T-Shirts, Singlets, Other Vests, Knitted Or Crocheted, Of Cotton |
| 30613 | 2.80 | -3.36 | 5.25 | Shrimps And Prawns, Including In Shell, Frozen |
| 940320 | 2.72 | -1.75 | Metal Furniture, NESOI | |
| 620520 | 2.66 | -1.04 | 5.24 | Men's Or Boys' Shirts, Of Cotton |
| 843149 | 2.63 | -0.33 | 2.57 | Parts Of Derricks, Cranes, Graders, Levellers, Scrapers Or Pile-Drivers |
| 903289 | 2.61 | -0.79 | 1.72 | Automatic Regulating Or Controlling Instruments & Apparatus |
| 950410 | 2.52 | -1.67 | Video Games Of A Kind Used With A Television Receiver | |
| 940161 | 2.48 | -1.06 | 2.17 | Seats With Wooden Frames, Upholstered, NESOI |
| 847989 | 2.46 | -0.29 | 21.75 | Air-Coolers, Air Purifiers Of Other Machines And Mechanical Appliances |
| 300439 | 2.31 | -0.56 | 4.10 | Medicaments Containing Other Hormones |
| 847340 | 2.07 | -0.43 | Parts And Accessories Of Office Machines, NESOI | |
| 901819 | 1.92 | -0.39 | 28.58 | Electro-Diagnostic Apparatus Nesoi, And Parts |
| 853669 | 1.75 | -0.56 | 1.99 | Plugs And Sockets, For A Voltage Not Exceeding 1,000V |
Table 3a. Quality Scope Estimates for Selected Export Products (Top 15 Largest Quality Products by Value (U.S. Exports))
| HS6 | 2005 Export Value ($bn) | Description |
|---|---|---|
| 854221 | 22.2 | Digital Monolithic Integrated Circuits |
| 870323 | 12.6 | Passenger Vehicles, Spark-Ignition, Engine>1,500CC |
| 870324 | 9.8 | Passenger Vehicles, Spark-Ignition, Engine>3,000CC |
| 271019 | 9.7 | Light Petroleum Distillates, NESOI |
| 854229 | 6.2 | Monolithic Itegrated Circuits, Other Than Digital |
| 300210 | 4.1 | Antisera And Other Blood Fractions |
| 520100 | 3.9 | Cotton, Not Carded Or Combed |
| 841199 | 3.8 | Gas Turbine Parts, NESOI |
| 851750 | 3.7 | Telecommunications Apparatus For Line Systems |
| 847149 | 2.9 | Digital Automated Processing Machines And Units |
| 847150 | 2.9 | Digital Processing Units, NESOI |
| 840991 | 2.9 | Spark-Ignition Internal Combustion Piston Engine Parts |
| 760612 | 2.1 | Aluminum Alloy Rectangular Plates, Over .2MM Thick |
| 848180 | 2.1 | Other Valves And Appliances For Pipes, Tanks And Vats |
| 470321 | 2.0 | Wood Pulp, Soda Or Sulphate, Coniferous, Bleached |
Table 3b. Quality Scope Estimates for Selected Export Products (Top 15 Largest Cost Products by Value (U.S. Exports))
| HS6 | 2005 Export Value ($bn) | Description |
|---|---|---|
| 847330 | 12.2 | Parts & Accessories For Automated Data Processing Machines |
| 870899 | 10.2 | Parts & Accessories For Motor Vehicles, NESOI |
| 870829 | 8.6 | Parts & Accessories Of Bodies Of Motor Vehicles, NESOI |
| 841191 | 7.8 | Turbojet And Turbopropelor Parts |
| 100590 | 4.9 | Maize, Except Seed Corn |
| 847989 | 4.6 | Machines And Mechanical Appliances With Individual Function, NESOI |
| 841112 | 4.5 | Turbojets Of A Thrust Exceeding 25 Knots |
| 840734 | 3.9 | Reciprocating Piston Engines For Vehicles, Exceeding 1,000CC |
| 870840 | 3.5 | Gear Boxes For Motor Vehicles |
| 851790 | 3.5 | Parts Of Electrical Apparatus For Line Telephony Or Line Telegraphy |
| 382200 | 3.5 | Composite Diagnostic Or Laboratory Reagents, NESOI |
| 392690 | 3.4 | Plastic Articles, NESOI |
| 840820 | 3.4 | Compression-Ignition Internal Combustion Piston Engine |
| 852520 | 3.3 | Transmission Apparatus Incorporating Reception Apparatus |
| 270112 | 3.1 | Bituminous Coal, Not Agglomerated |
Table 4a. The Correlation of Item Price and Wage (Wage Elasticity of Item, Prices, Pooled Across Quantiles)
| Skewness>0 Products: 15th | Skewness>0 Products: 85th | Skewness>0 Products: N | Skewness<0 Products: 15th | Skewness<0 Products: 85th | Skewness<0 Products: N | |||
|---|---|---|---|---|---|---|---|---|
| Animal & Animal Products | -0.06 | -0.09 | 3,404 | 0.03 | 0.05 | 5,174 | ||
| Vegetable Products | 0.34* | 0.64* | 2,747 | 0.33* | 0.62* | 1,801 | ||
| Plastics / Rubber | -0.04 | 2.63* | 5,176 | -0.39 | 0.65 | 703 | ||
| Textiles | 0.06 | 0.48* | 2,633 | -0.59* | -0.02 | 3,132 | ||
| Metals | 0.22* | 0.36* | 2,816 | 1.91* | 0.05 | 2,200 | ||
| Mechanical & Computers | 0.40* | 0.58* | 7,992 | 0.16 | 1.06* | 8,550 | ||
| Transportation | 0.70* | 0.09 | 22,531 | 2.47* | 2.30* | 6,504 | ||
Table 4b. The Correlation of Item Price and Wage (Wage Elasticity of Item Prices With Additional Controls)
| Skewness>0 Products: 15th | Skewness>0 Products: 85th | Skewness>0 Products: N | Skewness<0 Products: 15th | Skewness<0 Products: 85th | Skewness<0 Products: N | |
|---|---|---|---|---|---|---|
| Wage: Animal & Animal Products | -0.70* | -0.66 | 3,154 | 0.11 | 0.09* | 5,591 |
| Wage: Vegetable Products | 0.56* | 0.31* | 2,384 | 0.29* | 0.25* | 1,529 |
| Wage: Mechanical & Computers | -0.51 | -0.93 | 7,427 | 1.45* | 1.84* | 8,221 |
| Wage: Transportation | 0.01 | 0.07 | 22,483 | 1.41* | 0.93* | 5,997 |
| Market Transfer: Animal & Animal Products | 0.21* | 0.11 | ||||
| Market Transfer: Vegetable Products | 0.07 | 0.05 | 0.73* | 1.04* | ||
| Market Transfer: Mechanical & Computers | 0.16 | -1.43* | -1.42* | 0.12 | ||
| Market Transfer: Transportation | -0.13 | -0.17* | -2.61* | -1.94* | ||
| Cost Transfer: Animal & Animal Products | ||||||
| Cost Transfer: Vegetable Products | 0.12 | -0.11 | 1.32* | 0.72* | ||
| Cost Transfer: Mechanical & Computers | 1.30 | -1.35* | -0.18 | 1.30* | ||
| Cost Transfer: Transportation | 0.54* | -0.01 | 1.04* | 1.73* | ||
| Irregular Discontintuation: Animal & Animal Products | -0.09* | -0.04* | 0.08* | 0.03* | ||
| Irregular Discontintuation: Vegetable Products | -0.35* | -0.16* | -0.07* | -0.02 | ||
| Irregular Discontintuation: Mechanical & Computers | -0.39* | 0.02 | -0.26* | 0.28* | ||
| Irregular Discontintuation: Transportation | 0.05 | 0.01 | 0.01 | -0.36* |
Notes: Shown are estimated coefficients for the wage elasticity and other controls in equation (18). An asterisk denotes significance at the 10 percent level.
Table 5. Estimated Country Relative Prices for Exporters in the Textiles Sector at the 15th and 85th Quantiles of the Price Distribution
| Skewness>0 Products: 15th | Skewness>0 Products: 85th | Skewness<0 Products: 15th | Skewness<0 Products: 85th | |
|---|---|---|---|---|
| Pakistan | -1.68 | 1.15 | -0.82 | 1.39 |
| Bangladesh | -1.53 | 1.11 | -0.32 | 1.39 |
| Egypt | -1.13 | 0.47 | 1.13 | 1.33 |
| Costa Rica | -1.56 | 0.34 | 0.57 | 0.08 |
| China | -1.12 | 0.26 | -0.20 | 1.43 |
| India | -1.18 | -0.22 | -1.52 | -0.47 |
| Malaysia | -1.27 | -0.77 | 0.84 | 0.05 |
| Turkey | -0.91 | -0.78 | 1.96 | 1.62 |
| Thailand | -1.56 | -0.79 | 0.33 | 1.47 |
| Philippines | -1.27 | -0.88 | 0.17 | 0.04 |
| Colombia | -1.37 | -0.90 | 0.35 | 0.20 |
| Italy | -0.48 | -1.15 | 1.28 | 0.38 |
| Korea | -1.76 | -1.68 | 0.98 | -0.06 |
| Macao | -1.38 | -1.76 | 1.33 | -0.06 |
| Hong Kong | -1.44 | -1.83 | 1.40 | 0.04 |
Notes: Shown are estimated coefficients for α2c in equation (18). Quantile regressions are estimated separately for Quality and Cost products. All estimates are significant at the 10 percent level.
Table 6. Real Exchange Rate Pass-Through to Constant-Quality and Quality-Inclusive Import Prices (Annual, 1994-2004), Dep. Variable: Import Price Index
| Cost Industries: Constant-Quality (Transaction-Level), (I) | Cost Industries: Constant-Quality (Transaction-Level), (II) | Cost Industries: Quality-Inclusive (Unit Value), (III) | Cost Industries: Quality-Inclusive (Unit Value), (IV) | All Industries: Constant-Quality (Transaction-Level), (V) | All Industries: Constant-Quality (Transaction-Level), (VI) | All Industries: Quality-Inclusive (Unit Value), (VII) | All Industries: Quality-Inclusive (Unit Value), (VIII) | Quality Industries: Constant-Quality (Transaction-Level), (IX) | Quality Industries: Constant-Quality (Transaction-Level), (X) | Quality Industries: Constant-Quality (Transaction-Level), (XI) | Quality Industries: Constant-Quality (Transaction-Level), (XII) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Real Exch. Rate (w/ 2 lags) | 0.07** (0.01) |
0.06** (0.01) |
0.09 (0.06) |
0.11 (0.06) |
0.08** (0.01) |
0.08** (0.01) |
0.21** (0.04) | 0.21** (0.05) | 0.10** (0.01) |
0.10** (0.01) |
0.27** (0.08) |
0.27** (0.08) |
| Export Price | 0.17** (0.02) |
0.15** (0.02) | 0.21* (0.10) | 0.20 (0.11) |
0.17** (0.01) |
0.16** (0.01) |
0.27** (0.08) | 0.27** (0.08) | 0.16** (0.02) |
0.16** (0.02) | 0.30* (0.12) | 0.27* (0.12) |
| Tariff | 0.04** (0.01) |
-0.01 (0.07) |
0.00 (0.01) | 0.03 (0.06) |
-0.05** (0.01) | 0.06 (0.10) | ||||||
| China Share | 0.00** (0.00) |
0.01* (0.01) | 0.00 (0.01) | 0.00 (0.00) |
0.00 (0.00) | 0.00 (0.01) | ||||||
| Observations | 4,530 | 4,500 | 4,530 | 4,500 | 13,012 | 12,892 | 13,012 | 12,892 | 7,035 | 6,989 | 7,035 | 6,989 |
| R-squared | 0.76 | 0.76 | 0.82 | 0.82 | 0.75 | 0.75 | 0.75 | 0.75 | 0.75 | 0.75 | 0.72 | 0.72 |
Notes: Shown are estimates for (19) using ordinary least squares and classification group fixed effects. Standard errors are reported in parentheses, and stars denote the 5 and 1 percent significance levels.
Table 7. Real Exchange Rate Pass-Through to Constant-Quality and Quality-Inclusive Import Prices (Annual, 1994-2004): Dep. Variable: Import Price Index
| HS 84 & 85 Only: Cost Industries, Constant Quailty (I) | HS 84 & 85 Only: Cost Industries, Quality-Inclusive (II) | HS 84 & 85 Only: All Industries, Constant-Quality (III) | HS 84 & 85 Only: All Industries, Quality-Inclusive (IV) | HS 84 & 85 Only: Quality Industries, Constant-Quality (V) | HS 84 & 85 Only: Quality Industries, Quality-Inclusive (VI) | Export-Based Quality Scope Measure: Cost Industries, Constant-Quality (VII) | Export-Based Quality Scope Measure: Cost Industries, Quality-Inclusive (VIII) | Export-Based Quality Scope Measure: All Industries, Constant-Quality (IX) | Export-Based Quality Scope Measure: All Industries, Quality-Inclusive (X) | Export-Based Quality Scope Measure: Quality Industries, Constant-Quality (XI) | Export-Based Quality Scope Measure: Quality Industries, Quality-Inclusive (XII) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Real Exch. Rate (w/ 2 lags) | 0.11** (0.02) | -0.03 (0.22) | 0.08** (0.01) | 0.30** (0.15) | 0.06** (0.01) | 0.43** (0.19) | 0.07** (0.01) | 0.08 (0.12) |
0.07** (0.01) | 0.23* (0.11) | 0.08** (0.01) | 0.38* (0.19) |
| Export Price | 0.21** (0.03) | 0.72* (0.32) | 0.20** (0.02) | 0.13 (0.24) | 0.19** (0.02) | -0.13 (0.31) | 0.20** (0.02) | 0.08 (0.22) | 0.18** (0.01) | 0.22 (0.19) | 0.17** (0.02) | 0.29 (0.29) |
| Tariff | 0.30** (0.06) | -2.06** (0.71) | 0.20** (0.02) | 0.79** (0.50) | 0.11** (0.04) | 1.84** (0.63) | 0.05* (0.02) | -0.49* (0.22) | 0.04* (0.01) | -0.17 (0.19) | 0.03 (0.02) |
0.04 (0.30) |
| China Share | 0.00* (0.00) | -0.02 (0.02) | 0.00** (0.00) | -0.01 (0.01) | 0.00* (0.00) | 0.00 (0.02) |
0.00* (0.00) | -0.01 (0.01) | 0.00** (0.00) | 0.22 (0.19) |
0.00** (0.00) | 0.01 (0.01) |
| Observations | 902 | 902 | 3,515 | 3,515 | 2,613 | 2,613 | 2,139 | 2,139 | 4,154 | 4,154 | 2,015 | 2,015 |
| R-squared | 0.88 | 0.87 | 0.86 | 0.72 | 0.85 | 0.66 | 0.82 | 0.73 | 0.82 | 0.69 | 0.83 | 0.66 |
Notes: Shown are estimates for (19) using ordinary least squares and classification group fixed effects. Standard errors are reported in parentheses, and stars denote the 5 and 1 percent significance levels.
Footnotes
** Division of International Finance, Board of Governors of the Federal Reserve System, Washington, D.C. 20551 U.S.A. Email: [email protected]. I especially thank Robert Feenstra for guidance and constructive suggestions, David Hummels and James Harrigan for insightful discussant comments, as well as Robert McClelland and Rozi Ulics at BLS. I gratefully acknowledge helpful feedback by seminar participants at BLS, FRBNY, Federal Reserve Board, Georgetown, Johns Hopkins SAIS, UC Davis, UCSD IRPS, UVA, UW Madison, and the 2008 conferences of EIIT and ITFA. The views in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or any other person associated with the Federal Reserve System. Return to text
1. Quality differentiation is suggested by Schott (2004) and Hummels and Klenow (2005) to explain increasing unit values in exporter income, invoked by Baldwin and Harrigan (2007) to explain increasing unit value prices in exporter distance, by Kugler and Verhoogen (2008) to explain plant-level size-price correlations, and by Manova and Zhang (2009) and Crozet, Head and Mayer (2009) to analyze correlations of export price with several destination characteristics. Return to text
2. In models of that sort, firms differ across an array of productivity levels and compete in a monopolistically competitive industry. See Melitz (2003). Herein I refer to the absence of quality differentiation with the descriptor: 'cost.' Return to text
3. For example, a price increase for an upgraded model of automobile may be reflecting its more desirable features relative to its predecessor. Alternatively, a shift in demand into higher priced goods would increase an average (non-quality-adjusted) price even if each underlying price went unchanged. The distinction and large potential differences between constant quality and non-quality-adjusted price indexes is discussed and illustrated in Alterman (1991). Return to text
4. For instance, see Auer and Chaney's (2007) discussion of quality and exchange rate pass-through where varieties of different quality (within an industry) have different price sensitivity to exchanage rates. Return to text
5. Note the distinction between vertical quality differentiation and the standard assumption in monopolistic competition models of differentiated varieties (i.e., horizontal differentiation). In the horizontal case, varieties are distinct but provide equal value to the consumer's utility. In the vertical case, as will be made explicit in the model below, varieties enter asymmetrically into utility. Return to text
6. The IPP collects prices for roughly 20,000 imported items and 20,000 exported items per month. Over the course of the sample, approximately 60,000 imported items were observed. Return to text
7. The IPP data has also been used for the measurement of the frequency of price changes as well as exchange rate pass through. For detailed descriptions of the data, see: BLS (2009); Nakamura & Steinsson (2009); Gopinath & Rigobon (2008); and Gopinath, Itskhoki & Rigobon (2007). Return to text
8. The IPP tracks unique varieties of product groups over time and then aggregates the varieties using fixed weights. Therefore, the composition of item characteristics is held literally constant in the aggregation of each period's index. Return to text
9. The reason that the BLS uses slightly more aggregate groups is that not every group (particularly smaller ones) are represented in the IPP sample. Return to text
10. Although the frequency of the sample is monthly, actual price observations may not be available each period and are imputed by the BLS; this either means that the item price remains unchanged or is imputed linearly based on group price changes. For a typical item, prices are relatively stable with occasional changes. For a typical classif group, certain items are observed only sporadically while others enter or exit over the course of the data span; this creates several issues for aggregation which will be addressed separately for the uses of the data described below. For our purposes it will often be convenient to leave imputed price values in the sample, as the BLS does when it computes import price deflators. Leaving in imputations contrasts with other uses of the IPP data, such as the examination of the frequency of price changes. Whereas in frequency calculations imputations can cause biased statistics, imputed values actually add stability to the sample over time when computing the distribution at low levels of aggregation. Return to text
11. Due to changing classification categories over time, the number of groups in any given month is less than 7,000. Return to text
12. In the analysis of classification group price distribution, the reported units of sale are also controlled for; I distinguish between goods sold by the ton versus those sold by container which would be priced non-comparably. Also removed from the sample are those items not priced in dollars. Return to text
13. Sector categorization is defined by HS2: Animal and animal products (1-5); Vegetable products (6-15); Foodstuffs (16-24); Mineral products (25-27); Chemicals & allied industries (28-38); Plastics & rubber (39-40); Raw hides, skins & leather (41-43); Wood & wood products (44-49); Textiles (50-63); Footwear/Headgear (64-67); Stone/glass (68-71); Metals (72-83); Mechanical and computers (84); Electric machinery (85); Transportation (86-89); Miscellaneous (90-96). Return to text
14. It is not obvious a priori that export price distributions should be similar to import price distributions: U.S. exporters compete in a different set of products and within products U.S. exporters may optimally specialize on a distinct portion of the quality ladder (as suggested by Khandelwal (2008) and Schott (2008)). Moreover, there may exist non-monotonicities in export participation (as in Hallak and Sivadasan (2008)) that would affect the price distribution of exports versus imports. Return to text
15. High outliers are defined as prices greater than one standard deviation above the median price. Low outliers are defined as prices less than one standard deviation below the median price. Return to text
16. A more specific interpretation of monitoring costs could be as the costs of quality-differentiated inputs (whose quality level is complementary to that of the output), as in Kugler and Verhoogen (2008). Here, the particular reason for increasing returns to quality is not as relevant, so I will proceed with the more general specification. Return to text
17. In Kremer (1993), production is separated into a set of tasks undertaken by workers of varying skill. The equilibrium outcome is that workers of the same skill are matched together in firms, with higher skill firms paying a higher wage bill. Moreover, when technology choice is endogenous (i.e., firms choose the number of tasks, and hence complexity, associated with production), higher skill firms choose more complex production processes. Verhoogen (2007) employs an O-ring production function to explicitly show returns to skilled and unskilled labor. Return to text
18. ILO Yearbook wage data are available at the SIC 4-digit industry level, a courser level of aggregation. Return to text
19. Note that the level of U.S. firm size (as a proxy for productivity) is not being applied to foreign exporters, but rather the skewness of the size distribution. If the true underlying distribution of firm size in the U.S. and abroad is in the power law family (such as a Pareto) then the measured skewness will be scale invariant; applying these measures to foreign exporters invokes the weaker assumption that the shape of the U.S. firm size distribution is the same as that in the rest of the world. Return to text
20. The high number of products with close to symmetric distributions may reflect the small number of firms that the BLS samples within certain HS10 product groups. Figure 2 and the regression estimates below are not substantially different if the minimum number of firms per product included is increased. Return to text
21. Technically it is possible to estimate the quality cost parameters at the classification/HS10 level (as opposed to HS6). However, since the BLS classification and HS10 codes are identical at the HS6 level, for ease of interpretation I use the slightly more aggregate codes. Return to text
22. Seasonality does not appear to be a very important driver of variation in the import price distribution. Despite monthly import sales being quite volatile due to lumpiness, prices from month-to-month are quite rigid. Figure 1 illusrates how a change in the average price for an HS10 is not necessarily driven by a corresponding change in the price distribution. Moreover, IPP imputation techniques tend to reinforce the stability of the distribution at higher frequencies. Return to text
23. Robust standard errors, clustering HS10 estimates within HS6 groups, barely alter the number of precisely estimated scope measures. Return to text
24. For a fair comparison, the estimates
are recomputed for the whole sample with wage skewness on the
left-hand side (i.e.,
![]() ) and then
compared to the restricted sample. Return to text
) and then
compared to the restricted sample. Return to text
25. The interpretation of sales value sums across cost and quality products may be dubious due to the reliance of the estimates on product category definitions, as discussed above. For instance, if certain highly differentiated technology industries have very narrowly defined HS10 categories and also large sales, then too large a weight would be assigned to low scope industries despite the underlying quality heterogeneity of the industry. The assumption necessary to believe the sales sums (or any cross-product analysis for that matter) is that the agency determining the breadth of product categories defines them 'correctly,' where a correct product definition exactly matches the consumers' notion of the variety characteristics within a product. e.g., If consumers agree that PDA's are distinct products from cellular telephones, then the agency would be correct in defining a new product code. Given this limitation, the applications in this paper will focus on the characteristics of varieties within products. Return to text
26. By only considering products traded throughout the sample time frame, panel (b) ignores the creation of new categories, where a lot of the action may be in terms of quality composition, as well as some rather large reclassifications in product codes over the period. What we can take away from this selection of products is the absence of large shifts in the intensive margin towards products with long quality ladders. Return to text
27. The quantile regression does not function well for large numbers of righthand side variables nor for sparsely populated cells. To cope with this limitation, I divide the sample into the 16 sectors listed in Table 1 (for notational convenience, I suppress sector subscript in (18)). Then, each regression uses only the 5 largest classification groups (by observations) by sector-skewness and only includes countries with at least 75 observations over the course of the sample. Running the quantile regression command in Stata on the resulting restricted samples, convergence of the algorithm is achieved in 7 sectors (listed below). Return to text
28. Note that since the products of different skewness are produced by a different mix of countries, the coefficients shown are those for which a country produces products in industries with both positively and negatively skewed prices. Not shown are those countries in positively skewed industries only or in negatively skewed industries only. Return to text
29. The figure illustrates the estimates for the seven sectors listed in Table 4(a). Return to text
30. There is also an identifier for whether the item price was imputed for the purpose of index construction. Omitting the imputations does not affect the price distribution statistics systematically. Return to text
31. In the description above, the model is not closed to solve for the endogenously determined productivity cut-off, though the exact location of the marginal firm will not matter for the results obtained in this section. It is only important to know that there is some well-defined, unique equilibrium in which the firm on the margin of entry into the international market earns zero profits. Return to text
32. In cases where the classification group is more aggregate than HS10, country-HS10 unit value changes are calculated and then aggregated to the classification level (i.e., as opposed to first summing across values and potentially non-comparable quantities in order to calculate classification level unit values). Return to text
33. Since the IPP data frequency if monthly, once the monthly cumulative index is constructed at the classification level, annual averages are taken to make this series comparable to the lower frequency unit value index. Return to text
34. Theoretically the coefficient should be zero for small importers and negative for large importers, so it will depend on the size of the US in each particular product market. Return to text
35. Since the IPP data is a sample and the data does span the entire set of HS10 product-country groups, unit values were only computed for the sampled product-country groups in the constant-quality price indexes. This ensures that the comparison of HS10 indexes is not itself contaminated by different underlying HS10-country product composition. Return to text
36. This distinction is based solely on
the sign of the estimated scope for quality differentiation. Cost
industries are those with
![]() while quality industries
are those with
while quality industries
are those with
![]() . Using only the subset
of scope estimates that are significantly different than zero does
not affect the results. Return to
text
. Using only the subset
of scope estimates that are significantly different than zero does
not affect the results. Return to
text
37. In a broad set of empirical studies, estimated average pass-through of nominal exchange rates to U.S. import prices is approximately 0.5 in the 1980's, declining to approximately 0.2 in the 1990's (among others, see Goldberg and Knetter (1997), Olivei (2002), Marazzi et al. (2005), Gust et al. (2006), and Bergin and Feenstra (2007)). One explanation for the measured decline in average pass-through, posited by Campa and Goldberg (2005), attributes much of the decline to the changing composition of import bundles, from sectors with relatively high pass-through such as energy to sectors with relatively low pass-through such as manufactures. Following this line of reasoning a step further, sectoral pass-through itself is just the average elasticity across products with disparate scope for differentiation, reflecting the underlying microfoundations of the firms choice of product characteristics. The seemingly low pass-through estimates here likely reflect the low annual frequency of the data relative to other studies. However, the results are not vastly different from pass-through estimates in the 1990's of 20 percent. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text