
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1022, July 2011 --- Screen Reader
Version*
Forecasting the Price of Oil**
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
We address some of the key questions that arise in forecasting the price of crude oil. What do applied forecasters need to know about the choice of sample period and about the tradeoffs between alternative oil price series and model specifications? Are real or nominal oil prices predictable based on macroeconomic aggregates? Does this predictability translate into gains in out-of-sample forecast accuracy compared with conventional no-change forecasts? How useful are oil futures markets in forecasting the price of oil? How useful are survey forecasts? How does one evaluate the sensitivity of a baseline oil price forecast to alternative assumptions about future demand and supply conditions? How does one quantify risks associated with oil price forecasts? Can joint forecasts of the price of oil and of U.S. real GDP growth be improved upon by allowing for asymmetries?
Keywords: Asymmetries, demand and supply, forecasting, oil price, predictability
JEL classification: C53, Q43
1. Introduction
There is widespread agreement that unexpected large and persistent fluctuations in the real price of oil are detrimental to the welfare of both oil-importing and oil-producing economies. Reliable forecasts of the price of oil are of interest for a wide range of applications. For example, central banks and private sector forecasters view the price of oil as one of the key variables in generating macroeconomic projections and in assessing macroeconomic risks. Of particular interest is the question of the extent to which the price of oil is helpful in predicting recessions. For example, Hamilton (2009), building on the analysis in Edelstein and Kilian (2009), provides evidence that the recession of late 2008 was amplified and preceded by an economic slowdown in the automobile industry and a deterioration in consumer sentiment. Thus, more accurate forecasts of the price of oil have the potential of improving forecast accuracy for a wide range of macroeconomic outcomes and of improving macroeconomic policy responses.
In addition, some sectors of the economy depend directly on forecasts of the price of oil for their business. For example, airlines rely on such forecasts in setting airfares, automobile companies decide their product menu and product prices with oil price forecasts in mind, and utility companies use oil price forecasts in deciding whether to extend capacity or to build new plants. Likewise, homeowners rely on oil price forecasts in deciding the timing of their heating oil purchases or whether to invest in energy-saving home improvements.
Finally, forecasts of the price of oil (and the price of its derivatives such as gasoline or heating oil) are important in modeling purchases of energy-intensive durables goods such as automobiles or home heating systems.1 They also play a role in generating projections of energy use, in modeling investment decisions in the energy sector, in predicting carbon emissions and climate change, and in designing regulatory policies such as automotive fuel standards or gasoline taxes.2
This paper provides a comprehensive analysis of the problem of forecasting the price of oil. In section 2 we compare alternative measures of the price of crude oil. In section 3 we discuss the rationales of alternative specifications of the oil price variable in empirical work. Section 4 studies the extent to which the nominal price of oil and the real price of oil are predictable based on macroeconomic aggregates. We document strong evidence of predictability in population. Predictability in population, however, need not translate into out-of-sample forecastability. The latter question is the main focus of sections 5 through 8.
In sections 5, 6 and 7, we compare a wide range of out-of-sample forecasting methods for the nominal price of oil. For example, it is common among policymakers to treat the price of oil futures contracts as the forecast of the nominal price of oil. We focus on the ability of daily and monthly oil futures prices to forecast the nominal price of oil in real time compared with a range of simple time series forecasting models. We find some evidence that the price of oil futures has additional predictive content compared with the current spot price at the 12-month horizon; the magnitude of the reduction in mean-squared prediction error (MSPE) is modest even at the 12-month horizon, however, and there are indications that this result is sensitive to fairly small changes in the sample period and in the forecast horizon. There is no evidence of significant forecast accuracy gains at shorter horizons, and at the long horizons of interest to policymakers, oil futures prices are clearly inferior to the no-change forecast.
Similarly, forecasting models based on the dollar exchange rates of major commodity exporters, models based on the Hotelling (1931), and a variety of simple time series regression models are not successful at significantly lowering the MSPE at short horizons. There is evidence, however, that recent percent changes in the nominal price of industrial raw materials other than oil can be used to substantially and significantly reduce the MSPE of the no-change forecast of the nominal price of oil at horizons of 1 and 3 months. The gains may be as large as 22% at the 3-month horizon. The predictive success of expert survey forecasts of the nominal price of oil proved disappointing. Only the one-quarter-ahead EIA forecast significantly improved on the no-change forecast and none of the survey forecasts we studied significantly improved on the MSPE of the no-change forecast at the one-year horizon. Finally, at horizons of several years, forecasts based on adjusting the current spot price for survey inflation expectations systematically outperform the no-change forecast by a wide margin. At intermediate horizons, none of these alternative forecasting approaches outperforms the no-change forecast of the nominal price of oil.
The best econometric forecast need not coincide with the price expectations of market participants. The latter expectations data are rarely observed with the exception of data in the Michigan consumer survey on gasoline price expectations. We evaluate this survey forecast of the nominal retail price of gasoline against the no-change forecast benchmark. We also contrast this survey forecast with the price of the corresponding futures contracts. Following Anderson, Kellogg and Sallee (2010), we document that, after controlling for inflation, long-term household gasoline price expectations are well approximated by a random walk. This finding has immediate implications for modeling purchases of energy-intensive consumer durables.
Although the nominal price of crude oil receives much attention in the press, the variable most relevant for economic modeling is the real price of oil. Section 8 compares alternative forecasting models for the real price of oil. We provide evidence that reduced-form autoregressive and vector autoregressive models of the global oil market are more accurate than the random walk forecast of the real price of oil at short horizons. Even after taking account of the constraints on the real-time availability of predictors, the MSPE reductions can be substantial in the short run. These gains tend to diminish at longer horizons, however, and, beyond one or two years, the no-change forecast of the real price of oil is the predictor with the lowest MSPE in general. Moreover, the extent of these MSPE reductions depends on the definition of the oil price series.
An important limitation of reduced-form forecasting models from a policy point of view is that they provide no insight into what is driving the forecast and do not allow the policymaker to explore alternative hypothetical forecast scenarios. In section 9, we illustrate how recently developed structural vector autoregressive models of the global oil market may be used to generate conditional projections of how the oil price forecast would deviate from the unconditional forecast benchmark, given alternative scenarios such as a surge in speculative demand similar to previous historical episodes, a resurgence of the global business cycle, or increased U.S. oil production.
Much of the work on forecasting the price of oil has focused on the dollar price of oil. This is natural because crude oil is typically traded in U.S. dollars, but there also is considerable interest in forecasting the real price of oil faced by other oil-importing countries such as the Euro area, Canada, or Japan. In section 10, we discuss the changes required in forecasting the real price of oil in that case and show that accurate forecasts may require different forecasting models for different countries, given the important role of exchange rate fluctuations.
Section 11 focuses on the problem of jointly forecasting U.S. macroeconomic aggregates such as real GDP growth and the price of oil. Of particular interest is the forecasting ability of nonlinear transformations of the price of oil such as the nominal net oil price increase or the real net oil price increase. The net oil price increase is a censored predictor that assigns zero weight to net oil price decreases. There is little evidence that this type of asymmetry is reflected in the responses of U.S. real GDP to innovations in the real price of oil, as documented in Kilian and Vigfusson (2010a,b), but Hamilton (2010) suggests that the net oil price increase specification is best thought of as a parsimonious forecasting device. We provide a comprehensive analysis of this conjecture.
Point forecasts of the price of oil are important, but they fail to convey the large uncertainty associated with oil price forecasts. That uncertainty is captured by the predictive density. In section 12 we discuss various approaches of conveying the information in the predictive density including measures of price volatility and of tail conditional expectations with particular emphasis on defining appropriate risk measures. Section 13 contains a discussion of directions for future research. The concluding remarks are in section 14.
2. Alternative Oil Price Measures
Figure 1 plots alternative measures of the nominal price of oil. The longest available series is the West Texas Intermediate (WTI) price of crude oil. Data on U.S. refiners' acquisition cost for domestically produced oil, for imported crude oil and for a composite of these series are available starting in 1974.1. Figure 1 highlights striking differences in the time series process for the price of oil prior to 1973 and after 1973. The WTI data until 1973 tend to exhibit a pattern resembling a step-function. The price remains constant for extended periods, followed by discrete adjustments. The U.S. wholesale price of oil for 1948-1972 used in Hamilton (1983) is numerically identical with this WTI series. As discussed in Hamilton (1983, 1985) the discrete pattern of crude oil price changes during this period is explained by the specific regulatory structure of the oil industry during 1948-72. Each month the Texas Railroad Commission and other U.S. state regulatory agencies would forecast demand for oil for the subsequent month and would set the allowable production levels for wells in the state to meet demand. As a result, much of the cyclically endogenous component of oil demand was reflected in shifts in quantities rather than prices. The commission was generally unable or unwilling to accommodate sudden disruptions in oil production, preferring instead to exploit these events to implement sometimes dramatic price increases (Hamilton 1983, p. 230).
Whereas the WTI price is a good proxy for the U.S. price for oil during 1948-72, when the U.S. was largely self-sufficient in oil, it becomes less representative after 1973, when the share of U.S. imports of oil rapidly expanded. The price discrepancy between unregulated foreign oil and regulated domestic oil created increasing pressure to deregulate the domestic market. As regulatory control weakened in the mid-1970s, adjustments to the WTI price became much more frequent and smaller in magnitude, as shown in the right panel of Figure 1. By the mid-1980s, the WTI had been deregulated to the point that there was strong comovement between all three oil price series most of the time.
Figure 2 shows the corresponding oil price data adjusted for U.S. CPI inflation. The left panel reveals that in real terms the price of oil had been falling considerably since the late 1950s. That decline was corrected only by the sharp rise in the real price of oil in 1973/74. There has been no pronounced trend in the real price of oil since 1974, but considerable volatility. The definition of the real price of oil is of lesser importance after 1986. Prior to 1986, one key difference is that the refiners' acquisition cost for imported crude oil fell in 1974-76, whereas the real WTI price rose. A second key difference is that the real WTI price spiked in 1980, whereas the real price of oil imports remained largely stable. That pattern was only reversed with the outbreak of the Iran-Iraq War in late 1980.
Figure 3 once more highlights the striking differences between the pre- and post-1973 period. It shows the percent growth rate of the real price of oil. A major structural change in the distribution of the price of oil in late 1973 is readily apparent.3 Whereas the pre-1973 period is characterized by long periods of low volatility interrupted by infrequent large positive price spikes, the post-1973 period is characterized by high month-to-month volatility. It has been suggested that perhaps this volatility has increased systematically after the collapse of OPEC in late 1985. The answer is somewhat sensitive to the exact choice of dates. If one were to date the OPEC period as 1973.10-1985.12, for example, there is no evidence of an increase in the variance of the percent change in the real WTI price of oil. The volatility in the OPEC period is virtually identical to that in the post-OPEC period of 1986.1-2010.6. Shifting the starting date of the OPEC period to 1974.1, in contrast, implies a considerable increase in volatility after 1985. Extending the ending date of the OPEC period to include the price collapse in 1986 induced by OPEC actions, which seems reasonable, on the other hand, renders the volatility much more similar across subperiods. Finally, combining the earlier starting date and the later ending date, there is evidence of a reduction in the real price volatility after the collapse of OPEC rather than an increase. Below we therefore treat the post-1973 data as homogeneous.
Which price series is more appropriate for the analysis of post-1973 data depends in part on the purpose of the study. The WTI price data (as well as other measures of the domestic U.S. price of oil) are questionable to the extent that these prices were regulated until the mid-1980s and do not reflect the true scarcity of oil or the price actually paid by U.S. refiners. The refiners' acquisition cost for imported crude oil provides a good proxy for oil price fluctuations in global oil markets, but may not be representative for the price that U.S. refineries paid for crude oil. The latter price may be captured better by a composite of the acquisition cost of domestic and imported crude oil, neither of which, however, is available before January 1974. The real price of oil imports, nevertheless, is the price relevant for theories interpreting oil price shocks as terms-of-trade shocks. Theories that interpret oil price shocks as allocative disturbances, on the other hand, require the use of retail energy prices, for which the composite refiners' acquisition cost may be a proxy. Below we will consider several alternative oil price series.4
3. Alternative Oil Price Specifications
Although an increasing number of empirical studies of the post-1973 data focuses on the real price of oil, many other studies have relied on the nominal price of oil. One argument for the use of nominal oil prices has been that the nominal price of oil - unlike the real price of oil - is exogenous with respect to U.S. macroeconomic conditions and hence linearly unpredictable on the basis of lagged U.S. macroeconomic conditions.5 This argument may have some merit for the pre-1973 period, but is implausible for the post-1973 period. If the U.S. money supply unexpectedly doubles, for example, then, according to standard macroeconomic models, so will all nominal prices denominated in dollars (including the nominal price of oil), leaving the relative price or real price of crude oil unaffected (see Gillman and Nakov 2009). Clearly, one would not want to interpret such an episode as an oil price shock involving a doubling of the nominal price of oil. Indeed, economic models of the impact of the price of oil on the U.S. economy correctly predict that such a nominal oil price shock should have no effect on the U.S. economy because theoretical models inevitably are specified in terms of the real price of oil, which has not changed in this example.
Another argument in the literature has been that the nominal price of oil can be considered exogenous after 1973 because it is set by OPEC. This interpretation is without basis. First, there is little evidence to support the notion that OPEC has been successfully acting as a cartel in the 1970s and early 1980s, and the role of OPEC has diminished further since 1986 (see, e.g., Skeet 1988; Smith 2005; Almoguera, Douglas and Herrera 2010). Second, even if we were to accept the notion that an OPEC cartel sets the nominal price of oil, economic theory predicts that this cartel price will endogenously respond to U.S. macroeconomic conditions. This theoretical prediction is consistent with anecdotal evidence of OPEC oil producers raising the price of oil (or equivalently lowering oil production) in response to unanticipated U.S. inflation, low U.S. interest rates and the depreciation of the dollar. Moreover, as observed by Barsky and Kilian (2002), economic theory predicts that the strength of the oil cartel itself (measured by the extent to which individual cartel members choose to deviate from cartel guidelines) will be positively related to the state of the global business cycle (see Green and Porter 1984). Thus, both nominal and real oil prices must be considered endogenous with respect to the global economy, unless proven otherwise.
A third and distinct argument has been that consumers of refined oil products choose to respond to changes in the nominal price of oil rather than the real price of oil, perhaps because the nominal price of oil is more visible. In other words, consumers suffer from money illusion. There is no direct empirical evidence in favor of this behavioral argument at the micro level. Rather the case for this specification, if there is one, has to be based on the predictive success of such models; a success that, however, has yet to be demonstrated empirically. We will address this question in section 11.
Even proponents of using the nominal price in empirical models
of the transmission of oil price shocks have concluded that there
is no stable dynamic relationship between percent changes in the
nominal price of oil and in U.S. macroeconomic aggregates. There is
evidence from in-sample fitting exercises, however, of a predictive
relationship between suitable nonlinear transformations of the
nominal price of oil and U.S. real output, in particular. The most
successful of these transformations is the net oil price increase
measure of Hamilton (1996, 2003). Let ![]() denote
the nominal price of oil in logs and
denote
the nominal price of oil in logs and ![]() the
difference operator. Then the net oil price increase is defined
as:
the
difference operator. Then the net oil price increase is defined
as:
where![]() is the highest oil price in the
preceding 12 months or, alternatively, the preceding 36
is the highest oil price in the
preceding 12 months or, alternatively, the preceding 36
months. This transformation involves two distinct ideas. One is that consumers in oil-importing economies respond to increases in the price of oil only if the increase is large relative to the recent past. If correct, the same logic by construction should apply to decreases in the price of oil, suggesting a net change transformation that is symmetric in increases and decreases.
The second idea implicit in Hamilton's definition is that consumers do not respond to net decreases in the price of oil, allowing us to omit the net decreases from the model. In other words, consumers respond asymmetrically to net oil price increases and net oil price decreases and they do so in a very specific fashion. Although there are theoretical models that imply the existence of an asymmetry in the response of the economy to oil price increases and decreases, these models do not imply the specific nonlinear structure embodied in the net increase measure nor do they imply that the net decrease measure should receive zero weight. Nevertheless, Hamilton's nominal net oil price increase variable has become one of the leading specifications in the literature on predictive relationships between the price of oil and the U.S. economy. Hamilton (2010), for example, interprets this specification as capturing nonlinear changes in consumer sentiment in response to nominal oil price increases.6
As with other oil price specifications there is reason to expect lagged feedback from global macroeconomic aggregates to the net oil price increase. Whereas Hamilton (2003) made the case that net oil price increases in the 1970s, 1980s and 1990s were capturing exogenous events in the Middle East, Hamilton (2009) concedes that the net oil price increase of 2003-08 was driven in large part by a surge in the demand for oil. Kilian (2009a,b; 2010), on the other hand, provides evidence based on structural VAR models that in fact most net oil price increases have contained a large demand component driven by global macroeconomic conditions, even prior to 2003. This finding is also consistent with the empirical results in Baumeister and Peersman (2010).
For now we set aside all nonlinear transformations of the price of oil and focus on linear forecasting models for the nominal price of oil and for the real price of oil. Nonlinear joint forecasting models for U.S. real GDP and the price of oil based on net oil price increases are discussed in section 11.
4. Granger Causality Tests
Much of the existing work on predicting the price of oil has focused on testing for the existence of a predictive relationship from macroeconomic aggregates to the price of oil. The existence of predictability in population is a necessary precondition for out-of-sample forecastability (see Inoue and Kilian 2004a). Within the linear VAR framework the absence of predictability from one variable to another in population may be tested using Granger non-causality tests.
4.1. Nominal Oil Price Predictability
4.1.1. The Pre-1973 Evidence
Granger causality from macroeconomic aggregates to the price of oil has received attention in part because Granger non-causality is one of the testable implications of strict exogeneity. The notion that the percent change in the nominal price of oil may be considered exogenous with respect to the U.S. economy was bolstered by evidence in Hamilton (1983), who observed that there is no apparent Granger causality from U.S. domestic macroeconomic aggregates to the percent change in the nominal price of oil during 1948-1972. Of course, the absence of Granger causality is merely a necessary condition for strict exogeneity. Moreover, a failure to reject the null of no Granger causality is at best suggestive; it does not establish the validity of the null hypothesis. Hamilton's case for the exogeneity of the nominal price of oil with respect to the U.S. economy therefore rested primarily on the unique institutional features of the oil market during this period, discussed in section 2, and on historical evidence that unexpected supply disruptions under this institutional regime appear to be associated with exogenous political events in the Middle East, allowing us to treat the resulting price spikes as exogenous with respect to the U.S. economy. For a more nuanced view of these historical episodes see Kilian (2008b; 2009a,b; 2010). Even if we accept Hamilton's interpretation of the pre-1973 period, the institutional conditions that Hamilton (1983) appeals to ceased to exist in the early 1970s, and Hamilton's results for the 1948-1972 period are mainly of historical interest. The real question for our purposes is to what extent there is evidence that oil prices can be predicted from macroeconomic aggregates in the post-1973 period.
4.1.2. The Post-1973 Evidence
There is widespread agreement among oil economists that, starting in 1973, nominal oil prices must be considered endogenous with respect to U.S. macroeconomic variables (see Kilian 2008a). Whether this endogeneity makes the nominal price of oil predictable on the basis of lagged U.S. macroeconomic aggregates depends on whether the price of oil behaves like a typical asset price or not. In the former case, one would expect the nominal price of oil to incorporate information about expected U.S. macroeconomic conditions immediately, rendering the nominal price of oil linearly unpredictable on the basis of lagged U.S. macroeconomic aggregates. This line of reasoning is familiar from the analysis of stock and bond prices as well as exchange rates.7 In the latter case, the endogeneity of the nominal price of oil with respect to the U.S. economy implies that lagged changes in U.S. macroeconomic aggregates have predictive power for the nominal price of oil in the post-1973 data (see, e.g., Cooley and LeRoy 1985).
A recent study by Kilian and Vega (2010) helps resolve the question of which interpretation is more appropriate. Kilian and Vega find no evidence of systematic feedback from news about a wide range of U.S. macroeconomic aggregates to the nominal price of oil within a month. This lack of evidence is in sharp contrast to the evidence for typical asset prices, so lack of power cannot explain the absence of significant feedback from U.S. macroeconomic news to the nominal price of oil. These two results in conjunction allow us to rule out the pure asset price interpretation of the nominal price of oil. We conclude that, if the nominal price of oil is endogenous with respect to lagged U.S. macroeconomic aggregates, then these macroeconomic aggregates must have predictive power at least in population.
Predictability in the context of linear vector autoregressions may be tested using Granger causality tests. Table 1a investigates the evidence of Granger causality from selected nominal U.S. macroeconomic variables to the nominal price of oil. All results are based on pairwise vector autoregressions. The lag order is fixed at 12. Similar results would have been obtained with 24 lags. We consider four alternative nominal oil price series. The evaluation period is alternatively 1973.1-2009.12 or 1975.1-2009.12.8 It is not clear a priori which oil price series is best suited for finding predictability. On the one hand, one would expect the evidence of predictability to be stronger for oil price series that are unregulated (such as the refiners' acquisition cost for imported crude oil) than for partially regulated domestic price series. On the other hand, to the extent that the 1973/74 oil price shock episode was driven by monetary factors, as proposed by Barsky and Kilian (2002), one would expect stronger evidence in favor of such feedback from the WTI price series that includes this episode.
There are several reasons to expect the dollar-denominated nominal price of oil to respond to changes in nominal U.S. macroeconomic aggregates. One channel of transmission is purely monetary and operates through U.S. inflation. For example, Gillman and Nakov (2009) stress that changes in the nominal price of oil must occur in equilibrium just to offset persistent shifts in U.S. inflation, given that the price of oil is denominated in dollars. Indeed, the Granger causality tests in Table 1a indicate highly significant lagged feedback from U.S. headline CPI inflation to the percent change in the nominal WTI price of oil for the full sample, consistent with the findings in Gillman and Nakov (2009). The evidence for the other oil price series is somewhat weaker with the exception of the refiners' acquisition cost for imported crude oil, but that result may simply reflect a loss of power when the sample size is shortened.9
Gillman and Nakov view changes in inflation in the post-1973 period as rooted in persistent changes in the growth rate of money.10 Thus, an alternative approach of testing the hypothesis of Gillman and Nakov (2009) is to focus on Granger causality from monetary aggregates to the nominal price of oil. Given the general instability in the link from changes in monetary aggregates to inflation, one would not necessarily expect changes in monetary aggregates to have much predictive power for the price of oil, except perhaps in the 1970s (see Barsky and Kilian 2002). Table 1a nevertheless shows that there is considerable lagged feedback from narrow measures of money such as M1 for the refiners' acquisition cost and the WTI price of oil based on the 1975.2-2009.12 evaluation period. The much weaker evidence for the full WTI series may reflect the stronger effect of regulatory policies on the WTI price during the early 1970s. The evidence for broader monetary aggregates such as M2 having predictive power for the nominal price of oil is much weaker, with only one test statistically significant.
A third approach to testing for a role for U.S. monetary conditions relies on the fact that rising dollar-denominated non-oil commodity prices are thought to presage rising U.S. inflation. To the extent that oil price adjustments are more sluggish than adjustments in other industrial commodity prices, one would expect changes in nominal Commodity Research Bureau (CRB) spot prices to Granger cause changes in the nominal price of oil. Indeed, Table 1a indicates highly statistically significant lagged feedback from CRB sub-indices for industrial raw materials and for metals.
In contrast, neither short-term interest rates nor trade-weighted exchange rates have significant predictive power for the nominal price of oil. According to the Hotelling model, one would expect the nominal price of oil to grow at the nominal rate of interest, providing yet another link from U.S. macroeconomic aggregates to the nominal price of oil. Table 1a, however, shows no evidence of statistically significant feedback from the 3-month T-Bill rate to the price of oil. This finding is not surprising as the price of oil clearly was not growing at the rate of interest even approximately (see Figure 1). Nor is there evidence of significant feedback from lagged changes in the trade-weighted nominal U.S. exchange rate. This does not mean that all bilateral exchange rates lack predictive power. In related work, Chen, Rossi and Rogoff (2010) show that the floating exchange rates of small commodity exporters (including Australia, Canada, New Zealand, South Africa and Chile) with respect to the dollar have remarkably robust forecasting power for global prices of their commodity exports. The explanation is that these exchange rates are forward looking and embody information about future movements in commodity export markets that cannot easily be captured by other means.
Although Chen et al.'s analysis cannot be extended to oil exporters such as Saudi Arabia because Saudi Arabia's exchange rate has not been floating freely, the bilateral dollar exchange rates of Australia, Canada, New Zealand and South Africa may serve as a proxy for expected broad-based movements in industrial commodity prices that may also be helpful in predicting changes in the nominal price of oil. According to Chen et al., the share of nonagricultural commodity exports is largest in South Africa, followed by Australia, Canada and New Zealand. In general, the larger the share of nonagricultural exports, the higher one would expect the predictive power for industrial commodities to be. For the price of oil, the share of energy exports such as crude oil, coal and natural gas may be an even better indicator of predictive power, suggesting that Canada should have the highest predictive power for the price of oil, followed by Australia, South Africa, and New Zealand. Table 1b shows strong evidence of predictability for all bilateral exchange rates but that of New Zealand, consistent with this intuition. Moreover, when using the dollar exchange rate of the Japanese Yen and of the British Pound as a control group, there is no significant evidence of Granger causality from exchange rates to the price of oil.11 The results in Table 1b are also very much in line with the direct evidence of predictive power from nonagricultural commodity price indices in Table 1a.
4.1.3. Reconciling the Pre- and Post-1973 Evidence on Predictability
Tables 1a and 1b suggest that indicators of U.S. inflation have significant predictive power for the nominal price of oil. This result is in striking contrast to the pre-1973 period. As shown in Hamilton (1983) using quarterly data and in Gillman and Nakov (2009) using monthly data, there is no significant Granger causality from U.S. inflation to the percent change in the nominal price of oil in the 1950s and 1960s. This difference in results is suggestive of a structural break in late 1973 in the predictive relationship between the price of oil and the U.S. economy.
One reason that the pre-1973 predictive regressions differ from the post-1973 regressions is that prior to 1973 the nominal price of oil was adjusted only at discrete intervals (see Figure 1). Because the nominal oil price data was generated by a discrete-continuous choice model, conventional vector autoregressions by construction are not appropriate for testing predictability. One way of illustrating this problem is by fitting a random walk model with drift to these data and plotting randomly generated draws from the fitted model against the actual data. Figure 4 shows one such sequence. Without loss of generality, Figure 4 illustrates that the fitted time series model model - like any conventional time series model - is unable to replicate the discontinuous adjustment process underlying the pre-1973 WTI data. This is true even allowing for leptokurtic error distributions. In other words, autoregressive or moving average time series processes are inappropriate for these data and tests based on such models have to be viewed with caution.
This problem with the pre-1973 data may be ameliorated by deflating the nominal price of oil, which renders the oil price data continuous and more amenable to VAR analysis (see Figure 2). Additional problems arise, however, when combining oil price data generated by a discrete-continuous choice process with data from the post-Texas Railroad Commission era that are fully continuous. Concern over low power has prompted many applied researchers to combine oil price data for the pre-1973 and post-1973 period in the same model when studying the predictive relationship from macroeconomic aggregates to the price of oil. This approach is obviously inadvisable when dealing with nominal oil price data, as already discussed. Perhaps less obviously, this approach is equally unappealing when dealing with vector autoregressions involving the real price of oil. The problem that the nature and speed of the feedback from U.S. macroeconomic aggregates to the real price of oil differs by construction, depending on whether the nominal price of oil is temporarily fixed or not. This instability manifests itself in a structural break in the predictive regressions commonly used to test for lagged potentially nonlinear feedback from the real of price of oil to real GDP growth (see, e.g., Balke, Brown and Yücel 2002). The p-value for the null hypothesis that there is no break in 1973.Q4 in the coefficients of this predictive regression is 0.001 (see Kilian and Vigfusson 2010b).12 For that reason, regression estimates of the relationship between the real price of oil and domestic macroeconomic aggregates obtained from the entire post-war period are not informative about the strength of these relationships in post-1973 data.13 In the analysis of the real price of oil below we therefore restrict the evaluation period to start no earlier than 1973.1.
4.2. Real Oil Price Predictability in the Post-1973 Period
It is well established in natural resource theory that the real price of oil increases in response to low expected real interest rates and in response to high real aggregate output.14 Any analysis of the role of expected real interest rates is complicated by the fact that inflation expectations are difficult to pin down, especially at longer horizons, and that the relevant horizon for resource extraction is not clear. We therefore focus on the predictive power of fluctuations in real aggregate output. Table 2 reports p-values for tests of the hypothesis of Granger non-causality from selected measures of real aggregate output to the real price of oil.
A natural starting point is U.S. real GDP. Economic theory implies that U.S. real GDP and the real price of oil are mutually endogenous and determined jointly. For example, one would expect an unexpected increase in U.S. real GDP, all else equal, to increase the flow demand for crude oil and hence the real price of oil. Unless the real price of oil is forward looking and already embodies all information about future U.S. real GDP, a reasonable conjecture therefore is that lagged U.S. real GDP should help predict the real price of oil. Recent research by Kilian and Murphy (2010) has shown that the real price of oil indeed contains an asset price component, but that this component most of the time explains only a small fraction of the historical variation in the real price of oil. Thus, we would expect fluctuations in U.S. real GDP to predict the real price of oil at least in population. Under the assumption that the joint process can be approximated by a linear vector autoregression, this implies the existence of Granger causality from U.S. real GDP to the real price of oil.
Notwithstanding this presumption, Table 2 indicates no evidence of Granger causality from U.S. real GDP growth to the real price of oil. This finding is robust to alternative methods of detrending and alternative lag orders. In the absence of instantaneous feedback from U.S. real GDP to the real price of oil, a finding of Granger noncausality from U.S. real GDP to the real price of oil - in conjunction with evidence that the real price of oil Granger causes U.S. real GDP - would be consistent with the real price of oil being strictly exogenous with respect to U.S. real GDP. It can be shown, however, that the evidence of Granger causality from the real price of oil to U.S. real GDP is not much stronger. When linear detrending (LT), Hodrick-Prescott-filtering (HP) and log-differencing (DIF) the data, which each transformation applied symmetrically to both time series in a bivariate VAR(4) model, there is only one marginal rejection at the 10% level. This rejection occurs for the real WTI price in differences when evaluated on the 1973.I-2009.IV period. There are no rejections using other data transformations or shorter evaluation periods. The fact that there are few rejections, if any, in either direction suggests that the Granger noncausality test may simply lack power for samples of this length. In fact, this is precisely the argument that prompted some researchers to combine data from the pre-1973 and post-1973 period - a strategy that we do not recommend for the reasons discussed in section 4.1.3.
Another likely explanation of the failure to reject the null of no predictability is model misspecification. It is well known that Granger causality in a bivariate model may be due to an omitted third variable, but equally relevant is the possibility of Granger noncausality in a bivariate model arising from omitted variables (see Lütkepohl 1982). This possibility is more than a theoretical curiosity in our context. Recent models of the determination of the real price of oil after 1973 have stressed that this price is determined in global markets (see, e.g., Kilian 2009a; Kilian and Murphy 2010). In particular, the demand for oil depends not merely on U.S. demand, but on global demand. The bivariate model for the real price of oil and U.S. real GDP by construction omits fluctuations in real GDP in the rest of the world. The relevance of this point is that offsetting movements in real GDP abroad can easily offset the effect of changes in U.S. real GDP, obscuring the dynamic relationship of interest and lowering the power of the Granger causality test. Only when real GDP fluctuations are highly correlated across countries would we expect U.S. real GDP to be a good proxy for world real GDP.15 In addition, as the U.S. share in world GDP evolves, by construction so do the predictive correlations underlying Table 2. In this regard, Kilian and Hicks (2010) have documented dramatic changes in the PPP-adjusted share in GDP of the major industrialized economies and of the main emerging economies in recent years that cast further doubt on the U.S. real GDP results in Table 2. For example, today, China and India combined have almost as high a share in world GDP as the United States.
A closely related third point is that fluctuations in real GDP are a poor proxy for business-cycle driven fluctuations in the demand for oil. It is well known, for example, that in recent decades the share of services in U.S. real GDP has greatly expanded at the cost of manufacturing and other sectors. Clearly, real GDP growth driven by the non-service sector will be associated with disproportionately higher demand for oil and other industrial commodities than real GDP growth in the service sector. This provides one more reason why one would not expect a strong or stable predictive relationship between U.S. real GDP and the real price of oil.
An alternative quarterly predictor that partially addresses these last two concerns is quarterly world industrial production from the U.N. Monthly Bulletin of Statistics. This series has recently been introduced by Baumeister and Peersman (2010) in the context of modeling the demand for oil. Although there are serious methodological concerns regarding the construction of any such index, as discussed in Beyer, Doornik and Hendry (2001), one would expect this series to be a better proxy for global fluctuations in the demand for crude oil than U.S. real GDP. Indeed, Table 2 shows strong evidence of Granger causality from world industrial production to the real WTI price in the full sample period for the LT model. For the four shorter series there are three additional rejections for the LT model; the other p-value is not much higher than 0.1. The reduction in p-values compared with U.S. real GDP is dramatic. The fact that there is evidence of predictability only for the linearly detrended series makes sense. As discussed in Kilian (2009b), the demand for industrial commodities such as crude oil is subject to long swings. Detrending methods such as HP filtering (and even more so first differencing) eliminate much of this low frequency covariation in the data, removing the feature of the data we are interested in testing.
Additional insights may be gained by focusing on monthly rather than quarterly predictors. The first contender in Table 3 is the Chicago Fed National Activity Index (CFNAI). This is a broad measure of monthly real economic activity in the United States obtained from applying principal component analysis to a wide range of monthly indicators of real activity expressed in growth rates (see Stock and Watson 1999). As in the case of quarterly U.S. real GDP, there is no evidence of Granger causality. If we rely on U.S. industrial production as the predictor, there is weak evidence of feedback to the domestic price of oil for the LT model. For other measures of the real price of oil, none of the test statistics is significant, although we again note the sharp drop in p-values as we replace the CFNAI by industrial production.
There are no monthly data on world industrial production, but the OECD provides an industrial production index for OECD economies and six selected non-OECD countries. As expected, the rejections of Granger noncausality become much stronger when we focus on OECD+6 industrial production. Table 3 indicates strong and systematic Granger causality, especially for the LT specification. Even OECD+6 industrial production, however, is an imperfect proxy for business-cycle driven fluctuations in the global demand for industrial commodities such as crude oil.
One alternative is the index of global real activity recently proposed in Kilian (2009a). This index does not rely on any country weights and has truly global coverage. It has been constructed with the explicit purpose of measuring fluctuations in the broad-based demand for industrial commodities associated with the global business cycle.16 As expected, the last row of Table 3 indicates even stronger evidence of Granger causality from this index to the real price of oil, regardless of the definition of the real price of oil. It also highlights a fourth issue. There is evidence that allowing for two years worth of lags rather than one year often strengthens the significance of the rejections. This finding mirrors the point made in Hamilton and Herrera (2004) that it is essential to allow for a rich lag structure in studying the dynamic relationship between the economy and the price of oil.
Although none of the proxies for global fluctuations in demand is without limitations, we conclude that there is a robust pattern of Granger causality, as we correct for problems of model misspecification and of data mismeasurement that undermine the power of the test. This conclusion is further strengthened by evidence in Kilian and Hicks (2010) based on distributed lag models that revisions to professional real GDP growth forecasts have significant predictive power for the real price of oil during 2000.11-2008.12 after weighting each country's forecast revision by its PPP-GDP share. Predictability in population, of course, does not necessarily imply out-of-sample forecastability (see Inoue and Kilian 2004a). The next two sections therefore examine alternative approaches to forecasting the nominal and the real price of oil out-of-sample.
5. Short-Horizon Forecasts of the Nominal Price of Oil
The most common approach to forecasting the nominal price of oil is to treat the price of the oil futures contract of maturity h as the h-period forecast of the price of oil.17 In particular, many central banks and the International Monetary Fund (IMF) use the price of NYMEX oil futures as a proxy for the market's expectation of the spot price of crude oil. A widespread view is that prices of NYMEX futures contracts are not only good proxies for the expected spot price of oil, but also better predictors of oil prices than econometric forecasts. Forecasts of the spot price of oil are used as inputs in the macroeconomic forecasting exercises that these institutions produce. For example, the European Central Bank (ECB) employs oil futures prices in constructing the inflation and output-gap forecasts that guide monetary policy (see Svensson 2005). Likewise the IMF relies on futures prices as a predictor of future spot prices (see, e.g., International Monetary Fund 2005, p. 67; 2007, p. 42). Futures-based forecasts of the price of oil also play a role in policy discussions at the Federal Reserve Board. This is not to say that forecasters do not recognize the potential limitations of futures-based forecasts of the price of oil. Nevertheless, the perception among many macroeconomists, financial analysts and policymakers is that oil futures prices, imperfect as they may be, are the best available forecasts of the spot price of oil. Such attitudes have persisted notwithstanding recent empirical evidence to the contrary and notwithstanding the development of theoretical models aimed at explaining the lack of predictive ability of oil futures prices and spreads (see, e.g., Knetsch 2007; Alquist and Kilian 2010).
Interestingly, the conventional wisdom in macroeconomics and finance is at odds with long-held views about storable commodities in agricultural economics. For example, Peck (1985) emphasized that "expectations are reflected nearly equally in current and in futures prices. In this sense cash prices will be nearly as good predictions of subsequent cash prices as futures prices", echoing in turn the discussion in Working (1942) who was critical of the "general opinion among economists that prices of commodity futures are ...the market expression of consciously formed opinions on probable prices in the future" whereas "spot prices are not generally supposed to reflect anticipation of the future in the same degree as futures prices". Working specifically criticized the error of "supposing that the prices of futures ...tend to be more strongly influenced by these anticipations than are spot prices". The next section investigates the empirical merits of these competing views in the context of oil markets.
5.1. Forecasting Methods Based on Monthly Oil Futures Prices
Alquist and Kilian (2010) recently provided a comprehensive
evaluation of the forecast accuracy of models based on monthly oil
futures prices using data ending in 2007.2. Below we update their
analysis until 2009.12 and expand the range of alternative
forecasting models under consideration.18 In this subsection,
attention is limited to forecast horizons of up to one year. Let
![]() denote the current nominal price
of the futures contract that matures in h periods,
denote the current nominal price
of the futures contract that matures in h periods,
![]() the current nominal spot price of oil,
and
the current nominal spot price of oil,
and
![]() the expected future spot
price at date t+h conditional on information available at
t.
the expected future spot
price at date t+h conditional on information available at
t.
A natural benchmark for forecasts based on the price of oil futures is provided by the random walk model without drift. This model implies that changes in the spot price are unpredictable, so the best forecast of the spot price of crude oil is simply the current spot price:
| (1) |
This forecast is also known as the no-change forecast. In contrast, the common view that oil futures prices are the best available predictor of future oil prices implies the forecasting model:
| (2) |
A closely related approach to forecasting the spot price of oil is
to use the spread between the futures price and the spot price as
an indicator of whether the price of oil is likely to go up or
down. If the futures price equals the expected spot price, the
spread should be an indicator of the expected change in spot
prices. The rationale for this approach is clear from dividing
![]() by
by ![]() which results in
which results in
![]() We explore the forecasting accuracy of the spread based on several
alternative forecasting models. The simplest model is:
We explore the forecasting accuracy of the spread based on several
alternative forecasting models. The simplest model is:
| (3) |
To allow for the possibility that the spread may be a biased predictor, it is common to relax the assumption of a zero intercept:
| (4) |
Alternatively, one can relax the proportionality restriction:
| (5) |
Finally, we can relax both the unbiasedness and proportionality restrictions:
| (6) |
Here
![]() and
and
![]() denote least-squares estimates
obtained in real time from recursive regressions.
denote least-squares estimates
obtained in real time from recursive regressions.
The objective is to compare the real-time forecast accuracy of models (1)-(6). Our empirical analysis is based on daily prices of crude oil futures traded on the NYMEX from the commercial provider Price-Data.com. The time series begins in March 30, 1983, when crude oil futures were first traded on the NYMEX, and extends through December 31, 2009. Contracts are for delivery at Cushing, OK. Trading ends four days prior to the 25th calendar day preceding the delivery month. If the 25th is not a business day, trading ends on the fourth business day prior to the last business day before the 25th calendar day. A common problem in constructing monthly futures prices of a given maturity is that an h-month contract may not trade on a given day. We identify the h-month futures contract trading closest to the last trading day of the month and use the price associated with that contract as the end-of-month value. Our approach is motivated by the objective of computing in a consistent manner end-of-month time series of oil futures prices for different maturities. This allows us to match up end-of-month spot prices and futures prices as closely as possible. The daily spot price data are obtained from the webpage of the Energy Information Administration and refer to the price of West Texas Intermediate crude oil available for delivery at Cushing, OK.
Tables 4 through 8 assess the predictive accuracy of various forecasting models against the benchmark of a random walk without drift for horizons of 1, 3, 6, 9, and 12 months. The forecast evaluation period is 1991.1-2009.12 with suitable adjustments, as the forecast horizon is varied. The assessment of which forecasting model is most accurate may depend on the loss function of the forecaster (see Elliott and Timmermann 2008). We report results for the MSPE and the relative frequency with which a forecasting model correctly predicts the sign of the change in the spot price based on the success ratio statistic of Pesaran and Timmermann (2009). We formally test the null hypothesis that a given candidate forecasting model is as accurate as the random walk without drift against the alternative that the candidate model is more accurate than the no-change forecast. Suitably constructed p-values are shown in parentheses (as described in the notes to Table 4). It should be noted that commonly used tests of equal predictive accuracy for nested models (including the tests we rely on in this chapter) by construction are tests of the null of no predictability in population rather than tests of equal out-of-sample MSPEs (see, e.g., Inoue and Kilian 2004a,b; Clark and McCracken 2010). This means that these tests will reject the null of equal predictive accuracy more often than they should under the null, suggesting caution in interpreting test results that are only marginally statistically significant. We will discuss this point in more detail further below. This concern does not affect nonnested forecast accuracy comparisons.
Row (2) of Tables 4 through 8 shows that the oil futures price has lower MSPE than the no-change forecast at all horizons considered, but the differences are mostly marginal and none of the differences is statistically significant. For all practical purposes, the forecasts are equally accurate. Nor do futures forecasts have important advantages when it comes to predicting the sign of the change in the nominal price of oil. Only at the 12-month horizon is the success ratio significant at the 10 percent level. The improvement in this case is 5.7%. At the 1-month and 3-month horizon, the success ratio of the futures price forecast actually is inferior to tossing a coin. Similarly, rows (3)-(6) in Tables 4 through 8 show no systematic difference between the MSPE of the spread-based forecasts and that of the random walk forecast. In no case is there a statistically significant reduction in the MSPE from using the spread model. In the rare cases in which one of the spread models significantly helps predict the direction of change, the gains in accuracy are quite moderate. No spread model is uniformly superior to the others.
We conclude that there is no compelling evidence that, over this sample period, monthly oil futures prices were more accurate predictors of the nominal price of oil than simple no-change forecasts. Put differently, a forecaster using the most recent spot price would have done just as well in forecasting the nominal price of oil. This finding is broadly consistent with the empirical results in Alquist and Kilian (2010). To the extent that some earlier studies have reported evidence more favorable to oil futures prices, the difference in results can be traced to the use of shorter samples.19
5.2. Other Forecasting Methods
The preceding subsection demonstrated that simple no-change forecasts of the price of oil tend to be as accurate in the MSPE sense as forecasts based on oil futures prices, but this does not rule out that there are alternative predictors with even lower MSPE. Next we broaden the range of forecasting methods to include some additional predictors that are of practical interest. One approach is the use of parsimonious regression-based forecasting models of the spot price of crude oil. Another approach is the use of survey data. While economists have used survey data extensively in measuring the risk premium embedded in foreign exchange futures, this approach has not been applied to oil futures, with the exception of recent work by Wu and McCallum (2005). Yet another approach is to exploit the implication of the Hotelling (1931) model that the price of oil should grow at the rate of interest. Finally, we also consider forecasting models that adjust the no-change forecast for inflation expectations and for recent percent changes in other nominal prices.
5.2.1. Parsimonious Econometric Forecasts
One example of parsimonious econometric forecasting models is the random walk model without drift introduced earlier. An alternative is the double-differenced forecasting model proposed in Hendry (2006). Hendry observed that when time series are subject to infrequent trend changes, the no-change forecast may be improved upon by extrapolating today's oil price at the most recent growth rate:
| (7) |
where
![]() denotes the percent growth rate
between
denotes the percent growth rate
between ![]() and
and ![]() In other words, we
apply the no-change forecast to the growth rate rather than the
level. Although there are no obvious indications of structural
change in our sample period, it is worth exploring this alternative
method, given the presence of occasional large fluctuations in the
price of oil. Row (7) in Tables 4
through 8 shows that the double-differenced specification does not
work well in this case. Especially at longer horizons, this
forecasting method becomes erratic and suffers from very large
MSPEs. Nor is this method particularly adept at predicting the sign
of the change in the nominal price of oil.
In other words, we
apply the no-change forecast to the growth rate rather than the
level. Although there are no obvious indications of structural
change in our sample period, it is worth exploring this alternative
method, given the presence of occasional large fluctuations in the
price of oil. Row (7) in Tables 4
through 8 shows that the double-differenced specification does not
work well in this case. Especially at longer horizons, this
forecasting method becomes erratic and suffers from very large
MSPEs. Nor is this method particularly adept at predicting the sign
of the change in the nominal price of oil.
Yet another strategy is to extrapolate from longer-term trends. Given that oil prices have been persistently trending upward (or downward) at times, it is natural to consider a random walk model with drift. One possibility is to estimate this drift recursively, resulting in the forecasting model:
| (8) |
Alternatively, a local drift term may be estimated using rolling regressions:
| (9) |
where
![]() is the forecast of the
spot price at t+h; and
is the forecast of the
spot price at t+h; and
![]() is the percent
change in the spot price over the most recent h months. This
local drift model postulates that traders extrapolate from the spot
price's recent behavior when they form expectations about the
future spot price. The local drift model is designed to capture
"short-term forecastability" that arises from local trends in the
oil price data.
is the percent
change in the spot price over the most recent h months. This
local drift model postulates that traders extrapolate from the spot
price's recent behavior when they form expectations about the
future spot price. The local drift model is designed to capture
"short-term forecastability" that arises from local trends in the
oil price data.
Rows (8)-(9) in Tables 4 through 8 document that allowing for a drift typically increases the MSPE and in no case significantly lowers the MSPE relative to the no-change forecast, whether the drift is estimated based on rolling regressions or is estimated recursively. Nor does allowing for a drift significantly improve the ability to predict the sign of the change in the nominal price of oil.
5.2.2. Forecasts Based on the Hotelling Model
Another forecasting method is motivated by Hotelling's (1931) model, which predicts that the price of an exhaustible resource such as oil appreciates at the risk-free rate of interest:
| (10) |
where
![]() refers to the annualized interest
rate at the relevant maturity h.20 Although the
refers to the annualized interest
rate at the relevant maturity h.20 Although the
Hotelling model may seem too stylized to generate realistic predictions, we include it in this forecast accuracy comparison. We employ the Treasury bill rate as a proxy for the risk free rate.21 Row (10) in Tables 5, 6, and 8 shows no evidence that adjusting the no-change forecast for the interest rate significantly lowers the MSPE. The Hotelling model is better at predicting the sign of the change in the nominal price of oil than the no-change forecast, although we cannot assess the statistical significance of the improvement, given that there is no variability at all in the sign forecast.
5.2.3. Survey Forecasts
Given the significance of crude oil to the international economy, it is surprising that there are few organizations that produce monthly forecasts of spot prices. In the oil industry, where the spot price of oil is critical to investment decisions, producers tend to make annual forecasts of spot prices for horizons as long as 15-20 years, but these are not publicly available. The U.S. Department of Energy's Energy Information Administration (EIA) has published quarterly forecasts of the nominal price of oil since 1983. The Economist Intelligence Unit has produced annual forecasts since the 1990s for horizons of up to 5 years. None of these sources provides monthly forecasts.
A source of monthly forecasts of the price of crude oil is Consensus Economics Inc., a U.K.-based company that compiles private sector forecasts in a variety of countries. Initially, the sample consisted of more than 100 private firms; it now contains about 70 firms. Of interest to us are the survey expectations for the 3- and 12-month ahead spot price of West Texas Intermediate crude oil, which corresponds to the type and grade delivered under the NYMEX futures contract. The survey provides the arithmetic average, the minimum, the maximum, and the standard deviation for each survey month beginning in October 1989 and ending in December 2009. We use the arithmetic mean at the relevant horizon:
| (11) |
Row (11) in Tables 5 and 8 reveals that this survey forecast does not significantly reduce the MSPE relative to the no-change forecast and may increase the MSPE substantially. The survey forecast is particularly poor at the 3-month horizon. At the 12-month horizon the survey forecast has a lower MSPE than the no-change forecast, but the gain in accuracy is not statistically significant. There also is a statistically significant but negligible gain in directional accuracy.
Further analysis shows that until 2008.12 the consensus survey forecast had a much higher MSPE than the no-change forecast at both the 3-month and 12-month horizons. This pattern changes only toward the end of the sample. There is evidence that the accuracy of the consensus survey forecasts improves at the 12-month horizon, especially in 2009 as the oil market recovers from its collapse in the second half of 2008. It appears that professional forecasters correctly predicted a long-term price recovery in this instance, although they were not successful at predicting the timing of the 2009 recovery. Notwithstanding these caveats, there is no compelling evidence overall that survey forecasts outperform the no-change forecast.
We conclude that the no-change forecasts of the nominal price of oil not only are as accurate as forecasts based on monthly futures prices, but tend to be at least as accurate as forecasts based on simple econometric models or monthly survey forecasts. This result is consistent with common views among oil experts. For example, Peter Davies, chief economist of British Petroleum, has noted that "we cannot forecast oil prices with any degree of accuracy over any period whether short or long" (see Davies 2007).
5.2.4. Predictors Based on Other Nominal Prices
The evidence on Granger causality in section 4.1.2 suggests that some asset prices may have predictive power in real time for the nominal price of oil. The last rows of Tables 4 through 8 explore that question. One approach building on Chen, Rossi and Rogoff (2010) is to use recent percent changes in the bilateral nominal dollar exchange rate of selected commodity exporters:
| (12) |
where
![]() We
do not include New Zealand given its poor showing in section 4.1.2.
Tables 4 through 8 show that this approach does not significantly
reduce the out-of-sample MSPE regardless of the exchange rate
choice. There is some evidence that the Australian exchange rate
has significant predictive power for the sign of the change in the
nominal price of oil, but not at all horizons. For the other
exchange rates, the evidence is even weaker. We also considered the
alternative specification
We
do not include New Zealand given its poor showing in section 4.1.2.
Tables 4 through 8 show that this approach does not significantly
reduce the out-of-sample MSPE regardless of the exchange rate
choice. There is some evidence that the Australian exchange rate
has significant predictive power for the sign of the change in the
nominal price of oil, but not at all horizons. For the other
exchange rates, the evidence is even weaker. We also considered the
alternative specification
| (13) |
based on the percent change in the exchange rate over the most recent h months. That specification produces similar results for directional accuracy. For the MSPE, there are significant MSPE gains of about 13% up to horizon 3 for the Australian dollar and of about 7% up to horizon 6 for the Canadian dollar. The Rand performs less well. The directional accuracy results for all three alternative models are somewhat erratic with no model performing well consistently. These results are not shown in the tables to conserve space.
Another approach is to explore the forecasting value of recent percent changes in non-oil CRB commodity prices. One such forecasting model is
| (14) |
It can be shown that model (14) does not produce statistically significant reductions in the MSPE, presumably because month-to-month changes in commodity prices tend to be noisy. In fact, model (14) tends to worsen the MSPE ratio at long horizons, although it significantly improves directional accuracy at horizons up to 9 months for metals prices and up to 12 months for prices of industrial raw materials. An alternative model specification is based on the percent change in the CRB price index over the most recent h months:
| (15) |
Model (15) is designed to capture persistent changes in commodity prices in the recent past. This specification is less successful at predicting the direction of change at horizons beyond 6 months, but can yield significant reductions in the MSPE at short horizons. For example, the model using metals prices significantly lowers the MSPE at horizon 3 and the model using prices of industrial raw materials significantly reduces the MSPE at horizons 1 and 3. The MSPE reductions may be as large as 25% at horizon 3. That result, of course, reflects the importance of global demand pressures across all industrial commodities during the forecast evaluation period. To the extent that the price of oil sometimes is driven by other shocks, one would expect the accuracy gains from using model (15) to be less favorable.
Finally, in Table 8, we include results for forecasts that adjust the no-change forecast of the nominal price of oil for the 1-year inflation expectations in the Michigan Survey of Consumers.
| (16) |
There are no similar survey expectations for shorter horizons. This more direct approach does
not reduce the MSPE relative to the no-change forecast. The same result holds when using suitably scaled 10-year inflation forecasts from the Survey of Professional Forecasters.
| (17) |
The fact that these results are weaker than those obtained using inflation measures in Granger causality tests likely means that there was not much variation in inflation expectations in our sample period, but considerable variation historically.
We conclude that despite some success of the asset price approach in predicting the sign of the change in the nominal price of oil, only persistent changes in CRB industrial commodity prices significantly reduce the MSPE of the no-change forecast and even those accuracy gains are limited to very short horizons. Beyond the 3-month horizon, based on the MSPE criterion, the no-change forecast for all practical purposes remains the most accurate model for forecasting the nominal price of oil in real time.
5.3. Short-Horizon Forecasts Based on Daily Oil Futures Prices
Following the extant literature, our analysis so far has relied on monthly data for oil futures prices and spreads constructed from daily observations. The construction of monthly data allows one to compare the accuracy of these forecasts to that of alternative forecasts based on data only available at monthly frequency. A complementary approach is to utilize all daily oil future prices and compare their forecasting accuracy to the no-change forecast only. This alternative approach makes use of all oil-futures price data and hence may have more accurate size and higher power. It is not without drawbacks, however. Ideally, one would like to compare the price of a futures contract for delivery in h months with the price of delivery exactly h months later, where one month corresponds to 21 business days. That price, however, is not observed. The spot price quoted on the day of delivery instead will be the price for delivery sometime in the month following the date on which the futures contract matures. In fact, the date of delivery associated with a given spot price can never be made exact. We therefore follow the convention of evaluating futures price forecasts against the spot price prevailing when the futures contract matures. A reasonable case can be made that this is what practitioners view as the relevant forecasting exercise.
Note that the daily data are sparse in that there are many days for which no price quotes exist. We eliminate these dates from the sample and stack the remaining observations similar to the approach taken in Kilian and Vega (2010) in the context of modeling the impact of U.S. macroeconomic news on the nominal price of oil. Table 9 summarizes our findings. The MSPE ratios in Table 9 indicate somewhat larger gains in forecasting accuracy from using oil futures prices than in Tables 4 through 8. There are a number of caveats, however. First, the h-month oil futures forecasts are not forecasts for a horizon of h months, as in Tables 4 through 8, but rather for a horizon that may vary arbitrarily between h and h+1 months. For example, an oil futures contract quoted on August 13 for delivery starting on October 1 would be considered a 1-month contract for the purpose of Table 9, but so would an oil-futures contract quoted on August 25 for delivery starting on October 1. This is an inherent limitation of working with daily oil futures price data. This concern suggests caution in interpreting short-horizon results, but obviously becomes less important as h increases. A second concern is that the sample period spanned by the daily data extends back to January 1986, whereas the data in Tables 4 through 8 start in 1990. This difference is not driving the results in Table 9. It can be shown that making the sample period compatible with that in the earlier Tables would yield substantively identical results.
The third and most important concern is the statistical significance of the results in Table
9. Given that the sample size in Table 9 is larger than in
Tables 4 through 8 by a factor of about 10, care must be exercised
in interpreting the p-values. As is well known, for
sufficiently large sample sizes, any null hypothesis is bound to be
rejected at conventional significance levels, making it
inappropriate to apply the same significance level as in Tables 4
through 8. In recognition of this problem, Leamer (1978, p.
108-120) proposes a rule for constructing sample-size dependent
critical values. For example, for the F-statistic, the
appropriate level of statistical significance is
![]() For
For ![]() as in Table 4, this rule of thumb
implies a threshold for rejecting the null hypothesis of
as in Table 4, this rule of thumb
implies a threshold for rejecting the null hypothesis of
![]() In contrast, for
In contrast, for ![]() the same rule implies a much higher threshold of
the same rule implies a much higher threshold of
![]() Applying this rule to the
p-values in Table 9, none of the MSPE reductions are
statistically significant except at the 12-month horizon. The MSPE
ratio at the 12-month horizon of 0.93 is similar to the ratio of
0.94 reported in Table 8 based on monthly data. The statistical
significance of these MSPE gains in Table 9 is likely to be due to
the larger sample size, illustrating the power gains from using
daily data. There also is evidence that at horizons 6, 9 and 12,
the oil futures price has statistically significant directional
accuracy, but the gains are quantitatively negligible except
perhaps at horizon 12.
Applying this rule to the
p-values in Table 9, none of the MSPE reductions are
statistically significant except at the 12-month horizon. The MSPE
ratio at the 12-month horizon of 0.93 is similar to the ratio of
0.94 reported in Table 8 based on monthly data. The statistical
significance of these MSPE gains in Table 9 is likely to be due to
the larger sample size, illustrating the power gains from using
daily data. There also is evidence that at horizons 6, 9 and 12,
the oil futures price has statistically significant directional
accuracy, but the gains are quantitatively negligible except
perhaps at horizon 12.
These results lead us to revise somewhat our earlier findings. We conclude that there is statistically significant evidence that oil futures prices improve on the accuracy of the no-change forecast of the nominal price of oil at the 1-year horizon, but not at shorter horizons. The magnitude of these gains in accuracy is modest - at least by the standards of the literature on forecasting macroeconomic aggregates such as inflation rates. Moreover, there are indications that this result is sensitive to changes in the sample period and may not be robust as more data accumulate. After eliminating the data beyond March 2008, for example, the MSPE ratio of the 12-month futures price exceeds 1 and only when extending the sample period beyond July 2008 is the MSPE reduction statistically significant. This result, together with the lack of evidence for slightly shorter or slightly longer futures contracts, suggests caution in interpreting the evidence for the 12-month contract in Table 9.
6. Long-Horizon Forecasts of the Nominal Price of Oil
For oil industry managers facing investment decisions or for policymakers pondering the medium-term economic outlook a horizon of one year is too short. Crude oil futures may have maturities as long as seven years. Notwithstanding the low liquidity of oil futures markets at such long horizons, documented in Alquist and Kilian (2010), it is precisely these long horizons that many policymakers focus on. For example, Greenspan (2004a) explicitly referred to the 6-year oil futures contract in assessing effective long-term supply prices. For similar statements also see Greenspan (2004b), Gramlich (2004) and Bernanke (2004). In this section we focus on forecasting the nominal price of oil at horizons up to seven years.
It can be shown that the daily data are too sparse at horizons beyond one year to allow the construction of time series of end-of-month observations for oil futures prices. However, we can instead evaluate each daily futures price quote for contracts of any given maturity against the spot price that is realized on the day the contract expires. We already used this approach in Table 9 for horizons up to one year. One drawback of extending this approach to longer horizons is that the evaluation period for long-horizon contracts may exclude many of the particularly informative observations at the end of our sample period. Another drawback is that long-horizon futures prices are sparsely quoted, greatly reducing the sample size as the horizon is lengthened. For that reason, one would expect the results to be far less reliable than the earlier short-horizon results. Nevertheless, they provide the only indication we have of the usefulness of oil futures prices at the horizons at which they are employed by many policymakers.
Table 10 shows the results for horizons of 2, 3, 4, 5, 6, and 7 years. In sharp contrast with Table 9 the MSPE ratios are consistently above 1, indicating that oil futures prices are less accurate than the no-change forecast. In no case is there evidence of significant reductions in the MSPE. The test for directional accuracy is statistically significant at the two-year horizon, but not at longer horizons. In fact, in many cases the success ratios at longer horizons are distinctly worse than tossing a coin. Table 10 provides no evidence in support of the common practice at central banks of appealing to the price of long-horizon oil futures contracts as an indication of future spot prices. In particular, at a horizon of six years, which figures prominently in policy statements and speeches, central bankers would have been much better off relying on the no-change forecast than on oil futures prices.
An interesting question is whether the poor accuracy of forecasts from oil futures prices beyond one year simply reflects a sharp drop-off in the liquidity of oil futures markets at longer horizons. This does not appear to be the case. Figure 5 plots two measures of the liquidity of the oil futures market by horizon. Open interest is the total number of futures contracts, either long or short, that have been entered into for a given delivery month and have not yet been offset by another transaction or by physical delivery of oil. It measures the total number of contracts outstanding for delivery in a specific month. Volume is the total number of contracts traded during a specific period of time. Contracts are denoted in units of 1,000 barrels of crude oil. Although both average open interest and average trading volume drop off quickly with increasing maturity, it is not the case that average liquidity at the daily frequency is discontinuously lower at horizons beyond one year than at the 12-month horizon. Rather the decline in average liquidity is smooth.
One concern with the results in Table 10 is that the most traded oil futures contracts are the June and December contracts. This suggests focusing on the most liquid daily contracts rather than averaging results across all daily contracts, as we did in Table 10. Below we report sensitivity analysis for this subset of daily oil futures contracts. Because long-term futures contracts only became available in recent years and because their use greatly reduces the effective sample size, we focus on June and December contracts with maturities of one, two and three years. Based on the evaluation period of 1998-2010, we find that one-year contracts have an MSPE ratio of 0.91 compared with the no-change forecast, two-year contracts an MSPE ratio of 1.01 and three-year contracts an MSPE ratio of 1.27. These results are qualitatively similar to those in Table 10 for the same maturities, suggesting that there are no gains in forecast accuracy from restricting the sample.
Finally, we note that these results may not have been apparent in the years when longer-term oil futures contracts were first introduced. As recently as in the late 1990s, a forecaster employing the same methods that we used in this section, would have found that the monthly price of oil futures contracts with one-year maturity is much more accurate than the no-change forecast, although the MSPE reductions declined steadily throughout the 1990s, as more information became available, and the ratio has oscillated about 1 since then. Even two- and three-year daily contracts, which were introduced much more recently, initially seemed to forecast more accurately than the no-change forecast, but these MSPE reductions have been reversed more recently. Given that the forecast errors become more highly serially correlated, the higher the data frequency, very long samples are required for reliable estimates of relative MSPEs. Clearly, an evaluation period of fifteen years, for example, is insufficient to learn about the forecasting ability of oil futures prices, as illustrated by the repeated sharp reversals in forecast rankings over time. Even our results must be considered tentative and could be reversed as more data become available.
One possible explanation for the unexpectedly low out-of-sample accuracy of oil futures-based forecasts may be the presence of transaction costs impeding arbitrage. An alternative forecasting strategy in which one uses the futures price only if the futures spread exceeds 5% in absolute terms and uses the spot price otherwise, yields MSPE reductions between 0% and 6% at short horizons. Notably the MSPE reductions at horizons of 3 and 6 months are statistically significant in both the daily and the monthly data. At horizons beyond one year, this alternative method is much less accurate than the no-change forecast, however.
7. Do Survey Expectations Track Econometric Forecasts of Nominal Energy Prices?
Models of purchases of energy-intensive durables depend not on the price of crude oil, but on the retail price of energy. A case in point is the demand for automobiles. Although there can be substantial discrepancies between the evolution of the price of crude oil and the price of gasoline in the short run, long-horizon forecasts of the price of gasoline will track long-horizon forecasts of the price of crude oil (see Kilian 2010). In modeling automobile purchases researchers often need to take a stand on consumers' expectations of gasoline prices. A variety of modeling strategies has been explored, often with widely different results. Candidates include ARIMA models, no-change forecasts, oil futures prices and gasoline futures prices (see, e.g., Kahn 1986; Davis and Kilian 2010; Allcott and Wozny 2010). The issue is not only one of finding a forecasting method that achieves the smallest possible out-of-sample forecast error, but of understanding how consumers form their price expectations. An obvious concern is that actual consumer expectations may differ from the predictions generated by the forecasting methods considered so far. Unfortunately, time series data on consumer expectations of gasoline prices are rare, which has prevented a systematic investigation of this important question.
Recently, Anderson, Kellogg and Sallee (2010) obtained a previously unused data set from the Michigan Survey of Consumers on U.S. households' expectations of gasoline prices. The survey asks consumers about how many cents per gallon they think gasoline prices will increase or decrease during the next five years compared to now. Median responses are available for 1984.10-2010.1, but there are gaps in the data, preventing the construction of a continuous monthly time series. Expectations data may be constructed by adding the expected change in the price of gasoline to the current monthly U.S. city average retail price of gasoline (quoted in cents per gallon including taxes), as reported by the Energy Information Administration (EIA). The upper panel of Figure 6 shows that the median 5-year survey forecast systematically exceeds the current gasoline price. The magnitude of the gap varies over time.
As Anderson et al. observe, a likely explanation of this pattern is that households form their expectations by adding long-term inflation expectations to the current price of gasoline. If we adjust the survey gasoline price forecast for the 10-year inflation forecast in the Survey of Professional Forecasters (suitably scaled to the 5-year horizon), the two series line up rather well on average, implying that households' expectations of gasoline prices closely resemble a random walk forecast for the real price of gasoline (see second panel of Figure 6).22 Only on rare occasions such as immediately before the peak of the nominal price of oil in mid-2008 and near the oil price trough of 2008/2009 do household expectations depart from the no-change forecast. In the first instance, households predicted an even higher price of oil; in the second instance, they did not expect the price of oil to drop as sharply as it did.
The evidence in Figure 6 supports the view that the no-change forecast for the real price of gasoline is a better proxy than alternative forecasting models for modeling durables purchases. That evidence also is of interest more generally, given the finding in Edelstein and Kilian (2009) that fluctuations in retail energy prices are dominated by fluctuations in gasoline prices. Finally, the absence of money illusion in households' gasoline price forecasts is of independent interest.
An out-of-sample forecast accuracy comparison between the survey forecast and the no- change forecast of the nominal price of gasoline shows that survey data are quite accurate with an MSPE ratio of only 0.765 (see Table 11). The p-value for the null hypothesis of equal predictive accuracy is 0.000. The success ratio of 0.907 is also extraordinarily high.23 The reason for these rather strong improvements on the no-change forecast is that at such long horizons the inflation component of the nominal price of gasoline becomes very large and cannot be ignored. In other words, it is a fairly safe bet that the price of gasoline must increase in nominal terms over a five-year horizon.24
The same logic applies to the nominal price of oil. As we showed in section 4, predicting the price of oil at the one-year horizon based on expected inflation (much like households apparently predict the price of gasoline), would not have been more successful than the no-change forecast. Repeating that exercise at the 5-year horizon, however, using the same SPF inflation expectations data as in Figure 6, produces a highly significant MSPE ratio of 0.855 and a very high success ratio of 0.811 for the nominal price of oil as well (see Table 11). This simple forecasting rule is also much more accurate than the forecast implied by the 5-year oil futures price.
The last panel of Figure 6 shows that, notwithstanding this improved long-horizon forecast accuracy, households committed systematic forecast errors during the most recent oil price surge. Between 1998 and 2004, households persistently underestimated the price of gasoline. This evidence may help explain the continued popularity of SUVs, light trucks and other energy-inefficient automobiles during this period. Presumably, consumers would not have chosen to buy as many SUVs, had they foreseen the subsequent increase in gasoline prices at the time of their purchase decision.
There are no household surveys of oil price expectations, but, as discussed earlier, there are monthly data on the views of professional forecasters in the Consensus Economics forecast. Figure 7 highlights some systematic differences between these professional forecasts and the corresponding household gasoline price expectations. Whereas households' gasoline price forecast tends to exceed the current gasoline price by the expected inflation rate, professional oil price forecasts most of the time are below the current price of oil. The upper panel of Figure 7 shows that professional forecasters tend to smooth the predicted path relative to the current price. This smoothing is especially apparent during large oil price fluctuations such as those in 1990/91, in 1999/2000, and in 2003-2009. This tendency contributes to the large and persistently negative forecast errors shown in the lower panel of Figure 7 and helps explain why the consensus forecast does not significantly improve on the no-change forecast (see Table 11).
One possible explanation of the less than satisfactory accuracy of these survey forecasts in section 4 is that professional macroeconomic forecasters may not be experts on the oil market. Figure 8 therefore focuses on an alternative time series of 1-quarter and 4-quarters-ahead forecasts of the U.S. nominal refiners' acquisition cost for imported crude oil. These data were collected from the EIA's Short-term Economic Outlook, which is published by the U.S. Department of Energy. Given the difference in frequency and oil price definition the results are not strictly speaking comparable with our earlier analysis of the monthly WTI price. Nevertheless, these data are illuminating. Figure 8 illustrates that even these expert forecasts generally underpredicted the price of crude oil between 2004 and mid-2008, especially at longer horizons, while overpredicting it following the collapse of the price of oil in mid-2008 and underpredicting it again more recently. A natural question is how the EIA forecasts compare to the no-change forecast on the basis of the EIA's preliminary data releases for the current refiners' acquisition cost for imported crude oil. The latter data are provided by the same source. The DM test for equal predictive accuracy in Table 11 suggests that the MSPE ratio of 0.92 for the 1-quarter-ahead forecast is statistically significant at the 10% level, but the MSPE ratio of 0.97 for the 4-quarters-ahead forecast is not. We conclude that even the EIA has had at best modest success in forecasting the nominal price of oil in the short run and none at longer horizons.
8. Short-Horizon Forecasts of the Real Price of Oil
Our analysis in section 4 suggests that we stand a better chance of forecasting the real price of oil out-of-sample using monthly data, given the availability of more appropriate predictors at the monthly frequency. A natural benchmark for all forecasting models of the real price of oil is again the no-change forecast. At short horizons, inflation is expected to be at best moderate and it may seem that there is every reason to expect the high forecast accuracy of the random walk model without drift relative to less parsimonious regression models to carry over to the real price of oil (see Kilian 2010).25 On the other hand, in forecasting the real price of oil we may rely on additional economic structure and on additional predictors that could potentially improve forecast accuracy. Section 8 explores a number of such models. In addition to focusing on the real WTI price, we also present results for the real refiners' acquisition cost for oil imports.
8.1. Real U.S. Refiners' Acquisition Cost for Imported Crude Oil
8.1.1. Unrestricted AR, ARMA and VAR Models
A useful starting point is a forecast accuracy comparison of selected monthly AR and ARMA models for the real price of oil in log levels and in log differences. Both classes of models are evaluated in terms of their ability to predict the log level of the real price of oil in recursive settings.
Below we consider two alternative measures of the real price of
oil: The U.S. refiners' acquisition cost for imported crude oil,
which may be thought of as a proxy for the price of oil in global
oil markets, and the WTI price; in both cases the deflator is the
U.S. CPI. First consider the refiners' acquisition cost. Estimation
starts in 1973.2, and the evaluation period is 1991.12-2009.8 to
facilitate direct comparisons with VAR models of the global market
for crude oil in this and the next section.26 All MSPE results
are expressed as fractions of the MSPE of the no-change forecast.
Some models are based on fixed lag orders of 12 or 24, whereas
others rely on the Schwarz Information Criterion (SIC) or the
Akaike Information Criterion (AIC) for lag order selection (see
Inoue and Kilian 2006; Marcellino, Stock and Watson 2006). We
search over
![]() The forecast
accuracy results are robust to allowing for a larger upper
bound.
The forecast
accuracy results are robust to allowing for a larger upper
bound.
There are no theoretical results in the forecasting literature on how to assess the null of equal predictive accuracy when comparing iterated AR or ARMA forecasts to the no-change forecast. In particular, the standard tests discussed in Clark and McCracken (2001, 2005) or Clark and West (2007) are only designed for direct forecasts. Below we assess the significance of the MSPE reductions based on bootstrap p-values for the MSPE ratio constructed under the null of a random walk model without drift.27 The upper panel of Table 12 suggests that AR and ARMA models in log levels have lower recursive MSPE than the no-change forecast at short horizons. The accuracy gains may approach 17% in some cases and are highly statistically significant. Beyond the six-month horizon, all gains in forecast accuracy evaporate. There also are statistically significant gains in directional accuracy at horizons 1 and 3, and in some cases at horizon 6. There is little to choose between the AR(12), ARMA(1,1), AR(SIC) and AR(AIC) specifications overall. The AR(24) model has slightly better directional accuracy at longer horizons, but at the cost of a higher MSPE ratio.
The lower panel of Table 12 shows the corresponding forecasting models in log differences. Note that after imposing the unit root, the autoregressive lag order is reduced by one. For example, an ARMA(1,1) model in levels corresponds to an MA(1) model in differences. We find that models in log differences generally are about as accurate as models in log levels. There is robust evidence of statistically significant MSPE reductions at horizons 1 and 3 and there are statistically significant gains in directional accuracy at horizons of up to 6 months in some cases. There is little to choose between the five forecasting models in log differences.
We conclude (1) that forecasting the real price of oil based on models in log levels is by no means inferior to forecasting based on models in log differences; (2) that simple AR or ARMA models with fixed lag orders perform quite well; and (3) that the no-change forecast of the real price of oil can be improved upon at horizons of 1 month and 3 months, but generally not at horizons beyond half a year.
All models in Table 12 have in common that the information set is restricted to past values of the real price of oil. The question we turn to next is whether suitably chosen macroeconomic predictors can be used to improve further on the no-change forecast. Recently, a number of structural vector autoregressive models of the global market for crude oil have been proposed (see, e.g., Kilian 2009). These models produce empirically plausible estimates of the impact of demand and supply shocks in the oil market. A natural conjecture is that such models may also have value for forecasting. Here we focus on the reduced-form representation of the VAR model in Kilian and Murphy (2010). The sample period is 1973.2-2009.8. The variables in this model include the percent change in global crude oil production, the global real activity measure we already discussed in section 4, the log of the real price of oil, and a proxy for the change in global above-ground crude oil inventories. For further discussion of the data see Kilian and Murphy (2010). The VAR model may be consistently estimated without taking a stand on whether the real price of oil is I(0) or I(1) (see Sims, Stock and Watson 1990). We focus on recursive rather than rolling regression forecasts throughout this section. This approach makes sense in the absence of structural change, given the greater efficiency of recursive regressions and the small sample size.28
A natural starting point for the forecast accuracy comparison is the unrestricted VAR model. An obvious concern with forecasting from unrestricted vector autoregressions is that these highly parameterized models are subject to considerable estimation uncertainty which tends to inflate the out-of-sample MSPE. For that reason unrestricted VAR models are rarely used in applied forecasting. They nevertheless provide a useful point of departure. The upper panel of Table 13 shows results for unrestricted VAR models with 12 lags. Column (1) corresponds to the four-variable model used in Kilian and Murphy (2010). Table 13 shows that this unrestricted VAR forecast has lower recursive MSPE than the no-change forecast at all horizons but one and nontrivial directional accuracy.29 Despite the lack of parsimony, the reductions in the MSPE are somewhat larger than for the AR and ARMA models in Table 12. Bootstrap p-values for the MSPE ratio constructed under the null of a random walk model without drift indicate statistically significant reductions in the MSPE at horizons 1, 3, and 6. At longer horizons it becomes harder to beat the no-change forecast benchmark and there are no statistically significant reductions in the MSPE. There also is evidence of statistically significant gains in directional accuracy at horizons 1 and 3.
The forecasting success of the VAR approach clearly depends on the choice of variables and of the lag length. The remaining columns of the upper panel of Table 13 show analogous results for five other unrestricted VAR(12) models obtained by dropping one or more of the variables included in model (1). None of these models performs as well as the original four-variable model with two exceptions. The bivariate model (4) which includes only the change in oil inventories and the real price of oil has slightly lower MSPE than the four-variable VAR(12) model and similar directional accuracy, as does the trivariate model (6) specification that drops oil production from the baseline model.
The lower panel of Table 13 suggests that including 24 lags in the unrestricted model tends to reduce the MSPE reductions. All VAR(24) models but model (2) still significantly improve on the MSPE of the no-change forecast at horizons 1 and 3, but their MSPE ratio tends to exceed unity at higher horizons. Likewise, all six VAR(24) models yield statistically significant gains in directional accuracy at short horizons. Only the four VAR(24) models that include the global real activity variable in the model, however, retain their superior directional accuracy at all horizons. Unlike in the corresponding VAR(12) models, the gains in directional accuracy are statistically significant at all horizons.
We conclude that there is important predictive information in the change in oil inventories and in global real activity in particular, whereas the inclusion of oil production growth appears less important for forecasting. Moreover, based on the MSPE metric, suitably chosen VAR models systematically outperform the no-change forecast at short horizons. At longer horizons, the no-change forecast remains unbeaten, except based on the sign metric. This result immediately extends to longer horizons because none of the VAR forecasting models are suitable for extrapolating to long horizons.
It is important to keep in mind, however, that Table 13 may overstate the true statistical significance of the short-horizon MSPE reductions. One indication of this problem is that Table 13 sometimes indicates statistically significant rejections of the no-change forecast benchmark even when the MSPE ratio exceeds 1, indicating that the VAR has a strictly higher recursive MSPE. The reason for this counterintuitive result is that, as discussed earlier, standard tests of equal predictive accuracy do not test the null of equal out-of-sample MSPEs, but actually test the null of no predictability in population - much like the Granger causality tests we applied earlier - as pointed out by Inoue and Kilian (2004a). This point is readily apparent from the underlying proofs of asymptotic validity as well as the way in which critical values are simulated.
The distinction between population predictability and out-of-sample predictability does not matter asymptotically under fixed parameter asymptotics, but fixed parameter asymptotics typically provide a poor approximation to the finite-sample accuracy of forecasting models. Under more appropriate local asymptotics (designed to mimic the weak predictive power of many regressors) it can be shown that the null of no predictability in population is distinct from the null of equal out-of-sample MSPEs. It is always easier to reject the former than the latter. In other words, conventional tests of equal predictive accuracy test the wrong null hypothesis and may spuriously reject the no-change forecast in favor of the alternative. This is the deeper reason for the very low p-value obtained, for example, for model (1) with 24 lags at horizon 3. The intuition for this rejection is that under the null that the real price of oil is unpredictable one would expect much higher MSPE ratios than 1.047, so the fact that the MSPE of the VAR model is so close to 1 actually is evidence in favor of the VAR model being the population model.
Which model is the population model, of course, is irrelevant for the question of which model generates more accurate forecasts in finite samples, so we have to interpret this rejection with some caution. This type of insight recently has prompted the development of alternative tests of equal predictive accuracy based on local-to-zero asymptotic approximations to the predictive regression. Clark and McCracken (2010) for the first time proposed a correctly specified test of the null of equal out-of-sample MSPEs. Their analysis is limited to direct forecasts from much simpler forecasting models, however, and cannot be applied in Table 13.30 This caveat suggests that we discount only marginally statistically significant rejections of the no predictability null hypothesis in Table 13 and focus on the highly statistically significant test results. The tests for directional accuracy are not affected, of course.
8.1.2. Real-Time Forecasts
The results so far are encouraging in that they suggest that VAR models (even more so than AR or ARMA models) may produce useful short-horizon forecasts of the real price of oil. An important caveat regarding the results in Tables 12 and 13 is that the forecast accuracy comparison is not conducted in real time. There are two rather distinct concerns. One is that not all useful predictors may be available to the forecaster in real time. The other concern is that many predictors and indeed some measures of the price of oil are subject to data revisions. This caveat applies even to the no-change forecast. The reason is that the refiners' acquisition cost data become available only with a delay of about three months and the CPI data used to deflate the refiners' acquisition cost become available only with a one-month delay.
Additional caveats apply to the VAR evidence. Although the dry cargo shipping rate data underlying the real activity index are available in real time and not subject to revisions, the construction of the real activity index involves real-time CPI data as well real-time estimates of the trend in real shipping rates. Moreover, the data on global crude oil production only become available with a delay of 4 months and the data used to approximate global crude oil inventories with a delay of five months. This is less of a concern for the oil production data which tend to evolve rather smoothly than for the more volatile data on changes in crude oil inventories for which there is no good real time proxy. How imposing these real-time data constraints alters the relative accuracy of no-change benchmark model compared with VAR models is not clear a priori because both the benchmark model and the alternative model are affected.
The first study to investigate this question is Baumeister and Kilian (2011) who recently developed a real-time data set for the variables in question. They find (based on a data set extending until 2010.6) that VAR forecasting models of the type considered in this section can generate substantial improvements in real-time forecast accuracy. The MSPE reduction for unrestricted VAR models may be as high as 25% at the one-month horizon and as high as 9% at the three-month horizon. At longer horizons the MSPE reductions diminish even for the best VAR models. Beyond one year, the no-change forecast usually has lower MSPE than the VAR model. Baumeister and Kilian also show that VAR forecasting models based on Kilian and Murphy (2010) exhibit significantly improved directional accuracy. The improved directional accuracy persists even at horizons at which the MSPE gains have vanished. The success ratios range from 0.51 to 0.60, depending on the model specification and horizon.
8.2. Real WTI Price
Tables 14 and 15 show the corresponding results based on the real WTI price of oil instead of the real U.S. refiners' acquisition cost for imported crude oil. These results are not so much intended to validate those in Tables 12 and 13, given the inherent differences in the definition of the oil price data, but are of independent and complementary interest. The estimation and evaluation periods are unchanged to allow direct comparisons. The nominal WTI price is available without delay and is not subject to revisions, reducing concerns over the real-time availability of the oil price data.
Table 14 provides robust evidence that AR and ARMA models improve on the no-change forecast of the real WTI price of oil at horizons 1 and 3 with the exception of models with 24 lags. The largest MSPE reductions are only 5%, however, and all such accuracy gains vanish at longer horizons. The VAR results in Table 15 paint a similar picture. None of the VAR(12) models has significantly lower MSPE than the no-change forecast beyond horizon 6. In general the reductions in MSPEs are smaller than in Table 13. The largest MSPE reduction is 16% at horizon 3. Likewise, the evidence that forecasts from VAR models with 24 lags have directional accuracy is weaker than in Table 13. By the MSPE metric, only in rare cases are the VAR(24) models more accurate than the no-change forecast of the real WTI price of oil. This finding highlights that the definition of the real price of oil matters for the degree of forecastability. Clearly, the real price of WTI crude oil is more difficult to forecast in the short run than the real U.S. refiners' acquisition cost for imported crude oil.
Broadly similar results would be obtained with real-time data (see Baumeister and Kilian 2011). Unlike for the real refiners' acquisition cost, the differences between real-time forecasts of the real WTI price and forecasts based on ex-post revised data tend to be small.
8.3. Restricted VAR Models
Although the results for the unrestricted VAR models in Tables 13 and 15 are encouraging, there is reason to believe that alternative estimation methods may reduce the MSPE of the VAR forecast even further. One candidate is the use of Bayesian shrinkage estimation methods. In the VAR model at hand a natural starting point would be to shrink all lagged parameters toward zero under the maintained assumption of stationarity. This leaves open the question of how to determine the weights of the prior relative to the information in the likelihood. Giannone, Lenza and Primiceri (2010) recently proposed a simple and theoretically founded data-based method for the selection of priors in recursively estimated Bayesian VARs (BVARs). Their recommendation is to select priors using the marginal data density (i.e., the likelihood function integrated over the model parameters), which only depends on the hyperparameters that characterize the relative weight of the prior and the information in the data. They provide empirical examples in which the forecasting accuracy of that model in recursive settings is not only superior to unrestricted VAR models, but is comparable to that of single-equation dynamic factor models (see Stock and Watson 1999).
Table 16 compares the forecasting accuracy of this approach with that of the unrestricted VAR models considered in Tables 13 and 15. In all cases, we shrink the model parameters toward a white noise prior mean with the desired degree of shrinkage being determined by the data-based procedure in Giannone et al. (2010). For models with 12 lags, there is no strong evidence that shrinkage estimation reduces the MSPE. Although there are some cases in which imposing Bayesian priors reduces the MSPE slightly, in other cases it increases the MSPE slightly. For models with 24 lags, however, shrinkage estimation often greatly reduces the MSPE ratio and typically produces forecasts about as accurate as forecasts from the corresponding model with 12 lags. As in Tables 12 and 14, there is evidence of MSPE reductions at horizons of up to 6 months. For example, model (1) with 12 lags yields MSPE reductions of 20% at horizon 1, 12% at horizon 3, and 3% at horizon 6 with no further gains at longer horizons. Model (1) with 24 lags yields gains of 20%, 12% and 1%, respectively. Again, it can be shown that similar gains in accuracy are feasible even using real-time data (see Baumeister and Kilian 2011).
In addition, such VAR models can also be useful for studying how baseline forecasts of the real price of oil must be adjusted under hypothetical forecasting scenarios, as illustrated in the next section. This does require the VAR model to be fully identified, however.
9. Structural VAR Forecasts of the Real Price of Oil
Recent research has shown that historical fluctuations in the real price of oil can be decomposed into the effects of distinct oil demand and oil supply shocks associated with unpredictable shifts in global oil production, real activity and a forward-looking or speculative element in the real price of oil (see, e.g., Kilian and Murphy 2010). Changes in the composition of these shocks help explain why conventional regressions of macroeconomic aggregates on the price of oil tend to be unstable. They also are potentially important in interpreting oil price forecasts.
In section 8 we showed that recursive forecasts of the real price of oil based on the type of oil market VAR model proposed in Kilian and Murphy (2010) for the purpose of structural analysis are not necessarily inferior to simple no-change forecasts. The case for the use of VAR models, however, does not rest on their predictive accuracy alone. Policymakers expect oil price forecasts to be interpretable in light of an economic model. They also expect forecasters to be able to generate projections conditional on a variety of hypothetical economic scenarios. Questions of interest include, for example, what effects an unexpected slowing of Asian growth would have on the forecast of the real price of oil; or what the effect would be of an unexpected decline in global oil production associated with peak oil. Answering questions of this type is impossible using reduced-form time series models. It requires a fully structural VAR model (see Waggoner and Zha 1999).
In this section we illustrate how to generate such projections from the structural moving average representation of the VAR model of Kilian and Murphy (2010) estimated on data extending to 2009.8. The discussion closely follows Baumeister and Kilian (2011). This model allows the identification of three structural shocks: (1) a shock to the flow of the production of crude oil ("flow supply shock), (2) a shock to the flow demand for crude oil and other industrial commodities ("flow demand shock") that reflects unexpected fluctuations in the global business cycle, and (3) a shock to the demand for oil inventories arising from forward-looking behavior ("speculative demand shock"). The structural demand and supply shocks in this model are mainly identified by a combination of sign restrictions and bounds on impact price elasticities. This model is set-identified, but the admissible models can be shown to be quite similar, allowing us to focus on one such model with little loss of generality. We focus on the same model that Kilian and Murphy use as the basis for their historical decompositions.
There is a strict correspondence between standard reduced-form VAR forecasts and forecasts from the structural moving representation. The reduced-form forecast corresponds to the expected change in the real price of oil conditional on all future shocks being zero. Departures from this benchmark can be constructed by feeding pre-specified sequences of future structural shocks into the structural moving-average representation. A forecast scenario is defined as a sequence of future structural shocks. The implied movements in the real price of oil relative to the baseline forecast obtained by setting all future structural shocks to zero correspond to the revision of the reduced-form forecast implied by this scenario.
We consider three scenarios of economic interest. The forecast horizon is 24 months for illustrative purposes. The first scenario involves a successful stimulus to U.S. oil production, as had been considered by the Obama administration prior to the 2010 oil spill in the Gulf of Mexico. Here we consider the likely effects of a 20% increase in U.S. crude oil output in 2009.9, after the estimation sample of Kilian and Murphy (2010) ends. This is not to say that such a dramatic and sudden increase would be feasible, but that it would be a best-case scenario. Such a U.S. oil supply stimulus would translate to a 1.5% increase in world oil production, which is well within the variation of historical data. We simulate the effects of such a stimulus by calibrating a one-time structural oil supply shock such that the impact response of global oil production growth in 2009.9 is 1.5%. All other future structural shocks are set to zero. Figure 9 shows that the resulting reduction in the real price of oil expressed in percent relative to the baseline forecast is negligible. Even a much larger U.S. oil supply stimulus would do little to affect the forecast of the real price of oil, suggesting that policies aimed at creating such a stimulus will be ineffective at lowering the real price of oil.
The second scenario involves a recovery of global demand for oil and other industrial commodities. We ask how an unexpected surge in the demand for oil similar to that occurring during 2007.1-2008.6, but starting in 2009.9, would affect the real price of oil. This scenario involves feeding into the structural moving average representation future flow demand shocks corresponding to the sequence of flow demand shocks that occurred in 2007.1-2008.6, while setting all other future structural shocks equal to their expected value of zero. Figure 9 shows a persistent increase in the real price of oil starting in early 2010 that peaks in early 2011 about 50% above the price of oil in 2009.8. Taking the no-change forecast as the baseline forecast, this means that the peak occurs at a price of about 100 dollars. Alternatively, one could express these results relative to the unconditional VAR forecast.
Finally, we consider the possibility of a speculative frenzy such as occurred starting in mid-1979 after the Iranian Revolution (see Kilian and Murphy 2010). This scenario involves feeding into the model future structural shocks corresponding to the sequence of speculative demand shocks that occurred between 1979.1 and 1980.2 and were a major contributor to the 1979/80 oil price shock episode. Figure 9 shows that this event would raise the baseline forecast temporarily by as much as 30%. Most of the effects would have dissipated by mid-2011.
These results, while necessarily tentative, illustrate how structural models of oil markets may be used to assess risks in oil price forecasts and to investigate the sensitivity of reduced- form forecasts to specific economic events, possibly in conjunction with the formal risk measures discussed in section 12. Conditional projections, of course, are only as good as the underlying structural models. Our example highlights the importance of refining these models and of improving structural forecasting methods, perhaps in conjunction with Bayesian methods of estimating VAR forecasting models.
10. Forecasting the Real Price of Oil in Other Countries
It is natural to focus on forecasting the real price of oil in dollars because crude oil is traded in dollars. This perspective, however, is too limited. From the point of European oil importers, for example, it is the real price of oil in Euros that matters. Figure 10 shows the real price of oil between 1991.1 and 2009.12 in the U.S., the Euro zone, Japan, the U.K. and Canada. These data have been constructed from the U.S. refiners' acquisition cost for imported crude oil with the help of data on nominal exchange rates and consumer prices. For expository purposes all data have been expressed in log deviations from their mean over this sample period. Although the overall picture is similar, Figure 10 illustrates that there can be substantial differences in the real price of oil across countries at times. For example, the real exchange rate cushioned the increase in the real price of oil experienced by the Euro area in 2007/08, but amplified it in 2000/01.
These differences in the evolution of the real price of oil across countries shown in Figure 10 suggest that there is no a priori reason to expect the accuracy of alternative forecasting models of the real price of oil to be the same across countries. A model that works well for one country need not work well for other countries. Table 17 explores this question for Japan, the U.K. and Canada. We focus on the AR(12) model for illustrative purposes. The estimation and evaluation periods are the same as in Tables 12 and 14, allowing direct comparisons. The upper panel shows results based on the U.S. refiners' acquisition cost for imported crude oil and the lower panel results based on the WTI price. For each country we fit an AR(12) model to the price of oil expressed in terms of domestic consumer goods. These prices are obtained by multiplying the U.S. real price of crude oil by the appropriate monthly real exchange rates. The results in the upper panel are quite similar to those in Table 12. For all three countries the AR(12) model has significantly lower MSPE than the no-change forecast at horizons 1 and 3 and in some cases at horizon 6 as well. At longer horizons, the no-change forecast is more accurate. The results in the lower panel are similar to those in Table 14 in that the evidence against the no-change forecast is somewhat weaker. For Japan and Canada the no-change forecast is rejected at horizons 1 and 3, but for the U.K. there is no rejection at any horizon. The gains in accuracy, even if statistically significant, tend to be smaller than in the upper panel. This example suggests that - subject to the earlier caveats - the forecast accuracy gains we documented for the U.S. real price of oil continue to hold for other countries. We defer to future work the question of whether the relative accuracy of alternative AR and ARMA forecasting methods is the same for other countries as for the United States.
Extending the VAR approach of section 8 to other countries raises additional complications. One simple approach would be to augment the baseline reduced-form forecasting model for the real price of oil in dollars by including the real exchange rate. This approach, however, may cost too many degrees of freedom in practice. A simple alternative approach is to leave unchanged the VAR model, but to convert all forecasts of the real price of oil at the real exchange rate as of the date from which the forecasts are generated. This amounts to imposing a no-change forecast for the real exchange rate. At short horizons, the real exchange rate is dominated by fluctuations in the nominal exchange rate. It is well known that the change in the nominal exchange rate is unforecastable in real time. This suggests that the no-change forecast of the real exchange rate will provide a good approximation at least at short horizons. The same approach may be used in constructing the conditional predictions from structural VAR models discussed in section 9, which avoids having to reconsider the identification of the structural VAR shocks.
11. The Ability of Oil Prices to Forecast U.S. Real GDP
One of the main reasons the price of oil is considered important by many macroeconomists is its perceived predictive power for U.S. real GDP. Assessing that predictive power requires a joint forecasting model for the price of oil and for domestic real activity. In this section we first examine the forecasting accuracy of linear models and then examine a variety of nonlinear forecasting models. The baseline results are for the U.S. refiners' acquisition cost for imported crude oil. Toward the end of the section we discuss how these results are affected by other oil price choices. Our discussion draws on results in Kilian and Vigfusson (2010c).
11.1. Linear Autoregressive Models
A natural starting point is a linear VAR(p) model for the
real price of oil and for U.S. real GDP expressed in quarterly
percent changes. The general structure of the model is
![]() , where
, where
![]()
![]() denotes the log of real price of oil,
denotes the log of real price of oil, ![]() the log of real GDP,
the log of real GDP, ![]() is the
difference operator,
is the
difference operator, ![]() the regression error,
and
the regression error,
and
![]() The
benchmark model for real GDP growth is the AR(p) model
obtained with
The
benchmark model for real GDP growth is the AR(p) model
obtained with
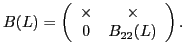
The specification of the components of ![]() marked as
marked as
![]() is irrelevant for this forecasting
model. We determined the lag order of this benchmark model based
on a forecast accuracy comparison involving all combinations of
horizons
is irrelevant for this forecasting
model. We determined the lag order of this benchmark model based
on a forecast accuracy comparison involving all combinations of
horizons
![]() and lag orders
and lag orders
![]() The AR(4) model for real
GDP growth proved to have the lowest MSPE or about the same MSPE as
the most accurate model at all horizons. The same AR(4) benchmark model
has also been used by Hamilton (2003) and others, facilitating
comparisons with existing results in the literature.
The AR(4) model for real
GDP growth proved to have the lowest MSPE or about the same MSPE as
the most accurate model at all horizons. The same AR(4) benchmark model
has also been used by Hamilton (2003) and others, facilitating
comparisons with existing results in the literature.
We compare the benchmark model with two alternative models. One model is the unrestricted VAR(p) model obtained with
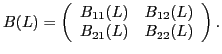
The other is a restricted VAR model of the form
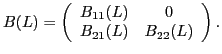
The restriction
![]() is implied by the hypothesis of
exogenous oil prices. Although that restriction is not literally
true, in section 4 we mentioned that in linear models the
predictive content of U.S. real GDP for the real price of oil,
while not zero, appears to be weak. Thus, a natural conjecture is
that the added parsimony from imposing zero feedback from lagged
real GDP to the real price of oil may help reduce the out-of-sample
MSPE of multi-step ahead real GDP forecasts.
is implied by the hypothesis of
exogenous oil prices. Although that restriction is not literally
true, in section 4 we mentioned that in linear models the
predictive content of U.S. real GDP for the real price of oil,
while not zero, appears to be weak. Thus, a natural conjecture is
that the added parsimony from imposing zero feedback from lagged
real GDP to the real price of oil may help reduce the out-of-sample
MSPE of multi-step ahead real GDP forecasts.
The real price of oil is obtained by deflating the refiners' acquisition cost for imported crude oil by the U.S. CPI. All three models are estimated recursively on data starting in 1974.Q1.
The initial estimation period ends in 1990.Q1, right before the
invasion of Kuwait in August of 1990. The forecast evaluation ends
in 2010.Q2. The maximum length of the recursive sample is
restricted by the end of the data and the forecast horizon. We
evaluate the MSPE of each model for the cumulative growth rates at
horizons
![]() corresponding to
the horizons of interest to policymakers.
corresponding to
the horizons of interest to policymakers.
The first column of Table 18 shows that, at horizons of three quarters and beyond, including the real price of oil in the autoregressive models may reduce the MSPE for real GDP growth by up to 8% relative to the AR(4) model for real GDP growth. The unrestricted VAR(4) model for the real price of oil is about as accurate as the restricted VAR(4) model in the second column. Imposing exogeneity marginally reduces the MSPE at some horizons, but the differences are all negligible. This fact is remarkable given the greater parsimony of the model with exogenous oil prices. We conclude that there are no significant gains from imposing exogeneity in forecasting from linear models. Next consider a similar analysis for the nominal price of oil. Although the use of the nominal price of oil in predicting real GDP is not supported by standard economic models, it is useful to explore this alternative approach in light of the discussion in section 3. Table 18 shows that the unrestricted VAR(4) model based on the real price of oil is consistently at least as accurate as the same model based on the nominal price of oil. We conclude that in linear models there are no gains in forecast accuracy from replacing the real price of oil by the nominal price. Imposing exogeneity, as shown in the last column, again makes little difference.
MSPE ratios are informative about relative forecasting accuracy, but are not informative about how accurate these models are in practice. Figure 11 focuses on the ability of recursively estimated AR(4) and VAR(4) models based on the real price of oil imports to predict the recessions of 1991, 2001, and 2007/8. The upper panel plots the one-quarter-ahead forecasts against the forecast realizations. AR and VAR forecasts are generally quite similar. Neither model is able to forecast the large economic declines in 1990/91, 2001, and 2008/09. The forecast accuracy deteriorates further at the one-year horizon, as shown in the lower panel.
One possible explanation is that this forecast failure simply reflects our inability to forecast more accurately the real price of oil. Put differently, the explanation could be that the real GDP forecasts would be more accurate if only we had more accurate forecasts of the real price of oil. Conditioning on realized values of the future price of oil, however, does not greatly improve the forecast accuracy of the linear VAR model for cumulative real GDP growth, so this explanation can be ruled out. An alternative explanation could be that the predictive relationship between the price of oil and domestic macroeconomic aggregates is time-varying. One source of time variation is that the share of energy in domestic expenditures has varied considerably over time. This suggests that we replace the percent change in the real price of oil in the linear VAR model by the percent change in the real price of oil weighted by the time-varying share of oil in domestic expenditures, building on the analysis in Edelstein and Kilian (2009). Hamilton (2009) reported some success in employing a similar strategy.31 Another source of time variation may be changes in the composition of the underlying oil demand and oil supply shocks, as discussed in Kilian (2009). Finally, yet another potential explanation investigated below is that the linear forecasting model may be inherently misspecified. Of particular concern is the possibility that nonlinear dynamic regression models may generate more accurate out-of-sample forecasts of cumulative real GDP growth.
11.2. Nonlinear Dynamic Models
In this regard, Hamilton (2003) suggested that the predictive relationship between oil prices and U.S. real GDP is nonlinear in that (1) oil price increases matter only to the extent that they exceed the maximum oil price in recent years and that (2) oil price decreases do not matter at all. This view was based on the in-sample fit of a single-equation predictive model of the form:
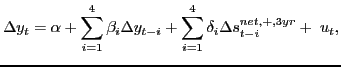 |
(18) |
where ![]() denotes the log of the nominal price of
oil and
denotes the log of the nominal price of
oil and
![]() the corresponding
3-year net
the corresponding
3-year net
increase in the nominal price of oil.
Hamilton's line of reasoning has prompted many researchers to construct asymmetric
responses to positive and negative oil price innovations from
censored oil price VAR models. Censored oil price VAR models refer
to linear VAR models for
![]() possibly augmented by other variables. Recently, Kilian and
Vigfusson (2010a) have shown that impulse response estimates from
VAR models involving censored oil price variables are inconsistent
even when equation (18) is correctly
specified. Specifically, that paper demonstrated, first, that
asymmetric models of the transmission of oil price shocks cannot be
represented as censored oil price VAR models and are fundamentally
misspecified whether the data generating process is symmetric or
asymmetric. This misspecification renders the parameter estimates
inconsistent and inference invalid. Second, standard approaches to
the construction of structural impulse responses in this literature
are invalid, even when applied to correctly specified models.
Instead, Kilian and Vigfusson proposed a modification of the
procedure discussed in Koop, Pesaran and Potter (1996). Third,
standard tests for asymmetry based on the slope coefficients of
single-equation predictive models are neither necessary nor
sufficient for judging the degree of asymmetry in the structural
response functions, which is the question of ultimate interest to
users of these models. Kilian and Vigfusson proposed a direct test
of the latter hypothesis and showed empirically that there is no
statistically significant evidence of asymmetry in the response
functions for U.S. real GDP.
possibly augmented by other variables. Recently, Kilian and
Vigfusson (2010a) have shown that impulse response estimates from
VAR models involving censored oil price variables are inconsistent
even when equation (18) is correctly
specified. Specifically, that paper demonstrated, first, that
asymmetric models of the transmission of oil price shocks cannot be
represented as censored oil price VAR models and are fundamentally
misspecified whether the data generating process is symmetric or
asymmetric. This misspecification renders the parameter estimates
inconsistent and inference invalid. Second, standard approaches to
the construction of structural impulse responses in this literature
are invalid, even when applied to correctly specified models.
Instead, Kilian and Vigfusson proposed a modification of the
procedure discussed in Koop, Pesaran and Potter (1996). Third,
standard tests for asymmetry based on the slope coefficients of
single-equation predictive models are neither necessary nor
sufficient for judging the degree of asymmetry in the structural
response functions, which is the question of ultimate interest to
users of these models. Kilian and Vigfusson proposed a direct test
of the latter hypothesis and showed empirically that there is no
statistically significant evidence of asymmetry in the response
functions for U.S. real GDP.
Hamilton (2010) agrees with Kilian and Vigfusson on the lack of validity of impulse response analysis from censored oil price VAR models, but suggests that nonlinear predictive models such as model (18) may still be useful for out-of-sample forecasting. We explore this conjecture below. We consider both one-quarter-ahead forecasts of real GDP growth and forecasts of the cumulative real GDP growth rate several quarters ahead. The latter forecasts require a generalization of the single-equation forecasting approach proposed by Hamilton (2010). In implementing this approach, there are several potentially important modeling choices to be made.
First, even granting the presence of asymmetries in the predictive model, one question is whether the predictive model should be specified as
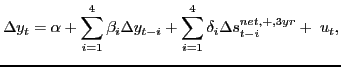 |
(18) |
as in Hamilton (2003), or rather as:
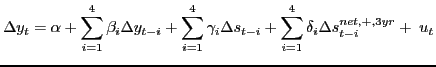 |
(19) |
as in Balke, Brown and Yücel (2002) or Herrera, Lagalo and
Wada (2010), for example. The latter specification encompasses the
linear reduced-form model as a special case. Kilian and Vigfusson
prove that dropping the lagged percent changes from model (19) will cause an
inconsistency of the OLS estimates, except in the theoretically
implausible case that there is no lagged feedback from percent
changes in the price of oil to real GDP. Hamilton, in contrast,
argues in effect that
![]() or, alternatively,
that the slopes
or, alternatively,
that the slopes
![]() are close enough to zero for the
misspecified (but more parsimonious) nonlinear predictive model
(18) to have
lower out-of-sample MSPE in finite samples than the unrestricted
encompassing model (19). This
motivation for the use of model (18) is new in that
heretofore the focus in the literature - including Hamilton's own
work - has been on establishing nonlinear predictability in
population rather than out-of-sample. Hamilton (2010) is, of
course, correct that there is a tradeoff between estimation
variance and bias. Indeed, in many other contexts parsimony has
been shown to help reduce the out-of-sample MSPE, but no systematic
evidence has been presented to make this case for this model. Below
we explore the merits of imposing
are close enough to zero for the
misspecified (but more parsimonious) nonlinear predictive model
(18) to have
lower out-of-sample MSPE in finite samples than the unrestricted
encompassing model (19). This
motivation for the use of model (18) is new in that
heretofore the focus in the literature - including Hamilton's own
work - has been on establishing nonlinear predictability in
population rather than out-of-sample. Hamilton (2010) is, of
course, correct that there is a tradeoff between estimation
variance and bias. Indeed, in many other contexts parsimony has
been shown to help reduce the out-of-sample MSPE, but no systematic
evidence has been presented to make this case for this model. Below
we explore the merits of imposing
![]() not only in the
context of single-equation models designed for one-step ahead
forecasting, but for multivariate nonlinear models as well.
not only in the
context of single-equation models designed for one-step ahead
forecasting, but for multivariate nonlinear models as well.
A second point of contention is whether nonlinear forecasting models should be specified in terms of the nominal price of oil or the real price of oil. For linear models, a strong economic case can be made for using the real price of oil. For nonlinear models, the situation is less clear, as noted by Hamilton (2010). Because the argument for using net oil price increases is behavioral, one specification appears as reasonable as the other. Below we therefore will consider models specified in real as well as in nominal oil prices.
A third issue that arises only in constructing iterated forecasts for higher horizons is how to specify the process governing the price of oil. The case can be made that treating this process as exogenous with respect to real GDP might help reduce the out-of-sample MSPE, even if that restriction is incorrect. Below we therefore consider specifications with and without imposing exogeneity.
In Table 19, we investigate whether there are MSPE reductions
associated with the use of censored oil price variables at horizons
![]() drawing on the
analysis in Kilian and Vigfusson (2010b, c). For completeness, we
also include results for the percent increase specification
proposed in Mork (1989), the forecasting performance of which has
not been investigated to date. We consider nonlinear models based
on the real price of oil as in Kilian and Vigfusson and nonlinear
models based on the nominal price of oil as in Hamilton (2003). The
unrestricted multivariate nonlinear forecasting model takes the
form
drawing on the
analysis in Kilian and Vigfusson (2010b, c). For completeness, we
also include results for the percent increase specification
proposed in Mork (1989), the forecasting performance of which has
not been investigated to date. We consider nonlinear models based
on the real price of oil as in Kilian and Vigfusson and nonlinear
models based on the nominal price of oil as in Hamilton (2003). The
unrestricted multivariate nonlinear forecasting model takes the
form
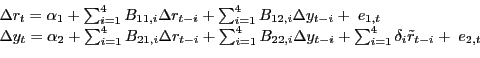 |
(20) |
where
![]()
![]() as
in Mork (1989), and I() denotes the indicator function. Analogous nonlinear forecasting models may
be constructed based on the nominal price of oil, denoted in logs
as
as
in Mork (1989), and I() denotes the indicator function. Analogous nonlinear forecasting models may
be constructed based on the nominal price of oil, denoted in logs
as ![]()
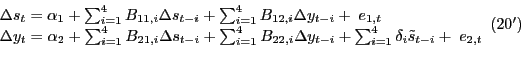 |
(20') |
where
![]()
In addition, we consider a restricted version of models
(20) and
(![]() ) which imposes the hypothesis that the
price of oil is exogenous such that:
) which imposes the hypothesis that the
price of oil is exogenous such that:
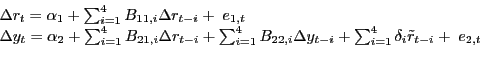 |
(21) |
and
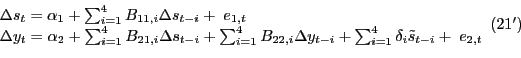 |
(21') |
Alternatively, we may restrict the feedback from lagged percent
changes in the price of oil, as suggested by Hamilton (2003). After
imposing
![]() the baseline nonlinear
forecasting model reduces to:
the baseline nonlinear
forecasting model reduces to:
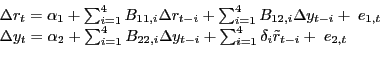 |
(22) |
and
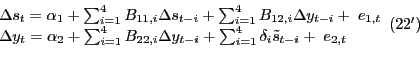 |
(22') |
Finally, we can combine the restrictions
![]() and
and
![]() resulting in
forecasting models (23) and
(
resulting in
forecasting models (23) and
(![]() ):
):
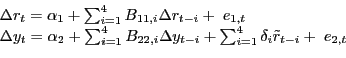 |
(23) |
and
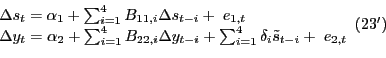 |
(23') |
At the one-quarter horizon, real GDP growth forecasts from model
(![]() ) and (
) and (![]() ) only depend on
the second equation, which is equivalent to using Hamilton's model
(1). All models are estimated by least squares, as is standard in the literature.
The forecasts are constructed by Monte Carlo integration based on
10,000 draws. The estimation and evaluation periods are the same as
in Table 18.
) only depend on
the second equation, which is equivalent to using Hamilton's model
(1). All models are estimated by least squares, as is standard in the literature.
The forecasts are constructed by Monte Carlo integration based on
10,000 draws. The estimation and evaluation periods are the same as
in Table 18.
Table 19 displays the MSPE ratios for all eight models by horizon. All results are normalized relative to the AR(4) model for real GDP growth. No tests of statistical significance have been conducted, given the computational cost of such tests. The first result is that no nonlinear model is more accurate than the AR(4) benchmark model at the one-quarter horizon except for models (22) and (23). The reduction in MSPE is 9%. At longer horizons, model (23') which combines Hamilton's assumptions with that of exogenous oil prices and embeds all these assumptions in a multivariate dynamic framework, yields even larger gains in accuracy relative to the benchmark model. At the one-year horizon, the reduction in MSPE reaches 26% compared with 15% for the unrestricted nonlinear model (22). The use of nominal as opposed to real net oil price increases (accounting for 11 percentage points by itself) and the omission of lagged percent changes in the nominal price of oil (accounting for 4 percentage points by itself) are mainly responsible for the additional gain in accuracy; the imposition of exogeneity plays no role. Accuracy gains at slightly shorter or longer horizons are closer to 10%.
Second, neither the percent increase model based on Mork (1989) nor the one-year net increase model motivated by Hamilton (1996) is more accurate than the AR(4) benchmark at the one-quarter horizon. This is true regardless of whether the price of oil is specified in nominal or real terms and regardless of what additional restrictions we impose. At longer horizons, there is weak evidence that some of these specifications reduce the MSPE at some horizons, but in no case as much as for the three-year net oil price increase.
Third, there is no clear ranking between forecasting models based on the real price of oil and models based on the nominal price of oil. For example, models (22) and (23) based on the real price of oil are more accurate at the one-quarter horizon than models (22') and (23') based on the nominal price, but at longer horizons the ranking is reversed.
An obvious question of interest is to what extent allowing for nonlinearities improves our ability to forecast major economic downturns in the U.S. The one-quarter ahead results in the upper panel of Figure 12 indicate that the nominal net increase model has considerable success in forecasting the 2008 recessions, about half of which is forecast by the model, but the model's performance during other episodes is less impressive. For example, its performance during the oil price shock episode of 1990/91 is erratic. Although the model forecasts a recession, the timing is off and the model forecasts sharp subsequent oscillations in economic growth that did not materialize.
The corresponding lower panel in Figure 12 shows that the net increase model (23') is even more successful at forecasting the downturn of 2008 and the subsequent recovery four quarters ahead. If anything, this nonlinear model appears too successful in that it seems to leave little independent role for the financial crisis. The forecasting success in 2008, however, comes at a price because model (23') on earlier occasions forecast a number of economic declines that did not materialize or were not nearly as severe as predicted by the model. For example, in panel (b), the net increase model incorrectly forecast pronounced declines in economic growth relative to average growth in 2005/06 and the economic decline of 1990/91 began long before the forecasted decline.
Plots of the recursive MSPE of these nonlinear models show that much of the forecasting success of nonlinear models is driven by one episode, namely the economic collapse in 2008/09 following the financial crisis. This point is illustrated in Figure 13. The left panel of Figure 13 is based on the nominal PPI used in Hamilton's original analysis; the right panel shows the corresponding results for the nominal refiners' acquisition cost for crude oil imports. The plot of the cumulative recursive MSPE for the PPI model (23') reveals that the overall gain in accuracy in this example is driven entirely by the 2008/09 recession. Excluding this episode, model (23') has higher MSPE than the linear AR model throughout the evaluation period. Given this evidence a strong case can be made that few forecasters would have had the courage to stick with the predictions of this nonlinear model given the sustained failure of the model in the years leading up to the financial crisis.
The corresponding results for the refiners' acquisition cost for imported crude oil in the right panel are somewhat more favorable, but reveal the same tendency of the net oil price increase model to have a higher recursive MSPE than the AR(4) benchmark model for real GDP growth throughout much of the pre-crisis period. Both in 1990 and between 1998 and 2008 the nonlinear forecasting model proved persistently less accurate out of sample than the AR(4) benchmark. Only in 2009 is that ranking reversed again in favor of the nonlinear model. Given that the financial crisis occurred immediately after a major surge in the price of oil, but itself was presumably not caused by that oil price surge, the obvious concern is that the nonlinear model may have forecast the 2008 recession for the wrong reasons.
It is usually thought that out-of-sample forecasts protect against overfitting. The example of 2008/09 illustrates that this need not be the case. Under quadratic loss the ability of the nonlinear model to predict correctly the sharp economic decline associated with the financial crisis may more than offset the sustained poor forecasting accuracy of this nonlinear model during earlier episodes not involving smaller forecasting errors. Only additional data will ultimately resolve this question. If the near-simultaneous occurrence of the financial crisis and the oil price surge is coincidental, then the forecasting accuracy of the nonlinear model can be expected to worsen, as the sample is extended. If the forecasting success of the nonlinear model were to persist even after the financial crisis is over, this would add credibility to the nonlinear real GDP growth forecasts.
The same concern regarding the financial crisis episode arises to varying degrees with other oil price series. Table 20 provides a systematic comparison of the performance of nonlinear forecasting models relative to the AR(4) benchmark model for real GDP growth for different oil price series and evaluation periods. To conserve space, we focus on models (23) and (23') which tend to be the most accurate nonlinear forecasting models. Table 20 shows that the relative MSPE of nonlinear forecasting models can be highly sensitive to the choice of oil price series. The first two columns of Table 20 focus on the evaluation period 1990.Q1-2010.Q2. Column (1) shows that, for eight of ten model specifications, the one-quarter ahead nonlinear forecasting model proposed by Hamilton (2010) fails to outperform the AR(4) benchmark model for real GDP. Only for the real refiners' acquisition cost for imported crude oil and for the nominal WTI specification are there any gains in forecast accuracy. In particular, the nominal PPI specification favored by Hamilton (2010) on the basis of in-sample diagnostics is less accurate than the AR benchmark model. Much more favorable results are obtained at the one-year horizon in column (2) of Table 20. All but one nonlinear forecasting model yields reductions in the MSPE, although the extent of these reductions greatly differs across models and can range from negligible to substantial. However, all evidence of forecast accuracy gains vanishes if the financial crisis episode is excluded, as shown in columns (3) and (4) of Table 20. Some nonlinear forecasting models have more than twice the MSPE of the AR benchmark model. We conclude that the evidence that nonlinear oil price transformation help forecast cumulative U.S. real GDP growth is mixed at best.
The results in Tables 19 and 20 were constructed from fully revised data that would not have been available to forecasters in real time. As in our analysis of real oil price forecasts, an obvious additional question would be how the results of the forecast accuracy comparison for U.S. real GDP growth would have changed, had we only used data sets actually available as of the time the forecast is generated. This remains an open question at this point.32
11.3. Nonparametric Approaches
Our approach in this section has been parametric. Alternatively, one could have used nonparametric econometric models to investigate the forecasting ability of the price of oil for real GDP. In related work, Bachmeier, Li and Liu (2008) used the integrated conditional moment test of Corradi and Swanson (2002, 2007) to investigate whether oil prices help forecast real GDP growth one-quarter ahead. The advantage of this approach is that - while imposing linearity under the null - it allows for general nonlinear models under the alternative; the disadvantage is that the test is less powerful than the parametric approach if the parametric structure is known. Bachmeier et al. report a p-value of 0.20 for the null that nominal net increases in the WTI price of oil do not help forecast U.S. real GDP. The p-value for percent changes in the WTI price of crude oil is 0.77. Similar results are obtained for real net increases and for percent changes in the real WTI price. These findings are broadly consistent with ours. Bachmeier et al. (2008) also report qualitatively similar results using a number of fully nonparametric approaches. An obvious caveat is that their analysis is based on data since 1949, which is not appropriate for the reasons discussed earlier, and ends before the 2008/09 recession. Using their nonparametric techniques on our much shorter sample period does not seem advisable, however, because there is no way of controlling the size of the test.
12. The Role of Oil Price Volatility
Point forecasts of the price of oil are important, but they fail to convey the uncertainty associated with oil price forecasts. That uncertainty is captured by the predictive density. Figure 14 plots the 12-month ahead predictive density for the real price of oil as of 2009.12, generated from the no-change forecasting model. Although it is obvious that there is tremendous uncertainty about the future real price of oil, even when using the best available forecasting methods, it is less obvious how to convey and interpret that information. For example, standard questions in the financial press about whether the price of oil could increase to $200 a barrel, at the risk of being misunderstood, inevitably and always must be answered in the affirmative because the predictive distribution has infinite support. That answer, however, is vacuous because it does not convey how likely such an event is or by how much the price of oil is expected to exceed the $200 threshold in that event.
12.1. Nominal Oil Price Volatility
One seemingly natural way of summarizing the information in the predictive distribution is to report the variability of the forecasts. Interest in oil price volatility measures arises, for example, from financial analysts interested in pricing options and from portfolio managers interested in diversifying risks. Given that at short horizons CPI inflation is negligible, it is customary in financial applications to focus on nominal oil price volatility. One approach to measuring oil price volatility is to rely on the implied volatilities of put and call options, which are available from January 1989 on. Implied volatility measures are computed as the arithmetic average of the daily implied volatilities from the put and call options associated with a futures contract of a given maturity. The upper panel of Figure 15 shows the 1-month implied volatility time series for 2001.1-2009.12, computed from daily CRB data, following the same procedure as for the spot and futures prices in section 5. Alternatively, we may use daily percent changes in the nominal WTI price of oil to construct measures of realized volatility, as shown in the second panel of Figure 15 (see, e.g., Bachmeier, Li and Liu 2008). Finally, yet another measure of volatility can be constructed from parametric GARCH or stochastic volatility models. The bottom panel of Figure 15 shows the 1-month-ahead conditional variance obtained from recursively estimated Gaussian GARCH(1,1) models.33 The initial estimation period is 1974.1-2000.12. The estimates are based on the percent change in the nominal WTI price; the corresponding results for the real WTI price are almost indistinguishable at the 1-month horizon.34
Figure 15 plots all three volatility measures on the same scale. Although all three measures agree that by far the largest volatility peak occurred near the end of 2008, there are important differences. For example, the implied volatility measure increases steadily starting in early 2008 and peaks in December 2008. Realized volatility also peaks in December 2008, but does not increase substantially the second half of 2008. Finally, GARCH volatility is even slower to increase in 2008 and only peaks in January 2009. This ranking is consistent with the view that implied volatility is the most forward-looking volatility measure and GARCH volatility the most backward-looking volatility estimate (and hence the least representative measure of real time volatility). Similarly, the implied volatility and realized volatility measures indicate substantial secondary spikes in volatility in 2001/02 and 2003, whereas the spikes in the GARCH volatility estimate are much smaller and occur only with a delay.
It may seem that fluctuations in oil price volatility, defined in this manner, would be a good indicator of changes in oil price risks. It is important not to equate risk and uncertainty, however. Whereas the latter may be captured by the volatility of oil price forecasts, the former cannot. The standard risk that financial markets in oil-importing economies are concerned with is the risk of excessively high oil prices. That risk in general will be at best weakly correlated with the volatility of oil price forecasts because any reduction in risk, as the price of oil falls, all else equal, will be associated with increased oil price volatility. This is why in 1986, for example, oil price volatility increased, as OPEC collapsed and the price of oil dropped sharply, whereas by all accounts consumers were pleased with lower oil prices and the diminished risk of an OPEC induced supply disruption. Hence, standard volatility measures are of limited use as summary statistics for the predictive distribution of oil price forecasts. We defer to section 12.3 for a more detailed exposition of how appropriate risk measures may be computed from the predictive distribution of the price of oil.
12.2. Real Oil Price Volatility
Interest in the volatility of oil prices also has been prompted by research aimed at establishing a direct link from oil price volatility to business cycle fluctuations in the real economy. For example, Bernanke (1983) and Pindyck (1991) showed that the uncertainty of the price of oil (measured by the volatility of the price of oil) matters for investment decisions if firms contemplate an irreversible investment, the cash flow of which depends on the price of oil. An analogous argument holds for consumers considering the purchase of energy-intensive durables such as cars. Real options theory implies that, all else equal, an increase in expected volatility will cause marginal investment decisions to be postponed, causing a reduction in investment expenditures. Kellogg (2010) provides evidence that such mechanisms are at work in the Texas oil industry, for example.
Unlike in empirical finance, the relevant volatility measure in these models is the volatility of the real price of oil at horizons relevant to purchase and investment decisions, which is typically measured in years or even decades rather than days or months, making standard measures of short-term nominal price volatility inappropriate. Measuring the volatility of the real price of oil at such long forecast horizons is inherently difficult given how short the available time series are, and indeed researchers in practice have typically asserted rather than measured these shifts in real price volatility or they have treated short-horizon volatility as a proxy for longer-horizon volatility (see, e.g., Elder and Serletis 2010).35 This approach is unlikely to work. Standard monthly or quarterly GARCH model cannot be used to quantify changes in the longer-run expected volatility of the real price of oil because GARCH forecasts of the conditional variance quickly revert to their time invariant unconditional expectation, as the forecasting horizon increases. If volatility at the economically relevant horizon is constant by construction, it cannot explain variation in real activity over time, suggesting that survey data may be better suited for characterizing changes in forecast uncertainty over time. Some progress in this direction may be expected from ongoing work conducted by Anderson, Kellogg and Sallee (2010) based on the distribution of Michigan consumer expectations of 5-year-ahead gasoline prices. For further discussion of this point also see Kilian and Vigfusson (2010b).
12.3. Quantifying Oil Price Risks
Although oil price volatility shifts play an important role in discussions of the impact of oil price shocks, it is important to keep in mind that volatility measures are not in general useful measures of the price risks faced by either producers or consumers of crude oil (or of refined products). Consider an oil producer capable of producing crude oil from existing wells as long as the price of oil exceeds his marginal cost of $25 a barrel. One risk faced by that oil producer is that he will go out of business if the price of oil falls below that threshold. Excessively high oil prices, in contrast, are of no concern until they reach the point of making replacement technologies economically viable. That might be the case at a threshold of $120 a barrel, for example, at which price major oil producers risk inducing the large-scale use of alternative technologies with adverse consequences for the long-run price of crude oil.36 Thus, the oil producer will care about the risk of the price of oil not being contained in the range between $25 and $120, and the extent to which he is concerned with violations of that range depends on his risk aversion, which need not be symmetric in either direction.37 There is no reason why oil producers should necessarily be concerned with a measure of the variability of the real price of oil. In fact, it can be shown that risk measures are not only quantitatively different from volatility measures, but in practice may move in the opposite direction.
Likewise, a consumer of retail motor gasoline (and hence indirectly of crude oil) is likely to be concerned with the price of gasoline exceeding what he can afford to spend each month (see Edelstein and Kilian 2009). The threshold at which consumers might trade in their SUV for a more energy-efficient car is near $3 a gallon perhaps. The threshold at which commuters may decide to relocate closer to their place of work might be at a price near $5 a gallon. The possibility that the price of gasoline could fall below $2, in contrast, is of comparatively little consequence to consumers' economic choices, making the volatility of oil prices and related statistics such as the value at risk irrelevant to the typical consumer.
In both examples above, the appropriate specification of these
agents' decision problem is in terms of upside and downside price
risks. The literature on risk management postulates that risk
measures must satisfy two basic requirements. One requirement is
that the measure of risk must be related to the probability
distribution ![]() of the random variable of
interest; the other requirement is that it must be linked to the
preferences of the user, typically parameterized by a loss function
(see Machina and Rothschild 1987). Except in special cases these
requirements rule out commonly used measures of risk based on the
predictive distribution alone such as the sample moments, sample
quantiles or the value at risk. In deriving appropriate risk
measures that characterize the predictive distribution for the real
price of oil, it is useful to start with the loss function. A
reasonably general class of loss functions
of the random variable of
interest; the other requirement is that it must be linked to the
preferences of the user, typically parameterized by a loss function
(see Machina and Rothschild 1987). Except in special cases these
requirements rule out commonly used measures of risk based on the
predictive distribution alone such as the sample moments, sample
quantiles or the value at risk. In deriving appropriate risk
measures that characterize the predictive distribution for the real
price of oil, it is useful to start with the loss function. A
reasonably general class of loss functions ![]() that encompasses the two empirical examples above
is:
that encompasses the two empirical examples above
is:
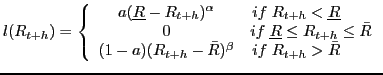
where ![]() denotes the real price of oil in
dollars
denotes the real price of oil in
dollars ![]() periods from date
periods from date ![]()
![]() is the weight attached to
downside risks, and
is the weight attached to
downside risks, and
![]() and
and
![]() measure the user's degree of
risk aversion. Risks are associated with the event of
measure the user's degree of
risk aversion. Risks are associated with the event of ![]() exceeding an upper threshold of
exceeding an upper threshold of ![]() or falling below the lower threshold of
or falling below the lower threshold of
![]() It can be shown that under
this loss function, the expected loss is a weighted average of
upside and downside risks of the form
It can be shown that under
this loss function, the expected loss is a weighted average of
upside and downside risks of the form
where
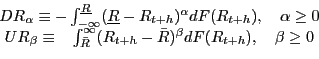
are the downside risk and upside risk, respectively. This
definition encompasses a variety of risk definitions familiar from
the finance literature. For example, for the special case of
![]() these expressions reduce to
the (target) probabilities
these expressions reduce to
the (target) probabilities
![]() and
and
![]() and for
the special case of
and for
the special case of
![]() they reduce to the tail
conditional expectations
they reduce to the tail
conditional expectations
![]() and
and
![]()
![]() Note that the
latter definition not only is concerned with the likelihood of a
tail event, but also with how far the real price of oil is expected
to be in the tail. The latter term is also known as the expected
shortfall (or expected excess). The expectations and probabilities
in question in practice can be estimated by their sample
equivalent.38
Note that the
latter definition not only is concerned with the likelihood of a
tail event, but also with how far the real price of oil is expected
to be in the tail. The latter term is also known as the expected
shortfall (or expected excess). The expectations and probabilities
in question in practice can be estimated by their sample
equivalent.38
This digression highlights that the volatility of the real price of oil in general is not the relevant statistic for the analysis of risks. In particular, if and only if the loss function is quadratic and symmetric about zero, the variance of the price of oil about zero provides an adequate summary statistic for the risk in oil price forecasts. Even that target variance, however, is distinct from conventionally used measures of oil price volatility, defined as the variance about the sample mean of the predictive distribution. The latter measure under no circumstances can be interpreted as a risk measure because it depends entirely on the predictive distribution of the price of oil and not at all on the user's preferences.
Risk measures can be computed for any predictive distribution.
The construction of the predictive distribution from regression
forecasting models typically relies on bootstrap methods applied to
the sequence of forecast errors obtained from fitting the
forecasting model to historical data. This requires the forecast
errors to be serially uncorrelated, as would typically be the case
in forecasting models at horizon h = 1. For example, when
fitting a random walk model of the form
![]() , the
forecast errors at horizon 1 may be resampled using standard
bootstrap methods for homoskedastic or conditionally
heteroskedastic data (see, e.g., Gonçalves and Kilian
2004).
, the
forecast errors at horizon 1 may be resampled using standard
bootstrap methods for homoskedastic or conditionally
heteroskedastic data (see, e.g., Gonçalves and Kilian
2004).
At longer horizons, one option is to fit the forecasting model on nonoverlapping observations and proceed as for h = 1. This approach is simple, but may involve a considerable reduction in estimation precision. For example, in constructing the predictive distribution of one-year-ahead no-change forecasts from monthly data, one would construct for the current month the sequence of year-on-year percent changes relative to the same month in the preceding year and approximate the predictive distribution by resampling this sequence of year-on-year forecast errors. The other option is to construct forecast errors from overlapping observations and to recover the underlying white noise errors by fitting an MA(h-1) process to the sequence of h-step- ahead forecast errors. This allows the construction of bootstrap approximations of the predictive density by first resampling the serially uncorrelated white noise residuals using suitable bootstrap methods such as the wild bootstrap and then constructing bootstrap replicates of the h-month-ahead forecast errors from the implied moving averages. The risk measures are constructed directly from the bootstrap estimate of the predictive distribution, as discussed above. Below we implement this approach in the context of a 12-month-ahead no-change forecast of the real WTI price of oil.
Figure 16 plots the risk that the price of oil (expressed in
2009.12 dollars) exceeds $80 one year later
![]() and the risk that it drops
below $45 one year later
and the risk that it drops
below $45 one year later
![]() These thresholds have
been chosen for illustrative purposes. The upper panel of Figure 16
plots the upside and downside risks for
These thresholds have
been chosen for illustrative purposes. The upper panel of Figure 16
plots the upside and downside risks for
![]() whereas the lower panel
plots the corresponding results for
whereas the lower panel
plots the corresponding results for
![]() Note that by convention
the downside risks have been defined as a negative number to
improve the readability of the plots. Although the upside risks and
downside risks respond to sustained changes in the conditional mean
forecast by construction, the relationship is not one-for-one.
Figure 16 shows that the ex ante probability of the real price of
oil exceeding $80 one year later was small except during 2005-08
and after mid-2009; high probabilities of the real price of oil
falling below $45 occurred only in 2001-04 and 2009. The lower
panel shows the corresponding tail conditional expectations.
Allowing for some risk aversion in the form of
Note that by convention
the downside risks have been defined as a negative number to
improve the readability of the plots. Although the upside risks and
downside risks respond to sustained changes in the conditional mean
forecast by construction, the relationship is not one-for-one.
Figure 16 shows that the ex ante probability of the real price of
oil exceeding $80 one year later was small except during 2005-08
and after mid-2009; high probabilities of the real price of oil
falling below $45 occurred only in 2001-04 and 2009. The lower
panel shows the corresponding tail conditional expectations.
Allowing for some risk aversion in the form of
![]() the upside risks in
2007-08 become disproportionately larger relative to earlier upside
risks and relative to the downside risks. Regardless of the choice
of
the upside risks in
2007-08 become disproportionately larger relative to earlier upside
risks and relative to the downside risks. Regardless of the choice
of ![]() and
and ![]() the
balance of risks since mid-2009 has been tilted in the upside
direction. Recent upside risks are comparable to those in 2006.
the
balance of risks since mid-2009 has been tilted in the upside
direction. Recent upside risks are comparable to those in 2006.
It is immediately evident that the three standard volatility measures in Figure 15 are not good proxies for either of the two risks shown in Figure 16. For example, in the second half of 2008 volatility skyrockets while the upside risk plummets. The upside risk peaks in mid-2008, when the real price of oil peaked, but volatility only peaks in December 2008 or January 2009, when the real price of oil had reached a trough, much to the relief of oil consumers. Moreover, the spikes in volatility in 2001/02 and 2003 are not mirrored by increases in upside risk, while the sustained increase in upside risk after 2004 is not mirrored by a sustained increase in volatility. Nor is volatility systematically related to downside oil price risks. Although both downside risks and volatility peak in 2001/02, the sustained increase in volatility in early and mid-2008 is not mirrored by an increase in downside risk. Furthermore, the decline in downside risks during 2004 and 2005 is not reflected in systematic changes in volatility.
It is worth emphasizing that none of these 12-month-ahead risk forecasts provided any warning of the collapse of the real price of oil in late 2008. To the extent that the collapse in the real price of oil was unpredictable based on past data, this is not surprising. The problem is not with the risk measures but rather with the underlying predictive distribution that these risk measures have been applied to. Although the predictive distribution based on the no-change forecast is among the best available approaches to forecasting the real price of oil, this is a useful reminder that even the best available approach need not be very accurate in practice.
13. Avenues for Future Research
There are a number of directions for future research on forecasting oil prices. One relates to the use of additional industry-level predictors not commonly considered by economists. Although crude oil is one of the more homogeneous commodities traded in global markets, not all refineries may process all grades of crude oil. Moreover, different grades of crude oil yield different mixes of refined products. Hence, shifts in the demand for one type of refined product, say, diesel fuel, have implications for the product mix of refined products (diesel, gasoline, kerosene, heating oil, etc.) and hence for the demand for different grades of crude oil, depending on the capacity utilization rates of different refineries. Situations can arise in which excess demand for one grade of crude oil may result in rising prices, while excess supply of another grade of crude oil is associated with falling prices. Models that incorporate information about such spreads or about the underlying determinants of demand have the potential of improving forecasts of the price of a given grade of crude oil.
A second issue of interest is the role played by heterogenous oil price and gasoline price expectations in modeling the demand for energy-intensive durables (see Anderson, Kellogg and Sallee 2010). There is strong evidence that not all households share the same expectations, casting doubt on standard rational expectations models with homogeneous agents. This also calls into question the use of a single price forecast in modeling purchasing decisions in the aggregate. This problem is compounded to the extent that different market participants (households, refiners, oil producers) in the same model may have very different risk assessments based on the same predictive oil price distribution. Both of these effects may undermine the predictive power of the price of oil for macroeconomic aggregates as well as the explanatory power of theoretical models based on oil price forecasts.
Third, we have deliberately refrained from exploring the use of factor models for forecasting the price of oil. In related work, Zagaglia (2010) reports some success in using a factor model in forecasting the nominal price of oil at short horizons, although his evaluation period is limited to early 2003 to early 2008, given the data limitations, and it is unclear how sensitive the results would be to extending the evaluation period. An obvious concern is that there are no price reversals over the evaluation period, so any predictor experiencing sustained growth is likely to have some forecasting power. Moreover, we have shown in section 5 that much simpler forecasting models appear capable of generating equally substantial reductions in the MSPE of the nominal price of oil at short horizons and do so for extended periods. The more important problem from an economic point of view, in any case, is forecasting the real price of oil. It seems unlikely that approximate factor models could be used to forecast the real price of oil. The variables that matter most for the determination of the real price of oil are global. Short of developing a comprehensive worldwide data set of real aggregates at monthly frequency, it is not clear whether there are enough predictors available for reliable real-time estimation of the factors. For example, drawing excessively on U.S. real aggregates as in Zagaglia (2010) is unlikely to be useful for forecasting the global price of oil for the reasons discussed in section 4. Using a cross-section of data on energy prices, quantities, and other oil-market related indicators may be more promising, but almost half of the series used by Zagaglia are specific to the United States and unlikely to be representative of global markets.
14. Conclusions
Although there are a fair number of papers dealing with the problem of predicting the price of oil, it is difficult to reconcile the seemingly conflicting results in this literature. The problem is not only the precise definition of the oil price variable, but whether the price of oil is expressed in nominal or in real terms, what estimation and evaluation periods are chosen, how forecast accuracy is evaluated, whether the conditional mean, conditional variance or conditional density is being forecast, whether the analysis is conducted in-sample or out-of-sample, whether the methods are parametric or nonparametric, and whether tests of statistical significance are provided or not. The most common problem in the literature is that results are sensitive to the choice of sample period and vanish when the sample period is extended.
In this chapter, our objective has been to provide a benchmark based on data that include the recent collapse of the price of oil in 2008 and its subsequent recovery. We started by discussing problems with combining data from the pre-1973 and post-1973 period, highlighting the need to discard the pre-1973 data because these data cannot be represented by standard time series models. We documented a structural break in the time series process of both the nominal and the real price of oil in late 1973. We also noted the presence of a structural break in the dynamic correlations between changes in the real price of oil and U.S. real GDP growth. That structural break invalidates predictive regressions based on data extending back further than 1973.
A natural starting point for our analysis was the question of whether the price of oil is inherently unpredictable, as is sometimes claimed. We provided strong evidence that after 1973 the nominal price of oil is predictable in population, consistent with economic theory. The most successful predictors are recent percent changes in U.S. consumer prices and monetary aggregates as well as global non-oil industrial commodity prices. An even better predictor is the recent percent change in the bilateral dollar exchange rate of major commodity exporters.
We also found strong evidence that after 1973 the real price of oil is predictable in population based on fluctuations in global real output, as suggested by standard economic theory. We illustrated how problems of omitted variables and of mismeasurement can obscure this predictive relationship. We emphasized the importance of accounting for structural changes in the composition of real output, of using measures with broad geographic coverage, and of using methods of detrending that can capture long swings in the demand for industrial commodities.
These results demonstrate that neither the nominal nor the real price of oil follows a random walk. Predictability in population need not translate into out-of-sample forecast accuracy, however. One concern is that in small samples simple parsimonious forecasting models such as the no-change forecast often have lower MSPE than forecasts from larger-dimensional models suggested by economic theory. This may occur even if the large-dimensional model is correctly specified, provided the increase in the forecast variance from estimating the unknown parameters of the correctly specified model exceeds the reduction in the (squared) forecast bias from eliminating the model misspecification.
We provided evidence that at horizons up to six months suitably designed unrestricted vector autoregressive models estimated recursively on ex-post revised data tend to be more accurate out of sample than the no-change forecast of the real price of oil. There also is strong evidence that recursively estimated AR and ARMA models have lower MSPE than the no-change forecast, especially at horizons of 1 and 3 months. At longer horizons, the no-change forecast of the real price of oil typically is the predictor with the lowest MSPE. These results are robust to the use of real time data.
Forecasting the nominal price of oil is a comparatively easier task. There is strong evidence of statistically significant MSPE reductions in forecasting the nominal price of oil at horizons of 1 and 3 months based on recent percent changes in the price of non-oil industrial raw materials, for example. The gains in accuracy at the 3-month horizon are 22%. There also is evidence that simply adjusting the no-change forecast for the real price of oil for expected inflation yields much more accurate forecasts of the nominal price of oil than the no-change forecast at horizons of several years. There is no evidence against the no-change forecast for the nominal price of oil at intermediate horizons, however.
More commonly used methods of forecasting the nominal price of oil based on the price of oil futures or the spread of the oil futures price relative to the spot price cannot be recommended. There is no reliable evidence that oil futures prices significantly lower the MSPE relative to the no-change forecast at short horizons, and long-term futures prices often cited by policymakers are distinctly less accurate than the no-change forecast. One possible explanation for the unexpectedly low out-of-sample accuracy of oil futures-based forecasts may be the presence of transaction costs impeding arbitrage. An alternative forecasting strategy in which one uses the futures price only if the futures spread exceeds 5% in absolute terms and uses the spot price otherwise, yields MSPE reductions between 0% and 6% at short horizons (some of which are statistically significant), but performs much worse than the no-change forecast at longer horizons. Likewise professional and government forecasts of the nominal price of oil do not significantly improve on the no-change forecast, except in some cases in the very short run, and can be much less accurate.
One of the main reasons for the importance that many macroeconomists attach to the price of oil is its perceived predictive power for U.S. real GDP. Assessing that predictive power requires a joint forecasting model for the price of oil and for domestic real activity. We showed that there are only small gains in using the price of oil in forecasting cumulative real GDP growth from VAR models. This finding is robust to whether the price of oil is specified in nominal or in real terms and whether it is treated as exogenous or endogenous. More importantly, linear autoregressive models fail to predict major economic downturns. One possible explanation of this forecast failure is that the predictive relationship is nonlinear. We therefore evaluated and compared a wide range of nonlinear joint forecasting models for the price of oil and real GDP growth. Except for the three-year net oil price increase specification, we found no evidence at all of substantially improved forecast accuracy for real GDP growth. Even for the three-year net increase model, the evidence was mixed at best. For example, we found no evidence that the nominal PPI three-year net increase model is more accurate than linear models for real GDP growth at the one-quarter horizon. A multivariate generalization of the model proposed by Hamilton (2003, 2010) tended to provide MSPE gains of up to 12% relative to the AR(4) benchmark model at longer horizons. Even more accurate results were obtained with some alternative oil price series. All these forecasting successes, however, were driven entirely by the 2008/09 recession. Excluding that episode from the evaluation period, even the most accurate nonlinear model was less accurate than the benchmark AR(4) model for real GDP growth.
We showed that there is reason to be skeptical of the seeming forecasting success of many nonlinear models during the recent financial crisis. In particular, if the one-year forecasts are to be believed, the financial crisis played almost no role in the economic decline of 2008/09, which does not seem economically plausible. An alternative explanation is that the evaluation sample is too short for reliable inference and that these results reflect overfitting. We observed that net oil price increase models have a tendency to predict major economic declines anytime the price of oil has increased substantially. Although such predictions repeatedly proved incorrect, most notably in 2005/06, the ability of some three-year net increase models to forecast the extreme decline of 2008/09 under quadratic loss more than compensates for earlier forecasting errors and accounts for the higher average out-of-sample forecast accuracy of these models for U.S. real GDP growth.
We also discussed the use of structural forecasting models for the real price of oil. An important limitation of reduced-form forecasting models of the real price of oil from a policy point of view is that they provide no insight into what is driving the forecast and do not allow the policymaker to explore alternative hypothetical forecasting scenarios. We illustrated how recently developed structural vector autoregressive models of the global oil market not only generate quite accurate out-of-sample forecasts, but may be used to generate projections of how the oil price forecast would deviate from the unconditional baseline forecast, conditional on alternative economic scenarios such as a surge in speculative demand similar to previous historical episodes, a resurgence of the global business cycle, or increased U.S. oil production. The proposed method allows users to assess the risks associated with reduced-form oil price forecasts.
Finally, we showed that oil price volatility measures commonly used to characterize predictive densities for the price of oil are not adequate measures of the risks faced by market participants. We demonstrated how appropriate risk measures can be constructed. Those risk measures, however, are only as good as the underlying forecasting models and would not have provided any advance warning of the collapse of the real price of oil in late 2008, for example.
References
Allcott, H., and N. Wozny (2010), "Gasoline Prices, Fuel Economy, and the Energy Paradox", mimeo, MIT.
Almoguera, P.A., Douglas, C., and A.M. Herrera (2010), "Testing for the Cartel in OPEC: Noncooperative Collusion or Just Noncooperative?", mimeo, Department of Economics, Michigan State University.
Alquist, R., and L. Kilian (2010), "What Do We Learn from the Price of Crude Oil Futures?" Journal of Applied Econometrics, 25, 539-573.
Anatolyev, S. (2007), "Inference about Predictive Ability When There Are Many Predictors," mimeo, New Economic School, Moscow.
Anderson, S., Kellogg, R., and J. Sallee (2010), "What Do Consumers Know (or Think They Know) About the Price of Gasoline?" mimeo, Department of Economics, University of Michigan.
Artzner, P., F. Delbaen, J.-M. Eber, and D. Heath (1999), "Coherent Measures of Risk," Mathematical Finance, 9, 203-228.
Bachmeier, L., Li, Q., and D. Liu (2008), "Should Oil Prices Receive So Much Attention? An Evaluation of the Predictive Power of Oil Prices for the US Economy," Economic Inquiry, 46, 528-539.
Balke, N.S., Brown, S.P.A., and M.K. Yücel (2002), "Oil Price Shocks and the U.S. Economy: Where Does the Asymmetry Originate?" Energy Journal, 23, 27-52.
Barsky, R.B., and L. Kilian (2002), "Do We Really Know that Oil Caused the Great Stagflation? A Monetary Alternative," in: NBER Macroeconomics Annual 2001, B.S. Bernanke and K. Rogoff (eds.), MIT Press: Cambridge, MA, 137-183.
Basak, S., and A. Shapiro (2001), "Value-at-Risk Based Management: Optimal Policies and Asset Prices," Review of Financial Studies, 14, 371-405.
Baumeister, C., and L. Kilian (2011), "Real-Time Forecasts of the Real Price of Oil," mimeo, Department of Economics, University of Michigan.
Baumeister, C., and G. Peersman (2010), "Sources of the Volatility Puzzle in the Crude Oil Market," mimeo, Department of Economics, Ghent University.
Bernanke, B.S. (1983), "Irreversibility, Uncertainty, and Cyclical Investment," Quarterly Journal of Economics, 98, 85-106.
Bernanke, B.S (2004), "Oil and the Economy," Speech presented at Darton College, Albany, GA, http://www.federalreserve.gov/boarddocs/speeches/2004/20041021/default.htm.
Beyer, A., Doornik, J.A. and Hendry, D.F. (2001), "Constructing
Historical Euro-Zone Data,"
Bollerslev, T., Chou, R.Y., and K.F. Kroner (1992), "ARCH Modeling in Finance," Journal of Econometrics, 52, 5-59.
Busse, M., Knittel, C., and F. Zettelmeyer (2010), "Pain at the Pump: How Gasoline Prices Affect Automobile Purchasing," mimeo, Northwestern University.
Calhoun, G. (2010), "Limit Theory for Comparing Overfit Models Out-of-Sample," mimeo, Department of Economics, Iowa State University.
Carlton, A.B. (2010), "Oil Prices and Real-Time Output Growth," mimeo, Department of Economics, University of Houston.
Chen, Y.-C., Rogoff, K., and B. Rossi (2010), "Can Exchange Rates Forecast Commodity Prices?" forthcoming: Quarterly Journal of Economics.
Clark, T.E., and M. McCracken (2001), "Tests of Equal Predictive Accuracy and Encompassing for Nested Models," Journal of Econometrics, 105, 85-101.
Clark, T.E., and M. McCracken (2005), "Evaluating Direct Multistep Forecasts," Econometric Reviews, 24, 369-404.
Clark, T.E., and M. McCracken (2010), "Nested Forecast Model Comparisons: A New Approach to Testing Equal Accuracy," mimeo, Federal Reserve Bank of St. Louis.
Clark, T.E, and K.D. West (2006), "Using Out-of-Sample Mean Squared Prediction Errors to Test the Martingale Difference Hypothesis," Journal of Econometrics, 135, 155-186.
Clark, T.E., and K.D. West (2007), "Approximately Normal Tests for Equal Predictive Accuracy in Nested Models," Journal of Econometrics, 138, 291-311.
Cooley, T.F., and S. LeRoy (1985), "Atheoretical Macroeconometrics: A Critique," Journal of Monetary Economics, 16, 283-308.
Corradi, V., and N.R. Swanson (2002), "A Consistent Test for Nonlinear Out of Sample Predictive Accuracy," Journal of Econometrics, 110, 353-381.
Corradi, V., and N.R. Swanson (2007), "Nonparametric Bootstrap Procedures for Predictive Inference Based on Recursive Estimation Schemes," International Economic Review, 48, 67-109.
Dargay, J.M., and D. Gately (2010), "World Oil Demand's Shift toward Faster Growing and Less Price-Responsive Products and Regions," Energy Policy, 38, 6261-6277.
Davies, P. (2007), "What's the Value of an Energy Economist?" Presentation at the 30th Annual Conference of the International Association for Energy Economics, Wellington, New Zealand, February 18.
Davis, L.W., and L. Kilian (2011), "The Allocative Cost of Price Ceilings in the U.S. Residential Market for Natural Gas", forthcoming: Journal of Political Economy.
Diebold, F.X., and R.S. Mariano (1995), "Comparing Predictive Accuracy," Journal of Business and Economic Statistics, 13, 253-263.
Dolado, J.J., and H. Lütkepohl (1996), "Making Wald Tests Work for Cointegrated VAR Systems," Econometric Reviews, 15, 369-386.
Dvir, E., and K. Rogoff (2010), "Three Epochs of Oil," mimeo, Harvard University.
Edelstein, P., and L. Kilian (2009), "How Sensitive are Consumer Expenditures to Retail Energy Prices?" Journal of Monetary Economics, 56, 766-779.
Elder, J., and A. Serletis (2010), "Oil Price Uncertainty," Journal of Money, Credit and Banking, 42, 1138-1159.
Elliott, G., and A. Timmermann (2008), "Economic Forecasting," Journal of Economic Literature, 46, 3-56.
Engle, R.F., and C.T. Brownlees (2010), "Volatility, Correlation and Tails for Systemic Risk Measurement," mimeo, Stern School of Business, New York University.
Farrell, A.E., and A.R. Brandt (2006), "Risks of the Oil Transition," Environmental Research Letters, 1, 1-6.
Fishburn, P.C. (1977), "Mean-Risk Analysis with Risk Associated with Below-Target Returns," American Economic Review, 67, 116-26.
Giannone, D., Lenza, M. and G. Primiceri (2010), "Prior Selection for Vector Autoregressions," mimeo, Department of Economics, Free University of Brussels.
Gillman, M., and A. Nakov (2009), "Monetary Effects on Nominal Oil Prices," North American Journal of Economics and Finance, 20, 239-254.
Goldberg, P. (1998), "The Effects of the Corporate Average Fuel Economy Standards in the U.S.," Journal of Industrial Economics, 46, 1-33.
Gonçalves, S., and L. Kilian (2004), "Bootstrapping Autoregressions in the Presence of Conditional Heteroskedasticity of Unknown Form," Journal of Econometrics, 123, 89-120.
Gramlich, E.M. (2004), "Oil Shocks and Monetary Policy," Annual Economic Luncheon, Federal Reserve Bank of Kansas City, Kansas City, Missouri.
Green, E.J., and R.H. Porter (1984), "Noncooperative Collusion under Imperfect Price Information," Econometrica, 52, 87-100.
Greenspan, A. (2004a), "Energy" Remarks by Chairman Alan Greenspan Before the Center for Strategic & International Studies, Washington, D.C. http://www.federalreserve.gov/boarddocs/speeches/2004/20040427/default.htm.
Greenspan, A. (2004b), "Oil," Speech presented at the National Italian American Foundation, Washington, DC. htttp://www.federalreserve.gov/boarddocs/speeches/2004/200410152/default.htm.
Hamilton, J.D. (1983), "Oil and the Macroeconomy Since World War II," Journal of Political Economy, 91, 228-248.
Hamilton, J.D. (1985), "Historical Causes of Postwar Oil Shocks and Recessions," Energy Journal, 6, 97-116.
Hamilton, J.D. (1994), Time Series Analysis, Princeton, NJ: Princeton University Press.
Hamilton, J. D. (1996). "This is What Happened to the Oil Price-Macroeconomy Relationship," Journal of Monetary Economics, 38, 215-220.
Hamilton, J. D. (2003) "What is an Oil Shock?" Journal of Econometrics, 113, 363-398.
Hamilton, J.D. (2009), "Causes and Consequences of the Oil Shock of 2007-08," Brookings Papers on Economic Activity, 1, Spring, 215-261.
Hamilton, J.D. (2010), "Nonlinearities and the Macroeconomic Effects of Oil Prices," forthcoming: Macroeconomic Dynamics.
Hamilton, J.D., and A.M. Herrera (2004), "Oil Shocks and Aggregate Economic Behavior: The Role of Monetary Policy," Journal of Money, Credit and Banking, 36, 265-286.
Hendry, D. (2006), "Robustifying Forecasts from Equilibrium-Correction Systems," Journal of Econometrics, 135, 399-426
Herrera, A.M., Lagalo, L.G., and T. Wada (2010), "Oil Price Shocks and Industrial Production: Is the Relationship Linear?" forthcoming: Macroeconomic Dynamics.
Holthausen, D.M. (1981), "A Risk-Return Model with Risk and Return Measured in Deviations from Target Return," American Economic Review, 71, 182-88.
Hotelling, H. (1931), "The Economics of Exhaustible Resources," Journal of Political Economy, 39, 137-175.
Inoue, A., and L. Kilian (2004a), "In-Sample or Out-of-Sample Tests of Predictability: Which One Should We Use?" Econometric Reviews, 23, 371-402.
Inoue, A., and L. Kilian (2004b), "Bagging Time Series Models," CEPR Discussion Paper No. 4333.
Inoue, A., and L. Kilian (2006), "On the Selection of Forecasting Models," Journal of Econometrics, 130, 273-306.
Isserlis, L. (1938), "Tramp Shipping Cargoes and Freights," Journal of the Royal Statistical Society, 101(1), 53-134.
International Monetary Fund 2005. World Economic Outlook, Washington, DC.
International Monetary Fund 2007. World Economic Outlook, Washington, DC.
Kahn, J.A. (1986), "Gasoline Prices and the Used Automobile Market: A Rational Expectations Asset Price Approach," Quarterly Journal of Economics, 101, 323-340.
Kellogg, R. (2010), "The Effect of Uncertainty on Investment: Evidence from Texas Oil Drilling," mimeo, Department of Economics, University of Michigan.
Kilian, L. (1999), "Exchange Rates and Monetary Fundamentals: What Do We Learn from Long-Horizon Regressions?" Journal of Applied Econometrics, 14, 491-510.
Kilian, L. (2008a), "The Economic Effects of Energy Price Shocks," Journal of Economic Literature, 46(4), 871-909.
Kilian, L. (2008b), "Exogenous Oil Supply Shocks: How Big Are They and How Much Do They Matter for the U.S. Economy?" Review of Economics and Statistics, 90, 216-240.
Kilian, L. (2009a), "Not all Oil Price Shocks Are Alike: Disentangling Demand and Supply Shocks in the Crude Oil Market," American Economic Review, 99, 1053-1069.
Kilian, L. (2009b), ""Comment on `Causes and Consequences of the Oil Shock of 2007-08' by James D. Hamilton," Brookings Papers on Economic Activity, 1, Spring 2009, 267-278.
Kilian, L. (2010), "Explaining Fluctuations in U.S. Gasoline Prices: A Joint Model of the Global Crude Oil Market and the U.S. Retail Gasoline Market," Energy Journal, 31, 87-104.
Kilian, L., and B. Hicks (2010), "Did Unexpectedly Strong Economic Growth Cause the Oil Price Shock of 2003-2008?" mimeo, Department of Economics, University of Michigan.
Kilian, L., and S. Manganelli (2007), "Quantifying the Risk of Deflation," Journal of Money, Credit and Banking, 39, 561-590.
Kilian, L., and S. Manganelli (2008), "The Central Banker as a Risk Manager: Estimating theFederal Reserve's Preferences under Greenspan," Journal of Money, Credit and Banking, 40, 1103-1129.
Kilian, L., and D. Murphy (2010), "The Role of Inventories and Speculative Trading in the Global Market for Crude Oil," mimeo, University of Michigan.
Kilian, L., Rebucci, A., and N. Spatafora (2009), "Oil Shocks and External Balances," Journal of International Economics, 77, 181-194.
Kilian, L., and C. Vega (2010), "Do Energy Prices Respond to U.S. Macroeconomic News? A Test of the Hypothesis of Predetermined Energy Prices," Review of Economics and Statistics, 93, 660-671.
Kilian, L., and R. Vigfusson (2010a), "Are the Responses of the U.S. Economy Asymmetric in Energy Price Increases and Decreases?" mimeo, Department of Economics, University of Michigan.
Kilian, L., and R. Vigfusson (2010b), "Nonlinearities in the Oil Price-Output Relationship," forthcoming: Macroeconomic Dynamics.
Kilian, L., and R. Vigfusson (2010c), "Do Net Oil Price Increases Help Forecast U.S. Real GDP?" mimeo, Department of Economics, University of Michigan.
Knetsch, T.A. (2007), "Forecasting the Price of Oil via Convenience Yield Predictions," Journal of Forecasting, 26, 527-549.
Koop, G., Pesaran M.H., and S.M. Potter (1996), "Impulse Response Analysis in Nonlinear Multivariate Models," Journal of Econometrics, 74, 119-147.
Leamer, E.E. (1978), Specification Searches: Ad hoc Inference with Nonexperimental Data, New York: Wiley-Interscience.
Lütkepohl, H. (1982), "Non-Causality due to Omitted Variables," Journal of Econometrics, 19, 367-378.
Machina, M.J., and M. Rothschild (1987), "Risk," in Eatwell, J., Millgate, M., and P. Newman (eds.), The New Palgrave Dictionary of Economics, London: MacMillan, 203-205.
Marcellino, M., Stock, J.H., and M.W. Watson (2006), "A Comparison of Direct and Iterated Multistep AR Methods for Forecasting Macroeconomic Time Series," Journal of Econometrics, 135, 499-526.
Mork, K.A. (1989), "Oil and the Macroeconomy. When Prices Go Up and Down: An Extension of Hamilton's Results," Journal of Political Economy, 97, 740-744.
Peck, A.E. (1985), "Economic Role of Traditional Commodity Futures Markets," in A.E. Peck (ed.): Futures Markets: Their Economic Role, Washington, DC: American Enterprise Institute for Public Policy Research, 1-81.
Pesaran, M.H., and A. Timmermann (2009), "Testing Dependence Among Serially Correlated Multicategory Variables," Journal of the American Statistical Association, 104, 325- 337.
Pindyck, R.S. (1991), "Irreversibility, Uncertainty and Investment," Journal of Economic Literature, 29, 1110-1148.
Ramey, V.A., and D.J. Vine (2010), "Oil, Automobiles, and the U.S. Economy: How Much Have Things Really Changed," forthcoming: NBER Macroeconomics Annual.
Ravazzolo, F., and P. Rothman (2010), "Oil and U.S. GDP: A Real Time Out-of-Sample Examination," mimeo, Norges Bank.
Ravn, M.O., and H. Uhlig (2002), "On Adjusting the Hodrick-Prescott Filter for the Frequency of Observations," Review of Economics and Statistics, 84, 371-380.
Reichlin, L., Giannone, D., and D. Small (2008), "Nowcasting GDP and Inflation: The Real Time Informational Content of Macroeconomic Data Releases," Journal of Monetary Economics, 55, 665-676.
Sims, C.A., Stock, J.H., and M.W. Watson (1990), "Inference in Linear Time Series Models with Some Unit Roots," Econometrica, 58, 113-144.
Skeet, I. (1988), OPEC: Twenty-Five Years of Prices and Politics. Cambridge: Cambridge University Press.
Smith, J.L. (2005), "Inscrutable OPEC? Behavioral Tests of the Cartel Hypothesis," Energy Journal, 26, 51-82.
Stock, J.H., and M.W. Watson (1999), "Forecasting Inflation," Journal of Monetary Economics, 44, 293-335.
Svensson, L.E.O. (2005), "Oil Prices and ECB Monetary Policy," mimeo, Department of Economics, Princeton University. See: http://www.princeton.edu/svensson/
Tinbergen, J. (1959). "Tonnage and Freight" in: Jan Tinbergen Selected Papers, Amsterdam: North Holland, 93-111.
Waggoner, D.F., and T. Zha (1999), "Conditional Forecasts in Dynamic Multivariate Models," Review of Economics and Statistics, 81, 639-651.
Working, H. (1942), "Quotations on Commodity Futures as Price Forecasts," Econometrica, 16, 39-52.
Wu, T., and A. McCallum (2005), "Do Oil Futures Prices Help Predict Future Oil Prices?" Federal Reserve Bank of San Francisco Economic Letter, 2005-38.
Zagaglia, P. (2010), "Macroeconomic Factors and Oil Futures Prices: A Data-Rich Model," Energy Economics, 32, 409-417.
Figure 1: The Nominal Price of Oil
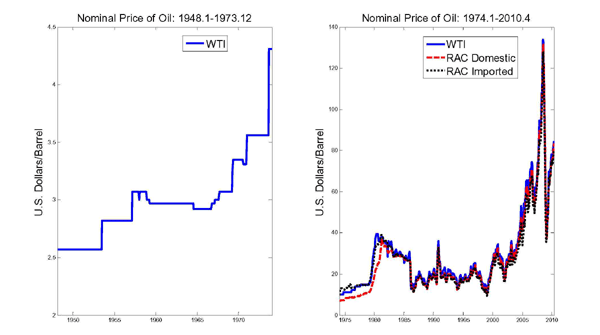
NOTES: WTI stands for the West Texas Intermediate price of crude oil and RAC for the U.S. refiners' acquisition cost.
Figure 2: The Real Price of Oil
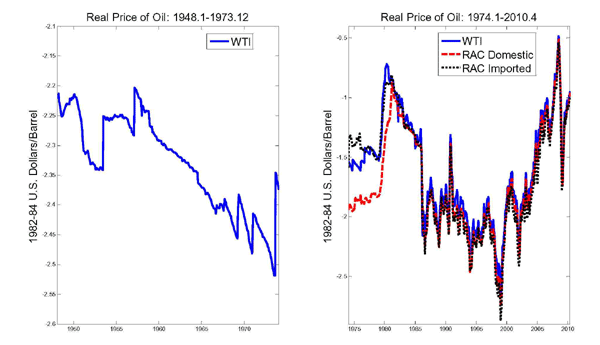
NOTES: Log scale. See Figure 1.
Figure 3: Percent Changes in the Real Price of Oil
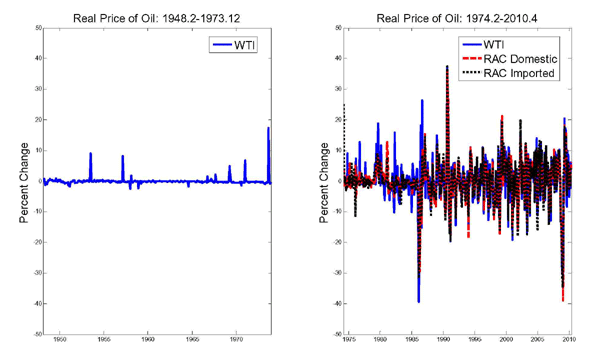
NOTES: See Figure 1.
Figure 4: The Impossibility of Modeling Pre-1973 WTI Data as an ARMA Process
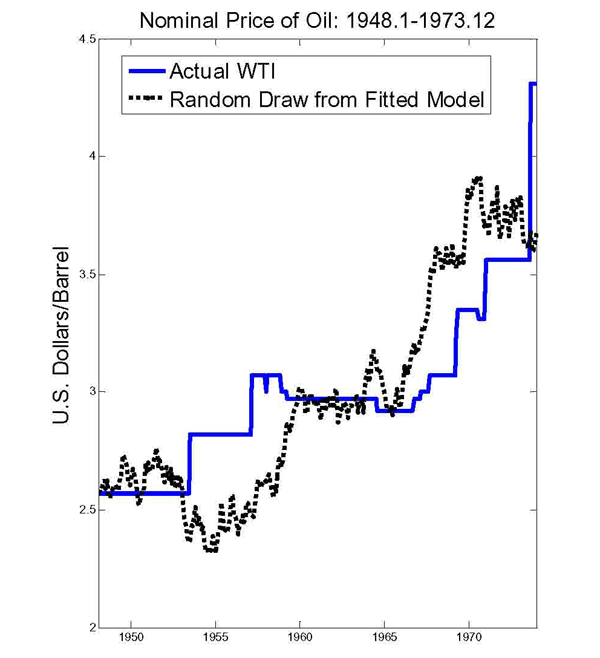
NOTES: The fitted model is a random walk with drift in logs. The fitted values have been exponentiated. The figure illustrates that unlike the original data - the data generated at random from the fitted model will never remain unchanged for extended periods of time. Hence, the class of ARMA processes is not suitable for modeling this data set.
Figure 5: Measures of Liquidity in the Oil Futures Market (by Maturity)
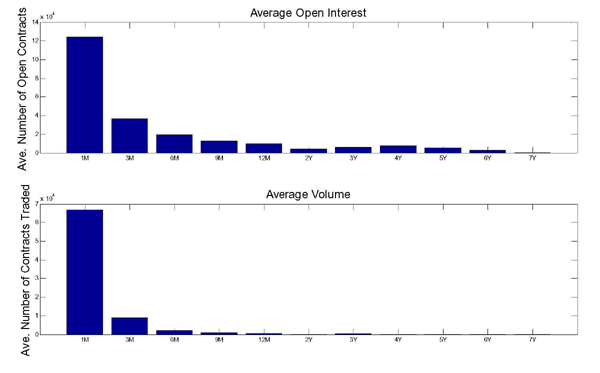
NOTES: Computations by the authors based on CRB data.
Figure 6: Household Expectations of U.S. Retail Gasoline Prices
(Cents/Gallon)
1992.11-2011.1
NOTES: Computations by the authors based on Michigan Consumer Survey Expectations, SPF 10-year CPI inflation forecasts, and EIA data for the city average of retail motor gasoline prices. This analysis draws on Anderson, Kellogg and Sallee (2010).
Figure 7: Consensus Economics Expectations of Nominal Price
of Oil (Dollars/Barrel)
1989.10-2009.12
NOTES: Computations by the authors based on data from Consensus Economics Inc.
Figure 8: EIA Forecasts of the U.S. Refiners' Acquisition
Cost for Imported Crude Oil
1983.Q1-2009.Q4
NOTES: The quarterly price forecasts were collected manually from the EIA's Short-Term Economic Outlook and compared with the ex-post realizations of the average quarterly nominal refiners' acquisition cost for imported crude oil. The plot shows the price realizations together with the EIA forecasts made for the same point in time one and four quarters earlier.
Figure 9: Forecasting Scenarios for the Real Price of Oil based on the Structural VAR Model of Kilian and Murphy (2010) Conditional Projections Expressed Relative to Baseline Forecast
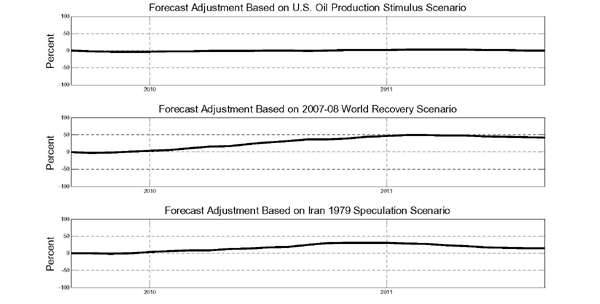
NOTES: All results are based on the structural oil market model of Kilian and Murphy (2010). The U.S. oil production stimulus involves a 20% increase in U.S. oil production in 2009.9, which translates to a 1.5% increase in world oil production. For this purpose, a one-time structural oil supply shock is calibrated such that the impact response of global oil production is 1.5%. The 2007-08 world recovery scenario involves feeding in as future shocks the sequence of flow demand shocks that occurred in 2007.1-2008.6. The Iran 1979 speculation scenario involves feeding in as future shocks the speculative demand shocks that occurred between 1979.1 and 1980.2 and were a major contributor to the 1979/80 oil price shock episode.
Figure 10: Real Price of Oil in
Different Currencies
1999.1-2009.12
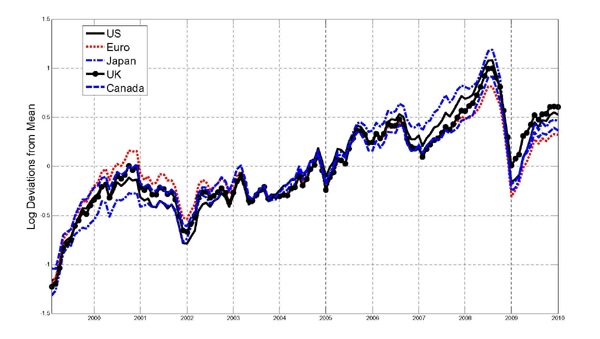
NOTES: Computations by the authors based on the U.S. refiners' acquisition cost for imported crude oil.
Figure 11: Autoregressive Forecasts of Cumulative Real GDP Growth based on the Real Price of Oil U.S. Refiners' Acquisition Cost for Imports
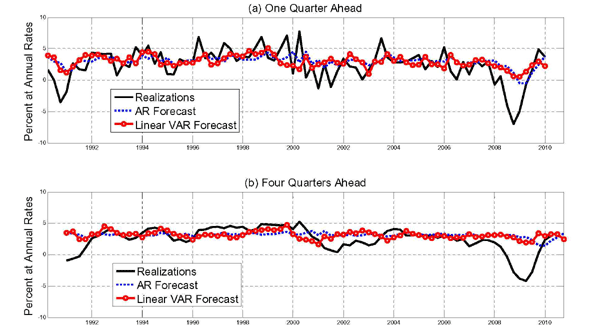
NOTES: The benchmark model is an AR(4) for real GDP growth. The alternative is an unrestricted linear VAR(4) model for real GDP growth and the percent change in the real price of oil. The price of oil is defined as the U.S. refiners' acquisition cost for imports.
Figure 12: Nonlinear Forecasts of Cumulative Real GDP Growth from Models (23) and (23') U.S. Refiners' Acquisition Cost for Imports
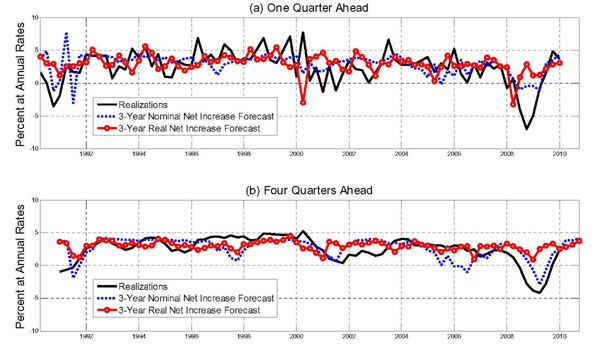
NOTES: One forecasting model is a suitably restricted VAR(4) model for real GDP growth and the percent change in the real price of oil augmented by four lags of the 3-year real net oil price increase. The other model is a similarly restricted VAR(4) model for real GDP growth and the percent change in the nominal price of oil augmented by four lags of the 3-year nominal net oil price increase.
Figure 13: Nonlinear Forecasts of Cumulative Real GDP Growth from Model (23')
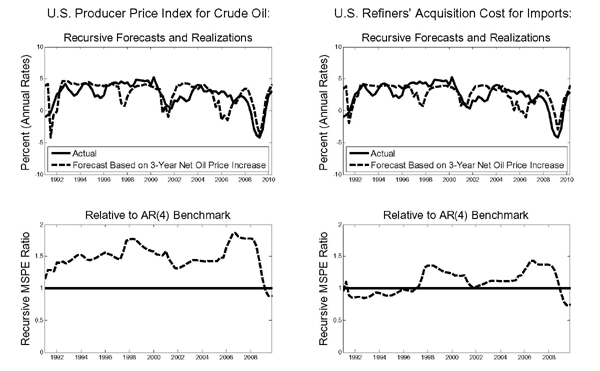
NOTES: The nonlinear forecasting model is a suitably restricted VAR(4) model for real GDP growth and the percent change in the nominal price of crude oil augmented by four lags of the corresponding 3-year nominal net oil price increase.
Figure 14: 12-Month Ahead Predictive Density of the Real WTI Price of Oil as of 2009.12 Based on No-Change Forecast
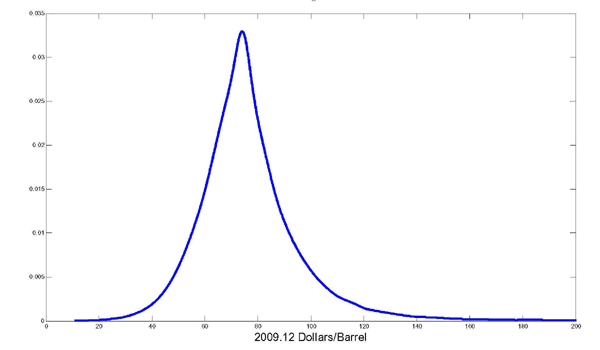
Figure 15: Alternative Measures of Nominal Oil Price Volatility
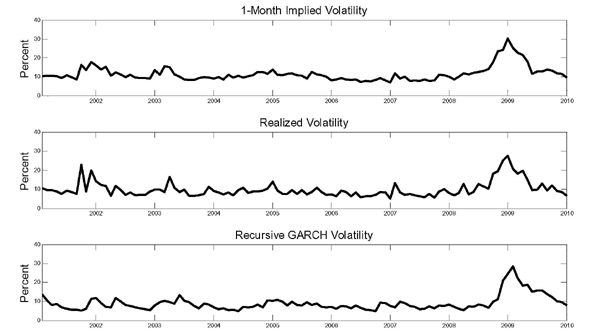
NOTES: The GARCH volatility estimate is for the percent change in the nominal WTI price. The realized volatility was obtained from daily WTI prices. The implied volatility measure refers to the arithmetic average of the daily implied volatilities from at-the-money put and call options associated with 1-month oil futures contracts and was constructed by the authors from CRB data. All volatility estimates are monthly and expressed as standard deviations, following the convention in the literature.
Figure 16: 12-Month Ahead Upside and Downside Risks in the Real WTI Price Based on No-Change Forecast
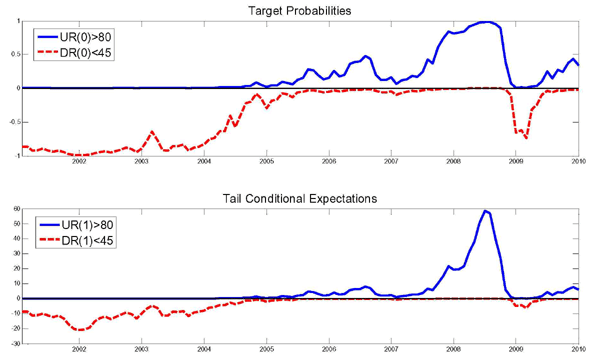
NOTES: Risks are defined in terms of the event that the price of oil (in 2009.12 dollars) exceeds 80 dollars or falls below 45 dollars. For further discussion of these risk measures see Kilian and Manganelli (2007).
Table 1a: Predictability from Selected Nominal U.S. Aggregates to the Nominal Price of Oil (p-values of the Wald test statistic for Granger Non-Causality)
| Monthly Predictors: | Evaluation Period: 1973.2-2009.12 WTI | Evaluation Period: 1975.2-2009.12 WTI | Evaluation Period: 1975.2-2009.12 RAC Oil Imports | Evaluation Period: 1975.2-2009.12 RAC Domestic Oil | Evaluation Period: 1975.2-2009.12 RAC Composite |
|---|---|---|---|---|---|
| CPI | 0.004 | 0.108 | 0.021 | 0.320 | 0.161 |
| M1 | 0.181 | 0.039 | 0.010 | 0.000 | 0.000 |
| M2 | 0.629 | 0.234 | 0.318 | 0.077 | 0.209 |
| CRB Industrial Raw Materials Index | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| CRB Metals Index | 0.001 | 0.002 | 0.006 | 0.001 | 0.006 |
| 3-Month T-Bill Rate | 0.409 | 0.712 | 0.880 | 0.799 | 0.896 |
| Trade-Weighted Exchange Rate | - | 0.740 | 0.724 | 0.575 | 0.746 |
NOTES: Boldface indicates significance at the 10% level. RAC stands for U.S. refiners' acquisition cost and CRB for the Commodity Research Bureau. All variables but the interest rate are expressed in percent changes. In some cases, one needs to consider the possibility of cointegration in levels. All rejections above remain significant if we follow Dolado and Lütkepohl (1996) in conducting a lag-augmented Granger non-causality test. All test results are based on bivariate VAR(12) models. Similar results are obtained with bivariate VAR(24) models.
Table 1b: Predictability from Selected Bilateral Nominal Dollar Exchange Rates to the Nominal Price of Oil (p-values of the Wald test statistic for Granger Non-Causality)
| Monthly Predictors: | Evaluation Period: 1973.1-2009.12 WTI | Evaluation Period: 1975.2-2009.12 WTI | Evaluation Period: 1975.2-2009.12 RAC Oil Imports | Evaluation Period: 1975.2-2009.12 RAC Domestic Oil | Evaluation Period: 1975.2-2009.12 RAC Composite |
|---|---|---|---|---|---|
| Australia | 0.038 | 0.066 | 0.073 | 0.017 | 0.044 |
| Canada | 0.004 | 0.003 | 0.002 | 0.006 | 0.002 |
| New Zealand | 0.128 | 0.291 | 0.309 | 0.045 | 0.169 |
| South Africa | 0.017 | 0.020 | 0.052 | 0.021 | 0.037 |
NOTES: Boldface indicates significance at the 10% level. RAC stands for U.S. refiners' acquisition cost. All variables are expressed in percent changes. All test results are based on bivariate VAR(12) models.
Table 2: Predictability from Selected Real Aggregates to the Real Price of Oil (p-values of the Wald test statistic for Granger Non-Causality)
| Quarterly Predictors: | Evaluation Period: 1973.I-2009.IV WTI | Evaluation Period: 1975.II-2009.IV WTI | Evaluation Period: 1975.II-2009.IV RAC Oil Imports | Evaluation Period: 1975.II-2009.IV RAC Domestic Oil | Evaluation Period: 1975.II-2009.IV RAC Composite |
|---|---|---|---|---|---|
| U.S. Real GDP: LT | 0.353 | 0.852 | 0.676 | 0.397 | 0.561 |
| U.S. Real GDP: HP | 0.253 | 0.821 | 0.653 | 0.430 | 0.573 |
| U.S. Real GDP: DIF | 0.493 | 0.948 | 0.705 | 0.418 | 0.578 |
| World Industrial Production1: LT | 0.032 | 0.095 | 0.141 | 0.081 | 0.098 |
| World Industrial Production1: HP | 0.511 | 0.766 | 0.800 | 0.665 | 0.704 |
| World Industrial Production1: DIF | 0.544 | 0.722 | 0.772 | 0.668 | 0.691 |
NOTES: Boldface indicates significance at the 10% level. LT
denotes linear detrending, HP denotes HP filtering with smoothing
parameter
![]() and DIF denotes first
differencing. RAC stands for U.S. refiners' acquisition cost. All
test results are based on bivariate VAR(4) models. Similar
results are obtained with bivariate VAR(8) models. In the
baseline specification the real price of oil is expressed in log
levels. Similar results are obtained when both variables are
detrended by the same method.
and DIF denotes first
differencing. RAC stands for U.S. refiners' acquisition cost. All
test results are based on bivariate VAR(4) models. Similar
results are obtained with bivariate VAR(8) models. In the
baseline specification the real price of oil is expressed in log
levels. Similar results are obtained when both variables are
detrended by the same method.
1Data source: U.N. Monthly Bulletin of Statistics. These data end in 2008.III because the U.N. has temporarily suspended updates of this series, resulting in a shorter evaluation period.
Table 3: Predictability from Selected Real Aggregates to the Real Price of Oil (p-values of the Wald test statistic for Granger Non-Causality)
| Monthly Predictors: | Evaluation Period: 1973.1-2009.12, WTI p=12 | Evaluation Period: 1973.1-2009.12, WTI p=24 | Evaluation Period: 1976.2-2009.12, WTI p=12 | Evaluation Period: 1976.2-2009.12, WTI p=24 | Evaluation Period: 1976.2-2009.12, RAC Oil Imports p=12 | Evaluation Period: 1976.2-2009.12, RAC Oil Imports p=24 | Evaluation Period: 1976.2-2009.12, RAC Domestic Oil p=12 | Evaluation Period: 1976.2-2009.12, RAC Domestic Oil p=24 | Evaluation Period: 1976.2-2009.12, RAC Composite p=12 | Evaluation Period: 1976.2-2009.12, RAC Composite p=24 |
|---|---|---|---|---|---|---|---|---|---|---|
Chicago Fed | 0.823 | 0.951 | 0.735 | 0.952 | 0.881 | 0.998 | 0.707 | 0.979 | 0.784 | 0.995 |
Chicago Fed | 0.411 | 0.633 | 0.370 | 0.645 | 0.410 | 0.746 | 0.091 | 0.421 | 0.182 | 0.510 |
Chicago Fed | 0.327 | 0.689 | 0.357 | 0.784 | 0.415 | 0.878 | 0.110 | 0.549 | 0.194 | 0.668 |
Chicago Fed | 0.533 | 0.859 | 0.458; | 0.866 | 0.473 | 0.909 | 0.114 | 0.490 | 0.222 | 0.699 |
OECD+6 Industrial | 0.028 | 0.001 | 0.009 | 0.033 | 0.023 | 0.199 | 0.021 | 0.187 | 0.018 | 0.230 |
OECD+6 Industrial | 0.195 | 0.034 | 0.072 | 0.278 | 0.138 | 0.714 | 0.121 | 0.530 | 0.114 | 0.706 |
OECD+6 Industrial | 0.474 | 0.060 | 0.130 | 0.353 | 0.182 | 0.741 | 0.174 | 0.604 | 0.209 | 0.757 |
Global Real Activity Index2 | 0.041 | 0.000 | 0.055 | 0.020 | 0.141 | 0.034 | 0.004 | 0.004 | 0.028 | 0.018 |
NOTES: Boldface indicates significance at the 10% level. LT
denotes linear detrending, HP denotes HP filtering with smoothing
parameter
![]() (see Ravn and Uhlig
2002), and DIF denotes first differencing. The CFNAI and the global
real activity index are constructed to be stationary. RAC stands
for U.S. refiners' acquisition cost. All test results are based on
bivariate VAR(p) models. In the baseline specification the
real price of oil is expressed in log levels. Similar results are
obtained when both variables are detrended by the same method.
(see Ravn and Uhlig
2002), and DIF denotes first differencing. The CFNAI and the global
real activity index are constructed to be stationary. RAC stands
for U.S. refiners' acquisition cost. All test results are based on
bivariate VAR(p) models. In the baseline specification the
real price of oil is expressed in log levels. Similar results are
obtained when both variables are detrended by the same method.
1Data source: OECD Main Economic Indicators.
2Data source: Updated version of the index developed in Kilian
(2009a).
Table 4: 1-Month Ahead Forecast Error Diagnostics for Nominal WTI Price of Oil
| | MSPE (p-value) | Success Ratio (p-value) |
|---|---|---|
| 20.325 | N.A. | |
| | 0.988 (0.108) | 0.465 (0.780) |
| | 1.001 (0.326) | 0.539 (0.209) |
| | 0.995 (0.125) | 0.531 (0.090) |
| | 1.002 (0.408) | 0.513 (0.576) |
| | 0.988 (0.108) | 0.465 (0.780) |
| | 1.397 (0.945) | 0.504 (0.488) |
| | 1.006 (0.513) | 0.531 (0.428) |
| | 1.397 (0.518) | 0.504 (0.488) |
| | 0.865 (0.212) | 0.513 (0.394) |
| | 0.930 (0.163) | 0.478 (0.739) |
| | 0.976 (0.425) | 0.482 (0.626) |
| | 0.913 (0.266) | 0.583 (0.008) |
| | 1.031 (0.566) | 0.579 (0.017) |
| | 0.913 (0.008) | 0.583 (0.008) |
| | 1.031 (0.404) | 0.579 (0.017) |
NOTES: All MSPE results are presented as ratios relative to the
benchmark no-change forecast model, for which we report the level
of the MSPE. The forecast evaluation period is 1991.1-2009.12. The
initial estimation window is 1986.1-1990.12. For regressions based
on 6-month futures prices the estimation window begins in 1983.10;
for the 9-month futures price in 1986.12; for the 12-month futures
price in 1989.1.
![]() is the futures price that
matures in h periods;
is the futures price that
matures in h periods; ![]() is the
m month interest rate;
is the
m month interest rate; ![]() is the
percent change in
is the
percent change in ![]() in the most recent
month; and
in the most recent
month; and
![]() is the percent
change in the spot price over the most recent h months. All
p-values refer to pairwise tests of the null of equal
predictive accuracy with the no-change forecast. Comparisons of
nonnested models without estimated parameters are based on the
DM-test of Diebold and Mariano (1995) using N(0,1) critical
values; p-values for other nonnested comparisons are
obtained by bootstrapping the loss differential. Nested model
comparisons with estimated parameters are obtained by bootstrapping
the DM-test statistic as in Clark and McCracken (2005) and
Clark and West (2006, 2007). The success ratio is defined as the
fraction of forecasts that correctly predict the sign of the change
in the price of oil. The sign test in the last column is based on
Pesaran and Timmermann (2009). This test cannot be applied when
there is no variability in the predicted sign. In such cases the
p-value is reported as N.A.
is the percent
change in the spot price over the most recent h months. All
p-values refer to pairwise tests of the null of equal
predictive accuracy with the no-change forecast. Comparisons of
nonnested models without estimated parameters are based on the
DM-test of Diebold and Mariano (1995) using N(0,1) critical
values; p-values for other nonnested comparisons are
obtained by bootstrapping the loss differential. Nested model
comparisons with estimated parameters are obtained by bootstrapping
the DM-test statistic as in Clark and McCracken (2005) and
Clark and West (2006, 2007). The success ratio is defined as the
fraction of forecasts that correctly predict the sign of the change
in the price of oil. The sign test in the last column is based on
Pesaran and Timmermann (2009). This test cannot be applied when
there is no variability in the predicted sign. In such cases the
p-value is reported as N.A.
Table 5: 3-Month Ahead Forecast Error Diagnostics for Nominal WTI Price of Oil
| | MSPE (p-value) | Success Ratio (p-value) |
|---|---|---|
| 95.451 | N.A. | |
| | 0.998 (0.467) | 0.465 (0.727) |
| | 1.044 (0.490) | 0.531 (0.493) |
| | 0.990 (0.215) | 0.474 (0.668) |
| | 1.026 (0.323) | 0.518 (0.727) |
| | 0.998 (0.478) | 0.465 (0.727) |
| | 2.325 (0.997) | 0.535 (0.168) |
| | 1.032 (0.570) | 0.561 (N.A.) |
| | 1.678 (0.656) | 0.539 (0.219) |
| | 1.000 (0.507) | 0.575 (N.A.) |
| | 1.519 (0.994) | 0.447 (0.760) |
| | 0.811 (0.173) | 0.553 (0.071) |
| | 0.918 (0.207) | 0.496 (0.570) |
| | 1.180 (0.851) | 0.518 (0.231) |
| | 0.802 (0.143) | 0.605 (0.001) |
| | 0.942 (0.422) | 0.636 (0.000) |
| | 0.782 (0.013) | 0.601 (0.012) |
| | 0.750 (0.004) | 0.601 (0.018) |
NOTES: See Table 4.
Table 6: 6-Month Ahead Forecast Error Diagnostics for Nominal WTI Price of Oil
| | MSPE (p-value) | Success Ratio (p-value) |
|---|---|---|
| 222.28 | N.A. | |
| | 0.991 (0.411) | 0.509 (0.322) |
| | 1.051 (0.422) | 0.535 (0.151) |
| | 0.978 (0.140) | 0.535 (0.151) |
| | 1.024 (0.269) | 0.544 (0.398) |
| | 0.995 (0.445) | 0.509 (0.322) |
| | 8.580 (0.992) | 0.539 (0.153) |
| | 1.057 (0.563) | 0.557 (N.A.) |
| | 2.225 (0.734) | 0.504 (0.547) |
| | 1.002 (0.533) | 0.575 (N.A.) |
| | 1.071 (0.745) | 0.561 (0.048) |
| | 0.966 (0.351) | 0.526 (0.225) |
| | 1.370 (0.985) | 0.544 (0.080) |
| | 0.976 (0.433) | 0.614 (0.001) |
| | 1.574 (0.899) | 0.592 (0.005) |
| | 1.055 (0.660) | 0.583 (0.054) |
| | 1.219 (0.673) | 0.623 (0.007) |
NOTES: See Table 4.
Table 7: 9-Month Ahead Forecast Error Diagnostics for Nominal WTI Price of Oil
| | MSPE (p-value) | Success Ratio (p-value) |
|---|---|---|
| 282.32 | N.A. | |
| | 0.978 (0.328) | 0.548 (0.121) |
| | 1.042 (0.355) | 0.583 (0.120) |
| | 0.989 (0.192) | 0.553 (0.070) |
| | 1.019 (0.242) | 0.561 (0.202) |
| | 0.985 (0.378) | 0.548 (0.121) |
| | 29.179 (0.940) | 0.509 (0.430) |
| | 1.066 (0.500) | 0.447 (0.980) |
| | 2.816 (0.743) | 0.487 (0.658) |
| | 1.352 (0.965) | 0.583 (0.011) |
| | 0.990 (0.455) | 0.539 (0.080) |
| | 1.471 (0.986) | 0.535 (0.102) |
| | 1.402 (0.887) | 0.570 (0.042) |
| | 3.374 (0.964) | 0.561 (0.054) |
| | 1.076 (0.679) | 0.553 (0.212) |
| | 1.304 (0.683) | 0.575 (0.113) |
NOTES: See Table 4.
Table 8: 12-Month Ahead Forecast Error Diagnostics for Nominal WTI Price of Oil
| | MSPE (p-value) | Success Ratio (p-value) |
|---|---|---|
| 302.54 | N.A. | |
| | 0.941 (0.139) | 0.557 (0.064) |
| | 1.240 (0.461) | 0.537 (0.396) |
| | 1.052 (0.706) | 0.528 (0.442) |
| | 1.281 (0.391) | 0.528 (0.442) |
| | 0.950 (0.177) | 0.557 (0.064) |
| | 179.77 (0.886) | 0.496 (0.584) |
| | 1.093 (0.478) | 0.407 (0.999) |
| | 3.746 (0.765) | 0.439 (0.934) |
| | 0.998 (0.482) | 0.566 (N.A.) |
| | 0.944 (0.382) | 0.539 (0.081) |
| | 1.678 (0.969) | 0.583 (0.010) |
| | 1.144 (0.795) | 0.504 (0.443) |
| | 1.911 (0.997) | 0.491 (0.489) |
| | 1.846 (0.906) | 0.566 (0.048) |
| | 7.170 (0.966) | 0.548 (0.112) |
| | 1.035 (0.594) | 0.548 (0.190) |
| | 1.278 (0.655) | 0.539 (0.254) |
| | 1.047 (0.764) | 0.566 (N.A.) |
| | 1.016 (0.667) | 0.579 (N.A.) |
NOTES: See Table 4.
Table 9: Short-Horizon Forecasts of the Nominal WTI Price of Oil from Daily Oil Futures Prices since January 1986, Start of Evaluation Period January 1986
| h=1 MSPE | h=1SR | h=3MSPE | h=3SR | h=6MSPE | h=6SR | h=9MSPE | h=9SR | h=12MSPE | h=12SR | |
|---|---|---|---|---|---|---|---|---|---|---|
| | 0.963 (0.009) | 0.522 (0.040) | 0.972 (0.053) | 0.516 (0.072) | 0.973 (0.077) | 0.535 (0.002) | 0.964 (0.063) | 0.534 (0.001) | 0.929 (0.001) | 0.562 (0.000) |
NOTES: There are 5968, 5926, 5861, 5744, and 5028 daily observations at horizons of 1 through 12 months, respectively. Following Leamer's (1978) rule for adjusting the threshold for statistical significance with changes in the sample size, p-values below about 0.0035 are considered statistically significant and are shown in boldface.
Table 10: Long-Horizon Forecasts of the Nominal WTI Price of Oil from Daily Oil Futures Prices
| | Starting date | Sample size | MSPE | SR |
|---|---|---|---|---|
| 2 | 11/20/90 | 3283 | 1.159 (1.000) | 0.515 (0.000) |
| 3 | 05/29/91 | 515 | 1.168 (0.996) | 0.518 (0.281) |
| 4 | 11/01/95 | 194 | 1.212 (1.000) | 0.294 (N.A.) |
| 5 | 11/03/97 | 154 | 1.280 (1.000) | 0.247 (N.A.) |
| 6 | 11/03/97 | 134 | 1.158 (0.999) | 0.276 (N.A.) |
| 7 | 11/21/97 | 22 | 1.237 (0.957) | 0.500 (N.A.) |
NOTES: Following Leamer's (1978) rule for adjusting the threshold for statistical significance with changes in the sample size, p-values below 0.0044 for a horizon of two years are considered statistically significant and are shown in boldface.
Table 11: Accuracy of Survey Forecasts Relative to No-Change Forecast
| h=3 MSPE Ratio | h=3 Success Ratio | h=12 MSPE Ratio | h=12 Success Ratio | h=60 MSPE Ratio | h=60 Success Ratio | |
|---|---|---|---|---|---|---|
| | 1.519 | 0.447 | 0.944 | 0.539 | - | - |
| | 0.918 | 0.417 | 0.973 | 0.562 | - | - |
| | - | - | - | - | 0.765 | 0.9071 |
| | - | - | 1.047 | 0.5661 | - | - |
| | - | - | 1.016 | 0.5791 | 0.855 | 0.8111 |
NOTES: Boldface indicates statistical significance at the 10%
level.1 No significance test possible due to lack of variation in
success ratio. MSC denotes the Michigan Survey of Consumers, SPF
the Survey of Professional Forecasters, EIA the Energy Information
Administration and CE denotes Consensus Economics Inc.
![]() stands for the expected
inflation rate between
stands for the expected
inflation rate between ![]() and
and ![]()
Table 12: Recursive Forecast Error Diagnostics for the Real Price of Oil from Selected AR and ARMA Models U.S. Refiners' Acquisition Cost for Imported Crude Oil, Evaluation Period: 1991.12-2009.8
| h=1 MSPE | h=1 SR | h=3 MSPE | h=3 SR | h=6 MSPE | h=6 SR | h=9 MSPE | h=9 SR | h=12 MSPE | h=12 SR | |
|---|---|---|---|---|---|---|---|---|---|---|
| AR(12) | 0.849 (0.000) | 0.599 (0.001) | 0.921 (0.000) | 0.552 (0.081) | 0.969 (0.042) | 0.522 (0.370) | 1.034 (0.374) | 0.441 (0.915) | 1.022 (0.279) | 0.517 (0.472) |
| AR(24) | 0.898 (0.000) | 0.576 (0.023) | 0.978 (0.010) | 0.557 (0.062) | 1.008 (0.133) | 0.565 (0.073) | 1.056 (0.373) | 0.446 (0.871) | 1.058 (0.344) | 0.453 (0.859) |
| AR(SIC) | 0.826 (0.000) | 0.613 (0.001) | 0.936 (0.000) | 0.557 (0.130) | 1.015 (0.374) | 0.488 (0.796) | 1.039 (0.483) | 0.515 (0.602) | 1.007 (0.257) | 0.532 (0.519) |
| AR(AIC) | 0.842 (0.000) | 0.613 (0.001) | 0.940 (0.001) | 0.562 (0.090) | 0.983 (0.082) | 0.483 (0.826) | 1.013 (0.273) | 0.500 (0.690) | 0.989 (0.170) | 0.527 (0.549) |
| ARMA(1,1) | 0.837 (0.001) | 0.580 (0.009) | 0.932 (0.000) | 0.514 (0.560) | 0.982 (0.094) | 0.493 (0.767) | 1.006 (0.266) | 0.510 (0.644) | 0.992 (0.201) | 0.527 (0.572) |
| ARI(11) | 0.856 (0.000) | 0.604 (0.000) | 0.939 (0.003) | 0.571 (0.024) | 1.003 (0.224) | 0.517 (0.243) | 1.095 (0.969) | 0.471 (0.671) | 1.091 (0.937) | 0.512 (0.279) |
| ARI(23) | 0.898 (0.000) | 0.561 (0.037) | 0.978 (0.015) | 0.538 (0.139) | 1.009 (0.183) | 0.546 (0.027) | 1.068 (0.694) | 0.500 (0.248) | 1.068 (0.654) | 0.508 (0.120) |
| ARI(SIC) | 0.833 (0.000) | 0.594 (0.003) | 0.951 (0.002) | 0.605 (0.001) | 1.041 (0.951) | 0.546 (0.101) | 1.053 (0.908) | 0.505 (0.570) | 1.016 (0.423) | 0.527 (0.377) |
| ARI(AIC) | 0.849 (0.000) | 0.604 (0.002) | 0.958 (0.006) | 0.605 (0.002) | 1.008 (0.366) | 0.556 (0.050) | 1.042 (0.806) | 0.500 (0.610) | 1.015 (0.375) | 0.527 (0.377) |
| ARIMA(0,1) | 0.841 (0.001) | 0.599 (0.001) | 0.945 (0.000) | 0.581 (0.004) | 1.009 (0.464) | 0.546 (0.093) | 1.032 (0.767) | 0.515 (0.463) | 1.017 (0.410) | 0.512 (0.575) |
NOTES: ARI and ARIMA, respectively, denote AR and ARMA models in log differences. The SIC and AIC are implemented with an upper bound of 12 lags. MSPE is expressed as a fraction of the MSPE of the no-change forecast. SR stands for success ratio. The p-values for the sign test are computed following Pesaran and Timmermann (2009); those for the test of equal MSPEs are computed by bootstrapping the VAR model under the null, adapting the bootstrap algorithm in Kilian (1999).
Table 13: Recursive Forecast Error Diagnostics for the Real Price of Oil from Selected Unrestricted VAR Models U.S. Refiners' Acquisition Cost for Imported Crude Oil, Evaluation Period: 1991.12-2009.8
| Model: p | h | (1) MSPE | (1) SR | (2) MSPE | (2) SR | (3) MSPE | (3) SR | (4) MSPE | (4) SR | (5) MSPE | (5) SR | (6) MSPE | (6) SR |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 12 | 1 | 0.814 (0.000) | 0.561 (0.030) | 0.876 (0.000) | 0.594 (0.004) | 0.863 (0.000) | 0.613 (0.000) | 0.801 (0.000) | 0.613 (0.000) | 0.863 (0.000) | 0.580 (0.017) | 0.798 (0.000) | 0.585 (0.006) |
| 12 | 3 | 0.834 (0.000) | 0.567 (0.080) | 0.960 (0.008) | 0.562 (0.078) | 0.947 (0.003) | 0.576 (0.040) | 0.833 (0.000) | 0.614 (0.005) | 0.944 (0.003) | 0.524 (0.267) | 0.833 (0.000) | 0.586 (0.033) |
| 12 | 6 | 0.940 (0.011) | 0.546 (0.173) | 1.011 (0.184) | 0.507 (0.523) | 0.991 (0.086) | 0.536 (0.294) | 0.920 (0.006) | 0.551 (0.148) | 0.996 (0.123) | 0.527 (0.329) | 0.922 (0.007) | 0.511 (0.161) |
| 12 | 9 | 1.047 (0.314) | 0.564 (0.125) | 1.085 (0.596) | 0.534 (0.339) | 1.060 (0.470) | 0.539 (0.314) | 0.999 (0.148) | 0.544 (0.231) | 1.063 (0.555) | 0.471 (0.781) | 1.000 (0.130) | 0.569 (0.111) |
| 12 | 12 | 0.985 (0.111) | 0.632 (0.004) | 1.055 (0.391) | 0.562 (0.154) | 1.036 (0.313) | 0.567 (0.132) | 0.948 (0.059) | 0.617 (0.012) | 1.045 (0.397) | 0.503 (0.593) | 0.931 (0.039) | 0.647 (0.002) |
| 24 | 1 | 0.961 (0.000) | 0.561 (0.033) | 0.954 (0.000) | 0.552 (0.086) | 0.912 (0.000) | 0.580 (0.010) | 0.892 (0.000) | 0.571 (0.034) | 0.912 (0.000) | 0.561 (0.052) | 0.895 (0.000) | 0.561 (0.046) |
| 24 | 3 | 1.081 (0.073) | 0.614 (0.006) | 1.151 (0.708) | 0.591 (0.024) | 1.048 (0.186) | 0.619 (0.002) | 0.924 (0.000) | 0.591 (0.012) | 1.005 (0.038) | 0.548 (0.100) | 0.978 (0.004) | 0.605 (0.019) |
| 24 | 6 | 1.298 (0.852) | 0.604 (0.023) | 1.271 (0.945) | 0.585 (0.081) | 1.078 (0.431) | 0.594 (0.038) | 1.052 (0.237) | 0.546 (0.163) | 1.073 (0.523) | 0.522 (0.261) | 1.129 (0.467) | 0.585 (0.081) |
| 24 | 9 | 1.476 (0.925) | 0.583 (0.080) | 1.441 (0.962) | 0.593 (0.085) | 1.153 (0.656) | 0.632 (0.015) | 1.150 (0.614) | 0.431 (0.900) | 1.158 (0.765) | 0.422 (0.881) | 1.255 (0.747) | 0.593 (0.086) |
| 24 | 12 | 1.415 (0.820) | 0.647 (0.013) | 1.407 (0.919) | 0.612 (0.049) | 1.137 (0.515) | 0.642 (0.010) | 1.137 (0.505) | 0.468 (0.782) | 1.169 (0.700) | 0.458 (0.718) | 1.208 (0.565) | 0.617 (0.044) |
NOTES: MSPE is expressed as a fraction of the MSPE of the no-change forecast. SR stands for success ratio. The p-values for the sign test are computed following Pesaran and Timmermann (2009); those for the test of equal MSPEs are computed by bootstrapping the VAR model under the null, adapting the bootstrap algorithm in Kilian (1999). Model (1) includes all four variables used in the VAR model of Kilian and Murphy (2010); model (2) excludes oil inventories; model (3) excludes both oil inventories and oil production; model (4) excludes real activity and oil production; model (5) excludes real activity and oil inventories; and model (6) excludes oil production.
Table 14: Recursive Forecast Error Diagnostics for the Real Price of Oil from Selected AR and ARMA Models WTI, Evaluation Period: 1991.12-2009.8
| h=1 MSPE | h=1 SR | h=3 MSPE | h=3 SR | h=6 MSPE | h=6 SR | h=9 MSPE | h=9 SR | h=12 MSPE | h=12 SR | |
|---|---|---|---|---|---|---|---|---|---|---|
| AR(12) | 0.972 (0.015) | 0.500 (0.525) | 0.974 (0.032) | 0.533 (0.813) | 1.011 (0.279) | 0.459 (0.813) | 1.037 (0.461) | 0.441 (0.920) | 1.034 (0.403) | 0.478 (0.747) |
| AR(24) | 1.035 (0.130) | 0.486 (0.666) | 0.994 (0.048) | 0.500 (0.474) | 0.995 (0.090) | 0.502 (0.503) | 1.008 (0.173) | 0.461 (0.806) | 1.019 (0.230) | 0.473 (0.720) |
| AR(SIC) | 0.947 (0.002) | 0.505 (0.667) | 0.979 (0.047) | 0.491 (0.813) | 1.022 (0.375) | 0.464 (0.896) | 1.052 (0.519) | 0.471 (0.844) | 1.058 (0.488) | 0.508 (0.610) |
| AR(AIC) | 0.949 (0.002) | 0.505 (0.656) | 0.980 (0.050) | 0.491 (0.813) | 1.022 (0.375) | 0.464 (0.896) | 1.046 (0.463) | 0.471 (0.844) | 1.047 (0.420) | 0.508 (0.610) |
| ARMA(1,1) | 0.956 (0.008) | 0.500 (0.774) | 0.982 (0.058) | 0.491 (0.815) | 1.010 (0.302) | 0.473 (0.857) | 1.036 (0.420) | 0.476 (0.420) | 1.040 (0.402) | 0.508 (0.610) |
| ARI(11) | 0.978 (0.024) | 0.505 (0.436) | 0.985 (0.069) | 0.529 (0.234) | 1.032 (0.704) | 0.517 (0.278) | 1.081 (0.924) | 0.456 (0.703) | 1.083 (0.875) | 0.433 (0.848) |
| ARI(23) | 1.034 (0.150) | 0.524 (0.216) | 0.988 (0.039) | 0.538 (0.127) | 0.988 (0.088) | 0.594 (0.006) | 1.016 (0.275) | 0.534 (0.100) | 1.026 (0.345) | 0.522 (0.177) |
| ARI(SIC) | 0.944 (0.001) | 0.528 (0.267) | 0.971 (0.020) | 0.571 (0.060) | 1.013 (0.529) | 0.546 (0.305) | 1.023 (0.556) | 0.505 (0.836) | 1.020 (0.403) | 0.517 (0.743) |
| ARI(AIC) | 0.947 (0.003) | 0.524 (0.333) | 0.976 (0.036) | 0.552 (0.180) | 1.018 (0.584) | 0.517 (0.761) | 1.031 (0.619) | 0.466 (1.000) | 1.026 (0.469) | 0.488 (0.996) |
| ARIMA(0,1) | 0.952 (0.006) | 0.524 (0.301) | 0.975 (0.028) | 0.600 (0.006) | 1.009 (0.390) | 0.527 (0.574) | 1.021 (0.513) | 0.500 (0.927) | 1.019 (0.382) | 0.517 (0.817) |
NOTES: See Table 12.
Table 15: Recursive Forecast Error Diagnostics for the Real Price of Oil from Selected Unrestricted VAR Models WTI, Evaluation Period: 1991.12-2009.8
| Model: p | h | (1): MSPE | (1): SR | (2): MSPE | (2): SR | (3): MSPE | (3): SR | (4): MSPE | (4): SR | (5): MSPE | (5): SR | (6): MSPE | (6): SR |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 12 | 1 | 0.896 (0.000) | 0.519 (0.279) | 0.981 (0.017) | 0.467 (0.885) | 0.976 (0.014) | 0.481 (0.810) | 0.893 (0.000) | 0.547 (0.056) | 0.983 (0.024) | 0.505 (0.461) | 0.882 (0.000) | 0.547 (0.053) |
| 12 | 3 | 0.843 (0.000) | 0.538 (0.208) | 0.979 (0.034) | 0.524 (0.336) | 0.968 (0.022) | 0.548 (0.181) | 0.877 (0.000) | 0.552 (0.119) | 0.994 (0.092) | 0.529 (0.266) | 0.841 (0.000) | 0.548 (0.165) |
| 12 | 6 | 0.988 (0.063) | 0.517 (0.331) | 1.035 (0.353) | 0.541 (0.279) | 1.011 (0.209) | 0.551 (0.226) | 0.984 (0.070) | 0.541 (0.206) | 1.037 (0.520) | 0.464 (0.785) | 0.973 (0.043) | 0.541 (0.207) |
| 12 | 9 | 1.053 (0.334) | 0.534 (0.230) | 1.080 (0.587) | 0.485 (0.688) | 1.049 (0.436) | 0.510 (0.507) | 1.021 (0.257) | 0.564 (0.132) | 1.067 (0.639) | 0.441 (0.919) | 1.014 (0.184) | 0.539 (0.216) |
| 12 | 12 | 1.007 (0.178) | 0.562 (0.125) | 1.062 (0.450) | 0.498 (0.557) | 1.041 (0.363) | 0.498 (0.578) | 0.988 (0.152) | 0.602 (0.045) | 1.059 (0.518) | 0.438 (0.909) | 0.968 (0.098) | 0.592 (0.053) |
| 24 | 1 | 1.109 (0.006) | 0.509 (0.419) | 1.118 (0.127) | 0.491 (0.672) | 1.053 (0.060) | 0.538 (0.192) | 1.011 (0.003) | 0.552 (0.037) | 1.063 (0.182) | 0.500 (0.487) | 1.013 (0.002) | 0.509 (0.451) |
| 24 | 3 | 1.112 (0.072) | 0.581 (0.037) | 1.185 (0.701) | 0.552 (0.191) | 1.017 (0.055) | 0.562 (0.134) | 0.970 (0.005) | 0.562 (0.060) | 1.049 (0.265) | 0.481 (0.663) | 0.962 (0.002) | 0.619 (0.003) |
| 24 | 6 | 1.369 (0.843) | 0.570 (0.074) | 1.312 (0.938) | 0.541 (0.306) | 1.030 (0.147) | 0.594 (0.062) | 1.107 (0.475) | 0.483 (0.605) | 1.075 (0.515) | 0.488 (0.541) | 1.127 (0.317) | 0.589 (0.043) |
| 24 | 9 | 1.455 (0.854) | 0.564 (0.134) | 1.340 (0.938) | 0.520 (0.484) | 1.060 (0.261) | 0.583 (0.115) | 1.160 (0.602) | 0.446 (0.815) | 1.106 (0.602) | 0.490 (0.484) | 1.153 (0.373) | 0.583 (0.084) |
| 24 | 12 | 1.369 (0.691) | 0.562 (0.190) | 1.378 (0.870) | 0.503 (0.572) | 1.054 (0.249) | 0.592 (0.084) | 1.167 (0.570) | 0.478 (0.649) | 1.119 (0.568) | 0.478 (0.599) | 1.086 (0.214) | 0.602 (0.056) |
NOTES: See Table 13.
Table 16: Recursive MSPE Ratios for the Real Price of Oil from Selected Bayesian VAR Models, Evaluation Period: 1991.12-2009.8
| Model: p | h | (1): RAC | (1): WTI | (2): RAC | (2): WTI | (3): RAC | (3): WTI | (4): RAC | (4): WTI | (5): RAC | (5): WTI | (6): RAC | (6): WTI |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 12 | 1 | 0.800 | 0.892 | 0.825 | 0.938 | 0.828 | 0.945 | 0.798 | 0.896 | 0.827 | 0.951 | 0.795 | 0.883 |
| 12 | 3 | 0.876 | 0.886 | 0.929 | 0.954 | 0.930 | 0.957 | 0.855 | 0.890 | 0.921 | 0.972 | 0.867 | 0.870 |
| 12 | 6 | 0.967 | 0.990 | 0.988 | 1.008 | 0.987 | 1.006 | 0.943 | 0.985 | 0.971 | 1.011 | 0.962 | 0.984 |
| 12 | 9 | 1.052 | 1.036 | 1.053 | 1.036 | 1.054 | 1.037 | 1.033 | 1.037 | 1.031 | 1.029 | 1.050 | 1.036 |
| 12 | 12 | 1.004 | 1.005 | 1.024 | 1.024 | 1.028 | 1.028 | 0.994 | 1.008 | 1.015 | 1.022 | 1.004 | 1.003 |
| 24 | 1 | 0.801 | 0.894 | 0.826 | 0.939 | 0.828 | 0.947 | 0.800 | 0.902 | 0.829 | 0.952 | 0.795 | 0.886 |
| 24 | 3 | 0.883 | 0.875 | 0.939 | 0.945 | 0.944 | 0.948 | 0.860 | 0.877 | 0.924 | 0.958 | 0.876 | 0.859 |
| 24 | 6 | 0.993 | 0.990 | 1.012 | 1.007 | 1.015 | 1.000 | 0.955 | 0.980 | 0.970 | 0.991 | 0.991 | 0.986 |
| 24 | 9 | 1.095 | 1.038 | 1.093 | 1.034 | 1.096 | 1.032 | 1.044 | 1.028 | 1.028 | 1.005 | 1.097 | 1.037 |
| 24 | 12 | 1.059 | 1.002 | 1.073 | 1.016 | 1.078 | 1.018 | 1.016 | 1.010 | 1.026 | 1.008 | 1.058 | 0.998 |
NOTES: The Bayesian VAR forecast relies on the data-based procedure proposed in Giannone, Lenza and Primiceri (2010) for selecting the optimal degree of shrinkage in real time. MSPE is expressed as a fraction of the MSPE of the no-change forecast. Boldface indicates MSPE ratios lower than for the corresponding unrestricted VAR forecasting model in Tables 12 and 14. RAC refers to the U.S. refiners' acquisition cost for imported crude oil and WTI to the price of West Texas Intermediate crude oil. Model (1) includes all four variables used in the VAR model of Kilian and Murphy (2010); model (2) excludes oil inventories; model (3) excludes both oil inventories and oil production; model (4) excludes real activity and oil production; model (5) excludes real activity and oil inventories; and model (6) excludes oil production.
Table 17a: Recursive Forecast Error Diagnostics for the Real Price of Oil (by Country), Evaluation Period: 1991.12-2009.8 - U.S. Refiners' Acquisition Cost for Imported Crude Oil
| h=1 MSPE | h=1 SR | h=3 MSPE | h=3 SR | h=6 MSPE | h=6 SR | h=9 MSPE | h=9 SR | h=12 MSPE | h=12 SR | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Japan: AR(12) | 0.811 (0.000) | 0.604 (0.005) | 0.917 (0.001) | 0.548 (0.112) | 0.986 (0.100) | 0.483 (0.741) | 1.035 (0.445) | 0.520 (0.429) | 1.026 (0.355) | 0.493 (0.714) | |
| U.K.: AR(12) | 0.929 (0.000) | 0.585 (0.010) | 0.965 (0.009) | 0.567 (0.042) | 0.988 (0.097) | 0.567 (0.042) | 1.040 (0.394) | 0.461 (0.856) | 1.042 (0.370) | 0.547 (0.233) | |
| Canada: AR(12) | 0.872 (0.000) | 0.599 (0.004) | 0.941 (0.002) | 0.533 (0.207) | 0.948 (0.019) | 0.531 (0.266) | 1.007 (0.210) | 0.461 (0.808) | 0.990 (0.159) | 0.503 (0.534) | |
Table 17b: Recursive Forecast Error Diagnostics for the Real Price of Oil (by Country), Evaluation Period: 1991.12-2009.8 - WTI
| h=1 MSPE | h=1 SR | h=3 MSPE | h=3 SR | h=6 MSPE | h=6 SR | h=9 MSPE | h=9 SR | h=12 MSPE | h=12 SR | |
|---|---|---|---|---|---|---|---|---|---|---|
| Japan: AR(12) | 0.943 (0.003) | 0.531 (0.197) | 0.955 (0.011) | 0.498 (0.567) | 1.008 (0.276) | 0.370 (0.998) | 1.027 (0.417) | 0.424 (0.957) | 1.034 (0.431) | 0.416 (0.964) |
| U.K.: AR(12) | 1.024 (0.358) | 0.540 (0.110) | 1.014 (0.262) | 0.469 (0.760) | 1.028 (0.392) | 0.476 (0.720) | 1.041 (0.440) | 0.459 (0.828) | 1.044 (0.416) | 0.495 (0.626) |
| Canada: AR(12) | 0.986 (0.030) | 0.526 (0.297) | 0.983 (0.053) | 0.502 (0.414) | 0.987 (0.122) | 0.486 (0.633) | 1.009 (0.257) | 0.459 (0.767) | 0.998 (0.213) | 0.515 (0.444) |
NOTES: All MSPE results have been normalized relative to the no-change forecast of the country in question. The sample period is the same as in Tables 11 and 13. The foreign real price is obtained by converting the U.S. real price at the real exchange rate.
Table 18: MSPE Ratios of Linear Autoregressive Models Relative to the AR(4) Benchmark Model Cumulative U.S. Real GDP Growth Rates
| Horizon | Real RAC Price of Imports: Oil Price Endogenous | Real RAC Price of Imports: Oil Price Exogenous | Nominal RAC Price of Imports: Oil Price Endogenous | Nominal RAC Price of Imports: Oil Price Exogenous |
|---|---|---|---|---|
| 1 | 1.09 | 1.09 | 1.10 | 1.10 |
| 2 | 1.03 | 1.03 | 1.04 | 1.04 |
| 3 | 0.99 | 0.98 | 1.00 | 0.99 |
| 4 | 0.97 | 0.96 | 0.98 | 0.97 |
| 5 | 0.96 | 0.95 | 0.97 | 0.95 |
| 6 | 0.95 | 0.94 | 0.95 | 0.94 |
| 7 | 0.92 | 0.92 | 0.92 | 0.92 |
| 8 | 0.92 | 0.92 | 0.92 | 0.92 |
NOTES: The benchmark model is an AR(4) for U.S. real GDP growth. The first alternative is a VAR(4) model for real GDP growth and the percent change in the price of oil that allows for unrestricted feedback from U.S. real GDP growth to the price of oil. The second alternative is a restricted VAR(4) model that treats the price of oil as exogenous. Boldface indicates gains in accuracy relative to the benchmark model. No tests of statistical significance have been conducted, given that these models are economically indistinguishable.
Table 19a1: MSPE Ratios of Nonlinear Dynamic Models Relative to the AR(4) Benchmark Model Cumulative U.S. Real GDP Growth Rates - Real Refiners' Acquisition Cost for Imported Crude Oil
| Horizon | Unrestricted Model (20): Mork Increase | Unrestricted Model (20): Hamilton Net Increase 1 Year | Unrestricted Model (20): Hamilton Net Increase 3 Year | Exogenous Model (21): Mork Increase | Exogenous Model (21): Hamilton Net Increase 1 Year | Exogenous Model (21): Hamilton Net Increase 3 Year |
|---|---|---|---|---|---|---|
| 1 | 1.51 | 1.59 | 1.26 | 1.50 | 1.59 | 1.26 |
| 2 | 1.53 | 1.69 | 1.16 | 1.51 | 1.68 | 1.16 |
| 3 | 1.41 | 1.69 | 1.10 | 1.40 | 1.67 | 1.10 |
| 4 | 1.41 | 1.78 | 1.11 | 1.40 | 1.75 | 1.11 |
| 5 | 1.42 | 1.90 | 1.25 | 1.39 | 1.87 | 1.26 |
| 6 | 1.40 | 1.65 | 1.19 | 1.36 | 1.62 | 1.19 |
| 7 | 1.41 | 1.46 | 1.13 | 1.36 | 1.42 | 1.12 |
| 8 | 1.43 | 1.33 | 1.06 | 1.37 | 1.29 | 1.06 |
Table 19a2: MSPE Ratios of Nonlinear Dynamic Models Relative to the AR(4) Benchmark Model Cumulative U.S. Real GDP Growth Rates - Nominal Refiners' Acquisition Cost for Imported Crude Oil
| Horizon | Unrestricted Model (20'): Mork Increase | Unrestricted Model (20'): Hamilton Net Increase 1 Year | Unrestricted Model (20'): Hamilton Net Increase 3 Year | Exogenous Model (21'): Mork Increase | Exogenous Model (21'): Hamilton Net Increase 1 Year | Exogenous Model (21'): Hamilton Net Increase 3 Year |
|---|---|---|---|---|---|---|
| 1 | 1.12 | 1.20 | 1.09 | 1.12 | 1.20 | 1.09 |
| 2 | 1.10 | 1.10 | 0.84 | 1.10 | 1.10 | 0.84 |
| 3 | 1.04 | 1.18 | 0.88 | 1.04 | 1.17 | 0.88 |
| 4 | 1.04 | 1.15 | 0.79 | 1.04 | 1.14 | 0.78 |
| 5 | 1.05 | 1.23 | 0.91 | 1.04 | 1.21 | 0.90 |
| 6 | 1.05 | 1.15 | 0.91 | 1.04 | 1.13 | 0.91 |
| 7 | 1.05 | 1.06 | 0.91 | 1.04 | 1.05 | 0.89 |
| 8 | 1.05 | 1.02 | 0.90 | 1.05 | 1.01 | 0.89 |
NOTES: The benchmark model is an AR(4) for U.S. real GDP growth. The nonlinear dynamic models are described in the text. Boldface indicates gains in accuracy relative to benchmark model. The exogenous model suppresses feedback from lagged real GDP growth to the current price of oil.
Table 19b1: MSPE Ratios of Nonlinear Dynamic Models Relative to the AR(4) Benchmark Model Cumulative U.S. Real GDP Growth Rates - Real Refiners' Acquisition Cost for Imported Crude Oil
| Horizon | Restricted Model (22): Mork Increase | Restricted Model (22): Hamilton Net Increase 1 Year | Restricted Model (22): Hamilton Net Increase 3 Year | Restricted Exogenous Model (23): Mork Increase | Restricted Exogenous Model (23): Hamilton Net Increase 1 Year | Restricted Exogenous Model (23): Hamilton Net Increase 3 Year |
|---|---|---|---|---|---|---|
| 1 | 1.14 | 1.12 | 0.91 | 1.14 | 1.12 | 0.91 |
| 2 | 1.12 | 1.03 | 0.86 | 1.11 | 1.04 | 0.85 |
| 3 | 1.07 | 1.10 | 0.90 | 1.07 | 1.09 | 0.90 |
| 4 | 1.04 | 1.05 | 0.85 | 1.03 | 1.05 | 0.85 |
| 5 | 1.03 | 1.07 | 0.88 | 1.02 | 1.07 | 0.88 |
| 6 | 1.02 | 1.02 | 0.87 | 1.00 | 1.01 | 0.87 |
| 7 | 1.02 | 0.97 | 0.86 | 1.00 | 0.95 | 0.85 |
| 8 | 1.01 | 0.95 | 0.85 | 1.01 | 0.95 | 0.85 |
Table 19b2: MSPE Ratios of Nonlinear Dynamic Models Relative to the AR(4) Benchmark Model Cumulative U.S. Real GDP Growth Rates - Nominal Refiners' Acquisition Cost for Imported Crude Oil
| Horizon | Restricted Model (22'): Mork Increase | Restricted Model (22'): Hamilton Net Increase 1 Year | Restricted Model (22'): Hamilton Net Increase 3 Year | Restricted Exogenous Model (23'): Mork Increase | Restricted Exogenous Model (23'): Hamilton Net Increase 1 Year | Restricted Exogenous Model (23'): Hamilton Net Increase 3 Year |
|---|---|---|---|---|---|---|
| 1 | 1.12 | 1.12 | 1.01 | 1.12 | 1.11 | 1.01 |
| 2 | 1.08 | 0.99 | 0.79 | 1.08 | 0.98 | 0.79 |
| 3 | 1.04 | 1.03 | 0.81 | 1.04 | 1.03 | 0.81 |
| 4 | 1.00 | 0.98 | 0.74 | 1.00 | 0.98 | 0.74 |
| 5 | 0.99 | 1.03 | 0.85 | 0.99 | 1.02 | 0.85 |
| 6 | 0.99 | 0.99 | 0.87 | 0.97 | 0.98 | 0.86 |
| 7 | 0.98 | 0.94 | 0.86 | 0.97 | 0.93 | 0.85 |
| 8 | 0.98 | 0.93 | 0.86 | 0.97 | 0.92 | 0.85 |
NOTES: The benchmark model is an AR(4) for U.S. real GDP growth. The nonlinear dynamic models are described in the text. Boldface indicates gains in accuracy relative to benchmark model. The restricted model suppresses feedback from lagged percent changes in the price of oil to current real GDP growth, as proposed by Hamilton (2003, 2010). The restricted exogenous model combines this restriction with that of exogenous oil prices, further increasing the parsimony of the model.
Table 20: MSPE Ratios for Cumulative U.S. Real GDP Growth Rate Relative to AR(4) Benchmark Model: Models (23) and (23') for Alternative Oil Price Specifications and Evaluation Periods
Oil Price Series | 1990.Q1-2010.Q2 Horizon: h=1 | 1990.Q1-2010.Q2 Horizon: h=4 | 1990.Q1-2007.Q4 Horizon: h=1 | 1990.Q1-2007.Q4 Horizon: h=1 |
|---|---|---|---|---|
Real: RAC imports | 0.91 | 0.85 | 1.11 | 1.71 |
Real: RAC composite | 1.16 | 0.99 | 1.49 | 2.05 |
Real: RAC domestic | 1.23 | 0.89 | 1.55 | 1.73 |
Real: WTI | 1.03 | 0.70 | 1.23 | 1.22 |
Real: PPI | 1.24 | 1.09 | 1.63 | 2.28 |
Nominal: RAC imports | 1.01 | 0.74 | 1.22 | 1.37 |
Nominal: RAC composite | 1.26 | 0.82 | 1.58 | 1.54 |
Nominal: RAC domestic | 1.23 | 0.80 | 1.50 | 1.40 |
Nominal: WTI | 0.92 | 0.66 | 1.02 | 1.08 |
Nominal: PPI | 1.23 | 0.88 | 1.59 | 1.78 |
NOTES: To conserve space, we focus on the most accurate nonlinear forecasting models. The models are described in the text. Boldface indicates gains in accuracy relative to AR(4) benchmark model for real GDP growth.
Footnotes
** We thank Christiane Baumeister for providing access to the world and OECD industrial production data and Ryan Kellogg for providing the Michigan survey data on gasoline price expectations. We thank Domenico Giannone for providing the code generating the Bayesian VAR forecasts. We have benefited from discussions with Christiane Baumeister, Mike McCracken, James Hamilton, Ana Mar�a Herrera, Ryan Kellogg, Simone Manganelli, and Keith Sill. We thank David Finer and William Wu for assisting us in collecting some of the data. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of the Bank of Canada or of any other person associated with the Federal Reserve System or with the Bank of Canada. Correspondence to: Lutz Kilian, Department of Economics, 611 Tappan Street, Ann Arbor, MI 48109-1220, USA. Email: [email protected]. Return to text
a1 Bank of Canada Return to text
a2 University of Michigan, CEPR Return to text
a3 Federal Reserve Board Return to text
1. See, e.g., Kahn (1986), Davis and Kilian (2010). Return to text
2. See, e.g., Goldberg (1998), Allcott and Wozny (2010), Busse, Knittel and Zettelmeyer (2010), Kellogg (2010). Return to text
3. In related work, Dvir and Rogoff (2010) present formal evidence of a structural break in the process driving the annual real price of oil in 1973. Given this evidence of instability, combining pre- and post-1973 real oil price data is not a valid option. Return to text
4. For further discussion of the trade-offs between alternative oil price definitions from an economic point of view see Kilian and Vigfusson (2010b). Return to text
5. For a review of the relationship between the concepts of (strict) exogeneity and predictability in linear models see Cooley and LeRoy (1985). Return to text
6. Interestingly, the behavioral rationale for the net oil price increase measure applies equally to the nominal price of oil and the real price of oil. Although Hamilton (2003) applied this transformation to the nominal price of oil, several other studies have recently explored models that apply the same transformation to the real price of oil (see, e.g., Kilian and Vigfusson 2010a; Herrera, Lagalo and Wada 2010). Return to text
7. Hamilton (1994, p. 306) illustrates this point in the context of a model of stock prices and expected dividends. Return to text
8. In the former case, the pre-1974.1 observations are only used as pre-sample observations. Return to text
9. It can be shown that similar results hold for the CPI excluding energy, albeit not for the CPI excluding food and energy. Return to text
10. For an earlier exposition of the role of monetary factors in determining the price of oil see Barsky and Kilian (2002). Both Barsky and Kilian (2002) and Gillman and Nakov (2009) view the shifts in U.S. inflation in the early 1970s as caused by persistent changes in the growth rate of the money supply, but there are important differences in emphasis. Whereas Barsky and Kilian stress the real effects of unanticipated monetary expansions on real domestic output, on the demand for oil and hence on the real price of oil, Gillman and Nakov stress that the relative price of oil must not decline in response to a monetary expansion, necessitating a higher nominal price of oil, consistent with anecdotal evidence on OPEC price decisions (see, e.g., Kilian 2008b). These two explanations are complementary. Return to text
11. Although the U.K. has been exporting crude oil starting in the late 1970s, its share of petroleum exports is too low to consider the U.K. a commodity exporter (see Kilian, Rebucci and Spatafora 2009). Return to text
12. Even allowing for the possibility of data mining, this break remains statistically significant at the 5% level. Return to text
13. This situation is analogous to that of combining real exchange rate data for the pre- and post-Bretton Woods periods in studying the speed of mean reversion toward purchasing power parity. Clearly, the speed of adjustment toward purchasing power parity will differ if one of the adjustment channels is shut down, as was the case under the fixed exchange rate system, than when both prices and exchange rates are free to adjust as was the case under the floating rate system. Thus, regressions on long time spans of real exchange rate data produce average estimates that by construction are not informative about the speed of adjustment in the Bretton Woods system. Return to text
14. For a review of this literature see Barsky and Kilian (2002). Return to text
15. For example, the conjunction of rising growth in emerging Asia with unchanged growth in the U.S. all else equal would cause world GDP growth and hence the real price of oil to increase, but would imply a zero correlation between U.S. real GDP growth and changes in the real price of oil. Alternatively, slowing growth in Japan and Europe may offset rising growth in the U.S., keeping the real price of oil stable and implying a zero correlation of U.S. growth with changes in the real price of oil. This does not mean that there is no feedback from lagged U.S. real GDP. Indeed, with lower U.S. growth the increase in the real price of oil would have slowed in the first example and without offsetting U.S. growth the real price of oil would have dropped in the second example. Return to text
16. This index is constructed from ocean shipping freight rates. The idea of using fluctuations in shipping freight rates as indicators of shifts in the global real activity dates back to Isserlis (1938) and Tinbergen (1959). The panel of monthly freight-rate data underlying the global real activity index was collected manually from Drewry's Shipping Monthly using various issues since 1970. The data set is restricted to dry cargo rates. The earliest raw data are indices of iron ore, coal and grain shipping rates compiled by Drewry's. The remaining series are differentiated by cargo, route and ship size and may include in addition shipping rates for oilseeds, fertilizer and scrap metal. In the 1980s, there are about 15 different rates for each month; by 2000 that number rises to about 25; more recently that number has dropped to about 15. The index was constructed by extracting the common component in the nominal spot rates. The resulting nominal index is expressed in dollars per metric ton, deflated using the U.S. CPI and detrended to account for the secular decline in shipping rates. For this paper, this series has been extended based on the Baltic Exchange Dry Index, which is available from Bloomberg. The latter index, which is commonly discussed in the financial press, is essentially identical to the nominal index in Kilian (2009a), but only available since 1985. Return to text
17. Futures contracts are financial instruments that allow traders to lock in today a price at which to buy or sell a fixed quantity of the commodity at a predetermined date in the future. Futures contracts can be retraded between inception and maturity on a futures exchange such as the New York Mercantile Exchange (NYMEX). The NYMEX offers institutional features that allow traders to transact anonymously. These features reduce individual default risk and ensure homogeneity of the traded commodity, making the futures market a low-cost and liquid mechanism for hedging against and for speculating on oil price risks. The NYMEX light sweet crude contract is the most liquid and largest volume market for crude oil trading. Return to text
18. Because the Datastream data for the daily WTI spot price of oil used in Alquist and Kilian (2010) were discontinued, we rely instead on data from the Energy Information Administration. As a result the estimation window for the forecast comparison is somewhat shorter in some cases than in Alquist and Kilian (2010). Return to text
19. Although we have focused on the WTI price of oil, qualitatively similar results would also be obtained on the basis of Brent spot and Brent futures prices, which are available from the same data sources. The evaluation period for the Brent price series, however, is much shorter, casting doubt on the reliability of the results, which is why we focus on the WTI data. Return to text
20. Assuming perfect competition, no arbitrage, and no uncertainty, oil companies extract oil at a rate that equates: (1) the value today of selling the oil less the costs of extraction; (2) and the present value of owning the oil, which, given the model's assumptions, is discounted at the risk free rate. In competitive equilibrium, oil companies extract crude oil at the socially optimal rate. Return to text
21. Specifically, we use the 3-month, 6-month, and 12-month constant-maturity Treasury bill rates from the Federal Reserve Board's website http://federalreserve.gov/releases/H15/data.htm Return to text
22. The corresponding 5-year Michigan survey inflation expectations are only available back to mid-2004, making the Survey of Professional Forecasters (SPF) data the best available proxy for 5-year inflation expectations (after suitable scaling). These data were obtained from the Federal Reserve Bank of Philadelphia. Although the SPF data are quarterly, the data evolve so smoothly that assigning the same quarterly value to each month in that quarter is likely to provide a good approximation. Return to text
23. The Pesaran-Timmermann test for directional accuracy cannot be applied because there is no variability in the predicted sign, making it impossible to judge the statistical significance of the success ratio. Return to text
24. A question of obvious interest is how the survey predictor compares with the price of gasoline futures. That comparison is not feasible due to data limitations. The longest maturity in the NYMEX gasoline futures market is 3 years, and the 3-year futures contract only became available in 2007. Return to text
25. Such a finding would not necessarily imply that the real price of oil actually follows a random walk. It could merely reflect the fact that the bias-variance tradeoff favors parsimonious forecasting models in small samples. The local-to-zero asymptotic approximation of predictive models suggests that using the no-change forecast may lower the asymptotic MSPE even relative to the correctly specified non-random walk model, provided the local drift parameter governing the predictive relationship is close enough to zero (see, e.g., Inoue and Kilian (2004b), Clark and McCracken 2010). Return to text
26. The refiners' acquisition cost was extrapolated back to 1973.2 as in Barsky and Kilian (2002). Return to text
27. Because there is no reason to expect the limiting distribution of the DM test statistic to be pivotal in this context, we bootstrap the average loss differential instead. Return to text
28. Rolling regression forecasts would not protect us from structural change in any case. It has been shown that the presence of structural breaks at unknown points in the future invalidates the use of forecasting model rankings obtained in forecast accuracy comparisons whether one uses rolling or recursive regression forecasts (see Inoue and Kilian 2006). Return to text
29. It also outperforms the random walk model with drift in both of these dimensions, whether the drift is estimated recursively or as the average growth rate over the most recent h months. These results are not shown to conserve space. Return to text
30. The size problem of conventional tests of equal predictive accuracy gets worse, when the number of extra predictors under the alternative grows large relative to the sample size. This point has also been discussed in a much simpler context by Anatolyev (2007) who shows that modifying conventional test statistics for equal predictive accuracy may remove these size distortions. Related results can be found in Calhoun (2010) who shows that standard tests of equal predictive accuracy for nested models such as Clark and McCracken (2001) or Clark and West (2007) will choose the larger model too often when the smaller model is more accurate in out-of-sample forecasts and also proposes alternative asymptotic approximations based on many predictors. None of the remedies is directly applicable in the context of Table 12, however. Return to text
31. In related work, Ramey and Vine (2010) propose an alternative adjustment to the price of gasoline that reflects the time cost of queuing in gasoline markets during the 1970s. That adjustment as well serves to remove a nonlinearity in the transmission process. Both the nonlinearity postulated in Edelstein and Kilian (2009) and that postulated in Ramey and Vine (2010) is incompatible with the specific nonlinearity embodied in the models of Mork (1989) and Hamilton (1996, 2003). In fact, the aforementioned papers rely on linear regressions after adjusting the energy price data. Return to text
32. Some preliminary evidence on this question has been provided by Ravazzolo and Rothman (2010) and by Carlton (2010). It is not straightforward to compare their results to those in Tables 19 and 20, however. Not only is their analysis based on one-step-ahead real GDP growth forecasts from single-equation predictive models evaluated at the relevant forecasting horizon (rather than iterated forecasts from multivariate models), but it is based on a sample period that includes pre-1973 data. Return to text
33. The standard GARCH model is used for illustrative purposes. An alternative would be a GARCH-in-Mean model. Given that oil is only one of many assets handled by portfolio managers, however, it is not clear that the GARCH-in-Mean model for single-asset markets is appropriate in this context, while more general multivariate GARCH models are all but impossible to estimate reliably on the small samples available for our purposes (see, e.g., Bollerslev, Chou and Kroner 1992). Return to text
34. We deliberately focus on oil price volatility at the 1-month horizon. Although from an economic point of view volatility forecasting at longer horizons would be of great interest, the sparsity of options price data makes it difficult to extend the implied volatility approach to longer horizons. Likewise, GARCH volatility estimates quickly converge to the unconditional variance at longer horizons. Return to text
35. In rare cases, the relevant forecast horizon may be short enough for empirical analysis. For example, Kellogg (2010) makes the case that for the purpose of drilling oil wells in Texas, as opposed to Saudi Arabia, a forecast horizon of only 18 months is adequate. Even at that horizon, however, there are no oil-futures options price data that would allow the construction of implied volatility measures. Kellogg (2010) therefore converts the one-month volatility to 18-month volatilities based on the term structure of oil futures. That approach relies on the assumption that oil futures prices are reliable predictors of future oil prices. Return to text
36. A similar irreversible shift in OECD demand occurred after the oil price shocks of the 1970s when fuel oil was increasingly replaced by natural gas. The fuel oil market never recovered, even as the price of this fuel fell dramatically in the 1980s and 1990s (see Dargay and Gately 2010). Return to text
37. The threshold of $120 in this example follows from adjusting the cost estimates for shale oil production in Farrell and Brandt (2006) for the cumulative inflation rate since 2000. Return to text
38. Measures of risk of this type were first introduced by Fishburn (1977), Holthausen (1981), Artzner, Delbaen, Eber and Heath (1999), and Basak and Shapiro (2001) in the context of portfolio risk management and have become a standard tool in recent years (see, e.g., Engle and Brownlees 2010). For a general exposition of risk measures and risk management in a different context see Kilian and Manganelli (2007, 2008). Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text