
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1027, April 2011 --- Screen Reader
Version*
Housing Wealth and Consumption1
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
Housing wealth is about one half of household net worth, and consumption is a considerable fraction (about two thirds) of Gross Domestic Product in the United States. Empirically, movements in housing wealth are associated with movements in consumption in the same direction. This observation has led many economists, commentators and policy makers to study how housing wealth and consumption are linked together. A sizeable portion of the comovement between housing wealth and consumption reflects common factors driving both variables, rather than the "wealth effect" of the former on the latter; however, a growing body of evidence suggests that the comovement is larger in developed financial markets and in the presence of liquidity constraints.
Keywords: Borrowing constraints, consumption, consumption function, household budget
JEL classification: C2, E2, G1, R2
1. Introduction: What is Housing Wealth?
At the aggregate level, housing wealth measures the market value of all the residential assets located in a particular country. According to this definition, housing wealth of U.S. households at the end of 2008 was 25.4 trillion dollars. Housing wealth is about one half of total household net worth (which is 52.9 trillion dollars), and is larger than the Gross Domestic Product (14.4 trillion dollars). Moreover, since financial wealth is more unequally distributed than housing wealth, housing wealth accounts for almost two thirds of the total wealth of the median household. Table 1.1 lists the balance sheet of the household sector in the United States at the end of 2008 using data from the Flow of Funds Accounts of the United States (FOF), using a breakdown of total household assets that differentiates housing capital from other forms of wealth. A large fraction (80 percent) of housing wealth is made up by the stock of owner-occupied homes. The remaining 20 percent (residential real estate held by nonfarm noncorporate businesses) is made up by the rental housing stock.
Figure 1 plots household consumption expenditures in the United States along with wealth divided into housing wealth and non-housing wealth. The series have been converted in 2005 billions of dollars using the deflator for personal consumption expenditures. The stock of housing wealth is large and moves slowly over time, but it exhibits a sharp increase between 1997 and 2005, followed by a bust between 2005 and 2008: size and persistence explain why changes in housing wealth are potentially an important candidate for understanding trends and cycles in aggregate consumption expenditures.
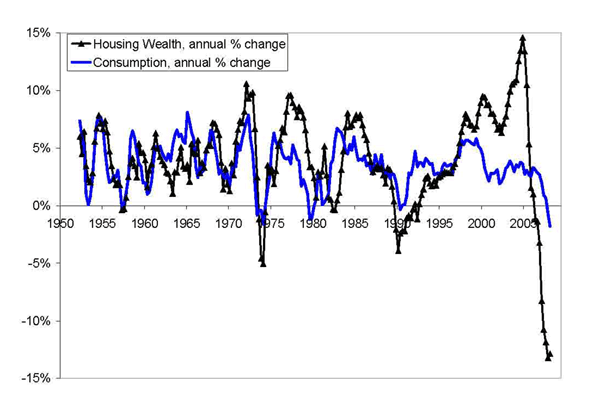
Figure 2 plots annual changes in housing wealth and personal consumption expenditures in the United States from 1952 to 2008. The two variables tend to move together in post-world war II U.S. history. Their contemporaneous correlation is 0.47. This correlation is larger than the correlation between consumption and the residual components of household wealth: for instance, the contemporaneous correlation between changes in financial wealth and consumption equals 0.38.
The comovement between housing wealth and consumption poses a challenging question for macroeconomists, policymakers and commentators. Do fluctuations in consumption reflect fluctuations in housing wealth, or are both variables determined by some other macroeconomic factor that moves them, such as technological change, movements in interest rates, or other factors that contribute to business cycle fluctuations?
Table 1.1: Composition of Household Wealth in the United States
| U.S. Households' Balance Sheet | 2008 Billion $ | FOF entry |
|---|---|---|
| A Assets | 67,134 | B.100:1 |
| B Real Estate (Owner-Occupied Homes) | 20,398 | B.100:3 |
| C Residential Real Estate of Noncorporate Business (Rented Homes) | 4,964 | B.103:4 |
| D Other Tangible Assets | 4,779 | B.100:2 less B.100:3 |
| E Financial Assets less Residential Real Estate of Noncorp. Business | 36,992 | B.100:8 less B.103:4 |
| F Liabilities | 14,216 | B.100:31 |
| G Household net worth | 52,917 | A |
| G Household net worth: Housing wealth | 25,362 | B+C |
| G Household net worth: Non housing wealth | 27,555 | D+E |
Figure 1.1: Housing Wealth, Consumption and Non-Housing Wealth in the United States From 1952 to 2008. The Series are Expressed in 2005 Billiions of Dollars.
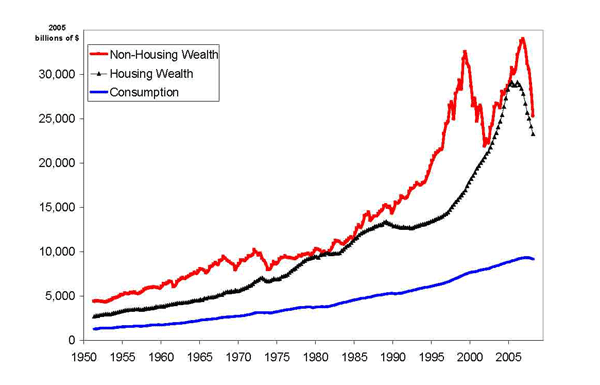
Figure 1.2: Annual Changes in Housing Wealth and Consumption in the U.S., From 1952 to 2008.
2. Housing Wealth and Consumption
A standard macroeconomics textbook contains a section presenting
the economy's consumption function. In this consumption function,
the standard determinants of consumption are wealth ![]() and
permanent income
and
permanent income ![]() , and the consumption function reads
as follows:
, and the consumption function reads
as follows:
| (1) |
where ![]() and
and ![]() measure
respectively the marginal propensity to spend out of wealth and
permanent income. This equation can be obtained as the solution to
a problem where individuals maximize utility over time given a set
of intertemporal trading opportunities, under very special
assumptions about the set of trading opportunities and about the
nature of the income process that the individual faces. An equation
such as (1) dates back in the history of
economic thought to at least Keynes, and was given prominence in
the seminal work of Milton Friedman and Franco Modigliani.
measure
respectively the marginal propensity to spend out of wealth and
permanent income. This equation can be obtained as the solution to
a problem where individuals maximize utility over time given a set
of intertemporal trading opportunities, under very special
assumptions about the set of trading opportunities and about the
nature of the income process that the individual faces. An equation
such as (1) dates back in the history of
economic thought to at least Keynes, and was given prominence in
the seminal work of Milton Friedman and Franco Modigliani.
When total wealth is broken down into housing ![]() and non-housing wealth
and non-housing wealth ![]() , a generalization
of the above equation that allows for different marginal
propensities to consume of housing and non-housing wealth can be
written as:
, a generalization
of the above equation that allows for different marginal
propensities to consume of housing and non-housing wealth can be
written as:
| (2) |
It is typical to interpret the coefficient ![]() in equation (2) as measuring the "housing
wealth effect" . At the basic level, in fact, this equation states
that if housing wealth were to change by, say, 1 dollar, consumption should change by
in equation (2) as measuring the "housing
wealth effect" . At the basic level, in fact, this equation states
that if housing wealth were to change by, say, 1 dollar, consumption should change by ![]() dollars. This equation provides the basis to think about the
connection between housing wealth and consumption. However, it is
entirely silent about the reasons why housing wealth moves. One
important caveat in interpreting the results from this equation is
that, while it is reasonable to interpret part of changes in the
two right-hand side variables as exogenous at the individual
level (bequests, lottery winnings, unemployment spells,
gentrification and deterioration of a neighborhood are somewhat
outside the control of the individual), the interpretation of this
equation at the aggregate level is more complicated, since,
to a large extent, all variables of equation (2) are jointly determined.
dollars. This equation provides the basis to think about the
connection between housing wealth and consumption. However, it is
entirely silent about the reasons why housing wealth moves. One
important caveat in interpreting the results from this equation is
that, while it is reasonable to interpret part of changes in the
two right-hand side variables as exogenous at the individual
level (bequests, lottery winnings, unemployment spells,
gentrification and deterioration of a neighborhood are somewhat
outside the control of the individual), the interpretation of this
equation at the aggregate level is more complicated, since,
to a large extent, all variables of equation (2) are jointly determined.
Movements in non-housing wealth, for instance, might either reflect a new view of future profits or occur because market participants apply a different set of discount factors to those expected profits, where the discount factors incorporate both risk-free interest rates and equity premiums. From a theoretical standpoint, these movements could have different effects on household spending. The same reasoning applies to housing wealth: changes in the value of the housing stock might reflect genuine shifts in tastes between housing and consumption goods, or could result from changes in availability of residential land, or from movements in sectoral technologies. It is reasonable to assume that all these changes could affect consumption, but their effects might differ.
The empirical literature (surveyed in the next section) grapples with the obvious identification problem of separating endogenous from exogenous movements in housing wealth. The theoretical literature studies instead the question of whether a housing wealth effect exists, what it means, and how to think about it.
3. The Theory
3.1 A Basic Model
To illustrate the ideas, this section considers a simple model
of consumption and housing choice. A household lives forever and
has preferences defined over current and future non-housing
consumption ![]() and housing services
and housing services ![]() That is, the household problem is defined by:
That is, the household problem is defined by:
| (3) |
where ![]() is the household discount factor, and
is the household discount factor, and
![]() is the expectation operator. This
preference specification is standard in models of household
behavior. Life-cycle and bequest considerations, endogenous labor
supply, non-separability between housing and consumption, and
housing tenure choice are ignored here. The household faces the
following budget constraint in any period
is the expectation operator. This
preference specification is standard in models of household
behavior. Life-cycle and bequest considerations, endogenous labor
supply, non-separability between housing and consumption, and
housing tenure choice are ignored here. The household faces the
following budget constraint in any period ![]() :
:
| (4) |
where ![]() is the price of housing,
is the price of housing, ![]() is non-housing wealth (for instance, shares in a firm or
holdings of government debt),
is non-housing wealth (for instance, shares in a firm or
holdings of government debt), ![]() is the return on
non-housing wealth,
is the return on
non-housing wealth, ![]() is labor income. In
equation
(4), the right-hand side measures
total resources available to the household at the end of the period
is labor income. In
equation
(4), the right-hand side measures
total resources available to the household at the end of the period
![]() These resources, in the absence of
portfolio adjustment costs, can be used for consumption, housing
wealth accumulation and non-housing wealth accumulation. Setting
aside general equilibrium considerations, one can treat
These resources, in the absence of
portfolio adjustment costs, can be used for consumption, housing
wealth accumulation and non-housing wealth accumulation. Setting
aside general equilibrium considerations, one can treat ![]()
![]() and
and ![]() as
exogenous (and possibly random), and assume that the household
chooses plans for consumption
as
exogenous (and possibly random), and assume that the household
chooses plans for consumption ![]() housing
housing
![]() and financial wealth
and financial wealth ![]() In this simple framework, random changes in
In this simple framework, random changes in ![]()
![]() and
and ![]() can proxy
respectively for housing wealth shocks, non-housing wealth shocks,
and income shocks. For given initial conditions, the solution to
the household problem can then be rearranged to express optimal
household consumption as a function of lagged non-housing wealth
can proxy
respectively for housing wealth shocks, non-housing wealth shocks,
and income shocks. For given initial conditions, the solution to
the household problem can then be rearranged to express optimal
household consumption as a function of lagged non-housing wealth
![]() , housing wealth
, housing wealth ![]() and innovations to
and innovations to ![]()
![]() and
and ![]() It has the interpretation of a
consumption function.
It has the interpretation of a
consumption function.
What are the implications for non-housing consumption of a shock
to housing wealth in this model? To gain some intuition, consider
the simplest possible case where the household, because of large
adjustment costs to housing, does not change house between two
consecutive periods:
![]() for every
for every ![]() .
It is easy to see that changes in
.
It is easy to see that changes in ![]() are
irrelevant for consumption behavior of this household, since
are
irrelevant for consumption behavior of this household, since
![]() in every period, so
that housing wealth disappears from the household budget
constraint. Intuitively, higher housing values (
in every period, so
that housing wealth disappears from the household budget
constraint. Intuitively, higher housing values (![]() ) result in higher housing costs (
) result in higher housing costs (![]() ) that exactly offset the housing wealth effect on
non-housing consumption; when
) that exactly offset the housing wealth effect on
non-housing consumption; when ![]() rises, wealth in
units of consumption increases, but, unless the individual changes
housing expenditures, housing wealth does not imply larger
consumption. This basic logic is what leads Buiter (2008) to assert
that housing wealth is not net wealth, unless individuals decrease
their housing consumption in response to housing price changes.
rises, wealth in
units of consumption increases, but, unless the individual changes
housing expenditures, housing wealth does not imply larger
consumption. This basic logic is what leads Buiter (2008) to assert
that housing wealth is not net wealth, unless individuals decrease
their housing consumption in response to housing price changes.
If the household can change housing consumption between two
periods (![]() needs not to equal
needs not to equal ![]() ), an additional effect kicks in. When house prices
rise, the so-called substitution effect will cause households to
reduce their demand for housing, and will free up resources that
can be spent on non-housing consumption. In this scenario, the
immediate effect of an increase in housing wealth is that of
stimulating consumption. The interpretation of the rise in
consumption, however, is subtle: part of the rise in consumption
does reflect the result that wealth, measured in units of
consumption, is larger, so that the individual will optimally
reallocate part of the larger wealth among all expenditure
categories. Part of the rise in consumption, instead, simply
reflects the economics of asset substitution: the household can now
achieve higher utility by consuming less housing and more
non-housing consumption goods than before.
), an additional effect kicks in. When house prices
rise, the so-called substitution effect will cause households to
reduce their demand for housing, and will free up resources that
can be spent on non-housing consumption. In this scenario, the
immediate effect of an increase in housing wealth is that of
stimulating consumption. The interpretation of the rise in
consumption, however, is subtle: part of the rise in consumption
does reflect the result that wealth, measured in units of
consumption, is larger, so that the individual will optimally
reallocate part of the larger wealth among all expenditure
categories. Part of the rise in consumption, instead, simply
reflects the economics of asset substitution: the household can now
achieve higher utility by consuming less housing and more
non-housing consumption goods than before.
3.2 Extensions
What is missing from the basic theory above?
- The simple theory above makes the extreme assumption that changes in the price of housing are purely exogenous. To see why modifying this assumption might change the results, consider the case where changes in the price of housing are the consequence of a shift in tastes between non-housing and housing goods: for instance, individuals might decide that they prefer to live in larger and nicer homes rather than dining out: under this assumption, it is possible that increases in the price of housing are associated with lower consumption, since the change in house prices is the consequence of a shift in preferences away from consumption goods. Empirically, evidence in favor of a mechanism of this kind comes from the observation (at least in the United States) that movements in housing prices are positively correlated with movements in housing investment: this evidence would seem to support the idea that movements in housing prices (and wealth) are the consequence of shifts in housing demand, rather than housing supply.
- Another consideration that is missing from the basic story is the presence of borrowing constraints. The structure of financial markets in many developed economies implies that households have easy access to housing wealth through second mortgages, home equity loans, or home equity lines of credit. If liquidity-constrained households - who are believed to have a high marginal propensity to spend on average - can borrow more whenever their housing wealth rises, this channel is likely to lead to a larger correlation between movements in housing wealth and movements in aggregate consumption. Moreover, one can expect larger aggregate effects from changes in housing wealth since housing wealth is more evenly distributed across the population than non-housing wealth: if relatively poor people have higher than average propensity to consume, the aggregate consumption response to changes in housing wealth might be larger than otherwise.
- The basic model also sidesteps life-cycle and housing tenure considerations. The representative household of the model displays a profile of housing consumption that is constant over time. In reality, the way consumption is connected to movements in housing wealth should also depend on whether individuals expect to modify their housing consumption in the future. Cross-sectional data show that housing wealth typically increases over the life cycle, before flattening out at a relatively old age. This is true both at the extensive margin (home ownership rates increase with age) and at the intensive margin (the average size of owner-occupied houses increases with age). Taking these elements into consideration, one should expect that life-cycle considerations should imply a negative response of consumption to increases in aggregate housing prices, since - to the extent that renters plan to become homeowners at some point of their life, or homeowners plan to move to larger homes - higher housing prices require larger savings than otherwise if individuals are planning to buy a larger home.
- A final aspect to consider is how persistent changes in housing wealth are relative to changes in other forms of wealth. Historically, changes in housing returns have been more persistent than changes in the return to, say, stockmarket wealth. Households consumption might respond more to a given size change in housing wealth if this change is not expected to reverse quickly.
3.3 Taking Stock
A message from the basic theory is that, after solving the household intertemporal optimization problem, one can derive an aggregate consumption function where consumption is expressed as a function of income and wealth, and where the marginal propensity to consume out of housing wealth is positive or negative depending on the underlying characteristics of the economy.
In a more realistic setting, however, especially when the goal is to model the economy as a whole (rather than the behavior of a single economic agent), one should assume that wealth is endogenous, and that its fluctuations are driven by current or expected movements in technology, tastes, taxes, or some other unidentified economic fundamentals. These fundamentals, in turn, may affect at the same time both consumption and wealth itself, thus making any statement about links from wealth to consumption (or vice versa) hard to interpret.
Yet central bankers, practitioners and policymakers routinely think of movements in wealth as exogenous, mostly because these movements are hard to predict or explain based on movements in readily available observable variables that one can regard as purely exogenous.
4. Empirical Studies
4.1 The Conventional Wisdom
A simple regression on quarterly United States data for the period 1952.I-2008.IV of:
![]()
where ![]() ,
, ![]() and
and ![]() measure
respectively consumption, housing wealth and non-housing wealth,
and
measure
respectively consumption, housing wealth and non-housing wealth,
and ![]() is the first difference operator,
yields the following coefficients (standard errors below):
is the first difference operator,
yields the following coefficients (standard errors below):
More sophisticated regressions yield similar results, at least qualitatively if not quantitatively. This simple regression has the virtue of being simple, easy to estimate, replicable and straightforward to interpret. According to this regression, the elasticity of consumption to housing wealth is 0.14, after controlling for movements in non-housing wealth (the elasticity of consumption to non-housing wealth is lower, at 0.06). These estimates are more often converted into dollar-to-dollar estimates using the fact that, in the sample in question, the average ratio of housing wealth to annual consumption is about 2.3, and the average ratio of non-housing wealth to annual consumption is about 2.75. A one dollar increase in housing wealth then generates an increase in annualized consumption of about 6 cents, and one dollar increase in non-housing wealth generates an increase in consumption of about 2 cents.
The results of this simple regression are the basis for a series of wisdoms about wealth effects and the basis for thinking about housing wealth and consumption. In particular, the larger sensitivity of consumption to housing wealth is one of the many reasons why policymakers might be more worried about changes in housing than non-housing wealth.
4.2 Studies Based on Aggregate Time-Series Data
Perhaps one of the most prominent studies of the link between housing wealth and consumption is the FRB/US model, which is one of the econometric models of the U.S. economy used by the Federal Reserve. One of the model blocks describes household consumption behavior as a function of total wealth and its composition. This model predicts, among other things, a marginal propensity to consume out of net tangible assets (housing wealth and consumer durables less home mortgages) which ranges between 5 and 10 cents on the dollar (see for instance Brayton and Tinsley, 1996).
Several studies have reviewed the literature and provided additional estimates of the so-called housing wealth effect. The broad consensus from the literature based on time-series data is not very different from the FRB/US model, with some studies finding larger elasticities for housing wealth, and some other studies finding the opposite. Poterba (2000) surveys a variety of estimates from the literature.
More recent studies corroborate the findings from the empirical literature of the 1990s. Carroll, Otsuka and Slacalek (2006) propose a time-series based method that exploits the sluggishness of consumption growth to distinguish between immediate and eventual wealth effects. Using U.S. data, they estimate that the immediate (next-quarter) marginal propensity to consume from a $1 change in housing wealth is about 2 cents, with an eventual effect around 9 cents, substantially larger than the effect of shocks to financial wealth.
Case, Quigley and Shiller (2005) find a strong correlation between aggregate house prices and aggregate consumption in a panel of developed countries. According to the central estimates, a 1 percent increase in housing wealth increases consumption by roughly 0.11 percent in the international panel. For a panel of U.S. states, an updated version of their 2005 paper (Case, Quigley and Shiller, 2011) reports elasticities of consumption to housing wealth that range from 0.03 to 0.18, with a central estimate of 0.08.
The main problem with studies based on aggregate data is that such data do not rule out alternative explanations for the time series correlation: either indirect wealth effects or reverse causation running from changes in household saving to changes in wealth. Iacoviello and Neri (2010) address this problem in a structural equilibrium model where both consumption and housing wealth are endogenous, and are driven by movements in technology, preferences, monetary policy. They show that their model quantitatively replicates the positive correlation in the data between consumption growth and housing wealth growth. The bulk of this correlation simply captures common factors that move the two variables in the same direction, such as shifts in preferences, interest rates, or technology. However, a non-negligible portion of this correlation reflects the contribution of liquidity constraints. This result echoes the conclusions of Muellbauer and Murphy (2008), who argue that housing collateral and downpayment constraints are the key to understanding the role of house-price variations in explaining medium-term consumption fluctuations.
4.3 Studies Based on Micro Data
A growing literature has used household-level data to connect movements in consumption and movements in housing wealth. One of the main questions in this literature is to study how households respond to changes in the value of their housing wealth. A central issue concerns how to identify movements in housing wealth that are orthogonal to other factors that might also affect consumption.
Campbell and Cocco (2007) study micro data from the UK Family Expenditure Survey from 1988-2000. They use repeated cross-sections of household expenditure data and regional home price information to estimate a small, positive consumption response to home prices for young homeowners, and a large positive response for old homeowners. Using mean home values and consumption as reported in their paper, this translates into marginal propensities to consume out of housing wealth of 0.06 for young homeowners, and 0.11 for old homeowners.
Mian and Sufi (2009) investigate how existing homeowners respond to the rising value of their home equity, which they refer to as the home equity-based borrowing channel. They use land topography-based housing supply elasticities in order to identify exogenous variations in house price growth across different geographical areas and individual-level data on homeowner debt and defaults from 1997 to 2008. They show that existing homeowners increase their borrowing significantly in response to changes in their home equity, and use the extra borrowing mainly for real outlays, such as consumption or home improvements.
5 Conclusions
Housing wealth is a major component of household wealth. Housing wealth is linked to non-housing consumption through the logic and algebra of the budget constraint: by moving to a smaller or larger house, a household can free up or use resources that would otherwise go into non-housing consumption or other forms of saving. Empirically, housing wealth and consumption tend to move together: this could happen because some third factor moves both variables, or because there is a more direct effect going from one variable to the other. Studies based on time-series data, on panel data and on more detailed, recent micro data point suggest that a considerable portion of the effect of housing wealth on consumption reflects the influence of changes in housing wealth on borrowing against such wealth.
References
Brayton, Flint, and Peter Tinsley (1996) 'A guide to frb/us: a macroeconomic model of the united
states.' Finance and Economics Discussion Series 96-42, Board of Governors of the Federal Reserve System (U.S.), October
Buiter, Willem H (2008) 'Housing wealth isn't wealth.' CEPR Discussion Papers 6920, C.E.P.R. Discussion Papers, July
Campbell, John Y., and Joao F. Cocco (2007) 'How do house prices affect consumption? evidence from micro data.' Journal of Monetary Economics 54(3), 591–621
Carroll, Christopher D., Misuzu Otsuka, and Jirka Slacalek (2006) 'How large is the housing wealth effect? a new approach.' NBER Working Papers 12746, National Bureau of Economic Research, Inc, December
Case, Karl E., John M. Quigley, and Robert J. Shiller (2005) 'Comparing wealth effects: The stock
market versus the housing market.' Advances in Macroeconomics 5(1), 1235–1235
____(2011) 'Wealth effects revisited 1978-2009.' NBER Working Papers 16848, National Bureau of
Economic Research, Inc, March
Davis, Morris A., and Jonathan Heathcote (2007) 'The price and quantity of residential land in the united states.' Journal of Monetary Economics 54(8), 2595–2620
Davis, Morris A., and Michael G. Palumbo (2001) 'A primer on the economics and time series econometrics of wealth effects.' Finance and Economics Discussion Series 2001-09, Board of Governors of the Federal Reserve System (U.S.)
Iacoviello, Matteo (2005) 'House prices, borrowing constraints, and monetary policy in the business cycle.' American Economic Review 95(3), 739–764
Iacoviello, Matteo, and Stefano Neri (2010) 'Housing market spillovers: Evidence from an estimated dsge model.' American Economic Journal: Macroeconomics 2(2), 125–64
Mian, Atif R., and Amir Su… (2009) 'House prices, home equity-based borrowing, and the u.s. house-hold leverage crisis.' NBER Working Papers 15283, National Bureau of Economic Research, Inc, August
Muellbauer, John, and Anthony Murphy (2008) 'Housing markets and the economy: the assessment.' Oxford Review of Economic Policy 24(1), 1–33
Poterba, James M. (2000) 'Stock market wealth and consumption.' Journal of Economic Perspectives 14(2), 99–118
Footnotes
1. This paper was written for the "International Encyclopedia of Housing and Home," to be published by Elsevier in 2011. I thank Andrea Raffo, Matteo Cacciatore, Morris Davis and Kim Kyung-Hwan for helpful discussions. The views in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
2. Matteo Iacoviello, Division of International Finance, Federal Reserve Board, 20th and C St. NW, Washington, DC 20551. Email: [email protected]. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text