
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1035, November 2011--- Screen Reader
Version*
The Variance Risk Premium Around the World
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
This paper investigates the variance risk premium in an international setting. First, I provide new evidence on the basic stylized facts traditionally documented for the US. I show that while the variance premiums in several other countries are, on average, positive and display significant time variation, they do not predict local equity returns. Then, I extend the domestic model in Bollerslev, Tauchen and Zhou (2009) to an international setting. In light of the qualitative implications of my model, I provide empirical evidence that the US variance premium outperforms that of all other countries in predicting local and foreign equity returns.
JEL classification:JEL Classification: E44, F36, G12, G13, G15.
Keywords:Variance risk premium, economic uncertainty, interdependence, international integration, comovements, return predictability
1 Introduction
Traditional asset pricing models have mainly focused on characterizing the reward for equity risk. However, such models typically fail to capture the reward for bearing variance risk. The variance risk premium is formally defined as the difference between the risk neutral and the physical expectation of the total return variation. It can be estimated using model-free measures as the difference between the option implied variance and the expected realized variance. The observed variance premium in the US is large and varies significantly over time. In order to generate a time-varying variance premium, standard asset pricing models have been adjusted in different ways. One strand of the literature, and the one that will be followed in this paper, links the variance risk premium to macroeconomic uncertainty. This strand follows the intuition behind the long-run risk model in Bansal and Yaron (2004) (BY hereafter), and the idea that agents have a preference for an early resolution of uncertainty in Bansal et. al. (2005). Extending BY's model, Bollerslev, Tauchen and Zhou (2009) (BTZ hereafter) show that the variance premium predicts equity returns; an implication for which they find empirical evidence for the US. An alternative strand of the literature relates the variance premium to agents' attitudes towards non-normalities in the distribution of returns. In Bakshi and Madam (2006), for example, the variance risk premium is explained by the desire of risk averse agents to buy protection against extreme events. In a similar vein, Bekaert and Engstrom (2010), Todorov (2010), and Gabaix (2009), using different methodologies, focus on the interplay between returns, risk aversion and extreme events to explain many asset pricing regularities, including the variance risk premium.
Existing work, both theoretical and empirical, has predominantly focused on the US market. This paper adds to the literature by extending the variance premium analysis to an international setting. The contribution is threefold. First, I provide new evidence on the basic stylized facts related to the variance premium for a total of eight countries. I show that while the variance premiums display significant time variation in all countries analyzed, the local return predictability does not hold internationally. Then, I extend the domestic model in Bollerslev, Tauchen and Zhou (2009) to an international setting. My model links the variance premium to local and aggregate macroeconomic uncertainty and yields a qualitative explanation for the local predictability puzzle. Finally, I provide new empirical evidence to investigate the main qualitative implications of my model. The empirical evidence suggests that the US variance premium predicts the equity returns in the US as well as in any other country in the sample. In addition, the evidence also suggest that the US variance premium plays a key role in predicting the variance premium correlations as well as the equity return correlations across countries. The different parts and contributions of the paper are discussed in more detail in turn.
In the first part, I investigate the main stylized facts related to the variance premium previously documented for the US in an international setting. In particular, I investigate whether the time-varying and positive nature of the variance premium as well as its capacity to predict returns holds internationally. In order to do so, I collect data for the US, Germany, UK, Japan, Switzerland, The Netherlands, Belgium, and France for the sample period between 2000 and 2009. As it has become standard in the literature, the variance premiums for all countries are estimated using model-free measures of the expected variance of returns. Thus, the (squared of the) model-free implied volatility (IV) index for each equity market approximates the expectation of the total return variation under the risk neutral measure (Carr and Madan, (1998), and Britten-Jones and Neuberger, (2000)) while the expectation under the physical measure is approximated by a conditional forecast of the actual realized variance.
The single-country evidence shows that the variance premiums display significant time variation and are, on average, positive for all countries in the sample. This international evidence is in line with previous findings for the US.1 However, I show that the local variance premium can predict local equity returns only in the US and Belgium. For any other country analyzed, the evidence suggests that the local variance premiums cannot predict local equity returns. This finding suggests a puzzle that cannot be solved by the existing domestic models where the variance premium implicitly explains the variation in the local equity premium. 2
The strictly domestic nature of the existing models motivates the theoretical contribution of this paper. In the second part, I propose a model to investigate the role of the variance premium in explaining the interactions across international equity and option markets. The model is a two-country extension of that in BTZ and extends the intuition that agents have a preference for an early resolution of uncertainty to an international setting. The macroeconomic uncertainty is characterized in my model by the dynamics of the consumption growth volatility of each country and is allowed to be transmitted across countries given a unique representative agent endowed with recursive preferences. In such a setting, the shocks to macroeconomic uncertainty in any country characterize the variance premium in all countries. In particular, the variance premiums of the two countries reveal the volatility of volatility of consumption generated in both countries. Given that changes in the volatility of volatility also explain a portion of the total risk premiums of any country, the model not only implies that variance risk is priced but also provides the intuition for the potential role of the variance premium of any country in predicting local and foreign equity returns. In other words, agents demand a reward for the existing local and foreign sources of risk (i.e., the volatility and the volatility of volatility of consumption). Although this uncertainty transmission mechanism is bidirectional, the model explicitly features a leader economy. The consumption process of this leader economy is entirely driven by local shocks. However, the shocks of the leader country consumption process can be partially transmitted to a second country, the follower.
My model yields several qualitative implications for the interactions across international equity and option markets that explain the inability of the variance premium to predict local equity returns in countries other than the US. The first main implication of my model is that the variance premium in each country is uniquely characterized by the volatility of volatility of consumption (VoV) of the two countries. The load of each country's VoV increases with the relative size of its economy and the degree of economic dependence among countries (leader-follower relation). As a consequence of having common components, the variance premiums are highly correlated across countries; and the cross-country variance premium correlation is mainly driven by the VoV generated in the leader country. Thus, the leader country variance premium plays the key role in predicting the variance premium correlations across countries. The second main implication of my model is that the VoV of the two countries also load on all countries' equity premiums. Similar to the implication for the variance premiums, the load of VoV increases with the relative size of each economy and the implied correlation of the consumption processes. This second implication links the variance premium to all countries' equity premiums. As a consequence, this implication explains the possibility that the variance premium of a leader economy predicts other countries' equity returns which in turn implies that the leader country variance premium plays the key role in predicting equity return correlations across countries.
The third contribution of this paper is that it provides new empirical evidence on the two main qualitative implications of my model. That is, I investigate the fundamental linkages between the variance premiums across countries as well as the interplay between the variance premiums and international equity returns. To do so, I first provide evidence that the variance premiums are highly correlated across countries as suggested by the common loads of volatility of volatility in the variance premiums suggested by my model. Then, I investigate the second main implication of my model which suggests that the leader country variance premium plays the key role in predicting local and foreign equity returns. On the one hand, I confront the evidence on the poor performance of the local variance premiums in predicting local returns for countries other than the US. Thus, I provide new evidence that only the US variance premium predicts equity returns for all countries in the sample except perhaps for Japan. The predictive power of the US variance premium over international equity returns holds for horizons between 1 to 6 months, and reaches its maximum at the quarterly horizon. In addition, I show that the US variance premium outperforms all other countries' variance premiums in predicting local and foreign equity returns. On the other hand, I provide evidence that international equity returns tend to comove more intensely following episodes of increasing US variance premium. The predictive power of the variance premium for both equity returns and cross-country return correlations holds for horizons between 3 and 6 months and is additional to that of traditional (local or US) variables such as the term spread and the dividend yield.
The remainder of the paper is organized as follows: Section 2 introduces the main definitions and data used throughout the paper. Section 3 provides international single-country evidence on the regularities related to the variance premium. Section 4 introduces the international consumption based general equilibrium model and analyzes its qualitative implications. Section 5 investigates the empirical evidence in light of the implications of my model. Finally, Section 6 concludes.
2 Data and Definitions
In this section, I introduce the data used to estimate the
monthly variance premiums for the following countries: US, Germany,
Japan, UK, Switzerland, The Netherlands, Belgium and France. The
variance premium is defined as the difference between the risk
neutral and the physical expectation of the market return variation
between time ![]() and one month forward
and one month forward ![]() for each market. It is estimated, as it has become standard in the
related literature, using model-free measures for the expectations
of the total return variation.
for each market. It is estimated, as it has become standard in the
related literature, using model-free measures for the expectations
of the total return variation.
I approximate the risk neutral expectation of the market return variation as (the square of) the model-free options implied volatility (IV) index for each market. The methodology for the IV index was initially proposed by Carr and Madan (1998) and Britten-Jones and Neuberger (2000). The IV index has shown to provide a much better approximation to the expected risk neutral return variation than previously Black-Scholes based measures (Bollerslev, Gibson and Zhou, (2011)). The IV indices are constructed from a portfolio of European calls where the underlying is a representative market index for each country as in
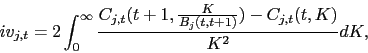
where ![]() are the prices of calls with strikes
from zero to infinity, and
are the prices of calls with strikes
from zero to infinity, and ![]() are the
local prices of zero-coupon bonds with one month ahead maturity.
are the
local prices of zero-coupon bonds with one month ahead maturity.
The availability of the IV index for the countries analyzed is limited by the recent development of their option markets. The index was first reported for the US by the Chicago Board Options Exchange (CBOE), the VIX, in 1993 (with data from 1990). The VIX was adapted to the model-free methodology in 2003, and was then called the New-VIX. An index for the German market, the VDAX, was released by the German Stock Exchange (Deutsche Beurse and Goldman Sachs) in 1994 (with data from 1992). The Swiss Exchange introduced the index for Switzerland, the VSMI, in 2005. Currently, Eurex estimates and reports both VDAX and VSMI following a unified New-VIX methodology. The Center for the Study of Finance and Insurance (CSFI) at Osaka University launched an index for Japan, the VXJ, with data from 1995. Finally, in 2007, Euronext announced IV indices for France (VCAC), Belgium (VBEL), the UK (VFTSE, in partnership with FTSE), and The Netherlands (VAEX) with data from 2000.3 Considering the data restrictions for the European markets, the empirical analysis in this paper is centered on the sample period between 2000 and 2009.
In order to construct the variance premiums, an expectation of the total return variation under the physical measure has to be estimated. I estimate a measure based on the first order autoregressive forecast of the total realized return variation or realized variance from the following equation:
where the realized variance is calculated summing the squared daily equity returns for each market as in
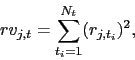
where ![]() are daily local returns within
month
are daily local returns within
month ![]() . I rely on daily returns since data at a
higher frequency are not available for all countries in the
sample.4
. I rely on daily returns since data at a
higher frequency are not available for all countries in the
sample.4
In order to make the results comparable to those in the
literature, and as a preventive solution to the possible
underperformance of this benchmark measure, all results are checked
using three alternative approximations of the expected realized
variance. In the first measure, I use the martingale measure where
the expected realized variance is approximated as the current
realized variance
![]() . In the second one, I
estimate a forecast of the realized variance that includes the
local IV index as in the following equation:
. In the second one, I
estimate a forecast of the realized variance that includes the
local IV index as in the following equation:
Finally, in the third one, I estimate a forecast of the realized variance that includes the range-based variance for each country as in
where ![]() is the range-based variance
calculated as
is the range-based variance
calculated as
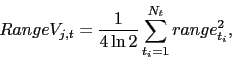
where ![]() is the daily difference between
the highest and the lowest price of the index.5, 6
is the daily difference between
the highest and the lowest price of the index.5, 6
In order to estimate the variance premiums, the monthly data (end of the month) for the IV indices as well as the daily returns for the underlying index returns for all countries are obtained from Datastream. All returns are expressed in local currencies.7 In order to obtain the local excess returns to investigate the return predictability, I consider the 3-months T-bill rates for each country. Finally, I also control for two variables traditionally used to predict excess returns, the dividend yield and the term spread, calculated as the difference between the 1 year T-bill and the 3-months T-bill rate for each country. The T-bill rates as well as the dividend yields for all countries are also obtained from Datastream.
3 Variance Premium: Single-Country Evidence
In this section, I investigate whether the stylized facts observed for the variance premium in the US also hold internationally. In a first step, I analyze the positive and time-varying nature of the variance premium. Then, I investigate the ability of the local variance premium in predicting equity returns in each country separately.
In order to get an idea of the magnitude and the time-varying
nature of the variance premiums, Figure 1 displays the
(benchmark) time series for all countries considered. The main
statistics of these series are summarized in Table 1. This table
also displays the IV indices and their underlying
equity market indices for each country. The volatility premiums [
![]() ] are also
included in the table in order to visualize the magnitude of the
premiums in annual percentages. The average volatility premium
ranges between 1.7% for Belgium to 3.8% for Japan. In order to get
an intuitive idea of these magnitudes in terms of one month
maturity at-the-money put options, the 3.8% volatility premium in
Japan translates into a price difference of 18% in a Black Scholes
world. That is, one month at-the-money put options priced at 26.75%
implied volatility, which is the average IV index for Japan, are
18% more expensive than the same options priced at 22.87% implied
volatility, which is the average realized volatility for this
country in this sample.
] are also
included in the table in order to visualize the magnitude of the
premiums in annual percentages. The average volatility premium
ranges between 1.7% for Belgium to 3.8% for Japan. In order to get
an intuitive idea of these magnitudes in terms of one month
maturity at-the-money put options, the 3.8% volatility premium in
Japan translates into a price difference of 18% in a Black Scholes
world. That is, one month at-the-money put options priced at 26.75%
implied volatility, which is the average IV index for Japan, are
18% more expensive than the same options priced at 22.87% implied
volatility, which is the average realized volatility for this
country in this sample.
Figure 1: Estimated (Model-Free) Variance Premiums
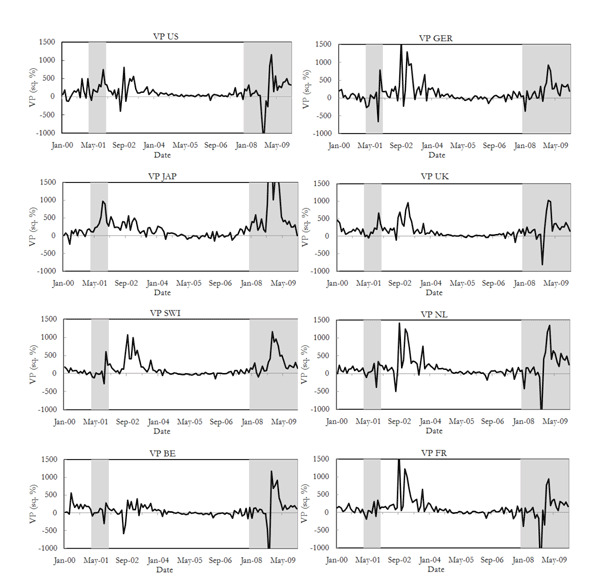
The figure shows the Variance Premiums vpt in annual squared percentages for the eight countries in the sample (see Table 1) for the sample period between 2000 and 2009. The variance premium in each country is estimated as ![]() , where the benchmark specification for the expected realize variance is its first order autoregressive forecast. The shaded areas represent NBER recession episodes for the US.
, where the benchmark specification for the expected realize variance is its first order autoregressive forecast. The shaded areas represent NBER recession episodes for the US.
Table 1:Summary Statistics. Variance (And Volatility) Premiums
|
The table reports the average volatility premiums (in annual percentages) calculated monthly as volpj,t=ivj,t-Et(rvj,t+1) for the eight countries considered for the sample period 2000 to 2009. It also reports the summary statistics for the variance premiums (in annual squared percentages). The variance premium in each country is estimated as , where the benchmark specification for the expected realized variance is its first order autoregressive forecast. AR(1) is the estimated first-order autoregressive coefficient of the variance premium. *, ** and *** represent significance at the standard 1, 5 and 10% confidence levels, both for the significance of the mean and the AR(1) coefficient. For the average volatility and variance premium, I perform a standard mean test and correct the standard deviations using Newey-West with 12 lags (given the evidence on the significance of the autoregressive coefficient). The standard errors to assess the significance of the AR(1) coefficient are also corrected using the Newey-West HAC (Heteroskedasticity and autocorrelation correction) with 12 monthly lags (Newey and West, 1987).
The information in Table 1 and Figure 1 suggests that the variance premiums display significant time variation. In particular, the premiums show several episodes of high volatility and notorious spikes around the same periods of time which translate into large Kurtosis for all series. The first high-variance-premiums episode occurs around the end of the technological boom in 2000. A second episode occurs at the end of 2002. This second episode coincides with the high macroeconomic uncertainty reported in the second semester of 2002 in the US (first semester of 2003 for Germany. An episode also related to the corporate accounting scandals around those years). Finally, the most notorious variance premium spikes occur around the recent subprime crisis. Not surprisingly, the minimum and maximum values for all series, except for Germany, occur in the last quarter of 2008. For Japan, for example, the variance premium reached 3,398.2 (annual percentage squared) in October 2008.8
In order to assess the positive nature of the average variance premiums, Figure 2 summarizes the results for a test on the significance of the mean variance premium for all countries. This figure displays the average variance premiums and their respective confidence intervals for the four alternative measures introduced in Section 2. The evidence suggests that the average variance premium is positive and significant for all countries analyzed and all alternative measures considered, except perhaps when the martingale measure is used.9 This evidence supports the idea that agents also price market volatility in countries other than the US. These results are new evidence that extends that found for the US by Britten-Jones and Neuberger (2000), Jiang and Tian (2005), Bakshi and Madan (2006), Carr and Wu (2009), Todorov (2010), Bollerslev, Gibson and Zhou (2011), Bekaert and Engstrom (2010), and BTZ, among others.10 This paper is, to the best of my knowledge, the first to show that these stylized facts also hold in other developed markets. 11
Figure 2: Significance of the Average Variance Premiums. Alternative Specifications
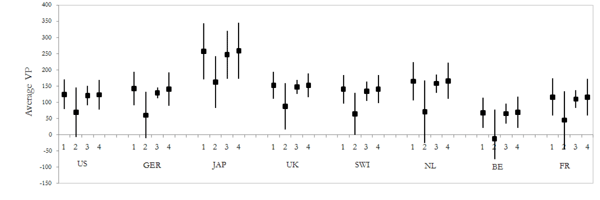
The figure reports the average variance premiums for each country for 4 alternative specifications (in bold squares) for the sample period 2000 to 2009. For each measure and each country, I also report the 95% confidence intervals for the significance of the average variance premium. Measure 1 is the benchmark measure (AR(1)) where the expected realized variance is estimated as its first order autoregressive forecast. Measure 2 assumes that the expectation of the volatility under the physical measure is well-proxied by rvt or martingale assumption. In measure 3, the expected realized variance is estimated from the regression that includes the IV indices as in ![]() . Finally, in measure 4, the expected realized variance is estimated from a regression that includes the monthly range-based variance for each country as in
. Finally, in measure 4, the expected realized variance is estimated from a regression that includes the monthly range-based variance for each country as in ![]() , where RangeVj,t is the range based variance calculated as
, where RangeVj,t is the range based variance calculated as ![]() , where
, where ![]() is the daily difference between he highest and the lowest price of the index.
is the daily difference between he highest and the lowest price of the index.
In the rest of this section, I test another US-based stylized fact, namely that the local variance premium predicts local equity returns.12 Given the new evidence presented above on the existence of a volatility premium in all countries analyzed, I investigate the role of the variance premium in predicting returns for all countries in the sample. To do so, Figure 3 reports the estimation results for the following regressions:
where
![]() represents future
compounded annualized excess returns
represents future
compounded annualized excess returns ![]() -months ahead,
-months ahead,
![]() is the local dividend yield, and
is the local dividend yield, and
![]() is the local term spread.
is the local term spread.
Figure 3: The Role of the Local Variance Premium in Predicting Local Equity Returns

The figure reports the estimated coefficients ![]() in the following regressions:
in the following regressions:
![]() where
where ![]() are h-months (compounded annualized) excess returns, dyj,t are the local dividend yields and tsj,t are the local term spreads calculated as the difference between the 1 year T-bill and the 3 months t-bill rate. I consider monthly forecasting horizons up to 12 months. The shaded areas represent the 95% confidence intervals for the Newey-West corrected standard errors with a number of lags l = max{2h, 12}. The figure also reports in the secondary axis the R2 for each regression. In order to separately identify the predictive power of the variance premium, the R2 and reported for regression in which only the variance premiums are considered as in
are h-months (compounded annualized) excess returns, dyj,t are the local dividend yields and tsj,t are the local term spreads calculated as the difference between the 1 year T-bill and the 3 months t-bill rate. I consider monthly forecasting horizons up to 12 months. The shaded areas represent the 95% confidence intervals for the Newey-West corrected standard errors with a number of lags l = max{2h, 12}. The figure also reports in the secondary axis the R2 for each regression. In order to separately identify the predictive power of the variance premium, the R2 and reported for regression in which only the variance premiums are considered as in ![]() .
.
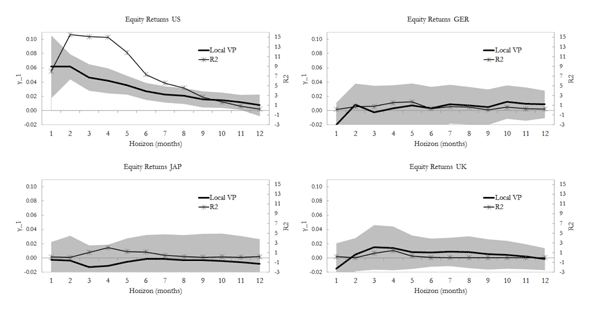
The evidence in Figure 3 confirms most of the results previously found in the literature for the US. That is, the US variance premium predicts returns specially for horizons between 3 to 6 months. In fact, the evidence shows that the US variance premium explains up 15% of the total variation in future equity returns at the quarterly frequency. The predictive power, as well as the coefficient of the variance premium in these regressions, follows a hump-shaped pattern and becomes irrelevant for horizons around one year.
However, the evidence suggests that the local variance premium plays a modest or insignificant role in predicting returns in any other country analyzed except perhaps for Belgium. For example, the results show that for Germany, Japan, the UK and the Netherlands, the R2 is modest and hardly ever above 1%. Not surprisingly, for these countries, the variance premium does not predict equity returns for any horizon considered. For Belgium the R2 is as high as 10% for the one-month horizon; and the predictive power of the variance premium follows a linearly decreasing pattern as the horizon increases.13 Finally, for France, although the R2 are also modest, the predictability follows a pattern similar to that found for the US. In the case of France however, both the R2 and the variance premium coefficient are only significant at the 2-months horizon.14
In sum, although this is, to the best of my knowledge, the first paper to present evidence on the role of the variance premium in predicting returns for countries other than the US, the single-country evidence is puzzling. My findings are on the one hand consistent with the existence of time-varying variance premiums for a large sample of countries. On the other hand, they suggests that the variance premium does not predict returns in countries other than the US. The concurrence of these two findings cannot be explained by the existing domestic models where the variance premium implicitly explains the variation in the local equity premium. This puzzling evidence is nonetheless the motivation for the international general equilibrium model introduced in the following section. The model proposed is able to qualitatively explain the poor evidence for the role of the local variance premium in predicting returns outside the US. This model suggests that the variance premium of a leader country plays a dominant role in predicting returns for all other countries; a key implication for which I provide empirical evidence in the subsequent section.
4 A Two-Country Model for the Role of the Variance Premium in International Equity Markets
The domestic nature of the existing models in the literature prohibits the analysis of the variance premium in an international setting. These models cannot provide an explanation for the poor role of the local variance premium in predicting returns in countries other than the US as shown in the previous section. Therefore, I propose an international consumption-based general equilibrium (GE) model where the variance risk is priced in the global as well as in the local portfolios. My model yields several new qualitative implications for the role of the variance premium in international markets. The most relevant implication of the model is that the variance premium of a leader economy plays a dominant role in predicting equity returns in all portfolios. In addition, the model implies that the leader country variance premium also plays a role in explaining equity and option markets correlations across countries.
In this section, I present the basic setup of the model as well as its main implications.15 I do not attempt to estimate nor to test my model but rather to use its qualitative implications to investigate the inability of the variance premium to predict local equity returns in countries other than the US. Therefore, I propose a numerical simulation of the model in order to understand its implications and illustrate the mechanism behind it. These numerical simulations provide the link between the single-country evidence, the implications of the model and the empirical evidence presented in the following section.
4.1 Model Setup and Assumptions
The model presented here is a two-country extension of that in BTZ. It preserves two key ingredients in BTZ's model: the use of recursive preferences, and the time-varying nature of macroeconomic uncertainty characterized by the volatility of consumption. However, my model adds to the literature by extending the intuition that financial markets dislike macroeconomic uncertainty (BY and Bansal, et. al., (2005)) to an international setting. Therefore, I include the additional sources of risk embedded in the consumption process of each country, namely the country-specific time-varying volatility and the volatility of volatility (VoV) of consumption.16 The setup of the model requires several additional assumptions. First, the two countries are assumed to be of a "considerable" size. That is, they both play a role in determining the global consumption growth which is a weighted average of the two countries' consumption growth. Second, one of the countries is assumed to be "the leader". The consumption process for the leader country is assumed to be entirely driven by local shocks, while the consumption process for the second country, "the follower", is also affected by the shocks generated in the leader country. Finally, I assume fully integrated equity markets. That is, there exists a unique representative agent holding a global portfolio with positions in the two equity markets. The assumptions of fully integrated equity markets and potentially integrated economies seem adequate given the particular characteristics of the sample considered in this paper.
Formally, each country consumption process is modeled similar to
BTZ. The log of the consumption growth ![]() for the
leader country (labeled as 1) follows
for the
leader country (labeled as 1) follows
|
(1) |
whereas the consumption process for the follower country (labeled as 2) follows
|
(2) |
The global consumption growth is a weighted average of the two countries' consumption process as in
where ![]() is the weight of the leader country in
the global economy.
is the weight of the leader country in
the global economy.
In order to simplify the model, the parameters in the volatility
and VoV processes in Eqs. (1) and
(2)
are assumed to be the same across countries. I also assume that
there are neither within nor cross-country statistical correlations
in the shocks. The only correlations assumed in my model are those
implied by the parameters ![]() (level) and
(level) and
![]() (volatility) in Eq. (2).
These two parameters control the extent to which the follower
country is affected by the shocks generated in the leader country.
In particular,
(volatility) in Eq. (2).
These two parameters control the extent to which the follower
country is affected by the shocks generated in the leader country.
In particular,
![]() implies that the consumption
process of the follower country is affected not only by the local
macroeconomic uncertainty, but also by that generated in the leader
economy. More importantly, the fact that both economies are exposed
to the same sources of macroeconomic uncertainty yields the
systematic component in both countries' variance premiums.17
implies that the consumption
process of the follower country is affected not only by the local
macroeconomic uncertainty, but also by that generated in the leader
economy. More importantly, the fact that both economies are exposed
to the same sources of macroeconomic uncertainty yields the
systematic component in both countries' variance premiums.17
The unique world representative agent is endowed with Epstein Zin Weil preferences (Epstein and Zin, 1989; and Weil, 1989). That is, her life-time utility function is given by the following equation:
| (3) |
where ![]() is the time discount rate,
is the time discount rate,
![]() is the risk aversion parameter,
and
is the risk aversion parameter,
and
![]() for
for ![]() is the intertemporal elasticity
of substitution (IES).18 These preferences have the property
of assigning non-zero market prices to shocks not directly related
to aggregate consumption. This property is crucial to investigate
other risk factors such as news related to volatility which is the
main objective of this paper.
is the intertemporal elasticity
of substitution (IES).18 These preferences have the property
of assigning non-zero market prices to shocks not directly related
to aggregate consumption. This property is crucial to investigate
other risk factors such as news related to volatility which is the
main objective of this paper.
4.2 Model-Implied Variance Premiums
Given the solution of the model in Appendix A, it can be shown that the two countries' VoV isolate the variance premium in the global and the local portfolios. The expression for the global portfolio's variance premium is given by19
where ![]() is the conditional variation of
returns between time
is the conditional variation of
returns between time ![]() and
and ![]() for
portfolio
for
portfolio ![]() for
for ![]() (see appendix A).
The variance premium can be approximated as20
(see appendix A).
The variance premium can be approximated as20
| (4) |
where
![]() represents the
load of
represents the
load of ![]() on
on ![]() . For the
global portfolio, these loads are characterized by the following
expressions:
. For the
global portfolio, these loads are characterized by the following
expressions:
where ![]()
![]()
![]() and
and ![]() are respectively the loads of
the risk factors
are respectively the loads of
the risk factors
![]()
![]()
![]()
![]() on the wealth-consumption ratio of each portfolio. These loads are
derived in detail in Appendix A.
on the wealth-consumption ratio of each portfolio. These loads are
derived in detail in Appendix A.
For the leader country, the variance premium is given by
| (5) | |||
while for the follower country
| (6) | |||
Eqs. (4)
to (6) imply that the
VoV of both countries are the unique sources of the variance
premiums in all portfolios. Actually, for ![]() , the two countries' VoV load positively on the
variance premiums. That is,
, the two countries' VoV load positively on the
variance premiums. That is,
![]() for
for ![]() (see appendix A). Consequently,
the global and local variance premiums are positive if
(see appendix A). Consequently,
the global and local variance premiums are positive if ![]() . Note that while the load of foreign VoV in the
leader country variance premium is explained by the recursive
nature of the utility function given fully integrated equity
markets, the leader country VoV load on the follower country
variance premium has the following two sources: the recursive
nature of the preferences, and the implied sensitivity to the
leader country macroeconomic uncertainty (See Eq. (2)).
. Note that while the load of foreign VoV in the
leader country variance premium is explained by the recursive
nature of the utility function given fully integrated equity
markets, the leader country VoV load on the follower country
variance premium has the following two sources: the recursive
nature of the preferences, and the implied sensitivity to the
leader country macroeconomic uncertainty (See Eq. (2)).
As an immediate consequence of the common components in the variance premium of all portfolios, the variance premium covariance across countries is uniquely characterized by the two countries' VoV. The expression for the variance premium covariance derived from Eqs. (5) and (6) can be written as follows:
| (7) |
where the VoV of both countries loads positively on the variance
premium covariance across countries as long as ![]() .
.
4.3 Model-Implied Equity Premiums
In order to understand the relation between the variance premiums and the dynamics of returns, in this section, I find the expressions for the equity premiums.
The global equity premium is characterized by the following expression:
| (8) | |||
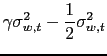 |
|||
where ![]() is the (log) gross return for
portfolio
is the (log) gross return for
portfolio ![]() (
(![]() ),
), ![]() is the global risk-free rate,
is the global risk-free rate,
![]() is the volatility of the world consumption, and
is the volatility of the world consumption, and
![]() is the
geometric adjustment term. The term
is the
geometric adjustment term. The term
![]() represents the load
of
represents the load
of ![]() on
on ![]() . For the
global portfolio these loads are given by
. For the
global portfolio these loads are given by
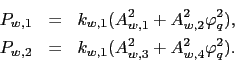
Equation (8)
shows the three model-implied components of the global risk
premium. The first component is the classic risk-return trade-off
![]() . This first
component is also present when the agents are endowed with CRRA
preferences. There are two additional components, one for the VoV
generated in each country. The VoV components of the equity premium
represent the true premium for variance risk since they are driven
by the shocks to the volatility and the volatility of volatility of
consumption in both countries. In the case of the global portfolio,
the VoV of both countries load positively on the equity premium if
. This first
component is also present when the agents are endowed with CRRA
preferences. There are two additional components, one for the VoV
generated in each country. The VoV components of the equity premium
represent the true premium for variance risk since they are driven
by the shocks to the volatility and the volatility of volatility of
consumption in both countries. In the case of the global portfolio,
the VoV of both countries load positively on the equity premium if
![]() . That is,
. That is,
![]() , for
, for
![]() (see Appendix A).
These positive loads are in line with the concept that, at least
for the global portfolio, agents are positively compensated for the
risk generated by the time-varying nature of the VoV.
(see Appendix A).
These positive loads are in line with the concept that, at least
for the global portfolio, agents are positively compensated for the
risk generated by the time-varying nature of the VoV.
The expressions for the equity premiums for each country are given by
| (9) | |||
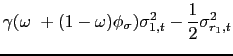 |
|||
and
| (10) | |||
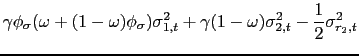 |
|||
where
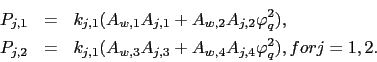
As for the global portfolio, the equity premium in each country is characterized by a volatility of consumption component, and two VoV components, one for each country. In particular, the VoV components in Eqs. (9) and (10) represent the true premium for local and foreign variance risk. Comparing the expressions for the Variance premium (Eqs. (5) and (6)) with those for the equity premiums (Eqs. (9) and (10)) yields the basic intuition for the role of local and foreign variance premium in predicting equity returns in any country. The intuition is as follows: the VPs reveal the VoV in both countries which in turn drives (in part) the time variation in the equity premiums. It is important to bear in mind that although the VoV is not a necessary condition to generate a variance risk premium, introducing the VoV isolates the risk premium on volatility and differentiate it from the consumption risk premium.
It seems natural from Eqs. (8) to (10) to expect the VoV to also explain the time variation in the covariance of returns across countries. The expression for the covariance of returns is given by
| (11) |
where ![]() is the load of
is the load of ![]() on
the covariance of returns. These loads are given by
on
the covariance of returns. These loads are given by
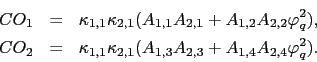
4.4 Numerical Implications of the Two-Country Model
In this section, I present some numerical simulations of my model in order to investigate the mechanism of transmission of VoV shocks across countries. The purpose of these simulations is to analyze the qualitative implications of my model for the variance premiums and for the interaction between the variance premiums and the equity returns. Understanding these qualitative implications provides a natural step between the model and the empirical evidence presented in the next section.
The base scenario for the numerical simulations is displayed in
Table 2. In this
scenario, the parameters in the preference function are calibrated
as in BTZ. In order to simplify the interpretation of results, I
consider the hypothetical case where the world is composed of only
two countries: the US, and Germany. Just for the purpose of
illustrating the mechanism behind the model, the US is considered
as the leader economy.21 For these two countries, the
parameters in Eqs. (1) and (2) are
calibrated as follows:![]() is estimated as
the average IP growth in each country during the period 1973-2009;
is estimated as
the average IP growth in each country during the period 1973-2009;
![]() is estimated as the
IP growth unconditional variance for the same period; and the rest
of the parameters are taken from BTZ (homogeneous parameters for
the two countries). The Campbell and Shiller constants
is estimated as the
IP growth unconditional variance for the same period; and the rest
of the parameters are taken from BTZ (homogeneous parameters for
the two countries). The Campbell and Shiller constants ![]() and
and ![]() are estimated using data for
the Price-Dividend (PD) ratio for each country as well as for the
Datastream world portfolio. The log-linearization constants are
estimated as
are estimated using data for
the Price-Dividend (PD) ratio for each country as well as for the
Datastream world portfolio. The log-linearization constants are
estimated as
![]() , where
, where
![]() is the unconditional mean of the (log)
PD ratio, and
is the unconditional mean of the (log)
PD ratio, and
![]() (Campbell and
Cochrane, 1999). Bear in mind that
(Campbell and
Cochrane, 1999). Bear in mind that ![]() and
and
![]() should actually be made dependent on
the theoretical wealth-consumption ratio (see Appendix A).
However, I use the unconditionally expected PD ratio, to make these
two parameters independent from the set of parameters considered in
each case.22
should actually be made dependent on
the theoretical wealth-consumption ratio (see Appendix A).
However, I use the unconditionally expected PD ratio, to make these
two parameters independent from the set of parameters considered in
each case.22
Table 2: Base Scenario for the Numerical Implications of the Two-Country Model
| Param. | Value: Global | Value: US | Value: GER. | Description |
|---|---|---|---|---|
| μg | 1.6 x 10-3 | 8.3 x 10-4 | Mean consumption growth | |
| aσ | 1.2 x 10-6 | 6.6 x 10-6 | Long-run consumption volatility | |
| pσ | 0.98 | 0.98 | Speed of reversion consumption volatility | |
| aq | 2.0 x 10-7 | 2.0 x 10-7 | Long-run VoV | |
| pq | 0.80 | 0.80 | Speed of reversion VoV | |
| k0 | 0.12 | 0.13 | 0.12 | Campbell-Shiller k0 |
| k1 | 0.97 | 0.97 | 0.97 | Campbell-Shiller k1 |
| ψ | 2.50 | Intertemporal elasticity of substitution | ||
| log δ | 1.00 | Discount factor |
The table reports the values for the
two-country model parameters considered as the base scenario to
test its numerical implications. In this scenario, all parameters
in the preference function (Eq. (3)) are
taken from BTZ. The country-specific parameters in Eqs. (1) and
(2)
are estimated as follows: ![]() is estimated as the average IP growth for the
sample 1973-2009;
is estimated as the average IP growth for the
sample 1973-2009;
![]() is estimated as the IP growth unconditional variance for
the sample 1973-2009. Finally, the parameters
is estimated as the IP growth unconditional variance for
the sample 1973-2009. Finally, the parameters ![]() and
and ![]() in the log-linearization of returns (Eq.
(12))
are estimated using data for the Price-Dividend (PD) ratio for each
country as well as for the Datastream world portfolio. The
log-linearization constants are estimated as
in the log-linearization of returns (Eq.
(12))
are estimated using data for the Price-Dividend (PD) ratio for each
country as well as for the Datastream world portfolio. The
log-linearization constants are estimated as
![]() ,
where
,
where ![]() is the
unconditional mean of the (log) PD ratio, and
is the
unconditional mean of the (log) PD ratio, and
![]() (Campbell and Cochrane, 1999).
(Campbell and Cochrane, 1999).
4.4.1 Variance Premium Dynamics
According to the first main implication of my model, both
countries' VoV load positively on all portfolios' variance premiums
(see Eqs. (4)
to (6)). In order to
show this implication, Figure 4 displays the
(unconditionally expected) VoV loads on the variance premium for
all portfolios. The figure shows the components of the variance
premiums for alternative values of the risk aversion (![]() ), the weight of the leader country (
), the weight of the leader country (![]() ), and the correlation of consumption (
), and the correlation of consumption (
![]() ). The simulations show that
the implied size of the US VoV load dominates that of Germany in
all cases considered. The dominance of the US VoV increases with
the relative size of the leader economy (
). The simulations show that
the implied size of the US VoV load dominates that of Germany in
all cases considered. The dominance of the US VoV increases with
the relative size of the leader economy (![]() ),
and with the relative dependence of the follower economy (
),
and with the relative dependence of the follower economy (
![]() ). The contribution of the
follower economy VoV in the variance premiums, on the other hand,
is almost insignificant no matter the size nor the independence of
the consumption process in this economy.
). The contribution of the
follower economy VoV in the variance premiums, on the other hand,
is almost insignificant no matter the size nor the independence of
the consumption process in this economy.
Figure 4: loads of VoV on the Variance Premiums. Alternative Parameters
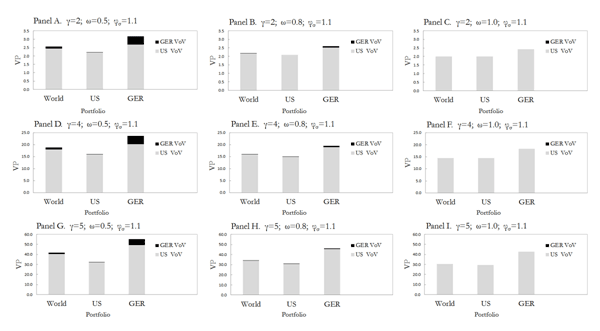

The figure reports the total unconditional loads of the two countries� volatility of volatility (VoV) on the variance premium of each portfolio as implied by Eqs. (4) to (6) for alternative values of parameters γ, ω, and φσ. The unconditional loads are calculated as ![]() and
and ![]() for k=US,GER, and j each one of the three possible portfolios: US, GER, and the global portfolio. Given the parameters in the base scenario (Table 2), the average VoV is given by
for k=US,GER, and j each one of the three possible portfolios: US, GER, and the global portfolio. Given the parameters in the base scenario (Table 2), the average VoV is given by ![]() .
.
The simulations also suggest that the magnitude of the expected variance premiums monotonously increases with the risk aversion, and decreases with the relative size of the riskiest market.23 The riskiest market is assumed, for coherence, to be that in the follower country. However, for all cases considered, the average variance premium is quantitatively far from that empirically observed for these two countries (see Table 1). The limitation to quantitatively reflect the observed premium in models with recursive preferences has been previously documented by Drechsler and Yaron (2011) in a single-country setting.
In unreported results, I show that the model-implied variance
premium correlation across the two countries is above 0.98 for all
simulations. This results is to be expected given the high common
component of the leader country VoV in all variance premiums.
Actually, for all cases considered, the model implies that the
leader country VoV accounts for more than 99 of the total
cross-country variance premium covariance. Surprisingly, the result
on the dominant role of the leader country's VoV holds no matter
the relative size of the follower economy (
![]() ) or its implied
correlation with the leader economy.
) or its implied
correlation with the leader economy.
In sum, the numerical simulations show that the VoV generated in the leader economy accounts for most of the systematic component of the variance premiums. Therefore, the VoV generated in the leader economy plays the key role in explaining the variance premium for all portfolios. This in turn implies that the leader country VoV is also the key driver of the expected variance premium correlation across countries.
4.4.2 Return Dynamics
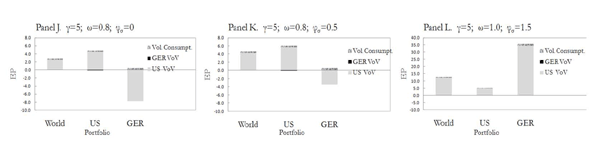
According to the second main implication of my model, the two countries' VoV that uniquely characterize the variance premiums also drive the time variation in equity premiums. Figure 5 displays the model-implied components of the equity premium for the global and the local portfolios for alternative sets of parameters. The simulations show that the leader country VoV load dominates that of the follower country in all portfolios' equity premiums for all cases considered. They also reveal that in some cases the VoV of the leader country loads negatively on the follower country's equity premium. This case only occurs when economies are poorly correlated as can be seen in Panel J and K. However, the follower country VoV loads negatively on the leader country's equity premium for all cases considered, except of course for the extreme case where the size of the follower economy is insignificant (Panels C,F,I, and L).
Figure 5: Consumption Volatility and VoV Loads of Equity Premiums. Alternate Parameters
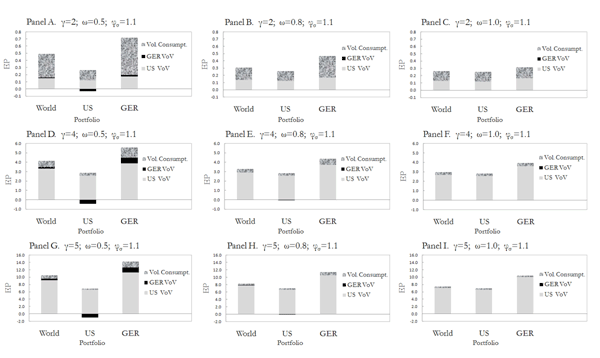
The figure reports the total unconditional components of all possible portfolio�s equity premiums as implied by Eqs. (8) to (10) for alternative values of parameters γ, ω, and φσ. In order to facilitate the interpretation, the exponential adjustment term ![]() is excluded from the figure. Given the parameters in the base scenario in Table 2, the loads of the volatility of consumption are calculated by assuming that (the average volatility of consumption)
is excluded from the figure. Given the parameters in the base scenario in Table 2, the loads of the volatility of consumption are calculated by assuming that (the average volatility of consumption) ![]() . The loads of VoV are calculated by assuming that (the average VoV)
. The loads of VoV are calculated by assuming that (the average VoV) ![]() .
.
The possibility of VoV loading negatively on the equity premiums can actually be explained by the mechanism of transmission of shocks to VoV implied by the model. According to this mechanism, a positive shock to VoV in the follower country has a negative impact on the leader country's equity premium. This effect can be interpreted as a macroeconomic uncertainty induced flight-to-safety from the follower to the leader economy. The possibility of an uncertainty flight-to-safety in this direction is actually generated by the fact that the leader country consumption process is, by construction, not sensitive to the shocks generated in the follower country (Eq. (1)). Investing in equities in the leader country is then expected to become a more attractive investment alternative with respect to this foreign source of risk. In contrast, an uncertainty flight-to-safety in the other direction (leader to follower) is not always possible. This is due to the fact that the follower country consumption process is affected by the shocks in the leader economy (Eq. (2)). Therefore, a flight-to-safety in this direction is only possible if the economies are assumed to be quite independent from each other. For example, in the case of totally independent economies in Panel J, any equity market is free from the uncertainty risk generated in the foreign economy. Thus, in this extreme case, the VoV of one country will always load negatively on the other country's equity premium.
As a consequence of the second main implication of my model,
both countries' VoV also play a role in explaining the covariance
of equity returns across countries. As expected, even if the
follower economy has a large (relative) size, the VoV of the leader
country dominates. The dominance of the leader country VoV
increases with the relative size of its economy (![]() ), and the degree of dependence across the two
economies (
), and the degree of dependence across the two
economies (
![]() ). In line with the
simulations in Figure 5 the VoV
generated in the follower country may even load negatively on the
covariance of returns. Actually, in the case of totally independent
or mildly correlated economies, the simulations confirm that even
VoV generated in the leader economy might load negatively on the
covariance of returns.24
). In line with the
simulations in Figure 5 the VoV
generated in the follower country may even load negatively on the
covariance of returns. Actually, in the case of totally independent
or mildly correlated economies, the simulations confirm that even
VoV generated in the leader economy might load negatively on the
covariance of returns.24
Finally, the simulations in Figure 6 show the
relation between the correlation of the economies and the
model-implied correlation across equity markets. These simulations
reflect the documented disparity between the correlation of equity
markets and the correlation of economies. They show that the equity
return correlation is in some cases higher than the implied
correlation of consumption. In particular, the simulations suggest
that for moderately risk averse agents (![]() )
and moderately correlated economies, the implied correlation across
equity markets is larger than that implied by the correlation of
consumption. This result arrives as a direct consequence of the
recursive nature of the representative agent's preferences.
)
and moderately correlated economies, the implied correlation across
equity markets is larger than that implied by the correlation of
consumption. This result arrives as a direct consequence of the
recursive nature of the representative agent's preferences.
Figure 6: Cross-Country Return Correlations and Model-Implied Correlation of Consumption
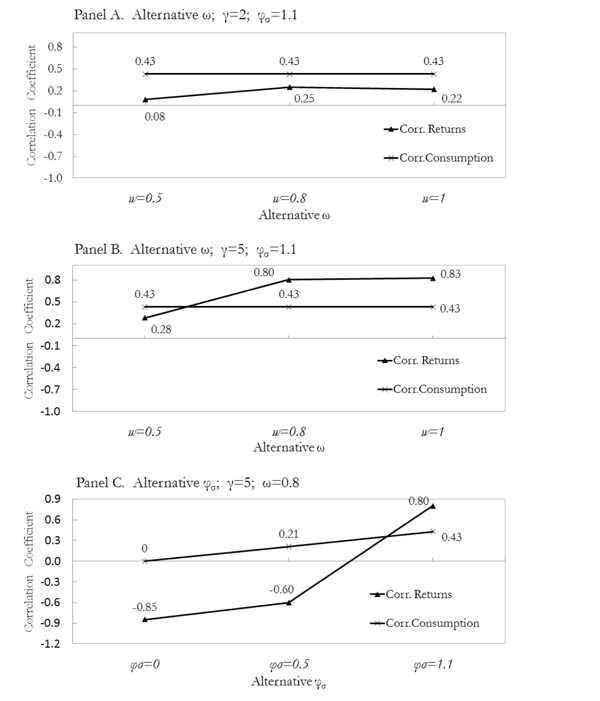
The figure shows the model-implied unconditional correlation of consumption ![]() and the
model-implied equity return correlation
and the
model-implied equity return correlation ![]() between Germany and the US for several alternative values of parameters γ, ω, and φσ.
between Germany and the US for several alternative values of parameters γ, ω, and φσ.
In sum, the numerical simulations show that the VoV generated in the leader economy plays the key role in explaining the time variation in the equity premium of all portfolios. As a consequence of this implication, the leader economy VoV also plays a dominant role in explaining the time variation in equity return correlations across countries. The simulations also show some consequences derived from the model setup. In particular, from the assumptions of integrated markets where the representative agent is endowed with recursive preferences and one economy behaves as a follower. For example, the model introduces the possibility of a macroeconomic uncertainty induced flight-to safety, which in turn introduces the possibility that the VoV of one country covaries negatively with the equity premium of another country.
5 The Variance Premium and International Equity and Option Markets: Empirical Evidence
In this section, I present the empirical evidence based on the qualitative implications of the GE model analyzed in Section 4. Using the variance premiums for all countries in the sample, I investigate their role in (i) explaining the time variation in the variance premium for all other countries, (ii) predicting the variance premium correlations across countries, (iii) predicting not only the local equity returns, but also those in other countries, and (iv) predicting the correlation of equity returns across countries.
5.1 Cross-Country Variance Premium Correlations
A first implication of my model is that the variance premiums are highly correlated across countries. The high variance premium correlation is due to the common load of the leader country VoV in all variance premiums (leader, follower, and global portfolio). This in turn implies that the leader country variance premium plays a key role in predicting the variance premium correlations across countries. In order to analyze this implication, I first provide evidence for the variance premium correlations across countries. Then, I investigate the role of each country's variance premium in predicting the variance premium correlations with any other country.
Table 3 displays the variance premium correlations across all countries in the sample. In line with the first implication of my model, all countries but Japan show correlations above 0.5. In particular, the US and the UK show a high correlation coefficient of 0.73. Among European markets, France and The Netherlands show the highest correlation coefficient in the sample: 0.89. However, Japan's variance premium shows a relatively low, or even negative, correlation with the variance premium of any other market excepts perhaps with Switzerland. 25 The evidence for Japan stands in sharp contrast to the implications of the model. In fact, my model can only accommodate positive variance premium correlations. This is in turn derived from the ability of my model to characterize only positive variance premiums.
Table 3:Variance Premium Correlations Across Countries
| US | GER | JAP | UK | SWI | NL | BE | FR | |
|---|---|---|---|---|---|---|---|---|
| US | 1.00 | 0.56 | -0.08 | 0.74 | 0.37 | 0.76 | 0.62 | 0.78 |
| GER | 1.00 | 0.24 | 0.74 | 0.79 | 0.82 | 0.42 | 0.78 | |
| JAP | 1.00 | 0.18 | 0.61 | 0.07 | 0.07 | -0.14 | ||
| UK | 1.00 | 0.70 | 0.67 | 0.48 | 0.51 | |||
| SWI | 1.00 | 0.67 | 0.48 | 0.51 | ||||
| NL | 1.00 | 0.72 | 0.89 | |||||
| BE | 1.00 | 0.57 | ||||||
| FR | 1.00 |
The table reports the correlation coefficients among the monthly variance premiums for all countries for the sample period 2000 to 2009.
The results on the high variance premium correlations has been previously documented in the literature for a shorter sample of countries. For example, Bekaert, Hoerova and Scheicher (2009) find evidence of high risk aversion and uncertainty correlation between Germany and the US. Although their measures are not directly the variance premiums, their empirical methodology uncovers the risk aversion and uncertainty time series using the observed IV and realized volatilities for these two countries. Sugihara (2010) also finds evidence of strong linkages in volatility premiums between the US, Germany and Japan. He actually finds empirical evidence that the correlation between these three markets is stronger around certain episodes; in particular, after the subprime crisis. However, in this paper, I not only extend the evidence for a larger sample of countries but also provide a fundamental explanation for the dynamics of the variance premium correlation across countries. In particular, my model relates the high variance premium correlation across countries to a systematic component which is mainly driven by the leader country variance premium.
A direct consequence of the common component in all variance
premiums is that the variance premium correlations are predicted by
the leader country's variance premium. In order to test this
consequence, Table 4 reports the
estimated coefficients
![]() for the following
regressions:
for the following
regressions:
where the correlation coefficient for the period ![]() to
to ![]() is calculated using daily data for the
variance premiums of the two countries for the month starting
immediately after the realization of
is calculated using daily data for the
variance premiums of the two countries for the month starting
immediately after the realization of ![]() .
26
.
26![]() 27 The
evidence suggests that the US variance premium predicts the
one-month-ahead variance premium correlation between the US,
Germany, and Japan (first horizontal block of results). 28 The
results also show that the US variance premium does not necessarily
outperform all other countries' variance premium. For example, the
first vertical block of results in the table suggests that the
variance premiums in Germany, Japan, the UK, Switzerland and The
Netherlands can also forecast the variance premium correlation
between these countries and the US.29
27 The
evidence suggests that the US variance premium predicts the
one-month-ahead variance premium correlation between the US,
Germany, and Japan (first horizontal block of results). 28 The
results also show that the US variance premium does not necessarily
outperform all other countries' variance premium. For example, the
first vertical block of results in the table suggests that the
variance premiums in Germany, Japan, the UK, Switzerland and The
Netherlands can also forecast the variance premium correlation
between these countries and the US.29
Table 4 : Predicting Variance Premium Correlations across Countries
| vpk,t-1 | ρ(vpj,t,t+1, vpk,t,t+1): US | ρ(vpj,t,t+1, vpk,t,t+1): GER | ρ(vpj,t,t+1, vpk,t,t+1): JAP | ρ(vpj,t,t+1, vpk,t,t+1): UK | ρ(vpj,t,t+1, vpk,t,t+1): SWI | ρ(vpj,t,t+1, vpk,t,t+1): NL | ρ(vpj,t,t+1, vpk,t,t+1): BE | ρ(vpj,t,t+1, vpk,t,t+1): FR | Avg. R2 |
|---|---|---|---|---|---|---|---|---|---|
| US | 50.52** (2.05) |
45.53** (2.03) |
28.62 (1.58) |
26.54 (1.42) |
30.34 (1.61) |
46.40 (1.48) |
8.22 (0.41) |
||
| US: R2 | 4.57 | 2.50 | 1.88 | 1.16 | 2.04 | 2.30 | 0.14 | 2.08 | |
| GER | 38.23*** (3.52) |
22.16 (1.40) |
31.31*** (2.58) |
6.52 (0.62) |
19.22* (1.84) |
24.32 (1.07) |
10.32 (0.89) |
||
| GER: R2 | 4.40 | 0.96 | 3.51 | 0.17 | 1.91 | 1.29 | 0.53 | 1.82 | |
| JAP | 37.45** (2.31) |
30.90*** (2.77) |
46.63*** (3.51) |
55.76*** (4.21) |
36.99*** (2.67) |
47.99*** (3.08) |
37.84*** (2.98) |
||
| JAP: R2 | 4.52 | 2.95 | 6.46 | 7.98 | 4.24 | 5.71 | 4.04 | 5.13 | |
| UK | 39.45*** (3.28) |
27.25* (1.77) |
66.80*** (2.94) |
3.24 (0.25) |
24.88* (1.84) |
-0.23 (-0.01) |
-8.33 (-0.57) |
||
| UK: R2 | 4.32 | 1.91 | 6.00 | 0.03 | 2.15 | 0.00 | 0.23 | 2.09 | |
| SWI | 21.49** (2.31) |
16.95 (1.60) |
42.14** (2.09) |
15.16* (1.78) |
18.70* (1.74) |
2.23 (0.07) |
8.79 (0.93) |
||
| SWI: R2 | 1.12 | 1.02 | 2.52 | 0.83 | 1.22 | 0.01 | 0.26 | 1.00 | |
| NL | 21.32** (2..13) |
21.08** (2.21) |
14.66 (0.58) |
22.71** (1.97) |
15.80 (1.18) |
29.42 (1.55) |
5.20 (0.58) |
||
| NL: R2 | 1.63 | 2.22 | 0.40 | 2.40 | 0.95 | 1.84 | 0.17 | 1.37 | |
| BE | -6.40 (-0.17) |
-6.08 (-0.13) |
-14.92 (-0.33) |
-13.84 (-0.36) |
-18.32 (-0.50) |
-34.07 (-0.64) |
-25.70 (-0.60) |
||
| BE: R2 | 0.03 | 0.03 | 0.15 | 0.18 | 0.31 | 1.09 | 0.58 | 0.34 | |
| FR | -0.59 (-0.04) |
-1.99 (-0.18) |
19.24 (0.87) |
-6.72 (-0.48) |
-21.20 (-1.33) |
-5.95 (-0.52) |
-2.48 (-0.12) |
||
| FR: R2 | 0.00 | 0.01 | 0.49 | 0.15 | 1.28 | 0.18 | 0.01 | 0.30 |
The table reports teh estimated coefficients γ1,j,k in the following regression:
ρt(vpj,t,t+1, vpk,t,t+1) = γ0,jk + ε1,j,kvpk,t-1+εj,k,t,
where j are the countries in teh columns and k, the countries in teh rows. For example, the information under the column JAP shows how the variance permium correlation between Japan (j) adn any other country in the rows (k) is forecasted by teh latter country variance premium. The correlation coefficient for the period t to t+1 is calculated using daily data for the variance premiums of the two countries for the month starting immediately after the realization of vpk,t-1. The standard errors in all regressions are corrected by Newey-West with 12 lags. In order to make the coefficients easier to interpret, the variance premiums are taken in montly squared percentages.
In sum, the evidence in this section suggests that the variance premium correlations across countries increase following episodes of increasing variance premiums. It also suggests that the model-implied dominant role of a leader country variance premium might restrict the interpretation of the potential ability of other countries in predicting one-month ahead variance premium correlations.
5.2 Cross-Country Equity Return Correlations
The second main implication of my model is that the variance premiums covary with the equity premiums (Eqs. (9) and (10)). This is due to the fact that the VoV shocks that uniquely characterize the variance premiums also load on both countries' equity premiums. In particular, the model implies that the leader country's VoV dominates that of the follower country in all equity premiums. As a consequence, the variance premium of a leader country should outperform that of the follower country in predicting local and foreign returns. In this section, I provide evidence for the role of foreign variance premiums in predicting equity returns for all countries in the sample.
Table 5 reports the estimation results for the following regressions:
where
![]() represents future
compounded annualized excess returns 3-months ahead,
represents future
compounded annualized excess returns 3-months ahead,
![]() is the local dividend yield, and
is the local dividend yield, and
![]() is the local term spread.30 On
top of the local predictability evidence discussed in Section 3,
the results in Table 5 suggest that only the US variance premium plays a significant role
in predicting equity returns for all other countries in the sample.
Nevertheless, for other pairs of countries, the predictive power of
the foreign variance premium over international equity returns
holds. This is the case for the significant predictive power of the
Japanese variance premium over the equity returns of Belgium and
France. It is also the case for the (often borderline) predictive
power of the variance premium of all countries, except for
Switzerland and Japan, over the US equity returns. 31
is the local term spread.30 On
top of the local predictability evidence discussed in Section 3,
the results in Table 5 suggest that only the US variance premium plays a significant role
in predicting equity returns for all other countries in the sample.
Nevertheless, for other pairs of countries, the predictive power of
the foreign variance premium over international equity returns
holds. This is the case for the significant predictive power of the
Japanese variance premium over the equity returns of Belgium and
France. It is also the case for the (often borderline) predictive
power of the variance premium of all countries, except for
Switzerland and Japan, over the US equity returns. 31
Table 5: Predicting International Equity Returns
| vpk,t-1 | (r-rf)j,t,t+h: US | (r-rf)j,t,t+h: GER | (r-rf)j,t,t+h: JAP | (r-rf)j,t,t+h: UK | (r-rf)j,t,t+h: SWI | (r-rf)j,t,t+h: NL | (r-rf)j,t,t+h: BE | (r-rf)j,t,t+h: FR | Avg. R2 |
|---|---|---|---|---|---|---|---|---|---|
| US | 0.05*** (4.94) | 0.04** (2.50) | 0.03* (1.67) | 0.03*** (3.85) | 0.03*** (2.61) | 0.03* (1.96) | 0.04** (2.50) | 0.04** (2.53) | |
| US: R2 | 22.87 | 10.94 | 7.93 | 15.16 | 11.39 | 6.84 | 9.11 | 12.77 | 12.13 |
| GER | 0.02* (1.70) | 0.00 (-0.12) | -0.01 (-0.54) | 0.01 (0.65) | 0.00 (0.17) | -0.01 (-0.95) | 0.00 (0.25) | 0.00 (0.29) | |
| GER: R2 | 13.05 | 5.24 | 4.30 | 7.66 | 6.13 | 4.22 | 2.86 | 5.87 | 6.17 |
| JAP | -0.01 (-1.15) | -0.03* (-1.71) | -0.01 (-0.82) | 0.00 (-0.58) | -0.01 (-1.01) | -0.02 (-1.45) | -0.02** (-2.00) | -0.02** (-2.75) | |
| JAP: R2 | 10.80 | 9.67 | 5.05 | 7.57 | 7.74 | 5.78 | 5.78 | 9.87 | 7.78 |
| UK | 0.03** (2.37) | 0.01 (0.26) | 0.00 (0.09) | 0.02 (0.95) | 0.02 (0.96) | 0.00 (-0.03) | 0.02 (0.53) | 0.02 (0.91) | |
| UK: R2 | 14.14 | 5.39 | 4.03 | 8.63 | 7.30 | 3.57 | 3.42 | 7.30 | 6.72 |
| SWI | 0.00 (0.35) | -0.04 (-1.45) | -0.02 (-0.76) | 0.00 (-0.31) | -0.01 (-0.55) | -0.03 (-1.39) | -0.01 (-0.58) | -0.01 (-0.99) | |
| SWI: R2 | 9.84 | 7.92 | 4.75 | 7.28 | 6.35 | 5.73 | 3.22 | 6.43 | 6.44 |
| NL | 0.03*** (2.86) | 0.02 (0.90) | 0.01 (0.60) | 0.02 (1.49) | 0.01 (1.09) | 0.00 (0.24) | 0.02 (1.21) | 0.02 (1.14) | |
| NL: R2 | 17.70 | 6.64 | 4.78 | 10.05 | 7.79 | 3.67 | 5.46 | 7.94 | 8.00 |
| BE | 0.01* (1.65) | 0.01 (0.84) | 0.01 (0.59) | 0.01 (1.50) | 0.01 (1.05) | 0.01 (0.65) | 0.03*** (3.06) | 0.01 (0.93) | |
| BE: R2 | 11.02 | 5.68 | 4.42 | 8.10 | 6.61 | 3.80 | 6.53 | 6.42 | 6.57 |
| FR | 0.03*** (2.84) | 0.02 (0.99) | 0.01 (0.77) | 0.02 (1.64) | 0.01 (1.29) | 0.01 (0.66) | 0.02 (1.27) | 0.02 (1.57) | |
| FR: R2 | 19.14 | 7.27 | 5.16 | 10.47 | 8.07 | 4.17 | 5.55 | 9.86 | 8.71 |
The Table reports the estimated coefficient γ1,j,k in the following regressions: where are 3-months (compounded annualized) excess returns, dyj,t are the (local) dividend yields and tsj,t the (local) term spreads calculated as the difference between the 1 year T-bill and the 3 months t-bill rate. The standard errors are corrected by Newey-West with a number of lags l=12. The table also reports the average R2 for th epredictive power of each country's variance premium.
In order to investigate more in depth the predictive power of the US variance premium over international equity returns, Figure 7 reports the estimation results for the following regressions:
where
![]() represents future
compounded annualized excess returns
represents future
compounded annualized excess returns ![]() -months ahead.
-months ahead.
The results suggest that he predictive power of the US variance premium for all countries except perhaps for Japan resembles the hump-shaped pattern found by BTZ for the US (local return predictability). This pattern reflects the fact that the variance premium should be a dominant predictor for horizons where the VoV is the main source of variation in equity returns. The extension of this evidence for other countries indicates that the US VoV is the dominant source of variation in all countries' equity returns for horizons between 3 and 6 months. The figure also suggests that the predictive power of the US variance premium is complementary to that of local term spreads and dividend yields.32 When compared to Figure 3, the evidence also suggest that the US variance premium outperforms the local variance premiums in predicting equity returns for all countries considered. In unreported results, I show that the ability of the US variance premium to predict one-quarter ahead foreign returns holds if a noise signal is added to the original variance premium. For all countries, except perhaps for the Netherlands and Japan, the standard deviation of the noise signal has to be at least 50% that of the original US variance premium before its predictive power disappears.33 Moreover, the predictive power of the US variance premium holds for all alternative variance premium specifications considered, except perhaps for the range-based estimation.34,35
Figure 7: The role of the US Variance Premium in Predicting International Equity Returns
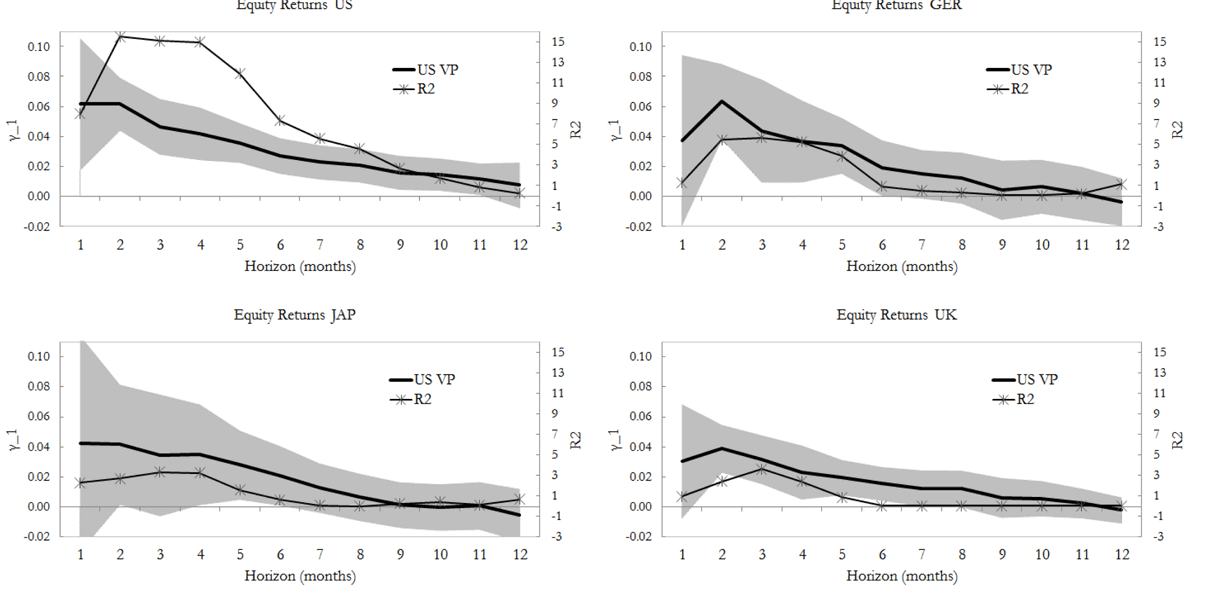
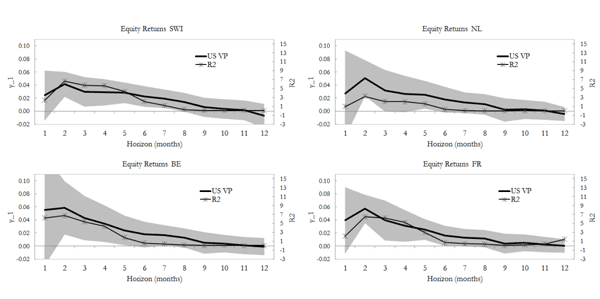
The Figure reports the estimated coefficient γ1,j,h in the following regressions:
![]() where
where ![]() are h-months (compounded annualized) excess returns, dyj,t are the local dividend yields and tsj,t are the local term spreads calculated as the difference between the 1 year T-bill and the 3 months t-bill rate. I consider monthly forecasting horizons up to 12 months. The shaded areas represent the 95% confidence intervals for the Newey-West corrected standard errors with a number of lags l=max{2h, 12}. The figure also reports in the secondary axis the R2 for each regression. In order to separately identify the predictive power of the variance premium, the R2 are reported for regressions in which only the US variance premium is considered as in
are h-months (compounded annualized) excess returns, dyj,t are the local dividend yields and tsj,t are the local term spreads calculated as the difference between the 1 year T-bill and the 3 months t-bill rate. I consider monthly forecasting horizons up to 12 months. The shaded areas represent the 95% confidence intervals for the Newey-West corrected standard errors with a number of lags l=max{2h, 12}. The figure also reports in the secondary axis the R2 for each regression. In order to separately identify the predictive power of the variance premium, the R2 are reported for regressions in which only the US variance premium is considered as in ![]() .
.
As a consequence of the systematic component of equity premiums, the leader country variance premium should also be a useful predictor of equity return correlations across countries (Eq. (11)). In order to test this consequence, Figure 8 reports the estimation results for the following regressions:
where
![]() is the
is the
![]() -months ahead equity return correlation
between any country and the US. The results suggest that the US
variance premium predicts equity return correlations between the US
and any other country in the sample except for Japan and Belgium.
As for the equity returns, the ability of the US variance premium
to forecast return correlations holds for horizons between 3 and 6
months for most of the countries. Actually, for the equity
correlation between the US and Germany, the US variance premium has
predictive power for horizons up to 12 months. In unreported
results, I also show that the US variance premium outperforms all
other countries in the sample in predicting equity return
correlations.
-months ahead equity return correlation
between any country and the US. The results suggest that the US
variance premium predicts equity return correlations between the US
and any other country in the sample except for Japan and Belgium.
As for the equity returns, the ability of the US variance premium
to forecast return correlations holds for horizons between 3 and 6
months for most of the countries. Actually, for the equity
correlation between the US and Germany, the US variance premium has
predictive power for horizons up to 12 months. In unreported
results, I also show that the US variance premium outperforms all
other countries in the sample in predicting equity return
correlations.
Figure 8: The role fo the US Variance Premium in Predicting Equity Return Correlations across countries
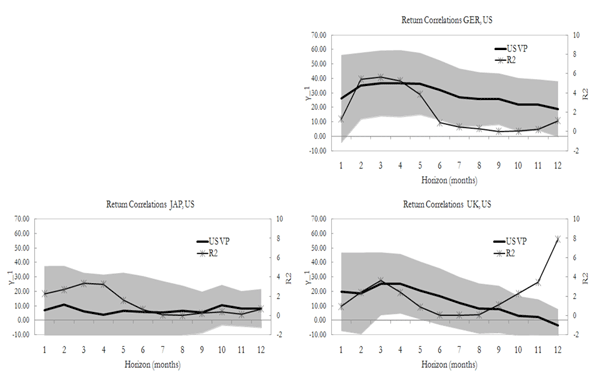
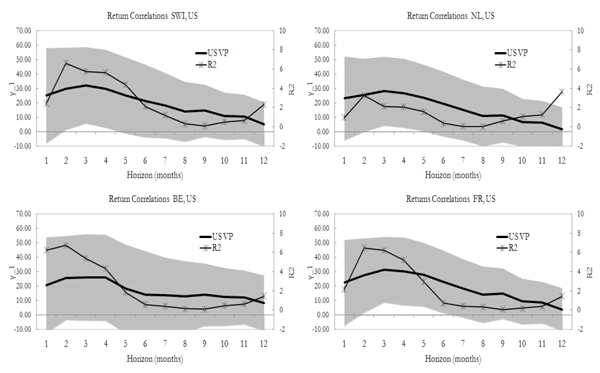
The table shows the estimated coefficients γ1,j,US the following regression:
![]() where
where ![]() is the h-months ahead equity return correlation between any country and the US. The correlation coefficient for the period t to t+1 is calculated using daily equity returns for the two countries for the month starting immediately after the realization of vpk,t-1. The shaded areas represent the 95% confidence intervals for the Newey-West corrected standard errors with a number of lags l=max{2h, 12}. The figure also reports in the secondary axis the R2 for each regression.
is the h-months ahead equity return correlation between any country and the US. The correlation coefficient for the period t to t+1 is calculated using daily equity returns for the two countries for the month starting immediately after the realization of vpk,t-1. The shaded areas represent the 95% confidence intervals for the Newey-West corrected standard errors with a number of lags l=max{2h, 12}. The figure also reports in the secondary axis the R2 for each regression.
In sum, the evidence in this section supports the qualitative implications of my model for the role of the variance premium in predicting international equity returns. In particular, this evidence confirms the predominant role of the US variance premium in predicting foreign equity returns and return correlations across countries. Therefore, the evidence supports the theoretical solution implied by my model to the local return predictability puzzle in Section 3. That is, the local variance premium cannot predict returns in countries other than the US because the role of the variance premium in those countries is dominated by the variance premium in a leader country: the US.
6 Conclusions
This paper presents several new findings related to the variance risk premium for a total of eight countries. First, I provide new evidence that the variance premiums display significant time variation and are, on average, positive for all countries analyzed. However, I also provide evidence that except for the US and Belgium, the local variance premiums do not predict local equity returns. This evidence is in sharp contrast to the existing theoretical models where the variance premium explains the time variation in equity returns.
Motivated by the puzzling single-country evidence, I propose an international model to understand the role of the variance premium in explaining international equity returns. My model is a two-country general equilibrium model which extends that in Bollerslev, Tauchen and Zhou (2009). It yields relevant qualitative implications that explain the inability of the variance premium in predicting local returns in countries other than the US. In particular, my model implies that the variance premium generated in a leader economy plays a key role in explaining the time variation in equity returns in the two countries. Therefore, the leader country variance premium outperforms the follower country variance premium in predicting not only equity returns, but also equity return correlations across countries. The dominant role of the leader country variance is a consequence of the common components in the variance premiums of all countries. In particular, a consequence of the dominant load of macroeconomic uncertainty shocks generated in the leader economy in the variance premiums of both countries.
Finally, I provide new empirical evidence for the qualitative implications of my model for the eight countries in the sample. I show that the US variance premium has predictive power over the equity returns for all countries in the sample. The predictive power of the US variance premium over international equity returns is (i) stronger for horizons between 3 and 6 months, (ii) additional to that of traditional local (or US) variables, and (iii) clearly outperforms the local variance premium themselves. Finally, I also show that the US variance premium predicts the correlation of equity returns between the US and all countries in the sample, except for Japan and Belgium.
Appendix
A Detailed Solution of the Two-country Model
This appendix explains in detail the solution to the model in Section 4.
Each country return process is assumed to be a claim on the
local consumption growth, while the global portfolio return is a
claim on the weighted global consumption
![]() , where
, where
![]() is the weight of the leader country.
Following Campbell and Shiller (1988), the returns are linearized
as
is the weight of the leader country.
Following Campbell and Shiller (1988), the returns are linearized
as
| (12) |
where ![]() denotes the log of the
wealth-consumption ratio of the asset that pays the consumption
endowment
denotes the log of the
wealth-consumption ratio of the asset that pays the consumption
endowment
![]() .
As it is standard in the asset pricing literature, I conjecture a
solution for
.
As it is standard in the asset pricing literature, I conjecture a
solution for ![]() as a function of the state
variables of both countries as follows:
as a function of the state
variables of both countries as follows:
| (13) |
Based on this solution, the basic asset pricing equation is imposed
in order to determine the components of ![]() . The
basic asset pricing equation is the first order condition from the
agent maximization problem given by
. The
basic asset pricing equation is the first order condition from the
agent maximization problem given by
where ![]() is the (log of) intertemporal
marginal rate of substitution. For the case of Epstein-Zin-Weil
preferences, and given that markets are assumed to be perfectly
integrated, the unique marginal rate of substitution is given by
is the (log of) intertemporal
marginal rate of substitution. For the case of Epstein-Zin-Weil
preferences, and given that markets are assumed to be perfectly
integrated, the unique marginal rate of substitution is given by
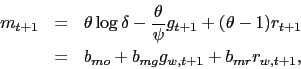
where ![]() is the time discount rate,
is the time discount rate,
![]() is the risk aversion parameter,
and
is the risk aversion parameter,
and
![]() for
for ![]() is the intertemporal elasticity
of substitution (IES).
is the intertemporal elasticity
of substitution (IES).
Solving for the world portfolio yields the following expressions
for the components of ![]() :
:
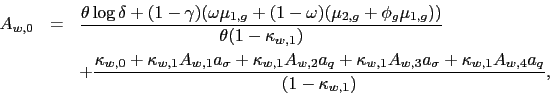
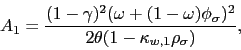
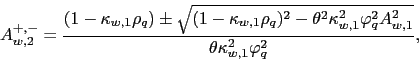
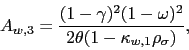
and
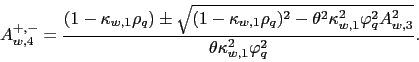
To avoid the load of time-varying volatilities ![]() , and
, and ![]() from growing
without bounds, I only keep
from growing
without bounds, I only keep ![]() (
(![]() ). The positive root discarded is
explosive in
). The positive root discarded is
explosive in ![]() , i.e.,
, i.e.,
![]() (
(
![]() ).
).
![]() (
(![]() )
will be a solution to the model as long as
)
will be a solution to the model as long as
![]() (
(
![]() ). It is easy to show from these expressions that all state
variables load negatively on the global wealth-consumption ratio.
That is,
). It is easy to show from these expressions that all state
variables load negatively on the global wealth-consumption ratio.
That is, ![]() ,
, ![]() ,
, ![]() ,
, ![]() as long as
as long as ![]() .
.
Solving for the leader country ![]() yields the
following expressions:
yields the
following expressions:
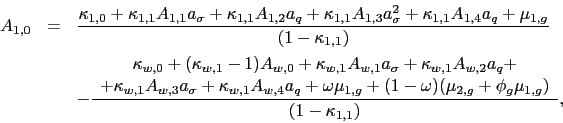

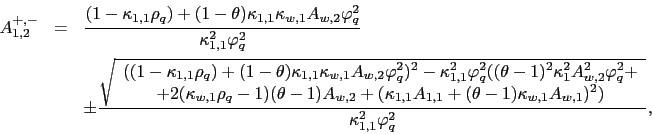
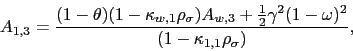
and
![\begin{eqnarray*} A_{1,4}^{+,-} &=&\frac{(1-\kappa _{1,1}\rho _{q})+(1-\theta )\kappa _{1,1}\kappa _{w,1}A_{w,4}\varphi _{q}^{2}}{\kappa _{1,1}^{2}\varphi _{q}^{2} } \ &&\pm \frac{\sqrt{ \begin{array}{c} ((1-\kappa _{1,1}\rho _{q})+(1-\theta )\kappa _{1,1}\kappa _{w,1}A_{w,4}\varphi _{q}^{2})^{2}-\kappa _{1,1}^{2}\varphi _{q}^{2}[(\theta -1)^{2}\kappa _{w,1}^{2}\varphi _{q}^{2}A_{w,4}^{2}+ \ +2(\kappa _{w,1}\rho _{q}-1)(\theta -1)A_{w,4}+(\kappa _{1,1}A_{1,3}+(\theta -1)\kappa _{w,1}A_{w,3})^{2}] \end{array}}}{\kappa _{1,1}^{2}\varphi _{q}^{2}}. \end{eqnarray*}](img233.gif)
Finally, for the follower country ![]() solving the
basic asset pricing equation yields
solving the
basic asset pricing equation yields
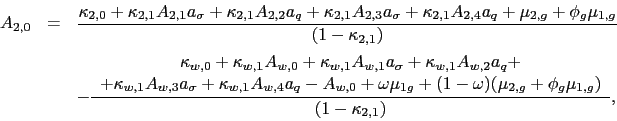
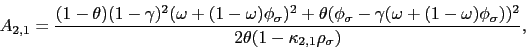
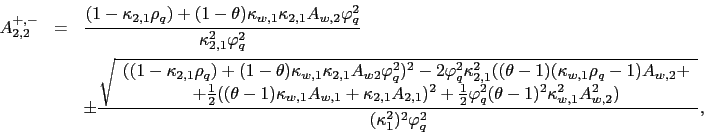
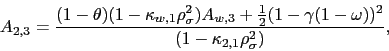
and
![\begin{eqnarray*} A_{2,4}^{+,-} &=&\frac{(1-\kappa _{2,1}\rho _{q})+(1-\theta )\kappa _{w,1}\kappa _{2,1}A_{w,4}\varphi _{q}^{2}}{\kappa _{2,1}^{2}\varphi _{q}^{2} } \ &&\pm \frac{\sqrt{ \begin{array}{c} ((1-\kappa _{2,1}\rho _{q})+(1-\theta )\kappa _{1}\kappa _{2,1}A_{w,4}\varphi _{q}^{2})^{2}-2\varphi _{q}^{2}\kappa _{2,1}^{2}[2(\kappa _{w,1}\rho _{q}-1)(\theta -1)A_{w,4}+ \ +[(\theta -1)\kappa _{w,1}A_{w,3}+\kappa _{2,1}A_{w,3}]^{2}+\varphi _{q}^{2}(\theta -1)^{2}\kappa _{w,1}^{2}A_{w,4}^{2}] \end{array}}}{\kappa _{2,1}^{2}\varphi _{q}^{2}}. \end{eqnarray*}](img239.gif)
Again, following the reasoning for the world portfolio, it only
makes sense to keep ![]() and
and ![]() .
.
References
Andersen, T., Bollerslev, F., and Diebold, F., 2001, The Distribution of Realized Stock Return Volatility, Journal of Financial Economics Vol. 61, 43-76.
Baele, L., and Inghelbrecht, K., 2010, Time-Varying Integration, Interdependence and Contagion, Journal of International Money and Finance Vol. 29, Nr. 5, 791-818.
Bakshi, G., Cao, Z., and Chen, Z., 2000, Pricing and Hedging Long-term Options, Journal of Econometrics, Vol. 94, 277-318.
Bakshi, G., and Madam, D., 2006, A Theory of Volatility Spreads, Management Science, No. 52, Issue 12, 1945-1956.
Bansal, R., Khatchatrian, V., and Yaron, A., 2005, Interpretable asset markets?, European Economic Review Vol. 49 , 531-560.
Bansal, R., and Yaron, A., 2004, Risks for the long-run: A potential Resolution of Asset Pricing Puzzles, The Journal of Finance Vol. 59, Nr. 5, 1481-1509.
Barndorff-Nielsen, O., and Shephard, N., 2002, Econometric Analysis of Realized Volatility and its use in Estimating Stochastic Volatility Models, Journal of Royal Statistical Society, 64, 253-280.
Bekaert, G., and Engstrom, E., 2010, Asset Return Dynamics under Bad Environment-Good Environment Fundamentals, Working Paper, NBER.
Bekaert, G., Engstrom, E., and Xing, Y., 2009, Risk, Uncertainty, and Asset Prices, Journal of Financial Economics Vol. 91 (1), 59-82.
Bekaert, G., Harvey, C., and Ng, A., 2005, Market Integration and Contagion, Journal of Business 78, 39-69.
Bekaert, G.,Hodrick,R., and Zhang,X., 2009, International Stock Return Comovements, Journal of Finance, Vol. 64, 2591-2626.
Bekaert, G., Hoerova, M., and Scheicher, M., 2009, What Do Asset Prices Have to Say About Risk Appetite and Uncertainty?, Working Paper, European Central Bank.
Bollerslev, T., Gibson, M., and Zhou, H., 2011, Dynamic Estimation of Volatility Risk Premiums and Investor Risk Aversion from Option-Implied and Realized Volatilities, Journal of Econometrics, Vol. 160, 235-245.
Bollerslev, T., Marrone, J., Xu, L., and Zhou, H., 2011, Stock Return Predictability and Variance Risk Premia: Statistical Inference and International Evidence, Working paper, NBER.
Bollerslev, T., Tauchen, G., and Zhou, H., 2009, Expected Stock Returns and Variance Risk Premiums, Review of Financial Studies Vol. 22, Nr. 11, 4463-4492.
Bollerslev, T., and Zhou, H., 2006, Volatility puzzles: a unified framework for gauging return-volatility regressions, Journal of Econometrics, Vol. 131, 123-150.
Britten-Jones, M., and Neuberger, A., 2000, Option Prices, Implied Prices Processes, and Stochastic Volatility, Journal of Finance Vol. 55, Nr. 2, 839-866.
Campbell, J., and Cochrane, J., 1999, By Force of Habit: A Consumption based explanation of Aggregate Stock Market Behavior, Journal of Political Economy, Vol. 107, 205-251.
Campbell, J., and Shiller, R., 1988, Stock Prices, Earnings, and Expected Dividends, Journal of Finance Vol. 43 , 661-676.
Carr, P., and Madan, D., 1998, Towards a Theory of Volatility Trading, in Jarrow, R. (ed.), Volatility: New Estimation Techniques for Pricing Derivatives, chapter 29, 417-427.
Carr, P., and Wu, L., 2009, Variance Risk Premiums, Review of Financial Studies Vol. 22, Issue 3, 1311-1341.
Christoffersen, P., Heston, S., and Jacobs, K., 2006, Option Valuation with Conditional Skewness, Journal of Econometrics Vol. 131, 253-84.
Corradi, V., Distaso, W., and Mele, A., 2009, Macroeconomic Determinants of Stock Market Volatility and Volatility Risk Premiums, Working Paper, University of Warwick, Imperial College Business School, London School of Economics.
Driessen, J., and Maenhout, P., 2006, The World Price of Jump and Volatility Risk, Working Paper, University of Amsterdam, INSEAD.
Drechsler, I., Yaron, A., 2011, What's Vol Got To Do with it, Review of Financial Studies, Vol. 24, 1-45.
Epstein, L., and Zin, S., 1989, Substitution, Risk Aversion, and the Intertemporal Behavior of Consumption and Asset Returns: A Theoretical Framework, Econometrica Vol. 57, 937-969.
Forbes, K., and Rigobon, R., 2002, No Contagion, Only Interdependence: Measuring Stock Market Comovements, Journal of Finance Vol. 57, 2223-2261.
Gabaix, X., 2009, Variable Rare Disasters: An Exactly Solved Framework for Ten Puzzles in Macro-Finance, NBER Working Paper.
Gagnon, L., and Karolyi, G., 2006, Price and Volatility Transmission across Borders, Financial Markets, Institutions and Instruments Vol. 15, 107-158.
Gemmill, G. , and Kamiyama, N., 2000, International Transmission of Option Volatility and Skewness: When You're Smiling Does the Whole World Smile?, Working Paper, Warwick Business School.
Hodrick, R., 1992, Dividend Yields and Expected Stock Returns: Alternative Procedures for Inference and Measurements, Review of Financial Studies Vol. 5, 357-386.
Jacob, J., and Vipul, 2008, Estimation and Forecasting of Stock Volatility with Range-Based Estimators, Journal of Futures Markets, Vol. 28, No. 6, 561-581.
Jiang, G., Konstantinidi, E., and Skiadopoulos, G., 2010, The Impact of News announcements on Volatility Spillovers: International Evidence from Implied Volatility Markets, Working Paper, University of Arizona, University of Piraeus.
Jiang, G., and Tian, Y., 2005, Model-Free Implied Volatility and Its Information Content, Review of Financial Studies Vol. 18, 1305-1342.
Konstantinidi, E., Skiadopoulos, G., and Tzagkaraki, E., 2008, Can the Evolution of Implied Volatility be Forecasted? Evidence from European and US implied Volatility Indices, Journal of Banking and Finance Vol. 32, 2401-2411.
Martens, M., and Van Dijk, D., 2007, Measuring Volatility with the Realized Range, Journal of Econometrics, Vol. 138, 181-207.
Meddahi, N., 2002, Theoretical Comparison Between Integrated and Realized Volatility, Journal of Applied Econometrics Vol. 17, 479-508.
Mehra, R., and Prescott, E., 1985, The Equity Premium: a Puzzle, Journal of Monetary Economics, Vol. 15, 145-161.
Mo, H., and Wu, L., 2007, International Capital Asset Pricing: Evidence from Options, Journal of Empirical Finance, Vol. 14 , No. 4, 465-498.
Newey, W., and West, K., 1987, A Simple Positive Semi-Definite, Heteroskedasticity and Autocorrelation Consistent Covariance Matrix, Econometrica Vol. 55, 703-708.
Siriopoulos, C., and Fassas, A., 2009, Implied Volatility Indices - A Review', Working Paper, University of Patras.
Sugihara, Y., 2010, Global Contagion of Volatilities and Volatility Risk Premiums, Working Paper, Institute for Monetary and Economic Studies, Bank of Japan.
Tang, J., 2001, Contagion: en Empirical Test, Working Paper, Duke University.
Todorov, V., 2010, Variance Risk Premium Dynamics: The Role of Jumps, Review of Financial Studies Vol. 23, 345-383.
Wagner, N., and Szimayer, A., 2004, Local and Spillover Shocks in Implied Market Volatility: Evidence for the US and Germany, Research in International Business and Finance Vol. 18, 237-251.
Weil, P., 1989, The Equity Premium Puzzle and the Risk-Free Rate Puzzle, Journal of Monetary Economics Vol. 24, 401-421.
Zhou, H., 2010, Variance Risk Premiums, Asset Predictability Puzzles, and Macroeconomic Uncertainty,, Working Paper, Board of Governors of the Federal Reserve System.
Footnotes
1. See for instance Britten-Jones and Neuberger (2000), Jiang and Tian (2005), Bakshi and Madan (2006), Carr and Wu (2009), Bollerslev, Gibson and Zhou (2011), and BTZ, among others. Return to text
2. BTZ, Zhou (2010), and Drechsler and Yaron (2011) find empirical evidence for their respective model-implied return predictability. However, Bekaert and Engstrom (2010) find weak evidence of return predictability. Return to text
3. Both, the UK (FTSE) and France (French March des Options Negociables de Paris) had previously introduced IV indices separately. Return to text
4. It has been shown in the literature that the use of intradaily returns outperforms lower frequency data in the estimation of the realized variance (Andersen et. al., (2001), Barndorff-Nielsen and Shephard, (2002); and Meddahi, (2002)). Return to text
5. Martens and van Dijk (2007) provide a description of the range based estimation of volatility. Jacob and Vipul (2008) analyze the extension of the range based measure to forecast the variance. Return to text
6. Also as a preventive measure to reduce the noise implicit in country-specific variance premiums, I also check the robustness of my results to considering a proxy for the world VP (with and without the US) similar to that in Bollerslev, et. al. (2011). Return to text
7. The results are checked for robustness when all returns are expressed in US dollars. Return to text
8. See Bollerslev, Gibson and Zhou (2011), and Corradi, et. al. (2009) for a more detailed analysis of the relation between the variance premium and the business cycle in the US. Return to text
9. The martingale measure is the benchmark measure in BTZ and Bollerslev, et. al. (2011). Return to text
10. A group of papers have also provided preliminary evidence of this regularity using Black-Scholes-based implied volatility. See, for instance, Bakshi, Cao and Chen (2000), Christoffersen, Heston and Jacobs (2006), and Bollerslev and Zhou (2006). Return to text
11. This is certainly not the first one in analyzing the informational content of option markets internationally. Some preliminary evidence that volatiliy risk is priced in an international setting can be found in Mo and Wu (2007) and Driessen and Maenhout (2006). Implied volatility in international markets has also been analyzed in Konstantinidi, Skiadopoulos, and Tzagkaraki (2008), Siriopoulos and Fassas (2009), and Jiang, Konstantinidi and Skiadopoulos (2010). Return to text
12. See for instance BTZ, Zhou (2010) and Drechsler and Yaron (2011). Return to text
13. It is worth pointing out that the variance premium in Belgium shows the lowest Sharpe ratio (almost half that for the rest of the countries). This could preliminary suggest that the variance premium is particularly volatile in Belgium. This in turn implies a somehow noisier measure in this country, potentially driven by the liquidity of the Belgian option market. Return to text
14. The empirical evidence on the inability of the local VP to predict local excess returns for all countries in our sample except for Belgium and the Netherlands has also been obtained in independent concurrent work by Bollerslev, et. al. (2011). Return to text
15. In order to save space, the detailed solution of my model is presented in Appendix A Return to text
16. Bekaert, Engstrom and Xing (2009) survey the evidence on time-varying volatility of consumption for the US. Bansal, et. al. (2005) provide empirical evidence of time-varying macroeconomic uncertainty for the US, Germany, Japan, and the UK. BTZ also find preliminary empirical evidence on the existence of time-varying VoV for the US. Return to text
17. The parameters ![]() , and
, and
![]() can of course be set to 0; a
case that I will also analyze in the numerical simulation of the
model. Now, although
can of course be set to 0; a
case that I will also analyze in the numerical simulation of the
model. Now, although ![]() turns out to have an
insignifcant effect on the role of international variance premium,
it is kept to maintain the possibility of a common level component
in consumption. Alternative ways of characterizing the systematic
component of the variance premiums outside the simplifications of a
two-country model are being explored in my current research
agenda. Return to text
turns out to have an
insignifcant effect on the role of international variance premium,
it is kept to maintain the possibility of a common level component
in consumption. Alternative ways of characterizing the systematic
component of the variance premiums outside the simplifications of a
two-country model are being explored in my current research
agenda. Return to text
18. To be coherent with the idea of
agents that fear an increase in macroeconomic uncertainty,
![]() is assumed to be higher than 1. This
assumption accomodates some empirical asset pricing regularities,
among them: (i) a positive variance premium; (ii) the feedback
effect between PD ratios and consumption volatility; and (iii) a
low risk-free rate (BY and BTZ). See also Mehra and Prescott (1985)
for reasonable values of
is assumed to be higher than 1. This
assumption accomodates some empirical asset pricing regularities,
among them: (i) a positive variance premium; (ii) the feedback
effect between PD ratios and consumption volatility; and (iii) a
low risk-free rate (BY and BTZ). See also Mehra and Prescott (1985)
for reasonable values of ![]() . Return to text
. Return to text
19. It is important to keep in mind that
this is actually the drift difference of the conditional variance
between the two measures. In the case of Gaussian shocks, the level
difference
![]() would be
zero (see Drechsler and Yaron, (2011)). I intentionally omit the
use of models that generate a level difference in the variance
premium to maintain the simplicity of the expressions specially
given that the main attention will be centered on the qualitative
implications of my model and not on the calibration of its
parameters. Return to text
would be
zero (see Drechsler and Yaron, (2011)). I intentionally omit the
use of models that generate a level difference in the variance
premium to maintain the simplicity of the expressions specially
given that the main attention will be centered on the qualitative
implications of my model and not on the calibration of its
parameters. Return to text
20. The risk neutral probability is replaced by its log-linear approximation:
Bear in mind that a closed form solution to the risk neutral variance cannot be obtained in this setting. Return to text
21. In the following section, the identification of the leader economy will be fully given by the empirical evidence. Return to text
22. A full calibration of my model is out of the scope of this paper. My attention is rather centered in its qualitative implications. These implications explain in turn the main empirical findings of this paper such as the local predictability puzzle and the ability of the US variance premium to predict all other countries equity returns. Return to text
23. It is easy to show that the same
monotonous relation holds for the IES ![]() . Results
for the relation between
. Results
for the relation between ![]() and the model
implications are available upon request. Return to text
and the model
implications are available upon request. Return to text
24. These simulations are left unreported in order to save space. Return to text
25. The highly idiosyncratic dynamic of the variance premium in Japan has been previously documented in the literature (see, for instance, Driessen and Maenhout, (2006)). Return to text
26. The following month (![]() ) is assumed to be the period 22 days after
the realization of
) is assumed to be the period 22 days after
the realization of ![]() . Return to text
. Return to text
27. Equation (7) actually has an implication on the variance premium covariance. To avoid a potential scale problem, and make results easier to interpret, I only report cross-country correlations. An expression for the variance premium correlation from Eq. (7) is direct, although not necessarily linear in VoV. Return to text
28. In unreported results, I actually show that, except for the variance premium measure based on the martingale assumption, the predictive role of the US variance premium over its correlation with Germany and Japan holds for all alternative variance premium specifications considered. Return to text
29. Given the high correlation in
![]() across countries, it would be hard to
disentangle the simultaneous role of
across countries, it would be hard to
disentangle the simultaneous role of ![]() with
any other
with
any other ![]() since multiple regressions will
be highly affected by multicolinearity. Return to text
since multiple regressions will
be highly affected by multicolinearity. Return to text
30. The evidence suggests that the predictive power of the variance premium is stronger at the quarterly horizon. This result is in line with the findings in BTZ for the US and is discussed in detail in the international setting below. Return to text
31. In fact, in unreported results, I show that not even a proxy for the world variance premium (with and without the US) is able to significantly predict equity returns for all other countries in the sample. This evidence is in contrast with that in Bollerslev, et.al. (2011). They find a value weighted VP, where the VP is measured using the Martingale assumption as in BTZ, to have predictive power over future equity returns for all countries in our sample except for Belgium and the Netherlands for a sample period between 2000 and 2010. Return to text
32. The hump-shaped predictability pattern, as well as the significance of the US variance premium in predicting foreign equity returns is robust to considering the US term spread and dividend yield. Results for these regressions are available upon request. Return to text
33. For the Netherlands and Japan, adding any noise to the US variance premium almost immediately weakens its predictive power. In contrast, for the UK, the standard deviation of the noise signal has to be at least 70% that of the original variance premium before its predictive power disappears. Return to text
34. When the range based forecast of realized volatility is used, the US variance premium predicts returns only for the UK, Belgium and France. Return to text
35. Results for the robustness tests are left unreported in order to save space and center the discussion. The results for the noise stress tests, the alternative variance premium specifications, samples, currencies, as well as for alternative variance covariance matrix approximations (In particular, Hodrick, (1992)) are available upon request. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text