
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1056, October 2012 --- Screen Reader
Version*
Evaluating a Global Vector Autoregression for Forecasting
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
Global vector autoregressions (GVARs) have several attractive features: multiple potential channels for the international transmission of macroeconomic and financial shocks, a standardized economically appealing choice of variables for each country or region examined, systematic treatment of long-run properties through cointegration analysis, and flexible dynamic specification through vector error correction modeling. Pesaran, Schuermann, and Smith (2009) generate and evaluate forecasts from a paradigm GVAR with 26 countries, based on Dées, di Mauro, Pesaran, and Smith (2007). The current paper empirically assesses the GVAR in Dées, di Mauro, Pesaran, and Smith (2007) with impulse indicator saturation (IIS)--a new generic procedure for evaluating parameter constancy, which is a central element in model-based forecasting. The empirical results indicate substantial room for an improved, more robust specification of that GVAR. Some tests are suggestive of how to achieve such improvements
Keywords: Cointegration, error correction, forecasting, GVAR, impulse indicator saturation, model design, model evaluation, model selection, parameter constancy, VAR
JEL classification: C32, F41
Introduction
The recent financial crisis and ensuing Great Recession have highlighted the importance and pervasiveness of international linkages in the world economy--and the importance of capturing those linkages in empirical macroeconomic models that are used for economic analysis, forecasting, and policy analysis. Pesaran, Schuermann, and Weiner (2004) propose and implement global vector autoregressions (or GVARs) as an ingenious approach for capturing international linkages between country- or region-specific error correction models. Dées, di Mauro, Pesaran, and Smith (2007) (hereafter DdPS) extend that work to a larger number of countries and regions; and Pesaran, Schuermann, and Smith (2009) assess the forecasting properties of the GVAR implemented in DdPS.
The GVAR methodology has several attractive features:
- a versatile structure for characterizing international macroeconomic and financial linkages though multiple channels,
- a standardized economically appealing choice of variables (both domestic and foreign) for each country or region,
- a systematic treatment of long-run properties through cointegration analysis, and
- flexible dynamic specification through vector error correction modeling.
These features are very appealing, and they balance naturally the roles of data and economic theory in empirical modeling. The GVAR explicitly aims to capture international economic linkages, especially linkages between the macroeconomic and financial sides of economies. Weak exogeneity plays an important role through allowing conditional subsystem analysis on a country-by-country basis. Data aggregation--empirically implemented but based on economic theory--achieves a high degree of parsimony in the estimated models.
The current paper re-examines some of the empirical underpinnings for global vector autoregressions, focusing on parameter constancy because of the intimate connections between it and forecast performance. To test parameter constancy, this paper uses impulse indicator saturation, which is a recent generic approach to evaluating constancy. The empirical results indicate substantial room for an improved, more robust specification of DdPS's GVAR; and some tests are suggestive of how to achieve such improvements. See Clements and Hendry (1998, 1999, 2002) and Hendry (2006) for discussions on the relationships between parameter constancy, forecast performance, and forecast failure.
In related work, Ericsson (2012) discusses the theory of reduction and exogeneity in the context of GVARs, thereby providing the background for tests of parameter constancy, data aggregation, and weak exogeneity in GVARs. Using those tests, Ericsson (2012) then evaluates the equations for the United States, the euro area, the United Kingdom, and China in DdPS's GVAR. Ericsson and Reisman (2012) provide parallel results for equations for all 26 countries in DdPS's GVAR.
This paper is organized as follows. The second section describes a prototypical GVAR and, in the context of that prototypical GVAR, summarizes the current approach taken to modeling GVARs, as developed in Pesaran, Schuermann, and Weiner (2004) and DdPS inter alia. The third section reviews the procedure for testing parameter constancy called impulse indicator saturation, which utilizes the computer-automated model selection algorithm in Autometrics. The fourth section empirically evaluates DdPS's GVAR for parameter constancy, using impulse indicator saturation. The final section concludes.
The GVAR
To motivate the use of GVARs in practice, this section describes a prototypical GVAR (first subsection) and relates it to the GVAR in DdPS (second subsection).
The current approach to modeling GVARs has been developed in Pesaran, Schuermann, and Weiner (2004) and DdPS inter alia. For further research on GVARs, see Garratt, Lee, Pesaran, and Shin (2006); Pesaran and Smith (2006); Dées, Holly, Pesaran, and Smith (2007); Pesaran, Smith, and Smith (2007); Hieberta and Vansteenkiste (2009); Pesaran, Schuermann, and Smith (2009); Castrén, Dées, and Zaher (2010); Chudik and Pesaran (2011); and the comments and rejoinders to Pesaran, Schuermann, and Weiner (2004) and Pesaran, Schuermann, and Smith (2009). Juselius (1992) provides a conceptual precursor to GVARs in her sector-by-sector analysis of the Danish economy to obtain multiple long-run feedbacks entering an equation for domestic inflation. Smith and Galesi (2011) have designed and documented an easy-to-use Excel-based interface that accesses Matlab procedures to implement GVARs.
A Prototypical GVAR
This subsection describes a prototypical GVAR that has three countries, with two variables per country and a single lag on each variable in the underlying vector autoregression (VAR). For ease of exposition, global variables (such as oil prices) and deterministic variables (such as an intercept and trend) are ignored. This prototypical GVAR highlights key features that are important to the remainder of this paper. In the exposition below, this prototypical GVAR is considered first in its generic form, then in its error correction representation, then on a country-by-country basis, and finally on a variable-by-variable basis for each country. While the prototypical GVAR may well be unrealistically simple for empirical use, it conveys important aspects of the GVAR without undue algebraic complication, and it allows a straightforward description of the GVAR in DdPS. Ericsson (2012) provides a more complete description of the structure of GVARs, the notation used, and the underlying assumptions.
The underlying VAR for the prototypical GVAR is:
(1) ![]()
for ![]() and
and
![]() , where
, where ![]() is the
country index,
is the
country index, ![]() is the time index,
is the time index, ![]() is
the number of observations,
is
the number of observations, ![]() is the vector
of domestic variables for country
is the vector
of domestic variables for country ![]() at time
at time
![]() ,
, ![]() is the vector of
corresponding foreign aggregates (i.e., foreign relative to country
is the vector of
corresponding foreign aggregates (i.e., foreign relative to country
![]() ) at time
) at time ![]() ,
, ![]() is the matrix of coefficients on the lagged domestic
variables,
is the matrix of coefficients on the lagged domestic
variables, ![]() and
and ![]() are the
matrices of coefficients on the contemporaneous and lagged foreign
aggregates, and
are the
matrices of coefficients on the contemporaneous and lagged foreign
aggregates, and ![]() is the error term induced by
having conditioned on those foreign variables. Empirically, one
interesting triplet of countries is as follows: the United States
(
is the error term induced by
having conditioned on those foreign variables. Empirically, one
interesting triplet of countries is as follows: the United States
(![]() ), the euro area (
), the euro area (![]() ), and
China (
), and
China (![]() ). Each subsystem in (1) is also a VARX*
model--that is, a VAR model that conditions on a set of (assumed)
exogenous variables and their lags.
). Each subsystem in (1) is also a VARX*
model--that is, a VAR model that conditions on a set of (assumed)
exogenous variables and their lags.
In error correction representation, the prototypical GVAR in (1) is:
(2)
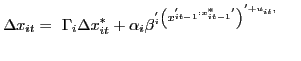
for ![]() and
and
![]() , where
, where ![]() is
the difference operator,
is
the difference operator,
![]() is the matrix of coefficients on
the change in contemporaneous foreign aggregates, and
is the matrix of coefficients on
the change in contemporaneous foreign aggregates, and
![]() and
and
![]() are the matrices of adjustment
coefficients and cointegrating vectors for country
are the matrices of adjustment
coefficients and cointegrating vectors for country ![]() .
The matrices
.
The matrices
![]() ,
,
![]() , and
, and
![]() in (2) are functions
of the matrices
in (2) are functions
of the matrices ![]() ,
, ![]() , and
, and
![]() in (1).
in (1).
The explicit country-by-country structure of the GVAR in equation (2) is as follows:
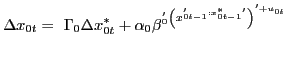
|
(1) |
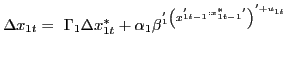
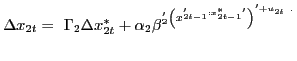
In equation (3),
a country's domestic variables respond to the foreign aggregates
and to lagged disequilibria involving the domestic and foreign
variables. Country 0's foreign aggregate ![]() is a weighted sum of
is a weighted sum of ![]() and
and![]() , which are the foreign variables for country 0.
Likewise,
, which are the foreign variables for country 0.
Likewise, ![]() is a weighted sum of
is a weighted sum of ![]() and
and![]() , and
, and ![]() is a weighted sum of
is a weighted sum of ![]() and
and![]() . The weights might be chosen to reflect the relative
economic importance of the foreign countries to the domestic
country. So, the weights for one country's foreign aggregates need
not (and generally would not) be the same as the weights for
another country's foreign aggregates.
. The weights might be chosen to reflect the relative
economic importance of the foreign countries to the domestic
country. So, the weights for one country's foreign aggregates need
not (and generally would not) be the same as the weights for
another country's foreign aggregates.
To further illuminate the structure of the GVAR, suppose that
![]() in equation (3) comprises two
variables:
in equation (3) comprises two
variables: ![]() (the log of country
(the log of country ![]() 's real GDP), and
's real GDP), and
![]() (country
(country ![]() 's
CPI inflation). Because
's
CPI inflation). Because
![]() and
and
![]() ,
equation (3)
can thus be written explicitly in six equations.
,
equation (3)
can thus be written explicitly in six equations.
(4)
![]()
The subscripts ![]() and
and ![]() refer to the
two variables
refer to the
two variables ![]() and
and ![]() . The GVAR
itself is thus a vector error correction model in which the
individual conditional error correction models for all of the
countries are stacked, one on top of the other.
. The GVAR
itself is thus a vector error correction model in which the
individual conditional error correction models for all of the
countries are stacked, one on top of the other.
Consider the interpretation of (4). In the first
equation of (4),
the growth of GDP in country 0 depends on the growth of GDP and
inflation in countries 1 and 2 through
![]() and
and
![]() , and on lagged
disequilibria involving both domestic and foreign variables through
the cointegrating relationships
, and on lagged
disequilibria involving both domestic and foreign variables through
the cointegrating relationships
![]() . In each remaining equation, the domestic variable likewise
depends on the foreign variables through the change in their
contemporaneous aggregates and through the error correction
terms.
. In each remaining equation, the domestic variable likewise
depends on the foreign variables through the change in their
contemporaneous aggregates and through the error correction
terms.
Some potential cointegrating relationships include the following: domestic and foreign GDP are cointegrated; domestic GDP is cointegrated with domestic inflation; domestic GDP is stationary, or is trend-stationary if a trend is included in the cointegrating space; domestic and foreign inflation are cointegrated; and domestic inflation is stationary. Even in this simple two-variable example, many long-run relationships are possible. Yet more (and more complicated) long-run relationships may exist in multivariate settings such as the GVAR in DdPS, described below.
While the prototypical GVAR in (4) has a remarkable simplicity of structure, it still shows how domestic and foreign variables may influence each other through multiple channels, and in both the short run and the long run. As (4) illustrates, a GVAR provides a versatile structure for characterizing multiple international linkages for a standardized economically appealing choice of variables with a systematic and flexible treatment of long-run and short-run properties through cointegration analysis and vector error correction modeling.
In practice, GVARs have many potential uses, such as private-firm policy regarding risk, banking supervision and regulation, central bank policy, and forecasting; cf. Pesaran, Schuermann, and Weiner (2004), Dées, di Mauro, Pesaran, and Smith (2007), and Pesaran, Schuermann, and Smith (2009). In some of these situations, strong exogeneity, super exogeneity, or both may be required for valid analysis; see Ericsson, Hendry, and Mizon (1998) and Ericsson (2012).
The GVAR in DdPS
To provide a sense of the empirical aspects involved in modeling a global vector autoregression, consider the GVAR in DdPS.
The set of domestic variables ![]() is as follows
(with a few exceptions for specific countries, as noted in DdPS):
real GDP (
is as follows
(with a few exceptions for specific countries, as noted in DdPS):
real GDP (![]() ), CPI inflation (
), CPI inflation (
![]() ), real equity prices
(
), real equity prices
(![]() ), the real exchange rate
(
), the real exchange rate
(![]() ), the short-term interest rate
(
), the short-term interest rate
(![]() ), and the long-term interest rate
(
), and the long-term interest rate
(![]() ). DdPS focus on 25 countries plus
one region (the euro area); see DdPS for details. For convenience,
both countries and regions are referred to as "countries" below.
The country-specific aggregated foreign variables (
). DdPS focus on 25 countries plus
one region (the euro area); see DdPS for details. For convenience,
both countries and regions are referred to as "countries" below.
The country-specific aggregated foreign variables (![]() ) are constructed from the full set of domestic
variables across all countries, using fixed trade weights.
) are constructed from the full set of domestic
variables across all countries, using fixed trade weights.
The VARX* for each country initially has two lags on domestic variables and on the foreign aggregates. In some instances, however, shorter lags are selected, based on standard information criteria. Also, the VARX* includes a global variable (oil prices) and deterministic variables (an intercept and trend).
Cointegration in the VARX* is tested, following the procedure in
Harbo, Johansen, Nielsen, and Rahbek (1998) and using critical
values from MacKinnon, Haug, and Michelis (1999); see also Johansen
(1992, 1995) and Juselius (2006). The number of cointegrating
vectors may differ from country to country. In the conditional
error correction model, the country's cointegrating vectors are
written in their reduced form, i.e., with
![]() beginning with an identity
matrix.
beginning with an identity
matrix.
The data are quarterly, mainly taken from the IMF's
International Financial Statistics; see DdPS. Estimation is
typically over 1979Q4-2003Q4 (![]() ). This GVAR from
DdPS provides the empirical illustration examined below.
). This GVAR from
DdPS provides the empirical illustration examined below.
Impulse Indicator Saturation
This section describes the procedure called impulse indicator saturation, which the subsequent section uses to test parameter constancy of the GVAR in DdPS.
Impulse indicator saturation (IIS) uses zero-one impulse
indicator dummies to analyze properties of a model. There are
![]() such dummies, one for each observation in
the sample. While inclusion of all
such dummies, one for each observation in
the sample. While inclusion of all ![]() dummies in an
estimated model is infeasible, blocks of dummies can be included;
and that insight provides the basis for IIS. A simple example with
two equal-sized blocks motivates the generic approach in IIS. See
Hendry, Johansen, and Santos (2008), Johansen and Nielsen (2009),
and Hendry and Santos (2010) for further discussion and recent
developments.
dummies in an
estimated model is infeasible, blocks of dummies can be included;
and that insight provides the basis for IIS. A simple example with
two equal-sized blocks motivates the generic approach in IIS. See
Hendry, Johansen, and Santos (2008), Johansen and Nielsen (2009),
and Hendry and Santos (2010) for further discussion and recent
developments.
Imagine estimating a model specification such as the GVAR in
(4) in three
steps. First, estimate that model, including impulse indicator
dummies for the first half of the sample. That estimation is
equivalent to estimating the model over the second half of the
sample, ignoring the first half. Drop all statistically
insignificant impulse indicator dummies and retain the
statistically significant dummies. Second, repeat this process, but
start by including impulse indicator dummies for the second half of
the sample; and retain the statistically significant ones. Third,
re-estimate the original model, including all dummies retained in
the two block searches; and select the statistically significant
dummies from that combined set. Hendry, Johansen, and Santos (2008)
and Johansen and Nielsen (2009) have shown that, under the null
hypothesis of correct specification, the fraction of impulse
indicator dummies retained is roughly ![]() , where
, where
![]() is the target size. For instance, if
is the target size. For instance, if
![]() and the target size is 1%, then (on
average) only one impulse indicator dummy is retained when the
model is correctly specified.
and the target size is 1%, then (on
average) only one impulse indicator dummy is retained when the
model is correctly specified.
If the model is mis-specified such that its implied coefficients are nonconstant over time, IIS has power to detect that nonconstancy. See Hendry and Santos (2010, Section 4) for an example. Interestingly, the residuals of the estimated model without any impulse indicator dummies need not lie outside their estimated 95% confidence region, even with a statistically and economically large break in the underlying parameters of the data generation process. Also, the IIS procedure can have high power to detect the break, even though the nature of the break was not utilized in the procedure itself.
In practice, IIS in the Autometrics routine of Doornik and Hendry's (2009) OxMetrics utilizes many blocks, and the partitioning of the sample into blocks may vary over iterations of searches; see also Hendry and Krolzig (1999, 2001, 2005), Hoover and Perez (1999, 2004), and Krolzig and Hendry (2001). IIS is a statistically valid procedure for integrated, cointegrated data; see Johansen and Nielsen (2009). IIS can also serve as a diagnostic statistic for many forms of mis-specification.
Many existing procedures can be interpreted as "special cases" of IIS in that they represent particular algorithmic implementations of IIS. Such special cases include recursive estimation, rolling regression, the Chow (1960) predictive failure statistic (including the 1-step, breakpoint, and forecast versions implemented in OxMetrics), the Andrews (1993) unknown breakpoint test, the Bai and Perron (1998) multiple breakpoint test, intercept correction (in forecasting), and robust estimation. IIS thus provides a general and generic procedure for analyzing a model's constancy, allowing for an unknown number of structural breaks occurring at unknown times with unknown duration and magnitude anywhere in the sample.
Algorithmically, IIS also solves the problem of having more regressors than observations by testing and selecting over blocks of variables. That block approach permits testing the aggregation assumption implied by the use of foreign aggregates in the GVAR; see Ericsson (2012) for a discussion of the underlying theory and for implementation in Autometrics.
Evaluation of DdPS's GVAR with IIS
This section implements the parameter constancy test associated
with impulse indicator saturation, using the GVAR in DdPS to
illustrate. Tests on individual equations and on country-specific
subsystems are both feasible. Specifically, the subsystem for a
given country is unrestricted (either as an unrestricted VARX*, or
as an unrestricted cointegrated VARX* conditional on the subsystem
estimate of
![]() ), so OLS estimation equation by
equation is maximum likelihood estimation of the subsystem VARX*
model. Valid omitted-variables test statistics can be calculated
either on the VARX* as a subsystem, or on the individual equations
of the VARX*. These two approaches may imply different alternative
hypotheses, even while the null hypothesis is the same. This
section discusses these test statistics for the equation-equation
approach for the cointegrated VARX*; Ericsson (2012) and Ericsson
and Reisman (2012) examine inter alia the IIS test
statistics for the subsystem approach.
), so OLS estimation equation by
equation is maximum likelihood estimation of the subsystem VARX*
model. Valid omitted-variables test statistics can be calculated
either on the VARX* as a subsystem, or on the individual equations
of the VARX*. These two approaches may imply different alternative
hypotheses, even while the null hypothesis is the same. This
section discusses these test statistics for the equation-equation
approach for the cointegrated VARX*; Ericsson (2012) and Ericsson
and Reisman (2012) examine inter alia the IIS test
statistics for the subsystem approach.
The first subsection discusses the IIS test results, focusing in detail on selected equations for the United States, Japan, Sweden, and Brazil. The second subsection compares these results with those reported in DdPS, and it discusses various implications and extensions.
Selected Highlights
To illustrate the use of impulse indicator saturation, Table 1
reports results from IIS at the 0.1% target level for four selected
equations: for U.S. output, for Japanese output, for the Swedish
real exchange rate, and for Brazilian inflation. This table lists
the ![]() -statistics for the significance of the
retained impulse indicator dummies, the associated
-statistics for the significance of the
retained impulse indicator dummies, the associated ![]() -values, and the dates of the retained impulse indicator
dummies.
-values, and the dates of the retained impulse indicator
dummies.
Parameter constancy is rejected by IIS in all four equations. In the first three equations, the retained impulse indicator dummies reflect known historical events associated with major changes in the behavior of the variable being modeled. In the equation for U.S. output, IIS retains impulse indicator dummies for 1980Q2 and 1982Q1, reflecting the fall of U.S. output growth after the second OPEC oil price increase and tightening of U.S. monetary policy. In the equation for Japanese output, IIS retains an impulse indicator dummy for 1989Q2, which marks the beginning of decades-long lower growth in Japan. In the equation for the Swedish real exchange rate, IIS retains an impulse indicator dummy for 1982Q4, which captures a 15.9% devaluation of the Swedish krona on October 8, 1982.
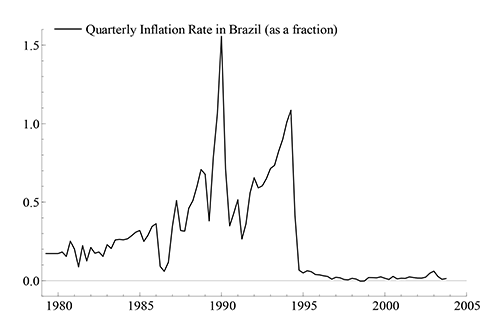
IIS for the fourth equation--of Brazilian inflation--is
particularly revealing. IIS detects 14 dummies--all prior to
1995--with an ![]() -statistic of 75.1 for the significance
of those dummies. As is evident from Figure 1, Brazilian inflation
changed its behavior radically after 1994, resulting in
historically very low inflation rates and much less variability,
and in line with marked changes in government policies.
Economically and statistically, IIS for this equation implies that
a VARX* model is inadequate to capture the essential features of
Brazilian inflation.
-statistic of 75.1 for the significance
of those dummies. As is evident from Figure 1, Brazilian inflation
changed its behavior radically after 1994, resulting in
historically very low inflation rates and much less variability,
and in line with marked changes in government policies.
Economically and statistically, IIS for this equation implies that
a VARX* model is inadequate to capture the essential features of
Brazilian inflation.
Table 1 reports results for four of the 134 equations in DdPS's GVAR. Impulse indicator dummies are found at the 0.1% target level in 99 of those 134 equations--over two thirds of them; see Ericsson and Reisman (2012). That result is particularly impressive because the target level is 0.1% and the sample size is 97, implying an only one-in-ten probability of retaining an impulse indicator dummy in a given equation by chance.
Table 1: Impulse Indicator Saturation at the 0.1% Target Level for Certain Equations for the United States, Japan, Sweden, and Brazil
| Country and Dependent variable | F-Statistic [p-value] d.f. Impulse Dates |
|---|---|
| United States | 9.50** [0.0002] 1980Q2, 1982Q1 |
| Japan | 13.1** [0.0005] 1989Q2 |
| Sweden | 12.1** [0.0008] 1982Q4 |
| Brazil | 75.1** [0.0000] 14 dummies |
Notes. The four entries within a given block of numbers are (i) the
![]() -statistic for the significance of the
retained impulse indicator dummies, (ii) the tail probability
associated with that value of the
-statistic for the significance of the
retained impulse indicator dummies, (ii) the tail probability
associated with that value of the ![]() -statistic (in
square brackets), (iii) the degrees of freedom (d.f.) for the
-statistic (in
square brackets), (iii) the degrees of freedom (d.f.) for the
![]() -statistic (inparentheses), and (iv) the
dates of the retained impulse indicator dummies or (for Brazil) the
number of retained impulse indicator dummies. The two superscript
asterisks ** on the
-statistic (inparentheses), and (iv) the
dates of the retained impulse indicator dummies or (for Brazil) the
number of retained impulse indicator dummies. The two superscript
asterisks ** on the ![]() -statistics denote
significance at the 1% level.
-statistics denote
significance at the 1% level.
Figure 1. The Quarterly Inflation Rate in Brazil (
![]() ), As a
Fraction
), As a
Fraction
Remarks
Several implications follow directly from the rejections described above. First, DdPS (Table V) evaluate their GVAR using tests for structural breaks and find little evidence of mis-specification. DdPS's results contrast with the evidence from IIS. The explanation of these differences lies in the tests employed. For evaluating parameter constancy, impulse indicator saturation may have more power than the structural break tests in DdPS for the range of relevant alternatives, particularly for breaks near the ends of the sample. Hence, the results above represent new information about the GVAR's properties; and they need not be related to other diagnostic tests such as those for residual autocorrelation. Equally, the rejections from IIS are unsurprising in that IIS was not incorporated as a design criterion in the building of DdPS's GVAR; see Hendry (1987) on the role of design criteria in model construction.
Second, rejection of a given null hypothesis does not imply the alternative hypothesis. For instance, the IIS test of parameter constancy may reject because of omitted-variable bias due to improper data aggregation and changing data moments. More generally, the presence of retained impulse indicator dummies may have any of a number of possible implications for modeling. It may be appropriate to simply include the retained impulse indicator dummies, as in the equation for the Swedish real exchange rate, where the dummy captures information beyond the scope of the model's structure. Or, one might add economic variables that the impulse indicator dummies proxy, as perhaps is the case for U.S. and Japanese output. Or, one might treat the presence of the impulse indicator dummies as evidence for a much more fundamental sort of mis-specification being present in the model, as with the equation for Brazilian inflation.
Third, while the large number of rejections by IIS in DdPS's
GVAR may be discouraging at first blush, they are also encouraging
because they imply substantial potential for model improvement; and
they may provide some guidance in finding a better-specified model.
Some of the test statistics above indicate clear directions for
model redesign, as with impulse indicator saturation of the
equation for
![]() detecting 1982Q4. This
modeling approach is consistent with a progressive research
strategy; see Hendry (1987), White (1990), and Doornik (2008)
inter alia.
detecting 1982Q4. This
modeling approach is consistent with a progressive research
strategy; see Hendry (1987), White (1990), and Doornik (2008)
inter alia.
Fourth, and relatedly, IIS in conjunction with automatic model selection may be used constructively in model building. In particular, Castle, Fawcett, and Hendry (2009), Choi and Varian (2012), and Castle and Hendry (2010) show how automatic model selection among a plethora of variables can improve nowcasting of important economic time series.
Fifth, inclusion of impulse indicator dummies can and does have significant consequences for the rest of the model's coefficients--economically, as well as statistically and numerically; see Ericsson (2012).
Sixth, impulse indicator saturation can be applied to any empirical model to assess parameter constancy and model specification of that model. Given the central and substantive roles of invariance and constancy in economic model interpretation, forecasting, and policy analysis, IIS would be of particular interest to apply to dynamic stochastic general equilibrium (DSGE) models, new Keynesian Phillips curve models, Markov switching models, and statistical time series models inter alia. For DSGE models in particular, see the analysis in Edge and Gürkaynak (2010); and note Erceg, Guerrieri, and Gust (2006), Smets and Wouters (2007), and Erceg and Lindé (2010).
Finally, discovering test rejections for a given equation has no implications for the properties of a well-specified equation. For instance, the latter may have constant parameters, even though the former does not.
Conclusions
A global vector autoregression is an ingenious structure for capturing international linkages between country- or region-specific error correction models. A GVAR is a versatile structure for characterizing international macroeconomic and financial linkages through multiple channels; it embodies a standardized economically appealing choice of variables for each country or region; it treats long-run properties through cointegration analysis in a systematic fashion; and it permits flexible dynamic specification through vector error correction modeling. The current paper re-examines the empirical underpinnings for GVARs, focusing on tests of parameter constancy that use impulse indicator saturation. Recent developments in computer-automated model selection allow implementation of impulse indicator saturation, even though historically IIS would have been viewed as infeasible. Empirical results from impulse indicator saturation show scope for improving the GVAR in DdPS and suggest directions to pursue for doing so.
References
Andrews, D. W. K. (1993) "Tests for Parameter Instability and Structural Change with Unknown Change Point", Econometrica, 61, 4, 821-856.
Bai, J., and P. Perron (1998) "Estimating and Testing Linear Models with Multiple Structural Changes", Econometrica, 66, 1, 47-78.
Castle, J. L., N. W. P. Fawcett, and D. F. Hendry (2009) "Nowcasting Is Not Just Contemporaneous Forecasting", National Institute Economic Review, 210, October, 71-89.
Castle, J. L., and D. F. Hendry (2010) "Nowcasting from Disaggregates in the Face of Location Shifts", Journal of Forecasting, 29, 1-2, 200-214.
Castrén, O., S. Dées, and F. Zaher (2010) "Stress-testing Euro Area Corporate Default Probabilities Using a Global Macroeconomic Model", Journal of Financial Stability, 6, 2, 64-78.
Choi, H., and H. Varian (2012) "Predicting the Present with Google Trends" , Economic Record, 88, s1, 2-9.
Chow, G. C. (1960) "Tests of Equality Between Sets of Coefficients in Two Linear Regressions", Econometrica, 28, 3, 591-605.
Chudik, A., and M. H. Pesaran (2011) "Infinite-dimensional VARs and Factor Models", Journal of Econometrics, 163, 1, 4-22.
Clements, M. P., and D. F. Hendry (1998) Forecasting Economic Time Series, Cambridge University Press, Cambridge.
Clements, M. P., and D. F. Hendry (1999) Forecasting Non-stationary Economic Time Series, MIT Press, Cambridge.
Clements, M. P., and D. F. Hendry (2002) "Explaining Forecast Failure in Macroeconomics", Chapter 23 in M. P. Clements and D. F. Hendry (eds.) A Companion to Economic Forecasting, Blackwell Publishers, Oxford, 539-571.
Dées, S., S. Holly, M. H. Pesaran, and L. V. Smith (2007) "Long Run Macroeconomic Relations in the Global Economy", Economics: The Open-Access, Open-Assessment E-Journal, 1, 2007-3, 1-57.
Dées, S., F. di Mauro, M. H. Pesaran, and L. V. Smith (2007) "Exploring the International Linkages of the Euro Area: A Global VAR Analysis", Journal of Applied Econometrics, 22, 1, 1-38.
Doornik, J. A. (2008) "Encompassing and Automatic Model Selection", Oxford Bulletin of Economics and Statistics, 70, supplement, 915-925.
Doornik, J. A. (2009) "Autometrics", Chapter 4 in J. L. Castle and N. Shephard (eds.) The Methodology and Practice of Econometrics: A Festschrift in Honour of David F. Hendry, Oxford University Press, Oxford, 88-121.
Doornik, J. A., and D. F. Hendry (2009) PcGive 13, Timberlake Consultants Press, London (3 volumes).
Edge, R. M., and R. S. Gürkaynak (2010) "How Useful Are Estimated DSGE Model Forecasts for Central Bankers?", Brookings Papers on Economic Activity, 2010, Fall, 209-244 (with comments and discussion).
Erceg, C. J., L. Guerrieri, and C. Gust (2006) "SIGMA: A New Open Economy Model for Policy Analysis", International Journal of Central Banking, 2, 1, 1-50.
Erceg, C. J., and J. Lindé (2010) "Asymmetric Shocks in a Currency Union with Monetary and Fiscal Handcuffs", International Finance Discussion Paper No. 1012, Board of Governors of the Federal Reserve System, Washington, D.C., December.
Ericsson, N. R. (2012) "Improving Global Vector Autoregressions", International Finance Discussion Paper, Board of Governors of the Federal Reserve System, Washington, D.C., in preparation.
Ericsson, N. R., D. F. Hendry, and G. E. Mizon (1998) "Exogeneity, Cointegration, and Economic Policy Analysis", Journal of Business and Economic Statistics, 16, 4, 370-387.
Ericsson, N. R., and E. L. Reisman (2012) "Evaluating Global Vector Autoregressions", International Finance Discussion Paper, Board of Governors of the Federal Reserve System, Washington, D.C., in preparation.
Garratt, A., K. Lee, M. H. Pesaran, and Y. Shin (2006) Global and National Macroeconometric Modelling: A Long-Run Structural Approach, Oxford University Press, Oxford.
Harbo, I., S. Johansen, B. Nielsen, and A. Rahbek (1998) "Asymptotic Inference on Cointegrating Rank in Partial Systems", Journal of Business and Economic Statistics, 16, 4, 388-399.
Hendry, D. F. (1987) "Econometric Methodology: A Personal Perspective", Chapter 10 in T. F. Bewley (ed.) Advances in Econometrics: Fifth World Congress, Volume 2, Cambridge University Press, Cambridge, 29-48.
Hendry, D. F. (2006) "Robustifying Forecasts from Equilibrium-correction Systems", Journal of Econometrics, 135, 1-2, 399-426.
Hendry, D. F., S. Johansen, and C. Santos (2008) "Automatic Selection of Indicators in a Fully Saturated Regression", Computational Statistics, 23, 2, 317-335, 337-339.
Hendry, D. F., and H.-M. Krolzig (1999) "Improving on `Data Mining Reconsidered' by K. D. Hoover and S. J. Perez", Econometrics Journal, 2, 2, 202-219.
Hendry, D. F., and H.-M. Krolzig (2001) Automatic Econometric Model Selection Using PcGets 1.0, Timberlake Consultants Press, London.
Hendry, D. F., and H.-M. Krolzig (2005) "The Properties of Automatic Gets Modelling", Economic Journal, 115, 502, C32-C61.
Hendry, D. F., and C. Santos (2010) "An Automatic Test of Super Exogeneity", Chapter 12 in T. Bollerslev, J. R. Russell, and M. W. Watson (eds.) Volatility and Time Series Econometrics: Essays in Honor of Robert F. Engle, Oxford University Press, Oxford, 164-193.
Hieberta, P., and I. Vansteenkiste (2009) "International Trade, Technological Shocks and Spillovers in the Labour Market: A GVAR Analysis of the US Manufacturing Sector", Applied Economics, 42, 24, 3045-3066.
Hoover, K. D., and S. J. Perez (1999) "Data Mining Reconsidered: Encompassing and the General-to-specific Approach to Specification Search", Econometrics Journal, 2, 2, 167-191 (with discussion).
Hoover, K. D., and S. J. Perez (2004) "Truth and Robustness in Cross-country Growth Regressions", Oxford Bulletin of Economics and Statistics, 66, 5, 765-798.
Johansen, S. (1992) "Cointegration in Partial Systems and the Efficiency of Single-equation Analysis", Journal of Econometrics, 52, 3, 389-402.
Johansen, S. (1995) Likelihood-based Inference in Cointegrated Vector Autoregressive Models, Oxford University Press, Oxford.
Johansen, S., and B. Nielsen (2009) "An Analysis of the Indicator Saturation Estimator as a Robust Regression Estimator", Chapter 1 in J. L. Castle and N. Shephard (eds.) The Methodology and Practice of Econometrics: A Festschrift in Honour of David F. Hendry, Oxford University Press, Oxford, 1-36.
Juselius, K. (1992) "Domestic and Foreign Effects on Prices in an Open Economy: The Case of Denmark", Journal of Policy Modeling, 14, 4, 401-428.
Juselius, K. (2006) The Cointegrated VAR Model: Methodology and Applications, Oxford University Press, Oxford.
Krolzig, H.-M., and D. F. Hendry (2001) "Computer Automation of General-to-specific Model Selection Procedures", Journal of Economic Dynamics and Control, 25, 6-7, 831-866.
MacKinnon, J. G., A. A. Haug, and L. Michelis (1999) "Numerical Distribution Functions of Likelihood Ratio Tests for Cointegration", Journal of Applied Econometrics, 14, 5, 563-577.
Pesaran, M. H., T. Schuermann, and L. V. Smith (2009) "Forecasting Economic and Financial Variables With Global VARs", International Journal of Forecasting, 25, 4, 642-715 (with comments and rejoinder).
Pesaran, M. H., T. Schuermann, and S. M. Weiner (2004) "Modeling Regional Interdependencies Using a Global Error-correcting Macroeconometric Model", Journal of Business and Economic Statistics, 22, 2, 129-181 (with comments and rejoinder).
Pesaran, M. H., L. V. Smith, and R. Smith (2007) "What if the UK or Sweden Had Joined the Euro in 1999? An Empirical Evaluation Using a Global VAR", International Journal of Finance and Economics, 12, 1, 55-87.
Pesaran, M. H., and R. Smith (2006) "Macroeconometric Modelling With a Global Perspective", The Manchester School, 74, supplement, 24-49.
Smets, F., and R. Wouters (2007) "Shocks and Frictions in US Business Cycles: A Bayesian DSGE Approach", American Economic Review, 97, 3, 586-606.
Smith, L. V., and A. Galesi (2011) GVAR Toolbox 1.1 User Guide, CFAP & CIMF, University of Cambridge, Cambridge.
White, H. (1990) "A Consistent Model Selection Procedure Based
on ![]() -testing", Chapter 16 in C. W. J. Granger
(ed.) Modelling Economic Series: Readings in Econometric
Methodology, Oxford University Press, Oxford, 369-383.
-testing", Chapter 16 in C. W. J. Granger
(ed.) Modelling Economic Series: Readings in Econometric
Methodology, Oxford University Press, Oxford, 369-383.
Footnotes
** Forthcoming in the International Advances in Economic Research. The first author is a staff economist in the Division of International Finance, Board of Governors of the Federal Reserve System, Washington, D.C. 20551 U.S.A. ([email protected]) and a Research Professor in the Department of Economics, The George Washington University, Washington, D.C. 20052 U.S.A. ([email protected]); and the second author was a research assistant in the Division of International Finance, Board of Governors of the Federal Reserve System, Washington, D.C. 20551 U.S.A. ([email protected]) at the time that this research was initially undertaken. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. The authors are grateful to David Hendry, Jesper Lindé, Jaime Marquez, Filippo di Mauro, Hashem Pesaran, Tara Rice, and Vanessa Smith for helpful discussions and comments; and additionally to Vanessa Smith for invaluable guidance in replicating estimation results from Dées, di Mauro, Pesaran, and Smith (2007). All numerical results were obtained using PcGive Version 13.30 and Autometrics Version 1.5e in OxMetrics 6.30: see Doornik and Hendry (2009) and Doornik (2009). Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text