
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1073, February 2013 --- Screen Reader
Version*
A Theory of Rollover Risk, Sudden Stops, and Foreign Reserves
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
Emerging economies, unlike advanced economies, have accumulated large foreign reserve holdings. We argue that this policy is an optimal response to an increase in foreign debt rollover risk. In our model, reserves play a key role in reducing debt rollover crises "sudden stops", akin to the role of bank reserves in preventing bank runs. We find that a small, unexpected, and permanent increase in rollover risk accounts for the outburst of sudden stops in the late 1990s, the subsequent increase in foreign reserves holdings, and the salient resilience of emerging economies to sudden stops ever since. Finally, we show that a policy of pooling reserves can substantially reduce the reserves needed by emerging economies.
Keywords: Rollover risk, reserves, sudden stops
JEL classification: F42, F34, H63
1 Introduction
Since the turn of the century, emerging economies have accumulated massive amounts of international reserves. According to Bernanke (2005), this has been the most important channel through which the global "savings glut" widened the U.S. current account deficit. For instance, in 2007, the foreign reserve holdings of China (1.5 trillion US dollars) alone represented approximately 65 percent of the (negative) net foreign asset position of the United States. While massive from an absolute perspective, China's reserves as a percentage of GDP, which averaged 33 percent from 2002-2007, are comparable to that of other emerging economies such as Korea (25 percent), Malaysia (47 percent), and Russia (23 percent).
This raises the question of why emerging economies have accumulated such large amounts of reserves. One strand of the literature focuses on reserves as a form of precautionary savings in economies where crises occur exogenously (Alfaro and Kanczuk 2009; Bianchi et al. 2012; Caballero and Panageas 2007; Jeanne and Ranciere 2011). These theories imply that reserves should be higher when crises are more frequent. However, Gourinchas and Obstfeld (2012) find that reserves are negatively associated with crises in the data. Another strand of the literature considers the role of a country's net foreign asset (NFA) position in preventing crises, without explicitly modeling reserves (Surdu et al. 2009; Mendoza 2010). In contrast, we document that a country's NFA is not significantly associated with crises in the data.
In this paper, we develop a theory in which reserves endogenously preventcrises. In particular, we focus on sudden stops (unusually large reversals of external capital inflows) because they are a common symptom of financial crises such as currency crises, banking crises, and default crises in emerging economies.1 In this theory, sudden stops occur when foreign lenders choose not to roll over a country's external liabilities. We consider the problem of a small open economy that borrows short-term from foreign lenders to finance long-term investments. This maturity mismatch gives rise to rollover risk: in the interim, a random fraction of creditors can choose to roll over while the other creditors cannot.2 Rollover risk in this environment is endogenous because the actual amount of debt that is rolled over is determined by the optimal debt arrangement. Faced with stochastic interim liquidity needs, the government may pay with the reserves it had set aside or liquidate its investment. For small enough liquidity shocks, interim payments are optimally paid with reserves and no sudden stop occurs. For sufficiently large shocks, the government cannot finance its debt obligations without liquidation. Sufficiently large shocks therefore result in a sudden stop as all lenders refuse to roll over. Reserves in turn reduce the probability of sudden stops and increase with rollover risk.
This paper makes empirical, theoretical, and quantitative contributions. First, using the panel discrete-choice approach of Gourinchas and Obstfeld (2012), we show that reserves are negatively associated with sudden stops in addition to default crises, banking crises, and currency crises. In contrast, we document that a country's net debt is not associated with most crises in emerging economies. These results suggest that reserves should be modeled explicitly to understand financial crises. Second, we develop a tractable model in which reserves endogenously reduce the probability of a sudden stop. Using closed form solutions, we show that both the optimal reserves-to-debt ratio and the induced probability of sudden stop increase as the rollover risk rises.
The model is then calibrated for two quantitative applications. First, a small but unanticipated, and permanent increase in rollover risk can account for the short-lived outburst of sudden stops in the late 1990s, and the large accumulation of foreign reserves since then. A model in which reserves do not affect the probability of a sudden stop cannot jointly match these facts. Second, mutual insurance across emerging economies could reduce the amount of reserves needed by as much as two-thirds: pooling or swapping reserves lowers rollover risk across the board.
This paper builds on a large body of literature on reserves, sudden stops, and debt crises. In particular, it relates to other papers on reserves (Aizenman and Lee 2007; Calvo et al. 2012; Frenkel and Jovanovic 1981; Heller 1966; Obstfeld et al. 2010), and on sudden stops (Calvo et al. 2004; Kehoe et al. 2012; Mendoza 2010). Our work departs from the literature by explicitly modeling the rollover decision of foreign lenders, thereby crucially endogenizing the probability of a sudden stop. The endogenous relationship between reserves, rollover risk, and sudden stops is precisely what allows our model to generate an outburst of sudden stops with a small but unexpected increase in rollover risk.
Our paper is also related to the literature on coordination problems and self-fulfilling crises (Cole and Kehoe 2000; Chang and Velasco 2001). In contrast, this paper focuses on debt rollover crises that arise from an optimal arrangement between a borrower and its lenders. Morris and Shin (2006) and Kim (2008) alternatively use the global games framework of Morris and Shin (1998) to study optimal external bailout and optimal reserves. In these coordination games, information dispersion across creditors and aggregate risk interact to induce rollover risk. This paper generates rollover risk from heterogeneous liquidity shocks and can quantitatively account for both the large buildup in reserves and the outburst of sudden stops in the data.
This paper is structured as follows. Section 2 empirically analyzes foreign reserves and sudden stops in emerging economies from 1990 to 2007. In section 3, we present a model of rollover risk, sudden stops, and reserves, and characterize optimal reserves and endogenous sudden stop probabilities. In section 4, we calibrate a multi-country dynamic extension of the model applied to emerging economies. Section 5 concludes.
2 Reserves and Sudden Stops in Emerging Economies
In this section, we document a set of stylized facts regarding foreign reserves, external debt liabilities, and sudden stops in 23 emerging economies during 1990-2007.3 We use the International Financial Statistics (IFS) dataset in conjunction with the updated and extended version of the dataset constructed by Lane and Milesi-Ferretti (2007).
The list of emerging economies used in this paper includes Argentina, Brazil, Chile, China, Colombia, the Czech Republic, Egypt, Hungary, India, Indonesia, Malaysia, Mexico, Morocco, Pakistan, Peru, Philippines, Poland, Romania, Russia, South Africa, South Korea, Thailand, and Turkey. This list includes countries appearing in most classifications of emerging countries.
2.1 Sudden Stops in Emerging Economies
Following Calvo et al. (2004), we define a sudden stop episode as a spell with exceptionally large current account reversals and a recession. We find 13 sudden stop experiences during 1990-2007 across the 23 emerging economies with an outburst of 10 sudden stops between 1997 and 2001.4
To highlight the outburst of sudden stops after the mid-1990s, we divide this time frame into three periods as shown in Figure 1: 1990-1996 is a period of low-frequency sudden stops (with 3 occurrences), 1997-2001 is a period of high-frequency sudden stops (with 10 occurrences), and 2002-2007 is a period of low-frequency sudden stops (with no occurrence).
2.2 Foreign Reserves
In the IFS dataset, foreign reserves are defined as all official public sector foreign assets, except gold, that are readily available to and controlled by the monetary authorities. We highlight two notable facts regarding foreign reserves holdings.
Figure 1. Sudden Stops in Emerging Economies
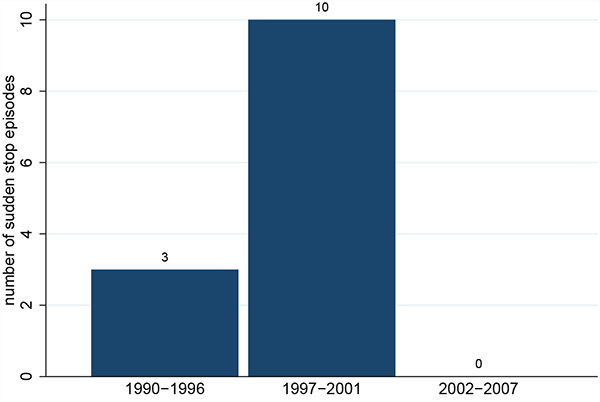
The first fact is that foreign reserves in emerging economies, both as a percent of GDP and and as a percent of external debt liabilities, are significantly higher than those in advanced economies5. The second fact is that these ratios have increased in emerging economies while they have decreased in advanced economies. These facts are summarized in Figures 2 and 3.
Figure 2. Foreign Reserves (Percent of GDP)
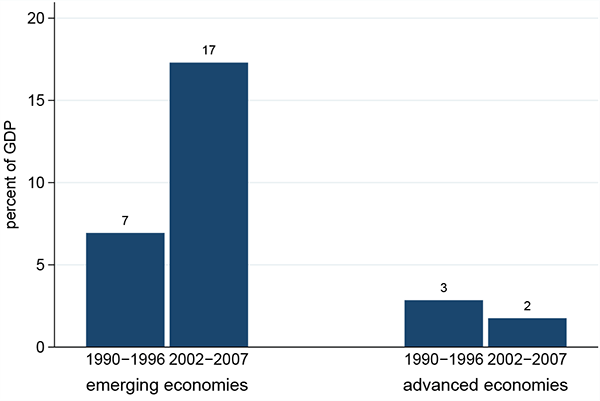
Note: The value for each period and each bloc is the median across economies of the period-average for each economy.
It is worth noting that this phenomenon of increasing reserves is not limited to just a few countries. In fact, foreign reserves are increasing in almost all emerging economies with Chile being the only case in which reserves are decreasing in both measures. This robust observation is shown in Table A.1 (see appendix) of average foreign reserves by country and period.
Figure 3. Foreign Reserves (Percent of External Debt Liabilities)
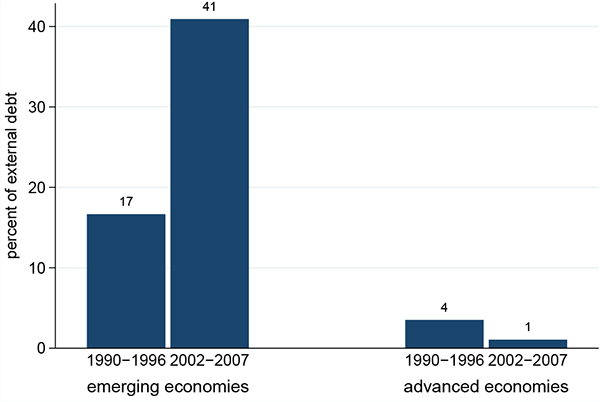
Note: The value for each period and each bloc is the median across economies of the period-average for each economy.
2.3 Reserves and Sudden Stop Probabilities
Following Gourinchas and Obstfeld (2012), we use a panel discrete-choice model to document the effect of foreign reserves on sudden stops. They documented that foreign reserves are associated with reduced banking crisis, currency crisis, or sovereign default. We further document that higher foreign reserves are also associated with reduced sudden stop likelihood. In contrast, net foreign assets are not typically associated with a reduced probability of a crisis.
We use a panel logit model with country fixed effects:
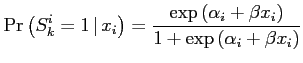
where ![]() denotes whether country
denotes whether country ![]() is in a sudden stop episode in the next
is in a sudden stop episode in the next ![]() years and
years and ![]() are foreign reserves and net
foreign assets in country
are foreign reserves and net
foreign assets in country ![]() during a year that
is not 0 to 3 years after a sudden stop episode (that is,
"tranquil" times using the terminology of Gourinchas and Obstfeld (2012)). The sample is
restricted to "tranquil" times to avoid post-crisis bias.
during a year that
is not 0 to 3 years after a sudden stop episode (that is,
"tranquil" times using the terminology of Gourinchas and Obstfeld (2012)). The sample is
restricted to "tranquil" times to avoid post-crisis bias.
The results of the panel logit estimation are reported in Table 1. Foreign reserves are significantly associated with a reduced probability of sudden stops. For instance, an increase of one standard deviation in the ratio of foreign reserves to external debt liabilities (around 20 percent) is associated with a fall of 7 percent in the probability of a sudden stop over the next two years. The results in Table 1 therefore extend the findings in Gourinchas adn Obstfeld (2012) on the importance of foreign reserves. Table 1 also shows that, unlike foreign reserves, net foreign assets are not commonly associated with crises.6 These findings therefore suggest that foreign reserves should be explicitly modeled to understand financial crises in emerging economies. We develop a theory of rollover risk, sudden stops, and foreign reserves in the next section.
3 Model
3.1 Environment
We consider a small open economy model with three stages:
s=0 (initial), 1 (interim), 2 (final). There is a unit measure of risk
neutral foreign lenders who can lend to the domestic country.7 The domestic country has a
representative agent who has linear preferences ![]() over final stage consumption
over final stage consumption ![]() . The
government chooses allocations and debt arrangements to maximize
the expected utility of the domestic agent. An overview of the
sequence of actions taken by the government and the lenders is
presented in Figure 4.
. The
government chooses allocations and debt arrangements to maximize
the expected utility of the domestic agent. An overview of the
sequence of actions taken by the government and the lenders is
presented in Figure 4.
Table 1. Panel Logit Estimation Across Emerging Economies
| S.D. | 1-2 Years: δp | 1-2 Years: ∂p/∂x | 1-3 Years: δp | 1-3 Years: ∂p/∂x | |
|---|---|---|---|---|---|
Panel A: Sudden Stops: Reserves | 20.16 | -7.13*** | -0.52*** | -10.43*** | -0.68*** |
| Panel A: Sudden Stops: Reserves over External Debt | (1.45) | (0.14) | (2.28) | (0.19) | |
| Panel A: Sudden Stops: Net Foreign Assets | 10.07 | -3.86* | 0.46 | -8.33** | -1.00** |
| Panel A: Sudden Stops: Net Foreign Assets over GDP | (2.30) | (0.32) | (2.87) | (0.42) | |
| Panel A: Sudden Stops: Probability in percent (p) | 11.76 | 20.37 | |||
Panel B: Default Crises: Reserves | 21.58 | -8.08*** | -0.71*** | -12.41*** | -1.11*** |
| Panel B: Default Crises: Reserves over External Debt | (2.15) | (0.21) | (3.10) | (0.29) | |
| Panel B: Default Crises: Net Foreign Assets | 7.79 | -3.95* | 0.63 | -6.16** | -0.98* |
| Panel B: Default Crises: Net Foreign Assets over GDP | (2.34) | (0.47) | (2.88) | (0.56) | |
| Panel B: Default Crises: Probability in percent (p) | 10.11 | 15.01 | |||
Panel C: Banking Crises: Reserves | 27.98 | -3.92 | -0.42** | -7.12** | -0.69*** |
| Panel C: Banking Crises: Reserves over External Debt | (2.47) | (0.17) | (3.00) | (0.18) | |
| Panel C: Banking Crises: Net Foreign Assets | 7.42 | -0.89 | -0.14 | -1.64 | 0.25 |
| Panel C: Banking Crises: Net Foreign Assets over GDP | (0.95) | (0.16) | (1.45) | (0.24) | |
| Panel C: Banking Crises: Probability in percent (p) | 4.12 | 7.67 | |||
Panel D: Currency Crises: Reserves | 24.54 | -2.00 | -0.36* | -4.52* | -0.70** |
| Panel D: Currency Crises: Reserves over External Debt | (1.65) | (0.21) | (2.49) | (0.25) | |
| Panel D: Currency Crises: Net Foreign Assets | 8.60 | -0.43 | 0.04 | 1.95 | 0.19 |
| Panel D: Currency Crises: Net Foreign Assets over GDP | (0.94) | (0.09) | (2.10) | (0.18) | |
| Panel D: Currency Crises: Probability in percent (p) | 2.02 | 4.62 |
Note: *, **, and *** denote significance at the 10, 5, and 1 percent level. ∂p/∂x is the marginal effect in percentage at "tranquil" sample mean. s.d.(x) is the unconditional standard deviation of x over "tranquil" times. Robust standard errors in parentheses are computed using the delta-method. The estimation sample is an unbalanced panel that spans 20 emerging countries between 1990 and 2007. Currency, banking, and default crises dates follow Gourinchas and Obstfeld (2012).
Figure 4. Timeline
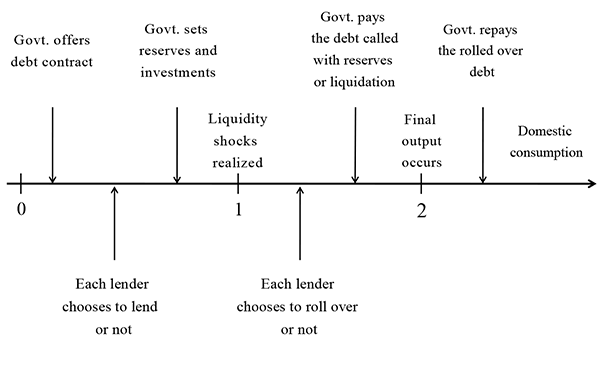
The domestic country has access to two technologies á la Diamond and Dybvig (1983). The first technology transforms the
investment ![]() made in the initial stage into
made in the initial stage into
![]() units in the final stage if production is
uninterrupted. However, if production is interrupted in the interim
through the liquidation of
units in the final stage if production is
uninterrupted. However, if production is interrupted in the interim
through the liquidation of ![]() units of
investment, the technology yields
units of
investment, the technology yields ![]() in
the interim and
in
the interim and ![]() in the final stage. We assume
that liquidation is costly,
in the final stage. We assume
that liquidation is costly,
| (1) |
Further, we impose that there is no partial interim liquidation,
| (2) |
This assumption of full liquidation is made for analytical tractability and is relaxed in the next section. The second technology stores resources (reserves) across stages without depreciation. These technologies are summarized by the following table:
| Technologies | s=0 | s=1 | s=2 |
|---|---|---|---|
| Production and liquidation | -K investment | λL liquidation | A(K-L) final output |
| Reserves | -R1 initial reserves | R1 | |
| -R2 interim reserves | R2 |
In the initial stage, the domestic government borrows
![]() from foreign lenders to finance its initial
stage investments,
from foreign lenders to finance its initial
stage investments,
| (3) |
In the interim, a random fraction ![]() of the
foreign lenders receive liquidity shocks denoted by
of the
foreign lenders receive liquidity shocks denoted by
![]() , meaning that they must call
the loan and be repaid back. The remaining fraction
, meaning that they must call
the loan and be repaid back. The remaining fraction
![]() of lenders with
of lenders with
![]() can call or roll over their
loans. The random aggregate liquidity shock
can call or roll over their
loans. The random aggregate liquidity shock
![]() has a cumulative distribution
function that follows the bounded Pareto distribution given by
has a cumulative distribution
function that follows the bounded Pareto distribution given by
![]() with
with
![]() .
.
We denote
![]() if lender
if lender ![]() rolls
over the loan and
rolls
over the loan and
![]() otherwise. The fraction of lenders
calling the loan is:
otherwise. The fraction of lenders
calling the loan is:
![]() . We assume
that individual lenders cannot coordinate on rollover decisions. We
call it a sudden stop when all lenders refuse to roll over
in the interim (
. We assume
that individual lenders cannot coordinate on rollover decisions. We
call it a sudden stop when all lenders refuse to roll over
in the interim (![]() ). However, all lenders may
panic and refuse to roll over regardless of the state of the
economy. In this paper, we rule out these self-fulfilling "panic"
runs, and instead focus on "rational" sudden stops that occur as
part of the optimal contract depending on the state of the economy.8
). However, all lenders may
panic and refuse to roll over regardless of the state of the
economy. In this paper, we rule out these self-fulfilling "panic"
runs, and instead focus on "rational" sudden stops that occur as
part of the optimal contract depending on the state of the economy.8
We allow the debt repayment of the debt ![]() to be
contingent on whether or not the economy is facing a sudden stop.
During normal times, foreign lenders receive
to be
contingent on whether or not the economy is facing a sudden stop.
During normal times, foreign lenders receive ![]() if they call the loan in the interim, and
if they call the loan in the interim, and
![]() in the final
stage if they roll over the loan.9 During a sudden stop,
however, all the lenders call the debt and receive
in the final
stage if they roll over the loan.9 During a sudden stop,
however, all the lenders call the debt and receive
![]() in the interim.
The debt repayment schedule can be summarized as:
in the interim.
The debt repayment schedule can be summarized as:
| Interim payment P1 | Final payment P2 | |
|---|---|---|
| Normal times (ψ<1) | D | (1+rN)D |
| Sudden stop (ψ=1) | (1+rS)D | 0 |
Because the interest rate can be different when the economy is
in sudden stop, the government can choose to partially default
during sudden stop episodes by setting
![]() . However, there is a limit to
the haircut the lenders can suffer because they can collectively
bargain and extract a fraction
. However, there is a limit to
the haircut the lenders can suffer because they can collectively
bargain and extract a fraction ![]() of the interim
resources available
of the interim
resources available
![]() .10 The
constraint arising from this collective bargaining outcome is given
by:
.10 The
constraint arising from this collective bargaining outcome is given
by:
| (4) |
In this section, we impose ![]() . This assumption is relaxed in the next
section.
. This assumption is relaxed in the next
section.
3.2 Feasible Debt Contracts
We now define the feasibility constraints that the debt contract offered by the government must satisfy in this environment. First, we define a debt contract as a list of:
- four scalars:
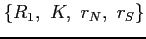 representing the initial reserves, the invested capital, the normal
interest rate, and the sudden stop interest rate, and
representing the initial reserves, the invested capital, the normal
interest rate, and the sudden stop interest rate, and - four state-contingent functions:
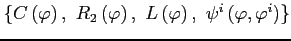 , which denote the final consumption, the interim reserves, the
interim liquidation, and the individual rollover policies,
respectively.
, which denote the final consumption, the interim reserves, the
interim liquidation, and the individual rollover policies,
respectively.
Resource feasibility A debt contract is resource feasible if it satisfies equations (2) and (3) as well as the following constraints:
| (5) |
| (6) |
| 0 | (7) |
Equation (5) requires that interim debt payments and interim reserves cannot exceed initial reserves and interim liquidation, while equation (6) requires that final debt payments and consumption cannot exceed interim reserves and final output.
Interim individual rationality
A debt contract is interim individually rational if, for
each aggregate liquidity shock ![]() and
individual liquidity shock
and
individual liquidity shock
![]() ,
,
| (8) | ||
| where | ![\begin{displaymath}V(\psi^{i}\vert\varphi,\varphi^{i})=\left\{ \begin{array}[c]{ll} P_{1}(\psi(\varphi)) & \text{if }\psi^{i}=1\ & \ 1_{\varphi_{i=0}}\cdot P_{2}(\psi(\varphi)) & \text{if }\psi^{i}=0 \end{array}\right. \end{displaymath}](img3a.gif) |
|
This condition requires that the rollover policy yields a payoff
at least as high as that from deviating. The lender payoff is given
by
![]() when calling, and
when calling, and
![]() when rolling over, if the lender did not receive a liquidity
shock.
when rolling over, if the lender did not receive a liquidity
shock.
Ex ante participation constraint A debt contract satisfies the ex ante participation
constraint if ex ante the debt contract is as profitable as
investing at the world interest rate ![]() :
:
| (9) |
Ex post renegotiation proofness Finally, a debt contract is ex post renegotiation-proof if it satisfies equation (4). This condition limits the haircut suffered by lenders in a sudden stop.
3.3 Optimal Debt Contract
An optimal debt contract is a tuple,
which maximizes the expected utility of the domestic agent subject to resource feasibility, interim individual rationality, the ex ante participation constraint, and ex post renegotiation-proofness. In other words, the government solves:
![]()
subject to (2)-(9)
3.4 Characterization
We now characterize the solution to the optimal debt contract problem.
Proposition 1. Optimal Debt Contract
An optimal debt contract ![]() satisfies:
satisfies:
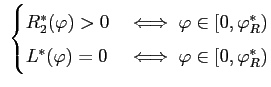
Furthermore, the optimal reserves ratio is:
![$ \varphi_{R}^{*}=\dfrac{R_{1}^{*}}{D}=1-\left[\dfrac{A-1}{A-\lambda}\left(\dfrac{\sigma}{\sigma+1}\right)\right]^{\sigma}$](img89.gif) .
.
(ii) For sufficiently large aggregate shocks, all lenders call their loans:
![$ \;\begin{cases} \psi(\varphi)=\varphi & \forall\varphi\in[0,\varphi_{S})\ \psi(\varphi)=1 & \forall\varphi\in[\varphi_{S},1] \end{cases}$](img91.gif)
Furthermore, sudden stops occur whenever reserves are
depleted:
![]() .
.
Proof: See appendix.
Proposition 1(i) and 1(ii) establish that there are cutoff rules
for reserves, liquidation, and sudden stops. In Proposition 1(i),
![]() is the liquidity shock at
which reserves are depleted and the government must liquidate the
invested capital to meet the promised payments. Because
is the liquidity shock at
which reserves are depleted and the government must liquidate the
invested capital to meet the promised payments. Because ![]() , the government uses existing reserves to meet
payments before eventually liquidating the invested capital.
Proposition 1(i) also establishes that the optimal
reserves-to-liabilities ratio is
, the government uses existing reserves to meet
payments before eventually liquidating the invested capital.
Proposition 1(i) also establishes that the optimal
reserves-to-liabilities ratio is
![]() .
.
In Proposition 1(ii),
![]() is the liquidity shock above
which all lenders exit. We identify this debt rollover crisis as a
sudden stop. The sudden stop cutoff
is the liquidity shock above
which all lenders exit. We identify this debt rollover crisis as a
sudden stop. The sudden stop cutoff
![]() is equal to the optimal
reserves-to-debt ratio
is equal to the optimal
reserves-to-debt ratio
![]() because we assumed there is
no partial liquidation. A sudden stop therefore occurs as soon as
the normal interim payments cannot be met using reserves. We later
relax the full liquidation assumption. With partial liquidation,
the sudden stop cutoff and the reserves cutoff no longer
coincide.
because we assumed there is
no partial liquidation. A sudden stop therefore occurs as soon as
the normal interim payments cannot be met using reserves. We later
relax the full liquidation assumption. With partial liquidation,
the sudden stop cutoff and the reserves cutoff no longer
coincide.
The following corollary establishes the endogenous relation between the optimal reserves and the probability of sudden stops. In this environment, reserves are set to balance the sudden stop risks incurred when reserves are not high enough and the cost of holding idle reserves.
Corollary 1. Endogenous Sudden Stop Probability
The optimal contract ![]() induces a
positive probability
induces a
positive probability
![]() that a sudden
stop occurs. Furthermore,
that a sudden
stop occurs. Furthermore,
![]() .
.
Proof: This follows immediately from Proposition 1.
3.5 Comparative Statics
In this subsection, we discuss how reserves and sudden stop
probabilities are affected by changes in the underlying liquidity
risk, that is: changes in ![]() .
.
Proposition 2. Reserves, Sudden Stop Probability, and Debt Rollover Risk
(i) The optimal reserves ratio is increasing in the aggregate liquidity risk. That is:
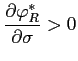
(ii) The sudden stop probability is also increasing in the aggregate liquidity risk. That is:
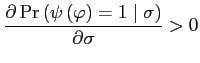
Proof: See appendix.
Proposition 2 establishes that both the optimal reserves and the
implied sudden stop probability are increasing in the liquidity
risk. A larger liquidity risk ![]() induces
larger interim shocks and prompts the domestic government to invest
in additional reserves. However, the increase in reserves does not
completely offset the higher probability of larger shocks, thus
leading to an increase in the debt rollover risk. Based on this
proposition, we simply refer to the aggregate liquidity risk
parameter
induces
larger interim shocks and prompts the domestic government to invest
in additional reserves. However, the increase in reserves does not
completely offset the higher probability of larger shocks, thus
leading to an increase in the debt rollover risk. Based on this
proposition, we simply refer to the aggregate liquidity risk
parameter ![]() as "rollover risk" throughout
the paper.
as "rollover risk" throughout
the paper.
Figure 5. Sudden Stop and Debt Rollover Risk
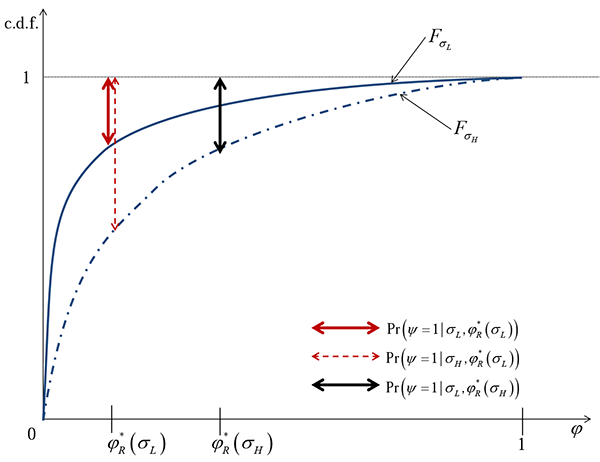
A central question that we address using Proposition 2 is: what
happens during an unexpected increase in rollover risk, say in the
wake of globalization? Figure 5 shows how an
unexpected increase in ![]() from
from
![]() to
to
![]() leads to a increase
in sudden stop probability as represented by the dashed vertical
line. Obviously, the government does not hold enough reserves,
given the unexpected increase in rollover risk. We later show
quantitatively that a small, but unanticipated increase in rollover
risk leads to a short-lived outburst of sudden stops and a dramatic
rise in reserves as seen in the data.
leads to a increase
in sudden stop probability as represented by the dashed vertical
line. Obviously, the government does not hold enough reserves,
given the unexpected increase in rollover risk. We later show
quantitatively that a small, but unanticipated increase in rollover
risk leads to a short-lived outburst of sudden stops and a dramatic
rise in reserves as seen in the data.
3.6 Self-Insurance Versus Mutual Insurance
In the self-insurance setup above, a government faces aggregate uncertainty stemming from its debt rollover risk. An individual government may over-accumulate reserves compared to a world in which governments can pool reserves and mutually insure against their idiosyncratic rollover risk. We now characterize the extent of reserves over-accumulation.
For simplicity, consider the problem of a planner who can swap
resources across a continuum of countries facing i.i.d.
idiosyncratic liquidity shocks
![]() with c.d.f.
with c.d.f.
![]() . By the law of large numbers, the
total measure of lenders who must call the debt is
. By the law of large numbers, the
total measure of lenders who must call the debt is
![]() .
In that sense, there is no aggregate uncertainty across countries
as they insure each other.11
.
In that sense, there is no aggregate uncertainty across countries
as they insure each other.11
In fact, the planner could set reserves to
![]() and thereby
prevent any sudden stop from occurring in any country. This policy
is indeed optimal when the liquidity risk is sufficiently low.
and thereby
prevent any sudden stop from occurring in any country. This policy
is indeed optimal when the liquidity risk is sufficiently low.
Proposition 3. Self-Insurance Versus Mutual Insurance
Consider a continuum of countries subject to i.i.d. liquidity
shocks. Each country individually over-accumulates reserves
compared to the mutual insurance outcome
![]() . That is:
. That is:
Proof: See appendix.
Proposition 3 establishes that countries hold more reserves than needed if they could mutually insure against idiosyncratic liquidity shocks. The mutual insurance problem has similarities with the liquidity provision problem studied by Holmström and Tirole (1998). Under mutual insurance, economies that face large liquidity shocks in the interim can access the reserves of economies with small liquidity needs, thereby reducing the overall debt rollover risk and the reserves required to manage it. In the next section, we quantify the over-accumulation of reserves after calibrating the liquidity risk faced by emerging economies.
4 A Multi-Country Dynamic Application
The previous section highlighted the relationship between rollover risk, sudden stops, and reserves. In this section, we extend this model along two dimensions.
First, the model is extended to an infinite horizon environment
in which each period ![]() contains the three stages,
contains the three stages,
![]() , of the basic model. At the end of
each period
, of the basic model. At the end of
each period ![]() , the government chooses how much
reserves to transfer to the next period. Second, the model is
extended to a multi-country environment in which agents learn about
the underlying rollover risk,
, the government chooses how much
reserves to transfer to the next period. Second, the model is
extended to a multi-country environment in which agents learn about
the underlying rollover risk,
![]() , using information on the sudden
stop occurrences each period.
, using information on the sudden
stop occurrences each period.
4.1 Environment
We consider ![]() identical small economies indexed
by
identical small economies indexed
by
![]() . Time is infinite, discrete,
and indexed by
. Time is infinite, discrete,
and indexed by
![]() . Each country is
populated by an infinitely-lived representative agent and a
welfare-maximizing government. The agents in country
. Each country is
populated by an infinitely-lived representative agent and a
welfare-maximizing government. The agents in country ![]() order consumption sequences according to
order consumption sequences according to
![]() where
where ![]() is the discount factor. There is a
continuum of infinitely lived risk-neutral foreign lenders indexed
by
is the discount factor. There is a
continuum of infinitely lived risk-neutral foreign lenders indexed
by
![]() . An overview of the
timeline of this extended model is showed in Figure 6.
. An overview of the
timeline of this extended model is showed in Figure 6.
Figure 6. Extended Timeline
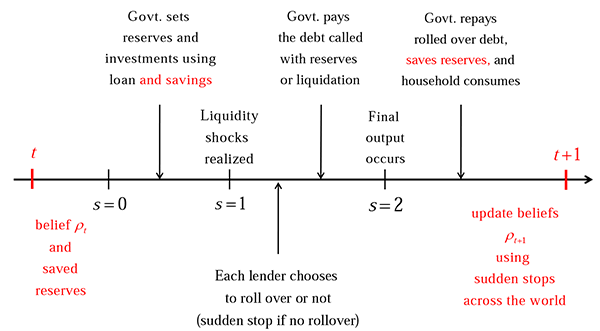
Each time period ![]() is divided into three
stages,
is divided into three
stages, ![]() , and encapsulates the three stages
of the previous model:
, and encapsulates the three stages
of the previous model:
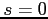 is the initial contracting stage,
is the initial contracting stage,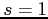 is the interim stage when liquidity
shocks occur and rollovers decided,
is the interim stage when liquidity
shocks occur and rollovers decided,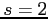 is the final production and consumption
stage.
is the final production and consumption
stage.
The aggregate interim liquidity shock in country ![]() at time
at time ![]() is denoted by
is denoted by
![]() . As in
the basic model, this means that a fraction
. As in
the basic model, this means that a fraction
![]() of country
of country ![]() 's creditors must call the debt in the interim while the
others can roll over or call the debt. The aggregate shocks
's creditors must call the debt in the interim while the
others can roll over or call the debt. The aggregate shocks
![]() are independent and identically distributed across countries and
time, with cumulative distribution function
are independent and identically distributed across countries and
time, with cumulative distribution function
![]() . We assume
. We assume
![]() with
with
![]() .
.
This rollover risk parameter
![]() is unobserved and unknown to the
agents. However, all agents share a common belief
is unobserved and unknown to the
agents. However, all agents share a common belief ![]() at time
at time ![]() :
:
At the end of each period ![]() , agents observe
the sudden stop occurrences in the
, agents observe
the sudden stop occurrences in the ![]() countries.
Using these sudden stop occurrences and the endogenous sudden stop
probabilities, agents update their beliefs according to Bayes' rule
as detailed in section 4.3.
countries.
Using these sudden stop occurrences and the endogenous sudden stop
probabilities, agents update their beliefs according to Bayes' rule
as detailed in section 4.3.
Within each period ![]() , the technologies available
at a stage
, the technologies available
at a stage ![]() are identical to those in the previous
section.12 In addition, at the end of each
period, the government can save
are identical to those in the previous
section.12 In addition, at the end of each
period, the government can save
![]() reserves for the next period
using the remaining reserves
reserves for the next period
using the remaining reserves
![]() :
:
We now allow for partial liquidation in the interim:
This implies that sudden stops may not occur as soon as reserves are depleted.
4.2 Optimal Recursive Debt Contracts
We represent the government's infinite horizon problem as a
recursive dynamic programming problem. The problem has one
endogenous state, the level of incoming saved reserves,
![]() , and one exogenous state, the
common belief,
, and one exogenous state, the
common belief, ![]() . The state of economy
. The state of economy
![]() at time
at time ![]() is then given by
is then given by
![]() .
.
The optimal recursive debt contract,
![]() , is a set of
policy functions for initial reserves:
, is a set of
policy functions for initial reserves:
![]() , invested
capital:
, invested
capital:
![]() , normal interest
rates:
, normal interest
rates:
![]() , sudden stop
interest rates:
, sudden stop
interest rates:
![]() , sudden stop
cutoffs:
, sudden stop
cutoffs:
![]() ,
consumption:
,
consumption:
![]() , interim
reserves:
, interim
reserves:
![]() ,
liquidation:
,
liquidation:
![]() , saved
reserves:
, saved
reserves:
![]() , and
rollover policies:
, and
rollover policies:
![]() which
satisfy the functional equation:
which
satisfy the functional equation:
![\begin{displaymath} \begin{array}{ccc} W\left(R_{0};\rho\right)= & \underset{B\in\Gamma\left(R_{0}\right)}{\max} & \mathbf{E}{}_{\varphi\vert\,\rho}\,\left[u\left(C\left(\varphi\right)\right)+\beta W\left(R_{0}';\rho\right)\right]\end{array}\end{displaymath}](img176.gif)
As in the previous section a debt contract is feasible, that is,
![]() , if it
satisfies resource feasibility, interim individual rationality, the
ex ante participation constraint, and ex post renegotiation
proofness. Resource feasibility is modified to allow for saved
reserves and partial liquidation. The initial
, if it
satisfies resource feasibility, interim individual rationality, the
ex ante participation constraint, and ex post renegotiation
proofness. Resource feasibility is modified to allow for saved
reserves and partial liquidation. The initial ![]() resource constraint, which incorporates incoming
reserves saved (
resource constraint, which incorporates incoming
reserves saved (![]() ), is now:
), is now:
| (10) |
The final ![]() resource constraint, modified to
allow for inter-temporal reserves savings (
resource constraint, modified to
allow for inter-temporal reserves savings (
![]() ), is now:
), is now:
| (11) |
Also, saved reserves and liquidation must satisfy
| (12) | |||
| (13) |
4.3 Bayesian Learning
The common belief
![]() is
dynamically updated using the sudden stop occurrences and sudden
stop probabilities in the
is
dynamically updated using the sudden stop occurrences and sudden
stop probabilities in the ![]() countries.13 Let us denote
countries.13 Let us denote
![]() as the
vector of sudden stops where
as the
vector of sudden stops where
![]() denotes that country
denotes that country
![]() experienced a sudden stop in period
experienced a sudden stop in period
![]() . For each country
. For each country ![]() , given
the incoming reserves
, given
the incoming reserves
![]() , the probability of a sudden
stop
, the probability of a sudden
stop
![]() is
endogenously determined by the optimal policy for the prevailing
belief
is
endogenously determined by the optimal policy for the prevailing
belief ![]() .
.
Bayes' Rule implies that:
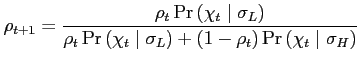
with the joint endogenous sudden stop probabilities
![]() given by:
given by:
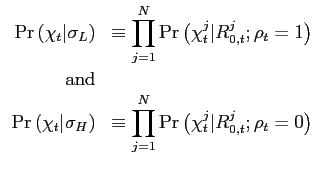
where
![]()
and
![]() .
.
4.4 Quantitative Analysis
In this section, we use the calibrated model to establish how a small but unexpected increase in debt rollover risk can explain the sharp increase in reserves and the temporary outburst in sudden stops documented in section 2. Based on our theory, an unexpected increase in the rollover risk will temporarily cause an underinvestment in reserve holdings which increases the probability of sudden stops. Governments and investors, seeing the rise in sudden stops, rationally update their common belief about the prevailing debt rollover risk. Once agents have fully learned the new regime, reserves remain steadily higher and sudden stops subside.
Calibration A period in the model is assumed to be a quarter. We choose
![]() as we have 23 emerging economies in our
dataset. We assume the aggregate liquidity shock distributions
as we have 23 emerging economies in our
dataset. We assume the aggregate liquidity shock distributions
![]() belong to the class of Pareto distributions on
belong to the class of Pareto distributions on
![]() :
:
![]() . An increase in
. An increase in ![]() shifts the cumulative
distribution function
shifts the cumulative
distribution function
![]() to the right as illustrated in
Figure 5. An
increase from
to the right as illustrated in
Figure 5. An
increase from
![]() to
to
![]() therefore represents an increase
in the underlying debt rollover risk.
therefore represents an increase
in the underlying debt rollover risk.
The discount factor ![]() is set to match average
interest rates of two percent in emerging economies over 1990-2007
and the world interest rate
is set to match average
interest rates of two percent in emerging economies over 1990-2007
and the world interest rate ![]() is set to
match a risk-free rate of one percent. The bargaining parameter
is set to
match a risk-free rate of one percent. The bargaining parameter
![]() is set to match the average haircut
of 19.4 percent in sovereign defaults from 1990 to 2007 using the
data from Benjamin and Wright (2009). The debt rollover risk parameter
is set to match the average haircut
of 19.4 percent in sovereign defaults from 1990 to 2007 using the
data from Benjamin and Wright (2009). The debt rollover risk parameter
![]() and
and
![]() are set to match median
reserves-to-debt ratios in the emerging economies for the periods
of 1990-1996 and 2002-2007 respectively. We set the liquidation
cost
are set to match median
reserves-to-debt ratios in the emerging economies for the periods
of 1990-1996 and 2002-2007 respectively. We set the liquidation
cost ![]() to be 25 percent, which is
conservative relative to the range of estimates and values used in
the literature.14 The long-term technology
productivity
to be 25 percent, which is
conservative relative to the range of estimates and values used in
the literature.14 The long-term technology
productivity ![]() is set to 1.2.15 The parameters
are summarized in Table 2. See the
computation appendix in section 6.2 for
details on the computation and calibration strategy.
is set to 1.2.15 The parameters
are summarized in Table 2. See the
computation appendix in section 6.2 for
details on the computation and calibration strategy.
Table 2. Calibration Values
| Name | Symbol | Value | Target |
|---|---|---|---|
| Discount factor | β | 0.98 | average interest rates (emerging) |
| World interest rate | rW | 0.01 | risk-free rate |
| Low rollover risk | σL | 0.061 | average reserves-to-debt, 1990-1996 |
| High rollover risk | σH | 0.172 | average reserves-to-debt, 2002-2007 |
| Divestment parameter | λ | 0.75 | see discussion |
| Productivity | A | 1.2 | - |
| Bargaining parameter | θ | 0.965 | average haircut on sovereign debt |
| Number of economies | N | 23 | emerging countries in sample |
Quantitative Results We assume that after 1996, there was an unexpected increase from
a
![]() -regime to a
-regime to a
![]() -regime. This is motivated by the
idea that globalization and widespread financial liberalization led
to an unprecedented increase in capital mobility and debt rollover
risk.
-regime. This is motivated by the
idea that globalization and widespread financial liberalization led
to an unprecedented increase in capital mobility and debt rollover
risk.
The ![]() ex ante identical economies experience
different aggregate liquidity shock paths
ex ante identical economies experience
different aggregate liquidity shock paths
![]() . As a
result, their reserves holdings and sudden stops paths also evolve
differently. The results shown are the average across a large
number of simulated paths for these
. As a
result, their reserves holdings and sudden stops paths also evolve
differently. The results shown are the average across a large
number of simulated paths for these ![]() countries.
countries.
Table 3 summarizes our key results. The calibration reveals that the debt
rollover risk ![]() increased from 0.061 to 0.172. This is a small increase in
the sense that the implied sudden stop probabilities only rise from
0.06 percent to 0.19 percent, compared to a 1.58 percent
probability during the transition. Despite this small increase in
debt rollover risk, there is an outburst of sudden stops with the
mode across simulations reaching 7 before subsiding
(see Figure 7).
In the meantime, the optimal reserves-to-debt ratios climbed from
17 percent to 41 percent.
The temporary surge in sudden stops is consistent with our
discussion of Proposition 2 in the simple model (see Figure 5): as governments
learn the higher rollover risk, they choose to hold a higher level
of reserves, thus returning sudden stop probabilities to lower
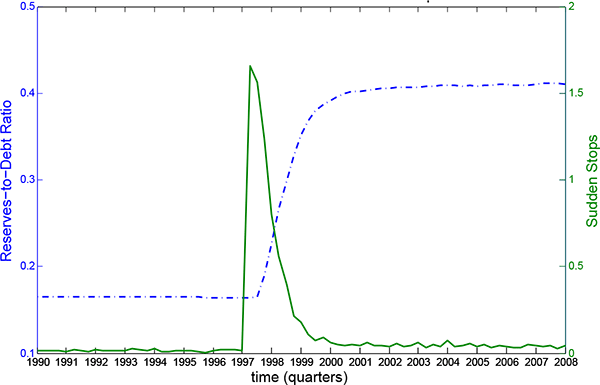
levels. The calibration establishes quantitatively how a small
increase in rollover risk can explain the surge we observed in the
data. As can be seen in Figure 8, our model can
jointly generate the temporary outburst of sudden stops in the
transition (1997-2001) along with the permanent rise in reserves
ever since.
increased from 0.061 to 0.172. This is a small increase in
the sense that the implied sudden stop probabilities only rise from
0.06 percent to 0.19 percent, compared to a 1.58 percent
probability during the transition. Despite this small increase in
debt rollover risk, there is an outburst of sudden stops with the
mode across simulations reaching 7 before subsiding
(see Figure 7).
In the meantime, the optimal reserves-to-debt ratios climbed from
17 percent to 41 percent.
The temporary surge in sudden stops is consistent with our
discussion of Proposition 2 in the simple model (see Figure 5): as governments
learn the higher rollover risk, they choose to hold a higher level
of reserves, thus returning sudden stop probabilities to lower
levels. The calibration establishes quantitatively how a small
increase in rollover risk can explain the surge we observed in the
data. As can be seen in Figure 8, our model can
jointly generate the temporary outburst of sudden stops in the
transition (1997-2001) along with the permanent rise in reserves
ever since.
Table 3. Summary of Results
| 1990-1996 | 1997-2001 | 2002-2007 | |
|---|---|---|---|
| Data: Reserves-to-External Debt Liabilities | 0.17 | 0.28 | 0.41 |
| Data: Sudden Stops | 2 | 10 | 0 |
| Model: Reserves-to External Debt Liabilities | 0.17 | 0.33 | 0.41 |
| Model: Sudden Stops | 0.40 | 7.28 | 1.10 |
| Model: Rollover Risk (σ) | 0.061 | 0.172 | 0.172 |
| Model: Sudden Stop Probabilities (percent) | 0.06 | 1.58 | 0.19 |
International Mutual Insurance and Reserves Proposition 3 showed that countries over-accumulate reserves compared to an allocation with mutual insurance with other countries. We now use the calibrated parameters to quantify the magnitude of the over-accumulation of reserves due to self-insurance.
Given the calibrated parameter values and using Proposition 3,
the international planner facing no aggregate uncertainty will
optimally set reserves to the mean liquidity shock because
![]() . Therefore, in
the higher rollover risk
. Therefore, in
the higher rollover risk
![]() regime, the
international planner optimally sets the reserves-to-debt ratio at:
regime, the
international planner optimally sets the reserves-to-debt ratio at:
![]() percent. This amounts to nearly one-thirds of the level of
41 percent in reserves-to-debt that emerging
economies held from 2002 to 2007.16
percent. This amounts to nearly one-thirds of the level of
41 percent in reserves-to-debt that emerging
economies held from 2002 to 2007.16
This result clearly underscores the importance of mutual insurance or international coordination across governments facing uninsurable idiosyncratic debt rollover risk. In fact, during the recent global financial crisis, reserves swap agreements such as the ASEAN+3 Chiang Mai Initiative were expanded. The U.S. and Japan also extended swap lines to emerging economies such as Korea.
The IMF could in principle assume the role of an international planner for rollover risk insurance. However, many economists and policymakers argue (see Ito (2012)) that emerging economies still bear the scar and the stigma from the inadequate liquidity assistance provided by the IMF during the crises of the late 1990s.
Figure 7. Histogram of Sudden Stops Frequencies by Era
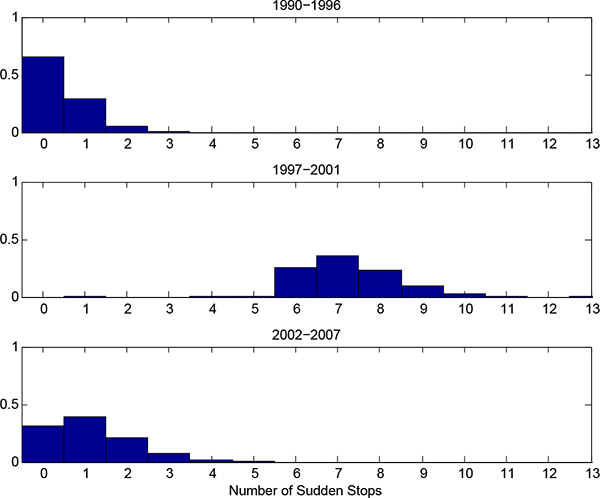
Figure 8. Results - Reserves and Sudden Stops
Reserves in the Euro Area Periphery Economies Interestingly, before 1999, the Euro Area Periphery economies (Greece, Ireland, Italy, Portugal, Spain) held the same levels of reserves as the 23 emerging economies we consider. However, upon joining the Euro Area, these economies slashed their reserves holdings, as illustrated in Figure 9.17
The common currency certainly explains part of the reduction in foreign reserves. However, to the extent that these economies still faced debt rollover risk, they may have under-invested in reserves. For instance, they may have mistakenly believed that they no longer faced rollover risk as they joined the Euro. Alternatively, the Periphery economies ex ante may have counted on a mutual insurance policy against liquidity needs which showed its limits during the Euro crisis.
In the meantime, self-insurance through reserves helped emerging economies weather the global financial crisis as noted by Dominguez et al. (2012) as well as Gourinchas and Obstfeld (2012). This is also consistent with our findings on the preventive role of reserves.
Figure 9. Foreign Reserves in the Euro Area Periphery
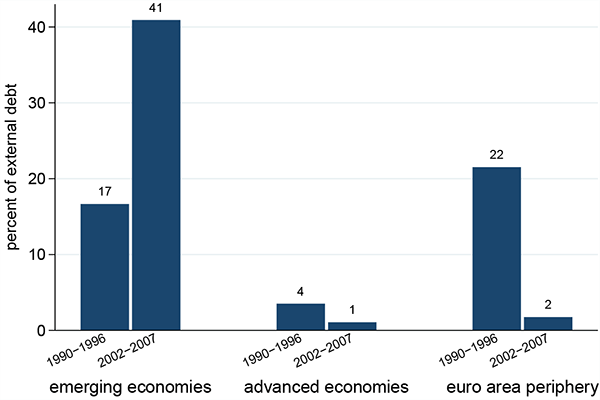
Note: The value for each period and each bloc is the median across economies of the period-average for each economy.
5 Conclusion
In this paper, we developed a theory of rollover risk, sudden stops, and reserves that can jointly account for the dynamics of foreign reserves and sudden stops in emerging economies.
In our theory, governments choose reserves to prevent "patient" foreign creditors from refusing to rollover their claims and inducing a sudden stop. We calibrate a dynamic multi-country extension of the model with Bayesian learning to emerging economies. A small, unexpected, but permanent change in rollover risk leads to the surge in sudden stops in the late 1990s, the subsequent rise in reserves, and the salient fall in sudden stops ever since. We also find that a policy of international mutual insurance can substantially reduce the reserves held by emerging economies.
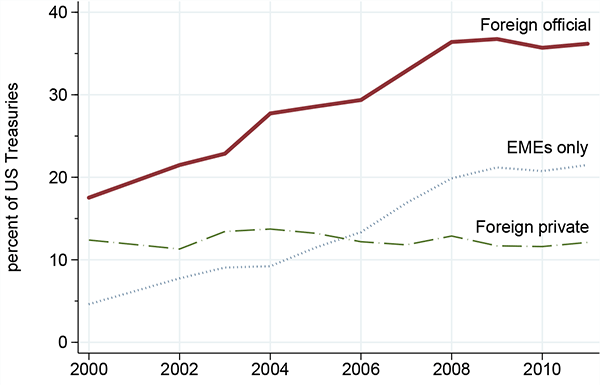
Several caveats are in order. Our model ignores the decision to issue reserve assets. In particular, U.S. Treasuries, the most popular reserve asset, are being increasingly held by foreign officials as they accumulate reserves (see Figure 10). Can the U.S. sustainably issue large amounts of reserve assets? Moreover, our model does not consider the maturity composition of a country's debt. We leave these interesting considerations for future research.
Figure 10: Foreign Holdings of U.S. Treasuries
Bibliography
Aizenman, Joshua, and Lee, Jaewoo. 2007. "International Reserves: Precautionary versus Mercantilist views, Theory and Evidence." Open Economies Review, 18(2): 191-214.
Alderson, Michael J., and Brian L. Betker. 1996. "Liquidation costs and accounting data." Financial Management, 25(2): 25-36.
Alfaro, Laura and Kanczuk, Fabio. 2009. "Optimal Reserve Management and Sovereign Debt." Journal of International Economics, 77(1):23-36.
Akinci, Ozge. 2012. "Global Financial Conditions, Country Spreads and Macroeconomic Fluctuations in Emerging Countries: A Panel VAR Approach."Working Paper.
Arellano, Cristina, and Ananth Ramanarayanan. 2012. "Default and the Maturity Structure in Sovereign Bonds." Journal of Political Economy, 120(2): 187-232.
Benjamin, David, and Mark L. J. Wright. 2009. "Recovery Before Redemption: A Theory of Delays in Sovereign Debt Renegotiations." Working Paper.
Bernanke, Ben. 2005. "The Global Saving Glut and the U.S. Current Account Deficit." Remarks at the Sandridge Lecture, Virginia Association of Economists, Richmond, Virginia, March 10, 2005.
Brown, Richard A., and Seth Epstein. 1992. "Resolution costs of bank failures: An update of the FDIC historical loss model." FDIC Banking Review, 5(2): 1-16.
Bianchi, Javier, Juan Carlos Hatchondo, and Leonardo Martinez. 2012. "International Reserves and Rollover Risk." Working paper.
Broner, Fernando A., Guido Lorenzoni, and Sergio L. Schmukler. 2007. "Why do Emerging Economies Borrow Short Term?" NBER Working Paper No. w13076.
Buera, Francisco J., Alexander Monge-Naranjo, and Giorgio E. Primiceri. 2011. "Learning the Wealth of Nations." Econometrica, 79(1): 1-45.
Caballero, Ricardo, and Stavros Panageas. 2007. "A Quantitative Model of Sudden Stops and External Liquidity Management." NBER Working Paper No. w11293.
Calvo, Guillermo A., Alejandro Izquierdo, and Rudy Loo-Kung. 2012. "Optimal Holdings of International Reserves: Self-Insurance Against Sudden Stops." NBER Working Paper No. w18219.
Calvo, Guillermo A., Alejandro Izquierdo, and Luis-Fernando Mejia. 2004. "On the Empirics of Sudden Stops: The Relevance of Balance-Sheet Effects." NBER Working Paper No. 10520.
Chang, Roberto, and Andres Velasco. 2001. "A model of financial crises in emerging markets." The Quarterly Journal of Economics, 116(2): 489-517.
Cole, Hal L. and Timothy J. Kehoe. 2000. "Self-Fulfilling Debt Crises." Review of Economic Studies, 67(1): 91–116.
Diamond, Douglas W., and Philip H. Dybvig. 1983. "Bank Runs, Deposit Insurance, and Liquidity." Journal of Political Economy, 91(3): 401–419.
Dominguez, Kathryn ME, Yuko Hashimoto, and Takatoshi Ito. 2012. "International reserves and the global financial crisis." Journal of International Economics, 88(2): 388-406.
Dooley, Michael P., David Folkerts-Landau, and Peter Garber. 2004. "The Revived Bretton Woods System." International Journal of Finance and Economics, 9(4): 307-313.
Durdu, Ceyhun Bora, Enrique G. Mendoza, and Marco E. Terrones. 2009. "Precautionary Demand for Foreign Assets in Sudden Stop Economies: An Assessment of the New Mercantilism." Journal of Development Economics, 89(2): 194-209.
Ennis, Huberto M., and Todd Keister. 2003. "Economic Growth, Liquidity, and Bank Runs." Journal of Economic Theory, 109(2): 220–245.
Frenkel, Jacob, and Boyan Jovanovic. 1981. "Optimal International Reserves: A Stochastic Framework." The Economic Journal, 91(362): 507-514.
Gendreau, Brian C., and Scott S. Prince. 1986. "The Private Costs of Bank Failures: Some Historical Evidence." Federal Reserve Bank of Philadelphia Business Review, March/April: 3-14.
Gourinchas, Pierre-Olivier and Maurice Obstfeld. 2012. "Stories of the Twentieth Century for the Twenty-First." American Economic Journal: Macroeconomics, 4(1): 226–65.
Heller, Heinz Robert. 1966. "Optimal International Reserves." The Economic Journal, 76(302): 296-311.
Holmström, Bengt, and Jean Tirole. 1998. "Private and Public Supply of Liquidity."The Journal of Political Economy, 106(1): 1-40.
International Monetary Fund. 2012. "Assessing the Need for Foreign Currency Reserves."IMF Survey Magazine: Policy.
Ito, Takatoshi. 2012. "Can Asia Overcome the IMF Stigma?" American Economic Review, 102(3): 198-202.
James, Christopher. 2012. "The losses realized in bank failures." The Journal of Finance, 46(4):1223-1242.
Jeanne, Olivier and Romain Ranciere. 2011. "The Optimal Level of International Reserves for Emerging Market Countries: A New Formula and Some Applications."The Economic Journal, 121: 905–930.
Kehoe, Timothy J., Kim J. Ruhl, and Joe Steinberg. 2012. "A Sudden Stop to the Savings Glut and the Future of the U.S. Economy," Federal Reserve Bank of Minneapolis Research Department Staff Report.
Kim, Jun Il. 2008. "Sudden Stops and Optimal Self-Insurance." IMF Working Papers, No 8144.
Lane, Philip R., and Gian Maria Milesi-Ferretti (2007). "The External Wealth of Nations Mark II: Revised and Extended Estimates of Foreign Assets and Liabilities, 1970–2004." Journal of International Economics, 73(4): 223–25.
Mendoza, Enrique G. 2010. "Sudden stops, financial crises, and leverage." American Economic Review, 100(5): 1941-1966.
Morris, Stephen, and Hyun Song Shin. 1998. "Unique equilibrium in a model of self-fulfilling currency attacks." American Economic Review, 88(3): 587-597.
Morris, Stephen, and Hyun Song Shin. 2006. "Catalytic finance: When does it work?" Journal of international Economics, 70(1): 161-177.
Obstfeld, Maurice, Jay C. Shambaugh, and Alan M. Taylor. 2010. "Financial Stability, the Trilemma, and International Reserves." American Economic Journal: Macroeconomics, 2(2): 57-94.
Yue, Vivian. 2010. "Sovereign Default and Debt Renegotiation." Journal of International Economics, 80(2): 176-187.
6 Appendix
6.1 Tables
Table A.1. Foreign Reserves
| (percent of GDP) 1990-1996 | (percent of GDP) 2002-2007 | (percent of External Debt Liabilities) 1990-1996 | (percent of External Debt Liabilities) 2002-2007 | |
|---|---|---|---|---|
| Argentina | 4.9 | 13.5 | 14.3 | 21.4 |
| Brazil | 4.9 | 8.6 | 19.5 | 35.3 |
| Chile | 20.4 | 16.5 | 50.9 | 39.0 |
| China | 8.4 | 33.2 | 54.3 | 271.4 |
| Colombia | 9.9 | 10.8 | 35.6 | 35.1 |
| Czech Republic | 17.4 | 25.3 | 57.2 | 77.5 |
| Egypt | 20.9 | 19.8 | 35.2 | 65.5 |
| Hungary | 15.5 | 16.6 | 26.6 | 26.2 |
| India | 3.5 | 18.4 | 11.8 | 101.0 |
| Indonesia | 6.5 | 12.4 | 11.7 | 25.2 |
| Korea | 5.4 | 24.6 | 28.0 | 97.4 |
| Malaysia | 28.5 | 47.1 | 77.0 | 125.6 |
| Mexioc | 4.6 | 8.2 | 12.2 | 40.9 |
| Morocco | 10.4 | 28.6 | 15.9 | 99.1 |
| Pakistan | 1.8 | 10.4 | 4.3 | 28.2 |
| Peru | 11.2 | 18.4 | 16.7 | 49.1 |
| Philippines | 8.0 | 17.3 | 13.3 | 28.4 |
| Poland | 6.9 | 14.2 | 15.9 | 35.8 |
| Romania | 4.2 | 18.5 | 22.7 | 53.9 |
| Russia | 3.0 | 23.2 | 7.3 | 68.5 |
| South Africa | 1.0 | 7.1 | 4.7 | 34.9 |
| Thailand | 19.3 | 30.6 | 41.8 | 112.1 |
| Turkey | 3.9 | 10.9 | 13.0 | 25.5 |
Table A.2. Sensitivity Analysis
| 1990-1996 | 1997-2001 | 2002-2007 | |
|---|---|---|---|
| λ = 0.7: Reserves-to External Debt Liabilities | 0.17 | 0.32 | 0.41 |
| λ = 0.7: Sudden Stops | 0.40 | 7.56 | 1.22 |
| λ = 0.7: Rollover Risk (σ) | 0.058 | 0.161 | 0.161 |
| λ = 0.7: Suddent Stop Probabilities (percent) | 0.06 | 1.64 | 0.21 |
| λ = 0.8: Reserves-to External Debt Liabilities | 0.17 | 0.33 | 0.41 |
| λ = 0.8: Sudden Stops | 0.26 | 7.60 | 1.69 |
| λ = 0.8: Rollover Risk (σ) | 0.061 | 0.198 | 0.198 |
| λ = 0.8: Suddent Stop Probabilities (percent) | 0.04 | 1.65 | 0.19 |
Computational Appendix
The computation strategy involves solving for policy functions
and simulating the induced equilibrium paths with Bayesian
learning. The government problem has two state variables: (i) the
incoming reserves, ![]() , and (ii) the belief,
, and (ii) the belief, ![]() . The policy functions are : (i) the
initial reserves,
. The policy functions are : (i) the
initial reserves, ![]() , (ii) the sudden stop
policy,
, (ii) the sudden stop
policy, ![]() ,18 (iii) the liquidation
policy,
,18 (iii) the liquidation
policy, ![]() , and (iv) the saved reserves,
, and (iv) the saved reserves,
![]() , where
, where ![]() is
the interim aggregate liquidity shock. These policy functions are
solved by value function iteration. We discretize the state space
and decision variables by choosing a finite grid, and use
interpolation methods.
is
the interim aggregate liquidity shock. These policy functions are
solved by value function iteration. We discretize the state space
and decision variables by choosing a finite grid, and use
interpolation methods.
Algorithm for Solving Equilibrium and Calibration
- Guess a vector of parameters
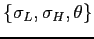
- For each belief on the belief grid, using value function iteration, solve for value functions and policy functions.
- Set initial reserves for
 countries
countries
 , and
initial belief
, and
initial belief 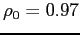
- For
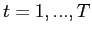 ,
,
- Set
![\begin{displaymath}\sigma_{t}=\left\{ \begin{array}[c]{lll} \sigma_{L} & & \text{if }t<T_{1}\ & & \ \sigma_{H} & & \text{if }t\geq T_{1} \end{array}\right. \end{displaymath}](img1c.gif)
- Draw aggregate liquidity shocks
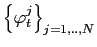 from
from
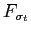
- Using distribution of incoming reserves,
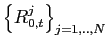 ,
policy functions,
,
policy functions,
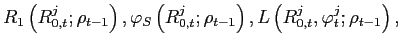
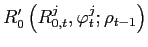 , and
shock realizations,
, and
shock realizations,
 ,
compute distribution of saved reserves,
,
compute distribution of saved reserves,
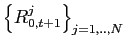
- using sudden stop probabilities and realizations, compute posterior as detailed in section 4.3
- Set
- Repeat step 4
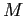 times, compute averages over
times, compute averages over 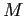 simulations. When
computing averages, exclude
simulations. When
computing averages, exclude 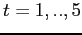 .
. - Repeat steps 1-5 until the difference between model moments and corresponding data targets are less than a specified threshold.
6.3 Proofs
PROOF OF PROPOSITION 1:
We proceed in eight steps.
Step 1: Interest rates satisfy
| (14) |
![]() follows from equation
(8). Equation
(3) and
follows from equation
(8). Equation
(3) and ![]() imply that
imply that
![]() . Since
. Since ![]() , equation (4) implies
, equation (4) implies
![]() .
Hence
.
Hence
![]() .
.
Step 2: If
![]() , then
, then
| (15) | |||
| (16) | |||
| (17) |
By definition, if
![]() , then
, then
![]() .
From step 1, we have that
.
From step 1, we have that
![]() .
Equations (5) and
(7) imply equations (15) and (16). Then
equation (17) follows
from equations (6)
and (7) .
.
Equations (5) and
(7) imply equations (15) and (16). Then
equation (17) follows
from equations (6)
and (7) .
Step 3: If
![]() , then
, then
| (18) | |||
| (19) | |||
| (20) |
By definition, if
![]() , then
, then
![]() and
and
![]() .
Suppose for contradiction that
.
Suppose for contradiction that
![]() . Then equation (5) implies
. Then equation (5) implies
![]() . Then we
have that
. Then we
have that
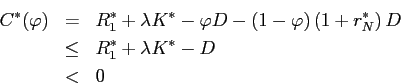
where the first equality comes from equation (6), the second
inequality comes from
![]() , and the third inequality
comes from (3) and
, and the third inequality
comes from (3) and ![]() . This violates equation (7). Hence equation
(18) holds. Then
equation (19) follows from equation (5), and equation
(20) follows from
(6).
. This violates equation (7). Hence equation
(18) holds. Then
equation (19) follows from equation (5), and equation
(20) follows from
(6).
Step 4: If
![]() , then
, then
| (21) | |||
| (22) |
Equation (19)
implies that
![]() . Similarly, step 3 implies that
. Similarly, step 3 implies that
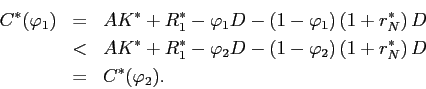
Step 5: Sudden stop policy satisfies
![\begin{displaymath}\exists\varphi_{S}^{\ast}\in\lbrack0,1]s.t.\left\{ \begin{array}[c]{lll} \psi^{\ast}(\varphi)=\varphi & & \forall\varphi\in\left[ 0,\varphi _{S}\right) \ & & \ \psi^{\ast}(\varphi)=1 & & \forall\varphi\in\left[ \varphi_{S},1\right] \end{array}\right. \end{displaymath}](img2d.gif)
First, note that
![]() , which
follows from symmetry. Then, suppose, without loss of generality,
that the optimal debt contract
, which
follows from symmetry. Then, suppose, without loss of generality,
that the optimal debt contract ![]() has
has
![]() such
that
such
that
![\begin{displaymath}\psi^{\ast}(\varphi)=\left\{ \begin{array}[c]{lll} \varphi & & \forall\varphi\in\left[ 0,\varphi_{1}\right) \ & & \ 1 & & \forall\varphi\in\left[ \varphi_{1},\varphi_{2}\right) \ & & \ \varphi & & \forall\varphi\in\left[ \varphi_{2},\varphi_{3}\right) \end{array}\right. \end{displaymath}](img3c.gif)
Then consider an alternative debt contract ![]() that is identical to
that is identical to ![]() except
that
except
that
![]() for some
for some ![]() . From equations (7) and (22), we know that
. From equations (7) and (22), we know that
![]() . By
continuity,
. By
continuity,
![]() for
for ![]() small enough. In contrast, from step
2,
small enough. In contrast, from step
2,
![]() . Similarly, from equations (7) and (21), we know that
. Similarly, from equations (7) and (21), we know that
![]() .
By continuity,
.
By continuity,
![]() for
for ![]() small enough. It remains to show that
equation (9) holds. This
is obvious since
small enough. It remains to show that
equation (9) holds. This
is obvious since
![]() . Hence
. Hence ![]() is feasible, yet has strictly higher
consumption than
is feasible, yet has strictly higher
consumption than ![]() , which is a contradiction.
, which is a contradiction.
Step 6: Reserves and Liquidation policies satisfy
![\begin{displaymath}\exists\varphi_{R}^{\ast}\in\lbrack0,1]s.t.\left\{ \begin{array}[c]{lll} R_{2}^{\ast}(\varphi)>0 & \Leftrightarrow & \varphi\in\left[ 0,\varphi _{R}\right) \ & & \ L^{\ast}(\varphi)=0 & \Leftrightarrow & \varphi\in\left[ 0,\varphi _{R}\right) \end{array}\right. \end{displaymath}](img4c.gif)
From step 5, we know that
![\begin{displaymath}\exists\varphi_{S}^{\ast}\in\lbrack0,1]s.t.\left\{ \begin{array}[c]{lll} \psi^{\ast}(\varphi)=\varphi & & \forall\varphi\in\left[ 0,\varphi _{S}\right) \ & & \ \psi^{\ast}(\varphi)=1 & & \forall\varphi\in\left[ \varphi_{S},1\right] \end{array}\right. \end{displaymath}](img5d.gif)
Let
![]() . Then the
result follows from steps 2 and 3. It also follows that
. Then the
result follows from steps 2 and 3. It also follows that
![]() .
.
Step 7: The Optimal Reserves-to-Debt ratio satisfies
The cutoff conditions imply that the state-contingent policy and payment functions can be written as:
![\begin{displaymath} \begin{array}[c]{lll} L^{\ast}(\varphi) & = & \left\{ \begin{array}[c]{lll} 0 & & \text{if }\varphi<\varphi_{R}^{\ast}\ & & \ K^{\ast} & & \text{otherwise} \end{array}\right. \ R_{2}^{\ast}(\varphi) & = & \left\{ \begin{array}[c]{lll} R_{1}^{\ast}-\varphi D & & \text{if }\varphi<\varphi_{R}^{\ast}\ & & \ 0 & & \text{otherwise} \end{array}\right. \ \psi_{i}^{\ast}(\varphi,\varphi_{i}) & = & \left\{ \begin{array}[c]{lll} 0 & \text{if }\varphi<\varphi_{R}^{\ast} & \text{and }\varphi_{i}=0\ & & \ 1 & & \text{otherwise} \end{array}\right. \ P_{1}^{\ast}(\varphi) & = & \left\{ \begin{array}[c]{lll} D & & \text{if }\varphi<\varphi_{R}^{\ast}\ & & \ R_{1}^{\ast}+\lambda K^{\ast} & & \text{otherwise} \end{array}\right. \ P_{2}^{\ast}(\varphi) & = & \left\{ \begin{array}[c]{lll} (1+r_{N}^{\ast})D & & \text{if }\varphi<\varphi_{R}^{\ast}\ & & \ 0 & & \text{otherwise} \end{array}\right. \end{array}\end{displaymath}](img7c.gif)
The participation constraint, holding with equality, can be
written as
![]() where
where
![]() .
.
Substituting the resource constraints and the condition
![]() , the optimal debt contract
problem can be written as:
, the optimal debt contract
problem can be written as:
The first order condition is given by:
Using the bounded Pareto distribution, we get:
Step 8: To verify the equilibrium, it suffices to show that
Since
![\begin{displaymath} \begin{array}[c]{lll} C^{\ast}(0) & = & (A(1-\varphi_{R}^{\ast})+\varphi_{R}^{\ast})D+\frac {G(\varphi_{R}^{\ast})+(1-F(\varphi_{R}^{\ast}))(\lambda+(1-\lambda )\varphi_{R}^{\ast})-(1+r_{W})}{F(\varphi_{R}^{\ast})-G(\varphi_{R}^{\ast} )}D\ & = & (A-1)(1-\varphi_{R}^{\ast})D-\frac{(1-\lambda)(1-\varphi_{R}^{\ast })(1-F(\varphi_{R}^{\ast}))+r_{W}}{F(\varphi_{R}^{\ast})-G(\varphi_{R}^{\ast })}D\ & = & (A-1)(1-\varphi_{R}^{\ast})D-(\sigma+1)\frac{(1-\lambda)(1-\varphi _{R}^{\ast})(1-\varphi_{R}^{\ast})^{\frac{1}{\sigma}}+r_{W}}{1-(1-\varphi _{R}^{\ast})^{\frac{1}{\sigma}+1}}D\ & = & (A-1)\left[ \frac{A-1}{A-\lambda}(\frac{\sigma}{\sigma+1})\right] ^{\sigma}D-(\sigma+1)\frac{(1-\lambda)(\frac{A-1}{A-\lambda}(\frac{\sigma }{\sigma+1}))^{\sigma+1}+r_{W}}{1-(\frac{A-1}{A-\lambda}(\frac{\sigma} {\sigma+1}))^{\sigma+1}}D \end{array}\end{displaymath}](img11c.gif)
Note that
![$ \underset{A\rightarrow\infty}{\lim}\left[ (A-1)\left[ \frac{A-1}{A-\lambda }(\frac{\sigma}{\sigma+1})\right] ^{\sigma}-(\sigma+1)\frac{(1-\lambda )(\frac{A-1}{A-\lambda}(\frac{\sigma}{\sigma+1}))^{\sigma+1}+r_{W}} {1-(\frac{A-1}{A-\lambda}(\frac{\sigma}{\sigma+1}))^{\sigma+1}}\right] =+\infty$](img12c.gif)
Hence
![]() such that
such that
![]() ,
, ![]() .
.
PROOF OF PROPOSITION 2:
(i) From Proposition 1, we know that
Then,
![\begin{displaymath} \begin{array}[c]{lll} \partial\varphi_{R}^{\ast} & > & 0\ & \Leftrightarrow & \ -\left\{ \log\left[ \frac{A-1}{A-\lambda}(\frac{\sigma}{\sigma+1})\right] +\left. \frac{1}{\sigma+1}\right\} \left[ \frac{A-1}{A-\lambda} (\frac{\sigma}{\sigma+1})\right] ^{\sigma}\right. & > & 0\ & \Leftrightarrow & \ \log\left[ \frac{A-1}{A-\lambda}(\frac{\sigma}{\sigma+1})\right] +\frac {1}{\sigma+1} & < & 0 \end{array}\end{displaymath}](img14c.gif)
Since ![]() , it suffices to show
, it suffices to show
, which is true since
(ii) From Corollary 1, we know that
Substituting for
![]() , we get
, we get
The result is obvious.
PROOF OF PROPOSITION 3:
Reserves Shortfall Before writing the planner's problem, it is useful to derive how
many countries have to suffer a crisis for a given level of
reserves shortfall. Suppose all countries coordinate to set
![]() reserves aside and invest
reserves aside and invest
![]() 19. The interim
shortfall is:
19. The interim
shortfall is: ![]() .
.
Some countries will have to (fully) liquidate to pay
![]() since their normal interim payments cannot be met. Let us denote
since their normal interim payments cannot be met. Let us denote
![]() , the measure of
countries that face a crisis. We have:
, the measure of
countries that face a crisis. We have:
where:
So:
The reserves decision ![]() determines the
probability
determines the
probability
![]() that a country
is in a sudden stop. The shortfall limits the interim insurance
since the interim debt repayment of some countries, the ones with
the largest shocks, cannot be met. We know:
that a country
is in a sudden stop. The shortfall limits the interim insurance
since the interim debt repayment of some countries, the ones with
the largest shocks, cannot be met. We know:
-
 and
and
-
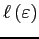 is strictly
increasing in
is strictly
increasing in 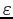
-
![$G_{\sigma}\left(\varphi\right)=\frac{\sigma}{\sigma+1}\left[1-\left(1-\frac{1}{\sigma}\varphi\right)\left(1-\varphi\right)^{\frac{1}{\sigma}}\right]\quad\Rightarrow\quad\ell\left(\varepsilon\right)=\left[1-G_{\sigma}^{-1}\left(\bar{\varphi}-\varepsilon\right)\right]^{\frac{1}{\sigma}}$](img140b.gif)
Planner's Problem Noting that the interim decision has been solved above, the planner's problem is:
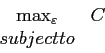
| (23) | |||
![$\displaystyle C+\left[\int_{0}^{\widehat{\varphi}\left(\varepsilon\right)}\left(1-\varphi\right)dF_{\sigma}\left(\varphi\right)\right]\left(1+r_{N}\right)D-A\left(1-\ell\left(\varepsilon\right)\right)\left(\bar{K}+\varepsilon D\right)$](img145b.gif) |
(24) | ||
![$\displaystyle \ell\left(\varepsilon\right)\left(1+r_{S}(\epsilon)\right)+\int_{0}^{\widehat{\varphi}\left(\varepsilon\right)}\left[\varphi+\left(1-\varphi\right)\left(1+r_{N}\right)\right]dF_{\sigma}\left(\varphi\right)-\left(1+r_{W}\right)$](img148b.gif) |
(25) | ||
| (26) | |||
| (27) |
Equations (23) - (27) represent initial resource constraint, final resource constraint, participation constraint, renegotiation proofness, and non-negativity constraint, which are analogous to equations (3), (6), (9), (4) , and (7), respectively. This simplifies to:
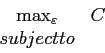
| (28) | |||
![$\displaystyle \ell\left(\varepsilon\right)\left(1+r_{S}(\epsilon)\right)+\int_{0}^{\widehat{\varphi}\left(\varepsilon\right)}\left[\varphi+\left(1-\varphi\right)\left(1+r_{N}\right)\right]dF_{\sigma}\left(\varphi\right)-\left(1+r_{W}\right)$](img161b.gif) |
(29) | ||
| (30) | |||
| (31) |
Equation (29) can be written as20:
| (32) |
Substituting (32) into (28) yields:
The planner's problem can then be written as:
![\begin{displaymath} \begin{array}[c]{ll} \max_{\varepsilon} & A(1-l(\varepsilon))(\frac{\overline{K}}{D}+\varepsilon )-((1+r_{W})-(\overline{\varphi}-\varepsilon)-l(\varepsilon)(1+r_{S} (\varepsilon)))\ & \Leftrightarrow\ \max_{\varepsilon} & -l(\varepsilon)A\frac{\overline{K}}{D}+A(1-l)(\varepsilon ))\varepsilon-\varepsilon+l(\varepsilon)(1+r_{S}(\varepsilon))+A\frac {\overline{K}}{D}+\overline{\varphi}-(1-r_{W})\ & \Leftrightarrow\ \max_{\varepsilon} & -l(\varepsilon)A\frac{\overline{K}}{D}+A(1-l)(\varepsilon ))\varepsilon-\varepsilon+l(\varepsilon)\left[ \overline{\varphi} +\lambda\frac{\overline{K}}{D}-(1-\lambda)\varepsilon\right] \end{array}\end{displaymath}](img19c.gif)
This is not a linear problem in ![]() since
since
![]() is not linear.
However, we know that:
is not linear.
However, we know that:
![\begin{displaymath} \begin{array}[c]{llll} l(\varepsilon) & = & 1-F_{\sigma}\left[ G_{\sigma}^{-1}(\overline{\varphi }-\varepsilon)\right] & \ & \Downarrow & & \ l^{\prime}(\varepsilon) & = & -F_{\sigma}^{^{\prime}}\left[ G_{\sigma} ^{-1}(\overline{\varphi}-\varepsilon)\right] \times\left( \frac{1} {G_{\sigma}^{^{\prime}}\left[ G_{\sigma}^{-1}(\overline{\varphi} -\varepsilon)\right] }\right) \times(-1) & \ & = & \frac{F_{\sigma}^{^{\prime}}\left[ G_{\sigma}^{-1}(\overline{\varphi }-\varepsilon)\right] }{G_{\sigma}^{^{\prime}}\left[ G_{\sigma}^{^{\prime} }(\overline{\varphi}-\varepsilon)\right] } & \ & = & \frac{f\left[ G_{\sigma}^{-1}(\overline{\varphi}-\varepsilon)\right] }{\left[ G_{\sigma}^{-1}(\overline{\varphi}-\varepsilon)\right] f\left[ G_{\sigma}^{-1}(\overline{\varphi}-\varepsilon)\right] } & \text{as }F^{\prime}=f\text{ and }G^{\prime}(\varphi)=\varphi f(\varphi)\ & = & \frac{1}{G_{\sigma}^{-1}(\overline{\varphi}-\varepsilon)} & \ & = & \frac{1}{\widehat{\varphi}(\varepsilon)} & \end{array}\end{displaymath}](img20c.gif)
The F.O.C. w.r.t. ![]() gives:
gives:
with equality if ![]() . Rearranging
yields:
. Rearranging
yields:
![\begin{displaymath} \begin{array}[c]{ll} -l^{^{\prime}}(\varepsilon)A\left( \frac{\overline{K}}{D}+\varepsilon\right) +A(1-l(\varepsilon))-(1-\lambda)l(\varepsilon)+l^{^{\prime}}(\varepsilon )(1+r_{S}(\varepsilon))-1 & \geq0\ & \Leftrightarrow\ (A-1)-(A+1-\lambda)l(\varepsilon)-l^{^{\prime}}(\varepsilon)\left[ A\left( \frac{\overline{K}}{D}+\varepsilon\right) -(1+r_{S}(\varepsilon))\right] & \geq0\ & \Leftrightarrow\ (A+1-\lambda)F_{\sigma}(\widehat{\varphi}(\varepsilon))-\frac{A\left( \frac{\overline{K}}{D}+\varepsilon\right) -\left( \overline{\varphi} +\lambda\frac{\overline{K}}{D}-(1-\lambda)\varepsilon\right) } {\widehat{\varphi}(\varepsilon)}-(2-\lambda) & \geq0\ & \Leftrightarrow\ (A+1-\lambda)F_{\sigma}(\widehat{\varphi}(\varepsilon))-\frac{A(1-\overline {\varphi}+\varepsilon)-(\overline{\varphi}+\lambda-\lambda\overline{\varphi }-(1-\lambda)\varepsilon)}{\widehat{\varphi}(\varepsilon)}-(2-\lambda) & \geq0\ & \Leftrightarrow\ (A+1-\lambda)F_{\sigma}(\widehat{\varphi}(\varepsilon))-\frac{(A-\lambda )-(A+1-\lambda)(\overline{\varphi}-\varepsilon)}{\widehat{\varphi} (\varepsilon)}-(2-\lambda) & \geq0 \end{array}\end{displaymath}](img22c.gif)
At ![]() , the L.H.S. of the F.O.C.
is:
, the L.H.S. of the F.O.C.
is:
![\begin{displaymath} \begin{array}[c]{l} (A+1-\lambda)-\left[ (A-\lambda)-(A+1-\lambda)(\overline{\varphi})\right] -(2-\lambda)\ =(A+1-\lambda)\overline{\varphi}-(1-\lambda)\ >0\text{ iff }\sigma>\frac{1-\lambda}{A} \end{array}\end{displaymath}](img23c.gif)
Therefore,
![]() if and only if
if and only if
![]() .
Otherwise,
.
Otherwise,
![]() . Obviously,
in any case:
. Obviously,
in any case:
![]() .
.
Finally, given that
![]() and
and
![]() :
:
Since
This is always true for
![]() .
.
Footnotes
** Sewon Hur (University of Pittsburgh): [email protected] | Illenin O. Kondo (Federal Reserve Board): [email protected]. We thank Cristina Arellano, Andrew Atkeson, V.V. Chari, Daniele Coen-Pirani, Bora Durdu, Tim Kehoe, Enrique Mendoza, Fabrizio Perri, Marla Ripoll, and John Rogers for many valuable comments. We have also benefited from comments by seminar participants at the University of Minnesota, Washington University in St. Louis, the Society for Economic Dynamics 2011 meetings, the Cantabria Nobel Campus 2012 meetings, the University of Pittsburgh, the Federal Reserve Board, the Midwest Macroeconomics 2012 Fall Meetings, and the Federal Reserve Bank of Minneapolis. The data used in this paper are available online. First draft: September 2010. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. All errors and shortcomings are ours alone. Return to text
1. While acknowledging other potential motives for holding reserves such as foreign exchange management (see for example Dooley et al. 2004), we focus on the role of reserves as a buffer (and preventive measure) against sudden stops. This is consistent with the view of policymakers. For example, Ben Bernanke stated that "foreign reserves have been used as a buffer against potential capital outflows" (Bernanke 2005) and a recent IMF survey of reserve managers found that building a "buffer for liquidity needs" was the foremost reason for building reserves (International Monetary Fund 2011). Return to text
2. Arellano and Ramanarayanan (2012) and Broner et al. (2007) explore models of debt maturity and why emerging economies issue short-term debt. Return to text
3. The dataset stops in 2007 because the external debt liabilities series constructed by Lane and Milesi-Ferretti (2007) stops in 2007. Other data on these emerging economies after 2007 indicates that sudden stops were still rare and reserves remained high compared to the late 1990s. The dataset starts after 1990 because of data availability, especially for current account data. Moreover, financial liberalization in emerging economies was largely still ongoing in the late 1980s, as documented by Buera et al. (2011). Return to text
4. Our sudden stop episodes are: Turkey (1994), Argentina, Mexico (1995), Thailand (1997), Czech Republic, Indonesia, Philippines, South Korea (1998), Chile, Peru, Russia (1999), Argentina, Turkey (2001). Durdu et al. (2009) report other episodes: Malaysia (1997), Brazil, Colombia, Pakistan (1999). In any case, there was an outburst in sudden stops between 1997 and 2001. Our methodology for constructing sudden stop episodes is explained in the data appendix. Return to text
5. Advanced economies here include the major reserve currencies: France, Germany, U.K., and U.S. Return to text
6. We obtain similar results when we separately estimate the model for each variable. The findings are also similar using alternative measures of reserves such as the reserves-to-GDP ratio used by Gourinchas and Obstfeld (2012). We prefer reserves as a fraction of external debt liabilities since it is a measure consistent with our theory. Return to text
7. We assume that the foreigners' capital endowment is finite and large enough. Return to text
8. This is in contrast to Diamond and Dybvig (1983) who focus on the limits to optimal risk-sharing among creditors that arise from self-fulfilling "panic" runs. More generally, one can allow for both "panic" crises and "rational" sudden stops to occur using a sunspot variable. Our restriction is without loss of generality if crisis payoff for the government is zero as is the case in this section. Return to text
9. The assumption that lenders receive zero net return on debt called in the interim is not essential. Return to text
10. The sovereign debt literature (see Yue 2010) documents the use of collective action during debt renegotiation. Return to text
11. Clearly, to the extent that liquidity shocks are correlated across countries, the i.i.d. case overstates the gains from mutual insurance. Akinci (2012) finds that global factors account for 20 percent of movements in aggregate activity in emerging economies. Return to text
12. The superscript ![]() and the subscript
and the subscript ![]() are therefore added to the
variables from the previous model to denote the country and the
period. We keep the subscripts indicating the stage
are therefore added to the
variables from the previous model to denote the country and the
period. We keep the subscripts indicating the stage ![]() when necessary. Return to text
when necessary. Return to text
13. Alternatively, agents can update
their priors using the realized liquidity shocks,
![]() .
This specification yields similar results with the only noticeable
difference being that the speed of learning is faster, and
therefore slightly fewer sudden stops in the interim. However,
there is still an outburst of sudden stops during the transition.
We find it more appealing to have countries learn using sudden stop
occurrences around the world instead. Return to text
.
This specification yields similar results with the only noticeable
difference being that the speed of learning is faster, and
therefore slightly fewer sudden stops in the interim. However,
there is still an outburst of sudden stops during the transition.
We find it more appealing to have countries learn using sudden stop
occurrences around the world instead. Return to text
14. For example, estimates for
liquidation costs include 30.5 percent (James 2012) and 49.9 percent
(Brown and Epstein 1992) in bank failures, and 37 percent (Alderson and Betker 1996) in Chapter 7
liquidations, while Ennis and Keister 2003 use liquidation costs of 60 percent and 70
percent in their analysis. We also run sensitivity analysis with
different values of ![]() , and find little
variation in the main results. See Table A.2 in the appendix for
details. Return to text
, and find little
variation in the main results. See Table A.2 in the appendix for
details. Return to text
15. The results hold as long as the productivity is sufficiently high. Return to text
16. Technically, a planner with a discrete number of countries still faces aggregate uncertainty. The case of a continuum of countries is more tractable and corresponds to an upper bound on the over-accumulation of reserves. Return to text
17. Reserves relative to GDP show exactly the same pattern. Return to text
18. For computational convenience, we
impose that the cutoff rule such that sudden stops occur if and
only if
![]() .
While this condition was an equilibrium result in the basic model,
we cannot analytically prove the cutoff rule in the extended model.
The cutoff rule significantly lowers the computational burden. We
find that this restriction is not binding in our simulations.
Return to text
.
While this condition was an equilibrium result in the basic model,
we cannot analytically prove the cutoff rule in the extended model.
The cutoff rule significantly lowers the computational burden. We
find that this restriction is not binding in our simulations.
Return to text
20. This is assuming the shortfall is not too high. Otherwise, the consumption would be negative due to the high interest implied by the high reserves shortfall. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text