A Robust Neighborhood Truncation Approach to Estimation of Integrated Quarticity

Torben Andersen, Dobrislav Dobrev, and Ernst Schaumburg^**

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

We provide a first in-depth look at robust estimation of integrated quarticity (IQ) based on high frequency data. IQ is the key ingredient enabling inference about volatility and the presence of jumps in financial time series and is thus of considerable interest in applications. We document the significant empirical challenges for IQ estimation posed by commonly encountered data imperfections and set forth three complementary approaches for improving IQ based inference. First, we show that many common deviations from the jump diffusive null can be dealt with by a novel filtering scheme that generalizes truncation of individual returns to truncation of arbitrary functionals on return blocks. Second, we propose a new family of efficient robust neighborhood truncation (RNT) estimators for integrated power variation based on order statistics of a set of unbiased local power variation estimators on a block of returns. Third, we find that ratio-based inference, originally proposed in this context by Barndorff-Nielsen and Shephard (2002), has desirable robustness properties in the face of regularly occurring data imperfections and thus is well suited for empirical applications. We confirm that the proposed filtering scheme and the RNT estimators perform well in our extensive simulation designs and in an application to the individual Dow Jones 30 stocks.

Keywords: Robust neighborhood truncation estimator, functional filtering, integrated quarticity, inference on integrated variance, inference on jumps, high-frequency data

JEL classification: C14; C15; C22; C80; G10

1 Introduction

Important progress in measuring and forecasting return volatility has been obtained through techniques exploiting the information in intraday price movements. The use of high-frequency data is, however, not without its problems. The main complication is the pronounced inhomogeneity of the intraday return series as diurnal patterns interspersed with news events and market microstructure frictions complicate direct modeling of the high frequency dynamics and introduce a variety of idiosyncratic features that are largely irrelevant for inference about inter-daily volatility. The realized volatility (RV) approach "solves" this problem by aggregating the intraday return observations to a daily frequency in a manner that retains the majority of the inherent volatility information while mitigating the impact of noise and diurnal patterns. The RV approach has been widely adopted ever since its formal introduction as a nonparametric estimator of the return variation in Andersen and Bollerslev (1998).¹ In parallel, a large body of theoretical work on model-free estimation and inference for components of the realized return variation process has arisen. Initial econometric issues are addressed in Andersen, Bollerslev, Diebold and Labys (2001, 2003) and Barndorff-Nielsen and Shephard (henceforth BNS) (2002).²

Conceptually, realized volatility differs from the standard notion of volatility by focusing on ex-post measurement of the realization of the (stochastic) return variation rather than the (ex-ante) return variance. Once attention shifts to the actual volatility realizations, new questions arise. For example, how do we assess the accuracy of our (daily) ex-post measures of the integrated return variation and how do we identify the impact of jump components. Such features are critical for a variety of issues in real-time financial management, including volatility forecasting, analysis of the dynamic properties of jumps and news events, derivatives pricing, estimation of return correlations, determination of return-volatility asymmetries (the leverage effect), and developing insights into the interplay between return volatility and the macroeconomic environment.

The key ingredient for inference regarding the return variation and the presence of jumps is the so-called integrated quarticity (IQ). To illustrate the importance of accurate IQ measures we review a few results from the RV literature. We denote the continuously evolving log-price for a financial asset by . Under general conditions, the log-price constitutes a semi-martingale with respect to an underlying filtered probability space. The associated ex-post realized quadratic variation, , for over may be decomposed into an integrated (diffusive) volatility, , and a residual (jump) component, ,

$\displaystyle dY_{t} \,\,$	$\displaystyle =$	$\displaystyle \,\, a_{t~}dt \, + \, \sigma _{t~}dB_{t} \, + \, dJ_{t}$	(1)
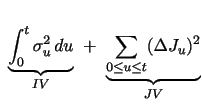
$\displaystyle QV_t \,\,$	$\displaystyle =$	$\displaystyle \,\, \underset{IV}{\underbrace{ \ST\int_0^t\sigma^2_u\,du}} \,\, + \,\, \underset{JV}{\underbrace{\sum_{0\le u\le t}(\Delta J_{u})^2}}$

where and $\sigma_t$ denote the instantaneous drift and diffusion coefficients, while and $J_{t}$ are adapted Wiener and finite activity jump processes, respectively.

For a given trading day, $t \in [0,1]$ , we consider the ideal scenario in which we observe equally-spaced (log) returns, $r_i = Y_\frac{i}{N} - Y_\frac{i-1}{N}$ , $i=1, \, \cdots , N$ . In this case, the realized volatility (RV) is a consistent nonparametric estimator of QV, as the number of intraday observations diverges, $N \rightarrow \infty$ (in-fill asymptotics),

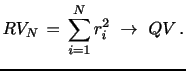
$\displaystyle RV_N \, = \, \sum_{i=1}^N r_i^2 \,\, \rightarrow \,\, QV \, .$

Moreover, absent price jumps, the limiting distribution is a Gaussian mixture,

$\displaystyle \sqrt{N} \, (RV_N - IV)$

$\displaystyle \, \, \rightarrow \,\,\, \mathcal{N}(0, 2 \, IQ)$

where $\, IQ \, = \, \int_0^1 \,\sigma^4_u \,du \,$ , which, as observed by BNS (2002), can be consistently estimated from the high-frequency data themselves via the Realized Quarticity (RQ) statistic:

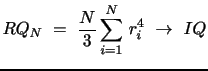
$\displaystyle RQ_N \, \, = \,\, \frac{N}{3} \sum_{i=1}^N \, r_i^4 \,\, \rightarrow \,\, IQ$

Clearly, accurate inference about the integrated variance hinges on reliable estimates for IQ. Unfortunately, IQ estimation is challenging. It involves estimating fourth order return moments from noisy intraday return series impacted by the confounding effects of market microstructure frictions, diurnal patterns, outliers, and other data irregularities. For example, it is well known that the RQ estimator is highly imprecise and non-robust to such features, even if jumps are absent. Moreover, when discrete price changes do occur, RV is no longer consistent for IV, and the RQ statistic diverges: $RQ_N \, \rightarrow \, \infty$ as $N \, \rightarrow \, \infty$ . Given the compelling evidence for jumps, this is critical in practice. In response, various jump-robust IQ estimators have been developed, but they are subject to potentially serious finite sample biases. At present, there simply is no systematic evidence regarding the performance of alternative jump-robust procedures for empirically realistic scenarios.

Recognizing these issues, a variety of ad hoc IQ estimation procedures have been implemented in the empirical literature. Before the jump-robust theory was developed, the RQ statistic was used, but only with relatively coarse sampling. For example, BNS (2004a) exploit 10-minute foreign exchange returns, while Bandi and Russell (2008) recommend computing RQ from 15- or 20-minute returns, as sparse sampling mitigates the impact of outliers and microstructure noise. Later, BNS (2004b) and Huang and Tauchen (2005) rely on 5-minute returns for constructing jump-robust estimators of IQ.³ Finally, due to the distortions arising from market microstructure effects, Jiang and Oomen (2008) opt for simply squaring their jump-robust IV estimator to obtain an IQ estimator, thus settling for a substantial Jensen inequality bias, but aiming to reduce estimation uncertainty.

To illustrate the practical importance of jump robustness, consider drawing inference about the IV of IBM stock returns across three days in February 2008 using the non-jump robust RQ/RV measures versus a pair of jump robust measures, as shown on Figure 1.⁴

Figure 1: IV inference using non-jump robust RQ/RV measures versus jump-robust MedRQ/MedRV measures.

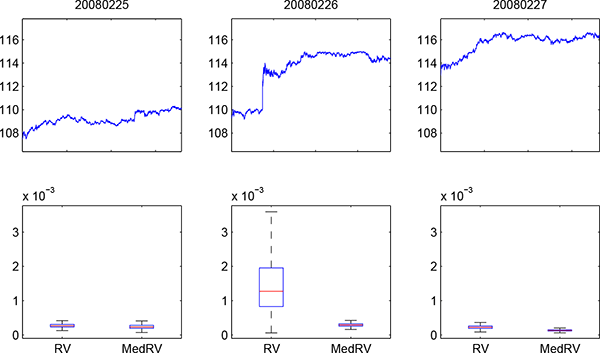
Figure 1: Figure 1 illustrates inference about the IV of IBM stock returns across three days in February 2008. On February 25, 2008 (first column) the IBM price increases from about $108 to $110 without any instantaneous large jumps (top row) and hence the point estimates of daily IV based on RV and MedRV (bottom row) are very close to each other with tight confidence bounds around 0.00025 based on RQ and MedRQ respectively. On February 26, 2008 (second column) the IBM price further increases from $110 to about $114 but now exhibits a clear large jump of more than $3 just before the end of the first quarter of the trading day (top row). As a result, the non-robust estimate of daily IV 0.00125 based on RV (bottom row) is about five times larger than the robust estimate of daily IV 0.00025 based on MedRV (bottom row). Moreover, the confidence bounds around the RV estimate based on RQ are invalid because of the jump and are more than five times larger than the still valid confidence bounds around the jump-robust MedRV estimate based on MedRQ (bottom row). On February 27, 2008 (third column) the IBM price increases a bit more from $114 to about $116 without any visible large jumps (top row), thereby reverting again to the agreement between the point estimates of daily IV based on RV and MedRV (bottom row) and their confidence bounds based respectively on RQ and MedRQ (bottom row) as initially observed on February 25, 2008 (first column).

We plot prices (blue line), the IV point estimate (red line), the inter-quartile range (blue box) as well as two standard deviation IV confidence bands (black whiskers) for IBM for three trading days in February 2008.

The jump on 2/26/2008 is readily identified visually and easily detected using a jump robust test statistic. In fact, the robust MedRV estimates and associated standard error bands, based on MedRQ, suggest a relative stable volatility process across the three trading days. In contrast, the regular RV estimate for IV is greatly inflated on 2/26/2008, and the confidence band is huge, reflecting a diverging RQ statistic. Hence, the reliance on non jump-robust statistics has two consequences. First, when jumps are present the IV estimate is upward biased because the jump component in QV is attributed to IV.⁵ Second, the associated confidence band is grossly overstated, indicating very poor estimation precision whereas, in fact, the robust estimate appears quite reliable. Hence, non-robust inference may produce excessively erratic IV estimates and convey a sense of exaggerated imprecision associated with these techniques. While the misleading inference afforded by the regular RV and RQ estimators is apparent in Figure 1, at least when contrasted with the robust inference and a depiction of the price path, it can be less obvious in cases with higher volatility levels and relatively smaller jumps. As such, it is important to develop feasible robust and efficient procedures for estimating IQ and conducting inference for IV.

One main contribution of this paper is to provide a first in-depth exploration of the virtues and drawbacks of alternative jump-robust estimation procedures for IQ, including their robustness to a variety of realistic features of the return generating process. A point of emphasis is the use of wide pre-averaging windows for controlling the impact of microstructure noise on the inference. This enhances robustness and simplifies the distribution theory as the impact of noise is annihilated asymptotically. A second contribution is the development of a new class of robust neighborhood truncation (RNT) estimators that generalize existing nearest neighbor and Quantile RV estimators. They involve the application of a second layer of order statistics to suitably chosen return functionals, thus robustifying the inference for IQ with only a minor loss of efficiency. We find such RNT estimators to perform admirably, especially when used in combination with the ratio statistic, , which is known to provide improved finite sample inference for IV. Moreover, these principles apply generally and can be used to enhance the robustness of inference from alternative classes of estimators. A third novelty is the use of an outlier filtering procedure that operates directly on an estimation functional of interest rather than on individual returns. This functional filtering principle adapts the filter to the specific assumptions underlying a given estimator. Hence, it controls the impact, and potential distortion, of abnormal outliers within the exact metric in which they contribute to the ultimate estimator. In applications to individual equity return data we find this filter indispensable for rendering entire classes of promising candidate IQ estimators viable. The unifying theme behind our new estimators and universal filtering procedure is to operate directly on the functional space of local power variation estimates rather than the individual returns. Nonetheless, the latter, and common, approach may be obtained as a special case of our procedure.

The remainder of the paper is structured as follows. Section 2 reviews the modern approach to robust estimation of integrated power variation. Section 3 develops our robust neighborhood truncation estimators. In Section 4, we discuss additional procedures applied to obtain robustness against jumps and noise. Section 5 illustrates the importance of common data features for IQ inference through an extensive simulation study. Finally, Section 6 provides evidence using high-frequency returns on the Dow Jones 30 stocks, while Section 7 concludes. All proofs are relegated to the Appendix.

2 Overview of Jump-Robust Power Variation Estimation

This section summarizes the modern approach to power variation estimation. We outline the theoretical setting and review some existing estimators which are later used in our simulation study and empirical investigation. In the process, we discuss practical trade-offs that must be confronted in estimating objects involving high powers of volatility.

2.1 The Theoretical Setting

We focus on a single asset traded continuously in a frictionless market over the period , referred to as a trading day. If it is a limited-liability asset with an expected positive payoff at some future date, the price will remain strictly positive. No-arbitrage conditions then ensure that the log-price process constitutes a semimartingale with respect to the underlying filtered probability space, see, e.g., Back (1991) and Andersen, Bollerslev and Diebold (2010). Hence, for most of our analysis we invoke the following conditions.

Assumption 1 The continuously compounded return process, $r_t \, ,$ is governed by a jump-diffusive semimartingale,

$\displaystyle r_t$

$\displaystyle =$

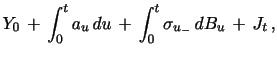
$\displaystyle Y_0 \, + \, \int_0^t a_u\,du \, + \, \int_0^t \sigma_{u_-} \, dB_u \, + \, J_{t}\, ,$

(2)

where is a locally bounded and predictable process, $\sigma$ is an adapted cadlag process bounded away from zero, and is a finite activity jump process.

Assumption 1A The volatility process, $\sigma_t$ , follows a jump-diffusive semimartingale,

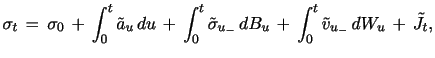
$\displaystyle \sigma_t \, = \, \sigma_0 \,+\, \int_0^t \tilde{a}_u \, du \, + \, \int_0^t \tilde{\sigma}_{u_-} \,dB_u \, + \, \int_0^t \tilde{v}_{u_-} \,dW_u \, + \, \tilde{J}_{t} ,$

where $\tilde{a}$ is locally bounded and predictable, $\tilde{\sigma}, \, \tilde{v}$ are cadlag, the Brownian motions $B, \, W$ are uncorrelated, and $\tilde{J}$ is a finite activity jump process.

If the Brownian component in Assumption 1 is non-zero, the return innovation is an order of magnitude larger than the expected return over short time intervals, implying that the drift term typically does not affect the asymptotic distribution of power variation estimators based on high-frequency data. Hence, we ignore the drift term in this section.⁶

Another key implication of Assumptions 1 and 1A is that we may derive the asymptotic properties of many relevant estimators assuming that the intraday returns are locally Gaussian. To operationalize this approach, the trading period is broken into smaller blocks. For each block, we treat volatility as constant, even if the actual return variation evolves stochastically and the price path contains finite activity jumps. If equally-spaced continuously compounded returns are available, and each block contains $m \geq 1$ returns, we assume, without loss of generality, that $N = K \cdot m$ . Notice that each block covers $\tfrac{1}{K}^{\text{th}}$ of the trading period and each return reflects the price evolution over an interval length of $\tfrac{1}{N}$ .

The above insight simplifies matters greatly, as nonparametric jump-robust estimators now are easy to devise. One simply selects a suitable unbiased estimator for the (power of) volatility within each block under the null hypothesis of i.i.d. Gaussian returns, and then cumulate the estimates across blocks to obtain the overall power variation. The distribution theory is developed using standard in-fill asymptotics, letting grow indefinitely, while requiring $\tfrac{m}{K} \to 0$ . In most cases, is fixed and diverges proportionally with .

2.2 Estimating Power Variation under the Diffusive Null Hypothesis

We first consider the case where there is no jump component. Given the assumptions invoked above, we focus on the null hypothesis that the returns within a small block are i.i.d. Gaussian. A generic estimator of the $p^{\text{th}}$ order return variation, for an even positive integer, is now obtained as the average of local estimates of $\sigma^{\,p}$ based on a functional operating on blocks of adjacent returns. For each integer $i, \, 1 \leq i \leq N-m+1$ , we have a return block, $\underline{r}_{i,m} = \left( r_{i}, r_{i+1\,}, \, \ldots \, , r_{i+m-1\,} \right)$ . Under the null, these returns are i.i.d. $\mathcal{N}(0,\, \sigma_{i}^{\,2} / \, N)$ . We let $f_{i} \, = \, f \left( \underline{r}_{i,m} \right)$ denote the functional exploited by a given estimator to obtain an unbiased estimate of $\sigma_{i}^{\,p}$ for the 'th block. If Assumption 1 holds, the power variation estimator is consistent. Heuristically, the law of large numbers implies, as $N \rightarrow \infty$ ,

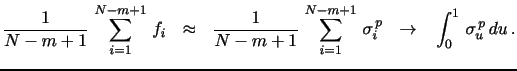
$\displaystyle \frac{1}{N-m+1} \, \sum_{i=1}^{N-m+1} \, f_{i} ~~ \approx ~~ \frac{1}{N-m+1} \, \sum_{i=1}^{N-m+1} \, \sigma_{i}^{\,p} ~~ \rightarrow ~~ \int_0^1 \, \sigma_u^{\,p}\,du \, .$

A corresponding central limit theory may typically be devised if we invoke Assumption 1A.

The simplest estimator within this framework is the realized Power Variation (PV) measure. It does not exploit multi-return blocks, so . It takes the form,

$\displaystyle f_{i}^{PV}(p;N) ~ = ~ f(r_{i\,}) ~ = ~ \mu_p^{\,-1} ~ \, N^{\frac{p}{2}} \, r_{i}^{\,p} \, , ~~~~~$ where $\displaystyle ~~~ \mu_p ~=~ E\vert Z\vert^p \, , ~~~$ for $\displaystyle ~~ Z \, \sim \, \mathcal{N}(0,1) \, .$

The normalization constant is given by $\, \mu_p \,\, = \,\, 2^{p/2} \, \frac{\, \Gamma((p+1)/2) \,}{\Gamma(1/2)} \,$ , for any .

For , this produces the regular RV, or PV(2), estimator with $\mu_2 = 1$ , while yields the RQ, or PV(4), estimator from Section 1 with normalizing constant $\mu_4 = 3$ .

A couple of comments are warranted. First, the setting ignores data errors and market microstructure frictions. Higher order return moments are particularly sensitive to faulty price observations or inappropriate assumptions regarding the evolution of the high frequency returns. We discuss these issues in the context of the simulation and empirical sections below. Second, in contrast to the realized power variation estimator, the functional will in the following be designed to be jump-robust, i.e., provide valid asymptotic inference for the power variation, even in the presence of finite activity jumps. However, jumps often have a severe adverse effect on the finite sample properties of the estimators, especially for . Many of the practical complications below arise from this feature.

2.3 Jump-Robust Power Variation Estimation

We now outline the basic principles behind the construction of power variation estimators that are robust to the presence of finite activity jump processes. Asymptotically, as the block sizes shrink towards zero and the number of blocks grows indefinitely, there will be a finite number of blocks containing one single jump each. Hence, in the limit, the power variation associated with the blocks containing jumps is negligible. It follows that the power variation can be estimated consistently as long as the contribution from the "jump blocks" is an order of magnitude less than the overall power variation measure which, of course, is . However, the jumps are also of order , so the functional must ensure that the jumps are dampened sufficiently to eliminate their impact asymptotically.

Formally, for any given sampling frequency, we denote the set of indices corresponding to returns for which the associated block contains a jump by . Thus, for $i \in I_J$ , there is a jump in the return block $\underline{r}_{i,m}$ . We then write the generic power variation estimator as,

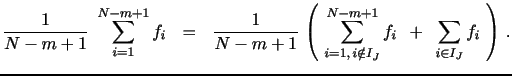
$\displaystyle \frac{1}{N-m+1} \,\, \sum_{i=1}^{N-m+1} f_{i} ~~ = ~~ \frac{1}{N-m+1} \, \left( \,\, \sum_{i=1, \, i \notin I_J}^{N-m+1} f_{i} ~\,+~ \sum_{i \in I_J} f_{i} \,\, \right) \, .$

The first term estimates the integrated power variation consistently, i.e.,

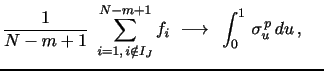$\displaystyle \frac{1}{N-m+1} \,\, \sum_{i=1, \, i \notin I_J}^{N-m+1} f_{i} ~ \longrightarrow ~ \int_0^1 \, \sigma_u^{\,p} \, du \, , ~~~$ as $\displaystyle ~ N \, \longrightarrow \, \infty \, .$

The contribution from the blocks containing jumps is negligible, in the limit, only if each such block is of order less than . Thus, the associated power variation estimator is consistent as long as $f_i \, \sim \, o(N),\,$ for $\, i \in I_J$ .⁷. This is accomplished in different ways by alternative jump-robust estimators. Moreover, their practical effectiveness is largely determined by the degree to which they accomplish sufficient dampening of the jump contributions in finite samples.

2.4 Alternative Jump-Robust Power Variation Estimators

2.4.1 Multi-Power Variation Estimators

The first (finite activity) jump-robust power variation estimators were the Realized Multi-Power Variation (MPV) statistics, inspired by BNS (2002). Expressed in terms of the functional applied to successive return blocks, the estimator takes the form,

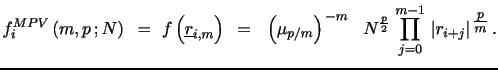
$\displaystyle f_{i}^{MPV}\left(m,p\,; N\right) ~ = ~ f\left(\underline{r}_{i,m}\right) ~ = ~ \, \left(\mu_{p/m}\right)^{\,-m} \,\,\,\, N^{\frac{p}{2}} \, \prod_{j=0}^{m-1} \, \vert r_{i+j}\vert^{\,\tfrac{p}{m}} \, .$

For and or , the estimator reduces to the (non jump-robust) RV or RQ estimator, respectively. Prominent (jump robust) special cases include , which defines the bipower variation statistic, and various IQ estimators, such as tripower , quadpower , and quintpower .

As described earlier, the actual estimator is now obtained by averaging the value of the functional across the available blocks,

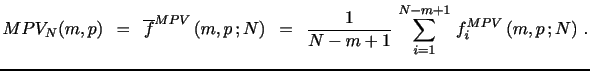
$\displaystyle MPV_N(m,p) \,\,\, = \,\,\, \overline{f}^{MPV}\left(m,p\,; N\right) \,\,\, = \,\,\, \frac{1}{N-m+1} \, \sum_{i=1}^{N-m+1} \, f_{i}^{MPV}\left(m,p\,; N\right) \, .$

The MPV estimator is consistent and affords an associated CLT, as long as is chosen sufficiently large relative to . This produces an inevitable bias-variance trade-off. A larger implies more dampening of the jump term, so the finite sample bias induced by the jump is alleviated. On the other hand, for a given sampling frequency, a larger block size, , implies that the functional is less localized, so the constant volatility assumption provides a poorer approximation, and the estimator becomes less efficient.

2.4.2 Truncated Power Variation Estimators

An estimator closely related to the PV and MPV statistics is the Realized Truncated Power Variation (TPV) measure. Mancini (2009) introduces the threshold realized volatility and quarticity estimators, while Corsi, Pirino and Reno (2010), henceforth CPR, consider a bipower variant of these statistics. These estimators achieve jump robustness by truncating observations exceeding a pre-specified threshold. Under in-fill asymptotics, we may stipulate that the threshold converges toward zero slowly enough (slower than $\frac{1}{N}\log(N)$ ) that the limiting distribution of the resulting estimators is identical to their non-truncated counterparts. In particular, Truncated RV, or TRV, is asymptotically most efficient among all jump robust IV estimators, and similarly the Truncated RQ, or TRQ, is the most efficient jump-robust estimator for IQ. Moreover, it is evident that the (finite sample) jump distortion is determined by the size of the truncation threshold and thus is under direct control in designing the estimator. The block-functional defining the truncation multi-power variation estimator of order with truncation threshold, $\vartheta_{i-j} > 0$ , takes the form,

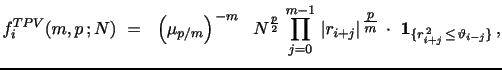
$\displaystyle f_i^{TPV}(m,p\,; N) ~ = ~ \, \left( \mu_{p/m} \right)^{\,-m} \,\,\,\, N^{\frac{p}{2}} \, \prod_{j=0}^{m-1} \, \vert r_{i+j}\vert^{\,\tfrac{p}{m}} \, \cdot \,\, \mathbf{1}_{\{r_{i+j}^{\,2} \, \le \, \vartheta_{i-j}\}} \, ,$

where $\mathbf{1}_{\{A\}}$ is an indicator function, taking the value of one if the statement A is true, and zero otherwise. As before, the actual TPV(m,p) estimator is obtained by averaging the functional values across the available return blocks for the trading period.

The choice of threshold can be delicate. It is beneficial to truncate aggressively to reduce the jump distortion by choosing a low threshold, but the non-jump returns are then also truncated with non-trivial probability. CPR suggest a finite-sample scaling to correct for this bias. They develop an iterative scheme aiming to obtain a fixed point at which the expectation of the truncated estimator equals the true (estimated) volatility under the null hypothesis. The approach is conceptually appealing, but has drawbacks. First, the modified estimator is no longer linear in the unobserved $\sigma^{2}$ and thus suffers from a downwards bias, due to Jensen's inequality, even in the ideal Brownian case. Second, they use a sizeable two-sided window (e.g., 50 observations) to obtain a local volatility estimate, thereby rendering it susceptible to an additional bias due to time variation in volatility across the block.

2.4.3 Neighborhood Truncation Estimators

Andersen, Dobrev and Schaumburg, henceforth ADS, (2012) introduce a couple of IV estimators, MinRV and MedRV, designed to improve on the trade-off between jump robustness and efficiency confronting the MPV estimators. MinRV and MedRV are based on an endogenous "nearest neighbor" truncation which is particularly helpful in alleviating the finite-sample impact of isolated large jumps. We now extend this theory to cover general power variation estimation. We start out by introducing notation that allows us to identify various order statistics associated with a given return block.

First, we denote the th block, consisting of absolute returns raised to the $p^{\text{th}}$ power, by $\vert\underline{r}_{\, i,m}^{\,p}\vert = ( \, \vert r_i\vert^{\,p} \, , \, \cdots \, , \, \vert r_{i+m-1}\vert^{\,p} \, ), \,\, i=1, \ldots , \, N-m+1. \,$ Next, $\, q_j\left(\vert\underline{r}_{\, i,m}^{\,p}\vert\right), ~ j=1, \, \cdots \, , \, m, \,$ indicates the $j^{\text{th}}$ order statistic of the block $\vert\underline{r}_{\, i,m}^{\,p}\vert$ , so $\, q_1(\vert\underline{r}_{\, i,m}^{\,p}\vert) \, \leq \, \ldots \, \leq \, q_m(\vert\underline{r}_{\, i,m}^{\,p}\vert) \,$ . As the returns are assumed $i.i.d. \, \mathcal{N}(\, 0, \, \sigma_i^2/N \, ), \,$ we may also write $\, N^{\frac{p}{2}} \cdot \vert\underline{r}_{\, i,m}^{\,p}\vert \, = \, \sigma_i^{\,p} \cdot \, \vert\underline{Z}_{\, i,m}^{\,p}\vert$ , highlighting the fact that all estimators for the block ultimately are functionals operating on the realization of an -dimensional standard normal random vector.

We now readily obtain separate unbiased estimators for $\sigma_i^{\,p}$ , namely one for each order statistic. We denote these "Neighborhood Truncation" estimators, or NT(j,m,p). As before, we construct them by averaging the appropriate block functional across the trading period. The functional takes the form,

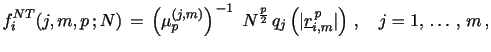
$\displaystyle f_i^{NT}(j,m,p \,; N) \, = \, \left( \mu_p^{(j,m)} \right)^{\,-1} \,\, N^{\frac{p}{2}} \, q_j\left(\vert\underline{r}_{i,m}^{\,p}\vert \right) \, , \,\,\,\,\,\, j = 1, \, \ldots \, , \, m \, ,$

where $\mu_p^{(j,m)} = E\left[ q_j \left( \vert Z_1\vert^p, \, \cdots \, , \, \vert Z_m\vert^p \right) \right], \,\, Z_{i} \sim i.i.d. \, \mathcal{N}(0,1), \,\, i=1, \, \ldots \, , m.$ This normalization ensures that the functional provides an unbiased estimator for $\sigma_i^{\,p}$ . Since the scaling factors are inversely related to the expected value of the order statistics, we have the ranking, $\mu_p^{(1,m)} \, > \ldots \, > \, \mu_p^{(m,m)}$ . For high values of and , these factors become quite large for the lower order statistics, while they are very small for the higher order statistics.⁸

The class of neighborhood truncation estimators generalize the MinRV and MedRV estimators, as we have, and .⁹ Under appropriate conditions the NT estimators are consistent and afford a CLT. We confirm this result when we introduce an even wider class of robust estimators in Section 3.

2.4.4 Combining Power Variation Estimators

It seems natural to combine some of the estimators introduced above to obtain superior asymptotic properties and, possibly, improved finite-sample performance. It is, however, outside the scope of the current paper to pursue this topic in depth. Nonetheless, we do develop the framework and notation to accommodate such combination estimators, as it is useful for our introduction of a new class of robust estimators in the next section.

Assume we have a candidate set of separate jump-robust power variation estimators which all are unbiased, consistent and afford a CLT under the local Gaussian null hypothesis. We denote this set of estimators, $\, \mathcal{E} \, = \, \{ \, \mathcal{E}_1, \, \ldots \, , \, \mathcal{E}_K \, \}. \,$ Almost trivially, it is then, in theory, feasible to improve the performance of any single estimator by combining it with others.¹⁰

We formalize the selection of a subset of the estimators by introducing a "selection" vector, identifying the elements in $\mathcal{E}$ used to construct a given (combination) estimator. Hence, we let the x vector $\textbf{\emph{I}} \,=\, (\, k_{1\,}, \, \ldots \, k_{H\,} ), \, 1 \leq H \leq K \, ,$ consisting of an ordered subset of integers from $\{1, \, \cdots \, , \, K \}, \,$ indicate that the combination estimator is based on the set $\mathcal{E}_{\emph{I}} = \left( \mathcal{E}_{k_1}, \, \cdots \, , \, \mathcal{E}_{k_H} \right)$ . Denoting the set of all possible selector vectors $\mathcal{I}$ , any subset is now uniquely identified by $\textbf{\emph{I}} \in \mathcal I$ , where $\textbf{\emph{I}}$ ranges from a scalar (using a single estimator), at the one extreme, to the full vector $\{1, \, \cdots \, , \, K \} \,$ (using them all), at the other extreme.

A natural way to preserve the desirable properties of the individual estimators is to exploit linear combinations with non-negative weights that sum to unity. For example, focusing exclusively on a set of NT estimators constructed using a return block of size , we have $\, \mathcal{E} \, = \, \{ \, \mathcal{E}_1, \, \ldots \, , \, \mathcal{E}_m \, \}$ , where each element represents an unbiased estimator based on the corresponding (absolute return) order statistic. Picking a specific NT estimator amounts to, a priori, selecting a given integer $j \in \{1, \, \cdots \, , \, m \}. \,$ There are a total of distinct non-empty subsets of $\mathcal{E}$ from which to construct a combination estimator. It is a routine exercise to extend our asymptotic results to cover the case of any such linear combination of NT estimators.¹¹ Conceptually, it is likewise straightforward to derive corresponding results for linear combinations involving alternative types of jump-robust estimators.

In summary, within the ideal setting of Assumptions 1 and 1A, superior asymptotic performance can be obtained by combining the information associated with all available estimators. However, this must be weighed against the robustness objective of ensuring reliable finite sample inference in the presence of jumps as well as other potential sources of noise. Such robustness concerns motivate the introduction of an even broader class of combination estimators in the following section, obtained by nonlinearly combining suitably chosen unbiased estimators via a second layer of order statistics.

3 Robust Neighborhood Truncation Estimation

Our major objective is to develop a reliable jump-robust procedure for estimating measures associated with the integrated quarticity. Most of the estimators reviewed in the previous section were developed for IV, even if they can be adapted for higher order power variation measures. It is worth recognizing that the relative importance of factors impacting the trade-off between statistical efficiency and robustness changes substantially as we estimate higher order power variation measures. In fact, our simulation evidence demonstrates, quite strikingly, that the most suitable approach for IV estimation is unlikely to be preferable when estimating IQ. Consequently, we now introduce a novel inference procedure which enhances the robustness to common sources of finite-sample distortions and allows for a great deal of flexibility in implementation so that the estimator can be tailored to the specific features of a given return series and market environment.

3.1 Theory

This section proposes estimating integrated power variation via a nonlinear combination of existing unbiased estimators, obtained by invoking an additional layer of order statistics. We develop the theory for neighborhood truncation estimators, but the principles apply for any set of unbiased estimators. The emphasis is on finite sample robustness to microstructure noise and jumps, so we label them "Robust Neighborhood Truncation," or RNT, estimators.

For a return block of size , there are distinct NT estimators, namely one for each order statistic. One may combine any subset of these to produce an estimator that exploits more sampling information than can be utilized by any individual one. The set of alternative selections is the set, $\mathcal{I}$ , of non-empty subsets of $\{1, \, \cdots \, , \, m\}$ . A specific choice is given by $\textbf{\emph{I}} \,=\, (\, k_{1\,}, \, \ldots \, k_{H\,} ), \, 1 \leq H \leq m.$ The corresponding NT estimators are defined via the functionals they apply to the underlying return blocks. To facilitate the exposition, we use the following short-hand notation for these functionals, applied to the $i^{\text{th}}$ return block,

$\displaystyle \underline{f}_{\,i,\mathbf{I}}^{NT}(m,p \,; N) \, = \, \left( f_i^{NT}(k_1,m,p \,; N), \, \ldots \, , f_i^{NT}(k_H,m,p \,; N) \right)\,.$

The rationale behind the NT estimators is to alleviate the impact of extreme returns - large or small - which may be incompatible with the i.i.d. Gaussian assumption. The robust neighborhood truncation principle takes the reasoning one step further by producing an estimator for $\sigma_i^{\,p}$ based on a suitable order statistic among the subset of selected NT estimators. Formally, we have,

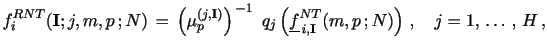
$\displaystyle f_i^{RNT}(\mathbf{I}; j,m,p \,; N) \, = \, \left( \mu_p^{(j,\mathbf{I})} \right)^{\,-1} \,\, q_j \left( \underline{f}_{\,i,\mathbf{I}}^{NT}(m,p \,; N) \right) \, , \,\,\,\,\,\, j = 1, \, \ldots \, , \, H \, ,$

where $\, \mu_p^{(j,\mathbf{I})} \,=\, E\left[ \, q_j \left( \vert Z_1\vert^p, \, \cdots \, , \, \vert Z_H\vert^p \right) \, \right], \,\,\,\, Z_{h} \sim i.i.d. \,\, \mathcal{N}(0,1), \,\,\,\, h=1, \, \ldots \, , H.$

Normalization is required, even if each NT estimator is individually unbiased, because selection conditional on observed realizations induces a bias. This is corrected by scaling with (the inverse of) the expected value of the corresponding order statistic for a standard normal x vector. This normalization factor is not available in closed form, but may be determined, to any degree of accuracy, by numerical integration or simulation.

As before, the actual estimator is obtained by averaging the estimates across all blocks in the trading periods, so we have,

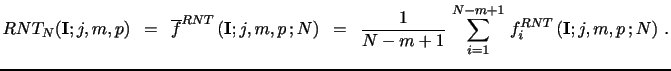
$\displaystyle RNT_N(\mathbf{I}; j,m,p) \,\,\, = \,\,\, \overline{f}^{RNT} \left( \mathbf{I}; j,m,p \,; N \right) \,\,\, = \,\,\, \frac{1}{N-m+1} \, \sum_{i=1}^{N-m+1} \, f_i^{RNT} \left(\mathbf{I}; j,m,p \,; N \right) \, .$

Notice that the RNT procedure involves two layers of order statistics: we first construct consistent NT estimators from the order statistics of a block of absolute returns (which readily may be extended to any set of consistent estimators), and then obtain the RNT estimator from another order statistic applied to a subset of these NT estimators. This provides a great deal of flexibility in alleviating the impact of extreme returns. In line with the logic behind the MinRV and MedRV measures, the RNT estimator is consistent if we exclude the largest order statistic from $\emph{I}$ . Asymptotically, this ensures that none of the NT estimators are generated from a (scaled) jump return. Alternatively, this is also guaranteed if we avoid constructing the RNT estimator from the largest realization of the NT estimators, i.e., in the second step.

Proposition 1 Let a family of distinct NT estimators, indexed by $\emph{I}$ , be generated from absolute return blocks of size . The largest order statistic used for constructing any of these NT estimators is denoted , $k_H \leq m$ . Next, consider the RNT estimator obtained from the $j^{\text{th}}$ order statistic applied to this family of NT estimators, $j < H \,$ $j \leq H$ .

If (i) Assumption 1 holds; (ii) and/or ; and (iii) is a positive, even integer; then, as $N\rightarrow\infty,$

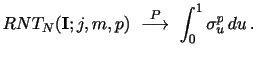
$\displaystyle RNT_N(\mathbf{I}; j,m,p) \,\, \overset{P}{\longrightarrow} \,\, \int_{0}^{1} \sigma_{u}^{p}\, du \, .$

If, in addition, Assumptions 1A applies, we obtain, for $\eta\left( \mathbf{I}; j,m,p \right)$ a known constant,

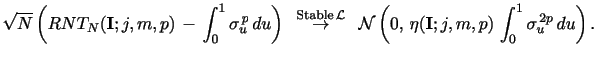
$\displaystyle \sqrt{N} \left( RNT_N(\mathbf{I}; j,m,p) \, - \, \int_0^1 \sigma_u^{\,p} \, du \right) \,\,\, \overset{\text{Stable} \, \mathcal{L}}{\rightarrow} \,\,\, \mathcal{N}\left(0,\, \eta(\mathbf{I}; j,m,p) \, \int_0^1 \sigma^{\, 2p}_u \, du \right).$

The proposition warrants a few comments. First, the distributional convergence is stable with a mixed Gaussian limit, i.e., a normal distribution conditional on the realization of the integrated power variation, $PV(q) = \int_{0}^{1} \sigma _{u}^{q} \,du$ , where, importantly, the limiting normal variate is independent of the (random) power variation process.¹² Second, the convergence result is qualitatively similar to those established for existing power variation estimators, with the "efficiency factor" $\eta(\mathbf{I}; j,m,p)$ determining the relative asymptotic efficiency of the estimator. Third, the main objective is not efficiency per se, but good performance along with (finite sample) robustness to jumps, noise, and other data irregularities. Fourth, the results apply for the Neighborhood Truncation and Nearest Neighbor Truncation estimators, as these constitute special cases involving a particular choice for the vector I. Fifth, the results are likely to extend to the infinite activity jump case, given suitably tight constraint on the size of the associated (jump) activity index.¹³

3.2 Illustration

The simulation and empirical work in the following sections exploit fairly small blocks of $m \leq 5$ in order to retain resiliency relative to rapidly changing volatility levels during the trading day. In addition, we find it useful to eliminate estimators that stem from the lowest order statistics of the absolute returns as these are relatively more affected by market microstructure noise such as price discreteness and bid-ask bounce. This is a particular concern, because these estimates are bias-corrected by scaling the original small returns by a large factor, implying that microstructure distortions may be amplified. Likewise, we typically satisfy the formal constraint on the order statistics by picking , so we avoid basing the RNT estimator on the largest realization among the relevant NT estimators.

For a -dimensional return block, the construction of the $RNT_N((\textbf{3,4,5}); 1,5,4 )$ and $RNT_N((\textbf{3,4,5}); 2,5,4)$ estimators are exemplified in Figure 2. The notation becomes quite involved so, for brevity, we refer to the two estimators in the diagram as and , respectively.¹⁴ Both play a significant role in our subsequent exposition. For these estimators, the two smallest absolute returns are discarded, while the remaining three are used to compute the corresponding NT estimators. Among those, we pick the lowest, respectively median, realization and scale it to construct the associated RNT estimator.

Figure 2: Schematic representation of the construction of the and estimators of $\sigma^{4}$ on a block of five adjacent returns.

Figure 2: Figure 2 provides a schematic flowchart representation of the construction of the RMinRQ (first column) and RMedRQ (second column) estimators of ï³4 on a block of five adjacent returns. The starting point for both estimators is an ordered set of five absolute returns {0.0, 3.0, 4.0, 4.5, 5.5} given in the first row of the flowchart. Of these the three largest absolute returns {4.0, 4.5, 5.5} are retained by both estimators as shown in blue in the second row of the flowchart. These are raised to the fourth power obtaining {256.0, 410.1, 915.1} as shown in blue in the third row of the flowchart. Each of these fourth-power terms is then scaled to an unbiased estimator of ï³4 applying the scaling factors given in Table 1, Panel B. The resulting values {369.0, 163.3, 78.9} are given in blue in the fourth row of the flowchart. Then by definition RMinRQ takes the minimum 78.9 among these, while RMedRQ takes their median 163.3, as shown in the fifth row of the flowchart. The last step applies the corresponding scaling factors from Table 1, Panel D to obtain the final unbiased estimates of 206.1 for RMinRQ and 198.3 for RMedRQ, as given in the last sixth row of the flowchart.

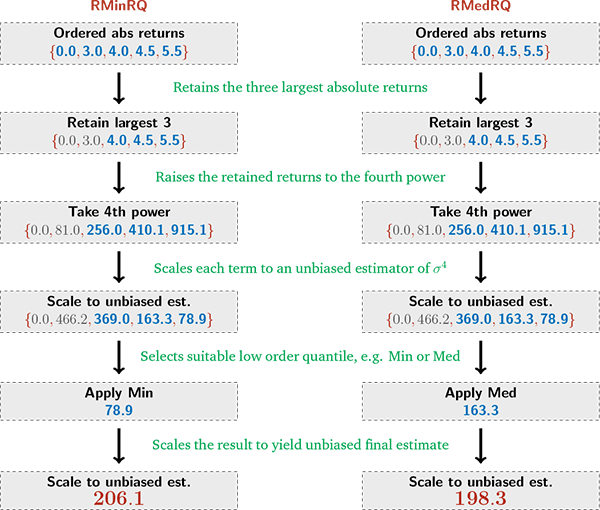
A few features are worth emphasizing. First, we display the NT estimators obtained from the first two order statistics along with the rest, even if they are excluded from the construction of the estimator. Hence, the third box displays all five returns taken to the fourth power. An extreme right skew is evident, with values spanning 0 to 915.1, even if the initial returns are not particularly scattered. A zero return is, of course, common due to the discreteness of the price grid. Second, between box 3 and 4 we apply the relevant scaling factors for the NT estimators, see Panel B of Table 1. Strikingly, the large factor (5.74 = (0.1741) $^{-1}$ ) for the second order statistic produces, by far, the largest realized estimator in box 4 (466.2). Finally, excluding the NT estimators originating from the two smallest absolute returns (0, 466.2), we pick the minimum and median of the remainder and scale these statistics (78.9 and 163.3) suitably with the scaling factors provided in Panel D of Table 1 (2.611 = (0.38303) $^{-1}$ and 1.214 = (0.82367) $^{-1}$ ) to obtain the local RNT estimators for $\, \sigma_i^{\,4 \,}$ of 206.1 given by , respectively 198.3 given by . These realizations happen to stem from the two largest order statistic of the original return block (5.5 and 4.5), but the low scaling factors for these order statistics (0.086 = (11.59249) $^{-1}$ and 0.398 = (2.51102) $^{-1}$ ) imply that the associated (unbiased) NT estimators in box 4 are the smallest among the relevant subset. It reflects the relatively low spread between the three largest absolute return realizations of 4.0, 4.5, and 5.5. In general, these procedures tend to moderate the local estimates relative to estimators which rely more directly on the raw fourth powers in box 3.

Table 1a: Tabulation of Moments of Order Statistics for Standard Gaussian Return Blocks of up to Five Returns - Panel A: 2nd Moments Defining the Inverse Scaling Factors for Corresponding NTV Estimators

Block Size	Z²₍₁₎	Z²₍₂₎	Z²₍₃₎	Z²₍₄₎	Z²₍₅₎
2	µ₂^(1,2) ≈1.6366198 =π - 2/π	µ₂^(2,2) ≈0.36338023 =2 + π/π
3	µ₂^(1,3) ≈0.19279847 =-6+2√3+π/π	µ₂^(2,3) ≈0.70454374 =6-4√3+π/π	µ₂^(3,3) ≈ 2.1026578 =1+2√3/π
4	µ₂^(1,4) ≈0.12070214 =1+4(4√3-9)/3π	µ₂^(2,4) ≈0.40908747 =12-8√3+π/π	µ₂^(3,4) ≈1	µ₂^(4,4) ≈2.4702104 = 1 + 8/ √ 3π
5	µ₂^(1,5)≈0.083077313	µ₂^(2,5)≈0.271201456	µ₂^(3,5)≈0.61591649	µ₂^(4,5)≈1.2560557	µ₂^(5,5)≈2.7737491

Table 1b: Tabulation of Moments of Order Statistics for Standard Gaussian Return Blocks of up to Five Returns - Panel B: 4th Moments Defining the Inverse Scaling Factors for Corresponding NTQ Estimators

Block Size	Z⁴₍₁₎	Z⁴₍₂₎	Z⁴₍₃₎	Z⁴₍₄₎	Z⁴₍₅₎
2	µ₄^(1,2)≈0.45352091 =3-8/π	µ₄^(2,2)≈5.5464791 =3+8/π
3	µ₄^(1,3)≈0.13874649 =3+26-24√3/√3π	µ₄^(2,3)≈1.0830697 =72-52√3+9π/3π	µ₄^(3,3)≈7.7781838 =3+26/√3π
4	µ₄^(1,4)≈ 0.057664089 =3+4(4(13√3-27)π-9/9π²	µ₄^(2,4)≈0.38199370 =3+4(9+(36-26√3)π)//3π²	µ₄^(3,4)≈1.7841458 =3-12/π²	µ₄^(4,4)≈9.7761964 =3+4(9+26√3π)/9π²
5	µ₄^(1,5)≈0.028554808	µ₄^(2,5)≈0.17410122	µ₄^(3,5)≈0.69383242	µ₄^(4,5)≈2.5110214	µ₄^(5,5)≈11.592490

Table 1c: Tabulation of Moments of Order Statistics for Standard Gaussian Return Blocks of up to Five Returns - Panel C: 2nd Moments Defining the Inverse Scaling Factors for Corresponding RNTV Estimators

Block Size	min( Z²₍₃₎ / µ₂^(3,5) ,Z²₍₄₎ / µ₂^(4,5) ,Z²₍₅₎ / µ₂^(5,5) )	med( Z²₍₃₎ / µ₂^(3,5) ,Z²₍₄₎ / µ₂^(4,5) ,Z²₍₅₎ / µ₂^(5,5) )
5	µ₂^(1,(3,4,5)) ≈0.62084	µ₂^(2,(3,4,5)) ≈ 0.94544

Table 1d: Tabulation of Moments of Order Statistics for Standard Gaussian Return Blocks of up to Five Returns - Panel D: 4th Moments Defining the Inverse Scaling Factors for Corresponding RNTQ Estimators

Block Size	min( Z⁴₍₃₎ / µ₄^(3,5) ,Z⁴₍₄₎ / µ₄^(4,5) ,Z⁴₍₅₎ / µ₄^(5,5) )	med( Z⁴₍₃₎ / µ₄^(3,5) ,Z⁴₍₄₎ / µ₄^(4,5) ,Z⁴₍₅₎ / µ₄^(5,5) )
5	µ₄^(1,(3,4,5)) ≈0.38303	µ₄^(2,(3,4,5)) ≈ 0.82367

We compute the second and fourth moments of order statistics based on blocks of powers of independent standard normals, Zi~N(0, 1), whose inverse represent the scaling factors of the NT and RNT estimators defined in sections 2.4.3 and 3.1. Panel A: Expectation of order statistics of squared normals (NTV estimators). Panel B: Expectation of order statistics of normals raised to the 4th power (NTQ estimators). Panel C: Expectation of quantiles of rescaled squared order statistics of normals (RNTV estimators). Panel D: Expectation of quantiles of rescaled order statistics of normals raised to the 4th power (RNTQ estimators).

4 Robustification Towards Noise and Errors

In estimating higher order return power variation measures, we deal with procedures that can be highly sensitive to erroneous outliers as well as the presence of noise. Hence, we adopt various techniques that mitigate the impact of such features on the inference. Our strategy includes standard pre-filtering for obvious data errors, pre-averaging to reduce the magnitude of the noise in the returns, and conducting inference on the ratio of versus rather than directly for . However, most inference techniques continue to display excessive sensitivity to data irregularities. Consequently, we supplement the above steps with a novel filtering method, specifically designed for robust power variation estimators operating on return blocks. This section reviews the techniques we employ to enhance the robustness of our inference towards data errors and noise.

4.1 Eliminating Obvious Errors in the Tick-by-Tick Data

Any large set of raw transactions data is invariably subject to recording errors that infuse noise into the high-frequency returns. Most dramatically, faulty prices create artificial outliers, causing so-called "bounce-backs" in returns, as there is a "jump" both when the flawed price first appears and later, often shortly thereafter, when the price reverts to the correct level. Hence, the need for effective cleaning procedures has long been acknowledged. BNHLS (2009) lay out a systematic framework for dealing with trade data from NYSE-TAQ. In their terminology, we apply the filters P1-P3 and T1-T4.¹⁵ These filters are arguably mild and uncontroversial and simply aim to eliminate obvious data errors.

4.2 Pre-Averaging

The assumption that (observed) high-frequency returns embody a diffusive component is systematically violated at the tick-by-tick level due to various market microstructure features, including the finite price grid and the bid-ask spread. As a result, tick-by-tick price changes are often an order of magnitude larger than what is consistent with a diffusive characterization. One effective approach to mitigating the impact of such noise is to apply pre-averaging, as originally suggested by Podolskij and Vetter (2009a). This is achieved by transforming the noisy observations on ultra high-frequency returns into a smaller set of kernel-averaged, and thus less erratic, "smoothed" returns. In particular, each of the returns within a block are obtained via kernel-averaging based on separate, non-overlapping subsets of tick-by-tick returns. The benefit is a reduction in the impact of idiosyncratic noise and, especially, distortions induced by bounce-backs. The drawback is a substantial drop in the underlying sampling frequency. The latter impacts the choice of the window width, , as the (diffusive) volatility fluctuates more widely across longer blocks.

Our implementation of pre-averaging, detailed in Appendix 6, is based on a relatively conservative choice of sampling frequency. This has the effect of emphasizing noise robustness over efficiency. Importantly, it also simplifies the analysis, as the impact of noise may be largely ignored in the asymptotic theory. First, the pre-averaging estimator has an asymptotic bias, but if the (pre-averaged) returns are not sampled at very high frequencies, the bias is, effectively, negligible. Second, if there are original high-frequency returns, the optimal convergence rate for pre-averaged estimators in the presence of noise is typically $N^{1/4}$ . The associated asymptotic variance reflects both the sampling variance of the true returns and the noise variance. This result is obtained if the number of returns per pre-averaging block, $2 \cdot K$ , grows at the asymptotic rate $N^{1/2}$ , so that the total number of pre-averaged returns without overlap, , also is of order $N^{1/2}$ . This allows the convergence rate - as usual - to equal the square-root of the number of (pre-averaged) returns, i.e., $\sqrt{n} = N^{1/4}$ . But if is larger, asymptotically rising at the rate for $\frac{1}{2} < q < 1$ , the number of pre-averaged returns grows more slowly, $n \sim N^{1-q}$ , implying a convergence rate of $\sqrt{n} = N^{\frac{1-q}{2}}$ , e.g., $N^{\frac{1}{5}}$ for $q=\frac{3}{5}$ . At the same time, the noise will be averaged more aggressively and vanishes asymptotically at a faster rate. The bottom line is that, by appealing to a slower asymptotic convergence rate relative to the number of original high-frequency returns, the (asymptotic) efficiency is lower, but the asymptotic variance of the pre-averaging estimator becomes identical to the one for the no-noise case with returns. However, this equivalence holds only for pre-averaged return series based on non-overlapping blocks without sub-sampling. The additional efficiency gain attainable by sub-sampling, as in Appendix C, is not identical with and without pre-averaging, differs from one estimator to another, and generally is not known in closed form.¹⁶ Nonetheless, the efficiency of each pre-averaged and sub-sampled estimator in the presence of noise is very close to its efficiency in the absence of noise, as long as the pre-averaging window size is sufficiently large relative to sample size. We monitor the latter prediction in the simulations below to verify that it provides a useful characterization of the relevant features of the finite sample distribution.

In summary, we appeal to an asymptotic theory guided by a slightly slower convergence rate than the "optimal" $N^{1/4}$ for pre-averaged estimators. This enhances robustness to noise while allowing the asymptotic theory for the no-noise case to be the relevant benchmark. In practice, we choose a relatively large return block so our procedure is compatible with the theoretical setting in this regard. This has the convenient implication that the theory in Sections 2 and 3 provides the appropriate basis for assessing the limiting behavior of our estimators computed from pre-averaged returns, even if it ignores the presence of noise. Thus, henceforth, we simply treat the pre-averaged returns as if they were the original raw returns and, with slight abuse of notation, we redefine to denote the relevant number of (pre-averaged) returns, while accommodating the effect of sub-sampling in the conventional fashion.

4.3 Filtering via Truncation of Return Functionals

Even for returns based on pre-averaged tick data and sampled at moderate frequencies, microstructure features and other data irregularities may induce inhomogeneous and serially correlated observations that blatantly violate our distributional assumptions. For quarticity estimation, in particular, it is paramount to control the impact of this type of data imperfections to achieve a beneficial trade-off between robustness and efficiency.

This section briefly outlines a general truncation principle for return functionals that enhances the robustness of integrated power variation estimators operating on return blocks. It provides an extension of existing techniques that employ truncation to alleviate the impact of jumps or data errors. However, the philosophy and implementation are very different. Existing procedures truncate returns based on whether a single observation constitutes a significant outlier under the local Brownian null. Moreover, the truncation is an essential step in rendering the estimator robust as it dampens, and asymptotically eliminates, the distortion induced by price jumps on the estimated power variation. For this to be effective, the detection of larger jumps must be reliable, and it is common to apply a threshold for jumps that correspond to "three sigmas" or a p-value of about 0.3%. As a result, the procedure generates a non-trivial incidence of type I errors because diffusive returns based on high-frequency return data inevitably are subjected to unwarranted truncation.¹⁷

In contrast, we develop a filtering procedure that operates directly on the jump-robust functional and more broadly alleviates distortions induced by deviations from the null that the block consists of i.i.d. draws from a normal distribution. In this scenario, jump robustness is, in principle, already assured by the choice of an appropriate functional. Hence, the filtering is merely intended to eliminate truly excessive ex post estimates of local power variation, driven by functional values incompatible with the maintained null hypothesis. As such, we rely on an extremely conservative threshold for truncation, typically with p-values around $10^{-6}$ or below. This is sufficiently low that we expect, under the null hypothesis, to truncate less than a single realization of the return functional across our entire sample. In practice, the underlying assumptions are violated and truncation occurs with non-trivial frequency which helps control the associated distortion in the power variation estimators.

To introduce this filtering procedure, we recall that $\, f_{i} \, = \, f(\underline{r}_{\, i,m}) \,$ is a functional providing an unbiased estimator of the local power variation, $\sigma_{i}^{\,p}$ under the null hypothesis. Next, for a sufficiently small $\alpha$ , e.g., $10^{-6}$ , we let $Q^{\,(1-\alpha)}[g]$ denote the $(1-\alpha)^$ th-quantile of the distribution of a random variable . We then define the corresponding truncated functional $f^{(1-\alpha)}_{i}$ ,

$\displaystyle f^{\,(1-\alpha)}_{i} ~ = ~ \left\{ \begin{array}{ll} \, f_{i} & \mbox{\, if } \,\,\,\, f_{i} ~ \sigma_{i}^{-p} \, \leq \, Q^{\,(1-\alpha)\,}[\, f_{i} \cdot \sigma_{i}^{-p \,}] \\ \, 0 & \mbox{\, else.} \end{array} \right.$

Accordingly, the realized truncated estimator based on $f^{\,(1-\alpha)}$ is given by,

$\displaystyle \frac{1}{\sum_{i=1}^{N-m+1} \,\, \mathbf{I}\{\, f_{i} \cdot \sigma^{-p} < Q^{\,(1-\alpha)}[\, f_{i} \cdot \sigma^{-p \,}]\} \,} ~ \sum_{i=1}^{N-m+1} f^{\,(1-\alpha)}_{i} \,\, ,$

where $\mathbf{I}\{\mathbf{A} \}$ equals one if the expression $\mathbf{A}$ is true and zero otherwise. Setting $\alpha=0$ we obtain the usual realized estimator based on without truncation. Moreover, if our functional filtering is equivalent to the usual return filtering at the significance level $\alpha$ .

A feasible version of the filter is developed in Andersen, Dobrev and Schaumburg (2011). The procedure exploits a local estimate of volatility based on preceding observations to provide the appropriate truncation level - exactly as done for the standard truncation RV estimator - while simulation is performed to obtain the critical values, taking into account the presence of estimation error for local volatility.

4.4 Using the Ratio 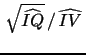$\, \sqrt{\widehat{IQ}} \, / \, {\widehat{IV}} \,$ for Robust IV Inference

The primary applications of IQ estimation is to draw inference about IV and to test for jumps under the null hypothesis of no jumps. For these procedures to perform well, it is essential that the IQ estimator has good efficiency and finite sample jump robustness.

Let $\widehat{IV}$ , $\widehat{IQ}$ be suitable jump-robust estimators of IV and IQ. A natural approach for drawing inference about IV follows directly from its limiting distribution,

$\displaystyle \frac{\sqrt{N} \, \left[\, \widehat{IV} - IV \, \right]}{\sqrt{ \, \eta \, \widehat{IQ} \,}} \,\,\, \overset{\text{Stable} \, \mathcal{L}}{\rightarrow} \,\,\, \mathcal{N}(0,\,1) \, ,$

where the "efficiency" factor, $\eta$ , depends on the specific choice of estimator.

Letting RV denote the realized volatility estimator, which is the efficient estimator of IV under the null, the natural Hausman test statistic for the presence of jumps, see BNS (2004) and Huang and Tauchen (2005), is given by

$\displaystyle \frac{\sqrt{N} \, \left[ \, \widehat{RV} - \widehat{IV} \, \right]} {\sqrt{ \, (\eta-2) \,\, \widehat{IQ}}} \,\,\, \overset{\text{Stable} \mathcal{L}}{\rightarrow} \,\,\, \mathcal{N}(0,\,1) \,.$

An asymptotically equivalent set of test statistics with better finite sample properties, proposed by BNS (2002), can be derived by applying the delta method to the log-transform of the volatility measures. This has the benefit that IQ enters only in terms of the ratio $\, \sqrt{IQ}/IV \,$ which, as also demonstrated in our empirical investigation below, has a stabilizing effect on the variance of log $\widehat{IV}$ .

$\displaystyle \frac{ \sqrt{N} \, [ \, \log ( \, \widehat{IV} \, ) - \log (IV) \, ] } { \sqrt{ \, \frac{ \, \eta \, \widehat{IQ} \, } { \, \widehat{IV}^{\,2} \,} } } \,\,\, \overset{\text{Stable} \, \mathcal{L}}{\rightarrow} \,\,\, \mathcal{N}(0, \, 1) \,.$

The corresponding Hausman test statistic for the presence of jumps is

$\displaystyle \frac{ \sqrt{N} \, [ \, \log ( \, \widehat{RV} \, ) - \log (\widehat{IV}) \, ] } { \sqrt{ (\eta-2) \, \frac{ \widehat{IQ} } { \, \widehat{IV}^{\,2} \, } } } \,\,\, \overset{\text{Stable} \mathcal{L}}{\rightarrow} \,\,\, \mathcal{N}(0, \, 1) \,.$

While the literature has documented superior performance of this ratio for jump-robust inference in a frictionless setting, it is evident that the ratio also will impact the way market microstructure noise affects the inference. In Appendix B, we provide an illustration based on computations involving the non-robust versions of the IQ and IV estimators. The findings point towards favorable properties of the ratio statistic relative to the raw statistic along this dimension as well. The intuition is as before: the realized and statistics tend to be impacted by noise in similar ways so the ratio provides a partial cancelation of errors. The issue is further pursued within the simulation set-up entertained in the following section.

5 Finite Sample Simulation Evidence

We design a series of Monte Carlo experiments, each focusing on a distinct feature of the data generating process that may affect the finite sample behavior of the estimators. The emphasis is on the qualitative impact of each feature in isolation. In reality, multiple features interact, creating complex patterns in tick-by-tick data. The joint presence of various factors, partially reinforcing or counteracting each other, render it difficult to infer the significance of individual features. Hence, our simulation design is not intended to replicate the empirical results in all dimensions, but to assist in identifying the features that create differential patterns in the results obtained from alternative estimators.

5.1 Estimators

We adopt the novel filtering procedure, based on (mildly) truncating the local power variation functional, for all estimators except those already truncating individual returns more aggressively, i.e., the truncation power variation estimators. For the latter, the impact of an additional layer of mild truncation is negligible.¹⁸ For the truncation estimators, we follow the approach advocated by CPR, as they document it improves on existing implementations. Overall, we consider the following IV and IQ estimators,

Multi-Power Variation: We denote MPV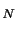(m,2) by MPVm and MPV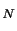(m,4) by MPQm. We include MPV3 and MPV5, as well as MPQ3 and MPQ5 in our analysis. This type of estimators was introduced by BNS (2004);
Truncated Power Variation: We use TRV = TPV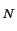(1,2) and TRQ = TPV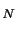(1,4), as well as Truncated Bipower Variation, TBV = TPV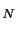(2,2) and Truncated Bipower Quarticity, TBQ = TPV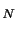(2,4). They are discussed by, e.g., Mancini (2009) and CPR;
Neighborhood Truncation: We consider MedRV = NT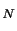(2,3,2) and the corresponding quarticity estimator MedRQ = NT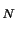(2,3,4). They are developed in ADS (2012) and in this paper;
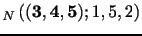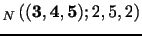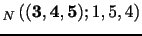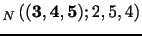Robust Neighborhood Truncation: We use = RNT $_N\left( \mathbf{(3,4,5)};1,5,2 \right)$ , = RNT $_N\left( \mathbf{(3,4,5)};2,5,2 \right)$ , = RNT $_N\left(\mathbf{(3,4,5)};1,5,4 \right)$ , and = RNT $_N\left(\mathbf{(3,4,5)};2,5,4 \right)$ . They are developed in this paper.

In addition, when investigating IV estimators, we include the standard RV estimator, serving as a non jump-robust benchmark, along with the QRV estimator of COP (2010). We omit an IQ counterpart of QRV from our analysis because we find the block size of 20 or more returns, necessary in order to establish the quantiles, to be prohibitively large for reliable inference on actual data subject to irregular sampling and pronounced intraday variation in volatility. Moreover, as discussed previously, one may interpret our NT estimators as modified QRV estimators based on the absolute returns over very small blocks.

Finally, taking into account the need to apply suitable noise-reduction technique when conducting inference in practice, we focus our Monte Carlo analysis exclusively on the pre-averaged implementation of all estimators, as defined in detail in Appendix C, including the efficiency gain from sub-sampling. The use of pre-averaging necessitates a somewhat conservative choice of sampling frequency. We report results based on 30, 120 and 600 second return observations.¹⁹

5.2 Simulation Results

We largely follow the comprehensive simulation design in ADS (2012) adopted for comparing IV estimators. We calibrate the unconditional daily IV to , or roughly 20% per year, across all scenarios. For each scenario we simulate 250,000 trading days, corresponding to about 1,000 years, from 9:30 am to 4:00 pm with new prices arriving every 3 seconds on average, so we have 7,800 distinct prices each day.

We consider three major departures from the Gaussian benchmark: (i) microstructure noise: bid-ask bounce, recording errors, irregular trade intervals, and price decimalization (discreteness); (ii) time-varying volatility: stochastic and deterministic (diurnal) variation in volatility along with volatility jumps; (iii) jumps in returns: one or multiple intraday price jumps. Each scenario is briefly described below, with additional details available in ADS (2012). We focus on estimators of , , and the ratio $\sqrt{IQ}/IV$ , with the latter computed using the same type of estimator for the numerator and denominator.²⁰ For brevity, we often - including in the tables - refer to the ratio as estimated by, say, , when it is estimated by $\sqrt{MPQ3}/MPV3$ .

5.2.1 The Brownian Motion Benchmark

This is our baseline scenario with sampling on an equispaced time grid. It is an ideal setting in which we expect the finite sample performance of all estimators to closely mimic the underlying asymptotic theory. Panel A of Tables 2 and 3 verify that most of the estimators are unbiased for IV and IQ. The exception is the minor downward bias in TRV, TBV, TRQ and TBQ. This stems from noise in the truncation and bias-correction procedures applied in constructing these estimators. They truncate individual returns at three (estimated) standard deviations, so a scaling is needed to mitigate the impact of erroneous truncation of diffusive returns and this introduces some estimation error, even under the BM null. All other estimators rely on the very conservative truncation level (p-value of $10^{-6}$ ) associated with our functional filtering, described in Section 4.3. As intended, the impact of this filter is negligible under the null hypothesis, so the estimators remain unbiased.

In terms of efficiency, the ordering of the jump-robust estimators is as prescribed by theory, with TRV superior in terms of RMSE for IV (matching RV), followed by , QRV, , and TBV. For IQ, TRQ is best, followed very closely by , and then , and TBQ at the higher frequencies.²¹ In summary, the RNT estimators perform well and, in particular, come close to matching the efficiency of TRQ for IQ. It suggests that this type of estimator can enhance robustness to noise and jumps without any significant loss of efficiency in general.

Finally, turning to the estimates for $\sqrt{IQ}/IV$ in Table 4, Panel A, we notice a small downward bias at the lowest sampling frequency in almost all cases. This is caused by a finite sample Jensen effect.²² More remarkably, in terms of efficiency, the TRQ estimator now performs relatively poorly. Instead, and outperform the alternatives by a substantial margin. The dramatic shift in relative efficiency reflects the fact that cancelation of outlier terms in the numerator and denominator is particularly effective under the robust neighborhood truncation principle where the largest return realizations are prevented from exerting any significant impact. Likewise, the MPQ5 estimator performs quite well due to the effective dampening of outliers. We conclude that, even under ideal circumstances, the RNT estimators provide an attractive alternative to existing procedures, especially for inference and jump tests based on the $\sqrt{IQ}/IV$ ratio.

Table 2a: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of IV. Panel A: BM

Relative Bias: Estimator	Relative Bias RV	Relative Bias MPV3	Relative Bias MPV5	Relative Bias TRV	Relative Bias TBV	Relative Bias QRV	Relative Bias MedRV	Relative Bias RMinRV	Relative Bias RMedRV	Relative MSE RV	Relative MSE MPV3	Relative MSE MPV5	Relative MSE TRV	Relative MSE TBV	Relative MSE QRV	Relative MSE MedRV	Relative MSE RMinRV	Relative MSE RMedRV
30 sec	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	0.26	0.35	0.38	0.27	0.32	0.29	0.34	0.31	0.29
120 sec	1.00	1.00	1.00	1.00	0.99	1.00	1.00	1.00	1.00	1.08	1.42	1.56	1.08	1.29	1.26	1.41	1.26	1.18
600 sec	1.00	1.00	1.00	0.99	0.97	1.00	1.00	1.00	1.00	5.52	7.51	8.44	5.53	6.60	7.91	7.47	6.87	6.42

Table 2b: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of IV. Panel B: BM + 1 Jump

Relative Bias: Estimator	Relative Bias RV	Relative Bias MPV3	Relative Bias MPV5	Relative Bias TRV	Relative Bias TBV	Relative Bias QRV	Relative Bias MedRV	Relative Bias RMinRV	Relative Bias RMedRV	Relative MSE RV	Relative MSE MPV3	Relative MSE MPV5	Relative MSE TRV	Relative MSE TBV	Relative MSE QRV	Relative MSE MedRV	Relative MSE RMinRV	Relative MSE RMedRV
30 sec	1.25	1.01	1.01	1.01	1.00	1.01	1.00	1.00	1.01	37.02	0.41	0.41	0.28	0.32	0.30	0.35	0.32	0.30
120 sec	1.25	1.03	1.03	1.03	1.01	1.02	1.01	1.02	1.02	38.37	1.87	1.81	1.30	1.38	1.37	1.50	1.39	1.36
600 sec	1.25	1.08	1.06	1.08	1.03	1.06	1.05	1.06	1.07	45.63	10.71	10.79	8.47	7.66	9.93	8.80	8.79	8.85

Table 2c: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of IV. Panel C: BM + 4 Jumps

Relative Bias: Estimator	Relative Bias RV	Relative Bias MPV3	Relative Bias MPV5	Relative Bias TRV	Relative Bias TBV	Relative Bias QRV	Relative Bias MedRV	Relative Bias RMinRV	Relative Bias RMedRV	Relative MSE RV	Relative MSE MPV3	Relative MSE MPV5	Relative MSE TRV	Relative MSE TBV	Relative MSE QRV	Relative MSE MedRV	Relative MSE RMinRV	Relative MSE RMedRV
30 sec	1.25	1.03	1.03	1.03	1.02	1.02	1.01	1.02	1.02	18.64	0.62	0.53	0.42	0.38	0.40	0.39	0.38	0.40
120 sec	1.25	1.07	1.06	1.07	1.05	1.06	1.04	1.05	1.06	19.95	2.78	2.48	2.47	1.94	2.16	1.93	1.99	2.20
600 sec	1.25	1.14	1.12	1.16	1.10	1.14	1.12	1.13	1.15	27.04	14.30	14.26	14.30	10.79	15.36	12.55	13.04	13.86

Table 2d: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of IV. Panel D: SV-U

Relative Bias: Estimator	Relative Bias RV	Relative Bias MPV3	Relative Bias MPV5	Relative Bias TRV	Relative Bias TBV	Relative Bias QRV	Relative Bias MedRV	Relative Bias RMinRV	Relative Bias RMedRV	Relative MSE RV	Relative MSE MPV3	Relative MSE MPV5	Relative MSE TRV	Relative MSE TBV	Relative MSE QRV	Relative MSE MedRV	Relative MSE RMinRV	Relative MSE RMedRV
30 sec	1.00	1.00	0.99	1.00	0.99	0.98	1.00	0.99	0.99	0.30	0.39	0.42	0.30	0.36	0.41	0.39	0.35	0.33
120 sec	0.99	0.98	0.98	0.99	0.98	0.94	0.98	0.97	0.98	1.21	1.56	1.70	1.21	1.46	1.90	1.55	1.42	1.33
600 sec	0.98	0.95	0.93	0.96	0.92	0.90	0.95	0.93	0.93	5.78	7.38	8.25	5.74	7.13	8.31	7.34	6.89	6.48

Table 2e: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of IV. Panel E: BM + 1 Volatility Jump

Relative Bias: Estimator	Relative Bias RV	Relative Bias MPV3	Relative Bias MPV5	Relative Bias TRV	Relative Bias TBV	Relative Bias QRV	Relative Bias MedRV	Relative Bias RMinRV	Relative Bias RMedRV	Relative MSE RV	Relative MSE MPV3	Relative MSE MPV5	Relative MSE TRV	Relative MSE TBV	Relative MSE QRV	Relative MSE MedRV	Relative MSE RMinRV	Relative MSE RMedRV
30 sec	1.00	1.00	1.00	1.00	1.00	0.99	1.00	1.00	1.00	0.40	0.53	0.58	0.41	0.48	0.51	0.52	0.47	0.44
120 sec	1.00	0.99	0.99	0.99	0.98	0.97	0.99	0.99	0.99	1.64	2.13	2.35	1.66	1.98	2.67	2.13	1.94	1.82
600 sec	0.99	0.96	0.94	0.93	0.92	0.90	0.96	0.95	0.96	8.23	10.34	11.81	8.17	9.89	16.15	10.38	10.10	9.53

Table 2f: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of IV. Panel F: BM + IID Noise

Relative Bias: Estimator	Relative Bias RV	Relative Bias MPV3	Relative Bias MPV5	Relative Bias TRV	Relative Bias TBV	Relative Bias QRV	Relative Bias MedRV	Relative Bias RMinRV	Relative Bias RMedRV	Relative MSE RV	Relative MSE MPV3	Relative MSE MPV5	Relative MSE TRV	Relative MSE TBV	Relative MSE QRV	Relative MSE MedRV	Relative MSE RMinRV	Relative MSE RMedRV
30 sec	1.03	1.03	1.03	1.03	1.03	1.03	1.03	1.03	1.03	0.44	0.52	0.56	0.41	0.46	0.47	0.52	0.47	0.46
120 sec	1.00	1.00	1.00	1.00	0.99	1.00	1.00	1.00	1.00	1.08	1.42	1.56	1.08	1.29	1.26	1.42	1.27	1.19
600 sec	1.00	1.00	1.00	0.99	0.97	1.00	1.00	1.00	1.00	5.49	7.47	8.40	5.50	6.57	7.88	7.43	6.83	6.39

Table 2g: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of IV. Panel G: BM + 1 Bounceback

Relative Bias: Estimator	Relative Bias RV	Relative Bias MPV3	Relative Bias MPV5	Relative Bias TRV	Relative Bias TBV	Relative Bias QRV	Relative Bias MedRV	Relative Bias RMinRV	Relative Bias RMedRV	Relative MSE RV	Relative MSE MPV3	Relative MSE MPV5	Relative MSE TRV	Relative MSE TBV	Relative MSE QRV	Relative MSE MedRV	Relative MSE RMinRV	Relative MSE RMedRV
30 sec	1.01	1.01	1.00	1.00	1.00	1.00	1.00	1.00	1.00	0.39	0.36	0.38	0.27	0.32	0.30	0.35	0.31	0.29
120 sec	1.00	1.00	1.00	1.00	0.99	1.00	1.00	1.00	1.00	1.08	1.42	1.56	1.08	1.29	1.26	1.42	1.26	1.19
600 sec	1.00	1.00	1.00	0.99	0.97	1.00	1.00	1.00	1.00	5.55	7.53	8.47	5.55	6.62	7.96	7.51	6.90	6.46

Table 2h: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of IV. Panel H: BM + Sparcity

Relative Bias: Estimator	Relative Bias RV	Relative Bias MPV3	Relative Bias MPV5	Relative Bias TRV	Relative Bias TBV	Relative Bias QRV	Relative Bias MedRV	Relative Bias RMinRV	Relative Bias RMedRV	Relative MSE RV	Relative MSE MPV3	Relative MSE MPV5	Relative MSE TRV	Relative MSE TBV	Relative MSE QRV	Relative MSE MedRV	Relative MSE RMinRV	Relative MSE RMedRV
30 sec	1.00	0.96	0.96	0.99	0.97	0.97	0.96	0.97	0.98	0.30	0.61	0.75	0.31	0.54	0.43	0.66	0.53	0.42
120 sec	1.00	0.99	0.99	1.00	0.99	0.99	0.99	0.99	0.99	1.11	1.43	1.56	1.11	1.33	1.27	1.43	1.28	1.20
600 sec	1.00	1.00	1.00	0.99	0.97	1.00	1.00	1.00	1.00	5.55	7.49	8.41	5.56	6.60	7.94	7.45	6.87	6.44

Table 2i: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of IV. Panel I: BM + Discrete Pricing

Relative Bias: Estimator	Relative Bias RV	Relative Bias MPV3	Relative Bias MPV5	Relative Bias TRV	Relative Bias TBV	Relative Bias QRV	Relative Bias MedRV	Relative Bias RMinRV	Relative Bias RMedRV	Relative MSE RV	Relative MSE MPV3	Relative MSE MPV5	Relative MSE TRV	Relative MSE TBV	Relative MSE QRV	Relative MSE MedRV	Relative MSE RMinRV	Relative MSE RMedRV
30 sec	1.02	1.00	0.94	1.02	1.01	1.02	1.02	1.01	1.02	0.34	0.36	1.08	0.32	0.35	0.37	0.43	0.34	0.36
120 sec	1.00	1.00	1.00	1.00	0.99	1.00	1.00	1.00	1.00	1.08	1.42	1.56	1.08	1.29	1.26	1.41	1.27	1.19
600 sec	1.00	1.00	1.00	0.99	0.97	1.00	1.00	1.00	1.00	5.49	7.47	8.40	5.50	6.57	7.87	7.43	6.83	6.39

We report the relative bias (left half of the table) and MSE (right half of the table) factors for different estimators of IQ for the following models: BM (Panel A), BM + 1 Jump (Panel B), BM + 4 Jumps (Panel C), SV-U (Panel D), BM + 1 Volatility Jump (Panel E), BM + IID Noise (Panel F), BM + 1 Bounceback (Panel G), BM + Sparcity (Panel H), BM + Discrete Pricing (Panel I). The rows in each panel correspond to each of the following pre-averaging window sizes: 30, 120, 600 seconds. The table columns represent the different estimators, with the abbreviations defined in the text. The relative MSE is computed using baseline window size of 120-seconds as the sample mean of 195(IV âˆ’IV )²/IV², where IV is the true simulated integrated variance on each day. The MSE factor for 120-sec pre-averaged RV in Panel A has the known theoretical value of 151/140 â‰ˆ 1.08, see Jacod et al. (2009).

Table 3a: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of IQ. Panel A: BM

Relative Bias: Estimator	Relative Bias MPQ3	Relative Bias MPQ5	Relative Bias TRQ	Relative Bias TBQ	Relative Bias MedRQ	Relative Bias RMinRQ	Relative Bias RMedRQ	Relative MSE MPQ3	Relative MSE MPQ5	Relative MSE TRQ	Relative MSE TBQ	Relative MSE MedRQ	Relative MSE RMinRQ	Relative MSE RMedRQ
30 sec	1.00	1.00	0.99	0.99	1.00	1.00	1.00	1.55	1.68	1.22	1.41	1.55	1.29	1.23
120 sec	1.00	1.00	0.98	0.99	1.00	1.00	1.00	6.37	6.96	4.84	5.71	6.40	5.32	5.05
600 sec	1.00	1.00	0.97	0.96	1.00	1.00	1.00	33.81	37.87	24.11	28.37	33.72	29.06	27.46

Table 3b: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of IQ. Panel B: BM + 1 Jump

Relative Bias: Estimator	Relative Bias MPQ3	Relative Bias MPQ5	Relative Bias TRQ	Relative Bias TBQ	Relative Bias MedRQ	Relative Bias RMinRQ	Relative Bias RMedRQ	Relative MSE MPQ3	Relative MSE MPQ5	Relative MSE TRQ	Relative MSE TBQ	Relative MSE MedRQ	Relative MSE RMinRQ	Relative MSE RMedRQ
30 sec	1.09	1.04	1.02	1.01	1.01	1.01	1.02	5.34	2.47	1.38	1.51	1.66	1.42	1.45
120 sec	1.16	1.08	1.09	1.05	1.04	1.05	1.07	22.87	11.30	8.30	7.23	7.74	7.00	7.69
600 sec	1.26	1.17	1.28	1.13	1.13	1.16	1.20	100.90	66.83	71.15	48.15	53.36	52.29	59.93

Table 3c: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of IQ. Panel C: BM + 4 Jumps

Relative Bias: Estimator	Relative Bias MPQ3	Relative Bias MPQ5	Relative Bias TRQ	Relative Bias TBQ	Relative Bias MedRQ	Relative Bias RMinRQ	Relative Bias RMedRQ	Relative MSE MPQ3	Relative MSE MPQ5	Relative MSE TRQ	Relative MSE TBQ	Relative MSE MedRQ	Relative MSE RMinRQ	Relative MSE RMedRQ
30 sec	1.16	1.08	1.09	1.05	1.04	1.05	1.07	9.35	3.77	3.33	2.19	2.20	2.08	2.69
120 sec	1.26	1.16	1.27	1.15	1.13	1.15	1.20	31.64	16.95	24.29	13.47	14.69	13.13	19.65
600 sec	1.39	1.31	1.54	1.32	1.33	1.35	1.42	120.66	93.47	142.43	86.62	113.01	94.73	121.22

Table 3d: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of IQ. Panel D: SV-U

Relative Bias: Estimator	Relative Bias MPQ3	Relative Bias MPQ5	Relative Bias TRQ	Relative Bias TBQ	Relative Bias MedRQ	Relative Bias RMinRQ	Relative Bias RMedRQ	Relative MSE MPQ3	Relative MSE MPQ5	Relative MSE TRQ	Relative MSE TBQ	Relative MSE MedRQ	Relative MSE RMinRQ	Relative MSE RMedRQ
30 sec	0.98	0.97	0.98	0.98	0.98	0.97	0.97	3.22	3.33	2.52	2.96	3.22	2.62	2.47
120 sec	0.94	0.91	0.94	0.94	0.94	0.91	0.91	10.45	10.38	7.80	9.52	10.42	8.38	7.98
600 sec	0.82	0.78	0.84	0.81	0.82	0.78	0.78	32.41	33.49	25.47	30.26	32.20	27.88	26.69

Table 3e: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of IQ. Panel E: BM + 1 Volatility Jump

Relative Bias: Estimator	Relative Bias MPQ3	Relative Bias MPQ5	Relative Bias TRQ	Relative Bias TBQ	Relative Bias MedRQ	Relative Bias RMinRQ	Relative Bias RMedRQ	Relative MSE MPQ3	Relative MSE MPQ5	Relative MSE TRQ	Relative MSE TBQ	Relative MSE MedRQ	Relative MSE RMinRQ	Relative MSE RMedRQ
30 sec	0.99	0.99	0.97	0.99	0.99	0.99	0.99	4.20	4.53	3.25	3.83	4.22	3.52	3.34
120 sec	0.97	0.96	0.94	0.95	0.97	0.96	0.96	15.08	16.19	11.67	13.76	15.15	12.91	12.34
600 sec	0.88	0.83	0.75	0.79	0.88	0.85	0.86	55.05	59.42	41.28	46.56	55.39	49.76	47.93

Table 3f: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of IQ. Panel F: BM + IID Noise

Relative Bias: Estimator	Relative Bias MPQ3	Relative Bias MPQ5	Relative Bias TRQ	Relative Bias TBQ	Relative Bias MedRQ	Relative Bias RMinRQ	Relative Bias RMedRQ	Relative MSE MPQ3	Relative MSE MPQ5	Relative MSE TRQ	Relative MSE TBQ	Relative MSE MedRQ	Relative MSE RMinRQ	Relative MSE RMedRQ
30 sec	1.06	1.06	1.04	1.05	1.06	1.06	1.06	2.38	2.52	1.65	2.08	2.38	2.05	2.01
120 sec	1.00	1.00	0.99	0.99	1.00	1.00	1.00	6.43	7.01	4.86	5.74	6.44	5.36	5.09
600 sec	1.00	1.00	0.97	0.96	1.00	1.00	1.00	33.58	37.63	23.98	28.22	33.47	28.90	27.26

Table 3g: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of IQ. Panel G: BM + 1 Bounceback

Relative Bias: Estimator	Relative Bias MPQ3	Relative Bias MPQ5	Relative Bias TRQ	Relative Bias TBQ	Relative Bias MedRQ	Relative Bias RMinRQ	Relative Bias RMedRQ	Relative MSE MPQ3	Relative MSE MPQ5	Relative MSE TRQ	Relative MSE TBQ	Relative MSE MedRQ	Relative MSE RMinRQ	Relative MSE RMedRQ
30 sec	1.02	1.01	1.01	1.01	1.01	1.01	1.01	1.76	1.77	1.30	1.46	1.62	1.36	1.33
120 sec	1.00	1.00	0.99	0.99	1.00	1.00	1.00	6.40	6.98	4.84	5.72	6.44	5.34	5.07
600 sec	1.00	1.00	0.98	0.96	1.00	1.00	1.00	34.07	38.05	24.26	28.54	34.06	29.32	27.77

Table 3h: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of IQ. Panel H: BM + Sparcity

Relative Bias: Estimator	Relative Bias MPQ3	Relative Bias MPQ5	Relative Bias TRQ	Relative Bias TBQ	Relative Bias MedRQ	Relative Bias RMinRQ	Relative Bias RMedRQ	Relative MSE MPQ3	Relative MSE MPQ5	Relative MSE TRQ	Relative MSE TBQ	Relative MSE MedRQ	Relative MSE RMinRQ	Relative MSE RMedRQ
30 sec	0.96	0.93	1.05	0.98	0.97	0.97	0.99	1.90	2.46	2.01	1.64	1.91	1.59	1.41
120 sec	0.99	0.98	1.00	0.99	0.99	0.99	1.00	6.49	6.92	5.22	5.91	6.58	5.47	5.23
600 sec	1.00	1.00	0.98	0.96	1.00	1.00	1.00	33.98	37.90	24.58	28.57	33.96	29.30	27.79

Table 3i: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of IQ. Panel I: BM + Discrete Pricing

Relative Bias: Estimator	Relative Bias MPQ3	Relative Bias MPQ5	Relative Bias TRQ	Relative Bias TBQ	Relative Bias MedRQ	Relative Bias RMinRQ	Relative Bias RMedRQ	Relative MSE MPQ3	Relative MSE MPQ5	Relative MSE TRQ	Relative MSE TBQ	Relative MSE MedRQ	Relative MSE RMinRQ	Relative MSE RMedRQ
30 sec	1.04	1.02	1.02	1.03	1.04	1.03	1.04	1.92	1.83	1.35	1.69	2.00	1.53	1.58
120 sec	1.00	1.00	0.99	0.99	1.00	1.00	1.00	6.42	7.00	4.86	5.73	6.42	5.35	5.08
600 sec	1.00	1.00	0.97	0.96	1.00	1.00	1.00	33.58	37.63	23.99	28.20	33.47	28.87	27.25

We report the relative bias (left half of the table) and MSE (right half of the table) factors for different estimators of IQ for the following models: BM (Panel A), BM + 1 Jump (Panel B), BM + 4 Jumps (Panel C), SV-U (Panel D), BM + 1 Volatility Jump (Panel E), BM + IID Noise (Panel F), BM + 1 Bounceback (Panel G), BM + Sparcity (Panel H), BM + Discrete Pricing (Panel I). The rows in each panel correspond to each of the following pre-averaging window sizes: 30, 120, 600 seconds. The table columns represent the different estimators, with the abbreviations defined in the text. The relative MSE is computed using a baseline window size of 120-seconds as the sample mean of 195(IQ - IQ)²/IQ², where IQ is the true simulated integrated quarticity for each day.

Table 4a: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of √IQ/IV. Panel A: BM

Relative Bias: Estimator	Relative Bias MPQ3	Relative Bias MPQ5	Relative Bias TRQ	Relative Bias TBQ	Relative Bias MedRQ	Relative Bias RMinRQ	Relative Bias RMedRQ	Relative MSE MPQ3	Relative MSE MPQ5	Relative MSE TRQ	Relative MSE TBQ	Relative MSE MedRQ	Relative MSE RMinRQ	Relative MSE RMedRQ
30 sec	1.00	1.00	1.00	1.00	1.00	1.00	1.00	0.05	0.04	0.05	0.05	0.06	0.03	0.02
120 sec	1.00	1.00	0.99	1.00	1.00	1.00	1.00	0.18	0.15	0.18	0.18	0.22	0.11	0.10
600 sec	0.98	0.98	0.98	1.00	0.98	0.98	0.98	0.76	0.64	0.75	0.76	0.89	0.48	0.42

Table 4b: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of √IQ/IV. Panel B: BM + 1 Jump

Relative Bias: Estimator	Relative Bias MPQ3	Relative Bias MPQ5	Relative Bias TRQ	Relative Bias TBQ	Relative Bias MedRQ	Relative Bias RMinRQ	Relative Bias RMedRQ	Relative MSE MPQ3	Relative MSE MPQ5	Relative MSE TRQ	Relative MSE TBQ	Relative MSE MedRQ	Relative MSE RMinRQ	Relative MSE RMedRQ
30 sec	1.03	1.01	1.00	1.00	1.00	1.00	1.00	0.43	0.09	0.05	0.05	0.06	0.03	0.04
120 sec	1.03	1.01	1.02	1.01	1.00	1.00	1.01	1.09	0.30	0.25	0.23	0.26	0.16	0.19
600 sec	1.01	0.99	1.03	1.02	0.99	1.00	1.00	1.60	0.79	1.12	1.01	1.12	0.64	0.70

Table 4c: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of √IQ/IV. Panel C: BM + 4 Jumps

Relative Bias: Estimator	Relative Bias MPQ3	Relative Bias MPQ5	Relative Bias TRQ	Relative Bias TBQ	Relative Bias MedRQ	Relative Bias RMinRQ	Relative Bias RMedRQ	Relative MSE MPQ3	Relative MSE MPQ5	Relative MSE TRQ	Relative MSE TBQ	Relative MSE MedRQ	Relative MSE RMinRQ	Relative MSE RMedRQ
30 sec	1.04	1.01	1.02	1.01	1.01	1.01	1.01	0.59	0.12	0.12	0.07	0.09	0.05	0.09
120 sec	1.04	1.01	1.04	1.02	1.01	1.01	1.02	1.01	0.32	0.59	0.34	0.51	0.26	0.51
600 sec	1.01	0.99	1.04	1.02	1.01	1.00	1.01	1.24	0.75	1.24	1.16	1.56	0.74	0.92

Table 4d: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of √IQ/IV. Panel D: SV-U

Relative Bias: Estimator	Relative Bias MPQ3	Relative Bias MPQ5	Relative Bias TRQ	Relative Bias TBQ	Relative Bias MedRQ	Relative Bias RMinRQ	Relative Bias RMedRQ	Relative MSE MPQ3	Relative MSE MPQ5	Relative MSE TRQ	Relative MSE TBQ	Relative MSE MedRQ	Relative MSE RMinRQ	Relative MSE RMedRQ
30 sec	0.99	0.99	0.99	0.99	0.99	0.99	0.99	0.27	0.26	0.22	0.25	0.28	0.20	0.19
120 sec	0.98	0.97	0.97	0.98	0.98	0.97	0.97	0.71	0.66	0.56	0.64	0.75	0.53	0.50
600 sec	0.94	0.93	0.94	0.95	0.94	0.94	0.94	1.81	1.74	1.55	1.44	1.94	1.45	1.36

Table 4e: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of √IQ/IV. Panel E: BM + 1 Volatility Jump

Relative Bias: Estimator	Relative Bias MPQ3	Relative Bias MPQ5	Relative Bias TRQ	Relative Bias TBQ	Relative Bias MedRQ	Relative Bias RMinRQ	Relative Bias RMedRQ	Relative MSE MPQ3	Relative MSE MPQ5	Relative MSE TRQ	Relative MSE TBQ	Relative MSE MedRQ	Relative MSE RMinRQ	Relative MSE RMedRQ
30 sec	1.00	0.99	0.99	0.99	1.00	0.99	1.00	0.35	0.36	0.31	0.34	0.38	0.28	0.26
120 sec	0.98	0.98	0.97	0.98	0.98	0.98	0.98	1.14	1.21	1.17	1.13	1.20	0.97	0.92
600 sec	0.93	0.91	0.90	0.93	0.93	0.92	0.93	4.07	4.75	5.14	3.88	4.22	4.02	3.75

Table 4f: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of √IQ/IV. Panel F: BM + IID Noise

Relative Bias: Estimator	Relative Bias MPQ3	Relative Bias MPQ5	Relative Bias TRQ	Relative Bias TBQ	Relative Bias MedRQ	Relative Bias RMinRQ	Relative Bias RMedRQ	Relative MSE MPQ3	Relative MSE MPQ5	Relative MSE TRQ	Relative MSE TBQ	Relative MSE MedRQ	Relative MSE RMinRQ	Relative MSE RMedRQ
30 sec	1.00	1.00	1.00	1.00	1.00	1.00	1.00	0.05	0.04	0.05	0.05	0.05	0.03	0.02
120 sec	1.00	1.00	0.99	1.00	1.00	1.00	1.00	0.18	0.15	0.17	0.18	0.22	0.11	0.10
600 sec	0.98	0.98	0.98	1.00	0.98	0.98	0.98	0.76	0.64	0.75	0.76	0.89	0.48	0.42

Table 4g: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of √IQ/IV. Panel G: BM + 1 Bounceback

Relative Bias: Estimator	Relative Bias MPQ3	Relative Bias MPQ5	Relative Bias TRQ	Relative Bias TBQ	Relative Bias MedRQ	Relative Bias RMinRQ	Relative Bias RMedRQ	Relative MSE MPQ3	Relative MSE MPQ5	Relative MSE TRQ	Relative MSE TBQ	Relative MSE MedRQ	Relative MSE RMinRQ	Relative MSE RMedRQ
30 sec	1.00	1.00	1.00	1.00	1.00	1.00	1.00	0.06	0.04	0.05	0.05	0.06	0.03	0.03
120 sec	1.00	1.00	0.99	1.00	1.00	1.00	1.00	0.18	0.15	0.18	0.18	0.22	0.11	0.10
600 sec	0.98	0.98	0.98	1.00	0.98	0.98	0.98	0.76	0.64	0.75	0.76	0.90	0.48	0.42

Table 4h: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of √IQ/IV. Panel H: BM + Sparcity

Relative Bias: Estimato	Relative Bias MPQ3	Relative Bias MPQ5	Relative Bias TRQ	Relative Bias TBQ	Relative Bias MedRQ	Relative Bias RMinRQ	Relative Bias RMedRQ	Relative MSE MPQ3	Relative MSE MPQ5	Relative MSE TRQ	Relative MSE TBQ	Relative MSE MedRQ	Relative MSE RMinRQ	Relative MSE RMedRQ
30 sec	1.02	1.01	1.03	1.02	1.03	1.02	1.02	0.13	0.07	0.27	0.17	0.20	0.10	0.11
120 sec	1.00	1.00	1.00	1.01	1.00	1.00	1.00	0.19	0.16	0.17	0.20	0.24	0.12	0.11
600 sec	0.98	0.98	0.98	1.00	0.98	0.98	0.99	0.76	0.64	0.75	0.77	0.90	0.48	0.42

Table 4i: Relative bias and relative mean squared error (MSE) factors for pre-averaged estimators of √IQ/IV. Panel I: BM + Discrete Pricing

Relative Bias: Estimator	Relative Bias MPQ3	Relative Bias MPQ5	Relative Bias TRQ	Relative Bias TBQ	Relative Bias MedRQ	Relative Bias RMinRQ	Relative Bias RMedRQ	Relative MSE MPQ3	Relative MSE MPQ5	Relative MSE TRQ	Relative MSE TBQ	Relative MSE MedRQ	Relative MSE RMinRQ	Relative MSE RMedRQ
30 sec	1.02	1.07	1.00	1.00	1.00	1.00	1.00	0.11	1.06	0.05	0.05	0.05	0.03	0.02
120 sec	1.00	1.00	0.99	1.00	1.00	1.00	1.00	0.18	0.15	0.18	0.18	0.22	0.11	0.10
600 sec	0.98	0.98	0.98	1.00	0.98	0.98	0.98	0.76	0.64	0.75	0.76	0.89	0.48	0.42

We report the relative bias (left half of the table) and MSE (right half of the table) factors for different estimators of IQ for the following models: BM (Panel A), BM + 1 Jump (Panel B), BM + 4 Jumps (Panel C), SV-U (Panel D), BM + 1 Volatility Jump (Panel E), BM + IID Noise (Panel F), BM + 1 Bounceback (Panel G), BM + Sparcity (Panel H), BM + Discrete Pricing (Panel I). The rows in each panel correspond to each of the following pre-averaging window sizes: 30, 120, 600 seconds. The table columns represent the different estimators, with the abbreviations defined in the text. The relative MSE is computed using baseline window size of 120-seconds as the sample mean of 195( √IQ/cIV - √Q/IV )²/(√IQ/IV)², where IV and IQ are the true simulated integrated variance and integrated quarticity for each day.

5.2.2 Jumps in Returns

To assess finite sample jump-robustness, we augment the BM model with return jumps of the Poisson-Gaussian type that are independent of volatility and account for 20% of the daily QV (25% of IV). We focus on two cases, one with a single jump per day, the "BM + 1 Jump" scenario, and one with four jumps per day, the "BM + 4 Jumps" scenario, but the overall jump contribution to the daily variance is identical for the two cases.

Panels B and C in Table 2 show that TRV, TBV, QRV, RMinRV and RMedRV provide the best robust IV inference in terms of RMSE. Moreover, the relative performance within this group shifts as we move from a single to four jumps with, in particular, RMinRV and TBV improving their standing as the jump intensity increases. This tendency is even more pronounced for IQ estimation, where panels B and C in Table 3 reveal that RMinRQ is the best performer in both jump scenarios at the 2-minute frequency.

Finally, and very strikingly, panels B and C of Table 4 show that the pairing of RMinRQ and RMinRV dominate all other estimators by a significant margin in terms of estimating the ratio $\sqrt{IQ}/IV$ , which governs the precision of log(IV). Thus, from the perspective of finite sample jump-robustness, the RNT estimators seem to offer attractive efficiency improvements, especially for the estimation of IQ and $\sqrt{IQ}/IV$ .

Juxtaposing Panel B or C in Tables 3 and 4, we also note that the distortions induced by jumps are much less pronounced for the ratio statistic than for IQ. Again, the partial cancelation of the (upward) bias in the numerator and the denominator is operative. Thus, ratio-based inference is likely preferable regardless of the choice of estimator. In summary, estimating the ratio statistic using RMinRQ emerges as a natural part of practical jump-robust inference for IV or testing for jumps. Below, we explore whether this estimator is robust to other common "irregularities" in high-frequency return data as well.

5.2.3 Time-Varying Volatility

Pronounced intraday variation as well as seemingly abrupt changes (jumps) in spot volatility are prevalent in high-frequency returns. This poses a challenge for power variation estimation, as jump-robust estimators may not be able to distinguish sharply between rapidly shifting volatility and return jumps. For example, in the context of IV estimation, ADS (2012) document sizeable finite sample distortion in IV estimators when the intraday volatility is stochastic and subject to a diurnal U-shaped pattern. This section extends this analysis and draws broader conclusions for estimation of IQ and $\sqrt{IQ}/IV$ by exploring two distinct scenarios that violate the (locally) constant volatility assumption.

Our first scenario, "SV-U," is a modification of the corresponding design in ADS (2012). The diurnal pattern is calibrated to the average volatility of tick-time sampled trades of the stocks analyzed in the next section. In particular, we simulate a two-factor affine stochastic volatility model and superimpose an asymmetric diurnal pattern (Hasbrouck, 1999) for which the variance at the open is more than four times the midday and end-of-day variance.

The second scenario, "BM + 1 Volatility Jump," involves a six-fold spike in the intraday variance at a random point in time, uniformly distributed across the trading day. Volatility is constant before the jump, and then constant at the new higher level following the jump. In this way, the scenario approximates the effect of sudden bursts in market activity that have inspired the development of alternative volatility jump specifications.

The striking similarity between Panels D and E of Tables 2-4 indicates that these two distinct forms of time variation in volatility have a qualitatively similar impact on the estimators in terms of finite sample bias and RMSE. Effectively, both scenarios render neighboring returns inhomogeneous, resulting in a downward bias due to scaling factors that are incorrectly sized as well as inappropriate truncation of diffusive returns that are misclassified as jumps due to the fluctuating level of the return variance. The less "local" estimators are more exposed to such heterogeneity. This explains the ordering of the biases of the IV and IQ estimators in Panels D and E of Tables 2 and 3, with estimators relying on block size one to three being the least biased, those based on blocks of four or five returns being slightly more biased, and finally the estimators relying on substantially larger block sizes (such as 20 for QRV in Table 2) being most biased.

In summary, Panels D and E of Table 3 provide evidence against the use of sparser sampling frequencies, such as ten minutes or lower, for IQ estimation. This runs counter to suggestions in the literature, indicating that biases in IQ estimation may be alleviated through sparse sampling. We find, in contrast, that the bias is much lower, and quite tolerable, at the two minute frequency, regardless of the block size of the IQ estimator.

Most importantly, Panels D and E in Table 4, confirm that the biases for the ratio $\sqrt{IQ}/IV$ are less pronounced and more uniform across the full range of estimators, as may be expected given that we obtain partial cancelation of the downward biases which affect both the numerator and denominator. Moreover, the ratio estimator based on and again performs best from an efficiency standpoint in spite of the block size of five. For comparison, increasing the block size of the MPQ and MPV estimators from three to five enlarges the RMSE for $\sqrt{IQ}/IV$ in the "BM + 1 Volatility Jump" scenario. Consequently, the superior efficiency in estimating $\sqrt{IQ}/IV$ stems from the design of the robust neighborhood truncation principle rather than from the increased block size.

We conclude that inference based on the ratio $\sqrt{IQ}/IV$ appears to be attractive also under time-varying volatility. Moreover, the estimator provides quite compelling performance in this setting as well for the higher sampling frequencies.

5.2.4 Microstructure Noise

There is a tradeoff in the choice of sampling frequency with jump robustness improving and resiliency to microstructure noise deteriorating as the return interval shrinks. We now explore the effectiveness in dealing with the adverse impact of various noise features by applying pre-averaging, as detailed in Appendix C, and sampling at moderate frequencies. In fact, as outlined in Section 4.2, our asymptotic theory is developed in a noise-free setting, so we seek to determine whether this provides a suitable approximation for practical inference.

We consider four separate market imperfections. First, in our "BM + IID Noise" scenario, Panel F, Tables 2-4, we simulate Gaussian i.i.d. noise with a noise-to-signal ratio of $\lambda = 0.25$ , in line with what is typical for trade data on individual stocks. Second, we consider a "BM + 1 Bounceback" scenario, Panel G, Tables 2-4, in which (isolated) errors in the recorded price induce so-called "bounce-backs" in returns, i.e., two large adjacent jumps of opposite sign due to immediate price reversals. We calibrate the magnitude of the bounce-back to match 20% of the daily QV (25% of IV). The third source of noise is irregular sampling, and the associated results are captured by our "BM + Sparcity" scenario, Panel H, Tables 2-4. It is generated via random arrivals of the 7,800 distinct quotes by sampling without replacement from the numbers in the range of 1 through 23,400. While not necessarily realistic, this model is helpful in exploring the potential distortion of the estimators when applied on non-homogeneously sampled returns, effectively inducing spurious variations in their volatility. Finally, in our "BM + Discrete Pricing" scenario, Panel I, Tables 2-4, we mimic price decimalization by rounding all intraday prices to the nearest cent with a starting price of $50. Price discreteness is a major reason for the presence of multiple zero returns in high-frequency samples, leading to pronounced downward biases of many jump-robust estimators.²³

First, the reported relative biases in Panels F, G, H, and I of Tables 2-4 reveal that, irrespective of the noise scenario, it is necessary to avoid sampling at the highest frequency, i.e., 30 seconds, to obtain reasonably unbiased estimates of IV and IQ, while the ratio $\sqrt{IQ}/IV$ is unbiased for all scenarios except the "sparsity" setting. However, once we reach 2 minutes, all the relevant quantities are estimated without bias, except for a minor bias for IQ in the sparsity scenario.

Second, for the 2-minute frequency, the MSE is nearly identical for the Brownian motion case and the various noise scenarios, highlighting the efficacy of the pre-averaging, filtering and subsampling procedures. In particular, for the ratio statistic, the MSE is literally identical across all scenarios and estimators at the 2-minute frequency except for the sparse sampling case. That is, noise has no discernible impact on the asymptotic errors of the estimators at this moderate frequency, apart from minor distortions arising from inhomogeneous sampling of the returns. In the empirical work below, we mitigate this effect by sampling in tick time which renders the return variability more uniform across observations.

Third, across all noise scenarios, the relative bias and MSE for the ratio $\sqrt{IQ}/IV$ are dramatically lower than for the IQ estimators. Thus, the cancelation of outliers in the numerator and denominator helps robustify the ratio statistic in the presence of noise.

Finally, we note that the pre-averaging is extremely effective for the "BM + 1 Bounceback" scenario. This is due to the near perfect cancelation of adjacent jumps of opposite sign when constructing the individual pre-averaged returns. In what follows, we rely on pre-averaging as implemented in our simulation experiments to suppress the impact of noise also in our empirical illustrations on real market data.

6 An Illustration for the Dow Jones 30 Stocks

Since the "true" values of IV and IQ are latent, there is no simple way to directly compare the performance of alternative estimators. Moreover, for IQ in particular, there is a great deal of uncertainty regarding the actual precision of existing estimation procedures. The preceding analysis has focused on bringing out the features that render estimation inaccurate as well as non-robust, and then developing new approaches that should improve the inference. We now seek to establish whether the issues we have identified actually do pose a challenge for practical estimation and if the suggestions and procedures we have proposed appear helpful.

Consequently, this section explores properties of competing estimators of , , and $\sqrt{IQ}/IV$ for the Dow Jones 30 stocks using tick time sampling of NYSE/TAQ trade data.²⁴ We split our sample period into a low volatility period, January 2005 - May 2007, and a high volatility period, June 2007 - July 2009. This serves as a robustness check against different noise-to-signal ratios and liquidity levels in the two periods.²⁵ The focus is on the estimates for and $\sqrt{IQ}/IV$ , while the results provide a benchmark for assessing the RNT estimators as well as the impact of our new filtering scheme relative to prior findings.

6.1 Truncation of Return Functionals

As documented in Section 5.2.4, power variation estimators can be quite sensitive to deviations from the local diffusive null, arising from microstructure features or recording errors. Common data filtering procedures may eliminate extreme outliers, but they are not sufficient to ensure sensible IQ estimates in practice for many candidate estimators of interest.

Figure: 3: IQ Signature Plots

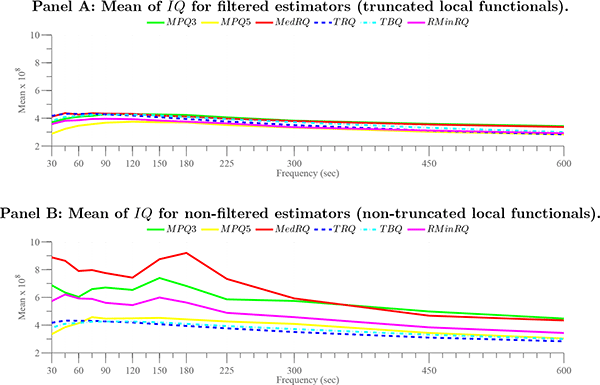
Data for Figure 3 immediately follows

In Panel A, the estimation is performed as described in the paper and, in particular, all estimators, except TRQ and TBQ, are subject to the functional filtering procedure detailed in Section 4.3. In contrast, Panel B depicts the estimators without functional filtering. TRQ and TBQ are identical in the two panels, as they are based solely on truncation of individual returns. The average is across all stocks in the DJ30 index during January 2005-May 2007 and all estimates are pre-averaged and sub-sampled based on tick-time sampling.

Data for Figure 3, Panel A: Mean (x 10^8) of IQ for Filtered Estimators (Truncated Local Functionals)

Frequency (sec)	MPQ3	MPQ5	MedRQ	TRQ	TBQ	RMinRQ
30	3.720052514	2.882352867	4.112050783	4.169505815	3.818405666	3.577058332
45	3.96284425	3.233797842	4.365354983	4.328077841	4.097223671	3.817202615
60	4.102844248	3.463292385	4.263463079	4.308726968	4.158315036	3.858885348
75	4.167514311	3.571950206	4.361093916	4.312173156	4.248558974	3.94681871
90	4.286646907	3.676661753	4.331868069	4.269108127	4.264827533	3.960426747
120	4.296451455	3.74681628	4.315920155	4.190058557	4.266466997	3.930647661
150	4.271745768	3.705585243	4.189331996	4.065456989	4.195995383	3.833907777
180	4.234479083	3.691167127	4.119015655	3.942195463	4.092137306	3.750333772
225	4.063206141	3.506383059	3.967354564	3.77018488	3.934918866	3.626068863
300	3.82431234	3.322212776	3.792300309	3.504637654	3.715902125	3.351887742
450	3.597318717	3.02007369	3.547721962	3.106425695	3.31046994	3.118577729
600	3.429539062	2.833001672	3.368716961	2.836167193	3.002191115	2.917494906

Data for Figure 3, Panel B: Mean (x 10^8) of IQ for Non-Filtered Estimators (Non-Truncated Local Functionals)

Frequency (sec)	MPQ3	MPQ5	MedRQ	TRQ	TBQ	RMinRQ
30	6.87416483	3.348265637	8.884153873	4.169505815	3.818405666	5.727073845
45	6.349350447	3.85440939	8.63416259	4.328077841	4.097223671	6.204619289
60	6.03193449	4.1343941	7.899762717	4.308726968	4.158315036	5.923854596
75	6.593049391	4.572805461	7.964916605	4.312173156	4.248558974	5.891482615
90	6.70745045	4.467455878	7.749278786	4.269108127	4.264827533	5.609135727
120	6.534065317	4.487924556	7.419890263	4.190058557	4.266466997	5.441359872
150	7.393709164	4.523397832	8.74598091	4.065456989	4.195995383	5.98917296
180	6.818907836	4.41435621	9.198128198	3.942195463	4.092137306	5.627193569
225	5.85539223	4.261182136	7.3295521	3.77018488	3.934918866	4.884044066
300	5.743823156	4.088405367	5.923765616	3.504637654	3.715902125	4.573054409
450	4.983318115	3.436828686	4.677684464	3.106425695	3.31046994	3.841105603
600	4.47526915	3.041055095	4.339880334	2.836167193	3.002191115	3.437396771

Panel A of Figure 3 depicts signature plots for a group of IQ estimators, obtained by averaging the daily IQ estimates across the entire sample period and all of the thirty stocks. By construction, the figure speaks to mean and bias effects rather than efficiency. It shows that the estimators generally are quite similar although it also reveals some significant variation. First, at the highest frequencies a few estimators, especially MPQ5, appear severely downward biased. Hence, the noise-reduction associated with pre-averaging, sub-sampling and filtering has been successful in stemming the upward bias of the raw estimators. The remaining effects are consistent with the impact of irregular or sparse sampling of the returns at the highest frequencies, see Table 3, Panel H. The other striking feature is the slow decline in the plots as we move towards lower frequencies. The most likely explanation is the impact of time-varying volatility within the sampling interval, as indicated by the results in Table 3, Panels D and E. We pursue this issue in detail in the following section. Nonetheless, it is noteworthy that the signature plots are quite flat and largely coincide for the various estimators in the range of 90-150 seconds.

By contrast, Panel B of Figure 3 offers widely diverging results. Here, none of the estimators are subject to functional filtering, so only TRQ and TBQ provide uniform truncation of stark outliers. The consequence is apparent. Apart from the extreme dampening achieved by MPQ5, the remaining estimators are wildly upward biased at the higher frequencies. This speaks to the lack of robustness of IQ estimators that do not exploit direct truncation of individual returns. The problem of excessive variability, or noise, in IQ estimates has been noted sporadically in the empirical literature and it has motivated some authors to rely on low, and relatively inefficient but less error prone, frequencies for IQ estimation, e.g., BNS (2004a) and Bandi and Russell (2008). Similarly, Jiang and Oomen (2008) uses the squared IV as a simple approximation to IQ, thereby accepting a significant bias in exchange for variance reduction of the IQ estimator.

Thus, it is very encouraging that the functional filtering regularizes the IQ estimators. The nominal size of our filter is $10^{-6}$ , so only gross violations of the Gaussian null is flagged. However, obviously, the null hypothesis is not satisfied for actual high-frequency data, so the truncation frequency is substantially larger in practice. For our equity data, the fraction of observations filtered ranges from $0.01\%$ to $0.05\%$ for the 60-180 second range, depending on the frequency and sample period. Overall, more than 70% of the stock days are untouched by our functional truncation. In contrast, TBQ truncates at least one observation on 99.9% of the days.²⁶ Overall, the evidence is compatible with our objective, namely that the functional filtering should control major data irregularities while avoiding excessively intrusive, and potentially distorting, truncation of the underlying returns.

6.2 The Intraday Volatility Pattern

One benefit of tick-time sampling of transactions data is that it tends to mitigate the intra-day U-shape pattern in volatility. Figure 4 demonstrates that the tick-time sampling succeeds in straightening the volatility pattern across the main part of the trading day, but there is little impact on the elevated level of volatility in the first 60-90 minutes of trading. Our Monte Carlo experiments found such intraday volatility variation to be a potent source of systematic biases in power variation estimates, with the ratio statistic $\sqrt{IQ}/IV$ being less sensitive to such distortions than the raw and measures.

Figure 4: Diurnal volatility pattern for intraday trade data across the DJ30 stocks between January 1, 2005 and May 31, 2007.

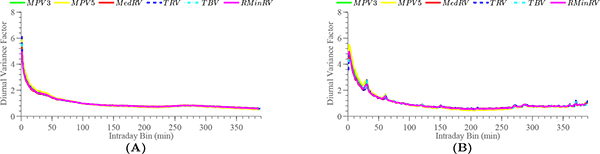
We plot the diurnal U-shape variance factors across stock-days based on local estimates of $\sigma^{2}$ in one minute buckets using tick time (Panel A) or calendar time (Panel B) sampling. On each stock-day, the factor in each one-minute bucket is computed by normalizing by the average of the 390 variance estimates on that day. The average variance factor is then computed by averaging across all stock-days

Data for Figure 4, Panel A: Tick Time

Intraday Bin (min)	MPV3	MPV5	MedRV	TRV	TBV	RMinRV
1	6.064729982	6.022776011	5.341480764	6.164035434	5.777039144	5.004557031
2	4.613565484	4.882487692	4.169216556	4.454525454	4.403919085	4.142636973
3	4.084005134	4.337520533	3.673024203	3.890645523	3.891508601	3.714971954
4	3.780395522	3.937862803	3.403077789	3.517630798	3.570706647	3.426637816
5	3.506969572	3.677154387	3.221589471	3.364749558	3.374114756	3.233007102
6	3.267677058	3.499849224	3.012623121	3.163501366	3.173633628	3.065716301
7	3.093526251	3.324252024	2.828995683	2.993073099	2.963303811	2.89460483
8	2.959586019	3.235256365	2.7008724	2.798166335	2.840572381	2.777552384
9	2.843499457	3.043338114	2.616089934	2.701745173	2.745091074	2.674407739
10	2.753303917	2.921953112	2.541200946	2.642641651	2.63482782	2.593835087
11	2.607607721	2.830135698	2.40635473	2.526060076	2.550188722	2.495426477
12	2.527600851	2.692385034	2.362544699	2.448782731	2.446077956	2.412963322
13	2.44955126	2.572271387	2.27571698	2.333683131	2.358744897	2.326788387
14	2.384465484	2.523862332	2.214671271	2.314846403	2.336624934	2.260742323
15	2.284930017	2.41514381	2.163225949	2.269376317	2.252272265	2.197086703
16	2.219770939	2.361207251	2.062121631	2.153187051	2.143612188	2.137509463
17	2.154926618	2.323151138	2.045166434	2.134803291	2.150363973	2.12183224
18	2.12863631	2.281723383	1.979768603	2.098052291	2.056446669	2.075473317
19	2.08747205	2.210894078	1.953128198	1.987996162	2.012154711	2.033085551
20	2.077482269	2.190707709	1.96420105	1.994568794	2.028905116	2.009589393
21	2.041917845	2.184298198	1.924936855	1.988238035	2.004059556	1.979040903
22	2.018129197	2.141443598	1.910358598	1.965989605	1.967640645	1.955905014
23	1.993637509	2.07286322	1.880109851	1.901085625	1.941615837	1.920921853
24	1.948927115	2.028504283	1.828125057	1.864218195	1.90552374	1.884011271
25	1.904632673	2.016084587	1.807464668	1.874103006	1.896089194	1.852760088
26	1.849826117	1.968689969	1.761693733	1.831899175	1.828594129	1.834099072
27	1.829757518	1.958663154	1.736175711	1.780875062	1.78428099	1.800323376
28	1.82491881	1.930477232	1.724054015	1.769055121	1.776376324	1.78789884
29	1.827960611	1.954213682	1.716579262	1.760321616	1.763630811	1.777254617
30	1.8209282	1.968023005	1.709991848	1.721954478	1.76720133	1.779292681
31	1.804548083	1.962643952	1.714283934	1.727049299	1.761461176	1.778709346
32	1.801821742	1.915146493	1.702068939	1.753121313	1.748199099	1.765887984
33	1.795758994	1.876877507	1.702644778	1.662108498	1.727391864	1.757239536
34	1.79778912	1.869808156	1.709012691	1.729752976	1.750542213	1.741131745
35	1.752540222	1.855105318	1.70199856	1.716478522	1.736422154	1.726154209
36	1.726994938	1.840855521	1.643513403	1.69513222	1.690101947	1.714808957
37	1.694095711	1.856223734	1.631958524	1.681018864	1.672103811	1.710465175
38	1.721163978	1.836336679	1.629358835	1.635864252	1.636273486	1.688399664
39	1.72436076	1.788772264	1.631005903	1.635711574	1.676229061	1.683861655
40	1.705467333	1.809832904	1.623944847	1.66134682	1.680092318	1.679422869
41	1.660650218	1.791071363	1.578582792	1.644143242	1.638521649	1.653240657
42	1.683891311	1.769933551	1.597288334	1.589464952	1.597020722	1.626355896
43	1.680157348	1.7531881	1.594193687	1.579436933	1.640393218	1.606804628
44	1.654379468	1.723502436	1.561082818	1.619203232	1.628674094	1.587814124
45	1.593169138	1.664343538	1.533317966	1.549926713	1.564845776	1.558810123
46	1.565620551	1.634144283	1.516620091	1.523269948	1.538248256	1.537039869
47	1.524130087	1.604629903	1.488526042	1.499681391	1.502518185	1.516667073
48	1.522978048	1.599818722	1.480837745	1.486209955	1.495305177	1.497418333
49	1.513444478	1.572962598	1.442312163	1.467533618	1.486847493	1.468895612
50	1.483929856	1.551094663	1.418349876	1.454030072	1.458162533	1.456255108
51	1.474694267	1.537144598	1.397262004	1.419461809	1.447853838	1.442377522
52	1.449493739	1.496033654	1.377755252	1.402583829	1.409665643	1.427677699
53	1.425656454	1.481856932	1.389670032	1.378111143	1.411060539	1.399687103
54	1.420637605	1.465760587	1.365262103	1.382436403	1.394402854	1.386084074
55	1.39778158	1.438308217	1.351397355	1.376732392	1.385432775	1.367253583
56	1.375205613	1.400733665	1.315731151	1.355752551	1.355041385	1.33726062
57	1.330809327	1.374923611	1.302294972	1.312109051	1.330563902	1.316620474
58	1.321031456	1.377600697	1.276626229	1.302223255	1.307406951	1.313068879
59	1.299486101	1.351832209	1.264951513	1.300893959	1.286863667	1.308990925
60	1.307347206	1.343865335	1.268215957	1.260610089	1.277584017	1.298476334
61	1.318354422	1.361837511	1.269006212	1.27571242	1.299444804	1.299428313
62	1.288785753	1.355890605	1.270342929	1.274801086	1.286946821	1.288077696
63	1.293812028	1.347095813	1.271605672	1.252751242	1.269503556	1.284965186
64	1.298657247	1.349930462	1.260809332	1.261070125	1.276610497	1.292905736
65	1.293666032	1.331554438	1.25821166	1.261697157	1.27920466	1.277354777
66	1.290083641	1.301687497	1.246686877	1.245738999	1.259321623	1.27038105
67	1.25468691	1.294865077	1.244572873	1.247926202	1.25945725	1.256375147
68	1.26577821	1.305356313	1.232668255	1.236556587	1.236907937	1.259125339
69	1.251988057	1.276933223	1.224568964	1.208649929	1.237079825	1.237755853
70	1.259512277	1.280212295	1.226165306	1.218090515	1.235300782	1.226836822
71	1.229897737	1.247469223	1.210250172	1.223270051	1.246310079	1.222111696
72	1.221010848	1.241222012	1.190503769	1.227629561	1.213757218	1.202002821
73	1.185878762	1.217340485	1.161583531	1.160935262	1.17173275	1.202463482
74	1.204479608	1.213876044	1.188381427	1.178127296	1.190187185	1.209053522
75	1.198479256	1.205152157	1.194933179	1.172162943	1.199233582	1.205409648
76	1.192342893	1.189468461	1.194437691	1.186185689	1.189668885	1.19153043
77	1.185546332	1.19194341	1.160545584	1.177928366	1.189120285	1.187227057
78	1.171534703	1.19143832	1.168068298	1.169158836	1.171684011	1.179937998
79	1.171392307	1.187703893	1.144432968	1.140946143	1.154657707	1.159661812
80	1.157895167	1.175767035	1.125309332	1.125993087	1.140843741	1.147873068
81	1.155529186	1.161841365	1.150080206	1.158953531	1.148227195	1.144739957
82	1.142085436	1.153346688	1.129121639	1.121672526	1.130633208	1.138589997
83	1.143299601	1.168033265	1.129155109	1.135443789	1.140109003	1.129968589
84	1.118995223	1.144210787	1.0997482	1.108420975	1.11408785	1.114175711
85	1.123980789	1.149215482	1.102230807	1.109245344	1.120863574	1.106935542
86	1.112133561	1.134469474	1.099104823	1.083770288	1.097256208	1.107082411
87	1.119038941	1.137165223	1.100659058	1.086746639	1.116358466	1.09897768
88	1.09892889	1.117556787	1.086778373	1.084272471	1.093938899	1.093015162
89	1.099424907	1.085823016	1.078557306	1.062903217	1.080136096	1.087617609
90	1.080745505	1.071731821	1.073932646	1.068679712	1.084140203	1.072073304
91	1.054665259	1.075511854	1.059165357	1.06859905	1.069260244	1.059772617
92	1.045655426	1.048687165	1.049740324	1.05256547	1.047980326	1.053186407
93	1.039679399	1.039578387	1.039864115	1.019436545	1.035901017	1.03844283
94	1.04827344	1.041724905	1.048854607	1.031448906	1.049629749	1.039747391
95	1.026012176	1.006883455	1.031169757	1.013641328	1.03425028	1.020822009
96	1.011951973	1.0027134	1.020311474	1.023801037	1.019975637	1.021228394
97	0.9967061	0.981609944	1.009224404	1.003939262	1.008563811	1.005281682
98	0.993736328	0.985098088	1.000389978	1.003754132	1.006866834	0.9958858
99	0.971389736	0.962382956	0.978318433	0.989256488	0.982428382	0.988425397
100	0.968371996	0.949000372	0.974232537	0.968263118	0.974366209	0.976644143
101	0.953848606	0.946874781	0.968067979	0.972655564	0.969487847	0.978709256
102	0.957184032	0.945686181	0.97278091	0.959370092	0.960072564	0.970273096
103	0.956515717	0.947521893	0.968337996	0.961392298	0.960478987	0.967900011
104	0.951682285	0.944712877	0.96050819	0.957015126	0.966223412	0.957089644
105	0.943032276	0.939303924	0.952551213	0.965105613	0.951822488	0.957762808
106	0.936691126	0.925204159	0.94534084	0.937622548	0.933321244	0.952604519
107	0.950569044	0.942597283	0.955318297	0.942161629	0.948424628	0.95702096
108	0.947249606	0.941338958	0.946728019	0.939271888	0.949692738	0.949404478
109	0.940845251	0.923357094	0.940369439	0.937103432	0.938489657	0.947005163
110	0.931787438	0.912509282	0.947118484	0.938400888	0.946730917	0.937194578
111	0.919546132	0.907975835	0.932147092	0.938762625	0.930217837	0.933039272
112	0.915751057	0.907403985	0.923828675	0.922596305	0.920179574	0.927793983
113	0.900918837	0.908106074	0.924045875	0.916468631	0.920294033	0.929196967
114	0.908368862	0.905297304	0.92863022	0.920312278	0.915984867	0.922235378
115	0.911626769	0.888801568	0.927236323	0.913708117	0.912590259	0.91293104
116	0.905056274	0.894860591	0.92736248	0.918776142	0.914643811	0.917057282
117	0.892888437	0.891278446	0.919487338	0.916132405	0.908235461	0.907461917
118	0.896021885	0.875275499	0.911604378	0.889454058	0.891751049	0.895213474
119	0.884495764	0.878596989	0.901594507	0.892556748	0.904905186	0.899203312
120	0.88152932	0.859240337	0.906352479	0.91724525	0.888595627	0.902006957
121	0.893545457	0.870482303	0.902529343	0.875673143	0.882901964	0.898888702
122	0.876513005	0.875935268	0.893604843	0.89196468	0.899328114	0.891797054
123	0.890489284	0.883262093	0.897340468	0.897219576	0.882568507	0.886834878
124	0.870069857	0.865019374	0.875506965	0.872642427	0.88685755	0.883431908
125	0.878516602	0.849982686	0.886518357	0.886240983	0.875397979	0.878441833
126	0.859183433	0.829321726	0.887258383	0.869301727	0.868635947	0.868393284
127	0.861100811	0.841741021	0.886180893	0.875101675	0.877682463	0.871753446
128	0.852099254	0.84554405	0.860411265	0.875520073	0.867128015	0.861473148
129	0.843807057	0.825773208	0.863475772	0.861142461	0.847249051	0.856944107
130	0.847052819	0.811539221	0.860772967	0.844544964	0.85043947	0.853047368
131	0.83600604	0.812427864	0.86189307	0.869320202	0.857680568	0.853149861
132	0.826709184	0.808181836	0.859146085	0.849315342	0.839745665	0.852726988
133	0.841257808	0.817022673	0.85375294	0.844851696	0.847637075	0.854355832
134	0.832855286	0.817897165	0.863423161	0.855863054	0.849515503	0.850458881
135	0.836445373	0.82715027	0.859568879	0.85242015	0.845832346	0.854978339
136	0.835598529	0.810082212	0.860782936	0.836543521	0.837792724	0.854570271
137	0.845045019	0.798277578	0.862702055	0.844706495	0.845188038	0.845369992
138	0.826888779	0.785944284	0.855120991	0.845098721	0.851516266	0.833210663
139	0.815683465	0.80061502	0.841967645	0.854975646	0.844419422	0.835346239
140	0.799920634	0.793972006	0.822677097	0.826878209	0.812962358	0.833865326
141	0.815003329	0.797957185	0.829796518	0.812139555	0.81309233	0.825632701
142	0.825488397	0.783410793	0.843999378	0.820415874	0.831382135	0.829929208
143	0.819858468	0.795240667	0.838245629	0.834383062	0.843045808	0.834388201
144	0.805588925	0.768551516	0.831755999	0.846772487	0.830475868	0.831056887
145	0.809517499	0.772069863	0.830961121	0.808239732	0.804789775	0.827452565
146	0.801261928	0.793784593	0.838821987	0.80750168	0.822401529	0.836256783
147	0.82495157	0.805368721	0.847815077	0.837689051	0.828277019	0.838136195
148	0.824620796	0.788932237	0.84464601	0.814242684	0.826865528	0.827387703
149	0.824146438	0.795928697	0.857700897	0.834724103	0.840506119	0.831899375
150	0.799897279	0.775963122	0.829121055	0.837067286	0.835825794	0.824302519
151	0.802750819	0.773381792	0.822124473	0.824288129	0.805052776	0.817697271
152	0.80583139	0.786465382	0.825807395	0.809805757	0.815594016	0.815136684
153	0.807289829	0.771256268	0.834198133	0.823422704	0.817919441	0.814601707
154	0.810736041	0.772401631	0.830012435	0.819232534	0.818750099	0.818803572
155	0.791516777	0.767774302	0.822862171	0.81349675	0.820256107	0.815635264
156	0.801170638	0.769035635	0.823248387	0.801841662	0.804438129	0.816335912
157	0.810644072	0.783220422	0.824940183	0.798646475	0.811504185	0.813556428
158	0.801506517	0.771156809	0.818751667	0.802753957	0.81766244	0.810442138
159	0.796546252	0.766177487	0.821081351	0.809971122	0.806362468	0.802724873
160	0.79633251	0.786544112	0.823263515	0.810192519	0.810639282	0.807735225
161	0.790320203	0.78812903	0.818563732	0.814772075	0.807773475	0.81899645
162	0.795030761	0.771412636	0.824419999	0.80263092	0.793480396	0.809171469
163	0.80942368	0.781770459	0.831656302	0.801387371	0.811754311	0.816424389
164	0.798488408	0.777559967	0.823876318	0.810782265	0.822671438	0.81634541
165	0.799620945	0.7676444	0.819209495	0.820168813	0.807114228	0.810436639
166	0.792101932	0.748705153	0.819270321	0.785906945	0.794918029	0.800923558
167	0.796488195	0.771857297	0.823007314	0.822127762	0.81804312	0.80522581
168	0.774522098	0.748778909	0.807115971	0.796378409	0.792972881	0.799616081
169	0.782631228	0.752501124	0.809227844	0.8001179	0.789468962	0.805222349
170	0.783406686	0.755363339	0.824057884	0.788813022	0.802392734	0.810455244
171	0.790764199	0.755879707	0.818496701	0.80761689	0.804345907	0.807547645
172	0.789714373	0.750866432	0.820287783	0.788667001	0.798303065	0.800719339
173	0.776878935	0.741981159	0.810681353	0.798663042	0.801644364	0.794831858
174	0.768422167	0.735961756	0.806382769	0.809576749	0.791878825	0.793535325
175	0.763099093	0.725927283	0.791449046	0.778875676	0.768222822	0.795691515
176	0.770208394	0.745941262	0.806199915	0.790335914	0.789589798	0.791025915
177	0.765504707	0.755518384	0.809102865	0.78618778	0.78433895	0.785809907
178	0.763959987	0.761806453	0.797235701	0.78048978	0.783468508	0.788570012
179	0.765175309	0.746465029	0.797024361	0.795250333	0.774233069	0.787324527
180	0.771033939	0.735430035	0.794168874	0.765381411	0.778453255	0.786789645
181	0.770998996	0.73857868	0.803203832	0.790693926	0.790311687	0.785483116
182	0.763796547	0.742068462	0.796044354	0.787764961	0.784795036	0.784174736
183	0.769139576	0.752261063	0.79444705	0.796242265	0.784058517	0.779292189
184	0.761126405	0.721558996	0.783198679	0.761419684	0.758739334	0.771811777
185	0.756472882	0.7378471	0.787375637	0.763550895	0.775797718	0.771953847
186	0.75815827	0.733278601	0.793492436	0.779570791	0.778638459	0.779666934
187	0.757566326	0.72727677	0.786527206	0.778938372	0.772146932	0.779235158
188	0.748070667	0.712381159	0.786536514	0.780806113	0.764763221	0.77383896
189	0.753077944	0.69306916	0.787111383	0.76174315	0.76154787	0.764478624
190	0.758121132	0.697179223	0.789678025	0.769656243	0.779539907	0.760095831
191	0.727964876	0.703754535	0.770057482	0.773389905	0.763224126	0.757549789
192	0.731935364	0.716864826	0.770582762	0.765775764	0.747632228	0.756720545
193	0.740165119	0.700248257	0.771500451	0.74494325	0.747170305	0.751370502
194	0.747018152	0.700157378	0.769920822	0.752237906	0.761584709	0.749525999
195	0.730186823	0.699058925	0.76822291	0.767636665	0.753983136	0.748543379
196	0.726920289	0.691692039	0.770982136	0.753581786	0.753761703	0.754777637
197	0.732109332	0.689367452	0.764687408	0.749727461	0.742542324	0.747376838
198	0.7396009	0.70607879	0.770624807	0.739174995	0.752964177	0.752111784
199	0.722494414	0.692891141	0.769103231	0.745350664	0.749128981	0.75458529
200	0.736743783	0.704207834	0.760069531	0.754852562	0.739002533	0.751883888
201	0.72560778	0.684609961	0.758871559	0.741075495	0.750597421	0.747181355
202	0.732635676	0.684512764	0.755819751	0.756917091	0.742906872	0.746651362
203	0.725783898	0.692984379	0.759344726	0.747251286	0.744839233	0.73941781
204	0.723565054	0.698320317	0.762968878	0.748161258	0.742867458	0.741150631
205	0.715656539	0.689702773	0.751205281	0.733179949	0.733732041	0.736818
206	0.72530679	0.672144964	0.75523153	0.745463834	0.736043368	0.729750818
207	0.714763353	0.673552882	0.756679847	0.738543964	0.742267425	0.727991879
208	0.710136698	0.688702643	0.752598703	0.739347926	0.736682025	0.732834782
209	0.707496749	0.684958312	0.747603398	0.742349361	0.724954416	0.733734832
210	0.71021615	0.681324702	0.747461154	0.730027269	0.715212166	0.735428949
211	0.721557346	0.679849841	0.754194033	0.727636116	0.733036984	0.73929539
212	0.719396971	0.677771059	0.75600904	0.743048897	0.738328092	0.739517569
213	0.71552984	0.673250702	0.757872044	0.747078074	0.732347489	0.73946054
214	0.712606062	0.675214693	0.753597143	0.74144773	0.736000154	0.733241278
215	0.705757861	0.672774779	0.757921408	0.74834308	0.732629724	0.73163258
216	0.711227695	0.681361498	0.745463116	0.728643619	0.72433668	0.732808981
217	0.71422595	0.683571932	0.749042261	0.731959289	0.730090532	0.73032651
218	0.714554462	0.678938189	0.75371688	0.725708665	0.728309363	0.732267782
219	0.722238669	0.668623725	0.760913922	0.742467353	0.741341369	0.72877607
220	0.711475538	0.664580987	0.742708379	0.74518694	0.735487894	0.732044404
221	0.704018366	0.661464323	0.745329668	0.730516123	0.726333651	0.727558795
222	0.703983061	0.668488077	0.74714143	0.741732871	0.723568304	0.728486886
223	0.704815315	0.678116015	0.747948811	0.706607449	0.71671718	0.727333085
224	0.711474116	0.692602938	0.755281134	0.74134977	0.738146918	0.734206756
225	0.729332401	0.69686167	0.755100824	0.736000902	0.735949443	0.736668969
226	0.72365209	0.68558394	0.753752513	0.740282437	0.741416543	0.736252272
227	0.722324029	0.680268364	0.749672789	0.73889908	0.738902535	0.737165538
228	0.708693248	0.672480064	0.753324901	0.739233344	0.732959765	0.741420174
229	0.711341994	0.67295485	0.751481086	0.740232371	0.732356962	0.73966533
230	0.713001139	0.681411138	0.757455997	0.734527042	0.732270839	0.739731108
231	0.717126885	0.686113311	0.755177122	0.732418851	0.730251358	0.741157651
232	0.726996798	0.694392242	0.755182066	0.741343369	0.741966788	0.74961419
233	0.726442625	0.691494129	0.764038723	0.740334104	0.740239725	0.750321262
234	0.733868339	0.701113962	0.765863077	0.74689107	0.746395483	0.753416194
235	0.725243512	0.693252887	0.764984625	0.745005908	0.74286371	0.750820821
236	0.733793373	0.696554958	0.776542216	0.752103051	0.746773773	0.756333778
237	0.731326801	0.697136578	0.76992454	0.756926734	0.748553778	0.756585036
238	0.73522597	0.70417305	0.776090814	0.759539148	0.747213093	0.754346293
239	0.72892768	0.699419599	0.772645498	0.748384549	0.748752133	0.753923998
240	0.730874103	0.698029852	0.762713892	0.758753543	0.749388759	0.747529423
241	0.732115141	0.707933596	0.768879711	0.75783636	0.747586108	0.751752562
242	0.737675213	0.718732496	0.767065803	0.748790104	0.750438027	0.759170832
243	0.748309472	0.723406253	0.771682379	0.757438307	0.753800611	0.766144863
244	0.752277014	0.737382944	0.783838935	0.765581881	0.76549259	0.764509581
245	0.761548243	0.749976176	0.779780011	0.766805002	0.767800682	0.770983613
246	0.758331607	0.734525368	0.778422008	0.765226835	0.765853297	0.779437975
247	0.7758565	0.753128532	0.797363746	0.776931127	0.77780327	0.783209634
248	0.772245641	0.758136531	0.801800518	0.781634738	0.787598832	0.786517336
249	0.77018602	0.740718735	0.791404385	0.78064799	0.778969291	0.781613572
250	0.778920674	0.744488087	0.791835895	0.778530471	0.778328544	0.781939615
251	0.768856676	0.74800365	0.794156065	0.779404466	0.788596242	0.782885554
252	0.769160916	0.757548917	0.794494325	0.779040368	0.776600752	0.787909771
253	0.781742694	0.770388824	0.794888	0.773877659	0.787697085	0.794147093
254	0.778390302	0.757114712	0.807580522	0.784963753	0.780582657	0.803786303
255	0.794003138	0.772869962	0.809106077	0.785764518	0.801840087	0.800424627
256	0.78800507	0.752950352	0.810067711	0.803811303	0.800124515	0.80619084
257	0.788871929	0.75589208	0.815359773	0.801245313	0.804298575	0.80296775
258	0.778327358	0.766121679	0.810928941	0.802381227	0.793653386	0.809616845
259	0.77613774	0.767702908	0.811986675	0.794092355	0.79145535	0.806077604
260	0.796891336	0.770939628	0.829229024	0.810114044	0.796743301	0.813092861
261	0.796664496	0.778155287	0.824496405	0.802153424	0.814096116	0.815027233
262	0.797537534	0.794524113	0.826368909	0.825327671	0.811664485	0.818563749
263	0.80448571	0.793319863	0.831739534	0.801805373	0.807060296	0.823500396
264	0.815389831	0.785021437	0.83143744	0.81763527	0.825516724	0.823060058
265	0.807100672	0.783392389	0.83486675	0.814872917	0.816904537	0.82303206
266	0.799381212	0.781586213	0.831639234	0.807269459	0.812854029	0.81709168
267	0.807840593	0.793407074	0.834747242	0.814982005	0.814606227	0.818597005
268	0.797534497	0.782319727	0.820570968	0.812340506	0.810555598	0.822429697
269	0.80651888	0.793971914	0.828241083	0.820020386	0.813025641	0.822157793
270	0.801242504	0.790225575	0.832571616	0.810624522	0.814870613	0.818814151
271	0.805268447	0.786469455	0.834779992	0.826125259	0.813434465	0.821924778
272	0.8044399	0.772822724	0.827440095	0.814722378	0.819021163	0.816374685
273	0.793560664	0.768924415	0.829096233	0.821354504	0.818960845	0.822306853
274	0.791469812	0.769872886	0.823518352	0.805747037	0.79474911	0.822432825
275	0.790971963	0.767357003	0.827681681	0.802145554	0.803436619	0.817247738
276	0.810184568	0.78557662	0.829909188	0.808248431	0.816206406	0.821888184
277	0.803828835	0.790908752	0.824182983	0.823453456	0.826625947	0.824336273
278	0.806535897	0.794499184	0.821806097	0.81745532	0.803051413	0.824904718
279	0.807057485	0.801363789	0.833002052	0.79886399	0.811644421	0.818277809
280	0.810065326	0.788497318	0.836925056	0.817719666	0.825151524	0.818176496
281	0.809096508	0.789770926	0.824751057	0.833592683	0.817560003	0.81646948
282	0.790306114	0.772886176	0.815164685	0.795659969	0.801616318	0.809036043
283	0.80031496	0.779340595	0.828759084	0.807680397	0.804660894	0.814804529
284	0.803457611	0.782926745	0.814682959	0.794423084	0.806683508	0.80335104
285	0.807374608	0.768519445	0.815257338	0.81416603	0.808662462	0.805116384
286	0.789859669	0.759489556	0.812047221	0.79281351	0.796712414	0.800141057
287	0.779450186	0.751598245	0.813516501	0.794882726	0.801857289	0.802910157
288	0.781148898	0.747712062	0.810888313	0.804078399	0.793851359	0.7988179
289	0.771726718	0.739393763	0.804640696	0.781748199	0.791482834	0.799751855
290	0.778654719	0.758159005	0.802582696	0.811848915	0.795332962	0.800713718
291	0.773971597	0.751542701	0.811701441	0.790198478	0.785181406	0.80008535
292	0.775205875	0.749549075	0.806566949	0.787143025	0.787891507	0.796858168
293	0.779235339	0.762298138	0.801025983	0.797160557	0.786271258	0.798259333
294	0.780382149	0.763353874	0.807765104	0.78856793	0.790384109	0.793011907
295	0.788702679	0.749644685	0.801829166	0.783023548	0.793392851	0.785257131
296	0.773447576	0.736000596	0.805719167	0.790260475	0.792562556	0.776239165
297	0.757427408	0.726847942	0.78774369	0.791239452	0.780868559	0.774533379
298	0.752770215	0.727388822	0.779089801	0.77123491	0.766098849	0.76993422
299	0.755373541	0.714387611	0.788077459	0.76144255	0.765328802	0.765094934
300	0.750852751	0.716427817	0.782974357	0.769173011	0.771744196	0.764347426
301	0.73663583	0.703709265	0.770522683	0.777311671	0.767748622	0.760614291
302	0.733286672	0.700397075	0.769771405	0.762975018	0.747608051	0.757129138
303	0.736972894	0.700431569	0.770615115	0.750613854	0.748147673	0.751243821
304	0.732496775	0.702815923	0.770092554	0.758203133	0.754524012	0.752348045
305	0.742209544	0.713462867	0.770732598	0.764164605	0.758271356	0.757168889
306	0.745178763	0.723072625	0.771069468	0.762759125	0.762983209	0.759691284
307	0.747600714	0.715687756	0.769503065	0.758979551	0.757251979	0.75578832
308	0.743426016	0.704320297	0.776822437	0.751589198	0.75092229	0.75295013
309	0.735026664	0.716833964	0.763416214	0.757606558	0.76210203	0.757284136
310	0.729492366	0.702263528	0.754733393	0.75854404	0.74189654	0.756186358
311	0.727673529	0.706782494	0.763919979	0.746859966	0.739781831	0.754262049
312	0.733999191	0.692251549	0.769241893	0.751780703	0.747974985	0.745273249
313	0.734431956	0.694804457	0.760185154	0.756030043	0.753881792	0.744085469
314	0.718937488	0.681326531	0.755230057	0.756020248	0.746096671	0.739202279
315	0.711377042	0.682980421	0.745768977	0.741823792	0.729256427	0.737653278
316	0.708600021	0.666225654	0.740633241	0.733416619	0.726539009	0.741044208
317	0.713890095	0.67509292	0.750293705	0.742243807	0.72866359	0.742962035
318	0.707914591	0.692202019	0.750801902	0.733710547	0.735411692	0.742018148
319	0.72602678	0.696384085	0.756757273	0.749797295	0.737315146	0.746270804
320	0.731584724	0.695766949	0.756316224	0.736924182	0.739837738	0.741476998
321	0.725333697	0.688437398	0.752761027	0.739150852	0.739416919	0.737378289
322	0.724601328	0.688773091	0.760114412	0.739857744	0.738796267	0.730894569
323	0.71830528	0.685551357	0.752531759	0.743969395	0.737995048	0.725605526
324	0.70764498	0.661037612	0.737524276	0.728665429	0.726755242	0.720485825
325	0.693315558	0.646385087	0.737161395	0.722623908	0.717136883	0.718282459
326	0.686950183	0.632998402	0.729216017	0.723749686	0.713021626	0.71105237
327	0.687692331	0.643141019	0.718883532	0.714159927	0.704894052	0.708313421
328	0.674204057	0.637270374	0.722584411	0.711699237	0.702880561	0.710366089
329	0.677192307	0.637233378	0.719697652	0.704959247	0.693846469	0.703254428
330	0.694241973	0.651248934	0.719146844	0.710442929	0.711574414	0.710664787
331	0.683860138	0.653436584	0.72212674	0.711326056	0.710793945	0.709535865
332	0.676475492	0.646744455	0.715667432	0.711634524	0.699117746	0.70746114
333	0.683210811	0.652560497	0.714438834	0.701808676	0.698034219	0.708759391
334	0.679433196	0.657035126	0.713623675	0.712144285	0.701888832	0.706017945
335	0.691025694	0.647195982	0.720133612	0.708406277	0.707897353	0.699173434
336	0.688011263	0.641308106	0.710598908	0.709685332	0.701686015	0.698211255
337	0.667218441	0.639751644	0.704043312	0.713141299	0.697859775	0.691744725
338	0.671677957	0.638411703	0.713613909	0.713632105	0.68826696	0.696798586
339	0.664495282	0.635886296	0.699303608	0.690362547	0.688106131	0.692869225
340	0.681287044	0.631543896	0.709454402	0.704870758	0.694158017	0.688776684
341	0.66809626	0.630415428	0.704155658	0.686293664	0.693986067	0.684764629
342	0.661736156	0.618431295	0.700167835	0.708544382	0.690738333	0.685337585
343	0.655928572	0.61889661	0.694733234	0.693752763	0.674432954	0.680464521
344	0.652094712	0.612851941	0.686881258	0.676925912	0.668188552	0.676936853
345	0.652847882	0.616564527	0.688701009	0.685077086	0.677712519	0.670540499
346	0.64749631	0.603703793	0.693652393	0.685901134	0.671054531	0.667105867
347	0.636562148	0.599764383	0.678201305	0.680230749	0.662847725	0.661717776
348	0.643236215	0.604302233	0.679852481	0.67251794	0.656248486	0.657676837
349	0.640973127	0.613965938	0.675675708	0.666682015	0.665942297	0.660034052
350	0.637281567	0.607143655	0.670385705	0.676808076	0.655081792	0.659908595
351	0.646600747	0.602071355	0.666624407	0.666859477	0.657862451	0.658502301
352	0.640837928	0.595797374	0.677917235	0.660348845	0.659032686	0.660174297
353	0.640178802	0.604447899	0.683071267	0.672725931	0.668688764	0.658344137
354	0.643672724	0.59717748	0.682664092	0.669672691	0.656946335	0.654177998
355	0.636845532	0.599731677	0.675412594	0.672892943	0.657042071	0.65165466
356	0.629589951	0.602254042	0.669941846	0.661581076	0.649528436	0.644018439
357	0.632261927	0.578343574	0.662890774	0.660941212	0.652529824	0.644018516
358	0.628107306	0.568984535	0.660804634	0.659455397	0.646102327	0.647908558
359	0.60651037	0.577252516	0.654078721	0.646666027	0.640831653	0.640205611
360	0.612716807	0.572272005	0.657080775	0.651767596	0.629280195	0.639590846
361	0.619847168	0.575405962	0.654678842	0.640859902	0.636606244	0.642093033
362	0.61727699	0.586610931	0.659639557	0.658177142	0.648690168	0.641453824
363	0.616285663	0.573558451	0.652192007	0.650740769	0.628245469	0.638855219
364	0.626221272	0.595019695	0.657808138	0.644416801	0.641024052	0.635364669
365	0.620685086	0.589522875	0.658299609	0.656351491	0.643386215	0.636563117
366	0.61809636	0.578012178	0.651705627	0.644449145	0.635540649	0.630985417
367	0.623596767	0.581979039	0.651940162	0.64706723	0.638606784	0.631927543
368	0.616151966	0.561953127	0.649382251	0.646392706	0.636196335	0.63153405
369	0.621138165	0.557220858	0.649018363	0.650910985	0.637850164	0.63102922
370	0.600483516	0.556210942	0.644761761	0.642982849	0.62582224	0.62003803
371	0.59276026	0.552911099	0.640016008	0.631178465	0.622235427	0.617220926
372	0.593147865	0.554177168	0.631856026	0.635382424	0.61693815	0.621058239
373	0.590340759	0.55007655	0.628890505	0.614968133	0.608103634	0.615268626
374	0.584943783	0.533906973	0.623694691	0.622661151	0.59973259	0.609904904
375	0.595784526	0.539406471	0.624678442	0.625137494	0.610139896	0.608203073
376	0.578553019	0.52745636	0.626651187	0.624811728	0.610781407	0.604959117
377	0.575881316	0.524289291	0.62240805	0.627673615	0.602300894	0.600577942
378	0.561744204	0.51912926	0.620182509	0.611609995	0.589484275	0.600014796
379	0.574488828	0.536456465	0.622007984	0.620770347	0.594513191	0.598571526
380	0.574543319	0.538486863	0.613668272	0.604776911	0.592016383	0.596279318
381	0.574904932	0.540168383	0.617469968	0.618813349	0.596922532	0.60243711
382	0.575776608	0.530777555	0.615161873	0.601939016	0.588449739	0.594689561
383	0.583464541	0.536175648	0.620147877	0.60345079	0.596724107	0.593586578
384	0.578864728	0.528911413	0.609187308	0.609718522	0.599228616	0.587035227
385	0.566138947	0.519124844	0.597614759	0.609002629	0.585980059	0.57771974
386	0.549496178	0.514909189	0.5902328	0.586160505	0.572021829	0.5748271
387	0.551348977		0.586479256	0.580961629	0.568486331
388	0.554351766		0.59337917	0.583518044	0.563606878
389				0.57898305	0.56991143
390				0.585796718

Data for Figure 4, Panel B: Calendar Time

Intraday Bin (min)	MPV3	MPV5	MedRV	TRV	TBV	RMinRV
1	4.370750452	4.740400589	4.415640969	3.535681778	3.979219486	4.711224092
2	5.096028845	5.495976812	4.804845927	4.745766509	4.832355928	4.975000362
3	4.978970841	5.420605325	4.619514077	4.631032096	4.678912041	4.732803131
4	4.799709973	5.17386223	4.379182316	4.356979799	4.500051249	4.438126301
5	4.530036308	4.858448561	4.14345153	4.131012902	4.276160913	4.176638391
6	4.283695514	4.591605905	3.878935417	3.973897984	4.051173738	3.90299568
7	4.024179101	4.396814438	3.628113564	3.735934186	3.850716237	3.692340596
8	3.750360485	4.169432076	3.391783842	3.487498181	3.570746266	3.507736574
9	3.547199992	3.852017863	3.275500902	3.309199003	3.408131381	3.301734789
10	3.435392502	3.71526857	3.127165843	3.160676964	3.262484033	3.151696797
11	3.221545708	3.654800483	2.994680095	3.070634345	3.179994132	3.077771437
12	3.119706194	3.534587789	2.806663306	2.982788255	2.955143091	3.00533546
13	3.052378701	3.342916458	2.774808232	2.727407881	2.832205027	2.897035575
14	3.077459544	3.294895303	2.838819906	2.753292768	2.922409015	2.831341638
15	2.949673678	3.1669668	2.733727096	2.785069294	2.883728196	2.747802727
16	2.797483483	3.007793704	2.590304132	2.700423165	2.726459812	2.620995914
17	2.675331151	2.939417307	2.445761737	2.538486359	2.585918156	2.540147455
18	2.602733557	2.861665958	2.414334814	2.454487657	2.509338452	2.472094033
19	2.542286366	2.811739604	2.338501018	2.334751739	2.443253819	2.391561173
20	2.503801503	2.701412923	2.305351827	2.365098246	2.415249911	2.354452072
21	2.426831585	2.614674893	2.237223888	2.296480598	2.362183616	2.276254735
22	2.371027858	2.502593783	2.211096369	2.290120889	2.296967587	2.22519356
23	2.255507474	2.457271065	2.091852719	2.127953495	2.221585983	2.16023039
24	2.206364606	2.445704144	2.068136238	2.159790685	2.162007109	2.163673539
25	2.161942307	2.391539393	2.003535911	2.0041421	2.070441371	2.124264104
26	2.204480355	2.391846672	2.055116556	2.026225463	2.087597799	2.112079367
27	2.191184872	2.57954148	2.047124717	2.045189815	2.136063933	2.267105526
28	2.181115812	2.68430498	2.041648265	2.113279677	2.129903036	2.34009
29	2.391360451	2.709440624	2.199925907	2.006455767	2.052041914	2.386400507
30	2.581795829	2.801785126	2.402063826	1.989506043	2.42149054	2.42929785
31	2.747171617	2.782025889	2.540069246	2.777379988	2.72691115	2.419613627
32	2.428764192	2.486295596	2.254657623	2.361368005	2.380063324	2.218938595
33	2.166819282	2.296224432	2.058688504	2.179409365	2.199729418	2.068056342
34	2.068993516	2.181331153	1.955120374	2.03770089	2.005805106	1.958994012
35	1.948671382	2.077446174	1.842091423	1.878158767	1.920121324	1.892198487
36	1.952106241	2.030273877	1.835218458	1.924256618	1.893887435	1.848410292
37	1.836201822	1.960480529	1.755988072	1.775506826	1.81981658	1.777629081
38	1.791771935	1.885543681	1.712846922	1.756516813	1.762901122	1.741165708
39	1.766896988	1.854657737	1.683575604	1.69553675	1.717414982	1.701152201
40	1.711521138	1.792912397	1.627309445	1.661569384	1.709529547	1.667210265
41	1.682804126	1.755493502	1.606474064	1.678349997	1.663808923	1.62545956
42	1.622134576	1.72885357	1.559098386	1.575509843	1.593132381	1.607758142
43	1.612800268	1.719393268	1.549012345	1.570859849	1.590926113	1.59352112
44	1.606544074	1.68969764	1.556654264	1.550283059	1.557438302	1.586746019
45	1.592764237	1.669273042	1.537064179	1.514268185	1.583852311	1.544086307
46	1.597242273	1.62137349	1.52920635	1.590205838	1.579106289	1.518194938
47	1.542682992	1.575589453	1.478651983	1.502538993	1.534463956	1.493303363
48	1.46550299	1.520567672	1.416526175	1.497189641	1.486586059	1.465287889
49	1.435098027	1.501706026	1.376549253	1.398648936	1.388144883	1.432167274
50	1.44641766	1.484799233	1.390037165	1.364944228	1.425906259	1.432996748
51	1.444817275	1.486042831	1.401327028	1.447113817	1.44933454	1.432743518
52	1.412934681	1.444165811	1.383049929	1.408000378	1.403665433	1.396922385
53	1.389498283	1.455212021	1.373975201	1.370779923	1.382961924	1.383621329
54	1.371236173	1.428972124	1.348144884	1.380255182	1.385369707	1.362941047
55	1.371249008	1.397172573	1.324514796	1.352974657	1.344603824	1.348613423
56	1.34215223	1.367408764	1.311052073	1.298136357	1.329062174	1.315879795
57	1.360959721	1.457409446	1.322952546	1.352956457	1.347315486	1.40042066
58	1.325460798	1.506811944	1.294514756	1.281602506	1.322513366	1.424970329
59	1.438528389	1.558250365	1.3717351	1.323137357	1.307257245	1.472509521
60	1.521076745	1.582393928	1.479166484	1.255302666	1.44545754	1.495132601
61	1.680764852	1.658847204	1.579378356	1.687860843	1.656781499	1.515696887
62	1.518404559	1.502350175	1.449268515	1.476440055	1.51659152	1.406180635
63	1.402144895	1.418761173	1.346279377	1.42651716	1.419136888	1.335999695
64	1.332139835	1.319117233	1.297011827	1.326451962	1.32751943	1.292723157
65	1.274361608	1.280217553	1.243693386	1.278198772	1.280128965	1.256546722
66	1.250078254	1.294595613	1.225965848	1.258477582	1.250925366	1.240651105
67	1.217440125	1.235641965	1.198758396	1.23616333	1.214168632	1.21904302
68	1.221878613	1.215450296	1.192052155	1.200156036	1.207146493	1.211243374
69	1.189317848	1.207574786	1.190155956	1.212189473	1.211418878	1.194487741
70	1.176307232	1.194795006	1.17467703	1.176989547	1.168581511	1.170466657
71	1.169364129	1.189625006	1.153263767	1.16266101	1.16770972	1.165973678
72	1.147195151	1.200816111	1.13172754	1.150100041	1.14253845	1.161638639
73	1.155741477	1.207240511	1.123109811	1.130770394	1.130903138	1.153797638
74	1.159733567	1.165093785	1.146847731	1.118145474	1.13856331	1.144671899
75	1.185772809	1.163927936	1.156279411	1.139028571	1.174087854	1.121961457
76	1.130554169	1.12187516	1.122327297	1.181467897	1.161672021	1.099522059
77	1.08394247	1.067259005	1.074617979	1.105467935	1.095371112	1.076894073
78	1.038419928	1.045274733	1.028073278	1.052952944	1.048567223	1.06464555
79	1.047259372	1.042287235	1.054135488	1.051141565	1.048167207	1.060514051
80	1.040685103	1.024154738	1.05297941	1.030819638	1.050460616	1.048871671
81	1.042150438	1.022535361	1.045837206	1.065716884	1.05855571	1.046772805
82	1.033001259	1.02609781	1.040306946	1.044633009	1.045643556	1.042948262
83	1.021575766	1.006668905	1.027506494	1.046007961	1.035626194	1.024961041
84	1.032268329	1.020519682	1.02134954	1.039287239	1.029195922	1.019292953
85	0.991256103	0.998040696	0.998973299	1.010084859	1.014681155	0.994746408
86	1.007926267	0.989177881	0.998090896	0.994745481	0.988913558	0.989778823
87	0.973645324	0.996460576	0.975859489	0.95531899	0.985948758	0.996040686
88	0.980063693	1.005612767	0.988303685	1.016998827	0.978949671	1.010369592
89	1.017101635	0.988985671	1.007475759	0.970643888	0.98420553	1.004998221
90	1.011940196	0.987619365	1.018536679	0.991281975	1.026878029	0.998996291
91	1.012913837	0.97426623	1.010178031	1.058684152	1.033161105	0.984395504
92	0.957288746	0.930187487	0.970661001	0.980283663	0.968060254	0.94789139
93	0.924399703	0.91182428	0.937680254	0.968318432	0.959521872	0.94789614
94	0.917513263	0.908774643	0.92880912	0.950422167	0.922404277	0.938092114
95	0.916317248	0.907229913	0.915173595	0.907603599	0.910575652	0.927347956
96	0.926607955	0.900074482	0.924968966	0.928315591	0.931825822	0.931232316
97	0.9196575	0.887860463	0.930373121	0.944187117	0.935059913	0.926673597
98	0.911989897	0.873118915	0.908866648	0.930111043	0.922475547	0.910497735
99	0.895911622	0.851662827	0.918238422	0.932621248	0.909721983	0.896754678
100	0.878104154	0.840385812	0.888792011	0.898749151	0.901945103	0.879105887
101	0.879375823	0.83538847	0.881529427	0.911311868	0.888536564	0.863899726
102	0.842501903	0.829157416	0.859694466	0.848925281	0.854192143	0.864874463
103	0.846443667	0.828074677	0.858602282	0.879097294	0.868772329	0.860802817
104	0.847229368	0.810477281	0.86682723	0.863343885	0.847939604	0.85762273
105	0.83355738	0.809113533	0.858835506	0.847033459	0.852831438	0.852173748
106	0.844135876	0.817575559	0.868450823	0.869105749	0.861146456	0.858158527
107	0.842656796	0.806424519	0.859154697	0.864605135	0.850622001	0.850207161
108	0.840611761	0.793975256	0.853044683	0.857567166	0.858821201	0.845494804
109	0.833543745	0.781136633	0.847857373	0.864410902	0.850312128	0.839915741
110	0.811322673	0.784755104	0.840787563	0.853433386	0.83524293	0.834259382
111	0.814920883	0.7814142	0.839430834	0.833350507	0.831637115	0.834274069
112	0.823197059	0.768714	0.841519907	0.853896325	0.832836811	0.817318065
113	0.801602835	0.757847121	0.819989006	0.823767892	0.819516267	0.822074741
114	0.787700566	0.77128678	0.82558776	0.831103429	0.814367975	0.819287892
115	0.794595228	0.792187154	0.823852052	0.824925842	0.806252583	0.821337473
116	0.805864389	0.795757921	0.814765923	0.81594703	0.806005215	0.824518562
117	0.815493487	0.813897248	0.836380304	0.808577479	0.815441542	0.845772915
118	0.816255203	0.817470311	0.843572163	0.827484518	0.839342392	0.845543058
119	0.848415618	0.83066023	0.862932402	0.83493409	0.824613848	0.840764749
120	0.846457286	0.807838155	0.863007436	0.825285977	0.867580097	0.823673992
121	0.837582455	0.775064512	0.852172862	0.90793077	0.862457293	0.812494135
122	0.780636039	0.727926717	0.801975588	0.815855712	0.812905763	0.780392372
123	0.763956402	0.718484627	0.786970026	0.812264637	0.787445617	0.774075729
124	0.739336256	0.711862668	0.772806056	0.768983377	0.758823379	0.756981613
125	0.731597916	0.688442386	0.767625817	0.761408014	0.753692806	0.746321292
126	0.743466648	0.695272803	0.760591654	0.773197088	0.753256674	0.7465051
127	0.718398254	0.681464142	0.752611387	0.752282945	0.752848929	0.741941077
128	0.717747344	0.679884199	0.758352604	0.768288317	0.734486101	0.739490806
129	0.714551	0.6744388	0.745752328	0.737738669	0.734277865	0.73086118
130	0.712703984	0.679454269	0.749311775	0.756199063	0.732698901	0.735430943
131	0.702247185	0.681912867	0.736635019	0.717777308	0.707710437	0.72970257
132	0.722664806	0.696484878	0.753305745	0.728970641	0.731412955	0.743185831
133	0.721212835	0.679687215	0.748187205	0.743352766	0.74631857	0.737609132
134	0.723005816	0.675419132	0.753201456	0.740823217	0.72642838	0.735502678
135	0.714010072	0.663058668	0.750403989	0.73160689	0.748149598	0.723522142
136	0.712870265	0.646046218	0.741789756	0.773503425	0.736589967	0.725612291
137	0.676750629	0.631425964	0.724104593	0.723122726	0.712404549	0.717751974
138	0.681615418	0.626194204	0.732358952	0.731525174	0.699729399	0.716125425
139	0.688535354	0.641994124	0.73828294	0.698985973	0.697610013	0.711268443
140	0.687731363	0.627157942	0.731058057	0.740233091	0.727844164	0.70792774
141	0.685725267	0.628544475	0.718212854	0.734390054	0.704007851	0.701866727
142	0.682916347	0.628805716	0.707107141	0.709466547	0.704285516	0.691723716
143	0.678096703	0.629714916	0.705500086	0.727659679	0.702108872	0.694171291
144	0.653700746	0.609962869	0.692498123	0.690867907	0.668848401	0.690404962
145	0.660318152	0.608634388	0.699286879	0.678487388	0.67607269	0.693767115
146	0.669057532	0.623905009	0.704676146	0.708341426	0.694595242	0.703776414
147	0.670199941	0.648030787	0.715784026	0.69858164	0.687072466	0.722884915
148	0.683636979	0.684174913	0.717598159	0.710513057	0.70066461	0.740030023
149	0.708947422	0.688572694	0.750486022	0.716486777	0.700406105	0.760256203
150	0.759520344	0.712803833	0.793759759	0.71410317	0.760200669	0.772780186
151	0.792924163	0.716035406	0.82309402	0.839994167	0.809362073	0.770475691
152	0.746182272	0.667473635	0.783855908	0.767691446	0.766669288	0.743714166
153	0.707685403	0.658477948	0.748673534	0.77614699	0.75376572	0.730817585
154	0.683790917	0.642472613	0.728842063	0.741189533	0.707359036	0.712397338
155	0.684561957	0.628839649	0.736313688	0.714202806	0.697279939	0.696440962
156	0.708977454	0.642852459	0.737776373	0.734250912	0.720592434	0.696977227
157	0.673636569	0.635752218	0.702785116	0.728059816	0.709436301	0.686452654
158	0.656328308	0.619955739	0.687544529	0.699302013	0.673653515	0.672069595
159	0.662380788	0.609288646	0.692519875	0.655762993	0.655920755	0.668701962
160	0.665544413	0.611246339	0.696164672	0.692849276	0.696299505	0.676446983
161	0.645386861	0.599900163	0.683306236	0.703557143	0.675268615	0.665050801
162	0.641671152	0.588738068	0.681601817	0.660681278	0.650975037	0.655774276
163	0.640343491	0.583418111	0.684773558	0.681894223	0.66789016	0.656194856
164	0.633631864	0.568752811	0.67664955	0.677985164	0.657536317	0.648800609
165	0.624721274	0.559334914	0.674719256	0.66512191	0.649569601	0.635471682
166	0.615218468	0.530825032	0.664320575	0.685113132	0.654551611	0.62762916
167	0.597931784	0.53073436	0.643416364	0.660694057	0.629761893	0.619905102
168	0.583130478	0.527289104	0.633540136	0.646327064	0.61738744	0.615283285
169	0.582347604	0.521079484	0.636245228	0.615348665	0.603265635	0.607624707
170	0.595760488	0.529108189	0.646639126	0.647966695	0.624021795	0.615690956
171	0.571283033	0.528077578	0.628844177	0.624915357	0.606324677	0.617975747
172	0.575135162	0.529914634	0.626400422	0.620847969	0.590901077	0.614733391
173	0.589437242	0.539309199	0.632380045	0.616930271	0.605198714	0.612727753
174	0.587469761	0.537593316	0.643866391	0.637845226	0.618717515	0.608115854
175	0.601234506	0.527508068	0.637095536	0.656445065	0.624795503	0.605117289
176	0.5814406	0.526117537	0.624544828	0.629319027	0.613246731	0.599906845
177	0.566111628	0.522423433	0.626225495	0.613627951	0.59587226	0.614208062
178	0.569599338	0.525083972	0.62265688	0.605561566	0.589029149	0.613334622
179	0.600114595	0.534908065	0.646542831	0.613206246	0.605988242	0.619139641
180	0.59639542	0.535680185	0.646182994	0.625065743	0.631950849	0.616236594
181	0.6019282	0.533033743	0.640635589	0.69060794	0.630762035	0.607333172
182	0.559605843	0.5025924	0.611594892	0.59734472	0.587068767	0.585781002
183	0.559347648	0.501404977	0.616537085	0.619642688	0.59262091	0.580988192
184	0.563089875	0.490454833	0.614180719	0.603891787	0.590866333	0.57612839
185	0.538671343	0.471725259	0.589645869	0.597904883	0.582251655	0.568799436
186	0.539155439	0.474658479	0.596060882	0.599401475	0.558675338	0.562920245
187	0.531333557	0.466286666	0.591481967	0.56569858	0.566660165	0.557980192
188	0.530444633	0.466109292	0.59193014	0.597741348	0.566976716	0.553930589
189	0.53075476	0.467925059	0.576871637	0.568020788	0.554751227	0.554319473
190	0.518419113	0.462990006	0.570353247	0.579768087	0.554128865	0.552493003
191	0.523569863	0.465970778	0.577142042	0.567338236	0.551645272	0.543628175
192	0.525185421	0.470570321	0.57356928	0.571414882	0.553528589	0.557734274
193	0.523914032	0.46405494	0.576328377	0.596596605	0.55895748	0.557904571
194	0.517856247	0.452134972	0.580273108	0.558440237	0.536865839	0.550061723
195	0.526965316	0.443627226	0.591306487	0.564755252	0.56336409	0.553904791
196	0.532513422	0.453819359	0.586791607	0.612953623	0.580662088	0.553231042
197	0.512626315	0.451611631	0.569225412	0.580726502	0.539473266	0.552588014
198	0.506532923	0.453939699	0.565987427	0.53937829	0.533183339	0.552692176
199	0.534321916	0.471382556	0.594699199	0.584450336	0.551418391	0.561551388
200	0.541567866	0.459308446	0.597293968	0.567150847	0.565535722	0.555162608
201	0.546940448	0.478679095	0.604346754	0.617065687	0.592405175	0.567549165
202	0.517741024	0.45055476	0.575107138	0.583006069	0.552730814	0.542624254
203	0.522591739	0.450585445	0.580861601	0.572038287	0.542004399	0.539390224
204	0.512848041	0.448546103	0.561601508	0.568139197	0.553652985	0.534087643
205	0.50577804	0.437105381	0.562391528	0.585104195	0.53815519	0.530763082
206	0.48860268	0.436123864	0.54439799	0.525724865	0.513469662	0.528629455
207	0.510763253	0.463916207	0.559453704	0.553640645	0.538203491	0.561478723
208	0.516521589	0.480148404	0.577656869	0.565741162	0.544114974	0.575310667
209	0.55335668	0.488116011	0.609920571	0.57478411	0.561149948	0.586483114
210	0.579447562	0.491213727	0.630347028	0.584875159	0.595313383	0.587723575
211	0.582077606	0.50493049	0.634414966	0.670676065	0.627364097	0.592069452
212	0.543900701	0.485918608	0.594565586	0.6069179	0.576479537	0.56890312
213	0.542559446	0.476001511	0.594941	0.591681219	0.564049504	0.565517236
214	0.549536457	0.471362319	0.598674093	0.574673991	0.568902183	0.565901374
215	0.540413756	0.461142297	0.598954608	0.591627829	0.575536192	0.56750493
216	0.544022443	0.477685435	0.598087454	0.601363135	0.578366563	0.571107482
217	0.533351858	0.47475617	0.587796784	0.589303454	0.569036728	0.567602829
218	0.541778567	0.477838691	0.600112117	0.577657069	0.554365084	0.564067062
219	0.536344781	0.46976365	0.590258035	0.574018225	0.566792053	0.561815353
220	0.536195754	0.467842886	0.602125414	0.591656427	0.567354382	0.565873698
221	0.541339032	0.463379846	0.596175428	0.593333092	0.575798146	0.562315891
222	0.535883487	0.472070294	0.586393217	0.594233613	0.557431272	0.559870579
223	0.529809057	0.488683362	0.586938637	0.572165486	0.562044924	0.562196623
224	0.535329514	0.482011614	0.589535804	0.582006189	0.561082086	0.563872875
225	0.549422367	0.469991134	0.6018867	0.585183033	0.562204398	0.562188149
226	0.540613691	0.473838722	0.593310481	0.580054699	0.583411295	0.570088596
227	0.521742749	0.478443571	0.586514558	0.600076541	0.562584892	0.572448618
228	0.533775403	0.483829022	0.596730232	0.571279375	0.548575305	0.578343829
229	0.559705785	0.500006226	0.614357345	0.577082807	0.578297513	0.581962522
230	0.571463755	0.50454936	0.62246233	0.614337862	0.600660121	0.588577991
231	0.562970276	0.503856554	0.612360014	0.618805212	0.599476536	0.583344638
232	0.543749066	0.497517859	0.597622241	0.607544174	0.577023098	0.577204251
233	0.550706107	0.488633743	0.601313704	0.59639042	0.573179472	0.57208028
234	0.540663266	0.477254055	0.598812003	0.591268926	0.568512679	0.57122221
235	0.543121128	0.481446187	0.601721167	0.596568705	0.576064235	0.572211849
236	0.545460006	0.491552001	0.600120957	0.59968081	0.574110708	0.571570343
237	0.53267829	0.485491838	0.582136067	0.57807943	0.561120186	0.574240798
238	0.542340504	0.493678977	0.596061515	0.592956763	0.566874871	0.583092677
239	0.538542286	0.488841256	0.598239116	0.577963847	0.55985935	0.58094556
240	0.570522672	0.507133739	0.610460935	0.59371217	0.580423379	0.589139558
241	0.575521517	0.507554872	0.617817758	0.627049476	0.606474412	0.596510019
242	0.550003418	0.497857832	0.613651655	0.592761817	0.575795729	0.590975543
243	0.569089589	0.527833781	0.623871612	0.6078071	0.594802358	0.596467327
244	0.578770862	0.525566187	0.616822699	0.635132363	0.600294437	0.593078862
245	0.568543053	0.52166135	0.611522321	0.609263009	0.594635098	0.590644148
246	0.556230931	0.523973753	0.60216378	0.614976953	0.588183089	0.595261839
247	0.568903733	0.527507222	0.618421689	0.610508582	0.583830193	0.60489848
248	0.592619084	0.53099999	0.639881376	0.609132158	0.608919878	0.61980164
249	0.588388899	0.518301478	0.647577824	0.62857014	0.630582739	0.617638592
250	0.58862675	0.510462218	0.6483683	0.645880705	0.613839466	0.612272613
251	0.585646705	0.509626537	0.629198265	0.631781252	0.62705627	0.608778851
252	0.569929447	0.510757774	0.618483052	0.655948186	0.607613904	0.614399984
253	0.565130028	0.513431556	0.624367953	0.611322896	0.584406353	0.608133125
254	0.588728582	0.546169056	0.637125407	0.6165618	0.613754719	0.625040272
255	0.59337741	0.548543251	0.646387201	0.642795809	0.623884146	0.630094232
256	0.611991847	0.545617792	0.65320603	0.646251445	0.62451238	0.621904994
257	0.600551096	0.550092925	0.647036106	0.633028618	0.627802749	0.62914779
258	0.592416278	0.558027497	0.641164494	0.664395008	0.635395441	0.629395064
259	0.600316512	0.555183807	0.64467571	0.641096414	0.609072876	0.62927102
260	0.592319671	0.555823248	0.648072842	0.609587278	0.622990904	0.632794161
261	0.618994062	0.577687512	0.662658716	0.684889563	0.638908269	0.653059618
262	0.622551813	0.562602301	0.664921006	0.637543077	0.635388679	0.640617082
263	0.641914861	0.568593992	0.689852134	0.672188637	0.662291473	0.651176141
264	0.61196353	0.557211998	0.662605782	0.682671031	0.663251239	0.641191166
265	0.607938171	0.559564784	0.660412575	0.678902749	0.629827798	0.639020886
266	0.600761767	0.567713822	0.653337629	0.656564021	0.633209376	0.642965211
267	0.613031767	0.61012477	0.654536362	0.669307961	0.635817979	0.682432063
268	0.623145858	0.649634959	0.662244035	0.650502648	0.640461871	0.727439793
269	0.683605571	0.683352009	0.712099005	0.668670703	0.653875628	0.766191965
270	0.772591266	0.755323796	0.828783154	0.681943067	0.742979595	0.818437127
271	0.848688277	0.795897382	0.87114901	0.897052535	0.887299437	0.833284572
272	0.826354355	0.760932867	0.838169051	0.864043669	0.821973776	0.797504471
273	0.769263106	0.726128837	0.7896885	0.775161589	0.795372713	0.762508595
274	0.756400124	0.717285704	0.7827293	0.822171057	0.779249465	0.760397667
275	0.715904463	0.681956882	0.738470227	0.732826956	0.729887424	0.735669059
276	0.732182442	0.66584528	0.763678962	0.747996111	0.736698255	0.739726014
277	0.722043557	0.668882301	0.758005221	0.753943832	0.761372975	0.737952925
278	0.710170167	0.682053572	0.752385823	0.771892585	0.740081842	0.739925119
279	0.699883977	0.677228999	0.740495452	0.724819873	0.712578947	0.732843994
280	0.731722449	0.685600416	0.758120051	0.737665542	0.747235482	0.743222307
281	0.728519369	0.689763887	0.748734267	0.758722529	0.749578119	0.745522598
282	0.72069198	0.709042137	0.762592141	0.767641163	0.739057595	0.766803959
283	0.710852354	0.736248384	0.745384253	0.743160894	0.728556488	0.789528807
284	0.762160305	0.771179109	0.794334754	0.745936808	0.737976804	0.820469453
285	0.838387942	0.820268207	0.865915889	0.769053782	0.825638457	0.868113568
286	0.878899335	0.849857446	0.884623668	0.889117117	0.896703171	0.89740651
287	0.866322146	0.861205977	0.88658229	0.870765142	0.856881151	0.903631796
288	0.874778034	0.857593686	0.900149816	0.86286148	0.876863774	0.891903052
289	0.912084315	0.853080427	0.918293147	0.861460631	0.877738101	0.882371729
290	0.860899078	0.797642126	0.896154034	0.874039148	0.909132414	0.853482559
291	0.838444378	0.763905624	0.866023801	0.902639199	0.860411157	0.829113081
292	0.77564604	0.738347317	0.804862782	0.82107974	0.832293258	0.79781566
293	0.76143571	0.747274459	0.791652245	0.836728986	0.778471322	0.782226166
294	0.753303622	0.740702143	0.762635202	0.756927475	0.750308596	0.769097268
295	0.775090996	0.737232527	0.796011064	0.767524681	0.773744562	0.777289687
296	0.764834762	0.716192763	0.797367412	0.773376808	0.786854001	0.782229395
297	0.757113114	0.737233546	0.792387184	0.782532767	0.768865666	0.785213244
298	0.762957584	0.724551728	0.79690757	0.78929791	0.784227338	0.774605529
299	0.767674404	0.735843068	0.797810627	0.785083116	0.774462576	0.775129428
300	0.750834288	0.726522376	0.766986256	0.783067019	0.782150342	0.768697072
301	0.753881145	0.725634457	0.780977028	0.812347953	0.76142969	0.769691639
302	0.733422498	0.72531578	0.766221431	0.732485835	0.738385034	0.770150942
303	0.759406137	0.733546718	0.788911748	0.782364622	0.769096774	0.781253136
304	0.772685085	0.718460807	0.8002766	0.765616831	0.777636841	0.772486828
305	0.774207584	0.704059304	0.779216082	0.783924595	0.789100976	0.7695162
306	0.749483896	0.705904492	0.77946012	0.797055967	0.774766114	0.759139688
307	0.728091011	0.708840527	0.767427778	0.75793303	0.743008399	0.750916282
308	0.726969798	0.709575913	0.75916829	0.754148823	0.751213214	0.755760098
309	0.738009747	0.716360016	0.76191609	0.74844499	0.743778946	0.766755297
310	0.740913738	0.741392917	0.767045236	0.758237033	0.762006311	0.769432785
311	0.756249384	0.715088176	0.779110287	0.782660864	0.762659337	0.764593957
312	0.772407711	0.727926821	0.788069254	0.778878285	0.77171031	0.773731118
313	0.747788996	0.73691835	0.775911489	0.783164443	0.789133893	0.772253213
314	0.759562404	0.724645617	0.774651105	0.799078122	0.75762376	0.77407463
315	0.741623049	0.703630638	0.771659681	0.747799848	0.756768479	0.759992377
316	0.764388339	0.719307937	0.787486687	0.805613803	0.782809167	0.758167736
317	0.732445588	0.691231884	0.761294447	0.74776151	0.749450586	0.746084166
318	0.720127701	0.674157088	0.764695456	0.785014576	0.760470197	0.743194007
319	0.708296675	0.670454106	0.737357747	0.74042943	0.721208731	0.731198045
320	0.71068899	0.680176003	0.745064727	0.727802269	0.731375372	0.734756718
321	0.728347971	0.702878969	0.748228735	0.763928626	0.74820784	0.743441872
322	0.72975552	0.681706695	0.753512133	0.744115161	0.736553891	0.737452756
323	0.725015972	0.693916196	0.761936393	0.749099345	0.750038374	0.754288207
324	0.703335974	0.700323209	0.738824587	0.744752078	0.724703311	0.76005687
325	0.737744878	0.717600745	0.762930932	0.749198088	0.730616001	0.762102717
326	0.760988278	0.718208411	0.796204287	0.744529106	0.772695415	0.76210916
327	0.757762121	0.733677711	0.790993523	0.809976758	0.79030582	0.785463001
328	0.72936972	0.734626904	0.762009789	0.780391364	0.75903741	0.776876339
329	0.750882612	0.724321528	0.773835856	0.739903105	0.72828647	0.771611962
330	0.784567655	0.739183345	0.806001678	0.73319733	0.785269111	0.776343996
331	0.789803623	0.740918875	0.804779041	0.863381998	0.83418876	0.781923391
332	0.747528647	0.738281923	0.77940183	0.792605642	0.765419779	0.773768231
333	0.744474626	0.742009932	0.769579027	0.760718389	0.767830755	0.775158257
334	0.762947564	0.731215273	0.779040367	0.774376205	0.754309744	0.774479291
335	0.767462378	0.74008368	0.790121697	0.74340967	0.783499671	0.773868868
336	0.782824399	0.743500106	0.796856665	0.845503769	0.81737938	0.779549208
337	0.757064705	0.717796807	0.766452598	0.773095395	0.765482352	0.75670792
338	0.749043662	0.731069161	0.754435411	0.754789675	0.759108428	0.763163618
339	0.755255385	0.733393306	0.763834067	0.75720811	0.75616708	0.774326238
340	0.750323258	0.718185452	0.779534552	0.778193844	0.762455496	0.784624736
341	0.768795681	0.736939785	0.789232556	0.759150137	0.772141472	0.782278523
342	0.775160704	0.731750325	0.80610777	0.807345756	0.803223639	0.783932103
343	0.764989201	0.716263502	0.7923078	0.820489502	0.790029406	0.763852227
344	0.74182041	0.682807483	0.764401139	0.777512264	0.760943376	0.745956028
345	0.734584859	0.689619943	0.75779717	0.766046999	0.761816897	0.743865245
346	0.71502092	0.687646883	0.744106291	0.76522026	0.74639596	0.737171361
347	0.707347011	0.690590539	0.742972113	0.732035771	0.721288321	0.737932442
348	0.722664461	0.724043196	0.74123399	0.742153489	0.735026349	0.753021471
349	0.728810553	0.726682451	0.749030703	0.755015718	0.740438908	0.760198614
350	0.757935128	0.726534296	0.772427912	0.743855258	0.741829652	0.765984948
351	0.775020116	0.721970366	0.781939455	0.761428969	0.780169057	0.765427691
352	0.761887224	0.719519987	0.776722702	0.801644912	0.790429954	0.758968931
353	0.721242504	0.690431941	0.744945322	0.767601917	0.749483723	0.74607919
354	0.716757999	0.671036995	0.742421193	0.754391946	0.725602274	0.741939049
355	0.715076541	0.684868514	0.751780403	0.722836146	0.733298843	0.747539917
356	0.725414338	0.700431162	0.754763289	0.765352545	0.743478277	0.756691636
357	0.71954093	0.750622518	0.751427359	0.752597838	0.736704704	0.798376919
358	0.749930441	0.783190872	0.777949888	0.751949605	0.752614481	0.820162564
359	0.839859807	0.82004847	0.84017772	0.779043913	0.788443517	0.84831993
360	0.835219854	0.793059241	0.848709112	0.803073744	0.855645833	0.84751578
361	0.863166058	0.809590735	0.872538276	0.928395989	0.878791087	0.836187822
362	0.806938319	0.786735556	0.819269176	0.839635302	0.838986858	0.806008694
363	0.781755123	0.768925795	0.795865606	0.84228248	0.800817243	0.793522853
364	0.775265564	0.741462519	0.791698101	0.790650487	0.781927795	0.77934784
365	0.781156824	0.7325042	0.78653376	0.786738403	0.789244105	0.771765274
366	0.753981869	0.74073614	0.777081349	0.808346397	0.793530223	0.769142472
367	0.738542829	0.830063251	0.760562385	0.778411951	0.752353555	0.868275985
368	0.741185045	0.855959354	0.756478563	0.742734212	0.736849753	0.899500837
369	0.937000433	0.894964255	0.922821024	0.790670199	0.785349767	0.920358715
370	0.970885442	0.918590598	0.984670891	0.780874721	1.013633543	0.931668421
371	1.017242598	0.961027484	0.991167775	1.324132463	1.097880157	0.955286153
372	0.850546787	0.870953385	0.851702594	0.90025031	0.862842937	0.870752431
373	0.826608881	0.85549523	0.835207273	0.813310275	0.822506986	0.872258275
374	0.866231456	0.892465342	0.864961986	0.828340747	0.844078603	0.882457822
375	0.911703278	0.911174225	0.897257645	0.847017744	0.898972484	0.883038039
376	0.902988413	0.861571437	0.881058709	0.898193409	0.913011981	0.870922619
377	0.864449892	0.855026074	0.855741372	0.90906174	0.879826727	0.870660551
378	0.821759573	0.873495884	0.834450761	0.843124968	0.841014295	0.883847286
379	0.837133098	0.888670282	0.842212142	0.834997176	0.814206439	0.891064366
380	0.88956662	0.89340839	0.890165042	0.81921164	0.855400623	0.894967954
381	0.926815684	0.913398124	0.913506248	0.906866649	0.931672184	0.916178449
382	0.925094363	0.92858022	0.89956463	0.951840977	0.931163706	0.913462153
383	0.885764899	0.906557645	0.870948784	0.878848414	0.8690517	0.884325619
384	0.890318601	0.917630052	0.864887482	0.848224047	0.86183044	0.880407348
385	0.886374938	0.967170415	0.866270852	0.87233449	0.895331386	0.91060029
386	0.882363428	1.094630465	0.855879891	0.887131294	0.853703314	1.004989555
387	0.917457014		0.888657438	0.794851879	0.842269623
388	1.122619896		1.080891943	0.854240014	0.935431661
389				0.96772791	1.166262093
390				1.253702191

To systematically assess the empirical relevance of intra-day volatility fluctuations, and in particular the diurnal volatility pattern, we split our equity sample into sub-groups consisting of stock-day combinations representing the top and bottom deciles with respect to a simple scale-free proxy for the intraday variation in volatility. This proxy, denoted (volatility-of-volatility), is constructed by splitting the trading day into 26 blocks, and then obtaining the median 30 second absolute returns within each block after first having eliminated all zero returns. Our proxy is then defined as the coefficient of variation (standard deviation divided by mean) of these 26 medians.²⁷ Importantly, the measure is designed to pick up any significant variation in intra-day volatility and not just the commonly occurring U-shape. In the following section, we provide signature plots that broadly support our interpretation of the simulation evidence.

6.3 Signature Plots for Integrated Power Variation

Panel A of Figure 5 provides signature plots for the IV estimates averaged across all days and stocks. They are plotted as a function of the sampling frequency implied by the size of the pre-averaging window and the intensity of the transactions (in tick time). The RV estimator is included as a reference point and, as expected, lies above the jump-robust IV estimators which are bundled closely together across most of the frequencies.²⁸ The main outliers are MPV5 at frequencies higher than 120 seconds and QRV at frequencies lower than 90 seconds. At high frequencies, the drop in MPV5 and, to a lesser extent, MPV3 may be explained by the presence of zero returns, due to discreteness, which has a pronounced impact on these estimators. Consistent with this explanation, RV is the only estimator not to display a tendency to fall off at the highest frequencies. At lower frequencies, the striking downward bias of QRV is in line with the evidence from the simulation experiments. While all the jump-robust measures feature downward sloping signature plots, QRV is, by far, subject to the most significant distortion.

The IQ estimators, shown in Panel A of Figure 6, display a similar but more pronounced pattern of decline at the lowest sampling frequencies, consistent with the simulation scenarios that incorporate time-varying volatility. In particular, the estimators are roughly ordered by block size, with the 5-block estimators at the bottom and the 3-block estimators at the top. The truncation based IQ estimators, although nominally based on a short block, are disproportionately impacted by time variation in volatility due to the wide window necessary for determining the truncation thresholds, explaining the relatively sharp decline in their signature plots. We do not include an IQ analogue to the QRV estimator as it displays downward biases that are an order of magnitude larger than for the others.

The signature plot for the $\sqrt{IQ}/IV$ ratio in Panel A of Figure 7 displays a relatively flat but distinct monotonically declining pattern. This suggests that the microstructure effects, afflicting estimators at the highest frequencies, cancel out quite effectively at moderate frequencies consistent with the simulation evidence. The multi-power variation estimators display clear abnormalities at the highest frequencies, primarily due to an imperfect offset of the zero returns in the denominator. At sampling frequencies of 60 seconds or lower, however, all the estimators are tightly clustered and downward sloping in accordance with the findings from the simulation scenarios with time-varying volatility.

To further explore the impact of time-varying volatility, Panels B and C of each figure depict signature plots, respectively, for the top and bottom deciles with respect to our volatility-of-volatility proxy, , across the combined stock-day sample. It is evident that both the IQ and IV signature plots on high VoV days are dramatically more steeply sloped than on low VoV days, corroborating the hypothesis that the slope is caused primarily by time-varying volatility due to factors like the intraday U-shape pattern, volatility jumps, and volatility bursts associated with news effects. For the ratio statistic in Figure 7, the signature plot for low VoV days is essentially flat, with the exception of the multi-power estimators, when viewed on the scale of the high VoV days, highlighting the fact that time variation in volatility also has a significant impact on the ratio statistic.

While the above evidence makes a fairly compelling case that VoV has a pronounced impact on the slope of the signature plots, it is based on grand averages across stocks and days and does not allow for formal statements about statistical significance. To provide a more rigorous analysis, controlling for the potential impact of a few outlier stocks, we have also run a series of panel regressions with stock fixed effects, capturing the average effect of VoV on the slope of the signature plot for each individual stock. These regressions confirm the strong significance of VoV on the slope of the signature plots.²⁹

Given the accumulated evidence we consider a sampling frequency around 90-120 seconds as a sensible choice for inference about IV and jump tests based on the $\sqrt{IQ}/IV$ ratio across most of the estimators. At higher frequencies, the microstructure effects start impacting the estimators quite severely, while employing lower frequencies entails a significant loss of efficiency and ultimately also generates a severe downward bias, especially for days with turbulent market conditions when volatility-of-volatility fluctuates greatly. Furthermore, among the set of estimators we consider, the RNT estimators, and , appear to possess advantages in both efficiency and robustness.

Figure 5: Average Estimates of IV Across the DJ30 Stocks Between January 1, 2005 and May 31, 2007

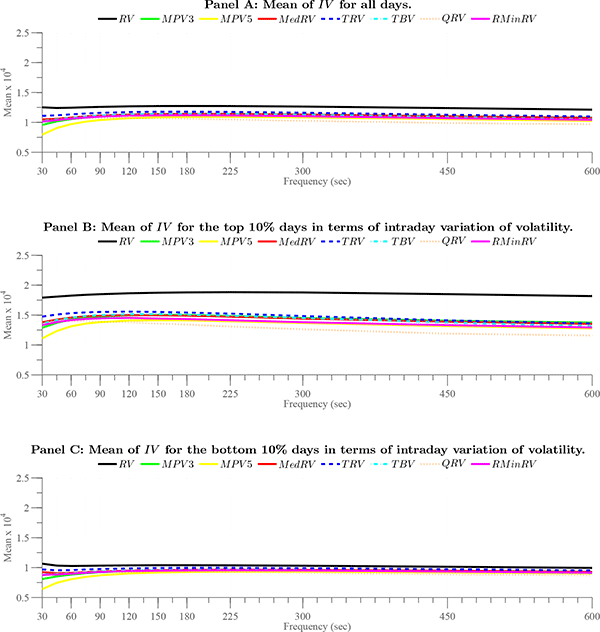
We provide signature plots for the mean of each pre-averaged estimator of IV as a function of pre-averaging window size matching the sampling frequency (measured in seconds on the x-axis). Panel A plots the mean across all days. Panel B plots the mean across the top 10% days with respect to intraday variation in volatility. Panel C plots the mean across the bottom 10% days with respect to intraday variation in volatility. Intraday variation in volatility is measured by the V oV measure of volatility of volatility described in Section 6.

Data for Figure 5, Panel A: Mean (x 10^4) of IV For All Days

Frequency (sec)	RV	MPV3	MPV5	MedRV	TRV	TBV	QRV	RMinRV
30	1.251884583	0.958551049	0.794837137	1.050386554	1.108841871	1.021009036	1.050368286	1.011301061
45	1.240427788	1.015900953	0.905233404	1.061270742	1.116815868	1.051249276	1.048687263	1.0373291
60	1.245180899	1.054981825	0.970684965	1.081438625	1.133234936	1.078672784	1.057689488	1.061914918
75	1.252532164	1.082041457	1.012162791	1.100383368	1.147583156	1.099965949	1.065566161	1.081304584
90	1.25903186	1.101218647	1.039562458	1.114048418	1.158290921	1.114885241	1.070461982	1.095103259
120	1.2680465	1.123873114	1.070614799	1.132082931	1.171693346	1.132898599	1.072164372	1.111266901
150	1.272537466	1.134766757	1.084669682	1.139628165	1.177157883	1.140914767	1.067865734	1.117304693
180	1.274062492	1.139652713	1.091031384	1.142783284	1.178085612	1.142917754	1.061406503	1.118967025
225	1.272713985	1.139434501	1.092115561	1.14171477	1.174619809	1.140426198	1.048426017	1.11616094
300	1.264602949	1.130578613	1.083323964	1.131335189	1.160997601	1.126193892	1.026726498	1.103180975
450	1.238713518	1.103201283	1.053442306	1.102535903	1.127560864	1.087865084	0.989489818	1.071352117
600	1.212630859	1.07727044	1.024563562	1.075803988	1.098021964	1.052253891	0.968514422	1.0424071

Data for Figure 5, Panel B: Mean (x 10^4) of IV for the Top 10% Days in Terms of Intraday Variation of Volatility

Frequency (sec)	RV	MPV3	MPV5	MedRV	TRV	TBV	QRV	RMinRV
30	1.791308526	1.28832395	1.109858253	1.379652254	1.474582587	1.357855589	1.385674883	1.332443208
45	1.808395937	1.36966899	1.233389255	1.425229399	1.509050078	1.417710152	1.393857513	1.382516833
60	1.825636059	1.425067337	1.312078123	1.4585819	1.531895237	1.459318265	1.399377542	1.416900981
75	1.839286468	1.455663491	1.356757493	1.479419676	1.544269167	1.485873165	1.399885101	1.435761221
90	1.849269302	1.476240167	1.382050553	1.489296872	1.551836014	1.498829328	1.394505684	1.445393125
120	1.864338254	1.496091624	1.409454643	1.500399676	1.557248506	1.513628464	1.379177435	1.451926121
150	1.873893928	1.501409369	1.412835636	1.494248369	1.551952373	1.515325927	1.359331111	1.442332755
180	1.879515242	1.500622253	1.411383763	1.489619882	1.541556205	1.507034983	1.34193356	1.433314958
225	1.88292431	1.482199717	1.395997252	1.472438277	1.523515411	1.488578865	1.307610203	1.413496149
300	1.878663654	1.451867085	1.367440507	1.439637528	1.48313302	1.450070889	1.262404469	1.380603429
450	1.849924495	1.40630547	1.315660776	1.388536935	1.411109831	1.376042037	1.188980342	1.332148809
600	1.816754692	1.374067481	1.277159656	1.352763392	1.358194549	1.312988669	1.158099485	1.292541786

Data for Figure 5, Panel C: Mean (x 10^4) of IV for the Bottom 10% Days in Terms of Intraday Variation of Volatility

Frequency (sec)	RV	MPV3	MPV5	MedRV	TRV	TBV	QRV	RMinRV
30	1.064453186	0.808401941	0.63944721	0.923949842	0.968292186	0.880766271	0.930248805	0.876132417
45	1.032398946	0.85268469	0.744624692	0.906240363	0.952690049	0.891556499	0.909594605	0.883767604
60	1.026416935	0.882320488	0.804331714	0.91103945	0.957266407	0.906735756	0.911336901	0.897698073
75	1.028838898	0.905278379	0.843978628	0.923324475	0.967302336	0.922738742	0.920267602	0.912815121
90	1.0317358	0.921134382	0.870431614	0.933955688	0.974988916	0.933904004	0.924939003	0.924588799
120	1.036663109	0.941568242	0.902112339	0.948157048	0.986868364	0.948836198	0.931165084	0.940793712
150	1.038761362	0.95147137	0.917081798	0.956034978	0.992809489	0.956542772	0.931747254	0.947183656
180	1.038800034	0.957645367	0.925342794	0.96098025	0.995418964	0.960751063	0.92995458	0.951781305
225	1.037083671	0.961733579	0.932318162	0.96456372	0.995250643	0.961887961	0.923971107	0.954821329
300	1.031355213	0.959019955	0.931353631	0.961688764	0.989846395	0.955404304	0.912235765	0.950804045
450	1.013458778	0.947926465	0.918609213	0.947701279	0.972184923	0.934043604	0.885822933	0.933863524
600	0.99400008	0.929011307	0.900639918	0.928322869	0.951593867	0.909432162	0.870820867	0.913544516

Figure 6: Average Estimates of √IQ Across the DJ30 Stocks Between January 1, 2005 and May 31, 2007

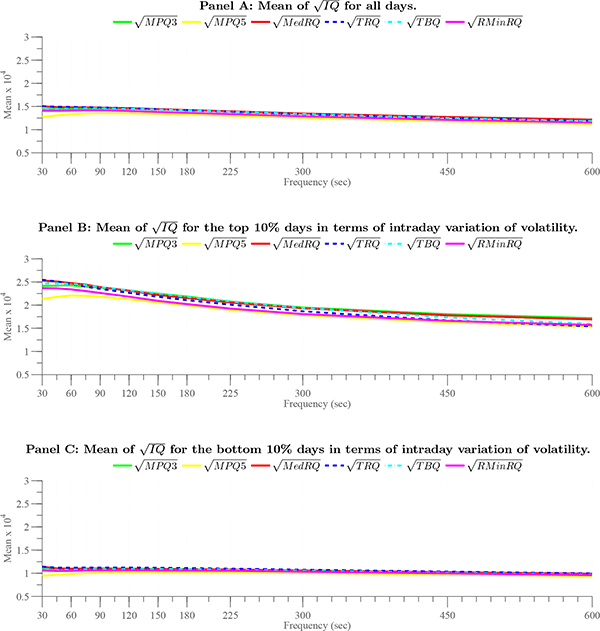
We provide signature plots for the mean of each pre-averaged estimator of √IQ as a function of pre-averaging window size matching the sampling frequency (measured in seconds on the x-axis). Panel A plots the mean across all days. Panel B plots the mean across the top 10% days with respect to intraday variation in volatility. Panel C plots the mean across the bottom 10% days with respect to intraday variation in volatility. Intraday variation in volatility is measured by the V oV measure of volatility of volatility described in Section 6.

Data for Figure 6, Panel A: Mean (x 10^4) of sqrt(IQ) For All Days

Frequency (sec)	sqrt(MPQ3)	sqrt(MPQ5)	sqrt(MedRQ)	sqrt(TRQ)	sqrt(TBQ)	sqrt(RMinRQ)
30	1.442376695	1.271094357	1.50213521	1.504948667	1.444731101	1.407577956
45	1.444610388	1.307127859	1.485826066	1.49324215	1.448247294	1.408467014
60	1.452406498	1.331527593	1.480005654	1.489189791	1.454337115	1.412584774
75	1.456050694	1.345995836	1.480198261	1.483994876	1.459416869	1.414846807
90	1.458908677	1.353859658	1.474429668	1.477593141	1.459394652	1.413456046
120	1.451633657	1.35302455	1.462847805	1.460877787	1.450830461	1.402183023
150	1.437650566	1.341985334	1.443333611	1.440123597	1.435805524	1.383074686
180	1.420556028	1.326830613	1.423955646	1.419035361	1.417242032	1.363768566
225	1.390721105	1.299967575	1.395086586	1.387299716	1.388898641	1.33589928
300	1.345483541	1.256945533	1.347919167	1.335407628	1.337876703	1.288199082
450	1.269947515	1.179696407	1.271543387	1.250640528	1.249169191	1.211242228
600	1.214550642	1.121440971	1.215479447	1.188109624	1.18259545	1.153606787

Data for Figure 6, Panel B: Mean (x 10^4) of sqrt(IQ) For the Top 10% Days in Terms of Intraday Variation of Volatility

Frequency (sec)	sqrt(MPQ3)	sqrt(MPQ5)	sqrt(MedRQ)	sqrt(TRQ)	sqrt(TBQ)	sqrt(RMinRQ)
30	2.414740215	2.131835896	2.529935902	2.546686961	2.468925337	2.366451326
45	2.420568695	2.176680926	2.50887977	2.511243842	2.473547662	2.362449527
60	2.429457688	2.209532142	2.475168122	2.456280306	2.456847426	2.339163034
75	2.399010398	2.200776601	2.443093202	2.39928646	2.43300215	2.303167315
90	2.378259469	2.181394988	2.389039727	2.350623616	2.389946912	2.262629619
120	2.312344377	2.125137108	2.312115428	2.264330651	2.320651894	2.180939663
150	2.247092381	2.057203767	2.221097096	2.180940004	2.252617282	2.091878004
180	2.186278118	1.997357848	2.156025381	2.107443178	2.179336298	2.022320003
225	2.074451936	1.896801638	2.057565038	2.010745134	2.080771114	1.92552261
300	1.949026038	1.782661999	1.932553109	1.867569482	1.939285464	1.806456873
450	1.801909048	1.629143347	1.779328859	1.668547958	1.734506235	1.660187785
600	1.717754237	1.535824664	1.691467327	1.54234234	1.592346649	1.570102974

Data for Figure 6, Panel C: Mean (x 10^4) of sqrt(IQ) For the Bottom 10% Days in Terms of Intraday Variation of Volatility

Frequency (sec)	sqrt(MPQ3)	sqrt(MPQ5)	sqrt(MedRQ)	sqrt(TRQ)	sqrt(TBQ)	sqrt(RMinRQ)
30	1.090740691	0.946622293	1.139040823	1.141013853	1.089748749	1.061179101
45	1.07110994	0.965648165	1.103721548	1.119139565	1.072358894	1.047801578
60	1.071849801	0.982760021	1.096716227	1.118325466	1.074127235	1.049474111
75	1.077733714	0.998254846	1.09861362	1.121553326	1.082446844	1.056759469
90	1.08192871	1.009411932	1.100501898	1.122008225	1.085647361	1.060421738
120	1.085857229	1.021904627	1.096876864	1.122263116	1.087921338	1.064571332
150	1.083122395	1.024420811	1.091681302	1.117110224	1.086362856	1.060617879
180	1.080635847	1.024169381	1.087006936	1.111299634	1.084712838	1.058277823
225	1.072625041	1.020861563	1.079842314	1.098481188	1.074911694	1.054189024
300	1.053372014	1.00387738	1.058810539	1.075018636	1.052173614	1.033618461
450	1.022146184	0.972097321	1.022660943	1.033864489	1.009762647	0.997645627
600	0.984909963	0.937265354	0.987750397	0.995117265	0.970799129	0.959921452

Figure 7: Average Estimates of √IQ/IV Across the DJ30 Stocks Between January 1, 2005 and May 31, 2007

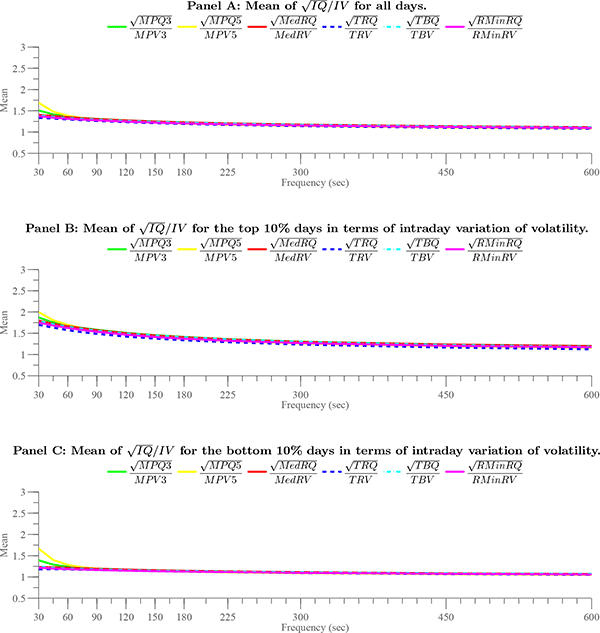
We provide signature plots for the mean of each pre-averaged estimator of √IQ/IV as a function of pre-averaging window size matching the sampling frequency (measured in seconds on the x-axis). Panel A plots the mean across all days. Panel B plots the mean across the top 10% days with respect to intraday variation in volatility. Panel C plots the mean across the bottom 10% days with respect to intraday variation in volatility. Intraday variation in volatility is measured by the V oV measure of volatility of volatility described in Section 6.

Data for Table 7, Panel A: Mean of sqrt(IQ)/IV For All Days

Frequency (sec)	sqrt(MPQ3)/MPV3	sqrt(MPQ5)/MPV5	sqrt(MedRQ)/MedRV	sqrt(TRQ)/TRV	sqrt(TBQ)/TBV	sqrt(RMinRQ)/RMinRV
30	1.507107116	1.688520391	1.404610311	1.333432815	1.39682524	1.372414188
45	1.415373352	1.48084126	1.377412284	1.315776639	1.358444536	1.339494557
60	1.365901129	1.384631033	1.350467704	1.29561673	1.330886944	1.313878287
75	1.333151781	1.332468752	1.328276659	1.276388978	1.310060192	1.292631281
90	1.309737645	1.29804305	1.30761283	1.25971896	1.292462826	1.275175229
120	1.274756732	1.25391734	1.275058403	1.231385714	1.263612388	1.245655383
150	1.249296936	1.224467131	1.249958514	1.208625869	1.241402007	1.222468807
180	1.228192509	1.201834695	1.22944161	1.190278298	1.223588791	1.203707929
225	1.203203523	1.176295435	1.205695507	1.167386557	1.201719466	1.181676008
300	1.173216794	1.145827553	1.176052292	1.138743558	1.173502872	1.154103509
450	1.134413428	1.107867389	1.1386597	1.101003192	1.136386898	1.118946506
600	1.11122577	1.083654651	1.115551977	1.076910652	1.114104639	1.096331805

Data for Table 7, Panel B: Mean of sqrt(IQ)/IV for the Top 10% Days in Terms of Intraday Variation of Volatility

Frequency (sec)	sqrt(MPQ3)/MPV3	sqrt(MPQ5)/MPV5	sqrt(MedRQ)/MedRV	sqrt(TRQ)/TRV	sqrt(TBQ)/TBV	sqrt(RMinRQ)/RMinRV
30	1.869772906	1.996228824	1.796450552	1.696402124	1.792326917	1.749964552
45	1.758004101	1.805429889	1.723958424	1.632565288	1.71478982	1.682568868
60	1.687659347	1.697808089	1.665577579	1.572967575	1.652188984	1.625985966
75	1.627424848	1.620863016	1.619109269	1.523349664	1.603359539	1.576199203
90	1.582478584	1.564781002	1.573784151	1.485077037	1.560275903	1.536602538
120	1.509960938	1.480947096	1.504130427	1.421401529	1.493874943	1.466579861
150	1.455961758	1.421286795	1.450322205	1.372759061	1.446281291	1.411986319
180	1.41476323	1.373692593	1.411000922	1.333901413	1.406450929	1.371972336
225	1.361373786	1.321218166	1.359959206	1.288107781	1.35865779	1.322928517
300	1.302423076	1.261113023	1.299854272	1.232724758	1.301405497	1.268472521
450	1.233709268	1.194729351	1.236934173	1.162867292	1.225713283	1.202619253
600	1.199779429	1.157911717	1.19962003	1.120995303	1.182343855	1.170356688

Data for Table 7, Panel C: Mean of sqrt(IQ)/IV for the Bottom 10% Days in Terms of Intraday Variation of Volatility

Frequency (sec)	sqrt(MPQ3)/MPV3	sqrt(MPQ5)/MPV5	sqrt(MedRQ)/MedRV	sqrt(TRQ)/TRV	sqrt(TBQ)/TBV	sqrt(RMinRQ)/RMinRV
30	1.390598436	1.66766297	1.23369788	1.180117752	1.248479554	1.218386657
45	1.289474933	1.400654313	1.228630236	1.181470229	1.216147175	1.198347103
60	1.240935776	1.284651078	1.217473453	1.177749366	1.200256028	1.183473185
75	1.214108691	1.229014611	1.205639107	1.171032638	1.190426406	1.173717965
90	1.197194467	1.197478017	1.195587597	1.162899062	1.18087963	1.164091418
120	1.172654296	1.161143029	1.174362496	1.148153688	1.163542539	1.147244041
150	1.155875825	1.139176304	1.15951379	1.134994194	1.150328581	1.135334708
180	1.143499694	1.124863049	1.145710064	1.125046599	1.141698091	1.125265033
225	1.126905012	1.107731499	1.132027953	1.110534543	1.12896346	1.114049269
300	1.108840734	1.088584894	1.113738203	1.091127156	1.111981387	1.095780815
450	1.083647284	1.065574076	1.085655326	1.066502664	1.088201084	1.074401761
600	1.066042116	1.047476475	1.069893784	1.049288809	1.074252286	1.057151672

7 Conclusion

We provide a first in-depth look at robust estimation of integrated quarticity (IQ) based on high frequency data. The sensitivity of many existing IQ estimators to pervasive data irregularities inspires us to introduce a novel set of jump-robust estimators that are defined in terms of order statistics of suitable return functionals and generalize the existing nearest neighbor truncation estimators of ADS (2012). This new class of robust neighborhood truncation (RNT) estimators can be designed to enhance the robustness properties vis-à-vis microstructure noise features of the data as well as reducing the finite sample sensitivity to outliers. The identical principle can more generally be applied also to other consistent estimators to enhance jump- and noise-robustness. We find that the novel RNT estimators outperform existing estimators by a considerable margin in terms of finite sample efficiency in estimating the key ratio of . This quantity is extremely useful for robust inference regarding IV and for testing for price jumps.

In the empirical implementation, we emphasize the importance of appropriate filtering for gross violations of the particular null hypothesis associated with a given estimation procedure. In particular, we apply a novel functional filtering scheme for local power variation estimators, which generalizes truncation of individual returns to truncation of return functionals and is easy to apply for a broad range of popular estimators. By invoking this approach at the level of the local power variation estimators, the threshold can be set very conservatively, thereby avoiding systematic biases arising from aggressive truncation and thus eliminating the need for ex-post bias correction. We also emphasize the use of pre-averaging based on a wide pre-averaging window. This allows for important robustness to extreme outliers, like the so-called bounce-backs, and it simplifies the associated distribution theory as the impact of noise vanishes asymptotically.

The unifying theme behind the new class of estimators, as well as the universal filtering procedure applied to them, is to operate directly on the functional space of local power variation estimates instead of restricting attention to the underlying individual returns. In fact, we may view the latter as a special case, arising from a block size of unity. Combining the functional filtering with the novel RNT class of estimators enables efficient inference in an extensive simulation design and generates supportive evidence from an empirical application using the Dow Jones 30 stocks. Overall, the study provides a set of new guidelines for the construction of practical robust and efficient estimation and inference regarding IV and IQ.

References

Andersen, T. G. and T. Bollerslev (1998). Answering the skeptics: Yes, standard volatility models do provide accurate forecasts. International Economic Review 39, 885-905.

Andersen, T. G., T. Bollerslev, and F. X. Diebold (2007). Roughing it up: Including jump components in the measurement, modeling, and forecasting of return volatility. Review of Economics and Statistics 89, 701-720.

Andersen, T. G., T. Bollerslev, and F. X. Diebold (2010). Parametric and Nonparametric Volatility Measurement. North Holland. In Handbook of Financial Econometrics, Volume 1 - Tools and Techniques; Yacine Ait-Sahalia, Lars P. Hansen, and Jose A. Scheinkman (Eds.).

Andersen, T. G., T. Bollerslev, F. X. Diebold, and P. Labys (2001). The distribution of realized exchange rate volatility. Journal of the American Statistical Association 96, 42-55.

Andersen, T. G., T. Bollerslev, F. X. Diebold, and P. Labys (2003). Modeling and forecasting realized volatility. Econometrica 71, 579-625.

Andersen, T. G., T. Bollerslev, and D. Dobrev (2007). No-arbitrage semi-martingale restrictions for continuous-time volatility models subject to leverage effects, jumps and i.i.d. noise: Theory and testable distributional implications. Journal of Econometrics 138, 125-180.

Andersen, T. G., D. P. Dobrev, and E. Schaumburg (2008). Duration based volatility estimation. Manuscript, Northwestern University.

Andersen, T. G., D. P. Dobrev, and E. Schaumburg (2011). A functional filtering and neighborhood truncation approach to integrated quarticity estimation. NBER Working Paper 17152.

Andersen, T. G., D. P. Dobrev, and E. Schaumburg (2012). Jump-robust volatility estimation using nearest neighbor truncation. Journal of Econometrics 169, 75-93.

Back, K. (1991). Asset pricing for general processes. Journal of Mathematical Economics 20, 371-395.

Bandi, F. M. and J. R. Russell (2008). Microstructure noise, realized variance, and optimal sampling. Review of Economic Studies 75, 339-369.

Barndorff-Nielsen, O. E., S. E. Graversen, J. Jacod, M. Podolskij, and N. Shephard (2006). A central limit theorem for realized power and bipower variations of continuous semimartingales. in From stochastic calculus to mathematical finance : the Shiryaev Festschrift, Springer Verlag.

Barndorff-Nielsen, O. E., S. E. Graversen, J. Jacod, and N. Shephard (2006). Limit theorems for bipower variation in financial econometrics. Econometric Theory 22, 677-719.

Barndorff-Nielsen, O. E., P. R. Hansen, A. Lunde, and N. Shephard (2008). Designing realized kernels to measure the ex post variation of equity prices in the presence of noise. Econometrica 76, 1481-1536.

Barndorff-Nielsen, O. E., P. R. Hansen, A. Lunde, and N. Shephard (2009). Realised kernels in practice: Trades and quotes. Econometrics Journal 12, C1-C32.

Barndorff-Nielsen, O. E. and N. Shephard (2002). Estimating quadratic variation using realized variance. Journal of Applied Econometrics 17, 457-477.

Barndorff-Nielsen, O. E. and N. Shephard (2004a). Econometric analysis of realized covariation: High frequency based covariance, regression, and correlation in financial economics. Econometrica 72, 885-925.

Barndorff-Nielsen, O. E. and N. Shephard (2004b). Power and bipower variation with stochastic volatility and jumps. Journal of Financial Econometrics 2, 1-37.

Barndorff-Nielsen, O. E. and N. Shephard (2006). Econometrics of testing for jumps in financial economics using bipower variation. Journal of Financial Econometrics 4, 1-30.

Barndorff-Nielsen, O. E., N. Shephard, and M. Winkel (2006). Limit theorems for multipower variation in the presence of jumps. Stochastic Processes and Their Applications 116, 796-806.

Christensen, K., R. Oomen, and M. Podolskij (2008). Realized quantile-based estimation of integrated variance. Working paper; CREATES, University of Aarhus, Denmark.

Christensen, K., R. Oomen, and M. Podolskij (2010). Realized quantile-based estimation of integrated variance. Journal of Econometrics 159, 74-98.

Corsi, F., D. Pirino, and R. RenÃ² (2010). Threshold bipower variation and the impact of jumps on volatility forecasting. Journal of Econometrics 159, 276-288.

Hasbrouck, J. (1999). The dynamics of discrete bid and ask quotes. Journal of Finance 54, 2109-2142.

Hautsch, N. and M. Podolskij (2010). Pre-averaging based estimation of quadratic variation in the presence of noise and jumps: Theory, implementation, and empirical evidence. Journal of Business and Economic Statistics forthcoming.

Hsieh, D. A. (1991). Chaos and nonlinear dynamics: Applications to financial markets. Journal of Finance 46, 1839-1878.

Huang, X. and G. Tauchen (2005). The relative contribution of jumps to total price variance. Journal of Financial Econometrics 3, 456-499.

Jacod, J., Y. Li, P. Mykland, M. Podolskij, and M. Vetter (2009). Mirostructure noise in the continuous case: the pre-averaging approach. Stochastic Processes and Their Applications 26, 2803-2831.

Jacod, J. and P. Protter (1998). Asymptotic error distributions for the euler method for stochastic differential equations. Annals of Probability 26, 267-307.

Jacod, J. and A. N. Shiryaev (2003). Limit theorems for stochastic processes (2nd ed.). Grundlehren der mathematischen Wissenschaften. Berlin; New York: Springer.

Jiang, G. J. and R. C. Oomen (2008). Testing for jumps when asset prices are observed with noise - a â€œswap varianceâ€ approach. Journal of Econometrics 144, 352-370.

Mancini, C. (2009). Non-parametric threshold estimation for models with stochastic diffusion coefficient and jumps. Scandinavian Journal of Statistics 36, 270-296.

Mykland, P. A. and L. Zhang (2009). Inference for continuous semimartingales observed at high frequency. Econometrica 77, 1403-1445.

Podolskij, M. and M. Vetter (2009a). Bipower-type estimation in a noisy diffusion setting. Stochastic Processes and Their Applications 119, 2803-2831.

Podolskij, M. and M. Vetter (2009b). Estimation of volatility functionals in the simultaneous presence of microstructure noise and jumps. Bernoulli 15, 634-658.

Schwert, G. W. (1989). Why does stock market volatility change over time? The Journal of Finance 44, 1115-1153.

Zhang, L., P. A. Mykland, and Y. Ait-Sahalia (2005). A tale of two time scales: Determining integrated volatility with noisy high-frequency data. Journal of the American Statistical Association 100, 1394-1411.

Zhou, B. (1996). High-frequency data and volatility in foreign-exchange rates. Journal of Business and Economic Statistics 14, 45-52.

A Proofs of Propositions

This appendix provides proofs of Proposition 1 and related results for the general case of estimating the integrated power variation of order , where is a positive and even integer. The proofs are initially given for the MinPV and MedPV type estimators and subsequently shown to extend to the RNT estimators in Lemma 9 below.

The (integrated) power variation, , is formally defined as,

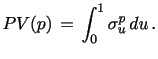
$\displaystyle PV(p) \, = \, \int_{0}^{1} \sigma _{u}^{p} \,du \,.$

(3)

Obviously, corresponds to the theoretical quantity relevant for the and estimators while refers to the integrated variance underlying the and estimators. The higher order integrated power variation estimators are less commonly used but do appear in the recent literature. For example, is required to assess the (asymptotic) precision of integrated quarticity estimators.

A.1 Basic Setting

Let be the log price process following a Brownian semimartingale

$\displaystyle Y_t$

$\displaystyle =$

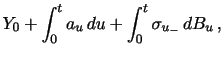
$\displaystyle Y_0 + \int_0^t a_u\,du+\int_0^t \sigma_{u_-} \, dB_u\, ,$

(4)

where is a locally bounded and predictable process and $\sigma$ is adapted, cadlag and bounded away from zero. Without loss of generality, we further assume that the functions $a, \, \sigma$ are uniformly bounded and $\inf_{t>0}\sigma_t\, > \, 0$ a.s.³⁰ The extension allowing for finite activity jumps in is dealt with Section A.6 below.

When discussing central limit theorems (CLTs) we require in addition that the volatility process follows a generalized Itô process:

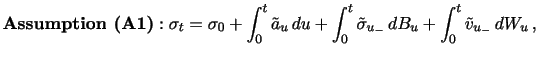
$\displaystyle \textbf{Assumption (A1)}: \sigma_t = \sigma_0+\int_0^t \tilde{a}_u\,du+\int_0^t\tilde{\sigma}_{u_-}\,dB_u+\int_0^t\tilde{v}_{u_-}\,dW_u \, ,$

where $\tilde{a}$ is locally bounded and predictable and $\tilde{\sigma}, \, \tilde{v}$ are cadlag and the Brownian motions $B, \, W$ are uncorrelated. We impose, without loss of generality, that the functions $\tilde{a}, \, \tilde{\sigma},$ and $\tilde{v}$ are uniformly bounded as well as $\inf_{t>0} \, \tilde\sigma_t>0$ and $\inf_{t>0} \, \tilde\nu_t>0$ a.s. We further note that, when the volatility process $\{\sigma_{t}\}_{t\ge0}$ satisfies Assumption A1, then the power variation process, $\{\sigma_{t}^{2}\}_{t\ge0}$ , also conforms to this general characterization.

We assume is observed at evenly spaced time points spanning the interval . Below, we denote these observations by $Y_{i/N}$ , $i=0,\ldots,N$ , and the associated log-returns by $\Delta_i^N Y = Y_{i/N} - Y_{(i-1)/N}$ , $i=1,\ldots,N$ . The proofs involve sequences of standardized return observations and corresponding approximating sequences for which volatility is fixed across one or more returns. Hence, we introduce non-overlapping blocks of $M \geq 1$ returns for which the volatility process is constant. We assume we have such blocks in the sample. Consequently, we define the quantities,

$\displaystyle \chi_i^N \,\,$	$\displaystyle =$	$\displaystyle \,\, \sqrt{N} \, \Delta_i^N Y \,\, ,$	(5)
$\displaystyle \beta_i^{N,M}\,\,$	$\displaystyle =$	$\displaystyle \,\, \sqrt{N} \, \sigma_{\frac{\lfloor \, (i-1)/M \, \rfloor \, M}{N}} \, \Delta_i^N B \,\, = \,\, \sqrt{N} \, \sigma_{\frac{\lfloor \, (i-1)/M \, \rfloor}{K}} \, \Delta_i^N B \, ,$	(6)

where $\lfloor\cdot\rfloor$ indicates the integer part of an expression. Hence, for each of the return blocks, corresponding to $\beta_i^{N,M}$ , the volatility remains fixed at the value it attains at the beginning of the block.

A.2 The Min and Med Power Variation Estimators

Let be a fixed positive even integer and let $g_{min,p}:\mathbb{R}^2\mapsto\mathbb{R}_+$ be given by,

$\displaystyle g_{min,p}(\mathbf{a}) \,\,$	$\displaystyle =$	$\displaystyle \,\, d_{min,p} \,\, \min \, (\,\vert a_1\vert^p,\vert a_2\vert^p\,) \, , \,\,\,\,\,\,$ where the scaling constant takes the form,	(7)
$\displaystyle d_{min,p}\,\,$	$\displaystyle =$	$\displaystyle \,\,(\,E\,[\,min \, (\,\vert Z_1\vert^{p},\,\vert Z_2\vert^{p}\, ) \,] \,)^{\,-1} \, , \,\,\,\,\,\,$ and $\displaystyle \,\,\,\,\, Z_{1}, Z_{2}\, \sim \, i.i.d. \mathcal{N}(0,1)$

For example, we have $d_{min,2} \, = \, \frac{\pi}{\pi-2} \,\,\,$ and $\,\,\, d_{min,4} \, = \, \frac{\pi}{3 \pi-8}$ .

Similarly, we define the median-based function $g_{med,p}:\mathbb{R}^3\mapsto\mathbb{R}_+$ and scaling factors,

$\displaystyle g_{med,p}(\mathbf{a}) \,\,$	$\displaystyle =$	$\displaystyle \,\, d_{med,p} \,\, \med \, (\,\vert a_1\vert^p,\,\vert a_2\vert^p,\,\vert a_3\vert^p \,) \, , \,\,\,\,$ where
$\displaystyle d_{med,p} \,$	$\displaystyle =$	$\displaystyle \, (\,E\,[\,med \,(\,\vert Z_1\vert^{p},\,\vert Z_2\vert^{p}\,), \,\vert Z_3\vert^{p}) \,] \,)^{\,-1} \, , \,\,\,\,\,$ and $\displaystyle \,\,\,\,\, Z_{1}, Z_{2}, Z_{3}\sim i.i.d. \mathcal{N}(0,1) \,.$

In this case, $d_{med,2} \,\, = \,\, \frac{\pi}{6 - 4 \sqrt{3} + \pi} \,\,\,$ and $\,\,\, d_{med,4} \,\, = \,\, \frac{3 \pi}{9 \pi + 72 - 52 \sqrt{3}}$ .

For any even positive integer, , we define the nearest neighbor truncation estimators of the 'th order power variation by,

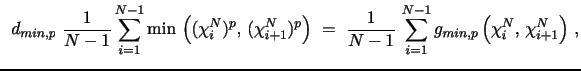
MinPV $\displaystyle _N(p)~\,=$	$\displaystyle ~\,d_{min,p} \,\, \frac{1}{N-1} \sum_{i=1}^{N-1} \min \, \left((\chi_i^N)^{p}, \, (\chi_{i+1}^N)^{p}\right) \,\, = \,\, \frac{1}{N-1} \, \sum_{i=1}^{N-1} g_{min,p}\left(\chi_i^N, \, \chi_{i+1}^N\right) \, ,$
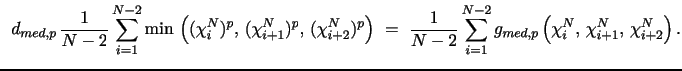
MedPV $\displaystyle _N(p)~\,=$	$\displaystyle ~\,d_{med,p} \, \frac{1}{N-2} \sum_{i=1}^{N-2} \min \, \left((\chi_i^N)^{p}, \, (\chi_{i+1}^N)^{p}, \, (\chi_{i+2}^N)^{p}\right) \,\, = \,\, \frac{1}{N-2} \sum_{i=1}^{N-2} g_{med,p} \left(\chi_i^N, \, \chi_{i+1}^N, \, \chi_{i+2}^N \right).$

For the cases of primary interest, i.e., and , these estimators are identical to the and estimators introduced in Section 2.1. Specifically, we have

MinPV $\displaystyle _N(2) \, = \,$ MinRV $\displaystyle _N \, , \,\,\,\,\,\,\,\,\,$ MedPV $\displaystyle _N(2) \, = \,$ MedRV $\displaystyle _N \, ,$

MinPV $\displaystyle _N(4) \, = \,$ MinRQ $\displaystyle _N \, , \,\,\,\,\,\,\,\,\,$ MedPV $\displaystyle _N(2) \, = \,$ MedRQ $\displaystyle _N \, .$

A.3 Additional Notation and Preliminary Results

We provide a detailed proof of the results in Propositions 1 and 2 concerning the MinPV estimator. The proofs for MedPV may be derived similarly. Moreover, we henceforth consider a fixed even, positive integer, , so the $g_{\text{min},p}$ function is uniquely defined. We refer to it simply as below.

First, we observe that, for any bivariate vectors, $\mathbf{a}=(a_1,a_2)$ and $\mathbf{b}=(b_1,b_2)$ , we have the following useful bound,

$\displaystyle \vert\,g(\mathbf{a}) \, - \, g(\mathbf{b})\,\vert \,\, \leq \,\, d_{min,p} \, \left(\, \vert\,a_1^{p}-b_1^{p}\,\vert \,+\, \vert\, a_2^{p}-b_2^{p} \,\vert \, \right) \, ,$

(8)

and furthermore that, except on the null set $\{(a_{1},a_{2})\in\mathbb{R}^{2}\vert a_{1}=a_{2}\}$ , we have

$\displaystyle \lim_{{\varepsilon\rightarrow0}} \,\, \frac{1}{\varepsilon} \,\, \left[\,\min(\,a_1^{p},\,a_2^{p} \, + \, \varepsilon \, z) \, \, - \, \min(\,a_1^{p},\, a_2^{p}\,)\,\right] \,\,\, = \,\,\, \left\{ \begin{array}{ll} z&\text{if } \,\,\,\,\, \vert a_2\vert \, < \, \vert a_1\vert \\ 0& \text{if } \,\,\,\,\, \vert a_2\vert \, > \, \vert a_1\vert \end{array}\right.$

(9)

The proofs of Propositions 1 and 2 revolve around the sequences,

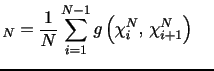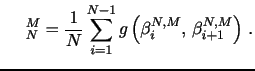
$\displaystyle \V_{N}=\frac{1}{N}\sum_{i=1}^{N-1} g\left(\chi_{i}^N, \, \chi_{i+1}^N \right) \,\,\,\,\,\,\,$ and $\displaystyle \,\,\,\,\,\,\,\, \U_{N}^M=\frac{1}{N}\sum_{i=1}^{N-1} g\left(\beta_{i}^{N,M}, \, \beta_{i+1}^{N,M}\right) \, .$

Since MinPV $_N(p) = \frac{N}{N-1} V_N \, , \,$ the sequence is asymptotically equivalent to our estimator, while is an approximating sequence as, for large $\, N, \,\, \chi_i^N \approx\ \beta_i^{N,M} \,$ .

For any adapted, integrable, -dimensional cadlag process, $\, X \,$ , and for $\, N \geq j>i-1 \geq 0 \,$ , we define the expectation conditional on information at time $\, \frac{i-1}{N}\,$ :

$\displaystyle E_{i-1} \left[\, X_{\frac{j}{N}} \, \right] \, = \, E\left[ \, X_{\frac{j}{N}} \vert \mathcal{F}_{\frac{i-1}{N}} \,\right]$

(10)

A useful implication of our ability to focus on the case with uniformly bounded drift and volatility functions is that, using the Burkholder-Davis-Grundy inequalities, we have,

$\displaystyle E_{i-1} \left[ \,\, \vert\chi_{i}^N\vert^q \, \right] \,\, \leq \,\, C \,\,\,\,\,$ and $\displaystyle \,\,\,\,\,\,\, E_{i-1} \left[ \,\, \vert\, \beta_{i}^{N,M} \,\vert^q \, \right] \,\, \leq \,\, C \, ,$

(11)

where $\, q > 0 \,$ and $\, C \,$ denotes a generic positive constant which we (with slight abuse of notation) allow to take on disparate values in different places.

We decompose our estimators for the power variation, , into a sum of conditional expectations and the associated martingale difference sequences: $V_N=V_{1N}+V_{2N}$ and $U_N^M=U_{1N}^M+U_{2N}^M$ where,

$\displaystyle \V_{1N}=\frac{1}{N}\sum_{i=1}^{N-1} E_{i-1} \left[g \left( \chi_{i}^N,\chi_{i+1}^N \right) \right], \,\,\,\,\,\,\,\,\,\, \V_{2N}=$	$\displaystyle \frac{1}{N}\sum_{i=1}^{N-1} \left\{ g(\chi_{i}^N,\chi_{i+1}^N) - E_{i-1} \left[g(\chi_{i}^N,\chi_{i+1}^N) \right]\right\}$
$\displaystyle \U_{1N}^M=\frac{1}{N}\sum_{i=1}^{N-1} E_{\lfloor\frac{i-1}{M}\rfloor M} \left[ g \left (\beta_i^{N,M},\beta_{i+1}^{N,M} \right) \right], \,\,\, \U_{2N}^M=$	$\displaystyle \frac{1}{N}\sum_{i=1}^{N-1} \left\{ g(\beta_{i}^{N,M}, \beta_{i+1}^{N,M}) - E_{\lfloor\frac{i-1}{M}\rfloor M} \left[ g(\beta_{i}^{N,M}, \beta_{i+1}^{N,M}) \right] \right\}.$

When we will use the shorthand $\beta_i^{N} \equiv \beta_i^{N,1}, \,\U_{N} \equiv \U_{N}^1$ and similarly for the individual pieces $\U_{1N}$ and $\U_{2N}$ . These definitions allow us to decompose the main estimator:

$\displaystyle \V_N$

$\displaystyle =$

$\displaystyle \U_{1N} + \U_{2N} + (\V_{1N}-\U_{1N}) + (\V_{2N}-\U_{2N})$

(12)

Consistency of $V_{N}$ can then be obtained by showing consistency of the estimator applied to the approximating Brownian path with piecewise constant volatility ( $\U_{N}= \U_{1N} + \U_{2N}$ ) and then showing that the difference $V_{N}-U_{N}$ (the last two terms in (12) above) is asymptotically negligible. This is what we do in Section A.4 below. To prove a CLT, we exploit a different decomposition (similar to Mykland and Zhang (2007)), in which we show the CLT for our estimator applied to an approximating Brownian motion for which volatility is piecewise constant over blocks of length . We then proceed to show that the difference between the original estimator and the estimator applied to the approximating process is negligible. This analysis is carried out in Section A.5 based on the decomposition:

$\displaystyle \sqrt{N} \, \left(\, \V_N-PV(p) \, \right) \,$	$\displaystyle =$	$\displaystyle \, \sqrt{N} \, (\V_{1N}-\U_{1N}) \, + \, \sqrt{N} \, (\, \V_{2N} \, - \, \U_{2N}) \, + \, \sqrt{N} \, (\, \U_{1N} \, - \,PV(p) \, )$
	$\displaystyle \, + \,$	$\displaystyle \sqrt{N} \, (\, \U_{2N} \,-\, \U^M_{2N} \,) \,+\, \sqrt{N}\,\U^M_{2N}$	(13)

A.4 Proposition 2: Consistency

We proceed by analyzing equation (12) term by term through a series of lemmas. For brevity, we focus on the features that are specific to our estimator, while referring to proofs in the extant literature when feasible. This also serves to highlight the underlying structural similarities between our measure and previously proposed power variation estimators and, in particular, and estimators.

Lemma 2 Under the maintained assumptions we have,

$\displaystyle \U_{1N} \,\, \overset{P}\rightarrow \,\, PV(p)$

(14)

Moreover, if Assumption (A1) holds we obtain,

$\displaystyle \sqrt{N} \, \left(\, U_{1N}-PV(p) \, \right) \,\, \overset{P}{\rightarrow} \,\, 0$

(15)

Proof. First, note that

$\displaystyle g\left (\beta_i^{N}, \beta_{i+1}^{N} \right) \,$

$\displaystyle =$

$\displaystyle \, \left[ \, g\left (\beta_i^{N}, \beta_{i+1}^{N} \right)\,-\,g\left(\, \beta_i^{N}, \, \sqrt{N}\sigma_{\frac{i-1}{N}} \, \Delta_{i+1}^{N}B \, \right) \, \right] \, + \, g\left (\, \beta_i^{N}, \, \sqrt{N} \sigma_{\frac{i-1}{N}} \, \Delta_{i+1}^{N}B \, \right)$

so we may write

$\displaystyle \U_{1N}\,$

$\displaystyle =$

$\displaystyle \, \frac{1}{N}\sum_{i=1}^{N-1}\E_{i-1}\left[\,g\left (\beta_i^{N}, \beta_{i+1}^{N} \right)\, - \, g\left (\beta_i^{N}, \sqrt{N}\sigma_{\frac{i-1}{N}} \, \Delta_{i+1}^{N}B \, \right)\, \right] \, + \, \frac{1}{N} \sum_{i=1}^{N-1} \sigma^{p}_{\frac{i-1}{N}}$

(16)

The first sum in (16) tends to zero in probability. To see this, note that the bound (8) implies the following limit in -norm:

$\displaystyle \E\left\vert\, \frac{1}{N}\sum_{i=1}^{N-1}\E_{i-1}\left[g\left (\beta_i^{N}, \beta_{i+1}^{N} \right)-g\left (\beta_i^{N}, \sqrt{N}\sigma_{\frac{i-1}{N}}\Delta_{i+1}^{N}B \right)\right]\, \right\vert^{\,2} \,\, \leq \,\, \frac{C}{N} \,\, \E \left[ \, \sum_{i=1}^{N-1} \vert\sigma^{p}_{\frac{i}{N}} - \sigma^{p}_{\frac{i-1}{N}}\vert^{\,2} \, \right] \,\, \rightarrow \,\, 0$

(17)

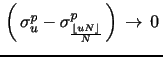where the convergence (17), and thus also convergence in probability, follows from the fact that $\sigma^{p}_{t}$ has finite quadratic variation (since $\sigma_{t}$ is a cadlag semimartingale). In addition, since $\{\sigma^{p}_{t}\}_{\,t\ge0}$ is uniformly bounded and cadlag, the pointwise dominated convergence of $\, \left( \, \sigma_{u}^p - \sigma_{\frac{\lfloor uN\rfloor}{N}}^p \, \right) \, \rightarrow \, 0 \,$ for $\, u\in[0;1] \,$ follows and Lebesgue's theorem yields

$\displaystyle \sum_{i=1}^{N-1} \left[ \, \int_{\frac{(i-1)}{N}}^{\frac{i}{N}} \left(\sigma_{u}^{p} -\sigma^{p}_{ \frac{(i-1)}{N}}\right)\,du \, \right] \, \overset{a.s.}{\rightarrow} \, 0$

(18)

Together (17) and (18) imply $PV(p)-U_{1N} ~ {\rightarrow} ~ 0 \, , \,$ which establishes (14). To show (15) we need the stronger assumption (A1). Define the sequence of independent standard normals $\, Z_{i} \, = \, \sqrt{N} \, \Delta_{i}^{N}B \,$ , then Assumption (A1) yields

$\displaystyle \E_{i-1}\left[\,(\sigma^{\, p}_{\frac{i}{N}} - \sigma^{\, p}_{\frac{i-1}{N}}) \, Z_{i+1}^{p}\mathbf{1}_{\vert Z_{i+1}\vert<\vert Z_{i}\vert} \, \right] \, = \, \E_{i-1}\left[\,(\sigma^{\, p}_{\frac{i}{N}}-\sigma^{\, p}_{\frac{i-1}{N}})\, \varphi(Z_{i}) \, \right] \, = \, O_{P \,}(1/N)$

(19)

since $\, \varphi(Z_{i})=\E_{i}[\, Z_{i+1}^{p} \mathbf{1}_{\vert Z_{i+1}\vert<\vert Z_{i}\vert} \,]\,$ ce is an even function of the Brownian path $\, \{B_{t}\}_{(i-1)/N<t<i/N}$ . Now the property (9) yields

$\displaystyle \E_{i-1}\left[\, g\left (\beta_i^{N}, \, \beta_{i+1}^{N} \right)-g\left (\beta_i^{N}, \, \sqrt{N}\sigma_{\frac{i-1}{N}} \Delta_{i+1}^{N}B \right) \, \right] \, = \, O_{P \,}(1/N)$

(20)

This ensures that the first term in (16) is asymptotically negligible, even when scaled up by $\sqrt{N}$ . Hence, the remaining task is to show,

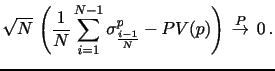
$\displaystyle \sqrt{N} \, \left( \frac{1}{N} \sum_{i=1}^{N-1} \sigma^{p}_{\frac{i-1}{N}} - PV(p) \right) \, \overset{P}\rightarrow \, 0 \, .$

However, this is analogous to the common task of showing that

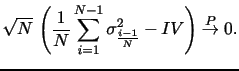
$\displaystyle \sqrt{N} \, \left( \frac{1}{N} \sum_{i=1}^{N-1} \sigma^{2}_{\frac{i-1}{N}} - IV \right) \overset{P}\rightarrow 0.$

in the IV literature and the method of proof is, by now, well established; see, e.g., BNGJPS where the result is shown in a general setting (allowing for infinite activity jumps) of which the current framework is a special case. A more intuitive and detailed exposition is provided by Barndorff-Nielsen, Graversen, Jacod, and Shephard (2006), henceforth BNGJS.

Lemma 3 Under the maintained assumptions, we have

$U_{2N}\overset{p}{\rightarrow}0$

(21)

Proof. To simplify notation, define the martingale difference sequence $\left\{ \frac{1}{N} \eta_{i}^{N}, \, \mathcal{F}_{\frac{i}{N}} \right\}_{i\ge0}$ :

$\displaystyle \eta_{i}^{N} \,\, = \,\, g(\beta_{i}^{N }, \, \beta_{i+1}^{N }) \, - \, E_{i-1} \left[ \, g(\beta_{i}^{N }, \, \beta_{i+1}^{N }) \, \right]$

Note that $\, \E[ \, (\eta_i^N)^2\vert\mathcal{F}_{\frac{i-1}{N}} \, ] \, \leq \, C \,$ , so applying the Cauchy-Schwartz inequality,

$\displaystyle \V\left[\frac{1}{N} \sum_{i=1}^N \eta_i^N\right] \, = \, \frac{1}{N} \, \E\left[ \, \frac{1}{N} \sum_{i=1}^N \left( (\eta_i^N)^2 \, + \, 2 \eta_i^N \eta_{i+1}^N \right) \, \right] \, \le \, \frac{C}{N} \, \E\left[ \, \frac{1}{N}\sum_{i=1}^N \E [ \, (\eta_i^N)^2\vert \mathcal{F}_{\frac{i-1}{N}} \,] \, \right] \, \le \, \frac{C}{N} \, \rightarrow \, 0 \,.$

The convergence implies . $\qedsymbol$ $\, \frac{1}{N} \sum_{i=1}^N \eta_i^N \, \overset{P}{\rightarrow} \, 0 \,$ .

Lemma 4 Under the maintained assumptions, we have,

$\displaystyle \left(\, \V_{1N} \, - \, \U_{1N} \, \right) \, \overset{P}\rightarrow \, 0 \, .$

(22)

Under Assumption (A1), we obtain,

$\displaystyle \sqrt{N} \, \left( \, \V_{1N} \, - \, \U_{1N} \, \right) \, \overset{P}\rightarrow \, 0 \, .$

(23)

Proof. We must show,

$\displaystyle V_{1N} - U_{1N} \, = \, \frac{1}{N} \sum_{i=1}^{N-1} \E_{i-1} \left[ \, \left( g(\chi_{i}^N,\,\chi_{i+1}^N) - g(\beta_{i}^N,\,\beta_{i+1}^N) \right) \, \right] \, \rightarrow \, 0 \,\,\,$ as $\displaystyle \,\,\, N \, \rightarrow \, \infty\,.$

(24)

Using the bound (8), it follows that,

$\displaystyle V_{1N} - U_{1N} \,\,\,\, \leq$	$\displaystyle \,\,\,\, \frac{1}{N} \E\left[\, \sum_{i=1}^{N-1} \, \vert\,g(\chi_{i}^N\,,\chi_{i+1}^N) \, - \, g(\beta_{i}^{N }, \, \beta_{i+1}^{N})\,\vert \, \right]$
$\displaystyle \leq$	$\displaystyle \,\,\,\, \frac{C}{N} \,\, \E\left[\, \sum_{i=1}^N \, \left\vert \, (\chi_i^N)^p - (\beta_i^N)^p \, \right\vert \, \right] \,\, = \,\, \frac{C}{N} \,\, \sum_{i=1}^N \, \left( \, \E_{i-1} \left\vert \, h(\sqrt{N} \Delta_i^N Y) \, - \, \sigma_{\frac{i-1}{N}}^p \, \right\vert \, \right)$

where we have defined the function . This formulation maps directly into the setting of BNGJPS where the results of this lemma are proven in a more general setting and for a generic function subject to regularity conditions. In particular, our function trivially satisfies the continuous differentiability and polynomial growth conditions necessary for the applicability of their analysis. An accessible, albeit lengthy, account of the steps of the argument may be found in BNGJS (2006, pp. 713-719). So while this proof is quite involved, the above reformulation of the relevant inequalities, as they arise within our specific setting, allows us to simply refer to previously published work for the result. $\qedsymbol$

Lemma 5 Under the maintained assumptions, we have,

$(V_{2N}-U_{2N})\overset{p}{\rightarrow}0$

(25)

Moreover, we may strengthen this result further to obtain,

$\displaystyle \sqrt{N} \, \left(\, \V_{2N} \, - \, \U_{2N} \, \right) \,\, \overset{P}\rightarrow \,\, 0 \, .$

(26)

Proof. In order to demonstrate the second result of the lemma, which obviously implies the first, we define,

$\displaystyle \xi_i^N \, = \, (1 / \sqrt{N}) \, \left[ \, g \left( \chi_{i}^N, \, \chi_{i+1}^N \right) \, - \, g \left( \beta_i^N, \, \beta_{i+1}^N \right) \, \right] \, ,$

and we must then prove that,

$\displaystyle \sum_{i=1}^{N-1} \, \left( \, \xi_i^N - \E_{i-1} [ \, \xi_i^N \, ] \, \right) \,\, \overset{P}\rightarrow \,\, 0 \, .$

This is a martingale difference sequence with respect to the filtration $\, \mathcal{F}_{\frac{i}{N}} \,$ , so it suffices to show,

$\displaystyle \sum_{i=1}^{N-1} \, \E \left[ \, (\xi_i^N)^2 \, \right] \,\, = \,\, \E \left[ \, \sum_{i=1}^{N-1} \E_{i-1} \left[ \, (\xi_i^N)^2 \, \right] \, \right] \, \rightarrow \, 0 \,\,\,\,\,\,$ as $\displaystyle \,\,\,\,\,\, N \, \rightarrow \, \infty \,.$

Mimicking the type of steps undertaken in the proof of the previous lemma, including application of the uniform bound on moments of $\, \chi_i^N \,$ and $\, \beta_i^N \,$ , we obtain,

$\displaystyle \sum_{i=1}^{N-1} \, \E \left[ \,(\xi_i^N)^2 \, \right] \,\,\,$	$\displaystyle =$	$\displaystyle \,\,\, \frac{1}{N} \,\, \E \left[ \, \sum_{i=1}^{N-1} \, \E_{i-1} \left\vert \, g( \, \chi_{i}^N, \, \chi_{i+1}^N) \, - \, g(\beta_i^N, \, \beta_{i+1}^N \, ) \, \right\vert^2 \, \right]$
	$\displaystyle \leq$	$\displaystyle \,\, \frac{C}{N} \,\, \E \left[ \sum_{i=1}^{N} \E_{i-1} \left[ \, \left( \, h(\chi_i^N) - h(\beta_i^N) \, \right)^2 \, \right] \, \right] \, .$

As for the previous lemma, our reformulation of the task maps the problem into the corresponding task in BNGJPS (2006) who prove a corresponding lemma in a more general setting. A detailed account of the requisite steps to complete this part of the proof may again be gleaned from BNGJS (2006, pp. 704-706).

Taken together, Lemma 2-3 and the first parts of Lemma 4-5 simply the consistency of our estimator under the minimal maintained assumptions. The second parts of Lemmas 4-5 are critical for the proof of the central limit theorem below.

A.5 Proposition 3: The CLT

Lemma 6 Under assumption (A1), we have

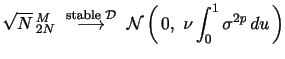
$\displaystyle \sqrt{N} \, \U^M_{2N} \,\, \overset{\text{stable }\mathcal{D}} \longrightarrow \,\, \mathcal{N}\left(\, 0, \,\, \nu\int_{0}^{1} \sigma^{2p}\,du \, \right)$

(27)

where the constant $\nu=\Var\left[g(Z_{0},Z_{1}\right]+2\,\Cov\left[g(Z_{0},Z_{1}),g(Z_{1},Z_{2})\right] \,$ for $\, Z_{0}, Z_{1}, Z_{2} \, \sim \, i.i.d. \mathcal{N}(0,1)$ .

Proof. Consider splitting the scaled return observations into blocks, the $k^{\text{th}}$ of which is the vector $\mathbf{\chi}_{k}^{M}= \{\sqrt{N}\Delta_{i}^{N}Y\}_{i\in\{(k-1)M+1,\ldots, kM\}}$ . The corresponding vector of observations from the approximating Brownian motion where volatility is held constant over the block is $\mathbf{\beta}_{k}^{N,M}=\{\beta_{i}^{N,M}\}_{i\in\{(k-1)M+1,\ldots, kM\}}$ . Next, define by $g_{M}(\cdot):\mathbb{R}^{M}\mapsto\mathbb{R}$ the block estimator of volatility:

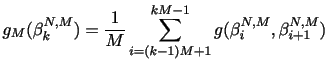
$\displaystyle g_{M}(\mathbf{\beta}_{k}^{N,M})=\frac{1}{M}\sum_{i=(k-1)M+1}^{kM-1}g(\beta_{i}^{N,M},\beta_{i+1}^{N,M})$

(28)

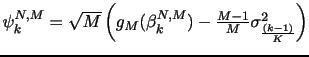We wish to apply Theorem IX.7.28 in Jacod and Shiryaev (2003) to $\sqrt{N} \, \U^{M}_{2N}$ . Defining the martingale difference sequence $\psi_{k}^{N,M}=\sqrt{M}\left(g_M(\mathbf{\beta}_k^{N,M})-\frac{M-1}{M} \sigma_{\frac{(k-1)}{K}}^{2}\right)$ we can write

$\displaystyle \sqrt{N} \, \U^{M}_{2N} \,\,$	$\displaystyle =\,\, \frac{1}{\sqrt{K}} \, \sum_{k=1}^{K} \psi_{k}^{N,M} \, + \, \frac{1}{\sqrt{N}} \, \sum_{k=1}^{K-1} \, \left(g(\,\beta_{kM}^{N,M},\,\beta_{kM+1}^{N,M}) \,-\, \E_{\frac{k-1}{K}}\left[g(\,\beta_{kM}^{N,M},\,\beta_{kM+1}^{N,M})\,\right]\,\right)$
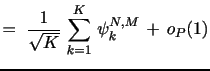
	$\displaystyle = \,\, \frac{1}{\sqrt{K}} \, \sum_{k=1}^{K} \, \psi_{k}^{N,M}\, + \, o_{P}(1)$	(29)

The last equality follows from the fact that each term in the second sum is centered and has bounded variance (given the uniform bound on $\sigma_t$ ). Thus the sum divided by $\sqrt{N}$ will tend to zero provided $K=o_{P}(N)$ .

We must now verify conditions (7.27)-(7.31) of Theorem IX.7.28. First note that $E[\,\psi_{k}^{N,M} \,\vert\,\mathcal{F}_{\frac{k-1}{K}} \,] \, = \, 0 \,$ so that condition (7.27) is trivially satisfied. Condition (7.28) follows from the fact that

$\displaystyle \frac{1}{K}\, \sum_{k=1}^{K} E\left[ \left\{ \, \sqrt{M} \left( \, g_M( \, \mathbf{\beta}_k^{M} \, ) \, - \, \frac{M-1}{M} \sigma_{\frac{(k-1)}{K}}^{\,p} \, \right) \, \right\}^{2} \, \vert \, \mathcal{F}_{\frac{k-1}{K}} \, \right] \, = \, \frac{\nu}{K} \, \sum_{k=1}^{K} \, \sigma^{2p}_{\frac{k-1}{K}} \, \overset{P}{\rightarrow} \, \nu \, \int_{0}^{1} \sigma^{2p}_{u}\,du$

(30)

where the convergence in probability (and in fact a.s.) is a consequence of the volatility process being cadlag and uniformly bounded. Next, we turn to condition (7.29). Let 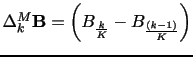$\Delta_{k}^{M}\mathbf{B}=\left(B_\frac{k}{K}-B_\frac{(k-1)}{K}\right)$ , then $E\left[\left.\psi_{k}^{N,M}\Delta_{k}^{M}\mathbf{B}\right\vert\mathcal{F}_{\frac{k-1}{K}}\right]=0$ , which follows from the fact that the variables $\psi_{k}^{N,M}$ are centered and that $g_{M}$ is an even function. Condition (7.30), stating that $E\left[(\psi_{k}^{N,M})^{2}\,\mathbf{1}_{\vert\psi_{k}^{N,M}\vert>\varepsilon}\right]\overset{P}{\rightarrow}0$ , follows straightforwardly from the fact that $\sigma$ is uniformly bounded.

Finally, let $\{N_{t}\}_{t\in[0;1]}$ be a bounded martingale orthogonal to (i.e. the covariation $\langle B,N\rangle_{t}=0\,\,a.s.$ ). We want to show that, for each block , $E[\psi_{k}^{N,M}\left(N_\frac{k}{K}-N_\frac{(k-1)}{K}\right)\vert\mathcal{F}_{\frac{k-1}{K}}]=0$ . For $t>\frac{k-1}{K}$ consider the martingale difference sequence $M_{t}=E\left[\left.\psi_{k}^{N,M}\right\vert\mathcal{F}_{t}\right]$ . 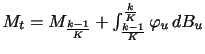By the martingale representation theorem, $M_{t}=M_{\frac{k-1}{K}}+\int_{\frac{k-1}{K}}^{\frac{k}{K}}\varphi_{u}\,dB_{u}$ for some predictable process $\varphi_{u}$ . Therefore the processes $\{M_{t}\}_{t>\frac{k-1}{K}}$ and $\{N_{t}-N_{\frac{k-1}{K}}\}_{t>\frac{k-1}{K}}$ are orthogonal and the product, $\{M_{t}(N_{t}-N_{\frac{k-1}{K}})\}$ is again a martingale which must then have mean zero. This verifies condition (7.31) and Theorem IX.7.28 in Jacod and Shiryaev (2003) states that as (and hence and ) tend to infinity:

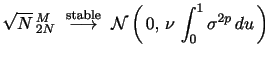
$\displaystyle {\sqrt{N}} \, \U_{2N}^{M} \,\, \overset{\text{stable}}{\longrightarrow} \,\, \mathcal{N}\left(\, 0, \, \nu \, \int_{0}^{1} \sigma^{2p}\,du \, \right)$

(31)

Lemma 7 Under the maintained assumptions, we have

$\displaystyle \sqrt{N} \, \left( \, \U_{2N} \, - \, \U^M_{2N} \, \right) \,\, \overset{P}\rightarrow \,\, 0$

(32)

Proof. Defining $\eta_{i}^{N,M}=g(\beta_i^{N,M},\beta_{i+1}^{N,M})-\E_{\lfloor(i-1)/M\rfloor M}\left[g(\beta_i^{N,M},\beta_{i+1}^{N,M})\right]$ , we note that $\left\{\frac{1}{\sqrt{N}}(\eta_i^{N}-\eta_i^{N,M})\right\}_{i\ge1}$ is a martingale difference sequence with respect to the filtration $\{\mathcal{F}_{i/N}\}$ . To show that $\sqrt{N}\left(\U_{2N}-\U^M_{2N}\right)=\sum_{i=1}^{N-1}(\eta_i^{N}-\eta_i^{N,M})/\sqrt{N}\rightarrow 0$ in probability, it therefore suffices (by Doobs inequality, e.g. Revuz and Yor (1999)) to show that

$\displaystyle \frac{1}{N} \,\, \E\left[\,\sum_{i=1}^{N-1}\left\vert g(\beta_i^{N},\,\beta_{i+1}^{N})\, - \, g(\beta_i^{N,M},\,\beta_{i+1}^{N,M})\right\vert^2\right] \,\, \rightarrow \,\, 0$

(33)

By the bound of $g(\cdot)$ we have

$\displaystyle \frac{1}{N} \, \E \left[\, \sum_{i=1}^{N-1}\left\vert\, g(\beta_i^{N},\, \beta_{i+1}^{N}) \, - \, g(\beta_i^{N,M},\,\beta_{i+1}^{N,M})\, \right\vert^2 \, \right] \, \leq \, \frac{C}{N} \, \E\left[\, \sum_{i=1}^{N} \, \E_{i-1}\left\vert\, (\beta_i^{N})^p \,-\, (\beta_i^{N,M})^p \, \right\vert^2 \, \right]$
$\displaystyle \leq \,\, \frac{C}{N} \, \E\left[\, \sum_{i=1}^{N} \left\vert\, \sigma_{\frac{i-1}{N}}^p \,-\, \sigma^p_{\frac{\lfloor(i-1)/M\rfloor M}{N}} \, \right\vert^2 \, \right] \,\, = \,\, C \,\, \E \int_0^1 \left(\, \sigma_{\frac{\, \lfloor uN \, \rfloor}{N}}^p \, - \, \sigma_{\frac{\, \lfloor uK \, \rfloor}{K}}^p \right)^2 \,du \,\, = \,\, o_P(1) \, ,$	(34)

where the last inequality follows from the uniform boundedness of $\sigma_t$ and Lebesgues theorem. $\qedsymbol$

Importantly, the specification of the volatility process in Assumption (A1) may be extended to include finite as well as infinite activity jump processes subject only to the regularity conditions stipulated in BNGJPS. This follows from the fact that the only terms in (13) affected by the inclusion of jumps are the terms $\sqrt{N}(V_{1N}-U_{1N})$ and $\sqrt{N}(V_{2N}-U_{2N})$ which map into the corresponding terms in BNGJPS as outlined in the proofs above. As such, the distributional results of the paper cover a wide range of underlying return generating processes.

A.6 The Asymptotic Distribution under Jump Alternatives

Suppose now the log price process is given as , where is a Brownian semimartingale of the form (4) while is a finite activity jump process. We show below that the above results continue to hold.³¹The key is that $\sqrt{N} \vert Y_{\frac{i}{N}}-Y_{\frac{i-1}{N}}\vert = O_{P}(\vert\log(N)\vert^{1/2})$ , which follows readily from Levy's modulus of continuity theorem for Brownian motion. This immediately yields:

Proposition 8 When is a finite activity jump process, the asymptotic distribution of the and estimators applied to the processes $\{X_t\}$ and $\{Y_t\}$ are identical.

Proof. As before, we deal only with the case as the case is analogous. On a given realization of the path there is a finite number of jumps, so (asymptotically) at most one of the terms $\, \vert \, X_{\frac{i}{N}} \, - \, X_{\frac{i-1}{N}} \,\vert \,$ or $\, \vert \, X_{\frac{i+1}{N}} \, - \, X_{\frac{i}{N}} \, \vert$ includes a jump. Therefore, each term in the estimator (up to a normalizing constant) is

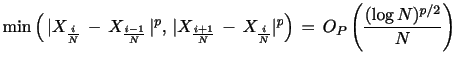
$\displaystyle \min \left( \, \vert X_{\frac{i}{N}} \, - \, X_{\frac{i-1}{N}} \, \vert^{p}, \, \vert X_{\frac{i+1}{N}} \, - \, X_{\frac{i}{N}}\vert^p\right) \, = \, O_{P}\left( \frac{(\log N)^{p/2}}{N} \right)$

regardless of whether a (single) jump occurred or not over $\, [\, \frac{i-1}{N}, \, \frac{i+1}{N} \,]$ . Since only finitely many terms differ,

$\displaystyle \sum_{j=1}^N\left[ \min \left(\vert X_{\frac{i}{N}}-X_{\frac{i-1}{N}}\vert^p, \vert X_{\frac{i+1}{N}}-X_{\frac{i}{N}}\vert^p\right) \, - \, \min \left(\vert Y_{\frac{i}{N}}-Y_{\frac{i-1}{N}}\vert^p, \vert Y_{\frac{i+1}{N}}-Y_{\frac{i}{N}}\vert^p\right) \right]\,$

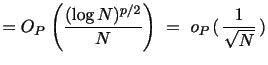
$\displaystyle = O_{P \,}\left( \frac{(\log N)^{p/2}}{N} \right) \,\, = \,\, o_{P \,}( \, \frac{1}{\sqrt{N}} \, )$

so neither consistency nor convergence in distribution is affected by the presence of finite activity jumps. $\qedsymbol$

A.7 Robust Neighborhood Truncation Estimators

We consider the family of robust neighborhood truncation (RNT) estimators on a block of i.i.d. $\mathcal{N}(0,\sigma^{2})$ returns, $\{Z_{1},\ldots,Z_{m}\}$ . The estimator is then constructed by taking the $j^{\text{th}}$ quantile of unbiased estimators of $\sigma^{p}$ on the block. Denoting these primitive estimators by $\mathcal{E}_{1},\ldots,\mathcal{E}_{H}$ , we can write the RNT estimator as

$\displaystyle RNT_N^{(j,\textbf{\emph{I}})}(p) \, = \, d_{(j,\textbf{\emph{I}})}(p) \, \frac{1}{(N-m+1)} \, \sum_{i=1}^{N-m+1} q_{j \,} \left[ \, \mathcal{E}_{1 \,}, \ldots , \, \mathcal{E}_{H \,} \right]$

where the $d_{(j,\textbf{\emph{I}})}(p)$ is a scaling factor.

Lemma 9 Let be a positive even integer and assume that the estimators $\mathcal{E}_{1},\ldots,\mathcal{E}_{H}$ satisfy the conditions of Proposition 1 and Proposition 2, then the robust neighborhood truncation estimator, $RNT_N^{(j,\textbf{\emph{I}})}(p)$ , defined in (35) is consistent for $\sigma^{p}$ and satisfies a CLT.

Proof. We need to verify the three properties,(8)-(9) and symmetry, of the $g(\cdot)$ function used in the theorem are satisfied when $g(\cdot)=RNT_N^{(j,\textbf{\emph{I}})}(p)$ . We deal with each condition in turn.

Clearly, if each primitive estimator $\mathcal{E}_{i}$ is symmetric, so is $RNT_N^{(j,\textbf{\emph{I}})}(p)$ . Moreover, if each $\mathcal{E}_{i}$ satisfies a bound of the type (8), so will $RNT_N^{(j,\textbf{\emph{I}})}(p)$ as it is simply an order statistic of such bounded functionals. Finally, assume that each $\mathcal{E}_{i}$ satisfies (9). Except on a null set, there exists a neighborhood around each m-tuple $(z_{1},\ldots,z_{m})$ , on which $RNT_N^{(j,\textbf{\emph{I}})}(p)=\mathcal{E}_{i}(z_{1}^{p},\ldots,z_{m}^{p})$ for some $1\le i\le H$ . Therefore it follows that also $RNT_N^{(j,\textbf{\emph{I}})}(p)$ satisfies (9). $\qedsymbol$

Remark 10 Since the NT estimators (up to a scale factor) essentially are a special case of RNT, the lemma applies to these as well.

B Noise Robustness Properties of the Ratio 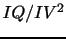$IQ/IV^{2}$

The ratio $IQ/IV^{2}$ plays an important role for both IV inference and jump attribution in finite samples. This section extends the analysis of Huang and Tauchen (2005) to show that the ratio $IQ/IV^{2}$ has certain desirable robustness features in the presence of microstructure noise. Following Ait-Sahalia and Mykland (2005), we assume that the true price process ( $p^{*}_{i}$ ) is observed at discrete points in time with an independent stationary (possibly autocorrelated) measurement error ( $u_{i}$ ) that results in an MA error structure in observed returns:

$\displaystyle p_{i} = p^{*}_{i} + u_{i} \,\,\Rightarrow\,\,r_{i}=r^{*}_{i}+\varepsilon_{i}\,\,$ where $\displaystyle \,\varepsilon_{i}=u_{i}-u_{i-1}$

For simplicity, we focus the discussion here on the (RV,RQ) pairing and denote:

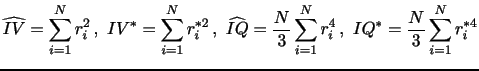
$\displaystyle \widehat{IV}=\sum_{i=1}^{N}r_{i}^{2}\,,\,\,IV^{*}=\sum_{i=1}^{N}r^{*2}_{i}\,,\,\, \widehat{IQ}=\frac{N}{3}\sum_{i=1}^{N}r_{i}^{4}\,,\,\,IQ^{*}=\frac{N}{3}\sum_{i=1}^{N}r^{*4}_{i}$

The presence of microstructure noise produces a bias in both the IQ and IV estimators of the form:

$\displaystyle E[\widehat{IQ}]$	$\displaystyle =$	$\displaystyle E[IQ^{}]+\frac{N^{2}}{3}E[\varepsilon_{i}^{4}]+2NE[IV^{}]E[\varepsilon_{i}^{2}]$
$\displaystyle E[\widehat{IV}^{2}]$	$\displaystyle =$	$\displaystyle E[IV^{2}] + NE[\varepsilon_{i}^{4}] + N(N-1)(E[\varepsilon_{i}^{2}])^{2}+2(N+2)E[IV^{}]E[\varepsilon_{i}^{2}]$
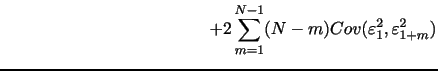
		$\displaystyle \hspace{1.8in}+2\sum_{m=1}^{N-1}(N-m)Cov(\varepsilon^{2}_{1},\varepsilon_{1+m}^{2})$	(35)

In the special case where $u_{i}\sim \mathcal{N}(0,\sigma^{2}_{u})$ is serially uncorrelated and denoting the noise to signal ratio $\lambda=\sigma_{u}^{2}/(\frac{1}{N}E[IV^{*}])$ , the expressions above simplify to,

$\displaystyle E[\widehat{IQ}]$	$\displaystyle =$	$\displaystyle E[IQ^{}]+4E[IV^{2}] (\lambda+\lambda ^2)$
$\displaystyle E[\widehat{IV}^{2}]$	$\displaystyle =$	$\displaystyle E[IV^{2}] + 4E[IV^{2}] (\lambda+\lambda ^2) + O\left(\frac{1}{N}\right)$	(36)

Under the null of no jumps, $\hat{IQ}, \hat{IV}$ are asymptotically unbiased and consistent and,

$\displaystyle \frac{\widehat{IQ}}{\widehat{IV}^{2}}$

$\displaystyle \overset{P}{\longrightarrow}$

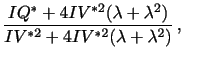$\displaystyle \frac{IQ^{*}+4IV^{*2}(\lambda+\lambda^{2})}{IV^{*2}+4IV^{*2}(\lambda+\lambda^{2})} \, , ~~$ as $\displaystyle \, N\rightarrow\infty$

The downward bias of the limiting ratio depends on the noise-to-signal ratio $\lambda$ and preaveraging of returns therefore plays an important role in reducing $\lambda$ and the associated distortions.³² Moreover, for sufficiently pre-averaged returns, there is very little evidence of serial correlation, as pointed out by COP (2010), and the serially uncorrelated noise case considered above is therefore the empirically most relevant case.³³In finite samples, this downward bias is further compounded by a pure Jensen (concavity) effect as readily seen from the Monte Carlo results for the Brownian motion scenario Path by path, the Cauchy-Schwartz inequality of course implies that $\widehat{IQ}/\widehat{IV}^{2}\ge\frac{1}{3}$ must hold regardless of the noise structure or other imperfections.

In the presence of other deviations from the Brownian null, forming the ratio $\widehat{IQ}/\widehat{IV}^{2}$ may have a stabilizing effect provided that the resulting distortion is uniform and roughly proportional to squared returns since this will lead to a cancelation in numerator and denominator. We see this effect at work in the simulations with price discreteness but in other instances, e.g., sparsity, it clearly fails. In cases involving additive distortions such as jumps, there will be no cancelation of biases and the ratio will tend to (in the case of upward biases) diverge at high frequencies due to the scaling by N in the numerator.

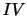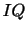C and estimators based on pre-averaged returns

Given equally-spaced (log) returns, $r_i = Y_\frac{i}{N} - Y_\frac {i-1}{N}$ , $i=1, \, \cdots , N$ , we define corresponding pre-averaged returns for any pre-averaging window size $2K \leq N$ :

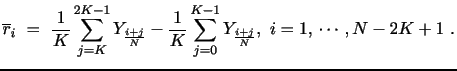
$\displaystyle \overline{r}_i ~=~ \frac{1}{K}\sum_{j=K}^{2K-1}Y_\frac{i+j}{N} - \frac {1}{K}\sum_{j=0}^{K-1}Y_\frac{i+j}{N}, \,\, i=1, \, \cdots , N-2K+1 ~.$

(37)

An equivalent definition with analytically more tractable expression is given by:

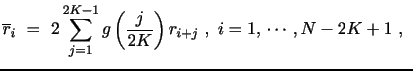
$\displaystyle \overline{r}_i ~=~ 2 \sum_{j=1}^{2K-1} g\left(\frac{j}{2K}\right) r_{i+j} ~,~i=1, \, \cdots , N-2K+1 ~,~$

(38)

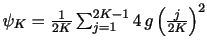where $g(x)=x\wedge(1-x)~,~x\in[0,1]$ is the pre-averaging kernel. We further define $\psi_{K} = \frac{1}{2K}\sum_{j=1}^{2K-1} 4 \, g\left(\frac {j}{2K}\right)^2$ as the finite sample analog of the variance scaling factor $\psi = \int_{0}^{1} 4 \, g(u)^2 du = \frac{1}{3}$ induced by the pre-averaging kernel.³⁴

Consider the following sub-samples of non-overlapping pre-averaged returns:

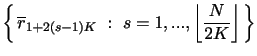
$\displaystyle \overline{S}_{1}$	$\displaystyle =$	$\displaystyle \left \{ \, \overline{r}_{1+2(s-1)K}~:~s=1,..., \left \lfloor \frac {N}{2K} \right \rfloor \, \right \}$
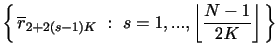
$\displaystyle \overline{S}_{2}$	$\displaystyle =$	$\displaystyle \left \{ \, \overline{r}_{2+2(s-1)K}~:~s=1,..., \left \lfloor \frac {N-1}{2K} \right \rfloor \, \right \}$
	$\displaystyle ...$
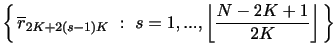
$\displaystyle \overline{S}_{2K}$	$\displaystyle =$	$\displaystyle \left \{ \, \overline{r}_{2K+2(s-1)K}~:~s=1,..., \left \lfloor \frac {N-2K+1}{2K} \right \rfloor \, \right \}$

Let $\widehat{IV}\left[\overline{S}_{i}\right]$ and $\widehat{IQ}\left [\overline{S}_{i}\right]$ , $i=1, \, \cdots , 2K$ denote the raw and estimates obtained on each sub-sample of pre-averaged returns. Then the pre-averaged (and sub-sampled) estimators $\widehat{IV}\left[ \overline {r}_{\cdot} \right]$ and $\widehat{IQ}\left[ \overline{r}_{\cdot} \right]$ for the full set of pre-averaged returns $\overline{r}_{\cdot} = \{\overline{r}_i\}_{i=1}^{N-2K+1}$ can be defined as follows:

$\displaystyle \widehat{IV}\left[ \overline{r}_{\cdot} \right]$	$\displaystyle =$	$\displaystyle \frac{1}{2K} \sum_{i=1}^{2K} {\frac{1}{\psi}\widehat{IV}\left[\overline{S}_{i}\right]}$
$\displaystyle \widehat{IQ}\left[ \overline{r}_{\cdot} \right]$	$\displaystyle =$	$\displaystyle \frac{1}{2K} \sum_{i=1}^{2K} {\frac{1}{\psi^{2}}\widehat{IQ}\left[\overline {S}_{i}\right]}$

After incorporating finite sample bias correction, these take the following final form that we use in our pre-averaged implementation of all estimators:

$\displaystyle \widehat{IV}^{Adj}\left[ \overline{r}_{\cdot} \right]$	$\displaystyle =$	$\displaystyle \frac{1}{2K} \sum_{i=1}^{2K} {\frac{1}{\psi_{K}} \, \frac{\frac{N}{2K}} { \left \lfloor \frac{N-i+1}{2K} \right \rfloor } \widehat{IV} \left[\overline{S}_{i}\right]}$
$\displaystyle \widehat{IQ}^{Adj}\left[ \overline{r}_{\cdot} \right]$	$\displaystyle =$	$\displaystyle \frac{1}{2K} \sum_{i=1}^{2K} {\frac{1}{\psi_{K}^{2}} \, \frac{\left(\frac{N}{2K}\right)^ {2}}{ \left \lfloor \frac{N-i+1}{2K} \right \rfloor^{2}} \, \widehat{IQ}\left[\overline {S}_{i}\right]}$

Consistency and asymptotic normality are clearly preserved by pre-averaging and sub-sampling, while noise-robustness improves. In particular, bounce-backs are near perfectly annihilated given that adjacent returns are subject to almost identical kernel weights. For further details on pre-averaging please refer to Podolskij and Vetter (2009) and Jacod, Li, Mykland, Podolskij and Vetter (2009) among others.

Footnotes

** Torben G. Andersen, Kellogg School of Management, Northwestern University, 2001 Sheridan Road, Evanston, IL 60208, USA; NBER; CREATES; t-andersen@northwestern.edu.
Dobrislav Dobrev: Federal Reserve Board of Governors, 20th Street and Constitution Avenue NW, Washington, DC 20551, USA; Dobrislav.P.Dobrev@frb.gov.
Ernst Schaumburg: Federal Reserve Bank of New York, 33 Liberty Street, New York, NY 10045, USA; Ernst.Schaumburg@gmail.com.
We are grateful to two anonymous referees as well as the editor, Jun Yu, for comments. We also thank participants at the 2010 SETA Conference at Singapore Management University and the "Nonlinear and Financial Econometrics Conference: A Tribute to A. Ronald Gallant," Toulouse, France, May 2011, the NBER-NSF Time Series Conference, Michigan State University, September 16-17, 2011, the 5th International Conference on Computational and Financial Econometrics, London, December 17-19, 2011, the 5th Annual SoFiE Conference - Oxford-Man Institute, June 20-22, 2012, the North American Summer Meeting of the Econometric Society, Evanston, June 28 - July 1, 2012, along with Federico Bandi, Peter R. Hansen, Andrew Patton, Peter C. B. Phillips and Kevin Sheppard for comments on an earlier draft. Excellent research assistance was provided by Patrick Mason.
Andersen gratefully acknowledges financial support from the NSF through a grant to the NBER and by CREATES funded by the Danish National Research Foundation.
The views in this paper are solely those of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System, the Federal Reserve Bank of New York or of any other person associated with the Federal Reserve System. Return to text

1. Corresponding measures were previously considered on an ad hoc basis, see, e.g., Schwert (1989), Hsieh (1991) and Zhou (1996). Return to text

2. Additional work regarding inference on the jump and continuous components of the return variation is developed in BNS (2004b, 2006), while general methodological insights were provided by Jacod and Protter (1998). Subsequently, market microstructure complications were addressed as part of the drive to exploit tick level data, see, e.g., Zhang, Mykland and Ait-Sahalia (2005), Bandi and Russell (2008), and Barndorff-Nielsen, Hansen, Lunde and Shephard, henceforth BNHLS, (2008). Return to text

3. Both studies explore the reliability of the procedures, but only under relatively ideal circumstances and not with a focus on the IQ estimator but rather the jump test statistic. Return to text

4. We rely on the MedRV/MedRQ estimators of Andersen, Dobrev and Schaumburg (2009) here, but any other sensible pair of robust IV and IQ estimators would suffice in this particular case as the evidence for a single significant jump is compelling and the associated empirical inference problem thus very straightforward. The robust estimators will be introduced later in the paper. Return to text

5. As a consequence, real-time predictions regarding the expected volatility over the following trading days will likely also be exaggerated on 2/26/2008 because the jump component of QV typically is much less persistent than the IV component, see, e.g., Andersen, Bollerslev and Diebold (2007). Return to text

6. Of course, the proofs for all our new results, provided in Appendix A, allow for a general drift term. Return to text

7. Naturally, additional dampening is required to establish a CLT for the power variation measures. In this case, 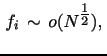$\, f_i \, \sim \, o(N^{\tfrac{1}{2}}),\,$ for $\, i \in I_J$ Return to text

8. For IQ estimation based on a block with five returns, we have $\mu_4^{(1,5)} = 35.0, \, \mu_4^{(2,5)} = 5.74, \, \mu_4^{(3,5)} = 1.44, \, \mu_4^{(4,5)} = 0.40, \, and \, \mu_4^{(5,5)} = 0.086$ . Hence, the largest normalization constant exceeds the smallest one by a factor of several hundred; see Table 1 for additional information. Return to text

9. For the integrated variance, these estimators may be interpreted as a redesigned version of the original Quantile Realized Variation, or QRV, estimator of Christensen, Oomen and Podolskij (COP) (2008), where it is applied to quantiles based on absolute rather than raw returns. The adaptation of QRV to cover the ADS (2012) nearest neighbor truncation estimators is discussed in COP (2010). This was also previously proposed during a conference discussion of COP (2010) by Kevin Sheppard, see also the comments in the realized_quantile_variance function in his Oxford MFE Toolbox. Return to text

10. In practice, finite sample complications can render the procedure less successful. One may want to avoid estimators that are highly sensitive to microstructure noise or jumps. Likewise, high correlation across estimators can generate optimal combinations that are extreme which may induce a degree of instability. Return to text

11. This is analogous to the use of linear combinations for the QRV estimator explored by COP (2008). Return to text

12. See, e.g., Jacod and Shiryaev (2003), Chapter IX, for an introduction to stable convergence. Return to text

13. We intend to apply these estimators in a setting with microstructure noise. As discussed in Section 4.2, this can be accommodated in the finite activity jump scenario via pre-averaging with a relatively large window size, resulting in a suboptimal convergence rate, but added robustness to noise. The literature on inference in the presence of infinite activity jumps and noise is limited. However, the findings for MPV estimators in Podolskij and Vetter (2009) and Hautsch and Podolskij (2010) suggest constructive results are feasible. Establishing formal results for this case falls outside the scope of the present paper. Return to text

14. In this notation, the initial "R" references the RNT estimator, "Min" ("Med") signals that we exploit the smallest (median) realization of the underlying NT estimators, and "RQ" ("RV") indicates realized quarticity (realized variance) estimation, that is (). It remains implicit that we take , but retain only the three largest absolute returns in constructing the estimator. Return to text

15. P1: Retain only observations with time stamps between 9:30am and 4:00pm. P2: Retain only trades with positive prices. P3: Retain only trades originating from the main exchange (NYSE for all stocks except MSFT and INTL for which it is NASDAQ). T1: Delete entries with corrected trades. T2: Delete entries with abnormal sale condition. T3: If multiple trades occurred with the same time stamp, use the median price. T4: Delete entries with prices above the ask (or under the bid) by more than one bid-ask spread. Return to text

16. Analogous to the scaling factors induced by the pre-averaging kernel, the efficiency with subsampling depends on the pre-averaging scheme as well as the length of the pre-averaging window relative to sample size. Hence, applications involving subsampling must develop a suitable estimate of the terms involving the efficiency factor $\eta$ in Section 3. One feasible approach is simulation. Return to text

17. Recognizing the downward bias, CPR develop an iterative rescaling procedure to alleviate this effect. Return to text

18. We confirm that our filtering procedure under the BM null, applied to pre-averaged returns, is active for about 1-in- $10^{6}$ return blocks, while the CPR filter is applied to roughly 1-in- $10^{3}$ returns on average. Return to text

19. These return intervals span the range that is relevant for our empirical application. Findings based on a more comprehensive set of frequencies are reported in ADS (2011). Return to text

20. This choice facilitates effective cancelation of noise and outliers across the numerator and denominator. Return to text

21. Recall, we abandon the QRV style estimators for IQ due to the rapidly deteriorating performance in estimating higher order return variation under realistic market conditions. Return to text

22. The improved performance for TBQ is due to a fortuitous cancelation of the biases of the numerator and denominator under the BM null. Return to text

23. MPV and MPQ, in particular, as they are based on products of adjacent (absolute) returns. Return to text

24. When using tick sampled data, we are implicitly converting the calendar time scale to a tick scale, where time evolves linearly in tick time. This implies that the estimators are consistent for IQ in tick time, but not in calendar time. Importantly, in this setting the (tick time) IQ represents the relevant quantity for assessing the asymptotic variance of the (tick time based) IV estimator and for inference regarding jumps. Return to text

25. Ex post, we find no qualitative differences in results between the two samples, so we only report findings for the initial sample. The full set of results may be gleaned from ADS (2011). Return to text

26. Of course, this reflects the different philosophy behind the mild functional truncation filtering relative to TRQ and TBQ. The latter employ truncation of single returns as the primary tool for achieving jump robustness, and thus need to ensure that - asymptotically - all jumps are prevented from impacting the IQ estimator. This requires aggressive truncation and, inevitably, some truncation of diffusive returns, motivating the CPR adjustment to mitigate the resulting finite-sample bias, as discussed in Section 5. Return to text

27. We confirm that alternative robust volatility-of-volatility measures lead to qualitatively similar results. Return to text

28. The distance from the (non-functional filtered) RV curve to the set of robust IV measures provides an estimate of the average jump contribution to the quadratic return variation. Return to text

29. For each individual robust estimator, we regressed the difference of the daily realized power variation estimate across the distinct frequencies against the daily VoV measure, allowing for a separate intercept term but enforcing a common slope across the stocks. The detailed results are available in ADS (2011). Return to text

30. As argued in Barndorf-Nielsen, Graversen, Podolskij, Jacod and Shephard (2006), henceforth BNGJPS, this follows from working with the stopped versions of the processes: $T_t^{(k)}=Y_{t\wedge T_k}$ and $\sigma_t^{(k)}=\sigma_{t\wedge T_k}$ where $T_k=\inf\{t\vert \vert a_t\vert+\vert\sigma_{t_-}\vert\ge k\}$ and $T_k\nearrow\infty$ a.s. Return to text

31. As for the volatility process, the specification may be generalized to infinite activity jump processes along the lines of Barndorff-Nielsen et al (2006c). Return to text

32. By Hölder's inequality, $IQ\ge IV^{2}$ , so that the distortion due to microstructure noise in general will result in a downward bias in the limiting ratio. Return to text

33. In the general case where $\varepsilon_{i}$ is a MA(q) process: $\varepsilon_{i}=\nu_{i}+\sum_{k=1}^{q}\theta_{k}\nu_{i-k}$ , we have

$\displaystyle E[\widehat{IQ}]$ $\displaystyle =$ $\displaystyle E[IQ^{*}]+E[IV^2] \left(\theta _1^2+\ldots+\theta _q^2+1\right){}^2 \lambda ^2+2 E[IV^2] \left(\theta _1^2+\ldots+\theta _q^2+1\right) \lambda$

$\displaystyle E[\widehat{IV}^{2}]$ $\displaystyle =$ $\displaystyle E[IV^{*2}] + E[IV^2] \left(\theta _1^2+\ldots+\theta _q^2+1\right){}^2 \lambda ^2+2 E[IV^2] \left(\theta _1^2+\ldots+\theta _q^2+1\right) \lambda+ O\left(\frac{1}{N}\right)$

Return to text

34. Note that the factor 4 arises from the multiplication by 2 in equation (38). Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

$\displaystyle E[\widehat{IQ}]$	$\displaystyle =$	$\displaystyle E[IQ^{*}]+E[IV^2] \left(\theta _1^2+\ldots+\theta _q^2+1\right){}^2 \lambda ^2+2 E[IV^2] \left(\theta _1^2+\ldots+\theta _q^2+1\right) \lambda$
$\displaystyle E[\widehat{IV}^{2}]$	$\displaystyle =$	$\displaystyle E[IV^{*2}] + E[IV^2] \left(\theta _1^2+\ldots+\theta _q^2+1\right){}^2 \lambda ^2+2 E[IV^2] \left(\theta _1^2+\ldots+\theta _q^2+1\right) \lambda+ O\left(\frac{1}{N}\right)$

A Robust Neighborhood Truncation Approach to Estimation of Integrated Quarticity

1 Introduction

2 Overview of Jump-Robust Power Variation Estimation

2.1 The Theoretical Setting

2.2 Estimating Power Variation under the Diffusive Null Hypothesis

2.3 Jump-Robust Power Variation Estimation

2.4 Alternative Jump-Robust Power Variation Estimators

2.4.1 Multi-Power Variation Estimators

2.4.2 Truncated Power Variation Estimators

2.4.3 Neighborhood Truncation Estimators

2.4.4 Combining Power Variation Estimators

3 Robust Neighborhood Truncation Estimation

3.1 Theory

3.2 Illustration

4 Robustification Towards Noise and Errors

4.1 Eliminating Obvious Errors in the Tick-by-Tick Data

4.2 Pre-Averaging

4.3 Filtering via Truncation of Return Functionals

4.4 Using the Ratio for Robust IV Inference

5 Finite Sample Simulation Evidence

5.1 Estimators

5.2 Simulation Results

5.2.1 The Brownian Motion Benchmark

5.2.2 Jumps in Returns

5.2.3 Time-Varying Volatility

5.2.4 Microstructure Noise

6 An Illustration for the Dow Jones 30 Stocks

6.1 Truncation of Return Functionals

6.2 The Intraday Volatility Pattern

6.3 Signature Plots for Integrated Power Variation

7 Conclusion

References

A Proofs of Propositions

A.1 Basic Setting

A.2 The Min and Med Power Variation Estimators

A.3 Additional Notation and Preliminary Results

A.4 Proposition 2: Consistency

A.5 Proposition 3: The CLT

A.6 The Asymptotic Distribution under Jump Alternatives

A.7 Robust Neighborhood Truncation Estimators

B Noise Robustness Properties of the Ratio

C and estimators based on pre-averaged returns

Footnotes

4.4 Using the Ratio $\, \sqrt{\widehat{IQ}} \, / \, {\widehat{IV}} \,$ for Robust IV Inference

B Noise Robustness Properties of the Ratio $IQ/IV^{2}$