
Board of Governors of the Federal Reserve System
International Finance Discussion Papers
Number 1092, November 2013 --- Screen Reader
Version*
Can Structural Reforms Help Europe?1
NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.
Abstract:
Structural reforms that increase competition in product and labor markets are often indicated as the main policy option available for peripheral Europe to regain competitiveness and boost output. We show that, in a crisis that pushes the nominal interest rate to its lower bound, these reforms do not support economic activity in the short run, and may well be contractionary. Absent the appropriate monetary stimulus, reforms fuel expectations of prolonged deflation, increase the real interest rate, and depress aggregate demand. Our findings carry important implications for the current debate on the timing and the design of structural reforms in Europe.
Keywords: Structural reforms, zero lower bound, monetary union
JEL classification: E52, E58, F33, F41
"...the biggest problem we have for growth in Europe is the problem of lack of competitiveness that has been accumulated in some of our Member States, and we need to make the reforms for that competitiveness.
...to get out of this situation requires...structural reforms, because there is an underlying problem of lack of competitiveness in some of our Member States."
José Manuel Durão Barroso
President of the European Commission
Closing Remarks following the State of the Union 2012
Strasbourg, September 12, 2012
1 Introduction
As the European Monetary Union (EMU) struggles to recover from the global financial crisis and the European debt crisis, conventional wisdom among academics and policymakers suggests that structural reforms that increase competition in product and labor markets are the main policy option to foster growth in the region.
This paper is bad news: In a standard dynamic stochastic general equilibrium model calibrated to match salient features of the EMU economy, we show that structural reforms do not improve output during a crisis. In fact, these reforms may entail near-term contractionary effects when monetary policy is constrained by the zero lower bound (ZLB). Even more disappointingly, if agents foresee that such reforms may be reversed (which may quite likely be the case, as several interest groups have strong incentives to oppose wide-ranging liberalizations), these policies can generate large short-term output losses, further deepening the ongoing recession.
Figure 1: Real GDP
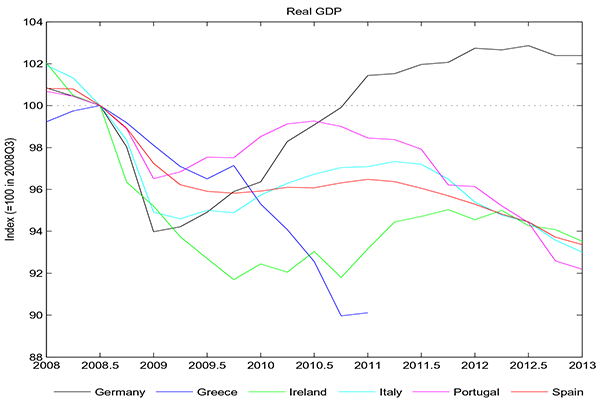
Real GDP (= 100 in 2008Q3) in Germany (black), Greece (blue), Ireland (green), Italy (cyan), Portugal (magenta) and Spain (red).
Data for Figure 1
| GE | GR | IR | IT | PT | SP | |
|---|---|---|---|---|---|---|
| 2008 - Q1 | 1.008 | 0.992 | 1.020 | 1.019 | 1.007 | 1.008 |
| 2008 - Q2 | 1.005 | 0.997 | 1.005 | 1.013 | 1.005 | 1.008 |
| 2008 - Q3 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 2008 - Q4 | 0.980 | 0.992 | 0.963 | 0.984 | 0.989 | 0.989 |
| 2009 - Q1 | 0.940 | 0.981 | 0.952 | 0.949 | 0.965 | 0.972 |
| 2009 - Q2 | 0.942 | 0.971 | 0.937 | 0.946 | 0.968 | 0.962 |
| 2009 - Q3 | 0.949 | 0.965 | 0.927 | 0.950 | 0.975 | 0.959 |
| 2009 - Q4 | 0.959 | 0.971 | 0.917 | 0.949 | 0.975 | 0.958 |
| 2010 - Q1 | 0.964 | 0.953 | 0.924 | 0.957 | 0.985 | 0.959 |
| 2010 - Q2 | 0.983 | 0.941 | 0.920 | 0.963 | 0.991 | 0.961 |
| 2010 - Q3 | 0.991 | 0.926 | 0.930 | 0.967 | 0.993 | 0.961 |
| 2010 - Q4 | 0.999 | 0.900 | 0.918 | 0.970 | 0.990 | 0.963 |
| 2011 - Q1 | 1.014 | 0.901 | 0.932 | 0.971 | 0.985 | 0.965 |
| 2011 - Q2 | 1.015 | 0.944 | 0.973 | 0.984 | 0.964 | |
| 2011 - Q3 | 1.020 | 0.947 | 0.972 | 0.979 | 0.961 | |
| 2011 - Q4 | 1.021 | 0.950 | 0.965 | 0.962 | 0.957 | |
| 2012 - Q1 | 1.027 | 0.946 | 0.954 | 0.961 | 0.953 | |
| 2012 - Q2 | 1.027 | 0.950 | 0.948 | 0.952 | 0.948 | |
| 2012 - Q3 | 1.029 | 0.943 | 0.944 | 0.944 | 0.945 | |
| 2012 - Q4 | 1.024 | 0.941 | 0.936 | 0.926 | 0.937 | |
| 2013 - Q1 | 1.024 | 0.935 | 0.930 | 0.922 | 0.934 | |
| 2013 - Q2 | 1.031 | 0.939 | 0.927 | 0.932 | 0.933 |
The 2008-9 global financial crisis hit the EMU hard, resulting in large and widespread output contractions (Figure 1). While core EMU countries, such as Germany, have mostly recovered their output losses, the aftermath has been particularly difficult for peripheral countries (Greece, Ireland, Italy, Portugal, and Spain). These countries have remained in severe recessions ever since 2008, eventually triggering doubts about the sustainability of their public finances and putting in danger the entire Euro project. Understanding the reasons for this asymmetric response between the core and the periphery of the EMU and what kind of policies can address this situation are thus questions of first-order importance in the current debate.
Figure 2: Current Account and Real Exchange Rate (Relative to Germany)
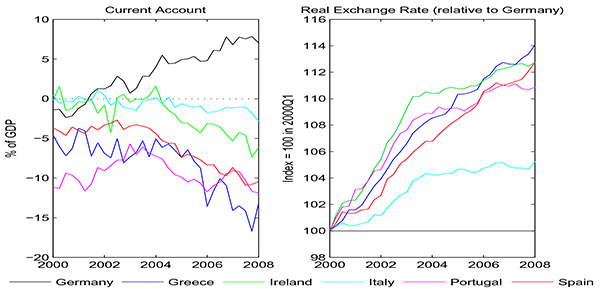
Balance on the current account in % of GDP (left panel) and real exchange rate relative to Germany normalized to 100 in 2000Q1 (right panel) for Germany (black), Greece (blue), Ireland (green), Italy (cyan), Portugal (magenta) and Spain (red).
Data for Figure 2: Current Account
| Germany | Greece | Ireland | Italy | Portugal | Spain | Netherlands | France | |
|---|---|---|---|---|---|---|---|---|
| 2000 - Q1 | -1.4 | -4.6 | -0.2 | 0.5 | -11.2 | -3.7 | 2.9 | 1.7 |
| 2000 - Q2 | -1.4 | -6.0 | 1.5 | -0.6 | -11.3 | -4.1 | 2.4 | 2.1 |
| 2000 - Q3 | -2.4 | -7.2 | -1.5 | -0.3 | -9.4 | -4.7 | -1.3 | 1.2 |
| 2000 - Q4 | -2.2 | -6.3 | -1.2 | -0.4 | -9.7 | -3.6 | 4.3 | 0.8 |
| 2001 - Q1 | -1.2 | -3.7 | -0.4 | 0.3 | -10.3 | -4.0 | 2.0 | 1.6 |
| 2001 - Q2 | -0.7 | -4.1 | -0.5 | -0.1 | -11.6 | -4.4 | 1.4 | 1.1 |
| 2001 - Q3 | 0.6 | -7.2 | -0.1 | -0.2 | -10.8 | -3.5 | 4.4 | 2.3 |
| 2001 - Q4 | 1.3 | -5.6 | -1.8 | 1.1 | -8.7 | -3.9 | 2.7 | 2.0 |
| 2002 - Q1 | 1.2 | -6.9 | -0.8 | 0.4 | -9.1 | -3.3 | 3.0 | 1.3 |
| 2002 - Q2 | 1.6 | -7.5 | -4.3 | -0.8 | -8.5 | -3.1 | -0.4 | 1.3 |
| 2002 - Q3 | 2.8 | -5.0 | 0.1 | -0.3 | -7.7 | -2.7 | 4.0 | 1.1 |
| 2002 - Q4 | 2.2 | -8.1 | 0.6 | -1.1 | -7.7 | -3.9 | 4.0 | 1.3 |
| 2003 - Q1 | 0.7 | -7.4 | -0.5 | -1.3 | -5.7 | -3.5 | 2.3 | 0.8 |
| 2003 - Q2 | 1.3 | -6.8 | 0.0 | -1.5 | -7.1 | -3.3 | 6.0 | 0.7 |
| 2003 - Q3 | 2.8 | -5.3 | -0.1 | -0.3 | -6.1 | -3.5 | 6.3 | 0.6 |
| 2003 - Q4 | 2.8 | -7.3 | 0.3 | -0.2 | -6.9 | -3.7 | 7.7 | 0.9 |
| 2004 - Q1 | 4.0 | -5.1 | 1.6 | 0.2 | -7.3 | -4.4 | 6.3 | 0.8 |
| 2004 - Q2 | 5.5 | -6.1 | -0.6 | -0.7 | -7.6 | -5.3 | 7.4 | 1.0 |
| 2004 - Q3 | 4.4 | -5.7 | -1.5 | 0.2 | -8.8 | -5.6 | 7.2 | 0.2 |
| 2004 - Q4 | 4.5 | -6.5 | -2.0 | -1.1 | -9.6 | -5.7 | 9.8 | 0.3 |
| 2005 - Q1 | 4.9 | -7.4 | -3.0 | -0.7 | -9.9 | -7.4 | 7.3 | -0.6 |
| 2005 - Q2 | 5.0 | -6.4 | -3.1 | -0.9 | -10.5 | -7.0 | 8.0 | -0.2 |
| 2005 - Q3 | 5.3 | -7.9 | -3.7 | -1.1 | -10.2 | -7.3 | 7.5 | -0.4 |
| 2005 - Q4 | 4.7 | -8.8 | -4.3 | -0.9 | -10.7 | -7.7 | 6.9 | -0.7 |
| 2006 - Q1 | 4.8 | -13.6 | -3.1 | -1.8 | -11.8 | -8.4 | 10.2 | -0.4 |
| 2006 - Q2 | 6.1 | -11.6 | -3.2 | -1.7 | -11.0 | -8.3 | 10.0 | -0.9 |
| 2006 - Q3 | 6.1 | -10.1 | -3.6 | -1.5 | -10.5 | -9.4 | 9.4 | -0.7 |
| 2006 - Q4 | 7.8 | -11.0 | -4.5 | -1.1 | -9.5 | -9.7 | 7.8 | -0.3 |
| 2007 - Q1 | 6.8 | -14.1 | -5.3 | -1.2 | -9.1 | -8.7 | 8.2 | -0.1 |
| 2007 - Q2 | 7.8 | -13.5 | -4.3 | -1.1 | -9.2 | -9.7 | 6.3 | -1.5 |
| 2007 - Q3 | 7.5 | -14.2 | -4.6 | -1.1 | -10.3 | -10.9 | 5.2 | -0.9 |
| 2007 - Q4 | 7.8 | -16.7 | -7.4 | -1.9 | -11.7 | -10.8 | 7.0 | -1.5 |
| 2008 - Q1 | 7.1 | -13.2 | -6.2 | -2.8 | -11.9 | -10.5 | 5.7 | -1.4 |
| 2008 - Q2 | 6.9 | -15.8 | -5.4 | -1.9 | -12.5 | -10.2 | 4.7 | -2.2 |
| 2008 - Q3 | 5.8 | -16.1 | -7.8 | -3.2 | -13.4 | -9.0 | 5.4 | -2.1 |
| 2008 - Q4 | 5.0 | -14.9 | -3.4 | -3.6 | -12.8 | -8.9 | 1.2 | -1.3 |
| 2009 - Q1 | 4.4 | -10.3 | -2.7 | -2.5 | -11.1 | -5.7 | 2.7 | -0.9 |
| 2009 - Q2 | 5.5 | -11.6 | -2.3 | -2.1 | -10.3 | -4.0 | 6.3 | -1.9 |
| 2009 - Q3 | 6.5 | -11.5 | -2.3 | -2.1 | -10.1 | -4.1 | 5.7 | -0.6 |
| 2009 - Q4 | 7.4 | -11.3 | -2.1 | -1.3 | -12.1 | -5.5 | 5.8 | -1.9 |
| 2010 - Q1 | 6.0 | -13.5 | 0.5 | -3.0 | -10.3 | -4.1 | 7.6 | -1.0 |
| 2010 - Q2 | 5.7 | -7.0 | 0.6 | -3.8 | -12.8 | -5.2 | 7.3 | -1.3 |
| 2010 - Q3 | 6.1 | -10.9 | 1.9 | -3.7 | -9.3 | -4.3 | 8.4 | -1.9 |
| 2010 - Q4 | 6.8 | -8.9 | 1.5 | -3.7 | -10.0 | -4.7 | 7.7 | -2.2 |
| 2011 - Q1 | 6.9 | -10.2 | -1.9 | -3.9 | -8.0 | -4.3 | 9.5 | -2.3 |
| 2011 - Q2 | 5.8 | -10.7 | 2.3 | -3.6 | -9.9 | -3.5 | 10.0 | -2.1 |
| 2011 - Q3 | 6.2 | -10.6 | 1.9 | -3.0 | -5.9 | -3.0 | 10.5 | -2.1 |
| 2011 - Q4 | 6.1 | -8.4 | 2.0 | -1.9 | -4.2 | -3.6 | 10.3 | -1.4 |
| 2012 - Q1 | 6.8 | -5.3 | 0.4 | -1.5 | -4.4 | -3.4 | 10.6 | -2.4 |
| 2012 - Q2 | 6.9 | -4.0 | 9.0 | -0.6 | -1.0 | -1.6 | 9.2 | -2.7 |
| 2012 - Q3 | 7.6 | -0.9 | 5.5 | -0.5 | -0.4 | -0.1 | 10.0 | -2.1 |
| 2012 - Q4 | 7.0 | -1.1 | 0.2 | -0.4 | 1.9 | 9.9 | -2.5 |
Data for Figure 2: Real Exchange Rate (Relative to Germany)
| GERMANY | GREECE | IRELAND | ITALY | PORTUGAL | SPAIN | |
|---|---|---|---|---|---|---|
| 2000 - Q1 | 100 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| 2000 - Q2 | 100 | 100.40 | 101.21 | 100.34 | 101.04 | 100.59 |
| 2000 - Q3 | 100 | 100.79 | 102.10 | 100.59 | 101.83 | 101.45 |
| 2000 - Q4 | 100 | 101.59 | 102.29 | 100.40 | 101.87 | 101.32 |
| 2001 - Q1 | 100 | 101.59 | 102.31 | 100.41 | 103.12 | 101.35 |
| 2001 - Q2 | 100 | 101.94 | 102.97 | 100.56 | 103.17 | 101.60 |
| 2001 - Q3 | 100 | 102.70 | 103.81 | 100.67 | 103.78 | 101.65 |
| 2001 - Q4 | 100 | 103.40 | 104.76 | 101.23 | 104.55 | 102.38 |
| 2002 - Q1 | 100 | 103.93 | 105.38 | 101.15 | 104.62 | 102.67 |
| 2002 - Q2 | 100 | 104.65 | 106.67 | 101.70 | 105.53 | 103.91 |
| 2002 - Q3 | 100 | 105.43 | 107.25 | 102.25 | 106.58 | 104.28 |
| 2002 - Q4 | 100 | 105.98 | 108.19 | 102.69 | 107.38 | 105.06 |
| 2003 - Q1 | 100 | 106.60 | 109.24 | 102.92 | 107.60 | 105.43 |
| 2003 - Q2 | 100 | 107.40 | 110.16 | 103.79 | 108.37 | 105.95 |
| 2003 - Q3 | 100 | 107.82 | 110.17 | 104.01 | 108.64 | 106.34 |
| 2003 - Q4 | 100 | 108.22 | 110.51 | 104.33 | 108.89 | 106.78 |
| 2004 - Q1 | 100 | 108.54 | 110.40 | 104.23 | 108.87 | 106.75 |
| 2004 - Q2 | 100 | 108.69 | 110.40 | 104.23 | 109.36 | 107.28 |
| 2004 - Q3 | 100 | 108.82 | 110.74 | 104.34 | 109.19 | 107.72 |
| 2004 - Q4 | 100 | 109.31 | 110.86 | 104.34 | 109.26 | 108.13 |
| 2005 - Q1 | 100 | 110.33 | 110.74 | 104.66 | 109.29 | 108.44 |
| 2005 - Q2 | 100 | 110.36 | 110.75 | 104.66 | 109.06 | 108.82 |
| 2005 - Q3 | 100 | 110.47 | 110.97 | 104.45 | 109.41 | 109.10 |
| 2005 - Q4 | 100 | 110.69 | 110.97 | 104.45 | 109.66 | 109.53 |
| 2006 - Q1 | 100 | 111.49 | 111.40 | 104.76 | 110.46 | 110.55 |
| 2006 - Q2 | 100 | 111.83 | 111.62 | 104.86 | 110.57 | 110.80 |
| 2006 - Q3 | 100 | 112.45 | 112.16 | 105.17 | 110.83 | 111.19 |
| 2006 - Q4 | 100 | 112.74 | 112.27 | 105.16 | 111.02 | 111.00 |
| 2007 - Q1 | 100 | 112.61 | 112.36 | 104.85 | 110.94 | 111.12 |
| 2007 - Q2 | 100 | 112.58 | 112.57 | 104.75 | 111.12 | 111.30 |
| 2007 - Q3 | 100 | 113.06 | 112.67 | 104.75 | 110.75 | 111.46 |
| 2007 - Q4 | 100 | 113.35 | 112.43 | 104.65 | 110.67 | 112.06 |
| 2008 - Q1 | 100 | 114.06 | 112.74 | 105.24 | 110.86 | 112.73 |
| 2008 - Q2 | 100 | 114.54 | 113.24 | 105.43 | 111.08 | 113.10 |
| 2008 - Q3 | 100 | 114.71 | 112.81 | 105.52 | 110.61 | 113.26 |
| 2008 - Q4 | 100 | 114.87 | 112.92 | 105.92 | 110.58 | 112.89 |
| 2009 - Q1 | 100 | 115.30 | 112.00 | 105.92 | 109.85 | 112.47 |
| 2009 - Q2 | 100 | 115.27 | 111.27 | 106.11 | 109.60 | 112.10 |
| 2009 - Q3 | 100 | 116.04 | 110.24 | 106.11 | 109.39 | 112.60 |
| 2009 - Q4 | 100 | 116.77 | 109.52 | 106.30 | 109.39 | 112.81 |
| 2010 - Q1 | 100 | 117.98 | 108.49 | 106.49 | 109.24 | 113.07 |
| 2010 - Q2 | 100 | 119.86 | 107.78 | 106.58 | 109.57 | 113.48 |
| 2010 - Q3 | 100 | 121.09 | 107.69 | 106.77 | 110.23 | 113.60 |
| 2010 - Q4 | 100 | 120.73 | 107.20 | 106.75 | 110.26 | 113.82 |
| 2011 - Q1 | 100 | 120.72 | 107.03 | 106.73 | 110.74 | 114.30 |
| 2011 - Q2 | 100 | 120.66 | 106.46 | 106.81 | 110.76 | 114.26 |
| 2011 - Q3 | 100 | 120.49 | 106.08 | 106.80 | 110.75 | 113.95 |
| 2011 - Q4 | 100 | 120.66 | 106.11 | 107.72 | 111.51 | 113.84 |
| 2012 - Q1 | 100 | 119.85 | 106.24 | 107.89 | 111.60 | 113.69 |
| 2012 - Q2 | 100 | 119.53 | 106.25 | 108.34 | 111.55 | 114.07 |
| 2012 - Q3 | 100 | 119.01 | 106.37 | 108.32 | 111.75 | 114.79 |
| 2012 - Q4 | 100 | 118.95 | 105.81 | 108.39 | 111.62 | 115.12 |
A popular narrative for the poor performance of the European periphery is that this reflects the accumulation of "macroeconomic imbalances" since the introduction of the common currency (see, among others, Eichengreen, 2010; Chen et al., 2012). As shown in the left panel of Figure 2, peripheral euro-area countries persistently maintained current account deficits over the past decade, whereas core countries (represented in the chart by Germany, but Austria and the Netherlands followed a similar pattern) ran current account surpluses. This steep deterioration in the periphery's external borrowing position was associated with sizeable competitiveness losses. As shown in the right panel of Figure 2, the real exchange rate of peripheral countries appreciated, relative to Germany, between 6% (Italy) and 15% (Greece) over the period 2000-2008.2 Importantly, these appreciations largely reflect outsized increases in non-tradable good prices, such as housing and other services (see, for instance, Gaulier and Vicard, 2012).
Figure 3: Economic Rigidities
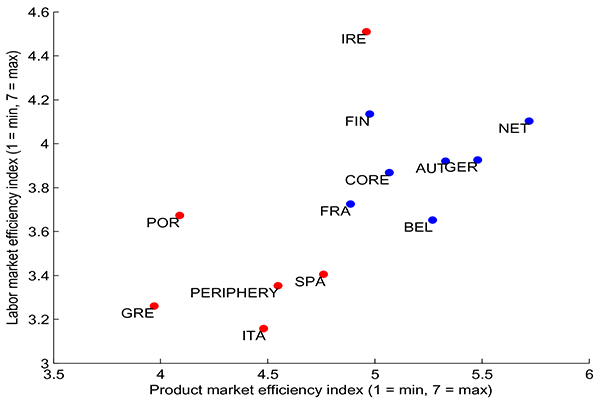
Scatter plot of product market (horizontal axis) and labor market (vertical axis) efficiency indexes (1 = minimum efficiency, 7 = maximum efficiency) for core (blue dots) and periphery (red dots) EMU countries.
Data for Figure 3
| PMR | LMR | |
|---|---|---|
| AUT | 5.33 | 3.92 |
| BEL | 5.27 | 3.65 |
| FIN | 4.98 | 4.14 |
| FRA | 4.89 | 3.73 |
| GER | 5.48 | 3.93 |
| NET | 5.72 | 4.10 |
| CORE | 5.07 | 3.87 |
| GRE | 3.97 | 3.26 |
| IRE | 4.96 | 4.51 |
| ITA | 4.48 | 3.16 |
| POR | 4.09 | 3.67 |
| SPA | 4.76 | 3.41 |
| PERIPHERY | 4.55 | 3.35 |
Amid limited policy options, including the impossibility of devaluing the currency, a broad consensus has emerged: Peripheral euro-area countries need to urgently adopt structural reforms that increase competition in product and labor markets. Such reforms would directly aim at the source of these macroeconomic imbalances, trying to achieve two complementary objectives in the context of the current crisis. First, reforms would effectively trigger a "real devaluation" of the periphery relative to the core, contributing to a reduction in the competitiveness gap accumulated over the past decade. Second, reforms would boost expectations about future growth prospects and stimulate current demand via wealth effects. This view is supported by the extensive empirical and survey-based evidence pointing to significantly higher economic rigidities in the periphery. Figure 3, for instance, presents indexes of economic flexibility obtained from the World Economic Forum (2012) that capture the degree of competition in product and labor markets.3 Indeed, peripheral countries score poorly along both dimensions.4 In light of these arguments--and evidence--it is perhaps not surprising that structural reforms are the cornerstone of both academics and international agencies' policy advice, as exemplified in the quote by the President of the European Commission Jose M.D. Barroso, reported above.
This paper investigates the effectiveness of structural reforms in an open economy version of the standard New-Keynesian model, with two sectors (tradable and non-tradable) and two countries that form a currency union. These two countries differ only in the extent to which policy barriers grant monopoly power to firms and unions. Structural reforms in one country (the "periphery" ) are introduced as a permanent reduction in product and labor market markups, in line with what is typically assumed in the literature (see, for instance, Bayoumi et al., 2004; Forni et al., 2010).
In our simulations, the long-run effects of structural reforms are unambiguously positive. A permanent reduction of product and labor market markups by 10 percentage points in the periphery service sector increases the level of output in that region by more than 5%, with positive spillovers to the core country.5 As output in the service sector expands and its prices fall, the periphery experiences a real exchange rate depreciation of more than 8%. Thus, these figures suggest that ambitious reforms implemented in peripheral EMU countries could greatly reduce the income and competitiveness gap observed between core and periphery.
Notwithstanding these long-run benefits, we find that the short-run transmission mechanism of these reforms critically depends on the ability of the central bank to provide policy accommodation. In normal times, reforms increase agents' permanent income and stimulate consumption. Amid falling aggregate prices, the central bank cuts the nominal interest rate and the currency union experiences a vigorous short-term boom.6 These effects, however, are completely overturned in crisis times. When the nominal interest rate is at the ZLB, reforms are contractionary, as expectations of prolonged deflation increase the real interest rate and depress consumption. In our simulations, the short-run output losses associated with the ZLB constraint are increasing with the magnitude of the reforms and become particularly large when reforms are not fully credible (and are later undone).
We next consider two experiments in order to disentangle the short-run transmission of reforms at the ZLB. In the spirit of Eggertsson (2012), we first study the effects of temporarily granting firms and unions higher monopoly power. In spite of the absence of long-run changes to output (income effect), these temporary reforms are expansionary when implemented at the ZLB. The main intuition for this surprising result is that such a policy would create inflationary expectations, thus reducing the real interest rate beyond the direct stimulus provided by monetary policy and providing incentives to households to front-load their consumption.
In a second experiment, we follow the recent work by Fernandez-Villaverde et al. (2012) and study the effects of announcements to credibly implement structural reforms at some future date. This policy delivers a sizeable income effect thanks to the permanent increase in the long-run level of output but avoids the short-term costs of prolonged deflation, as reforms are implemented when the ZLB stops binding. The net effect is a significant boost in output, even in the short term.
Our research contributes to a growing literature that studies the implications of the ZLB constraint for the short-run transmission of shocks and policies. Eggertsson (2012) argues that New Deal policies facilitated the recovery from the Great Depression by temporarily granting monopoly power to firms and unions. Our work differs from his in two important respects. First, we consider the transmission of (markup) shocks in an open economy environment which features tradable and non-tradable goods, thus involving significant cross-sector and cross-country spillovers. Second, we focus on shocks that are permanent, emphasizing the horse race between sizeable increases in long-run income and short-run deflationary effects. A number of studies have also studied the transmission of fiscal shocks at the ZLB (see, for example, Christiano et al., 2011; Eggertsson, 2011; Erceg and Linde, 2012), often concluding that fiscal multipliers change greatly when the central bank's nominal interest rate is at its lower bound. While we leave a full investigation of the interaction between structural reforms and fiscal policy for future research, our findings do suggest that the magnitude, and possibly the sign, of the structural reform "multiplier" may change as well at the ZLB.7
The rest of the paper is organized as follows. Section 2 outlines a simplified closed economy model to illustrate the two offsetting effects that are critical for our evaluation: The perverse effect of structural reforms due to deflationary expectations, and the positive effect due to a permanent increase in long-run income. Section 3 presents the full two-country model and its calibration. Section 4 discusses the effects of structural reforms in normal times. Section 5 introduces the crisis and re-evaluates the effects of structural reforms in that context. Section 6 studies two alternative policies that avoid the perverse short-run effects of structural reforms. Finally, Section 7 concludes.
2 An Illustrative Model
We begin our analysis by studying the effects of structural reforms in a linearized version of a standard closed economy model with monopolistic competition and sticky prices. The basic New Keynesian structure of this model is also at the heart of the open economy DSGE model that we use in our quantitative experiments. While we study the full non-linear dynamics of our multi-country model, the simple intuition that arises from the linearized closed economy provides insights about the main tradeoffs associated with structural reforms when monetary policy is constrained by the ZLB.
The linearized version of the prototype New-Keynesian model can be summarized by the following two equations
| (1) | |||
| (2) |
where ![]() is inflation
is inflation![]()
![]() is output in deviation from its
first best level,
is output in deviation from its
first best level, ![]() is an exogenous
disturbance,
is an exogenous
disturbance, ![]() is the slope of the Phillips
curve (a convolution of structural parameters),
is the slope of the Phillips
curve (a convolution of structural parameters), ![]() is the coefficient of relative risk aversion,
is the coefficient of relative risk aversion,
![]() , where
, where
![]() is the inverse Frisch elasticity of
labor supply, and
is the inverse Frisch elasticity of
labor supply, and
![]() is the expectation operator
conditional on all information available at time
is the expectation operator
conditional on all information available at time ![]() .
The variable
.
The variable
![]() denotes a wedge between output
under flexible prices and the first best level of output. In the
microfoundation of the model, this wedge could either be driven by
the market power of firms (due to monopolistic competition in
product markets) or markups in the labor markets. We interpret
structural reforms as policies that aim at reducing this wedge by
promoting competition in product and labor markets, for instance
through lower entry barriers in industries, removal of restrictions
on working hours, and privatization of government-owned enterprises
with corresponding increase in the number of operating firms in
protected sectors.
denotes a wedge between output
under flexible prices and the first best level of output. In the
microfoundation of the model, this wedge could either be driven by
the market power of firms (due to monopolistic competition in
product markets) or markups in the labor markets. We interpret
structural reforms as policies that aim at reducing this wedge by
promoting competition in product and labor markets, for instance
through lower entry barriers in industries, removal of restrictions
on working hours, and privatization of government-owned enterprises
with corresponding increase in the number of operating firms in
protected sectors.
Consider a regime where
![]() that is, the central bank manages
to target zero inflation at all times. Under this assumption, the
model becomes static. In particular, we can think of the short and
long-run equilibrium separately. Denote short-run variables by
that is, the central bank manages
to target zero inflation at all times. Under this assumption, the
model becomes static. In particular, we can think of the short and
long-run equilibrium separately. Denote short-run variables by
![]() and long-run variables by
and long-run variables by ![]() Then, equation (2) reduces to
Then, equation (2) reduces to
| (3) |
Equations (3) reveals two
important insights. First, structural reforms have an unambiguous
impact on output, whose magnitude depends on ![]() In particular, a reduction in the wedge increases
output. Second, under zero-inflation targeting, aggregate demand
(equation 1) plays no
role in determining short-run output. It is simply a pricing
equation that pins down the level of the interest rate
In particular, a reduction in the wedge increases
output. Second, under zero-inflation targeting, aggregate demand
(equation 1) plays no
role in determining short-run output. It is simply a pricing
equation that pins down the level of the interest rate ![]() consistent with zero inflation.
consistent with zero inflation.
The dynamics significantly change when monetary policy is
constrained by the ZLB. Consider the following shock, common in the
literature on the zero bound due to its analytic simplicity: At
time zero, the shock ![]() takes value
takes value
![]() but then, in each period, it
reverts back to steady state with probability
but then, in each period, it
reverts back to steady state with probability ![]() . Once in steady state, the shock stays there forever.
We can consider both long- and short-run structural reforms in this
framework. In particular, consider reforms such that
. Once in steady state, the shock stays there forever.
We can consider both long- and short-run structural reforms in this
framework. In particular, consider reforms such that
![]() when the
when the
![]() and
and
![]() when the shock is back to
steady state (i.e.
when the shock is back to
steady state (i.e.
![]() ). Under these
assumptions, the model can still be conveniently split into long
run and short run by exploiting the forward-looking nature of the
equations. Moreover, as long as
). Under these
assumptions, the model can still be conveniently split into long
run and short run by exploiting the forward-looking nature of the
equations. Moreover, as long as
![]() and the policy
and the policy
![]() is sufficiently
close to the point around which we approximate, the ZLB is binding
only in the short run.
is sufficiently
close to the point around which we approximate, the ZLB is binding
only in the short run.
This shock dramatically changes the short-run equilibrium. When
the nominal interest rate is at zero, the economy becomes
completely demand-determined and equation (1) becomes
relevant for the determination of output. Using our assumptions
about the interest rate shock, and taking the solution once the
shock is over as given (which we continue to denote by ![]() ), we can rewrite equation (1) and equation
(2) as
), we can rewrite equation (1) and equation
(2) as
| AD: |
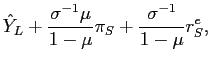 |
(4) | |
| AS: |
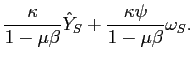 |
(5) |
Figure 4: Short-Run Equilibrium of Aggregate Demand (AD) and Aggregate Supply (AS) at the ZLB
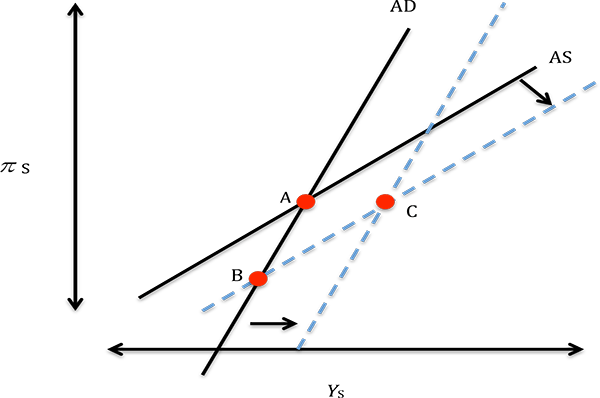
Short-run equilibrium at the ZLB under permanent structural reforms in the illustrative model.
Given the policy
![]() the short-run
equilibrium is a pair
the short-run
equilibrium is a pair
![]() that satisfies these
two equations. Graphically, the equilibrium corresponds to the
intersection of the aggregate supply (AS) and the aggregate demand
(AD) "curves," as shown by point A in Figure 4. Note that, when
the ZLB binds, the aggregate demand curve becomes upward-sloping,
as higher inflation stimulates demand through lower real interest
rates.8
that satisfies these
two equations. Graphically, the equilibrium corresponds to the
intersection of the aggregate supply (AS) and the aggregate demand
(AD) "curves," as shown by point A in Figure 4. Note that, when
the ZLB binds, the aggregate demand curve becomes upward-sloping,
as higher inflation stimulates demand through lower real interest
rates.8
Figure 4 shows the
impact of permanent structural reforms (i.e. a reduction in
![]() and
and
![]() ) on short-run output and
inflation. A product or labor market liberalization generates two
effects. First, it shifts the AS curve down, as firms can produce
more output for any given level of inflation. Perhaps somewhat
surprisingly, this effect turns out to be contractionary in the
short run. At the ZLB, reforms amplify deflationary pressures,
resulting in a higher real interest rate and contracting aggregate
demand. Given that the interest rate is stuck at zero, the central
bank cannot provide enough monetary stimulus to offset this effect
and output declines.9
) on short-run output and
inflation. A product or labor market liberalization generates two
effects. First, it shifts the AS curve down, as firms can produce
more output for any given level of inflation. Perhaps somewhat
surprisingly, this effect turns out to be contractionary in the
short run. At the ZLB, reforms amplify deflationary pressures,
resulting in a higher real interest rate and contracting aggregate
demand. Given that the interest rate is stuck at zero, the central
bank cannot provide enough monetary stimulus to offset this effect
and output declines.9
As shown in equation (4), however,
reforms also have a second effect on short-run output
![]() through
through
![]() , thus shifting the aggregate
demand schedule outward (see again Figure 4). As structural
reforms increase permanent income, output and inflation move up in
the short term as well. Thus, depending on the relative strength of
these two effects, reforms may be contractionary or expansionary in
the short run. For instance, if structural reforms do not have much
"credibility" (i.e. agents expect a policy reversal at some
point in the future, such that
, thus shifting the aggregate
demand schedule outward (see again Figure 4). As structural
reforms increase permanent income, output and inflation move up in
the short term as well. Thus, depending on the relative strength of
these two effects, reforms may be contractionary or expansionary in
the short run. For instance, if structural reforms do not have much
"credibility" (i.e. agents expect a policy reversal at some
point in the future, such that
![]() but
but
![]() ), the AS curve shifts down
whereas the AD curve does not change, and the reforms are clearly
contractionary (point B in Figure 4). In contrast,
ambitious reforms that are gradually implemented and become more
credible over time are associated with large permanent income
effects, shifting the AD curve more than the AS curve (point C in
Figure 4).
), the AS curve shifts down
whereas the AD curve does not change, and the reforms are clearly
contractionary (point B in Figure 4). In contrast,
ambitious reforms that are gradually implemented and become more
credible over time are associated with large permanent income
effects, shifting the AD curve more than the AS curve (point C in
Figure 4).
The question of which effect dominates is ultimately quantitative. For this purpose, in the next section, we develop and calibrate a two-country model of a monetary union that we then use as a laboratory to evaluate the effects of different structural reforms experiments.
The open-economy dimension of the model is important to make our analysis concrete with respect to two key features that are relevant for the debate on the European crisis. First, the evidence in Figure 3 suggests that structural reforms are mostly needed in the periphery, to favor a catch-up in competitiveness with the core. Second, and related, structural reforms may prove helpful in closing the imbalances in external borrowing and relative prices that have received so much attention since the onset of the crisis. Our analysis sheds light on the short-run interaction between the role of structural reforms in correcting these imbalances and monetary policy when the nominal interest rate is constrained by the ZLB.
3 The Full Model
The world economy consists of two countries, the periphery
(![]() ) and the core (
) and the core (![]() ), that belong
to a currency union whose population size is normalized to one. The
common central bank sets monetary policy for the union targeting
zero inflation.
), that belong
to a currency union whose population size is normalized to one. The
common central bank sets monetary policy for the union targeting
zero inflation.
A continuum of households of measure ![]() inhabits
country
inhabits
country ![]() . Each household derives utility from
consumption of tradable and non-tradable goods and disutility from
hours worked. Households supply sector-specific differentiated
labor inputs. A representative labor agency combines these inputs
in sector-specific aggregates, while households set the wage for
each input on a staggered basis.
. Each household derives utility from
consumption of tradable and non-tradable goods and disutility from
hours worked. Households supply sector-specific differentiated
labor inputs. A representative labor agency combines these inputs
in sector-specific aggregates, while households set the wage for
each input on a staggered basis.
Firms in each country produce tradable and a non-tradable goods using labor, which is immobile across countries. Production takes place in two stages. In each sector (tradable and non-tradable), a representative retailer combines differentiated intermediate goods to produce the final consumption good. Monopolistic competitive wholesale producers set the price of each differentiated intermediate good on a staggered basis.
In each country, we assume the existence of a full set of transfers that completely insure against the idiosyncratic income risk arising from staggered price and wage setting. Across countries, the only asset traded is a one-period nominal bond denominated in the common currency. One-period changes in the net foreign asset position define the current account.
This section presents the details of the model from the
perspective of the periphery (country ![]() ). Variables
for the core (country
). Variables
for the core (country ![]() ) are denoted by an
asterisk.
) are denoted by an
asterisk.
3.1 Retailers
A representative wholesale producer in the tradable (![]() ) and non-tradable (
) and non-tradable (![]() ) sector combines
raw goods according to a technology with constant elasticity of
substitution
) sector combines
raw goods according to a technology with constant elasticity of
substitution
![]()
![$\displaystyle Y_{kt}=\left[ \left( \frac{1}{\gamma _{k}}\right) ^{\frac{1}{\theta _{k}} }\int_{0}^{\gamma _{k}}Y_{kt}(j)^{\frac{\theta _{k}-1}{\theta _{k}}}dj\right] ^{\frac{\theta _{k}}{\theta _{k}-1}},$](img64.gif) |
(6) |
where ![]() indexes an intermediate goods producer and
indexes an intermediate goods producer and
![]() is the size
of the tradable and non-tradable sector, respectively.
is the size
of the tradable and non-tradable sector, respectively.
The representative retailer in sector ![]() maximizes profits subject to its technological constraint (6)
maximizes profits subject to its technological constraint (6)
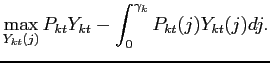 |
(7) |
The first order condition for this problem yields the standard demand function
![$\displaystyle Y_{kt}(j)=\frac{1}{\gamma _{k}}\left[ \frac{P_{kt}(j)}{P_{kt}}\right] ^{-\theta_k}Y_{kt},$](img69.gif) |
(8) |
where ![]() is the price of the
is the price of the ![]() variety of the good produced in sector
variety of the good produced in sector ![]() .
The zero profit condition implies that the price index in sector
.
The zero profit condition implies that the price index in sector
![]() is
is
![$\displaystyle P_{kt}=\left[ \frac{1}{\gamma _{k}}\int_{0}^{\gamma _{k}}P_{kt}(j)^{1-\theta_k}dj\right] ^{\frac{1}{1-\theta_k}}.$](img74.gif) |
(9) |
3.2 Labor Agencies
In each sector, a representative labor agency combines
differentiated labor inputs provided by each household ![]() into a sector-specific homogenous aggregate
according to a technology with constant elasticity of substitution
into a sector-specific homogenous aggregate
according to a technology with constant elasticity of substitution
![]()
![$\displaystyle L_{kt}=\left[ \left( \frac{1}{\gamma _{k}n}\right) ^{\frac{1}{\phi _{k}} }\int_{0}^{\gamma _{k}n}L_{kt}(i)^{\frac{\phi _{k}-1}{\phi _{k}}}di\right] ^{ \frac{\phi _{k}}{\phi _{k}-1}}.$](img77.gif) |
(10) |
The representative labor agency in sector ![]() maximizes profits subject to its technological constraint (10)
maximizes profits subject to its technological constraint (10)
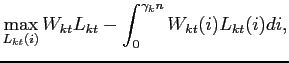 |
(11) |
where ![]() is the wage index in sector
is the wage index in sector
![]() and
and ![]() is the wage
specific to type-
is the wage
specific to type-![]() labor input. The first order
condition for this problem is
labor input. The first order
condition for this problem is
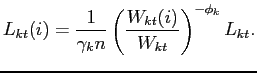 |
(12) |
The zero profit condition implies that the wage index is
![$\displaystyle W_{kt}=\left[ \frac{1}{\gamma _{k}n}\int_{0}^{\gamma_k n}W_{kt}(i)^{1-\phi_k}di\right] ^{\frac{1}{1-\phi_k}}.$](img85.gif) |
(13) |
3.3 Intermediate Goods Producers
A continuum of measure
![]() of intermediate goods producers
operate in each sector using the technology
of intermediate goods producers
operate in each sector using the technology
| (14) |
where ![]() is an exogenous productivity shock.
is an exogenous productivity shock.
Intermediate goods producers are imperfectly competitive and
choose the price for their variety ![]() , as
well as the optimum amount of labor inputs
, as
well as the optimum amount of labor inputs ![]() ,
to maximize profits subject to their technological constraint
(14) and the demand
for their variety (8).
,
to maximize profits subject to their technological constraint
(14) and the demand
for their variety (8).
As customary, we can separate the intermediate goods producers problem in two steps. First, for a given price, these firms minimize labor costs subject to their technology constraint. The result of this step is that the marginal cost (the Lagrange multiplier on the constraint) equals the nominal wage scaled by the level of productivity
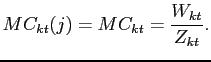 |
(15) |
This condition also shows that the marginal cost is independent of firm-specific characteristics. However, because of nominal price and wage rigidities, aggregate labor demand in each sector depends on price dispersion. We can use the demand function (8) and the production function (14) to write an aggregate production function as
| (16) |
where equilibrium in the labor market implies
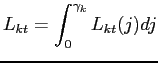 |
and
![]() is an index of price dispersion
defined as
is an index of price dispersion
defined as
![$\displaystyle \Delta_{kt} \equiv \frac{1}{\gamma_k} \int_0^{\gamma_k} \left[\frac{P_{kt}(j) }{P_{kt}} \right]^{-\theta_k} dj.$](img95.gif) |
The second step of the intermediate goods producers' problem is
the optimal price setting decision, given the expression for the
marginal cost. We assume that firms change their price on a
staggered basis. Following Calvo (1983), the
probability of not being able to change the price in each period is
![]() . The optimal price setting
problem for a firm
. The optimal price setting
problem for a firm ![]() that is able to reset its
price at time
that is able to reset its
price at time ![]() is
is
![$\displaystyle \max_{\widetilde{P}_{kt}(j)}\mathbb{E}_{t} \left\{ \underset{s=0}{\overset{ \infty }{\sum }}\xi_p^s Q_{t,t+s}\left[ (1 - \tau^p_{kt+s}) \widetilde{P} _{kt}(j) - MC_{kt+s} \right] Y_{kt+s}(j) \right\},$](img99.gif) |
(17) |
subject to the demand for their variety (8) conditional on
no price change between ![]() and
and ![]() .
Households in each country own a diversified non-traded portfolio
of domestic tradable and non-tradable intermediate goods producing
firms. Therefore, firms discount future profits using
.
Households in each country own a diversified non-traded portfolio
of domestic tradable and non-tradable intermediate goods producing
firms. Therefore, firms discount future profits using ![]() --the individual stochastic discount factor for a
nominal asset between period
--the individual stochastic discount factor for a
nominal asset between period ![]() and period
and period
![]() (such that
(such that ![]() ).
The time-varying tax
).
The time-varying tax
![]() is the policy instrument that
the government can use to affect the degree of competitiveness in
each sector. Ceteris paribus, a lower tax reduces the firms'
effective markup and increases output. We discuss government policy
in more details below.
is the policy instrument that
the government can use to affect the degree of competitiveness in
each sector. Ceteris paribus, a lower tax reduces the firms'
effective markup and increases output. We discuss government policy
in more details below.
In equilibrium, all firms that reset their price at time
![]() choose the same strategy (
choose the same strategy (
![]() ).
After some manipulations, we can write the optimality condition
as
).
After some manipulations, we can write the optimality condition
as
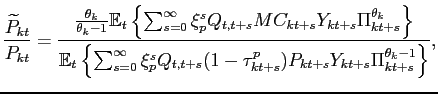 |
(18) |
where
![]() is the
inflation rate in sector
is the
inflation rate in sector ![]() . Firms that are not able to
adjust, on average, keep their price fixed at the previous period's
level. The price index (9) for sector
. Firms that are not able to
adjust, on average, keep their price fixed at the previous period's
level. The price index (9) for sector
![]() yields a non-linear relation between the
optimal relative reset price and the inflation rate
yields a non-linear relation between the
optimal relative reset price and the inflation rate
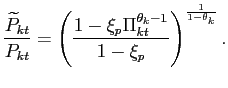 |
(19) |
Moreover, from the price index (9) and the assumption of staggered price setting, we can also derive the law of motion for the index of price dispersion
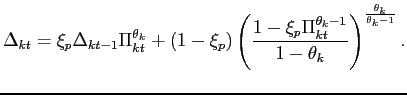 |
(20) |
In steady state, there is no price dispersion (
![]() ) and the price in sector
) and the price in sector
![]() is a markup over the marginal cost
is a markup over the marginal cost
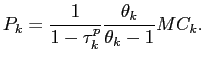 |
(21) |
The government can choose a value of
![]() that fully offsets firms'
monopolistic power--or, more generally, set a desired markup level
in the goods market.
that fully offsets firms'
monopolistic power--or, more generally, set a desired markup level
in the goods market.
3.4 Households
In country ![]() , a continuum of households of measure
, a continuum of households of measure
![]() derive utility from consumption and supply
differentiated labor inputs while setting wages on a staggered
basis (Calvo, 1983). Consumption is a composite of
tradable and non-tradable goods with constant elasticity of
substitution
derive utility from consumption and supply
differentiated labor inputs while setting wages on a staggered
basis (Calvo, 1983). Consumption is a composite of
tradable and non-tradable goods with constant elasticity of
substitution
![]()
![$\displaystyle C_{t}(i)=\left[ \gamma ^{\frac{1}{\varphi }}C_{Tt}(i)^{\frac{\varphi -1}{ \varphi }}+(1-\gamma )^{\frac{1}{\varphi }}C_{Nt}(i)^{\frac{\varphi -1}{ \varphi }}\right] ^{\frac{\varphi }{\varphi -1}},$](img122.gif) |
(22) |
where
![]() is the share of tradables
in total consumption. The associated expenditure minimization
problem is
is the share of tradables
in total consumption. The associated expenditure minimization
problem is
| (23) |
subject to (22). The first order condition for this problem yields the demand for the tradable and non-tradable goods
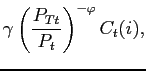 |
(24) | ||
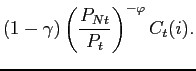 |
(25) |
The associated price index is
![$\displaystyle P_{t}=\left[ \gamma P_{Tt}^{1-\varphi }+(1-\gamma )P_{Nt}^{1-\varphi }\right] ^{\frac{1}{1-\varphi }}.$](img131.gif) |
(26) |
Consumption of tradables includes goods produced in the two
countries combined according to a constant elasticity of
substitution (
![]() ) aggregator
) aggregator
![$\displaystyle C_{Tt}(i)=\left[ \omega ^{\frac{1}{\epsilon }}C_{Ht}(i)^{\frac{\epsilon -1}{ \epsilon }}+(1-\omega )^{\frac{1}{\epsilon }}C_{Ft}(i)^{\frac{\epsilon -1}{ \epsilon }}\right] ^{\frac{\epsilon }{\epsilon -1}},$](img133.gif) |
(27) |
where
![]() is the share of tradable
goods produced in country
is the share of tradable
goods produced in country ![]() . We assume that
the law of one price holds for internationally tradable goods
. We assume that
the law of one price holds for internationally tradable goods
| (28) | |||
| (29) |
The expenditure minimization problem is
| (30) |
subject to (27). The first order conditions for this problem yield the standard demand functions for tradable goods
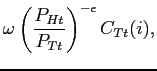 |
(31) | ||
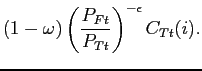 |
(32) |
The zero profit condition implies that the price index for tradable goods is
![$\displaystyle P_{Tt}=\left[ \omega P_{Ht}^{1-\epsilon }+(1-\omega )P_{Ft}^{1-\epsilon } \right] ^{\frac{1}{1-\epsilon }}.$](img149.gif) |
(33) |
While the the law of one price holds, home bias in tradable
consumption (![]() ) implies that the price
index for tradable goods differs across countries (
) implies that the price
index for tradable goods differs across countries (
![]() ). Consumer price
indexes (CPI) further differ across countries because of the
presence of non-tradable goods. Therefore, purchasing power parity
fails (
). Consumer price
indexes (CPI) further differ across countries because of the
presence of non-tradable goods. Therefore, purchasing power parity
fails (
![]() ) and the real
exchange rate (
) and the real
exchange rate (
![]() ) endogenously moves.
) endogenously moves.
Conditional on the allocation between tradable and non-tradable
goods and between tradable goods produced in country ![]() and
and ![]() , the problem of a generic household
, the problem of a generic household
![]() in country
in country ![]() is
is
![$\displaystyle \max_{C_{t+s}(i),B_{t+s}(i),W_{kt+s}(i)}\mathbb{E}_{t}\left\{ \sum_{s=0}^{\infty }\beta ^{s}\varsigma _{t+s}\left[ \frac{ C_{t+s}(i)^{1-\sigma }}{1-\sigma }-\frac{L_{kt+s}(i)^{1+\nu }}{1+\nu }\right] \right\} ,$](img158.gif) |
(34) |
subject to the demand for labor input (12) and the budget constraint
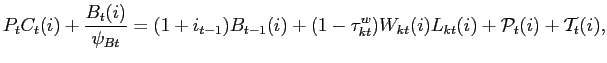 |
(35) |
where ![]() represents nominal debt,
represents nominal debt,
![]() indicates profits from
intermediate goods producers and
indicates profits from
intermediate goods producers and
![]() represents lump-sum
tranfers. As for the goods market, the sector-specific and
time-varying tax
represents lump-sum
tranfers. As for the goods market, the sector-specific and
time-varying tax
![]() is the policy instrument that
the government can use to affect the degree of competitiveness in
the labor market of each sector. Ceteris paribus, a lower tax
reduces workers' monopoly power and increases labor supply. The
variable
is the policy instrument that
the government can use to affect the degree of competitiveness in
the labor market of each sector. Ceteris paribus, a lower tax
reduces workers' monopoly power and increases labor supply. The
variable
![]() is a preference shock that
makes agents more or less impatient. For instance, positive
preference shocks (an increase in the desire to save) may capture
disruptions in financial markets that force the monetary authority
to lower the nominal interest rate to zero. Finally, as in Erceg et al. (2006), the intermediation cost
is a preference shock that
makes agents more or less impatient. For instance, positive
preference shocks (an increase in the desire to save) may capture
disruptions in financial markets that force the monetary authority
to lower the nominal interest rate to zero. Finally, as in Erceg et al. (2006), the intermediation cost
![]() ensures stationarity of the net
foreign asset position
ensures stationarity of the net
foreign asset position
![$\displaystyle \psi _{Bt}\equiv \exp \left[ -\psi _{B}\left( \frac{nB_{t}}{P_{t}Y_{t}} \right) \right] ,$](img166.gif) |
(36) |
where
![]() and
and
![]() corresponds to nominal GDP
corresponds to nominal GDP
| (37) |
Only domestic households pay the transaction cost while foreign households collect the associated fees. Moreover, while we assume that the intermediation cost is a function of the net foreign asset position, domestic households do not internalize this dependency.10
The existence of a full set of transfers that completely insure
against the idiosyncratic income risk arising from staggered price
and wage setting and an appropriate normalization of initial wealth
levels implies that all households make the same consumption and
savings decisions (
![]() ,
,
![]() ). Hence, from now
on, we will suppress the index
). Hence, from now
on, we will suppress the index ![]() from consumption
variables. The consumption-saving optimality conditions yield
from consumption
variables. The consumption-saving optimality conditions yield
![$\displaystyle 1=\beta \psi _{Bt}(1+i_{t})\mathbb{E}_{t}\left[ \frac{\varsigma _{t+1}}{ \varsigma _{t}}\left( \frac{C_{t+1}}{C_{t}}\right) ^{-\sigma }\frac{1}{\Pi _{t+1}}\right] .$](img174.gif) |
(38) |
From expression (38), we
can denote the stochastic discount factor for nominal assets
(![]() ) as
) as
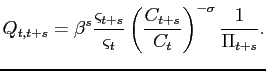 |
(39) |
Each household has a probability of being able to reset the wage
at time ![]() equal to
equal to ![]() . The
optimal wage setting problem in case of adjustment for household
. The
optimal wage setting problem in case of adjustment for household
![]() working in sector
working in sector ![]() is
is
![$\displaystyle \max_{\widetilde{W}_{kt}(i)}\mathbb{E}_{t}\left\{ \underset{s=0}{\overset{ \infty }{\sum }}(\beta \xi _{w})^{s}\left[ (1-\tau _{kt+s}^{w})C_{t+s}^{-\sigma }\frac{\widetilde{W}_{kt}(i)}{P_{t+s}} L_{kt+s}(i)-\frac{L_{kt+s}(i)^{1+\nu }}{1+\nu }\right] \right\} ,$](img181.gif) |
(40) |
subject to the demand for the specific labor variety (12) conditional on
no wage change between ![]() and
and ![]() .
.
In equilibrium, all households who reset their wage at time
![]() choose the same strategy (
choose the same strategy (
![]() ).
After some manipulations, we can rewrite the first order condition
for optimal wage setting as
).
After some manipulations, we can rewrite the first order condition
for optimal wage setting as
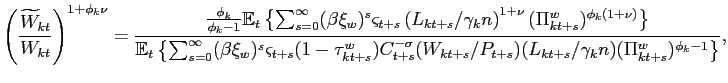 |
(41) |
where
![]() is the
wage inflation rate in sector
is the
wage inflation rate in sector ![]() . The remaining
households, who are not able to adjust, on average keep their wages
fixed at the previous period's level. The wage index (13) for sector
. The remaining
households, who are not able to adjust, on average keep their wages
fixed at the previous period's level. The wage index (13) for sector
![]() yields a non-linear relation between the
optimal relative reset wage and the wage inflation rate
yields a non-linear relation between the
optimal relative reset wage and the wage inflation rate
![$\displaystyle \frac{\widetilde{W}_{kt}}{W_{kt}}=\left[ \frac{1-\xi _{w}(\Pi _{kt}^{w})^{\phi _{k}-1}}{1-\xi _{w}}\right] ^{\frac{1}{1-\phi _{k}}}.$](img190.gif) |
(42) |
In steady state, the real wage in sector ![]() is a
markup over the marginal rate of substitution between labor and
consumption
is a
markup over the marginal rate of substitution between labor and
consumption
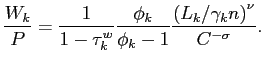 |
As in the case of prices, the government can choose a tax that fully offsets workers' monopolistic power--or, more generally, set a desired markup level in the labor market.
3.5 Fiscal and Monetary Policy
We assume that the government in each country rebates goods and labor market taxes via lump-sum transfers
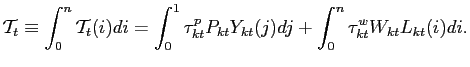 |
(43) |
Using (37) and its foreign counterpart, we construct a union-wide level of output as a population-weighted geometric average of the levels of output in the two countries
| (44) |
In the same spirit, we define the union-wide price index
![]() as a population-weighted
geometric average of the CPIs in the two countries11
as a population-weighted
geometric average of the CPIs in the two countries11
| (45) |
Consequently, the inflation rate in the currency union is
| (46) |
We assume that a single central bank sets the nominal interest rate in the entire union to implement a strict inflation target
However, we take explicitly into account the possibility that the nominal interest rate cannot fall below some lower bound
In the aftermath of shocks that take the economy to the lower
bound, the central bank keeps the nominal interest rate at
![]() until inflation reaches its target
again. Our results would be unchanged if we were to specify an
interest rate rule that responds to inflation, the output gap
and/or the natural rate of interest.
until inflation reaches its target
again. Our results would be unchanged if we were to specify an
interest rate rule that responds to inflation, the output gap
and/or the natural rate of interest.
3.6 Equilibrium
An imperfect competitive equilibrium for this economy is a sequence of quantities and prices such that the optimality conditions for households and firms in the two countries hold, the markets for final non-tradable goods and for labor inputs in each sector clear at the country level, and the markets for tradable goods and financial assets clear at the union level. Because of nominal rigidities, intermediate goods producers and workers who cannot adjust their contracts stand ready to supply goods and labor inputs at the price and wage prevailing in the previous period. An appendix available upon request contains the detailed list of equilibrium conditions. Here we note that goods market clearing in the tradable and non-tradable sectors satisfies
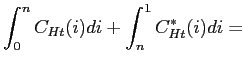 |
(47) | ||
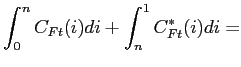 |
(48) |
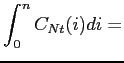 |
(49) | ||
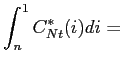 |
(50) |
Integrating the budget constraint across households in country
![]() and using the zero profit conditions for
labor agencies and retailers, as well as the government budget
constraint and the equilibrium conditions for tradable and
non-tradable goods, implies that net foreign assets evolve
according to
and using the zero profit conditions for
labor agencies and retailers, as well as the government budget
constraint and the equilibrium conditions for tradable and
non-tradable goods, implies that net foreign assets evolve
according to
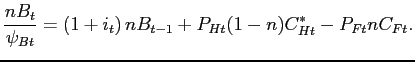 |
(51) |
Finally, asset market clearing requires
| (52) |
3.7 Calibration and Solution Strategy
In our experiments, we model structural reforms as changes in
the tax rates
![]() and
and
![]() that affect, permanently or
temporarily, the markups in the labor and product markets (i.e. the
degree of competition in the two markets). We run deterministic
non-linear simulations that allow us to quantify the steady state
effects and trace the dynamic evolution of the endogenous variables
in response to the policy experiment.12
that affect, permanently or
temporarily, the markups in the labor and product markets (i.e. the
degree of competition in the two markets). We run deterministic
non-linear simulations that allow us to quantify the steady state
effects and trace the dynamic evolution of the endogenous variables
in response to the policy experiment.12
Table 1: Product market markup estimates by sector.
| Periphery ( | Core ( | |
|---|---|---|
| Total private firms | 1.36 | 1.25 |
| Manufacturing (Tradable) | 1.17 | 1.14 |
| Services (Nontradable) | 1.48 | 1.33 |
Note: Source: OECD (2005). Periphery: Italy and Spain. Core: France and Germany.
We set the initial levels of price markups in the periphery and the core following the estimates produced by the OECD (2005) for peripheral and core EMU, reported in Table 1. We consider the manufacturing sector as a proxy for the tradable sector in the model and the service sector as a proxy for the non-tradable sector. The OECD estimates for price markups show two interesting patterns. First, markups in the periphery are higher than in the core, consistent with the evidence provided in Figure 3. Second, this difference is largely accounted for by higher markups in the service sector of the periphery, whereas markups in the manufacturing sector are similar across regions. These data support the view that peripheral European countries could greatly benefit from the implementation of liberalization measures in the product market.
In order to calibrate the elasticity of substitution ![]() in sector
in sector ![]() of each region, we start
from the expression of the total markup in the steady state
of each region, we start
from the expression of the total markup in the steady state
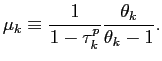 |
(53) |
For the manufacturing sector, we assume symmetry across countries
and no policy-induced distortions (i.e.
![]() ).
Targeting a steady state net markup of 15%, this
strategy allows us to pin down the elasticity of substitution in
the tradable sector (
).
Targeting a steady state net markup of 15%, this
strategy allows us to pin down the elasticity of substitution in
the tradable sector (
![]() ). For
the service sector, we assume no policy distortion in the core (
). For
the service sector, we assume no policy distortion in the core (
![]() ). The estimate in Table 1 then implies
). The estimate in Table 1 then implies
![]() . We assume that the
elasticity is the same in the periphery (
. We assume that the
elasticity is the same in the periphery (
![]() ) and
attribute the difference in the OECD markup estimates to policy
distortions (
) and
attribute the difference in the OECD markup estimates to policy
distortions (
![]() ).
).
Empirical studies point to similar patterns for wage markups across countries and sectors. Although direct estimates of wage markups are more difficult to obtain, data on wage premia (Jean and Nicoletti, 2002) and evidence on wage bargaining power in Europe (Everaert and Schule, 2006) indicate that wage markups are likely to be higher in peripheral countries than in core countries because of higher markups in the service sector. Furthermore, the point estimates of the implied wage markups so computed are not too different from the figures presented in Table 1. Thus, we set the wage elasticities and taxes across sectors and regions equal to the corresponding values for the product market.13
Table 2. Parameter Values
| Parameter | Value |
|---|---|
| Households: Country size | |
| Households: Individual discount factor | |
| Households: Inverse Frisch elasticity | |
| Households: Elasticity of intertemporal substitution | |
| Households: Home bias | |
| Households: Consumption share of tradable goods | |
| Households: Elasticity of substitution tradables-nontradables | |
| Households: Elasticity of substitution H-F tradables | |
| Price and Wage Setting: Probability of not being able to adjust prices | |
| Price and Wage Setting: Probability of not being able to adjust wages | |
| Monetary Policy: Inflation target | |
| Monetary Policy: Effective lower bound on nominal interest rate |
The remaining parameters used in our simulations are relatively
standard (Table 2). In our benchmark experiment, the core and the periphery have the
same size (![]() ). The individual discount factor
). The individual discount factor
![]() equals 0.99, implying an annualized
real interest rate of about 4%. The coefficient of relative risk
aversion
equals 0.99, implying an annualized
real interest rate of about 4%. The coefficient of relative risk
aversion ![]() is equal to 0.5, which is within the
range of estimates provided in Hansen adn Singleton (1983) and slightly higher than Rotembert and Woodford (1997). The inverse Frisch elasticity
is equal to 0.5, which is within the
range of estimates provided in Hansen adn Singleton (1983) and slightly higher than Rotembert and Woodford (1997). The inverse Frisch elasticity
![]() is equal to 2, a value commonly used in
the New-Keynesian literature (see, for instance, Erceg and Linde, 2012). We calibrate the degree of home bias
is equal to 2, a value commonly used in
the New-Keynesian literature (see, for instance, Erceg and Linde, 2012). We calibrate the degree of home bias
![]() and the size of the tradable
sector
and the size of the tradable
sector
![]() to match (i) a steady state
import share of 15% (corresponding to the average within-eurozone
import share for France, Germany, Italy, and Spain) and (ii) a
steady state output share of 38% in manufacturing (from the
EU-KLEMS database). We set the elasticity of substitution between
tradable and non-tradable goods
to match (i) a steady state
import share of 15% (corresponding to the average within-eurozone
import share for France, Germany, Italy, and Spain) and (ii) a
steady state output share of 38% in manufacturing (from the
EU-KLEMS database). We set the elasticity of substitution between
tradable and non-tradable goods ![]() equal to
0.5, consistent with the estimates for industrialized countries in Mendoza (1991), and the elasticity of substitution
between tradable goods produced in the core and in the periphery
equal to
0.5, consistent with the estimates for industrialized countries in Mendoza (1991), and the elasticity of substitution
between tradable goods produced in the core and in the periphery
![]() to 1.5, as in Backus et al. (1994). Finally, the probabilities of not being able to
reset prices and wages in any given quarter (
to 1.5, as in Backus et al. (1994). Finally, the probabilities of not being able to
reset prices and wages in any given quarter (![]() and
and ![]() , respectively) equal
0.66, implying an average frequency of price and wages changes of 3
quarters. We assume that the ECB targets zero inflation (
, respectively) equal
0.66, implying an average frequency of price and wages changes of 3
quarters. We assume that the ECB targets zero inflation (
![]() ) and consider an effective lower
bound of the short term interest rate of 1%, annualized consistent
with the evidence that the ECB has been resistant to lower nominal
rates below that threshold throughout the crisis.14
) and consider an effective lower
bound of the short term interest rate of 1%, annualized consistent
with the evidence that the ECB has been resistant to lower nominal
rates below that threshold throughout the crisis.14
4 The Effects of Structural Reforms in Normal Times
We begin our analysis by investigating the consequences of structural reforms in normal times. Specifically, we study the effects of a permanent reduction in the tax component of steady-state price and wage markups by one percentage point in the periphery non-tradable sector. Figure 5 presents the dynamics of the main economic variables following the implementation of these reforms.
Figure 5: Response of Output, Inflation, and Sectoral Output
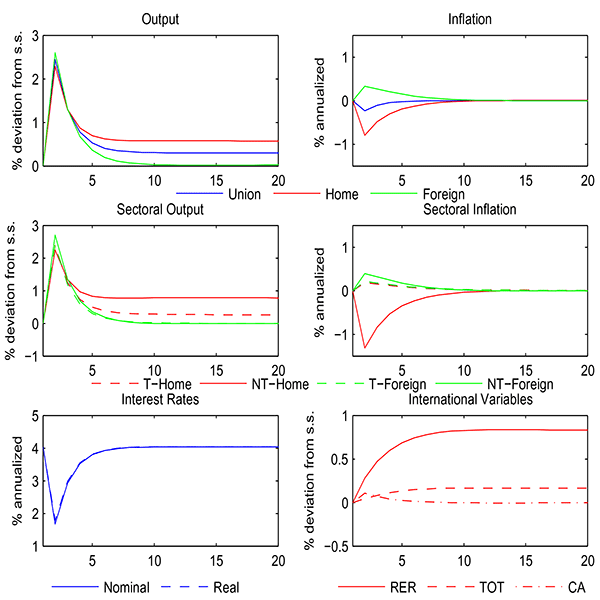
Response of output (top-left), inflation (top-right), sectoral output (middle-left), sectoral inflation (middle-right), interest rates (bottom-left) and international variables (bottom-right) to a permanent increase in labor and product market subsidies by one percentage point.
Data for Figure 5: Panel 1. Output
| Union | Home | Foreign | |
|---|---|---|---|
| 1 | 0.00 | 0.00 | 0.00 |
| 2 | 2.13 | 1.99 | 2.27 |
| 3 | 1.13 | 1.13 | 1.14 |
| 4 | 0.67 | 0.75 | 0.59 |
| 5 | 0.46 | 0.60 | 0.31 |
| 6 | 0.35 | 0.53 | 0.17 |
| 7 | 0.30 | 0.51 | 0.10 |
| 8 | 0.28 | 0.50 | 0.06 |
| 9 | 0.27 | 0.50 | 0.04 |
| 10 | 0.26 | 0.50 | 0.03 |
| 11 | 0.26 | 0.50 | 0.02 |
| 12 | 0.26 | 0.50 | 0.02 |
| 13 | 0.26 | 0.50 | 0.02 |
| 14 | 0.26 | 0.50 | 0.02 |
| 15 | 0.26 | 0.50 | 0.02 |
| 16 | 0.26 | 0.50 | 0.02 |
| 17 | 0.26 | 0.50 | 0.02 |
| 18 | 0.26 | 0.50 | 0.02 |
| 19 | 0.26 | 0.50 | 0.02 |
| 20 | 0.26 | 0.49 | 0.02 |
Data for Figure 5: Panel 2. Inflation
| Union | Home | Foreign | |
|---|---|---|---|
| 1 | 0.00 | 0.00 | 0.00 |
| 2 | -0.20 | -0.69 | 0.28 |
| 3 | -0.10 | -0.43 | 0.24 |
| 4 | -0.05 | -0.27 | 0.18 |
| 5 | -0.02 | -0.17 | 0.13 |
| 6 | -0.01 | -0.11 | 0.09 |
| 7 | 0.00 | -0.07 | 0.06 |
| 8 | 0.00 | -0.04 | 0.04 |
| 9 | 0.00 | -0.03 | 0.02 |
| 10 | 0.00 | -0.02 | 0.01 |
| 11 | 0.00 | -0.01 | 0.01 |
| 12 | 0.00 | 0.00 | 0.00 |
| 13 | 0.00 | 0.00 | 0.00 |
| 14 | 0.00 | 0.00 | 0.00 |
| 15 | 0.00 | 0.00 | 0.00 |
| 16 | 0.00 | 0.00 | 0.00 |
| 17 | 0.00 | 0.00 | 0.00 |
| 18 | 0.00 | 0.00 | 0.00 |
| 19 | 0.00 | 0.00 | 0.00 |
| 20 | 0.00 | 0.00 | 0.00 |
Data for Figure 5: Panel 3. Sectoral Output
| T_H | NT_H | T_F | NT_F | |
|---|---|---|---|---|
| 1 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 2.06 | 1.95 | 2.09 | 2.36 |
| 3 | 1.08 | 1.17 | 1.03 | 1.19 |
| 4 | 0.63 | 0.85 | 0.52 | 0.61 |
| 5 | 0.43 | 0.72 | 0.26 | 0.31 |
| 6 | 0.33 | 0.68 | 0.14 | 0.16 |
| 7 | 0.29 | 0.68 | 0.07 | 0.08 |
| 8 | 0.26 | 0.68 | 0.04 | 0.04 |
| 9 | 0.25 | 0.68 | 0.02 | 0.01 |
| 10 | 0.24 | 0.69 | 0.01 | 0.00 |
| 11 | 0.24 | 0.69 | 0.00 | -0.01 |
| 12 | 0.24 | 0.69 | 0.00 | -0.01 |
| 13 | 0.23 | 0.69 | 0.00 | -0.01 |
| 14 | 0.23 | 0.69 | 0.00 | -0.01 |
| 15 | 0.23 | 0.69 | 0.00 | -0.01 |
| 16 | 0.23 | 0.69 | 0.00 | -0.01 |
| 17 | 0.23 | 0.69 | 0.00 | -0.01 |
| 18 | 0.22 | 0.69 | -0.01 | 0.00 |
| 19 | 0.22 | 0.69 | -0.01 | 0.00 |
| 20 | 0.22 | 0.69 | -0.01 | 0.00 |
Data for Figure 5: Panel 4. Sectoral Inflation
| T_H | NT_H | T_F | NT_F | |
|---|---|---|---|---|
| 1 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.16 | -1.18 | 0.18 | 0.34 |
| 3 | 0.13 | -0.75 | 0.15 | 0.28 |
| 4 | 0.10 | -0.48 | 0.12 | 0.21 |
| 5 | 0.08 | -0.32 | 0.09 | 0.15 |
| 6 | 0.06 | -0.21 | 0.07 | 0.10 |
| 7 | 0.04 | -0.14 | 0.05 | 0.07 |
| 8 | 0.03 | -0.09 | 0.04 | 0.04 |
| 9 | 0.03 | -0.06 | 0.03 | 0.02 |
| 10 | 0.02 | -0.04 | 0.02 | 0.01 |
| 11 | 0.02 | -0.02 | 0.02 | 0.00 |
| 12 | 0.01 | -0.01 | 0.01 | 0.00 |
| 13 | 0.01 | -0.01 | 0.01 | 0.00 |
| 14 | 0.01 | -0.01 | 0.01 | -0.01 |
| 15 | 0.01 | 0.00 | 0.01 | -0.01 |
| 16 | 0.01 | 0.00 | 0.01 | -0.01 |
| 17 | 0.01 | 0.00 | 0.01 | -0.01 |
| 18 | 0.01 | 0.00 | 0.01 | -0.01 |
| 19 | 0.01 | 0.00 | 0.01 | -0.01 |
| 20 | 0.01 | 0.00 | 0.01 | -0.01 |
Data for Figure 5: Panel 5. Interest Rate
| Nominal | Real | |
|---|---|---|
| 1 | 4.04 | 4.04 |
| 2 | 1.98 | 2.07 |
| 3 | 3.07 | 3.12 |
| 4 | 3.58 | 3.61 |
| 5 | 3.83 | 3.84 |
| 6 | 3.94 | 3.94 |
| 7 | 3.99 | 3.99 |
| 8 | 4.02 | 4.02 |
| 9 | 4.03 | 4.03 |
| 10 | 4.03 | 4.03 |
| 11 | 4.04 | 4.04 |
| 12 | 4.04 | 4.04 |
| 13 | 4.04 | 4.04 |
| 14 | 4.04 | 4.04 |
| 15 | 4.04 | 4.04 |
| 16 | 4.04 | 4.04 |
| 17 | 4.04 | 4.04 |
| 18 | 4.04 | 4.04 |
| 19 | 4.04 | 4.04 |
| 20 | 4.04 | 4.04 |
Data for Figure 5: Panel 6. International Variables
| RER | TOT | CA | |
|---|---|---|---|
| 1 | 0.00 | 0.00 | 0.00 |
| 2 | 0.24 | 0.04 | 0.10 |
| 3 | 0.41 | 0.07 | 0.06 |
| 4 | 0.52 | 0.10 | 0.04 |
| 5 | 0.60 | 0.12 | 0.02 |
| 6 | 0.65 | 0.13 | 0.01 |
| 7 | 0.68 | 0.14 | 0.01 |
| 8 | 0.70 | 0.14 | 0.00 |
| 9 | 0.72 | 0.15 | 0.00 |
| 10 | 0.72 | 0.15 | 0.00 |
| 11 | 0.73 | 0.15 | 0.00 |
| 12 | 0.73 | 0.15 | 0.00 |
| 13 | 0.73 | 0.15 | 0.00 |
| 14 | 0.73 | 0.14 | 0.00 |
| 15 | 0.73 | 0.14 | 0.00 |
| 16 | 0.73 | 0.14 | 0.00 |
| 17 | 0.73 | 0.14 | 0.00 |
| 18 | 0.73 | 0.14 | 0.00 |
| 19 | 0.73 | 0.14 | 0.00 |
| 20 | 0.72 | 0.14 | 0.00 |
In response to lower markups in the non-tradable sector, peripheral output sharply expands on impact and subsequently decreases before converging to a higher long-run steady state (top-left panel). Trade linkages between the two regions of the monetary union propagate this expansion in the periphery through higher demand for goods produced in the core, thus stimulating a large short-run increase of output in the core. Overall, output in the monetary union expands almost 2.5% in the near term and the price level declines a touch, as deflation in the periphery outweighs the modest demand-driven increase of prices in the core (top-right panel). Crucially, the common central bank accommodates the effects of structural reforms by lowering policy rates (bottom-left panel).
As for developments across sectors, lower markups in the
non-tradable sector generate a sizeable short-term increase of
non-tradable and tradable output in the periphery as well as in the
core country (middle-left panel). Lower markups also induce a
decline of non-tradable prices but an increase in the price of
tradable goods as well as of prices indices in the core country
(middle-right panel). International relative prices in the
periphery depreciate, but most of the movement in the real exchange
rate (
![]() ) is accounted for by
changes in the relative price of nontradables, whereas changes in
the terms of trade (
) is accounted for by
changes in the relative price of nontradables, whereas changes in
the terms of trade (
![]() ) are
comparatively small (bottom-right panel). The same panel also shows
that the current account (
) are
comparatively small (bottom-right panel). The same panel also shows
that the current account (
![]() , where
, where
![]() ) responds little to
structural reforms, as permanent changes in the income of the
periphery reduce the incentive to smooth consumption through the
trade balance.
) responds little to
structural reforms, as permanent changes in the income of the
periphery reduce the incentive to smooth consumption through the
trade balance.
In the long run, this one-percentage point reduction in price and wage markups implemented by the periphery increases domestic output by 0.56%. This gain mostly reflects the permanent expansion of production in the non-tradable sector. Notwithstanding the modest size of the reforms considered, measures of competitiveness typically observed by policymakers improve substantially, with the real exchange rate in the periphery depreciating by 0.85% in the long run. The relative price of nontradables drives the depreciation, whereas the terms of trade only accounts for about 20% of the total adjustment in the real exchange rate.
While the dynamics explicitly take into account the non-linearities of the model, the steady state effects are approximately log-linear. Therefore, the numbers just reported can be interpreted as elasticities. For example, permanent reduction in markups by 10 percentage points increases output in the domestic country by about 5.5% and depreciates its real exchange rate by about 8.5%. This finding, which is consistent with other studies in the literature (Bayoumi et al., 2004; Forni et al., 2010), supports the policy prescription that higher competition in product and labor markets can generate sizable permanent gains in peripheral countries'output, possibly boosting their near-term growth prospects as well through substantial wealth effects.
5 The Effects of Structural Reforms in a Crisis
We next investigate how the short-run transmission mechanism of structural reforms changes in the presence of the ZLB constraint. The motivation for this analysis is twofold. First, a legacy of the 2008-09 global financial crisis is that policy rates have been at the ZLB in many countries for several years. This development has prompted a large debate on the role of alternative policies at the ZLB, the impact of the ZLB on the recovery, and the ability of monetary policy to deal with unexpected adverse events (such as the European debt crisis). Second, a growing literature finds that the effects of shocks in the presence of the ZLB can be qualitatively and quantitatively very different than in normal circumstances. For instance, Erceg and Linde (2012) find that tax-based fiscal consolidations may entail lower output losses in the short run than expenditure-based fiscal consolidations, thus overturning findings previously established in the literature (see, for instance, ALesina and Ardagna, 2010). Closer to our work, Eggertsson (2012) argues that a temporary increase in the monopoly power of firms and unions helped the U.S. recovery during the Great Depression by relaxing the ZLB constraint on monetary policy. This result is in contrast with the conventional wisdom that these policies increased the persistence of the recession (see, for instance, Cole and Ohanian, 2004).
5.1 The Crisis and the ZLB
Figure 6: Crisis
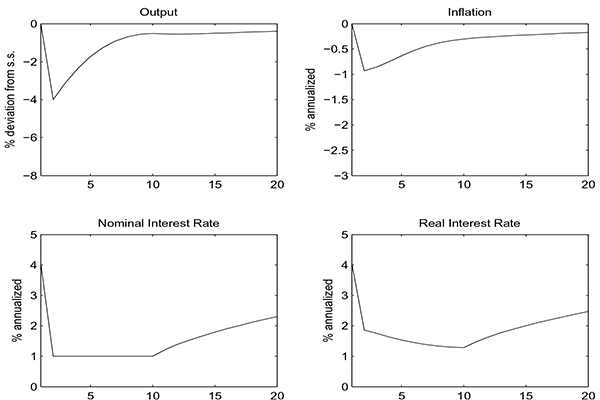
Response of output (top-left), inflation (top-right), nominal interest rates (bottom-left) and real interest rate (bottom-right) to the crisis.
Data for Figure 6
| GDP | Inflation | Nom Int Rate | Real Int Rate | |
|---|---|---|---|---|
| 1 | 0.00 | 0.00 | 4.04 | 4.04 |
| 2 | -4.00 | -0.93 | 1.00 | 1.86 |
| 3 | -3.10 | -0.86 | 1.00 | 1.75 |
| 4 | -2.35 | -0.75 | 1.00 | 1.64 |
| 5 | -1.74 | -0.63 | 1.00 | 1.53 |
| 6 | -1.27 | -0.53 | 1.00 | 1.45 |
| 7 | -0.92 | -0.45 | 1.00 | 1.38 |
| 8 | -0.69 | -0.38 | 1.00 | 1.34 |
| 9 | -0.56 | -0.33 | 1.00 | 1.30 |
| 10 | -0.51 | -0.30 | 1.00 | 1.28 |
| 11 | -0.55 | -0.28 | 1.21 | 1.48 |
| 12 | -0.55 | -0.26 | 1.39 | 1.64 |
| 13 | -0.54 | -0.25 | 1.54 | 1.77 |
| 14 | -0.53 | -0.24 | 1.67 | 1.89 |
| 15 | -0.50 | -0.22 | 1.79 | 2.01 |
| 16 | -0.48 | -0.21 | 1.91 | 2.11 |
| 17 | -0.46 | -0.20 | 2.01 | 2.21 |
| 18 | -0.44 | -0.19 | 2.12 | 2.30 |
| 19 | -0.42 | -0.18 | 2.21 | 2.39 |
| 20 | -0.40 | -0.17 | 2.30 | 2.47 |
In our crisis scenarios, we follow the recent literature (see, for example, Eggertsson and Woodford, 2003) and assume that an aggregate preference shock hits the monetary union, depressing output and generating deflation. The common central bank attempts to provide monetary stimulus, but the ZLB constraint prevents it from completely offsetting the recession.
Figure 6 displays the impact of the crisis. We calibrate the size of the shock so that we can reproduce the peak-to-trough decline of euro-area output of about 4% following the collapse of Lehman Brothers in September 2008 (top-left panel). Interestingly, under our baseline calibration, prices drop nearly 1% (top-right panel), in line with the data. The central bank immediately cuts the nominal interest rate to its effective lower bound of 1% and keeps this accommodative stance for 10 quarters (bottom-left panel). The crisis' deflationary pressures, combined with the lower bound constraint, imply that the real interest rate remains relatively high (bottom-right panel).15
Having described the crisis environment, we next study the response of the economy to structural reforms considered in Section 4.
5.2 The Effects of Structural Reforms at the ZLB
Table 3: Impact effects of structural reforms at the ZLB
|
|
Output | Inflation | Real Rate |
|---|---|---|---|
| 0 | -4.00 | -0.93 | 1.86 |
| 1 | -4.13 | -1.47 | 2.22 |
| 5 | -4.56 | -3.59 | 3.56 |
| 10 | -5.07 | -6.25 | 5.13 |
Note: Response (in %) to a permanent reduction in price and wage markups in the periphery non-tradable sector.
Table 3 summarizes the main findings of our analysis. As shown in the first column, we consider permanent structural reforms in the periphery's non-tradable sector ranging from no change in labor and product market markups (crisis scenario) to a 10 percentage point reduction in both markups (crisis scenario + ambitious reforms). The last three columns of the table present the impact response of union-wide output (second column), prices (third column), and the real interest rate (fourth column) to these policy experiments. Amid contracting output and falling prices due to the crisis, the implementation of reforms in a ZLB environment further reduces aggregate output between 13 basis points (in the case of a 1 percentage point markup reduction) and 1.07 percentage points (in the case of a markup reduction of 10 percentage points).
The fall in periphery output primarily explains the union-wide contraction. In the periphery, production collapses both in the tradable and non-tradable sector. As marginal costs decrease, firms in the non-tradable sector cut prices, thus worsening the deflationary pressures associated with the crisis and contributing to an increase in the real interest rate. This effect slows down demand even further, with consequences also for the tradable sectors of both countries. Conversely, core aggregate production is roughly unchanged. In that region, the slowdown in tradables is approximately compensated by an increase in the production of nontradables, driven by a favorable adjustment in relative prices.
The short-run perverse effects of reforms are quantitatively even more remarkable when compared to the standard effects of reforms in normal times. A markup reduction by one percentage point generates an increase in union output of about 2.5% in normal times (see Figure 5 above), but an output drop of 13 basis points in a crisis. This change in the sign of the output response suggests that the short-run transmission of structural reforms critically depends on the ability of monetary policy to provide stimulus. When the ZLB constrains monetary policy, the income and substitution effects of reforms may work in opposite directions. On the one hand, agents anticipate that income will be permanently higher, resulting in strong wealth effects and higher consumption. On the other hand, these policies stimulate production and competitiveness through lower domestic prices that result in higher real interest rates. While in normal times the central bank accommodates deflation by reducing the policy rate, higher real rates at the ZLB further depress consumption and output. Not surprisingly, more ambitious reform efforts are associated with a deeper output contraction as deflationary pressures become even more acute.
Figure 7: Effects of Reforms in Crisis
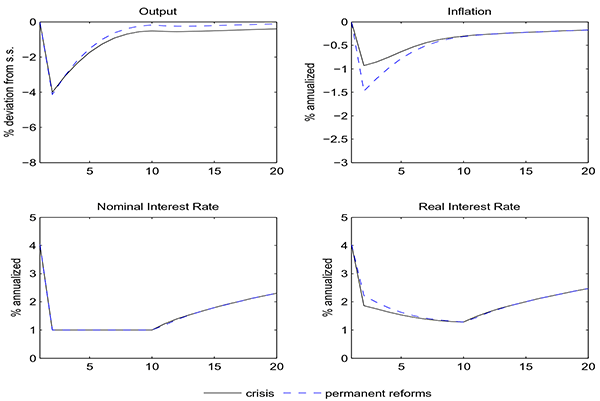
Response of output (top-left), inflation (top-right), nominal interest rates (bottom-left) and real interest rate (bottom-right) to the crisis without reforms (continuous black line) and with a permanent increase in labor and product market subsidies by one percentage point (dashed blue line).
Data for Figure 7
| GDP | Inflation | Nom Int Rate | Real Int Rate | |
|---|---|---|---|---|
| 1 | 0.00 | 0.00 | 4.04 | 4.04 |
| 2 | -4.14 | -1.47 | 1.00 | 2.22 |
| 3 | -3.07 | -1.21 | 1.00 | 1.98 |
| 4 | -2.20 | -0.98 | 1.00 | 1.79 |
| 5 | -1.52 | -0.78 | 1.00 | 1.63 |
| 6 | -1.00 | -0.62 | 1.00 | 1.51 |
| 7 | -0.63 | -0.50 | 1.00 | 1.42 |
| 8 | -0.38 | -0.41 | 1.00 | 1.35 |
| 9 | -0.23 | -0.35 | 1.00 | 1.31 |
| 10 | -0.18 | -0.31 | 1.00 | 1.29 |
| 11 | -0.22 | -0.29 | 1.17 | 1.44 |
| 12 | -0.25 | -0.27 | 1.37 | 1.62 |
| 13 | -0.25 | -0.25 | 1.53 | 1.76 |
| 14 | -0.23 | -0.24 | 1.67 | 1.89 |
| 15 | -0.21 | -0.22 | 1.79 | 2.00 |
| 16 | -0.19 | -0.21 | 1.91 | 2.11 |
| 17 | -0.17 | -0.20 | 2.01 | 2.21 |
| 18 | -0.15 | -0.19 | 2.12 | 2.30 |
| 19 | -0.13 | -0.18 | 2.21 | 2.39 |
| 20 | -0.11 | -0.17 | 2.30 | 2.47 |
Granted, the long-run benefits of structural reforms remain unchanged, and union-wide output improves relative to the crisis after a few quarters (Figure 7). Yet, in the short run, structural reforms do not contribute to alleviate the consequences of a deep crisis. The main point of the paper, on which we elaborate in the next section, is not to deny the long-term gains associated with these reforms. In contrast, our analysis underscores that, absent the appropriate monetary stimulus, ambitious reforms may be detrimental for the near-term growth prospects of vulnerable euro-area countries, contrary to what is often advocated in policy and academic environments.
5.3 The Effects of Temporary Reforms at the ZLB
Under our baseline calibration (as well as in several robustness checks discussed in the next subsection), permanent reforms at the ZLB do not contribute to support economic activity in the immediate aftermath of a demand-driven crisis. In practice, other impediments--such as social unrest, political economy considerations, reallocation of factors across sectors, uncertainty about the implementation and gains of reforms--may actually exacerbate the short-term costs of reforms and limit their long-term benefits. The Greek and Spanish strikes over the recent austerity measures, as well as the pledge of some parties to undo the labor market reforms undertaken by the technocratic government during the 2013 elections in Italy, are clear examples of these issues.
We model these complex socio-political dynamics by considering an experiment in which the reforms are perceived as (and in fact turn out to be) temporary. Governments in the periphery implement labor and product market reforms as the crisis hits. However, the short-run costs in terms of deflation and the absence of output gains lead to social unrest and imply that the reforms are eventually undone. We make the simplifying assumptions that this outcome is perfectly anticipated at the time of implementation and the reforms are unwound when the ZLB stops binding.16
Figure 8: Effects of Temporary Reforms in Crisis
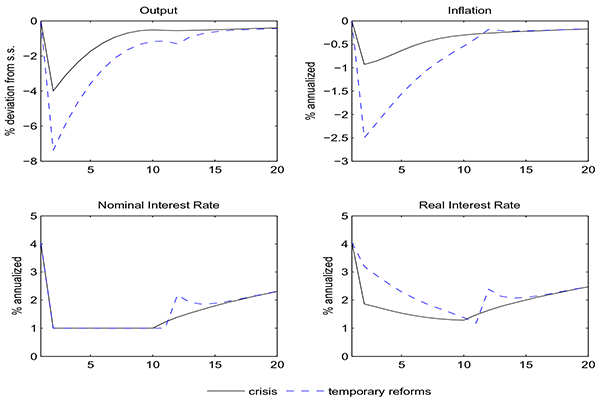
Response of output (top-left), inflation (top-right), nominal interest rates (bottom-left) and real interest rate (bottom-right) to the crisis without reforms (continuous black line) and with a temporary increase in labor and product market subsidies by one percentage point (dashed blue line).
Data for Figure 8
| GDP | Inflation | Nom Int Rate | Real Int Rate | |
|---|---|---|---|---|
| 1 | 0.00 | 0.00 | 4.04 | 4.04 |
| 2 | -7.37 | -2.50 | 1.00 | 3.20 |
| 3 | -5.88 | -2.18 | 1.00 | 2.87 |
| 4 | -4.62 | -1.86 | 1.00 | 2.57 |
| 5 | -3.58 | -1.56 | 1.00 | 2.30 |
| 6 | -2.75 | -1.29 | 1.00 | 2.07 |
| 7 | -2.11 | -1.06 | 1.00 | 1.87 |
| 8 | -1.64 | -0.87 | 1.00 | 1.70 |
| 9 | -1.33 | -0.70 | 1.00 | 1.54 |
| 10 | -1.17 | -0.54 | 1.00 | 1.38 |
| 11 | -1.16 | -0.37 | 1.00 | 1.19 |
| 12 | -1.31 | -0.19 | 2.17 | 2.39 |
| 13 | -0.93 | -0.21 | 1.92 | 2.13 |
| 14 | -0.73 | -0.22 | 1.85 | 2.07 |
| 15 | -0.63 | -0.21 | 1.88 | 2.09 |
| 16 | -0.56 | -0.21 | 1.95 | 2.15 |
| 17 | -0.52 | -0.20 | 2.04 | 2.23 |
| 18 | -0.49 | -0.19 | 2.13 | 2.31 |
| 19 | -0.46 | -0.18 | 2.22 | 2.39 |
| 20 | -0.44 | -0.17 | 2.31 | 2.47 |
Figure 8 compares the response of output (top-left panel), inflation (top-right panel), the nominal interest rate (bottom-left panel) and the real interest rate (bottom-right panel) to the crisis without reforms (continuous black line) against the case of a temporary reduction in labor and product market markups by one percentage point (dashed blue line).
When monetary policy is constrained by the ZLB, temporary reforms entail large output losses in the short-run. At the union level, output drops by 7.4% on impact, almost doubling the output costs associated with the crisis. As in the case of permanent reforms, reducing markups increases the deflationary pressures generated by the crisis. However, the temporary nature of the reforms creates much more severe short-run deflationary pressures. This result reflects two mechanisms. First, as in the case of permanent reforms, lower prices increase the short-term real interest rate. However, temporary reforms are associated with much smaller wealth effects as long-run output is unchanged, thus providing stronger incentives for agents to postpone their consumption. Second, households understand that the eventual unwinding of reforms (i.e. higher markups) when the crisis has almost completely vanished will have inflationary consequences, triggering a sharp increase in the nominal and real interest rate. Anticipating the future tightening, aggregate demand contracts immediately, contributing to a deeper crisis. This effect adds to the initial deflationary pressures and creates a perverse feedback loop, as the real interest rate further increases. Moreover, the economy suffers a policy-induced double-dip recession when the ZLB stops binding. Under temporary reforms, the absence of long-run wealth effects together with higher short-run output losses imply that, differently from the case of permanent reforms, the periphery borrows from abroad and runs a current account deficit (not shown).
In sum, our experiments suggest that when monetary policy is at the ZLB, ambitious and credible structural reforms may have undesirable short-run effects. In addition, when political economy factors, such as electoral outcomes and social unrest, undermine the credibility of the reforms and cast doubts on their long-lasting impact, these perverse effects are likely to be magnified.
5.4 Robustness
In this section, we briefly discuss the sensitivity of the perverse effects of structural reforms at the ZLB to three factors, namely the elasticity of intertemporal substitution, the size of the economy implementing the reforms, and the nature of the shock generating the crisis.17
Elasticity of Intertemporal Substitution. An important
parameter governing the short-run response of consumption to
changes in the real interest rate is the elasticity of
intertemporal substitution (
![]() ). As shown in Table 2, in our
benchmark calibration we set
). As shown in Table 2, in our
benchmark calibration we set
![]() , implying that the elasticity of
intertemporal substitution is above one
, implying that the elasticity of
intertemporal substitution is above one![]() Although
several authors provide evidence in support of our calibration
(Hansen and Singleton, 1983; Summers, 1984; Attanasio and Weber, 1989; Rotembert and Woodford, 1997; Gruber, 2006), other macroeconomists would consider
such a value for
Although
several authors provide evidence in support of our calibration
(Hansen and Singleton, 1983; Summers, 1984; Attanasio and Weber, 1989; Rotembert and Woodford, 1997; Gruber, 2006), other macroeconomists would consider
such a value for ![]() as a low estimate for this
parameter (Hall, 1988). Thus, given the
disagreement on the appropriate value for the elasticity of
intertemporal substitution in the literature, we repeat our
simulations with
as a low estimate for this
parameter (Hall, 1988). Thus, given the
disagreement on the appropriate value for the elasticity of
intertemporal substitution in the literature, we repeat our
simulations with ![]() and
and ![]() .18 A smaller elasticity of
intertemporal substitution implies a smaller negative output effect
of permanent reforms in the short run. Moreover, and contrary to
our benchmark results, larger reforms lead to smaller output
losses. Yet, when
.18 A smaller elasticity of
intertemporal substitution implies a smaller negative output effect
of permanent reforms in the short run. Moreover, and contrary to
our benchmark results, larger reforms lead to smaller output
losses. Yet, when ![]() , a permanent
reduction in labor and product markups by 10 percentage points (our
most ambitious reforms considered in Table 3) still leads to output
gains of only 0.6 percentage point relative to the crisis scenario.
Given the size of the reforms, these gains are quite small,
especially if compared to the 25% output increase experienced in
normal times, pointing once again to the critical role played by
(the lack of) monetary policy accommodation for the short-run
transmission of reforms.
, a permanent
reduction in labor and product markups by 10 percentage points (our
most ambitious reforms considered in Table 3) still leads to output
gains of only 0.6 percentage point relative to the crisis scenario.
Given the size of the reforms, these gains are quite small,
especially if compared to the 25% output increase experienced in
normal times, pointing once again to the critical role played by
(the lack of) monetary policy accommodation for the short-run
transmission of reforms.
Country Size. The effects of reforms during crisis times are robust to changes in country size. Our calibration assumes that the currency union consists of two equal-sized regions, which represents a good approximation to the relative weight of core and peripheral countries in the EMU.19 Our experiments reflect the idea that all peripheral countries are currently being encouraged to implement ambitious reform programs. In practice, however, the implementation of reforms may occur at different times in each country. To check if the size of the country that implements the reforms matters for our results, we run simulations assuming that the periphery country accounts for only 10% of union-wide output.20
Perhaps not surprisingly, the main difference relative to the symmetric case is the smaller output decline experienced by the union as a whole. However, this difference simply reflects the smaller weight of the periphery in aggregate variables. The relevant real interest rate for the consumption decisions of the representative household in the periphery is a function of the nominal interest rate set by the common monetary authority, which is at the ZLB during the crisis, and the periphery's CPI inflation rate, which is approximately independent of the country size.21 Structural reforms that make the non-tradable sector in the periphery more competitive impact the domestic CPI almost identically, no matter whether the periphery is large or small. Therefore, the additional output contraction in the periphery due to the reforms compared to the crisis scenario remains essentially unaffected.
Asymmetric Shock. In our main experiment, we considered the crisis as a shock that hits symmetrically both countries in the currency union. However, the recovery from the global financial crisis in core and peripheral European countries reveals a great deal of asymmetry between the two regions, perhaps reflecting the "macroeconomic imbalances" accumulated in the early 2000s.
Motivated by this observation, we investigate the robustness of our main findings to a crisis shock that is not symmetric. We consider a scenario where the shock only hits the periphery. As in the previous exercise, we continue to calibrate the shock to match a 4% decline in union-wide output. This crisis is still associated with the nominal interest rate stuck at the ZLB for about three years. We then study the effects of structural reforms implemented in the periphery in the context of this crisis.
The main difference in case of an asymmetric shock is the large adjustment in international variables. The periphery runs a large current account surplus and the terms of trade significantly contributes to the depreciation of the real exchange rate. However, these movements primarily reflect the asymmetric nature of the crisis shock and occur also in the absence of structural reforms.
That said, structural reforms that permanently reduce product and labor market markups in the periphery continue to be contractionary in the short run, as more protracted deflation at the ZLB results in higher real interest rates. With an asymmetric crisis, the magnitudes of the additional output losses is smaller--twenty basis points in the case of a 10 percentage points reduction in markups. Yet, our main conclusion is qualitatively unchanged.
6 Disentangling the Effects of Reforms at the ZLB
So far, we have argued that the short-run transmission of reforms depends critically on the ability of the central bank to provide monetary policy accommodation. In normal times, the nominal interest rate falls, providing stimulus against deflationary pressures. However, in a severe crisis, whereby the central bank runs into the ZLB constraint, the deflationary pressures associated with structural reforms lead to higher real rates and further depress economic activity. In this section, we consider two experiments that shed light on the mechanism behind these findings.
In the first experiment, which we label "New Deal," we assume
that the government sets
![]() and
and
![]() to temporarily increase the
monopolistic power of firms and unions. This experiment is in the
spirit of Eggertsson (2012), who claims that
policies of this kind contributed to end the Great Depression, or
can be interpreted as an application of unconventional fiscal
policies that provide monetary stimulus at the ZLB as in Correia et al. (2013).22 In essence, this policy aims at
generating expectations of price increases in the short run without
any implication for the long-run level of output. Thus, we
interpret this experiment as isolating the substitution effect
associated with expectations of higher prices at the ZLB.
to temporarily increase the
monopolistic power of firms and unions. This experiment is in the
spirit of Eggertsson (2012), who claims that
policies of this kind contributed to end the Great Depression, or
can be interpreted as an application of unconventional fiscal
policies that provide monetary stimulus at the ZLB as in Correia et al. (2013).22 In essence, this policy aims at
generating expectations of price increases in the short run without
any implication for the long-run level of output. Thus, we
interpret this experiment as isolating the substitution effect
associated with expectations of higher prices at the ZLB.
In our simulations, the government increases distortionary taxes on firms and workers as long as the "shadow" nominal interest rate (i.e. the nominal interest rate absent the ZLB constraint) stays in negative territory
where
![]() is a parameter that
controls how aggressively the government increases the taxes in
response to the crisis.23
is a parameter that
controls how aggressively the government increases the taxes in
response to the crisis.23
Our second experiment, which we label "Delay" , aims at retaining the long-run benefits of structural reforms without imposing the short-run costs in terms of deflation. Thus, we interpret this experiment as isolating the wealth effect associated with expectations of higher permanent income at the ZLB.
When the crisis hits, the government (credibly) announces that it will implement structural reforms when the ZLB stops binding
The Delay rule differs from the New Deal rule because the permanent
change in the tax needs to be consistent with the final steady
state. Therefore, the coefficient
![]() is constrained to be equal to
is constrained to be equal to
![]() .
.
The idea that news about future supply increases may stimulate subdued aggregate demand in an economy facing a liquidity trap is not new. In their discussion about the Japanese ZLB experience of the late 1990s, Krugman (1998) argues that an expected drop in productivity due to population aging contributed to the persistence of the ZLB, while Rogoff (1998) suggests that future productivity gains ought to be the solution to the ZLB constraint. More recently, Fernandez-Villaverde et al. (2012) formalize this argument in a two-period New-Keynesian model. Our Delay policy can be interpreted as a state-contingent application of these arguments.
Figure 9: Disentangling the Effects of Reforms in Crisis
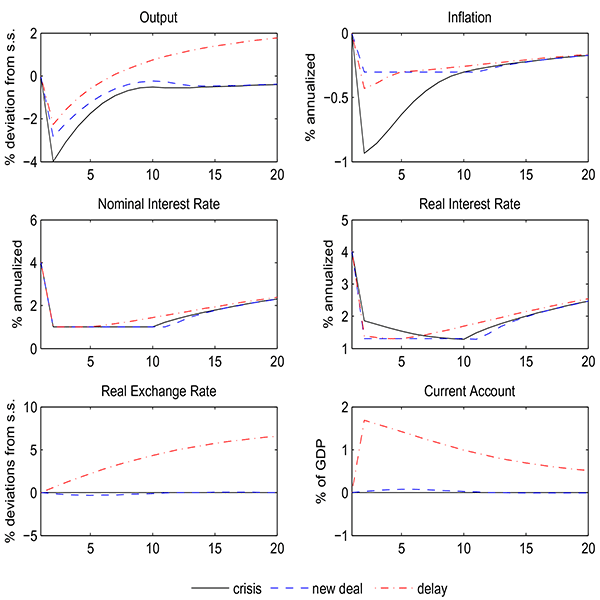
Response of output (top-left), inflation (top-right), nominal interest rate (middle-left), real interest rate (middle-right), real exchange rate (bottom-left) and current account (bottom-right) in the crisis without reforms (continuous black line), under the "new deal" rule (dashed blue line) and under the "delay" rule (dashed-dotted red line).
Data for Figure 9: Crisis
| GDP | GDP % | Inflation | Nom Int Rate | Real Int Rate | RER | CA | |
|---|---|---|---|---|---|---|---|
| 1 | 0.40 | 0.00 | 0.00 | 4.04 | 4.04 | 0.00 | 0.00 |
| 2 | 0.39 | -4.00 | -0.93 | 1.00 | 1.86 | 0.00 | 0.00 |
| 3 | 0.39 | -3.10 | -0.86 | 1.00 | 1.75 | 0.00 | 0.00 |
| 4 | 0.39 | -2.35 | -0.75 | 1.00 | 1.64 | 0.00 | 0.00 |
| 5 | 0.40 | -1.74 | -0.63 | 1.00 | 1.53 | 0.00 | 0.00 |
| 6 | 0.40 | -1.27 | -0.53 | 1.00 | 1.45 | 0.00 | 0.00 |
| 7 | 0.40 | -0.92 | -0.45 | 1.00 | 1.38 | 0.00 | 0.00 |
| 8 | 0.40 | -0.69 | -0.38 | 1.00 | 1.34 | 0.00 | 0.00 |
| 9 | 0.40 | -0.56 | -0.33 | 1.00 | 1.30 | 0.00 | 0.00 |
| 10 | 0.40 | -0.51 | -0.30 | 1.00 | 1.28 | 0.00 | 0.00 |
| 11 | 0.40 | -0.55 | -0.28 | 1.21 | 1.48 | 0.00 | 0.00 |
| 12 | 0.40 | -0.55 | -0.26 | 1.39 | 1.64 | 0.00 | 0.00 |
| 13 | 0.40 | -0.54 | -0.25 | 1.54 | 1.77 | 0.00 | 0.00 |
| 14 | 0.40 | -0.53 | -0.24 | 1.67 | 1.89 | 0.00 | 0.00 |
| 15 | 0.40 | -0.50 | -0.22 | 1.79 | 2.01 | 0.00 | 0.00 |
| 16 | 0.40 | -0.48 | -0.21 | 1.91 | 2.11 | 0.00 | 0.00 |
| 17 | 0.40 | -0.46 | -0.20 | 2.01 | 2.21 | 0.00 | 0.00 |
| 18 | 0.40 | -0.44 | -0.19 | 2.12 | 2.30 | 0.00 | 0.00 |
| 19 | 0.40 | -0.42 | -0.18 | 2.21 | 2.39 | 0.00 | 0.00 |
| 20 | 0.40 | -0.40 | -0.17 | 2.30 | 2.47 | 0.00 | 0.00 |
Data for Figure 9: New Deal
| GDP | Inflation | Nom Int Rate | Real Int Rate | RER | CA | |
|---|---|---|---|---|---|---|
| 1 | 0.00 | 0.00 | 4.04 | 4.04 | 0.00 | 0.00 |
| 2 | -2.85 | -0.30 | 1.00 | 1.30 | -0.13 | 0.00 |
| 3 | -2.22 | -0.30 | 1.00 | 1.30 | -0.23 | 0.00 |
| 4 | -1.68 | -0.30 | 1.00 | 1.30 | -0.29 | 0.00 |
| 5 | -1.23 | -0.30 | 1.00 | 1.30 | -0.31 | 0.00 |
| 6 | -0.87 | -0.30 | 1.00 | 1.30 | -0.30 | 0.00 |
| 7 | -0.60 | -0.30 | 1.00 | 1.30 | -0.27 | 0.00 |
| 8 | -0.40 | -0.30 | 1.00 | 1.30 | -0.22 | 0.00 |
| 9 | -0.28 | -0.30 | 1.00 | 1.30 | -0.16 | 0.00 |
| 10 | -0.24 | -0.30 | 1.00 | 1.30 | -0.10 | 0.00 |
| 11 | -0.26 | -0.30 | 1.00 | 1.28 | -0.05 | 0.00 |
| 12 | -0.37 | -0.28 | 1.20 | 1.46 | -0.01 | 0.00 |
| 13 | -0.45 | -0.26 | 1.45 | 1.69 | 0.01 | 0.00 |
| 14 | -0.47 | -0.24 | 1.63 | 1.85 | 0.02 | 0.00 |
| 15 | -0.47 | -0.23 | 1.77 | 1.98 | 0.03 | 0.00 |
| 16 | -0.46 | -0.21 | 1.89 | 2.10 | 0.03 | 0.00 |
| 17 | -0.44 | -0.20 | 2.01 | 2.20 | 0.03 | 0.00 |
| 18 | -0.43 | -0.19 | 2.11 | 2.29 | 0.03 | 0.00 |
| 19 | -0.41 | -0.18 | 2.21 | 2.38 | 0.03 | 0.00 |
| 20 | -0.39 | -0.17 | 2.30 | 2.47 | 0.02 | 0.00 |
Data for Figure 9: Delay
| GDP | Inflation | Nom Int Rate | Real Int Rate | RER | CA | |
|---|---|---|---|---|---|---|
| 1 | 0.00 | 0.00 | 4.04 | 4.04 | 0.00 | 0.00 |
| 2 | -2.26 | -0.43 | 1.00 | 1.39 | 0.60 | 0.02 |
| 3 | -1.59 | -0.39 | 1.00 | 1.34 | 1.17 | 0.02 |
| 4 | -1.03 | -0.34 | 1.00 | 1.30 | 1.71 | 0.02 |
| 5 | -0.59 | -0.30 | 1.01 | 1.31 | 2.21 | 0.01 |
| 6 | -0.23 | -0.29 | 1.07 | 1.36 | 2.70 | 0.01 |
| 7 | 0.07 | -0.29 | 1.15 | 1.43 | 3.15 | 0.01 |
| 8 | 0.33 | -0.28 | 1.24 | 1.51 | 3.58 | 0.01 |
| 9 | 0.55 | -0.27 | 1.34 | 1.60 | 3.97 | 0.01 |
| 10 | 0.74 | -0.26 | 1.44 | 1.69 | 4.34 | 0.01 |
| 11 | 0.91 | -0.25 | 1.54 | 1.78 | 4.67 | 0.01 |
| 12 | 1.05 | -0.24 | 1.64 | 1.87 | 4.97 | 0.01 |
| 13 | 1.18 | -0.23 | 1.74 | 1.96 | 5.25 | 0.01 |
| 14 | 1.29 | -0.22 | 1.85 | 2.05 | 5.50 | 0.01 |
| 15 | 1.39 | -0.21 | 1.94 | 2.14 | 5.73 | 0.01 |
| 16 | 1.48 | -0.20 | 2.04 | 2.23 | 5.94 | 0.01 |
| 17 | 1.56 | -0.19 | 2.13 | 2.31 | 6.12 | 0.01 |
| 18 | 1.64 | -0.18 | 2.22 | 2.39 | 6.29 | 0.01 |
| 19 | 1.71 | -0.17 | 2.31 | 2.47 | 6.45 | 0.01 |
| 20 | 1.77 | -0.16 | 2.39 | 2.55 | 6.58 | 0.01 |
Figure 9 presents the response of the main variables to the New Deal policy (dashed blue line) and to the Delay policy (dashed-dotted red line). Notwithstanding the absence of monetary accommodation due to the ZLB, both policies are closer to the short-run transmission mechanism of reforms operating in normal times: On impact, output in the currency union is well above the crisis scenario and, as a consequence, the permanent reform scenario discussed in Section 5.2. Under the New Deal policy, the initial drop in output is about 2.5%, much less than the 4% contraction experienced in the absence of announced reforms. Under the Delay policy, which is calibrated to a long-run reduction in markups of 10 percentage points, the output gains are somewhat larger (although still significantly less than in normal times). In particular, output recovers from the crisis and monetary policy exits the ZLB after only six quarters.
These experiments highlight the main tradeoffs associated with the implementation of reforms at the ZLB. The New Deal policy attempts to offset the deflationary effects of the crisis by creating expectations for positive inflation through higher, albeit temporary, monopoly power. Thus, this policy operates mainly through the substitution effect of lower real interest rates and has no effect on long-run income. In the case of the Delay policy, the expectation that reforms will be permanent, though implemented in the future, generates a large wealth effect that stimulates aggregate demand, thus limiting the short-run output drop due to the crisis and supporting domestic prices.
As for the open-economy variables, the permanent effects associated with the Delay policy result in a gradual depreciation of the real exchange rate and a current account surplus, similarly to what was observed in normal times. The New Deal policy, in contrast, has very little impact on international variables. The temporary nature of this policy does not bring about any realignment in international prices or permanent gain in competitiveness. In the short-run, the real exchange rate modestly appreciates and the current account turns slightly positive. These responses reflect higher output and prices in the periphery relative to the core, where no policy is implemented.
We close this section with an important caveat. The two policies discussed in this section present serious political economy challenges. Increasing markups in a crisis may combat deflationary pressures, but the same interest groups that oppose permanent reforms in a crisis could fight to make the temporary change indeed permanent. Similarly, crises are times when external forces may render unpleasant reforms acceptable. Announcing at the beginning of a crisis that the ambitious reforms will be implemented when the ZLB stops being binding poses obvious time-inconsistencies problems. For these reasons, we interpret the "New Deal" and "Delay" policies as illustrative of the key mechanisms at play in our model, rather than normative statements on the actual implementation of structural reforms.
7 Conclusions
Structural reforms can greatly reduce the competitiveness gap between the EMU core and periphery and boost income prospects in the region. However, the timing of such reforms is crucial. If undertaken during a crisis that takes monetary policy rates to the ZLB, structural reforms can deepen the recession by worsening deflation and increasing real rates. This effect becomes even stronger if the public expects policymakers to later unwind these reforms.
Our paper contributes to the recent literature on the implications of the ZLB for the transmission of shocks. We expand on the existing results by investigating the effects of permanent markup changes at the ZLB in an open economy environment, thus focusing on the domestic and international transmission of shocks.
In addressing the effects of reforms at the ZLB, we have abstracted from important considerations that are likely to shape the policy debate in Europe. First, our analysis features only inputs of production that cannot be accumulated over time. As argued by Fernandez-Villaverde (2013) in his discussion of this paper, the presence of physical capital may in principle preserve the standard transmission mechanism of reforms. However, in their simulations, Gavin et al. (2013) find that technology shocks at the ZLB continue to have perverse effects, at least in a closed economy environment. Moreover, if physical capital (or other assets, such as housing) can relax borrowing limits through their collateral value, perverse debt-deflation dynamics at the ZLB are likely to be amplified (see, for instance, Eggertsson and Krugman, 2012). Second, while our analysis has solely focused on the short-run transmission of reforms, the policy debate in Europe involves important political economy considerations (Blanchard adn Giavazzi, 2003). The social and political opposition faced by governments in peripheral Europe to adopt relatively small reform packages in times of financial turbulence reveals the difficulties of changing these policies in practice. Our findings emphasize a relevant macroeconomic tradeoff associated with the absence of sufficient monetary policy stimulus to support reform efforts. Future research efforts could embed the pure macroeconomic forces discussed in this paper in a political economy environment, with the objective of drawing serious welfare implications.
References
Adao, B., I. Correia, and P. Teles (2009). On the Relevance of Exchange Rate Regimes for Stabilization Policy. Journal of Economic Theory 144, 1468-188.
Alesina, A. and S. Ardagna (2010). Large Changes in Fiscal Policy: Taxes versus Spending. In J. Brown (Ed.), Tax Policy and the Economy, Chapter 3, pp. 35-68. University of Chicago Press.
Attanasio, O. and G. Weber (1989). Intertemporal Substitution, Risk Aversion, and the Euler Equation for Consumption. Economic Journal 99, 59-73.
Backus, D., P. Kehoe, and F. Kydland (1994). The Dynamics of the Trade Balance and the Terms of Trade: The J-Curve? American Economic Review 84, 84-103.
Bayoumi, T., D. Laxton, and P. Pesenti (2004). Benefits and Spillovers of Greater Competition in Europe: A Macroeconomic Assessment. NBER Working Paper 10416.
Blanchard, O. and F. Giavazzi (2003). The Macroeconomic Effects of Regulation and Deregulation in Goods and Labor Markets. Quarterly Journal of Economics 118, 879-909.
Cacciatore, M. and G. Fiori (2012). The Macroeconomic Effects of Goods and Labor Markets Deregulation. Unpublished, HEC Montreal.
Cacciatore, M., G. Fiori, and F. Ghironi (2012). Market Deregulation and Optimal Monetary Policy in a Monetary Union. Unpublished, HEC Montreal.
Calvo, G. (1983). Staggered Prices in a Utility-Maximizing Framework. Journal of Monetary Economics 12, 383-398.
Chen, R., G. M. Milesi-Ferretti, and T. Tressel (2012). External Imbalances in the Euro Area. IMF Working Paper 12/36.
Christiano, L., M. Eichenbaum, and S. Rebelo (2011). When Is the Government Spending Multiplier Large? Journal of Political Economy 119, 78-121.
Cole, H. and L. Ohanian (2004). New Deal Policies and the Persistence of the Great Depression: A General Equilibrium Analysis. Journal of Political Economy 112, 779-816.
Correia, I., E. Farhi, J. P. Nicolini, and P. Teles (2013). Unconventional Fiscal Policy at the Zero Bound. American Economic Review Forthcoming.
Corsetti, G., P. Martin, and P. Pesenti (2013). Varieties and the Transfer Problem. Journal of International Economics 89, 1-12.
Corsetti, G. and H. Pesaran (2012). Beyond Fiscal Federalism: What Does It Take to Save the Euro? http://www.voxeu.org/article/beyond-fiscal-federalism-what-will-it-take-save-euro.
Eggertsson, G. (2011). What Fiscal Policy Is Effective at Zero Interest Rates? In D. Acemoglu and M. Woodford (Eds.), NBER Macroeconomics Annual 2010, Volume 25, Chapter 2, pp. 59-112. University of Chicago Press.
Eggertsson, G. (2012). Was the New Deal Contractionary? American Economic Review 102, 524-555.
Eggertsson, G. and P. Krugman (2012). Debt, Deleveraging, and the Liquidity Trap: A Fisher-Minsky-Koo Approach. Quarterly Journal of Economics 127, 1469-1513.
Eggertsson, G. and M. Woodford (2003). The Zero Bound on Interest Rates and Optimal Monetary Policy. Brookings Papers on Economic Activity 34, 139-235.
Eichengreen, B. (2010). Imbalances in the Euro Area. Unpublished, University of California at Berkeley.
Erceg, C., L. Guerrieri, and C. Gust (2006). SIGMA: A New Open Economy Model for Policy Analysis. International Journal of Central Banking 2, 1-50.
Erceg, C. and J. Linde (2012). Fiscal Consolidation in an Open Economy. American Economic Review 102, 186-191.
Everaert, L. and W. Schule (2006). Structural Reforms in the Euro Area: Economic Impact and Role of Synchronization Across Markets and Countries. IMF Working Paper 06/137.
Farhi, E., G. Gopinath, and O. Itskhoki (2012). Fiscal Devaluations. Unpublished, Harvard
University.
Fernandez-Villaverde, J. (2013). Discussion of "Can Structural Reforms Help Europe?". Unpublished, University of Pennsylvania.
Fernandez-Villaverde, J., P. Guerron-Quintana, and J. Rubio-Ramirez (2012). Supply-Side Policies and the Zero Lower Bound. Unpublished, University of Pennsylvania.
Forni, L., A. Gerali, and M. Pisani (2010). Macroeconomic Effects of Greater Competition in the Service Sector: The Case of Italy. Macroeconomic Dynamics 14, 677-708.
Gaulier, G. and V. Vicard (2012). The Signatures of Euro Area Imbalances. Unpublished, Banque de France.
Gavin, W., B. Keen, A. Richter, and N. Throckmorton (2013). Global Dynamics at the Zero Lower Bound. Federal Reserve Bank of St. Louis Working Paper 2013-007A.
Gerali, A., A. Notarpietro, and M. Pisani (2013). Potential Outout and Structural Reforms after the Crisis: The Case of Italy. Unpublished, Bank of Italy.
Gruber, J. (2006). A Tax-Based Estimate of the Elasticity of Intertemporal Substitution. NBER Working Paper 11945.
Hall, R. (1988). Intertemporal Substitution in Consumption. Journal of Political Economy 96, 339-357.
Hansen, L.-P. and K. Singleton (1983). Stochastic Consumption, Risk Aversion, and the Temporal Behavior of Asset Returns. Journal of Political Economy 91, 249-265.
Jean, S. and G. Nicoletti (2002). Product Market Regulation and Wage Premia in Europe and North America: An Empirical Investigation. OECD Economics Department Working 318.
Krugman, P. (1998). It's Baaack: Japan's Slump and the Return of the Liquidity Trap. Brookings Papers on Economic Activity 2, 137-187.
Lipinska, A. and L. von Thadden (2012). On the (In)effectiveness of Fiscal Devaluations in a Monetary Union. FEDS Working Papers 2012-71.
Mendoza, E. (1991). Real Business Cycles in a Small Open Economy. American Economic Review 81, 797-818.
Rogoff, K. (1998). Discussion of: "It's Baaack: Japan's Slump and the Return of the Liquidity Trap". Brookings Papers on Economic Activity 2, 194-199.
Rotemberg, J. and M. Woodford (1997). An Optimization-Based Econometric Framework for the Evaluation of Monetary Policy. In B. Bernanke and J. Rotemberg (Eds.), NBER Macroeconomics Annual 1997, Volume 12, Chapter 6, pp. 297-361. MIT Press.
Summers, L. (1984). The After-Tax Rate of Return Affects Private Savings. American Economic Revie 74, 249-253.
World Economic Forum (2012). Global Competitiveness Report.
Footnotes
1. Prepared for the 2013 Carnegie-NYU-Rochester Conference on "Fiscal Policy in the Presence of Debt Crises." We thank our discussants Jesus Fernadez-Villaverde, T. Braun, Anna Lipinska, and Ricardo M. Félix for insightful comments, as well as seminar participants at the Carnegie-NYU-Rochester Conference, the Federal Reserve Bank of New York, the Federal Reserve Board, the University of Maryland, the Spring 2013 SCIEA Meetings, the 2013 Midwest Macroeconomic Meetings, the 2013 SED Meetings, the 2013 NBER Summer Institute, the Central Bank of Hungary/CEPR/Bank of Italy Conference on "Growth, Rebalancing, and Macroeconomic Adjustment after Large Shocks," and King's College London. M. Henry Linder provided excellent research assistance. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the view of the Board of Governors of the Federal Reserve System or of any other person associated with the Federal Reserve System. Return to text
2. Corsetti and Pesaran (2012) note how inflation differentials between EMU members and Germany--effectively the rate of change of the real exchange rate--are a much more reliable proxy for interest rate differentials than sovereign debt-to-GDP differentials. To the extent that current account deficits are correlated with real exchange rate appreciations, the external balance of periphery countries is also tightly related to sovereign yield spreads. In sum, according to this view, fiscal and external imbalances, as well as the relative competitive position, are different sides of the same underlying problem (Eichengreen, 2010). Return to text
3. The product market efficiency index is an average of the scores in the categories related to market competition, such as "Extent of market dominance" and "Effectiveness of anti-monopoly policy." The labor market efficiency index is an average of the scores in the categories related to wage flexibility, such as "Flexibility in wage determination" and "Redundancy costs in weeks of salary." See World Economic Forum (2012) for more details. Return to text
4. OECD estimates of business markups and regulations burden paint a similar picture. We make explicit use of these estimates in our quantitative exercises. Return to text
5. These large long-run gains are consistent with the existing literature (Bayoumi et al., 2004; Forni et al., 2010), although the exact numbers may be sensitive to the introduction of entry and exit in the product market and search and matching frictions in the labor market (Cacciatore and Fiori, 2012; Corsetti et al., 2013). Return to text
6. Cacciatore et al. (2012) study optimal monetary policy in a monetary union under product and labor market deregulation in a model with endogenous entry and exit and search frictions. As in our "normal times" scenario, the Ramsey plan in that setup also calls for monetary policy accommodation during the transition period. Return to text
7. In a small open economy calibrated to Italian data, Gerali et al. (2013) find that strong complementarities between structural reforms and fiscal consolidations can give rise to substantial output benefits. Like our experiments that temporarily increase markups or announce reforms at later stages, however, political economy considerations may hinder several aspects of such a coordinated plan and reduce the combined gains of these supply-side policies. Return to text
8. When the ZLB does not bind, the AD curve is horizontal in a zero-inflation targeting regime. Return to text
9. Eggertsson (2010) calls this effect the "paradox of toil." His analysis, however, is restricted to temporary reforms, whereas our focus here is on the effects of permanent reforms on the equilibrium. Return to text
10. We use the intermediation cost only
to ensure stationarity of the net foreign asset position. We set
the parameter ![]() small enough as to have no
discernible effects on the transition dynamics. Return to text
small enough as to have no
discernible effects on the transition dynamics. Return to text
11. This definition is the model-equivalent of the Harmonized Index of Consumer Prices (HICP), the measure of consumer prices published by Eurostat. Return to text
12. We perform our simulations using Dynare, which relies on a Newton-Rapson algorithm to compute non-linear transitions between an initial point and the final steady state. Return to text
13. Bayoumi et al. (2004) and Forni et al. (2010) follow a similar calibration strategy. Return to text
14. The exact level of either the
inflation target or the bound on the interest rate is not central
for our results. What we need is that a lower bound for the policy
rate exists, thus preventing the monetary authority from providing
additional stimulus. To implement the zero-inflation targeting
regime in the simulations, we assume the policy reaction
function
![]()
where
![]() is the feedback
coefficient on inflation and
is the feedback
coefficient on inflation and
![]() is the effective lower bound
for the interest rate. A high enough value for
is the effective lower bound
for the interest rate. A high enough value for
![]() approximates a
zero-inflation targeting regime well. We set
approximates a
zero-inflation targeting regime well. We set
![]() , although higher values
would make no difference. Lower values can still approximate a
zero-inflation targeting in the model if we were to assume that the
ECB also responds to the output gap and/or the natural rate of
interest. Return to text
, although higher values
would make no difference. Lower values can still approximate a
zero-inflation targeting in the model if we were to assume that the
ECB also responds to the output gap and/or the natural rate of
interest. Return to text
15. The real interest rate is high relative to a counterfactual world in which the nominal interest rate could go below its lower bound, and possibly into negative territory. Return to text
16. These assumptions, while obviously extreme, make the analysis particularly stark. More realistically, the unwinding may occur with some probability at time of implementation, which would likely lead to a smaller output drop. At the same time, the unwinding may be decoupled from the duration of the crisis--in particular, the reforms could be reversed a few quarters after the ZLB stops being binding--which would entail more severe output losses. Return to text
17. Tables and figures associated with these experiments are available upon request. Return to text
18. In each experiment, we recalibrate the size of the preference shock to ensure that aggregate output contracts 4% in the crisis episode. Return to text
19. In the data, Italy and Spain account for 17% and 12% of euro-area output, respectively, whereas Greece, Ireland, and Portugal each account for about 2% of total output. Thus, peripheral countries account for about 35% of euro-area output in total. Return to text
20. In this experiment, we adjust the
parameters governing home bias ![]() and the
share of tradable goods
and the
share of tradable goods ![]() to match the same
targets as in the benchmark simulation. Return to text
to match the same
targets as in the benchmark simulation. Return to text
21. Country size may have an indirect effect on the domestic CPI via the terms of trade. Return to text
22. Given the severe fiscal constraints faced by peripheral countries and the lack of exchange rate flexibility, a recent academic literature (see Adao et al., 2009; Farhi et al., 2012) has focused on the scope for fiscal devaluations, that is, revenue-neutral changes in the composition of taxes that mimic an exchange rate devaluation. However, quantitatively, the potential gains associated with these policies for reasonable changes in tax rates appear to be limited (Lipinska and von Thadden, 2012). Return to text
23. We calibrate the parameter
![]() in the New Deal policy to
minimize deflation on impact. Qualitatively, a constant increase in
taxes would achieve the same objective as the state-contingent
rule. However, if taxes remain high for too long, the nominal
interest rate may endogenously spike up even if the crisis is not
over yet. Return to text
in the New Deal policy to
minimize deflation on impact. Qualitatively, a constant increase in
taxes would achieve the same objective as the state-contingent
rule. However, if taxes remain high for too long, the nominal
interest rate may endogenously spike up even if the crisis is not
over yet. Return to text
This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text