The Federal Reserve Board eagle logo links to home page

Uncovered Equity Parity and Rebalancing in International Portfolios**

Stephanie E. Curcurua, Charles P. Thomasa, Francis E. Warnockb, and Jon Wongswanc

NOTE: International Finance Discussion Papers are preliminary materials circulated to stimulate discussion and critical comment. References in publications to International Finance Discussion Papers (other than an acknowledgment that the writer has had access to unpublished material) should be cleared with the author or authors. Recent IFDPs are available on the Web at http://www.federalreserve.gov/pubs/ifdp/. This paper can be downloaded without charge from the Social Science Research Network electronic library at http://www.ssrn.com/.

Abstract:

Portfolio rebalancing is a key driver of the Uncovered Equity Parity (UEP) condition. According to UEP, when foreign equity holdings outperform domestic holdings, domestic investors are exposed to higher exchange rate exposure and hence repatriate some of the foreign equity to decrease their exchange rate risk. By doing so, foreign currency is sold, leading to foreign currency depreciation. We examine the relationship between U.S. investors' portfolio reallocations and returns and find some evidence consistent with UEP: Portfolio shifts are related to past returns in the underlying equity markets. But we argue that a motive other than reducing currency risk exposure is likely behind this rebalancing. In particular, U.S. investors may be exploiting mean reversion in underlying equity markets, rebalancing away from equity markets that recently performed well and moving into equity markets market just prior to relatively strong performance. Such behavior suggests tactical reallocations to increase returns rather than reduce risk.

Keywords: Exchange rate determination, international returns, equity portfolios

JEL classification: G11, G12, F21


1.  Introduction

A new parity condition has emerged in the international finance literature, the uncovered equity parity condition (UEP) of Cappiello, Lorenzo, and De Santis (2005, 2007), Hau and Rey (2006), and Kim (2011). UEP is exciting in part because it provides another way of thinking about exchange rate movements, which have been notoriously difficult to predict (Meese and Rogoff 1983; Cheung, Chinn, and Pascual 2005).

The main intuition behind the UEP condition is one of portfolio rebalancing. There are two distinct steps. First, when foreign equity holdings outperform domestic holdings, domestic investors are exposed to higher relative exchange rate exposure and decide to repatriate some of the foreign equity to decrease exchange rate risk. Second, the associated selling of foreign currency leads to foreign currency depreciation.

Evidence supporting the second step of UEP is abundant, as order flow has been shown to impact exchange rates (Evans and Lyons 2002; Dunne, Hau, and Moore 2010; Filipe 2012). However, evidence supporting the first step does not exist; we attempt to fill this void by examining the evidence on the mechanisms behind UEP. One part of the mechanism has investors rebalancing international equity portfolios away from (toward) countries whose markets have recently done well (poorly). Do they? Or do they continue to purchase the equities of countries whose markets have recently performed well? UEP presumes the former, but this behavior would seem to be counter to the presumed behavior driving carry trades in which a high yielding currency is expected to appreciate and continue to appreciate, or returns chasing in general.1

We examine this issue from an empirical perspective, using the most recent update of the Bertaut and Tryon (2007) data on U.S. investors' monthly equity positions across 42 markets from 1990 to 2010. We find strong evidence supporting the second leg of UEP: equity flows are contemporaneously positively correlated with currency movements, a relationship consistent with price pressure. This finding is neither controversial nor surprising, as many others have found such evidence.

More elusive has been evidence supporting the first leg of UEP, which itself has two parts. One part is that when foreign equity holdings outperform domestic holdings, domestic investors decide to repatriate some of the foreign equity. The second part is why investors do this. In particular, UEP presumes that the selling of foreign equity holdings that recently outperformed owes to a desire to reduce the now higher exchange rate exposure.

We tackle these two subcomponents in turn. First, we find strong evidence--once appropriate techniques and data are used--that investors do indeed sell foreign equity markets that recently performed well. This behavior is asymmetric, as we do not find increased flows into markets that recently performed very poorly, and so only constitutes partial evidence supporting a condition behind UEP, but it is nonetheless robust evidence.

The second subcomponent, why investors engage in this behavior, is somewhat more difficult to ascertain. UEP suggests investors reallocate to lessen the increased risk of currency exposure. An indirect test of this is to see if investors reallocate because of past currency movements. They do not. U.S. investors react to changes in underlying equity market returns in a manner consistent with partial equity rebalancing, trading away from equity markets that recently performed well and into ones that subsequently perform well. But we find that past currency movements have no influence on these portfolio shifts.

That investors do not react to currency movements is not damning evidence against UEP, as UEP is about returns translated back into a common currency and hence concerns what we will call total returns, the combination of the underlying equity returns and the currency returns. And, indeed, as found in Curcuru et al. (2011), an examination of total returns provides evidence of selling past winners. We find that this behavior is due to movements in the underlying equity returns, not currency movements.

We then explore another way to assess the motive behind the reallocations. We find that equity returns, much more than currency returns, exhibit some mean reversion, so investors might be opportunistically exploiting dynamics in the underlying equity returns, consistent with De Bondt and Thaler 1985 and many others. We find this in country-by-country returns--the underlying equity returns of ten countries have negative and significant autocorrelation coefficients at the six-month horizon--but also when dividing countries in quartiles based on past returns, as the top quartile markets never dominate the middle quartiles in horizons up to six months. The worst quartile (based on past returns) continues to perform poorly up to three months out, perhaps why our rebalancing results are asymmetric (top performers come back to earth, but the worst performers do not quickly turn around) and only begin to perform well at longer horizons.

We then examine how well the reallocations performed. Here we find pretty strong evidence against the notion that investors reallocate to reduce risk. In fact, we find evidence that U.S. investors switched into the right equity markets: for horizons of one, two and three months those markets outperformed. This switching to markets that subsequently outperformed owes to exploiting movements in the underlying equity returns and seems to have nothing to do with currency movements. Thus, the evidence based on country-by-country returns autocorrelations, portfolios constructed based on past returns, and how well the reallocations predict future returns all suggest that the reallocations were tactical decisions to increase expected returns, not measures to reduce currency exposure.

Overall, our assessment of the evidence is that two mechanisms behind UEP--price pressure and reallocating away from past winners--are strongly supported in the data, but the evidence does not support the behavior proposed in the UEP literature. Rather than finding evidence consistent with a desire to reduce currency exposure driving reallocations, the evidence we find is consistent with tactical reallocations toward equity markets that will subsequently outperform. In that sense the returns-seeking behavior we find is more consistent with the carry trade--moving into high yielding currencies that have performed well and, absent a sharp increase in risk aversion, will continue to perform well--that puts the uncovered interest parity directly at odds with reality.2 Our conclusion is that while evidence of the mechanics behind UEP is strong enough, it seems this is due to positioning to earn higher returns, not to mitigate risk.

Our results are important for the growing area of international macroeconomic research on gross financial flows and international portfolio allocation. Theoretical models of international portfolio choice are being constructed with ever-increasing frequency; see, among many others, Kraay and Ventura (2000, 2003), Van Nieuwerburgh and Veldkamp (2009), Coeurdacier, Kollmann, and Martin (2007), Tille and van Wincoop (2008, 2010), Hnatkovska (2010), Pavlova and Rigobon (2010), Devereaux and Sutherland (2010, 2011), and Dumas, Lewis, and Osambela (2010). One could very well imagine such models to begin incorporating UEP. Our results would suggest that some mechanisms behind UEP are supported by data, but the assumed behavior of risk mitigation is not. In addition, any study of the returns on international positions is worthwhile, as valuation effects have become ever more important determinants of changes in the external wealth of nations as gross international positions have become ever larger. But even though empirical research on this topic has skyrocketed with the improved availability of data on international positions, made possible in large part by the datasets created in Lane and Milesi-Ferretti (2001, 2007), Obstfeld (2010) paints a bleak picture of the extent of our knowledge. This limited knowledge is due at least in part to the fact that most datasets have a disconcertingly limited ability to provide accurate information on valuation gains and losses in international portfolios. In this paper we strive to add to our understanding of valuation gains and losses by delving deeply into one aspect: the relationship between portfolio reallocations and past and prospective equity and currency returns within U.S. investors' foreign equity portfolios.

The paper proceeds as follows. In the next section we discuss theory on how equity portfolios should react to currency movements, as well as evidence from practitioners. In Section 3 we present data, methodologies, and main results, focusing on the relationship between reallocations and past, contemporaneous, and future returns. In Section 4 we present similar evidence for a sample that excludes countries with the Kim (2011) notion of market risk. We conclude in Section 5.


2.  Uncovered Equity Parity and the Existing Evidence

There are a number of theories on how international equity investors should react to currency movements. Adler and Dumas (1983) suggests that investors will hedge the currency exposure inherent in international equity positions by altering their nominal bond portfolios or through forward contracts. International equity positions should not adjust based on past currency movements, because the currency exposure is hedged elsewhere. In contrast, the existence of a carry trade in currencies (Burnside, Eichenbaum, and Rebelo 2010; Brunnermeier Nagel and Pederson 2010; Lustig and Verdelhan 2007; Lustig, Roussanov, and Verdelhan 2011) might suggest that investors should increase their allocations to the equities of countries whose currency recently appreciated. In this framework currency movements are largely a function of slow-moving interest rate differentials, so investors should add to their exposure of currencies that recently appreciated, a form of returns chasing, and those currencies should continue to appreciate.

A third alternative is uncovered equity parity (UEP), suggested by the work of Hau and Rey (2004, 2006, 2008), Cappiello and De Santis (2005, 2007), and Kim (2011). In those models, investors have an optimal currency exposure in mind and cannot perfectly hedge against currency movements. To minimize currency risk, investors rebalance away from equity markets that recently performed well. This rebalancing is a reaction to movements in the currency, the underlying equity market, or some combination of the two. Moreover, rebalancing away from a foreign market will appreciate the home currency. The argument is laid out informally in Hau and Rey (2004), with the theoretical underpinnings developed more fully in Hau and Rey (2006). At the heart of the UEP condition is portfolio rebalancing due to increased currency exposure: Whenever foreign equity holdings outperform domestic holdings, domestic investors have increased foreign exchange rate exposure. In reaction, they repatriate some of the foreign equity wealth to decrease their exchange rate risk and, by doing so, they sell the foreign currency which then depreciates.

Thus, the UEP of Hau and Rey (2006) and Kim (2011) provides a set of mechanisms that we can explore in the data.3 But other theories are consistent with international equity investors not reacting to currency movements (because they are already hedged) or adding to the equity positions of countries whose currency recently appreciated (for carry trade reasons). In the absence of a theoretical consensus, the obvious question is: What do investors actually do?

The first thing to note about how investors actually react to currency exposure is that in practice it is impossible to tell with publicly available data, for the simple reason that there is no dataset that allows us to discern the true exposure faced by investors. Consider amounts for one snapshot as of end-2010 (Table 1). U.S. investors' international equity holdings totaled $4,647 billion. Added to that is a small amount ($500 billion) of U.S. holdings of foreign-currency denominated bonds issued by foreign entities.4 U.S. investors also hold foreign currency debt issued by U.S. entities, but the vast majority of such debt ($817 billion of the $1,019 billion) is held by foreigners. U.S. investors also hold the equities of U.S. multinationals that have operations in many foreign countries; one can back out those holdings and attempt to estimate the inherent currency exposure (see Cai and Warnock 2012). In addition to all those are derivatives positions--forward, options, and others--for which the data problems are even more daunting; only summary data on the fair-market value of U.S. cross-border derivatives is available, with no data on exposures to specific equities or currencies (Curcuru 2007). So though we know the value of U.S. investors' equity and bond positions in many countries and can back out their holdings of U.S.-issued foreign currency bonds and of U.S. multinationals' equities, these data offer an incomplete picture of currency exposure.

Surveys of investors suggest that while international bond positions might be hedged, international equity positions are typically unhedged (Levich et. al 1999). One reason might be that the currency exposure of an international bond is easily quantified because the currency of the bond's periodic coupon payments and final payment is well defined. In contrast, it is difficult to ascertain ex ante the currency exposure associated with a foreign equity. The actual currency exposure of a firm's assets and liabilities is unknown, as is the exposure of its off-balance sheet products such as derivatives that could be in place specifically to alter the firm's currency exposure.5 Even for well-measured equity positions it is impossible to ascertain the true currency exposure.

So available data cannot ascertain the extent of currency exposure, and theory allows for all possibilities of investors reactions to currency movements--they might ignore currency movements, chase them, or in the case of UEP rebalance away from them--and evidence from practitioners suggests little reaction of international equity investors to currency movements. We turn next to empirical evidence from U.S. investors' international equity portfolios.


3.  Empirical Assessment of UEP

We will assess the various legs in the UEP condition in three steps by examining the relationships between flows or portfolio reallocations and current, past, and future returns.

3.1  Flows and Contemporaneous Returns: An Assessment of Price Pressure on Exchange Rates

There is a substantial literature that shows using high frequency data that flows impact exchange rates (Evans and Lyons 2002; Dunne, Hau, and Moore 2010; Filipe 2012). In the UEP literature, some work has utilized the TIC (Treasury International Capital) flow data, the official capital flows data for the United States. For example, Hau and Rey (2004) use bilateral net TIC flows scaled by gross trading (that is, the sum of purchases and sales), while Hau and Rey (2006) use normalized "net-net" TIC flows: net U.S. purchases of foreign equities minus net foreign purchases of U.S. equities, normalized by the average absolute level of the net increase in foreign stock ownership by U.S. residents over the previous 12 months. In Table 2 we recreate such analysis and find some evidence of a positive contemporaneous correlation between flows and currency movements. In eleven countries the correlation is positive and significant; for no country is it negative and significant. While we do not know the timing of purchases within a month and so cannot perfectly disentangle return-chasing from price pressure, the positive contemporaneous correlations are consistent with the third leg of UEP: equity flows cause exchange rate movements.

3.2  Analysis of Past Returns: Do Investors Rebalance?

Analysis of flows can assess price pressure (subject to not knowing the timing of within-period flows), but any attempt to discern trading behavior from flow data is subject to the Curcuru et al (2011) critique: Flow data are influenced by changes in financial wealth. Thus, while we can observe flows and past returns, a negative relationship between the two is not necessarily evidence of rebalancing, neither is a positive relationship necessarily evidence of returns chasing.

Portfolio data are, however, well suited to assess the existence of such trading behavior.6 We use the Bertaut and Tryon (2007), henceforth BT, estimates of the monthly bilateral positions of U.S. investors in the equities of a large set of foreign countries. The country-level dataset includes, for example, a monthly time series of U.S. holdings of German equities (as well as of the U.S. holdings of equities in many other foreign countries). The BT data are formed by combining high-quality but infrequent readings on positions (from security-level benchmark surveys) with more frequent flow data. In the process of combining positions and flows data, the reported-flow data are adjusted to alleviate well-known country attribution problems (the financial center bias of Warnock and Cleaver 2003, among others). Specifically, the BT monthly bilateral positions are formed by starting with an initial position as given by a benchmark survey, creating naïve monthly positions until the next benchmark survey by using flow data and valuation adjustments (from, for foreign equity markets, MSCI indexes), and then adjusting the estimates to eliminate the financial center bias and other wedges between flows-based estimates and survey-based readings. The resulting dataset is entirely consistent with reported data on U.S. holdings of foreign equities. In fact, an earlier version of the dataset formed the basis for the official U.S. entries in the IMF's Coordinated Portfolio Investment Survey in 2002, a year in which the United States did not conduct a benchmark asset survey.7

The bilateral holdings data provide the country weights in U.S. investors' portfolios.8 Another important piece of our dataset is the returns earned by U.S. investors within each foreign market. This is currently unknowable; returns series based on U.S. investors' foreign holdings do not exist. While directly measured country-level returns series do not exist, the literature is pretty clear on the type of firms that should be in such an index. A long line of research has shown that investors--be they Americans, Swedes, Finns, or others--tend to hold the largest and most liquid foreign stocks (Kang and Stulz (1997), Dahlquist and Robertsson (2001), Grinblatt and Keloharju (2001), Edison and Warnock (2004), and Leuz, Lins, and Warnock (2009)). This suggests the use of the publicly available country-level MSCI returns indices, which are comprised of the largest and most liquid firms in each country. Moreover, a one-time comparison of MSCI firms and actual U.S. investment at a point in time (December 1997) showed that MSCI firms represent almost 80 percent of U.S. investors' foreign equity investment and that in the 12,000-firm universe of foreign stocks in Ammer et al. (2012), the correlation between weights in the MSCI World Ex US and U.S. investors' foreign equity portfolios is quite high at 0.77. MSCI returns indices, while not direct measurements, should be reasonable representations of the returns U.S. investors earn within each foreign market.

Armed with the time series of country weights from the BT dataset, and assuming that within each country the market (as represented by MSCI firms) is held, we are able to compute the (unhedged) dollar returns earned by U.S. investors on their foreign equity portfolios. We note that the dollar returns U.S.-based investors face in foreign equity markets are comprised of two components: returns on the currency and returns on the underlying local-currency equity market. Our final working dataset is monthly 1990 - 2010 for 42 foreign markets for which we have both U.S. portfolio weights and monthly equity returns. These markets, listed in Table 2, comprise $4,161 billion of the $4,647 billion in U.S. foreign equity holdings as of December 2010.9

Armed with data on bilateral portfolio reallocations and currency and equity returns, we can use of the Grinblatt, Titman, and Wermers (1995) techniques to assess whether reallocations and past returns are related negatively (as in UEP) or positively (as in returns-chasing behavior).

We use three measures (LM, BM, and SM) to assess the degree to which U.S. investors actively change their portfolio holdings in the direction of previous currency or underlying stock returns. The key, as demonstrated in Curcuru et al. (2011), is to use not flow data but the active change in the weight of country i in U.S. investors' foreign portfolio at time t, X$ {}_{i,t}$:

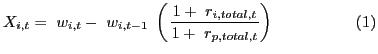
$\displaystyle X_{i,t}=\ w_{i,t}-\ w_{i,t-1\ }\left(\left.\frac{1+\ r_{i,total,t}}{1+\ r_{p,total,t}}\right)\right.\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1)$

where r$ {}_{i,}$ $ {}_{total,}$$ {}_{t}$ is the total dollar return on country i equities from period t-1 to t; r$ {}_{p}$ $ {}_{,total}$$ {}_{,t}$ is the total dollar return on U.S. investors' foreign portfolio, defined as $ r_{p,total,t}=\ \ \sum^{Nt}_{i=1}{w_{i,t-1}r_{i,total,t}}\ $; and w$ {}_{i,t}$ is the weight of country i at time t in U.S. investors' portfolio. If investors followed a buy-and-hold strategy, X$ {}_{i,t}$ would equal zero. The momentum statistic LM$ {}_{k}$ is:

$\displaystyle {LM}_k=\ \frac{1}{T}\ \sum^T_{t=1}{\ \sum^{N_t}_{i=1}{X_{i,t}}}\ \left(r_{i,m,t-k}-\ r_{p,m,t-k}\right)\ \ \ \ (2)$

where N$ {}_{t}$ is the number of countries held in the portfolio at time t , m denotes whether returns are total dollar returns, underlying equity returns, or currency returns, and k is the number of months (k=1, 2, 3, or 6) the returns are lagged. If X$ {}_{i,t}$ is positively related to past returns the LM statistic will be positive and significant, indicating momentum trading: U.S. investors on average increased the weights on countries whose equities or currencies performed well (relative to the other countries) k periods ago. A significantly negative value of LM would be evidence of contrarian trading or portfolio rebalancing, consistent with UEP. Two additional momentum statistics isolate trading when investors increase country weights (the BM measure) from when they decrease country weights (the SM measure).

Table 3 shows results.10 Focusing on all portfolio reallocations (i.e., the LM measure), only two LM statistics are significant at the 5% level. In the Equity Returns block, LM$ {}_{3}$ and LM$ {}_{6}$ are both negative and significant. The SM and BM lines in the Equity Returns block indicate that this rebalancing is due to selling past winners (SM statistic for all lags is negative and significant), not to buying past losers.

Turning to the relationship between reallocations and currency returns (the middle panel), we find no evidence that U.S. investors consider past currency movements when adjusting their international equity portfolios. At no lag are portfolio reallocations related to currency movements at the 5% level of significance, and the one coefficient that is significant at the 10% level is positive. This could be because the currency risk is already hedged, unknowable ex ante, or that investors are reallocating solely in response to the underlying equity moves.11 But at some level this behavior does not appear to be consistent with the uncovered equity parity theory in which investors actively reallocate away from currencies that have appreciated.

Overall, the evidence in Table 3 indicates that U.S. investors reallocate out of equity markets that recently performed well--in line with UEP--and that this behavior owes to reactions to underlying equity returns, not to currency movements.

3.3  Portfolio Reallocations and Future Returns: Are Investors Positioning to Reduce Exposure or to Increase Future Returns?

The above analysis is supportive of UEP in that rebalancing away from past winners seems to be a feature of U.S. international equity portfolios. UEP might struggle to reconcile the facts that none of the reallocations seem to owe to currency movements and that the reallocations are asymmetric (i.e., no evidence of buying of past losers), but the results are robust and largely in support of mechanisms proposed to underlie UEP.

We next tackle what is arguably more difficult to ascertain empirically: What exactly is the motivation behind investor behavior observed in Table 3? By UEP, it should be that the reallocations are done to reduce mounting currency risk. An alternative hypothesis is that the reallocations are tactical decisions to increase future returns. We assess these competing behaviors in a number of ways.

First, we ascertain whether there is mean reversion in currency or equity returns that could prompt relatively mechanical reallocations out of past winners (Table 4). We find substantial mean reversion in equities at the six-month horizon, with equity market returns in eleven countries having significantly negative autocorrelation coefficients at that horizon. In contrast, at short horizons (one-month) both currency and equity returns have some persistence. Beyond the 1-month horizon currency returns show no real tendency for persistence or reversion. We take the results in Table 4 to suggest that at the 6-month horizon there may well be some predictability in equity returns, but not in currency returns.12

Table 4 is country-by-country. We turn next to portfolio analysis similar to Richards (1997) that segments the sample into portfolios based on past returns (Table 5). Portfolios are formed based on the returns over ranking periods of the past k months, where k=1, 2, 3, 6, or 12. The worst performing countries during the ranking period form Portfolio 1; the best performing countries form Portfolio 4. "Test period returns" then shows the performance of those ranking period portfolio in the subsequent k months. For total USD equity returns (top panel), during the test period the best ranking period performers (Portfolio 4) underperforms the next best (Portfolio 3) for horizons of one, two, and six months (and is roughly equal over the 3-month horizon). The worst ranking period performers (Portfolio 1) continue to perform poorly for three more months, improving at the 6- and 12-month horizons. One interpretation of the top block of Table 5 is that the strategy uncovered in the LM, BM, SM analysis of Table 3--that of selling equity markets that performed well in the past--seems supported in the returns data. A similar analysis of local equity returns (middle block) is less supportive. The bottom panel of Table 5 shows similar results for currency returns. For currencies, the poor performers continue to do poorly (at all horizons), and for short horizons the best performers continue to perform strongly. For currency returns, there is little evidence to suggest it would be profitable to rebalance away from the best performers.

We next move to two more direct ways to assess the behavior that might be behind the reallocations out of past winners that we have documented. In both we assess the relationship between portfolio reallocation and future returns. If the behavior posited in the UEP condition is actually occurring, we should not see a positive relationship between today's reallocations and future returns, as the reallocations would occur to reduce exposure, not to position portfolios for stronger returns.

The first way we assess this is with the conditional weight-based measure (CWM), a portfolio-based measure developed by Grinblatt and Titman (1989, 1993), Eckbo and Smith (1998), and Ferson and Khang (2002). The CWM is based on an estimate of the sum of the covariances between active changes in portfolio weights and future abnormal returns (that is, the component of the return that is not forecastable using public information). The CWM is often used in the literature as a gauge of private information or an informational advantage; under time-varying expected returns, a risk-averse investor with non-increasing absolute risk aversion would move into (out of) the market when private information indicates a positive (negative) abnormal return relative to that predicted using public information. When the private information signals are on average correct, the estimate of the sum of the conditional covariances between changes in portfolio weight and future abnormal returns will be positive.

We set up the CWM as follows. Define the estimate of the sum of the conditional covariances as

$\displaystyle \sum^{N_t}_{i=1}{Co\nu (w_{i,t}},\ r_{i,\ m,t+1}\left\vert{\Omega }_{{\rm t}}\right){\rm =\ }\sum^{N_t}_{i=1}{E}\left[{(w}_{i,t}-\ w^b_{i,t}\right)\left(r_{i,m,t+1}-\ E\left(r_{i,m,t+1}\mathrel{\left\vert\vphantom{r_{i,m,t+1} {\Omega }_{{\rm t}}}\right.\kern-\nulldelimiterspace}{\Omega }_{{\rm t}}\right)\right)\left\vert{\Omega }_{{\rm t}}\right]{\rm\ \ \ \ \ \ \ (3)}$

where $ w^b_{i,t}$ is the benchmark weight of country i at time t and m denotes whether returns are total dollar returns, underlying equity returns, or currency returns. Let the benchmark be a buy-and-hold weight of lag k defined as

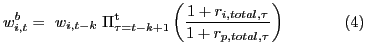
$\displaystyle w^b_{i,t}=\ w_{i,t-k\ }{\Pi }^{{\rm t}}_{\tau =t-k+1}\left(\frac{1+r_{i,total,\tau }}{1+r_{p,total,\tau }}\right)\ \ \ \ \ \ \ \ \ \ \ (4)$

Estimate the conditional portfolio weight-based measure via GMM:

$\displaystyle e_{i,t+1}=\ r_{i,m,t+1}-\ {{\mathbf b}}^{{\mathbf \ /}}_{{\mathbf i}}{{\mathbf Z}}_{{\mathbf t}}{\mathbf \ \ \ \ \ \ \ \ \ \ \ \ \ }(5)$

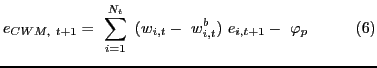
$\displaystyle e_{CWM,\ t+1}=\ \sum^{N_t}_{i=1}{\ (w_{i,t}}-\ w^b_{i,t})\ e_{i,t+1}-\ {\varphi }_p\ \ \ \ \ \ \ \ \ (6)$

With the one distinction of allowing for different types of returns (total, underlying equity, and currency) the implementation follows Curcuru et al. (2011). Equation (5) is an N vector of errors from estimating a linear function of future excess returns on information variables when N is the maximum value of N$ {}_{t}$ for the full sample. Z$ {}_{t}$, a subset of $ {{\mathbf \Omega }}_{{\mathbf t}}$, arepublic information variables.13 Each error in equation (5) has an interpretation of an abnormal return. Equation (6) is the error from estimating an average of the conditional covariances between changes in portfolio weights and future abnormal returns. $ \varphi $$ {}_{p}$ is the average of conditional weight measure across the full sample. See Curcuru et al. (2011) for estimation details.

Table 6 shows the results of the CWM analysis; the top panel includes our full sample of 42 countries, whereas the bottom panel is for the "floating" sample. The Equity Returns lines show positive and significant CWM coefficients for horizons of one, two, and three months. U.S. investors switched into equity markets that subsequently performed abnormally well (compared to their predicted returns), which is consistent with tactical reallocations to increase future returns rather than attempts to reduce exposure to certain currencies. Moreover, the Currency Returns lines in Table 6 show that U.S. investors' reallocations are not associated with future currency appreciations or depreciations.

The CWM statistic is widely used to ascertain the extent to which investors successfully use private information when reallocating their portfolios, but the statistic is not directly related to performance. A portfolio could evolve in a way that produces a positive and significant CWM statistic but does not actually produce higher returns. In other words, the CWM is positive if the investor switched into country x just before country x had higher than expected returns (specifically, positive abnormal returns), but if the switch meant foregone returns in country y just before it had even higher returns, the switch into x need not have improved portfolio performance. Curcuru et al. (2011) showed that U.S. investors switched into markets that subsequently had high abnormal returns, and we have shown that this owes to timing the underlying equity markets, but did these reallocations lead to exceptional portfolio performance?14

We construct a new measure to ascertain whether reallocations actually led to higher total portfolio returns. Consider a measure, which we refer to as timing or TM, that captures the degree to which U.S. investors correctly anticipate future returns within the context of their entire foreign equity portfolio, rather than just at the country-level. The construction of TM is similar to the LM measure, but is forward looking:

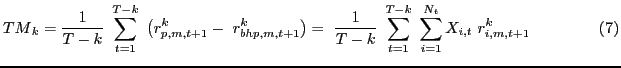
$\displaystyle {TM}_k=\frac{1}{T-k}\ \sum^{T-k}_{t=1}{\ \left(r^k_{p,m,t+1}-\ r^k_{bhp,m,t+1}\right)}=\ \frac{1}{T-k}\ \sum^{T-k}_{t=1}{\ \sum^{N_t}_{i=1}{X_{i,t}}}\ r^k_{i,m,t+1}\ \ \ \ \ \ \ \ \ \ \ \ \ (7)$

where X$ {}_{i,t}$ is the active portfolio shift defined in (1); m denotes whether returns are total dollar returns, underlying equity returns, or currency returns; r$ {}_{i}$$ {}_{,}$$ {}_{m,}$$ {}_{t,}$$ {}_{t}$ is the k-month return on country i equities at time t; and r$ {}_{bhp,}$$ {}_{m,}$$ {}_{t+k}$ is the return that would have been realized at time t on the buy-and-hold portfolio (specifically, U.S. investors' foreign portfolio had there not been an active shift at time t). A significantly positive value of TM would indicate that U.S. investors on average increased the weights on countries whose equities were set to outperform the buy-and-hold benchmark.

As was the case with the momentum measure, the main TM measure combines investors' actions when they buy with their actions when they sell. We also jointly compute separate timing measures for buys (BTM) and sells (STM). Specifically, the BTM statistic will indicate whether returns are correctly anticipated when investors increase country weights; STM applies when investors decrease country weights.

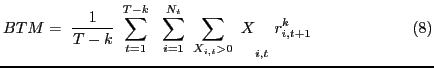
$\displaystyle BTM=\ \frac{1}{T-k}\ \sum^{T-k}_{t=1}{\ \ \sum^{N_t}_{i=1}{{\ \sum_{X_{i,t}>0}{\ }X}_{i,t}}}\ r^k_{i,t+1}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (8)$
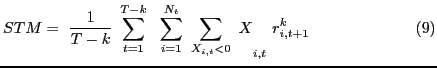
$\displaystyle STM=\ \frac{1}{T-k}\ \sum^{T-k}_{t=1}{\ \ \sum^{N_t}_{i=1}{{\ \sum_{X_{i,t}<0}{\ }X}_{i,t}}}\ r^k_{i,t+1}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (9)$

where BTM (STM) is a measure of correct anticipation when investors buy (sell) securities. The timing measures (TM, BTM, and STM) capture the degree to which U.S. investors correctly anticipate future returns within the context of their entire foreign equity portfolio, rather than just at the country-level; a significantly positive value of TM would indicate that U.S. investors on average increased the weights on countries whose equities were set to outperform the buy-and-hold benchmark.

The TM line in Table 7 shows results for the main timing measure for dollar returns, underlying equity returns, and currency returns. The TM measure is positive and significant for one-month total returns and one- and two-month equity returns. TM for currency returns is never significant. Overall, the evidence suggests that when U.S. investors reallocate within their foreign equity portfolios, their reallocations improved short-term portfolio performance.15 The results that focus on instances in which U.S. investors increased the portfolio weight on country i (BTM Buy Only) are even stronger. U.S. investors reallocate into equities that are set to outperform a buy-and-hold portfolio at return horizons of one, two, three and six months. In contrast, when they decreased the weight on country i (STM Sell Only), the results are insignificant.

Taken together, the evidence in Tables 6 and 7 indicates that U.S. investors systematically switch into markets that are about to experience high abnormal returns (or higher than their average returns), and that these portfolio reallocations improved near-term portfolio performance. By UEP, reallocations should be done to reduce mounting currency risk. But the alternative hypothesis that the reallocations are tactical decisions to increase future returns seems to be more supported by the data.


4.  Limiting the Sample to Advanced Economies

Market risks might help explain failure of UEP (Kim 2011), so in this section we limit the sample to countries unlikely to have substantial market risks. Market risks in Kim (2011) are associated with emerging markets, as they "can be justified by incomplete institutional reforms, weaker macroeconomic fundamentals, more volatile economic conditions, shallow financial markets, and imperfect market integration" and include, specifically, "the degree of market integration, transaction costs, the distance between capital markets, and the size of the market". Moreover, "market risk after the liberalization of financial markets is expected to decrease gradually along the path of market integration."16 Thus, market risk in Kim (2011) is an emerging market phenomenon that helps explain failure of UEP in such economies.

To assess whether our conclusions are subject to the market-risk phenomenon of Kim (2011), we re-estimate our main evidence limiting the sample to a set of countries not subject to the Kim (2011) notion of market risk: advanced economies. Tables 8-10 show that the full sample results also hold for AEs: Trading patterns in U.S. investors' advanced economies' foreign equity portfolios are due to a relationship between reallocations and returns of the underlying equity markets, not currency returns. Specifically, the rebalancing we find in the AE portfolio is not due to past currency movements, but to movements in underlying equity markets (Table 8), and seems to be more about positioning for future returns rather than rebalancing to reduce risk exposure (Tables 9 and 10). Even in the sample of countries not subject to Kim (2011) market risk, the behavior proposed in the UEP literature--rebalancing in order to reduce currency exposure--does not seem supported by the evidence.


5.  Conclusion

Using portfolio data on international equity holdings and portfolio-based techniques, we find evidence that trading patterns in U.S. investors' foreign equity portfolios arise from a relationship between reallocations and returns of the underlying equity markets. We find no such evidence of a particular trading strategy with respect to currency movements.

We cannot rule out the uncovered equity parity theory, nor is it our intent to, because at its heart is a statement about overall currency exposure and subsequent portfolio reallocations. Overall currency exposure comes from some combination of currency movements and changes in the underlying equity prices, as well as changes in the value of other assets and positions in derivatives. While our analysis shows that within their international equity portfolio U.S. investors do not react to currency movements, it does not necessarily mean that they do not react to currency exposure. As we note, data limitations preclude an analysis of currency exposure.

We provide an assessment of the uncovered equity parity condition (UEP) by examining the mechanisms that have been posited to lead to UEP. For some of the mechanisms behind UEP, we find strong support. We found a positive contemporaneous relationship between equity returns and portfolio adjustments, which could be due to price pressure, consistent with one leg of UEP. We find substantial evidence that investors reallocate away from equity markets that recently performed well, consistent with the rebalancing leg of UEP. But for other aspects of UEP, our evidence is not supportive. The rebalancing we find is not due to past currency movements, but to movements in underlying equity markets. This is not damning, but does raise questions about UEP. More troubling is that the rebalancing we find seems to be more about positioning for future equity returns rather than rebalancing to reduce risk exposure, the behavior proposed in the UEP literature. Overall, our assessment is that while data are consistent with some legs of UEP (price pressure and rebalancing), the behavior proposed in the UEP literature--rebalancing in order to reduce currency exposure--does not seem supported by the evidence. Indeed, if the rebalancing that we observe is to better position one's portfolio for higher future returns, then that rebalancing shares more in common with the uncovered interest parity's antithesis, the carry trade: Neither is to reduce exposure, both are to earn higher future returns.

We note that our results are not inconsistent with other empirical work on the predictability of currency movements and equity prices. Because currency movements are notoriously difficult to predict at short horizons (Meese and Rogoff 1983, Cheung, Chinn, and Pascual 2005), it would be surprising to find that U.S. investors reallocated based on past currency movements or were able to time future currency movements. In contrast, there is existing evidence of equity return predictability, especially for one market relative to another. Ferson and Harvey (1993) find some predictability of international equity returns, Kasa (1992) finds mean reversion (and, hence, some predictability) in two-country equity portfolios, and Richards (1995) and Balvers, Wu, and Gilliland (2000) find that country-specific returns relative to a world index exhibit mean reversion, suggesting that the contrarian strategy of DeBondt and Thaler (1985) and Richards (1997) might be profitable. Thus, both the partial rebalancing we find--the selling of equity markets that performed well in the recent past--and the switching into markets that subsequently have high abnormal returns are consistent with the literature on the predictability of international equity market returns.


References

Adler, M., and B. Dumas, 1983. International Portfolio Choice and Corporation Finance: A Synthesis. Journal of Finance 38(3): 925-984.

Ammer, J., S. Holland, D. Smith, and F. Warnock, 2012. U.S. International Equity Investment. Journal of Accounting Research 50(5): 1109-1139

Balvers, R., Y. Wu, and E. Gillilland, 2000. Mean Reversion across National Stock Markets and Parametric Contrarian Investment Strategies. Journal of Finance 55(2): 745-772.

Bekaert, G., and C.R. Harvey, 1997. Emerging equity market volatility. Journal of Financial Economics 43, 29-77.

Bertaut, Carol C., and Ralph W. Tryon, 2007. Monthly Estimates of U.S. Cross-Border Securities Positions. FRB International Finance Discussion Paper No. 910.

Bohn, Henning, and Linda L. Tesar, 1996. "US Equity Investment in Foreign Markets: Portfolio Rebalancing or Return Chasing?" American Economic Review, 86(2): 77-81.

Brennan, Michael J., and H. Henry Cao, 1997. "International Portfolio Investment Flows." Journal of Finance, 52(5): 1851-80.

Brunnermeier, Markus K., Stefan Nagel and Lasse H. Pederson, 2010. Carry Trades and Currency Crashes, in J. Frankel and C. Pissarides (ed) NBER International Seminar on Macroeconomics 2008. University of Chicago Press, 314-347.

Burger, J., F. Warnock, and V. Warnock, 2012. Emerging local currency bond markets. Financial Analysts Journal 68(4): 73-93.

Burnside, Craig, Martin Eichenbaum and Sergio Rebelo, 2010. Carry Trade: The Gains of Diversification. Journal of the European Economic Association 6, 581-588.

Cai, F., and F. Warnock, 2012. Foreign Exposure through Domestic Equities. Finance Research Letters 9: 8-20.

Cappiello, Lorenzo, and Roberto De Santis, 2005. Explaining Exchange Rate Dynamics: The Uncovered Equity Return Parity Condition. ECB Working Paper 529.

Cappiello, Lorenzo, and Roberto De Santis, 2007. The Uncovered Return Parity Condition. ECB Working Paper 812.

Cheung, Yin-Wong, Menzie D. Chinn, and Antonio Garcia Pascual, 2005. Empirical exchange rate models of the nineties: Are any fit to survive? Journal of International Money and Finance 24: 1150-1175.

Coeurdacier, Nicolas, Robert Kollmann, and Philippe Martin, 2007. International portfolios with supply, demand and redistributive shocks. NBER International Seminar on Macroeconomics (ISOM). University of Chicago Press.

Curcuru, Stephanie E., 2007. U.S. Cross-Border Derivatives Data: A User's Guide. Federal Reserve Bulletin vol. 93 (May).

Curcuru, Stephanie E., Tomas Dvorak, and Francis E. Warnock, 2008. Cross-Border Returns Differentials. Quarterly Journal of Economics 123(4): 1495-1530.

Curcuru, Stephanie E., Tomas Dvorak, and Francis E. Warnock, 2010. The Decomposition of the U.S. External Returns Differential. Journal of International Economics 80: 22-32.

Curcuru, S., C. Thomas, and F. Warnock, 2009. Current Account Sustainability and Relative Reliability. in J. Frankel and C. Pissarides (ed) NBER International Seminar on Macroeconomics 2008. University of Chicago Press, pgs 67-109.

Curcuru, Stephanie E., Charles Thomas, Jon Wongswan, and Francis E. Warnock, 2011. U.S. International Equity Investment and Past and Prospective Returns. American Economic Review 101: 3440-3455.

Dahlquist, M., and G. Robertsson, 2001. Direct foreign ownership, institutional investors, and firm characteristics. Journal of Financial Economics 59: 413-440.

DeBondt , W., and R. Thaler, 1985. Does the stock market overreact? Journal of Finance 40: 793-805.

Devereux, Michael, and Alan Sutherland, 2010. Valuation Effects and the Dynamics of Net External Assets. Journal of International Economics 80: 129-143.

Devereux, Michael, and Alan Sutherland, 2011. Country Portfolios in Open Economy Macro Models. Journal of the European Economic Association 9: 337-369.

Dumas, Bernard, Karen K. Lewis, and Emilio Osambela, 2010. Differences of Opinion and International Equity Markets. SSRN Working Paper 1570168.

Dunne, P., H. Hau, and M. Moore, 2010. International order flows: explaining equity and exchange rate returns. Journal of International Money and Finance 29: 358-386.

Eckbo, E., and D. Smith, 1998. The conditional performance of insider trades. Journal of Finance 53(2), 467-498.

Edison, H. J., and F. Warnock, 2004. U.S. Investors' Emerging Market Equity Portfolios: A Security-Level Analysis, Review of Economics and Statistics 84(3), 691-704.

Engel, Charles, 1996, The forward discount anomaly and the risk premium: a survey of recent evidence, Journal of Empirical Finance 3, 123-191.

Engel, Charles, 2014. Exchange Rates and Interest Parity. Handbook of International Economics vol. 4 (Elsevier)

Evans, M., and Lyons, R., 2002. Order flow and exchange rate dynamics. Journal of Political Economy 110 (1), 170-180.

Fama, E. F., 1984. Forward and spot exchangerates. Journal of Monetary Economics 14, 319-338.

Ferson, W., and C. R. Harvey, 1993. The risk and predictability of international equity returns. Review of Financial Studies 6, 527-566.

Ferson, W., and K. Khang, 2002. Conditional performance measurement using portfolio weights: evidence for pension funds. Journal of Financial Economics 65, 249-282.

Filipe, Sara Ferreira, 2012. Equity order flow and exchange rate dynamics. Journal of Empirical Finance 19(3) 359-381.

Grinblatt, M., and M. Keloharju, 2001. How distance, language, and culture influence stockholdings and trades. Journal of Finance 56: 1053-67.

Grinblatt, M., S. Titman, 1989. Portfolio performance evaluation: Old issues and new insights. Review of Financial Studies 2, 393-421.

Grinblatt, M., S. Titman, 1993. Performance measurement without benchmarks: An examination of mutual fund returns. Journal of Business 60, 97-112.

Grinblatt, M., S. Titman, and R. Wermers, 1995. Momentum investment strategies, portfolio performance, and herding: a study of mutual fund behavior. American Economic Review 85(5), 1088-1105.

Harvey, C., 1991. The World Price of Covariance Risk, Journal of Finance 46, 111-157.

Hau, H., and H. Rey, 2004. Can Portfolio Rebalancing Explain the Dynamics of Equity Returns, Equity Flows, and Exchange Rates? American Economic Review 96(2): 126-133.

Hau, H., and H. Rey, 2006. Exchange Rate, Equity Prices, and Capital Flows. Review of Financial Studies 19: 273-317.

Hau, H., and H. Rey, 2008. Global Portfolio Rebalancing Under the Microscope. NBER Working Paper No. 14165.

Hnatkovska, Viktoria, 2010. Home bias and high turnover: Dynamic portfolio choice with incomplete markets. Journal of International Economics 80: 113-128.

Hodrick, R., 1987. The Empirical Evidence on the Efficiency of Forward and Futures Foreign Exchange Markets. HarwoodAcademicPublishers, Chur,Switzerland.

Kang, J., and R. Stulz, 1997. Why is there a home bias? An analysis of foreign portfolio equity ownership in Japan. Journal of Financial Economics 46:3-28.

Kasa, K., 1992. Common Stochastic Trends in International Stock Markets. Journal of Monetary Economics 29, 95-124.

Kim, Heeho, 2011. The risk adjusted uncovered equity parity. Journal of International Money and Finance 30(7) 1491-1505.

Kraay, Aart, Ventura, Jaume, 2000. Current accounts in debtor and creditor countries. Quarterly Journal of Economics XCV, 1137-1166.

Kraay, Aart, Ventura, Jaume, 2003. Current accounts in the long and short run. NBER Macroeconomics Annual 2002.

Lane, Philip R., and Gian Maria Milesi-Ferretti, 2001. The External Wealth of Nations: Measures of Foreign Assets and Liabilities for Industrial and Developing Countries. Journal of International Economics 55: 263-294.

Lane, Philip R., and Gian Maria Milesi-Ferretti, 2007. The external wealth of nations mark II: Revised and extended estimates of foreign assets and liabilities, 1970-2004. Journal of International Economics 73: 223-250.

Leuz, C., Lins, K., and F. Warnock, 2009. Do foreigners invest less in poorly governed firms? Review of Financial Studies, 22, 3245-3285.

Levich, R. M., G. S. Hayt, and B. A. Ripston, 1999. 1998 Survey of Derivative and Risk Management Practices by U.S. Institutional Investors. Survey conducted by the NYU Salomon Center, CIBC World Markets, and KPMG, available at http://www.stern.nyu.edu/rlevich/.

Lustig, H.N., A. Verdelhan, 2007. The cross section of foreign currency risk premia and consumption growth risk. American Economic Review 97(1), 89-117.

Lustig, H., N. Roussanov, and A. Verdelhan, 2011. Common Risk Factors in Currency Markets. Review of Financial Studies 24 (11): 3731-3777.

Meese, R., Rogoff, K., 1983. Empirical exchange rate models of the seventies: do they fit out of sample? Journal of International Economics 14, 3e24.

Newey, W. K., and K. D. West, 1987. A simple, positive semi-definite, heteroskedasticity and autocorrelation consistent covariance matrix, Econometrica 55, 703-708.

Obstfeld, M., 2010. Expanding Gross Asset Positions and the International Monetary System. Remarks at the Federal Reserve Bank of Kansas City symposium on "Macroeconomic Challenges: The Decade Ahead," Jackson Hole, Wyoming, August 26-28, 2010.

Pavlova, Anna, and Roberto Rigobon, 2010. An Asset-Pricing View of External Adjustment. Journal of International Economics 80: 144-156.

Richards, A., 1995. Comovements in National Stock Market Returns: Evidence of Predictability, but not Cointegration. Journal of Monetary Economics 36: 631-654.

Richards, A., 1997. Winner-loser Reversals in National Stock Market Indices: Can They Be Explained? Journal of Finance 52: 2129-2144.

Tille, Cedric, and Eric van Wincoop, 2008. International Capital Flows under Dispersed Information: Theory and Evidence. NBER Working Paper 14390.

Tille, Cedric, and Eric van Wincoop, 2010. International Capital Flows. Journal of International Economics 80: 157-175.

Treasury Department, Federal Reserve Bank of New York, and Board of Governors of the Federal Reserve System, 2011a. Report on U.S. Portfolio Holdings of Foreign Securities as of December 31, 2010.

Treasury Department, Federal Reserve Bank of New York, and Board of Governors of the Federal Reserve System, 2011b. Report on Foreign Portfolio Holdings of U.S. Securities as of June 30, 2010.

Van Nieuwerburgh, S., and L. Veldkamp, 2009. Information Immobility and the Home Bias Puzzle. Journal of Finance 64(3):1187-215.

Warnock, Francis E. and Chad Cleaver, 2003. Financial Centers and the Geography of Capital Flows. International Finance 6(1): 27-59.

Table 1: International Positions

The table shows amounts in billions of U.S. dollars as of end-2010. U.S. investment in foreign equities foreign-currency denominated foreign bonds are from Tables 1 and 9, respectively, of Treasury Department et al. (2011a). Outstanding foreign-currency debt issued by U.S. entities is from data that underlie BIS Quarterly Review Tables 14a and 14b; note that the amount is much smaller than the $6 trillion listed in those tables because they include roughly $5 trillion in US-issued "international" bonds that are denominated in U.S. dollars. Foreign-held US-issued foreign-currency debt is as of June 2010 from tables 15a and 15b of Treasury Department et al. (2011b).

 Billions of U.S. Dollars
US Holdings of: Foreign Equities4,647
US Holdings of Foreign-Currency Denominated Debt Securities500
Memo: Outstanding US-Issued Foreign-Currency Debt1,019
Memo: Outstanding US-Issued Foreign-Currency Debt of Which, Held by Foreigners817

Table 2a: Correlation Between Exchange Rates and Flows (Advanced Economies)

CountryCorrelation Between the Log Exchange Rate Return and the Change in "Net-Net" Equity Outflows
Australia0.018
Austria0.137**
Belgium0.155**
Canada0.033
Denmark-0.044
Finland0.038
France-0.015
Germany-0.019
Greece0.181***
Hong Kong0.124
Ireland0.031
Israel0.113*
Italy0.051
Japan-0.009
Korea0.090
Netherlands0.022
Norway0.007
Portugal0.145**
Singapore0.074
Spain0.101
Sweden0.021
Switzerland0.108*
Taiwan0.085
United Kingdom0.056
Euro-0.006

Table 2b: Correlation Between Exchange Rates and Flows (Emerging Market Economies)

CountryCorrelation Between the Log Exchange Rate Return and the Change in "Net-Net" Equity Outflows
Argentina0.060
Brazil0.208***
Chile0.008
China0.042
Colombia-0.019
Czech Republic-0.081
Hungary-0.019
India0.113*
Indonesia0.025
Malaysia0.362***
Mexico0.014
Peru-0.039
Philippines0.105
Poland0.062
Russia-0.036
South Africa0.129**
Thailand0.112*
Turkey-0.052

Correlations between the log exchange rate return and the change in "net-net" equity outflows (the change in outflows minus the change in inflows, scaled by the average change in flows) are for 42 foreign countries for the period from January 1990 to December 2010 and for 1999-2010 for the Euro Area aggregate. ***, **, and * denote statistically significant at the 1, 5 and 10 percent levels, respectively.

Table 3a: The Relationship between Reallocations and Past Equity and Currency Returns (Total Returns)

 Lag 1Lag 2Lag 3Lag 6
LM-0.017-0.136-0.215*-0.090
LM: (Buy and Sell)(0.129)(0.138)(0.129)(0.164)
BM0.1110.059-0.0160.125
BM: (Buy Only)(0.110)(0.102)(0.092)(0.151)
SM-0.123**-0.187**-0.197**-0.223**
SM: (Sell Only)(0.051)(0.059)(0.057)(0.058)

Table 3b: The Relationship between Reallocations and Past Equity and Currency Returns (Currency Returns)

 Lag 1Lag 2Lag 3Lag 6
LM-0.054-0.0040.0490.140*
LM: (Buy and Sell)(0.061)(0.065)(0.063)(0.081)
BM-0.041-0.0080.0200.092
BM: (Buy Only)(0.046)(0.045)(0.045)(0.066)
SM-0.0130.0060.0320.044
SM: (Sell Only)(0.029)(0.031)(0.027)(0.028)

Table 3c: The Relationship between Reallocations and Past Equity and Currency Returns (Equity Returns)

 Lag 1Lag 2Lag 3Lag 6
LM0.034-0.134-0.255**-0.237**
LM: (Buy and Sell)(0.123)(0.122)(0.122)(0.122)
BM0.1470.064-0.0330.027
BM: (Buy Only)(0.090)(0.089)(0.085)(0.101)
SM-0.108**-0.192**-0.223**-0.267**
SM: (Sell Only)(0.050)(0.050)(0.056)(0.056)

The analysis in this table is for the 42 foreign countries listed in Table 2 for the period from January 1990 to December 2010. The LM statistic is a measure of momentum based on deviations of portfolio weights from a passive buy-and-hold strategy.The BM statistic is a measure of momentum based on the positive portfolio weight deviations from a passive buy-and-hold strategy.The SM statistic is a measure of momentum based on the negative portfolio weight deviations from a passive buy-and-hold strategy. Lag 1, Lag 2, Lag 3, and Lag 6 correspond to the measure of momentum based on returns lagged 1, 2, 3, and 6 months, respectively. Newey and West (1987) standard errors are in parentheses. **, * denote statistically significant at the 5 and 10 percent levels, respectively.

Table 4a: Time Series Properties of Returns (Currency Returns: Developed Countries)

 1 Month3 Month6 Month
Australia0.117*-0.1220.074
Austria0.1020.098-0.119
Belgium0.1040.128-0.143
Canada-0.014-0.042-0.128
Denmark0.1030.132-0.128
Finland0.112*0.115-0.105
France0.0850.116-0.126
Germany0.0980.103-0.119
Greece0.1020.091-0.078
Hong Kong0.0580.0660.993*
Ireland0.0770.063-0.178
Israel0.044-0.0740.177
Italy0.124**0.059-0.256
Japan0.0320.299***-0.394**
Korea0.0650.0990.105
Netherlands0.1020.110-0.117
Norway0.140**-0.057-0.083
Portugal0.0750.119-0.103
Singapore0.0930.152-0.082
Spain0.0970.072-0.142
Sweden0.151**0.023-0.190
Switzerland0.0590.165-0.188
Taiwan0.162**-0.0420.157
United Kingdom0.152**-0.0420.087
Euro0.0770.109-0.207
USn.a.n.a.n.a.

Table 4b: Time Series Properties of Returns (Local Equity Returns Returns: Developed Countries)

 1 Month3 Month6 Month
Australia0.036-0.017-0.369**
Austria0.198***-0.006-0.138
Belgium0.225***-0.005-0.306*
Canada0.134**-0.045-0.203
Denmark0.0280.044-0.257
Finland0.211***0.150-0.285*
France0.110*0.002-0.379**
Germany0.048-0.112-0.392**
Greece0.114*0.090-0.265
Hong Kong0.107*0.0680.098
Ireland0.198***0.152-0.060
Israel0.0620.050-0.387**
Italy0.0040.073-0.266
Japan0.0900.053-0.122
Korea0.0570.065-0.001
Netherlands0.0840.027-0.262
Norway0.107*0.075-0.107
Portugal0.155**0.117-0.244
Singapore0.092-0.131-0.102
Spain0.1010.105-0.195
Sweden0.0920.053-0.282
Switzerland0.167***0.037-0.373**
Taiwan0.0850.026-0.099
United Kingdom0.073-0.024-0.324*
Euro0.122-0.131-0.493**
US0.0720.054-0.137

Table 4c: Time Series Properties of Returns (Currency Returns: Developing Countries)

 1 Month3 Month6 Month
Argentina0.138-0.1040.300
Brazil0.011-0.227*0.278
Chile0.230***-0.072-0.106
China0.426***0.0190.624
Colombia0.194***-0.0110.205
Czech Republic0.056-0.140-0.017
Hungary0.086-0.1180.109
India0.152**0.075-0.012
Indonesia0.074-0.197*0.127
Malaysia0.1070.018-0.280
Mexico0.146**0.203*-0.054
Peru0.323***0.1590.322*
Philippines0.130*-0.0960.184
Poland0.137**-0.267**0.221
Russia0.531***0.0220.027
South Africa0.0910.208*-0.198
Thailand0.182***0.1150.133
Turkey0.322***0.296***0.426**

Table 4d: Time Series Properties of Returns (Local Equity Returns Returns: Developing Countries)

 1 Month3 Month6 Month
Argentina0.134**0.019-0.062
Brazil0.514***0.529***0.221
Chile0.157**0.029-0.007
China0.116*0.0140.220
Colombia0.140**-0.045-0.184
Czech Republic0.0480.094-0.093
Hungary0.0900.105-0.203
India0.084-0.0430.027
Indonesia0.044-0.1320.378**
Malaysia0.146**0.0770.207
Mexico0.0050.159-0.336**
Peru-0.0320.090-0.202
Philippines0.1030.0580.280
Poland0.0300.0010.141
Russia0.160**-0.089-0.019
South Africa-0.0510.071-0.378**
Thailand-0.022-0.011-0.256
Turkey0.0360.071-0.054

The table shows the autocorrelation coefficient for the indicated returns for 42 foreign countries for the period from January 1990 to December 2010 and from 1999-2010 for Euro Area aggregate. Developed/developing country classifications from IMF World Economic Outlook database for April 2005. Statistics are computed using non-overlapping samples. ***, **, * denote statistically significant at the 1, 5 and 10 percent levels, respectively.

Table 5a: Excess Returns From Contrarian Strategy (Ranking Period Returns)

HorizonPort 1Port 2Port 3Port 4Contrarian
Total Returns: 1-72.5%-13.3%26.1%92.0%-164.5%
Total Returns: 2-51.7%-6.4%22.0%67.7%-119.4%
Total Returns: 3-41.2%-3.5%19.2%55.5%-96.7%
Total Returns: 6-26.3%-0.4%16.5%42.4%-68.6%
Total Returns: 12-17.0%1.6%14.4%33.5%-50.6%
Local Equity Returns: 1-63.7%-11.1%25.1%90.3%-154.0%
Local Equity Returns: 2-44.6%-5.6%21.8%67.7%-112.2%
Local Equity Returns: 3-35.7%-2.9%19.1%57.4%-93.1%
Local Equity Returns: 6-21.8%0.3%16.6%44.4%-66.2%
Local Equity Returns: 12-14.0%2.6%14.6%37.8%-51.8%
Currency Returns: 1-32.9%-9.0%7.1%29.3%-62.1%
Currency Returns: 2-26.1%-6.5%5.0%21.0%-47.2%
Currency Returns: 3-23.5%-5.3%4.4%17.1%-40.6%
Currency Returns: 6-19.1%-4.1%3.1%12.4%-31.5%
Currency Returns: 12-16.5%-3.4%1.8%8.8%-25.3%

Table 5b: Excess Returns From Contrarian Strategy (Test Period Returns)

HorizonPort 1Port 2Port 3Port 4Contrarian
Total Returns: 11.9%6.9%8.8%6.7%-4.8%
Total Returns: 23.4%7.5%10.3%4.8%-1.4%
Total Returns: 35.5%7.1%8.0%8.1%-2.7%
Total Returns: 68.2%6.0%9.4%6.8%1.4%
Total Returns: 1212.1%8.0%8.2%9.4%2.7%
Local Equity Returns: 12.9%6.9%7.6%10.9%-8.0%
Local Equity Returns: 25.0%5.1%10.4%12.5%-7.5%
Local Equity Returns: 35.6%4.3%7.6%11.3%-5.7%
Local Equity Returns: 66.4%6.5%8.2%15.7%-9.3%
Local Equity Returns: 128.8%8.8%9.6%14.9%-6.2%
Currency Returns: 1-5.1%0.4%1.1%1.9%-6.9%
Currency Returns: 2-3.1%0.1%0.9%1.1%-4.3%
Currency Returns: 3-3.5%1.4%1.7%0.2%-3.7%
Currency Returns: 6-0.4%1.0%0.3%-0.3%-0.1%
Currency Returns: 12-1.9%1.2%0.4%-0.8%-1.1%

The analysis in this table is for the 42 foreign countries listed in Table 2 for the period from January 1990 to December 2010. Portfolios are constructed using the technique of Richards (1997). Portfolio returns are market-cap-weighted and annualized. Portfolios are based on quartiles set during the ranking period, with Portfolio 1 being returns on a portfolio comprised of returns from the worst-performing quartile and Portfolio 4 being for the best-performing quartile. Returns are total USD returns (top panel) or of underlying equity markets (middle panel) or currencies (bottom panel). The horizon indicates the number of months of returns used to compute ranking period and test period returns. Annualized percent return shown.

Table 6: The Relationship between Reallocations and Prospective Equity and Currency Returns

 k=1k=2k=3k=6
Total Returns0.311**
(0.126)		0.493**
(0.199)		0.422**
(0.247)		0.161
(0.391)
Currency Returns0.070
(0.058)		0.006
(0.096)		0.025
(0.126)		-0.058
(0.206)
Equity Returns0.202*
(0.113)		0.431**
(0.178)		0.525**
(0.229)		0.105
(0.364)
Floating Sample: Total Returns0.230**
(0.109)		0.461**
(0.155)		0.452**
(0.190)		0.093
(0.338)
Floating Sample: Currency Returns0.065
(0.058)		0.008
(0.093)		-0.044
(0.132)		0.005
(0.206)
Floating Sample: Equity Returns0.180*
(0.096)		0.421**
(0.142)		0.482**
(0.180)		0.141
(0.315)

The table reports CWM statistics, a measure of the relationship between portfolio reallocation and future abnormal returns, for holding periods of k=1, 2, 3, or 6 months. The analysis in the top panel of this table is for the 42 foreign countries listed in Table 2 for the period from January 1990 to December 2010. In the bottom panel we use a "floating sample" that excludes countries without freely floating exchange rates for most of the sample period according to IMF AREAER reports, such as Greece (prior to its joining the Euro area), Argentina, China, Hong Kong, Malaysia, Peru, Singapore, Taiwan, and Brazil (prior to 1995) and treats the Euro area as one country starting in 1999. Total Returns refer to total (dollar) returns. The second and third lines in each panel reports statistics when currency or equity market returns are used. Newey and West (1987) standard errors are in parentheses. **,* denotes statistically significant at the 5 percent and 10 percent level, respectively.

Table 7: The Relationship Between Reallocations and Future Portfolio Returns

 k=1k=2k=3k=6
Total Returns: TM0.223**0.2710.352-0.071
Total Returns: TM (Buy and Sell)(0.098)(0.207)(0.250)(0.530)
Total Returns: BTM0.415**0.826**0.7451.258*
Total Returns: BTM (Buy Only)(0.163)(0.363)(0.498)(0.764)
Total Returns: STM-0.191-0.555-0.393-1.328
Total Returns: STM (Sell Only)(0.176)(0.355)(0.506)(0.910)
Currency Returns: TM0.018-0.069-0.016-0.503
Currency Returns: TM (Buy and Sell)(0.052)(0.108)(0.178)(0.308)
Currency Returns: BTM0.015-0.051-0.153-0.251
Currency Returns: BTM (Buy Only)(0.083)(0.144)(0.260)(0.454)
Currency Returns: STM0.002-0.0180.137-0.252
Currency Returns: STM (Sell Only)(0.070)(0.112)(0.194)(0.354)
Equity Returns: TM0.212**0.357*0.3670.497
Equity Returns: TM (Buy and Sell)(0.094)(0.197)(0.240)(0.533)
Equity Returns: BTM0.390**0.908**0.908*1.558*
Equity Returns: BTM (Buy Only)(0.138)(0.352)(0.464)(0.801)
Equity Returns: STM-0.178-0.551-0.542-1.061
Equity Returns: STM (Sell Only)(0.157)(0.348)(0.455)(0.844)

This table uses an alternative timing measure:

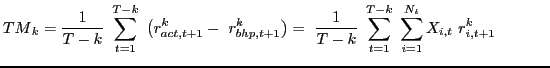
$\displaystyle {TM}_k=\frac{1}{T-k}\ \sum^{T-k}_{t=1}{\ \left(r^k_{act,t+1}-\ r^k_{bhp,t+1}\right)}=\ \frac{1}{T-k}\ \sum^{T-k}_{t=1}{\ \sum^{N_t}_{i=1}{X_{i,t}}}\ r^k_{i,t+1}\ \ \ \ \ \ \ \ \ \ $

A positive and significant TM$ {}_{k}$ statistic indicates that investors' reallocations improved portfolio returns over a k-month horizon (k=1, 2, 3, or 6). BTM and STM limit the sample to positive and negative reallocations, respectively. Averages are of non-overlapping returns. Data are for January 1990 through December 2010 for the "floating sample" of countries with freely floating currencies and combined euro area countries; see Table 6 for details. Newey and West (1987) standard errors are in parentheses. **, * denote statistically significant at the 5 and 10 percent levels, respectively.

Table 8: The Relationship between Reallocations and Past Equity and Currency Returns: Advanced Economies

 Lag 1Lag 2Lag 3Lag 6
Total Returns: LM-0.099-0.200-0.249*-0.189
Total Returns: LM (Buy and Sell)(0.127)(0.134)(0.140)(0.163)
Total Returns: BM-0.006-0.065-0.1210.020
Total Returns: BM (Buy Only)(0.109)(0.093)(0.099)(0.138)
Total Returns: SM-0.098*-0.136**-0.127**-0.209**
Total Returns: SM (Sell Only)(0.053)(0.059)(0.059)(0.058)
Currency Returns: LM-0.065-0.0230.0320.120
Currency Returns: LM (Buy and Sell)(0.067)(0.066)(0.073)(0.081)
Currency Returns: BM-0.044-0.025-0.0010.088
Currency Returns: BM (Buy Only)(0.049)(0.045)(0.052)(0.066)
Currency Returns: SM-0.0230.0020.0330.031
Currency Returns: SM (Sell Only)(0.031)(0.030)(0.026)(0.028)
Equity Returns: LM-0.035-0.178-0.275**-0.314**
Equity Returns: LM (Buy and Sell)(0.122)(0.124)(0.130)(0.122)
Equity Returns: BM0.038-0.042-0.122-0.076
Equity Returns: BM (Buy Only)(0.092)(0.086)(0.089)(0.094)
Equity Returns: SM-0.073-0.136**-0.154**-0.238**
Equity Returns: SM (Sell Only)(0.051)(0.051)(0.056)(0.058)

The analysis in this table is for 24 advanced foreign countries for the period from January 1990 to December 2010. See Table 3 for details. Newey and West (1987) standard errors are in parentheses. ** and * denote statistically significant at the 5 and 10 percent levels, respectively.

Table 9: The Relationship Between Reallocations and Prospective Equity and Currency Returns: Advanced Economies

 k=1k=2k=3k=6
Total Returns0.210*
(0.120)		0.341**
(0.173)		0.373*
(0.229)		0.115
(0.369)
Currency Returns0.032
(0.062)		-0.018
(0.099)		-0.063
(0.139)		0.059
(0.219)
Equity Returns0.122
(0.108)		0.241
(0.160)		0.402*
(0.224)		0.130
(0.358)
Floating Only: Total Returns0.139
(0.103)		0.309**
(0.140)		0.306*
(0.175)		0.066
(0.304)
Floating Only: Currency Returns0.015
(0.062)		-0.047
(0.097)		-0.121
(0.141)		-0.029
(0.209)
Floating Only: Equity Returns0.097
(0.094)		0.287**
(0.130)		0.357**
(0.175)		0.020
(0.311)

The analysis in this table is for 24 advanced foreign countries for the period from January 1990 to December 2010. See Table 6 for details. Newey and West (1987) standard errors are in parentheses. ** and * denote statistically significant at the 5 and 10 percent levels, respectively.

Table 10: The Relationship Between Reallocations and Future Portfolio Returns, AEs

 k=1k=2k=3k=6
Total Returns: TM0.158*0.0980.153-0.431
Total Returns: TM (Buy and Sell)(0.095)(0.217)(0.280)(0.651)
Total Returns: BTM0.342**0.715*0.6781.251*
Total Returns: BTM (Buy Only)(0.158)(0.365)(0.456)(0.760)
Total Returns: STM-0.185-0.618*-0.524-1.681*
Total Returns: STM (Sell Only)(0.173)(0.371)(0.507)(0.933)
Currency Returns: TM0.013-0.112-0.047-0.362
Currency Returns: TM (Buy and Sell)(0.054)(0.112)(0.181)(0.282)
Currency Returns: BTM0.0430.031-0.008-0.022
Currency Returns: BTM (Buy Only)(0.088)(0.149)(0.268)(0.406)
Currency Returns: STM-0.030-0.143-0.039-0.340
Currency Returns: STM (Sell Only)(0.074)(0.109)(0.177)(0.357)
Equity Returns: TM0.1450.2270.2150.031
Equity Returns: TM (Buy and Sell)(0.093)(0.212)(0.241)(0.515)
Equity Returns: BTM0.290**0.723**0.7141.347*
Equity Returns: BTM (Buy Only)(0.138)(0.359)(0.444)(0.785)
Equity Returns: STM-0.145-0.497-0.500-1.316
Equity Returns: STM (Sell Only)(0.155)(0.353)(0.475)(0.890)

Data are for January 1990 through December 2010 for 24 advanced foreign countries with freely floating currencies and a combined euro area starting in 1999. See Table 7 for details. Newey and West (1987) standard errors are in parentheses. ** and * denote statistically significant at the 5 and 10 percent levels, respectively.

Footnotes

**   Also released as NBER Working Paper 19963. The authors are thankful for comments from Galina Hale, Richard Levich, Assaf Razin, Giorgio Valente, and participants in seminars or conferences at BIS, Clemson University, De Nederlandsche Bank, ECB, Federal Reserve Bank of Dallas, Federal Reserve Board, Georgetown University, Hong Kong Monetary Authority, Trinity College Dublin, Universiteit van Amsterdam, University of Oregon, and University of Virginia. We thank James Albertus for excellent research assistance. Warnock thanks the Darden School Foundation for generous support and the Asian Institute of Management for its hospitality. The views in this paper are solely the responsibility of the authors and should not be interpreted as reflecting the views of the Federal Reserve Bank of Dallas, the Board of Governors of the Federal Reserve System, or of any other person associated with the Federal Reserve System. Return to text

a  Board of Governors of the Federal Reserve System Return to text

b  Darden Graduate School of Business, University of Virginia; Institute for International Integrations Studies, Trinity College Dublin; Globilization and Monetary Policy Institute, Federal Reserve Bank of Dallas; National Bureau of Economic Research Return to text

c  Phatra Securities Public Company Limited Return to text

1.   By carry trade, we mean simultaneously shorting one or more low-interest rate currencies and buying one or more high interest rate currencies. See, among many others, Lustig, Roussanov and Verdelhan (2011).This strategy will be profitable as long as the low interest rate currencies do not appreciate too much against the high interest rate currencies. On returns chasing in international equity markets, see Bohn and Tesar (1996), Brennan and Cao (1997), and Curcuru et al. (2011), among others. Return to text

2.  For evidence on the failure of UIP, see the surveys of Hodrick (1987) and Engel (1996, 2014). Return to text

3.  Cappiello and De Santis (2005, 2007) present another mechanism for UEP: expected returns on risky assets, when expressed in a common currency, should be equal. Return to text

4.  See Burger, Warnock and Warnock (2012) for analysis of these bond holdings. Return to text

5.  This is true in national statistics but also at the level of individual equities. Consider, for example, that for an international investor the simple categorization of the Swiss firm Roche as a Swiss equity might suggest its currency exposure is based solely on movements in the Swiss franc. But in practice Roche's exposure is spread throughout the world. Even if it is known exactly how Roche's assets and liabilities (and income and cost streams) are distributed throughout the world, corporate hedging programs are typically flexible enough that it is not possible to determine ex ante how Roche will choose to hedge its currency risk over the short- to medium-term. If the currency exposure of international equity investors is difficult to discern and what exposure they have might or might not be hedged by the firm, it is impossible for national statistics on international portfolio positions to speak to exposure.  Return to text

6.  Hau and Rey (2008) use mutual fund data for four source countries and find evidence of currency risk rebalancing behavior. Return to text

7.  The BT dataset is currently the best available for monthly U.S. investment in foreign equities. That said, data quality could improve even more in the near future. For example, positions estimates could be further improved by incorporating more direct measures of the returns U.S. investors earn in each foreign market; such direct returns measures do not currently exist but could be constructed for the portion of holdings that is in individual equities. Moreover, since June 2011, some monthly securities positions data have been collected by the U.S. Department of the Treasury through its Treasury International Capital (TIC) system. To date, post-WWII benchmark asset surveys occurred as of March 1994, year-ends of 1997 and 2001, and annually at year-end starting 2003. During World War II the Treasury Department conducted a survey of all foreign assets owned by U.S. citizens and residents as of May 1943, but the primary purpose was to identify U.S. assets abroad in preparation for the war settlements phase of peace negotiations; the 1943 survey is sufficiently removed in time and different in scope, methods, and purpose that the 1994 benchmark survey is considered to be the first of its kind. Return to text

8.  The bilateral data we use in this paper are the basis for Curcuru et al. (2011). Aggregate BT data---specifically, aggregate foreign positions in U.S. securities and aggregate U.S. positions in foreign securities---have been used in Curcuru, Dvorak, and Warnock (2008, 2010) and Curcuru, Thomas, and Warnock (2009) to show that (i) previous estimates of the differential between returns on U.S. investors' foreign portfolios and returns on foreigners' U.S. positions were biased upward and (ii) foreigners' U.S. portfolio returns were reduced by ill-timed switching between U.S. bonds and U.S. equities. Return to text

9.  Of the $486 billion in end-2010 U.S. holdings of foreign equities not included in our study, 94 percent is in financial centers of the Caribbean, Jersey, Guernsey, and Luxembourg. Return to text

10.  In Tables 3-7, countries enter the dataset in January 1990 or at the time of the first data point on equity returns. For all Advanced Economies (except Hong Kong and Israel), equity returns are available by January 1990. EME equity returns tend to start in the mid-1990s. Return to text

11.  We note that the Adler and Dumas (1983) notion that nominal bond positions are altered to hedge currency risk would mean that U.S. investors are shorting foreign bonds. We have no way to tell if this is occurring. Return to text

12.  The lact of predictability of currency returns is a feature of a long literature spanning Meese and Rogoff (1983) and Cheung, Chinn, and Pascual (2005). Return to text

13.  As in Curcuru et al. (2011), we use three variables to proxy for public information: (1) lagged changes in the short-term interest rate (U.S. Treasury three-month yield), (2) lagged changes in term structure spread (U.S. Treasury 10-year yield minus U.S. Treasury 3-month yield), and (3) lagged world excess returns. These information variables have been found to have robust predictive power for aggregate country-level expected returns (Harvey, 1991; Ferson and Harvey, 1993; and Bekaert and Harvey, 1997). Return to text

14.  Because the information variables have a low predictive power (that is, it is difficult to predict one-month ahead equity returns, whether local variables are included or not), the Curcuru et al. (2011) results would have been nearly identical had information variables been excluded. In that case, those results would be interpreted as "switching into markets just prior to higher than their time-series average returns" Return to text

15.  While Table 7 suggests that U.S. investors' reallocations their foreign equity portfolios improved short-term portfolio performance, Curcuru, Dvorak, and Warnock (2010) found no evidence of timing ability when U.S. investors reallocate between foreign debt and foreign equity. Return to text

16.  Quotes are from Kim (2011, pg. 1492). Return to text

This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to text

Home | Economic research and data | Publications and education resources
Accessibility | Contact us
Last update: June 3, 2014