An example calling the MATLAB Implementation of AIM
This example uses a simple two-equation model to demonstrate how to use the MATLAB implementation of the Anderson-Moore Algorithm.
The Firm Value Model
We investigate the solution of a simple linear model which describes the value of a firm. We investigate the solution of a simple linear model which describes the value of a firm.
The model consists of two equations:
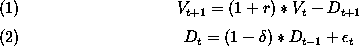
where V is the value of the firm, D is the dividend, r is the interest rate,  is the growth rate of the dividend (here, negative). E is the error term for stochastic shocks.
is the growth rate of the dividend (here, negative). E is the error term for stochastic shocks.
Using the Anderson Moore Algorithm
The AIM routine requires three input files:
- A model file in syntax called MODELEZ
- A parameter file.
- The setup script to execute AIM.
Model Representation in MDLEZ
Here is what the MODELEZ file for our example looks like.
Below we will explain each line of the file.
MODEL> FIRMVALUE
ENDOG>
V
DIV
e_
one
EQUATION> VALUE
EQ> LEAD(V,1) = (1+R)*V - LEAD(DIV,1)
EQUATION> DIVIDEND
EQ> DIV = (1-DELTA)*LAG(DIV,1)
EQUATION> e_
EQ> e_ = 0 * one
EQUATION> ONE
EQ> one = LAG(one,1)
END
MODEL>
The name of the model.
ENDOG>
The names of the endogenous variables. In the AIM formulation, models must completely describe the long-run behavior of the system. Thus all variables are endogenous. "Exogenous variables must have, at least, a trivial forecasting equation.
EQUATION>
The name of the equation.
EQ>
The model equation definition.
The parameter file for our example is called firmparms.m:
R = 0.10; DELTA = 0.60;
The following script, which we call runfirm.m, executes AIM for the firmvalue model:
dirnam='./'; % directory of this example parnam='firmparms'; modnam='firmvalue'; [cof, scof, cofb, param_, eqname_,... endog_, eqtype_, vtype_, neq, nlag, nlead, rts, lgrts,aimcode]=... SPSolve(dirnam, modnam, parnam);
Sample run of the firmvalue model on Unix:
Change the directory to the directory where the script resides:
The script to run aim is: runfirm.m
The model file name is: firmvalue
The parameter file name is: firmparms.m
mqmx3(174)% cd ~/yourPathTo/examples/firm
Call matlab and execute the run script
msulx1(124)% matlab -nodesktop
< M A T L A B >
Copyright 1984-2005 The MathWorks, Inc.
Version 7.0.4.352 (R14) Service Pack 2
January 29, 2005
To get started, type one of these: helpwin, helpdesk, or demo.
For product information, visit www.mathworks.com.
>> addpath('~/sp_solve')
addpath('~/sp_solve')
>> runfirm
runfirm
SPSolve version:($Name: $,$Revision: 1.4 $)
ans =
found Aim on system classpath
initializing parsers
Aim Java Parser Version 1.03: Reading from file ./firmvalue...
Aim Java Parser Version 1.03: No syntactic errors found.
Checking for errors......
No semantic errors found.
chose modelez parser
>>
Displaying the results:
In the output below:
"cof" is the structural coefficients matrix (neqs by neqs*(nlag+nlead+1))
"cofb" is the reduced form coefficients matrix (neqs by neqs * nlag)
"scof" is the observable structure matrix (neqs by neqs*(nlag+1))
"rts" returns the eigenvector
"aimerr(aimcode)" returns a diagnostic message about the model
where: "neq" = number of equations
"nlag" =number of lags
"nlead" =number of leads
> cof
cof
cof =
Columns 1 through 7
0 0 0 0 -1.1000 0 0
0 -0.4000 0 0 0 1.0000 -1.0000
0 0 0 0 0 0 1.0000
0 0 0 -1.0000 0 0 0
Columns 8 through 12
0 1.0000 1.0000 0 0
0 0 0 0 0
0 0 0 0 0
1.0000 0 0 0 0
> cofb
cofb
cofb =
0 0.2286 0 0
0 0.4000 0 0
0 0 0 0
0 0 0 1.0000
> scof
scof
scof =
Columns 1 through 7
0 0 0 0 -1.1000 0.6286 0
0 -0.4000 0 0 0 1.0000 -1.0000
0 0 0 0 0 0 1.0000
0 0 0 -1.0000 0 0 0
Column 8
0
0
0
1.0000
> rts
rts
rts =
1.1000
1.0000
0.4000
> aimerr(aimcode)
aimerr(aimcode)
ans =
Aim: unique solution.
References
1 Gary Anderson. A reliable and computationally efficient algorithm for imposing the saddle point property in dynamic models. Unpublished Manuscript, Board of Governors of the Federal Reserve System, 1997.
2 Gary Anderson and George Moore. A linear algebraic procedure for solving linear perfect foresight models. Economics Letters, 17, 1985.
3 Michael W. Berry. Large scale sparse singular value computations. University of Tennessee, Department of Computer Science, 1996.
4 Olivier Jean Blanchard and C. Kahn. The solution of linear difference models under rational expectations. Econometrica, 48, 1980.
5 Gene H. Golub and Charles F. van Loan. Matrix Computations. Johns Hopkins, 1989.
6 E. V. Krishnamurthy. Parallel Processing: Principles and Practice. Addison-Wesley, 1989.
7 David G. Luenberger. Time-invariant descriptor systems. Automatica, 14:473-480, 1978.
8 Ben Noble. Applied Linear Algebra. Prentice-Hall, Inc., 1969.
9 J. Taylor. Conditions for unique solutions in stochastic macroeconomic models with rational expectations. Econometrica, 45:1377-1385, |SEP| 77.
10 C. H. Whiteman. Linear Rational Expectations Models: A User's Guide. University of Minnesota, 1983.