IFDP Notes
February 8, 2016
The Dollar in the U.S. International Transactions (USIT) Model
Joseph Gruber, Andrew McCallum, and Robert Vigfusson
The dollar's 20 percent climb against a broad index of foreign currencies since the middle of 2014 has led to an increased focus on how dollar fluctuations affect the U.S. economy. In a recent speech, "The Transmission of Exchange Rate Changes to Output and Inflation," Vice Chairman Fischer discussed estimates of the dollar's effect on U.S. trade, GDP, and inflation in the context of the U.S. International Transactions (USIT) model, one of a suite of econometric models used by Federal Reserve Board staff to assess the dollar's effect on the U.S. economy.1 This note provides further detail on the structure and estimation of the trade block of the USIT model.2 In the context of the model, we present the estimated effect of a 10 percent dollar appreciation on U.S. trade flows and trade prices. We conclude with an assessment of the model's performance since the dollar began its steep appreciation in the summer of 2014.
A Partial-Equilibrium Model
One of the main conceptual features of the USIT model is that it is partial equilibrium inasmuch as there is no feedback from U.S. trade volumes and prices to the assumed determinants of these variables (such as domestic GDP, foreign GDP, other prices, or exchange rates). To better illustrate this point, consider a hypothetical appreciation of the dollar. As the higher dollar increases the price of U.S. products relative to foreign goods, the model predicts that foreign demand for U.S. exports will decline while U.S. demand for imports will rise, both of which would--all else equal--act to reduce U.S. GDP. In assessing the partial-equilibrium effects of a dollar appreciation, we stop here. In a general-equilibrium context, of course, the decline in U.S. GDP that would be predicted by the partial-equilibrium framework would have a number of additional effects on the economy, some of which would work to mitigate the negative effect on GDP. For example, a decline in GDP (and hence in domestic incomes) should tend to depress import demand, thereby reversing some of the dollar-induced increase in imports. In addition, lower U.S. GDP would tend to result in more-accommodative monetary policy, which would in turn would also act to offset some of the negative impact of the higher dollar identified in our partial approach. To capture these effects, Board staff also maintain a number of general-equilibrium models--such as the SIGMA and FRB/US models--that explicitly incorporate and provide a full accounting of these additional channels. On balance, the real effects of a change in the exchange value of the dollar tend to be larger in absolute terms in a partial-equilibrium framework than in a general-equilibrium model, since the feedback mechanisms incorporated into a general-equilibrium model tend to attenuate the influence of the dollar on real activity.
The USIT model has eight key trade equations corresponding to price and volume equations for exports and imports of core goods and exports and imports of services.3 We will limit our discussion to five of these equations, focusing first on the equations for trade volumes before turning to core import prices. For reference, note that the main independent variables that we treat as exogenous in the model include U.S. and foreign real GDP growth and inflation rates, oil and non-fuel commodity prices, and the dollar exchange rate.
Trade Volume Equations
The model specifications for import and export volumes can be interpreted as demand equations, with the log volume of trade (exports or imports), v, modelled as a function of log income, y, and the log of the real exchange rate, e, which captures the relative price of foreign and domestic goods:
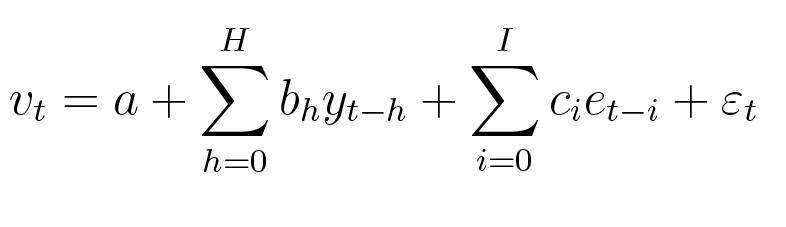
For the import equations, the relevant income measure is U.S. GDP. For the export equations, the income measure is a composite of foreign countries' GDPs weighted by each country's respective share in overall U.S. exports. The real exchange rate captures the competitiveness of domestic compared to foreign production and is calculated as a nominal effective exchange rate multiplied by the ratio of U.S. and foreign consumer price indexes.4
The measure of import and export volumes used to estimate the model are constructed using nominal trade on a Balance of Payments (BOP) basis deflated by trade prices as reported in the National Income and Product Accounts (NIPAs). These equations of the model are estimated in logs using generalized least squares (GLS) on an equation-by-equation basis at a quarterly frequency, with a Cochrane-Orcutt correction for first-order residual serial correlation.5 In addition, the coefficients on lagged relative price terms are estimated with a polynomial distributed lag, in part to smooth the quarterly volatility of the model's output. The number of income and exchange rate terms included in each equation is determined by empirical fit. Coefficient estimates and the estimated serial correlation coefficient for each equation are presented in Table 1.
| Table 1. Model Coefficient Estimates |
|---|
| Exports | Imports | |||
|---|---|---|---|---|
| Core Goods | Services | Core Goods | Services | |
| (1) | (2) | (3) | (4) | |
| yt | 1.393 | 1.688 | 1.220 | 1.456 |
| yt-1 | 0.845 | |||
| et | -0.023 | -0.146 | 0.033 | 0.065 |
| et-1 | -0.041 | -0.128 | 0.059 | 0.049 |
| et-2 | -0.056 | -0.110 | 0.075 | 0.033 |
| et-3 | -0.068 | -0.092 | 0.084 | 0.016 |
| et-4 | -0.075 | -0.073 | 0.084 | |
| et-5 | -0.079 | -0.055 | 0.075 | |
| et-6 | -0.079 | -0.037 | 0.059 | |
| et-7 | -0.075 | -0.018 | 0.033 | |
| et-8 | -0.068 | |||
| et-9 | -0.056 | |||
| et-10 | -0.041 | |||
| et-11 | -0.023 | |||
| pĀ | 0.859 | 0.813 | 0.828 | 0.950 |
As can be seen from the table, changes in real exchange rates are estimated to have persistent effects on trade flows. The core goods export equation (column 1) includes three years of lagged real exchange rates. The core goods import equation (column 3) includes two years of lagged exchange rates. Similarly, the services export equation (column 2) also has two years of lagged exchange rates, with most of the impact felt in the near-term. Lastly, the equation for service imports (column 4) has only one year of exchange rate lags.
In contrast to exchange rates, the effect of income on trade volumes tends to be felt relatively quickly: The export equations include only the contemporaneous quarter of the foreign GDP composite; likewise, services imports are estimated to respond to contemporaneous U.S. GDP while goods imports respond to the contemporaneous value and first lag of U.S. GDP.
Table 2 provides a summary of the model's trade volume elasticities. Two regularities identified in the economics literature are evident in these estimates: First, there is a considerable asymmetry in income elasticities between the United States and its foreign trading partners; second, exports respond more than imports to exchange rate movements.6 (In part, the weak response of imports to exchange rate changes likely reflects the relatively small degree of pass-through of exchange rates to U.S. import prices.)
| Table 2. Summary of Trade Volume Elasticities |
|---|
| Exports | Imports | |||
|---|---|---|---|---|
| Income | Ex. Rate | Income | Ex. Rate | |
| (1) | (2) | (3) | (4) | |
| 1. Core goods | 1.39 | -0.69 | 2.06 | 0.5 |
| 2. Services | 1.69 | -0.66 | 1.46 | 0.16 |
| 3. Weighted average | 1.45 | -0.68 | 1.93 | 0.43 |
Note: Weighted averages are calculated using NIPA nominal shares for 2014.
Core Import Prices
The USIT model equation for core import prices relates the log of these prices, p, to a log composite of foreign CPIs (p*), the nominal exchange rate (s), and log commodity prices (cp).7 As in the volume equations, the foreign CPIs and nominal exchange rates are weighted by source-country shares of U.S. non-oil imports. Commodity prices are measured by an import-weighted aggregate of the International Monetary Fund's price indexes for agricultural materials, beverages, foods, and metals.8 The equation is estimated from 1990:Q1 to 2013:Q4; the exact specification and coefficient estimates are:
The model equation is structured so that the initial effects of the commodity prices on import prices are somewhat stronger than subsequent effects.
In addition to a direct effect, dollar movements also indirectly affect import prices through commodity prices. When the dollar appreciates, many commodities decrease in price. These lower commodity prices result in lower U.S. import prices. Taking these direct and indirect effects together, the overall exchange-rate elasticity of core import prices is estimated to be about 0.3, such that only about a third of movements in the dollar is passed through to import prices.
Response to a 10 Percent Real Dollar Appreciation
Observed movements in the dollar can reflect an array of underlying fundamental shocks. While the effect of a change in the dollar on domestic variables will typically depend on the ultimate source of the movement in the dollar, it is still useful to consider the predicted partial equilibrium effect treating dollar movements as exogenous. Table 3 presents the partial effect on real exports, real imports, real GDP, and core import prices following an assumed permanent 10 percent appreciation of the real exchange value of the dollar. These estimates are derived from the equations in the model described above and, again, are partial inasmuch as they do not allow for feedback effects on GDP or any response of monetary policy.9
| Table 3. Partial Equilibrium Effects of a 10 Percent Real Dollar Appreciation |
|---|
| Percent Deviations from Baseline without GDP or monetary policy responses | After 1 year | After 2 years | After 3 years | |
|---|---|---|---|---|
| 1 | Level of real exports | -2.9 | -5.7 | -7.1 |
| 2 | Level of real imports | 2.1 | 3.9 | 3.9 |
| 3 | Level of real U.S. GDP | -0.7 | -1.3 | -1.5 |
| 4 | Level of core import prices | -3.0 | -3.0 | -3.0 |
The equations for goods and services exports predict that a 10 percent appreciation of the real dollar would reduce the level of overall real exports by about 7 percent after three years (line 1). After three years, the model predicts that real imports would be almost 4 percent higher (line 2). In total, therefore, a 10 percent dollar appreciation would reduce the level of real GDP by about 1-1/2 percent relative to its baseline path after three years (line 3).
The model predicts that a 10 percent increase in the value of the dollar would result in a 3 percent decline in the level of core import prices.10 As discussed in Vice Chairman Fischer's November speech, a reduction in core import prices of this magnitude is likely to reduce the level of core PCE prices by about 0.3 percent.11
Recent Performance of the Model
The USIT model has done a fairly good job of predicting the response of U.S trade volumes in the wake of the dollar's recent appreciation. Table 4 summarizes the model's prediction for real export and import growth over the period between 2014:Q3 to 2015:Q3, shown in column 2, compared to the actual realizations of the data, shown in column 1. As shown in the first line, from 2014:Q3 to 2015:Q3 net exports subtracted 0.7 percentage point from U.S. real GDP growth, a bit less than the almost 1 percentage point drag predicted by the model over the same period taking realized observations on income, CPIs, and exchange rates as inputs. As shown on line 2, the real export growth over this period has been in line with the model's projection. However, the model does identify some anomalies relative to historical experience. Services exports (line 4) have continued to grow robustly, despite the model's prediction of only a subdued increase. In contrast, goods exports have been even weaker than would have been expected given the historical relationships embodied in the model. As shown in line 5, real imports have responded less positively to the dollarís appreciation than the model has predicted, particularly as imports of goods have disappointed.
| Table 4. Actual and Model-Implied Real Trade Growth 2014:Q3 to 2015:Q3 |
|---|
| Data | Model | Error = Data - Model | |
|---|---|---|---|
| (1) | (2) | (3) | |
| Contribution to Real GDP Growth (percentage points, a.r.) | |||
| 1. Net Exports | -0.7 | -0.9 | 0.2 |
| Real Growth Rates (percent, a.r., NIPA basis) | |||
| 2. Exports of Goods and Services | 1.2 | 1.2 | 0.0 |
| 3. Exports of Goods | -0.8 | 1.3 | -2.1 |
| 4. Exports of Services | 5.6 | 0.9 | 4.7 |
| 5. Imports of Goods and Services | 5.6 | 7.1 | -1.7 |
| 6. Imports of Goods | 5.4 | 7.2 | -1.8 |
| 7. Imports of Services | 6.7 | 6.8 | -0.1 |
Note: Reported model prediction for exports of goods includes actual realizations of exports of computers and semiconductors. Reported model prediction for imports of goods includes actual realizations of imports of computers, semiconductors, oil, and natural gas. Also reported model predictions include actual realizations of adjustments between data on a BOP and NIPA basis.
In regard to import prices, the model has also generally matched the data. From 2014:Q3 to 2015:Q3 the Bureau of Labor Statistics' measure of goods import prices excluding computers, semiconductors, and petrol (similar to model's definition of core imports) declined 3.1 percent. Over the same period the model predicted a slightly steeper 3.6 percent fall in core import prices.
Conclusion
The USIT model is one of several quantitative tools that Board staff use to interpret the effects of foreign developments on the U.S. economy. The equations that govern the model are based on economic theory and estimated to fit historical patterns. As such, the model is a helpful tool to gauge the effect of changes in the exchange value of the dollar on exports, imports, and domestic price inflation relative to historical norms. Following the sharp appreciation of the dollar since the summer of 2014, the evolution of net exports has more or less matched the model's predictions, suggesting that overall the response of the U.S. economy to the change in the dollar up to this point has not been significantly at odds with historical experience.
References
Bertaut, Carol C., Steven B. Kamin, and Charles P. Thomas, 2009. "How Long Can the Unsustainable U.S. Current Account Deficit be Sustained?" IMF Staff Papers, vol. 56, no. 3, pp. 596-632.
Fischer, Stanley, 2015. "The Transmission of Exchange Rate Changes to Output and Inflation." Speech delivered at the conference "Monetary Policy Implementation and Transmission in the Post-Crisis Period," Board of Governors of the Federal Reserve System, Washington D.C. (November 12).
Loretan, Mico. 2005. "Indexes of the Foreign Exchange Value of the Dollar." Federal Reserve Bulletin, vol. 91 (Winter), pp. 1-8.
1. The speech was delivered at the conference "Monetary Policy Implementation and Transmission in the Post-Crisis Period," which was held at the Board of Governors of the Federal Reserve System in Washington D.C. on November 12, 2015. Return to text
2. In its entirety, the USIT model is comprised of nearly 500 equations and encompasses both trade and financial flows for the U.S. external sector, providing a framework for examining and forecasting the U.S. current account balance and all its components. As mentioned above, this note focuses on the block of the model that encompasses the trade balance. Many aspects regarding the non-trade parts of the USIT model not covered here are discussed in Bertaut, et al (2009). Return to text
3. Core goods exports are defined as exports of goods excluding computers and semiconductors; core goods imports are defined as nonfuel goods imports excluding computers and semiconductors. The excluded categories are modelled separately, since their response to economic fundamentals differs significantly from that of core goods; in particular, the model assumes that real imports of energy products and exports and imports of computers and semiconductors do not respond to changes in the exchange value of the dollar. Return to text
4. The country weights used to construct an aggregate real exchange rate index vary with each equation and are allowed to vary over time. In the import equations, relative prices are weighted by country shares of either U.S. imports of goods or of services. In the core goods export model, country weights are an equally weighted aggregation of bilateral export weights and third party competitiveness weights. In the services export model, weights are determined using country shares of U.S. services exports. (See Loretan, 2005, for additional discussion.) Return to text
5. The equation estimation periods range from 1975:Q1 to 2013:Q4 for core goods exports, from 1980:Q1 to 2013:Q4 for services exports, from 1973:Q1 to 2013:Q4 for core goods imports, and from 1980:Q1 to 2013:Q4 for services imports. Return to text
6. The asymmetry in income elasticities is a well-documented empirical regularity that is often referred to as the "Houthakker-Magee" effect. Return to text
7. The core import price index covers goods imports excluding computers, semiconductors, oil, and natural gas. Return to text
8. These subindexes come from the "IMF Primary Commodity Prices" website, with quarterly values defined as the averages of the reported monthly data. The raw data can be accessed from http://www.imf.org/external/np/res/commod/External_Data.xls ![]() . Return to text
. Return to text
9. As mentioned earlier, staff models such as SIGMA do take into account general equilibrium effects, including the response of monetary policy. In SIGMA, the negative effect of a 10 percent appreciation is substantially mitigated by the reaction of monetary policy, with an overall effect that is roughly half of the amount reported here. Return to text
10. Since import prices respond quickly to the dollar in the model equations, the effect after 1 year is the same as the effect after 3 years. Return to text
11. The core PCE price index excludes food and energy prices. Return to text
Please cite as:
Gruber, Joseph, Andrew McCallum, and Robert Vigfusson (2016). "The Dollar in the U.S. International Transactions (USIT) Model," IFDP Notes. Washington: Board of Governors of the Federal Reserve System, February 08, 2016. https://doi.org/10.17016/2573-2129.16
Disclaimer: IFDP Notes are articles in which Board economists offer their own views and present analysis on a range of topics in economics and finance. These articles are shorter and less technically oriented than IFDP Working Papers.
